- 1Water Research Laboratory, School of Civil and Environmental Engineering, UNSW Sydney, Sydney, NSW, Australia
- 2School of Environment, Faculty of Science, University of Auckland, Auckland, New Zealand
Sandy beaches comprise approximately 31% of the world's ice-free coasts. Sandy coastlines around the world are continuously adjusting in response to changing waves and water levels at both short (storm) and long (climate-driven, from El-Nino Southern Oscillation to sea level rise) timescales. Managing this critical zone requires robust, advanced tools that represent our best understanding of how to abstract and integrate coastal processes. However, this has been hindered by (1) a lack of long-term, large-scale coastal monitoring of sandy beaches and (2) a robust understanding of the key physical processes that drive shoreline change over multiple timescales. This perspectives article aims to summarize the current state of shoreline modeling at the sub-century timescale and provides an outlook on future challenges and opportunities ahead.
1. Introduction
Beaches provide essential ecosystem services, including the natural buffering of inland areas from the damaging impacts of waves and elevated water levels during storm events. The coastal zone also provides major economic benefits. The challenge in many coastal areas is that, due to historical planning decisions and perhaps a persistent lack of understanding of the complex dynamic coastline, infrastructure has been inappropriately sited within the active coastal zone. Hence, many new and on-going coastal management projects are needed to deal with the risks associated with coastal erosion.
Coastal erosion can be episodic (storm-driven), show long-term patterns (from seasons to decades) or be chronic (when a trend is established) as a result of both natural (due to changes in water levels and wave characteristics) and anthropogenic causes. Extra-tropical and tropical events can cause widespread and rapid erosion over large areas of the coastline in a matter of hours to days (Castelle et al., 2015; Masselink et al., 2016b; Harley et al., 2017), whereas longer term climate variability (e.g., El-Nino Southern Oscillation, ENSO) can also cause enhanced erosion (or accretion) on time scales of 2–7 years (e.g., Barnard et al., 2015). The issue of changes induced by sea-level rise is also hotly debated (Vitousek et al., 2017a; Cooper et al., 2020; Vousdoukas et al., 2020) because we still lack a clear modeling framework to deal with this even longer temporal scale. For improved shoreline forecasting and coastal management in a dynamic and changing system like the nearshore there is an outstanding need for both long-term, large-scale continuous data sets and improved coastal shoreline prediction models.
2. Data
Data is fundamental for expanding our understanding of the coastline. Importantly, data also underpins all of our modeling efforts. This is particularly true for hybrid modeling approaches as described in section 3, that train specific predefined relationships to data. High quality data is even more important for future endeavors to develop predictive models entirely based on data (e.g., machine learning algorithms).
2.1. Shorelines
Historically, a key challenge in our ability to fully understand coastal change has been the lack of long-term, large-scale, high-resolution (in time and space) coastal data sets (Turner et al., 2016; Ludka et al., 2019; Castelle et al., 2020). The result is that many studies on coastal shoreline dynamics have been based on a select few sites and span specific timeframes, thus limiting the universality of the findings. Despite the rather lack of data, we have learned about general principles that control shoreline behavior and the key drivers, including the effects of changing sea-levels (e.g., Brunel and Sabatier, 2009), storminess (e.g., Frazer et al., 2009), climate-driven responses (Barnard et al., 2015), inter-annual variability (e.g., Pianca et al., 2015) and embayment rotation (e.g., Harley et al., 2015).
Recently, the public release of satellite images has provided significant new opportunities for large-scale coastal change studies based on shoreline observations (Luijendijk et al., 2018; Mentaschi et al., 2018; Vos et al., 2019a). Recent open-source toolboxes, for example CoastSat (Vos et al., 2019b) or CASSIE (Almeida et al., 2021), allow for high resolution (order 10 m) bi-weekly shoreline measurements to be obtained at most sandy beaches around the world over the last 30 years. This spatio-temporal resolution of data is a necessary component in shoreline model development and calibration (Splinter et al., 2013). Newer satellites are continuously being added to the data stream providing higher spatial and temporal resolution into the future. As such, satellite data will most likely play an increasing and ongoing role in future, regional scale shoreline modeling efforts via data assimilation (e.g., Vitousek et al., 2017a).
2.2. Waves and Water Levels
When looking at the past, data of the “drivers” of shoreline change, for example waves and water levels, are often readily available as direct observations or numerical hindcasts. A recent paper outlining the priorities for wind-waves research highlighted the need for enhanced buoy networks and high quality bathymetry for nearshore wave predictions (Greenslade et al., 2019). Topographic and bathymetric data collection was also recently listed as a top priority by the Coastal Geosciences community (Power et al., 2021) due to the importance of the links between nearshore bathymetry and beach response, including sediment exchange as well as wave transformation processes. With respect to waves, some coastlines may be considered quite data rich, such as the USA with the NOAA network of buoys, while others rely entirely on global wave models. On complex coastlines, more refined models are needed to capture the complex wave transformation processes from offshore to nearshore in the absence of nearshore buoy networks. These models in turn, require high quality bathymetry data that is expensive to acquire.
The problem becomes insurmountable when looking at the future. Rates of sea-level rise over the next few decades are unknown and available projections depend on global climate models and therefore on the emission scenarios considered, which are also deemed uncertain. Similarly, our ability to predict the details of decadal oscillations in climate variability is extremely limited. However, efforts are being made within the shoreline community to address these (e.g., Antolinez et al., 2016; Montaño et al., 2021). A specific challenge for shoreline prediction is the need for continuous timeseries of forcing conditions. While the wave climate can be derived from global climate models, at present the projections of wave characteristics provide only one temporal sequence of wave conditions. This limits the possibility of assessing, for example, the effect of clustering or chronology of storms on future beach erosion that previous authors have shown to be important (e.g., Coco et al., 2014; Karunarathna et al., 2014; Castelle et al., 2015; Dissanayake et al., 2015; Masselink et al., 2016a,b; Splinter et al., 2016; Angnuureng et al., 2017).
3. Models
Models may incorporate a variety of processes, such as those described in Figure 1. While models can take on many forms, here we focus on simple models used for daily to multi-year shoreline prediction which form a subset of reduced complexity models. These encompass the “microscale” problem on understanding our coastline at engineering timescales of years to decades and spatial scales of kilometers to tens of kilometers (Wolinsky, 2009). More complex, process-based models, such as XBeach or SBeach are well-suited for short-term (e.g., individual storm response) scenarios but at present they are still not capable of providing robust and reliable predictions of multi-year shoreline change. This model typology, based on the fundamental equations of momentum and mass conservation, could eventually be used to model long-term coastal response, but at present it requires significant computational resources, making it almost impossible to assess how predictions are affected by model uncertainties (in parameters and drivers, for example). The more complex, process-based models also require more calibration data and input data, including the bottom boundary (i.e., bathymetry), tidal currents, and wave-driven currents, making them unsuitable for large regional studies of shoreline change. Here we categorize shoreline models used at engineering timescales into three types: ones that focus on cross-shore process; ones that focus on alongshore processes; and ones that combine these.

Figure 1. Considerations relevant to shoreline modeling at a variety of timescales of interest. (1) Water levels; (2) Waves; (3) Sediment Supply; (4) Human Impact. These may be considered separately, in a combination, or all of them depending on the circumstances. Models can also consider these processes as deterministic or probabilistic.
3.1. Cross-Shore Models
The most common models used to predict and understand multi-year shoreline change are semi-empirical models (Yates et al., 2009; Davidson et al., 2013; Splinter et al., 2014) based around the equilibrium assumption. The primary forcing component that drives onshore/offshore shoreline movement is waves at the timescales of days to decades. A generalized form of a model considering cross-shore process may take the form:
where Δx(t) refers to the cross-shore change in shoreline position (x) as a function of the time-dependant wave height (H(t)), wave period (T(t)), wave direction (θ(t)), and shoreline position (x(t)). Shoreline change at the timescales of hours to days is often quite noisy, such that models are often trained on the resulting time-integral of shoreline change [i.e., shoreline position x(t)].
Due to the simplicity of Equation (1), these models require several years of high-resolution data to properly calibrate (Yates et al., 2009; Splinter et al., 2013) and show reasonable skill at predicting shoreline evolution on timescales of individual storms to decades. A key aspect in these models is the inclusion of hysteresis in the system, whereby shoreline change is a function of the present shoreline position (or proxy) in relation to the present wave forcing. The models also assume an unlimited sediment supply is available, with the beach not obstructed by human intervention or other geological features that might limit erosion (e.g., Doria et al., 2016). Approaches to explicitly incorporate the active profile and following the equilibrium principle have also been proposed (e.g., Miller and Dean, 2004; Davidson, 2021). These particular models explicitly include the influence of time-varying water levels, which may be important along coastlines with large tidal variability, large storm surge, or at longer timescales where changes in the mean water level may be important.
At these longer timescales (50–100 year time frames), where changes in mean sea-level may be considered the main driver of shoreline evolution, approaches such as the Bruun Rule (Bruun, 1962) are often employed. These models often consider geomorphic descriptors of the beach profile, such as slope (β), berm/dune height (B) relative to a water level (WL) and may take the form:
This overly simplistic approach, which only considers retreat from rising water levels has been criticized by a number of researchers (e.g., Cooper and Pilkey, 2004; Ranasinghe et al., 2012). Alternative approaches to account for the cross-shore movement of the shoreline due to changes in water levels have also been discussed (e.g., Wolinsky and Murray, 2009; Gutierrez et al., 2011; Rosati et al., 2013; D'Anna et al., 2021b; Davidson-Arnott and Bauer, 2021; McCarroll et al., 2021).
3.2. Alongshore Models
One-line models provide a simplified representation of the beachface and focus on shoreline change as a result of the gradients in alongshore transport resulting from oblique wave action (θ) relative to the orientation of the coastline. These models typically estimate alongshore transport based on breaking waves using the CERC (USACE and Coastal Engineering Research Center, 1984) or Kamphuis (Kamphuis, 1991) formulas and take a simplified form similar to:
where both input and output variables are dependant on the alongshore (y) location. However, it is widely accepted that these equations offer an order of magnitude estimate, with local calibration and tuning providing improved results (e.g., Smith et al., 2009; Ruggiero et al., 2010). These models are most suitable for coastlines with significant gradients in alongshore transport, which may be due to sediment supply, natural features (such as headlands) or human impacts (such as harbors, breakwaters, and groins). Given that gradients in alongshore transport are often relatively small, these models are best suited for long-term (decadal-scale and beyond) studies of shoreline change (e.g., Ruggiero et al., 2010; Anderson et al., 2018).
Other researchers have proposed equilibrium approaches to model the planform of embayed beaches (e.g., Turki et al., 2013; Jaramillo et al., 2021). Much like their sister cross-shore equilibrium models described above, they rely on data to develop simplified relationships between the existing alongshore distribution of the shoreline and the prevailing wave forcing with the underlying physical assumption that beaches will tend to align with the prevailing wave climate direction.
3.3. Combined Approaches to Shoreline Modeling
Building off of established models as described above, a number of simple shoreline models have been proposed that encompass the impacts of cross-shore and alongshore processes (e.g., Vitousek et al., 2017b; Robinet et al., 2018; Antolínez et al., 2019; Roelvink et al., 2020; Alvarez-Cuesta et al., 2021). These models are well-suited for complex coastlines, where the influences of humans, sediment supply, and both alongshore and cross-shore processes contribute to the observed shoreline change. They may take the generalized form of:
As these models also encompass a variety of processes that act at different timescales, these models have also been used for long-term assessment of shoreline variability/change (e.g., Vitousek et al., 2017a; Alvarez-Cuesta et al., 2021).
4. Model Advances
4.1. Deterministic vs. Probabilistic Approaches
Many of the above models were developed as deterministic descriptors of shoreline change over time. However, it is critically important to acknowledge that both inputs (i.e., forcing) and model structure (i.e., equations) contain a certain level of error and uncertainty that needs to be included in future shoreline predictions (Ranasinghe, 2020). To that effect, there is a growing body of literature related to predicting future shoreline change that acknowledges the cascades of uncertainty and how these effect long-term shoreline predictions (Le Cozannet et al., 2019; D'Anna et al., 2020, 2021a; Kroon et al., 2020; Toimil et al., 2020, 2021).
To emphasize the importance of acknowledging the uncertainty in wave forcing, Greenslade et al. (2019) listed ensemble and probabilistic wave modeling and forecasting as one of the top 5 priorities for wind-wave research at present. As a start, over the past few decades wave emulators have been developed to address this issue (Davidson et al., 2010, 2017; Antolinez et al., 2016; Anderson et al., 2019; Cagigal et al., 2020). Wave emulators allow for a probabilistic description of wave conditions using techniques such as Monte Carlo sampling. Also with the perspective of providing probabilistic estimates of long-term shoreline change, D'Anna et al. (2021a) developed a framework to address uncertainty related to the unknown future changes in the mean sea level. We believe this is an area where much more work needs to be done to allow for robust future shoreline predictions in an uncertain future.
Uncertainty and error due to model structure has been less well-studied, with the most common approach being an equal-weight ensemble used to estimate the mean and spread of a range of models for a given input scenario (Montaño et al., 2020). While equally weighting all available models provides improved estimates compared to a single model, it has also been acknowledged that certain shoreline models perform better under certain conditions (Montaño et al., 2020; D'Anna et al., 2021a) such that a more dynamic weighting approach to ensemble model output may provide improved model results and more robust estimates of uncertainty and should be considered in future shoreline prediction efforts.
4.2. Timescales of Change
At present the most widely used coastal models assume stationary processes when considering the timescales of days to multi-decade, which by proxy assumes that the systems they model vary within a constrained envelope based on past observations (Yates et al., 2009) or that trends of the past will continue into the future (Luijendijk et al., 2018; Vousdoukas et al., 2020). These assumptions are likely challenged in the face of climate change. Recently, a number of approaches to address non-stationary forcing and model adaptation timescales have been proposed, acknowledging that beaches may adapt over a variety of timescales (e.g., Frazer et al., 2009; Splinter et al., 2016). Many of these have been included acknowledging the simplistic equilibrium-type shoreline models may not be suitable for long-term shoreline prediction (Ranasinghe, 2020). For example, Ibaceta et al. (2020) suggested an ensemble Kalman Filter assimilation technique could track changes in model structure due to changing wave-shoreline feedback. Montaño et al. (2021) and Schepper et al. (2021) separately proposed two different multi-scale model approaches. Montaño et al. (2021) used a Complete Ensemble Empirical Mode Decomposition method that linked different timescales of forcing to the corresponding timescales in the shoreline change. In contrast, Schepper et al. (2021) included upscaling, downscaling and direct forcing methods to link forcing to various timescales of shoreline evolution. These advances hint at ways forward to robustly predict future shoreline changes in a changing and uncertain climate using these simplified reduced complexity models.
5. Future Opportunities
Two recent priority setting exercises (Greenslade et al., 2019; Power et al., 2021) found that a number of key priorities in the coastal geosciences and engineering community were related to the need to better understand our coasts now and in the future. Specifically, high quality temporal and spatial data of both the forcing (waves) and coastlines, enhanced quantification of shoreline change, and improved understanding of extreme events and the quantification of future impacts of climate change on our coasts were listed among the top priorities.
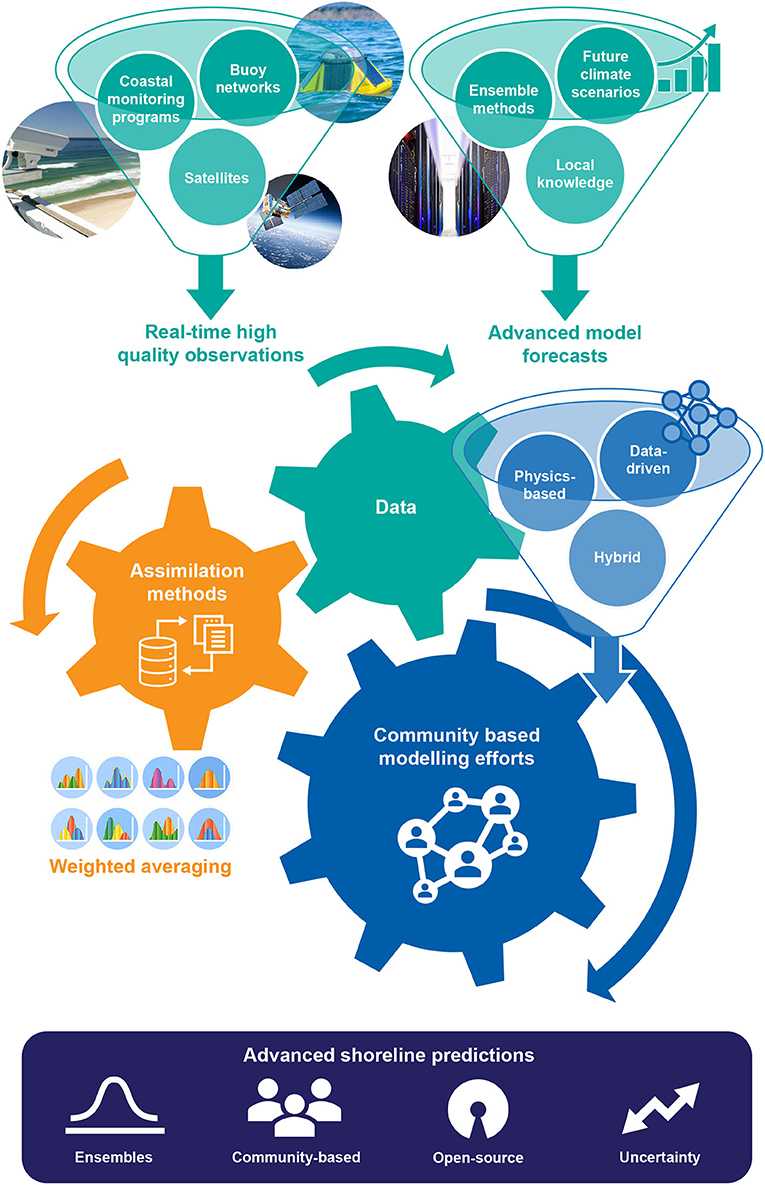
One of the biggest challenges in coastal shoreline forecasting is the ability to predict how coasts may adapt to a range of possible futures. At multiple timescales, planning decisions—be it “do we need to evacuate that house due to risk of an impending storm?” to—“will this stretch of coast become uninhabitable before the end of the century?” require reliable and robust predictions of shoreline position. To address this, over the last 20 years advancements into modeling of shoreline change at timescales of individual storms to century level predictions have been proposed. To develop more accurate forecast tools for future coastal shoreline change, we recommend the following (also summarized in Figure 2):
1. Data is key
• A continued push for real-time, high frequency and high quality in-situ coastal monitoring programs at relevant temporal and spatial scales to better understand the complex ocean/land boundary with a focus to capture the shoreline and nearshore bathymetry.
• Improved spatial and temporal resolution of the necessary metocean forcing (waves, water levels).
• Increasing accessibility to the ever growing network of satellite missions and the data they provide.
• Benchmark data sets openly available for the community to test their models against.
2. Advanced forecasts
• Reliable and robust forecasts of future wave conditions, in the form of continuous timeseries mode, based on the best climate projections that account for changes in storminess and clustering of storms. This may include the use of alternative approaches, such as surrogate models and emulators.
• Improved and more frequent use of ensemble methods to bring different forecasts together and address uncertainty associated to model structure.
• Continue to seek local (traditional) knowledge, particularly at sites that are data poor.
• Consider new ways of model calibration—based on the ensemble, rather than individual models.
3. Collaboration beats competition
• A push for more diverse groups to work together to advance the science—this may include engineers, geomorphologists, oceanographers, climatologists, and data scientists for example.
• An open source approach to improve both process-based models and reduced complexity models on the timescales of interest.
• Ensemble approaches that use advanced weighting techniques.
4. Learn from new data
• Acknowledging model structure error and including this in the assimilation process.
• Incorporating new data streams as they become available.
• Models that adapt in time to changes in forcing.
Much like the advancements that have been made in climate modeling and wave forecasting on a global scale, workshops and working groups will help to foster the community spirit and rapidly advance the science. We have seen evidence of this already, such as the international ShoreShop (Montaño et al., 2020) and through various national-level programs such as iCOASST (UK), and the National Assessment of Shoreline Change (USA). These models will need to be open source to maximize uptake and development of the community-based efforts. Platforms, such as GitHub and the Community Surface Dynamics Modeling system (https://csdms.colorado.edu/) will become necessary for models to be integrated and developed with proper version control. The community models will ultimately include an “ensemble of ensembles” of shoreline predictions with uncertainty bounds based on the uncertainty of both the inputs (waves/water levels) and of the individual models.
Today's model predictions, no matter which shape or type of model is considered, remain hampered by a variety of uncertainty sources that in some cases can only be partially reduced (e.g., the future wave climate and the large uncertainties associated with the uncertainty in the various emission scenarios used to drive the GCMs). As a result predictions of shoreline change will need to be cast in a probabilistic framework and will require a joint community effort.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author Contributions
KS and GC came up with the ideas for this perspectives. All authors contributed to the writing and editing of the article.
Funding
All authors would like to acknowledge the various funding agencies who in the past have supported their research in shoreline prediction and modeling. These include the Australian Research Council (Discovery and Linkage Program), and the NZ National Hazard Platform.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors wish to thank Anna Blacka (UNSW) for her assistance with the graphics and many colleagues that have contributed to shoreline modeling over the past decade and continue to do so in an open and collaborative manner for the further advancement in our field. We also wish to thank the reviewers for their insightful feedback that has improved the manuscript.
References
Almeida, L. P., de Oliveira, I. E., Lyra, R., Dazzi, R. L. S., Martins, V. G., and da Fontoura Klein, A. H. (2021). Coastal analyst system from space imagery engine (CASSIE): shoreline management module. Environ. Modell. Softw. 140:105033. doi: 10.1016/j.envsoft.2021.105033
Alvarez-Cuesta, M., Toimil, A., and Losada, I. J. (2021). Modelling long-term shoreline evolution in highly anthropized coastal areas. Part 1: model description and validation. Coast. Eng. 169:103960. doi: 10.1016/j.coastaleng.2021.103960
Anderson, D., Rueda, A., Cagigal, L., Antolinez, J., Mendez, F., and Ruggiero, P. (2019). Time-varying emulator for short and long-term analysis of coastal flood hazard potential. J. Geophys. Res. Oceans 124, 9209–9234. doi: 10.1029/2019JC015312
Anderson, D., Ruggiero, P., Antolinez, J. A. A., Mendez, F. J., and Allen, J. (2018). A climate index optimized for longshore sediment transport reveals interannual and multi-decadal littoral cell rotations. J. Geophys. Res. Earth Surface 123, 1958–1981. doi: 10.1029/2018JF004689
Angnuureng, D. B., Almar, R., Senechal, N., Castelle, B., Addo, K. A., Marieu, V., et al. (2017). Shoreline resilience to individual storms and storm clusters on a meso-macrotidal, barred beach. Geomorphology 290, 256–276. doi: 10.1016/j.geomorph.2017.04.007
Antolínez, J. A., Méndez, F. J., Anderson, D., Ruggiero, P., and Kaminsky, G. M. (2019). Predicting climate-driven coastlines with a simple and efficient multiscale model. J. Geophys. Res. Earth Surface 124, 1596–1624. doi: 10.1029/2018JF004790
Antolinez, J. A. A., Mendez, F. J., Camus, P., Vitousek, S., Gonzales, E. M., Ruggiero, P., et al. (2016). A multiscale climate emulator for long-term morphodynamics (MUSCLE-morpho). J. Geophys. Res. Oceans 121, 775–791. doi: 10.1002/2015JC011107
Barnard, P., Short, A. D., Harley, M. D., Splinter, K. D., Vitousek, S., Turner, I. I. L., et al. (2015). Coastal vulnerability across the Pacific dominated by El Ni no/southern oscillation. Nat. Geosci. 8, 1–8. doi: 10.1038/ngeo2539
Brunel, C., and Sabatier, F. (2009). Potential influence of sea-level rise in controlling shoreline position on the French Mediterranean Coast. Geomorphology 107, 47–57. doi: 10.1016/j.geomorph.2007.05.024
Bruun, P. (1962). Sea-level rise as a cause of shore erosion. J. Waterways Harbors Coast. Eng. Divis. 1, 117–130. doi: 10.1061/JWHEAU.0000252
Cagigal, L., Rueda, A., Anderson, D., Ruggiero, P., Merrifield, M. A., Montano, J., et al. (2020). A multivariate, stochastic, climate-based wave emulator for shoreline change modelling. Ocean Modell. 154:101695. doi: 10.1016/j.ocemod.2020.101695
Castelle, B., Bujan, S., Marieu, V., and Ferreira, S. (2020). 16 years of topographic surveys of rip-channelled high-energy meso-macrotidal sandy beach. Sci. Data 7, 1–9. doi: 10.1038/s41597-020-00750-5
Castelle, B., Marieu, V., Bujan, S., Splinter, K. D., Robinet, A., Sénéchal, N., et al. (2015). Impact of the winter 2013-2014 series of severe Western Europe storms on a double-barred sandy coast: beach and dune erosion and megacusp embayments. Geomorphology 238, 135–148. doi: 10.1016/j.geomorph.2015.03.006
Coco, G., Senechal, N., Rejas, A., Bryan, K. R., Capo, S., Parisot, J. P., et al. (2014). Beach response to a sequence of extreme storms. Geomorphology 204, 493–501. doi: 10.1016/j.geomorph.2013.08.028
Cooper, J., Masselink, G., Coco, G., Short, A., Castelle, B., Rogers, K., et al. (2020). Sandy beaches can survive sea-level rise. Nat. Clim. Change 10, 993–995. doi: 10.1038/s41558-020-00934-2
Cooper, J. A. G., and Pilkey, O. H. (2004). Sea-level rise and shoreline retreat: time to abandon the Bruun Rule. Glob. Planet. Change 43, 157–171. doi: 10.1016/j.gloplacha.2004.07.001
D'Anna, M., Castelle, B., Idier, D., Rohmer, J., Le Cozannet, G., Thieblemont, R., et al. (2021a). Uncertainties in shoreline projections to 2100 at Truc Vert Beach (France): role of sea-level rise and equilibrium model assumptions. J. Geophys. Res. Earth Surface 126, 1–26. doi: 10.1029/2021JF006160
D'Anna, M., Idier, D., Castelle, B., Le Cozannet, G., Rohmer, J., and Robinet, A. (2020). Impact of model free parameters and sea-level rise uncertainties on 20-years shoreline hindcast: the case of Truc Vert beach (SW France). Earth Surface Process. Landforms 45, 1895–1907. doi: 10.1002/esp.4854
D'Anna, M., Idier, D., Castelle, B., Vitousek, S., and Le Cozannet, G. (2021b). Reinterpreting the Bruun Rule in the context of equilibrium shoreline models. J. Marine Sci. Eng. 9:974. doi: 10.3390/jmse9090974
Davidson, M. (2021). Forecasting coastal evolution on time-scales of days to decades. Coast. Eng. 168:103928. doi: 10.1016/j.coastaleng.2021.103928
Davidson, M., Lewis, R., and Turner, I. (2010). Forecasting seasonal to multi-year shoreline change. Coast. Eng. 57, 620–629. doi: 10.1016/j.coastaleng.2010.02.001
Davidson, M., Splinter, K., and Turner, I. (2013). A simple equilibrium model for predicting shoreline change. Coast. Eng. 73, 191–202. doi: 10.1016/j.coastaleng.2012.11.002
Davidson, M., Turner, I., Splinter, K. D., and Harley, M. D. (2017). Annual prediction of shoreline erosion and subsequent recovery. Coast. Eng. 130, 14–25. doi: 10.1016/j.coastaleng.2017.09.008
Davidson-Arnott, R. G., and Bauer, B. O. (2021). Controls on the geomorphic response of beach-dune systems to water level rise. J. Great Lakes Res. (in press). doi: 10.1016/j.jglr.2021.05.006
Dissanayake, P., Brown, J., Wisse, P., and Karunarathna, H. (2015). Effects of storm clustering on beach/dune evolution. Marine Geol. 370, 63–75. doi: 10.1016/j.margeo.2015.10.010
Doria, A., Guza, R., O'Reilly, W. C., and Yates, M. (2016). Observations and modeling of San Diego beaches during El Ni no. Continent. Shelf Res. 124, 153–164. doi: 10.1016/j.csr.2016.05.008
Frazer, L. N., Anderson, T. R., and Fletcher, C. H. (2009). Modeling storms improves estimates of long-term shoreline change. Geophys. Res. Lett. 36:L20404. doi: 10.1029/2009GL040061
Greenslade, D., Hemer, M., Babanin, A., Lowe, R., Turner, I., Power, H., et al. (2019). 15 priorities for wind-waves research: an Australian perspective. Bull. Am. Meteorol. Soc. 101, E446–E461. doi: 10.1175/BAMS-D-18-0262.1
Gutierrez, B. T., Plant, N. G., and Thieler, E. R. (2011). A Bayesian network to predict coastal vulnerability to sea level rise. J. Geophys. Res. Earth Surface 116, 1–15. doi: 10.1029/2010JF001891
Harley, M., Turner, I., Kinsela, M., Middleton, J., Mumford, P., Splinter, K., et al. (2017). Extreme coastal erosion enhanced by anomalous extratropical storm wave direction. Sci. Rep. 7:6033. doi: 10.1038/s41598-017-05792-1
Harley, M. D., Turner, I. L., and Short, A. D. (2015). New insights into embayed beach rotation: the importance of wave exposure and cross-shore processes. J. Geophys. Res. F Earth Surface 120, 1470–1484. doi: 10.1002/2014JF003390
Ibaceta, R., Splinter, K. D., Harley, M. D., and Turner, I. L. (2020). Enhanced coastal shoreline modeling using an ensemble Kalman filter to include nonstationarity in future wave climates. Geophys. Res. Lett. 47:e2020GL090724. doi: 10.1029/2020GL090724
Jaramillo, C., González, M., Medina, R., and Turki, I. (2021). An equilibrium-based shoreline rotation model. Coast. Eng. 163:103789. doi: 10.1016/j.coastaleng.2020.103789
Kamphuis, J. W. (1991). Alongshore sediment transport rate. J. Waterway Port Coast. Ocean Eng. 117, 624–640. doi: 10.1061/(ASCE)0733-950X(1991)117:6(624)
Karunarathna, H., Pender, D., Ranasinghe, R., Short, A. D., and Reeve, D. E. (2014). The effects of storm clustering on beach profile variability. Mar. Geol. 348, 103–112. doi: 10.1016/j.margeo.2013.12.007
Kroon, A., de Schipper, M. A., van Gelder, P. H., and Aarninkhof, S. G. (2020). Ranking uncertainty: wave climate variability versus model uncertainty in probabilistic assessment of coastline change. Coast. Eng. 158:103673. doi: 10.1016/j.coastaleng.2020.103673
Le Cozannet, G., Bulteau, T., Castelle, B., Ranasinghe, R., Wöppelmann, G., Rohmer, J., et al. (2019). Quantifying uncertainties of sandy shoreline change projections as sea level rises. Sci. Rep. 9, 1–11. doi: 10.1038/s41598-018-37017-4
Ludka, B. C., Guza, R. T., O'Reilly, W. C., Merrifield, M. A., Flick, R. E., Bak, A. S., et al. (2019). Sixteen years of bathymetry and waves at San Diego beaches. Sci. Data 6, 1–13. doi: 10.1038/s41597-019-0167-6
Luijendijk, A., Hagenaars, G., Ranasinghe, R., Baart, F., Donchyts, G., and Aarninkhof, S. (2018). The state of the world's beaches. Sci. Rep. 8, 1–11. doi: 10.1038/s41598-018-24630-6
Masselink, G., Castelle, B., Scott, T., Dodet, G., Suanez, S., Jackson, D., et al. (2016a). Extreme wave activity during 2013/2014 winter and morphological impacts along the Atlantic coast of Europe. Geophys. Res. Lett. 43, 2135–2143. doi: 10.1002/2015GL067492
Masselink, G., Scott, T., Poate, T., Russell, P., Davidson, M., and Conley, D. (2016b). The extreme 2013/2014 winter storms: hydrodynamic forcing and coastal response along the southwest coast of England. Earth Surface Process. Landforms 41, 378–391. doi: 10.1002/esp.3836
McCarroll, R. J., Masselink, G., Valiente, N. G., Scott, T., Wiggins, M., Kirby, J. A., et al. (2021). A rules-based shoreface translation and sediment budgeting tool for estimating coastal change: ShoreTrans. Mar. Geol. 435:106466. doi: 10.1016/j.margeo.2021.106466
Mentaschi, L., Vousdoukas, M. I., Pekel, J.-F., Voukouvalas, E., and Feyen, L. (2018). Global long-term observations of coastal erosion and accretion. Sci. Rep. 8:12876. doi: 10.1038/s41598-018-30904-w
Miller, J. K., and Dean, R. G. (2004). A simple new shoreline change model. Coast. Eng. 51, 531–556. doi: 10.1016/j.coastaleng.2004.05.006
Montaño, J., Coco, G., Antolínez, J. A., Beuzen, T., Bryan, K. R., Cagigal, L., et al. (2020). Blind testing of shoreline evolution models. Sci. Rep. 10, 1–10. doi: 10.1038/s41598-020-59018-y
Montaño, J., Coco, G., Cagigal, L., Mendez, F., Rueda, A., Bryan, K. R., et al. (2021). A multiscale approach to shoreline prediction. Geophys. Res. Lett. 48:e2020GL090587. doi: 10.1029/2020GL090587
Pianca, C., Holman, R., and Siegle, E. (2015). Shoreline variability from days to decades: results of long-term video imaging. J. Geophys. Res. C Oceans 120, 2159–2178. doi: 10.1002/2014JC010329
Power, H. E., Pomeroy, A. W., Kinsela, M. A., and Murray, T. P. (2021). Research priorities for coastal geoscience and engineering: a collaborative exercise in priority setting from Australia. Front. Mar. Sci. 8:645797. doi: 10.3389/fmars.2021.645797
Ranasinghe, R. (2020). On the need for a new generation of coastal change models for the 21st century. Sci. Rep. 10, 1–6. doi: 10.1038/s41598-020-58376-x
Ranasinghe, R., Callaghan, D., and Stive, M. J. F. (2012). Estimating coastal recession due to sea level rise: beyond the Bruun Rule. Clim. Change 110, 561–574. doi: 10.1007/s10584-011-0107-8
Robinet, A., Idier, D., Castelle, B., and Marieu, V. (2018). A reduced-complexity shoreline change model combining longshore and cross-shore processes: the LX-Shore model. Environ. Modell. Softw. 109, 1–16. doi: 10.1016/j.envsoft.2018.08.010
Roelvink, D., Huisman, B., Elghandour, A., Ghonim, M., and Reyns, J. (2020). Efficient modeling of complex sandy coastal evolution at monthly to century time scales. Front. Mar. Sci. 7:535. doi: 10.3389/fmars.2020.00535
Rosati, J. D., Dean, R. G., and Walton, T. L. (2013). The modified Bruun Rule extended for landward transport. Mar. Geol. 340, 71–81. doi: 10.1016/j.margeo.2013.04.018
Ruggiero, P., Buijsman, M., Kaminsky, G. M., and Gelfenbaum, G. (2010). Modeling the effects of wave climate and sediment supply variability on large-scale shoreline change. Mar. Geol. 273, 127–140. doi: 10.1016/j.margeo.2010.02.008
Schepper, R., Almar, R., Bergsma, E., de Vries, S., Reniers, A., Davidson, M., et al. (2021). Modelling cross-shore shoreline change on multiple timescales and their interactions. J. Mar. Sci. Eng. 9:582. doi: 10.3390/jmse9060582
Smith, E. R., Wang, P., Ebersole, B. A., and Zhang, J. (2009). Dependence of total longshore sediment transport rates on incident wave parameters and breaker type. J. Coast. Res. 253, 675–683. doi: 10.2112/07-0919.1
Splinter, K., Turner, I., and Davidson, M. (2013). How much data is enough? The importance of morphological sampling interval and duration for calibration of empirical shoreline models. Coast. Eng. 77, 14–27. doi: 10.1016/j.coastaleng.2013.02.009
Splinter, K., Turner, I. L., Davidson, M., Barnard, P., Castelle, B., and Oltman-Shay, J. (2014). A generalized equilibrium model for predicting daily to interannual shoreline response. J. Geophys. Res. Earth Surface 119, 1936–1958. doi: 10.1002/2014JF003106
Splinter, K. D., Turner, I. L., Reinhardt, M., and Ruessink, G. (2016). Rapid adjustment of shoreline behavior to changing seasonality of storms: Observations and modelling at an open-coast beach. Earth Surface Process. Landforms. 42, 1186–1194. doi: 10.1002/esp.4088
Toimil, A., Camus, P., Losada, I. J., and Alvarez-Cuesta, M. (2021). Visualising the uncertainty cascade in multi-ensemble probabilistic coastal erosion projections. Front. Mar. Sci. 8:683535. doi: 10.3389/fmars.2021.683535
Toimil, A., Camus, P., Losada, I. J., Le Cozannet, G., Nicholls, R. J., Idier, D., et al. (2020). Climate change-driven coastal erosion modelling in temperate sandy beaches: methods and uncertainty treatment. Earth Sci. Rev. 202:103110. doi: 10.1016/j.earscirev.2020.103110
Turki, I., Medina, R., Coco, G., and Gonzalez, M. (2013). An equilibrium model to predict shoreline rotation of pocket beaches. Mar. Geol. 346, 220–232. doi: 10.1016/j.margeo.2013.08.002
Turner, I., Harley, M., Short, A., Simmons, J., Bracs, M., Phillips, M., et al. (2016). A multi-decade dataset of monthly beach profile surveys and inshore wave forcing at Narrabeen, Australia. Sci. Data 3:160024. doi: 10.1038/sdata.2016.24
USACE and Coastal Engineering Research Center (1984). Shore Protection Manual. US Army Corps of Engineers, Washington, DC.
Vitousek, S., Barnard, P. L., and Limber, P. (2017a). Can beaches survive climate change? J. Geophys. Res. Earth Surface 122, 1060–1067. doi: 10.1002/2017JF004308
Vitousek, S., Barnard, P. L., Limber, P., Erikson, L., and Cole, B. (2017b). A model integrating longshore and cross-shore processes for predicting long-term shoreline response to climate change. J. Geophys. Res. Earth Surface 122, 782–806. doi: 10.1002/2016JF004065
Vos, K., Harley, M. D., Splinter, K. D., Simmons, J. A., and Turner, I. L. (2019a). Sub-annual to multi-decadal shoreline variability from publicly available satellite imagery. Coast. Eng. 150, 160–174. doi: 10.1016/j.coastaleng.2019.04.004
Vos, K., Splinter, K. D., Harley, M. D., Simmons, J. A., and Turner, I. L. (2019b). CoastSat: a Google Earth Engine-enabled Python toolkit to extract shorelines from publicly available satellite imagery. Environ. Modell. Software 122:104528. doi: 10.1016/j.envsoft.2019.104528
Vousdoukas, M. I., Ranasinghe, R., Mentaschi, L., Plomaritis, T. A., Athanasiou, P., Luijendijk, A., et al. (2020). Sandy coastlines under threat of erosion. Nat. Clim. Change 10, 260–263. doi: 10.1038/s41558-020-0697-0
Wolinsky, M. A. (2009). A unifying framework for shoreline migration: 1. Multiscale shoreline evolution on sedimentary coasts. J. Geophys. Res. 114:F01008. doi: 10.1029/2007JF000855
Wolinsky, M. A., and Murray, A. B. (2009). A unifying framework for shoreline migration: 2. Application to wave-dominated coasts. J. Geophys. Res. 114:F01009. doi: 10.1029/2007JF000856
Keywords: shoreline, sandy coastline, prediction, waves, uncertainty, equilibrium models, ensemble modeling
Citation: Splinter KD and Coco G (2021) Challenges and Opportunities in Coastal Shoreline Prediction. Front. Mar. Sci. 8:788657. doi: 10.3389/fmars.2021.788657
Received: 03 October 2021; Accepted: 29 November 2021;
Published: 20 December 2021.
Edited by:
Felice D'Alessandro, University of Milan, ItalyReviewed by:
Ali Dastgheib, IHE Delft Institute for Water Education, NetherlandsAlessandro Romano, Roma Tre University, Italy
Copyright © 2021 Splinter and Coco. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kristen D. Splinter, ay5zcGxpbnRlckB1bnN3LmVkdS5hdQ==
 Kristen D. Splinter
Kristen D. Splinter Giovanni Coco
Giovanni Coco