Development of the global tsunami forecasting system considering the dynamic interaction of tide-tsunami around the Korean Peninsula

Dang, Hai Van; Lee, Eunju; Ahn, Seongho; Kim, Kyeong Ok; Shin, Sungwon; Ha, Taemin

doi:10.3389/fmars.2023.1258552

ORIGINAL RESEARCH article

Front. Mar. Sci., 13 November 2023

Sec. Physical Oceanography

Volume 10 - 2023 | https://doi.org/10.3389/fmars.2023.1258552

This article is part of the Research Topic Recent Advances in Computational Technologies to Improve Understanding of Water Environments View all 8 articles

Development of the global tsunami forecasting system considering the dynamic interaction of tide-tsunami around the Korean Peninsula

Hai Van Dang¹

Eunju Lee¹

Seongho Ahn²

Kyeong Ok Kim³

Sungwon Shin¹

Taemin Ha^4*

¹Department of Marine Science and Convergent Engineering, Hanyang University ERICA, Ansan, Republic of Korea
²Department of Civil Engineering, Jeju National University, Jeju, Republic of Korea
³Marine Environmental Research Center, Korea Institute of Ocean Science and Technology, Busan, Republic of Korea
⁴Department of Civil Engineering, Kangwon National University, Samcheok, Republic of Korea

Tsunamis are extreme natural events that pose a significant threat to coastal communities, making a comprehensive understanding of tsunami propagation mechanisms necessary for forecasting and evacuation purposes. While previous forecasting models have successfully examined several factors influencing tsunami propagation, the impact of the dynamic interaction between tides and tsunamis has yet to be investigated thoroughly. The Yellow Sea is characterized by high tidal elevations and strong tidal currents, which can accelerate the tsunami impacts on the Korean coasts. This study developed a regional tide-tsunami interaction model based on the shallow water equation model to quantitatively investigate the dynamic tide-tsunami interaction and evaluate its influence on tsunami propagation and amplification mechanism. High-resolution numerical tests were conducted for two worst-case tsunami scenarios that occurred in the Korean Peninsula, including the 2010 Chilean tsunami (far-field forecasting) and the 2011 Tohoku tsunami (near-field forecasting). The performance of the numerical model was validated utilizing the observational tide data collected along the Korean coasts. The numerical model effectively reproduces the horizontal distribution of instantaneous free surface displacement and velocity. The results reveal that the dynamic tide-tsunami interaction induced by these tsunamis generally reduces the water level and velocity in the ocean while amplifying these quantities as the tsunamis approach the coastal regions. However, due to the complex and arbitrary features of the topography, the impact of the dynamic tide and tsunami interaction on water elevation and velocity is inconsistent even compared with measurements from the adjacent tidal gauges, which suggests that the dynamic interaction can play an opposite role during the propagation and amplification process. Furthermore, the different arrival times of tsunamis along the Korean coasts are dominated by the corresponding phase of the local tidal currents that develop in each region.

1 Introduction

Tsunamis pose a severe hazard to coastal communities and are widely recognized as one of the most perilous natural disasters due to their potential to cause extensive damage to marine ecosystems, coastal infrastructures, and loss of life (Giles et al., 2021). Numerous studies have investigated the impact of tsunami-induced inundation and overland flow in coastal regions; however, previous studies on transoceanic tsunamis are still limited. Transoceanic tsunamis, although they typically do not cause significant inundation on coastlines, can have an adverse impact on marine infrastructures (Lynett et al., 2014) and populations (Heidarzadeh et al., 2022). For instance, the 1960 Chilean tsunami resulted in damage to several facilities in Japan, Hawaii, and the Philippines after traveling a distance of 17,000 km across the Pacific Ocean. Similarly, the 2004 Sumatra tsunami had a profound impact, causing over 230,000 deaths locally and in Africa (Igarashi et al., 2011). In addition, the 2010 Chilean tsunami induced strong currents that caused damage to docks in San Diego Bay and Ventura Harbor (Lynett et al., 2014). In January 2022, a significant tsunami induced by volcanic activities of Hunga Tonga–Hunga Haapai (HTHH) in the Tonga region propagated with remarkable speeds of 312 m/s, reaching distant coastlines in the Indian Ocean and the Mediterranean Sea. Consequently, this event resulted in at least five casualties and approximately $USD 90.4 million in damage (Heidarzadeh et al., 2022).

Moreover, the Korean Peninsula is particularly vulnerable to tsunamis that originate in the Sea of Japan and the Ring of Fire around the Pacific Ocean Basin. Since the 1900s, five historical earthquake-induced tsunamis have been observed on the Korean Peninsula. The first tsunami occurred in 1940 due to the Shakotan-oki earthquake (M_w = 7.5), resulting in severe damage to several houses and fishing vessels but no fatalities (Satake, 1986). In 1964, the Niigata earthquakes (M_w = 7.5) generated a tsunami, reaching the Korean coasts without damage (Satake and Abe, 1983). The most destructive tsunami occurred due to the Akita-oki earthquake in 1983 (Miyoshi, 1986), causing a maximum runup height of 4 m measured at Imwon Harbor on the eastern coasts of the Korean Peninsula. As a consequence, three casualties and significant damage to infrastructures were reported during this event (Kim et al., 2016). Another tsunami was generated by the 1993 Hokkaido earthquake with the same magnitude as the Akita-oki earthquake (Tanioka et al., 1995). However, the center of the Hokkaido tsunami source was further from the Korean coastlines than the Akita-oki tsunami, causing less influence to be observed in the Korean peninsula compared to the 1983 event. Three historical tsunami events were induced by earthquakes located in the Sea of Japan with a magnitude less than 8; however, the Ring of Fire around the Pacific Basin is characterized by various earthquake sources capable of producing earthquakes with a magnitude greater than 9.0 (Parsons et al., 2012). In recent years, the Tohoku-oki earthquake (M_w = 9.0~9.1) was generated in the forearc region of Japan, inducing tsunami heights of approximately 0.2 m recorded by tidal gauges installed along Jeju Island. In the Ring of Fire positions near the Korean coasts, such as the Nankai Trough area, a high possibility of large earthquakes occurring repeatedly at intervals of 100 to 200 years was witnessed (Ishibashi and Satake, 1998), which may induce significant impacts on Korean coastlines. Tsuji et al. (2014) confirmed that the 1707 Hoei earthquake, the largest earthquake in the Nankai trough, produced a large tsunami that killed over 20,000 people (Lee et al., 2015) and damaged the Korean coasts. Generally, the Korean Peninsula is prone to distant tsunamis throughout the Pacific Basin and other transoceanic tsunamis. The resulting tsunamis from the Pacific Ocean require between 1 hour and 4 hours to reach the Korean coasts, whereas transoceanic tsunamis from further distant locations, such as Chile or USA can take up to 12 hours (Yoon et al., 2019).

The propagation of tsunamis across long distances in the open sea is a complex process influenced by several factors, including the tsunami source characteristics, the distance between the original source and the affected coastlines, the coastal topography, and the presence of submarine features (Iglesias et al., 2014; Ayca and Lynett, 2016). Another critical factor influencing the precise forecasting of tsunami propagation is the interaction between tides and tsunamis (Ayca and Lynett, 2016). However, most previous studies overlooked the influence of tidal effects when predicting tsunami propagation, primarily because the water motions induced by tsunamis are relatively stronger than other “background water motions” (Kowalik and Proshutinsky, 2010 Lee et al., 2015). Moreover, the effects of the dynamic interaction of tides and tsunamis have been neglected in simulating tsunami transportation along the coasts partly due to the lack of computational resources. Therefore, the dynamic interaction was mostly considered as a linear superposition from the sea level change caused by tides and tsunamis (Kowalik and Proshutinsky, 2010). Mofjeld et al. (2007) investigated the probabilistic distribution of the effects on maximum tsunami heights at Seaside, Oregon. Their methodology involved an examination of linearly superimposed exponentially decaying tsunami events, coupled with the prediction of tidal behavior along the open coast at Seaside. It is worth noting that their investigation did not consider nearshore modeling characterized by the introduction of complex topographic features; however, the results proposed statistical properties, including means, standard deviations, and probability distribution functions, of the maximum tsunami height that changed in response to tidal patterns in the offshore region of the Seaside. In the report Coastal Disaster Prevention Council released in 2012, eleven scenarios of extreme earthquake tsunamis (M_w = 9) along the Pacific coasts of Japan were simulated to investigate tsunami propagation. The results show that the maximum tsunami heights, reaching up to 20 m along the coastlines, are measured at the maximum high tides by linearly superposing two peak values (Lee et al., 2015); however, the dynamic interaction between tides and tsunamis is not considered. On the other hand, several recent studies have recognized the significant impact of tides on the tsunami patterns near coastal areas. Zhang et al. (2011) reported that although a negligible influence was observed in the open coasts, the dynamic effects of tides during the 1964 Alaska tsunami had a substantial impact on the runup and inundation around some estuaries and rivers. The results indicate that the dynamic effects of tides accounted for approximately 50% of maximum wave runup and 100% of inundation depths during the 1964 Prince William Sound (Alaska). Kowalik and Proshutinsky (2010) conducted numerical experiments to examine the coupling effects of strong tides and frequent tsunamis in Anchor Point and Anchorage at Cook Inlet, Alaska. The results indicated that the tides could considerably affect the tsunami propagation, resulting in an amplification of up to six times the tsunami magnitude in Anchor Point. In contrast, the Anchorage location experienced damping by 5% and amplification by 35%, depending on the phase of the tides. Lee et al. (2015) investigated the influence of tides on tsunami propagation in five scenarios of potential earthquakes in the Nankai trough under four different tide phases for flood, ebb, high, and low tides. The results showed that the changing water depths induced by tides generated higher tsunami heights and earlier tsunami arrivals at high tide than in low tide conditions. Moreover, the findings emphasized that the level of tide impacts on tsunami propagation significantly depends on the individual basin, bathymetry, and coastal topography. Furthermore, Ayca and Lynett (2016) investigated to what degree the inclusion of tides in tsunami simulations has any impact on tsunami-generated currents. The findings indicate that the variability attributable to tidal effects on event-maximum tsunami currents ranges from 10% to 25%. Ayca and Lynett (2016) also pointed out that there is no general rule in estimating the tidal effects on tsunami currents for a specific location, even in the neighboring harbors. The patterns of tidal effects on tsunami transportation in harbors are highly influenced by the physical characteristics of individual site-specific harbors. However, it should be noted that the previous findings neglect the tide effects or are specific to case studies such as Alaska, California, and the Nankai trough, which may not be generalizable to other regions around the world.

The Yellow Sea and East China Sea are known to experience the development of strong tides. Kim et al. (2021) also confirmed that sea-level rise increases the tidal amplitude in shallow water regions, which can have a significant impact on tsunami propagation. Therefore, the consideration of the tide effect is crucial when predicting the process of tsunami propagation in the Korean Peninsula (Heo et al., 2019a; Heo et al., 2019b). Weisz and Winter (2005) further support the statement that tides can increase the water depth in nearshore regions, which should be taken into account when calculating the tsunami run-up. Thus, investigating the dynamic interaction of tides and tsunamis during the propagation of tsunamis in Korean coastal regions is of great importance. Such investigations can provide valuable insight into the development of coastal hazard mitigation strategies.

Shallow water equation models have gained popularity among scientists and engineers as effective tools for simulating tsunami propagation and run-up due to their computational efficiency and acceptable accuracy. Numerous previous studies (e.g., Apotsos et al., 2011; Cheung et al., 2011; Lee et al., 2015) have utilized the shallow water equation models to simulate case studies of historical tsunamis successfully. A well-known model is the COMCOT model (COrnell Multigrid COupled Tsunami model), which is based on the shallow water theory. The recently updated version of the COMCOT model has been enhanced to include the dispersion effects (Wang and Liu, 2011), improving the ability of the COMCOT model to simulate tsunami behaviors accurately. The developed COMCOT model, v1.7, the latest available online version, has been effectively applied to various tsunami scenarios in previous studies (e.g., Lynett et al., 2012; Wijetunge, 2012; Chai et al., 2014; Heo et al., 2019a). Therefore, the COMCOT version 1.7 was also utilized to simulate the tsunami propagation in this study.

The primary objective of this study is to develop a new algorithm based on the COMCOT model to enhance the tsunami forecasting system. This algorithm considers the interaction between tides and tsunamis, specifically applied to the propagation of tsunamis in the Korean Peninsula. A series of numerical experiments utilizing this algorithm were conducted to provide valuable insights into the tsunami patterns interacting with strong tides and tidal currents along the Korean coasts. Apart from the introduction section, the remainder of this study is constructed into the three following sections. Section [2] provides a comprehensive description of the regional tide-tsunami model developed for this study. Moreover, detailed information on the regional tide and global tsunami models, utilized to extract the boundary conditions for the regional tide-tsunami model, was also introduced. Furthermore, this section presents details of the numerical model setup. In Section [3], the numerical model results of the regional tide model and the regional tide-tsunami model are presented. This section also further evaluates the predictive performance of the regional tide-tsunami interaction model by comparing its free surface displacements to those extracted from the conventional method (Linear Superimposed Tide-Tsunami) and observation data obtained by several tidal gauges installed along the Korean coasts of the past tsunamis. Finally, Section [4] summarizes the findings and highlights the limitations of the study.

2 The global tsunami forecasting system including tide-tsunami interactions

In this section, a detailed description of the research methodology for modeling tide-tsunami interactions will be presented in the following. Previously, Heo et al. (2019a) proposed a fundamental concept of a tsunami forecasting algorithm that includes dynamic tide–tsunami interactions in the tsunami model. The algorithm was basically constructed according to three different numerical domains, and the numerical results were efficiently manipulated to be applied as initial and boundary conditions to the corresponding numerical domains. However, the original algorithm was barely applicable to certain virtual tsunami cases and led to unexpected numerical errors on open boundaries of the numerical domain due to a lack of handling radiation conditions.

To address numerical errors that remained in Heo et al. (2019a), a newly improved algorithm was developed by remedying the radiation conditions of the model. This enhanced numerical algorithm is implemented to establish the global tsunami forecasting system, which includes the dynamic tide–tsunami interactions. Firstly, the global tsunami forecasting system is structured using three different numerical domains, each consisting of corresponding modeling systems, defined as the global tsunami model, the regional tide model, and the regional tide–tsunami model. Secondly, a novel numerical module has been developed to facilitate the manipulation of numerical results, enabling their application as initial and boundary conditions on smaller numerical domains. Lastly, the modeling systems can be connected effectively using a corresponding numerical module. Detailed explanations of the new algorithm for simulating the dynamic interaction between tides and currents will be presented in the following subsections.

2.1 The regional tide model

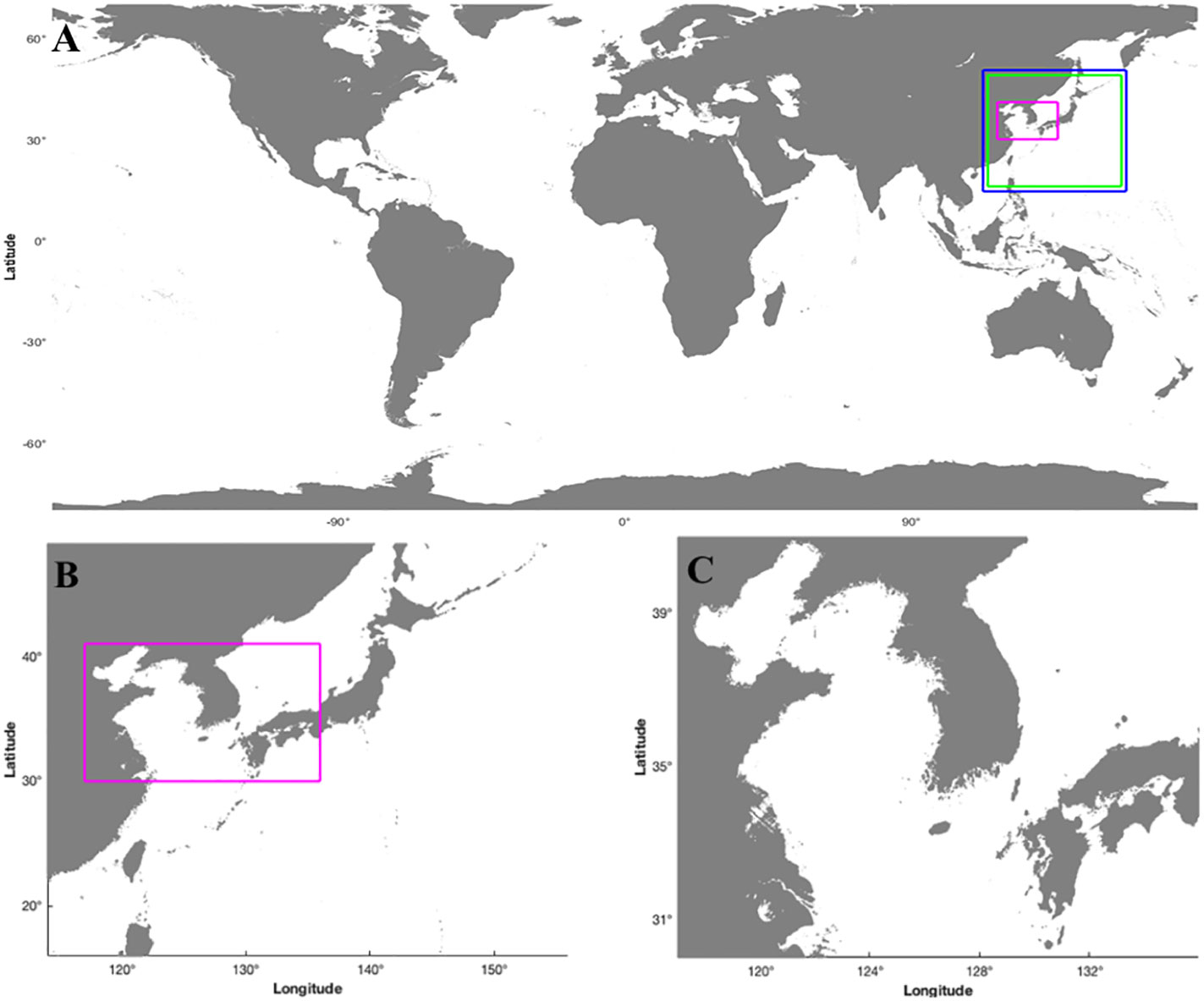
The regional modeling system of tides and tidal currents, referred to as ROSI (Regional mOdeling System of tIdes and tidal currents), is established in the second numerical domain, R2DI (Regional 2^nd Domain for tIde and tsunami modeling), and followed by the subsequent regional numerical domains (Figure 1A). The updated COMCOT model (ver. 1.7; Wang and Liu, 2011) is significantly improved through source code manipulation and utilized to simulate tides and tidal currents in the Korean Peninsula. Although the original COMCOT model can handle nested grids, enabling the efficient simulation of distant tsunamis in a large numerical domain, it also employs simple radiation conditions on open boundaries of the numerical domain (Ha and Cho, 2015). As a result, the original model can effectively manage outgoing tsunami wave energy on open boundaries but struggles with incoming wave energy. Furthermore, the original model occasionally encounters problems with controlling outgoing wave energy, resulting in reflection back into the computational domain.

FIGURE 1

Figure 1 Numerical model domains (A) global domain G1D, (B) R2DU domain, and (C) R3DN domain.

In tide modeling, the identification of appropriate initial conditions and time-varying boundary conditions is of great importance on the entire computational grids and open boundaries, respectively. The COMCOT model includes an embedded “hotstart” module to address initial conditions and an embedded “boundaries” module to manage the time-varying boundary conditions. However, the utilization of the embedded module for time-varying boundary conditions requires the computation domain set to be closed, resulting in the accumulation of tide energy inside the numerical domains due to the reflection back into the domains. To mitigate this undesired accumulation, the original COMCOT model was improved by adding robust radiation conditions to handle incoming-outgoing wave energy on the open boundaries. In the original COMCOT model, the following radiation condition is employed to mimic outgoing wave energy on open boundaries.

\begin{array}{l} H \vec{U} \pm c_{e} η = 0 & (1) \end{array}

Where $H$ is the water depth, $\vec{U}$ represents velocities in the horizontal directions, $c_{e}$ is the celerity under the long wave assumption, and $η$ is the free surface displacement. As reported in several numerical experiments, it is confirmed that the original radiation condition resulted in unexpected reflection back to the computational domains. Since the governing equations are numerically computed in the COMCOT model by first calculating the continuity equations and then the momentum equations during one cycle of computation, time-varying conditions for tides and tidal currents, which are determined in each time step, may generate an artificial wall condition on open boundaries without any radiation conditions. To minimize the numerical errors, several typical radiation conditions were tested, and two different conditions were employed to handle the outgoing wave energy on open boundaries.

\begin{array}{l} \frac{\partial η}{\partial t} \pm c_{e} \frac{\partial η}{\partial x} = 0 & (2) \end{array}

\begin{array}{l} \frac{\partial \vec{U}}{\partial t} \pm c_{e} \frac{\partial \vec{U}}{\partial x} = 0 & (3) \end{array}

Eq. 2 is applied to the COMCOT model after the computation of the continuity equation, and Eq. 3 follows the computation of the momentum equations in each time step. The continuity equation calculates the free surface displacement of a current time step by utilizing the free surface displacement and the horizontal velocity of the previous time step. However, the momentum equation updates the horizontal velocity of the current time step by using the free surface displacement at the present time step and the horizontal velocity at the previous time step. The radiation conditions consider the newly updated values, effectively preventing the occurrence of artificial wall conditions on open boundaries.

The regional tidal model generates a substantial amount of data, reaching hundreds of Gigabytes, and is generated by creating boundary conditions that match the computational time intervals of the ROSI model. This process consumes a considerable amount of time, even when utilizing high-performance computing servers with large memory capacities. Therefore, a newly constructed numerical model is required to reduce computational storage and processing time. In the ROSI model, the boundary conditions can be interpolated from the boundary conditions applied before and after the calculated time. The interval at which the boundary condition is applied at the boundary of the numerical domain decreases to a certain extent while producing negligible changes in the results. As a result, the time interval of the boundary conditions was set to 15 minutes for efficient operation of the prediction system, which can achieve satisfaction in both the data processing speed and the accuracy of the results.

2.2 The global tsunami model

The Global mOdeling System of tsUnamis, known as GOSU, is established in the first numerical domain, G1D (Global 1^st Domain for tsunami modeling), followed by the next regional numerical domains (Figure 1A). The simulation of the global tsunami model using the COMCOT model has been widely applied in previous studies (e.g., Lynett et al., 2012; Wijetunge, 2012; Ha and Cho, 2015). The original COMCOT model was slightly modified to handle the cyclic boundary condition, and the new model is employed to simulate tsunami propagation in the global numerical domain, G1D. In the global domain, the eastern and western boundaries are connected, in which the cyclic boundary conditions are implemented to ensure the continuous propagation of tsunamis from either boundary to the opposite boundary (Lee et al., 2015). On the other hand, land boundary conditions were applied to facilitate the reflection of tsunamis in Antarctica at the southern boundary; however, as the northern boundary is connected to the sea area, the open boundary conditions were employed to prevent energy accumulation within the numerical domain.

2.3 The regional tide-tsunami model

A regional modeling system has been developed to simulate the tide, tidal current, and tsunami, taking into account the dynamic interaction between tides and tsunamis. This system, named ROSES (Regional mOdeling System of tidEs, tidal currents, and tSunamis), is established in the third numerical domain, R2DU (Regional 2^nd Domain for tide–tsUnami modeling), and followed by the next regional numerical domains (R3DN). The R3DN domain is utilized for the global tsunami forecasting system organized by the Korean Meteorological Administration, which provides the highest resolution, mainly focusing on the Korean coasts (Figure 1B). R3DN and R2DU represent the domains of the numerical model utilized for the regional tsunami-tide interaction model (ROSES), which mainly focuses on the Korean Peninsula. R3DN is the nested grid included in the upper grid domain R2. In the whole system, R2 domains are divided into two types of domains, which have the same grid resolution and are employed in corresponding numerical models. The first one, R2DI, is used in GOSU and ROSI as the R2 domain, and the other one, R2DU, is employed in ROSES. The R2DU domain has dimensions less than 1.5 degrees in both longitudes and latitudes compared to those of the R2DI domain. Since the boundary conditions of ROSES are generated from the numerical results of GOSU and ROSI, we carefully selected the boundaries of the R2DU domain to give some distance from each boundary of the R2DI domain. Consequently, the boundary conditions of ROSES are properly generated to include sufficient spatial tidal mixing from ROSI and to avoid unexpected numerical errors that can be induced near the nested grid boundary. The primary objective of ROSES is to perform numerical modeling that considers the dynamic interaction between tides and tsunamis through the application of boundary conditions over time in the numerical domain. In addition, the initial condition of tides is required at the time when the tsunami is generated simultaneously to predict the impact of the tsunami effectively. Similar to the regional tidal model, the application of lateral boundary conditions is critical in preventing re-reflections back to numerical domains during the numerical modeling. The ROSES model is specifically configured to prevent the accumulation of tsunami and tide energy by utilizing incoming-outgoing boundary conditions established in the regional tidal model (ROSI). The initial and boundary conditions used in ROSES are determined by the integration of the ROSI and GOSU (Figure 2), which involves the following three steps:

(1) The initial and boundary conditions employed in ROSI were generated utilizing the Global Tidal Database (GTB) model (TPXO Global Tidal Models: Egbert et al., 1994; and Egbert and Erofeeva, 2002).

(2) The regional tidal model (ROSI) determines the tides and tidal currents in the numerical domain as a function of time, while the global tsunami model (GOSU) was utilized to simulate the tsunami generation, propagation, and inundation in the still water level, thereby enabling the acquisition of the water level and flow velocity over time in the entire numerical domain. The water level and flow velocity may be interfered with at the boundary conditions, causing numerical errors in the ROSES model. Thus, as discussed above, to minimize the numerical errors, the size of the numerical domain of ROSES was set to be 1.5 degrees smaller in both longitude and latitude compared to the numerical domain of both ROSI and GOSU.

(3) Initial and boundary conditions of ROSES are calculated by combining the results of the regional tidal model (ROSI) and the global tsunami model (GOSU). By conducting these three steps, the initial and boundary conditions could be obtained. Finally, ROSES is capable of simulating the dynamic interaction of tide-tsunami and the effects of tides on tsunami propagation around the Korean Peninsula.

FIGURE 2

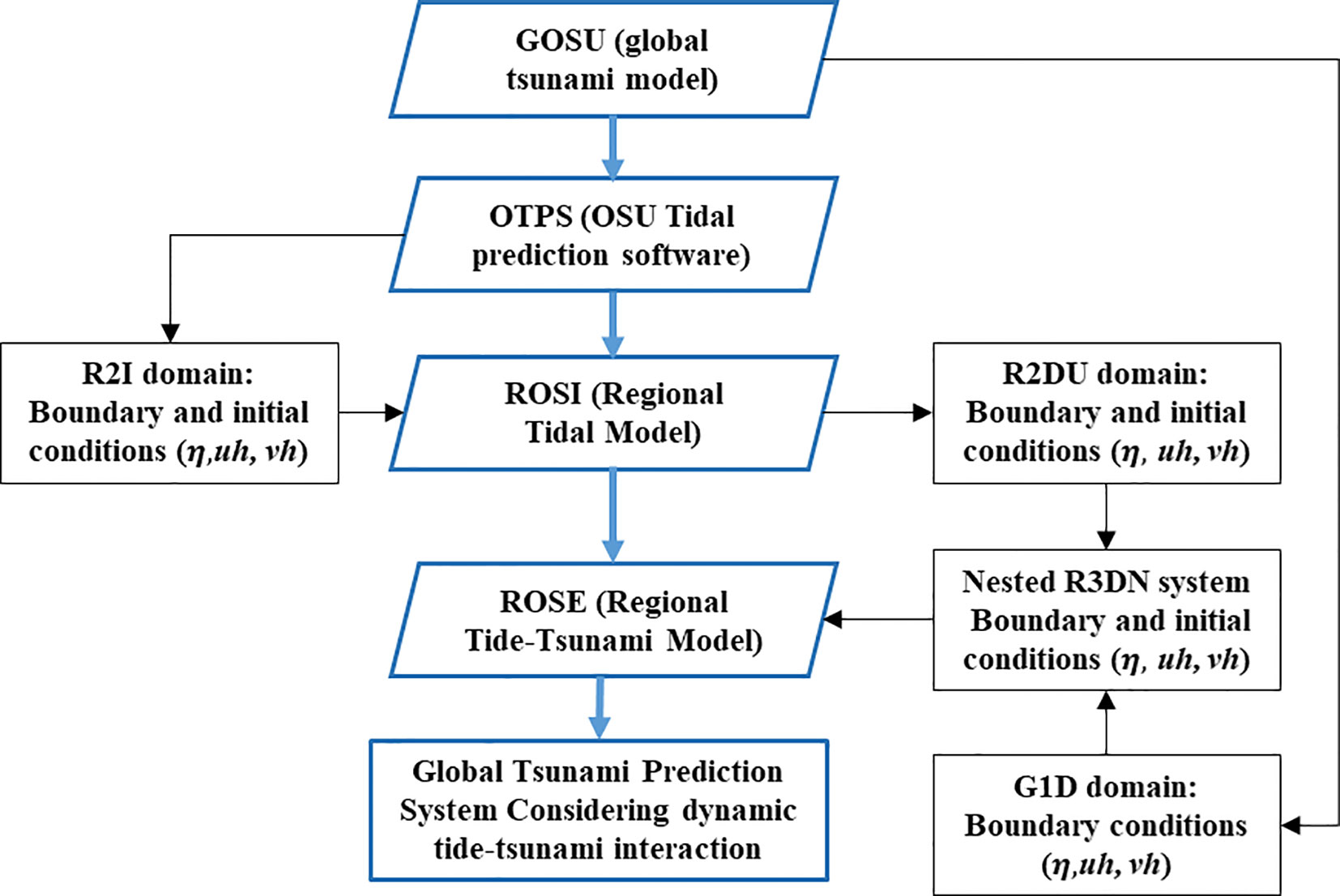
Figure 2 A new algorithm for investigating the effects of tide-tsunami interaction on global tsunami prediction system.

This global tsunami prediction model was designed with the ultimate objective of real-time operation and automation. After calculating the boundary conditions of ROSI from the global tidal model, a module based on Fortran codes was developed to extract the results of ROSI and GOSU as input for the boundary conditions of ROSES. Finally, an algorithm for the tsunami prediction system was constructed to enable the autonomous exaction of the calculation modules on each server so the results could be mutually transmitted. The modules developed for the implementation of real-time operation and automation are summarized as follows:

- OTPS2toCOMCOT: The boundary condition of ROSI is extracted from the global tidal model

- TStoCOMCOT: The boundary condition of ROSES is derived from the calculation results of both ROSI and GOSU models. Since the ROSES model considers the interaction between tides and tsunamis by simultaneously simulating both tides and tsunamis, the results of both models are required to apply the boundary conditions. Hence, the TStoCOMCOT module is responsible for extracting and synthesizing the water level and velocity data corresponding to the boundary conditions of ROSES from the results of each model to provide the superimposed data.

- Hotstart: The initial conditions of ROSES are calculated by synthesizing the results of ROSI and GOSU, enabling the tsunami prediction system to operate with the generation of the tsunami in ROSES simultaneously.

2.4 Numerical domain and nested grid system

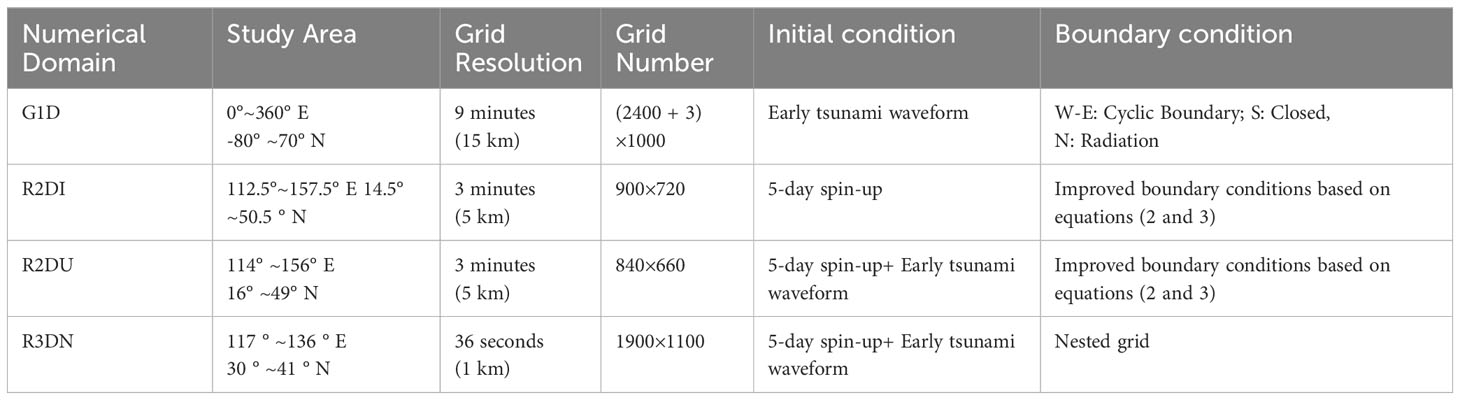
The international project GEBCO (General Bathymetric Chart of the Oceans) has been operated by the International Hydrographic Organization (IHO) and the Intergovernmental Oceanographic Commission (IOC) under the leadership of the United Nations Educational Scientific and Cultural Organization (UNESCO). The representative product of GEBCO, a GEBCO_2020, provides the bathymetry data of the entire world at 15-arc-second intervals (~0.5 km), and the recently released GEBCO_2021 (GEBCO Compilation Group, 2021) has improved the bathymetry data by adding various regional data around the world to the existing dataset. Detailed information on GEBCO can be referred to this website (https://www.gebco.net/data_and_products/gridded_bathymetry_data/). For the regional dataset in the Korean peninsula, the Korea Meteorological Administration (KMA) has established and utilized bathymetric data around the South Korean Peninsula with a 36-arcsecond interval grid (~1.1 km) for the tsunami warning system (Lee et al., 2015). Furthermore, the Korea Hydrographic and Oceanographic Agency (KHOA) recently improved bathymetric data for the same region with 150 m intervals to enhance the utility and reliability of the recent ocean numerical model (Yoo et al., 2019). In this study, numerical bathymetry data was constructed for the global tsunami prediction system using the global bathymetry data, GEBCO_2021, at a 15-arcsecond interval. To improve the accuracy of the area near the Korean Peninsula, a 150 m horizontal interval database provided by the KHOA was incorporated. Furthermore, to more accurately represent the complex coastal and island regions of the southwestern coasts of the Korean Peninsula, all available data, including the regional terrain data, were also considered. The numerical topographic map used in this study was compared to the reproduction of topographic maps according to Pixel registration and Grid registration techniques. The co-registration technique ensures precise georeferencing of data points, enabling accurate and consistent representation of ocean topographic mapping. The technique was also utilized for the ETOPO1 Ice Surface and Bedrock global relief models, comprehensively described in Amante and Eakins (2009). The Pixel registration technique induced relatively few errors in the Finite Difference Method (FDM) (Wessel and Watts, 1988; Wessel and Smith, 2004), enabling the production of the topographic map effectively. Since the topographic data were synthesized from various sources, the numerical topographic maps were generated using GMT modules (Generic Mapping Tool) ver. 5.4.5 (Wessel et al., 2019). The land masking and ocean bathymetry data was processed and then validated using the actual topographic map to improve the reliability of the numerical topographic maps. The grid information, the initial conditions, and the boundary conditions of each module are shown in Table 1, and the map is illustrated in Figure 1.

TABLE 1

Table 1 Initial and boundary condition setup for numerical model.

3 Numerical results and discussion

3.1 The regional tide model (ROSI)

To validate the reliability of ROSI, the regional tide modeling was performed using initial and boundary conditions extracted from the GTB model. The initial conditions were obtained by calculating the tidal elevations and currents for the entire numerical domain of the regional tidal model, while the boundary conditions were applied by computing the tidal elevations and currents overtime at the boundaries of the numerical domain. A spin-up time of three days has been commonly used in previous studies (e.g., Federico et al., 2016; Pratama, 2019) to allow tides to propagate adequately throughout the entire numerical domain. However, tides on the East and South coasts of the Korean Peninsula are weak even with a 3-day spin-up time, compared to the strong tides that occur on the West and South coasts. Therefore, the spin-up time was extended to five days to ensure that the influence of the tides could be sufficiently propagated into the entire numerical domain.

To analyze the results of the regional tidal model (ROSI), we carried out tidal modeling to investigate the impact of the highest tide event that occurred around August 15^th, 2019, which induced the most pronounced effects along coasts in the Korean Peninsula (Figure 3). A 5-day spin-up was implemented to observe the quantitative changes of the tide effects in the vicinity of the Korean coast from August 13^th at 0:00 to August 17^th at 0:00. Generally, tides rotate around the center of the Yellow Sea, where the Chinese mainland and the Korean Peninsula are situated on either side (Fang et al., 2004). The tidal currents develop by rotating counterclockwise in the Yellow Sea, originating from Jeju Island, following the southwestern coast of the Korean Peninsula, passing through North Korea, and eventually reaching China (Choi et al., 2003). A recurring phenomenon occurs at regular intervals, in which tidal currents simultaneously enter the narrow strait from the southwest and northwest directions of the Taiwan Strait. However, it is worth noting that there is a possibility of numerical errors resulting from abnormal accumulation of tidal energy, such as in the vicinity of the Taiwan Strait, which are reported in some previous studies (e.g., Jan et al., 2004; and Choi et al., 2013). However, upon examining the results of the tidal modeling performed by the ROSI model, it can be seen that tidal levels and currents are well reproduced over time without numerical errors near the vicinity of Taiwan Strait, and the tidal currents pass through the narrow Taiwan Strait and finally exists from the numerical domain (Figures 3A–D). Furthermore, the regional tidal model ROSI quantitatively replicates the development of tides and tidal currents that rotate counterclockwise with a specific period in the Yellow Sea over time (Figures 3A–F).

FIGURE 3

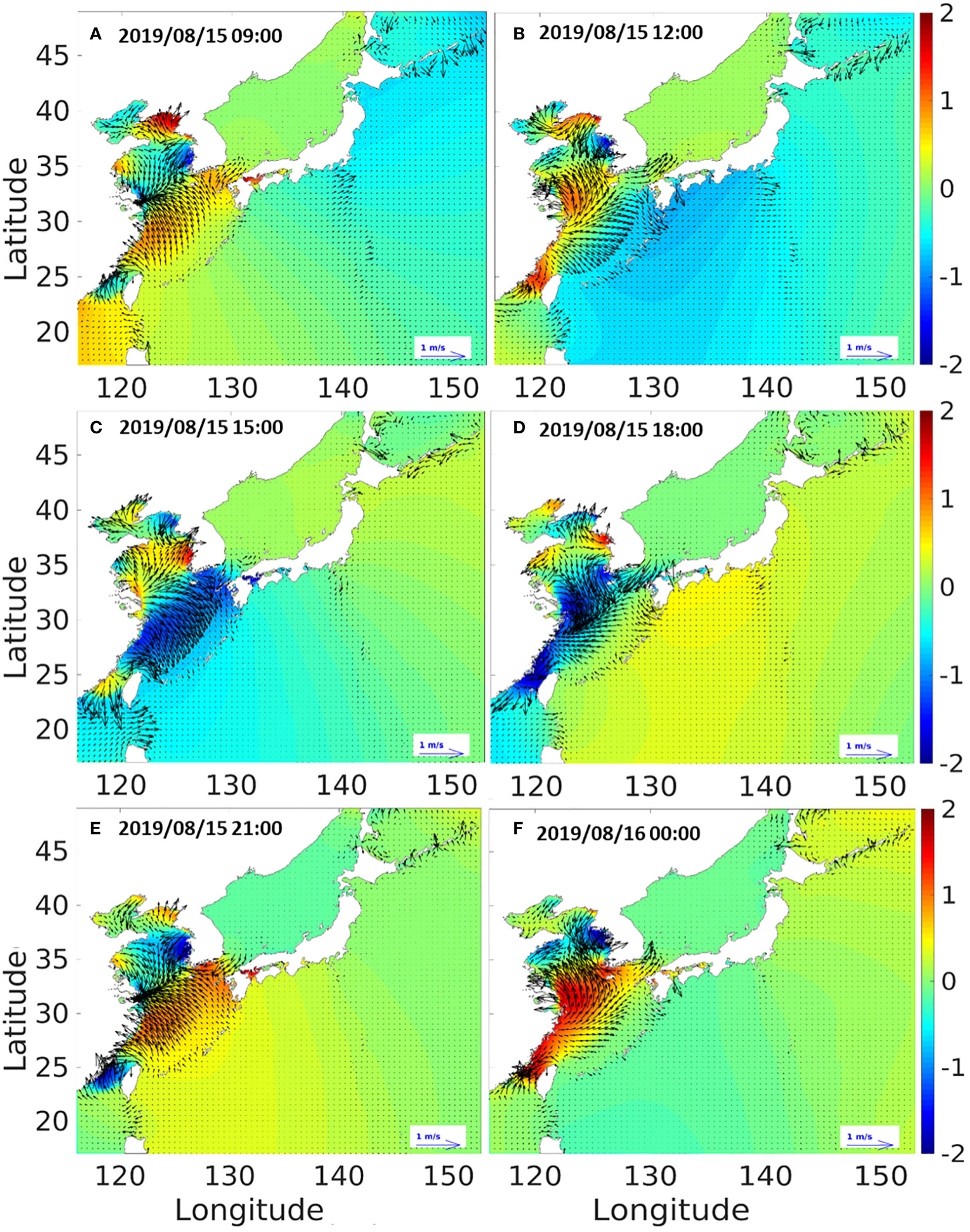
Figure 3 Tidal modeling results of the regional tidal model (ROSI) for the highest tide (August 15^th, 2019) in the Korean Peninsula for specific time instants: 2019/08/15 09:00 (A), 2019/08/15 12:00 (B), 2019/08/15 15:00 (C), 2019/08/15 18:00 (D), 2019/08/15 21:00 (E), 2019/08/16 00:00 (F).

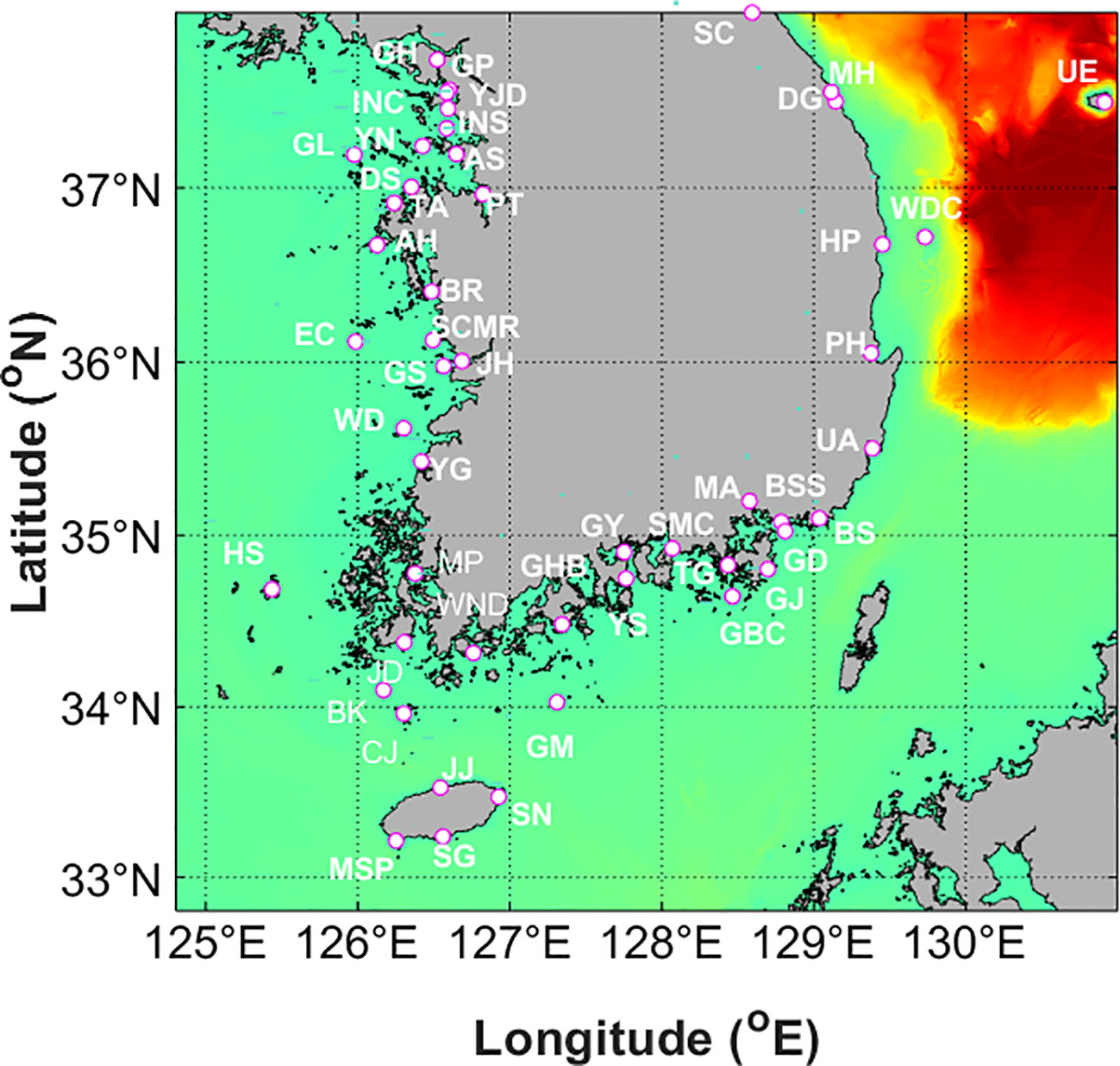
For quantitative verification of the ROSI results, tidal modeling was performed during a four-year period spanning from 2010 to 2011 and 2018 to 2019, which encompassed significant events such as the 2010 Chilean earthquake and the 2011 Tohoku earthquakes, which had the most substantial impact on the Korean Peninsula in the last 20 years. The boundary conditions of ROSI were extracted from the GTB Model (TPXO9), and the changes in tides and currents over the four years were recorded and statistically analyzed to validate the ROSI results. Currently, the tsunami prediction system that has been established is not parallelized, requiring one year of numerical modeling time on a single server to perform tidal modeling for four years. This processing time makes it impossible to conduct a study for model validation and improvement. The alternative approach is to divide the 4-year tidal modeling period into 48 monthly segments and to utilize 48 nodes of the computation server to perform the calculation simultaneously. The clock time required to simulate the one day of tidal modeling is approximately 20 hours by utilizing a single core of the Power Edge Dell R640 server. In order to maintain the continuity of the calculated results from each node, a 7-day spin-up time was used before the analysis to ensure that the tides were adequately reproduced in all data used for the analysis. For example, we can divide the 2011 year into 12 months from January to December. Then, each month has 7 days of mixing time before the first day of the month. In detail, the first segment is January 2011, and we simulated from 25 December 2010 for the initial tidal mixing. After the 48 simulations were completed, we performed a combination of each segment into continuous profiles by removing the tidal mixing part from each segment. As a result, the continuity of the data was maintained at the beginning and end of each divided data segment. The regional tidal model was optimized by determining tidal boundary conditions by combining harmonic constants under various conditions to obtain the best quantitative results (Byun et al., 2023). The tidal modeling was performed according to the tidal boundary conditions, and the observation data was compared with the numerical modeling results to optimize tidal boundary conditions. The tide observation data is extracted from 49 tide stations located along the Korean Peninsula, presented in Figure 4, while the abbreviations for the different station locations illustrated in Figure 4 are clarified in Table A1 in the Appendix section.

FIGURE 4

Figure 4 Locations of 49 tidal observation stations along the Korean Peninsula.

Four harmonic combinations of tidal constants, including [Whole: 58 harmonic constants; 4 main constituents: (M2+S2+K1+O1); 6 main constituents: (M2+S2+K1+O1+N2+K2); each component of 6 mains: (M2, S2, K1, O1, N2, K2)], were calculated to validate the ROSI results by comparing tidal amplitudes with those measured in the observation stations for each condition. The PSMSL/POL Tidal Analysis Software Kit 2000 (TASK-2000 Package) was developed for the harmonic analysis of data (such as from tidal gauges), and the harmonic analysis was also performed using the observation data gathered from 49 tide gauges from 2010 to 2011 and 2018 to 2019. Figure 5 compares the tidal amplitudes derived from the measured tidal results of the observation stations and the regional tide model (ROSI) through harmonic analysis with the main tidal constituents of M2, S2, K1, O1, N2, and K2. Three ocean tidal stations, including Wangdolcho, Boksacho, and Gyoboncho stations, are excluded from the comparison because there are missing datasets in 2019. Generally, the numerical model effectively reproduces the tidal amplitudes measured at the 46 observation stations during given periods. Table 2 presents the statistical comparison of simulated tidal constituents (TCs) and measured results from observation data in 46 tide gauge stations. The predictive performance of ROSI is evaluated using statistical metrics, including bias, root-mean-square-error (RMSE), and correlation coefficient (R). The bias factor represents the tendency of the predicted tidal constituents, in which the positive bias shows parameter overestimation, in contrast to the negative bias for underestimation. The RMSE factor is utilized to compute the goodness of fit between the predicted and observed values, whereas the correlation coefficient (R) ranges from 0 to 1, indicating the agreement of these values. The statistical values are expressed as follows:

FIGURE 5

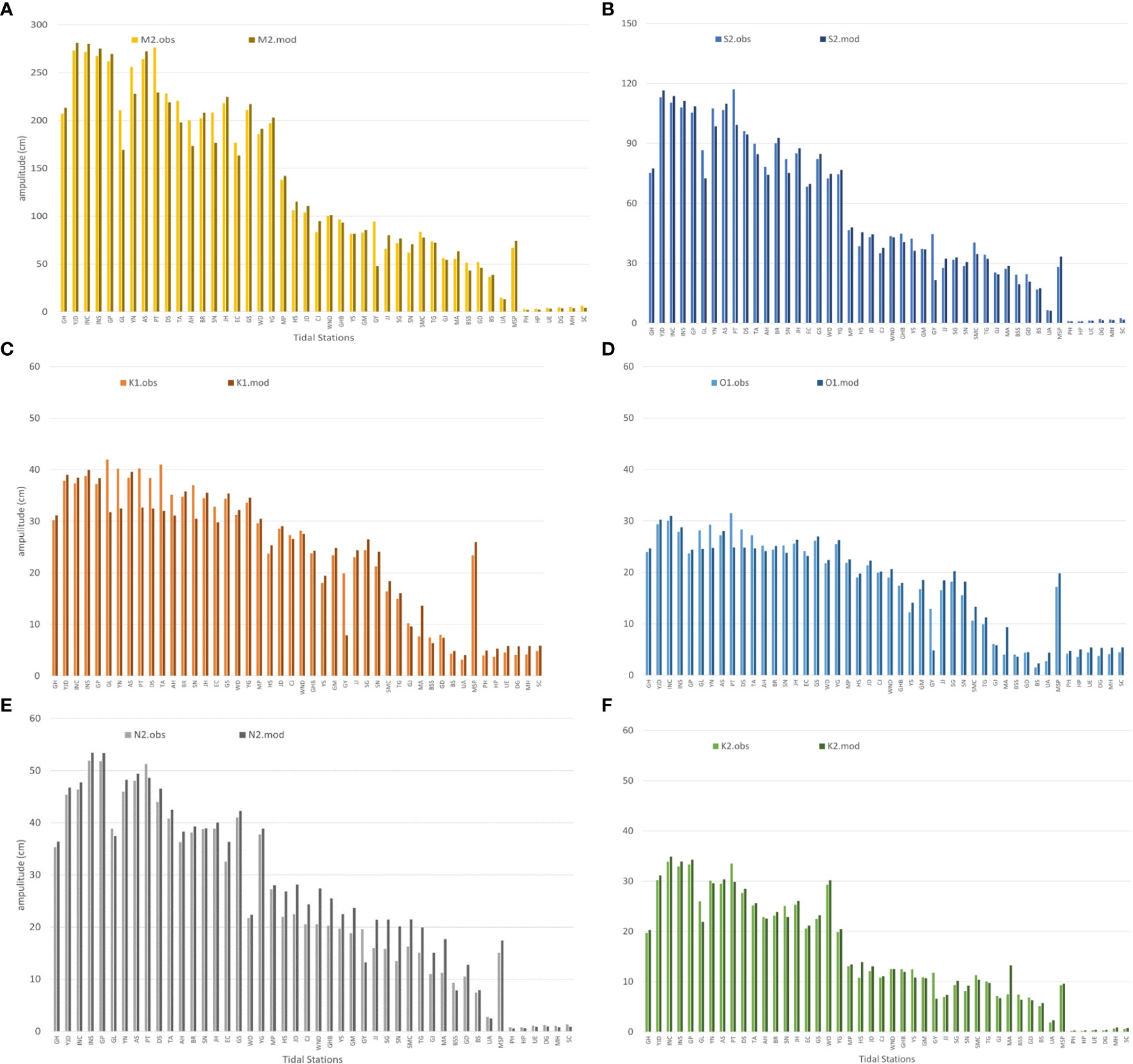
Figure 5 Comparison of observed and modelled amplitude distribution through harmonic analysis for six harmonic constants in each tide stations (A) M2, (B) S2, (C) K1, (D) O1, (E) N2, and (F) K2.

TABLE 2

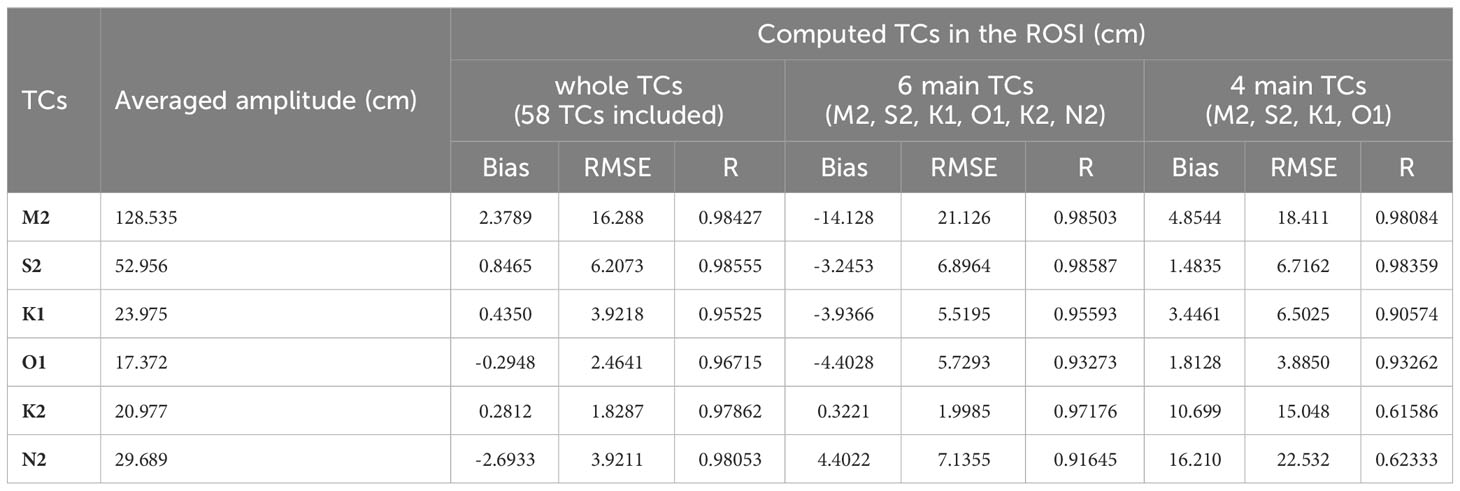
Table 2 Statistical comparison of the tidal constituents (TCs) in the ROSI with the observed data in 49 tidal stations around the Korean Peninsula.

\begin{array}{l} B i a s = \frac{1}{N} \sum_{i = 1}^{N} (η_{O, i} - η_{S, i}) & (4) \end{array}

\begin{array}{l} R M S E = \sqrt{\frac{1}{N} \sum_{i = 1}^{N} {(η_{O, i} - η_{S, i})}^{2}} & (5) \end{array}

\begin{array}{l} R = \frac{\sum_{i = 1}^{N} (η_{O, i} - \bar{η_{O}}) (η_{O, i} - \bar{η_{S}})}{\sqrt{\sum_{i = 1}^{N} {(η_{O, i} - \bar{η_{O}})}^{2} \sum_{i = 1}^{N} {(η_{S, i} - \bar{η_{S}})}^{2}}} & (6) \end{array}

where N is the number of elevations measured in different tidal constituents, $η_{O, i}$ and $η_{S, i}$ are observed and simulated elevations for data point i. Moreover, $\bar{η_{O}} and \bar{η_{S}}$ represent the mean values of observed and simulated elevations. For the harmonic combination of whole 58 tidal constituents (58 TCs), the computed amplitudes show the best agreement between measured amplitudes compared to the four main TCs and six main TCs combinations, with the correlation coefficient (R) ranging from 0.95525 to 0.9855. Moreover, the absolute bias and RMSE values derived from whole 58TCs are less than those calculated in the 6 main TCs and 4 main TCs. The combination of six main TCs (M2, S2, K1, O1, N2, K2) also fit the measured amplitudes with R higher than 0.93273. For 4 main TCs (M2, S2, K1, and O1), the correlation factors were witnessed above 0.90574, indicating reasonable agreement with the observed tidal amplitudes. Generally, the results of ROSI slightly overestimated the tidal amplitudes in comparison to the observation data, while the discrepancy in average amplitudes of each harmonic constant was less than 10%.

3.2 The regional tide-tsunami model (ROSES)

Over the past two decades, two tsunamis had a significant impact on the Korean Peninsula, including the 2010 Chilean and 2011 Tohoku tsunamis. The tsunami propagation model is initialized according to the Okada model (Okada, 1985). In the context of finite fault models derived through seismic inversion techniques, the Okada model was applied to numerous subfaults based on the inverted slip distribution (Yoon et al., 2019). Since the occurrence of the 2010 Chilean tsunami and the 2011 Tohoku tsunami, numerous inverted slip distributions have been published. Among these distributions, the final US Geological Survey (USGS: https://earthquake.usgs.gov/data/finitefault/) demonstrated the closest alignment with the data obtained using our model. First, on 27 February 2010, the earthquake occurred at an original position of 36.122°S and 72.898°W, as a result of the shallow thrust faulting processes at the Nazca plate beneath the South America plate. The fault rupture, predominantly situated offshore, was measured to be more than 100 km in width and extended to over 500 km parallel to the coastlines (Hayes et al., 2017). Furthermore, the rupture began approximately 22.9 km deep, propagating in the westward, northward, and southward directions and generating a fault slip of up to 15 m. Consequently, a massive earthquake (M_w = 8.8) was generated along the fault rupture area, which shook and warped the seafloor, generating a significant tsunami. The detailed information on fault parameters for the 2010 Chilean tsunami utilized in this study can be found on the USGS link (https://earthquake.usgs.gov/earthquakes/eventpage/official20100227063411530_30/finite-fault : latest access on 17 October 2018). Second, the 2010 Tohoku tsunami also resulted from a significant earthquake (M_w = 9.1) derived from the shallow thrust fault between the Pacific and North American plates. The fault depth was observed to be 29 km, while the fault movement ranged from 50 m to 60 m, affecting the fault region of 400 km in length and 150 km in width (Hayes et al., 2017). The detailed input source parameters of the historical tsunami event are comprehensively described on the USGS finite fault distribution website (https://earthquake.usgs.gov/earthquakes/eventpage/official20110311054624120_30/origin/detail: latest access on 21 June 2019). Two earthquake tsunamis were simulated and utilized to validate the global and regional tsunami prediction systems. The validation process required different application methods for the two tsunamis, for they occurred in different domains of ROSES and ROSI models. Particularly, the 2010 Chilean tsunami, which occurred in the external domain of the two models, can be applied to assess the behavior of a transoceanic tsunami propagating from a distant location (far-field forecasting) and encountering the strongly developed tidal currents near the Korean Peninsula. On the other hand, the 2011 Tohoku tsunami, which occurred in the internal domain (near-field forecasting), was investigated for the following two purposes. The first is to validate the behavior of a tsunami generated from a strong earthquake occurring within the numerical domain, integrated with considerable tidal currents, and the second one is to identify the potential numerical errors caused by the energy of the internal tsunami near the boundary of the numerical domain. Therefore, using the actual near-field and far-field tsunami scenarios can be sufficient in evaluating the predictive performance of ROSES.

The validation of tsunami prediction can be conducted through integrated modeling of the tides and tsunamis using ROSI, GOSU, and ROSES models. Firstly, the tide and tsunami were extracted from the ROSI and GOSU, respectively, and utilized as initial and boundary conditions for ROSES. These initial and boundary conditions were calculated by summarizing the results of the ROSI and GOSU models, and the ROSES model performed 30 hours of the regional tsunami modeling, including tide-tsunami interactions dynamically without a spin-up simulation, by using the “hotstart” module embedded in the COMCOT model. The results of the ROSES model were compared with the results of the regional tidal modeling ROSI and the global tsunami modeling GOSU to confirm that the ROSES model can dynamically reproduce the propagation of tsunamis and the development of tides in the vicinity of the Korean Peninsula. A quantitative analysis was also conducted to determine how the dynamic interaction between tsunamis and tides influences tsunami propagation and evolution.

3.2.1 Numerical simulation of the 2010 Chilean tsunami

The generation and propagation of the 2010 Chilean tsunami were simulated using the regional tide- tsunami around the Korean Peninsula. Figure 6 presents the horizontal distribution of the free surface displacements of tides and tsunamis in the regional tide-tsunami model ROSES. At 14:00, strong tides with maximum amplitudes of up to approximately 2.5 m were generated in the Yellow Sea. The 2010 Chilean tsunami arrived at the eastern coast of Japan and propagated along the east coast of Japan, reaching the northwestern part of the Yellow Sea at 18:00. The tsunami and tide combination continued to develop widely during this event. The original source of the 2010 Chilean tsunami is very far from the Northwestern Pacific Ocean, including the Korean Peninsula; thus, the Chilean tsunami propagated across the ocean and arrived in the region with an approximately slight wave amplitude of 0.2 m (Kato et al., 2011). Therefore, the elevation of tides was significantly larger than that of tsunami-only, making the propagation of the distant tsunami not clearly observable in this figure. The tidal elevation was excluded from the model results to clarify the transformation of the 2010 Chilean tsunami around the Korean coasts.

FIGURE 6

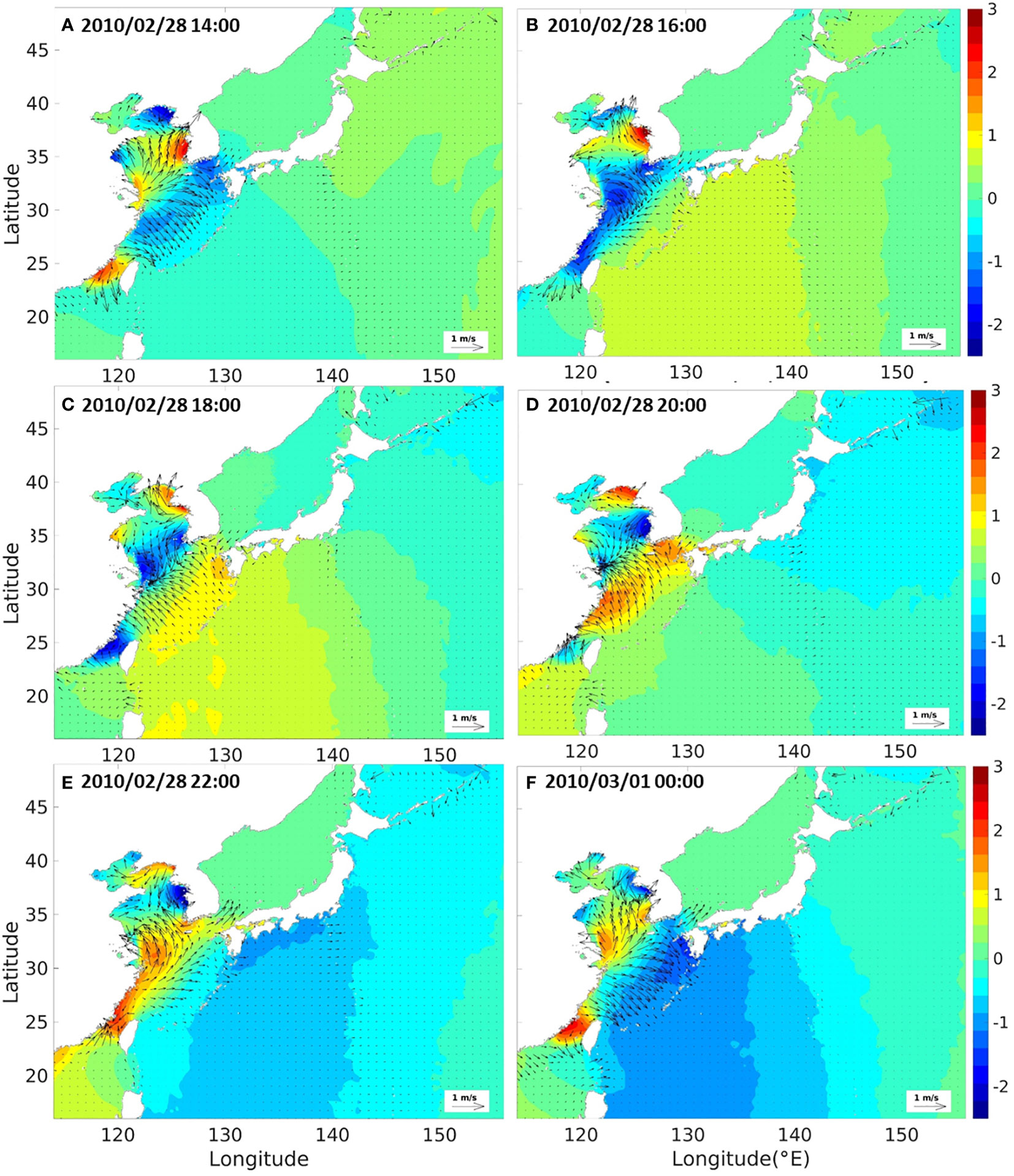
Figure 6 Snapshots of tide and tsunami elevations extracted from the regional tidal-tsunami model for the 2010 Chilean tsunami for specific time instants: 2010/02/28 14:00 (A), 2010/02/28 16:00 (B), 2010/02/28 18:00 (C), 2010/02/28 20:00 (D), 2010/02/28 22:00 (E), 2010/03/01 00:00 (F).

Figure 7 shows the dynamic modeling results of the regional tide-tsunami model, ROSES, indicating the free surface displacement of the tsunami and tide-tsunami interaction components (A), tsunami-only (B), and tide-tsunami interaction components (C) corresponding to the time steps. Figures 7A, B show similar patterns of free surface displacement distribution over different time instants. The tsunami arrived and mainly influenced the southern coast of the Korean Peninsula initially, propagating along the west coasts and quickly dissipating towards the Yellow Sea. By the time the tsunami reached the Yellow Sea, the phases of tidal currents were at the stage developing toward the northwest (Figure 6C), and consequently, the tsunami experienced strong tidal currents in almost a similar direction during propagation over the Yellow Sea (see Figures 6, 7). Therefore, the arrival time of the tsunami along the southwestern coast of the Korean Peninsula, including Jeju Island, was advanced proportionally as the tsunami propagated while being delayed along the southeastern coast due to tidal currents in the opposite direction to the tsunami propagation. On the other hand, only a slight difference was observed in the free surface displacement between the tsunami-tide effects and tsunami-only near the Korean coasts since the wave amplitude of the tsunami and the corresponding potential energy were small in absolute quantity (Kim and Son, 2018; Kim and Son, 2019). Behera et al. (2011) identified that the interaction of the tide and the tsunami is influenced by the magnitude of the tide-induced current and the phase velocity of the tsunami, similar to linear waves that interact with currents (Li and Herbich, 1984; Kaihatu, 2009). It has long been recognized that the interaction produces the Doppler effect, resulting in a reduction in the wavelength and an increase in the wave height for opposing currents and vice versa (Behera et al., 2011; Løvholt et al., 2015). The Doppler effect involves a shift in the frequency (or wavelength) of waves due to the relative motion between the source of waves and an observer (Seddon and Bearpark, 2003). In the context of tsunamis and tides in the current study, the Doppler effect occurred; however, this effect is usually not the primary factor that influences their interaction compared to other critical factors. In Figures 7, 8, the dynamic interaction of tide and the tsunami displays the Doppler effect, which resulted in a reduction of the tsunami elevations and earlier arrival time along the southwestern coast of the Korean Peninsula while amplifying tsunami elevations and delaying arrival time along the southeastern coast. Furthermore, the dynamic interaction had a negative impact on the amplification of tsunami elevations on the southeastern coasts of the Chinese mainland (the sea around the Shanghai coast). The probable intensity of the tidal effects is observed in Figure 7C, in which a significant impact is concentrated around the coast of Shanghai. While the maximum tsunami elevation was recorded as less than 0.2 m on the Shanghai coast, a peak difference of free surface displacements derived from the tsunami elevations of dynamic modeling and tsunami-only in this area was measured at approximately 0.15 m, which was relatively over 75% high. Figure 8 compares the velocities recorded in the dynamic model, ROSES, of the tsunami and tide-tsunami interaction components (A), tsunami-only (B), and only the tide-tsunami interaction components (C). Similar to the patterns of the free surface displacement distribution, the effects of tidal currents considerably decreased the maximum velocity of the tsunami propagation near the Chinese east coasts due to the Doppler effect; the tide-tsunami interaction components had minor impacts along the Korean coasts since the wave velocities of the tsunami and the corresponding kinetic energy were small in absolute quantity (Kim and Son, 2018; Kim and Son, 2019). Overall, the simulated horizontal distribution of the free surface displacement and velocity qualitatively reproduced the 2010 Chilean tsunami propagation, considering the tidal effects on the Korean Peninsula effectively.

FIGURE 7

Figure 7 The regional tide-tsunami model results in the Korean Peninsula over time for the Chilean tsunami: (A) dynamic modeling results indicating the elevation of tsunami considering tidal effects; (B) tsunami-only; (C) tidal effects.

FIGURE 8

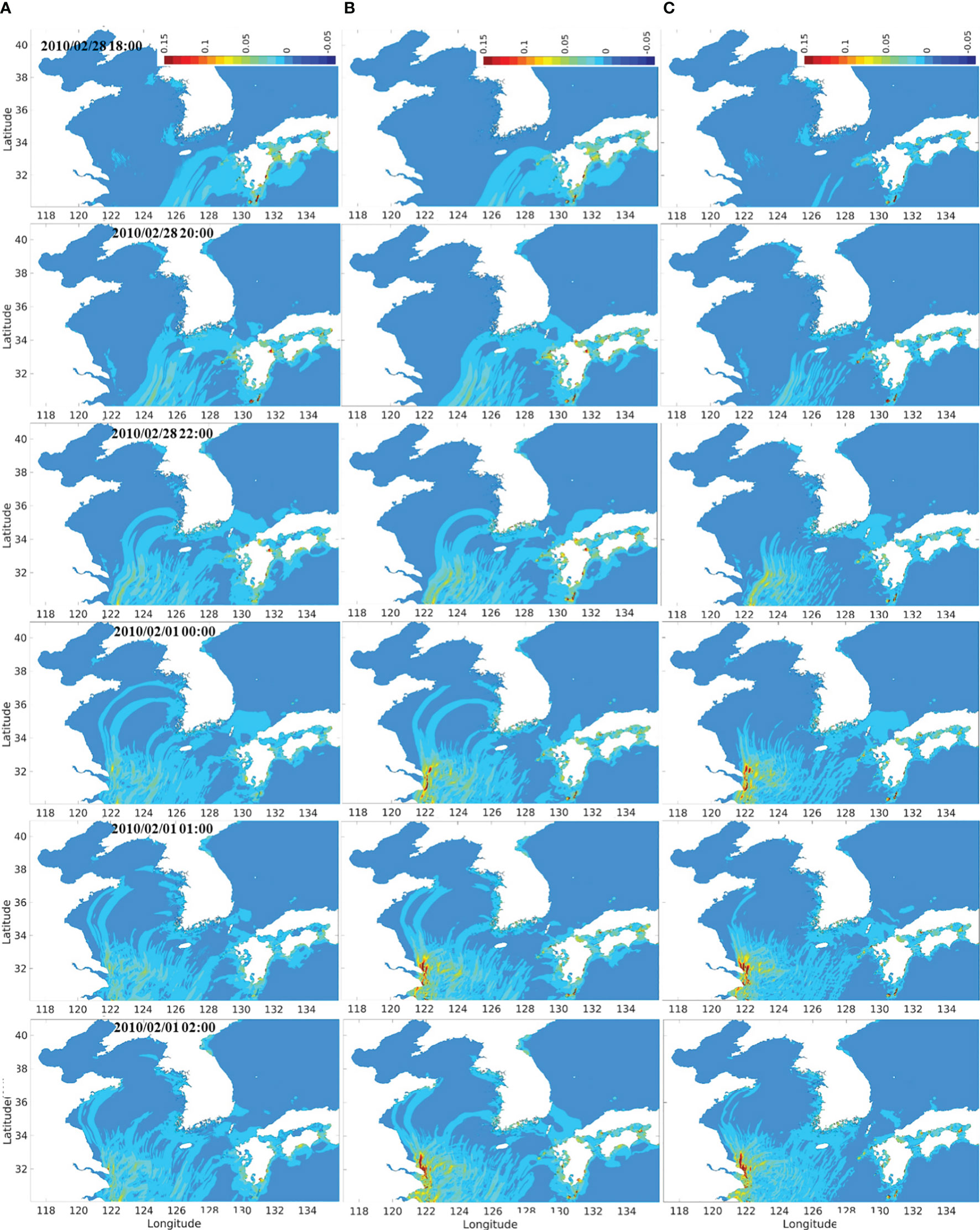
Figure 8 The comparison of velocity results extracted from the regional tide-tsunami model in the Korean Peninsula over time for the Chilean tsunami: (A) dynamic modeling results indicating the velocities of tsunami considering tidal effects; (B) tsunami-only; (C) tidal effects.

3.2.2 Numerical simulation of the 2011 Tohoku tsunami

The propagation of the 2011 Tohoku tsunami that occurred on 11^th March 2011, considering the interaction with tides, was computed using the dynamic tide-tsunami interaction model ROSES. Firstly, the generation and propagation of the Tohoku tsunami and tides in the Yellow Sea were simultaneously simulated. Figure 9 shows the snapshots of the horizontal distribution of the free surface displacement of tsunamis and tides in various time instants. The initial tsunami was generated at approximately 15:00 on the east coast of Tohoku; meanwhile, strong tide currents were concurrently observed in both the west coast and east coast of the Korean Peninsula and the Chinese mainland, respectively. The tsunami propagated along Japanese coasts, and its amplitude markedly decreased before reaching the Korean south coast at 21:00. The tide currents developed towards the south and southwest of Korean coasts. Generally, the high-resolution numerical model, ROSES, qualitatively represented the distribution of the free surface displacement effectively. However, the issue of tsunami wave reflection at the boundaries for the 2011 Tohoku tsunami simulation occurred in this model, as seen at 17:00 in Figure 9B. This numerical error is attributed to the nested grid technique employed in the existing COMCOT model. Several previous studies (e.g., Ha et al., 2013; Lynett et al., 2017) attempted to consider and handle the typical numerical errors in the tsunami simulation. Additional boundary conditions introduced by previous studies (e.g., Son et al., 2011; Ha and Cho, 2015; Son and Lynett, 2020), which were reported to potentially reduce the wave reflection issue, were applied in the COMCOT model utilized in the current study. However, the absolute amount of numerical error is not relatively significant in this study, and it could not be eliminated completely even with the introduction of the additional boundary conditions accompanied by the inevitably longer simulation time. Moreover, the 2011 Tohoku tsunami is an unprecedentedly large-scale event in history and occurred near the boundary of the numerical domain where wave reflection was generated. As a consequence, there were limitations in achieving complete control of wave reflection when a large amount of tsunami energy reached the boundaries. However, a quantitative examination shows that the tsunami prediction system, considering the tide-tsunami interaction, well reproduces the propagation of the tsunami in the vicinity of the Korean Peninsula. Furthermore, since the 2011 Tohoku tsunami generated the water elevation still smaller than the tide level near the Korean Peninsula; therefore, the propagation of tsunami is not prominently distinguished from tides in the ROSES results, whereas the changes in the water surface displacement caused by the tsunami with the tidal elevation removed can be seen in Figure 10.

FIGURE 9

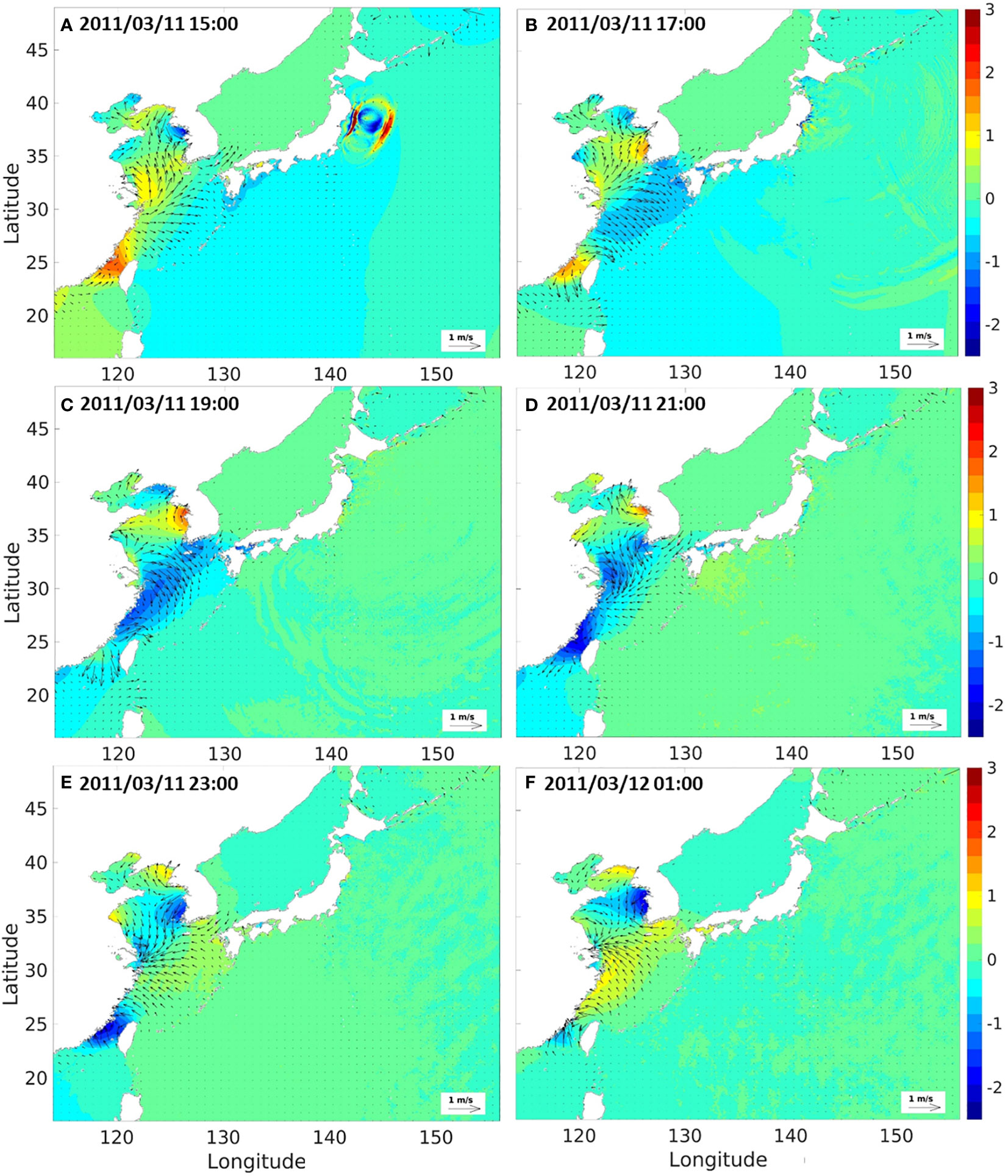
Figure 9 Snapshots of tide and tsunami elevations extracted from the regional tidal-tsunami model for the 2011 Tohoku tsunami for specific time instants: 2011/03/11 15:00 (A), 2011/03/11 17:00 (B), 2011/03/11 19:00 (C), 2011/03/11 21:00 (D), 2011/03/11 23:00 (E), 2011/03/12 01:00 (F).

FIGURE 10

Figure 10 The regional tide-tsunami model results in the Korean Peninsula over time for the Tohoku tsunami: (A) dynamic modeling results indicating the elevation of tsunami considering tidal effects; (B) tsunami-only; (C) tidal effects.

Figure 10 presents the comparison of the horizontal distribution of free surface displacement computed by the dynamic tide-tsunami interaction model, ROSES. Figure 10A shows the transformation of the tsunami considering the tide-tsunami interaction component, while Figure 10B indicates the tsunami modeling only. Additionally, Figure 10C illustrates the difference in computed free surface displacement between the 2011 Tohoku tsunami with tidal modeling and tsunami modeling only. In the 2011 Tohoku tsunami event, the mechanism of tsunami propagation in the Yellow Sea was quite similar to that of the 2010 Chilean tsunami event, regardless of whether or not tidal modeling was used. Although Figures 10A, B show almost similar distribution patterns of free surface displacement, the presence of tidal currents induced further amplification or reduction of the tsunami elevations and differences in arrival time depending on the phase of tide development during the time that the 2011 Tohoku tsunami impacted the Korean Peninsula. In Figures 10, 11, the dynamic interaction of the tide and the tsunami clearly displays the Doppler effects, which resulted in a reduction of the tsunami elevations and earlier arrival time along the southwestern coast of the Korean Peninsula with amplification of the tsunami elevations and delayed arrival time along the southeastern coast.

FIGURE 11

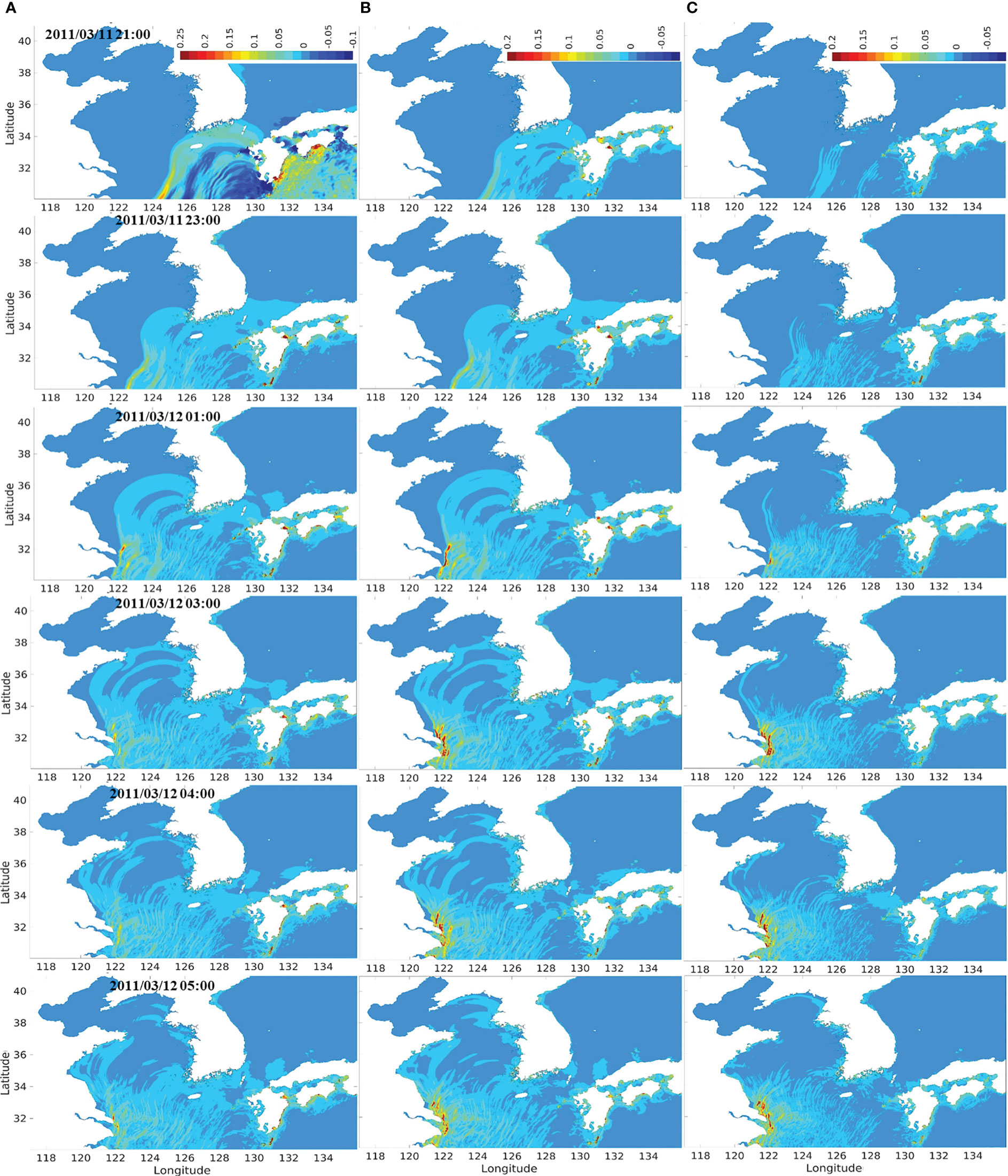
Figure 11 The comparison of velocity results extracted from the regional tide-tsunami model in the Korean Peninsula over time for the Tohoku tsunami: (A) dynamic modeling results indicating the velocities of tsunami considering tidal effects; (B) tsunami-only; (C) tidal effects.

Figure 10A shows slightly higher tsunami elevations and slower spreading speed than Figure 10B during the tsunami propagation along the southwestern coast of the Korean Peninsula toward the Yellow Sea, and the resulting differences between the two figures gradually increase from the initial stage at 21:00 when the 2011 Tohoku tsunami arrived on the south coast. Meanwhile, as the tsunami experienced positive tidal impacts along the southeastern coast of the Korean Peninsula, the tsunami elevations were reduced, and the arrival time of the tsunami was advanced due to the Doppler effect. Similarly, the tidal currents around the eastern sea of the Shanghai coasts were directed to the northwest when the tsunami arrived in the area, resulting in positive tidal effects on the propagation of the 2011 Tohoku tsunami. Therefore, the amplification of the potential tsunami energy was moderated in the eastern sea of the Shanghai region, and Figure 10C indicates the strong intensity of the tidal effects, which is represented by the significant differences between the tsunami elevations of dynamic modeling and tsunami-only modeling. Numerical results of the horizontal velocities recorded in the dynamic model, ROSES, of the tsunami and the tide-tsunami effects (A), tsunami-only (B), and only the tide-tsunami interaction component (C) are illustrated in Figure 11. Similar to the horizontal distribution patterns of the tsunami elevations, the velocities of the tsunami developed towards the southwestern sea of the Korean Peninsula, slightly amplified and delayed due to the influence of positive tidal currents. Meanwhile, the velocities of the tsunami propagating on the eastern sea of Shanghai were considerably reduced due to the Doppler effect, and the dynamic tide-tsunami interaction components had some impacts along the Korean coasts since the wave velocities of the tsunami and the corresponding kinetic energy were relatively increased when comparing with those of the 2010 Chilean tsunami (Figure 11C). Overall, the numerical model considering the dynamic tide-tsunami interaction reasonably represented well the propagation and transformation of the 2011 Tohoku tsunami with the strong tidal currents in the Yellow Sea.

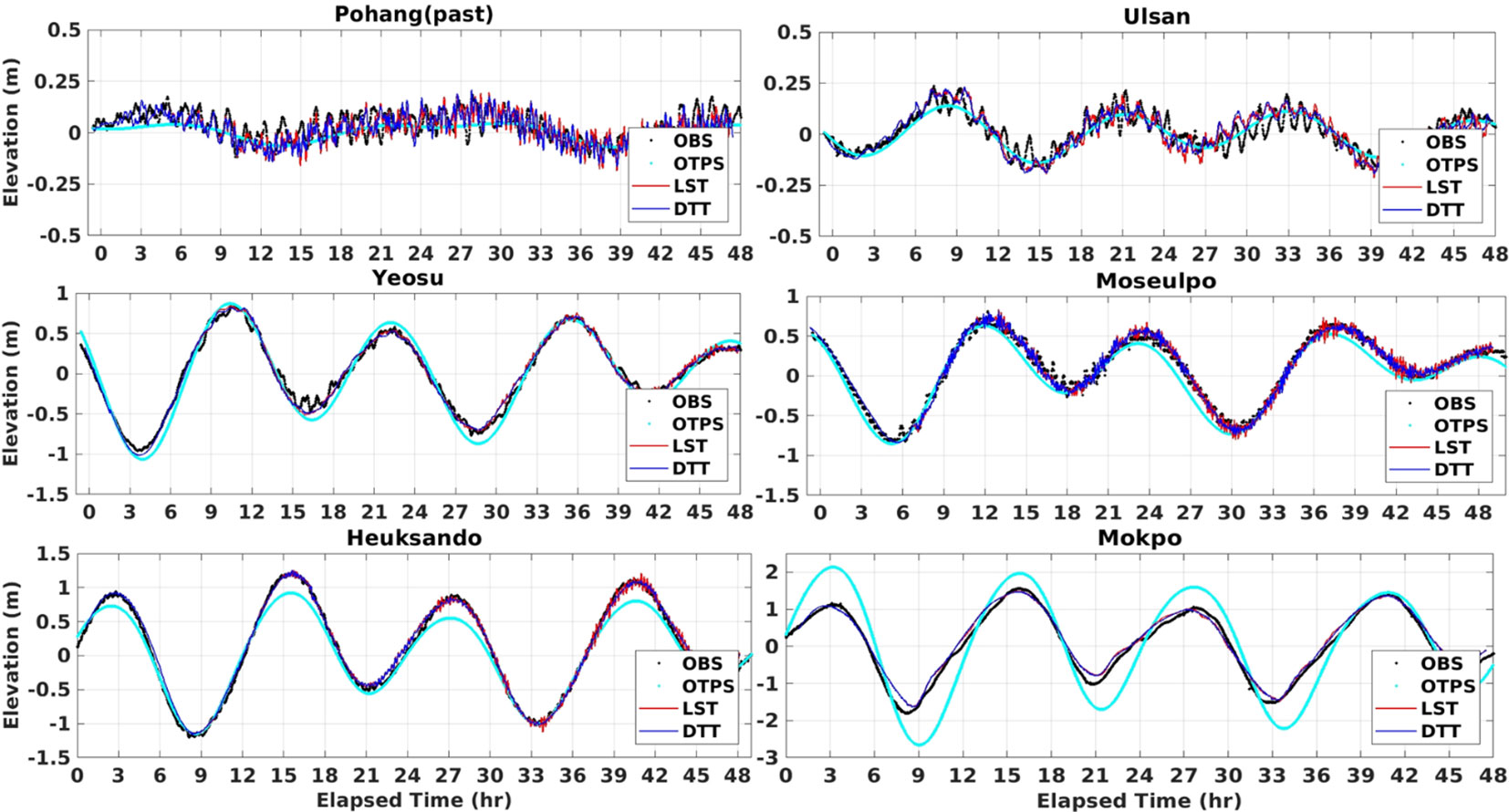
Quantitative validation of the predictive performance of the tsunami prediction system was carried out by comparing the time series of tsunami elevation measured from the numerical models to the observation results obtained from several representative tidal gauges along the southeast and southwest coasts of the Korean Peninsula during the 2011 Tohoku tsunami event (Figure 12). The results of the newly established model for tide-tsunami interaction (ROSES) and synthesized results from ROSI and GOSU models were also presented to examine the influence of the interaction between tides and tsunamis. In the Korean Peninsula, strong tides occurred and dominated the tsunami elevation from the previous tsunami events. Thus, to visually clarify the difference between the elevation of tsunami-only and tsunami with dynamic effects of tide-tsunami interaction, the tidal elevation is excluded from the time series of tsunami elevation shown in Figure 12. The detailed comparison of both tide and tsunami elevation extracted from numerical models and observation datasets is presented in Figure A1 in the Appendix. The blue line (DTT: Dynamic Tide-Tsunami) and the red line (LST: Linear Superposition of Tide-Tsunami) indicate the dynamic modeling results of ROSES for the tsunami elevation with consideration of the effects of tide-tsunami interaction and the tsunami-only extracted from the GOSU model, respectively, while the black dotted line shows the observation data that was filtered by the high-pass filter technique at a cut-off frequency of 3 hours. Overall, the results obtained from ROSES exhibited better agreement with the results from tidal gauges than the GOSU model, albeit a slight difference in phase and amplitude was observed in some regions. Since the R3DN domain is the highest resolution with a 36-second interval (about 1 km) in both the longitude and latitude coordinate system, there are some differences in the peak values measured in the numerical domain and observed in the tide stations due to the relatively coarse grid size which hardly represent the detailed topography near the tide stations located inside the harbors. The ROSES results quantitatively reproduced the tide observation, considering the difference in physical distance and bathymetry. However, the arrival time of the tide and tsunami increases roughly in proportion to the travel distance, causing the phase difference when compared to the tide observation due to the physical distance difference between the numerical domain and the actual location of the tide observation. Hence, the tsunami arrival time affected by tide could not be compared quantitatively due to the significant differences in arrival times between the tide station points in the numerical domain and the actual locations.

FIGURE 12

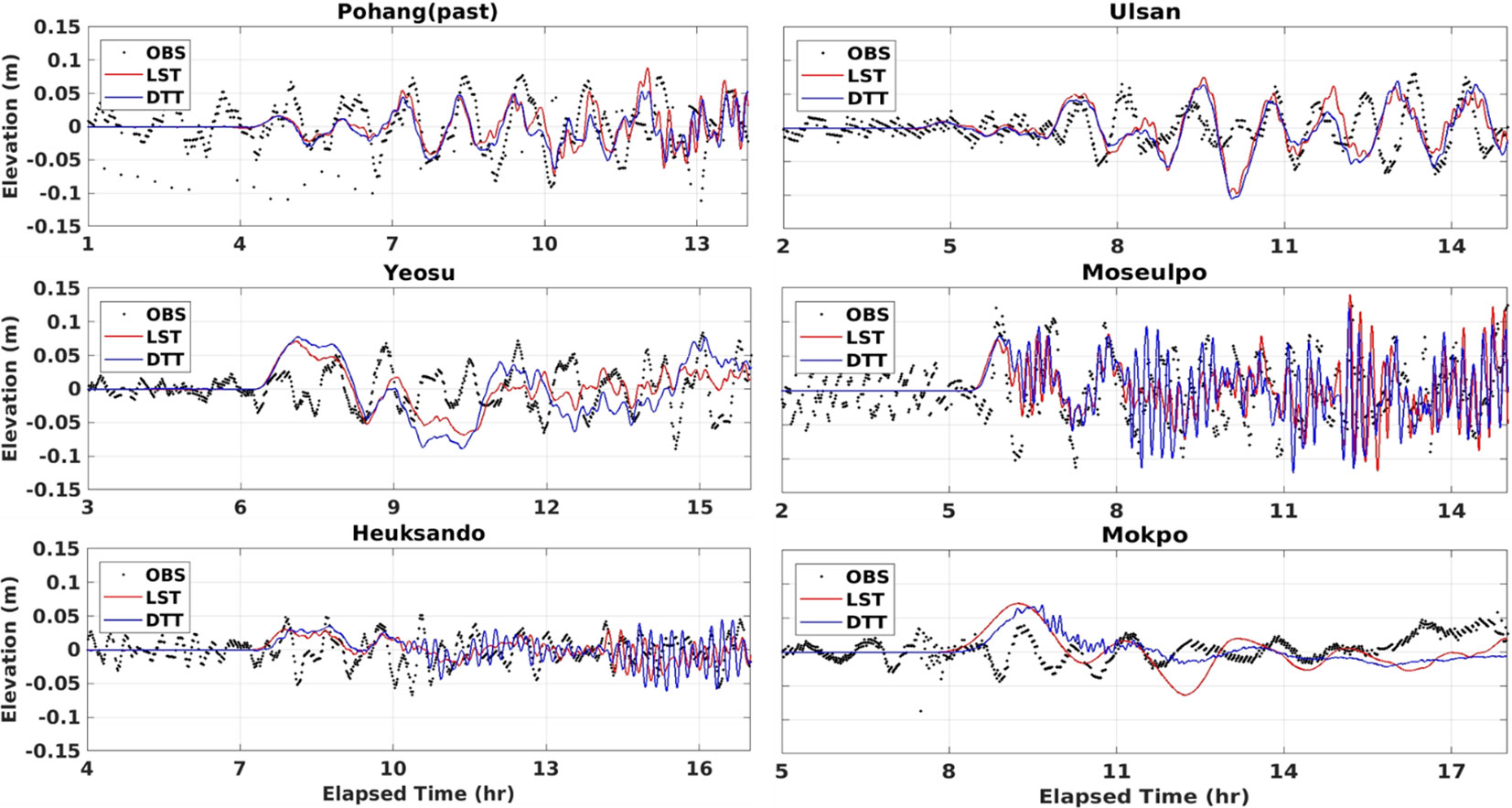
Figure 12 Comparison of time series of tsunami elevation measured from ROSES (DTT), linearly synthesized results (LST) to the observation data measured in typical tide gauge stations located in the southeast to southwest coasts during the Tohoku tsunami event.

On the other hand, Figure 12 demonstrates that both the dynamic model for tide-tsunami interaction (DTT) and the global tsunami model (LST) reasonably reproduce the time series of elevation measured by tidal observation stations. The Pohang station (PH), which is located on the southeast coast of the Korean Peninsula, is less affected by the significant effects of strong tides, inducing little difference in the time series of tsunami elevation between cases with and without considering the tidal effects in both maximum wave heights and phases (Figure 12). The maximum observed tsunami elevation measured in the Pohang tide gauge is about 0.09 m, similar to the maximum elevation results computed in the ROSES and GOSU models. Although the forecasted results show slightly earlier arrival times than observation data, both model results generally agreed with the observed results in the maximum wave height, arrival time, and wave period. By contrast, the dynamic model for tide-tsunami interaction (ROSES) is significantly better than the global tsunami model (GOSU) in simulating the maximum elevations and phases when compared to the observed results in the Ulsan tide gauge (UA). In detail, GOSU overestimated the maximum tsunami amplitude of 0.12 m, while both ROSES and observed results show a similar value of 0.098 m. For the tsunami elevation data measured in the southwest coasts of the Korean Peninsula, the tsunami is significantly influenced by the tide effects, causing shorter periods than those in the southeast regions. It is interesting to note that at the isolated position of Moseulpo (MSP) and Heuksando (HS), the dynamic effect of the tide-tsunami interaction is considerable compared to the tsunami-only elevation and shows a difference of maximum elevation with observed results of less than 10%. As a result, compared to GOSU results, the ROSES model has good agreement with the observation results. Despite some numerical errors, the tsunami prediction system effectively replicates the influence of tides and is quantitatively suitable for tsunami prediction with consideration of the tide-tsunami interaction near the Korean coasts.

4 Conclusion and discussion

A series of high-resolution numerical investigations were carried out to examine the generation and evolution of tsunamis occurring in the Korean Peninsula, considering the influence of the tide and tidal currents. The regional tide and tsunami interaction model (ROSES) is proposed with the initial and boundary conditions obtained from the global tsunami model (GOSU) and regional tide model (ROSI) to examine the tidal effects on the horizontal distribution of tsunami free surface displacement and velocity around the Korean coasts. Two actual far-field and near-field tsunamis, including the 2010 Chilean tsunami and the 2011 Tohoku tsunami, were employed to evaluate the performance of the dynamic tide-tsunami interaction model. The numerical results indicate that the regional forecasting model ROSES well represented the tsunami transformation and amplification mechanisms when interacting with strong tides and tidal currents developed in the Korean Peninsula. The predictive performance of models was validated using the tidal observation dataset collected in tide stations along the Korean coasts. The free surface displacement time series extracted from the ROSES model was compared with the time series of observed elevation and linearly superimposed elevation between tsunamis and tides (traditional method). The results show that the proposed dynamic model shows better agreement than the linear superimposed method in both the peak elevation and phase, with a maximum difference of less than 10% compared to the observation data. Although the tides that occurred in the Yellow Sea induced dominant elevations compared to the tsunami elevations, the dynamic effects of tides generally influence the tsunami propagation directions and amplitudes around the Korean regions. The arrival time of tsunami propagation highly depends on the corresponding phase of local tidal currents.

While the ROSES model effectively represents the dynamic interaction between tides and tsunamis along the Korean coasts, it is important to note that the results cannot be generalized in quantifying the tide effects on tsunami propagation in any specific location. Firstly, each location exhibits complex and unique topographic features, leading to variations in the patterns of tidal effects on tsunami elevation and velocity, even among neighboring tide stations. Secondly, the presence of mitigation structures constructed along the Korean coasts further complicates the influence of tides. Oetjen et al. (2022) conducted a comprehensive review on gray structures, such as seawalls and offshore breakwaters, to physically prevent tsunami impacts by reducing the inundation level, and green structures to focus on coastal resilience, vulnerable reduction, and nature-based solutions for tsunami mitigation. Moreover, Gijsman et al. (2021) have demonstrated that countermeasures, such as mangroves, can significantly impact arrival times, inundation depths, and maximum run-up in inland areas. Therefore, it is highly recommended to conduct similar investigations but only focus on specific locations and consider the presence of countermeasures. This approach will enable more accurate predictions of the significant impacts of tides on tsunami currents. Finally, the two actual tsunami cases used in this study are intense in the original sources but had a slight effect on the Korean Peninsula. Also, the arrival time of tsunamis is dominated by the corresponding phase of tides, inducing unclear observation of the impact of the dynamic interaction between tides and tsunamis on tsunamis in the Yellow Sea. Hence, it is necessary to simulate additional tsunami scenarios to understand further the interaction between tides and tsunamis in different positions along the Korean coasts.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding author.

Author contributions

HD: Conceptualization, Formal Analysis, Investigation, Methodology, Writing – original draft, Writing – review & editing. EL: Conceptualization, Investigation, Methodology, Writing – review & editing. SA: Conceptualization, Data curation, Formal Analysis, Investigation, Writing – review & editing. KOK: Conceptualization, Data curation, Investigation, Methodology, Writing – review & editing. SS: Conceptualization, Funding acquisition, Investigation, Methodology, Supervision, Writing – review & editing. TH: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Supervision, Visualization, Writing – review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research was funded by the Basic Science Research Program through the National Research Foundation of Korea (NRF), funded by the Ministry of Science and ICT, South Korea (RS-2023-00209256), and the Korea Meteorological Administration Research and Development Program under Grant KMI2018-02410. This study was based upon work partially supported by Korea Institute of Marine Science & Technology Promotion (KIMST) funded by the Ministry of Oceans and Fisheries (RS-2023-00256687).

Acknowledgments

We thank KHOA (Korean Hydrographic and Oceanographic Agency) and KMA (Korea Meteorological Administration) for providing the observation tide gauge dataset.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Amante C., Eakins B. W. (2009). ETOPO1 arc-minute global relief model: procedures, data sources and analysis. NOAA technical memorandum NESDIS NGDC 24, 1–25. Available at: https://repository.library.noaa.gov/view/noaa/1163/noaa_1163_DS1.pdf.

Google Scholar

Apotsos A., Jaffe B., Gelfenbaum G. (2011). Wave characteristic and morphologic effects on the onshore hydrodynamic response of tsunamis. Coast. Eng. 58, 1034–1048. doi: 10.1016/j.coastaleng.2011.06.002