Assessment of the stoichiometry and efficiency of CO2 fixation coupled to reduced sulfur oxidation

Chemolithoautotrophic sulfur oxidizing bacteria (SOB) couple the oxidation of reduced sulfur compounds to the production of biomass. Their role in the cycling of carbon, sulfur, oxygen, and nitrogen is, however, difficult to quantify due to the complexity of sulfur oxidation pathways. We describe a generic theoretical framework for linking the stoichiometry and energy conservation efficiency of autotrophic sulfur oxidation while accounting for the partitioning of the reduced sulfur pool between the energy generating and energy conserving steps as well as between the main possible products (sulfate vs. zero-valent sulfur). Using this framework, we show that the energy conservation efficiency varies widely among SOB with no apparent relationship to their phylogeny. Aerobic SOB equipped with reverse dissimilatory sulfite reductase tend to have higher efficiency than those relying on the complete Sox pathway, whereas for anaerobic SOB the presence of membrane-bound, as opposed to periplasmic, nitrate reductase systems appears to be linked to higher efficiency. We employ the framework to also show how limited rate measurements can be used to estimate the primary productivity of SOB without the knowledge of the sulfate-to-zero-valent-sulfur production ratio. Finally, we discuss how the framework can help researchers gain new insights into the activity of SOB and their niches.

Introduction

Autotrophic sulfur oxidizing bacteria (SOB) comprise a phylogenetically diverse group of microbes that obtain the energy required for growth from the oxidation of reduced sulfur compounds. Prominent natural habitats of SOB are hydrothermal vents, where these bacteria live in symbiotic association with invertebrates or, when free-living, form microbial mats (e.g., Sievert and Vetriani, 2012). SOB are found also on top of organic-rich marine sediments, where they typically form conspicuous and often quite extensive mats. For instance, on the continental shelf off the Namibian coast, such mats cover an area comparable to the size of Austria (>80,000 km²; Brüchert et al., 2006). In addition to natural habitats, SOB are important also in industrial applications, where they are used, for instance, for waste water treatment by biodesulfurisation (Janssen et al., 2009).

A common feature of environments inhabited by SOB is the encounter of sulfide or other reduced sulfur species with a terminal electron acceptor (TEA) such as oxygen or nitrate. This encounter creates a chemical disequilibrium from which energy can be harvested and conserved in the form of biomass. While the general validity of this concept is well established, there are still significant gaps in our understanding of systems driven by chemical energy derived from reduced sulfur oxidation. This is because the reactions performed by autotrophic SOB are highly complex and the assessment of the stoichiometry of sulfur oxidation is not trivial, even for cultivated SOB.

In chemolithoautotrophic SOB known to date the energy gained from the reduced sulfur oxidation drives reverse electron transport within the membrane, which generates sufficiently negative electron potential to reduce an electron carrier (e.g., NAD⁺) with the reduced sulfur compound as the electron donor (e.g., Harold, 1986). Thus, the reduced sulfur compound is used as the electron donor for the reduction of both CO₂ (via the electron carrier) and TEA. The partitioning of the reduced sulfur pool between these two reductive processes, which is related to the efficiency of energy conservation and the growth rate per substrate utilized, is poorly understood and varies substantially among the different cultivated SOB (Kelly, 1999). Additionally, the end product of sulfur oxidation (e.g., sulfate vs. zero-valent sulfur) is also variable and appears to exhibit a degree of flexibility even within individual organisms, as shown for several Beggiatoa strains (Nelson et al., 1986; Hagen and Nelson, 1997; Berg et al., 2014).

This complexity is echoed in the diversity of pathways by which SOB oxidize the reduced sulfur compound. As summarized in Figure 1, three main pathways have been identified so far (reviewed, e.g., by Ghosh and Dam, 2009): (i) the Sox pathway mediated by the thiosulfate-oxidizing multi-enzyme (TOMES) complex, (ii) the tetrathionate (SI₄) pathway of thiosulfate oxidation, and (iii) the rather recently described “branched” pathway. The occurrence of individual enzymes of the traditional pathways does not appear to be linked to the phylogenetic identity of SOB. This phenomenon is generally explained by horizontal gene transfer, which is possibly also responsible for the co-occurrence and linkage of specific enzymes or even several complete pathways in the same organism (e.g., Ghosh and Dam, 2009). In addition to the diverse sulfur oxidation pathways, the complexity of autotrophic sulfur oxidation by SOB is further increased by the fact that they can employ different terminal oxidases for TEA reduction and two possible pathways for CO₂ fixation (namely the Calvin-Benson-Bassham cycle, hereafter referred to as the Calvin cycle, or the reverse tricarboxylic acid (rTCA) cycle; e.g., Hügler and Sievert, 2011; Sievert and Vetriani, 2012).

FIGURE 1

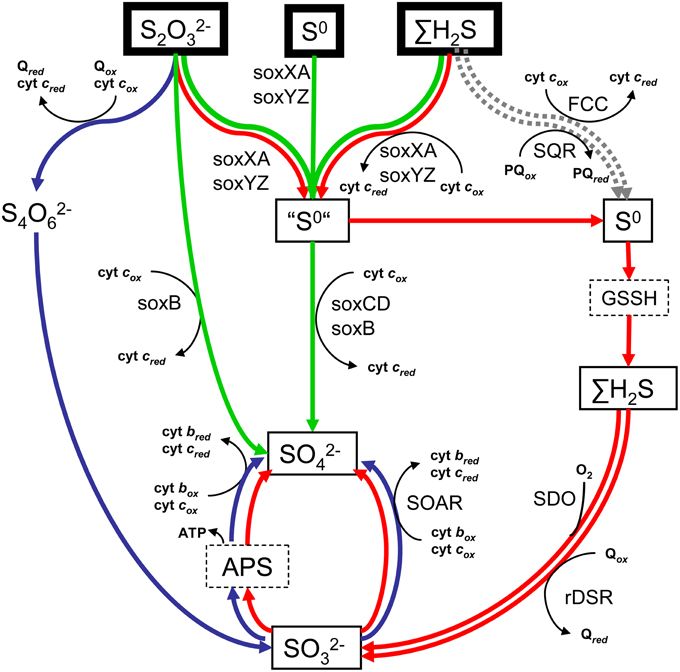
Figure 1. Scheme of the main pathways of reduced sulfur oxidation. Green arrows indicate the traditional Sox pathway, blue arrows the tetrathionate (SI₄) pathway and red arrows correspond to the branched pathway for thiosulfate oxidation. Possible entry sites of H₂S that are not part of these traditional pathways are shown with a gray dotted arrow. FCC = flavocytochrome c:oxidoreductase; SQR = sulfide:quinine:oxidoreductase; GSSH = S-sulfanylglutathione; APS = adenosine-5′-phosphosulfate; SOAR = sulfite:cyt c:oxidoreductase; rDSR = reverse dissimilatory sulfate reductase; SDO = sulfur dioxygenase; soxXA, soxYZ, and soxB are subunits of the thiosulfate-oxidizing multi-enzyme (TOMES) complex.

The complexity of SOB physiology and sulfur oxidation biochemistry hampers our ability to quantify the contribution of SOB to sulfur, carbon, nitrogen, and oxygen cycling in a given environment, as well as to understand their niches. This is especially true for environments with fluctuating conditions, where also the products and intermediates of sulfur oxidation vary. Additionally, this complexity hinders the development of industrial applications that use SOB for processes such as waste water biodesulfurisation, which require precise control and predictability of SOB activity.

In this study we describe a generic theoretical framework for a rapid quantitative assessment of chemolithoautotrophic sulfur oxidation. First, we demonstrate how to use it for the quantification of the stoichiometry and energy conservation efficiency of autotrophic sulfur oxidation from rate measurements of the reactants involved. Second, we apply it on literature data and identify possible links between the energy conservation efficiency and the different oxidative and reductive pathways employed by SOB. Third, we suggest how it can be used to estimate chemolithoautotrophic primary productivity by SOB from limited rate measurements. Finally, we discuss how our framework makes it possible to formally relate the capabilities of SOB (e.g., stoichiometry and efficiency) to their environment and thus gain insight into the differentiation of their niches.

Materials and Methods

Generalized Equations for Aerobic Sulfide Oxidation

The generalized mass-balanced equations for aerobic sulfide oxidation coupled to CO₂ fixation are derived by considering the energy generating and energy conserving steps separately. The energy generating step is performed with zero-valent sulfur (S⁰) and sulfate (SO²⁻₄) as two possible end products. The corresponding reactions are written as (Nelson et al., 1986; Kelly, 1999)

$\begin{array}{cc}{\text{H}}_2\text{S}+0.5{\text{O}}_2\to {\text{S}}^0{+\text{H}}_2\text{O},& (1)\end{array}$

$\begin{array}{cc}{\text{H}}_2\text{S}+2{\text{O}}_2\to {\text{SO}}_4^{2-}{+0\text{H}}^{+}.& (2)\end{array}$

When both reactions occur simultaneously, the generalized equation for the energy generating step is

$\begin{array}{cc}\begin{array}{l}{\text{H}}_2\text{S}+(2-1.5x){\text{O}}_2\to \\ x{\text{S}}^0+(1-x){\text{SO}}_4^{2-}+x{\text{H}}_2\text{O}+(2-2x){\text{H}}^{+},\end{array}& (3)\end{array}$

where x and (1–x) are the parts of the total H₂S pool oxidized to S⁰ and SO²⁻₄, respectively (0≤x≤1).

In SOB, H₂S serves not only as the energy source but also as the electron donor for the reduction of CO₂. Analogously to the energy generating step, this can occur with S⁰ or SO²⁻₄ as two possible end products, i.e.,

$\begin{array}{cc}{\text{H}}_2\text{S}+0.5{\text{CO}}_2\to {\text{S}}^0+0.{5\text{CH}}_2\text{O}+0.{5\text{H}}_2\text{O},& (4)\end{array}$

$\begin{array}{cc}{\text{H}}_2\text{S}+2{\text{CO}}_2+2{\text{H}}_2\text{O}\to {\text{SO}}_4^{2-}+{2\text{CH}}_2\text{O}+{2\text{H}}^{+}.& (5)\end{array}$

A critical assumption in our derivation is that the S⁰:SO²⁻₄ product ratio (defined by x) is the same for both the energy generating and CO₂ fixing steps. Consequently, the generalized equation for the CO₂ fixing step is written as

$\begin{array}{cc}\begin{array}{l}{\text{H}}_2\text{S}+(2-1.5x){\text{CO}}_2+(2-2.5x){\text{H}}_2\text{O}\to \\ x{\text{S}}^0+(1-x){\text{SO}}_4^{\text{2}-}+(2-1.5x){\text{CH}}_2\text{O}+(2-2x){\text{H}}^{+}.\end{array}& (6)\end{array}$

To arrive at a generalized equation for the complete aerobic sulfide oxidation coupled to CO₂ reduction, we assume that part y (0≤y≤1) of the total H₂S pool is used for energy generation (Equation 3) while the remaining part 1–y is used for CO₂ reduction (Equation 6). Thus, by summing Equation (3) multiplied with y and Equation (6) multiplied with 1–y we obtain

$\begin{array}{cc}\begin{array}{l}{\text{H}}_2\text{S}+{\nu }_{O2}{\text{O}}_2+{\nu }_{CO2}{\text{CO}}_2\to \\ {\nu }_{S0}{\text{S}}^0+{\nu }_{SO4}{\text{SO}}_4^{2-}+{\nu }_{orgC}{\text{CH}}_2\text{O}+{\nu }_{H2O}{\text{H}}_2\text{O}\\ +{\nu }_{H+}{\text{H}}^{+},\end{array}& (7)\end{array}$

where the stoichiometric coefficients of the reactants involved are ν_O2 = y(2 − 1.5x), ν_CO2 = ν_orgC = (1 − y)(2 − 1.5x), ν_S0 = x, ν_SO4 = (1 − x), ν_H2O = yx−(1 − y)(2 − 2.5x) and ν_H+ = 2(1 − x). Equation (7) is the general mass-balanced equation for aerobic sulfide oxidation coupled to CO₂ fixation.

Efficiency of Energy Conservation: The Traditional Calculation Approach

The thermodynamic efficiency of energy conservation, ε, is generally defined as the ratio between the Gibbs free energies of the endergonic (energy-consuming) and exergonic (energy-generating) reactions. Specifically for aerobic sulfide oxidation, where CO₂ reduction (Equation 6 multiplied by 1−y) and O₂ reduction (Equation 3 multiplied by y) are the endergonic and exergonic reactions, respectively, ε is written as

$\begin{array}{cc}{\epsilon }_{\text{I}}=\frac{(1-y)\Delta G_r({\text{CO}}_2\text{red})}{-y\Delta G_r({\text{O}}_2\text{red})},& (8)\end{array}$

where ΔG_r is expressed per mole of H₂S oxidized. At non-standard conditions, the Gibbs free energy of a reaction is calculated as

$\begin{array}{cc}\Delta G_r=\Delta G_r^0+\text{RT}\text{ln}Q,& (9)\end{array}$

where ΔG⁰_r is ΔG_r at standard biochemical conditions (pH = 7, reactant concentrations 1 M, temperature 25°C), R is the universal gas constant, T is temperature, and Q is the ratio of the activity coefficients of the products and substrates involved, which can be approximated by the ratio of the corresponding concentrations (Thauer et al., 1977). Using Equations (3) and (6), the respective ΔG_r values in Equation (8) are calculated as

$\begin{array}{cc}\begin{array}{l}\Delta G_r({\text{O}}_2\text{red})=\text{}\text{}\text{}\text{}x\Delta G_f^0({\text{S}}^0)+(1-x)\Delta G_f^0({\text{SO}}_4^{2-})\\ +\text{}\text{}\text{}\text{}x\Delta G_f^0({\text{H}}_2\text{O})-\Delta G_f^0({\text{H}}_2\text{S})\\ -\text{}\text{}\text{}\text{}(2-1.5x)\Delta G_f^0({\text{O}}_2)+\text{RT}\text{ln}{Q}_1,\end{array}& (10)\end{array}$

$\begin{array}{cc}\begin{array}{l}\Delta G_r({\text{CO}}_2\text{red})=\text{}\text{}\text{}\text{}x\Delta G_f^0({\text{S}}^0)+(1-x)\Delta G_f^0({\text{SO}}_4^{2-})\\ -\text{}\text{}\text{}\text{}\Delta G_f^0({\text{H}}_2\text{S})-(2-2.5x)\Delta G_f^0({\text{H}}_2\text{O})\\ +\text{}\text{}\text{}\text{}(2-1.5x)[\Delta G_f^0({\text{CH}}_2\text{O})-\Delta G_f^0({\text{CO}}_2)]\\ +\text{}\text{}\text{}\text{}\text{RT}\text{ln}{Q}_2,\end{array}& (11)\end{array}$

where the Gibbs free energies of formation of the respective reactants at standard biochemical conditions, ΔG⁰_f, are tabulated in Thauer et al. (1977) and the quotients Q₁ and Q₂ are given by

$\begin{array}{cc}{Q}_1=\frac{{[{\text{SO}}_4^{2-}]}^{(1-x)}{[{\text{H}}^{+}]}^{(2-2x)}}{[{\text{H}}_2\text{S}]{[{\text{O}}_2]}^{(2-1.5x)}},& (12)\end{array}$

$\begin{array}{cc}{Q}_2=\frac{{[{\text{SO}}_4^{2-}]}^{(1-x)}{[{\text{H}}^{+}]}^{(2-2x)}}{[{\text{H}}_2\text{S}]{[{\text{CO}}_2]}^{(2-1.5x)}}.& (13)\end{array}$

Equations (8–13) summarize the traditional approach for the calculations of the energy conservation efficiency of autotrophic aerobic sulfide oxidation (e.g., Nelson and Hagen, 1995).

Factorization of the Traditional Energy Conservation Efficiency

The general aim of calculating the efficiency of energy conservation is to gain insights into how the energy generated by an exergonic reaction is converted into the biochemical currency ATP and how this ATP is further utilized to drive endergonic reactions. For the specific case of autotrophic sulfur oxidation, we divide the flow of energy into three steps: conversion of the Gibbs free energy released by sulfur oxidation into ATP, transfer of this ATP to the site of CO₂ reduction (that is, not for processes associated with “cell maintenance”), and ATP utilization for driving CO₂ reduction (see Figure S1). The efficiency of the first step, ε_SO, characterizes the efficiency of the sulfur oxidation pathway. It is calculated as

$\begin{array}{cc}{\epsilon }_{\text{SO}}=\frac{\Delta E_r({\text{O}}_2\text{red})}{\Delta G_r({\text{O}}_2\text{red})},& (14)\end{array}$

where ΔE_r(O₂ red) describes the energy gained, in the form of ATP, from the reduction of O₂. Analogously, the efficiency of ATP utilization for the reduction of CO₂, ε_u, is calculated as

$\begin{array}{cc}{\epsilon }_{\text{u}}=\frac{\Delta G_r({\text{CO}}_2\text{red})}{\Delta E_r({\text{CO}}_2\text{red})},& (15)\end{array}$

where ΔE_r(CO₂ red) describes the energy requirements, in the form of ATP, of CO₂ reduction. Finally, the efficiency of the energy transfer, ε_t, is calculated as

$\begin{array}{cc}{\epsilon }_{\text{t}}=\frac{(1-y)\Delta E_r({\text{CO}}_2\text{red})}{-y\Delta E_r({\text{O}}_2\text{red})},& (16)\end{array}$

where, as above, y and 1–y describe the fractions of the total H₂S pool used for energy generation and CO₂ reduction, respectively. Note that the values of ΔE_r and ΔG_r in Equations (14–16) are expressed per mole of H₂S.

As follows from Equations (8, 14–16), the overall thermodynamic efficiency ε_I can be expressed as a product of the partial efficiencies of the three steps involved in the energy flow associated with autotrophic sulfur oxidation, namely

$\begin{array}{cc}{\epsilon }_{\text{I}}={\epsilon }_{\text{SO}}{\epsilon }_{\text{u}}{\epsilon }_{\text{t}}.& (17)\end{array}$

Because ε_I can be calculated from thermodynamic data based on the stoichiometry of autotrophic sulfur oxidation, this means that Equation (17) can be used to calculate any one of the efficiencies ε_SO, ε_u or ε_t provided that the other two are known. Although this is not possible at the current state of knowledge, Equation (17) makes it possible to estimate their minimal values. Specifically, the minimal value of ε_SO is reached when both ε_u and ε_t are maximal (i.e., ε_u = ε_t = 1), which gives ε_{SO, I, min} = ε_I. Analogously, ε_{u, min} = ε_{t, min} = ε_I. Thus, ε_I represents the minimal value of the partial efficiencies ε_SO, ε_u and ε_t.

Efficiency of Energy Conservation: The New Calculation Approach

The traditional approach of efficiency calculation does not consider that sulfide oxidation and CO₂ reduction in SOB are coupled via redox couples such as NAD⁺/NADH, FAD/FADH₂ and oxidized/reduced Ferredoxin (Fd_ox/Fd_red). In our new approach we account for this coupling explicitly. Also, we distinguish between two possible CO₂ fixation pathways observed in SOB: the Calvin cycle and the reverse tricarboxylic acid (rTCA) cycle. In accordance with Bar-Even et al. (2010), we chose glyceraldehyde-3-phosphate (GA3P) as the primary product of both CO₂ fixation pathways, even though phosphoenolpyruvate is considered the output of the rTCA cycle (Buchanan and Arnon, 1990). The choice of phosphoenolpyruvate would result in small numerical differences that would, however, not alter significantly our conclusions.

In the SOB employing the Calvin cycle, CO₂ fixation occurs according to reaction

$\begin{array}{cc}6\text{NADH}+3{\text{CO}}_2+{\text{P}}_{\text{i}}\to 6{\text{NAD}}^{+}+\text{GA3P}+7{\text{H}}_2\text{O}.& (18)\end{array}$

This reaction requires conversion of ATP into ADP and P_i, and its energy requirement is ΔG_r(CO₂ fix) = 69.7 kJ CO⁻¹₂ (Supplemental material of Bar-Even et al., 2010). The reducing equivalents NADH required for the reduction of CO₂ in Equation (18) are produced via membrane-associated reverse electron transport (RET) reactions with zero-valent sulfur (S⁰) or sulfate (SO²⁻₄) as two possible end products:

$\begin{array}{cc}{\text{H}}_2\text{S}+{\text{NAD}}^{+}\to S^0+\text{NADH}+{\text{H}}^{+},& (19)\end{array}$

$\begin{array}{cc}{\text{H}}_2\text{S}+4{\text{NAD}}^{+}+4{\text{H}}_2\text{O}\to {\text{SO}}_4^{2-}+4\text{NADH}+6{\text{H}}^{+}.& (20)\end{array}$

These two endergonic reactions are driven by proton motive force, which is generated either directly by the exergonic reaction given by Equation (3) or by utilizing ATP. When both of them occur simultaneously, the generalized equation for the RET reaction is

$\begin{array}{cc}\begin{array}{l}{\text{H}}_2\text{S}+(4-3x){\text{NAD}}^{+}+(4-4x){\text{H}}_2\text{O}\to \\ x{\text{S}}^0+(1-x){\text{SO}}_4^{2-}+(4-3x)\text{NADH}+(6-5x){\text{H}}^{+},\end{array}& (21)\end{array}$

where x again describes the S⁰: SO²⁻₄ product ratio, and its energy requirement is calculated as

$\begin{array}{cc}\begin{array}{l}\Delta G_r(\text{RET})=x\Delta G_f^0({\text{S}}^0)+(1-x)\Delta G_f^0({\text{SO}}_4^{2-})-\Delta G_f^0({\text{H}}_2\text{S})\\ -4(1-x)\Delta G_f^0({\text{H}}_2\text{O})+(4-3x)\\ [\Delta G_f^0(\text{NADH})-\Delta G_f^0({\text{NAD}}^{+})]+\text{RT}\text{ln}{Q}_3.\end{array}& (22)\end{array}$

Here the difference ΔG⁰_f(NADH)–ΔG⁰_f(NAD⁺) = 60.99 kJ (mol NADH)⁻¹ (Alberty, 1998) and the reaction quotient Q₃ is given by

$\begin{array}{cc}{Q}_3=\frac{{[{\text{SO}}_4^{2-}]}^{(1-x)}{[\text{NADH}]}^{(4-3x)}{[{\text{H}}^{+}]}^{(6-5x)}}{[{\text{H}}_2\text{S}]{[{\text{NAD}}^{+}]}^{(4-3x)}}.& (23)\end{array}$

In the SOB employing the rTCA cycle, CO₂ fixation occurs according to reaction

$\begin{array}{cc}\begin{array}{l}3\text{NADH}+4{\text{Fd}}_{\text{red}}+{\text{FADH}}_2+3{\text{CO}}_2\to \\ 3{\text{NAD}}^{+}+4{\text{Fd}}_{\text{ox}}+\text{FAD}+\text{GA3P}+7{\text{H}}_2\text{O}.\end{array}& (24)\end{array}$

Energy requirement of this reaction is ΔG_r(CO₂ fix) = 64.3 kJ CO⁻¹₂ (Bar-Even et al., 2010). The reducing equivalents NADH, FADH₂ and Fd_red required for the reduction of CO₂ in Equation (24) are produced by the reduction of the corresponding redox couples with H₂S according to two possible reactions:

$\begin{array}{cc}\begin{array}{l}{\text{H}}_2\text{S}+0.5{\text{NAD}}^{+}+0.67{\text{Fd}}_{\text{ox}}+0.17\text{FAD}\to \\ {\text{S}}^0+0.5\text{NADH}+0.67{\text{Fd}}_{\text{red}}+0.17{\text{FADH}}_2+1.17{\text{H}}^{+},\end{array}& (25)\end{array}$

$\begin{array}{cc}\begin{array}{l}{\text{H}}_2\text{S}+2{\text{NAD}}^{+}+2.67{\text{Fd}}_{\text{ox}}+0.67\text{FAD}+4{\text{H}}_2\text{O}\to \\ {\text{SO}}_4^{2-}+2\text{NADH}+2.67{\text{Fd}}_{\text{red}}+0.67{\text{FADH}}_2+6.67{\text{H}}^{+}.\end{array}& (26)\end{array}$

When both of these reactions occur simultaneously, the generalized equation for the RET reaction is

$\begin{array}{cc}\begin{array}{l}{\text{H}}_2\text{S}+(2-1.5x){\text{NAD}}^{+}+(2.67-2x){\text{Fd}}_{\text{ox}}+(0.67-0.5x)\\ \text{FAD}+(4-4x){\text{H}}_2\text{O}\to \\ x{\text{S}}^0+(1-x){\text{SO}}_4^{2-}+(2-1.5x)\text{NADH}+(2.67-2x){\text{Fd}}_{\text{red}}\\ +(0.67-0.5x){\text{FADH}}_2+(6.67-5.5x){\text{H}}^{+}\end{array}& (27)\end{array}$

and its energy requirement is calculated as

$\begin{array}{cc}\begin{array}{l}\Delta G_r(\text{RET})=x\Delta G_f^0({\text{S}}^0)+(1-x)\Delta G_f^0({\text{SO}}_4^{2-})-\Delta G_f^0({\text{H}}_2\text{S})\\ -4(1-x)\Delta G_f^0({\text{H}}_2\text{O})+(2-1.5x)\\ [\Delta G_f^0(\text{NADH})-\Delta G_f^0({\text{NAD}}^{+})]+(2.67\text{}-\text{}2x)\\ [\Delta G_f^0({\text{Fd}}_{\text{red}})-\Delta G_f^0({\text{Fd}}_{\text{ox}})]+(0.67-0.5x)\\ [\Delta G_f^0({\text{FADH}}_2)\text{}-\text{}\Delta G_f^0(\text{FAD})]\text{}+\text{}\text{RT}\text{ln}{Q}_4.\end{array}& (28)\end{array}$

Here, ΔG⁰_f(NADH) − ΔG⁰_f(NAD⁺) = 60.99 kJ (mol NADH)⁻¹, ΔG⁰_f(FADH₂) − ΔG⁰_f(FAD) = 42.65 kJ (mol FADH₂)⁻¹, ΔG⁰_f(Fd_red) − ΔG⁰_f(Fd_ox) = 38.88 kJ (mol Fd_red)⁻¹ (Alberty, 1998) and the reaction quotient Q₄ is given by

$\begin{array}{cc}{Q}_4=\frac{\begin{array}{l}{[{\text{SO}}_4^{2-}]}^{(1-x)}{[\text{NADH}]}^{(2-1.5x)}{[{\text{Fd}}_{\text{red}}]}^{(2.67-2x)}\hfill \\ {[{\text{FADH}}_2]}^{(0.67-0.5x)}{[{\text{H}}^{+}]}^{(6.67-5.5x)}\hfill \end{array}}{[{\text{H}}_2\text{S}]{[{\text{NAD}}^{+}]}^{(2-1.5x)}{[{\text{Fd}}_{\text{ox}}]}^{(2.67-2x)}{[\text{FAD}]}^{(0.67-0.5x)}}.& (29)\end{array}$

Taken together, CO₂ reduction in SOB comprises two steps: production of the reducing equivalents (Equations 21 or 27) and the actual CO₂ fixation (Equations 18 or 24), as already pointed out by Kelly (1999). Thus, the total energy requirement of CO₂ reduction is given by the sum of ΔG_r(RET) and ΔG_r(CO₂ fix). Analogously to Equation (8), in our new approach we therefore calculate the thermodynamic energy conservation efficiency of autotrophic sulfur oxidation as

$\begin{array}{cc}{\epsilon }_{\text{II}}=\frac{(1-y)[\Delta G_r(\text{RET})+\Delta G_r({\text{CO}}_2\text{fix})]}{-y\Delta G_r({\text{O}}_2\text{red})},& (30)\end{array}$

where the corresponding ΔG_r values are calculated as described above. It should be noted that ε_II > ε_I because ΔG_r(CO₂ red) calculated by the traditional approach (Equation 11) is always lower than the sum ΔG_r(RET) + ΔG_r(CO₂ fix).

Factorization of the New Energy Conservation Efficiency

Analogously to the factorization of the traditional thermodynamic efficiency (see Equation 17), the new thermodynamic efficiency ε_II defined by Equation (30) can also be written as a product of partial efficiencies characterizing the processes involved in the autotrophic sulfur oxidation. Specifically, because CO₂ reduction in our new approach is divided into RET and CO₂ fixation, expression (15) for the efficiency of ATP utilization must be written as

$\begin{array}{cc}{\epsilon }_{\text{u},\text{II}}=\frac{\Delta G_r(\text{RET})+\Delta G_r({\text{CO}}_2\text{fix})}{\Delta E_r(\text{RET})+\Delta E_r({\text{CO}}_2\text{fix})},& (31)\end{array}$

where ΔE_r(RET) and ΔE_r(CO₂ fix) describe the energy requirements, in the form of ATP, of the RET and CO₂ fixation reactions, respectively. This implies that ε_II can be factorized as

$\begin{array}{cc}{\epsilon }_{\text{II}}={\epsilon }_{\text{SO}}{\epsilon }_{\text{u},\text{II}}{\epsilon }_{\text{t}}.& (32)\end{array}$

To make the influence of the RET and CO₂ fixation reactions more explicit, we define their corresponding efficiencies as

$\begin{array}{cc}{\epsilon }_{\text{RET}}=\frac{\Delta G_r(\text{RET})}{\Delta E_r(\text{RET})}& (33)\end{array}$

and

$\begin{array}{cc}{\epsilon }_{\text{CO2}}=\frac{\Delta G_r({\text{CO}}_2\text{fix})}{\Delta E_r({\text{CO}}_2\text{fix})}.& (34)\end{array}$

This makes it possible to write ε_II as a product

$\begin{array}{cc}{\epsilon }_{\text{II}}={\epsilon }_{\text{SO}}{\epsilon }_{\text{t}}{\epsilon }_{\text{CO2}}{\epsilon }_{\text{RET}}{[\alpha {\epsilon }_{\text{RET}}+(1-\alpha ){\epsilon }_{\text{CO2}}]}^{-1}& (35)\end{array}$

where the parameter α is defined as

$\begin{array}{cc}\alpha =\frac{\Delta G_r({\text{CO}}_2\text{fix})}{\Delta G_r(\text{RET})+\Delta G_r({\text{CO}}_2\text{fix})}.& (36)\end{array}$

Previous work has already characterized the realistic ATP requirements of CO₂ fixation. Assuming 0% oxygenase activity of RuBisCO, ATP requirements of the Calvin cycle are 3 ATP per CO₂, whereas ATP requirements of the rTCA cycle are ~1.67 ATP per CO₂ (Bar-Even et al., 2010). As pointed out by Kelly (1999), these requirements can be considered constant. Assuming the ATP energy content of 41 kJ (mol ATP)⁻¹, this translates into ΔE_r(CO₂ fix) of 123 kJ (mol CO₂)⁻¹ and 68.3 kJ (mol CO₂)⁻¹ for the Calvin and rTCA cycle, respectively. Considering the ΔG_r(CO₂ fix) values calculated by Bar-Even et al. (2010) (see Section Efficiency of Energy Conservation: The New Calculation Approach), the energy conservation efficiency of the CO₂ fixation can therefore be considered as a known parameter: ε_CO2 = 0.57 for the Calvin cycle and ε_CO2 = 0.94 for the rTCA cycle (Bar-Even et al., 2010). Similarly, the parameter α has also a known value depending on the parameter x and on the CO₂ fixation pathway employed by the SOB, as follows from Equations (22), (28) and (36).

Taken together, this means that although the efficiencies ε_SO, ε_t and ε_RET are generally unknown, they are related through Equation (35). This makes it possible to calculate any one of these efficiencies provided that the other two are known. Since this is not possible at the current state of knowledge, Equation (35) can be used to estimate their minimal values. Of specific interest in this study is the minimal value of the efficiency of the sulfur oxidation pathway, ε_SO. This value is reached when the efficiencies ε_RET and ε_t are maximal (i.e., ε_RET = ε_t = 1), which gives

$\begin{array}{cc}\begin{array}{l}{\epsilon }_{\text{SO},\text{II},\text{min}}={\epsilon }_{\text{II}}\left[\frac{\alpha }{{\epsilon }_{\text{CO2}}}+(1-\alpha )\right]\\ =\frac{(1-y)[\Delta G_r(\text{RET})+\Delta E_r({\text{CO}}_2\text{fix})]}{-y\Delta G_r({\text{O}}_2\text{red})},\end{array}& (37)\end{array}$

as follows from Equations (30), (35) and (36). It should be noted that ε_{SO, II, min} > ε_{SO, I, min}. Our new approach therefore provides a more constrained range of possible efficiencies of sulfur oxidation coupled to O₂ reduction in comparison to the traditional approach.

Generalized Equations and Efficiencies for other Reduced Sulfur Oxidation Processes

Many SOB can use alternative reduced sulfur species for the reduction of O₂ and CO₂, such as thiosulfate. Additionally, in anoxic environments or habitats that are characterized by fluctuating conditions, such as hydrothermal vents, also the reduction of NO⁻₃ has to be considered as a possible sink of electrons during reduced sulfur oxidation. NO⁻₃ can either be reduced partially to N₂ by denitrification or completely to NH⁺₄ by dissimilatory nitrate reduction to ammonia (DNRA) to generate energy for CO₂ fixation. The generalized mass-balanced equations for these processes are derived analogously as Equations (1–7) and are given in the Table S1. Furthermore, the corresponding energy conservation efficiencies ε_I, ε_II and ε_{SO, II, min} are calculated from expressions similar to Equations (8), (30), and (37) with the exception that the ΔG_r values in the nominator and denominator are calculated based on the stoichiometry of the corresponding energy-conserving and energy-generating reaction. We implemented these calculations in R (www.cran.r-project.org) as functions and scripts that can be freely downloaded from the internet (http://nanosims.geo.uu.nl/SOX; Supplement 1).

Results

Stoichiometry of Autotrophic Sulfur Oxidation from Rate Measurements

Here we demonstrate how the generic theoretical framework can be used to rapidly evaluate the stoichiometry of autotrophic reduced sulfur oxidation from rate measurements of the reactants involved. Additional examples are provided in Supplement 2.

The first example involves marine Beggiatoa strain MS-81-6. Nelson et al. (1986) reported that this strain performed aerobic sulfide oxidation coupled to CO₂ fixation with the O₂:ΣH₂S consumption ratio of ~1.65 and the CO₂:ΣH₂S consumption ratio of 0.35. Using Table S1A, these experimental values lead to equations ν_O2/ν_H2S = y(2−1.5x) = 1.65 and ν_CO2/ν_H2S = (1−y)(2−1.5x) = 0.35, which yield y = 0.825 and x = 0. As follows from Table S1A, this implies that (i) the aerobic oxidation of sulfide in this strain was performed according to equation

$\begin{array}{l}{\text{H}}_2\text{S}+1.65{\text{O}}_2+0.35{\text{CO}}_2+0.35{\text{H}}_2\text{O}\to \\ {\text{SO}}_4^{2-}+0.35{\text{CH}}_2\text{O}+2{\text{H}}^{+},\end{array}$

(ii) sulfate was the exclusive product, and (iii) 82.5% of the sulfide pool was used in the energy gaining reaction with oxygen (Equation 3) while the remaining 17.5% was used for CO₂ fixation (Equation 6). This is consistent with the conclusions of Nelson et al. (1986).

The second example deals with SOB that live in symbiosis with tubeworms Riftia. Girguis et al. (2002) reported that the sulfide consumption rate of 6.75 μmol ΣH₂S g⁻¹ h⁻¹ by the whole-worm symbiosis was accompanied by the total rates of O₂ and CO₂ consumption of 12.4 μmol O₂ g⁻¹ h⁻¹ and 12.45 μmol CO₂ g⁻¹ h⁻¹, respectively. Assuming that host respiration constitutes 25% of the whole-worm O₂ consumption (see Supplement 3), the estimated rates of O₂ and CO₂ consumption by the symbionts are 9.3 μmol O₂ g⁻¹ h⁻¹ and 15.55 μmol CO₂ g⁻¹ h⁻¹, respectively. This directly translates into equations ν_O2/ν_H2S = y(2−1.5x) = 9.3/6.75 = 1.38 and ν_CO2/ν_H2S = (1−y)(2−1.5x) = 15.55/6.75 = 2.3, which yield x = −1.12, y = 0.375 and the corresponding equation

$\begin{array}{l}{\text{H}}_2\text{S}+1.12{\text{S}}^0+1.38{\text{O}}_2+2.3{\text{CO}}_2+3.42{\text{H}}_2\text{O}\to \\ 2.12{\text{SO}}_4^{2-}+2.3{\text{CH}}_2\text{O}+4.24{\text{H}}^{+}.\end{array}$

This means that during the particular experiment reported by Girguis et al. (2002) the Riftia symbionts probably oxidized not only H₂S but also a relatively large amount of stored zero-valent sulfur to fix CO₂, with 37.5% of this total pool of reduced sulfur used for energy generation. This result is reasonable considering that the sum of the O₂ and CO₂ consumption rates cannot be larger than double the sulfide consumption rate if aerobic sulfide oxidation is performed with H₂S and SO²⁻₄ as the only reduced and oxidized sulfur species, respectively (see Table S1A).

Energy Conservation Efficiency from Stoichiometry

The energy conservation efficiency of autotrophic sulfur oxidation can be calculated once the stoichiometry of the generalized equation is known. First, we demonstrate this calculation for Beggiatoa strain MS-81-6 analyzed above using the traditional calculation approach and assuming standard biochemical conditions. Substitution of x = 0 and of the ΔG⁰_f values tabulated in Thauer et al. (1977) to Equations (10) and (11) yields ΔG⁰_r(O₂ red) = −829 kJ mol⁻¹ and ΔG⁰_r(CO₂ red) = 145 kJ mol⁻¹. Subsequent substitution of these values together with y = 0.825 obtained above to Equation (8) yields ε_I = 0.037. This is consistent with the efficiency value of 0.038 obtained by Nelson and Hagen (1995). The small discrepancy is most likely due to the fact that Nelson and Hagen (1995) used ΔG⁰_f(O₂) = 0 kJ mol⁻¹ for the standard Gibbs energy of formation of O₂, which corresponds to O₂ gas, while we used the value of 16.4 kJ mol⁻¹, which corresponds to dissolved O₂.

Traditionally, the efficiency value of 0.037 is interpreted such that Beggiatoa strain MS-81-6 conserves 3.7% of the energy gained by aerobic sulfide oxidation into biomass. Based on our analysis above (Equation 17), a more accurate interpretation is that 0.037 is the product of the partial efficiencies of (i) ATP generation by O₂ reduction (ε_SO), (ii) ATP utilization for CO₂ fixation (ε_u) and (iii) the transfer of ATP gained by O₂ reduction for CO₂ fixation and thus not for cellular maintenance (ε_t). For example, an assumption that Beggiatoa strain MS-81-6 uses ATP exclusively for CO₂ fixation and not for any other biochemical reaction (ε_t = 1), and that its ATP utilization for CO₂ fixation occurs without loss of energy (ε_u = 1), would imply that the efficiency of ATP generation by O₂ reduction (see Equation 14) in this strain is ε_SO = ε_I/(ε_tε_u) = 0.037.

In the second example we analyse the difference between the efficiency values calculated according to the traditional (ε_I; Equation 8) and our new approach (ε_II; Equation 30). We do this for aerobic thiosulfate oxidizers Sulfurimonas denitrificans and Thioalkalivibrio versutus, which fix CO₂ using the rTCA cycle (Hügler et al., 2005) and the Calvin cycle, respectively. Based on the substrate consumption rates reported by Hoor (1981) and Sorokin et al. (2001) we calculated x = 0 and y = 0.833 for S. denitrificans and x = 0 and y = 0.844 for T. versutus (see Supplement 4). Using these values in the traditional approach, we obtained the efficiency of ε_I = 0.0314 for S. denitrificans and ε_I = 0.0289 for T. versutus, whereas our new approach gave values ε_II = 0.0799 for S. denitrificans and ε_II = 0.0796 for T. versutus.

We see that our new approach yields substantially larger efficiency values than the traditional approach. This is generally because the new approach accounts for the fact that CO₂ reduction by SOB is performed in two separate steps (i.e., the reduction of an electron carrier via reverse electron transport followed by the reduction of CO₂ coupled to the electron carrier oxidation in the respective CO₂ fixation pathway) and because the theoretical energy requirements of these two steps [ΔG_r(RET) + ΔG_r(CO₂ fix); see Equation (30)] are substantially larger than the theoretical energy requirement of the net CO₂ reduction reaction [ΔG_r(CO₂ red); see Equation (8)] considered in the traditional approach. Additionally we see that the relative difference between the efficiency values of the compared SOB depends on the choice of the approach, particularly if the SOB employ different CO₂ fixation pathways. In this specific case the efficiency ε_I of S. denitrificans is by about 8% larger than that of T. versutus, whereas their ε_II values are practically identical. This is related to the fact that the ΔG_r values of the RET and CO₂ fixation reactions (Equation 30) depend on the type of the electron carriers involved in the CO₂ fixation pathways, which differ between the rTCA and Calvin cycle (compare Equations 18 and 21 vs. Equations 24 and 27).

As a last point, we illustrate an additional insight that can be gained from the factorized form of ε_II (see Equation 35). The fact that S. denitrificans and T. versutus have practically identical values of the overall efficiency ε_II might be misinterpreted by concluding that their corresponding partial efficiencies ε_SO, ε_RET, ε_CO2, and ε_t are also the same. However, we know that the efficiency ε_CO2 of the rTCA cycle used by S. denitrificans to fix CO₂ is almost two-fold larger than that of the Calvin cycle employed by T. versutus. This implies that at least one of the efficiencies ε_SO, ε_RET, and ε_t must differ between the two SOB. By calculating the minimum values of these efficiencies using Equations (35–37) we found that all of them are higher for T. versutus (ε_{SO, II, min} = ε_{t, II, min} = 0.1030 and ε_{RET, II, min} = 0.052) than for S. denitrificans (ε_{SO, II, min} = ε_{t, II, min} = 0.0818 and ε_{RET, II, min} = 0.051). This suggests that T. versutus has a more efficient sulfur oxidation pathway (larger ε_SO or ε_RET) or lower cellular maintenance requirements (larger ε_t) than S. denitrificans. It should be noted that this conclusion can only be drawn based on our new calculation approach but not based on the traditional approach. Therefore, our new approach, and particularly the value of ε_{SO, II, min}, is better suited to identify differences between sulfur oxidation pathways among SOB, particularly if the compared SOB employ different CO₂ fixation pathways.

Sensitivity of the Calculated Efficiency Toward Reactant Concentrations

Until now our calculations assumed standard biochemical conditions. However, as pointed out by Nelson and Hagen (1995) and Kelly (1999), the actual experimental conditions should be used when calculating the ΔG_r values for the energy gaining and energy conserving reactions. In the literature on SOB activity these concentrations are in most cases not reported or not well constrained. Thus, it is important to evaluate possible errors introduced by this uncertainty in the calculation of the energy conservation efficiency. This is achieved through sensitivity analysis.

To perform this analysis, we varied the concentration of one of the reactants between 1 M and 1 nM, or the pH between 2 and 12, while keeping the other reactant concentrations as well as the stoichiometry of the reaction mediated by an SOB unchanged. In our formalism the variations of the reactant concentrations and pH are captured in the variation of the quotients Q (see Equations 12, 13, 23, and 29). As examples, we used the aerobic sulfide oxidizing bacteria Thermithiobacillus tepidarius and Halothiobacillus neapolitanus, which employ the Calvin cycle for CO₂ fixation, and the denitrifying thiosulfate oxidizing bacteria Sulfurimonas hongkongensis and Sulfurimonas denitrificans, which employ the rTCA cycle for CO₂ fixation.

This analysis revealed that the calculated efficiency values are most sensitive to the concentrations of CO₂ (ε_I) and of the electron carriers such as NAD⁺/NADH (ε_{SO, II, min}), whereas the sensitivity toward the concentration of the terminal electron acceptor (TEA) is lowest (Figure S2). Sensitivities toward pH, the reduced sulfur compound (e.g., S₂O₃²⁻ or H₂S) and SO²⁻₄ (Figure S2) as well as toward temperature between 0 and 30°C (data not shown) are intermediate but also rather small. For instance, for the aerobic sulfide oxidizing bacteria T. tepidarius and H. neapolitanus a change in the concentration of NAD⁺ by three orders of magnitude would change the calculated value of ε_{SO, II, min} by ~14%, while the same change in the concentration of CO₂ would change ε_I by ~24%. In contrast the calculated values of ε_{SO, II, min} and ε_I would only change by ~4% if the concentration of O₂ changed by three orders of magnitude. The errors introduced by uncertainties in the reactant concentrations are similar for the denitrifying thiosulfate oxidizing bacteria S. hongkongensis and S. denitrificans (Figure S2).

As the aim of this study is to compare efficiencies among SOB, it is important to evaluate how the errors introduced by the uncertainties in the reactant concentrations would affect this comparison. To do this we considered two SOB whose efficiencies calculated at standard conditions differ, and determined the change in the reactant concentrations required to make the efficiencies equal. We illustrate the result on the same pairs of aerobic and anaerobic SOB as above. When using the traditional approach, the efficiency ε_I calculated for T. tepidarius would become equal to that of H. neapolitanus if the former were calculated with a 10⁶-fold lower SO²⁻₄ concentration than the standard concentration of 1 M or at pH = 10 instead of pH = 7. In contrast, the difference in the SO²⁻₄ concentration or pH would need to be considerably larger (~10²⁰-fold for SO²⁻₄, or at a pH≈11) to achieve the same effect for the efficiency ε_{SO, II, min} calculated by our new approach (Figure S2A). Similar conclusion can be drawn for S. hongkongensis and S. denitrificans (Figure S2B) as well as for SOB that perform other types of autotrophic sulfur oxidation (data not shown). We therefore conclude that, although the sensitivities toward reactant concentrations are similar for both approaches, our new approach is more robust to resolve differences between SOB with respect to their energy conservation efficiency if the calculations are affected by an uncertainty in the concentrations of the reactants involved.

Efficiency of Autotrophic Sulfur Oxidation in different Strains of SOB

The reason for different efficiencies of autotrophic sulfur oxidation is generally assumed to lie in the different biochemical pathways that the SOB employ for the oxidation of the reduced sulfur compound (e.g., Hagen and Nelson, 1997; Kelly, 1999). To gain more insights into this possible relationship, we compiled literature data on cultivated strains of SOB, calculated their energy conservation efficiencies, and listed them together with the available information on the identified sulfur oxidation and carbon fixation pathways and selected specific enzymes. To follow the outcomes of the above analyses, we used ε_{SO, II, min} to compare the SOB. Specifically, we first calculated the complete stoichiometry of sulfur oxidation coupled to TEA and CO₂ reduction based on rates reported in the literature. As for most SOB these rates were obtained under not well-constrained experimental conditions, we could not include the concentration dependency of the ΔG_r values (in the form of the reaction quotient Q) in our efficiency calculations. Thus, to still make a comparison possible, we chose to calculate the efficiency values at standard biochemical conditions.

The results of this compilation are summarized in Table 1 and Figure 2. First, they show that the efficiencies cover a wide range with no apparent clustering according to the SOB phylogeny. Furthermore, they suggest possible links between the efficiency, the sulfur oxidation pathway and/or the type of TEA reductase. This is quite astonishing considering that the efficiency values were calculated from rate measurements performed under different experimental settings (e.g., batch reactor studies, continuous cultivation) and that coherent data on both stoichiometry and biochemical pathways employed by SOB are rather limited.

TABLE 1

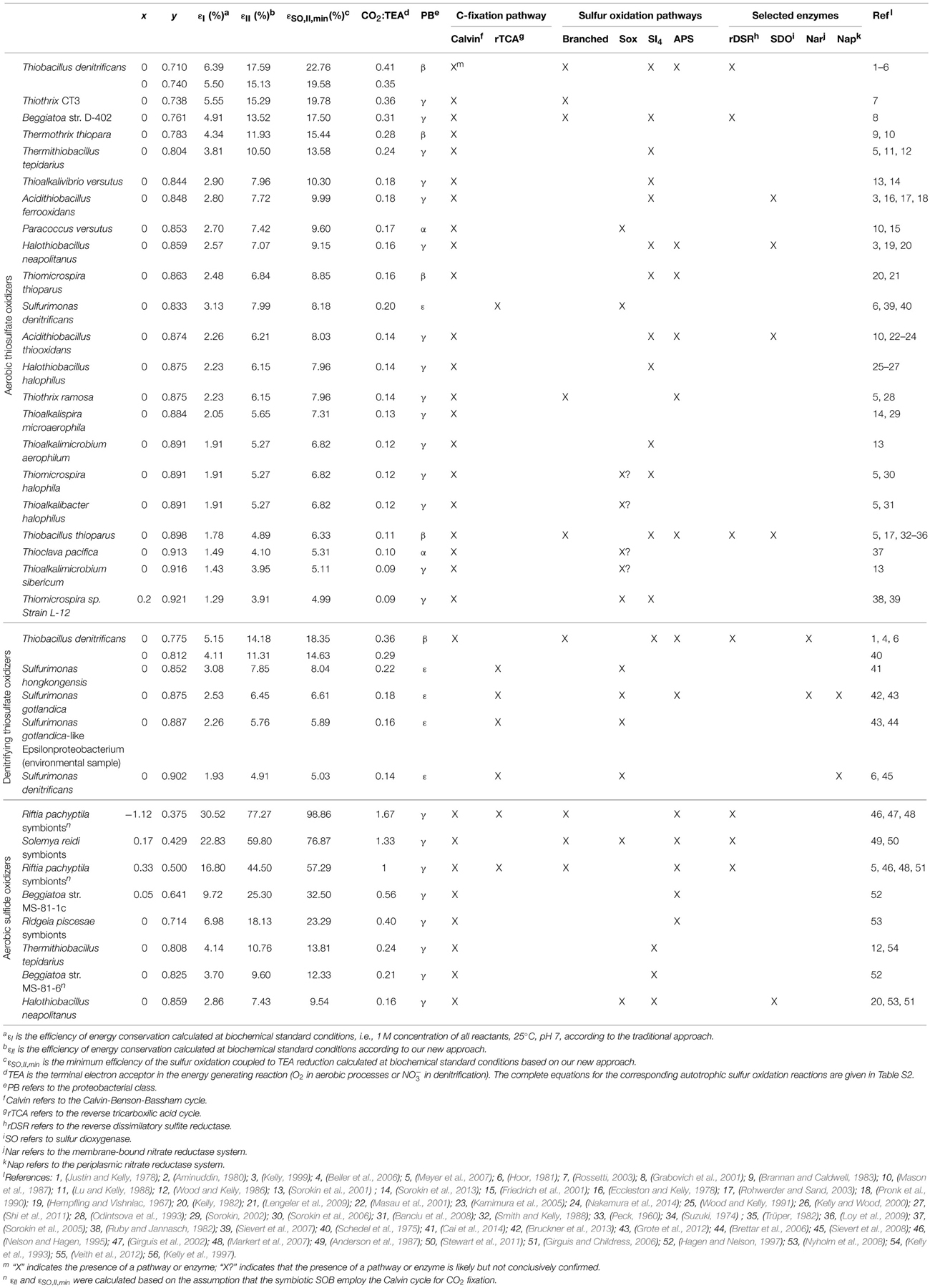
Table 1. Characteristics of autotrophic sulfur oxidizing bacteria (SOB) derived from literature data and calculated in this study (ε_I, ε_II, ε_{SO, II, min}, CO₂:TEA).

FIGURE 2

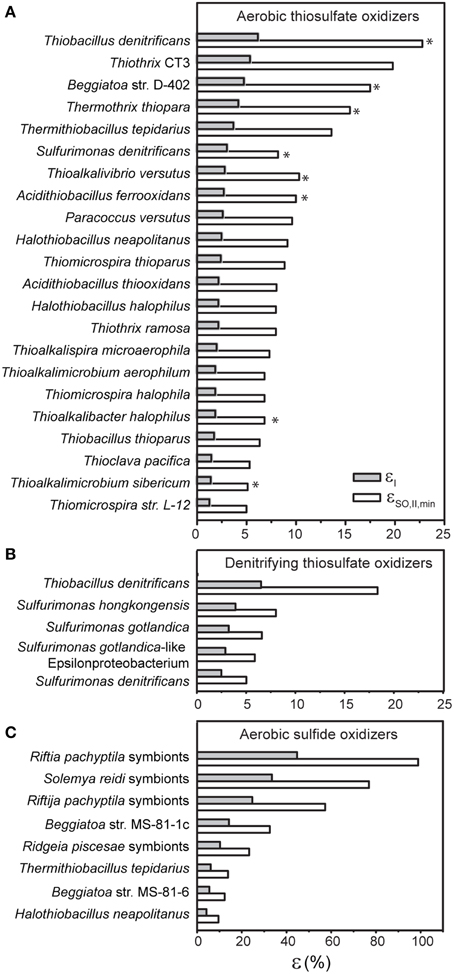
Figure 2. Energy conservation efficiencies of SOB performing aerobic thiosulfate oxidation (A), thiosulfate oxidation coupled to denitrification (B) and aerobic sulfide oxidation (C). Values were calculated using experimental data in the literature (see Table 1) based on the traditional approach (ε_I) and our new approach (ε_{SO, II, min}). Asterisks in panel A indicate that the SOB are facultatively anaerobic.

With regard to aerobic thiosulfate oxidizing bacteria, for which the available literature data is most abundant, our analysis shows that autotrophic thiosulfate oxidation measured under aerobic conditions appears to be performed with the highest efficiency if the SOB are facultatively anaerobic (indicated by asterisk in Figure 2), a trend noticed already, for instance, by Kelly (1982). Concerning the pathways of thiosulfate oxidation, SOB equipped with the enzyme reverse dissimilatory sulfite reductase (rDSR), which is involved in the branched pathway (red arrows in Figure 1), tend to have the highest efficiencies among the aerobic thiosulfate oxidizers, whereas those relying on the Sox pathway (green arrows in Figure 1) appear to have the lowest efficiencies. In contrast, no clear patterns are apparent for the SOB employing the SI₄ pathway (blue arrows in Figure 1), whose efficiencies span from low to high values. The same is true for the APS pathway for sulfite oxidation, which can be part of both the branched and SI₄ pathways (Figure 1).

Aerobic sulfide oxidizing bacteria employing pathways that involve oxidation of zero-valent sulfur (black arrows in Figure 1) to sulfite via rDSR (red arrows in Figure 1) have the highest efficiency (Table 1). This is similar to the pattern identified for the aerobic thiosulfate oxidizing bacteria. Most strikingly, extremely high efficiencies of energy conservation are found among aerobic sulfide oxidizers that live in symbiotic association with invertebrates such as the Riftia tubeworm. Note that these high values are not the consequence of the fact that they were calculated at standard biochemical conditions. Specifically, the concentrations of the substrates and products involved would have to be in the kilomolar and picomolar range, respectively, to obtain efficiency values comparable to those of the other, less efficient SOB. Since it is unlikely that the host regulates the substrates and products in such an extreme range of concentrations, the high efficiency values of the symbiotic SOB are realistic.

With respect to SOB that couple thiosulfate oxidation to denitrification, the data available in the literature is very limited. Nevertheless, the present data indicate that SOB equipped with a membrane-bound nitrate reductase system (Nar) have in general high efficiencies whereas those relying exclusively on a periplasmic nitrate reductase system (Nap), namely S. denitrificans, have a very low energy conservation efficiency (Table 1).

Stoichiometry from the Efficiency of Energy Conservation and Limited Rate Measurements

Most stoichiometries and efficiency values listed in Table 1 and Table S2 were calculated based on rate measurements during which the studied SOB oxidized the sulfur compound completely to sulfate. However, for many SOB main products of sulfur oxidation may include also other sulfur species, such as zero-valent sulfur (e.g., Ghosh and Dam, 2009). To calculate the stoichiometry of autotrophic sulfur oxidation at an arbitrary S⁰:SO²⁻₄ production ratio, one generally needs to provide gross rates of three reactants involved. However, accurate quantification of three gross rates is often experimentally difficult. Here we demonstrate that the stoichiometry of autotrophic sulfur oxidation can be estimated if the consumption/production rates of only two reactants involved are measured, provided that certain additional conditions characterizing the activity of an SOB are known.

Our framework shows that the stoichiometry is completely determined by the values of the parameters x and y. To find these values, two constraints are needed. The first constraint is obtained by measuring the rates of two reactants involved, whereby their ratio directly provides a relationship between x and y, as follows from the generalized mass balanced equations in Table S1. The second constraint is obtained from the knowledge of how the CO₂:TEA consumption ratio (essentially the parameters y; see Table S1) or the energy conservation efficiency (e.g., ε_II) varies depending on the S⁰:SO²⁻₄ production ratio, i.e., on the parameter x. Unfortunately, such information is presently not available because, to the best of our knowledge, the complete stoichiometry of autotrophic sulfur oxidation has never been measured over variable x in an isolated SOB. Therefore, to illustrate the general approach based on our generic framework, we first assume that either the CO₂:TEA ratio or the efficiency ε_II is independent of x and equal to the value calculated from the known stoichiometry at x = 0 (see Table 1). We use the aerobic sulfide oxidizing Beggiatoa str. MS-81-6 as an example.

Based on the experimental data reported by Nelson et al. (1986) we showed above that this SOB performs aerobic sulfide oxidation to SO²⁻₄ (i.e., x = 0) with the CO₂:O₂ consumption ratio of 0.21, O₂:ΣH₂S ratio of 1.65 and, when accounting for the energy requirements of the CO₂ fixation pathway, with the efficiency of ε_II = 9.60% (Table 1 and Table S2). Let us now suppose that in a separate experiment the O₂:ΣH₂S consumption ratio by this strain would be 0.5. What would be the corresponding stoichiometry?

As follows from Table S1A, the generalized stoichiometric coefficients must be related as ν_O2/ν_H2S = O₂:ΣH₂S = 0.5, which yields the first relationship between x and y, namely y(2−1.5x) = 0.5. If we additionally assume that the energy conservation efficiency ε_II is independent of x and equal to the value at x = 0 (i.e., 9.60%; Table 1), the second relationship between x and y is provided by Equation (30). By solving these two equations numerically (implemented in a script written in R available on the internet at http://nanosims.geo.uu.nl/SOX; Supplement 1) we obtained x = 0.920 and y = 0.807 and thus the stoichiometry

$\begin{array}{l}{\text{H}}_2\text{S}+0.5{\text{O}}_2+0.12{\text{CO}}_2\to \\ 0.08{\text{SO}}_4^{2-}+0.92{\text{S}}^0+0.12{\text{CH}}_2\text{O}+0.8{\text{H}}_2\text{O}+0.16{\text{H}}^{+}.\end{array}$

As mentioned above and applied in the work of Nelson et al. (1986), the alternative approach assumes that the growth yield per mole of TEA utilized is independent of x and equal to the value determined at x = 0 (i.e., CO₂:O₂ = 0.21). Using the generalized stoichiometric coefficients (see Table S1), this implies ν_CO2/ν_O2 = (1−y)/y = 0.21 and thus the value of y = 0.826. Combination of this value with the first constraint (i.e., y(2–1.5x) = 0.5; see above) then yields x = 0.929 and thus the stoichiometry

$\begin{array}{l}{\text{H}}_2\text{S}+0.5{\text{O}}_2+0.11{\text{CO}}_2\to \\ 0.07{\text{SO}}_4^{2-}+0.93{\text{S}}^0+0.11{\text{CH}}_2\text{O}+0.82{\text{H}}_2\text{O}+0.14{\text{H}}^{+}.\end{array}$

We see that the efficiency-based and CO₂:TEA-based approach give a very similar stoichiometry of the overall sulfide oxidation reaction, suggesting that they are almost equivalent. To verify this, we performed the same calculations over all possible values of x as well as for different aerobic and anaerobic SOB. If the two approaches were equivalent, the calculated CO₂:TEA consumption ratios would not change with x. As shown in Figures 3A,B, this is approximately the case, since the calculated CO₂:TEA ratios vary by less than ~20% over the complete interval of x. Additionally, this variability is decreased if the reactant concentrations are decreased from values at standard biochemical conditions to a more environmentally relevant range (compare solid and dashed lines in Figures 3A,B). This means that the possible error made when determining the stoichiometric coefficients (for an arbitrary value of x) based on the CO₂:TEA-based approach or the efficiency-based approach will be relatively small (<20%).

FIGURE 3

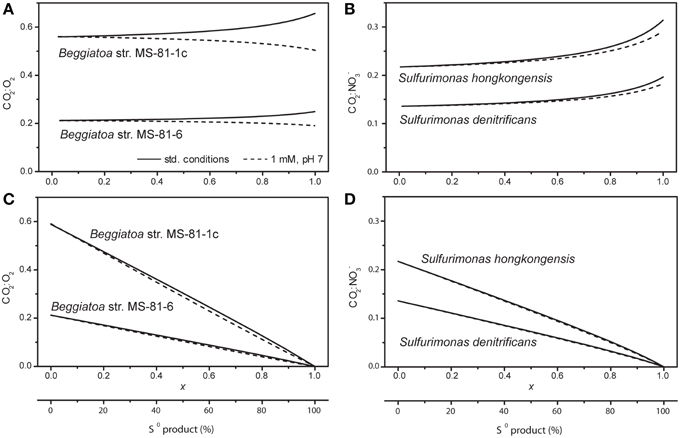
Figure 3. CO₂:TEA ratios in selected SOB calculated over the complete range of S⁰:SO²⁻₄ production ratios (represented by 0<x<1). Calculations were done for two aerobic (A,C) and two anaerobic (B,D) SOB at standard biochemical conditions (solid lines) and with all reactant concentrations equal to 1 mM and pH = 7 (dashed lines), assuming that the energy conservation efficiency ε_II is constant (A,B) or linearly decreasing from the maximum reached at x = 0 toward zero reached at x = 1 (C,D).

The assumption that either the CO₂:TEA ratio or the efficiency ε_II is independent of x is likely not generally applicable to all SOB. Indeed, gslund (Høgslund et al. 2009) showed that sulfide oxidation to S⁰ in bundles of Thioploca spp. is completely decoupled from CO₂ fixation (CO₂:TEA = 0), implying y = 1 and ε_II = 0 at x = 1. It is therefore likely that in some SOB the variability of the CO₂:TEA ratio or of the efficiency ε_II with the parameter x is better approximated by a linear function that, for instance, reaches a maximum at x = 0 and some other value, such as zero, at x = 1. By assuming that this is the case for the efficiency ε_II, we found that the calculated CO₂:TEA ratio also very closely follows a linear trend (Figures 3C,D). This means that, again, the possible error made when determining the stoichiometric coefficients (for an arbitrary value of x) based on the CO₂:TEA-based approach or the efficiency-based approach will be very small.

Overall, these examples demonstrate how our framework can be applied to calculate the stoichiometry of autotrophic sulfur oxidation reactions from two experimentally determined rates (e.g., the consumption rates of the oxidant and of the reduced sulfur species) at an arbitrary S⁰:SO²⁻₄ production ratio. Prerequisite for such calculations is the knowledge of a function that describes the dependency of the CO₂:TEA yield or of the energy conservation efficiency on the S⁰:SO²⁻₄ production ratio parameterized by x. When, due to the lack of experimental data, these functions need to be approximated based on experiments performed at only one or two values of x, the results obtained from the CO₂:TEA-based approach and the efficiency-based approach will be very similar.

Discussion

Calculation of Energy Conservation Efficiency in SOB

The aim of calculating the energy conservation efficiency is to gain insights into the relationship between the ATP requirements and ATP yields of microbially mediated processes (Baas-Becking and Parks, 1927; Hoor, 1981). For chemolithoautotrophic sulfur oxidation the efficiency is calculated as the ratio between the Gibbs free energy required to fix CO₂ and the Gibbs free energy gained from the oxidation of the reduced inorganic sulfur compound (Kelly, 1982, 1990). However, this ratio is generally difficult to interpret because of the complexity of the ATP-consuming and ATP-producing pathways involved. Specifically, ATP is gained during the transfer of electrons from the reduced sulfur compound to the TEA (e.g., O₂ or NO⁻₃) in the diverse sulfur oxidation pathways (Figure 1) and additionally during substrate-level phosphorylation (e.g., in the APS pathway, Figure 1). In contrast, ATP is required during the reverse electron transport from the sulfur compound to the electron carrier such as NAD⁺ (Elbehti et al., 2000), the reduction of CO₂ by the electron carrier in the carbon fixation pathway, and for all other biochemical pathways associated with cell maintenance. Since each of the enzymes involved in the diverse steps of sulfur compound oxidation has a specific electron acceptor in the electron transport chain, the amount of proton-motive-force, and thus ATP, generated per electron transferred depends on the level at which the electron enters the transport chain and the type of TEA reductase. Similarly, the ATP requirement of the electron carrier reduction depends on the level at which electrons enter the transport chain. Last but not least, ATP requirements of the CO₂ fixation also depend on the specific carbon fixation pathway used.

The traditional calculation approach of the energy conservation efficiency is based on the Gibbs free energy of the net reactions involved in energy consumption (Equation 6) and energy generation (Equation 3) (Nelson and Hagen, 1995; Kelly, 1999). Since this approach does not consider the above-mentioned complexity of the pathways involved in the autotrophic sulfur oxidation, especially the influence of the CO₂ fixation pathway and reverse electron transport reactions, it cannot identify which biochemical pathway or reaction has the highest impact on the calculated efficiency. In contrast, our new approach makes this differentiation at least partially possible. Specifically, the calculated value of ε_II represents the overall energy conservation efficiency of sulfur oxidation that accounts for the efficiency of the CO₂ fixation pathway employed by the SOB. Additionally, by formulating this overall efficiency as a product of partial efficiencies of sulfur oxidation coupled to TEA reduction (ε_SO), energy utilization for reverse electron transfer and CO₂ fixation (ε_RET and ε_CO2) and the “transfer efficiency” (ε_t) (see Equation 35 and Figure S1B), our new approach makes it possible to constrain the range of values that these partial efficiencies can have. Of particular utility is the minimum efficiency of sulfur oxidation coupled to TEA reduction (ε_{SO, II, min}), which allows the comparison of SOB with respect to the efficiency of their sulfur oxidation pathways independent of the type and efficiency of their CO₂ fixation pathway.

Variability of Energy Conservation Efficiencies Amongst SOB

Possible links between the energy conservation efficiency and pathways of sulfur oxidation have been extensively discussed before (Kelly, 1982, 1999, 2003; Nelson and Hagen, 1995; Hagen and Nelson, 1997). By combining the efficiency values calculated by our new approach with additional information derived from diverse research approaches (e.g., physiological studies, enzyme assays and genome sequencing), our analysis provides new insights in this discussion. Specifically, it identifies the importance of rDSR and of the TEA reduction step and questions the role of the APS pathway.

Role of rDSR

As noticed by Kelly (1982), facultative anaerobic SOB appear to generally have a higher energy conservation efficiency than obligate aerobic SOB, a trend clearly supported also by our results (Figure 2). This pattern can be understood by noticing that most facultative anaerobic thiosulfate oxidizing SOB are equipped with the “branched” pathway for thiosulfate oxidation (red arrows in Figure 1; Table 1), which is characterized by a truncated Sox system. In SOB that possess a Sox system that is not truncated (green arrows in Figure 1) a thiosulfate-oxidizing multi-enzyme (TOMES) complex catalyzes the complete oxidation of thiosulfate to sulfate, whereby the oxidation of the intermediate zero-valent sulfur is catalyzed by the soxCD enzymes of this complex (e.g., Ghosh and Dam, 2009). However, these enzymes are missing in the branched pathway and, instead, the transiently stored zero-valent sulfur is oxidized, after its reactivation to glutathione persulfide (GSSH), by other enzymes such as rDSR or the oxygen-dependent sulfur dioxygenase (SDO) (Rohwerder and Sand, 2003). While the complete TOMES complex directly channels all electrons derived from thiosulfate oxidation into the electron transport chain at the level of cyt c (Kelly et al., 1997), rDSR catalyzes the cytoplasmic oxidation of GSSH to sulfite and donates the 6 electrons into the electron transport chain eventually at the level of quinone (Holkenbrink et al., 2011). This rDSR-mediated mechanism might therefore provide more ATP and thus eventually lead to a higher energy conservation efficiency as compared to the Sox pathway.

rDSR is suspected to be the most ancient enzyme equipment of SOB and was probably employed by anaerobic anoxygenic phototrophs already in the early Archean era (Meyer and Kuever, 2007). The fact that rDSR is only conserved in extant facultative anaerobic SOB (and phototrophs) might therefore explain the apparent link between the high energy conservation efficiency and the capability of an anaerobic life style.

Role of the Terminal Electron Acceptor Reduction Step

The importance of the type of TEA reductase for the energy conservation efficiency is suggested by our data compiled for the denitrifying SOB (Table 1). Namely, Sulfurimonas denitrificans exclusively relies on a periplasmically oriented nitrate reductase system (Nap) and does not possess a membrane-bound cytoplasmically oriented nitrate reductase system (Nar) (Sievert et al., 2008). Nitrate oxidation via Nap was shown not to contribute to the generation of proton-motive-force and thus ATP (Stewart et al., 2002), which is consistent with the rather poor energy conservation efficiency of this Epsilonproteobacterium. Most other known important denitrifying SOB, such as the large marine Beggiatoa and Thioploca, are equipped with a membrane-bound nitrate reductase system (Nar) (e.g., Crossman, 2007), which oxidizes nitrate on the cytoplasmic side of the membrane and thus contributes to the generation of proton motive force (Simon et al., 2008; Simon and Klotz, 2013). This is consistent with their generally higher energy conservation efficiency (Table 1). Thus, in denitrifying SOB the enzymes directly involved in TEA (NO⁻₃) reduction appear to have at least a similar impact on the energy conservation efficiency as the sulfur oxidation pathway.

Role of the APS Pathway

The role of the pathway of sulfite oxidation to sulfate, where the sulfite is derived, e.g., from sulfide oxidation by rDSR (Figure 1), has been extensively discussed in the past (e.g., Kelly, 2003). This oxidation step can be mediated either by sulfite:cyt c:oxidoreductase (SOAR) or via the APS pathway (Figure 1). Depending on the pathway of sulfur oxidation, SOARs are either associated with the TOMES complex or are complex-independent (Figure 1). While SOARs have been identified in all sulfite oxidizing free-living SOB, the APS pathway appears to be an “extra” pathway that is not crucial for the operation of complete sulfur oxidation (Kappler and Dahl, 2001). It is known that the APS pathway allows additional ATP gain via substrate level phosphorylation before the electrons enter the electron transport chain (Aminuddin, 1980), and its use should thus lead to a higher overall energy conservation efficiency. However, we did not identify a clear link between the efficiency and the presence of the APS pathway in our present data (Table 1), suggesting that the electron transport processes are more important than this substrate level phosphorylation step.

Nevertheless, the presence of the APS pathway might still be the cause of variations in efficiency among closely related species, such as Beggiatoa spp., as suggested by Nelson and Hagen (1995) and Hagen and Nelson (1997). Also, it has to be considered that the APS pathway in the anoxygenic phototroph Allochromatium vinosum only contributes to energy generation at high irradiances (Sánchez et al., 2001), which correspond to saturating availability of TEA and sulfur compound in chemolithotrophic SOB when sulfite oxidation via SOR might become the rate limiting step. Thus, also in SOB the APS pathway might operate only under certain growth conditions. It was not shown for all SOB listed in Table 1 that the APS pathway was active during the rate measurements, which might disguise a possible link between the calculated efficiency and the APS pathway.

Sulfur Oxidation at a Variable Sulfate-To-Zero-Valent-Sulfur Product Ratio

An interesting outcome of our analysis was the way to calculate the stoichiometry of autotrophic sulfur oxidation at a variable S⁰:SO²⁻₄ production ratio from the rates of only two reactants involved (see Section Stoichiometry from the efficiency of energy conservation and limited rate measurements). This calculation relied on an additional information about the activity of the SOB, namely on the relationship between the S⁰:SO²⁻₄ production ratio (parameter x) and the energy conservation efficiency or the CO₂:TEA consumption ratio. Ideally, this relationship should be determined experimentally; however, since such data are presently not available for an isolated SOB, our calculation assumed two specific forms of this relationship: a constant or a linearly decreasing or increasing function of x. In the following we clarify the biochemical interpretation and limitations of these assumptions.

The assumption of a constant CO₂:TEA consumption ratio is equivalent to the assumption that the amount of ATP generated per electron transported to the TEA and the amount of ATP consumed per electron transported to the electron carrier (e.g., NAD⁺) are independent of the origin of the electrons, i.e., whether the electrons are derived from the first (S⁰ production) or second (S⁰ to SO²⁻₄) oxidation step. This is because the rate of TEA reduction linearly correlates with the rate of electrons transported (e.g., 4 electrons per O₂). In contrast, the assumption of a constant energy conservation efficiency implicitly assumes that both the first (reduced sulfur compound to S⁰) and second (S⁰ to SO²⁻₄) oxidation steps have the same efficiency, i.e., the amount of ATP gained from TEA reduction and required for the electron carrier reduction per kJ of the calculated Gibbs free energy is the same for both oxidation steps.

The assumption of a linear dependency of the CO₂:TEA consumption ratio on x considers that the amount of ATP generated during electron transport to the TEA and the amount of ATP required during electron transport to the electron carriers depend on the origin of the electrons. Since the transported electrons derived from each oxidation reaction will have a specific constant potential to generate ATP, a linear dependency of the CO₂:TEA ratio on x will result from the linear “mixing” of the electrons originating from the first and second oxidation step. Similarly, the assumption of a linear dependency of the efficiency on x is a consequence of the linear “mixing” of the efficiencies specific for the complete and incomplete sulfur oxidation reactions.

It should be noted that a major shortcoming of the CO₂:TEA-based approach is that it does not consider the experimental conditions, such as reactant concentrations or the effect of the oxygen concentration on the efficiency of the CO₂ fixation pathway (ε_CO2). These conditions are expected to affect the ATP yield and ATP consumption per transported electron. In contrast, the efficiency-based approach does allow to account for this. Specifically, if the conditions were well-constrained during the experimental determination of the relation between the efficiency and x, and during the independent measurement of two reactant rates, our framework would make it possible, at least theoretically, to precisely predict the complete stoichiometry of autotrophic sulfur oxidation, and thus primary productivity, at any experimental condition.

Interpretation of Reactant Fluxes in the Environment

In mixed microbial communities different processes that utilize the same reactants often spatially overlap, which hampers our ability to interpret the measured net consumption/production rates of the reactants involved. To illustrate how our framework can aid such interpretation, we consider microbial mats inhabited by one dominant SOB in addition to other bacteria. In such mats, it is often observed that, in the zone where sulfide is oxidized with oxygen, the ratio between the steady-state O₂ and ΣH₂S consumption rates is 2 (e.g., Jørgensen et al., 2010). What does this ratio suggest about the S, O, and C cycling in the system?

Knowing that under steady-state conditions SOB exclusively produce SO²⁻₄ and no S⁰ (Nelson et al., 1986), the O₂:ΣH₂S ratio of 2 suggests complete aerobic sulfide oxidation to sulfate (e.g., Jørgensen et al., 2010). Although this interpretation is correct, it ignores carbon cycling within the sulfide oxidation zone. If carbon cycling is taken into account, as it should be because the SOB that mediate the aerobic sulfide oxidation must also grow, this interpretation must be reevaluated.

Our framework implies that the general stoichiometry of aerobic sulfide oxidation coupled to CO₂ fixation under steady state is (Table S1A)

$\begin{array}{l}{\text{H}}_2\text{S}+2\text{y}{\text{O}}_2+2(1-y){\text{CO}}_2+2(1-y){\text{H}}_2\text{O}\to \\ {\text{SO}}_4^{2-}+2(1-y){\text{CH}}_2\text{O}+2{\text{H}}^{+}.\end{array}$

Thus, the O₂:ΣH₂S ratio due to the SOB activity is 2y, which is generally lower than 2 because 0<y<1 (Table S2). This means that in the mixed community part of the observed O₂ consumption must be due to another kind of activity. A plausible candidate is aerobic respiration according to the stoichiometry

$\begin{array}{l}2(1-y){\text{O}}_2+2(1-y){\text{CH}}_2\text{O}\to \\ 2(1-y){\text{CO}}_2+2(1-y){\text{H}}_2\text{O}.\end{array}$

This shows that when the two processes occur simultaneously the O₂:ΣH₂S ratio of 2 can be achieved only if the stoichiometric coefficient for CO₂ in the SOB-driven reaction is the same as that in the aerobic respiration reaction [i.e., 2(1−y)]. Thus, assuming that the steady-state conditions are met, the O₂:ΣH₂S ratio of 2 suggests that the biomass built up by the dominant SOB through aerobic sulfide oxidation is completely recycled within the sulfide oxidation zone via aerobic respiration. Note that this argument is independent of y and thus of the energy conservation efficiency of the dominant SOB. The efficiency only determines the fraction of the O₂ flux that is used for organic carbon recycling.

This analysis can be extended to cases when the O₂:ΣH₂S consumption ratio in the sulfide oxidation zone is different from 2 while the stoichiometry of the SOB activity remains unchanged. Specifically, O₂:ΣH₂S<2 would suggest export of the SOB-generated biomass out of the sulfide oxidation zone (e.g., for degradation by anaerobic processes), whereas O₂:ΣH₂S>2 would indicate import of an external reductant (e.g., organic carbon) into, and its aerobic oxidation within, the zone.

Implications for Niche differentiation among SOB

Past and present research on SOB revealed that (i) sulfur oxidation pathways are highly diverse and characterized by a degree of redundancy (Figure 1), (ii) the product of sulfide oxidation can vary substantially (between S⁰ and SO²⁻₄) even in one SOB dependent on growth conditions and phase, (iii) the energy conservation efficiency of SOB varies widely (Table 1), and (iv) SOB possessing one of the most ancestral enzymes involved in sulfur oxidation (rDSR) appear to be also the most efficient (Table 1). In the following we attempt a synthesis of these findings in the context of niche differentiation among SOB.

To understand the apparent diversification toward lower energy conservation efficiency, it needs to be realized that efficiency is generally not the only measure of success in a given environment. Generally, the success is determined by the growth rate, which is a product of the substrate uptake rate and the growth yield (i.e., the amount of organic carbon synthesized per unit of substrate utilized). Since the growth yield and efficiency are directly related (as follows from Table S1 and Equations 8 and 30), being efficient is only one of the possibilities for being successful. If organisms compensate their inefficient energy conservation by speed with which they utilize the substrate, they can be equally or even more successful than the efficient ones (e.g., Sorokin and Kuenen, 2005). These strategies are, however, likely dominant only in environments with unlimited substrates.

The situation is different in environments where the substrates are limited, e.g., because of a limited external supply. In the context of SOB this can occur if the flux of the reduced sulfur compound (S_red) or of the TEA into the sulfur oxidizing zone is capped, e.g., by the rate of diffusion or by the substrate concentration in the seeping water delivering the substrate through advection. Under such circumstances, the flux of the external substrate supply will define the maximum substrate uptake rate. Ignoring the role of other phenotypes such as motility, this implies that the success of a specific SOB in the sulfur oxidizing zone will depend only on its energy utilization efficiency.

A possible strategy for an SOB to become successful under such circumstances is to match its substrate uptake stoichiometry to the TEA:S_red ratio fixed by the environment. Such an SOB will utilize the available substrates completely, leaving nothing for potential competitors. Table S1 and Equation (30) show that this can be achieved essentially by “adjusting” two parameters: y, and thus the energy conservation efficiency, and x, i.e., the S⁰:SO²⁻₄ product ratio. Which of the parameters is “adjusted” depends on the time-scale at which the environmental setting (the TEA:S_red ratio) varies.

Specifically, a long-term stable environment with a low TEA:S_red ratio should select for an SOB with a high efficiency, and vice versa. This could, for example, provide a possible explanation why SOB living in symbiotic association with invertebrates are highly efficient (Table 1). Specifically, symbiotic SOB need to compete with the host for O₂ and thus likely face O₂ limitation, which requires them to have evolved highly efficient substrate utilization. On the other hand, they can “afford” to be highly efficient because they do not have to retain flexibility in the presumably stable environment regulated by the host.

In contrast, environments with short-term TEA:S_red fluctuations should select for SOB that possess mechanisms for rapid optimization of the substrate utilization stoichiometry. Phenotypic traits operating on short time-scales, such as motility coupled to chemotaxis or the ability to store TEA (nitrate), will likely play a role. However, another important mechanism could be the ability to perform sulfur oxidation at a variable S⁰: SO²⁻₄ ratio. Our framework formulates this ability through the parameter x while the overall stoichiometry of the autotrophic sulfur oxidation reaction is additionally dependent on the parameter y. This makes it possible to predict the optimal range of sulfur oxidation efficiencies that an SOB should have to be successful in a given fluctuating environment. Specifically, this range should be such that the corresponding TEA:S_red utilization ratios during the incomplete (at x = 1) and complete (at x = 0) oxidation of S_red would match the range of the TEA:S_red fluctuations imposed by the environment.

To illustrate this, we assume that the O₂:ΣH₂S flux ratio available in the environment rapidly fluctuates between 0.45 and 1.7. To optimally utilize the available O₂ and total sulfide (ΣH₂S) pool at all times, the SOB should vary the product of its sulfide oxidation between two extremes: S⁰ when the O₂:ΣH₂S ratio reaches 0.45, and SO²⁻₄ when the O₂:ΣH₂S ratio reaches 1.7. As follows from Table S1, the O₂:ΣH₂S ratio is equal to y(2-1.5x), which yields y = 0.9 to satisfy the condition O₂:ΣH₂S = 0.45 at x = 1 (incomplete sulfide oxidation) and y = 0.85 to satisfy the condition O₂:ΣH₂S = 1.7 at x = 0 (complete sulfide oxidation). Assuming standard conditions and Calvin cycle, the efficiency of the most successful SOB should therefore vary between ε_II = 4.3% and ε_II = 8% for the incomplete and complete aerobic sulfide oxidation, respectively, with the corresponding stoichiometries varying between

${\text{H}}_2\text{S}+0.45{\text{O}}_2+0.05{\text{CO}}_2\to {\text{S}}^0+0.05{\text{CH}}_2\text{O}+0.95{\text{H}}_2\text{O}$

and

$\begin{array}{l}{\text{H}}_2\text{S}+1.7{\text{O}}_2+0.3{\text{CO}}_2+0.3{\text{H}}_2\text{O}\to \\ {\text{SO}}_4^{2-}+0.3{\text{CH}}_2\text{O}+2{\text{H}}^{+}.\end{array}$

There are possibly other strategies that SOB living in fluctuating environments employ to become successful, including minimization of S⁰ production to prevent cell bursting (if S⁰ is stored intra-cellularly) or maximization of the growth yield. Although they can be explored within our theoretical framework, their thorough theoretical analysis would go beyond the scope of this study. Nevertheless, the examples and analyses discussed above demonstrate that the concepts and equations put forward in this study provide a generic theoretical framework that can help researchers gain new insights into the activity of sulfur oxidizing bacteria in a wide range of environments and their niches.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank Dirk de Beer and Tim Ferdelman of the Max-Planck-Institute for Marine Microbiology for fruitful discussions. We thank the reviewers for valuable comments that helped improve the manuscript. This work was financially supported by the Max-Planck-Society.

Supplementary Material

The Supplementary Material for this article can be found online at: http://journal.frontiersin.org/article/10.3389/fmicb.2015.00484/abstract

References

Alberty, R. A. (1998). Calculation of standard transformed formation properties of biochemical reactants and standard apparent reduction potentials of half reactions. Arch. Biochem. Biophys. 358, 25–39. doi: 10.1006/abbi.1998.0831

CrossRef Full Text | Google Scholar

Aminuddin, M. (1980). Substrate level versus oxidative phosphorylation in the generation of ATP in Thiobacillus denitrificans. Arch. Microbiol. 128, 19–25. doi: 10.1007/BF00422300

PubMed Abstract | CrossRef Full Text | Google Scholar

Anderson, A. E., Childress, J. J., and Favuzzi, J. A. (1987). Net uptake of CO₂ driven by sulphide and thiosulphate oxidation in the bacterial symbiont-containing clam Solemya reidi. J. Exp. Biol. 133, 1–31.

Google Scholar

Baas-Becking, L. G. M., and Parks, G. S. (1927). Energy relations in the metabolism of autotrophic bacteria. Physiol. Rev. 7, 85–106.

Google Scholar

Banciu, H. L., Sorokin, D. Y., Tourova, T. P., Galinski, E. A., Muntyan, M. S., Kuenen, J. G., et al. (2008). Influence of salts and pH on growth and activity of a novel facultatively alkaliphilic, extremely salt-tolerant, obligately chemolithoautotrophic sufur-oxidizing Gammaproteobacterium Thioalkalibacter halophilus gen. nov., sp. nov. from South-Western Siber. Extremophiles 12, 391–404. doi: 10.1007/s00792-008-0142-1

CrossRef Full Text | Google Scholar

Bar-Even, A., Noor, E., Lewis, N. E., and Milo, R. (2010). Design and analysis of synthetic carbon fixation pathways. Proc. Natl. Acad. Sci. U.S.A. 107, 8889–8894. doi: 10.1073/pnas.0907176107

PubMed Abstract | CrossRef Full Text | Google Scholar

Beller, H. R., Letain, T. E., Chakicherla, A., Kane, S. R., Legler, T. C., and Coleman, M. A. (2006). Whole-genome transcriptional analysis of chemolithoautotrophic thiosulfate oxidation by Thiobacillus denitrificans under aerobic versus denitrifying conditions. J. Bacteriol. 188, 7005–7015. doi: 10.1128/JB.00568-06

CrossRef Full Text | Google Scholar

Berg, J. S., Schwedt, A., Kreutzmann, A.-C., Kuypers, M. M. M., and Milucka, J. (2014). Polysulfides as intermediates in the oxidation of sulfide to sulfate by Beggiatoa spp. Appl. Environ. Microbiol. 80, 629–636. doi: 10.1128/AEM.02852-13

PubMed Abstract | CrossRef Full Text | Google Scholar

Brannan, D. K., and Caldwell, D. E. (1983). Growth kinetics and yield coefficients of the extreme thermophile Thermothrix thiopara in continuous culture. Appl. Environ. Microbiol. 45, 169–173.

PubMed Abstract | Google Scholar

Brettar, I., Labrenz, M., Flavier, S., Bötel, J., Kuosa, H., Christen, R., et al. (2006). Identification of a Thiomicrospira denitrificans-like epsilonproteobacterium as a catalyst for autotrophic denitrification in the central Baltic Sea. Appl. Environ. Microbiol. 72, 1364–1372. doi: 10.1128/AEM.72.2.1364-1372.2006

PubMed Abstract | CrossRef Full Text | Google Scholar

Brüchert, V., Currie, B., Peard, K. R., Lass, U., Endler, R., Dübecke, A., et al. (2006). “Biogeochemical and physical control on shelf anoxia and water column hydrogen sulphide in the Benguela coastal upwelling system off Namibia,” in Past and Present Water Column Anoxia ed L. N. Neretin (Dordrecht: Springer), 161–193. doi: 10.1007/1-4020-4297-3_07

CrossRef Full Text

Bruckner, C. G., Mammitzsch, K., Jost, G., Wendt, J., Labrenz, M., and Jürgens, K. (2013). Chemolithoautotrophic denitrification of epsilonproteobacteria in marine pelagic redox gradients. Environ. Microbiol. 15, 1505–1513. doi: 10.1111/j.1462-2920.2012.02880.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Buchanan, B. B., and Arnon, D. I. (1990). A reverse Krebs cycle in photosynthesis: consensus at last. Photosynth. Res. 24, 47–53. doi: 10.1007/BF00032643

CrossRef Full Text | Google Scholar

Cai, L., Shao, M.-F., and Zhang, T. (2014). Non-contiguous finished genome sequence and description of Sulfurimonas hongkongensis sp. nov., a strictly anaerobic denitrifying, hydrogen- and sulfur-oxidizing chemolithoautotroph isolated from marine sediment. Stand. Genomic Sci. 9, 1302–1310. doi: 10.4056/sigs.4948668

PubMed Abstract | CrossRef Full Text | Google Scholar

Crossman, L. C. (2007). Sink or swim. Nat. Rev. Microbiol. 5, 834–835. doi: 10.1038/nrmicro1777

PubMed Abstract | CrossRef Full Text | Google Scholar

Eccleston, M., and Kelly, D. P. (1978). Oxidation kinetics and chemostat growth kinetics of Thiobacillus ferrooxidans on tetrathionate and thiosulfate. J. Bacteriol. 134, 718–727.

PubMed Abstract | Google Scholar

Elbehti, A., Brasseur, G., and Lemesle-Meunier, D. (2000). First evidence for existence of an uphill electron transfer through the bc(1) and NADH-Q oxidoreductase complexes of the acidophilic obligate chemolithotrophic ferrous ion-oxidizing bacterium Thiobacillus ferrooxidans. J. Bacteriol. 182, 3602–3606. doi: 10.1128/JB.182.12.3602-3606.2000

PubMed Abstract | CrossRef Full Text | Google Scholar

Friedrich, C. G., Rother, D., Bardischewsky, F., Quentmeier, A., and Fischer, J. (2001). Oxidation of reduced inorganic sulfur compounds by bacteria: emergence of a common mechanism? Appl. Environ. Microbiol. 67, 2873–2882. doi: 10.1128/AEM.67.7.2873-2882.2001

PubMed Abstract | CrossRef Full Text | Google Scholar

Ghosh, W., and Dam, B. (2009). Biochemistry and molecular biology of lithotrophic sulfur oxidation by taxonomically and ecologically diverse bacteria and archaea. FEMS Microbiol. Rev. 33, 999–1043. doi: 10.1111/j.1574-6976.2009.00187.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Girguis, P. R., and Childress, J. J. (2006). Metabolite uptake, stoichiometry and chemoautotrophic function of the hydrothermal vent tubeworm Riftia pachyptila: responses to environmental variations in substrate concentrations and temperature. J. Exp. Biol. 209, 3516–3528. doi: 10.1242/jeb.02404

PubMed Abstract | CrossRef Full Text | Google Scholar

Girguis, P. R., Childress, J. J., Freytag, J. K., Klose, K., and Stuber, R. (2002). Effects of metabolite uptake on proton-equivalent elimination by two species of deep-sea vestimentiferan tubeworm, Riftia pachyptila and Lamellibrachia cf luymesi: proton elimination is a necessary adaptation to sulfide-oxidizing chemoautotrophic symbiont. J. Exp. Biol. 205, 3055–3066.

PubMed Abstract | Google Scholar

Grabovich, M. Y., Patritskaya, V. Y., Muntyan, M. S., and Dubinina, G. A. (2001). Lithoautotrophic growth of the freshwater strain Beggiatoa D-402 and energy conservation in a homogeneous culture under microoxic conditions. FEMS Microbiol. Lett. 204, 341–345. doi: 10.1111/j.1574-6968.2001.tb10908.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Grote, J., Schott, T., Bruckner, C. G., Glöckner, F. O., Jost, G., Teeling, H., et al. (2012). Genome and physiology of a model Epsilonproteobacterium responsible for sulfide detoxification in marine oxygen depletion zones. Proc. Natl. Acad. Sci. U.S.A. 109, 506–510. doi: 10.1073/pnas.1111262109

PubMed Abstract | CrossRef Full Text | Google Scholar

Hagen, K. D., and Nelson, D. C. (1997). Use of reduced sulfur compounds by Beggiatoa spp.: enzymology and physiology of marine and freshwater strains in homogeneous and gradient cultures. Appl. Environ. Microbiol. 63, 3957–3964.

PubMed Abstract | Google Scholar

Harold, F. M. (1986). The Vital Force: A Study of Bioenergetics. New York, NY: W.H.Freeman & Co Ltd.

Google Scholar

Hempfling, W. P., and Vishniac, W. (1967). Yield coefficients of Thiobacillus neapolitanus in continuous culture. J. Bacteriol. 93, 874–878.

PubMed Abstract | Google Scholar

Høgslund, S., Revsbech, N. P., Kuenen, J. G., Jørgensen, B. B., Gallardo, V. A., van de Vossenberg, J., et al. (2009). Physiology and behaviour of marine Thioploca. ISME J. 3, 647–657. doi: 10.1038/ismej.2009.17

PubMed Abstract | CrossRef Full Text | Google Scholar

Holkenbrink, C., Barbas, S. O., Mellerup, A., Otaki, H., and Frigaard, N.-U. (2011). Sulfur globule oxidation in green sulfur bacteria is dependent on the dissimilatory sulfite reductase system. Microbiology 157, 1229–1239. doi: 10.1099/mic.0.044669-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Hoor, A. T. (1981). Cell yield and bioenergetics of Thiomicrospira denitrificans compared with Thiobacillus denitrificans. Antonie Van Leeuwenhoek 47, 231–243. doi: 10.1007/BF00403394

PubMed Abstract | CrossRef Full Text | Google Scholar

Hügler, M., and Sievert, S. M. (2011). Beyond the Calvin cycle: autotrophic carbon fixation in the ocean. Ann. Rev. Mar. Sci. 3, 261–289. doi: 10.1146/annurev-marine-120709-142712

PubMed Abstract | CrossRef Full Text | Google Scholar

Hügler, M., Wirsen, C. O., Fuchs, G., Taylor, C. D., and Sievert, S. M. (2005). Evidence for autotrophic CO₂ fixation via the reductive tricarboxylic acid cycle by members of the epsilon subdivision of proteobacteria. J. Bacteriol. 187, 3020–3027. doi: 10.1128/JB.187.9.3020-3027.2005

PubMed Abstract | CrossRef Full Text | Google Scholar

Janssen, A. J. H., Lens, P. N. L., Stams, A. J. M., Plugge, C. M., Sorokin, D. Y., Muyzer, G., et al. (2009). Application of bacteria involved in the biological sulfur cycle for paper mill effluent purification. Sci. Total Environ. 407, 1333–1343. doi: 10.1016/j.scitotenv.2008.09.054

PubMed Abstract | CrossRef Full Text | Google Scholar

Jørgensen, B. B., Dunker, R., Grünke, S., and Røy, H. (2010). Filamentous sulfur bacteria, Beggiatoa spp., in arctic marine sediments (Svalbard, 79 degrees N). FEMS Microbiol. Ecol. 73, 500–513. doi: 10.1111/j.1574-6941.2010.00918.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Justin, P., and Kelly, D. P. (1978). Growth kinetics of Thiobacillus denitrificans in anaerobic and aerobic chemostat culture. J. Gen. Microbiol. 107, 123–130. doi: 10.1099/00221287-107-1-123

CrossRef Full Text | Google Scholar

Kamimura, K., Higashino, E., Kanao, T., and Sugio, T. (2005). Effects of inhibitors and NaCl on the oxidation of reduced inorganic sulfur compounds by a marine acidophilic, sulfur-oxidizing bacterium, Acidithiobacillus thiooxidans strain SH. Extremophiles 9, 45–51. doi: 10.1007/s00792-004-0420-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Kappler, U., and Dahl, C. (2001). Enzymology and molecular biology of prokaryotic sulfite oxidation. FEMS Microbiol. Lett. 203, 1–9. doi: 10.1111/j.1574-6968.2001.tb10813.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Kelly, D. P. (1982). Biochemistry of the chemolithotrophic oxidation of inorganic sulphur. Philos. Trans. R. Soc. Lond. B. Biol. Sci. 298, 499–528. doi: 10.1098/rstb.1982.0094

PubMed Abstract | CrossRef Full Text | Google Scholar

Kelly, D. P. (1990). “Energetics of chemolithotrophs,” in Bacterial Energetics, ed T. A. Krulwich (San Diego, CA: Academic Press), 479–501. doi: 10.1016/B978-0-12-307212-2.50020-X

CrossRef Full Text

Kelly, D. P. (1999). Thermodynamic aspects of energy conservation by chemolithotrophic sulfur bacteria in relation to the sulfur oxidation pathways. Arch. Microbiol. 171, 219–229. doi: 10.1007/s002030050703

CrossRef Full Text | Google Scholar

Kelly, D. P. (2003). “Microbial inorganic sulfur oxidation: the APS pathway,” in Biochemistry and Physiology of Anaerobic Bacteria, eds L. G. Ljungdahl, M. W. Adams, L. L. Barton, J. G. Ferry, and M. K. Johnson (New York, NY: Springer), 205–219. doi: 10.1007/0-387-22731-8_15

CrossRef Full Text

Kelly, D. P., Lu, W.-P., and Poole, R. K. (1993). Cytochromes in Thiobacillus tepidarius and the respiratory chain involved in the oxidation of thiosulphate and tetrathionate. Arch. Microbiol. 160, 87–95. doi: 10.1007/BF00288708

CrossRef Full Text | Google Scholar

Kelly, D. P., Shergill, J. K., Lu, W. P., and Wood, A. P. (1997). Oxidative metabolism of inorganic sulfur compounds by bacteria. Antonie Van Leeuwenhoek 71, 95–107. doi: 10.1023/A:1000135707181

PubMed Abstract | CrossRef Full Text | Google Scholar

Kelly, D. P., and Wood, A. P. (2000). Reclassification of some species of Thiobacillus to the newly designated genera Acidithiobacillus gen. nov., Halothiobacillus gen. nov. and Thermithiobacillus gen. nov. Int. J. Syst. Evol. Microbiol. 50, 511–516. doi: 10.1099/00207713-50-2-511

PubMed Abstract | CrossRef Full Text | Google Scholar

Lengeler, J. W., Drews, G., and Schlegel, H. G. (eds.). (2009). “Oxidation of inorganic compounds by chemolithotrophs,” in Biology of the Prokaryotes (Oxford, UK: Blackwell Science Ltd), 234–260.

Google Scholar

Loy, A., Duller, S., Baranyi, C., Mussmann, M., Ott, J., Sharon, I., et al. (2009). Reverse dissimilatory sulfite reductase as phylogenetic marker for a subgroup of sulfur-oxidizing prokaryotes. Environ. Microbiol. 11, 289–299. doi: 10.1111/j.1462-2920.2008.01760.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, W.-P., and Kelly, D. P. (1988). Cellular Location and Partial Purification of the “Thiosulphate-oxidizing Enzyme” and “Trithionate Hydrolyase” from Thiobacillus tepidarius. Microbiology 134, 877–885. doi: 10.1099/00221287-134-4-877

CrossRef Full Text | Google Scholar

Markert, S., Arndt, C., Felbeck, H., Becher, D., Sievert, S. M., Hügler, M., et al. (2007). Physiological proteomics of the uncultured endosymbiont of Riftia pachyptila. Science 315, 247–250. doi: 10.1126/science.1132913

PubMed Abstract | CrossRef Full Text | Google Scholar

Masau, R. J. Y., Oh, J. K., and Suzuki, I. (2001). Mechanism of oxidation of inorganic sulfur compounds by thiosulfate-grown Thiobacillus thiooxidans. Can. J. Microbiol. 47, 348–358. doi: 10.1139/cjm-47-4-348

PubMed Abstract | CrossRef Full Text | Google Scholar

Mason, J., Kelly, D. P., and Wood, A. P. (1987). Chemolithotrophic and autotrophic growth of Thermothrix thiopara and some thiobacilli on thiosulphate and polythionates, and a reassessment of the growth yields of Thx. thiopara in chemostat culture. Microbiology 133, 1249–1256. doi: 10.1099/00221287-133-5-1249

CrossRef Full Text | Google Scholar

Meyer, B., Imhoff, J. F., and Kuever, J. (2007). Molecular analysis of the distribution and phylogeny of the soxB gene among sulfur-oxidizing bacteria - evolution of the Sox sulfur oxidation enzyme system. Environ. Microbiol. 9, 2957–2977. doi: 10.1111/j.1462-2920.2007.01407.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Meyer, B., and Kuever, J. (2007). Phylogeny of the alpha and beta subunits of the dissimilatory adenosine-5′-phosphosulfate (APS) reductase from sulfate-reducing prokaryotes–origin and evolution of the dissimilatory sulfate-reduction pathway. Microbiology 153, 2026–2044. doi: 10.1099/mic.0.2006/003152-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Nakamura, K., Kuribayashi, S., Kurosawa, H., and Amano, Y. (2014). Pathway of sulfite oxidation in Thiobacillus thiooxidans JCM 7814. Biosci. Biotechnol. Biochem. 56, 261–263. doi: 10.1271/bbb.56.261

CrossRef Full Text | Google Scholar

Nelson, D. C., and Hagen, K. D. (1995). Physiology and biochemistry of symbiotic and free-living chemoautotrophic sulfur bacteria. Integr. Comp. Biol. 35, 91–101. doi: 10.1093/icb/35.2.91

CrossRef Full Text | Google Scholar

Nelson, D. C., Jørgensen, B. B., and Revsbech, N. P. (1986). Growth pattern and yield of a chemoautotrophic Beggiatoa sp. in oxygen-sulfide microgradients. Appl. Environ. Microbiol. 52, 225–233.

PubMed Abstract | Google Scholar

Nyholm, S. V., Robidart, J., and Girguis, P. R. (2008). Coupling metabolite flux to transcriptomics: insights into the molecular mechanisms underlying primary productivity by the hydrothermal vent tubeworm Ridgeia piscesae. Biol. Bull. 214, 255–265. doi: 10.2307/25470667

PubMed Abstract | CrossRef Full Text | Google Scholar

Odintsova, E. V., Wood, A. P., and Kelly, D. P. (1993). Chemolithoutotrophic growth of Thiothrix ramosa. Arch. Microbiol. 160, 152–157. doi: 10.1007/BF00288718

PubMed Abstract | CrossRef Full Text | Google Scholar

Peck, H. D. (1960). Adenosine 5′-phosphosulfate as an intermediate in the oxidation of thiosulfate by Thiobacillus thioparus. Proc. Natl. Acad. Sci. U.S.A. 46, 1053–1057. doi: 10.1073/pnas.46.8.1053

PubMed Abstract | CrossRef Full Text | Google Scholar

Pronk, J. T., Meulenberg, R., Hazeu, W., Bos, P., and Kuenen, J. G. (1990). Oxidation of reduced inorganic sulphur compounds by acidophilic thiobacilli. FEMS Microbiol. Lett. 75, 293–306. doi: 10.1111/j.1574-6968.1990.tb04103.x

CrossRef Full Text | Google Scholar

Rohwerder, T., and Sand, W. (2003). The sulfane sulfur of persulfides is the actual substrate of the sulfur-oxidizing enzymes from Acidithiobacillus and Acidiphilium spp. Microbiology 149, 1699–1710. doi: 10.1099/mic.0.26212-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Rossetti, S. (2003). Phylogenetic and physiological characterization of a heterotrophic, chemolithoautotrophic Thiothrix strain isolated from activated sludge. Int. J. Syst. Evol. Microbiol. 53, 1271–1276. doi: 10.1099/ijs.0.02647-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Ruby, E. G., and Jannasch, H. W. (1982). Physiological characteristics of Thiomicrospira sp. Strain L-12 isolated from deep-sea hydrothermal vents. J. Bacteriol. 149, 161–165.

PubMed Abstract | Google Scholar

Sánchez, O., Ferrera, I., Dahl, C., and Mas, J. (2001). In vivo role of adenosine-5′-phosphosulfate reductase in the purple sulfur bacterium Allochromatium vinosum. Arch. Microbiol. 176, 301–305. doi: 10.1007/s002030100327

PubMed Abstract | CrossRef Full Text | Google Scholar

Schedel, M., Legall, J., and Baldensperger, J. (1975). Sulfur metabolism in Thiobacillus denitrificans. Arch. Microbiol. 105, 339–341. doi: 10.1007/BF00447155

PubMed Abstract | CrossRef Full Text | Google Scholar

Shi, J., Lin, H., Yuan, X., and Zhao, Y. (2011). Isolation and characterization of a novel sulfur-oxidizing chemolithoautotroph Halothiobacillus from Pb polluted paddy soil. Afr. J. Biotechnol. 10, 4121–4126. doi: 10.5897/AJB10.2406

CrossRef Full Text | Google Scholar

Sievert, S. M., Hügler, M., Taylor, C. D., and Wirsen, C. O. (2007). “Sulfur oxidation at deep-sea hydrothermal vents,” in Microbial Sulfur Metabolism, eds C. Dahl and C. G. Friedrich (Berlin; Heidelberg: Springer), 238–258. doi: 10.1007/978-3-540-72682-1_19

CrossRef Full Text

Sievert, S. M., Scott, K. M., Klotz, M. G., Chain, P. S. G., Hauser, L. J., Hemp, J., et al. (2008). Genome of the epsilonproteobacterial chemolithoautotroph Sulfurimonas denitrificans. Appl. Environ. Microbiol. 74, 1145–1156. doi: 10.1128/AEM.01844-07

PubMed Abstract | CrossRef Full Text | Google Scholar

Sievert, S., and Vetriani, C. (2012). Chemoautotrophy at deep-sea vents: past, present, and future. Oceanography 25, 218–233. doi: 10.5670/oceanog.2012.21

CrossRef Full Text | Google Scholar

Simon, J., and Klotz, M. G. (2013). Diversity and evolution of bioenergetic systems involved in microbial nitrogen compound transformations. Biochim. Biophys. Acta 1827, 114–135. doi: 10.1016/j.bbabio.2012.07.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Simon, J., van Spanning, R. J. M., and Richardson, D. J. (2008). The organisation of proton motive and non-proton motive redox loops in prokaryotic respiratory systems. Biochim. Biophys. Acta 1777, 1480–1490. doi: 10.1016/j.bbabio.2008.09.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Smith, N. A., and Kelly, D. P. (1988). Mechanism of oxidation of dimethyl disulphide by Thiobacillus thioparus Strain E6. Microbiology 134, 3031–3039. doi: 10.1099/00221287-134-11-3031

CrossRef Full Text | Google Scholar

Sorokin, D. Y. (2002). Thioalkalispira microaerophila gen. nov., sp. nov., a novel lithoautotrophic, sulfur-oxidizing bacterium from a soda lake. Int. J. Syst. Evol. Microbiol. 52, 2175–2182. doi: 10.1099/ijs.0.02339-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Sorokin, D. Y., Banciu, H., Robertson, L. A., Kuenen, J. G., Muntyan, M. S., and Muyzer, G. (2013). “Halophilic and haloalkaliphilic sulfur-oxidizing bacteria,” in The Prokaryotes, eds E. Rosenberg, E. F. DeLong, S. Lory, E. Stackebrandt, and F. Thompson (Berlin; Heidelberg: Springer), 529–554. doi: 10.1007/978-3-642-30141-4_77

CrossRef Full Text

Sorokin, D. Y., and Kuenen, J. G. (2005). Haloalkaliphilic sulfur-oxidizing bacteria in soda lakes. FEMS Microbiol. Rev. 29, 685–702. doi: 10.1016/j.femsre.2004.10.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Sorokin, D. Y., Lysenko, A. M., Mityushina, L. L., Tourova, T. P., Jones, B. E., Rainey, F. A., et al. (2001). Thioalkalimicrobium aerophilum gen. nov., sp. nov. and Thioalkalimicrobium sibericum sp. nov., and Thioalkalivibrio versutus gen. nov., sp. nov., Thioalkalivibrio nitratis sp.nov., novel and Thioalkalivibrio denitrificancs sp. nov., novel obligately alkaliphilic and obligately chemolithoautotrophic sulfur-oxidizing bacteria from soda lakes. Int. J. Syst. Evol. Microbiol. 51, 565–580. doi: 10.1099/00207713-51-2-565

PubMed Abstract | CrossRef Full Text | Google Scholar

Sorokin, D. Y., Tourova, T. P., Kolganova, T. V, Spiridonova, E. M., Berg, I. A., and Muyzer, G. (2006). Thiomicrospira halophila sp. nov., a moderately halophilic, obligately chemolithoautotrophic, sulfur-oxidizing bacterium from hypersaline lakes. Int. J. Syst. Evol. Microbiol. 56, 2375–2380. doi: 10.1099/ijs.0.64445-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Sorokin, D. Y., Tourova, T. P., Spiridonova, E. M., Rainey, F. A., and Muyzer, G. (2005). Thioclava pacifica gen. nov., sp. nov., a novel facultatively autotrophic, marine, sulfur-oxidizing bacterium from a near-shore sulfidic hydrothermal area. Int. J. Syst. Evol. Microbiol. 55, 1069–1075. doi: 10.1099/ijs.0.63415-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Stewart, F. J., Dmytrenko, O., Delong, E. F., and Cavanaugh, C. M. (2011). Metatranscriptomic analysis of sulfur oxidation genes in the endosymbiont of Solemya velum. Front. Microbiol. 2:134. doi: 10.3389/fmicb.2011.00134

PubMed Abstract | CrossRef Full Text | Google Scholar

Stewart, V., Lu, Y., and Darwin, A. J. (2002). Periplasmic nitrate reductase (NapABC enzyme) supports anaerobic respiration by Escherichia coli K-12. J. Bacteriol. 184, 1314–1323. doi: 10.1128/JB.184.5.1314-1323.2002

PubMed Abstract | CrossRef Full Text | Google Scholar

Suzuki, I. (1974). Mechanisms of inorganic oxidation and energy coupling. Annu. Rev. Microbiol. 28, 85–101. doi: 10.1146/annurev.mi.28.100174.000505

PubMed Abstract | CrossRef Full Text | Google Scholar

Thauer, R. K., Jungermann, K., and Decker, K. (1977). Energy conservation in chemotrophic anaerobic bacteria. Bacteriol. Rev. 41, 100–180.

PubMed Abstract | Google Scholar

Trüper, H. G. (1982). “Microbial processes in the sulfur cycle through time,” in Mineral Deposits and the Evolution of the Biosphere, eds H. D. Holland and M. Schidlowski (Berlin, Heidelberg: Springer Berlin Heidelberg), 5–30.

Veith, A., Botelho, H. M., Kindinger, F., Gomes, C. M., and Kletzin, A. (2012). The sulfur oxygenase reductase from the mesophilic bacterium Halothiobacillus neapolitanus is a highly active thermozyme. J. Bacteriol. 194, 677–685. doi: 10.1128/JB.06531-11

CrossRef Full Text | Google Scholar

Wood, A. P., and Kelly, D. P. (1986). Chemolithotrophic metabolism of the newly-isolated moderately thermophilic, obligately autotrophic Thiobacillus tepidarius. Arch. Microbiol. 144, 71–77. doi: 10.1007/BF00454959

CrossRef Full Text | Google Scholar

Wood, A. P., and Kelly, D. P. (1991). Isolation and characterisation of Thiobacillus halophilus sp. nov., a sulphur-oxidising autotrophic eubacterium from a Western Australian hypersaline lake. Arch. Microbiol. 156, 277–280. doi: 10.1007/BF00262998

CrossRef Full Text | Google Scholar