- 1RIKEN Center for Sustainable Resource Science, Yokohama, Japan
- 2Department of Bioscience and Biotechnology, Graduate School of Bioresource and Bioenvironmental Science, Kyushu University, Fukuoka, Japan
The high-throughput acquisition of metabolome data is greatly anticipated for the complete understanding of cellular metabolism in living organisms. A variety of analytical technologies have been developed to acquire large-scale metabolic profiles under different biological or environmental conditions. Time series data are useful for predicting the most likely metabolic pathways because they provide important information regarding the accumulation of metabolites, which implies causal relationships in the metabolic reaction network. Considerable effort has been undertaken to utilize these data for constructing a mathematical model merging system properties and quantitatively characterizing a whole metabolic system in toto. However, there are technical difficulties between benchmarking the provision and utilization of data. Although, hundreds of metabolites can be measured, which provide information on the metabolic reaction system, simultaneous measurement of thousands of metabolites is still challenging. In addition, it is nontrivial to logically predict the dynamic behaviors of unmeasurable metabolite concentrations without sufficient information on the metabolic reaction network. Yet, consolidating the advantages of advancements in both metabolomics and mathematical modeling remain to be accomplished. This review outlines the conceptual basis of and recent advances in technologies in both the research fields. It also highlights the potential for constructing a large-scale mathematical model by estimating model parameters from time series metabolome data in order to comprehensively understand metabolism at the systems level.
Introduction
Systems biology has become an important research field to fully understand the complex metabolism of cells in living organisms in toto (Kitano, 2002a,b; Aderem, 2005; Kirschner, 2005). It involves numerous techniques including -omics to systematically identify, analyze, control, and design metabolic systems (Ukai and Ueda, 2010) at gene, transcript, protein, and metabolite levels. Among the -omics, metabolomics is one of the newest -omics sciences (Rochfort, 2005; Preidis and Hotez, 2015). The metabolome, which is affected by changes in the transcriptome and proteome, is considered to be downstream in the layer of multi-omics. It is also most directly related to the visible phenotype of biological systems. A complete understanding of metabolism through use of metabolome data is greatly anticipated. This involves the development of high-throughput analytical instruments to provide a wide range of metabolic profiles along with the improvement of data processing techniques to accurately identify or annotate metabolites from mass spectra and precisely measure their quantities in a living cell (Fiehn, 2002; Weckwerth, 2003; Bain et al., 2009). This information can then be implemented to advance intuitive and functional concepts for designing and engineering ideal metabolic systems.
An assortment of statistical methods have been developed and utilized to identify correlations or differences among metabolome data of biological samples. Nevertheless, novel strategies are required to systematically elucidate the regulatory mechanisms of metabolites in greater detail. Time series metabolome data is suited for this task. Time series data of the response of a metabolic system to internal and/or external stimuli contain important information of different aspects of the dynamic characteristics (Voit, 2013) of the metabolic system regardless of the type of organism. For example, time series metabolic data were used to elucidate regulatory mechanisms of respiratory oscillations of yeast (Murray et al., 2007) and their adaptation to temperature stress (Strassburg et al., 2010). Time series metabolome data were also used to understand adaptation mechanisms of plants to cold (Espinoza et al., 2010), salinity (Kim et al., 2007), dehydration (Urano et al., 2008), and thermal stress such as to heat- and cold-shocks (Kaplan et al., 2004). In humans, time series metabolome data were collected to determine metabolic profile responses of stored red blood cells to hypoxia (Kinoshita et al., 2007), which included monitoring ATP levels, as well as to validate mathematical models of dynamic characteristics and behaviors of erythrocyte metabolism (Nishino et al., 2013). Time series data is not only useful for validating simulated metabolic behaviors predicted from a mathematical model generated using enzyme kinetics, but these data are also a powerful component for directly generating a kinetic model to systematically understand metabolic behaviors and characteristics of a metabolism of interest. Kinetic models can be used to further predict possible unknown regulatory mechanisms controlling a metabolic pathway.
An overview of mathematical modeling using metabolome data is illustrated in Figure 1. In general, the workflow begins with sampling biological data consisting of simultaneously-acquired metabolic profiles. The profiles are processed and utilized for constructing a mathematical model, which can be exploited to analyze metabolic systems as well as to design an optimal system of interest. In this review, we address the basic concepts of advancements in both metabolomics and mathematical modeling. We review the methods for metabolome analyses and nature of metabolome data (Section Nature of Metabolome Data) as well as current mathematical modeling approaches (Section Current Status of Modeling Metabolic Reaction Networks), and then describe the procedures to construct a kinetic model from those data (Section Kinetic Models from Time Series Metabolome Data) and use it for system analysis (Section Systems Analysis). Finally, we pinpoint the potential of combining mathematical techniques to construct a large-scale dynamic model for further understanding of biological systems.
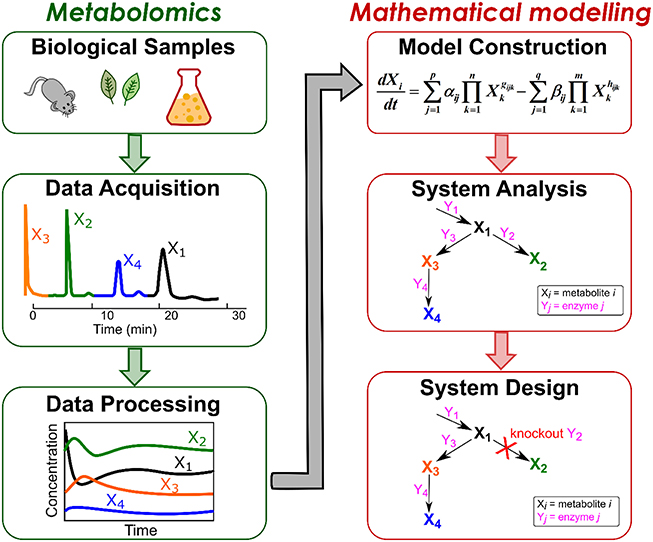
Figure 1. Outline for mathematical modeling using metabolome data. The workflow includes metabolomics approaches for acquiring and processing metabolic data from biological samples as well as mathematical approaches for constructing and analyzing mathematical model to design an optimal system.
Nature of Metabolome Data
A living cell contains thousands of metabolites, which differ greatly in their chemical property and abundance (Luca and Pierre, 2000; Griffin and Shockcor, 2004; Prescher and Bertozzi, 2005); therefore, no single analytical instrument is suitable to measure all metabolites (Saito and Matsuda, 2010; Weckwerth, 2011). A combination of different high-throughput instruments, including nuclear magnetic resonance (NMR) spectroscopy, and gas chromatography (GC), liquid chromatography (LC), or capillary electrophoresis (CE) coupled to mass spectrometry (MS), is required to analyze a whole metabolome (Villas-Boas et al., 2005; Pan and Raftery, 2007).
In most cases, analytical procedures to generate metabolome data start with sample preparation, which includes quenching and metabolite extraction (Fukushima and Kusano, 2013). Sample preparation methods are important because they have an effect on the coverage and content of metabolites that can be analyzed (Vuckovic, 2012). Depending on the metabolites-of-interest and instruments used, sample preparation may include derivatization to chemically modify compounds to produce derivatives which have properties suitable for analysis. The spectra and intensities of metabolites are then acquired using suitable instruments. These data are pre-processed to determine the quantity and identity of metabolites. Core technologies for detection can be classified into two types: non-targeted and targeted methods for top-down and bottom-up approaches, respectively (Bain et al., 2009; Hiller et al., 2009).
Non-targeted methods generally aim to identify as many metabolites as possible in a biological sample at once. The identification of metabolites involves instruments (Dunn et al., 2012; Fuhrer and Zamboni, 2015; Sèvin et al., 2015) to detect spectra, i.e., patterns representing the distribution of ions by mass-to-charge ratio (m/z), across wide coverage ranges. Spectra are subsequently pre-processed for base-line correction, peak detection, and peak alignment (Lommen, 2009; Lommen and Kools, 2012) to appropriately identify peaks and mass spectra (Tsugawa et al., 2015) as well as annotate metabolites (Matsuda et al., 2009; Horai et al., 2010). Although non-targeted methods have an advantage in covering a greater percentage of the metabolome, they usually provide only qualitative data. Accordingly, the application of data from non-targeted methods is usually subject to statistical analysis to normalize data by the original mass of the sample and/or by an internal standard to reduce the influence of experimental factors on the data set (Summer et al., 2007). These data can be used to investigate correlations among metabolite intensities due to different environmental conditions (Wechwerth et al., 2004), the existence of metabolites in mutants compared to wide-type specimens (Jonsson et al., 2005; Kim et al., 2015), and for multivariate comparative analysis of metabolic phenotypes (Tikunov et al., 2005).
In contrast to non-targeted methods, targeted methods detect specific metabolites (Badawy et al., 2008; Sawada et al., 2009; Kato et al., 2012); however, targeted methods can be applied to analyze hundreds of metabolites in a semi-quantitative or quantitative manner (Shulaev, 2006). Targeted methods provide quantitative data in absolute concentrations typically by using stable isotope-labeled standard compounds (Birkemeyer et al., 2005). Isotope labeling also permits the quantification of cell fluxomes through metabolic flux analysis (You et al., 2014). Both absolute metabolite concentrations and rates of flux are potential components for building a large-scale mathematical model, which can reveal dynamic associations of metabolites in an entire metabolic system. However, isotope labeling-assisted metabolomics is costly and isotope-labeled compounds are limited. Consequently, most studies, wherein large-scale targeted metabolomics were performed, report metabolic abundances in relative concentrations, or peak intensities rather than in absolute concentrations. Although, both non-targeted and targeted analyses can be used to determine a large number of metabolic profiles at once, it does not necessarily indicate the detection and measurement of all metabolites in a particular metabolic pathway. This presents a challenge for constructing precise mathematical models, which typically require absolute concentrations of all metabolites in a specific pathway.
Current Status of Modeling Metabolic Reaction Networks
Mathematical models permit the investigation of metabolic characteristics and behaviors, including of regulatory mechanisms and responses to internal and external environments, to comprehensively understand metabolism. Table 1 tabulates methods commonly used for mathematical modeling. Model types vary from large-scale qualitative models, such as topological and stoichiometric models, to small-scale quantitative models, such as kinetic models (Hartmann and Schreiber, 2015; Novere, 2015). As the stoichiometric and kinetic models seem to have a potential to handle large-scale dynamic systems, they will be discussed in more details.
Stoichiometric modeling typically uses a static model based on the assumption of steady-state; therefore, it does not require kinetic information and can handle a large-scale system. A well-known stoichiometric model is genome-scale metabolic reconstruction using flux balance analysis (Orth et al., 2010; Palsson, 2015). It is a constraint-based model using linear programming to optimize metabolic fluxes based on stoichiometric coefficients of each reaction throughout the entire metabolic network; it principally requires only steady-state absolute concentrations for optimization. Genome-scale metabolic reconstruction is straightforward and can be used for the prediction of cellular phenotypes, analysis of biological network properties, as well as metabolic engineering (McCloskey et al., 2013). Thus, it has been applied in the analysis of various organisms, including Escherichia coli (Edwards and Palsson, 2000; Orth et al., 2011), Saccharomyces cerevisiae (Herrgård et al., 2008), Arabiodopsis thaliana (Poolman et al., 2009; de Oliveira Dal'Molin et al., 2010; Mintz-Oron et al., 2012), and humans (Thiele et al., 2013).
In contrast, kinetic modeling, which generates a dynamic model, requires kinetic rate equations, and model parameters to provide detailed quantitative description, quantitative prediction and dynamic behaviors. These requirements make kinetic modeling more complicated and limit its application to only small-scale systems. Dynamic models can be classified into two classes: stochastic and deterministic (Puchalka and Kierzek, 2004; Shmulevich and Aitchison, 2009). Stochastic or probabilistic models incorporate randomness or uncertainty to characterize the performance of a system, and use values generated from probability distributions rather than a fixed unique value. In contrast, deterministic models capture the collective behaviors of the elements constituting the network. Again, they require a set of variable states uniquely determined by parameters using optimization methods and experimental data.
Recent efforts have been made to implement dynamic characteristics into genome-scale reconstruction models in order to consider the entire dynamic system. The common approach to observe dynamic characteristics is to use dynamic flux balance analysis (dFBA). For example, dFBA has been used to link a Monod kinetic model and genome-scale flux balance analysis to analyze the dynamic metabolism of environmentally important bacterium (Feng et al., 2012). Although this method cannot offer a fully dynamic state, it can still provide pseudo-dynamic characteristics to predict directions of metabolic fluxes with changes in gene expression or enzyme activities. Alternatively, genome-scale metabolic reconstruction models can also be integrated with in vivo metabolome data via the differential biochemical Jacobian (Nägele et al., 2014) to define a metabolic interaction matrix. The differential Jacobian is calculated using a metabolic reaction matrix and covariance of metabolome data. It combines dynamic modeling strategies with large-scale steady state profiling approaches without explicit knowledge of individual kinetic parameters. The Jacobian might permit design parameter optimization strategies for ODE-based kinetic models of metabolic systems in the near future.
Kinetic Models from Time Series Metabolome Data
Kinetic models comprise two components: symbolic formulas of model equations and numerical values of model parameters. Most model equations are expressed as ordinary differential equations (ODEs) of various forms (Table 1), such as linear approximations, enzyme kinetic rate laws using Michaelis-Menten kinetics (Bajzer and Strehler, 2012), linear-logarithmic approximations (Hatzimanikatis and Bailey, 1996; Visser and Heijnen, 2002), and power-law equations based on metabolic control analysis (MCA; Kacser and Burns, 1973; Heinrich and Rapoport, 1974) or biochemical systems theory (BST; Savageau, 1969; Voit, 2000). Regardless of the chosen format of model equations, numerical values determining metabolite concentrations and reaction rates are required. This involves inverse problems using experimental data (or results) to calculate model parameters (or causes). Since experimental data contain not only a wealth of information but also biological variation and analytical errors, parameter estimation from actual biological data remains a challenging task, which usually represents a bottleneck in the modeling process (Voit, 2012).
Parameter Estimation
Typical approaches for estimating parameter values include determining enzymatic kinetic rates through in vitro enzymatic assays (bottom-up) or indirectly estimating from metabolic time series data (top-down). The bottom-up method is a conventional method in which each model parameter is experimentally determined and then integrated into a final model. It has been applied to several organisms; however, it requires considerable time and financial support to conduct experiments to obtain parameter values of every individual reaction.
As an alternative and with the aim of constructing kinetic models using limited data sets and requiring less time, theoretical researchers have proposed new algorithms for simultaneously estimating model parameters using only time series data of metabolite concentrations. In general, parameter values are determined by minimizing an objective function measuring the difference between experimental data (time series data) and model predictions (predicted data). Various optimization algorithms to find global or local optima were previously reviewed in detail (Mendes and Kell, 1998; Chou and Voit, 2009). Standard optimization methods for global optimization in metabolic modeling include genetic algorithms (Michalewicz, 1994), evolutionary programming (Fogel et al., 1992), and simulated annealing (Corana et al., 1987), whereas those for local optimization include Newton-Raphson (Press et al., 2002, 2007) for linear least-squares analysis and Levenberg-Marquardt (Levenberg, 1944; Marquardt, 1963; Gavin, 2011) for non-linear least-squares analysis. Both global and local optimization algorithms have their advantages and disadvantages. In short, most global optimization algorithms search for the global minimum across all inputs, which require a set of functions, boundaries, constraints, and high computational costs. Local optimization algorithms search only for the local minimum but are computationally less expensive. Some researchers have even reduced these constraints to the no free lunch theorem in search and optimization (Wolpert and MacReady, 1997), claiming that there is no perfect algorithm that can guarantee a solution in a reasonable time and space unless the model equations and experimental data are optimally suited to solve a problem. Consequently, although various tools for kinetic modeling have been used (Alves et al., 2006), selecting an optimization method still depends on data characteristics, types of model equations, or even the preferences and experiences of the modeler.
The fewer the number of model parameters, parameter estimation becomes simpler and more accurate. Several research groups have been working on the development of mathematical approaches to reduce the number of parameters in parameter estimation by taking advantage of the simplification of S-system formulation (approximate power law representation) within biochemical systems theory (BST). Numerous approaches to estimate parameter values using S-system formulation together with time series data of metabolic concentrations have been proposed. This includes alternative regression (Chou, 2006), automated procedure (Marino and Eberhard, 2006), Newton flow (Kutalik et al., 2007), automated smoother for decoupling (Vilela et al., 2007), neutral (Vilela et al., 2009), two-phase dynamic (Jia et al., 2011), estimation of dynamic flux profiles (Chou and Voit, 2012), Newton-Raphson (Iwata et al., 2014), and PENDISC method (Sriyudthsak et al., 2014a). In addition, approximate estimation methods for large-scale analysis include coarse (Iwata et al., 2013) and U-system (Sriyudthsak et al., 2014b) approaches, which were proposed for predicting coarse metabolic parameters, including those of unmeasurable metabolites.
In general, these optimization algorithms perform well with training data generated in silico with low noise. Unfortunately, biological data is characterized by high variance from both biological variation and analytical errors. In addition, larger-sized models involve the estimation of more parameters. The majority of metabolome data are also reported in relative concentration units, which sometimes result in problems when balancing the absolute amounts and stoichiometry of parameter values. Ultimately, a useful model must be able to reproduce biological observations before being used to predict different biological scenarios. Thus, a reasonable number of model equations and model parameters are required, even though a compromise between model accuracy and model size remains a challenge.
Systems Analysis
Once a given metabolic reaction system has been described using a mathematical model, systems analysis can be performed to characterize the following characteristics of the reaction network.
Eigenvalues
The stability and oscillatory behavior of a system is usually identified by means of eigenvalues, which are originally a special set of scalars associated with a linear system of equations. The same concept can be employed for nonlinear systems expressed by differential equations describing the time rate of change in metabolite concentrations. In this case, a steady state is commonly used as an operating point to approximately linearize the systems. The eigenvalues are the roots of the characteristic equations derived from the differential equations under a steady state assumption. In general, n differential equations for metabolite concentrations provide the same number of eigenvalues. The eigenvalue is generally a complex number with real and imaginary parts, which can reveal at least four different network behaviors. First, if all the real parts are negative, the nominal steady state is locally stable and the system will return to steady state following small perturbations. Second, if at least one imaginary part is nonzero, metabolite concentrations may oscillate under certain conditions. Third, if the absolute value of the ratio of maximum to minimum values of the real parts, i.e., stiffness ratio, is very large, metabolite concentrations vary at significantly different rates, and some may require very long times to reach steady state (Shiraishi and Savageau, 1992c). For example, if the stiffness ratio is >104, the system is judged to be stiff (Shiraishi and Savageau, 1992a), which makes it difficult to numerically solve relevant differential equations. Fourth, the absolute value of the minimum value of the real parts can be approximately regarded as the rate constant of a first-order reaction and therefore can be expressed in units of time. Consequently, the reciprocal of the value provides an approximate time at which all metabolite concentrations return to the previous steady state following perturbations (it would take about three-folds of the estimated time until all metabolite concentrations sufficiently return to steady state).
Steady State Sensitivity
The sensitivity of a reaction network at steady state is an essential measure to characterize the reaction network. BST defines several kinds of sensitivities (logarithmic gain, rate-constant sensitivity, and kinetic-order sensitivity) (Shiraishi and Savageau, 1992a,b,c,1993; Savageau, 2009). The most important and commonly used sensitivity value is the logarithmic gain, which expresses the percentage change of a dependent variable (metabolite concentration Xi and flux Vi) in response to the infinitesimal percentage change of an independent variable (enzyme activity Yj). The equations for metabolite concentration and flux are:
where, the * symbol indicates that results are evaluated at the nominal steady state. A larger absolute logarithmic gain value indicates that the dependent variable is more strongly affected by the independent variable. A positive value of L(Xi,Yj) indicates that the dependent variable (metabolite concentration) at a new steady state achieved by a change in an independent variable (enzyme activity) takes a value larger than that at the previous steady state, whereas a negative value indicates the opposite response. The software, COSMOS (Shiraishi et al., 2014), performs calculations of steady-state metabolite concentrations, transformations of differential equations with various types of flux expressions into those with power-law flux expressions in S-system or GMA-system form (Table 1), and calculations of logarithmic gains and eigenvalues with high accuracy. It achieves high accuracy by implementing the complex-step method (Lyness and Moler, 1967), by which numerical derivatives can be calculated to 14–16 significant digits of accuracy in double precision. Thus, all calculated values are reliable even when the number of differential equations is very large. Moreover, COSMOS can find steady-state metabolite concentrations accurately, even for a large-scale system, by first numerically solving differential equations until metabolite concentrations do not change remarkably and then using those values as initial estimates in root-finding iterations.
Dynamic Sensitivity
When there is no steady state or when there exists a steady state but the objective is to observe and analyze the dynamics of a system, metabolite concentrations that vary with time must be considered. In these cases, steady state sensitivities can no longer be calculated. Hence, time-varying sensitivities, i.e., dynamic sensitivities (dynamic logarithmic gains), must be calculated (Shiraishi et al., 2005, 2009; Sriyudthsak et al., 2015). The first step of this calculation is to partially differentiate the differential equations for metabolite concentrations with an independent or dependent variable of interest in order to obtain the differential equations for sensitivities, i.e., sensitivity equations (Dickinson and Gelinas, 1976). This mathematical operation is laborious and mistakes are trivial to make especially when the system is large. This problem can be overcome by utilizing the function of symbolic differentiation in the commercially available software, Matlab, or the open-source software, Python together with SymPy package. On the other hand, if one can utilize highly accurate numerical methods, it is possible to develop software without being constrained by the above software. SoftCADS (Shiraishi et al., 2009) is one such software for calculating dynamic sensitivities with high accuracy, which achieves its accuracy through a combination of highly-accurate numerical differentiation methods (Shiraishi et al., 2007) and Taylor-series methods (Shiraishi et al., 2011). The sensitivity equations are automatically derived from the differential equations for metabolite concentrations and the sensitivities can always be obtained with reliable accuracy.
Bottleneck Ranking Indicator (BR Indicator)
When there is an enzyme reaction that strongly restricts the formation of a desired product in a reaction network (i.e., when there is a bottleneck enzyme), the productivity of the desired product may be augmented by increasing the activity of the bottleneck enzyme. Identification of the bottleneck enzyme is necessary for this purpose. The BR indicator expresses the degree of the “bottleneck” and can be used to identify the bottleneck enzyme (Sriyudthsak and Shiraishi, 2010a,b,c;Sriyudthsak et al., 2015). The BR indicator is calculated by:
Larger absolute values of the BR indicator indicate that the relevant enzyme indirectly restricts the formation of the desired product more strongly. The absolute values of BR indicators are ranked to determine which enzyme represents the bottleneck. The effectiveness of the BR indicator has been demonstrated in penicillin V and ethanol fermentation (Sriyudthsak and Shiraishi, 2010a,b,c). When microbial cells grow or a reactor is operated at non-steady state, the ranking of enzymes and therefore the designation of the bottleneck enzyme may vary with time (Sriyudthsak and Shiraishi, 2010a; Sriyudthsak et al., 2015).
Network Prediction
Metabolome data may also be used for the discovery of unknown metabolic pathways and their regulatory mechanisms. Rather than dealing with model construction, this deals with network analysis (Fukushima et al., 2014), which include correlation and causation networks. Metabolic profiles from different biological conditions can be used to build a correlation network, whereas the profiles of time series metabolic data can be utilized to generate a causation network. The correlation structure which is typically built by statistical methods using discrete data links the elements or nodes (i.e., metabolites) by their relations or edges (i.e., enzymatic reactions) of the metabolic networks. The correlation allows us to decrease the actual dimensionality of the system and qualitatively generate a probable network without comprehensive understanding of enzymatic reactions. For example, a system dynamics can be extracted from experimental time-series data using Takens theorem (Broomhead and King, 1986). In the case of large-scale metabolome data, the sample data obtained on different measurement scales can be processed using principal component analysis (Giuliani et al., 2004). Correlation network (Steuer et al., 2003) can also be visualized to understand relations among metabolites.
On the other hand, causation network links metabolites on the basis of their causal relationships. Two common approaches for generating a causal network are dynamic Bayesian network inference and Granger causality approaches for short and long length of time series data (Zou and Feng, 2009). More specific approaches, which combine mathematical and statistical approaches such as BST-loglem (Sriyudthsak et al., 2013a,b), were also proposed to predict metabolic pathways together with their regulatory mechanisms.
Challenges and Future Perspectives
Regardless of past progress, there are still major challenges regarding the advantages and weaknesses of metabolomics integration and mathematical modeling. From our point of view, two major keystones that remain to be tackled are (1) the development of hybrid mathematical approaches for predicting a probable unknown pathway or regulatory mechanism from available metabolome data and (2) the integration of multilayer-omics data into large-scale kinetic models for designing optimal metabolic systems.
For the former issue (1), a challenge lies in the fact that there are thousands of metabolites inside of a cell, whereas metabolomics and mathematical modeling can usually handle hundreds of metabolites and it is, therefore, difficult to precisely predict which metabolite has an effect on a specific reaction pathway. A mathematical model in current approaches often gives several candidates for key regulatory metabolites, so that we still needs trial-and-error experiments in laboratory to narrow down the candidates on the basis of knowledge-based, but not data-driven, hypotheses. Thus, hybrid mathematical approaches combining existing and novel algorithms are expected to solve the issue.
For the latter issue (2), a significant challenge is the systematic integration of large-scale multilayer-omics data to understand metabolism not as a static system but as a dynamic one by capturing the dynamic behaviors and characteristics of all components inside a cell. Currently, it is possible to obtain metabolome, proteome, and transcriptome data. However, the systematic integration of those data by mathematical modeling approaches is still difficult. The selection of a suitable model type to deal with this circumstance has been long debated. A small-scale quantitative kinetic model can provide a detailed regulatory mechanism but only be applicable to a specific pathway. In contrast, a large-scale qualitative static model can offer the correlations among metabolites in a large-scale system but not clarify the detailed mechanism and dynamic behaviors. Thus, instead of selecting either approach exclusively, an improvement in a hybrid approach is desired for the construction of a large-scale kinetic model as well as the modeling of a multilayer-omics (or trans-omic) network, through the integration of the metabolome, proteome, and transcriptome (Yugi et al., 2014). It is anticipated that large-scale kinetic models for handling a trans-omic network would ultimately provide a holistic perspective with much greater insights into complex metabolic systems (Horgan and Kenny, 2011) to design and engineer the metabolism of a whole cell. An appropriated model will permit the precise prediction of dynamic behaviors and provide enormous possibilities for simulating entire cellular metabolisms, before practically exploiting the information to practical applications. Improved approaches to be established will pave the ways to computationally design an entire cellular metabolism and to simulate the behaviors, functions, and mechanisms of its components, like we can design a car and simulate the functions in each compartment.
Author Contributions
All authors listed, have made substantial, direct and intellectual contribution to the work, and approved it for publication.
Funding
This research was supported in part by RIKEN Incentive Research Grant to KS, MEXT KAKENHI grant number 25119719 to FS, and JSPS KAKENHI grant number 25660084 to MYH.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Aderem, A. (2005). Systems biology: its practice and challenges. Cell 121, 511–513. doi: 10.1016/j.cell.2005.04.020
Alves, R., Antunes, F., and Salvador, A. (2006). Tools for kinetic modeling of biochemical networks. Nat. Biotech. 24, 667–672. doi: 10.1038/nbt0606-667
Badawy, A. A.-B., Morgan, C. J., and Turner, J. A. (2008). Application of the phenomenex EZ:faast™ amino acid analysis kit for rapid gas-chromatographic determination of concentrations of plasma tryptophan and its brain uptake competitors. Amino Acids 34, 587–596. doi: 10.1007/s00726-007-0012-7
Bain, J. R., Stevens, R. D., Wenner, B. R., Ilkayeva, O., Muoio, D. M., and Newgard, C. B. (2009). Metabolomics applied to diabetes research: moving from information to knowledge. Diabetes 58, 2429–2443. doi: 10.2337/db09-0580
Bajzer, Z., and Strehler, E. E. (2012). About and beyond the Henri-Michaelis-Menten rate equation for single-substrate enzyme kinetics. Biochem. Biophys. Res. Commun. 417, 982–985. doi: 10.1016/j.bbrc.2011.12.051
Baldan, P., Cocco, N., Marin, A., and Simeoni, M. (2010). Petri nets for modelling metabolic pathways: a survey. Nat. Comput. 9, 955–989. doi: 10.1007/s11047-010-9180-6
Birkemeyer, C., Luedemann, A., Wagner, C., Erban, A., and Kopka, J. (2005). Metabolome analysis: the potential of in vivo labeling with stable isotopes for metabolite profiling. Trends Biotechnol. 23, 28–33. doi: 10.1016/j.tibtech.2004.12.001
Broomhead, D. S., and King, G. P. (1986). Extracting qualitative dynamics from experimental-data. Physica D 20, 217–236. doi: 10.1016/0167-2789(86)90031-X
Chou, I.-C. (2006). Parameter estimation in biochemical systems models with alternating regression. Theor. Biol. Med. Model. 3, 1–11. doi: 10.1186/1742-4682-3-25
Chou, I.-C., and Voit, E. O. (2009). Recent developments in parameter estimation and structure identification of biochemical and genomic systems. Math. Biosci. 219, 57–83. doi: 10.1016/j.mbs.2009.03.002
Chou, I.-C., and Voit, E. O. (2012). Estimation of dynamic flux profiles from metabolic time series data. BMC Syst. Biol. 6:84. doi: 10.1186/1752-0509-6-84
Corana, A., Marchesi, M., Martini, C., and Ridella, S. (1987). Minimizing multimodal functions of continuous variables with the ‘simulated annealing’ algorithm. ACM Trans. Math. Softw. 13, 262–280. doi: 10.1145/29380.29864
de Oliveira Dal'Molin, C. G., Quek, L.-E., Palfreyman, R. W., Brumbley, S. M., and Nielsen, L. K. (2010). AraGEM, a genome-scale reconstruction of the primary metabolic network in Arabidopsis. Plant Physiol. 152, 579–589. doi: 10.1104/pp.109.148817
Dickinson, R. P., and Gelinas, R. J. (1976). Sensitivity analysis of ordinary differential equation systems - a direct method. J. Comput. Phys. 21, 123–143. doi: 10.1016/0021-9991(76)90007-3
Dunn, W. B., Erban, A., Weber, R. J. M., Creek, D. J., Brown, M., Breitline, R., et al. (2012). Mass appeal: metabolite identification in mass spectrometry-focused untargeted metabolomics. Metabolomics 9, 44–66. doi: 10.1007/s11306-012-0434-4
Edwards, J. S., and Palsson, B. O. (2000). The Escherichia coli MG1655 in silico metabolic genotype: its definition, characteristics, and capabilities. Proc. Natl. Acad. U.S.A. 97, 5528–5533. doi: 10.1073/pnas.97.10.5528
Espinoza, C., Degenkolbe, T., Caldana, C., Zuther, E., Leisse, A., Willmitzer, L., et al. (2010). Interaction with diurnal and circadian regulation results in dynamic metabolic and transcriptional changes during cold acclimation in Arabidopsis. PLoS ONE 5:e14101. doi: 10.1371/journal.pone.0014101
Feng, X., Xu, Y., Chen, Y., and Tang, Y. J. (2012). Integrating flux balance analysis into kinetic models to decipher the dynamic metabolism of Shewanella oneidensis MR-1. PLoS Comput. Biol. 8:e1002376. doi: 10.1371/journal.pcbi.1002376
Fiehn, O. (2002). Metabolomics - the link between genotypes and phenotypes. Plant Mol. Biol. 48, 155–171. doi: 10.1023/A:1013713905833
Fogel, D. B., Fogel, L. J., and Atmar, J. W. (1992). “Meta-evolutionary programming,” in 25th Asilomar Conference on Signals, Systems and Computers, ed R. R. Chen (Pacific Grove, CA: IEEE Computer Society), 540–545.
Fuhrer, T., and Zamboni, N. (2015). High-throughput discovery metabolomics. Curr. Opin. Biotechnol. 31, 73–78. doi: 10.1016/j.copbio.2014.08.006
Fukushima, A., Kanaya, S., and Nishida, K. (2014). Integrated network analysis and effective tools in plant systems biology. Front. Plant Sci. 5:598. doi: 10.3389/fpls.2014.00598
Fukushima, A., and Kusano, M. (2013). Recent progress in the development of metabolome databases for plant systems biology. Front. Plant Sci. 4:73. doi: 10.3389/fpls.2013.00073
Gavin, H. (2011). The Levenberg-Marguardt Method for Nonlinear Least Squares Curve-Fitting Problems. Department of Civil and Environmental Engineering, Duke University. 1–15.
Giuliani, A., Zbilut, J. P., Conti, F., Manetti, C., and Miccheli, A. (2004). Invariant features of metabolic networks: a data analysis application on scaling properties of biochemical pathways. Physica A-Stat. Mech. Appl. 337, 157–170. doi: 10.1016/j.physa.2004.01.053
Griffin, J. L., and Shockcor, J. P. (2004). Metabolic profiles of cancer cells. Nat. Rev. Cancer 4, 551–561. doi: 10.1038/nrc1390
Hartmann, A., and Schreiber, F. (2015). Integrative analysis of metabolic models – from structure to dynamics. Front. Bioeng. Biotechnol. 2:91. doi: 10.3389/fbioe.2014.00091
Hatzimanikatis, V., and Bailey, J. E. (1996). MCA Has More to Say. J. Theor. Biol. 182, 223–242. doi: 10.1006/jtbi.1996.0160
Heinrich, R., and Rapoport, T. A. (1974). A linear steady-state treatment of enzymatic chains: general properties, control and quantitative analysis. Eur. J. Biochem. 42, 89–95. doi: 10.1111/j.1432-1033.1974.tb03318.x
Herrgård, M. J., Swainston, N., Dobson, P., Dunn, W. B., Arga, K. Y., Arvas, M., et al. (2008). A consensus yeast metabolic network reconstruction obtained from a community approach to systems biology. Nat. Biotech. 26, 1155–1160. doi: 10.1038/nbt1492
Hiller, K., Hangebrauk, J., Jäger, C., Spura, J., Schreiber, K., and Schomburg, D. (2009). Metabolitedetector: comprehensive analysis tool for targeted and nontargeted GC/MS based metabolome analysis. Anal. Chem. 81, 3429–3439. doi: 10.1021/ac802689c
Horai, H., Arita, M., Kanaya, S., Nihei, Y., Ikeda, T., Suwa, K., et al. (2010). MassBank: a public repository for sharing mass spectral data for life sciences. J. Mass. Spectrom. 45, 703–714. doi: 10.1002/jms.1777
Horgan, R. P., and Kenny, L. C. (2011). “Omic” technologies: genomics, transcriptomics, proteomics and metabolomics. SAC Rev. 13, 189–195. doi: 10.1576/toag.13.3.189.27672
Horn, F., and Jackson, R. (1972). General mass action kinetics. Arch. Ration. Mech. Anal. 47, 81–116. doi: 10.1007/BF00251225
Iwata, M., Shiraishi, F., and Voit, E. O. (2013). Coarse but efficient identification of metabolic pathway system. Int. J. Syst. Biol. 4, 57–72.
Iwata, M., Sriyudthsak, K., Hirai, M. Y., and Shiraishi, F. (2014). Estimation of kinetic parameters in an S-system equation model for a metabolic reaction system using the Newton-Raphson method. Math. Biosci. 248, 11–21. doi: 10.1016/j.mbs.2013.11.002
Jia, G. S., Gregory, N., and Gunawan, R. (2011). Parameter estimation of kinetic models from metabolic profiles: two-phase dynamic decoupling method. Bioinformatics 27, 1964–1970. doi: 10.1093/bioinformatics/btr293
Jonsson, P., Johansson, A. I., Gullberg, J., Trygg, J., A, J., Grung, B., et al. (2005). High-theoughput data analysis for detecting and identifying differences between samples in GC/MS-based metabolomics analyses. Anal. Chem. 77, 5635–5642. doi: 10.1021/ac050601e
Kaplan, F., Kopka, J., Haskell, D. W., Zhao, W., Schiller, K. C., Gatzke, N., et al. (2004). Exploring the temperature-stress metabolome of Arabidopsis. Plant Physiol. 136, 4159–4168. doi: 10.1104/pp.104.052142
Kato, H., Izumi, Y., Hasunuma, T., Matsuda, F., and Kondo, A. (2012). Widely targeted metabolic profiling analysis of yeast central metabolites. J. Biosci. Bioeng. 113, 665–673. doi: 10.1016/j.jbiosc.2011.12.013
Kim, J. K., Bamba, T., Harada, K., Fukusaki, E., and Kobayayashi, A. (2007). Time-course metabolic profiling in Arabidopsis thaliana cell cultures after salt stress treatment. J. Exp. Bot. 58, 415–424. doi: 10.1093/jxb/erl216
Kim, T., Dreher, K., Nilo-Poyanco, R., Lee, I., Fiehn, O., Lange, B. M., et al. (2015). Patterns of metabolite changes identified from large-scale gene perturbations in Arabidopsis using a genome-scale metabolic network1. Plant Physiol. 167, 1685–1698. doi: 10.1104/pp.114.252361
Kinoshita, A., Tsukada, K., Soga, T., Hishiki, T., Ueno, Y., Nakayama, Y., et al. (2007). Roles of hemoglobin allostery in hypoxia-induced metabolic alterations in erythrocytes. J. Biol. Chem. 282, 10731–10741. doi: 10.1074/jbc.M610717200
Kirschner, M. W. (2005). The meaning of systems biology. Cell 121, 503–504. doi: 10.1016/j.cell.2005.05.005
Kitano, H. (2002b). Systems biology: a brief overview. Science 295, 1662–1664. doi: 10.1126/science.1069492
Kutalik, Z., Tucker, W., and Moulton, V. (2007). S-system parameter estimation for noisy metabolic profiles using Newton-flow analysis. IET Syst. Biol. 1, 174–180. doi: 10.1049/iet-syb:20060064
Levenberg, K. (1944). A method for the solution of certain problems in least squares. Q. J. Appl. Math. 2, 164–168.
Lommen, A. (2009). MetAlign: interface-driven, versatile metabolomics tool for hyphenated full-scan mass spectrometry data preprocessing. Anal. Chem. 81, 3079–3086. doi: 10.1021/ac900036d
Lommen, A., and Kools, H. J. (2012). MetAlign 3.0: performance enhancement by efficient use of advances in computer hardware. Metabolomics 8, 719–726. doi: 10.1007/s11306-011-0369-1
Luca, V. D., and Pierre, B. S. (2000). The cell and developmental biology of alkaloid biosynthesis. Trends Plant Sci. 5, 168–173. doi: 10.1016/S1360-1385(00)01575-2
Lyness, J. N., and Moler, C. B. (1967). Numerical differentiation of analytic functions. SIAM J. Num. Anal. 4, 202–210. doi: 10.1137/0704019
Ma, H. W., and Zeng, A. P. (2003). The connectivity structure, giant strong component and centrality of metabolic networks. Bioinformatics 19, 1423–1430. doi: 10.1093/bioinformatics/btg177
Marino, S. V., and Eberhard, O. (2006). An automated procedure for the extraction of metabolic network information from time series data. J. Bioinform. Comput. Biol. 4, 665–691. doi: 10.1142/S0219720006002259
Marquardt, D. (1963). An algorithm for least-squares estimation of nonlinear parameters. SIAM J. Appl. Math. 11, 431–441. doi: 10.1137/0111030
Matsuda, F., Yonekura-Sakakibara, K., Niida, R., Kuromori, T., Shinozaki, K., and Saito, K. (2009). MS/MS spectral tag-based annotation of non-targeted profile of plant secondary metabolites. Plant J. 57, 555–577. doi: 10.1111/j.1365-313X.2008.03705.x
McCloskey, D., Palsson, B. Ø., and Feist, A. M. (2013). Basic and applied uses of genome-scale metabolic network reconstructions of Escherichia coli. Mol. Syst. Biol. 9, 661. doi: 10.1038/msb.2013.18
Mendes, P., and Kell, D. B. (1998). Non-linear optimization of biochemical pathways: applications to metabolic engneering and parameter estimation. Bioinformatics 14, 869–883. doi: 10.1093/bioinformatics/14.10.869
Michalewicz, Z. (1994). Genetic Algorithms + Data Structures = Evolution Programs, 3rd Edn. Berlin: Springer-Verlag.
Mintz-Oron, S., Meir, S., Malitsky, S., Ruppin, E., Aharoni, A., and Shlomi, T. (2012). Reconstruction of Arabidopsis metabolic network models accounting for subcellular compartmentalization and tissue-specificity. Proc. Natl. Acad. U.S.A. 109, 339–344. doi: 10.1073/pnas.1100358109
Murray, D. B., Beckmann, M., and Kitano, H. (2007). Regulation of yeast oscillatory dynamics. Proc. Natl. Acad. Sci. U.S.A 104, 2241–2246. doi: 10.1073/pnas.0606677104
Nagele, T., Mair, A., Sun, X., Fragner, L., Teige, M., and Weckwerth, W. (2014). Solving the differential biochemical jacobian from metabolomics covariance data. PLoS ONE 9:e92299. doi: 10.1371/journal.pone.0092299
Nishino, T., Yachie-Kinoshita, A., Hirayama, A., Soga, T., Suematsu, M., and Tomita, M. (2013). Dynamic simulation and metabolome analysis of longterm erythrocyte storage in adenine–guanosine solution. PLoS ONE 8:e71060. doi: 10.1371/journal.pone.0071060
Novère, N. (2015). Quantitative and logic modelling of molecular and gene networks. Nat. Rev. Genet. 16, 146–158. doi: 10.1038/nrg3885
Orth, J. D., Conrad, T. M., Na, J., Lerman, J. A., Nam, H., Feist, A. M., et al. (2011). A comprehensive genome-scale reconstruction of Escherichia coli metabolism—2011. Mol. Syst. Biol. 7, 535. doi: 10.1038/msb.2011.65
Orth, J. D., Thiele, I., and Palsson, B. Ø. (2010). What is flux balance analysis? Nat. Biotech. 28, 245–248. doi: 10.1038/nbt.1614
Palsson, B. O. (2015). Systems Biology: Constraint-based Reconstruction and Analysis. Cambridge, UK: Cambridge University Press.
Pan, Z., and Raftery, D. (2007). Comparing and combining NMR spectroscopy and mass spectrometry in metabolomics. Anal. Bioanal. Chem. 287, 525–527. doi: 10.1007/s00216-006-0687-8
Poolman, M. G., Miguet, L., Sweetlove, L. J., and Fell, D. A. (2009). A genome-scale metabolic model of Arabidopsis and some of its properties. Plant Physiol. 151, 1570–1581. doi: 10.1104/pp.109.141267
Preidis, G. A., and Hotez, P. J. (2015). The newest “omics”—metagenomics and metabolomics—enter the battle against the neglected tropical diseases. PLoS Negl. Trop. Dis. 9:e0003382. doi: 10.1371/journal.pntd.0003382
Prescher, J. A., and Bertozzi, C. R. (2005). Chemistry in living systems. Nat. Chem. Biol. 1, 13–21. doi: 10.1038/nchembio0605-13
Press, W. H. T., Saul, A., Vetterling, W. T. F., and Brian, P. (2002). Numerical Recipes in C: The Art of Scientific Computing. New York, NY: Cambridge University Press.
Press, W. H. T., Saul, A., Vetterling, W. T. F., and Brian, P. (2007). Numerical Recipes: The Art of Scientific Computing. New York, NY: Cambridge University Press.
Puchalka, J., and Kierzek, A. M. (2004). Bridging the gap between stochastic and deterministic regimes in the kinetic simulations of the biochemical reaction networks. Biophys. J. 86, 1357–1372. doi: 10.1016/S0006-3495(04)74207-1
Rochfort, S. (2005). Metabolomics reviewed: a new “omics” platform technology for systems biology and implications for natural products research. J. Nat. Prod. 68, 1813–1820. doi: 10.1021/np050255w
Saito, K., and Matsuda, F. (2010). Metabolomics for functional genomics, systems biology, and biotechnology. Annu. Rev. Plant Biol. 61, 463–489. doi: 10.1146/annurev.arplant.043008.092035
Savageau, M. A. (1969). Biochemical systems analysis I: some mathematical properites of the rate law for the component enzymatic reactions. J. Theor. Biol. 25, 365–369. doi: 10.1016/S0022-5193(69)80026-3
Savageau, M. A. (2009). Biochemical Systems Analysis: A Study of Function and Design in Molecular Biology. Reading, MA: Addison-Wesley Publishing Company.
Sawada, Y., Akiyama, K., Sakata, A., Kuwahara, A., Otsuki, H., Sakurai, T., et al. (2009). Widely targeted metabolomics based on large-scale MS/MS data for elucidating metabolite accumulation patterns in plants. Plant Cell Physiol. 50, 37–47. doi: 10.1093/pcp/pcn183
Schuster, S., Dandekar, T., and Fell, D. A. (1999). Detection of elementary flux modes in biochemical networks: a promising tool for pathway analysis and metabolic engineering. Trends Biotechnol. 17, 53–60. doi: 10.1016/S0167-7799(98)01290-6
Sèvin, D. C., Kuehne, A., Zamboni, N., and Sauer, U. (2015). Biological insights through nontargeted metabolomics. Curr. Opin. Biotechnol. 34, 1–8. doi: 10.1016/j.copbio.2014.10.001
Shiraishi, F., Egashira, M., and Iwata, M. (2011). Highly accurate computation of dynamic sensitivities in metabolic reaction systems by a Taylor series method. Math. Biosci. 233, 59–67. doi: 10.1016/j.mbs.2011.06.004
Shiraishi, F., Furuta, S., Ishimatsu, T., and Akhter, J. (2007). A simple and highly accurate numerical differentiation method for sensitivity analysis of large-scale metabolic reaction systems. Math. Biosci. 208, 590–606. doi: 10.1016/j.mbs.2006.11.007
Shiraishi, F., Hatoh, Y., and Irie, T. (2005). An efficient method for calculation of dynamic logarithmic gains in biochemical systems theory. J. Theor. Biol. 234, 79–85. doi: 10.1016/j.jtbi.2004.11.015
Shiraishi, F., and Savageau, M. A. (1992a). The tricarboxylic acid cycle in Dictyostelium discoideum. II. Evaluation of model consistency and robustness. J. Biol. Chem. 267, 22919–22925.
Shiraishi, F., and Savageau, M. A. (1992b). The tricarboxylic acid cycle in Dictyostelium discoideum. III. Analysis of steady state and dynamic behavior. J. Biol. Chem. 267, 22926–22933.
Shiraishi, F., and Savageau, M. A. (1992c). The tricarboxylic acid cycle in Dictyostelium discoideum: IV. Resolution of discrepancies between alternative methods of analysis. J. Biol. Chem. 267, 22934–22943.
Shiraishi, F., and Savageau, M. A. (1993). The tricarboxylic acid cycle in Dictyostelium discoideum: V. Systemic effects of including protein turnover in the current model. J. Biol. Chem. 268, 16917–16928.
Shiraishi, F., Tomita, T., Iwata, M., and Berrada, A. A. (2009). A reliable Taylor series-based computational method for the calculation of dynamic sensitivities in large-scale metabolic reaction systems: algorithmic and software evaluation. Math. Biosci. 222, 73–85. doi: 10.1016/j.mbs.2009.09.001
Shiraishi, F., Yoshida, E., and Voit, E. O. (2014). An efficient and very accurate method for calculating steady-state sensitivities in metabolic reaction systems. IEEE/ACM Trans. Comput. Biol. Bioinform. 11, 1077–1086. doi: 10.1109/TCBB.2014.2338311
Shmulevich, I., and Aitchison, J. D. (2009). Deterministic and stochastic models of genetic regulatory networks. Methods Enzymol. 467, 335–356. doi: 10.1016/S0076-6879(09)67013-0
Shulaev, V. (2006). Metabolomics technology and bioinformatics. Brief. Bioinform. 7, 128–139. doi: 10.1093/bib/bbl012
Sriyudthsak, K., Iwata, M., Hirai, M. Y., and Shiraishi, F. (2014a). PENDISC: a simple method for constructing a mathematical model from time-series data of metabolite concentrations. Bull. Math. Biol. 76, 1333–1351. doi: 10.1007/s11538-014-9960-8
Sriyudthsak, K., Sawada, Y., Chiba, Y., Yamashita, Y., Kanaya, S., Onouchi, H., et al. (2014b). A U-system approach for predicting metabolic behaviors and responses based on an alleged metabolic reaction network. BMC Syst. Biol. 8:S4. doi: 10.1186/1752-0509-8-S5-S4
Sriyudthsak, K., and Shiraishi, F. (2010a). Identification of bottleneck enzymes with negative dynamic sensitivities: ethanol fermentation systems as case studies. J. Biotechnol. 149, 191–200. doi: 10.1016/j.jbiotec.2010.01.015
Sriyudthsak, K., and Shiraishi, F. (2010b). Instantaneous and overall indicators for determination of bottleneck ranking in metabolic reaction networks. Ind. Eng. Chem. Res. 49, 2122–2129. doi: 10.1021/ie901531d
Sriyudthsak, K., and Shiraishi, F. (2010c). Selection of best indicators for ranking and determination of bottleneck enzymes in metabolic reaction systems. Ind. Eng. Chem. Res. 49, 9738–9742. doi: 10.1021/ie100911h
Sriyudthsak, K., Shiraishi, F., and Hirai, M. Y. (2013a). “BST-loglem: parameter and network estimations based on BST modeling using LOESS, Granger Causality and Levenberg-Marquardt Method,” in The 25th Annual Meeting of the Thai Society for Biotechnology and International Conference (Bangkok).
Sriyudthsak, K., Shiraishi, F., and Hirai, M. Y. (2013b). Identification of a metabolic reaction network from time-series data of metabolite concentrations. PLoS ONE 8:e51212. doi: 10.1371/journal.pone.0051212
Sriyudthsak, K., Uno, H., Gunawan, R., and Shiraishi, F. (2015). Using dynamic sensitivities to characterize metabolic reaction systems. Math. Biosci. 269, 153–163. doi: 10.1016/j.mbs.2015.09.002
Steuer, R., Kurths, J., Fiehn, O., and Weckwerth, W. (2003). Observing and interpreting correlations in metabolomic networks. Bioinformatics 19, 1019–1026. doi: 10.1093/bioinformatics/btg120
Strassburg, K., Walther, D., Takahashi, H., Kanaya, S., and Kopka, J. (2010). Dynamic transcriptional and metabolic responses in yeast adapting to temperature stress. OMICS 14, 249–259. doi: 10.1089/omi.2009.0107
Summer, L. W., Urbanczyk-Wochniak, E., and Broeckling, C. D. (2007). “Metabolomics data analysis, visualization, and integration,” in Plant Bioinformatics: Methods and Protocols, ed D. Edwards (Totowa, NJ: Humana Press), 409–436.
Thiele, I., Swainston, N., Fleming, R. M. T., Hoppe, A., Sahoo, S., Aurich, M. K., et al. (2013). A community-driven global reconstruction of human metabolism. Nat. Biotech. 31, 419–425. doi: 10.1038/nbt.2488
Tikunov, Y., Lommen, A., de Vos, C. H., Verhoeven, H. A., Bino, R. J., Hall, R. D., et al. (2005). A novel approach for nontargeted data analysis for metabolomics. Large-scale profiling of tomato fruit volatiles. Plant Physiol. 139, 1125–1137. doi: 10.1104/pp.105.068130
Tsugawa, H., Cajka, T., Kind, T., Ma, Y., Higgins, B., Ikeda, K., et al. (2015). MS-DIAL: data-independent MS/MS deconvolution for comprehensive metabolome analysis. Nat. Methods 12, 523–526. doi: 10.1038/nmeth.3393
Ukai, H., and Ueda, H. R. (2010). Systems biology of mammalian circadian clocks. Annu. Rev. Physiol. 72, 579–603. doi: 10.1146/annurev-physiol-073109-130051
Urano, K., Maruyama, K., Ogata, Y., Morishita, Y., Takeda, M., Sakurai, N., et al. (2008). Characterization of the ABA-regulated global responses to dehydration in Arabidopsis by metabolomics. Plant J. 57, 1065–1078. doi: 10.1111/j.1365-313X.2008.03748.x
Vilela, M., Borges, C. C., Vinga, S., Vasconcelos, A. T., Santos, H., Voit, E. O., et al. (2007). Automated smoother for the numerical decoupling of dynamics models. BMC Bioinformatics 8:305. doi: 10.1186/1471-2105-8-305
Vilela, M., Vinga, S., Maia, M. A., Voit, E. O., and Almeida, J. S. (2009). Identification of neutral biochemical network models from time series data. BMC Syst. Biol. 3:47. doi: 10.1186/1752-0509-3-47
Villas-Boas, S. G., Mas, S., Akesson, M., Smedsgaard, J., and Nielsen, J. (2005). Mass spectrometry in metabolome analysis. Mass Spectrom. Rev. 2005, 613–646. doi: 10.1002/mas.20032
Visser, D., and Heijnen, J. J. (2002). The mathematics of metabolic control analysis revisited. Metab. Eng. 4, 114–123. doi: 10.1006/mben.2001.0216
Voit, E. O. (2000). Computational Analysis of Biochemical Systems: A Practical Guide for Biochemists and Molecular Biologists. Cambridge, UK: Cambridge University Press.
Voit, E. O. (2012). A First Course in Systems Biology. New York, NY: Garland Science, Taylor & Francis Group.
Voit, E. O. (2013). Characterizability of metabolic pathway systems from time series data. Math. Biosci. 246, 315–325. doi: 10.1016/j.mbs.2013.01.008
Vuckovic, D. (2012). Current trends and challenges in sample preparation for global metabolimcs using liquid chromatography-mass spectrometry. Anal. Bioanal. Chhem. 403, 1523–1548. doi: 10.1007/s00216-012-6039-y
Weckwerth, W. (2003). Metabolomics in systems biology. Annu. Rev. Plant Biol. 54, 669–689. doi: 10.1146/annurev.arplant.54.031902.135014
Weckwerth, W. (2011). Unpredictability of metabolism–the key role of metabolomics science in combination with next-generation genome sequencing. Anal. Bioanal. Chem. 400, 1967–1978. doi: 10.1007/s00216-011-4948-9
Wechwerth, W., Loureino, M. E., Wenzel, K., and Fiehn, O. (2004). Differential metabolic networks unravel the effects of silent plant phenotypes. Proc. Natl. Acad. Sci. U.S.A 101, 7809–7814. doi: 10.1073/pnas.0303415101
Wolpert, D. H., and MacReady, W. G. (1997). No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1, 67–82. doi: 10.1109/4235.585893
Wu, L., Wang, W. M., van Winden, W. A., van Gulik, W. M., and Heijnen, J. J. (2004). A new framework for the estimation of control parameters in metabolic pathways using lin-log kinetics. Eur. J. Biochem. 271, 3348–3359. doi: 10.1111/j.0014-2956.2004.04269.x
You, L., Zhang, B., and Tang, Y. J. (2014). Application of stable isotope-assisted metabolomics for cell metabolism studies. Metabolites 4, 142–165. doi: 10.3390/metabo4020142
Yugi, K., Kubota, H., Toyoshima, Y., Noguchi, R., Kawata, K., Komori, Y., et al. (2014). Reconstruction of insulin signal flow from phosphoproteome and metabolome data. Cell Rep. 8, 1171–1183. doi: 10.1016/j.celrep.2014.07.021
Keywords: biochemical systems theory, bottleneck ranking indicator, dynamic simulation, mathematical model, metabolic reaction network, metabolome, sensitivity analysis, time series data
Citation: Sriyudthsak K, Shiraishi F and Hirai MY (2016) Mathematical Modeling and Dynamic Simulation of Metabolic Reaction Systems Using Metabolome Time Series Data. Front. Mol. Biosci. 3:15. doi: 10.3389/fmolb.2016.00015
Received: 30 December 2015; Accepted: 12 April 2016;
Published: 03 May 2016.
Edited by:
Thomas Nägele, University of Vienna, AustriaReviewed by:
Alessandro Giuliani, Istituto Superiore di Sanità, ItalyLaurent Simon, New Jersey Institute of Technology, USA
Copyright © 2016 Sriyudthsak, Shiraishi and Hirai. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Fumihide Shiraishi, ZnVtaXNoaXJhQGJycy5reXVzaHUtdS5hYy5qcA==;
Masami Yokota Hirai, bWFzYW1pLmhpcmFpQHJpa2VuLmpw
 Kansuporn Sriyudthsak
Kansuporn Sriyudthsak Fumihide Shiraishi2*
Fumihide Shiraishi2* Masami Yokota Hirai
Masami Yokota Hirai