- 1Institute for Chemical Reaction Design and Discovery, Hokkaido University, Sapporo, Japan
- 2PRESTO, Japan Science and Technology Agency (JST), 4-1-8 Honcho, Kawaguchi, Japan
- 3Graduate School of Frontier Biosciences, Osaka University, Suita, Japan
- 4Institute for Open and Transdisciplinary Research Initiatives, Osaka University, Suita, Japan
Paraspeckles are nuclear bodies scaffolded by RNP complexes of NEAT1_2 RNA transcripts and multiple RNA-binding proteins. The assembly of paraspeckles is coupled with the transcription of NEAT1_2. Paraspeckles form the core-shell structure, where the two terminal regions of NEAT1_2 RNP complexes compose the shell of the paraspeckle and the middle regions of these complexes compose the core. We here construct a theoretical model of paraspeckles by taking into account the transcription of NEAT1_2 in an extension of the theory of block copolymer micelles. This theory predicts that the core-shell structure of a paraspeckle is assembled by the association of the middle region of NEAT1_2 RNP complexes due to the multivalent interactions between RBPs bound to these regions and by the relative affinity of the terminal regions of the complexes to the nucleoplasm. The latter affinity results in the effective repulsive interactions between terminal regions of the RNA complexes and limits the number of complexes composing the paraspeckle. In the wild type, the repulsive interaction between the middle and terminal block dominates the thermal fluctuation. However, the thermal fluctuation can be significant in a mutant, where a part of the terminal regions of NEAT1_2 is deleted, and distributes the shortened terminal regions randomly between the shell and the core, consistent with our recent experiments. With the upregulated transcription, the shortened terminal regions of NEAT1_2 in a deletion mutant is localized to the core to decrease the repulsive interaction between the terminal regions, while the structure does not change with the upregulation in the wild type. The robustness of the structure of paraspeckles in the wild type results from the polymeric nature of NEAT1_2 complexes.
Introduction
A cell nucleus is not a uniform solution of DNA and proteins, but there are a number of nuclear bodies in the interchromatin space (Chujo et al., 2016; Nakagawa et al., 2018; Palikyaras and Papantonis 2019; Banani et al., 2017; Berry et al., 2015; Van Treeck and Parker 2018). Some nuclear bodies are scaffolded by RNAs that make ribonucleoprotein (RNP) complexes with RNA-binding proteins (RBPs). A class of RNAs that are essential in assembling nuclear bodies are called architectural RNAs (arcRNAs) (Chujo et al., 2016). Growing number of evidences suggest that nuclear bodies are condensates assembled by liquid-liquid phase separation (LLPS) because of the multivalent interactions between the intrinsically disordered regions of RBPs that are bound to arcRNAs (Chujo et al., 2016; Nakagawa et al., 2018; Palikyaras and Papantonis 2019; Banani et al., 2017; Berry et al., 2015; Van Treeck and Parker 2018). Condensates produced by LLPS are thought to act as reaction crucibles of specific biochemical reactions, molecular sponges that sequester specific proteins and RNAs from the nucleoplasm, and hubs to organize the 3D structure of genome (Shin and Brangwynne 2017). It is of interest to study the assembly mechanism of nuclear bodies due to the possible relationship with their physiological functions.
Paraspeckles are nuclear bodies that are scaffolded by NEAT1_2 arcRNA (Sunwoo et al., 2008; Clemson et al., 2009; Sasaki et al., 2009). Paraspeckles act as molecular sponges that sequester some types of RNA transcripts and proteins (Chen and Carmichael 2009; Hirose et al., 2014; Imamura et al., 2014; Hu et al., 2015; West et al., 2016; Nakagawa et al., 2018; Wang et al., 2018; Yap et al.,2022) and interact with chromatin regions, enriched in active promoters and enhancers (West et al., 2014; Li et al., 2017; Sridhar et al., 2017; Fang et al., 2019; Bonetti et al., 2020; Cai et al., 2020). De novo assembled paraspeckles are often observed at the proximity to the transcription site of NEAT1_2 and are disassembled when the transcription of arcRNA is suppressed (Clemson et al., 2009; Sasaki et al., 2009; Mao et al., 2011). The number of paraspeckles increases when transcription of NEAT1_2 is upregulated (Clemson et al., 2009; Hirose et al., 2014). These results imply that the assembly of paraspeckles is coupled with the transcription of NEAT1_2. RNA-binding proteins can be bound to nascent NEAT1_2 transcripts, which are still connected to the transcription site via RNA polymerase II (Pol II). The array of nascent NEAT1_2 RNAs produced during a transcription burst probably act as a nucleation site of paraspeckles (Chujo and Hirose 2017; Yamazaki et al., 2020).
We have recently extended the Flory-Huggins theory, which is the standard theory of phase separation of polymers in a solution (Doi 1996), to predict the phase separation driven by the production of arcRNAs due to transcription (Yamamoto et al., 2020). The condensates assembled by this mechanism are disordered liquids of complexes of arcRNAs and RBPs. However, paraspeckles are not condensates of disordered liquid, but form a characteristic core-shell structure (Souquere et al., 2010; West et al., 2016): the two terminal regions and the middle region of NEAT1_2 form the shell and the core of paraspeckles, respectively. The structure of paraspeckles is analogous to micelles of ABC triblock copolymers in a selective solvent, where two polymer chains (A and C blocks) composed of hydrophilic units are chemically bonded to the two ends of a chain (B block) composed of hydrophobic units (Monzen et al., 2000; Mai and Eisenberg 2012; Moughton et al., 2012). The ordered structure and the transcription driven formation of paraspeckles are two features that distinguish paraspeckles from condensates assembled by the classical phase separation, such as LLPS, in the thermodynamic equilibrium.
In our recent experiments, we have constructed mutant NEAT1_2 cell lines, in which the terminal regions of NEAT1_2 were partly deleted by CRISPR/Cas9 and have observed paraspeckles in such cell lines with the super-resolution optical microscope and the electron microscope (Yamazaki et al., 2018, 2021). Our experiments have shown that the terminal regions of NEAT1_2 RNAs were localized in the shells of paraspeckles in the wild type (WT) (Figure 1A), whereas the terminal regions were distributed both to the core and the shell in the mutant cells (Figure 1B) (the schematics of NEAT1_2 for each case is shown in Figure 1C). Motivated by this result, we here construct a model of paraspeckles by taking into account the transcription dynamics of NEAT1_2 in an extension of the theory of micelles of ABC triblock copolymers. The A and C blocks correspond to the terminal regions of NEAT1_2 RNP complexes and the B block corresponds to their middle region. The B blocks are associative due to the multivalent interactions between RBPs, such as NONO and FUS, that specifically bind to this B block region due to its sequence (Yamazaki et al., 2018).
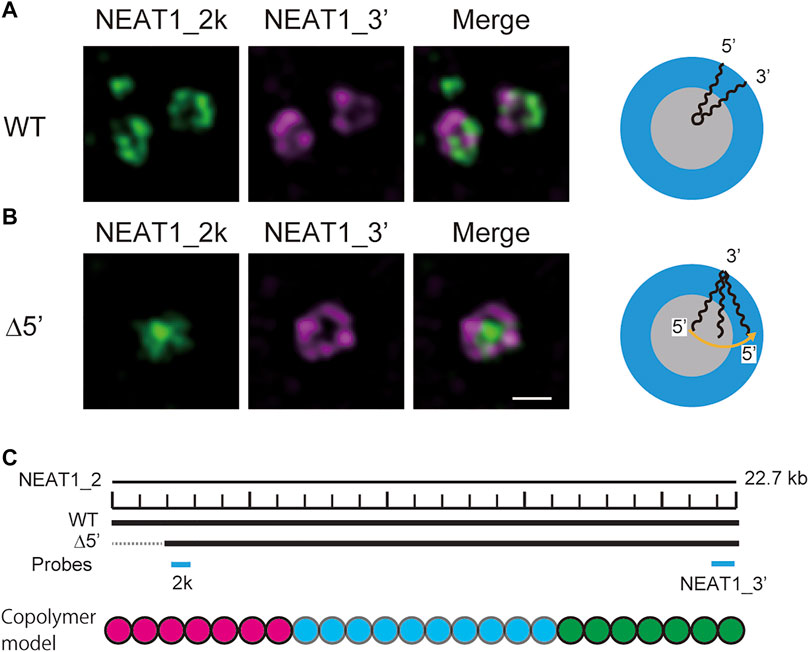
FIGURE 1. Super-resolution microscopic images of paraspeckles in HAP1 NEAT1 wild type (A) and D5′ mutant cells lacking their NEAT1 0–1.8 kb regions (B) detected by NEAT1_2k FISH probes against 5′ terminal region of NEAT1 (green) and NEAT1_3′ FISH probes (magenta) in the presence of MG132 (5 mM for 6 h). Scale bar, 500 nm. (C) The schematics of WT NEAT1_2 and mutants with deletions in the 5′ terminal regions. The positions of NEAT1 probes (NEAT1_2k and NEAT1_3′) are shown by the blue bars. See Yamazaki et al. 2021 for experimental details. Copolymer model is schematic and the borders of A, B, and C blocks remain to be experimentally characterized.
In many cases, paraspeckles are approximately spherical, whereas cylindrical paraspeckles are also observed, for example, when NEAT1_2 transcription is upregulated (Hirose et al., 2014). The analysis of cylindrical paraspeckles greatly complicates the theory, while the essence of the biophysical mechanism of the assembly of paraspeckles is already in the theory of spherical paraspeckles. Not to hide the essence behind the complexity of analysis, in this paper, we limit our discussion to spherical paraspeckles.
Our theory predicts the distribution of terminal blocks (A blocks) and the size of paraspeckles in wild type and mutant with deleted terminal blocks and also the effect of the upregulation of NEAT1_2 transcription. Our prediction is consistent with our recent experiments (Yamazaki et al., 2018, 2021), implying that the assembly of paraspeckles can be understood as micellization. Our theory provides biophysical insight into the assembly of WT and mutant paraspeckles. The sequences of arcRNAs determine the arrangements of RBPs along these arcRNAs and thus play a role in the blueprints of nuclear bodies, while their assembly is fine-tuned by the transcription dynamics of arcRNAs. Our theory can be extended to understand the mechanism of the assembly of other nuclear bodies once the arrangements of RBPs along arcRNAs are determined by experiments.
Materials and methods
Model
We treat the NEAT1_2 RNP complexes as ABC triblock copolymers (Figure 2A). Different RBPs are bound to A, B, and C blocks and this makes the magnitudes of interactions between units in the same blocks different from the magnitudes of the interactions between different blocks. Treating a complex as one polymer, instead of treating arcRNA and RBPs separately, is effective for the case in which the binding affinity of RNA-binding proteins to these blocks is relatively large (Yamamoto et al., 2020). The A, B, and C blocks are composed of
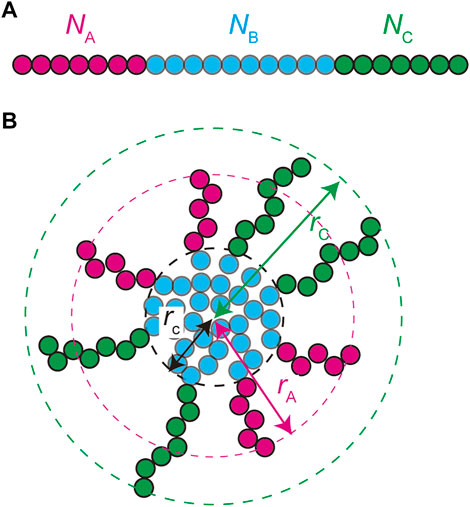
FIGURE 2. A spherical paraspeckle is modeled as a micelle of ABC block copolymers. The A, B, and C blocks are composed of
In the thermodynamic equilibrium, the most stable state is the one at the minimum of the free energy of the system. The free energy of a micelle of block copolymers is composed of 1) the stretching free energy of the blocks in the core, 2) the surface free energy at the interface between the core and the shell, and 3) the free energy of the blocks in the shell (Halperin and Alexander 1989; Semenov et al., 1995; Zhulina et al., 2005). The growth of polymer micelles decreases the surface free energy and increases the stretching free energy of blocks in the core and the free energy due to the excluded volume interactions between blocks in the shell (Halperin and Alexander 1989; Semenov et al., 1995; Zhulina et al., 2005). The stable size of spherical micelles is determined by the balance of these free energy contributions. Most theories predict the distribution of the size of polymer micelles that are assembled uniformly in a block copolymer solution at the thermodynamic equilibrium (Annianson and Wall 1974; Safran 2003; Hadgiivanova et al., 2011; Mysona et al., 2019). We extend the theory of polymer micelles by taking into account the fact that paraspeckles are assembled locally at the transcription site of NEAT1_2 and their assembly is coupled with the transcription of NEAT1_2.
Free energy
The free energy quantifies the stability of the system at the thermodynamic equilibrium. We here derive the free energy of a paraspeckle by taking into account the fact that the terminal blocks of NEAT1_2 are distributed both to the shell and the core in an extension of the free energy of a polymer micelle (Halperin and Alexander 1989; Semenov et al., 1995; Zhulina et al., 2005). The free energy of a paraspeckle composed of
where
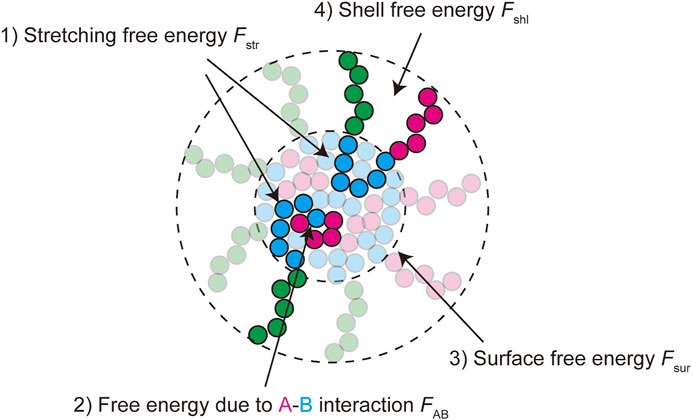
FIGURE 3. The free energy of a paraspeckle is composed of five terms: 1) the stretching free energy of blocks in the core
The free energy of the core has the form
The first and second terms are the stretching free energy of the B blocks in the core and are derived in the spirit of Semenov 1985, see Supplementary Section S1. The third term is the free energy due to the interactions between the A and B units in the core. For cases in which the number
where
The surface free energy has the form
The interaction parameter
Theories of block copolymer micelles treat blocks in the shell as a polymer brush on a curved surface (Halperin and Alexander 1989; Semenov et al., 1995; Zhulina et al., 2005). There are elaborate approaches to treat polymer brushes on planer (Netz and Schick 1998) and curved surfaces (Zhulina et al., 2006), however, for simplicity, we here use the scaling theory of polymer brush (Alexander 1977; de Gennes 1980). With this approach, the free energy of the shell has the form
with
Eqn. 6 includes the stretching free energy of the A blocks in the shell and the free energy due to the excluded volume interactions between A units in the shell. Eqn. 7 is the corresponding free energy for the C blocks. We neglected the excluded volume interaction between the A and C units because the 3′ and 5’ terminal regions are segregated in separate domains in the shell of wild type paraspeckles (West et al., 2016). Eqs. 6, 7 are derived by using so-called Daoud-Cotton scaling theory (Daoud and Cotton 1982), assuming that the solution is a good solvent to both A and C blocks, following the usual treatment of block copolymer micelles (Halperin and Alexander 1989; Semenov et al., 1995; Zhulina et al., 2005), see also in Supplementary Section S2.1
Eqn. 8 is derived by using the fact that the osmotic pressure in the domains of A blocks is equal to the osmotic pressure in the domains of C blocks, see Supplementary Section S2.1.
The mixing free energy represents the entropic contribution that distributes the A blocks randomly to the shell and the core and has the form
The free energy
Association and dissociation dynamics of NEAT1_2
Most theories of polymer micelles predict the most stable size and the distribution of the size of polymer micelles that are assembled uniformly in a block copolymer solution at the thermodynamic equilibrium (Annianson and Wall 1974; Safran 2003; Hadgiivanova et al., 2011; Mysona et al., 2019). In contrast, the assembly of paraspeckles is coupled with the transcription of NEAT1_2 (Mao et al., 2011). RBPs can bind to nascent NEAT1_2 transcripts, which are still connected to the transcription site via Pol II, and an array of complexes of nascent NEAT1_2 transcripts and RBPs during a transcription burst act as a nucleation site of paraspeckles. Once a paraspeckle is nucleated, nascent NEAT1_2 transcripts are added to the paraspeckle one by one as nascent transcripts are produced by Pol II. This situation may be somewhat analogous to the assembly of micelles due to the association of side chains that are attached to a main chain, except for the fact that these side chains are not produced and released dynamically. The side chains assemble micelles without translational entropy cost, in contrast to the micellization of polymer chains freely diffusing in the solution (Borisov and Halperin 1995). We thus derive the time evolution equation of a paraspeckle at the transcription site by taking into account the facts that 1) nascent NEAT1_2 transcripts are associated with the paraspeckle without the translational entropy cost and 2) paraspeckles are assembled locally at the transcription site. Because of these features, paraspeckles are different from block copolymer micelles assembled in the thermodynamic equilibrium (Annianson and Wall 1974; Safran 2003; Hadgiivanova et al., 2011; Mysona et al., 2019).
We treat the probability
The flux
The first term of Eqn. 14 is the rate with which transcripts diffusing in the solution are spontaneously associated with the paraspeckle. The second term is the rate with which a transcript is spontaneously dissociated from the paraspeckle. The third term is the rate with which a nascent transcript during production is added to the paraspeckle through transcription.
For cases in which the transcription is suppressed,
Substituting Eqn. 15 into Eqn. 14 leads to
In the steady state,
The effective free energy
where
The number of transcripts composing a paraspeckle with the maximum probability in the steady state is derived by minimizing the effective free energy
Results
Transcription dynamics regulates the structure of paraspeckles
We first discuss the dependence of the fraction
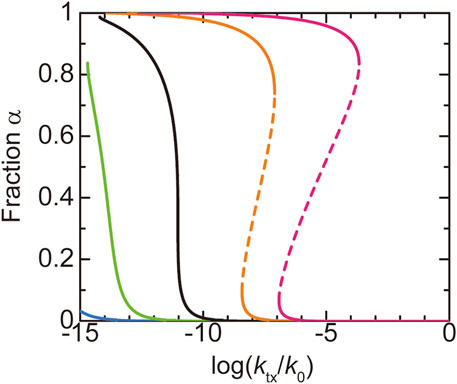
FIGURE 4. The fraction
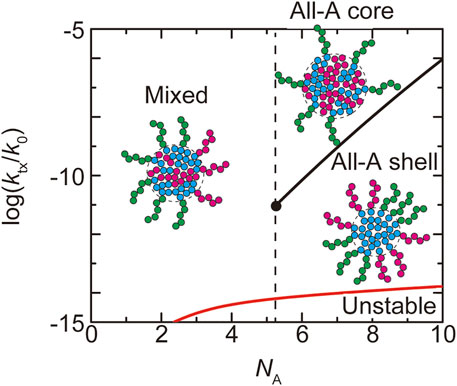
FIGURE 5. The phase diagram of paraspeckles is shown for the (natural) logarithm of production rate
In the WT, most of the terminal regions of NEAT1_2 are localized at the shell (Souquere et al., 2010; West et al., 2016; Yamazaki et al., 2018, 2021). This implies that paraspeckles in the WT are in the ‘all-A shell’ state, which happens for
Our theory predicts the biophysical mechanism of the assembly of paraspeckles. The fact that all the terminal blocks are localized at the shell in the WT paraspeckles results from the strong repulsive interaction between A and B blocks, where its influence to the structures of paraspeckles is quantified by the free energy
The number
Repulsive interactions of terminal blocks and entropic elasticity of middle blocks limit the number of transcripts in paraspeckles
The size of paraspeckles in the WT and deletion mutants is experimentally accessible. The radius
where the heights,
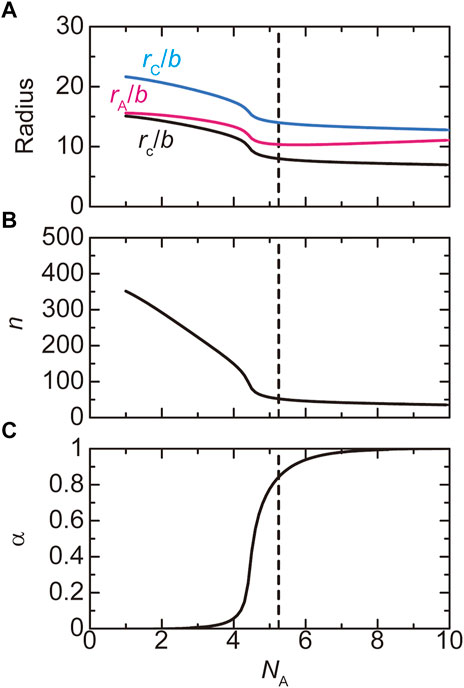
FIGURE 6. The radius (A), the number
The number of transcripts in a paraspeckle is limited by the free energy
Paraspeckles are assembled by the association of the middle regions
Paraspeckles are assembled by the attractive interactions between the B blocks of NEAT1_2 RNP complexes. As expected, the radius
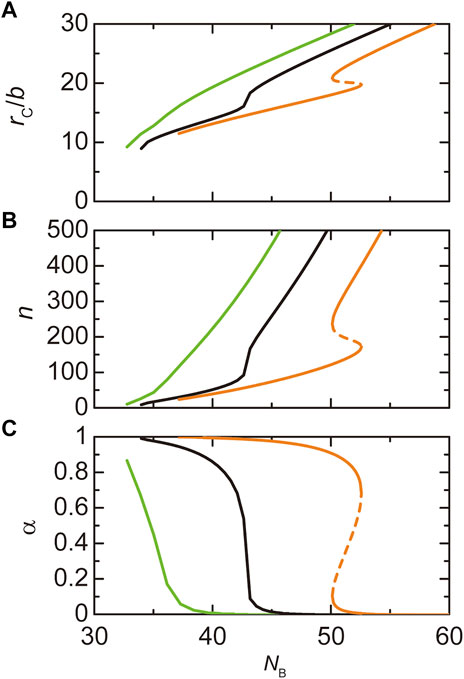
FIGURE 7. The radius
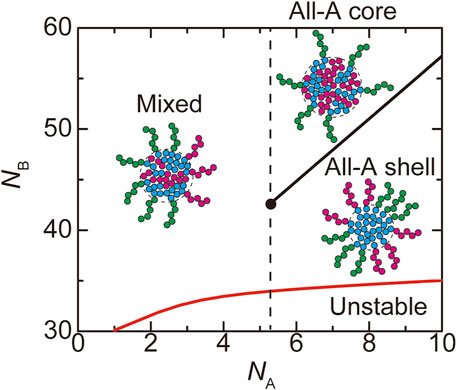
FIGURE 8. The phase diagram of paraspeckles is shown for the number
Discussion
We have constructed a theory of paraspeckle assembly by taking into account the transcription dynamics of NEAT1_2 in an extension of the theory of ABC triblock copolymer micelles. This model captures two features of paraspeckles: paraspeckles form the characteristic core-shell structure and the assembly of paraspeckles is coupled with the transcription of NEAT1_2. Our theory provides a biophysical insight into the assembly of paraspeckles. Paraspeckles are assembled by multivalent interactions between the middle blocks of the NEAT1_2 RNP complexes (Yamazaki et al., 2018). The repulsive interactions between A and B blocks, quantified by the interaction free energy
Our recent experiments have revealed that (I) the 5′ terminal regions of NEAT1_2 transcripts were distributed randomly between the shell and the core in paraspeckles of Δ5′ deletion mutants, where the 5′ terminal region of NEAT1_2 was deleted by
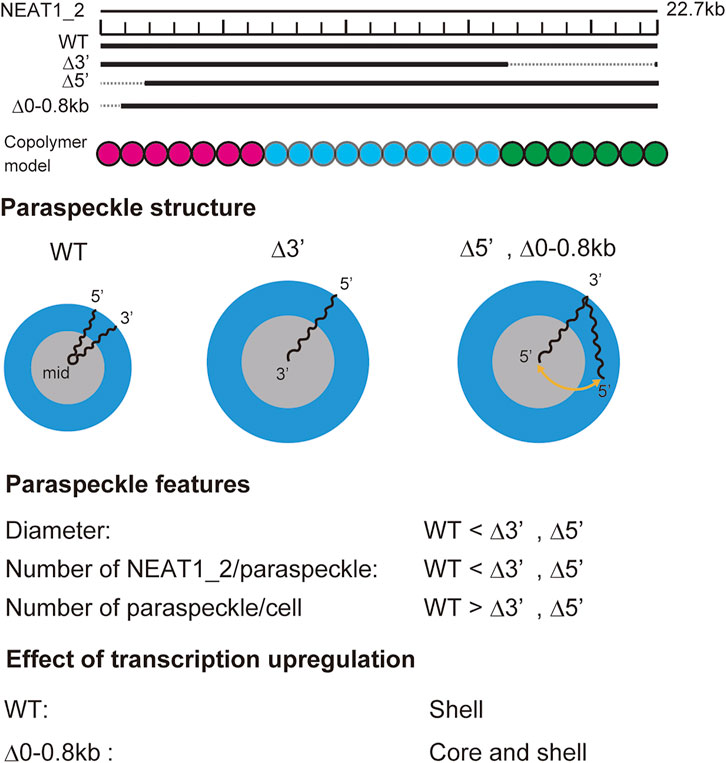
FIGURE 9. Summary of experimental results on paraspeckles in wild type and deletion mutants (Yamazaki et al., 2021). Copolymer model is schematic and the borders of A, B, and C blocks remain to be experimentally characterized.
Our theory provides a biophysical insight into our experimental results: In the WT, all the A blocks are localized in the shell because the free energy
In our approach, we take into account only the essential features to understand the mechanism of the assembly of paraspeckles, instead of doing computer simulations by including all known things. It is indeed the strategy of theoretical physics. Our theory is certainly an important first step, but there are a couple of remaining mysteries. First, we focused on the analysis of spherical paraspeckles, not to hide the essence of the assembly of paraspeckles behind the complexity in treating cylindrical paraspeckles. We thus did not explain the sphere-cylinder morphological transition of paraspeckles. The fact that the fraction of cylindrical paraspeckles increases with the upregulation of NEAT1_2 transcription is indeed consistent with our conclusion that paraspeckles are assembled by micellization. Second, in the WT, 3′ and 5’ terminal regions are not randomly mixed, but are separated in microdomains (West et al., 2016). Our present theory takes into account this feature in the free energy
Conclusion
By the combination of theory and experiments, we have shown that paraspeckles are assembled by micellization, not liquid-liquid phase separation. One important feature of micelles is that their size is regulated by the balance between the surface free energy
Our theory and experiments provide insight into the general principle of the assembly of nuclear bodies: The pattern of RBPs binding to arcRNAs is tailored into their RNA sequences and the RNP complexes behave as copolymers that direct the ordering in the internal structures of nuclear bodies. Our theory can be therefore extended to understand the mechanism of the assembly of other nuclear bodies by using the experimentally determined arrangement of RBPs along arcRNAs. The assembly of nuclear bodies is facilitated by the transcription of arcRNAs. The number of arcRNAs per nuclear body is controlled by both the interactions and connectivity of RBPs bound to the arcRNAs and the transcription dynamics. Chemical engineers control the stability and size of liquid condensates by using surfactants. Life takes the same strategy by using RNA.
Data availability statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://doi.org/10.6084/m9.figshare.20209202.
Author contributions
All authors designed the research and wrote the manuscript. TeY constructed the model and performed the calculations.
Funding
This research was supported by KAKENHI grants from the Ministry of Education, Culture, Sports, Science, and Technology (MEXT) of Japan [TeY (18K03558, 19H05259, 20H05934, 21H00241, 21K03479), to ToY (19K06479, 19H05250, 21H00253, 22H02545), and TH (20H00448, 20H05377, 21H05276 22K19293)], JST, PRESTO Grant Number JPMJPR18KA (to TeY), JST CREST Grant Number JPMJCR20E6 (To TH), the Mochida Memorial Foundation for Medical and Pharmaceutical Research (to ToY), the Naito Foundation (to ToY), and the Takeda Science Foundation (to ToY).
Acknowledgments
TeY is grateful for the fruitful discussion with Takashi Uneyama (Nagoya University).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmolb.2022.925058/full#supplementary-material
References
Alexander, S. (1977). Adsorption of chain molecules with a polar head a scaling description. J. Phys. Fr. 28, 983–987. doi:10.1051/jphys:01977003808098300
Annianson, E. A. G., and Wall, S. N. (1974). On the kinetics of step-wise micelle association. J. Phys. Chem. 78, 1024–1030. doi:10.1021/j100603a016
Banani, S. F., Lee, H. O., Hyman, A. A., and Rosen, M. K. (2017). Biomolecular condensates: Organizers of cellular biochemistry. Nat. Rev. Mol. Cell. Biol. 18, 285–298. doi:10.1038/nrm.2017.7
Berry, J., Weber, S. C., Vaidya, N., Haataja, M., and Brangwynne, C. P. (2015). RNA transcription modulates phase transition-driven nuclear body assembly. Proc. Natl. Acad. Sci. U. S. A. 112, E5237–E5245. doi:10.1073/pnas.1509317112
Bonetti, A., Agostini, F., Suzuki, A. M., Hashimoto, K., Pascarella, G., Gimenez, J., et al. (2020). RADICL-seq identifies general and cell type–specific principles of genome-wide RNA-chromatin interactions. Nat. Commun. 11, 1018. doi:10.1038/s41467-020-14337-6
Borisov, O. V., and Halperin, A. (1995). Micelles of polysoaps. Langmuir 11, 2911–2919. doi:10.1021/la00008a012
Cai, Z., Cao, C., Ji, L., Ye, R., Wang, D., Xia, C., et al. (2020). RIC-seq for global in situ profiling of RNA-RNA spatial interactions. Nature 582, 432–437. doi:10.1038/s41586-020-2249-1
Chen, L. L., and Carmichael, G. G. (2009). Altered nuclear retention of mRNAs containing inverted repeats in human embryonic stem cells: Functional role of a nuclear noncoding RNA. Mol. Cell. 35, 467–478. doi:10.1016/j.molcel.2009.06.027
Chujo, T., and Hirose, T. (2017). Nuclear bodies built on architectural long noncoding RNAs: Unifying principles of their construction and function. Mol. Cells 40, 889–896. doi:10.14348/molcells.2017.0263
Chujo, T., Yamazaki, T., and Hirose, T. (2016). Architectural RNAs (arcRNAs): A class of long noncoding RNAs that function as the scaffold of nuclear bodies. Biochim. Biophys. Acta 1859, 139–146. doi:10.1016/j.bbagrm.2015.05.007
Clemson, C. M., Hutchinson, J. N., Sara, S. A., Ensminger, A. W., Fox, A. H., Chess, A., et al. (2009). An architectural role for a nuclear noncoding RNA: NEAT1 RNA is essential for the structure of paraspeckles. Mol. Cell. 33, 717–726. doi:10.1016/j.molcel.2009.01.026
Daoud, M., and Cotton, J. P. (1982). Star shaped polymers: A model for the conformation and its concentration dependence. J. Phys. Fr. 43, 531–538. doi:10.1051/jphys:01982004303053100
de Gennes, P. G. (1980). Conformations of polymers attached to an interface. Macromolecules 13, 1069–1075. doi:10.1021/ma60077a009
Fang, J., Ma, Q., Chu, C., Huang, B., Li, L., Cai, P., et al. (2019). PIRCh-seq: Functional classification of non-coding RNAs associated with distinct histone modifications. Genome Biol. 20, 292. doi:10.1186/s13059-019-1880-3
Hadgiivanova, R., Diamant, H., and Andelman, D. (2011). Kinetics of surfactant micellization: A free energy approach. J. Phys. Chem. B 115, 7268–7280. doi:10.1021/jp1073335
Halperin, A., and Alexander, S. (1989). Polymeric micelles: Their relaxation kinetics. Macromolecules 22, 2403–2412. doi:10.1021/ma00195a069
Hirose, T., Virnicchi, G., Tanigawa, A., Naganuma, T., Li, R., Kimura, H., et al. (2014). NEAT1 long noncoding RNA regulates transcription via protein sequestration within subnuclear bodies. Mol. Biol. Cell. 25, 169–183. doi:10.1091/mbc.E13-09-0558
Hu, S. B., Xiang, J. F., Li, X., Xu, Y., Xue, W., Huang, M., et al. (2015). Protein arginine methyltransferase CARM1 attenuates the paraspeckle-mediated nuclear retention of mRNAs containing IRAlus. Genes Dev. 29, 630–645. doi:10.1101/gad.257048.114
Imamura, K., Imamachi, N., Akizuki, G., Kumakura, M., Kawaguchi, A., Nagata, K., et al. (2014). Long noncoding RNA NEAT1-dependent SFPQ relocation from promoter region to paraspeckle mediates IL8 expression upon immune stimuli. Mol. Cell. 53, 393–406. doi:10.1016/j.molcel.2014.01.009
Li, X., Zhou, B., Chen, L., Gou, L. T., Li, H., Fu, X. D., et al. (2017). GRID-seq reveals the global RNA-chromatin interactome. Nat. Biotechnol. 35, 940–950. doi:10.1038/nbt.3968
Mai, Y., and Eisenberg, A. (2012). Self-assembly of block copolymers. Chem. Soc. Rev. 41, 5969–5985. doi:10.1039/c2cs35115c
Mangenot, S., Raspaud, E., Tribet, C., Belloni, L., and Livolant, F. (2002). Interactions between isolated nucleosome core particles: A tail-bridging effect? Eur. Phys. J. E 7, 221–231. doi:10.1140/epje/i200101151
Mao, Y. S., Sunwoo, H., Zhang, B., and Spector, D. L. (2011). Direct visualization of the co-transcriptional assembly of a nuclear body by noncoding RNAs. Nat. Cell. Biol. 13, 95–101. doi:10.1038/ncb2140
Monzen, M., Kawakatsu, T., and Doi, M. (2000). Micelle formation in triblock copolymer solutions. Comput. Theor. Polym. Sci. 10, 275–280. doi:10.1016/s1089-3156(99)00052-5
Moughton, A., Hillmyer, M. A., and Lodge, T. P. (2012). Multicompartment block polymer micelles. Macromolecules 45, 2–19. doi:10.1021/ma201865s
Mysona, J. A., McCormick, A. V., and Morse, D. C. (2019). Mechanism of micelle birth and death. Phys. Rev. Lett. 123, 038003. doi:10.1103/PhysRevLett.123.038003
Nakagawa, S., Yamazaki, T., and Hirose, T. (2018). Molecular dissection of nuclear paraspeckles: Towards understanding the emerging world of the RNP milieu. Open Biol. 8, 180150. doi:10.1098/rsob.180150
Netz, R. R., and Schick, M. (1998). Polymer brushes: From self-consistent field theory to classical theory. Macromolecules 31, 5105–5122. doi:10.1021/ma9717505
Oohashi, T., Inoue, K., and Nakamura, Y. (2014). Second and third virial coefficients of low-molecular-weight polyisoprene in 1, 4-dioxane. Polym. J. 46, 699–703. doi:10.1038/pj.2014.43
Palikyaras, S., and Papantonis, A. (2019). Modes of phase separation affecting chromatin regulation. Open Biol. 9, 190167. doi:10.1098/rsob.190167
Safran, S. A. (2003). Statistical thermodynamics of surfaces, interfaces, and membranes. USA: Westview Press, CO.
Sasaki, Y. T. F., Ideue, T., Sano, M., Mituyama, T., and Hirose, T. (2009). MENepsilon/beta noncoding RNAs are essential for structural integrity of nuclear paraspeckles. Proc. Natl. Acad. Sci. U. S. A. 106, 2525–2530. doi:10.1073/pnas.0807899106
Semenov, A. N. (1985). Contribution to the theory of microphase layering in block-copolymer melts. Sov. Phys. JETP 61, 733–742. http://www.jetp.ras.ru/cgi-bin/e/index/e/61/4/p733?a=list.
Semenov, A. N., Nyrkova, I. A., and Khokhlov, A. R. (1995). Polymers with strongly interacting Groups: Theory for nonspherical multiplets. Macromolecules 28, 7491–7500. doi:10.1021/ma00126a029
Shin, Y., and Brangwynne, C. P. (2017). Liquid phase condensation in cell physiology and disease. Science 357, eaaf4382. doi:10.1126/science.aaf4382
Souquere, S., Beauclair, G., Harper, F., Fox, A., and Pierron, G. (2010). Highly ordered spatial organization of the structural long noncoding Neat1 RNAs within paraspeckle nuclear bodies. Mol. Biol. Cell. 21, 4020–4027. doi:10.1091/mbc.E10-08-0690
Sridhar, B., Rivas-Astroza, M., Nguyen, T. C., Chen, W., Yan, Z., Cao, X., et al. (2017). Systematic mapping of RNA-chromatin interactions in vivo. Curr. Biol. 20, 602–609. doi:10.1016/j.cub.2017.01.011
Sunwoo, H., Dinger, M. E., Wilusz, J. E., Amaral, P. P., Mattick, J. S., Spector, D. L., et al. (2008). MEN epsilon/beta nuclear-retained non-coding RNAs are up-regulated upon muscle differentiation and are essential components of paraspeckles. Genome Res. 19, 347–359. doi:10.1101/gr.087775.108
Wang, Y., Hu, S. B., Wang, M. R., Yao, R. W., Wu, D., Yang, L., et al. (2018). Genome-wide screening of NEAT1 regulators reveals cross-regulation between paraspeckles and mitochondria. Nat. Cell. Biol. 20, 1145–1158. doi:10.1038/s41556-018-0204-2
West, J. A., Davis, C. P., Sunwoo, H., Simon, M. D., Sadreyev, R., Wang, P. I., et al. (2014). The long noncoding RNAs NEAT1 and MALAT1 bind active chromatin sites. Mol. Cell. 55, 791–802. doi:10.1016/j.molcel.2014.07.012
West, J. A., Mito, M., Kurosaka, S., Takumi, T., Tanegashima, C., Chujo, T., et al. (2016). Structural, super-resolution microscopy analysis of paraspeckle nuclear body organization. J. Cell. Biol. 214, 817–830. doi:10.1083/jcb.201601071
Yamamoto, T., Yamazaki, T., and Hirose, T. (2020). Phase separation driven by production of architectural RNA transcripts. Soft Matter 16, 4692–4698. doi:10.1039/c9sm02458a
Yamazaki, T., Nakagawa, S., and Hirose, T. (2020). Architectural RNAs for membraneless nuclear body formation. Cold Spring Harb. Symp. Quant. Biol. 84, 227–237. doi:10.1101/sqb.2019.84.039404
Yamazaki, T., Souquere, S., Chujo, T., Kobelke, S., Chong, Y. S., Fox, A. H., et al. (2018). Functional domains of NEAT1 architectural lncRNA induce paraspeckle assembly through phase separation. Mol. Cell. 70, 1038–1053. doi:10.1016/j.molcel.2018.05.019
Yamazaki, T., Yamamoto, T., Yoshino, H., Souquere, S., Nakagawa, S., Pierron, G., et al. (2021). Paraspeckles are constructed as block copolymer micelles. EMBO J. 40, e107270. doi:10.15252/embj.2020107270
Yap, K., Chung, T. H., and Makeyev, E. V. (2022). Hybridization-proximity labeling reveals spatially ordered interactions of nuclear RNA compartments. Mol. Cell. 82, 463–478.e11. doi:10.1016/j.molcel.2021.10.009
Zhulina, E. B., Adam, M., LaRue, I., Sheiko, S. S., and Rubinstein, M. (2005). Diblock copolymer micelles in a dilute solution. Macromolecules 38, 5330–5351. doi:10.1021/ma048102n
Keywords: paraspeckle, NEAT1_2, architectural RNA, micellization, transcription
Citation: Yamamoto T, Yamazaki T and Hirose T (2022) Triblock copolymer micelle model of spherical paraspeckles. Front. Mol. Biosci. 9:925058. doi: 10.3389/fmolb.2022.925058
Received: 21 April 2022; Accepted: 11 July 2022;
Published: 22 August 2022.
Edited by:
Silvia ML Barabino, University of Milano-Bicocca, ItalyReviewed by:
Abbul Bashar Khan, Jamia Millia Islamia, IndiaLeonard Atanase, Apollonia University, Romania
Copyright © 2022 Yamamoto, Yamazaki and Hirose. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Tetsuya Yamamoto, dHlhbWFtb3RvQGljcmVkZC5ob2t1ZGFpLmFjLmpw
†These authors contributed equally to this work
 Tetsuya Yamamoto
Tetsuya Yamamoto Tomohiro Yamazaki
Tomohiro Yamazaki Tetsuro Hirose3,4
Tetsuro Hirose3,4