- 1Department of Electrical and Computer Engineering, The University of Texas at Austin, Austin, TX, United States
- 2Sandia National Laboratories, Albuquerque, NM, United States
- 3Sandia National Labs, Livemore, CA, United States
Bayesian neural networks (BNNs) combine the generalizability of deep neural networks (DNNs) with a rigorous quantification of predictive uncertainty, which mitigates overfitting and makes them valuable for high-reliability or safety-critical applications. However, the probabilistic nature of BNNs makes them more computationally intensive on digital hardware and so far, less directly amenable to acceleration by analog in-memory computing as compared to DNNs. This work exploits a novel spintronic bit cell that efficiently and compactly implements Gaussian-distributed BNN values. Specifically, the bit cell combines a tunable stochastic magnetic tunnel junction (MTJ) encoding the trained standard deviation and a multi-bit domain-wall MTJ device independently encoding the trained mean. The two devices can be integrated within the same array, enabling highly efficient, fully analog, probabilistic matrix-vector multiplications. We use micromagnetics simulations as the basis of a system-level model of the spintronic BNN accelerator, demonstrating that our design yields accurate, well-calibrated uncertainty estimates for both classification and regression problems and matches software BNN performance. This result paves the way to spintronic in-memory computing systems implementing trusted neural networks at a modest energy budget.
1 Introduction
The powerful ability of deep neural networks (DNNs) to generalize has driven their wide proliferation in the last decade to many applications. However, particularly in applications where the cost of a wrong prediction is high, there is a strong desire for algorithms that can reliably quantify the confidence in their predictions (Jiang et al., 2018). Bayesian neural networks (BNNs) can provide the generalizability of DNNs, while also enabling rigorous uncertainty estimates by encoding their parameters as probability distributions learned through Bayes’ theorem such that predictions sample trained distributions (MacKay, 1992). Probabilistic weights can also be viewed as an efficient form of model ensembling, reducing overfitting (Jospin et al., 2022). In spite of this, the probabilistic nature of BNNs makes them slower and more power-intensive to deploy in conventional hardware, due to the large number of random number generation operations required (Cai et al., 2018a). Some proposals to increase the energy efficiency of digital BNNs via pipelining have been made (Cai et al., 2018b), but ultimately these approaches hit an efficiency wall due to the serial nature of random number generation. In contrast, emerging memory devices pose an attractive set of possible options for true random number generators (TRNGs) at a less than 1 pJ/bit energy footprint (Carboni and Ielmini, 2019).
In recent years, in-memory computing has also emerged to enable orders-of-magnitude more efficient processing of data-intensive DNN algorithms. These systems alleviate the memory wall problem in conventional architectures, while also leveraging the efficiency and parallelism of analog computation (Sebastian et al., 2020; Xiao et al., 2020). A variety of computational memory devices have been proposed as artificial synapses for DNNs: resistive random access memories (ReRAM) (Li et al., 2018; Yao et al., 2020), phase change memories (Barbera et al., 2018; Joshi et al., 2020), electrochemical memories (Gkoupidenis et al., 2015; Lin et al., 2016; Li et al., 2021; Kireev et al., 2022), designer ionic/electronic thin films (Robinson et al., 2022), magnetic memories (Jung et al., 2022), and others. However, these synaptic devices cannot directly implement BNN weights, which are not static but are sampled from trained probability distributions.
Spintronic devices possess properties that make them promising for data storage, in-memory computing for DNNs, and probabilistic computing. Spintronic devices typically use the magnetic tunnel junction (MTJ) as the building block (Ikeda et al., 2010) and have demonstrated high energy efficiency, scalability, and endurance (Xue et al., 2018; Grollier et al., 2020; Raymenants et al., 2021). Magnetic spin textures such as domain walls (Akinola et al., 2019; Siddiqui et al., 2020; Leonard et al., 2021; Brigner et al., 2022) and skyrmions (Jadaun et al., 2020; Song et al., 2020) can implement complex, tunable behaviors that can realize higher-order neurons and synapses. Spintronic devices also have unique intrinsic stochastic properties (Sengupta et al., 2016; Srinivasan et al., 2016; Liu et al., 2021). Recently, stochasticity in MTJs has been experimentally demonstrated to produce conductance noise due to thermal fluctuations in magnetization experienced by the free ferromagnetic layer. Importantly, the distribution of conductance noise is dictated by the magnetic energy landscape, which can be manipulated using a variety of methods including magnetic field (Hayakawa et al., 2021), spin transfer torque (Borders et al., 2019), spin orbit torque (Ostwal and Appenzeller, 2019), and voltage-controlled magnetic anisotropy (VCMA) (Cai et al., 2019; Safranski et al., 2021). As a result, the tunable random bitstream readout of stochastic MTJs can be used to implement Boltzmann machines for probabilistic computing (Kaiser et al., 2022). While proposals for spin-based BNNs have been made (Yang et al., 2020; Lu et al., 2022), they relied upon either streaming generated RNGs from the periphery into each array or using digital circuitry to fully compose the weight used in the sampling step. These decisions majorly reduce the efficiency of a hardware spintronic BNN design by increasing the energy cost of the basic sampling operation. Lastly, ReRAM devices have also been used to implement probabilistic weights (Lin et al., 2019; Malhotra et al., 2020; Dalgaty et al., 2021), but required many devices per weight since the weight’s mean and standard deviation cannot be independently encoded at the device level.
In this work, we introduce a novel array design for efficient probabilistic matrix-vector multiplication (MVM) sample steps with the inference operation fully supported by in-situ analog spintronic device electrical operation. We target BNNs that are trained using the variational inference method to represent each weight as a normal distribution with a trained mean (μ) and standard deviation (σ). The BNNs are deployed on a spintronic system where each weight is encoded by a domain-wall memory with multi-bit precision in μ, and a stochastic spintronic memory that independently encodes σ with multi-bit precision. The devices are directly integrated in the same array, and are used together in a probabilistic MVM. The accuracy and quality of uncertainty predictions from the proposed hardware are evaluated using realistic in-memory computing simulations, based on stochastic device properties obtained from micromagnetic simulations. We show that the proposed spintronic implementations of BNNs give accurate, well-calibrated uncertainty estimates for complex classification and regression problems that match software BNN implementations, and are superior to comparable DNNs. These BNN predictions require 10–100× less energy than conventional hardware by efficiently combining the RNG and MVM operations in the analog domain.
2 Artificial synapses for encoding probability distributions
2.1 Bayes-magnetic tunnel junction noise encoder
To encode a BNN’s weight probability distributions, our fully spintronic Bayesian artificial synapse compactly integrates a tunable noise source with a programmable artificial synapse that encodes the mean component of the weight. The tuning range of the conductance noise should ideally cover a large range in order to encode both wide (highly noisy) and narrow (nearly deterministic) weight probability distributions. The proposed Bayes-MTJ utilizes the physical stochasticity and voltage controllability of magnetic materials to realize this functionality, and further uses magneto-ionics to ensure that the encoded noise properties are non-volatile.
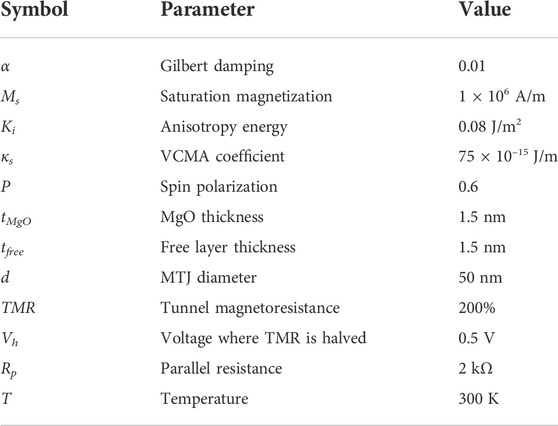
The Bayes-MTJ structure is shown in Figure 1A, and based on a cylindrical in-plane MTJ. Both of the in-plane axes (i.e., the x-y plane) are easy axes for the free layer’s magnetization, and thus thermal fluctuations can readily cause random changes in the free layer’s in-plane magnetization. These fluctuations generate noise in the conductance across the MTJ, and this noise fully spans the range between the maximum conductance state (free and reference layers parallel) and the minimum conductance state (free and reference layers anti-parallel). Experiments validating this effect in cylindrical in-plane magnetic systems have been shown previously (Debashis et al., 2016). Since the noise always spans the full conductance range of the device, the magnitude of conductance noise can be controlled by modulating the MTJ’s tunnel magnetoresistance (TMR) ratio via the voltage-controlled magnetic anisotropy (VCMA) effect. Modulation of the TMR ratio using an applied voltage across the oxide layer has has been demonstrated previously, both experimentally and theoretically (Shiota et al., 2011; Li et al., 2014; Zhang et al., 2020; Krizakova et al., 2021).
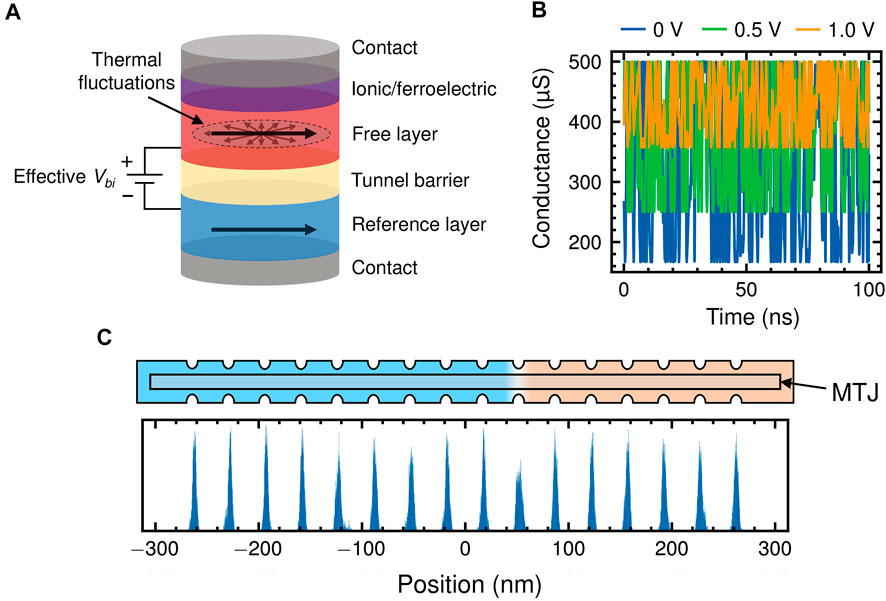
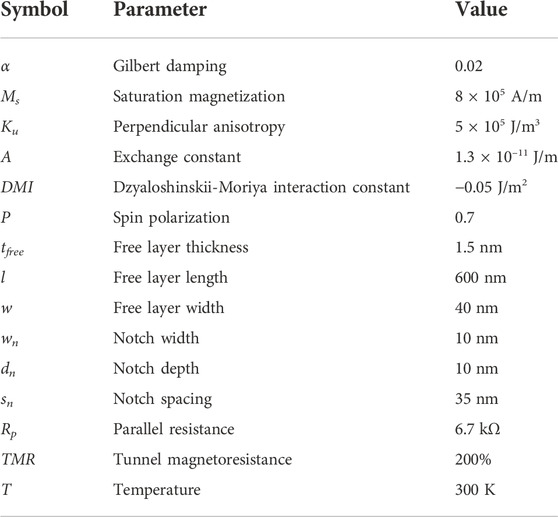
FIGURE 1. (A) Structure of the Bayes-MTJ. Thermal fluctuations cause random changes in the in-plane magnetization of the free layer that manifest as noise in the tunnel magnetoresistance, (B) Simulated noise in the Bayes-MTJ conductance. The applied voltage modulates the TMR and the magnitude of the noise via the VCMA effect. (C) Structure of a notched DW-MTJ synapse. Bottom shows the distribution of DW position over 25 ns after being initialized in each of 16 notches.
An externally applied voltage is not an efficient implementation of tunable noise because each device encodes a unique probability distribution and thus would require an independent VCMA voltage during an inference operation. However, there are at least two ways that non-volatile encoding of the noise magnitude can be accomplished. Firstly, a ferroelectric or multiferroic layer can be introduced to the stack to induce a polarization field at the interface, implementing an effective electric field that can be modulated to an appropriate state using applied voltage (Chen et al., 2019; Fang et al., 2019; Wang et al., 2021). Another option is to introduce an ion-conductive layer to reversibly modulate the oxidation state of the free layer. Ion migration is induced using an electric field, resulting in non-volatile changes in magnetic properties such as the magnetic anisotropy (Bauer et al., 2015; Baldrati et al., 2017; Tan et al., 2019; Xue et al., 2019) and magnetoresistance (Wei et al., 2019; Nichterwitz et al., 2020; Long et al., 2021). Oxidation of the free layer has been shown to reduce the TMR of MTJ stacks (Joo et al., 2012). In this paper, these effects will be approximated using an effective built-in voltage Vbi across the MgO tunnel barrier that is set during programming.
The Bayes-MTJ can be represented by a macrospin Landau-Lifshitz-Gilbert (LLG) model described as follows (Shiota et al., 2011):
where
where
The VCMA effect modulates the anisotropy field as well as the resistance when a voltage is applied. The anisotropy field is modeled with the following:
where Ki is the anisotropy energy, tfree and tox are the thickness of the free layer and oxide layer respectively, κs is the VCMA coefficient, and Vbi is the built-in voltage. The resistance of the MTJ can be expressed as:
where Rp is resistance when the magnetizations of free and reference layers are parallel, Vh is the voltage at which the TMR ratio is halved, and θ and ϕ are the polar coordinates for the unit vector magnetization of the free layer.
In Figure 1B, the conductance of the Bayes-MTJ device is sampled for 100 ns at a VCMA voltage of 0, 0.5, and 1 V. In each case, the conductance varies randomly and continuously between the fully parallel and fully anti-parallel states of the MTJ. Increasing the VCMA voltage decreases the TMR ratio, which narrows the range of allowed output conductance and thus reduces the magnitude of conductance noise. This device acts as a tunable noise source that is used by the cell design in Section 2.3 to encode the standard deviation of a probability distribution.
2.2 Domain wall static weight encoder
To encode the static or mean value of a weight probability distribution, we use a domain wall-magnetic tunnel junction (DW-MTJ) artificial synapse (Leonard et al., 2021; Liu et al., 2021). This three-terminal device has previously been shown to have extremely low read and write noise, an important feature for the precise encoding of static weights. The DW-MTJ device contains a ferromagnetic rectangular wire that produces a magnetic domain wall (DW). The wire lies underneath a tunnel barrier and a reference magnetic layer to form an MTJ. The DW-MTJ can encode multiple conductance states based on the DW position, which controls the proportion of the free layer that is parallel or anti-parallel to the reference layer. Notches are also lithographically defined along the edges of the wire to provide linearly spaced, repeatable states and reduce drift of the DW due to thermal fluctuations. A write operation is performed by passing current in the direction of the desired DW motion, in-plane to the stack, while a read operation is performed by measuring resistance perpendicular to the stack (through the tunnel barrier). DW motion is mediated by spin transfer torque (STT) and an additional spin orbit torque (SOT) component provided by the heavy metal layer underneath the free layer. A top-down schematic of the device is shown in Figure 1C.
To model the more complicated physical dynamics of the DW in the free layer, the MuMax3 micromagnetics solver is used (Vansteenkiste et al., 2014). The finite temperature LLG equation described previously is solved for each timestep for a multi-spin system. The constants used for the perpendicular magnetic anisotropy CoFeB/MgO/CoFeB system in this simulation are shown in Table 2. To characterize the intrinsic noise of a DW-MTJ, a DW is created at a notch within the track and the position of the DW is sampled over 25 ns at 300 K. This is repeated for all 16 levels to characterize the variation in DW position, shown in Figure 1C. On average, the DW-MTJ’s conductance noise is approximately 0.335% of the full conductance range dictated by its TMR.
2.3 Probabilistic in-memory matrix-vector multiplication
We propose a novel cell design shown in Figure 2A to combine the Bayes-MTJ tunable noise source with a DW-MTJ static weight, collectively encoding the trained weight probability distributions in BNNs. The cell uses the difference in conductance of two DW-MTJs to represent both positive and negative weight means. All three devices are connected on one end to the same metal column so that their output currents add. The fabrication challenges of simultaneously integrating both types of devices are important to note. Since the proposed cell centers around the use of the in-plane magnetization Bayes-MTJ, one solution is to use in-plane magnetization DW-MTJ devices (Currivan-Incorvia et al., 2016) to enable monolithic integration of both devices on the same material stack. However, when scaling and energy efficiency is a concern, out-of-plane magnetic systems are typically desired for the DW-MTJ device. This is because in-plane domain walls are generally wider and more sensitive to track roughness (Catalan et al., 2012), limiting scaling in contrast to out-of-plane systems. In this case, heterogenous integration of two different magnetic material stacks is necessary. One solution is for different stacks to be grown in different areas of the wafer for integration during the growth phase (Chavent et al., 2020). Another possibility is to use flip chip integration, allowing devices to be fabricated on two different magnetic substrates before being bonded together for final integration (Lau, 2016).
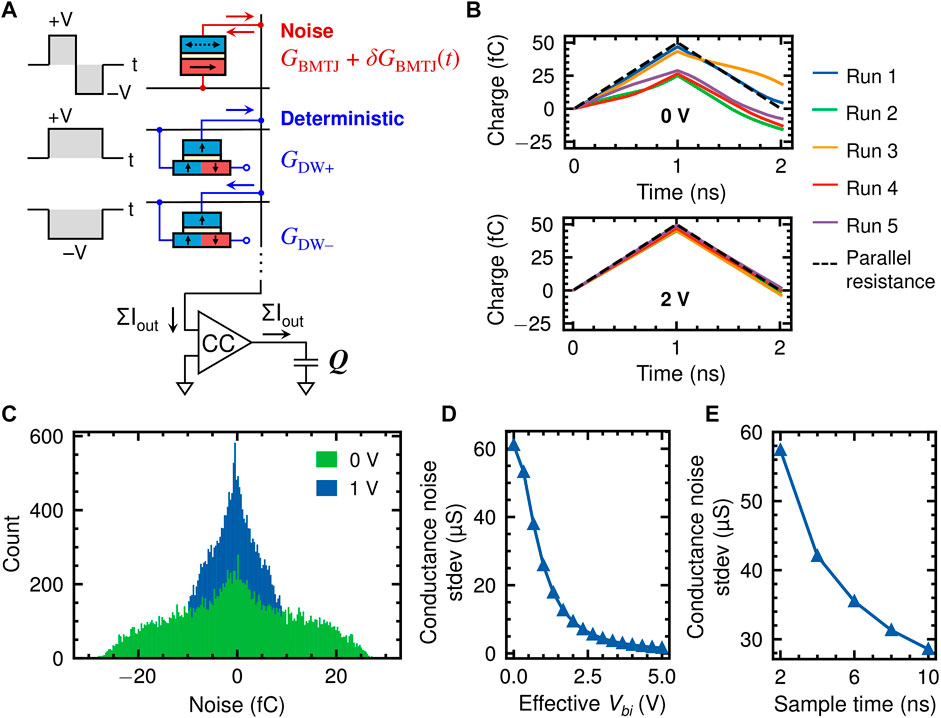
FIGURE 2. (A) Probabilistic cell with one Bayes-MTJ and two DW-MTJ devices to encode a programmable Gaussian distribution. The third DW-MTJ terminal is used only during programming. Currents on a column are integrated on a capacitor. (B) Charge on the capacitor Q vs. time due to the Bayes-MTJ current at two values of Vbi. Each run is an independent read using a 2 ns bipolar volage pulse. (C) Distribution of the final capacitor charge Q (T =2ns) induced by noise in the Bayes-MTJ, at two values of Vbi with 20,000 samples each. (D) Standard deviation of Q (T =2ns) vs. Vbi on the Bayes-MTJ, (E) Q(T) vs. the total pulse length T at Vbi =0 V.
To realize independent control of the weight means by the DW-MTJs and the weight standard deviations by the Bayes-MTJ, the time-averaged conductance of the Bayes-MTJ must be canceled out so that the device contributes only zero-centered random noise. To accomplish this, a bipolar volage pulse is applied to the Bayes-MTJ device consisting of two pulses of equal duration and amplitude but opposite polarity. The resulting bipolar current is integrated over the full duration on a capacitor at the bottom of a column, using a current conveyor (CC) circuit. The CC acts as a current buffer with large output resistance while maintaining a virtual ground on the column (Marinella et al., 2018). The time-averaged conductance of the Bayes MTJ contributes equal but opposite currents during the two halves of the pulse, and gets canceled out in the final capacitor charge so that only the noise contribution remains. An important advantage of this approach is that the cancellation does not depend on the value of the time-averaged conductance, so that device-to-device MTJ variations can be tolerated.
Figure 2B shows the accumulated charge from the output of a Bayes-MTJ alone during a read pulse with length tread = 2 ns, for five independent pulses. The dashed black line depicts the output of a deterministic resistor with Rp = 2 kΩ. Each run with a Bayes-MTJ is an independent sample from the encoded weight probability distribution. There is a clear difference in the noise distribution at different applied voltage, where the final accumulated charge has a much tighter distribution around 0C when 2 V is applied due to the reduced TMR. Figure 2C shows the distribution of the charge noise after 2 ns for two effective Vbi, with 20,000 samples each. The distribution is not Gaussian, but can effectively approximate BNNs trained with normally distributed weights, as shown in the next section.
The integrated charge Q from a Bayes-MTJ can then be converted to an effective conductance noise via δGBMTJ = Q/Vread tread, where Vread is the read voltage (note that Q scales linearly with Vread so δGBMTJ is independent of Vread). The dependence of the conductance noise standard deviation on built-in voltage is shown in Figure 2D, for tread = 2 ns. The range of modulation between maximum and minimum noise standard deviation is 38.9:1. Figure 2E shows how the noise standard deviation depends on the pulse length at 0 V built-in voltage. A 2 ns sample time is chosen to maximize the cycle-to-cycle fluctuations in capacitor charge. A longer integration time averages out the effective conductance noise.
The two DW-MTJs are driven by unipolar pulses of the same amplitude and total duration as the bipolar pulse: one positive and one negative, so that their currents are subtracted. Currents from multiple cells of this type can be summed on the same column, and the same read pulses can be broadcast to a row of cells. This implements a fully analog, in-memory MVM where every matrix element is sampled simultaneously from an independent probability distribution. The amplitude of the three pulses applied to each row is proportional to the corresponding element of the input vector. The integrated charge can be read out as a capacitor voltage that represents the final probabilistic matrix-vector product.
3 Uncertainty quantification with the Bayes-magnetic tunnel junction
3.1 Bayesian neural networks
A Bayesian neural network uses probabilistic weights to make predictions with a quantified uncertainty. Though there are other ways to quantify uncertainty, a BNN produces well-calibrated uncertainties by learning the weight probability distributions using Bayes’ theorem (MacKay, 1992):
During the training phase, computing the right-hand side of this equation is computationally expensive. Furthermore, the posterior distribution for a weight can be an arbitrarily complex distribution that is difficult to implement in analog hardware. For these reasons, we approximate Bayes’ theorem using variational inference (VI) (Blei et al., 2017). VI is used to constrain the distribution for each weight to be a Gaussian distribution
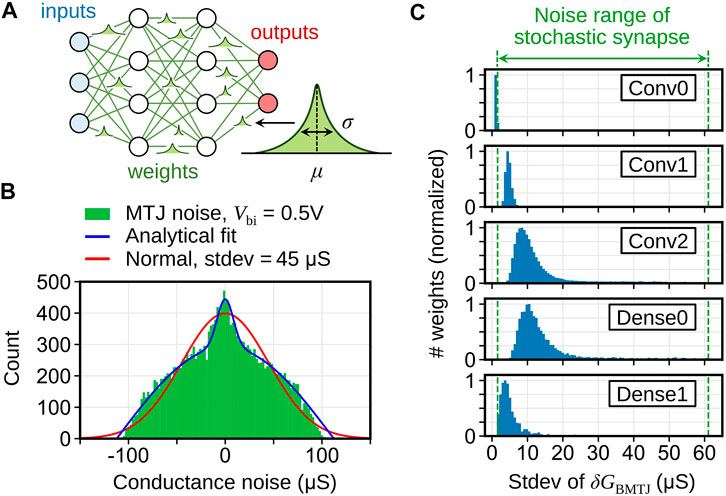
FIGURE 3. (A) Schematic of a Bayesian neural network where each weight follows a Gaussian distribution
3.2 Mapping Bayesian neural networks to Bayes-magnetic tunnel junction arrays
For each probabilistic weight in the trained BNNs, the mean μ is mapped to the difference in conductance (GDW+ − GDW-) of a DW-MTJ device pair. The standard deviation σ is encoded in the effective conductance noise of the Bayes-MTJ tunable noise source, defined in Section 2.3. The simulated Bayes-MTJ noise distribution in Figure 2C does not exactly follow a Gaussian distribution. The Bayes-MTJ noise distribution is zero-symmetric, strictly bounded, and has the same shape regardless of Vbi, which controls the width of the distribution. To compactly model this distribution for large arrays, the following analytical distribution is used, up to a normalization constant:
where A = 0.9298 and B = 0.0367 are fitting parameters, and x is a random variable in the range (−1, +1). For a desired value of σ, a random value x is sampled from this distribution and is converted to a conductance fluctuation by:
where 61.06 µS is the maximum Bayes-MTJ effective conductance noise at Vbi = 0V (using Vread = 0.1 V, tread = 2 ns, and Rp = 2 kΩ). The constant 2.379 accounts for the difference in the standard deviation between P(x) and the standard normal
Figure 3B shows the simulated Bayes-MTJ noise distribution at a voltage of 0.5 V alongside its analytical distribution (blue) and a Gaussian distribution with the same standard deviation (red). Figure 3C shows the distribution of σ, expressed in terms of the target Bayes-MTJ conductance standard deviation, for a five-layer Fashion MNIST BNN to be described in Section 3.3.1. The range between the green dashed lines represents the σ values that can be encoded by the Bayes-MTJ having Vbi between 0 V and 5V, which will be the range used through the rest of the paper unless otherwise stated. Excluding the first layer, the vast majority (99.5%) of the σ values in the BNN can be encoded by the Bayes-MTJ, with outliers clipped to the nearest value inside the range. The first layer’s σ values are almost entirely zero, so it is implemented by a standard array where no read pulses are delivered to the Bayes-MTJ rows.
For the spintronic hardware simulations of BNNs in the following sections, we extend the CrossSim modeling framework (Xiao et al., 2022) for analog accelerators to model in-memory computations with tunable stochastic elements. The Bayes-MTJ is modeled using the analytical distribution above. The μ values were linearly quantized to be compatible with 4 bits of precision in each DW-MTJ conductance (16 notches), and the σ values were nonlinearly quantized to support 4 bits of precision in the VCMA voltage.
3.3 Quantifying classification uncertainty
For classification problems, a DNN typically has a softmax output layer, which can be interpreted as a vector of probabilities
The uncertainty of a BNN is based on sampling N predictions, each yielding a probability vector
where
Aleatoric uncertainty Haleatoric originates from randomness or ambiguity inherent in the data, and the epistemic uncertainty Hepistemic originates from the model’s lack of knowledge (Hüllermeier and Waegeman, 2021). Aleatoric uncertainty tends to be high when the input data is noisy, while epistemic uncertainty tends to be high if the input is out of distribution, i.e., has properties that are distinct from the training data. Epistemic uncertainty is particularly useful in enabling the neural network to make safe extrapolations to out-of-distribution data (Kendall and Gal, 2017). Thus, the BNN offers two potential advantages over the DNN baseline: 1) better calibrated uncertainty estimates, and 2) meaningful decomposition of uncertainty.
The loss function used for variational inference is a sum of the prediction’s categorical cross entropy and the Kullback-Leibler (KL) divergence of each posterior distribution with the prior, aggregated over all the weights. The KL divergence term is responsible for approximating Bayes’ theorem (Blundell et al., 2015), while for the DNN baseline only the categorical cross entropy loss is used.
3.3.1 Fashion MNIST experiments
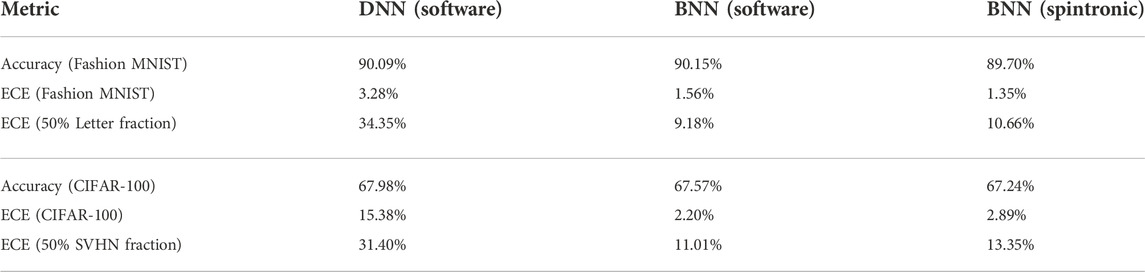
A DNN and a BNN were trained on the Fashion MNIST dataset (Xiao et al., 2017) with ten classes, both using the LeNet-5 architecture (Lecun et al., 1998), but with sigmoids replaced by Rectified Linear Unit (ReLU) activations and average pooling replaced by max pooling. The DNN has 61.7 K parameters and the BNN has 123.2 K parameters, since each weight has two parameters (μ and σ). The bias weights in the BNN are left deterministic so that they can be implemented digitally within the accelerator. The same optimizer (Adam), number of epochs (20), and learning rate (10–3) are used for both models. Figure 3C shows the distribution of trained σ values in the BNN for each layer.
First, both networks were evaluated on the Fashion MNIST test set (10,000 images) and the EMNIST-Letters test set (10,000 images) of handwritten letters (Cohen et al., 2017), representing out-of-distribution data where the network should predict high uncertainty. The BNN was evaluated both in software and simulated on the spintronic hardware, and was sampled 100 times unless otherwise specified. Figures 4A,B show that all cases predict low uncertainty on Fashion MNIST and higher uncertainty on EMNIST-Letters. However, the DNN still has a prominent peak at low uncertainty for letters, whereas the BNN has a much higher uncertainty overall, as expected.
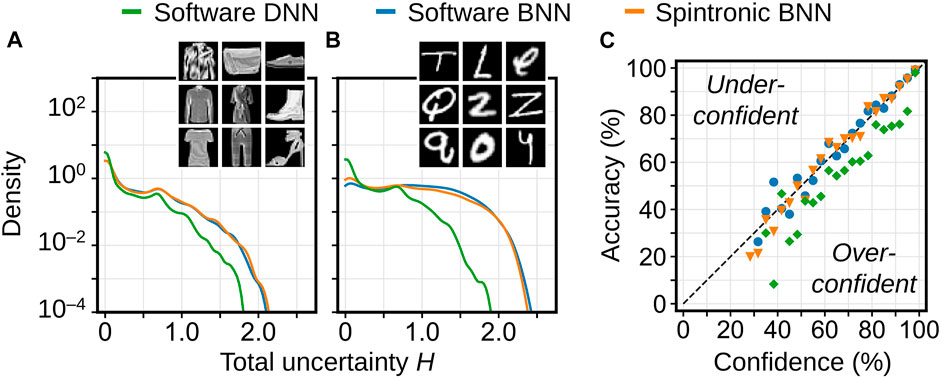
FIGURE 4. Distribution of predicted uncertainty (kernel density estimation) by the software DNN, software BNN, and BNN simulated on spintronic hardware, on (A) the Fashion MNIST test set, and (B) the EMNIST-Letters test set. Both the DNN and BNN were trained on Fashion MNIST. Uncertainties are in units of information entropy. (C) Uncertainty calibration curve of the three cases on the Fashion MNIST test set. Note that most of the predictions lie in the highest confidence bands.
To more quantitatively assess the quality of these uncertainty estimates, a calibration curve (Guo et al., 2017) is used, shown in Figure 4C. For each network, the Fashion MNIST test set is split into bins based on the confidence of the prediction. If the uncertainty is well calibrated, the confidence should match the accuracy of the images in the bin: e.g., for images where the network has 50% confidence, it should ideally be correct 50% of the time. Figure 4C shows that the BNN is better calibrated than the DNN, which is over-confident, and that the spintronic BNN closely implements the software BNN despite the limited noise range, limited noise precision, and the difference in distribution shape. An overall metric for the quality of the uncertain estimate is the expected calibration error (Guo et al., 2017):
where
We further probe the differences between the BNN and DNN by experimenting with images that are linear superpositions of Fashion MNIST clothing items and EMNIST letters. This is parameterized by the letter fraction, where 0% is a Fashion MNIST image and 100% is a letter image, as shown in Figure 5A. Figure 5B shows the ECE vs. letter fraction, where 1,000 random clothing-letter pairs were generated for each letter fraction from 0% to 90%, separated by 10% intervals. The label for each image is the original Fashion MNIST label. The ECE is less meaningful at very high letter fractions where the image is very weakly related to its label. The BNNs, including the spintronic implementation, have lower ECE at all values of the letter fraction, indicating better calibrated uncertainties. Figure 5C shows how the spintronic hardware’s ECE changes as the noise On/Off ratio of the Bayes-MTJ is decreased below what can be achieved with Vbi = 5 V (Figure 2D). A ratio larger than 10 can accurately capture the small σ values in the network.
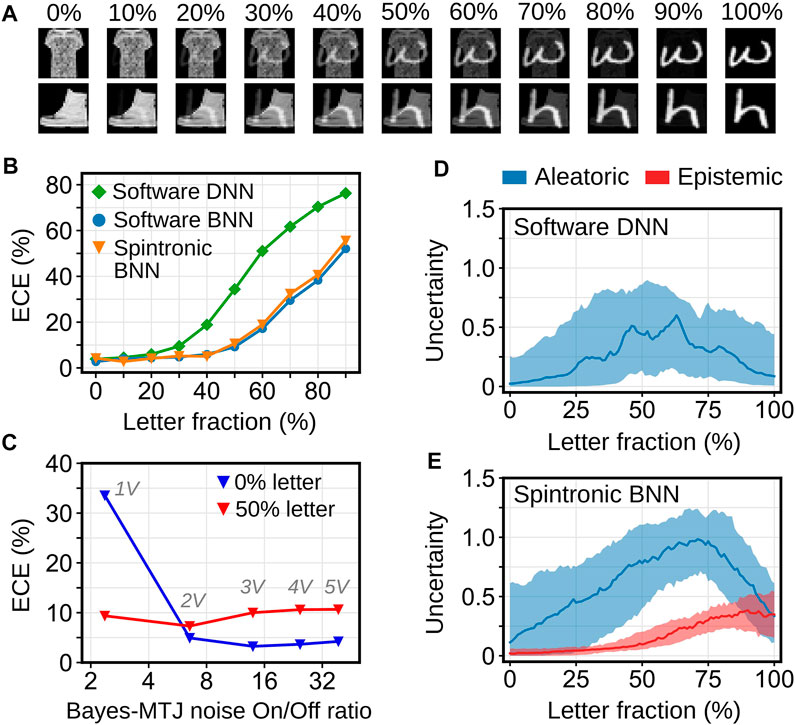
FIGURE 5. (A) Continuous transformation from Fashion MNIST to EMNIST-Letters images by varying the letter fraction, (B) ECE vs. letter fraction for the software DNN, software BNN, and spintronic implementation of the BNN, (C) Dependence of the ECE on the Bayes-MTJ noise On/Off ratio (δGBMTJ,max/δGBMTJ,min). The maximum value of Vbi needed to achieve the On/Off ratio is labeled. (D) Uncertainty vs. letter fraction predicted by the DNN, (E) Uncertainty vs. letter fraction predicted by the BNN, decomposed into aleatoric and epistemic uncertainty components. Uncertainties are in units of information entropy and the shaded regions contain the middle 50% of 100 FMNIST-to-Letters transformations tested.
Finally, Figures 5D,E compare the decomposed uncertainty components of the DNN and spintronic BNN, respectively. The DNN baseline is deterministic, so it cannot predict a non-zero epistemic uncertainty. For both models, the aleatoric uncertainty peaks at an intermediate letter fraction, though this is more evident in the BNN. This is hypothesized to be due to the fact that images with near-equal mixtures of letters and clothing items have the greatest number of overlapping spatial features and thus appear more noisy. Meanwhile, the BNN’s predicted epistemic uncertainty increases nearly monotonically with letter fraction, which matches the fact that a higher letter fraction means that the image is farther away from the training distribution. The epistemic uncertainty is important for increasing the BNN’s uncertainty for images with large letter fraction where the original Fashion MNIST label is harder to predict.
3.3.2 CIFAR-100 experiments
To demonstrate the feasibility of the spintronic BNN accelerator on a more complex problem and a larger-scale algorithm, deep residual networks (ResNets) (He et al., 2016) were trained on the CIFAR-100 image classification dataset with 100 classes (Krizhevsky and Hinton, 2009). The ResNet topology in Figure 6A was used to train both a DNN and a BNN having 1.25 and 2.50 M parameters, respectively. To improve accuracy, both networks were trained with data augmentation (random horizontal flips, random horizontal shifts ≤10%, and random vertical shifts ≤10%) applied to the training images. Both networks were trained for 100 epochs with the same optimizer (Adam) and learning rates. Figure 6B shows the distribution of σ values in the BNN for each layer. To facilitate mapping to the Bayes-MTJ, a maximum value constraint was imposed on σ during training.
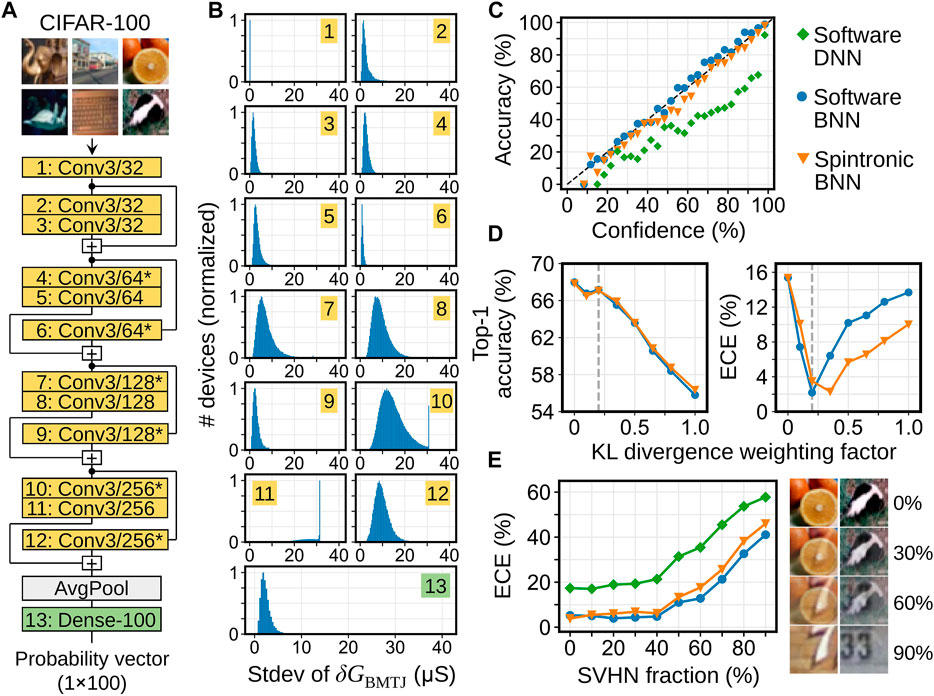
FIGURE 6. (A) ResNet topology for CIFAR-100 image classification, used for both the DNN and BNN. An asterisk denotes a stride of two. Convolutions other than layers 6, 9, and 12 are followed by batch normalization. (B) Distribution of trained σ values for each layer of the ResNet, mapped to Bayes-MTJ conductance noise. (C) Comparison of uncertainty calibration curves for the ResNet DNN, BNN, and BNN simulated on spintronic hardware, for the CIFAR-100 test set. (D) Accuracy and ECE on the CIFAR-100 test set for various BNNs trained with different weighting factors on the KL divergence term of the loss function. Each network is evaluated both in software and simulated on the spintronic accelerator. (E) ECE vs SVHN fraction for CIFAR-100 images continuously mixed with SVHN images. Results in (C,E) used a BNN with a KL divergence weighting factor of 0.2 and 100 samples per prediction. Results in (D) are based on 25 samples per prediction.
The spintronic hardware implementation of the BNN used the same assumptions as for Fashion MNIST, except that we represent μ values with 8 bits of precision using bit slicing (Xiao et al., 2020): each μ value uses two pairs of DW-MTJ devices with 16 notches per device. One pair encodes the higher 4 bits and is integrated with the Bayes-MTJ that encodes the 4-bit σ value. The other pair encodes the lower 4 bits in a separate array where the Bayes-MTJ rows are left unused. The Bayes-MTJ is not used for the first convolution layer where most of the σ values are near zero. To improve energy efficiency, the batch normalization operation is folded into the convolution μ and σ values (Jacob et al., 2018).
The ECEs of the trained ResNets on the CIFAR-100 test set (Table 3) are larger than for Fashion MNIST due to the greater complexity of the task: correct predictions with high confidence were less dominant in CIFAR-100. The BNN reduces the ECE by 7×, at a cost of just 0.41% in top-1 accuracy. Figure 6C shows the calibration curves. The spintronic implementation of the BNN tends to be more confident than the software BNN. We hypothesize that this is because the analog accelerator resamples the Bayes-MTJ noise on every probabilistic MVM, and thus each instance of weight re-use in a convolution layer independently resamples the posterior weight distributions. Averaged across the ResNet, a given weight is re-sampled 51× per image in the analog accelerator. By contrast, the software (TensorFlow Proability) implementation only resamples weights once per batch of 32 images to reduce RNG overheads. The much more frequent resampling allows for greater cancellation of the noise in the subsequent layer, reducing the overall variance in the network’s predictions and leading to greater confidence.
Figure 6D shows that by varying the weighting factor on the KL divergence loss term relative to categorical cross entropy, BNNs can be trained at different points along the trade-off between accuracy and ECE. The ECE does not directly track this hyperparameter but rather has a minimum; the BNN is over-confident to the left of the minimum and under-confident to the right. The ECE minimum lies further to the right for the spintronic implementation. This is because the analog hardware is slightly more confident, so it tends to be well-calibrated where the software BNN is slightly under-confident.
As with Fashion MNIST, uncertainties far away from the training set were evaluated by continuously blending CIFAR-100 images with a different dataset: the Street View House Numbers (SVHN) dataset (Netzer et al., 2011), which uses 32 × 32 RGB images similar to CIFAR-100. The ECE vs SVHN fraction is shown in Figure 6E. The ResNet BNN and its spintronic hardware implementation produce significantly better-calibrated uncertainties on out-of-distribution data than a conventional classification ResNet.
3.4 Quantifying regression uncertainty
The proposed spintronic BNN accelerator can also be used to efficiently quantify uncertainty with regression models, where a continuous quantity is predicted rather than a discrete class. We use the Auto MPG dataset (Quinlan, 1993), where the task is to predict an automobile’s fuel efficiency given eight other attributes of the car which can be continuous (e.g., horsepower, weight) or discrete (e.g., model year, number of cylinders). The dataset of 398 cars is divided into 255 training, 64 validation, and 78 test examples. A simple BNN is trained for 500 epochs using VI with three dense layers that have 128, 32, and 1 output, respectively. Unlike the classification case, a negative log-likelihood loss function is used that assumes a normal distribution for the fuel efficiency y:
where ypred is the predicted fuel efficiency, ytrue is the true efficiency, and σ0 is a hyperparameter that is used to calibrate the estimated uncertainty of the model. For this network topology, which produces point predictions, the corresponding DNN does not provide any uncertainty estimate because the output has no probabilistic interpretation.
The model’s predictive uncertainty is obtained by defining confidence intervals (CIs) that contain some percentage of the 1000 BNN point predictions for each input. Figure 7A shows the mean prediction and 90% CIs for the examples in the test set, where blue indicates that the true fuel efficiency lies within the 90% CI. For a model that produces well-calibrated uncertainties, a CI containing α% of the predictions should contain the true output for α% of the test inputs. Figure 7B shows that the BNN gives well-calibrated uncertainties across the full range of CIs (values of α), and the spintronic hardware closely matches the ideal software results.
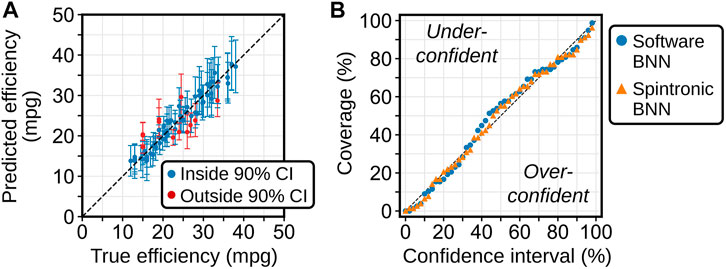
FIGURE 7. (A) Spintronic BNN regression results on the Auto MPG test set, comparing the predicted to true efficiency. Error bars show the 90% confidence interval obtained from sampling 100 BNN predictions. Blue indicates points where the true values lies inside the 90% confidence interval. (B) Calibration curve for the software and spintronic implementation of the regression BNN on the Auto MPG test set.
3.5 Energy efficiency
Compared to conventional digital implementations of BNNs, the proposed MTJ-based probabilistic MVM engine saves considerable energy by performing multi-bit RNG and multiply-accumulate (MAC) operations using low-voltage magnetic devices in the analog domain. Furthermore, the proposed hardware can be more efficient than previously proposed MTJ-based accelerators (Lu et al., 2022; Yang et al., 2020b) by integrating the two functions within the same array, without the need for intermediate digital processing to compute a probabilistic MVM.
Figure 8A shows how the energy consumption per probabilistic MAC operation scales for the proposed spintronic accelerator. Circuit energies were computed based on a 40 nm transistor process, assuming 8-bit precision for the analog-to-digital converter (ADC) and shared digital-to-analog converter (DAC). To reduce the current consumption of the CC, MTJs with higher resistance than listed in Tables 1, 2 are assumed (Bayes-MTJ Rp = 10 kΩ, DW-MTJ Rp = 56 kΩ). We also consider the efficiency of a system that uses the highest MTJ resistances demonstrated in the literature (Doevenspeck et al., 2020) (Bayes-MTJ Rp = 1 MΩ, DW-MTJ Rp = 5.6 MΩ). Since the CC, ADC, or DAC dominate the energy, higher efficiency can be obtained in large arrays where these costs can be amortized over more MACs. Meanwhile, the cost of true RNG in state-of-the-art CMOS circuits is about 1.6 pJ/bit (Bae et al., 2017), or 6.4 pJ to generate a 4-bit random value that matches the assumed programming precision of the Bayes-MTJ. Multiplication of 4-bit values incurs an additional ∼0.05 pJ/MAC (Horowitz, 2014). The spintronic accelerator can yield more than 100× energy improvement at large array sizes.
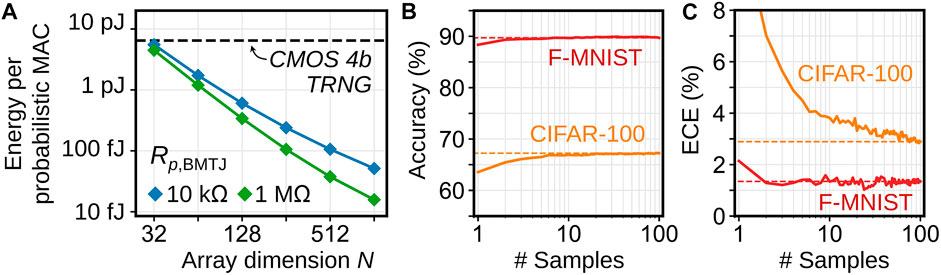
FIGURE 8. (A) Energy consumption per probabilistic MAC operation within an N × N probabilistic MVM executed by the spintronic in-memory computing accelerator (blue). Two values of the Bayes-MTJ parallel resistance are considered. The black dashed line shows the efficiency of performing the same probabilistic MACs using the CMOS True RNG from Bae et al. (2017). (B,C) Accuracy and ECE vs. number of sampled predictions from the spintronic BNN on the Fashion MNIST and CIFAR-100 datasets.
An energy cost associated with BNNs, whether implemented in digital software or a spintronic accelerator, is the cost of randomly sampling the prediction multiple times. Resampling the noisy weights is needed to produce well-calibrated uncertainties, and also improves accuracy by ensembling the predictions of multiple weight samples. Figures 8B,C show how the accuracy and ECE on Fashion MNIST and CIFAR-100 depend on the number of samples for the spintronic BNN. The number of samples needed for convergence of accuracy and ECE depends on the task, and this number is the overhead factor of a BNN prediction over a DNN prediction on the same analog hardware.
4 Conclusion
Our results confirm that a Bayes-MTJ noise encoder (programmable standard deviation σ) and a pair of DW-MTJ devices constructing a spintronic synapse (programmable mean μ) can collectively encode expressive probability distributions with sufficient quality for real BNN operations. The two types of devices can be co-integrated within a compact nanofabric, paving the way to one-shot probabilistic matrix-vector multiplications in the analog domain. The proposed hardware can be 10 − 100× more efficient than performing the same computation using conventional RNGs, and can be made even more so with more resistive MTJ devices. We simulated classification and regression Bayesian neural networks whose trained probabilistic weights are encoded using the novel spintronic technology. Despite device non-idealities (non-Gaussian noise distribution, limited range and precision in representing σ and μ), the spintronic BNN implementation produces well-calibrated and decomposable uncertainty estimates on CIFAR-100, Fashion MNIST, and perturbed versions of these datasets. The spintronic hardware yields high-fidelity accuracy and ECE metrics that are nearly identical or superior to those produced by a software BNN. To demonstrate feasibility on more complex tasks and to relax device programming precision and range requirements, future work will investigate closer co-design of the algorithm and device by integrating device properties into the VI training of the BNN.
Data availability statement
The metrics and methodologies used to obtain the data shown it the tables/figures in this work are included in the article itself. Data science tasks used in evaluation of these ideas are open-access and have been referenced throughout the draft. Any further inquiries can be directed to the corresponding authors.
Author contributions
SL, TX, and CB conceived the stochastic device, circuit, and system concepts. SL performed micromagnetic device simulations. TX and CB trained the neural networks. TX conducted simulations of the spintronic neural network accelerator. All authors contributed to the writing of the manuscript. CB and JI supervised the project.
Funding
This work was supported by the National Science Foundation Graduate Research Fellowship under Grant No. 2021311125 (SL), the Laboratory Directed Research and Development Program at Sandia National Laboratories (TX, CB, SA, and BD), and by the Department of Energy Office of Science through the COINFLIPS project (JK).
Licenses and Permissions
This article has been authored by employees of National Technology and Engineering Solutions of Sandia, LLC under Contract No. DENA0003525 with the US Department of Energy (DOE). These employees own all right, title and interest in and to the article and are solely responsible for its contents. The United States Government retains and the publisher, by accepting the article for publication, acknowledges that the United States Government retains a nonexclusive, paid-up, irrevocable, world-wide license to publish or reproduce the published form of this article or allow others to do so, for United States Government purposes. The DOE will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan https://www.energy.gov/downloads/doe-public-access-plan.
Conflict of interest
PT, CB, BD, and SA are all employees of Sandia National Labs, operated by NTESS LLC.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Author’s Disclaimer
This paper describes objective technical results and analysis. Any subjective views or opinions that might be expressed in the paper do not necessarily represent the views of the U.S. Department of Energy or the United States Government.
References
Akinola, O., Hu, X., Bennett, C. H., Marinella, M., Friedman, J. S., and Incorvia, J. A. C. (2019). Three-terminal magnetic tunnel junction synapse circuits showing spike-timing-dependent plasticity. J. Phys. D. Appl. Phys. 52, 49LT01. doi:10.1088/1361-6463/ab4157
Bae, S.-G., Kim, Y., Park, Y., and Kim, C. (2017). 3-Gb/s high-speed true random number generator using common-mode operating comparator and sampling uncertainty of D flip-flop. IEEE J. Solid-State Circuits 52, 605–610. doi:10.1109/JSSC.2016.2625341
Baldrati, L., Tan, A. J., Mann, M., Bertacco, R., and Beach, G. S. D. (2017). Magneto-ionic effect in CoFeB thin films with in-plane and perpendicular-to-plane magnetic anisotropy. Appl. Phys. Lett. 110, 012404. doi:10.1063/1.4973475
Barbera, S. L., Ly, D. R. B., Navarro, G., Castellani, N., Cueto, O., Bourgeois, G., et al. (2018). Narrow heater bottom electrode-based phase change memory as a bidirectional artificial synapse. Adv. Electron. Mat. 4, 1800223. doi:10.1002/aelm.201800223
Bauer, U., Yao, L., Tan, A. J., Agrawal, P., Emori, S., Tuller, H. L., et al. (2015). Magneto-ionic control of interfacial magnetism. Nat. Mat. 14, 174–181. doi:10.1038/nmat4134
Blei, D. M., Kucukelbir, A., and McAuliffe, J. D. (2017). Variational inference: A review for statisticians. J. Am. Stat. Assoc. 112, 859–877. doi:10.1080/01621459.2017.1285773
Blundell, C., Cornebise, J., Kavukcuoglu, K., and Wierstra, D. (2015). “Weight uncertainty in neural network,”Proc. 32nd Int. Conf. Mach. Learn., France: PMLR. Editors F. Bach, D. Blei, and Lille, 37, 1613–1622.
Borders, W. A., Pervaiz, A. Z., Fukami, S., Camsari, K. Y., Ohno, H., and Datta, S. (2019). Integer factorization using stochastic magnetic tunnel junctions. Nature 573, 390–393. doi:10.1038/s41586-019-1557-9
Brigner, W. H., Hassan, N., Hu, X., Bennett, C. H., Garcia-Sanchez, F., Cui, C., et al. (2022). Domain wall leaky integrate-and-fire neurons with shape-based configurable activation functions. IEEE Trans. Electron Devices 69, 2353–2359. doi:10.1109/TED.2022.3159508
Cai, J., Fang, B., Zhang, L., Lv, W., Zhang, B., Zhou, T., et al. (2019). Voltage-controlled spintronic stochastic neuron based on a magnetic tunnel junction. Phys. Rev. Appl. 11, 034015. doi:10.1103/PhysRevApplied.11.034015
Cai, R., Ren, A., Liu, N., Ding, C., Wang, L., Qian, X., et al. (2018a). Vibnn: Hardware acceleration of bayesian neural networks. ASPLOS. International Conference on Architectural Support for Programming Languages and Operating Systems (ASPLOS), ’18. New York, NY, USA: Association for Computing Machinery, 476–488. doi:10.1145/3173162.3173212
Cai, R., Ren, A., Liu, N., Ding, C., Wang, L., Qian, X., et al. (2018b). Vibnn: Hardware acceleration of bayesian neural networks. SIGPLAN Not. 53, 476–488. doi:10.1145/3296957.3173212
Carboni, R., and Ielmini, D. (2019). Stochastic memory devices for security and computing. Adv. Electron. Mat. 5, 1900198. doi:10.1002/aelm.201900198
Catalan, G., Seidel, J., Ramesh, R., and Scott, J. F. (2012). Domain wall nanoelectronics. Rev. Mod. Phys. 84, 119–156. doi:10.1103/RevModPhys.84.119
Chavent, A., Iurchuk, V., Tillie, L., Bel, Y., Lamard, N., Vila, L., et al. (2020). A multifunctional standardized magnetic tunnel junction stack embedding sensor, memory and oscillator functionality. J. Magnetism Magnetic Mater. 505, 166647. doi:10.1016/j.jmmm.2020.166647
Chen, A., Wen, Y., Fang, B., Zhao, Y., Zhang, Q., Chang, Y., et al. (2019). Giant nonvolatile manipulation of magnetoresistance in magnetic tunnel junctions by electric fields via magnetoelectric coupling. Nat. Commun. 10, 243. doi:10.1038/s41467-018-08061-5
Cohen, G., Afshar, S., Tapson, J., and Van Schaik, A. (2017). “Emnist: Extending MNIST to handwritten letters,” in 2017 international joint conference on neural networks (IJCNN IEEE), 2921. –2926.
Currivan-Incorvia, J. A., Siddiqui, S., Dutta, S., Evarts, E. R., Zhang, J., Bono, D., et al. (2016). Logic circuit prototypes for three-terminal magnetic tunnel junctions with mobile domain walls. Nat. Commun. 7, 10275–10279. doi:10.1038/ncomms10275
Dalgaty, T., Esmanhotto, E., Castellani, N., Querlioz, D., and Vianello, E. (2021). Ex situ transfer of Bayesian neural networks to resistive memory-based inference hardware. Adv. Intell. Syst. 3, 2000103. doi:10.1002/aisy.202000103
Debashis, P., Faria, R., Camsari, K. Y., Appenzeller, J., Datta, S., and Chen, Z. (2016). Experimental demonstration of nanomagnet networks as hardware for Ising computing. IEEE) 34, 3. doi:10.1109/IEDM.2016.7838539
Doevenspeck, J., Garello, K., Verhoef, B., Degraeve, R., Van Beek, S., Crotti, D., et al. (2020). SOT-MRAM based analog in-memory computing for DNN inference. IEEE symposium on VLSI Technology, 1. –2. doi:10.1109/VLSITechnology18217.2020.9265099
Fang, M., Zhang, S., Zhang, W., Jiang, L., Vetter, E., Lee, H. N., et al. (2019). Nonvolatile multilevel states in multiferroic tunnel junctions. Phys. Rev. Appl. 12, 044049. doi:10.1103/PhysRevApplied.12.044049
Gkoupidenis, P., Schaefer, N., Garlan, B., and Malliaras, G. G. (2015). Neuromorphic functions in PEDOT:PSS organic electrochemical transistors. Adv. Mat. 27, 7176–7180. doi:10.1002/adma.201503674
Grollier, J., Querlioz, D., Camsari, K. Y., Everschor-Sitte, K., Fukami, S., and Stiles, M. D. (2020). Neuromorphic spintronics. Nat. Electron. 3, 360–370. doi:10.1038/s41928-019-0360-9
Guo, C., Pleiss, G., Sun, Y., and Weinberger, K. Q. (2017). On calibration of modern neural networks. Proc. 34th Int. Conf. Mach. Learn. - Volume 70 ICML’17, 1321–1330. JMLR.org).
Hayakawa, K., Kanai, S., Funatsu, T., Igarashi, J., Jinnai, B., Borders, W., et al. (2021). Nanosecond random telegraph noise in in-plane magnetic tunnel junctions. Phys. Rev. Lett. 126, 117202. doi:10.1103/PhysRevLett.126.117202
He, K., Zhang, X., Ren, S., and Sun, J. (2016). “Deep residual learning for image recognition,” in Conf. On computer vision and pattern recognition (CVPR), 770. –778.
Horowitz, M. (2014). Computing’s energy problem (and what we can do about it). IEEE international solid-state circuits conference digest of technical papers (ISSCC). 10–14. doi:10.1109/ISSCC.2014.6757323
Hüllermeier, E., and Waegeman, W. (2021). Aleatoric and epistemic uncertainty in machine learning: An introduction to concepts and methods. Mach. Learn. 110, 457–506. doi:10.1007/s10994-021-05946-3
Ikeda, S., Miura, K., Yamamoto, H., Mizunuma, K., Gan, H. D., Endo, M., et al. (2010). A perpendicular-anisotropy CoFeB–MgO magnetic tunnel junction. Nat. Mat. 9, 721–724. doi:10.1038/nmat2804
Jacob, B., Kligys, S., Chen, B., Zhu, M., Tang, M., Howard, A., et al. (2018). “Quantization and training of neural networks for efficient integer-arithmetic-only inference,” in Conf. On computer vision and pattern recognition. (CVPR). 2704–2713.
Jadaun, P., Cui, C., Liu, S., and Incorvia, J. A. C. (2020). Adaptive cognition implemented with a context-aware and flexible neuron for next-generation artificial intelligence. doi:10.48550/ARXIV.2010.15748
Jiang, H., Kim, B., Guan, M., and Gupta, M. (2018). “To trust or not to trust a classifier,”. Advances in neural information processing systems. Editors S. Bengio, H. Wallach, H. Larochelle, K. Grauman, N. Cesa-Bianchi, and R. Garnett (Curran Associates, Inc.), 31.
Joo, S., Jung, K. Y., Lee, B. C., Kim, T.-S., Shin, K. H., Jung, M.-H., et al. (2012). Effect of oxidizing the ferromagnetic electrode in magnetic tunnel junctions on tunneling magnetoresistance. Appl. Phys. Lett. 100, 172406. doi:10.1063/1.4704557
Joshi, V., Gallo, M. L., Haefeli, S., Boybat, I., Nandakumar, S., Piveteau, C., et al. (2020). Accurate deep neural network inference using computational phase-change memory. Nat. Commun. 11, 2473. doi:10.1038/s41467-020-16108-9
Jospin, L. V., Laga, H., Boussaid, F., Buntine, W., and Bennamoun, M. (2022). Hands-on bayesian neural networks—A tutorial for deep learning users. IEEE Comput. Intell. Mag. 17, 29–48. doi:10.1109/MCI.2022.3155327
Jung, S., Lee, H., Myung, S., Kim, H., Yoon, S. K., Kwon, S.-W., et al. (2022). A crossbar array of magnetoresistive memory devices for in-memory computing. Nature 601, 211–216. doi:10.1038/s41586-021-04196-6
Kaiser, J., Borders, W. A., Camsari, K. Y., Fukami, S., Ohno, H., and Datta, S. (2022). Hardware-aware in situ learning based on stochastic magnetic tunnel junctions. Phys. Rev. Appl. 17, 014016. doi:10.1103/PhysRevApplied.17.014016
Kendall, A., and Gal, Y. (2017). “What uncertainties do we need in Bayesian deep learning for computer vision?” in Proceedings of the 31st international conference on neural information processing systems (NY, USANeurIPS’17: Red HookCurran Associates Inc.), 5580–5590.
Kireev, D., Liu, S., Jin, H., Xiao, T. P., Bennett, C. H., Akinwande, D., et al. (2022). Metaplastic and energy-efficient biocompatible graphene artificial synaptic transistors for enhanced accuracy neuromorphic computing. doi:10.48550/ARXIV.2203.04389
Krizakova, V., Grimaldi, E., Garello, K., Sala, G., Couet, S., Kar, G. S., et al. (2021). Interplay of voltage control of magnetic anisotropy, spin-transfer torque, and heat in the spin-orbit-torque switching of three-terminal magnetic tunnel junctions. Phys. Rev. Appl. 15, 054055. doi:10.1103/PhysRevApplied.15.054055
Lau, J. H. (2016). Recent advances and new trends in flip chip technology. J. Electron. Packag. 138. doi:10.1115/1.4034037
Lecun, Y., Bottou, L., Bengio, Y., and Haffner, P. (1998). Gradient-based learning applied to document recognition. Proc. IEEE 86, 2278–2324. doi:10.1109/5.726791
Leonard, T., Liu, S., Alamdar, M., Cui, C., Akinola, O. G., Xue, L., et al. (2021). Shape-dependent multi-weight magnetic artificial synapses for neuromorphic computing. doi:10.48550/ARXIV.2111.11516
Li, C., Hu, M., Li, Y., Jiang, H., Ge, N., Montgomery, E., et al. (2018). Analogue signal and image processing with large memristor crossbars. Nat. Electron. 1, 52–59. doi:10.1038/s41928-017-0002-z
Li, P., Chen, A., Li, D., Zhao, Y., Zhang, S., Yang, L., et al. (2014). Electric field manipulation of magnetization rotation and tunneling magnetoresistance of magnetic tunnel junctions at room temperature. Adv. Mat. 26, 4320–4325. doi:10.1002/adma.201400617
Li, Y., Xiao, T. P., Bennett, C. H., Isele, E., Melianas, A., Tao, H., et al. (2021). In situ parallel training of analog neural network using electrochemical random-access memory. Front. Neurosci. 15, 636127. doi:10.3389/fnins.2021.636127
Lin, Y.-P., Bennett, C. H., Cabaret, T., Vodenicarevic, D., Chabi, D., Querlioz, D., et al. (2016). Physical realization of a supervised learning system built with organic memristive synapses. Sci. Rep. 6, 31932–32012. doi:10.1038/srep31932
Lin, Y., Zhang, Q., Tang, J., Gao, B., Li, C., Yao, P., et al. (2019). Bayesian neural network realization by exploiting inherent stochastic characteristics of analog RRAM.6.1–14.6.4. IEEE International Electron Devices Meeting (IEDM), 14. doi:10.1109/IEDM19573.2019.8993616
Liu, S., Xiao, T. P., Cui, C., Incorvia, J. A. C., Bennett, C. H., and Marinella, M. J. (2021). A domain wall-magnetic tunnel junction artificial synapse with notched geometry for accurate and efficient training of deep neural networks. Appl. Phys. Lett. 118, 202405. doi:10.1063/5.0046032
Long, G., Xue, Q., Li, Q., Shi, Y., Li, L., Cheng, L., et al. (2021). Interfacial control via reversible ionic motion in battery-like magnetic tunnel junctions. Adv. Electron. Mat. 7, 2100512. doi:10.1002/aelm.202100512
Lu, A., Luo, Y., and Yu, S. (2022). An algorithm-hardware co-design for Bayesian neural network utilizing SOT-MRAM’s inherent stochasticity. IEEE J. Explor. Solid-State Comput. Devices Circuits 8, 27–34. doi:10.1109/JXCDC.2022.3177588
MacKay, D. J. C. (1992). A practical Bayesian framework for backpropagation networks. Neural Comput. 4, 448–472. doi:10.1162/neco.1992.4.3.448
Malhotra, A., Lu, S., Yang, K., and Sengupta, A. (2020). Exploiting oxide based resistive ram variability for bayesian neural network hardware design. IEEE Trans. Nanotechnol. 19, 328–331. doi:10.1109/tnano.2020.2982819
Marinella, M. J., Agarwal, S., Hsia, A., Richter, I., Jacobs-Gedrim, R., Niroula, J., et al. (2018). Multiscale co-design analysis of energy, latency, area, and accuracy of a ReRAM analog neural training accelerator. IEEE J. Emerg. Sel. Top. Circuits Syst. 8, 86–101. doi:10.1109/JETCAS.2018.2796379
Netzer, Y., Wang, T., Coates, A., Bissacco, A., Wu, B., and Ng, A. Y. (2011). “Reading digits in natural images with unsupervised feature learning,” in NIPS workshop on deep learning and unsupervised feature learning 2011.
Nichterwitz, M., Honnali, S., Zehner, J., Schneider, S., Pohl, D., Schiemenz, S., et al. (2020). Control of positive and negative magnetoresistance in iron oxide–iron nanocomposite thin films for tunable magnetoelectric nanodevices. ACS Appl. Electron. Mat. 2, 2543–2549. doi:10.1021/acsaelm.0c00448
Ostwal, V., and Appenzeller, J. (2019). Spin–orbit torque-controlled magnetic tunnel junction with low thermal stability for tunable random number generation. IEEE Magn. Lett. 10, 1–5. doi:10.1109/LMAG.2019.2912971
Quinlan, J. R. (1993). Combining instance-based and model-based learning. Proc. Tenth Int. Conf. Int. Conf. Mach. Learn. ICML’93. San Francisco, CA, USA: Morgan Kaufmann Publishers Inc., 236–243.
Raymenants, E., Bultynck, O., Wan, D., Devolder, T., Garello, K., Souriau, L., et al. (2021). Nanoscale domain wall devices with magnetic tunnel junction read and write. Nat. Electron. 4, 392–398. doi:10.1038/s41928-021-00593-x
Robinson, D. A., Foster, M. E., Bennett, C. H., Bhandarkar, A., Webster, E. R., Celebi, A., et al. (2022). Tunable intervalence charge transfer in ruthenium prussian blue analogue enables stable and efficient biocompatible artificial synapses. arXiv e-printsarXiv–2207.
Safranski, C., Kaiser, J., Trouilloud, P., Hashemi, P., Hu, G., and Sun, J. Z. (2021). Demonstration of nanosecond operation in stochastic magnetic tunnel junctions. Nano Lett. 21, 2040–2045. doi:10.1021/acs.nanolett.0c04652
Sebastian, A., Gallo, M. L., Khaddam-Aljameh, R., and Eleftheriou, E. (2020). Memory devices and applications for in-memory computing. Nat. Nanotechnol. 15, 529–544. doi:10.1038/s41565-020-0655-z
Sengupta, A., Panda, P., Wijesinghe, P., Kim, Y., and Roy, K. (2016). Magnetic tunnel junction mimics stochastic cortical spiking neurons. Sci. Rep. 6, 30039. doi:10.1038/srep30039
Shiota, Y., Murakami, S., Bonell, F., Nozaki, T., Shinjo, T., and Suzuki, Y. (2011). Quantitative evaluation of voltage-induced magnetic anisotropy change by magnetoresistance measurement. Appl. Phys. Express 4, 043005. doi:10.1143/APEX.4.043005
Siddiqui, S. A., Dutta, S., Tang, A., Liu, L., Ross, C. A., and Baldo, M. A. (2020). Magnetic domain wall based synaptic and activation function generator for neuromorphic accelerators. Nano Lett. 20, 1033–1040. doi:10.1021/acs.nanolett.9b04200
Smith, L., and Gal, Y. (2018). “Understanding measures of uncertainty for adversarial example detection,”Proceedings of the Thirty-Fourth Conference on Uncertainty in Artificial Intelligence, UAI 2018. August 6-10, 2018. Editors A. Globerson,, and R. Silva (Monterey, California, USA: AUAI Press), 560–569.
Song, K. M., Jeong, J. S., Pan, B., Zhang, X., Xia, J., Cha, S., et al. (2020). Skyrmion-based artificial synapses for neuromorphic computing. Nat. Electron. 3, 148–155. doi:10.1038/s41928-020-0385-0
Srinivasan, G., Sengupta, A., and Roy, K. (2016). Magnetic tunnel junction based long-term short-term stochastic synapse for a spiking neural network with on-chip STDP learning. Sci. Rep. 6, 29545. doi:10.1038/srep29545
Tan, A. J., Huang, M., Avci, C. O., Büttner, F., Mann, M., Hu, W., et al. (2019). Magneto-ionic control of magnetism using a solid-state proton pump. Nat. Mat. 18, 35–41. doi:10.1038/s41563-018-0211-5
Vansteenkiste, A., Leliaert, J., Dvornik, M., Helsen, M., Garcia-Sanchez, F., and Waeyenberge, B. V. (2014). The design and verification of mumax3. AIP Adv. 4, 107133. doi:10.1063/1.4899186
Wang, J., Chen, A., Li, P., and Zhang, S. (2021). Magnetoelectric memory based on ferromagnetic/ferroelectric multiferroic heterostructure. Materials 14, 4623. doi:10.3390/ma14164623
Wei, Y., Matzen, S., Quinteros, C. P., Maroutian, T., Agnus, G., Lecoeur, P., et al. (2019). Magneto-ionic control of spin polarization in multiferroic tunnel junctions. npj Quantum Mat. 4, 62. doi:10.1038/s41535-019-0201-0
Wen, Y., Vicol, P., Ba, J., Tran, D., and Grosse, R. (2018). Flipout: Efficient pseudo-independent weight perturbations on mini-batches. arXiv preprint arXiv:1803.04386.
Xiao, H., Rasul, K., and Vollgraf, R. (2017). Fashion-MNIST: A novel image dataset for benchmarking machine learning algorithms. arXiv preprint arXiv:1708.07747.
Xiao, T. P., Bennett, C. H., Feinberg, B., Agarwal, S., and Marinella, M. J. (2020). Analog architectures for neural network acceleration based on non-volatile memory. Appl. Phys. Rev. 7, 031301. doi:10.1063/1.5143815
Xiao, T. P., Bennett, C. H., Feinberg, B., Marinella, M. J., and Agarwal, S. (2022). CrossSim: Accuracy simulation of analog in-memory computing. Available at:https://github.com/sandialabs/cross-sim.
Xue, F., Sato, N., Bi, C., Hu, J., He, J., and Wang, S. X. (2019). Large voltage control of magnetic anisotropy in CoFeB/MgO/OX structures at room temperature. Apl. Mater. 7, 101112. doi:10.1063/1.5101002
Xue, L., Ching, C., Kontos, A., Ahn, J., Wang, X., Whig, R., et al. (2018). Process optimization of perpendicular magnetic tunnel junction arrays for last-level cache beyond 7 nm node, 2018 IEEE Symposium on VLSI Technology. 18-22 June 2018. Honolulu, HI, USA. 117–118. doi:10.1109/VLSIT.2018.8510642
Yang, K., Malhotra, A., Lu, S., and Sengupta, A. (2020). All-spin bayesian neural networks. IEEE Trans. Electron Devices 67, 1340–1347. doi:10.1109/ted.2020.2968223
Yao, P., Wu, H., Gao, B., Tang, J., Zhang, Q., Zhang, W., et al. (2020). Fully hardware-implemented memristor convolutional neural network. Nature 577, 641–646. doi:10.1038/s41586-020-1942-4
Keywords: spintronics, probabilistic computation, Bayesian inference, neuromorphic computing, domain wall (DW) control, magnetic tunnel junction, analog accelerator design, micromagnetic simulation
Citation: Liu S, Xiao TP, Kwon J, Debusschere BJ, Agarwal S, Incorvia JAC and Bennett CH (2022) Bayesian neural networks using magnetic tunnel junction-based probabilistic in-memory computing. Front. Nanotechnol. 4:1021943. doi: 10.3389/fnano.2022.1021943
Received: 17 August 2022; Accepted: 23 September 2022;
Published: 17 October 2022.
Edited by:
Ying-Chen Chen, Northern Arizona University, United StatesReviewed by:
Mei-Chin Chen, Intel, United StatesJiyong Woo, Kyungpook National University, South Korea
© 2022 Liu, Xiao, Kwon, Debusschere, Agarwal, Incorvia and Bennett. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Samuel Liu, bGl1a3RzQHV0ZXhhcy5lZHU=; T. Patrick Xiao, dHhpYW9Ac2FuZGlhLmdvdg==; Christopher H. Bennett, Y2Jlbm5ldEBzYW5kaWEuZ292
†These authors have contributed equally to this work and share first authorship
 Samuel Liu
Samuel Liu T. Patrick Xiao
T. Patrick Xiao Jaesuk Kwon1
Jaesuk Kwon1 Bert J. Debusschere
Bert J. Debusschere Sapan Agarwal
Sapan Agarwal Jean Anne C. Incorvia
Jean Anne C. Incorvia Christopher H. Bennett
Christopher H. Bennett