Towards computational polar-topotronics: Multiscale neural-network quantum molecular dynamics simulations of polar vortex states in SrTiO3/PbTiO3 nanowires

Recent discoveries of polar topological structures (e.g., skyrmions and merons) in ferroelectric/paraelectric heterostructures have opened a new field of polar topotronics. However, how complex interplay of photoexcitation, electric field and mechanical strain controls these topological structures remains elusive. To address this challenge, we have developed a computational approach at the nexus of machine learning and first-principles simulations. Our multiscale neural-network quantum molecular dynamics molecular mechanics approach achieves orders-of-magnitude faster computation, while maintaining quantum-mechanical accuracy for atoms within the region of interest. This approach has enabled us to investigate the dynamics of vortex states formed in PbTiO₃ nanowires embedded in SrTiO₃. We find topological switching of these vortex states to topologically trivial, uniformly polarized states using electric field and trivial domain-wall states using shear strain. These results, along with our earlier results on optical control of polar topology, suggest an exciting new avenue toward opto-electro-mechanical control of ultrafast, ultralow-power polar topotronic devices.

Introduction

Topological structures of matter such as skyrmions and merons are emergent quantized defects that carry a topological charge, which is invariant under continuous deformation or external field. Originally conceptualized in particle physics, these topological objects have since been realized as magnetic spin textures in ferromagnetic materials and have found great interest due to their potential applications in next-generation spintronic devices such as racetrack memory (Tokura and Kanazawa, 2021). In the analogous field of ferroelectrics, there has been a growing effort to realize similar topological features in their inherent polarization fields. Recent experiments have shown success in generating skyrmion bubbles and vortex structures in SrTiO₃ (STO)/PbTiO₃ (PTO) based superlattices (Das et al., 2019) as well as creation of meron structures in strained PTO thin films grown on SmScO₃ (Wang et al., 2020). These structures emerge from a subtle balance of strain and polarization energies within interfacial materials, which in turn can be controlled by external optical, electrical and mechanical forces. Such rich controllability makes these polar topological structures an ideal enabler of the next-generation polar “topotronic” devices (Tian et al., 2021). Since these topological structures are protected against thermal noise, different states only need to be separated by low energy barriers, thus allowing polar topotronic devices to operate at ultralow power.

Despite the great prospect of polar topotronics, it remains an open question how these topological structures can be optically, electrically and mechanically manipulated. The primary challenge is to computationally describe their complex polarization dynamics extending many spatiotemporal scales as they emerge, while retaining quantum-mechanical accuracy. This challenge could be met by recent successes in machine learning based interatomic potentials to perform neural-network quantum molecular dynamics (NNQMD) simulations with ab initio accuracy but at a fraction of computational cost (Behler, 2015; Krishnamoorthy et al., 2021). In fact, we have successfully studied optical control of polar topological structures in PTO using NNQMD simulations on massively parallel supercomputers, which were trained by excited-state quantum molecular dynamics (QMD) simulations (Linker et al., 2022). However, electrical and mechanical control of topology in more realistic interfacial structures still remains a challenge. To address this challenge, we propose to combine NNQMD with a multiscale simulation approach that embeds high-accuracy but more compute-intensive simulation in coarser simulation only where high fidelity is required (Warshel and Levitt, 1976; Ogata et al., 2001), which was the topic of 2013 Nobel Chemistry prize (Warshel, 2014). We use the resulting multiscale NNQMD/molecular mechanics (MM) framework, or simply NN/MM method, to study electrical and mechanical manipulation of ferroelectric topological structures formed in ferroelectric/paraelectric heterostructures. Specifically, a scalable neural network is trained to accurately represent the potential energy surface of ferroelectric material, which is embedded in a classical force-field model to describe appropriate strain and dielectric boundary conditions imposed by paraelectric material.

In this paper, we present NN/MM simulations to study the dynamics of topological states in a ferroelectric PTO nanowire embedded in STO matrix. We find the formation of a vortex state in the nanowire in the ground state. To study electrical and mechanical manipulation of the vortex state, we examine two cases: 1) dynamics under an electric field in the vortex plane; and 2) dynamics under shear stress. In both cases, we find transformations from a vortex state to trivial domains with zero topological charge. These results demonstrate an exciting new framework for exploring control of ferroelectric topologies for development of next generation topotronic devices.

Materials and methods

We use a NNQMD approach to model the potential energy surface and forces within the PTO nanowire (Linker et al., 2022). NNQMD employs a feed-forward neural network architecture, which consists of an input layer, multiple hidden layers, and an output layer (Figure 1). The input is a multidimensional feature vector for each atom that represents its local environment through permutationally, translationally and rotationally invariant functions within a cutoff distance. Eq 1 and 2 show the radial and angular features for the ith atom, respectively:

$G_i^{\text{rad}}={\displaystyle {\sum }_j{e}^{-\eta {\left(R_{ij}-R_{\text{S}}\right)}^2}}\cdot f_{\text{c}}\left(R_{ij}\right),(1)$

$G_i^{\text{ang}}=2^{1-\varsigma }{\displaystyle {\sum }_{j,k\ne i}{\left(1+\lambda \cos {\vartheta }_{ijk}\right)}^{\varsigma }{e}^{-\eta \left(R_{ij}^2+R_{jk}^2+R_{ik}^2\right)}}\cdot f_{\text{c}}\left(R_{ij}\right)\cdot f_{\text{c}}\left(R_{jk}\right)\cdot f_{\text{c}}\left(R_{ik}\right),(2)$

where R_ij is the interatomic distance between the atomic pair (i, j) and the cutoff function $f_{\text{c}}\left(R_{ij}\right)$ smoothly truncates $G_i^{\text{rad}}$ and $G_i^{\text{ang}}$ functions at the cutoff distance R_c:

$f_{\text{c}}\left(R_{ij}\right)=1/2(\text{cos}\left(\pi R_{ij}/R_{\text{c}}\right) +1)\left(R_{ij}\le R_{\text{c}}, \right); 0 \left(\text{else}\right).(3)$

FIGURE 1

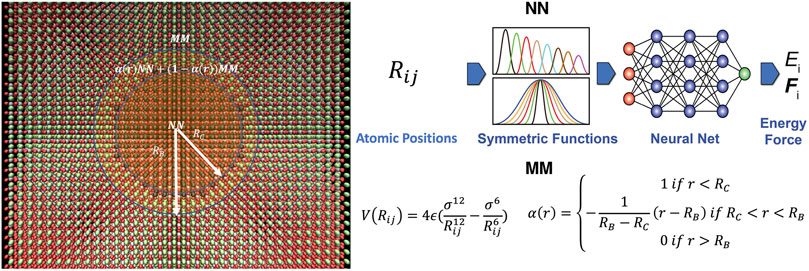
FIGURE 1. NN/MM method. (Left panel) Spatial decomposition into NN and MM domains to study PTO nanowire, where black, green, silver and red spheres represent Pb, Sr, Ti and O atoms, respectively. Within the nanowire domain defined by radius R_C, molecular dynamics is governed by the NNQMD model for PTO. For atoms within $R_{\text{C}}<r<R_{\text{B}}$, forces are linearly mixed between NN and MM models for STO and PTO. Beyond $R_{\text{B}}$, the dynamics is purely MM (Right panel) NNQMD for PTO. Atomic positions are used to compute symmetric functions for feature vectors that act as an input to a feed-forward neural network. The network is trained using DFT to predict quantum-mechanically accurate energies and forces on atoms. The MM model for STO is a simple LJ model that reproduces correct lattice constants for STO.

We used R_c = 0.75 nm in this study. Hyperparameters $\eta$, $R_S$, $\varsigma$ and $\lambda$ are determined to accurately describe the atomic local environment. For the PTO system, we found that the feature function G^rad with a set of hyperparameters, $\eta =\left\{0.5,1.0,3.0\right\}$ and $R_{\text{s}}=\left\{1.0,2.0,3.0,4.0\right\}$, provides sufficient accuracy and computational efficiency.

The network nodes are interconnected by adjustable weight matrices that are trained to reproduce a ground-truth QMD training dataset. We use two hidden layers and twenty nodes in each layer with modified hyperbolic tangent as the activation function. Eq. 4 shows the loss function L, i.e., the mean square error (MSE) of the system energy and the total sum of the atomic forces, to improve both the model fidelity and robustness.

$L=\frac{p_E}{2}\frac{1}{N_I}{\displaystyle {\sum }_I^{N_I}{\left(E_I^{\text{QMD}}-E_I^{\text{NN}}\right)}^2}+\frac{p_{\text{F}}}{2}\frac{1}{N_I}{\displaystyle {\sum }_I^{N_I}\frac{1}{3N_{\text{atom}}}}{\displaystyle {\sum }_i^{N_{\text{atom}}}{\left({\mathit{F}}_{I,i}^{\text{QMD}}-{\mathit{F}}_{I,i}^{\text{NN}}\right)}^2}.(4)$

The loss function compares the system energy E and the atomic forces F_i between NNQMD prediction and ground truth obtained by QMD. Here, N_I is the number of frames of the training dataset, N_atom is the number of atoms in each frame. The coefficients p_E and p_F are adjustable parameters to control the relative importance of the two terms as model training progresses. We used an equal weight for the energy and force loss functions and the L-BFGS-B scheme to minimize the loss function.

Training data was generated using density functional theory (DFT) based QMD simulations in the canonical (NVT) ensemble at temperature 300 K performed for a 4 $\times$ 4 $\times$ 4 PTO tetragonal supercell using the gamma-point for Brillouin-zone sampling. QMD simulations were performed using the QXMD software (Shimojo et al., 2019). A plane-wave basis was used with a cutoff energy of 30 Ry (410 eV) for wave functions and 250 Ry (3,400 eV) for charge density. Vanderbilt-style ultrasoft pseudopotentials were used, and local density approximation was used for the exchange-correlation functional. The training and test root mean-square error values converged within a few meV per atom, and the NNQMD model was validated using QMD data through comparison of radial distribution functions and bond-angle distribution. Details on model generation, training and validation are provided in (Linker et al., 2022).

To model the paraelectric and strain boundary conditions imposed by large STO matrix, we use a Lennard-Jones (LJ) force field, which is much less compute-intensive than the neural network inference in NNQMD:

$V\left(r_{ij}\right)=4\mathit{ϵ}\left({\left(\frac{{\sigma }_{ab}}{r_{ij}}\right)}^{12}-{\left(\frac{{\sigma }_{ab}}{r_{ij}}\right)}^6\right) \left(a,b\in \left\{\text{Sr}, \text{Ti},\text{O}\right\}\right),(5)$

where $r_{ij}$ is the interatomic distance between ith and jth atoms, $\mathit{ϵ}$ is an interaction energy scale and ${\sigma }_{ab}$ are element-dependent length scales. We fit the adjustable parameters ${\sigma }_{ab}$ to reproduce the experimental lattice constants, while $\mathit{ϵ}$ is taken to be on the order of STO’s melting temperature.

We perform multiscale NN/MM simulations in a core + buffer approach analogous to divide-and-conquer approaches commonly used in linear-scaling QMD simulations (Shimojo et al., 2014). Here, a NNQMD region is defined with a core radius $R_{\text{C}}$ and additional buffer radius $R_{\text{B}}$ ($>R_{\text{C}}$). The forces on atoms from the NN and MM models are then determined using a linear support function $\alpha \left(r\right)$ to form a partition of unity over the entire simulation box:

${\mathbf{F}}_i\left(r\right)=\alpha \left(r\right){\mathbf{F}}_i^{NNQMD}\left(r\right)+\left(1-\alpha \left(r\right)\right){\mathbf{F}}_i^{MM}\left(r\right),(6)$

$\alpha \left(r\right)=\{\begin{array}{c}1\left(r<R_{\text{C}}\right)\\ -\frac{1}{R_{\text{B}}-R_{\text{C}}}\left(r-R_{\text{B}}\right)\left(R_{\text{C}}\le r<R_{\text{B}}\right)\\ 0\left(r\ge R_B\right)\end{array}.(7)$

Forces on the atoms are determined by the NNQMD model inside the core region within $R_{\text{C}}$, linearly mixed in the buffer region ($R_{\text{C}}\le r<R_{\text{B}}$) and purely MM outside. In general, The NN region and corresponding support function $\alpha \left(r\right)$ can be defined in 1, 2 or 3D depending on the geometry of the problem. For the case of a PTO nanowire, $\alpha \left(r\right)$ is confined to 2D such that $R_{\text{C}}$ is the radius of the PTO nanowire, whereas $R_{\text{B}}$ is $R_{\text{C}}$ plus the neural-network cutoff distance (Figure 1). We perform NN/MM simulations on nanowires of radius 2.7 and 5.5 nm. The 2.7 nm nanowire is embedded in a matrix of 36 $\times$ 36 STO unit cells in the lateral directions, while the 5.5 nm nanowire in a 72 $\times$ 72 unit-cell STO matrix. Both systems are 4-unit cells thick along the nanowire axis, which coincides with the PTO polarization direction. The lattice constants are made compliant to the STO matrix. To stabilize NNQMD simulations, a small LJ repulsion equal to 8% of the STO $1/r^{12}$ interaction is added to the NNQMD force field for PTO. Such a physically constrained network is effective in preventing atoms from getting too close in highly strained systems.

Results

We first investigate the ground-state polarization field in the nanowire by performing molecular dynamics simulation at a low temperature of 10 K until polarization field becomes steady and only slightly oscillates due to harmonic oscillation within 4 ps. The formation of a vortex state is illustrated in Figure 2A with Sr atoms colored in green, Pb black, O red, Ti silver and the arrows representing Ti polar displacements creating the vortex state. Formation of a similar vortex state has been computationally studied in BaTiO₃ embedded within a STO matrix (Nahas et al., 2015). The center of the vortex is found to occur in the Pb-O plane of four neighboring unit-cells with finite polarization, drawing similar resemblance to Pb-O styled domain walls (Behera et al., 2011). We find the vortex core displaced from the center of the nanowire, despite the cylindrical symmetry of boundary conditions. A similar spontaneous symmetry breaking was observed experimentally and in phase-field modeling in STO/PTO heterostructures (Behera et al., 2022), where off centering of vortex cores in alternating clockwise and counter-clockwise vortex pair states led to a net polarization and emergent net chirality of vortex pair states. The nanowire system possesses no preferred location to pin the emergence of the vortex core such as a domain wall or oxygen vacancy. While the radial location of the vortex core is dictated by the energetics, its angular location is stochastic, depending on the initial velocities of the simulation.

FIGURE 2

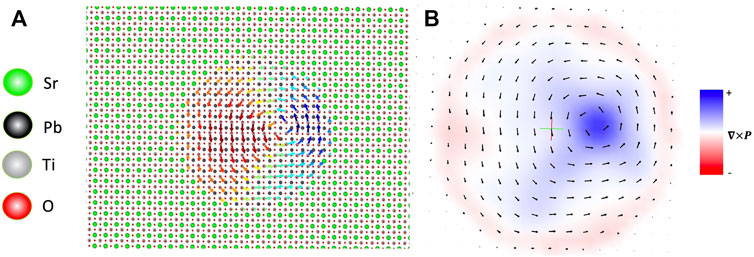
FIGURE 2. Vortex formation. (A) Formation of a vortex state in the PTO nanowire after 4 ps of NNQMD simulation at a temperature of 10 K. Black, green, silver and red spheres are Pb, Sr, Ti and O atoms, respectively, whereas arrows represent Ti polar displacements. (B) Vorticity map of the polar vortex state.

For our 2-dimensional system, the chirality of the vortex in can be determined by its circulation

$\mathrm{\Gamma }={\displaystyle {\iint }_S\left(\mathbf{\nabla }\times \mathbf{P}\right)}\cdot \mathit{d}\mathbf{S}={\displaystyle {\iint }_S\mathbf{\omega }\cdot \mathit{d}\mathbf{S}},(8)$

where P is the polarization. We compute the pseudovector vorticity $\mathit{\omega }=\omega \widehat{z}$ using finite differencing of the integrand of Eq. (8) on an interpolated fine grid of the Ti polar displacements (Figure 2B). We observe a clear positive spike at the center of the vortex, corresponding to its right-hand orientation. When Eq. (8) is integrated over the surface encompassed by the radius of PTO nanowire, a finite positive circulation is found corresponding to the vortex’s chirality (Behera et al., 2022).

We next study the dynamics of the vortex state under electric field, to examine the possibility of electric manipulation of the vortex state. We apply an electric field of 1 V/nm parallel to the vortex plane (Figure 3A). Figures 3B–D show progression of the vortex state after turning on the field at time $t=0$. Within the first 300 fs, the vortex state is quickly corrupted as the polarization begins to curl to comply with the electric field. After 700 fs, almost all signature of the vortex state has been lost with only small curl of the polarization remaining. Within 1 ps, the entire vortex state has been annihilated, forming a topologically trivial, uniformly polarized domain in the direction of the electric field. This is consistent with experimental and phase-field study of electric field annihilation of polar topological structures in STO/PTO (Das et al., 2021). Upon turning off the electric field subsequently, the vortex state is restored within 3 ps (Figure 3E), with relaxation found to be similar to that of initial creation of the vortex. The vortex core moves from its initial position before the application of the electric field. This further corroborates the stochastic nature of the vortex core position discussed before. Overall, these results demonstrate the possibility of field-induced reversible topological switching in a PE/FE nanowire.

FIGURE 3

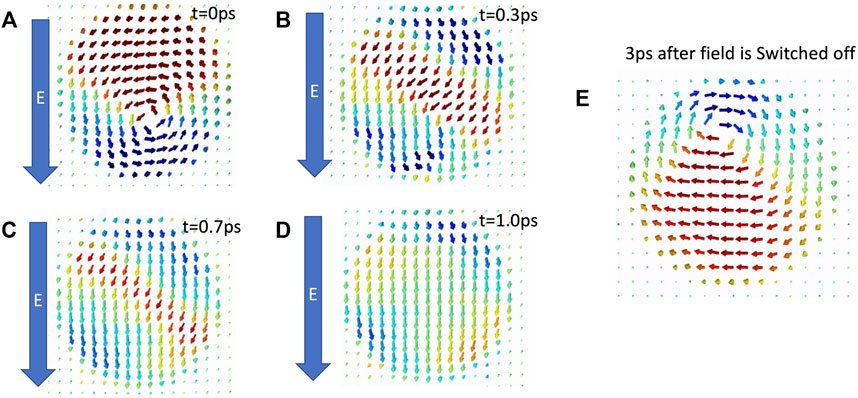
FIGURE 3. Electric-field-induced annihilation of vortex. (A)–(D) Evolution of a topological vortex state to a topologically trivial, uniformly polarized state under electric field. (E) Restoration of the vortex state upon subsequent turning-off of the electric field.

To examine the possibility of mechanical manipulation of vortex states, we next study the dynamics of the vortex state under shear strain. Figure 4A shows the initial vortex state in a 5.5 nm PTO nanowire embedded in STO matrix. We simulate shear dynamics by reducing the yz box angle at a rate of ${10}^{-5}$ fs⁻¹. Under 4 ps of continuous shear strain and at box angle $\alpha =$ 86$°$, the vortex state is still intact (Figure 4B). After 8 ps of continuous shear and resulting box angle $\alpha =$ 82$°$, the vortex state has become corrupted, resulting in a domain wall structure with a small curl in the polarization near the edge of the nanowire (Figure 4C). Upon further shearing, this small amount of curl is lost, forming a trivial domain wall state (Figure 4D), which demonstrates the ability to mechanically annihilate the vortex topology.

FIGURE 4

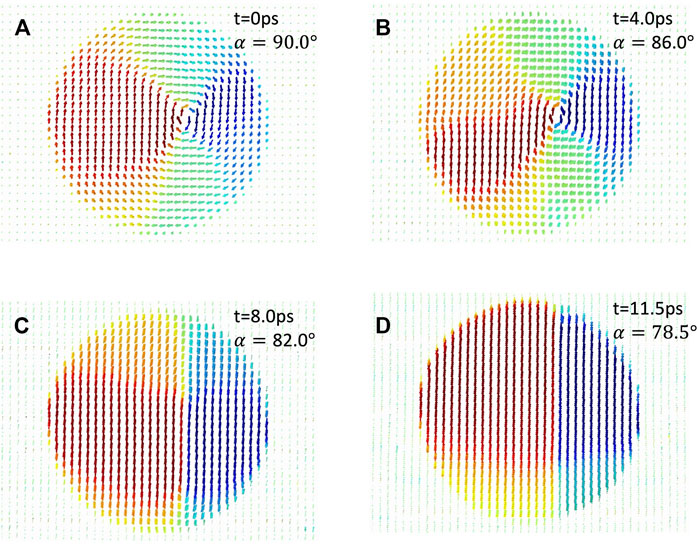
FIGURE 4. Shear-induced annihilation of vortex state. (A) Original vortex state prior to shear deformation. (B)–(D) Gradual transformation to a trivial domain-wall state under shear strain at different times t and lattice angles $\alpha$.

Discussion

Overall, our results demonstrate the controllability of topological vortex states in PTO nanowires embedded in STO through electrical and mechanical means. This work also demonstrates the ability of the new multiscale NN/MM method to model the emergence of topological vortices and their erasure under electric field and shear strain, highlighting its potential to investigate complex topological phase transitions in ferroelectric materials. Ultimately, deterministic control of polar topologies requires a precise understanding of the switching dynamics on sub nanosecond time scales (Tian et al., 2021), which is currently lacking. Atomistic methods like the new NN/MM simulations performed here could help provide valuable insight in this vein. Along with a recently developed multiscale approach that combines Maxwell equations, real-time timed-dependent density functional theory, nonadiabatic and Fermi-occupation QMD, and excited state NNQMD (Linker et al., 2022) to study optical control of topological structures, the proposed NN/MM method will form the basis of the promising new area of “computational topotronics” to explore optical, electrical and mechanical control of topological states in next generation toptronics devices.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

RK, AN, FS, and PV designed the work. KN and KS developed the NNQMD code. TL and AK developed the force fields. TL performed the NNQMD simulations. TL, SF, and AK analyzed the results.

Funding

This work was supported as part of the Computational Materials Sciences Program funded by the US Department of Energy, Office of Science, Basic Energy Sciences, under Award Number DE-SC0014607.

Acknowledgments

Simulations were performed at the Argonne Leadership Computing Facility under the DOE INCITE and Aurora Early Science programs and at the Center for Advanced Research Computing of the University of Southern California.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Behera, P., May, M. A., Gomez-Ortiz, F., Susarla, S., Das, S., Nelson, C. T., et al. (2022). Electric field control of chirality. Sci. Adv. 8 (1), eabj8030. doi:10.1126/sciadv.abj8030

PubMed Abstract | CrossRef Full Text | Google Scholar

Behera, R. K., Lee, C. W., Lee, D., Morozovska, A. N., Sinnott, S. B., Asthagiri, A., et al. (2011). Structure and energetics of 180° domain walls in PbTiO₃by density functional theory. J. Phys. Condens. Matter 23 (17), 175902. doi:10.1088/0953-8984/23/17/175902

PubMed Abstract | CrossRef Full Text | Google Scholar

Behler, J. (2015). Constructing high-dimensional neural network potentials: A tutorial review. Int. J. Quantum Chem. 115 (16), 1032–1050. doi:10.1002/qua.24890

CrossRef Full Text | Google Scholar

Das, S., Tang, Y. L., Hong, Z., Goncalves, M. A. P., McCarter, M. R., Klewe, C., et al. (2019). Observation of room-temperature polar skyrmions. Nature 568 (7752), 368–372. doi:10.1038/s41586-019-1092-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Das, S., Hong, Z., Stoica, V. A., Goncalves, M. A. P., Shao, Y. T., Parsonnet, E., et al. (2021). Local negative permittivity and topological phase transition in polar skyrmions. Nat. Mater. 20, 94–201.

CrossRef Full Text | Google Scholar

Krishnamoorthy, A., Nomura, K., Baradwaj, N., Shimamura, K., Rajak, P., Mishra, A., et al. (2021). Dielectric constant of liquid water determined with neural network quantum molecular dynamics. Phys. Rev. Lett. 126 (21), 216403. doi:10.1103/PhysRevLett.126.216403

PubMed Abstract | CrossRef Full Text | Google Scholar

Linker, T., Nomura, K., Aditya, A., Fukshima, S., Kalia, R. K., Krishnamoorthy, A., et al. (2022). Exploring far-from-equilibrium ultrafast polarization control in ferroelectric oxides with excited-state neural network quantum molecular dynamics. Sci. Adv. 8 (12), eabk2625. doi:10.1126/sciadv.abk2625

PubMed Abstract | CrossRef Full Text | Google Scholar

Nahas, Y., Prokhorenko, S., Louis, L., Gui, Z., Kornev, I., and Bellaiche, L. (2015). Discovery of stable skyrmionic state in ferroelectric nanocomposites. Nat. Commun. 6, 8542. doi:10.1038/ncomms9542

PubMed Abstract | CrossRef Full Text | Google Scholar

Ogata, S., Lidorikis, E., Shimojo, F., Nakano, A., Vashishta, P., and Kalia, R. K. (2001). Hybrid finite-element/molecular-dynamics/electronic-density-functional approach to materials simulations on parallel computers. Comput. Phys. Commun. 138 (2), 143–154. doi:10.1016/S0010-4655(01)00203-X

CrossRef Full Text | Google Scholar

Shimojo, F., Fukushima, S., Kumazoe, H., Misawa, M., Ohmura, S., Rajak, P., et al. (2019). QXMD: An open-source program for nonadiabatic quantum molecular dynamics. SoftwareX 10, 100307. doi:10.1016/j.softx.2019.100307

CrossRef Full Text | Google Scholar

Shimojo, F., Kalia, R. K., Kunaseth, M., Nakano, A., Nomura, K., Ohmura, S., et al. (2014). A divide-conquer-recombine algorithmic paradigm for multiscale materials modeling. J. Chem. Phys. 140 (18), 18A529. doi:10.1063/1.4869342

PubMed Abstract | CrossRef Full Text | Google Scholar

Tian, G., Yang, W. D., Gao, X. S., and Liu, J. M. (2021). Emerging phenomena from exotic ferroelectric topological states. Apl. Mater. 9 (2), 020907. doi:10.1063/5.0039139

CrossRef Full Text | Google Scholar

Tokura, Y., and Kanazawa, N. (2021). Magnetic skyrmion materials. Chem. Rev. 121 (5), 2857–2897. doi:10.1021/acs.chemrev.0c00297

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Y. J., Feng, Y. P., Zhu, Y. L., Tang, Y. L., Yang, L. X., Zou, M. J., et al. (2020). Polar meron lattice in strained oxide ferroelectrics. Nat. Mat. 19 (8), 881–886. doi:10.1038/s41563-020-0694-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Warshel, A., and Levitt, M. (1976). Theoretical studies of enzymic reactions: Dielectric, electrostatic and steric stabilization of the carbonium ion in the reaction of lysozyme. J. Mol. Biol. 103 (2), 227–249. doi:10.1016/0022-2836(76)90311-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Warshel, A. (2014). Multiscale modeling of biological functions: From enzymes to molecular machines (Nobel lecture). Angew. Chem. Int. Ed. 53 (38), 10020–10031. doi:10.1002/anie.201403689

PubMed Abstract | CrossRef Full Text | Google Scholar