STeP-CiM: Strain-Enabled Ternary Precision Computation-In-Memory Based on Non-Volatile 2D Piezoelectric Transistors

We proposed 2D piezoelectric FET (PeFET)–based compute-enabled non-volatile memory for ternary deep neural networks (DNNs). PeFETs hinge on ferroelectricity for bit storage and piezoelectricity for bit sensing, exhibiting inherently amenable features for computation-in-memory of dot products of weights and inputs in the signed ternary regime. PeFETs consist of a material with ferroelectric and piezoelectric properties coupled with a transition metal dichalcogenide channel. We utilized (a) ferroelectricity to store binary bits (0/1) in the form of polarization (−P/+P) and (b) polarization-dependent piezoelectricity to read the stored state by means of strain-induced bandgap change in the transition metal dichalcogenide channel. The unique read mechanism of PeFETs enables us to expand the traditional association of +P (−P) with low (high) resistance states to their dual high (low) resistance depending on read voltage. Specifically, we demonstrated that +P (−P) stored in PeFETs can be dynamically configured in (a) a low (high) resistance state for positive read voltages and (b) their dual high (low) resistance states for negative read voltages, without afflicting a read disturb. Such a feature, which we named as polarization-preserved piezoelectric effect reversal with dual voltage polarity (PiER), is unique to PeFETs and has not been shown in hitherto explored memories. We leveraged PiER to propose a Strain-enabled Ternary Precision Computation-in-Memory (STeP-CiM) cell with capabilities of computing the scalar product of the stored weight and input, both of which are represented with signed ternary precision. Furthermore, using multi-word line assertion of STeP-CiM cells, we achieved massively parallel computation of dot products of signed ternary inputs and weights. Our array-level analysis showed 91% lower delay and improvements of 15% and 91% in energy for in-memory multiply-and-accumulate operations compared to near-memory design approaches based on 2D FET–based SRAM and PeFET, respectively. We also analyzed the system-level implications of STeP-CiM by deploying it in a ternary DNN accelerator. STeP-CiM exhibits 6.11× to 8.91× average improvement in performance and 3.2$\times$ average improvement in energy over SRAM-based near-memory design. We also compared STeP-CiM to near-memory design based on PeFETs showing 5.67× to 6.13× average performance improvement and 6.07$\times$ average energy savings.

1 Introduction

Deep neural networks (DNNs) have transformed the field of machine learning and are deployed in many real-world products and services (Lecun et al., 2015). However, enormous storage and computational demands limit their application in energy-constrained edge devices (Venkataramani et al., 2016). Precision reduction in DNNs has emerged as a popular approach for energy-efficient realization of hardware accelerators for these applications (Courbariauxécole and Bengio, 2015; Mishra et al., 2017; Choi et al., 2018; Colangelo et al., 2018; Wang et al., 2018). State-of-the-art DNN hardware for inference employs 8-bit precision, and recent algorithmic efforts have shown the pathway for aggressive scaling up to binary precision (Choi et al., 2018; Colangelo et al., 2018). However, accuracy suffers significantly at binary precision. Interestingly, ternary precision networks offer a near-optimal design point in the low precision regime with significant accuracy boost compared to binary DNNs (Li et al., 2016; Zhu et al., 2016) and large energy savings with mild accuracy loss compared to higher precision DNNs (Mishra et al., 2017; Wang et al., 2018). Due to these features, ternary precision networks have garnered interest for their hardware realizations (Jain et al., 2020; Thirumala et al., 2020). Ternary DNNs can be implemented using classical accelerator architectures (e.g., tensor processing unit and graphical processing unit) by employing specialized processing elements and on-chip scratchpads to improve energy efficiency, but they are nevertheless limited by memory bottleneck. In this regard, computing-in-memory (CiM) brings a new opportunity that can greatly enhance efficiency of DNN accelerators by reducing power-hungry data transfer between memory and processors.

1.1 Related Works on Low Precision Computing-In-Memory for DNNs

Several previous works have explored hardware realization of low-precision CiM for DNN workloads. For example, binary networks such as XNOR-RRAM (Sun et al., 2018) and XNOR-SRAM (Yin et al., 2020) feature large parallel vector-matrix multiplication capability, but they suffer from low accuracies due to aggressive quantization of weights and inputs to binary values. At the other end of the spectrum, DNNs with 4–8 bits have attained high accuracies, albeit at the cost of considerably increased energy consumption and reduction in throughput (Liu et al., 2015; Chi et al., 2016). In this regard, ternary DNNs are attractive as they achieve a remarkably large upswing in accuracy compared to the binary networks while significantly reducing the energy consumption compared to higher precision networks (Mishra et al., 2017; Wang et al., 2018). In other words, ternary DNNs yield a near-optimal design point in the context of energy–accuracy trade-offs for energy-constrained applications, which has motivated several ternary CiM designs. Yoo et al. (2019) proposed eDRAM-based ternary CiM. However, the repetitive refresh operations add burden to the energy-constrained edge devices. Emerging technologies such as resistive RAM (RRAM) (Chen et al., 2018; Liu et al., 2020; Doevenspeck et al., 2021) and spin transfer/orbit torque magnetic RAM (STT/SOT-MRAM) (Doevenspeck et al., 2020; Bian et al., 2021) are also being actively explored for ternary precision networks due to their high density and low leakage power. However, their power-hungry current driven write (Si et al., 2021) lowers their favorability as a candidate for ternary CiM hardware targeted for energy-constrained environments. The common aspect in all the aforementioned works is that they used signed ternary weights with binary inputs and do not attempt to exploit the accuracy benefits of pure signed ternary networks, that is, with weights = {−1, 0, 1} and inputs = {−1, 0, 1}. Recent works have brought attention to hardware accelerator designs for pure signed ternary regime with static random access memory (SRAM) and non-volatile ferroelectric transistor–based DNN architectures (Jain et al., 2020; Thirumala et al., 2020). These works report high parallelism, low energy, and small accuracy loss, making a case for hardware architectures for signed ternary CiM. However, a downside of both designs is the requirement of hardware additions for achieving ternary CiM functionality. SRAM-based ternary CiM implementations, such as those by Jain et al. (2020), raise concerns for area efficiency and leakage energy. The use of non-volatile ferroelectric transistors in the ternary CiM design (Thirumala et al., 2020) remits area cost and leakage energy. However, existing ferroelectric-based non-volatile memories suffer from other disadvantages that are discussed subsequently.

1.2 Background of Ferroelectric-Based Memories

Ferroelectric RAM or FERAM (Kim et al., 2007) is one of the earliest memories based on ferroelectric materials. It utilizes a ferroelectric capacitor along with an access transistor in a 1T-1C configuration. FERAMs feature high density, large endurance, high retention, and electric field–driven write, which is more energy efficient compared to current-based write in other non-volatile memories (Si et al., 2021). However, it suffers from issues such as destructive read and low distinguishability between the memory states. Ferroelectric FETs (FEFETs), in which the ferroelectric material is integrated within the gate stack of a transistor (Yu et al., 2021), offer appealing attributes that mitigate the concerns of FERAMs. For instance, FEFETs feature separation of read-write paths, non-destructive read, and high distinguishability while retaining the benefits of electric field–driven write (Yu et al., 2021) and offering other advantages such as multilevel storage (Ni et al., 2018; Dutta et al., 2020; Kazemi et al., 2020; Liao et al., 2021). However, they are known to suffer from variability, endurance, and retention concerns due to traps at the ferroelectric–dielectric interface and depolarization fields in the ferroelectric. Moreover, it is challenging to scale their write voltage. In order to achieve write voltage reduction, ferroelectric-metal-FETs (FEMFETs) were proposed by Ni et al. (2018) and Kazemi et al. (2020) which connect a ferroelectric capacitor with the gate of a transistor, allowing independent optimization of the cross-sectional area of two components. This is helpful in scaling the write voltage to logic-compatible levels. The ferroelectric capacitor can be formed directly on the gate stack or at the back-end of the line. In addition to write-voltage reduction, FEMFETs mitigate the variability concerns of FEFETs due to the presence of metal between the ferroelectric and the dielectric of the transistor, which addresses the trap-related issues (Ni et al., 2018; Kazemi et al., 2020). However, this inter-layer metal (ILM) is floating and therefore is susceptible to potential changes due to gate leakage, which leads to bit-sensing challenges (Thirumala and Gupta, 2018).

To address the issues of FERAM, FEFETs, and FEMFETs, while still retaining the advantages of electric field–driven write, we (Thakuria et al., 2020) had explored another flavor of a ferroelectric material–based memory called piezoelectric FET (PeFET). PeFET utilizes both ferroelectric and piezoelectric properties of the ferroelectric material. PeFET consists of a ferroelectric capacitor coupled with a 2D transition metal dichalcogenide (TMD) FET in a four-terminal structure with gate, drain, source, and back contacts. The capacitor is designed with a material exhibiting strong ferroelectric and piezoelectric properties. PeFET utilizes polarization retention of the ferroelectric capacitor for bit storage. Its write operation involves applying suitable voltage across the ferroelectric capacitor to switch the polarization, similar to that of an FERAM. Therefore, PeFETs inherit the advantages of low power electric field–driven switching, large endurance, and high retention. Also, since the ferroelectric layer is controlled by metal layers on both ends, it does not suffer from severe trap-related issues observed in FEFETs. For read, PeFETs employ a unique mechanism based on dynamic bandgap change in the TMD FET induced by voltage-dependent strain of the ferroelectric/piezoelectric capacitor. This leads non-destructive read and separation of read-write paths (discussed later). Furthermore, there is no floating metal in PeFETs (unlike FEMFETs). This prevents issues related to gate leakage. One design challenge in PeFETs is limited distinguishability, which can be improved by choosing ferroelectric material exhibiting high piezoelectricity, for example, PZT-5H (Malakooti and Sodano, 2013) and TMD material with high sensitivity of bandgap change to pressure, for example, MoS₂ (Peña-Álvarez et al., 2015) and geometry optimization such as hammer and nail effect (Newns et al., 2012) to focus the strain on the TMD channel. These aspects are discussed in detail later. In summary, PeFETs address several important challenges observed in existing ferroelectric-based memories while retaining the key advantage of electric field–driven write. In addition, as proposed in this work, they exhibit unique properties associated with polarization-induced strain that make them amenable for designing compute-enabled memories in the pure signed ternary regime.

1.3 Previous Works on Piezoelectric-Based FETs

Initial proposals of piezoelectric-based FETs were made in the context of steep-switching devices (Newns et al., 2012; Hueting et al., 2015; Das, 2016; Wang et al., 2018; Alidoosty-Shahraki et al., 2019). A material with high piezoelectric coefficient, such as lead magnesium niobate–lead titanate (commonly known as PMN-PT) is utilized in such devices to modulate the resistance of a piezoresistive material (Newns et al., 2012) or bandgap of the Si/TMD channel (Hueting et al., 2015; Das, 2016; Alidoosty-Shahraki et al., 2019). Our proposal of PeFET (Thakuria et al., 2020) extends the idea of piezoelectricity-driven bandgap modulation of TMD beyond steep-switching devices to non-volatile memory (NVM) design. As already introduced, it stores bit information in a piezoelectric/ferroelectric material and leverages polarization-dependent piezoelectric response to modulate the bandgap of the TMD channel for sensing. As shown by Thakuria et al. (2020) and discussed later, positive ferroelectric polarization (+P) leads to bandgap reduction in TMD and thus low resistance state (LRS). On the other hand, negative polarization (−P) yields bandgap increase and high resistance state (HRS). The drain current of PeFET can be used to sense the memory. Contrary to previous proposals of piezoelectric-based FETs, PeFET NVM uses lead zirconate titanate (PZT-5H) as piezoelectric (PE) to satisfy the following requirements: (i) sufficiently wide hysteresis of polarization–voltage response for non-volatile memory functionality (ferroelectric property) and (ii) large strain–voltage characteristics (piezoelectric property) for achieving effective bandgap modulation in TMD NVM. Various experiments have demonstrated monotonic bandgap reduction in TMD on the application of out-of-plane pressure (Nayak et al., 2014; Peña-Álvarez et al., 2015). For example, multilayer molybdenum disulfide (MoS₂) subjected to out-of-plane uniaxial stress has experimentally shown a bandgap reduction of ∼80 meV/GPa and achieves semiconductor-to-metal transistor at ∼20 GPa (Nayak et al., 2014). Monolayer MoS₂ achieves bandgap reduction of up to ∼800 meV/GPa (Peña-Álvarez et al., 2015). We use monolayer MoS₂ in this work due to its high bandgap coefficient.

1.4 Contributions in This Work

In this study, we identified that the unique read mechanism of PeFET can be extended beyond standard memory implementation proposed in Thakuria et al. (2020). We build on this understanding to present PeFET-enabled signed ternary CiM design. The key contributions of this study are as follows:

1. We established through simulations that LRS of +P can be swapped to HRS while HRS of −P to LRS by reversing the polarity of applied voltage across the piezoelectric during sensing. We named this feature as polarization preserved piezoelectric effect reversal with dual voltage polarity (PiER).

2. We explored PiER for ternary input encoding. We show that PiER motivates exploration of PeFET-based non-volatile memory that naturally supports signed ternary CiM.

3. We proposed a ternary compute-enabled non-volatile memory (STeP-CiM) using PeFET and PiER functionality that performs scalar multiplication of signed inputs and weights without extra transistors.

4. We showed parallel in-memory dot product computation with STeP-CiM based on current sensing, as opposed to voltage sensing in the previous ternary designs by Jain et al. (2020) and Thirumala et al. (2020). We discussed the implications of current sensing for signed ternary CiM and evaluated the energy and delay of STeP-CiM in comparison to near-memory (NM) baselines based on PeFET (PeFET-NM) and SRAM (SRAM-NM).

5. We evaluated the system-level implications of STeP-CiM by implementing it in a DNN accelerator and quantify its energy, performance benefits and tradeoffs over PeFET-NM and SRAM-NM baseline designs.

2 Device Structure, Materials, and Methods of Modeling and Simulation

2.1 Device Structure and Operation of PeFET

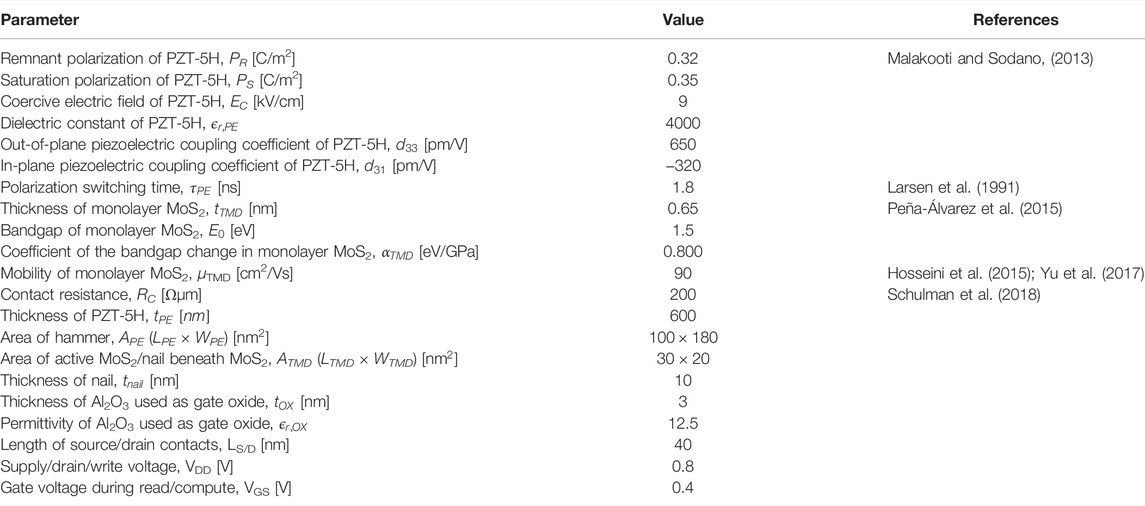
PeFET is a four-terminal non-volatile device consisting of drain (D), gate (G), source (S), and back (B) contacts. We present the structure and schematic of a PeFET device in Figures 1A,B. Its non-volatility is enabled by a ferroelectric material (PE) positioned between G and B, which also functions as the write port of the device, as illustrated in Figure 1A. In addition to ferroelectricity, PE, which is PZT-5H in this work, exhibits good piezoelectric response (high piezoelectric coefficient value, d₃₃ = 650 p.m./V (Malakooti and Sodano, 2013) for successful sensing. On the other side of G, an oxide layer of Al₂O₃ is deposited and a 2D-TMD channel of monolayer MoS₂ is grown over it. The monolayer MoS₂ undergoes bandgap change caused by the transfer of polarization-induced strain from PE to TMD. We select MoS₂ due to its high coefficient of bandgap change for applied pressure, ${\alpha }_{TMD}$₌ 800 meV/GPa (Peña-Álvarez et al., 2015).

FIGURE 1

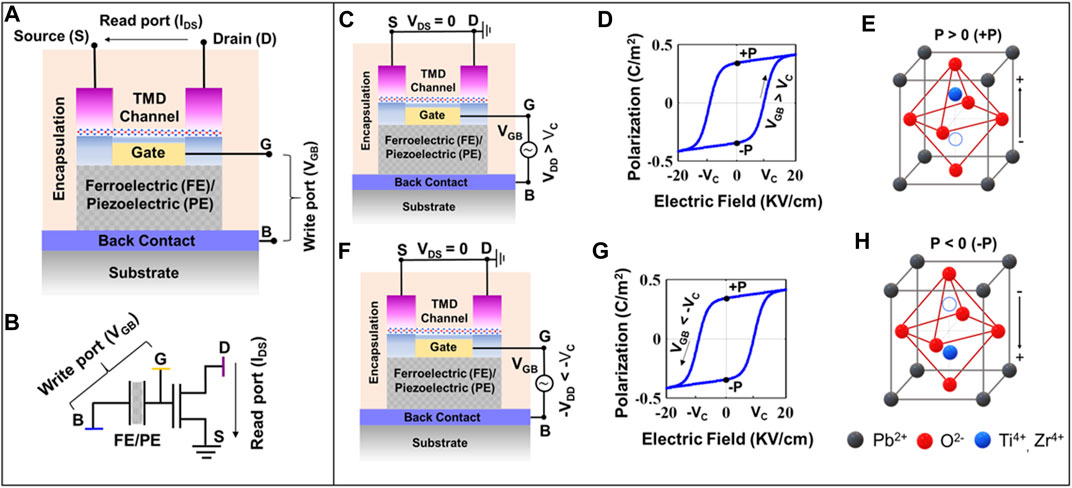
FIGURE 1. (A) Device structure of PeFET showing its four terminals, namely, back (B), drain (D), gate (G), and source (S). Ferroelectric or piezoelectric (FE/PE) material that extends non-volatile feature to PeFET is placed between G and B terminals. (B) Schematic representation of PeFET. Ferroelectric-based storage in PeFET. (C) Bias conditions of PeFET for +P polarization switching. (D) Polarization vs. electric field response showing +P switching behavior for V_GB > V_C in PZT-5H, extracted from the experimental result by Malakooti and Sodano (2013). (E) Structure of PZT in the +P stable state. (F) Bias conditions of PeFET for −P polarization switching. (G) Polarization vs. electric field response showing −P switching behavior for V_GB < −V_C in PZT-5H, extracted from the experimental result by Malakooti and Sodano (2013). (H) Structure of PZT in the −P stable state.

PE stores binary bit information (1 or 0) in the form of stable polarization states (+P or −P). The polarization state is controlled by voltage at the write port or gate to back voltage (V_GB) as illustrated by Figures 1C–H. To write +P (logic 1), we apply V_GB = V_DD > V_C, where V_C is the coercive voltage of PZT-5H (Figure 1C). V_GB > V_C induced +P switching is shown by the polarization–electric field (P-E) response in Figure 1D. On the contrary, application of V_GB < −V_C causes polarization to switch to −P state (or logic 0), as signified in Figures 1F,G. At a structural level, a perovskite material such as PZT-5H exist in +P (or −P) polarized state due to upward (or downward) displacement of Ti⁴⁺/Zr⁴⁺ from their centrosymmetric position, as depicted in Figures 1E,H.

To read the stored polarization in FE, we apply a positive voltage (V_R) across G and B. We present a description of the read mechanism in PeFET through Figure 2. First, V_R < |V_C| is applied to ensure that current state of polarization in PE is not disturbed. V_R has the following role: (i) it actuates strain (piezoelectric effect) in the PE, which is in turn transduced to the TMD channel and (ii) simultaneously turns on the TMD channel. If +P had been stored in the PE, V_R enhances charge separation along the direction of polarized charge, as shown in Figure 2A. This causes an increase in PE thickness ($\text{Δ}{t}_{PE}>0$) and yields positive strain ($S_{PE}= \frac{\text{Δ}{t}_{PE}}{t_{PE}}>0$). The experimentally characterized strain–electric field (S-E) response of PZT-5H reported by Malakooti and Sodano (2013) reflects this effect (see the S-E plot in Figure 2A). As pointed by the arrow, PZT-5H in +P demonstrates positive strain on experiencing a voltage that is positive but lower than V_C (similar to V_R). In case of −P, V_R, being opposite in polarity compared to the stored polarization, diminishes charge separation (Figure 2B). This constricts PE thickness ($\text{Δ}{t}_{PE}<0$) resulting in negative strain ($S_{PE}<0$, as also highlighted in the S-E plot of Figure 2B). Strain in PE translates to stress (σ_PE) which is induced as pressure in TMD (σ_TMD) and is responsible for dynamic modulation of bandgap in TMD (ΔE_G). Positive strain in PE ($S_{PE}$ > 0) transduces as positive pressure in (σ_TMD > 0) causing bandgap reduction (ΔE_G > 0). Contrarily, negative strain expands the bandgap (ΔE_G < 0). Note, even for S_PE = 0, TMD can experience stress from components in the device structure other than that due to the piezoelectric effect, leading the bandgap reduction from its intrinsic value. While positive S_PE further reduces the bandgap, negative S_PE relaxes this pressure leading to bandgap expansion toward the intrinsic value. The effect of reduced/expanded bandgap change reflects in drain current as low/high resistance states (LRS/HRS), respectively. Hence, enhanced drain to source current (I_DS = I_LRS) is sensed for +P and I_DS = I_HRS is for −P during read.

FIGURE 2

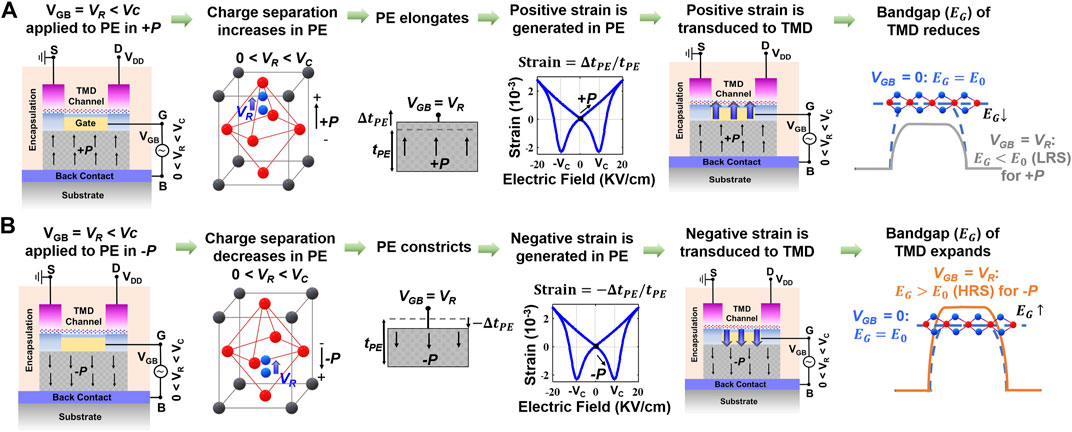
FIGURE 2. Mechanism of polarization-dependent strain transduction in PE that enables read operation in PeFET. (A) PeFET with +P showing bandgap reduction and (B) PeFET with −P showing bandgap expansion from intrinsic position on application of read voltage that is 0 < V_R < V_C. The baseline for bandgap comparison is PeFET with V_GB = 0.

2.2 Modeling and Simulation

To perform circuit simulations of PeFET, we employ a simulation framework that integrates HSPICE, COMSOL, and Verilog A–based models of various components in PeFETs. A representation of the modeling framework is provided in Figure 3. First, we discuss the HSPICE-based circuit-compatible model, Miller model, used for capturing the ferroelectric behavior of PE. The equivalent circuit of the PE is shown in Figure 3. We utilize Eqs 1, 2 to simulate the polarization–electric field switching behavior of PE. Figure 4A presents calibration of the simulated P-E characteristics with experimental characterization of PZT-5H by Malakooti and Sodano (2013). The hysteresis window of P-E response of PZT-5H is 18 kV/cm with E_C = 9 kV/cm (Malakooti and Sodano, 2013). The calibrated values of saturation polarization (P_S), remnant polarization (P_R), coercive electric field (E_C), and dielectric permittivity (${\mathit{ϵ}}_{r,PE}$) used in our model are provided in Table 1. The polarization switching delay, ${\tau }_{PE}$, is incorporated using a resistor ($R_{PE}$)—capacitor ($C_{PE}$) network (Figure 3), wherein $R_{PE}={\tau }_{PE}/C_{PE}$ and C_PE is given by Eq. 3. For thickness of PE used in this work (t_PE = 600 nm), V_C = E_C × t_PE ∼ 0.54 V. Based on this, we select the write voltage of PeFET to be V_GB = 0.8 V > V_C. We use ${\tau }_{PE}$ = 1.8 ns, as reported by Larsen et al. (1991) for PZT.

$P=P_S\mathit{tanh}\left(\frac{E\pm E_C}{2\delta }\right)+{\mathit{ϵ}}_0{\mathit{ϵ}}_{r,PE}E,(1)$

$\delta =\alpha {\left[\ln \left(\frac{P_S+P_R}{P_S-P_R}\right)\right]}^{-1},(2)$

$C_{PE}=A_{PE}\left(\frac{dP}{dE}\right).(3)$

FIGURE 3

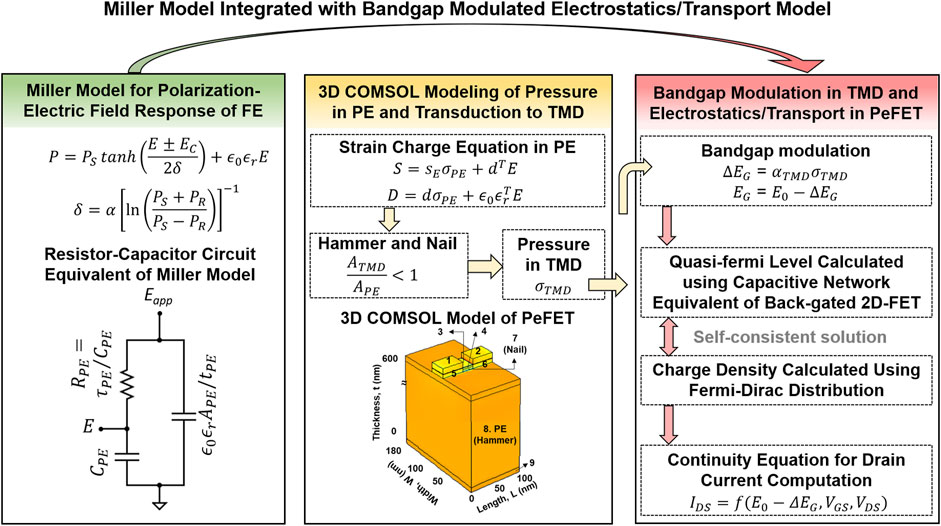
FIGURE 3. HSPICE-compatible model of PeFET formed by integrating (i) Miller model of polarization–electrical field behavior of PE, (ii) 3D COMSOL model of PeFET simulating pressure in PE and its transduction to TMD on application of gate voltage, and (iii) electrostatics and transport model of TMD augmented with bandgap modulation behavior.

FIGURE 4

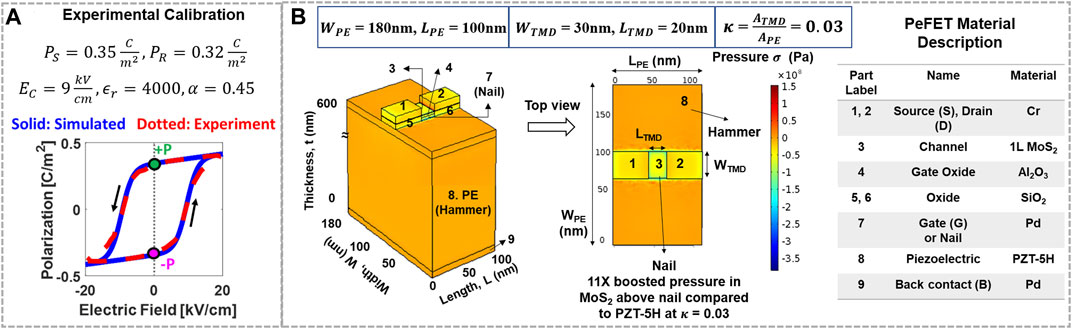
FIGURE 4. (A) Calibration of simulated polarization-electrical response with experiments. (B) 3D COMSOL model of PeFET with components labeled, their material specification, and top view of PeFET signifying hammer which is the top surface area of PE (8) and nail which is the gate below active MoS₂ (7). Pressure in MoS₂ in the active/nail region is ∼11× higher than PE.

TABLE 1

TABLE 1. Parameters used in the PeFET model.

Next, we model a 3D structure of PeFET in COMSOL Multiphysics Suite (Figure 3) that integrates solid mechanics, electrostatics, and their couplings using Eqs 4–7. Using this model, we analyze piezoelectric effect in PE and transduction of stress to 2D-TMD during read. We employ strain–charge Eqs 4, 5 to our 100 nm × 180 nm × 600 nm PE composed of PZT-5H. To obtain strain in PE (S_PE), we provide V_R = 0.4 V to the gate contact (labeled as 7 in Figure 4B). Therefore, E across PE = V_R/t_PE = 6.7 kV/cm. E translates to strain by means of piezoelectric coupling coefficients, d. We use parameter values of d (d₃₃ and d₃₁) that are reported in Malakooti and Sodano (2013) based on experimentally characterized strain vs. electric field response of PZT-5H. Stress in PE ${\sigma }_{PE}$ (Eq. 4), generated due to interactions of various materials in the model (Eq. 7), contribute to S_PE by means of the compliance parameter, s_E. Electric displacement field, D, caused by ${\sigma }_{PE}$ and E is modeled using Eq. 5.

$S_{PE}=s_E{\sigma }_{PE}+d^{T}E,(4)$

$D=d{\sigma }_{PE}+{\mathit{ϵ}}_0{\mathit{ϵ}}_{r,PE}^{T}E,(5)$

$\nabla .D=\rho ,(6)$

$\nabla .{\sigma }_{PE}=0.(7)$

Furthermore, to boost efficiency of transduction of stress from PE (σ_PE) to TMD (σ_TMD), we incorporate the hammer and nail effect. Hammer and nail is effective when the area of nail/2D-TMD (A_TMD) is sufficiently smaller than that of PE (A_PE), that is, A_TMD < A_PE. Smaller A_TMD than A_PE allows stress from PE (hammer labeled as 8 in Figure 4B) to be better localized to TMD that lies above the nail (label 3, 7 in Figure 4B), thereby facilitating efficient transfer. We define a device parameter $\kappa$ in Eqs 8, 9 to help us later analysis of this principle.

$\kappa =\frac{A_{TMD}}{A_{PE}},(8)$

$=\frac{L_{TMD}{W}_{TMD}}{L_{PE}{W}_{PE}}<1.(9)$

Here, $L_{TMD}$ = 20 nm is the feature size of PeFET and W_TMD is the width of TMD. We use minimum width of TMD as per design rules, W_PE = W_TMD = 1.5 × L_TMD = 30 nm, to maintain low $\kappa$ and maximize σ_TMD. We choose a wide PE (W_PE) while leveraging the total device length of PeFET including contacts for L_PE. Such a design consideration allows us to achieve L_PE = 100 nm > L_TMD that assists in further diminishing $\kappa$, without incurring additional overhead. Details about W_PE are provided in Section 3.1. Moreover, we choose metals with high stiffness (e.g., Pd and Cr) for the gate (beneath the nail) and bottom contact of PE and source/drain contacts (Figure 4B). We surround the PeFET including the source/drain contacts and TMD with an encapsulant material that has high elastic modulus (e.g., Al₂O₃) (Schulman Daniel S., 2019). The purpose of the capping layer is to restrain the expansion of the whole PE/gate stack/TMD structure (Newns et al., 2012). By constraining the TMD from the top, it helps to localize the piezoelectricity-induced strain in PE toward compressing the TMD material (via by the gate stack).

We use σ_TMD obtained from the COMSOL model as input to the Verilog A model of 2D-TMD FET. This model first converts σ_TMD to a bandgap change, $\text{Δ}{E}_G={\alpha }_{TMD}{\sigma }_{TMD}$, where ${\alpha }_{TMD}$ is the bandgap coefficient of TMD (Table 1). We use a capacitive network–based model (Suryavanshi and Pop, 2016) modified for a back-gated device to model the electrostatics of the 2D FET. The charge density and source/drain quasi-Fermi level of a TMD material are self-consistently solved in the model (Suryavanshi and Pop, 2016). We incorporate the effect of bandgap modulation (ΔE_G) induced by transduction of piezoelectric strain (Eq. 10) in the calculation for quasi-Fermi level. Next, the continuity equation is used to derive drain to source current of TMD (Suryavanshi and Pop, 2016). The drain to source current (Eq. 11) reflects not only the effect of electrostatics but also that of bandgap modulation in PeFET device characteristics.

$E_G=E_0-\text{Δ}{E}_G,(10)$

$I_{DS}=f(E_G, V_{GS}, V_{DS}),(11)$

where E₀ is the bandgap of TMD at zero gate to back voltage.

Finally, the HSPICE compatible model of PeFET is a combination of Miller equation for PE/FE with the polarization-induced piezoelectric response incorporated 2D-TMD FET model. The parameters used in our simulations are based on prior literature and experiments (Table 1).

3 Characteristics of 2D Piezoelectric FET

3.1 Strain Transfer Through the Hammer-and-Nail Principle

To analyze the hammer and nail principle in our 3D COMSOL model of PeFET (Figure 4B), we use W_PE = 180 nm that results in $\kappa$ = 0.03 <1 according to Eq. 9. We show ∼11× increase in σ_TMD compared to σ_PE for V_R = V_GB = 0.4 V in Figure 4B. At this V_R, σ_TMD causes bandgap of TMD to decrease (increase) by 48.4 mV when PE is in +P/−P state.

Tuning of $\kappa$ enables design time optimization of the distinguishability of memory states in PeFET. We know from Section 2.1 that positive stress appears in a +P polarized PeFET on application of V_GB = V_R. By decreasing $\kappa$, we further enhance the hammer and nail effect or localization of positive stress on TMD. As a result, resistance of TMD decreases to a greater extent. Hence, I_LRS increases. Contrarily, for −P, negative stress caused by V_R is accentuated for smaller $\kappa$. This results in a more resistive HRS in TMD (I_HRS decreases). The combined effect of improved I_LRS and diminished I_HRS improves distinguishability (= $I_{LRS}/I_{HRS}$) significantly. According to our approach in Section 2.2, we increase W_PE, keeping other dimensions fixed, to achieve lower $\kappa$. This leads to a tradeoff between improved distinguishability and area increase which, in turn, can potentially increase latency and energy. Considering these aspects, we design our PeFET here with $\kappa =0.03$ that provides us with a distinguishability of 5$\times$ (details in next section) and sufficient drain current for desirable sense margin for dot product computations (elaborate discussion in Section 5.3).

3.2 Device Characteristics of PeFET

Let us start with a brief discussion on the biases required for $\pm P$ storage in PeFET. To write +P (or 1), we provide V_GB with 0.8 V = V_DD > V_C of PZT-5H (= 0.54 V at $t_{PE}$ of 600 nm as per Figure 4A). Similarly, −P (0) is stored at V_GB = −0.8 V < −V_C.

Now, we divulge into the polarization/strain-dependent transfer characteristics (I_DS-V_GS) of PeFET. To avoid polarization switching while obtaining transfer characteristics, we apply a positive gate voltage V_G = V_R = 0.4 V (< V_C of PZT-5H = 0.54 V at $t_{PE}$ = 600 nm) while the back contact (V_B) is kept at 0 V akin to Figure 5A. Note that V_R at the gate turns on the channel (controls electrostatics) while triggering piezoelectric response by dint of V_GB = V_R across PE. For comparison, we also simulate a device with V_GB = 0 (sweeping V_G and V_B at the same time), from which we obtain polarization-independent nominal transfer characteristics of MoS₂-based 2D FET.

FIGURE 5

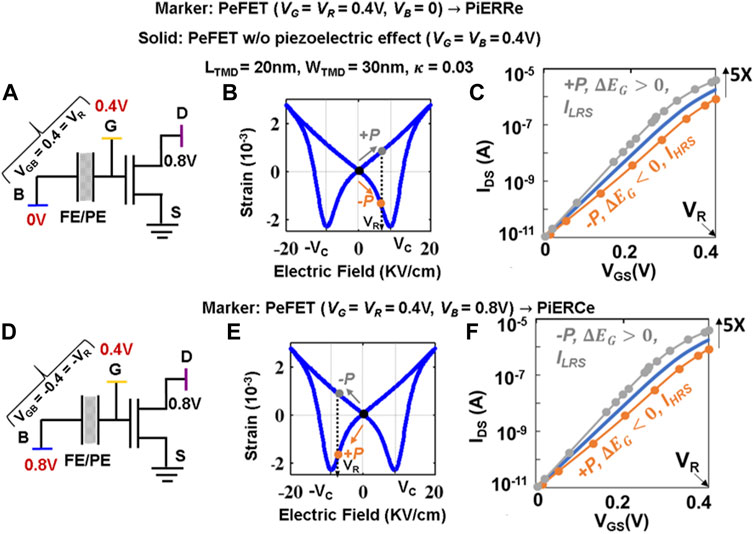
FIGURE 5. (A) Schematic representation of PeFET for V_G = 0.4 V, V_B = 0 V, V_GB = 0.4 V > 0, or PiERRe mode. (B) Strain–electric field response for V_GB = V_R > 0. (C) Device characteristics for V_GB > 0. (D) Schematic representation of PeFET for V_G = 0.4 V, V_B = 0.8 V, V_GB = −0.4 V < 0, or PiERCe mode. (E) Strain–electric field response for V_GB = −V_R < 0. (F) Device characteristics for V_GB < 0.

When V_GB = V_R = 0.4 V is applied, PeFET with +P undergoes positive strain in PE (follow gray arrow in Figure 5B) that results in bandgap reduction $\Delta$ E_G = 48.4 mV, yielding 2.3× enhanced I_DS (= I_LRS) compared to the baseline (MoS₂-FET with V_GB = 0), as shown in Figure 5C. Contrarily, when a −P state PeFET receives the same V_R, I_DS diminishes by 2.2× compared to baseline which we refer to as I_HRS (Figure 5C). This is because of negative strain (follow orange arrow in Figure 5B) in PE, which ultimately reflects as increase of bandgap toward the intrinsic value. Note that these results correspond to V_DS = 0.8 V and = 0.03. Overall, the distinguishability or I_LRS/I_HRS = ∼5×.

Let us now present the PiER characteristics of PeFETs, which is associated with the dependence of PeFET characteristics on the polarity of V_GB and eventually enables us to design signed ternary CiM.

3.3 Polarization Preserved Piezoelectric Effect Reversal With Dual Voltage Polarity

Until now, our analyses focused on piezoelectric response generated when PE is subjected to V_GB = V_R > 0. Recall that we maintain V_B = 0, while sweeping V_G to V_R to achieve the same. With this bias, PeFET in +P yields LRS whereas −P leads to HRS (Figure 5C).

Interestingly, the sensed resistance states with $\pm P$ are reversed when voltage across PE is negative, that is, V_GB = −V_R < 0. Again, since V_R < |V_C|, stored state of polarization is undisturbed. For the same polarization stored in PE, negative V_GB induces opposite piezoelectric response in PE compared to positive V_GB. This allows the same polarization to induce opposite resistance states in TMD for V_GB = −V_R compared to V_GB = V_R. Note that we bias V_G = V_R =V_DD/2 and V_B = V_DD, respectively, such that V_GB = −V_DD/2 = −V_R, also illustrated in Figure 5D. Since V_G controls electrostatics in TMD apart from piezoelectricity in PE, we ensure that a positive gate voltage greater than the device threshold voltage is applied, to keep the PeFET ON even when V_GB < 0.

We elucidate the reversal of piezoelectric effect and its impact on the TMD resistance now. Let the stored polarization in PE be −P. When V_GB = −V_R, charge separation occurs in the same direction as that of initial polarization. This causes $t_{PE}$ to elongate, thereby generating positive strain in PE for −P (follow gray arrow in Figure 5E). We know from our previous understanding that bandgap reduction of TMD occurs when it receives positive strain. Hence, PeFET is in LRS for the −P state. For +P, negative V_GB (= −V_R) bias reduces the polarization. This causes $t_{PE}$ to constrict, and negative strain (orange arrow in Figure 5E) is generated that leads to bandgap increase. Hence, HRS is observed for +P. Thus, +P (−P) stored in PeFETs can be configured in a low (high) resistance state by applying V_GB > 0 (i.e., V_B = 0, V_G = V_R = V_DD/2). On the other hand, +P (−P) induces high (low) resistance states with V_GB < 0 (i.e., V_B = V_DD, V_G = V_R = V_DD/2) during sensing (read/compute). We name this unique property as Polarization Preserved Piezoelectric Effect Reversal with Dual Voltage Polarity (PiER). We will refer to piezoelectric effect pertaining to V_GB = −V_R as PiERCe, where Ce signifies that negative V_GB mode is used exclusively for ternary compute (Section 5), whereas PiERRe identifies piezoelectric effect for positive V_GB (used for standard read as well as compute). We summarize this discussion in Table 2.

TABLE 2

TABLE 2. Summary of bias conditions and the PeFET resistance state with PiERRe and PiERCe modes.

From our analysis of PeFET device characteristics in PiERCe configuration (Figure 5F: V_G = 0.4 V, V_B = 0.8 V, and V_GB = −0.4 V), we observe that PeFET with −P exhibit 2.3× larger drain current (I_LRS) whereas that with +P shows 2.2× lower drain current (I_HRS) compared to baseline (i.e., PeFET without bandgap modulation: V_GB = 0). Overall, distinguishability = ∼5× is achieved, which is similar to that for read described in Section 3.2, but with polarization state mapping to LRS and HRS swapped.

Note that we use strain-independent electron mobility, ${\mu }_e=$ 90 cm²/Vs. for MoS₂ in our PeFET model (Hosseini et al., 2015; Yu et al., 2017). However, studies have shown that mobility of MoS₂ improves (degrades) subject to positive (negative) uniaxial strain such as that experienced by PeFET (Hosseini et al., 2015). Note that in PeFET, LRS and HRS are outcome of positive and negative strain, respectively. This implies improvement of I_LRS (due to enhanced ${\mu }_e$) and degradation of I_HRS (caused by lowered ${\mu }_e$). Consequently, a higher distinguishability of PeFET may be expected than the reported value in this work.

4 Ternary Compute–Enabled Memory Based on Pefet

In this section, we propose a PeFET-based non-volatile memory with the capability to perform dot product computations in the signed ternary regime. We refer to the proposed memory as Strain-enabled Ternary Precision Computation-in-Memory (STeP-CiM).

4.1 STeP-CiM Cell

STeP-CiM presented in Figures 6A,B consists of two PeFET-based bit cells (M₁ and M₂). M₁ and M₂ store bit information (1/0) in the form of +P/−P polarization. M₁ and M₂ use 2D TMD FET–based access transistors (AX_1, AX₂, RAX₁, and RAX₂) that are switched on/off using word line (WL). Access transistors AX₁ and AX₂ connect bit lines BL₁ and BL₂ with the gate terminals (G₁ and G₂) of the respective PeFETs M₁ and M₂. Recall that the gate terminal is a common control knob for the channel of the 2D-TMD FET and PE in M₁/M₂. Hence, BL₁ and BL₂ can actuate ferroelectric switching for write as well as piezoelectric response in PE for read/compute depending on the voltage they are driven to. The bias conditions of BL₁/BL₂ and impact on write-read-compute operation are discussed in detail in Section 4.2 and Section 5. Note that RAX₁ and RAX₂ are read access transistors that connect drains (D₁ and D₂) of PeFETs in M₁ and M₂ to read bit lines RBL₁ and RBL₂, respectively. The back terminals of PeFETs in M₁ and M₂ are shared and connected to compute word line, CWL. Read and compute are achieved by sensing strain-induced resistance changes in the PeFETs (more in Section 4.2.2 and Section 5) in terms of RBL₁ and RBL₂ currents. During hold, voltages of BL₁, BL₂, RBL₁, RBL₂, CWL, and WL are 0 V.

FIGURE 6

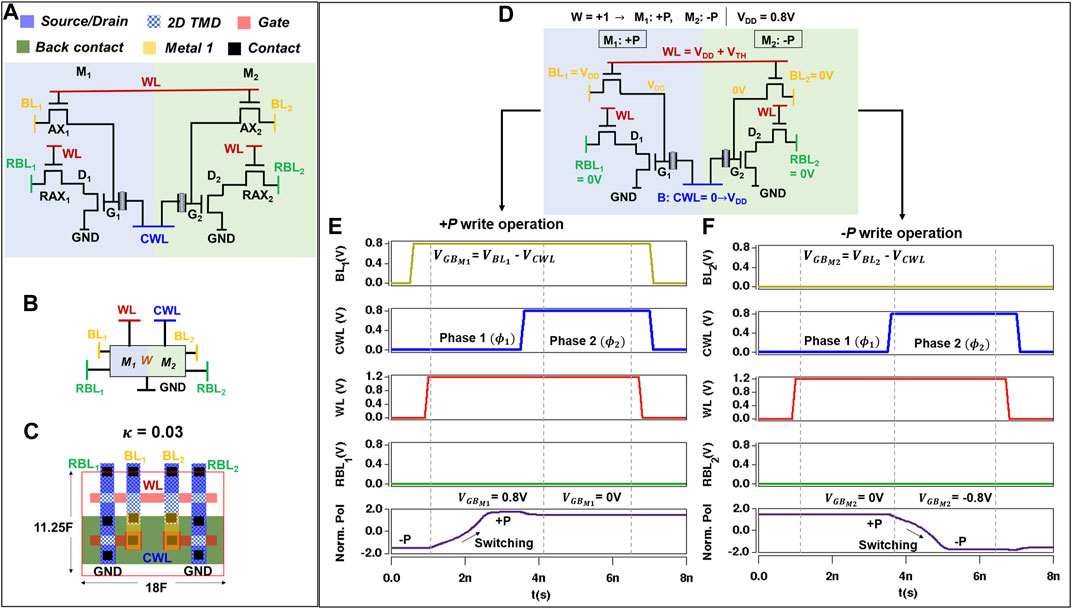
FIGURE 6. Non-volatile memory cell for STeP-CiM showing (A) Schematic illustration, (B) symbol, and (C) layout. (D) Schematic representation of the STeP-CiM cell with an example of biases for write operation (ternary 1). Two-phase write operation depicting in (E) −P $\to$ +P polarization switching when V_GB = 0.8 V > V_C and (F) +P $\to$ −P polarization switching when V_GB = −0.8 V < −V_C. +P and −P states being written to M₁ and M₂ constitute ternary storage of W = +1.

It should be noted that M₁/M₂ of STeP-CiM cell can be used as standard memory with binary storage. Hence, STeP-CiM cell can be reconfigured to serve as a standard memory (with 2 bit cells) or a compute-enabled memory for ternary precision as per application needs (further discussion on this in Section 6). Using two access transistors (such as AX₁ and RAX₁ in M₁) does not lead to any area penalty in the layout shown in Figure 6C. This is because the layout area is dictated by the PeFET footprint arising from the wide PE requirement for hammer and nail effect. As per our layout analysis, both AX and RAX can be accommodated within the PE layout area.

The access transistors in STeP-CiM cell (AX₁, AX₂, RAX₁, and RAX₂) serve two other purposes, in addition to achieving selective access to the cells in a memory array. First, AX₁/AX₂ of the un-accessed cells disconnect BL_1/2 from the respective PE capacitance, which is large due to high dielectric permittivity of PZT-5H, ${\mathit{ϵ}}_{r,PE}=4000$ (Malakooti and sodano., 2013). This averts the increase in the total BL capacitance due to large PE capacitance (C_PE) and improves write energy efficiency and performance. Second, RAX₁/RAX₂ provides means to disconnect un-accessed PeFET from RBLs, thereby avoiding unwanted RBL currents. It is an important aspect in this design as floating gate terminals of PeFETs in the un-accessed cells (disconnected from BL_1/2 by AX₁/AX₂) may develop a potential greater than the threshold voltage of TMD FET due to noise and leakage, leading to spurious currents on RBLs. The advantage of using two access transistors (AX and RAX) per PeFET is decoupling of write and read/compute operations, which enhances the design margins, especially for the dot product computation. With this background, we now describe the write and read operations next, and CiM operations in the subsequent section.

4.2 Write and Read Operations of STeP-CiM Cell

4.2.1 Write

The encoding for signed ternary weights stored in a STeP-CiM cell is provided in Table 3A. To store ternary “1” in STeP-CiM, +P and −P are written in M₁ and M₂ as per Table 3A. This operation is depicted by Figures 6D–F. First, BL₁ is driven to V_DD > V_C and BL₂ to 0 V. RBL_1/2 are kept at 0 V. Next, WL is asserted to V_DD + V_TH (boosted to compensate for threshold voltage V_TH drop in write access transistors). Finally, CWL is supplied with a two-phase signal ($0\to V_{DD}$), wherein the voltage in the first phase $\left({\text{Φ}}_1\right)$ is 0 V, while it is V_DD in the second phase $\left({\text{Φ}}_2\right)$. The two-phase signal (Li et al., 2019) facilitates writing “1” and “0” states to multiple PeFETs as follows. PeFET in M₁ (Figure 6E) experiences V_GB = V_BL1−V_CWL = 0.8 V during ${\text{Φ}}_1$ since V_BL1 = 0.8 V and V_CWL = 0 V. This results in $-P\to +P$ switching. M₂ (Figure 6F) experiences V_{GB =} V_BL2−V_CWL = 0 (as V_BL2 = 0 V and V_CWL = 0 V) during ${\text{Φ}}_1$ and the previous polarization state is preserved. During ${\text{Φ}}_2,$ M₁ retains its state of ${\text{Φ}}_1$ (V_GB = 0) while M₂ switches to $-P$ after receiving V_GB = −0.8 V (V_BL2 = 0 V and V_CWL = 0.8 V). Similarly, for ternary “−1”, −P and +P should be written to M₁ and M₂ (Table 3A). The process is similar except that now, BL₁ is driven to 0 V and BL₂ to 0.8 V. Finally, ternary “0” corresponds to −P in both M₁ and M₂, which is stored by having BL₁ and BL₂ at 0 V.

TABLE 3

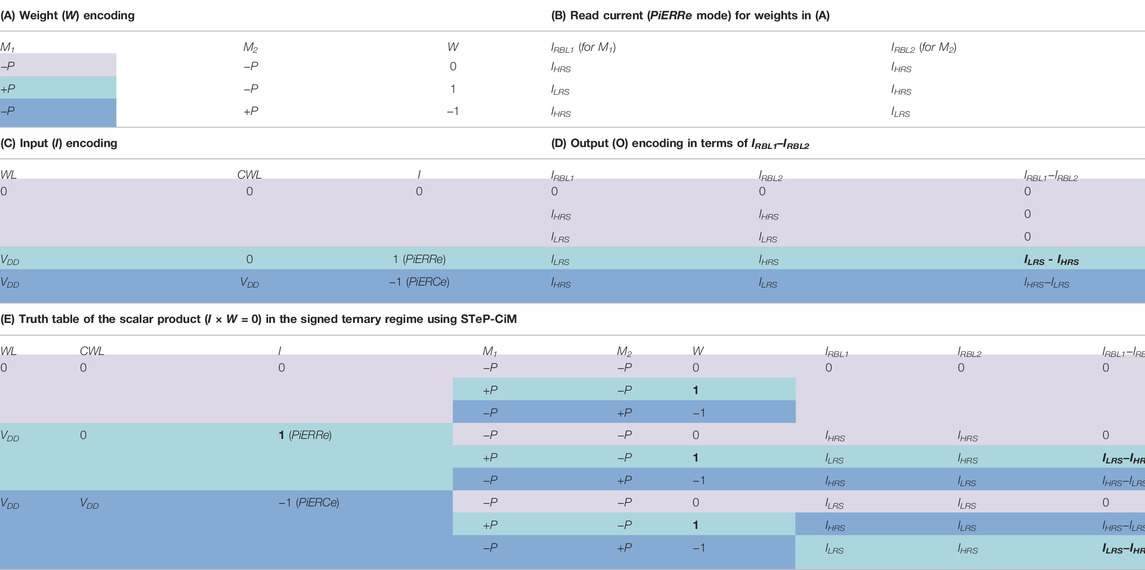
TABLE 3. Signed ternary scheme of {−1, 0, 1} in (A) weights (W) represented in terms of polarization stored in PeFETs M₁ and M₂. (B) Sensed states of weights. (C) Inputs (I) encoded utilizing biases in word line (WL) and read word line (CWL). It should be noted that the inputs place PeFETs M₁ and M₂ into different resistance regimes, PiERCe and PiERRe. (D) Outputs (O) used for MAC computation in STeP-CiM. Subtracted currents on read bit lines RBL₁ and RBL₂ signify ternary outputs. (E) Truth table of the scalar product in the signed ternary regime using STeP-CiM.

4.2.2 Read

In order to sense the stored polarization value in the STeP-CiM cell, a positive V_GB (= V_R < V_C) need to be applied across the PEs of M₁ and M₂ for them to be in PiERRe condition (refer to Table 2). Moreover, gates G₁ and G₂ of M₁ and M₂ should receive V_R for PeFETs to conduct. To achieve this, we drive BL₁ and BL₂ to V_R = 0.4 V while CWL is kept at 0 V. In addition, RBL₁ and RBL₂ are switched to V_DD = 0.8 V to facilitate drain to source conduction of PeFETs. The schematic with biases for the read operation and waveform are demonstrated in Figures 7A,B.

FIGURE 7

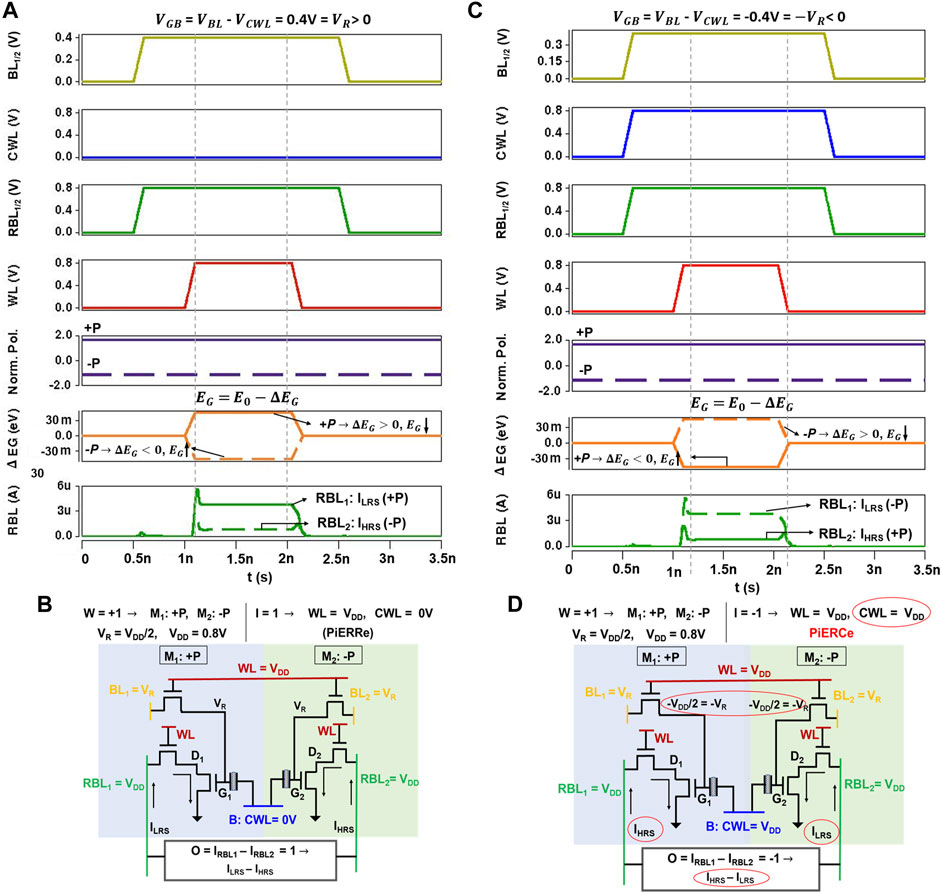
FIGURE 7. Waveform of (A) read operation showing I_LRS for +P and I_HRS for −P when V_GB = V_R (PiERRe mode). This waveform and schematic representation in (B) show scalar product with W = 1 (+P in M₁ and −P in M₂) and I = 1 (corresponding to CWL = 0 V and WL = V_DD), resulting in I_LRS on RBL₁ due to +P in M₁ and I_HRS on RBL₂ due to −P in M₂. (C) Waveform and schematic representation in (D) depicting the scalar product with W = 1 (+P in M₁ and −P in M₂) and I = −1 (in the PiERCe mode corresponding to CWL = V_DD and WL = V_DD). This results in I_HRS on RBL₁ due to +P in M₁ being sensed as HRS due to I = −1 and I_LRS on RBL₂ due to −P in M₂ being sensed as LRS due to I = −1. For the same weights, currents on RBL₁ and RBL₂ for I = 1 (waveform A) are swapped for I = −1 (waveform B) due to difference in CWL (highlighted with red circles).

On asserting WL with V_DD = 0.8 V, V_GB = V_BL1/BL2−V_CWL = 0.4 V for both M₁ and M₂. Let us explore the sensing of ternary “1”. In this case, as +P is stored in M₁, bandgap reduces ($\text{Δ}{E}_G$ < 0) in response to V_GB = 0.4 V and I_LRS is sensed on RBL₁ (corroborating with Table 2). Contrarily, for −P in M₂, bandgap expands with V_R, that is, $\text{Δ}{E}_G$ > 0 (dotted line of Figure 7A), leading to increased resistance of M₂ or I_HRS on RBL₂. I_LRS on RBL₁ and I_HRS on RBL₂ indicate ternary “1” storage, as also listed in Table 3B. For ternary “−1” (−P in M₁ and +P in M₂), we obtain I_HRS on RBL₁ and I_LRS on RBL_2. For ternary “0”, which is encoded by −P in both M₁ and M₂, I_HRS is observed on RBL₁ and RBL₂.

4.3 Segmented Architecture of STeP-CiM

If standard memory array architecture is followed for STeP-CiM cell wherein CWL runs throughout the row, C_PE from all cells in the row add to CWL capacitance. This could lead to large energy overheads (Thakuria and Gupta, 2022), since C_PE for PZT-5H is large (as discussed before). To mitigate this, we design an array for STeP-CiM that employs segmentation similar to FERAMs (Rickes et al., 2002). Figure 8 illustrates the segmented array architecture of STeP-CiM-based cells. Segmentation may not be required for CiM in DNNs that utilize high parallelism by computing the dot products for all the columns simultaneously. However, if this proposed array is used as a standard memory (as discussed before), segmentation will be important for high energy efficiency, especially in edge devices. Therefore, we employ the segmented architecture with an objective to support the reconfiguration of the proposed design from a compute-enabled ternary memory for DNNs to a standard memory, as per the application needs.

FIGURE 8

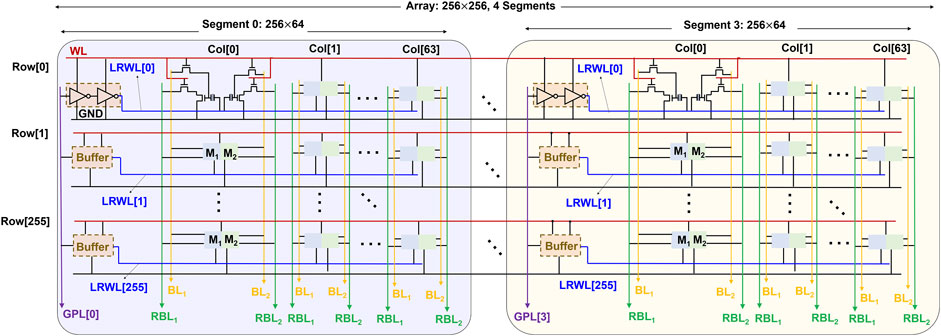
FIGURE 8. Segmented array of STeP-CiM of size 256 × 256, comprising 4 segments, each of size 64 × 256.

A segment in the segmented array (Thakuria and Gupta, 2022) is sized as 64 × 256 (Figure 8). Each segment has an exclusive global plate line (GPL) that runs along the column direction. GPL acts as an input to buffers in each local row of the segment. The output of the buffers is used to drive a local read word line LCWL for each local row comprised of 64 STeP-CiM cells. Notice that, the capacitance on LCWL is from C_PE of 64 STeP-CiM cells instead of the entire row, which enhances the energy efficiency. WL provides the supply voltage to the buffers and also activates access transistors of each STeP-CiM in the accessed segment. Bit lines BL₁, BL₂, RBL_1, and RBL₂ run along the column. The 64 STeP-CiM cells in a segmented row are accessed simultaneously for read and write.

Appropriate biasing of GPL during write and read operations is important to ensure that LCWL voltage is identical to CWL voltage discussed in Section 4.2. For write, we apply the two phase 0 → V_DD signal to GPL, instead of CWL in Section 4.2.1. When WL is asserted with V_DD + V_TH, LCWL is driven to 0 → V_DD + V_TH by the active buffers connected to GPL and LCWL. V_GB = V_DD in ${\text{Φ}}_1$ and $-P\to +P$ write occurs, while $+P\to -P$ occurs in ${\text{Φ}}_2$ when V_GB = −V_DD, similar to Section 4.2.1. During read, GPL voltage is 0 V with WL = V_DD such that LCWL is at 0, as in Section 4.2.2. Other lines are biased in an identical fashion as described in Section 4.2.1 (for write) and Section 4.2.2 (for read). WL is de-asserted for all un-accessed rows of an accessed segment. An unaccessed segment is put on hold by pulling its GPL, WLs (other than that of the row accessed by another segment) and all RBLs, BLs to 0 V.

5 In-Memory Ternary Computation Using STeP-CiM

In this section, we explain ternary in-memory scalar multiplication and dot product computation using STeP-CiM. We target signed ternary precision for weights, inputs, and the scalar product having values {−1, 0, 1} (Li et al., 2016). As discussed in Section 4.2.1, combination of polarization states of M₁ and M₂ in STeP-CiM constitute a ternary weight (Table 3A). The ternary inputs encoded with WL and CWL voltages to utilize the resistance states of both conditions, PiERRe (CWL = 0) and PiERCe (CWL = V_DD = 0.8 V), are indicated in Table 3C. More details on this are as follows. BL₁ and BL₂ are driven to V_R = 0.4 V so that V_GB < |V_C| appears across PE of M₁ and M₂ (similar to Section 4.2.2). RBL₁ and RBL₂ are driven to V_DD during compute. In accordance with the ternary weights and applied input, different instances of RBL₁ and RBL₂ currents (I_RBL1 and I_RBL2) are observed. Finally, the scalar product or output is obtained as O = I_RBL1−I_RBL2. Notice from Table 3D that O = {−1, 0, 1} is interpreted as {(I_HRS–I_LRS), 0, (I_LRS–I_HRS)}, respectively.

5.1 Ternary Scalar Multiplication Using STeP-CiM

Before delving into details of ternary scalar multiplication with STeP-CiM, we elaborate on what the input encoding (I) in Table 3C represents in terms of resistance states. Subsequently, we evaluate examples of ternary scalar multiplication. The truth table for scalar product is available in Table 3E.

5.1.1 Ternary input (I) = +1

I = +1 corresponds to CWL = 0 and WL being asserted with V_DD. With BL₁ and BL₂ being V_R during compute (as mentioned before), we have V_GB1,2 = V_BL1,2−V_CWL = V_R for I = +1. Note that V_GB, being a positive voltage here, puts PeFETs in PiERRe resistance regime (corroborating with Table 2). That is, +P is read as LRS (I_LRS) and −P as HRS (I_HRS). With this background, we elaborate the scalar products for different weight (W) conditions with I = +1 (for which PeFETs are in PiERRe). Please refer to Table 3E for further clarity on the descriptions of W, I, and corresponding O.

(a) W = +1: According to this weight encoding, M₁ and M₂ store +P and −P, respectively. Since, PeFETs are in PiERRe because of I = +1, M₁ and M₂ are in LRS and HRS, respectively. Hence, I_RBL1 = I_LRS, I_RBL2 = I_HRS, and O = W×I = I_LRS–I_HRS. O corresponds to scalar product of +1 in Table 3E. Figures 7A,B shows the waveform for this example.

(b) W = −1: M₁ and M₂ are written with −P and +P, respectively; hence, they exhibit HRS and LRS for I = 1. Hence, I_RBL1 = I_HRS, I_RBL2 = I_LRS, and O = I_HRS–I_LRS corresponding to scalar product = −1.

(c) W = 0: Both M₁ and M₂ have −P stored in them and are in HRS for I = 1. Thus, I_RBL1 = I_HRS, I_RBL2 = I_HRS, and O = I_HRS−I_HRS = 0 (corresponding to scalar product of 0).

5.1.2 Ternary input (I) = −1

For I = −1, CWL and WL are both switched to V_DD. Since, BL₁ and BL₂ remain at V_R (= V_DD/2) during compute, we have V_GB1,2 = V_BL1,2−V_CWL = −V_DD/2 = −V_R for I = −1. With V_GB < 0, now PeFETs M₁ or M₂ are in PiERCe resistance regime. Hence, +P and −P are sensed as HRS (I_HRS) and LRS (I_LRS). Note that the sensed states are reversed for the same stored polarization compared to previous example due to PiERCe (refer to Section 3.3 for detailed mechanism). The scalar products with I = −1 for varying weights are evaluated as follows.

(a) W = +1: Although M₁ and M₂ have +P and −P stored in them [same as in example 5.1(a)], they now exhibit HRS and LRS, respectively, now due to PeFETs being in PiERCe. This is caused by interaction of the stored polarization with negative V_GB (refer to Table 2) when I = −1. Ultimately, I_RBL1 = I_HRS, I_RBL2 = I_LRS, and O = I_HRS–I_LRS = −1 (Table 3E). Figures 7C,D represent this example with waveforms, highlighting the differences from I = 1 and W = 1.

(b) W = −1: In this case, polarization in M₁ and M₂ is −P and +P, respectively. Due to PiERCe, I_RBL1 = I_LRS, I_RBL2 = I_HRS, and O = I_LRS–I_HRS = +1.

(c) W = 0: With M₁ and M₂ both storing −P and −P. Hence, O = I_LRS−I_LRS = 0.

5.1.3 Ternary Input (I) = 0

In this case, CWL and WL are de-asserted with 0 V. PeFETs are non-conducting. I_RBL1 and I_RBL2 are 0V, hence O = 0, irrespective of the weights.

5.2 Ternary Multiply-and-Accumulate With STeP-CiM

In this section, we elaborate on the design details of a STeP-CiM array for achieving ternary MAC, with reference to the schematic in Figure 9A. Prior to the operation, weight vector with W_is is mapped and programmed to M_1i and M_2i of each row of STeP-CiM, following the procedure discussed in Section 4.2.1. The input vector (I_i) encoded as WL and CWL voltages is applied to the rows accessed for MAC. Currents flowing through RBL₁ and RBL₂ due to scalar product of I_i and W_i add up on the respective lines. These currents are used to evaluate the dot product. Our method for current-based sensing is as follows: first, we compare I_RBL1 and I_RBL2 to determine which branch has higher current. The output of the comparator in Figure 9B determines the sign (Sn) of the final MAC output. If I_RBL1 > I_RBL2, Sn = 1, whereas for I_RBL1 < I_RBL2, Sn = −1. Next, the comparator output is fed to a current subtractor circuit (Figure 9C), which determines the magnitude of the difference of bit currents, I_RBL1−I_RBL2. The output of the subtractor is actually an integer multiple of I_LRS–I_HRS, that is, I_RBL1−I_RBL2 = a (I_LRS–I_HRS), where “a” is the integer multiple. To determine the value of “a”, we employ a flash analog to digital converter (ADC), as in Figure 9D. Finally, the dot product is computed as O = Sn $\times$ a = $\pm$ a depending on which of I_RBL1 and I_RBL2 is greater, as discussed earlier. Notice that our method of subtracting of RBL currents before digitization of the sensed current from the array saves us an ADC compared to other ternary designs that employ ADCs on each bit line (Jain et al., 2020; Thirumala et al., 2020) due to their use of voltage-based sensing. The benefits of this are evidenced at the system-level results.

FIGURE 9

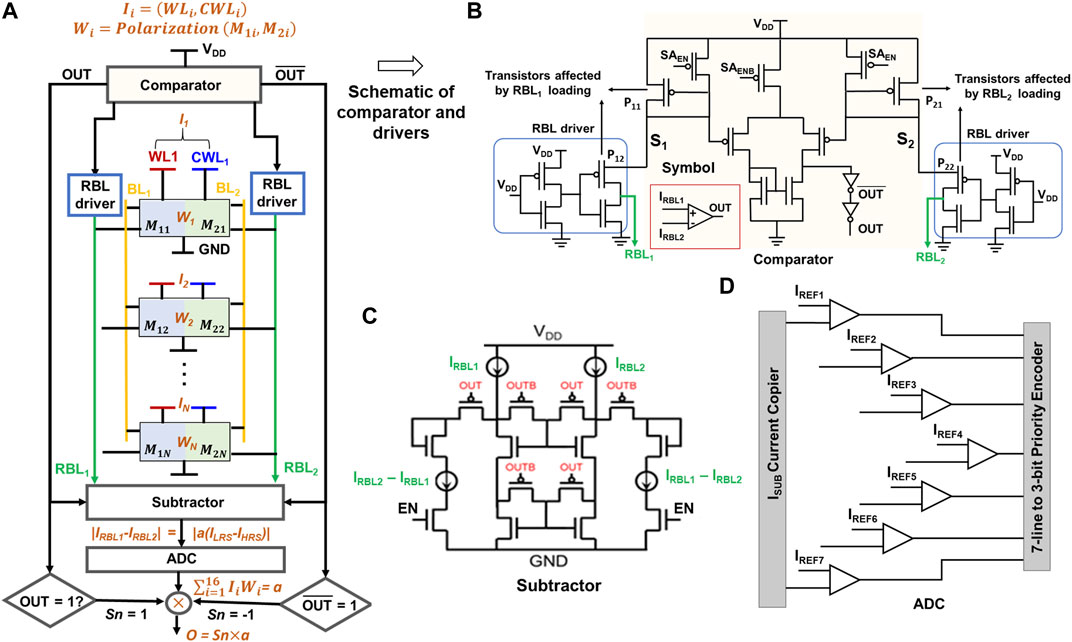
FIGURE 9. (A) Column of the STeP-CiM cell for MAC operation. In the schematic representation, we labeled weights (W) as combination of polarization in M_1i and M_2i conforming to encoding in Table 3A, while inputs of a cell are encoded utilizing WL and CWL, according to Table 3C. Peripherals used in the simulation of a MAC operation such as comparators, read drivers, subtractors, and ADC are shown. Schematic representation of (B) read drivers interacting with RBL and comparator. (C) Subtractor and (D) 3-bit ADC represented using symbol in inset of (B).

Next, we throw light on the design of our peripherals and the non-idealities caused by their interaction with current-based sensing scheme for MAC. The read bit line drivers in Figures 9A,B used for biasing RBL₁ and RBL₂ to V_DD during MAC operation (as per the biasing scheme discussed in Section 5) are the primary source of non-idealities. Note in Figure 9B that the transistor P₁₁ (P₂₁) of the comparator is connected in series to transistor P₁₂ (P₂₂) of read bit line driver, with drain of P₁₂ (P₂₂) connected to RBL₁ (RBL₂). Although this configuration is necessary for mirroring RBL₁ and RBL₂ current to the comparator required for MAC (whose functionality we have discussed previously), rising current on RBL₁ (RBL₂) with multiple row access causes voltage on the source node S₁ (or S₂) of P₁₂ (P₂₂) to be pulled to value less than V_DD by resistive divider action of the pull up transistors of comparator/read bit line and access transistors on RBL. This leads to non-ideal current on RBL₁ and RBL₂. We reference this as loading effect in the future. In other words, RBL_1/2 is biased at a value less than V_DD due to the loading effect, and this value is dependent on RBL current. Higher the RBL current, larger is the voltage drop across the biasing transistors, and lower is the RBL voltage. In our analysis presented in the subsequent section, we discuss the loading effect for STeP-CiM array and how it can alter the sense margin from one output to another, which is an undesirable effect.

Before proceeding to investigate the sense margin for different outputs, it is important to reflect on the number of cells that can be accessed together robustly while performing the MAC operation. We decide the same on the basis of ADC precision and sparsity of input and weight vectors. Higher ADC precision has been shown to overshadow energy efficiency achieved at the array level with CiM (Jain et al., 2020). Therefore, following their energy estimations, we consider the 3-bit flash ADC of Figure 9D. Moreover, DNNs are known to exhibit >50% sparsity. Considering this into account, we assert N_V = 16 cells simultaneously to obtain a maximum dot product output of 8, which can also be robustly computed by the 3-bit ADC. This analysis and the design decisions have been borrowed from our earlier work on ternary memories (Jain et al., 2020; Thirumala et al., 2020). It is noteworthy that outputs >8 (rare due to sparsity >50%) are interpreted as eight by the system (due to limited ADC precision). However, this has negligible impact on the overall system accuracy, as confirmed by our system analysis described later.

5.3 Sense Margin and Variation Analysis for Signed Ternary MAC

We evaluate the robustness of signed ternary MAC operation performed in a column of 16 rows. We study different instances of accessing word lines 1–16 to understand their effect on RBLs loading and its translation to sense margin. In essence, we want to establish combinations of I_i and W_i that reflect minimum loading (best case) and maximum loading (worst case) of RBLs to define sense margin.

(A) Let us first consider the case where the loading effect is minimum (i.e., with lowest RBL current). To start with, we first analyze the condition for scalar product, O = 1. Corroborating with our previous understanding of scalar product computation in Section 5.1, we expect I_LRS on RBL₁ and I_HRS on RBL₂ for this output. We provide an input sequence where a row (say row₁) receives I₁ = 1 and the remaining 15 rows (e.g., rows_{2 … 16}) receive I_{2 ... 16} = 0. This is achieved with W₁ = 1 for I₁ = 1. Rows_{2 … 16} do not contribute significantly to currents on RBLs as I_{2 ... 16} = 0 (WL = 0V, which disconnects PeFETs from RBLs). Similarly, to obtain a MAC output of “a”, “a” number of rows store W_{1 … a} = 1 and receive I_{1 … a} = 1. The remaining rows receive input, I_{a+1 … 16} = 0. Ws of rows a..16 are not of much significance here since they are non-contributing by dint of their inputs I = 0. Hence, I_RBL1 = aI_LRS, I_RBL2 = aI_HRS and O_a = a (I_LRS–I_HRS) = a. Here, a = number of rows with I = 1 and a ≤ 16. Note that the RBLs in this example are loaded with currents only from the rows having I = 1, which is akin to a scenario of minimum loading of RBL for a desired output. This example is illustrated in Figure 10A.

(B) Next, we consider another example whose expected outcome is similar to the case study in (A), but with Wi and Ii different from example (A). Here, our intent is to obtain the combinations of W_i and I_i that maximizes current on RBLs to mimic a worst-case example of loading effect. Again, starting with O = 1, we program the weight of row₁ as W₁ = 1 (i.e., M₁:+P, M₂: −P) and remaining rows_{2 … 16} with W_{2 … 16} = 0 (their M₁: −P, M₂: −P). The inputs corresponding to row₁ I₁ = 1 and rows_{2 … 16} I_{2 … 16} = −1. We expect a MAC output = 1 using these combinations. Let us analyze what this means in terms of scalar product from each row, and the resultant MAC output.

FIGURE 10

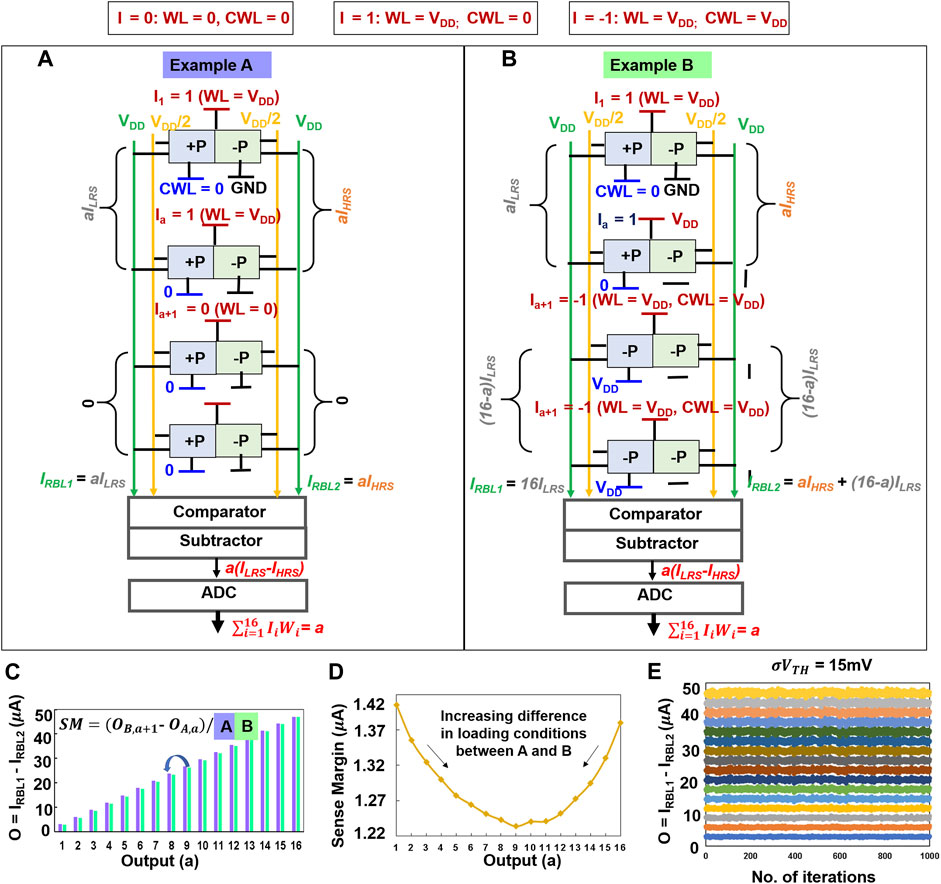
FIGURE 10. Examples of STeP-CiM for (A) best-case and (B) worst-case loading effect, (C) computation of sense margin, (D) sense margin, and (E) variation analysis for 16 activations.

The cell in row₁ with I₁ = 1 is in PiERRe mode. This implies that for W₁ = 1, M₁ is in LRS and M₂ in HRS. Correspondingly, the contribution to I_RBL1 and I_RBL2 is I_LRS and I_HRS. Rows_{2 … 16} with I = −1 are in PiERCe. Hence, for W_{2 … 16} = 0 (−P, −P as per Table 3A), both M₁ and M₂ are in LRS (Table 2), we observe I_LRS on RBL₁ and RBL_2. Ultimately, we obtain I_RBL1 = 16I_LRS and I_RBL2 = I_HRS+15I_LRS. Overall, O₁ = I_RBL1−I_RBL2 = I_LRS−I_HRS, which corresponds to output of 1. However, I_RBL1 and I_RBL2 in this scenario is significantly higher than example (A), reflecting worst-case loading effect.

Similarly, to obtain a MAC output of “a” while loading the RBLs maximally, “a” number of rows get input and weight as 1 (i.e., I_{1 … a} = 1, W_{1 … a} = 1) which contribute as I_RBL1 = aI_LRS and I_RBL2 = aI_HRS. The remaining rows receive input of −1 and weight 0 (i.e., I_{a+1 … 16} = −1, W_{a+1 … 16} = 0). Hence, from these rows we receive I_RBL1 = (16-a)I_LRS and I_RBL2 = (16-a)I_LRS. For all the 16 rows, I_RBL1 = 16I_LRS and I_RBL2 = 16I_LRS + a(I_HRS–I_LRS) and O_a = a × (I_LRS–I_HRS) = a.

From (A) and (B), it is clear that the former and latter have highest and lowest loading effects. We take these into account while determining the maximum and minimum currents for each output (Figures 10A,B). Based on this approach, we define the worst-case sense margin for an expected output “a” (say) to be = (O_{Min_load,a}–O_{Max_load,a-1})/2. Here, O_{Min_load,a} is based on minimal loading of RBL₁ and RBL₂ for output “a” calculated using the method in (A), while O_{Max_load,a-1} is the maximum loading of RBL₁ and RBL₂ for the prior output “a-1” using method in (B). Figure 10B depicts this method of calculating sense margin. The calculated sense margin is plotted in Figure 10C. Note that the minimum sense margin of >1 $\mu A$ is obtained by optimizing the widths of the loading transistors in the read bit line drivers.

We further perform variation analysis (Figure 10E) using Monte Carlo HSPICE simulations and analyze the sensing errors in ternary MAC based on sense margins in Figure 10D. We consider $\sigma {\mathrm{V}}_{\mathrm{TH}}=$ 15 mV. random variation of V_TH (Smets et al., 2019; Sebastian et al., 2021) in transistors in STeP-CiM. As the expected MAC output increases, we observe overlap of output currents with adjacent states resulting in an error magnitude of $\pm$ 1 and rising trend of sensing error probability. We calculate a total of such 10 errors from 16 outputs, each undergoing 1000 Monte Carlo iterations. Combined with occurrence probability of error for each state (Jain et al., 2020), the overall error is sufficiently small not to affect DNN accuracy.

5.4 Architecture for Increased Parallel Computation of MAC

Next, we discuss the STeP-CiM array used for performing parallel in-memory dot product computation between ternary inputs and weights. The size of our STeP-CiM array is 256 × 256 (= N_R × N_C). The array is segmented into 16 blocks, wherein each block consists of 16 × 256 (= N_V × N_C) STeP-CiM cells. All N_V rows and N_C columns of the block are asserted during a block access for dot product computation. Hence, a block can perform simultaneous ternary multiplication of input vector I with N_V elements and weight matrix W of size N_V × N_C. We follow a similar architecture as proposed in (Jain et al., 2020) to compute dot product with input vectors N_V > 16. In this case, partial sums are stored in a peripheral compute unit (PCU) using a sample and hold circuitry. The partial sums are accumulated after several block accesses to get the final dot product. The dot products are then quantized, and passed through an activation function to provide inputs to the next DNN layer (Jain et al., 2020). We use Q = 32 PCUs for the entire array (where Q < N_C = 256) to minimize area/energy overheads of the peripheral circuits (Jain et al., 2020).

6 Results and Analysis

6.1 Array-Level Analysis

Here, we present analysis of STeP-CiM for array-level metrics, namely cell area, latency and energy for write, read and MAC operations. We compare them with near-memory designs based on PeFETs (PeFET-NM) and 2D FET based SRAM (SRAM-NM). The STeP-CiM cell presented in Figure 6A can be readily repurposed for near-memory compute by maintaining CWL = 0 V (akin to PiERRe condition), during these operations. We name this mode as PeFET-NM. Whereas, during in-memory ternary dot product computations, STeP-CiM operate with either CWL = 0 (PiERRe) for I = 1 or CWL = V_DD (PiERCe) for I = −1. SRAM-NM cell is designed with two 2D FET SRAM bit cells for ternary weight storage. The 2D FETs have a feature size of 20 nm (similar to L_TMD of PeFET). Consistent with PeFET based NM/STeP-CiM, V_DD = 0.8 V and array size of 256 × 256 is used for SRAM-NM. For PeFET-NM and SRAM-NM, scratchpad memories are accessed row-by-row for performing vector-matrix multiplication (Jain et al., 2020). On the other hand, in STeP-CiM the same is performed by accessing 16 rows of a block simultaneously. We reiterate that the primary distinction between STeP-CiM and PeFET-NM is during compute, while they are identical for memory operations–write and read.

6.1.1 Area

We present our area analysis of STeP-CiM (or PeFET-NM) and SRAM-NM using thin-cell layout (Khare et al., 2002) based on scalable layout ($F$-based) rules, where F = feature size. In this work, F = 20 nm for PeFET and 2D FET based on which SRAMs are designed. We use these rules in conjunction with Intel defined 20 nm gate/metal pitch rules (Intel 20 nm Lithography). The area of PeFET-NM/STeP-CiM obtained from the layout in Figure 6C is 202.5F² while that of SRAM-NM is 378F². We estimate the area of SRAM-NM based on the layout analysis of 2D FET SRAM by (Thakuria et al., 2020). Finally, we report in Figure 11A that the layout footprint of PeFET-NM/STeP-CiM is 46% smaller than SRAM-NM.

FIGURE 11

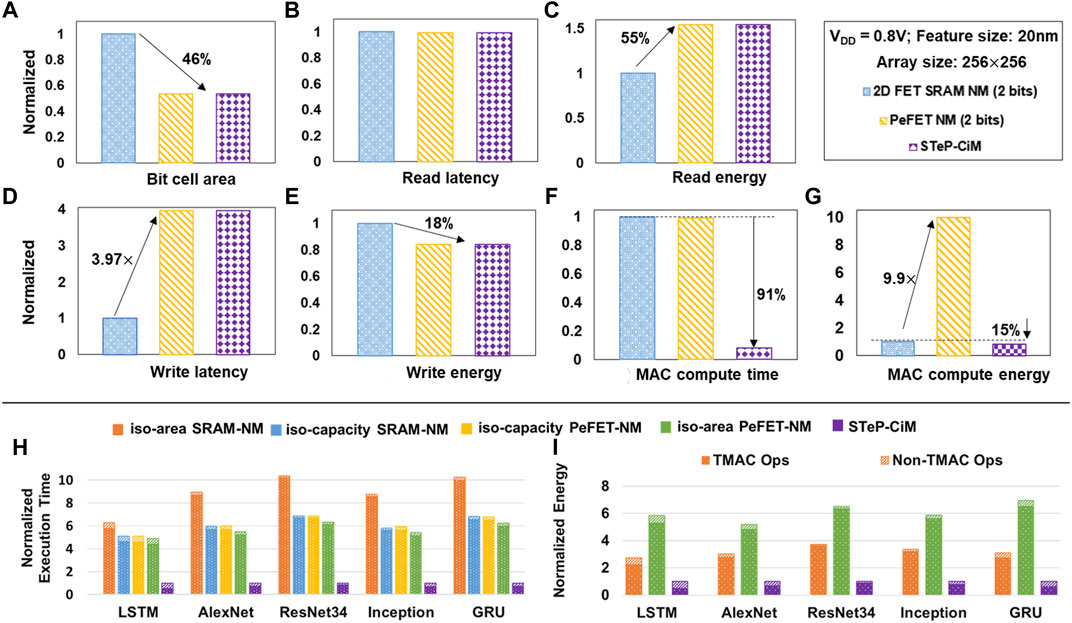
FIGURE 11. Array-level results of STeP-CiM vs. PeFET-NM and SRAM-NM shown for (A) bit cell area, (B) read latency, (C) read energy, (D) write latency, (E) write energy, (F) MAC compute time, and (G) MAC compute energy. System-level results for (H) normalized execution time. (I) Normalized energy of STeP-CiM with respect to iso-capacity and iso-area PeFET-NM and SRAM-NM.

6.1.2 Read and Write Comparisons

Performance and energy of STeP-CiM and PeFET-NM are identical since they are essentially the same bit cell during read/write operations, as also discussed earlier. Figure 11B indicates that the read latency of STeP-CiM/PeFET-NM is similar to SRAM-NM. We do not observe faster read in the former despite their compact cell area, since we must account for bit line charging time in current-based sensing mechanism employed during read. In case of SRAM-NM, where we utilize voltage-based sensing, this delay may be ignored since RBL₁/RBL₂ are pre-charged to V_DD.

Next, we elaborate our read energy results. We calculate the read energy in Figure 11C considering active energy for 20% utilization, as reported for L2 cache by (Park et al., 2012) and leakage energy for remaining 80% utilization. The active read energy of STeP-CiM/PeFET-NM is 9× higher compared to SRAM-NM. This is because, current-based sensing in STeP-CiM/PeFET-NM necessitate switching BL₁, BL₂ to V_DD/2 and RBL₁, RBL₂ to V_DD during read, causing energy overheads. In case of SRAM-NM, we utilize voltage-based sensing in which BL/BLB discharge by a small voltage of 50 mV from their pre-charged state. This incurs low active read energy in SRAM-NM than in current-based sensing of STeP-CiM and PeFET-NM. However, leakage energy from the 80% idle utilization dominates in SRAM-NM, while it is insignificant in STeP-CiM/PeFET-NM. This helps reduce the read energy overhead of STeP-CiM/PeFET-NM over SRAM-NM to 55% as shown in Figure 11C.

Now, we present the write analysis. Due to polarization switching delay in STeP-CiM/PeFET-NM, they show 3.97× higher write time over SRAM-NM (Figure 11D).

Interestingly, the write energy of STeP-CiM/PeFET-NM is 18% lower than SRAM-NM (Figure 11E). Note that, similar to read, total write energy is reported considering 20% active utilization and 80% leakage in an L2 cache (Park et al., 2012). Although the active energy of STeP-CiM/PeFET-NM is 2× higher than SRAM-NM due to polarization switching, we observe benefits in total write energy due to low utilization rates of modern day caches and dominating leakage energy in SRAM-NM (Park et al., 2012). In this scenario, SRAM-NM is leaking for the remaining 80% utilization, while PeFET-NM/STeP-CiM do not, resulting in overall improvement in the latter.

6.1.3 MAC

The highlight of STeP-CiM is that we can access 16 multiple rows parallelly. On the contrary, it needs to be done sequentially in NM baselines. This property benefits both performance and energy of MAC operations using STeP-CiM. Compared to SRAM-NM, we observe ∼91% benefits in MAC latency of STeP-CiM, while PeFET-NM shows comparable latency as SRAM-NM (Figure 11F).

With respect to MAC energy in Figure 11G, STeP-CiM shows 15% improvement over SRAM-NM. Note that we obtain benefits in MAC energy with STeP-CiM because of high parallelism mentioned earlier, despite overheads of current sensing. On the contrary, Figure 11G shows overhead of MAC energy of PeFET-NM over SRAM-NM. This is attributed to high energy consumption of current-based sensing in the former compared to low energy voltage-based sensing. It is important to mention that since >90% operations in DNNs are MACs, overheads in standard read and write operations are amortized due to significant MAC benefits of the proposed STeP-CiM design. Consequently, large improvements in system performance and energy is observed in STeP-CiM, which we discuss in system-level analysis next.

6.2 System Evaluation

Here, we evaluate the system-level energy and performance benefits of CiM using STeP-CiM in five state-of-the-art DNN benchmarks, viz. AlexNet, ResNet34, Inception, LSTM and GRU.

6.2.1 Simulation Framework

We design our compute-in-memory (CiM) architecture based on TiM-DNN (Jain et al., 2020) with 32 STeP-CiM arrays, where each array consists of 256 × 256 STeP-CiM cells, providing a total memory capacity of 2 mega ternary words (512 kB). By activating 16 rows simultaneously in each of these arrays, we can perform 8196 parallel vector MAC operations with a vector length of 16. The peripheral circuitry of the STeP-CiM array consists of ADCs (Figure 9) and small compute elements to sense the MAC outputs and perform partial-sum reduction (Jain et al., 2020). We compare the STeP-CiM system with two NM baseline architectures, SRAM-NM and PeFET-NM, constructed with the corresponding memory technologies. We perform the MAC computations and partial-sum reduction in the near-memory compute (NM) units, the inputs to which are read in a sequential row-by-row manner from each memory array. We design two variants of the near-memory baseline—(i) iso-capacity and (ii) iso-area. The iso-capacity SRAM-NM and PeFET-NM baselines contain 32 memory arrays of size 512 × 256 (identical to STeP-CiM system). We design the iso-area baseline architectures with 21 SRAM-NM and 35 PeFET-NM memory arrays, each of size 512 × 256. We design the SRAM-NM iso-area baseline with a smaller number of memory arrays compared to PeFET-NM because SRAM-NM suffers area overhead due to large footprint of SRAM cell. Further, the STeP-CiM array is 1.09× larger in area compared to PeFET-NM due to the area overhead of the ADCs. We leverage the lower area of PeFET-NM to place a larger number of memory arrays compared to STeP-CiM.

6.2.2 Performance

Figure 11H shows the performance benefits of STeP-CiM over iso-capacity and iso-area SRAM-NM and PeFET-NM baselines. We obtain 6.11× and 6.13× average speed-up over the iso-capacity SRAM-NM and PeFET-NM respectively, across the benchmarks considered. Similarly, the average speed-up over iso-area SRAM-NM and PeFET-NM is 8.91× and 5.67×, respectively. The performance improvements over the near-memory baselines arise from the massively parallel in-memory MAC computation capability of STeP-CiM. The SRAM-NM and PeFET-NM iso-capacity baselines have similar performances due to similar memory read latency (discussed in the array-level results). Note that, performance enhancement of STeP-CiM over iso-area SRAM-NM is greater than over iso-capacity SRAM-NM. This is due to higher throughput of STeP-CiM than SRAM-NM at iso-area, in addition to the benefits of massively parallel MAC operations. The boosted throughput follows from the larger number of memory arrays of STeP-CiM (32 vs. 21 of SRAM-NM) available for computation at iso-area. Contrarily, the performance benefits of STeP-CiM over PeFET-NM at iso-area is slightly diminished (relative to the iso-capacity case) because PeFET-NM has a comparatively larger number of memory arrays (35 arrays of PeFET-NM compared to 32 of STeP-CiM at iso-capacity).

6.2.3 Energy

We now present the system-level energy benefits of STeP-CiM compared to near-memory baselines in Figure 11I. We note that in this evaluation, the iso-area and iso-capacity baselines are equivalent since the total energy depends on the total number operations that remain the same across these baselines. Therefore, we report the energy benefits of STeP-CiM against the iso-area baselines. We achieve 3.2× and 6.07× average energy reduction compared to iso-area/capacity SRAM-NM and PeFET-NM respectively for the benchmarks considered. The superior energy efficiency of the proposed STeP-CiM system is due to the parallelism offered by the STeP-CiM arrays as a result of multi-word line assertion for in-memory computation. PeFET-NM consumes higher energy compared to SRAM-NM because of comparatively higher read-energy caused by switching of multiple bit lines required for current-based sensing (as discussed in Section 6.1). We would like to mention here that since the bit-cell for STeP-CiM is reused for PeFET-NM, it is optimized for ternary computation rather than read.

We compare the proposed architecture with existing state-of-the-art ternary DNN accelerators in Table 4. With respect to TeC DNN (Thirumala et al., 2020) and TiM-DNN (Jain et al., 2020), we achieve 2.45× and 4.9× improvement in TOPS/W respectively. Moreover, the benefits in TOPS/mm² are 7× and 15.15× compared to TeC DNN and TiM-DNN, respectively. The improvements are obtained due to compact size and scaled technology nodes used (20 vs. 45 nm and 32 nm) and superior compute energy efficiency. Compared to state-of-the-art GPUs, we observe up to 1486× and 5880× in TOPS/W and TOPS/mm², respectively. Note, however, that the comparisons are made between simulation and experimental results of GPUs.

TABLE 4

TABLE 4. System-level comparison with state-of-the-art DNNs.

7 Conclusion

In this work, we proposed a non-volatile memory (STeP-CiM) for ternary DNNs that has the ability to perform signed ternary dot product computation-in-memory. The CiM operation in our design is based on piezoelectric-induced dynamic bandgap modulation in PeFETs. We proposed a unique technique called Polarization Preserved Piezoelectric Effect Reversal with Dual Voltage Polarity (PiER) which we show is amenable for signed ternary computation-in-memory. Using this property along with multi-word line assertion, STeP-CiM performs massively parallel dot product computations between signed ternary inputs and weights. From our array-level analysis, we observed 91% lower delay and energy improvement of 15% and 91% for in-memory multiply-and-accumulate operations compared to near-memory approaches designed with 2D FET SRAM and PeFET, respectively. Our system-level evaluations show that STeP CiM achieves upto 6.13× and 8.91× average performance improvement; up to 6.07× and 3.2× reduction in energy compared to PeFET and SRAM based on near-memory baselines, respectively, across five state-of-the-art DNN benchmarks.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

NT and SG conceived the idea and designed the analysis. ST contributed to the idea of current-based sensing. NT and RE used the device and array and performed system-level simulations and analyses. NT, RE, and SG wrote the manuscript. NT, RE, ST, AR, and SG analyzed the data, discussed the results, agreed on their implications, and contributed to the preparation of the manuscript. AR and SG supervised the project.

Funding

This research was supported, in part, by the Army Research Office (W911NF-19-1-048) and the SRC/NSF-funded E2CDA program (1640020).

Conflict of Interest

At the time of research, ST was a student at School of Electrical and Computer Engineering, Purdue University, USA. Presently, he is employed by Intel Corporation, USA.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Al Bahou, A., Karunaratne, G., Andri, R., Cavigelli, L., and Benini, L. (2018). “XNORBIN: A 95 TOp/s/W Hardware Accelerator for Binary Convolutional Neural Networks,” in IEEE Symposium on Low-Power and High-Speed Chips and Systems, COOL Chips 2018 - Proceedings (Yokohama, Japan: Institute of Electrical and Electronics Engineers Inc.), 1–3. doi:10.1109/CoolChips.2018.8373076

CrossRef Full Text | Google Scholar

Alidoosty-Shahraki, M., Pourfath, M., and Esseni, D. (2019). An MoS2-Based Piezoelectric FET: A Computational Study of Material Properties and Device Design. IEEE Trans. Electron Devices 66, 1997–2003. doi:10.1109/TED.2019.2899371

CrossRef Full Text | Google Scholar

Bian, Z.-J., Guo, Y., Liu, B., and Cai, H. (2021). “In-MRAM Computing Elements with Single-step Convolution and Fully Connected for BNN/TNN,” in MRAM Computing Elements with Single-step Convolution and Fully Connected for BNN/TNN. In 2021 IEEE International Conference on Integrated Circuits, Technologies and Applications, ICTA 2021 (Zhuhai, China: Institute of Electrical and Electronics Engineers Inc.), 141–142. doi:10.1109/ICTA53157.2021.9661808

CrossRef Full Text | Google Scholar

Chen, W.-H., Li, K.-X., Lin, W.-Y., Hsu, K.-H., Li, P.-Y., Yang, C.-H., et al. (2018). “A 65nm 1Mb Nonvolatile Computing-In-Memory ReRAM Macro with Sub-16ns Multiply-And-Accumulate for Binary DNN AI Edge Processors,” in Digest of Technical Papers - IEEE International Solid-State Circuits Conference (San Francisco, CA, United States: Institute of Electrical and Electronics Engineers Inc.), 494–496. doi:10.1109/ISSCC.2018.8310400

CrossRef Full Text | Google Scholar

Chi, P., Li, S., Xu, C., Zhang, T., Zhao, J., Liu, Y., et al. (2016). “PRIME: A Novel Processing-In-Memory Architecture for Neural Network Computation in ReRAM-Based Main Memory,” in Proceedings - 2016 43rd International Symposium on Computer Architecture, ISCA 2016 (Seoul, South Korea: Institute of Electrical and Electronics Engineers Inc.), 27–39. doi:10.1109/ISCA.2016.13

CrossRef Full Text | Google Scholar

Choi, J., Wang, Z., Venkataramani, S., Chuang, P. I.-J., Srinivasan, V., and Gopalakrishnan, K. (2018). PACT: Parameterized Clipping Activation for Quantized Neural Networks. Available at: http://arxiv.org/abs/1805.06085.

Google Scholar

Colangelo, P., Nasiri, N., Nurvitadhi, E., Mishra, A., Margala, M., and Nealis, K. (2018). “Exploration of Low Numeric Precision Deep Learning Inference Using Intel FPGAs,” in Proceedings - 26th IEEE International Symposium on Field-Programmable Custom Computing Machines, FCCM 2018 (Boulder, CO, United States: Institute of Electrical and Electronics Engineers Inc.), 73–80. doi:10.1109/FCCM.2018.00020

CrossRef Full Text | Google Scholar

Courbariauxécole, M., and Bengio, Y. (2015). BinaryConnect: Training Deep Neural Networks with Binary Weights during Propagations. Montreal, Canada. doi:10.5555/2969442.2969588

CrossRef Full Text | Google Scholar

Das, S. (2016). Two Dimensional Electrostrictive Field Effect Transistor (2D-EFET): A sub-60mV/decade Steep Slope Device with High on Current. Sci. Rep. 6. doi:10.1038/srep34811

PubMed Abstract | CrossRef Full Text | Google Scholar

Doevenspeck, J., Degraeve, R., Fantini, A., Cosemans, S., Mallik, A., Debacker, P., et al. (2021). OxRRAM-Based Analog In-Memory Computing for Deep Neural Network Inference: A Conductance Variability Study. IEEE Trans. Electron Devices 68, 2301–2305. doi:10.1109/TED.2021.3068696

CrossRef Full Text | Google Scholar

Doevenspeck, J., Garello, K., Verhoef, B., Degraeve, R., van Beek, S., Crotti, D., et al. (2020). “SOT-MRAM Based Analog In-Memory Computing for DNN Inference,” in 2020 IEEE Symposium on VLSI Technology (IEEE), 1–2. doi:10.1109/VLSITechnology18217.2020.9265099

CrossRef Full Text | Google Scholar

Dutta, S., Ye, H., Chakraborty, W., Luo, Y.-C., Jose, M. S., Grisafe, B., et al. (20202020). Monolithic 3D Integration of High Endurance Multi-Bit Ferroelectric FET for Accelerating Compute-In-Memory. IEEE Int. Electron Devices Meet. 36, 4.1–36.4.4. doi:10.1109/IEDM13553.2020.9371974

CrossRef Full Text | Google Scholar

Hosseini, M., Elahi, M., Pourfath, M., and Esseni, D. (2015). Strain Induced Mobility Modulation in Single-Layer MoS2. J. Phys. D. Appl. Phys. 48, 375104. doi:10.1088/0022-3727/48/37/375104

CrossRef Full Text | Google Scholar

Hueting, R. J. E., van Hemert, T., Kaleli, B., Wolters, R. A. M., and Schmitz, J. (2015). On Device Architectures, Subthreshold Swing, and Power Consumption of the Piezoelectric Field-Effect Transistor ( ${\pi }$ -FET). IEEE J. Electron Devices Soc. 3, 149–157. doi:10.1109/JEDS.2015.2409303

CrossRef Full Text | Google Scholar

Jain, S., Gupta, S. K., and Raghunathan, A. (2020). TiM-DNN: Ternary In-Memory Accelerator for Deep Neural Networks. IEEE Trans. VLSI Syst. 28, 1567–1577. doi:10.1109/TVLSI.2020.2993045

CrossRef Full Text | Google Scholar

Kazemi, A., Rajaei, R., Ni, K., Datta, S., Niemier, M., and Hu, X. S. (2020). “A Hybrid FeMFET-CMOS Analog Synapse Circuit for Neural Network Training and Inference,” in 2020 IEEE International Symposium on Circuits and Systems(IEEE), 1–5. doi:10.1109/ISCAS45731.2020.9180722

CrossRef Full Text | Google Scholar

Khare, M., Ku, S. H., Donaton, R. A., Greco, S., Brodsky, C., Chen, X., et al. (2002). A High Performance 90nm SOI Technology with 0.992 μm/sup 2/6T-SRAM Cell. Tech. Dig. - Int. Electron Devices Meet., 407–410. doi:10.1109/IEDM.2002.1175865

CrossRef Full Text | Google Scholar

Kim, J.-H., Jung, D. J., Kang, Y. M., Kim, H. H., Jung, W. W., Kang, J. Y., et al. (2007). “A Highly Reliable FRAM (Ferroelectric Random Access Memory),” in 2007 IEEE International Reliability Physics Symposium Proceedings. 45th Annual (IEEE), 554–557. doi:10.1109/RELPHY.2007.369950

CrossRef Full Text | Google Scholar

Larsen, P. K., Kampschöer, G. L. M., Ulenaers, M. J. E., Spierings, G. A. C. M., and Cuppens, R. (1991). Nanosecond Switching of Thin Ferroelectric Films. Appl. Phys. Lett. 59, 611–613. doi:10.1063/1.105402

CrossRef Full Text | Google Scholar

Lecun, Y., Bengio, Y., and Hinton, G. (2015). Deep Learning. Nature 521, 436–444. doi:10.1038/nature14539

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, F., Zhang, B., and Liu, B. (2016). Ternary Weight Networks. Available at: http://arxiv.org/abs/1605.04711.

Google Scholar

Li, X., Wu, J., Ni, K., George, S., Ma, K., Sampson, J., et al. (2019). Design of 2T/Cell and 3T/Cell Nonvolatile Memories with Emerging Ferroelectric FETs. IEEE Des. Test. 36, 39–45. doi:10.1109/MDAT.2019.2902094

CrossRef Full Text | Google Scholar

Liao, C.-Y., Hsiang, K.-Y., Hsieh, F.-C., Chiang, S.-H., Chang, S.-H., Liu, J.-H., et al. (2021). Multibit Ferroelectric FET Based on Nonidentical Double HfZrO2 for High-Density Nonvolatile Memory. IEEE Electron Device Lett. 42, 617–620. doi:10.1109/LED.2021.3060589

CrossRef Full Text | Google Scholar

Liu, Q., Gao, B., Yao, P., Wu, D., Chen, J., Pang, Y., et al. (2020). “33.2 A Fully Integrated Analog ReRAM Based 78.4TOPS/W Compute-In-Memory Chip with Fully Parallel MAC Computing,” in 2020 IEEE International Solid- State Circuits Conference - (ISSCC) (San Francisco, CA, United States: IEEE), 500–502. doi:10.1109/ISSCC19947.2020.9062953

CrossRef Full Text | Google Scholar

Liu, X., Mao, M., Liu, B., Li, H., Chen, Y., Li, B., et al. (2015). “Reno,” in Proceedings - Design Automation Conference (Institute of Electrical and Electronics Engineers Inc.). doi:10.1145/2744769.2744900

CrossRef Full Text | Google Scholar

Malakooti, M. H., and Sodano, H. A. (2013). Noncontact and Simultaneous Measurement of the D33 and D31 Piezoelectric Strain Coefficients. Appl. Phys. Lett. 102, 061901. doi:10.1063/1.4791573

CrossRef Full Text | Google Scholar

Mishra, A., Nurvitadhi, E., Cook, J. J., and Marr, D. (2017). WRPN: Wide Reduced-Precision Networks. Available at: http://arxiv.org/abs/1709.01134.

Google Scholar

Nayak, A. P., Bhattacharyya, S., Zhu, J., Liu, J., Wu, X., Pandey, T., et al. (2014). Pressure-induced Semiconducting to Metallic Transition in Multilayered Molybdenum Disulphide. Nat. Commun. 5. doi:10.1038/ncomms4731

PubMed Abstract | CrossRef Full Text | Google Scholar

Newns, D. M., Elmegreen, B. G., Liu, X.-H., and Martyna, G. J. (2012). High Response Piezoelectric and Piezoresistive Materials for Fast, Low Voltage Switching: Simulation and Theory of Transduction Physics at the Nanometer-Scale. Adv. Mat. 24, 3672–3677. doi:10.1002/adma.201104617

CrossRef Full Text | Google Scholar

Ni, K., Smith, J. A., Grisafe, B., Rakshit, T., Obradovic, B., Kittl, J. A., et al. (2018). “SoC Logic Compatible Multi-Bit FeMFET Weight Cell for Neuromorphic Applications,” in 2018 IEEE International Electron Devices Meeting (IEEE), 13, 2.1–13.2.4. doi:10.1109/IEDM.2018.8614496

CrossRef Full Text | Google Scholar

NVIDIA (2022). NVIDIA V100 Tensor Core. Available at: https://www.nvidia.com/en-us/data-center/v100/ (Accessed January 26, 2022).

Google Scholar

Park, S. P., Gupta, S., Mojumder, N., Raghunathan, A., and Roy, K. (2012). “Future Cache Design Using STT MRAMs for Improved Energy Efficiency,” in Proceedings of the 49th Annual Design Automation Conference on - DAC ’12 (New York, New York, USA: ACM Press), 492. doi:10.1145/2228360.2228447

CrossRef Full Text | Google Scholar

Peña-Álvarez, M., del Corro, E., Morales-García, Á., Kavan, L., Kalbac, M., and Frank, O. (2015). Single Layer Molybdenum Disulfide under Direct Out-Of-Plane Compression: Low-Stress Band-Gap Engineering. Nano Lett. 15, 3139–3146. doi:10.1021/acs.nanolett.5b00229

PubMed Abstract | CrossRef Full Text | Google Scholar

Rickes, J. T., Mcadams, H., Grace, J., Fong, J., Gilbert, S., Wang, A., et al. (2002). A Novel Sense-Amplifier and Plate-Line Architecture for Ferroelectric Memories. Integr. Ferroelectr. 48, 109–118. doi:10.1080/713718311

CrossRef Full Text | Google Scholar

Schulman Daniel, S. (2019). Schulman Dissertation. Available at: https://www.proquest.com/docview/2432825234?pq-origsite=gscholar&fromopenview=true (Accessed March 25, 2022).

Google Scholar

Schulman, D. S., Arnold, A. J., and Das, S. (2018). Contact Engineering for 2D Materials and Devices. Chem. Soc. Rev. 47, 3037–3058. doi:10.1039/c7cs00828g

PubMed Abstract | CrossRef Full Text | Google Scholar

Sebastian, A., Pendurthi, R., Choudhury, T. H., Redwing, J. M., and Das, S. (2021). Benchmarking Monolayer MoS2 and WS2 Field-Effect Transistors. Nat. Commun. 12. doi:10.1038/s41467-020-20732-w

CrossRef Full Text | Google Scholar

Si, M., Cheng, H.-Y., Ando, T., Hu, G., and Ye, P. D. (2021). Overview and Outlook of Emerging Non-volatile Memories. MRS Bull. 46, 946–958. doi:10.1557/s43577-021-00204-2

CrossRef Full Text | Google Scholar

Smets, Q., Groven, B., Caymax, M., Radu, I., Arutchelvan, G., Jussot, J., et al. (2019). Ultra-scaled MOCVD MoS2 MOSFETs with 42nm Contact Pitch and 250µA/µm Drain Current. IEEE Int. Electron Devices Meet. 23, 2.1–23. doi:10.1109/IEDM19573.2019.8993650

CrossRef Full Text | Google Scholar

Sun, X., Yin, S., Peng, X., Liu, R., Seo, J.-s., and Yu, S. (2018). “XNOR-RRAM: A Scalable and Parallel Resistive Synaptic Architecture for Binary Neural Networks,” in Proceedings of the 2018 Design, Automation and Test in Europe Conference and Exhibition, DATE 2018 (Dresden, Germany: Institute of Electrical and Electronics Engineers Inc.), 1423–1428. doi:10.23919/DATE.2018.8342235

CrossRef Full Text | Google Scholar

Suryavanshi, S. v., and Pop, E. (2016). S2DS: Physics-Based Compact Model for Circuit Simulation of Two-Dimensional Semiconductor Devices Including Non-idealities. J. Appl. Phys. 120, 224503. doi:10.1063/1.4971404

CrossRef Full Text | Google Scholar

Thakuria, N., and Gupta, S. K. (2022). Piezoelectric Strain FET (PeFET) Based Non-volatile Memories. doi:10.48550/ARXIV.2203.00064

CrossRef Full Text | Google Scholar

Thakuria, N., Saha, A. K., Thirumala, S. K., Schulman, D., Das, S., and Gupta, S. K. (2020a). “Polarization-induced Strain-Coupled TMD FETs (PS FETs) for Non-volatile Memory Applications,” in 2020 Device Research Conference (DRC) (IEEE), 1–2. doi:10.1109/DRC50226.2020.9135172

CrossRef Full Text | Google Scholar

Thakuria, N., Schulman, D., Das, S., and Gupta, S. K. (2020b). 2-D Strain FET (2D-SFET) Based SRAMs-Part I: Device-Circuit Interactions. IEEE Trans. Electron Devices 67, 4866–4874. doi:10.1109/TED.2020.3022344

CrossRef Full Text | Google Scholar

Thirumala, S. K., and Gunta, S. K. (2018). “Gate Leakage in Non-volatile Ferroelectric Transistors: Device-Circuit Implications,” in Device Research Conference - Conference Digest, DRC (Santa Barbara, CA, United States: Institute of Electrical and Electronics Engineers Inc.). doi:10.1109/DRC.2018.8442186

CrossRef Full Text | Google Scholar

Thirumala, S. K., Jain, S., Gupta, S. K., and Raghunathan, A. (2020). “Ternary Compute-Enabled Memory Using Ferroelectric Transistors for Accelerating Deep Neural Networks,” in 2020 Design, Automation & Test in Europe Conference & Exhibition (DATE) (IEEE), 31–36. doi:10.23919/DATE48585.2020.9116495

CrossRef Full Text | Google Scholar

Venkataramani, S., Roy, K., and Raghunathan, A. (2016). “Efficient Embedded Learning for IoT Devices,” in Proceedings of the Asia and South Pacific Design Automation Conference, ASP-DAC (Macao, China: Institute of Electrical and Electronics Engineers Inc.), 308–311. doi:10.1109/ASPDAC.2016.7428029

CrossRef Full Text | Google Scholar

Wang, H., Jiang, X., Xu, N., Han, G., Hao, Y., Li, S.-S., et al. (2018a). Revised Analysis of Design Options and Minimum Subthreshold Swing in Piezoelectric FinFETs. IEEE Electron Device Lett. 39, 444–447. doi:10.1109/LED.2018.2791987

CrossRef Full Text | Google Scholar

Wang, P., Xie, X., Deng, L., Li, G., Wang, D., and Xie, Y. (2018b). HitNet: Hybrid Ternary Recurrent Neural Network.

Google Scholar

wiki chip (2012). Intel 20nm Lithography. Available at: https://en.wikichip.org/wiki/20_nm_lithography_process.

Google Scholar

Yin, S., Jiang, Z., Seo, J.-S., and Seok, M. (2020). XNOR-SRAM: In-Memory Computing SRAM Macro for Binary/Ternary Deep Neural Networks. IEEE J. Solid-State Circuits 55, 1–11. doi:10.1109/JSSC.2019.2963616

CrossRef Full Text | Google Scholar

Yoo, T., Kim, H., Chen, Q., Kim, T. T.-H., and Kim, B. (2019). “A Logic Compatible 4T Dual Embedded DRAM Array for In-Memory Computation of Deep Neural Networks,” in 2019 IEEE/ACM International Symposium on Low Power Electronics and Design (IEEE), 1–6. doi:10.1109/ISLPED.2019.8824826

CrossRef Full Text | Google Scholar

Yu, S., Hur, J., Luo, Y.-C., Shim, W., Choe, G., and Wang, P. (2021). Ferroelectric HfO2-Based Synaptic Devices: Recent Trends and Prospects. Semicond. Sci. Technol. 36, 104001. doi:10.1088/1361-6641/ac1b11

CrossRef Full Text | Google Scholar

Yu, Z., Ong, Z.-Y., Li, S., Xu, J.-B., Zhang, G., Zhang, Y.-W., et al. (2017). Analyzing the Carrier Mobility in Transition-Metal Dichalcogenide MoS2Field-Effect Transistors. Adv. Funct. Mat. 27, 1604093. doi:10.1002/adfm.201604093

CrossRef Full Text | Google Scholar

Zhu, C., Han, S., Mao, H., and Dally, W. J. (2016). Trained Ternary Quantization. Available at: http://arxiv.org/abs/1612.01064.

Google Scholar