- 1 Department of Computational Biology, Royal Institute of Technology, Stockholm, Sweden
- 2 Stockholm Brain Institute, Stockholm, Sweden
- 3 Neurocentre Magendie, Bordeaux University, Bordeaux Cedex, France
Computer simulation has been used to investigate several aspects of locomotion in salamanders. Here we introduce a three-dimensional forward dynamics mechanical model of a salamander, with physically realistic weight and size parameters. Movements of the four limbs and of the trunk and tail are generated by sets of linearly modeled skeletal muscles. In this study, activation of these muscles were driven by prescribed neural output patterns. The model was successfully used to mimic locomotion on level ground and in water. We compare the walking gait where a wave of activity in the axial muscles travels between the girdles, with the trotting gait in simulations using the musculo-mechanical model. In a separate experiment, the model is used to compare different strategies for turning while stepping; either by bending the trunk or by using side-stepping in the front legs. We found that for turning, the use of side-stepping alone or in combination with trunk bending, was more effective than the use of trunk bending alone. We conclude that the musculo-mechanical model described here together with a proper neural controller is useful for neuro-physiological experiments in silico.
1 Introduction
Locomotion is one of the most important behaviors in the animal kingdom and has been refined by evolution for hundreds of millions of years. The salamander, an amphibian with a sprawling posture and axial locomotion, provides opportunity for studying key elements in the transition from aquatic to terrestrial motion (Chevallier et al., 2008). It is a tetra-pod, representing vertebrates capable of both swimming and walking. The sprawling posture, in which the limbs extend laterally out from the body with the feet placed wide apart (see Figure 1A), make it easier to mimic for research in the field of biologically inspired robots or computer simulation (Ijspeert, 2000a; Ijspeert et al., 2005; Karakasiliotis and Ijspeert, 2009). In particular, this configuration poses less difficulties in maintaining balance compared to a more erect posture. Furthermore, the central nervous system of the salamander shows many similarities to that of the lamprey (Fetcho, 1987) where a large body of neuro-physiological studies and models is available for the swimming circuitry (Ijspeert et al., 1998; Ekeberg and Grillner, 1999; Saitoh et al., 2007; Grillner et al., 2008) providing an essential framework for understanding the salamander locomotor system. Thus, biologically realistic modeling and computer simulations would provide help in understanding the salamander locomotion from both a neurophysiological and a bio-mimetic standpoint.

Figure 1. (A) A picture of a real salamander, Spanish ribbed newt (Pleurodeles waltl). (B) Computer screen view of the three-dimensional salamander locomotion simulator.
In recent past, computer simulations have been used to model different aspects of locomotion in salamanders, including aquatic and terrestrial gaits, transition from swimming to walking, spinal central pattern generator networks, and visual tracking (reviewed in Chevallier et al., 2008). It has even been argued that a thorough understanding of the neural and bio-physical mechanisms that underlie locomotion can only be achieved by using computer simulations in parallel with physiological experiments (Pearson et al., 2006). Especially when the animal can not be forced to do some specific behavior or when isolation of muscular, sensory, or neuronal mechanisms are impossible in neuro-physiological experiments (Harischandra and Ekeberg, 2008), the computer models and simulations are very useful tools. Not only neural activities in nervous centers that are related to locomotion but also the bio-mechanics of the body and its interactions with the environment plays a major role in locomotion. The adaptive behavior could be best understood by looking at the interactions between the nervous system, body mechanics, and the dynamics of the environment (Chiel et al., 2009). Moreover, in silico experiments are essential in bridging the gap between neuro-physiological experiments and bio-mimetic/bio-mechanical robotic engineering.
In order to investigate such interactions in a biologically plausible manner, a three-dimensional (3D) musculo-mechanical model with realistic physical parameters is essential but has so far been lacking for the salamander. Previous computer simulation studies have been based on drastically simplified models of both the body and its actuators. The model and the simulation described here is inspired by the lamprey model developed by Ekeberg (1993). Pioneering work has been done by Ijspeert (2000a, 2001) on the salamander using both two and three-dimensional models. In this early 3D model, its trunk and tail segments are sliding on the ground when stepping (Ijspeert, 2000b), making it essentially 2D. Furthermore the model’s knee and elbow joints have axes of rotation perpendicular to the body axis making it unsuitable for mimicking lateral side-stepping that can be seen in real animals when turning (see Section 2.2.3). Therefore, here we introduce a 3D musculo-mechanical model of the salamander which has legs capable of bearing body weight without touching the ground and at the same time capable of lateral leg movements. The 3D model (see Figure 1B) is designed to match data from the Spanish ribbed newt, making it anatomically more precise. We have observed videos of freely moving salamanders simultaneously captured from top and side viewing directions and used measured anatomical parameters such as mass, width, height, and length variation along the body and limb segments when setting up the mechanical model.
The musculo-skeletal model was tested by driving the body (trunk and tail) and limb muscles with predefined patterns (see Section 2.2) that correspond to neural output to the muscles during ground stepping and underwater swimming. Furthermore, the model was used here to investigate the lateral turning strategies involving trunk bending and side-stepping and a combination of both. The same experiment was carried out for two different gaits: walking, where one limb at a time is in swing phase, and trotting, where diagonal limbs are simultaneously in swing (Ashley Ross, 1994b).
2 Materials and Methods
This section describes the musculo-mechanical model, implementation of muscle dynamics, neural activation patterns for locomotor gaits and modes, and the simulator program in detail.
2.1 Musculo-Mechanical Model
Mechanically, the body of the model incorporates four limbs, each actuated by six simulated muscles. The trunk and tail are divided into segments in the axial direction and the movement of each segment is also controlled by a set of simulated muscles representing the epaxial muscles of the salamander. The trunk and tail (head to tip of the tail) was made up of 15 rigid segments where each segment is connected to its neighbors with hinge joints with an axis of rotation in the vertical direction and one degree of freedom (DOF). The hind legs are attached to the trunk at the ninth segment (counting from the tail end) whereas front legs are connected to the 13th segment (see Figure 2). Each limb was modeled with two segments: thigh and shank with three DOFs. While knee or elbow had one DOF, the hip or shoulder had an additional DOF to enable abduction and adduction (up and down; see Figure 3) movements of the limb.

Figure 2. Schematic of the bio-mechanical model of the simulated salamander. The body; head, trunk, and tail, is composed of 15 rigid links that are connected by one DOF hinge joints with the vertical axis (coming out from the page) as the axis of rotation. The limbs are attached to the body with two DOF joints with one vertical axis of rotation and one horizontal (see Figure 3).
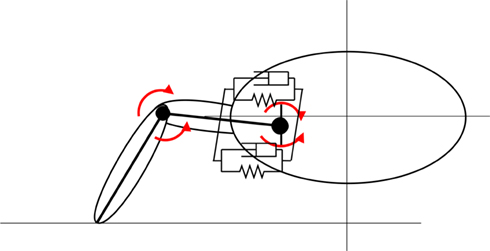
Figure 3. Limb geometry. Movements of the pelvis joint is generated by two pairs of muscles. The muscles acting on the vertical plain are shown here. See Figure 2 for the other pair. The knee joints have one DOF and they can rotate around a horizontal axis parallel to the animal trunk.
At a neutral posture, all the trunk and tail joints are set so that the body lies along a straight line. The joint connecting tail segments to the trunk (eighth from the tail end), has an additional DOF in order to make the tail slant down toward to the tip and has a maximum and minimum slope of 10° and 5°. The resting angle for this is 7.5°. At the resting position, limbs spread perpendicular to the body axis and each thigh is elevated about 14° from the horizontal plane and each limb has knee or elbow neutral angle of 106°. The maximum retraction or protraction angle is 55° from the neutral position.
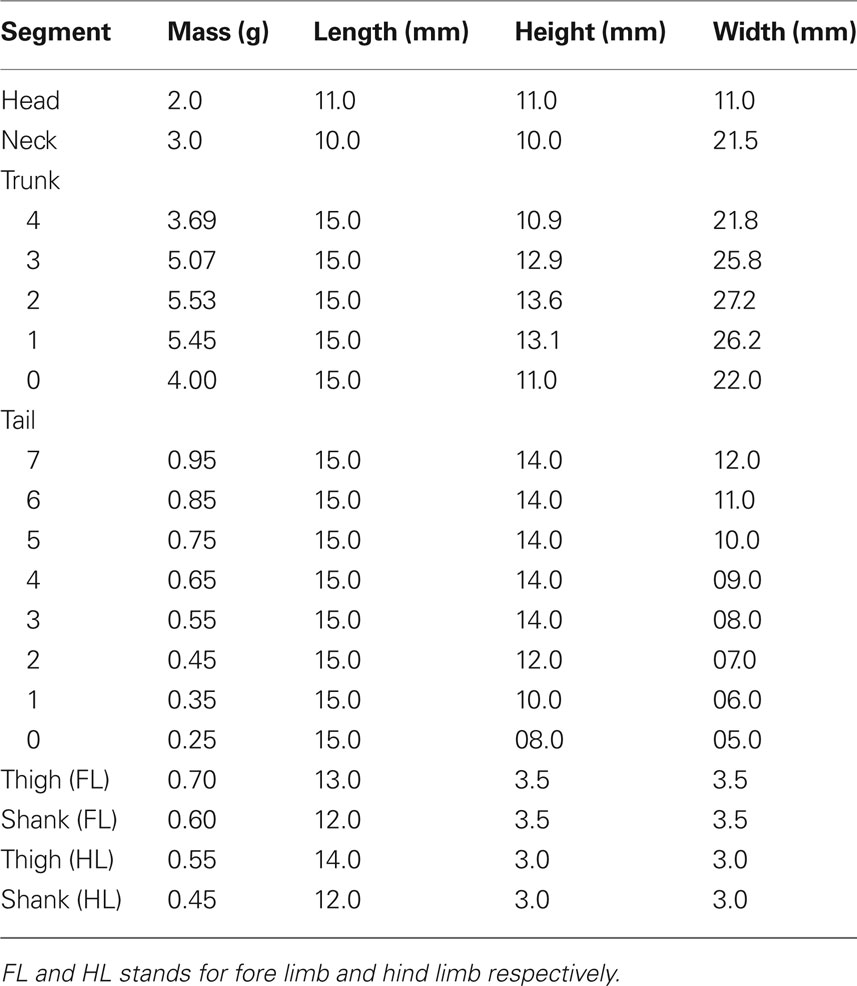
The total length of the model’s body is 21.6 cm and the snout to vent length (SVL) is 9.6 cm. Each segment, from head to tip of the tail, is 1.5 cm long and has an elliptical cross section where height and width depend on its position along the body. The head and the neck have slightly shorter segments (see Table 1). Each leg is composed of two cylindrical segments joined together by a hinge joint (elbow/knee joint). The mass and the geometrical parameters of the segments are chosen such that they match average values of five (n = 5) adult Spanish ribbed salamanders, Pleurodeles waltl. For instance, averaged total tail mass was distributed linearly among the eight equally long parts along the tail with the heaviest at the segment near the pelvic girdle. Similarly, total mass for the trunk was distributed among five equally long segments considering volume variations along the trunk.
The forces due to the environment depend on whether the salamander is on the ground or in water. It should be mentioned that this salamander specie does not contact the ground with its belly while stepping. Apart from the legs, only the last part of the tail touches the ground. Therefore, the contacts between the feet and the ground were subjected to coulomb friction in the model. During ground locomotion, the trunk segments are moving in the air whereas the tail segments are sliding on the ground with less friction. In water, we assume that the only environmental force acting on the salamander is inertial and hence the forces being proportional to the square of the speed of the segments relative to the water. In fact, this is true when the speed of the body relative to the water is sufficiently high. Although this is a simple model, it has been widely used in computer simulation experiments on swimming (Ekeberg, 1993; Ijspeert, 2001; Crespi and Ijspeert, 2006).
2.1.1 Simulating skeletal muscles
Movements of the body and limb segments are generated by skeletal muscles that are individually simulated as a combination of a spring in parallel with a damper. The resultant torque exerted on each joint is determined by a pair of antagonist muscles. These are the axial muscles on each side of the body (trunk and tail), the retractor and protractor muscles, the abductor and adductor muscles, and the elbow/knee extensor and elbow/knee flexor muscles of the limbs. The simulation of each muscle is based on the mathematical model introduced by Ekeberg (1993) in his neuromechanical lamprey model. The calculation of the muscle torque is based on the following equation. The torque acting at a particular joint is determined by the neural activation (“E”) of the muscle:

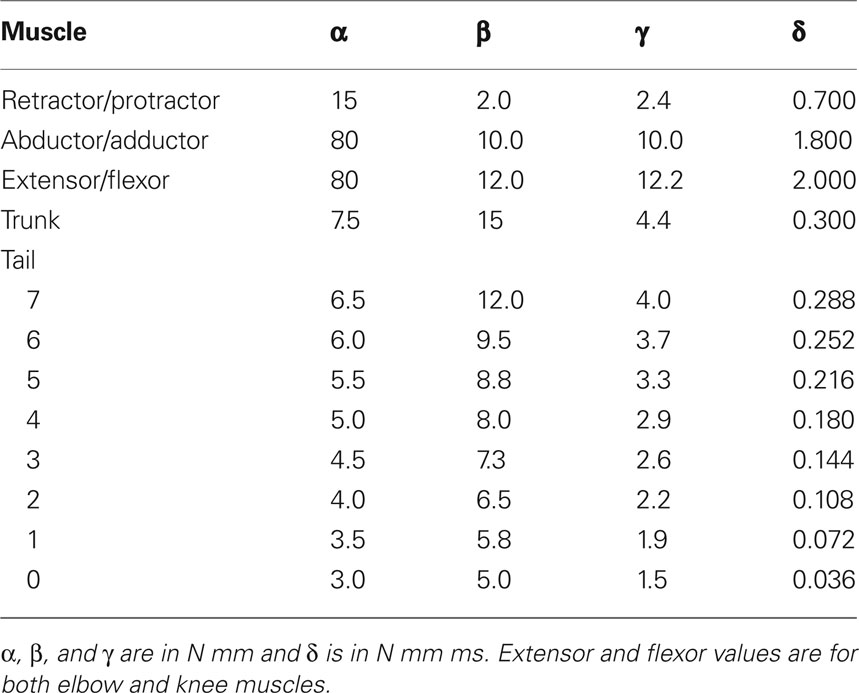
where Δφ is the difference between the actual angle of the joint and the resting angle. The coefficients α, β, γ, and δ determine the characteristics of the muscle and muscle-joint combination and are named the gain, the stiffness gain, intrinsic stiffness, and the damping coefficient respectively. Note that here, activation dynamics of the muscles are not included in the model. The parameter sets of the muscles are slightly different from muscle to muscle depending on the type of the joint on which the muscle is acting. Furthermore, stiffness of the muscles toward the tail end of the body is reduced to make them more flexible like in the real salamander. Additionally, the abductor/adductor and the extensor/flexor muscles were made strong compared to the retractor/protractor, since the animal can bear its own body weight in resting position. The parameter values are shown in Table 2. Note that the tail and the trunk segment numbering start from the rear. These parameters were tuned by trial and error to obtain a realistic stepping and swimming in the salamander simulation. The muscles can be contracted by input signals coming from a neural controller which in this case is a program that mimics the output of a central pattern generator (CPG).
2.2 Simulating Neural Activity
The model was tested in a computer simulated environment where we used prescribed neural output patterns to drive the activation of a set of linearly modeled skeletal muscles which in turn provide the forces to move the mechanical model. Our primary aim in this investigation was to test the musculo-mechanical system. Note that the use of prescribed patterns will make this study immune to all the uncertainties involved with trying to faithfully model the neural mechanisms underlying the muscle activation patterns. Therefore, the activation patterns are here generated using time driven functions rather than bio-physically detailed neural networks or coupled oscillators. The muscle pairs along the trunk and tail are activated by pairs of such segmental pattern generators which are oscillating with 180° phase shift. Similarly, muscles controlling movements of the limbs are activated by a separate set of similar pattern generators. The output from these pattern generators are transformed (cubed) sinusoidal functions. For the limb muscles:
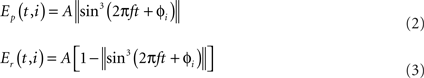
where Ep(t,i) and Er(t,i) are the inputs to the protractor (extensor) and retractor (flexor) muscles for joint i at time t. The maximum amplitude of the signal is given by A which may vary from joint to joint. f and φi correspond to the frequency of oscillation and the phase at joint i, respectively. Similarly the muscles controlling the body (trunk and tail) receive an activity pattern which is of the form Ep(t,i). Note that all functional units that generate activity patterns for all the muscles, have the same frequency of oscillation f.
2.2.1 Activity patterns for stepping
On ground, the salamander uses mainly its limbs and trunk to obtain the thrust to move forward. In general, a trotting salamander adopts an “S”-shaped standing wave pattern along the body (Roos, 1964; Frolich and Biewener, 1992; Delvolve et al., 1997). However several gait patterns are possible in different conditions such as underwater stepping or at different speeds of locomotion (Ashley-Ross, 1994b; Ashley-Ross et al., 2009). In the model, elbow and knee flexors and extensors are tonically activated to make the elbow/knee joints a bit stiff. Moreover, each limb is lifted using its abductor muscle slightly before the protractor muscle gets activated (8−10% phase shift), which causes the initiation of the swing phase of the leg.
Walking gait. This gait can be seen when the salamander is moving on ground at slow speeds. The main characteristic of this gait is to have three legs on the ground most of the time throughout the step cycle. This was often seen in the videos of real salamanders walking on level ground. The pattern of activity used in the model for controlling the limb muscles are shown in Figure 4A. The major difference in the activity patterns for limb muscles compared with that of the trotting gait is that here the opposite contralateral legs have a slight phase shift. In order to accommodate that, the phase of the activity patterns for trunk segments needs to be shifted from each other, causing a traveling wave of neural activity along the trunk segments (see Figure 4B).
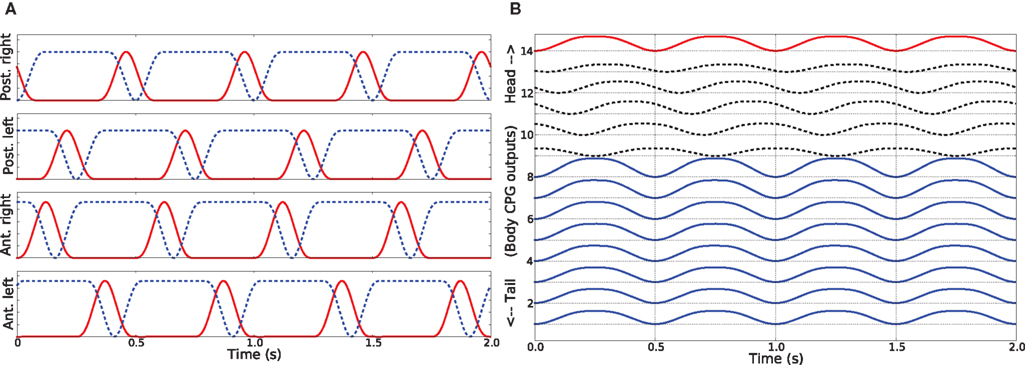
Figure 4. (A) Activity patterns of the retractor and protractor muscles of the four limbs during walking gait of the salamander. Post. and Ant. are abbreviations for posterior and anterior respectively and the dotted lines represent the retractor muscles. (B) The pattern of activity in the trunk and tail muscles during walking. Dotted lines correspond to trunk muscles and the red line represent the neck muscle of which the activity is in phase with that of the tail muscles.
Trotting gait. The trotting gait is produced in the model by a pattern of activity in limb musculature in which all the muscles controlling the trunk joints are activated in synchrony (φi = 0°) and at the same time out of phase compared to the muscles in the tail segments (φi = 180°). The muscles causing the movements of the joint at the neck also oscillate out of phase relative to the trunk muscles and has the effect of keeping the head approximately straight (see Figure 5B). As shown in Figure 5A, limb muscles (protractor and retractor) receive inputs from the neural controller such that diagonally opposite contralateral limbs move in phase and are out of phase compared to both ipsilateral and contralateral adjacent limbs. Previous computer models of the salamander locomotion have exclusively used this kind of gait for the ground stepping (Ijspeert, 2001; Bem et al., 2003; Ijspeert et al., 2005).
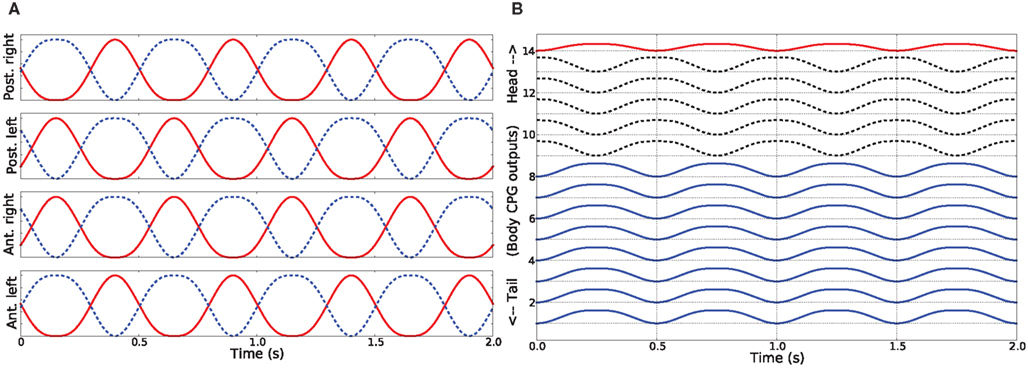
Figure 5. (A) Activity patterns of the retractor and protractor muscles of the four limbs for the trotting gait during level ground stepping of the salamander. (B) The pattern of activity in the trunk and tail muscles during trotting. The abbreviations and the legend are same as for the Figures 4A,B.
2.2.2 Activity patterns for swimming
In water, the salamander uses a swimming mode where a mechanical wave is traveling from head to tail (anguilliform gait) along the body (Frolich and Biewener, 1992; Delvolve et al., 1997; Chevallier et al., 2008). This traveling wave is obtained in the model by setting the phase of the activity patterns for muscles between consecutive segments such that the body makes a complete wave, with a constant phase lag between the spinal cord segments (see Figure 6). During ordinary swimming (in certain situations, real animal can use its limbs to produce additional thrust against water) the limbs are kept against the sides of the body through contraction of the retractor muscles at the pelvic and scapular girdles. In this study, we simulate only this type of swimming. Turning was achieved by increasing the activity of all the muscles of the side (either left or right) in the steering direction, while the traveling wave activity (the phase shift) was left intact. The amount of asymmetric activation determines the amount of bending.
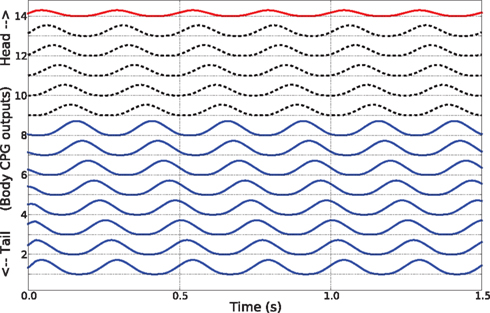
Figure 6. Activity patterns of the trunk and tail muscles during swimming of the simulated salamander. These patterns correspond to the neural outputs coming from body CPGs that are located along the spinal cord.
2.2.3 Simulating side-stepping
In all previous computer simulation models, turning of the salamander during over ground stepping has been achieved by bending the trunk in the desired direction (Ijspeert, 2001; Ijspeert et al., 2005; Crespi and Ijspeert, 2006). This can be done by increasing the magnitude of contraction in the axial muscles situated along the side of the body ipsilateral to the turning direction. However, while observing videos of freely moving salamanders, it became clear that they use their front limbs actively for turning. Correspondingly, from the studies of insects, it is known that the stick insect does move its fore limbs in the lateral direction in order to turn sideways (Dürr and Ebeling, 2005; Rosano and Webb, 2007). We hypothesize that a similar method may be utilized by the salamander, i.e., that it uses its fore legs in a coordinated manner to step aside in the lateral direction, i.e., turning by side-stepping. Side-stepping achieves turning by stretching the front leg shank to the side of the turning direction when the leg is in swing phase while pushing against the ground with the other front leg. Then, after touch down, the leg on the ground is flexed so that the animal is pulled in the direction of the leg while the other leg starts to swing and in contrast it is flexed so that when it touches the ground it has moved a bit further side ways in the direction of turning. In our model, elbow extensor and flexor muscles are used to move the shank (outer limb segment) around the elbow joint (see Figure 3). When turning, activation patterns for these muscles (not shown) have a phase advance of 8% relative to the activity of protractor and retractor muscles. Maximum stretching angle of the elbow joint is 125° and the minimum is 80°.
2.3 Simulator Program
The simulator is programmed using the Python language and a set of open source libraries. The mechanical body dynamics of the salamander is simulated using the open dynamics engine (ODE, http://www.ode.org), which is an open source, high performance library for simulating rigid body dynamics. 3D graphical animation is done by a separate module that was programmed using OpenGL and Qt libraries. Modular structure and the object oriented programming technique was used to increase the changeability, i.e., modules can easily be modified without altering the entire program, and allow easy access to the model parameters of the simulator. In particular, the controller module providing the activation of muscles can be replaced by a neuronal network (network of CPGs) with neurons (Ekeberg, 1993; Inoue et al., 2007) or a network of simple oscillators (Ijspeert, 2001). Furthermore, the musculo-mechanical model can be equipped with sensory feedback affecting the locomotion. In this study, as mentioned above, a time driven set of pattern generators is used for mimicking neural activity of limb and trunk/tail muscles. In these simulations, the time-step was set to 1 ms. After the simulation, logged data were written into text files and the analysis and plotting were done using the tools in Matlab 7.0.4 (R14).
3 Results
The musculo-mechanical model of the salamander successfully produced the two stepping gaits, walking and trotting, and swimming in water. After tuning the parameters of the limb and body (trunk and tail) muscles and of the activity patterns for those muscles, stepping and swimming were obtained which matched the video recordings of real salamanders. By changing the frequency of the oscillatory patterns, different speeds of locomotion were obtained. With low frequencies, i.e., from about 0.5 to 2.0 Hz, over ground stepping was smooth and in addition the inter-limb and body coordination was stable. In fact, these frequencies are in agreement with those observed in the real salamander. However, with high frequencies (more than 3 Hz) in the activity patterns, limb and body coordination started to deteriorate and this destabilized the locomotion. On the other hand, swimming was possible for a wider range of oscillatory frequencies (from 1 to 6 Hz) in activation patterns. Therefore higher velocities of locomotion were possible during swimming.
Different gaits were achieved by activating limbs in proper coordination not only with each other but also with the trunk and tail. Figures 7A,B show the phase relationship among the four limbs of the simulated salamander during the two gaits. Each cycle has a duration of 500 ms. Both gaits showed a shorter swing phase and a longer stance phase for all the four limbs. In general, the walking gait has a duty factor of stepping (percentage of stance duration over a cycle) of about 76% and that for the trotting gait is about 60%. By visual comparison of the videos of the real salamander with the simulation, walking gait (Figure 7C) showed more natural locomotor movements compared to the trotting gait (Figure 7D). With the model, we were also able to successfully mimic underwater stepping and swimming on a slippery surface (results are not shown here). Especially, underwater stepping with the walking gait showed more natural and stable locomotion.

Figure 7. Gait diagrams for the terrestrial locomotion of the salamander. (A) This shows the diagram for the walking gait. (B) Shows the gait diagram for the trotting (see the Section 2.2.1). Bars indicate periods during which the foot is on ground. PL, left hind foot; AL, left front foot; AR, right front foot; PR, right hind foot. (C,D) shows sequential frames from the simulator, covering one step while walking and trotting respectively. Time duration between two frames is 70 ms.
Next we used the model to investigate the ability to turn by modifying the stepping pattern (see the Section 2.2.3). Three different strategies were tested; only bending the trunk, only using side-stepping of the front legs, and a combination of both bending and side-stepping. Figure 8 shows a comparison of front limb movement during normal stepping and the side-stepping when the gait is trotting. The sideways extension of the front leg, in the direction of the turn, during the swing phase is clearly visible. The other leg makes a corresponding flexion during its swing. All these experiments were repeated for both walking and trotting gaits using a simulation time of 5.0 s for each trial. In each trial, the turning pattern was driving the corresponding muscles for 3.0 s after 1.0 s delay. Too high activation of axial muscles on one side to generate the bend tends to destabilize the locomotion, mainly because the model tips over to the side. Similarly, too high amplitudes in elbow flexor and extensor muscles will destabilize the stepping movements. Thus, for the comparison, activation increments in axial muscles and/or activity amplitudes in elbow muscles were set so that we could observe smooth locomotion in the 3D model during turning as well. In other words, maximum curvature without breaking down the gait was used in each case. The results, as stick diagrams, are shown in Figures 9A,B for the walking and trotting gait respectively. In both cases, turning by side-stepping was more efficient than by bending alone. Here, efficiency is measured and compared as the deviation of the direction of locomotion from the initial orientation, at the end of the stimulation. The combination of bending and side-stepping gave improved efficiency for turning when the model used trotting gait. However, with the walking gait, the combination gave slightly less efficiency than when using side-stepping alone but was still much better than when using bending alone.
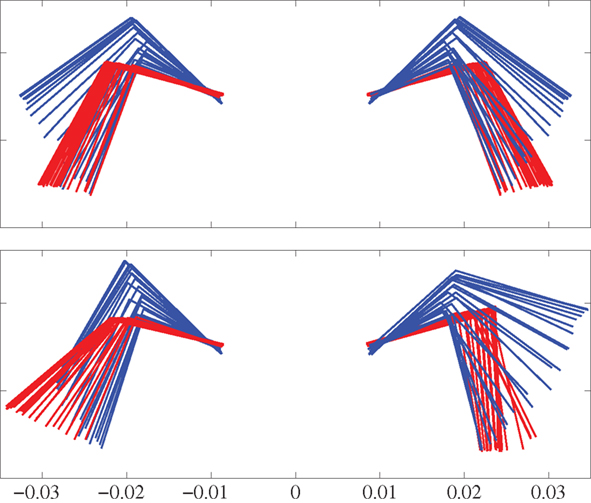
Figure 8. Front view of the front legs using a body-centered coordinate system anchored at the front girdle. Top panel shows steps during straight trotting. Bottom panel shows turning (to the left) steps during side-stepping while trotting. Red indicates the stance phase while blue indicates the swing phase. Time duration between each frame is 10 ms.
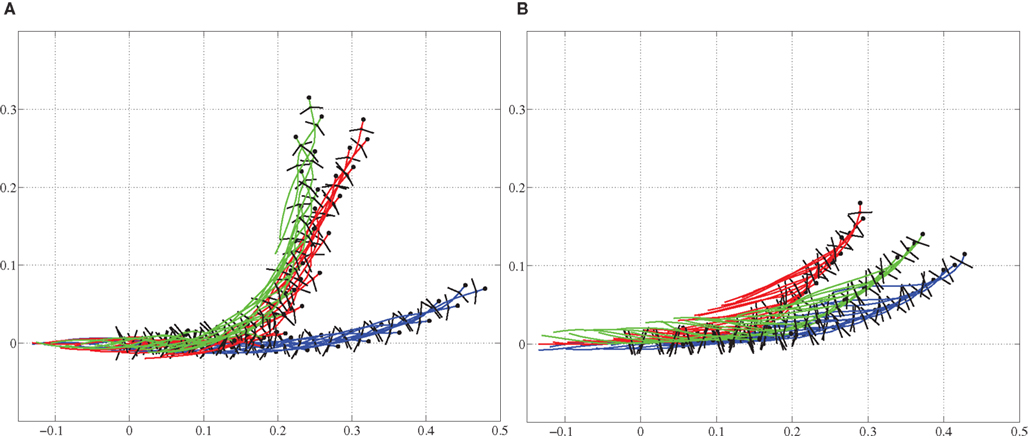
Figure 9. Trajectories are shown for comparison of turning (steering) strategies during level ground stepping. (A) For the walking gait, the side-stepping is more pronounced than the bending only. (B) For the trotting gait, bending and side-stepping combination is more pronounced. Blue: bending only, Green: side-stepping only, and Red: combination of both. Axes values are in meters, representing coordinates in space.
During swimming, steering or turning of the model is possible by increasing the neural activity of the muscles along the desired side of the body (trunk and tail) causing it to bend in that direction. Figure 10 shows a stick plot (viewing from top) of the model turning to the left while swimming at a speed of about 0.5 m/s.
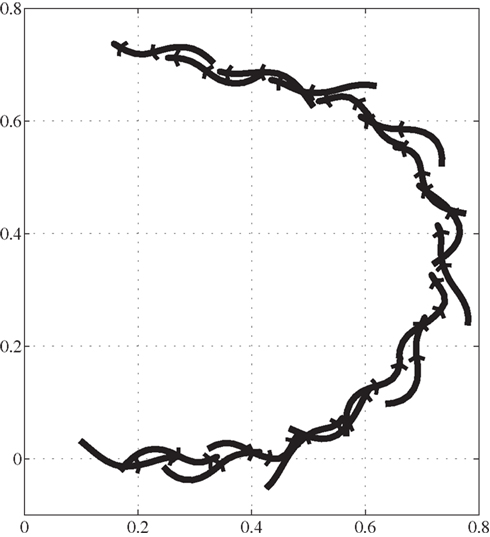
Figure 10. Trajectory of salamander’s turning during swimming, viewing from the above. Axes represent the same as in the Figure 9. Time duration between consecutive frames is 150 ms.
4 Discussion
Due to its amphibian nature, the salamander is capable of both swimming and terrestrial stepping and it has a locomotor system which is, in general, similar to, but less complex than that of other vertebrates. The two locomotor modes, swimming and stepping, differ in their patterns of activation of epaxial musculature (inter-segmental coordination) and limb muscles (Frolich and Biewener, 1992; Delvolve et al., 1997). The same spinal neuronal network of CPGs is presumably responsible for producing the patterns of muscle activity (along the body) for both modes with the coupling of the limb CPGs (Delvolve et al., 1997; Ijspeert et al., 2007). In the same way, different gaits are also possible with proper timing and rhythmic activation of limb muscles in a coordinated manner.
During over ground stepping, the salamander uses horizontal body movements which generate an “S”-shaped standing wave pattern along the body with zero movement (in the lateral direction) points at the girdles, to increase the stride length (Frolich and Biewener, 1992; Ashley-Ross and Bechtel, 2004). This condition is ideal for the limb coordination used in a trotting like gait. However, for the walking gait, since the front and contralateral hind limb muscle pairs have a slight phase shift in their activation (see Figure 4A), it is advantageous to have a phase shift in the activation of trunk muscles along the body. Therefore in this gait, a slight deviation from the “S”-shaped movement pattern could be seen corresponding to a traveling wave of activation (see Figure 4B) of the trunk muscles between the two girdles of the animal. This differs from the previous observations of Edwards (1977) or Ashley-Ross (1994a), see the review Chevallier et al. (2008). However, a traveling wave has been observed in some lower tetra-pods like Chalcides occellatus and it has been argued that the resulting placement of the limbs on the ground closer to the center of the body curvatures would be most efficient (Daan and Belterman, 1968). Here, we were able to successfully reproduce this kind of walking gait with the musculo-mechanical model for salamander locomotion.
The traveling and standing waves of body curvature are reflected in electromyographic (EMG) patterns (Frolich and Biewener, 1992; Delvolve et al., 1997). In lampreys, trouts, or other fish, waves of muscle activity travel faster than waves of body undulation (Williams et al., 1989) and the relative timing between these two waves is related to the efficiency of locomotion. It is realistic to assume that the same phenomena can be seen in the salamander as well. In the case of the locomotor model, this can affect the coordination of the limbs and the trunk. Especially during over ground stepping, high frequency of oscillations in the axial muscle activity will generate a neural wave traveling fast compared to that of the body undulations (kinematic wave). Hence, due to the different speed of propagation, locomotion can become unstable. Here, when mimicking the walking gait with a traveling wave between the girdles, activation for the hind limb muscles were given 14% lag in order to match with the body undulations, that is, to make the forward swing (protraction) of the hind limb synchronous with the outward bending of the trunk (swing starts when the trunk stretches) at the pelvic girdle. This lag was added to overcome the slow propagation of the kinematic wave along the mechanical body. Hence, in general, we can conclude that the stepping works best at relatively low speeds in the current locomotor model.
Rhythmic patterns of EMG activity in the axial muscles of the salamander and lamprey or other lower vertebrates exhibit a rostrocaudal traveling wave of contractions during swimming (Frolich and Biewener, 1992; Delvolve et al., 1997; Ekeberg and Grillner, 1999). As shown in Figure 6, a pair of axial muscles which are responsible for the generation of bending of a segment in the locomotor model received activation with a phase lag relative to that of the next rostral muscle pair. This activity creates the lateral undulations of the body, as observed in kinematic studies of real animals (Frolich and Biewener, 1992; Ashley-Ross and Bechtel, 2004), generating the forward thrust needed for swimming.
In the walking gait, most of the time the locomotor model has support from three or four legs (see Figure 7C). However, there are periods of the stride (around 10%) during which the modal is supported by only two legs. A recent kinematic study on California newts has shown a similar gait pattern when the newt is moving forward slowly on the ground with a duty factor of 77% (Ashley-Ross et al., 2009) which is almost the same for the walking gait observed in this study (76%). In contrast, during trotting gait, the duty factor is reduced and most of the time the body is supported by only two legs. Furthermore, the model is supported by all four legs at about the same percentage (around 20%) as with the walking gait. This stride characteristic, classified as trot according to Ashley-Ross (1994a), is similar to the newt’s underwater stepping except the overlapping ground contact (Ashley-Ross et al., 2009). It is likely that the animal uses walking rather than trotting in terrestrial stepping at slow speeds.
A recent study of in vivo EMG recordings during underwater stepping have shown that a traveling wave can exist from head to tail together with the rhythmic limb muscle activity (Lamarque et al., 2009). In fact, the salamander model with the walking gait which has a traveling wave of activity in the muscles between the girdles showed more realistic underwater stepping than that of the trotting gait with its standing wave of activity.
The only way to turn the salamander when swimming is to bend the body. The model was able to successfully turn, while swimming at several speeds, by bending the body (see Figure 10). Furthermore, the same strategy can be used for turning during over ground stepping (Ijspeert, 2000a, 2001). This was tested on the locomotor model for both gaits. The second method, described in the Section 2.2.3 and which has not been explored earlier in salamander locomotor models, is to use side-steps of the front limbs. The 3D model and the simulation environment helped to investigate this behavior in a physiologically plausible way. With the proper timing and co-activation of limb musculature, the model produced natural turning behavior. In fact we have compared the model with the videos of freely moving salamanders. As a third strategy, a combination of both bending and side-stepping was used in the turning experiments. In general, a combination of both techniques can be used for turning during both gaits. However, it can be clearly seen that the turning by side-stepping or the combination is more efficient during walking than trotting. From this study, we can conclude that the side-stepping with properly coordinated trunk bending would increase the efficiency of the turning behavior at least in simulated or robotic salamander locomotor models. It is likely that this would be the case for the real animal as well. However, it should be mentioned that the role of the tail in the turning behavior was not thoroughly investigated in this study. The results of this investigation would definitely help to find control solutions in steering for robotic artifacts that resemble salamander locomotion (Crespi and Ijspeert, 2006; Ijspeert et al., 2007; Inoue et al., 2007; Sfakiotakis and Tsakiris, 2007). Furthermore, we conclude that the described musculo-mechanical model and the simulator has proven useful for mimicking neuro-physiological phenomena and will be useful in experiments on salamander locomotion in future in silico investigations.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank the Swedish International Development Cooperation Agency (SIDA), EU FP7 (LAMPETRA), and VINNOVA for the financial support. We are grateful to H. Didier and S. Lamarque for video recordings and anatomical measurements of the real salamanders.
References
Ashley-Ross, M. (1994a). Hindlimb kinematics during terrestrial locomotion in a salamander (Dicamptodan tenebrosus). J. Exp. Biol. 193, 255–283.
Ashley-Ross, M. (1994b). Metamorphic and speed effects on hindlimb kinematics during terrestrial locomotion in the salamander Dicamptodon tenebrosus. J. Exp. Biol. 193, 285–305.
Ashley-Ross, M., and Bechtel, B. (2004). Kinematics of the transition between aquatic and terrestrial locomotion in the newt Taricha torosa. J. Exp. Biol. 207, 461–474.
Ashley-Ross, M., Lundin, R., and Johnson, K. (2009). Kinematics of level terrestrial and underwater walking in the California newt, Taricha torosa. J. Exp. Zool. 311A, 240–257.
Bem, T., Cabelguen, J., Ekeberg, Ö., and Grillner, S. (2003). From swimming to walking: a single basic network for two different behaviors. Biol. Cybern. 88, 79–90.
Chevallier, S., Ijspeert, A., Ryczko, D., Nagy, F., and Cabelguen, J. (2008). Organisation of the spinal central pattern generators for locomotion in the salamander: biology and modelling. Brain Res. Rev. 57, 147–161.
Chiel, H., Ting, L., Ekeberg, Ö., and Hartmann, M. (2009). The brain in its body: motor control and sensing in a biomechanical context. J. Neurosci. 29, 12807–12814.
Crespi, A., and Ijspeert, A. (2006). “Amphibot ii: an amphibious snake robot that crawls and swims using a central pattern generator,” in Proceedings of the 9th International Conference on Climbing and Walking Robots (CLAWAR 2006), Brussels, 19–27.
Daan, S., and Belterman, T. (1968). Lateral bending in locomotion of some lower tetrapods, i and ii. Proc. K. Ned. Akad. Wet. C 71, 245–266.
Delvolve, I., Bem, T., and Cabelguen, J. (1997). Epaxial and limb muscle activity during swimming and terrestrial stepping in the adult newt, Pleurodeles waltl. J. Neurophysiol. 78, 638–650.
Dürr, V., and Ebeling, W. (2005). The behavioural transition from straight to curve walking: kinetics of leg movement parameters and the initiation of turning. J. Exp. Biol. 208, 2237–2252.
Edwards, J. (1977). “The evolution of terrestrial locomotion,” in Major Patterns in Vertebrate Evolution, eds M. Hecht, P. Goody, and B. Hecht (New York: Plenum), 553–576.
Ekeberg, Ö. (1993). A combined neuronal and mechanical model of fish swimming. Biol. Cybern. 69, 363–374.
Ekeberg, Ö., and Grillner, S. (1999). Simulations of neuromuscular control in lamprey swimming. Philos. Trans. R. Soc. Lond., B, Biol. Sci. 354, 895–902.
Fetcho, J. (1987). A review of the organization and evolution of motoneurons innervating the axial musculature of vertebrates. Brain Res. Rev. 12, 243–280.
Frolich, L., and Biewener, A. (1992). Kinematic and electromyographic analysis of the functional role of the body axis during terrestrial and aquatic locomotion in the salamander Ambystoma tigrinum. J. Exp. Biol. 162, 107–130.
Grillner, S., Wallen, P., Saitoh, K., Kozlov, A., and Robertson, B. (2008). Neural bases of goal-directed locomotion in vertebrates – an overview. Brain Res. Rev. 57, 2–12.
Harischandra, N., and Ekeberg, Ö. (2008). System identification of muscle-joint interactions of the cat hind limb during locomotion. Biol. Cybern. 99, 125–138.
Ijspeert, A. (2000a). “A 3-d biomechanical model of the salamander,” in Proceedings of the Second International Conference on Virtual Worlds, ed. J. Heudin (London: Springer), 225–234.
Ijspeert, A. (2000b). “A neuromechanical investigation of salamander locomotion,” in Proceedings of the International Symposium on Adaptive Motion of Animals and Machines, Montreal, 8–12.
Ijspeert, A. (2001). A connectionist central pattern generator for the aquatic and terrestrial gaits of a simulated salamander. Biol. Cybern. 84, 331–348.
Ijspeert, A., Crespi, A., and Cabelguen, J. (2005). Simulation and robotics studies of salamander locomotion. Neuroinformatics 3, 171–196.
Ijspeert, A., Crespi, A., Ryczko, D., and Cabelguen, J. (2007). From swimming to walking with a salamander robot driven by a spinal cord model. Science 315, 1416–1419.
Ijspeert, A., Hallam, J., and Willshaw, D. (1998). “From lampreys to salamanders: evolving neural controllers for swimming and walking,” in From Animals to Animats, Proceedings of the Fifth International Conference of The Society for Adaptive Behavior (SAB98), eds R. Pfeifer, B. Blumberg, J.-A. Meyer, S.W. Wilson (Cambridge, MA: MIT Press), 390–399.
Inoue, K., Sumi, T., and Ma, S. (2007). “Cpg-based control of a simulated snake-like robot adaptable to changing ground friction,” in Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, CA, 1957–1962.
Karakasiliotis, K., and Ijspeert, A. (2009). “Analysis of the terrestrial locomotion of a salamander robot,” in IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis.
Lamarque, S., Ryczko, D., Didier, H., and Cabelguen, J. (2009). “Dynamics of the axial locomotor network in intact, freely moving salamanders,” in 31st International Symposium of the GRSNC, Montreal.
Pearson, K., Ekeberg, Ö., and Buschges, A. (2006). Assessing sensory function in locomotor systems using neuro-mechanical simulations. Trends Neurosci. 29, 625–631.
Rosano, H., and Webb, B. (2007). A dynamic model of thoracic differentiation for the control of turning in the stick insect. Biol. Cybern. 97, 229–246.
Saitoh, K., Menard, A., and Grillner, S. (2007). Tectal control of locomotion, steering, and eye movements in lamprey. J. Neurophysiol. 97, 3093–3108.
Keywords: computer simulation, musculo-mechanical model, pattern generators, salamander locomotion,side-stepping, walking gait
Citation: Harischandra N, Cabelguen J-M and Ekeberg Ö (2010) A 3D musculo-mechanical model of the salamander for the study of different gaits and modes of locomotion. Front. Neurorobot. 4:112. doi: 10.3389/fnbot.2010.00112
Received: 04 October 2010;
Paper pending published: 25 October 2010;
Accepted: 01 December 2010;
Published online: 16 December 2010
Edited by:
Ricardo Chavarriaga, Ecole Polytechnique Fédérale de Lausanne, SwitzerlandReviewed by:
Poramate Manoonpong, Georg-August-Universität GÖttingen, GermanyMiriam Ashley-Ross, Wake Forest University, USA
Copyright: © 2010 Harischandra, Cabelguen and Ekeberg. This is an open-access article subject to an exclusive license agreement between the authors and the Frontiers Research Foundation, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Örjan Ekeberg, Department of Computational Biology, School of Computer Science and Communication, Royal Institute of Technology, S-10044 Stockholm, Sweden. e-mail:b3JqYW5AbmFkYS5rdGguc2U=