- 1 LISV, University of Versailles St Quentin, Vélizy, France
- 2 ETIS, UMR 8051CNRS-ENSEA-UCP, University of Cergy Pontoise, Cergy-Pontoise, France
This paper presents the use of Rowat and Selverston-type of central pattern generator (CPG) to control locomotion. It focuses on the role of afferent exteroceptive and proprioceptive signals in the dynamic phase synchronization in CPG legged robots. The sensori-motor neural network architecture is evaluated to control a two-joint planar robot leg that slips on a rail. Then, the closed loop between the CPG and the mechanical system allows to study the modulation of rhythmic patterns and the effect of the sensing loop via sensory neurons during the locomotion task. Firstly simulations show that the proposed architecture easily allows to modulate rhythmic patterns of the leg, and therefore the velocity of the robot. Secondly, simulations show that sensori-feedbacks from foot/ground contact of the leg make the hip velocity smoother and larger. The results show that the Rowat–Selverston-type CPG with sensory feedbacks is an effective choice for building adaptive neural CPGs for legged robots.
Introduction
What has become apparent in recent years is that the questions that biologists have about how walking is generated and controlled in animals are the same questions that any engineer or researcher must answer in order to build a functioning legged robot especially humanoid biped robots. In his review paper Ijspeert (2008) explains that advancing in the fundamental understanding of the functioning of the locomotor nervous system is indispensable in the fields of robotics, biology, and medicine. As in a robot, a biological mechanical apparatus, consisting of a series of articulated legs, must produce coordinated movements allowing animal walking, even on an irregular terrain or even if damages occur to part of its body. A central command is generated and sensors allow online corrections necessary to adapt the movements to the internal or external constraints (Nadim and Manor, 2000; Marder and Bucher, 2001).
It is well-known that biological neural architectures dedicated to locomotion in animals are very complex (see Cattaert and Le Ray, 2001 for a review of the neural organization complexity of one crayfish leg). Nevertheless, for many years, great progress has been made in the understanding of how the central nervous system works. This is the case for swimming with the lamprey spinal cord preparation (Grillner et al., 1995; Di Prisco et al., 2000; Grillner and Wallen, 2002). However, the questions are much more complex when addressed to walking systems for which the central neuronal networks must generate complex patterned activities and control multi-joint appendages. In the nervous systems of invertebrates (mainly insects), the organization of neural networks and sensory signals mediating coordination of multi-segmental organs for locomotion has been studied (for a review, see Büschges, 2005). Many neurons have been identified and their properties and synaptic contacts analyzed. Several recent trials have been made to simulate realistic simulation models of insect walking (Cruse et al., 1995, 1998). For example, in the crayfish walking system, biologists have shown that the organization of the walking system is largely modular (Gill and Skorupski, 1996; Cattaert and Le Ray, 2001). Each leg is controlled by its own central neuronal network, and there are a large number of neurons for one joint articulation. Biologists have identified different types of neurons that are fundamental to produce a coherent rhythmic pattern: rhythmic neurons, premotor interneurons, and motoneurons. Motoneurons induce the muscle control signal to the muscle fibers. Rhythmic neurons can produce oscillations that are modulated by premotor interneurons. Interneurons are involved in local joint control. Some interneurons which have the role of sensory neurons measure angular position, velocity, or forces of the joint. Other interneurons coordinate interneurons. They activate monosynaptic excitatory synapses onto motoneurons of different joints and establish disynaptic inhibitory connections with antagonistic motoneurons. Most of these interneurons are non-spiking neurons.
As for neuronal connections, biologists have proved that connections among the neuronal network controlling an articular joint of a crayfish leg are of three kinds: a classical chemical synapse activated by the occurrence of a presynaptic activity (some are excitatory, others are inhibitory depending on neurotransmitter and post-synaptic receptors); a tonic chemical synapse that does not require the spike to liberate the neurotransmitter; and electrical connections described between motoneurons of the same pool between sensory terminals of the same sensory organ (Marchand et al., 1997) and between premotor interneurons and motoneurons.
Despite this complexity, it is possible to reduce the architecture of an articular joint of a biological neuronal network to a model that respects its fundamental properties. Mc Crea and Ryback (2008) suggest an interesting neural organization in which a central pattern generator (CPG) is built with a rhythmic generator (RG) level based on oscillatory neurons, and a pattern formation (PF) circuit level based on interneurons responsible for motoneuron activation (motoneurons are connected to extensor and flexor muscles). In their architecture, the locomotor rhythm and the durations of flexor and extensor phases are determined by the RG network which controls the activity of the PF network by a combination of direct excitation and inhibition mediated by the afferent sensory inputs. Locomotion is initiated by a tonic excitatory drive signal from mesencephalic locomotor region (MLR). Indeed, the architecture of Rybak and McCrea seems very efficient to control the articulation of a robot.
Biologists have shown the fundamental role of rhythmic neurons in CPG architectures. They pointed out the four main behaviors of a biological rhythmic neuron: quiescent, plateau potentials, damped oscillating, and oscillating. For many years, artificial neural networks have been studied to control biped or other legged robot, in robotics. Many studies have focused on dynamic neural controllers based on continuous-time recurrent neural networks (CTRNN) because of their ability to be universal approximators (Beer and Chiel, 1992; Gallagher et al., 1996; Brunel, 2000; Vogels and Abbott, 2005; Beer, 2006). CTRNNs are also of interest in bio-inspired control, thanks to their capability to reproduce the full range of nerve cell phenomenology qualitatively. In CTRNNs (which are a type of RNN) the activities of neurons are determined by current synaptic inputs and by the history of neural states. This property allows CTRNNs to be superior to discrete time RNN models in the production of continuous sensori-motor sequences (Yamashita and Tani, 2008). CTRNNs make it possible to show adaptivity properties based on homeostatic plastic mechanisms (Hoinville and Henaff, 2004; Williams, 2007). Nevertheless, the neuron model used in CTRNN does not seem realistic enough for locomotion genesis because it is not an intrinsic rhythmic model. Indeed, as has shown Beer, the probability of oscillations of a CTRNN depends on the number of neurons and on certain synaptic connections.
Another well-known neuron model was suggested by Matsuoka (1985). This model has been largely used for many years in locomotion especially in bipedal walking (Taga et al., 1991; Endo et al., 2005; Matsubara et al., 2006; Lei et al., 2008; Woosung et al., 2008). This model is more biological than the CTRNN because it takes into account the adaptation mechanism of neurons which is critical in the generation of oscillations. However, in this model, it is not easy to control its rhythmic behavior to have the four main behaviors of a biological rhythmic neuron.
To get a flexible and dynamical legs coordination to generate the ongoing motion Pitti et al. (2009) show that CPGs can be seen as chaotic controllers that maintain the dynamical phase synchronization between them and the robot body dynamics. One way to achieve this aim is to use relaxation oscillators. This type of CPG models has been used frequently to control biped robots (Dutra et al., 2003; De Pine Filho et al., 2005), quadruped (Buchli et al., 2006; Liu et al., 2009), or snake robot (Conradt and Varshavskaya, 2003). Nevertheless, to our knowledge, the robot is often in an open-loop relative to its environment; there are no sensory neurons to improve the rhythmic activity, especially no sensory feedback from the ground. Then, from our point of view, the fundamental biological principle of sensory/motor loop that maintains the dynamical phase synchronization between the controller and the robot interacting with its environment is not respected.
The originality of this paper resides in the introduction of afferent exteroceptive and proprioceptive signals on a CPG controller based on intrinsic chaotic rhythmic neurons. The CPG follows the three levels organization of Rybak and McCrea (pattern generation level, PF level, and motor level). This architecture seems very efficient to control the articulation of a robot. Due to the number of articulations (a biped robot usually has six joints on each leg), it is much too complex to design a global neural controller of a biped robot. Nevertheless, we suggest to preliminarily study how one can control, with such kind of neurocontroller, the rhythmic pattern, and the velocity of a two-joint planar robot leg that slips on a rail. The rhythmic neuron is modeled as the one proposed by Rowat and Selverston (1993, 1997) which is a generalization of the Van der Pol’s relaxation oscillator. This model is interesting because one single neuron is intrinsically capable to generate different kinds of oscillatory signals. Indeed, it has two state-parameters which allow to control and modify the neuron phase among the four biological cited above. RS neurons were used for the first time in a robotic locomotion problem in order to design (with genetic algorithms) neurocontrollers for various multi-legged robots (Hoinville, 2007). This work showed that the RS neuron model is very well suited to generate adaptive rhythmic locomotion for legged robots because it may show properties of plasticity through its parameters.
This paper is organized as follows. In the second section, the model of neuron proposed by Rowat and Selverston is briefly described and simulations that illustrate its efficiency are carried out. First, an architecture based on two RS neurons is proposed for a one-joint neurocontroller and then for a two-joint planar leg that slips on a rail. In Section “Results and Discussion,” simulations show the interest of RS model: firstly, the easiness to control the rhythmic of the walking gait of the leg, and secondly the importance of ground/foot sensory feedback in the fluidity of rhythmic activity. In Section “Conclusion,” conclusion and future works are presented.
Materials and Methods
Rowat–Selverston Rhythmic Neuron Model
A reminder on RS model
Biological neurons with several ionic channels are complex, hence difficult to model. Rowat and Selverston (1993) present a simple model of a neuron for which two groups of currents are identified: a fast current and a slow current, each defined by a first order differential equation. Fast current is defined by Eq. 1 and slow current by Eq. 2.


with τm < τs. τm, is the time constant of the neuron membrane, τs is the time constant of slow currents activation. Iinj, is the injected current, V the cellular membrane voltage, and q the slow current.
F(V, σf), defined in Eq. 3, is a non-linear current–voltage function for the fast current. We see in Figure 1 that the fast current shape F(V, σf) can be linear (σf = 0), non-linear but bijective (σf = 1), and non-linear and non-bijective (σf = 2). F(V, σf) is a fundamental part of the RS model because this function induces different behaviors for the neuron (damped oscillating, plateau potentials, or oscillating) following the value of the fast current gain, σf.
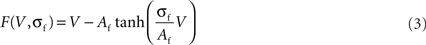
Meanwhile, the steady-state value of the slow current is linear in V, with conductance σs:

In Eqs. 1 and 2, q, V, and Iinj have the dimension of an electrical current. It means that a current is represented by enough potential to drive the current through the membrane leak conductance, gL, which is a constant. For deep mathematical study of the model please refer to (Rowat and Selverston, 1993, 1997).
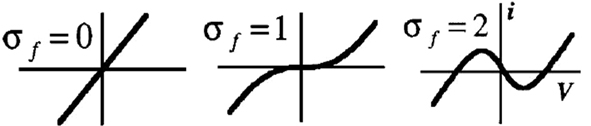
Figure 1. Effect of σf parameter on the fast current (extract from Rowat and Selverston, 1997). Af adjusts the width of the N-shape (right) without affecting the degree of N-shape.
Simulation and study of the cell model
Studying the equations of current for the cell model shows that the frequency of oscillation is basically determined by the value of σs, and its amplitude determined by the value of Af. Moreover, if σf is reduced to σf < 1 while σs is large enough, the cell does not oscillate anymore. However, if σf > 1, but σs is reduced below a certain value, the model does not oscillate but shows plateau potentials.
In the following, the neuron model of Rowat and Selverston is simulated under MATLAB-Simulink. The activity of this model for different values of variables σs, σf, τs, and τm is explained. The primary values of these variables are τs = 1 s, τm = 0.05 s, and Af = 2. Input Iinj is a pulse of amplitude 1 and duration of 1 s. In Figure 2 (up) it can be seen that for a rather high value of σf (=2.2 in this case), but small values of σs, the cell does not oscillate and shows plateau potentials. As the value of this parameter increases above one, the cell starts to oscillate, and the frequency of this oscillation is proportional to the value of σs. On the other hand, if σs is large but σf small, the neuron output shows damped oscillations (see Figure 2, bottom).
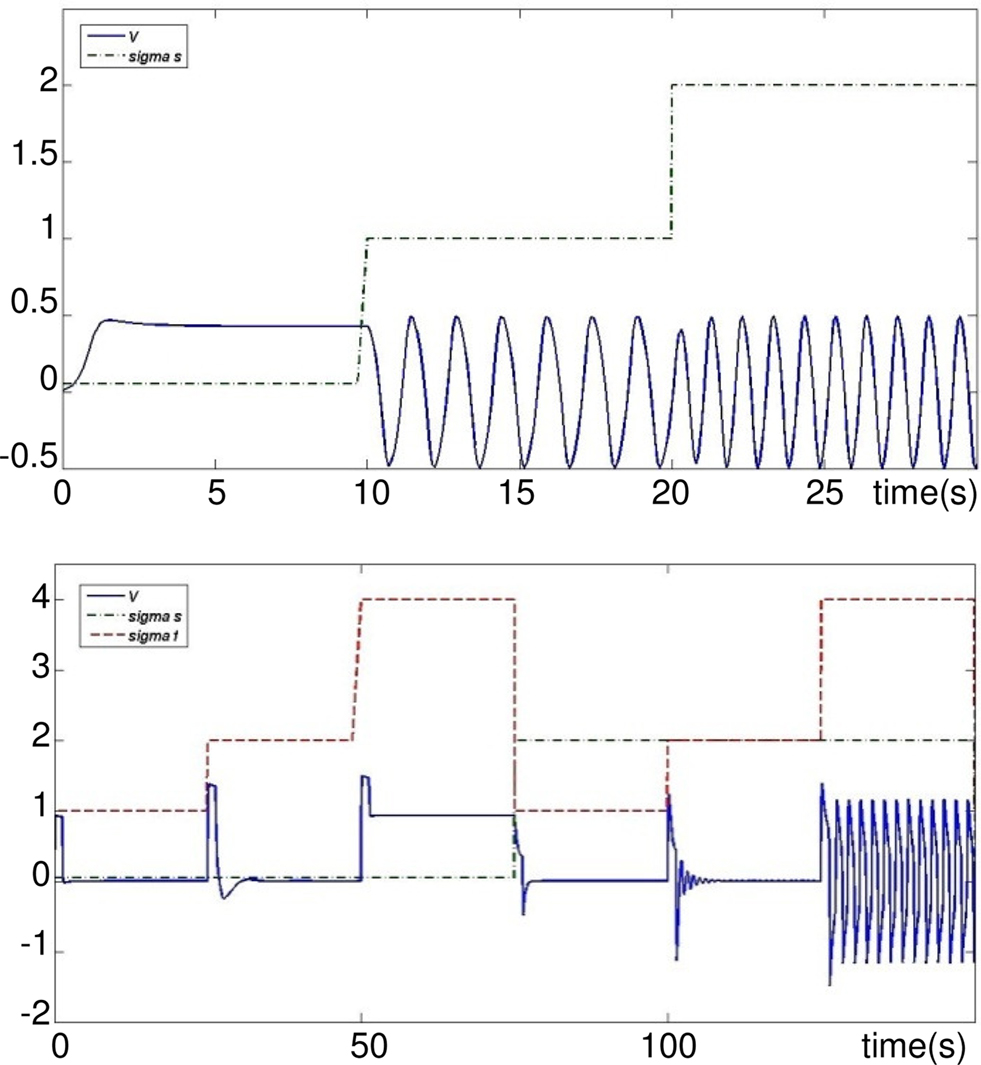
Figure 2. Activity mode and frequency w. r.t different values of σs and σf. Top: σf = 2.2 and σs ∈ [0.05,1,2]. Bottom: σf ∈ [1,2,4] and σs = 0.05 then σs = 2 and σf ∈ [1,2,4]. Iinj occurs simultaneously to each change of σs or σf.
With different combinations values of σs and σf, the neuron shows different modes of activity (quiescent, damped oscillating, plateau potentials, or oscillating). Different zones of this activity can be defined as shown in the bifurcation figure diagram of Figure 3.
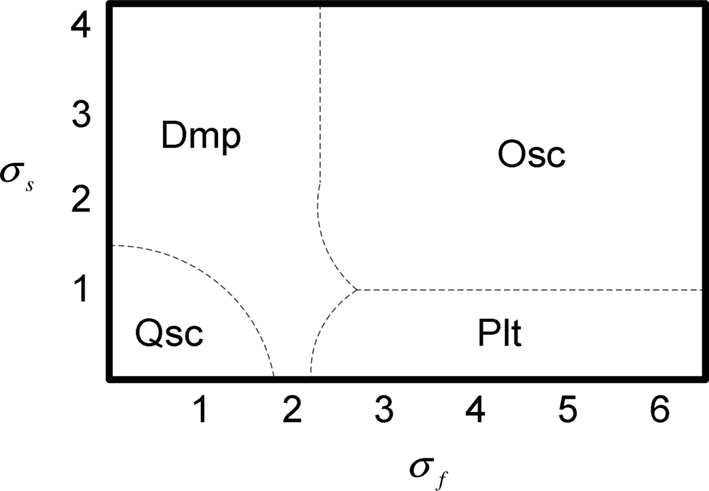
Figure 3. Bifurcation diagram for values of σf and σs. Qsc, quiescent; Dmp, damped oscillating; Plt, plateau potentials; Osc, oscillating. τs = 1 s, τm = 0.05 s, Af = 2.
This diagram has been obtained manually and through a detailed study of different combinations of values for parameters σf and σs. Note that in this bifurcation study, the transition time to toggle from one activity mode to another is not taken into account. Nevertheless, one can see in Figure 2 that this time seems rather short. Therefore, the RS model allows for the simulation of the fundamental intrinsic functional properties met in biological networks which generate rhythmic gaits. In particular, it is a plastic intrinsic model through its parameters σf, and σs, which can be modulated by internal or external signals. In Section “Conclusion” we will show that this plasticity is very efficient to produce adaptive walking gaits for legged robot.
CPG Model for One Joint Articulation
The neural architecture suggested in this paper (see Figure 4) uses two Rhythmic Neurons, two Sensory Neurons for feedback from angular position, and two Velocity Sensory Neurons that code velocity feedback of the joint. Two cells which we call Motoneurons modulate the output of each Rhythmic Neurons depending on Sensor Neuron outputs.
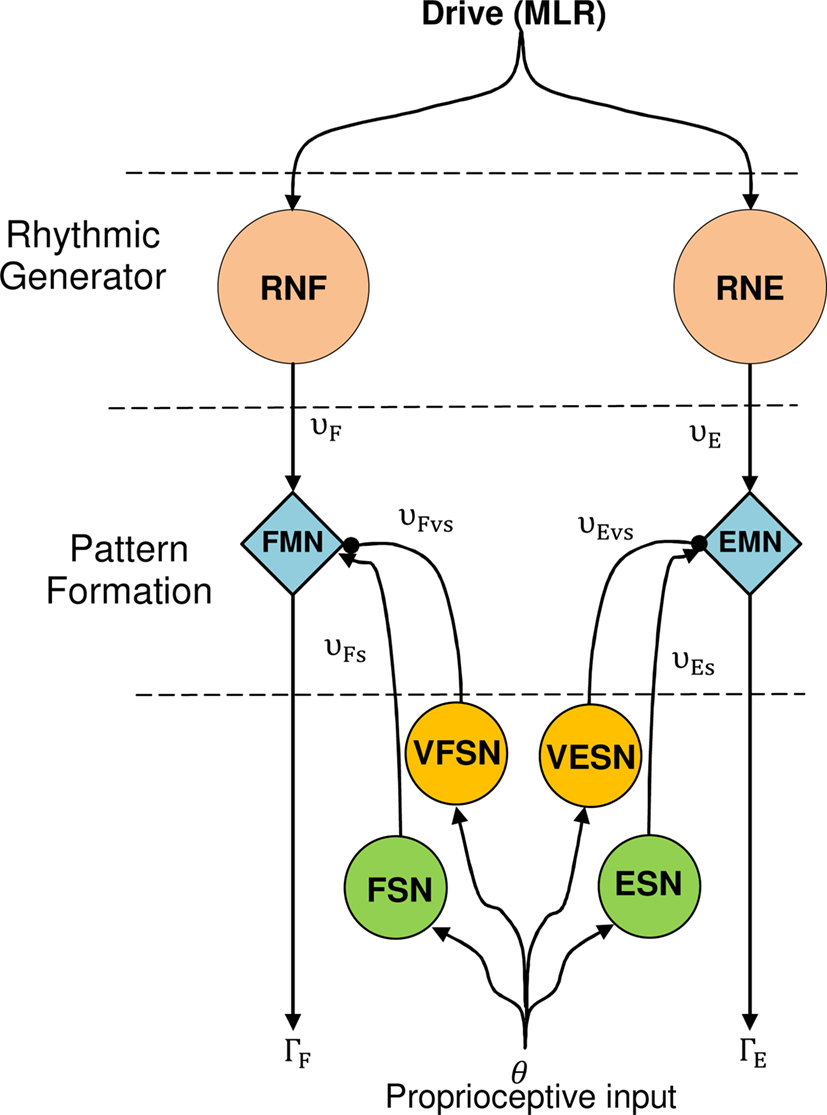
Figure 4. The CPG model for one articulation. Proprioceptive inputs come from the angular position of the articular joint. RNF and RNE are Rowat–Selverston rhythmic neurons (flexor and extensor). EMN and FMN are extensor and flexor motor neurons, ESN and FSN are extensor, and flexor sensory neurons. VFSN and VESN are the velocity extensor and flexor sensory neurons.
Sensory neurons are modeled as stretch receptors similar to those in (Geng et al., 2006; Wörgötter et al., 2006; Manoonpong et al., 2008). This is a model inspired by a sensor neuron proposed by Wadden and Ekeberg (1998).
Outputs from position sensor neurons are given by:


Where the parameter θES limits the joint articulation to maximum angle of extension, θFS defines the minimum value of flexion and kp = 5.
Outputs from velocity sensor neurons are given by:


Where kd = 5.
Like in (Wörgötter et al., 2006), the torque applied on the articulation is given by:

Where extensor and flexor torques are produced by motoneurons FMN and EMN:


Simulation of 1-DOF
In this subsection, the architecture described in the previous sub-section is applied to a leg with 1-DOF, in MATLAB-Simulink (Figure 5). All simulations in this paper are in the plane.
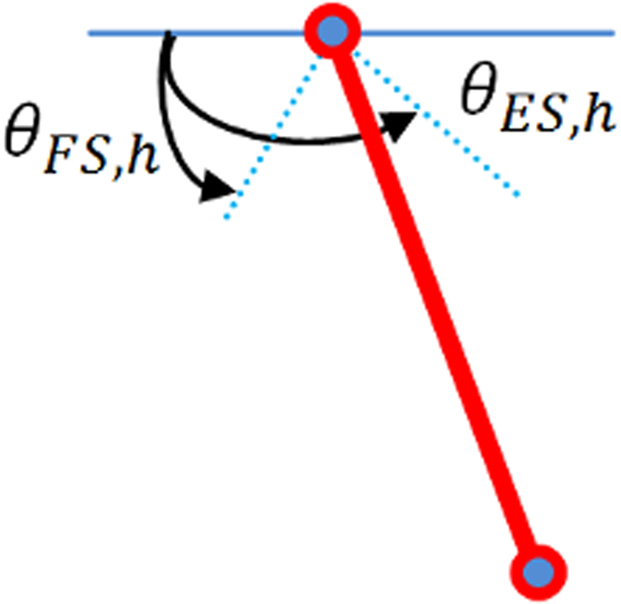
The leg is simulated like a pendulum, fixed on the hip and is not in contact with the ground. θES,h and θFS,h define respectively maximum extension and flexion angles of the hip.
Drive MLR is an one pulse signal of 0.1 s that is sufficient enough to trigger the CPG. Outputs of the two motor neurons RNE and RNF are shown Figure 6, torque and angular joint on Figure 7.
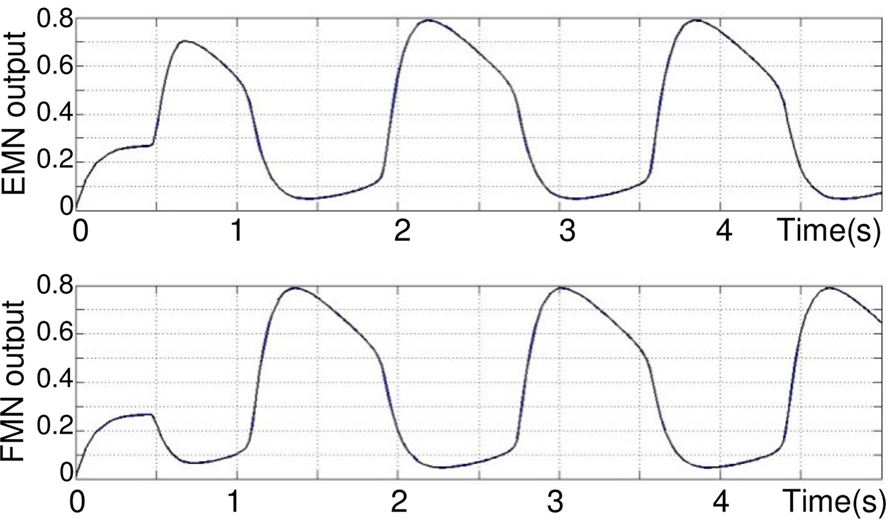
Figure 6. Oscillations in Rowat–Selverston-type neurons implemented in extensor and flexor joint controllers, respectively. The output is normalized. τm = 0.05 s, τs = 1 s, τm = 0.05 s, σf = σs = 3, Af = 5.
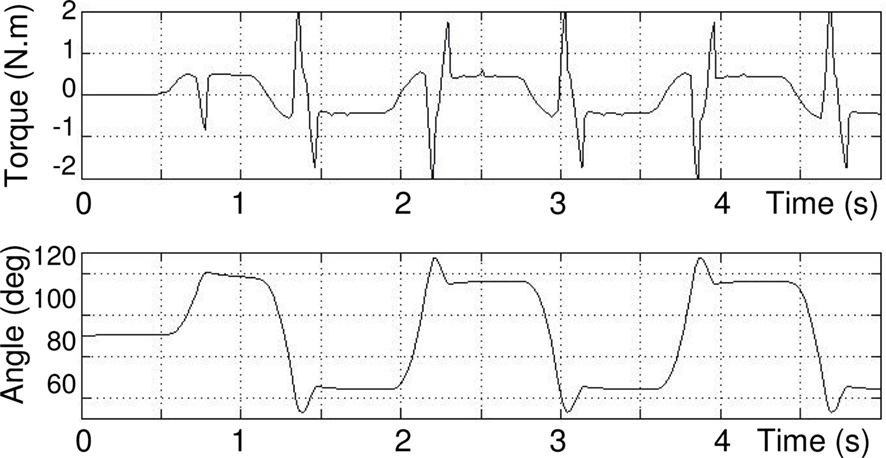
Figure 7. Commanded torque (above) and angular position (below) of joint measured by sensory neurons, θES = 120°, θFS = 60°.
It can be seen (on Figure 6) that after a transition phase, the two motor neurons EMN and FMN oscillate in opposite phase on a stable regime. This transition is also visible on Figure 7 takes 0.75 s. The torque applied to the hip and its angle show that, after the transition, the joint maintains in a stable behavior the defined extension and flexion angular constraints θES = 120°, θFS = 60°. In addition, one can clearly see how the torque is synchronized to the sensory neuron. Note that this oscillation maintains itself indefinitely, which means that our CPG generates a robust limit cycle.
CPG Model for One Leg with Two Planar Joints
Locomotion problem
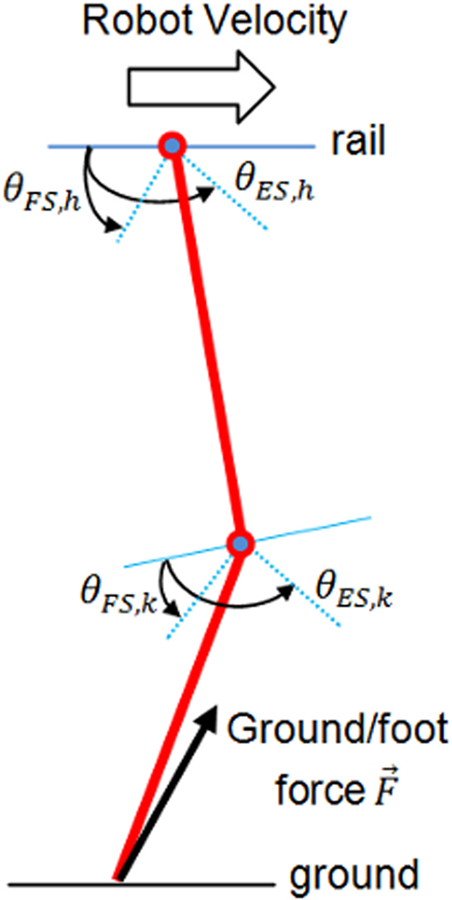
In this section, the aim is to control a planar leg which slides on a rail (see Figure 8). This leg has a punctual foot, one joint at hip level, and another on the knee. The hip is joined to an ideal rail (no friction), and slides forward by pushing the point foot on to the ground (like in skating). Thigh and tibia are both 20 cm long and weight 1 kg. The problem is similar to Wörgötter et al.’s (2006) experiment, in the way that both models are in the sagittal plane and are based on sensory feedback from the ground (forces) and articular joints.
Leg CPG model with afferent sensory inputs
To control this leg with two articulations, one CPG presented before (Figure 4) is needed for each articulation. It is necessary here to coordinate the angular movement of the knee with the hip. For this purpose, two sensory neurons are used (see Eqs 8 and 9 respectively and Figure 9).
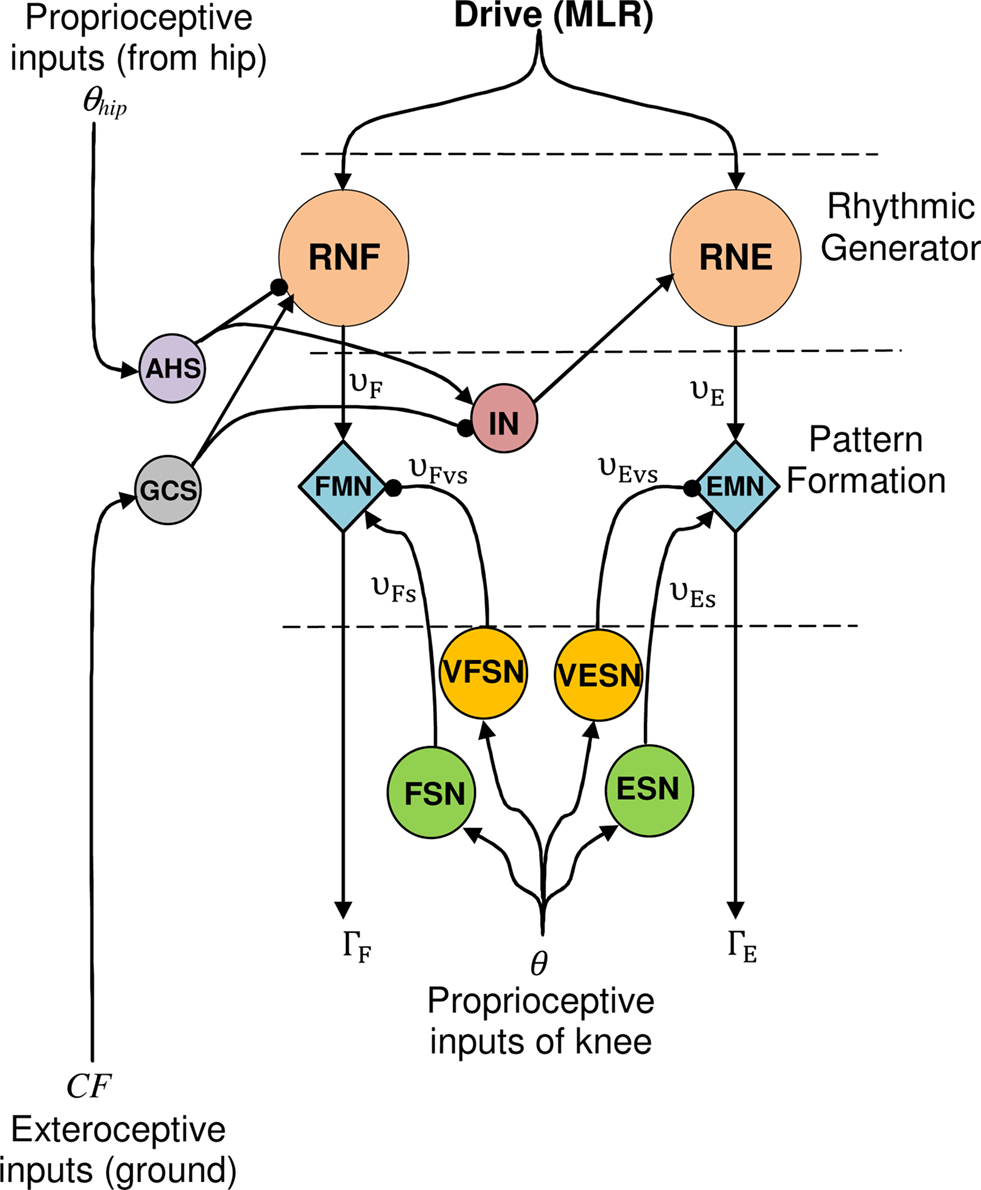
Figure 9. CPG model for the knee articulation (for more clarity, the hip level is not depicted). Proprioceptive inputs come from the hip (θhip: angular extension) and exteroceptive from the ground (CF: intensity of vertical component 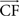 of the contact force
of the contact force 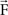 ).
).
The first one, the anterior hip sensor (AHS), measures the anterior hip angle and excites the RG level of the knee. The second, called ground contact sensor (GCS), is a force sensor neuron that senses the intensity of vertical component 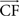 of the contact force
of the contact force 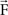 between the ground and the foot. GCS excites knee Rhythmic Flexor Neuron and inhibits knee Rhythmic Extensor Neuron. Outputs of AHS and GCS neurons are given by:
between the ground and the foot. GCS excites knee Rhythmic Flexor Neuron and inhibits knee Rhythmic Extensor Neuron. Outputs of AHS and GCS neurons are given by:


These two sensory loops work as follows. As long as the hip angle is smaller than its extreme value (θES,h), the AHS fires and inhibits the knee extensor (if θhip < θES,h, then υAHS > 0 and inhibits the RNF). When the hip reaches its maximum extension AHS liberates the knee extensor and consequently the knee starts to extend. Meanwhile, the GCS is activated by the ground force applied to the foot as soon as the foot touches the ground GCS is activated, inhibits the knee extensor and strengthens the knee flexor. So the knee extensor neuron is inhibited, either when the foot is in contact with the ground or when the thigh is not at its maximum extension phase. Thus, an interneuron IN is introduced. It is activated if at least one of the two sensory neurons AHS and GCS is active. This neuron is defined as Eq. 14 and its output Σ has a value between 0 and 1 according to its input v
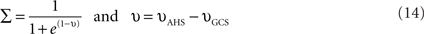
In case of a two legged robot, sensory neurons at hips level are also needed to coordinate the two legs. In this paper the architecture is limited to a single leg, then sensory neurons are not added to the hip and its architecture is the same as the one described in the previous Section “Results and Discussion.”
Results and Discussion
In Figure 10 the applied torque and the correspondent angle of each joint (hip and knee) are presented.
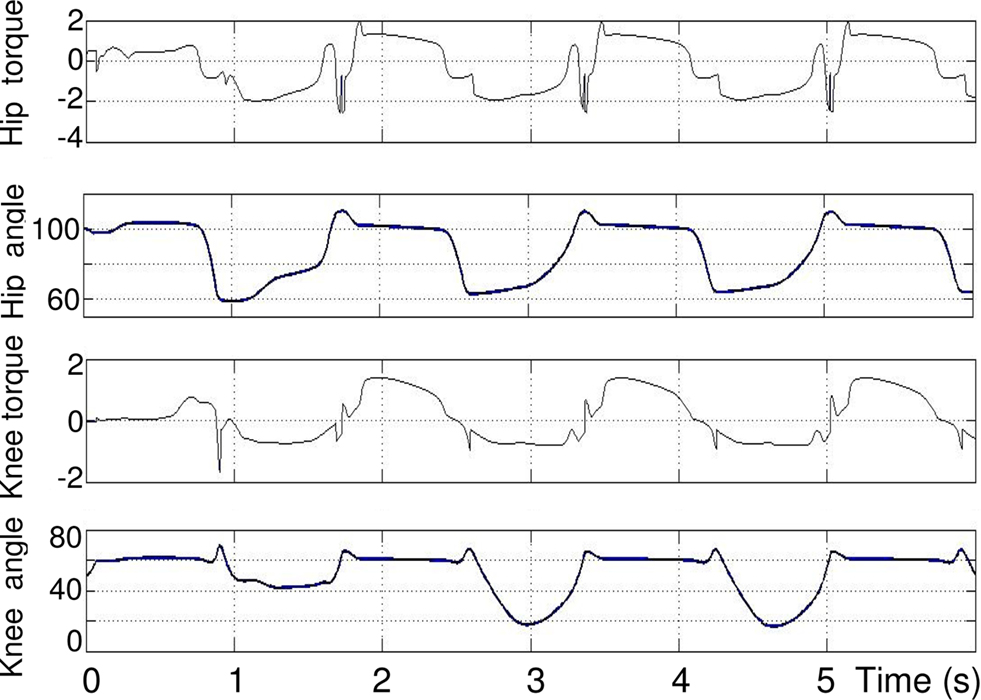
Figure 10. From top to bottom: torque (N. m) and angle (degree) of hip and knee. θES,h = 105°, θFS,h = 50°, θES,k = 90°, θFS,k = 10°.
As it can be seen in the second and third plots, when the hip reaches its maximum extension angle (θES,h), the extensor in the knee is activated and thus the torque applied to knee joint increases. As for one articulation, there exists a transitory phase, that lasts about 2 s, which is the time needed to stabilize the permanent rhythmic activity. The length of this temporary phase also depends on the initial position and angle. The hip rhythmic activity has the same appearance as the one in Section “Modulation of the Rhythmic Activity” except frequency and amplitude that changed because of coordination setting. The rhythmic activity of the knee has the same frequency as that of the hip. In the extension phase of the knee cycle, the foot touches the ground, so the tibia stops extending before reaching its maximum extension angle θES,k = 90.
Ground/Foot Contact Effect on the Rhythmic Activity
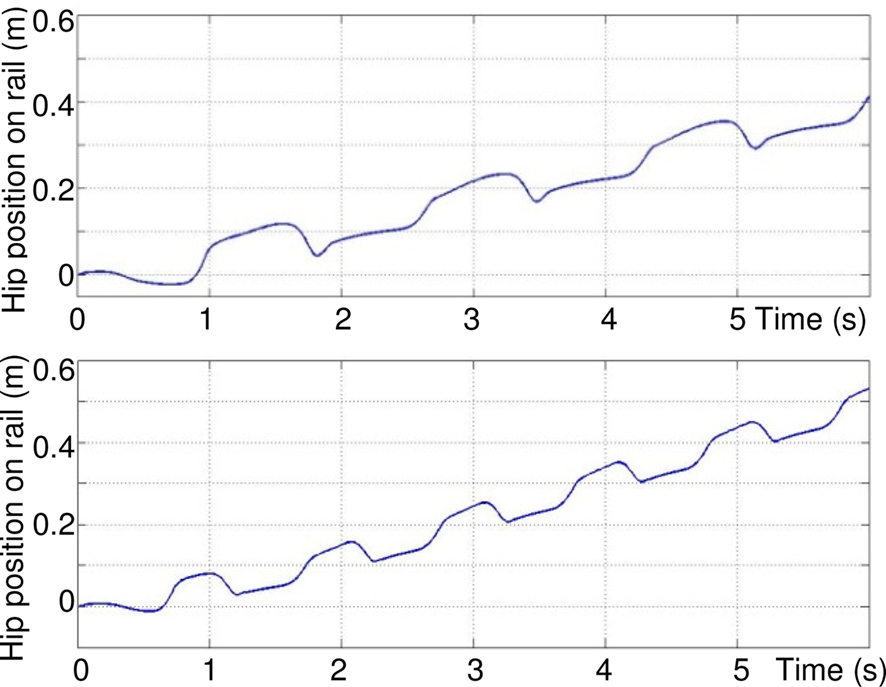
Figure 11 compares the hip position and velocity in presence of ground contact neuron GCS (dashed lines) and without GCS (solid lines). This figure illustrates the importance of the GCS in the leg, already proven to exist in biology (Cattaert and Le Ray, 2001). The figure (top) shows that the movement of the hip is smoother and faster in presence of GCS. After six seconds, the distance reached by the hip on the rail is longer with GCS than without. The figure (bottom) shows that there is less variation of speed when there is a GCS sensory loop.
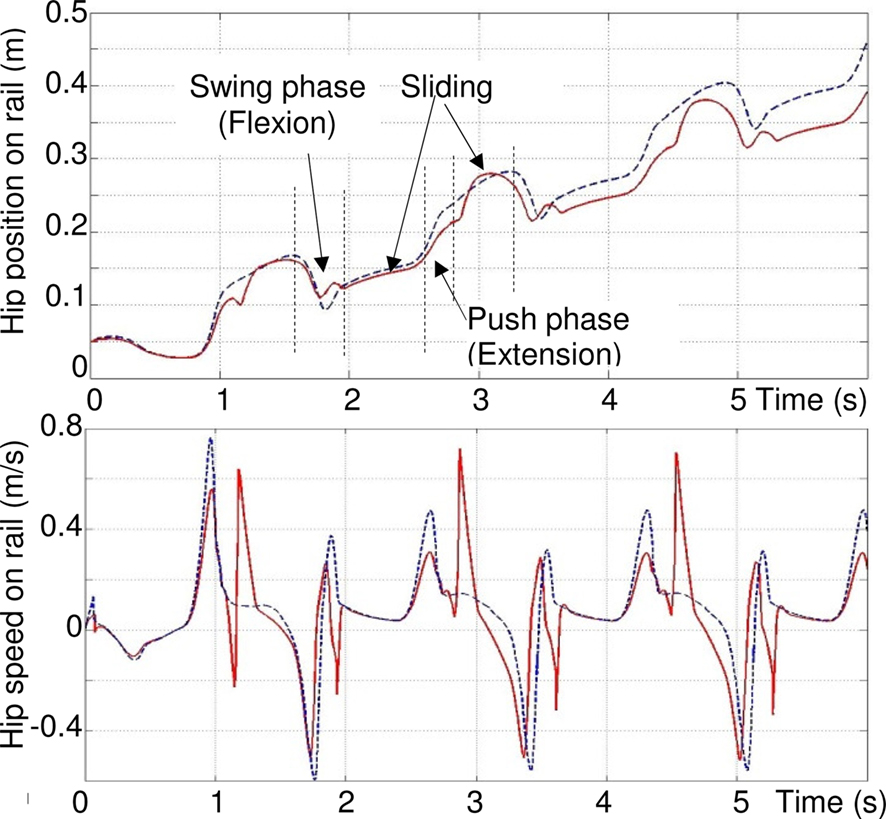
Figure 11. Effect of feedback from ground sensor GCS on the rhythmic activity of the leg. Top: distance reached by the hip on the rail. Bottom: speed of the hip. Dashed lines: with GCS. Solid lines, without.
There are three phases in one walking cycle. From 0.8 to 1.7 s, due to the push of the foot against the ground (extension of articulations), the hip velocity on the rail increases rapidly (acceleration): and the hip slips on the rail. The maximum velocity is highest with GCS. Then, from 1.7 to 2 s, it is the swing phase of the leg. In this phase, the rapid flexion of the two articulations induces (without GCS, at around 1.3, 1.7 and 1.9 s and 1.7 s with GCS) an inverse dynamic effect which moves back the hip (negative speed) because the friction forces on the rail are low. Finally, from 2 to 2.6 s, the hip continues to slip and the foot is in contact with the ground and pushes again (positive speed). The sudden oscillation (rapid negative/positive peaks at t = 1.3, 1.9, 3.6 s…) are rejected with GCS. Other negative peaks (t = 1.7, 3.5, 5.1 s) are the same with and without GCS, because of the rapid flexion of the leg.
Figure 12 shows that the effect of the GCS is statistically larger when the initial conditions are varied. Two hundred forty-seven initial conditions of the leg are simulated with and without the contact sensor: the hip angle is incremented from 60° to 120°, with intervals of 5° and the knee angle, with respect to the thigh, for a range of 0–90°. Simulation is run for 6 s in each case, for eight integer values of σs varying from 3 to 10. The average speed and the final position of the hip are measured. Results show that in more than 93% of the trials (red bars in Figure 12), the model with the contact feedback slides ahead on the rail (for some difficult trials, the leg remains blocked), while this number is a little lower for the model without GCS, yet around 90% (not depicted). The average improvement between the final position reached at t = 6 s in the presence of CGS is at least 20%, and can go up to 80% for certain values of σs (blue bars). There have been some cases where, without GCS, the leg does not slide ahead (difficult initial configuration), like the one depicted in Figure 13.
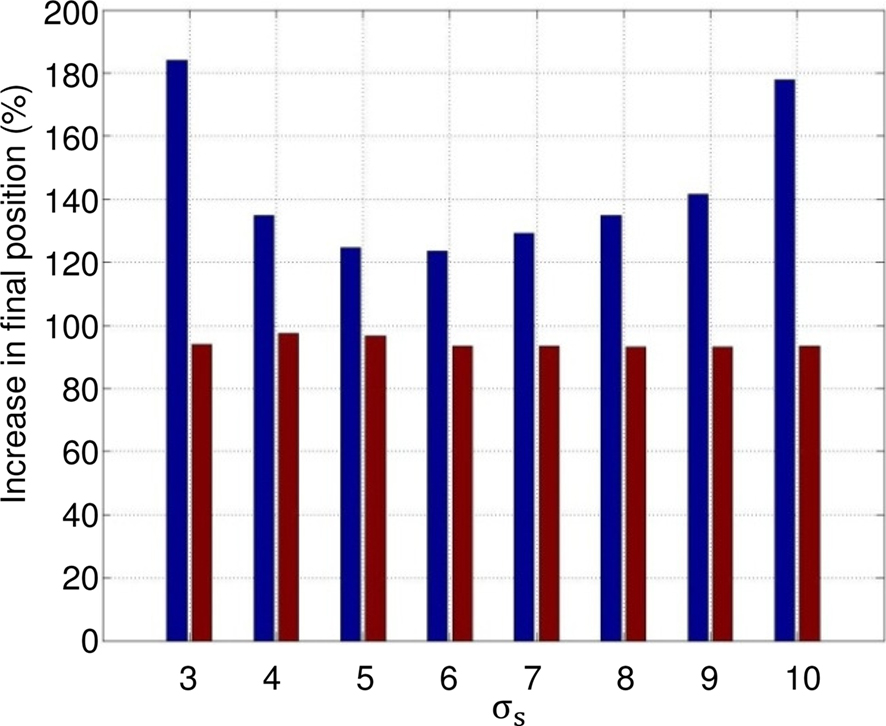
Figure 12. Statistical analysis: 247 different initial conditions of the leg for eight values of σs. Red bars: percentage of trials the model with the contact feedback slides ahead on the rail; leg is not blocked due to initial conditions. Blue bars: mean value of improvement in presence of GCS (final position with GCS/final position without GCS).
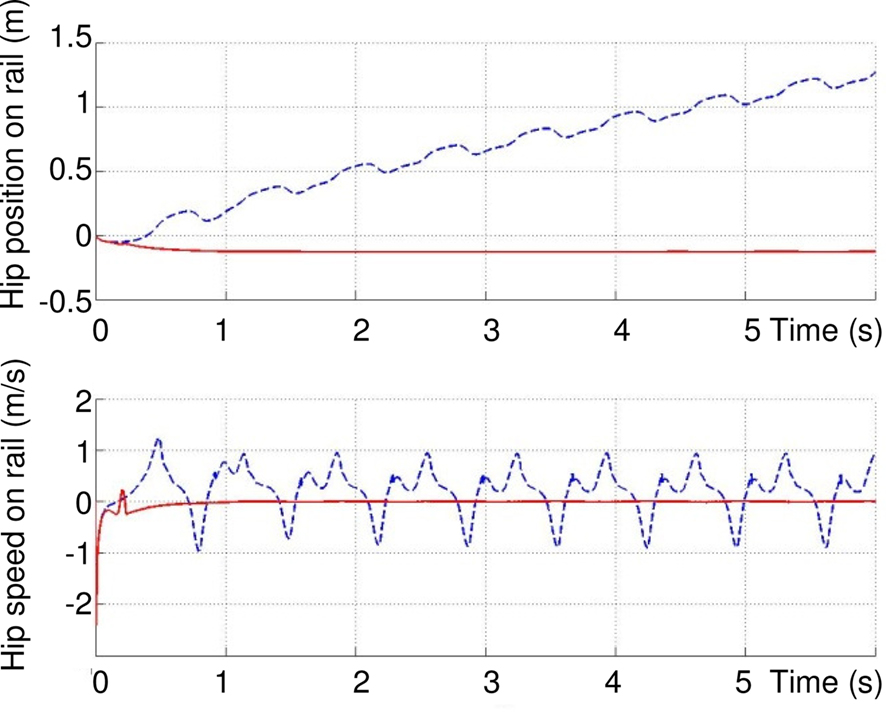
Figure 13. In several difficult initial conditions like this one (hip = 95°, knee = 85°), the leg does not slide ahead without GCS.
All these results show that the sensory feedback improves the dynamic coordination of the leg. Therefore, the dynamical interaction between the CPGs, the robot and the environment favors rhythm production and phase synchronization as mentioned in (Pitti et al., 2009).
Modulation of the Rhythmic Activity
Figure 14 shows the influence of conductance σs values on the walking cycle. By increasing the value of this parameter for the four rhythmic neurons, the frequency of the walk increases.
In Figure 15, at time t = 3 s, the value of this parameter decreases from 5 to 0.5, so that the activity mode of the motor neurons change from oscillatory to plateau potentials. This switch in activity mode stops the sliding of the leg.
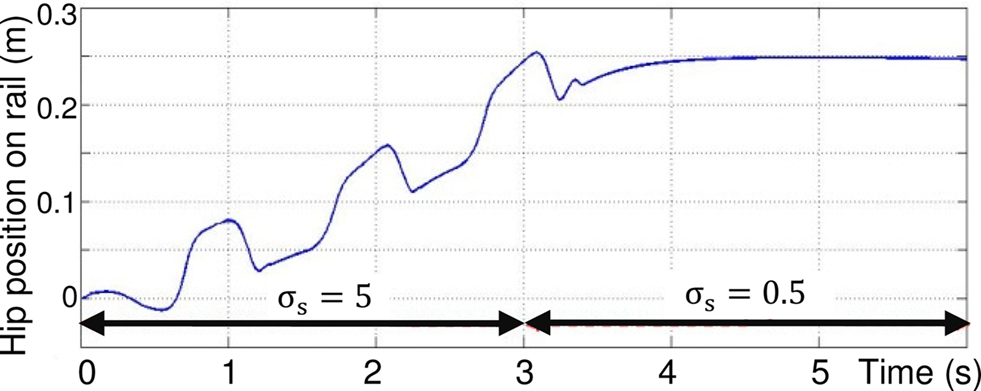
Figure 15. Control of the walking pattern due to change in value of σs from 5 to 0. 5 at time t = 3 s.
These last two simulations show that the walking cycle can easily be controlled by the modulation of a single parameter in rhythmic neurons of the proposed architecture of Figure 9, and then stops the robot walking.
Note that the transition from one walking gait to another is continuous and stable because of the robustness of the Rowat–Selverston neuron model. Hence, it is logical to assume that this modulation can be applied from a high-level controller to modify, for example, the desired velocity of the legged robot.
Figure 16 shows the walk on an uneven terrain, for values of σs that increase robot velocity. Three vertical stairs appear between t = 4 and 8 s. This simulation clearly shows the robustness of the neural controller. Indeed, the rhythmic pattern is not much disturbed, the velocity decreases, and the neural CPG finds a normal rhythmic activity when the ground level is 0 cm at t = 8 s.
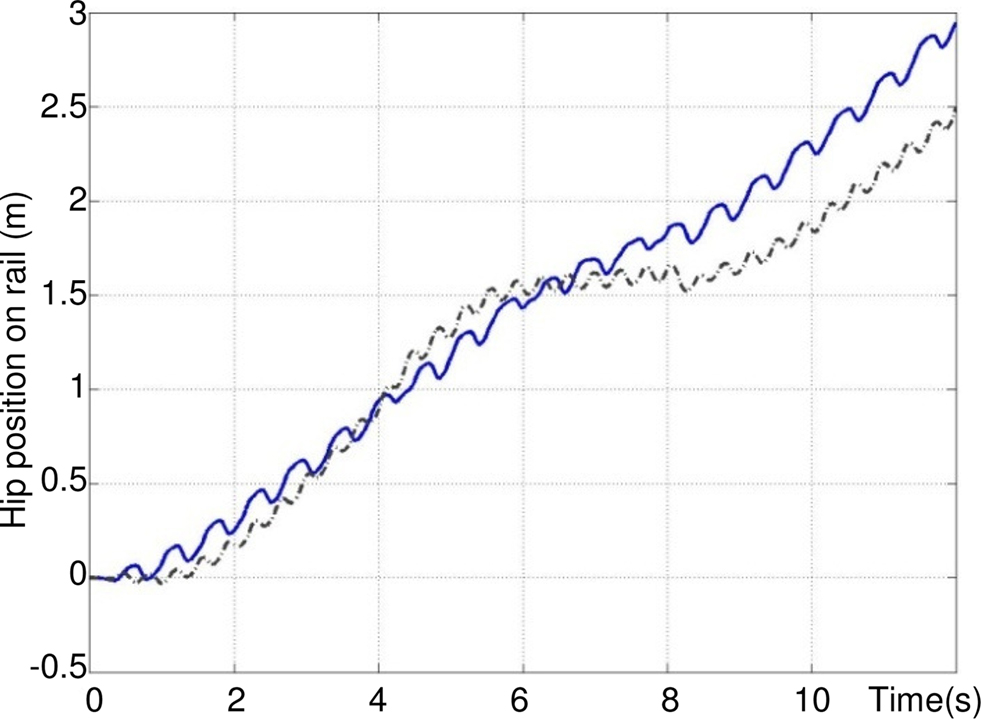
Figure 16. Control of the walking pattern on an uneven terrain for σs = 10 (dashed black) and σs = 20 (solid blue). At time t = 4 s a vertical up stair of 7 cm appears (ground is at +7 cm), at t = 6 s, a vertical down stair of 4 cm appears (ground is at +3 cm), at t = 8 s, a vertical down stair of 3 cm appears (ground is at 0 cm).
Compared to Figure 14, for σs = 20 the speed is three times greater than for σs = 5.
Conclusion
This paper presents and reproduces the functioning mechanism of a neural CPG architecture based on Rowat and Selverston neuron. First, we have shown that this model can be easily used to produce a controllable walking gait by modulation of the single conductance parameter σs of each rhythmic neuron. The proposed CPG architecture is based on fundamental biological principles consisting of rhythmic level, PF level, proprioceptive, and exteroceptive sensory loops. Second, through simulations, we have shown that the ground force sensory feedback has an important role in the quality of the rhythmic activity.
Future work will be to extend this architecture to a biped robot for which the modulation of a membrane neuron conductance could create adaptive locomotion. For this purpose, this parameter must be modulated with respect to external parameters of the robot, such as contact forces of each foot, as well as internal properties, like coordination between the legs and balance.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Beer, R. (2006). Parameter space structure of continuous-time recurrent neural networks. Neural Comput. 18, 3009–3051.
Beer, R., and Chiel, H. (1992). A distributed neural network for hexapod Robot Locomotion. Neural Comput. 4, 356–365.
Brunel, N. (2000). Dynamics of networks of randomly connected excitatory and inhibitory spiking neurons. J. Physiol. 94, 445–463.
Buchli, J., Iida F., and Ijspeert A. (2006). “Finding resonance: adaptive frequency oscillators for dynamic legged locomotion,” in Proceeding of IEEE International Conference on Intelligent Robots and Systems (IROS), Beijing, 3903–3910.
Büschges, A. (2005). Sensory control and organization of neural networks mediating coordination of multisegmental organs for locomotion. J. Neurophysiol. 93, 1127–1135.
Cattaert, D., and Le Ray, D. (2001). Adaptive motor control in the crayfish. Prog. Neurobiol. 63, 199–240.
Conradt, J., and Varshavskaya, P. (2003). “Distributed central pattern generator control for a serpentine robot,” in Proceedings of the International Conference on Artificial Neural Networks (ICANN) (Istanbul, Turkey), 338–341.
Cruse, H., Bartling, C., Cymbalyuk, G., Dean, J., and Dreifert, M. (1995). A modular artificial neural net for controlling a six-legged walking system. Biol. Cybern. 72, 421–430.
Cruse, H., Kindermann, T., Schumm, M., Dean, J., and Schmitz, J. (1998). Walknet-a biologically inspired network to control six-legged walking. Neural Netw. 11, 1435–1447.
De Pine Filho, A. C., Dutra, M. S., and Raptopoulos, L. S. C. (2005). Modeling of a bipedal robot using mutually coupled Rayleigh oscillators. Biol. Cybern. 92, 1–7.
Di Prisco, G. V., Pearlstein, E., Le Ray, D., Robitaille, R., and Dubuc, R. (2000). A cellular mechanism for the transformation of a sensory input into a motor command. J. Neurosci. 20, 8169–8176.
Dutra, M. S., De Pina Filho, A. C., and Romano, V. F. (2003). Modeling of a bipedal locomotor using coupled nonlinear oscillators of Van der Pol. Biol. Cybern. 88, 286–292.
Endo, G., Nakanishi, J., Morimoto, J., and Cheng, G. (2005). “Experimental studies of a neural oscillator for biped locomotion with QRIO,” in Proceedings of IEEE International Conference on Robotics and Automation, (ICRA) 2005, Barcelona, 596–602.
Gallagher, J., Beer., R., Espenschied, K., and Quinn, R. (1996). Application of evolved locomotion controllers to a hexapod robot. Rob. Auton. Syst. 19, 95–103.
Geng, T., Porr, B., and Wörgötter, F. (2006). A reflexive neural network for dynamic biped walking control. Neural Comput. 18, 1156–1196.
Gill, M. D., and Skorupski, P. (1996). Modulation of spontaneous and reflex activity of crayfish leg motor neurons by octopamine and serotonin. J. Neurophysiology 76, 3535–3549.
Grillner, S., Deliagina, T., Ekeberg, O., El Manira, A., Hill, R. H., Lansner, A., Orlovsky, G. N., and Wallen, P. (1995). Neural networks coordinating locomotion and body orientation in lamprey – biological and mathematical models. J. Neurophysiol. 18, 270–279.
Grillner, S., and Wallen, P. (2002). Cellular bases of a vertebrate locomotor system-steering, intersegmental and segmental co-ordination and sensory control. Brain Res. Rev. 40, 92–106.
Hoinville, T. (2007). évolution de contrôleurs neuronaux plastiques. De la locomotion adaptée vers la locomotion adaptative. Ph.D. thesis (In French), University of Versailles St Quentin, Vélizy.
Hoinville, T., and Henaff, P. (2004). “Comparative study of two homeostatic mechanisms in evolved neural controllers for legged locomotion,” in Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems, Sendai, 2624–2629.
Ijspeert, A. (2008). Central pattern generators for locomotion control in animals and robots: a review. Neural Netw. 21, 642–653.
Lei, L. G., Habib, M. K., Watanabe, K., and Izumi, K. (2008). Central pattern generators based on Matsuoka oscillators for the locomotion of biped robots. Artif. Life Rob. 12, 264–269.
Liu, C., Qijun, C., and Jiaqi, Z. (2009). “Coupled Van Der Pol oscillators utilised as central pattern generators for quadruped locomotion,” in Proceedings of International Conference on Chinese control and Decision Conference, Shanghai, 3677–3682.
Manoonpong, P., Pasemann, F., and Wörgötter, F. (2008). Sensor-driven neural control for omnidirectional locomotion and versatile reactive behaviors of walking machines. Rob. Auton. Syst. 56, 265–288.
Marchand, A. R., Barnes, W. J. P., and Cattaert, D. (1997). Primary afferent depolarizations of sensory origin within contact- sensitive mechanoreceptive afferents of a crayfish leg. J. Neurophysiol. 77, 3340–3354.
Marder, E., and Bucher, D. (2001). Central pattern generators and the control of rhythmic movements. Curr. Biol. 11, 986–996.
Matsubara, T., Morimoto, J., Nakanishi, J., Sato, M., and Doya, K. (2006). Learning CPG-based biped locomotion with a policy gradient method. Rob. Auton. Syst. 54, 911–920.
Matsuoka, K. (1985). Sustained oscillations generated by mutually inhibiting neurons with adaptation. Biol. Cybern. 52, 367–376.
Mc Crea, D. A., and Ryback, I. A. (2008). Organization of mammalian locomotor rhythm and pattern generation. Brain Res. Rev. 57, 134–146.
Nadim, F., and Manor, Y. (2000). The role of short-term synaptic dynamics in motor control. Curr. Opin. Neurobiol. 10, 683–690.
Pitti, A., Lungarella, M., and Kuniyoshi, Y. (2009). Generating spatiotemporal joint torque patterns from dynamical synchronization of distributed pattern generators. Front. Neurorobotics 3:2. doi: 10.3389/neuro. 12.002.2009
Rowat, F., and Selverston, I. (1993). Modeling the gastric mill central pattern generator of the lobster with a relaxation-oscillator network. Neurophysiology 70, 1030–1053.
Rowat, P., and Selverston, A. (1997). Oscillatory mechanisms in Pairs of neurons connected with fast inhibitory synapses. J. Comput. Neurosci. 4, 103–127.
Taga, G., Yamaguchi, Y., and Shimizu, H. (1991). Self-organized control of bipedal locomotion by neural oscillators in unpredictable environment. Biol. Cybern. 65, 147–159.
Vogels, T. P., and Abbott, L. F. (2005). Signal propagation and logic gating in networks of integrated-and-fire neurons. J. Neurosci. 25, 10786–10795.
Wadden, T., and Ekeberg, O. (1998). A neuro-mechanical model of legged locomotion: single leg control. Biol. Cybern. 79, 161–173.
Williams, H. J. (2007). Homeostatic plasticity improves signal propagation in continuous-time recurrent neural networks. Biosystems 87, 252–259.
Woosung, Y., Chong, N. Y., Ra, S., Chang, H. K., and Bum, J. Y. (2008). “Self-stabilizing bipedal locomotion employing neural oscillators,” in Proceedings of 8th IEEE-RAS International Conference on Humanoid robots, Daejeon, 8–15.
Keywords: central pattern generator, legged locomotion, sensorimotor coordination, Rowat–Selverston
Citation: Amrollah E and Henaff P (2010) On the role of sensory feedbacks in Rowat–Selverston CPG to improve robot legged locomotion. Front. Neurorobot. 4:113. doi: 10.3389/fnbot.2010.00113
Received: 14 March 2010;
Accepted: 06 December 2010;
Published online: 29 December 2010.
Edited by:
Jun Tani, RIKEN Brain Science Institute, JapanCopyright: © 2010 Amrollah and Henaff. This is an open-access article subject to an exclusive license agreement between the authors and the Frontiers Research Foundation, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Patrick Henaff, ETIS, UMR CNRS 8051, Université de Cergy-Pontoise, Site de ST Martin, 2 rue A. Chauvin, 95302 Cergy-Pontoise Cedex, France e-mail:cGF0cmljay5oZW5hZmZAdS1jZXJneS5mcg==