- 1 The Bionic Ear Institute, Melbourne, VIC, Australia
- 2 NICTA Victoria Research Lab, The University of Melbourne, Melbourne, VIC, Australia
- 3 Department of Electrical and Electronic Engineering, The University of Melbourne, Melbourne, VIC, Australia
- 4 Physik Department T35 and BCCN-Munich, Technische Universität München, Garching bei München, Germany
Recent results about spike-timing-dependent plasticity (STDP) in recurrently connected neurons are reviewed, with a focus on the relationship between the weight dynamics and the emergence of network structure. In particular, the evolution of synaptic weights in the two cases of incoming connections for a single neuron and recurrent connections are compared and contrasted. A theoretical framework is used that is based upon Poisson neurons with a temporally inhomogeneous firing rate and the asymptotic distribution of weights generated by the learning dynamics. Different network configurations examined in recent studies are discussed and an overview of the current understanding of STDP in recurrently connected neuronal networks is presented.
Introduction
Ten years after spike-timing-dependent plasticity (STDP) appeared (Gerstner et al., 1996; Markram et al., 1997), a profusion of publications have investigated its physiological basis and functional implications, both on experimental and theoretical grounds (for reviews, see Dan and Poo, 2006; Caporale and Dan, 2008; Morrison et al., 2008). STDP has led to a re-evaluation by the research community about Hebbian learning (Hebb, 1949), in the sense of focusing on causality between input and output spike trains, as an underlying mechanism for memory. Following preliminary studies that suggested the concept of STDP (Levy and Steward, 1983; Gerstner et al., 1993), the model initially proposed by Gerstner et al. (1996) and first observed by Markram et al. (1997) based on a pair of pre- and postsynaptic spikes has been extended to incorporate additional physiological mechanisms and account for more recent experimental data. This includes, for example, biophysical models based on calcium channels (Hartley et al., 2006; Graupner and Brunel, 2007; Zou and Destexhe, 2007) and more elaborate experimental stimulation protocols such as triplets of spikes (Sjöström et al., 2001; Froemke and Dan, 2002; Froemke et al., 2006; Pfister and Gerstner, 2006; Appleby and Elliott, 2007). In order to investigate the functional implications of STDP, previous mathematical studies (Kempter et al., 1999; van Rossum et al., 2000; Gütig et al., 2003) have used simpler phenomenological models to relate the learning dynamics to the learning parameters and input stimulation. However, a lack of theoretical results even for the original pairwise STDP with recurrently connected neurons persisted until recently, mainly because of the difficulty of incorporating the effect of feedback loops in the learning dynamics. The present paper reviews recent results about the weight dynamics induced by STDP in recurrent network architectures with a focus on the emergence of network structure. Note that we constrain STDP to excitatory glutamatergic synapses, although there is some experimental evidence for a similar property for inhibitory GABAergic connections (Woodin et al., 2003; Tzounopoulos et al., 2004).
Due to its temporal resolution, STDP can lead to input selectivity based on spiking information at the scale of milliseconds, namely spike-time correlations (Gerstner et al., 1996; Kempter et al., 1999). To achieve this, STDP can regulate the output firing rate in a regime that is neither quiescent nor saturated by means of enforcing stability upon the mean incoming synaptic weight and in this way establishing a homeostatic equilibrium (Kempter et al., 2001). In addition, a proper weight specialization requires STDP to generate competition between individual weights (Kempter et al., 1999; van Rossum et al., 2000; Gütig et al., 2003). In the case of several similar input pathways, a desirable outcome is that the weight selection corresponds to a splitting between (but not within) the functional input pools, hence performing symmetry breaking of an initially homogeneous weight distribution that reflects the synaptic input structure (Kempter et al., 1999; Song and Abbott, 2001; Gütig et al., 2003; Meffin et al., 2006).
In this review, we examine how the concepts described above extend from a single neuron (or feed-forward architecture) to recurrent networks, focusing on how the corresponding weight dynamics differs in both cases. The learning dynamics causes synaptic weights to be either potentiated or depressed. Accordingly, STDP can lead to the evolution of different network structures that depend on both the correlation structure of the external inputs and the activity of the network In particular, we relate our recent body of analytical work shortcite (Gilson et al., 2009a–c, 2010) to other studies with a view to illustrating how theory applies to the corresponding network configurations.
Models
In the present paper, we use a model of STDP that contains two key features: the dependence upon relative timing for pairs of spikes via a temporally asymmetric learning window W (Gerstner et al., 1996; Markram et al., 1997; Kempter et al., 1999), as illustrated in Figure 1, and upon the current strength of the synaptic weight (Bi and Poo, 1998; van Rossum et al., 2000; Gütig et al., 2003; Morrison et al., 2007; Gilson et al., 2010). In this review we will therefore consider the STDP learning window as a function of two variables: W(Jij,u). The spike-time difference u in Figure 1B corresponds to the times when the effect of the presynaptic and the postsynaptic spike reaches the synapse, which involves the axonal and back-propagation delays, respectively 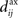 and
and 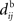 , in Figure 1A. Although the present theoretical framework is suited to account for individual STDP properties for distinct synapses (Froemke et al., 2005), we only consider a single function W for all synapses in the present paper for the purpose of clarity. We note that the continuity of the curve for W in Figure 1B does not play any significant role in the following analysis.
, in Figure 1A. Although the present theoretical framework is suited to account for individual STDP properties for distinct synapses (Froemke et al., 2005), we only consider a single function W for all synapses in the present paper for the purpose of clarity. We note that the continuity of the curve for W in Figure 1B does not play any significant role in the following analysis.
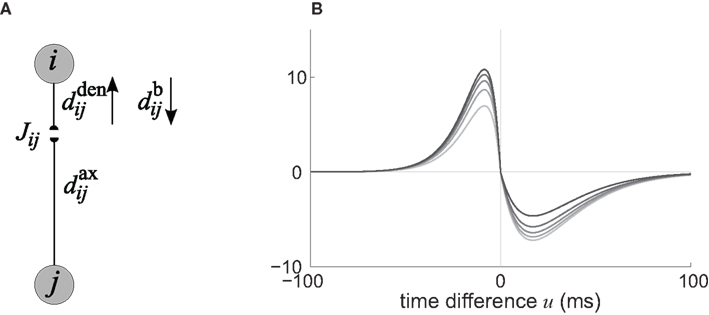
Figure 1. (A) Schematic representation of a synapse from the source neuron j to the target neuron i. The synaptic weight is Jij and axonal delay 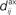 ;
; 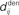 accounts for the conduction of the postsynaptic response along the dendritic tree toward the soma while the
accounts for the conduction of the postsynaptic response along the dendritic tree toward the soma while the 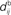 accounts for the back-propagation of action potential to the synapse. Here
accounts for the back-propagation of action potential to the synapse. Here 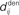 and
and 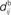 are distinguished, but they can be considered to be equal if the conduction along the dendrite in both directions is passive. (B) Examples of STDP learning window function; the vertical scale (dimensionless) indicates the change of synaptic strength arising from the occurrence of a pair of pre- and postsynaptic spikes with time difference u. The darker curves correspond to stronger values for the current weight, indicating the effect of weight dependence.
are distinguished, but they can be considered to be equal if the conduction along the dendrite in both directions is passive. (B) Examples of STDP learning window function; the vertical scale (dimensionless) indicates the change of synaptic strength arising from the occurrence of a pair of pre- and postsynaptic spikes with time difference u. The darker curves correspond to stronger values for the current weight, indicating the effect of weight dependence.
In addition to the learning window function W, a number of studies (Kempter et al., 1999; Gilson et al., 2009a) have included rate-based terms win and wout, namely modifications of the weights for each pre- and postsynaptic spike (Sejnowski, 1977; Bienenstock et al., 1982). This choice leads to a general form of synaptic plasticity (van Hemmen, 2001; Gerstner and Kistler, 2002) that incorporates changes for both single spikes and pairs of spikes. The choice of the Poisson neuron model with temporally inhomogeneous firing rate and with a linear input–output function for the firing rates makes it possible to incorporate such rate-based terms in order to obtain homeostasis (Turrigiano, 2008).
In order to study the evolution of plastic weights in a given network configuration, it is necessary to define the stimulating inputs. For pairwise STDP, spiking information is conveyed in the firing rates and cross-correlograms, and Poisson-like spiking is often used to reproduce the variability observed in experiments (Gerstner et al., 1996; Kempter et al., 1999; Song et al., 2000; Gütig et al., 2003). Spike coordination or rate covariation can be combined to generate correlated spike trains (Staude et al., 2008). The present review will focus on narrowly correlated inputs (almost synchronous) that are partitioned in pools; in this configuration, correlated inputs belong to a common pathway (e.g., monocular visual processing). We will also discuss more elaborate input correlation structures that use narrow spike-time correlations (Krumin and Shoham, 2009; Macke et al., 2009), oscillatory inputs (Marinaro et al., 2007), and spike patterns (Masquelier et al., 2008). Our series of papers has also made minimal assumptions about the network topology, namely mainly considering recurrent connectivity to be homogeneous. The starting situation consists in unorganized (input and/or recurrent) weights that are randomly distributed around a given value.
Once the input and network configuration is fixed, it is necessary to evaluate the spiking activity in the network in order to predict the evolution of the weights. The Poisson neuron model has proven to be quite a valuable tool (Kempter et al., 1999; Gütig et al., 2003; Burkitt et al., 2007; Gilson et al., 2009a,d), although recent progress has been made toward a similar framework for integrate-and-fire neurons (Moreno-Bote et al., 2008). In the Poisson neuron model, the output firing mechanism for a given neuron i is approximated by an inhomogeneous Poisson process with rate function or intensity λi(t) that evolves over time according to the presynaptic activity received by the neuron:
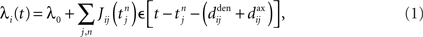
where 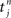 , 1 ≤ n, are the spike times for neuron j, and λ0 describes background excitation/inhibition from synapses that are not considered in detail. The kernel function ε describes the time course of the postsynaptic response (chosen identical for all synapses here), such as an alpha function. We also discriminate between axonal and dendritic components for the conduction delay, cf. Figure 1A. Although only coarsely approximating real neuronal firing mechanisms, this model transmits input spike-time correlations and leads to a tractable mathematical formulation of the input–output correlogram, which allows the analytical description of the evolution of the plastic weights.
, 1 ≤ n, are the spike times for neuron j, and λ0 describes background excitation/inhibition from synapses that are not considered in detail. The kernel function ε describes the time course of the postsynaptic response (chosen identical for all synapses here), such as an alpha function. We also discriminate between axonal and dendritic components for the conduction delay, cf. Figure 1A. Although only coarsely approximating real neuronal firing mechanisms, this model transmits input spike-time correlations and leads to a tractable mathematical formulation of the input–output correlogram, which allows the analytical description of the evolution of the plastic weights.
Analysis of Synaptic Weight Dynamics
Before starting we quickly explain what STDP means and how Poisson neurons function in the present context. Then we focus on the asymptotics of an analytic description for the development of synaptic strengths by means of a set of coupled differential equations and introduce the notion of “almost-additive” STDP. In so doing we will also see how a population of recursively connected neurons influences the synaptic development in the population as a whole so that one gets a “grouping” of the synapses on the neurons. Input by itself and input in conjunction with or, more interestingly, versus recurrence play an important role in this game. Finally, we will see how the form of the learning window influences the neuron-to-input and neuron-to-neuron spike-time correlations. This is a preparation of the next section where we will analyze emerging network structures and their functional implications.
Spike-Timing-Dependent Plasticity
The barn owl (Tyto alba) is able to determine the prey direction in the dark by measuring interaural time differences (ITDs) with an azimuthal accuracy of 1–2° corresponding to a temporal precision of a few microseconds, a process of binaural sound localization. The first place in the brain where binaural signals are combined to ITDs is the laminar nucleus. A temporal precision as low as a few microseconds was hailed by Konishi (1993) as a paradox – and rightly so since at a first sight it contradicts the slowness of the neuronal “hardware,” viz., membrane time constants of the order of 200 μs. In addition, transmission delays from the ears to laminar nucleus scatter between 2 and 3 ms (Carr and Konishi, 1990) and are thus in an interval that greatly exceeds the period of the relevant oscillations (100–500 μs). The key to the solution (Gerstner et al., 1996) is a Hebbian learning process that tunes the hardware so that only synapses and, hence, axonal connections with the right timing survive. Genetic coding is implausible because 3 weeks after hatching, when the head is full-grown, the young barn owl cannot perform azimuthal sound localization. Three weeks later it can. So what happens in between? The solution to the paradox involves a careful study of how synapses develop during ontogeny (Gerstner et al., 1996; Kempter et al., 1999). The inputs provided by many synapses decide what a neuron does but, once it has fired, the neuron determines whether each of the synaptic efficacies will increase or decrease, a process governed by the synaptic learning window, a notion that will be introduced shortly. Each of the terms below in Eq. 2 has a neurobiological origin. The process they describe is what we call infinitesimal learning in that synaptic increments and decrements are small. Consequently it takes quite a while before the organism has built up a “noticeable” effect. Though processes that happen in the long term are not fully understood yet, their effect is well described by Eq. 2.
For the sake of definiteness we are going to study waxing and waning of synaptic strengths associated with a single neuron i; cf. Figure 2A. Here we ignore the weight dependence to focus on the temporal aspect and thus use W(·,u) as the STDP learning window function. The 1 ≤ j ≤ N synapses provide their input at times 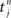 , where n is a label denoting the sequential spikes. The firing times of the neuron are denoted by
, where n is a label denoting the sequential spikes. The firing times of the neuron are denoted by 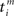 , it being understood that m is a label like n. Given the firing times, the change ΔJij(t): = Jij(t) − Jij(t − T) of the weight of synapse j → i (synaptic strength) during a learning session of duration T and ending at time t is governed by several factors,
, it being understood that m is a label like n. Given the firing times, the change ΔJij(t): = Jij(t) − Jij(t − T) of the weight of synapse j → i (synaptic strength) during a learning session of duration T and ending at time t is governed by several factors,
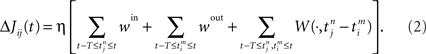
Here the firing times 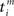 of the postsynaptic neuron may, and in general will, depend on Jij. We now focus on the individual terms. The prefactor 0 < η ≪ 1 reminds us explicitly of learning being slow on a neuronal time scale. This condition is usually referred to as the “adiabatic hypothesis.” It holds in numerous biological situations and has been a mainstay of computational neuroscience ever since. It may also play a beneficial role in an applied context. If it is does not hold, a numerical implementation of the learning rule (Eq. 2) is straightforward, but an analytical treatment is not.
of the postsynaptic neuron may, and in general will, depend on Jij. We now focus on the individual terms. The prefactor 0 < η ≪ 1 reminds us explicitly of learning being slow on a neuronal time scale. This condition is usually referred to as the “adiabatic hypothesis.” It holds in numerous biological situations and has been a mainstay of computational neuroscience ever since. It may also play a beneficial role in an applied context. If it is does not hold, a numerical implementation of the learning rule (Eq. 2) is straightforward, but an analytical treatment is not.
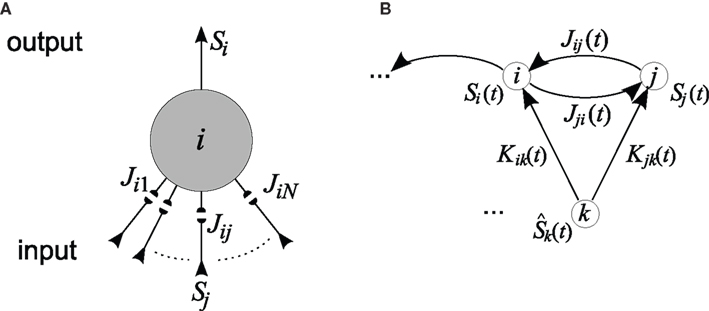
Figure 2. (A) Single neuron. Spike-timing-dependent plasticity (STDP) refers to the development of synaptic weights Jij (small filled circles, 1 ≤ j ≤ N) of a single neuron (large circle) in dependence upon the arrival times of presynaptic spikes (input) and firing times of the postsynaptic neuron (output). Here the neuron receives input spike trains denoted by Sj and produces output spikes denoted by Si. The collective interaction of all the input spikes determines the firing times of the postsynaptic neuron they are all sitting on and in this way the input spike times at different synapses influence the latter’s waxing and waning. (B) Recurrently connected network. Schematic representation of two neurons i and j stimulated by one external input k with spike train 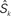 . Input and recurrent weights are denoted by K and J, respectively.
. Input and recurrent weights are denoted by K and J, respectively.
Each incoming spike and each action potential of the postsynaptic neuron change the synaptic efficacy by ηwin and ηwout, respectively. The last term in Eq. 2 represents the learning window W(·,u), which indicates the synaptic change in dependence upon the time difference 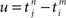 between an incoming spike
between an incoming spike 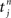 and an outgoing spike
and an outgoing spike 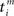 . When the former precedes the latter, we have
. When the former precedes the latter, we have 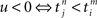 , and the result is W(·,u) > 0, implying potentiation. This seems reasonable since NMDA receptors, which are important for long-term potentiation (LTP), need a strongly positive membrane voltage to become “accessible” by loosing the Mg2+ ions that block their “gate.” A postsynaptic action potential induces a fast retrograde “spike” doing exactly this (Stuart et al., 1997). Because the presynaptic spike arrived slightly earlier, neurotransmitter is waiting to obtain access, which is allowed after the Mg2+ ions are gone. The result is Ca2+ influx. On the other hand, if the incoming spike comes “too late,” then u > 0 and W(·,u) < 0, implying depression – in agreement with a general rule in politics, discovered two decades ago: “Those who come too late shall be punished.” In neurobiological terms, there is no neurotransmitter waiting to be admitted.
, and the result is W(·,u) > 0, implying potentiation. This seems reasonable since NMDA receptors, which are important for long-term potentiation (LTP), need a strongly positive membrane voltage to become “accessible” by loosing the Mg2+ ions that block their “gate.” A postsynaptic action potential induces a fast retrograde “spike” doing exactly this (Stuart et al., 1997). Because the presynaptic spike arrived slightly earlier, neurotransmitter is waiting to obtain access, which is allowed after the Mg2+ ions are gone. The result is Ca2+ influx. On the other hand, if the incoming spike comes “too late,” then u > 0 and W(·,u) < 0, implying depression – in agreement with a general rule in politics, discovered two decades ago: “Those who come too late shall be punished.” In neurobiological terms, there is no neurotransmitter waiting to be admitted.
Poisson Neurons
Since Poisson neurons (Kempter et al., 1999; van Hemmen, 2001) are cardinal to obtaining analytically exact solutions and at the same time effortlessly reflect uncertainty in response to input stimuli, which we then interpret as “stochastic,” we first quickly discuss what “inhomogeneous Poisson” is all about.
A general Poisson process with intensity λi(t) is defined by three properties:
(i) the probability of finding a spike between t and t + Δt is λi(t)Δt,
(ii) the probability of finding two or more spikes there is o(Δt),
(iii) the process has independent increments, i.e., events in disjoint intervals are independent.
In a neuronal context it is fair to call property (ii) a mathematical realization of a neuron’s refractory behavior. Property (iii) makes it all exactly soluble (cf. van Hemmen, 2001, App. B). When the “membrane potential” λi(t) in Eq. 1 is high/low, the probability of getting a spike is high/low too. For those who like an explicit non-linearity better, the clipped Poisson neuron with

where ϑ1 is a given threshold and Θ is the Heaviside step function [Θ(t) = 0 for t < 0 and Θ(t) = 1 for t ≥ 0], is a suitable substitute that also allows an exact disentanglement (Kistler and van Hemmen, 2000). For λi(t) ≡ λ0 where λ0 is a constant we regain the classical Poisson process. The information content of the single number λ0 is rather restricted and so is that of a spike sequence generated by a classical Poisson process. If, on the other hand, λi(t) is a periodic function with high maxima, steep slopes, and low (≈0) minima, then we get a pronounced periodic-like but not exactly periodic response. The latter property is convenient to simulate, e.g., neuronal response to periodic input.
Dynamical System and Asymptotic Solution
We now turn to general pre- and postsynaptic spike trains, with no reference to a neuronal model or a specific input structure. The only assumption here is that the learning is sufficiently slow so that averaging over the spike trains can be performed (van Hemmen, 2001); note that significant weight evolution over tens of minutes still satisfies this requirement. For pairwise (possibly weight-dependent) STDP, the evolution of the mean weight averaged over all trajectories (drift of the stochastic process) results in a learning-dynamics equation of the general form
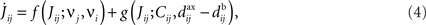
where the dependence of the variables upon time has been omitted. In Eq. 4 the spiking information conveyed by the spike trains Si(t) and Sj(t) for neurons i and j, respectively, is contained in the firing rates

and the spike-time covariance coefficient
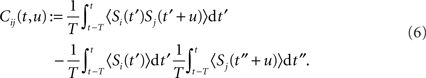
This separation of time scales (involving the averaging duration T) is dictated by the STDP learning window W (cf. Figure 1): typically, phenomena “faster” than 10 Hz (i.e., 100 ms) will be captured by W as spike effects through Cij, such as oscillatory activity (Marinaro et al., 2007) and spike patterns (Masquelier et al., 2008). The formulation in Eq. 6 is slightly more general than that used by Gerstner and Kistler (2002) and Gilson et al. (2009a); it can account for covariation of underlying rate functions (Sprekeler et al., 2007) as well as (stochastic) spike coordination (Kempter et al., 1999; Gütig et al., 2003; see also Staude et al., 2008). Finally, we note that the averaging 〈…〉 in Eqs 5 and 6 comes for free as the “learning time” T is so large and the temporal correlations in naturally generated stochastic processes in Eq. 2 have so small a range that we can apply a law of large numbers (van Hemmen, 2001, App. A) so as to end up with the averages as indicated. That is, we need not explicitly average as it all comes, so to speak, for free.
For a given network configuration, predicting the evolution of the weight distribution requires the evaluation of the neuronal variables involved in Eq. 4 as functions of the parameters for the stimulating inputs. For all network neurons, the output spike trains are constrained by the neuron model and input spike trains: the key to the analysis is the derivation of self-consistency equations that describe this relationship for the firing rates and spike-time correlations. In particular, recurrent connectivity implies non-linearity in the network input–output function for the neuronal firing rates. The interplay between the spiking activity and network connectivity, where the latter is modified by plasticity on a slower time scale, is crucial to understanding the effect of STDP. A network of Poisson neurons with input weights K and recurrent weights J as in Figure 2B leads to the following system of matrix equations (Gilson et al., 2009a,d):
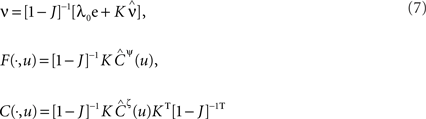
The vector of neuronal firing rates ν is expressed in terms of the input firing rates 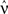 and the weight matrices K and J. Vector e has all element equal to ones and the superscript T denotes the transposition. Matrices C and F respectively contain the neuron-to-neuron and neuron-to-input spike-time covariances, cf. Eq. 6. Only their dependence upon u is considered here and they are expressed in terms of the input-to-input covariance matrix Ĉ convolved with the following functions (indicated by the superscript):
and the weight matrices K and J. Vector e has all element equal to ones and the superscript T denotes the transposition. Matrices C and F respectively contain the neuron-to-neuron and neuron-to-input spike-time covariances, cf. Eq. 6. Only their dependence upon u is considered here and they are expressed in terms of the input-to-input covariance matrix Ĉ convolved with the following functions (indicated by the superscript):

where e is the postsynaptic response kernel for the Poisson neuron; cf. Eq. 1. The dependence upon time t has been omitted, as the time-averaged firing rates and spike-time covariances practically only vary at the same pace as the plastic weights. In this framework, the effect of the recurrence is taken into account in the inverse of the matrix 1 − J in Eq. 7. For the rates ν and the neuron-to-input covariances F, this leads to a linear feedback, whereas the dependence is quadratic-like for the neuron-to-neuron covariances C. These equations allow the analysis of the learning equation (Eq. 4) for recurrent weights J, as well as an equivalent expression for input weights K with the neuron-to-input spike-time covariance F in place of C.
For both a single neuron and recurrently connected network, the learning equation (Eq. 4) can lead to a double dynamics that operates upon the incoming synaptic weights for each neuron (Kempter et al., 1999; Gilson et al., 2009a,d, 2010):
• a partial (homeostatic) equilibrium that stabilizes the mean incoming weight, and hence the output firing rate, through the constraint 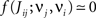 for each neuron i;
for each neuron i;
• competition between individual weights based on the spike-time covariances embedded in 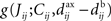 , which can result in splitting the weight distribution.
, which can result in splitting the weight distribution.
Note that this discrimination between rate and spike effects is valid irrespective of the neuron model. The following analysis, which is based on the Poisson neuron model, can be extended to more elaborate models, such as the integrate-and-fire neuron when it is in a (roughly) linear input-output regime.
Several features have been used to ensure a stable and realizable homeostatic equilibrium. That is, the mean incoming weight Jav for each neuron has a stable fixed point between the bounds [Jmin, Jmax]. This is important so as to ensure proper weight specialization in that, if the fixed point is not realizable (outside the bounds) or unstable, all weights will tend to cluster at one of the bounds and no effective selection is then possible, as is illustrated by Figure 3A. On the other hand, in Figure 3B splitting of the weights occurs on each side of the stable value for the mean weight (thick black line). If rate-based terms can be added to obtain a polynomial form of f (Kempter et al., 1999; Gilson et al., 2009a,d), weight dependence can also be chosen to bring stability (Gütig et al., 2003; Gilson et al., 2010), as is illustrated in Figure 3. Such features preserve the local character of the plasticity rule and homeostasis is then a consequence of local plasticity (Kempter et al., 2001). In contrast, additional mechanisms such as synaptic scaling (or normalization) can be enforced to constrain the mean incoming weight (van Rossum et al., 2000). In any case, only if 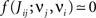 for all synapses j → i is the weight specialization determined by the spike-time covariance. Otherwise, firing rates are likely to take part in the weight competition and the dichotomy between rate and spike effects may not be effective.
for all synapses j → i is the weight specialization determined by the spike-time covariance. Otherwise, firing rates are likely to take part in the weight competition and the dichotomy between rate and spike effects may not be effective.
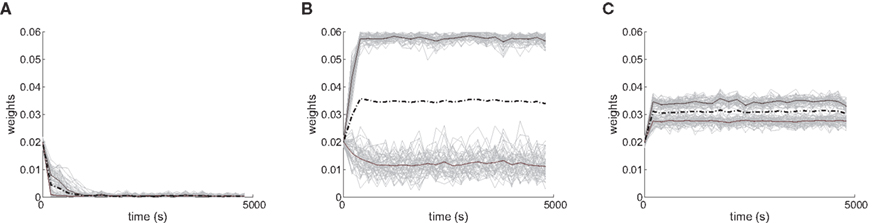
Figure 3. Evolution of synaptic weights. In each plot individual weights are represented (gray traces) as well as their overall mean Jav (thick solid black line) and the two means over each input pool (thick dashed and dashed-dotted black lines). In the simulations, one pool had spike-time correlation while the other had none while win = win = 0. (A) Case of non-realizable (but stable) fixed point 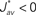 . (B) Stability of the mean incoming weight (
. (B) Stability of the mean incoming weight (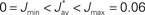 ) and competition between individual weights when using almost-additive STDP. (C) Similar plot to (B) with medium weight dependence, which implies weaker competition.
) and competition between individual weights when using almost-additive STDP. (C) Similar plot to (B) with medium weight dependence, which implies weaker competition.
Lack of proper homeostatic stability can lead to dramatic changes in the spiking activity when slightly modifying some parameters in simulations, such as an “explosive” behavior where the neuron saturates at a very high firing rate (Song et al., 2000). Non-linear activation mechanisms (e.g., sigmoidal rate function, integrate-and-fire) may play a role in the weight dynamics and possibly affect the correlograms. In particular, stable homeostatic equilibrium can be obtained without use of rate-based terms win and wout for additive STDP through integrate-and-fire neurons (this is not possible with Poisson neuron), but the range of adequate learning parameters, in particular the value of W~, was found to be smaller (Song et al., 2000) than when using rate-based plasticity terms (Kempter et al., 1999; Gilson et al., 2009a).
After the homeostatic equilibrium has been reached, spike-time correlations become the dominating term in the learning-dynamics equation (Eq. 4) and hence determine the subsequent weight specialization. The rule of thumb for the weight splitting after reaching the homeostatic equilibrium is that synapses j → i with larger coefficients 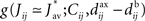 will be potentiated at the expense of the others. The function g involves the convolution of the correlogram Cij, such as those in Figures 4B,C, with the STDP function W
will be potentiated at the expense of the others. The function g involves the convolution of the correlogram Cij, such as those in Figures 4B,C, with the STDP function W
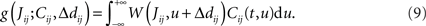
This implies that the STDP learning function W is shifted by the difference between the axonal and the dendritic back-propagation delays Δdij in Eq. 4,

Hence a purely dendritic delay implies Δdij < 0, which is equivalent to shifting the STDP learning window function (solid line) in Figure 4D to the right (dashed line), i.e., toward more potentiation. Conversely, a purely axonal delay shifts the curve to the left (dashed-dotted line) and thus toward more depression since Δdij < 0. A previous analysis of this effect (Gilson et al., 2010) assumed 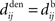 but the conclusions can be straightforwardly adapted to the more general case; the respective roles played by the delays in determining the spike-time correlations and learning dynamics is highlighted below.
but the conclusions can be straightforwardly adapted to the more general case; the respective roles played by the delays in determining the spike-time correlations and learning dynamics is highlighted below.
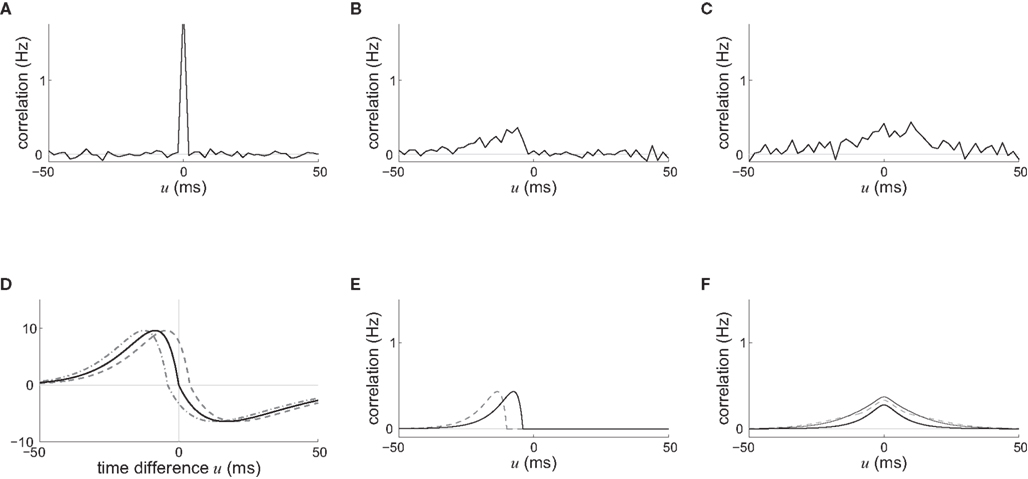
Figure 4. Spike-time correlograms between (A) two inputs, (B) an input and a neuron, and (C) two neurons. These three plots correspond to Eq. 6 for randomly chosen pairs of inputs/neurons in a network of 100 neurons excited by 100 inputs (30% probability of connection; no learning was applied) and simulated over 1000 s with the sum of delays 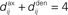 ms; the time bin is 2 ms. (D) Learning window function
ms; the time bin is 2 ms. (D) Learning window function 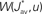 with no delay (solid line, Δdij = 0 ms), purely dendritic delay
with no delay (solid line, Δdij = 0 ms), purely dendritic delay 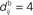 ms (dashed line, Δdij = −4 ms) and purely axonal delay
ms (dashed line, Δdij = −4 ms) and purely axonal delay 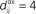 ms (dashed-dotted line, Δdij = 4 ms). (E,F) Theoretical curves of ψ and ζ corresponding to approximation at the first order of the correlograms in (B,C), respectively, with short (4 ms, solid lines) and large (10 ms, dashed lines) values for
ms (dashed-dotted line, Δdij = 4 ms). (E,F) Theoretical curves of ψ and ζ corresponding to approximation at the first order of the correlograms in (B,C), respectively, with short (4 ms, solid lines) and large (10 ms, dashed lines) values for 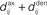 ; cf. Eq. 8. The two curves (for 4 and 10 ms) are superimposed for ζ and the thin lines represent the corresponding predictions when incorporating a further order in the recurrent connectivity. The agreement with the spreading and amplitude of the curves in (B,C), which correspond to 4 ms, is only qualitative.
; cf. Eq. 8. The two curves (for 4 and 10 ms) are superimposed for ζ and the thin lines represent the corresponding predictions when incorporating a further order in the recurrent connectivity. The agreement with the spreading and amplitude of the curves in (B,C), which correspond to 4 ms, is only qualitative.
The weight dependence ensuing from STDP modulates the weight specialization. This can lead to either a unimodal or bimodal distribution at the end of the learning epoch (van Rossum et al., 2000; Gütig et al., 2003; Gilson et al., 2010); see Figures 3C,B, respectively. We will refer to almost-additive STDP in the case where the weight-dependence is small, i.e., small values of the μ > 0 parameter of Gütig et al. (2003). Almost-additive STDP can generate effective weight competition including partial stability whenever the weight dependence leads to more depression and/or less potentiation for higher values of the current weight and the homeostatic equilibrium (Gilson et al., 2010). In general, stronger weight dependence implies more stability for both the mean incoming weight and individual weights, whereas competition is more effective for almost-additive STDP.
Input Versus Recurrent Connections
An interesting example illustrates the difference in the weight dynamics when stepping from a single neuron to a recurrently connected network. We consider neurons that are excited by external synaptic inputs with narrow spike-time correlations (i.e., almost-synchronous spiking), as illustrated in Figure 4A. We also assume homogeneous input and recurrent connectivity, which can be partial. We compare the effect of STDP for an input connection from an external input to a given network neuron on the one hand, and a recurrent connection between two neurons on the other hand. In so doing we recall that a positive (resp. negative) value for the convolution in Eq. 9 implies potentiation (depression) of the more correlated input pathways (Gilson et al., 2009a) and outgoing recurrent connections for more correlated neuronal groups (Gilson et al., 2009d). Typical correlograms are illustrated in Figures 4B,C for input and recurrent connections, respectively. For the input connection the distribution is clearly non-symmetrical, whereas it is roughly symmetrical for recurrently connected neurons (in a homogeneous network). The shifted STDP curve W in Figure 4D depends on the delays 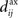 and
and 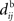 , which we assumed to be of the same order as
, which we assumed to be of the same order as 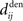 . The correlograms in Figures 4B,C can be evaluated with first-order approximations by the following functions ψ and ζ in Eq. 8, respectively. In Figure 4E, the theoretical correlogram ψ that corresponds to Figure 4B is shifted to the left by the sum of the delays
. The correlograms in Figures 4B,C can be evaluated with first-order approximations by the following functions ψ and ζ in Eq. 8, respectively. In Figure 4E, the theoretical correlogram ψ that corresponds to Figure 4B is shifted to the left by the sum of the delays 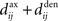 ; it follows that the curve always overlaps with the potentiation side of W, irrespective of the axonal/dendritic ratio (assuming
; it follows that the curve always overlaps with the potentiation side of W, irrespective of the axonal/dendritic ratio (assuming 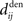 and
and 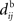 to be of the same order). However, for the recurrent connection in Figure 4F, the delays affect only higher-order approximations of the correlogram ζ in Eq. 8, namely by increasing the spread of the distribution (thin lines); the distribution of φ remains symmetrical and similar to the simulated distribution in Figure 4C, while the convolution with W can give a positive or negative value, depending upon the shift of W.
to be of the same order). However, for the recurrent connection in Figure 4F, the delays affect only higher-order approximations of the correlogram ζ in Eq. 8, namely by increasing the spread of the distribution (thin lines); the distribution of φ remains symmetrical and similar to the simulated distribution in Figure 4C, while the convolution with W can give a positive or negative value, depending upon the shift of W.
The effect of the delay difference Δdij upon the dynamical evolution of the input and recurrent weights induced by STDP becomes clearer in Figure 5, where the dashed and dashed-dotted curves represent the convolutions in Eq. 9 for the two corresponding correlograms plotted as a function of Δdij. For an input connection (dashed curve), delays do not qualitatively change the specialization scheme for input plastic connections, viz., the sign of the dashed curve in the range of Δdij considered (between −4 and 4 ms here). Delays, however, are found to crucially determine the sign of the dashed-dotted curve for recurrent weights (dashed-dotted curve) around Δdij = 0: a predominantly dendritic component (Δdij ≪ 0) favors strengthening of feedback connections for synchronous neurons. On the other hand, predominantly axonal delays (Δdij ≫ 0) lead to decorrelation, viz., weakening of self-feedback connections. Note that these conclusions apply to positively correlated input spike trains.
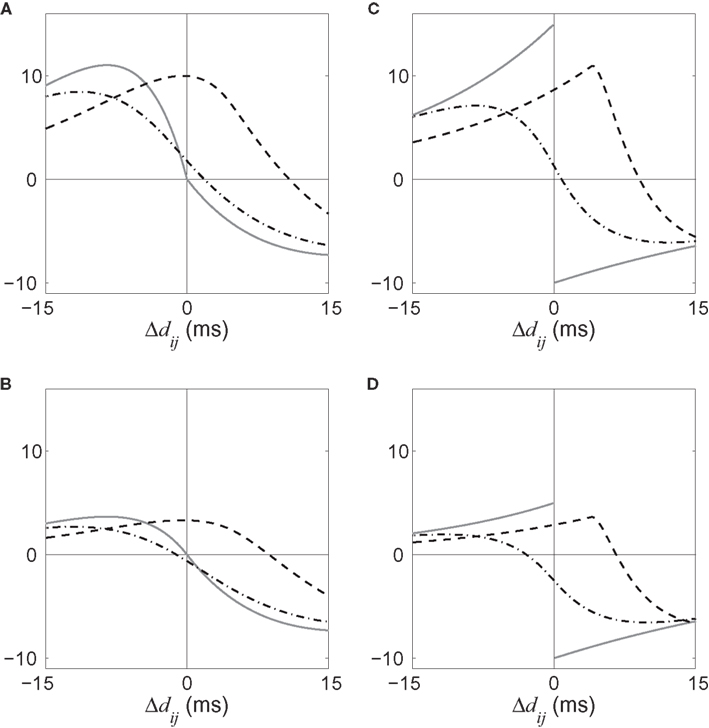
Figure 5. Four illustrative plots of the STDP learning window W (gray solid line) and its convolutions in Eq. 9: W*ψ for input connections (dashed line) and W*ζ for recurrent connections (dashed-dotted line). The theoretical spike-time correlograms ψ and ζ in Eq. 8 can be found in Figures 4E,F, respectively. The sign of the function resulting from the convolution for the argument Δdij predicts the weight evolution. The curves correspond to delays such that 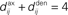 ms and the effect of Δdij can be read on the horizontal axis (technically, it should be read −4 ≤ Δdij ≤ 4). Comparison between an STDP learning window
ms and the effect of Δdij can be read on the horizontal axis (technically, it should be read −4 ≤ Δdij ≤ 4). Comparison between an STDP learning window 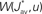 that induces (A) more potentiation than depression for small values of u and (B) the converse situation. We note that the integral is negative in both cases, which means more overall depression (for uncorrelated inputs), which is required for stability. (C,D) Similar plots to (A,B) with a discontinuous curve W in u = 0.
that induces (A) more potentiation than depression for small values of u and (B) the converse situation. We note that the integral is negative in both cases, which means more overall depression (for uncorrelated inputs), which is required for stability. (C,D) Similar plots to (A,B) with a discontinuous curve W in u = 0.
The shape of W around 0 is also important to determine the sign of the convolution in Eq. 9: stronger potentiation than depression strengthens self-feedback for correlated groups of neurons and thus favors synchrony, as illustrated in Figures 5A,B. In general this effect is more pronounced when using a non-continuous W function since the discrepancies around u = 0 are larger; see Figures 5C,D. In conclusion, a suitable typical choice for W involves a longer time constant for depression but higher amplitude for potentiation, which is in agreement with previous experimental results (Bi and Poo, 1998).
Another difference between plasticity for input and recurrent connections lies in stability issues for the spiking activity: (“soft” or “hard”) bounds on the weights must be chosen such that recurrent feedback does not become too strong (in particular, at the homeostatic equilibrium). Otherwise, potentiation of synapses may lead to an “explosive” spiking behavior, where all neurons saturate at a high firing rate (Morrison et al., 2007).
Extension of Results to More Elaborate STDP Rules
The analysis presented above does not depend on precise quantitative values, but rather the conclusions depend on qualitative properties, namely the signs of functions within some range. The methods are also valid for non-strictly pairwise STDP. For restrictions on the spike interactions that contribute to STDP (Sjöström et al., 2001; Izhikevich and Desai, 2003; Burkitt et al., 2004), an effective correlogram can be evaluated to be convolved with the STDP window function W. When the interaction restrictions do not modify the global shape of the correlograms, the predicted trends for the weight specialization should still hold and the effect of parameters such as dendritic/axonal delays should be similar for more elaborate STDP rules.
In other words, only non-linearities that would significantly change the qualitative properties of the correlograms in Figure 4 are important; for example, those that alter their (non-)symmetrical character. It has been shown that the rate-based contribution for STDP can be significantly affected by the restriction scheme (Izhikevich and Desai, 2003; Burkitt et al., 2004); STDP can then exhibit a BCM-like behavior (Bienenstock et al., 1982) with respect to the input firing rate and lead to depression below a given threshold and potentiation above that threshold.
Further work is necessary to understand the implications of interaction restrictions for an arbitrary correlation structure. More biophysically accurate plasticity rules that exhibit a STDP profile for spike pairs (Graupner and Brunel, 2007; Zou and Destexhe, 2007) are also expected to exhibit qualitatively similar behavior when stimulated by spike trains with pairwise spike-time correlations. The rule proposed by Appleby and Elliott (2006) is an exception where higher-order correlations are necessary to obtain competition. Other synaptic plasticity rules involving a temporal learning window, such as “burst-time-dependent plasticity” that corresponds to the longer time scale of a second (Butts et al., 2007), can be analyzed using the same framework and similar dynamical ingredients are expected to participate to the weight evolution (stabilization and competition).
Emergence of Network Structure and Functional Implications
Finally, we illustrate how the interplay between STDP, connectivity topology, and input correlation structure can lead to the emergence of synaptic structure in a recurrently connected network. First we describe how the weight dynamics presented above can shape synaptic pathways using the simple example of narrowly (or delta) correlated inputs. Second we extend the analysis to more elaborate input structures, such as oscillatory spiking activity. We also discuss the link between these results and the resulting processing of spiking information performed by trained neurons and networks.
Organizing Synaptic Pathways
We start by focusing on a specific configuration of the external stimulating inputs, viz., two pools of external inputs that can have within-pool, but no between-pool spike-time correlations; see Figure 6 where filled bottom circles indicate input pools with narrowly distributed spike-time correlations, in a similar fashion to Figure 3. Each pool represents a functional pathway and the spiking information is mainly contained in the spike-time correlations between pairs of neurons. This scheme has been used in many studies to examine input selectivity, such as how a neuron can become sensitive to only a portion of its stimulating inputs, hence specializing to a given pathway (Kempter et al., 1999; Song and Abbott, 2001; Gütig et al., 2003).
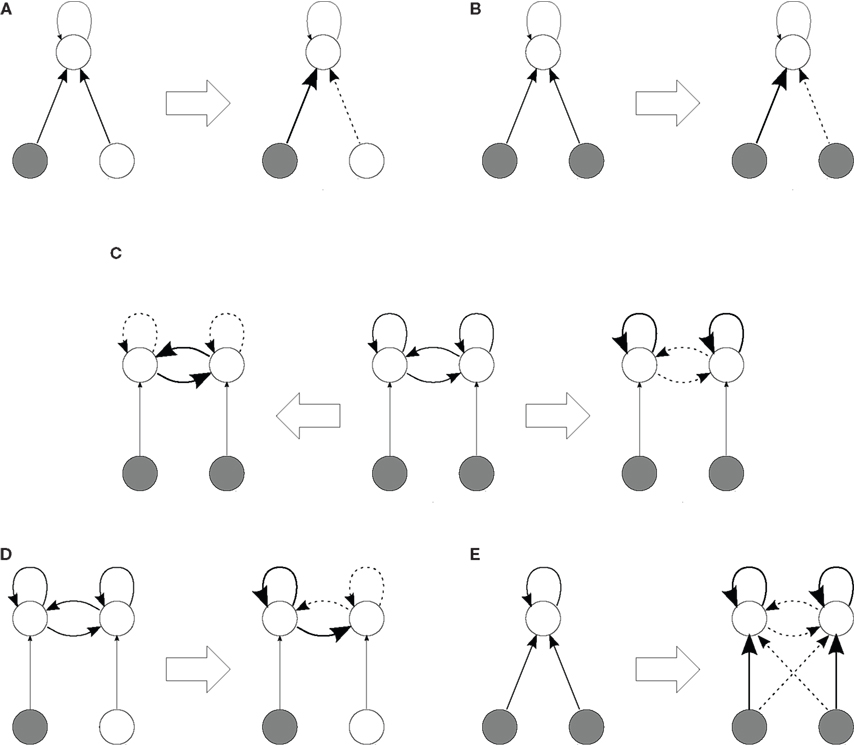
Figure 6. Self-organization scheme in a network (top circles) stimulated by two correlated pools of external inputs (bottom circles). The diagrams represent the connectivity before and after learning (indicated by the block arrows, ⇒ and ⇐). For initial configurations, thin arrows represent fixed connections while thick arrows denote plastic connections. After learning, very thick (resp. dashed) arrows indicate potentiated (depressed) weights. In case (C) two different network topologies that can emerge are represented, depending on the particular learning and neuronal parameters. A mathematical analysis of the weight dynamics for configurations in (A), (B), (C,D), and (E) can be found in Gilson et al. (2009a), Gilson et al. (2009b), Gilson et al. (2009d), and Gilson et al. (2010), respectively.
For a single neuron, input pathways with a narrow spike-time correlation distribution are potentiated by Hebbian STDP (Kempter et al., 1999; Song et al., 2000), as explained in Section “Input Versus Recurrent Connections.” This conclusion still holds when we train input connections for recurrently connected neurons, as illustrated in Figure 6A. When the spike-time correlations have a broader distribution, their widths matter and the more peaked pool is selected (Kistler and van Hemmen, 2000).
When two input pathways have similar correlation strengths, additive-like STDP induces sufficient competition to lead to a winner-take-all situation where only one pool is selected (Song and Abbott, 2001; Gütig et al., 2003). When using STDP without the rate-based terms win and wout, a stricter condition on the weight dependence has been found to ensure a similar behavior (Meffin et al., 2006). Then two STDP modes can be distinguished depending on the strength of weight dependence: Either the competition is sufficiently strong to induce a splitting of the weight distribution (additive-like STDP) or the asymptotic weight remains unimodal (Gütig et al., 2003).
The limit between the above two classes of behavior also depends on the strength of the input correlation, so there exists a parameter range for which proper weight specialization only occurs when there is spiking information in the sense of spike-time correlations for two or more input pools (Meffin et al., 2006; Gilson et al., 2010). During this symmetry breaking of initially homogeneous input connections, recurrent connections may play a role (irrespective of their plasticity) so that recurrently connected neurons with excitatory synapses tend to specialize preferably to the same input pathway (Gilson et al., 2009b); this effect is more pronounced for stronger recurrent connections. In Figure 6B, only one of the two input correlated pools is selected (with 50% probability in the case of two pools). This group specialization is important to obtain consistent input selectivity within areas with strong local feedback, and not “salt-and-pepper” organization where neurons would become selective independently of each other.
Specialization within a network with recurrent connections requires that neurons receive different inputs in terms of firing rates and correlations (Gilson et al., 2009d), which can be obtained after the emergence of input selectivity. As mentioned above, different learning parameters can lead to a strengthening or weakening of feedback within neuronal groups when they receive correlated input. This phenomenon is illustrated in Figure 6C by the right and left arrows (⇒ and ⇐) that correspond to Figures 5A,B, respectively. In other words, for recurrent delays, a prominent dendritic component favors emergence of strongly connected neuronal groups, whereas a prominent axonal component leads to the converse evolution. Likewise, parameters corresponding to strengthening feedback lead to dominance by the group that receives stronger correlated input than the “other” neurons, which results in the emergence of a feed-forward pathway in an initially homogeneous recurrent network, as illustrated in Figure 6D.
The above conclusions describe conditions on the parameters for which the results presented by Song and Abbott (2001) are valid: the rewiring of recurrent connections corresponded to favoring groups that receive more correlated inputs; cf. Figures 6C(⇒),D. In a more realistic network with different populations of neurons, such as one with excitatory and inhibitory connections (Morrison et al., 2007) but with different delay components for distinct sets of connections (e.g., dendritic for short-range connections and axonal for medium-range ones), a combination of synchronization and decorrelation between neurons, depending on their spatial location, may well be obtained.
When input and recurrent connections are both plastic, it is possible to arrive at input selectivity as well as specialization of recurrent connections as described above (Gilson et al., 2010). This requires weight-dependent STDP in order to stabilize the mean weights for both input and recurrent connections, and relates to the fact that all incoming plastic weights compete with each other, irrespectively of their input or recurrent nature, and firing rates may play a role here too. For additive STDP the learning dynamics causes the sets of input and recurrent weights to diverge from each other (Gilson et al., 2010). Splitting of weight distributions, however, is impaired for medium weight dependence (Gütig et al., 2003; Gilson et al., 2010). There is thus a trade-off between stability and competition to obtain proper weight specialization in the sense of separating input weights into distinct groups. In Figure 6E, the input structure consisting of the two pools lead the network neurons to organize into two groups in a similar manner to Figure 6B, each specialized to only one pool; in addition, the recurrent connections within each neuronal group are strengthened at the expense of the between-group connections, cf. Figure 6C (⇒). An interesting point here is that such self-organization does not require a prerequisite network topology since STDP alone can cause neurons to separate into two groups and preserve the consistency of the two input pathways. By this we mean that the information of both input pathways is represented by the synaptic structure after learning and processed by the two resulting neuronal groups.
All typical weight evolution scenarios described in this section hold when applying STDP to homogeneous initial weights. The initial weight distribution can also be of importance, at least for additive-like STDP (Gilson et al., 2009a,c); it was observed in numerical simulation that even weak weight dependence can lead to palimpsest behavior, where previous weight specialization is forgotten after some duration of stimulation using uncorrelated inputs (Gilson et al., 2010).
External Stimulation Using Oscillatory and “Pacemaker” Activity
We now consider two types of stimulating input that have been widely used in conjunction with STDP in recurrent networks, viz., pacemaker-like and oscillatory activity. One reason for their success is that these global periodic phenomena (applied on a whole network, not locally) constrain the spike-time correlograms and, consequently, a global trend for the weight evolution can be sketched. For two neurons chosen arbitrarily in a network with homogeneous and partial connectivity, the stimulating signals we just described induce strong neuron-to-neuron correlation with peaks corresponding to the frequency, as illustrated in Figure 7. We can thus predict the synaptic-weight evolution using the convolution of the STDP learning window W and an idealization of such correlograms, in a similar fashion to Figure 5, since the periodicity overpowers other correlation effects in the recurrent network, even for medium coupling between them.
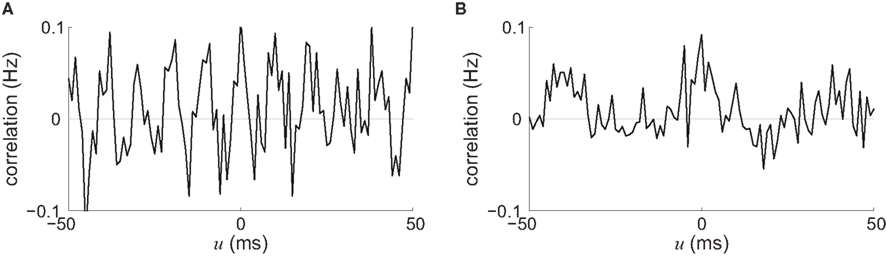
Figure 7. Spike-time cross-correlograms Cij(·,u) for 2 out of 100 recurrently connected neurons with 30% probability that receive (A) oscillatory stimulation at 100 Hz and (B) pacemaker-like activity (regular pulse train at 25 Hz). Both input and recurrent delays were chosen equal to 4 ± 1 ms (uniformly distributed in the interval [3,5] ms).
For a global “pacemaker” activity with a low frequency (below the time scale of STDP, say, 10 Hz), the effect of delays is similar to the exposition in Section “Input Versus Recurrent Connections” in that purely dendritic delays lead to an increase of within-group connections (Morrison et al., 2007) whereas purely axonal delays can cause STDP to decouple neurons during population bursts (Lubenov and Siapas, 2008). Comparison between the situations where input/output spike trains are uncorrelated and time-locked (i.e., highly correlated) shows that STDP can behave as a BCM rule (Bienenstock et al., 1982) for a single neuron (Standage et al., 2007). Frequency may play a similar role for oscillations, although this does not appear to have been studied in detail. When the intrinsic properties of neurons subject to oscillations determine a specific phase response that tend to desynchronize these neurons (e.g., positive phase-response curve), a network with axonal delays can become partitioned into groups that have no self-feedback, but connections between some of them (Câteau et al., 2008); cf. Figure 6C(⇐).
In an all-to-all connected network of heterogeneous oscillators, STDP tends to break coupling between neurons, which can result in asymmetry in the sense of the emergence of feed-forward pathways (Karbowski and Ermentrout, 2002; Masuda and Kori, 2007), in a similar fashion to Figure 6D. When this happens, the neuron with highest frequency may end up driving of the rest of the population of oscillators at its own frequency (Takahashi et al., 2009). The propensity of STDP for such time locking is supported by a study of Nowotny et al. (2003b) using a real neuron and a simulated plastic synapse, which showed that STDP can compensate intrinsic neuronal mechanisms to enable synchronization with a stimulating pacemaker. UP and DOWN states of network spiking activity consist in depolarization and hyperpolarization, respectively, for a large portion of the neurons; they can be related to two levels of correlation at the scale of the network. A recurrently connected network with spontaneous UP and DOWN states can organize in a more a feed-forward structure (Kang et al., 2008). Interestingly, the synaptic structure that emerged preserved the transitions between the two states.
Emerging Synchronization between Recurrent Neurons
Synchronous firing activity has been discussed as a basis of neuronal information, although a comprehensive understanding of such a mechanism is yet to be elucidated. Since STDP is by essence sensitive to temporal coordination in spike trains, its study is an important aspect of such correlation-based neuronal coding. As evidence of its synchronizing properties, STDP has been demonstrated to shape spike-time correlograms both for a single neuron (Song et al., 2000) and within a recurrent network (Morrison et al., 2007), in contrast to other (non-temporally asymmetric) versions of Hebbian learning (Amit and Brunel, 1997). In a population of synapses with varying properties, STDP can perform delay selection (Gerstner et al., 1996; Kempter et al., 2001; Leibold et al., 2002; Senn, 2002). Here we review recent results on the implications at different topological and temporal scales.
At the mesoscopic scale in a recurrent network, the weight specialization as described in Figure 6C can be related to the increase or decrease of synchronization when the recurrent delays 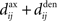 are small. Depending on the learning parameters, neurons that receive synchronously correlated input tend to reinforce or eliminate their coupling, which then determines the probability of firing at almost coincident times. In this way a number of studies (cited below) have aimed at understanding how the spiking activity of recurrently connected neurons can be constrained by synaptic plasticity. An increase in synchrony arises from the strengthening of within-group recurrent connections when receiving correlated input (Gilson et al., 2009d), cf. Figure 6C(⇒). Typical connectivity matrices before and after a learning epoch are represented in Figures 8A,B, respectively. The corresponding spike-time correlograms in the absence of external stimulation (i.e., intrinsic to the recurrent connectivity) show stronger “coincident” firing within a range of several times the postsynaptic response (here tens of milliseconds) for two neurons that do not have direct connections but belong to the same group, as illustrated in Figure 8C. Likewise, when the network receives external stimulation from two correlated input pools as in Figure 6C, the neuronal spike-time correlation is higher for stronger recurrent connections, see Figure 8D. This can also be related to a reduction in the variability of the neural response for a single neuron due to STDP, as analyzed using information theory techniques (Bohte and Mozer, 2007). Global synchrony has been obtained by repeatedly stimulating recurrently connected neurons with given spike trains, which resulted in the network behaving as a pacemaker. This evolution of network structure is also related to the concept of synfire chains, where neuronal groups successively activate one another within a feed-forward architecture (Hosaka et al., 2008); see Figures 8E,F for an illustrative example with three groups. Similarly, the repeating stimulation of a group of neurons can lead to a synfire chain structure in an initially homogeneous recurrent network provided the divergent growth of outgoing connections due to potentiation by STDP is prevented from taking over the whole network (Jun and Jin, 2007). In contrast, a population of neurons can become decorrelated through synchronous stimulation, as happens when the neurons involved in the burst are not the same for each burst. Then no causal (feed-forward) network structure emerges since synchronization does not involve a growing population of neurons (Lubenov and Siapas, 2008); cf. Figure 6C(⇐) for different neuronal subgroups of the network at each burst time. In agreement with the theory in Section “Input Versus Recurrent Connections,” the time constants of the STDP learning window can also determine whether the network is constrained to synchronized (e.g., successive firing of several groups) or asynchronous activity (Kitano et al., 2002).
are small. Depending on the learning parameters, neurons that receive synchronously correlated input tend to reinforce or eliminate their coupling, which then determines the probability of firing at almost coincident times. In this way a number of studies (cited below) have aimed at understanding how the spiking activity of recurrently connected neurons can be constrained by synaptic plasticity. An increase in synchrony arises from the strengthening of within-group recurrent connections when receiving correlated input (Gilson et al., 2009d), cf. Figure 6C(⇒). Typical connectivity matrices before and after a learning epoch are represented in Figures 8A,B, respectively. The corresponding spike-time correlograms in the absence of external stimulation (i.e., intrinsic to the recurrent connectivity) show stronger “coincident” firing within a range of several times the postsynaptic response (here tens of milliseconds) for two neurons that do not have direct connections but belong to the same group, as illustrated in Figure 8C. Likewise, when the network receives external stimulation from two correlated input pools as in Figure 6C, the neuronal spike-time correlation is higher for stronger recurrent connections, see Figure 8D. This can also be related to a reduction in the variability of the neural response for a single neuron due to STDP, as analyzed using information theory techniques (Bohte and Mozer, 2007). Global synchrony has been obtained by repeatedly stimulating recurrently connected neurons with given spike trains, which resulted in the network behaving as a pacemaker. This evolution of network structure is also related to the concept of synfire chains, where neuronal groups successively activate one another within a feed-forward architecture (Hosaka et al., 2008); see Figures 8E,F for an illustrative example with three groups. Similarly, the repeating stimulation of a group of neurons can lead to a synfire chain structure in an initially homogeneous recurrent network provided the divergent growth of outgoing connections due to potentiation by STDP is prevented from taking over the whole network (Jun and Jin, 2007). In contrast, a population of neurons can become decorrelated through synchronous stimulation, as happens when the neurons involved in the burst are not the same for each burst. Then no causal (feed-forward) network structure emerges since synchronization does not involve a growing population of neurons (Lubenov and Siapas, 2008); cf. Figure 6C(⇐) for different neuronal subgroups of the network at each burst time. In agreement with the theory in Section “Input Versus Recurrent Connections,” the time constants of the STDP learning window can also determine whether the network is constrained to synchronized (e.g., successive firing of several groups) or asynchronous activity (Kitano et al., 2002).
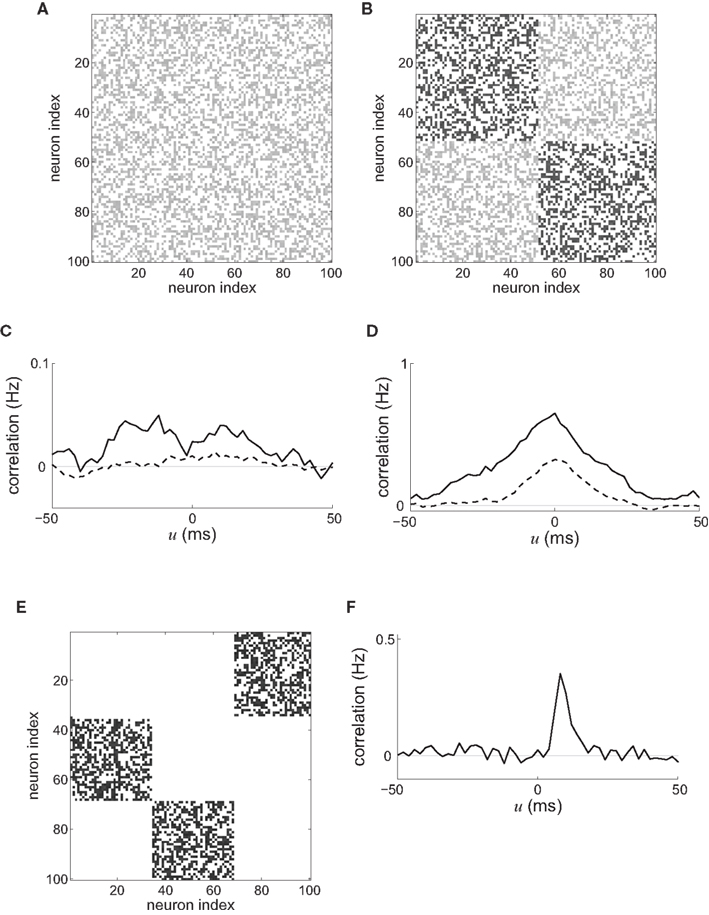
Figure 8. Typical connectivity matrices for recurrent connections (A) before and (B) after a learning epoch during which the weight specialization due to STDP corresponds to Figure 6C(⇒). Darker pixels indicate stronger weights. (C) Resulting spike-time correlograms for two neurons within the same emerged group in the recurrently connected network that only receives spontaneous (homogeneous) excitation before (dashed curve) and after (solid curve) the above mentioned weight specialization. These neurons do not have direct synaptic connections between each other. (D) Similar to (C) with external stimulation from two delta-correlated pools similar to Figure 6C. (E) Connectivity matrix corresponding to three groups forming a feed-forward loop. (F) Spike-time correlogram (averaged over several neurons) between two successively connected groups when the first group receives correlated external stimulation.
In the case of inhomogeneous delays in a recurrent network, STDP can lead to distributed synchronization over time for neuronal groups at the microscopic scale (Izhikevich, 2006). This concept has been coined as polychronization and consists of neuronal groups whose firing is time locked in accordance to the synaptic delays of the connections between these neurons. In a network, such functional groups of, say, tens of neurons then fire sequences of spikes; note that a neuron can take part in several groups and the synaptic connections for a given group may be cyclic or not. A group is tagged as active when a large portion (e.g., 50%) of its members fires with the corresponding timing. Such self-organization can occur even without external stimulation, but then one crucial feature in obtaining stable functional groups that persist over time is the degree of coupling between individual neurons. Such spike-time precision can also be obtained in parallel to oscillatory spiking activity at the scale of a population of neurons, hence providing two different levels of synchrony (Shen et al., 2008).
Input Representation and Applications
The same dynamical ingredients highlighted above have been used to train single neurons and networks for classification and/or detection tasks, many of which involved more elaborate input spike trains than the pools of narrowly correlated spikes considered above (although most of these studies where done using numerical simulations). We briefly review some of these studies as an illustration of applications for the theoretical framework presented above.
Note that learning based on the covariance between firing rates has been used to extract most significant features (in the sense of a principal component analysis) within input stimuli (Sejnowski, 1977; Oja, 1982). In the case of STDP, such features mainly relate to spike-time correlations (van Rossum and Turrigiano, 2001; Gilson et al., 2009a,d). When input spike trains have reliable spike times down to the scale of a millisecond, they convey temporal information that can be picked up by a suitable temporal plasticity rule (Delorme et al., 2001). It has been demonstrated that STDP can train a single neuron to detect a given spike pattern with no specific structure once the pattern is repeatedly presented among noisy spike trains that have similar firing rates (Masquelier et al., 2008). This propensity of STDP to capture spiking information and generate proper input selectivity can explain the storage of sequences of spikes and their retrieval using cues (namely the start of the sequences) using a network with (all-to-all) plastic recurrent connections (Nowotny et al., 2003a). Similarly, patterns relying on oscillatory spiking activity have also been successfully learnt in a recurrent network of oscillatory neurons (Marinaro et al., 2007). STDP can also be used for phase coding in networks with oscillatory activity (Lengyel et al., 2005; Masquelier et al., 2009). Such theoretical studies are further steps toward a better understanding of recent experimental findings with neurons in the auditory pathway known to experience STDP: these neurons can change their spectrum responses after receiving stimulation using combinations of their preferred/non-preferred frequencies (Dahmen et al., 2008).
Self-organizing neural maps provide an interesting example of how networks can build a representation of many input stimuli, though they need not always rely on neuronal characteristics (Kohonen, 1982). STDP has been shown capable of generating such a topological unsupervised organization in a recurrent neuronal network with spatial extension; for example, to detect ITDs (Leibold et al., 2002) and to reproduce an orientation map similar to that observed in the visual cortex (Wenisch et al., 2005). Training lateral (internal recurrent) connections crucially determines the shape of orientation fields in such maps (Bartsch and van Hemmen, 2001). When several sensory neuronal maps have been established, STDP can further learn mappings between these maps (Davison and Frégnac, 2006; Friedel and van Hemmen, 2008), in this way performing multimodal integration of sensory stimuli.
Another abstract concept to learn and detect general spiking signals has appeared recently, which does not rely on an emerging topological organization. For instance, in the liquid-state machine a recurrently connected network behaves as a reservoir that performs many arbitrary operations on the inputs, which allows simple supervised training to discriminate between different classes of input (Maass et al., 2002). Recent studies have shown that STDP applied on the recurrent network can boost the performance of the detection by such a system, by tuning the operations performed by the reservoir, which can be seen as a projection of the input signals onto a large-dimensional space (Henry et al., 2007; Carnell, 2009; Lazar et al., 2009). The resulting information encoding is then distributed, but hidden, in the learned synaptic structure, which can be analyzed in the spiking activity at a fine time scale, e.g., by polychronized groups (Paugam-Moisy et al., 2008). Altogether, STDP is capable of organizing a recurrent neuronal network to exhibit specific spiking activity depending on the presentation of input stimuli, as illustrated in Figure 9.
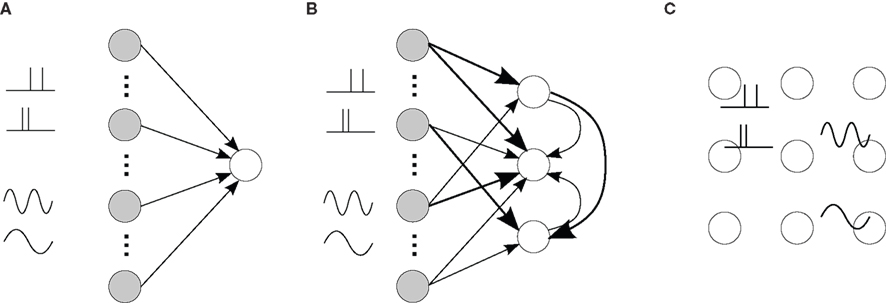
Figure 9. (A) Single neuron (open circle) excited by external input neurons (filled circles) that correspond to specific spike-time correlation structure, such as oscillatory activity and spike patterns. The four thumbnail sketches on the LHS of the plot represent two different types of input correlation structure: inputs containing a repeated spike patterns (top two thumbnails) and inputs with an oscillating firing rate (bottom two thumbnails). (B) Strengthening of some input and recurrent connections (thick arrows) for several such neurons. (C) Resulting specialization of some areas (neighbor neurons) in the network to some of the presented stimuli (thumbnails), which implies differentiated topological spiking activity depending on the presented stimulus. External inputs are not represented in (C).
Finally, a number of studies focused on linking STDP to more abstract schemes of processing neuronal (spiking) information. A plasticity rule with probabilistic change for the weights has been found to modulate the speed of learning/forgetting (Fusi, 2002). A similar concept of non-deterministic modification in the weight strength for STDP proved to be fruitful in terms of capturing multi-correlation between input and output spike trains (Appleby and Elliott, 2007). STDP has also been demonstrated to be capable of training a single neuron to perform a broad range of operations for input–output mapping on the spike trains (Legenstein et al., 2005). Recently, STDP has been used to perform an independent component analysis on input signals that mimic retinal influx (Clopath et al., 2010). Using information theory, STDP has been related to optimality in supervised and unsupervised learning (Toyoizumi et al., 2005, 2007; Pfister et al., 2006; Bohte and Mozer, 2007). These contributions are important steps toward a global picture of the functional implications of STDP at a higher level of abstraction.
Conclusion
Spike-timing-dependent plasticity has led to a re-evaluation of our understanding of Hebbian learning, in particular by discriminating between rate-based and spike-based contributions to synaptic plasticity for which temporal causality plays a crucial role. The resulting learning dynamics appears richer than what can be obtained by rate-based plasticity rules, in the sense that STDP alone can generate a mixture of stability and competition on different time scales. For neurons communicate through spikes and not rates, a procedure such as STDP is quite natural, whereas rates are an afterthought.
In a recurrently connected neuronal network, the weight evolution is determined by an interplay between the STDP parameters, neuronal properties, input correlation structure and network topology. The functional implications of the resulting organization, which can be unsupervised or supervised, have been the subject of intense research recently. For both single neurons and recurrent networks, it has been demonstrated how STDP can generate a network structure that accurately reflects the synaptic input representation for a broad range of stimuli, which can lead to neuronal sensory maps or implicit representation in networks. In particular, the study of the emerging (pairwise or higher-order) correlation structure has started to uncover some interesting properties of trained networks that are hypothesized to play an important role in information encoding schemes.
It is not yet clear, however, what underlying algorithm on the stimuli signals is performed through the weight dynamics, and how STDP encodes the input structure into the synaptic weight. This research may establish links between physiological learning mechanisms and the more abstract domain of machine learning, hence expanding our understanding of the functional role of synaptic plasticity in the brain.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Matthieu Gilson was funded by scholarships from the University of Melbourne and NICTA. J. Leo van Hemmen is partially supported by the BCCN–Munich. Funding is acknowledged from the Australian Research Council (ARC Discovery Projects #DP0771815 and #DP1096699). The Bionic Ear Institute acknowledges the support it receives from the Victorian Government through its Operational Infrastructure Support Program.
References
Amit, D. J., and Brunel, N. (1997). Dynamics of a recurrent network of spiking neurons before and following learning. Netw. Comput. Neural Syst. 8, 373–404.
Appleby, P. A., and Elliott, T. (2006). Stable competitive dynamics emerge from multispike interactions in a stochastic model of spike-timing-dependent plasticity. Neural Comput. 18, 2414–2464.
Appleby, P. A., and Elliott, T. (2007). Multispike interactions in a stochastic model of spike-timing-dependent plasticity. Neural Comput. 19, 1362–1399.
Bartsch, A. P., and van Hemmen, J. L. (2001). Combined Hebbian development of geniculocortical and lateral connectivity in a model of primary visual cortex. Biol. Cybern. 84, 41–55.
Bi, G. Q., and Poo, M. M. (1998). Synaptic modifications in cultured hippocampal neurons: dependence on spike timing, synaptic strength, and postsynaptic cell type. J. Neurosci. 18, 10464–10472.
Bienenstock, E. L., Cooper, L. N., and Munro, P. W. (1982). Theory for the development of neuron selectivity – orientation specificity and binocular interaction in visual-cortex. J. Neurosci. 2, 32–48.
Bohte, S. M., and Mozer, M. C. (2007). Reducing the variability of neural responses: a computational theory of spike-timing-dependent plasticity. Neural Comput. 19, 371–403.
Burkitt, A. N., Gilson, M., and van Hemmen, J. L. (2007). Spike-timing-dependent plasticity for neurons with recurrent connections. Biol. Cybern. 96, 533–546.
Burkitt, A. N., Meffin, H., and Grayden, D. B. (2004). Spike-timing-dependent plasticity: the relationship to rate-based learning for models with weight dynamics determined by a stable fixed point. Neural Comput. 16, 885–940.
Butts, D. A., Kanold, P. O., and Shatz, C. J. (2007). A burst-based “Hebbian” learning rule at retinogeniculate synapses links retinal waves to activity-dependent refinement. PLoS Biol. 5, e61. doi:10.1371/journal.pbio.0050061.
Caporale, N., and Dan, Y. (2008). Spike timing-dependent plasticity: a Hebbian learning rule. Annu. Rev. Neurosci. 31, 25–46.
Carnell, A. (2009). An analysis of the use of Hebbian and anti-Hebbian spike time dependent plasticity learning functions within the context of recurrent spiking neural networks. Neurocomputing 72, 685–692.
Carr, C. E., and Konishi, M. (1990). A circuit for detection of interaural time differences in the brain-stem of the barn owl. J. Neurosci. 10, 3227–3246.
Câteau, H., Kitano, K., and Fukai, T. (2008). Interplay between a phase response curve and spike-timing-dependent plasticity leading to wireless clustering. Phys. Rev. E 77, 051909.
Clopath, C., Büsing, L., Vasilaki, E., and Gerstner, W. (2010). Connectivity reflects coding: a model of voltage-based STDP with homeostasis. Nat. Neurosci. 13, 344–352.
Dahmen, J. C., Hartley, D. E., and King, A. J. (2008). Stimulus-timing-dependent plasticity of cortical frequency representation. J. Neurosci. 28, 13629–13639.
Dan, Y., and Poo, M. M. (2006). Spike timing-dependent plasticity: from synapse to perception. Physiol. Rev. 86, 1033–1048.
Davison, A. P., and Frégnac, Y. (2006). Learning cross-modal spatial transformations through spike timing-dependent plasticity. J. Neurosci. 26, 5604–5615.
Delorme, A., Perrinet, L., and Thorpe, S. J. (2001). Networks of integrate-and-fire neurons using rank order coding B: spike timing dependent plasticity and emergence of orientation selectivity. Neurocomputing 38, 539–545.
Friedel, P., and van Hemmen, J. L. (2008). Inhibition, not excitation, is the key to multimodal sensory integration. Biol. Cybern. 98, 597–618.
Froemke, R. C., and Dan, Y. (2002). Spike-timing-dependent synaptic modification induced by natural spike trains. Nature 416, 433–438.
Froemke, R. C., Poo, M. M., and Dan, Y. (2005). Spike-timing-dependent synaptic plasticity depends on dendritic location. Nature 434, 221–225.
Froemke, R. C., Tsay, I. A., Raad, M., Long, J. D., and Dan, Y. (2006). Contribution of individual spikes in burst-induced long-term synaptic modification. J. Neurophysiol. 95, 1620–1629.
Fusi, S. (2002). Hebbian spike-driven synaptic plasticity for learning patterns of mean firing rates. Biol. Cybern. 87, 459–470.
Gerstner, W., Kempter, R., van Hemmen, J. L., and Wagner, H. (1996). A neuronal learning rule for sub-millisecond temporal coding. Nature 383, 76–78.
Gerstner, W., and Kistler, W. M. (2002). Mathematical formulations of Hebbian learning. Biol. Cybern. 87, 404–415.
Gerstner, W., Ritz, R., and van Hemmen, J. L. (1993). Why spikes? Hebbian learning and retrieval of time-resolved excitation patterns. Biol. Cybern. 69, 503–515.
Gilson, M., Burkitt, A. N., Grayden, D. B., Thomas, D. A., and van Hemmen, J. L. (2009a). Emergence of network structure due to spike-timing-dependent plasticity in recurrent neuronal networks. I: input selectivity – strengthening correlated input pathways. Biol. Cybern. 101, 81–102.
Gilson, M., Burkitt, A. N., Grayden, D. B., Thomas, D. A., and van Hemmen, J. L. (2009b). Emergence of network structure due to spike-timing-dependent plasticity in recurrent neuronal networks. II: input selectivity – symmetry breaking. Biol. Cybern. 101, 103–114.
Gilson, M., Burkitt, A. N., Grayden, D. B., Thomas, D. A., and van Hemmen, J. L. (2009c). Emergence of network structure due to spike-timing-dependent plasticity in recurrent neuronal networks. III: partially connected neurons driven by spontaneous activity. Biol. Cybern. 101, 411–426.
Gilson, M., Burkitt, A. N., Grayden, D. B., Thomas, D. A., and van Hemmen, J. L. (2009d). Emergence of network structure due to spike-timing-dependent plasticity in recurrent neuronal networks. IV: structuring synaptic pathways among recurrent connections. Biol. Cybern. 101, 427–444.
Gilson, M., Burkitt, A. N., Grayden, D. B., Thomas, D. A., and van Hemmen, J. L. (2010). Emergence of network structure due to spike-timing-dependent plasticity in recurrent neuronal networks. V: self-organization schemes and weight dependence. Biol. Cybern (accepted).
Graupner, M., and Brunel, N. (2007). STDP in a bistable synapse model based on CaMKII and associated signaling pathways. PLoS Comput. Biol. 3, 2299–2323. doi:10.1371/journal.pcbi.0030221.
Gütig, R., Aharonov, R., Rotter, S., and Sompolinsky, H. (2003). Learning input correlations through nonlinear temporally asymmetric Hebbian plasticity. J. Neurosci. 23, 3697–3714.
Hartley, M., Taylor, N., and Taylor, J. (2006). Understanding spike-time-dependent plasticity: a biologically motivated computational model. Neurocomputing 69, 2005–2016.
Henry, F., Dauce, E., and Soula, H. (2007). Temporal pattern identification using spike-timing dependent plasticity. Neurocomputing 70, 2009–2016.
Hosaka, R., Araki, O., and Ikeguchi, T. (2008). STDP provides the substrate for igniting synfire chains by spatiotemporal input patterns. Neural Comput. 20, 415–435.
Jun, J. K., and Jin, D. Z. (2007). Development of neural circuitry for precise temporal sequences through spontaneous activity, axon remodeling, and synaptic plasticity. PLoS ONE 2, e723. doi:10.1371/journal.pone.0000723.
Kang, S., Isomura, Y., Takekawa, T., Câteau, H., and Fukai, T. (2008). Multi-neuronal dynamics in rat neocortex and hippocampus during natural sleep. Neurosci. Res. 61, S189–S189.
Karbowski, J., and Ermentrout, G. B. (2002). Synchrony arising from a balanced synaptic plasticity in a network of heterogeneous neural oscillators. Phys. Rev. E 65, 031902.
Kempter, R., Gerstner, W., and van Hemmen, J. L. (1999). Hebbian learning and spiking neurons. Phys. Rev. E 59, 4498–4514.
Kempter, R., Gerstner, W., and van Hemmen, J. L. (2001). Intrinsic stabilization of output rates by spike-based Hebbian learning. Neural Comput. 13, 2709–2741.
Kistler, W. M., and van Hemmen, J. L. (2000). Modeling synaptic plasticity in conjunction with the timing of pre- and postsynaptic action potentials. Neural Comput. 12, 385–405.
Kitano, K., Câteau, H., and Fukai, T. (2002). Self-organization of memory activity through spike-timing-dependent plasticity. Neuroreport 13, 795–798.
Kohonen, T. (1982). Self-organized formation of topologically correct feature maps. Biol. Cybern. 43, 59–69.
Krumin, M., and Shoham, S. (2009). Generation of spike trains with controlled auto- and cross-correlation functions. Neural Comput. 21, 1642–1664.
Lazar, A., Pipa, G., and Triesch, J. (2009). SORN: a self-organizing recurrent neural network. Front. Comput. Neurosci. 3:23. doi:10.3389/neuro.10.023.2009.
Legenstein, R., Naeger, C., and Maass, W. (2005). What can a neuron learn with spike-timing-dependent plasticity? Neural Comput. 17, 2337–2382.
Leibold, C., Kempter, R., and van Hemmen, J. L. (2002). How spiking neurons give rise to a temporal-feature map: from synaptic plasticity to axonal selection. Phys. Rev. E 65, 051915.
Lengyel, M., Kwag, J., Paulsen, O., and Dayan, P. (2005). Matching storage and recall: hippocampal spike timing-dependent plasticity and phase response curves. Nat. Neurosci. 8, 1677–1683.
Levy, W. B., and Steward, O. (1983). Temporal contiguity requirements for long-term associative potentiation depression in the hippocampus. Neuroscience 8, 791–797.
Lubenov, E. V., and Siapas, A. G. (2008). Decoupling through synchrony in neuronal circuits with propagation delays. Neuron 58, 118–131.
Maass, W., Natschlager, T., and Markram, H. (2002). Real-time computing without stable states: a new framework for neural computation based on perturbations. Neural Comput. 14, 2531–2560.
Macke, J. H., Berens, P., Ecker, A. S. Tolias, A. S., and Bethge, M. (2009). Generating spike trains with specified correlation coefficients. Neural Comput. 21, 397–423.
Marinaro, M., Scarpetta, S., and Yoshioka, M. (2007). Learning of oscillatory correlated patterns in a cortical network by a STDP-based learning rule. Math. Biosci. 207, 322–335.
Markram, H., Lübke, J., Frotscher, M., and Sakmann B. (1997). Regulation of synaptic efficacy by coincidence of postsynaptic APs and EPSPs. Science 275, 213–215.
Masquelier, T., Guyonneau, R., and Thorpe, S. J. (2008). Spike timing dependent plasticity finds the start of repeating patterns in continuous spike trains. PLoS ONE 3, e1377. doi:10.1371/journal.pone.0001377.
Masquelier, T., Hugues, E., Deco, G., and Thorpe, S. J. (2009). Oscillations, phase-of-firing coding, and spike-timing-dependent plasticity: an efficient learning scheme. J. Neurosci. 29, 13484–13493.
Masuda, N., and Kori, H. (2007). Formation of feedforward networks and frequency synchrony by spike-timing-dependent plasticity. J. Comput. Neurosci. 22, 327–345.
Meffin, H., Besson, J., Burkitt, A. N., and Grayden, D. B. (2006). Learning the structure of correlated synaptic subgroups using stable and competitive spike-timing-dependent plasticity. Phys. Rev. E 73, 041911.
Moreno-Bote, R., Renart, A., and Parga, N. (2008). Theory of input spike auto-and cross-correlations and their effect on the response of spiking neurons. Neural Comput. 20, 1651–1705.
Morrison, A., Aertsen, A., and Diesmann, M. (2007). Spike-timing-dependent plasticity in balanced random networks. Neural Comput. 19, 1437–1467.
Morrison, A., Diesmann, M., and Gerstner, W. (2008). Phenomenological models of synaptic plasticity based on spike timing. Biol. Cybern. 98, 459–478.
Nowotny, T., Rabinovich, M. I., and Abarbanel, H. D. I. (2003a). Spatial representation of temporal information through spike-timing-dependent plasticity. Phys. Rev. E 68, 011908.
Nowotny, T., Zhigulin, V. P., Selverston, A. I., Abarbanel, H. D. I., and Rabinovich, M. I. (2003b). Enhancement of synchronization in a hybrid neural circuit by spike-timing dependent plasticity. J. Neurosci. 23, 9776–9785.
Oja, E. (1982). A simplified neuron model as a principal component analyzer. J. Math. Biol. 15, 267–273.
Paugam-Moisy, H., Martinez, R., and Bengio, S. (2008). Delay learning and polychronization for reservoir computing. Neurocomputing 71, 1143–1158.
Pfister, J.-P., and Gerstner, W. (2006). Triplets of spikes in a model of spike timing-dependent plasticity. J. Neurosci. 26, 9673–9682.
Pfister, J.-P., Toyoizumi, T., Barber, D., and Gerstner, W. (2006). Optimal spike-timing-dependent plasticity for precise action potential firing in supervised learning. Neural Comput. 18, 1318–1348.
Sejnowski, T. J. (1977). Storing covariance with nonlinearly interacting neurons. J. Math. Biol. 4, 303–321.
Senn, W. (2002). Beyond spike timing: the role of nonlinear plasticity and unreliable synapses. Biol. Cybern. 87, 344–355.
Shen, X., Lin, X. B., and De Wilde, P. (2008). Oscillations and spiking pairs: behavior of a neuronal model with STDP learning. Neural Comput. 20, 2037–2069.
Sjöström, P. J., Turrigiano, G. G., and Nelson, S. B. (2001). Rate, timing, and cooperativity jointly determine cortical synaptic plasticity. Neuron 32, 1149–1164.
Song, S., and Abbott, L. F. (2001). Cortical development and remapping through spike timing-dependent plasticity. Neuron 32, 339–350.
Song, S., Miller, K. D., and Abbott, L. F. (2000). Competitive Hebbian learning through spike-timing-dependent synaptic plasticity. Nat. Neurosci. 3, 919–926.
Sprekeler, H., Michaelis, C., and Wiskott, L. (2007). Slowness: an objective for spike-timing-dependent plasticity? PLoS Comput. Biol. 3, 1136–1148. doi:10.1371/journal.pcbi.0030112.
Standage, D., Jalil, S., and Trappenberg, T. (2007). Computational consequences of experimentally derived spike-time and weight dependent plasticity rules. Biol. Cybern. 96, 615–623.
Staude, B., Rotter, S., and Grun, S. (2008). Can spike coordination be differentiated from rate covariation? Neural Comput. 20, 1973–1999.
Stuart, G., Spruston, N., Sakmann, B., and Häusser, M. (1997). Action potential initiation and backpropagation in neurons of the mammalian CNS. Trends Neurosci. 20, 125–131.
Takahashi, Y. K., Kori, H., and Masuda, N. (2009). Self-organization of feed-forward structure and entrainment in excitatory neural networks with spike-timing-dependent plasticity. Phys. Rev. E 79, 051904.
Toyoizumi, T., Pfister, J.-P., Aihara, K., and Gerstner, W. (2005). Generalized Bienenstock–Cooper–Munro rule for spiking neurons that maximizes information transmission. Proc. Natl. Acad. Sci. U.S.A. 102, 5239–5244.
Toyoizumi, T., Pfister, J.-P., Aihara, K., and Gerstner, W. (2007). Optimality model of unsupervised spike-timing-dependent plasticity: synaptic memory and weight distribution. Neural Comput. 19, 639–671.
Turrigiano, G. G. (2008). The self-tuning neuron: synaptic scaling of excitatory synapses. Cell 135, 422–435.
Tzounopoulos, T., Kim, Y., Oertel, D., and Trussell, L. O. (2004). Cell-specific, spike timing-dependent plasticities in the dorsal cochlear nucleus. Nat. Neurosci. 7, 719–725.
van Hemmen, J. L. (2001). “Theory of synaptic plasticity (Chapter 18),” in Handbook of Biological Physics, Vol. 4, Neuro-informatics and Neural Modelling, eds F Moss and S Gielen (Amsterdam: Elsevier), 771–823.
van Rossum, M. C. W., Bi, G. Q., and Turrigiano, G. G. (2000). Stable Hebbian learning from spike timing-dependent plasticity. J. Neurosci. 20, 8812–8821.
van Rossum, M. C. W., and Turrigiano, G. G. (2001). Correlation based learning from spike timing dependent plasticity. Neurocomputing 38, 409–415.
Wenisch, O. G., Noll, J., and van Hemmen, J. L. (2005). Spontaneously emerging direction selectivity maps in visual cortex through STDP. Biol. Cybern. 93, 239–247.
Woodin, M. A., Ganguly, K., and Poo, M. M. (2003). Coincident pre- and postsynaptic activity modifies GABAergic synapses by postsynaptic changes in Cl− transporter activity. Neuron 39, 807–820.
Keywords: recurrent neuronal network, network structure, STDP, spike-time correlations, self-organization / unsupervised learning
Citation: Gilson M, Burkitt A and van Hemmen JL (2010) STDP in recurrent neuronal networks. Front. Comput. Neurosci. 4:23. doi: 10.3389/fncom.2010.00023
Received: 01 March 2010;
Paper pending published: 18 May 2010;
Accepted: 28 June 2010;
Published online: 10 September 2010
Edited by:
Wulfram Gerstner, Ecole Polytechnique Fédérale de Lausanne, SwitzerlandReviewed by:
Christian Leibold, Ludwig Maximilians University, GermanyGuillaume Hennequin, Brain-Mind Institute, Switzerland
Copyright: © 2010 Gilson, Burkitt and van Hemmen. This is an open-access article subject to an exclusive license agreement between the authors and the Frontiers Research Foundation, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Matthieu Gilson, Lab for Neural Circuit Theory, Riken Brain Science Institute, Hirosawa 2-1, Wako-shi, Saitama 351-0198, Japan. e-mail:Z2lsc29ubUB1bmltZWxiLmVkdS5hdQ==


