- 1 Institute of Physics at São Carlos, University of São Paulo, São Carlos, São Paulo, Brazil
- 2 National Institute of Science and Technology of Complex Systems, Niterói, Rio de Janeiro, Brazil
- 3 St. Catharine’s College, University of Cambridge, Cambridge, UK
- 4 Department of Chemistry, University of Cambridge, Cambridge, UK
This article proposes the concept of neuromorphological space as the multidimensional space defined by a set of measurements of the morphology of a representative set of almost 6000 biological neurons available from the NeuroMorpho database. For the first time, we analyze such a large database in order to find the general distribution of the geometrical features. We resort to McGhee’s biological shape space concept in order to formalize our analysis, allowing for comparison between the geometrically possible tree-like shapes, obtained by using a simple reference model, and real neuronal shapes. Two optimal types of projections, namely, principal component analysis and canonical analysis, are used in order to visualize the originally 20-D neuron distribution into 2-D morphological spaces. These projections allow the most important features to be identified. A data density analysis is also performed in the original 20-D feature space in order to corroborate the clustering structure. Several interesting results are reported, including the fact that real neurons occupy only a small region within the geometrically possible space and that two principal variables are enough to account for about half of the overall data variability. Most of the measurements have been found to be important in representing the morphological variability of the real neurons.
1 Introduction
Despite the continuing scientific and technological advances in neuroscience, the understanding of the nervous system of living organisms still remains largely incipient. Among the several problems which have constrained the advances in this area, one of the most prominent issues regards the relationship between shape and functioning of neuronal cells (Costa et al., 2002; Schierwagen, 2008; Wen and Chklovskii, 2008). Remarkably, the nervous systems of most animals are composed by neuronal cells exhibiting a large variety of shapes. This was first realized through the pioneering work of Cajal (1989), who went so far as to assign human intelligence to the “unaccustomed” variety of neuronal morphology. Indeed, neuronal cells vary from relatively simple structures such as the bipolar cells of the retina, to the exuberant complexity of Purkinje and some pyramidal cells (Masland, 2004; Bota and Swanson, 2007). The emerging dynamics in neuronal systems is ultimately the consequence of established synaptic connections, which are to a large extent defined by the neuronal branching pattern (Kreindler, 1965; Elston and Rosa, 2000), relative position of the neuronal cells, and the respective history of dynamical response to stimuli presentation. For instance, cells which are very simple and separated from each other tend to make a smaller number of synapses. Therefore, the proper understanding of the connectivity patterns in the nervous system demands the analysis of neuronal morphology. In addition, the dynamical operation of neurons is also intrinsically constrained and even defined by their respective shapes (Koch et al., 1982; Fukuda et al., 1984; Agmon-Snir et al., 1998; Segev, 1998; Jan and Jan, 2003; Pérez-Reche et al., 2010). For all such reasons, it becomes exceedingly important to investigate neuronal morphology in a systematic and comprehensive way.
Following the works of Ramón-y-Cajal, the main interest in neuroscience was shifted to electrophysiology, which dominated much of the research in this area for many decades thereon. The relatively few approaches to neuromorphometry developed along this period include the Sholl (1953) analysis, fractal dimension characterization (Montague and Friedlander, 1991), influence area analysis (Toris et al., 1995), and dendrogram representation (Poznanski, 1992). More recently, the scientific community resumed interest on neuromorphological research. Improvements in high definition visualization (Hosking and Schwartz, 2009), as well as in the methodology used for analysis paved the way for the development of computational neuromorphometry (Costa et al., 2002), a research field aimed at quantifying the shape of these cells. At the same time, the development of new methods and measurements (Costa, 2003; Rodrigues et al., 2005) complemented the characterization and modeling of neuronal systems. Neuromorphological analysis comprises both characterization (Costa and Velte, 1999; Costa et al., 2007) and classification (Bota and Swanson, 2007) of neuronal cells through multivariate techniques, which require choosing appropriate measurements (Costa, 1995) and the application of pattern recognition methods. A particularly relevant approach involves the grouping of neuronal cells into categories according to their morphological similarity. Such an approach is important for understanding the heterogeneity of the groups, as well as for unveiling the relationship between neuronal structure and function, and can be applied to comparative anatomy, developmental neurobiology, and diagnosis.
One of the most promising recent trends in neuroscience has been the advent of public data repository such as the NeuroMorpho Database1 (Ascoli et al., 2007). Initiated in 2006, this database has grown steadily to become what is the most complete database of neuronal morphology, comprising currently 5673 cells of several types and species. It includes 3-D reconstructions, measurements, softwares, and general information about the cells, such as reference papers, animal species, brain region, neuron class, amongst many others.
The current work explores the availability of such welcomed public repositories in order to perform a systematic and comprehensive investigation of the morphological characteristics of a large and representative set of neurons. More specifically, we use optimal multivariate statistical approaches in order to investigate the distribution of neuronal geometry as characterized by the several measurements available in the NeuroMorpho database. The multidimensional measurement space where the cells are mapped is henceforth called the neuromorphological space, NS for short.
In this paper, we address the following important questions: (i) What are the most populated areas in the NS and where are their boundaries? (ii) Out of the set of possible tree-like structures, which are actually found in biological neurons? (iii) Do the cells of the same type, tissue, or species tend to cluster together? (iv) Are there redundancies between the available geometrical features, as quantified by their pairwise correlations? (v) What are the features contributing more decisively for the variability of the cell morphologies and separation of different types of cells?
Each of the neuronal cells in NeuroMorpho is characterized by 20 available features quantifying different aspects of the respective morphology. In order to allow the visualization of the distribution of the cells in the NS, we resort to two optimal projection methods, namely, principal component analysis (PCA) and canonical analysis. While the former defines the projection axes so as to maximize the variability of the data, the latter performs the projection so as to maximize the separation between the several imposed categories. We also propose a simple reference model of tree-like structures, which is capable of generating the most diverse types of trees. This model is used in order to identify, in the projected spaces, the overall region of almost every possible tree-like structures with unbiased branching. So, we can compare how the biological neurons are distributed within this wide region of geometrically possible shapes. The application of the projection methods also paved the way to identifying the contribution of every considered feature for the variability of the original data as well as for the separation between the groups of cells (type, tissue, or species). We also performed a density analysis in the original 20-D space, in order to complement the clustering structures observed in the projection approach.
Several relevant results are obtained. The most remarkable finding is that the biological neurons occupy only a rather small portion of the larger space of the unbiased branched structures. The article starts by presenting the several involved basic concepts, methods and models, and follows by presenting and discussing the results.
2 Materials and Methods
In this section, we describe the NeuroMorpho database and the characteristics (measurements) of neural cells available from this repository. Then, the concept of morphospace is introduced and the statistical methods of its analysis are briefly described. In particular, a new approach to analysis of the morphospace based on use of radial density function is discussed in detail. Finally, a numerical model for generating diverse branching tree-like structures is developed and used for exploring the morphospace.
2.1 The Neuromorpho Database
NeuroMorpho (Ascoli et al., 2007) is an on-line public repository of reconstructed neurons, obtained from available WWW databases and direct peer-to-peer requests to individual laboratories and researchers. The purpose of this repository is to facilitate neuronal data access and sharing in the scientific community. New data is only uploaded by administrators, who first standardize the data format. The Computational Neuroanatomy Group (Krasnow Institute for Advanced Study, George Mason University), under the direction of Prof. Giorgio Ascoli, is the developer and maintainer of NeuroMorpho. This repository integrates the Neuroscience Information Framework (NIF) consortium (Halavi et al., 2008), which include several academic institutions, such as Cornell, Stanford, and California Universities. The first version of NeuroMorpho (Alpha) was released on August 01, 2006, with 932 neurons. Since then, it has being continuously updated to include more neurons and to improve the site functionality (Halavi et al., 2008; Figure 1). At the present version (4.0), it has 5673 neurons. The available data includes 3-D reconstructions and measurements (volume, diameter, etc.), as well as general information such as the data provider (researcher and laboratory), reference papers and URLs related to the data, experiment setup (protocol, staining method, etc.), animal type (species, age, etc.), brain region and sub-region, neuron class and sub-class, and methods and software used in the reconstruction.
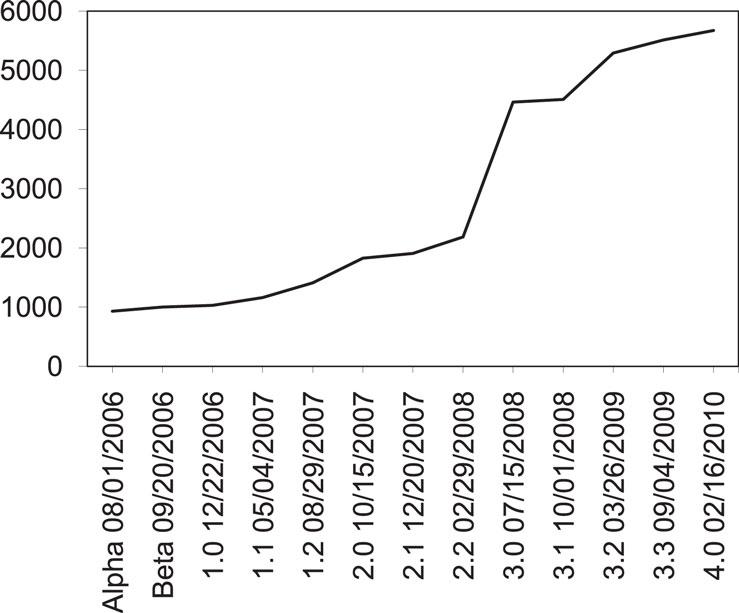
Figure 1. Version releases and evolution of the number of neurons in the NeuroMorpho database: since its release in 2006, data has being continuously added and currently it is the largest database of neuronal morphology, containing 5673 cells.
Usually, neuronal morphology data acquisition involves the sectioning of the neuron and their serial reconstruction. It is well known that this process can potentially introduce artifacts (Horcholle-Bossavit et al., 2000; Hamam and Kennedy, 2003), such as shrinkage and distortion caused by fixation, dehydration, loss of tissue parts during sectioning, and misalignment of slices during reconstruction. Also, the image segmentation and the connection of the neuronal parts between sections in the reconstruction are challenging tasks (Meijering, 2010). Because each of these artifacts will imply specific, different bias on the estimation of each of the possible neuromorphological measurements, a comprehensive study would need to be carried out at quantifying and characterizing such biases. At any rate, such problems tend to be reduced with the advances in experimental procedures and equipment.
2.2 Measurements
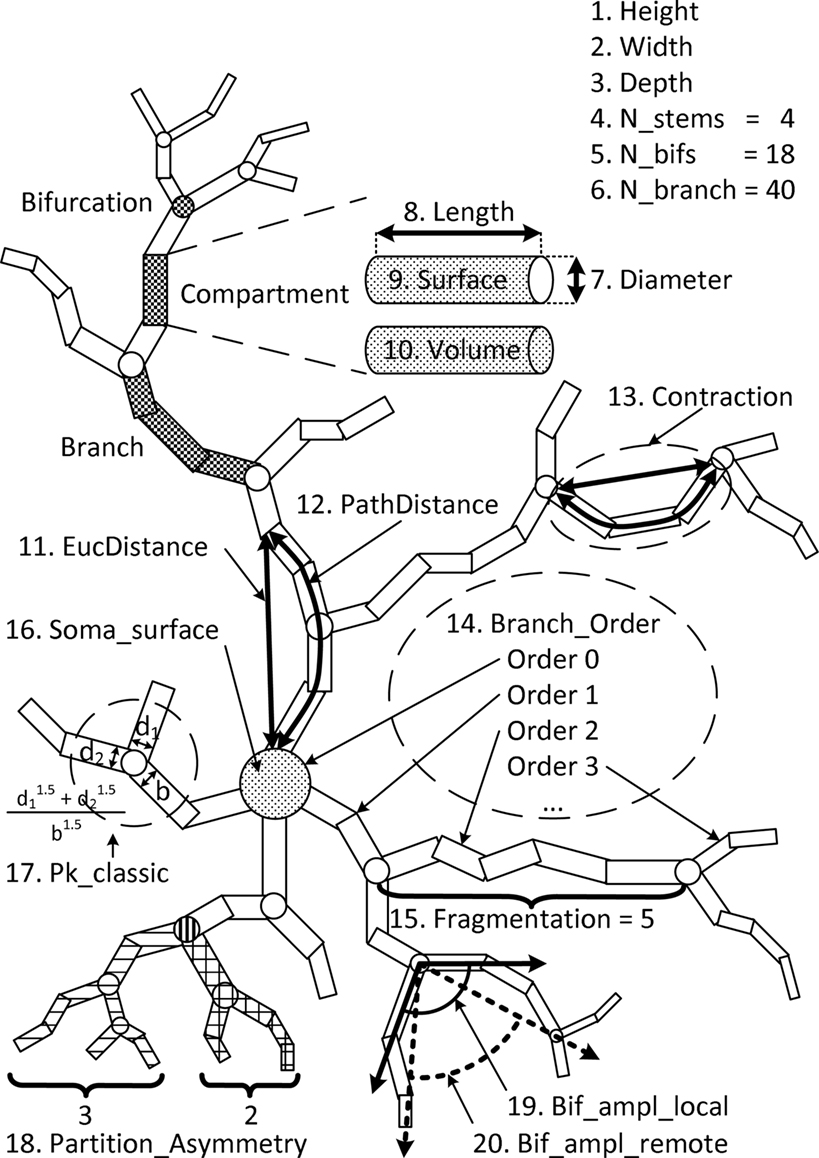
In order to study the morphology of neurons, it is necessary to represent and characterize them in some way suitable for processing and analysis. NeuroMorpho provides the L-Measure (Scorcioni et al., 2008), a tool to extract several measurements from the neurons in the database. The measurements used in this work are illustrated in Figure 2, numbered from 1 to 20 and named as in the software documentation.
The concepts of compartment, branch, and bifurcation are illustrated in Figure 2. Compartments are segments represented as cylinders with diameter and extremity points coordinates. Branches are formed with one or more compartments between the soma, the bifurcations, and the tips. Bifurcations are points where a branch splits into two other branches. Measurements 1, 2, and 3 are the height, width, and depth of a neuron, calculated after its alignment along the principal axis obtained by PCA. The number of stems, bifurcations, and branches in a neuron correspond to the measurements 4, 5, and 6. The feature 7 is the diameter averaged over all compartments. Features from 8 to 10 are length, surface area, and volume, respectively, which are summed over all compartments.
The branches have their associated measurements numbered from 11 to 15. Measurement 11 is the maximum Euclidean distance between a compartment and the soma, while the path distance (12) is the maximum of the sums of the lengths of the compartments between two endpoints. Contraction (13) is the average ratio between the Euclidean distance and its path distance. Measure 14 is the maximum branching order with respect to the soma, which has order 0. This measurement corresponds to the topological distance of a branch to the soma. Fragmentation (15) is the total sum of compartments in a branch. Only compartments between bifurcations or between a bifurcation and a tip are considered.
Measurement 16 is the soma surface area. The soma can be of two types: a sphere or a set of compartments. In the latter case, the area is calculated as the sum of the area surfaces of the soma compartments.
The other measurements are related to bifurcations. Pk_classic (17) is the average ratio 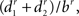 where r is the Rall’s power law value, set in this measure as 1.5, and b, d1, and d2 are the diameters of the bifurcation compartments (the parent and the two daughters, respectively). The partition asymmetry (18) considers the average number of tips on the left and on the right daughter subtrees of a bifurcation as n1 and n2 in the expression |n1 − n2|/(n1 + n2 − 2). In Figure 2, the analyzed bifurcation has vertical stripes, while the left daughter subtree has horizontal stripes and the right one has a pattern of squares. Then, in this example, n1 = 3 and n2 = 2 gives |3 − 2|/(3 + 2 − 2) = 0.33. Measurement 19 is the angle between two daughter compartments in a bifurcation averaged over all bifurcation points, while measurement 20 is the angle regarding the endpoints of two daughter branches also averaged over all bifurcation points.
where r is the Rall’s power law value, set in this measure as 1.5, and b, d1, and d2 are the diameters of the bifurcation compartments (the parent and the two daughters, respectively). The partition asymmetry (18) considers the average number of tips on the left and on the right daughter subtrees of a bifurcation as n1 and n2 in the expression |n1 − n2|/(n1 + n2 − 2). In Figure 2, the analyzed bifurcation has vertical stripes, while the left daughter subtree has horizontal stripes and the right one has a pattern of squares. Then, in this example, n1 = 3 and n2 = 2 gives |3 − 2|/(3 + 2 − 2) = 0.33. Measurement 19 is the angle between two daughter compartments in a bifurcation averaged over all bifurcation points, while measurement 20 is the angle regarding the endpoints of two daughter branches also averaged over all bifurcation points.
2.3 Modeling the Hyperspace of Biological Forms
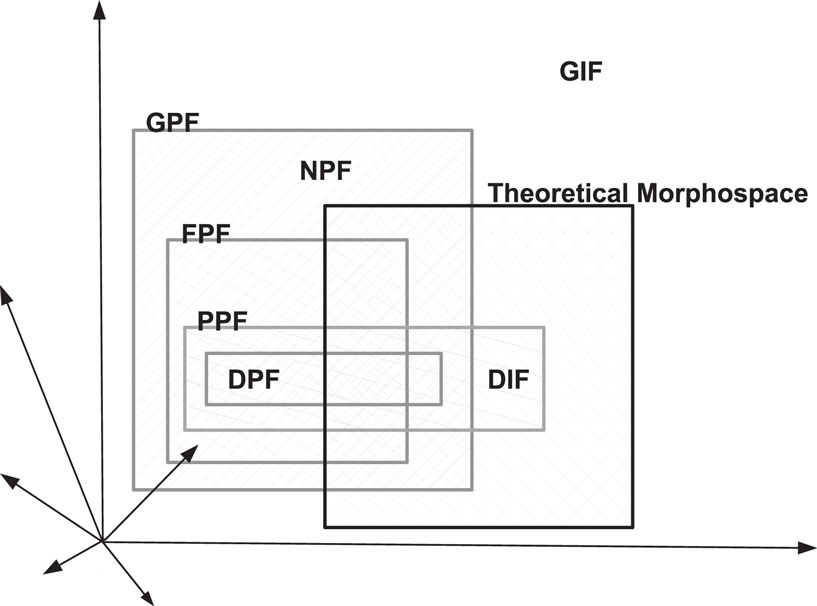
A theoretical shape-hyperspace, in an analogy with geometrical concepts, can be understood as a n-dimensional space, which axes are associated respectively with some measurements. In biology, particularly for morphological analysis, these measurements refer to shape properties, such as length, height, depth, or volume of a living organism or structure. Ideally, the morphospace can be constructed by modeling biological entities through variations of these parameters and considering all possible individuals whose existence is deemed possible. So, although continuous, the morphospace is ultimately reduced as a consequence of several constraints imposed by specific properties of the organisms and their habitat.
By using the morphospace, it becomes possible to define regions and boundaries corresponding to allowed geometrical, functional, phylogenetically, and developmental properties of the investigated biological entities ( McGhee, 2006; see Figure 3). An important subset of the shape-hyperspace corresponds to the set of geometrically possible forms (GPF), in the sense that the points outside this region belong to the set of geometrically impossible forms (GIF). There are two exclusive sub-regions within the GPF subspace distinguished by the functionality of the forms, namely, between those that are functionally viable and allow the biological entity to survive (functional possible forms – FPF) and those that are not functionally viable (nonfunctional possible forms – NPF).
These four classifications (GPF, GIF, FPF, and NPF) are based on the extrinsic constraints that are imposed by physical or geometrical laws, in contrast to the intrinsic constraints which refer to the biology of a specific organism. The region defined by the intrinsic properties can be subdivided further into developmental (developmentally possible form – DPF) and phylogenetic (phylogenetically possible forms – PPF) constraints for a given species, respectively limited by its potential for development and its genetic coding. It is possible to have overlaps between the PPF region and the NPF and GIF spaces. The set defined by the overlaps of these regions comprises the theoretical shape-hyperspace, denoted by morphospace. As an example, a set of cells which are related to genetic diseases must belong to the phylogenetic possible region, but its respective developmental region (DPF) is constrained by the viability of the life of the organism, so that a shorter life implies for that individual to be assigned to the impossible developmental region (DIF).
In addition, there is an empirical morphospace which is defined as the space of the experimental measurements extracted from real individuals. The investigation of the empirical morphospace can help us to make hypotheses such as what factors along both evolutionary and developmental stages affect the subsequent trajectories inside the morphospace.
In order to simulate a possible representation of theoretical morphospace, algorithms aimed at producing a set of artificial neurons can be implemented. They are based on statistical models which select some morphological features and vary the corresponding measurements, checking their existence or even fitness. Of course, this method is unable to reproduce accurately the natural processes of life creation and development. At the same time, we should take into account that the adopted set of empirical individuals contains only a fraction of the natural neurons. Nevertheless, both these subsets will provide insights, as well as an estimate for the density and location of the empirical data within the simulated theoretical hyperspace. It is important to note that several models for generation of tree-like neuronal structures have been proposed before, which some of them are based on stochastic sampling of real features (Ascoli and Krichmar, 2000; van Ooyen and van Pelt, 2002; van Pelt and Uylings, 2007), entropy maximization (Wen et al., 2009), and diffusion-limited aggregation process (Luczak, 2006).
As proposed in this work, the morphological theoretical approach can be applied to neuroscience in order to model the hyperspace of neuronal shapes (neuronal morphospace). Considering a set of measurements extracted from some real set of neuronal cells by using the available measurements in NeuroMorpho database, we can model the empirical morphospace and verify the behavior (boundaries and overlaps) of each of the above defined regions.
2.4 Principal Component Analysis
Principal component analysis (Duda et al., 2001; Härdle and Simar, 2007) is a powerful statistical method aiming to reduce the dimension of problems with many measurements. In several applications, PCA promotes the elimination of redundancies, transforming a system described by a set of possibly correlated variables into a new fully uncorrelated system. The technique changes the orientation of the axes in the original space, and then project the measurements space to the subspace characterized by the first principal axes with maximal dispersion.
The data can be arranged as a N × M matrix W, where each row corresponds to a feature vector 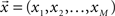 associated with one of N neuronal cells. Each element of these vectors is related to a particular measure. It is important to note that these measures can be at different scales and a data standardization is therefore required. The next step is to define the covariance matrix V as (Härdle and Simar, 2007):
associated with one of N neuronal cells. Each element of these vectors is related to a particular measure. It is important to note that these measures can be at different scales and a data standardization is therefore required. The next step is to define the covariance matrix V as (Härdle and Simar, 2007):
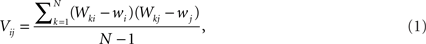
where 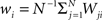 is the mean value of the i-th measure. Now, we define the correlation matrix R as follows
is the mean value of the i-th measure. Now, we define the correlation matrix R as follows

Next, we calculate the eigenvalues λ and eigenvectors 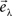 of R. The M eigenvalues are sorted in descending order and the first P values are chosen (P < M) for PCA. Linear transformation with the use of the restricted eigenvector basis,
of R. The M eigenvalues are sorted in descending order and the first P values are chosen (P < M) for PCA. Linear transformation with the use of the restricted eigenvector basis,

reduces the size of original data matrix from N × M to N × P. The amount of the variance explained by the P chosen eigenvectors can be quantified by the following value:

All these characteristics were used for analysis of the organization of neuronal cells in the morphospace.
2.5 Canonical Variable Analysis
Canonical Variable Analysis (McLachlan, 2004; Costa et al., 2007) is an algebraic method to find the data projection that best separates predefined data classes. This can be achieved through the maximization of the interclass dispersion, i.e., dispersion between classes, while minimizing the intraclass dispersion inside each class. Let us suppose that each element can be classified into a class Ci containing ni elements, where i = 1,2,…Nc and Nc is the maximum number of classes. Using these definitions, we can express the interclass scatter matrix (Equation 5) and the intraclass scatter matrix (Equation 6) as:
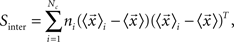

where 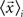 is the mean feature vector of the elements in class Ci,
is the mean feature vector of the elements in class Ci, 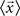 is the mean feature vector of all elements, and Si is the dispersion of the measurements inside each class (scatter matrix for each class Ci):
is the mean feature vector of all elements, and Si is the dispersion of the measurements inside each class (scatter matrix for each class Ci):
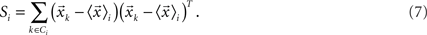
Then, we can calculate the eigenvalues and eigenvectors of the matrix 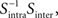 where
where 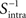 is the inverse of Sintra. After that, the eigenvalues must be ordered in descending order. Afterwards, we can pick up the eigenvectors corresponding to the highest eigenvalues to build up the new data projections. For example, if we choose the three eigenvectors corresponding to the three highest eigenvalues, we can reduce the data-space dimensionality to 3, allowing us to visualize the data.
is the inverse of Sintra. After that, the eigenvalues must be ordered in descending order. Afterwards, we can pick up the eigenvectors corresponding to the highest eigenvalues to build up the new data projections. For example, if we choose the three eigenvectors corresponding to the three highest eigenvalues, we can reduce the data-space dimensionality to 3, allowing us to visualize the data.
2.6 Analysis of the Hyperspace Density
Although, in the present work, we mainly focus on analysis of the 2-D spaces obtained from the projections of 20-D original spaces, we can also investigate the relationship between the several neuronal cells in the original high-dimensional space using a radial density approach. This will be done by evaluating a radial density function around each neuron in the original space. The radial function f(R) gives the number of neurons that are located between distance R and R + ΔR from a particular neuron (with ΔR = 1 used below).
Each neuron, represented by a vector with components given by the respective morphological measurements, is taken as the centre of a n-dimensional sphere, whose radius is progressively increased, as showed in Figure 4A. For each step, the number of neurons inside the shell of the hypersphere is computed, as a function of R. Because each of such functions reflects the surrounding distribution of neighbours Figure 4B, it is expected that two neurons with similar geometrical features and thus mapped nearby in the feature space, will yield similar radial density functions. In addition, because of the finite size of the space occupied by the neurons in the feature space, it is expected that the radial functions will have a peak at some value of R′. In particular, neurons near the border of the occupied space will tend to have such a peak displaced to the larger values of R (corresponding to outliers), while the more central neurons will produce peaks at smaller values of R.
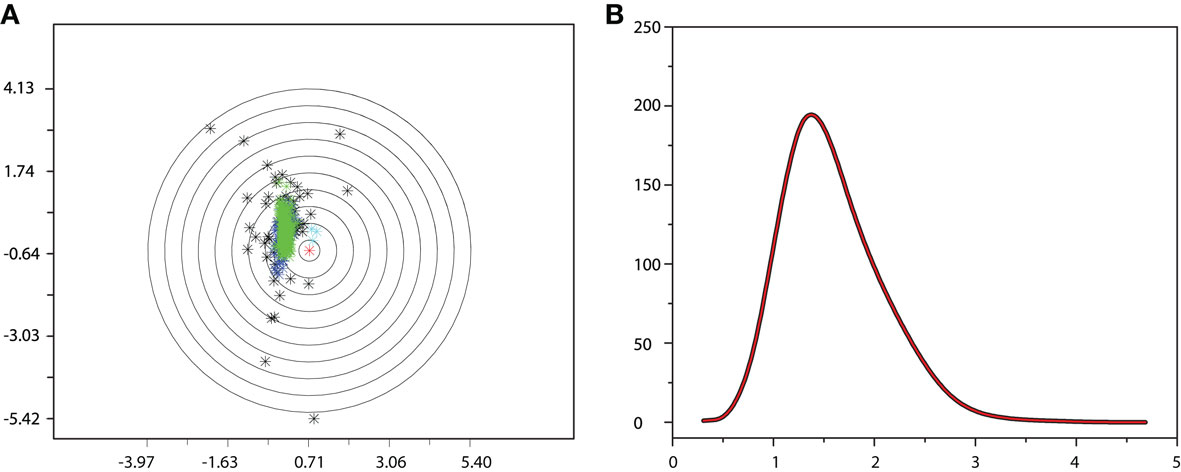
Figure 4. Example of radial density function. (A) Distribution of real neurons in the 2-D feature space. (B) Respective radial density function for the central neuron (in red).
2.7 Simple Reference Model
In this section, we describe a simple reference model to represent the locus of the possible tree-like shapes. The artificial tree-like structures were constructed in the following way. We start with a single straight branch represented by a vector 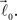 The end of this vector is a bifurcation point at which two other vectors (branches),
The end of this vector is a bifurcation point at which two other vectors (branches), 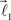 and
and 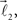 are added to the structure. All these three vectors are coplanar and bifurcation is symmetric so that vectors
are added to the structure. All these three vectors are coplanar and bifurcation is symmetric so that vectors 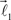 and
and 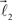 form equal angles with vector
form equal angles with vector 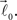 The bifurcation angle, θ (angle between vectors
The bifurcation angle, θ (angle between vectors 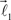 and
and 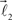 ) is a random variable distributed according to truncated normal distribution in the interval θ ∈ [0, π],
) is a random variable distributed according to truncated normal distribution in the interval θ ∈ [0, π],
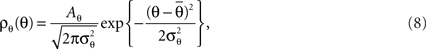
where Aθ is the normalization constant and 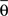 and
and 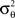 are the parameters of the distribution approaching mean value and variance in the case of sufficiently narrow distribution. Once created, the vectors
are the parameters of the distribution approaching mean value and variance in the case of sufficiently narrow distribution. Once created, the vectors 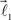 and
and 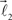 are then simultaneously rotated about vector
are then simultaneously rotated about vector 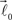 by random angle φ ∈ [−φ*, φ*] distributed according to the truncated normal distribution given by Equation (8) with theta replaced everywhere by φ. Such a rotation is redundant for the first bifurcation point but becomes significant for the subsequent branching points because it enables appearance of 3-D rather than 2-D structures.
by random angle φ ∈ [−φ*, φ*] distributed according to the truncated normal distribution given by Equation (8) with theta replaced everywhere by φ. Such a rotation is redundant for the first bifurcation point but becomes significant for the subsequent branching points because it enables appearance of 3-D rather than 2-D structures.
The ends of the vectors 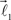 and
and 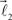 serve as new bifurcation points. For example, the vectors
serve as new bifurcation points. For example, the vectors 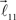 and
and 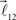 are added to the end of vector
are added to the end of vector 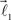 but now with additional constrain such that both vectors
but now with additional constrain such that both vectors 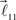 and
and 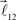 are coplanar with vector
are coplanar with vector 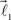 and original vector
and original vector 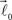 (this original vector is always coplanar to the new branches added to the structure). The other rules are similar to those described for the first branching point.
(this original vector is always coplanar to the new branches added to the structure). The other rules are similar to those described for the first branching point.
In order to account for existence of not necessarily straight branches between bifurcation points, at each bifurcation point, one of the new branches is allowed to be randomly removed with probability pr. The growth process terminates once the predefined number of branches, Nb, both straight and curved, is reached. The lengths of the vectors, 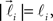 are random discrete variables, ℓ = 0, 1,…, distributed with the following probabilities,
are random discrete variables, ℓ = 0, 1,…, distributed with the following probabilities,

where p(ℓ) is the probability for length of the vector to be equal to ℓ (≥1), pg(ℓ)is the parameter of the model and has the meaning of probability of further growth for a branch of length ℓ. It was assumed that pg(0) = 1, pg(ℓ) = pg if 0 < ℓ < φmax and pg(ℓ) = 0 if ℓ ≥ φmax, so that the maximum branch length is restricted by parameter φmax.
By using this procedure, we generated N = 6000 artificial neurons considering almost all possible values of free parameters according to the real data, i.e., 1 ≤ Nb ≤ 8000, 0 ≤ pg ≤ 1, 0 ≤ pr ≤ 1, 0 ≤ 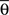 ≤ π, φ* = π, φ* = 0,
≤ π, φ* = π, φ* = 0, 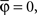 φmax = 100. For the variables σθ and σφ, we considered the ranges [0, π/6] and [0, π/9], respectively. All variables were chosen at random, except for Nb and
φmax = 100. For the variables σθ and σφ, we considered the ranges [0, π/6] and [0, π/9], respectively. All variables were chosen at random, except for Nb and  which were chosen according to the distribution of the real data. It is relevant to note that, because of the generality of our model, we believe it covers the GPF in an almost ideal way. Such a generality of our model is that each of the morphological parameters are covered independently one another in a uniform way. Therefore, provided a large enough number of samples are adopted, the shapes produced by this model can include all cases, even those characterized by interdependence of morphological features. For instance, even if real neurons were characterized by dendritic segments whose length diminished along the branching hierarchy, such a type of neurons would also be generated by our model as a consequence of the independent choice of lengths.
which were chosen according to the distribution of the real data. It is relevant to note that, because of the generality of our model, we believe it covers the GPF in an almost ideal way. Such a generality of our model is that each of the morphological parameters are covered independently one another in a uniform way. Therefore, provided a large enough number of samples are adopted, the shapes produced by this model can include all cases, even those characterized by interdependence of morphological features. For instance, even if real neurons were characterized by dendritic segments whose length diminished along the branching hierarchy, such a type of neurons would also be generated by our model as a consequence of the independent choice of lengths.
3 Results and Discussion
In this section, we present the main findings regarding the morphological neuronal space and its organization. First, the simple reference model is applied for generation of artificial cells used for obtaining the boundaries of the theoretical space. Next, we show how the real cells are distributed in this space. In this analysis, we consider seven measurements and their projections onto 2-D space by using PCA.
Next, we analyze the correlations between all the 20 measurements available in the NeuroMorpho database. These measurements are also analyzed using PCA and canonical projections. Finally, we check how the cells are located in the high-dimensional and projected spaces.
3.1 Modeling the Morphologically Possible Space
In order to demonstrate the feasibility of delineating the boundaries for theoretically possible neuronal forms in the morphospace, we used the reference model presented in Section 2.7. By using this model, we generated 6000 artificial neurons, which then had the following seven features extracted: width, height, and depth of the neurons, number of bifurcations and branches, branch order, and angle between branches. Considering that artificial and real neurons have different length scales, the first three measurements were used in order to generate another three dimensionless measurements, denoted by: L1 = Height/Width, L2 = Depth/Width, and L3 = Depth/Height. The distributions of these variables for thus created artificial neurons are presented by red curves in Figures 5A–G. For comparison, corresponding distributions for real neurons are shown in black. It can be seen that they are quite similar in shape and scale. Partly, this was achieved by using experimentally available values for some of the free parameters in the model, such as the mean number of branches (see Figure 5E) and mean bifurcation angle (G).
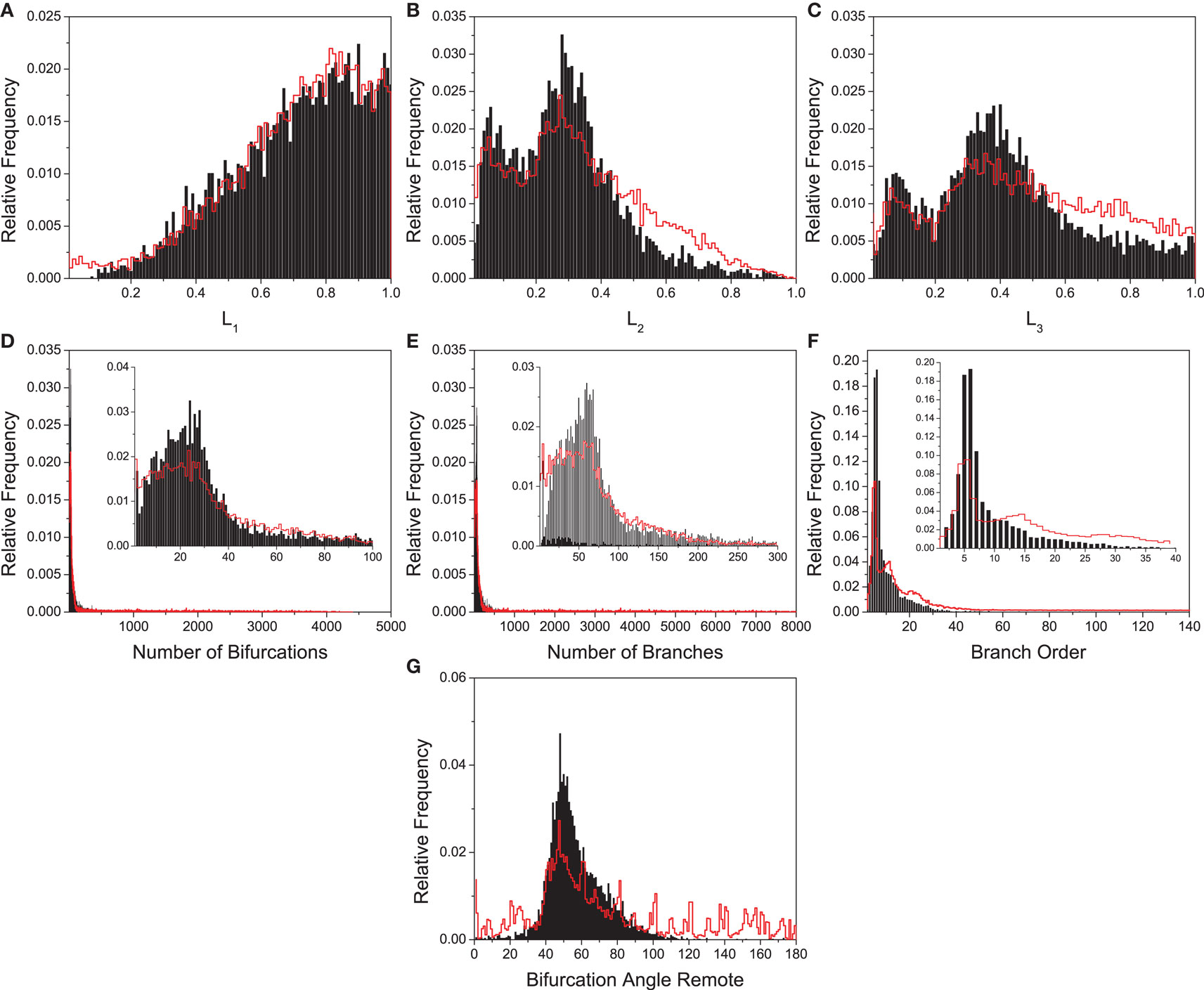
Figure 5. Distribution of (A) L1, (B) L2, (C) L3, (D) number of bifurcations, (E) number of branches, (F) branch orders, and (G) bifurcation angle remote. The red lines correspond to the distribution for the artificial neurons generated by using the model described in this paper. The insets are magnifications of the interest peak regions.
The 7-D space was projected onto two dimensions by using PCA. The results are shown in Figure 6. As we can see, the proposed model (gray points) successfully spanned the entire real morphospace (black open circles). By analyzing the distribution of the real neurons in the morphospace in Figure 6, we can see that the neurons tend to become more 3-D as one moves upwards along the right-hand border of the distribution (i.e., neuron (B) is more 3-D than neuron (A), and so on). A similar effect is observed for artificial neurons shown in Figure 7, where one can also identify the dense globular-type structures typical for the region of morphospace not containing any real neurons.
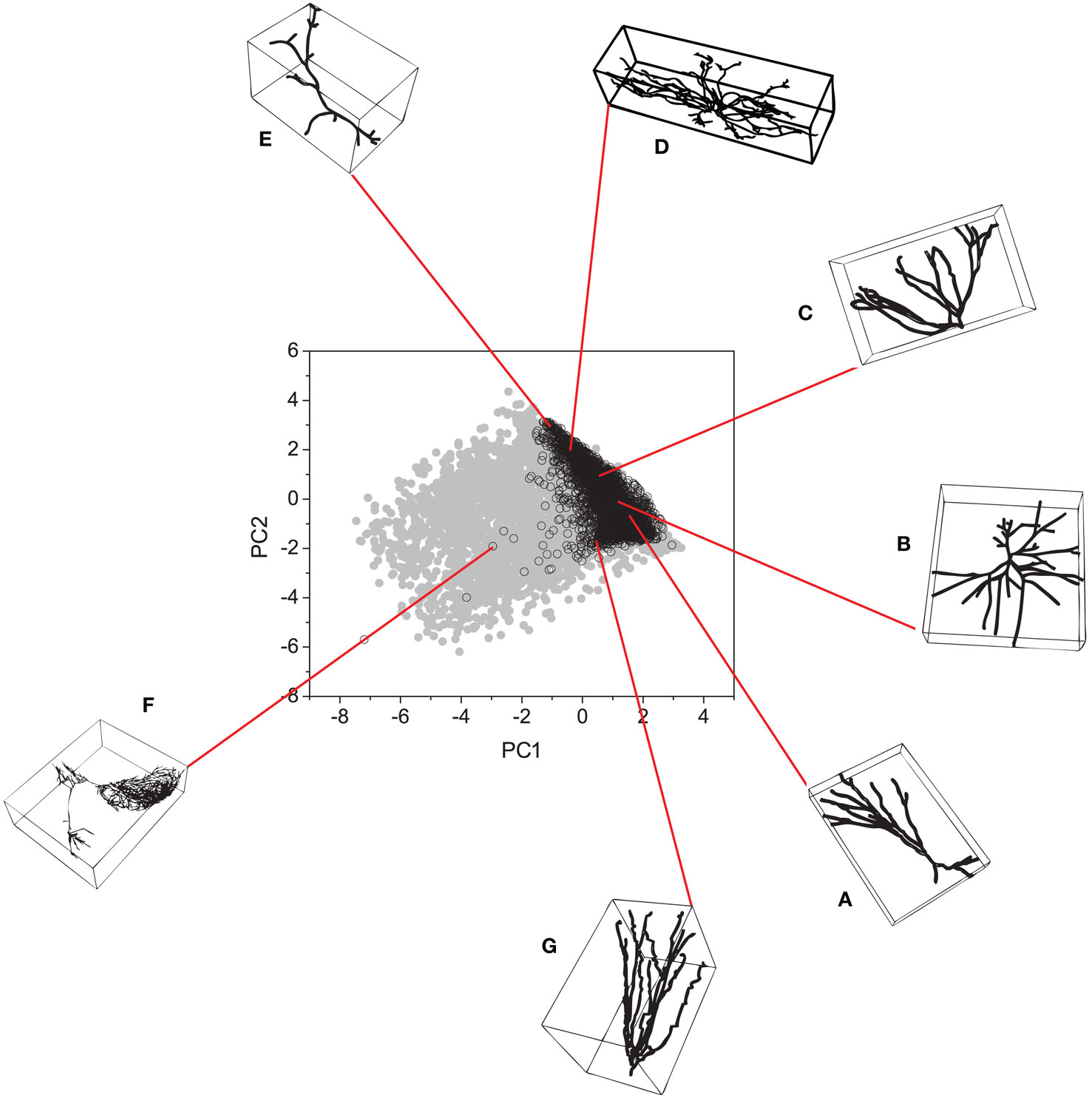
Figure 6. Principal component analysis obtained by considering both real (black open circles) and artificial neurons (grey circles). (A–G) Some real neurons are presented around the plot.
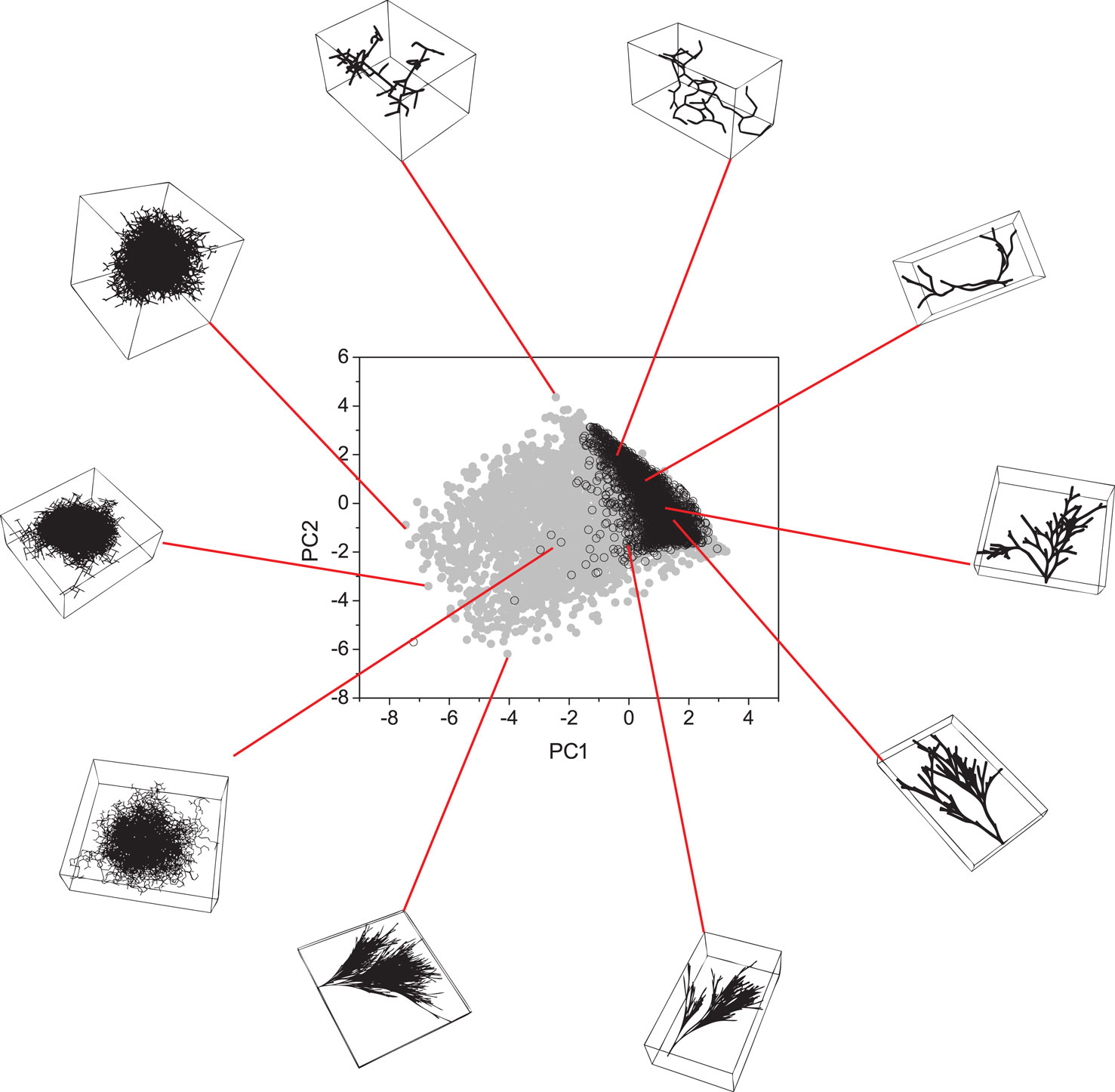
Figure 7. Principal component analysis considering both real (black open circles) and artificial neurons (gray circles). Some artificial neurons are presented around the plot.
We verified that the first principal variable covers 38.3% of the total variance, while the second adds another 25.4%, which means that 63.7% of the total data variation is accounted for by the first two principal components in the PCA. Table 1 shows the PCA weights given by the respective eigenvector components of the two principal main axes. In the first axis, almost all variables have a significant contribution. On the other hand, in the second axis, the variables L3 and L2 have a slight dominance while branch order and bifurcation angle remote have little influence.
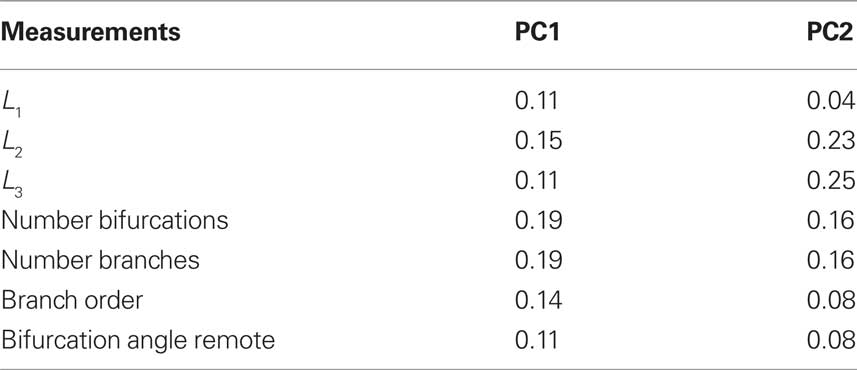
Table 1. Principal component analysis weights considering both real and artificial neurons (see projections in Figures 6 and 7): the seven considered measurements and their respective percentage weights in each principal component axis (PC1 and PC2) are presented. A higher value means that the measurement has a larger contribution to the data variance on the axis.
3.2 Measurements Interrelationship and PCA Analysis
We now focus on the organization of the DPF space, which contains the real neurons. In order to do so, we used all 20 measurements available in NeuroMorpho database. First, we analyzed the interrelationship between these measurements by calculating the Pearson’s correlation coefficient (Härdle and Simar, 2007) between them. The results are represented in gray scale in Figure 8. Particularly high positive values of correlations can be observed between the branch order and the Number of branch and Number of Bifurcation. In principle, provided there is a high number of branching orders, a larger number of branches and bifurcations could be expected. However, this is only true in case most of the orders are well-populated by branches, unlike what would be observed in more linear chains of branchings. Therefore, these two correlations seem to indicate that most of the branching orders are well-populated by branches. Other particularly high correlations can be noticed between the Euclidean distance and the width, height, and depth measurements, which was inherently expected. The three latter measurements are also strongly correlated one another.
Figure 9 presents the PCA results for the cells grouped by cell type (A), brain regions (B), and species (C). For the cell type, we selected the 15 largest groups from among the original 39 features. The neurons in these 15 groups correspond to 95% of the total number of cells. As we can observe in Figure 9A, only the Uniglomerular Projected Neurons (cyan solid circles) constitute a compact cluster.
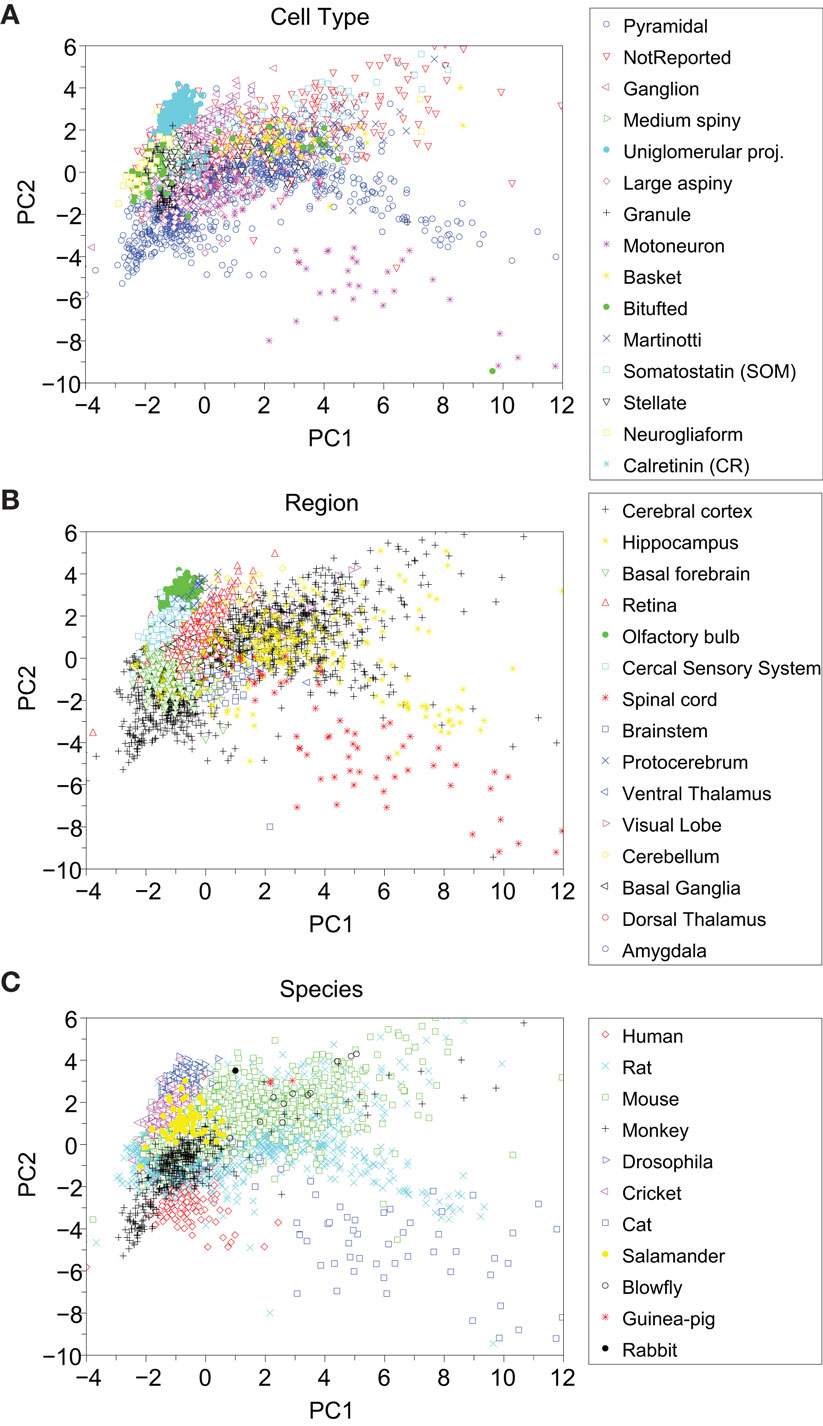
Figure 9. Principal component analysis visualization of the categories grouped by: (A) cell type, (B) brain region, and (C) animal species. There are 39 cell types (only 15 shown here), 15 regions, and 11 species.
Neurogliaform (yellow squares), Calretinin (bright blue star), and Bitufted (green solid circles) exhibit most part of their cells grouped together on the left, while the other categories are not grouped in very-well-defined clusters. The Pyramidal cells (open blue circles), the most numerous group, can be found in many areas of this PCA projection. On the lower right part of the diagram, it is possible to distinguish some cells of the Motoneuron (purple stars) and some Pyramidal cells (blue open circles) forming two separated and scattered subgroups.
In Figure 9B, a larger number of grouped categories can be observed, such as Protocerebrum (blue crosses), Cercal Sensory System (cyan squares), Retina (red upward-pointing triangles), Brainstem (blue squares), Basal Forebrain (green downward-pointing triangles), and Olfactory Bulb (green solid circles). The latter remained well-separated from the others and can be found to correspond to the Uniglomerular cell type. The Cerebral Cortex cells (black plus signs) correspond mainly to the Pyramidal cells and includes some not reported cells. The regions of Spinal Cord (red stars) and Brainstem (Blue squares) are mostly composed by Motoneuron cell type.
Figure 9C, which shows the distinction between cell groups according to the species in which they are found. We can distinguish three well-separated clusters: drosophila (blue right-pointing triangles), human (red diamonds), and cat (blue squares). Cricket (purple left-pointing triangles), salamander (yellow solid circles), and monkey (black plus signs) also have well-defined regions, but they overlap with mouse (green squares) and rat (cyan crosses), which are the two larger categories.
Figure 10 shows the variance accounted for by each of the principal axes. This was calculated using the eigenvalues: higher values contribute more. In this plot, the eigenvalues were converted into percentages and presented in a cumulative sequence of bars, highlighting the cumulative contribution of each variable for the data variability. The first two eigenvalues used in the PCA plots explained 46% of the variance.
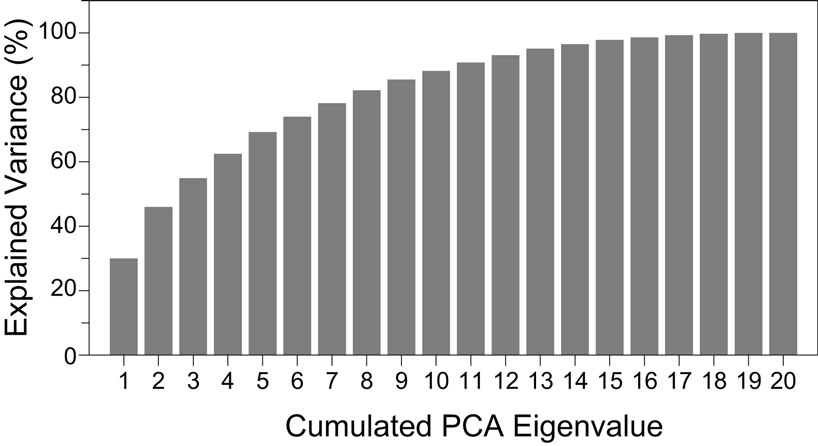
Figure 10. Cumulative explained variance in the PCA, sorted in descending order of their contribution.
Analyzing Table 2, it is possible to see that data variance is distributed amongst several measurements. In the first principal variable, Length and Euclidean Distance have the higher contributions, 0.089 and 0.083, respectively. The largest weights in the second principal variable are the Bifurcation Angle Local (0.090) and Bifurcation Angle Remote (0.093).
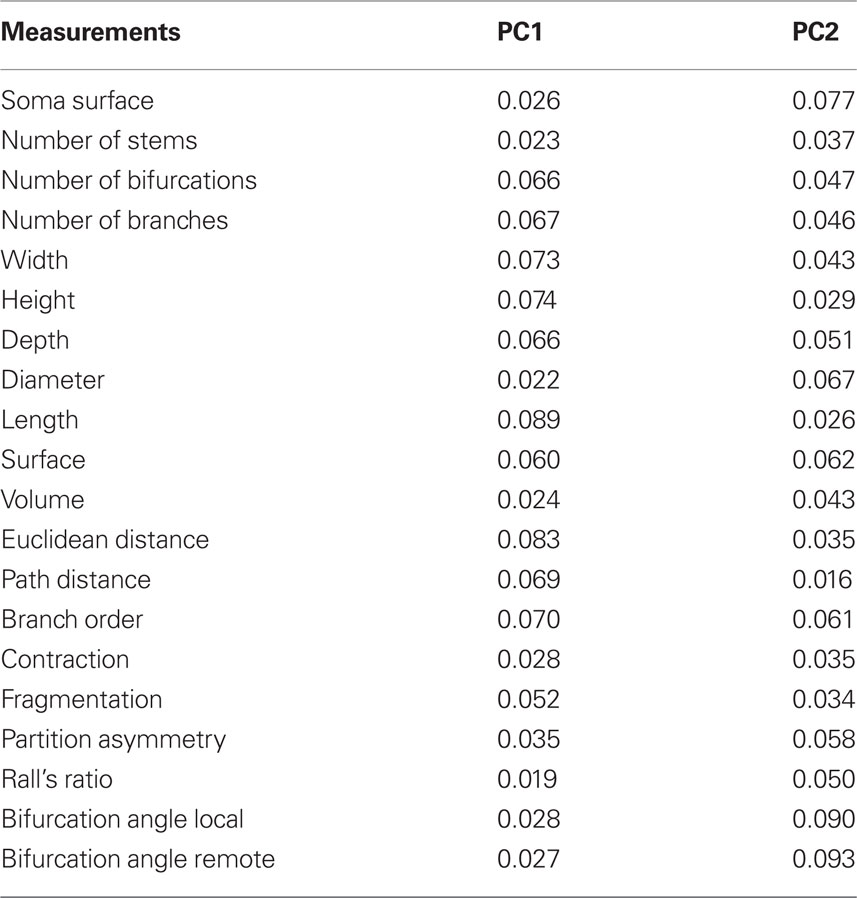
Table 2. Principal component analysis weights regarding the real neurons in NeuroMorpho database (see projections in Figure 9): the percentage weights of the 20 measurements in each principal component axis (PC1 and PC2) are shown. Recall that higher values correspond to measurements which most contribute to the data variance on the axis.
3.3 Distribution of Categories
The canonical variable analysis is a suitable method to visualize and investigate the distribution of categories in the NeuroMorpho database. Figure 11A shows the results for cell type, Figure 11B depicts the results for brain region, and Figure 11C gives the results for species classifications. We used the same 15 types of cells as described in the previous section.
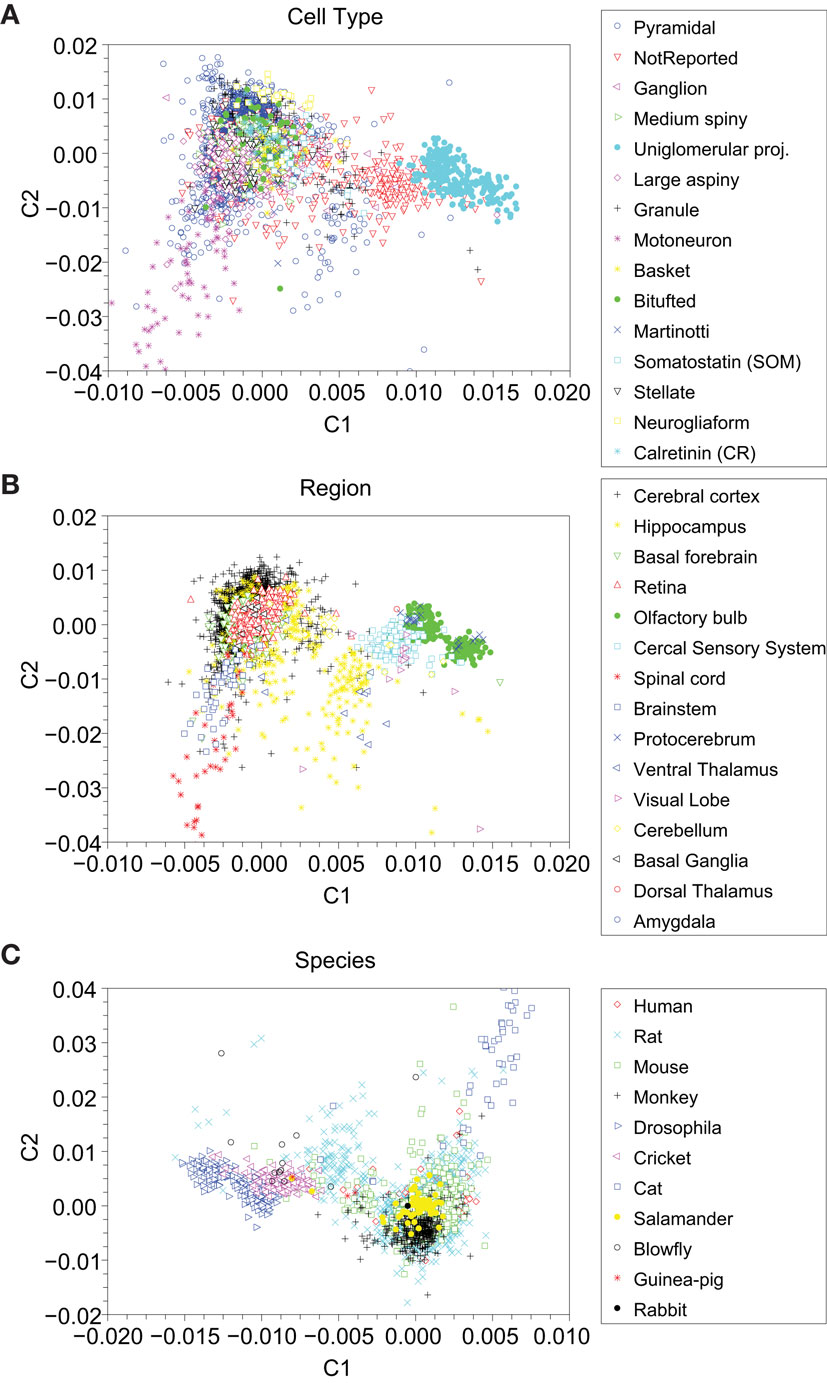
Figure 11. Canonical variable analysis visualization of the categories, grouped by (A) cell type, (B) brain region, and (C) animal species. There are 39 cell types (only 15 shown here), 15 regions, and 11 species.
As could be expected, the canonical analysis revealed a better separation between the considered groups. In Figure 11A, the Uniglomerular Projection Neuron class (cyan circles) remained compact in a specific region and some Motoneuron cells (pink asterisk) are found in the left-hand (middle and bottom) of the graph. In both PCA and canonical analysis, the not reported cells (upside down red triangles) overlapped other cell categories, but on the latter analysis one can observe a well-defined dense core. Also similar as in PCA, the Granule (black crosses), Basket (yellow circles), Bitufted (green solid circles), Somatostatin (cyan square), and Stellate cells (upside down black triangles) are clustered in the same region.
In Figure 11B, we can see a good separation of neuronal cells according to their respective brain regions. Cercal Sensory System (cyan squares), Olfactory Bulb (green circles), and Brainstem (blue squares) yielded well-separated groups. Some regions were split into two sub-regions, particularly cells from Olfactory Bulb (green solid circles), Protocerebrum (blue crosses), and Hippocampus (yellow stars). Basal Forebrain (upside down triangles), Retina (red triangles), and Hippocampus (yellow circles) overlap one another within the greater cluster.
The projection that better allowed the identification of the groups of neuronal cells and their respective regions are given with respect to animal species in Figure 11C. It is clear from this figure that cells from the same animal species tended to group together. Again, we observed splitting of groups into two subgroups for both drosophilas (blue right-pointing triangles) and rats (cyan crosses). Mice (green squares) are scattered between principal cluster and other regions.
3.4 Radial Function
In order to investigate the data directly in the 20-D feature space, we used the radial functions as defined in Section 2.6. Figure 12 demonstrates the radial density functions for four cell types and the PCA projections with both real and artificial neurons. Some representative types of cells were selected in order to investigate for coherence between the densities in the 20-D space and the respective 2-D projections. Purkinje, stellate, Martinotti cells, and lateral horn neuron were selected for this analysis, appearing highlighted within the region of the morphospace (Figure 12E). The radial density functions of the neurons within each of these groups tend to be similar, defining respective clusters in the 20-D space.
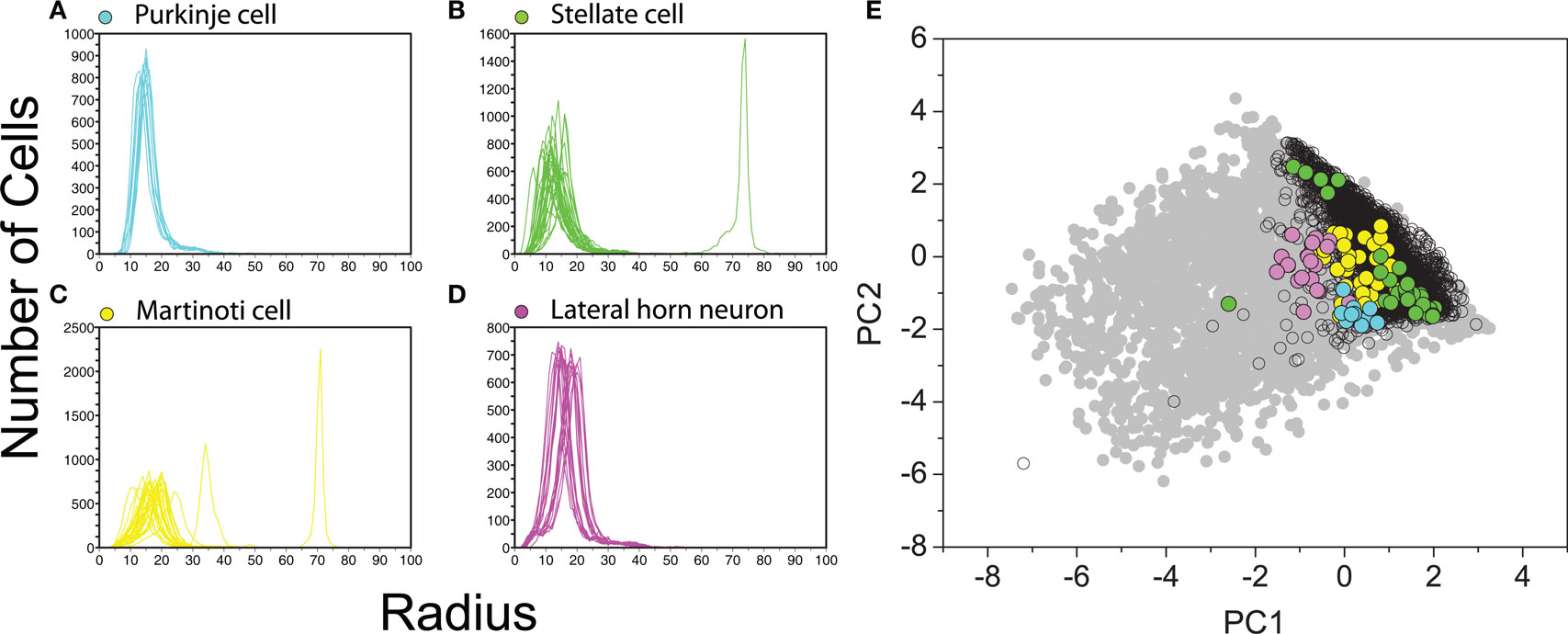
Figure 12. Radial density functions for (A) Purkinje cells, (B) stellate cells, (C) Martinotti cells, and (D) lateral horn cells. Note that cells of the same type tend to have similar radial curves, meaning that they are located around the same region in the 20-D multidimensional feature space. This behavior is also observed when the dimension is reduced by using PCA (E), where cells of the same type tend to be close.
It is interesting to observe the presence of outliers curves in Figures 12B,C. In the first case, we can easily identify the corresponding outlier point in the 2-D projection space. This is not the case of the outlier curves observed in 12(C), where we cannot identify the correspondent outlier points in the projection space. Moreover, stellate neurons are an exception in sense that all of them are close in 20-D space, but give rise to separated clusters in 2-D.
4 Conclusions
Several connectivity and functional properties of the nervous system are ultimately determined or strongly affected by the morphology of the involved individual cells. Given that thousands of neurons became recently available in the public NeuroMorpho database, it is now possible to investigate general morphological properties of neuronal cells. This was the main purpose of the current article. More specifically, we have analyzed the whole public repository NeuroMorpho, which currently contains 5673 cataloged neurons. We resorted to an extension of McGhee’s theoretical framework (morphospace) in order to formalize our approach (McGhee, 2006). Twenty measurements, readily available from NeuroMorpho, were used in order to describe the morphological space in which the neurons are embedded. For the visualization of the morphospace, we applied PCA and canonical analysis over the original 20-D measurement space, yielding the respective 2-D projections. Seven of the original measurements were used in order to compare the real cells with artificial neurons generated by using the reference model proposed in this paper. This allowed us to compare the region of geometrically possible neurons with those neurons which actually appear in nature.
Our results indicate that there is only one single region in the morphological space defined by a density peak. Also, we observed a large empty region extending away from the real neuron cluster. These regions therefore correspond to the geometrically possible neurons, generated by the reference model, which are not found in nature. The neurons belonging to these regions are characterized by significantly greater number of branches.
Regarding the measurements provided by the NeuroMorpho database, we found that some of them are strongly correlated. In particular, measurements that involve euclidean measurements, such as depth × length and euclidean distance × path distance have Pearson correlations above 0.75. All of these correlations were eliminated by using the PCA, which was used to decrease the dimensionality of our data. Yet, the two principal axes were found to depend strongly on almost all the 20 considered measurements. Even so, the two principal axes explained almost 50% the total variance in the original measurement space.
One particularly interesting result is that, with a few exceptions, the neuronal cells tend to cluster together when taken by type, region, and species. This clustering was substantially increased as a result of applying the canonical analysis. We also verified, by using the radial functions, that the clusters in the original 20-D space tended to remain separated in the respective 2-D projections.
The morphology of neurons provides potentially valuable insights not only for neuronal function, but for species evolution, ecology, and functional differences between brain areas. However, the current database size only allows global studies. Important questions, such as “how neuronal morphology evolved along species” or “have neurons become more or less branched along the phylogenetic scale,” remain intractable. Our findings indicate a trend of morphological similarity among neurons from the same species, such as monkey and humans, and rats and mice, but it is not enough to predict any general behavior. The database growth also could help to answer questions regarding ecology, such as “would the neurons of interrelated species share any morphological traits as implied by co-existence and sharing of habitats.” These topics can be considered in future works as well as the improvement of the proposed model, incorporating a larger number of measures in order to decrease the degree of degeneracy implied by using just a few morphological features.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
5 Acknowledgments
Luciano Da Fontoura Costa is grateful to FAPESP (05/00587-5) and CNPq (301303/06-1 and 573583/2008-0) for sponsorship. Krissia Zawadzki is grateful to FAPESP sponsorship (2010/01994-1). Mauro Miazaki thanks FAPESP (07/50988-1) for financial support. Matheus Viana is grateful to FAPESP sponsorship (07/50882-9).
Footnote
References
Agmon-Snir, H., Carr, C. E., and Rinzel, J. (1998). The role of dendrites in auditory coincidence detection. Nature 393, 268–272.
Ascoli, G. A., Donohue, D. E., and Halavi, M. (2007). NeuroMorpho.Org: a central resource for neuronal morphologies. J. Neurosci. 27, 9247–9251.
Ascoli, G. A., and Krichmar, J. L. (2000). L-neuron: a modeling tool for the efficient generation and parsimonious description of dendritic morphology. Neurocomputing 32, 1003.
Costa, L. d. F. (1995). Computer vision based morphometric characterization of neural cells. Rev. Sci. Instrum. 66, 3770–3773.
Costa, L. d. F., Manoel, E. T. M., Faucereau, F., Chelly, J., van Pelt, J., and Ramakers, G. (2002). A shape analysis framework for neuromorphometry. Netw. Comput. Neural Syst. 13, 283–310.
Costa, L. d. F., Rodrigues, F. A., Travieso, G., and Villas Boas, P. R. (2007). Characterization of complex networks: a survey of measurements. Adv. Phys. 56, 167–242.
Costa, L. d. F., and Velte, T. J. (1999). Automatic characterization and classification of ganglion cells from salamander retina. J. Comp. Neurol. 404, 33–51.
Duda, R. O., Hart, P. E., and Stork, D. G. (2001). Pattern Classification. New York: Wiley-Interscience.
Elston, G. N., and Rosa, M. G. P. (2000). Pyramidal cells, patches, and cortical columns: a comparative study of infragranular neurons in TEO, TE, and the superior temporal polysensory area of the macaque monkey. J. Neurosci. 20, RC117.
Fukuda, Y., Hsiao, C. F., Watanabe, M., and Ito, H. (1984). Morphological correlates of physiologically identified y-, x-, and w-cells in cat retina. J. Neurophysiol. 52, 999–1013.
Halavi, M., Polavaram, S., Donohue, D. E., Hamilton, G., Hoyt, J., Smith, K. P., and Ascoli, G. A. (2008). NeuroMorpho.Org implementation of digital neuroscience: dense coverage and integration with the NIF. Neuroinformatics 6, 241–252.
Hamam, B. N., and Kennedy, T. E. (2003). Visualization of the dendritic arbor of neurons in intact 500 μm thick brain slices. J. Neurosci. Methods 123, 61–67.
Härdle, W. K., and Simar, L. (2007). Applied Multivariate Statistical Analysis, 2nd Edn. Berlin/Heidelberg: Springer.
Horcholle-Bossavit, G., Gogan, P., Ivanov, Y., Korogod, S., and Tyc-Dumont, S. (2000). The problem of the morphological noise in reconstructed dendritic arborizations. J. Neurosci. Methods 95, 83–93.
Hosking, C. R., and Schwartz, J. L. (2009). The future’s bright: imaging cell biology in the 21st century. Trends Cell Biol. 9, 553–554.
Koch, C., Poggio, T., and Torre, V. (1982). Retinal ganglion cells: a functional interpretation of dendritic morphology. Philos. Trans. R. Soc. Lond., B, Biol. Sci. 298, 227–264.
Kreindler, A. (1965). Experimental Epilepsy. Progress in Brain Research. New York: Elsevier Publishing Company.
Luczak, A. (2006). Spatial embedding of neuronal trees modeled by diffusive growth. J. Neurosci. Methods 157, 132.
McGhee, G. R. (2006). The Geometry of Evolution: Adaptive Landscapes and Theoretical Morphospaces. New York: Cambridge University Press.
McLachlan, G. J. (2004). Discriminant Analysis and Statistical Pattern Recognition. New York: Wiley-Interscience.
Montague, P. R., and Friedlander, M. J. (1991). Morphogenesis and territorial coverage by isolated mammalian retinal ganglion cells. J. Neurosci. 11, 1440–1457.
Pérez-Reche, F. J., Taraskin, S. N., Costa, L. d. F., Neri, M. F., and Gilligan, A. C. (2010). Complexity and anisotropy in host morphology make populations less susceptible to epidemic outbreaks. J. R. Soc. Interface 7, 1083.
Poznanski, R. R. (1992). Modelling the electronic structure of starburst amacrine cells in the rabbit retina: functional interpretation of dendritic morphology. Bull. Math. Biol. 54, 905–928.
Rodrigues, E. P., Barbosa, M. S., and Costa, L. d. F. (2005). Self-referred approach to lacunarity. Phys. Rev. E 72, 016707.
Schierwagen, A. (2008). Neuronal morphology: shape characteristics and model. Neurophysiology 40, 310–315.
Scorcioni, R., Polavaram, S., and Ascoli, G. (2008). L-measure: a web-accessible tool for the analysis, comparison and search of digital reconstructions of neuronal morphologies. Nat. Protoc. 3, 866–876.
Sholl, D. A. (1953). Dendritic organization in the neurons of the visual and motor cortices of the cat. J. Anat. 87, 387–406.
Toris, C. B., Eiesland, J. L., and Miller, R. F. (1995). Morphology of ganglion cells in the neotenous tiger salamander retina. J. of Comp. Neurol. 352, 535–559.
van Ooyen, A., and van Pelt, J. (2002). Computational Neuroanatomy: Principles and Methods. Totowa, NJ: Humana Press.
van Pelt, J., and Uylings, H. B. M. (2007). “Modeling neuronal growth and shape,” in Modeling Biology – Structures, Behaviors, Evolution, eds M. D. Laubichler and G. B. Müller (The MIT Press, Cambridge, Massachusetts), 195–215.
Wen, Q., and Chklovskii, D. B. (2008). A cost-benefit analysis of neuronal morphology. J. Neurophysiol. 99, 497–500.
Keywords: neuromorphological space, NeuroMorpho, neural morphology, neuroscience
Citation: Costa LDF, Zawadzki K, Miazaki M, Viana MP and Taraskin SN (2010) Unveiling the neuromorphological space. Front. Comput. Neurosci. 4:150. doi: 10.3389/fncom.2010.00150
Received: 13 August 2010;
Accepted: 09 November 2010;
Published online: 02 December 2010.
Edited by:
Jaap van Pelt, Vrije Universiteit Amsterdam, NetherlandsReviewed by:
Jaap van Pelt, Vrije Universiteit Amsterdam, NetherlandsHerbert Jelinek, Charles Sturt University, Australia
Copyright: © 2010 Costa, Zawadzki, Miazaki, Viana and Taraskin. This is an open-access article subject to an exclusive license agreement between the authors and the Frontiers Research Foundation, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Luciano Da Fontoura Costa, Institute of Physics at São Carlos, University of São Paulo, PO Box 369, São Carlos, São Paulo 13.560-970, Brazil. e-mail:bHVjaWFub0BpZnNjLnVzcC5icg==

 Krissia Zawadzki1
Krissia Zawadzki1