- Center for Biological and Computational Learning, McGovern Institute for Brain Research, Massachusetts Institute of Technology, Cambridge, MA, USA
Learning by temporal association rules such as Foldiak's trace rule is an attractive hypothesis that explains the development of invariance in visual recognition. Consistent with these rules, several recent experiments have shown that invariance can be broken at both the psychophysical and single cell levels. We show (1) that temporal association learning provides appropriate invariance in models of object recognition inspired by the visual cortex, (2) that we can replicate the “invariance disruption” experiments using these models with a temporal association learning rule to develop and maintain invariance, and (3) that despite dramatic single cell effects, a population of cells is very robust to these disruptions. We argue that these models account for the stability of perceptual invariance despite the underlying plasticity of the system, the variability of the visual world and expected noise in the biological mechanisms.
1. Introduction
A single object can give rise to a wide variety of images. The pixels (or photoreceptor activations) that make up an image of an object change dramatically when the object is moved relative to its observer. Despite these large changes in sensory input, the brain's ability to recognize objects is relatively unimpeded. Temporal association methods are promising solutions to the problem of how to build computer vision systems that achieve similar feats of invariant recognition (Foldiak, 1991; Wallis and Rolls, 1997; Wiskott and Sejnowski, 2002; Einhauser et al., 2005; Spratling, 2005; Wyss et al., 2006; Franzius et al., 2007; Masquelier and Thorpe, 2007; Masquelier et al., 2007). These methods associate temporally adjacent views under the assumption that temporal adjacency is usually a good cue that two images are of the same object. For example, an eye movement from left to right causes an object to translate on the visual field from right to left; under such a rule, the cells activated by the presence of the object on the right will be linked with the cells activated by the presence of the object on the left. This linkage can be used to signal that the two views represent the same object—despite its change in retinal position.
Recent experimental evidence suggests that the brain may also build invariance with this method. Furthermore, the natural temporal association-based learning rule remains active even after visual development is complete (Wallis and Bulthoff, 2001; Cox et al., 2005; Li and DiCarlo, 2008, 2010; Wallis et al., 2009). This paper addresses the wiring errors that must occur with such a continually active learning rule due to regular disruptions of temporal contiguity (from lighting changes, sudden occlusions, or biological imperfections, for example).
Experimental studies of temporal association involve putting observers in an altered visual environment where objects change identity across saccades. Cox et al. (2005) showed that after about an hour of exposure to an altered environment, where objects changed identity at a specific retinal position, the subjects mistook one object for another at the swapped position while preserving their ability to discriminate the same objects at other positions. A subsequent physiology experiment by Li and DiCarlo using a similar paradigm showed that individual neurons in primate anterior inferotemporal cortex (AIT) change their selectivity in a position-dependent manner after less than an hour of exposure to the altered visual environment (Li and DiCarlo, 2008).
The Li and DiCarlo experiment did not include a behavioral readout, so the effects of the manipulation on the monkey's perception are not currently known, however, the apparent robustness of our visual system suggests it is highly unlikely that the monkey would really be confused between such different looking objects (e.g., a teacup and a sailboat) after such a short exposure to the altered visual environment. In contrast, the Cox et al. psychophysics experiment had a similar timecourse (a significant effect was present after 1 h of exposure) but used much more difficult to discriminate objects (“Greebles” Gauthier and Tarr, 1997).
In this paper, we describe a computational model of invariance learning that shows how strong effects at the single cell level, like those observed in the experiments by Li and DiCarlo do not necessarily cause confusion on the neural population level, and hence do not imply perceptual effects. Our simulations show that a population of cells is surprisingly robust to large numbers of mis-wirings due to errors of temporal association.
2. Materials and Methods
2.1. Hierarchical Models of Object Recognition
We examine temporal association learning with a class of cortical models inspired by Hubel and Wiesel's famous studies of visual cortex (Hubel and Wiesel, 1962). These models contain alternating layers of simple S cells or feature detectors to build specificity, and complex C cells that pool over simple cells to build invariance (Fukushima, 1980; Riesenhuber and Poggio, 1999; Serre et al., 2007). We will focus on one particular such model, HMAX (Serre et al., 2007). The differences between these models are likely irrelevant to the issue we are studying, and thus our results will generalize to other models in this class.
2.2. The HMAX Model
In this model, simple (S) cells compute a measure of their input's similarity to a stored optimal feature via a gaussian radial basis function (RBF) or a normalized dot product. Complex (C) cells pool over S cells by computing the max response of all the S cells with which they are connected. These operations are typically repeated in a hierarchical manner, with the output of one C layer feeding into the next S layer and so on. The model used in this report had four layers: S1 → C1 → S2 → C2. The caption of Figure 1 gives additional details of the model's structure.
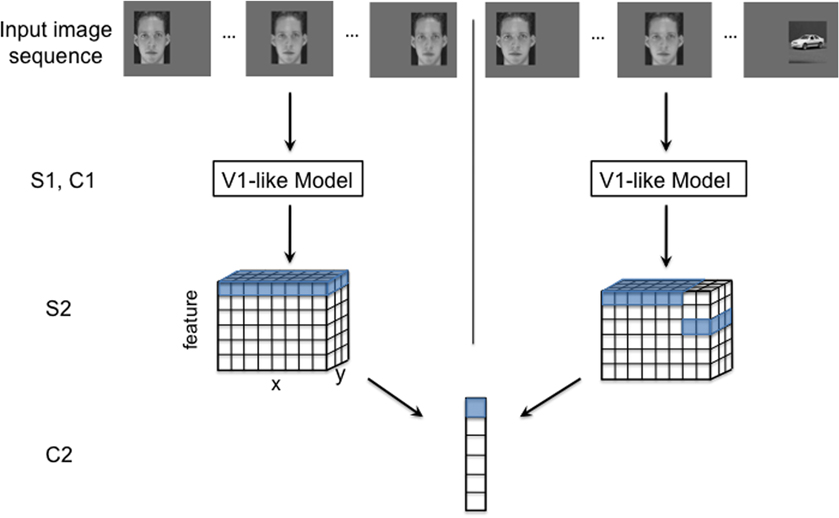
Figure 1. An illustration of the HMAX model with two different input image sequences: a normal translating image sequence (left), and an altered temporal image sequence (right). The model consists of four layers of alternating simple and complex cells. S1 and C1 (V1-like model): The first two model layers make up a V1-like model that mimics simple and complex cells in the primary visual cortex. The first layer, S1, consists of simple orientation-tuned Gabor filters, and cells in the following layer, C1, pool (maximum function) over local regions of a given S1 feature. S2: The next layer, S2, performs template matching between C1 responses from an input image and the C1 responses of stored prototypes (unless otherwise noted, we use prototypes that were tuned to, C1 representations of, natural image patches). Template matching is implemented with a radial basis function (RBF) network, where the responses have a Gaussian-like dependence on the Euclidean distance between the (C1) neural representation of an input image patch and a stored prototype. The RBF response to each template is calculated at various spatial locations for the image (with half overlap). Thus, the S2 response to one image (or image sequence) has three dimensions: x and y, corresponding to the original image dimensions, and feature, the response to each template. C2: Each cell in the final layer, C2, pools (maximum function) over all the S2 units to which it is connected. The S2 to C2 connections are highlighted for both the normal (left) and altered (right) image sequences. To achieve ideal transformation invariance, the C2 cell can pool over all positions for a given feature as shown with the highlighted cells.
In our implementation of the HMAX model, the response of a C2 cell—associating templates w at each position t—is given by:
In the hardwired model, each template wt is replicated at all positions, thus the C2 response models the outcome of a previous temporal association learning process that associated the patterns evoked by a template at each position. The C2 responses of the hardwired model are invariant to translation (Serre et al., 2007; Leibo et al., 2010). The remainder of this report is focused on the model with learned pooling domains. Section 2.3 describes the learning procedure and Figure 2 compares the performance of the hardwired model to an HMAX model with learned C2 pooling domains.
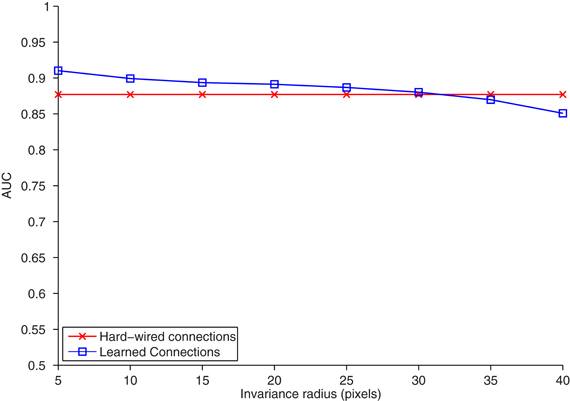
Figure 2. The area under the ROC curve (AUC) (ordinate) plotted for the task of classifying (nearest neighbors) objects appearing on an interval of increasing distance from the reference position (abscissa). The model was trained and tested on separate training and testing sets, each with 20 car and 20 face images. For temporal association learning, one C2 unit is learned for each association period or training image, yielding 40 learned C2 units. One hard-wired C2 unit was learned from each natural image patch that S2 cells were tuned to, yielding 10 hard-wired C2 units. Increasing the number of hard-wired features has only a marginal effect on classification accuracy. For temporal association learning, the association period τ was set to the length of each image sequence (12 frames), and the activation threshold θ was empirically set to 3.9 standard deviations above the mean activation.
As in Serre et al. (2007), we typically obtain S2 templates from patches of natural images (except where noted in Figure 3). The focus of this report is on learning the pooling domains. The choice of templates, i.e., the learning of selectivity (as opposed to invariance) is a separate issue with a large literature of its own1.
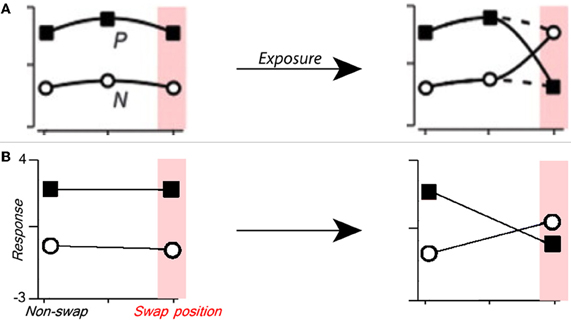
Figure 3. Manipulating single cell translation invariance through altered visual experience. (A) Figure from Li and DiCarlo (2008) summarizing the expected results of swap exposure on a single cell. P is the response to preferred stimulus, and N is that to non-preferred stimulus. (B) The response of a C2 cell tuned to a preferred object before (left) and after (right) altered visual training where the preferred and non-preferred objects were swapped at a given position. To model the experimental paradigm used in Wallis and Bulthoff (2001), Cox et al. (2005), and Li and DiCarlo (2008, 2010), altered training and final testing were performed on the same altered image sequence. The C2 cell's relative response (Z-score) to the preferred and non-preferred objects is shown on the ordinate, and the position (swap or non-swap) is shown on the abscissa.
2.3. Temporal Association Learning
Temporal association learning rules provide a plausible way to learn transformation invariance through natural visual experience (Foldiak, 1991; Wallis and Rolls, 1997; Wiskott and Sejnowski, 2002; Einhauser et al., 2005; Spratling, 2005; Wyss et al., 2006; Franzius et al., 2007; Masquelier and Thorpe, 2007; Masquelier et al., 2007). Objects typically move in and out of our visual field much slower than they transform due to changes in pose and position. Based on this difference in timescale we can group together cells that are tuned to the same object under different transformations.
Our model learns translation invariance from a sequence of images of continuously translating objects. During a training phase prior to each simulation, the model's S2 to C2 connections are learned by associating the patterns evoked by adjacent images in the training sequence as shown in Figure 1, left.
The training phase is divided into temporal association periods. During each temporal association period the highly active S2 cells become connected to the same C2 cell. One C2 cell is learned during each association period. When modeling “standard” (undisrupted) visual experience, as in Figure 2, each association period contains all views of a single object at each retinal position. If temporally adjacent images really depict the same object at different positions, then this procedure will group all the S2 cells that were activated by viewing the object, no matter what spatial location elicited the response. The outcome of this learning procedure in one association period is illustrated in Figure 1, left. The C2 cell produced by this process pools over its connected S2 cells. The potential effect of a temporally altered image sequence is illustrated in Figure 1, right. This altered training will likely result in mis-wirings between the S2 and C2 neurons, which could ultimately alter the system's performance.
2.3.1. Learning rule
In Foldiak's original trace rule, shown in Equation 2, the weight of a synapse wij between an input cell xj and output cell yi is strengthened proportionally to the input activity and the trace or average of recent output activity at time t. The dependence of the trace on previous activity decays over time with the δ term (Foldiak, 1991).
Foldiak trace rule:
In the HMAX model, connections between S and C cells are binary. Additionally, in our training case we want to learn connections based on image sequences of a known length, and thus for simplicity should include a hard time window rather than a decaying time dependence. Thus we employed a modified trace rule that is appropriate for learning S2 to C2 connections in the HMAX model.
Modified trace rule for the HMAX model:
With this learning rule, one C2 cell with index i is produced for each association period. The length of the association period is τ.
3. Results
3.1. Training for Translation Invariance
We model natural invariance learning with a training phase where the model learns to group different representations of a given object based on the learning rule in Equation 3. Through the learning rule, the model groups continuously translating images that move across the field of view over each association period τ. An example of a translating image sequence is shown at the top, left of Figure 1. During this training phase, the model learns the domain of pooling for each C2 cell.
3.2. Accuracy of Temporal Association Learning
To test the performance of the HMAX model with the learning rule in Equation 3, we train the model with a sequence of training images. Next, we compare the learned model's performance to that of the hard-wired HMAX (Serre et al., 2007) on a translation-invariant recognition task. In standard implementations of the HMAX model, the S2 to C2 connections are hard-wired, each C2 cell pools all the S2 responses for a given template globally over all spatial locations. This pooling gives the model translation invariance and mimics the outcome of an idealized temporal association process.
The task is a 20 face and 20 car identification task, where the target images are similar (but not identical) for different translated views2. We collect hard-wired C2 units and C2 units learned from temporal sequences of the faces and cars. We then used a nearest neighbor classifier to compare the correlation of C2 responses for translated objects to those in a given reference position. The accuracy of the two methods (hard-wired and learned from test images) versus translation is shown in Figure 2. The two methods performed equally well. This confirms that the temporal associations learned from this training yield correct invariance.
3.3. Manipulating the Translation Invariance of a Single Cell
In their physiology experiments Li and DiCarlo identified AIT cells that responded preferentially to one object over another, they then performed altered temporal association training where the two objects were swapped at a given position (Li and DiCarlo, 2008). To model these experiments we perform temporal association learning (described by Equation 3) with a translating image of one face and one car. For this simulation, the S2 units are tuned to the same face and car images (see Figure 1 caption) to mimic object-selective cells that are found in AIT. Next we select a “swap position” and perform completely new, altered training with the face and car images swapped only at that position (see Figure 1, top right). After the altered training, we observe the response (of one C2 cell) to the two objects at the swap position and another non-swap position in the visual field that was unaltered during training.
As shown in Figure 3, the C2 response for the preferred object at the swap position (but not the non-swap position) is lower after training, and the C2 response to the non-preferred object is higher at the swap position. As in the physiology experiments performed by Li and DiCarlo, these results are object and position specific. Though unsurprising, this result draws a parallel between the response of a single C2 unit and the physiological response of a single cell.
3.4. Individual Cell Versus Population Response
In the previous section we modeled the single cell results of Li and DiCarlo, namely that translation-invariant representations of objects can be disrupted by a relatively small amount of exposure to altered temporal associations. However, single cell changes do not necessarily reflect whole population or perceptual behavior and no behavioral tests were performed on the animals in this study.
A cortical model with a temporal association learning rule provides a way to model population behavior with swap exposures similar to the ones used by Li and DiCarlo (2008, 2010). A C2 cell in the HMAX model can be treated as analogous to an AIT cell (as tested by Li and DiCarlo), and a C2 vector as a population of these cells. We can thus apply a classifier to this cell population to obtain a model of behavior or perception.
3.5. Robustness of Temporal Association Learning with a Population of Cells
We next model the response of a population of cells to different amounts of swap exposure, as illustrated in Figure 1, right. The translating image sequence with which we train the model replicates visual experience, and thus jumbling varying amounts of these training images is analogous to presenting different amounts of altered exposure to a test subject as in (Li and DiCarlo, 2008, 2010). These disruptions also model the mis-associations that may occur with temporal association learning due to sudden changes in the visual field (such as light, occlusions, etc.), or other imperfections of the biological learning mechanism. During each training phase we randomly swap different face and car images in the image sequences with a certain probability, and observe the effect on the response of a classifier to a population of C2 cells. The performance, as measured by area under the ROC curve (AUC), versus different neural population sizes (number of C2 cells) is shown in Figure 4 for several amounts of altered exposure. We measured altered exposure by the probability of flipping a face and car image in the training sequence.
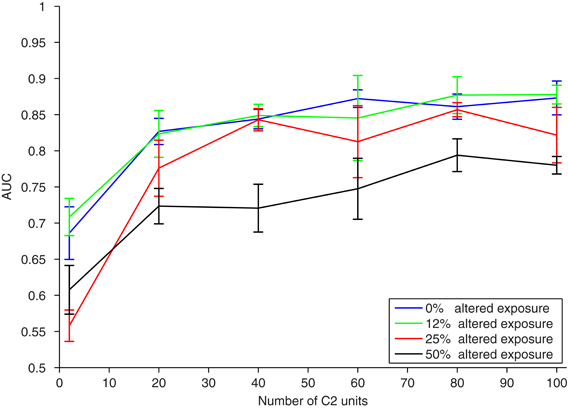
Figure 4. Results of a translation invariance task (±40 pixels) with varying amounts of altered visual experience. To model the experimental paradigm used in (Wallis and Bulthoff, 2001; Cox et al., 2005; Li and DiCarlo, 2008, 2010; Wallis et al., 2009), training and testing were performed on the same altered image sequence. The performance (AUC) on the same translation-invariant recognition task as in Figure 2, with a nearest neighbor classifier, versus the number of C2 units. Different curves have a different amount of exposure to altered visual training as measured by the probability of swapping a car and face image during training. The error bars show ± one standard deviation over runs using different natural image patches as S2 templates.
A small amount of exposure to altered temporal training (0.125 probability of flipping each face and car) has negligible effects, and the model under this altered training performs as well as with normal temporal training. A larger amount of exposure to altered temporal training (0.25 image flip probability) is not significantly different than perfect temporal training, especially if the neural population is large enough. With enough C2 cells, each of which is learned from a temporal training sequence, the effects of small amounts of jumbling in training images are insignificant. Even with half altered exposure (0.5 image flip probability), if there are enough C2 cells, then classification performance is still reasonable. This is likely because with similar training (multiple translating faces or cars) redundant C2 cells are formed, creating robustness to association errors that occurred during altered training. Similar redundancies are likely to occur in natural vision. This indicates that in natural learning mis-wirings do not have a strong effect on learning translation invariance, particularly with familiar objects or tasks.
4. Discussion
We use a cortical model inspired by Hubel and Wiesel (1962), where translation invariance is learned through a variation of Foldiak's trace rule (Foldiak, 1991) to model the visual response to altered temporal exposure. We first show that this temporal association learning rule is accurate by comparing its performance to that of a similar model with hard-wired translation invariance (Serre et al., 2007). This extends previous modeling results by Masquelier et al. (2007) for models of V1 to higher levels in the visual recognition architecture. Next, we test the robustness of translation invariance learning on single cell and whole population responses. We show that even if single cell translation invariance is disrupted, the whole population is robust enough to maintain invariance despite a large number of mis-wirings.
The results of this study provide insight into the evolution and development of transformation invariance mechanisms in the brain. It is unclear why a translation invariance learning rule, like the one we modeled, and those confirmed by Cox et al. (2005) and Li and DiCarlo (2008, 2010), would remain active after development. We have shown that the errors associated with a continuously active learning rule are negligible, and thus it may be simpler to leave these processes active than to develop a mechanism to turn them off.
Extending this logic to other transformations is interesting. Translation is a generic transformation; all objects translate in the same manner, so translation invariance, in principle, can be learned during development for all types of objects. This is not true of “non-generic” or class-specific transformations, such as rotation in depth, which depends on the 3-D structure of an individual object or class of objects (Vetter et al., 1995; Leibo et al., 2010, 2011). For example, knowledge of how 2-D images of faces rotate in depth can be used to predict how a new face will appear after a rotation. However, knowledge of how faces rotate is not useful for predicting the appearance of non-face objects after the same 3-D transformation. Many transformations are class-specific in this sense3. One hypothesis as to why invariance-learning mechanisms remain active in the mature visual system could be a continuing need to learn and refine invariant representations for more objects under non-generic transformations.
Disrupting rotation in depth has been studied in psychophysics experiments. Wallis and Bulthoff showed that training subjects with slowly morphing faces, disrupts viewpoint invariance after only a few instances of altered training (Wallis and Bulthoff, 2001; Wallis et al., 2009). This effect occurs with a faster time course than observed in the translation invariance experiments (Cox et al., 2005). One possible explanation for this time discrepancy is that face processing mechanisms are higher-level than those for the “greeble objects” and thus easier to disrupt. However, we conjecture that the strong, fast effect has to do with the type of transformation rather than the specific class of stimuli.
Unlike generic transformations, class-specific transformations cannot be generalized between objects with different properties. It is even possible that we learn non-generic transformations of novel objects through a memory-based architecture that requires the visual system to store each viewpoint of a novel object. Therefore, it is logical that learning rules for non-generic transformations should remain active as we are exposed to new objects throughout life.
In daily visual experience we are exposed more to translations than rotations in depth, so through visual development or evolutionary mechanisms there may be more cells dedicated to translation-invariance than rotation-invariance. We showed that the size of a population of cells has a significant effect on its robustness to altered training, see Figure 4. Thus rotation invariance may also be easier to disrupt, because there could be fewer cells involved in this process.
Two plausible hypotheses both point to rotation (class-specific) versus translation (generic) being the key difference between the Wallis and Bulthoff and Cox et al. experiments. We conjecture that if an experiment controlled for variables such as the type and size of the stimulus, class-specific invariances would be easier to disrupt than generic invariances.
This study shows that despite unavoidable disruptions, models based on temporal association learning are quite robust and therefore provide a promising solution for learning invariance from natural vision. These models will also be critical in understanding the interplay between the mechanisms for developing different types of transformation invariance.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work was supported by the following grants: NSF-0640097, NSF-0827427, NSF-0645960, DARPA-DSO, AFSOR FA8650-50-C-7262, AFSOR FA9550-09-1-0606.
Footnotes
- ^See Leibo et al. (2010) for a discussion of the impact of template-choice on HMAX results with a similar translation-invariant recognition task to the one used here.
- ^The invariance-training and testing datasets come from a concatenation of two datasets from: ETH80 (http://www.d2.mpi-inf.mpg.de/Datasets/ETH80) and ORL (http://www.cl.cam.ac.uk/research/dtg/attarchive/facedatabase.html). Except when noted, the image patches used to obtain the S2 templates were obtained from a different, unrelated, collection of natural images; see Serre et al. (2007) for details.
- ^Changes in illumination are another example of a class-specific transformation. These depend on both 3-D structure and material properties of objects (Leibo et al., 2011).
References
Cox, D., Meier, P., Oertelt, N., and DiCarlo, J. J. (2005). ‘Breaking’ position-invariant object recognition. Nat. Neurosci. 8, 1145–1147.
Einhauser, W., Hipp, J., Eggert, J., Korner, E., and Konig, P. (2005). Learning viewpoint invariant object representations using a temporal coherence principle. Biol. Cybern. 93, 79–90.
Franzius, M., Sprekeler, H., and Wiskott, L. (2007). Slowness and sparseness lead to place, head-direction, and spatial-view cells. PLoS Comput. Biol. 3:e166. doi: 10.1371/journal.pcbi.0030166
Fukushima, K. (1980). Neocognitron: a self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biol. Cybern. 36, 193–201.
Gauthier, I., and Tarr, M. (1997). Becoming a “greeble” expert: exploring mechanisms for face recognition. Vision Res. 37, 1673–1682.
Hubel, D. H., and Wiesel, T. N. (1962). Receptive fields, binocular interaction and functional architecture in the cats visual cortex. J. Physiol. 160, 106–154.
Leibo, J. Z., Mutch, J., and Poggio, T. (2011). “Why the brain separates face recognition from object recognition,” in Advances in Neural Information Processing Systems (NIPS), (Cambridge, MA).
Leibo, J. Z., Mutch, J., Rosasco, L., Ullman, S., and Poggio, T. (2010). Learning generic invariances in object recognition: translation and scale. MIT-CSAIL-TR-2010–2061.
Li, N., and DiCarlo, J. J. (2008). Unsupervised natural experience rapidly alters invariant object representation in visual cortex. Science 321, 1502–1507.
Li, N., and DiCarlo, J. J. (2010). Unsupervised natural visual experience rapidly reshapes size-invariant object representation in inferior temporal cortex. Neuron 67, 1062–1075.
Masquelier, T., Serre, T., Thorpe, S., and Poggio, T. (2007). Learning complex cell invariance from natural videos: a plausible proof. MIT-CSAIL-TR-2007–2060.
Masquelier, T., and Thorpe, S. J. (2007). Unsupervised learning of visual features through spike timing dependent plasticity. PLoS Comput. Biol. 3:e31. doi: 10.1371/journal.pcbi.0030031
Riesenhuber, M., and Poggio, T. (1999). Hierarchical models of object recognition in cortex. Nat. Neurosci. 2, 1019–1025.
Serre, T., Wolf, L., Bileschi, S., Riesenhuber, M., and Poggio, T. (2007). Robust object recognition with cortex-like mechanisms. IEEE Trans. Pattern Anal. Mach. Intell. 29, 411–426.
Spratling, M. (2005). Learning viewpoint invariant perceptual representations from cluttered images. IEEE Trans. Pattern Anal. Mach. Intell. 27, 753–761.
Vetter, T., Hurlbert, A., and Poggio, T. (1995). View-based models of 3D object recognition: invariance to imaging transformations. Cereb. Cortex 3, 261–269.
Wallis, G., Backus, B. T., Langer, M., Huebner, G., and Bulthoff, H. (2009). Learning illumination- and orientation-invariant representations of objects through temporal association. J. Vis. 96, 1–8.
Wallis, G., and Bulthoff, H. (2001). Effects of temporal association on recognition memory. Proc. Natl. Acad. Sci. U.S.A. 98, 4800–4804.
Wallis, G., and Rolls, E. T. (1997). Invariant face and object recognition in the visual system. Prog. Neurobiol. 51, 167–194.
Wiskott, L., and Sejnowski, T. J. (2002). Slow feature analysis: unsupervised learning of invariances. Neural Comput. 14, 715–770.
Keywords: object recognition, invariance, vision, trace rule, cortical models, inferotemporal cortex, visual development
Citation: Isik L, Leibo JZ and Poggio T (2012) Learning and disrupting invariance in visual recognition with a temporal association rule. Front. Comput. Neurosci. 6:37. doi: 10.3389/fncom.2012.00037
Received: 01 November 2011; Accepted: 27 May 2012;
Published online: 25 June 2012.
Edited by:
Evgeniy Bart, Palo Alto Research Center, USAReviewed by:
Peter Konig, University of Osnabrück, GermanyJay Hegdé, Georgia Health Sciences University, USA
Copyright: © 2012 Isik, Leibo and Poggio. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Leyla Isik, Center for Biological and Computational Learning, McGovern Institute for Brain Research, Massachusetts Institute of Technology, Bldg. 46-5155, 77 Massachusetts Avenue, Cambridge, MA, USA. e-mail:bGlzaWtAbWl0LmVkdQ==
† These authors contributed equally to this work.


