Recurrent network of perceptrons with three state synapses achieves competitive classification on real inputs

1. Introduction

Work on attractor network models with Hebbian learning mechanisms has spanned almost three decades (Hopfield, 1982; Amit, 1989; Amit and Brunel, 1997; Wang, 1999; Brunel and Wang, 2001; Curti et al., 2004). Most work has focused on the mathematical and biological properties of attractor networks with very naive assumptions on the distribution of the input data; few have attempted to test these on highly variable realistic data. Such data may violate the simple assumptions of the models; they may have correlation between class prototypes or highly variable class coding levels. Some attempts have been made to bridge this gap between theory and practice. Amit and Mascaro (2001), in order to deal with the complexity of real inputs, propose a two layer architecture with a non-recurrent feature layer feeding into a recurrent attractor layer. In the attractor layer, random subsets of approximately the same size were assigned to each class. The main role of learning was to update the feedforward connections from the feature layer to the attractor layer. Classification was expressed through a majority vote in the attractor layer; actual attractor dynamics proved to be unstable. Assuming a fixed threshold for all neurons in the attractor layer, it was necessary to introduce a field-dependent learning rule that controlled the number of potentiated synapses that could feed into a single neuron. Furthermore, to achieve competitive classification rates, it was necessary to perform a boosting operation with multiple networks. Subsequent work (Senn and Fusi, 2005) provided an analysis of field-dependent learning, and experiments were performed on the Latex database. This analysis was further pursued in Brader et al. (2007) using complex spike-driven synaptic dynamics. In both cases majority voting was used for classification.

The contribution of this paper is two-fold. First, we achieve classification through recurrent dynamics in the attractor layer which is stabilized with recurrent inhibition. Second, we employ three state synapses with feedforward inhibition, allowing us to achieve competitive classification rates with one network without the boosting required in Amit and Mascaro (2001). The advantage of a three state feedforward synapse with feedforward inhibition over a two state synapse stems from the ability to give a positive effective weight to features with high probability on class and low probability off class and a negative effective weight to features with low probability on class and high off class. Both types of features are informative for class/non-class discrimination. The intermediate “control” level of less informative features is assigned an effective zero weight. This modification in the number of synaptic states coupled with the appropriate feedforward inhibition leads to dramatic increases in classification rates. The use of inhibition to create effective negative synapses was proposed in Scofield and Cooper (1985) in a model of learning in primary visual cortex. An inhibitory interneuron receives input from the presynaptic neuron and feeds into the postsynaptic neuron. This type of feedforward system has since then been used in many models. Recently in Parisien et al. (2008) a more general approach is proposed to achieve effective negative weights avoiding a dedicated interneuron for each synapse. This is the approach taken here.

That synapses have a limited number of states has been advocated in a number of papers, see for example, Petersen et al. (1998), O'Connor et al. (2005a,b). Experimental reports on LTP and LTD typically show three synaptic levels for any given synapse. These include a control level, a depressed state, and a potentiated state, see Mu and Poo (2006), Dong et al. (2008), and Collingridge et al. (2010), although the distribution of the strengths of the potentiated states over the population of synapses has a significant spread, see Brunel et al. (2004). In our model the three states are uniformly set at 0, depressed; 1, control; and 2, potentiated.

There has been some work on analyzing the advantages of multi-state synapses versus binary synapses for feedforward systems. This work has mainly been in the context of memory capacity with the assumption of standard uncorrelated random type inputs with some coding level. See for example Ben Dayan Rubin and Fusi (2007), Leibold and Kempter (2008). In broad terms, it appears that multiple level synapses do not provide a significant increase in memory capacity for low coding levels. Here the question is quite different. We are interested in the discriminative power of the individual perceptrons on real-world data with significant overlap between the features of competing classes and significant noise in terms of the presence or absence of a feature in any given class.

2. Materials and Methods

The network architecture consists of two layers, a retinotopic input feature layer F and an attractor layer A that contains random populations A_c coding for the different classes. The attractor layer has recurrent connections labeled J_ij, between presynaptic neuron a_i ∈ A and post-synaptic neuron a_j ∈ A. The input layer has only feedforward connections labeled J_kj between feature f_k and attractor neuron a_j, see Figure 1. The two-layer separation was initially motivated in Amit and Mascaro (2001) by the failure to obtain stable attractor behavior in recurrent networks of neurons coding input features such as edges or functions of edges on real images. The variability in the number of high probability features among the different classes was too large as well as the overlap of features between classes. The coding of classes and the memory retrieval phenomena—the important characteristics in attractor networks—are therefore pushed to an “abstract” attractor layer with random subsets of neurons coding for each class. These subsets do not have any inherent relation to the sensory or visual input. In Figure 1 the different color nodes in the attractor layer A represent different class populations A_c, showing only a subset of the potentiated synapses connecting them. All neurons in the network are binary, taking only values of 0 or 1. All synapses in the network can take on three states, 1, baseline; 0, depressed; and 2, potentiated.

FIGURE 1

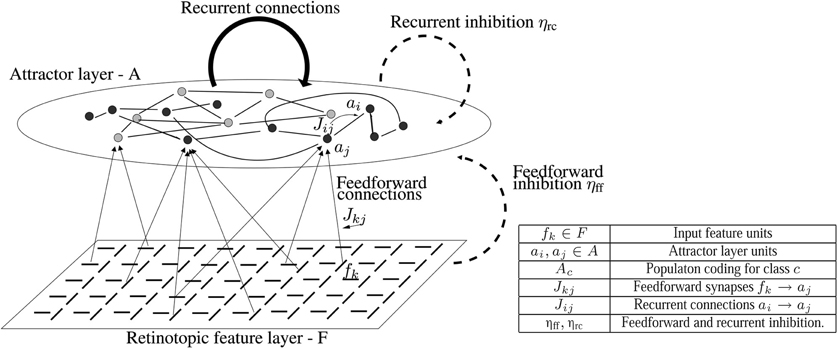
Figure 1. Architecture of network. Input retinotopic feature layer oriented edge features with units denoted f_k. Attractor layer A with units a_i, aj. Units of different colors correspond to different class populations A_c. Feedforward connections (F → A) denoted J_kj and recurrent connections A → A denoted J_ij. Feedforward inhibition η_ff and recurrent inhibition η_rc.

2.1. The Input Layer

The input layer consists of retinotopic arrays of local features computed from the input image. There are no connections between neurons in the input layer, only feedforward connections to attractor neurons. Each neuron in the input layer corresponds to a particular visual feature at some location. If a feature is detected at a location, activation is spread to the surrounding neighborhood. Spreading introduces more robustness to local shape variability and is analogous to the abstraction of the complex neuron. This was first employed in the neo-cognitron (Fukushima and Miyake, 1982). It is a special case of the MAX operation from Riesenhuber and Poggio (1999). Most experiments were performed with binary oriented edge features. These are selective to discontinuity orientation at eight orientations—multiples of π/4, at each location in the image. The neuron activates at a location if an edge is present with an angle that is within π/8 of the neuron's defined orientation. The neuron thus has a step function tuning curve as opposed to the traditional bell-shaped tuning curve. The input may be compared to an abstraction of the retinotopic map of complex cells in V1 (Hubel, 1988). In Figure 2 we show the eight edge orientations, an example of an edge detected on an image and illustrate the notion of spreading.

FIGURE 2

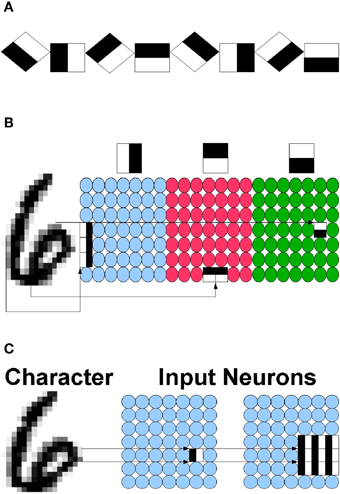
Figure 2. (A) Eight oriented edges. (B) Neurons respond to a particular feature at a particular location. (C) If an edge feature is detected at some pixel, neurons in the neighborhood are also activated. In this case, the neighborhood is 3 × 3.

We also experimented with higher level features called edge pairs. These are spatial conjunctions of two different edges, a center edge and another edge, in five possible relative orientations, (± π/2, ± π/4, 0) anywhere in an adjacent constrained region. The size of the area searched for the second edge was nine pixels. The set of edge pairs centered at a horizontal edge is illustrated in Figure 3. Similar conjunctions are proposed in Riesenhuber and Poggio (2000). Neurons receptive to such features can be viewed as coarse curvature selectors and are are analogous to curvature detectors found in Hegde and Van Essen (2000) and Ito and Komatsu (2004). Edge pairs are more sparsely distributed in generic images than single edges and are quite stable at particular locations on the object. A detailed study of the statistics of such features in generic images can be found in Amit (2002). The edge pairs are used without the input edge features since for each orientation the first pair shown in Figure 3 detects orientation, but with higher specificity. The increase in feature specificity allows for an increase in the range of spreading, yielding more invariance. Increased spreading also allows for greater subsampling of the feature locations to a coarser grid. The end result is an improvement in the classification rate.

FIGURE 3

Figure 3. Illustration of five edge pairs centered at a horizontal edge. There are five similar pairs for each of the other seven edge orientations.

Feedforward connections to the attractor layer are random; a connection is established between an input neuron f_k and attractor neuron a_j with probability p_ff independently for each input neuron. The set of input neurons feeding into unit a_j is denoted ℱ_j. Each attractor neuron therefore functions as a perceptron with highly constrained weights {0, 1, 2}, which classifies between its assigned class and “all the rest.” The random distribution of the feedforward connections is one way to ensure that these perceptrons constitute different and hopefully weakly correlated classifiers [see Amit and Geman (1997)]. They respond to different subsets of features (Amit and Mascaro, 2001), whose size is determined by p_ff. This is one motivation for using multiple perceptrons as opposed to one unit per class. However, as we will see below, the primary motivation is the ability to code classification as the sustained activity of this population in a recurrent network.

A complementary approach to randomizing the perceptrons is through the learning process, as opposed to the physical network architecture. With full feedforward connectivity—p_ff = 1—this is achieved through randomization in the potentiation and depression coupled with the field dependent learning, as detailed in Section 2.4.

2.2. The Attractor Layer

Classification takes place in the attractor layer which is fully connected. Classes are represented by a population of attractor neurons selected at random with probability p_cl. Because of the random selection there will be some overlap between the populations. Learning of synaptic connections in the attractor layer is done prior to the presentation of any input images. A class label is chosen at random, the units coding for that class are activated, and the synapses are updated based on the learning rule described in Section 2.4. The synapses connecting units within the same class population end up potentiated with high probability, and synapses from units of a class population to non-class units end up depressed with high probability.

Classification is represented as the stable sustained activity of the elements of one population and the elimination of activity in the others. Upon presentation of an image to the network, the attractor layer is initialized with the response of each of the perceptrons to the stimulus coming from the input layer. Let ℱ_j ⊂ F be the set of input neurons connected to a_j. The feedforward field h^ff at a_j is computed as:

$\begin{array}{cc}\begin{array}{c}{h}_j^{\text{ff}}={\displaystyle \sum }_{k\in {ℱ}_j}{J}_{kj}{f}_k-{\eta }_{\text{ff}}{\displaystyle \sum }_{k\in {ℱ}_j}{f}_k,\\ a_j^{\text{initial}}=\{\begin{array}{cc}1& \text{if }{h}_j^{\text{ff}}>\theta \\ 0& \text{otherwise}\end{array}\end{array}& (1)\end{array}$

The inhibition term is local, namely depends on the activity in the set ℱ_j connected to a_j.

Typically the number of neurons in the correct class, initialized as in (1) by the feedforward connections, will be larger than that in other classes. The initialized activity a^initial is in itself sufficient for classifying the input, by assigning it to the population with the majority of active units, as in Amit and Mascaro (2001). However, classification through a win or take all process of convergence to an attractor is more biologically plausible and more powerful as a tool for sustained short-term memory, for pattern completion and noise elimination. After the initialization step the feedforward input is removed, and the updates in the recurrent layer proceed through stochastic asynchronous dynamics. At step t a random neuron j is selected for update, the field h^rc_j is computed only from the recurrent layer inputs and compared to the threshold.

$\begin{array}{cc}\begin{array}{c}{h}_j^{\text{rc}}={\displaystyle \sum }_{i\ne j}{J}_{ij}{a}_i^{(t)}-{\eta }_{\text{rc}}{\displaystyle \sum }_i{a}_i^{(t)}\\ a_j^{(t+1)}=\{\begin{array}{cc}1& \text{if }{h}_j^{\text{rc}}>\theta \\ 0& \text{otherwise}\end{array}\end{array}& (2)\end{array}$

Stable convergence to an attractor state is only possible with the recurrent inhibition, the second term of the field computation above. The essential role of inhibition in stabilizing a recurrent network of integrate and fire neurons has been well established since Amit and Brunel (1997). More recently in Amit and Huang (2010) this has been demonstrated in the context of networks of binary neurons, and has been shown to increase the memory capacity of these networks. Once the network converges, activity in all classes but the winner class is eliminated and the activity of the population of the winning class can be sustained for a very long time, even in the presence of noise.

2.3. Three State Synapses

As indicated above, feedforward inhibition in the network is local with each attractor neuron a_j having its own pool of local inhibitory neurons, which are all connected to the set of inputs ℱ_j that feeds into a_j. If the synaptic states are constrained to J=0, 1, 2, when η_ff = 1 the effect of these local inhibitory circuits is simply a constant subtraction of 1 from the synaptic state of every input neuron in ℱ_j. Thus, (1) can be rewritten as $h_j^{\text{ff}}={\displaystyle {\sum }_{k\in {ℱ}_j}(J_{kj}-1)fk}$, or the effective feedforward synaptic weights become −1,0,1. We note that feedforward inhibitory circuits, with presynaptic neurons having both direct excitatory and interneuron inhibitory connections to post-synaptic neurons, have been found in the hippocampus (Buzsak, 1984), the LGN (Blitz and Regehr, 2005), and the cerebellum (Mittmann et al., 2005). Models involving such circuits can be found in Scofield and Cooper (1985) but would require an interneuron for each synapse. Our approach is similar to that of Parisien et al. (2008) using a pool of inhibitory neurons receiving non-specific input from the afferent neurons of each attractor neuron. Moreover with full connectivity from the input layer to the attractor layer, only one non-specific inhibitory pool of neurons is needed that receives input from the feature layer and is connected to all neurons in the attractor layer. Regarding the discrete state synapses, there appears to be experimental evidence that individual synapses exhibit “three” states: depressed, control, and potentiated. See for example O'Connor et al. (2005a,b), Mu and Poo (2006), Dong et al. (2008), and Collingridge et al. (2010).

The three synaptic states play a crucial role in distinguishing features that are low probability on the class and higher probability on other classes. More specifically, imagine dividing the input features for the given class into three broad categories. “Positive” features are high probability on the class and lower probability on the rest, “negative” features are low probability on the class and higher probability on the rest, and all the remaining “null” features have more or less the same probability on the class and on the rest. The first two categories contain informative features that can assist in classification. Features from the third category are not useful for classification. Any reasonable linear classifier would assign the first category of features a positive weight, the second category a negative weight and ignore the third category. This is achieved with the three state synapses combined with local inhibition.

For each perceptron of a given class, the randomized learning process described in Section 2.4, effectively potentiates the synapses coming from some subset of “positive” features and depresses the synapses from some subset of “negative” features. In Figure 4 we show the histograms of log [P(f_k = 1| Class c)/P(f_k = 1| Class not c)] (log probability ratio of feature on for image from class c to feature on for image not from class c), for those synapses at state 2 at the end of the learning process. For state 2 synapses, we specifically focused on features for which p(f_k) > 0.3. We also show the histograms of the same quantity for all synapses at state 0 (bottom row). The former are skewed towards the positive side, namely state 2 synapses correspond to “positive” features that have higher probability on class than off class. The state 0 synapses are skewed toward the negative side of the axis corresponding to features that have higher probability off class than on class. Both types of synapses are informative for class/non-class discrimination. With only two synaptic states it is impossible to separate these two types of features. Performance with two state feedforward synapses with the local inhibition is significantly worse, since the non-informative “null” features get confounded with either the “positive” ones or the “negative” ones.

FIGURE 4

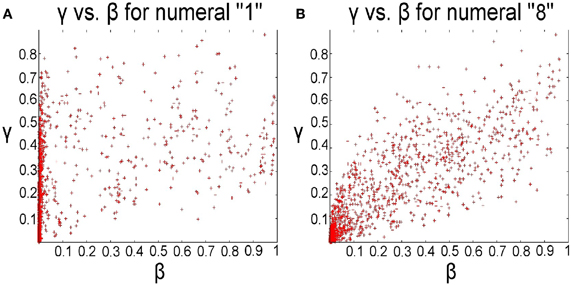
Figure 4. Histograms of log probability ratios log [P(f_k = 1|Class c)/P(f_k = 1|Class not c)] for potentiated synapses J=2 and depressed synapses J = 0 after learning. (A) Class c = 0. (B) Class c = 4. Top: distribution for state 2 synapses. Bottom: distribution for state 0 synapses. For state 2 synapses the log-probability ratios are mostly positive, for state 0 synapses mostly negative.

2.4. Learning

Learning in the network is Hebbian and field-dependent. As in previous models with binary synapses, Amit and Fusi (1994), Senn and Fusi (2005), Romani et al. (2008), and Amit and Huang (2010), learning is stochastic. If both the pre-synaptic and the post-synaptic neuron are active, then the synapse will increase in state with probability p_LTP. If the pre-synaptic neuron is active but the post-synaptic neuron is not, then the synapse will decrease in state with probability p_LTD. Since there are only three discrete synaptic states, both potentiation and depression probabilities are kept small in order to avoid frequent oscillations. In field dependent learning potentiation stops when the field is above threshold by a margin of Δ_LTP. Similarly when the field is below threshold by a margin of Δ_LTD depression stops. This is summarized as follows:

• If f_k = 1, a_j = 1, J_kj < 2, h^ff_j < θ + Δ_LTP then J_kj → J_kj + 1, with probability p_LTP
• If f_k = 1, a_j = 0, J_kj > 0, h^ff_j > θ − Δ_LTD then J_kj → J_kj − 1, with probability p_LTD.

All transitions are mutually independent.

2.4.1. Attractor layer

As indicated above, learning in the attractor layer occurs first and involves activating class populations A_c in random order and updating the synapses according to the rule above. The coding level in the attractor layer is fixed and the overlaps of the random A_c subsets are small, thus learning is very stable and effectively ends up with almost all synapses between neurons within A_c potentiated at level 2 and all synapses from neurons in A_c to those outside depressed at 0.

2.4.2. Feedforward synapses

The feedforward synapses are learned by choosing a training image at random, say from class c, activating its input features and activating the population A_c of neurons corresponding to its class in the attractor layer. No dynamics occurs in the attractor layer—the units in A_c are assumed “clamped” to the on state, and all the other units to the off state. All feedforward synapses are then updated according the rule above. In order for a synapse connecting to a unit in A_c to potentiate, it must correspond to a high probability “positive” feature for images of class c, and this will occur with high probability only with a large number of presentations. However, it will only remain potentiated if it is low probability for images not from class c. Similarly, in order for a synapse to depress it must correspond to a low probability “negative” feature for class c, with high probability on images not from class c. This will occur with high probability only with a large number of presentations. As proposed in Senn and Fusi (2005), we set the parameters at p_LTP = p_LTD = 0.01. These parameters coincidentally were found to yield optimal performance in our experiments (see below).

Field-dependent learning keeps the average input for all neurons in the network roughly the same, allowing the use of a global threshold. Without this constraint it would be difficult to adjust one threshold to simultaneously accommodate classes with different numbers of “positive” and “negative” features. Indeed this was the original motivation for the introduction of field-dependent learning in Amit and Mascaro (2001), see also the discussion and comparison with other synaptic normalization methods. The distribution of features in the different classes varies significantly as shown in Figure 5. In Figure 6 we show the distribution of the number of synapses at state 2 and state 0 for each of the 10 classes. These are all very similar, despite the variability in feature distributions.

FIGURE 5

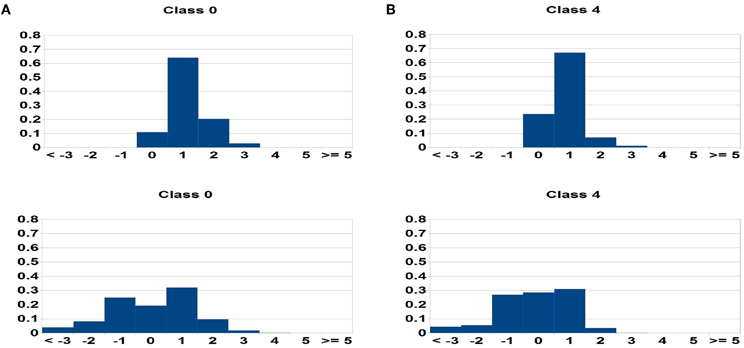
Figure 5. Scatter plots of on-class γ and off-class β feature probabilities for all input features. (A) Class 1, (B) Class 8. There are significant differences between the two classes in the fraction of positive and negative features.

FIGURE 6

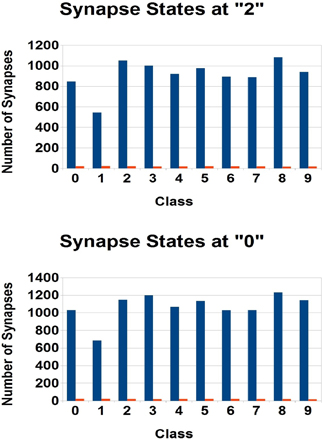
Figure 6. Means (blue) and standard deviations (red) of the number of synapses in the two informative states (2/0) connected to attractor neurons after learning with the base parameters. Mean over perceptrons in each class. The field dependent learning mechanisms generally create a stable number of potentiated and depressed synapses across classes.

From its very definition the field-dependent learning yields an algorithm reminiscent of the classical perceptron learning rule, except that it is randomized and the synapses are constrained to a small set of values. Specifically, in perceptron learning weight modification takes place only if the current example is wrongly classified, i.e., its field is on the wrong side of the threshold. This has been analyzed in detail in Senn and Fusi (2005). However, an additional outcome of this form of learning, coupled with the stochastic nature of potentiation and depression, is that even with the same set of features, each learning run creates a different classifier. Thus multiple randomized perceptrons are generated, even with full connectivity between the input layer and the attractor layer. Without field-dependent learning, even with stochastic potentiation and depression, asymptotically as the number of pattern presentations for each class grows, all “positive” features for that class would be potentiated with high probability. As mentioned above the feedforward connectivity probability p_ff determines the average size of the subset of features for each randomized perceptron. Subsets that are too small will not contain enough information for the neurons to distinguish classes. Performance initially increases quickly and then slows down as p_ff reaches around 30%. Indeed, the percentage of synapses with state 0 or 2 does not vary significantly as p_ff varies between 20 and 100%. It remains around 17–20%. Performance thus almost solely rests on choosing an appropriate threshold and learning probabilities. For this reason in the experiments we used full connectivity between the input layer and each perceptron.

3. Results

The network was tested on the MNIST handwritten digit dataset (Lecun, 2010). The 28 × 28 images were first treated with a basic form of slant correction. The network was then trained on 10,000 randomly ordered examples, 1000 from each digit class, and tested on another 10,000 examples. Attractor neurons were randomly assigned to classes. For convenience, the learning phase of the attractor classes was skipped. All the in-class attractor synapses were thus assigned a state of 2 and the rest 0. This shortcut has no effect on the final behavior of the network. During feedforward training, the attractor neurons of a given classes were clamped on, while all other neurons in the layer were inactive. Learning of the feedforward synapses then took place after the input pattern was presented and the field of each neuron in the attractor layer was calculated. Field-dependent learning implied that potentiation stopped if the feedforward field exceeded Δ_LTP units above threshold, and depression stopped if the field was less than Δ_LTD units below threshold.

Testing began with an initial presentation of a pattern that activated the attractor neurons without any recurrent dynamics. Typically many attractor neurons of the correct class were activated together with a number of neurons in other classes. Then the input was removed, and classification was represented by the convergence to an attractor corresponding to a single class. Sustained activity is present only among neurons coding for one class. Neuron updates in the attractor layer were asynchronous, and continued until convergence to a steady state occurred–no changes in neural states. Base parameters are in Table 1. When using a training set of 10,000 images (1000 per class) each image was presented three times—all in random order. With smaller training sets the number of presentations was rescaled accordingly. For example with 1000 images (100 per class) we used 30 presentations per image. The base classification rate was 96.0%.

TABLE 1

Table 1. Base parameters for experiments.

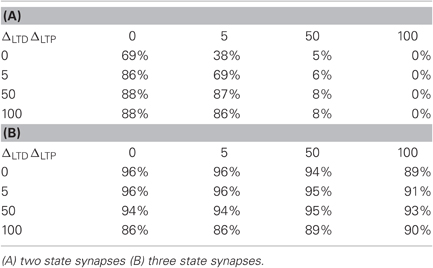
3.1. Two State vs. Three State Synapses

To compare two state vs. three state synapses we kept all base parameters listed in Table 1 the same and modified only the two inhibition levels. Feedforward inhibition for two states was set at 0.05 instead of 1 in the three state network, and attractor inhibition was set at 0.75 instead of 1.5. Using one perceptron per class the classification rates were 48.1% for two states and 81.2% for three states. For the full size attractor layer, with two state synapses there is a drastic difference between performance of classification with straightforward voting and using attractor dynamics. Voting yields a 90.0% classification rate whereas the recurrent dynamics produced the much lower rate of 64.4%. In contrast the three state network yields similar performance with voting or attractor dynamics once the size of the class populations A_c is on the order of several tens. For lower population sizes the attractor dynamics is less stable and voting performs much better. The classification rate at 96.0%., with the base parameter settings (Table 1), is comparable to support vector machines. For the full size attractor layer, convergence failed only with eight examples out of 10,000.

Of particular interest is the fact that with two state synapses there was significant sensitivity to the size of the margins. It is clear that the three state system not only performs better, but is also much more stable to the margin settings and is nearly symmetric. For the two state system there is a marked preference for a larger depression margin, meaning that it is “easier” to achieve depression. In this scenario, synapses corresponding to the less informative features will most likely be depressed. It is possible that the errors incurred by non-informative features “voting” for a class are larger than when they “vote” against. The results for classification using a set of different margin values are shown in Table 2 for both two state and three state synapses.

TABLE 2

Table 2. Classification results with different margin values.

3.2. Sensitivity to Parameter Settings

Keeping all other parameters constant at the base level, each parameter was modified over some range. The classification rate based on recurrent dynamics was then compared. The network seems to be fairly robust to changes in parameters in a neighborhood of the base parameters.

3.2.1. Size of attractor layer and size of class population

Each class population is chosen randomly with proportion p_cl, yielding some overlaps between class populations. When the size of the population coding for each class in the attractor layer is too small classification degrades due to a combination of the lack of sufficient randomized perceptrons and instability in the attractor dynamics. Thus with 100 neurons in A, namely 10 per class on average, the rate is 81%, with 250 neurons the classification rate rises to 93%. In contrast when the proportion of each class gets too large (e.g., p_cl =0.2) with the size of A held fixed, the overlaps are too large and recurrent dynamics collapses. These results are summarized in Table 3.

TABLE 3

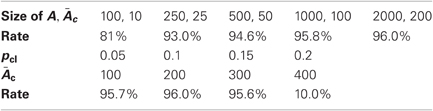
Table 3. Dependence of classification rates on size of attractor layer and mean size Ā_c of class populations.

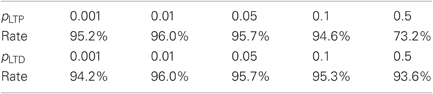
3.2.2. Learning rate

We also see that slow learning is preferable. If the potentiation probability is high many irrelevant features can get potentiated, and as mentioned above the randomizing effect on the perceptrons is lost. Sensitivity to the depression rate is not as pronounced, which may reflect the fact that most of the information for classification lies in “negative features”, namely features that are low probability on class and high probability on the rest. See Table 4.

TABLE 4

Table 4. Dependence of classification rate on learning rates.

3.2.3. Other parameters

Feedforward connectivity affects the number of features used in each randomized perceptron. The baseline is full connectivity so that randomization is only a result of the combination of stochastic and field-dependent learning. Lowering the connectivity does not have a major effect until it drops by an order of magnitude at which point there are not enough input features to generate sufficiently good classifiers. The performance does not seem to depend significantly on the threshold in a reasonable range. We also see that some advantage is gained from spreading. See Table 5.

TABLE 5

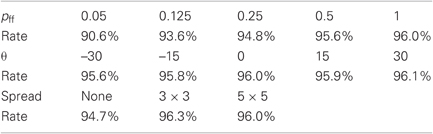
Table 5. Classification rates as feedforward connectivity, the threshold and the spreading vary individually around baseline given in Table 1.

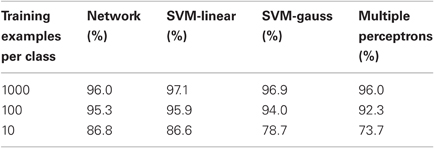
3.3. Comparison to Other Classifiers

The network performs at a level comparable to state of the art classifiers such as support vector machines, which interestingly performed optimally with the simple linear kernel (see Table 6). The network performed slightly better with the smaller training sets of 1000 (100 per class) or 100 (10 per class). The software for the SVMs was a specialized version of libsvm (Huang et al., 2011) that used one-versus-all classification. The input layer was treated as an n-dimensional vector of 1s and 0s. All other libsvm parameters were set at the default level.

TABLE 6

Table 6. Comparison of classifiers with edges.

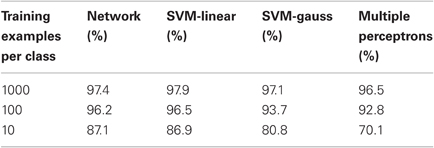
To assess the loss involved in using discrete three state synapses and a classification decision based on convergence to a single stable population (as opposed to simple voting) we experimented with a voting scheme among large numbers of classical perceptrons, 200 per class, each classifying one class against the rest. Each perceptron was fully connected to the input layer and trained using the classical perceptron learning rule, with continuous unbounded weights. Training data was presented in random order, with a step size of 0.001 for edges and 0.0001 for edge-pairs. The randomization of the presentation order of the training data produced the randomization in the different perceptrons assigned to the same class. Classification was based on the group of perceptrons with the highest aggregate output. The perceptrons were also trained on three iterations of the training data for 10,000 examples, 30 iterations for 1000, and 300 iterations for 100 examples. The results seem to indicate that nothing is lost in using constrained perceptrons with discrete three state synapses. On the other hand the linear SVM, which is also a perceptron, albeit trained somewhat differently, achieves its high classification rate with only one unit per class, showing that with a different learning scheme and unconstrained synapses a large pool of perceptrons is not really needed—as long as classification is read out directly from the output of the units and not through the sustained activity of a class-population in the attractor layer.

Also in Table 7 observe that performance is improved with the more informative edge-pair features. It is to be expected that even further improvements could be achieved with even more complex features; however, it is at this point unclear how these should be defined. Using all triples, for example, is combinatorially prohibitive; there thus needs to be some mechanism for selection of complex features.

TABLE 7

Table 7. Comparison of classifiers with edge-pairs.

4. Discussion

We find it encouraging that competitive classification rates can be achieved with a highly constrained network of binary neurons, discrete three state synapses and simple field dependent Hebbian learning. Moreover classification is successfully coded in the dynamics of the attractor layer through the sustained activity of a class population. The use of a population of neurons to code for a class together with the stochastic learning rule turn out to be an asset in the sense that we gain a collection of weakly correlated randomized classifiers whose aggregate classification rate is much higher than that of any individual one. However, it should be noted that for mere classification, using simple voting, only 10–20 units per class are needed to achieve competitive rates. The larger number of units is needed to stabilize the attractor dynamics.

Of further interest is the comparison to the outcome of full perceptron learning with multiple perceptrons. Here the only randomization is the order of the training example presentations, not the decision whether to modify a weight or not. It may be that this does not introduce sufficient randomness in the classifiers. Another point is that no weight penalization occurs in the perceptron learning rule, whereas the network we propose has a drastic penalization in that weights are constrained to three states. Note that the best performance was recorded with linear SVM's with only one unit per class. In other words, there exists a set of weights for the synapses that can achieve very low error rates with only 10 linear classifiers of class against non-class. This, however, requires the weight penalization incorporated in the SVM loss function, which does not appear in ordinary perceptron learning.

The advantage of three state synapses with feedforward inhibition for feedforward processing is apparent already in the behavior of a single perceptron. For simple recurrent networks with random input patterns the advantage of signed synapses in terms of capacity was noted in Nadal (1990). Recently, there has been interest in the distribution of synaptic weights in Purkinjee cells in cerebellum (Brunel et al., 2004). The analysis of this distribution made the assumption that all weights were positive. Based on the experiments reported here this would seem rather wasteful. The experiments reported in Brunel et al. (2004) report on the role of inhibition achieved by an individual interneuron, in forcing inputs to be highly coincident in time. However, they do not show the behavior of the post-synaptic neuron in the presence of stimulation of a large number of input neurons, which would trigger the collective inhibitory correction to the synapses, yielding an effective negative effect for depressed synapses. The assumption in Brunel et al. (2004) is that the silent synapses correspond to those with lowest weights. A provocative but not impossible alternative is that the silent synapses correspond to those that would have had no effect after factoring in the inhibitory effect of the full array of stimuli, and that the spike in the distribution is actually located somewhere in middle of the distribution.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Partially supported by NSF DMS-0706816.

References

Amit, D. J. (1989). Modelling Brain Function: the World of Attractor Neural Networks. Cambridge, UK: Cambridge University Press.

Amit, Y. (2002). 2d Object Detection and Recognition: Models, Algorithms and Networks. Cambridge, MA: MIT Press.

Amit, D. J., and Brunel, N. (1997). Model of global spontaneous activity and local structured activity during delay periods in the cerebral cortex. Cereb. Cortex 7, 237–252.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Amit, D. J., and Fusi, S. (1994). Learning in neural networks with material synapses. Neural Comput. 6, 957–982.

Amit, Y., and Geman, D. (1997). Shape quantization and recognition with randomized trees. Neural Comput. 9, 1545–1588.

Amit, Y., and Huang, Y. (2010). Precise capacity analysis in binary networks with multiple coding level inputs. Neural Comput. 22, 660–688.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Amit, Y., and Mascaro, M. (2001). Attractor networks for shape recognition. Neural Comput. 13, 1415–1442.

Pubmed Abstract | Pubmed Full Text

Ben Dayan Rubin, D. D., and Fusi, S. (2007). Long memory lifetimes require complex synapses and limited sparseness. Front. Comput. Neurosci. 1:7. doi: 10.3389/neuro.10.007.2007

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Blitz, D. M., and Regehr, W. G. (2005). Timing and specificity of feed-forward inhibition within the LGN. Neuron 45, 917–928.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Brader, J. M., Senn, W., and Fusi, S. (2007). Learning real-world stimuli in a neural network with spike-driven synaptic dynamics. Neural Comput. 19, 2881–912.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Brunel, N., Hakim, V., Isope, P., Nadal, J.-P., and Barbour, B. (2004). Optimal information storage and the distribution of synaptic weights: perceptron versus purkinje cell. Neuron 43, 745–757.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Brunel, N., and Wang, X.-J. (2001). Effects of neuromodulation in a cortical network model of object working memory dominated by recurrent inhibition. J. Comput. Neurosci. 11, 63–85.

Pubmed Abstract | Pubmed Full Text

Buzsak, G. (1984). Feed-forward inhibition in the hippocampal formation. Prog. Neurobiol. 22, 131–153.

Pubmed Abstract | Pubmed Full Text

Collingridge, G. L., Peineau, S., Howlang, J. G., and Wang, Y. T. (2010). Long-term depression in the cns. Nat. Rev. Neurosci. 11, 459–473.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Curti, E., Mongillo, G., La Camera, G., and Amit, D. J. (2004). Mean field and capacity in realistic networks of spiking neurons storing sparsely coded random memories. Neural Comput. 16, 2597–2637.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Dong, Z., Han, H., Cao, H., Zhang, X., and Xu, L. (2008). Coincident activity of converging pathways enables simultaneous long-term potentiation and long-term depression in hippocampal ca1 network in vivo. PLoS ONE 3:e2848. doi: 10.1371/journal.pone.0002848

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Fukushima, K., and Miyake, S. (1982). Neocognitron: a new algorithm for pattern recognition tolerant of deformations and shifts in position. Pattern Recogn. 15, 455–469.

Hegde, J., and Van Essen, D. C. (2000). Selectivity for complex shapes in primate visual area v2. J. Neurosci. 20, RC61.

Pubmed Abstract | Pubmed Full Text

Hopfield, J. J. (1982). Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. U.S.A. 79, 2554–2558.

Pubmed Abstract | Pubmed Full Text

Huang, T.-K., Weng, R., and Lin, C. J. (2011). libsvm. www.csie.ntu.edu.tw/cjlin/libsvmtools/

Hubel, D. H. (1988). Eye, Brain, and Vision. New York, NY: Scientific American Library.

Ito, M., and Komatsu, H. (2004). Angle representation in area v2. J. Neurosci. 24, 3313–3324.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lecun, Y. (2010). Mnist Database. yann.lecun.com/exdb/mnist/.

Leibold, C., and Kempter, R. (2008). Sparseness constrains the prolongation of memory lifetime via synaptic metaplasticity. Cereb. Cortex 18, 67–77.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Mittmann, W., Koch, U., and Häusser, M. (2005). Feed-forward inhibition shapes the spike output of cerebellar Purkinje cells. J. Physiol. 563(Pt 2), 369–378.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Mu, Y., and Poo, M. (2006). Spike timing-dependent ltp/ltd mediates visual experience-dependent plasticity in a developing retinotectal system. Neuron 50, 115–125.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Nadal, J.-P. (1990). On the storage capacity with sign-constrained synaptic couplings. Network 1, 463–466.

O'Connor, D. H., Wittenberg, G. M., and Wang, S. S. (2005a). Dissection of biderctional synaptic plasticity into saturable unidirectional processes. J. Neurophysiol. 94, 1565–1573.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

O'Connor, D. H., Wittenberg, G. M., and Wang, S. S. (2005b). Graded bidirectional synaptic plasticity is composed of switch-like unitary events. Proc. Natl. Acad. Sci. U.S.A. 102, 9679–9684.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Parisien, C., Anderson, C. H., and Eliasmith, C. (2008). Solving the problem of negative synaptic weights in cortical models. Neural Comput. 20, 1473–1494.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Petersen, C. C. H., Malenka, R. C., Nicoll, R. A., and Hopfield, J. J. (1998). All-or-none potentiation at ca3-ca1 synapses. Proc. Natl. Acad. Sci. U.S.A. 95, 4732–4737.

Pubmed Abstract | Pubmed Full Text

Riesenhuber, M., and Poggio, T. (1999). Hierarchical models of object recognition in cortex. Nat. Neurosci. 2, 1019–1025.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Riesenhuber, M., and Poggio, T. (2000). Models of object recognition. Nat. Neurosci. 3, 1199–1204.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Romani, S., Amit, D. J., and Amit, Y. (2008). Optimizing one-shot learning with binary synapses. Neural Comput. 20, 1920–1958.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Scofield, C. L., and Cooper, L. N. (1985). Development and properties of neural networks. Contemp. Phys. 26, 125–145.

Senn, W., and Fusi, S. (2005). Convergence of stochastic learning in perceptrons with binary synapses. Phys. Rev. E 71, 61907.1–61907.12.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wang, X. J. (1999). Synaptic basis of cortical persistent activity: the importance of NMDA receptors to working memory. J. Neurosci. 19, 9587–9603.

Pubmed Abstract | Pubmed Full Text