Cues to Opening Mechanisms From in Silico Electric Field Excitation of Cx26 Hemichannel and in Vitro Mutagenesis Studies in HeLa Transfectans

Connexin channels play numerous essential roles in virtually every organ by mediating solute exchange between adjacent cells, or between cytoplasm and extracellular milieu. Our understanding of the structure-function relationship of connexin channels relies on X-ray crystallographic data for human connexin 26 (hCx26) intercellular gap junction channels. Comparison of experimental data and molecular dynamics simulations suggests that the published structures represent neither fully-open nor closed configurations. To facilitate the search for alternative stable configurations, we developed a coarse grained (CG) molecular model of the hCx26 hemichannel and studied its responses to external electric fields. When challenged by a field of 0.06 V/nm, the hemichannel relaxed toward a novel configuration characterized by a widened pore and an increased bending of the second transmembrane helix (TM2) at the level of the conserved Pro87. A point mutation that inhibited such transition in our simulations impeded hemichannel opening in electrophysiology and dye uptake experiments conducted on HeLa tranfectants. These results suggest that the hCx26 hemichannel uses a global degree of freedom to transit between different configuration states, which may be shared among the whole connexin family.

Introduction

Connexins are topologically conserved proteins composed of four transmembrane (TM) helixes connected by two extracellular loops (EC1, EC2) and one cytoplasmic (CL) loop. Connexin hemichannels, also known as connexons, are hexameric arrays of connexins. They can function as regular membrane channels (Bennett et al., 2003; Sáez and Leybaert, 2014), or dock in the extracellular space to form gap junction channels that support direct cell-to-cell communication by connecting adjacent cytoplasmic spaces (Goodenough and Paul, 2009). Gap junction channels cluster in plaques by the thousands, and have been identified in virtually all tissues (Evans and Martin, 2002). It has been estimated that over 35.000 members of the human metabolome can be transferred through gap junction channels, or exchanged through unpaired connexons (Esseltine and Laird, 2016). In recent years, it has been discovered that also small, non-coding RNA (siRNAs or miRNAs) can diffuse through connexin-made channels (Esseltine and Laird, 2016). The relevance of connexins and their tightly regulated function is highlighted by their implication in pathological states of completely different character, such as cancer (Tsai et al., 2018), inflammation (Li et al., 2018), and neurodegenerative diseases (Belousov et al., 2018). For this reason, modulation of connexin hemichannels is becoming increasingly interesting for the treatment of several diseases including Alzheimer Disease (Yi et al., 2017), skin disorders, or X-linked Charcot Marie Tooth disease (Sáez and Leybaert, 2014; Carrer et al., 2017; Xu et al., 2017).

The only X-ray structures available at atomistic resolution for the connexin protein family are those corresponding to Ca²⁺-free (Maeda et al., 2009; Bennett et al., 2016) and Ca²⁺-bound (Bennett et al., 2016) forms of the hCx26 gap junction channel. The two structures, which have been associated with conductive and non-conductive states, respectively, overlap almost completely. For this reason, it has been recently hypothesized that the non-conductive state is associated with an electrostatic barrier created by bound calcium ions in the outer vestibule of the connexon (Bennett et al., 2016). However, this explanation meets some difficulties: (i) in the Ca²⁺-free configuration the pore seems not wide enough to allow the passage of small non-coding RNAs or relatively large molecules such as ATP, NADP, prostaglandins, etc., which are rapidly released from the cytoplasm to mediate autocrine/paracrine signaling (Kar et al., 2012); (ii) in the Ca²⁺-bound configuration, the pore is too wide to prevent the flux of small neutral molecules, such as water or glucose, that interact negligibly with the electrostatic barrier and therefore would diffuse freely through undocked connexons. Moreover: (iii) atomic force microscopy identified a significantly enlarged conformation of the extracellular mouth of the connexon in the Ca²⁺-free state (Müller et al., 2002); (iv) spontaneous transitions between non-conductive and conductive states of Cx32 and Cx26 hemichannels have been observed by electrophysiology and dye-uptake experiments under resting conditions (Fasciani et al., 2013). Indeed, single Cx26 hemichannel recordings show frequent alternation between conductive and non-conductive states at TM potentials (ΔV_m, inside minus outside) ≤ −30 mV even in zero extracellular Ca²⁺ concentration ([Ca²⁺]_o) (Sanchez et al., 2013, 2016). This behavior has been attributed to the so-called “loop gate” of Cx26, which is thought to remain constitutively active at all voltages (Sanchez et al., 2016). The same behavior is not observed in hemichannels formed by other connexins (e.g., connexin 46 and 50), which remain stably open in low [Ca²⁺]_o and close only if subjected to robust hyperpolarization (Trexler et al., 1996; Srinivas et al., 2005). Finally, (v) early molecular dynamics simulations questioned whether the published structures represent a fully open channel, since permeation and conductance properties could be reproduced only partially(Kwon et al., 2011; Zonta et al., 2012).

Our working hypothesis, based on the above considerations, is that connexin hemichannels may undergo yet uncharacterized conformational transitions, which we sought to explore using theoretical methods. Several approaches have been implemented to the study of membrane proteins mimicking a cell membrane potential (Cohen and Venkatachalam, 2014) using MD simulations (Delemotte et al., 2011; Bernardi et al., 2015; Escalona et al., 2016; Villanelo et al., 2017). A comprehensive review of the different theoretical approaches that have contributed to the study of connexin channels has been recently published (Villanelo et al., 2017). In particular, it has been recently shown that relatively high electric field pulses in combination with time-resolved X-ray crystallography can unravel details on the conformation and mechanics of proteins (Hekstra et al., 2016). Inspired by this technique, we used coarse-grained (CG) molecular dynamics using the SIRAH force field (Darré et al., 2015) to explore the conformational behavior of the hCx26 connexon in the presence and absence of an external field aligned with the pore axis. This computational technique applies a force perpendicular to the membrane to all charged particles. Because of the features of the SIRAH force field, all but hydrophobic CG particles beads carry a (partial) charge. Hence, the electric field will impact on all degrees of freedom with non-zero components along the membrane perpendicular. In this sense, we can expect the electric field to act like a biasing potential, in rough analogy to enhanced sampling methods used in combination with molecular dynamics (Grübmuller, 1995; Laio and Parrinello, 2002). Applying an electric field to a CG membrane protein allowed us to speed up simulations significantly while avoiding the use of ad-hoc biases and keeping a more realistic explicit representation of the membrane and solvent environment.

Materials and Methods

CG simulations were performed using the SIRAH force field (Darré et al., 2015) (www.sirahff.com), which is sensitive to variations in ionic strength and protein sequence (Surdo et al., 2017), and the lipid parameterization presented in Astrada et al. (2016).

The starting positions for the atoms of the Ca²⁺ free hCx26connexon were obtained from our previously published all-atom (AA) model (Zonta et al., 2012, 2013, 2014, 2015), and comprised also the amino acids not present in the experimental structure (such as the intracellular loop). Following the same procedure, we generated a model of the Ca²⁺-bound conformation using the X-ray structure by Bennett et al. (2016) as template for the TM region, and that of Maeda et al. (2009) for the part that were not resolved in the former. These AA models were converted to CG using SIRAH tools (Machado and Pantano, 2016) and inserted in a square membrane patch containing 230 phospholipid (DMPC) molecules. The systems were then solvated with 2377 CG solvent molecules called WT4 (Darre et al., 2010), comprising 115 Chloride, 31 Potassium, and 30 Sodium ions, altogether accounting for an ionic strength of approximately 150 mM. For charge neutralization, six Potassium and six Sodium ions were removed from the Ca²⁺-bound system. Ca²⁺ parameters were the same recently introduced and tested in Cali et al. (2017). After stabilization, the simulation box converged to sizes of 9.9, 9.9, and 13.5 nm for x, y, and z coordinates, respectively.

The simulation protocol for CG simulations consisted of 5,000 steps of unconstrained energy minimization followed by 10 ns of MD performed in the presence of positional constraints of 1,000 kJ/mol/nm² on all the protein beads with a time step of 10 fs. This was followed by 10 ns of unconstrained simulation with a time step of 15 fs. Production runs were performed for at least 1 μs. All CG simulations were performed in the NPT ensemble at 300 K coupling protein, phospholipids and water/ions to three separate v-rescale thermostats (Bussi et al., 2007). Pressure was fixed at 1 bar using semi anisotropic coupling using Parrinello-Rahman barostats (Parrinello and Rahman, 1981). A timestep of 20 fs and a direct cutoff for non-bonded interactions of 1.2 nm was used. Long-range electrostatics was calculated with Particle Mesh Ewald summation method (Darden et al., 1993). All simulations were performed with Gromacs 4.6.7 (Pronk et al., 2013).

When indicated, an external electric field was applied in the direction perpendicular to the membrane plane (arbitrarily chosen as the Z direction) as implemented in Gromacs. Backmapping of CG conformers of wild type (wt) hCx26 and its T86L mutant was performed using SIRAH tools (Machado and Pantano, 2016).

Calculated Properties

Root mean square deviations were calculated on Cα atoms (or beads) in all cases. According to our previous results, the maximum constriction point of the channel is located at the level of Lys41 (Zonta et al., 2012). Hence, the minimum diameter of the pore was estimated as the average distance on the three pairs of opposed Lys 41 minus the van der Waals (vdW) radii of each bead (0.55 nm; Darré et al., 2015). The kink angle at TM2 was measured as the angle formed between the Cα atoms of amino acids Gln80, Pro87, and His94, i.e., two helix turns before and after the kink introduced by Pro87.

Cx26T86L Mutagenesis

The QuikChange II Site-Directed Mutagenesis Kit (Agilent, cat. no. 200523) was used to mutagenize the Threonine in position 86 of wt hCx26 to Leucine using the Cx26WTVenus pcDNA3.1 construct (Beltramello et al., 2005) as template. The primers were the followings:

Cx26T86Lf: 5′–CTGATCTTCGTGTCCCTGCCAGCGCTCCTAGTG−3′

Cx26T86Lr: 5′–CACTAGGAGCGCTGGCAGGGACACGAAGATCAG−3′. The correct insertion of the mutation was verified by DNA Sanger Sequencing.

Patch Clamp and Dye-Uptake Assays

HeLa DH cells (Sigma-Aldrich, Cat. No. 96112022) were seeded onto round glass coverslips (Fisher Scientific, Cat. No. FIS#12-542A). Cells were maintained in Dulbecco's modified Eagle's medium (ThermoFisher, Cat.No. 41965039) containing 10% (v/v) FBS (Gibco-Invitrogen, Cat.No. 10270-106) and 1% penicillin/streptomycin (Gibco-Invitrogen, Cat.No. 15070-063). Twenty four hours after plating, a transfection reagent (Lipofectamine 2000, Cat. No. 11668-019) was used to transiently transfect cells at 25–30% confluence with wild type hCx26–Venus construct or its T86L mutant.

A double stage vertical puller (PP-830, Narishige) was used to fabricate patch pipettes from glass capillaries (G85150T-4, Harvard Apparatus, Edenbridge, UK). Pipettes were filled with a potassium aspartate (KAsp)-based intracellular solution (ICS_KAsp) containing (in mM): 115 KAsp, 10 NaCl, 10 KCl, 1 MgCl₂, 10 HEPES, 1 CaCl₂, and 5 BAPTA tetrapotassium salt (pH 7.2, 311 mOsm) and filtered through 0.22-mm pores (Millipore). Filled pipettes had resistances of 4-6 MΩ when immersed in a NaCl-based extracellular solution (ECS_NaCl) containing a reduced (0.2 mM) Ca²⁺ concentration ([Ca²⁺]₀) and (in mM): 140 NaCl, 5 KCl, 10 HEPES, 2 sodium pyruvate, 4 tetraethylammonium chloride (TEA-Cl), 4 CsCl and 5 glucose (pH 7.4, 323 mOsm).

Twenty four hours after transfection, glass coverslips with adherent cells were transferred to the stage of an upright fluorescence microscope (BX51, Olympus) equipped with differential interference contrast (DIC) optics. Cells were continuously superfused at 2 ml/min at 20–23°C with ECS_NaCl. Hemichannel currents were assayed in ECS_NaCl while keeping cells near their zero-current potential (between −20 and 0 mV) under whole cell patch clamp recording conditions. Cells were transiently depolarized to +40 mV for 20 s followed by a 1 s ramp down −40 or −60 mV and subsequently held at this negative potential for up to 1 min before stepping back to the zero-current potential. Alternatively, they were stimulated with slow (8 min) voltage ramps from +60 to −60 mV. To measure junctional currents, pairs of HeLa DH cells visibly connected by a gap junction plaque were selected, patch clamped with two separate amplifiers and initially held at 0 mV. Then one of the two cells (cell 1) was stimulated by voltage commands while recording the whole cell current from the unstimulated cell (cell 2). For dye uptake assays, HeLaDH cells were seeded at 40% confluence and transfected 24 h later with Cx26Venus constructs (wt and T86L). Control cells were treated with Lipofectamine 2000 alone.

Six hours after transfection, cells were washed three times with D-PBS (Thermo Fisher Scientific, cat. no.14190250), incubated at room temperature for 1 h with propidium iodide (PI, ThermoFisher, Cat No. P1304MP, 0.25 mM dissolved in D-PBS). Cells were then washed in HBSS, fixed in PFA 2%, mounted onto glass slides with a mounting medium (FluorSave™ Reagent, cat. 345789, Merk Millipore) and observed using a confocal microscope (TCS SP5, Leica) equipped with an oil–immersion objective (63 × HCX PL APO 1.4 N.A., Leica). Samples were excited with Argon laser 488 (Venus) and 561 (PI) lines.

Results

CG Molecular Dynamics of the hCx26 Connexon Reproduce Atomistic Simulations in the Absence of External Electric Fields

The CG simulations performed as described in the Material and Methods section produced stable trajectories on a timescale spanning several microseconds. During the initial equilibration phase, the Root Mean Square Deviation (RMSD) of the whole hemichannel (shown in Figure 1A) underwent a rapid increase and stabilized near 0.55 nm (0.45 nm when considering only the TM region, Figure 1B). The increase in RMSD during the first 100 ns was mirrored by the trajectory of the AA simulation (Zonta et al., 2012) (Figure 1C, inset). This indicates that the time evolution of the CG simulation is comparable to that produced by state-of-the-art fully atomistic simulations within the time scale explored.

FIGURE 1

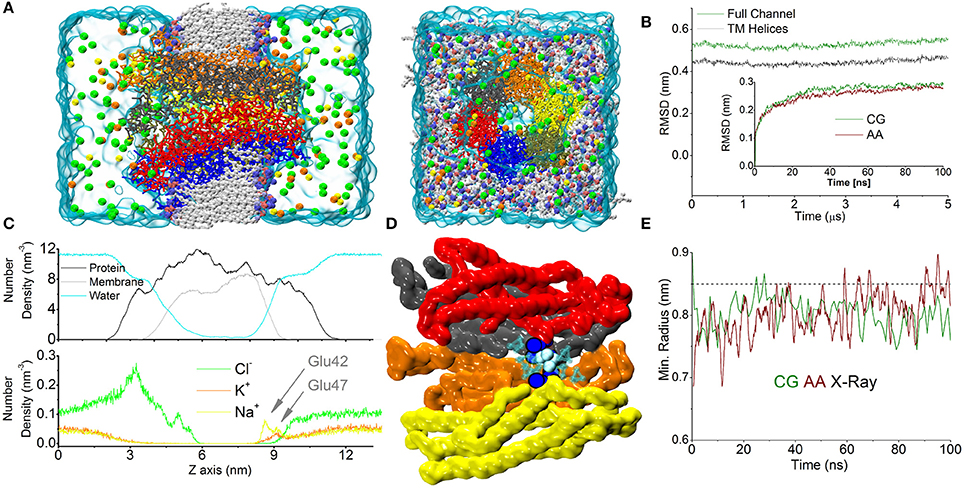
Figure 1. CG simulation of the Cx26 unperturbed hemichannel. (A) Molecular representation of the CG Connexon showing the different constituents of the computational system on side and top (extracellular) views. Electrolytes are shown with their actual solvated size. Chloride, Sodium, and Potassium are shown in green, yellow, and orange, respectively. (B) RMSD calculated along the dynamics on the Cα positions on the full Connexon and considering only the TM helices (dark green and black, respectively). The inset shows a comparison with the same quantity calculated from an AA trajectory during the first 100 ns of simulation reported in Zonta et al. (2015). (C) Lateral density profiles of different components of the system. Protein (black), membrane (including all beads, gray), and water (cyan) are shown in the top panel, while electrolytes are shown on the bottom to facilitate the visualization. Arrows indicate the cation's peaks in the density profile corresponding to the position of Glu42 and 47. (D) The point of maximum constriction is found at the level of Lys41 (blue spheres), consistently with the AA simulation. In this point a single coarse-grained molecule can be accommodated (cyan spheres). (E) Plot of minimum radius vs. time at the level of the Lys41 in the first 100 ns for CG and AA simulations (green and dark red traces, respectively). The dashed line corresponds to the X-ray structure.

Calculation of the averaged density profiles of the CG system's components within the simulation box showed correct partitioning of the different species (protein, water, phospholipids, Figure 1C). In particular, Cl⁻ ions accumulated in the mouth of the channel, attracted by the numerous Lysine residues present in the intracellular loops that form the outer backbone of the cytoplasmic vestibule. In contrast, cationic species showed a marked depletion in this region. Conversely, in the extracellular vestibule, acidic residues (Glu42, 47 and Asp 46, 50) favored the accumulation of cations. In particular, the distribution of Na⁺ ions showed two peaks, roughly corresponding to the positions of Glu42 and Glu47, which coordinate six Ca²⁺ ions in the Ca²⁺-bound X-ray structure (Bennett et al., 2016). Owing to the larger size of K⁺ (compared to Na⁺), the density of K⁺ ions peaked only at the more external position of the extracellular vestibule (Figure 1C). In agreement with our published atomistic simulations, the maximal constriction of the pore corresponds to the position of the six Lys41 (Zonta et al., 2012), whose side chains leave enough room to accommodate a single CG water molecule (Figure 1D) in the center of the pore. The minimum pore diameters of the X-ray crystallographic structures, the AA and CG models are indistinguishable from each other (Figure 1E), once statistical fluctuations and experimental resolution are taken into account. In the course of this simulation, lasting 5 μs, we did not detect any net flux of water or ions across the TM region, consistent with the fact that we were simulating equilibrium conditions.

Temperature effects in atomistic simulations affect the conformation of each connexin independently, resulting in a loss of symmetry (Kwon et al., 2011). This is particularly evident at the N-terminal helices, where amino acids 1 to 14 display a high mobility with averaged helical contents varying from nearly 0% for one chain to ~80% for others (Figure 2).

FIGURE 2

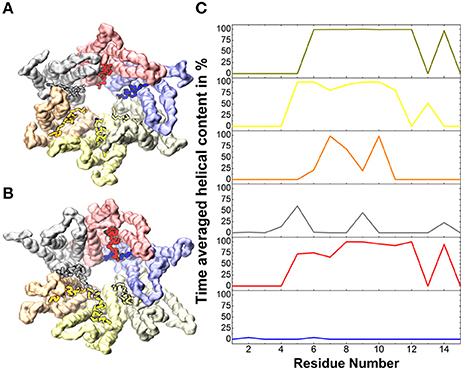
Figure 2. Helical content in the N-terminal helices. (A) Solvent accessible surface of the backbone beads of the Cx26 Connexon colored by chain for the initial conformer. (B) Same as (A) for the final conformer after 5 μs. Vivid colors indicate residues 1 to 14 on which the averaged helical content is calculated in (C).

Altogether, these results suggest that the conformations sampled by the CG model in a multi-μs timescale equilibrium simulation are consistent with the experimental structures, and supply a dynamical description comparable to that provided by AA models.

External Electric Fields Reshape the hCx26 Hemichannel Structure and Widen Its Pore

In time-resolved X-ray crystallography, electric field pulses of about 1 MV/cm have been successfully applied to protein crystals to promote conformational changes throughout the protein structure and observe them in spatial and temporal detail (Hekstra et al., 2016). Building upon this idea, we sought to explore possible alternative conformations of the hCx26 hemichannel, by imposing in silico a constant electric field in the direction of the pore axis, and performed CG simulations starting from the configuration of the equilibrated system described in the previous section. In the following, we denote as “positive” an electric field that drives a cation from the cytoplasmic to the extracellular side of the plasma membrane and “negative” in the opposite direction. Furthermore, for the sake of convenience, we will hereafter express the electric field in V/nm units (1 MV/cm = 0.1 V/nm). We explored a range of electric field amplitudes around those used in Hekstra et al. (2016) and determined that values of approximately ± 0.1 V/nm resulted in a rapid (from few ns up to 1 μs) destruction of the molecular structure and membrane electroporation (Supplementary Movie SM1). Amplitudes between ± 0.1 and 0.07 V/nm resulted in conformational distortions, which included the separation of the connexin chains within few μs. These results can be in phenomenological agreement with electrophysiology experiments, since high TM potentials above ~180–200 mV invariably destroy biological membranes (Teissié and Rols, 1993). At the other extreme of the scale, electric field amplitudes below ± 0.03 V/nm did not elicit any evident effect on the structure of the hCx26connexon, within a timescale of 10 μs. In contrast, we observed a more interesting behavior for intermediate values of the electric field, i.e., induction of mild and reproducible conformational changes, which depended on the polarity of the applied field (see Figure 3 for a summary). Specifically, a negative field of 0.06 V/nm produced a smooth increase of the RMSD (Figure 3A, red trace) within few hundred nanoseconds, accompanied by an increase in the minimum internal radius of the hemichannel measured at the level of Lys41 (Figure 3B, red trace). A positive electric field of equal amplitude produced milder effects on the overall structure of the hemichannel and elicited a smaller increase in the minimum radius, mostly due to rotation of Lys41 side chains (Figure 3B, blue trace). Comparison of the solvent accessible surfaces between initial and final conformers in all three simulations (Figure 3C) shows that the small opening present in the X-ray structure at the level of the six Lys41 was maintained in the presence of the positive field, vanished in the absence of an electric field and increased upon application of a negative electric field (Figure 3C).

FIGURE 3

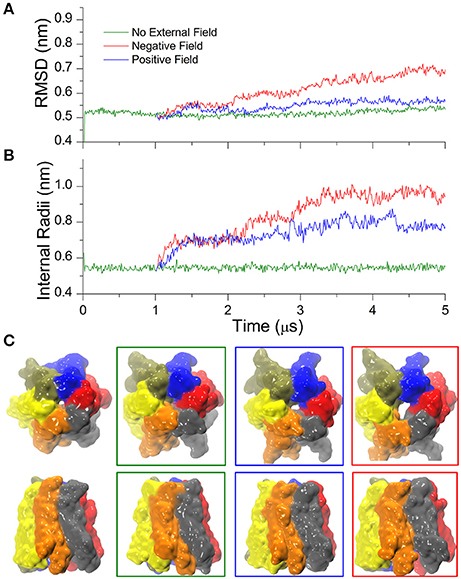
Figure 3. Cx26 under external electric field. (A) RMSD on the Cx26 Connexon in absence (green) and presence of an external field (red: negative or polarizing; blue: positive or depolarizing). The external field in either direction was applied after 1 μs of simulation in the absence of an external field. The green trace corresponds to the same simulation presented in Figure 1, which is shown here as a reference. (B) Time series of the maximum constriction size at the pore lumen measured at the level of Lys41 in the absence and in the presence of external field. (C) Solvent accessible surfaces of initial (left) and final conformers colored by chain in top and side views. The color code of the external frames is the same as in (A,B).

It is worth emphasizing that the observed relatively fast (μs) configuration transition must not be confused with the “loop gating” mechanism, as the latter closes the hemichannel for negative potentials and occurs on a far longer time scale (ms) (Sanchez et al., 2013, 2016). The transition uncovered by our CG simulations, instead, leads the hemichannel to a new stable configuration distinct from the crystallographic structures. Repeating the simulation using slightly different starting conditions reproduced qualitatively the open conformation, underlining the robustness of our approach (Figure SM1).

Ca²⁺ Inhibits the Pore Widening of the Hemichannel

It is well-established that extracellular Ca²⁺ ions stabilize the closed state of connexin hemichannels (Verselis and Srinivas, 2008). To explore this effect we started from the Ca²⁺ bound crystal structure of the hCx26 hemichannel and used CG simulations to follow its dynamics for 1 μs in absence of external field. Thereafter we applied either positive or negative electric fields for 4 μs (± 0.06 V/nm, respectively). Trajectories were stable in the absence of electric fields, although characterized by a slightly higher value of RMSD compared with Ca²⁺-free simulations (compare Figure 4A and Figure 3A; these small differences can be ascribed to the different initial configurations of Ca²⁺-free and Ca²⁺-bound simulations).

FIGURE 4

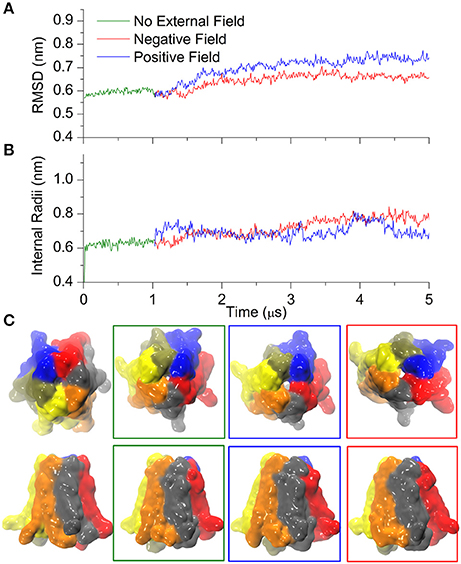
Figure 4. Calcium bound Cx26 under external electric field. (A) RMSD on the Cx26 Connexon in absence (green) and presence of an external field (red: negative or polarizing; blue: positive or depolarizing). The external field in either direction was applied after 1 μs of simulation in the absence of an external field. (B) Internal radii as a function of the simulation time in the absence and in the presence of external field measured at the level of Lys41. (C) Solvent accessible surfaces of Cx26 conformers at different point of the simulations. From left to right: initial, after 1 μs in absence of external field, after 4 μs under depolarizing field, and after 4 μs of polarizing field. The apparent differences in the external diameter are originated by the flexible C-terminal tails.

The introduction of the external field in either direction caused a small increase in RMSD that stabilized after ~3 μs (Figure 4A), whereas the internal radii remained rather insensitive to the perturbation (Figure 4B), in line with the stabilizing role of Ca²⁺. Indeed, only a small orifice is observed in both cases (Figure 4C) at the level of the Lys41 girdle, which did not allow the permeation of any coarse grained ions (which are equivalent to hydrated ions of AA simulations). Therefore, these computational results suggest that Ca²⁺ coordination within the extracellular vestibule of the channel (Figure 5) inhibits the transition to the wider pore state described in the previous paragraph.

FIGURE 5

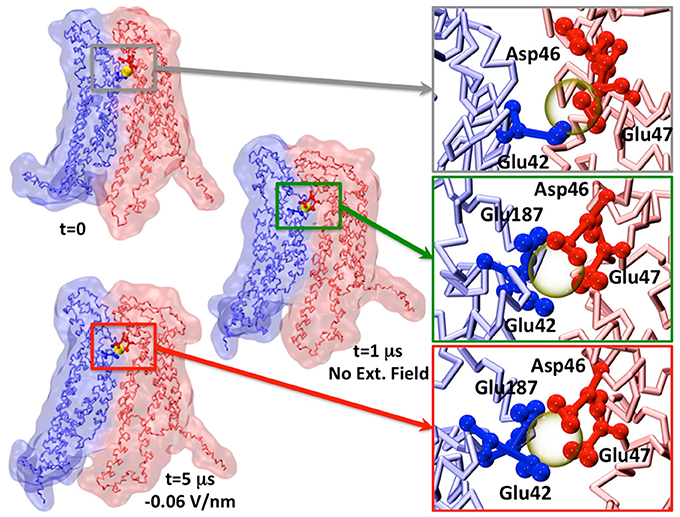
Figure 5. Representative snapshot of two apposed connexins coordinating one Calcium ion. The insets show the change in Calcium coordination. For the sake of visual clarity, only the amino acids within 0.5 nm of Calcium (semitransparent yellow sphere) are shown and colored by chain.

We also notice that Ca²⁺ coordination was lost during the dynamics already during the equilibration phase (Figure 5), in agreement with previous AA simulation results (Bennett et al., 2016; Lopez et al., 2016). This is likely due to the low affinity of Ca²⁺ for the extracellular domain (in the millimolar range, Gómez-Hernández et al., 2003).

Pore Widening of the Ca²⁺-Free Structure Depends on TM2 Rearrangement at the Level of Pro87

To understand the molecular mechanism leading to the widened pore configuration of the hemichannel, we examined in further detail the transition pathway. We thus noted that the final state achieved after 5 μs of CG simulation, in the presence of the negative field and in the absence of Ca²⁺, was asymmetrical and that the six protomers responded differently to the applied field during the dynamics. Moreover, RMSD computed along the transition for each protomer remained below 0.3 nm. This figure should be compared to the 0.55 and 0.75 nm RMSDs of the whole hemichannel in absence and presence of a negative electric field, respectively, indicating that the change in quaternary structure exceeded that of the individual subunits.

At the level of the single connexin, amino acids 41 to 43 experienced a reduction in the average alpha helix content between 12 and 23% in the presence of a negative field (Figure 6). This effect does not reflect a stable conformational change but an increased structural disorder, in agreement with the proposal that this region behaves like a labile “parahelix” (Tang et al., 2009). More importantly, we noted a shift toward lower angle values (comprised between 120 and 140°), in the TM2 kink, which is due to the presence of a conserved Pro at position 87 (Figures 7A,B). To explore this phenomenon in further detail, we used the backmapping capabilities of the SIRAH force field (Machado and Pantano, 2016) to generate pseudo-atomistic models of the initial and final CG conformers. In the backmapped conformations, the side chain of Thr86 in TM2 interacted with Phe31 in an adjacent connexin, (see insets in Figures 7A,B). Mutation of this Threonine has been shown to shift the dependence of Cx32 gap junction channels on the transcellular voltage (V_j gating) (Ri et al., 1999). Therefore, we predicted that the Thr86Leu (T86L) mutation should impair the electric field-driven conformational transition. We confirmed this prediction by performing a CG simulation on the hCx26T86L mutant. The mutated hemichannel evolved toward a more linear configuration of TM2 regardless of the application of an external field (Figures 7C,D) and remained in a state very similar to the conformation of the WT hCx26 connexon in the absence of an external field.

FIGURE 6

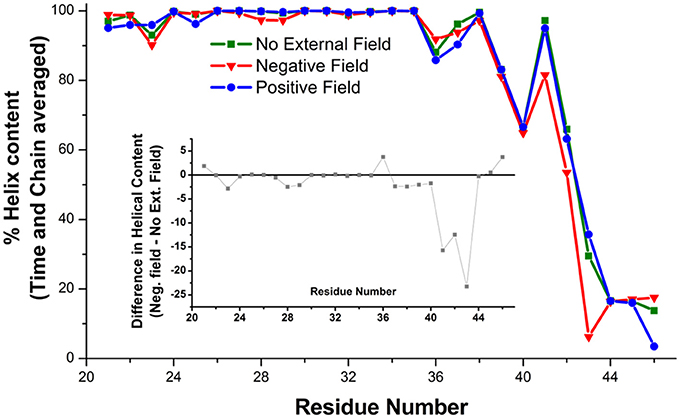
Figure 6. Helical content on the amino acids of the TM1 averaged on six Connexin chains and over the last μs of the simulation. The inset shows the difference between the simulations in absence (green squares) and presence (red triangles) of a hyperpolarizing electric field.

FIGURE 7

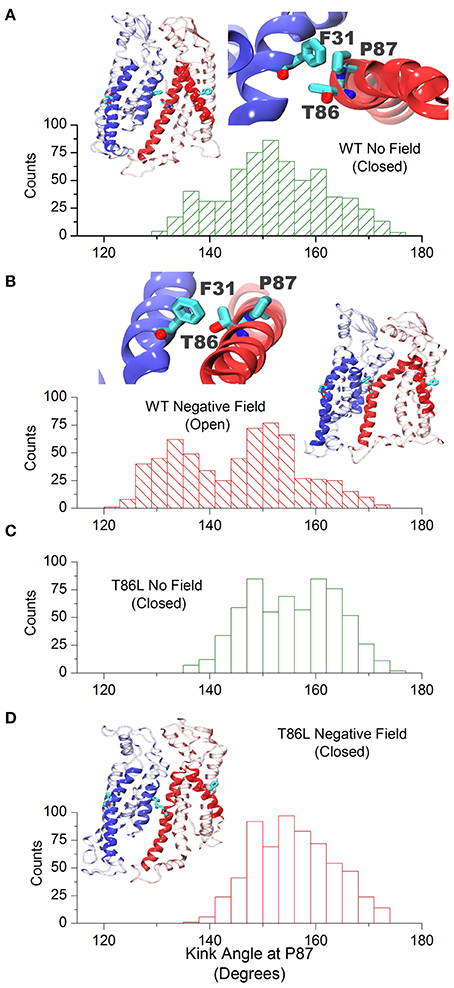
Figure 7. Cx26 in the open conformation. (A) Angle distribution of the kink at TM2 in the closed hemichannel in absence of electric field measured along the last μs of simulation. The molecular drawings show two adjacent backmapped connexins (left) and the interaction between Phe31, Thr86, and Pro87 looking from the extracellular side (right). (B) Same as (A) for the open configuration. (C,D) Angle distribution of the kink at TM2 for the Thr86Leu mutated Cx26 in the absence and presence of a polarizing field, respectively. The molecular drawing in (D) corresponds to backmapped, mutated connexins (to be compared with those in A,B).

To substantiate these computational findings, we performed patch clamp and dye-uptake assays in HeLa DH cells transiently transfected with WT hCx26 or its T86L mutant (Figure 8). Although mutant proteins trafficked correctly to the cell plasma membrane, where they also formed gap junction plaques (Figure 8A), cells remained electrically uncoupled (Figure 8B). Likewise, prominent hemichannel currents were elicited in cells expressing only the WT connexin (Figure 8C). These voltage-clamp experiments were performed in 0.2 mM Ca²⁺, a condition, which favors hemichannel opening (González et al., 2006; Sanchez et al., 2010, 2014; Fasciani et al., 2013). The absence of measurable hemichannel conductance in cells expressing the mutant connexin was confirmed by measuring the whole cell current as a function of TM potential (Figure 8D). Consistent with these findings, cells expressing the T86L mutant failed to uptake Propidium Iodide in nominally Ca²⁺-free extracellular medium, whereas cells expressing WT hemichannels readily up took the dye (Figure 8E).

FIGURE 8

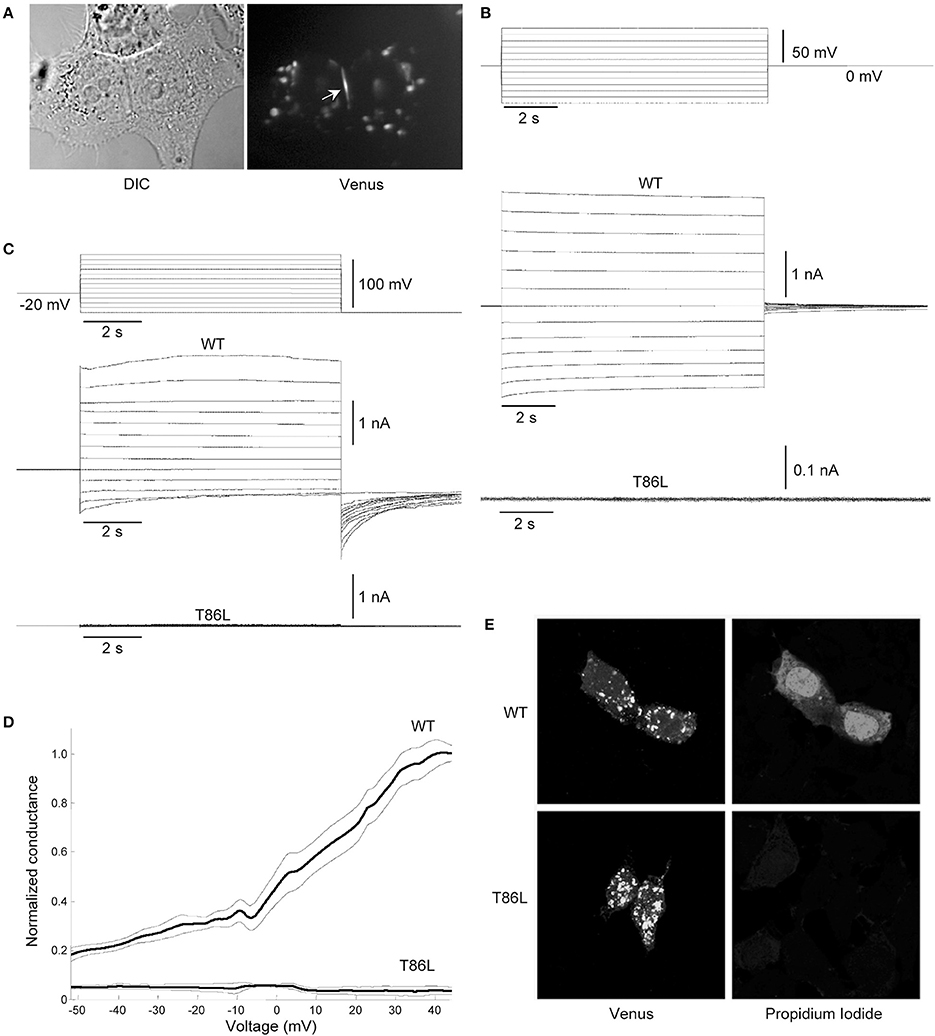
Figure 8. Patch clamp and dye-uptake assays in HeLa DH transfectants. (A) Left: differential contrast image (DIC) of HeLa DH cells transiently transfected with hCx26T86L fused in frame with the GFP color mutant Venus; right: same field of view under fluorescence illumination, highlighting a gap junction plaque between a pair of adjacent cells (arrow). Cytosolic fluorescent puncta are consistent with previous analysis of connexin trafficking en route to the plasma membrane (Thomas et al., 2005). (B) Voltage commands applied to cell 1 (top traces) elicited junctional currents in the adjacent cell (cell 2) of a pair of HeLa DH cells transiently trasfected with wild type (WT) hCx26 (middle traces); junctional currents were undetectable in T86L transfectants (bottom traces). (C) Representative measurements of hemichannel currents elicited by voltage commands (top traces) in HeLa DH cells transiently trasfected with wild type (WT) hCx26 (middle traces); hemichannel currents were undetectable in T86L transfectants (bottom traces). (D) Membrane conductance in response to slow (400 s) voltage ramps from nominal +60 to −60 mV; ordinates were normalized by the mean conductance of WT hCx26 at +40 mV; abscissas were corrected for the voltage drop due to the access resistance (18 ± 3 MOhm for T86L, n = 6; 19 ± 5 MOhm for WT, n = 6); measurements in (B,C) were performed in 0.2 mM extracellular Ca²⁺. (E) Incubating HeLa DH cells for 60 min in nominally Ca²⁺-free extracellular solution containing Propidium Iodide 0.25 mM promoted dye uptake in cells expressing WT hCx26 (top), whereas cells expressing the T86L mutant failed to uptake the dye (bottom).

Discussion and Conclusions

Achieving a reliable theoretical framework for the study and prediction of permeation properties in connexin hemichannels represents a milestone in the understanding of cell communication and membrane biophysics. While molecular dynamics simulations can be regarded, in principle, as a suitable tool, in practice they are limited by the difficulty of sampling adequately the configuration space accessible to the system composed by the hemichannel and the molecules that permeate it. In particular, AA simulations failed to reproduce any of the configuration transitions, which are expected on the basis of known gating mechanisms.

In this article, we mimicked the experimental technique proposed in Hekstra et al. (2016), and applied external electric fields on a CG representation of the hCx26 hemichannel in a phospholipid membrane. Converting the electric field module to transmembrane voltages and considering the box dimensions, the applied potential was nearly 800 mV, i.e., roughly four-fold larger than the rupture voltage for biological membranes (Chen et al., 2006). Although similarly large voltages are routinely used in simulations studies (Delemotte et al., 2011; Escalona et al., 2016), a direct comparison between the energetics of real systems with their CG representations is impossible due to the loss of degrees of freedom inherent in the coarse-graining process. Consequently, the results obtained in the present study should be considered at the qualitative level, at least as far as membrane potential is concerned.

Based on the SIRAH force field, the electric field promoted a conformational change only in the wt channel under negative field direction. Positive electric field, Calcium or an ad-hoc point mutation showed no sensitivity to the external field.

The conformational transition toward a new stable state of the hemichannel characterized by an increased pore diameter took place within the microsecond timescale. This transition required the increase of the TM2 kink angle at the level of Pro87, which faces Phe31 in TM1. Although qualitative, our simulation scheme resulted accurate enough to predict that an amino acid bulkier than Threonine in position 86 should impair pore widening by creating steric hindrance with Phe31 (Figure 7). We verified this prediction by dye uptake experiments in HeLa cells transfected with hCx26WT and hCx26T86L mutant hemichannels (Figure 8) (Ri et al., 1999). Pro87 and Phe31 are conserved in all human connexins, with the notable exception of Cx40.1 (Figure 9). On the other hand, Thr86 is replaced only by small amino acids (i.e., Ala, Cys, Val, and Ser), suggesting that the size of the side chains in this position is a key determinant of channel function. In fact, the only connexin featuring a bulkier amino acid is, again, Cx40.1, which has a Leu instead of Thr86, suggesting that the presence of a larger side chain at position 86 must be compensated by a smaller (Phe to Leu) side chain at position 31 in order to decrease steric hindrance and to allow the conformational transition. Hence, our results suggest that the collective degree of freedom that enables the transition described above is shared among the whole connexin family.

FIGURE 9

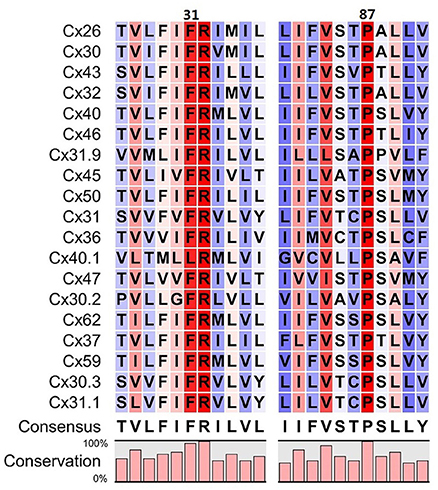
Figure 9. Sequence alignment around residues 31 and 87 of the 19 human connexins that are known to be translated into proteins. Colors refer to the percentage of consensus, from blue (30%) to red (100%), numbering refers to the amino acid sequence of Cx26. Amino acids in positions 86 always have a small side chain (T, A, C, V, S), with the only exception of Cx40.1 (L). In this connexin, the phenylalanine in position 31 is replaced by a leucine, whose side chain is smaller, assuring that the overall steric hindrance of the two opposed amino acids is conserved along the family.

Nevertheless, a direct connection between such electric field-driven transition and hCx26 hemichannel gating mechanisms should not be made at this point. Indeed, multiple experiments show that, in the absence of Ca²⁺ and at negative potentials, hCx26 hemichannel exhibit active loop gating events i.e., open-close transitions, which can last even seconds (see for example single channels recording in Sanchez et al., 2016 or Sanchez et al., 2013). At most, it could be speculated that the combination of the external electric field with the CG force field excited a collective degree of freedom, which might also be used by one of the hemichannel gating mechanisms.

While hinted by several experimental studies, our model shows for the first time how a connexin hemichannel can rearrange the quaternary structure in response to an external field. The cost-effective characteristic of our simulation scheme could allow for a large-scale mutagenesis studied on one or more members of the connexin family, to facilitate the rationalization of spontaneously arising mutations or polymorphisms.

Author Contributions

FZ and SP designed research. FZ, SP, and DB performed computer simulations. FB, AC, and GC performed experiments. FM designed and supervised experiments. FZ, DB, SP, GY, and FM analyzed data. FZ, SP, and FM wrote the paper.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer UZ and handling Editor declared their shared affiliation.

Acknowledgments

Simulations were partially performed at the Informatics Platform of SIAIS, Shanghaitech University (FZ) and at the Institut Pasteur the Montevideo (SP). Some of the Tesla K40 GPUs used for this research were donated by the NVIDIA Corporation to SP. This work was supported by: National Science Foundation of China (Grant N 31770776 to FZ), FOCEM (MERCOSUR Structural Convergence Fund), COF 03/11 to SP; Fondazione Telethon (grant GGP13114 to FM); CNR (Project DSB.AD009.001.004/INVECCHIAMENTO IBCN to FM); Science and Technology Commission of Shanghai Municipality (grant 16DZ1910299 to GY). SP is part of the Uruguayan National Scientific Research Program of ANII (SNI). FM is a recipient of a Shanghai Thousand Talent Program award for Foreign Experts.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fnmol.2018.00170/full#supplementary-material

Figure SM1. Independent replicas of the Cx26 under external electric field. (Top) RMSD on the Cx26 hemichannel in absence (green) and presence of an external field (red: negative; blue: positive). The two columns identify independent replicas. The external field in either direction was applied immediately after the stabilization period re-generating a temperature distribution using different random seeds. (Bottom) time dependence of the internal radii measured at the level of Lys41.

Supplementary Movie SM1. Excessively high electric fields destroy protein and membrane systems. The simulation was carried out applying an external field in the -z direction during 100 ns.

References

Astrada, S., Gomez, Y., Barrera, E., Obal, G., Pritsch, O., Pantano, S., et al. (2016). Comparative analysis reveals amino acids critical for anticancer activity of peptide CIGB-552. J. Pept. Sci. 22, 711–722. doi: 10.1002/psc.2934

PubMed Abstract | CrossRef Full Text | Google Scholar

Belousov, A. B., Nishimune, H., Denisova, J. V., and Fontes, J. D. (2018). A potential role for neuronal connexin 36 in the pathogenesis of amyotrophic lateral sclerosis. Neurosci. Lett. 666, 1–4. doi: 10.1016/j.neulet.2017.12.027

PubMed Abstract | CrossRef Full Text | Google Scholar

Beltramello, M., Piazza, V., Bukauskas, F. F., Pozzan, T., and Mammano, F. (2005). Impaired permeability to Ins(1,4,5)P3 in a mutant connexin underlies recessive hereditary deafness. Nat. Cell Biol. 7, 63–69. doi: 10.1038/ncb1205

PubMed Abstract | CrossRef Full Text | Google Scholar

Bennett, B. C., Purdy, M. D., Baker, K. A., Acharya, C., McIntire, W. E., Stevens, R. C., et al. (2016). An electrostatic mechanism for Ca²⁺ -mediated regulation of gap junction channels. Nat. Commun. 7:8770. doi: 10.1038/Ncomms9770

PubMed Abstract | CrossRef Full Text | Google Scholar

Bennett, M. V., Contreras, J. E., Bukauskas, F. F., and Sáez, J. C. (2003). New roles for astrocytes: gap junction hemichannels have something to communicate. Trends Neurosci. 26, 610–617. doi: 10.1016/j.tins.2003.09.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Bernardi, R. C., Melo, M. C. R., and Schulten, K. (2015). Enhanced sampling techniques in molecular dynamics simulations of biological systems. Biochim. Biophys. Acta 1850, 872–877. doi: 10.1016/j.bbagen.2014.10.019

PubMed Abstract | CrossRef Full Text | Google Scholar

Bussi, G., Donadio, D., and Parrinello, M. (2007). Canonical sampling through velocity rescaling. J. Chem. Phys. 126:014101. doi: 10.1063/1.2408420

PubMed Abstract | CrossRef Full Text | Google Scholar

Cali, T., Frizzarin, M., Luoni, L., Zonta, F., Pantano, S., Cruz, C., et al. (2017). The ataxia related G1107D mutation of the plasma membrane Ca²⁺ ATPase isoform 3 affects its interplay with calmodulin and the autoinhibition process. Biochim. Biophys. Acta 1863, 165–173. doi: 10.1016/j.bbadis.2016.09.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Carrer, A., Leparulo, A., Crispino, G., Ciubotaru, C. D., Marin, O., Zonta, F., et al. (2017). Cx32 hemichannel opening by cytosolic Ca²⁺ is inhibited by the R220X mutation that causes Charcot-Marie-Tooth disease. Hum. Mol. Genet. 27, 80–94. doi: 10.1093/hmg/ddx386

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, C., Smye, S. W., Robinson, M. P., and Evans, J. A. (2006). Membrane electroporation theories: a review. Med. Biol. Eng. Comput. 44, 5–14. doi: 10.1007/s11517-005-0020-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Cohen, A. E., and Venkatachalam, V. (2014). Bringing bioelectricity to light. Annu. Rev. Biophys. 43, 211–232. doi: 10.1146/annurev-biophys-051013-022717

PubMed Abstract | CrossRef Full Text | Google Scholar

Darden, T., York, D., and Pedersen, L. (1993). Particle mesh Ewald: an N·log(N) method for Ewald sums in large systems. J. Chem. Phys. 98, 10089–10093. doi: 10.1063/1.464397

CrossRef Full Text | Google Scholar

Darré, L., Machado, M. R., Brandner, A. F., González, H. C., Ferreira, S., and Pantano, S. (2015). SIRAH: a structurally unbiased coarse-grained force field for proteins with aqueous solvation and long-range electrostatics. J. Chem. Theory Comput. 11, 723–739. doi: 10.1021/ct5007746

PubMed Abstract | CrossRef Full Text | Google Scholar

Darre, L., Machado, M. R., Dans, P. D., Herrera, F. E., and Pantano, S. (2010). Another coarse grain model for aqueous solvation: WAT FOUR? J. Chem. Theory Comput. 6, 3793–3807. doi: 10.1021/ct100379f

CrossRef Full Text | Google Scholar

Delemotte, L., Tarek, M., Klein, M. L., Amaral, C., and Treptow, W. (2011). Intermediate states of the Kv1.2 voltage sensor from atomistic molecular dynamics simulations. Proc. Natl. Acad. Sci. U.S.A. 108, 6109–6114. doi: 10.1073/pnas.1102724108

PubMed Abstract | CrossRef Full Text | Google Scholar

Escalona, Y., Garate, J. A., Araya-Secchi, R., Huynh, T., Zhou, R., and Perez-Acle, T. (2016). Exploring the membrane potential of simple dual-membrane systems as models for gap-junction channels. Biophys. J. 110, 2678–2688. doi: 10.1016/j.bpj.2016.05.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Esseltine, J. L., and Laird, D. W. (2016). Next-generation connexin and pannexin cell biology. Trends Cell Biol. 26, 944–955. doi: 10.1016/j.tcb.2016.06.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Evans, W. H., and Martin, P. E. (2002). Gap junctions: structure and function (Review). Mol. Membr. Biol. 19, 121–136. doi: 10.1080/09687680210139839

PubMed Abstract | CrossRef Full Text | Google Scholar

Fasciani, I., Temperán, A., Pérez-Atencio, L. F., Escudero, A., Martínez-Montero, P., Molano, J., et al. (2013). Regulation of connexin hemichannel activity by membrane potential and the extracellular calcium in health and disease. Neuropharmacology 75, 479–490. doi: 10.1016/j.neuropharm.2013.03.040

PubMed Abstract | CrossRef Full Text | Google Scholar

Gómez-Hernández, J. M., de Miguel, M., Larrosa, B., González, D., and Barrio, L. C. (2003). Molecular basis of calcium regulation in connexin-32 hemichannels. Proc. Natl. Acad. Sci. U.S.A. 100, 16030–16035. doi: 10.1073/pnas.2530348100

PubMed Abstract | CrossRef Full Text | Google Scholar

González, D., Gómez-Hernández, J. M., and Barrio, L. C. (2006). Species specificity of mammalian connexin-26 to form open voltage-gated hemichannels. FASEB J. 20, 2329–2338. doi: 10.1096/fj.06-5828com

PubMed Abstract | CrossRef Full Text | Google Scholar

Goodenough, D. A., and Paul, D. L. (2009). Gap junctions. Cold Spring Harb. Perspect. Biol. 1:a002576. doi: 10.1101/cshperspect.a002576

PubMed Abstract | CrossRef Full Text | Google Scholar

Grübmuller, H. (1995). Predicting slow structural transitions in macromolecular systems: conformational flooding. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 52, 2893–2906.

PubMed Abstract | Google Scholar

Hekstra, D. R., White, K. I., Socolich, M. A., Henning, R. W., Šrajer, V., and Ranganathan, R. (2016). Electric-field-stimulated protein mechanics. Nature 540, 400–405. doi: 10.1038/nature20571

PubMed Abstract | CrossRef Full Text | Google Scholar

Kar, R., Batra, N., Riquelme, M. A., and Jiang, J. X. (2012). Biological role of connexin intercellular channels and hemichannels. Arch. Biochem. Biophys. 524, 2–15. doi: 10.1016/j.abb.2012.03.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Kwon, T., Harris, A. L., Rossi, A., and Bargiello, T. A. (2011). Molecular dynamics simulations of the Cx26 hemichannel: evaluation of structural models with Brownian dynamics. J. Gen. Physiol. 138, 475–493. doi: 10.1085/jgp.201110679

PubMed Abstract | CrossRef Full Text | Google Scholar

Laio, A., and Parrinello, M. (2002). Escaping free-energy minima. Proc. Natl. Acad. Sci. U.S.A. 99, 12562–12566. doi: 10.1073/pnas.202427399

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, W., Bao, G., Chen, W., Qiang, X., Zhu, S., Wang, S., et al. (2018). Connexin 43 hemichannel as a novel mediator of sterile and infectious inflammatory diseases. Sci. Rep. 8:166. doi: 10.1038/s41598-017-18452-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Lopez, W., Ramachandran, J., Alsamarah, A., Luo, Y., Harris, A. L., and Contreras, J. E. (2016). Mechanism of gating by calcium in connexin hemichannels. Proc. Natl. Acad. Sci. U.S.A. 113, E7986–E7995. doi: 10.1073/pnas.1609378113

PubMed Abstract | CrossRef Full Text | Google Scholar

Machado, M. R., and Pantano, S. (2016). SIRAH Tools: mapping, backmapping and visualization of coarse-grained models. Bioinformatics 32, 1568–1570. doi: 10.1093/bioinformatics/btw020

PubMed Abstract | CrossRef Full Text | Google Scholar

Maeda, S., Nakagawa, S., Suga, M., Yamashita, E., Oshima, A., Fujiyoshi, Y., et al. (2009). Structure of the connexin 26 gap junction channel at 3.5 A resolution. Nature 458, 597–602. doi: 10.1038/nature07869

PubMed Abstract | CrossRef Full Text | Google Scholar

Müller, D. J., Hand, G. M., Engel, A., and Sosinsky, G. E. (2002). Conformational changes in surface structures of isolated connexin 26 gap junctions. EMBO J. 21, 3598–3607. doi: 10.1093/emboj/cdf365

PubMed Abstract | CrossRef Full Text | Google Scholar

Parrinello, M., and Rahman, A. (1981). Polymorphic transitions in single crystals: a new molecular dynamics method. J. Appl. Phys. 52, 9.

Google Scholar

Pronk, S., Páll, S., Schulz, R., Larsson, P., Bjelkmar, P., Apostolov, R., et al. (2013). GROMACS 4.5: a high-throughput and highly parallel open source molecular simulation toolkit. Bioinformatics 29, 845–854. doi: 10.1093/bioinformatics/btt055

PubMed Abstract | CrossRef Full Text | Google Scholar

Ri, Y., Ballesteros, J. A., Abrams, C. K., Oh, S., Verselis, V. K., Weinstein, H., et al. (1999). The role of a conserved proline residue in mediating conformational changes associated with voltage gating of Cx32 gap junctions. Biophys. J. 76, 2887–2898. doi: 10.1016/S0006-3495(99)77444-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Saez, J. C., and Leybaert, L. (2014). Hunting for connexin hemichannels. FEBS Lett. 588, 1205–1211. doi: 10.1016/j.febslet.2014.03.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Sanchez, H. A., Bienkowski, R., Slavi, N., Srinivas, M., and Verselis, V. K. (2014). Altered inhibition of Cx26 hemichannels by pH and Zn²⁺ in the A40V mutation associated with keratitis-ichthyosis-deafness syndrome. J. Biol. Chem. 289, 21519–21532. doi: 10.1074/jbc.M114.578757

PubMed Abstract | CrossRef Full Text | Google Scholar

Sanchez, H. A., Mese, G., Srinivas, M., White, T. W., and Verselis, V. K. (2010). Differentially altered Ca²⁺ regulation and Ca²⁺ permeability in Cx26 hemichannels formed by the A40V and G45E mutations that cause keratitis ichthyosis deafness syndrome. J. Gen. Physiol. 136, 47–62. doi: 10.1085/jgp.201010433

PubMed Abstract | CrossRef Full Text | Google Scholar

Sanchez, H. A., Slavi, N., Srinivas, M., and Verselis, V. K. (2016). Syndromic deafness mutations at Asn 14 differentially alter the open stability of Cx26 hemichannels. J. Gen. Physiol. 148, 25–42. doi: 10.1085/jgp.201611585

PubMed Abstract | CrossRef Full Text | Google Scholar

Sanchez, H. A., Villone, K., Srinivas, M., and Verselis, V. K. (2013). The D50N mutation and syndromic deafness: altered Cx26 hemichannel properties caused by effects on the pore and intersubunit interactions. J. Gen. Physiol. 142, 3–22. doi: 10.1085/jgp.201310962

PubMed Abstract | CrossRef Full Text | Google Scholar

Srinivas, M., Kronengold, J., Bukauskas, F. F., Bargiello, T. A., and Verselis, V. K. (2005). Correlative studies of gating in Cx46 and Cx50 hemichannels and gap junction channels. Biophys. J. 88, 1725–1739. doi: 10.1529/biophysj.104.054023

PubMed Abstract | CrossRef Full Text | Google Scholar

Surdo, N. C., Berrera, M., Koschinski, A., Brescia, M., Machado, M. R., Carr, C., et al. (2017). FRET biosensor uncovers cAMP nano-domains at β-adrenergic targets that dictate precise tuning of cardiac contractility. Nat. Commun. 8:15031. doi: 10.1038/ncomms15031

PubMed Abstract | CrossRef Full Text | Google Scholar

Tang, Q., Dowd, T. L., Verselis, V. K., and Bargiello, T. A. (2009). Conformational changes in a pore-forming region underlie voltage-dependent “loop gating” of an unapposed connexin hemichannel. J. Gen. Physiol. 133, 555–570. doi: 10.1085/jgp.200910207

PubMed Abstract | CrossRef Full Text | Google Scholar

Teissié, J., and Rols, M. P. (1993). An experimental evaluation of the critical potential difference inducing cell membrane electropermeabilization. Biophys. J. 65, 409–413. doi: 10.1016/S0006-3495(93)81052-X

PubMed Abstract | CrossRef Full Text | Google Scholar

Thomas, T., Jordan, K., Simek, J., Shao, Q., Jedeszko, C., Walton, P., et al. (2005). Mechanisms of Cx43 and Cx26 transport to the plasma membrane and gap junction regeneration. J. Cell Sci. 118 (Pt 19), 4451–4462. doi: 10.1242/jcs.02569

PubMed Abstract | CrossRef Full Text | Google Scholar

Trexler, E. B., Bennett, M. V., Bargiello, T. A., and Verselis, V. K. (1996). Voltage gating and permeation in a gap junction hemichannel. Proc. Natl. Acad. Sci. U.S.A. 93, 5836–5841.

PubMed Abstract | Google Scholar

Tsai, C. F., Cheng, Y. K., Lu, D. Y., Wang, S. L., Chang, C. N., Chang, P. C., et al. (2018). Inhibition of estrogen receptor reduces connexin 43 expression in breast cancers. Toxicol. Appl. Pharmacol. 338, 182–190. doi: 10.1016/j.taap.2017.11.020

PubMed Abstract | CrossRef Full Text | Google Scholar

Verselis, V. K., and Srinivas, M. (2008). Divalent cations regulate connexin hemichannels by modulating intrinsic voltage-dependent gating. J. Gen. Physiol. 132, 315–327. doi: 10.1085/jgp.200810029

PubMed Abstract | CrossRef Full Text | Google Scholar

Villanelo, F., Escalona, Y., Pareja-Barrueto, C., Garate, J. A., Skerrett, I. M., and Perez-Acle, T. (2017). Accessing gap-junction channel structure-function relationships through molecular modeling and simulations. BMC Cell Biol. 18 (Suppl. 1):5. doi: 10.1186/s12860-016-0121-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, L., Carrer, A., Zonta, F., Qu, Z., Ma, P., Li, S., et al. (2017). Design and characterization of a human monoclonal antibody that modulates mutant connexin 26 hemichannels implicated in deafness and skin disorders. Front. Mol. Neurosci. 10:298. doi: 10.3389/fnmol.2017.00298

PubMed Abstract | CrossRef Full Text | Google Scholar

Yi, C., Ezan, P., Fernández, P., Schmitt, J., Sáez, J. C., Giaume, C., et al. (2017). Inhibition of glial hemichannels by boldine treatment reduces neuronal suffering in a murine model of Alzheimer's disease. Glia 65, 1607–1625. doi: 10.1002/glia.23182

PubMed Abstract | CrossRef Full Text | Google Scholar

Zonta, F., Buratto, D., Cassini, C., Bortolozzi, M., and Mammano, F. (2014). Molecular dynamics simulations highlight structural and functional alterations in deafness-related M34T mutation of connexin 26. Front. Physiol. 5:85. doi: 10.3389/fphys.2014.00085

PubMed Abstract | CrossRef Full Text | Google Scholar

Zonta, F., Girotto, G., Buratto, D., Crispino, G., Morgan, A., Abdulhadi, K., et al. (2015). The p.Cys169Tyr variant of connexin 26 is not a polymorphism. Hum. Mol. Genet. 24, 2641–2648. doi: 10.1093/hmg/ddv026

PubMed Abstract | CrossRef Full Text | Google Scholar

Zonta, F., Polles, G., Sanasi, M. F., Bortolozzi, M., and Mammano, F. (2013). The 3.5 angstrom X-ray structure of the human connexin26 gap junction channel is unlikely that of a fully open channel. Cell Commun. Signal. 11:15. doi: 10.1186/1478-811X-11-15

PubMed Abstract | CrossRef Full Text | Google Scholar

Zonta, F., Polles, G., Zanotti, G., and Mammano, F. (2012). Permeation pathway of homomeric connexin 26 and connexin 30 channels investigated by molecular dynamics. J. Biomol. Struct. Dyn. 29, 985–998. doi: 10.1080/073911012010525027

PubMed Abstract | CrossRef Full Text | Google Scholar