Coupling of the Monte Carlo iMC and OpenFoam codes for multiphysics calculations of molten salt reactors

This paper presents the development of a multiphysics coupled framework of Monte Carlo neutronics iMC and OpenFOAM Computational Fluid Dynamics codes for molten salt reactor (MSR) analysis. The overall coupling scheme is handled, including the framework structure and iteration scheme. Also, related techniques to enhance the accuracy and efficiency of the coupling are introduced, such as delayed neutron precursor tracking. The framework is applied to a simple molten salt reactor model and achieves a converged solution. In addition, sensitivity studies on the neutronics mesh are performed. The research demonstrates the capability of the iMC-OpenFOAM coupled framework to achieve a converged solution and provides significant insights into the analysis of the MSRs.

1 Introduction

Molten Salt Reactor (MSR) is an advanced nuclear reactor concept gaining significant attention. MSRs offer distinct advantages over conventional reactor designs. Since the MSR employs liquid fuel, it leads to continuous refueling and removal of noble fission products by utilizing helium bubbling. In addition, the MSR provides inherent safety and long-term operation. Given these advantages, MSRs are being actively developed worldwide, with several experimental and commercial designs progressing toward deployment. Despite the benefits, an accurate analysis of MSR is an ongoing challenge that requires a multiphysics simulation framework. Unlike traditional reactor systems, where the phenomenon can often be treated separately, MSR requires tightly coupled simulations, especially its delayed neutron precursors (DNP) flow and neutron-induced heating. This complexity has led to ongoing efforts in developing MSR-specific multiphysics models, including coupled neutronics, fluid dynamics, and thermal-mechanical analysis. Although multiphysics solvers for MSRs have been proposed, most rely on deterministic neutronics and simplified CFD, limiting their accuracy in capturing key MSR phenomena (Křepel et al., 2007; Aufiero et al., 2014; Ridley et al., 2017; Yang et al., 2022). Regarding the neutronics, deterministic solvers are preferred due to their simplicity and computing efficiency. However, deterministic methods rely on simplifying assumptions and cannot fully capture effects such as secondary photon transport.

To address these challenges, we propose a novel MSR-specialized multiphysics analysis scheme by coupling an in-house neutron transport code, iMC (Kim and Kim, 2021), with the OpenFOAM CFD framework (Weller et al., 1998). iMC code is a Monte Carlo neutron transport code developed at KAIST, which has previous efforts to develop and implement the MSR-specialized analysis, including DNP shift and nuclide control in depletion (Kim et al., 2024; Kim et al., 2025). The iMC method offers an accurate and flexible approach to solving neutron transport problems. Unlike previous approaches that utilized a deterministic neutronics solver, this work aims to evaluate reactor power distribution based solely on Monte Carlo neutron transport analysis with secondary photon transport. Monte Carlo methods enable high-fidelity modeling of coupled phenomena, making them particularly suitable for MSR analysis. At the same time, OpenFOAM is an open-source and accurate CFD code for simulating complex fluid flow and thermal-hydraulic phenomena. By integrating these two codes, we aim to develop a computational framework capable of capturing the tightly coupled physics of MSRs, including neutron transport, temperature feedback, and fuel salt circulation.

This paper presents the development and implementation of the multiphysics coupling scheme for MSR analysis. Section 2 details the coupling framework by the coupling mechanism, mesh control strategies, and treatment of MSR-specific flow characteristics. Section 3 describes the problem setup and demonstrates the results of the developed scheme applied to benchmark MSR configurations. Finally, Section 4 concludes the study by summarizing key findings and discussing future improvements in MSR multiphysics simulation.

2 Methods

2.1 Coupling framework

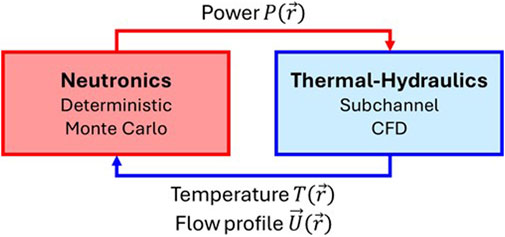
The paper discusses a coupled framework of the iMC and OpenFOAM codes to provide a multiphysics solution for the MSR. Figure 1 describes the physics to be considered in the MSR analysis and data transferred between the schemes. The framework comprises three parts: neutronics, CFD, and an intermediate coupler. The neutronics, Monte Carlo neutron transport using the iMC code, has temperature T, density ρ, and flow profile $\overrightarrow{U}$ from the CFD code as inputs and tallies heat distribution from the neutron. The CFD code, OpenFOAM, utilizes the heat distribution from the neutronics to compute temperature and velocity distributions in the reactor domain. The results are then transferred to the neutronics part. The coupler is a script that handles data transfer and iterations. Since the neutronics and fluid dynamics are tightly coupled, a certain level of iterations is required to provide a converged result. The coupler performs a fixed-point iteration by handling the data from both sides and halting the simulation when the result is sufficiently converged.

Figure 1

Figure 1. Coupling scheme between neutronics and thermal-hydraulics.

A contribution of the neutronics to the coupled framework is the production of a heat distribution induced by the neutron. In detail, neutron heating can be classified into direct and indirect heating via secondary photons. Regarding conventional Monte Carlo simulation, fission heating data can be scaled to include secondary photon heating without additional photon transport. On the other hand, the spatial distribution of the heating is required for the coupling scheme. Therefore, secondary photon production and transport simulation are necessary to obtain an accurate spatial distribution of the heating. A photon transport module has been newly implemented in the iMC code and internally verified against OpenMC and Serpent results (Lund and Romano, 2018; Kaltiaisenaho, 2020). The power distribution is generated from the coupled neutron-photon transport, which serves as the source term for CFD simulations.

The OpenFOAM evaluates the temperature distribution $T\left(\overrightarrow{r}\right)$ and flow profile $U\left(\overrightarrow{r}\right)$ based on the transferred power distribution. The temperature distributions of the fuel and the moderator are applied to the iMC Monte Carlo analysis, based on the on-the-fly Doppler broadening. Section 2.2 expresses the on-the-fly Doppler broadening’s theoretical basis and its usage in the iMC code. The fuel flow profile affects the delayed neutron precursor and perturbs the reactivity and kinetic parameters. Section 2.3 introduces an approach used in the iMC code to simulate the delayed neutron precursor on the fuel flow.

One practical difference between the iMC and OpenFOAM codes is the mesh size. Since OpenFOAM solves fluid dynamics using the finite volume method, a sufficiently small mesh is required for an accurate result. On the other hand, the iMC code provides a heat distribution based on a tally on the mesh. Therefore, there is a mismatch in the mesh size, and the data needs to be collapsed when transferred from the OpenFOAM to the iMC. In the framework, the CFD data is converted to a coarser mesh by utilizing the OpenFOAM post-processing feature, which utilizes volume averaging. On the other hand, the power distribution on the coarser mesh is transferred to the OpenFOAM code and directly applied to the fine CFD mesh without interpolation.

2.2 Temperature treatment

After the CFD analysis from OpenFOAM, the temperature distribution is transferred to the iMC. In the iMC code, the temperature treatment simulates the target velocity. Equation 1 gives the Doppler-broadened cross-section $\sigma \left(y,T\right)$ evaluated from a base temperature T₀ (Cullen and Weisbin, 1976).

$\sigma \left(y,T\right)=\frac{1}{y^2\sqrt{\pi }}{\displaystyle \underset{0}{\overset{\infty }{\int }}}dx{x}^2\sigma \left(x,T_0\right)\left[e^{-{\left(x-y\right)}^2}-e^{-{\left(x+y\right)}^2}\right],(1)$

where x and y are defined as in Equation 2.

$\alpha =\frac{A}{k\left(T-T_0\right)},x=\sqrt{\alpha E_r},y=\sqrt{\alpha E},(2)$

where E and E_r are incident neutron energy and relative neutron energy concerning target velocity sampled from the target temperature, respectively. A and k are the relative target mass to neutron mass and the Boltzmann coefficient, respectively. In the iMC code, Equation 1 integral is evaluated using a modified Gauss-Hermite Quadrature, which provides sufficient accuracy (Jo and Cho, 2017). This method requires a single temperature point, suitable for thermo-coupled analysis that varies in temperature range.

Some nuclides require additional thermal scattering data. Unlike the cross-section data, the Doppler broadening is unavailable for the thermal scattering. Therefore, the thermal scattering data linearly interpolates the cross-section at different temperature points.

In the iMC neutron tracking, the particle stops at the material or geometry boundaries. As temperature change leads to the cross-section change, the particle should also stop at the temperature grid boundary. When the particle crosses the temperature grid boundaries, the material temperature and density are updated based on the CFD results. Therefore, the size of the temperature mesh affects the computing time, especially for the fine temperature mesh. When the temperature distribution is obtained from the OpenFOAM, computing time increases significantly. The coupling scheme collapses the temperature distribution into the coarser mesh. The mesh sensitivity regarding accuracy and computing time will be investigated in a subsequent section.

2.3 Delayed neutron tracking

One unique aspect of the MSR analysis is its flowing fuel. As mentioned, the MSR utilizes the liquid fuel as a coolant, achieving thermal balance. Furthermore, the flowing fuel affects the neutronics by shifting the delayed neutron distribution. The shift changes the contribution to the fission chain by simply moving the precursor position. The contribution becomes negligible when the precursor moves out of the active core and decays.

The iMC code has a feature to simulate the delayed neutron precursor shifts on the given fuel flow (Kim et al., 2024). During the neutron tracking, if the neutron undergoes fission, the resulting fission neutrons are tested to determine whether they are delayed or not based on the delayed neutron fission yield. If the fission neutron is considered delayed, the delayed group is also determined, and the corresponding emission time, t_emit is sampled based on Equation 3, using constant $\lambda$ and uniform random number $\gamma$,

$t_{emit}=-\frac{\ln \gamma }{\lambda }.(3)$

Then, given the emission time and position, its shifted position is sampled. Based on the velocity field provided by the CFD code, the precursors move toward the top of the active core. Since the velocity field is not provided in a functional form, the precursor tracking is performed numerically. Equation 4 shows a basic tracking scheme. From fission site $\overrightarrow{r}\left(0\right)$, the position of the precursor is numerically obtained based on the velocity field $U\left(\overrightarrow{r},t\right)$ and fine time step dt. The current framework defines the velocity field for the finite volume and assumes constant velocity within the volume. Therefore, dt is automatically determined based on the current position and distance to the velocity grid boundary.

$\overrightarrow{r}\left(t+dt\right)=\overrightarrow{r}\left(t\right)+\overrightarrow{U}\left(\overrightarrow{r},t\right)dt.(4)$

The tracking is performed until the precursor decays or reaches the top of the active core. If the precursor reaches the top of the active core, the precursor is considered to recirculate and return to the bottom. In the current recirculation scheme in the iMC code, the out-of-core model is simplified: the precursor decayed out of the core is neglected from the analysis, and the precursor recirculated into the core is uniformly distributed. The iMC code set the weight of the delayed neutron produced out of the active core to zero.

The conventional fraction of the delayed neutron is about 0.7%. Since the Monte Carlo analysis requires numerous simulations for better precision, the precision of the delayed neutron-related results is often insufficient due to the low concentration of the delayed neutron. To enhance statistical precision, delayed neutron precursor splitting is introduced. The splitting intentionally splits the delayed neutron precursors from the fission while adjusting the corresponding weight to avoid bias. The delayed neutron precursors are then tracked based on the fuel flow profile.

Prompt or delayed neutrons are determined from the neutron yield when the neutron undergoes fission. Instead of producing a single delayed neutron precursor with unity weight, n_split delayed neutron precursors are produced with the weight of 1/n_split. The scheme leads to multiple samplings of the delayed neutron precursor groups and the corresponding precursor shift. Note that the method needs to be unbiased and thus requires some attention regarding its normalization. Recalling a typical Monte Carlo neutron transport procedure, after cycle i ends, the next cycle’s neutron weight w_i+1 is adjusted to Equation 5:

$w_{i+1}=N/M,(5)$

where N and M are the initial number of histories per cycle and the total weight of fission neutrons produced from cycle i, respectively. However, the weight of the delayed neutron should be adjusted as in Equation 6, for unbiased evaluation:

$w_{d,i+1}=\frac{N}{M{n}_{split}}.(6)$

In addition, the delayed neutron leaks from the core should be adequately considered by setting their initial weight to zero. Therefore, the initial total weight will be slightly smaller than N if some precursors decay out of the core.

The method is ineffective for static fuel since the delayed neutron fraction is solely determined by the delayed neutron yield and fission rate. On the other hand, the technique enhances precision for the moving fuel where the produced delayed neutron precursors are shifted. While sampling without splitting results in a single position moved due to the flow, splitting provides a distribution of the delayed neutron production for varying emission times. In this paper, n_split is set to 10 for every fission reaction. Improvement in the precision, accuracy, and computing time will be discussed in Section 3.

Adjoint neutron flux is a measure of the contribution of the phase space to the fission chain, which needs to be considered while producing the effective kinetic parameters. The iMC code was previously developed and implemented using the iterated fission probability (IFP) method, which was introduced to obtain adjoint-weighted factors during the Monte Carlo simulation (Oh et al., 2025). The IFP method is utilized to get the adjoint-weighted kinetic parameters, with 10 latent cycles.

2.4 Iteration scheme

Due to the nonlinear relation between the neutronics and the fluid dynamics, multiple coupled calculations are required to obtain a converged solution. However, unlike deterministic neutronics code, the results from the Monte Carlo method contain uncertainty due to its statistical nature. The uncertainty complicates the convergence criteria, as the solutions are expected to oscillate within a specific range.

In this study, the heat distribution from the Monte Carlo analysis is applied with an under-relaxation. When the heat distribution H_i is obtained from the ith iteration, actual input for the OpenFOAM code, H_i’ can be estimated as in Equation 7:

$H_i^{\prime }=w_i{H}_i+\left(1-w_i\right)H_{i-1},(7)$

where the weight w_i can be determined using Equation 8:

${\mathrm{w}}_{\mathrm{i}}=\frac{1}{i}.(8)$

The selection of the w_i is heuristic and intended to stabilize the solution gradually. The convergence is determined by comparing the temperature distribution with the previous results. In this paper, the convergence criteria for the temperature are set to a maximum absolute difference of 0.1 K for both regions.

3 Numerical results

3.1 Problem description

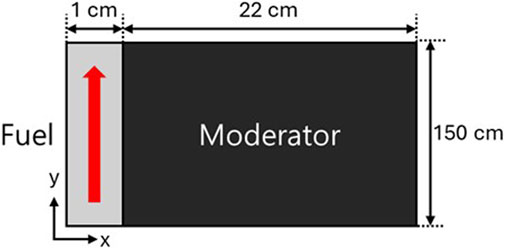
We adopt a newly proposed 2D thermal MSR benchmark developed by Pfhal (2025), which features a 1 cm-wide fuel channel adjacent to a 22 cm graphite moderator slab and extends 1.5 m in height. The total power of the model is considered to be 0.35 MW. As this benchmark is recent, no reference solution is available for direct comparison.

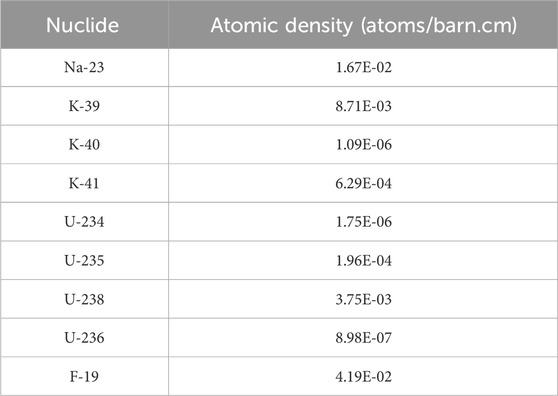
Figure 2 shows a geometry of the MSR model. Table 1 denotes an isotope-wise composition of the fuel. The initial temperature of the fuel and the graphite is assumed to be 873.15 K. The moderator is considered pure natural carbon. Table 2 shows a fundamental thermo-physical properties.

Figure 2

Figure 2. 2D MSR model (not to scale).

Table 1

Table 1. Atomic number density of the fuel in atoms/barn.cm

Table 2

Table 2. Thermo-physical properties of the fuel and moderator.

In OpenFOAM, the problem is solved on 47,600 meshes. The fuel-side mesh contains 14,200 mesh divided into 142 and 100 meshes horizontally and vertically. Note that the mesh becomes finer as it approaches the fuel-moderator interface. Due to the lower heat transfer in the fuel region, a drastic temperature increase is expected near the interface. The conjugate heat transfer, a heat transfer between fluid and solid, is a complex phenomenon in terms of the CFD code. Therefore, a finer mesh is required near the interface. Similarly, the moderator region contains 33,400 mesh divided into 334 and 100 meshes horizontally and vertically, which becomes finer near the interface.

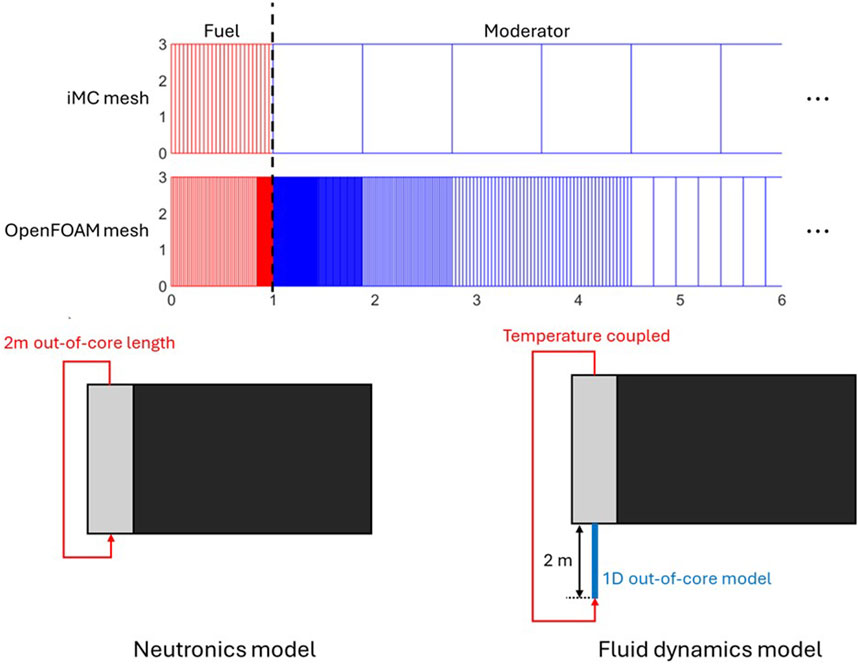
On the other hand, iMC produces heat distribution for 1,250 meshes for both regions. The mesh size is equivalent in an area since the heat distribution is relatively smoother than the fluid dynamics. Due to the use of different mesh sizes, sensitivity analysis of the mesh collapse will be performed. Mesh conversion is done with a post-processing tool equipped with the OpenFOAM.

For the iMC, reflective boundary conditions are applied horizontally, and vacuum boundary conditions are applied vertically. Regarding the OpenFOAM, slip boundary conditions are applied for the interface between the fuel and the moderator. The top and bottom boundaries of the moderator are set to be adiabatic, while fuel is set to be inlet and outlet. Initial velocity and temperature conditions are set to be 0.2 m/s upward and 873.15 K, respectively.

Instead of explicitly modeling an out-of-core model, the fuel flow is assumed to stay out of the core for 10 s and undergo cooling. In this problem, the cooling is simplified as a temperature transfer to the reference temperature defined as Equation 9:

$\frac{dT}{dt}=-{\gamma }_{cool}\left(T-T_{ref}\right),(9)$

where ${\gamma }_{cool}$ and $T_{ref}$ are 0.2 s^-1 and 873.15 K, respectively.

The out-of-core model is not directly modeled in both codes but is simplified differently. Figure 3 describes different approaches to the out-of-core model. Regarding the OpenFOAM, the out-of-core model is simplified to a 1D axial model, subdivided into 200 equivalent meshes. The inlet temperature of the 1D model is set to the average outlet temperature of the active core. In detail, the average outlet temperature is defined as the mass flow rate-weighted average, representing a heat addition in the active core. Outlet temperature is set to a zero gradient and transferred uniformly to the inlet of the active core. Inlet, outlet, and internal velocities are set to be 0.2 m/s upward. For each cell in the model, temperature-dependent cooling is added. In the iMC code, the only consideration for the out-of-core model is its residence time. Therefore, the delayed neutron precursor is considered lost when it escapes through the top of the active core and emits within 10 s. Otherwise, if the emission time left is longer than 10 s, the precursor position is sampled uniformly at the bottom of the active core.

Figure 3

Figure 3. Mesh and out-of-core modeling used in the iMC and OpenFOAM codes.

OpenFOAM steady-state analysis is performed with a conjugate heat transfer solver, chtMultiRegionSimpleFoam (OpenFOAM, 2025). For the first iteration, which starts with a uniform temperature, the evaluation required roughly 50,000 iterations to achieve a sufficient convergence since the temperature rise at the moderator is extremely slow. From the next iteration, the OpenFOAM requires fewer steps for convergence. For the iMC calculation, 500,000 particles per cycle are utilized for 200 inactive cycles and 500 active cycles. It results in 5–6 pcm uncertainty in the infinite multiplication factor k_eff. ENDF-B/VII.1 nuclear data library is utilized (Chadwick et al., 2011), including general neutron-induced cross-section, thermal scattering for the graphite, and photon cross-section.

3.2 Computation result

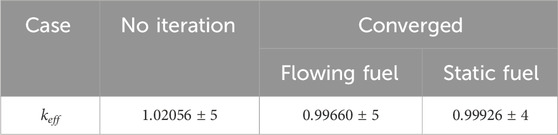
As discussed in Section 2.4, the iteration is terminated when the maximum temperature difference between the previous trial is below 0.1 K. With the temperature convergence criteria, the convergence is achieved in 11 iterations. Table 3 compares the initial k_eff value before the iteration and after the convergence. Note that the initial case uses a uniform temperature distribution of 873.15 K for fuel and moderator. In addition, the problem is solved with the static fuel flow and converged temperature distribution, which can be found as static fuel case.

Table 3

Table 3. k_eff values for initial and converged states.

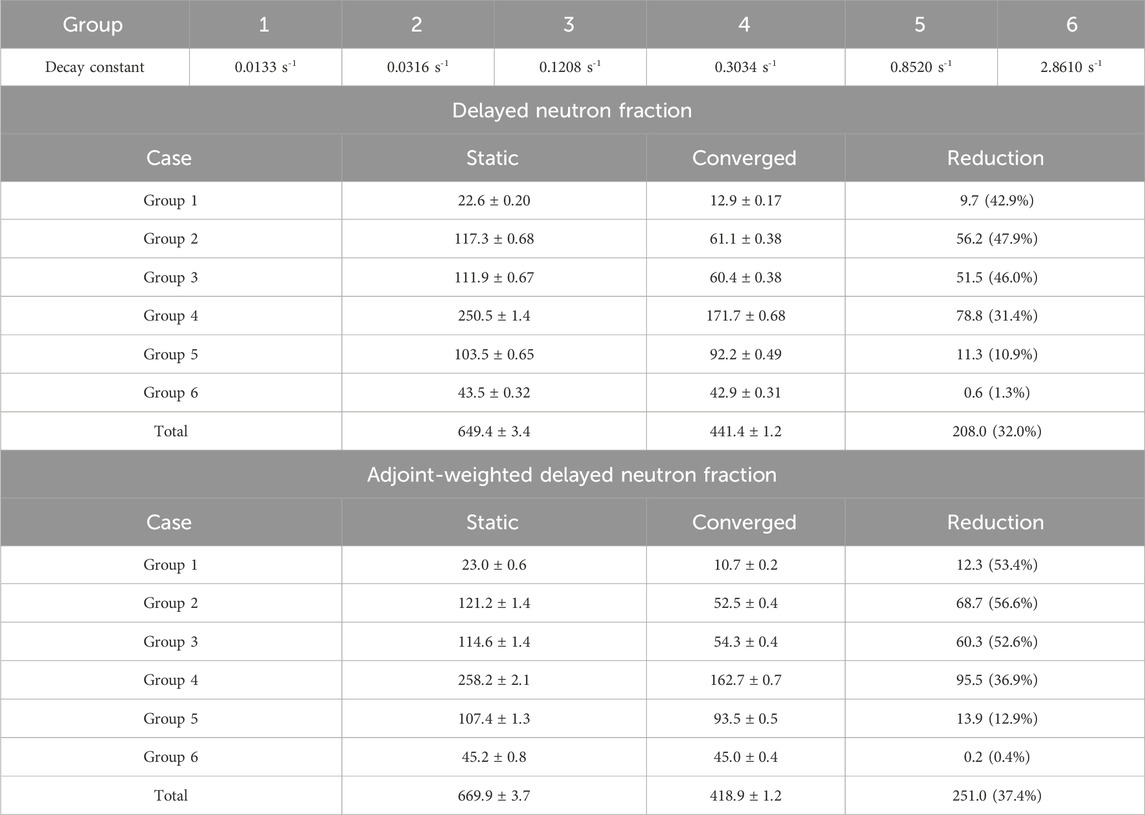
Table 4 compares unweighted and adjoint-weighted delayed neutron fractions from the static and flowing fuel by delayed neutron precursor groups (Anoussis et al., 1973). Upper table stands for the unweighted fractions and lower table stands for the adjoint-weighted fractions based on the IFP. The upper half shows a fraction of the resulting delayed neutrons compared to the total neutron population. Delayed neutron fractions significantly decrease due to precursor drift, particularly in long-lived groups, underscoring the importance of modeling flow-induced spectral shifts.

Table 4

Table 4. Group-wise precursor decay constants and delayed neutron fractions in pcm.

The third column of Table 4 is the reduction of the group-wise fraction in pcm, and its fraction compared to the static case. By comparing groups 1 and 2, a more considerable reduction is observed for group 2, while its half-life is shorter than that of group 1. The phenomenon is due to the recirculation. Although both groups 1 and 2 precursors are likely to escape the active core, precursors of group 1 are more likely to return to the active core. According to the comparison between delayed neutron fractions and the effective fractions, more significant reductions in the effective delayed neutron fractions are observed. For the delayed neutron population, it reduces only when the delayed neutron precursors escape from the active core. However, for the effective delayed neutron fractions, the reduction occurs when it escapes from the active core and shifts from the region with higher importance. According to the nature of the adjoint neutron flux, the central region is more likely to contribute to the fission chain. Regarding the nature of the model, the axial distribution of the delayed neutron and the adjoint neutron flux are cosine-shaped. When the delayed neutron distribution shifts upward due to the flow, most of the delayed neutron precursors move to neutronically less important regions. The delayed neutrons from those regions have a smaller contribution to the fission chain, resulting in a greater reduction in β_eff compared to β.

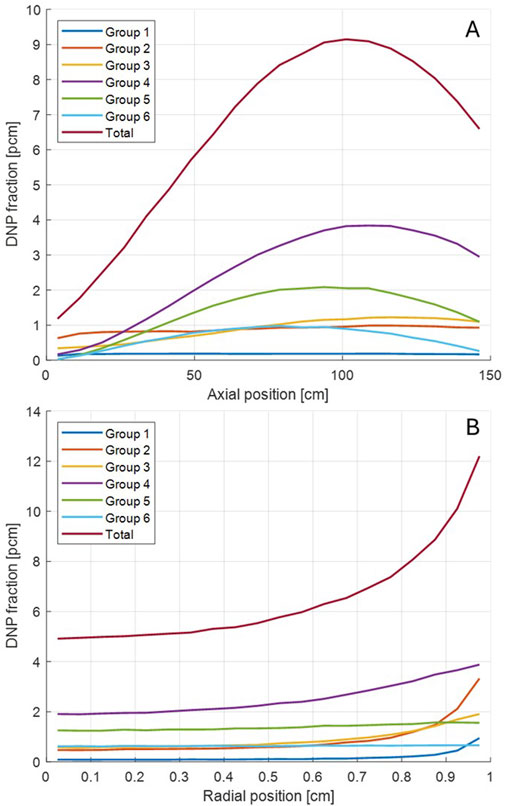
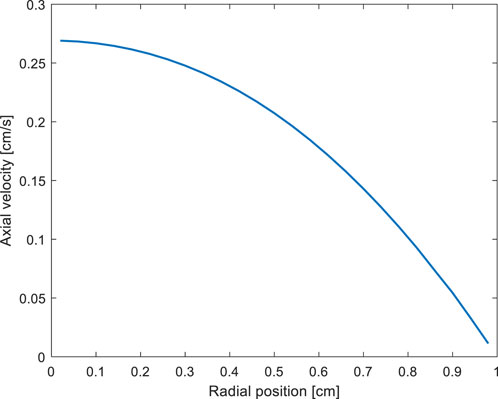
Figure 4 shows the axial and radial distributions of the delayed neutron precursors. According to the axial distribution, the distribution is shifted upward, and 32.0% of delayed neutron precursors decay out of the active core. Regarding the radial distribution, according to the velocity field from Figure 5, delayed neutron precursor concentration is higher at the peripheral region due to lower axial velocity. Although the current model has nearly uniform radial importance, the higher precursor concentration near the interface will cause a more significant impact on other MSR cores.

Figure 4

Figure 4. Axial (A) and radial (B) distribution of the delayed neutron precursors.

Figure 5

Figure 5. Axial velocity profile.

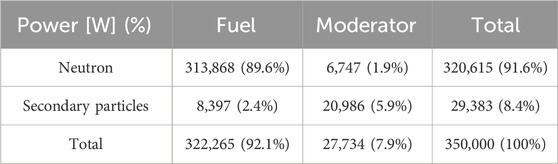
Table 5 tabulates the contributions of each region and particle to the total heating of 0.35 MWth based on the coupled neutron-gamma transport. The table shows that secondary particle transport is necessary for an accurate heat distribution, especially in the graphite region. Figures 6A,B are 2-dimensional heat distributions in the fuel and the moderator regions, respectively. The fuel heating shows a flat distribution along the x-axis due to the narrow fuel channel size. Figure 6C is an axial distribution of the fuel heating, averaged along the x-axis. Similarly, Figure 6D is a radial distribution of the graphite heating, averaged along the y-axis. Regarding graphite heating, the majority is from secondary photon heating. The graphite heat distributions show that the heat distribution reduces exponentially due to the short traveling distance of the photon in the moderator.

Table 5

Table 5. Heating tallied from each region and particle type.

Figure 6

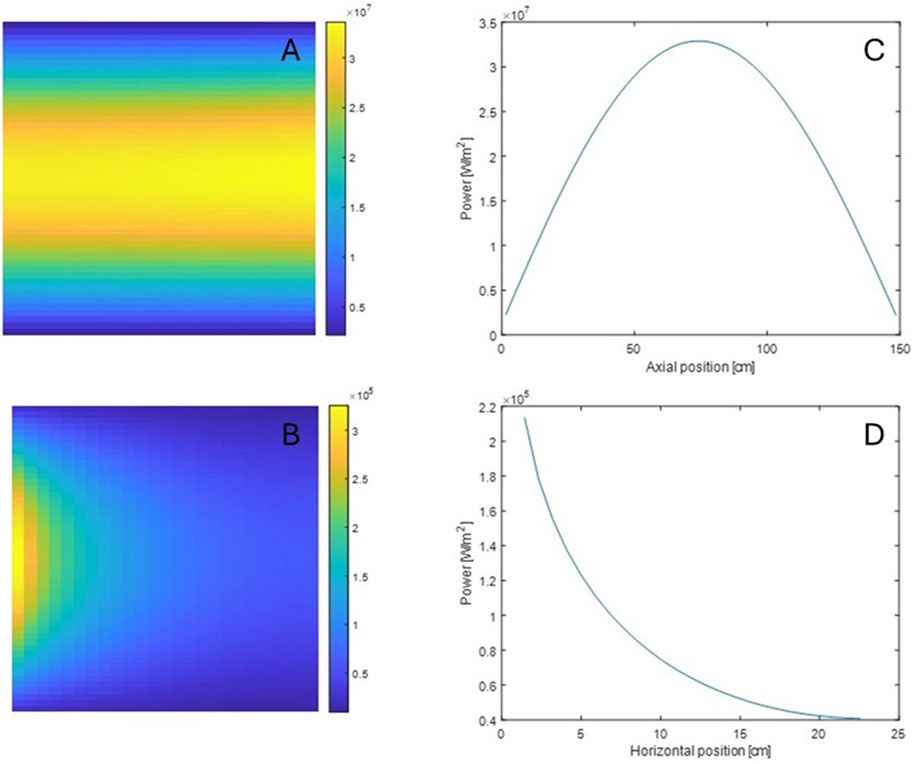
Figure 6. 2D heat distribution in fuel (A) and moderator (B). Axial fuel heat distribution (C) and Radial moderator heat distribution (D).

The inlet and outlet average temperatures are obtained: 1065.9 and 1108.6 K, respectively. The temperatures are obtained from the 1-D out-of-core model. For a fixed out-of-core time of 10 s, inlet temperature can be estimated analytically with outlet temperature T_out (Equation 10), which also returns 1065.9 K for outlet temperature 1108.6 K. This implies accuracy in the 1-D numerical solver.

$T\left(t\right)=\left(T_{out}-T_{ref}\right)e^{-\gamma t}+T_{ref}.(10)$

Figure 7 shows the temperature distributions along the axial midline of the fuel channel, the axial midline of the moderator, and the horizontal midline across the fuel and the moderator regions.

Figure 7

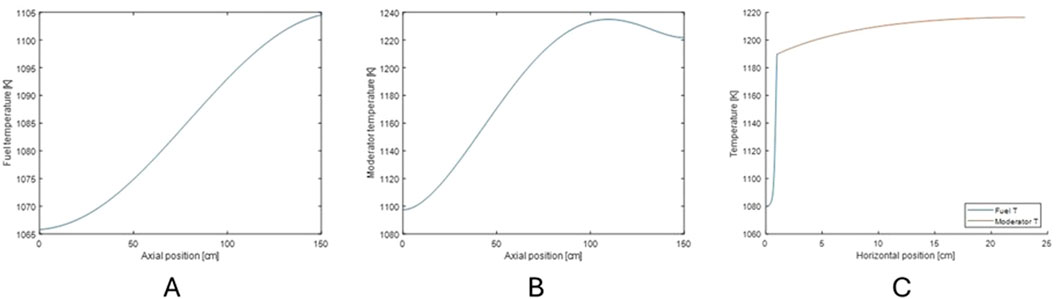
Figure 7. Axial temperature along fuel (A) and moderator (B) midlines, and radial temperature along the midline (y = 75 cm) (C).

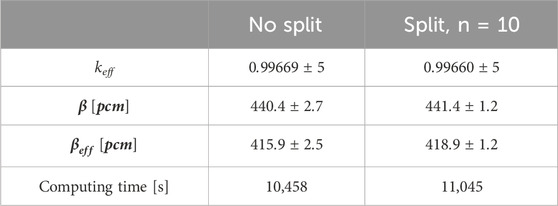
In section 2.3, the delayed neutron precursor splitting is introduced. The method aims to enhance the precision of the delayed neutron-related tallies, including delayed neutron fraction and distribution, without a noticeable computing burden. At the end of the iteration, the temperature and velocity profiles are utilized again without delayed neutron precursor splitting. Both calculations are performed on five computing nodes with 28 cores of Intel^® Xeon^® CPU E5-2697. Table 6 compares the results regarding k_eff, delayed neutron fraction β, effective delayed neutron fraction β_eff, and computing time to check the effectiveness of the splitting scheme. The comparison clearly shows that the splitting scheme increases the computing time 5% for n = 10, while halving the uncertainty of the delayed neutron-related quantities.

Table 6

Table 6. Effective delayed neutron fractions.

3.3 Mesh size sensitivity analysis

Since the iMC code does not adopt delta-tracking, the number of the temperature mesh is powerfully relevant to the computing time. Therefore, in the coupling process, the temperature fields of the fuel and the moderator are collapsed into coarser meshes. Hence, coarser meshes are utilized to decrease computing time, although this may potentially lead to inaccuracies. This section measures the impact of the mesh size on the neutronics analysis.

Two meshes are additionally defined: fine and bulk meshes. The fine mesh utilizes mesh for the OpenFOAM directly. As mentioned earlier, 47,600 meshes are utilized where vertical mesh size is fixed to 1.5 cm, and horizontal mesh size varies from 0.22 cm to 0.0008 cm. On the other hand, the bulk mesh runs a similar procedure as the normal mesh, but one mesh is used for each fuel and moderator region. The difference in the mesh is applied both to the temperature and the velocity mesh.

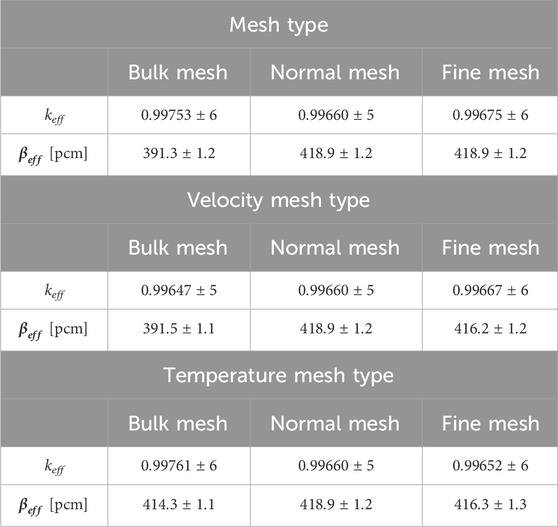
First, the multiplication factors are compared for three types of meshes. Mesh types are visualized in Figure 8A. Table 7 tabulates the k_eff values for fine, normal, and bulk mesh. The comparison shows a statistically significant increase in the k_eff value and a reduction in the effective delayed neutron fraction found for bulk mesh compared to other mesh types.

Figure 8

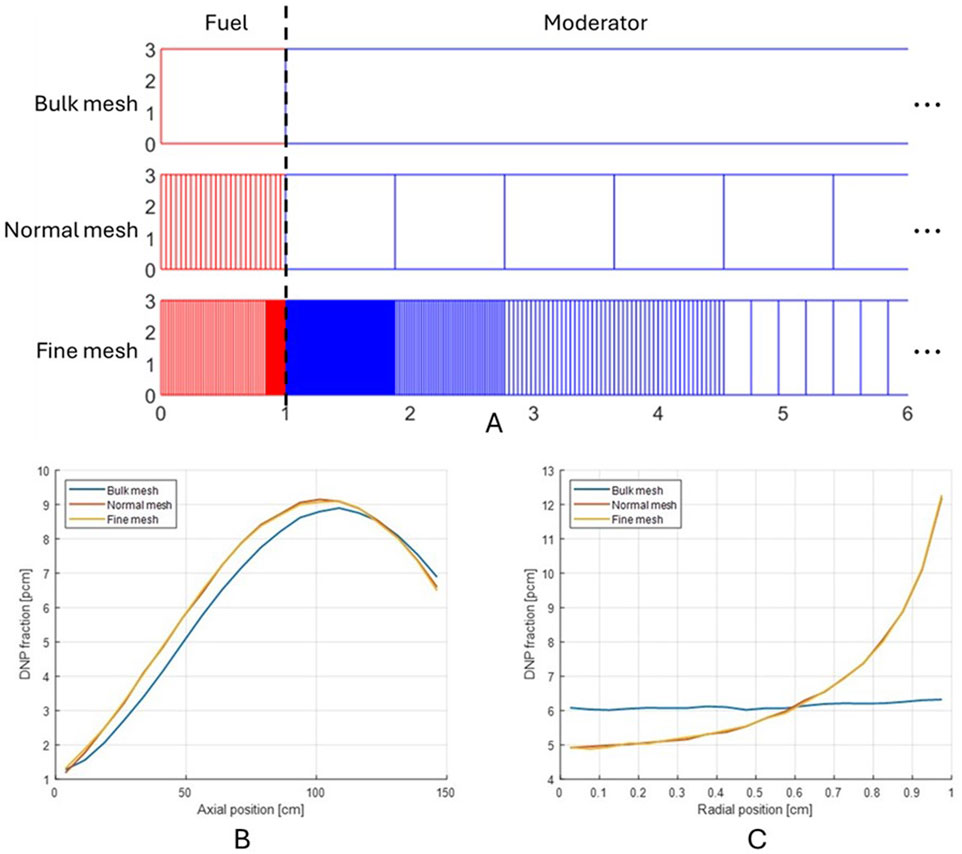
Figure 8. (A) Comparison of each mesh type (B,C) axial and radial distributions of the delayed neutron precursors with varying mesh types.

Table 7

Table 7. Mesh-dependent k_eff values.

Table 7 compares the k_eff and ${\beta }_{eff}$ to investigate and compare the effect of the velocity and temperature mesh. Regarding the velocity mesh case, the temperature meshes are fixed to the normal mesh, while the velocity mesh varies. The tests show that the impact of the velocity mesh size on the k_eff value is statistically negligible, while applying the bulk temperature will result in a biased result.

Figure 8 shows radial description of mesh types, and each mesh type’s delayed neutron precursor distributions, plotted similarly with Figure 4. Comparison between the fine and the normal meshes clarifies that no significant difference exists between the two mesh types. Nevertheless, apparent discrepancies are found for the bulk mesh for axial and radial distributions. As shown in the axial distribution, a more shifted distribution can explain the larger reduction in the effective delayed neutron fraction in Table 7. However, its impact on the k_eff value is not visible due to comparable uncertainty.

4 Conclusions and future work

This work develops and demonstrates a high-fidelity coupled Monte Carlo–CFD framework for MSR multiphysics analysis. The iMC Monte Carlo code provides a heat distribution based on neutron transport, including its secondary photon transport. The OpenFOAM CFD code performs thermal analysis to obtain the model’s temperature profile and the fuel flow’s velocity field. The overall coupling scheme and related techniques are covered in this study, including delayed neutron precursor tracking and iteration scheme. By solving the 2D MSR model, a sufficiently converged solution from both iMC and OpenFOAM codes is obtained.

The analysis showed that the reduction in the delayed neutron fraction is underestimated compared to the effective fractions, which denotes an actual impact on the fission chain. The research emphasizes the necessity of evaluating adjoint-weighted kinetic parameters, especially for MSRs. According to the mesh type comparison, the appropriate selection of the mesh size is essential for an accurate evaluation. Despite the overall mass flow rate being conserved in terms of fluid dynamics, its impact deviates from the actual behavior when applied as a single quantity. Recalling that the 2D model in this research has a narrow fuel channel, the impact will be critical for the MSRs with a broader channel.

This paper considers a steady-state case, while one of the tasks of the MSRs is its transient behavior, such as unprotected loss of flow (ULOF). Future development will extend this steady-state coupling to transient scenarios such as unprotected loss-of-flow (ULOF) using dynamic Monte Carlo. Moreover, integrating CMFD-based acceleration and depletion capabilities will enable full-cycle MSR simulations with reduced variance and improved efficiency.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

IK: Writing – original draft, Writing – review and editing. TO: Writing – review and editing. YK: Supervision, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by the Korea Institute of Energy Technology Evaluation and Planning (KETEP) and the Ministry of Trade, Industry and Energy (MOTIE) of the Republic of Korea (No. RS-2023-00304393 and No. RS-2024-00439210).

Acknowledgments

The authors thank Philip Pfahl and Bent Lauritzen for advising the usage of OpenFOAM and providing a 2D MSR benchmark model.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Anoussis, J. N., Perricos, D. C., Chrysochoides, N. G., and Mitsonias, C. A. (1973). Relative abundances for six delayed neutron groups from reactor neutron-induced fission of 281Pa. Radiochim. Acta 20 (3), 118–119. doi:10.1524/ract.1973.20.3.118

CrossRef Full Text | Google Scholar

Aufiero, M., Cammi, A., Geoffroy, O., Losa, M., Luzzi, L., Ricotti, M. E., et al. (2014). Development of an OpenFOAM model for the molten salt fast reactor transient analysis. Chem. Eng. Sci. 111, 390–401. doi:10.1016/j.ces.2014.03.003

CrossRef Full Text | Google Scholar

Chadwick, M. B., Herman, M., Oblozinsky, P., Dunn, M., Danon, Y., Kahler, A., et al. (2011). ENDF/B-VII.1 nuclear data for science and technology: cross sections, covariances, fission product yields and decay data. Nucl. Data Sheets 112 (12), 2887–2996. doi:10.1016/j.nds.2011.11.002

CrossRef Full Text | Google Scholar

Cullen, D., and Weisbin, C. (1976). Exact Doppler broadening of tabulated cross sections. Nucl. Sci. Eng. 60, 199–229. doi:10.13182/nse76-1

CrossRef Full Text | Google Scholar

Jo, Y., and Cho, N. (2017). “Refinements of on-the-fly Doppler broadening via Gauss-Hermite quadrature in Monte Carlo reactor analysis,” in Transactions of the Korea nuclear society spring meeting (Jeju, Korea: Korean Nuclear Society).

Google Scholar

Kaltiaisenaho, T. (2020). Photon transport physics in Serpent 2 Monte Carlo code. Comput. Phys. Commun. 252, 107143. doi:10.1016/j.cpc.2020.107143

CrossRef Full Text | Google Scholar

Kim, H., and Kim, Y. (2021). Unstructured mesh–based neutronics and thermomechanics coupled steady-state analysis on advanced three-dimensional fuel elements with Monte Carlo Code iMC. Nucl. Sci. Eng. 195 (5), 464–477. doi:10.1080/00295639.2020.1839342

CrossRef Full Text | Google Scholar

Kim, I., Oh, T., and Kim, Y. (2024). “Development of a delayed neutron precursor tracking module for molten salt reactors in the iMC Monte Carlo code,” in Proceedings of the International Conference on Physics of Reactors, PHYSOR 2024, San Francisco, United States, 21 Apr 2024-24 Apr 2024.

Google Scholar

Kim, I., Oh, T., and Kim, Y. (2025). Development and verification of depletion capabilities in the iMC Monte Carlo code. Ann. Nucl. Energy 216, 111260. doi:10.1016/j.anucene.2025.111260

CrossRef Full Text | Google Scholar

Křepel, J., Rohde, U., Grundmann, U., and Weiss, F. P. (2007). DYN3D-MSR spatial dynamics code for molten salt reactors. Ann. Nucl. Energy 34 (6), 449–462. doi:10.1016/j.anucene.2006.12.011

CrossRef Full Text | Google Scholar

Lund, A. L., and Romano, P. K. (2018). Implementation and validation of photon transport in OpenMC. Technical Report ANL/MCS-TM-381.

Google Scholar

Oh, T., Kim, I., and Kim, Y. (2025). Evaluation of effective kinetic parameters and adjoint flux distribution using iterated fission probability in the iMC Monte Carlo code. Ann. Nucl. Energy 210, 110878. doi:10.1016/j.anucene.2024.110878

CrossRef Full Text | Google Scholar

OpenFOAM (2025). OpenFOAM: user guide: CHTMultiRegionFoam. Available online at: https://www.openfoam.com/documentation/guides/latest/doc/guide-applications-solvers-heat-transfer-chtMultiRegionFoam.html.

Google Scholar

Pfhal, P. (2025). Thermal MSR benchmark multi-physics benchmark for a thermal molten salt reactor, submitted to nuclear engineering and design.

Google Scholar

Ridley, G., Huff, K., Turk, M., and Lindsay, A. (2017). Multiphysics analysis of molten salt reactor transients. Technical Report No. UIUC-ARFC-2017-01.

Google Scholar

Weller, H. G., Tabor, G., Jasak, H., and Fureby, C. (1998). A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 12 (6), 620–631. doi:10.1063/1.168744

CrossRef Full Text | Google Scholar

Yang, G., Jaradat, M. K., Sik Yang, W., and Lee, C. (2022). Development of coupled PROTEUS-NODAL and SAM code system for multiphysics analysis of molten salt reactors. Ann. Nucl. Energy 168, 108889. doi:10.1016/j.anucene.2021.108889

CrossRef Full Text | Google Scholar