A Hahn-Ramsey scheme for dynamical decoupling of single solid-state qubits

Spin systems in solid state materials are promising qubit candidates for quantum information in particular as quantum memories or for quantum sensing. A major prerequisite here is the coherence of spin phase oscillations. In this work, we show a control sequence which, by applying RF pulses of variable detuning, allows to increase the visibility of spin phase oscillations. We experimentally demonstrate the scheme on single NV centers in diamond and analytically describe how the NV electron spin phase oscillations behave in the presence of classical noise models. We hereby introduce detuning as the enabling factor that modulates the filter function of the sequence, in order to achieve a visibility of the Ramsey fringes comparable to or longer than the Hahn-echo T₂ time and an improved sensitivity to DC magnetic fields in various experimental settings.

1 Introduction

Solid-state qubits are of central importance within the quantum technologies due to their outstanding performance in key fields such as quantum information processing (Stajic, 2013) and quantum magnetic field sensing (Jones et al., 2009; Bal et al., 2012). Several physical systems have been exploited to experimentally realize solid-state qubits such as quantum dots (Hanson and Awschalom, 2008; Shulman et al., 2012; Veldhorst et al., 2017; Strauß et al., 2019; Carmele and Reitzenstein, 2019), superconductive qubits (Wendin, 2017; Dicarlo et al., 2009), nuclear spins in materials (Pla et al., 2013) and electronic spins in molecules or defect-centers in crystals (Smeltzer et al., 2009; Pla et al., 2012; D. et al., 2007; Schlegel et al., 2008). Among the latter, the nitrogen-vacancy (NV) color center in diamond has been extensively investigated due to its exceptional stability and properties observed even at room temperature and in ambient conditions (Kurtsiefer et al., 2000). The NV center has an electron spin triplet that can be optically initialized, readout via fluorescence intensity measurement and controlled with appropriate radiofrequency (RF) pulse trains (Jelezko and Wrachtrup et al., 2006; Kennedy et al., 2003; Ryan et al., 2010). This has allowed the demonstration of quantum information storage (Dutt et al., 2007; Maurer et al., 2012) and of magnetic field measurements with high sensitivity and spatial resolution (Degen et al., 2017; Sushkov et al., 2014; Mamin et al., 2012; Loretz et al., 2014). Furthermore, electron spin relaxometry has also been used to probe the behavior of single magnetic domain particles (Gould et al., 2014; Sadzak et al., 2018) and small ensembles of molecules (Ermakova et al., 2013) on the nanoscale. In order to perform sensing in complex physical environments, dynamical decoupling (DD) schemes have been implemented to filter-out the background magnetic noise from the specific target signals. These schemes rely on sequences of precisely timed RF pulses that act as frequency filters and bandwidth selectors. Some basic DD measurements are Ramsey (1950) and Hahn (1950) schemes, that have been followed by a manifold of other techniques often derived from the nuclear magnetic resonance (NMR) field (Degen et al., 2017), such as CPMG (Naydenov et al., 2011), XY-n (de Lange et al., 2010), UDD (Uhrig, 2007; Wang et al., 2012). Most of the currently available decoupling schemes are focused on prolonging the T₂ coherence time and are primarly applied to AC magnetometry. Concerning DC magnetometry, the current approaches are based on using isotopically pure diamonds (Ishikawa et al., 2012), diamond material engineering (Barry et al., 2020) or elaborated schemes that circumvent the problem by using spin bath driving, ancillary spins or diamond mechanical rotation (Wood et al., 2018; Liu et al., 2019; Barry et al., 2020). As these solutions rely on specific experimental configurations, a robust dynamical-decoupling alternative would be particularly interesting for a manifold of applications. Motivated by recent experiments on trapped atoms (Vitanov et al., 2015), we propose here an extension of the Hahn-Ramsey dynamical decoupling scheme, where the detuning of the RF spin control pulses is used to obtain an increased visibility of the electron spin phase oscillations. We demonstrate the protocol on single NV centers in bulk diamond, and show a pronounced increase in the spin oscillations coherence time. Furthermore, we give an analytical description of the filter function and of the sequence and provide an estimation of the scheme sensitivity for DC magnetometry, thereby proving that it can be of great importance in a broad range of applications such as quantum sensing, quantum information processing (Nielsen and Chuang, 2000) and synchronization (Hodges et al., 2013).

2 Theory and methods

We make use of two experimental procedures in order to observe the Hahn-Ramsey properties and demonstrate its effects on NV centers under different conditions and parameters. In the first, we select a stable defect center with long electron spin $T_2^{*}$ time and apply the Ramsey and Hahn-Ramsey schemes - in a low detuning condition - in order to establish the effectiveness of the latter in extending the spin phase visibility above the Ramsey limit. In the second approach, we instead use high detuning-to-Rabi ratios to induce complex spin oscillation fringes and show the fitness of our theoretical framework in explaining the observed patterns. By successively adding a source of known artificial noise, we are able to compare the spin phase oscillation visibility and envelope changes for Ramsey and Hahn-Ramsey sequences, under a well defined noise pattern that is added to the baseline environment random fluctuations the NV center is subject to. We analyse our measurement results using the spectral decomposition approach, in order to extract information about the noise suppression effectiveness for different detunings and noise specifications, as well as to obtain a more accurate picture of the spin trajectory in noisy environments. In the following section, we lay out the framework for the experiments underlying physical phenomena, describing how a pseudo spin-1/2 system, such as the NV center’ m_s = 0, − 1 states, behaves under the spin manipulation schemes we are exploring. Typically, phase oscillations of the NV electron spin are detected via Ramsey spectroscopy. In this technique, the defects electron spin is initalized in the m_s = 0 state, generally via a long off-resonant laser pulse at 532 nm wavelength. This is followed by two detuned radiofrequency π/2 pulses separated by a free precession interval, where the electron spin picks up a phase proportional to the external magnetic fields oriented along the NV center quantization axis. The observed signal is represented by a measurement of the σ_z spin projection, that is the expectation value of the σ_z operator $s\left(\tau \right)=\mathrm{Tr}\left[\rho \left(\tau \right){\sigma }_z\right]$:

$s\left(\tau \right)=⟨\uparrow |R^{†}\left(\theta ,{\omega }_1{t}_p\right)U^{†}\left(0,\tau \right)R^{†}\left(\theta ,{\omega }_1{t}_p\right){\sigma }_{z}R\left(\theta ,{\omega }_1{t}_p\right)U\left(0,\tau \right)R\left(\theta ,{\omega }_1{t}_p\right)|\uparrow ⟩,(1)$

where σ_z is the Pauli spin matrix, U (0, τ) is the free evolution operator, $R\left(\theta ,{\omega }_1{t}_p\right)$ the rotation operator for an off-resonant pulse (see Supplementary Material) and θ = arctan$\left({\omega }_1/\mathrm{\Delta }\right)$ the rotation angle (Levitt, 2000). Here ${\omega }_1=\sqrt{{\omega }_0^2+{\mathrm{\Delta }}^2}$ is the effective precession frequency, with Δ being the detuning in the RF driving field, ω₀ the resonant Rabi frequency and t_p the effective pulse duration. In the case of noisy environments, a fluctuating time dependent detuning shift arises from the noise contribution to the total magnetic field acting on the NV centers spin. In this situation, the rotating-wave free evolution operator can assume different forms, with the most general one being:

$U_{\mathrm{\Delta }}\left(0,\tau \right)=\exp \left[-i\frac{{\sigma }_z}{2}{\int }_0^{\tau }\left(\mathrm{\Delta }+f\left(t\right)\right)dt\right],(2)$

Where $f\left(t\right)$ represents the local σ_z field at the free precession time t and Δ is the detuning term leading to the observation of Ramsey fringes. It is the stochastic process describing the noise term $f\left(t\right)$ that determines the shape of the signal decay. In general, few considerations can be made. If $f\left(t\right)$ is a drift-less, zero-mean random process which occurs on much faster timescales than the free evolution time acquisition, then this will average out in the final signal. If $f\left(t\right)$ instead changes on a time comparable or larger than each acquisition time τ, then the observed signal will show a characteristic coherence decay pattern. Nevertheless, in this case a composite pulse sequence may be used to compensate the random phase accumulated for each τ measurement. This is the principle of the Hahn-echo, where a spin transition resonant refocusing pulse, applied at the center of the free evolution period, is used to reverse the precession in the second half of the sequence, canceling the effect of static fields and low-frequency noise but removing spin phase oscillations as well. The Hahn-Ramsey scheme uses the same temporal distribution of Hahn-echo pulses, but adds a detuning pattern. Specifically, the sequence consists of an initial and final π/2 pulse having a Δ detuning, separated by a free precession time τ and a central pulse of length π having instead opposite detuning − Δ. Under this definition, the general expression of the Hahn-Ramsey signal is:

$\begin{array}{ll}\hfill s\left(2\tau \right)& =\langle \uparrow |R^{†}\left(\theta ,\pi /2\right)U^{†}\left(0,\tau \right)R^{†}\left(-\theta ,\pi \right)U^{†}\left(\tau ,2\tau \right)\times R^{†}\left(\theta ,\pi /2\right){\sigma }_{z}R\left(\theta ,\pi /2\right)\hfill \\ \hfill & \times U\left(\tau ,2\tau \right)R\left(-\theta ,\pi \right)U\left(0,\tau \right)R\left(\theta ,\pi /2\right)|\uparrow \rangle .\hfill \end{array}(3)$

Here, the pulse length is assumed to be ideal (that is, τ_p is tuned so that ω₁τ_p = π/2 or ω₁τ_p = π). The central, inversely detuned π pulse, separates the free precession time in two parts, with the first being described by the operator U_Δ(0, τ) and the second by U_−Δ(τ, 2τ). Given the form of Eq. 2, this implies that the slow contribution of f(t) is canceled out, leaving nevertheless an oscillating spin phase dependent on Δ only. While quantum interactions with other single spins are typically represented via specific interaction operators, such as hyperfine interaction, spin-spin coupling and so on, bath interactions or fluctuating environment fields of classical nature are included in the term f(t) and treated as a stochastic process. For solid-state spin centers, it is appropriate to treat f(t) as a classical magnetic noise described by a compound Poisson process, where the jump times have an exponentially decaying probability density function with a correlation time of 1/λ and the jump intensities have a Gaussian distribution with zero average and Γ variance. By including this in Eq. 3, we obtain an expression that links the fringes decoherence process to detuning and Rabi frequencies, and also to the noise parameters here introduced (see Supplementary Material). After switching to the frequency domain, the expected signal can be expressed as an exponentially decaying function $s\left(\tau \right)=\exp \left[-\chi \left(\tau \right)\right]$ (Biercuk et al., 2011), where the exponential argument is the frequency convolution between the control sequence filter function and the spectral density function of the external field or noise process. It can be seen, from Eq. 3, that the opposite detuning for the refocusing pulse with respect to the π/2 pulses leads to a signal that is the sum of two detuning-induced oscillating components and one non-oscillating component, each one displaying a different decaying behavior. The overall signal can then be written as:

$\begin{array}{ll}\hfill s_{\theta }\left(2\tau \right)& =\frac{a^4}{2}\left(1-2b^2\right)+\frac{a^2{b}^4}{2}\exp \left[-\frac{2\lambda {\mathrm{\Gamma }}^2}{\pi }{\int }_0^{\infty }\frac{d\omega /{\omega }^2}{{\omega }^2+{\lambda }^2}{\sin }^2\left(\omega \tau \right)\right]\hfill \\ \hfill & -2a^4{b}^2\cos \left(\mathrm{\Delta }\tau \right)\exp \left[-\frac{2\lambda {\mathrm{\Gamma }}^2}{\pi }{\int }_0^{\infty }\frac{d\omega /{\omega }^2}{{\omega }^2+{\lambda }^2}{\sin }^2\left(\frac{\omega \tau }{2}\right)\right]\hfill \\ \hfill & +\frac{b^4}{2}\left(a^2+1\right)\cos \left(2\mathrm{\Delta }\tau \right)\exp \left[-\frac{8\lambda {\mathrm{\Gamma }}^2}{\pi }{\int }_0^{\infty }\frac{d\omega /{\omega }^2}{{\omega }^2+{\lambda }^2}{\sin }^4\left(\frac{\omega \tau }{2}\right)\right],\hfill \end{array}(4)$

With a = cos(θ) and b = sin(θ). These three components are weighted in the final signal by detuning-related coefficients (see Figure 1). The term with the spin phase oscillating as $\cos \left(2\mathrm{\Delta }\tau \right)$ is associated with a Hahn-Echo-type filter function, that means the coherence decays as in the standard Hahn-echo sequence, while the non-oscillating term shows a Ramsey-like decoherence. The term oscillating instead as $\cos \left(\mathrm{\Delta }\tau \right)$ has a different nature; its filter function has a similar periodicity of the Hahn-Echo but different magnitude, and gives a longer decoherence time. By choosing an opportune detuning one can select how each component is contributing to the total signal, which will then lead to different behavior but also potential application of the sequence. In the following experimental part, we will demonstrate the fitness of our theoretical approach and draw some conclusions regarding the physical dynamics and the implications for DC magnetometry.

FIGURE 1

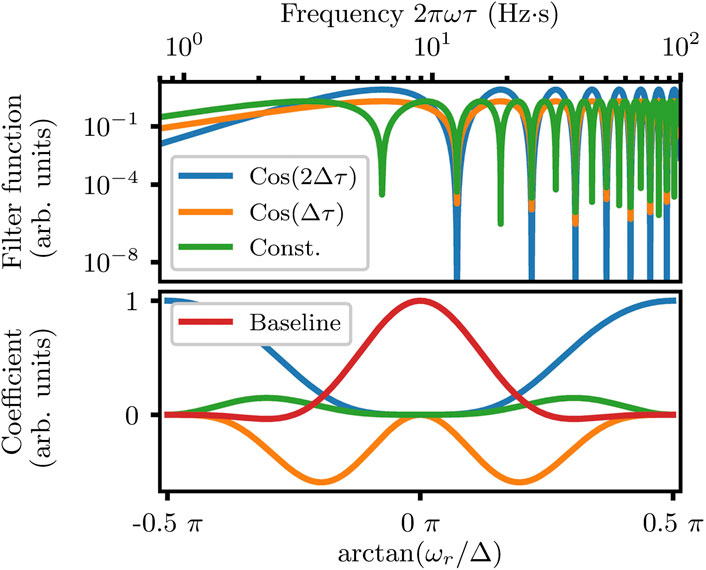
FIGURE 1. The top figure shows the filter functions contributing to the Hahn-Ramsey signal; the colors represent respectively the non-oscillating part (green), the component oscillating in $\cos \left(\mathrm{\Delta }\tau \right)$ (orange) and the component oscillating in $\cos \left(2\mathrm{\Delta }\tau \right)$ (blue). The first and the last terms are equivalent to the Ramsey and Hahn-Echo filter functions, while the $\cos \left(\mathrm{\Delta }\tau \right)$ has the same periodicity of the Hahn-echo but different filter function amplitudes. The contribution to the overall signal is given by the detuning-dependent weighting coefficients depicted in the bottom figure with their respective colors, with the red line (denoted as baseline) showing the constant term dependent only on the ratio between Rabi frequency and detuning.

3 Experimental results

For our experiment, we use a type [111] CVD-grown delta-doped diamond plate with a ¹⁵NV center rich layer. The diamond is placed on a microwave waveguide and the RF pulses are delivered via a 50 µm thick copper wire closely located to the surface. From the bottom side, the diamond is accessible via a high numerical aperture (NA = 1.4) oil immersion objective Olympus UPLANSAPO ×60, that is used to optically initialize the nitrogen-vacancies with a 532 nm diode laser source pulsed by an acousto-optic modulator. The same objective collects the fluorescence light that is sent to a confocal setup and a beamsplitter, and finally collimated on two Perkin-Elmer single photon detectors. The experimental setup and basic ODMR measurements are shown in Figure 2. In order to perform the first demonstration, we carry out several acquisitions of Ramsey and Hahn-Ramsey signals on different NV centers in the diamond plate. After identifying a single NV center via autocorrelation measurements, we apply a ≈ 500 G static magnetic field parallel to the defects quantization axis to achieve a nuclear spin hyperpolarization (Jacques et al., 2009) of 80%–90% (see Figure 2), that allows us to work with an approximate two-level spin-1/2 system. We then proceed to record the Ramsey and Hahn-Ramsey fringes for a specific radiofrequency detuning, as shown in Figure 3. By testing the sequence directly on the NV centers in the natural diamond environment, we would expect this to be effective in prolonging spin phase fringes only if the surrounding is characterized by a non-negligible sub-MHz noise dynamics that affects the spin coherence. The measurements results confirm this picture and show that the Hahn-Ramsey is effective in increasing the visibility of electron spin phase oscillations and the T_2,HR time. This is depicted in Figure 3, where an exponential fit shows a change in the oscillation decay timescale from $T_2^{*}$ (1.9 ± 0.1) µs to T_2,HR (3.1 ± 0.1) µs. In this case, the Δ < ω₁ condition leads to a trajectory on the Bloch sphere as depicted in Figure 4, where the spin rotates closely and symmetrically around the zy plane; the dominant oscillation frequency is $\cos \left(2\mathrm{\Delta }\tau \right)$, but a weak beating appears due to a proximal spin that induces an energy splitting of approximatively 500 kHz, as shown by low-power ODMR. We then proceed to the second experimental part, for which we select an NV center that intrinsically displays comparable $T_2^{*}$ and T_2,HR times. For this specific center, the Ramsey $T_2^{*}$ decay time is measured as (1.6 ± 0.1) µs. Here we add an external source of controlled magnetic noise, created by a programmable function generator that is connected to an amplifier feeding a solenoid located around the diamond. The antenna produces a magnetic field parallel to the NV center quantization axis. After setting a 3 MHz detuning, we proceed in measuring again the Ramsey and Hahn-Ramsey signal profiles, which assume the form displayed in Figure 5. While the Ramsey signal shows a single-frequency regular pattern, the Hahn-Ramsey displays more complex features, which are nevertheless well fitted by our theoretical model. These features arise from the combination of spin phase oscillations taking place at different frequencies, and the different decay each one of these components experiences under the existing noise. Adding artificial noise reduces as expected the spin phase coherence, but in a more pronounced way for the Ramsey measurement. The Hahn-Ramsey shows longer fringes, mainly due to the stronger low frequency noise suppression for the $\cos \left(2\mathrm{\Delta }\tau \right)$ component. Another effect that becomes more relevant when Δ/Ω_Rabi ≈ 1 or Δ/Ω_Rabi > 1 is the mixing with $\cos \left(\mathrm{\Delta }\tau \right)$. This second term can provide, in certain cases, a longer spin phase coherence time than the resonant Hahn-echo (see Figure 6), due to the higher angle of precession with respect to the (xz) plane of the Bloch sphere, which in turn limits the amplitude of the acquired phase and protects the phase oscillations induced by the constant detuning (See Figure 5). Interestingly, this component is also sensitive to small DC magnetic fields that shift the detuning of the π and π/2 pulses asymmetrically. While the $\cos \left(2\mathrm{\Delta }\tau \right)$ term cancels these shifts, the $\cos \left(\mathrm{\Delta }\tau \right)$ part of the signal allows them to be detected in amplitude and envelope. In this case, it is possible to derive (see Supplementary Material) that the sensitivity, maximized for θ_p ≈ 0.2π, is:

${\eta }_{HR}\propto \frac{1}{3\pi {\gamma }_e\sqrt{T_{2,HR}}}(5)$

FIGURE 2

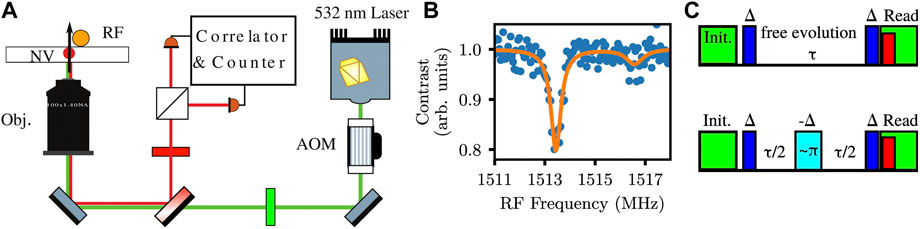
FIGURE 2. (A) Schematic representation of the experimental setup; a [111] diamond plate is illuminated by an AOM-pulsed 532 nm green laser. The emission from the NV centers is collected via an oil immersion objective (NA = 1.40) and sent to a confocal filter and a beamsplitter, terminating on two avalanche photodiodes used for autocorrelation and photon counting measurements. The spins are manipulated by radiofrequency pulses delivered on the diamond by an impedance matched stripline. By applying a static field of ≈ 500 G along the NV centers axis, the ¹⁵N nitrogen nuclear spin of the NV center is hyperpolarized in one of its two states with a polarization ratio $>$ 0.80 (B) as confirmed by the resonance measurement. The scheme in (C) shows the Ramsey (top) and Hahn-Ramsey (bottom) sequences, with the green areas representing the polarization and readout laser pulses, and the blue areas representing the microwave pulses controlling the NV centers electron spin, with their detuning indicated as ±Δ.

FIGURE 3

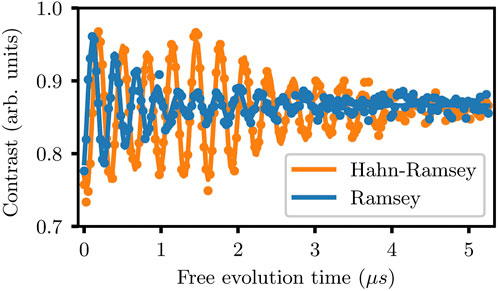
FIGURE 3. Ramsey (blue) and Hahn-Ramsey (orange) measurements on a single NV center in diamond, with the solid lines showing the fit functions. The beatings are due to a second spin weakly interacting with the NV electron spin. The Hahn-Ramsey fit is performed via Eqs 3, 4 as given in the Supplementary Material, provided a nominal detuning of Δ = 4 MHz and θ ≈ 1.10 (corresponding to Ω_Rabi = 6 MHz) that follows the condition Δ < Ω_Rabi. An exponentially decaying fit of the form $\exp \left[-{\left(t/{\tau }_c\right)}^2\right]$ allows to obtain a coherence time $T_2^{*}$ = (1.9±0.1) µs for the Ramsey and T_2,HR = (3.1±0.1) µs for the Hahn-Ramsey.

FIGURE 4

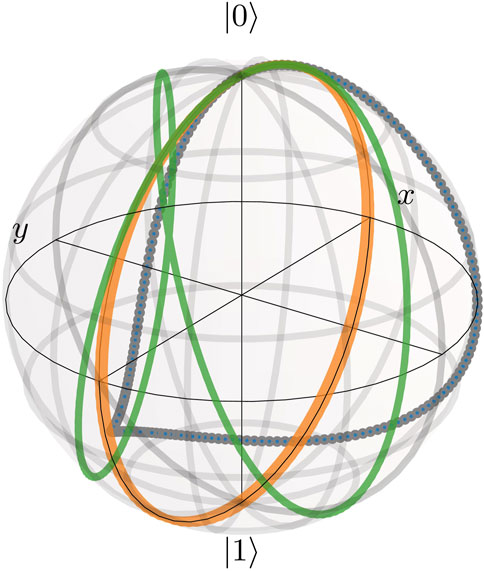
FIGURE 4. Simulations of different trajectories for a single Hahn-Ramsey fringe on the Bloch sphere, given three possible θ = ω₁/Δ values. The green line depicts the case of θ ≈ π/2, the orange line θ ≈ 0.4 ⋅ π while the blue dotted line shows the case where θ = 0.2π. By shifting Δ/ω₁ away from the ≪ 1 limit, the spin rotation takes place around an off-equator axis, where phase oscillations show a more complex pattern and are less sensitive to noise.

FIGURE 5

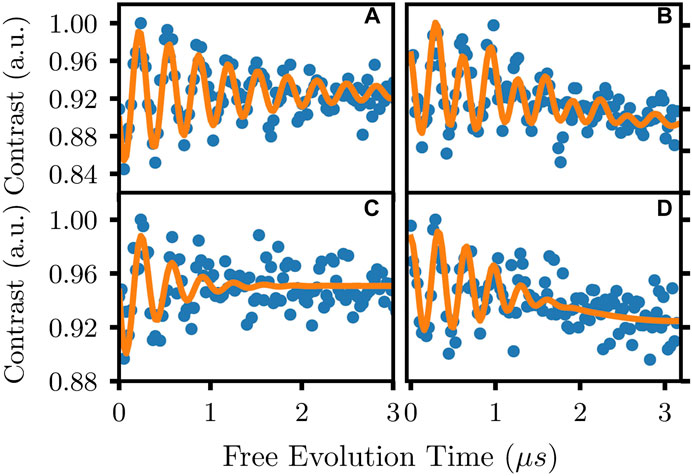
FIGURE 5. The outcomes of Ramsey (A) and Hahn-Ramsey (B) measurements on a single NV center in the diamond compared with (C,D), where the Ramsey and Hahn-Ramsey signals are acquired after adding artificial magnetic noise with Poissonian statistics and correlation time of 0.5 µs, corresponding to a −3 dB bandwidth of 2 MHz, and a strength of Γ ≈ 200 kHz. The complex pattern displayed by the Hahn-Ramsey measurements is well fitted by the model, which shows as well the more pronounced decay for the Ramsey signal after applying the additional noise.

FIGURE 6

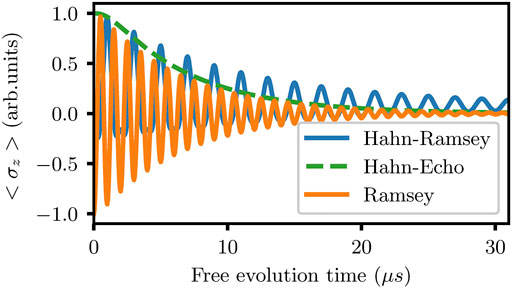
FIGURE 6. Simulation showing the Ramsey, Hahn-Ramsey and Hahn-echo measurements given the parameters of λ = 2.5 1/t, Γ = 2π ⋅ 0.1 1/t and θ = 0.2π. For a detuning comparable to the Rabi frequency, the $\cos \left(\mathrm{\Delta }\tau \right)$ component contributes significantly to the signal leading to an improved visibility for spin phase oscillations, with a T_2,HR time longer than the Ramsey and Hahn-echo times.

Compared to the classic Ramsey interferometry, the Hahn-Ramsey sensitivity scales with the respective T_2,HR time and offers an improved performance for physical situations where low-intensity noises are an important contribution to the sensitivity deterioration, and as well in situations where low-power RF are available for the spin manipulation pulses, with improvement factors of up to $\approx 1.5$ for environments with comparable Poissonian noise characteristics.

4 Conclusion

We have described and experimentally demonstrated a Hahn-Ramsey type of dynamical decoupling sequence on NV centers in diamond. By opportunely inverting the detunings in the RF control sequence, we are able to show that the HR scheme is effective in providing a better suppression of low-frequency noise with respect to the Ramsey scheme, approaching the Hahn-echo limit when the detuning is smaller than the Rabi frequency. This can be exploited to effectively improve the spin phase oscillation visibility. When the detuning magnitude is instead comparable to the Rabi frequency, the Hahn-Ramsey can provide even longer Ramsey fringes decay times. This in turn may be used for DC magnetometry, providing a better sensitivity than the standard Ramsey interferometry.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

NS conceived the experiment and performed measurements and simulations. AC developed the theoretical analysis. All authors made substantial contributions to the work and to the manuscript preparation.

Acknowledgments

AK and AC gratefully acknowledge support from the Deutsche Forschungsgemeinschaft (DFG) through the project B2 of the SFB 910 and from the European Union’s Horizon 2020 research and innovation program under the SONAR Grant Agreement No. 734690. NS gratefully acknowledges funding from the Deutsche Forschungsgemeinschaft (DFG) through the SFB 951.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphot.2022.932944/full#supplementary-material

References

Bal, M., Deng, C., Orgiazzi, J.-L., Ong, F., and Lupascu, A. (2012). Ultrasensitive magnetic field detection using a single artificial atom. Nat. Commun. 3, 1324. doi:10.1038/ncomms2332

PubMed Abstract | CrossRef Full Text | Google Scholar

Barry, J. F., Schloss, J. M., Bauch, E., Turner, M. J., Hart, C. A., Pham, L. M., et al. (2020). Sensitivity optimization for nv-diamond magnetometry. Rev. Mod. Phys. 92, 015004. doi:10.1103/RevModPhys.92.015004

CrossRef Full Text | Google Scholar

Biercuk, M. J., Doherty, A. C., and Uys, H. (2011). Dynamical decoupling sequence construction as a filter-design problem. J. Phys. B At. Mol. Opt. Phys. 44, 154002. doi:10.1088/0953-4075/44/15/154002

CrossRef Full Text | Google Scholar

Carmele, A., and Reitzenstein, S. (2019). Non-markovian features in semiconductor quantum optics: Quantifying the role of phonons in experiment and theory. Nanophotonics 8, 655–683. doi:10.1515/nanoph-2018-0222

CrossRef Full Text | Google Scholar

de Lange, G., Wang, Z. H., Ristè, D., Dobrovitski, V. V., and Hanson, R. (2010). Universal dynamical decoupling of a single solid-state spin from a spin bath. Science 330, 60–63. doi:10.1126/science.1192739

PubMed Abstract | CrossRef Full Text | Google Scholar

Degen, C. L., Reinhard, F., and Cappellaro, P. (2017). Quantum sensing. Rev. Mod. Phys. 89, 035002. doi:10.1103/RevModPhys.89.035002

CrossRef Full Text | Google Scholar

Dicarlo, L., Chow, J. M., Gambetta, J. M., Bishop, L. S., Johnson, B. R., Schuster, D. I., et al. (2009). Demonstration of two-qubit algorithms with a superconducting quantum processor. Nature 460, 240–244. doi:10.1038/nature08121

PubMed Abstract | CrossRef Full Text | Google Scholar

Dutt, M. V. G., Childress, L., Jiang, L., Togan, E., Maze, J., Jelezko, F., et al. (2007). Quantum register based on individual electronic and nuclear spin qubits in diamond. Science 316, 1312–1316. doi:10.1126/science.1139831

PubMed Abstract | CrossRef Full Text | Google Scholar

Ermakova, A., Pramanik, G., Cai, J. M., Algara-Siller, G., Kaiser, U., Weil, T., et al. (2013). Detection of a few metallo-protein molecules using color centers in nanodiamonds. Nano Lett. 13, 3305–3309. doi:10.1021/nl4015233

PubMed Abstract | CrossRef Full Text | Google Scholar

Gould, M., Barbour, R. J., Thomas, N., Arami, H., Krishnan, K. M., and Fu, K. M. C. (2014). Room-temperature detection of a single 19nm super-paramagnetic nanoparticle with an imaging magnetometer. Appl. Phys. Lett. 105, 072406. doi:10.1063/1.4893602

CrossRef Full Text | Google Scholar

Hahn, E. L. (1950). Spin echoes. Phys. Rev. 80, 580–594. doi:10.1103/PhysRev.80.580

CrossRef Full Text | Google Scholar

Hanson, R., and Awschalom, D. D. (2008). Coherent manipulation of single spins in semiconductors. Nature 453, 1043–1049. doi:10.1038/nature07129

PubMed Abstract | CrossRef Full Text | Google Scholar

Hodges, J. S., Yao, N. Y., Maclaurin, D., Rastogi, C., Lukin, M. D., and Englund, D. (2013). Timekeeping with electron spin states in diamond. Phys. Rev. A . Coll. Park. 86, 032118. doi:10.1103/PhysRevA.87.032118

CrossRef Full Text | Google Scholar

Ishikawa, T., Fu, K. M. C., Santori, C., Acosta, V. M., Beausoleil, R. G., Watanabe, H., et al. (2012). Optical and spin coherence properties of nitrogen-vacancy centers placed in a 100 nm thick isotopically purified diamond layer. Nano Lett. 12, 2083–2087. doi:10.1021/nl300350r

PubMed Abstract | CrossRef Full Text | Google Scholar

Jacques, V., Neumann, P., Beck, J., Markham, M., Twitchen, D., Meijer, J., et al. (2009). Dynamic polarization of single nuclear spins by optical pumping of nitrogen-vacancy color centers in diamond at room temperature. Phys. Rev. Lett. 102, 057403. doi:10.1103/PhysRevLett.102.057403

PubMed Abstract | CrossRef Full Text | Google Scholar

Jelezko, F., and Wrachtrup, J. (2006). Single defect centres in diamond: A review. Phys. Stat. Sol. 203, 3207–3225. doi:10.1002/pssa.200671403

CrossRef Full Text | Google Scholar

Jones, J. A., Karlen, S. D., Fitzsimons, J., Ardavan, A., Benjamin, S. C., Briggs, G. A. D., et al. (2009). Magnetic field sensing beyond the standard quantum limit using 10-spin noon states. Science 324, 1166–1168. doi:10.1126/science.1170730

PubMed Abstract | CrossRef Full Text | Google Scholar

Kennedy, T. A., Colton, J. S., Butler, J. E., Linares, R. C., and Doering, P. J. (2003). Long coherence times at 300 k for nitrogen-vacancy center spins in diamond grown by chemical vapor deposition. Appl. Phys. Lett. 83, 4190–4192. doi:10.1063/1.1626791

CrossRef Full Text | Google Scholar

Kurtsiefer, C., Mayer, S., Zarda, P., and Weinfurter, H. (2000). Stable solid-state source of single photons. Phys. Rev. Lett. 85, 290–293. doi:10.1103/PhysRevLett.85.290

PubMed Abstract | CrossRef Full Text | Google Scholar

Levitt, M. H. (2000). Spin dynamics : Basics of nuclear magnetic resonance. New York, United States: John Wiley & Sons.

Google Scholar

Liu, Y. X., Ajoy, A., and Cappellaro, P. (2019). Nanoscale vector dc magnetometry via ancilla-assisted frequency up-conversion. Phys. Rev. Lett. 122, 100501. doi:10.1103/PhysRevLett.122.100501

PubMed Abstract | CrossRef Full Text | Google Scholar

Loretz, M., Pezzagna, S., Meijer, J., and Degen, C. L. (2014). Nanoscale nuclear magnetic resonance with a 1.9-nm-deep nitrogen-vacancy sensor. Appl. Phys. Lett. 104, 033102. doi:10.1063/1.4862749

CrossRef Full Text | Google Scholar

Mamin, H. J., Sherwood, M. H., and Rugar, D. (2012). Detecting external electron spins using nitrogen-vacancy centers. Phys. Rev. B 86, 195422. doi:10.1103/PhysRevB.86.195422

CrossRef Full Text | Google Scholar

Maurer, P. C., Kucsko, G., Latta, C., Jiang, L., Yao, N. Y., Bennett, S. D., et al. (2012). Room-temperature quantum bit memory exceeding one second. Science 336, 1283–1286. doi:10.1126/science.1220513

PubMed Abstract | CrossRef Full Text | Google Scholar

Naydenov, B., Dolde, F., Hall, L. T., Shin, C., Fedder, H., Hollenberg, L., et al. (2011). Dynamical decoupling of a single-electron spin at room temperature. Phys. Rev. B 83, 081201. doi:10.1103/PhysRevB.83.081201

CrossRef Full Text | Google Scholar

Nielsen, M. A., and Chuang, I. L. (2000). Quantum computation and quantum information. Cambridge: Cambridge University Press.

Google Scholar

Pla, J. J., Tan, K. Y., Dehollain, J. P., Lim, W. H., Morton, J. J., Jamieson, D. N., et al. (2012). A single-atom electron spin qubit in silicon. Nature 489, 541–545. doi:10.1038/nature11449

PubMed Abstract | CrossRef Full Text | Google Scholar

Pla, J. J., Tan, K. Y., Dehollain, J. P., Lim, W. H., Morton, J. J., Zwanenburg, F. A., et al. (2013). High-fidelity readout and control of a nuclear spin qubit in silicon. Nature 496, 334–338. doi:10.1038/nature12011

PubMed Abstract | CrossRef Full Text | Google Scholar

Ramsey, N. F. (1950). A molecular beam resonance method with separated oscillating fields. Phys. Rev. 78, 695–699. doi:10.1103/PhysRev.78.695

CrossRef Full Text | Google Scholar

Ryan, C. A., Hodges, J. S., and Cory, D. G. (2010). Robust decoupling techniques to extend quantum coherence in diamond. Phys. Rev. Lett. 105, 200402. doi:10.1103/PhysRevLett.105.200402

PubMed Abstract | CrossRef Full Text | Google Scholar

Sadzak, N., Héritier, M., and Benson, O. (2018). Coupling a single nitrogen-vacancy center in nanodiamond to superparamagnetic nanoparticles. Sci. Rep. 8, 8430. doi:10.1038/s41598-018-26633-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Schlegel, C., Van Slageren, J., Manoli, M., Brechin, E. K., and Dressel, M. (2008). Direct observation of quantum coherence in single-molecule magnets. Phys. Rev. Lett. 101, 147203. doi:10.1103/PhysRevLett.101.147203

PubMed Abstract | CrossRef Full Text | Google Scholar

Shulman, M. D., Dial, O. E., Harvey, S. P., Bluhm, H., Umansky, V., and Yacoby, A. (2012). Demonstration of entanglement of electrostatically coupled singlet-triplet qubits. Science 336, 202–205. doi:10.1126/science.1217692

PubMed Abstract | CrossRef Full Text | Google Scholar

Smeltzer, B., McIntyre, J., and Childress, L. (2009). Robust control of individual nuclear spins in diamond. Phys. Rev. A . Coll. Park. 80, 050302. doi:10.1103/PhysRevA.80.050302

CrossRef Full Text | Google Scholar

Stajic, J. (2013). The future of quantum information processing. Science 339, 1163. doi:10.1126/science.339.6124.1163

PubMed Abstract | CrossRef Full Text | Google Scholar

Strauß, M., Carmele, A., Schleibner, J., Hohn, M., Schneider, C., Höfling, S., et al. (2019). Wigner time delay induced by a single quantum dot. Phys. Rev. Lett. 122, 107401. doi:10.1103/PhysRevLett.122.107401

PubMed Abstract | CrossRef Full Text | Google Scholar

Sushkov, A. O., Chisholm, N., Lovchinsky, I., Kubo, M., Lo, P. K., Bennett, S. D., et al. (2014). All-optical sensing of a single-molecule electron spin. Nano Lett. 14, 6443–6448. doi:10.1021/nl502988n

PubMed Abstract | CrossRef Full Text | Google Scholar

Uhrig, G. S. (2007). Keeping a quantum bit alive by optimized π-pulse sequences. Phys. Rev. Lett. 98, 100504. doi:10.1103/PhysRevLett.98.100504

PubMed Abstract | CrossRef Full Text | Google Scholar

Veldhorst, M., Eenink, H. G., Yang, C. H., and Dzurak, A. S. (2017). Silicon cmos architecture for a spin-based quantum computer. Nat. Commun. 8, 1766. doi:10.1038/s41467-017-01905-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Vitanov, N. V., Gloger, T. F., Kaufmann, P., Kaufmann, D., Collath, T., Tanveer Baig, M., et al. (2015). Fault-tolerant hahn-ramsey interferometry with pulse sequences of alternating detuning. Phys. Rev. A . Coll. Park. 91, 033406. doi:10.1103/PhysRevA.91.033406

CrossRef Full Text | Google Scholar

Wang, Z. H., De Lange, G., Ristè, D., Hanson, R., and Dobrovitski, V. V. (2012). Comparison of dynamical decoupling protocols for a nitrogen-vacancy center in diamond. Phys. Rev. B 85, 155204. doi:10.1103/PhysRevB.85.155204

CrossRef Full Text | Google Scholar

Wendin, G. (2017). Quantum information processing with superconducting circuits: A review. Rep. Prog. Phys. 80, 106001. doi:10.1088/1361-6633/aa7e1a

PubMed Abstract | CrossRef Full Text | Google Scholar

Wood, A. A., Aeppli, A. G., Lilette, E., Fein, Y. Y., Stacey, A., Hollenberg, L. C., et al. (2018). T2-limited sensing of static magnetic fields via fast rotation of quantum spins. Phys. Rev. B 98, 174114. doi:10.1103/PhysRevB.98.174114

CrossRef Full Text | Google Scholar