- 1Roche Pharma Research and Early Development, Pharmaceutical Sciences, Roche Innovation Center Basel, F. Hoffmann-La Roche Ltd., Basel, Switzerland
- 2Department of Computer Science, University of Oxford, Oxford, United Kingdom
- 3Centre for Mathematical Medicine and Biology, School of Mathematical Sciences, University of Nottingham, Nottingham, United Kingdom
Computational models of the electrical potential across a cell membrane are longstanding and vital tools in electrophysiology research and applications. These models describe how ionic currents, internal fluxes, and buffering interact to determine membrane voltage and form action potentials (APs). Although this relationship is usually expressed as a differential equation, previous studies have shown it can be rewritten in an algebraic form, allowing direct calculation of membrane voltage. Rewriting in this form requires the introduction of a new parameter, called Γ0 in this manuscript, which represents the net concentration of all charges that influence membrane voltage but are not considered in the model. Although several studies have examined the impact of Γ0 on long-term stability and drift in model predictions, there has been little examination of its effects on model predictions, particularly when a model is refit to new data. In this study, we illustrate how Γ0 affects important physiological properties such as action potential duration restitution, and examine the effects of (in)correctly specifying Γ0 during model calibration. We show that, although physiologically plausible, the range of concentrations used in popular models leads to orders of magnitude differences in Γ0, which can lead to very different model predictions. In model calibration, we find that using an incorrect value of Γ0 can lead to biased estimates of the inferred parameters, but that the predictive power of these models can be restored by fitting Γ0 as a separate parameter. These results show the value of making Γ0 explicit in model formulations, as it forces modellers and experimenters to consider the effects of uncertainty and potential discrepancy in initial concentrations upon model predictions.
1 Introduction
Since the seminal work by Hodgkin and Huxley (1952), mathematical models of electrophysiology have been developed for many different cell types, including neurons, cardiomyocytes, gastric smooth muscle cells, and many more (Noble, 1962; Dodge and Cooley, 1973; Corrias and Buist, 2007). Differences in ionic concentrations across cell membranes lead to a transmembrane voltage (Vm). Its evolution over time is usually calculated in mathematical models by numerically integrating the effects of the ionic currents passing through the membrane. Since the late 90s, several authors have showed that Vm can also be computed directly from intra- and extracellular concentrations of charges, due to a conservation principle in the models (Guan et al., 1997; Varghese and Sell, 1997; Endresen et al., 2000; Hund et al., 2001; Jacquemet, 2007; Livshitz and Rudy, 2009; Pan et al., 2018). In this work, we investigate further the implications of using this second expression for Vm in terms of numerical stability, we highlight its impact on electrophysiological predictions, and we discuss the benefits to using this approach in model calibration.
First, in this section we present a brief overview of relevant work that leads to different ways of computing the voltage in AP models, based on a conservation of charge principle hidden in the equations, as well as how this conservation of charge relates to the steady state of the AP models. Section 2 then highlights how the accuracy of solutions is improved by the algebraic expression for voltage. In Section 3, we show that model outputs are sensitive to the net concentration of charge across the cell membrane, which varies because of high variability and/or uncertainty in initial concentrations. We finally show in Section 4 that Γ0, a parameter characterising the relationship between Vm and the intra- and extracellular concentrations of charges, can be inferred from experimental data to produce the desired steady-state behaviour of the AP model, despite being challenging to estimate experimentally.
In this study, we explore the consequences of writing Vm algebraically using the Ten Tusscher-Panfilov model of human ventricular cells (TTP06) (Ten Tusscher and Panfilov, 2006) and the CiPA version of the O’Hara-Rudy model by Dutta et al. (2017) (ORd-CiPA). Beyond these two models, our findings apply to any model tracking the intracellular concentrations of all charge-carriers, which make up the majority of modern electrophysiology models.
1.1 Membrane Voltage and Ionic Concentrations in AP Models
Major variables in AP models include Vm, channel and pump/transporter state variables and, in later models, concentrations of ions, buffers, and signalling molecules. The relationship between these variables, grouped together in a vector X, is expressed as a system of ordinary differential equations (ODEs) of the form
where the vector function f(X) describes the rate of change of X, which can be subdivided into Vm, the ionic concentrations C and all other variables g. The first equation in f is usually the one that defines the rate of change in Vm, using an ideal capacitor equation:
where Cm is the membrane capacitance (usually in pF), and Ij are the N different ionic currents flowing across the cell membrane (in pA). Note that the currents depend non-linearly on voltage, concentration, and time, so that all the state variables are coupled together in a non-linear system.
The earliest AP models (e.g. Hodgkin and Huxley, 1952; Noble, 1962; McAllister et al., 1975) approximated intracellular concentrations as constants, arguing that the relatively small ionic currents would not alter concentrations significantly. This assumption holds well for the K+ and Na+ currents included in these models, which have relatively large internal concentrations which do not show significant variations during a single AP. In addition, simulating longer time spans during which these small changes could build up, was computationally infeasible at the time. But after the discovery of Ca2+ currents in the 60s, it was quickly realised that
Later, DiFrancesco and Noble (1985) proposed a model where the current-induced changes in
1.2 Algebraic Expressions for Vm
A study by Varghese and Sell (1997) showed that models in which all membrane currents are assigned to a charge-carrying species, and in which the intracellular ionic concentrations vary accordingly, will implicitly satisfy a conservation of charge principle. As a result, Vm can be computed algebraically as a function of the concentrations, so that the ODE for Vm Eq. 1 is redundant. Applying the approach of Varghese & Sell to the Luo and Rudy (1994) model as an example, we obtain
where V0 is an integration constant (called C0 in the original publication), F is the Faraday constant,
Endresen et al. (2000) proposed an expression very similar to that of Varghese and Sell but with a strong assumption: that all charges contributing to Vm are carried by K+, Na+, and Ca2+. This assumption leads to
where [X]o is the extracellular concentration of species X. In other words, Vm is simply proportional to the difference between total intracellular and extracellular concentrations of these three species. Endresen et al. acknowledged that their approach omitted anions, but justified this with the observation that the total concentrations of anions are approximately the same inside and outside the cell and that most currents are carried by cations. However, this framework needs to be extended for models which include Cl−, e.g., Hund and Rudy (2004); Grandi et al. (2010); Tomek et al. (2020): Eqs 2, 3 can be combined and generalised to any number of modelled species and compartments as follows
where A represents each charged species in the model, zA its valence,
Note that the total concentration of any ion A is denoted here as [A]total,k. Some models include buffering of ions which alters free ionic concentrations, but as binding to buffers does not cause current flow over the membrane it should not change membrane voltage. So the [A]total notation in Eq. 4 serves as a reminder that the total concentration carried by A is given by the sum of any buffered and free concentrations. For example, in many models
However, various other charge-carriers—ions, compounds and charged proteins—are known to be present at different concentrations on either side of the membrane, but are omitted from models. If these omitted charge carriers lead to a net transmembrane voltage, then an extra parameter is needed to account for the contribution of their charge imbalance to Vm. For example, the Hund and Rudy (2004) dog action potential model includes Cl− ions and an extra offset parameter would be needed to compensate the strong imbalance between intracellular (
We can modify Eq. 4 to explicitly allow for transmembrane imbalance of species that are not included in the model:
Here, ΔV corresponds to the transmembrane potential due to the difference in charge of all un-modelled species on either side of the membrane. As the contribution of these species to Vm is not modelled as varying, ΔV remains constant through the simulations. Equivalently, we can express the offset constant as a concentration that we denote Γ0:
where
Expressing the offset as a concentration rather than voltage may help in assessing whether the values implicitly attributed to Γ0 by ODE models could be realistic. If positive, Γ0 could be interpreted as the net concentration of 1 + charged intracellular ions carried by species omitted in the model (or equivalently the net extracellular concentration of 1 − charged ions), and if negative it could be interpreted as a net intracellular concentration of 1 − charged omitted ions—but in reality it will reflect the sum of concentrations of a wide range of intra and extracellular un-modelled charged species. The smaller the magnitude of Γ0, the smaller the transmembrane imbalance of charge carried by un-modelled species. As a consequence, a value of Γ0 = 0 mM does not necessarily imply that no charge is missing in the model; but it does imply that any external missing charge is balanced exactly by an internal missing charge. Thus, the value of Γ0 must be interpreted in the light of which charged species are included in each model. Throughout this manuscript, we will use the Γ0 symbol to represent these missing charges, but the results hold equally well for its mathematically equivalent representation as voltage (Endresen et al., 2000), concentration of charge (Hund et al., 2001), or electrical charge (Jacquemet, 2007). Further detail on these expressions and their interpretation is provided in Supplementary Material Section S1-2.
A value for Γ0 can be found by substituting in the initial conditions for the concentrations and the initial value of Vm from the ODE formulation. This highlights an important point: models that express Vm in ODE form “hide” the value of this model parameter within their initial conditions. So when a set of initial conditions is chosen, perhaps arbitrarily from within the bounds of physiological realism, a hidden assumption is being made about the (im)balance of un-modelled charges in the cell. As we will show in this study, this net imbalance in un-modelled charge, captured by Γ0, is a key parameter in determining the behaviour of AP models.
1.3 Γ0 and Stable Behaviour
In Figure 1 we show the stable behaviour of the O’Hara-Rudy CiPA model when paced for a long time at 1 Hz. The solution converges to a pattern under which all variables in the system take the same trajectory (to within numerical simulation tolerances) every time a stimulus is applied. The resulting periodic orbit in the state variable space (as shown in Figure 1E) is called a “stable limit cycle” in the study of dynamical systems, but is often referred to as a “steady state” for shorthand in electrophysiology modelling. Figure 1 also shows how a change in pacing to 2 Hz results in a transient shift to a new limit cycle. Similar transients to different limit cycles will also occur when other parameters in the model are changed (e.g., those representing maximal ion channel conductances being altered by drug block, or a change in extracellular concentrations). A model at a limit cycle has settled to a stable behaviour where each ionic concentration is in a dynamic equilibrium—any depletion/accumulation due to ions flowing down concentration gradients is restored before the next pace by pumps and exchangers (see Figure 1C).
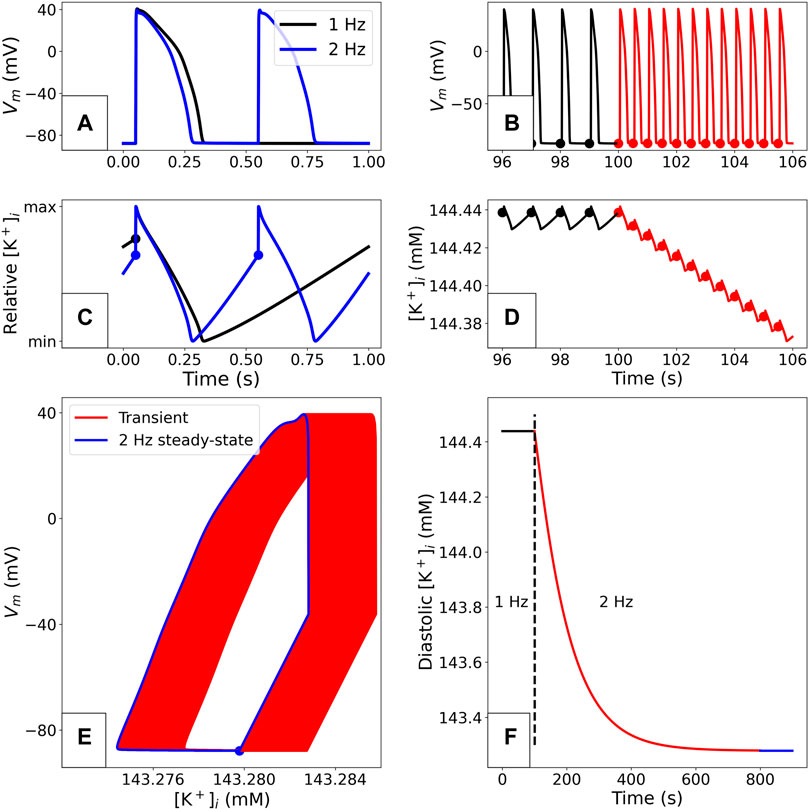
FIGURE 1. Example of a limit cycle in the O’Hara-Rudy CiPA 2017 model (Dutta et al., 2017), using the initial conditions from the published CellML model. The simulation methods are detailed in “Simulation”. (A): Comparison of paced steady-state APs with 1 and 2 Hz pacing. (B): Adaptation of the voltage profile when the pacing rate is suddenly changed from 1 to 2 Hz. The dots plotted on the traces correspond to the end of the diastolic phase in each AP. (C): Comparison of periodic steady-state
Convergence to a stable limit cycle of the same period as the pacing (a “period-1” orbit) is not guaranteed: some models’ variables/concentrations may simply keep drifting (perhaps reaching unrealistic levels); exhibit more complex behaviour such as alternans (a stable “period-2” limit cycle in which we arrive back at the same state after two stimuli periods rather than one); or even chaotic behaviour (Qu, 2011). If pacing is stopped altogether, model variables may converge to stable values—a “stable steady state”. In models that exhibit automaticity, a limit cycle can be reached without any periodic forcing applied by a stimulus current. In this manuscript, we will use either “limit cycle” or “periodic steady state” when referring to stable limit cycles, and “quiescent steady state” when referring to stable steady states without any periodic forcing by a stimulus current.
Many published models do not exhibit a periodic steady state. Hund et al. (2001); Jacquemet (2007) showed that models where variables drift can often be ‘fixed’ to produce periodic steady states by ensuring that all currents through the membrane, including the stimulus current, are taken into account in the concentration updates, i.e. by ensuring that charge is conserved (as well as other conservation laws, see Pan et al., 2018).
Even when a model does have a periodic steady state, for any models where Vm is written as a redundant ODE, the charge represented by Γ0 is defined by the initial conditions. As a result, arbitrarily varying initial conditions in the presence of this redundant ODE alters the parameterisation of the model (changes the amount of charge in the system), and any quiescent steady states or limit cycles can alter accordingly. Or in other words, when a redundant ODE is included there can be no unique periodic steady state, it will vary depending on the initial conditions. Conversely, when the redundant ODE is removed there is often a unique stable limit cycle or quiescent steady state; that is, the same quiescent steady state or limit cycle is reached for any initial conditions.
Some authors such as Livshitz and Rudy (2009) have gone a step further, and suggested that uniqueness of limit cycles/quiescent steady states is guaranteed once conservation of charge is met. An analysis by Jacquemet (2007), however, shows that more than one stable quiescent steady state can exist for a charge-conserving model with a given value of Γ0. Examining the atrial model by Nygren et al. (1998), Jacquemet found that for some values of Γ0 the model had a stable steady state where Vm is polarised at rest (−60 to −90 mV), a stable steady state where the cell is depolarised to about −30 mV, and an unstable periodic steady state where the model displays automaticity. In the course of this study we also found examples of more than one stable limit cycle in other analytic-Vm models, which are discussed below.
Although undoubtedly important for reproducible modelling, it is reasonable to question the physiological relevance of quiescent steady states and limit cycles. Convergence to a perfect limit cycle seems unlikely to occur in real cells, as channel activity and other chemical processes are inherently stochastic and will perturb each orbit differently. The idea of a limit cycle, however, overlaps well with biological concepts of homeostasis and robustness. Even though the cell’s environment is constantly altering to some degree, it would be ideal for a cell to exist in close proximity to a stable limit cycle such that small stochastic perturbations converge back to the same behaviour—at least while energetic demands are met.
2 Impact of the Algebraic Voltage Formulation on Numerical Solutions
2.1 Models and Simulation
CellML files for the TTP06 and ORd-CiPA models were obtained from the Physiome Model Repository (Yu et al., 2011). The TTP06 model has epi-, endo- and mid-myocardial variants; where not stated otherwise we used the epicardial variant in this study. The units in the obtained CellML files for TTP06 had to be corrected before the algebraic-Vm form could be applied, as described in Supplementary Material Section S1.1. The algebraic-Vm forms of the TTP06 and ORd-CiPA models were derived, and model variants that employ this form were created for comparison with the original derivative-Vm form. A detailed overview of the conversion of a model to its algebraic-Vm form is given in Supplementary Material Section S1.3, along with a guide to performing this translation in other models.
Simulations were performed using Myokit (Clerx et al., 2016) which imported the CellML models, and using solver tolerances stated in the section below. Unless stated otherwise, figures were created after 2000 pre-pacing stimuli at a frequency of 1 Hz. In the TTP06 model, the stimulus current was modelled as a K+ current of amplitude −52 A/F lasting 0.5 ms. In the ORd-CiPA model, the stimulus current was also attributed to K+ ions and its amplitude was set at −50 A/F and its duration at 1 ms.
All code used for this article is publicly available and open source (see Data Availability at the end of the article).
2.2 Accuracy of Solutions
Simulations in Myokit are performed using the CVODES software package (Hindmarsh et al., 2005) to numerically integrate the differential equations. CVODES has two “tolerance” settings that control the accuracy of the numerical solutions (Cohen et al., 1996). To visualise the influence of solver tolerance on AP simulations and find suitable tolerances to use in this study, simulations were run for 2000 paces with the ORd-CiPA model in its derivative-Vm form, using a coarse setting (10–6 and 10–4 for absolute and relative tolerance, respectively) and a fine setting (10–8 and 10–6). The resting membrane potential (RMP) was measured as the Vm 1 ms before application of the stimulus, and plotted for the final 1750 paces in Figure 2.
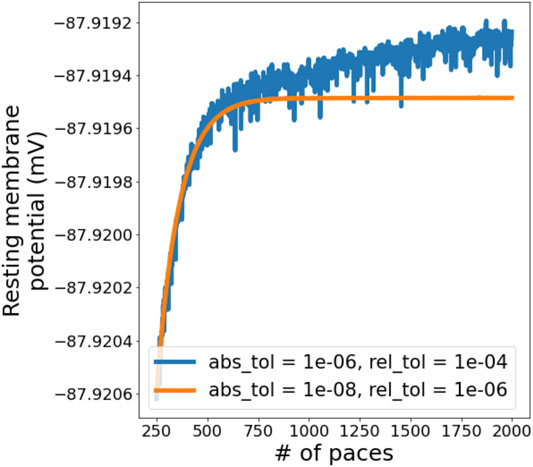
FIGURE 2. Evolution of resting membrane potential (RMP) in a simulation with the derivative-Vm ORd-CiPA model, starting from the published initial conditions. 2000 paces were simulated, we are showing paces 250 onwards to examine the behaviour close to periodic steady state. A slight drift is observed when using a coarse solver tolerance, but this disappears when tolerances are tightened.
As expected, using coarse tolerances results in (a small) numerical error in the solution, but the figure also shows a slight drift in Vm, even after 1,000 paces. When tightening the solver tolerance, the numerical noise is significantly reduced, and Vm stabilises after around 700 paces. The other state variables show a similar pattern, as can be seen for
To further investigate the long term stability of the solutions, 3,000 paces were simulated with the ORd-CiPA and TTP06 models, in both the derivative and the algebraic-Vm forms. Since, with fine tolerances, the system had stabilised after 2000 paces (see Figure 2), the variation in the state variables after 2000 paces could safely be attributed to numerical error and not to electrophysiological phenomena. We quantified this variation by measuring the standard deviation in the final 1,000 paces in
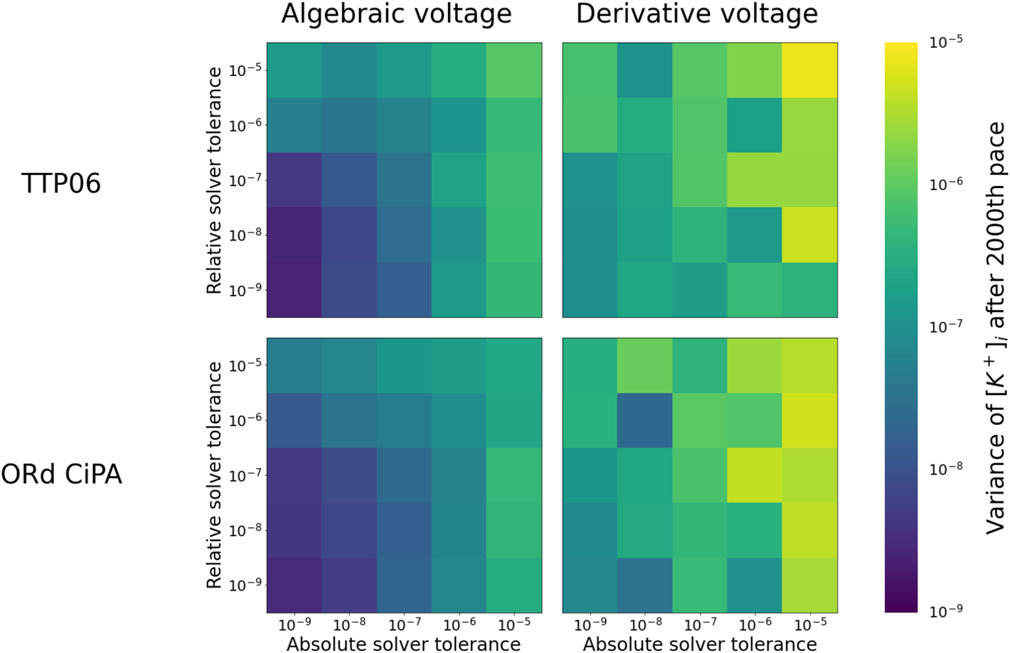
FIGURE 3. Numerical stability of
For both models, numerical solutions appear less stable when using the derivative-Vm form Eq. 1. We believe this is because the intracellular ionic concentrations and Vm are updated without the numerical method having any knowledge of Γ0. This can lead to numerical errors that break conservation of charge, effectively introducing variations in Γ0, and allowing the periodic steady state of the system to change. By contrast, when explicitly incorporating the algebraic constraint on Vm (Eq. 6) and fixing Γ0, conservation of charge is guaranteed, so that the periodic steady state stays the same and the stability of the solution is improved.
For the remainder of this manuscript, we therefore used the algebraic-Vm form and absolute and relative solver tolerances of 10–8 and 10–6, respectively.
2.3 Computation Time
We also investigated whether computation time was affected by switching to the algebraic-Vm form of the model. One might have expected an improvement in simulation time due to a smaller and better conditioned system with the redundant ODE removed (avoiding a singular Jacobian as Varghese and Sell (1997) suggested), but there was no significant (if any) change in computation time, see Supplementary Figure S5 in the Supplementary Material.
3 Physiological Impact of Γ0
3.1 Γ0,
The algebraic-Vm form of the model (Eq. 6) gives the voltage in terms of the total intra- and extra-cellular ionic concentrations. The impact of variations in these parameters and variables across ventricular models was investigated by computing Γ0 for several literature models using the published initial conditions. This work could be carried out only for models which obey the conservation of charge principle. The results are shown in Table 1 which reports Γ0 (Eq. 6), the corresponding C0 as defined by Endresen et al., and the corresponding voltage offset ΔV for each of the investigated models.
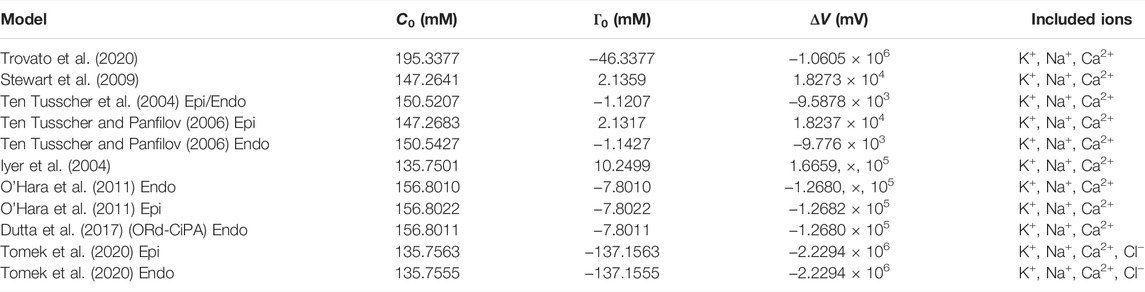
TABLE 1. The integration constant for a range of human AP models, written as C0 (Hund et al., 2001)—see Section 1.2—, net un-modelled species concentration Γ0 Eq. 6, and voltage offset ΔV Eq. 5. The Trovato et al. (2020) and Stewart et al. (2009) models are Purkinje fibre models, while the remaining models represent ventricular cells.
These parameters contain information about the difference between the un-modelled intra- and extracellular charged species (e.g. H+, Mg2+, cations, phosphates, proteins). In the TTP06 Epi model, for example, the intra- and extra-cellular charges of these missing species are responsible for a voltage offset of 18.2 V. In the ORd-CiPA model, the voltage offset is of −126.8 V.
The Tomek et al. (2020) model (an update of the 2019 version to conserve charge) has a very high Γ0 constant due to the inclusion of chloride ions, for which there is a very large difference between intra- and extracellular concentrations. In the Ten Tusscher et al. (2004) model, the epicardial and endocardial versions were assumed to have the same initial conditions, so their missing charge concentrations are the same. The 2006 epi/endo variants of the Ten Tusscher model (Ten Tusscher and Panfilov, 2006) have minor differences in the initial conditions and buffered Ca2+ concentrations. As a result, there are slight differences in Γ0 between the various versions of the Ten Tusscher et al. model.
It remains to be seen whether the Γ0 value (net concentration of un-modelled charge) is biologically as variable as the values it has been implicitly assigned within models, or whether this simply reflects lack of information on real concentrations and subsequent uncertainty in what initial conditions should be used.
Comparing the magnitudes of Γ0 and ΔV in Table 1 shows that a 20 mV variation one might observe in resting potential between models corresponds to Γ0 variations of approximately 0.002 mM, much smaller than the variation in the offset constants between models. So what we observe is not influenced much by the precise value of the initial condition for the RMP (this is the same reason initial gating variable values have negligible effects) but instead by how the various possible initial concentrations cause longer term system behaviour to change via altered Nernst potential (or GHK flux equations) and resulting currents, as well as any explicit concentration-dependence in gating kinetics. So the impact of initial RMP on Γ0 can be neglected in comparison to that of initial concentrations (RMP is also much easier to measure to within a few millivolts in experiments). As a consequence, variation of the initial voltage used to compute Γ0 from Eq. 6 was neglected in this study and the initial voltage as published in the original models was used to compute Γ0 in simulations of the sections below.
3.2 Γ0 and Ranges of K+ and Na+
In this section, we estimate the variability of Γ0 from literature and observe how this variability might impact the AP predicted by the model. The values that can be taken by Γ0 are, for a large part, dictated by the uncertainty in intracellular concentrations in intact myocytes. Extracellular concentrations are fixed parameters in most AP models that are more reliably estimated (at least in in vitro experiments); we therefore investigate the effect of only the initial conditions of intracellular state variables on long-term model behaviour.
A literature search was carried out to find the range of intracellular K+ and Na+ concentrations observed experimentally in human cardiomyocytes and/or used in simulations. The contribution of Ca2+ to total intracellular charge at the end of the resting phase of the AP is much smaller, so its variation can be neglected compared to K+ and Na+, and Γ0 variation between the models is mainly due to different intra- and extra-cellular K+ and Na+. The concentrations of
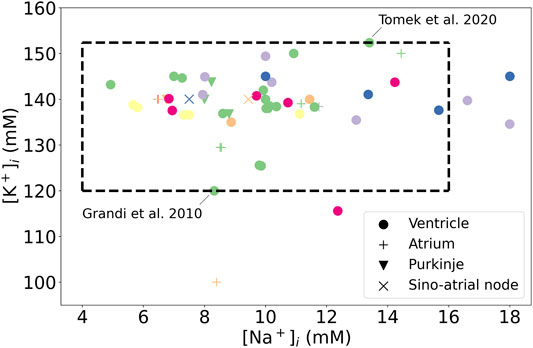
FIGURE 4. Initial concentrations published for cardiac AP models, for a range of species and tissues. Green: human, Purple: canine, Orange: rabbit, Yellow: Guinea pig, Blue: mammalian, Pink: murine. The dotted box highlights the extreme values of intracellular concentrations, estimated from the work of Bers et al. (2003) for Na+ and from the Grandi et al. (2010) and the Tomek et al. (2020) models for K+.
In human ventricular cardiomyocytes the intracellular sodium concentration (
The extreme K+ and Na+ concentrations from Figure 4 were used to initialise
In simulations in sections below where the value of Γ0 is imposed by the user, the initial intracellular concentrations must be changed to satisfy the algebraic constraint of Eq. 6 and leave the initial voltage unchanged. Otherwise, the high variations of Γ0 reported in Table 1 would lead to voltage offsets of up to several kilovolts. The intracellular concentration of K+ was therefore adjusted with Eq. 6 so that the initial voltage remains untouched and consistent with the required value of Γ0. Alternatively, Na+ could be adjusted; but the degree of variation of Γ0 could lead to negative values of
The ORd-CiPA model has extra ionic variables compared to the TTP06 model: variables were added for the concentrations of sodium and potassium in the subspace domain, denoted by [Na+]SS and [K+]SS. At the limit cycle, the difference between diastolic concentrations of ions in the subspace and in the intracellular compartment were observed to be smaller than 0.1 mM, even when initial conditions were set to very different values (results not shown). Furthermore, there is no physical structure delimiting the subspace from the bulk intracellular space. Thus, K+ and Na+ concentrations in the subspace are very close to concentrations in the main intracellular compartments at the end of the resting phase of the AP, i.e., when state variables are initialised in simulations. To avoid introducing big differentials in K+ and Na+ concentrations between the subspace and the bulk cytosol compartment in simulations where the user introduced changes to initial conditions for
The limit cycle APs, observed after 2,000 paces, are plotted in Figure 5. The difference in Γ0 induces important changes in the limit cycle AP, especially for the TTP06 model. For instance, the TTP06 model does not have a physiological AP when simulated with a very low Γ0 value, the cell does not depolarise. In the ORd-CiPA model, the RMP is particularly impacted, decreasing from −82 mV for Γ0 = −24.4 mM to −88 mV for Γ0 = 20.9 mM. This shows that Γ0 variations have a strong impact on the model output, which is investigated further below.
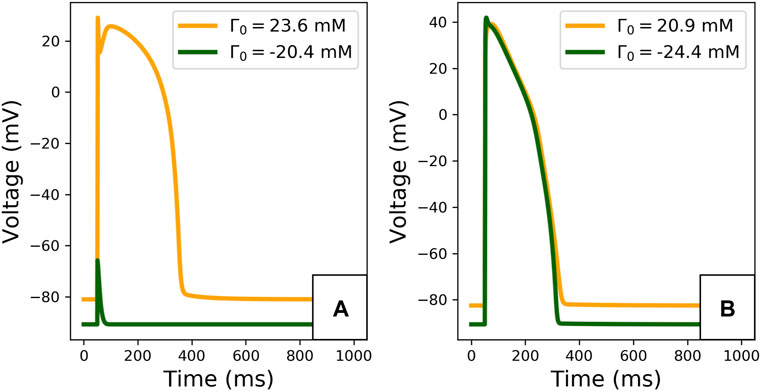
FIGURE 5. Limit cycle APs for extreme initial conditions for the TTP06 model (A) and for the ORd-CiPA model (B). Extreme Γ0 values covering approximately 44 mM are computed from the extreme
3.3 Effect of Γ0 on Steady States
Several authors have asserted that Γ0 (or its equivalents from the literature) defines the steady states of various models, both under paced and unpaced conditions (Hund et al., 2001; Jacquemet, 2007; Livshitz and Rudy, 2009; Pan et al., 2018). Here we investigate the steady states and limit cycles reached by the TTP06 and ORd-CiPA models for initial conditions that sample the range of physiologically-plausible Γ0 values (Section 3.2).
The range of experimental concentrations determined in the previous section was sampled at 10 linearly spaced Γ0 values. For each Γ0 value, the
The quiescent steady state and the 1 Hz limit cycle diastolic intracellular concentrations are shown in Figure 6. For each Γ0 value, all the simulations converged to the same quiescent or periodic steady state. The steady states that can be reached by the models for the various Γ0 values align on these plots.
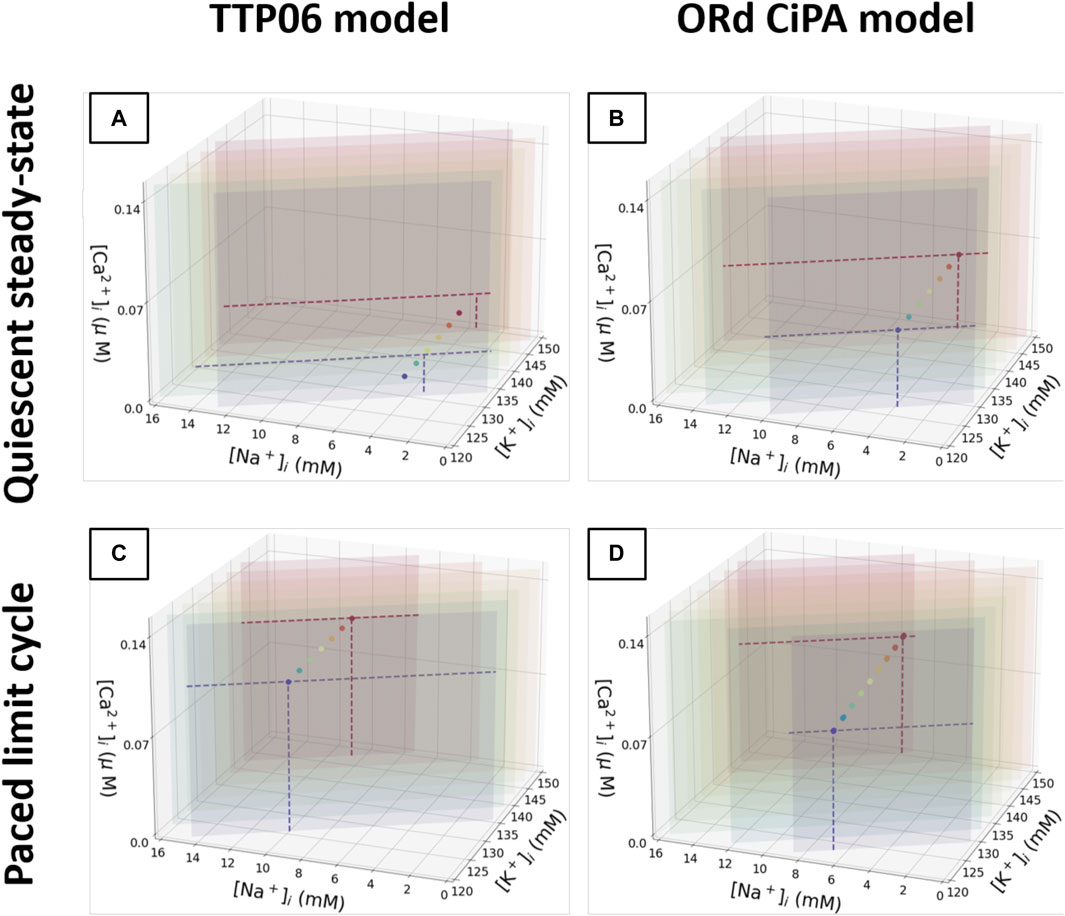
FIGURE 6. Plot of the quiescent steady state and limit cycle values for
Note how some of the points in Figure 6A appear to move outside the Γ0 plane. Only
For both models, regardless of the initial conditions used for the state variables, a unique quiescent steady state and a unique 1 Hz limit cycle were observed for each value of Γ0. Thus, the solution of the model under quiescence and for prolonged regular pacing is defined by the value of Γ0. This observation is consistent with the studies mentioned previously, with constants equivalent to Γ0. As a conclusion, Γ0 can be used as a single model parameter to summarise the intracellular concentrations in these models at these pacing conditions and parameter values. Moreover, the initial conditions for the gating variables did not impact the limit cycle or steady-state outputs, so their initial conditions were not altered in further simulations. When calibrating an AP model based on its limit cycle or steady state outputs, it appears sufficient to establish the correct value of Γ0, regardless of how K+, Na+ and Ca2+ concentrations and gating variables are individually initialised as long as they remain physiologically plausible. Thus, when exploring values of Γ0 in a derivative-Vm model the changes could be attributed to a single intracellular concentration (K+ for example) without loss of generality.
3.4 Model Predictions Are Sensitive to Γ0
The influence of Γ0 on the limit cycle outputs and on the APD restitution portrait was evaluated in the TTP06 and ORd-CiPA models. The models’ outputs were recorded with Γ0 values varying by 30 mM. Intracellular concentrations were initialised so that Eq. 6 is satisfied with the initial voltage set to its published value. The state variables other than intracellular concentrations were initialised to their originally published initial values. 2000 paces were simulated to approach the limit cycle. The inward rectifier potassium current (IK1) and the sodium potassium exchanger current (INaK), the currents which showed the highest sensitivity to Γ0 change, were recorded at 1 Hz pacing, together with Vm.
The AP duration restitution portrait at limit cycle was investigated using the Cardiac Electrophysiology Web Lab (https://chaste.cs.ox.ac.uk/WebLab) (Cooper et al., 2016; Daly et al., 2018). There, the models were loaded as CellML files, using the public protocol “Steady State Restitution”. In this protocol, 2000 paces are applied (bringing models close to their limit cycles) at various pacing periods ranging from 250 to 2000 ms. Two consecutive APs are then recorded, and their APD90s measured. The limit cycle outputs at 1 Hz and the restitution plots are shown in Figure 7.
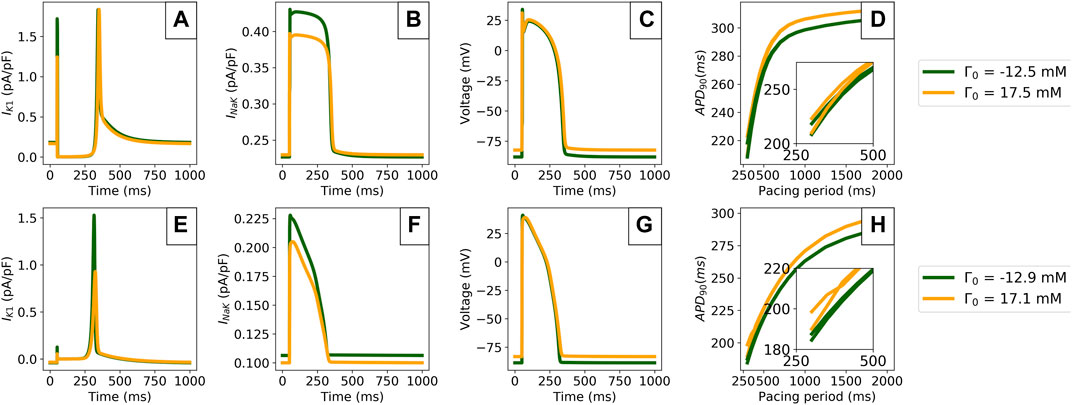
FIGURE 7. Comparison of model predictions in the periodic steady state outputs for the extreme values of Γ0 computed from Section 3.2. Data is shown for the TTP06 (top row) and ORd-CiPA models (bottom row). (A,E): IK1 current. (B,F): Sodium-Potassium exchanger (INaK) current. (C,G): AP. (D,H): Limit cycle restitution portraits showing APD90 variation with the pacing period. The insets show pacing cycle lengths of 500 ms and shorter.
Γ0 variations impacted the IK1 current particularly strongly in both models, with faster IK1 activation kinetics for lower Γ0 values, see Figures 7A,E. In addition, peak IK1 is decreased by 45% when increasing Γ0 by 30 mM in the ORd-CiPA model. INaK is also shown to be sensitive to Γ0, see Figures 7B,F. When using a low Γ0 value, INaK is reduced by approximately 15% in both the TTP06 and the ORd-CiPA models. The consequences for the simulated AP are important, see Figures 7C,G. When looking at the resting membrane potential (RMP) and the APD at 90% repolarisation (APD90) for example, RMP is increased from −88 mV to −82 mV for the TTP06 model, and from −88 mV to −83 mV in the ORd-CiPA model when increasing Γ0 by 30 mM. APD90 is increased from 299 to 306 ms for the TTP06 model, and is increased from 265 to 273 ms in the TTP06 ORd-CiPA model, when increasing Γ0 by 30 mM.
Figures 7D,H show that Γ0 has an effect on the APD90 steady state restitution portraits. The bifurcation of APD90 in the restitution portrait is particularly important as it is characteristic of alternans, when two consecutive APs do not have the same APD90 but the model outputs are still periodic. Note that when stable alternans occurs, the limit cycle no longer follows the trajectory of the state variables over a single pacing period, but over two consecutive pacing periods.
There is a bifurcation of APD90 for pacing periods at 700 ms for the TTP06 model and at 400 ms for the ORd-CiPA model. The pacing periods generating this bifurcation appear to be independent of Γ0. However, the steepness of the restitution slope as well as the size of the bifurcation depend on Γ0 used for the simulation, especially for the ORd-CiPA model. In the studied models, higher values of Γ0 generate wider bifurcations in the APD90 restitution portrait. The impact of Γ0 on characteristics of the alternans predicted by the TTP06 and ORd-CiPA models stresses the need to carefully consider the value of Γ0 used in AP models.
4 Calibration of AP Models and Γ0
The dependency of model outputs to Γ0 observed in Figure 7 is also expected have an impact when fitting parameter values to whole traces of Vm, or their derived biomarkers. Indeed, if Γ0 is fixed to a value that incorrectly summarises the experimental concentrations under which the data were generated, we might expect a fitting process to return parameter values which are skewed away from their correct values. A fitting of the ORd-CiPA model to synthetic (simulated) data was performed to examine this effect.
The synthetic datasets used in model training were generated by running the ORd-CiPA model for 2000 pre-paces (1 Hz pacing), and recording the 2001th AP, with one data point per 0.05 ms, no noise was added. The “true” scaling parameters for conductances were then “forgotten” and re-calibrated to the synthetic AP data, as in Johnstone et al. (2016). The parameters used for the simulations are expressed as: gsimulation = θ × goriginal, with gsimulation the value of the conductance used for the simulation, θ the scaling factor, and goriginal the original value of the conductance parameter. Thus, a scaling factor of θ = 1 corresponds to the conductance used in the original published model (the “true” value in this synthetic study).
Three cases were explored to assess the influence of Γ0 in the fitting process. In the first case, the initial conditions were unaltered (assumed to be known/exactly correct), therefore the value of Γ0 during the fitting was set to the “true” value, i.e. the one used for synthetic data generation. In the second case, the model was fitted with a fixed and incorrect Γ0 value computed from initial concentrations and voltage published for the TTP06 model, a different but still plausible value. The third fitting is the same as the second case, but Γ0 was added to the set of parameters to be fitted, to allow compensation for discrepancy in the initial intracellular ion concentrations provided by the user (in terms of Figure 6 this allows flexibility in the plane upon which intracellular concentrations will settle). The initial conditions used for the fittings are reported in the Table 2.
When using initial concentrations from the TTP06 model, calcium concentrations,
The optimisation problem was defined as the minimisation of the sum of square errors between the synthetic data and the fitted model AP. The fitting algorithm uses the PINTS Python package (https://github.com/pints-team/pints) (Clerx et al., 2019), to run the Covariance Matrix Adaptation-Evolution Strategy (CMA-ES) (Hansen et al., 2003). The scaling factor parameters θCaL, θKr, θKs, θNa, θNaL of the ORd-CiPA model were fitted. The initial guesses for scaling factors were taken from the range 0.2–5, while the boundaries were set to 0.1 to 10. The CMA-ES hyper-parameter Σ0, the initial proposal covariance for new parameter samples, was set to 0.1 along the diagonal for all parameters and zero otherwise.
The value of scaling parameters retrieved by the three fittings are compared in Table 3, and the corresponding APs are plotted in Figure 8. In the case of the first fitting with the correct Γ0, the true parameter values are retrieved as expected due to these model parameters being identifiable. In the case of the second fitting with a discrepancy in Γ0, the model cannot converge to the right limit cycle. The optimal AP is still very similar to the synthetic data, the only difference being a small shift in the resting membrane potential, as seen in Figure 8A. However, the discrepancy in ionic concentrations is compensated by a dramatic shift in the retrieved scaling parameters, especially for gKs (0.522) and gNaL (1.585). This impacts the response of the model to perturbation: for example 50% block of IKr as shown in Figure 8B, where we see a 14 ms difference in the predicted APD90 which would be significant in many drug effect prediction settings.

TABLE 3. Parameters retrieved from fittings in the investigated cases. The fitting process with an incorrect Γ0 value yields incorrect values for model parameters. Such a model suffers from poor predictive power, this can be corrected by fitting Γ0 together with the other model parameters.
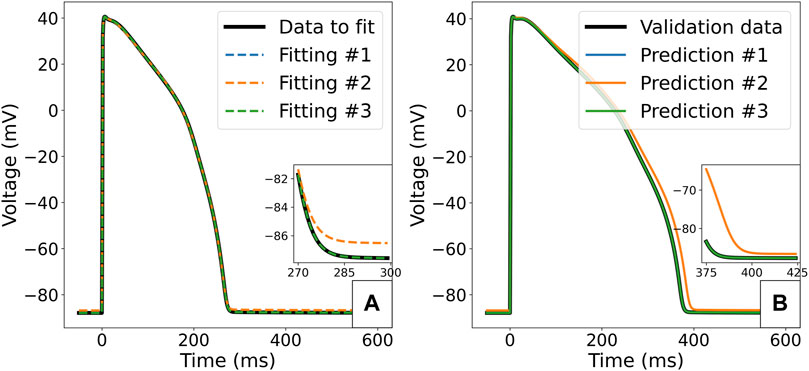
FIGURE 8. Predicted APs for the ORd-CiPA model fitted to synthetic data. (A) Comparison of the synthetic data with APs obtained from optimal parameterisations in the different fitting cases. (B) Prediction of response of the model to 50% block of IKr. Predictions of model with parameter fittings #1, #3 and the true parameters set overlay.
In the case of the third fitting with Γ0 as an inferred parameter, the true values for all scaling parameters could be recovered. The fact that the value of Γ0 could also be accurately retrieved from fitting supports its identifiability as a model parameter, at least in the absence of model misspecification/discrepancy.
4.1 Calibration When Multiple Stable Limit Cycles Exist for a Single Γ0 Value
It was shown in Section 3.3 that the ORd-CiPA model, with published parameters, has a unique limit cycle for any particular value of Γ0 that has been used (implicitly) in previous models. As shown by previous studies, under certain conditions there are possibly multiple quiescent steady state (Guan et al., 1997; Jacquemet, 2007) and/or limit cycle (Surovyatkina et al., 2010) solutions for the same value of Γ0.
For instance, with 95% reduction of IKr, Γ0 = −20 mM, and 1 Hz pacing, the ORd-CiPA model has two stable limit cycle APs, shown in Figure 9. With the initial Na+ concentration as originally published in the ORd-CiPA model, the limit cycle AP has an early after-depolarisation (EAD), whereas the limit cycle AP with higher initial Na+ concentration exhibits alternans and an EAD. This is characteristic of a bifurcation of the limit cycle for the same value of Γ0, which is investigated further in this section.
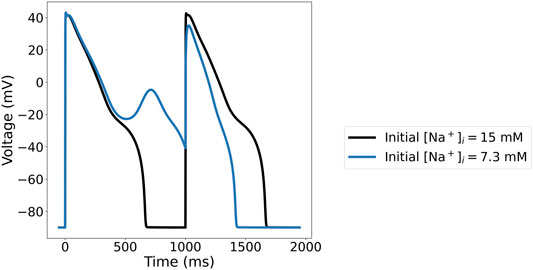
FIGURE 9. Limit cycle APs for the ORd-CiPA model under 95% of IKr reduction, generated with the same value for Γ0=−20 mM, but different initial Na+ concentrations. With the initial Na+ concentration set to 15 mM (Black), the limit cycle AP shows no early after-depolarisation (EAD). With a lower initial Na+ concentration of 7.3 mM (Blue), the limit cycle AP exhibits alternans with an EAD.
Various conditions of IKr block (0, 90 and 95%) were applied to the ORd-CiPA model to test for the presence of multiple limit cycles for a single value of Γ0. As in Section 3.3, the ORd-CiPA model was paced to its limit cycle for various initial conditions that sample the physiological range of concentrations reported in Section 3.2, but variations of initial conditions were considered only for
The limit cycle diastolic concentrations reached for the various Γ0 values with various IKr block conditions are represented in Figure 10. For IKr block lower than 90% across the range of initial conditions we studied, the limit cycle is unique for a given value of Γ0. In such situations, fitting Γ0 would be sufficient to fully inform the intracellular concentrations.
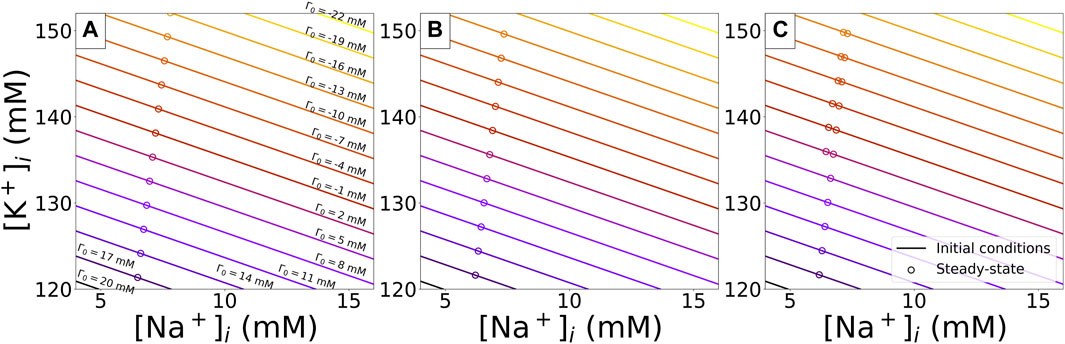
FIGURE 10. Limit cycle concentrations of
In the extreme case of 95% of IKr block, a bifurcation is observed for the ORd-CiPA model—see Figure 10C. A second stable limit cycle appears, and intracellular concentrations converge to one or the other limit cycle value depending on their initial conditions, despite corresponding to the same Γ0 value. The multiple limit cycles at a fixed Γ0 value are observed for Γ0 values ranging from −13 to 2 mM—see Figure 10C. In such cases, Γ0 does not solely determine which limit cycle will be reached, and one needs to consider
As observed in Figure 10, multiple stable limit cycles can be found for the same value of Γ0 under particular conditions. In this section, we investigate how the bifurcations of the limit cycle can impact the fitting process. Under 95% of IKr reduction, there are two stable limit cycle APs for the ORd-CiPA model for the same value of Γ0: one with early after-depolarisation (EAD) generated with low initial
The synthetic data was generated with the ORd-CiPA model under 95% of IKr block, with intracellular concentrations initialised at
During the fitting process, the initial concentration of Na+ was fixed to its published value
Note that for Γ0 = −20 mM,
The parameters retrieved from the fitting are reported in Table 4. The limit cycle AP under 95% IKr reduction for the calibrated model is compared to the synthetic data (Figure 11A) and its prediction of AP without IKr block is compared to that of the true model that generated the synthetic data in the validation case of Figure 11B.

TABLE 4. Rescaling factors for conductance parameters retrieved from fitting to data generated under conditions where several stable limit cycles coexist for the same value of Γ0 = −20 mM.
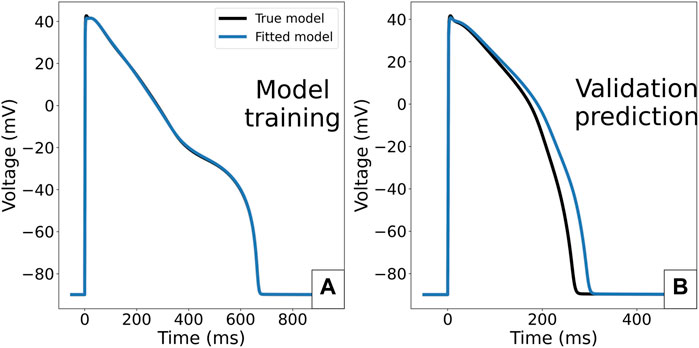
FIGURE 11. Consequence of fitting the ORd-CiPA model in case of multiple stable limit cycles for the same Γ0 value. (A): ORd-CiPA fitted with initial
The optimal values of θKr and θNa are close to their true values, but θNaL and θKs have considerable differences to their true values, 57 and 26% too large respectively. This explains why even though the synthetic data AP is well reproduced (Figure 11A), the fitted model makes an incorrect prediction in the validation case with no IKr block (Figure 11B). The optimal value of Γ0 is interestingly close to its true value. However, one cannot conclude from this example alone that Γ0 value will still be correctly recovered in the case of bifurcation.
In this case with bifurcation, fitting initial conditions for both
5 Discussion
We investigated the consequences of computing voltage in AP models directly from concentrations, using an algebraic-Vm formulation (Eq. 6). This method for computing voltage increases the numerical accuracy of solutions, compared to the canonical derivative-Vm method of integrating the sum of trans-membrane currents. The computation time of simulations is not impacted significantly by the choice of expression for the voltage. Changing to the algebraic-Vm form of the model did not reduce the computational time required for AP simulations, as it does not change the stiffness of the model (the main driver for the computational cost).
Γ0 is a constant representing the net concentration of un-modelled charge present in the model, needed to ensure the consistency of initial values for concentrations and voltage. In most cases, the value of Γ0 defines the steady-state behaviour of the model, regardless of the combination of initial values for state variables such as concentrations in the simulations. Given the high variability of intracellular concentrations that have been used in action potential models, with less variability in extracellular concentrations, Γ0 is also highly variable. Extreme variations of Γ0 lead to very different steady-state behaviours and substantially impact their outputs, making it important to establish the value of Γ0 as accurately as possible.
Measurements of intracellular ionic concentrations in intact myocytes are not generally available alongside recordings of electrophysiological activity used to calibrate AP models. We showed that this issue could potentially be addressed by inferring Γ0 from the data, along with other parameters of the AP model.
With the algebraic-Vm form of the model, the algebraic constraint on the variables appears explicitly. At each time-step, this constraint is therefore rigorously applied to the system. With the derivative-Vm form of the model, the constraint is mathematically satisfied by the system—by design in AP models which satisfy the conservation of charge principle—but during the numerical integration of the equations, the constraint is not verified at each time step. Therefore, the numerical errors that appear during the integration allow the constraint to be violated. This violation of conservation of charge explains that with a coarse solver tolerance, the model does not properly converge to a limit cycle—see Figure 2. Livshitz & Rudy noted that AP models are often mistaken as Ordinary Differential Equation (ODE) systems when they are actually Differential-Algebraic Equation (DAE) systems—ODE systems with algebraic constraints. With the algebraic-Vm form of the model, all constraints of the DAEs appear explicitly, which is best practice (Livshitz and Rudy, 2009). In theory, the differential and algebraic representations of the membrane voltage are still mathematically equivalent, so modellers could use either of them as preferred (Hund et al., 2001). In practice, we recommend to use the algebraic-Vm formulation.
Using the algebraic-Vm form of the model makes also Γ0 appear as a model parameter, highlighting the need to consider its value explicitly. We propose to infer Γ0 from the experimental data on which the model is calibrated. Endresen et al. (2000) reported with the derivative-Vm form of the model that “the observer tracks only the variations in the number of ions, but then an initial concentration must be guessed”. Livshitz & Rudy proposed criteria for validation against experimental data and adequate comparison between dynamic models (Livshitz and Rudy, 2009). Among these criteria, the use of “a consistent set of initial conditions for state variables (Vm, intracellular ion concentrations)” is recommended. Smirnov et al. (2020) also noted that the question of initial conditions for ionic concentrations is often overlooked when fitting AP models, when they fitted the O’Hara Rudy model (O’Hara et al., 2011) to AP recordings from optical mapping experiments in human ventricular wedges.
The errors induced in conductance fits when using a fixed but incorrect Γ0—see Section 4—emphasise the importance of using the correct initial conditions for concentrations when fitting to AP data. An AP model calibrated using an incorrect representation of concentrations (i.e. an incorrect but plausible value for Γ0) is badly parameterised with up to ±50% error in some maximal conductance parameters, and has a reduced predictive power.
Our results show that Γ0 can be fitted to compensate for errors in assumed intracellular concentrations, at least when fitting to synthetic (simulated) AP data. So we recommend inferring Γ0 from the training data during model calibration, following the methods of Section 4. When using real data, discrepancy in the AP model may cause additional problems, but still the possibility for uncertainty in Γ0 should be explicitly considered.
In our study, we show that due to the conservation law: 1) a consistent Γ0 value should be used throughout the model calibration, and 2) it is sufficient to fit the value of Γ0 to capture the input of intracellular concentrations on steady state outputs, unless bifurcations are present. The second point is supported by observations on other models reported in the literature (Hund et al., 2001; Jacquemet, 2007; Livshitz and Rudy, 2009; Pan et al., 2018). For example, Smirnov et al. (2020) have included initial values for
It remains important to consider that the uniqueness of the limit cycle for a single Γ0 value cannot be always guaranteed (Guan et al., 1997; Jacquemet, 2007). The methods presented in Section 3.3 can be reused to verify that Γ0 solely defines the limit cycle for a model under a given set of studied experimental conditions. If the uniqueness of a limit cycle is verified, it is reasonable to fit Γ0 alone to summarise the initial conditions of intracellular ionic concentrations. Otherwise, in case of bifurcation of the limit cycle, we would recommend fitting Γ0 and the initial condition of
5.1 Limitations
As mentioned above and in the literature (Guan et al., 1997; Jacquemet, 2007), the uniqueness of the steady states for a single Γ0 value is not always guaranteed. In cases of bifurcation, where several stable solutions exist for the model with a single value of Γ0, Γ0 (as well as other parameters) can be incorrectly determined. We observed in this study that for the ORd-CiPA model, the limit cycle is unique in most physiologically-plausible cases. However, this property does not always hold if parameters are changed. A method to investigate thoroughly the uniqueness of the limit cycle for a given value of Γ0 for all parameterisations of an AP model could be extremely costly computationally. Still, we have demonstrated for the ORd-CiPA model, as originally published, that Γ0 is identifiable and could be correctly estimated. We observed consistent findings for Γ0 in the TTP06 model, which has a very different model structure to the ORd-CiPA model—data not shown. We therefore expect this behaviour to be replicated for all AP models that conserve charge. Hence we recommend to consider calibrating Γ0 as a parameter that usually encapsulates both the initial conditions of the modelled ionic species and the un-modelled charge. In the cases where there are multiple steady states for the same Γ0, the unidentifiability could be resolved by fitting initial conditions for ionic concentrations as well.
To define the physiologically-plausible range of concentrations, we used the extreme values of
When AP models are used to investigate changes in extracellular concentrations (e.g. when simulating hypo/er-kalemia or ischaemia—pathological changes to extracellular concentrations such as [K+]) care is needed with Eq. 6. In such situations, as the extracellular ion of interest changes concentration, opposite charges will be introduced into the same solution to maintain electrical neutrality (e.g. if we experimentally use the salt KCl to change
5.2 Possible Extensions to This Study
Although this study was focused on ventricular AP models, the conservation law that binds together the voltage and intracellular ionic concentrations applies to all cellular electrophysiology models: other cardiac cell types, neural, gastric, skeletal muscle etc.
The improvement in numerical accuracy enabled by the algebraic-Vm form of the model was shown to reduce the numerical error that can lead to deviation of state variables after reaching the periodic steady state—see Figure 3 and Supplementary Material Section S1.4. The computational efficiency was similar with the algebraic-Vm form of the model when using the same solver tolerance.
The extent to which intracellular concentrations are well established has been somewhat overlooked (Smirnov et al., 2020). Our study, showed the importance of the correct estimation of Γ0 in specifying concentrations. In literature models, there is significant variation between the assumed initial concentrations, and therefore variation in Γ0, as shown in Section 3.2. In papers on action potential model development, we have not found any discussion of the choice of Γ0, or equivalently the choice of the offset between concentrations and voltage in initial conditions, perhaps suggesting somewhat arbitrary choices. It remains to be seen whether Γ0 exhibits significant physiological variation to contribute to inter-cell and/or inter-individual differences in electrophysiology, or whether it is a well-constrained biological quantity—which would be the case if the un-modelled missing ions that Γ0 represents do not vary significantly between cells or individuals. In either case, Γ0 strongly influences model behaviour and a concerted effort should be made to identify its value alongside other key model parameters. The recent emergence of cell-specific models (Groenendaal et al., 2015) may offer an approach to quantify Γ0 more accurately.
6 Conclusion
We advocate here for the use of the algebraic-voltage form of AP models, as it improves the stability of numerical solutions by enforcing a hidden algebraic constraint in the models. Furthermore, the algebraic-voltage form ensures that the model conserves charge. It also requires the modeller to think carefully about initial conditions for intracellular concentrations and to acknowledge their effects on the model output. We recommend consideration of the potential discrepancy and uncertainty in intra- and extracellular concentrations of ions, as model outputs and model fitting are dependent on these. The Γ0 value summarises these factors into one parameter which can be fitted alongside the rest of a model.
Data Availability Statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories can be found below: Github: https://github.com/CardiacModelling/Gamma_0. Zenodo (permanent archive of Github): http://dx.doi.org/10.5281/zenodo.6423387.
Author Contributions
Y-SB, JS, DW, MC, DG, and GM designed the investigation. Y-SB wrote the codes and performed the simulations under the supervision of MC, KW, LP, DG, and GM. Y-SB, MC, DG, and GM wrote the manuscript. All authors read and approved the final version of the manuscript.
Funding
This work was supported by the UK Engineering and Physical Sciences Research Council (grant number EP/S024093/1); the Biotechnology and Biological Sciences Research Council (grant number BB/P010008/1); and the Wellcome Trust (grant number 212203/Z/18/Z). Y-SB. acknowledges support from F. Hoffmann-La Roche Ltd. for studentship support via the EPSRC and MRC Centre for Doctoral Training in Systems Approaches to Biomedical Science. GM, JS, MC, and DW acknowledge support from the Wellcome Trust via a Wellcome Trust Senior Research Fellowship to GM, MC, and GM acknowledge support from a BBSRC project grant. DG. gratefully acknowledges support from the EPSRC Centres for Doctoral Training Programme. This research was funded in whole, or in part, by the Wellcome Trust (212203/Z/18/Z). For the purpose of open access, the author has applied a CC-BY public copyright licence to any Author Accepted Manuscript version arising from this submission.
Conflict of Interest
Authors KW and LP were employees of F. Hoffmann-La Roche Ltd. and KW is a shareholder.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphys.2022.879035/full#supplementary-material
References
Beeler G. W., Reuter H. (1977). Reconstruction of the Action Potential of Ventricular Myocardial Fibres. J. Physiol. 268, 177–210. doi:10.1113/jphysiol.1977.sp011853
Bers D., Barry W., Despa S. (2003). Intracellular Na+ Regulation in Cardiac Myocytes. Cardiovasc. Res. 57, 897–912. doi:10.1016/S0008-6363(02)00656-9
Clerx M., Collins P., de Lange E., Volders P. G. A. (2016). Myokit: A Simple Interface to Cardiac Cellular Electrophysiology. Prog. Biophys. Mol. Biol. 120, 100–114. doi:10.1016/j.pbiomolbio.2015.12.008
Clerx M., Robinson M., Lambert B., Lei C. L., Ghosh S., Mirams G. R., et al. (2019). Probabilistic Inference on Noisy Time Series (PINTS). J. Open Res. Softw.. doi:10.5334/jors.252
Cohen S. D., Hindmarsh A. C., Dubois P. F. (1996). CVODE, a Stiff/nonstiff ODE Solver in C. Comput. Phys. 10, 138–143. doi:10.1063/1.4822377
Cooper J., Scharm M., Mirams G. R. (2016). The Cardiac Electrophysiology Web Lab. Biophysical J. 110, 292–300. doi:10.1016/j.bpj.2015.12.012
Cooper J., Spiteri R. J., Mirams G. R. (2015). Cellular Cardiac Electrophysiology Modeling with Chaste and Cellml. Front. Physiol. 5, 511. doi:10.3389/fphys.2014.00511
Corrias A., Buist M. L. (2007). A Quantitative Model of Gastric Smooth Muscle Cellular Activation. Ann. Biomed. Eng. 35, 1595–1607. doi:10.1007/s10439-007-9324-8
Daly A. C., Clerx M., Beattie K. A., Cooper J., Gavaghan D. J., Mirams G. R. (2018). Reproducible Model Development in the Cardiac Electrophysiology Web Lab. Prog. Biophys. Mol. Biol. 139, 3–14. doi:10.1016/j.pbiomolbio.2018.05.011
Demir S. S., Clark J. W., Murphey C. R., Giles W. R. (1994). A Mathematical Model of a Rabbit Sinoatrial Node Cell. Am. J. Physiology-Cell Physiol. 266, C832–C852. doi:10.1152/ajpcell.1994.266.3.c832
Dibb K., Trafford A., Zhang H., Eisner D. (2015). A Model Model: A Commentary on DiFrancesco and Noble (1985) 'A Model of Cardiac Electrical Activity Incorporating Ionic Pumps and Concentration Changes'. Phil. Trans. R. Soc. B 370, 20140316. doi:10.1098/rstb.2014.0316
DiFrancesco D., Noble D. (1985). A Model of Cardiac Electrical Activity Incorporating Ionic Pumps and Concentration Changes. Philos. Trans. R. Soc. Lond. B Biol. Sci. 307, 353–398. doi:10.1098/rstb.1985.0001
Dodge F. A., Cooley J. W. (1973). Action Potential of the Motorneuron. IBM J. Res. Dev. 17, 219–229. doi:10.1147/rd.173.0219
Dokos S., Celler B., Lovell N. (1996). Ion Currents Underlying Sinoatrial Node Pacemaker Activity: A New Single Cell Mathematical Model. J. Theor. Biol. 181, 245–272. doi:10.1006/jtbi.1996.0129
Dutta S., Chang K. C., Beattie K. A., Sheng J., Tran P. N., Wu W. W., et al. (2017). Optimization of an In Silico Cardiac Cell Model for Proarrhythmia Risk Assessment. Front. Physiol. 8, 616. doi:10.3389/fphys.2017.00616
Endresen L. P., Hall K., Høye J. S., Myrheim J. (2000). A Theory for the Membrane Potential of Living Cells. Eur. Biophys. J. 29, 90–103. doi:10.1007/s002490050254
Fry C. H., Ward J. P. T., Twist V. W., Powell T. (1986). Determination of Intracellular Potassium Ion Concentration in Isolated Rat Ventricular Myocytes. Biochem. Biophysical Res. Commun. 137, 573–578. doi:10.1016/0006-291X(86)91249-0
Grandi E., Pasqualini F. S., Bers D. M. (2010). A Novel Computational Model of the Human Ventricular Action Potential and Ca Transient. J. Mol. Cell Cardiol. 48, 112–121. doi:10.1016/j.yjmcc.2009.09.019
Groenendaal W., Ortega F. A., Kherlopian A. R., Zygmunt A. C., Krogh-Madsen T., Christini D. J. (2015). Cell-Specific Cardiac Electrophysiology Models. Plos Comput. Biol. 11, e1004242. doi:10.1371/journal.pcbi.1004242
Guan S., Lu Q., Huang K. (1997). A Discussion about the DiFrancesco-Noble Model. J. Theor. Biol. 189, 27–32. doi:10.1006/jtbi.1997.0486
Hansen N., Müller S. D., Koumoutsakos P. (2003). Reducing the Time Complexity of the Derandomized Evolution Strategy with Covariance Matrix Adaptation (CMA-ES). Evol. Comput. 11, 1–18. doi:10.1162/106365603321828970
Hilgemann D., Noble D. (1987). Excitation-Contraction Coupling and Extracellular Calcium Transients in Rabbit Atrium: Reconstruction of Basic Cellular Mechanisms. Proc. R. Soc. Lond. B. 230, 163–205. doi:10.1098/rspb.1987.0015
Hindmarsh A. C., Brown P. N., Grant K. E., Lee S. L., Serban R., Shumaker D. E., et al. (2005). SUNDIALS: Suite of Nonlinear and Differential/Algebraic Equation Solvers. ACM Trans. Math. Softw. 31, 363–396. doi:10.1145/1089014.1089020
Hodgkin A. L., Huxley A. F. (1952). A Quantitative Description of Membrane Current and its Application to Conduction and Excitation in Nerve. J. Physiol. 117, 500–544. doi:10.1113/jphysiol.1952.sp004764
Hund T. J., Kucera J. P., Otani N. F., Rudy Y. (2001). Ionic Charge Conservation and Long-Term Steady State in the Luo-Rudy Dynamic Cell Model. Biophysical J. 81, 3324–3331. doi:10.1016/S0006-3495(01)75965-6
Hund T. J., Rudy Y. (2004). Rate Dependence and Regulation of Action Potential and Calcium Transient in a Canine Cardiac Ventricular Cell Model. Circulation 110, 3168–3174. doi:10.1161/01.CIR.0000147231.69595.D3
Iyer V., Mazhari R., Winslow R. L. (2004). A Computational Model of the Human Left-Ventricular Epicardial Myocyte. Biophysical J. 87, 1507–1525. doi:10.1529/biophysj.104.043299
Jacquemet V. (2007). Steady-State Solutions in Mathematical Models of Atrial Cell Electrophysiology and Their Stability. Math. Biosciences 208, 241–269. doi:10.1016/j.mbs.2006.10.007
Johnstone R. H., Chang E. T. Y., Bardenet R., De Boer T. P., Gavaghan D. J., Pathmanathan P., et al. (2016). Uncertainty and Variability in Models of the Cardiac Action Potential: Can We Build Trustworthy Models? J. Mol. Cell Cardiol. 96, 49–62. doi:10.1016/j.yjmcc.2015.11.018
Lindblad D. S., Murphey C. R., Clark J. W., Giles W. R. (1996). A Model of the Action Potential and Underlying Membrane Currents in a Rabbit Atrial Cell. Am. J. Physiology-Heart Circulatory Physiol. 271, H1666–H1696. doi:10.1152/ajpheart.1996.271.4.H1666
Livshitz L., Rudy Y. (2009). Uniqueness and Stability of Action Potential Models during Rest, Pacing, and Conduction Using Problem-Solving Environment. Biophysical J. 97, 1265–1276. doi:10.1016/j.bpj.2009.05.062
Lovell N. H., Cloherty S. L., Celler B. G., Dokos S. (2004). A Gradient Model of Cardiac Pacemaker Myocytes. Prog. Biophys. Mol. Biol. 85, 301–323. doi:10.1016/j.pbiomolbio.2003.12.001
Luo C. H., Rudy Y. (1994). A Dynamic Model of the Cardiac Ventricular Action Potential. I. Simulations of Ionic Currents and Concentration Changes. Circ. Res. 74, 1071–1096. doi:10.1161/01.RES.74.6.1071
McAllister R. E., Noble D., Tsien R. W. (1975). Reconstruction of the Electrical Activity of Cardiac Purkinje Fibres. J. Physiol. 251, 1–59. doi:10.1113/jphysiol.1975.sp011080
Noble D. (1962). A Modification of the Hodgkin-Huxley Equations Applicable to Purkinje Fibre Action and Pacemaker Potentials. J. Physiol. 160, 317–352. doi:10.1113/jphysiol.1962.sp006849
Noble D., Noble S. J., Bett G. C. L., Earm Y. E., Ho W. K., So I. K. (1991). The Role of Sodium - Calcium Exchange during the Cardiac Action Potential. Ann. NY Acad. Sci. 639, 334–353. doi:10.1111/j.1749-6632.1991.tb17323.x
Nygren A., Fiset C., Firek L., Clark J. W., Lindblad D. S., Clark R. B., et al. (1998). Mathematical Model of an Adult Human Atrial Cell: the Role of K+ Currents in Repolarization. Circ. Res. 82, 63–81. doi:10.1161/01.RES.82.1.63
O'Hara T., Virág L., Varró A., Rudy Y. (2011). Simulation of the Undiseased Human Cardiac Ventricular Action Potential: Model Formulation and Experimental Validation. Plos Comput. Biol. 7, e1002061. doi:10.1371/journal.pcbi.1002061
Pan M., Gawthrop P. J., Tran K., Cursons J., Crampin E. J. (2018). Bond Graph Modelling of the Cardiac Action Potential: Implications for Drift and Non-Unique Steady States. Proc. R. Soc. A. 474, 20180106. doi:10.1098/rspa.2018.0106
Pohl A., Wachter A., Hatam N., Leonhardt S. (2016). A Computational Model of a Human Single Sinoatrial Node Cell. Biomed. Phys. Eng. Express 2, 035006. doi:10.1088/2057-1976/2/3/035006
Qu Z. (2011). Chaos in the Genesis and Maintenance of Cardiac Arrhythmias. Prog. Biophys. Mol. Biol. 105, 247–257. doi:10.1016/j.pbiomolbio.2010.11.001
Smirnov D., Pikunov A., Syunyaev R., Deviatiiarov R., Gusev O., Aras K., et al. (2020). Genetic Algorithm-Based Personalized Models of Human Cardiac Action Potential. PLoS ONE 15, e0231695. doi:10.1371/journal.pone.0231695
Stewart P., Aslanidi O. V., Noble D., Noble P. J., Boyett M. R., Zhang H. (2009). Mathematical Models of the Electrical Action Potential of Purkinje Fibre Cells. Phil. Trans. R. Soc. A. 367, 2225–2255. doi:10.1098/rsta.2008.0283
Surovyatkina E., Noble D., Gavaghan D., Sher A. (2010). Multistability Property in Cardiac Ionic Models of Mammalian and Human Ventricular Cells. Prog. Biophys. Mol. Biol. 103, 131–141. doi:10.1016/j.pbiomolbio.2010.01.004
Ten Tusscher K. H. W. J., Noble D., Noble P. J., Panfilov A. V. (2004). A Model for Human Ventricular Tissue. Am. J. Physiology-Heart Circulatory Physiol. 286, H1573–H1589. doi:10.1152/ajpheart.00794.2003
Ten Tusscher K. H. W. J., Panfilov A. V. (2006). Alternans and Spiral Breakup in a Human Ventricular Tissue Model. Am. J. Physiology-Heart Circulatory Physiol. 291, H1088–H1100. doi:10.1152/ajpheart.00109.2006
Tomek J., Bueno-Orovio A., Rodriguez B. (2020). ToR-ORd-dynCl: An Update of the ToR-ORd Model of Human Ventricular Cardiomyocyte with Dynamic Intracellular Chloride. BioRxiv. doi:10.1101/2020.06.01.127043
Trovato C., Passini E., Nagy N., Varró A., Abi-Gerges N., Severi S., et al. (2020). Human Purkinje In Silico Model Enables Mechanistic Investigations into Automaticity and Pro-Arrhythmic Abnormalities. J. Mol. Cell Cardiol. 142, 24–38. doi:10.1016/j.yjmcc.2020.04.001
Varghese A., Sell G. R. (1997). A Conservation Principle and its Effect on the Formulation of Na-Ca Exchanger Current in Cardiac Cells. J. Theor. Biol. 189, 33–40. doi:10.1006/jtbi.1997.0487
Whittaker D. G., Clerx M., Lei C. L., Christini D. J., Mirams G. R. (2020). Calibration of Ionic and Cellular Cardiac Electrophysiology Models. Wires Syst. Biol. Med. 12, e1482. doi:10.1002/wsbm.1482
Wilders R., Jongsma H. J., Van Ginneken A. C. (1991). Pacemaker Activity of the Rabbit Sinoatrial Node. A Comparison of Mathematical Models. Biophysical J. 60, 1202–1216. doi:10.1016/s0006-3495(91)82155-5
Keywords: action potential, electrophysiology, mathematical model, conservation of charge, parameter fitting, calibration
Citation: Barral Y-SHM, Shuttleworth JG, Clerx M, Whittaker DG, Wang K, Polonchuk L, Gavaghan DJ and Mirams GR (2022) A Parameter Representing Missing Charge Should Be Considered when Calibrating Action Potential Models. Front. Physiol. 13:879035. doi: 10.3389/fphys.2022.879035
Received: 18 February 2022; Accepted: 16 March 2022;
Published: 26 April 2022.
Edited by:
Gernot Plank, Medical University of Graz, AustriaReviewed by:
Richard A. Gray, United States Food and Drug Administration, United StatesSanjay Ram Kharche, Western University, Canada
Copyright © 2022 Barral, Shuttleworth, Clerx, Whittaker, Wang, Polonchuk, Gavaghan and Mirams. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Gary R. Mirams, Z2FyeS5taXJhbXNAbm90dGluZ2hhbS5hYy51aw==
 Yann-Stanislas H. M. Barral
Yann-Stanislas H. M. Barral Joseph G. Shuttleworth
Joseph G. Shuttleworth Michael Clerx
Michael Clerx Dominic G. Whittaker
Dominic G. Whittaker Ken Wang
Ken Wang Liudmila Polonchuk
Liudmila Polonchuk David J. Gavaghan
David J. Gavaghan Gary R. Mirams
Gary R. Mirams