Deriving Snow Depth From ICESat-2 Lidar Multiple Scattering Measurements

Introduction

Snowpack is one of the most important wintertime land-surface characteristics (Zeng et al., 2018), and it is one of the hardest features that can be accurately observed and quantified on a global scale (Robinson et al., 1993). Seasonal snow and glaciers provide water resources for over one billion people worldwide, and it is also important for weather, climate, and ecosystem functioning through a variety of different mechanisms (e.g., Vavrus 2007; Lawrence and Slater 2010; Betts et al., 2014; Broxton et al., 2017; Musselman et al., 2017). While satellite passive remote sensing has successfully measured the snow cover extent (Frei et al., 2012), its measurements of snow water equivalent (SWE) and snow depth are much more challenging (e.g., Dawson et al., 2018). For these reasons, the recent Earth Science Decadal Survey (National Academies of Sciences, 2018) recommended snow mass and depth among the seven targeted observables for the NASA Earth System Explorer satellite mission competitions.

While lidar altimetry has been used in airborne measurements of snow depth as the difference between the measured snow top and snow-free ground heights (Deems et al., 2013; Painter et al., 2016), its applicability in space-borne measurements is more challenging due to stringent ground track requirements. For snow over sea ice, while space-borne lidar measurements (e.g., ICESat-2; Markus et al., 2017) can provide the snow top height above sea water, the broad consensus is that space-borne radar measurements are needed for the retrieval of the actual snow depth over sea ice. For these reasons, most of the explorations of space-borne measurements of SWE and snow depth have focused on radar measurements (and its combination with other measurements) (e.g., Lemmetyinen et al., 2018; Oveisgharan et al., 2020; Derksen et al., 2021; Lievens et al., 2022).

The scientific and technological question is as follows: can space-borne lidar measure snow depth (and SWE) over land and over sea ice? If yes, the latter measurement in combination of the measurement of snow top over sea ice would also enable the global estimate of sea ice thickness, which is of substantial importance in the Earth system and national defense (e.g., Laxon et al., 2003; Kwok 2018).

The purpose of this study is to combine radiative transfer theory with Monte Carlo simulations to derive analytical relations of snow depth and optical properties directly from the space-borne lidar measurements of vertical backscatter profiles of snow. This would provide the theoretical foundation for space-borne lidar measurements of snow depth for the first time. We will address the robustness of our method by assessing the agreement among three derived relations and the convergence of the relations using a different approach. As a preliminary application, these relations are then used to retrieve snow depth over the Antarctic ice sheet and Arctic sea ice from ICESat-2 lidar measurements. The retrieval of SWE and comparison of SWE and snow depth with observations will be reported in separate articles.

Radiative Transfer Simulations of ICESat-2 Lidar Measurements

In this section, we will introduce the simple relationships among the average path length, snow depth, and diffuse scattering coefficient.

Inspired by biological studies of the spatial distributions of ant colonies (Theraulaz et al., 2002), an intriguing theory of photon diffusion suggests that for uniform illumination, the averaged traveling path length of photon diffusion, <L>, between the entry and exit of a diffusive, non-absorbing medium is equal to 4 V/S, with V and S being volume and surface area of any 3-dimensional diffusion medium, respectively (Blanco and Fournier, 2003). Such a relationship also applies to a hypothetical 2-dimensional random walk process as well if we replace V and S by the area and the circumference, respectively. It is also suggested that the mean free path (inverse of the diffuse scattering coefficient) is related to the higher-order moment of the path length distribution (Blanco and Fournier, 2006). The theory was proven true for diffusive radiative transfer with uniform light incidence from the entire boundary of the scattering medium. The question is as follows: Will this simple theory also be true when the snow is illuminated by a laser while observation is made by measuring the near-nadir viewing backscatter of snow using a receiver with its footprint on the ground thousands of times larger than the mean free path to cover most multiple scattering events?

At 532 nm, pure snow is a weakly absorbing, diffusive scattering medium. Photons bounce inside the snow many times before exiting the snow. Thus, the high vertical resolution measurements from the ICESat-2 mission (Markus et al., 2017) provide a great opportunity to quantify the path distributions of photons traveling inside snow. Path length distributions can provide important physical information about snow because the average path length (first moment of the path length distribution) and low-order moments of the path length distribution can be linked to snow depth and mean free path of scattering. This study intends to address the following questions: 1) Does the relationship between snow depth (H, which equals half of 4 V/S when the surface area is far greater than H²) and the average path length <L> hold for pencil beam point source lidar measurements as it does for uniform incidence? 2) What are the relationships among the higher moments (<L²>, <L³>) of the path length distribution, snow depth, and diffuse scattering mean free path f (1/scattering coefficient k_d)?

Here, we try to answer the aforementioned equations through radiative transfer simulations and introduce an algorithm to derive snow depth directly from space lidar measurements of the scattering path length distributions. For the first time, snow depths are estimated directly from lidar measurements of vertical backscatter profiles of snow. These snow depth estimates are different from the existing laser altimetry measurements (Deems et al., 2013), such as the two-survey methods, from which snow depths are estimated from the difference of snow top heights measured by lidar and the known height of the land surfaces below the snow.

Monte Carlo Simulations

The backscatter path length is the distance a photon has traveled inside the snow. It starts when a photon enters the snow and ends when the same photon exits the snow in the backward direction. In this subsection, we use Monte Carlo simulations to evaluate the validity of <L> = 2H, <L²>/k_sd = H³, <L³>/k_sd² = H⁵ (where k_sd is the diffuse scattering coefficient) and briefly introduce the snow depth retrieval algorithms.

Specifically, we will develop 1) a simple Monte Carlo simulation model to calculate the backscatter path length distribution p(L); 2) evaluate the relationship between average path length <L> (= $\underset{0}{\overset{\infty }{{\displaystyle \int }}}Lp\left(L\right)dL$) and snow depth, and 3) evaluate the relationship among second and third moments of the path length distribution < L²> = $\underset{0}{\overset{\infty }{{\displaystyle \int }}}{L}^{2}p\left(L\right)dL$, <L³> = $\underset{0}{\overset{\infty }{{\displaystyle \int }}}{L}^{3}p\left(L\right)dL$, mean free path f (f = 1/k_sd), and snow depth H.

The Monte Carlo simulation code we developed for this study is based on a semi-analytic Monte Carlo method that is similar to the lidar radiative transfer model developed for CALIPSO cloud measurements (Hu et al., 2001). Polarization is removed from the model to reduce computational time. The Monte Carlo code uses random walk processes to mimic photon pulses (hereafter referred to as photons for short) propagating in a turbid medium. The characteristics of photons include location (x,y,z) and direction of propagation ($\mu =\cos \theta ,\varphi$), where $\theta$ and $\varphi$ are the zenith and azimuth angles of the direction, respectively, and a variable L denoting its travel distance. The Monte Carlo code repeats the following steps for each photon until it exits the snow layer in the backward direction and enters the receiver field-of-view:

1) Finding the distance D, the photon will travel before it interacts with a snow particle; $D=f\ast log\left(\zeta \right)$, where $\zeta$ is a random number with uniform distribution between 0 and 1;

2) Estimating the new location of scattering interaction (x,y,z) from the old location and traveling direction and adding D to the photon traveling length L₀;

3) Estimating the probability of the photon scattered directly to the lidar receiver and adding that probability to the backscatter path length distribution while registering the altitude as L′ = L₀ + z;

4) Calculating the new traveling direction ($\mu =\cos \theta ,\varphi$) of the photon that will follow the statistics of the scattering phase function through random number generation and coordinate transformation.

We can choose between two types of surfaces below the snow: a) a sea-ice type of surface with specular reflectance following Fresnel’s theory; b) land surfaces with Lambertian reflectance. Each Monte Carlo calculation will take about 10 million photons to generate the backscatter path length distribution p(L). We can also calculate the attenuated backscatter profile $\beta \left(z\right)$ of lidar measurements by adding absorption to the path length distribution:$\beta \left(z\right)=p\left(L=2z\right)\text{exp}(-k_{a}L)dL$, where $k_a$ is the absorption coefficient of snow.

Figure 1 shows the simulated absorption-free snow backscatter profiles for 1) isotropic scattering (blue line) and for a diffuse scattering coefficient $k_{sd}=k_s=\frac{1}{f}$ = 200 m⁻¹; 2) anisotropic scattering with a Henyey–Greenstein phase function (g = 0.7, green line) (Henyey and Greenstein, 1941), and with a diffuse scattering coefficient of $k_{sd}=\left(1-g\right)k_s=\frac{1}{f}$ = 200 m⁻¹; 3) anisotropic scattering with a Henyey–Greenstein phase function (g = 0.88, red line) and diffuse scattering coefficient of 200 m⁻¹. Here, k_s is the scattering coefficient, $P\left(\text{Θ}\right)$ is single-scattering phase function, Θ is the scattering angle between incident light and scattered light, and g is the asymmetry factor, $g=\underset{-1}{\overset{1}{{\displaystyle \int }}}P\left(\text{Θ}\right)cos\text{ΘdcosΘ}$. The lidar backscatter profiles from the aforementioned three different types of scattering phase functions align very well, which suggests that backscatter path length distributions are insensitive to the details of the single-scattering phase functions as long as the diffuse scattering coefficients $k_{sd}=\left(1-g\right)\ast k_s$ are the same. This is in agreement with the general invariance property of diffusive random walks, supporting that the general theory applies to ICESat-2.

FIGURE 1

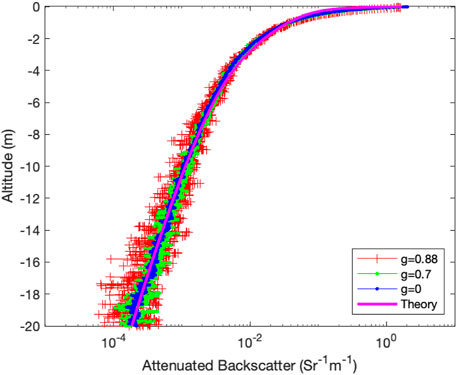
FIGURE 1. Monte Carlo simulation results of the lidar backscatter profile for isotropic (blue line) and anisotropic scattering with Henyey–Greenstein phase function (green: g = 0.7; red: g = 0.88) for snow depth 1 m and the same effective scattering coefficient k_sd = (1-g)k_s.

For snow, the mean free path of diffuse scattering is normally on the order of subcentimeter (Kokhanovsky and Zege, 2004). Thus, the diffuse scattering coefficient k_sd is of the order of a few hundreds per meter. For snow depth H greater than 10 cm, the diffuse scattering optical depth is far greater than 4 ($k_{sd}H\gg 4$). We can fit the lidar backscatter path length distribution using a simple Γ distribution (magenta line in Figure 1),

$p\left(L\right)=\frac{{\left[2H(\frac{k_{sd}H}{4}-1)\right]}^{-{(\frac{k_{sd}H}{4}-1)}^{-1}}}{\text{Γ}\left({(\frac{k_{sd}H}{4}-1)}^{-1}\right)}{L}^{{(\frac{k_{sd}H}{4}-1)}^{-1}-1}\exp \left[-\frac{L}{2H\left(\frac{k_{sd}H}{4}-1\right)}\right]=\text{Γ}\left(L,\alpha ,\beta \right)=\frac{{\beta }^{\alpha }}{\text{Γ}\left(\alpha \right)}{L}^{\alpha -1}\text{exp}(-\beta L) .(1)$

Here, $\alpha ={(\frac{k_{sd}H}{4}-1)}^{-1}$; $\beta ={\left[2H\left(\frac{k_{sd}H}{4}-1\right)\right]}^{-1}.$ Both α and β are far less than 1.

Monte Carlo simulations suggest that for snow with a variety of optical properties such as single-scattering phase functions and scattering coefficients, the average path length of the path length distribution is twice that of snow depth H (Figure 2A)

$<L> =\alpha /\beta =2H,(2)$

and the second moment of the path length distribution, <L²>, is (Figure 2B),

$<L^2> =\frac{\alpha \left(\alpha +1\right)}{{\beta }^2}=k_{sd}{H}^3.(3)$

Thus, scattering optical depth of the snow can be estimated from the higher moments of the path length distribution: ${\tau }_s=k_{sd}H= \frac{<L^2>}{H^2}=4 \frac{<L^2>}{<L{>}^2}$. It is also possible to estimate the diffuse scattering coefficient k_sd, or equivalently the transport mean free path f/(1-g) = 1/k_sd, using the first and second moments <L> and <L²> of the path length distribution.

${\tau }_s=k_{sd}H= \frac{<L^2>}{H^2}=4 \frac{<L^2>}{<L{>}^2}, \frac{1-g}{f}=k_{sd}=8\frac{<L^2>}{<L{>}^3}.(4)$

The Monte Carlo simulation also suggests that the third-order moment of the path length distribution is a simple function of diffuse scattering coefficient and snow depth (Figure 2C),

$<L^3> =\frac{\alpha \left(\alpha +1\right)\left(\alpha +2\right)}{{\beta }^3}\approx k_{sd}^2{H}^5 .(5)$

Thus, snow depth can be derived from all three lower order moments, respectively, In addition, we also found that $<L^N> =k_{sd}^{N-1}{H}^{2N-1}$ for all positive integers N that is greater than 1.

FIGURE 2

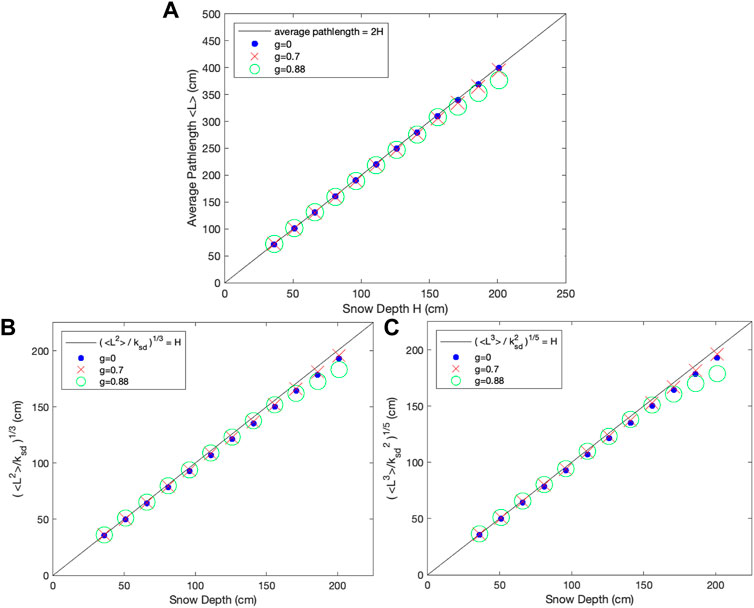
FIGURE 2. (A): Monte Carlo simulation results of the relationship between snow depth H and average backscatter path length <L> for various scattering phase functions and snow depths; (B): Monte Carlo simulation results of the relationship between H and [$<{\mathit{L}}^2>/{\mathit{k}}_{\mathit{d}}{]}^{1/3}$, or [$<{\mathit{L}}^2>\mathit{*f}{]}^{1/3}$; (C): the relationship between H and [$<{\mathit{L}}^3>/{\mathit{k}}_{\mathit{d}}^{\mathit{2}}{]}^{1/5}$ or [$<{\mathit{L}}^3>\mathit{*}{\mathit{f}}^2{]}^{1/5}$. Here, < L²> and <L³> are the second and third moments of the path length distribution, respectively; k_d is the effective scattering coefficient; and f is the mean free path.

Monte Carlo simulations using various combinations of snow depth H and diffusive scattering coefficient k_sd suggest that the multiple scatter signals measured by a space-based lidar, such as ICESat-2, always follow Γ-distribution p(L) = Γ(L,α,β), which is the distribution of maximum entropy $\underset{0}{\overset{\infty }{{\displaystyle \int }}}p\left(L\right)\text{ln}\left[p\left(L\right)\right]dL$ under the constraints of fixed <L> and fixed < ln(L)>: $<L>=\frac{\alpha }{\beta }=2H$, and $<\ln \left(L\right)>\approx <{\displaystyle \sum }_N{c}_N{L}^N>=f\left(k_{sd}\right)=\frac{dln\left[\text{Γ}\left(\alpha \right)\right]}{d\alpha }-\frac{dln\left[\text{Γ}\left(\beta \right)\right]}{d\beta }=\text{ψ}\left(\alpha \right)-\text{ψ}\left(\beta \right)$. Here, $\text{ψ}\left(x\right)$ is the so-called digamma function.

A Different Theoretical Explanation of <L> = 2H

To better understand the analytical results in Section 2.1, here, we use a different theoretical explanation of the average path length <L> and snow depth H relationship <L> = 2H using the weak absorption limit simulations from both Monte Carlo and DISORT (DIScrete Ordinate Radiative Transfer) (Stamnes et al., 1988) calculations, a general and versatile plane-parallel radiative transfer program.

When the absorption coefficient (k_a) approaches zero, the total absorption of the snow layer, A, will reduce the integrated backscatter of a non-absorbing medium by <L>*k_a,

$A\left(k_a\to 0\right)=1-\frac{R\left(k_a\right)}{R\left(k_a=0\right)}=\underset{0}{\overset{\infty }{{\displaystyle \int }}}p\left(L\right)(1-e^{-k_{a}L})dL \approx \underset{0}{\overset{\infty }{{\displaystyle \int }}}p\left(L\right)k_{a}LdL= <L>k_a,(6)$

where R (ka = 0) is the reflectance for a non-absorbing medium.

Both the Monte Carlo simulations (Figure 3A) and DISORT (DIScrete Ordinate Radiative Transfer) calculations (Figure 3B) suggest that

$A\left(k_a\to 0\right)=1-\frac{R\left(k_a\right)}{R\left(k_a=0\right)}\approx 2\ast \left(1-\omega \right)\tau =2\ast k_a\ast H.(7)$

Here, ω is single-scattering albedo and τ is total optical depth of snow. 1- ω is the fraction of absorption and (1-ω)*τ is the absorption optical depth, which equals k_a*H. From Eqs, 6,7, we can conclude that $<L>k_a= 2\ast k_a\ast H$. Thus, $<L>= 2H$.

FIGURE 3

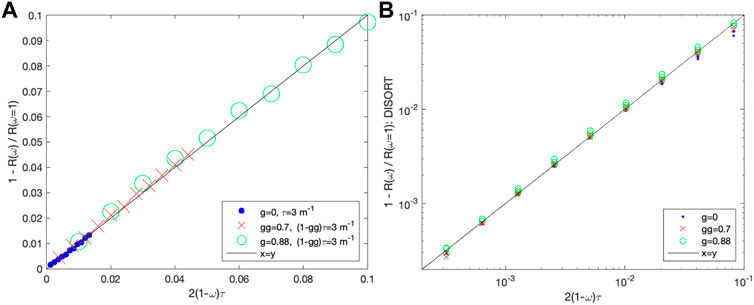
FIGURE 3. Monte Carlo simulations (A) and DISORT (B) suggest that when the absorption coefficient approaches zero, snow absorption $\mathit{A}\left({\mathit{k}}_{\mathit{a}}\to 0\right)$ equals 2*(1-ω)τ = 2*k_a*H. As $\mathit{A}\left({\mathit{k}}_{\mathit{a}}\to 0\right)\mathit{ }$ also equals <L> k_a. Thus, <L> = 2H.

An Iterative Procedure to Derive Snow Depth from ICESat-2 Measurements

With the theoretical development in Section 2.1 and Section 2.2, we will use the following iterative procedure to derive snow depth and snow albedo, snow grain size, absorption coefficient, and the diffuse scattering coefficient estimates:

1) The ICESat-2 attenuated backscatter profile of snow, β(z), is improved with a correction of instrument transient response: de-convolution of the ICESat-2 snow backscatter profile using the instrument transient response (Lu at al., 2021);

2) An initial guess of the snow absorption coefficient k_a (e.g., k_a = 0.07 m⁻¹) is made;

3) The absorption-free, snow backscattering path length distribution, p(L), is estimated by removing the impact of absorption from the ICESat-2 attenuated backscatter profile of snow: p (L = 2z) = β(L)exp (k_aL); and snow albedo a is derived: $a=\frac{{{\displaystyle \int }}_0^{\infty }\beta \left(L\right)dL}{{{\displaystyle \int }}_0^{\infty }P\left(L\right)dL}$;

4) Snow depth H from path length distribution is derived: $H=\frac{L}{2}=\underset{0}{\overset{\infty }{{\displaystyle \int }}}Lp\left(L\right)dL$;

5) The diffuse scattering coefficient $k_{sd}=\frac{<L^2>}{{(<L>/2)}^3}$is derived;

6) Snow particle grain size R and diffuse flux attenuation coefficient, k_d, are derived using the empirical relationship between snow albedo a and absorption coefficient k_a (Bohren and Barkstrom, 1974; Warren, 1982): $R=\frac{1}{k_a}{\left(\frac{1-a}{8.43}\right)}^2, k_d=0.65{(k_a/R)}^{1/2}$. The diffuse flux attenuation coefficient k_d is a function of diffuse scattering coefficient k_sd and absorption coefficient: $k_d=\sqrt{3k_a(k_{sd}+k_a)}\approx \sqrt{3k_a{k}_{sd}}$;

7) A new absorption coefficient, $k_a^{\prime },$ is derived using the diffuse scattering coefficient k_sd of step 5 and diffuse flux attenuation coefficient k_d of step 6: $k_a\prime =\frac{{\left(k_d\right)}^2}{3(k_{sd}+k_a)}\approx \frac{{\left(k_d\right)}^2}{3k_{sd}}$;

8) If abs (k_a′-k_a) > 0.001, k_a is replaced by k_a′ and procedures 3–7 are repeated until $k_a\prime =k_a$.

Preliminary Data Analysis Results Using ICESat-2 Measurements

To derive the backscatter path length distribution from the nighttime measurements of ICESat-2 photon heights (ATL03, version 5, Neumann et al., 2019), we need to correct for lidar receiver transient response and absorption by snow. Lidar receiver optic components and laser pulse shape can affect the ICESat-2 snow backscatter profile measurements. The results here are from the strong beam measurements of ICESat-2. To derive snow backscatter path length distribution, the lidar backscatter profile is corrected through a deconvolution using the lidar receiver transient response derived from ICESat-2 measurements of flat, hard targets (Lu et al., 2021).

After de-convolution, the attenuated lidar backscatter profile β(z = L/2), scaled by the snow layer–integrated attenuated backscatter, equals path length distribution p(L) reduced by absorption,

$p\left(L=2z\right)e^{-k_{a}L}=\beta \left(z\right)/\underset{0}{\overset{\infty }{{\displaystyle \int }}}\beta \left(z\right)dz.(8)$

p(L) is insensitive to radiometric calibration and atmospheric attenuation. We are testing a couple of algorithms for estimating the absorption coefficient (k_a) from the lidar measurements. For introduction, we first assume the 532-nm absorption coefficient around 0.07 m⁻¹ as a first guess for relatively weakly contaminated snow in the Arctic in springtime (Warren et al., 2006). Thus, snow backscatter path length distribution can be derived from the deconvoluted ICESat-2 snow measurements,

$p\left(L\right)=\beta (z=\frac{L}{2})e^{k_{a}L}/\underset{0}{\overset{\infty }{{\displaystyle \int }}}\beta \left(z\right)dz.(9)$

$<L^n>=\underset{0}{\overset{\infty }{{\displaystyle \int }}}{\left(2z\right)}^n\beta \left(z\right)e^{2k_{a}z}dz/\underset{0}{\overset{\infty }{{\displaystyle \int }}}\beta \left(z\right)dz\left(n=\mathrm{1,2,3},\dots \right).(10)$

Figure 4A shows the ICESat-2 snow measurements near the South Pole after correcting for the detector transient response with deconvolution. Snow depths over Antarctica derived from the three methods, <L>/2, (<L²>/k_sd)^1/3, and (<L³>/k²_sd)^1/5 (Figure 4B) agree reasonably well.

FIGURE 4

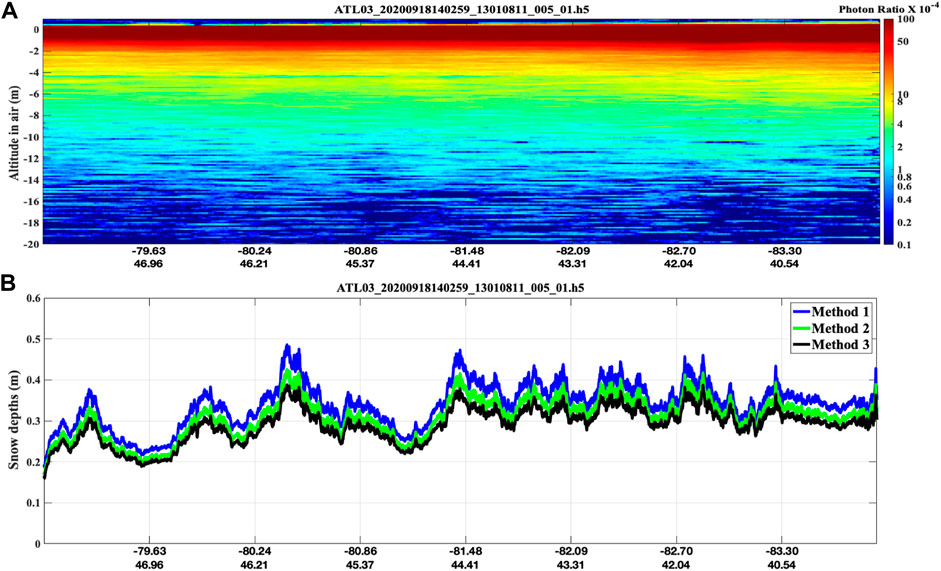
FIGURE 4. (A): ICESat-2 snow backscatter signal (Antarctica); (B): snow depth derived from the snow multiple scatter signal (blue: mean path length method: H=<L>/2; green: <L²> and diffuse scattering coefficient method: H = (<L²>/k_sd)^1/3; Black: <L³> and diffuse scattering coefficient method: H = (<L³>/k_sd²)^1/5.

Figure 5A is similar to Figure 4A, but from ICESat-2 measurements of snow above first-year sea-ice in the Arctic. The snow depths derived from the multiple scattering photon path length distribution [Figure 5B. Method 1: <L>/2; Method 2 (<L²>/k_sd)^1/3; Method 3: [<L³>*k_sd²]^1/5;) also show reasonable agreement of ICESat-2 freeboard measurements (altitude difference between sea water and snow top). The freeboard is defined as the total height of the snow cover and sea ice above the ocean. If proven, this technique will enable accurate lidar measurements of both freeboard and snow depth, and thus estimates of sea-ice depth directly without having to rely on radars to provide altitude of the snow/sea-ice interface. The purple data points of Figure 5 are snow depths from collocated AMSR-2 snow depth data product (Rostosky et al., 2018). The spatial resolution of the AMSR-2 snow depth data product is 25 km.

FIGURE 5

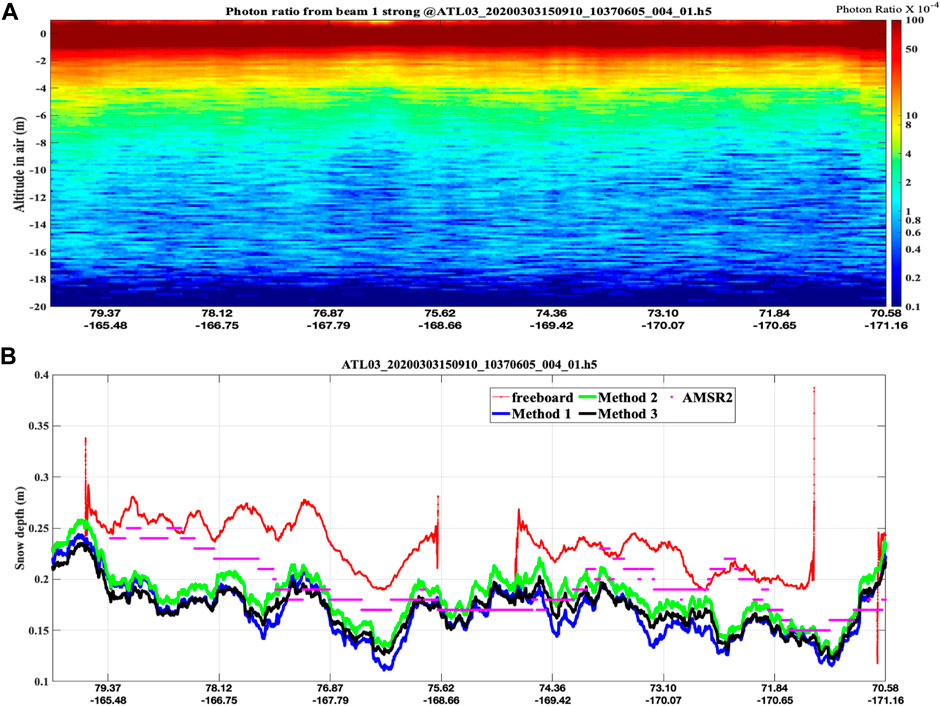
FIGURE 5. (A): ICESat-2 snow backscatter signal (Arctic, north of Chukchi Sea); (B): snow depth (blue, green, and black), AMSR-2 snow depth (purple) and freeboard data (red).

Snow grain size (blue line in Figure 6A), diffuse flux attenuation coefficient k_d (blue line in Figure 6B), and snow albedo (red lines in Figure 6) are estimated from the multiple scattering signal of the Arctic ICESat-2 flight as in Figure 5 and theoretical radiative transfer, as discussed in the previous section. The estimated diffuse flux attenuation coefficients are consistent with diffuse attenuation obtained from in situ measurements (e.g., Schwerdtfeger and Weller, 1977).

FIGURE 6

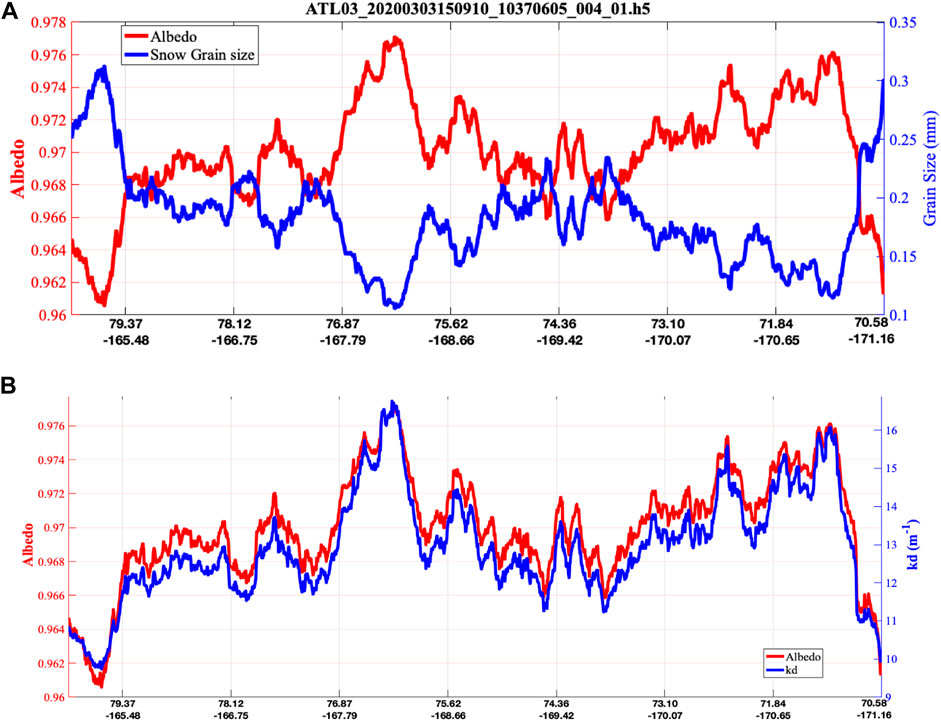
FIGURE 6. (A): Albedo distribution (red line) and snow grain size (radius, blue line) derived from the backscatter path length distribution. (B): snow albedo (red line) and diffuse flux attenuation coefficient k_d (blue line) estimated from the 532-nm lidar backscatter measurements. ${\mathit{k}}_{\mathit{d}}=\sqrt{\mathbf{3}{\mathit{k}}_{\mathit{a}}({\mathit{k}}_{\mathit{sd}}+{\mathit{k}}_{\mathit{a}})}$.

For snow thicker than 1 m, model simulations suggest that multiple scattering path lengths can last a hundred meters or more. Due to limited satellite downlink bandwidth and the finite number of detected photons, ICESat-2 does not send down all the snow multiple scattering signals. As a result, the long tail parts of the multiple scattering path lengths are truncated, and the amount of photons reaching the deeper part of the snow is under-estimated. We are assessing its impact on snow depth retrievals and testing different extrapolation methods using simulated data.

This technique retrieves the depths of snow layers comprising diffusively scattering snow particulates with large scattering coefficients and small single-scattering co-albedos (absorption coefficient/scattering coefficient) (Räisänen et al., 2015) at the 532-nm laser wavelength. More studies are needed to examine the sensitivity of the technique to lower layers of multiyear snow with reduced scattering coefficients due to melting, infiltration of rainwater, and retention of snowmelt (Boone and Etchevers, 2001). More theoretical studies and field measurements concerning ice sheets are needed to examine if the snow depth we derived here is the depths of first-year snow only.

Summary

Previous studies (Blanco and Fournier, 2003, 2006) suggested that when shining light uniformly from all angles into the entire surface of a given 3D diffusive scattering medium, the average path length between a photon entering and exiting the medium is equal to <L> = 4V/S. Here, V is the volume and S is the surface area of the medium. Inspired by these elegant results, we have addressed the relevant question for the snow depth estimate from ICESat-2 lidar measurements: Is it possible that the theory is also true when we illuminate snow from a space-based laser at a wavelength with relatively weak absorption and with receiver footprint diameter hundreds of times larger than the mean free path?

To answer this question, a Monte Carlo lidar radiative transfer model is developed for simulating ICESat-2 measurements of laser light propagation in snow. For normal incidence, the model results confirmed the theory predicting that 1) the average snow backscattering path length <L> = 4V/S derived from the ICESat-2 measurements equaled two times the snow depth H; 2) the diffuse scattering mean free path (1/k_sd) times the second moment of the path length distribution; <L²> equals the third power of snow depth (H³); (3) $<L^3> =k_{sd}^2{H}^5$. In addition, we also found that $<L^N> =k_{sd}^{N-1}{H}^{2N-1}$ for all positive integers N, when N is greater than 1. The simple relationships between snow depths and lower-order moments of the scattering path length distributions are valid for scattering media with different single-scattering properties such as scattering phase functions and scattering cross sections.

The path length distribution follows a simple Γ (L, α, β) distribution function and $\text{Γ}(\text{L},\text{α},\text{β})=\frac{{\beta }^{\alpha }}{\text{Γ}\left(\alpha \right)}{L}^{\alpha -1}\text{exp}(-\beta L)$, where $\alpha ={\left[\frac{k_{sd}H}{4}-1\right]}^{-1}$ and $\beta ={\left[2H(\frac{k_{sd}H}{4}-1)\right]}^{-1}.$ For a fixed snow depth (H) and diffuse scattering coefficient (k_sd), both <L> and <ln(L)> are fixed as well. The multiple scattering photon path length distribution p(L) maximizes entropy $\underset{0}{\overset{L}{{\displaystyle \int }}}p\left(L\right)\ln \left[p\left(L\right)\right]dL$ for fixed <L> and <ln(L)>.

For snow depth greater than a few centimeters, $\frac{k_{sd}H}{4}\gg 1$; thus, $\alpha ={\left[\frac{k_{sd}H}{4}-1\right]}^{-1}\approx \frac{4}{k_{sd}H}\ll 1$ and $\beta ={\left[2H(\frac{k_{sd}H}{4}-1)\right]}^{-1}\approx \frac{2}{k_{sd}{H}^2}.$ The long tail of the $\text{Γ}(L,\alpha ,\beta )$ distribution approaches $\frac{c}{L}{e}^{-\frac{2L}{k_{sd}{H}^2}}$, where c is a constant, which is useful in assessing the consistency of the deeper part of the lidar profiles.

Initial ICESat-2 data analysis suggests that snow depth can be derived from the average diffuse scattering path length derived from the ICESat-2 lidar measurements. More studies in retrieval algorithm improvements and validations are needed to mature the new retrieval concept. For example, we are working on improving solar background removal algorithms to reduce uncertainties in daytime snow depth retrievals. We are also working on robust along-track averaging algorithms to reduce snow depth retrieval uncertainties associated with snow surface roughness and various sampling errors.

This snow depth retrieval technique may open a new path for future remote sensing of snow globally.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

YH initiated the theoretical concept and conducted Monte Carlo modeling studies. XL provided ICESAT-2 data analysis under TN and NK guidance. XZ is the science advisor of the research. SS and KS provided DISORT modeling analysis. CW and all co-authors contributed various ideas during discussions.

Conflict of Interest

Authors CW and JL were employed by Ball Aerospace Corp.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors wish to thank the NASA ICESat-2 program, NASA Remote Sensing Theory program, and NASA ESTO’s IIP program for supporting this research. The ICESat-2 ATL03 data used in this study are available at the National Snow and Ice Data Center: https://nsidc.org/data/ATL03/versions/5.

References

Betts, A. K., Desjardins, R., Worth, D., Wang, S., and Li, J. (2014). Coupling of winter Climate Transitions to Snow and Clouds over the Prairies. J. Geophys. Res. Atmos. 119, 1118–1139. doi:10.1002/2013jd021168

CrossRef Full Text | Google Scholar

Blanco, S., and Fournier, R. (2003). An Invariance Property of Diffusive Random Walks. Europhys. Lett. 61 (2), 168–173. doi:10.1209/epl/i2003-00208-x

CrossRef Full Text | Google Scholar

Blanco, S., and Fournier, R. (2006). Short-path Statistics and the Diffusion Approximation. Phys. Rev. Lett. 97 (23), 230604. doi:10.1103/physrevlett.97.230604

PubMed Abstract | CrossRef Full Text | Google Scholar

Bohren, C. F., and Barkstrom, B. R. (1974). Theory of the Optical Properties of Snow. J. Geophys. Res. 79 (30), 4527–4535. doi:10.1029/jc079i030p04527

CrossRef Full Text | Google Scholar

Boone, A., and Etchevers, P. (2001). An Intercomparison of Three Snow Schemes of Varying Complexity Coupled to the Same Land Surface Model: Local-Scale Evaluation at an Alpine Site. J. Hydrometeor 2 (4), 374–394. doi:10.1175/1525-7541(2001)002<0374:aiotss>2.0.co;2

CrossRef Full Text | Google Scholar

Broxton, P. D., Zeng, X., and Dawson, N. (2017). The Impact of a Low Bias in Snow Water Equivalent Initialization on CFS Seasonal Forecasts. J. Clim. 30, 8657–8671. doi:10.1175/jcli-d-17-0072.1

CrossRef Full Text | Google Scholar

Dawson, N., Broxton, P., and Zeng, X. (2018). Evaluation of Remotely Sensed Snow Water Equivalent and Snow Cover Extent over the Contiguous United States. J. Hydrometeor. 19, 1777–1791. doi:10.1175/jhm-d-18-0007.1

CrossRef Full Text | Google Scholar

Deems, J. S., Painter, T. H., and Finnegan, D. C. (2013). Lidar Measurement of Snow Depth: A Review. J. Glaciol. 59 (215), 467–479. doi:10.3189/2013JoG12J154

CrossRef Full Text | Google Scholar

Derksen, C. H., Belair, S., Garnaud, C., Vionnet, V., Fortin, V., Lemmetyinen, J., et al. (2021). Development of the Terrestrial Snow Mass Mission. IEEE Int. Geosci. Remote Sensing Symp. IGARSS, 614–617. doi:10.1109/IGARSS47720.2021.9553496

CrossRef Full Text | Google Scholar

Frei, A., Tedesco, M., Lee, S., Foster, J., Hall, D. K., Kelly, R., et al. (2012). A Review of Global Satellite-Derived Snow Products. Adv. Space Res. 50 (8), 1007–1029. doi:10.1016/j.asr.2011.12.021

CrossRef Full Text | Google Scholar

Henyey, L. C., and Greenstein, J. L. (1941). Diffuse Radiation in the Galaxy. ApJ 93, 70–83. doi:10.1086/144246

CrossRef Full Text | Google Scholar

Hu, Y. X., Winker, D., Yang, P., Baum, B., Poole, L., and Vann, L. (2001). Identification of Cloud Phase from PICASSO-CENA Lidar Depolarization: A Multiple Scattering Sensitivity Study. J. quantitative Spectrosc. radiative transfer 70 (4-6), 569–579. doi:10.1016/s0022-4073(01)00030-9

CrossRef Full Text | Google Scholar

Kokhanovsky, A. A., and Zege, E. P. (2004). Scattering Optics of Snow. Appl. Opt. 43, 1589–1602. doi:10.1364/ao.43.001589

PubMed Abstract | CrossRef Full Text | Google Scholar

Kwok, R. (2018). Arctic Sea Ice Thickness, Volume, and Multiyear Ice Coverage: Losses and Coupled Variability (1958-2018). Environ. Res. Lett. 13, 105005. doi:10.1088/1748-9326/aae3ec

CrossRef Full Text | Google Scholar

Lawrence, D. M., and Slater, A. G. (2010). The Contribution of Snow Condition Trends to Future Ground Climate. Clim. Dyn. 34, 969–981. doi:10.1007/s00382-009-0537-4

CrossRef Full Text | Google Scholar

Laxon, S., Peacock, N., and Smith, D. (2003). High Interannual Variability of Sea Ice Thickness in the Arctic Region. Nature 425, 947–950. doi:10.1038/nature02050

PubMed Abstract | CrossRef Full Text | Google Scholar

Lemmetyinen, J., Derksen, C., Rott, H., Macelloni, G., King, J., Schneebeli, M., et al. (2018). Retrieval of Effective Correlation Length and Snow Water Equivalent from Radar and Passive Microwave Measurements. Remote Sensing 10, 170. doi:10.3390/rs10020170

CrossRef Full Text | Google Scholar

Lievens, H., Brangers, I., Marshall, H.-P., Jonas, T., Olefs, M., and De Lannoy, G. (2022). Sentinel-1 Snow Depth Retrieval at Sub-kilometer Resolution over the European Alps. Cryosphere Discussik 16, 159–177. doi:10.5194/tc-16-159-2022

CrossRef Full Text | Google Scholar

Lu, X., Hu, Y., Yang, Y., Vaughan, M., Palm, S., Trepte, C., et al. (2021). Enabling Value Added Scientific Applications of ICESat-2 Data with Effective Removal of Afterpulses. Earth Space Sci. 8 (6), e2021EA001729. doi:10.1029/2021EA001729

PubMed Abstract | CrossRef Full Text | Google Scholar

Markus, T., Neumann, T., Martino, A., Abdalati, W., Brunt, K., Csatho, B., et al. (2017). The Ice, Cloud, and Land Elevation Satellite-2 (ICESat-2): Science Requirements, Concept, and Implementation. Remote sensing Environ. 190, 260–273. doi:10.1016/j.rse.2016.12.029

CrossRef Full Text | Google Scholar

Musselman, K. N., Clark, M. P., Liu, C., Ikeda, K., and Rasmussen, R. (2017). Slower Snowmelt in a Warmer World. Nat. Clim Change 7, 214–219. doi:10.1038/nclimate3225

CrossRef Full Text | Google Scholar

National Academies of Sciences (2018). Engineering, and Medicine, Thriving on Our Changing Planet: A Decadal Strategy for Earth Observation from Space. Washington, DC: The National Academies Press. doi:10.17226/24938

CrossRef Full Text | Google Scholar

Neumann, T. A., Martino, A. J., Markus, T., Bae, S., Bock, M. R., Brenner, A. C., et al. (2019). The Ice, Cloud, and Land Elevation Satellite - 2 mission: A Global Geolocated Photon Product Derived from the Advanced Topographic Laser Altimeter System. Remote Sensing Environ. 233, 111325. doi:10.1016/j.rse.2019.111325

PubMed Abstract | CrossRef Full Text | Google Scholar

Oveisgharan, S., Esteban-Fernandez, D., Waliser, D., Friedl, R., Nghiem, S., and Zeng, X. (2020). Evaluating the Preconditions of Two Remote Sensing SWE Retrieval Algorithms over the US. Remote Sensing 12, 2021. doi:10.3390/rs12122021

CrossRef Full Text | Google Scholar

Painter, T. H., Berisford, D. F., Boardman, J. W., Bormann, K. J., Deems, J. S., Gehrke, F., et al. (2016). The Airborne Snow Observatory: Fusion of Scanning Lidar, Imaging Spectrometer, and Physically-Based Modeling for Mapping Snow Water Equivalent and Snow Albedo. Remote Sensing Environ. 184, 139–152. doi:10.1016/j.rse.2016.06.018

CrossRef Full Text | Google Scholar

Räisänen, P., Kokhanovsky, A., Guyot, G., Jourdan, O., and Nousiainen, T. (2015). Parameterization of Single-Scattering Properties of Snow. The Cryosphere 9 (3), 1277–1301. doi:10.5194/tc-9-1277-2015

CrossRef Full Text | Google Scholar

Robinson, D. A., Dewey, K. F., and Heim, R. R. (1993). Global Snow Cover Monitoring: An Update. Bull. Amer. Meteorol. Soc. 74, 1689–1696. doi:10.1175/1520-0477(1993)074<1689:gscmau>2.0.co;2

CrossRef Full Text | Google Scholar

Rostosky, P., Spreen, G., Farrell, S. L., Frost, T., Heygster, G., and Melsheimer, C. (2018). Snow Depth Retrieval on Arctic Sea Ice from Passive Microwave Radiometers-Improvements and Extensions to Multiyear Ice Using Lower Frequencies. J. Geophys. Res. Oceans 123 (10), 7120–7138. doi:10.1029/2018JC014028

CrossRef Full Text | Google Scholar

Schwerdtfeger, P., and Weller, G. E. (1977). “Radiative Heat Transfer Processes in Snow and Ice,” in Meteorological Studies at Plateau Station, Antarctica. Editors P. C. Dalrymple, A. J. Riordan, A. Riordan, A. J. Riordan, G. Weller, and H. H. Letta.

CrossRef Full Text | Google Scholar

Stamnes, K., Tsay, S.-C., Wiscombe, W., and Jayaweera, K. (1988). Numerically Stable Algorithm for Discrete-Ordinate-Method Radiative Transfer in Multiple Scattering and Emitting Layered media. Appl. Opt. 27 (12), 2502–2509. doi:10.1364/ao.27.002502

PubMed Abstract | CrossRef Full Text | Google Scholar

Theraulaz, G., Bonabeau, E., Nicolis, S. C., Solé, R. V., Fourcassié, V., Blanco, S., et al. (2002). Spatial Patterns in Ant Colonies. Proc. Natl. Acad. Sci. U.S.A. 99 (15), 9645–9649. doi:10.1073/pnas.152302199

PubMed Abstract | CrossRef Full Text | Google Scholar

Vavrus, S. (2007). The Role of Terrestrial Snow Cover in the Climate System. Clim. Dyn. 29, 73–88. doi:10.1007/s00382-007-0226-0

CrossRef Full Text | Google Scholar

Warren, S. G., Brandt, R. E., and Grenfell, T. C. (2006). Visible and Near-Ultraviolet Absorption Spectrum of Ice from Transmission of Solar Radiation into Snow. Appl. Opt. 45 (21), 5320–5334. doi:10.1364/ao.45.005320

PubMed Abstract | CrossRef Full Text | Google Scholar

Warren, S. G. (1982). Optical Properties of Snow. Rev. Geophys. 20 (1), 67–89. doi:10.1029/rg020i001p00067

CrossRef Full Text | Google Scholar

Zeng, X., Broxton, P., and Dawson, N. (2018). Snowpack Change from 1982-2016 over Conterminous United States. Geophys. Res. Lett. 15, 12940–12947. doi:10.1029/2018GL079621

CrossRef Full Text | Google Scholar