Analyzing Local Carbon Dioxide and Nitrogen Oxide Emissions From Space Using the Divergence Method: An Application to the Synthetic SMARTCARB Dataset

Since the Paris Agreement was adopted in 2015, the role of space-based observations for monitoring anthropogenic greenhouse gas (GHG) emissions has increased. To meet the requirements for monitoring carbon dioxide (CO₂) emissions, the European Copernicus programme is preparing a dedicated CO₂ Monitoring (CO2M) satellite constellation that will provide CO₂ and nitrogen dioxide (NO₂) observations at 4 km² resolution along a 250 km wide swath. In this paper, we adapt the recently developed divergence method to derive both CO₂ and nitrogen oxide (NO_x) emissions of cities and power plants from a CO2M satellite constellation by using synthetic observations from the COSMO-GHG model. Due to its long lifetime, the large CO₂ atmospheric background needs to be removed to highlight the anthropogenic enhancements before calculating the divergence. Since the CO₂ noise levels are large compared to the anthropogenic enhancements, we apply different denoising methods and compare the effect on the CO₂ emission estimates. The annual NO_x and CO₂ emissions estimated from the divergence maps using the peak fitting approach are in agreement with the expected values, although with larger uncertainties for CO₂. We also consider the possibility to use co-emitted NO_x emission estimates for quantifying the CO₂ emissions, by using source-specific NO_x-to-CO₂ emission ratios derived directly from satellite observations. In general, we find that the divergence method provides a promising tool for estimating CO₂ emissions, alternative to typical methods based on inverse modeling or on the analysis of individual CO₂ plumes.

1 Introduction

Using satellite data for estimating carbon dioxide (CO₂) emissions from anthropogenic sources has become increasingly important since the Paris Agreement was adopted in 2015, as satellites provide consistent observations with global coverage. The very first study that estimated CO₂ emissions from individual power plants using satellite data was published in 2017 (Nassar et al., 2017). Before that, Bovensmann et al. (2010) provided the first theoretical study on monitoring power plant CO₂ emissions from space. In recent years, the literature has been rapidly expanding with several new approaches and case studies (e.g., Reuter et al., 2019; Wu et al., 2020; Hakkarainen et al., 2021). One key success element has been the launch of NASA’s CO₂ mission, Orbiting Carbon Observatory-2 (OCO-2), in 2014 that has enabled many of these studies, even if its narrow swath (less than 10 km wide) is not optimal for the analysis of anthropogenic signals. Recently, NASA’s OCO-3 instrument, operating on the International Space Station, has been providing Snapshot Area Map (SAM) and target mode measurements for the analysis of emission hot spots like cities and power plants (Kiel et al., 2021).

In Europe, one of the key activities responding to the needs of the Paris Agreement to monitor anthropogenic CO₂, is the Copernicus CO₂ Monitoring (CO2M) mission (Janssens-Maenhout et al., 2020; Meijer et al., 2020). Currently, a two-to-three-satellite constellation is planned. The first two satellites are to be delivered in October 2025, with the first launch scheduled at the end of 2025. In addition to CO₂, the CO2M instrument will measure nitrogen dioxide (NO₂) and methane (CH₄). The requirement for the spatial resolution is 4 km² and for the imaging swath larger than 250 km. To support achieving the strict accuracy requirements of the GHG measurements, dedicated aerosol and cloud instruments are added to the payload.

Many of the proposed techniques for estimating CO₂ emissions from local sources are based on single satellite overpasses (e.g., Varon et al., 2018). Observations of NO₂, co-emitted with CO₂, are often used for detecting the emission plume and its shape (e.g., Kuhlmann et al., 2019; Reuter et al., 2019; Hakkarainen et al., 2021). The NO₂ signal-to-noise ratio is generally higher compared to CO₂ and the NO₂ plumes are easier to detect with current satellite instruments owing to their wider satellite swaths. Since the launch of TROPOMI/Sentinel 5p (S5p) in 2017, it has been possible to observe individual NO₂ emission plumes from single satellite overpasses (unlike its predecessors).

In comparison to CO₂, the lifetime of NO₂ is very short (only a few hours) and the signal-to-noise is higher. For these reasons, nitrogen oxide (NO_x = NO+NO₂) emission areas can be easily identified by averaging satellite NO₂ concentrations over a sufficiently long period of time. To estimate NO_x emissions from averaged NO₂ columns, methods based on the temporal averages of spatially co-located observations are often applied (Fioletov et al., 2015; Beirle et al., 2011, 2019; de Foy et al., 2014). The advantage of these methods is that they do not require complex atmospheric modeling and that they generally provide more robust emission estimates compared to individual satellite overpasses. In addition, these approaches have been successfully applied to instruments and locations, where the individual plumes are not detectable, but the emission signal becomes visible when multiple scenes are averaged (e.g., Ialongo et al., 2021).

Conversely, emission estimation methods based on temporal averaging have not yet been successfully applied to satellite-based observations of column-averaged CO₂ dry air mole fraction (XCO₂), although this option has been discussed by Hakkarainen et al. (2016) and Hill and Nassar (2019). The main challenges are related to the scarce coverage of current CO₂ measurement systems as well as the large background signal. To link the satellite XCO₂ observations to anthropogenic sources, we must define the XCO₂ anomalies as the difference to a regional background that accounts for the increasing CO₂ levels in the atmosphere and its spatio-temporal variability (Hakkarainen et al., 2016, 2019).

In this paper, we discuss the use of methods based on temporal averaging for estimating the CO₂ and NO_x emissions from satellite observations. In particular, we adapt the divergence method, developed originally for NO₂ (Beirle et al., 2019, 2021) to estimate CO₂ emissions. The method is applied to the SMARTCARB dataset of synthetic satellite observations, which was produced to closely mimic the CO₂ and NO₂ observations of the upcoming CO2M mission (Kuhlmann et al., 2020b). In addition, we estimate source-specific NO_x-to-CO₂ emission ratios for converting the satellite-based estimates of NO_x emissions into CO₂ emissions.

The paper is organized as follows. Section 2 describes the SMARTCARB dataset and the different emission estimation techniques. In Section 3 we apply the proposed emission estimation methods to the SMARTCARB dataset. We discuss the results in Section 4 and Section 5 concludes the paper.

2 Data and Methods

2.1 SMARTCARB Dataset

The synthetic observations used in this study were created within the ESA-funded SMARTCARB project to prepare for the upcoming CO2M mission. The dataset has been extensively described and used in previous works (Brunner et al., 2019; Kuhlmann et al., 2019, 2020a, 2021), and is openly available (Kuhlmann et al., 2020b).

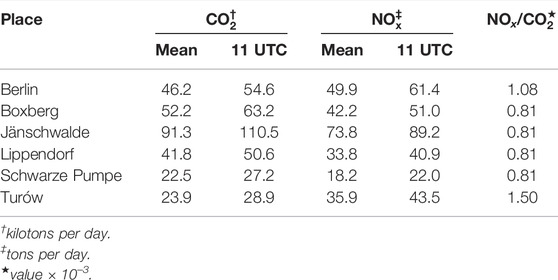
The synthetic NO₂ and CO₂ vertical columns are based on atmospheric transport model simulations obtained with the COSMO-GHG model at 1 km by 1 km resolution. The model domain covers parts of Germany, Poland and Czechia for the year 2015. The synthetic data were further averaged to 2 km by 2 km satellite pixels along the 250 km wide swath of simulated CO2M satellite orbits. In this study, we mainly use a constellation setup with two satellites, but we carry out additional tests with one to six satellites. Furthermore, we apply a Gaussian random noise with standard deviation of 1.5 × 10¹⁵ molec./cm² to the NO₂ simulations and 0.5 ppm to the XCO₂ simulations. The CO2M mission requirements indicate that the CO₂ precision shall be better than 0.7 ppm for vegetation scenario at solar zenith angle of 50 degrees and the NO₂ precision better than 1.5 × 10¹⁵ molec./cm² (Meijer et al., 2020). Figure 1 shows an example of XCO₂ observations on a 250 km wide CO2M orbit overlaid with the simulated XCO₂ field. The NO_x and CO₂ emissions used as input in the simulations are summarized in Table 1 for six large point sources and the city of Berlin (Figure 1). Table 1 includes also the annual emissions at 11 UTC, which approximately corresponds to the foreseen satellite overpass time of CO2M over Central Europe.

FIGURE 1

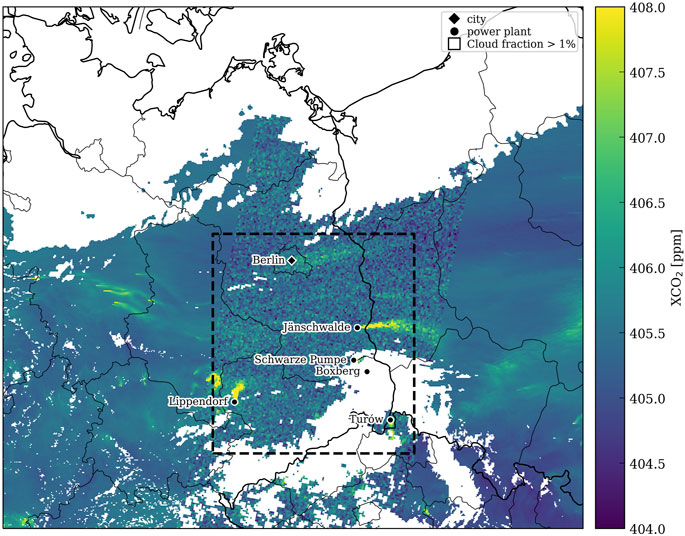
FIGURE 1. Synthetic XCO₂ observations on 23 April 2015 over a 250 km wide swath of the planned CO2M instrument (low-noise scenario). Simulated SMARTCARB XCO₂ field is illustrated on the background. Missing CO₂ measurements (cloud fraction larger than 1%) are shown in white. The black rectangle indicates the study area. The emission sources considered in the analysis (Berlin, Boxberg, Jänschwalde, Lippendorf, Schwarze Pumpe, and Turów) are highlighted.

TABLE 1

TABLE 1. Summary of the emissions used in the SMARTCARB dataset.

2.2 Divergence Method

Beirle et al. (2019), Beirle et al. (2021) introduced the divergence method to estimate the NO_x emissions from TROPOMI NO₂ retrievals. Here we provide an overview of the method applied to synthetic CO2M satellite retrievals of both NO₂ and CO₂ vertical columns. A more comprehensive theoretical discussion is given in the supplementary material, including more details on the different assumptions. The divergence method is based on the continuity equation (Jacob, 1999) at the steady state, where the divergence of vector field F (flux) is defined as the difference between emissions E and sinks S:

$\nabla \cdot F=E-S.(1)$

The flux F is defined as F = (F_x, F_y) = (V ⋅ u, V ⋅ v), where V is the vertical column density observed by satellite, and u and v are the eastward and northward winds, respectively, at the level of the enhanced concentrations. As discussed by Beirle et al. (2019), the NO_x sink can be calculated from the NO₂ columns as S = LV/τ, where τ is the NO_x lifetime generally assumed as 4 hours (as used also in the SMARTCARB simulations) and L is the constant NO_x-to-NO₂ ratio (typically assumed as 1.32 as in Beirle et al., 2011, 2019). In the follow-up paper by Beirle et al. (2021), the sink term is neglected due to the uncertainties in the assumed NO_x lifetime and only the divergence is analyzed. The divergence method can also be applied to CO₂ but since its lifetime is extremely long (in the order of centuries) as compared to NO_x, the sink term can be neglected as well.

For the flux calculation we use the wind information from the European Centre for Medium-Range Weather Forecasts (ECMWF) next-generation reanalysis ERA5 dataset (Hoffmann et al., 2019) given at 0.1° ×0.1° grid size resolution. Following the approach by Fioletov et al. (2015), we use the mean value from the layers at 900, 950 and 1000 hPa. For each satellite pixel, we take the closest point from the wind grid and then temporally interpolate the wind values to the measurement time.

As the divergence operator is linear, the divergence can be calculated from the mean F_x and F_y fields as reported by Beirle et al. (2019, 2021). However, due to missing values in the data, the averaging and divergence operators are not entirely commutative. In our analysis, we found that the divergence fields are less affected by missing data if the divergence operator is calculated before averaging, and thus this option was used throughout the paper. Supplementary Figure S1 in the supplement shows an example of the CO₂ divergence maps calculated before and after the temporal averaging, with the former option showing less noisy patterns.

The partial derivatives, needed for the divergence ∇ ⋅ F = (∂F_x/∂_x, ∂F_y/∂_y), are calculated using second-order central differences. For data points along the edges, the partial derivatives are calculated using single-sided differences. To adapt the original divergence approach (Beirle et al., 2019) to long-lived gases, such as CO₂, we remove the atmospheric background (e.g., as in Hakkarainen et al., 2016) before calculating the divergence as the flux is not linear with the column V due to the changing wind speed. Thus, before the calculation of the divergence, we derive the XCO₂ anomaly $({\mathrm{X}\mathrm{C}\mathrm{O}}_2^{\mathrm{a}})$ as

${\mathrm{X}\mathrm{C}\mathrm{O}}_2^{\mathrm{a}}\left(x,y,t\right)={\mathrm{X}\mathrm{C}\mathrm{O}}_2\left(x,y,t\right)-{\mathrm{X}\mathrm{C}\mathrm{O}}_2^{\text{bg}}\left(t\right).(2)$

Here we define the background ${\mathrm{X}\mathrm{C}\mathrm{O}}_2^{\text{bg}}$ for each orbit as the median over the area of interest. The definition of the background can be tuned case-by-case. The full theoretical derivation of the divergence method, the background removal and other aspects of the approach are discussed in the supplementary material.

2.3 Peak Fitting

In order to calculate source-specific emissions from the enhancements in the averaged divergence/emission fields, the peak fitting approach (as in Beirle et al., 2021) can be applied by fitting the following function, including a Gaussian and a linear term:

$\begin{array}{ll}\hfill P\left(x,y\right)& =\frac{A}{2\pi {\sigma }_x{\sigma }_y}\exp \left(-\frac{{\left(x-x_0\right)}^2}{2{\sigma }_x^2}\right)\exp \left(-\frac{{\left(y-y_0\right)}^2}{2{\sigma }_y^2}\right)\hfill \\ \hfill & +m_x\left(x-x_0\right)+m_y\left(y-y_0\right)+b,\hfill \end{array}(3)$

where A is the estimated source-specific flux. The variables σ_x and σ_y describe the width of the two-dimentional Gaussian function, and x₀ and y₀ indicate the location of the source. The terms m_x, m_y and b define the linear background field. Here we estimate all of the variables mentioned above using the Markov chain Monte Carlo (MCMC) toolbox developed by Laine (2008) (available online at https://mjlaine.github.io/mcmcstat/) using an adaptive Metropolis algorithm (Haario et al., 2001). We also estimate the statistical noise of the averaged divergence field using MCMC. The fitted parameters are estimated as the mean values of the posterior distribution and the fitting uncertainties as the standard deviation.

2.4 Exponentially-Modified Gaussian Method

As an alternative to the divergence method, we estimate the NO_x emissions also by fitting the synthetic observations with the exponentially-modified Gaussian (EMG) function (Beirle et al., 2011). Before fitting, we apply the wind rotation technique (Fioletov et al., 2015) by rotating each pixel around the point source according to the wind direction so that all scenes have wind direction from west to east. The resulting rotated mean field is then integrated along the latitudinal dimension to derive the NO₂ line densities. Those are then fitted with a 1D EMG model M (as in Beirle et al., 2011) as follows:

$M\left(x\right)=Q\times \left(e\ast G\right)\left(x\right)+B.(4)$

Here Q is the emission factor (E = Q × u), B is the background (both given in molec./m), u is the effective wind speed, and (e*G)(x) is the convolution between the Gaussian function G and the exponential decay

$e\left(x\right)=\left\{\begin{array}{c}\exp \left(-\left(x-X\right)/d\right),x\ge X\left(\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n}\mathrm{w}\mathrm{i}\mathrm{n}\mathrm{d}\right),\hfill \\ 0,x<X\left(\mathrm{u}\mathrm{p}\mathrm{w}\mathrm{i}\mathrm{n}\mathrm{d}\right).\hfill \end{array}\right.(5)$

The variable X is the distance along the wind direction between the line density peak and the point source. The NO_x lifetime can be obtained by dividing the e-folding distance d with the mean wind speed as τ = d/u. We estimate all together five parameters: Q, B, X, d, and the width of the Gaussian function. For the estimation of the parameters, we use the MCMC approach described in Section 2.3. The uncertainties related to this method have been discussed extensively in the literature (e.g., Beirle et al., 2011; Fioletov et al., 2015; Goldberg et al., 2019).

2.5 Source-Specific NO_x-to-CO₂ Emission Ratios

Since the signal-to-noise ratio for NO₂ is higher than that for CO₂, it is generally easier to estimate NO_x emissions than CO₂ emissions from satellite observations. In addition, NO₂ retrievals are less affected by the presence of clouds and more observations can be acquired. Thus, the CO₂ emissions can also be estimated by scaling the NO_x emissions obtained using the divergence method or the EMG fitting with a source-specific NO_x-to-CO₂ ratio. On the other hand, NO_x emissions depend on assumptions on the lifetime and the conversion from NO₂ to NO_x, that are not needed for CO₂.

Here we derive the NO_x-to-CO₂ emission ratio by calculating the NO₂-to-CO₂ ratios r(x) at multiple transects along matching NO₂ and CO₂ plumes (see Section 3.3). We calculate r(x) using linear fit between NO₂ and CO₂ columns at each transect. We then fit an exponential decay function (similarly to Kuhlmann et al., 2021):

$r\left(x\right)=r_0\exp \left(\frac{-x}{u\times \tau }\right),(6)$

where r₀ is the estimated NO_x-to-CO₂ emission ratio, u is the mean wind speed and τ is the lifetime. As noted by Kuhlmann et al. (2021), it is not always feasible to fit the exponential decay to the data if the number of transect is too small. In those cases, we take into account the value of the ratio at the transects near the source. This method is adapted from the approach proposed by Hakkarainen et al. (2021), where the NO_x-to-CO₂ emission ratios were derived from TROPOMI NO₂ and OCO-2 CO₂ observations at Matimba Power Station in South Africa. In that case, due to the narrow swath of OCO-2 observations, one cross-section per plume was used. If the entire plume is visible from the satellite observations, as for several orbits in the synthetic CO2M observations, we can calculate the ratios at multiple transects along the plume.

2.6 Denoising

The computation of the divergence is sensitive to systematic and random errors (see, e.g., Beirle et al., 2021). In this synthetic case study, particular errors are the single-sounding precision errors added to the data (see Section 2.1), and errors in the estimated effective wind fields. The temporal averaging of the divergence computations partially overcomes the influence of random errors, and the averaging increases the signal-to-noise ratio of the divergence map. However, we can additionally “denoise” the total vertical column density fields using computer vision techniques (Koene et al., 2021). In this study we analyse two denoising methods that are described shortly below.

A relatively simple technique for denoising is a mean filter. Here, we spatially convolve a gridded total vertical column density image V(x, y, t) with an N × N kernel $K_{N^2}$ whose elements have the value 1/N². For example, a convolution with the kernel

$K_9\left(x,y\right)=\frac{1}{9}\left[\begin{array}{ccc}\hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill \end{array}\right](7)$

effectively computes a filtered image based on the average of 3 × 3 regions in V(x, y, t). The expectation is that the mean filter suppresses random noise, varying from pixel to pixel. On the other hand, some signal will be lost in the process. In this paper, we refer to the filter of Eq. 7 as “mean filter 9.” We additionally considered the 5 × 5 kernel K₂₅ as “mean filter 25.”

An alternative denoising technique we applied exploits the colocated CO₂ and NO₂ observations in the synthetic CO₂ images. It is based on a method called block-matching and 3D filtering, or BM3D (Dabov et al., 2007), which performs around the upper bound of possible performance that a denoising technique can achieve (Levin and Nadler, 2011). In short, BM3D works by denoising an image patch-wise in two steps. First, 3D blocks are formed of similar-looking patches, which are collaboratively denoised using a hard thresholding step, and the collaboratively denoised patches are re-aggregated into an initial estimate of the denoised image. The second step takes place the same way, except that the hard thresholding is replaced with a Wiener filter based on the initially denoised image, with respect to a user-specified denoising level σ_BM3D. We refer to Dabov et al. (2007) and Lebrun (2012) for further details. A notable extension is that we set up BM3D to consider the joint information present in CO₂ and NO₂ images, by normalizing the two images to the same dynamic range and then linearly adding 0.75 times the scaled CO₂ image with 0.25 times the scaled NO₂ image, to form a joint image. The locations of the selected similar-looking patches were established in this joint image; while the denoising took place for both this joint image and an image consisting of 0.75 times the CO₂ image minus 0.25 times the scaled NO₂ image. After adding the two denoised images and rescaling, we obtain a new CO₂ image, while the filtering was helped by the higher signal-to-noise ratio of the NO₂ images during the patch selection and denoising steps. In this paper, we refer to “BM3D σ_BM3D,” for example “BM3D 5,” to indicate denoised images using a specified noise level in the Wiener filter.

3 Results

3.1 Divergence Method

Figure 2 illustrates the CO₂ divergence calculated from the CO₂ synthetic observations for the year 2015 simulated by the COSMO-GHG model in an optimal case without presence of noise or background field. We consider model simulations at 11:00 UTC assuming clear-sky conditions gridded at 0.05°×0.05° resolution. The largest point sources (Table 1), such as the individual power stations (Boxberg, Jänschwalde, Lippendorf, Schwarze Pumpe, and Turów) and the city of Berlin are visible as enhancements in the divergence map.

FIGURE 2

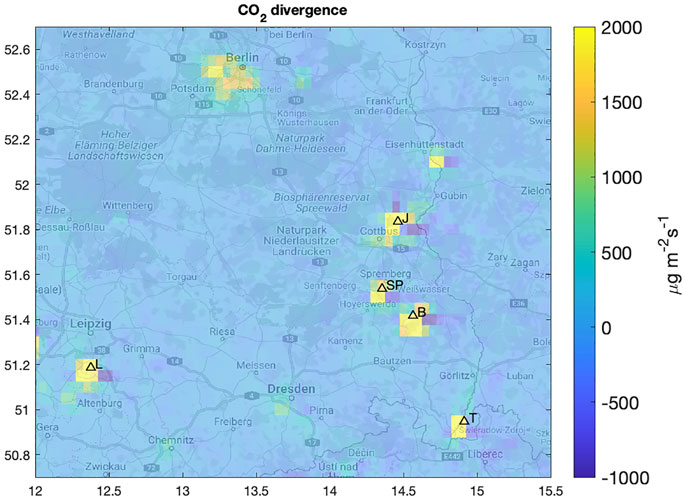
FIGURE 2. CO₂ divergence calculated from the COSMO-GHG model simulations. Only anthropogenic enhancements are considered. Positive values correspond to strong emissions sources such as power stations (Boxberg, Jänschwalde, Lippendorf, Schwarze Pumpe, and Turów marked with B, J, L, SP, and T, respectively) and the city of Berlin.

In practice, the situation is more complicated than illustrated in Figure 2 as several aspects affect the divergence calculation. For example, the amount of available data can be reduced due to the limited coverage of satellite observations and the persistence of cloudy conditions. The effect of clouds is more restricting for CO₂, as compared to NO_x, since almost completely clear sky conditions are needed for a successful CO₂ retrieval, while partially cloudy conditions (cloud fraction smaller than 30%) are considered suitable for reliable NO₂ retrievals. In addition, the calculation of the CO₂ divergence requires removing the background (about 400 ppm), with the anthropogenic enhancements in the order of 1 ppm. The highest challenge is posed by the instrument noise.

To mimic the analysis of satellite observations we consider different constellation options from the SMARTCARB dataset. The divergence is calculated for the full year 2015 with data filtering for cloud free conditions. Supplementary Figure S2 in the supplement shows the CO₂ divergence calculated for constellations with one up to six satellites. For the remaining part of this paper, we will use the setup with two satellites shown in Supplementary Figure S2B.

Figure 3 illustrates the divergence calculated with different model setups. Figure 3A shows the NO_x divergence calculated from simulations with added noise (standard deviation 1.5 × 10¹⁵ molec./cm²), without any background removal and with cloud fraction smaller than 0.3. Figure 3B shows the CO₂ divergence based on simulations without presence of background or noise, and with cloud fraction limit 0.01. Both NO_x and CO₂ divergence maps have similar spatial features, with enhancements close to the main emission sources, but the CO₂ fields are noisier and less sharp, as expected due to the longer lifetime and the more restrictive cloud fraction limit which reduces the number of available observations (Supplementary Figure S3 in the supplement). Figure 3C shows the CO₂ divergence map after adding artificial noise (standard deviation 0.5 ppm) to the simulations. Figure 3D shows the CO₂ divergence after adding the simulated background and subsequently removing it by calculating the anomaly as the difference from the background (i.e. the median for each orbit over the area covered in Figure 3). The noise addition has much larger effect to the divergence patterns than the background addition (and removal). Figure 3E combines Figures 3C,D, including both the noise and the background (and its removal). Finally, in Figure 3F the XCO₂ data are denoised by using a mean filter with constant 5-by-5 kernel before removing the background and calculating the CO₂ divergence. After denoising the data, the CO₂ divergence patterns in Figure 3F are similar to Figure 3B and Figure 3D. The effect of denoising is further discussed in Section 3.2. To calculate emission estimates for individual point sources we apply the peak fitting approach described in Section 2.3. For CO₂ we use the divergence map shown in Figure 3F, that includes the denoised data (with background removed) that would be available from a two-satellite constellation. We are able to calculate the CO₂ emission values for all the major sources in the area except for Turów Power Station, which does not appear as a point source in Figure 3F. For NO_x we fit the peaks from the emission map given as the sum of the divergence and the sink terms (Supplementary Figure S4).

FIGURE 3

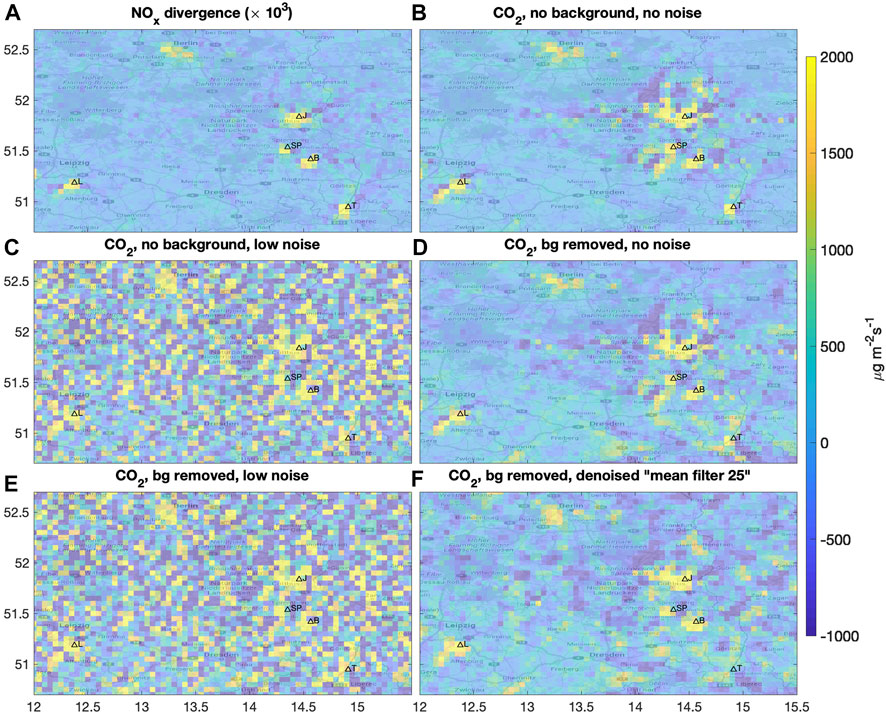
FIGURE 3. Divergence calculated with various setups. (A) shows the NO_x divergence and (B–F) the CO₂ divergence. The different setups are indicated in the title of each panel.

Figure 4 shows the comparison between the NO_x and CO₂ emissions estimates derived using peak fitting and the annual mean of the emissions at 11 UTC used as input in the model simulations for each source (orange symbols). The emission estimates are also presented in Table 2. The emission values sit generally close to the 1:1 line, with high correlation (correlation coefficients R = 0.94 and R = 0.97 for NO_x and CO₂, respectively) between our estimates and the 11 UTC emissions used as model input. Some differences can be related to the differences in emissions during different seasons which might be not homogeneously sampled.

FIGURE 4

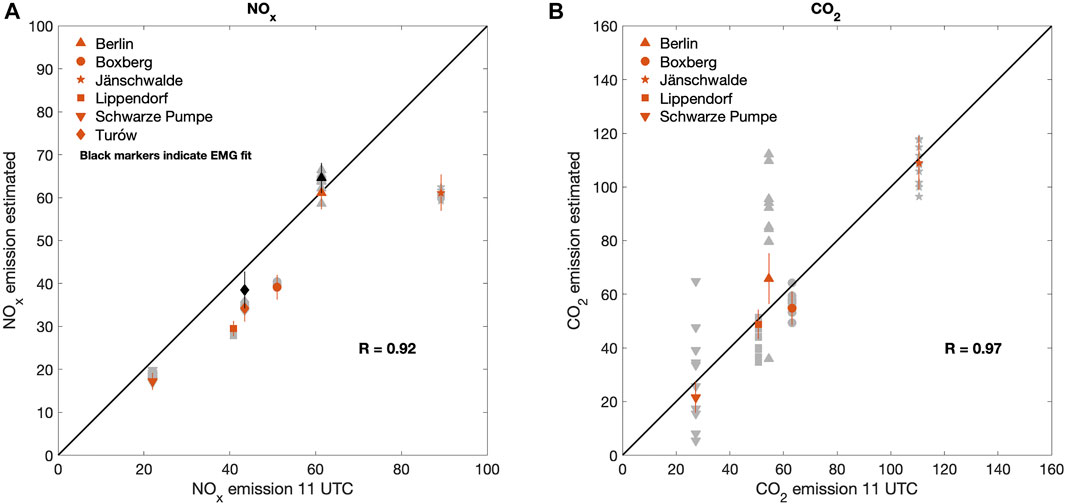
FIGURE 4. Source-specific emissions for NO_x (A) and CO₂ (B). Orange symbols indicate the emissions calculated from the CO₂ divergence map shown in Figure 3F (denoised and with background removed) and from the NO_x emission map shown in the Supplement (Supplementary Figure S4) using peak fitting. Grey symbols indicate emission values calculated with different realization of the measurement noise. Black markers show the NO_x emissions derived from the EMG fit for the Turów power station and the city of Berlin.

TABLE 2

TABLE 2. Summary of the estimated emissions.

To study the effect of the instrumental noise on the emission estimates, we sampled different realisations of the random noise for creating the observation error. The effect of the noise is rather small for the NO_x emission estimates, while it is more pronounced for CO₂, as shown in Figure 3. The different emission estimates (after denoising) are presented as grey symbols in Figure 4. The largest variability due to different random noise can be found for the city of Berlin (emission estimates ranging from 36 to 112 kton/day) and for Schwarze Pumpe power station (5–65 kton/day). Supplementary Figure S5 in the supplement shows two examples of the CO₂ divergence map with two different sets of random noise corresponding to very different outcomes in terms of emission estimates. Supplementary Figure S5A corresponds to CO₂ emission estimates of 36 kton/day for Berlin and 65 kton/day for Schwarze Pumpe, while in Supplementary Figure S5B Schwarze Pumpe CO₂ emissions are much smaller (5 kton/day) and the Berlin CO₂ emissions are about 85 kton/day.

The error bars in Figure 4 correspond to the fitting error (standard deviation of the posterior distribution) calculated using the MCMC sampling. This fitting error is only a statistical error estimate that describes how well the 2D Gaussian model fits the divergence/emission fields. Thus, the fitting error is likely to underestimate the true error as it does not include any systematic component.

The NO_x emissions can be also estimated by using the EMG method described in Section 2.4. This method is suitable for relatively isolated sources and it can be challenging to apply in the presence of strong neighboring sources. Dedicated algorithms have been developed to deal with this issue (Fioletov et al., 2017; Verstraeten et al., 2018; Liu et al., 2022). Here we apply the wind rotation technique around each source (Fioletov et al., 2015) and calculate the NO_x line densities. We obtain a successful fit to estimate the emissions only for the city of Berlin and Turów Power Station, which are both relatively distant from the other sources in the area of study. The resulting NO_x emission estimates for Berlin and Turów are 64.6 ± 3.5 ton/day and 38.5 ± 4.3 ton/day, respectively (Figure 4, black symbols). The estimates based on EMG fitting agree within the uncertainties with the emission estimates obtained from peak fitting from the emission maps. We also estimate the NO_x lifetime for Berlin and Turów as 1.9 ± 0.2 h and 1.7 ± 0.3 h, respectively. These values are about 50% lower than the lifetime used in the SMARTCARB simulations (4 h). The underestimation of NO_x lifetime using the wind rotation and EMG approach was also found by de Foy et al. (2014).

3.2 Effect of Denoising

As shown in Figure 3, denoising is an essential step when estimating the emissions from the CO₂ divergence fields. In Figure 4, we used a simple denoising based on a mean filter with constant 5-by-5 kernel. To further analyze the effect of denoising, we test also the BM3D method with various denoising parameters (σ_BM3D = 4, 8, 10, 15, 30) as well as the mean filter with 3-by-3 kernel before the calculation of the CO₂ divergence (Figure 5). As expected, increasing the denoising parameter σ_BM3D in the BM3D method leads to increasingly smoother divergence fields. Overall, the denoising with σ_BM3D = 15 (Figure 5D) produces similar patterns than the mean filter 25 (Figure 3F). The mean filter 9 (with 3-by-3 kernel, Figure 5F) remains quite noisy.

FIGURE 5

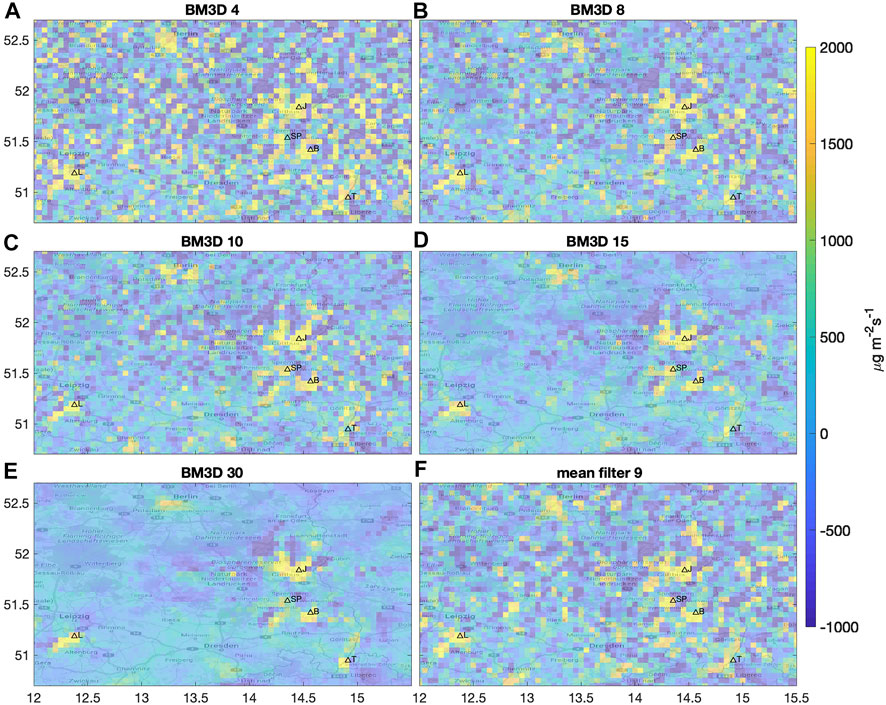
FIGURE 5. CO₂ divergence calculated with different denoising methods. The different setups are indicated in the title of each panel. We tested the BM3D method with various denoising parameters (σ_BM3D = 4, 8, 10, 15, 30) as well as the mean filter with 3-by-3 kernel. See also Figure 3 for comparison.

Figure 6 shows the comparison between the CO₂ emission estimates from peak fitting and the emissions at 11 UTC used as input in the model simulations with different setups for denoising. Here we use the same realization of the instrumental noise to test the effect of different denoising approaches. The emission estimates for Berlin show quite a large spread, while for the Schwarze Pumpe power station the spread is relatively smaller excluding one outlier (BM3D with σ_BM3D = 30). The correlation between the CO₂ emissions estimates from peak fitting and the assumed emissions is generally high, but the overestimation of the emissions for Berlin causes the correlation coefficients to become lower when the BM3D denoising method is applied. Figure 6 also show the CO₂ emission estimates in the cases where no noise and no CO₂ background are considered as well as the case where no denoising is applied.

FIGURE 6

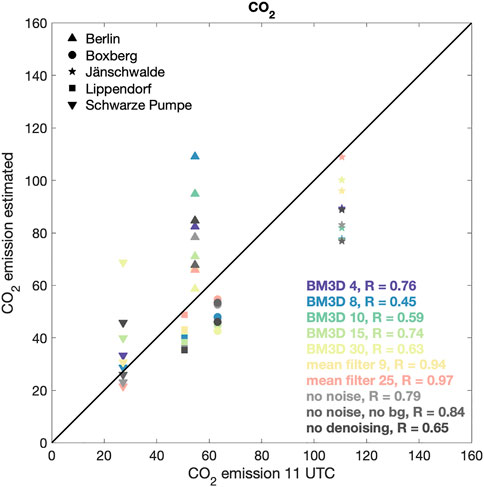
FIGURE 6. Source-specific CO₂ emissions calculated with different denoising methods (shown as different colors). See Figures 3, 5 for the corresponding divergence maps.

3.3 Source-Specific Emission Ratios

As alternative to the divergence approach, we also derive the CO₂ emissions by converting NO_x into CO₂ emissions, using a source-specific NO_x-to-CO₂ emission ratio calculated as described in Section 2.5. For each emission source listed in Table 1 we plot all the available overpasses from the SMARTCARB dataset and calculate the cross-sectional NO₂-to-CO₂ ratios along each observable plume (Hakkarainen et al., 2019, 2021). The ratios are calculated over several (0.1 degrees wide) transects perpendicular to the plume direction (white lines in Figure 7), located at regular distance downwind from the source (0.025 degrees intervals starting at 0.05 degrees from the source). We then fit the NO₂-to-CO₂ ratios using the exponential decay function (Eq. 6) to derive the NO_x-to-CO₂ emission ratio at the source as described in Section 2.5. Figure 7 shows an example of this approach for the Jänschwalde power station. In general, fitting an exponential decay to noisy data is challenging, and the estimates are highly influenced by the values near the emission source. This could potentially be an issue with real NO₂ satellite observations, if the NO emissions are not yet fully oxidised near the source.

FIGURE 7

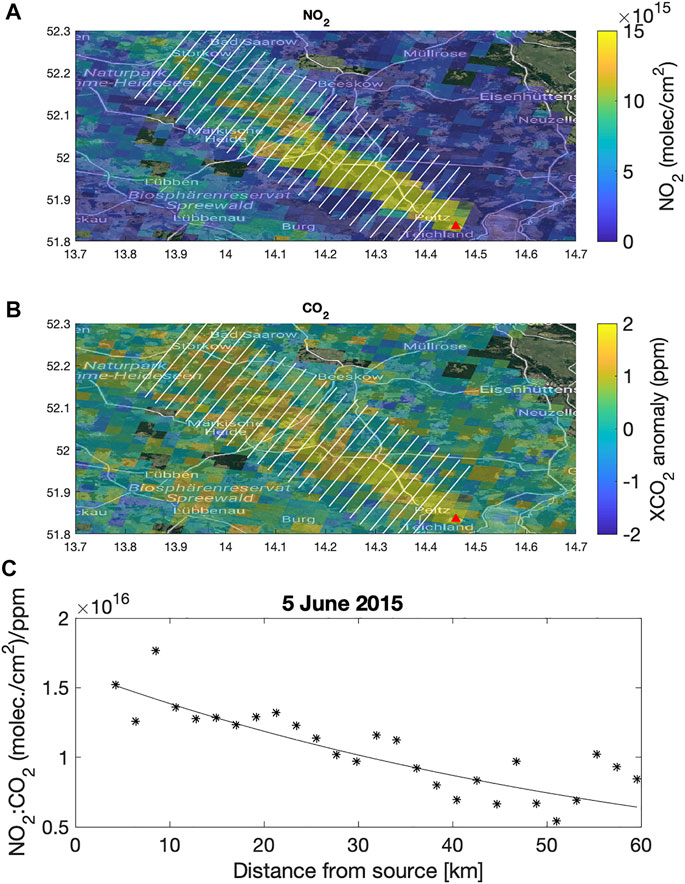
FIGURE 7. Example of the calculation of source-specific NO_x-to-CO₂ emission ratio for Jänschwalde power station on 5 June 2015. Panel (A) and (B) show the NO₂ and CO₂ plumes. Panel (C) shows the cross-sectional NO₂-to-CO₂ ratio calculated over several transects [white lines in panels (A) and (B)], located at regular distance downwind from the source. Black symbols and line indicate the ratios and the corresponding exponential decay, respectively.

Figure 8 includes the mean NO_x-to-CO₂ emission ratios obtained averaging the results from multiple plumes for each power station. In all cases, the true emission value is within the one-sigma error. The main challenge of this approach is the limited number of plumes available to derive the ratios. The estimation process was the most robust for the Jänschwalde power station, which has the largest CO₂ emissions in the area of study and several (13) detectable plumes available for the calculation of the ratios. On the other hand, we were able to identify only four plumes for Turów power station, which showed large variability, especially due to the low CO₂ signal compared to NO₂. Turów has the largest NO_x-to-CO₂ emission ratio, which appears to be captured by our estimates despite the large variability. We attempted a similar approach also for the city of Berlin, but it was difficult do identify clear CO₂ emission plumes from noisy simulations mainly because Berlin has to be considered as an area source, rather than a point source, and our results remained inconclusive.

FIGURE 8

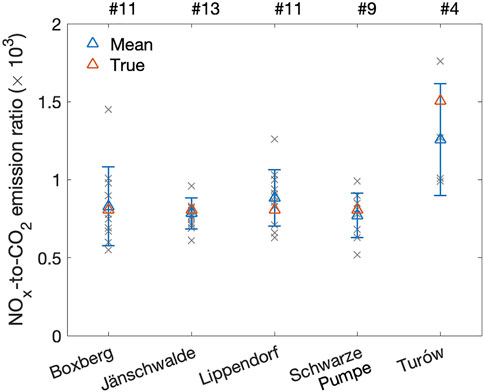
FIGURE 8. Source-specific NO_x-to-CO₂ emission ratios for each power station. Grey symbols indicate estimates from individual plumes while blue symbols show the mean value and the standard deviation. Orange symbols indicate the true emission ratio. The number of plumes analyzed are indicated above the figure.

Table 2 summarizes the NO_x and CO₂ emission values presented in Figure 3 and the mean NO_x-to-CO₂ emission ratios from Figure 8. The last column, includes the CO₂ emissions when the NO_x emissions obtained from peak fitting are converted into CO₂ emissions using the source-specific NO_x-to-CO₂ emission ratios. Overall, the results showed in Table 2 are mostly in agreement (within the uncertainties) with the emission values used as input in the simulations (Table 1). We note that systematic errors are not taken into account in the uncertainties. If the source-specific NO_x-to-CO₂ emission ratios are obtained with the same dataset as the NO_x emissions, possible biases in the NO₂ observations or the assumed constant NO_x-to-NO₂ ratio cancels out when the estimated ratios are applied to convert the NO_x emissions to CO₂ emissions.

4 Discussion

We showed how the divergence method developed for estimating NO_x emissions from satellite observations can be applied to CO₂ retrievals that will become available from the upcoming CO2M mission. There are several aspects that make the analysis of the CO₂ divergence more difficult than for NO_x. For example:

1) CO₂ has a long atmospheric lifetime which complicates the analysis and makes the divergence fields more blurry and causes mixing of the plume signal;

2) CO₂ has a large atmospheric background (of about 400 ppm, compared to the enhancements of about 1–3 ppm) that has to be removed before the divergence method can be applied;

3) CO₂ has a larger variety of sources and sinks;

4) The effect of clouds is more restricting for CO₂, as compared to NO_x, since almost completely clear sky conditions are needed for a successful CO₂ retrieval;

5) The CO₂ noise levels are large (0.5–1 ppm) compared to the anthropogenic enhancements and a denoising method has to be applied before the divergence can be calculated.

On the other hand, due to the long lifetime of CO₂, the sink term in Eq. 1 does not need to be accounted for and no assumptions on the lifetime need to be made.

The approach presented here can be extended to other regions or at global scale, which would require different considerations for the choice of the background. The source identification and peak fitting procedure can also be automated as described in previous studies (Fioletov et al., 2016; Beirle et al., 2021; Finch et al., 2022; Lauvaux et al., 2022). A different formulation of the divergence method has been also applied to TROPOMI methane observations (Liu et al., 2021). In principle, the divergence method could be applied to high-resolution retrievals that will become available from the upcoming MethaneSat and CarbonMapper instruments, assuming persistent emissions and sufficient spatio-temporal coverage. On the other hand, such high-resolution observations already have the capability to detect anthropogenic enhancements and methods based on the analysis of individual plumes might be more suitable for estimating emissions.

Several studies in the literature have suggested the use of co-emitted NO₂ observations to guide the detection of CO₂ emission plumes (e.g., Reuter et al., 2019; Kuhlmann et al., 2021) or to convert NO_x to CO₂ emissions using NO_x-to-CO₂ emission ratios (e.g., Liu et al., 2020; Hakkarainen et al., 2021). In this work we tested the latter approach and we were able to compute the source-specific NO_x-to-CO₂ emission ratio for all the power stations analyzed, but not for the city of Berlin. This allowed us to estimate CO₂ emissions also for the Turów power station, while it was not possible with the divergence method and peak fitting. In the case of Turów, the NO_x-to-CO₂ emission ratio was however based on a limited number (4) of plumes which produces a larger statistical uncertainty. In general, analysing NO_x-to-CO₂ emission ratios is quite challenging due to the large uncertainties, as also noted by Kuhlmann et al. (2021). Additional challenges are posed by the fact that the NO_x-to-CO₂ emission ratios might not be constant in time. In general, the NO_x emissions are decreasing faster than the CO₂ emissions due to the implementation of cleaner technologies (in terms of NO_x emissions), corresponding to decreasing NO_x-to-CO₂ emission ratios. This can be an issue also when considering emission ratios from slowly updating emission inventories. Furthermore, even when the NO_x emissions can be successfully estimated from (also quite small) emission sources, it can be challenging to obtain the NO_x-to-CO₂ emission ratios from the same space-based observations due to lack of detectable matching NO₂ and CO₂ plumes.

The emissions estimated from individual plumes correspond to the specific time at which the plume is observed and a factor accounting for changing conditions (such as the seasonal cycle) should be taken into account to derive annual values (Kuhlmann et al., 2020a, 2021). In principle, approaches based on temporal averaging like the divergence method do represent the mean conditions over a defined period of time, but the available observations might be scarce or unevenly distributed temporally and spatially. In any case, satellite observations from passive instruments will correspond to clear-sky conditions at the time of the satellite overpass, which means that few observations will be available under persistent cloudy conditions (e.g., in the winter), and no observations will be available during night-time.

An advantage of the divergence method is that it enables the detection of relatively small emission sources that could not be easily detected using individual plumes. In addition, the divergence method allows us to distinguish nearby sources that would be challenging to analyse using a simple method based on EMG fitting. On the other hand, a longer averaging period is required to detect a clear enhancement and to obtain a successful emission estimate from the divergence mean fields, as compared to the EMG fitting.

5 Summary

In this paper we demonstrated how anthropogenic CO₂ emissions may be estimated from (synthetic) satellite observations using the divergence method, originally developed for short-lived gases. We found that the divergence method applied to the CO2M synthetic observations provided robust estimates of the NO_x emissions for non-isolated sources (as highlighted by Beirle et al., 2019, 2021), even though the swath of the upcoming CO2M satellites will be much narrower (∼250 km) than the current TROPOMI swath (∼2,400 km). In general, the CO2M mission requirements are not dictated by applications based on temporal averaging, but are mostly designed to detect individual emission plumes. We found that the estimated CO₂ emissions are in agreement with the expected values, although with larger uncertainties compared to NO_x.

From a technical point of view, denoising the CO₂ observations before calculating the divergence is necessary to identify the emission sources from the divergence maps. The source-specific CO₂ emission estimates can vary depending on the denoising method applied. We noted that calculating the divergence before averaging rather than the reverse (as done in previous studies), reduces the effect of missing data and produces less noisy spatial patterns. The NO_x emission estimates derived by fitting the exponentially-modified Gaussian function are in excellent agreement with the divergence method, although the NO_x lifetime is underestimated (about 50% lower) as compared to the expected lifetime of 4 hours used in the SMARTCARB simulations. Overall, the divergence method offers a valuable tool for estimating CO₂ emissions from point sources, along with approaches based on inverse modeling and individual plume analysis (e.g., mass balance).

Data Availability Statement

Publicly available datasets were analyzed in the study. This data can be found here: https://doi.org/10.5281/zenodo.4048228.

Author Contributions

JH and II conducted the analysis and wrote the first draft. EK assisted in the analysis, provided the denoising algorithm and texts related to denoising and divergence method theory. MS provided input for analysing the NOx-to-CO₂ emission ratios. JT coordinated the work in the CoCO2 project (Task 4.2). GK and DB provided critical expertise on the SMARTCARB dataset. All authors provided comments and input to the final version of the manuscript.

Funding

The team acknowledge funding from the H2020 project CoCO2 (grant no. 958927). The FMI team also acknowledge the funding and support from the ESA-funded DACES project. The synthetic dataset used in this study was created in the ESA-funded SMARTCARB project. Funding from the Academy of Finland is also acknowledged (grant numbers 336798, 337552 and 331829).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frsen.2022.878731/full#supplementary-material

References

Beirle, S., Boersma, K. F., Platt, U., Lawrence, M. G., and Wagner, T. (2011). Megacity Emissions and Lifetimes of Nitrogen Oxides Probed from Space. Science 333, 1737–1739. doi:10.1126/science.1207824

PubMed Abstract | CrossRef Full Text | Google Scholar

Beirle, S., Borger, C., Dörner, S., Eskes, H., Kumar, V., de Laat, A., et al. (2021). Catalog of NO_x Emissions from Point Sources as Derived from the Divergence of the NO₂ Flux for TROPOMI. Earth Syst. Sci. Data 13, 2995–3012. doi:10.5194/essd-13-2995-2021

CrossRef Full Text | Google Scholar

Beirle, S., Borger, C., Dörner, S., Li, A., Hu, Z., Liu, F., et al. (2019). Pinpointing Nitrogen Oxide Emissions from Space. Sci. Adv. 5. doi:10.1126/sciadv.aax9800

CrossRef Full Text | Google Scholar

Bovensmann, H., Buchwitz, M., Burrows, J. P., Reuter, M., Krings, T., Gerilowski, K., et al. (2010). A Remote Sensing Technique for Global Monitoring of Power Plant CO₂ Emissions from Space and Related Applications. Atmos. Meas. Tech. 3, 781–811. doi:10.5194/amt-3-781-2010

CrossRef Full Text | Google Scholar

Brunner, D., Kuhlmann, G., Marshall, J., Clément, V., Fuhrer, O., Broquet, G., et al. (2019). Accounting for the Vertical Distribution of Emissions in Atmospheric CO₂ Simulations. Atmos. Chem. Phys. 19, 4541–4559. doi:10.5194/acp-19-4541-2019

CrossRef Full Text | Google Scholar

Dabov, K., Foi, A., Katkovnik, V., and Egiazarian, K. (2007). Image Denoising by Sparse 3-D Transform-Domain Collaborative Filtering. IEEE Trans. Image Process. 16, 2080–2095. doi:10.1109/TIP.2007.901238

PubMed Abstract | CrossRef Full Text | Google Scholar

de Foy, B., Wilkins, J. L., Lu, Z., Streets, D. G., and Duncan, B. N. (2014). Model Evaluation of Methods for Estimating Surface Emissions and Chemical Lifetimes from Satellite Data. Atmos. Environ. 98, 66–77. doi:10.1016/j.atmosenv.2014.08.051

CrossRef Full Text | Google Scholar

Finch, D. P., Palmer, P. I., and Zhang, T. (2022). Automated Detection of Atmospheric NO₂ Plumes from Satellite Data: A Tool to Help Infer Anthropogenic Combustion Emissions. Atmos. Meas. Tech. 15, 721–733. doi:10.5194/amt-15-721-2022

CrossRef Full Text | Google Scholar

Fioletov, V. E., McLinden, C. A., Krotkov, N., Li, C., Joiner, J., Theys, N., et al. (2016). A Global Catalogue of Large SO₂ Sources and Emissions Derived from the Ozone Monitoring Instrument. Atmos. Chem. Phys. 16, 11497–11519. doi:10.5194/acp-16-11497-2016

CrossRef Full Text | Google Scholar

Fioletov, V. E., McLinden, C. A., Krotkov, N., and Li, C. (2015). Lifetimes and Emissions of SO₂ from Point Sources Estimated from OMI. Geophys. Res. Lett. 42, 1969–1976. doi:10.1002/2015GL063148

CrossRef Full Text | Google Scholar

Fioletov, V., McLinden, C. A., Kharol, S. K., Krotkov, N. A., Li, C., Joiner, J., et al. (2017). Multi-Source SO₂ Emission Retrievals and Consistency of Satellite and Surface Measurements with Reported Emissions. Atmos. Chem. Phys. 17, 12597–12616. doi:10.5194/acp-17-12597-2017

CrossRef Full Text | Google Scholar

Goldberg, D. L., Lu, Z., Streets, D. G., de Foy, B., Griffin, D., McLinden, C. A., et al. (2019). Enhanced Capabilities of TROPOMI NO₂: Estimating NO_X from North American Cities and Power Plants. Environ. Sci. Technol. 53, 12594–12601. doi:10.1021/acs.est.9b04488

PubMed Abstract | CrossRef Full Text | Google Scholar

Haario, H., Saksman, E., and Tamminen, J. (2001). An Adaptive Metropolis Algorithm. Bernoulli 7, 223. doi:10.2307/3318737

CrossRef Full Text | Google Scholar

Hakkarainen, J., Ialongo, I., Maksyutov, S., and Crisp, D. (2019). Analysis of Four Years of Global XCO₂ Anomalies as Seen by Orbiting Carbon Observatory-2. Remote Sens. 11, 850. doi:10.3390/rs11070850

CrossRef Full Text | Google Scholar

Hakkarainen, J., Ialongo, I., and Tamminen, J. (2016). Direct Space‐Based Observations of Anthropogenic CO₂ Emission Areas from OCO‐2. Geophys. Res. Lett. 43, 11,400–11,406. doi:10.1002/2016GL070885

CrossRef Full Text | Google Scholar

Hakkarainen, J., Szeląg, M. E., Ialongo, I., Retscher, C., Oda, T., and Crisp, D. (2021). Analyzing Nitrogen Oxides to Carbon Dioxide Emission Ratios from Space: A Case Study of Matimba Power Station in South Africa. Atmos. Environ. X 10, 100110. doi:10.1016/j.aeaoa.2021.100110

CrossRef Full Text | Google Scholar

Hill, T., and Nassar, R. (2019). Pixel Size and Revisit Rate Requirements for Monitoring Power Plant CO₂ Emissions from Space. Remote Sens. 11, 1608. doi:10.3390/rs11131608

CrossRef Full Text | Google Scholar

Hoffmann, L., Günther, G., Li, D., Stein, O., Wu, X., Griessbach, S., et al. (2019). From ERA-Interim to ERA5: The Considerable Impact of ECMWF's Next-Generation Reanalysis on Lagrangian Transport Simulations. Atmos. Chem. Phys. 19, 3097–3124. doi:10.5194/acp-19-3097-2019

CrossRef Full Text | Google Scholar

Ialongo, I., Stepanova, N., Hakkarainen, J., Virta, H., and Gritsenko, D. (2021). Satellite-Based Estimates of Nitrogen Oxide and Methane Emissions from Gas Flaring and Oil Production Activities in Sakha Republic, Russia. Atmos. Environ. X 11, 100114. doi:10.1016/j.aeaoa.2021.100114

CrossRef Full Text | Google Scholar

Jacob, D. J. (1999). Introduction to Atmospheric Chemistry. Princeton, New Jersey: Princeton University Press.

Google Scholar

Janssens-Maenhout, G., Pinty, B., Dowell, M., Zunker, H., Andersson, E., Balsamo, G., et al. (2020). Toward an Operational Anthropogenic CO₂ Emissions Monitoring and Verification Support Capacity. Bull. Am. Meteorological Soc. 101, E1439–E1451. doi:10.1175/BAMS-D-19-0017.1

CrossRef Full Text | Google Scholar

Kiel, M., Eldering, A., Roten, D. D., Lin, J. C., Feng, S., Lei, R., et al. (2021). Urban-Focused Satellite CO₂ Observations from the Orbiting Carbon Observatory-3: A First Look at the Los Angeles Megacity. Remote Sens. Environ. 258, 112314. doi:10.1016/j.rse.2021.112314

CrossRef Full Text | Google Scholar

Koene, E., Brunner, D., Kuhlmann, G., Hakkkarainen, J., Le Brazidec, J. D., and Broque, G. (2021). Documentation of Plume Detection and Quantification Methods. Tech. Rep., Empa. CoCO2: Prototype System for a Copernicus CO2 Service. ECMWF. Available on https://www.coco2-project.eu/sites/default/files/2022-03/CoCO2-D4-3-V1-0.pdf.

Google Scholar

Kuhlmann, G., Broquet, G., Marshall, J., Clément, V., Löscher, A., Meijer, Y., et al. (2019). Detectability of CO₂ Emission Plumes of Cities and Power Plants with the Copernicus Anthropogenic CO₂ Monitoring (CO2M) Mission. Atmos. Meas. Tech. 12, 6695–6719. doi:10.5194/amt-12-6695-2019

CrossRef Full Text | Google Scholar

Kuhlmann, G., Brunner, D., Broquet, G., and Meijer, Y. (2020a). Quantifying CO₂ Emissions of a City with the Copernicus Anthropogenic CO₂ Monitoring Satellite Mission. Atmos. Meas. Tech. 13, 6733–6754. doi:10.5194/amt-13-6733-2020

CrossRef Full Text | Google Scholar

[Dataset] Kuhlmann, G., Clément, V., Marshall, J., Fuhrer, O., Broquet, G., Schnadt-Poberaj, C., et al. (2020b). Synthetic XCO₂, CO and NO₂ Observations for the CO2M and Sentinel-5 Satellites. Zenodo. doi:10.5281/zenodo.4048228

CrossRef Full Text | Google Scholar

Kuhlmann, G., Henne, S., Meijer, Y., and Brunner, D. (2021). Quantifying CO₂ Emissions of Power Plants with CO₂ and NO₂ Imaging Satellites. Front. Remote Sens. 2, 14. doi:10.3389/frsen.2021.689838

CrossRef Full Text | Google Scholar

Laine, M. (2008). Adaptive MCMC Methods with Applications in Environmental and Geophysical Models. Helsinki, Finland: Finnish Meteorological Institute Contributions.

Google Scholar

Lauvaux, T., Giron, C., Mazzolini, M., d’Aspremont, A., Duren, R., Cusworth, D., et al. (2022). Global Assessment of Oil and Gas Methane Ultra-Emitters. Science 375, 557–561. doi:10.1126/science.abj4351

PubMed Abstract | CrossRef Full Text | Google Scholar

Lebrun, M. (2012). An Analysis and Implementation of the BM3D Image Denoising Method. Image Process. Line 2, 175–213. doi:10.5201/ipol.2012.l-bm3d

CrossRef Full Text | Google Scholar

Levin, A., and Nadler, B. (2011). “Natural Image Denoising: Optimality and Inherent Bounds,” in CVPR 2011, Colorado Springs, CO, USA, 20-25 June 2011 (Piscataway, New Jersey: IEEE), 2833–2840. doi:10.1109/cvpr.2011.5995309

CrossRef Full Text | Google Scholar

Liu, F., Duncan, B. N., Krotkov, N. A., Lamsal, L. N., Beirle, S., Griffin, D., et al. (2020). A Methodology to Constrain Carbon Dioxide Emissions from Coal-Fired Power Plants Using Satellite Observations of Co-Emitted Nitrogen Dioxide. Atmos. Chem. Phys. 20, 99–116. doi:10.5194/acp-20-99-2020

CrossRef Full Text | Google Scholar

Liu, F., Tao, Z., Beirle, S., Joiner, J., Yoshida, Y., Smith, S. J., et al. (2022). A New Method for Inferring City Emissions and Lifetimes of Nitrogen Oxides from High-Resolution Nitrogen Dioxide Observations: A Model Study. Atmos. Chem. Phys. 22, 1333–1349. doi:10.5194/acp-22-1333-2022

CrossRef Full Text | Google Scholar

Liu, M., van der A, R., van Weele, M., Eskes, H., Lu, X., Veefkind, P., et al. (2021). A New Divergence Method to Quantify Methane Emissions Using Observations of Sentinel‐5P TROPOMI. Geophys. Res. Lett. 48, e2021GL094151. doi:10.1029/2021GL094151

CrossRef Full Text | Google Scholar

Meijer, Y., Boesch, H., Bombelli, A., Brunner, D., Buchwitz, M., Ciais, P., et al. (2020). Copernicus CO₂ Monitoring Mission Requirements Document. Tech. Rep., European Space Agency. Issue 3.0, EOP-SM/3088/YM-ym. ESA. Available at: https://esamultimedia.esa.int/docs/EarthObservation/CO2M_MRD_v3.0_20201001_Issued.pdf.

Google Scholar

Nassar, R., Hill, T. G., McLinden, C. A., Wunch, D., Jones, D. B. A., and Crisp, D. (2017). Quantifying CO₂ Emissions from Individual Power Plants from Space. Geophys. Res. Lett. 44, 10,045–10,053. doi:10.1002/2017GL074702

CrossRef Full Text | Google Scholar

Reuter, M., Buchwitz, M., Schneising, O., Krautwurst, S., O'Dell, C. W., Richter, A., et al. (2019). Towards Monitoring Localized CO₂ Emissions from Space: Co-Located Regional CO₂ and NO₂ Enhancements Observed by the OCO-2 and S5P Satellites. Atmos. Chem. Phys. 19, 9371–9383. doi:10.5194/acp-19-9371-2019

CrossRef Full Text | Google Scholar

Varon, D. J., Jacob, D. J., McKeever, J., Jervis, D., Durak, B. O. A., Xia, Y., et al. (2018). Quantifying Methane Point Sources from Fine-Scale Satellite Observations of Atmospheric Methane Plumes. Atmos. Meas. Tech. 11, 5673–5686. doi:10.5194/amt-11-5673-2018

CrossRef Full Text | Google Scholar

Verstraeten, W. W., Boersma, K. F., Douros, J., Williams, J. E., Eskes, H., Liu, F., et al. (2018). Top-Down NO_X Emissions of European Cities Based on the Downwind Plume of Modelled and Space-Borne Tropospheric NO₂ Columns. Sensors 18, 2893. doi:10.3390/s18092893

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, D., Lin, J. C., Oda, T., and Kort, E. A. (2020). Space-Based Quantification of Per Capita CO₂ Emissions from Cities. Environ. Res. Lett. 15, 035004. doi:10.1088/1748-9326/ab68eb

CrossRef Full Text | Google Scholar