Transport Properties of Critical Sulfur Hexafluoride From Multiscale Analysis of Density Fluctuations

1 Introduction

Phase transition reveals materials properties near the critical point, where the buoyancy that leads to the raising of the vapor bubbles and the gravitational pulling that determines the falling of the liquid droplets determines the formation of a flat meniscus by the gravity-induced coalescence of bubbles or droplets (Beysens et al., 2000; Beysens and Garrabos, 2000). Earth’s gravity limits both the spatial extent of the critical region and the duration over which critical fluctuations can be observed. Weightlessness near critical point experiments also benefits from the critical slowing down that enables the study of fast processes on a more accessible time scale. In addition to its practical material science applications, the study of critical fluctuations and phase separation processes leads to a better understanding of critical scaling universality and its generalization to all fluids.

The DECLIC (Dispositif pour l’Etude de la Croissance et des Liquides Critiques) is a multi-user facility to study critical fluids’ behavior and directional solidification of transparent alloys. The DECLIC is a joint NASA and CNES research program onboard the International Space Station (ISS). The compact design contains three inserts. We refer here only to the ALI (Alice Like Insert) dedicated to studying sulfur hexafluoride (SF₆) as a near-ambient temperature critical fluid. The program covers a complete characterization of SF₆, ranging from thermodynamic quantities measurements (thermal diffusivity, heat capacity, and turbidity near the critical point) to boiling effects studies (Pont et al., 2011).

We analyzed SF₆ critical fluctuations very near the critical point, within 0.2 mK, using high-resolution DECLIC images recorded in 2012. For this purpose, we used a supercritical SF₆ sample brought from an initial state, which is already in a liquid-vapor two-phase state very slightly below the critical temperature T_c = 45.557 297°C to a temperature 0.2 mK below its initial temperature by a temperature quench (Oprisan et al., 2012; Oprisan et al., 2014).

In the case of pure fluids near the critical point, their critical behavior is described by a single variable, i.e., the fluid’s density, which is the natural choice for the order parameter in such systems (Domb et al., 2001). The order parameter for pure fluids is defined as M^± = (ρ^± − ρ_c)/ρ_c, where ρ^± is the mean density of liquid and vapor phase, respectively, and ρ_c is the critical density (Beysens, 1997; Lecoutre et al., 2009). The gas-liquid coexistence curve is universal and given by $M=B{(1-T/T_c)}^{\beta }$, where B = 1.60 (Zappoli et al., 2015). Additionally, the volume fraction of the minority phase, ϕ, is determined by the lever rule (Beysens, 1997; Perrot et al., 1999; Oprisan, 2006; Oprisan et al., 2008):

$\varphi =\frac{M^{+}-M}{M^{+}-M^{-}}=\frac{1}{2}\left(1-{\left(1+\frac{\mathrm{\Delta }T}{\delta T}\right)}^{-\beta }\right),(1)$

where δT = T_c − T_f is the quench depth with respect to the critical temperature, T_c = 45.557 297°C, ΔT = T_c − T_cx is the coexistence temperature depth with T_cx = 46.0072°C, β = 0.32575 is a universal exponent and M^± are the order parameters (relative densities) of liquid and vapor phase, respectively. According to the generalized nucleation processes (Schmelzer et al., 2000; Schmelzer, 2001; Schmelzer and Schmelzer, 2001; Schmelzer et al., 2006), the volume fraction determines the evolution of large order parameter fluctuations. At large volume fractions, hydrodynamic flows during a coalescence process between domains can induce other coalescence events, and so on. In this case, the domain size grows as t¹, and the phase separating pattern is interconnected. A small volume fraction leads to domain collisions via purely Brownian motion. As a result, liquid droplets and vapor bubbles grow slower as t^1/3, and the pattern is disconnected as an assembly of drops or bubbles (Nikolayev et al., 1996; Beysens and Garrabos, 2000). The DECLIC uses light transmitted through a Direct Observation Cell (DOC) to record high-resolution images of SF₆ critical fluctuations.

Dynamic light scattering (DLS), has long used for measuring diffusivity in colloids (Nossal et al., 1971) and thermal diffusivity in fluids near their critical point or mutual diffusion coefficient in binary liquids near their miscibility critical point (see, e.g., (Levy et al., 1982)). DLS yields the normalized intermediate scattering function (ISF) (Berne and Pecora, 2000), which probes density relaxation processes at length scale 2π/q. The Dynamic Differential Microscopy (DDM) has been used for almost two decades and is a well-established method for analyzing images in a microscope setting. Among the early studies using DDM are the seminal works by Cerbino and Trappe (Cerbino and Trappe, 2008) The fundamental aspects of DDM method and its applications to microscopy were explained in by Giavazzi et al. (Giavazzi et al., 2009). Spectral analysis is a well-established method that applies to stationary and theoretically periodic signals to extract, for example, information regarding the characteristic size of fluctuations (Oprisan, 2006; Oprisan et al., 2008; Oprisan et al., 2011; Oprisan et al., 2012; Oprisan et al., 2014). Additional information regarding the temporal dynamics of fluctuations can be obtained by using the Dynamic Differential Microscopy (DDM) (see Supplementary Section S5.1 and (Vailati and Giglio, 1998; Bondarchuk et al., 2005; Croccolo, 2006)). For example, the DDM allows the computation of the dynamic structure factor and the relaxation time of dynamical phenomena (Cerbino and Trappe, 2008; Cerbino and Vailati, 2009; Vailati et al., 2011; Croccolo et al., 2016b). DDM has also been applied to investigating equilibrium fluctuations close to critical conditions in binary mixtures (Giavazzi et al., 2016a) and under nonequilibrium conditions in dense colloids (Cerbino and Trappe, 2008; Cerbino and Vailati, 2009; Vailati et al., 2011; Croccolo et al., 2016b; Giavazzi et al., 2016b). The DDM method has recently been applied to critical density fluctuations from light scattering images of systems approaching the liquid-gas critical point of pure fluids from the homogeneous domain (Oprisan et al., 2021a). In such experiments, the results of image processing performed with the DDM are consistent with the modern theory of critical phenomena (Oprisan et al., 2021a). When compared against the traditional light scattering method, the DDM has the advantage of a simpler setup and the possibility to observe fluctuations in the direct space, which facilitates the interpretation of phenomena. Additionally, the analysis of fluctuations in the reciprocal space, gives the normalized intermediate scattering function (ISF), which allows the investigations of dynamics of fluctuations and measurements of correlation time. However, the DDM requires a correction for the optical transfer function, except for some very special Schlieren optical setups (Croccolo et al., 2006). In practice, for sufficiently large wave vectors q, the DDM does not need data correction (Cerbino and Vailati, 2009).

For experiments performed within µK of the critical point, finite-size effects limit the wavenumbers range over which thermophysical properties can be accurately measured. Additionally, short recordings very near the critical point in the vicinity of the thermal quench that steps through T_c are affected by transient and non-stationary density fluctuations. Since spectral methods are not well-suited to analyze transient and non-stationary data, a necessary pre-processing step is the decomposition of the original signal into orthogonal and stationary IMFs (Huang et al., 1998a; Jean et al., 2003; Nunes et al., 2003; Huang et al., 2010; Liu and Chen, 2018). We previously applied the Bidimensional Empirical Mode Decomposition (BEMD) to separate density fluctuation images into multiple spatial scales and investigated their dynamics with the Fourier-based DDM method (Oprisan et al., 2021a). The BEMD decomposes the original fluctuation images into orthogonal images (see Supplementary Section S5.2 for more details and (Oprisan et al., 2021a)). Data-driven approaches, such as the BEMD, are concerned with identifying the relationship between the inputs and the outputs of a complex system without making any hypotheses regarding the internal processes that led to the observed output (Wang et al., 2006). The EMD method better describes the local time scale instantaneous frequencies and does not need any predetermined basis functions (Huang et al., 1998a; Li, 2006). The EMD-based techniques are suitable for analyzing nonlinear and nonstationary data. With the EMD-based methods, data are decomposed into a small number of intrinsic mode functions (IMFs), which are derived based on the local characteristic time (for time series) or spatial (for images) scale of the data itself and describe the dynamic behavior from high to low frequencies (Huang et al., 1998a; Huang et al., 2003; Wu and Huang, 2004). All the IMFs are orthogonal to each other (Huang et al., 1998a; Wu et al., 2015). The first EMD-based study analyzed the movement of the ocean waves (Huang et al., 1998a; Zhang et al., 2008). Subsequently, the EMD method was applied in social science to investigate dengue hemorrhagic fever (Cummings et al., 2004), the crude oil price (Zhang et al., 2008; Yu et al., 2010), and the financial markets. The EMD method has been used for describing the phase distribution and phase correlation of financial time series (Wu et al., 2006; Wu, 2012) and the damped oscillations in the ratios of stock market indices (Wu, 2012). Financial crisis forecasting and foreign exchange rate forecasting have been investigated with this method, and the results are significantly improved compared with those obtained with conventional neural networks (Yu et al., 2010; Lin et al., 2012). Among other relevant applications of time series analysis using EMD, we mention earthquake accelerograms (Raghukanth and Sangeetha, 2012), pulmonary blood pressure investigation (Huang et al., 1998b), and vibration analysis damage (Garcia-Perez et al., 2013). The BEMD has been extensively applied to image denoising (Ben Arfia et al., 2011; Liu and Chen, 2018), image analysis (Jean et al., 2003; Nunes et al., 2003), texture analysis (Nunes et al., 2005), facial image analysis (Saha et al., 2016), multispectral and panchromatic remote sensing (Dong et al., 2014), bamboo forest analysis (Liu et al., 2016), and gravity anomalies study for mining industry (Huang et al., 2010).

Thermophysical properties can be determined from fluctuation images at different spatial scales. Using this approach, one could investigate how the power-law exponents for structure factor scaling change with the wavenumber range. One can also explore the relationship between the correlation time of small versus large fluctuations and estimate the diffusion coefficient for fluctuations of different sizes (Oprisan et al., 2021a). Although there is no rule for selecting the number of orthogonal decompositions, called Intrinsic Mode Functions (IMFs), we used three IMFs and a residual in this study. The main reason for our choice is that the wavenumbers are separated in low (where we expect large sinusoidal fluctuations of the signal affected by the optical transfer function of the experimental setup and also poor Fourier space statistics), intermediate (where the optical transfer function may play negligible role and data do not need correction), and large (where the data might be recorded close to the spatial sampling resolution of the camera).

The paper is organized as follows. The DECLIC setup is reviewed in Section 2, and a brief description of optical features is given in Section 2.1. The detailed results obtained using the DDM method for extracting the structure factor and the correlation time of fluctuations are discussed in Section 3.1. The orthogonal separation of original images in IMFs and the corresponding thermophysical properties are discussed in Section 3.2. The concluding remarks in Section 4 offer a review and a context for the current multiscale analysis of critical fluctuations. The two subsections of the Appendix briefly review the main characteristic features of the DDM technique (Supplementary Section S5.1) and the BEMD method (Supplementary Section S5.2), with relevant references.

2 Experimental Setup

The DECLIC (Dispositif pour l‘Etude de la Croissance et des Liquides Critiques) has a flexible design with different inserts to accommodate a thermostat and a sample cell unit (SCU) with the fluid to be studied. It also contains most of the electronics associated with user-dedicated temperature sensors. The ALI (Alice Like Insert) has been used for studying phase transitions near the critical point at room temperature, critical fluids, and boiling crisis. DECLIC is a shared project by the CNES (Centre National d‘Etudes Spatiales) center of Toulouse (France) and NASA’s Marshall Space Flight Center (Huntsville, United States).

The DOC was filled with SF₆ at the (temperature, pressure, density) critical coordinates of the gas-liquid critical point, i.e., T_c = 45.557 297°C, p_c = 3.73 MPa, and ρ_c = 742.6 kg m⁻³. The design of this cell is briefly reviewed below (see also (Garrabos et al., 2010)).

The fluid sample volume observed by light transmission corresponds to a cylindrical volume of inner diameter D_cyl = 10.6 mm and inner thickness e_cyl = 4.115 mm. The total fluid volume of the cell is 0.463 cm³ (including a dead volume mainly due to filling holes), corresponding to a total SF₆ mass of 0.353 g. The mean density was ρ = ρ_c + (0.09 ± 0.01) %. Three small (250 µm bead diameter) thermistors are located inside the fluid volume so that three local temperatures are measured close to the gas-liquid interface in the microgravity environment. The thermistors are visible in Figures 1A,B. The DOC also allows collecting the light scattered at small angles and 90°. We analyzed 1,922 images taken very close to the critical point and recorded at 11.5 frames per second (approximately 173 s total recording). Based on our estimated value of the correlation length ξ ≈ (2.4 ± 0.2) µm (see Table 1), the first image in the series is 99 µK above critical temperature T_c = 45.557 297°C.

FIGURE 1

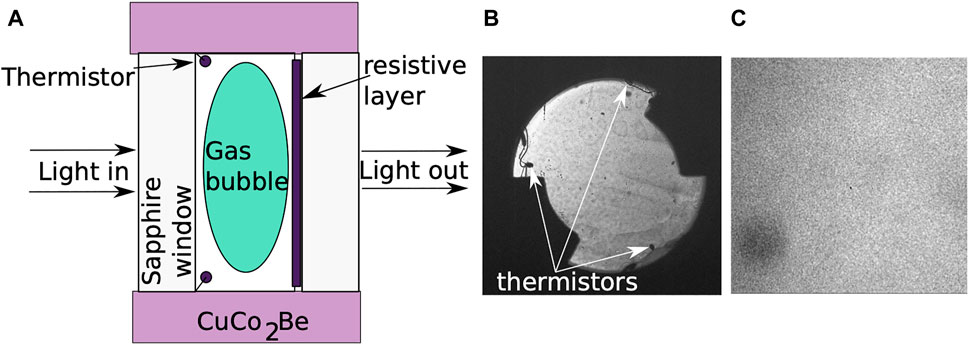
FIGURE 1. The Sample Cell Unit (SCU) schematic representation shows the SF₆ fluid in a CuCo₂Be cylinder sandwiched between two sapphire windows (A). There is a resistive layer on one window that generates a heat pulse for boiling studies. A full view of the transmitted light through the Direct Observation Cell (DOC) reveals the location of thermistors (B). A microscope objective was also used for recording a small 1 × 1 mm² object image from the center of the DOC (C).

TABLE 1

TABLE 1. Effective diffusion coefficient obtained by fitting the correlation time of fluctuations shown in Figure 3D with Eq. 4 at large wavenumbers (first row). The critical wavenumber was obtained from the peak of the smooth spline interpolation of correlation time data shown in Figure 3D (second row). The peak wavenumber q_peak of the structure factor S(q) shown in Figure 3C is shown on the third row. The correlation wavenumber, i.e., q_corr = 1/ξ, was obtained by fitting S(q) with Eq. 3 (fourth row). Based on the scaling law of the correlation length ξ given by Eq. 5, the estimated distance from critical temperature shows strong dependence on the IMF order.

2.1 Optical Setup

The following description of the optical characteristics is similar to ALICE 2 facility used on MIR experiments (see (Lecoutre et al., 2014; Garrabos et al., 2015; Lecoutre et al., 2015; Mota et al., 2015; Nikolayev et al., 2015; Garrabos et al., 2016; Durieux et al., 2017; Garrabos et al., 2018) and references therein). ALI insert has a modular optical design with a “source optical box” containing the laser, different filters, and photodiodes, the “thermostat box” that includes the sample cell unit, and a “collecting optical box” that contains the CCD and additional photodiodes (Lecoutre et al., 2009). The complete optical scheme is detailed in (Marcout et al., 1994), and the optical performances are precisely analyzed for other experiments, such as turbidity measurements (Lecoutre et al., 2009).

The fluid sample cell is visualized through light transmission normal to the windows using LED illumination with a spectrum centered around 660 nm. ALI instrumentation works with a wide field of view of 10 × 10 mm² object image at 30 µm resolution. It also records small field of view images of approximately 1 × 1 mm² object image from the center of the DOC with a microscope objective within Δx = 3.5 µm resolution. All images analyzed in this study were of the small field-of-view type obtained with the optical microscope at the focal plane in the middle of fluid layer, centered on the optical axis of the fluid sample. We analyzed N_img = 1,922 recorded with a sampling rate of f_s = 11.5 frames per second (the time interval between two successive images is t_s = 1/f_s ≈ 87 ms). All images $I(\vec{r},t)$ are digitized with a spatial vector given by $\vec{r}=\mathrm{\Delta }x(n_x,n_y)$, where n_x and n_y are integer numbers comprised between 1 and the image size M = 1,024 pixels.

Figure 2A1 shows an original image and its corresponding power spectrum in the Fourier space (q_x, q_y) = q_min(m_x, m_y), with m_x, m_y integers comprised between − M_w/2 and M_w/2, where M_w is the Fourier window size, and q_min = 2π/(MΔx) = 2π/W in which W ≈ 1 mm is the side of the small field-of-view image (see Figure 2A2). In general, the Fourier window size M_w is a power of two. In this study, the Fourier window size M_w was the same as the image size M = 1,024. The power spectrum has azimuthal symmetry, as illustrated by the “ring” surrounding the DC component at the center of Figure 2A2. Although all spectra have symmetry, the azimuthal symmetry is not perfect for all spectra. For some IMFs (see Figures 2C2–D2), the vertical and horizontal anisotropy of the objects present in these IMFs leads to a rounded square shape of the power spectra for some wavenumbers. Due to the azimuthal symmetry of the power spectra (see Figures 2A2–E2), only the azimuthal averages of the power spectra versus the magnitude of the wavenumber $q=\sqrt{q_x^2+q_y^2}$ = $q_{\min }\sqrt{m_x^2+m_y^2}$ were considered for the DDM analysis (see the red continuous line insets in Figures 2A2–E2). The azimuthal average is calculated over thin rings with nearly the same wave vector modulus $q=\sqrt{q_x^2+q_y^2}$. Each ring has a width of 1 unit in the discrete Fourier space. Since the DC component of the power spectrum near q = 0 is orders of magnitude larger than the rest of the power spectrum, and because it does not contribute any valuable information to the subsequent analysis, we removed it from the insets. The DC component leakage into adjacent wavenumbers and significantly affects the residual image’s power spectrum shown in Figure 2E2. The wavenumber resolution in Fourier space is q_min = 2π/W ≈ 62.8 cm⁻¹, where W ≈ 1 mm is the side of the small field-of-view image. At small wave vectors, the azimuthal averaging statistic is relatively poor, but for large wavenumbers, the number of independent samples in a single wavevector ring $q=\sqrt{q_x^2+q_y^2}$ = $q_{\min }\sqrt{m_x^2+m_y^2}$ increases proportionally to π × m, in which m is the number of the channel which varies from 1 to $M_w/\sqrt{2}$, where M_w is the window size of Fourier transform. Since our images are square, m = m_x = m_y. At the maximum wave vector $m\approx M_w/\sqrt{2}\approx$ 724, which results in over 2,000 statistically independent samples for the respective value of the wavevector q. The wavevector can be expressed either in Fourier space integers 1 ≤ m ≤ M_w for an M_w-point Fourier transform or in corresponding cm units by using the Fourier resolution formula q = m × q_min.

FIGURE 2

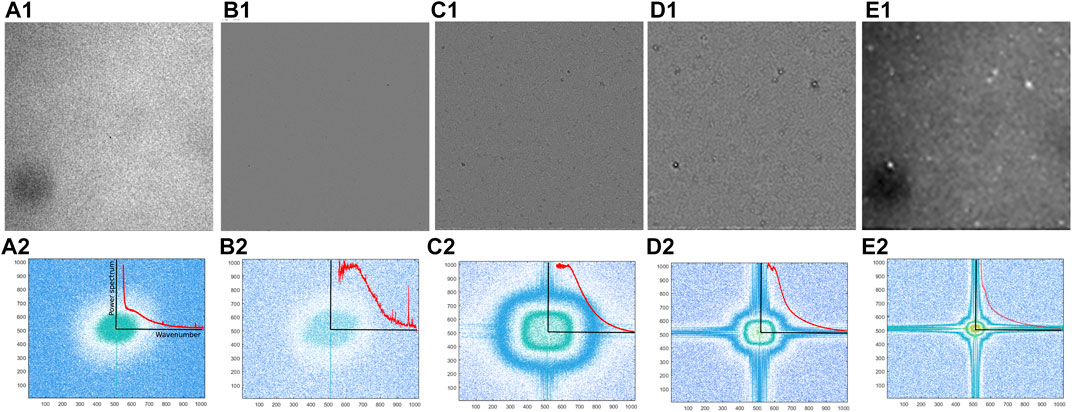
FIGURE 2. A small field of view original image (A1) was decomposed in three Intrinsic Mode Functions (IMFs) using the Bidimensional Empirical Mode Decomposition (BEMD) method. The IMFs are shown in panels (B1–D1) together with the residual image (E1). The M × M pixels image produced the corresponding M_w-point Fourier images in the Fourier space wavenumbers (q_x, q_y) shown in (A2–E2) (we considered M = M_w = 1,024). Each power spectrum shown in (A2–E2) has radial symmetry as indicated by the round spatial patterns. As a result of the azimuthal symmetry of power spectra, only radial averages of power spectra versus the magnitude of the wavenumber $q=\sqrt{q_x^2+q_y^2}$ were used for DDM analysis, and they are shown with the continuous line as an inset in (A2–E2). The very large values of the power spectrum near q = 0 (the DC component) were removed from the insets.

3 Results

Our approach to the multiscale investigation of thermal fluctuations very near the critical point of SF₆ was first to separate spatial scales using a data-driven BEMD method and then apply the DDM method to determine the structure factor and the correlation time of fluctuations at each spatial scale. Fourier-based methods rely on the data stationarity assumption and cannot be applied to transient phenomena (Hayes, 1996). However, our very short data set recorded near the thermal quench that stepped through the critical temperature most likely includes transient phenomena. A possible workaround is the use of wavelets (Blanco et al., 1998; Garcia-Perez et al., 2013; Sang, 2013) instead of the Fourier basis. However, the wavelet-based analysis of transient phenomena is strongly dependent on the selected mother wavelet. Furthermore, the EMD method outperforms the wavelet method for waveform reconstruction (Labate et al., 2013). The EMD does not assume any basis functions; the decomposition is data-driven and can be applied to transient, non-linear, and non-stationary signals (Huang et al., 1998a; Huang, 2005; Huang et al., 2009).

3.1 Dynamic Structure Factor From DDM Method for the Original Images

Without repeating the details of the almost two decades old Differential Dynamic Microscopy (DDM) method (see Supplementary Section S5.1 for a brief description and references (Cerbino and Trappe, 2008; Giavazzi et al., 2009)), we only mention novel results based on this revolutionary approach to the dynamic light scattering technique. The DDM is a spectral, Fourier-based image analysis method. The two-dimensional intensity images $I(\vec{r},t)$ are first normalized by the average image intensity to account for light source intensity fluctuations during the measurement, i.e, $i(\vec{r},t)=I(\vec{r},t)/{\overline{I(\stackrel{⃗}{r},t)}}_{\vec{r}}$. The fundamental quantity in DDM is the normalized image difference $\delta i(\vec{r},\mathrm{\Delta }t,t)=i(\vec{r},t+\mathrm{\Delta }t)-i(\vec{r},t)$, where Δt is a delay time between frames (Cerbino and Trappe, 2008). The advantage of considering the image difference is a significant reduction in static scattering coming from dust, scratches on the sample cell, or other static imperfections of the setup (Kessler et al., 2020).

The DDM also uses a moving average of the power spectrum of the fluctuating image $\delta i(\vec{q},\mathrm{\Delta }t,t)=|FFT[\delta i(\vec{r},\mathrm{\Delta }t,t)]{|}^2$ over different reference times t and the same delay Δt to reduce optical noise. Such a moving average is called the image structure function, i.e., $C_m(\vec{q},\mathrm{\Delta }t)={\overline{\delta i(\stackrel{⃗}{q},\mathrm{\Delta }t,t)}}_t$. The reason for the temporal average is to increase “the statistical accuracy of the data” (Cerbino et al., 2017). The number of reference times over which the average is computed N_avg is generally smaller than the correlation time of fluctuations such that fast relaxation processes are not averaged out. In practice, one uses a recursive selection process in which we start with a high enough number of averaged images to reduce the noise and obtain good statistics, e.g., N_avg = 32. Once the correlation time of fluctuations is determined, one can change N_avg and repeat the estimation of the correlation time. By varying the delay time Δt during image fluctuation calculations, one can extract the power spectrum both over the wavenumbers q and elapsed time Δt between frames. The dependence of the power spectrum on the elapsed time Δt between frames contains information on the correlation time of fluctuations. The two-dimensional image structure function probes the sample dynamics in different directions in the $\vec{q}$ plane. Whenever the image structure function bears a circular symmetry, the azimuthal averaging, i.e.,

$C_m\left(q,\mathrm{\Delta }t\right)={\overline{C_m\left(\stackrel{⃗}{q},\mathrm{\Delta }t\right)}}_{\vec{q}}$

is used to obtain the one-dimensional image structure function. The one-dimensional image structure function C_m(q, Δt) “rises until saturating when the images are totally decorrelated” as seen in Figure 3A (Lu et al., 2012).

FIGURE 3

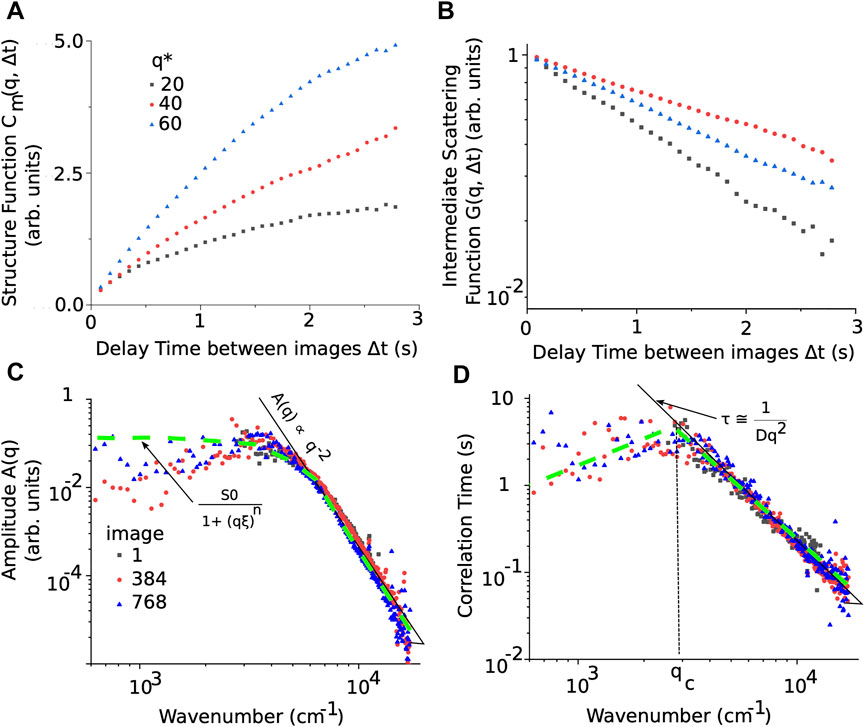
FIGURE 3. The time-dependent structure functions C_m(q, Δt) starts flattening around a delay of 1–3 s between successive images (A). The saturation delay time is determined by the relaxation time of fluctuations and depends on the wavenumber (here, dimensionless wavenumbers q* = q/q_min were used). (B) The linear-log plot of the Intermediate Scattering Function (ISF) represents the function G(q, Δt) in Eq. 2. (C) The amplitude A(q) from Eq. 2 is proportional to the structure factor S(q) for wavenumbers larger than q_cross = 850 cm⁻¹. At large wavenumbers, the amplitude A(q) obeys the power-law A(q) ∝ q⁻² (see the continuous solid black line). Over the range of wavenumbers where A(q) is proportional to S(q), Eq. 3 is a good fit for the experimental data (see thick dashed green line). (D) The correlation time of the fluctuations determines the critical wavenumber q_c and the effective diffusion coefficient D. At large wavenumbers, the correlation time can be approximated by Eq. 4 (see the continuous black line), which allows direct estimation of the effective diffusion coefficient D. The inflection point of the smooth spline interpolation of the correlation time gives a reasonable estimate of the critical wavenumber q_c (see the inflection of thick dashed green curve in panel (D)).

Examples of azimuthal averages of power spectra, such as those shown with the continuous red line in Figures 2A2–E2 insets, versus the delay time Δt for fixed wavenumbers q are shown in Figure 3A. The (one-dimensional) time-dependent structure functions C_m(q, Δt) describes how the spectral power changes with the delay time Δt between images for a fixed wavenumber q, and it is given by (Cerbino and Trappe, 2008; Giavazzi et al., 2009; Lu et al., 2012):

$Cm\left(q,\mathrm{\Delta }t\right)=2A\left(q\right)\left[1-G\left(q,\mathrm{\Delta }t\right)\right]+B\left(q\right),(2)$

where A(q) is an amplitude term that contains information about the static scattering from the sample and the optical system’s transfer function, B(q) is the background contribution to the time-dependent structure functions, and G(q, Δt) is “equivalent” (Lu et al., 2012) of the normalized ISF from the traditional dynamic light scattering experiments (see Figure 3B). For particular optical setups, such as Schlieren and Shadowgraph, the analytical form of the optical transfer function T(q) is known (see (Trainoff and Cannell, 2002; Croccolo et al., 2006; Cerbino and Trappe, 2008; Giavazzi et al., 2009; Oprisan and Leilani Payne, 2013; Croccolo et al., 2016a)).

The effect of DDM moving average on the structure factor and fluctuation correlation time. As mentioned above briefly, DDM relies on the temporal moving average of power spectra to reduce as much as possible the ubiquitous image noise (see (Vailati and Giglio, 1998; Croccolo, 2006; Croccolo et al., 2006; Croccolo et al., 2007; Cerbino and Vailati, 2009; Giavazzi et al., 2009; Vailati et al., 2011; Ortiz de Zárate et al., 2014; Cerbino et al., 2015; Croccolo et al., 2016a; Giavazzi et al., 2016a; Bataller et al., 2016; Croccolo et al., 2016b; Giavazzi et al., 2016b; Cerbino et al., 2017) and references therein) and to compute the structure factor and correlation times over averaged fluctuation images. The number of images over which denoising average is performed depends on the particular conditions of each experiment. As mentioned above, the general recommendations are (see (Vailati and Giglio, 1998; Croccolo, 2006; Croccolo et al., 2006; Croccolo et al., 2007; Cerbino and Vailati, 2009; Giavazzi et al., 2009; Vailati et al., 2011; Ortiz de Zárate et al., 2014; Cerbino et al., 2015; Croccolo et al., 2016a; Giavazzi et al., 2016a; Bataller et al., 2016; Croccolo et al., 2016b; Giavazzi et al., 2016b; Cerbino et al., 2017) and references therein) that the number of images averaged needs to be small enough to avoid averaging out fast-changing processes or completely de-correlating the images in a batch, and, at the same time, the number of images in an averaging batch must be large enough to provide good noise filtering. We based our selection of the number of images in an averaging batch on the delay time between frames Δt it takes for the time-dependent structure functions C_m(q, Δt) to begin saturating. As shown in Figure 3A, the time-dependent structure functions C_m(q, Δt) starts saturating around 1–3 s, corresponding to 20–70 consecutive images. In other words, the correlation between fluctuations becomes negligible after 20–70 successive images. In this study, we performed the N_avg = 32-image temporal moving average of power spectra since it was on the lower end of the above saturation range of time-dependent structure functions C_m(q, Δt). Such a value for the number of images in an averaging batch still captures short correlation times down to 1×10^–2 ms while producing decent image denoising (see Figure 3D). We found that a lower size of the moving average did not change the amplitude factor A(q) fitting nor the correlation time estimate (not shown). On the upper limit side, a N_avg = 64 images moving average batch could also work, but that would be towards the upper limit of the saturation time for the time-dependent structure functions C_m(q, Δt) (see Figure 3A) and has the potential of filtering out shorter saturation times. Additionally, such a large averaging batch size leads to fewer data points at low correlation times in Figure 3D and, therefore, a less precise estimation of the effective diffusion coefficient D. Since time-dependent structure functions C_m(q, Δt) were averaged over N_avg = 32 images, the image index and the corresponding recording time reported on all figures referring to C_m(q, Δt) or any quantity derived from it, such as the amplitude A(q), the ISF G(q, Δt), the correlation time of fluctuations τ(q), and the diffusion coefficient D, are for the first image in the batch.

DDM data correction to account for the optical transfer function T(q). The amplitude A(q) = S(q) × T(q) from Eq. 2 contains information on both the structure factor S(q) and the transfer function T(q) of the optical setup. As shown by Cerbino and Vailati (Cerbino and Vailati, 2009), “in the limit of coherently illuminated” optical field and “weakly scattering objects,” the transfer function is $T(q)={\sin }^2(\frac{q^{2}z\lambda }{4\pi })$, which has increasingly fast oscillations as the wavevector q increases. As noted by Cerbino and Vailati (Cerbino and Vailati, 2009), “in practice, for sufficiently large wave vectors q, the function T(q) may lose its oscillatory character and in some cases there is no need for data correction.” According to Cerbino and Vailati (Cerbino and Vailati, 2009), for wave vectors larger than the “crossover wave vector” $q_{\mathit{cross}}=\min \left\{\pi \sqrt{\frac{2}{e_{\mathit{cyl}}\lambda }},\frac{\pi L_{\mathit{sensor}}}{z\lambda }\right\}$, “there is no need for data correction” due to the transfer function T(q). In our experiment, the sample thickness is e_cyl = 4.115 mm, the sensor size L_sensor is given by sensor’s resolution Δx = 3.5 µm and the number M = 1,024 of pixels, i.e., L_sensor = Δx × M = 3.584 mm. The wavelength of the LED used was λ = 660 nm, and the estimated distance z for the microscopic view images is the order of 1 mm. The visualization distance z is measured between the sample and the plane imaged onto the sensor (Croccolo, 2006). With the above data, the crossover wavenumber due to sample thickness is q_cross ≈ 850 cm⁻¹. Note that this estimation of the crossover wave number q_cross due to the sample’s thickness still holds for all values of z up to 20 cm, which is well within the range of our microscope setup. For wavenumbers q larger than the crossover value q_cross ≈ 850 cm⁻¹, we used the amplitude A(q) and the structure factor S(q) interchangeably. To be on the conservative side, we only estimated the slope of the amplitude A(q) for wavenumbers larger than q_cross to ensure that there is no need for T(q) correction (see Figure 3). Based on the above estimate of the crossover wavenumber, the amplitude A(q) was also fitted with Eq. 3 in the large wavenumber range where there is no need for data correction (Cerbino and Vailati, 2009).

Another potential issue when estimating the slope and fitting the amplitude A(q) with Eq. 3 is the temporal moving average performed by DDM. In general, image averaging is equivalent to a lowpass filtering that attenuates high (spatial) frequencies and could change the slope of the structure factor or slightly shifts it along the wavenumber axis. We checked that the slope of the amplitude A(q) shown in Figure 3C with a denoising DDM average of N_avg = 32 did not change compared to the slope of A(q) for individual images. The variance for the slopes obtained without averaging was larger than when averaging over batches of N_avg = 32 images.

The experimental structure factor S(q) obtained by fitting the one-dimensional image structure function with Eq. 2 can be approximated with

$S\left(q\right)=\frac{S_0}{1+{\left(q\xi \right)}^n}=\frac{S_0}{1+{\left(q/q_{\mathit{corr}}\right)}^n},(3)$

where S₀ is the structure factor value at very low (q → 0) wavenumbers, ξ is the correlation distance of fluctuations, q_corr = 1/ξ is the correlation wavenumber given in Table 1, and n is a power-law exponent usually close to 2 for critical fluctuations (see also Figure 3A in Ref. (Oprisan et al., 2012; Oprisan et al., 2021a) for structure factors of equilibrium fluctuations near the critical point in other systems). The curve described in Eq. 3 is shown with a green dashed line in Figure 3C on top of the amplitude A(q) experimental data. Finally, we notice that the slope of the amplitude A(q) shown with a continuous black line changes with the wavenumber range considered. For example, near the peak of A(q), the slope, i.e., the power-law exponent n from Eq. 3, approaches zero, whereas, at large wavenumbers, it approaches −4. The existence of multiple power-law exponents for the structure factor was attributed to the fractal nature of the observed dynamics using scattered light (Sorensen, 2001). One should not give too much weight to data points at large wavenumbers as they represent data at the lower end of CCD camera resolution, which is around q_max = 2π/3.5 µm ≈ 18 ,000 cm⁻¹ in our experiment. Other factors that limit the wavenumber range are poor signal-to-noise ratio, inadequate sampling frequency, and recording duration. For a more detailed analysis of different limiting factors, see (Giavazzi et al., 2017).

The saturation of time-dependent structure functions C_m(q, Δt) shown in Figure 3A and the dependence of the amplitude A(q) on the wavenumber q shown in Figure 3C provide insight into the characteristic relaxation time of the density fluctuations (Oprisan et al., 2012). The corresponding ISF shown in Figure 3B exhibits an exponential relaxation for delay times shorter than 3 s. The slope of the ISF shown in Figure 3B gives the inverse of the correlation time of fluctuations shown in Figure 3D. At large wavenumbers, the log-log plot of correlation time is always linear with a slope of −2 (see the continuous black line in Figure 3D).

Theoretically, the relaxation time τ of critical fluctuations near critical temperature T_c should obey Kawasaki (Kawasaki, 1970) formula:

${\tau }^{-1}\approx D{q}^2,(4)$

when D is the thermal diffusivity coefficient. Such results are exemplified in Figure 4B, where the dashed green curve corresponds to a smooth spline interpolation of the correlation time of fluctuations in the original image (see the solid black square in Figure 4B) to highlight the inflection point at critical wavenumber q_c. In this case, the straight line with a slope of −2 (see the continuous white line in Figure 3) gives the effective diffusion coefficient D.

FIGURE 4

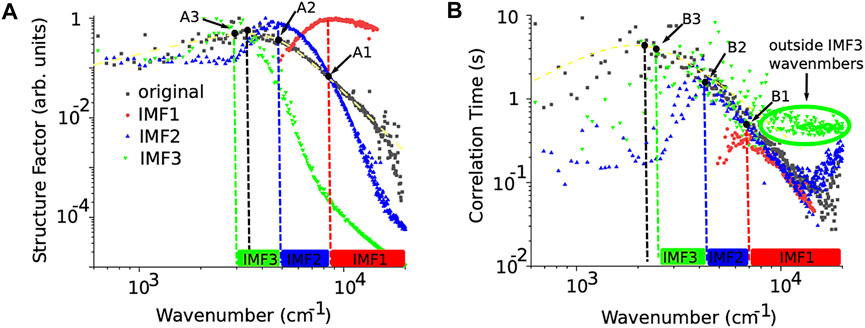
FIGURE 4. Normalized structure factor for the original (solid black rectangles), IMF1 (solid red circles), IMF2 (solid blue triangles), and IMF3 (solid inverted green triangles) (A). The structure factors were fitted with the general Eq. 3 (except for IMF3, which did not meet the most conservative criterion q > q_cross = 4,900 cm⁻¹) and only shown for the original image with a dashed green curve superimposed on the solid black squares (A). The corresponding dashed vertical lines mark the peak wavenumber for the original and each IMF image (except IMF3). The wavenumber ranges for each IMF are marked with correspondingly labeled solid rectangles along the wavenumber axis. The correlation time of density fluctuations (B) shows that each IMF has a maximum correlation time (marked by the corresponding points B1-B3). The correlation times over the range of wavenumbers appropriate for each IMF overlap with the correlation time for the original image (solid black squares). The green dashed curved line superimposed on the solid black squares represents a smooth spline interpolation of the data to highlight the inflection point that determines the critical wavenumber q_c. At wavenumbers outside the range of the IMF, the correlation time diverges from the theoretical formula (see the green solid inverted triangles marked outside the IMF3 wavenumber domain).

3.2 Spatial Scales Separation Using BEMD

Density fluctuations near critical points have a wide range of sizes limited only by the boundaries of the enclosing container (Beysens, 1986; Beysens et al., 1987; Beysens and Garrabos, 2000; Onuki, 2002; Barmatz et al., 2007; Midya and Das, 2017). Critical density fluctuations near critical points show fractal patterns (Guenoun et al., 1989; Schaefer et al., 1989; Antoniou et al., 1998; Antoniou et al., 2000; Oprisan et al., 2021a; Oprisan et al., 2021b). Nonequilibrium fluctuations can also lead to fractal patterns (Vailati et al., 2011). The fractal structures are usually described by a spectrum of fractal dimensions, which are power-law exponents associated with different spatial or temporal scales present in the data. How would a fluctuating image near the critical point look if we could break it into disjoint spatial scales, like decomposing white light into narrow-band, monochromatic waves? We noticed in the previous Section 3.1 that the amplitude A(q) factor in Eq. 2, which coincides with the structure factor S(q) above a crossover wavenumber that eliminates the need for optical transfer function correction of the data, scales as A(q) ∝ q⁻² (see Figure 3C). We also noticed that the amplitude A(q) slope changes for different wavenumber ranges. Could different power-law exponents required over different wavenumber ranges reflect the multifractal nature of critical fluctuations? What would such a multiscale analysis over disjoint wavenumber ranges reveal about the behavior of the fluctuations’ correlation time? The DDM-based results obtained in Section 3.1 from the original images indicate that the correlation time decreases with the wavenumber (see Figure 3D), i.e., the correlation time increases with the characteristic size of fluctuations. What happens to the slope of the structure factor over different spatial scales? What happens to the critical wavenumber q_c that marks the transition to a different fluctuation regime? Where is the critical wavenumber q_c located on images that only capture fluctuation over a limited wavenumber range? Do the scaling laws governing each spatial scale change when decomposing fluctuations into narrow wavenumber ranges? How are the relaxation times of fluctuations at each spatial scale related to the dynamics of fluctuations in the original image? We decomposed the original images over disjoint wavenumber ranges using the BEMD method to answer such questions. We then determined the correlation time of fluctuations and critical wavenumbers q_c using DDM as described in Section 3.1.

We used BEMD to break the original image (Figure 2A1) into three IMFs (Figures 2B1–D1) and a residual background (Figure 2E1). We performed the data analysis described in the previous subsection on all IMFs. To compare side-by-side the structure factors of the original image and the three IMFs shown in Figures 2A1–D1, we normalized each of them by their respective maximum values and plotted all four curves in Figure 4A. We notice that the amplitude factor A(q) of the original image (solid black squares in Figure 4A), which is proportional to the structure factor S(q) for wavenumbers larger than q_cross = 850 cm⁻¹, shows a power-law behavior with an exponent n close to −2 (see the yellow dashed line in Figure 4A). The theory of critical fluctuations predicts a power-law exponent equal to −2 (Beysens, 1986; Beysens and Garrabos, 2000; Domb et al., 2001).

As the BEMD decomposes the original image into orthogonal IMFs by separating the spatial scales of fluctuations, it only retains spatial structures larger than a characteristic size starting from the smallest (IMF1), then intermediate (IMF2) and large (IMF3). This means that each IMF has both a lower and upper boundary on the wavenumbers that it can capture. While there is no set rule for defining the exact boundaries of a given IMF order, we used the peak q_peak of the structure factor criterion, i.e., the lower wavenumber for a given IMF is the peak of the structure factor. The upper limit of the wavenumbers for a given IMF order is the lower boundary of the precedent IMF order. For example, q_maxIMF2 = q_minIMF1. Specifically, IMF1 only contains small-size objects from the original images, which means that its corresponding wavenumbers will start around the peak of the IMF1’s structure factor, which is q_minIMF1 ≈ 8,500 cm⁻¹ and expand up to the larges wavenumbers captured by the original images. IMF2 will only capture intermediate size objects, which means the wavenumbers over which its results are accurate cover q_minIMF2 ≈ 5,000 cm⁻¹ to q_maxIMF2 ≈ q_minIMF1. Ideally, if the IMFs are truly orthogonal decompositions of the original image, there should be no leakage between them and, therefore, the wavenumber ranges for each IMF should be disjoint. In such an ideal case, we would expect that the smallest wavenumber in IMF1 q_minIMF1 will be close to the largest wavenumber in IMF2 q_maxIMF2 and so on. Since we have a bit of leakage between IMFs, the wavenumber ranges may overlap, most likely due to image noise. The IMF3 will only capture large-size fluctuations, which means the wavenumbers over which its results are accurate cover q_minIMF3 ≈ 3,000 cm⁻¹ to q_maxIMF3 ≈ q_minIMF2. We note that the range of wavenumbers for IMF3 is well above the crossover wavenumber q_cross = 850 cm⁻¹ determined with the criterion from (Cerbino and Vailati, 2009).

Suppose we retain only the wavenumbers larger than the peak location of IMF1 in the structure factor of the original image (see point A1 in Figure 4A). In that case, the structure factor of the original image is determined mainly by the structure factor of IMF1 and IMF2. This is because, as seen in Figure 4A, for wavenumbers larger than those indicated by the peak A1 of IMF1, the structure factor of IMF2 is one order of magnitude smaller than IMF1, and IMF3 is at least three orders of magnitude smaller than IMF1. At the same time, the slope of the original image’s structure factor is intermediate between the slope of IMF1, which is on average −2.1 ± 0.6, and the slope of IMF2, which is on average −4.3 ± 0.3. The solid red rectangle marks the wavenumber range for IMF1 on the wavenumber axis in Figure 4A. The solid blue rectangle marks the corresponding wavenumber range for IMF2 on the wavenumber axis in Figure 4A.

Finally, at small wavenumbers, between the peak of the IMF2 (blue vertical dashed line in Figure 4A) and IMF3 (green dashed vertical line in Figure 4A), the structure factor of the original image lies between points A2 and A3 in Figure 4A. The structure factor of the original image is determined mainly by IMF2 and IMF3 as the structure factor for IMF1 is more than one order of magnitude smaller than the other two. Since the slope of the original image’s structure factor swings from positive (at low wavenumbers) to negative (at higher wavenumbers), it is a mix of IMF2, which has a positive slope, and IMF3, which has a very abrupt negative slope of −5.6 ± 1.1. The fact that the original image’s negative slope of the structure factor is not as steep as for IMF3 shows that the positive slope of IMF2 contributed significantly to the original image’s structure factor. The peak wavenumber decreases for successive IMFs, as shown in Figure 4A.

A similar picture emerges when analyzing the correlation time of fluctuation in the original image and the corresponding IMFs (see Figure 4B). We did not normalize the correlation times but retained the actual values in seconds as obtained from the intermediate scattering function (see Figure 3B) with Supplementary Appendix SEq. 7. We repeated the correlation time fitting for all IMFs following the procedure detailed in the previous section and determined the corresponding D and q_c. As we notice from Figure 4B, the peak location of the correlation time (q_c) for IMF1 (see point B1 in Figure 4B) determines the range of wavenumbers over which it overlaps with the correlation time of the original image (see the red rectangle marked IMF1 on the wavenumber axis in Figure 4B). Similarly, the IMF2 correlation time starts overlapping the correlation time of the original image at the onset of intermediate-range wavenumber (point B2 in Figure 4B). Finally, the IMF3 wavenumber range extends from low wavenumbers marked by point B3 in Figure 4B, and the overlap does not extend farther than B1. At large wavenumbers, the correlation time for IMF3 flattens out (solid green inverted triangles in Figure 4B), suggesting that we reached the limit of maximum acceptable wavenumber for the respective IMF. Similar behavior can be observed for IMF2 (blue solid upright triangles in Figure 4B). However, as seen in Figure 4B, the flattening out of the correlation time of IMF3 (solid inverted triangles in Figure 4B) is determined by the fact that the results past q_maxIMF3 are not accurate since there is no information in IMF3 regarding objects at such wavenumbers.

In addition, the correlation time of fluctuations (see Figure 4B) shows that the maximum correlation time τ_max increases with IMF’s order. In other words, large wavenumber fluctuations, i.e., small physical size fluctuations, have short correlation times. For example, the smallest spatial scale of IMF1 has a maximum correlation time of 0.2 s, the IMF2 reaches 2 s, and the largest spatial scale of IMF3 reaches a maximum correlation time of 10 s (see Figure 4B). This relationship between the maximum correlation time and the physical size of the fluctuations confirms the fractal nature of fluctuations (see also (Oprisan et al., 2021a)). Most of the focus of scaling laws near criticality was on spatial criticality, i.e., deriving the universal laws for correlation length of fluctuations (Moldover et al., 1979; Beysens, 1986; Beysens et al., 1990; Wilkinson et al., 1998; Barmatz et al., 2007). This study shows that near the critical point, the correlation time of fluctuations also separates in multiple domains, similar to the spatial separation of fluctuations.

Once we fit the correlation time of fluctuations (Figure 4B) with Eq. 4, one gets the effective diffusion coefficient D shown in Figure 5A. The critical wavenumber q_c is the inflection point of the correlation time (see the points B1, B2, and B3 in Figure 4B), and they are shown in Figure 5B. Based on the examples shown in Figure 4B, we expect that the correlation time slopes for the original images and their IMFs are almost identical within the experimental variability. Since the slopes of the correlation times at large wavenumber are virtually identical, we anticipate from Figure 4B that the effective diffusion coefficient is the same across the original images and all IMFs. Indeed, as we see from Figure 5A, the effective diffusion coefficients computer for each batch of N_avg = 32 images are very similar within experimental errors. We also notice from Figure 5A example and Table 1 that the effective diffusion coefficient variance increases with the IMF’s order.

FIGURE 5

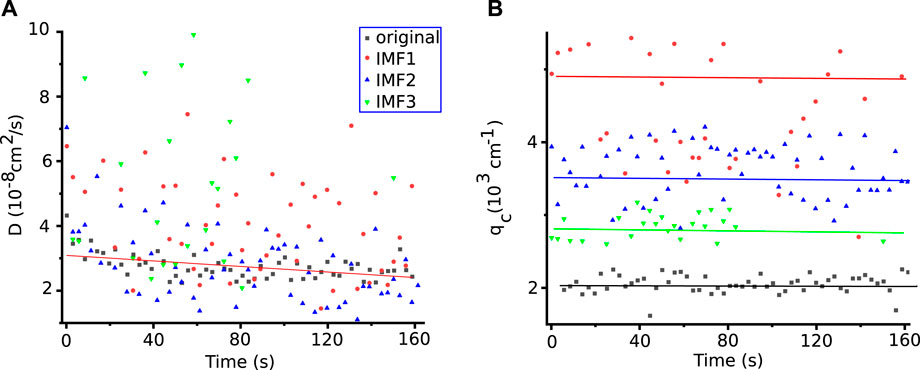
FIGURE 5. The experimental effective diffusion coefficients obtained using Eq. 4 for the original (solid black squares) and the first three IMFs show a slight slope (A). The data fitting variance increases with IMF’s order, as seen from Table 1. The critical wavenumber q_c decreases with the IMF’s order and reflects the characteristic length of larger and larger structures separated by BEMD from the original image (B).

The continuous black line that fits the effective diffusion coefficients for the original image in Figure 5A is given by equation D = (3.66 ± 0.06) 10^–8 + (−5.9 ± 0.6) 10^–11 × t (in cm s⁻¹), where t is the temporal variable shown in Figure 5. The above linear fit’s statistics show a χ² = 5.47 × 10^–18 and an adjusted coefficient of determination R² = 0.588. Given the significant data variance of the average diffusion coefficient D (see Table 1), even for the original image, the slight negative slope of −1.18×10^–10 cm² s⁻² might not be statistically significant. To determine that the effective diffusion coefficient decreases over time, as the fitting line for the original images in Figure 5A suggests, future studies need to include more experimental data.

We also extracted the value of the critical wavenumber q_c, i.e., the wavenumber for which the correlation time reached the peak in Figure 4B and plotted it in Figure 5B. As expected, the critical wavenumber decreases with the IMF’s order. The horizontal lines in Figure 5B show the average for the corresponding IMFs.

To conclude, using the BEMD decomposition over a narrow wavenumber range, we obtained structure factors with a single power-law exponent, e.g., IMF1 exponent is −2.1 ± 0.6, IMF2 exponent is −4.3 ± 0.3, and IMF3 exponent is −5.6 ± 1.1. We previously reported that depending on the wavenumber range, one gets different power-law exponents for the structure factor in the original image. Using BEMD we can trace those exponents to different IMFs.

3.3 Critical Temperature Estimation From the Correlation Length

To find the values of the correlation length wavenumber q_corr = 1/ξ, we fitted each structure factor with Eq. 3. Although the correlation length wavenumber q_corr seems to change over time slightly (data not shown), we estimated its average value and standard deviation in Table 1. Using q_corr = (4,088 ± 653) cm⁻¹ from the original image, we found that the corresponding correlation length ξ = 1/q_corr ≈ (2.4 ± 0.2) µm. This means q_c × ξ ≤ 1, which shows that we are in the hydrodynamic regime (Onuki, 2002), which justifies the use of the Kawasaki (Kawasaki, 1970) formula shown in Eq. 4 to determine the effective diffusion coefficient.

The experimentally estimated correlation length of ξ = 1/q_corr ≈ (2.4 ± 0.2) µm allowed us to determine the corresponding temperature distance from T_c by using the scaling law for correlation length (Domb et al., 2001):

$\xi ={\xi }_{+}{\left(\frac{T-T_c}{T_c}\right)}^{-\nu },(5)$

where ξ₊ = 1.892×10^–10 m, T_c = 318.733 K and the universal exponent is ν = 0.6304 (Moldover et al., 1979; Lecoutre et al., 2009). Our computations show that this 0.2 mK temperature quench stepped through T_c, which seems to be right in the middle of the quench with the first image in the 1922 series 73–121 µK above T_c.

If we assume that the same scaling law given by Eq. 5 applies to the IMFs, we can estimate their “temperatures.” The range of temperatures is as follows: IMF1 823–943 µK above T_c, IMF2 186–217 µK above T_c, and for IMF3 64–75 µK above T_c (see Table 1. Because the BEMD breaks the original image into different wavenumber ranges, the “temperature” of the first IMF will always be larger than the second, and so on.

4 Conclusion

In this study, we used DECLIC data from the ISS to study critical density fluctuation in SF₆ under microgravity conditions extremely close to critical temperature T_c, i.e., within 0.2 mK (see Figure 1) (Marcout et al., 1994; Lecoutre et al., 2009). The advantage of DECLIC data is the 1,024 × 1,space mission, and contributed to writing024-pixel high-resolution image recordings with a small field of view of 1 × 1 mm. To extract thermophysical properties, such as the effective diffusion coefficient, from recorded images of critical density fluctuations, we used the Differential Dynamic Microscopy (DDM) method (see Supplementary Appendix S5.1 and (Oprisan et al., 2012; Oprisan et al., 2021a)). Given that the thermal quench of 0.2 mK stepped through T_c and that we only investigate a relatively short set of images covering approximately 80 s of data, it is expected that many of the observed phenomena are transitory. To our knowledge, one of the best approaches to investigating transitory phenomena is the Empirical Mode Decomposition (EMD), which is a data-driven and fully unsupervised technique suitable for the analysis of locally nonlinear and nonstationary data (see Supplementary Section S5.2 and (Oprisan et al., 2021a)). We used a Bidimensional Empirical Mode Decomposition (BEMD) algorithm to separate the contribution to thermophysical properties of the fluid of different spatial scales of density fluctuations (see Figure 2). Once the original images are decomposed into orthogonal Intrinsic Mode Functions (IMFs) using BEMD, we extracted thermophysical properties from each IMF (see Figure 3). In this study, we only decomposed the original images in three IMFs and a final residual, which we did not include in the data analysis as it gives the correction for nonuniform illumination of the original image.

Due to the high resolution of the recorded images, it was possible to show that the structure factor has a well-defined range of wavenumbers over which it is valid (see Figure 4). The first order, IMF1, retains the smallest objects from the original image and has its natural upper limit of wavenumbers at the largest possible value q_max = 2π/3.5 µm ≈ 18 ,000 cm⁻¹. We set the cutoff wavenumber for IMF1 at the peak of the structure factor q_minIMF1. Similarly, the range of the wavenumbers covered by IMF2 has an upper limit q_maxIMF2 = q_minIMF1 and a lower limit q_minIMF2 determined by the peak of IMF2. Breaking the wavenumbers in disjoint intervals corresponding to each IMF allows us to identify the contribution of each spatial scale of fluctuation to the structure factor of the original image. We were able to identify multifractal exponents associated with the power-laws followed by structure factors at different spatial scales using the BEMD framework. Although we have known for a long time that the structure factor does not have a uniques power-law exponents but rather a whole spectrum of exponents for different ranges of wavenumbers, this is the first systematic study to reveal the multiscale components of the structure factor near T_c. We found that the linear portion of the IMF1 structure factor (in log-log coordinates) has an average slope of −2.1 ± 0.6, increases to −4.3 ± 0.3 for IMF2, and reaches −5.6 ± 1.1 for IMF3.

We found that all ISF for IMFs exhibit an exponential relaxation with a characteristic time. The correlation time of fluctuations has remarkably similar shapes with the distinction that they peak at durations that increase with the IMF orders.

From Figure 5A, the average value of the experimentally determined effective diffusion coefficients of the original images and their IMFs is D = (3.19 ± 0.36) 10^–8 cm² s⁻¹. This experimental value from high-resolution images recorded with DECLIC matches our previous results (Oprisan et al., 2012; Oprisan et al., 2021a). As we notice from Table 1, the effective diffusion coefficients of the original image and all its IMFs are statistically identical. The effective diffusion coefficient values for the original images seem to support a linear fitting with equation D = (3.66 ± 0.06) 10^–8 + (−1.18 ± 0.13) 10^–10 × t (in cm s⁻¹) with a χ² = 5.47 × 10^–18 and an adjusted coefficient of determination R² = 0.588. The very small slope of (−1.18 ± 0.13) 10^–10 cm² s⁻² of the effective diffusion coefficient versus time may not be statistically significant given the large standard deviation of the data shown in Table 1. As a result, more experimental data are needed in order to establish with certainty any temporal dependence of the effective diffusion coefficient during the quench through T_c.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: https://www.nasa.gov/PSI.

Author Contributions

AO performed image processing, contributed to writing and reviewing the manuscript. DM, DD, and SZ helped with the data fitting. SO performed numerical simulations and data analyses, contributed to writing and reviewing the manuscript. IH contributed to the experimental design and coordinated the space mission, and contributed to reviewing the manuscript YG, CL-C, and DB contributed to the experimental design and coordinated the space mission that acquired DECLIC data, contributed to writing and reviewing the manuscript.

Funding

AO acknowledges a mini-REAP and a Palmetto Academy grant from NASA South Carolina Space Grant/EPSCoR. AO acknowledges partial support from the Fulbright US Scholar Program. SO acknowledges a research and development grant from the College of Charleston and a Palmetto Academy grant from NASA South Carolina Space Grant/EPSCoR. YG, CL, and DB acknowledge a research grant from Centre National d’Études Spatiales (CNES) focused on DECLIC-ALI mission and a NASA grants NAG3-1906 and NAG3-2447. The research of IH was carried out at Jet Propulsion Laboratory, California Institute of Technology, under a contract with NASA.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frspt.2022.883899/full#supplementary-material

References

Antoniou, N. G., Contoyiannis, Y. F., and Diakonos, F. K. (2000). Fractal Geometry of Critical Systems. Phys. Rev. E. 62, 3125–3134. doi:10.1103/PhysRevE.62.3125

PubMed Abstract | CrossRef Full Text | Google Scholar

Antoniou, N. G., Contoyiannis, Y. F., Diakonos, F. K., and Papadopoulos, C. G. (1998). Fractals atT=Tcdue to Instantonlike Configurations. Phys. Rev. Lett. 81, 4289–4292. doi:10.1103/PhysRevLett.81.4289

CrossRef Full Text | Google Scholar

Barmatz, M., Hahn, I., Lipa, J. A., and Duncan, R. V. (2007). Critical Phenomena in Microgravity: Past, Present, and Future. Rev. Mod. Phys. 79, 1–52. doi:10.1103/RevModPhys.79.1

CrossRef Full Text | Google Scholar

Bataller, H., Giraudet, C., Croccolo, F., and Ortiz de Zárate, J. M. (2016). Analysis of Non-Equilibrium Fluctuations in a Ternary Liquid Mixture. Microgravity Sci. Technol. 28, 611–619. doi:10.1007/s12217-016-9517-6

CrossRef Full Text | Google Scholar

Ben Arfia, F., Sabri, A., Ben Messaoud, M., and Abid, M. (2011). “The Bidimensional Empirical Mode Decomposition with 2D-DWT for Gaussian Image Denoising,” in 2011 17th International Conference on Digital Signal Processing (DSP), 1–5. doi:10.1109/ICDSP.2011.6004908

CrossRef Full Text | Google Scholar

Berne, B., and Pecora, R. (2000). Dynamic Light Scattering: With Applications to Chemistry, Biology, and Physics. Mineola, New York: Dover Books on Physics Series Dover Publications.

Google Scholar

Beysens, D. A., Forgacs, G., and Glazier, J. A. (2000). Cell Sorting Is Analogous to Phase Ordering in Fluids. Proc. Natl. Acad. Sci. U.S.A. 97, 9467–9471. doi:10.1073/pnas.97.17.9467

PubMed Abstract | CrossRef Full Text | Google Scholar

Beysens, D. A., and Garrabos, Y. (2000). The Phase Transition of Gases and Liquids. Phys. A Stat. Mech. its Appl. 281, 361–380. doi:10.1016/s0378-4371(00)00030-3

CrossRef Full Text | Google Scholar

Beysens, D. A. (1997). Kinetics and Morphology of Phase Separation in Fluids: The Role of Droplet Coalescence. Phys. A Stat. Mech. its Appl. 239, 329–339. doi:10.1016/s0378-4371(97)00028-9

CrossRef Full Text | Google Scholar

Beysens, D. (1986). Critical Phenomena. Berlin: Springer, 191–224. doi:10.1007/978-3-642-82761-7_9

CrossRef Full Text | Google Scholar

Beysens, D., Guenoun, P., and Perrot, F. (1990). Direct Observation of Critical Fluctuations. J. Phys. Condens. Matter 2, SA127–SA133. doi:10.1088/0953-8984/2/s/015

CrossRef Full Text | Google Scholar

Beysens, D., Straub, J., and Turner, D. J. (1987). Phase Transitions and Near-Critical Phenomena. Berlin: Springer, 221–256.

CrossRef Full Text | Google Scholar

Blanco, S., Figliola, A., Quiroga, R. Q., Rosso, O. A., and Serrano, E. (1998). Time-frequency Analysis of Electroencephalogram Series. Iii. Wavelet Packets and Information Cost Function. Phys. Rev. E. 57, 932–940. doi:10.1103/PhysRevE.57.932

CrossRef Full Text | Google Scholar

Bondarchuk, O., Dougherty, D. B., Degawa, M., Williams, E. D., Constantin, M., Dasgupta, C., et al. (2005). Correlation Time for Step Structural Fluctuations. Phys. Rev. B. 71, 045426. doi:10.1103/PhysRevB.71.045426

CrossRef Full Text | Google Scholar

Cerbino, R., Piotti, D., Buscaglia, M., and Giavazzi, F. (2017). Dark Field Differential Dynamic Microscopy Enables Accurate Characterization of the Roto-Translational Dynamics of Bacteria and Colloidal Clusters. J. Phys. Condens. Matter 30, 025901. doi:10.1088/1361-648x/aa9bc5

CrossRef Full Text | Google Scholar

Cerbino, R., Sun, Y., Donev, A., and Vailati, A. (2015). Dynamic Scaling for the Growth of Non-equilibrium Fluctuations during Thermophoretic Diffusion in Microgravity. Sci. Rep. 5, 14486. doi:10.1038/srep14486

PubMed Abstract | CrossRef Full Text | Google Scholar

Cerbino, R., and Trappe, V. (2008). Differential Dynamic Microscopy: Probing Wave Vector Dependent Dynamics with a Microscope. Phys. Rev. Lett. 100, 188102. doi:10.1103/PhysRevLett.100.188102

PubMed Abstract | CrossRef Full Text | Google Scholar

Cerbino, R., and Vailati, A. (2009). Near-field Scattering Techniques: Novel Instrumentation and Results from Time and Spatially Resolved Investigations of Soft Matter Systems. Curr. Opin. Colloid & Interface Sci. 14, 416–425. doi:10.1016/j.cocis.2009.07.003

CrossRef Full Text | Google Scholar

Croccolo, F., Brogioli, D., Vailati, A., Giglio, M., and Cannell, D. S. (2006). Use of Dynamic Schlieren Interferometry to Study Fluctuations during Free Diffusion. Appl. Opt. 45, 2166–2173. doi:10.1364/AO.45.002166

PubMed Abstract | CrossRef Full Text | Google Scholar

Croccolo, F., Brogioli, D., Vailati, A., Giglio, M., and Cannell, D. S. (2007). Nondiffusive Decay of Gradient-Driven Fluctuations in a Free-Diffusion Process. Phys. Rev. E. 76, 041112. doi:10.1103/PhysRevE.76.041112

PubMed Abstract | CrossRef Full Text | Google Scholar

Croccolo, F. (2006). Dynamics of Non Equilibrium Fluctuations in Free Diffusion. Thesis. Milano, Italy: Universita degli Studi di Milano.

Google Scholar

Croccolo, F., Giraudet, C., Bataller, H., Cerbino, R., and Vailati, A. (2016a). Shadowgraph Analysis of Non-equilibrium Fluctuations for Measuring Transport Properties in Microgravity in the GRADFLEX Experiment. Microgravity Sci. Technol. 28, 467–475. doi:10.1007/s12217-016-9501-1

CrossRef Full Text | Google Scholar

Croccolo, F., Ortiz de Zárate, J. M., and Sengers, J. V. (2016b). Non-Local Fluctuation Phenomena in Liquids. Eur. Phys. J. E. 39, 125. doi:10.1140/epje/i2016-16125-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Cummings, D. A. T., Irizarry, R. A., Huang, N. E., Endy, T. P., Nisalak, A., Ungchusak, K., et al. (2004). Travelling Waves in the Occurrence of Dengue Haemorrhagic Fever in thailand. Nature 427, 344–347. doi:10.1038/nature02225

PubMed Abstract | CrossRef Full Text | Google Scholar

Domb, C., Lebowitz, J., and Lebowitz, J. (2001). Phase Transitions and Critical Phenomena. San Diego, USA London, UK: Academic Press.

Google Scholar

Dong, W., Li, X. e., Lin, X., and Li, Z. (2014). A Bidimensional Empirical Mode Decomposition Method for Fusion of Multispectral and Panchromatic Remote Sensing Images. Remote Sens. 6, 8446–8467. doi:10.3390/rs6098446

CrossRef Full Text | Google Scholar

Durieux, A., Martin, B., and Laubier, D. (2017). “Declic: Design, Integration and Testing of a Multi Configurable Instrument Using Optical Diagnostics to Study Directional Solidification and Critical Fluids,” in International Conference on Space Optics ? ICSO 2006. Editors E. Armandillo, J. Costeraste, and N. Karafolas (International Society for Optics and Photonics SPIE), 951–957. doi:10.1117/12.2308146

CrossRef Full Text | Google Scholar

Garcia-Perez, A., Amezquita-Sanchez, J. P., Dominguez-Gonzalez, A., Sedaghati, R., Osornio-Rios, R., and Romero-Troncoso, R. J. (2013). Fused Empirical Mode Decomposition and Wavelets for Locating Combined Damage in a Truss-type Structure through Vibration Analysis. J. Zhejiang Univ. Sci. A 14, 615–630. doi:10.1631/jzus.a1300030

CrossRef Full Text | Google Scholar

Garrabos, Y., Lecoutre, C., Beysens, D., Nikolayev, V., Barde, S., Pont, G., et al. (2010). Transparent Heater for Study of the Boiling Crisis Near the Vapor-Liquid Critical Point. Acta Astronaut. 66, 760–768. doi:10.1016/j.actaastro.2009.08.018

CrossRef Full Text | Google Scholar

Garrabos, Y., Lecoutre, C., Marre, S., Beysens, D., and Hahn, I. (2018). Liquid-Vapor Rectilinear Diameter Revisited. Phys. Rev. E. 97, 020101. doi:10.1103/PhysRevE.97.020101

PubMed Abstract | CrossRef Full Text | Google Scholar

Garrabos, Y., Lecoutre, C., Marre, S., Guillaument, R., Beysens, D., and Hahn, I. (2015). Crossover Equation of State Models Applied to the Critical Behavior of Xenon. J. Stat. Phys. 158, 1379–1412. doi:10.1007/s10955-014-1157-x

CrossRef Full Text | Google Scholar

Garrabos, Y., Lecoutre, C., Marre, S., LeNeindre, B., and Hahn, I. (2016). Critical Crossover Functions for Simple Fluids: Towards the Crossover Modelling Uniqueness. J. Stat. Phys. 165, 471–506. doi:10.1007/s10955-016-1627-4

CrossRef Full Text | Google Scholar

Giavazzi, F., Brogioli, D., Trappe, V., Bellini, T., and Cerbino, R. (2009). Scattering Information Obtained by Optical Microscopy: Differential Dynamic Microscopy and beyond. Phys. Rev. E. 80, 031403. doi:10.1103/PhysRevE.80.031403

PubMed Abstract | CrossRef Full Text | Google Scholar

Giavazzi, F., Edera, P., Lu, P. J., and Cerbino, R. (2017). Image Windowing Mitigates Edge Effects in Differential Dynamic Microscopy. Eur. Phys. J. E. 40, 97. doi:10.1140/epje/i2017-11587-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Giavazzi, F., Fornasieri, A., Vailati, A., and Cerbino, R. (2016a). Equilibrium and Non-Equilibrium Concentration Fluctuations in a Critical Binary Mixture. Eur. Phys. J. E 39, 103. doi:10.1140/epje/i2016-16103-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Giavazzi, F., Savorana, G., Vailati, A., and Cerbino, R. (2016b). Structure and Dynamics of Concentration Fluctuations in a Non-Equilibrium Dense Colloidal Suspension. Soft Matter 12, 6588–6600. doi:10.1039/C6SM00935B

PubMed Abstract | CrossRef Full Text | Google Scholar

Guenoun, P., Perrot, F., and Beysens, D. (1989). Microscopic Observation of Order-Parameter Fluctuations in Critical Binary Fluids: Morphology, Self-Similarity, and Fractal Dimension. Phys. Rev. Lett. 63, 1152–1155. doi:10.1103/physrevlett.63.1152

PubMed Abstract | CrossRef Full Text | Google Scholar

Hansen, J.-P., and McDonald, I. R. (2013). Theory of Simple Liquids. fourth edition edn. Oxford: Academic Press.

Google Scholar

Hayes, M. (1996). Statistical Digital Signal Processing and Modeling. United Kingdom: J.Wiley.

Google Scholar

Huang, J., Zhao, B., Chen, Y., and Zhao, P. (2010). Bidimensional Empirical Mode Decomposition (BEMD) for Extraction of Gravity Anomalies Associated with Gold Mineralization in the Tongshi Gold Field, Western Shandong Uplifted Block, Eastern china. Comput. Geosciences 36, 987–995. doi:10.1016/j.cageo.2009.12.007

CrossRef Full Text | Google Scholar

Huang, N. E. (2005). Hilbert-huang Transform and its Applications. Hackensack, NJ: World Scientific Publishing Co.

Google Scholar

Huang, N. E., Shen, Z., Long, S. R., Wu, M. C., Shih, H. H., Zheng, Q., et al. (1998a). The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-stationary Time Series Analysis. Proc. R. Soc. Lond. A 454, 903–995. doi:10.1098/rspa.1998.0193

CrossRef Full Text | Google Scholar

Huang, W., Shen, Z., Huang, N. E., and Fung, Y. C. (1998b). Use of Intrinsic Modes in Biology: Examples of Indicial Response of Pulmonary Blood Pressure to ± Step Hypoxia. Proc. Natl. Acad. Sci. U.S.A. 95, 12766–12771. doi:10.1073/pnas.95.22.12766

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, N. E., Wu, M.-L., Qu, W., Long, S. R., and Shen, S. S. P. (2003). Applications of Hilbert-Huang Transform to Non-Stationary Financial Time Series Analysis. Appl. Stoch. Models Bus. Ind. 19, 245–268. doi:10.1002/asmb.501

CrossRef Full Text | Google Scholar

Huang, N. E., Wu, Z., Long, S. R., Arnold, K. C., Chen, X., and Blank, K. (2009). On Instantaneous Frequency. Adv. Adapt. Data Anal. 01, 177–229. doi:10.1142/S1793536909000096

CrossRef Full Text | Google Scholar

Huang, S., Liu, Z., Liu, Z., and Wang, L. (2017). Sar Image Change Detection Algorithm Based on Different Empirical Mode Decomposition. J. Comput. Commun. 05, 9–20. doi:10.4236/jcc.2017.58002

CrossRef Full Text | Google Scholar

Jean, C., Bouaoune, Y., Eric, D., Oumar, N., and Bunel, P. (2003). Image Analysis by Bidimensional Empirical Mode Decomposition. Image Vis. Comput. 21, 1019–1026. doi:10.1016/S0262-8856(03)00094-5

CrossRef Full Text | Google Scholar

Kawasaki, K. (1970). Kinetic Equations and Time Correlation Functions of Critical Fluctuations. Ann. Phys. 61, 1–56. doi:10.1016/0003-4916(70)90375-1

CrossRef Full Text | Google Scholar

Kessler, R., Bräuer, D., Dreissigacker, C., Drescher, J., Lozano, C., Bechinger, C., et al. (2020). Direct-imaging of Light-Driven Colloidal Janus Particles in Weightlessness. Rev. Sci. Instrum. 91, 013902. doi:10.1063/1.5124895

PubMed Abstract | CrossRef Full Text | Google Scholar

Labate, D., Foresta, F. L., Occhiuto, G., Morabito, F. C., Lay-Ekuakille, A., and Vergallo, P. (2013). Empirical Mode Decomposition vs. Wavelet Decomposition for the Extraction of Respiratory Signal from Single-Channel Ecg: A Comparison. IEEE Sensors J. 13, 2666–2674. doi:10.1109/jsen.2013.2257742

CrossRef Full Text | Google Scholar

Lecoutre, C., Garrabos, Y., Beysens, D., Nikolayev, V., and Hahn, I. (2014). Boiling Phenomena in Near-Critical Sf6 Observed in Weightlessness. Acta Astronaut. 100, 22–29. doi:10.1016/j.actaastro.2014.03.012

CrossRef Full Text | Google Scholar

Lecoutre, C., Garrabos, Y., Georgin, E., Palencia, F., and Beysens, D. (2009). Turbidity Data of Weightless SF6 Near its Liquid-Gas Critical Point. Int. J. Thermophys. 30, 810–832. doi:10.1007/s10765-009-0582-6

CrossRef Full Text | Google Scholar

Lecoutre, C., Guillaument, R., Marre, S., Garrabos, Y., Beysens, D., and Hahn, I. (2015). Weightless Experiments to Probe Universality of Fluid Critical Behavior. Phys. Rev. E 91, 06010. doi:10.1103/PhysRevE.91.060101

PubMed Abstract | CrossRef Full Text | Google Scholar

Levy, M., Le Guillou, J.-C., and Zinn-Justin, J. (1982). Phase Transitions Cargese 1980. New York: Plenum.

Google Scholar

Li, X. (2006). Temporal Structure of Neuronal Population Oscillations with Empirical Model Decomposition. Phys. Lett. A 356, 237–241. doi:10.1016/j.physleta.2006.03.045

CrossRef Full Text | Google Scholar

Lin, C.-S., Chiu, S.-H., and Lin, T.-Y. (2012). Empirical Mode Decomposition-Based Least Squares Support Vector Regression for Foreign Exchange Rate Forecasting. Econ. Model. 29, 2583–2590. doi:10.1016/j.econmod.2012.07.018

CrossRef Full Text | Google Scholar

Liu, D., and Chen, X. (2018). Image Denoising Based on Improved Bidimensional Empirical Mode Decomposition Thresholding Technology. Multimed. Tools Appl. 78, 7381–7417. doi:10.1007/s11042-018-6503-6

CrossRef Full Text | Google Scholar

Liu, G., Li, L., Gong, H., Jin, Q., Li, X., Song, R., et al. (2016). Multisource Remote Sensing Imagery Fusion Scheme Based on Bidimensional Empirical Mode Decomposition (BEMD) and its Application to the Extraction of Bamboo Forest. Remote Sens. 9, 19. doi:10.3390/rs9010019

CrossRef Full Text | Google Scholar

Lu, P. J., Giavazzi, F., Angelini, T. E., Zaccarelli, E., Jargstorff, F., Schofield, A. B., et al. (2012). Characterizing Concentrated, Multiply Scattering, and Actively Driven Fluorescent Systems with Confocal Differential Dynamic Microscopy. Phys. Rev. Lett. 108, 218103. doi:10.1103/PhysRevLett.108.218103

PubMed Abstract | CrossRef Full Text | Google Scholar

Marcout, R., Zwilling, J., Laherrere, J., and Garrabos, Y. (1994). “ALICE 2, an Advanced Facility for the Analysis of Fluids Close to Their Critical Point in Microgravity,” in 45th Congress of the International Astronautical Federation (Jerusalem, Israel: International Astronautical Federation).

Google Scholar

Midya, J., and Das, S. K. (2017). Finite-size Scaling Study of Dynamic Critical Phenomena in a Vapor-Liquid Transition. J. Chem. Phys. 146, 044503. doi:10.1063/1.4974506

PubMed Abstract | CrossRef Full Text | Google Scholar

Moldover, M. R., Sengers, J. V., Gammon, R. W., and Hocken, R. J. (1979). Gravity Effects in Fluids Near the Gas-Liquid Critical Point. Rev. Mod. Phys. 51, 79–99. doi:10.1103/RevModPhys.51.79

CrossRef Full Text | Google Scholar

Mota, F. L., Bergeon, N., Tourret, D., Karma, A., Trivedi, R., and Billia, B. (2015). Initial Transient Behavior in Directional Solidification of a Bulk Transparent Model Alloy in a Cylinder. Acta Mater. 85, 362–377. doi:10.1016/j.actamat.2014.11.024

CrossRef Full Text | Google Scholar

Nikolayev, V., Garrabos, Y., Lecoutre, C., Charignon, T., Hitz, D., Chatain, D., et al. (2015). Boiling Crisis Dynamics: Low Gravity Experiments at High Pressure. Microgravity Sci. Technol. 27, 253–260. doi:10.1007/s12217-015-9447-8

CrossRef Full Text | Google Scholar

Nikolayev, V. S., Beysens, D., and Guenoun, P. (1996). New Hydrodynamic Mechanism for Drop Coarsening. Phys. Rev. Lett. 76, 3144–3147. doi:10.1103/physrevlett.76.3144

PubMed Abstract | CrossRef Full Text | Google Scholar

Nossal, R., Chen, S.-H., and Lai, C.-C. (1971). Use of Laser Scattering for Quantitative Determinations of Bacterial Motility. Opt. Commun. 4, 35–39. doi:10.1016/0030-4018(71)90122-2

CrossRef Full Text | Google Scholar

Nunes, J. C., Bouaoune, Y., Delechelle, E., Niang, O., and Bunel, P. (2003). Image Analysis by Bidimensional Empirical Mode Decomposition. Image Vis. Comput. 21, 1019–1026. doi:10.1016/S0262-8856(03)00094-5

CrossRef Full Text | Google Scholar

Nunes, J. C., Guyot, S., and Delechelle, E. (2005). Texture Analysis Based on Local Analysis of the Bidimensional Empirical Mode Decomposition. Mach. Vis. Appl. 16, 177–188. doi:10.1007/s00138-004-0170-5

CrossRef Full Text | Google Scholar

Onuki, A. (2002). Phase Transition Dynamics. Cambridge, UK: Cambridge University Press.

Google Scholar

Oprisan, A., Oprisan, S. A., Hegseth, J. J., Garrabos, Y., Lecoutre-Chabot, C., and Beysens, D. (2008). Universality in Early-Stage Growth of Phase-Separating Domains Near the Critical Point. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 77, 051118. doi:10.1103/PhysRevE.77.051118

PubMed Abstract | CrossRef Full Text | Google Scholar

Oprisan, A. (2006). Fluctuations, Phase Separation and Wetting Films Near Liquid-Gas Critical Point. New Orleans, LA: Ph.D. thesis.

Google Scholar

Oprisan, A., Garrabos, Y., Lecoutre-Chabot, C., and Beysens, D. (2021a). Multiscale Empirical Mode Decomposition of Density Fluctuation Images Very Near above and below the Critical Point of SF6. Phys. A Stat. Mech. its Appl. 561, 125293. doi:10.1016/j.physa.2020.125293

CrossRef Full Text | Google Scholar

Oprisan, A., Oprisan, S. A., Garrabos, Y., Lecoutre-Chabot, C., and Beysens, D. (2021b). Density Fluctuation Analysis Very Near above and below Critical Point Using Morphological and Spatiotemporal Information. Eur. Phys. J. Plus 136, 523. doi:10.1140/epjp/s13360-021-01531-8

CrossRef Full Text | Google Scholar

Oprisan, A., Hegseth, J. J., Smith, G. M., Lecoutre, C., Garrabos, Y., and Beysens, D. A. (2011). Dynamics of a Wetting Layer and Marangoni Convection in Microgravity. Phys. Rev. E. 84, 021202. doi:10.1103/PhysRevE.84.021202

PubMed Abstract | CrossRef Full Text | Google Scholar

Oprisan, A., and Leilani Payne, A. (2013). Dynamic Shadowgraph Experiments and Image Processing Techniques for Investigating Non-Equilibrium Fluctuations during Free Diffusion in Nanocolloids. Opt. Commun. 290, 100–106. doi:10.1016/j.optcom.2012.10.052

CrossRef Full Text | Google Scholar

Oprisan, A., Oprisan, S. A., Bayley, B., Hegseth, J. J., Garrabos, Y., Lecoutre-Chabot, C., et al. (2012). Dynamic Structure Factor of Density Fluctuations from Direct Imaging Very Near (Both Above and Below) the Critical Point of SF6. Phys. Rev. E 86, 061501. doi:10.1103/PhysRevE.86.061501

PubMed Abstract | CrossRef Full Text | Google Scholar

Oprisan, A., Oprisan, S. A., Hegseth, J. J., Garrabos, Y., Lecoutre-Chabot, C., and Beysens, D. (2014). Dimple Coalescence and Liquid Droplets Distributions During Phase Separation in a Pure Fluid under Microgravity. Eur. Phys. J. E. 37, 85. doi:10.1140/epje/i2014-14085-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Ortiz de Zárate, J. M., Giraudet, C., Bataller, H., and Croccolo, F. (2014). Non-Equilibrium Fluctuations Induced by the Soret Effect in a Ternary Mixture. Eur. Phys. J. E 37, 34. doi:10.1140/epje/i2014-14077-2

CrossRef Full Text | Google Scholar

Perrot, F., Beysens, D., Garrabos, Y., Fröhlich, T., Guenoun, P., Bonetti, M., et al. (1999). Morphology Transition Observed in a Phase Separating Fluid. Phys. Rev. E. 59, 3079–3083. doi:10.1103/PhysRevE.59.3079

CrossRef Full Text | Google Scholar

Pont, G., Barde, S., and Blonde, D. (2011). DECLIC, Soon Two Years of Successful Operations. Cape Town, SA: International Astronautical Federation.

Google Scholar

Raghukanth, S. T. G., and Sangeetha, S. (2012). Empirical Mode Decomposition of Earthquake Accelerograms. Adv. Adapt. Data Anal. 04, 1250022. doi:10.1142/S1793536912500227

CrossRef Full Text | Google Scholar

Saha, A., Pukhrambam, M., and Nath Pradhan, S. (2016). Facial Image Analysis for Expression Recognition by Bidimensional Empirical Mode Decomposition. Indian J. Sci. Technol. 9, 1–9. doi:10.17485/ijst/2016/v9i31/90495

CrossRef Full Text | Google Scholar

Sang, Y.-F. (2013). Improved Wavelet Modeling Framework for Hydrologic Time Series Forecasting. Water Resour. Manage 27, 2807–2821. doi:10.1007/s11269-013-0316-1

CrossRef Full Text | Google Scholar

Schaefer, D. W., Bunker, B. C., Wilcoxon, J. P., Rowlinson, J. S., Ball, R. C., Tildesley, D. J., et al. (1989). Fractals and Phase Separation. Proc. R. Soc. Lond. A 423, 35–53. doi:10.1098/rspa.1989.0040

CrossRef Full Text | Google Scholar

Schmelzer, J. W. P., Boltachev, G. S., and Baidakov, V. G. (2006). Classical and Generalized Gibbs' Approaches and the Work of Critical Cluster Formation in Nucleation Theory. J. Chem. Phys. 124, 194503. doi:10.1063/1.2196412

PubMed Abstract | CrossRef Full Text | Google Scholar

Schmelzer, J. W. P. (2001). Comments on the Nucleation Theorem. J. Colloid Interface Sci. 242, 354–372. doi:10.1006/jcis.2001.7798

CrossRef Full Text | Google Scholar

Schmelzer, J. W. P., Schmelzer, J., and Gutzow, I. S. (2000). Reconciling Gibbs and van der Waals: A new Approach to Nucleation Theory. J. Chem. Phys. 112, 3820–3831. doi:10.1063/1.481595

CrossRef Full Text | Google Scholar

Schmelzer, J. W. P., and Schmelzer, J. (2001). Kinetics of Condensation of Gases: A New Approach. J. Chem. Phys. 114, 5180–5193. doi:10.1063/1.1331570

CrossRef Full Text | Google Scholar

Sorensen, C. M. (2001). Light Scattering by Fractal Aggregates: A Review. Aerosol Sci. Technol. 35, 648–687. doi:10.1080/02786820117868

CrossRef Full Text | Google Scholar

Trainoff, S. P., and Cannell, D. S. (2002). Physical Optics Treatment of the Shadowgraph. Phys. Fluids. 14, 1340–1363. doi:10.1063/1.1449892

CrossRef Full Text | Google Scholar

Vailati, A., Cerbino, R., Mazzoni, S., Takacs, C. J., Cannell, D. S., and Giglio, M. (2011). Fractal Fronts of Diffusion in Microgravity. Nat. Commun. 2, 1–5. doi:10.1038/ncomms1290

PubMed Abstract | CrossRef Full Text | Google Scholar

Vailati, A., and Giglio, M. (1998). Nonequilibrium Fluctuations in Time-dependent Diffusion Processes. Phys. Rev. E. 58, 4361–4371. doi:10.1103/PhysRevE.58.4361

CrossRef Full Text | Google Scholar

Wang, W., Gelder, P. H. A. J. M. V., Vrijling, J. K., and Ma, J. (2006). Forecasting Daily Streamflow Using Hybrid Ann Models. J. Hydrology. 324, 383–399. doi:10.1016/j.jhydrol.2005.09.032

CrossRef Full Text | Google Scholar

Wilkinson, R. A., Zimmerli, G. A., Hao, H., Moldover, M. R., Berg, R. F., Johnson, W. L., et al. (1998). Equilibration Near the Liquid-Vapor Critical Point in Microgravity. Phys. Rev. E. 57, 436–448. doi:10.1103/PhysRevE.57.436

CrossRef Full Text | Google Scholar

Wu, M.-C. (2012). Damped Oscillations in the Ratios of Stock Market Indices. Europhys. Lett. 97, 48009. doi:10.1209/0295-5075/97/48009

CrossRef Full Text | Google Scholar

Wu, M.-C. (2015). “Damped Oscillatory Behaviors in the Ratios of Stock Market Indices,” in Proceedings of the International Conference on Social Modeling and Simulation, plus Econophysics Colloquium 2014. Editors H. Takayasu, N. Ito, I. Noda, and M. Takayasu (Cham: Springer International Publishing), 51–62. doi:10.1007/978-3-319-20591-5_5

CrossRef Full Text | Google Scholar

Wu, M.-C., Huang, M.-C., Yu, H.-C., and Chiang, T. C. (2006). Phase Distribution and Phase Correlation of Financial Time Series. Phys. Rev. E. 73, 016118. doi:10.1103/PhysRevE.73.016118

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, Z., and Huang, N. E. (2004). A Study of the Characteristics of White Noise Using the Empirical Mode Decomposition Method. Proc. R. Soc. Lond. A. 460, 1597–1611. doi:10.1098/rspa.2003.1221

CrossRef Full Text | Google Scholar

Yu, L., Wang, S., Lai, K. K., and Wen, F. (2010). A Multiscale Neural Network Learning Paradigm for Financial Crisis Forecasting. Neurocomputing 73, 716–725. doi:10.1016/j.neucom.2008.11.035

CrossRef Full Text | Google Scholar

Zappoli, B., Beysens, D., and Garrabos, Y. (2015). Heat Transfers and Related Effects in Supercritical Fluids. Heat Transfers Relat. Eff. Supercrit. Fluids 108, 44. doi:10.1007/978-94-017-9187-8

CrossRef Full Text | Google Scholar

Zhang, X., Lai, K. K., and Wang, S.-Y. (2008). A New Approach for Crude Oil Price Analysis Based on Empirical Mode Decomposition. Energy Econ. 30, 905–918. doi:10.1016/j.eneco.2007.02.012

CrossRef Full Text | Google Scholar