- 1O'Neill School of Public and Environmental Affairs, Indiana University, Bloomington, IN, United States
- 2Pacific Northwest Research Station, U. S. Forest Service, Corvallis, OR, United States
- 3U.S. Geological Survey, Reston, VA, United States
Headwater streams account for more than 89% of global river networks and provide numerous ecosystem services that benefit downstream ecosystems and human water uses. It has been established that changes in climate have shifted the timing and magnitude of observed precipitation, which, at specific gages, have been directly linked to long-term reductions in large river discharge. However, climate impacts on ungaged headwater streams, where ecosystem function is tightly coupled to flow permanence along the river corridor, remain unknown due to the lack of data sets and ability to model and predict flow permanence. We analyzed a network of 10 gages with 38–69 years of records across a 5th-order river basin in the U.S. Pacific Northwest, finding increasing frequency of lower low-flow conditions across the basin. Next, we simulated river network expansion and contraction for a 65-year period of record, revealing 24% and 9% declines in flowing and contiguous network length, respectively, during the driest months of the year. This study is the first to mechanistically simulate network expansion and contraction at the scale of a large river basin, informing if and how climate change is altering connectivity along river networks. While the heuristic model presented here yields basin-specific conclusions, this approach is generalizable and transferable to the study of other large river basins. Finally, we interpret our model results in the context of regulations based on flow permanence, demonstrating the complications of static regulatory definitions in the face of non-stationary climate.
Introduction
More than 89% of the global river network is headwaters (Downing et al., 2012; Allen et al., 2018), supporting ecosystem services and the health of downstream waters (Alexander et al., 2007; US EPA, 2015). These services are associated with the frequency with which streams have surface flow (hereafter “flow permanence”), and any declines in flow permanence will effectively disconnect larger rivers from their headwaters and their functions. Flow generated in headwater streams is highly sensitive to changes in precipitation timing, magnitude, and duration based on a small number of empirical studies over short timescales (Godsey and Kirchner, 2014; Jensen et al., 2017; Zimmer and McGlynn, 2017; Prancevic and Kirchner, 2019). However, no observational studies have covered a sufficient period of record to evaluate if and how changing climate has altered flow permanence across river networks. Consequently, numerical simulations parameterized with readily available data are needed to fill this knowledge gap (Gallart et al., 2016; Ward et al., 2018a).
Changes in flow permanence can alter the transport and transformation of water, energy, dissolved and suspended materials, and organisms throughout the river network (Larned et al., 2010; Gallart et al., 2012; Steward et al., 2012; Datry et al., 2016, 2017; Raymond et al., 2016). Evaluating how flow permanence has changed requires quantification of both the temporal variation (i.e., the frequency a given segment has surface flow) and spatial variation (i.e., the spatial connectivity of surface flow) (Covino, 2017; Wohl, 2017; Wohl et al., 2017). In headwater streams, flow permanence is controlled by the dynamic interaction of geologic setting with hydrologic forcing (Costigan et al., 2016; Prancevic and Kirchner, 2019). Climate change is primarily associated with changes to hydrologic forcing, such as altering the spatial distribution and within-year timing of precipitation. Geologic setting—such as valley width and slope, sinuosity, and hydraulic conductivity—will remain relatively static compared to the pace of climate change.
Changes in flow permanence complicate management and protection of headwater streams. Regulatory protections in the U.S. and E.U. are traditionally focused on perennially flowing waters, with emerging attention paid to temporarily flowing waters (US DoD, 1986; Nikolaidis et al., 2013; US DoD EPA, 2015; Fritz et al., 2018; US DoD US EPA, 2018; Walsh and Ward, 2019). Further complicating management, data on headwater streams, and particularly intermittent and ephemeral streams, are lacking. For example, only 3% of the rivers gaged in the U.S. are headwater streams, as gages are heavily biased toward larger rivers (Poff et al., 2006; Eng and Milly, 2007). A proposed rule would revise protected status to waters with contiguous surface flow in a “typical” 30-year period in the U.S., but does not address systematic changes in flow permanence (US DoD US EPA, 2018). The time-variable definition of the 30-year window does not consider the role of climate change and shifting norms, despite clear evidence that non-stationarity is prevalent in hydrologic systems (Milly et al., 2008). For example, systematic declines in streamflow, and particularly lower low-flows, have been observed across the U.S. Pacific Northwest (Luce and Holden, 2009). Subsequent study revealed that slowing westerlies during winter months reduced the orographic enhancement of precipitation in the region, changing both the amount of precipitation reaching the landscape and the timing for storage vs. export from catchments (Luce et al., 2013). A more recent example paints another dire picture for the future of streamflow in the Southwestern U.S. in response to shifting precipitation and temperature (Milly and Dunne, 2020).
Here we assess whether flow permanence in headwater streams has shifted over the past 65 years from the mid twentieth century baseline in response to observed changes in climate-driven hydrologic forcing. We investigate how timing and magnitude of discharge have shifted over a 65-yr period of record and yielded changes in flow permanence along mountain stream networks. Finally, we consider how our findings may inform current and future protections for streams under the proposed Waters of the U.S. (WOTUS) Rule (US DoD US EPA, 2018) and subsequently finalized in the Navigable Waters Protection Rule (US DoD US EPA, 2019). We selected the 5th-order Lookout Creek basin (Western Cascade Mountains, Oregon, USA) because of the extensive and long-term network of gages on low-order streams (Table S2). Furthermore, this basin is representative of the broader Pacific Northwest where climate change impacts on the timing and magnitude of moisture delivery to high elevation watersheds are known to cause declines in large rivers (Luce and Holden, 2009; Luce et al., 2013). Thus, reduced orographic enhancement of precipitation due to climate change is projected at the field site. This study considers the cascading impact of this change on stream discharge, and how discharge changes in headwaters may change flow permanence and connectivity in a river network.
Methods
Site Description and Available Data
The study was conducted at the H.J. Andrews Experimental Forest (HJA), a 5th-order basin in the Western Cascades, Oregon, USA (site map in Figure S1). The basin drains about 6,400 ha of forested landscape, with elevations ranging from about 410–1,630 m a.m.s.l, making it an ideal place to evaluate the impact of a changing climate on river networks of the broader Pacific Northwest. The basin has been a long-term study site for ecological and forest management research for more than 70 years and is relatively pristine with no urban land use, no dams or reservoirs, and minimal logging during the period of this study. At the longest currently operating meteorological station (CS2MET, elev. 485 m a.m.s.l.) annual precipitation averages 2,345 mm and average annual air temperature is 9.2 deg. C. Additional summaries of temperature and precipitation including trends for the period of record for each station are summarized in Table S1 and Figures S2–S15). In general, significant trends in monthly precipitation and air temperature are infrequently detected, due largely to the short observational records at the local meteorological network (Table S1). Further details about the local climate, morphology, geology, and ecology are comprehensively described elsewhere (Dyrness, 1969; Swanson and James, 1975; Swanson and Jones, 2001; Jefferson et al., 2004; Cashman et al., 2009; Deligne et al., 2017).
The HJA includes a network of 10 stream gages with drainage areas ranging from 8.5 to 6,241.9 ha, with records of 38–69 years of data across the gage network (Table S2). Additionally, a high quality digital elevation model derived from an airborne LiDAR survey is available for the entire basin, which has been reliably processed to extract topographic metrics including valley width, valley slope, and stream sinuosity (after Corson-Rikert et al., 2016; Schmadel et al., 2017; Ward et al., 2018a,b). For each gage we also calculated annual summary metrics of discharge including annual minimum discharge, mean discharge, maximum discharge, exceedance discharges (1, 5, 10, 25, 50, 75, 90, 95, 99th percentiles), total annual discharge, and the days elapsed to various cumulative fractions of discharge (1, 5, 10, 25, 50, 75, 90, 95, 99%).
Finally, an extensive data collection effort spanning the stream orders and lithologic regions of the basin was completed in 2015, providing a database of stream and valley morphologies and hydraulic conductivities to inform network-scale model parameterization (Ward et al., 2019b).
Simulation of the River Network
Simulation of network expansion and contraction followed the methods, data sources, and implementation described by Ward et al. (2018a). Briefly, the approach conceptualizes the river corridor in 1-D along the valley, with domains representing the surface stream and down-valley flow in the valley bottom. Critically, the down-valley subsurface flow (or “underflow”) is filled first, with surface flow representing only the volumetric flow in excess of what the valley bottom can transmit downstream (Figure 1). Put another way, surface flow occurs only when the valley's subsurface cannot accommodate all of the down-valley discharge.
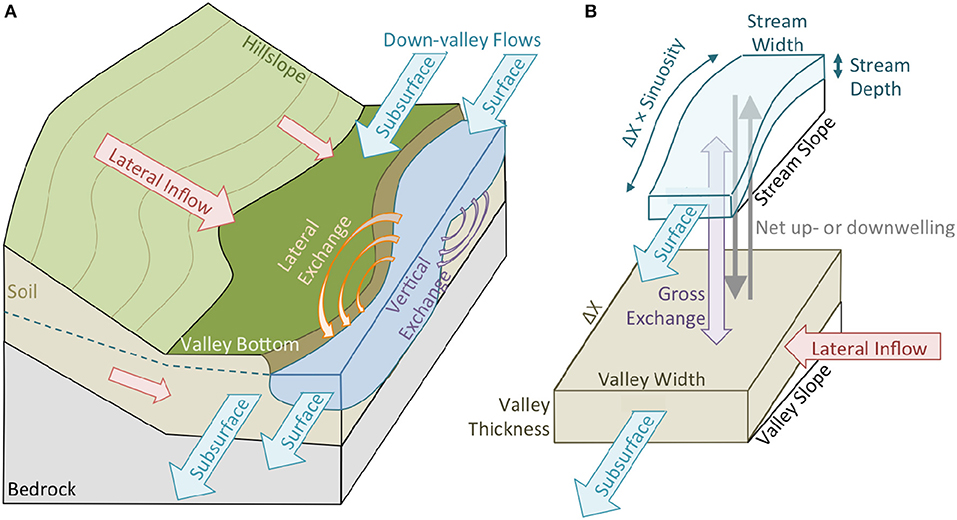
Figure 1. (A) Perceptual model of river corridor exchange showing the inflows and outflows considered in the model. (B) Representation of stores, fluxes, and key variables used in the model implementation. The key advance of this model is the representation of the river corridor as parallel transport in the subsurface and surface domains, with surface flow only activating when the subsurface cannot accommodate all down-valley flow. Reprinted with permission from Ward et al. (2018a).
Ward et al. (2018a) validated the model in a 2nd order catchment within our study basin, concluding the model was appropriate to represent network expansion and contraction based on correct prediction of flowing or dry streambed conditions for more than 95% of over 3.2 million observations. We proceed with implementation of this model across a 5th order basin on the basis of Ward's et al. (2018a) success within our study basin, particularly given the accuracy in representing network expansion and contraction in response to diurnal fluctuations driven by evapotranspiration, storms, and seasonal baseflow.
The model was intentionally derived and constructed to require geomorphic and hydrologic data that are readily estimated for unstudied catchments (Ward et al., 2018a), consistent with our application in this study. Valley width, valley slope, along-stream slope, sinuosity, and the lateral contributing area for each 10-m segment of the valley bottom were extracted from the LiDAR data using a modified version of the TopoToolbox (Schwanghart and Kuhn, 2010; Schwanghart and Scherler, 2014; Schmadel et al., 2017). Stream width at each location was estimated using a power-law regression of 62 observations collected in August 2015 (Ward et al., 2019b) as:
where b is the width of the channel (m) and UAA is the total drainage area (ha), and the best-fit relationship had a coefficient of determination of 0.84. We assigned a uniform Manning's n of 0.045 along the entire network based on visual inspection while working in the basin. Ward et al. (2018a) identified hydraulic conductivity as the largest source of uncertainty in the model. In response, we measured hydraulic conductivity of the streambed at 57 sites in August 2015 (Ward et al., 2019b) and assigned the geometric mean, 1.53 × 10−4 m s−1, across the network. Porosity was assigned as 0.3 at all locations, the midpoint of past studies (Dyrness, 1969; Kasahara and Wondzell, 2003; Wondzell et al., 2009; Ward et al., 2017) and the same value used in model validation (Ward et al., 2018a). We set valley colluvium depth to a minimum value of 1-m (Gooseff et al., 2006; Ward et al., 2018a), increasing as:
where h is colluvium depth (m) and w is valley width (m). This functional form was selected to reflect the limited measurements of subsurface colluvium depth that are available, including geophysical observations at several headwater locations (Crook et al., 2008; Ward et al., 2012) and along the 5th order reach of Lookout Creek (Wondzell, personal communication, and unpublished data).
To parameterize the total down-valley discharge at the upstream end of each 1st order segment, we calculated a unique power-law regression for the gage discharge and drainage area for each 15-min timestep simulated, and defined the discharge based on UAA. Thus, all available gage data, and their time variation, informed the upstream boundaries for model headwaters. Lateral inflows for each segment were estimated using the same power-law regression, where the change in UAA between the up- and downstream end of each segment was used to calculate the associated change in discharge attributed to the lateral area (Schmadel et al., 2017; Ward et al., 2018a,b). Finally, we used the threshold of at least 2.21 × 10−4 m3 s−1 to differentiate surface flow from dry streambeds after past studies in the basin (Ward et al., 2018a).
Consistent with Ward et al. (2018a), we underscore that reduced complexity models are intended to represent the dominant mechanisms and interactions in a system of interest. This necessarily comes at the expense of representation of complexity and heterogeneity within the system. While our model has been derived and validated for headwaters within the study basin, the parameterization detailed above requires simplifications. To that end, this model is most appropriately viewed as heuristic, consistent with common practice in the study of river corridors (e.g., Gooseff et al., 2006; Cardenas and Wilson, 2007; Trauth et al., 2013; Irvine and Lautz, 2015; Schmadel et al., 2016, 2017). At the scale of river networks, comparable models have been applied to study patterns and trends at large spatial scales at the expense of site-specific localized predictions (e.g., Gomez-Velez and Harvey, 2014; Kiel and Cardenas, 2014; Gomez-Velez et al., 2015; Schmadel et al., 2018). Thus, given the model's strong performance at the reach-scale within our study basin (Ward et al., 2018a), explicit design as a heuristic that can be implemented at minimally studied sites, the wealth of data available across our network, and the tradition of heuristic models to test hypotheses in river corridor science, we proceed with this approach.
Statistical Tests
All between-group differences were tested using one-way ANOVA, Kruskal-Wallis, and Mann-Whitney-Wilcoxson U tests. We report differences as significant only if p < 0.05 for all three tests.
For all trends in discharge metrics, flowing frequency, contiguous frequency, flowing length, and contiguous length, we used Mann-Kendall tests and Sen's slopes to define the significance and direction of trends. Decreasing trends are reported for p < 0.05 for the Mann-Kendall tests and a Sen's slope of < 0. Increasing trends are reported for p < 0.05 for the Mann-Kendall tests and a Sen's slope > 0. We report no significant trend for a Mann-Kendall test with p > 0.05 or if Sen's slope is zero.
Analysis of trends may be sensitive to the length of the data set and which years or timesteps are included (i.e., different starting or ending dates, or different trend lengths). Consequently, we analyzed trends for every moving window of 10 or more years for every metric considered in the study, including those related to discharge at gages as well as flowing and contiguous lengths. In the body of manuscript we report significance and direction based on overall trends for each analysis. In the supplemental information we also tabulate how many of the moving windows agree with the overall trends, the length of the single longest trend that opposes the overall trend, and the length of the single longest period with no significant trend. We also tabulated the mean, median, maximum, and minimum Sen's Slope for every analysis, and the number of trends that are increasing, decreasing, or exhibit no significant trend (see Table S4 for robustness of discharge trends, Table S5 for robustness of flowing length and connected length trends, and Figures S29, S30 for visualization of the annual flowing length and connected length trends).
Results and Discussion
Headwater Stream Discharge Is Declining During the Dry Season
Discharge is predominantly decreasing across all gages in the basin over a 65-year period of record (Figure 2). For example, the Lookout Creek gage at the basin outlet has decreasing discharge for 81% of the year (about 300 days), steady discharge for 4% of the year (about 15 days), and increasing discharge for 15% of the year (about 55 days) (Figure 2C; remaining sites in Figures S16–S24; Tables S2, S3). The largest and most consistently decreasing trends are during the summer season when discharge is lowest. We found no increasing discharge for the driest 7-months of the year (April through October; Figure 2D).
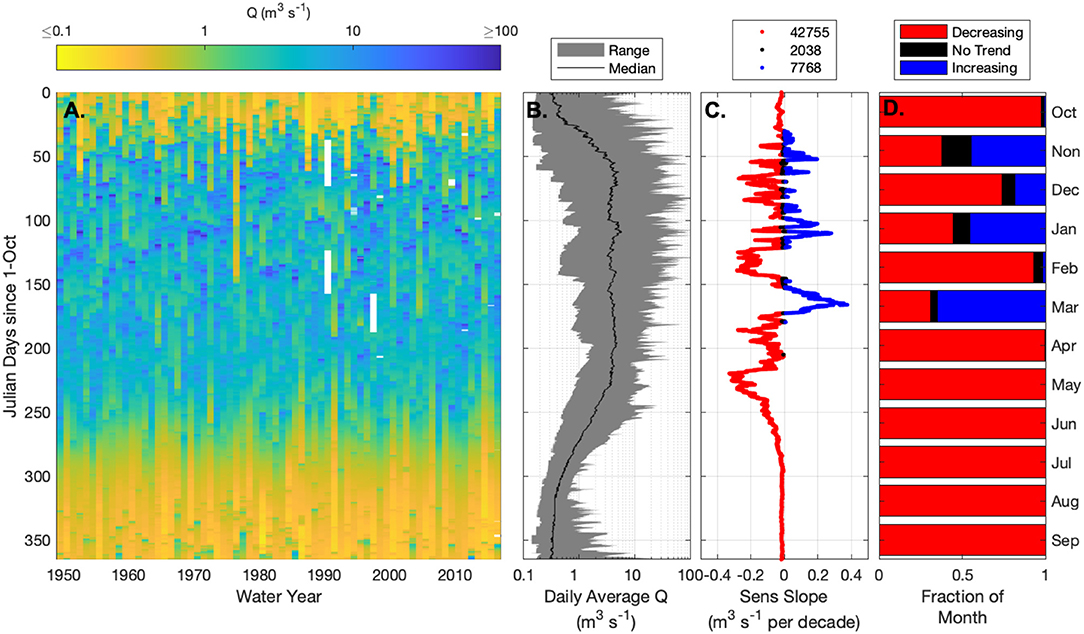
Figure 2. Ten minute discharge analysis for Lookout Creek gage near the outlet of the basin. (A) Discharge for every day, every year of record (white indicates missing data). (B) Range of discharges from the period of record. The median discharge for each 10-min is timestep displayed atop the range. (C) Sen's slope for each 10-min period. Color indicates trend is significantly decreasing (red; 81% of the year; n = 42,755; p < 0.05), not changing (black; 4% of the year; n = 2,038), or significantly increasing (blue; 15% of the year; n = 7,768; p < 0.05). (D) Fraction of each month with decreasing, no, or increasing discharge trends for the period of record. See Figures S6–S24 for comparable plots of all gages in this study.
Across the gage network, we find significant inter- and intra-annual changes in the timing and magnitude of discharge. Annual mean, median, and total discharge are all decreasing for 9 of 10 gages across their periods of record. We also found decreasing annual minimum and maximum discharges for 7 of 10 stream gages, declining annual low-flows (75–99% exceedance flows) at all gages, and declining annual high-flows (1–25% exceedance flows) at 7 of 10 gages (Table S3). Conceptually, the changes in moisture delivery is causing an increased export of water during winter months (Luce et al., 2013; Table S3), as evidenced by the more rapid time to export the first 10% of streamflow each year. Consequently, less water is stored during the rainy season, resulting in decreased dry-season baseflow, and extended times to export the last 10% of annual discharge.
Decreased Flow Permanence Has Reduced River Network Connectivity
Using the stream gage data, topographic analysis, and published data collected in the basin, we simulated dynamic expansion and contraction of the network (Figure 3 and Figure S25) (Ward et al., 2018a). For the 65-year simulation period, declining discharge, and increasing early season export of water within the basin result in an overall contraction of the flowing network (Figure 3). We found the flowing network reaches a maximum length of about 40-km during the wet winter months and contracts to as short as 15-km during the driest periods of record (Figure 3B and Figure S25). Flowing network length is a useful proxy for connectivity along the river corridor, where longer flowing lengths allow more rapid connection of hillslopes to downstream water and promote rapid export of energy and materials rather than internal transformation (van Meerveld et al., 2019).
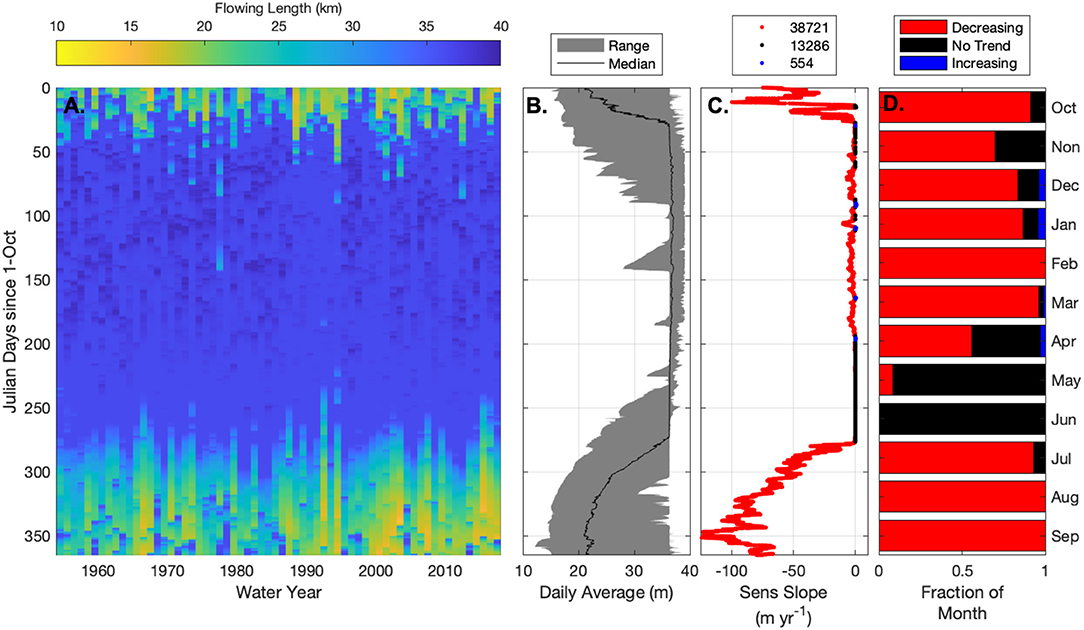
Figure 3. Summary of flowing lengths for the simulation period, including: (A) Flowing length for every 10-min period for water years 1953 through 2017; (B) annual flowing lengths; (C) Sen's slope for the period of record, calculated for every 10-min period of the year; and (D) fraction of each month that length is decreasing, increasing, or has no significant trend. A comparable plot of contiguously flowing length is provided in Figure S25.
Next, we found the connected network length plateaus at about 21-km during the wet winter months and contracts to as small as about 5-km under the lowest discharge conditions (Figure S10). The connected network represents an average of 57.4% of the flowing network across the entire simulation (median 55.9%; range 8.9–79.8%). The connected network defines the migration corridor through which aquatic organisms may travel upstream from the basin outlet without encountering a dry streambed location.
We found significant declines in flowing length for 75.7% of the year (about 276 days) compared to 23.6% of the year with no-trend (about 86 days), and <1% of the year (about 3 days) with increasing flowing length (Figure 3C). The decreasing trends are common throughout much of the year except for the highest discharge conditions associated with spring storms and snowmelt runoff (April through June) when the network length is more steady. Connected length exhibits similar trends, declining for 66.7% of the year (about 243 days), no trend for 33.1% of the year (about 121 days) and increasing trends for <1% of the year (about 2 days; Figure S25).
Decreasing flowing and connected lengths are not distributed evenly through the year. Flowing length declines by a long-term average rate of 21.0 m yr−1 (median 2.3 m yr−1 contraction; range 124.3 m yr−1 contraction to 1.1 m yr−1 expansion) and connected length declines by an average of 4.7 m yr−1 (median 0.6 m yr−1 decline; range 44.1 m yr−1 decline to 0.40 m yr−1 expansion). The largest average rate of flowing length decline, 94.2 m yr−1, is in September. Average September flowing length is 24.1% shorter in 2009–2018 than 1953–1962. Similarly, connected length averages a loss of 21.4 m/yr in August, and is 9.2% shorter in 2009–2018 than the 1953–1962 August average.
Network expansion and contraction exhibit threshold behavior, generally consistent with past studies (Ward et al., 2018a; Prancevic and Kirchner, 2019). When discharge at the Lookout Creek gage is greater than about 1 m3 s−1, the flowing and connected lengths are nearly constant at their plateau values (Figure 3B and Figure S27). Under these wet-season, high discharge conditions, the flowing length maximum reflects a geologic limitation on network expansion where the drainage network is sufficiently dense to drain additional precipitation from the landscape without developing additional channels. As discharge drops below 1 m3 s−1, the network dynamically expands and contracts in response to precipitation. Under these dynamic conditions, the capacity of the valley bottom is comparable to the down-valley discharge, resulting in the large variation in flowing length in response to minor fluctuations in discharge (Ward et al., 2018a).
Headwater Streams In Steeper and/or Wider Valleys Are the Most Sensitive to Climate Change
About 41% of the headwater stream network exhibits a decreasing surface flow frequency, with the remaining 59% exhibiting no change (Figure 4A). No location had increasing frequency of surface flow. Similarly, 27% of locations decrease in frequency of connected flow, 73% have no change, and no sites are more frequently connected across the period of record (Figure S11).
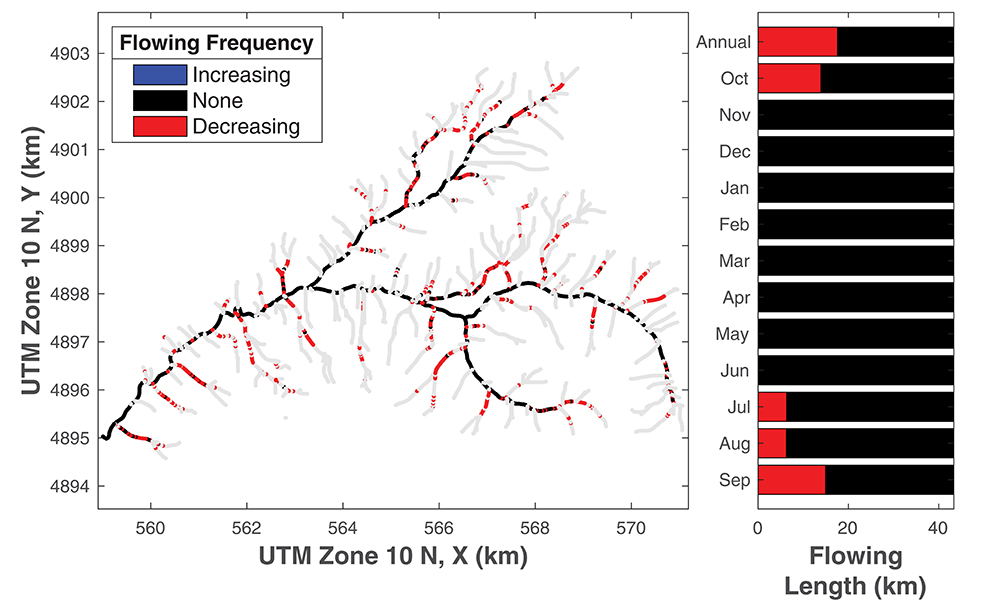
Figure 4. (A, left) Annual trends in flowing days for each segment. (B, right) Annual and monthly summary of model segments exhibiting increasing, decreasing, or no trends in flowing frequency. Panel B presents data discretized in space, while Figure 3D presents data lumped in time. A comparable plot for trends in contiguously flowing status is presented in Figure S26.
Declining trends in flowing and connected frequency are not evenly distributed through the year. Instead, we found few significant trends for any segment during the wet season (November through June) because maximum network extent is controlled by basin morphology and drainage density (Figure 4B). During the dry season (July–October) we found declining frequency of surface flow and contiguous flow in many network segments, due to declining discharge during this period. Similarly, trends in flowing and connected frequency are not evenly distributed in space. The reaches with the largest declines in flowing and connected frequency have significantly smaller drainage areas, steeper valley slopes, and/or wider valleys compared to locations with no trend (Figure S28), consistent with past findings in smaller catchments and the conceptual model (Costigan et al., 2015; Ward et al., 2018a; Prancevic and Kirchner, 2019). Decreasing trends in both flowing and connected frequency are most prevalent at the most upstream extents of the network, making the lowest-order streams “canaries in the coal mine” to first detect the impacts of climate change on flow permanence.
Changing Flow Permanence Challenges Current Regulatory Strategies
Non-stationarity is now the dominant paradigm in water resources (Milly et al., 2008). In our study system, the peak and average connected lengths are significantly larger in the first 30 years than the last 30 years. From a practical perspective, some waters that would have been federally jurisdictional (herafter “jurisdictional”) in 1982 (based on the period 1953–1982) may not be jurisdictional in 2018 (based on the period 1989–2018).
The revised definition for Waters of the United States, which defines the basis for a water receiving federal protections under the federal Clean Water Act, focuses on the frequency of surface flow (US DoD US EPA, 2018). The definition would establish jurisdiction over streams with surface water flow in a “typical year” based on precipitation during a rolling 30-year window absent extreme flood and drought events. Thus, flow permanence is a de facto standard for protection, but its systematic changes with climate are not accounted for in regulations. For example, if jurisdictional status is defined as flow during 29 of 30 years, jurisdictional network length would decline from about 29-km in 1982 to about 26-km in 2017 (horizontal range at Y = 29-year; Figure 5). As the minimum number of flowing years for regulatory protection decreases, changes due to climate become negligible (e.g., horizontal range at Y = 15-year; Figure 5). In contrast, if the Navigable Waters Protection Rule was intended to provide a constant-in-time determination, it must explicitly adjust the definition of “typical year” with climate. The systematic contraction in our study system, and thereby loss of federal protections for streams and their nearby wetlands, is only one response to changes in climate. In a landscape where flow permanence increases due to changing climate, federal jurisdictional scope could increase. Our critique here is consistent with draft comments from the US EPA's Science Advisory Board (Honeycutt and Board, 2019).
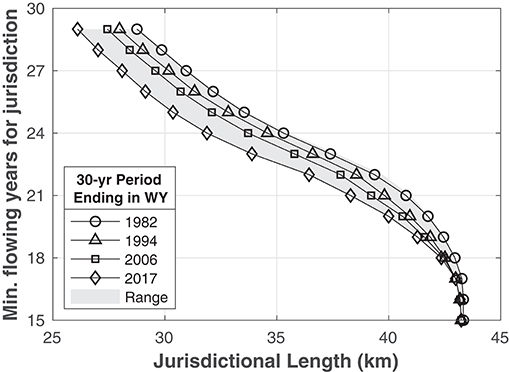
Figure 5. Federal jurisdictional length (x-axis) as a function of the minimum number of flowing years to establish jurisdiction (y-axis) and final year of rolling 30-year period. The horizontal range between the lines is the change in jurisdictional length for a fixed definition of “typical year” (e.g., must flow 25 of 30 years to be jurisdictional). The vertical range between lines is the reduction in threshold that would be required to protect the same length of stream.
Conclusions
While past studies have explored the reduction in discharge at downstream gages on large rivers (Luce and Holden, 2009), this study is the first to examine how known changes in precipitation (Luce et al., 2013) and discharge translate into changes in connectivity between mountain hillslopes and their headwaters. Compared to their 1953–1962 averages, the 2009–2018 network has contracted by 24.1% and 9.2% in flowing and connected length, respectively, during the driest months. The dynamic connections along the network underpin a host of ecosystem services that we expect to also vary with flowing frequency. The loss of ecological function of such streams could be irreversible, and time-variable jurisdictional protections complicate the protection of these important resources. These losses are relative to a mid twentieth century baseline, and while some function will be lost as flow permeance decreases, other functions could be amplified as a result of increased duration or frequency of non-flowing conditions. Decreases in streamflow during periods when water resources are in highest demand, as was recently observed across the western U.S. (e.g., Milly and Dunne, 2020), further highlights the need for the extending the approaches presented here to more river basins.
Simulations predict that reaches with smaller drainage areas and larger subsurface flow capacity are the most likely to change in their flowing and connected frequencies in response to climate change. Thus headwater locations with steep valley gradients, larger valley widths, and/or disproportionately high hydraulic conductivity (Wondzell, 2006; Ward et al., 2019a) should be closely monitored to assess catchment response to climate change. Importantly, there are a small number of critical locations within a valley that can cutoff entire upstream reaches from the contiguous network—one location with a wider- or steeper-than-average morphology can transition to entirely subsurface flow. We observed this threshold disconnection when the Lookout Creek gage discharge dropped below about 1 m3 s−1. While this threshold is the result of local geologic setting, we expect other systems will exhibit similar threshold behavior as a function of subsurface flow capacity and discharge. Finally, we underscore that current regulations are not designed with climate change-induced shifts in flowing and connected frequency, which will complicate policy enforcement for protection of headwater streams. The conclusions presented here are specific to one river basin in the Pacific Northwest, but the modeling approach and interpretation were intentionally designed to be transferable to other river networks, enabling extended analysis with modest, commonly-available data.
Data Availability Statement
Topographic data and stream discharge data are available from the H.J. Andrews Experimental Forrest LTER database (https://andrewsforest.oregonstate.edu/data) as data sets GI010 and HF004, respectively. Valley and stream geometries derived from the LiDAR are publicly available (Ward et al., 2019b). Model outputs including timeseries of flowing length, contiguous length, and flowing frequency for each modeled segment are archived in CUAHSI's HydroShare at: http://www.hydroshare.org/resource/2f9643bb5d85436ba997a466ba8ed653.
Author Contributions
AW conceived of the study and led the modeling, analysis, and writing. NS completed the topographic analyses and contributed to conceptual and numerical model development. AW and SW secured funding to support the research. AW, SH, SW, and NS participated in the data analysis and writing of the study.
Funding
This research was funded in part, by the National Science Foundation under Grant No. DEB-1440409. Additional support to individual authors is acknowledged from National Science Foundation (NSF) awards EAR 1652293, EAR 1417603, and EAR 1446328, Department of Energy award DE-SC0019377, and the Burnell and Barbara Fischer Faculty Fellowship at Indiana University. This research was sponsored by the Office of Biological and Environmental Research within the Office of Science of the U. S. Department of Energy (DOE), as part of the Mercury Science Focus Area project at Oak Ridge National Laboratory (ORNL), which is managed by UT-Battelle, LLC under Contract no. DE-AC05-00OR22725 with the DOE. NS was supported by the USGS Water Mission Area Mendenhall postdoctoral fellowship (NMS).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Data and facilities were provided by the H.J. Andrews Experimental Forest and Long Term Ecological Research program, administered cooperatively by the USDA Forest Service Pacific Northwest Research Station, Oregon State University, and the Willamette National Forest. The authors acknowledge this would not have been possible without support from their home institutions. Any use of trade, firm, or product names is for descriptive purposes only and does not imply endorsement by the U.S. Government nor the authors' institutions.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frwa.2020.00007/full#supplementary-material
References
Alexander, R. B., Boyer, E. W., Smith, R. A., Schwarz, G. E., and Moore, R. B. (2007). The role of headwater streams in downstream water quality. JAWRA. 43, 41–59. doi: 10.1111/j.1752-1688.2007.00005.x
Allen, G. H., Pavelsky, T. M., Barefoot, E. A., Lamb, M. P., Butman, D., Tashie, A., et al. (2018). Similarity of stream width distributions across headwater systems. Nat. Commun. 9:610. doi: 10.1038/s41467-018-02991-w
Cardenas, M. B., and Wilson, J. L. (2007). Exchange across a sediment-water interface with ambient groundwater discharge. J Hydrol. 346, 69–80. doi: 10.1016/j.jhydrol.2007.08.019
Cashman, K. V., Deligne, N. I., Gannett, M. W., Grant, G. E., and Jefferson, A. (2009). Fire and water: volcanology, geomorphology, and hydrogeology of the cascade range, central oregon. Field Guide. 15, 539–582. doi: 10.1130/2009.fld015(26)
Corson-Rikert, H. A., Wondzell, S. M., Haggerty, R., and Santelmann, M. V. (2016). Carbon dynamics in the hyporheic zone of a headwater mountain streamin the Cascade Mountains, Oregon. Water Resour. Res. 52, 7556–7576. doi: 10.1002/2016WR019303
Costigan, K. H., Daniels, M. D., and Dodds, W. K. (2015). Fundamental spatial and temporal disconnections in the hydrology of an intermittent prairie headwater network. J. Hydrol. 522, 305–316. doi: 10.1016/j.jhydrol.2014.12.031
Costigan, K. H., Jaeger, K. L., Goss, C. W., Fritz, K. M., and Goebel, P. C. (2016). Understanding controls on flow permanence in intermittent rivers to aid ecological research: integrating meteorology, geology and land cover. Ecohydrology. 9, 1141–1153. doi: 10.1002/eco.1712
Covino, T. (2017). Hydrologic connectivity as a framework for understanding biogeochemical flux through watersheds and along fluvial networks. Geomorphology. 277, 133–144. doi: 10.1016/j.geomorph.2016.09.030
Crook, N., Binley, A. M., Knight, R., Robinson, D. A., Zarnetske, J. P., and Haggerty, R. (2008). Electrical resistivity imaging of the architecture of substream sediments. Water Resour. Res. 44:W00D13. doi: 10.1029/2008WR006968
Datry, T., Bonda, N., and Boulton, A. J. (Eds.). (2017). Intermittent Rivers and Ephemeral Streams : Ecology and Management, 1st ed. London: Academic Press.
Datry, T., Pella, H., Leigh, C., Bonada, N., and Hugueny, B. (2016). A landscape approach to advance intermittent river ecology. Freshw. Biol. 61, 1200–1213. doi: 10.1111/fwb.12645
Deligne, N. I., Mckay, D., Conrey, R. M., Grant, G. E., Johnson, E. R., O'Connor, J., et al. (2017). Field-Trip Guide to Mafic Volcanism of the Cascade Range in Central Oregon - A Volcanic, Tectonic, Hydrologic, and Geomorphic Journey. U. S. Geological Survey Scientific Investigations Report 2017-5022-H. 94. doi: 10.3133/sir20175022H
Downing, J. A., Cole, J. J., Duarte, C. M., Middelburg, J. J., Melack, J. M., Prairie, Y. T., Tranvik, L. J., et al. (2012). Global abundance and size distribution of streams and rivers. Inland Waters. 2, 229–236. doi: 10.5268/IW-2.4.502
Dyrness, C. T. (1969). Hydrologic Properties of Soils on Three Small Watersheds in the Western Cascades of Oregon. USDA Forest Serv. Res. Note Pnw-111.
Eng, K., and Milly, P. C. D. (2007). Relating low-flow characteristics to the base flow recession time constant at partial record stream gauges. Water Resour. Res., 43, 1–8. doi: 10.1029/2006WR005293
Fritz, K. M., Schofield, K. A., Alexander, L. C., McManus, M. G., Golden, H. E., Lane, C. R., et al. (2018). Physical and chemical connectivity of streams and riparian wetlands to downstream waters: a synthesis. J. Am. Water Resour. Assoc. 54, 323–345. doi: 10.1111/1752-1688.12632
Gallart, F., Llorens, P., Latron, J., Cid, N., Rieradevall, M., and Prat, N. (2016). Validating alternative methodologies to estimate the regime of temporary rivers when flow data are unavailable. Sci. Total Environ. 565, 1001–1010. doi: 10.1016/j.scitotenv.2016.05.116
Gallart, F., Prat, N., Garca-Roger, E. M., Latron, J., Rieradevall, M., Llorens, P., Froebrich, J., et al. (2012). A novel approach to analysing the regimes of temporary streams in relation to their controls on the composition and structure of aquatic biota. Hydrol. Earth Syst. Sci. 16, 3165–3182. doi: 10.5194/hess-16-3165-2012
Godsey, S. E., and Kirchner, J. W. (2014). Dynamic, discontinuous stream networks: Hydrologically driven variations in active drainage density, flowing channels and stream order. Hydrol. Process. 28, 5791–5803. doi: 10.1002/hyp.10310
Gomez-Velez, J. D., and Harvey, J. W. (2014). A hydrogeomorphic river network model predicts where and why hyporheic exchange is important in large basins. Geophys. Res. Lett. 41, 6403–6412. doi: 10.1002/2014GL061099
Gomez-Velez, J. D., Harvey, J. W., Cardenas, M. B., and Kiel, B. (2015). Denitrification in the Mississippi River network controlled by flow through river bedforms. Nat. Geosci. 8, 1–8. doi: 10.1038/ngeo2567
Gooseff, M. N., Anderson, J. K., Wondzell, S. M., LaNier, J., and Haggerty, R. (2006). A modelling study of hyporheic exchange pattern and the sequence, size, and spacing of stream bedforms in mountain stream networks, Oregon, USA. Hydrol. Process. 20, 2443–2457. doi: 10.1002/hyp.6349
Honeycutt, M., and Board, U. E. S. A. (2019). Draft Commentary on the Proposed Rule Defining the Scope of Waters Federally Regulated Under the Clean. Water Act.
Irvine, D. J., and Lautz, L. K. (2015). High resolution mapping of hyporheic fluxes using streambed temperatures: Recommendations and limitations. J. Hydrol. 524, 137–146. doi: 10.1016/j.jhydrol.2015.02.030
Jefferson, A., Grant, G. E., and Lewis, S. L. (2004). “A river runs underneath it: geological control of spring and channel systems and management implications, cascade range, Oregon,” in Advancing the Fundamental Sciences Proceedings of the Forest Service: Proceedings of the Forest Service National Earth Sciences Conference, 1(October 2004), 18–22.
Jensen, C. K., McGuire, K. J., and Prince, P. S. (2017). Headwater stream length dynamics across four physiographic provinces of the Appalachian Highlands. Hydrol. Process. 31, 3350–3363. doi: 10.1002/hyp.11259
Kasahara, T., and Wondzell, S. M. (2003). Geomorphic controls on hyporheic exchange flow in mountain streams. Water Resour. Res. 39:1005. doi: 10.1029/2002WR001386
Kiel, B., and Cardenas, M. (2014). Lateral hyporheic exchange throughout the Mississippi River network. Nat. Geosci. 7, 413–417. doi: 10.1038/ngeo2157
Larned, S. T., Datry, T., Arscott, D. B., and Tockner, K. (2010). Emerging concepts in temporary-river ecology. Freshw. Biol. 55, 717–738. doi: 10.1111/j.1365-2427.2009.02322.x
Luce, C. H., Abatzoglou, J., and Holden, Z. A. (2013). The missing mountain water: slower westerlies decrease orographic enhancement in the Pacific Northwest USA. Science. 1360, 1360–1365. doi: 10.1126/science.1242335
Luce, C. H., and Holden, Z. A. (2009). Declining annual streamflow distributions in the Pacific Northwest United States, 1948-2006. Geophys. Res. Lett. 36, 2–7. doi: 10.1029/2009GL039407
Milly, P. C. D., Bentacourt, J., Falkenmark, M., Robert, M., Hirsch, R. M., Kundzewicz, Z. W., et al. (2008). Stationarity is dead: Whither water management? Science. 319, 573–574. doi: 10.1126/science.1151915
Milly, P. C. D., and Dunne, K. A. (2020). Colorado River flow dwindles as warming-driven loss of reflective snow energizes evaporation. Science. 9187:eaay9187. doi: 10.1126/science.aay9187
Nikolaidis, N. P., Demetropoulou, L., Froebrich, J., Jacobs, C., Gallart, F., Prat, N., et al. (2013). Towards sustainable management of Mediterranean river basins: policy recommendations on management aspects of temporary streams. Water Policy. 15, 830–849. doi: 10.2166/wp.2013.158
Poff, L. N., Bledsoe, B. P., and Cuhaciyan, C. O. (2006). Hydrologic variation with land use across the contiguous United States: geomorphic and ecological consequences for stream ecosystems. Geomorphology. 79, 264–285. doi: 10.1016/j.geomorph.2006.06.032
Prancevic, J. P., and Kirchner, J. W. (2019). Topographic controls on the extension and retraction of flowing streams. Geophys. Res. Lett. 46, 2084–2092. doi: 10.1029/2018GL081799
Raymond, P. A., Saiers, J. E., and Sobczak, W. V. (2016). Hydrological and biogeochemical controls on watershed dissolved organic matter transport: pulse- shunt concept. Ecology. 97, 5–16. doi: 10.1890/14-1684.1
Schmadel, N. M., Harvey, J. W., Alexander, R. B., Schwarz, G. E., Moore, R. B., Eng, K., et al. (2018). Thresholds of lake and reservoir connectivity in river networks control nitrogen removal. Nat. Commun. 9:2779. doi: 10.1038/s41467-018-05156-x
Schmadel, N. M., Ward, A. S., Lowry, C. S., and Malzone, J. M. (2016). Hyporheic exchange controlled by dynamic hydrologic boundary conditions. Geophys. Res. Lett. 43, 4408–4417. doi: 10.1002/2016GL068286
Schmadel, N. M., Ward, A. S., and Wondzell, S. M. (2017). Hydrologic controls on hyporheic exchange in a headwater mountain stream. Water Resour. Res. 53, 6260–6278. doi: 10.1002/2017WR020576
Schwanghart, W., and Kuhn, N. J. (2010). TopoToolbox: a set of Matlab functions for topographic analysis. Environ. Model. Softw. 25, 770–781. doi: 10.1016/j.envsoft.2009.12.002
Schwanghart, W., and Scherler, D. (2014). Short communication: topoToolbox 2 - MATLAB-based software for topographic analysis and modeling in Earth surface sciences. Earth Surface Dyn. 2, 1–7. doi: 10.5194/esurf-2-1-2014
Steward, A. L., Von Schiller, D., Tockner, K., Marshall, J. C., and Bunn, S. E. (2012). When the river runs dry: human and ecological values of dry riverbeds. Front. Ecol. Environ. 10, 202–209. doi: 10.1890/110136
Swanson, F. J., and James, M. E. (1975). Geology and geomorphology of the H.J. Andrews Experimental Forest, western Cascades, Oregon. Portland, OR.
Swanson, F. J., and Jones, J. A. (2001). Geomorphology and Hydrology of the H.J. Andrews Experimental Forest, Blue River, Oregon. 1–5.
Trauth, N., Schmidt, C., Maier, U., Vieweg, M., and Fleckenstein, J. H. (2013). Coupled 3-D stream flow and hyporheic flow model under varying stream and ambient groundwater flow conditions in a pool-riffle system. Water Resour. Res. 49, 5834–5850. doi: 10.1002/wrcr.20442
US DoD (1986). Final rule for regulatory programs of the corps of engineers. Fed. Regist. 51, 41206–41260.
US DoD and EPA (2015). Clean water rule: definition of “Waters of the United States.” Fed. Regist. 80, 37054–37127.
US DoD and US EPA (2018). Revised definition of “Waters of the United States” (pp. 253 pp. EPA-HQ-OW-2018-0149). pp. 253 pp. EPA-HQ-OW-2018-0149.
US DoD and US EPA (2019). Definition of '“Waters of the United States”'-Recodification of Pre-Existing Rules (Vol. 84).
US EPA (2015). Connectivity of Streams and Wetlands to Downstream Waters: A Review and Synthesis of the Scientific Evidence (Final Report).
van Meerveld, H. J. I., Kirchner, J. W., Vis, M. J. P., Assendelft, R. S., and Seibert, J. (2019). Expansion and contraction of the flowing stream network changes hillslope flowpath lengths and the shape of the travel time distribution. Hydrol. Earth System Sci. Discuss. 2006(September 2006), 1–18. doi: 10.5194/hess-2019-218
Walsh, R., and Ward, A. S. (2019). Redefining clean water regulations reduces protections for wetlands and jurisdictional uncertainty. Front. Water 1:1. doi: 10.3389/frwa.2019.00001
Ward, A. S., Fitzgerald, M., Gooseff, M. N., Voltz, T. J., Binley, A. M., and Singha, K. (2012). Hydrologic and geomorphic controls on hyporheic exchange during base flow recession in a headwater mountain stream. Water Resour. Res. 48:W04513. doi: 10.1029/2011WR011461
Ward, A. S., Schmadel, N. M., and Wondzell, S. M. (2018a). Simulation of dynamic expansion, contraction, and connectivity in a mountain stream network. Adv. Water Resour. 114, 64–82. doi: 10.1016/j.advwatres.2018.01.018
Ward, A. S., Schmadel, N. M., and Wondzell, S. M. (2018b). Time-variable transit time distributions in the hyporheic zone of a headwater mountain stream. Water Resour. Res. 54, 2017–2036. doi: 10.1002/2017WR021502
Ward, A. S., Schmadel, N. M., Wondzell, S. M., Gooseff, M. N., and Singha, K. (2017). Dynamic hyporheic and riparian flow path geometry through base flow recession in two headwater mountain streamcorridors. Water Resour. Res. 53, 3988–4003. doi: 10.1002/2016WR019875
Ward, A. S., Wondzell, S. M., Schmadel, N. M., Herzog, S., Zarnetske, J. P., Baranov, V., et al. (2019a). Spatial and temporal variation in river corridor exchange across a 5th order mountain stream network. Hydrol. Earth Syst. Sci. 23, 5199–5225. doi: 10.5194/hess-23-5199-2019
Ward, A. S., Zarnetske, J. P., Baranov, V., Blaen, P. J., Brekenfeld, N., Chu, R., et al. (2019b). Co-located contemporaneous mapping of morphological, hydrological, chemical, and biological conditions in a 5th order mountain stream network, Oregon, USA. Earth Syst. Sci. Data Discuss. 11, 1567–1581. doi: 10.5194/essd-11-1567-2019
Wohl, E. (2017). Connectivity in rivers. Progress Phys. Geogr. 41, 345–362. doi: 10.1177/0309133317714972
Wohl, E., Magilligan, F. J., and Rathburn, S. L. (2017). Introduction to the special issue: connectivity in Geomorphology. Geomorphology. 277, 1–5. doi: 10.1016/j.geomorph.2016.11.005
Wondzell, S. M. (2006). Effect of morphology and discharge on hyporheic exchange flows in two small streams in the Cascade Mountains of Oregon, USA. Hydrol. Process. 20, 267–287. doi: 10.1002/hyp.5902
Wondzell, S. M., LaNier, J., and Haggerty, R. (2009). Evaluation of alternative groundwater flow models for simulating hyporheic exchange in a small mountain stream. J. Hydrol. 364, 142-151. doi: 10.1016/j.jhydrol.2008.10.011
Keywords: river corridor, river network, intermittent, ephemeral, stream, hyporheic, climate
Citation: Ward AS, Wondzell SM, Schmadel NM and Herzog SP (2020) Climate Change Causes River Network Contraction and Disconnection in the H.J. Andrews Experimental Forest, Oregon, USA. Front. Water 2:7. doi: 10.3389/frwa.2020.00007
Received: 02 January 2020; Accepted: 20 March 2020;
Published: 23 April 2020.
Edited by:
Dipankar Dwivedi, Lawrence Berkeley National Laboratory, United StatesReviewed by:
Heather E. Golden, United States Environmental Protection Agency, United StatesZexuan Xu, Lawrence Berkeley National Laboratory, United States
Copyright © 2020 Ward, Wondzell, Schmadel and Herzog. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Adam S. Ward, YWRhbXdhcmRAaW5kaWFuYS5lZHU=
 Adam S. Ward
Adam S. Ward Steven M. Wondzell2
Steven M. Wondzell2 Noah M. Schmadel
Noah M. Schmadel