- 1School of Earth Systems and Sustainability, Southern Illinois University, Carbondale, IL, United States
- 2Illinois State Water Survey, University of Illinois, Champaign, IL, United States
Extreme precipitation contributes to widespread impacts in the U.S. Great Lakes region, ranging from agricultural losses to urban floods and associated infrastructure costs. Previous studies have reported historical increases in the frequency of extreme precipitation in the region and downscaled model projections indicate further changes as the climate system continues to warm. Here, we conduct trend analysis on the 5 km NOAA NClimDiv data for the U.S. Great Lakes region using both parametric (Ordinary Least Squares) and non-parametric methods (Theil-Sen/Mann-Kendall) and accounting for temporal autocorrelation and field significance to produce robust estimates of extreme precipitation frequency trends in the region. The approaches provide similar overall results and reflect an increase in extreme precipitation frequency in parts of the U.S. Great Lakes region. To relate the identified trends to large scale drivers, a bivariate self-organizing map (SOM) is constructed using standardized values of 500 hPa geo-potential height and 850 hPa specific humidity obtained from the ECMWF ERA-5 reanalysis. Using a Monte Carlo approach, we identify six SOM nodes that account for only 25.4% of all days, but 50.5% of extreme precipitation days. Composites of days with and without extreme precipitation for each node indicate that extreme events are associated with stronger features (height gradient and background humidity) than their non-extreme counterparts. The analysis also identifies a significant increase in the frequency of one SOM node often associated with extreme precipitation (accounting for 8.5% of all extreme precipitation days) and a significant increase in the frequency of extreme precipitation days relative to all days across the six extreme precipitation nodes collectively. Our results suggest that changes in atmospheric circulation and related moisture transport and convergence are major contributors to changes in extreme precipitation in the U.S. Great Lakes region.
Introduction
Extreme precipitation is associated with wide-reaching impacts in the Great Lakes region of the United States, including direct effects on localized and large-scale flooding (Winters et al., 2015), transportation and infrastructure (Angel et al., 2018) and agriculture, and many indirect effects, such as heightened risk of gastrointestinal illness (Drayna et al., 2010), impacts on disease vector habitats, and overall water quality. Improved understanding of the changing nature and drivers of extreme precipitation is therefore critical for reducing the impacts of current and future climate impacts in the region.
Extreme precipitation events occur in the absence of enhanced radiative forcing from greenhouse gases, but there is also a theoretical expectation, and growing observational evidence, of an increase in precipitation extremes associated with anthropogenically-driven global warming (Allan and Soden, 2008). The Clausius-Clapeyron (C-C) relation indicates an ~7% increase in saturation specific humidity per degree of warming under constant relative humidity. Because regional changes in extreme precipitation are determined not only by background humidity, but also by transport of atmospheric moisture to regions of convergence, local, and regional changes in extreme precipitation can differ substantially from the expected C-C scaling (Lenderink and Van Meijgaard, 2010), especially for the most extreme precipitation values and at the shortest time scales (Pendergrass, 2018).
Multi-decadal climate projections from ensembles of climate models indicate further increases in extreme precipitation over most land areas (IPCC, 2021) as the atmospheric continues to warm. Regional studies conducted with multiple generations of climate models, statistical and dynamical downscaling approaches, and mid- and late-century time horizons have similarly pointed to more frequent and intense precipitation events in the region under additional global and regional warming (Pryor et al., 2013; D'orgeville et al., 2014; Byun and Hamlet, 2018; Zhang et al., 2019).
The nature of historical and potential future changes in extreme precipitation in the U.S. Great Lakes region, as well as their drivers, need to be well-understood so that appropriate mitigation and adaptation strategies can be identified and implemented. Precipitation extremes results from processes occurring across spatial scales, ranging from the micro-scale to the upper end of the mesoscale (sometimes referred to as synoptic scale) (Orlanski, 1975). There is growing interest in identifying the mesoscale and synoptic scale conditions associated with events (Barlow et al., 2019), including those occurring at the regional scale (e.g., the Northeast USA by Agel et al., 2018). As noted by Barlow et al. (2019), the synoptic scale is particularly critical for understanding extreme precipitation events as synoptic scale processes are (1) important for producing extreme precipitation events, (2) associated with some medium-range predictability, and (3) resolved in both weather and climate models.
To contribute to a better understanding of changes in extreme precipitation in the U.S. Great Lakes region, we first conduct a historical trend analysis of daily extreme precipitation events identified using a peaks-over-threshold framework [section Bivariate Synoptic Classification Using the Self-Organizing Map (SOM)]. The trend analysis includes both parametric and non-parametric trend estimation techniques that account for temporal autocorrelation in the time series and field significance. We then develop a bivariate synoptic classification by applying the self-organizing map (SOM) technique (section Linking SOM Nodes and Regional Precipitation Extremes) to synoptic scale atmospheric circulation and humidity fields. Finally, we investigate relationships between trends in precipitation extremes and their associated synoptic patterns.
Study Region and Data
Study Region
The study region is defined as the states bordering the Laurentian Great Lakes, plus Iowa which is mostly contained within the convex hull of the lake-border states. The region therefore includes Illinois, Indiana, Iowa, Michigan, Minnesota, New York, Ohio, Pennsylvania, and Wisconsin (Figure 1) and includes parts of the drainage basin for the Great Lakes, but also for the Mississippi and Ohio Rivers. The general pattern of annual precipitation is characterized by a decreasing amounts from southeast to northwest (Pryor et al., 2013), driven primarily by variations in winter precipitation. Extreme precipitation has widespread impacts in the region, including those on agriculture, natural ecosystems, urban systems, and water quality, among others (Wuebbles et al., 2019).
Figure 1. Map showing Great Lakes region used for analysis of extreme precipitation and the ERA5 0.25° grid used for the synoptic classification using self-organizing map (SOM) algorithm.
Data
Precipitation Data
Our analysis of extreme precipitation is based on daily precipitation data from NOAAs NClimDiv data set (Vose et al., 2014), a 5 km resolution gridded temperature and precipitation product derived via climatologically aided interpolation (CAI; Willmott and Robeson, 1995) of station data from the daily Historical Climatological Network (HCN-D; Menne et al., 2012). Relative to previous divisional data sets, NClimDiv includes a larger number of stations, additional quality assurance tests, and bias adjustments for changes in observation technique as described in Vose et al. (2014). Daily precipitation grids are available from 1951 to present for the contiguous United States. The 5 km NClimDiv grid used in this study covers the labeled states shown in Figure 1.
Because NClimDiv is derived from interpolation of available station data, the product is spatially and serially complete. While NClimDiv does not provide information regarding sub-daily precipitation extremes, the consistent long-term perspective it provides regarding daily precipitation extremes is valuable for understanding regional changes in extreme precipitation over time. Additional details about the NClimDiv data set, including identification of extreme precipitation events is provided in section Precipitation Extremes.
Reanalysis Data
To characterize the synoptic environment as it relates to extreme precipitation events, we used the European Center for Medium-Range Weather Forecasts (ECMWF) ERA5 reanalysis (Hersbach et al., 2020). ERA5 represents an improvement over previous reanalysis products as a result of improved model accuracy and data assimilation techniques, resulting in more accurate estimates and at higher resolution. ERA5 currently provides global, hourly estimates of atmospheric and land surface variables at a resolution of 0.25° for pressure levels ranging for 1–1,000 hPa starting in 1979, with a plan to ultimately extend the analysis back to 1950. Our analysis of both precipitation extremes and their corresponding synoptic-scale patterns therefore starts in 1979 and ends in 2019.
Reanalysis data should be used cautiously in areas with sparse data. Because upper air conditions in the central and eastern United States are regularly observed using radiosondes, and these measurements are assimilated by ERA5, the reanalysis outputs should provide an excellent representation of the upper air conditions in the region. With high spatial resolution and spatial and serial completeness, ERA5 is ideal for investigating synoptic scale circulation variability and links with the surface extreme precipitation record. Previous studies (Junker et al., 1999; Schumacher and Johnson, 2005, 2006; Tryhorn and Degaetano, 2011; Kunkel et al., 2013; Nasri et al., 2016) have established that synoptic scale drivers of extreme precipitation include measures of circulation and atmospheric humidity. We therefore use 500-hPa geo-potential height to reflect circulation and 850-hPa specific humidity to characterize moisture availability. The ERA5 grid point used in this study are shown in Figure 1. For this application, the hourly ERA5 outputs were used to compute daily averages for use with the daily precipitation data described in section Precipitation Data.
Methods
Our research design includes several types of analysis designed to meet the stated research objectives. First, we define our extreme precipitation metric and explore the climatology of extreme precipitation events in the U.S. Great Lakes region, including a detailed analysis of trends in extreme event frequency. Second, we classify regional circulation and humidity data in a bivariate synoptic classification to investigate large-scale drivers of extreme precipitation. Finally, we examine changes in extreme precipitation through the lens of the resulting synoptic classes.
Precipitation Extremes
Identification of Precipitation Extremes
Extreme values in climate science have been traditionally investigated using either a block maximum approach, in which the maximum value from each time block is identified and then the collection of block maxima are studied, or by the peaks-over-threshold approach, in which exceedances of a pre-specified threshold are counted and explored. We chose to use the peaks-over-threshold to ensure that no extreme events were discarded, following Acero et al. (2011). An additional subjective decision is the choice of an absolute or relative threshold. Because extreme precipitation magnitude varies across the region, a relative threshold is used. Specifically, for each grid point in NClimDiv, the threshold applied is the magnitude of precipitation associated with a 1-year recurrence interval based on a partial duration series (PDS, see Bonnin et al., 2005). Since the record of study is 1979–2019 (41 years), this value is determined by ranking the daily precipitation values across all years from largest to smallest and identifying the 41st ordered value. We then use this threshold value with the daily NClimDiv data to compute the number of exceedances per year from at each grid point in the region.
Extreme Precipitation Trend Analysis
Changes in extreme precipitation in the U.S. Great Lakes region are quantified by applying trend analysis to the extreme precipitation counts from the analysis of precipitation extremes. Because ordinary least squares (OLS) regression is sensitive to outliers and extreme values at the series endpoints, we follow previous studies that have considered both parametric and non-parametric approaches (Huth and Pokorna, 2004; Asadieh and Krakauer, 2015). The non-parametric technique adopted is Theil-Sen estimation (Sen, 1968), which is equivalent to median-of-pairwise slopes regression (see Lanzante, 1996). Both approaches have advantages and disadvantage. Despite sensitivity to outliers, OLS regression is powerful approach for estimating trends and assessing their differences from 0. In OLS, the trend magnitude and statistical significance are determined simultaneously. In the non-parametric technique, a Mann-Kendall test (Kendall, 1975) is used to assess the statistical significance of the monotonic trend estimated by the Theil-Sen approach. Both techniques are applied with a significance level of 0.1 (α = 0.1) under the null hypothesis that there is no trend in the frequency of extreme precipitation events exceeding the magnitude associated with a 1-year recurrence interval. Rejection of the null hypothesis implies the existence of a monotonic trend.
The significance of a temporal trend in a time series can be inflated (deflated) in the presence of positive (negative) autocorrelation. Although our times series of frequencies of threshold exceedances are likely to be less persistent that the original daily series that they are derived from, they may still contain autocorrelation associated with persistence of large-scale modes of climate variability. Rather than assuming independence, modifications to the trend estimation technique can be implemented to better assess the trend significance (Santer et al., 2000; Yue and Wang, 2004). The modification is an adjustment on the sample variance. In both parametric and non-parametric techniques, this is a correction factor based on the effective sample size. That is,
where S is the sample variance, n is the sample size, and n* is the effective sample size, which is a function of the autocorrelation present in the time series. Because the trend can contaminate the estimate of sample autocorrelation, the estimate is based on the detrended time series. Here, the trend is removed by subtracting the product of the estimated trend (θ) and the position of that year within the time series from each year. In particular,
The lag-1 autocorrelation (ρ) is then determined from the detrended time series and the effective sample size is given by:
With a positive autocorrelation, the effective sample size is smaller than n, which increases the variance of the test statistic, leading to a failure to reject the null hypothesis when a naïve test may have found the presence of a significant trend. On the other hand, the presence of negative autocorrelation in the time series increases the effective sample size, decreasing the test statistic variance, and can therefore either sustain already significant grid points or bring the non-significant points past the threshold needed to reject the null hypothesis.
We assess the significance of the parametrically- and non-parametrically-derived trends at the local level. However, with such a large number of tests conducted, there is an increased chance of identifying a significant result by chance when it does not truly exist. To avoid these issues, Wilks (2006, 2016) recommend the use of the false discovery rate criterion (FDR). In this meta-test, a maximum number of significant points are determined such that a global test of significance at all local points is met. In this case, the FDR procedure is used to evaluate the field significance of trends in precipitation days per year with αglobal = 0.2 (see Wilks, 2006 for details). First, the p-values of each local hypothesis test result are ordered from the lowest to the highest (p1, p2, …, pn) and compared to the corresponding value (i/N)*αglobal. The maximum significant p-value is largest of the n p-values that satisfies the inequality:
Once this threshold is obtained, grid points with a lower p-value (p1, p2, …, pi) are designated as significant trends having satisfied the global meta-test.
Bivariate Synoptic Classification Using the Self-Organizing Map (SOM)
While several approaches exist for classification of atmospheric patterns, the self-organizing map, or SOM (Kohonen, 1998) has emerged as a leading approach in synoptic climatology. The SOM algorithm distributes a designated number of nodes across the multidimensional input space and sequentially moves each node toward the best matching input data based on a set learning rate and a predetermined number of iterations. The result is a two-dimensional map of nodes representative of the continuum of the input data (Hewitson and Crane, 2002; Sheridan and Lee, 2011). The SOM technique is also selected for its demonstrated skill in feature extraction and the interpretability of a map space (Liu et al., 2006; Agel et al., 2018).
Prior to classification with the SOM algorithm, several data preprocessing steps were necessary. First, the hourly ERA5 outputs of 500-hPa geo-potential height and 850-hPa specific humidity were aggregated to daily averages, producing 14,975 daily grids for the 1979–2019 study period. SOM results can be sensitive to the choice of spatial domain. We opted for a domain that closely corresponds to the Great Lakes region (Figure 1) to reduce the variability with the goal of better representation of rare patterns (Gibson et al., 2017), but with some additional grid points to the South and West, the predominant direction for approaching weather systems. Finally, to consider both geo-potential height and specific humidity, which differ by several orders of magnitude, each variable was standardized by subtracting the mean and dividing by the standard deviation. This standardization is applied to each day in the sample on the basis of calendar year means and standard deviations. This allows for equal weighting in the classification process, as both geo-potential height and specific humidity input data will have a mean of 0 and a standard deviation of 1. The data presented to the SOM are therefore the daily standardized values of 500-hPa geo-potential height and 850-hPa specific humidity at each of the 9,801 ERA5 grid points in the region on each of the 14,975 days, producing a 19,602 × 14,975 input array.
There are a number of additional subjective decisions required for SOM-based classifications. Among these is the desired size (number of nodes) in the resulting SOM space. Given the relative rarity of the events of interest (precipitation extremes exceeding the value associated with a 1-year recurrence interval), the SOM dimensions must be sufficiently large to isolate the large-scale signal associated with extremes. We investigated SOM architectures ranging from 4 to 45 nodes in various configurations and used two approaches to assess the viability of the SOM and find a balance of within-type and between-type variability. Specifically, we used the root-mean-square error (between a sample grid and its representative node) and Sammon mapping of the resulting SOM nodes to justify our selection following (Jiang et al., 2015). The difference between the sample grid and its representative node decreases as map size increases, whereas smaller node numbers contribute to a more cohesive mapping pattern across space. Using these approaches, we converged on a 20 node (5 × 4) SOM solution. Given the SOM size, the learning rate and number of iterations are also parameters that influence the result of the mapping algorithm. Defaulting to recommendations of the software (Matlab's Deep Learning Toolbox), the initial learning rate in this instance was set to 4. The number of iterations was then set to 1,000 to ensure the success of the training while minimizing the computation time of the algorithm.
Linking SOM Nodes and Regional Precipitation Extremes
The output of the SOM algorithm includes the centroid for each node, a distance matrix relating the node centroids, and an index of the closest node for each of the 14,975 daily ERA5 grids. These outputs allow the construction of a synoptic catalog in which each day is assigned to one node of the SOM, which can then be considered in the context of the extreme precipitation climatology. To this end, we establish a framework for connecting the large-scale meteorological patterns with the established extreme precipitation climatology by identifying the nodes most associated with extreme precipitation. We classify a day as an extreme precipitation day if at least 1% of the 81972.5km NClimDiv grid points in the region exceeds its threshold.
Once we have identified the extreme precipitation days belonging to each node, we conduct a Monte Carlo experiment to determine which nodes are associated with a greater than expected number of extreme precipitation days, following Agel et al. (2018). For each node, a random sample of days equal to the number of days within the node are selected and the number of extreme precipitation days in the random sample are noted. Resampling 1,000 times establishes a distribution for the expected number of extreme precipitation days corresponding to a specific node size. A node is then established as a node associated with extreme precipitation, and thus classified as an “extreme node,” if the number of extreme days associated with the node exceeds the 97.5th percentile of the resulting distribution.
Further analysis places these extreme nodes in the context of the entire SOM space and explores changes in node occurrence over time. First, the days belonging to each extreme node are separated into sets representing extreme and non-extreme days. Composites of these sets denote the differences in structure and magnitude due to internode variability and illustrate the characteristics of weather types favorable for extreme precipitation. After examining the structure of the extreme nodes, trend analysis is conducted to better understand the frequency of occurrence of extreme nodes over time, with the trend estimated by the Theil-Sen approach and the significance of the trend is assessed using a Mann-Kendall test.
Results
Extreme Precipitation Climatology and Trends
The threshold used to identify extreme precipitation days (the value associated with a 1-year recurrence interval) exhibits considerable spatial variability across the U.S. Great Lakes region (Figure 2). There is a general south to north gradient with the largest values, ~70 mm/day, occurring in southeastern NY and southern IL. The lowest values of the precipitation magnitude associated with a 1-year recurrence interval, around 35 mm/day, occur in the northern parts of MI and MN. The average value over all NClimDiv grid points in the region is 44.2 mm/day.
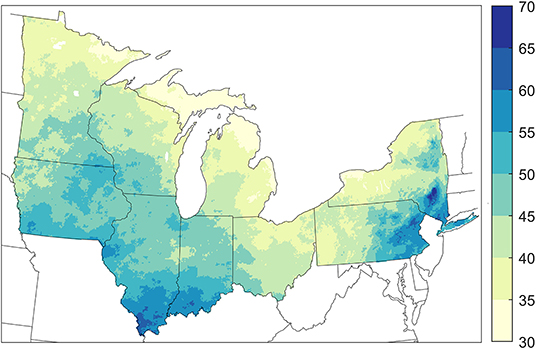
Figure 2. Map of the study region showing the threshold used for identification of extreme precipitation days (the magnitude of the daily precipitation associated with a 1-year recurrence interval (mm).
Our examination of precipitation extremes is based on a trend analysis designed to identify changes in Great Lakes extreme precipitation frequency over time. As described in section Extreme Precipitation Trend Analysis, our trend analysis includes both parametric (OLS) and non-parametric (Theil-Sen/Mann-Kendall) approaches for trend fitting and assessment of statistical significance. In both cases, additional considerations are made to account for autocorrelation in the time series and test multiplicity, and we draw additional comparisons between the parametric and non-parametric approaches at each step in the analysis. The non-parametric approach sometimes leads to a counterintuitive result when applied to time series containing many zeros (such as a time series of extreme event counts). Specifically, it is possible that the slope value will be 0, but the Mann-Kendall test will indicate significance. We therefore present our initial results only in terms of trend significance (binary) and discuss trend magnitude only for our final trend analysis results.
Significant trends in extreme precipitation frequency identified by the naïve Theil-Sen/Mann-Kendall and OLS approaches are shown in Figures 3A,B, respectively. Both approaches identify a large number of grid points in the U.S. Great Lakes region exhibiting significant trends (Figure 3, Table 1). The maps show strong qualitative similarity, with a slightly larger number of significant trends identified by the Theil-Sen/Mann-Kendall relative to OLS. Despite the greater extent of significant trends from the Theil-Sen/Mann-Kendall approach, the region of significance overlaps well. A total of 25,607 out of 79,679, or 32.1% of points within the region, are identified as having significant trends by either approach with 69.5% of these 25,607 points identified as having significant trends by both approaches. Spatially, the locations with significant extreme precipitation frequency trends are scattered in clusters across the region but tend to be more widespread in the western portion.
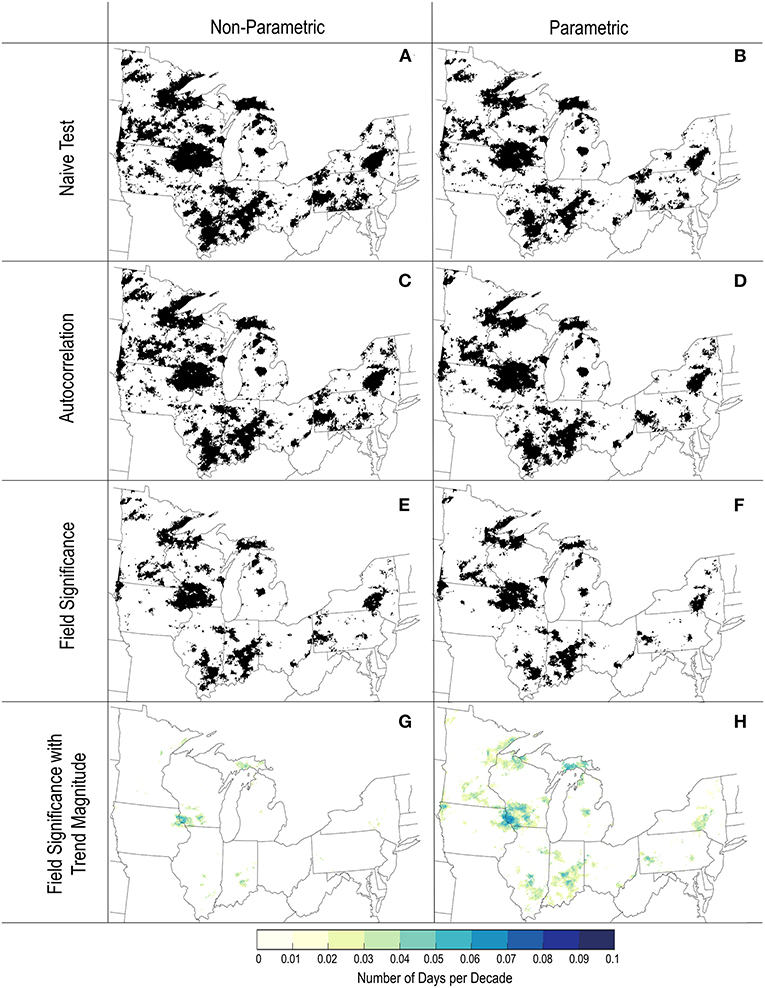
Figure 3. Results of trend analysis for extreme precipitation frequency in the Great Lakes region. The points shown reflect grid points with significant trends for the Theil-Sen/Mann-Kendall non-parametric approach (left column) and OLS parametric approach (right column). The rows show the trends from the natïve approach (first row, A,B) and after accounting for temporal autocorrelation (second row, C,D), and field significance (third row, E,F). The trend magnitude at points identified as field significant are shown in the fourth row (G,H).
To account for temporal autocorrelation in the time series, modified tests, which alter the sample variance based on the lag-1 autocorrelation, were conducted. As described in section Extreme Precipitation Trend Analysis, this correction is needed because an autocorrelated series violates the assumption that time series values are independent. The most common outcome is that significance is reduced by the presence of positive autocorrelation. However, in cases where the autocorrelation is negative, the effective sample size can be larger than the actual sample size. This can lead to points that were previously below the significance threshold becoming significant. Autocorrelation in our extreme precipitation time series (not shown) is highly variable over space and does not exhibit a clear spatial pattern. For the Theil-Sen/Mann-Kendall approach, accounting for autocorrelation reduced the number of points with significant trends in extreme precipitation frequency slightly (cf. Figures 3A,C, Table 1). The modified OLS approach, on the hand, led to virtually no change in the number of significant grid points (cf. Figures 3B,D, Table 1). In both cases, the maps before and after accounting for autocorrelation are qualitatively and quantitatively similar and agreement between the non-parametric and parametric approaches remains strong. A total of 25,145 grid points (31.5%) exhibit significant extreme precipitation frequency trends according to either approach and 65.9% of these points have significant trends under both approaches after accounting for autocorrelation.
When conducting a large number of hypothesis tests, there is potential for rejecting a substantial number of hypothesis incorrectly by chance or due to spatial autocorrelation. Consideration of field significance addresses these issues by using the false discovery rate (FDR) criterion. As described in section Extreme Precipitation Trend Analysis, for each approach, the number of field significant points is determined by ordering the p-values of the local tests and identifying their intersection with the false discovery rate threshold. Any grid point where the p-value is lower than the p-value at this intersection is said to have a regionally significant trend. For both the non-parametric and parametric approaches, accounting for field significance decreases the spatial extent of significant trends in extreme precipitation frequency (Figures 3E,F). For the Theil-Sen/Mann-Kendall approach, the ordered p-value curve intersects the FDR threshold at a p-value of 0.0328, so that 12,773 grid points in the region meet field significance criteria (i.e., those with p < 0.0328). In the OLS approach, the ordered p-value curve intersects the FDR threshold at a p-value of 0.0271, yielding 10,799 points meeting field significance criteria. Although accounting for field significance reduced the overall extent of significant trends in extreme precipitation frequency, there is still relatively strong agreement between the approaches with 65.5% of points with a significant result from either approach have a significant result from both approaches.
After accounting for both autocorrelation and field significance, we are left with considerable parts of the U.S. Great Lakes region exhibiting significant trends in extreme precipitation frequency regardless of the methodological approach used for trend analysis.
The magnitude of the estimated trends in extreme precipitation frequency is shown in Figures 3G,H. The greater spatial extent of the OLS-derived trends relative to those derived from the Theil-Sen/Mann-Kendall approach is related to the presence of significant trends with no magnitude, resulting from separately assessing the slope magnitude (Theil-Sen) and significance (Mann-Kendall) within this approach. As noted, this results from the time series being characterized by a relatively high proportion of zeros so that the median of pairwise slopes using in the Theil-Sen estimator is zero. Because of this, only a fraction (1,694 of 12,773, or 13.3%) of points with significant trends according to the Mann-Kendall test have a non-zero Theil-Sen slope estimate. These points are located primarily in a block along the Illinois-Iowa border, with some smaller regions of significance scattered in other parts of the domain. The average magnitude of significant non-zero trends is 0.328 days per decade, ranging from 0.125 to 0.556 days per decade. In the OLS approach, the trend magnitude and significance are more directly connected, so that any grid point found to be significant will have a non-zero slope. For the 10,799 points identified as having a significant trend in extreme precipitation frequency, the resulting trends varied from 0.085 to 0.706 days per decade, with an average of 0.324 days per decade.
Despite the differences resulting from the tendency of the Theil-Sen/Mann-Kendall approach to produce significant trends without magnitude, both parametric and non-parametric approaches indicate positive trends in the number of extreme precipitation days in the region, with strikingly similar location and magnitude. Overall, the clear indication from our trend analysis is that extreme precipitation frequency is increasing in the region, even when applying conservative approaches to account for temporal and spatial autocorrelation and test multiplicity. These robust changes can now be explored in the context of the large-scale climate influencing the region.
Weather Type Classification
To better understand the large-scale circulation and humidity regimes associated with extreme precipitation in the U.S. Great Lakes region, we applied a bivariate self-organizing map (SOM) to 500 hPa geo-potential height and 850 hPa specific humidity as described in section Bivariate Synoptic Classification Using the Self-Organizing Map (SOM). Following experimentation with the SOM architecture, we developed a 20-node (5 × 4) solution, which is displayed in Figure 4. The right-hand side of the SOM is largely characterized by patterns with negative height anomalies over the western (top rows), central or eastern (bottom rows) parts of the region. Conversely, the left side of the SOM space is characterized by generally characterized by positive height anomalies over the central and western parts of the region. In terms of 850 hPa specific humidity, nodes with positive anomalies tend to be clustered along the top of the SOM space with drier patterns along the bottom of the SOM space. Considering both variables together, the SOM allows for identification of patterns that couple high values of humidity with strong height gradients, leading the moisture transport into the study region (e.g., Node 3).
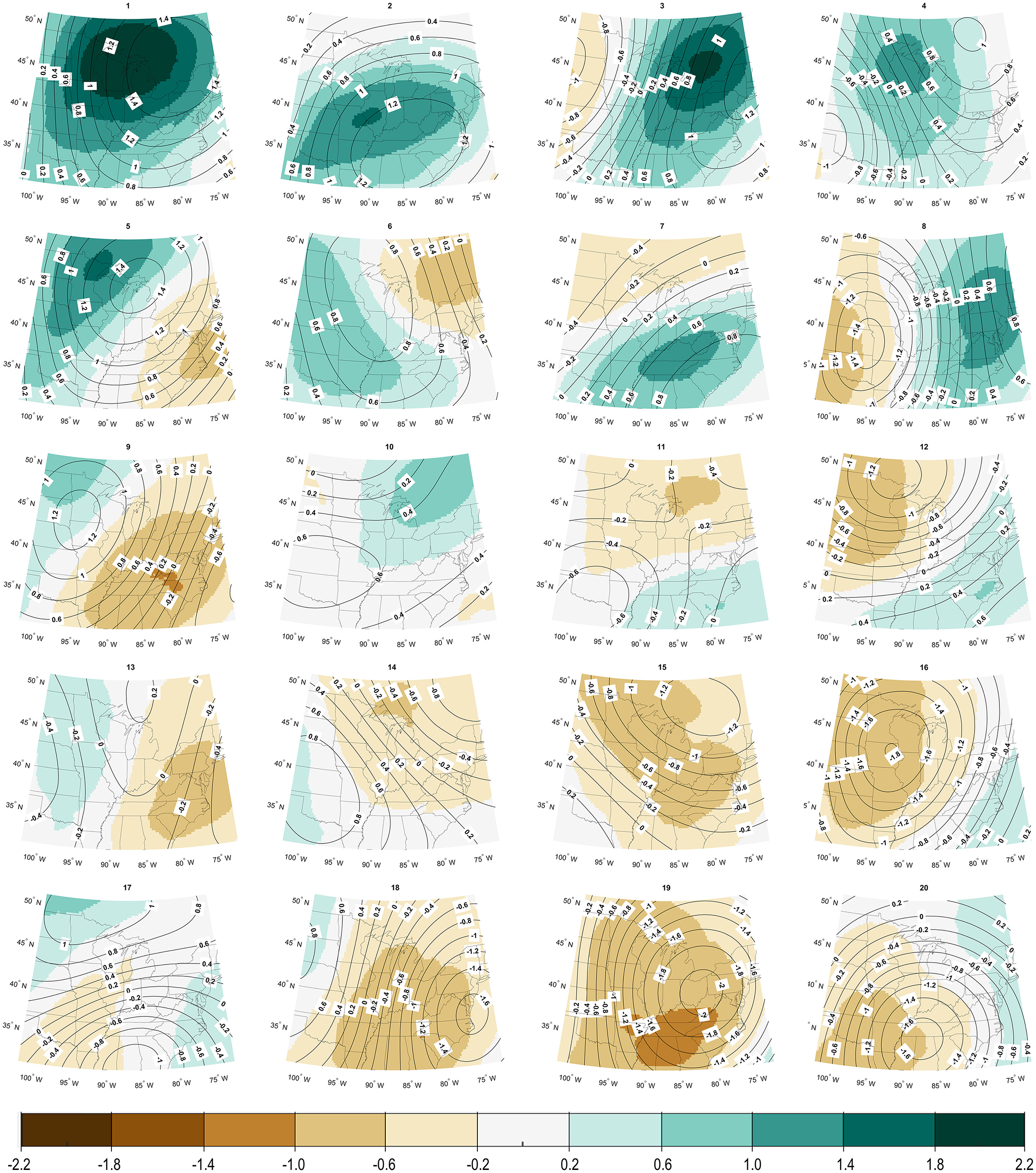
Figure 4. The 20-node (5 × 4) SOM solution showing standardized anomalies of 500 hPa geo-potential height (black contours) and 850 hPa specific humidity (shaded in color). Nodes are numbered 1–20 for reference within text.
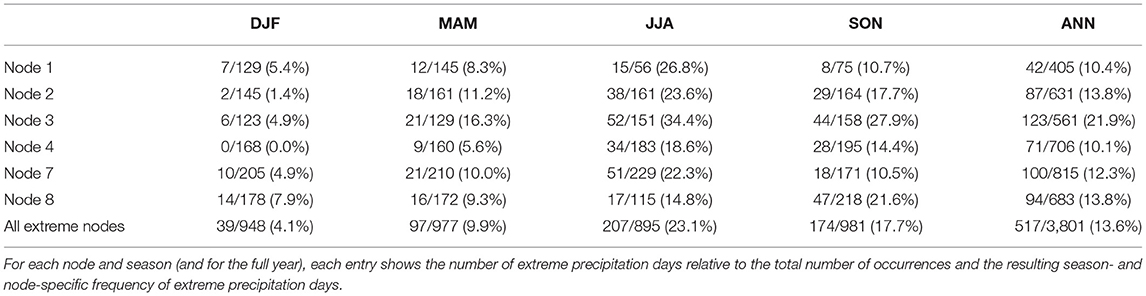
To determine the association between the SOM nodes and the extreme precipitation days, we first computed the distribution of total days by node and extreme precipitation days by node (Table 2). The SOM classifies the original 14,975 days into 20 nodes ranging in size from 405 days (2.70%, Node 1) to 965 days (6.44%, Node 18). Using the criteria in section Linking SOM Nodes and Regional Precipitation Extremes, we identified a total of 1,024 extreme precipitation days. The share of these days belonging to each node is also shown in Table 2 and ranges from just 15 days (1.46%, Nodes 9, 15, and 18) to 123 days (12.01%, Node 3). To identify nodes that are associated with a higher-than-expected share of extreme precipitation days, we apply a Monte Carlo approach (see section Linking SOM Nodes and Regional Precipitation Extremes), which identifies six nodes: 1, 2, 3, 4, 7, and 8, that account for 517 (50.5%) of the extreme precipitation days. More than half of the extreme precipitation days correspond to just 30% of the nodes that collectively represent 25.4% of all days.
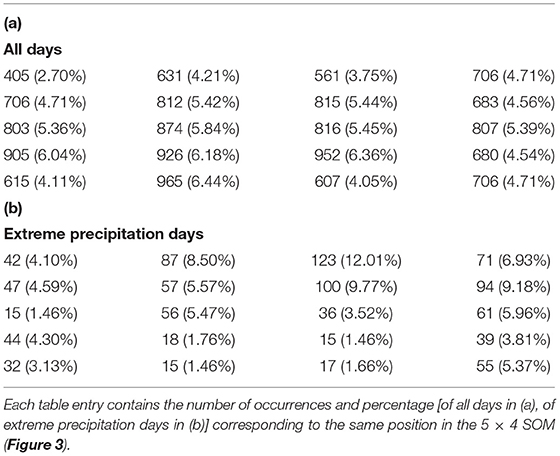
Table 2. (a) Frequency of occurrence for each SOM node (out of 14,975) and (b) frequency of occurrence of extreme precipitation days for each SOM node (out of 1,024).
Structurally, the nodes associated with extreme precipitation belong to the top portion of the SOM space and therefore have some common physical characteristics, including high standardized values of specific humidity across the domain. Aside from the nodes with the highest average specific humidity anomalies (1 and 2), the remaining nodes associated with extreme precipitation are characterized by high specific humidity anomalies and a geo-potential height gradient across the region with the lowest heights anomalies toward the west. This configuration leads to moisture transport into the region and may be reflective of mesoscale convective systems and/or frontal systems, which account for a large majority of the extreme precipitation events in the Central US (Schumacher and Johnson, 2005; Kunkel et al., 2012). While a majority of extreme precipitation days fall into the six extreme patterns, just 13.6% of the days within those patterns are classified as extreme, reflecting within-node variability. We therefore considered differences between non-extreme precipitation days and extreme precipitation days within each node using compositing. Figure 5 displays each extreme node, along with composites of the non-extreme and extreme precipitation days for that pattern. In each case, we found that the overall structure of the pattern in the node (i.e., the location of height/humidity extrema) does not differ between extreme and non-extreme days. However, we often identified a stark difference in the magnitude of those extrema. For each extreme precipitation node, extreme precipitation days are characterized by stronger 500 hPa geo-potential height gradients and similar or larger 850 hPa specific humidity anomalies (Figure 5).
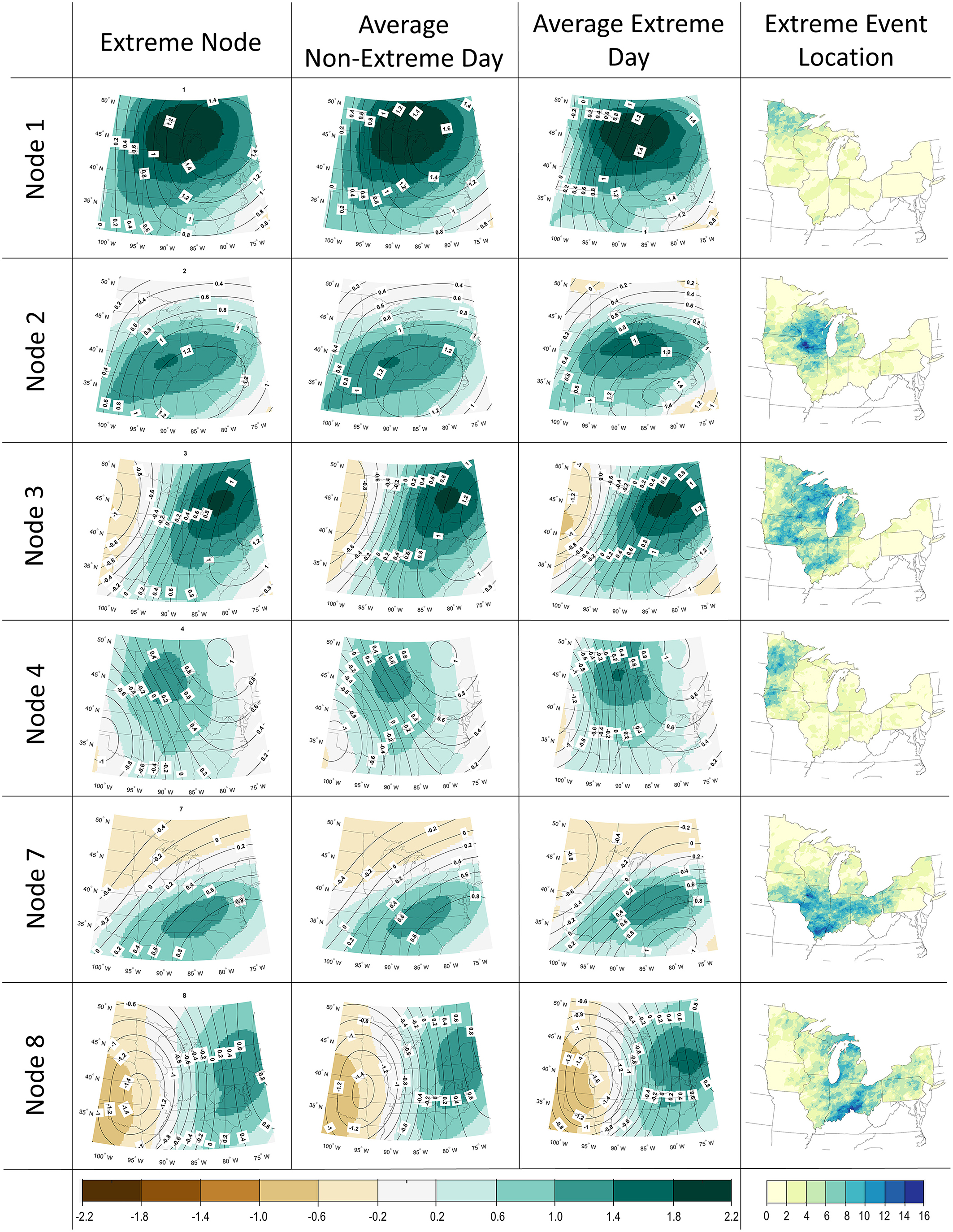
Figure 5. SOM nodes associated with extreme precipitation in the Great Lakes region. For each of the six nodes, the figure shows the original SOM node from Figure 4 (1st column), the composite pattern of days without extreme precipitation (2nd column), the composite pattern of days with extreme precipitation (3rd column), and the location of extreme precipitation associated with the SOM node events within the region, defined as the frequency of extreme precipitation at each NClimDiv grid cell on days belonging to the SOM node (4th column).
Examination of these specific nodes also reflects their association with extreme precipitation frequency across the U.S. Great Lakes region (Figure 5). As expected, for each node, the areas with the greatest extreme event frequency are located directly east of the negative geo-potential height center and near the area of positive specific humidity. Nodes 1 and 4 tend to produce extreme precipitation in the north-west part of the region, while Nodes 2, 3, and 7 produce extreme precipitation in the west-central part of the region, and Node 8 produces extreme precipitation in the east-central part of the region. Although (Schumacher and Johnson, 2005) use a much higher extreme precipitation threshold (the precipitation amount associated with the 50-year recurrence interval), our extreme nodes reflect some of the processes described in their work. For example, the circulation and humidity patterns characterized by Node 2 and Node 7 are consistent with the east-west orientation of the training line/adjoining stratiform (TL/AS) type of mesoscale convective system identified in their study. While a full analysis of node transitions is beyond our scope, we did assess the persistence of each node by examining the days preceding and following and extreme precipitation day. Nodes 2 and 7 were the most persistent nodes consistent with a stationary east-west moisture maximum across the region. Nodes 3 and 8, on the other hand, are the least persistent and are likely to be associated with faster moving synoptic systems and their associated fronts.
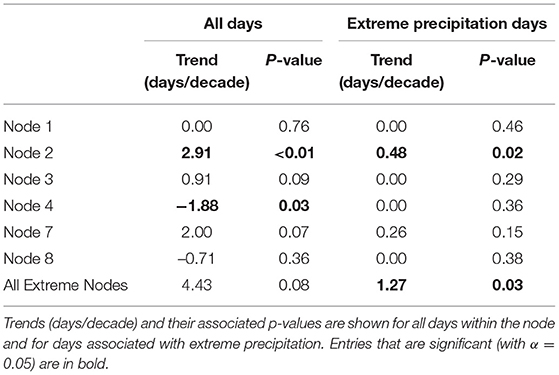
Extreme precipitation in the region exhibits notable seasonal variability which is evident in the seasonal frequencies of the associated SOM nodes. While the six specific nodes highlighted in Figure 5 occur approximately evenly across the seasons, 40.0% of the extreme precipitation events (207 of 517 events) occur during the summer and 33.6% (174 of 517 events) occur during the autumn (Table 3). Most of the remaining events (97 of 517 or 18.6%) occur in the spring and only 7.5% (39/517) occur during the winter. Therefore, even across the nodes associated with extreme precipitation, winter extreme precipitation events are relatively uncommon. This may result partially from the SOM design, which uses daily standardized values of 500-hPa geo-potential height and 850-hPa specific humidity. Even anomalously high 850-hPa specific humidity in winter may be insufficient to support extreme precipitation. However, our results are consistent with previous studies (e.g., Schumacher and Johnson, 2006) that have identified a strong summer maximum in extreme precipitation. During the winter, within-type variability is also larger, and the percentages of each node associated with extreme precipitation are at a minimum. During summer, the six key nodes produce extreme precipitation on nearly 25% of days on which they occur, and for Node 3, extreme precipitation occurs on more 1/3 of summer days. Trend analysis of the frequency of SOM nodes associated with extreme precipitation provides an initial perspective on how synoptic-scale variability and change may be related to changes in extreme precipitation. The number of extreme precipitation days in the U.S. Great Lakes region is increasing at a rate of 1.27 days/decade, which may be at least partially explained by variations in the frequency of days belonging to those specific SOM nodes associated with elevated extreme precipitation frequency. We find that two extreme precipitation nodes exhibit significant trends over time (Table 4). Node 2 has a significant positive trend of 2.91 days/decade (p < 0.01), while Node 4 has a significant negative trend of −1.88 days/decade (p ~ 0.03). The other nodes associated with extreme precipitation have positive trends that do not meet the criteria for significance (with α = 0.05). Finally, we assessed trends in the occurrence of extreme precipitation days within each extreme node and across all extreme nodes. Results indicate that across all extreme nodes, there is a significant trend of 1.27 extreme precipitation days per decade (p ~ 0.03). This is driven primarily by Node 2, which has a significant positive trend (p ~ 0.02) of 0.48 days/decade in days meeting the extreme precipitation criteria. The impact location associated with Node 2 (Figure 5) corresponds very well with the extreme precipitation trends presented in section Extreme Precipitation Climatology and Trends and Figure 3, suggesting a potentially substantive role for mesoscale and synoptic processes in the observed extreme precipitation increases.
Summary and Discussion
The objectives of this study were to quantify changes in extreme precipitation frequency in the U.S. Great Lakes region and their links with large-scale circulation and humidity. We first conducted an analysis of trends in extreme event frequency, using both parametric and non-parametric trend estimation techniques and accounting for autocorrelation and field significance. While accounting for autocorrelation and field significance reduced the spatial extent of the identified trends, we identified the existence of positive extreme frequency trends in the region using both techniques. No negative precipitation trends were identified in the region. To relate regional extreme precipitation events to atmospheric drivers, we applied a bivariate self-organizing map to assign each day in the record to one of 20 distinct nodes characterized by their standardized 500 hPa geo-potential height and 850 hPa specific humidity anomalies. A Monte Carlo approach was then used to identify six nodes associated with regional extreme precipitation occurrence. Each of these extreme nodes featured a unique structure, typically with a strong geo-potential height gradient and corresponding low-level humidity maximum. When considering only the extreme precipitation days within each node, we found these features to be exaggerated (i.e., a stronger gradient and higher humidity), indicating that structure and magnitude of these weather types are both essential for relating them to extreme precipitation. Finally, for each of the extreme nodes, and for all extreme nodes collectively, we quantified the trend in overall frequency and in the frequency of extreme precipitation days associated with the node. Collectively, the frequency of these extreme nodes is increasing over time (not significant) and the frequency of extreme days within the nodes is also increasing over time (significant with α = 0.05). Node 2 specifically exhibits significant increases in overall frequency and in the frequency of extreme days within Node 2. The spatial structure of extreme precipitation frequency under Node 2 qualitatively matches the observed trend structure.
Our results are consistent with results of previous students, such as the significant increase in the frequency of heavy precipitation over the central United States reported by Mallakpour and Villarini (2015). Because they used alternative data sources with different spatial resolutions and time periods, a direct comparison is not possible. However, the greater spatial extent of extreme precipitation trends in the parts of their domain that overlap with ours, could result from our consideration of autocorrelation in the time series. We recommend that time series studies account for autocorrelation to avoid overconfidence in identified trends. The results of our synoptic classification (and the identified nodes associated with extreme precipitation) are also in agreement with previous studies. For example, each of the nodes that we associated with extreme precipitation are instantiations of the “Midwest water hose” pattern denoted by Zhang et al. (2019). In that study, the authors used a broader domain to identify a connection between extreme precipitation and circulation. In the current study, we've used a narrower domain leading to a wider array of identified circulation/humidity types. As discussed in section Results, Nodes 2 and 7 are consistent with the east-west “training” events described by Schumacher and Johnson (2005) that are responsible for a large number of extreme precipitation events identified in their study.
The vast majority of previous synoptic classifications with the SOM algorithm have relied on a single classification variable, usually geo-potential height or sea level pressure, to reflect the primary circulation features. Our results, based on a bivariate SOM, demonstrate that consideration of additional variables, 850 hPa specific humidity in our case, can improve the interpretation of the resulting weather types and their associations with extreme precipitation. Each of the nodes that we associated with extreme precipitation occurrence is characterized by a combination of geo-potential height and specific humidity anomalies in specific geographic regions. The SOM nodes that are not associated with extreme precipitation occurrence may exhibit similar structure in either geo-potential height or specific humidity, but not both. We also found that the magnitude of both of these parameters is vital. Our study suggests that extreme days are related to both steepened geo-potential height gradients and amplified specific humidity. Agel et al. (2019) similarly reported that extreme precipitation events were related to enhanced moisture transport.
Previous studies focused on the central United States have identified disparate drivers of extreme precipitation changes. Specifically, Kunkel et al. (2012), attributed increasing extreme events to be related to frontal systems, while Schumacher and Johnson (2005, 2006) and Barlow et al. (2019) identified mesoscale convective systems occurring during spring and summer as a major cause. These differences may result from different definitions and the extreme nodes identified in this study are consistent with both mesoscale convective systems and frontal systems. While direct comparison with previous studies is difficult, our results indicate that extreme precipitation frequency is increasing in many parts of our region, with substantial contributions from unique combinations of large-scale circulation and humidity patterns. Future studies may benefit from including additional information from reanalyses, such as the convective vs. large-scale rain rates to better differentiate between the large-scale mechanisms that produce extreme precipitation. The strength of the links between SOM nodes and extreme precipitation may be further improved by incorporating greater specificity regarding regional precipitation drivers, perhaps including aspects of the Great Plains low-level jet (Junker et al., 1999) or consideration of multi-day events and their associated large-scale drivers.
While our results contribute to greater understanding of changes in precipitation extremes in the U.S. Great Lakes region, there are some limitations worth noting. In synoptic classification problems, the goal is to minimize within-type variability and maximize between-type variability, but resulting nodes often suffer from a large degree of within-type variability (Brinkmann, 1999). Although we identified six patterns that account for more than half of all extreme precipitation days, each of the nodes identified as an extreme precipitation node also includes a large number of days without extreme precipitation. This limitation is also noted by Gibson et al. (2017) in the context of using SOMs to explore extreme event environments. Our analysis of the difference between large-scale patterns associated with extreme and non-extreme precipitation days within the nodes, determined by simple compositing, indicates that the pattern magnitudes are greater on extreme precipitation days, reflecting within-type variability. Another limitation is related to our use of standardized anomalies. While this was necessary to include both geo-potential height and specific humidity which differ by several orders of magnitude, it can also mask important seasonal variations in extreme precipitation drivers. For example, anomalously high specific humidity during winter may still be insufficient to produce extreme precipitation. Specific analysis focused on each season may therefore provide greater insight into the physical processes involved. Despite these caveats, this study was successful in identifying trends in extreme precipitation in the U.S. Great Lakes region and relating them to specific circulation/humidity regimes. Key contributions of our work include insights gained from estimating trends using multiple techniques that account for autocorrelation and field significance and relating those trends to combinations of large-scale geo-potential height and humidity. The framework developed here could easily be expanded to other regions or to include more than two large-scale variables.
Projections from contemporary climate models indicate additional increases in the frequency of extreme precipitation under further large-scale warming (IPCC, 2021). However, regional changes in precipitation are still a challenge for climate models (Tabari et al., 2019), which often fail to produce the key precipitating systems, such as mesoscale convective systems (Gutowski et al., 2020). Analyses like those presented here can provide a basis for evaluation of climate models by specifically assessing the frequency with which they produce the large-scale conditions required for extreme precipitation. Studies in other regions (e.g., the NE by Agel et al., 2020) have begun to assess the ability of climate models to simulate extreme precipitation and its related circulation. Future work will expand upon these results to assess representation of the extreme precipitation nodes in contemporary climate models.
Data Availability Statement
Publicly available datasets were analyzed in this study. Daily NOAA NClimDiv data is available via file transfer protocol (FTP) from ftp.ncdc.noaa.gov; ECMWF ERA5 data can be accessed at https://www.ecmwf.int/en/forecasts/datasets/reanalysis-datasets/era5.
Author Contributions
Analysis was conducted by AP and JS with assistance from TF and JR. Writing was conducted by AP and JS. All authors contributed to the article and approved the submitted version.
Funding
The work was partially funded with support from NOAA (Grant #NA17OAR4310148).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We acknowledge two reviewers whose constructive comments improved the manuscript substantially.
References
Acero, F. J., Garcia, J. A., and Gallego, M. C. (2011). Peaks-over-threshold study of trends in extreme rainfall over the Iberian Peninsula. J. Clim. 24, 1089–1105. doi: 10.1175/2010JCLI3627.1
Agel, L., Barlow, M., Colby, F., Binder, H., Catto, J. L., Hoell, A., et al. (2019). Dynamical analysis of extreme precipitation in the US northeast based on large-scale meteorological patterns. Clim. Dynamics 52, 1739–1760. doi: 10.1007/s00382-018-4223-2
Agel, L., Barlow, M., Feldstein, S. B., and Gutowski, W. J. (2018). Identification of large-scale meteorological patterns associated with extreme precipitation in the US northeast. Clim. Dynamics 50, 1819–1839. doi: 10.1007/s00382-017-3724-8
Agel, L., Barlow, M., Polonia, J., and Coe, D. (2020). Simulation of northeast US extreme precipitation and its associated circulation by CMIP5 models. J. Clim. 33, 9817–9834. doi: 10.1175/JCLI-D-19-0757.1
Allan, R. P., and Soden, B. J. (2008). Atmospheric warming and the amplification of precipitation extremes. Science 321, 1481–1484. doi: 10.1126/science.1160787
Angel, J., Swanston, C., Bousted, B. M., Conlon, K. C., and Hall, K. R. J. L. (2018). “Midwest,” in Impacts, Risks, and Adaptation in the United States: Fourth National Climate Change Assessment, Volume II, eds. D. R. Reidmiller, C. W. Avery, D. R. Easterling, K. E. Kunkel, K. L. M. Lewis, T. K. Maycock, and B. C. Stewart (Washington, DC: U.S. Global Change Research Program). p. 872–940.
Asadieh, B., and Krakauer, N. Y. (2015). Global trends in extreme precipitation: climate models versus observations. Hydrol. Earth Syst. Sci. 19, 877–891. doi: 10.5194/hess-19-877-2015
Barlow, M., Gutowski, W. J., Gyakum, J. R., Katz, R. W., Lim, Y. K., Schumacher, R. S., et al. (2019). North American extreme precipitation events and related large-scale meteorological patterns: a review of statistical methods, dynamics, modeling, and trends. Clim. Dynamics 53, 6835–6875. doi: 10.1007/s00382-019-04958-z
Bonnin, G. M., Todd, D., Lin, B., Parzybok, T., Yekta, M., and Riley, D. (2005). “Precipitation-Frequency Atlas of the United States,” in: NOAA Atlas. (Silver Spring, MD: National Weather Service). p. 1–301.
Brinkmann, W. A. R. (1999). Within-type variability of 700 hPa winter circulation patterns over the Lake Superior basin. Int. J. Climatol. 19, 41–58. doi: 10.1002/(SICI)1097-0088(199901)19:1<41::AID-JOC349>3.0.CO;2-U
Byun, K., and Hamlet, A. F. (2018). Projected changes in future climate over the Midwest and Great Lakes region using downscaled CMIP5 ensembles. Int. J. Climatol. 38, E531–E553. doi: 10.1002/joc.5388
D'orgeville, M., Peltier, W. R., Erler, A. R., and Gula, J. (2014). Climate change impacts on Great Lakes Basin precipitation extremes. J. Geophys. Res. 119, 10799–10812. doi: 10.1002/2014JD021855
Drayna, P., Mclellan, S. L., Simpson, P., Li, S. H., and Gorelick, M. H. (2010). Association between Rainfall and Pediatric Emergency Department visits for acute gastrointestinal illness. Environ. Health Persp. 118, 1439–1443. doi: 10.1289/ehp.0901671
Gibson, P. B., Perkins-Kirkpatrick, S. E., Uotila, P., Pepler, A. S., and Alexander, L. V. (2017). On the use of self-organizing maps for studying climate extremes. J. Geophys. Res. 122, 3891–3903. doi: 10.1002/2016JD026256
Gutowski, W. J., Ullrich, P. A., Hall, A., Leung, L. R., O'brien, T. A., Patricola, C. M., et al. (2020). The ongoing need for high-resolution regional climate models: process understanding and stakeholder information. Bull. Am. Meteorol. Soc. 101, E664–E683. doi: 10.1175/BAMS-D-19-0113.A
Hersbach, H., Bell, B., Berrisford, P., Hirahara, S., Horanyi, A., Munoz-Sabater, J., et al. (2020). The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 146, 1999–2049. doi: 10.1002/qj.3803
Hewitson, B. C., and Crane, R. G. (2002). Self-organizing maps: applications to synoptic climatology. Clim. Res. 22, 13–26. doi: 10.3354/cr022013
Huth, R., and Pokorna, L. (2004). Parametric versus non-parametric estimates of climatic trends. Theor. Appl. Climatol. 77, 107–112. doi: 10.1007/s00704-003-0026-3
IPCC (2021). “Summary for Policymakers,” in Climate Change 2001: The Physical Scientific Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change, eds. V. Masson-Delmotte, P. Zhai, A. Pirani, S. L. Connors, C. Pean, S. Berger, N. Caud, Y. Chen, L. Goldfarb, M. I. Gomis, M. Huang, K. Leitzell, E. Lonnoy, J. B. R. Matthews, T. K. Maycock, T. Waterfield, O. Yelecki, R. Yu, and B. Zhou (Cambridge: Cambridge University Press). p. 1–30.
Jiang, N. B., Luo, K. H., Beggs, P. J., Cheung, K., and Scorgie, Y. (2015). Insights into the implementation of synoptic weather-type classification using self-organizing maps: an Australian case study. Int. J. Climatol. 35, 3471–3485. doi: 10.1002/joc.4221
Junker, N. W., Schneider, R. S., and Fauver, S. L. (1999). A study of heavy rainfall events during the great midwest flood of 1993. Weather Forecasting 14, 701–712. doi: 10.1175/1520-0434(1999)014<0701:ASOHRE>2.0.CO;2
Kohonen, T. (1998). The self-organizing map. Neurocomputing 21, 1–6. doi: 10.1016/S0925-2312(98)00030-7
Kunkel, K. E., Easterling, D. R., Kristvich, D. A. R., Gleason, B., Stoecker, L., and Smith, R. (2012). Meteorological causes of the secular variations in observed extreme precipitation events for the conterminous United States. J. Hydrometeorol. 13, 1131–1141. doi: 10.1175/JHM-D-11-0108.1
Kunkel, K. E., Karl, T. R., Easterling, D. R., Redmond, K., Young, J., Yin, X. G., et al. (2013). Probable maximum precipitation and climate change. Geophys. Res. Lett. 40:50334. doi: 10.1002/grl.50334
Lanzante, J. R. (1996). Resistant, robust and non-parametric techniques for the analysis of climate data: theory and examples, including applications to historical radiosonde station data. Int. J. Climatol. 16, 1197–1226. doi: 10.1002/(SICI)1097-0088(199611)16:11<1197::AID-JOC89>3.0.CO;2-L
Lenderink, G., and Van Meijgaard, E. (2010). Linking increases in hourly precipitation extremes to atmospheric temperature and moisture changes. Environ. Res. Lett. 5:025208. doi: 10.1088/1748-9326/5/2/025208
Liu, Y. G., Weisberg, R. H., and Mooers, C. N. K. (2006). Performance evaluation of the self-organizing map for feature extraction. J. Geophys. Res. Oceans 111, 1–14. doi: 10.1029/2005JC003117
Mallakpour, I., and Villarini, G. (2015). The changing nature of flooding across the central United States. Nat. Clim. Change 5, 250–254. doi: 10.1038/nclimate2516
Menne, M. J., Durre, I., Vose, R. S., Gleason, B. E., and Houston, T. G. (2012). An overview of the global historical climatology network-daily database. J. Atmos. Oceanic Technol. 29, 897–910. doi: 10.1175/JTECH-D-11-00103.1
Nasri, B., Tramblay, Y., El Adlouni, S., Hertig, E., and Ouarda, T. B. M. J. (2016). Atmospheric predictors for annual maximum precipitation in North Africa. J. Appl. Meteorol. Climatol. 55, 1063–1076. doi: 10.1175/JAMC-D-14-0122.1
Orlanski, I. (1975). Rational subdivision of scales for atmospheric processes. Bull. Am. Meteorol. Soc. 56, 527–530. doi: 10.1175/1520-0477-56.5.527
Pendergrass, A. G. (2018). What precipitation is extreme? Science 360, 1072–1073. doi: 10.1126/science.aat1871
Pryor, S. C., Barthelmie, R. J., and Schoof, J. T. (2013). High-resolution projections of climate-related risks for the Midwestern USA. Clim. Res. 56, 61–79. doi: 10.3354/cr01143
Santer, B. D., Wigley, T. M. L., Boyle, J. S., Gaffen, D. J., Hnilo, J. J., Nychka, D., et al. (2000). Statistical significance of trends and trend differences in layer-average atmospheric temperature time series. J. Geophys. Res. 105, 7337–7356. doi: 10.1029/1999JD901105
Schumacher, R. S., and Johnson, R. H. (2005). Organization and environmental properties of extreme-rain-producing mesoscale convective systems. Monthly Weather Rev. 133, 961–976. doi: 10.1175/MWR2899.1
Schumacher, R. S., and Johnson, R. H. (2006). Characteristics of US extreme rain events during 1999-2003. Weather Forecast. 21, 69–85. doi: 10.1175/WAF900.1
Sen, P. K. (1968). Estimates of regression coefficient based on Kendalls Tau. J. Am. Stat. Assoc. 63:1379. doi: 10.1080/01621459.1968.10480934
Sheridan, S. C., and Lee, C. C. (2011). The self-organizing map in synoptic climatological research. Progr. Phys. Geogr. 35, 109–119. doi: 10.1177/0309133310397582
Tabari, H., Hosseinzadehtalaei, P., Aghakouchak, A., and Willems, P. (2019). Latitudinal heterogeneity and hotspots of uncertainty in projected extreme precipitation. Environ. Res. Lett. 14:ab55fd. doi: 10.1088/1748-9326/ab55fd
Tryhorn, L., and Degaetano, A. (2011). A comparison of techniques for downscaling extreme precipitation over the Northeastern United States. Int. J. Climatol. 31, 1975–1989. doi: 10.1002/joc.2208
Vose, R. S., Applequist, S., Squires, M., Durre, I., Menne, M. J., Williams, C. N., et al. (2014). Improved historical temperature and precipitation time series for U.S. climate divisions. J. Appl. Meteorol. Climatol. 53, 1232–1251. doi: 10.1175/JAMC-D-13-0248.1
Wilks, D. S. (2006). On “field significance” and the false discovery rate. J. Appl. Meteorol. Climatol. 45, 1181–1189. doi: 10.1175/JAM2404.1
Wilks, D. S. (2016). The stippling shows statistically signficant grid points: how research results are routinely overstated and overinterpreted, and what to do about it. Bull. Am. Meteorol. Soc. 97:2263. doi: 10.1175/BAMS-D-15-00267.1
Willmott, C. J., and Robeson, S. M. (1995). Climatologically aided interpolation (CAI) of terrestrial air-temperature. Int. J. Climatol. 15, 221–229. doi: 10.1002/joc.3370150207
Winters, B. A., Angel, J., Ballerine, C., Byard, J., Flegel, A., Gambill, D., et al. (2015). Report for the Urban Flooding Awareness Act. Office of Water Resources, Illinois Department of Natural Resources, p. 1–97. Available Online at: https://www2.illinois.gov/dnr/waterresources/documents/final_ufaa_report.pdf
Wuebbles, D. J., Cardinale, B., Cherkauer, K., Davidson-Arnott, R., Hellmann, J., Infante, D., et al. (2019). An Assessment of the Impacts of Climate Change on the Great Lakes. Chicago, IL: ELP Center.
Yue, S., and Wang, C. Y. (2004). The Mann-Kendall test modified by effective sample size to detect trend in serially correlated hydrological series. Water Res. Manag. 18, 201–218. doi: 10.1023/B:WARM.0000043140.61082.60
Keywords: Great Lakes region, climate extremes, extreme precipitation, self-organizing maps, global change
Citation: Paxton A, Schoof JT, Ford TW and Remo JWF (2021) Extreme Precipitation in the Great Lakes Region: Trend Estimation and Relation With Large-Scale Circulation and Humidity. Front. Water 3:782847. doi: 10.3389/frwa.2021.782847
Received: 24 September 2021; Accepted: 06 December 2021;
Published: 24 December 2021.
Edited by:
Julie A. Winkler, Michigan State University, United StatesReviewed by:
Art DeGaetano, Cornell University, United StatesThomas Mote, University of Georgia, United States
Copyright © 2021 Paxton, Schoof, Ford and Remo. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Justin T. Schoof, anNjaG9vZkBzaXUuZWR1
 Andrew Paxton1
Andrew Paxton1 Justin T. Schoof
Justin T. Schoof Trent W. Ford
Trent W. Ford