A Brief Review on Deep Learning Applications in Genomic Studies

Deep learning is a powerful tool for capturing complex structures within the data. It holds great promise for genomic research due to its capacity of learning complex features in genomic data. In this paper, we provide a brief review on deep learning techniques and various applications of deep learning to genomic studies. We also briefly mention current challenges and future perspectives on using emerging deep learning techniques for ongoing and future genomic research.

1 Introduction

Deep learning has achieved great success in many areas such as computer vision and natural language processing. It leads the data-driven science into a new era due to its ability of learning complex structure from data without human intervention. With its success in many areas, there are increasing interests in using deep learning in genomic research. Genomic data are sophisticated in nature, and have complex relationship with responses (e.g., disease outcomes). While classical methods (e.g., linear regression) have commonly used in genomic data analysis to detect simple linear effects, deep learning can learn complex features from the genomic data, making it a powerful method for considering nonlinear and interaction effects. In this review paper, we provide a brief review on a variety of applications of deep learning to genomic research. Deep learning, as a class of machine learning approaches, can also be categorized into supervised learning and unsupervised learning. We start by introducing key concepts in supervised learning, unsupervised learningand semi-supervised learning, and then reviewing popular deep learning methods and their applications in genomic research. Due to a large number of available deep learning methods and limited space, the review mainly focused on classic deep learning methods, especially those having the potential to be applied to genomic data analysis.

2 2 Supervised, Unsupervised and Semi-Supervised Learning

2.1 Supervised Learning

Statistically speaking, there are three key elements in supervised learning: 1) a generator of random vectors $\mathit{X}$ from a fixed unknown distribution $P\left(\mathit{x}\right)$, 2) a supervisor (or a teacher) that returns $Y$ for every $\mathit{X}$ according to a conditional distribution $P\left(y|\mathit{x}\right)$, and 3) a class of learning machines $\left\{\mathit{f}\left(\mathit{x},\theta \right):\mathit{\theta }\in \text{Θ}\right\}$. This concept was introduced by Vapnik, (1998). The question is given independent and identically distributed (i.i.d.) pairs of data $\left({\mathit{X}}_{\mathrm{1}},{\mathit{Y}}_{\mathrm{1}}\right),\dots ,\left({\mathit{X}}_{\mathit{n}},{\mathit{Y}}_{\mathit{n}}\right)$, often known as the training data, from the joint distribution $\mathit{P}\left(\mathit{x},\mathit{y}\right)=P\left(y\text{|}\mathit{x}\right)\mathit{P}\left(\mathit{x}\right)$, how to choose from $\left\{\mathit{f}\left(\mathit{x},\mathit{\theta }\right):\mathit{\theta }\mathrm{\in }\text{Θ}\right\}$ an $\mathit{f}$ that predicts the supervisor’s response $Y$ in the “best” possible way. When $Y$ is continuous, the learning problem is often known as a regression problem. In a regression, we seek the best parameter $\theta$ that minimizes the quadratic loss function:

${\widehat{\mathit{\theta }}}_{\mathrm{1}}=\text{arg}\underset{\theta \in \text{Θ}}{\min }\frac{1}{\mathit{n}}{\displaystyle \sum }_{\mathit{i}=1}^n{\left({\mathit{Y}}_{\mathit{i}}-\mathit{f}\left({\mathit{X}}_{\mathit{i}},\mathit{\theta }\right)\right)}^2.$

When $Y$ is dichotomous, the learning problem is known as a classification or pattern recognition problem. In a classification problem, a commonly used loss function is the cross-entropy function,

${\widehat{\mathit{\theta }}}_2=\text{arg}\underset{\theta \in \text{Θ}}{\min }\frac{1}{\mathit{n}}{\displaystyle \sum _{\mathit{i}=1}^n\left[-Y_i\log f\left({\mathit{X}}_i,\theta \right)-\left(1-Y_i\right)\log \left(1-f\left({\mathit{X}}_i,\theta \right)\right)\right].}$

When $f\left(\mathit{x},\theta \right)={\mathit{x}}^T\theta$, ${\widehat{\theta }}_1$ becomes the classical least squares estimator in a linear regression. Similarly, ${\widehat{\theta }}_2$ is the estimator for coefficients in a logistic regression if $f\left(\mathit{x},\theta \right)={\left(1+e^{-{\mathit{x}}^T\theta }\right)}^{-1}$.

2.2 Neural Networks

Neural networks are algorithms that try to mimic the function of a human brain. A neural network is a collection of perceptrons. Therefore, another commonly used name for neural networks is multi-layer perceptrons. The basic structure of a perceptron is shown in Figure 1A. In a perceptron (Rosenblatt, 1958), a nonlinear activation function is applied to the linear combination of weights and input features to produce an output. Commonly used nonlinear activation functions in neural networks and in deep learning include:

• Hard-threshold (Heaviside) function: $\sigma \left(u\right)=\{\begin{array}{cc}1& \text{if} u\ge 0\\ 0& \text{if} u<0\end{array}$;

• Soft-threshold (Logistic) function: $\mathit{\sigma }\left(\mathit{u}\right)={\left(\mathrm{1}+{\mathit{e}}^{-u}\right)}^{-1}$;

• Hyperbolic tangent function: $\sigma \left(u\right)=\tanh \mathit{u}=\frac{{\mathit{e}}^{\mathit{u}}-{\mathit{e}}^{-\mathit{u}}}{{\mathit{e}}^{\mathit{u}}+{\mathit{e}}^{-\mathit{u}}}$;

• Normal cumulative distribution function: $\mathit{\sigma }\left(\mathit{u}\right)=\underset{-\infty }{\overset{\mathit{u}}{{\displaystyle \int }}}\frac{1}{\sqrt{\mathrm{2}\mathit{\pi }}}{\mathit{e}}^{-\frac{{\mathit{t}}^2}{2}}\mathit{dt}$; and

• Rectified linear unit (ReLU) function: $\sigma \left(u\right)=\text{max}\left(0, u\right)$ (Jarrett et al., 2009; Nair and Hinton, 2010; Glorot et al., 2011).

FIGURE 1

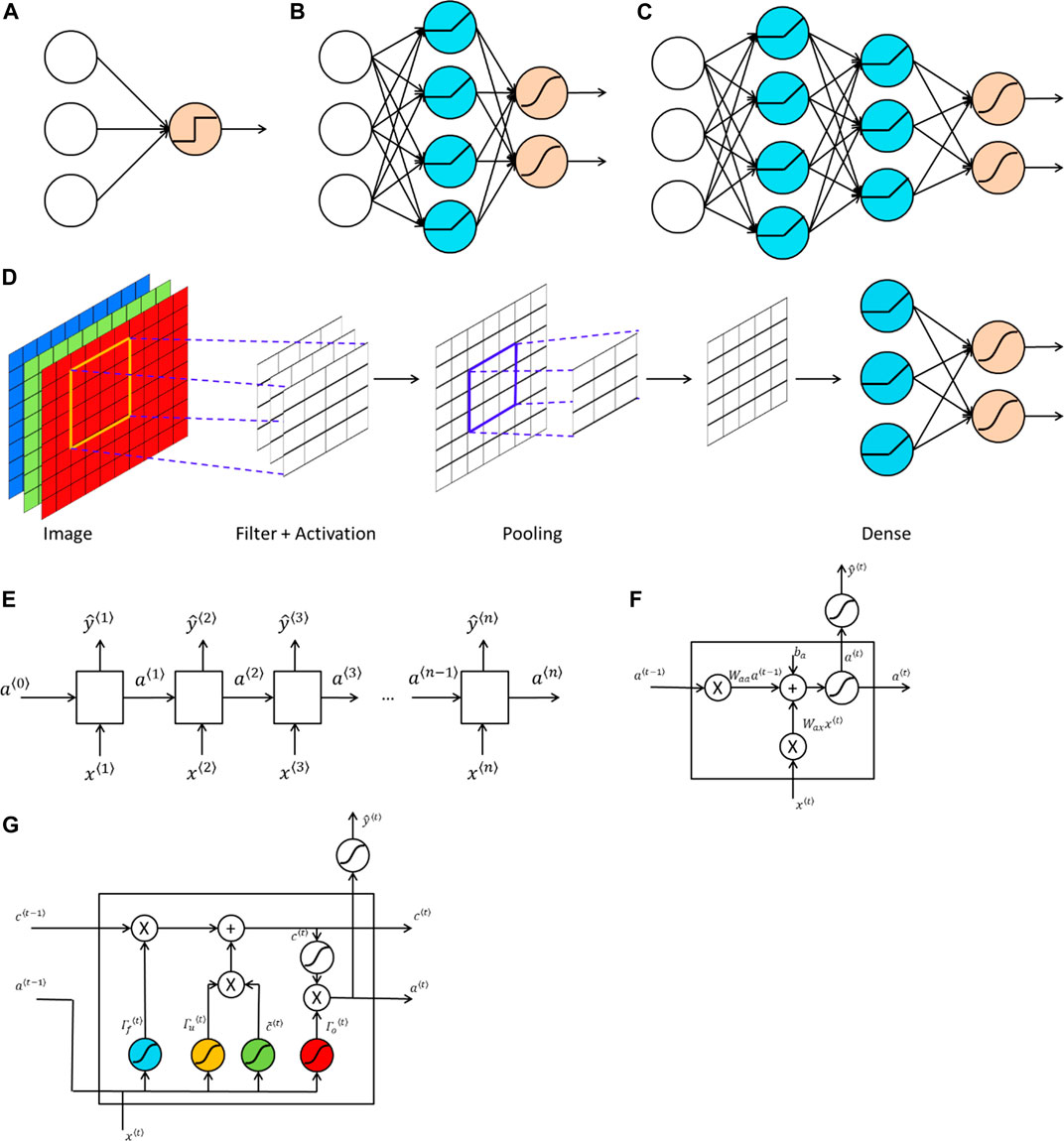
FIGURE 1. Structures of popular machine learning and deep learning models. (A) A perceptron where a nonlinear activation function (e.g., a hard-threshold function) is applied to the linear combination of inputs and weights to predict the output. (B) A neural network with one hidden layer, which consists of multiple perceptrons. The blue computation units are the hidden units, which are generated by applying a nonlinear activation function (e.g., a ReLU function) to the linear combination of inputs and weights. The output layer with computation units shown in orange, which uses an activation (e.g., a sigmoid or softmax function) to produce predicted values. (C) A deep neural network with two hidden layers, where computation units in each hidden layer apply a nonlinear activation function to the linear combination of weights and outputs from the previous layer. (D) A convolutional neural network (CNN), where the input is an image with three channels representing red, green and blue. The hidden layers of a CNN comprise two types of layers: convolutional layers and pooling layers. A convolutional layer consists of several filters, which have the same number of channels as the input data. Each filter acts as a sliding window and applies a nonlinear activation to the linear combination of filter entries and the outputs from the previous layer. Such an operation is known as convolution. A pooling layer is used to reduce the size of the representation to accelerate computations, as well as to make detected features more robust. A commonly used pooling layer is called max pooling, where a filter acts as a sliding window and produce the maximum elements from that part. After several convolutional layers and pooling layers, the output is vectorized as the input of a fully connected neural network. (E) A recurrent neural network, where both the input and the output are sequences with the same length. Each input $x^t$ (e.g., a word in a sentence) and the output $a^{t-1}$ from the previous neural network are used to predict ${\widehat{y}}^t$ and produce an output $a^t$, which then serves as the input for the next neural network. Typical structures of the neural network used in RNN are RNN cell or long short-term memory (LSTM) cell shown in (F,G), respectively.

While linear activation functions can be used in the output layer for regression types of problems, it is important to use nonlinear activation functions in hidden layers. The use of nonlinear activation functions makes it possible for neural networks to capture nonlinear relationships between input data and output data. If linear activation functions are used in hidden layers instead, a neural network then collapses to a linear regression or a logistic regression. Figure 1B shows a general structure of a neural network with one hidden layer. As we can see from the figure, the difference between a perceptron and a neural network with one hidden layer is an additional layer, known as the hidden layer, lies between the input layer and the output layer. Each hidden unit in the hidden layer is formed in the same way as the processor in a perceptron, which is generated by applying a nonlinear activation function to a linear combination of weights and inputs.

An important characteristic of a neural network is the universal approximation theorem (Hornik et al., 1989). The theorem says that a neural network with one hidden layer can approximate a continuous function defined on a compact set in ${\mathrm{ℝ}}^d$ arbitrarily well as long as the number of hidden units is large enough. Nevertheless, Györfi et al. (2006) and Shen et al. (2019) found that the number of hidden units cannot grow as fast as the sample size in order to make the neural network estimators reach statistical consistency. Therefore, there is a gap between theory and applications on this topic, which might worth further investigation.

2.3 Deep Neural Networks

A deep neural network is a neural network with more than one hidden layers. Figure 1C gives an example of a deep neural network with two hidden layers. One advantage of deep learning is that it requires much less number of hidden units to learn complex features, while a much larger number of hidden units may be needed for a shallow neural network. An example is to learn the XOR (i.e., exclusive OR) function. As shown in Figure 2, if we use a tree-structured deep neural network to learn the function, the number of hidden units required is $O\left(\log n\right)$. The number of hidden units increases exponentially in a neural network with one hidden layer as we need to enumerate all $2^n$ possible configurations of the input bits to learn the XOR function.

FIGURE 2

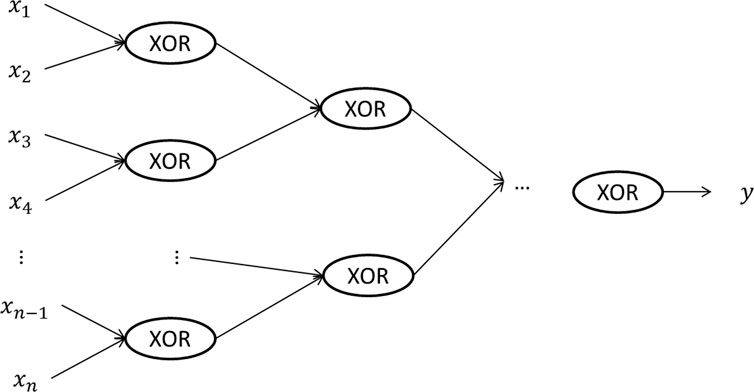
FIGURE 2. A tree structured deep neural network representing the XOR (i.e., exclusive or) function on the input data, where each input unit can only take two values, 0 and 1. By using a deep neural network, the depth of the network is $\left(\log n\right)$ , therefore we don’t need a large number of nodes to approximate the XOR function. However, if we approximate this function using only one hidden layer, then the number of units in this hidden layer can be exponentially large as we need to enumerate all $2^n$ possible configurations of the input bits.

Among all the nonlinear activation functions mentioned above, the ReLU activation function is one of the most popularly used functions in deep neural networks. For most of other nonlinear activation functions, the function value is almost unchanged when the input value is too large or too small. Therefore, when applying the back propagation algorithm, the gradient is close to zero which slows down the update of parameters (Rumelhart et al., 1988). ReLU avoids this vanishing gradient problem and is computationally efficient, which makes it ideal for training deep neural networks with many layers.

Besides the well-known fully connected feed-forward neural network, there are two other types of neural networks that have been widely used. One is known as the convolutional neural network (CNN) (LeCun, 1989) and the other is the recurrent neural network (RNN) (Rumelhart et al., 1988). CNN is commonly used for grid-like data structure such as images, while RNN is often used for sequence data such as a DNA sequence. The main feature of CNN is that convolution operations are used in place of matrix multiplications (Goodfellow et al., 2016) and the convolution operation captures spatial information in the data. Figure 1D provides a typical structure of CNN. Hidden layers in CNN usually consist of two parts. One type of hidden layer is the convolutional layer, where several filters having the same number of channels are applied to the output of previous layer. Each filter acts as a sliding window and a nonlinear activation function is applied to the linear combination of weights in the filter and elements in the “window” that come from the output of previous layer. The other type of hidden layer in CNN is called the pooling layer. A commonly used pooling layer is known as the max pooling layer, where a filter is served as a sliding window and the maximum element from that window is extracted. There are no parameters that need to be learned in a pooling layer. A Pooling layer is used to reduce the size of the representation, which speeds up the computation and makes detected features more robust.

While CNN can be used to capture spatial information in the data, RNN is used to capture the temporal dynamic behavior in the data. Figure 1E provides an example of RNN. In RNN, an input (e.g., a word in a sentence) is combined with the output from the last hidden layer of the previous neural network, to serve as inputs for the next successive neural network. The structure of commonly used RNN cells is shown in Figure 1F. Two unique features of RNNs are:

1) The input length and the output length can be different. Since the input of RNN is usually a sequence and the output can be a different sequence or a class label, it is likely that the length of the input is different from the length of the output. The structure of RNN is quite flexible, making it feasible to accommodate such scenarios.

2) Parameters are shared across neural networks. In an RNN, the weight matrices are shared across all neural networks, which greatly reduces the number of parameters to be estimated.

One issue of a classical RNN shown in Figure 1E is that it only uses the information earlier in the sequence, which can be addressed by using a bidirectional RNN (Schuster and Paliwal, 1997). Another drawback for a classical RNN is that it can run into a vanishing gradient problem, which makes it difficult to capture long range dependencies. To address this issue, two modifications of the classical RNN cells were proposed, one is the gated recurrent unit (GRU) (Cho et al., 2014) and the other one is the long short-term memory (LSTM) unit (Sak et al., 2014). Figure 1G shows the basic structure of an LSTM unit. The blue computation unit is known as the forget gate, which is used to get rid of previously stored memory value. The orange computation unit is known as the update gate. The updated value of the cell is given by $c^t={\text{Γ}}_f^t{c}^{t-1}+{\text{Γ}}_u^t{\tilde{c}}^t$, which is determined by the value from the update gate and the forget gate. Therefore, both the update gate and the forget gate control the update of the cell value.

With the increasing number of inputs, most learning algorithms need to deal with the over-fitting issue. One can build a sophisticated model on a training dataset with small training error but such a model may not have good generalizability. When applying this model to a different testing dataset, the model could be subject to high generalization error or testing error. Complex models usually have low bias but high variance. Therefore, the over-fitting issue is the same as the bias-variance tradeoff in statistics. Commonly used approaches for addressing the over-fitting issue in deep learning include regularization and dropout (Srivastava et al., 2014). For regularization approaches, a penalty term is often added to the loss function to solve the over-fitting issue. While the model increases its complexity to reduce the discrepancy between the estimated value and the true value, it can also increase the penalty. Therefore, minimizing the loss function with the penalty term helps to keep the balance between bias and variance. Dropout is another popularly used approach in neural networks. Figure 3 provides an illustration of the dropout approach. In dropout, we randomly delete hidden units with certain probability and remove all the in-and-out edges associated with those hidden units. The intuition behind the dropout is that since the “input” hidden units can be randomly dropout, the “output” hidden units cannot rely on any one of the features. Therefore, the weights have to be shrunk towards zero. As pointed out in Wager (Wager et al., 2013), when applied to linear regression, dropout is equivalent to the classical L₂-regularization.

FIGURE 3

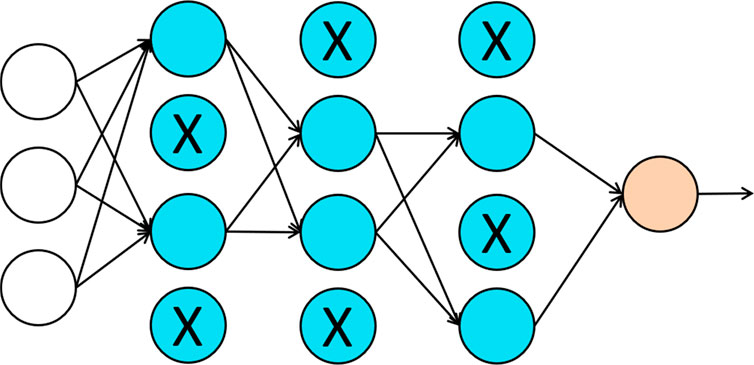
FIGURE 3. An illustration of dropout regularization. Each hidden unit is randomly deleted with some probability, marked by X in the figure, and the in-and-out edges associated with those hidden units are also removed.

2.4 Unsupervised Learning

In supervised learning, there is a teacher (i.e., labeled responses) supervising the performance of the learning machine through some metric quantifying the discrepancy. In unsupervised learning, however, there are no labeled responses. Instead, we are more interested in data compression by extracting useful information from the input data. The dimension of extracted features is usually much smaller than the dimension of the original input data. By doing so, we can not only reduce the cost of data storage, but also make the downstream analyses more efficient.

A commonly used unsupervised learning algorithm is the Principle Component Analysis (PCA). There is a counterpart of PCA in deep neural network, known as autoencoder (LeCun, 1987; Bourlard and Kamp, 1988; Hinton and Zemel, 1994). Figure 4A provides an illustration of an autoencoder. In an autoencoder, important features are extracted from the original data. To determine whether the extracted features represent the original input, we reconstruct the “original data” from the extracted features and use the difference between the reconstructed data and the original data as a guideline to train the network.

FIGURE 4

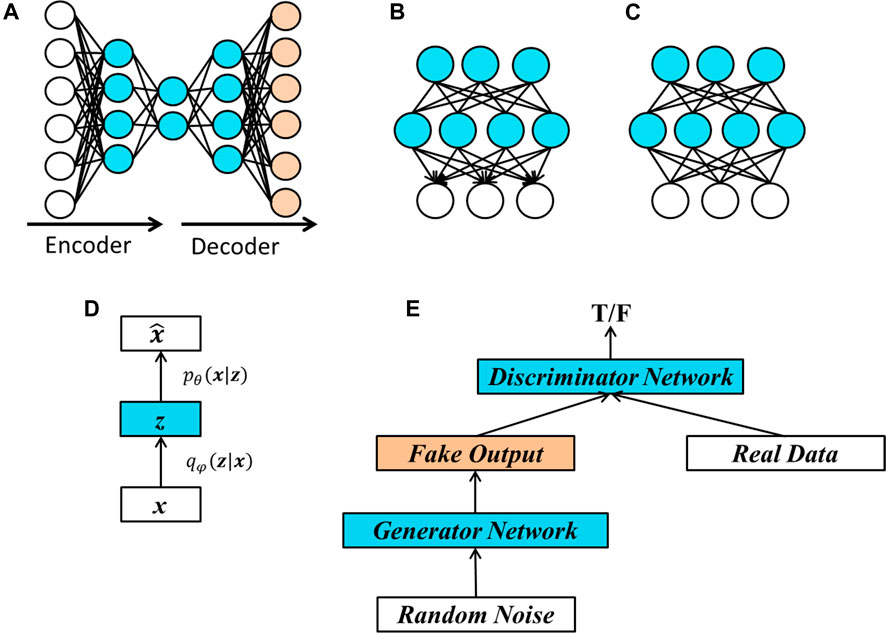
FIGURE 4. Structures of popular unsupervised learning methods. (A) Basic structure of an autoencoder. The three layers on the left represent encoding process, which extract important features from the input data and the two layers on the right represent decoding process, which tries to reproduce the original data. An autoencoder is usually learned by minimizing the discrepancy between the original data and the respective reproduced data. (B) A deep belief network (DBN) with two hidden layers. A main characteristic of a DBN is that the edges between the top two layers are undirected and the edges between all other layers are directed pointing towards the layer that is closest to the data. (C) A deep Boltzmann machine (DBM) is a generative model having similar structures with a DBN except that all the connections between layers are undirected. (D) A variational autoencoder (VAE) learns two conditional distributions, one is the conditional distribution of latent features given the input data $q_{\phi }\left(\mathit{z}\text{|}\mathit{x}\right)$ and the conditional distribution of outputs given the latent features $p_{\theta }\left(\mathit{x}\text{|}\mathit{z}\right)$, which is the target distribution used to generate new samples. (E) General structure of a generative adversarial network (GAN). A GAN starts with samples from a simple distribution such as random noises and uses a neural network (the generator network) to learn the complex transformation of the samples to create fake outputs and use a discriminator network to see if the generated outputs are close enough to the real data.

One of the most active research topics in unsupervised learning is generative models. The goal of these models is to learn the model distribution from the data so that we can generate new data from the distribution. Here are some most commonly used generative models:

• Boltzmann machines (BM) (Fahlman et al., 1983; Hinton et al., 1984) provide a way to model the joint distribution of a large number of binary random variables.

• Restricted Boltzmann machines (RBM) (Smolensky, 1986) is a bipartite undirected graph containing one visible layer and one hidden layer. Both layers contain nodes taking binary values, and the model is used to approximate any joint distribution of binary random variables. Therefore, RBM is often known as a stochastic neural network.

• Deep Belief Networks (DBN) (Hinton, 2009) are generative models that have multiple layers of latent binary variables. As we can see from Figure 4B, the connections between the top two hidden layers are undirected, while the connections between other layers are directed and point towards the layers closer to the visible data.

• Deep Boltzmann machines (DBMs) (Salakhutdinov and Hinton, 2009) are similar to deep belief networks except that all the edges in a DBM are undirected, as shown in Figure 4C.

• Variational autoencoders (VAE) (Kingma and Welling, 2014) is a probabilistic version of autoencoders, which allows us to sample data from the model. The structure of a VAE is shown in Figure 4D. In VAE, the hidden layers represent some latent factors, denoted by z in Figure 4D, which are used to generate the input data. The goal of VAE is to learn parameters in two conditional distributions. The first one [i.e., $q_{\phi }\left(\mathit{z}\text{|}\mathit{x}\right)$ in Figure 4D] is the conditional distribution of the latent factors given the input data, and the other one [i.e., $p_{\theta }\left(\mathit{x}\text{|}\mathit{z}\right)$ in Figure 4D] is the conditional distribution of the output given the latent factors, which is used to generate new samples.

• Generative adversarial networks (GAN) (Goodfellow et al., 2014) are popular methods that enable us sample data from complex, and high-dimensional training distributions even there is no direct way to do it. The basic structure of a GAN is shown in Figure 4E. A generator network is used to learn the complex transformation of the samples from a simple distribution such as random noise and to produce fake outputs. A discriminator network is then applied to the fake outputs and real data. The goal is to train the network so that the discriminator network cannot distinguish the fake data and the real data.

2.5 Semi-Supervised Learning

As suggested by its name, semi-supervised learning sits between supervised learning and unsupervised learning. In supervised learning, each data point in the training data has a label, which serves as a “teacher” to guide the performance of prediction (Chapelle et al., 2006; Zhu 2008). In many real-world problems, additional data points without labels may also be available. The goal of semi-supervised learning is to construct a learner by using both the labeled training data and the unlabeled data for improved performance. Although there is no guarantee that prediction performances will be improved by incorporating additional unlabeled data, empirical studies have shown consistent performance gain, compared with their supervised counterparts, by using semi-supervised learning methods based on neural networks. Therefore, semi-supervised learning methods using deep neural networks have been widely applied to genomic studies, especially for cell-type classification using single-cell RNA-seq data. We provide a detailed survey on this topic in Section 5.

Van Engelen and Hoos, (2020) provide a comprehensive survey on semi-supervised learning, where they taxonomize semi-supervised learning methods into two main categories: inductive methods and transductive methods. The goals of inductive methods are similar to those of supervised learning. A weak learner, mapping from the input space to the output space, is produced. In supervised learning, only labeled data is used, while in semi-supervised learning, both the labeled data and unlabeled data are used. On the other hand, the goal of transductive methods is to solely predict labels for the unlabeled data points.

As inductive methods share the same goals as supervised learning methods, these methods can be used for any supervised learners. Different inductive methods use different methods to incorporate unlabeled data. For example, one can use an autoencoder to extract important features from the unlabeled data and use these features to train the labeled data. This is known as unsupervised preprocessing in van Engelen and Hoos, (2020). One can also train a classifier using the labeled data and create pseudo-labels for unlabeled data. The classifier is then retrained on the labeled dataset and pseudo-labeled dataset. Such a method is called a wrapper method according to van Engelen and Hoos, (2020). Unlabeled data can also be incorporated by adding additional terms into the loss function, and such inductive methods are called intrinsically semi-supervised methods.

Since transductive methods only focus on predicting labels for unlabeled data without training a classifier, almost all transductive methods are graph-based, which mainly consist of three steps: 1) constructing a graph based on some similarity measures, 2) weighing the edges, and 3) drawing inference on the graph.

Figure 5 provides a block diagram showing some major deep learning methods to be discussed in the following sections.

FIGURE 5

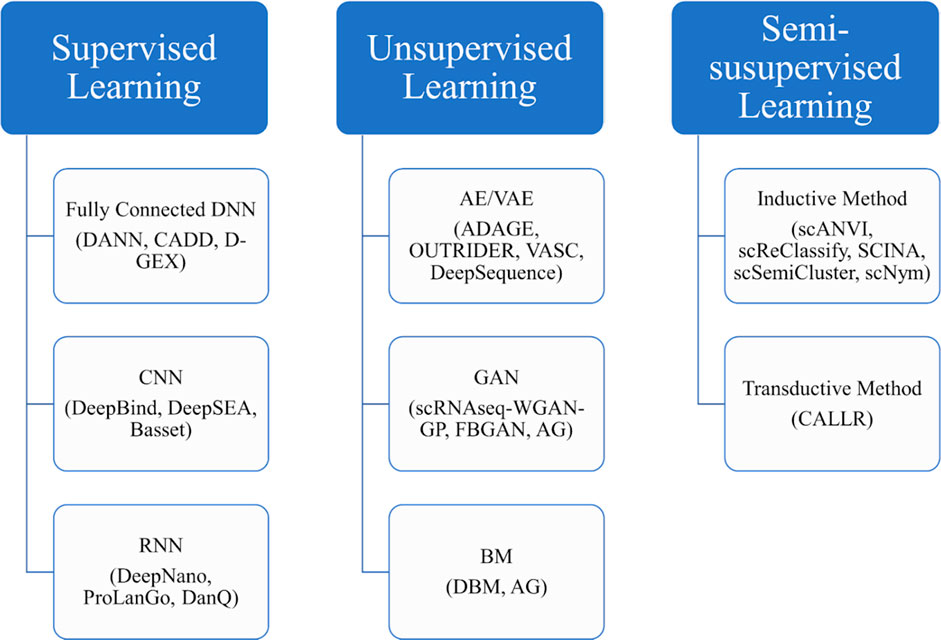
FIGURE 5. The block diagram of some main deep learning methods to be discussed in the rest of the review.

3 Applications of Supervised Deep Learning to Genomic Studies

In recent years, deep learning techniques have been successfully applied to various areas such as computer vision, natural language processing, autonomous driving, etc. Starting from the seminal studies in 2015, which established the applicability of deep learning to DNA sequence data (Alipanahi et al., 2015; Zhou and Troyanskaya, 2015; Eraslan et al., 2019), there is an increasing interest in using deep learning in genomic studies. As mentioned in Park and Kellis, (2015), deep learning holds great promise for genomic research since various levels of information and abstraction can be captured by different layers in deep learning.

Fully connected deep neural networks have been used in various genomic studies. For instance, Quang et al. (2014) proposed DANN, a method that makes predictions on the deleteriousness of genetic variants using deep neural networks. Compared with a commonly used algorithm known as combined annotation—dependent depletion (CADD) (Kircher et al., 2014), DANN reduces the relative error rate by 19%. The reason is that CADD uses a linear kernel support vector machine and only linear representation can be learned from the data. Another area of deep learning application is in gene expression inference. D-GEX (Chen et al., 2016), used a deep neural network to predict the expression of target genes from the expression of landmark genes. The relative performance of D-GEX, in terms of the overall error rate, improves 15.33% over linear regression and D-GEX also achieves lower error than linear regression through a gene-wise comparative analysis.

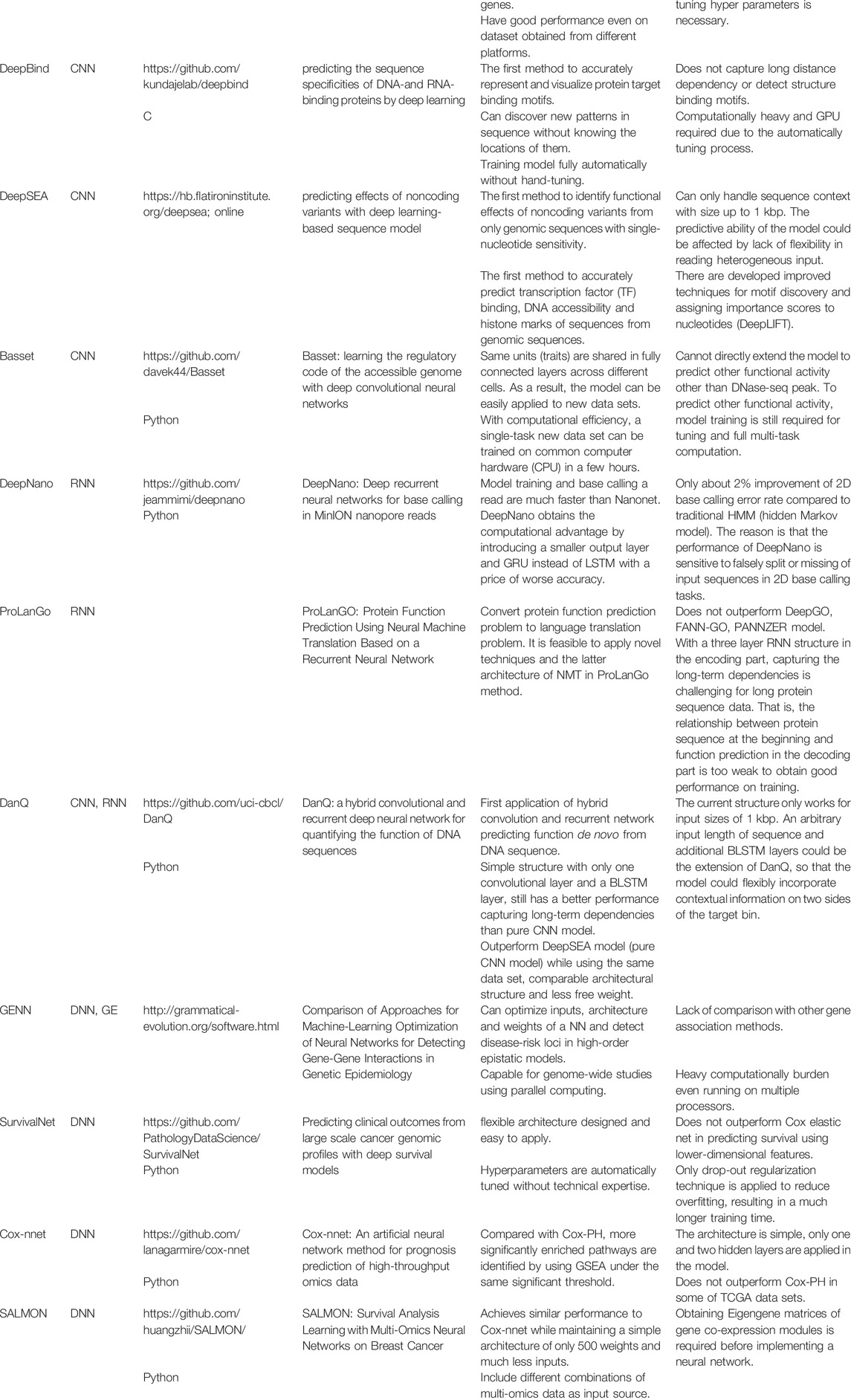
CNNs are great tools for analyzing data with spatial dependencies. It holds great promise for DNA sequence data as it can take linkage disequilibrium into account. Primary works on applying CNNs to genomic studies include DeepBind (Alipanahi et al., 2015), DeepSEA (Zhou and Troyanskaya, 2015) and Basset (Kelley et al., 2016). Since DNA sequence is a one-dimensional data, when applying CNNs, one-hot encoding is usually used to deal with the four DNA bases. For example, we can code each DNA base as A = [1,0,0,0], G = [0,1,0,0], C = [0,0,1,0], T = [0,0,0,1] so that a DNA sequence now becomes a matrix with four columns and a classical CNN can be applied. If there are any missing values in the DNA coding, one possible solution is to add an additional column, which corresponds to the missing value, to the DNA one-hot encoding matrix. For the purpose of classifying transcription factors, the filters in the first convolutional layers are actually the motif detectors, which are similar to position weight matrices without requiring the entries to be probabilities or log-odds ratios.

Besides CNNs, RNNs have also been applied to genomic studies. Pouladi et al. (2015) used matrix factorization and RNNs to construct a genotype imputation and phenotype sequences prediction system, which attained better performance than long short-term memory and spatial partial least squares models. Boža et al. (2017) proposed DeepNano, an RNN-based approach, which substantially improves the base calling accuracy for MinION sequencing data (Mikheyev and Tin, 2014). A combination of RNN and particle swarm optimization was proposed by Xu et al. (2007) to infer genetic regulatory networks and produce meaningful insights on the nonlinear dynamics of the gene expression time series. Recently, ProLanGo (Cao et al., 2017), a RNN-based model, was proposed for prediction of protein function.

As mentioned by Eraslan et al. (2019), an important area of applying deep learning to genomics is predicting the effect of non-coding regions. 98% of the human-genome is non-coding and 93% identified disease-associated variants from over 1,200 genome-wide association studies are located in the non-coding regions (Pennisi, 2011). DeepSEA (Zhou and Troyanskaya, 2015) and DanQ (Quang and Xie, 2016) are two important works in this area. DeepSEA is a CNN approach with three convolutional layers and two max pooling layers. The network structure of DanQ, as shown in Figure 6, is similar to that of DeepSEA. However, instead of applying two more convolutional layers and a max pooling layer, DanQ uses a bi-directional long short-term memory RNN after the first convolutional and max pooling layer. The outputs from the LSTM units are then flattened in DanQ and a dense layer of rectified linear units is applied followed by a multi-task sigmoid unit. Both methods attain great performances in terms of prediction accuracy, while DanQ outperforms DeepSEA and other methods (e.g., logistic regression) across several other metrics.

FIGURE 6

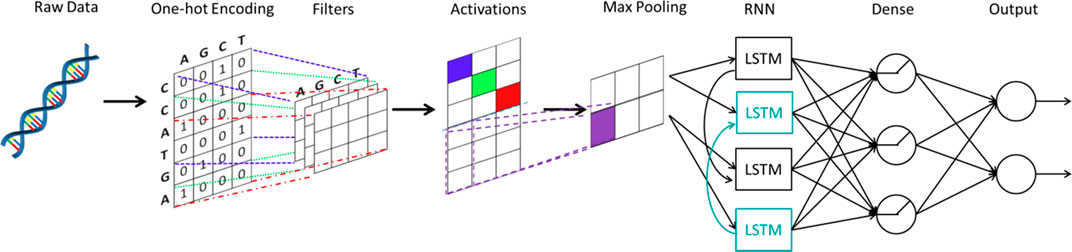
FIGURE 6. The structure of DanQ. One-hot encoding is applied to the original DNA sequence. A convolutional neural network is used, followed by a bidirectional recurrent neural network with long short-term memory units. The outputs from the bidirectional recurrent neural network are fed into a neural network to make final predictions.

Another area of using deep learning is in genetic association studies. In the past decade, genome-wide association studies (GWAS) have uncovered numerous genetic variants predisposing to human traits and diseases (Consortium, 2007; Scott et al., 2007; Sladek et al., 2007). Nevertheless, most of the identified variants are associated with small effects and account for only a small fraction of heritability (Maher, 2008). Part of the missing heritability can be explained by gene-gene interactions or epistatis (Manolio et al., 2009). While each genetic variant is associated with a small effect, it can interact with other variants to play an important role on diseases. This leads to many multi-locus interaction studies in order to understand the joint effects of multiple loci on complex diseases (Cordell, 2009; Gusareva et al., 2014).

Due to the large number of genetic markers in association studies, inference on gene-gene interactions is computational challenging for most classical statistical methods. Neural networks, on the other hand, can be used to model complex relations between traits and genetic markers without having to enumerate all the possible interactions between genetic markers. Researchers have used neural networks in genetic data analyses, but the results are inconsistent (Lucek and Ott, 1997; Lucek et al., 1998; Saccone et al., 1999; Curtis et al., 2001; Marinov and Weeks, 2001; North et al., 2003). One possible explanation is the existence of multiple local minima in the optimization and the selection of suboptimal neural network structures. Machine learning approaches, such as genetic programming neural networks (Motsinger et al., 2006) and grammatical evolution neural networks (GENN) (Motsinger-Reif et al., 2008) have been developed to address these issues by choosing the best neural network architectures based on a given data set. Motsinger et al. (2006) have demonstrated that GENN have higher power than the classical neural network using back-propagation. Furthermore, Motsinger-Reif et al. (2008) showed that the performance of GENN is better than that of GPNN when there exist high order gene-gene interactions. Besides classical neural networks, Bayesian neural networks (Beam et al., 2014) have also been used to detect gene-gene interactions. Studies showed that Bayesian neural networks are more powerful than other popularly used methods, such as ${\chi }^2$ test and Bayesian Epistasis Association Mapping (Zhang and Liu, 2007). Recently, Uppu et al. (2016a) and Uppu et al. (2016b) have applied deep neural network to detect gene-gene interactions in association studies and achieved promising results.

Deep learning-based survival prediction with gene expression profiles has recently emerged as a new research area. Primary works include SurvivalNet (Yousefi et al., 2017), Cox-nnet (Ching et al., 2018) and SALMON (Huang et al., 2019). These methods all adopt feedforward neural networks with an output of hazard ratio in the Cox proportional hazards model, and they use negative log partial likelihood as cost function for network training. The three methods differ in network design, regularization, and pre-training of gene expression data. Cox-nnet and SALMON are both single hidden layer neural networks, whereas SurvivalNet uses a Bayesian optimization technique to determine the network design. SurvivalNet and Cox-nnet adopt dropout (Srivastava et al., 2014) to prevent the neural networks from overfitting, whereas SALMON applies the LASSO penalty (Tibshirani, 1996) to the network weights in the cost function. Rather than using raw gene expression values as network inputs, as SurvivalNet and Cox-nnet do, SALMON performs a gene co-expression module analysis and uses the resulting eigengene matrices of gene co-expression modules as the inputs, which greatly reduces the number of parameters in the neural network. Through an empirical study based on real data, Huang et al. (2019) found that Cox-nnet and SALMON had comparable discriminative abilities and outperformed the elastic-net Cox regression (Simon et al., 2011) and the random survival forest (Ishwaran et al., 2008). No prediction performance comparison has been made between these two methods and SurvivalNet, though. Surprisingly, all these survival learning machines just output a prognostic index, namely the hazard ratio relative to the baseline, for each subject, not a predicted survival curve, although this drawback can be easily fixed by using Breslow’s estimator (Breslow, 1974) to generate a baseline hazard function. Also, it is worthwhile to extend deep neural networks to other popular survival models such as the accelerated failure time model.

Bellot et al. (2018) provides a comprehensive comparison on the predictive accuracy between deep learning methods (e.g., deep neural networks and CNNs) and classical methods (e.g., linear regression and Bayesian ridge regression). They applied both types of methods to the UKBiobank (www.ukbiobank.ac.uk) with 80,000 training samples and 20,221 testing samples. Using genotype data, they use different methods to predict five phenotypes: human height, bone heel mineral density (BHMD), body mass index (BMI), systolic blood pressure (SBP), and waist-hip ratio (WHR). They found that the performances of deep learning methods rely on the network architecture of deep learning. Depending on the trait, deep learning and classical methods may have different performances. For example, for human height, a highly polygenetic trait with a predominant additive genetic basis, there is not much performance differences among all methods. One reason is that in such scenario, linear models work pretty well. Through this empirical study, they also demonstrated that CNNs have comparable and slightly better performance than linear methods, except for human height. Since CNNs can capture spatial correlation of SNPs due to linkage disequilibrium, they suggest future research is needed on studying the performance of CNN in genetic predictions.

For convenience, we summarize the methods discussed in the section in Table 1.

TABLE 1

TABLE 1. Summary of reviewed supervised learning methods for genetic and genomic studies.

4 Applications of Unsupervised Deep Learning to Genomic Studies

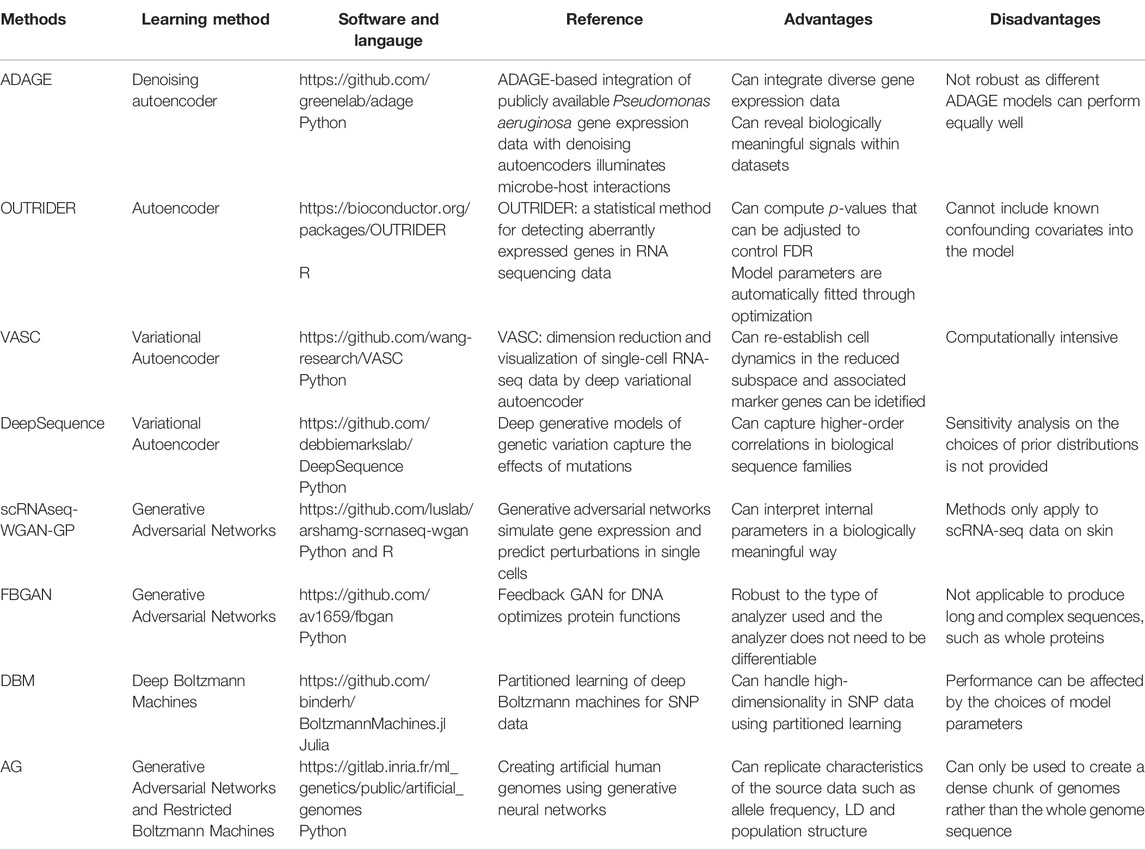
Besides the use of supervised deep learning methods in genomic studies, there are also many applications of using unsupervised deep learning methods in genomics. For instance, Scholz et al. (2005) used autoencoder to estimate missing values for metabolite data and gene expression data. Their results showed that autoencoders can better estimate missing values for nonlinear structured data as compared with linear methods. Similarly, Tan et al. (2016); Tan et al. (2017a); Tan et al. (2017b) proposed a method called ADAGE, which uses autoencoders to build gene expression signatures consistent with biological pathways. Through analysis of KEGG pathways, ADAGE and the popular gene set enrichment analysis (GSEA) (Subramanian et al., 2005) both detected five pathways. Moreover, ADAGE detected nine pathways that were not significantly enriched in GSEA.

There are also some applications of using generative models in genomics. A deep variational autoencoder for single-cell RNA sequencing data (VASC) (Wang and Gu, 2018) was developed to model the dropout events and to find the nonlinear hierarchical feature representations of the data. By comparing the results on 20 datasets with different numbers of cells included and sequencing protocols used, VASC outperformed other dimension reduction methods such as PCA, t-SNE, ZIFA (Pierson and Yau, 2015) and SIMLR (Wang and Gu, 2018). DeepSequence (Riesselman et al., 2018) used VAE to predict mutation effects and the results are significantly better than the existing method.

The first application of GAN to genomic studies is due to Ghahramani et al. (2018). They applied GAN to simulate single cell RNA-seq data. Not only can they provide biologically meaningful interpretation of their model parameters, the effect of cell state perturbation can be predicted as well. Recently, Gupta and Zou, (2019) proposed a generative model known as the feedback GAN (FBGAN) to produce synthetic gene sequences for desired properties. In FBGAN, a function analyzer is used to produce a score for the synthetic gene sequences generated from the generator in GAN and gradually replace the real data by the synthetic gene sequence with the highest score from the function analyzer. FBGAN has been applied to generate genes coding for antimicrobial peptides as well as to optimize synthetic genes for the secondary structure of the resulting peptides. The results demonstrated that proteins generated from FBGAN have good biophysical properties. Despite its good properties, applying GAN architectures to produce long and complex sequences is still challenging and worth further investigations. DBNs have also been used in genomic studies. For example, Ghasemi et al. (2018) proposed using DBNs to initialize parameters in a deep neural network for Quantitative Structure Activity Relationship (QSAR) studies. The results of their study showed that the prediction performance has been improved by using DBNs.

In terms of using unsupervised learning methods in genetic studies, Montañez et al. (2018) used both stacked autoencoders (SAE) and a deep neural network to classify extremely obese and non-obese individuals. In SAE, the output from a single layer autoencoder is used to train a second autoencoder and the process is repeated multiple times. The output of the final autoencoder is used to pre-trained the weights in a deep neural network. Based on a study of feature selection from a set of 2,465 SNPs (p-values <1e-2) and using extracted features to classify obese samples from normal control samples through a deep neural network, it is found that although the performance on validation set and testing set deteriorate according to classification accuracy when 50 features were extracted, the AUC was still over 85% and relatively low overfitting occurred in the study.

Directly applying a DBM is not a good option as in genetic studies, the number of SNPs often exceeds the number of individuals. To overcome this issue, Hess et al. (2017) first estimated the relation between SNPs using stagewise regression, where each SNP is regressed on all the other SNPs, and then apply a DBM to the small clusters of correlated SNPs. Such method is called partitioned DBM. The result demonstrated that the partitioned DBM can identify almost twice number of significant SNPs compared with univariate testing, while the type I error can also be controlled.

Recently, Yelmen et al. (2021) demonstrated that GANs and RBMs can be used to generate high quality artificial genomes and the outcomes are promising and the generated artificial genome can inherit genotype-phenotype associations. Since GWAS usually requires a huge number of samples and most research data are not publicly available due to privacy issues. The success of generating high quality artificial genomes provides a great substitute for those private databases.

The advances in spatially resolved transcriptomics (SRT) have enabled gene expression profiling with spatial location information in tissues (Asp et al., 2020). One important step before further analysis in SRT studies is to cluster the spots and this is accomplished in many recent studies with the help of deep learning. For example, one of the workflows of SpaCell (Tan et al., 2019) is for cell-type clustering using autoencoders by integrating pixel-intensity values with gene expression measurements from spots in a tissue. StLearn (Pham et al., 2020) uses a transfer learning deep neural network to extract features from pixel image tiles created from the hematoxylin and eosin-stained microscopy image containing tissue morphology information. A graph convolutional network is applied in SpaGCN (Li et al., 2020) to aggregate gene expression information from neighboring spots and then detects spatially variable genes based on the aggregated gene expression. We refer interested readers to Hu et al. (2021) for a review on statistical and machine learning methods for SRT with histology.

There are various other applications of deep learning in genomic studies. We refer interested readers to review papers on this topic (Angermueller et al., 2016; Jones et al., 2017; Min et al., 2017; Ching et al., 2018; Wainberg et al., 2018; Yue and Wang, 2018; Zou et al., 2018; Eraslan et al., 2019). Table 2 provides a brief summary of the reviewed recent unsupervised learning methods having applications to genomic studies.

TABLE 2

TABLE 2. Summary of reviewed unsupervised learning methods for genetic and genomic studies.

5 Applications of Semi-Supervised Learning for Single-Cell RNA-Seq Data

The fast-emerging technology has made it possible to collect global transcriptome profiling on the single cell level. Through accurate identification of cell types, the formation of complex organs and various cancers could be better understood (Kim et al., 2019). However, using single cell RNA-seq data to accurately identify cell types remains a challenging task (Stegle et al., 2015). Recently, semi-supervised learning has become a technique popularly used for single-cell RNA-seq data analysis. Table 3 provides a list of the semi-supervised learning methods for single-cell RNA-seq data discussed in this section.

TABLE 3

TABLE 3. Summary of reviewed semi-supervised learning methods for single-cell RNA-seq data.

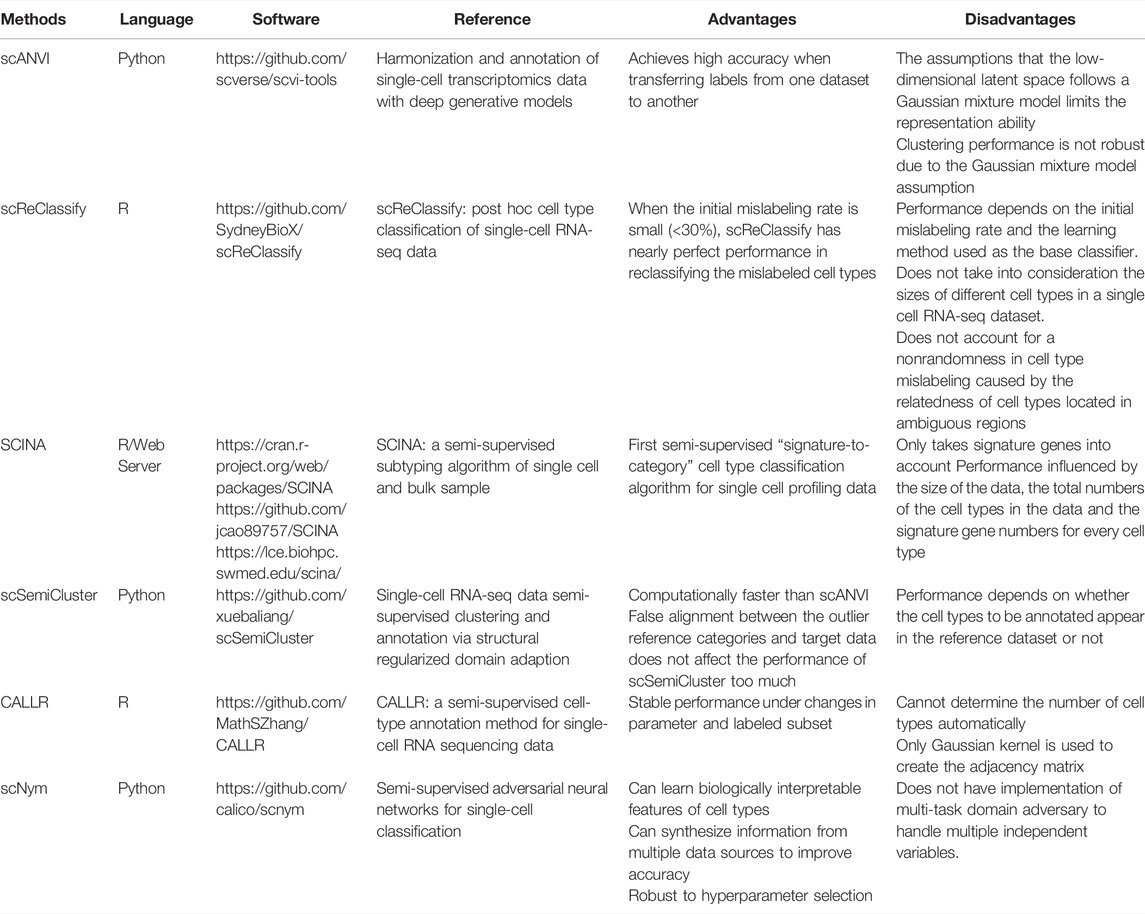
Before fully diving into the semi-supervised learning methods used for cell type annotations, it is worthwhile to mention single-cell Variational Inference (scVI) (Lopez et al., 2018) and its extension to single-cell ANnotation using Variational Inference (scANVI) (Xu et al., 2021). Both methods use variational inference and deep generative models to fully characterize the distribution of single-cell RNA-seq data. scANVI can also be used to annotate cell types and has been used as a baseline method for recently proposed methods, such as scSemiCluster (Chen et al., 2021) and scNym (Kimmel and Kelley, 2021).

scReClassify proposed by Kim et al. (2019) uses PCA to perform dimension reduction of the original single cell RNA-seq data, and then apply a semi-supervised learning method to reclassify the mislabeled cell types caused by human inspection. When the initial mislabeling rate is small, scReClassify can reclassify those mislabeled cell types to the correct ones. However, there is no gain in performance when the initial mislabeling rate is high. Moreover, scReClassify does not consider the sizes of different cell types in a single cell RNA-seq dataset and the non-randomness in cell type mislabeling due to the relatedness of the cell types located in ambiguous regions.

Zhang et al. (2019) developed the SCINA algorithm for cell type classifications in single cell RNA-seq data. The prior knowledge of signature genes is taken into account in the unsupervised estimation process. SCINA is the first semi-supervised “signature-to-category” cell type classification algorithm for single cell-RNA-seq data. Nonetheless, it only takes signature genes into consideration, and its performance depends on the size of the data, the total number of cell types in the data and the number of signature genes for every cell type.

scSemiCluster (Chen et al., 2021) and CALLR (Wei and Zhang, 2021) are two new cell type annotation methods based on semi-supervised learning. scSemiCluster is computationally faster than scANVI, and its performance will be less affected by the false alignment between the outlier reference categories and target data. Nevertheless, since the reference dataset is used in scSemiCluster to make predictions, its performance depends on whether the cell types to be annotated are contained in the reference dataset. CALLR is an optimization-based method that combines a graph Laplacian matrix constructed from all the cells with sparse logistic regression. While CALLR is robust to changes in parameters and labeled subset, it cannot determine the number of cell types automatically.

scNym (Kimmel and Kelley, 2020) is one of the newest semi-supervised methods for analyzing single cell RNA-seq data. Instead of relying on a reference dataset to annotate cell types, scNym uses an adversarial network to improve the classification performance. Moreover, scNym is robust to hyperparameter selection and can further improve accuracy by learning biologically interpretable features and synthesizing information from multiple data sources. However, the current method does not consider a multi-task domain, which makes it less useful when there are multiple independent variables.

6 Conclusion and Perspectives

With the rapid progress in graphical processing unit (GPU) technology, complex deep learning algorithms can be accomplished in rather short time, which leads to wide use of deep learning in many areas. One of the advantages of deep learning methods is the convenient and easy access of deep learning platforms such as Keras (https://keras.io/), TensorFlow (https://www.tensorflow.org/) and PyTorch (https://pytorch.org/). Benefiting from these well-developed platforms, researchers can implement deep learning algorithms without knowing the mathematical details behind them, which makes it feasible for researchers to focus more on applying deep learning to their own research fields.

In this paper, we have reviewed some important deep learning developments in genomics studies. Despite its great improvement in prediction performance compared to other classical statistical methods (LeCun et al., 2015), there are still many challenging issues in this research field. One challenge of deep learning is lack of interpretability. In genetic association studies, identifying and interpreting disease-associated genetic markers is of major interest. Nevertheless, deep learning has been considered as a black box, which hinders its application in genetic association studies. Shen et al. (2019) and Horel and Giesecke, (2020) have developed theories to address such an issue, but the applicability of the theories to real data applications remains a challenging task. To make the results from deep learning interpretable, DeepLIFT (Shrikumar et al., 2017) assigns importance scores to the input for a given response to determine the crucial features. Sundararajan et al. (2017) considered sensitivity and implementation invariance as two fundamental axioms and proposed an integrated gradients method for attributing the prediction of a deep network to its inputs.

On the other hand, root mean square error (RMSE) and the correlation between prediction and original data are often used as measurements to compare the performances of different methods. However, such measurements may become obsolete due to the discovery of double descent phenomena (Belkin et al., 2019) for deep neural networks. As long as the networks have been trained for a sufficiently long period, the training error will keep decreasing to zero, while the testing error will increase first and then decrease again to reach an even smaller testing error. The double descent phenomena suggest that a deep neural network has the potential to achieve RMSE close to zero and correlation close to one if it has been trained for a sufficiently long period. Therefore, new measurements for comparing performances from different methods need to be proposed in the future.

Besides the researches on interpreting deep learning models, transfer learning (Pan and Yang, 2009) is another promising research area. Generalizing knowledge learned in one setting (e.g., variants discovered from Caucasian population) to another setting (e.g., other minority populations) is the major goal of transfer learning. Given the knowledge gained from animal studies, transfer learning can be used to generalize findings learned from animal studies to human studies. In addition, natural language processing methods such as BERT (Devlin et al., 2019) showed that by adding only a few more layer to a pre-trained network and fine tuning the parameters, better prediction performance can be achieved. Given the easy implementation of deep learning algorithms and the flexible deep learning models, we believe that deep learning will play an important role in future genomic and genetic research.

Author Contributions

XS, CJ, and QL contributed to conception and design of the study. XS and CJ wrote the first draft of the manuscript. YW, CL, and QL wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This work is supported by NIH 1R01DA043501-01 and NIH 1R01LM012848-01.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fsysb.2022.877717/full#supplementary-material

References

Alipanahi, B., Delong, A., Weirauch, M. T., and Frey, B. J. (2015). Predicting the Sequence Specificities of DNA- and RNA-Binding Proteins by Deep Learning. Nat. Biotechnol. 33, 831–838. doi:10.1038/nbt.3300

PubMed Abstract | CrossRef Full Text | Google Scholar

Angermueller, C., Pärnamaa, T., Parts, L., and Stegle, O. (2016). Deep Learning for Computational Biology. Mol. Syst. Biol. 12, 878. doi:10.15252/msb.20156651

PubMed Abstract | CrossRef Full Text | Google Scholar

Asp, M., Bergenstråhle, J., and Lundeberg, J. (2020). Spatially Resolved Transcriptomes-Next Generation Tools for Tissue Exploration. BioEssays 42 (10), 1900221. doi:10.1002/bies.201900221

PubMed Abstract | CrossRef Full Text | Google Scholar

Beam, A. L., Motsinger-Reif, A., and Doyle, J. (2014). Bayesian Neural Networks for Detecting Epistasis in Genetic Association Studies. BMC Bioinforma. 15, 368. doi:10.1186/s12859-014-0368-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Belkin, M., Hsu, D., Ma, S., and Mandal, S. (2019). Reconciling Modern Machine-Learning Practice and the Classical Bias-Variance Trade-Off. Proc. Natl. Acad. Sci. U.S.A. 116 (32), 15849–15854. doi:10.1073/pnas.1903070116

PubMed Abstract | CrossRef Full Text | Google Scholar

Bellot, P., de los Campos, G., and Pérez-Enciso, M. (2018). Can Deep Learning Improve Genomic Prediction of Complex Human Traits? Genetics 210, 809–819. doi:10.1534/genetics.118.301298

PubMed Abstract | CrossRef Full Text | Google Scholar

Bourlard, H., and Kamp, Y. (1988). Auto-association by Multilayer Perceptrons and Singular Value Decomposition. Biol. Cybern. 59, 291–294. doi:10.1007/bf00332918

PubMed Abstract | CrossRef Full Text | Google Scholar

Boža, V., Brejová, B., and Vinař, T. (2017). DeepNano: Deep Recurrent Neural Networks for Base Calling in MinION Nanopore Reads. PloS One 12, e0178751. doi:10.1371/journal.pone.0178751

PubMed Abstract | CrossRef Full Text | Google Scholar

Brechtmann, F., Mertes, C., Matusevičiūtė, A., Yépez, V. A., Avsec, Ž., Herzog, M., et al. (2018). OUTRIDER: A Statistical Method for Detecting Aberrantly Expressed Genes in RNA Sequencing Data. Am. J. Hum. Genet. 103, 907–917. doi:10.1016/j.ajhg.2018.10.025

PubMed Abstract | CrossRef Full Text | Google Scholar

Breslow, N. (1974). Covariance Analysis of Censored Survival Data. Biometrics, 89–99. doi:10.2307/2529620

CrossRef Full Text | Google Scholar

Cao, R., Freitas, C., Chan, L., Sun, M., Jiang, H., and Chen, Z. (2017). ProLanGO: Protein Function Prediction Using Neural Machine Translation Based on a Recurrent Neural Network. Molecules 22, 1732. doi:10.3390/molecules22101732

PubMed Abstract | CrossRef Full Text | Google Scholar

Chapelle, O., Chi, M., and Zien, A. (2006). Semi-supervised Learning. 1st ed. Cambridge: The MIT Press.

Google Scholar

Chen, L., He, Q., Zhai, Y., and Deng, M. (2021). Single-cell RNA-Seq Data Semi-supervised Clustering and Annotation via Structural Regularized Domain Adaptation. Bioinformatics 37 (6), 775–784. doi:10.1093/bioinformatics/btaa908

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, Y., Li, Y., Narayan, R., Subramanian, A., and Xie, X. (2016). Gene Expression Inference with Deep Learning. Bioinformatics 32, 1832–1839. doi:10.1093/bioinformatics/btw074

PubMed Abstract | CrossRef Full Text | Google Scholar

Ching, T., Himmelstein, D. S., Beaulieu-Jones, B. K., Kalinin, A. A., Do, B. T., Way, G. P., et al. (2018). Opportunities and Obstacles for Deep Learning in Biology and Medicine. J. R. Soc. Interface. 15, 20170387. doi:10.1098/rsif.2017.0387

PubMed Abstract | CrossRef Full Text | Google Scholar

Cho, K., Van Merrienboer, B., Gulcehre, C., Bougares, F., Schwenk, H., Bengio, Y., et al. (2014). “Learning Phrase Representations Using RNN Encoder-Decoder for Statistical Machine Translation” in Conference on Empirical Methods in Natural Language Processing (EMNLP 2014). ArXiv Prepr. ArXiv14061078. doi:10.3115/v1/d14-1179

CrossRef Full Text | Google Scholar

Consortium, W. T. C. C. (2007). Genome-wide Association Study of 14,000 Cases of Seven Common Diseases and 3,000 Shared Controls. Nature 447, 661–678. doi:10.1038/nature05911

PubMed Abstract | CrossRef Full Text | Google Scholar

Cordell, H. J. (2009). Detecting Gene-Gene Interactions that Underlie Human Diseases. Nat. Rev. Genet. 10, 392–404. doi:10.1038/nrg2579

PubMed Abstract | CrossRef Full Text | Google Scholar

Curtis, D., North, B. V., and Sham, P. C. (2001). Use of an Artificial Neural Network to Detect Association between a Disease and Multiple Marker Genotypes. Ann. Hum. Genet. 65, 95–107. doi:10.1046/j.1469-1809.2001.6510095.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Devlin, J., Chang, M., Lee, K., and Toutanova, K., 2019. “BERT: Pre-Training of Deep Bidirectional Transformers for Language Understanding.” in Proceedings of NAACL. ArXiv Prepr. ArXiv181004805.

Google Scholar

Eraslan, G., Avsec, Ž., Gagneur, J., and Theis, F. J. (2019). Deep Learning: New Computational Modelling Techniques for Genomics. Nat. Rev. Genet. 20, 389–403. doi:10.1038/s41576-019-0122-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Fahlman, S. E., Hinton, G. E., and Sejnowski, T. J. (1983). “Massively Parallel Architectures for Al: NETL, Thistle, and Boltzmann Machines,” in Proceedings of the National Conference on Artificial Intelligence AAAI-83 (AAAI).

Google Scholar

Ghahramani, A., Watt, F. M., and Luscombe, N. M. (2018). Generative Adversarial Networks Simulate Gene Expression and Predict Perturbations in Single Cells. BioRxiv, 262501. doi:10.1101/262501

CrossRef Full Text | Google Scholar

Ghasemi, F., Mehridehnavi, A., Fassihi, A., and Pérez-Sánchez, H. (2018). Deep Neural Network in QSAR Studies Using Deep Belief Network. Appl. Soft Comput. 62, 251–258. doi:10.1016/j.asoc.2017.09.040

CrossRef Full Text | Google Scholar

Glorot, X., Bordes, A., and Bengio, Y. (2011). “Deep Sparse Rectifier Neural Networks,” in Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, 315–323.

Google Scholar

Goodfellow, I., Bengio, Y., and Courville, A. (2016). Deep Learning. MIT press.

Google Scholar

Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., et al. (2014). “Generative Adversarial Nets,” in Advances in Neural Information Processing Systems. Editors D. A. Cohn, M. S. Kearns, and S. A. Solla (MIT press), 2672–2680.

Google Scholar

Gupta, A., and Zou, J. (2019). Feedback GAN for DNA Optimizes Protein Functions. Nat. Mach. Intell. 1, 105–111. doi:10.1038/s42256-019-0017-4

CrossRef Full Text | Google Scholar

Gusareva, E. S., Carrasquillo, M. M., Bellenguez, C., Cuyvers, E., Colon, S., Graff-Radford, N. R., et al. (2014). Genome-wide Association Interaction Analysis for Alzheimer's Disease. Neurobiol. Aging 35, 2436–2443. doi:10.1016/j.neurobiolaging.2014.05.014

PubMed Abstract | CrossRef Full Text | Google Scholar

Györfi, L., Kohler, M., Krzyzak, A., and Walk, H. (2006). A Distribution-free Theory of Nonparametric Regression. Springer Science & Business Media.

Google Scholar

Hess, M., Lenz, S., Blätte, T. J., Bullinger, L., and Binder, H. (2017). Partitioned Learning of Deep Boltzmann Machines for SNP Data. Bioinformatics 33, 3173–3180. doi:10.1093/bioinformatics/btx408

PubMed Abstract | CrossRef Full Text | Google Scholar

Hinton, G. (2009). Deep Belief Networks. Scholarpedia 4, 5947. doi:10.4249/scholarpedia.5947

CrossRef Full Text | Google Scholar

Hinton, G. E., Sejnowski, T. J., and Ackley, D. H. (1984). Boltzmann Machines: Constraint Satisfaction Networks that Learn. Carnegie-Mellon University, Department of Computer Science Pittsburgh.

Google Scholar

Hinton, G. E., and Zemel, R. S. (1994). “Autoencoders, Minimum Description Length and Helmholtz Free Energy,” in Advances in Neural Information Processing Systems, 3–10.

Google Scholar

Horel, E., and Giesecke, K., 2020. Significance Tests for Neural Networks. J. Mach. Learn. Res. 21 (227), 1–29.

PubMed Abstract | Google Scholar

Hornik, K., Stinchcombe, M., and White, H. (1989). Multilayer Feedforward Networks Are Universal Approximators. Neural Netw. 2, 359–366. doi:10.1016/0893-6080(89)90020-8

CrossRef Full Text | Google Scholar

Hu, J., Schroeder, A., Coleman, K., Chen, C., Auerbach, B. J., and Li, M. (2021). Statistical and Machine Learning Methods for Spatially Resolved Transcriptomics with Histology. Comput. Struct. Biotechnol. J. 19, 3829–3841. doi:10.1016/j.csbj.2021.06.052

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, Z., Zhan, X., Xiang, S., Johnson, T. S., Helm, B., Yu, C. Y., et al. (2019). SALMON: Survival Analysis Learning With Multi-Omics Neural Networks on Breast Cancer. Front. Genet. 10, 166.

PubMed Abstract | CrossRef Full Text | Google Scholar

Ishwaran, H., Kogalur, U. B., Blackstone, E. H., and Lauer, M. S. (2008). Random Survival Forests. Ann. Appl. Stat. 2 (3), 841–860.

CrossRef Full Text | Google Scholar

Jarrett, K., Kavukcuoglu, K., Ranzato, M., and LeCun, Y. (2009). “What Is the Best Multi-Stage Architecture for Object Recognition?,” in 2009 IEEE 12th International Conference on Computer Vision (IEEE), 2146–2153.

Google Scholar

Jones, W., Alasoo, K., Fishman, D., and Parts, L. (2017). Computational Biology: Deep Learning. Emerg. Top. Life Sci. 1, 257–274. doi:10.1042/etls20160025

PubMed Abstract | CrossRef Full Text | Google Scholar

Kelley, D. R., Snoek, J., and Rinn, J. L. (2016). Basset: Learning the Regulatory Code of the Accessible Genome with Deep Convolutional Neural Networks. Genome Res. 26, 990–999. doi:10.1101/gr.200535.115

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, T., Lo, K., Geddes, T. A., Kim, H. J., Yang, J. Y. H., and Yang, P. (2019). scReClassify: Post Hoc Cell Type Classification of Single-Cell rNA-Seq Data. BMC genomics 20 (9), 1–10. doi:10.1186/s12864-019-6305-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Kimmel, J. C., and Kelley, D. R. 2021. Semisupervised Adversarial Neural Networks for Single-Cell Classification. Gen. Res. 31 (10), 1781–1793. bioRxiv.

CrossRef Full Text | Google Scholar

Kingma, D. P., and Welling, M., 2014. “Auto-Encoding Variational Bayes,” in Proceedings of the International Conference on Learning Representations (ICLR). ArXiv Prepr. ArXiv13126114.

Google Scholar

Kircher, M., Witten, D. M., Jain, P., O'Roak, B. J., Cooper, G. M., and Shendure, J. (2014). A General Framework for Estimating the Relative Pathogenicity of Human Genetic Variants. Nat. Genet. 46, 310–315. doi:10.1038/ng.2892

PubMed Abstract | CrossRef Full Text | Google Scholar

LeCun, Y., Bengio, Y., and Hinton, G. (2015). Deep Learning. nature 521, 436–444. doi:10.1038/nature14539

PubMed Abstract | CrossRef Full Text | Google Scholar

LeCun, Y. (1989). “Generalization and Network Design Strategies,” in Connectionism in Perspective. Editors F. Fogelman-Soulié, L. Steels, R. Pfeifer, and Z. Schreter (Elsevier Science). Citeseer.

Google Scholar

LeCun, Y. (1987). Modeles connexionnistes de lapprentissage (PhD Thesis), 6. Universite Paris, PhD thesis, These de Doctorat.

Google Scholar

Li, M., Hu, J., Li, X., Coleman, K., Schroeder, A., Irwin, D., et al. (2020). Integrating Gene Expression, Spatial Location and Histology to Identify Spatial Domains and Spatially Variable Genes by Graph Convolutional Network. Nat. Methods 18 (11), 1342–1351. doi:10.1038/s41592-021-01255-8

CrossRef Full Text | Google Scholar

Lopez, R., Regier, J., Cole, M. B., Jordan, M. I., and Yosef, N. (2018). Deep Generative Modeling for Single-Cell Transcriptomics. Nat. Methods 15 (12), 1053–1058. doi:10.1038/s41592-018-0229-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Lucek, P., Hanke, J., Reich, J., Solla, S. A., and Ott, J. (1998). Multi-locus Nonparametric Linkage Analysis of Complex Trait Loci with Neural Networks. Hum. Hered. 48, 275–284. doi:10.1159/000022816

PubMed Abstract | CrossRef Full Text | Google Scholar

Lucek, P. R., and Ott, J. (1997). Neural Network Analysis of Complex Traits. Genet. Epidemiol. 14, 1101–1106. doi:10.1002/(sici)1098-2272(1997)14:6<1101::aid-gepi90>3.0.co;2-k

PubMed Abstract | CrossRef Full Text | Google Scholar

Maher, B. (2008). Personal Genomes: The Case of the Missing Heritability. Nature 456, 18–21. doi:10.1038/456018a

PubMed Abstract | CrossRef Full Text | Google Scholar

Manolio, T. A., Collins, F. S., Cox, N. J., Goldstein, D. B., Hindorff, L. A., Hunter, D. J., et al. (2009). Finding the Missing Heritability of Complex Diseases. Nature 461, 747–753. doi:10.1038/nature08494

PubMed Abstract | CrossRef Full Text | Google Scholar

Marinov, M., and Weeks, D. E. (2001). The Complexity of Linkage Analysis with Neural Networks. Hum. Hered. 51, 169–176. doi:10.1159/000053338

PubMed Abstract | CrossRef Full Text | Google Scholar

Mikheyev, A. S., and Tin, M. M. Y. (2014). A First Look at the Oxford Nanopore MinION Sequencer. Mol. Ecol. Resour. 14, 1097–1102. doi:10.1111/1755-0998.12324

PubMed Abstract | CrossRef Full Text | Google Scholar

Min, S., Lee, B., and Yoon, S. (2017). Deep Learning in Bioinformatics. Brief. Bioinform. 18, 851–869. doi:10.1093/bib/bbw068

PubMed Abstract | CrossRef Full Text | Google Scholar

Curbelo Montañez, C. A., Fergus, P., Chalmers, C., and Hind, J., 2018. “Analysis of Extremely Obese Individuals Using Deep Learning Stacked Autoencoders and Genome-Wide Genetic Data,” in International Meeting on Computational Intelligence Methods for Bioinformatics and Biostatistics (Cham: Springer), 262–272. ArXiv Prepr. ArXiv180406262.

Google Scholar

Motsinger, A. A., Dudek, S. M., Hahn, L. W., and Ritchie, M. D. (2006). “Comparison of Neural Network Optimization Approaches for Studies of Human Genetics,” in Workshops on Applications of Evolutionary Computation (Springer), 103–114. doi:10.1007/11732242_10

CrossRef Full Text | Google Scholar

Motsinger-Reif, A. A., Dudek, S. M., Hahn, L. W., and Ritchie, M. D. (2008). Comparison of Approaches for Machine-Learning Optimization of Neural Networks for Detecting Gene-Gene Interactions in Genetic Epidemiology. Genet. Epidemiol. 32, 325–340. doi:10.1002/gepi.20307

PubMed Abstract | CrossRef Full Text | Google Scholar

Nair, V., and Hinton, G. E. (2010). “Rectified Linear Units Improve Restricted Boltzmann Machines,” in Proceedings of the 27th International Conference on Machine Learning (Omnipress, Madison: ICML-10), 807–814.

Google Scholar

North, B. V., Curtis, D., Cassell, P. G., Hitman, G. A., and Sham, P. C. (2003). Assessing Optimal Neural Network Architecture for Identifying Disease-Associated Multi-Marker Genotypes Using a Permutation Test, and Application to Calpain 10 Polymorphisms Associated with Diabetes. Ann. Hum. Genet. 67, 348–356. doi:10.1046/j.1469-1809.2003.00030.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Pan, S. J., and Yang, Q. (2009). A Survey on Transfer Learning. IEEE Trans. Knowl. Data Eng. 22, 1345–1359.

Google Scholar

Park, Y., and Kellis, M. (2015). Deep Learning for Regulatory Genomics. Nat. Biotechnol. 33, 825–826. doi:10.1038/nbt.3313

PubMed Abstract | CrossRef Full Text | Google Scholar

Pennisi, E. (2011). Disease Risk Links to Gene Regulation. American Association for the Advancement of Science.

Google Scholar

Pham, D., Tan, X., Xu, J., Grice, L. F., Lam, P. Y., Raghubar, A., and Nguyen, Q. 2020. stLearn: Integrating Spatial Location, Tissue Morphology and Gene Expression to Find Cell Types, Cell-Cell Interactions and Spatial Trajectories within Undissociated Tissues. BioRxiv. doi:10.1101/2020.05.31.125658

CrossRef Full Text | Google Scholar

Pierson, E., and Yau, C. (2015). ZIFA: Dimensionality Reduction for Zero-Inflated Single-Cell Gene Expression Analysis. Genome Biol. 16 (1), 1–10.

PubMed Abstract | CrossRef Full Text | Google Scholar

Pouladi, F., Salehinejad, H., and Gilani, A. M. (2015). “Recurrent Neural Networks for Sequential Phenotype Prediction in Genomics,” in 2015 International Conference on Developments of E-Systems Engineering (DeSE) (IEEE), 225–230. doi:10.1109/dese.2015.52

CrossRef Full Text | Google Scholar

Quang, D., Chen, Y., and Xie, X. (2014). DANN: a Deep Learning Approach for Annotating the Pathogenicity of Genetic Variants. Bioinformatics 31, 761–763. doi:10.1093/bioinformatics/btu703

PubMed Abstract | CrossRef Full Text | Google Scholar

Quang, D., and Xie, X. (2016). DanQ: a Hybrid Convolutional and Recurrent Deep Neural Network for Quantifying the Function of DNA Sequences. Nucleic Acids Res. 44, e107. doi:10.1093/nar/gkw226

PubMed Abstract | CrossRef Full Text | Google Scholar

Riesselman, A. J., Ingraham, J. B., and Marks, D. S. (2018). Deep Generative Models of Genetic Variation Capture the Effects of Mutations. Nat. Methods 15, 816–822. doi:10.1038/s41592-018-0138-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Rosenblatt, F. (1958). The Perceptron: a Probabilistic Model for Information Storage and Organization in the Brain. Psychol. Rev. 65, 386–408. doi:10.1037/h0042519

PubMed Abstract | CrossRef Full Text | Google Scholar

Rui Xu, R., Wunsch, D. C., and Frank, R. L. (2007). Inference of Genetic Regulatory Networks with Recurrent Neural Network Models Using Particle Swarm Optimization. IEEE/ACM Trans. Comput. Biol. Bioinf. 4, 681–692. doi:10.1109/tcbb.2007.1057

CrossRef Full Text | Google Scholar

Rumelhart, D. E., Hinton, G. E., and Williams, R. J. (1988). Learning Representations by Back-Propagating Errors. Cogn. Model. 5, 1.

Google Scholar

Saccone, N. L., Downey, T. J., Meyer, D. J., Neuman, R. J., and Rice, J. P. (1999). Mapping Genotype to Phenotype for Linkage Analysis. Genet. Epidemiol. 17, S703–S708. doi:10.1002/gepi.13701707115

PubMed Abstract | CrossRef Full Text | Google Scholar

Sak, H., Senior, A., and Beaufays, F. (2014). “Long Short-Term Memory Recurrent Neural Network Architectures for Large Scale Acoustic Modeling,” in Fifteenth Annual Conference of the International Speech Communication Association. doi:10.21437/interspeech.2014-80

CrossRef Full Text | Google Scholar

Salakhutdinov, R., and Hinton, G. (2009). “Deep Boltzmann Machines,” in Artificial Intelligence and Statistics, 448–455.

Google Scholar

Scholz, M., Kaplan, F., Guy, C. L., Kopka, J., and Selbig, J. (2005). Non-linear PCA: a Missing Data Approach. Bioinformatics 21, 3887–3895. doi:10.1093/bioinformatics/bti634

PubMed Abstract | CrossRef Full Text | Google Scholar

Schuster, M., and Paliwal, K. K. (1997). Bidirectional Recurrent Neural Networks. IEEE Trans. Signal Process. 45, 2673–2681. doi:10.1109/78.650093

CrossRef Full Text | Google Scholar

Scott, L. J., Mohlke, K. L., Bonnycastle, L. L., Willer, C. J., Li, Y., Duren, W. L., et al. (2007). A Genome-wide Association Study of Type 2 Diabetes in Finns Detects Multiple Susceptibility Variants. science 316, 1341–1345. doi:10.1126/science.1142382

PubMed Abstract | CrossRef Full Text | Google Scholar

Shen, X., Jiang, C., Sakhanenko, L., and Lu, Q. (2019). “Asymptotic Properties of Neural Network Sieve Estimators,”. ArXiv Prepr. ArXiv190600875.

Google Scholar

Shrikumar, A., Greenside, P., and Kundaje, A. (2017). “Learning Important Features through Propagating Activation Differences,” in Proceedings of the 34th International Conference on Machine Learning-Volume 70 (JMLR. org), 3145–3153.

Google Scholar

Simon, N., Friedman, J., Hastie, T., and Tibshirani, R. (2011). Regularization Paths for Cox’s Proportional Hazards Model via Coordinate Descent. J. Stat. Softw. 39 (5), 1.

PubMed Abstract | CrossRef Full Text | Google Scholar

Sladek, R., Rocheleau, G., Rung, J., Dina, C., Shen, L., Serre, D., et al. (2007). A Genome-wide Association Study Identifies Novel Risk Loci for Type 2 Diabetes. Nature 445, 881–885. doi:10.1038/nature05616

PubMed Abstract | CrossRef Full Text | Google Scholar

Smolensky, P. (1986). “Information Processing in Dynamical Systems: Foundations of Harmony Theory,” in Parallel Distributed Processing. Editors D. E. Rumelhart, and J. L. McClelland (Cambridge: MIT Press) 1.

Google Scholar

Stegle, O., Teichmann, S. A., and Marioni, J. C. (2015). Computational and Analytical Challenges in Single-Cell Transcriptomics. Nat. Rev. Genet. 16 (3, 133–145.

PubMed Abstract | CrossRef Full Text | Google Scholar

Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I., and Salakhutdinov, R. (2014). Dropout: a Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 15, 1929–1958.

Google Scholar

Subramanian, A., Tamayo, P., Mootha, V. K., Mukherjee, S., Ebert, B. L., Gillette, M. A., et al. (2005). Gene Set Enrichment Analysis: A Knowledge-Based Approach for Interpreting Genome-Wide Expression Profiles. Proc. Natl. Acad. Sci. 102 (43), 15545–15550.

PubMed Abstract | CrossRef Full Text | Google Scholar

Sundararajan, M., Taly, A., and Yan, Q. (2017). “Axiomatic Attribution for Deep Networks,” in Proceedings of the 34th International Conference on Machine Learning-Volume 70 (JMLR. org), 3319–3328.

Google Scholar

Tan, J., Hammond, J. H., Hogan, D. A., and Greene, C. S. (2016). ADAGE-based Integration of Publicly Available Pseudomonas aeruginosa Gene Expression Data with Denoising Autoencoders Illuminates Microbe-Host Interactions. MSystems 1, e00025–15. doi:10.1128/mSystems.00025-15

PubMed Abstract | CrossRef Full Text | Google Scholar

Tan, J., Doing, G., Lewis, K. A., Price, C. E., Chen, K. M., Cady, K. C., et al. (2017a). Unsupervised Extraction of Stable Expression Signatures from Public Compendia with an Ensemble of Neural Networks. Cell Syst. 5, 63–71. doi:10.1016/j.cels.2017.06.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Tan, J., Huyck, M., Hu, D., Zelaya, R. A., Hogan, D. A., and Greene, C. S. (2017b). ADAGE Signature Analysis: Differential Expression Analysis with Data-Defined Gene Sets. BMC Bioinforma. 18, 512. doi:10.1186/s12859-017-1905-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Tan, X., Su, A., Tran, M., and Nguyen, Q. (2019). SpaCell: Integrating Tissue Morphology and Spatial Gene Expression to Predict Disease Cells. Bioinformatics 36 (7), 2293–2294. doi:10.1093/bioinformatics/btz914

PubMed Abstract | CrossRef Full Text | Google Scholar

Tibshirani, R. (1996). Regression Shrinkage and Selection via the Lasso. J. R. Stat. Soc. B: Methodol. 58 (1), 267–288.

CrossRef Full Text | Google Scholar

Uppu, S., Krishna, A., and Gopalan, R. P. (2016a). “Towards Deep Learning in Genome-wide Association Interaction Studies,” in PACIS, 20.

Google Scholar

Uppu, S., Krishna, A., Krishna, A., and Gopalan, R. P. (2016b). A Deep Learning Approach to Detect SNP Interactions. JSW 11, 965–975. doi:10.17706/jsw.11.10.965-975

CrossRef Full Text | Google Scholar

Van Engelen, J. E., and Hoos, H. H. (2020). A Survey on Semi-supervised Learning. Mach. Learn 109 (2), 373–440. doi:10.1007/s10994-019-05855-6

CrossRef Full Text | Google Scholar

Vapnik, V. N. (1998). Statistical Learning Theory. 1 edition. New York: Wiley-Interscience.

Google Scholar

Wager, S., Wang, S., and Liang, P. S. (2013). “Dropout Training as Adaptive Regularization,” in Advances in Neural Information Processing Systems, 351–359.

Google Scholar

Wainberg, M., Merico, D., Delong, A., and Frey, B. J. (2018). Deep Learning in Biomedicine. Nat. Biotechnol. 36, 829–838. doi:10.1038/nbt.4233

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, D., and Gu, J. (2018). VASC: Dimension Reduction and Visualization of Single-Cell RNA-Seq Data by Deep Variational Autoencoder. Genomics, Proteomics Bioinforma. 16, 320–331. doi:10.1016/j.gpb.2018.08.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Wei, Z., and Zhang, S. (2021). CALLR: a Semi-supervised Cell-type Annotation Method for Single-Cell RNA Sequencing Data. Bioinformatics 37 (Suppl. ment_1), i51–i58. doi:10.1093/bioinformatics/btab286

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, C., Lopez, R., Mehlman, E., Regier, J., Jordan, M. I., and Yosef, N. (2021). Probabilistic Harmonization and Annotation of Single-Cell Transcriptomics Data with Deep Generative Models. Mol. Syst. Biol. 17 (1), e9620. doi:10.15252/msb.20209620

PubMed Abstract | CrossRef Full Text | Google Scholar

Yelmen, B., Decelle, A., Ongaro, L., Marnetto, D., Tallec, C., Montinaro, F., et al. 2021. Creating Artificial Human Genomes Using Generative Neural Networks. PLoS Genet. 17 (2), e1009303. bioRxiv 769091.

PubMed Abstract | CrossRef Full Text | Google Scholar

Yousefi, S., Amrollahi, F., Amgad, M., Dong, C., Lewis, J. E., Song, C., et al. (2017). Predicting Clinical Outcomes From Large Scale Cancer Genomic Profiles With Deep Survival Models. Sci. Rep. 7 (1), 1–11.

PubMed Abstract | CrossRef Full Text | Google Scholar

Yue, T., and Wang, H., 2018. Deep Learning for Genomics: A Concise Overview. ArXiv Prepr. ArXiv180200810.

Google Scholar

Zhang, Y., and Liu, J. S. (2007). Bayesian Inference of Epistatic Interactions in Case-Control Studies. Nat. Genet. 39, 1167–1173. doi:10.1038/ng2110

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Z., Luo, D., Zhong, X., Choi, J. H., Ma, Y., Wang, S., Mahrt, T., Guo, fnm., Stawiski, fnm., Modrusan, fnm., Seshagiri, fnm., Kapur, fnm., Hon, fnm., Brugarolas, fnm., and Wang, fnm. (2019). SCINA: Semi-supervised Analysis of Single Cells In Silico. Genes 10 (7), 531. doi:10.3390/genes10070531

CrossRef Full Text | Google Scholar

Zhou, J., and Troyanskaya, O. G. (2015). Predicting Effects of Noncoding Variants with Deep Learning-Based Sequence Model. Nat. Methods 12, 931–934. doi:10.1038/nmeth.3547

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, X. (2008). Semi-supervised Learning Literature Survey. Technical Report. University of Wisconsin-Madison, 1530.

Google Scholar

Zou, J., Huss, M., Abid, A., Mohammadi, P., Torkamani, A., and Telenti, A. (2018). A Primer on Deep Learning in Genomics. Nat. Genet. 1. doi:10.1038/s41588-018-0295-5

CrossRef Full Text | Google Scholar