Enhancing breast cancer treatment selection through 2TLIVq-ROFS-based multi-attribute group decision making

Introduction: Breast cancer is an extremely common and potentially fatal illness that impacts millions of women worldwide. Multiple criteria and inclinations must be taken into account when selecting the optimal treatment option for each patient.

Methods: The selection of breast cancer treatments can be modeled as a multi-attribute group decision-making (MAGDM) problem, in which a group of experts evaluate and rank alternative treatments based on multiple attributes. MAGDM methods can aid in enhancing the quality and efficacy of breast cancer treatment selection decisions. For this purpose, we introduce the concept of a 2-tuple linguistic interval-valued q-rung orthopair fuzzy set (2TLIVq-ROFS), a new development in fuzzy set theory that incorporates the characteristics of interval-valued q-rung orthopair fuzzy set (IVq-ROFS) and 2-tuple linguistic terms. It can express the quantitative and qualitative aspects of uncertain information, as well as the decision-makers' level of satisfaction and dissatisfaction.

Results: Then, the 2TLIVq-ROF weighted average (2TLIVq-ROFWA) operator and the 2TLIVq-ROF weighted geometric (2TLIVq-ROFWJ) operator are introduced as two new aggregation operators. In addition, the multi-attribute border approximation area comparison (MABAC) method is extended to solve the MAGDM problem with 2TLIVq-ROF information.

Discussion: To demonstrate the efficacy and applicability of the suggested model, a case study of selecting the optimal breast cancer treatment is presented. The results of the computations show that the suggested MAGDM model is able to handle imprecision and subjectivity in complicated decision-making scenarios and opens new research scenarios for scholars.

1 Introduction

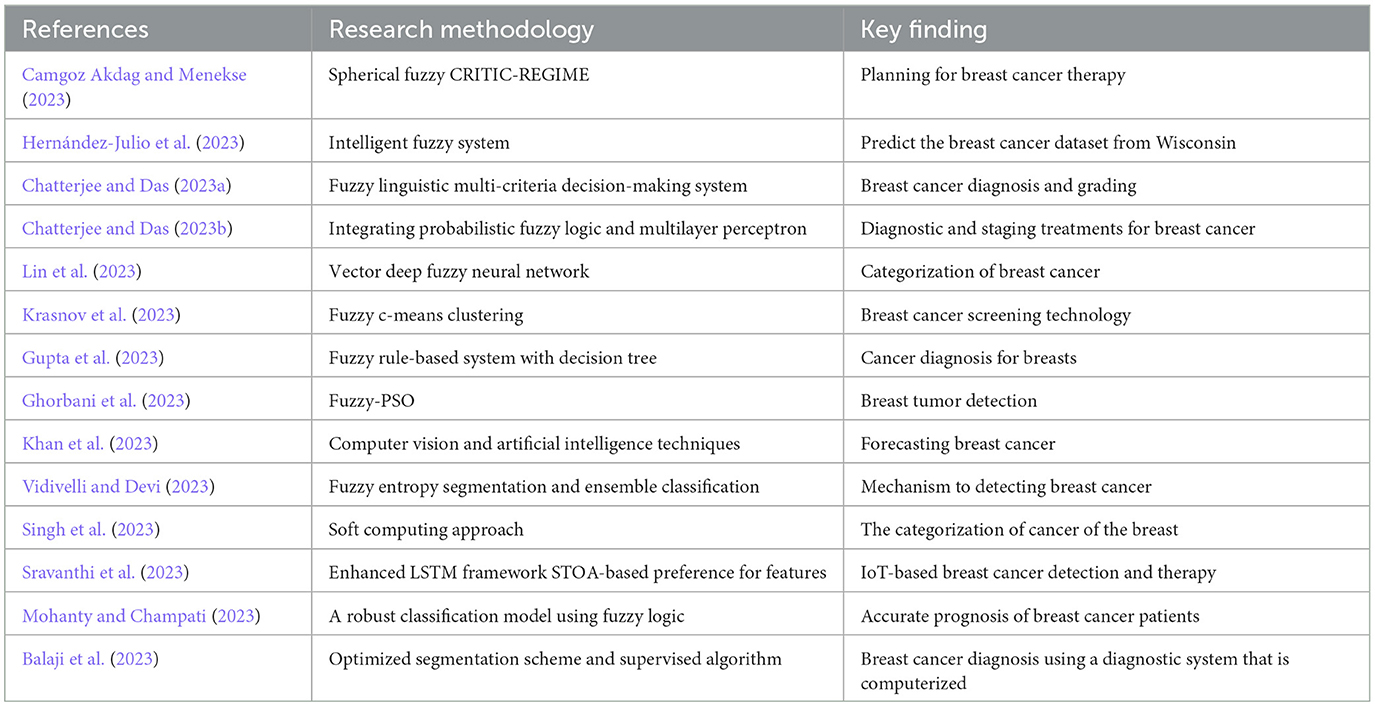
Treating breast cancer needs different kinds of treatment from different medical experts. Khajehkhasan and Fakheri (2020) evaluated mammographic images of patients' breasts with the help of doctors. Shastri et al. (2020) found how tumors turned into malignant or benign with the help of machine learning techniques. Several factors, including the stage and subtype of cancer, the patient's age and general health, the patient's preferences and values, and the availability and accessibility of diverse treatment options, influence the selection of the most suitable treatment for each individual. Among the most common treatments for breast cancer are surgery, radiation therapy, chemotherapy, hormone therapy, targeted therapy, and immunotherapy. Each of these treatments has its own benefits and risks, and they can be used individually or in combination with others. The goal of cancer treatment is to get rid of cancer cells, delay their return, and improve the patient's quality of life and chances of survival. The breast cancer treatment decision-making process entails a dialogue between the patient and the healthcare team, which may include oncologists, surgeons, radiologists, pathologists, nurses, social workers, and other specialists. The patient should be informed of the diagnosis, prognosis, treatment options, potential outcomes, adverse effects, and cost of each option. In addition, the patient should be encouraged to ask inquiries, express concerns and preferences, and seek a second opinion when necessary. Respecting and upholding the patient's autonomy and values throughout the treatment journey is the responsibility of the healthcare team. The most prevalent cancer in the globe, breast cancer is a global public health problem. Survival rates and patient wellbeing are increased by effective treatment plans. However, selecting a treatment for breast cancer is a complex and challenging utilization involving numerous considerations, alternatives, and stakeholders, consequently, it is a MAGDM issue. MAGDM is a branch of decision science that focuses on situations where multiple decision-makers (DMs) evaluate multiple alternatives based on multiple criteria. In the context of breast cancer treatment selection, alternatives refer to the available treatment options, including surgery, radiation therapy, endocrine therapy, chemotherapy, and immunotherapy. The criteria are the variables that influence the treatment outcomes, including survival rate, toxicity, cost, quality of life, and patient preference. The stakeholders are the individuals or groups who are involved in or affected by the treatment decision, such as patients, doctors, nurses, family members, and insurance companies. To address a MAGDM problem, various methods and tools can be utilized to aggregate the preferences and opinions of the stakeholders and to rank or select the optimal alternative(s) based on the attribute. Incorporating evidence-based data, expert knowledge, and patient values, this paper applies the MABAC method to 2TLIVq-ROFS information in order to provide clinical decision support for breast cancer treatment selection. Table 1 represents the summary of existing research on breast cancer treatment selection.

Table 1

Table 1. Summary of existing research on breast cancer treatment selection.

Multi-attribute decision making (MADM) refers to making preference decisions by evaluating and prioritizing a limited set of alternatives based on multiple conflict attributes (Nafei et al., 2021, 2023; Akram et al., 2023d; Farajpour Khanaposhtani, 2023). Soltanifar (2024) presented a hybrid method based on a linear programming model for solving MADM problems by combining two new methods, the COPRAS and the MOORA and also using the concept of discrimination intensity functions. Shakerian et al. (2023) selected the best contractor in one of the projects of dairy companies in Fars province, after holding a tender and completing a questionnaire by project experts, using AHP and VIKOR methods. In the field of decision sciences, MAGDM holds significant importance as it provides a fascinating framework for analyzing and resolving complex problems. In the modern era, decision-making is used in digital transformation for a more informed and effective approach (Haudi, 2024; Jones, 2024; Min and Kim, 2024). It examines how to encourage a panel of DMs in differing preferences and viewpoints to reach a consensus on a complex problem involving multiple criteria and options. MAGDM can be applied to numerous domains, including project management, resource allocation, environmental planning, social choice, and more. MAGDM methods typically involve four steps: defining the problem structure, soliciting the individual preferences, aggregating the preferences into a group preference, and choosing the best alternative(s) based on the group preference. There are numerous challenges and opportunities in MAGDM research, including how to handle uncertainty, inconsistency, and conflict among DMs, how to design effective and efficient preference induction and aggregation mechanisms, how to incorporate human factors and ethical considerations, and how to evaluate and compare various MAGDM methods. Regarding the circumstances of real-world MADM, intuitionistic fuzzy set (IFS) was conceptualized by Atanassov (1986) in this discussion, represent a valuable extension of fuzzy set (FS) (Zadeh, 1965). IFS is characterized by its capacity to assign each element both a membership degree (MD) and a non-membership degree (NMD), with the combined values' sum cannot be more than 1.

Rasoulzadeh et al. (2022) proposed a new combined Markowitz and the cross data envelopment analysis models utilizing the IF numbers. However, in practical decision-making scenarios, it can occur that the squared sum of an alternative's MD and NMD, as per the DMs criteria, exceeds 1. This presents a challenge for IFS but is effectively addressed by Pythagorean fuzzy set (PyFS) (Yager, 2013). Ismail et al. (2023) proposed the incorporation of a Bonferroni mean aggregation operator within a Pythagorean neutrosophic environment, illustrated through a numerical example applied to DEMATEL. PyFS ensures that the squared sum of their MD and NMD remains equal to or less than 1, as illustrated by example: A support for membership of DM in an alternative is $\frac{\sqrt{3}}{3}$, and his support against membership is ½. The sum of these values is indeed >1, underscoring the inadequacy of IFS to handle this situation. In contrast, PyFS, with ${\left(\frac{\sqrt{3}}{3}\right)}^2+{\left(\frac{1}{2}\right)}^2\le 1$, competently capture such ambiguity. Evidently, PyFS is better suited to model ambiguity in real-world MADM problems compared to IFS. Furthermore, development of q-rung orthopair fuzzy sets (q-ROFS) (Yager, 2016) has gained recognition as a valuable approach to capturing ambiguity in MADM situations. q-ROFS distinguish from other existing FSs due to its MD and NMD characteristics, where the total of the qth powers of MD and NMD does not exceed 1. For instance, when (0.8+0.1) ≤ 1, it represents an IFS and when (0.7 + 0.5)² ≤ 1, it denotes a PyFS, though it is not considered an IFS when the MD is 0.5. This scenario cannot be effectively described using either IFS or PyFS if the NMD is 0.8. In this case, (0.8, 0.7) represents a q-ROF number (q = 3), and the q-ROFS proves to be the suitable approach to address this situation. IFS and PyFS, both falling under the category of q-ROFS, shows the generality of q-ROFS. As the rung q increases, the scope of permissible orthopairs expands that adhere to the bounding constraint. This feature empowers q-ROFS to represent a wider range of fuzzy information. In essence, the diversity of data expression can be flexibly determined by varying the parameter q, making q-ROFS exceptionally adaptable and well-suited for handling uncertainty in various environments.

However, while q-ROFS has been utilized in numerous applications of MAGDM, its limitations are becoming increasingly evident. There are instances where DMs face challenges quantifying their judgments with precise numerical values due to incomplete information. In such scenarios, it becomes more practical for DMs to convey their assessments using a subset of the closed interval [0, 1]. In response to this need, Joshi et al. (2018) introduced IVq-ROFS, where membership and non-membership degrees are represented as intervals instead of single real numbers. This approach also involved the investigation of operations like negation, union, intersection, and set operations. Wan et al. (2023) devised an innovative integrated group decision-making method for evaluating the quality of systems using IVq-ROFS, particularly in the context of selecting the best software product from multiple alternatives. Gurmani et al. (2023) aimed to establish a novel methodology for determining expert weights through distance and similarity measures by using IVq-ROFNs. Luqman and Shahzadi (2023) developed the IVq-ROF superiority and inferiority technique, incorporating sine-trigonometric operational laws. Xu (2023) proposed a two-stage MADM method that used the IVq-ROF technique to address complex problems, such as the selection of a bike-sharing recycling supplier. Combining complex IVq-ROF information with linguistic sets, Qi et al. (2023) introduced the concept of complex interval-valued q-rung orthopair linguistic information, which is more generalized and exceptionally practical for representing challenging and unreliable information in complex situations. Ahemad et al. (2023) developed the COPRAS approach to address MAGDM problems using IVq-ROFNs.

It can be challenging to quantitatively present judgements in decision-making at times. Zadeh (1975) made a distinction between linguistic and numerical data to get around this problem. He introduced the idea that linguistic terms can be used to describe qualitative information and established the concept of linguistic variables. 2TL preference relations are useful instruments for resolving situations in which DMs are likely to employ linguistic variables to represent data for evaluation. To more clearly describe the qualitative information in MADM situations through linguistic terms, Herrera and Martínez (2000) suggested a new model called the 2TL representation model. The 2TL Fermatean FS is a useful tool that brings together the benefits of the reliable 2TL model and Fermatean FS. Akram et al. (2023a) set out to create new decision-making methods based on 2TL Fermatean FS that could deal with circumstances where linguistic labels were applied to specific data. Akram et al. (2023b) introduced a novel 2TLPyF-MULTIMOORA approach to solving the undergraduate teaching audit and evaluation problem, which depends on the the 2TLPyFS and the MULTIMOORA technique. Akram et al. (2023c) proposed and utilized the Dombi operations to develop certain aggregation operators: 2TL q-rung picture fuzzy Dombi weighted averaging operator and 2TL q-rung picture fuzzy Dombi weighted geometric operator. By combining cloud theory and rough approximations with a 2TL situation, Sarwar (2023) suggested a novel mathematical model. First, three novel language manipulation models, 2TL clouds, 2TL rough numbers, and Dual 2TL rough number clouds, were developed to handle unpredictability with randomness and multi-granularity at the same time. Jin et al. (2023) proposed a 2TL decision-making technique that coupled a consistency adjustment algorithm with a 2TL data envelopment analysis model in order to maintain the initial preference information of DMs.

In 2015, Pamučar and Ćirović (2015) proposed the MABAC method as a MADM technique. This method looks at different options by seeing how close they are to the best and worst values within a certain area called the border approximation area (BAA). Therefore, MABAC can manage conflicting attributes and provides a more precise ranking result than other MADM methods such as RAFSI, MAIRCA, VIKOR, or MARCOS. Demir et al. (2024) presented a comprehensive bibliometric analysis of MABAC method using the Biblioshiny application of the bibliometrix package, R program and VOSviewer tools to provide a holistic view of the research landscape by identifying its evolution, major contributors and most influential research areas. In light of numerous options and ambiguous, subjective, and unreliable data, Shang et al. (2023) sought to identify the optimal MADM method. The modified rough Z-number MABAC approach used Pugh's controlled convergence, rough number, Z-number, consistency theory, and Shannon entropy. Ran (2023) proposed the maximizing deviation method for determining the attribute weights for the single-valued neutrosophic set (SVNS), and the SVNN-MABAC method was designed for MAGDM under SVNS to evaluate the lending performance of sustainable microfinance organization. With the goal to establish the feasibility of the suggested methodology, Jana et al. (2023) presented a novel method to construct MABAC approach utilizing PyF numbers. To determine the most effective plastic waste management procedure in situations where the attribute weights and decision expert weights are completely unknown, Mandal and Seikh (2023) developed a hybrid MAGDM methodology combining the entropy method, deviation-based method, and MABAC method with interval-valued spherical FS. Given that risk assessment is complex and uncertain, and that cognitive fuzziness and psychological behavior of experts further complicate matters, combining prospect theory and the MABAC method in a fuzzy Fermatean environment, Tan et al. (2023) developed an integrated MAGDM risk investment evaluation framework. The modified MABAC method with Z-numbers was utilized by Božanic et al. (2023) to identify the most effective contingency strategy for managing oil release risks. Zorlu and Dede (2023) used CRITIC method to analyze criteria weights, while MABAC established their priority values for alternatives.

1.1 Motivation

Millions of women throughout the world are affected by the common and fatal disease known as breast cancer. To increase patient outcomes and survival rates, it is crucial to improve the decision-making process for choosing a course of treatment. It is difficult for doctors and DMs to choose a breast cancer treatment because there are different criteria and preferences. This hard subject can be approached methodically and completely using a structured MAGDM framework. The uncertainty and confusion in deciding on breast cancer treatment can make it hard for traditional methods to handle it well. By introducing the 2TLIVq-ROFS approach, assessments can be made more flexible and exact, which improves the representation of expert viewpoints. By ensuring that the final treatment choice is well-founded and takes into account all pertinent information, the development of novel aggregation operators further improves the precision of the decision-making process. By expanding the applicability of this well-known strategy and enabling it to be handled to the unique issues of breast cancer treatment selection, the MABAC method can be extended to the 2TLIVq-ROFS environment to make better decisions. Doctors and DMs can confidently use this strategy because the suggested model has shown it works well and is practical. Moreover, the sensitivity analysis can prove that the proposed method is wide and reliable. The proposed strategy can outperform over other techniques and contribute to better decision-making in the selection of breast cancer treatment by a comparative analysis with existing methodologies.

1.2 Objectives

The research study is done in order to accomplish the following objectives:

- The challenge of selecting the best treatment option for breast cancer patients is addressed by proposing a MAGDM framework.

- The concept of 2TLIVq-ROFS is introduced as a novel way for DMs to present their evaluations within a wider scope as well as improve their ability to handle uncertain knowledge more efficiently.

- A variety of novel aggregation operators are established, including the 2TLIVq-ROFWA and the 2TLIVq-ROFWJ operators, to improve the precision of current aggregation techniques while considering the interconnection of the 2TLIVq-ROF numbers (2TLIVq-ROFNs).

- The MABAC method is extended to handle the MAGDM problem under 2TLIVq-ROFS information, enabling better decision-making in breast cancer treatment selection.

- A case study of breast cancer treatment selection is demonstrated which shows the efficacy and practicability of proposed model in handling imprecision and subjectivity in complex decision-making environments.

- The resilience and adaptability of the proposed model is assessed by performing a sensitivity analysis to determine how the parameter q affects decision-making.

- Comparative analysis with existing decision-making approaches is done which shows that it improves breast cancer treatment selection.

1.3 Structure

Organization of this article is as follows: Section 2 discusses the definitions of 2TL representation model and IVq-ROFS. Section 3 introduces the 2TLIVq-ROFS, a new data representation concept. Additionally, this part discusses operational principles, the score function, and the accuracy function of 2TLIVq-ROFNs. Section 4 discusses the average and geometric operators with their weighted forms for 2TLIVq-ROFNs, as well as their properties. Section 5 examines the 2TLIVq-ROF-MABAC method for MAGDM problem-solving. Section 6 gives a breast cancer therapy case study to demonstrate the viability and effectiveness of the suggested methodology. Section 7 provide insights, acknowledge limitations, and suggest future study directions.

1.4 Nomenclature

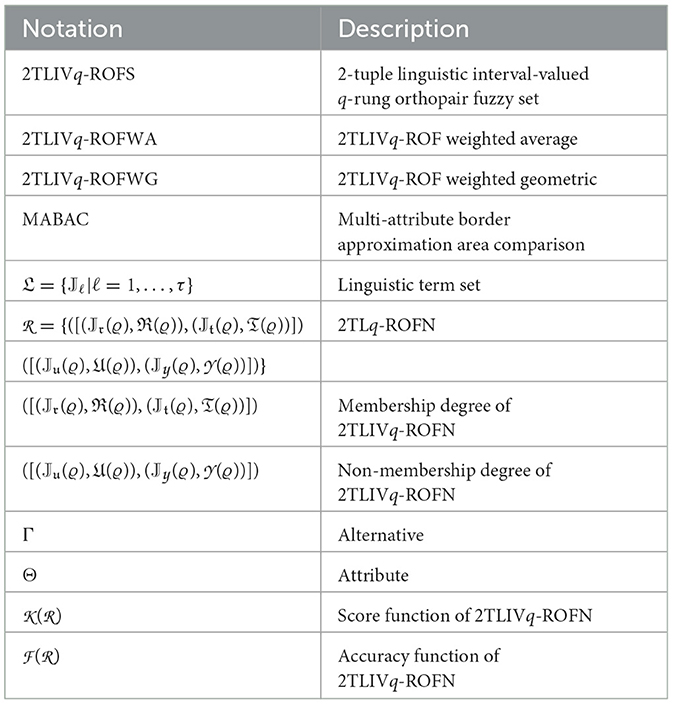
Nomenclature of the proposed work is shown in Table 2.

Table 2

Table 2. Nomenclature of the proposed work.

2 Preliminaries

In this section, we will explore key concepts related to our research study such as 2TL terms and IVq-ROFS.

Definition 1. Herrera and Martínez (2000) Let 𝔏 = {𝕁_ℓ|ℓ = 1, …, τ} be a linguistic term set (LTS), and ξ ∈ [0, τ] indicate the linguistic symbolic aggregation outcome. Description of the function Δ to acquire 2TL information identical to ξ:

$\begin{array}{l}\Delta :\left[0,\tau \right]\to 𝔏\times \left[-0.5,0.5\right),\\ \Delta \left(\xi \right)=\{\begin{array}{l}{𝕁}_{\ell },\ell =\text{round}\left(\xi \right),\\ \upsilon =\xi -\ell ,\upsilon \in \left[-0.5,0.5\right).\end{array}\end{array}$

Definition 2. Herrera and Martínez (2000) Let 𝔏 = {𝕁_ℓ|ℓ = 1, …, τ} be a LTS and (𝕁_ℓ, υ_ℓ) being a 2-tuple, then there is a function Δ⁻¹ that converts the 2-tuple to its analogous number ξ ∈ [0, τ]⊂R, where

$\begin{array}{r}{\Delta }^{-1}:𝔏\times \left[-0.5,0.5\right)\to \left[0,\tau \right],\\ {\Delta }^{-1}\left({𝕁}_{\ell },\upsilon \right)=\ell +\upsilon =\xi .\end{array}$

Definition 3. Joshi et al. (2018) An IVq-ROFS $A$ derived on the basis of the fixed set $P$ can be described as in the following Equation 1.

$\begin{array}{ll}A=\left\{\varrho ,{\mu }_A\left(\varrho \right),{\nu }_A\left(\varrho \right)|\varrho \in P\right\}& (1)\end{array}$

where ${\mu }_A\left(\varrho \right)$ and ${\nu }_A\left(\varrho \right)$ are two intervals, denoted as [u, v] and [x, y], respectively, representing the MD and NMD of the element $\varrho \in P$ with respect to the set $A$. These intervals meet the requirement $0\le \mathrm{\text{Sup}}{\left({\mu }_A\left(\varrho \right)\right)}^q+\mathrm{\text{Sup}}{\left({\nu }_A\left(\varrho \right)\right)}^q\le 1$ for all $\varrho \in P$. To achieve simplicity, we indicate to this pair of intervals as an IVq-ROFN, represented as ℜ = ([u, v], [x, y]).

3 2-Tuple linguistic interval-valued q-rung orthopair fuzzy set

In the field of FS theory, the 2TLIVq-ROFS is a novel development. This section illustrates the structure and operational laws of the proposed 2TLIVq-ROFS. Combining the concepts of 2TL terms and IVq-ROFS resulted in the innovative idea of 2TLIVq-ROFS. Considering that the qth power of MD as well as NMD is included, the proposed set is more flexible.

Definition 4. Assume 𝔏 = {𝕁_ℓ|ℓ = 0, 1, …, τ} indicates a LTS that has an odd cardinality. If ([(𝕁_𝔯(ϱ), ℜ(ϱ)), (𝕁_𝔱(ϱ), 𝔗(ϱ))], $[({𝕁}_{𝔲}(\varrho ),𝔘(\varrho )),({𝕁}_y(\varrho ),Y(\varrho ))])$ is defined for ${𝕁}_{𝔯}\left(\varrho \right),{𝕁}_{𝔱}\left(\varrho \right),{𝕁}_{𝔲}\left(\varrho \right),{𝕁}_y\left(\varrho \right),\in 𝔏,\Re \left(\varrho \right),𝔗\left(\varrho \right),𝔘\left(\varrho \right),Y\left(\varrho \right)\in \left[-0.5,0.5\right)$, where ([(𝕁_𝔯(ϱ), ℜ(ϱ)), (𝕁_𝔱(ϱ), 𝔗(ϱ))]) and $\left(\left[\left({𝕁}_{𝔲}\left(\varrho \right),𝔘\left(\varrho \right)\right),\left({𝕁}_y\left(\varrho \right),Y\left(\varrho \right)\right)\right]\right)$ indicate the MD and NMD with respective 2TL terms. The 2TLIVq-ROFS is characterized by the following Equation 2:

$\begin{array}{r}ℛ=\{\varrho ,([({𝕁}_r\left(\varrho \right),\Re \left(\varrho \right)),({𝕁}_t\left(\varrho \right),T\left(\varrho \right))],[({𝕁}_u\left(\varrho \right),U\left(\varrho \right)),\\ \left({𝕁}_y\right(\varrho ),Y(\varrho \left)\right)])|\varrho \in \mathcal{P}\},& (2)\end{array}$

where ${\Delta }^{-1}\left({𝕁}_{𝔯}\left(\varrho \right),\Re \left(\varrho \right)\right)$, ${\Delta }^{-1}\left({𝕁}_{𝔱}\left(\varrho \right),𝔗\left(\varrho \right)\right)$, ${\Delta }^{-1}\left({𝕁}_{𝔲}\left(\varrho \right),𝔘\left(\varrho \right)\right)$, ${\Delta }^{-1}\left({𝕁}_y\left(\varrho \right),Y\left(\varrho \right)\right)\in \left[0,\tau \right]$ and $0\le \mathrm{\text{Sup}}\left({\Delta }^{-1}\right[({𝕁}_{𝔯}\left(\varrho \right),\Re \left(\varrho \right)),$ $\left({𝕁}_{𝔱}\left(\varrho \right),𝔗\left(\varrho \right))\right]{)}^q+\mathrm{\text{Sup}}{({\Delta }^{-1}[({𝕁}_{𝔲}\left(\varrho \right),𝔘\left(\varrho \right)),\left({𝕁}_{\mathcal{y}}\left(\varrho \right),\mathcal{Y}\left(\varrho \right)\right)])}^q\le {\tau }^q.$

In order to compare any two 2TLIVq-ROFNs, their score and accuracy functions are described in the following Equations 3 and 4:

Definition 5. Let $R=\left(\left[\left({𝕁}_{𝔯},\Re \right),\left({𝕁}_{𝔱},𝔗\right)\right],\left[\left({𝕁}_{𝔲},𝔘\right),\left({𝕁}_y,Y\right)\right]\right)$ be a 2TLIVq-ROFN. Afterward, the score function $K$ and the accuracy function $F$ are established as:

$\begin{array}{r}\mathcal{K}(ℛ)=\Delta {\left(\frac{\tau }{4}\left(\right(1+(\frac{{\Delta }^{-1}({𝕁}_r,\Re )}{\tau }\right)}^q-{\left(\frac{{\Delta }^{-1}({𝕁}_u,U)}{\tau }\right)}^q)\\ +(1+{\left(\frac{{\Delta }^{-1}({𝕁}_t,T)}{\tau }\right)}^q-{\left(\frac{{\Delta }^{-1}({𝕁}_y,Y)}{\tau }\right)}^q)\left)\right),\\ {\Delta }^{-1}\left(\mathcal{K}\right(ℛ\left)\right)\in [0,\tau ],& (3)\end{array}$

$\begin{array}{r}ℱ(ℛ)=\Delta \left(\begin{array}{c}\frac{\tau }{4}{\left(\frac{{\Delta }^{-1}({𝕁}_r,\Re )}{\tau }\right)}^q+{\left(\frac{{\Delta }^{-1}({𝕁}_t,T)}{\tau }\right)}^q\\ +{\left(\frac{{\Delta }^{-1}({𝕁}_u,U)}{\tau }\right)}^q+{\left(\frac{{\Delta }^{-1}({𝕁}_y,\mathcal{Y})}{\tau }\right)}^q)\end{array}\right),\\ {\Delta }^{-1}\left(F\left(R\right)\right)\in \left[0,\tau \right].& (4)\end{array}$

Definition 6. Let $R_1=\left(\left[\left({𝕁}_{{𝔯}_1},{\Re }_1\right),\left({𝕁}_{{𝔱}_1},{𝔗}_1\right)\right],\left[\left({𝕁}_{{𝔲}_1},{𝔘}_1\right),\left({𝕁}_{y_1},Y_1\right)\right]\right)$ and $R_2=\left(\left[\left({𝕁}_{{𝔯}_2},{\Re }_2\right),\left({𝕁}_{{𝔱}_2},{𝔗}_2\right)\right],\left[\left({𝕁}_{{𝔲}_2},{𝔘}_2\right),\left({𝕁}_{y_2},Y_2\right)\right]\right)$ represent two 2TLIVq-ROFNs, and subsequently compare both utilizing the aforementioned principles:

(1) If $K\left(R_1\right)>K\left(R_2\right)$, then $R_1>R_2$;

(2) If $K\left(R_1\right)=K\left(R_2\right)$, then

- If $F\left(R_1\right)>F\left(R_2\right)$, then $R_1>R_2$;

- If $F\left(R_1\right)=F\left(R_2\right)$, then $R_1~R_2$.

Innovative operational principles of the 2TLIVq-ROFNs are described in Definition 7.

Definition 7. Let $R=\left(\left[\left({𝕁}_{𝔯},\Re \right),\left({𝕁}_{𝔱},𝔗\right)\right],\left[\left({𝕁}_{𝔲},𝔘\right),\left({𝕁}_y,Y\right)\right]\right)$, $R_1=\left(\left[\left({𝕁}_{{𝔯}_1},{\Re }_1\right),\left({𝕁}_{{𝔱}_1},{𝔗}_1\right)\right],\left[\left({𝕁}_{{𝔲}_1},{𝔘}_1\right),\left({𝕁}_{y_1},Y_1\right)\right]\right)$ and $R_2=\left(\left[\left({𝕁}_{{𝔯}_2},{\Re }_2\right),\left({𝕁}_{{𝔱}_2},{𝔗}_2\right)\right],\left[\left({𝕁}_{{𝔲}_2},{𝔘}_2\right),\left({𝕁}_{y_2},Y_2\right)\right]\right)$ are any three 2TLIVq-ROFNs and ε be a real positive integer, then

$\begin{array}{l}\text{1. }{R}_1\oplus R_2=\left(\begin{array}{l}\left[\begin{array}{l}\Delta \left(\tau \left(\sqrt[q]{{\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔯}_1},{\Re }_1\right)}{\tau }\right)}^q+{\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔯}_2},{\Re }_2\right)}{\tau }\right)}^q-{\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔯}_1},{\Re }_1\right)}{\tau }\right)}^q{\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔯}_2},{\Re }_2\right)}{\tau }\right)}^q}\right)\right),\\ \Delta \left(\tau \left(\sqrt[q]{{\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔱}_1},{𝔗}_1\right)}{\tau }\right)}^q+{\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔱}_2},{𝔗}_2\right)}{\tau }\right)}^q-{\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔱}_1},{𝔗}_1\right)}{\tau }\right)}^q{\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔱}_2},{𝔗}_2\right)}{\tau }\right)}^q}\right)\right)\end{array}\right],\\ \left[\begin{array}{l}\Delta \left(\tau \left(\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔲}_1},{𝔘}_1\right)}{\tau }\right)\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔲}_2},{𝔘}_2\right)}{\tau }\right)\right)\right),\Delta \left(\tau \left(\left(\frac{{\Delta }^{-1}\left({𝕁}_{y_1},Y_1\right)}{\tau }\right)\left(\frac{{\Delta }^{-1}\left({𝕁}_{y_2},Y_2\right)}{\tau }\right)\right)\right)\end{array}\right]\end{array}\right).\end{array}$

$\begin{array}{l}\text{2. }{R}_1\otimes R_2=\left(\begin{array}{l}\left[\begin{array}{l}\Delta \left(\tau \left(\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔯}_1},{\Re }_1\right)}{\tau }\right)\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔯}_2},{\Re }_2\right)}{\tau }\right)\right)\right),\Delta \left(\tau \left(\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔱}_1},{𝔗}_1\right)}{\tau }\right)\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔱}_2},{𝔗}_2\right)}{\tau }\right)\right)\right)\end{array}\right],\\ \left[\begin{array}{l}\Delta \left(\tau \left(\sqrt[q]{{\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔲}_1},{𝔘}_1\right)}{\tau }\right)}^q+{\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔲}_2},{𝔘}_2\right)}{\tau }\right)}^q-{\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔲}_1},{𝔘}_1\right)}{\tau }\right)}^q{\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔲}_2},{𝔘}_2\right)}{\tau }\right)}^q}\right)\right),\\ \Delta \left(\tau \left(\sqrt[q]{{\left(\frac{{\Delta }^{-1}\left({𝕁}_{y_1},Y_1\right)}{\tau }\right)}^q+{\left(\frac{{\Delta }^{-1}\left({𝕁}_{y_2},Y_2\right)}{\tau }\right)}^q-{\left(\frac{{\Delta }^{-1}\left({𝕁}_{y_1},Y_1\right)}{\tau }\right)}^q{\left(\frac{{\Delta }^{-1}\left({𝕁}_{y_2},Y_2\right)}{\tau }\right)}^q}\right)\right)\end{array}\right]\end{array}\right).\end{array}$

$\begin{array}{l}\text{3. }\epsilon R=\left(\begin{array}{l}\left[\begin{array}{l}\Delta \left(\tau \left(\sqrt[q]{1-{\left(1-{\left(\frac{{\Delta }^{-1}\left({𝕁}_{𝔯},\Re \right)}{\tau }\right)}^q\right)}^{\epsilon }}\right)\right),\Delta \left(\tau \left(\sqrt[q]{1-{\left(1-{\left(\frac{{\Delta }^{-1}\left({𝕁}_{𝔱},𝔗\right)}{\tau }\right)}^q\right)}^{\epsilon }}\right)\right)\end{array}\right],\\ \left[\begin{array}{l}\Delta \left(\tau \left({\left(\frac{{\Delta }^{-1}\left({𝕁}_{𝔲},𝔘\right)}{\tau }\right)}^{\epsilon }\right)\right),\Delta \left(\tau \left({\left(\frac{{\Delta }^{-1}\left({𝕁}_y,Y\right)}{\tau }\right)}^{\epsilon }\right)\right)\end{array}\right]\end{array}\right),\epsilon \ge 0.\end{array}$

$\begin{array}{l}\text{4. }{R}^{\epsilon }=\left(\begin{array}{l}\left[\begin{array}{l}\Delta \left(\tau \left({\left(\frac{{\Delta }^{-1}\left({𝕁}_{𝔯},\Re \right)}{\tau }\right)}^{\epsilon }\right)\right),\Delta \left(\tau \left({\left(\frac{{\Delta }^{-1}\left({𝕁}_{𝔱},𝔗\right)}{\tau }\right)}^{\epsilon }\right)\right)\end{array}\right],\\ \left[\begin{array}{l}\Delta \left(\tau \left(\sqrt[q]{1-{\left(1-{\left(\frac{{\Delta }^{-1}\left({𝕁}_{𝔲},𝔘\right)}{\tau }\right)}^q\right)}^{\epsilon }}\right)\right),\Delta \left(\tau \left(\sqrt[q]{1-{\left(1-{\left(\frac{{\Delta }^{-1}\left({𝕁}_y,Y\right)}{\tau }\right)}^q\right)}^{\epsilon }}\right)\right)\end{array}\right]\end{array}\right),\epsilon \ge 0.\end{array}$

Definition 8. Let $R_1=\left(\left[\left({𝕁}_{{𝔯}_1},{\Re }_1\right),\left({𝕁}_{{𝔱}_1},{𝔗}_1\right)\right],\left[\left({𝕁}_{{𝔲}_1},{𝔘}_1\right),\left({𝕁}_{y_1},Y_1\right)\right]\right)$ and $R_2=\left(\left[\left({𝕁}_{{𝔯}_2},{\Re }_2\right),\left({𝕁}_{{𝔱}_2},{𝔗}_2\right)\right],\left[\left({𝕁}_{{𝔲}_2},{𝔘}_2\right),\left({𝕁}_{y_2},Y_2\right)\right]\right)$ are two 2TLIVq-ROFNs. The 2TLIVq-ROF normalized Hamming distance is expressed as follows:

$\begin{array}{ll}d\left(R_1,R_2\right)=\Delta \left(\frac{\tau }{4}\left(\begin{array}{l}|{\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔯}_1},{\Re }_1\right)}{\tau }\right)}^q-{\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔯}_2},{\Re }_2\right)}{\tau }\right)}^q|+|{\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔱}_1},{𝔗}_1\right)}{\tau }\right)}^q-{\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔱}_2},{𝔗}_2\right)}{\tau }\right)}^q|\\ +|{\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔲}_1},{𝔘}_1\right)}{\tau }\right)}^q-{\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔲}_2},{𝔘}_2\right)}{\tau }\right)}^q|+|{\left(\frac{{\Delta }^{-1}\left({𝕁}_{y_1},Y_1\right)}{\tau }\right)}^q-{\left(\frac{{\Delta }^{-1}\left({𝕁}_{y_2},Y_2\right)}{\tau }\right)}^q|\end{array}\right)\right),& (5)\end{array}$

where $d\left(R_1,R_2\right)\in \left[0,\tau \right]$.

4 The 2TLIVq-ROF weighted aggregation operators

The following section describes the 2TLIVq-ROFWA and 2TLIVq-ROFWJ operators for weighted information aggregation. The two proposed AOs additionally possess the characteristics of idempotency, monotonicity, and boundedness.

Definition 9. Let ${\mathcal{R}}_{ȷ}=\left(\right[\left({𝕁}_{{𝔯}_{ȷ}},{\Re }_{ȷ}\right)$, (𝕁_𝔱ȷ, 𝔗_ȷ)], [(𝕁_𝔲ȷ, ${𝔘}_{ȷ}),({𝕁}_{{\mathcal{y}}_{ȷ}},{\mathcal{Y}}_{ȷ}\left)\right])\left(ȷ=1,2,\dots ,\beta \right)$ be a set of 2TLIVq-ROFNs. The 2TLIVq-ROFWA operator as represents in Equation 6 the transformation that ensures ⊺^β → ⊺ is transformed as follows:

$\begin{array}{ll}\text{2TLIV}q\text{-ROFWA}\left(R_1,R_2,\dots ,R_{\beta }\right)={\displaystyle \underset{ȷ=1}{\overset{\beta }{\oplus }}}{\varpi }_{ȷ}{R}_{ȷ},& (6)\end{array}$

in which ⊺ is the set of 2TLIVq-ROFNs, $\varpi ={\left({\varpi }_1,{\varpi }_2,\dots ,{\varpi }_{\beta }\right)}^T$ represents the weight vector of $R_{ȷ}\left(ȷ=1,2,\dots ,\beta \right)$, satisfies the criteria ϖ_ȷ ∈ [0, 1] as well as ${\displaystyle \sum _{ȷ=1}^{\beta }}{\varpi }_{ȷ}=1.$

Theorem 1. Consider $R_{ȷ}=([({𝕁}_{{𝔯}_{ȷ}},{\Re }_{ȷ}),({𝕁}_{{𝔱}_{ȷ}},{𝔗}_{ȷ})],[({𝕁}_{{𝔲}_{ȷ}},{𝔘}_{ȷ}),({𝕁}_{y_{ȷ}},Y_{ȷ})])(ȷ=1,2,\dots ,\beta )$ be a set of 2TLIVq-ROFNs regarding weight vector $\varpi ={({\varpi }_1,{\varpi }_2,\dots ,{\varpi }_{\beta })}^T$, in which ϖ_ȷ ∈ [0, 1] and ${\displaystyle \sum _{ȷ=1}^{\beta }}{\varpi }_{ȷ}=1$, then

$\begin{array}{l}\text{2TLIV}q\text{-ROFWA}\left(R_1,R_2,\dots ,R_{\beta }\right)=\\ \left(\begin{array}{l}\left[\begin{array}{l}\Delta \left(\tau \left(\sqrt[q]{1-{\displaystyle \prod _{ȷ=1}^{\beta }}{\left(1-{\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔯}_{ȷ}},{\Re }_{ȷ}\right)}{\tau }\right)}^q\right)}^{{\varpi }_{ȷ}}}\right)\right),\Delta \left(\tau \left(\sqrt[q]{1-{\displaystyle \prod _{ȷ=1}^{\beta }}{\left(1-{\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔱}_{ȷ}},{𝔗}_{ȷ}\right)}{\tau }\right)}^q\right)}^{{\varpi }_{ȷ}}}\right)\right)\end{array}\right],\\ \left[\begin{array}{l}\Delta \left(\tau {\displaystyle \prod _{ȷ=1}^{\beta }}{\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔲}_{ȷ}},{𝔘}_{ȷ}\right)}{\tau }\right)}^{{\varpi }_{ȷ}}\right),\Delta \left(\tau {\displaystyle \prod _{ȷ=1}^{\beta }}{\left(\frac{{\Delta }^{-1}\left({𝕁}_{y_{ȷ}},Y_{ȷ}\right)}{\tau }\right)}^{{\varpi }_{ȷ}}\right)\end{array}\right]\end{array}\right).& (7)\end{array}$

Proof. To prove that Equation (8) is valid for positive integer β, we use mathematical induction.

(a) Whenever β = 1, then the subsequent outcome is:

${\varpi }_1{R}_1=\left(\begin{array}{l}\left[\begin{array}{l}\Delta \left(\tau \left(\sqrt[q]{1-{\left(1-{\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔯}_1},{\Re }_1\right)}{\tau }\right)}^q\right)}^{{\varpi }_1}}\right)\right),\Delta \left(\tau \left(\sqrt[q]{1-{\left(1-{\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔱}_1},{𝔗}_1\right)}{\tau }\right)}^q\right)}^{{\varpi }_1}}\right)\right),\end{array}\right],\\ \left[\begin{array}{l}\Delta \left(\tau {\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔲}_1},{𝔘}_1\right)}{\tau }\right)}^{{\varpi }_1}\right),\Delta \left(\tau {\left(\frac{{\Delta }^{-1}\left({𝕁}_{y_1},Y_1\right)}{\tau }\right)}^{{\varpi }_1}\right)\end{array}\right]\end{array}\right).$

Thus, Equation (7) holds for β = 1.

(b) Assume that Equation (7) is valid when β = α,

$\begin{array}{l}\text{2TLIV}q\text{-ROFWA}\left(R_1,R_2,\dots ,R_{ȷ}\right)\\ =\left(\begin{array}{l}\left[\begin{array}{l}\Delta \left(\tau \left(\sqrt[q]{1-{\displaystyle \prod _{ȷ=1}^{\alpha }}{\left(1-{\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔯}_{ȷ}},{\Re }_{ȷ}\right)}{\tau }\right)}^q\right)}^{{\varpi }_{ȷ}}}\right)\right),\Delta \left(\tau \left(\sqrt[q]{1-{\displaystyle \prod _{ȷ=1}^{\alpha }}{\left(1-{\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔱}_{ȷ}},{𝔗}_{ȷ}\right)}{\tau }\right)}^q\right)}^{{\varpi }_{ȷ}}}\right)\right)\end{array}\right],\\ \left[\begin{array}{l}\Delta \left(\tau {\displaystyle \prod _{ȷ=1}^{\alpha }}{\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔲}_{ȷ}},{𝔘}_{ȷ}\right)}{\tau }\right)}^{{\varpi }_{ȷ}}\right),\Delta \left(\tau {\displaystyle \prod _{ȷ=1}^{\alpha }}{\left(\frac{{\Delta }^{-1}\left({𝕁}_{y_{ȷ}},Y_{ȷ}\right)}{\tau }\right)}^{{\varpi }_{ȷ}}\right)\end{array}\right]\end{array}\right).\end{array}$

Subsequently, when the value of β = α + 1, we can utilize the inductive assumption to establish the following:

$\begin{array}{r}\text{2TLIV}q\text{-ROFWA}\left(R_1,R_2,\dots ,R_{\alpha },R_{\alpha +1}\right)\\ =\text{2TLIV}q\text{-ROFWA}\left(R_1,R_2,\dots ,R_{\alpha }\right)\oplus {\varpi }_{\alpha +1}{R}_{\alpha +1}\end{array}$

$\begin{array}{l}=\left(\begin{array}{l}\left[\begin{array}{l}\Delta \left(\tau \left(\sqrt[q]{1-{\displaystyle \prod _{ȷ=1}^{\alpha }}{\left(1-{\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔯}_{ȷ}},{\Re }_{ȷ}\right)}{\tau }\right)}^q\right)}^{{\varpi }_{ȷ}}}\right)\right),\Delta \left(\tau \left(\sqrt[q]{1-{\displaystyle \prod _{ȷ=1}^{\alpha }}{\left(1-{\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔱}_{ȷ}},{𝔗}_{ȷ}\right)}{\tau }\right)}^q\right)}^{{\varpi }_{ȷ}}}\right)\right)\end{array}\right],\\ \left[\begin{array}{l}\Delta \left(\tau {\displaystyle \prod _{ȷ=1}^{\alpha }}{\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔲}_{ȷ}},{𝔘}_{ȷ}\right)}{\tau }\right)}^{{\varpi }_{ȷ}}\right),\Delta \left(\tau {\displaystyle \prod _{ȷ=1}^{\alpha }}{\left(\frac{{\Delta }^{-1}\left({𝕁}_{y_{ȷ}},Y_{ȷ}\right)}{\tau }\right)}^{{\varpi }_{ȷ}}\right)\end{array}\right]\end{array}\right)\\ \oplus \left(\begin{array}{l}\left[\begin{array}{l}\Delta \left(\tau \left(\sqrt[q]{1-{\left(1-{\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔯}_{\alpha +1}},{\Re }_{\alpha +1}\right)}{\tau }\right)}^q\right)}^{{\varpi }_{\alpha +1}}}\right)\right),\Delta \left(\tau \left(\sqrt[q]{1-{\left(1-{\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔱}_{\alpha +1}},{𝔗}_{\alpha +1}\right)}{\tau }\right)}^q\right)}^{{\varpi }_{\alpha +1}}}\right)\right)\end{array}\right],\\ \left[\begin{array}{l}\Delta \left(\tau {\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔲}_{\alpha +1}},{𝔘}_{\alpha +1}\right)}{\tau }\right)}^{{\varpi }_{\alpha +1}}\right),\Delta \left(\tau {\left(\frac{{\Delta }^{-1}\left({𝕁}_{y_{\alpha +1}},Y_{\alpha +1}\right)}{\tau }\right)}^{{\varpi }_{\alpha +1}}\right)\end{array}\right]\end{array}\right).\\ =\left(\begin{array}{l}\left[\begin{array}{l}\Delta \left(\tau \left(\sqrt[q]{1-{\displaystyle \prod _{ȷ=1}^{\alpha +1}}{\left(1-{\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔯}_{ȷ}},{\Re }_{ȷ}\right)}{\tau }\right)}^q\right)}^{{\varpi }_{ȷ}}}\right)\right),\Delta \left(\tau \left(\sqrt[q]{1-{\displaystyle \prod _{ȷ=1}^{\alpha +1}}{\left(1-{\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔱}_{ȷ}},{𝔗}_{ȷ}\right)}{\tau }\right)}^q\right)}^{{\varpi }_{ȷ}}}\right)\right)\end{array}\right],\\ \left[\begin{array}{l}\Delta \left(\tau {\displaystyle \prod _{ȷ=1}^{\alpha +1}}{\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔲}_{ȷ}},{𝔘}_{ȷ}\right)}{\tau }\right)}^{{\varpi }_{ȷ}}\right),\Delta \left(\tau {\displaystyle \prod _{ȷ=1}^{\alpha +1}}{\left(\frac{{\Delta }^{-1}\left({𝕁}_{y_{ȷ}},Y_{ȷ}\right)}{\tau }\right)}^{{\varpi }_{ȷ}}\right)\end{array}\right]\end{array}\right).\end{array}$

Thus, Equation (7) is valid for a non-negative integer β = α + 1. Therefore, utilizing the method of induction, it is concluded that Equation (7) has validity for any number of β ≥ 1.

Theorem 2. Let $R_{ȷ}=([({𝕁}_{{𝔯}_{ȷ}},{\Re }_{ȷ}),({𝕁}_{{𝔱}_{ȷ}},{𝔗}_{ȷ})],[({𝕁}_{{𝔲}_{ȷ}},{𝔘}_{ȷ}),({𝕁}_{y_{ȷ}},Y_{ȷ})])$ and $R_{ȷ}^{\prime }=([({𝕁}_{{𝔯}_{ȷ}}^{\prime },{\Re }_{ȷ}^{\prime }),({𝕁}_{{𝔱}_{ȷ}}^{\prime },{𝔗}_{ȷ}^{\prime })],[({𝕁}_{{𝔲}_{ȷ}}^{\prime },{𝔘}_{ȷ}^{\prime }),({𝕁}_{y_{ȷ}}^{\prime },Y_{ȷ}^{\prime })])(ȷ=1,2,\dots ,\beta )$ are distinct sets of 2TLIVq-ROFNs. The 2TLIVq-ROFWA operator consequently adheres to the following properties:

1. (Idempotency) When every $R_{ȷ}=([({𝕁}_{{𝔯}_{ȷ}},{\Re }_{ȷ}),({𝕁}_{{𝔱}_{ȷ}},{𝔗}_{ȷ})],[({𝕁}_{{𝔲}_{ȷ}},{𝔘}_{ȷ}),({𝕁}_{y_{ȷ}},Y_{ȷ})])(ȷ=1,2,\dots ,\beta )$ is identical with regard to each ȷ, then

$\begin{array}{l}\text{2TLIV}q\text{-ROFWA}\left(R_1,R_2,\dots ,R_{\beta }\right)=R.\end{array}$

2. (Monotonicity) If $R_{ȷ}\le R_{ȷ}^{\prime }$, for all ȷ, then

$\begin{array}{l}\text{2TLIV}q\text{-ROFWA}\left(R_1,R_2,\dots ,R_{\beta }\right)\le \\ \text{2TLIV}q\text{-ROFWA}\left(R_1^{\prime },R_2^{\prime },\dots ,R_{\beta }^{\prime }\right).\end{array}$

3. (Boundedness) Let ${\mathcal{R}}_{ȷ}=([({𝕁}_{{𝔯}_{ȷ}}$, ${\Re }_{ȷ}),({𝕁}_{{𝔱}_{ȷ}},{𝔗}_{ȷ})],[({𝕁}_{{𝔲}_{ȷ}},{𝔘}_{ȷ}),({𝕁}_{{\mathcal{y}}_{ȷ}},{\mathcal{Y}}_{ȷ})])(ȷ=1,2,\dots ,\beta )$ be a set of 2TLIVq-ROFNs, and let ${\mathcal{R}}^{-}=([\underset{ȷ}{min}({𝕁}_{{𝔯}_{ȷ}},{\Re }_{ȷ}),\underset{ȷ}{min}({𝕁}_{{𝔱}_{ȷ}},{𝔗}_{ȷ})],[\underset{ȷ}{max}({𝕁}_{{𝔲}_{ȷ}},{𝔘}_{ȷ})$, $\underset{ȷ}{max}({𝕁}_{{\mathcal{y}}_{ȷ}},{\mathcal{Y}}_{ȷ})])$ and $R^{+}=([\underset{ȷ}{max}({𝕁}_{{𝔯}_{ȷ}},{\Re }_{ȷ}),\underset{ȷ}{max}({𝕁}_{{𝔱}_{ȷ}},{𝔗}_{ȷ})],$ $[\underset{ȷ}{min}({𝕁}_{{𝔲}_{ȷ}},{𝔘}_{ȷ}),\underset{ȷ}{min}({𝕁}_{y_{ȷ}},Y_{ȷ})]$), then

$\begin{array}{l}{R}^{-}\le \text{2TLIV}q\text{-ROFWA}\left(R_1,R_2,\dots ,R_{\beta }\right)\le R^{+}.\end{array}$

Definition 10. Consider $R_{ȷ}=\left(\left[\left({𝕁}_{{𝔯}_{ȷ}},{\Re }_{ȷ}\right),\left({𝕁}_{{𝔱}_{ȷ}},{𝔗}_{ȷ}\right)\right],\left[\left({𝕁}_{{𝔲}_{ȷ}},{𝔘}_{ȷ}\right),\left({𝕁}_{y_{ȷ}},Y_{ȷ}\right)\right]\right)\left(ȷ=1,2,\dots ,\beta \right)$ be a set of 2TLIVq-ROFNs. The 2TLIVq-ROFWJ operator represents a transformation that ensures ⊺^β → ⊺ is transformed as follows in Equation 8:

$\begin{array}{ll}\text{2TL}T\text{-SFWJ}\left(R_1,R_2,\dots ,R_{\beta }\right)={\displaystyle \underset{ȷ=1}{\overset{\beta }{\otimes }}}{R}_{ȷ}^{{\varpi }_{ȷ}},& (8)\end{array}$

in which ⊺ is the set of 2TLIVq-ROFNs, $\varpi ={\left({\varpi }_1,{\varpi }_2,\dots ,{\varpi }_{\beta }\right)}^T$ is the weighting vector of $R_{ȷ}\left(ȷ=1,2,\dots ,\beta \right)$, such that ϖ_ȷ ∈ [0, 1] and ${\displaystyle \sum _{ȷ=1}^{\beta }}{\varpi }_{ȷ}=1.$

Theorem 3. Consider $R_{ȷ}=([({𝕁}_{{𝔯}_{ȷ}},{\Re }_{ȷ}),({𝕁}_{{𝔱}_{ȷ}},{𝔗}_{ȷ})],[({𝕁}_{{𝔲}_{ȷ}},{𝔘}_{ȷ}),({𝕁}_{y_{ȷ}},Y_{ȷ})])(ȷ=1,2,\dots ,\beta )$ be a group of 2TLIVq-ROFNs regarding a weight vector $\varpi ={({\varpi }_1,{\varpi }_2,\dots ,{\varpi }_{\beta })}^T$, such that ϖ_ȷ ∈ [0, 1] and ${\displaystyle \sum _{ȷ=1}^{\beta }}{\varpi }_{ȷ}=1$. The aggregate value obtained through the 2TLIVq-ROFWJ operator remains a 2TLIVq-ROFN, and the 2TLIVq-ROFWJ operator represents in the Equation 9.

$\begin{array}{l}\text{2TLIV}q\text{-ROFWJ}\left(R_1,R_2,\dots ,R_{\beta }\right)\\ =\left(\begin{array}{l}\left[\begin{array}{l}\Delta \left(\tau {\displaystyle \prod _{ȷ=1}^{\beta }}{\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔯}_{ȷ}},{\Re }_{ȷ}\right)}{\tau }\right)}^{{\varpi }_{ȷ}}\right),\Delta \left(\tau {\displaystyle \prod _{ȷ=1}^{\beta }}{\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔱}_{ȷ}},{𝔗}_{ȷ}\right)}{\tau }\right)}^{{\varpi }_{ȷ}}\right)\end{array}\right],\\ \left[\begin{array}{l}\Delta \left(\tau \left(\sqrt[q]{1-{\displaystyle \prod _{ȷ=1}^{\beta }}{\left(1-{\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔲}_{ȷ}},{𝔘}_{ȷ}\right)}{\tau }\right)}^q\right)}^{{\varpi }_{ȷ}}}\right)\right),\Delta \left(\tau \left(\sqrt[q]{1-{\displaystyle \prod _{ȷ=1}^{\beta }}{\left(1-{\left(\frac{{\Delta }^{-1}\left({𝕁}_{y_{ȷ}},Y_{ȷ}\right)}{\tau }\right)}^q\right)}^{{\varpi }_{ȷ}}}\right)\right)\end{array}\right]\end{array}\right).& (9)\end{array}$

The demonstration closely resembles the one found in Theorems 1 and 2.

5 Methodology

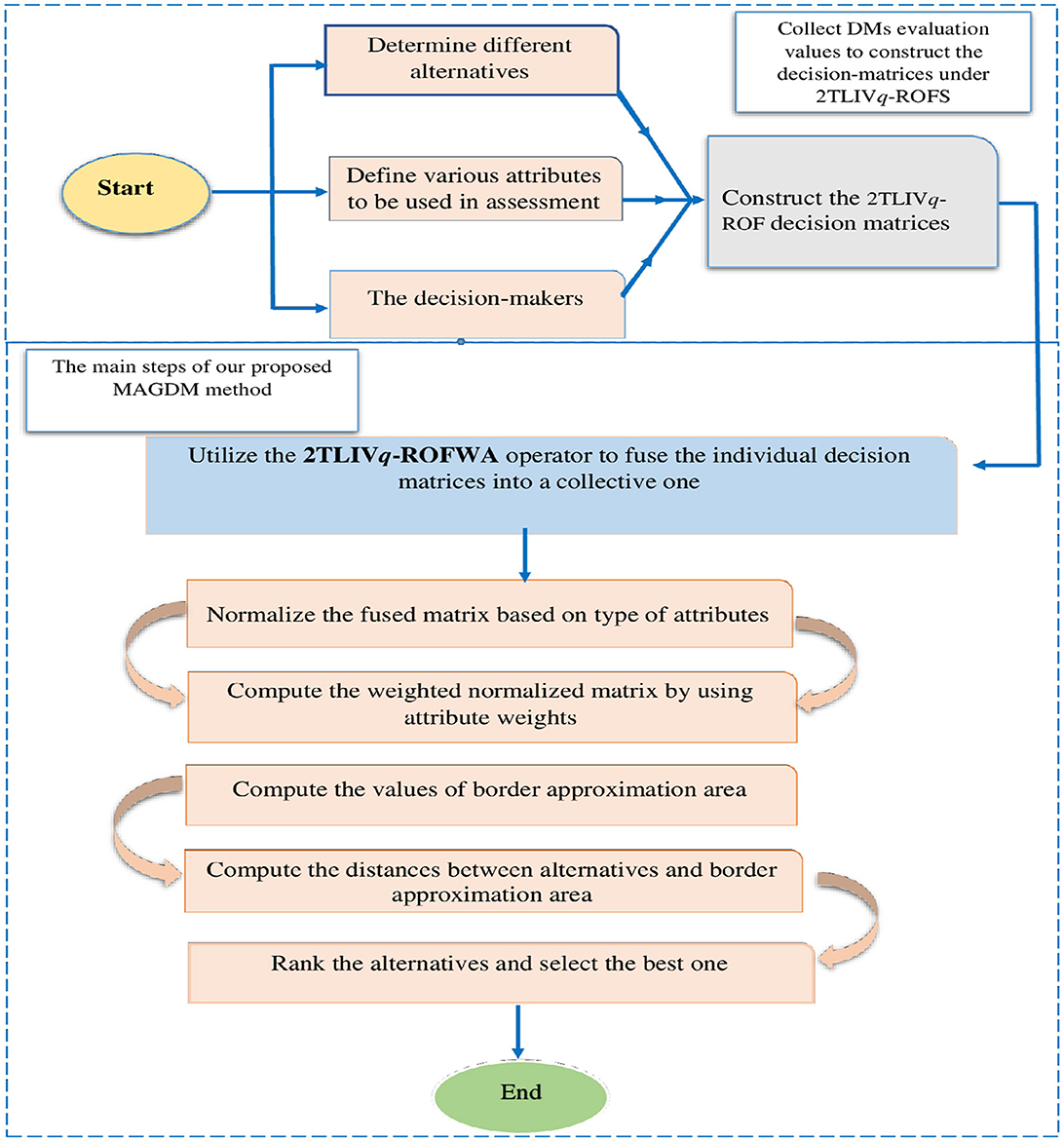
Research methodology in decision-making is the systematic process of gathering and analyzing information to inform a choice. It involves defining the problem, choosing a research design to collect data, analyzing that data, and using the results to weigh options and make a well-supported decision. An essential subfield of MADM research, MAGDM entails a group of DMs evaluating alternatives based on multiple competing attributes for ranking all the alternatives or choosing the most suitable one. Recent articles on MAGDM have emphasized methodological techniques for ambiguous situations in general (Ozcalici, 2022; Ashouri et al., 2023; Colombo et al., 2023; Kiptum et al., 2023; Lazarashouri and Najafi, 2024). Due to the severity of MAGDM challenges, it is difficult for DMs to collect all possible alternative information. Understanding how to deal with uncertainty and ambiguity is crucial for selecting the best option in practical decision-making challenges. Innovative MABAC method facilitates group decision-making by offering a structured framework that integrates multiple attributes, fostering collaboration and ensuring comprehensive evaluation of alternatives. MABAC helps consider uncertainties in preferences by incorporating fuzzy logic concepts, ultimately aiming to identify the best alternative through a structured comparison process. In order to assess the linguistic information, a novel 2TLIVq-ROF-MABAC method is constructed in which the collected data is aggregated by the 2TLIVq-ROFWA and 2TLIVq-ROFWJ operators. In particular, to cope with MAGDM problems, there is a set of α alternatives Γ = {Γ₁, Γ₂, …, Γ_α}, β attributes Θ = {Θ₁, Θ₂, …, Θ_β}, and 𝔣 experts $E=\left\{E_1,E_2,\dots ,E_{𝔣}\right\}$, and let $\varpi ={\left({\varpi }_1,{\varpi }_2,\dots ,{\varpi }_{\beta }\right)}^T$ and ${\omega }^{\prime }={\left({\omega }_1^{\prime },{\omega }_2^{\prime },\dots ,{\omega }_{𝔣}^{\prime }\right)}^T$ be the weight vector of the Θ_ȷ and weight vector of the $E_{\gamma }$ satisfy ϖ_ȷ ∈ [0, 1], ω_γ ∈ [0, 1], ${\displaystyle \sum _{ȷ=1}^{\beta }}{\varpi }_{ȷ}=1$, and ${\displaystyle \sum _{\gamma =1}^{𝔣}}{\omega }_{\gamma }=1$.

Step 1. For 2TLIVq-ROFS, the evaluation matrix is constructed as $R={[{\beth }_{ıȷ}^{\gamma }]}_{\alpha \times \beta }=$$({[(𝕁{𝔯}_{ıȷ},{\Re }_{ıȷ}),({𝕁}_{{𝔱}_{ıȷ}},{𝔗}_{ıȷ})]}^{\gamma },$ ${[({𝕁}_{{𝔲}_{ıȷ}},{𝔘}_{ıȷ}),({𝕁}_{y_{ıȷ}},Y_{ıȷ})]}^{\gamma })$ $(ı=1,2,\dots ,\alpha ,ȷ=1,2,\dots ,\beta ,\gamma =1,2,\dots ,𝔣)$. The 2TLIVq-ROFS conveys the information regarding alternatives ${\beth }_{ı}$ on attributes Θ_ȷ as evaluated by DMs $E_{\gamma }$.

Step 2. By utilizing the 2TLIVq-ROFWA operator from Equation (8), the combined 2TLIVq-ROFNs matrix r = [${\beth }_{ı}$_ȷ]_α×β is obatined, in which ${\beth }_{ıȷ}=([({𝕁}_{{𝔯}_{ıȷ}},{\Re }_{ıȷ}),({𝕁}_{{𝔱}_{ıȷ}},{𝔗}_{ıȷ})],[({𝕁}_{{𝔲}_{ıȷ}},{𝔘}_{ıȷ}),({𝕁}_{y_{ıȷ}},Y_{ıȷ})])$.

Step 3. Applying an attribute-based procedure, normalize the aggregated matrix r = [${\beth }_{ı}$_ȷ]_α×β by using Equations 10 and 11.

For benefit attributes:

$\begin{array}{c}{\mathbb{N}}_{ıȷ}={\beth }_{ıȷ}=([({𝕁}_{r_{ıȷ}},{\Re }_{ıȷ}),({𝕁}_{t_{ıȷ}},T_{ıȷ})],[({𝕁}_{u_{ıȷ}},\\ U_{ıȷ}),({𝕁}_{y_{ıȷ}},Y_{ıȷ})]), ıȷ=1,2,\dots ,\alpha , =1,2,\dots ,\beta & (10)\end{array}$

For cost attributes:

$\begin{array}{c}{\mathbb{N}}_{ıȷ}={\beth }_{ıȷ}^c=[({𝕁}_{u_{ıȷ}},U_{ıȷ}),({𝕁}_{y_{ıȷ}},Y_{ıȷ})],[({𝕁}_{r_{ıȷ}},{\Re }_{ıȷ}),({𝕁}_{t_{ıȷ}},\\ T_{ıȷ})],ıȷ=1,2,\dots ,\alpha ,=1,2,\dots ,\beta & (11)\end{array}$

Step 4. By using the obtained results of normalized matrix ${\mathbb{N}}_{ıȷ}=([({𝕁}_{{𝔯}_{ıȷ}},{\Re }_{ıȷ}),({𝕁}_{{𝔱}_{ıȷ}},{𝔗}_{ıȷ})],[({𝕁}_{{𝔲}_{ıȷ}},{𝔘}_{ıȷ}),({𝕁}_{y_{ıȷ}},Y_{ıȷ})])$ and attribute weights ϖ_ȷ(ȷ = 1, 2, …, β), the 2TLIVq-ROF weighted normalized matrix ${𝕎\mathbb{N}}_{ıȷ}=([({𝕁}_{{𝔯}_{ıȷ}}^{\prime },{\Re }_{ıȷ}^{\prime }),({𝕁}_{{𝔱}_{ıȷ}}^{\prime },{𝔗}_{ıȷ}^{\prime })],[({𝕁}_{{𝔲}_{ıȷ}}^{\prime },{𝔘}_{ıȷ}^{\prime }),({𝕁}_{y_{ıȷ}}^{\prime },Y_{ıȷ}^{\prime })])$ is put forward as in Equation 12:

$\begin{array}{ll}{𝕎\mathbb{N}}_{ıȷ}={\varpi }_{ȷ}\otimes {\mathbb{N}}_{ıȷ}==\left(\begin{array}{l}\left[\begin{array}{l}\Delta \left(\tau \left(\sqrt[q]{1-{\left(1-{\left(\frac{{\Delta }^{-1}\left({𝕁}_{𝔯},\Re \right)}{\tau }\right)}^q\right)}^{{\varpi }_{ȷ}}}\right)\right),\Delta \left(\tau \left(\sqrt[q]{1-{\left(1-{\left(\frac{{\Delta }^{-1}\left({𝕁}_{𝔱},𝔗\right)}{\tau }\right)}^q\right)}^{{\varpi }_{ȷ}}}\right)\right)\end{array}\right],\\ \left[\begin{array}{l}\Delta \left(\tau \left({\left(\frac{{\Delta }^{-1}\left({𝕁}_{𝔲},𝔘\right)}{\tau }\right)}^{{\varpi }_{ȷ}}\right)\right),\Delta \left(\tau \left({\left(\frac{{\Delta }^{-1}\left({𝕁}_{\mathcal{y}},\mathcal{Y}\right)}{\tau }\right)}^{{\varpi }_{ȷ}}\right)\right)\end{array}\right]\end{array}\right).& (12)\end{array}$

Step 5. Calculate BAA values as well as matrix G = [g_ȷ]_1×β is constructed into the following form by using Equation 13;

$\begin{array}{ll}{g}_{ȷ}={\left({\displaystyle \prod _{ı=1}^{\alpha }}{𝕎\mathbb{N}}_{ıȷ}\right)}^{1/\alpha }=\left(\begin{array}{l}\left[\begin{array}{l}\Delta \left(\tau {\displaystyle \prod _{ȷ=1}^{\beta }}{\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔯}_{ȷ}}^{\prime },{\Re }_{ȷ}^{\prime }\right)}{\tau }\right)}^{1/\alpha }\right),\Delta \left(\tau {\displaystyle \prod _{ȷ=1}^{\beta }}{\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔱}_{ȷ}}^{\prime },{𝔗}_{ȷ}^{\prime }\right)}{\tau }\right)}^{1/\alpha }\right)\end{array}\right],\\ \left[\begin{array}{l}\Delta \left(\tau \left(\sqrt[q]{1-{\displaystyle \prod _{ȷ=1}^{\beta }}{\left(1-{\left(\frac{{\Delta }^{-1}\left({𝕁}_{{𝔲}_{ȷ}}^{\prime },{𝔘}_{ȷ}^{\prime }\right)}{\tau }\right)}^q\right)}^{1/\alpha }}\right)\right),\\ \Delta \left(\tau \left(\sqrt[q]{1-{\displaystyle \prod _{ȷ=1}^{\beta }}{\left(1-{\left(\frac{{\Delta }^{-1}\left({𝕁}_{y_{ȷ}}^{\prime },Y_{ȷ}^{\prime }\right)}{\tau }\right)}^q\right)}^{1/\alpha }}\right)\right)\end{array}\right]\end{array}\right).& (13)\end{array}$

Step 6. The distance matrix $D={\left[d_{ıȷ}\right]}_{\alpha \times \beta }$ is constructed from the results of ${𝕎\mathbb{N}}_{ı}$_ȷ and G_ȷ matrices by calculating the 2TLIVq-ROF normalized Hamming distance described in Equation (5).

$\begin{array}{ll}{d}_{ıȷ}=\{\begin{array}{l}d({𝕎\mathbb{N}}_{ıȷ},g_{ȷ}),if{𝕎\mathbb{N}}_{ıȷ}>g_{ȷ}\\ 0,if{𝕎\mathbb{N}}_{ıȷ}=g_{ȷ}\\ -d({𝕎\mathbb{N}}_{ıȷ},g_{ȷ}),if{𝕎\mathbb{N}}_{ıȷ}<g_{ȷ}\end{array}& (14)\end{array}$

Step 7. The cumulative values of the $d_{ı}$_ȷ for each alternative can be calculated by using Equation 15.

$\begin{array}{ll}{S}_{ı}={\displaystyle \sum _{ȷ=1}^{\beta }}{d}_{ıȷ}& (15)\end{array}$

The comprehensive assessment result $S_{ı}$ can be used to establish the order of all alternatives; obviously, the better the decision, the greater the comprehensive assessment result $S_{ı}$.

Figure 1 provides a visual representation of the methodology.

Figure 1

Figure 1. A graphical representation illustrating the methodology.

6 Case study

A case study follows to demonstrate the usefulness and versatility of the proposed approach. We validate our strategy through the challenging process of choosing the best breast cancer treatment.

6.1 The problem description

Breast cancer is when cells in the breast tissue turn harmful and damage the tissue. Although it is more prevalent among women, men are not impervious to this particular form of cancer. A multidisciplinary treatment approach is required due to the complexity of breast cancer. Numerous factors play a role in the decision of which treatment is best for each patient. These include the stage and subtype of the cancer, the patient's age and overall health, the patient's personal preferences and values, as well as the availability and accessibility of diverse treatment options. Antineoplastic agents, targeted therapies, radiation therapy, chemotherapy, hormone therapy, and immunotherapy are among the most frequently used treatments for breast cancer. Each of these treatments possesses its own set of benefits and drawbacks and may be implemented individually or in combination with other therapies. The objectives of treatment are to eliminate or manage the cancer, safeguard against its recurrence or growth, and improve the overall wellbeing and survival of the patient. The formulation of a treatment plan for a patient with breast cancer is a complex and individualized process that considers numerous factors and potentialities. Different types of cancer treatment options are considered based on the cancer's type, stage, and characteristics, as well as the patient's preferences and overall health. Some people have access to the following possibilities for deciding how to treat their breast cancer:

1. Lumpectomy (Γ₁)

In this procedure, the majority of the breast is left untouched, and just the tumor and a narrow margin of healthy tissue surrounding it are removed. Radiation therapy is frequently used after a lumpectomy to eradicate any breast cancer cells that may still be present. If a patient has a tiny or early-stage tumor and wants to maintain the appearance and function of their breasts, a lumpectomy may be a possibility.

2. Mastectomy (Γ₂)

In this procedure, the entire breast-along with the nipple and areola is removed. Patients with big, aggressive, or multifocal tumors, those who have a high chance of recurrence, or those who have a genetic mutation that raises their risk of getting breast cancer may be advised to have a mastectomy. A mastectomy may be performed in conjunction with reconstructive surgery to reshape the breasts using implants or body tissue.

3. Chemotherapy (Γ₃)

The goal of this therapy is to eradicate cancer cells throughout the body via medication. Prior to surgery (neoadjuvant) to reduce the size of the tumor and make it simpler to remove, or after surgery (adjuvant) to lower the risk of growth or recurrence, chemotherapy may be administered. Chemotherapy can relieve symptoms and improve the quality of life in advanced or cancerous breast cancer patients.

4. Hormone therapy (Γ₄)

This therapy inhibits or reduces the levels of the hormones (estrogen and progesterone) that encourage the growth of some kinds of breast cancer cells. Whether used alone or in conjunction with other therapies, hormone therapy can be administered as tablets, injections, or implants. Patients identified as hormone receptor-positive breast tumors, constituting an estimated 70% of the total breast cancer cases, may qualify for hormone therapy.

5. Targeted therapy (Γ₅)

Drugs that specifically target substances or processes connected with the advancement and survival of cancer cells are used in this therapy. Since chemotherapy affects normal cells less, targeted treatment could have fewer negative effects than chemotherapy. Patients with particular forms of breast cancer, such as HER2-positive breast cancer, that have particular genetic alterations or indicators, may have the option of targeted therapy.

6. Immunotherapy (Γ₆)

The immune system is encouraged by the use of medicines in this therapy to identify and fight cancer cells. Immunotherapy may strengthen the body's natural defenses, and inhibit signals that enable cancer cells to avoid detection, or transfer poisons or radioactive materials directly to cancer cells. For individuals with certain kinds of breast cancer, such as triple-negative breast cancer, that has unique traits or mutations, immunotherapy may be a possibility.

7. Clinical trials (Γ₇)

These trials examine the safety and efficacy of novel medications, apparatus, methods, or treatment accumulation in humans. Access to novel or experimental medicines that are still only available in research settings may be provided via clinical trials. Patients who have tried all of the traditional therapies, have uncommon or difficult-to-treat kinds of breast cancer, or who want to help progress science and medicine may be candidates for clinical trials.

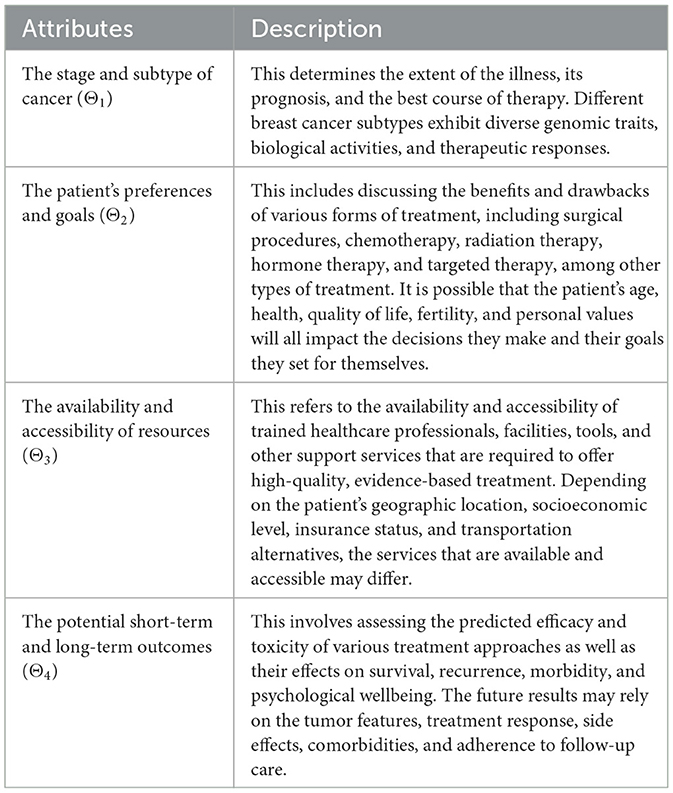
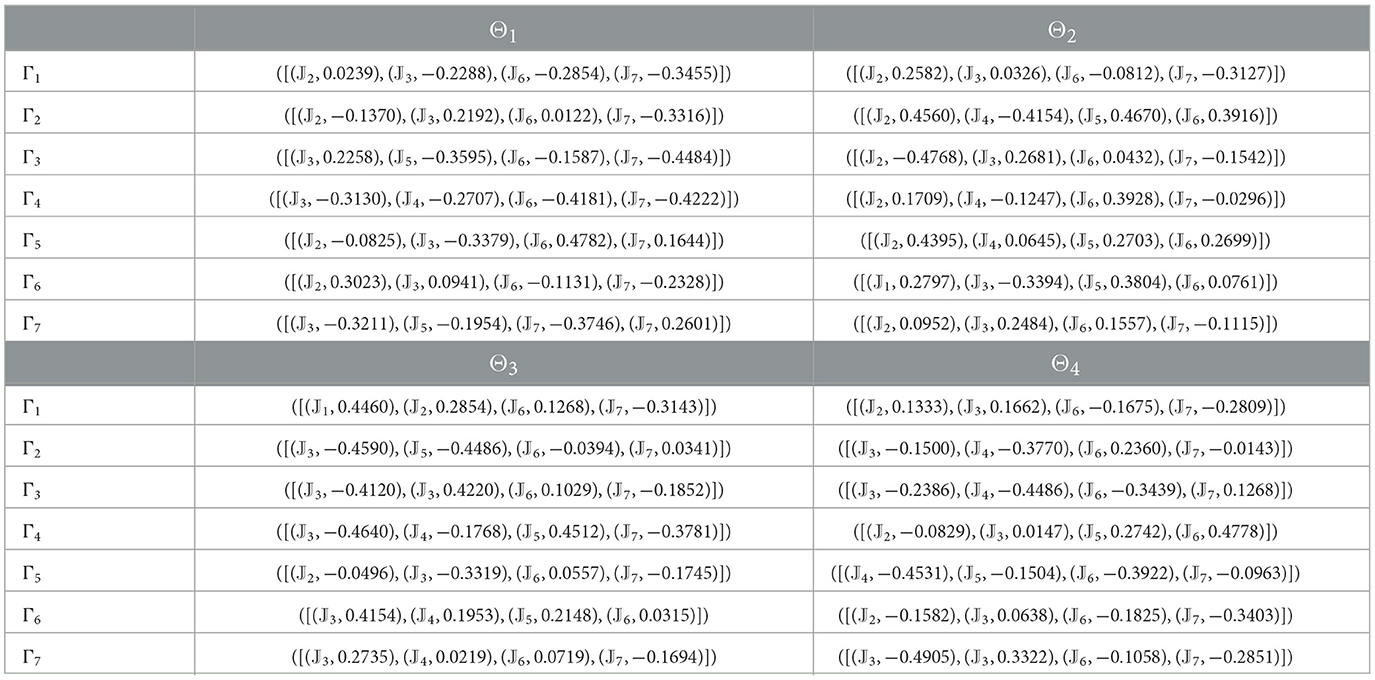
The selection of breast cancer treatments is an intricate procedure involving multiple factors and stakeholders. Consequently, breast cancer treatment selection can be regarded as a conventional MAGDM problem. We intend to evaluate breast cancer treatment utilizing the 2TLIVq-ROF-MABAC method that is suggested in this paper and data is aggregated by the proposed 2TLIVq-ROF aggregation operators. In this regard, seven distinct alternatives can be considered (a brief discussion of each is given above) Γ = {Γ₁, Γ₂, Γ₃, …, Γ₇}, evaluated by an advisory group of four DMs $E=\left\{E_1,E_2,E_3,E_4\right\}$ with weights ω′ = (0.2192, 0.2134, 0.1930, 0.1906)^T with the goal to deal with the problem described above. The four DMs choose an optimal alternative based on the four attributes Θ = {Θ₁, Θ₂, Θ₃, Θ₄} (as depicted in Table 3) and their corresponding weights are, ϖ = (0.2542, 0.2533, 0.2480, 0.2445)^T. To evaluate the significance of each LTS 𝔏, four DMs express their assessments. The LTS categories include 𝔏 = {𝕁₀: Immaterial, 𝕁₁: Low Suitability, 𝕁₂: Moderate Suitability, 𝕁₃: High Suitability, 𝕁₄: Reasonable, 𝕁₅: Low Efficacy, 𝕁₆: Moderate Efficacy, 𝕁₇: High Efficacy, 𝕁₈: Trustable }.

Table 3

Table 3. A synopsis of assessing attributes.

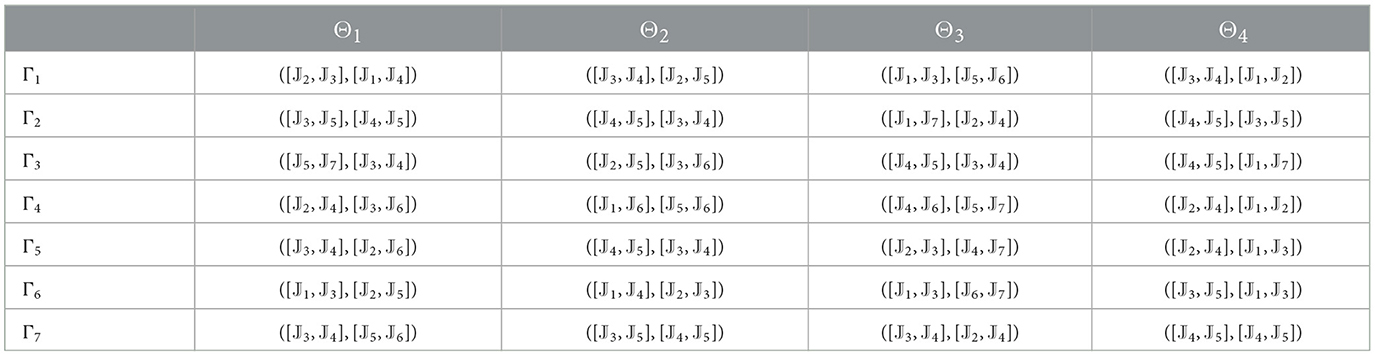
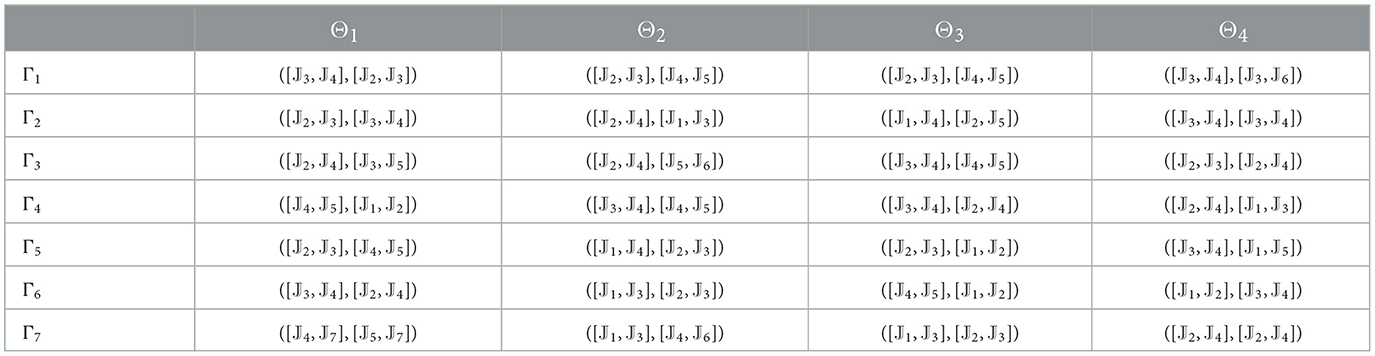
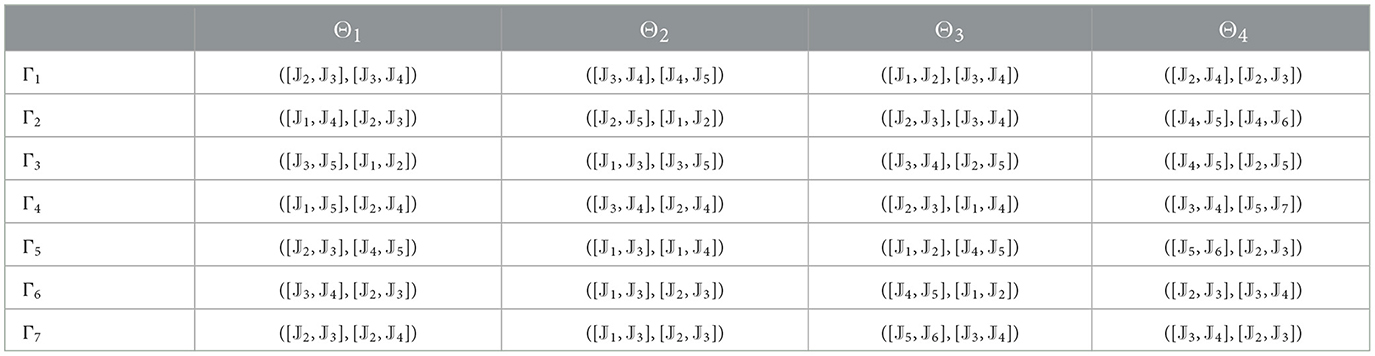
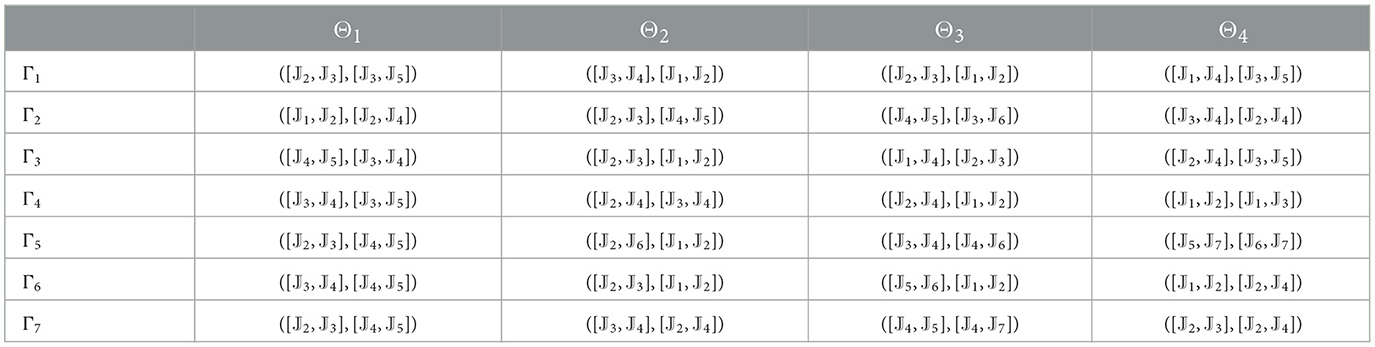
Tables 4–7 provide decision matrices determined by each of the four DMs' assessment values for all alternatives. In these tables, the 2TL term (𝕁_ℓ, 0) can be written as 𝕁_ℓ for convenience.

Table 4

Table 4. 2TLIVq-ROF decision matrix by $E_1$.

Table 5

Table 5. 2TLIVq-ROF decision matrix by $E_2$.

Table 6

Table 6. 2TLIVq-ROF decision matrix by $E_3$.

Table 7

Table 7. 2TLIVq-ROF decision matrix by $E_4$.

6.2 Evaluation of case study utilizing the proposed 2TLIVq-ROF approach

The 2TLIVq-ROF-MABAC approach based on the 2TLIVq-ROFWA operator is used in this subsection to illustrate the assessment procedure for selecting the best cancer treatment.

Step 1. We construct the 2TLIVq-ROF assessment matrices $R^{\kappa }={[{\beth }_{ıȷ}^{\kappa }]}_{7\times 4}=({[({𝕁}_{{𝔯}_{ıȷ}},{\Re }_{ıȷ}),({𝕁}_{{𝔱}_{ıȷ}},{𝔗}_{ıȷ})]}^{\gamma },{[({𝕁}_{{𝔲}_{ıȷ}},{𝔘}_{ıȷ}),({𝕁}_{y_{ıȷ}},Y_{ıȷ})]}^{\gamma })$ ($ı$ = 1, 2, …, 7, ȷ = 1, 2, 3, 4, γ = 1, 2, 3, 4) as shown in Tables 4–7.

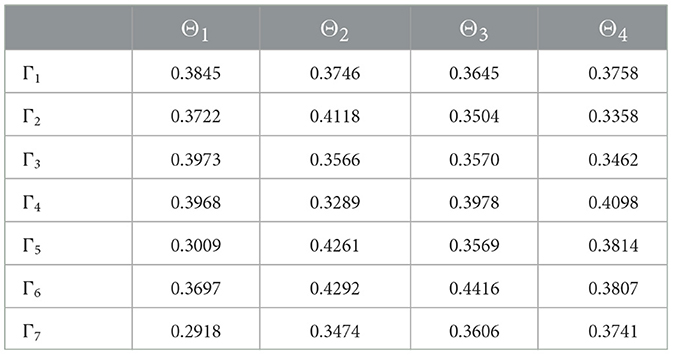
Step 2. The combined 2TLIVq-ROFNs matrix r = [${\beth }_{ı}$_ȷ]_7×4 is obtained utilizing the 2TLIVq-ROFWA aggregation operator, which is illustrated in Table 8 [assuming that q = 6, τ = 8, ω′ = (0.2192, 0.2134, 0.1930, 0.1906)^T].

Step 3. Normalization is unnecessary provided all of the attributes are of the benefit type. Consider the evaluation matrix presented in Table 8 to be the normalized version.

Step 4. In accordance with ${\mathbb{N}}_{ı}$_ȷ $=([({𝕁}_{{𝔯}_{ıȷ}},{\Re }_{ıȷ}),({𝕁}_{{𝔱}_{ıȷ}},{𝔗}_{ıȷ})]$, $[({𝕁}_{{𝔲}_{ıȷ}},{𝔘}_{ıȷ}),({𝕁}_{y_{ıȷ}},Y_{ıȷ})])$ $(ı=1,2,\dots ,7,ȷ=1,2,3,4)$ and weights ${\varpi }_{ȷ}={(0.2542,0.2533,0.2480,0.2445)}^T$, the 2TLIVq-ROF weighted normalized matrix ${𝕎\mathbb{N}}_{ıȷ}=({[({𝕁}_{{𝔯}_{ıȷ}}^{\prime },{\Re }_{ıȷ}^{\prime }),({𝕁}_{{𝔱}_{ıȷ}}^{\prime },{𝔗}_{ıȷ}^{\prime })]}^{\gamma },{[({𝕁}_{{𝔲}_{ıȷ}}^{\prime },{𝔘}_{ıȷ}^{\prime }),({𝕁}_{y_{ıȷ}}^{\prime },Y_{ıȷ}^{\prime })]}^{\gamma })$($ı$ = 1, 2, …, 7, ȷ = 1, 2, 3, 4) through Equation (13) can be found in Table 9.

The scores of 2TLIVq-ROF elements of weighted normalized matrix ${𝕎\mathbb{N}}_{ı}$_ȷ are shown in Table 10.

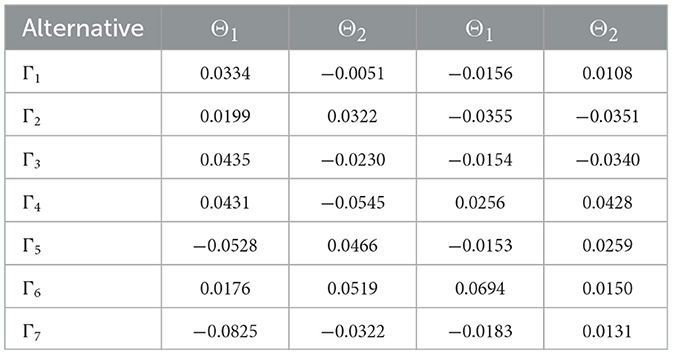
Step 5. Construct the BAA matrix G = [_gȷ]1×4 using Equation (14). Table 11 displays the results of the BAA matrix G.

Step 6. Compute the normalized Hamming distance $D={\left[d_{ıȷ}\right]}_{7\times 4}$ between ${𝕎\mathbb{N}}_{ı}$_ȷ and G_ȷ matrices through the Equation (6) as illustrated in the Table 12.

Step 7. The cumulative values of the $d_{ı}$_ȷ for each alternative are:

$\begin{array}{l}{S}_1={\displaystyle \sum _{ȷ=1}^4}{d}_{ıȷ}=0.0234,S_2={\displaystyle \sum _{ȷ=1}^4}{d}_{2ȷ}=-0.0184,\\ S_3={\displaystyle \sum _{ȷ=1}^4}{d}_{3ȷ}=-0.0289,S_4={\displaystyle \sum _{ȷ=1}^4}{d}_{4ȷ}=0.0569,\\ S_5={\displaystyle \sum _{ȷ=1}^4}{d}_{5ȷ}=0.0043,S_6={\displaystyle \sum _{ȷ=1}^4}{d}_{6ȷ}=0.1539,\\ S_7={\displaystyle \sum _{ȷ=1}^4}{d}_{7ȷ}=-0.1199\end{array}$

Table 8

Table 8. Combined 2TLIVq-ROFN matrix utilizing the 2TLIVq-ROFWA operator.

Table 9

Table 9. The evaluated ${𝕎\mathbb{N}}_{ı}$_ȷ matrix with 2TLIVq-ROFNs.

Table 10

Table 10. Score functions of weighted normalized matrix.

Table 11

Table 11. The evaluated G matrix with 2TLIVq-ROFNs.

Table 12

Table 12. Evaluated 2TLIVq-ROFN distance matrix.

Consequently, using the result of $S_{ı}$, alternatives ${\Gamma }_{ı}=(ı=1,2,\dots ,7)$) can be ordered accordingly. The alternative with the greatest $S_{ı}$ value is considered optimal. Following is the order of alternatives:

${\Gamma }_6>{\Gamma }_4>{\Gamma }_1>{\Gamma }_5>{\Gamma }_2>{\Gamma }_3>{\Gamma }_7$

As a result, Γ₆ is the most effective treatment for breast cancer.

6.3 Analyzing parameter effect on rankings

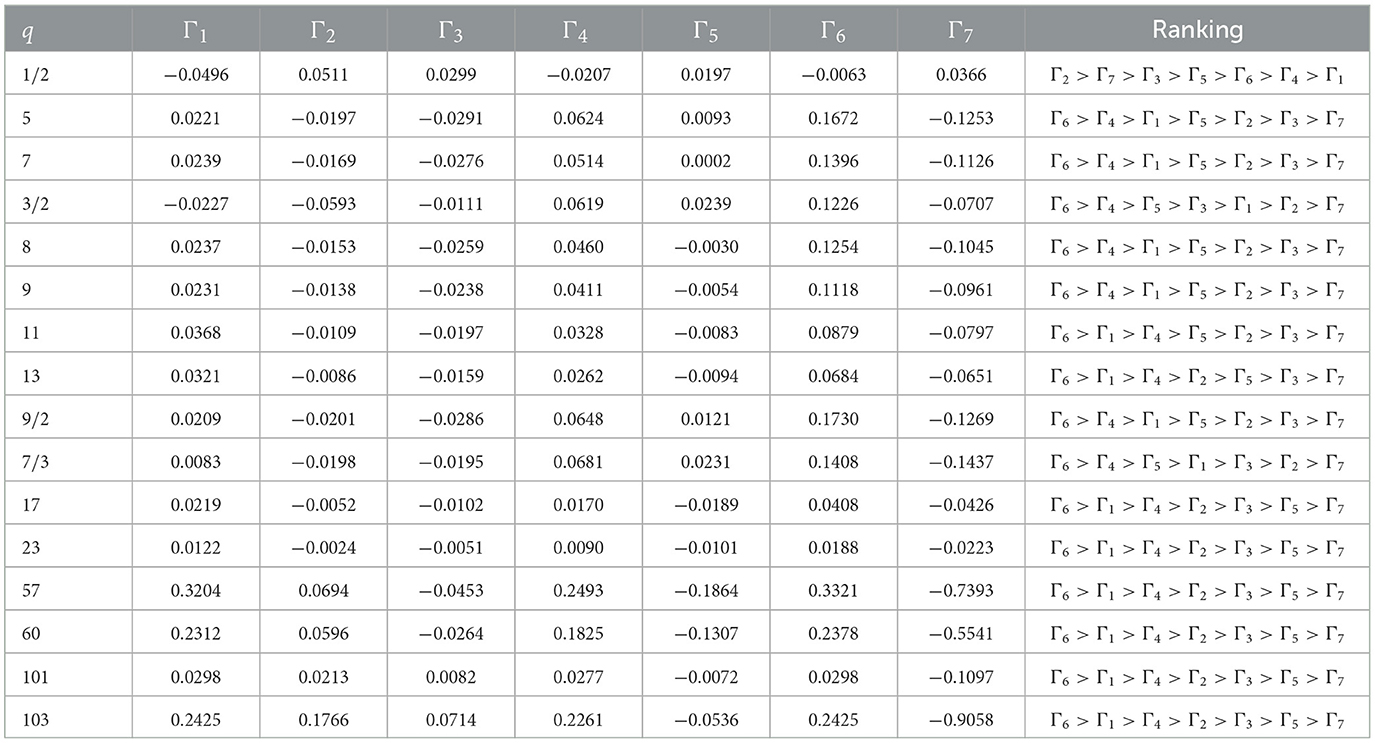
Cumulative values and rankings based on various q values in the 2TLIVq-ROFWA operator are provided in Table 13. This research reveals how q affects the performance and ranking of seven alternatives. q is the parameter of the 2TLIVq-ROFS and always has a positive value because it represents a quantity that cannot be negative (i.e., negative root values can distort the results and make the information complex to evaluate). In the proposed model the values of parameter q are chosen randomly considering their condition to be positive to observe its impact on the final ranking. Trends show that choice outcomes are sensitive to q. Cumulative values for each alternative vary greatly when q changes. Alternative Γ₆ regularly outperforms others, with cumulative values increasing with the q level. However, alternative Γ₇ typically has the lowest results for different q values, indicating poor performance. This sensitivity to q emphasizes the need to carefully select this parameter in the decision-making process to match context and criterion. Further examination of the Table 13 shows that ranks change with q. Different q values significantly affect the ranking of alternatives, demonstrating the 2TLIVq-ROFWA operator's responsiveness to parameter changes. Notably, alternative Γ₆ consistently ranks first for most q values, demonstrating its robust and beneficial performance under a variety of conditions. Conversely, alternative Γ₇ frequently gets ranked lower, suggesting its inferior performance in most situations. To make educated judgments using the 2TLIVq-ROFWA aggregation operator, the best q value must be carefully evaluated, taking into consideration the relationship between alternatives and preferences of DMs. To evaluate these rankings' stability under data fluctuations and uncertainties, robustness testing is advised. In summary, the q parameter significantly affects the outcomes utilizing the 2TLIVq-ROFWA operator operator, requiring sensitivity analysis, a deep understanding of decision-making implications, and robustness assessment to ensure reliable rankings under changing data conditions. The visual variation of parameters can be observed in Figure 2.

Table 13

Table 13. Ranking outcomes with different q in the 2TLIVq-ROFWA operator.

Figure 2

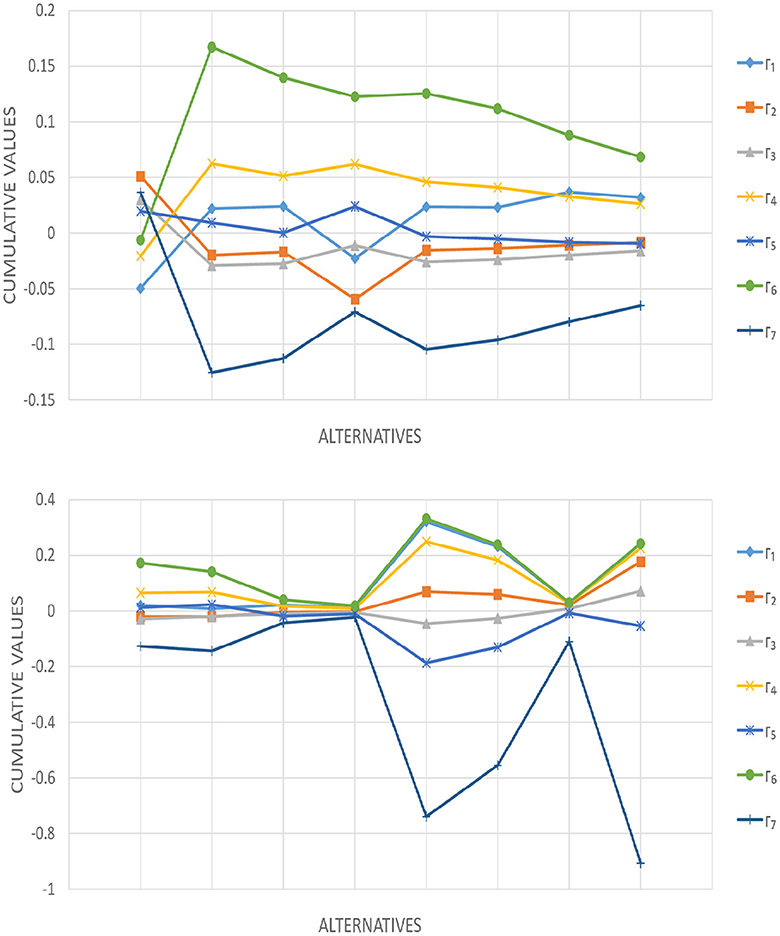
Figure 2. Cumulative values employing the 2TLIVq-ROFWA operator as depicted in Table 13.

6.4 Comparative analysis

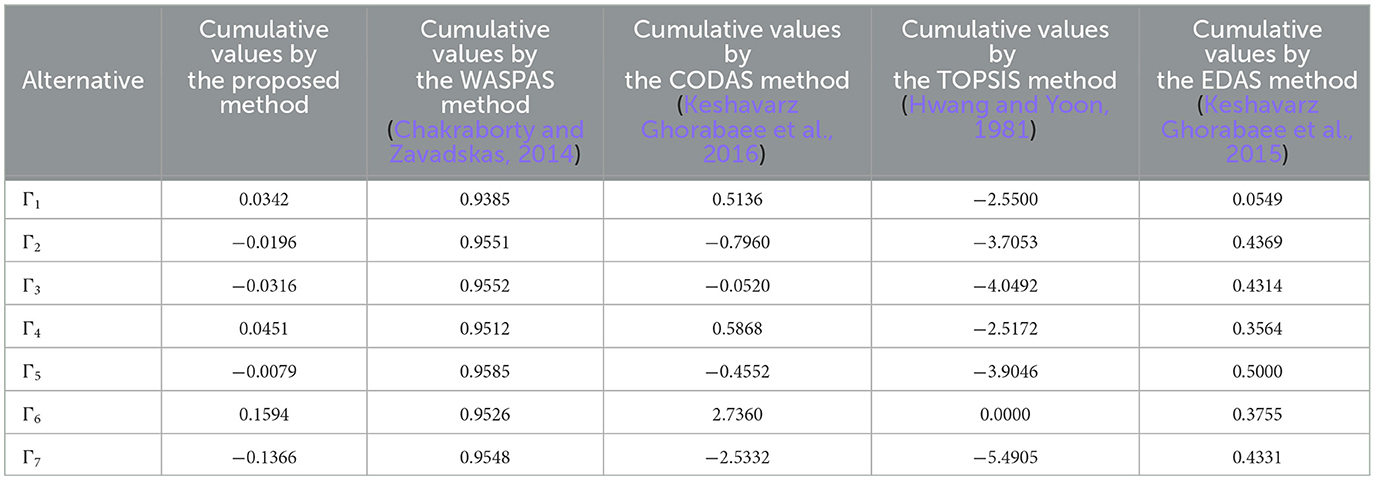
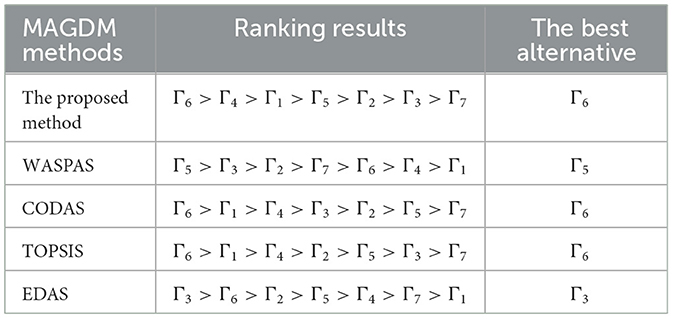
Comparative analysis between the proposed research and the existing literature is the objective of this subsection, with the intent of highlighting the benefits of the new proposed study in relation to the existing theories. In this study, we present a case study and address it using our proposed method in addition to a large number of MAGDM techniques already in use. In response to a variety of practical decision problems, we propose a novel decision strategy based on multiple theories, known as the 2TLIVq-ROFS. In the context of risk decision-making complexities, many existing methodologies must incorporate the psychological dynamics and behavioral aspects of DMs throughout information synthesis and choice analysis. Tables 14, 15 display the 2TLIVq-ROFWA operator's comparative analysis of breast cancer treatment selection utilizing different MAGDM methods. In Table 14, the cumulative values for various treatment options are displayed, with each column representing a unique MAGDM method. Notably, alternative Γ₆ consistently receives the highest cumulative value, whereas the rankings of the remaining alternatives differ across methods. For instance, the proposed method, the CODAS method (Keshavarz Ghorabaee et al., 2016), and the TOPSIS method (Hwang and Yoon, 1981) rank the same alternative as the best, whereas EDAS method (Keshavarz Ghorabaee et al., 2015) and the WASPAS method (Chakraborty and Zavadskas, 2014) produce distinct results, highlighting the significance of the chosen method for treatment selection. Table 15 provides a ranking of each MAGDM method's results to further illustrate these distinctions. According to each technique, the optimal solution is determined. Γ₆ is ranked highest in three methodologies, highlighting its potential as a preferred treatment option. Other alternatives, however, are ranked significantly differently. The EDAS method and WASPAS method distinguish themselves by selecting Γ₃ and Γ₅ as the best options, respectively, highlighting the method's distinctive criteria and decision-making priorities. This comparative analysis emphasizes the impact of the selected MAGDM method on the ranking and selection of breast cancer treatment alternatives. It stresses the significance of understanding the specific criteria and preferences of each method when making decisions in the complex realm of breast cancer treatment. When using MAGDM techniques, researchers and healthcare professionals should carefully consider these variations to ensure that each patient receives the optimal treatment for his or her specific requirements. The visual depiction of comparative analysis results is given in Figure 3.

Table 14

Table 14. Comparison with different MAGDM methods by the 2TLIVq-ROFWA operator.

Table 15

Table 15. Ranking results of comparative analysis.

Figure 3

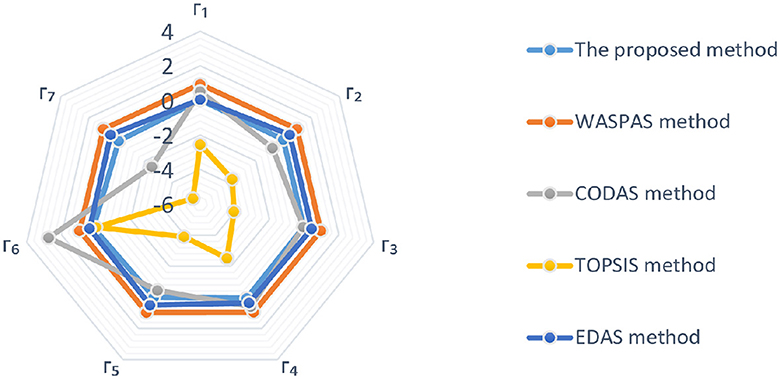
Figure 3. Cumulative values employing different MAGDM methods as depicted in Table 14.

7 Conclusions

Many women worldwide suffer from deadly breast cancer now-a-days. Choosing the optimal course of treatment for each patient can be quite challenging due to the numerous variables and individual preferences at play. To address this complexity, treatment selection for breast cancer can be regarded as a MAGDM problem, in which a group of doctors and DMs evaluate and rank numerous options based on numerous attributes. Utilizing MAGDM techniques can enhance the effectiveness and quality of breast cancer treatment selection decisions. In this study, we introduced the concept of a 2TLIVq-ROFS to assist DMs in handling ambiguous information and express their evaluations in a broader domain. To accomplish this, we proposed a collection of novel aggregation operators, such as the 2TLIVq-ROFWA and 2TLIVq-ROFWJ operators. In addition, by employing 2TLIVq-ROF information, we expanded the MABAC method to address the MAGDM issue. We conducted a case study of breast cancer treatment selection to demonstrate the efficacy and viability of the proposed methodology. In complex decision-making scenarios, the computational outcomes indicate that our MAGDM model is capable of handling ambiguity and uniqueness. A sensitivity analysis is also performed to ascertain whether the effects of the option are affected by varying the parameter q. DMs can gain insight into how this parameter influences results by observing its impact, and can then make informed adjustments as required. The results from the comparison with existing studies indicate that our method can handle the complexity and uncertainty associated with breast cancer treatment selection while still providing a positive outcome for both patients and medical professionals. Although, the proposed approach presents potential benefits in addressing the complexity of treatment selection by incorporating various attributes and preferences, some of its limitations are existed. There is no discussion on the ethical implications and potential biases associated with the use of MAGDM techniques in healthcare decision-making. The proposed approach does not address the challenges or limitations of integrating machine learning and artificial intelligence, including data privacy concerns and algorithmic biases. Future research opportunities may include integrating technologies such as machine learning and artificial intelligence into the MAGDM framework for selecting breast cancer treatments. This integration will increase the precision and efficacy of decision-making processes and contribute to improved patient outcomes. In various areas of healthcare decision-making, the proposed strategy will be extended to more informed choices and can benefit more individuals by discussing ethical implications and potential biases.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

MR: Writing – review & editing, Writing – original draft, Visualization, Validation, Supervision, Software, Resources, Project administration, Methodology, Investigation, Funding acquisition, Formal analysis, Data curation, Conceptualization. AM: Writing – review & editing, Writing – original draft, Visualization, Validation, Supervision, Software, Resources, Project administration, Methodology, Investigation, Funding acquisition, Formal analysis, Data curation, Conceptualization. ANM: Writing – review & editing, Writing – original draft, Project administration, Funding acquisition. IB: Writing – review & editing, Writing – original draft. ZA: Writing – review & editing, Writing – original draft. ZF: Writing – review & editing, Writing – original draft.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frai.2024.1402719/full#supplementary-material

References

Ahemad, F., Khan, A. Z., Mehlawat, M. K., Gupta, P., and Roy, S. K. (2023). Multi-attribute group decision-making for solid waste management using interval-valued q-rung orthopair fuzzy COPRAS. RAIRO Operat. Res. 57, 1239–1265. doi: 10.1051/ro/2023033

Crossref Full Text | Google Scholar

Akram, M., Bibi, R., and Deveci, M. (2023a). An outranking approach with 2-tuple linguistic Fermatean fuzzy sets for multi-attribute group decision-making. Eng. Appl. Artif. Intell. 121, 105–992. doi: 10.1016/j.engappai.2023.105992

Crossref Full Text | Google Scholar

Akram, M., Khan, A., and Ahmad, U. (2023b). Extended MULTIMOORA method based on 2-tuple linguistic Pythagorean fuzzy sets for multi-attribute group decision-making. Gran. Comp. 8, 311–332. doi: 10.1007/s41066-022-00330-5

Crossref Full Text | Google Scholar

Akram, M., Khan, A., Luqman, A., Senapati, T., and Pamucar, D. (2023c). An extended MARCOS method for MCGDM under 2-tuple linguistic q-rung picture fuzzy environment. Eng. Appl. Artif. Intell. 120, 105–892.

Google Scholar

Akram, M., Shah, S. M. U., Al-Shamiri, M. M. A., and Edalatpanah, S. A. (2023d). Extended DEA method for solving multi-objective transportation problem with Fermatean fuzzy sets. Aims Math. 8, 924–961. doi: 10.3934/math.2023045

Crossref Full Text | Google Scholar

Ashouri, M., Hadi-Vencheh, A., and Jamshidi, A. (2023). An interval valued fuzzy complex proportional assessment (IVF-COPRAS) method to solve MCDM problem with an application. J. Decis. Operat. Res. 8, 861–871. doi: 10.22105/dmor.2023.339388.1600

Crossref Full Text | Google Scholar

Atanassov, K. T. (1986). Intuitionistic fuzzy sets. Fuzzy Sets Syst. 20, 87–96. doi: 10.1016/S0165-0114(86)80034-3

Crossref Full Text | Google Scholar

Balaji, S., Arunprasath, T., Rajasekaran, M. P., Vishnuvarthanan, G., and Sindhuja, K. (2023). Computer-aided diagnostic system for breast cancer detection based on optimized segmentation scheme and supervised algorithm. Automatika 64, 1244–1254. doi: 10.1080/00051144.2023.2244307

Crossref Full Text | Google Scholar

Božanic, D., Pamucar, D., Badi, I., and Tešic, D. (2023). A decision support tool for oil spill response strategy selection: application of LBWA and Z MABAC methods. Opsearch 60, 24–58. doi: 10.1007/s12597-022-00605-0

Crossref Full Text | Google Scholar

Camgoz Akdag, H., and Menekse, A. (2023). Breast cancer treatment planning using a novel spherical fuzzy CRITIC-REGIME. J. Intell. Fuzzy Syst. 44, 8343–8356. doi: 10.3233/JIFS-222648

Crossref Full Text | Google Scholar

Chakraborty, S., and Zavadskas, E. K. (2014). Application of WASPAS method in manufacturing decision making. Informatica 25, 1–20. doi: 10.15388/Informatica.2014.01

PubMed Abstract | Crossref Full Text | Google Scholar

Chatterjee, S., and Das, A. (2023a). An ensemble algorithm using quantum evolutionary optimization of weighted type-II fuzzy system and staged pegasos quantum support vector classifier with multi-criteria decision-making system for diagnosis and grading of breast cancer. Soft Comp. 27, 7147–7178. doi: 10.1007/s00500-023-07939-x

Crossref Full Text | Google Scholar

Chatterjee, S., and Das, A. (2023b). An ensemble algorithm integrating consensus-clustering with feature weighting based ranking and probabilistic fuzzy logic-multilayer perceptron classifier for diagnosis and staging of breast cancer using heterogeneous datasets. Appl. Intell. 53, 13882–13923. doi: 10.1007/s10489-022-04157-0

Crossref Full Text | Google Scholar

Colombo, J. A., Akhter, T., Wanke, P., Azad, M. A. K., Tan, Y., Edalatpanah, S. A., et al. (2023). Interplay of cryptocurrencies with financial and social media indicators: An Entropy-weighted neural-MADM approach. J. Operat. Strat. Anal. 1, 160–172. doi: 10.56578/josa010402

Crossref Full Text | Google Scholar

Demir, G., Chatterjee, P., Zakeri, S., and Pamucar, D. (2024). Mapping the evolution of multi-attributive border approximation area comparison method: a bibliometric analysis. Decis. Making Appl. Manag. Eng. 7, 290–314. doi: 10.31181/dmame7120241037

Crossref Full Text | Google Scholar

Farajpour Khanaposhtani, G. (2023). A new multi-attribute decision-making method for interval data using support vector machine. Big Data Comp. Vis. 3, 137–145. doi: 10.22105/bdcv.2023.190406

Crossref Full Text | Google Scholar

Ghorbani, H., Lajmorak, S., Ghorbani, S., Ghorbani, P., Khlghatyan, N., Stepanyan, H., et al. (2023). “Application of a new hybrid machine learning (fuzzy-pso) for detection of breast's tumor,” in 2023 IEEE 21st World Symposium on Applied Machine Intelligence and Informatics (SAMI) (IEEE), 147–154.

Google Scholar

Gupta, V., Gaur, H., Vashishtha, S., Das, U., Singh, V. K., and Hemanth, D. J. (2023). A fuzzy rule-based system with decision tree for breast cancer detection. IET Image Process. 17, 2083–2096. doi: 10.1049/ipr2.12774

PubMed Abstract | Crossref Full Text | Google Scholar

Gurmani, S. H., Garg, H., Zulqarnain, R. M., and Siddique, I. (2023). Selection of unmanned aerial vehicles for precision agriculture using interval-valued q-rung orthopair fuzzy information based TOPSIS method. Int. J. Fuzzy Syst. 25, 2939–2953. doi: 10.1007/s40815-023-01568-0

Crossref Full Text | Google Scholar

Haudi, H. (2024). The impact of digital transformation on consumer behavior and marketing strategies. Int. J. Econ. Literat. 2, 167–179.

PubMed Abstract | Google Scholar

Hernández-Julio, Y. F., Díaz-Pertuz, L. A., Prieto-Guevara, M. J., Barrios-Barrios, M. A., and Nieto-Bernal, W. (2023). Intelligent fuzzy system to predict the wisconsin breast cancer dataset. Int. J. Environ. Res. Public Health 20, 5–103. doi: 10.3390/ijerph20065103

PubMed Abstract | Crossref Full Text | Google Scholar

Herrera, F., and Martínez, L. (2000). An approach for combining linguistic and numerical information based on the 2-tuple fuzzy linguistic representation model in decision-making. Int. J. Uncertainty Fuzziness Knowl. Based Syst. 8, 539–562. doi: 10.1142/S0218488500000381

Crossref Full Text | Google Scholar

Hwang, C. L., and Yoon, K. (1981). Methods for multiple attribute decision-making. Multip. Attrib. Decis. Making 186, 58–191. doi: 10.1007/978-3-642-48318-9_3

Crossref Full Text | Google Scholar

Ismail, J. N., Rodzi, Z., Hashim, H., Sulaiman, N. H., Al-Sharqi, F., Al-Quran, A., et al. (2023). Enhancing decision accuracy in DEMATEL using Bonferroni mean aggregation under Pythagorean neutrosophic environment. J. Fuzzy Extens. Appl. 4, 281–298. doi: 10.22105/jfea.2023.422582.1318

Crossref Full Text | Google Scholar

Jana, C., Garg, H., and Pal, M. (2023). Multi-attribute decision-making for power Dombi operators under Pythagorean fuzzy information with MABAC method. J. Ambient Intell. Humaniz. Comput. 14, 10761–10778. doi: 10.1007/s12652-022-04348-0

Crossref Full Text | Google Scholar

Jin, F., Guo, S., Cai, Y., Liu, J., and Zhou, L. (2023). 2-Tuple linguistic decision-making with consistency adjustment strategy and data envelopment analysis. Eng. Appl. Artif. Intell. 118, 105–671. doi: 10.1016/j.engappai.2022.105671

Crossref Full Text | Google Scholar

Jones, V. A. (2024). Business intelligence solutions for enhanced accounting decision-making in digital transformation. Eng. Sci. Lett. 3, 11–15. doi: 10.56741/esl.v3i01.468

Crossref Full Text | Google Scholar

Joshi, B. P., Singh, A., Bhatt, P. K., and Vaisla, K. S. (2018). Interval valued q-rung orthopair fuzzy sets and their properties. J. Intell. Fuzzy Syst. 35, 5225–5230. doi: 10.3233/JIFS-169806

PubMed Abstract | Crossref Full Text | Google Scholar

Keshavarz Ghorabaee, M., Zavadskas, E. K., Olfat, L., and Turskis, Z. (2015). Multi-criteria inventory classification using a new method of evaluation based on distance from average solution (EDAS). Informatica 26, 435–451. doi: 10.15388/Informatica.2015.57

Crossref Full Text | Google Scholar

Keshavarz Ghorabaee, M., Zavadskas, E. K., Turskis, Z., and Antucheviciene, J. (2016). A new combinative distance-based assessment (CODAS) method for multi-criteria decision-making. Econ. Comp. Econ. Cybern. Stud. Res. 50, 25–44. Available online at: https://etalpykla.vilniustech.lt/handle/123456789/116529

Google Scholar

Khajehkhasan, S., and Fakheri, S. (2020). A new method based on operational strategies for early detection of breast cancers. Innovat. Manag. Operat. Strat. 1, 187–201. doi: 10.22105/imos.2021.266543.1027

Crossref Full Text | Google Scholar

Khan, A. I., Abushark, Y. B., Alsolami, F., Almalawi, A., Alam, M. M., Kshirsagar, P., et al. (2023). Prediction of breast cancer based on computer vision and artificial intelligence techniques. Measurement 218, 113–230. doi: 10.1016/j.measurement.2023.113230

Crossref Full Text | Google Scholar

Kiptum, C. K., Bouraima, M. B., Badi, I., Zonon, B. I. P., Ndiema, K. M., and Qiu, Y. (2023). Assessment of the challenges to urban sustainable development using an interval-valued Fermatean fuzzy approach. Syst. Anal. 1, 11–26. doi: 10.31181/sa1120233

Crossref Full Text | Google Scholar

Krasnov, D., Davis, D., Malott, K., Chen, Y., Shi, X., and Wong, A. (2023). Fuzzy c-means clustering: a review of applications in breast cancer detection. Entropy 25:1021. doi: 10.3390/e25071021

PubMed Abstract | Crossref Full Text | Google Scholar

Lazarashouri, H., and Najafi, S. E. (2024). Enhancing emergency department efficiency through simulation and fuzzy multi-criteria decision-making integration. J. Operat. Strat. Anal. 2, 56–71. doi: 10.56578/josa020106

Crossref Full Text | Google Scholar

Lin, C. J., Wu, M. Y., Chuang, Y. H., and Lee, C. L. (2023). Vector deep fuzzy neural network for breast cancer classification. Sens. Mater. 35, 795–811. doi: 10.18494/SAM4121

Crossref Full Text | Google Scholar

Luqman, A., and Shahzadi, G. (2023). Multi-criteria group decision-making based on the interval-valued q-rung orthopair fuzzy SIR approach for green supply chain evaluation and selection. Gran. Comp. 8, 1937–1954. doi: 10.1007/s41066-023-00411-z

Crossref Full Text | Google Scholar

Mandal, U., and Seikh, M. R. (2023). Interval-valued spherical fuzzy MABAC method based on Dombi aggregation operators with unknown attribute weights to select plastic waste management process. Appl. Soft Comput. 145, 110–516. doi: 10.1016/j.asoc.2023.110516

Crossref Full Text | Google Scholar

Min, S., and Kim, B. (2024). Adopting artificial intelligence technology for network operations in digital transformation. Administr. Sci. 14:70. doi: 10.3390/admsci14040070

Crossref Full Text | Google Scholar

Mohanty, H., and Champati, S. (2023). “A robust classification model using fuzzy logic: successfully prediction of breast cancer patients,” in AIP Conference Proceedings (Vol. 2819, No. 1) (AIP Publishing).

Google Scholar

Nafei, A., Gu, Y., and Yuan, W. (2021). An extension of the TOPSIS for multi-attribute group decision making under neutrosophic environment. Miskolc Math. Notes 22, 393–405. doi: 10.18514/MMN.2021.3332

Crossref Full Text | Google Scholar

Nafei, A., Huang, C. Y., Chen, S. C., Huo, K. Z., Lin, Y. C., and Nasseri, H. (2023). Neutrosophic autocratic multi-attribute decision-making strategies for building material supplier selection. Buildings 13:1373. doi: 10.3390/buildings13061373

Crossref Full Text | Google Scholar

Ozcalici, M. (2022). Asset allocation with multi-criteria decision-making techniques. Decis. Making Appl. Manag. Eng. 5, 78–119. doi: 10.31181/dmame0305102022o

Crossref Full Text | Google Scholar

Pamučar, D., and Ćirović, G. (2015). The selection of transport and handling resources in logistics centers using multi-attributive border approximation area comparison (MABAC). Expert Syst. Appl. 42, 3016–3028. doi: 10.1016/j.eswa.2014.11.057

Crossref Full Text | Google Scholar

Qi, X., Ali, Z., Mahmood, T., and Liu, P. (2023). Multi-attribute decision-making method based on complex interval-valued q-rung orthopair linguistic Heronian mean operators and their application. Int. J. Fuzzy Syst. 25, 1338–1359. doi: 10.1007/s40815-022-01455-0

Crossref Full Text | Google Scholar

Ran, H. (2023). MABAC method for multiple attribute group decision-making under single-valued neutrosophic sets and applications to performance evaluation of sustainable microfinance groups lending. PLoS ONE 18:e0280239. doi: 10.1371/journal.pone.0280239

PubMed Abstract | Crossref Full Text | Google Scholar

Rasoulzadeh, M., Edalatpanah, S. A., Fallah, M., and Najafi, S. E. (2022). A multi-objective approach based on Markowitz and DEA cross-efficiency models for the intuitionistic fuzzy portfolio selection problem. Decis. Making Appl. Manag. Eng. 5, 241–259. doi: 10.31181/dmame0324062022e

Crossref Full Text | Google Scholar

Sarwar, M. (2023). Improved assessment model for health-care waste management based on dual 2-tuple linguistic rough number clouds. Eng. Appl. Artif. Intell. 123, 106–255. doi: 10.1016/j.engappai.2023.106255

Crossref Full Text | Google Scholar

Shakerian, S., Nezhad, Z., Raeiszadeh, M., and Qayumi, M. (2023). Selection of the best contractor by AHP and VIKOR method, a case study of an executive project in the dairy industry. Modern Res. Perform. Eval. 2, 79–90.

Google Scholar

Shang, B., Chen, Z., Ma, Q., and Tan, Y. (2023). A comprehensive mortise and tenon structure selection method based on Pugh's controlled convergence and rough Z-number MABAC method. PLoS ONE 18:e0283704. doi: 10.1371/journal.pone.0283704

PubMed Abstract | Crossref Full Text | Google Scholar

Shastri, R., Pradeep, N., Rao Mangalore, K. K., Rajpal, B., and Prasad, N. (2020). Breast cancer detection using machine learning algorithms. Int. J. Res. Ind. Eng. 9, 235–246. doi: 10.22105/riej.2020.259298.1155

Crossref Full Text | Google Scholar

Singh, L. K., Khanna, M., and Singh, R. (2023). Efficient feature selection for breast cancer classification using soft computing approach: a novel clinical decision support system. Multim. Tools Appl. 83, 43223–43276. doi: 10.1007/s11042-023-17044-8

Crossref Full Text | Google Scholar

Soltanifar, M. (2024). A new interval for ranking alternatives in multi-attribute decision making problems. J. Appl. Res. Ind. Eng. 11, 37–56.

Google Scholar

Sravanthi, V., Annapurna, T., Krishna, V. R., and Jyothi, B. (2023). “STOA based feature selection with improved LSTM model for breast cancer diagnosis in IoT,” in 2023 Fifth International Conference on Electrical, Computer and Communication Technologies (ICECCT). doi: 10.1109/ICECCT56650.2023.10179785

Crossref Full Text | Google Scholar

Tan, J., Liu, Y., Senapati, T., Garg, H., and Rong, Y. (2023). An extended MABAC method based on prospect theory with unknown weight information under Fermatean fuzzy environment for risk investment assessment in BandR. J. Ambient Intell. Humaniz. Comput. 14, 13067–13096. doi: 10.1007/s12652-022-03769-1

PubMed Abstract | Crossref Full Text | Google Scholar

Vidivelli, S., and Devi, S. S. (2023). Breast cancer detection model using fuzzy entropy segmentation and ensemble classification. Biomed. Signal Process. Control 80, 104–236. doi: 10.1016/j.bspc.2022.104236

Crossref Full Text | Google Scholar

Wan, B., Hu, Z., Garg, H., Cheng, Y., and Han, M. (2023). An integrated group decision-making method for the evaluation of hypertension follow-up systems using interval-valued q-rung orthopair fuzzy sets. Comp. Intell. Syst. 9, 4521–4554. doi: 10.1007/s40747-022-00953-w

PubMed Abstract | Crossref Full Text | Google Scholar

Xu, Y. (2023). A two-stage multi-criteria decision-making method with interval-valued q-rung orthopair fuzzy technology for selecting bike-sharing recycling supplier. Eng. Appl. Artif. Intell. 119, 105–827. doi: 10.1016/j.engappai.2023.105827

Crossref Full Text | Google Scholar

Yager, R. R. (2013). Pythagorean membership grades in multicriteria decision making. IEEE Transact. Fuzzy Syst. 22, 958–965. doi: 10.1109/TFUZZ.2013.2278989

PubMed Abstract | Crossref Full Text | Google Scholar

Yager, R. R. (2016). Generalized orthopair fuzzy sets. IEEE Transact. Fuzzy Syst. 25, 1222–1230. doi: 10.1109/TFUZZ.2016.2604005

Crossref Full Text | Google Scholar

Zadeh, L. A. (1965). Fuzzy sets. Inf. Control 8, 338–353. doi: 10.1016/S0019-9958(65)90241-X

Crossref Full Text | Google Scholar

Zadeh, L. A. (1975). The concept of a linguistic variable and its application to approximate reasoning-I. Inf. Sci. 8, 199–249. doi: 10.1016/0020-0255(75)90036-5

Crossref Full Text | Google Scholar

Zorlu, K., and Dede, V. (2023). The geomorphosite assessment by trapezoidal bipolar fuzzy information-based CRITIC-MABAC method. Geoheritage 15:94. doi: 10.1007/s12371-023-00859-0

Crossref Full Text | Google Scholar