Human vs. algorithmic auditors: the impact of entity type and ambiguity on human dishonesty

Introduction: Human-machine interactions become increasingly pervasive in daily life and professional contexts, motivating research to examine how human behavior changes when individuals interact with machines rather than other humans. While most of the existing literature focused on human-machine interactions with algorithmic systems in advisory roles, research on human behavior in monitoring or verification processes that are conducted by automated systems remains largely absent. This is surprising given the growing implementation of algorithmic systems in institutions, particularly in tax enforcement and financial regulation, to help monitor and identify misreports, or in online labor platforms widely implementing algorithmic control to ensure that workers deliver high service quality. Our study examines how human dishonesty changes when verification of statements that may be untrue is performed by machines vs. humans, and how ambiguity in the verification process influences dishonest behavior.

Method: We design an incentivized laboratory experiment using a modified die-roll paradigm where participants privately observe a random draw and report the result, with higher reported numbers yielding greater monetary rewards. A probabilistic verification process introduces risk of identifying a lie and punishment, with treatments varying by verification entity (human vs. machine) and degree of ambiguity in the verification process (transparent vs. ambiguous).

Results: Our results show that under transparent verification rules, cheating magnitude does not significantly differ between human and machine auditors. However, under ambiguous conditions, cheating magnitude is significantly higher when machines verify participants' reports, reducing the prevalence of partial cheating while leading to behavioral polarization manifested as either complete honesty or maximal overreporting. The same applies when comparing reports to a machine entity under ambiguous and transparent verification rules.

Discussion: These findings emphasize the behavioral implications of algorithmic opacity in verification contexts. While machines can serve as effective auditors under transparent conditions, their black box nature combined with ambiguous verification processes may unintentionally incentivize more severe dishonesty. These insights have practical implications for designing automated oversight systems in tax audits, compliance, and workplace monitoring.

1 Introduction

Human-machine interaction is ubiquitous in today's world, driven by increasing automation and the growing reliance on algorithms and artificial intelligence (AI) in decision-making. AI, algorithmic advisors, and computerized decision support systems are employed in various domains, where they often outperform human judgment. Notable examples include medicine and healthcare (Cheng et al., 2016; Gruber, 2019), public administration (Kouziokasa, 2017; Bignami, 2022), autonomous driving (Levinson et al., 2008), human resource management (Highhouse, 2008), investment decisions (Tao et al., 2021), insurance claim processing (Komperla, 2021), tax audits (Black et al., 2022; Baghdasaryan et al., 2022), and criminal jurisdiction (Kleinberg et al., 2018), among others. At the same time, demographic shifts and skilled labor shortages present pressing societal challenges, which are increasingly addressed through algorithmic and AI-based automation.

Despite algorithms often demonstrating superior predictive accuracy compared to human forecasters, people frequently prefer human input when given a choice between algorithmic and human forecasts (Dietvorst et al., 2015). Likewise, individuals regularly disregard algorithmic advice in favor of their own judgment, even when doing so is not rational and leads to inferior outcomes (Burton et al., 2019; Jussupow et al., 2024). Conversely, the perceived reliability, consistency, and objectivity of algorithms can lead to over-reliance on their advice, particularly in structured and predictable tasks (Klingbeil et al., 2024; Banker and Khetani, 2019). This duality in perception highlights the complexity of human attitudes toward machine-supported decision-making, as levels of algorithm acceptance and adherence typically vary widely across individuals and contexts (Fenneman et al., 2021).

Many of the fields of application mentioned at the beginning inherently involve moral considerations to which individual differences in the perception of humans vs. machines pertain. When algorithms act as ethical advisors, an asymmetry in their impact becomes apparent: algorithmic advice appears largely unsuccessful in promoting honest behavior, but is able to facilitate dishonest behavior (Leib et al., 2024). Similarly, AI agents can function as enablers of unethical behavior in decisions that can be delegated by offering individuals a means to outsource or share the moral load imposed by unethical behavior (Köbis et al., 2021; Bartling and Fischbacher, 2012). Regarding honesty, (Cohn et al. 2022) find significantly more cheating when individuals interact with machines than with humans, regardless of whether the machine has anthropomorphic features. Dishonest individuals actively prefer machine interaction when given an opportunity to cheat. Meanwhile, people cheat less in the presence of a robot (Petisca et al., 2022) or digital avatar (Mol et al., 2020) if it signals awareness of the situation than when being alone, even when it cannot intervene.

However, what happens to human dishonest behavior if machines can identify when someone lies or makes an untrue statement? Does behavior potentially change because of the machine entity itself or because of the ambiguity machines create through their “black box” nature? Concurrent with the tendency to use AI as advisors, algorithms are also used to monitor human conduct. For example, there is growing implementation of algorithmic systems in institutions, particularly in tax enforcement and financial regulation, to help monitor and verify misreports (e.g., Faúndez-Ugalde et al., 2020; Braun-Binder, 2020). It is therefore not surprising that companies started to strategically adjust language complexity, tone, and structure of written reports to optimize machine readability, ensuring that these systems accurately capture key parameter disclosures for various stakeholders including authorities and investors (Cao et al., 2023). Further, online labor platforms widely implement algorithmic control to ensure that workers consistently deliver high quality services (Wang et al., 2024). Despite the prevalence and impact of this form of human-machine interaction, we have limited understanding of how human dishonest behavior is shaped when their actions are subject to machine verification. We therefore ask the following research questions:

How does human dishonesty change when verification of statements that may be untrue is performed by machines vs. humans, and to what extent does ambiguity in the verification process influence dishonest behavior?

We hereby make two important contributions. First, our research extends findings from the dishonesty literature by investigating scenarios where machines serve not as advisors or partners but as entities that verify whether statements are true or not, an increasingly common human-machine interaction context. Generally, despite the topics of lying and cheating having been extensively studied in experimental psychology and behavioral economics, most research designs lack the real-world element of potential sanctions. This gap has recently been highlighted by a collaborative effort of leading researchers in the field (Shalvi et al., 2025), who also emphasize the growing importance of accounting for emerging technological advancements. Second, while institutions such as tax authorities have increasingly implemented algorithmic systems to identify suspicious patterns in tax reports, our research clarifies whether the use of such machines creates a deterrence effect that reduces dishonesty. These insights may also provide valuable information for organizations implementing monitoring systems, where research regularly shows that electronic surveillance systems are often perceived negatively by employees and can even be associated with increased employee intentions to engage in counterproductive workplace behaviors (e.g., Yost et al., 2019).

To answer our research questions, we conduct an incentivized one-shot laboratory experiment that employs a modified version of the die-roll paradigm introduced by (Fischbacher and Föllmi-Heusi 2013). Participants privately observe a random draw and report its outcome, with monetary payoffs tied to the reported number—creating an opportunity to profit from dishonesty. We introduce a two-stage verification process in which reports that may turn out to not coincide with the truth are sanctioned with a substantial monetary penalty. By incorporating elements of risk and uncertainty into the traditional dishonesty paradigm, our methodological approach maintains a generalizable framework that intentionally abstracts from domain-specific settings such as tax evasion or corruption. While these contexts share similar mechanisms of identifying and sanctioning deviant behavior, they frequently involve additional motivational factors such as civic duty, moral obligations, and imposing negative externalities on others that could confound the fundamental relationship between dishonest behavior and verification entity that we aim to isolate. We vary both the verification entity (Human vs. Machine) and the level of ambiguity involved in processing the die-roll reports (Black box vs. Transparent) to compare how participants' dishonest behavior is affected by who verifies their reports and how transparent the verification process is. We control for factors such as risk preferences, attitudes toward ethical dilemmas, perceived closeness to the auditor, and technology affinity.

The proceeding paper is structured as follows: Section 2.1 reviews prior research on perceptions of algorithmic entities, human dishonesty, and their intersection. With this context established, two hypotheses are derived for the experimental study. Subsequently, Section 2.2 outlines the experimental design and procedure in detail. Section 3 presents descriptive results, followed by hypothesis testing and multivariate regression analysis. Finally, Section 4 offers an interpretation of the findings and concludes with a discussion of the study's limitations and implications.

2 Materials and methods

2.1 Related literature and derivation of hypotheses

2.1.1 Literature overview

2.1.1.1 Algorithm perception

Recent advances in human-machine interaction research increasingly focus on how individuals perceive algorithms and AI, particularly in the context of algorithm aversion and algorithm appreciation (e.g., Mahmud et al., 2022; Jussupow et al., 2024; Dietvorst et al., 2015, 2018; Castelo et al., 2019; Logg et al., 2019; Fuchs et al., 2016).¹ Within this literature, the term algorithm is often used as a broad synonym, encompassing various technological systems, including decision support systems, automated advisors, robo-advisors, digital agents, machine agents, forecasting tools, chatbots, expert systems, and AI-generated decisions (Mahmud et al., 2022).² In line with this, we use the term “algorithm” to denote any technological system that applies a fixed stepwise process to decision-making that may or may not include stochastic elements (Dietvorst and Bharti, 2020).

Generally, attitudes toward algorithms vary widely among individuals. These attitudes are not fixed, but rather context-dependent, reflecting both algorithm aversion and algorithm appreciation (Fenneman et al., 2021; Hou and Jung, 2021). Algorithm aversion describes the tendency—whether conscious or unconscious – to resist relying on algorithms, even when they are demonstrably outperform human judgment. People frequently reject algorithmic advice in favor of their own or other humans' opinions, despite being aware of the algorithm's superior accuracy and incurring material costs for doing so (Dietvorst et al., 2015, 2018; Mahmud et al., 2022; Jussupow et al., 2024). Although people frequently attribute near-perfect performance to algorithms (Dzindolet et al., 2002), they are quicker to lose trust in them following errors, regardless of the error's context or severity (Renier et al., 2021). In contrast, equivalent human mistakes are more readily excused (Madhavan and Wiegmann, 2007). Conversely, algorithm appreciation refers to situations in which individuals are more likely to follow identical advice when it originates from an algorithm rather than a human, often displaying greater confidence in such recommendations despite having little to no insight into the algorithm's internal workings (Logg et al., 2019). This effect is especially pronounced when the algorithm signals expertise (Hou and Jung, 2021). A systematic literature review by (Mahmud et al. 2022) concludes that algorithm acceptance varies along several demographic lines: older individuals and women tend to show greater aversion, while higher education is associated with greater acceptance. Moreover, algorithm aversion is often more pronounced among domain experts (Logg et al., 2019; Jussupow et al., 2024). Similarly, as highlighted by (Chugunova and Sele 2022) in their review of 138 experimental studies on human interaction with automated agents in different decision-support roles, contextual factors, performance expectations and how decision-making responsibilities are shared between humans and automated systems all constitute important factors that systematically affect human acceptance of automated agents in decision-making.

Both these directions of biased algorithm perception may result in economic inefficiencies. On the one hand, algorithms, despite not being entirely free of errors, consistently provide more accurate decisions than human counterparts (Dawes et al., 1989; Logg et al., 2019). Yet, in decisions under risk and uncertainty, individuals often disregard even high-quality algorithmic advice due to heightened sensitivity to potential errors, leading to suboptimal outcomes (Dietvorst and Bharti, 2020; Prahl and Swol, 2017; Jussupow et al., 2024). This reluctance is particularly evident in morally salient domains – such as medicine, criminal justice, or military contexts—where algorithmic input is frequently rejected even when it aligns with human decisions and produces efficient outcomes (Bigman and Gray, 2018). On the other hand, unreflective algorithm appreciation may results in over-reliance, where individuals defer to algorithmic recommendations despite contradictory contextual knowledge or better judgment. This can lead to suboptimal decisions with unintended consequences for both the decision-maker and affected third parties (Klingbeil et al., 2024). For example, (Banker and Khetani 2019) find that consumers often rely too heavily on algorithmic recommendations, leading to inferior purchasing decisions. Similarly, (Krügel et al. 2022) demonstrate that individuals' decision-making in ethical dilemmas can be manipulated through overtrust in AI. Two key factors determining an individual's unique degree of algorithm adherence, i.e., their inclination to either use or avoid algorithms, are anticipated efficacy and trust placed in the algorithmic system (Fenneman et al., 2021). Perceived efficacy appears to have a stronger positive influence on willingness to rely on algorithms than discomfort or unease associated with using them (Castelo et al., 2019). In terms of trust, similar factors as in human relationships—perceived competence, benevolence, comprehensibility, and responsiveness—also apply to automation. Additionally, perceptions specific to technology, such as reliability, validity, utility, and robustness, play an important role (Hoffman et al., 2013).

2.1.1.2 Human dishonesty

People lie and cheat for their own benefit or for the benefit of others (Abeler et al., 2019; Jacobsen et al., 2018). However, despite being able to maximize their monetary payoffs, people often abstain from lying and cheating, for various reasons, e.g., general preferences for truth-telling, intrinsic lying costs, lying aversion, emotional discomfort and social image concerns (Abeler et al., 2014, 2019; Bicchieri and Xiao, 2009; Khalmetski and Sliwka, 2019). Additionally, lying behavior differs in magnitude, distinguishing between full liars (i.e., lying to the maximum extent possible), partial liars (i.e., exaggerating the actual outcome but not to the maximum), and fully honest individuals (Fischbacher and Föllmi-Heusi, 2013; Gneezy et al., 2018). Fittingly, previous experimental research (either in the lab or field) finds a considerable variance in cheating behavior among individuals with the opportunity to do so. Observed proportions of fully honest decision-making usually range between 40 (Fischbacher and Föllmi-Heusi, 2013) and close to 70 percent (Peer et al., 2014; Djawadi and Fahr, 2015; Gneezy et al., 2018), while (Abeler et al. 2014) observe close to no cheating at all. The large-scale meta-study by (Gerlach et al. 2019) finds cheating rates of approximately 50% across common experimental lying and cheating settings (sender-receiver games, die-roll tasks, matrix tasks). Meanwhile, similar heterogeneity can be found for the respective degree of dishonesty, as fractions of 2.5% and 3.5% lying to the maximum extent possible are observed by (Shalvi et al. 2011) and (Peer et al. 2014) respectively, while around 20% of individuals lie to the maximum extent possible in (Fischbacher and Föllmi-Heusi 2013). (Gneezy et al. 2018) find that up to 47% of subjects engage in dishonest behavior. Among those who lie, up to 91% do so to the maximum extent possible, with this proportion varying according to the specific reporting mechanism and the availability of opportunities to cheat. As shown in (Gerlach et al. 2019), the degree of cheating generally appears to vary considerably with personal and situational factors.

The possibility of lying and cheating in (nearly) all domains of human-machine interaction mentioned above imposes ethical challenges and financial costs to both businesses and society. (Cohn et al. 2022) find that individuals are more likely to engage in dishonest behavior when interacting with a machine rather than a human, regardless of whether the machine exhibits human-like characteristics. Moreover, individuals with an intention to cheat tend to prefer interacting with machines over humans. This related evidence suggests greater dishonesty when machines verify statements. However, there is also a substantial body of related literature in the domain of lie detection, which examines how accurately human judgment assesses whether the sender of a message (e.g., another person) lies or tells the truth (e.g., Vrij, 2000; Balbuzanov, 2019; Ioannidis et al., 2022). Various studies suggest that humans exhibit limited accuracy in identifying deception, with their judgments of others' truthfulness barely surpassing random guessing (Konrad et al., 2014; von Schenk et al., 2024; Bond and DePaulo, 2006). This indirect evidence would suggest that dishonesty should be more pronounced when humans verify statements. Thus, the conflicting predictions from the related dishonesty and lie detection literature necessitates empirical investigation of our specific context. Notably, our research differs substantially from the lie detection literature. Our focus is not on assessing the accuracy with which humans or machines judge whether a person who uses different facial expressions or words lies or tells the truth. Instead, our focus is on verifying a given statement against objective truth based on a predefined set of procedural steps that contain probabilistic elements leading to judgment. We examine how the sender of the statement changes behavior when humans vs. machines perform identical verification procedures, and whether transparency regarding the rules governing the verification process influences the sender's behavior.

2.1.2 Hypotheses

Referring to the literature on algorithm aversion and appreciation, it becomes evident that in numerous daily and economic contexts, functionally equivalent actions performed by humans and machines can be differently perceived by human recipients. For the examination of verifying statements and potentially sanctioning dishonest behavior, there also exist competing arguments regarding whether dishonesty rates might increase or not when machines rather than humans verify the statements' truthfulness.

On the one hand, algorithmic decisions are usually being perceived as more objective, consistent and less error-prone (Dzindolet et al., 2002, 2003; Renier et al., 2021), with machines being conceptualized as rigid rule-followers that usually lack affective capacities (Haslam, 2006; Bigman and Gray, 2018; Gogoll and Uhl, 2018; Niszczota and Kaszás, 2020). Referring to the related lie detection literature, as humans are shown to display limited accuracy in correctly judging whether a person lies or tells the truth (e.g., Serra-Garcia and Gneezy, 2025), this may also lead to perceptions that humans are worse in verifying statements than machines. This perception may be particularly pronounced in our context, as research suggests that human accuracy in detecting lies is generally lower than their ability to detect the truth (Holm, 2010). Human individuals intending to engage in dishonest behavior may therefore prefer human verification of their reports, anticipating a higher chance of avoiding discovery of their untrue statement and subsequent sanctions due to perceived limitations in human monitoring capabilities. Moreover, individuals may be more likely to act dishonestly when humans verify their statements because they believe humans exercise discretionary judgment based on empathy or fairness considerations. Such perceptions have been observed particularly in morally charged contexts (Dietvorst et al., 2015; Mahmud et al., 2022; Jauernig et al., 2022).

On the other hand, (Chugunova and Sele 2022) show in their review that human interactions with algorithms are generally less emotional, more rational, and less affected by social concerns than interactions with other humans. The findings reported in (Cohn et al. 2022) about the preference for interacting with machines when given an opportunity to cheat is attributed to social image concerns in interactions between humans, which have been previously identified as a key inhibitor of dishonesty (Abeler et al., 2019; Khalmetski and Sliwka, 2019). Similar findings are reported by (Biener and Waeber 2024), who observe greater honesty when participants report the outcomes of unobserved, payoff-relevant random draws to a human rather than a chatbot. The degree of perceived agency, as well as considerations of social image and norms, appear to drive this difference. Social image concerns represent a plausible factor in our setting as well. Being caught and sanctioned by another human may carry higher reputational consequences for the individual than when such identification occurs through algorithmic means, as machines are less likely to be perceived as forming judgments about character or moral worth. Consistent with this, (LaMothe and Bobek 2020) find that people are more willing to misreport to a computer software than to a human professional in a tax compliance context and show that this effect is driven by the reduced sense of social presence when interacting with machines. This asymmetry would suggest that algorithmic verification systems may inadvertently facilitate dishonest behavior by lowering the social costs that typically deter such conduct when human oversight is present. Given these competing arguments, we formulate our first hypothesis in a conservative manner without specifying the direction of potential behavioral differences:

Hypothesis 1: Human dishonest behavior will differ when their statements' truthfulness is verified by humans or machines.

As technological trends suggest that machines will increasingly be employed for automated verification processes, our second hypothesis focuses on machines as verification entities. Beyond psychological, biological, and ethical dimensions, perceptual differences between humans and machines are typically rooted in technological characteristics, where a central debate concerns whether algorithmic systems should operate through transparent rules or be deliberately kept ambiguous. There are indications that this discussion is also relevant for the human-machine interaction in our setting. As algorithms, by nature, tend to be opaque rather than transparent, they are frequently perceived as “black boxes” that convert some type of input into some type of output without revealing their internal logic (Burrell, 2016; Tschider, 2020). Commonly, humans neither understand nor are aware of how algorithms function, which constitutes a major reason for them rejecting algorithms and their advice (Yeomans et al., 2019; Dzindolet et al., 2002; Kayande et al., 2009). From the perspective of advice-taking, “opening the black box” through increasing transparency, accessibility, explainability, interactivity and tunability has been widely advocated to foster trust in and reduce aversion toward algorithms (Sharan and Romano, 2020; Chander et al., 2018; Holzinger et al., 2017; Litterscheidt and Streich, 2020; Shin, 2020).

However, it has been shown that even if an algorithm's underlying logic is disclosed to the decision-maker, it may remain unintelligible, especially to non-experts (Önkal et al., 2009). Decision context also plays a crucial role. (Sutherland et al. 2016) find that humans are more inclined to rely on algorithms in uncertain environments. Contrastingly, (Longoni et al. 2019) report greater aversion to algorithmic decision-making in high-stakes environments rife with uncertainty such as healthcare. These mixed findings reflect a distinction in how humans perceive decisions under ambiguity (i.e., uncertainty) differently from decisions under risk, where potential outcomes and related probabilities are known (Ellsberg, 1961; Einhorn and Hogarth, 1986; Fox and Tversky, 1995; Chow and Sarin, 2001). The influence of an algorithm's black box nature specifically on human dishonest behavior is therefore not straightforward. Under transparent verification rules, dishonesty may reflect a rational cost-benefit analysis based on known probabilities, on the basis of which partial cheating may reflect a rational outcome. Under ambiguity, however, where the likelihood of being caught and punished is unknown, such estimates become difficult. Therefore, transparency might actually encourage more dishonesty compared to an ambiguous verification process, as individuals can better assess these risks. In contrast, when probability parameters for identifying untrue statements are unavailable, ambiguity may lead individuals to adopt an “all-or-nothing” strategy: either being fully honest to avoid any negative consequence or fully dishonest as uncertainty about being identified as a liar applies equally to all untrue statements. In this vein, it is plausible to assume that if an individual decides to cheat under ambiguity they will do so more likely to the maximum extent possible. Whether the distribution under ambiguity consists of more honest than dishonest behavior is also not entirely clear. Literature has shown that ambiguity may intensify individual risk preferences (Ghosh and Ray, 1997) and as most individuals are assumed to be risk-averse, this could result in a higher proportion of honest behavior. Conversely, ambiguity may also enable greater self-justification for dishonest behavior (e.g., Pittarello et al., 2015).

In summary, individual dishonest behavior is likely not only affected by the nature of the verification entity itself but also by whether machines operate the verification process under transparent or non-transparent rules. As there are convincing arguments for both more and less dishonest behavior under each rule type, we refrain from a directional prediction in formulating our second hypothesis:

Hypothesis 2: Human dishonest behavior will differ when their statements' truthfulness is verified by machines under transparent or undisclosed rules.³

2.2 Experiment

We conducted a one-shot, incentivized laboratory experiment in which participants entered a prize draw with a potential payoff of up to €90. The final payoff depended on each subject's decision and the outcomes of up to two lotteries. Only one winner was drawn per session, in line with a random incentive system—a well-established approach in experimental economics that has been shown to produce similar behavior as under deterministic payoff schemes (Charness et al., 2016; Camerer and Hogarth, 1999; Bolle, 1990; Tversky and Kahneman, 1981).

2.2.1 Experimental design

The experiment comprised two main parts: the Choice Part and the Verification Part.

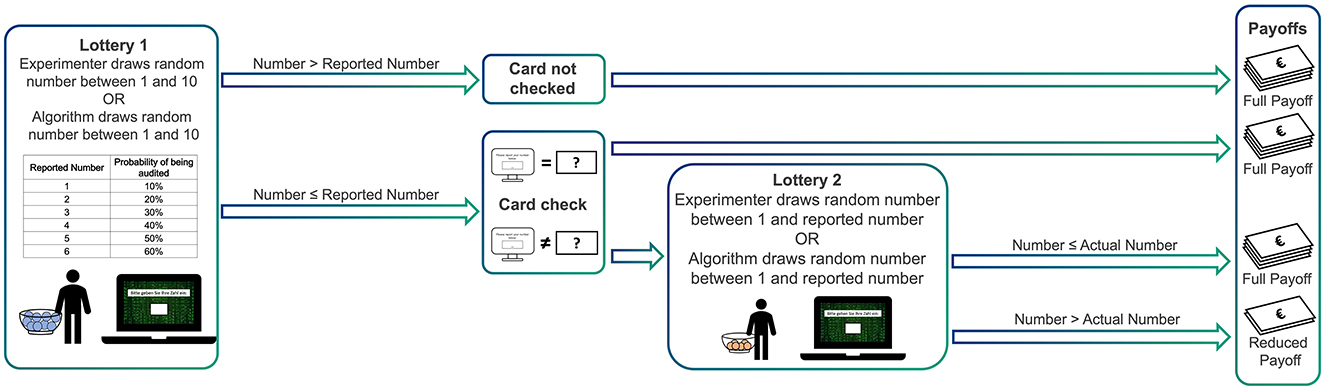
In the Choice Part, illustrated in Figure 1, subjects drew exactly one card randomly from an urn containing 100 cards numbered between 1 and 6. Subsequently, they confidentially reported their drawn number via a computer interface. Importantly, the reported number—in conjunction with Verification Part results—would later determine the prize payoff for one randomly selected winner, calculated as the reported number multiplied by €15 (payoff range: €15 to €90). This setup created the opportunity for subjects to increase their potential payoff by overreporting the drawn number. After submitting their report, participants completed a series of questionnaires (see Section 2.2.3), before the prize winner was determined.

Figure 1

Figure 1. Overview of the Choice Part of the experiment (all participants).

In the Verification Part, the winner underwent a verification procedure comprising up to two lotteries:

• In Lottery 1, a number between 1 and 10 was randomly drawn. If this number was greater than the subject's reported number, no additional check occurred, and the full payoff (reported number × €15) was paid. If the number was less than or equal to the reported number, the subject's actual drawn card was checked.

• In the check, if the reported and actual numbers matched, the prize winner received the full payoff.

• If they mismatched, Lottery 2 was triggered: An urn containing numbers from 1 up to the reported number was used to randomly draw one number. If this drawn number was less than or equal to the subject's actual number, the price winner still received the full payoff. Otherwise, the payoff was reduced to the actual number multiplied by €7.50 (payoff range: €7.50 to €37.50).

Thus, the verification procedure incorporated two central design features. First, the probability of a card check increased with the magnitude of the reported number – similar to materiality thresholds in accounting, where more conspicuous reports are subject to greater scrutiny. Second, the probability of punishment, conditional on being checked, increased with the discrepancy between the reported and actual number. This mechanism allowed subjects to potentially receive the full payoff despite overreporting, thereby mimicking discretionary tolerance in real-world verifications, where minor deviations may be overlooked while larger discrepancies are more likely to result in sanctions.

The structure of the Verification Part is illustrated in Figure 2.

Figure 2

Figure 2. Overview of the Verification Part of the experiment (only prize draw winner).

Theoretically, for a risk-neutral decision-maker, the payoff-maximizing strategy is to always report a 6, regardless of the actual number drawn. The design of Lottery 2 ensured that cheating of equal magnitude carried identical punishment probabilities—for instance, overstating a 3 as a 5 was punished with the same likelihood as overstating a 2 as a 4. Meanwhile, the likelihood of punishment increased with the extent of the misreport: for example, if two subjects both reported a 6, the subject who actually drew a 2 faced a higher probability of being penalized than one who drew a 5. The formal derivation of this utility function is provided in the Supplementary Table S1.

2.2.2 Treatment conditions

We implemented four experimental treatments: Human (H), Machine (M), Human Black Box (HB), and Machine Black Box (MB). In the Human treatment, the verification process was conducted by a human agent (i.e., the experimenter), whereas in the Machine treatment, it was executed by a computerized, rule-based algorithm. To emphasize the verification entity's role, both were visually represented using pictographs in the instructions (see Supplementary Figure S1). Procedures in the black box versions (HB and MB) mirrored their respective non-black box treatments (H and M), except that the verification rules were not disclosed to participants.

In the Human treatments, the lotteries of the verification part were physically implemented using numbered balls drawn from urns. In the Machine treatments, the process was simulated by a computer algorithm, with visual feedback (e.g., animations; see Supplementary Figures S2–S4) provided to convey the impression of data processing. Critically, the underlying verification rules and their associated probabilities were held constant across all treatments; only the entity who conducted the process (human vs. machine) varied.

In the black box conditions, the exact same procedures were applied (verification rules and probabilities remained identical). However, subjects were only informed that a human or machine would decide whether a card check would occur and, in the case of a mismatch, whether the payoff would be reduced. To reflect this lack of procedural transparency, the verification steps were referred to as “Decision 1” and “Decision 2” in the instructions.

In all treatments, while participants were informed the urn contained numbers 1–6, they were not told the actual distribution. The true composition of the urn was 95 cards displaying the number 2, while the numbers 1, 3, 4, 5, and 6 were each represented by a single card. This design ensured that most participants would draw a 2, allowing for individual-level analysis of dishonest behavior and increasing opportunities for overreporting. It would also largely prevent reduction of the sample size for the analysis due to subjects drawing a 6, which left them no opportunity to be dishonest. After each session, the remaining cards in the urn were counted to infer the actual distribution of numbers drawn. If all five non-2 cards remained, any report higher than 2 could be clearly identified as dishonest. If one or more of the five non-2 cards had been drawn, one observation with a report of a 6 would be randomly excluded from the dataset per card drawn, to obtain a conservative estimate of dishonest behavior.

This approach did not disadvantage any participant, as the distribution of cards was not disclosed in the instructions. The decision to equip the urn with a majority of cards numbered with a “2” instead of a “1” was made to avoid triggering “revenge cheating” (i.e., retaliation due to receiving the lowest possible draw) and to ensure participants faced a meaningful trade-off between honesty and financial gain. By drawing a “2” with the highest probability, truthful reporting would yield a €30 payoff for the prize winner, which is already substantial for an experiment participation of around 45-minutes, but could potentially be tripled through dishonest reporting. Moreover, a payoff-maximizing subject's utility function should not depend on the number drawn.

We note that omission of information about the exact card distribution in our experiment allowed us to collect individual-level data on dishonest behavior, which is rare in the literature yet important in real-life and would be prohibitively difficult to gather without this design feature.⁴ Dishonesty research has often relied on approaches that withhold certain information, or introduce ambiguity in their framing to create opportunities for participants to act dishonestly, for example, by employing unsolvable or overly time-consuming tasks for which a subject's claim to have solved them can automatically be identified as untruthful (Kaushik et al., 2022; Daumiller and Janke, 2019; Eisenberger and Shank, 1985). Other indirect measures of individual level dishonesty include using copy paper to track and compare actual to reported performance in a task (Ruedy and Schweitzer, 2010) or have a computerized random draw automatically recorded (Gneezy et al., 2018; Abeler et al., 2019).

2.2.3 Experimental procedure

The experiment was conducted in December 2023 at the Business and Economic Research Laboratory (BaER-Lab) at Paderborn University and computerized using oTree (Chen et al., 2016). Subjects were recruited via the online recruiting system ORSEE (Greiner, 2015) and were only allowed to participate in one session. In total, ten sessions were run (Human: 3, Machine: 3, Human Black Box: 2, Machine Black Box: 2). Each session lasted 30–45 min.

Participants were randomly assigned to individual computer workplaces in cubicles to ensure privacy and were instructed not to communicate during the session. After receiving written instructions (see Sections 1 and 2.2 in the Supplementary material) and being given time to read them carefully, participants completed extensive comprehension checks (see Section 1.1 in the Supplementary material) to ensure a sufficient understanding of the experimental rules and payoff conditions. They could only proceed after answering all questions correctly. Consequently, subjects were, at least implicitly, aware of the opportunity to misreport before making any decisions in the experiment.

The Choice Part began once all subjects had successfully completed the comprehension checks. The experimenter moved from cubicle to cubicle, presenting an urn containing the number cards to each subject. After the drawing process was completed, the experiment automatically advanced to the reporting screen, where subjects entered their reported number. To encourage thoughtful decision-making, participants were not subjected to any time limit.

After confirming their choice, subjects completed a series of questionnaires (see Section 1.2 in the Supplementary material). First, they were asked whether they generally preferred a human or a machine to perform the verification process. Second, subjects were asked which of the two entities they generally perceived as more error-prone and which they perceived to have greater discretion, in other words, the ability to make decisions based on one's own judgment. Subsequently, subjects answered standardized questionnaires on affinity for technology interaction (Franke et al., 2018), attitudes toward ethical dilemmas (adapted from Blais and Weber, 2006), a pictorial measure of interpersonal closeness (adapted for inter-entity comparison) [Schubert and Otten, 2002 based on (Aron et al. 1992)], the general risk preference measure by (Dohmen et al. 2011), as well as demographic questions.

Once all questionnaires were completed, one prize winner was randomly selected using the cubicle numbers. Non-winning participants received a fixed payment of €7.50⁵ in cash to compensate for their participation time and were then dismissed.

The Verification Part was conducted privately with the winner to preserve anonymity and minimize social influence (Bolton et al., 2021).⁶ The two lotteries were implemented based on the entity type of the respective treatment, following the procedure described in Section 2.2.1. The winner received their (full or reduced) payoff in cash, concluding the session.

3 Results

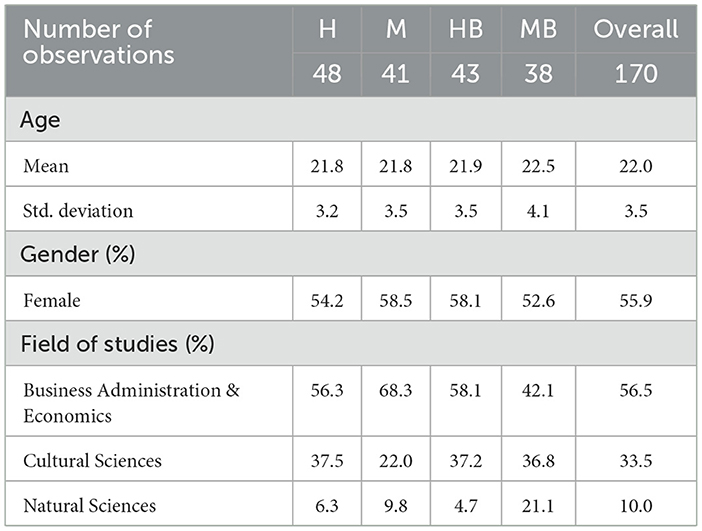
In total, one-hundred-seventy (N = 170) student subjects participated in the experiment. Of these, 48 were randomly assigned to the Human treatment (H), 41 to the Machine treatment (M), 43 to the Human Black Box treatment (HB), and 38 to the Machine Black Box treatment (MB) respectively. In the analysis, each subject constitutes one independent observation in the analysis. An overview of demographic characteristics is provided in Table 1. Participants were, on average, 22 years old, with ages ranging from 18 to 36. Women constituted 56% of the sample, and gender distribution did not differ significantly between treatments [Pearson χ²(3) = 0.43, p = 0.935]. Multiple fields of study were represented, with Business Administration & Economics (56.5%) being the most common. The distribution of fields of study did not differ significantly between treatments [Pearson χ²(6) = 11.14, p = 0.084].

Table 1

Table 1. Demographic statistics.

3.1 Dishonest behavior

Similarly to (Djawadi and Fahr 2015), our design enables a direct and relatively precise measurement of dishonest behavior—in contrast to prior experimental studies that infer dishonesty by comparing reported outcomes to theoretical distributions (see e.g., Abeler et al., 2014; Hao and Houser, 2008; Fischbacher and Föllmi-Heusi, 2013; Shalvi et al., 2011; Jacobsen and Piovesan, 2016) – by comparing the distribution of numbers drawn with the distribution of numbers reported. We use two dependent variables to measure cheating behavior: frequency and magnitude of overreporting, with the primary focus on the latter.

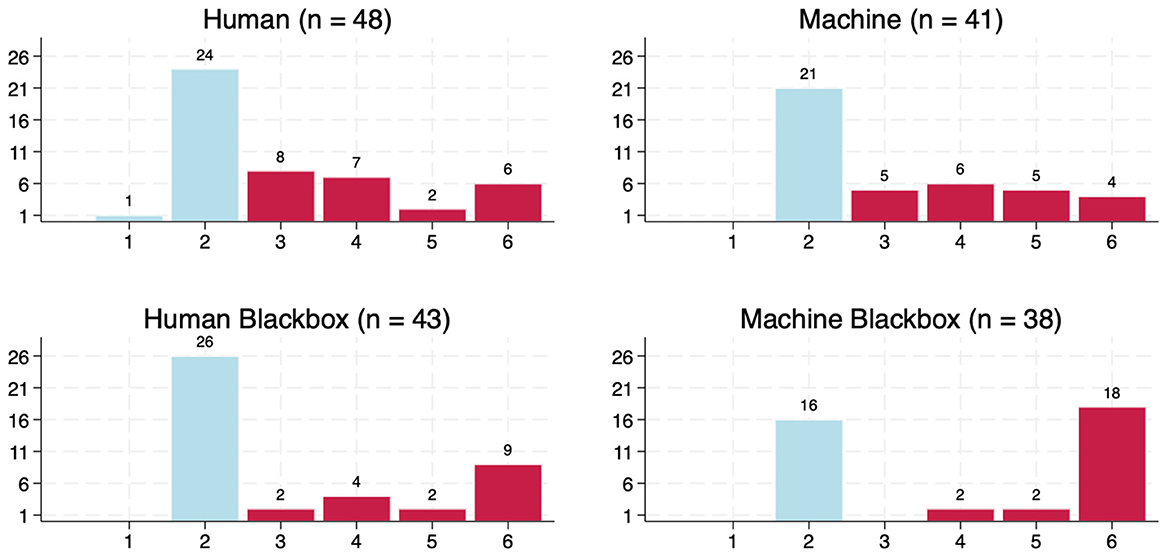
Figure 3 displays the frequency distributions of reported numbers by treatment. On average, subjects in the Human, Machine, and Human Black Box treatments reported numbers close to 3 (H: 3.06, M: 3.17, HB: 3.21), while subjects in the Machine Black Box treatment reported an average of 4.16. Reporting distributions differ significantly between groups (Kruskal-Wallis equality-of-populations rank test with ties: χ²(3) = 7.85, p = 0.049).

Figure 3

Figure 3. Frequency distributions of reported numbers, by treatment.

In all treatments except the Human condition, no other numbers than 2 were drawn. In the Human treatment, the number 1 was drawn and accurately reported. Therefore, no exclusions of observations from the reported distributions were necessary, and any reported number above 2 can be interpreted directly as cheating.

In the non-black box groups, nearly half of the participants overreported: 23 out of 48 (47.9%) in the Human treatment and 20 out of 41 (48.7%) in the Machine treatment reported a higher number than they actually drew. Overreporting was less prevalent in the Human Black Box group (17 out of 43, or 39.5%), while the highest rate occurred in the Machine Black Box group (22 out of 38, or 57.9%). However, these differences in reporting rates are not statistically significant [Pearson χ²(3) = 2.73, p = 0.435].

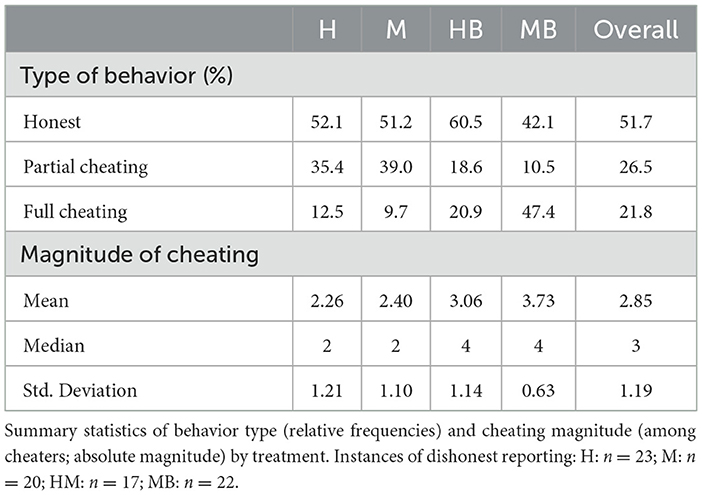
Following conventions in related studies, we classify participants who overreported to the maximum extent possible (i.e., reporting a “6”) as full cheaters, and those who overreported by a smaller margin as partial cheaters. Overall, the distribution of honest participants, partial cheaters, and full cheaters (see Table 2) differs significantly between treatments (Pearson χ²(6) = 25.93, p < 0.0001). In the non-black box groups, partial cheaters outnumber full cheaters. In the Human Black Box group, the proportions are roughly equal. In contrast, the Machine Black Box condition shows a substantially larger share of full cheaters, with partial cheaters being nearly absent. Notably, over half of participants were honest in the Human, Machine, and Human Black Box groups respectively, while the number of subjects who overreported to the maximum extent in the Machine Black Box group was higher than the number of honest subjects.

Table 2

Table 2. Summary statistics of cheating behavior by treatment.

Regarding the magnitude of cheating, among cheaters, the average overreporting exceeded two numbers in all conditions, but was markedly higher in the black box groups. Consistently, the median magnitude of cheating was 2 in the non-black box treatments and 4 in the black box treatments. A Kruskal-Wallis equality-of-populations rank test with ties reveals a statistically significant difference in cheating magnitude across groups (χ²(3) = 21.64, p = 0.0001). The Machine Black Box group not only shows the highest average cheating magnitude but also the lowest standard deviation, indicating more consistent and extreme overreporting, reflecting the group with the highest proportion of full liars.

Comparing magnitudes of cheating under transparent verification rules, we find no significant differences between the Human and Machine entity treatments (Mann-Whitney U-test: |z| = 0.48, p = 0.6357), as the average magnitude of cheating is only marginally higher in the Machine treatment. Under undisclosed rules, however, we observe a notable difference in cheating magnitude, as average overreporting is higher in the Machine Black Box group than in the Human Black Box group by 0.7 – a difference that is statistically significant (Mann-Whitney U-test: |z| = 2.09, p = 0.0442). Meanwhile, when pooling data across both verification rule conditions, the overall comparison between all human- and machine-audited individuals remains statistically insignificant (Mann-Whitney U-test: |z| = 1.82, p = 0.0704). Thus, we find partial support for Hypothesis 1, as the magnitude of cheating differs by verification entity, but only under undisclosed verification rules.

Focusing on the machine groups under transparent and undisclosed verification rules, we observe a substantial increase in the average extent of overreporting—by approximately 1.3—with the introduction of ambiguity about verification rules in the Machine Black Box group compared to the Machine group. The difference is highly statistically significant (Mann-Whitney U-test: |z| = 4.03, p < 0.0001). Therefore, we find support for Hypothesis 2: average magnitude of cheating toward a machine as verification entity differs between transparent and undisclosed processing rules, as ambiguity appears to lead to a higher magnitude of cheating. For comparison, overreporting toward a human as verification entity significantly increased by, on average, 0.8 from the Human to the Human Black Box (Mann-Whitney U-test: |z| = 2.02, p = 0.0469) as well as by 1.1 when pooled across both entities (Mann-Whitney U-test: |z| = 4.29, p = 0.000). ⁷

To compare effect sizes, we calculate Cohen's d with bootstrapped standard errors (see Supplementary Table S3). The entity effect is negligible in size under transparent verification rules (d = −0.12), while increasing to d = −0.75 under ambiguous rules, which can be classified as medium to large based on conventional benchmarks (Cohen, 1988). Analogously, the effect of ambiguity in machine verification can be considered (very) large (d = −1.50).

3.2 Control variables

The analysis of our questionnaire data provides strong support for the assumption that participants perceive humans as both more error-prone and more discretionary in their decision-making (illustrated in Figure 4). Binomial tests for both variables yield results significantly different from 0.5—which would indicate indifference – across all four treatment groups (p < 0.0000). Moreover, response distributions do not differ significantly between groups (error-proneness: Pearson χ²(3) = 1.50, p = 0.681; discretion: Pearson χ²(3) = 1.26, p = 0.739).

Figure 4

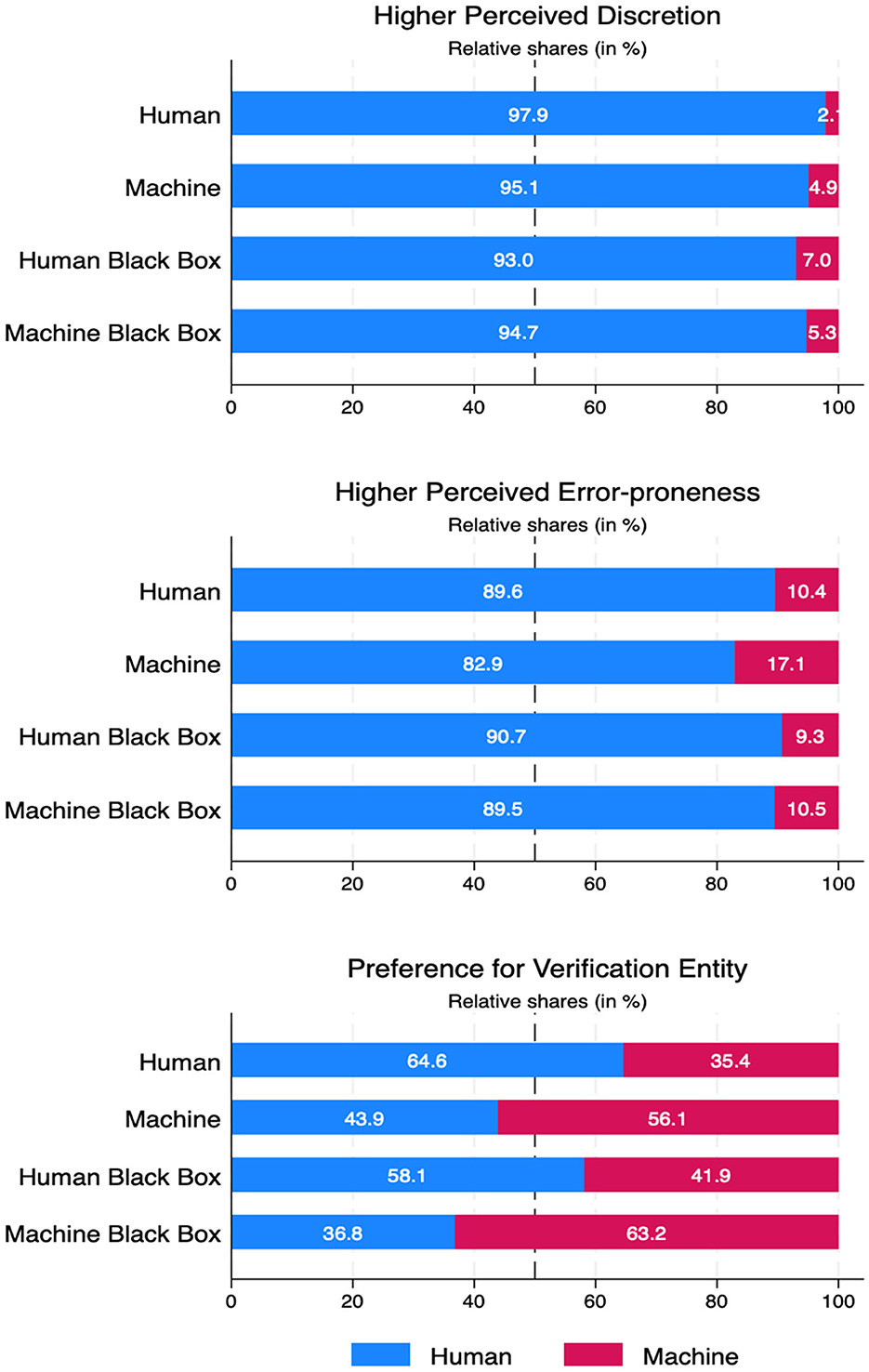
Figure 4. Comparison of stated perceived discretion, error-proneness, and verification entity preference, by treatment.

Findings are less conclusive regarding participants' preferred entity for verifying the reports (see also Figure 4). In both human treatment groups, participants tended to prefer a human as verification entity, whereas in the machine treatments, preferences leaned toward a machine as verification entity. However, in none of the groups did the distribution of preferences differ significantly from an even 50/50 split (see Supplementary Table S3 for Binomial test results by group). The apparent tendency to prefer the respective verification entity encountered during the experiment may reflect a default option effect (Johnson and Goldstein, 2003), as preferences were elicited post-experiment.

Furthermore, standardized questionnaire controls indicate that self-reported affinity for technology interaction, sensitivity to ethical dilemmas, perceived closeness to the verification entity, and stated risk preferences did not differ substantially across experimental groups as shown in Table 3 (see Supplementary Table S4 for pairwise treatment comparisons of cheating frequency and control variables).

Table 3

Table 3. Summary statistics and between-group comparison of questionnaire items.

Across all subjects, those who overreported and thus cheated reported a significantly higher willingness to take risks (Mann-Whitney U-test: |z| = 2.62, p = 0.0085). On average, cheaters indicated a general risk tendency of 6.4 (median: 7) on an 11-point scale, compared to 5.5 (median: 5.5) among honest participants. Also, the willingness to take risks was significantly positively correlated with the magnitude of cheating (Spearman's ρ = 0.355, p = 0.0011).

Also, gender differences were evident: women cheated significantly less frequently than men (Pearson χ²(1) = 13.36, p < 0.0001), with 35.8% of female and 64.0% of male participants overstating their drawn number. However, the magnitude of cheating did not differ significantly between genders (Mann-Whitney U-test: |z| = 0.67, p = 0.5032).

The other demographic and control variables did not differ significantly between honest and dishonest participants, nor were they significantly associated with the extent of cheating (see Supplementary Table S5).

3.3 Regression analysis

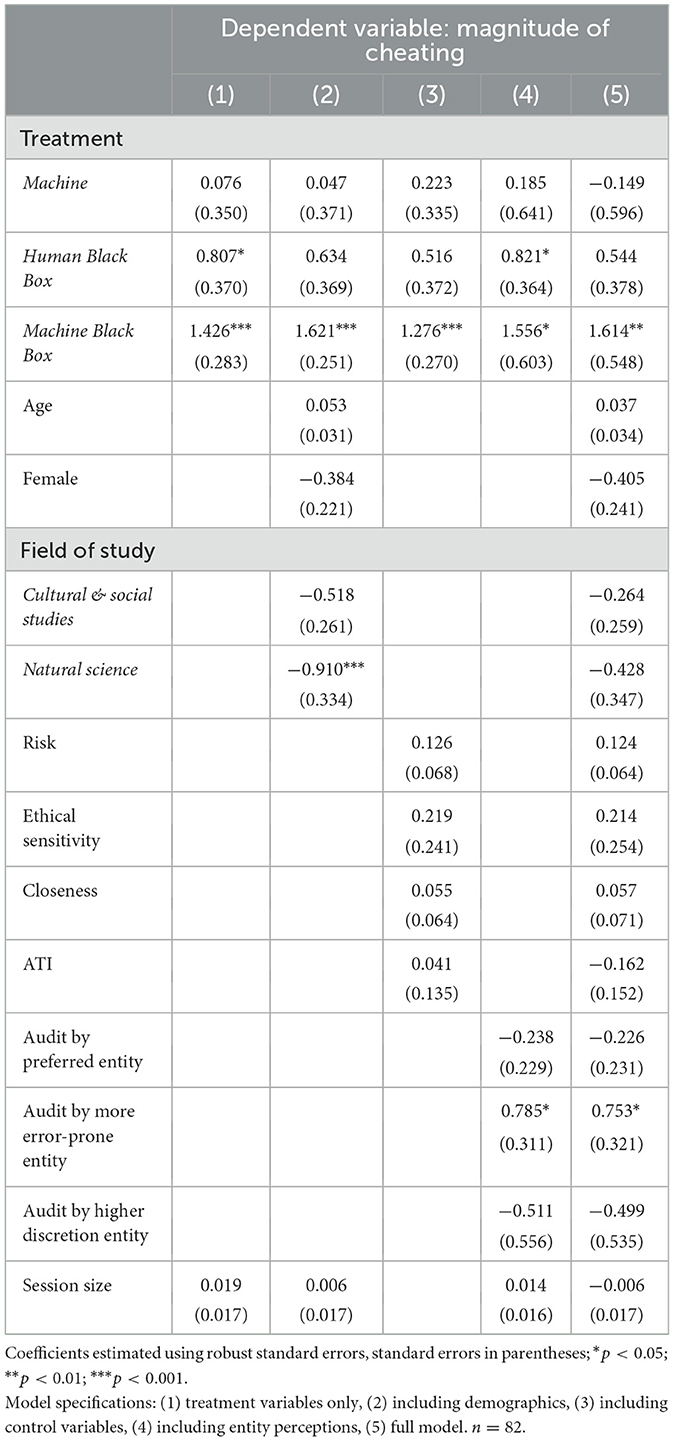
In addition to our non-parametric analysis, we conduct multivariate regression analysis to gain a deeper understanding of the relationship between dishonest behavior and its potential determinants. Specifically, we regressed likelihood and magnitude of cheating on the type of verification entity and the ambiguity level of verification rules, along with demographic, control, and entity-perception variables. Furthermore, a session size indicator was included in all models as each treatment was comprised of multiple experiment sessions of varying numbers of participants. Table 4 presents the average marginal effects from a logit regression analysis of the likelihood of cheating, comparing multiple model specifications (coefficients can be obtained from Supplementary Table S6).

Table 4

Table 4. Logit regression for likelihood of cheating—marginal effects.

The baseline model (Column 1) includes only treatment indicators as independent variables, while subsequent models add demographic variables (Column 2), control variables (Column 3), and dummy variables indicating matches between the assigned verification entity and participants' stated entity preferences, perceptions of error-proneness, and perceived discretion (Column 4) respectively. All available variables are included in the full model (Column 5). In models (3) and (5), affinity to technology interaction (ATI) and Closeness to the auditing entity are centered and interacted with the treatment variable, as the former is only relevant to the machine-audited treatments and the latter is directly related to the respective treatment's entity, while risk and ethical sensitivity were measured as general concepts unrelated to the main experiment.

The regression results are consistent with our non-parametric analysis, with gender and general risk preferences emerging as the only predictors of likelihood to cheat that are statistically significant and meaningful in size. For instance, being female is associated with a 27.1 percentage-point lower probability of overreporting [using the more conservative estimate from model (2)].

Based on the sub-sample of individuals who cheated (n = 82), we examined the factors influencing the extent to which participants overstated their drawn number. Table 5 presents the average marginal effects of the multivariate OLS regression, using the same model specifications as those employed in the logit regression for cheating likelihood (coefficients can be obtained from Supplementary Table S7).

Table 5

Table 5. OLS Regression for magnitude of cheating—marginal effects.

Among the model specifications, the full model (Column 5) demonstrates the highest coefficient of determination [R² = 0.5880], which is considerably high for studies based on observational data on human behavior. This indicates that the model explains a substantial portion of the variation in cheating magnitude. However, the adjusted R² is nearly 15 percentage points (p.p.) lower, reflecting the inclusion of numerous explanatory variables and their potential cost in model parsimony. The full model also yields the lowest Akaike information criterion (AIC) value among the five alternatives (see for the statistics Supplementary Table S7), supporting its superior fit. Predictably, the full model in return shows the highest Bayesian Information Criterion (BIC) value, given BIC's stronger penalty for model complexity. Nevertheless, in the relevant literature, the AIC is generally preferred for model selection in multivariate regression analysis with the goal of outcome prediction, especially when the sample size is smaller (see e.g., Burnham and Anderson, 2002; Yang, 2005; Chakrabarti and Ghosh, 2011). Accordingly, our interpretation focuses primarily on the results from the full model specification.

Consistent with the non-parametric findings, the Machine Black Box treatment stands out: its average marginal effect is substantially larger—indicating that overreports are higher by, on average, 1.6—and significantly different from that of the Human group, which serves as the reference category in the regression. In contrast, the effects for the Machine and Human Black Box treatments are smaller in magnitude—or even slightly negative in the case of the Machine treatment—and not significantly different from the Human group. This pattern suggests that it is specifically the combination of audit ambiguity and a machine auditor that drives the increase in dishonest reporting.

While being male is identified as the main predictor of the likelihood to cheat, gender does not significantly influence the magnitude of cheating. A similar pattern emerges for individual risk preferences: although significantly related to the decision to cheat, their effect on the extent of cheating becomes statistically insignificant (p = 0.057), despite a still meaningful marginal effect size. Specifically, a one-point increase in self-reported risk willingness to take risk is associated with an average increase of 0.12 in the magnitude of overreporting—an effect that accumulates across the 11-point scale. This divergence from non-parametric results can likely be attributed to the two interaction terms, whose inclusion inherently drives variance inflation through multicollinearity, which typically increases standard errors and may obscure statistical significance. This explanation is further supported by the results of an additional ordered logit regression (see below). As expected based on the non-parametric analysis, regression coefficients for other demographic and control variables—age, field of study, ethical sensitivity, perceived closeness to the verification entity, and affinity to technology interaction—are neither statistically significant nor meaningful in size.

Regarding the discussed psychological drivers of cheating, only the perception of the verification entity as more error-prone appears to be consequential. When the assigned auditor matches the participant's perception of being the more error-prone entity, while having been irrelevant for the likelihood to cheat, the magnitude of cheating increases by approximately 0.75. By contrast, whether the verification entity is perceived as having greater discretion does not have a significant impact on cheating magnitude.

For robustness, an additional ordered logit regression was conducted based on the full model (5), providing more detailed insights into the dynamics across individual levels of cheating magnitude. Due to space constraints, the marginal effects are reported in Supplementary Table S9 (the related coefficients can be found in Supplementary Table S8). The results reinforce findings from both the non-parametric and OLS regression analyses, particularly regarding the distinction between partial and full cheating. Specifically, the probability of a subject in the Machine Black Box treatment cheating to the maximum possible extent is significantly higher—by 66.3 p.p. (p = 0.000)—compared to the Human treatment, holding other variables constant. In contrast, the probabilities for partial overreporting by 1 and 2 units are significantly lower—by 31.6 p.p. (p = 0.023) and 28.0 p.p. (p = 0.000), respectively. Overreporting by 3 units is also less likely, though this effect remains marginally insignificant (−6.7 p.p., p = 0.078). A similar pattern can be observed for risk attitudes, for which a one-unit increase in the general willingness to take risks exerts a significant negative effect on the probability of overreporting by 1 unit (−3.4 p.p., p = 0.017), insignificant negative effects on the probabilities of overreporting by 2 and 3 units, and a significant positive effect on the probability of cheating to the maximum (5.8 p.p., p = 0.018)—despite no significant effect being identified in the OLS model. This suggests that a greater willingness to take risks is associated with an increased likelihood of maximum cheating, and decreased likelihood of partial cheating, which appears intuitively plausible. The effects of being audited by the entity perceived as more error-prone follow the same directional pattern and significance profile as the risk variable—1 unit: −2.7 p.p., p = 0.001; 2 units: −14.6 p.p., p = 0.076; 3 units: −3.8 p.p., p = 0.313; 4 units: 4.5 p.p., p = 0.008—indicating a stronger inclination to cheat fully rather than partially when the verification entity is perceived as error-prone. All other effects of treatment and covariate effects remain statistically insignificant in this analysis.

4 Discussion

Human-machine interactions become increasingly pervasive in daily life and professional contexts, motivating research to examine how human behavior changes when individuals interact with machines rather than other humans. While most of the existing literature focuses on human perceptions and actions toward algorithmic systems in advisory roles, our study examines a different yet equally important human-machine setting in which machines can verify the truthfulness of human statements and penalize fraudulent reporting. We incorporate elements of risk and uncertainty into the die-roll paradigm by (Fischbacher and Föllmi-Heusi 2013) and design four experimental conditions varying the verification entity (human vs. machines) and the transparency of processing rules (transparent vs. ambiguous) to identify and sanction dishonest behavior. The experimental design involved a clearly quantifiable reporting task in which participants could increase their earnings by overreporting the actual outcome of the die-roll, while facing either specified or unknown risks of discovery and punishment. Unlike many earlier studies where deception carried no consequences for the individual, our design reflects realistic decision environments where risk preferences matter, payoff incentives are substantial, and higher reported values face greater scrutiny.

Cheating was observed – at relatively high rates between roughly 40% and 60% – across all four experimental conditions. In each treatment, we observed the full spectrum of behavior: complete honesty, partial cheating, and full cheating. The obtained findings support our first hypothesis partially: behavioral differences in dishonesty between humans and machines as verification entities do not emerge in general, but specifically under conditions of ambiguous verification rules. Regarding our second hypothesis, we find strong evidence of higher average cheating magnitudes when machines verify under ambiguous rather than transparent rules. Specifically, the behavioral pattern under machine ambiguity exhibits increased polarization, with participants more likely to engage in either complete honesty or maximal dishonesty, rather than partial cheating. The fact that in aggregation these average cheating magnitudes are significantly higher than in the transparent condition indicates that ambiguity facilitates greater justification for dishonest behavior.

However, the results of our study should be interpreted with caution, given its methodological and contextual limitations. First, the number of participants per treatment group is relatively modest. This means that sub-samples of cheaters are even smaller, which may limit the statistical power of our analysis (see Supplementary Table S3). Consequently, findings based on medium effect sizes and p-values near the 0.05 threshold should be interpreted cautiously. Nonetheless, effects related to ambiguity (d>1) and the apparent absence of entity effects under transparent verification rules are sufficiently distinct to support clearer conclusions. Second, despite the machine verification procedure being framed as algorithmic, the experimenter remained involved in its administration. In particular, the drawn number was still checked by a human. While this setup does not entirely eliminate potential social image concerns toward the experimenter, the comparative statics should preserve the interpretability of between-group differences. Third, the Verification Part of our experiment can be viewed as a compound lottery, a design feature that has been subject to discussion in the elicitation literature (see e.g., Starmer and Sugden, 1991; Harrison et al., 2015). However, our design requires subjects to make only a single consequential decision, aligning with how individuals are typically found to approach compound lotteries (Holt, 1986). If the lottery design influences behavior at all, it is likely to do so by discouraging cheating due to incomplete understanding of the consequences—and could only do so in the transparent treatments, as the probabilistic structure of verification was undisclosed in the ambiguous conditions. Fourth, while internal validity appears relatively strong—a substantial part of regression model variation is explained by the covariates included— questions regarding external validity remain. In our experiment, punishment led to a loss within a larger gain frame. When identified as dishonest, the penalty reduced the monetary amount below what participants would have received had they been honest. However, this means that even those prize draw winners who were punished for overreporting exited the experiment with positive net payoffs. In real-world settings, penalties may outweigh gains and result in actual losses—conditions that are difficult to replicate in typical laboratory settings due to ethical and methodological constraints. Therefore, related experiments provide participants with an initial endowment subject to subsequent reductions (e.g., Konrad et al., 2014) or, as in our experimental design, require participants to weigh the gain of overreporting against the potential losses of being identified and punished at once. Nevertheless, despite these methodological challenges, since our implemented punishment scheme remained constant across all treatment conditions, it is highly unlikely that harsher punishment would have fundamentally altered our results. Finally, from a practical standpoint, while real-world verifications or audits typically do not operate under undisclosed or ambiguous rules due to legal constraints, perceived ambiguity often exists nonetheless, particularly among non-experts facing for example complex tax laws and legal regulations. Such perceived opacity may effectively replicate in practice the black box experience observed in our experimental conditions.

Our study aimed to examine how human dishonesty in verification processes is affected by the verifying entity and procedural transparency, providing several promising avenues for future research. Our findings suggest that different psychological mechanisms may operate under varying conditions. Consistent with prior work by (Cohn et al. 2022) and (Biener and Waeber 2024), whose experimental designs most closely parallel our black box conditions, differential social image concerns toward humans and machines could explain the observed differences between our “Human Black Box” and “Machine Black Box” treatments. However, social image concerns alone cannot explain the behavioral similarity between transparent human and machine treatments, where participants appear to converge toward rational responses to the underlying risk-reward structure regardless of the verification entity. Similarly, while participants perceived human verification entities as more discretionary than machines, these perceptions played only secondary roles in reporting decisions. Interestingly, perceiving verification entities as error-prone increased overreporting magnitude, yet the perception that humans are more error-prone than machines did not translate into greater dishonesty in transparent conditions. Treating our study as a starting point, future research would therefore benefit from systematically analyzing which mechanisms drive dishonest behavior and under what conditions specific factors become negligible. One valuable direction would be investigating situations where competing psychological forces cancel each other out, resulting in no behavioral differences between verification entities. For instance, if some individuals prioritize social image concerns while others focus on error-proneness, these competing motivations could explain why behavior remains similar across human and machine treatments under certain conditions. Further, the factors examined in our study likely represent only a subset of relevant mechanisms. Future research could explore additional dimensions, such as beliefs about detection risk, which may overlap with but remain distinct from error-proneness perceptions. Systematically eliciting these beliefs separately would clarify whether perceived detection risks vary consistently across entities and transparency conditions. Future studies could also address external validity concerns by examining whether our findings replicate in field settings with actual loss frames, different participant populations (e.g., Djawadi and Fahr, 2015; Jussupow et al., 2024), and varying stakes.

Nevertheless our study carries important practical implications, especially for domains, institutions or companies that have implemented or plan to implement enhanced automation in verification processes that minimize or even eliminate human oversight. When machines are planned as verification entities, we recommend that practitioners and policymakers prioritize addressing the black box problem by enhancing procedural transparency, i.e., “opening the black box” (Litterscheidt and Streich, 2020). The combination of ambiguous rules and machine verification clearly drives up the magnitude of cheating and thus the related economic damage. While transparency alone may not eliminate dishonest behavior, a lack of transparency is likely to exacerbate it significantly. Given that our results suggest that the magnitude of cheating under ambiguity is lower when a human is involved, automating verification processes in such settings could unintentionally increase the impact of dishonest behavior. These findings therefore cast skepticism on the expectations of authorities, such as tax agencies, that automation may produce deterrence effects simply because machines can better identify suspicious patterns in tax reports. Rather, in contexts where rule interpretation is complex or ambiguous, it may be advisable to revert automated (verification or auditing) processes back to humans, provided that the cost of human employment is offset by the averted damage from dishonest behavior. Beyond the binary perspective of our experiment, hybrid solutions such as human-in-the-loop process designs, may offer valuable alternatives for ostensibly routine tasks that hold large damage potential in exceptional cases. For instance, AI can be used to improve efficiency in insurance claim processing and fraud detection by identifying inconsistencies or suspicious patterns in claim submissions, which are then forwarded for further human assessment and final decision-making (Komperla, 2023).

Conversely, when processing rules are transparent, algorithmic verifications may offer a viable alternative without further sacrificing behavioral integrity. In such cases, the identity of the verification entity – human or machine – appears to have no meaningful effect on cheating behavior in terms of either frequency or magnitude. Natural areas of application include financial and tax audits, where algorithmic automation offers great potential for efficiency improvements (Bakumenko and Elragal, 2022; Li et al., 2025). These systems are already used to determine audit targets, with researchers working to increase purposive selection and algorithmic fairness (Black et al., 2022). For example, in some domains, such as tax administration, policy debates have emerged around requiring tax agencies to disclose their algorithmic procedures and inform taxpayers subjected to severe audits about the reasons for selection, thereby providing grounds for legal challenge (Faúndez-Ugalde et al., 2020).

However, our findings may be extended to all kinds of compliance, monitoring, and verification processes that hold potential for both automation and dishonest human behavior. For example, in settings where electronic surveillance are installed to monitor human conduct, these systems are perceived more negatively than human surveillance systems (Schlund and Zitek, 2024). While monitoring and surveillance are inherently unwelcome, ensuring that electronic surveillance systems are not perceived more negatively than human alternatives serves the interests of authorities and organizations. Empirical evidence suggests that electronic surveillance may trigger psychological reactance, a motivational state of resistance toward perceived restrictions on behavioral freedom, which frequently manifests in deviant behavior. For example, (Yost et al. 2019) find that electronic surveillance in organizations elicits reactance that correlates with increased employee intentions to engage in counterproductive workplace behaviors. Based on our results, one approach to mitigate this perceptual gap may be enhancing transparency in monitoring rules and procedures so that individuals view the electronic system as substitute for, rather than intensification of, human surveillance. In this regard, automated solutions can be implemented such that the benefits of reduced human labor costs are not offset by increased costs arising from more dishonest or counterproductive workplace behavior.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author/s.

Ethics statement

Ethical approval was not required for the studies involving humans because at the time of conducting our initial study, we did not seek formal ethics approval, as our laboratory adhered to the 10-item self-assessment checklist provided by the German Association for Experimental Economic Research (GfeW), which was widely used in the field and considered adequate for minimal-risk behavioral studies. Importantly, in compliance with laboratory rules, the study involved fully informed consent, anonymized data collection, and no deception or sensitive topics. For a planned field-based follow-up study using the same design and materials, we have since obtained formal ethics approval (see https://gfew.de/ethik/i6ZPYa4V). This reflects both the evolving standards in our field and our commitment to adhering to current best practices. The studies were conducted in accordance with the local legislation and institutional requirements. The participants provided their written informed consent to participate in this study.

Author contributions

MP: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Project administration, Resources, Software, Visualization, Writing – original draft. BD: Conceptualization, Funding acquisition, Investigation, Methodology, Project administration, Resources, Validation, Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This research was funded by the Deutsche Forschungsgemeinschaft (DFG) within the “SFB 901: On-The-Fly (OTF) Computing–Individualized IT-Services in Dynamic Markets” program (160364472). We acknowledge support for the publication cost by the Open Access Publication Fund of Paderborn University.

Acknowledgments

We thank session participants at the German Association for Experimental Economic Research e.V. (GfeW) Annual Meeting 2023, the Paderborn University Faculty of Business Administration and Economics Research Workshop 2023, and the Society for the Advancement of Behavioral Economics (SABE) Annual Meeting 2024, with special thanks to Nils Köbis, Sebastian Oelrich and Mathieu Chevrier, for valuable ideas and comments.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Gen AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frbhe.2025.1645749/full#supplementary-material

Footnotes

1. ^Empirical research in this field can be broadly categorized into two strands: (1) studies in which humans interact with algorithms, programs, chatbots, or AI systems through a computer interface (e.g., Cohn et al., 2022; Biener and Waeber, 2024; Dietvorst et al., 2015; Logg et al., 2019); and (2) studies involving humans interacting with anthropomorphic robots, focusing on perceived trustworthiness, intelligence, or reciprocity – often observed from a third-person perspective (e.g., Canning et al., 2014; Ullman et al., 2014; Sandoval et al., 2020). The present study is concerned solely with the former type of interaction.

2. ^From a technical standpoint, an algorithm is defined as a sequential logical process applied to a data set to accomplish a certain outcome. This process is automated and processes without human interference (Gillespie, 2016).

3. ^Note on preregistration of hypotheses: Research examining human dishonesty in verification processes conducted by human vs. machine entities is still in its infancy, with competing theoretical predictions from related literature and a need to remain open to unexpected empirical patterns that could inform future theory development. This exploratory nature is also reflected in our bi-directional hypotheses. We therefore deliberately chose not to preregister our hypotheses. This exploratory approach allowed us to conduct comprehensive analyses across multiple dimensions of dishonest behavior (incidence, magnitude, and behavioral patterns) without being constrained by predetermined theoretical and/or analytical frameworks, thereby enabling a more complete characterization of this understudied phenomenon.

4. ^For a broader discussion on the topic of information omission in the context of what may, and what should not, be considered subject deception, see, for example, (Charness et al. 2022), (Cooper 2014), (Krawczyk 2015), (Barrera and Simpson 2012), (Krasnow et al. 2020), (Jamison et al. 2008), and (Krawczyk 2019).

5. ^This is three times the amount of the laboratory's usual show-up fee in experiments with individual performance-dependent incentives.

6. ^While social image concerns toward the experimenter cannot be ruled out entirely, comparative statics ensure interpretability of treatment differences between groups.

7. ^We conducted hypothesis testing based on the sub-sample of individuals who engaged in dishonest behavior, i.e., overreported their drawn number, as we argue that including honest reports would dilute the true extent of damage caused by cheating. Naturally the average magnitude of overreporting declines when these are incorporated (H: 1.1; M: 1.2; HB: 1.2; MB: 2.2). Nevertheless, key statistical results would remain robust: under undisclosed verification rules, the entity effect remains statistically significant (Mann-Whitney U-test: |z| = 2.19, p = 0.0296), as does the effect of ambiguity with a machine verifying the reports (Mann-Whitney U-test: |z| = 2.28, p = 0.0214), while still no significant difference is observed between entities under transparent rules (Mann-Whitney U-test: |z| = 0.25, p = 0.8076).

References

Abeler, J., Becker, A., and Falk, A. (2014). Representative evidence on lying costs. J. Public Econ. 113, 96–104. doi: 10.1016/j.jpubeco.2014.01.005

Crossref Full Text | Google Scholar

Abeler, J., Nosenzo, D., and Raymond, C. (2019). Preferences for truth-telling. Econometrica 87, 1115–1153. doi: 10.3982/ECTA14673

Crossref Full Text | Google Scholar

Aron, A., Aron, E. N., and Smollan, D. (1992). Inclusion of other in the self scale and the structure of interpersonal closeness. J. Pers. Soc. Psychol. 63, 596–612. doi: 10.1037//0022-3514.63.4.596

PubMed Abstract | Crossref Full Text | Google Scholar

Baghdasaryan, V., Davtyan, H., Sarikyan, A., and Navasardyan, Z. (2022). Improving tax audit efficiency using machine learning: the role of taxpayer's network data in fraud detection. Appl. Artif. Intellig. 36:e2012002. doi: 10.1080/08839514.2021.2012002

Crossref Full Text | Google Scholar

Bakumenko, A., and Elragal, A. (2022). Detecting anomalies in financial data using machine learning algorithms. Systems 10:130. doi: 10.3390/systems10050130

Crossref Full Text | Google Scholar

Balbuzanov, I. (2019). Lies and consequences: The effect of lie detection on communication outcomes. Inte. J. Game Theory 48, 1203–1240. doi: 10.1007/s00182-019-00679-z

Crossref Full Text | Google Scholar

Banker, S., and Khetani, S. (2019). Algorithm overdependence: how the use of algorithmic recommendation systems can increase risks to consumer well-being. J. Public Policy Market. 38, 500–515. doi: 10.1177/0743915619858057

Crossref Full Text | Google Scholar

Barrera, D., and Simpson, B. (2012). Much ado about deception. Sociol. Methods Res. 41, 383–413. doi: 10.1177/0049124112452526

Crossref Full Text | Google Scholar

Bartling, B., and Fischbacher, U. (2012). Shifting the blame: on delegation and responsibility. Rev. Econ. Stud. 79, 67–87. doi: 10.1093/restud/rdr023

PubMed Abstract | Crossref Full Text | Google Scholar

Bicchieri, C., and Xiao, E. (2009). Do the right thing: but only if others do so. J. Behav. Decis. Mak. 22, 191–208. doi: 10.1002/bdm.621

Crossref Full Text | Google Scholar

Biener, C., and Waeber, A. (2024). Would i lie to you? How interaction with chatbots induces dishonesty. J. Behav. Exp. Econ. 112:102279. doi: 10.1016/j.socec.2024.102279

Crossref Full Text | Google Scholar

Bigman, Y. E., and Gray, K. (2018). People are averse to machines making moral decisions. Cognition 181:21–34. doi: 10.1016/j.cognition.2018.08.003

PubMed Abstract | Crossref Full Text | Google Scholar

Bignami, F. (2022). Artificial intelligence accountability of public administration. Am. J. Comp. Law 70, i312–i346. doi: 10.1093/ajcl/avac012

Crossref Full Text | Google Scholar

Black, E., Elzayn, H., Chouldechova, A., Goldin, J., and Ho, D. E. (2022). “Algorithmic fairness and vertical equity: Income fairness with IRS tax audit models,” in ACM Conference on Fairness, Accountability and Transparency (Seoul, Republic of Korea: ACM), 1479–1503.

Google Scholar

Blais, A.-R., and Weber, E. U. (2006). A domain-specific risk-taking (DOSPERT) scale for adult populations. Manage. Sci. 1:33–47. doi: 10.1017/S1930297500000334

PubMed Abstract | Crossref Full Text | Google Scholar

Bolle, F. (1990). High reward experiments without high expenditure for the experimenter. J. Econ. Psychol. 11, 157–167. doi: 10.1016/0167-4870(90)90001-P

Crossref Full Text | Google Scholar

Bolton, G., Dimant, E., and Schmidt, U. (2021). Observability and social image: On the robustness and fragility of reciprocity. J. Econ. Behav. Organiz. 191, 946–964. doi: 10.1016/j.jebo.2021.09.018

Crossref Full Text | Google Scholar

Bond, C. F., and DePaulo, B. M. (2006). Accuracy of deception judgments. Personal. Soc. Psychol. Rev. 10, 214–234. doi: 10.1207/s15327957pspr1003_2

PubMed Abstract | Crossref Full Text | Google Scholar

Braun-Binder, N. (2020). “Artificial intelligence and taxation: Risk management in fully automated taxation procedures,” in Regulating Artificial Intelligence, eds. T. Wischmeyer and T. Rademacher (Cham: Springer International Publishing), 295–306.

Google Scholar

Burnham, K. P., and Anderson, D. R. (2002). Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach. Cham: Springer-Verlag.

Google Scholar

Burrell, J. (2016). How the machine ‘thinks': understanding opacity in machine learning algorithms. Big Data Soc. 3, 1–12. doi: 10.1177/2053951715622512

Crossref Full Text | Google Scholar

Burton, J. W., Stein, M.-K., and Jensen, T. B. (2019). A systematic review of algorithm aversion in augmented decision making. J. Behav. Decis. Mak. 33, 220–239. doi: 10.1002/bdm.2155

PubMed Abstract | Crossref Full Text | Google Scholar

Camerer, C. F., and Hogarth, R. M. (1999). The effects of financial incentives in experiments: a review and capital-labor-production framework. J. Risk Uncertain. 19, 7–42. doi: 10.1023/A:1007850605129

Crossref Full Text | Google Scholar

Canning, C., Donahue, T. J., and Scheutz, M. (2014). “Investigating human perceptions of robot capabilities in remote human-robot team tasks based on first-person robot video feeds,” in International Conference on Intelligent Robots and Systems (IROS 2014) (New York, NY: Curran Associates), 4354–4361.

Google Scholar

Cao, S. S., Jiang, W., Yang, B., Zhang, A. L., and Ramadorai, T. (2023). How to talk when a machine is listening: corporate disclosure in the age of AI. Rev. Financ. Stud. 36, 3603–3642. doi: 10.1093/rfs/hhad021

Crossref Full Text | Google Scholar

Castelo, N., Bos, M. W., and Lehmann, D. R. (2019). Task-dependent algorithm aversion. J. Market. Res. 56, 809–825. doi: 10.1177/0022243719851788

Crossref Full Text | Google Scholar

Chakrabarti, A., and Ghosh, J. K. (2011). “Aic, bic and recent advances in model selection,” in Philosophy of Statistics, eds. P. S. Bandyopadhyay, and M. R. Forster (London: Elsevier), 583–605.

Google Scholar

Chander, A., Srinivasan, R., Chelian, S., Wang, J., and Uchino, K. (2018). “Working with beliefs: AI transparency in the enterprise,” in Joint Proceedings of the ACM IUI 2018 Workshops co-located with the 23rd ACM Conference on Intelligent User Interfaces (ACM IUI 2018) (Aachen: CEUR Workshop Proceedings), eds. A. Said, and T. Komatsu.

Google Scholar

Charness, G., Gneezy, U., and Halladay, B. (2016). Experimental methods: Pay one or pay all. J. Econ. Behav. Organiz. 131, 141–150. doi: 10.1016/j.jebo.2016.08.010

Crossref Full Text | Google Scholar

Charness, G., Samek, A., and van de Ven, J. (2022). What is considered deception in experimental economics? Exp. Econ. 25, 385–412. doi: 10.1007/s10683-021-09726-7

Crossref Full Text | Google Scholar

Chen, D. L., Schonger, M., and Wickens, C. (2016). oTree—an open-source platform for laboratory, online, and field experiments. J. Behav. Exp. Finance 9, 88–97. doi: 10.1016/j.jbef.2015.12.001

Crossref Full Text | Google Scholar

Cheng, J.-Z., Ni, D., Chou, Y.-H., Qin, J., Tiu, C.-M., Chang, Y.-C., et al. (2016). Computer-aided diagnosis with deep learning architecture: applications to breast lesions in us images and pulmonary nodules in CT scans. Sci. Rep. 6:24454. doi: 10.1038/srep24454

PubMed Abstract | Crossref Full Text | Google Scholar

Chow, C. C., and Sarin, R. K. (2001). Comparative ignorance and the ellsberg paradox. J. Risk Uncertain. 22, 129–139. doi: 10.1023/A:1011157509006

Crossref Full Text | Google Scholar

Chugunova, M., and Sele, D. (2022). We and it: an interdisciplinary review of the experimental evidence on how humans interact with machines. J. Behav. Exp. Econ. 99:101897. doi: 10.1016/j.socec.2022.101897

Crossref Full Text | Google Scholar

Cohen, J. (1988). Statistical Power Analysis for the Behavioral Sciences. New York: Academic Press.

Google Scholar

Cohn, A., Gesche, T., and Maréchal, M. A. (2022). Honesty in the digital age. Manage. Sci. 68, 809–1589. doi: 10.1287/mnsc.2021.3985

PubMed Abstract | Crossref Full Text | Google Scholar

Cooper, D. J. (2014). A note on deception in economic experiments. J. Wine Econ. 9, 211–219. doi: 10.1017/jwe.2014.18

PubMed Abstract | Crossref Full Text | Google Scholar

Daumiller, M., and Janke, S. (2019). The impact of performance goals on cheating depends on how performance is evaluated. AERA Open 5, 1–10. doi: 10.1177/2332858419894276

Crossref Full Text | Google Scholar

Dawes, R. M., Faust, D., and Meehl, P. E. (1989). Clinical versus actuarial judgment. Science 243, 1668–1674. doi: 10.1126/science.2648573

PubMed Abstract | Crossref Full Text | Google Scholar

Dietvorst, B. J., and Bharti, S. (2020). People reject algorithms in uncertain decision domains because they have diminishing sensitivity to forecasting error. Psychol. Sci. 31, 1302–1314. doi: 10.1177/0956797620948841

PubMed Abstract | Crossref Full Text | Google Scholar

Dietvorst, B. J., Simmons, J. P., and Massey, C. (2015). Algorithm aversion: People erroneously avoid algorithms after seeing them err. J. Exp. Psychol.: General 144, 114–126. doi: 10.1037/xge0000033

PubMed Abstract | Crossref Full Text | Google Scholar

Dietvorst, B. J., Simmons, J. P., and Massey, C. (2018). Overcoming algorithm aversion: people will use imperfect algorithms if they can (even slightly) modify them. Manage. Sci. 64, 1155–1170. doi: 10.1287/mnsc.2016.2643

PubMed Abstract | Crossref Full Text | Google Scholar

Djawadi, B. M., and Fahr, R. (2015). “...and they are really lying”: Clean evidence on the pervasiveness of cheating in professional contexts from a field experiment. J. Econ. Psychol. 48, 48–59. doi: 10.1016/j.joep.2015.03.002

Crossref Full Text | Google Scholar

Dohmen, T., Falk, A., Huffman, D., Sunde, U., Schupp, J., and Wagner, G. G. (2011). Individual risk attitudes: measurement, determinants, and behavioral consequences. J. Eur. Econ. Assoc. 9, 522–550. doi: 10.1111/j.1542-4774.2011.01015.x

Crossref Full Text | Google Scholar

Dzindolet, M. T., Pierce, L. G., Beck, H. P., and Dawe, L. A. (2002). The perceived utility of human and automated aids in a visual detection task. Hum. Factors 44, 79–94. doi: 10.1518/0018720024494856

PubMed Abstract | Crossref Full Text | Google Scholar

Dzindolet, M. T., Scott, A., Peterson, R. A. P., Pierce, L. G., and Beck, H. P. (2003). The role of trust in automation reliance. Econometrica 58, 697–718. doi: 10.1016/S1071-5819(03)00038-7

Crossref Full Text | Google Scholar

Einhorn, H. J., and Hogarth, R. M. (1986). Decision making under ambiguity. J. Busin. 4, S225–S250. doi: 10.1086/296364

Crossref Full Text | Google Scholar

Eisenberger, R., and Shank, D. M. (1985). Personal work ethic and effort training affect cheating. J. Pers. Soc. Psychol. 49, 520–528. doi: 10.1037//0022-3514.49.2.520

PubMed Abstract | Crossref Full Text | Google Scholar

Ellsberg, D. (1961). Risk, ambiguity, and the savage axioms. Q. J. Econ. 75, 643–669. doi: 10.2307/1884324

Crossref Full Text | Google Scholar

Faúndez-Ugalde, A., Mellado-Silva, R., and Aldunate-Lizana, E. (2020). Use of artificial intelligence by tax administrations: an analysis regarding taxpayers' rights in latin american countries. Comp. Law Security Rev. 38:105441. doi: 10.1016/j.clsr.2020.105441

Crossref Full Text | Google Scholar

Fenneman, A., Sickmann, J., Pitz, T., and Sanfey, A. G. (2021). Two distinct and separable processes underlie individual differences in algorithm adherence: Differences in predictions and differences in trust thresholds. PLoS ONE 16:e247084. doi: 10.1371/journal.pone.0247084

PubMed Abstract | Crossref Full Text | Google Scholar

Fischbacher, U., and Föllmi-Heusi, F. (2013). Lies in disguise - An experimental study on cheating. J. Eur. Econ. Assoc. 11, 525–547. doi: 10.1111/jeea.12014

Crossref Full Text | Google Scholar

Fox, C. R., and Tversky, A. (1995). Ambiguity aversion and comparative ignorance. Q. J. Econ. 110, 585–603. doi: 10.2307/2946693

Crossref Full Text | Google Scholar

Franke, T., Attig, C., and Wessel, D. (2018). A personal resource for technology interaction: Development and validation of the affinity for technology interaction (ATI) scale. Int. J. Human–Comp. Interact. 35, 456–467. doi: 10.1080/10447318.2018.1456150

Crossref Full Text | Google Scholar

Fuchs, C., Matt, C., Hess, T., and Hoerndlein, C. (2016). “Human vs. algorithmic recommendations in big data and the role of ambiguity,” in In for Information Systems (AIS), A., editor, 22nd Americas Conference on Information Systems (AMCIS 2016): Surfing the IT Innovation Wave. New York: Curran Associates.

Google Scholar

Gerlach, P., Teodorescu, K., and Hertwig, R. (2019). The truth about lies: A meta-analysis on dishonest behavior. Psychol. Bull. 145, 1–44. doi: 10.1037/bul0000174

PubMed Abstract | Crossref Full Text | Google Scholar

Ghosh, D., and Ray, M. R. (1997). Risk, ambiguity, and decision choice: some additional evidence. Deci. Sci. 28, 81–104. doi: 10.1111/j.1540-5915.1997.tb01303.x

Crossref Full Text | Google Scholar

Gillespie, T. (2016). “Algorithm,” in Digital Keywords: A Vocabulary of Information Society and Culture, eds. B. Peters (Princeton: Princeton University Press), 18–30.

Google Scholar

Gneezy, U., Kajackaite, A., and Sobel, J. (2018). Lying aversion and the size of the lie. Am. Econ. Rev. 108, 419–453. doi: 10.1257/aer.20161553

Crossref Full Text | Google Scholar

Gogoll, J., and Uhl, M. (2018). Rage against the machine: automation in the moral domain. J. Behav. Exp. Econ. 74, 97–103. doi: 10.1016/j.socec.2018.04.003

Crossref Full Text | Google Scholar

Greiner, B. (2015). Subject pool recruitment procedures: organizing experiments with ORSEE. J. Econ. Sci. Assoc. 1, 114–125. doi: 10.1007/s40881-015-0004-4

Crossref Full Text | Google Scholar

Gruber, K. (2019). Is the future of medical diagnosis in computer algorithms? Lancet Digital Health 1, E15–E16. doi: 10.1016/S2589-7500(19)30011-1

Crossref Full Text | Google Scholar

Hao, L., and Houser, D. (2008). Perceptions, intentions, and cheating. J. Econ. Behav. Organiz. 133, 52–73. doi: 10.1016/j.jebo.2016.10.010

Crossref Full Text | Google Scholar

Harrison, G. W., Martínez-Correa, J., and Swarthout, J. T. (2015). Reduction of compound lotteries with objective probabilities: theory and evidence. J. Econ. Behav. Organiz. 119, 32–55. doi: 10.1016/j.jebo.2015.07.012

Crossref Full Text | Google Scholar

Haslam, N. (2006). Dehumanization: An Integrative Review. Personal. Soc. Psychol. Rev. 10, 252–264. doi: 10.1207/s15327957pspr1003_4

PubMed Abstract | Crossref Full Text | Google Scholar

Highhouse, S. (2008). Stubborn reliance on intuition and subjectivity in employee selection. Ind. Organ. Psychol. 1, 333–342. doi: 10.1111/j.1754-9434.2008.00058.x

Crossref Full Text | Google Scholar

Hoffman, R. R., Johnson, M., and Bradshaw, J. M. (2013). Trust in automation. Human-Cent. Comp. 28, 84–88. doi: 10.1109/MIS.2013.24

Crossref Full Text | Google Scholar

Holm, H. J. (2010). Truth and lie detection in bluffing. J. Econ. Behav. Organiz. 76, 318–324. doi: 10.1016/j.jebo.2010.06.003

PubMed Abstract | Crossref Full Text | Google Scholar

Holt, C. A. (1986). Preference reversals and the independence axiom. Am. Econ. Rev. 76, 508–515.

PubMed Abstract | Google Scholar

Holzinger, A., Biemann, C., Pattichis, C. S., and Kell, D. B. (2017). What do we need to build explainable AI systems for the medical domain? arXiv [preprint] arXiv:1712.09923. doi: 10.48550/arXiv.1712.09923

Crossref Full Text | Google Scholar

Hou, Y. T.-Y., and Jung, M. F. (2021). Who is the expert? Reconciling algorithm aversion and algorithm appreciation in ai-supported decision making. Proc. ACM Human-Comp. Interact. 5, 1–25. doi: 10.1145/3479864

Crossref Full Text | Google Scholar

Ioannidis, K., Offerman, T., and Sloof, R. (2022). Lie detection: A strategic analysis of the verifiability approach. Am. Law Econ.Rev. 24, 659–705. doi: 10.1093/aler/ahac005

PubMed Abstract | Crossref Full Text | Google Scholar

Jacobsen, C., Fosgaard, T. R., and Pascual-Ezama, D. (2018). Why do we lie? A practical guide to the dishonesty literature. J. Econ. Surv. 32, 357–387. doi: 10.1111/joes.12204

Crossref Full Text | Google Scholar

Jacobsen, C., and Piovesan, M. (2016). Tax me if you can: an artifactual field experiment on dishonesty. J. Econ. Behav. Organiz. 124, 7–14. doi: 10.1016/j.jebo.2015.09.009

Crossref Full Text | Google Scholar

Jamison, J., Karlan, D., and Schechter, L. (2008). To deceive or not to deceive: The effect of deception on behavior in future laboratory experiments. J. Behav. Organiz. 68, 477–488. doi: 10.1016/j.jebo.2008.09.002

Crossref Full Text | Google Scholar

Jauernig, J., Uhl, M., and Walkowitz, G. (2022). People prefer moral discretion to algorithms: algorithm aversion beyond intransparency. Philosophy Technol. 35:2. doi: 10.1007/s13347-021-00495-y

Crossref Full Text | Google Scholar

Johnson, E. J., and Goldstein, D. (2003). Do defaults save lives? Science 302, 1338–1339. doi: 10.1126/science.1091721

PubMed Abstract | Crossref Full Text | Google Scholar

Jussupow, E., Benbasat, I., and Heinzl, A. (2024). An integrative perspective on algorithm aversion and appreciation in decision-making. MIS Quart. 48, 1575–1590. doi: 10.25300/MISQ/2024/18512

Crossref Full Text | Google Scholar

Kaushik, M., Singh, V., and Chakravarty, S. (2022). Experimental evidence of the effect of financial incentives and detection on dishonesty. Sci. Rep. 12:2680. doi: 10.1038/s41598-022-06072-3

PubMed Abstract | Crossref Full Text | Google Scholar

Kayande, U., Bruyn, A. D., Lilien, G. L., Rangaswamy, A., and van Bruggen, G. H. (2009). How incorporating feedback mechanisms in a DSS affects DSS evaluations. Inform. Syst. Res. 20, 527–546. doi: 10.1287/isre.1080.0198

PubMed Abstract | Crossref Full Text | Google Scholar

Khalmetski, K., and Sliwka, D. (2019). Disguising lies - Image concerns and partial lying in cheating games. Am. Econ. J.: Microeconom. 11, 79–110. doi: 10.1257/mic.20170193

Crossref Full Text | Google Scholar

Kleinberg, J., Lakkaraju, H., Ludwig, J., and Mullainathan, S. (2018). Human decisions and machine predictions. Quart. J. Econ. 133, 237–293. doi: 10.1093/qje/qjx032

PubMed Abstract | Crossref Full Text | Google Scholar

Klingbeil, A., Grützner, C., and Schreck, P. (2024). Trust and reliance on AI - An experimental study on the extent and costs of overreliance on AI. Comput. Human Behav. 160:108352. doi: 10.1016/j.chb.2024.108352

Crossref Full Text | Google Scholar

Köbis, N., Bonnefon, J. F., and Rahwan, I. (2021). Bad machines corrupt good morals. Nat. Hum. Behav. 5, 79–94. doi: 10.1038/s41562-021-01128-2

PubMed Abstract | Crossref Full Text | Google Scholar

Komperla, R. C. A. (2021). AI-enhanced claims processing: Streamlining insurance operations. J. Res. Administrat. 3, 95–106.

Google Scholar

Komperla, R. C. A. (2023). How can AI help in fraudulent claim identification. J. Res. Administrat. 5, 1539–1590.

Google Scholar

Konrad, K. A., Lohse, T., and Qari, S. (2014). Deception choice and self-selection-the importance of being earnest. J. Econ. Behav. Organiz. 107, 25–39. doi: 10.1016/j.jebo.2014.07.012

Crossref Full Text | Google Scholar

Kouziokasa, G. N. (2017). The application of artificial intelligence in public administration for forecasting high crime risk transportation areas in urban environment. Transport. Res. Procedia 24, 467–473. doi: 10.1016/j.trpro.2017.05.083

Crossref Full Text | Google Scholar

Krasnow, M. M., Howard, R. M., and Eisenbruch, A. B. (2020). The importance of being honest? Evidence that deception may not pollute social science subject pools after all. Behav. Res. Methods 52, 1175–1188. doi: 10.3758/s13428-019-01309-y

PubMed Abstract | Crossref Full Text | Google Scholar

Krawczyk, M. (2015). “Trust me, I am an economist.” a note on suspiciousness in laboratory experiments. J. Behav. Exp. Econ. 55, 103–107. doi: 10.1016/j.socec.2014.12.003

Crossref Full Text | Google Scholar

Krawczyk, M. (2019). What should be regarded as deception in experimental economics? evidence from a survey of researchers and subjects. J. Behav. Exp. Econ. 79, 110–118. doi: 10.1016/j.socec.2019.01.008

Crossref Full Text | Google Scholar

Krügel, S., Ostermaier, A., and Uhl, M. (2022). Zombies intheloop? Humans trustuntrust worthy AI-advisors for ethical decisions. Philos. Technol. 35, 1–37. doi: 10.1007/s13347-022-00511-9

Crossref Full Text | Google Scholar

LaMothe, E., and Bobek, D. (2020). Are individuals more willing to lie to a computer or a human? Evidence from a tax compliance setting. J. Busin. Ethics 167, 157–180. doi: 10.1007/s10551-019-04408-0

Crossref Full Text | Google Scholar

Leib, M., Köbis, N. C., Rilke, R. M., Hagens, M., and Irlenbusch, B. (2024). Corrupted by algorithms? How AI-generated and human-written advice shape (dis)honesty. Econ. J. 134, 766–784. doi: 10.1093/ej/uead056

PubMed Abstract | Crossref Full Text | Google Scholar

Levinson, J., Askeland, J., Becker, J., Dolson, J., Held, D., Kammel, S., et al. (2008). “Towards fully autonomous driving: systems and algorithms,” in 2011 IEEE Intelligent Vehicles Symposium (IV) (Baden-Baden: IEEE), 163–168.

Google Scholar

Li, J., Liu, W., and Zhang, J. (2025). Automating financial audits with random forests and real-time stream processing: a case study on efficiency and risk detection. Informatica 49, 1–20. doi: 10.31449/inf.v49i16.7805

Crossref Full Text | Google Scholar

Litterscheidt, R., and Streich, D. J. (2020). Financial education and digital asset management: What's in the black box? J. Behav. Exp. Econ. 87:101573. doi: 10.1016/j.socec.2020.101573

Crossref Full Text | Google Scholar

Logg, J. M., Minson, J. A., and Moore, D. A. (2019). Algorithm appreciation: People prefer algorithmic to human judgment. Organ. Behav. Hum. Decis. Process. 151:90–103. doi: 10.1016/j.obhdp.2018.12.005

Crossref Full Text | Google Scholar

Longoni, C., Bonezzi, A., and Morewedge, C. K. (2019). Resistance to medical artificial intelligence. J. Consum. Res. 46, 629–650. doi: 10.1093/jcr/ucz013

Crossref Full Text | Google Scholar

Madhavan, P., and Wiegmann, D. A. (2007). Similarities and differences between human–human and human–automation trust: an integrative review. Theoret. Issues Ergon. Sci. 8, 277–301. doi: 10.1080/14639220500337708

Crossref Full Text | Google Scholar

Mahmud, H., Islam, A. N., Ahmed, S. I., and Smolander, K. (2022). What influences algorithmic decision-making? A systematic literature review on algorithm aversion. Technol. Forecast. Soc. Change 175:121390. doi: 10.1016/j.techfore.2021.121390

Crossref Full Text | Google Scholar

Mol, J. M., van der Heijden, E. C. M., and Potters, J. J. M. (2020). (Not) alone in the world: Cheating in the presence of a virtual observer. Exp. Econ. 23, 961–978. doi: 10.1007/s10683-020-09644-0

Crossref Full Text | Google Scholar

Niszczota, P., and Kaszás, D. (2020). Robo-investment aversion. PLoS ONE 15:e0239277. doi: 10.1371/journal.pone.0239277

PubMed Abstract | Crossref Full Text | Google Scholar

Önkal, D., Goodwin, P., Thomson, M., Gönül, S., and Pollock, A. (2009). The relative influence of advice from human experts and statistical methods on forecast adjustments. J. Behav. Decis. Mak. 22, 390–409. doi: 10.1002/bdm.637

Crossref Full Text | Google Scholar

Peer, E., Acquisti, A., and Shalvi, S. (2014). “I cheated, but only a little”: Partial confessions to unethical behavior. J. Pers. Soc. Psychol. 106, 202–217. doi: 10.1037/a0035392

PubMed Abstract | Crossref Full Text | Google Scholar

Petisca, S., Leite, I., Paiva, A., and Esteves, F. (2022). Human dishonesty in the presence of a robot: The effects of situation awareness. Int. J. Soc. Robot. 14, 1211–1222. doi: 10.1007/s12369-022-00864-3

Crossref Full Text | Google Scholar

Pittarello, A., Leib, M., Gordon-Hecker, T., and Shalvi, S. (2015). Justifications shape ethical blind spots. Psychol. Sci. 26, 794–804. doi: 10.1177/0956797615571018

PubMed Abstract | Crossref Full Text | Google Scholar

Prahl, A., and Swol, L. V. (2017). Understanding algorithm aversion: When is advice from automation discounted? J. Forecast. 36, 691–702. doi: 10.1002/for.2464

Crossref Full Text | Google Scholar

Renier, L. A., Mast, M. S., and Bekbergenova, A. (2021). To err is human, not algorithmic – robust reactions to erring algorithms. Comput. Human Behav. 124, 1–12. doi: 10.1016/j.chb.2021.106879

Crossref Full Text | Google Scholar

Ruedy, N. E., and Schweitzer, M. E. (2010). In the moment: The effect of mindfulness on ethical decision making. J. Busin. Ethics 95, 73–87. doi: 10.1007/s10551-011-0796-y

Crossref Full Text | Google Scholar

Sandoval, E. B., Brandstatter, J., Yalcin, U., and Bartneck, C. (2020). Robot likeability and reciprocity in human robot interaction. Int. J. Soc. Robot. 13, 851–862. doi: 10.1007/s12369-020-00658-5

Crossref Full Text | Google Scholar

Schlund, R., and Zitek, E. M. (2024). Algorithmic versus human surveillance leads to lower perceptions of autonomy and increased resistance. Commun. Psychol. 2:53. doi: 10.1038/s44271-024-00102-8

PubMed Abstract | Crossref Full Text | Google Scholar

Schubert, T. W., and Otten, S. (2002). Overlap of self, ingroup, and outgroup: Pictorial measures of self-categorization. Self Identity 1, 353–376. doi: 10.1080/152988602760328012

Crossref Full Text | Google Scholar

Serra-Garcia, M., and Gneezy, U. (2025). Improving human deception detection using algorithmic feedback. Managem. Sci. doi: 10.1287/mnsc.2023.02792

PubMed Abstract | Crossref Full Text | Google Scholar

Shalvi, S., Dana, J., Handgraaf, M. J., and Dreu, C. K. D. (2011). Justified ethicality: Observing desired counterfactuals modifies ethical perceptions and behavior. Organ. Behav. Hum. Decis. Process. 115, 181–190. doi: 10.1016/j.obhdp.2011.02.001

Crossref Full Text | Google Scholar

Shalvi, S., Levine, E., Thielmann, I., Jayawickreme, E., van Rooij, B., Teodorescu, K., et al. (2025). “The science of honesty: A review and research agenda,” in Advances in Experimental Social Psychology. Cambridge: Academic Press.

Google Scholar

Sharan, N. N., and Romano, D. M. (2020). The effects of personality and locus of control on trust in humans versus artificial intelligence. Helyion 6:e04572. doi: 10.1016/j.heliyon.2020.e04572

PubMed Abstract | Crossref Full Text | Google Scholar

Shin, D. (2020). User perceptions of algorithmic decisions in the personalized AI system: perceptual evaluation of fairness, accountability, transparency, and explainability. J. Broadcast. Electronic Media 64, 541–565. doi: 10.1080/08838151.2020.1843357

Crossref Full Text | Google Scholar

Starmer, C., and Sugden, R. (1991). Does the random-lottery incentive system elicit true preferences? An experimental investigation. Am. Econ. Rev. 81, 971–978.

Google Scholar

Sutherland, S. C., Harteveld, C., and Young, M. E. (2016). Effects of the advisor and environment on requesting and complying with automated advice. ACM Trans. Interact. Intellig. Syst. 6, 1–36. doi: 10.1145/2905370

Crossref Full Text | Google Scholar

Tao, R., Su, C.-W., Xiao, Y., Dai, K., and Khalid, F. (2021). Robo advisors, algorithmic trading and investment management: Wonders of fourth industrial revolution in financial markets. Technol. Forecast. Soc. Change 163:120421. doi: 10.1016/j.techfore.2020.120421

Crossref Full Text | Google Scholar

Tschider, C. A. (2020). Beyond the 'black box'. Denver Law Rev. 98, 683–723.

Google Scholar

Tversky, A., and Kahneman, D. (1981). The framing of decisions and the psychology of choice. Science 211, 453–458. doi: 10.1126/science.7455683

PubMed Abstract | Crossref Full Text | Google Scholar

Ullman, D., Leite, I., Phillips, J., Kim-Cohen, J., and Scassellati, B. (2014). “Smart human, smarter robot: How cheating affects perceptions of social agency,” in Proceedings of the Annual Meeting of the Cognitive Science Society, 2996–3001.

Google Scholar

von Schenk, A., Klockmann, V., Bonnefon, J.-F., Rahwan, I., and Köbis, N. (2024). Lie detection algorithms disrupt the social dynamics of accusation behavior. Iscience 27:7. doi: 10.1016/j.isci.2024.110201

PubMed Abstract | Crossref Full Text | Google Scholar

Vrij, A. (2000). Detecting Lies and Deceit: The Psychology of Lying and Implications for Professional Practice. Chichester: Wiley.

Google Scholar

Wang, Y., Wang, Z., and Li, J. (2024). Does algorithmic control facilitate platform workers' deviant behavior toward customers? The ego depletion perspective. Comput. Human Behav. 156:108242. doi: 10.1016/j.chb.2024.108242

Crossref Full Text | Google Scholar

Yang, Y. (2005). Can the strengths of aic and bic be shared? Biometrika 92, 937–950. doi: 10.1093/biomet/92.4.937

Crossref Full Text | Google Scholar

Yeomans, M., Shah, A., Mullainathan, S., and Kleinberg, J. (2019). Making sense of recommendations. Inform. Syst. Res. 32, 403–414. doi: 10.1002/bdm.2118

Crossref Full Text | Google Scholar

Yost, A. B., Behrend, T. S., Howardson, G., Darrow, J. B., and Jensen, J. M. (2019). Reactance to electronic surveillance: a test of antecedents and outcomes. J. Bus. Psychol. 34, 71–86. doi: 10.1007/s10869-018-9532-2

Crossref Full Text | Google Scholar