From biophysics to cellular function: neural TELCs-membrane-anions capacitor transmembrane potential

Based on the transmembrane-electrostatically localized protons/cations charges (TELCs) theory, neural transmembrane potential including both resting and action potential is now well elucidated as the voltage contributed by the TELCs-membrane-anions capacitor biophysics in a neuron. Accordingly, neural transmembrane potential has an inverse relationship with TELCs surface density, which may represent a substantial progress in bettering the fundamental understanding of neuroscience. In this article, I will present a review on the latest development of the TELCs neural transmembrane potential theory and address Silverstein’s interesting arguments regarding the TELCs model that may constitute a complementary development to both the Hodgkin-Huxley classic cable theory and the Goldman-Hodgkin-Katz equation. A series of predictions from the TELCs model regarding crucial ion channels have exactly been experimentally observed in many well-established electrophysiological phenomena including (but not limited to): 1) The tetrodotoxin (TTX) sensitivity shows the complete blockade of action potentials by TTX; 2) Genetic knockout or mutation of critical ion channels abolishes action potential spike; and 3) The precise clustering of ion channels at the axonal initial segment and nodes of Ranvier underlies the ability to fire action potential spikes and the saltatory conduction along a myelinated axon. This indicates that the TELCs model can be well predictive and provide new opportunities as a theoretical tool for further research to better understand neurosciences.

GRAPHICAL ABSTRACT

GRAPHICAL ABSTRACT | The TELCs theory shows: Neural transmembrane potential has an inverse relationship with TELCs surface density.

Highlights

• Neural transmembrane potential is now elucidated as the voltage contributed by the TELCs membrane capacitor activity.

• The TELCs model is complementary to the Hodgkin-Huxley classic cable theory and the Goldman-Hodgkin-Katz equation.

• Application of the TELCs model enables calculation of TELCs surface density as a function of transmembrane potential.

• Action potential spikes can now be constructed through TELCs-based integral equations using transmembrane ion current data.

Introduction

The recently developed transmembrane-electrostatically localized proton(s)/cation(s) charge(s) [TELC(s)] model (Lee, 2019a; Lee, 2020a; Lee, 2021) provides a theoretical framework that can help explain protonic cell energetics including many experimental observations and elucidate bioenergetic systems including both delocalized and localized protonic couplings (Lee, 2023a; Lee, 2020b; Lee, 2020c). The term TELCs represent the “total transmembrane-electrostatically localized positive charges” including the “charges of both the transmembrane-electrostatically localized proton(s) (TELP(s)) and the associated transmembrane-electrostatically localized non-proton cations after the proton-cation exchanging process reaching equilibrium”. TELCs are immediately related to transmembrane potential that is now known as a function of TELCs population density within a TELCs-membrane-anions capacitor (Lee, 2019a; Lee, 2020c). Consequently, the excess positive charges of TELCs at one side of the membrane are balanced by the excess negative charges of transmembrane-electrostatically localized hydroxides anions (TELAs) at the other side of the membrane. The formation of a TELCs-membrane-TELAs capacitor has been experimentally demonstrated using a biomimetic anode water-Teflon membrane-water cathode system (Saeed and Lee, 2015; Saeed and Lee, 2018; Lee, 2025a) through two PhD thesis research projects (Saeed, 2016; Kharel, 2024).

The TELCs (TELPs) model (Lee, 2019a; Lee, 2020a; Lee, 2021), which may represent “a complementary development to Mitchell’s chemiosmotic theory”, is highly useful in helping to elucidate “real-world bioenergetic systems with both delocalized and localized protonic coupling”. For instance, the TELPs model has been successfully employed in “elucidating the decades-longstanding energetic conundrum (Guffanti and Krulwich, 1984; Krulwich et al., 1998; Krulwich et al., 2011) of ATP synthesis in alkalophilic bacteria” (Lee, 2020b; Lee, 2015; Lee, 2017a; Lee, 2019b; Lee, 2018; Lee, 2017b) and in “bettering the understanding of energetics in mitochondria” (Lee, 2020a; Lee, 2021). Its application has recently led to the discovery of the TELPs “thermotrophic function” as the “Type-B energetic process” (Lee, 2022a; Lee, 2022b; Lee, 2023b; Sheehan et al., 2023; Lee, 2024) which can isothermally utilize environmental heat energy to do useful work in helping drive the synthesis of ATP (Lee, 2021a; Lee, 2021b).

Consequently, it is now understood that neural transmembrane potential has an inverse relationship with TELCs surface density, which may represent a transformative progress in bettering the fundamental understanding of neuroscience (Lee, 2020c; Lee, 2023c). Application of the TELCs model enables calculation of TELCs surface density as a function of transmembrane potential (Lee, 2023c), which may represent a complementary development to both the Hodgkin-Huxley classic cable theory and the Goldman-Hodgkin-Katz equation. Using the TELCs model, the neural touch signal transduction responding time required to fire an action potential spike has now, for the first time, been calculated to be as short (fast) as 0.3 ms (Lee, 2025b), which led to a better understanding on the question of how the transient ion transport activity of touch receptors (PIEZO) could change the graded potential to stimulate an action potential firing.

However, probably due to the subtlety of the TELCs theory and due to the complexity of the neural systems and their associated energetics, currently, not necessarily everyone could easily understand the TELCs-based neural transmembrane potential theory and its implications (Lee, 2020c; Lee, 2023c). For example, Todd Silverstein previously presented his critiques (Silverstein, 2023a; Silverstein, 2025) on the TELCs model (Lee, 2020c; Lee, 2023c). The author (Lee) welcomes critiques and discussions as that can also be a part of the process for scientific progress and learning. As we recently discussed in a review article published in the current trends of neurology (Lee, 2023c), Silverstein’s critiques (Silverstein, 2023a; Silverstein, 2025) were largely stemmed from his own errors, misunderstanding, and/or mischaracterization of the TELCs model (Lee, 2025a). Certain independent researcher has now also pointed out that “Silverstein’s critiques are untenable” (Tamagawa, 2025). Since misunderstanding or mischaracterization could potentially cause confusions in the field, it is necessary to clarify here for the scientific community. Especially, Silverstein’s critiques (Silverstein, 2023a; Silverstein, 2025; Silverstein, 2024a; Silverstein, 2022) typically do not accurately describe the TELCs model and its associated equations.

Therefore, in this article, I will present a review on the latest development of the TELCs neural transmembrane potential theory and then address Silverstein’s interesting claims and arguments (Silverstein, 2025) point-by-point. I will also comparatively present some of the key tenets between the classic Goldman-Hodgkin-Katz (GHK) model vs the TELCs theory. Finally, we will discuss the opportunities and directions for further research on TELCs-based neuroscience.

Results and discursions

Neural TELCs-membrane-TELAs capacitor transmembrane potential model

The TELCs-based neural transmembrane potential theory (Lee, 2020c; Lee, 2023c) is built on the knowledge that liquid water can serve as a protonic conductor (Figure 1A), which well agrees with the fact that protons can use the “hops and turns” mechanism and quickly translocate among water molecules as first outlined by Grotthuss (de Grotthuss, 1806; Marx et al., 1999; Pomès and Roux, 2002; Marx, 2006) who developed this model to explain the enormous mobility of the H⁺ ion relative to other ions. This protonic conduction (Figure 1A) is much faster than the diffusive movement of a non-proton cation such as Na⁺ which tightly binds with water molecules. For a non-proton cation to move through liquid water, it must carry its bound water molecules and physically plough through the molecular array of liquid water. Consequently, protonic conduction is much faster that the movement of non-proton cations such as Na⁺, K⁺, and Mg²⁺.

Figure 1

Figure 1. Illustration of liquid water as a protonic conductor in relation to neural membrane capacitor formation. (A) Protons can quickly transfer among water molecules by the “hops and turns” mechanism [also known as the Grotthuss mechanism Marx (2006)] so that a microscopic water body may be thought as a protonic conductor (Adapted from Lee 2012 Bioenergetics 1: 104, 1–8); (B) Illustration of ATP-driven sodium/potassium (3Na⁺/2K⁺) pump in relation to TELCs-membrane-TELAs capacitor formation in a neuron: an ATP-driven sodium/potassium (3Na⁺/2K⁺) pump transporting 3 sodium cations across the cytoplasmic membrane from inside the cell to the outside while co-transporting 2 potassium cations across the membrane from the outside into the cell, which results in a TELCs-neural membrane-TELAs capacitor as illustrated by the TELCs at the liquid-membrane interface along the extracellular side while localized anions along the intracellular side. “E = 0” means the electric field in the liquid is zero. R and r are polar coordinates. dS is a surface differential element. The extracellular and intracellular bulk-liquid phase Na⁺, K⁺, Cl⁻, Ca²⁺ concentrations shown in the drawing are based on Hammond (2015). Reproduced from Lee (2025b).

According to certain neuroscience knowledge (Hammond, 2015) and the TELCs neural transmembrane potential theory (Lee, 2020c; Lee, 2023c), as illustrated in Figure 1B, an ATP-driven sodium/potassium (3Na⁺/2K⁺) pump transports every 3 sodium cations across the neuron cytoplasmic membrane from inside the cell to the outside while co-transports every 2 potassium cations across the membrane from the outside into the cell per ATP consumption (Hammond, 2015). Two of the 3 sodium cations transported out of the cell are charge-balanced by the 2 potassium cations transported into the cell whereas one of the 3 sodium cations (positive charges) is not charge-balanced, becoming an excess (extra) positive charge at the extracellular side. Consequently, this 3Na⁺/2K⁺ transporting process per ATP consumption results in a net translocation of one positive charge (e.g., Na⁺) across the cytoplasmic membrane from inside the neuronal cell to the outside leaving its countering anion (e.g., Cl⁻) inside the cell. As the electrogenic 3Na⁺/2K⁺ transporting process continues, it results in the accumulation of excess positive charges (cations) outside the neuron cell while accumulating excess anions (negative charges) inside the cell, which is important also in setting up and/or maintaining the ion concentration gradients of Na⁺ (high outside), K⁺ (high inside), and indirectly, Cl⁻ (high outside). By “excess cations” (or excess positive charges), it means that their positive charges are not balanced by their countering anions since their countering anions (excess negative charges) are on the other side of the membrane. The excess positive charges and the excess negative charges across the neural membrane will form a TELCs-membrane-TELAs capacitor (Figure 1B) which follows the principle of total charge neutrality.

During TELCs formation, any transmembrane-electrostatically localized excess non-proton cations may be exchanged out by the protons from the liquid phase. Any excess cations that are exchanged out of the TELCs layer into the bulk-liquid phase will fully interact (such as hydration) with water molecules and electrostatically repel protons (parts of water molecules) from the bulk aqueous phase through the “hops and turns” mechanism to the liquid-neural membrane interface to be transmembrane-electrostatically localized along the outside surface of the neuron cell membrane where the localized protons/cations transmembrane-electrostatically attract the excess anions such as hydroxide anions at the other side of the cell membrane as illustrated in Figure 1B.

The events of the transmembrane-electrostatically localized protons/cations (i.e., TELCs) occur beneath the membrane molecular backgrounds: the membrane-fixed surface charge-attracted ions including the “electrical double layers” along the membrane surfaces that exist even before the membrane is energized. One must not confuse the membrane fixed-charge-attached protons/cations with the TELCs at the water-membrane interface. It is the TELCs that are relevant to the transmembrane potential. Therefore, the fixed surface-charges-attracted ions including their associated electrical double layers that can be well described by the Gouy-Chapman theory (Mclaughlin, 1989) are not the focus of this paper and thus not shown in Figure 1B, which focuses on illustrating the fundamental concept of a TELCs-membrane-TELAs capacitor that is relevant to the neural transmembrane potential known also as the “resting and action potential”.

Also, unlike the charge-balanced “free protons” as reported previously in a bulk liquid volume (Bal et al., 2012), the transmembrane-electrostatically localized protons (TELPs) at the liquid-membrane interface are not entirely free (Lee, 2019a): they can move quickly along the membrane surface in a way somewhat similar to those postulated previously (Williams, 1988; Nagle and Tristramnagle, 1983; Mulkidjanian et al., 2005); but, they are not entirely free to move away from the membrane surface because of the transmembrane-electrostatic attraction between the excess positive charges (protons/cations) and the excess negative charges (anions) across the membrane as reported previously (Lee, 2020c; Lee, 2023c).

Since neural transmembrane potential is measured typically from a reference electrode outside a neuronal cell to a measuring electrode inside the cell, its calculation convention ($V_m=V_{cytosol}-V_{out}$, Azzone et al., 1993; Bertl et al., 1992) is opposite to the standard Mitchellian protonic bioenergetics convention for transmembrane potential calculation ($∆\psi ={∆\psi }_p-{∆\psi }_n$). Therefore, based on the TELC theory (Lee, 2020c; Lee, 2023c), the neural transmembrane potential (V) including the neural resting and action potential is mathematically expressed in relation to the TELCs density which is the sum of the steady-state TELP and transmembrane-electrostatically localized non-proton cations concentrations $\left(\left[H_L^{+}\right]+{\displaystyle {\sum }_{i=1}^n}\left[M_L^{i+}\right]\right)$ after cation exchange with TELPs as shown in the following equation with a voltage unit (V in volts):

$Neuraltransmembranepotential\left(V\right)=-\frac{S·l·F·\left(\left[H_L^{+}\right]+{\displaystyle {\sum }_{i=1}^n}\left[M_L^{i+}\right]\right)}{C}(1)$

where $S$ is the membrane surface area; $C$ is the membrane capacitance; $l$ is the thickness of TELC layer; $F$ is the Faraday constant; $\left[H_L^{+}\right]$ is the TELP concentration and ${\displaystyle {\sum }_{i=1}^n}\left[M_L^{i+}\right]$ is the sum of transmembrane-electrostatically localized non-proton cations (e.g., Na⁺ and K⁺) concentrations $\left[M_L^{i+}\right]$ at the liquid-membrane interface on the extracellular membrane surface after the proton-cation exchange reaching equilibrium.

With this TELCs-based neural transmembrane potential equation (Equation 1), the biophysics of action potential can now be better understood. For example, as reported previously (Lee, 2020c), upon stimulation by neurotransmitters, the neuron membrane potential may change positively and/or negatively resulting in a “graded potential”. When the graded potential reaches the threshold of −55 mV, an opening of voltage-gated sodium channels is triggered (Figure 2A), resulting in an flow of excess Na⁺ cations from outside into the neuronal cell so that the TELCs density $\left(\left[H_L^{+}\right]+{\displaystyle {\sum }_{i=1}^n}\left[M_L^{i+}\right]\right)$ at the extracellular membrane surface is reduced until becoming a negative value that represents a state of “depolarization”, thus dramatically changing the value of action potential according to the TELCs neural transmembrane potential equation (Equation 1). This explains the formation of an action potential spike: a rapid “depolarization” up to about +30 mV where the voltage-gated sodium channels rapidly inactivate, and the voltage-gated potassium channels will open (Figure 2B, Cook et al., 2016).

Figure 2

Figure 2. Illustration of protonic capacitor in relation to action potential in a neuron (“E = 0” means the electric field in the liquid is zero. R and r are polar coordinates. dS is a surface differential element.): (A) an opening of V-gated sodium (Na⁺) channels is triggered, resulting in the flow of the excess Na⁺ cations from the outside into the neuron cell so that the transmembrane-electrostatically localized protons/cation population density is dramatically reduced until becoming a state of “depolarization” as illustrated by the localized protons/cations at the liquid-membrane interface along the cytoplasmic (intracellular) side while anions at the liquid-membrane interface along the periplasmic (extracellular) side. (B) When the “depolarization” process reaches the membrane potential level of about +30 mV, the V-gated potassium (K⁺) channels open to allow the K⁺ cations flow out of the neural cell resulting in a rapid “repolarization” followed by a “undershoot” and then the activities of the leaky channels and the ATP-driven sodium/potassium (3Na⁺/2K+) pumps will equilibrate and re-establish the polarized state with a resting potential as commonly observed in a neuron as shown in Figure 1B. The extracellular and intracellular bulk-liquid phase Na⁺, K⁺, Cl⁻, Ca²⁺ concentrations shown in the drawing are based on Hammond (2015). Reproduced from Lee (2025b).

Note, the voltage-gated potassium channels (threshold potential around −40 mV) are believed to act as a type of “delayed rectifiers which activate after a delay following membrane depolarization and inactivate slowly” (Hammond, 2015). Consequently, the exit of K⁺ ions through the voltage-gated “delayed rectifier” potassium channels responsible for action potential repolarization does not occur at the same time as the entry of Na⁺ ions through the voltage-gated sodium channels. This enables the neural membrane to first depolarize in response to the entry of Na⁺ through voltage-gated sodium channels and then to repolarize as a consequence of the exit of K⁺ through open voltage-gated potassium channels.

As illustrated in Figure 2B, the opening of the voltage-gated potassium channels allows K⁺ cations flow out of the cell, which increases the population of excess cations (K⁺) charges outside the cell so that the TELCs density $\left(\left[H_L^{+}\right]+{\displaystyle {\sum }_{i=1}^n}\left[M_L^{i+}\right]\right)$ on the extracellular membrane surface will increase in accordance of Equation 1. This explains the rapid “repolarization” in returning to the polarized neural cell state followed by an “undershoot”. Then, the activities of other channels including certain leaky channels and the ATP-driven sodium/potassium (3Na⁺/2K⁺) pumps will equilibrate and re-establish a resting potential (Figure 1B) as commonly observed in neurons.

Therefore, with the TELCs neural transmembrane potential equation (Equation 1), the origin of the resting and action potential is now much better understood as a TELCs capacitor-related behavior that is driven by the activities of the ion transporters and channels across the neuron membrane. That is, as shown by Equation 1, the neural transmembrane potential (V) is a function of the TELCs density $\left(\left[H_L^{+}\right]+{\displaystyle {\sum }_{i=1}^n}\left[M_L^{i+}\right]\right)$ at the liquid-membrane interface in a neural membrane capacitor (Figures 1, 2). Consequently, it is the TELCs density $\left(\left[H_L^{+}\right]+{\displaystyle {\sum }_{i=1}^n}\left[M_L^{i+}\right]\right)$ at the liquid-membrane interface of the neural protonic-cationic capacitor system that biophysically constitutes/manifests the “neural resting and action potential”.

TELCs held by transmembrane-electrostatic attraction force with TELAs

As reported in our latest publication (Lee, 2025c), in a TELCs-membrane-TELAs capacitor, most of the TELCs (TELPs) are likely to be held within the first layer of water molecules on the alkane (hydrophobic) core membrane surface beneath lipid head groups. This is because TELCs are held on the alkane core membrane surface by the transmembrane-electrostatic attraction force with TELAs on the other side of the membrane. Note, the lipid head groups and the membrane lipids compositions have little to do with the transmembrane potential (Lee, 2025c).

Figure 3 illustrates a protonic capacitor (TELPs-membrane-TELAs) across the fully dehydrated alkane core membrane in a typical lipid bilayer which has three distinct regions: the fully hydrated headgroups (0.7–1.0 nm), the fully dehydrated alkane core membrane (2.5–3.5 nm thick) and a short (0.3 nm) intermediate region with partial hydration. As illustrated in Figure 3, transmembrane-electrostatically localized protons (H⁺, TELPs) are located likely within the 0.3-nm “intermediate” region with partial hydration on the surface of the fully dehydrated alkane core membrane; Meanwhile, their corresponding transmembrane-electrostatically localized hydroxide (OH⁻) anions (TELAs) are at the other side of the dehydrated alkane core membrane.

Figure 3

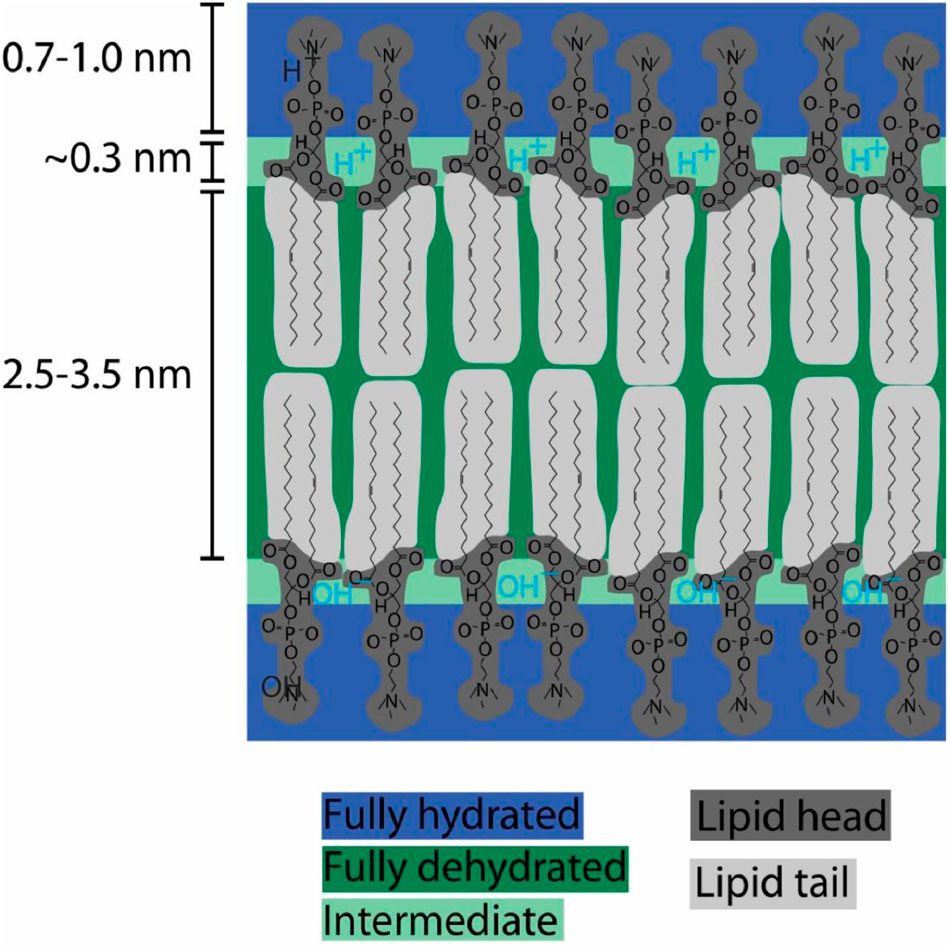
Figure 3. Schematic illustration of a protonic capacitor (TELPs-membrane-TELAs) across a fully dehydrated alkane core membrane in a typical lipid bilayer. There are three distinct regions in a typical lipid bilayer: a fully hydrated headgroups (0.7–1.0 nm), a fully dehydrated alkane core membrane (2.5–3.5 nm thick) and a short (0.3 nm) intermediate region with partial hydration. Transmembrane-electrostatically localized protons (H⁺, TELPs) are located within the 0.3 nm intermediate region with partial hydration on the surface of the fully dehydrated alkane core membrane while transmembrane-electrostatically localized hydroxides (OH⁻) anions (TELAs) are at the other side of the dehydrated alkane core membrane. Note, at a typical resting transmembrane potential of −70 mV, the separation distance between two adjacent TELPs is about 16 nm. The drawing of TELPs density here is not in scale. Adapted and modified from MDougM (2008), Lee (2025c).

Accordingly, TELPs and TELAs are held together across a fully dehydrated alkane core membrane (2.5–3.5 nm thick) by their mutual transmembrane-electrostatic attractive force as shown in a TELPs-membrane-TELAs capacitor (Figure 3). As reported in our latest publication (Lee, 2025c), the total transmembrane attractive force ($F$) of a transmembrane-electrostatically localized proton (H⁺) is from the transmembrane interactions with its multiple transmembrane-electrostatically localized hydroxide (OH⁻) anions (TELAs).

As reported in our latest publication (Lee, 2025c), we have recently calculated the associated TELCs surface density, the specific membrane area (nm²) per TELC, the mean separation distance between adjacent TELCs, and the transmembrane attractive force ($F$) of a transmembrane-electrostatically localized proton (H⁺) interacting with multiple transmembrane-electrostatically localized hydroxide (OH⁻) anions. As presented in Table 1, at a typical neural resting transmembrane potential with its absolute value of 70 mV, the transmembrane attractive force ($F$) was calculated to be in range from 2.03 × 10⁻¹¹ to 1.10 × 10⁻¹¹ N for a typical lipid bilayer, respectively with its alkane core membrane thickness in a range from 2.5 nm to 3.5 nm (Figure 3).

Table 1

Table 1. Transmembrane-electrostatically localized charges (TELCs/TELPs or TELAs) surface density, mean separation distance (b) between adjacent transmembrane-electrostatically localized hydroxide (OH⁻) anions, and the integrated protonic transmembrane attractive force ($F$) calculated as a function of transmembrane potential $∆\psi$ for a typical lipid bilayer assuming its hydrocarbon core membrane dielectric constant (κ) of 1.88 using the calculation method reported in Lee (2025c). TELCs density was calculated from transmembrane potential in a range from 10 to 100 mV through Equations 1, 2 using specific membrane capacitance $C/S$ of 9.2 mF/m² based on measured experimental data (Gentet et al., 2000). Mean separation distance b (nm) between adjacent transmembrane-electrostatically localized hydroxide (OH⁻) anions was calculated from the square root of 1/TELC density. Adapted and modified from Lee (2025c).

Accordingly, to move such a localized proton away from the membrane-liquid interface by 1 nm (say from 2.03 × 10⁻¹¹ N of 2.5 nm to 1.10 × 10⁻¹¹ N of 3.5 nm), it would require 1.56 × 10⁻²⁰ J of energy (=10⁻⁹ m × (2.03 × 10⁻¹¹ + 1.10 × 10⁻¹¹ N)/2), which is equivalent to 3.6 times as much as the Boltzmann kT thermal kinetic energy at a physiological temperature of 37 °C (310 K). These results (Table 1) again indicate that a TELPs-membrane-TELAs capacitor (Figure 3) can be quite stable. Thus, TELCs (TELPs) formation does not require any of the putative “potential well/barrier” proposed by Junge and Mulkidjanian (Cherepanov et al., 2003; Mulkidjanian et al., 2006) and recently advocated by Silverstein (Silverstein, 2023b) in liquid phase.

According to the understanding with the TELC(s) model (Lee, 2019a; Lee, 2020a; Lee, 2025c), TELCs (TELPs) activities “are likely to be local and dynamic”: TELPs can rapidly migrate along the membrane surface and they are also in dynamic communication with the bulk aqueous liquid phase through the cation-proton exchange process. Meanwhile (Lee, 2025c), most of the TELPs are likely to stay within the first layer of water molecules on the alkane core membrane surface which is beneath the membrane’s lipid head groups” (Figure 3). That is, TELPs likely are just hiding on the alkane core membrane surface beneath the lipid head groups.

As listed in Table 1, at a typical neural resting transmembrane potential with its absolute value of 70 mV, the calculated TELCs density (3.93 × 10³ TELCs per µm²) indicates that TELCs (TELPs) are quite sparsely distributed with an average separation distance of 15.9 nm between any two adjacent TELCs on the alkane core membrane surface. The current imaging and spectroscopy tools (e.g., AFM, SERS, cryo-EM) could not visualize such dynamic and sparsely distributed TELPs or TELCs on biological membrane surface for at least two reasons: 1) All of those imaging and spectroscopy tools do not have the required resolution to “see” a proton or sodium cation that is dynamic and sparsely distributed with an average separation distance of 16 nm; and 2) TELCs (TELPs) could hardly be retained in any conventional membrane sample preparation since they are dynamic and dependent on transmembrane potential. Currently, we are not aware of any artificial pH sensor that could be used to directly measure TELPs in in-vivo biomembrane systems; that probably could also explain why the existence of TELPs was never uncovered during the last 7 decades of the “delocalized vs. localized proton coupling debates” since the early 1960s (Mitchell, 1961; Mitchell and Moyle, 1965; Williams, 1978; Slater, 1967; Williams, 1975; Williams, 1988; Heberle et al., 1994; Dilley et al., 1987; Dilley, 2004; Mulkidjanian et al., 2006).

Only recently, TELPs were, for the first time, discovered through experimental demonstration of a protonic capacitor in a biomimetic cathode water-Teflon membrane-water anode system using an aluminum (Al) metal film as a protonic sensor (Lee, 2025a). Teflon (Tf) membrane which is an insulator with a dielectric constant of 2.1 is a reasonable mimic of the biological alkane core membrane, which is in the same way as how our bioenergetics founding Father Peter Mitchell had treated biological membrane as an insulator in his pioneering Chemiosmotic Theory (Mitchell and Moyle, 1967; Mitchell, 1985). The experimentally demonstrated TELPs activities with the Al metal film surface in comparison with the Tf membrane surface (Lee, 2025a) is well in line with the TELPs capacitor model. The experimental results indicate that most of the TELPs are indeed held within the first layer of water molecules on the hydrophobic surface of the Al-Tf-Al membrane system so that TELPs can directly react with the Al film atoms as part of the protonic sensing corrosion process.

TELCs model-based biophysics equations to enable better mathematical description of neural transmembrane potential

Application of the TELCs model can mathematically better describe neural transmembrane potential (Lee, 2020c; Lee, 2023c). Briefly, based on the neural transmembrane potential equation (Equation 1), the molar concentration of total transmembrane-electrostatically localized protons/cations charges $\left[TELC\right]$, which are the sum of the transmembrane-electrostatically localized protons and non-proton cations such as sodium $\left(\left[H_L^{+}\right]+{\displaystyle {\sum }_{i=1}^n}\left[M_L^{i+}\right]\right)$ at the liquid-membrane interface along neuronal extracellular membrane surface, was calculated using the following equation:

$\left[TELC\right]=\left[H_L^{+}\right]+{\displaystyle \sum _{i=1}^n}\left[M_L^{i+}\right]=-\frac{Neuraltransmembranepotential\left(V\right)·C}{S·l·F}(2)$

Where $S$ is the neural extracellular membrane surface area; $l$ is the TELC layer thickness; $F$ is the Faraday constant; $C$ is the neural membrane capacitance; and $V$ is the neural transmembrane potential.

Using a given molar TELC concentration [TELC] with extracellular membrane surface area ($S$) and TELC layer thickness ($l$), the TELC surface population density was calculated as the amounts (numbers) of transmembrane-electrostatically localized protons/cations charges (TELC) per extracellular membrane surface area ($S$, or per cell) according to the following equation:

$TELCnumbers=S·l·N_A·\left[TELC\right]=S·l·N_A·\left(\left[H_L^{+}\right]+{\displaystyle \sum _{i=1}^n}\left[M_L^{i+}\right]\right)(3)$

where $N_A$ is the Avogadro constant (6.02205 × 10²³ mol⁻¹).

The $TELCnumbers$ essentially represent the localized excess proton and cation charges (TELCs) population density per surface area ($S$). From here, one can also quite clearly understand that it is the localized excess proton and cation charges (TELCs but not the bulk phase ion concentrations) that physically form the instant transmembrane potential through the membrane capacitor effect as expressed in Equations 1–3.

Based on the understanding of TELCs-associated action potential theory (Lee, 2020c; Lee, 2023c), the TELC density change per cell surface area ($S$) as a result from an ionic flow across the neuronal membrane (such as the PIEZO-channel cationic conduction current) was calculated using the following equation:

$TELCchange/S=I·t/\left(e·S\right)(4)$

Where $I$ is a given transmembrane cationic-conduction current (outward: positive; inward: negative) in Amps across the neuronal membrane; $t$ is the transmembrane cationic-conduction time; $e$ is the elementary charge (1.60219 $\times$ 10⁻¹⁹ C); and $S$ is the neuronal extracellular membrane surface area.

Based on the TELCs action potential theory (Lee, 2020c; Lee, 2023c), the time-dependent transmembrane-electrostatically localized charge density (${TELC}_t$) with net time-dependent transmembrane current $I\left(t\right)$ was mathematically described by the following integration equation:

${TELC}_t=\frac{N_A}{S·F}{\int }_0^{t}I\left(t\right)dt+{TELC}_0(5)$

where $S$ is the extracellular membrane surface area; $F$ is the Faraday constant; $N_A$ is the Avogadro constant; $I\left(t\right)$ is the net time-dependent transmembrane cation conduction current (in Amps), which has a positive sign when cation flows out of the cell (negative sign when cation flows into the cell); and ${TELC}_0$ is the initial TELC surface density at time t = 0.

Conversely, the time-dependent transmembrane potential ($V_t$) was mathematically described by the following integral equation:

${V_t=-\frac{S·F}{C·N_A}TELC}_t=-\frac{1}{C}{\int }_0^{t}I\left(t\right)dt+V_0(6)$

where $C$ is the membrane capacitance and $V_0$ is the initial transmembrane potential at time t = 0.

Note, the net real-time transmembrane ion conduction current ($I\left(t\right)$) is the summation of all the time-dependent transmembrane ion currents including the time-dependent sodium current ($\left.I_{Na}\left(t\right)\right)$ from V-gated sodium channels, the time-dependent potassium current ($\left.I_K\left(t\right)\right)$ from the V-gated potassium channel, and the time-dependent other ions currents ($\left.I_l\left(t\right)\right)$ which is also known as the “leaky currents” including (but not limited to) certain “leaky” inward Cl⁻ flow through Cl⁻ channels (positive sign when anion (Cl⁻) flow into the cell; negative sign when anion (Cl⁻) flow out of the cell), ions current through certain mechanotransduction channels (such as PIEZO, Coste et al., 2010; Wu et al., 2017; Coste et al., 2012), and/or the miscellaneous other ions “leaky currents”. Note, when the net ($\left.I_l\left(t\right)\right)$ current value <0, it may be regarded as an excitatory (stimulation) current; On the other hand, when the net ($\left.I_l\left(t\right)\right)$ current value >0, it can be regarded as an inhibitor (suppression) current. Anyhow, real-time neural transmembrane action potential ($V_t$) can be further described by the following integral equation:

$V_t=-\frac{1}{C}{\int }_0^t\left\{I_{Na}\left(t\right)+I_K\left(t\right)+I_l\left(t\right)\right\}dt+V_0(7)$

TELCs density on membrane surface calculated

Table 2 lists the TELCs surface population density with the units of charges per µm² as calculated through Equations 2 and 3 using specific membrane capacitance $C/S$ of 9 mf/m² based on measured experimental data (G et al., 2000), in relation to the resting potential (−70 mV), stimulation threshold (−55 mV), and action potential peak level (about +30 mV) in a neuron.

Table 2

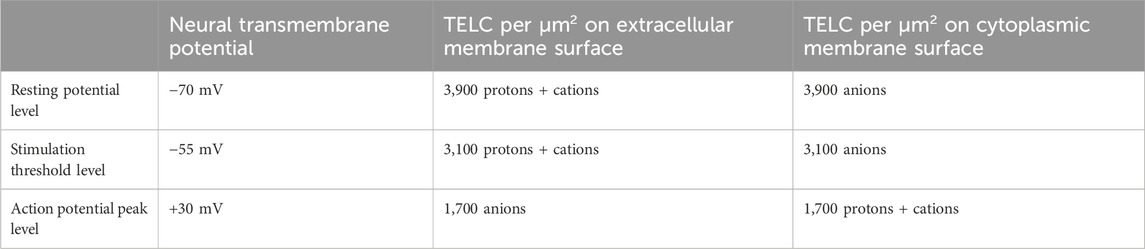
Table 2. TELCs density: The number of transmembrane-electrostatically localized charges (TELCs) per μm² of membrane surface area as calculated through Equations 2, 3 from the resting membrane potential (−70 mV), stimulation threshold (−55 mV), and action potential peak level (+30 mV) in a typical neural cell using specific membrane capacitance $C/S$ of 9 mf/m² based on measured experimental data (Gentet et al., 2000). Reproduced from Lee (2023c).

At the resting neural membrane potential of −70 mV, the TELCs density on extracellular membrane surface is now calculated to be 3,900 positive charges (protons + cations) per μm² meanwhile an equal amount (3,900) of transmembrane-electrostatically localized anions charges (negative charges) on cytoplasmic membrane surface.

At the stimulation threshold level (−55 mV), the calculated results (Table 2) show that the extracellular membrane surface typically has a TELCs density of 3,100 (protons + cations) per μm² while the cytoplasmic membrane surface has 3,100 transmembrane-electrostatically localized anions per μm².

These are significant results since they show, for the first time, that the change of neural membrane potential from the resting potential (−70 mV) to the stimulation threshold level (−55 mV) requires a change of TELCs density by −800 charges (protons + cations) per μm² from 3,900 to 3,100 TELC per μm² on the extracellular membrane surface, which is the TELCs density level to induce the firing of an action potential spike. This indicates that a TELCs density of 3,100 charges per μm² is required to trigger the V-gated sodium (Na⁺) channels for their opening (Figure 2A) to fire an action potential spike (Figure 4).

Figure 4

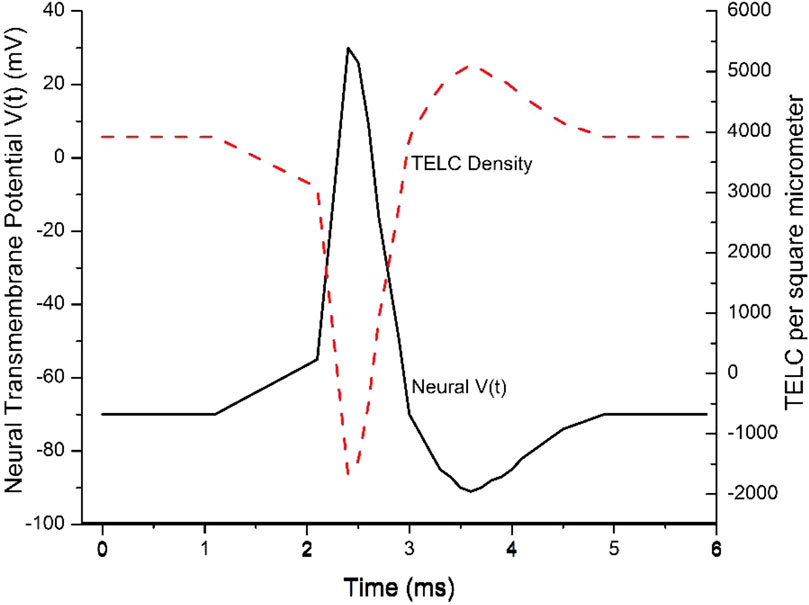
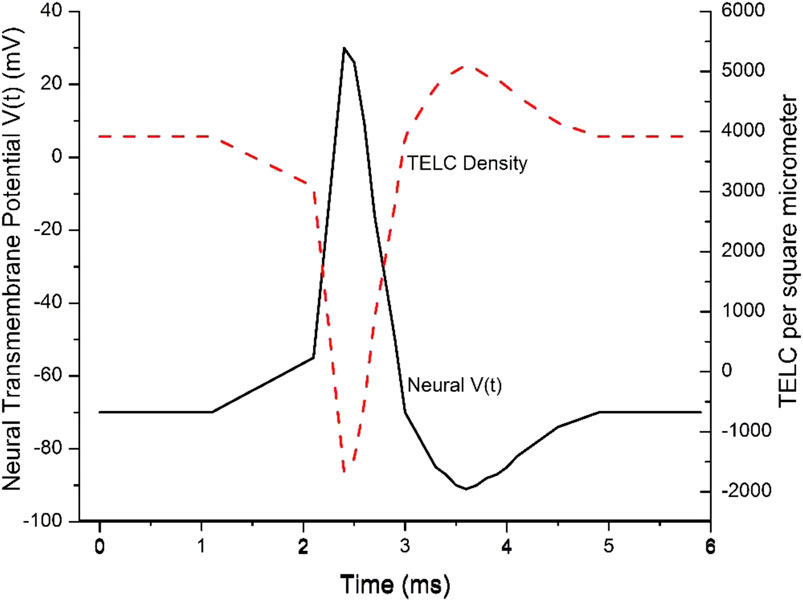
Figure 4. Transmembrane-electrostatically localized protons/cations charges (TELC) density is expected to appear as an inverse mirror image of an action potential spike in neurons. Reproduced from Lee (2023c).

The time-dependent TELCs and transmembrane potential better elucidated with integration equations

In this example, the time-dependent TELC (Equation 5) and time-dependent transmembrane potential (Equations 6 and 7) are employed to better explain an action potential spike. As shown in Figure 4, the initial TELCs surface density at time t = 0, ${TELC}_0$, is 3,900 (protons + cations) per µm² with its corresponding rest potential level (−70 mV). During the period from the time (t) of 0–1.1 ms at the resting state, the net transmembrane ion conduction current $I\left(t\right)$ is zero so that its integral as the first term of Equation 5 is zero and thus the ${TELC}_t$ remains as a flat curve at the ${TELC}_0$ level of 3,900 (protons + cations) per µm². Correspondingly, the neural transmembrane potential $V_t$ remains as a flat curve at the $V_0$ level of −70 mV.

During a “graded potential” period from time (t) of 1.1–2.1 ms, the net transmembrane ion conduction current $I\left(t\right)$ is the net leak current ($I_l\left(t\right)$) to serve as a stimulation current which has a negative “−” value owning to certain cation current “flows into the cell” as defined in Equation 6. The integration of $I\left(t\right)$ (=$I_l\left(t\right)$) at about −120 mA/m² (a reasonable number previously employed by Zeberg et al. (2010), equivalent to −0.12 pA/μm² or −7.5 × 10⁵ charges/s•µm²) with $dt$ (the first term of Equation 7) for the period from time (t) of 1.1–2.1 ms yields a TELC density change of −800 charges (protons + cations) per µm², thus reducing the ${TELC}_t$ level from the resting level of 3,900 to the stimulation level of 3,100 per µm² as shown in Figure 4. Correspondingly, in accordance with Equations 6 and 7, the transmembrane potential $V_t$ curve now as a “graded potential” rises from the resting level of −70 mV to the simulation level of −55 mV, which triggers an opening of voltage-gated sodium channels, resulting in an action potential firing (Figure 4).

During the “action potential firing depolarization” period from 2.1 to 2.4 ms, in this example, the transmembrane channel ion conduction current $I\left(t\right)$ is now the $I_{Na}\left(t\right)$ of −3,700 mA/m² (−3.7 pA/μm²) which is within a range employed in Wang and Liu (2019) and equivalent to −2.3 × 10⁷ Na⁺/s•µm² (−38 μmol/s/m²) from the opening of voltage-gated sodium channels that results in a substantial sodium (cation) conduction from the extracellular side to the intracellular side as illustrated in Figure 2A. Consequently, its integral from the time (t) from 2.1 to 2.4 ms as the first term of Equation 5 (for the TELC density change) is a large negative number (−4,800 charges per µm²) for ${TELC}_t$ to go down from 3,100 to −1,700 charges per µm² while the integral of Equation 7 (for the neural transmembrane potential change) is a large positive number (+85 mV) for $V_t$ to rise from −55 mV to 30 +mV. This result shows that it is the integration of $I_{Na}\left(t\right)$ with $dt$ over the period (from 2.1 to 2.4 ms) that drives the rising phase of an action potential spike. This also mathematically explains the inverse relationship between the ${TELC}_t$ curve and the $V_t$ curve as shown in Figure 4. As a result, the ${TELC}_t$ curve (Figure 4) shows a dramatic decline (corresponding to “depolarization”) in the TELCs density to a negative number well below zero (−1700, corresponding to the action potential peak of about +30 mV at the time of 2.4 ms) where the voltage-gated sodium channels will be shut and the voltage-gated potassium channels will open (Figure 2B).

During the “repolarization” period from the time of 2.4 ms–3.0 ms for the falling phase of the action potential spike, the transmembrane ion current $I\left(t\right)$ is now the $I_K\left(t\right)$ of about +2,200 mA/m² which is within a range employed in Wang and Liu (2019) and equivalent to 1.4 × 10⁷ K⁺/s•µm² (23 μmol/s/m²) from the opening of the V-gated potassium channels that allows K⁺ cations to flow out of the cell as shown in Figure 2B. Consequently, its integral from the time (t) of 2.4 ms–3.0 ms in the first term of Equation 5 (for TELC density change) is a large positive number (+5,600 charges per µm²) for ${TELC}_t$ to return from −1700 to 3,900 charges per µm²; while the integral of Equation 7 (for the transmembrane potential change) accumulates a substantial negative number (−100 mV) for $V_t$ to return from +30 mV to −70 mV by the time at 3.0 ms.

The repolarization is then followed by an “undershoot” (to about −90 mV with TELC density reaching as much as +5,100 charges per µm²) at the time of 3.6 ms and subsequently re-equilibrate to −70 mV (+3,900 charges per μm²) at the time of 4.9 ms. This phenomenon typically corresponds to the process of “repolarization” followed by re-equilibrating with the activities of the leaky channels of other ions likely including chloride channels and the ATP-driven sodium/potassium (Na⁺/K⁺) pumps (Figure 1B) to re-establish a TELCs surface density to about 3,900 per μm² (corresponding to a resting potential of −70 mV where the net transmembrane ion current $I\left(t\right)$ may return to zero) at the time of 4.9 ms. Subsequently, both ${TELC}_t$ and $V_t$ remain as flat curves for the re-established resting state thereafter from 4.9 to 5.9 ms as shown in Figure 4.

This example (Figure 4) explains the time-dependent TELC and transmembrane potential with the integral equations (Equations 5–7) for an action potential spike from its beginning to its end. It shows that our newly developed time-dependent TELC-based transmembrane potential integral equations (Equations 5–7) can be helpful to construct and analyze neural action potential spikes.

The TELC model predicts that if the V-gated sodium channel activity ($I_{Na}\left(t\right)$) is not temporally separated from the V-gated potassium channel activity ($I_K\left(t\right)$), their effect to drive the rising and falling phases of an action potential may cancel each other since the sign (−) of V-gated sodium channel activity ($I_{Na}\left(t\right)$) is opposite to that (+) of the V-gated potassium channel activity ($I_K\left(t\right)$). This feature as predicted by the TELC model (Equations 5–7) was observed exactly in the independent experimental study (Carter and Bean, 2009): “in fast-spiking GABAergic neurons (cerebellar Purkinje cells and cortical interneurons), twice as much sodium enters as the theoretical minimum. The extra entry occurs because sodium channel inactivation is incomplete during the falling phase of the spike”. Therefore, the TELC model (Equations 1–7) is well in line with the independent study of (Carter and Bean, 2009) on sodium entry during action potentials of mammalian central neurons and is in line also with the latest experimentally measured ion currents of human cortical pyramidal neurons (Beaulieu-Laroche et al., 2021).

Majority of neural TELCs are likely to be TELPs

Based on the TELCs model (Lee, 2020c; Lee, 2023c), the steady-state neural TELP concentration $\left[H_L^{+}\right]$ after cation-proton exchange with each of the cation species $M_{pB}^{i+}$ of the bulk liquid positive (p)-phase is,

$\left[H_L^{+}\right]=\frac{\left[TELC\right]}{{\displaystyle {\prod }_{i=1}^n}\{K_{Pi}\left(\frac{\left[M_{pB}^{i+}\right]}{\left[H_{pB}^{+}\right]}\right)+\left.1\right\}}(8)$

Where $\left[TELC\right]$ is the concentration of total transmembrane-electrostatically localized protons and cations ($\left[H_L^{+}\right]$ + ${\displaystyle {\sum }_{i=1}^n}\left[M_L^{i+}\right]$); $\left[M_{pB}^{i+}\right]$ represents the concentrations of non-proton cations in the bulk liquid p-phase, and $K_{Pi}$ is the equilibrium constant for the cation to exchange with TELP. The equilibrium constant $K_{Pi}$ is defined as the ratio of the delocalized proton concentration $\left[H_{pB}^{+}\right]$ to the cation concentration $\left[M_{pB}^{i+}\right]$ in the bulk aqueous p-phase when the cation-proton exchanging process reaches the midpoint at an equilibrium state where the steady-state TELP concentration $\left[H_L^{+}\right]$ is equal to the transmembrane-electrostatically localized cation concentration $\left[M_{pL}^{i+}\right]$ at the liquid-membrane interface.

Accordingly, the composition of neural TELCs in relation to TELPs is determined by the effect of the cation-proton exchange process as described mathematically in Equation 8. Based on the neural cell data from Hammond (2015), the concentrations of the extracellular cation species Na⁺, K⁺ and Ca²⁺ are the 140 mM Na⁺, 3 mM K⁺, and 1.5 mM Ca²⁺ in the neural extracellular liquid as shown in Figure 1B. The product of the cation-proton exchange reduction factors (the denominator of Equation 8) is now calculated to be 1.22 (see Table 3). As shown in Table 3, the cation-proton exchange reduction factors were calculated from the extracellular pH 7.3 and the Na⁺, K⁺ and Ca²⁺ concentrations, using the previously reported cation-proton exchange equilibrium constants K_Pi of 5.07 × 10⁻⁸ and 6.93 × 10⁻⁸ for Na⁺ and K⁺, respectively (Saeed and Lee, 2018); and 2.26 × 10⁻⁶ for Ca²⁺ recently determined experimentally by the Lee team in the lab. This calculation for the product (effect) of the cation-proton exchange reduction factors employed the same method as previously reported (Lee, 2019a).

Table 3

Table 3. The calculation for the product of cation-proton exchange reduction factors for the TELPs of TELCs in a neural cell with extracellular liquid ${pH}_{pB}$ = 7.3. Adapted and updated from Lee (2023c).

Using the calculated value of 1.22 for the product of the cation-proton exchange reduction factors with Equation 8, the ratio of TELPs to TELCs was calculated to be 1/1.22 = 0.82. This indicates that TELPs represent about 80% of TELCs in the neural cell. That is, the majority of neural TELCs is likely to be TELPs at the resting state with a neural transmembrane potential of −70 mV. Note, the ratio of TELPs to TELCs is merely a characteristics of TELCs, but it does not change the total TELCs since neural TELPs are also part of the neural TELCs population. It is the TELCs that represent the basis for the TELCs-charged membrane capacitor which gives rise to neural transmembrane potential as shown in the TELCs transmembrane potential equation (Equation 1).

TELCs-membrane-TELAs capacitor experimentally demonstrated

Recently, the formation of a TELC-membrane-TELAs capacitor has been experimentally demonstrated using a biomimetic anode water-Teflon^® membrane-water cathode system (Saeed and Lee, 2015; Saeed and Lee, 2018) through two PhD thesis research projects (Saeed, 2016; Kharel, 2024). In his “critiques” (Silverstein, 2023a; Silverstein, 2025; Silverstein, 2024a), Silverstein repeatedly claimed he (Silverstein, 2024b) has “challenged” our major conclusions on the experimental demonstration of TELPs (Saeed and Lee, 2015; Saeed and Lee, 2018). As shown in the latest peer-reviewed journal publication (Lee, 2025a), we have now found out that Silverstein’s “critiques” (Silverstein, 2023a; Silverstein, 2025; Silverstein, 2024a) were misconceived largely because of his own errors or misunderstandings such as his misconception on the aluminum (Al) film protonic sensing limit and his fallacy in distinguishing Al protonic (acidic) corrosion and Al hydroxide (alkaline) corrosion. The experimental demonstration and characterization of TELPs [29, 78] have now been affirmed successful (Lee, 2025a).

The “diffusion coefficients” and “radius of ionhydrate complex” may not be applicable to the excess protons in liquid water

In his “critiques” (Silverstein, 2023a; Silverstein, 2025; Silverstein, 2024a), Silverstein repeatedly applied “diffusion coefficients” and “radius of ionhydrate complex”, without any justification, to the conduction of excess protons in liquid water. For example, Silverstein used the diffusion coefficients listed in his “Table 1” of Silverstein, 2025 to argue: “the aqueous proton diffuses 4 to 13 times faster than other ions, due to its small size and the de Grotthuss mechanism”…“even with D_H+ = 9.3 nm²/ns, the aqueous proton’s diffusion speed is orders of magnitude slower than the velocity of an electron in an electrical circuit”. His “diffusion coefficients” argument there is questionable since he blindly treated “aqueous proton’s diffusion” (a concentration-driven random walk process) as a vectorial conduction of excess protons (driven by electric field of excess charges) in liquid water.

In his critique (Silverstein, 2025), Silverstein further argued: “Compared to the proton, the charge/radius ratio of the hydrated monovalent cations (Na⁺, K⁺) is only 25 – 30% lower; for the divalent cations (Ca²⁺, Mg²⁺), the ratio is actually 50 – 60% higher (Table 1). Hence, electrostatic considerations suggest that cation-proton exchange Keq values should be 10⁻² or higher for Na⁺ and K⁺, and >1 for Ca²⁺ and Mg²⁺”. Silverstein’s argument there was again misconceived since he apparently treated the charged-balanced protons (such as those in a HCl solution) as excess protons and improperly compared the excess protons with the non-proton cations. In accordance of the TELC theory and experimental demonstrations, excess protons can readily conduct into the first layer of water molecules on the membrane surface because the transmembrane attraction by the excess hydroxide anions on the other side of the membrane in forming a protonic (TELPs) capacitor. In contrast to Silverstein’s argument, it is now affirmed (Lee, 2025a): the sodium/TELPs exchange equilibrium constant $K_{p{Na}^{+}}$ was experimentally measured to be (5.07 ± 0.97) × 10⁻⁸ and the potassium/TELPs exchange equilibrium constant $K_{p{K}^{+}}$ was determined to be (6.93 ± 1.23) × 10⁻⁸.

Notably, excess protons have been studied in water with excess electric charge by independent laboratory research groups (Santos et al., 2011; Fuchs et al., 2016). Based on the TELCs theory (Lee, 2019a; Lee, 2020a; Lee, 2021) with liquid water as protonic conductor, it is expected that the excess protons will appear on the liquid water surface because of the mutual repulsion of excess protons that is known also as the Gauss law effect of electrostatics (Lee, 2023a; Lee, 2012; Lee, 2023d). This feature as expected was shown also by independent studies where the migration of excess protons to the liquid/air interface has been simulated (Petersen and Saykally, 2005) and observed experimentally (Fuchs et al., 2019).

The electrogenic process of 3Na⁺/2K⁺ ATPase

Since the activity of 3Na⁺/2K⁺ ATPase is electrogenic which actively pumps a positive excess charge from the intracellular side to the extracellular side per ATP consumption, it can help to generate and/or maintain a resting transmembrane potential in accordance of the TELC model; at the same time, the activity of 3Na⁺/2K⁺ ATPase, of course, can also generate and maintain the bulk liquid phase ion concentration gradients of Na⁺ (high outside), K⁺ (high inside), and indirectly, Cl⁻ (high outside) across the membrane. Once the electrochemical gradient is established, it can also be utilized to drive all kinds of ion transporting processes. For example, “adult mammalian central neurons maintain a low intracellular Cl⁻ concentration. Cl⁻ extrusion is achieved by K⁺–Cl⁻ cotransporters (KCC) fueled by K⁺. As all transporters, it does not directly consume ATP but derives its energy from ionic gradients, here the K⁺ gradient generated by the Na/K/ATPase” (Hammond, 2015).

Previously (Silverstein, 2023a), by repeatedly making his misconceived claim of “Cl⁻ flows out through channels, following the excess Na⁺”, Silverstein tried to deny the fact that the process of 3Na⁺/2K⁺ ATPase is electrogenic which can help to generate and/or maintain a resting transmembrane potential. His point was that “3Na⁺/2K⁺ ATPase pumping electrogenically pumps one net +1 charge out, but that one Cl⁻ follows this charge out through separate channels, thus neutralizing the excess +1 export”. In trying to defend his claim, Silverstein made another argument in his latest article (Silverstein, 2025): “plasma membrane ClC-1 channels are voltage-gated open above −100 mV (Stolting et al., 2014), and carry about 80% of the ionic current accounting for the neuronal resting membrane potential (Stauber et al., 2012; Stolting et al., 2014; Pedersen et al., 2016). This substantial Cl⁻ resting permeability of the neuronal plasma membrane (10–100% of the resting K⁺ permeability (Kuffler et al., 1984; Junge, 1992; Aidley, 1989), depending on tissue) has been known for more than half a century. The result is that Cl⁻ anions are exported through the open CLC-1 channels along with the excess Na⁺ cation, counter-balancing the +1 charge export of the Na/K ATPase pump”.

Note, based on the understating with the TELCs model, when a neural cell has a low plasmic chloride concentration [Cl⁻]_int, an opening of a chloride channel such as CLC1 (in some tissue) could allow some Cl⁻ flow into the neural cell, resulting in somewhat hyperpolarized transmembrane potential (about −80 mV) so that its graded potential could not be too easy to reach the stimulation threshold (−55 mV) to prevent from triggering an unwanted action potential spike. This is physiologically important to prevent from causing myotonia congenita or epilepsy (Adrian and Bryant, 1974; Stölting et al., 2014). When a neural cell has a high plasmic chloride concentration [Cl⁻]_int and/or under certain overly polarized state (such as in the “under shoot” phase when transmembrane potential is as negative as about −100 mV), an opening of a chloride channel such as CLC2 could allow Cl⁻ to flow out of the cell to help restore the transmembrane potential from an overly polarized state to the resting level of about −70 mV (Scholl et al., 2018). That is, both CLC1 and ClC2 are regulated chloride channels. Their activity could utilize their Cl⁻ electrochemical potential including the transmembrane potential, but none of them would change the transmembrane potential from the resting level (−70 mV) all the way to 0 mV. Therefore, Silverstein’s claim of “Cl⁻ flows out through channels, following the excess Na⁺” is again not supported.

Readers probably can also understand that a relative Cl⁻ permeability accounting for “about 80% of the ionic current” at the neuronal resting membrane potential does not necessarily have to translate to a large Cl⁻ flow, since the total ionic current at a neuronal resting membrane potential is typically quite small. Xu and Adams (Xu and Adams, 1992) reported: “The contribution of Na⁺, K⁺ and Cl⁻ to the resting membrane potential was examined and relative ionic permeabilities P_Na/P_K = 0.12 and P_Cl/P_K < 0.001 were calculated using the Goldman-Hodgkin-Katz voltage equation” in rat intracardiac neurons.

Zero “excess charges” in the bulk liquid phase

According to the TELCs capacitor model, “excess charges” will stay on membrane surface but not in the bulk liquid phase. Therefore, the TELCs-membrane-TELAs capacitor model predicts zero “excess charges” in the bulk liquid phase at the equilibrium state. This predicted feature is well in line with the contemporary textbook (Hammond, 2015) knowledge: “In spite of the unequal distribution of ions across the plasma membrane, intracellular and extracellular media are neutral ionic solutions: in each medium, the concentration of positive ions is equal to that of negative ions”.

Silverstein’s claim of “large positive value of excess charge in both internal and external phases of squid giant axon (≈+ 30 mM) and in muscle neuron cytoplasm (+150 mM)” (Silverstein, 2025) is just misguided, since that would violate the principle of total charge neutrality.

The contemporary neuroscience textbook (Hammond, 2015) teaches clearly: “In the intracellular compartment, anions other than chloride ions are present and compensate for the positive charges. These anions are HCO₃⁻, PO₄²⁻, amino acids, proteins, nucleic acids, etc. Most of these anions are organic anions that do not cross the membrane”.

Tamagawa and others identified the limitation and deficiency of the GHK equation

Although the Goldman-Hodgkin-Katz (GHK) equation is one of the most widely used equations in electrobiology (Xu and Adams, 1992; Huang et al., 2015; Perram and Stiles, 2010; Clay, 2009; Clay et al., 2008; Barry, 2006; Martin and Harvey, 1994; Weiss et al., 1992; Ohki, 1984; Bowman and Baglioni, 1984; Salas and Lopez, 1982), it also has certain limitations. Independent studies by the Tamagawa team (Tamagawa and Morita, 2014; Tamagawa and Ikeda, 2017; Tamagawa and Ikeda, 2018; Tamagawa, 2015; Tamagaw, 2019) have recently concluded that “the Goldman-Hodgkin-Katz equation is no reliable tool to determine permeabilities” (Tamagawa and Ikeda, 2018; Heimburg, 2018). That means, its relative membrane permeability coefficients ($P_K$, $P_{Na}$ and $P_{Cl}$) could not be measured directly through independent experiments without using the GHK equation per se. As Tamagawa and Ikeda pointed out (Tamagawa and Ikeda, 2018), “the permeability constant is not necessarily obtained by the direct measurement of membrane permeability to ions” (Wright and Diamond, 1968; Olschewski et al., 2001; Uteshev, 2010); They (Tamagawa and Ikeda, 2018) further explicated: “these permeability coefficients do not have any substantial meaning, but serve merely as a parameter matching the potential computed using the Goldman-Hodgkin-Katz equation and the experimentally measured potential”. Tamagawa’s another study (Tamagawa, 2019) also concluded that the GHK equation “does not necessarily provide us with a trustworthy enough membrane potential generation mechanism”.

Salas and Lopez (Salas and Lopez, 1982) reported: “The Goldman-Hodgkin-Katz equation has been extensively used to determine cationic/anionic permeability ratios in the paracellular pathways of the gallbladder epithelium. Nevertheless, new experimental evidence suggests that none of the theoretical assumptions of the equation hold for these pathways. In order to assess the experimental validity of the Goldman equation the permeability ratios were calculated from zero-current diffusion potentials by means of the Goldman equation and compared with the cationic/anionic permeability ratios measured by simultaneous determinations of cation and anion tracer fluxes in the same membranes. The results indicate that the Goldman equation is empirically valid for the tested salts (KCl and RbCI) within the experimental range of concentrations (25–200 mM) at an electrochemical-potential difference of zero”.

Chang (1983) noticed: “although the GHK equation can fit the V vs [K⁺]_o data well, it has difficulty explaining the observed dependence of V on [Na]_o when the axon is bathed in K⁺-free artificial sea water” and also showed “the GHK equation can fit the observed data only partially. Some of the ionic dependence of the resting potential is difficult to explain”.

Independent study by Bowman and Baglioni (1984) pointed out another deficiency of the GHK equation: “If the IV (current-voltage) curve involves more than one ion, then each ion must be replaced with a relatively impermeant ion in a systematic study to test the validity of use of the GHK current equation”.

In a review article (Clay, 2009), Clay 2009 also pointed out: “One final point concerning the utility of the GHK equation for models of membrane excitability is that it permits a straightforward determination of I_K when K_o⁺ = 0, conditions which are problematic for I_K ∼ (V − E_K) since E_K is undefined for K_o⁺ = 0”.

Therefore, the Tamagawa team (Tamagawa and Ikeda, 2017; Tamagawa and Ikeda, 2018; Tamagawa, 2015; Tamagaw and a, 2019) and other independent researchers (Clay, 2009; Bowman and Baglioni, 1984; Salas and Lopez, 1982; Chang, 1983) have made substantial scientific contributions to rightly identifying the limitation and deficiency of the GHK equation.

In his critique (Silverstein, 2025), Silverstein commented “Lee cited four papers (Heimburg, 2018; Wright and Diamond, 1968; Olschewski et al., 2001; Uteshev, 2010) that he claimed ‘concluded that the Goldman-Hodgkin-Katz equation is not a reliable tool to determine permeabilities. That is, its relative membrane permeability coefficients (P_K+, P_Na+, and P_Cl-) could not be measured directly through independent experiments (Lee, 2023a)’”. Readers can probably now see, Silverstein’s comment again appears to be improper, since it seems to have an appearance in trying to improperly credit the valuable contribution made by the Tamagawa team (Tamagawa and Ikeda, 2017; Tamagawa and Ikeda, 2018; Tamagawa, 2015; Tamagawa, 2019) to someone else (Lee); and since the three references “(Wright and Diamond, 1968; Olschewski et al., 2001; Uteshev, 2010)” were originally cited by Tamagawa and Ikeda (Tamagawa and Ikeda, 2018) to show examples (Wright and Diamond, 1968; Olschewski et al., 2001; Uteshev, 2010) of “the permeability constant is not necessarily obtained by the direct measurement of membrane permeability to ions” (Tamagawa and Ikeda, 2018).

Silverstein’s “pH_surface” may not represent TELPs

Silverstein’s “Table A1” of his article (Silverstein, 2025) lists “pH_surface” as “pH values reported within 1.5 nm of a water/hydrophobic interface, either measured experimentally with lipid-fluorophore proton sensors or calculated from molecular dynamics simulations or electrostatics”. However, none of them has any relevance to TELPs (transmembrane-electrostatically localized protons). For example, many of his numbers are apparently from some molecular dynamic simulations for the fixed interface property-enriched protons (at the liquid-decane interface or air-water interface) without any transmembrane potential and its membrane capacitor-associated TELP(s), thus having little relevance to the TELP(s) model.

According to the TELCs neural transmembrane potential equation (Equation 1), TELPs are instantly associated with the transmembrane potential (V). Many of the systems listed in Silverstein’s “Table A1” (Silverstein, 2025) have no transmembrane potential (V) and are thus irrelevant. For example, Silverstein’s “pH_surface” of “5.0 ± 0.2” in his “Table A1” as he claimed from the “lipid bilayer” system (Weichselbaum et al., 2017) without any transmembrane potential (V) obviously does not represent any TELPs. Similarly, the “lipid bilayer” of reference (Tocanne and Teissié, 1990) talking about “ionization of phospholipids” and surface potential (but not transmembrane potential) also has little relevance to TELPs either. Silverstein claimed “pH_surface” of “4.7” from his reference “5 (Wolf et al., 2014)” is also irrelevant to the TELCs (TELPs) model since the “molecular dynamic simulation study of (Wolf et al., 2014)” (Wolf et al., 2014) did not involve any transmembrane potential.

Xu et al. (2016) reports a quite interesting study of protonation dynamics on lipid nanodiscs with sophisticated fluorescence correlation spectroscopy using fluorescein-5-Maleimide (CAS number 75350-46-8) and DOPE-Flu (CAS number 799268-49-8), but without any transmembrane potential. Therefore, the “pH_surface” of “5.5” that Silverstein claimed from this Xu et al. (2016) is also irrelevant to TELPs.

Readers probably also know that a lipid fluorophore like fluorescein DHPE (CAS number 87706-98-7) or DOPE-Flu (CAS number 799268-49-8) whose fluorescent active site (polar carboxyfluorescein which is expected to stay in the bulk liquid phase) is located at a position above the lipid headgroup, likely more than 1.5 nm away from the first layer of water molecules (where most of the TELPs reside) on the alkane core membrane surface. Consequently, any of the “pH_surface” that Silverstein claimed from “lipid fluorophore”-based studies may not represent TELPs either.

Therefore, readers probably can also understand that Silverstein’s “critique” (Silverstein, 2025) with his largely irrelevant “Table A1” again seems to reflect his error or misunderstanding of the TELPs model.

As recently discussed (Lee, 2023a; Lee, 2025c) according to the size of the pH-sensitive GFP (Rieger et al., 2017) and its associated protein linker used in the mitochondrial pH measuring experiments (Rieger et al., 2014; Rieger et al., 2021; Toth et al., 2020), “the active site of its pH-sensitive chromophore is likely to be at least about 2–3 nm away from the membrane surface”. This separation distance (2–3 nm away from the mitochondrial membrane surface) is good to detect bulk-liquid phase pH; but too far away to sense TELPs on the alkane core membrane surface. Therefore, according to the TELPs model (Figures 1B, 3), we predict that the pH-sensitive GFP sensors can see the protons in the bulk liquid phase (around pH 7), but could not detect TELPs that stay primarily within the first layer of water molecules on the hydrophobic alkane core membrane surface. This TELPs-model-based prediction for the pH-sensitive GFP bulk-liquid phase pH measurement was observed exactly in the measured mitochondrial “pH 6.8–7.0” (Rieger et al., 2014) and “pH 7.0–7.1” (Toth et al., 2020) that Silverstein listed in his “Table 1” of his 2022 critique (Silverstein, 2022). Therefore, readers can now probably also see that the data listed in Silverstein’s “Table 1” of his 2022 critique (Silverstein, 2022) and his “Table A1” of his 2025 critique (Silverstein, 2025) are actually in line with the TELPs-model prediction.

According to our understanding with the TELC(s) model (Lee, 2019a; Lee, 2020a; Lee, 2021), TELCs (TELPs) activities are likely to be local and dynamic. Although they are in dynamic communication with the bulk aqueous liquid phase through the cation-proton exchange process, most of the TELPs are likely to stay within the first layer of water molecules on the hydrophobic core membrane surface which is beneath the membrane’s lipid head groups (Figure 3). That is, TELPs likely are just hiding on the alkane core membrane surface beneath the lipid head groups. Currently, we are not aware of any artificial pH sensor that could be used to directly measure TELPs in biomembrane systems, that probably could explain why the existence of TELPs was never uncovered during the last 7 decades of the “delocalized vs. localized proton coupling debates” since the early 1960s (Mitchell, 1961; Mitchell and Moyle, 1965; Williams, 1978; Slater, 1967; Williams, 1975; Williams, 1988; Heberle et al., 1994; Dilley et al., 1987; Dilley, 2004; Mulkidjanian et al., 2006). Only recently, TELPs were, for the first time, discovered through experimental demonstration of a protonic capacitor in a biomimetic cathode water-membrane-water anode system using an Al metal film as a protonic sensor (Lee, 2025a). However, the Al film-based protonic sensor would be not easy for use in micro/nanometer-scale biomembrane systems. Therefore, it is now important to develop “a new type of protonic sensors to directly observe TELPs within the first layer of water molecules on hydrophobic core membrane surface in biological membrane systems”. According to our analysis, two natural membrane protein complexes are now known to sense and use TELPs: the F_oF₁-ATP synthase (Lee, 2023a) and the melibiose transporter MelB (Hariharan et al., 2024). Therefore, I hereby encourage researchers “to take cue and inspiration from the natural TELPs-sensing biomolecules to better design and make the needed protonic probes for more direct detections of TELPs in biomembrane system”.

The transmembrane ion currents employed by Lee in teaching the applications of the TELCs model equations are valid

In contrast to Silverstein’s claims in his last five paragraphs of his article (Silverstein, 2025), the examples of transmembrane ion currents employed by Lee in teaching the applications of the TELCs neural transmembrane potential model (Lee, 2023c) are valid and the calculations were all correct. For example, the stimulation current values (e.g., I_stim of −120 mA/m²) employed by Lee (2023c) was proper, since the values were within a range from 0 to 1,200 mA/m² that had been well employed by other experts in theoretical studies [the stimulation current density values and their range can be found in the “Figures 1, 3, 8A and 10” of the cited Zeberg et al. (2010)]. For example, I_stim of −120 mA/m² was employed by Zeberg et al., 2010 in their “Figure 1B” and the vertical axis of their “Figure 8A” (Zeberg et al., 2010) shows a range from 0 to 1,200 mA/m² in a hippocampal neuron model. Therefore, our use of the “I_stim of −120 mA/m²” as one of the numbers within a range from 0 to 1,200 mA/m² in testing use of the newly developed TELCs-based time-dependent neural transmembrane potential integration equations (Equations 5‒7) was completely legitimate to numerically construct an action potential spike, for the first time. Similarly, the information about the “potassium and sodium channel current density in a range from −5 to +5 A/m²” (that Silverstein apparently missed) is provided in the vertical axis of “Figure 3B” and “Figure 5A” of the cited Wang and Liu (2019). Therefore, Silverstein’s unnecessary claims and arguments in his last five paragraphs of his article [16] were misconceived purely by his own errors or misunderstanding. It is now quite clear that the TELCs-membrane-TELAs capacitor-based transmembrane potential biophysics equations (Equations 1‒8) are indeed valid (Lee, 2020c; Lee, 2023c).

The dynamic and local nature of the TELCs capacitor model

Neural TELCs-membrane-TELAs capacitor is dynamic and local in nature. The entire surface of the cell membrane is not necessarily equipotential, and, especially, the action potential spike propagates along an axon. Therefore, the TELCs capacitor model is not necessarily identical to the technical concept of just simply a capacitor—namely, two equipotential surfaces separated by a dielectric insulating membrane. A live neuron is a dynamic (not necessarily static) system. As recently discussed in the application of the TELCs capacitor model to calculate for a neural touch signal transduction time (Lee, 2025b), “it may require a ‘graded potential’ only at a small specific area of neuronal membrane such as at an axon hillock (the initial segment of an axon) or a node of Ranvier to reach the stimulation threshold level (−55 mV, equivalent to 3,100 TELCs per μm² on extracellular membrane surface) to fire an action potential spike”. Action potential spikes can propagate along a myelinated axon which could be more than a meter long (such as the neural cell with its axon extended from brain to foot). The known saltatory propagation of action potential spikes along an axon indicates that the entire surface of the cell membrane is not necessarily equipotential since the neural TELCs-membrane-TELAs capacitor is local and dynamic in nature. That is, neural transmembrane potential including action potential can be local such as at the axonal initial segment and nodes of Ranvier where dense clusters of ion channels underlie action potential generation and rapid conduction (Hill et al., 2008; Elvira and Jenkins, 2025). Meanwhile, it can also be dynamic (migrating) along membrane surface in line with the saltatory conduction along an axon. Only under certain calm condition when the resting transmembrane potential is fully equilibrated throughout a neural cell, the entire surface of the cell membrane may be in an equipotential state. Therefore, the TELCs capacitor model is illustrated as a across section of an idealized neuron (Figure 1B), which represents a highly idealized model, especially when it is contrasted with the actual morphology of a neuronal cell.

Notably, the local specific membrane capacitance may vary dramatically along a myelinated axon and non-myelinated axon. As previously discussed (Lee, 2020c), the specific membrane capacitance at a myelinated section of an axon can be 40 times less than that at a node of Ranvier which is not myelinated. Consequently, according to the TELCs-based transmembrane potential equation (Equations 1 and 2), even at the same fully equilibrated resting transmembrane potential of 70 mV, the TELCs density (3,900/40 = 97.5 TELCs per μm²) at the neural liquid-membrane interface along a myelinated axon segment may be 40 times less than that (3,900 TELCs per μm²) at the node of Ranvier or non-myelinated axon segment. That is, a myelinated axon requires much less TELCs density (less ATP energy cost) to deliver the action potential spike signal than a non-myelinated axon. Therefore, based on the TELCs capacitor model (Equations 1 and 2), “the biological significance of axon myelination is now also elucidated as to provide protonic/cationic insulation and prevent any ions both inside and outside of the neuron from interfering with the action potential signal, so that the action potential can quickly propagate along the axon with minimal (e.g., 40 times less) energy requirement” as previously reported (Lee, 2020c). This also shows that the TELCs density (Equation 2) is not necessarily equal along the entire surface of the cell membrane either, since it depends not only on the local transmembrane potential but also on the local specific membrane capacitance.

Comparison of key tenets from Goldman-Hodgkin-Katz model vs TELCs theory

Table 4 lists a comparison of the key tenets from the classic Goldman-Hodgkin-Katz (GHK) model vs the TELCs Theory. As listed in Table 4, according to the classic GHK Model, the source of transmembrane potential is believed to be “somehow” generated by bulk-liquid phase ions concentration differences across the membrane with the selective ions permeability (Na⁺, K⁺, Cl⁻), apparently assuming excess charges staying in liquid as part of the bulk liquid phase ions concentrations. On the other hand, the TELCs model explains that the transmembrane potential is generated by the TELCs-membrane-TELAs capacitor formation as a result of transmembrane ion transport as shown in the integral equation (Equation 7) for the real-time neural transmembrane action potential ($V_t$), assuming excess positive changes as TELCs at one side of the membrane and excess negative charges as TELAs at the other side of the membrane as illustrated in Figures 1B, 2.

Table 4

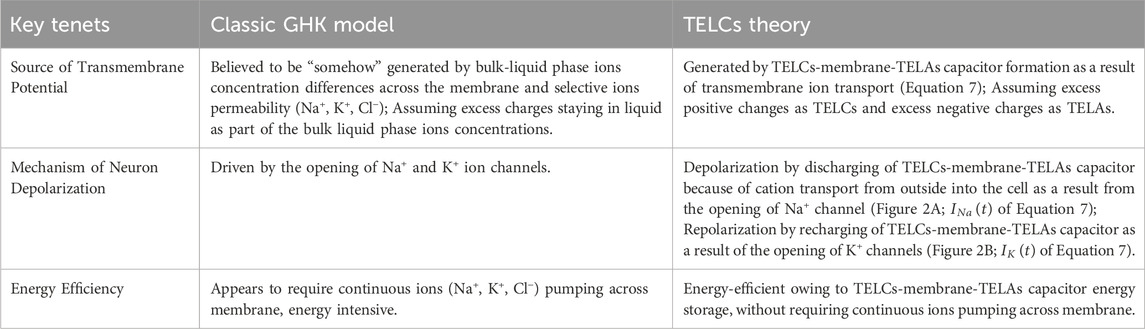
Table 4. Comparison of key tenets between Goldman-Hodgkin-Katz (GHK) Model vs TELCs Theory. Adapted and modified from Alharbi (2025).

Both the classic GHK model and the TELCs model agree that neuron depolarization is due to the opening of Na⁺ channels. The difference between the two models here is somewhat subtle. According to the GHK-equation model, neuron depolarization seems to be driven by the opening of Na⁺ and K⁺ ion channels with the selective ions permeability (Na⁺, K⁺, Cl⁻) to the bulk-liquid phase ions concentration differences across the membrane. On the other hand, the TELCs Theory can more clearly explain how neuronal cell depolarization occurs: by “discharging of TELCs-membrane-TELAs capacitor because of cation transport from outside into the cell as a result from the opening of Na⁺ ion channel” (Figure 2A; $I_{Na}\left(t\right)$ of Equation 7). The TELCs model further explains that neuron repolarization is through recharging the TELCs-membrane-TELAs capacitor as a result from the opening of K⁺ channels as shown in Figure 2B and $I_K\left(t\right)$ of Equation 7.

This understanding from the TELCs model with its integral equations (Equations 5–7) conceptually (Figures 1–3) and mathematically (Equation 7) affirms that ion channels are certainly part of the molecular basis in addition to the membrane capacitor property for action potential generation in neurons.

For example, the TELCs model with its integral equation (Equation 7) for the real-time neural transmembrane action potential ($V_t$) can make a series of experimentally testable predictions regarding ion channels: a) the voltage-gated Na⁺ channels ($I_{Na}\left(t\right)$ of Equation 7) are required to fire action potential spikes and a blockage of the required voltage-gated Na⁺ channels by an inhibitor like tetrodotoxin (TTX) would completely blockade action potentials; b) Genetic knockout (deletion) or mutation of critical ion channels such as required voltage-gated Na⁺ channels ($I_{Na}\left(t\right)$ of Equation 7) and/or the voltage-gated K⁺ channels ($I_K\left(t\right)$ of Equation 7) would abolish and/or affects action potential firing which in return could result in neurological disease (or conditions) such as certain neuropathic pain and epilepsy; and c) The genetic expression for the precise clustering of ion channels (such as the voltage-gated Na⁺ channels ($I_{Na}\left(t\right)$ of Equation 7) and the voltage-gated K⁺ channels ($I_K\left(t\right)$ of Equation 7) at the axonal initial segment and nodes of Ranvier would lay the biomolecular foundation for the ability to fire action potential spikes and saltatory conduction along a myelinated axon. All these predictions from the TELCs model have recently been experimentally observed exactly in many well-established electrophysiological phenomena including (but not limited to): 1) The tetrodotoxin (TTX) sensitivity shows the complete blockade of action potentials by TTX, which targets voltage-gated Na⁺ channels (Bean, 2007; Blair and Bean, 2002; Zou et al., 2024; Lee and Ruben, 2008; Harty and Waxman, 2007; Theile and Cummins, 2011; Hille, 2001); 2) Genetic knockout (deletion) or mutation of critical ion channels abolishes (or affects) action potential firing which in return may result in neurological disease (or conditions) such as certain neuropathic pain and epilepsy (Martinez-Espinosa et al., 2015; Oyrer et al., 2018; Veerman et al., 2015; Pinto et al., 2025; Derangeon et al., 2012; Ma et al., 2017; Quraishi et al., 2020; Hill et al., 2023; Eijkelkamp et al., 2012; Raouf et al., 2010; Yogi et al., 2025); and 3) The precise clustering of ion channels at the axonal initial segment and nodes of Ranvier underlies the ability to fire action potential spikes and saltatory conduction along a myelinated axon (Freeman et al., 2016; Freeman et al., 2015; Rasband and Peles, 2016; Feinberg et al., 2010; Rasband et al., 1999; Hill et al., 2008; Elvira and Jenkins, 2025; Arancibia-Carcamo and Attwell, 2014; Amor et al., 2017). Therefore, the TELCs model (with its Equations 1‒8) can well be predictive and may now provide universal applicability across cell types.

On energy efficiency, the GHK model appears to require continuous ions (Na⁺, K⁺, Cl⁻) pumping across membrane, which would be energy intensive. The TELCs model appears to be energy-efficient owing to TELCs-membrane-TELAs capacitor energy storage, without requiring continuous ions pumping across membrane.

Opportunities and directions for future research

Better computational and experimental demonstration of protonic capacitor and TELPs activity

So far, we have shown the existence of TELCs capacitor and TELPs activity through bioenergetic analyses based on physical sciences and experimental demonstrations using biomimetic membrane systems and protonic sensing aluminum (Al) films. It is now highly desirable to better visualize protonic capacitor and TELPs activity through both computational and experimental approaches to help better understand TELCs-based neuroscience. Future research for better experimental demonstration of TELCs-membrane-TELAs capacitor activity should be particularly encouraged. In addition to the protonic sensing Al films, innovative development and utilization of new tools and methods including proton-sensitive dye molecules and/or ratiometric pH-sensitive fluorescent proteins could make the visualization of TELPs activity on biological membrane possible. The technical challenges are to place an active site of a protonic probe within a quite sparsely distributed TELPs molecular layer that is likely to be mostly in the first layer of water molecules on the biological alkane core membrane surface. Both protonic probe and methodology development to overcome the technical challenges shall be encouraged. Hereby, I also encourage the development of proper computer simulation models such as molecular dynamics simulations for certain TELCs-membrane-TELAs capacitor comprising excess protons on one side of the membrane and excess hydroxide anions on the other side of the membrane to better understand protonic bioenergetics and neuroscience. The computational approach could be particularly important before more effective experimental methods and tools to analyze TELPs can become available.

Need a new generation of protonic sensors to directly observe TELPs on biological alkane core membrane surface

As mentioned previously, we currently are not aware of any artificial pH sensor that could be used to directly measure TELPs within the first layer of water molecules on the hydrophobic core biomembrane surface beneath the lipid head groups (Figure 3). Only recently, TELPs were, for the first time, discovered through experimental demonstration of a protonic capacitor in a biomimetic cathode water-membrane-water anode system using an Al metal film as a protonic sensor (Lee, 2025a). However, the Al film-based protonic sensor would be not easy for use in micro/nanometer-scale biomembrane systems. Therefore, it is now highly important to develop “a new type of protonic sensors” to directly observe TELPs within the first layer of water molecules on biological alkane core membrane surface. According to our analysis, two natural membrane protein complexes are now known to sense and use TELPs: the F_oF₁-ATP synthase (Lee, 2023a) and the melibiose transporter MelB (Hariharan et al., 2024). Therefore, I hereby again encourage researchers “to take cue and inspiration from the natural TELPs-sensing biomolecules to better design and make the needed protonic probes for more direct detections of TELPs in biomembrane system”.

Measuring the speed of excess proton conduction through liquid water

In liquid water, protonic conduction is through the Grotthuss “hops and turns” mechanism, which is substantially different from the non-proton cation (e.g., Na⁺) diffusion that must physically plough through liquid water molecular array. Recently, our calculation using the known diffusion coefficient D of 9.31 × 10⁻⁹ m²/s showed that the root mean square distance $\overline{x}$ traveled by excess protons produced by anode water electrolytic process in a 10-h experiment is only about 26 mm, which is apparently inadequate to explain the fast conduction of excess protons through liquid water as measured by the water electrolysis current in the experiments (Lee, 2025a). Recently, we noticed the excess protons can very quickly conduct through a large chamber liquid to an impermeable membrane to form a protonic capacitor in a time scale of seconds in the experiments (Saeed and Lee, 2015; Saeed and Lee, 2018). The evidences for such fast conduction of excess protons in liquid water are: 1) the measured water electrolysis current displays an “RC” protonic charging characteristics when a Teflon membrane was used (Saeed and Lee, 2015); 2) Observed excess protons-enabled Aluminum (Al) corrosion when Al films were used as a part of an impermeable membrane; and 3) the measured water electrolysis DC current is very substantial (about 50 µA) when the excess protons-enabled Al film corrosion is in progressing (Saeed and Lee, 2018). This indicates that the classic diffusion model is inadequate to describe the conduction of excess protons through liquid water. Therefore, it is important to physically measure the speed of excess proton conduction through liquid water, which is imperative to better understand neuroscience, especially the saltatory conduction of action potential spikes along a myelinated axon.

Further application of the TELCs model to better understand neuroscience

As shown above, the TELCs model (with its Equations 1‒8) can well be predictive and may now provide universal applicability across cell types. That is, the TELCs theory can be highly useful to better analyze and understand neural cell activities. For example, the TELCs model with Equation 7 may be applied to better elucidate how a stimulation by touch (Lee, 2025b) or a spicy chili taste can change the graded transmembrane potential to induce an action potential spike firing in a neural cell. Another fundamental neuroscience question to be answered is how an action potential spike can quickly propagate along a myelinated axon from brain to hand. It is now known that conventional ions (Na⁺, K⁺ and Cl⁻) diffusion is too slow to account for the fast saltatory conduction of action potential along a myelinated axon. Analysis with the TELCs model has suggested that the saltatory propagation of action potential spike may be through protonic conduction using liquid water along the axon as a protonic wire (Lee, 2020c; Lee, 2023c). Accordingly, human brain may be made of “protonic circuits” with neural cells that may communicate with their TELCs (TELPs) activities (Lee, 2020c; Lee, 2023c). Further research in this direction may help to address a centrally important question: What is the fundamental element of human memory? Could the TELCs-associated activities be part of the brain function and memory process? Therefore, the author hereby encourage more research efforts on TELCs-associated neuroscience.

Author contributions

JL: Supervision, Methodology, Investigation, Validation, Conceptualization, Data curation, Writing – review and editing, Visualization, Writing – original draft, Formal Analysis, Software, Project administration, Funding acquisition, Resources.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This research was supported in part by a Multidisciplinary Biomedical Research Seed Funding Grant from the Graduate School, the College of Sciences, and the Center for Bioelectrics at Old Dominion University, Norfolk, Virginia, United States.

Acknowledgments

The author thanks the Editor and peer reviewers for their highly valuable and constructive review comments that made this article better.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adrian, R. H., and Bryant, S. H. (1974). On the repetitive discharge in myotonic muscle fibres. J. Physiol. 240 (2), 505–515. doi:10.1113/jphysiol.1974.sp010620

PubMed Abstract | CrossRef Full Text | Google Scholar

Aidley, D. J. (1989). The physiology of excitable cells. 3rd edn. Cambridge, MA: Cambridge University Press.

Google Scholar

Alharbi, B. H. (2025). “PhD thesis chapter three: protonic probe for detecting protons in neuron cells and the transmembrane-electrostatically localized protons (TELPs),” in Chemistry and biochemistry (Virginia: Old Dominion University Norfolk). 23529.

Google Scholar

Amor, V., Zhang, C., Vainshtein, A., Zhang, A., Zollinger, D. R., Eshed-Eisenbach, Y., et al. (2017). The paranodal cytoskeleton clusters Na⁺ channels at nodes of Ranvier. eLife 6, e21392. doi:10.7554/eLife.21392

PubMed Abstract | CrossRef Full Text | Google Scholar

Arancibia-Carcamo, I. L., and Attwell, D. (2014). The node of Ranvier in CNS pathology. Acta Neuropathol. 128 (2), 161–175. doi:10.1007/s00401-014-1305-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Azzone, G., Benz, R., Bertl, A., Colombini, M., Crofts, A., Dilley, R., et al. (1993). Transmembrane measurements across bioenergetic membranes. Biochimica Biophysica Acta (BBA) - Bioenergetics 1183 (1), 1–3. doi:10.1016/0005-2728(93)90002-W

CrossRef Full Text | Google Scholar

Bal, W., Kurowska, E., and Maret, W. (2012). The final frontier of pH and the undiscovered country beyond. Plos One 7 (9), ARTN e45832. doi:10.1371/journal.pone.0045832

PubMed Abstract | CrossRef Full Text | Google Scholar

Barry, P. H. (2006). The reliability of relative anion-cation permeabilities deduced from reversal (dilution) potential measurements in ion channel studies. Cell Biochem. Biophysics 46 (2), 143–154. doi:10.1385/Cbb:46:2:143

PubMed Abstract | CrossRef Full Text | Google Scholar

Bean, B. P. (2007). The action potential in mammalian central neurons. Nat. Rev. Neurosci. 8 (6), 451–465. doi:10.1038/nrn2148

PubMed Abstract | CrossRef Full Text | Google Scholar

Beaulieu-Laroche, L., Brown, N. J., Hansen, M., Toloza, E. H. S., Sharma, J., Williams, Z. M., et al. (2021). Allometric rules for mammalian cortical layer 5 neuron biophysics. Nature 600 (7888), 274–278. doi:10.1038/s41586-021-04072-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Bertl, A., Blumwald, E., Coronado, R., Eisenberg, R., Findlay, G., Gradmann, D., et al. (1992). Electrical measurements on endomembranes. Science 258 (5084), 873–874. doi:10.1126/science.1439795

PubMed Abstract | CrossRef Full Text | Google Scholar

Blair, N. T., and Bean, B. P. (2002). Roles of tetrodotoxin (TTX)-sensitive Na⁺ current, TTX-resistant Na⁺ current, and Ca2⁺ current in the action potentials of nociceptive sensory neurons. J. Neurosci. 22 (23), 10277–10290. doi:10.1523/jneurosci.22-23-10277.2002

PubMed Abstract | CrossRef Full Text | Google Scholar

Bowman, C. L., and Baglioni, A. (1984). Application of the goldman-hodgkin-katz Current equation to membrane current voltage data. J. Theor. Biol. 108 (1), 1–29. doi:10.1016/S0022-5193(84)80165-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Carter, B., and Bean, B. (2009). Sodium entry during action potentials of mammalian neurons: incomplete inactivation and reduced metabolic efficiency in fast-spiking neurons. Neuron 64, 898–909. doi:10.1016/j.neuron.2009.12.011

PubMed Abstract | CrossRef Full Text | Google Scholar

Chang, D. C. (1983). Dependence of cellular-potential on ionic concentrations - data supporting a modification of the constant field equation. Biophysical J. 43 (2), 149–156. doi:10.1016/S0006-3495(83)84335-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Cherepanov, D. A., Feniouk, B. A., Junge, W., and Mulkidjanian, A. Y. (2003). Low dielectric permittivity of water at the membrane interface: effect on the energy coupling mechanism in biological membranes. Biophysical J. 85 (2), 1307–1316. doi:10.1016/S0006-3495(03)74565-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Clay, J. R. (2009). Determining k channel activation curves from k channel currents often requires the goldman-hodgkin-katz equation. Front. Cell. Neurosci. 3, 20. doi:10.3389/neuro.03.020.2009

PubMed Abstract | CrossRef Full Text | Google Scholar

Clay, J. R., Paydarfar, D., and Forger, D. B. (2008). A simple modification of the Hodgkin and Huxley equations explains type 3 excitability in squid giant axons. J. R. Soc. Interface 5 (29), 1421–1428. doi:10.1098/rsif.2008.0166

PubMed Abstract | CrossRef Full Text | Google Scholar

Cook, M., Draeger, K., Fietsam, A., and Reyes, R. (2016). “Voltage-Gated potassium channels,” in The nerve impulse. Available online at: https://eprojects.isucomm.iastate.edu/314-4-kbcm/2016/11/16/voltage-gated-potassium-channels/ (Accessed May 20, 2025).

Google Scholar

Coste, B., Mathur, J., Schmidt, M., Earley, T. J., Ranade, S., Petrus, M. J., et al. (2010). Piezo1 and Piezo2 are essential components of distinct mechanically activated cation channels. Science 330 (6000), 55–60. doi:10.1126/science.1193270

PubMed Abstract | CrossRef Full Text | Google Scholar

Coste, B., Xiao, B. L., Santos, J. S., Syeda, R., Grandl, J., Spencer, K. S., et al. (2012). Piezo proteins are pore-forming subunits of mechanically activated channels. Nature 483 (7388), 176–181. doi:10.1038/nature10812

PubMed Abstract | CrossRef Full Text | Google Scholar

de Grotthuss, C. J. T. (1806). Sur la décomposition de l’eau et des corps qu'elle tient en dissolution à l’aide de l'électricité galvanique. Ann. Chim. 58, 54–73.

Google Scholar

Derangeon, M., Montnach, J., Baró, I., and Charpentier, F. (2012). Mouse models of SCN5A-Related cardiac arrhythmias. Front. Physiol. 3, 210. doi:10.3389/fphys.2012.00210

PubMed Abstract | CrossRef Full Text | Google Scholar

Dilley, R. A. (2004). On why thylakoids energize ATP formation using either delocalized or localized proton gradients - a Ca2⁺ mediated role in thylakoid stress responses. Photosynth. Res. 80 (1-3), 245–263. doi:10.1023/B:PRES.0000030436.32486.aa

PubMed Abstract | CrossRef Full Text | Google Scholar

Dilley, R. A., Theg, S. M., and Beard, W. A. (1987). Membrane-proton interactions in chloroplast bioenergetics - localized proton domains. Annu. Rev. Plant Physiology Plant Mol. Biol. 38, 347–389. doi:10.1146/annurev.arplant.38.1.347

CrossRef Full Text | Google Scholar

Eijkelkamp, N., Linley, J. E., Baker, M. D., Minett, M. S., Cregg, R., Werdehausen, R., et al. (2012). Neurological perspectives on voltage-gated sodium channels. Brain 135 (9), 2585–2612. doi:10.1093/brain/aws225

PubMed Abstract | CrossRef Full Text | Google Scholar

Elvira, C. C., and Jenkins, P. M. (2025). Cytoskeletal scaffolding of NaVs and KVs in neocortical pyramidal neurons: implications for neuronal signaling and plasticity. Curr. Opin. Cell Biol. 96, 102570. doi:10.1016/j.ceb.2025.102570

PubMed Abstract | CrossRef Full Text | Google Scholar

Feinberg, K., Eshed-Eisenbach, Y., Frechter, S., Amor, V., Salomon, D., Sabanay, H., et al. (2010). A glial signal consisting of gliomedin and NrCAM clusters axonal Na⁺ channels during the formation of nodes of ranvier. Neuron 65 (4), 490–502. doi:10.1016/j.neuron.2010.02.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Freeman, S. A., Desmazières, A., Simonnet, J., Gatta, M., Pfeiffer, F., Aigrot, M. S., et al. (2015). Acceleration of conduction velocity linked to clustering of nodal components precedes myelination. Proc. Natl. Acad. Sci. U. S. A. 112 (3), E321–E328. doi:10.1073/pnas.1419099112

PubMed Abstract | CrossRef Full Text | Google Scholar

Freeman, S. A., Desmazières, A., Fricker, D., Lubetzki, C., and Sol-Foulon, N. (2016). Mechanisms of sodium channel clustering and its influence on axonal impulse conduction. Cell. Mol. Life Sci. 73 (4), 723–735. doi:10.1007/s00018-015-2081-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Fuchs, E. C., Sammer, M., Wexler, A. D., Kuntke, P., and Woisetschläger, J. (2016). A floating water bridge produces water with excess charge. J. Phys. D Appl. Phys. 49 (12), 125502. doi:10.1088/0022-3727/49/12/125502

CrossRef Full Text | Google Scholar

Fuchs, E. C., Yntema, D., and Woisetschläger, J. (2019). Raman spectroscopy and shadowgraph visualization of excess protons in high-voltage electrolysis of pure water. J. Phys. D Appl. Phys. 52 (36), 365302. doi:10.1088/1361-6463/ab252b

CrossRef Full Text | Google Scholar

Gentet, L. J., Stuart, G. J., and Clements, J. D. (2000). Direct measurement of specific membrane capacitance in neurons. Biophysical J. 79 (1), 314–320. doi:10.1016/S0006-3495(00)76293-X

PubMed Abstract | CrossRef Full Text | Google Scholar

Guffanti, A., and Krulwich, T. (1984). Bioenergetic problems of alkalophilic bacteria. Biochem. Soc. Trans. 12 (3), 411–412. doi:10.1042/bst0120411

PubMed Abstract | CrossRef Full Text | Google Scholar

Hammond, C. (2015). “Chapter 3 - ionic gradients, membrane potential and ionic currents,” in Cellular and molecular neurophysiology. Editor C. Hammond Fourth Edition (Boston: Academic Press). doi:10.1016/B978-0-12-397032-9.00003-0

CrossRef Full Text | Google Scholar

Hariharan, P., Bakhtiiari, A., Liang, R., and Guan, L. (2024). Distinct roles of the major binding residues in the cation-binding pocket of the melibiose transporter MelB. J. Biol. Chem. 300 (7), 107427. doi:10.1016/j.jbc.2024.107427

PubMed Abstract | CrossRef Full Text | Google Scholar

Harty, T. P., and Waxman, S. G. (2007). Inactivation properties of sodium Channel Na_v1.8 maintain action potential amplitude in small DRG neurons in the context of depolarization. Mol. Pain 3 (1), 1744-8069-3–12. doi:10.1186/1744-8069-3-12

CrossRef Full Text | Google Scholar

Heberle, J., Riesle, J., Thiedemann, G., Oesterhelt, D., and Dencher, N. A. (1984). Proton migration along the membrane-surface and retarded surface to bulk transfer. Nature 370 (6488), 379–382. doi:10.1038/370379a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Heimburg, T. (2018). Comment on Tamagawa and Ikeda's reinterpretation of the goldman-hodgkin-katz equation: are transmembrane potentials caused by polarization? Eur. Biophysics J. 47 (8), 865–867. doi:10.1007/s00249-018-1335-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Hill, A. S., Nishino, A., Nakajo, K., Zhang, G., Fineman, J. R., Selzer, M. E., et al. (2008). Ion channel clustering at the Axon initial segment and node of ranvier evolved sequentially in early chordates. PLoS Genet. 4 (12), e1000317. doi:10.1371/journal.pgen.1000317

PubMed Abstract | CrossRef Full Text | Google Scholar

Hill, S. F., Jafar-Nejad, P., Rigo, F., and Meisler, M. H. (2023). Reduction of Kcnt1 is therapeutic in mouse models of SCN1A and SCN8A epilepsy. Front. Neurosci. 17, 1282201. doi:10.3389/fnins.2023.1282201

PubMed Abstract | CrossRef Full Text | Google Scholar

Hille, B. (2001). Ion channels of excitable membranes. Oxford: Sinauer Associates is an imprint of Oxford University Press.

Google Scholar

Huang, S. W., Hong, S. H., and De Schutter, E. (2015). Non-linear leak currents affect mammalian neuron physiology. Front. Cell. Neurosci. 9, 432. doi:10.3389/fncel.2015.00432)

PubMed Abstract | CrossRef Full Text | Google Scholar

Junge, D. (1992). Nerve and muscle excitation. 3rd edn. Sunderland, MA: Sinauer Associates, 37–49.

Google Scholar

Kharel, G. (2024). “Chapter 4: investigation of calcium and magnesium cation-proton exchange with transmembrane electrostatically localized protons (TELP) at a liquid-membrane interface. In PhD thesis: exploring cation exchange: unveiling its significance in biochar and bioenergetics applications,” in Chemistry and biochemistry (Norfolk, VA: Old Dominion University).

Google Scholar

Krulwich, T. A., Ito, M., Gilmour, R., Hicks, D. B., and Guffanti, A. A. (1998). Energetics of alkaliphilic bacillus species: physiology and molecules. Adv. Microb. Physiol. 40, 401–438. doi:10.1016/s0065-2911(08)60136-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Krulwich, T. A., Liu, J., Morino, M., Fujisawa, M., Ito, M., and Hicks, D. B. (2011). Adaptive mechanisms of extreme alkaliphiles. Extrem. Handb., 119–139. doi:10.1007/978-4-431-53898-1_7

CrossRef Full Text | Google Scholar

Kuffler, S. W., Nicholls, D. G., and Martin, A. R. (1984). From Neuron to Brain. 2nd edn. Oxford, United Kingdom: Blackwell Scientific.

Google Scholar

Lee, J. W. (2012). Proton-electrostatics hypothesis for localized proton coupling bioenergetics. Bioenergetics 1 (104), 1–8. doi:10.4172/2167-7662.1000104

CrossRef Full Text | Google Scholar

Lee, J. W. (2015). Proton-electrostatic localization: explaining the bioenergetic conundrum in alkalophilic bacteria. Bioenergetics 4 (121), 1–8. doi:10.4172/2167-7662.1000121

CrossRef Full Text | Google Scholar

Lee, J. W. (2017a). Localized excess protons and methods of making and using the same. PCT International Patent Application Publication No. WO 2017/007762 A1. Switzerland, CH, Geneva: WIPO - World Intellectual Property Organization, 56.

Google Scholar

Lee, J. W. (2017b). Elucidating the 30-Year-Longstanding bioenergetic mystery in alkalophilic bacteria. Biophysical J. 112 (Suppl. 1), 278a–279a. doi:10.1016/j.bpj.2016.11.1509

CrossRef Full Text | Google Scholar

Lee, J. W. (2018). Proton motive force computation revealing latent heat utilization by localized protons at a liquid-biomembrane interface. Abstr. Pap. Am. Chem. Soc. 255.

Google Scholar

Lee, J. W. (2019a). Electrostatically localized proton bioenergetics: better understanding membrane potential. Heliyon 5 (7), e01961. doi:10.1016/j.heliyon.2019.e01961

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, J. W. (2019b). Physical chemistry of living systems: isothermal utilization of latent heat by electrostatically localized protons at liquid-membrane interface. Biophysical J. 116 (Suppl. 1), 317a. doi:10.1016/j.bpj.2018.11.1719

CrossRef Full Text | Google Scholar

Lee, J. W. (2020a). Protonic capacitor: elucidating the biological significance of mitochondrial cristae formation. Sci. Rep. 10, 10304. doi:10.1038/s41598-020-66203-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, J. W. (2020b). Isothermal environmental heat energy utilization by transmembrane electrostatically localized protons at the liquid-membrane interface. Acs Omega 5 (28), 17385–17395. doi:10.1021/acsomega.0c01768

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, J. W. (2020c). Protonic conductor: better understanding neural resting and action potential. J. Neurophysiology 124 (4), 1029–1044. doi:10.1152/jn.00281.2020

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, J. W. (2021a). Mitochondrial energetics with transmembrane electrostatically localized protons: do we have a thermotrophic feature? Sci. Rep. 11 (1), 14575. doi:10.1038/s41598-021-93853-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, J. W. (2022a). Type-B energy process: asymmetric function-gated isothermal electricity production. Energies 15 (19), 7020. doi:10.3390/en15197020

CrossRef Full Text | Google Scholar

Lee, J. W. (2022b). Type-B energetic processes and their associated scientific implication. J. Sci. Explor. 36 (3), 487–495. doi:10.31275/20222517

CrossRef Full Text | Google Scholar

Lee, J. W. (2023a). TELP theory: elucidating the major observations of Rieger et al. 2021 in mitochondria. Mitochondrial Commun. 1, 62–72. doi:10.1016/j.mitoco.2023.09.001

CrossRef Full Text | Google Scholar

Lee, J. W. (2023b). Thermotrophy exploratory study. J. Sci. Explor. 37 (1), 5–16. doi:10.31275/20232655

CrossRef Full Text | Google Scholar

Lee, J. W. (2023c). Application of TELC model to neurology: review and commentary responding to Silverstein’s critique. Curr. Trends Neurol. 17, 83–89.

Google Scholar

Lee, J. W. (2023d). Transient protonic capacitor: explaining the bacteriorhodopsin membrane experiment of Heberle et al. Biophys. Chem. 300, 107072. doi:10.1016/j.bpc.2023.107072

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, J. W. (2024). Type-B energetic processes: their identification and implications. Symmetry 16 (7), 808. doi:10.3390/sym16070808

CrossRef Full Text | Google Scholar

Lee, J. W. (2025a). Experimental demonstration and study of transmembrane-electrostatically localized protons prevail. Water - A Multidiscip. Res. J. 14, 35–58. doi:10.14294/WATER.2024.2

CrossRef Full Text | Google Scholar

Lee, J. W. (2025b). Application of TELC model to better elucidate neural stimulation by touch. Explor. Neurosci. 4, 100685. doi:10.37349/en.2025.100685

CrossRef Full Text | Google Scholar

Lee, J. W. (2025c). Calculation of proton transmembrane-electrostatic interaction force and elucidation of the water droplet experiment with a transient protonic front. RSC Adv. 15 (26), 21108–21120. doi:10.1039/D5RA03298A

CrossRef Full Text | Google Scholar

Lee, J. W. (2021). Energy Renewal: Isothermal utilization of environmental heat energy with asymmetric structures. Entropy 23 (6), 665. doi:10.3390/e23060665

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, C. H., and Ruben, P. C. (2008). Interaction between voltage-gated sodium channels and the neurotoxin, tetrodotoxin. Channels 2 (6), 407–412. doi:10.4161/chan.2.6.7429

PubMed Abstract | CrossRef Full Text | Google Scholar

Ma, Z., Saung, W. T., and Foskett, J. K. (2017). Action potentials and ion conductances in wild-type and CALHM1-knockout type II taste cells. J. Neurophysiol. 117 (5), 1865–1876. doi:10.1152/jn.00835.2016

PubMed Abstract | CrossRef Full Text | Google Scholar

Martin, F. G., and Harvey, W. R. (1994). Ionic circuit analysis of K⁺/H⁺ antiport and amino-acid K⁺ symport energized by a proton-motive force in manduca-sexta larval midgut vesicles. J. Exp. Biol. 196, 77–92. doi:10.1242/jeb.196.1.77

PubMed Abstract | CrossRef Full Text | Google Scholar

Martinez-Espinosa, P. L., Wu, J., Yang, C., Gonzalez-Perez, V., Zhou, H., Liang, H., et al. (2015). Knockout of Slo2.2 enhances itch, abolishes KNa current, and increases action potential firing frequency in DRG neurons. eLife 4, e10013. doi:10.7554/eLife.10013

PubMed Abstract | CrossRef Full Text | Google Scholar

Marx, D. (2006). Proton transfer 200 years after von Grotthuss: insights from ab initio simulations. ChemPhysChem 7 (9), 1848–1870. doi:10.1002/cphc.200600128

PubMed Abstract | CrossRef Full Text | Google Scholar

Marx, D., Tuckerman, M. E., Hutter, J., and Parrinello, M. (1999). The nature of the hydrated excess proton in water. Nature 397 (6720), 601–604. doi:10.1038/17579

CrossRef Full Text | Google Scholar

Mclaughlin, S. (1989). The electrostatic properties of membranes. Annu. Rev. Biophysics Biomol. Struct. 18, 113–136. doi:10.1146/annurev.biophys.18.1.113

PubMed Abstract | CrossRef Full Text | Google Scholar

MDougM. Public domain, via Wikimedia commons. (2008). Available online at: https://commons.wikimedia.org/wiki/File:Bilayer_hydration_profile.svg (Accessed May 20, 2025).

Google Scholar

Mitchell, P. (1961). Coupling of phosphorylation to electron and hydrogen transfer by a chemi-osmotic type of mechanism. Nature 191 (4784), 144–148. doi:10.1038/191144a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Mitchell, P. (1985). The correlation of chemical and osmotic forces in biochemistry. J. Biochem. 97 (1), 1–18. doi:10.1093/oxfordjournals.jbchem.a135033

PubMed Abstract | CrossRef Full Text | Google Scholar

Mitchell, P., and Moyle, J. (1965). Evidence discriminating between chemical and chemiosmotic mechanisms of electron transport phosphorylation. Nature 208 (5016), 1205. doi:10.1038/2081205a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Mitchell, P., and Moyle, J. (1967). Chemiosmotic Hypothesis of oxidative phosphorylation. Nature 213 (5072), 137–139. doi:10.1038/213137a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Mulkidjanian, A. Y., Cherepanov, D. A., Heberle, J., and Junge, W. (2005). Proton transfer dynamics at membrane/water interface and mechanism of biological energy conversion. Biochem. Mosc. 70 (2), 251–256. doi:10.1007/s10541-005-0108-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Mulkidjanian, A. Y., Heberle, J., and Cherepanov, D. A. (2006). Protons @ interfaces: implications for biological energy conversion. Biochimica Biophysica Acta-Bioenergetics 1757 (8), 913–930. doi:10.1016/j.bbabio.2006.02.015

PubMed Abstract | CrossRef Full Text | Google Scholar

Nagle, J. F., and Tristramnagle, S. (1983). Hydrogen-bonded chain mechanisms for proton conduction and proton pumping. J. Membr. Biol. 74 (1), 1–14. doi:10.1007/Bf01870590

PubMed Abstract | CrossRef Full Text | Google Scholar

Ohki, S. (1984). Membrane potential of squid axons: comparison between the goldman-hodgkin-kantz equation and the surface/diffusion potential equation. Bioelectrochemistry Bioenergetics 13 (4-6), 439–451. doi:10.1016/0302-4598(84)87045-2

CrossRef Full Text | Google Scholar

Olschewski, A., Olschewski, H., Brau, M. E., Hempelmann, G., Vogel, W., and Safronov, B. V. (2001). Basic electrical properties of in situ endothelial cells of small pulmonary arteries during postnatal development. Am. J. Respir. Cell Mol. Biol. 25 (3), 285–290. doi:10.1165/ajrcmb.25.3.4373

PubMed Abstract | CrossRef Full Text | Google Scholar

Oyrer, J., Maljevic, S., Scheffer, I. E., Berkovic, S. F., Petrou, S., and Reid, C. A. (2018). Ion channels in genetic epilepsy: from genes and mechanisms to disease-targeted therapies. Pharmacol. Rev. 70 (1), 142–173. doi:10.1124/pr.117.014456

PubMed Abstract | CrossRef Full Text | Google Scholar

Pedersen, T. H., Riisager, A., de Paoli, F. V., Chen, T. V., and Nielsen, O. B. (2016). Role of physiological ClC-1 Cl- ion channel regulation for the excitability and function of working skeletal muscle. J. Gen. Physiol. 147, 291–308.

PubMed Abstract | CrossRef Full Text | Google Scholar

Perram, J. W., and Stiles, P. J. (2010). A dynamical system for action potentials in the giant axon of the squid. J. Phys. Chem. C 114 (48), 20350–20361. doi:10.1021/jp1030637

CrossRef Full Text | Google Scholar

Petersen, P. B., and Saykally, R. J. (2005). Evidence for an enhanced hydronium concentration at the liquid water surface. J. Phys. Chem. B 109 (16), 7976–7980. doi:10.1021/jp044479j

PubMed Abstract | CrossRef Full Text | Google Scholar

Pinto, L. G., Vilar, B., and McNaughton, P. A. (2025). PGE2 and HCN2 ion channels are critical mediators of pain initiated by angiotensin II. Brain, Behav. Immun. 125, 268–279. doi:10.1016/j.bbi.2024.12.156

PubMed Abstract | CrossRef Full Text | Google Scholar

Pomès, R., and Roux, B. (2002). Molecular mechanism of H⁺ conduction in the single-file water chain of the gramicidin channel. Biophysical J. 82 (5), 2304–2316. doi:10.1016/s0006-3495(02)75576-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Quraishi, I. H., Mercier, M. R., McClure, H., Couture, R. L., Schwartz, M. L., Lukowski, R., et al. (2020). Impaired motor skill learning and altered seizure susceptibility in mice with loss or gain of function of the Kcnt1 gene encoding slack (KNa1.1) Na⁺-activated K⁺ channels. Sci. Rep. 10 (1), 3213. doi:10.1038/s41598-020-60028-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Raouf, R., Quick, K., and Wood, J. N. (2010). Pain as a channelopathy. J. Clin. Investigation 120 (11), 3745–3752. doi:10.1172/jci43158

PubMed Abstract | CrossRef Full Text | Google Scholar

Rasband, M. N., and Peles, E. (2016). The nodes of ranvier: molecular assembly and maintenance. Cold Spring Harb. Perspect. Biol. 8 (3), a020495. doi:10.1101/cshperspect.a020495

PubMed Abstract | CrossRef Full Text | Google Scholar

Rasband, M. N., Peles, E., Trimmer, J. S., Levinson, S. R., Lux, S. E., and Shrager, P. (1999). Dependence of Nodal sodium channel clustering on paranodal axoglial contact in the developing CNS. J. Neurosci. 19 (17), 7516–7528. doi:10.1523/jneurosci.19-17-07516.1999

PubMed Abstract | CrossRef Full Text | Google Scholar

Rieger, B., Junge, W., and Busch, K. B. (2014). Lateral pH gradient between OXPHOS complex IV and F0F1 ATP-synthase in folded mitochondrial membranes. Nat. Commun. 5, 3103. doi:10.1038/ncomms4103

PubMed Abstract | CrossRef Full Text | Google Scholar

Rieger, B., Shalaeva, D. N., Sohnel, A. C., Kohl, W., Duwe, P., Mulkidjanian, A. Y., et al. (2017). Lifetime imaging of GFP at CoxVIIIa reports respiratory supercomplex assembly in live cells. Sci. Rep. 7, 46055. doi:10.1038/srep46055

PubMed Abstract | CrossRef Full Text | Google Scholar

Rieger, B., Arroum, T., Borowski, M.-T., Villalta, J., and Busch, K. B. (2021). Mitochondrial F1FO ATP synthase determines the local proton motive force at cristae rims. EMBO Rep. 22 (12), e52727. doi:10.15252/embr.202152727

PubMed Abstract | CrossRef Full Text | Google Scholar

Saeed, H. (2016). Bioenergetics: experimental demonstration of excess protons and related features. PhD thesis. Norfolk, VA: Old Dominion University.

Google Scholar

Saeed, H. A., and Lee, J. W. (2015). Experimental demonstration of localized excess protons at a water-membrane interface. Bioenergetics 4 (127), 1–7. doi:10.4172/2167-7662.1000127

CrossRef Full Text | Google Scholar

Saeed, H., and Lee, J. (2018). Experimental determination of proton-cation exchange equilibrium constants at water-membrane interface fundamental to bioenergetics. WATER J. Multidiscip. Res. J. 9, 116–140. doi:10.14294/WATER.2018.2

CrossRef Full Text | Google Scholar

Salas, P. J. I, and Lopez, E. M. (1982). Validity of the Goldman-Hodgkin-Katz equation in paracellular ionic pathways of gallbladder epithelium. Biochimica Biophysica Acta (BBA) - Biomembr., 691(1), 178–182. doi:10.1016/0005-2736(82)90227-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Santos, L. P., Ducati, T. R. D., Balestrin, L. B. S., and Galembeck, F. (2011). Water with excess electric charge. J. Phys. Chem. C 115 (22), 11226–11232. doi:10.1021/jp202652q

CrossRef Full Text | Google Scholar

Scholl, U. I., Stölting, G., Schewe, J., Thiel, A., Tan, H., Nelson-Williams, C., et al. (2018). CLCN2 chloride channel mutations in familial hyperaldosteronism type II. Nat. Genet. 50 (3), 349–354. doi:10.1038/s41588-018-0048-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Sheehan, D. P., Moddel, G., and Lee, J. W. (2023). More on the demons of thermodynamics. Phys. Today 76 (3), 12–13. doi:10.1063/Pt.3.5186

CrossRef Full Text | Google Scholar

Silverstein, T. P. (2022). A critique of the capacitor-based “Transmembrane electrostatically localized proton” hypothesis. J. Bioenergetics Biomembr. 54 (2), 59–65. doi:10.1007/s10863-022-09931-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Silverstein, T. P. (2023a). Lee’s “Transmembrane electrostatically-localized proton” model does NOT offer a better understanding of neuronal transmembrane potentials. J. Neurophysiology 130 (1), 123–127. doi:10.1152/jn.00173.2023

PubMed Abstract | CrossRef Full Text | Google Scholar

Silverstein, T. P. (2023b). Lee's transient protonic capacitor cannot explain the surface proton current observed in bacteriorhodopsin purple membranes. Biophys. Chem. 301, 107096. doi:10.1016/j.bpc.2023.107096

PubMed Abstract | CrossRef Full Text | Google Scholar

Silverstein, T. P. (2024a). Oxidative phosphorylation does not violate the second law of thermodynamics. J. Phys. Chem. B 128 (35), 8448–8458. doi:10.1021/acs.jpcb.4c03047

PubMed Abstract | CrossRef Full Text | Google Scholar

Silverstein, T. P. (2024b). Serious problems with Saeed and Lee’s “Experimental Determination of proton-cation exchange equilibrium constants at water-membrane interface fundamental to bioenergetics”. Water 13, 103–114. doi:10.14294/WATER.2024.1

CrossRef Full Text | Google Scholar

Silverstein, T. P. (2025). Explaining neuronal membrane potentials: the Goldman equation vs. Lee’s TELC hypothesis. Neuroscience 567, 1–8. doi:10.1016/j.neuroscience.2024.12.065

PubMed Abstract | CrossRef Full Text | Google Scholar

Slater, E. C. (1967). An evaluation of the mitchell Hypothesis of chemiosmotic coupling in oxidative and photosynthetic phosphorylation. Eur. J. Biochem. 1 (3), 317–326. doi:10.1111/j.1432-1033.1967.tb00076.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Stauber, T., Weinert, S., and Jentsch, T. J. (2012). Cell biology and physiology of clc chloride channels and transporters. Compr. Physiol. 2 (3), 1701–1744. doi:10.1002/cphy.c110038

PubMed Abstract | CrossRef Full Text | Google Scholar

Stölting, G., Fischer, M., and Fahlke, C. (2014). CLC channel function and dysfunction in health and disease. Front. Physiol. 5, 378. doi:10.3389/fphys.2014.00378

PubMed Abstract | CrossRef Full Text | Google Scholar

Tamagawa, H. (2019). Mathematical expression of membrane potential based on Ling’s adsorption theory is approximately the same as the goldman-hodgkin-katz equation. J. Biol. Phys. 45 (1), 13–30. doi:10.1007/s10867-018-9512-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Tamagawa, H. (2015). Membrane potential generation without ion transport. Ionics 21 (6), 1631–1648. doi:10.1007/s11581-014-1333-7

CrossRef Full Text | Google Scholar

Tamagawa, H. (2025). Comment on the Silverstein’s critiques of Lee’s TELC theory as a membrane potential generation mechanism. Neuroscience 573, 381. doi:10.1016/j.neuroscience.2025.03.049

PubMed Abstract | CrossRef Full Text | Google Scholar

Tamagawa, H., and Ikeda, K. (2017). Generation of membrane potential beyond the conceptual range of Donnan theory and goldman-hodgkin-katz equation. J. Biol. Phys. 43 (3), 319–340. doi:10.1007/s10867-017-9454-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Tamagawa, H., and Ikeda, K. (2018). Another interpretation of the goldman-hodgkin-katz equation based on Ling’s adsorption theory. Eur. Biophysics J. 47 (8), 869–879. doi:10.1007/s00249-018-1332-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Tamagawa, H., and Morita, S. (2014). Membrane potential generated by ion adsorption. Membranes 4 (2), 257–274. doi:10.3390/membranes4020257

PubMed Abstract | CrossRef Full Text | Google Scholar

Theile, J. W., and Cummins, T. R. (2011). Recent developments regarding voltage-gated sodium channel blockers for the treatment of inherited and acquired neuropathic pain syndromes. Front. Pharmacol. 2, 54. doi:10.3389/fphar.2011.00054

PubMed Abstract | CrossRef Full Text | Google Scholar

Tocanne, J. F., and Teissié, J. (1990). Ionization of phospholipids and phospholipid-supported interfacial lateral diffusion of protons in membrane model systems. Biochim. Biophys. Acta 1031 (1), 111–142. doi:10.1016/0304-4157(90)90005-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Toth, A., Meyrat, A., Stoldt, S., Santiago, R., Wenzel, D., Jakobs, S., et al. (2020). Kinetic coupling of the respiratory chain with ATP synthase, but not proton gradients, drives ATP production in cristae membranes. Proc. Natl. Acad. Sci. 117 (5), 2412–2421. doi:10.1073/pnas.1917968117

PubMed Abstract | CrossRef Full Text | Google Scholar

Uteshev, V. V. (2010). Evaluation of Ca²⁺ permeability of nicotinic acetylcholine receptors in hypothalamic histaminergic neurons. Acta Biochimica Biophysica Sinica 42 (1), 8–20. doi:10.1093/abbs/gmp101

PubMed Abstract | CrossRef Full Text | Google Scholar

Veerman, C. C., Wilde, A. A. M., and Lodder, E. M. (2015). The cardiac sodium channel gene SCN5A and its gene product NaV1.5: role in physiology and pathophysiology. Gene 573 (2), 177–187. doi:10.1016/j.gene.2015.08.062

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, V. Q., and Liu, S. (2019). A general model of ion passive transmembrane transport based on ionic concentration. Front. Comput. Neurosci. 12, 110. doi:10.3389/fncom.2018.00110

PubMed Abstract | CrossRef Full Text | Google Scholar

Weichselbaum, E., Österbauer, M., Knyazev, D. G., Batishchev, O. V., Akimov, S. A., Hai Nguyen, T., et al. (2017). Origin of proton affinity to membrane/water interfaces. Sci. Rep. 7 (1), 4553. doi:10.1038/s41598-017-04675-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Weiss, J. N., Venkatesh, N., and Lamp, S. T. (1992). ATP-sensitive K⁺ channels and cellular K⁺ loss in hypoxic and ischaemic mammalian ventricle. J. Physiol. 447, 649–673. doi:10.1113/jphysiol.1992.sp019022

PubMed Abstract | CrossRef Full Text | Google Scholar

Williams, R. J. B. (1975). Proton-driven phosphorylation reactions in mitochondrial and chloroplast membranes. Febs Lett. 53 (2), 123–125. doi:10.1016/0014-5793(75)80001-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Williams, R. J. P. (1978). The history and the hypotheses concerning ATP-formation by energised protons. FEBS Lett. 85 (1), 9–19. doi:10.1016/0014-5793(78)81238-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Williams, R. J. P. (1988). Proton circuits in biological energy interconversions. Annu. Rev. Biophysics Biomol. Struct. 17, 71–97. doi:10.1146/annurev.biophys.17.1.71

CrossRef Full Text | Google Scholar

Wolf, M. G., Grubmüller, H., and Groenhof, G. (2014). Anomalous surface diffusion of protons on lipid membranes. Biophys. J. 107 (1), 76–87. doi:10.1016/j.bpj.2014.04.062

PubMed Abstract | CrossRef Full Text | Google Scholar

Wright, E. M., and Diamond, J. M. (1968). Effects of pH and polyvalent cations on the selective permeability of gall-bladder epithelium to monovalent ions. Biochimica Biophysica Acta (BBA) - Biomembr. 163 (1), 57–74. doi:10.1016/0005-2736(68)90033-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, J., Young, M., Lewis, A. H., Martfeld, A. N., Kalmeta, B., and Grandl, J. (2017). Inactivation of mechanically activated Piezo1 ion channels is determined by the C-Terminal extracellular domain and the inner pore helix. Cell Rep. 21 (9), 2357–2366. doi:10.1016/j.celrep.2017.10.120

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, Z. J., and Adams, D. J. (1992). Resting membrane potential and potassium currents in cultured parasympathetic neurones from rat intracardiac ganglia. J. Physiology 456, 405–424. doi:10.1113/jphysiol.1992.sp019343

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, L., Öjemyr, L., Bergstrand, J., Brzezinski, P., and Widengren, J. (2016). Protonation dynamics on lipid nanodiscs: influence of the membrane surface area and external buffers. Biophysical J. 110 (9), 1993–2003. doi:10.1016/j.bpj.2016.03.035

PubMed Abstract | CrossRef Full Text | Google Scholar

Yogi, A., Banderali, U., Moreno, M. J., and Martina, M. (2025). Preclinical animal models to investigate the role of Nav1.7 ion channels in pain. Life 15 (4), 640. doi:10.3390/life15040640

PubMed Abstract | CrossRef Full Text | Google Scholar

Zeberg, H., Blomberg, C., and Århem, P. (2010). Ion channel density regulates switches between regular and fast spiking in soma but not in axons. PLOS Comput. Biol. 6 (4), e1000753. doi:10.1371/journal.pcbi.1000753

PubMed Abstract | CrossRef Full Text | Google Scholar

Zou, X., Zhang, Z., Lu, H., Zhao, W., Pan, L., and Chen, Y. (2024). Functional effects of drugs and toxins interacting with NaV1.4. Front. Pharmacol. 15, 1378315. doi:10.3389/fphar.2024.1378315

PubMed Abstract | CrossRef Full Text | Google Scholar