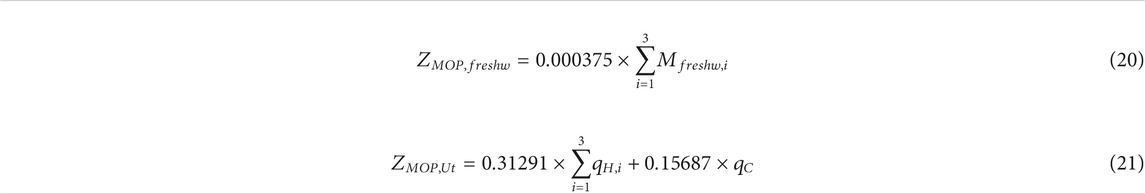Optimisation of Water-Energy Networks in Process Industry: Implementation of Non-Linear and Multi-Objective Models

The improvement of water and energy use in the industrial sector is an important concern to improve the overall techno-economic performance of single plants. The most recent EU strategy for energy system integration has been treating these issues in the redaction of its first pillar, which is based on the relations between the promotion of circular economy and energy efficiency and it has as specific objectives the promotion of waste heat recovery and energy recovery from wastewater. Although on the context of research and industrial appliance both waste heat recovery and water recycling and reuse have been extensively explored, it is still verifiable a lack of comprehension and application of methods to simultaneously improve the use of both water and energy in a plant. In this work, two approaches for the solving of an optimisation problem related to the improvement of water and energy use in a process industry plant (three water-using processes) are implemented. These approaches consist on the development of a mixed-integer non-linear programming (MINLP) model and a multi-objective programming (MOP) model using the Python language. In addition, a complementary approach based on the development of a non-linear programming (NLP) model for further heat integration is also developed. Within the three applied methodologies (MINLP, MOP and integrated MINLP and NLP), the integrated MINLP and NLP model was the one in which the most favourable results were obtained, with 33.7% freshwater savings, 73.2% energy savings and 67.2% total economic savings.

1 Introduction

Water and energy integration consist in a set of methods, measures and practices to improve the use of water and energy in industry (Gundersen, 2013; Alnouri et al., 2014), which are two of the most important resources used in a plant (Oliveira, 2018). The study of the water and energy integration is on the scope of the research area of process integration. Process integration (PI) may be defined as the study of the all potential interdependencies of industrial processes in a plant with the scope to improve the use of certain resources (Foo et al., 2017). The side of energy integration is traditionally heat integration, this is, based on the recirculation of thermal energy streams, and it is thus essentially based on the theoretical assumptions of waste heat recovery (WHR) (Rašković et al., 2010). While the heat integration has been heavily the scope of study by several authors, and its applicability in industry has been proved, there is currently an interest to proceed with more profound research on water integration, as well as combined water and energy integration.

The ultimate goal of this area of research is to study potential improvement of water and energy efficiency (Ahmetović et al., 2015). The study of energy efficiency has been the scope of the majority of international energy and environmental policies, namely the most recent European 2030 climate and energy framework (European Commission, 2014), European Green Deal (European Commission, 2019), European 2050 long-term strategy (European Commission, 2018) and the Paris Agreement (Horowitz, 2016). The interdependencies of water and energy resources, which includes the understanding of the improvement of water use through the understanding of the use of energy, have been studied on the scope of the water-energy nexus (Oliveira et al., 2019).

The water and energy integration methodology may be applied in a high number of industrial processes and also a high number of industrial sectors (Ahmetović et al., 2015). As such, many industrial systems may be studied in this scope. While the object of study of heat integration are only industrial thermal processes (Castro Oliveira et al., 2020), water integration approaches water recirculation and treatment systems (which encompasses both the processes to recycle water and treat wastewater) and combined water and energy integration approaches full water-energy networks (Savulescu and Alva-Argaez, 2013). The practice of Combined Water and Energy Integration passes by the simultaneous application of the principles of water recirculation and heat recovery (Savulescu and Alva-Argaez, 2013; Ahmetović et al., 2015; Chin et al., 2019). In practice, such may be process through the use of several water streams as waste heat streams (Savulescu and Alva-Argaez, 2013), forming in joint with the water-using processes a water-energy network (WEN).

The conceptualization of water-energy networks (WEN), also designated as Heat-Integrated Water Allocation Network (HIWAN) and Water Allocation and Heat Exchange Networks (WAHEN), through the application of the pinch methodology has been carried out by the development and implementation of several optimisation methodologies (including LP, MILP, NLP, MINLP and MOP) by several authors. These studies consistently present a focus on multiple contaminant problem-solving (Zheng et al., 2003; Ahmetović and Kravanja, 2013; Hong et al., 2018a), inclusion of multiple freshwater sources (Sahu and Bandyopadhyay, 2010; Hong et al., 2017; Hou et al., 2017; Hong et al., 2018a; Kermani et al., 2019; Souifi and Souissi, 2019), analysis of wastewater treatment units (Zhelev and Zheleva, 2002; Kermani et al., 2018; Dong et al., 2022), the inclusion of multiple utilities (Caballero et al., 2021) and large-scale industrial systems (Zhao et al., 2019; How et al., 2021; Ibrić et al., 2021; Kamat and Bandyopadhyay, 2021). In addition, several authors approach the performance of the characterization of the research gaps regarding the application of Combined Water and Energy Integration models and its applicability within several industrial sectors (Budak Duhbacı et al., 2021; Chijin et al., 2021). Overall, these approaches are inserted in two categories: sequential approaches (a three-step sequence is applied, in which the first step is based on utility use reduction, the second is based on interconnection reduction and the third one is based on cost reduction) and simultaneous approaches (in which all the performance indicators are simultaneously minimized). Each one of these types of approaches are characterized by limitation: while the sequential approaches are associated to the rank reversal issue (the selection of different alternatives may depend on different priority criteria) (Aires and Ferreira, 2018), the simultaneous approaches subsist on the consideration of several assumptions which limit the formulation of the problem in terms of the objective-function and equality constraints (Kermani et al., 2018).

In this work, two approaches for the solving of an optimisation problem related to the improvement of water and energy use in a process industry plant (three water-using processes) are described and implemented. These approaches consist of the development of a mixed-integer non-linear programming (MINLP) model and a multi-objective programming (MOP) model using the Python language, as well as a complementary approach based on the development of a non-linear programming (NLP) model for further heat integration. The two main approaches are compared, with such implementations converging on the conceptualization of several water-energy networks (WEN).

The presented modelling framework represents a novel methodology based on a different type of approach that the ones previously implemented by authors. For instance, the MINLP model is firstly implemented to solve the problem related to water use, hot and cold utility use and interconnection minimization based on the direct recirculation of wastewater streams and a second step subsisting on the application of a NLP model is implemented for the implementation of further heat integration (in which an additional heat exchanger is installed in the previously conceptualized WEN). The MOP model, in its turn, is implemented to serve as basis of comparison to the MINLP and integrated MINLP and NLP models, so to overall compare the proposed new approach and the one of previously work in which MOP is the first step of a two-step approach (Boix et al., 2012).

2 Description of Previous Modelling Approaches

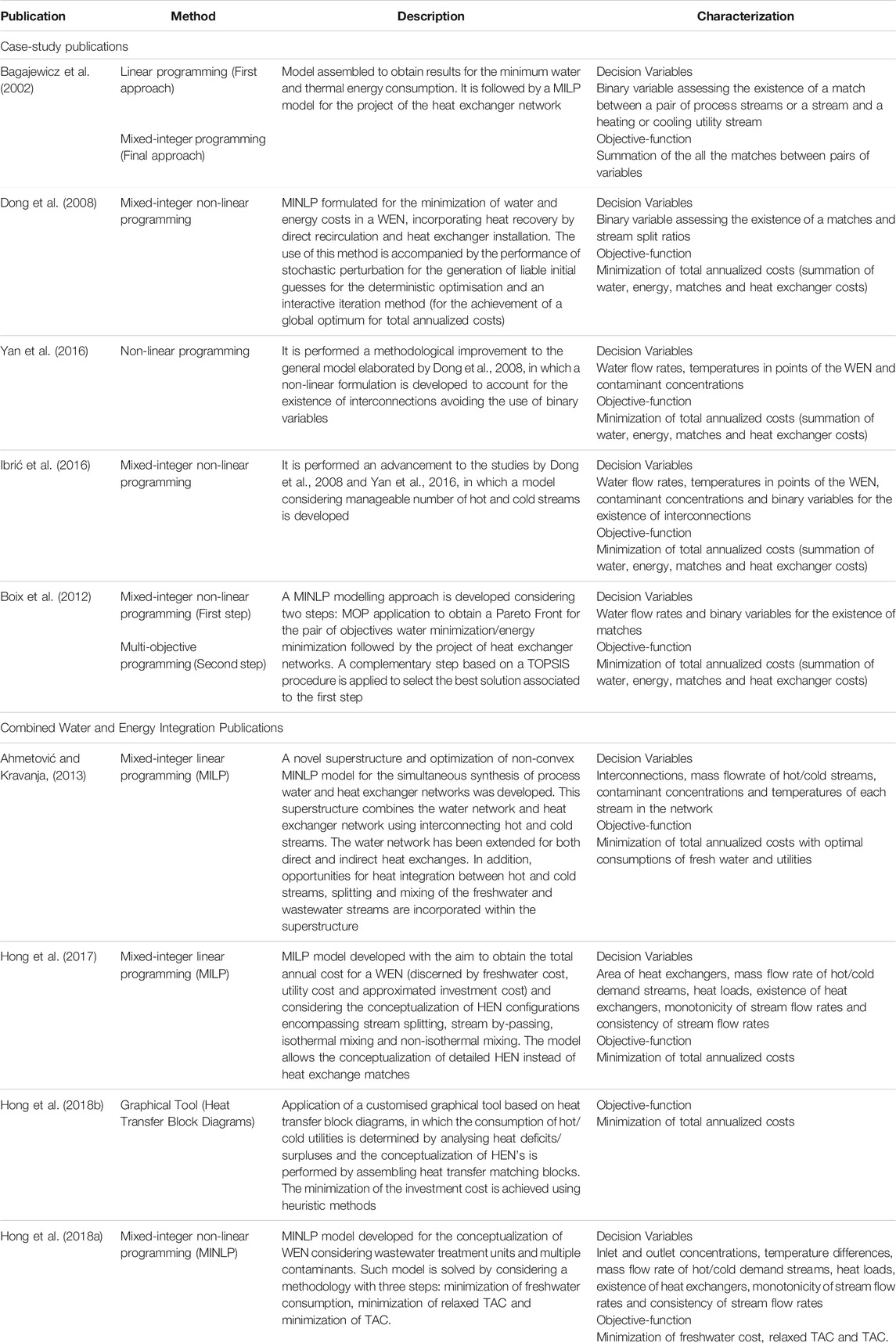
The conceptualization of this work is based on the analysis of the previous work Minimizing water and energy consumptions in water and heat exchange networks (Boix et al., 2012). The optimisation problem solved on this section is one of the problems approached by Boix et al. (2012). Nonetheless, the study developed by these authors have already been primarily performed by Bagajewicz et al. (2002) and Dong et al. (2008). In addition, improvements for the model of Dong et al., 2008 were further developed by Yan et al. (2016) and Ibrić et al. (2016). The set of approaches taken by the authors implement the general principles of Combined Water and Energy Integration, and as such make use of the theoretical principles of water recirculation and waste heat recovery. In Tables 1 and 2, previous studies are described, as well as relevant publications in respect to the use of analytical and graphical methods for the development of optimisation models for WEN conceptualization. The conceptual advantages and disadvantages associated to the target publication (Boix et al., 2012) are summarized in Table 3.

TABLE 1

TABLE 1. Brief Description of previous approaches.

TABLE 2

TABLE 2. Contextualization of recent studies regard Combined Water and Energy Integration.

TABLE 3

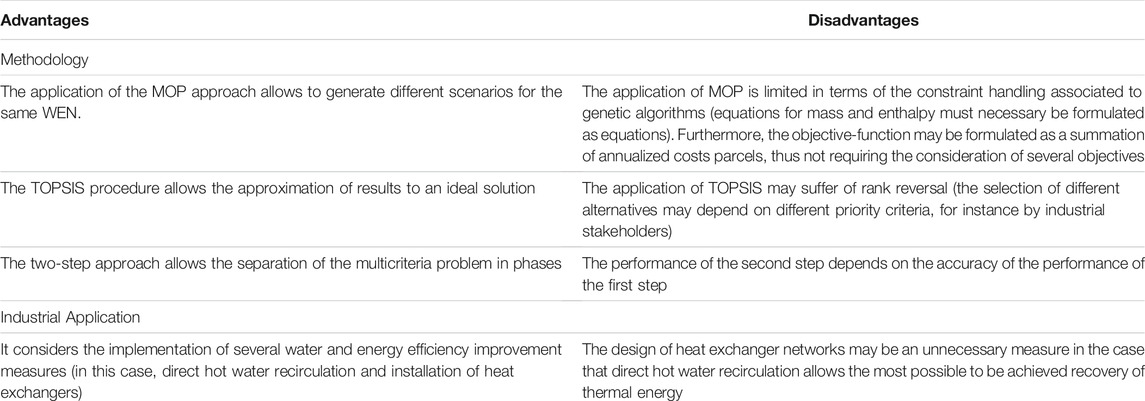
TABLE 3. Conceptual advantages and disadvantages associated to the approach by Boix et al., 2012.

3 Description of the Case-Study

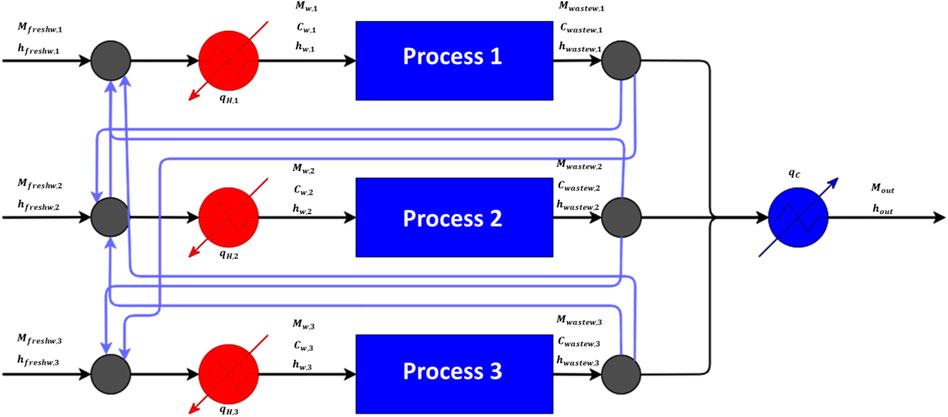
The approached case-study is applied to a process industry plant containing three water-consuming processes (conveniently designated in this article as Process 1, 2 and 3). To each one of these processes, it is fed a freshwater stream which is used to remove a certain amount of contaminants. Each one of the inlet water streams is heated up to the operational temperature of each water-consuming process with the transportation of these streams through heat exchangers (heaters). The outlet wastewater streams from the processes are then cooled down by passing through a single heat exchanger (cooler). Such processes of heating and cooling are processes through the supply of hot utilities and cold utilities to constitute the heat exchangers’ hot stream and cold stream, respectively.

The removal of contaminants requires limit concentration levels for the inlet water stream (although the inlet water streams do not necessarily have to be pure water streams, it exists a maximum level for each inlet concentration). The flow rates of the inlet water streams have also limit values (maximum flow rate levels to be fed to the water-consuming processes), as well as the concentration of the outlet wastewater stream. The described industrial system is represented in Figure 1, which also encompasses the data and limit values associated to each process.

FIGURE 1

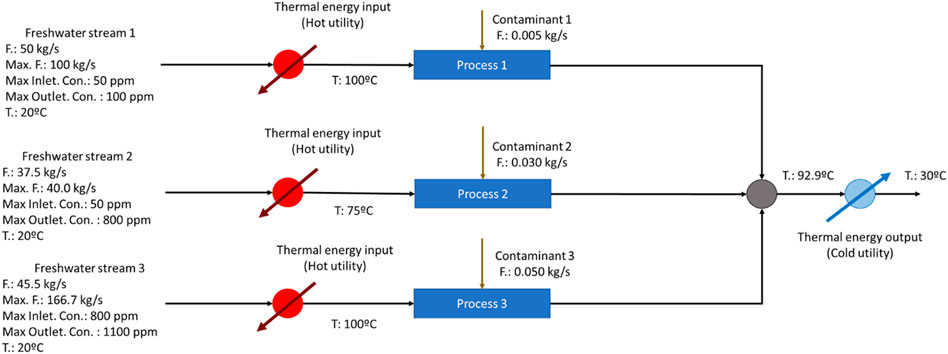
FIGURE 1. Flowsheet of the industrial system [adapted from (Boix et al., 2012)].

Currently, there is an interest to improve the water efficiency and energy efficiency of the plant. In practice, such may be performed by reducing the input of freshwater and the total supply of hot and cold utilities to the industrial system.

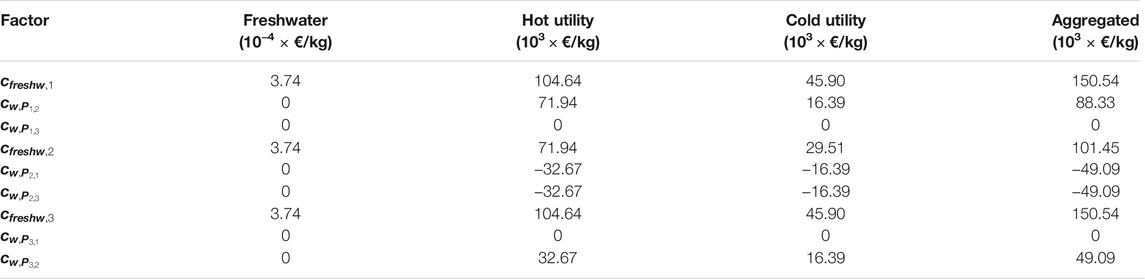
The solving of the optimisation problems formulated by the authors are set to find the optimal point in which the total network cost is the minimum possible. The optimisation problem is in practice solved by the minimization of the freshwater flow rate, hot and cold utilities, number of interconnections, number of heat exchangers and heat exchanger area, which are multiplied by a factor representing its respective unitary costs. The unitary values associated to each cost term are presented in Table 4. It is to note that these data was converted from dollar ($) to euro (€) base from the data presented by Boix et al. (2012), considering a conversion value of 0.83 €/$. In addition, the presented unitary cost values are converted in yearly units (the final value of the multiplication of each parcel has €/year units).

TABLE 4

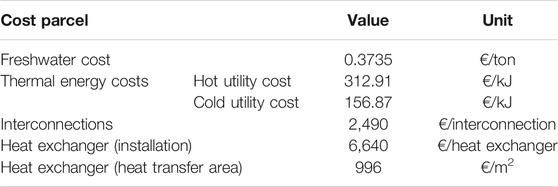
TABLE 4. Unitary costs associated to each total cost parcel (data gathered from Boix et al., 2012).

4 Modelling and Optimisation

The formulation of the optimisation problem to be solved on the scope of this work is to minimize the total network cost, based on the conceptualization of retrofitted industrial systems based on the principles of Combined Water and Energy Integration, in which a set of water streams are recirculated to be supplied water stream to water-consuming processes as well as waste heat streams. This new approach starts by performing a conceptualization of the industrial system in which all possible interconnections (water recirculation paths) are considered. The generic conceptualization of the water-energy network considering all the possible to be established water recirculation paths is represented in Figure 2.

FIGURE 2

FIGURE 2. Superstructure of the conceptualized Water-Energy Network.

4.1 Approach Contextualization

The overall modelling and optimisation procedure encompassed in this work is based on the application of three methodologies: mixed-integer non-linear programming (MINLP), multi-objective programming (MOP) and non-linear programming (NLP). While the MINLP and MOP models are set to be alternative approaches to solve the same optimisation problem, the NLP approach is applied as a complementary step. The development of the MINLP model is the primary target of the modelling and optimisation procedure, with the MOP model being developed to establish a comparison between the results of the two alternative methodologies. The contextualization of each one of the abovementioned methodologies is furtherly described in Table 5.

TABLE 5

TABLE 5. Contextualization of optimisation methodologies.

In a generalist view, the methodology developed for this work differs from the one by Boix et al., 2012 in the sense that the two-step approach is replaced by a primary-complementary approach. In respect to the MINLP model, although the method is the same as the one implemented by Dong et al. (2008) and Ibrić et al. (2016) and also the second step of Boix et al., 2012, the overall approach is not the same. For instance, while in the Dong et al., 2008 approach direct recirculation and heat exchanger installation are simultaneously considered on the formulation of the same problem, the approach taken in this work considers a different paradigm owing to an adopted order of priority. In this prospect, direct recirculation is in principle favoured in relation to heat exchanger installation (a primary step in which only direct recirculation is considered for heat recovery and then the installation of heat exchangers is considered in the formulation of the NLP model considered in the complementary step).

4.2 General Formulation of the Optimisation Problem

The assembling of a model to solve an optimisation problem related to the minimization of TAC in practice requires the consideration of equations involving the freshwater streams and the recirculated wastewater streams (the water streams at the outlet of each water-consuming process). For the approached case-study, these totalize three freshwater streams and six recirculated streams. In the context of this problem, the flow rate of these nine streams are the fundamental variables to be considered, since these streams are the one that contain usable water or thermal energy and thus are the ones in which the unitary costs presented in Table 4 fall on.

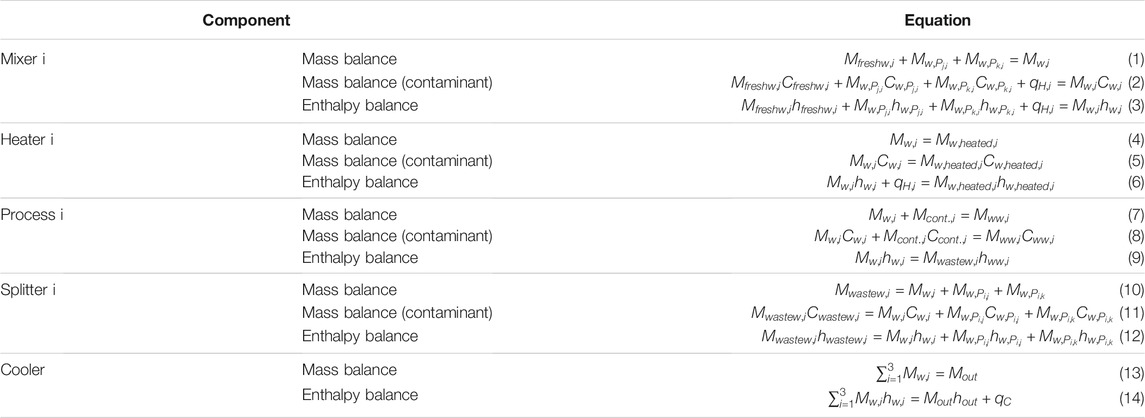
In the context of the conceptualized WEN, the equations that relate all the variables required to be considered are the mass and enthalpy balance equations. The generalized mass and enthalpy balance equations to which component of the conceptualized WEN are presented in Table 6.

TABLE 6

TABLE 6. Mass and Enthalpy Balances for each component of the industrial system.

The optimisation problem may be formulated based on the equations presented in Table 6 and the consideration of the unitary costs presented in Table 4. This problem must be formulated considering two types of constraints: the mass and enthalpy balances (which are set to be formulated as equality constraints) and operational constrains associated to limit values of supplied water, inlet concentrations, outlet concentrations and the supply of hot and cold utilities (which are set to be formulated as inequality constraints). The generalist formulation of the optimisation problem is represented in Eq. 12.

$Min. Z= {\displaystyle \sum }_{i=1}^3{c}_{freshw,i}{M}_{freshw,i}+{\displaystyle \sum }_{i=1}^3{\displaystyle \sum }_j{c}_{w,P_{i,j}}{M}_{w,P_{i,j}}+{\displaystyle \sum }_{i=1}^3{\displaystyle \sum }_j{d}_{i,j}{y}_{i,j}$

$s.t.: f\left(x\right)\le 0$ (Operational Constraints) $g\left(x\right)=0$ (Mass and Enthalpy Balances) and

$M_{freshw,i}\ge 0,\dots ,M_{w,P_{i,j}}\ge 0,\dots (15)$

The presented optimisation problem may be furtherly adapted considering the requirements for the implementation of each method in specific, as it will be demonstrated in the further section.

4.2.1 Definition of Decision Variables and Objective-Function

The overall optimisation problem is characterized by considering 18 continuous decision variables (three freshwater flow rates, six recirculated water flow rates, three total process inlet water flow rates, three inlet concentrations and three outlet concentrations) and six integer decision variables (which are six binary variables signifying the existence of interconnection). Moreover, the flow rate of a recirculated water stream is considered in the formulation of the optimisation problem whether such water pathway is established or not, with the binary variables being the model variables that secure the existence of those streams.

The objective-function may be defined according to the unitary cost terms defined in Table 3. Each one of the factors of the objective-function ($c_i$) may be defined for three terms: freshwater, hot utility and cold utility. In the context of the problem, these factors will have units of €/kg, since these depend only of the flow rates of the water streams (kg/s) on the objective function. It is to note that the unitary costs for thermal energy which are in per energy units (€/kW) are converted per quantity of water units (€/kg) considering the specific enthalpy values of each stream (kJ/kg), which are fixed values on the overall model to secure the required temperature constraints. Such determination results on aggregated values for the objective-function factors, which are the ones effectively used in the final objective function. The calculation method used to determine the aggregated values and the corresponding coefficients for hot and cold utilities in kg/s is represented in Eqs 13–15, in which $h_{iH,out}$ refers to the specific enthalpy associated to a certain stream at the outlet of the heater to which it is directed, $h_{iH,in}$ refers to the specific enthalpy associated to a certain stream at the inlet of the heater to which it is directed, $h_{iC,in}$ refers to the specific enthalpy associated to a certain stream at the inlet of the cooler, $h_{iC,out}$ refers to the specific enthalpy associated to a certain stream at the outlet of the cooler.

$c_{iHU}\left(€/kg\right)=c_{iHU}\left(€/kJ\right)\left(h_{iH,out}-h_{iH,in}\right)(16)$

$c_{iCU}\left(€/kg\right)=c_{iCU}\left(€/kJ\right)\left(h_{iC,in}-h_{iC,out}\right)(17)$

$c_{iaggregated}\left(€/kg\right)=c_{ifreshw}\left(€/kg\right)+c_{iHU}\left(€/kJ\right)\left(h_{iH,out}-h_{iH,in}\right)+c_{iCU}\left(€/kJ\right)\left(h_{iC,in}-h_{iC,out}\right)(18)$

The objective-function factors associated to each parcel are defined in Table 7.

TABLE 7

TABLE 7. Values for the factors of the objective-function.

The presented optimisation problem may be furtherly adapted considering the requirements for the implementation of each method in specific, as it will be demonstrated in the further sections.

4.2.2 Modelling Assumptions

The modelling assumptions taken to develop the optimisation models in this work are the same taken by Boix et al. (2012). These assumptions may be listed as the following:

• The operation of water-using process is considered isothermal;

• The whole water systems are adiabatic (no heat losses);

• Water losses are not considered (the inlet flow rate is equal to the outlet flow rate);

• The operation of heat exchangers is considered to be in counter-current;

• The performance of heat integration is based on the heat recovery from (or to) water streams (and hot and cold utilities);

• The properties associated to the streams are the ones of water, such as heat capacity [4.18 kJ/(°C·kg)] and specific enthalpies.

4.3 Mixed-Integer Non-Linear Programming Model

The solving of the optimisation problem whose general formulation was presented in Section 4.2 will be performed by the implementation of a mixed-integer non-linear programming (MINLP) approach. Such approach is necessary and adequate over a linear model approach considering that the concentrations associated to each water stream are considered as decision variables, taking into account the mass and enthalpy balances Eqs 1–11 that overall define the WEN model (in which the water flow rates are multiplied by the concentrations). Furthermore, as the existence of interconnections are also considered as decision variables, the involvement of integer variables on the overall model is strictly necessary.

For the solving of the optimisation problem using a MINLP approach, a model was developed using the existing Python package GEKKO (Beal et al., 2018). The APOPT solver was selected due to being the solver of selection within GEKKO package to handle mixed-integer problems (APMonitor, 2021). The developed MINLP model is presented in the Section 1 of the Supplementary Material.

4.3.1 Model Setup

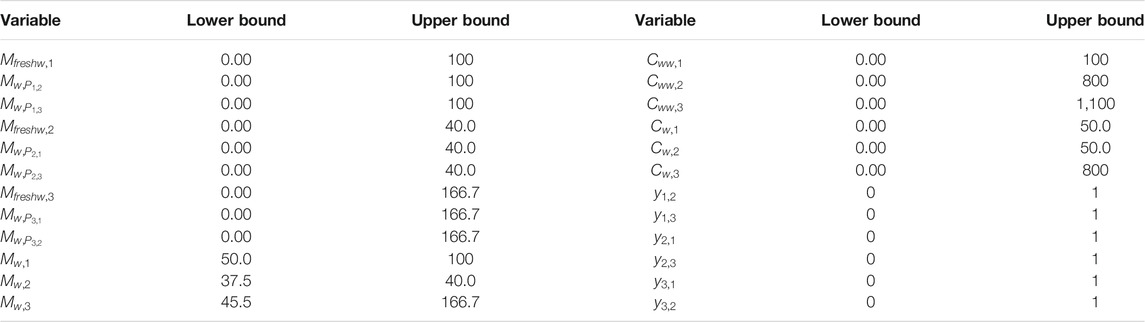
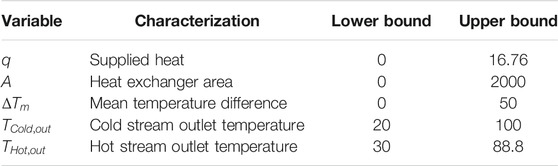
The MINLP model was developed considering the mass and enthalpy equations presented in Section 4.2 and the general setup of the optimisation problem defined in Eq. 16 and Sections 4.2.1, 4.2.2. The decision variables, as defined in Table 7, are characterized in Table 8, in which are presented the initialisation value, lower bound and upper bound used in the definition of the problem using the GEKKO package. The lower and upper bounds were defined according to the data presented in Figure 1.

TABLE 8

TABLE 8. Characterization of decision variables of the MINLP model.

The constraints of the optimisation problem were defined by recurring to the mass balance equations (as enunciated in Table 6) and operational requirements associated to the supplied hot and cold utilities and the minimum flow rates for the recirculation of water streams. It is to note that the operational requirements relative to concentrations and limit water flow rates are already defined by the lower and upper boundaries of the some of the respective decision variables.

The objective-function for this problem was defined according to the setup presented in Table 8. The objective-function is presented in Eq. 19.

$Z_{MINLP}=150.54\times M_{freshw,1}+88.33\times M_{w,P_{\mathrm{1,2}}}+101.45\times M_{w,P_{\mathrm{1,3}}}-49.09\times M_{w,P_{\mathrm{2,1}}}-49.09\times M_{w,P_{\mathrm{2,3}}}+150.54\hspace{0.17em}{M}_{freshw,3}+49.09\times M_{w,P_{\mathrm{3,2}}}+ 2.490\times {\displaystyle \sum }_{i=1}^3{\displaystyle \sum }_j{y}_i(19)$

4.3.2 Optimisation Results and Model Validation

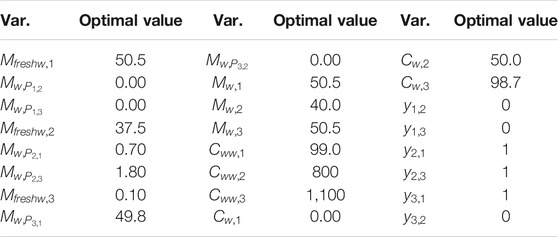
The obtained optimisation results converge on the project of a new WEN, in which the flow rates of the inlet freshwater and recirculated water streams are obtained. The results obtained for the decision variables obtained by the running of the MINLP model are presented in Table 9.

TABLE 9

TABLE 9. Values for the decision variables.

To ensure the consistency of the obtained results, it is necessary to proceed with the validation of the developed model. This is performed by calculating the residuals obtained for the enthalpy balances, considering that the hot and cold utility supplies were calculated based on slack variables of certain constraint equations. It is to note that these equations are formulated considering the freshwater flow rate and recirculated water flow rate variables, which were substituted from the corresponding variables for the inlet water flow rate at each process. As such, it is necessary to ensure that the consideration of the enthalpy balance equation as inequality constraints in the formulation of the optimisation problem effectively respect the overall enthalpy balances to the WEN. The residuals obtained for each enthalpy balance equations are presented in Table 10.

TABLE 10

TABLE 10. Residuals obtained for the enthalpy balance equations.

As may be observed, the residuals obtained for each enthalpy balance equation are considerably low. As such, it is possible to ensure the validity of the model to perform the required assessment.

4.3.3 Sensitivity Analysis

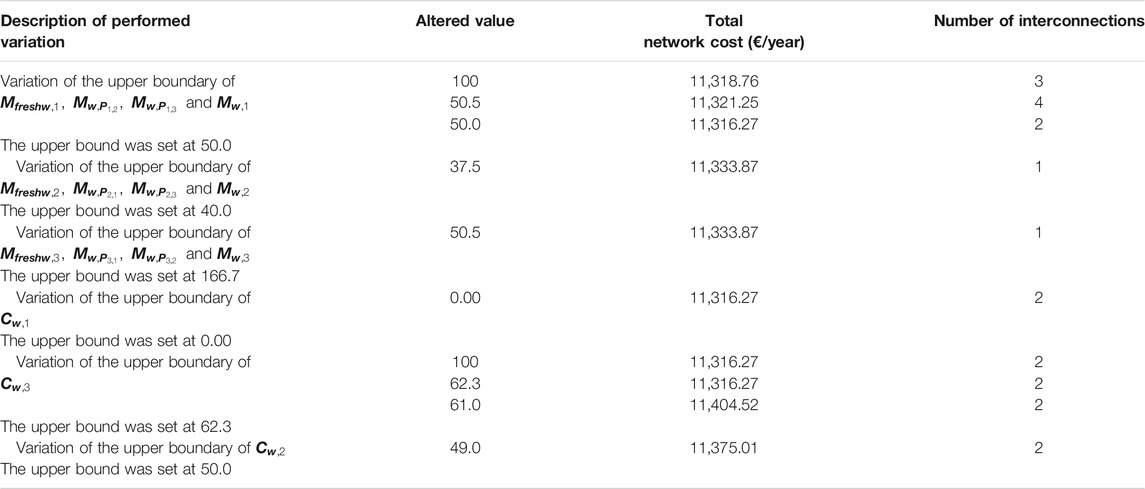
A sensitivity analysis was conducted to assess the robustness of the developed model in for the attainment of results for the minimization of total annualized cost. The adopted methodology was of a One-at-a-Time (OAT) sensitivity analysis. Specific parameters of the model were changed separately to analyse the impact of the variation of several inputs on the obtained solution of the optimisation problem. The selected parameters for this analysis were the upper limits of flow rates and concentrations of the freshwater, recirculated water and process inlet water streams. The results of the sensitivity analysis are presented in Table 11.

TABLE 11

TABLE 11. Results for the sensitivity analysis.

As may be observed in Table 11, the first parameter to be changed was the upper limit of the water stream at the inlet of process 1. This parameter was set at the given result for $M_{w,1}$ (as presented in Table 8), in which it was verified a considerable change in the obtained solution. The value for this parameter was furtherly decreased to match with the respective lower bound. It was verified a slight change in the initial solution, although it represents in practice a considerable change in terms of the WEN possible to be conceptualized, as the total annualized costs are reduced relative to the initial solution and the total number of interconnections in the WEN may be reduced from three to two.

In a next phase, it was changed the upper bound of the water stream flow rates at the inlet of process 2. The upper limit was set at the respective lower bound of $M_{w,2}$. The obtained solution considerably changes. Although the number of connections is decreased, the total annualized costs are increased, and as such this solution does not represent an improvement relative to the initial solution. The upper bound of the flow rates of the water streams at the inlet of process three was variated in the same manner, having been obtained similar results, in which the number of interconnections is reduced but the total network costs are increased.

The concentrations were changed similarly to the flow rates, in which the results obtained in Table 9 were set as the respective upper bound. By this variation, it was verified that no change occurs in the achievement of the previous solution. In the case of the concentrations of the water stream at the inlet of process 2 $\left(C_{w,2}\right)$ and process 3 $\left(C_{w,3}\right)$ it was verified that a slight decrease of the respective upper boundaries already produced a considerable change for the obtained solution.

4.4 Multi-Objective Programming Model

In this section, the optimisation problem presented in Section 4.1 will be solved using a different approach from the one of Section 4.2, by developing and using a multi-objective programming (MOP) model. Similar to the previous approach, this model will use a non-linear procedure to solve the optimisation problem, albeit considering two different objective-functions.

This MOP approach was implemented by using the pymoo package (Blank and Deb, 2020) in Python 3.9.4. For the attainment of results, the genetic algorithm NSGA-II was used, as defined in Table 12. The developed MOP model is presented in the Section 2 of the Supplementary Material.

TABLE 12

TABLE 12. Parameters for the genetic algorithm NSGA-II.

4.4.1 Model Setup

The MOP model was developed considering alterations on the paradigm of the general model presented in Section 4.2 and the MINLP model presented in Section 4.3. Such alterations are related to the requirements for the formulation of the MOP models, in which the constraints must be all preferably be formulated as inequality constraints, namely due to limitations of the handling of equality constraints by the genetic algorithm. Several tests developed using versions of this MOP model (developed using the pymoo package) containing constraints formulated as absolute values and squared expressions (so to approximate these constraints the most possible to equality constraints) have failed (the running of the model could not produce any result). As such, all constraints had to be formulated as inequations, which required several alterations to the previous models. For instance, the inlet water flow rates at each process and the outlet concentrations were not considered as decision variables and substituted by the thermal power values that are inputted our outputted in the heaters and cooler, respectively. Nonetheless, the limit values associated to these variables were inputted as inequality constraints. The formulation of the MOP model in terms of decision variables and objective-functions is presented in Tables 13, 14 respectively.

TABLE 13

TABLE 13. Characterization of decision variables of the MOP model.

TABLE 14

TABLE 14. Objective-functions of the MOP model optimisation problem.

4.4.2 Optimisation Results

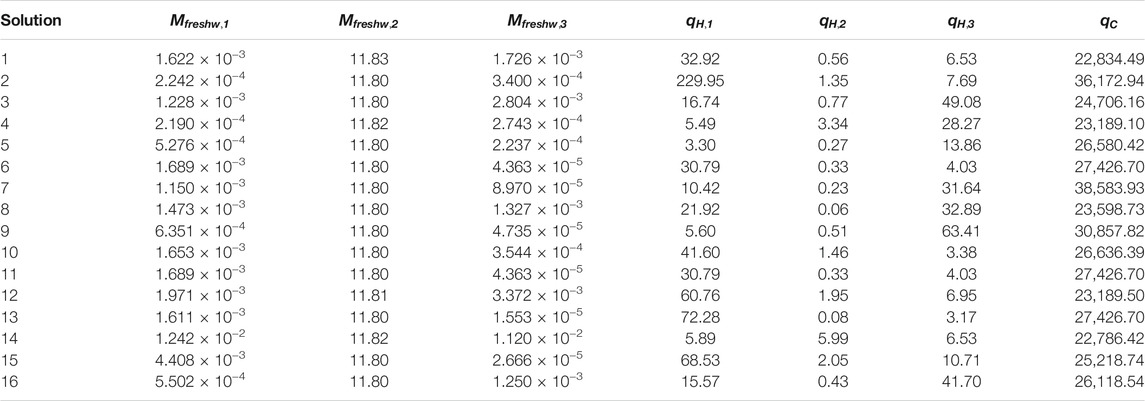
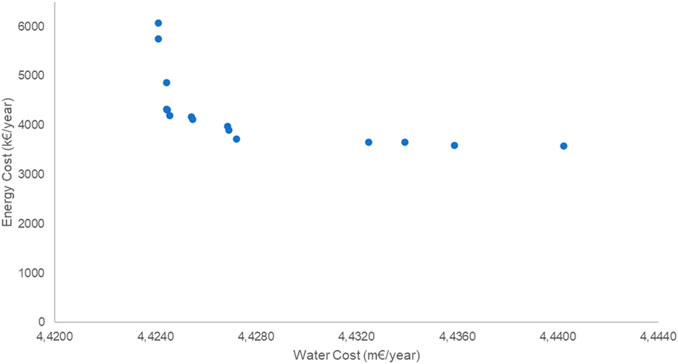
The running of the model presented in Section 4.4.1 allowed the obtainment of several results for water and energy consumption values. As in practice the MOP model was developed to be compared with the previously developed MINLP model, dividing both the objectives of minimizing water and energy costs, the running of this model resulted in a Pareto set for water mass flow rates and hot and cold utilities supply and a Pareto front for the water costs and energy costs (which are set to be the abscissa and ordinate of the Pareto front, respectively). The results for the Pareto set are presented in Table 15. The results for the Pareto front are presented in Figure 3.

TABLE 15

TABLE 15. Results for the Pareto set (Water and Energy Consumption).

FIGURE 3

FIGURE 3. Pareto front generated by the solving of the MOP model optimisation problem.

As may be verified by a general analysis of the results, the implementation of the MOP approach in alternative to the MINLP approach is able to lead to the attainment of results for water and energy costs that are overall more favourable. It is to note that the costs relative to the formation of interconnections are not considered in the formulation of the presented MOP model, and as such the running of the model is able to give solutions in which all the potential interconnections are considered. Such comparison between the MINLP and the MOP models is only possible since the overall term of the total annualized costs associated to energy is significantly higher than the interconnections costs.

As may be observed in Table 15, the non-dominated solutions obtained for the freshwater consumption variables are significantly lower than the corresponding results of the MINLP model. The solutions obtained with the MINLP model may be considered as dominated solutions of the MOP model. Overall, the results for freshwater consumption are consistent for all the 16 obtained solutions of the Pareto set, being verified a non-significant of values between different solutions. In specific, the results for freshwater consumption in Processes 1 and 3 are approximately null. Such non-significant variation may also be verified in the obtained Pareto front represented in Figure 3, in which for all the non-dominated solutions there is only a minor variation between solutions of the Water Cost on the abscissa of the graph. Nonetheless, such is not verified for the variables corresponding to hot and cold utility use, in which much higher variations are verified between different solutions. Such observation may be attributed to the inability to ensure the same validity of the MOP model in comparison to the MINLP model in terms of the modelling of mass and enthalpy balances, which in its turn is attributed to the difficulty of MOP-related solvers on the handling of equality constraints, despite the favourability of the obtained solutions in terms of water and energy use.

4.5 Implementation of Further Integration

The MINLP and MOP approaches previously presented in Sections 4.2, 4.3 respectively were based on the performance of heat recovery through the direct recirculation of wastewater streams, this is, the additional heat inputted in the heaters at the inlet of each water-using process is derived from the combination of the inlet cold freshwater streams and the hot wastewater streams, without the requirement for the installation of additional heat exchangers. The original methodology elaborated by the authors (Bagajewicz et al., 2002; Dong et al., 2008; Boix et al., 2012) considered the installation of heat exchangers in addition to direct water recirculation. Each author developed a different methodology for a further heat integration implementation based on heat exchanger installation, and as primarily referred in Section 4.1 this work in particular will also assess such implementation using its proper methodology.

The methodology used in this work is based on the development and implementation of a non-linear programming (NLP) model. Such represents a second step of the overall exercise of the solving of the proposed optimisation problem, and as such is developed over the layer of the previously described models. For instance, it is based on the further re-configuration of the obtained water-energy networks (heat exchangers are set to be added in several points of the WEN which already encompasses several pathways for water recirculation).

In this case, the installation of heat exchangers is only justifiable as an alternative measure for direct water recirculation (this is, freshwater streams that are not combined with wastewater stream in the heaters and may be heated up to avoid further consumption of hot utilities). Considering such assumption, the WEN obtained by the implementation of the MINLP model will be used for further heat integration. Such WEN configuration was selected since it was the only one from all the potential configurations obtained by the MINLP and MOP problems in which a freshwater stream was not combined with hot wastewater streams from the remaining water-using processes (in this case, the freshwater stream at the inlet of Process 1). As such, for further heat integration it was considered the installation of a heat exchanger for the heat transfer between the inlet water stream at the cooler (hot stream), which is the stream that results from the combination of the discharge streams of each process, and the inlet water stream at heater 1 (cold stream). For this complementary approach, a model was developed using the existing Python package GEKKO (Beal et al., 2018), using the APOPT solver. The developed NLP model is presented in the Section 3 of the Supplementary Material.

The proposed NLP model was developed considering the same theoretical assumptions of the MINLP and MOP models, namely in terms of mass and enthalpy balance equations. Furthermore, it also additionally considers the heat transfer equation for the modelling of the heat transfer phenomena in the heat exchanger. The heat transfer equation has the general formula of Eq. 22.

$q=U\times A\times \mathrm{\Delta }{T}_m(22)$

The mean temperature difference considered in Eq. 22 may be computed through the use of Chen’s approximation to the logarithmic mean temperature difference (Chen, 2019), as presented in Eq. 23. It is to note that although the consideration of a different method for the calculation of this parameter (such as the finite volume method) would potentially produce more accurate results, the use of such methods for the solving of the proposed problem is rather unnecessary.

$\mathrm{\Delta }{T}_m={\left(\left(T_{Hot,in}-T_{Cold,out}\right)\times \left(T_{Hot,out}-T_{Cold,in}\right)\times \frac{\left(T_{Hot,in}-T_{Cold,out}\right)+\left(T_{Hot,out}-T_{Cold,in}\right)}{2}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}(23)$

The characterization of the NLP model in terms of decision variables is presented in Table 16.

TABLE 16

TABLE 16. Characterization of decision variables of the NLP model.

The objective-function of this optimisation problem is represented in Eq. 24, which has units of 1,000 €. In Eq. 24, the constant factors have the following meaning: 2,672.22 is the cost associated to the part of water costs and energy costs that are not changed on the newly conceptualized WEN (which encompasses the three supplied freshwater streams, the hot utilities on heaters two and three and the previously formed interconnections), 6.64 denotates the newly formed interconnection (the water stream that is recirculated) and 2.46 is associated to the installation of a new heat exchanger. Once again, the capital costs associated to interconnections and heat exchanger installation such are summed to the time-variating operational costs associated to the water and hot and cold utilities in the objective-function due to a reason of convenience for the attainment of optimisation results.

$Z_{NLP}=2672.22+6.64+2.46+\left(16760-1000q\right)\times 0.31291+\left(21660-q\right)\times 0.15687+0.996\times A (24)$

The results for the implementation of heat integration are presented in Table 17.

TABLE 17

TABLE 17. Results for the implementation of heat integration.

4.6 Final Assessment of Results

The implementation of the previously presented optimisation models converges on the conceptualization of new WEN. The optimisation results may be represented pictorially by representing the flowsheet of the newly conceptualized WEN. Furthermore, the performance of the conceptualized system in terms of water and energy efficiency improvement potential may be assessed by analysing specific key performance indicators (KPI), which in this case consist of the reductions on water and energy consumption and total network costs. The newly conceptualized WEN obtained respectively by the implementation of the MINLP model and the combined MINLP/NLP models are pictorially represented in Figure 4. The results for several aggregated KPI’s are presented in Table 18.

FIGURE 4

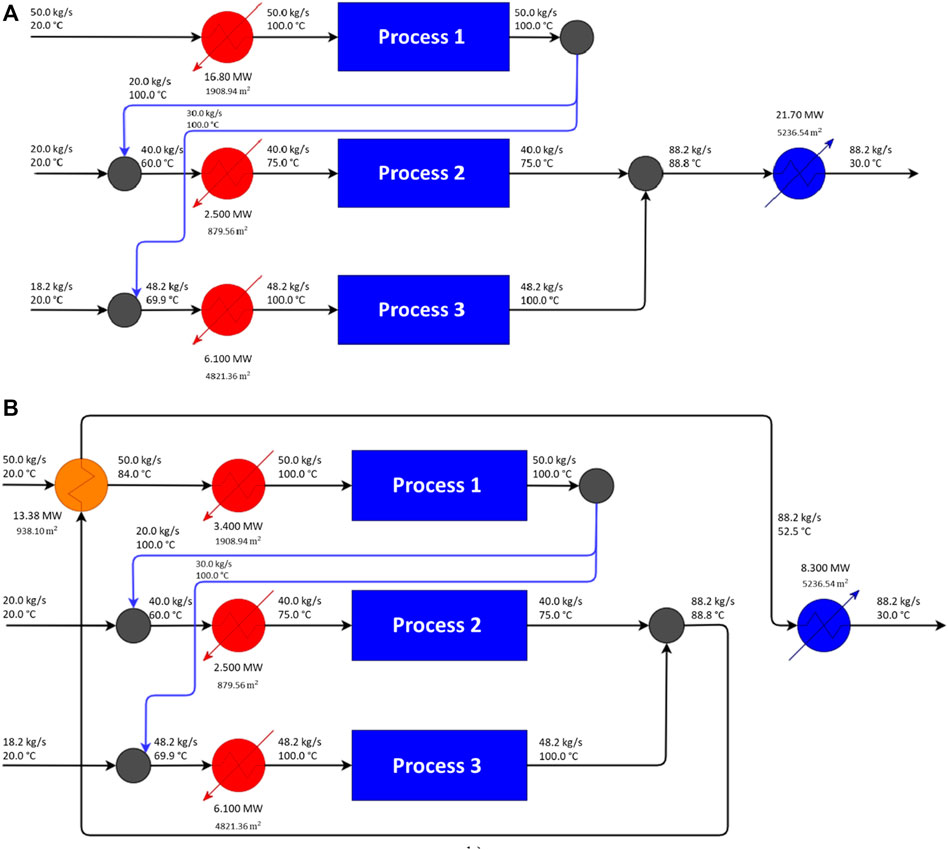
FIGURE 4. Flowsheet for (A) WEN configuration obtained by the implementation of the MINLP model (WEN1), (B) WEN configuration obtained by further heat integration (WEN2).

TABLE 18

TABLE 18. Determination of Key performance indicators (KPI).

5 Discussion

The approach considered in this work was based on the formulation of two different models (MINLP and MOP models) to solve an optimisation problem presented in literature. To assess the effectiveness of both these models associated to the solving of the proposed problem, it is necessary to compare the results of both these models, as well as with the results obtained by the previously referred author.

5.1 Comparison of MINLP and MOP Approaches

The MINLP approach was the initial approach to develop a model for the solving of the proposed optimisation problem. It was necessary to formulate the model as a mixed-integer one since it involved integer variables (namely the number of interconnections for water recirculation) and also non-linear since some decision variables do multiply with each other in several constraints of the problem, although the objective-function was formulated as a linear function. Such formulation considered a high number of decision variables (Eq. 24), which was effectively necessary for the case with such formulation highly assisting for the convergence of the final solution. The objective-function was formulated to only consider the decision variables that directly contributed to the total annualized costs (in this case, freshwater and recirculated water flow rates in addition to existence of interconnections).

The MINLP model was validated by determining the residuals associated to the enthalpy balances in the heaters and coolers, whose respective equations were formulated as inequality constraints. Such determination was necessary due to the consideration of a high number of decision variables in the model, and as such it is necessary to ensure that the mathematical relation between these variables in terms of mass and enthalpy balances is in accordance with the theoretical equations. The calculated residuals presented considerably low values, and as such the MINLP model may be considered overall valid. Furtherly, a one-at-a-time (OAT) based sensitivity analysis was performed, in which several parameters of the model were varied to test the robustness of the model. Overall, the performed sensitivity analysis revealed that determinate variations on the lower and upper boundaries of determinate decision variables led to slight changes in the obtained result, to the point that it is possible to obtain a more viable solution (an inferior value for the total annualized costs) by changing determinate parameters. As such, the sensitivity analysis revealed that although the model is overall robust (the solution is not considerably changed by the variation of parameters), it was still possible to improve the final solution. Such is particularly not in terms of the robustness of the developed mathematical model but rather in operational terms (lesser water and energy consumption and formed interconnections in the plant).

In a next phase, the MOP model was developed, considering a bi-objective problem for the minimization of water costs and energy costs. To implement such approach, the original approach taken for the MINLP has to be altered, so to surpass technical limitations associated to the use of the pymoo package of the Python language to implement the MOP approach. Such limitations were essentially related to the handling of equality constraints by the used genetic algorithm (NSGA-II). As such, all the constraints of this model were elaborated as inequality constraints. The running of the developed model allowed the obtainment of a Pareto set and a Pareto front of solutions for the proposed optimisation problem. The non-dominated solutions constituting the Pareto Front are overall inferior to the solution obtained by MINLP (the MINLP solution may be considered in fact one of the dominated solutions). Considering all these observations, it is possible to establish the following comparison between the MINLP and MOP approaches: although it is not possible to ensure the same validity of the MOP model in terms of the overall phenomena associated to the WEN (mass and enthalpy balances), the MOP approach is capable of assessing solutions that are even more potentially viable than the ones obtained by MINLP. Nonetheless, it is needed to take into account that such observation is valid only considering that energy costs represent the highest share of the total annualized costs, highly surpassing the representativity of water costs and interconnections costs (the latter which are not even considered in the formulation of the problem).

The overall optimisation and modelling work was finalized by analysing further heat integration, in specific through the installation of heat exchangers in determinate points of the WEN (an operational procedure was approached by Bagajewicz et al. (2002), Dong et al. (2008), Boix et al. (2012), Ibrić et al. (2016) and Yan et al. (2016). For such aim, it was developed a NLP model to analyse the installation of an heat exchanger to heat up a freshwater stream that is not combined with any recirculated stream in MINLP solution. The running of this model revealed that it is possible to obtain an even further improved configuration of the WEN, with lesser energy consumption (73.2%, compared to the previous 37.8% reduction) and total network costs (67.2% compared to the previously obtained 37.9% reduction). Considering that the integrated MINLP and NLP model (primary step followed by the complementary step) produces an overall more viable solution than the MOP model, it is possible to conclude that although the MINLP/direct water recirculation only approach may not be overall more successful compared to MOP, its coupling with the complementary NLP/further heat integration approach produces the most viable results.

5.2 Comparison to the Approaches of Previous Authors

This work seeks to advance on the studies carried on by Boix et al. (2012) and develop an alternative model that represents an advance to the one developed by the authors. In particular, it is set to surpass the faults carried on by the two-step approach developed by the authors, namely in respect to the handling of the MOP step and the intermediary TOPSIS step. In one side, it may be considered that the MOP step may suffer of the same limitations pointed in section 5.1 (in terms of the handling of equality constraints). Furthermore, the MOP approach by Boix et al. (2012) uses a MILP procedure, in contrast to the non-linear procedure taken in the MOP approach of this work, which lays a limit on the consideration of determinate decision variables (for instance, it is not possible to consider simultaneously water mass flow rates and concentrations as decision variables). On the other side, the TOPSIS procedure may suffer of rank reversal, in which the selection of different alternatives may depend on different priority criteria. In a next step, a MINLP approach was applied by the authors to proceed with further heat integration.

In this work, the first step of the Boix et al., 2012 overall approach is carried on by the implementation of the MINLP and MOP models, which serve as alternative approaches not depending one from the other. The second step is carried on by the complementary NLP model, as already mentioned in the previous sections. The carrying of the second step over the MINLP model instead of the MOP model disables the use of a decision-making procedure such as TOPSIS, and thus the avoidance of the rank reversal issue. The decision-making intermediary step is proceeded by analysing one single result and having as priority the summation of all the considered costs encompassed by the total network costs.

The WEN configuration obtained by the implementation of the MINLP model (WEN1) corresponds to one of the WEN configurations obtained by Boix et al. (2012) (this is, one of the configurations obtained by the two-step procedure). This configuration is associated to 33.7% water savings and 37.8% total energy savings. The second WEN configuration obtained by further heat integration (WEN2) allowed to obtained an even furtherly improved overall result, with 33.7% water savings and 73.2% total energy savings. As such, it is possible to conclude that this work is both an advancement and improvement to the work by Boix et al. (2012) in the sense that the same result was obtained by the implementation of a simpler procedure but also in the sense that the overall modelling and optimisation framework was able to assess even higher improvements at the level of water and energy efficiency.

In addition to the approach by Boix et al. (2012), a set of two different attempts were developed by Yan et al. (2016) and Ibrić et al. (2016) using, respectively, the NLP and the MINLP methodologies. As mentioned afore, these two works are more recent improvements over the MINLP model developed by Dong et al. (2008). These two models were developed using GAMS language considering the respective causal conditions for the existence of recirculation streams. Such modelling procedure was adopted to prepare the models for the solving of problems in different scales and for manageable number of hot and cold streams.

The procedure adopted for the handling of the MINLP approach in this work is different in the sense that the existence of a certain recirculation stream is determined by the values associated to binary variables which denotate the existence of these streams. These binary variables are considered in the linearized objective functions through its multiplication with the respective unitary costs for a single interconnection and within the constraints through its use in the mass and enthalpy balance parcels with adequate assigned to these streams. The process model is used in the optimization problem through the minimization of total network costs to determine the existence of a certain recirculation stream for the scenarios. Since the binary variable values are multiplied in additional constraints which relate the original variables and corresponding duplicate variables and considering that these duplicate variables are the ones that are effectively used in the objective function the model converges to a point in which the total network costs calculated by the multiplication of the unitary cost factors and the corresponding duplicate variables is minimum. Overall, such modelling procedure allows the avoidance of the use of conditional clauses, which may be difficult to be handled. The structure of the MINLP model in terms of the disposition of the original and duplicate real variables may be observed in Section 1 of Supplementary Material.

Therefore, a robust model was produced by only considering the equations for physical phenomena (mass and enthalpy balances and heat transfer). The developed model runs with a reasonable running time (an average 0.06 s in a machine using Python 3.9.6, Intel Core i5 processor and 8 GB RAM). Furthermore, the established general model by the same set of equations may be furtherly adapted to be used for different case-studies (namely ones with larger industrial scales) and for implementation in different software packages (in practice, the user must only change the structure of the physical phenomena equations and the conditions associated to different solvers).

5.3 Comparison With Other Literature Approaches

The analysis of the potential associated to the presented models for the project of water-energy networks may be performed by the comparison of the results of this work with the results obtained by the optimisation models developed by previous sequential and simultaneous approaches. In this sense, the results obtained in this work will be compared with the ones obtained by the sequential approach adopted by Kermani et al. (2019) and the simultaneous approach adopted by Hou et al. (2017).

The overall methodology developed by Kermani et al. (2019) subsisted on the formulation of three sub-problems for the conceptualization of WEN and its solving through the iterative generation of potential solutions by the implementation of integer cut constraints, overall using a multi-criteria approach. The solving of the proposed overall problem leads to the generation of several solutions which may be furtherly evaluated by decision-makers to be selected as the most favourable WEN configuration. The selection of a multi-criteria approach is attributed to the fact that the cost of heat exchanger networks (HEN) is taken as the main objective of previous optimisation models. Such rationale effectively leads to the consideration of the multiple objectives considered in the conceptualization of a WEN and also enables the choice of the most favourable configurations taking into account different criteria by different industrial decision-makers. Nonetheless, such modelling concept may still be associated to the issue of rank reversal. The integrated MINLP/NLP approach developed in this work surpasses such issue by considering a previously defined priority criteria in the conceptualization of the MINLP model followed by the NLP model, in which direct water recirculation is favoured as a practical measure over installation of heat exchangers. In this prospect, through the consideration of different models and different conceptualization steps, this work avoids the issue of rank reversal, it sequentially presents more favourable WEN configurations although it considers the role of further decision-making by industrial stakeholders by presenting several alternatives.

The methodology developed by Hou et al. (2017) subsists on a simultaneous approach for the minimization of water and energy use based on two design steps: the first one consists on the conceptualization of water allocation networks (WAN) (which corresponds to the direct water recirculation step encompassed by the MINLP and MOP models in this work) and the second one consists on the combination of the conceptualized network with a heat exchanger network (HEN), which is then optimised in the sense to minimize the number of heat exchangers. The procedure to assess the minimization of the number of heat exchangers is performed considering a heuristic procedure. The application of such methodology leads to the conceptualization of a WEN configuration with significantly low heating needs (about 4 MW) and null cooling needs for a studied example. The modelling procedure considered in the second design step may be associated to a set of limitations also appointed to the use of the pinch technique, namely in respect to the consideration of assumptions on physical properties and temperature profiles. The primary approach considered in this work (MINLP and MOP models) is similar to the one developed and implemented by Hou et al. (2017), leading to similar results in terms of minimization of freshwater and energy. The second design step considered by Hou et al. (2017) is taken into account in this work through the further heat integration complementary approach. In this case, heat exchanger installation is regarded as an alternative measure to direct water recirculation and conceptualized for the heating of freshwater streams at the inlet of heaters that are not combined with wastewater streams from other processes in the heaters in the initial WEN configuration. Such design option leads to the planning of the installation of heat exchangers in specific and defined points of the WEN. The heat transfer phenomena within the heat exchangers is then modelled through the heat transfer equation considering the Chen’s approximation to the logarithmic mean temperature difference. In this prospect, such conceptualization option in the complementary approach allows the assessment of further improvement at the level of water and energy use that are not attained in the initial WEN configuration by the development and implementation of a relatively accurate model for heat transfer.

Taking into account the aforementioned aspects, the overall methodology developed in this work is developed to create models that accurately compute the values associated to mass and enthalpy balances and heat transfer equations and assess the highest possible improvements at the level of water and energy use. Nonetheless, it considers the role of decision-making by presenting several alternatives and a sequence of WEN configurations that are gradually more favourable.

5.4 Comparison of Key Performance Indicators

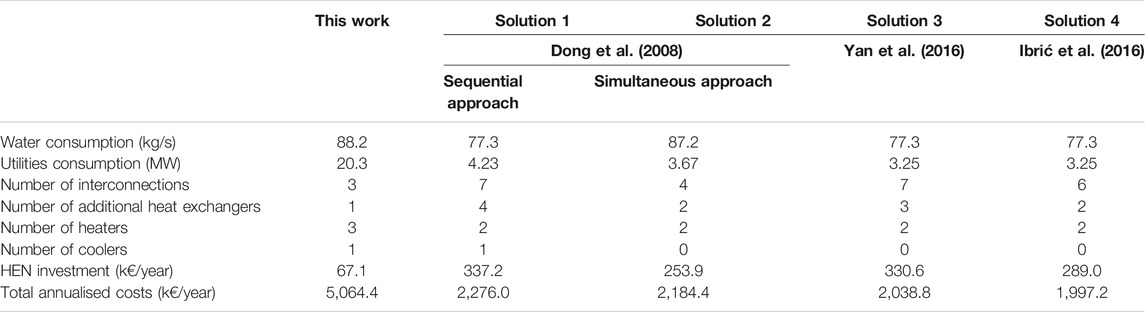
The numerical results obtained in this work related to the associated potential for water and energy efficiency improvement may be assessed by the comparison of determined key performance indicators (KPI) for different solutions for the same case-study. In this case, such is performed by comparing the results associated to the most favourable WEN configuration obtained in this work (WEN 2) and the results for the WEN configurations approached by previous authors (Bagajewicz et al., 2002; Dong et al., 2008; Boix et al., 2012; Ibrić et al., 2016; Yan et al., 2016). The comparison of different KPI’s in respect to the optimisation results obtained the present paper and the results obtained by previous authors is presented in Table 19.

TABLE 19

TABLE 19. Comparison of Key Performance Indicators (KPI) for the same approached case-study.

As may be verified by an overall analysis to the values presented in Table 19, the results obtained in this work for water and utilities consumption are considerably higher than the corresponding results obtained by previous authors. In this view, the corresponding values for annualised operating costs and total network costs are also considerably higher. Such may be explained in a primary basis and in accordance with the verifications of Section 5.3 by the definition of different criteria of WEN conceptualization between the different works. While in this work the priority criteria focused on the minimization of the water and utilities consumption and total networks costs, in this work were taken also as priority the impact of decision-making (namely the existence of operational conditions that are not considered in the conceptualization of the WEN superstructure) and the accuracy associated to the models in terms of considering physical phenomena such as heat transfer.

By establishing a comparison of the designated solutions 1–4 presented in Table 19, it is possible to verify that the results are consistently improved from solution 1 to 4, which correspond to gradually new solutions for the solving of the same problem. An exception would be the freshwater consumption from solution 1 to 2, although such may be considered a minor drawback since, as already mentioned above, the costs associated to the utilities are associated to a much higher order of magnitude than the costs associated to water, and also by comparing the HEN investment costs from solution 2 to 3, which is attributed to increased costs for investment on heat exchanger installation.

In a more specific analysis, it is to note that the conceptualization of WEN superstructures by the previous authors considered the existence of other water recirculation points (such as by-passes) and other points of installation of heaters in addition to the standard superstructure constituted by one heater per process inlet, one cooler for the whole WEN and water recirculation from one process outlet to the remaining ones. Considering the aforementioned criteria, a set of three models were developed in this work using the existing Python packages. These models were developed with the aim to be reproducible and adaptable for several case-studies with different industrial scales, by establishing a general model encompassing mass and enthalpy balance equations. As mentioned in previous sections, this general model was in the case adapted for the two considered initial approaches (MINLP and MOP). The existence of some points of water recirculation and installation of heaters is not considered, however, in the conceptualization of the WEN superstructure elaborated for this work. In its turn, the alternative MOP approach developed for this work can produce results which produce higher water and utilities savings, although, as mentioned afore, it is not possible to ensure the same validity of the developed model as for the integrated MINLP and NLP approach, in addition to the potential of existence of the rank reversal issue associated to the handling of the step of further heat integration. As such, it is possible to conclude that for the attainment of more favourable results for water consumption, utilities consumption and total annualised costs the aforementioned general model must be adapted to consider further points of water recirculation and installation of heaters.

6 Conclusion

This work approaches the solving of an optimisation problem present in literature related to the conceptualization of water-energy networks (WEN). These type of industrial energy systems encompass the recirculation of wastewater streams from water-using processes to be used as additional sources of both water and energy, to produce improvements in terms of water and energy efficiency in a perspective of integrated waste heat recovery and water recirculation, designated as Combined Water-Energy Integration. The case-study of this work consists on the analysis and assessment of a water system constituted by three water-using processes. Each process is feed with a freshwater stream, with a heater being installed in each respective inlet water pathway and then the discharge water streams being combined to be cooled down in a cooler. The aim adjacent of the proposed optimisation problem is based on the minimization of total annualized costs, encompassing water costs and energy costs (hot and cold utilities in the heaters and cooler, respectively), as well as capital costs for interconnections and the installation of heat exchangers.

For the solving of this general optimisation problem, two methods were proposed and used: mixed-integer non-linear programming (MINLP) and multi-objective programming (MOP). These two approaches only considered direct water recirculation as the operational method for heat recovery, and as such an additional method based on non-linear programming (NLP) for further heat integration based on heat exchanger installation was applied, being assembled over the overall layer of the MINLP model. Overall, the combined MINLP and NLP approach revealed to be more viable than the MOP approach (with obtained optimal total annualized costs of 5,131.5 k€). Nonetheless, the MOP approach considers a higher number of results translated on possible WEN configurations. In general, the WEN configurations obtained by the implementation of the MINLP model (WEN1) and further integration (WEN2) revealed the potential to improve water efficiency (33.7% water savings), energy efficiency (energy savings of 37.8% for WEN 1 and 73.2% for WEN2) and reduce total network costs (reduction of 37.9% for WEN1 and 67.2% for WEN2). The numerical results for water and utilities consumption are higher than the ones obtained by previous author approaches, as other priority criteria (in addition to the water and energy savings) was considered. The existence of several levels of decision-making by industrial stakeholders and model accuracy in respect to physical phenomena are considered. Although the assembled models are valid and robust for improved industrial water systems it still exists space for improving to include more specific criteria and solve other uncertainties regarding industrial decision-making.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

MO developed the models and elaborated the manuscript. SV, MI, and HM conceptualized the work and reviewed the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the European Union’s Horizon 2020 research and innovation programmes under grant agreement “No. 810764”, FCT, through IDMEC, under LAETA, project UIDB/50022/2020 and through CERENA under grant UIDB/04028/2020_UIDP/04028/2020.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fceng.2021.750411/full#supplementary-material

References

Ahmetović, E., Ibrić, N., Kravanja, Z., and Grossmann, I. E. (2015). Water and Energy Integration: A Comprehensive Literature Review of Non-isothermal Water Network Synthesis. Comput. Chem. Eng. 82, 144–171. doi:10.1016/j.compchemeng.2015.06.011

CrossRef Full Text | Google Scholar

Ahmetović, E., and Kravanja, Z. (2013). Simultaneous Synthesis of Process Water and Heat Exchanger Networks. Energy 57, 236–250. doi:10.1016/j.energy.2013.02.061

CrossRef Full Text | Google Scholar

Aires, R. F. d. F., and Ferreira, L. (2018). The Rank Reversal Problem in Multi-Criteria Decision Making: A Literature Review. Pesqui. Oper. 38, 331–362. doi:10.1590/0101-7438.2018.038.02.0331

CrossRef Full Text | Google Scholar

Alnouri, S. Y., Linke, P., and El-Halwagi, M. (2014). Water Integration in Industrial Zones: A Spatial Representation with Direct Recycle Applications. Clean. Techn Environ. Pol. 16, 1637–1659. doi:10.1007/s10098-014-0739-2

CrossRef Full Text | Google Scholar

APMonitor (2021). APM.SOLVER. Available at: https://apmonitor.com/wiki/index.php/Main/OptionApmSolver (Accessed May 7, 2021).

Google Scholar

Bagajewicz, M., Rodera, H., and Savelski, M. (2002). Energy Efficient Water Utilization Systems in Process Plants. Comput. Chem. Eng. 26, 59–79. doi:10.1016/S0098-1354(01)00751-7

CrossRef Full Text | Google Scholar

Beal, L., Hill, D., Martin, R., and Hedengren, J. (2018). GEKKO Optimization Suite. Processes 6, 106. doi:10.3390/pr6080106

CrossRef Full Text | Google Scholar

Blank, J., and Deb, K. (2020). Pymoo: Multi-Objective Optimization in Python. IEEE Access 8, 89497–89509. doi:10.1109/ACCESS.2020.2990567

CrossRef Full Text | Google Scholar

Boix, M., Pibouleau, L., Montastruc, L., Azzaro-Pantel, C., and Domenech, S. (2012). Minimizing Water and Energy Consumptions in Water and Heat Exchange Networks. Appl. Therm. Eng. 36, 442–455. doi:10.1016/j.applthermaleng.2011.10.062

CrossRef Full Text | Google Scholar

Budak Duhbacı, T., Özel, S., and Bulkan, S. (2021). Water and Energy Minimization in Industrial Processes through Mathematical Programming: A Literature Review. J. Clean. Prod. 284, 124752. doi:10.1016/j.jclepro.2020.124752

CrossRef Full Text | Google Scholar

Caballero, J. A., Pavão, L. V., Costa, C. B. B., and Ravagnani, M. A. S. S. (2021). A Novel Sequential Approach for the Design of Heat Exchanger Networks. Front. Chem. Eng. 3, 1. doi:10.3389/fceng.2021.733186

CrossRef Full Text | Google Scholar

Castro Oliveira, M., Iten, M., Cruz, P. L., and Monteiro, H. (2020). Review on Energy Efficiency Progresses, Technologies and Strategies in the Ceramic Sector Focusing on Waste Heat Recovery. Energies 13, 6096. doi:10.3390/en13226096

CrossRef Full Text | Google Scholar

Chen, J. J. J. (2019). Logarithmic Mean: Chen's Approximation or Explicit Solution? Comput. Chem. Eng. 120, 1–3. doi:10.1016/j.compchemeng.2018.10.002

CrossRef Full Text | Google Scholar

Chijin, Z., Congjing, R., Zuwei, L., Jingyuan, S., Jingdai, W., and Yongrong, Y. (2021). Recent Progresses on Optimal Design of Heat Integrated Water Allocation Network. China Pet. Process. Petrochemical Technol. 23, 69–75.

Google Scholar

Chin, H. H., Foo, D. C. Y., and Lam, H. L. (2019). Simultaneous Water and Energy Integration with Isothermal and Non-isothermal Mixing - A P-Graph Approach. Resour. Conservation Recycling 149, 687–713. doi:10.1016/j.resconrec.2019.05.007

CrossRef Full Text | Google Scholar

Dong, H.-G., Lin, C.-Y., and Chang, C.-T. (2008). Simultaneous Optimization Approach for Integrated Water-Allocation and Heat-Exchange Networks. Chem. Eng. Sci. 63, 3664–3678. doi:10.1016/j.ces.2008.04.044

CrossRef Full Text | Google Scholar

Dong, X., Zhang, C., Peng, X., Chang, C., Liao, Z., Yang, Y., et al. (2022). Simultaneous Design of Heat Integrated Water Allocation Networks Considering All Possible Splitters and Mixers. Energy 238, 121916. doi:10.1016/j.energy.2021.121916

CrossRef Full Text | Google Scholar

Elena Savulescu, L., and Alva-Argaez, A. (2013). Process Integration Concepts for Combined Energy and Water Integration. In: Woodhead Publishing Series in Energy, Handbook of Process Integration (PI). J.J. Kleme (Sawston, Cambridge: Woodhead Publishing), 461–483. doi:10.1533/9780857097255.4.461

CrossRef Full Text | Google Scholar

European Commission (2014). 2030 Climate & Energy Framework. Available at: http://data.consilium.europa.eu/doc/document/ST-169-2014-INIT/en/pdf (Accessed May 7, 2021).

Google Scholar

European Commission (2018). 2050 Long-Term Strategy. Available at: https://ec.europa.eu/clima/policies/strategies/2050_el (Accessed May 7, 2021).

Google Scholar

European Commission (2019). A European Green Deal | European Commission. Available at: https://ec.europa.eu/info/strategy/priorities-2019-2024/european-green-deal_en (Accessed May 7, 2021).

Google Scholar

Foo, D. C. Y., El-Halwagi, M. M., and Tan, R. R. (2017). Process Integration for Sustainable Industries. Encycl. Sustain. Technol., 117–124. doi:10.1016/B978-0-12-409548-9.10032-6

CrossRef Full Text | Google Scholar

Gundersen, T. (2013). Heat Integration: Targets and Heat Exchanger Network Design. In Woodhead Publishing Series in Energy, Handbook of Process Integration (PI). J.J. Kleme (Sawston, Cambridge: Woodhead Publishing), 129–167. doi:10.1533/9780857097255.2.129

CrossRef Full Text | Google Scholar

Hong, X., Liao, Z., Jiang, B., Wang, J., and Yang, Y. (2017). Targeting of Heat Integrated Water Allocation Networks by One-step MILP Formulation. Appl. Energ. 197, 254–269. doi:10.1016/j.apenergy.2017.04.003

CrossRef Full Text | Google Scholar

Hong, X., Liao, Z., Sun, J., Jiang, B., Wang, J., and Yang, Y. (2018a). Energy and Water Management for Industrial Large-Scale Water Networks: A Systematic Simultaneous Optimization Approach. ACS Sust. Chem. Eng. 6, 2269–2282. doi:10.1021/acssuschemeng.7b03740

CrossRef Full Text | Google Scholar

Hong, X., Liao, Z., Sun, J., Jiang, B., Wang, J., and Yang, Y. (2018b). Heat Transfer Blocks Diagram: A Novel Tool for Targeting and Design of Heat Exchanger Networks inside Heat Integrated Water Allocation Networks. ACS Sust. Chem. Eng. 6, 2704–2715. doi:10.1021/acssuschemeng.7b04315

CrossRef Full Text | Google Scholar

Horowitz, C. A. (2016). Paris Agreement. Int. Leg. Mater. 55, 740–755. doi:10.1017/s0020782900004253

CrossRef Full Text | Google Scholar

Hou, Y., Xie, W., Duan, Z., and Wang, J. (2017). A Conceptual Methodology for Simultaneous Optimization of Water and Heat with Non-isothermal Mixing. Front. Chem. Sci. Eng. 11, 154–165. doi:10.1007/s11705-016-1593-z

CrossRef Full Text | Google Scholar

How, B. S., Orosz, Á., Teng, S. Y., Lim, J. Y., and Friedler, F. (2021). Heat Integrated Water Regeneration Network Synthesis via Graph-Theoretic Sequential Method. Chem. Eng. Trans. 88, 49–54. doi:10.3303/CET2188008

CrossRef Full Text | Google Scholar

Ibrić, N., Ahmetović, E., Kravanja, Z., and Grossmann, I. E. (2021). Simultaneous Optimisation of Large-Scale Problems of Heat-Integrated Water Networks. Energy 235, 121354. doi:10.1016/j.energy.2021.121354

CrossRef Full Text | Google Scholar

Ibrić, N., Ahmetović, E., and Kravanja, Z. (2016). Mathematical Programming Synthesis of Non-isothermal Water Networks by Using a Compact/reduced Superstructure and an MINLP Model. Clean. Techn Environ. Pol. 18, 1779–1813. doi:10.1007/s10098-016-1152-9

CrossRef Full Text | Google Scholar

Kamat, S., and Bandyopadhyay, S. (2021). A Hybrid Approach for Heat Integration in Water Conservation Networks through Non-isothermal Mixing. Energy 233, 121143. doi:10.1016/j.energy.2021.121143

CrossRef Full Text | Google Scholar

Kermani, M., Kantor, I. D., and Maréchal, F. (2019). Optimal Design of Heat-Integrated Water Allocation Networks. Energies 12, 2174. doi:10.3390/en12112174

CrossRef Full Text | Google Scholar

Kermani, M., Kantor, I., and Maréchal, F. (2018). Synthesis of Heat-Integrated Water Allocation Networks: A Meta-Analysis of Solution Strategies and Network Features. Energies 11, 1158. doi:10.3390/en11051158

CrossRef Full Text | Google Scholar

Oliveira, M. C., Iten, M., Matos, H. A., and Michels, J. (2019). Water-energy Nexus in Typical Industrial Water Circuits. Water 11, 699. doi:10.3390/w11040699

CrossRef Full Text | Google Scholar

Oliveira, M. C. (2018). Optimization and Modelling of Industrial Water Circuits. Available at: https://fenix.tecnico.ulisboa.pt/cursos/meq/dissertacao/1409728525632167 (Accessed May 10, 2021).

Google Scholar

Rašković, P., Anastasovski, A., Markovska, L., and Meško, V. (2010). Process Integration in Bioprocess Indystry: Waste Heat Recovery in Yeast and Ethyl Alcohol Plant. Energy 35, 704–717. doi:10.1016/j.energy.2009.11.020

CrossRef Full Text | Google Scholar

Sahu, G. C., and Bandyopadhyay, S. (2010). Energy Conservation in Water Allocation Networks with Negligible Contaminant Effects. Chem. Eng. Sci. 65, 4182–4193. doi:10.1016/j.ces.2010.04.027

CrossRef Full Text | Google Scholar

Souifi, M., and Souissi, A. (2019). Simultaneous Water and Energy Saving in Cooling Water Networks Using Pinch Approach. Mater. Today Proc. 13, 1115–1124. doi:10.1016/j.matpr.2019.04.079

CrossRef Full Text | Google Scholar

Yan, F., Wu, H., Li, W., and Zhang, J. (2016). Simultaneous Optimization of Heat-Integrated Water Networks by a Nonlinear Program. Chem. Eng. Sci. 140, 76–89. doi:10.1016/j.ces.2015.09.036

CrossRef Full Text | Google Scholar

Zhao, H.-P., Yang, Y., and Liu, Z.-Y. (2019). Design of Heat Integrated Water Networks with Multiple Contaminants. J. Clean. Prod. 211, 530–536. doi:10.1016/j.jclepro.2018.11.210

CrossRef Full Text | Google Scholar

Zhelev, T. K., and Zheleva, S. R. (2002). Combined Pinch Analysis for More Efficient Energy and Water Resources Management in Beverage Industry. Waste Manag. Environ. 2002, 623–632.

Google Scholar

Zheng, X. S., Feng, X., and Cao, D. L. (2003). Design Water Allocation Network with Minimum Freshwater and Energy Consumption. Comput. Aided Chem. Eng. 15, 388–393. doi:10.1016/S1570-7946(03)80575-8

CrossRef Full Text | Google Scholar

Glossary

$A$ Heat transfer area (m²)

$c$ Unitary costs (€/kg)

$C$ Contaminant concentration (ppm)

$h$ Specific enthalpy (kJ/kg)

$M$ Mass flow rate (kg/s)

$q$ Supplied or withdrawn heat (MW)

$T$ Temperature (ºC)

$U$ Overall heat transfer coefficient (MW/(m²·ºC))

$y$ Existence of interconnection

$Z$ Total investment cost to be minimized (€/year)

$\Delta$ Variation

$\mathrm{1,2,3}$ Processes 1, 2 and three

$C$ Heat exchanger (cooler)

$Cold$ Cold Fluid Stream

$cont.$ Contaminant

$freshw$ Freshwater stream

$H$ Heat exchanger (heater)

$Hot$ Hot Fluid Stream

$in$ Heat exchanger inlet

$m$ Mean

$out$ Heat exchanger outlet

$P$ Water-using process

$Ut$ Utilities

$w$ Feed water to a Water-using process

$wastew$ Wastewater

HEN Heat exchanger network

HIWAN Heat-Integrated Water Allocation Network

KPI Key Performance Indicators

LP Linear programming

MILP Mixed-integer linear programming

MINLP Mixed-integer non-linear programming

MOP Multi-objective programming

NLP Non-linear programming

TAC Total annualized cost

WAHEN Water allocation and heat exchanger network

WAN Water allocation network

WEN Water-energy network

WHR Waste heat recovery

ZLD Zero-liquid discharge