Proportional Predictive Control of Networked Linear Switched Reluctance Machine System With Time-Varying Delay

In this article, a proportional predictive (PP) control strategy is proposed and a high-precision position tracking controller is designed for the networked linear switched reluctance machine system (NLSRMS) with time-varying delay. The closed-loop system model of the NLSRMS is constructed based on the PP control strategy. The stability conditions of the system are proposed by combining the optimal control value calculated by the cost function. The controller of the closed-loop NLSRMS is designed by using continuously updated predictive output equation information based on calculation. The comparative study of the proposed PP and PID control methods is presented by tracking several types of signals. The maximum steady errors of PP and PID control strategies are 0.2 mm and 2 mm under the sinusoidal signal, respectively. The maximum steady errors of PP and PID control strategies are 0.07 mm and 0.7 mm under the square signal, respectively. The simulation results show the effectiveness of the proposed PP control strategy.

1 Introduction

The linear switched reluctance machine (LSRM) system has many advantages, such as low manufacturing cost, stable performance, reliable and straightforward structure, and low loss (Daldaban and Ustkoyuncu, 2010; Yoon, 2016; Cao et al., 2020). There have been some research achievements about LSRM in recent years, such as for nonlinear LSRM; the linearized model of LSRM was obtained in the study by (Ahmad and Narayanan, 2016) by trying a variety of LSRM small-signal models. The system parameters are measured and optimized in the study by (Prasad et al., 2020) using the finite element analysis method. The parameters are tuned and optimized in the study by (Wang, 2018) by using the current-sharing method combined with some advanced algorithms. In addition, the optimal control strategies are proposed, such as the adaptive fuzzy controller designed in the study by (Masoudi et al., 2018) by obtaining the adaptive control law online to improve the robustness of the system. The fuzzy PID control was proposed in the study by (Pan et al., 2013a) to improve the stability performance of the LSRM system. An adaptive control strategy is proposed in the study by (Pan et al., 2013b) to deal with the double-sided LSRM model’s uncertainties and external disturbances.

The emergence of networked control systems (NCSs) effectively solves the problems in traditional control systems, such as the large number of point-to-point connections, maintenance difficulties, and inability to share information. The NCS is more convenient to update and renovate (Zhang et al., 2016). The closed-loop NCS uses the communication networks in forward and feedback transmission channels (Walsh et al., 2001), which can realize the connection between the network and the physical world and perform multiple task synchronization remotely. Therefore, the networked LSRM model is established by using the NCS method. Although the network has these undeniable advantages, network communication inevitably brings transmission delay, packet drop, and attacks (Tan et al., 2015); these drawbacks reduce system performance and even lead to system unsteadiness. The time delay is the usual occurrence in network communication. Therefore, it is of great significance to consider the communication delay in the network transmission of the NCS and design a delay compensation that reduces the effect of the communication delay on the NLRSMS.

There is much research on the NCS with communication delay. For example, the model predictive control (MPC) method has been frequently adopted in recent research. It has high application value, such as improving the operating efficiency of the motor (Miao et al., 2018; Yao et al., 2018) and enhancing the performance of the intelligent driving system (Song et al., 2019). The MPC strategy can perform forward prediction using the state information received from the sensor and combine the predicted future state information with the rolling optimization method to solve the optimal control value of the system to realize the control of the system. This method solves the problem when the controller cannot receive the state information due to the transmission delay; the control value can be solved by predicting the system state. It is better than the traditional method of letting the system control value remain unchanged or equal to zero to deal with the time delay problem. However, it also has a drawback, due to the calculation delay caused by a large number of calculations in forward prediction and rolling optimization (Findeisen and Allgöwer, 2004; Lan and Zhao, 2020). A time-varying networked predictive control method was proposed in the study by (Yang et al., 2014) for a network control system with communication delay. The MPC method (Liu et al., 2017) is investigated to solve the problems of the uncertainty model and the communication delay. The robust MPC control strategy was proposed in the study by (Han et al., 2008) to solve the model uncertainty system with delay. A centralized MPC method was proposed in the study by (Zhao et al., 2018) to reduce the impact of communication delays in the automatic power generation system on the interconnected grid. However, the MPC methods studied in these previous works of research to improve the performance of the system are achieved by modifying the cost function and the stability conditions. Inspired by the PID control method, the PP control strategy proposed in this article combines the proportional feedback control method with the MPC control method.

The networked predictive control method has been applied in multi-agent systems, but there is seldom research on applications in the LSRM tracking control. In a time delay multi-motor control system with uncertain models (Qiu et al., 2018a) and position disturbances (Qiu et al., 2018b), a networked control method is proposed to improve the position tracking accuracy of the motor control system. Therefore, the proposed PP control method is applied to the position tracking control of the NLSRMS with time delay in this article.

To verify the effectiveness of the proposed PP control method, we separately used the PP control method and the PID control method in the NLSRMS with time delay to track the sinusoidal signal, the square wave signal, the alternating signal of the sinusoidal, the square wave, and the sawtooth wave signal. The simulation results indicate that the proposed PP control method has higher precision tracking performance and better stability than the PID control method.

Motivated by the above observations, this article mainly focuses on the high-precision tracking control of the NLSRMS. The main contributions consist of three points:

i) The proposed PP strategy is used in the NLSRMS with time delay.

ii) Considering the influence of time delay in the feedback channel on system stability and control performance, the PP control strategy is proposed to make the system stable and improve control performance. Then, the cost function is designed to compute the value of optimal control to improve the accuracy of the NLSRMS.

iii) The stability of the closed-loop NLSRMS is analyzed, and the feedback controller is designed.

2 The Modeling of LSRM

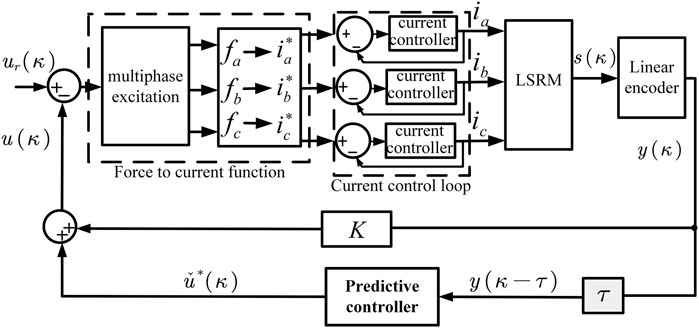
The operating principle of the LSRM is that the torque is distributed according to the real-time measurement of the relative displacement of the motor by the linear encoder, and the value of the electromagnetic force and the torque distribution function of each phase are obtained (Fu et al., 2019) through the force-current converter. The internal current controller generates each phase current required to drive the LSRM. Therefore, the PP control algorithm is proposed to reduce the affect of random delay on the control performance of LSRM. The structure of the NLSRMS is shown in Figure 1.

FIGURE 1

FIGURE 1. Structure of the NLSRMS with time-varying delay.

It should be noted that the meanings of the symbols in the structure of the NLSRMS shown in Figure 1 are presented in Table 1.

TABLE 1

TABLE 1. Meanings of symbols in the NLSRMS.

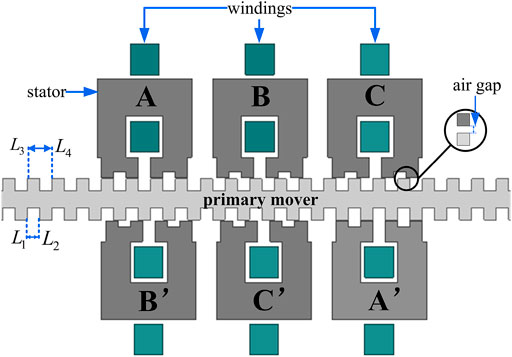
The structure of LSRM is mainly composed of a mover, stator, and winding. The basic parameters are as follows: mover mass and stator mass are 3.8 kg and 5 kg, respectively. The air gap width is 0.3 mm, the coil is 220 turns, and the pole pitch and width are 12 mm and 6 mm, respectively. In addition, the phase resistance and the damping coefficient are 2 Ω and 0.070, respectively. The external structure of the LSRM is shown in Figure 2.

FIGURE 2

FIGURE 2. Structure of LSRM.

The electromagnetic and mechanical motion equations of the LSRM are as follows, respectively (Pan et al., 2013b):

$F_l=\pi i_l^2\bar{L}\sin (\frac{2\pi s}{q})(1)$

$F=m\frac{d^{2}s}{d{t}^2}+\sigma \frac{ds}{dt}+f(2)$

where

$\bar{L}=\frac{L_{\max }-L_{\min }}{2}(3)$

m, s, and i_l are the mover mass, displacement, and phase current, respectively. l is one of the three phases of the LSRM, q is the total width of motor slot and tooth width, and σ is the speed resistance. f, F, and F_l are the load resistance, traction, and phase electromagnetic force, respectively. L_max and L_min are the maximum and minimum inductance values, respectively. The model of the LSRM system can be rewritten as follows (Qiu et al., 2018b):

$\left\{\begin{array}{c}x(\kappa +1)=Ax(\kappa )+Bu(\kappa )\hfill \\ y(\kappa )=Cx(\kappa )\hfill \end{array}\right.(4)$

where the LSRM system parameter matrices A and B are as follows:

$A=\left[\begin{array}{cc}\hfill 0\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill -\frac{b}{m}\hfill \end{array}\right],B=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill \frac{1}{m}\hfill \end{array}\right]$

and C is the system observation matrix. x(κ), y(κ), and u(κ) are the state vector, output vector, and control input vector, respectively. It should be noted that $x(\kappa )={[s{(\kappa )}^T\dot{s}{(\kappa )}^T]}^T$ in which s(κ) is displacement.

Remark: The LSRM studied in this article is the controlled object, and it works under zero load, so the load parameter of f is omitted in the study.

In order to facilitate analysis, we make some basic assumptions as follows:

1) The conditions that the system matrices satisfy include (A, B) being controllable, (A, C) being observable, and the state of the system can be observed.

2) m and p denote the predictive time horizon and the control time horizon, respectively. If m ≥ p, the control value u(κ) will remain unchanged when the condition p ≤ κ ≤ m is satisfied.

3) The time delay in the controller-actuator channel is bound that meets $0\le \underline{\tau }\le {\tau }_{\kappa }\le \bar{\tau }$, where $\underline{\tau }$ and $\bar{\tau }$ are the delay lower and upper bounds, respectively.

4) The reference input r is known.

3 Design of PP Controller and Stability Analysis

In this section, by combining the networked prediction method (Yang et al., 2014) and the proportional integral prediction control strategy (Liu, 2020), the PP control strategy is proposed for the NLSRMS, which is beneficial to the system to reduce position error and improve NLSRMS stability.

3.1 Proportional Predictive Controller

Considering the impact of time delay on the position tracking control performance of the NLSRMS, the PP controller can be designed as follows:

$u(\kappa )=Ky(\kappa )+ǔ(\kappa )(5)$

In which K is the proportional gain and $ǔ(\kappa )$ is the predictive control vector. The PP controller (5) is applied to the LSRM system (4) and the following model of the NLSRMS is obtained:

$\left\{\begin{array}{cc}\hfill x(\kappa +1)& =\bar{A}x(\kappa )+Bǔ(\kappa ),\hfill \\ \hfill y(\kappa )& =Cx(\kappa )\hfill \\ \hfill x({\kappa }_0)& ={\beta }_0,{\kappa }_0=-\bar{\tau },-\bar{\tau }+1,\dots ,0.\hfill \end{array}\right.(6)$

where $\bar{A}=A+BKC$, x(κ₀), β₀, and κ₀ represent the initial state, initial value, and initial delay of the system, respectively. Based on assumption 1, the system state is observed. Consider the following state observer adopted from the study by (An et al., 2018):

$\left\{\begin{array}{c}\bar{x}(\kappa +1)=\bar{A}\bar{x}(\kappa )+Bǔ(\kappa )+L(y(\kappa )-C\bar{x}(\kappa ))\hfill \\ \bar{y}(\kappa +1)=C\bar{x}(\kappa )\hfill \end{array}\right.(7)$

where $\bar{x}(\kappa ),\bar{y}(\kappa )$, and L denote the observed state vector, observed output vector, and observer gain, respectively. Moreover, according to the current received observed state, the strategy of predictive control can compute the state in the future prediction time horizon. System (6) predicts the future m + τ_k step based on the state up to κ moment, for n = 1, 2, … , m + τ_κ as follows (Chen and Liu, 2020):

$\begin{array}{ll}\hfill x̌(\kappa +1\mid \kappa )& =\bar{A}\bar{x}(\kappa )+Bǔ(\kappa )\hfill \\ \hfill x̌(\kappa +2\mid \kappa )& =\bar{A}x̌(\kappa +1\mid \kappa )+Bǔ(\kappa +1\mid \kappa )\hfill \\ \hfill & ={\bar{A}}^2\bar{x}(\kappa )+\bar{A}Bǔ(\kappa )+Bǔ(\kappa +1\mid \kappa )\hfill \\ \hfill & ⋮\hfill \\ \hfill x̌(\kappa +n\mid \kappa )& ={\bar{A}}^n\bar{x}(\kappa )+\sum _{i=0}^{n-1}{\bar{A}}^{i}Bǔ(\kappa +n-1-i\mid \kappa )\hfill \end{array}(8)$

where $x̌(\kappa +1\mid \kappa )$ denote the ahead step predicted state from step κ to step κ + 1. Let κ = κ − τ_κ. By considering the time-varying delay, Eq. 8 can be rewritten as follows:

$x̌\left(\kappa -{\tau }_{\kappa }+n\mid \kappa -{\tau }_{\kappa }\right)={\bar{A}}^n\bar{x}(\kappa -{\tau }_{\kappa })+\sum _{i=0}^{n-1}{\bar{A}}^{i}Bǔ\left(\kappa -{\tau }_{\kappa }+n-1-i\mid \kappa -{\tau }_{\kappa }\right)(9)$

for n = 1, 2, … , p + τ_κ. Based on assumption 2, as long as n ≥ p + τ_κ + 1, the predictive control values are equal to the following:

$ǔ\left(\kappa -{\tau }_{\kappa }+n\mid \kappa -{\tau }_{\kappa }\right)=ǔ\left(\kappa +p\mid \kappa -{\tau }_{\kappa }\right)(10)$

Then, Eq. 9 can be rewritten as follows:

$\begin{array}{cc}\hfill x̌\left(\kappa -{\tau }_{\kappa }+n\mid \kappa -{\tau }_{\kappa }\right)=& {\bar{A}}^n\bar{x}\left(\kappa -{\tau }_{\kappa }\right)+\sum _{i=0}^{n-p-{\tau }_{\kappa }-1}{\bar{A}}^{i}Bǔ\left(\kappa +p\mid \kappa -{\tau }_k\right)\hfill \\ \hfill & +\sum _{i=n-p-{\tau }_{\kappa }}^{n-1}{\bar{A}}^{i}Bǔ\left(\kappa -{\tau }_{\kappa }+n-1-i\mid \kappa -{\tau }_{\kappa }\right)\hfill \end{array}(11)$

for n = p + τ_κ + 1, p + τ_κ + 2, … , m + τ_κ. Via the system (6), the predicted output equation is obtained as follows:

$y̌\left(\kappa -{\tau }_{\kappa }+n\mid \kappa -{\tau }_{\kappa }\right)=Cx̌\left(\kappa -{\tau }_{\kappa }+n\mid \kappa -{\tau }_{\kappa }\right)(12)$

The m + τ_κ step predictive output vector and the p + τ_κ step control input vector are defined as follows (Miao et al., 2018):

$\begin{array}{c}Y̌\left(\kappa +M_y\mid \kappa -{\tau }_{\kappa }\right)=\left[\begin{array}{c}\hfill y̌\left(\kappa -{\tau }_{\kappa }+1\mid \kappa -{\tau }_{\kappa }\right)\hfill \\ \hfill y̌\left(\kappa -{\tau }_{\kappa }+2\mid \kappa -{\tau }_{\kappa }\right)\hfill \\ \hfill ⋮\hfill \\ \hfill y̌\left(\kappa +m\mid \kappa -{\tau }_{\kappa }\right)\hfill \end{array}\right]\\ Ǔ\left(\kappa +P_u\mid \kappa -{\tau }_{\kappa }\right)=\left[\begin{array}{c}\hfill ǔ\left(\kappa -{\tau }_{\kappa }\right)\hfill \\ \hfill ǔ\left(\kappa -{\tau }_{\kappa }+1\mid \kappa -{\tau }_{\kappa }\right)\hfill \\ \hfill ⋮\hfill \\ \hfill \breve{u}\left(\kappa +p\mid \kappa -{\tau }_{\kappa }\right)\hfill \end{array}\right]\end{array}$

Combining Eqs 9, 11, 12, the predicted m + τ_κ step output of the NLSRMS can be calculated through the equation of predicted output. Which means

$Y̌\left(\kappa +M_y\mid \kappa -{\tau }_{\kappa }\right)=S\bar{x}\left(\kappa -{\tau }_{\kappa }\right)+HǓ\left(\kappa +P_u\mid \kappa -{\tau }_{\kappa }\right)(13)$

where

$S=\left[\begin{array}{c}\hfill C\bar{A}\hfill \\ \hfill C{\bar{A}}^2\hfill \\ \hfill ⋮\hfill \\ \hfill C{\bar{A}}^{m+{\tau }_{\kappa }}\hfill \end{array}\right]H=C\left[\begin{array}{cccc}\hfill I\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill \bar{A}\hfill & \hfill I\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\bar{A}}^{p+{\tau }_{\kappa }-1}\hfill & \hfill {\bar{A}}^{p+{\tau }_{\kappa }-2}\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill {\bar{A}}^{p+{\tau }_{\kappa }}\hfill & \hfill {\bar{A}}^{p+{\tau }_{\kappa }-1}\hfill & \hfill \cdots \hfill & \hfill I\hfill \\ \hfill {\bar{A}}^{p+{\tau }_{\kappa }+1}\hfill & \hfill {\bar{A}}^{p+{\tau }_{\kappa }}\hfill & \hfill \cdots \hfill & \hfill \bar{A}+I\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill {\bar{A}}^{m+{\tau }_{\kappa }-1}\hfill & \hfill {\bar{A}}^{m+{\tau }_{\kappa }-2}\hfill & \hfill \cdots \hfill & \hfill \sum _{i=0}^{m-p}{\bar{A}}^i\hfill \end{array}\right]B(14)$

3.2 The Cost Function of NLSRMS

In order to make the output of the NLSRMS track the reference input signal precisely, the cost function is adopted as follows:

$\begin{array}{c}\hfill \underset{Ǔ(\kappa +P_u|\kappa -{\tau }_{\kappa })}{\min }J(\kappa )={\gamma }_y\Vert Y̌(\kappa +M_y|\kappa -{\tau }_{\kappa })-\mathfrak{R}(\kappa +M){\Vert }^2+{\gamma }_u\Vert Ǔ(\kappa +P_u|\kappa -{\tau }_{\kappa }){\Vert }^2\end{array}(15)$

where γ_y and γ_u are non-negative weighting factors. The reference input was defined in the study by (Yao et al., 2018) and presented as follows:

$\mathfrak{R}(\kappa +M)=\left[\begin{array}{c}\hfill r(\kappa -{\tau }_{\kappa }+1)\hfill \\ \hfill r(\kappa -{\tau }_{\kappa }+2)\hfill \\ \hfill ⋮\hfill \\ \hfill r(\kappa +m)\hfill \end{array}\right]$

where M is the dimension of the reference vector.

The local minimum control value of the NLSRMS can be obtained via the derivative of the cost function with respect to the control value. Let Eq. 13 be substituted into Eq. 15, the cost function can be rewritten as follows:

$\begin{array}{ll}\hfill \underset{Ǔ(\kappa +P_u|\kappa -{\tau }_{\kappa })}{\min }J=& {\gamma }_y\Vert S\bar{x}(\kappa -{\tau }_{\kappa })+HǓ(\kappa +P_u|\kappa -{\tau }_{\kappa })-\mathfrak{R}(\kappa +M){\Vert }^2\hfill \\ \hfill & +{\gamma }_u\Vert Ǔ(\kappa +P_u|\kappa -{\tau }_{\kappa }){\Vert }^2\hfill \\ =\hfill & {\left[\begin{array}{c}\hfill S\bar{x}(\kappa -{\tau }_{\kappa })+HǓ(\kappa +P_u|\kappa -{\tau }_{\kappa })-\mathfrak{R}(\kappa +M)\hfill \\ \hfill Ǔ(\kappa +P_u|\kappa -{\tau }_{\kappa })\hfill \end{array}\right]}^T\left[\begin{array}{cc}\hfill {\gamma }_{y}I\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\gamma }_{u}I\hfill \end{array}\right]\hfill \\ \hfill & \left[\begin{array}{c}\hfill S\bar{x}(\kappa -{\tau }_{\kappa })+HǓ(\kappa +P_u|\kappa -{\tau }_{\kappa })-\mathfrak{R}(\kappa +M)\hfill \\ \hfill Ǔ(\kappa +P_u|\kappa -{\tau }_{\kappa })\hfill \end{array}\right]\hfill \end{array}(16)$

Then, the derivative of the cost function is equal to zero, which means

$\frac{dJ(\kappa )}{dǓ(\kappa +P_u|\kappa -{\tau }_{\kappa })}=0(17)$

Therefore, the optimal control sequence at the moment is

$\begin{array}{c}\hfill U^{\ast }(\kappa +P_u|\kappa -{\tau }_{\kappa })={(H^T{\gamma }_{y}H+{\gamma }_{u}I)}^{-1}{H}^T{\gamma }_y\times (\mathfrak{R}(\kappa +M)-S\bar{x}(\kappa -{\tau }_{\kappa }))\end{array}(18)$

considering the predictive control scheme, selecting the first control value of the optimal control sequence works on the LSRM, which means that the optimal control can be gained

${ǔ}^{*}(\kappa -{\tau }_{\kappa })=K_{mpc}(\mathfrak{R}(\kappa +M)-S\bar{x}(\kappa -{\tau }_{\kappa }))(19)$

in which $K_{mpc}=\left[\begin{array}{cccc}\hfill I\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \end{array}\right]{(H^T{\gamma }_{y}H+{\gamma }_{u}I)}^{-1}{H}^T{\gamma }_y$. In the next instant, let κ = κ + 1, and the optimal control value can be solved by online rolling.

3.3 The Stability Analysis and Controller Design of NLSRMS

Define the error of the observer as $e(\kappa )=x(\kappa )-\bar{x}(\kappa )$. By substituting Eq. 19 into (6), the NLSRMS control system based on the PP control strategy can be rewritten as follows:

$\begin{array}{cc}\hfill x(\kappa +1-{\tau }_{\kappa })& =\bar{A}x(\kappa -{\tau }_{\kappa })+B{ǔ}^{\ast }(\kappa -{\tau }_{\kappa })\hfill \\ \hfill & =\bar{A}x(\kappa -{\tau }_{\kappa })+B{K}_{mpc}(\mathfrak{R}(\kappa +M)-S\bar{x}(\kappa -{\tau }_{\kappa }))\hfill \\ \hfill & =(\bar{A}-B{K}_{mpc}S)x(\kappa -{\tau }_{\kappa })+B{K}_{mpc}\mathfrak{R}(\kappa +M)+B{K}_{mpc}Se(\kappa -{\tau }_{\kappa })\hfill \end{array}(20)$

Therefore, the observer error is

$\begin{array}{cc}\hfill e(\kappa +1-{\tau }_{\kappa })& =x(\kappa +1-{\tau }_{\kappa })-\bar{x}(\kappa +1-{\tau }_{\kappa })\hfill \\ \hfill & =(\bar{A}-LC)e(\kappa -{\tau }_{\kappa })\hfill \end{array}(21)$

Let $\mathrm{\Psi }\left(\kappa -{\tau }_{\kappa }\right)=\left[\begin{array}{c}\hfill x(\kappa -{\tau }_{\kappa })\hfill \\ \hfill e(\kappa -{\tau }_{\kappa })\hfill \end{array}\right]$. Combining Eqs 20, 21 leads to

$\mathrm{\Psi }\left(\kappa -{\tau }_{\kappa }+1\right)=\left[\begin{array}{cc}\hfill \bar{A}-B{K}_{mpc}S\hfill & \hfill B{K}_{mpc}S\hfill \\ \hfill 0\hfill & \hfill \bar{A}-LC\hfill \end{array}\right]\mathrm{\Psi }\left(\kappa -{\tau }_{\kappa }\right)+\left[\begin{array}{c}\hfill B{K}_{mpc}\hfill \\ \hfill 0\hfill \end{array}\right]\mathfrak{R}(\kappa +M)(22)$

Definition: For linear discrete time-invariant control systems, the system is asymptotically stable when it satisfies the Schur stability condition.

Proof: If the system (22) satisfies the Schur stability definition, it means that all the eigenvalues of the system matrix in (22) are in the unit circle

$\left|\lambda \left(\left[\begin{array}{cc}\hfill \bar{A}-B{K}_{mpc}S\hfill & \hfill B{K}_{mpc}S\hfill \\ \hfill 0\hfill & \hfill \bar{A}-LC\hfill \end{array}\right]\right)\right|<1(23)$

where λ(A) represents the eigenvalue of matrix A. Therefore, lim _κ→∞ Ψ(κ) → 0, it implies x(κ) → 0 and e(κ) → 0, as κ → ∞. That is, the stability of the NLSRM system (6) with the PP control strategy is equal to the stability of the system (22).

According to the stability conditions of the system, there exists an appropriate proportional gain of K satisfied

$\left\{\begin{array}{c}\left|\lambda \left(\bar{A}-B{K}_{mpc}S\right)\right|<1\hfill \\ |\lambda \left(\bar{A}-LC\right)|<1\hfill \end{array}\right.(24)$

By the aid of the place function from Matlab, the state observer gain L can be designed.

4 Simulation Results Analysis

In order to verify the performance of the proposed PP control method, the LSRM with the following adopted coefficient matrices from the study by (Qiu et al., 2018b) is studied.

$A=\left[\begin{array}{cc}\hfill 1.0004\hfill & \hfill 0.0909\hfill \\ \hfill 0.0085\hfill & \hfill 0.8247\hfill \end{array}\right],B=\left[\begin{array}{c}\hfill 0.0047\hfill \\ \hfill 0.0909\hfill \end{array}\right],C=[10]$

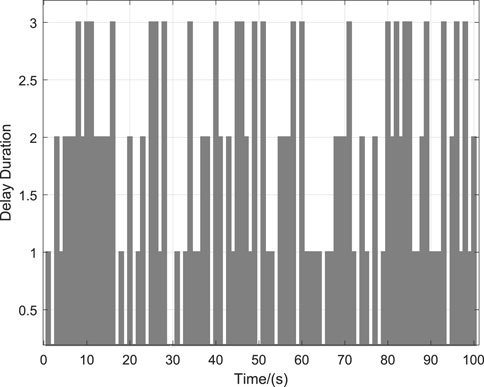
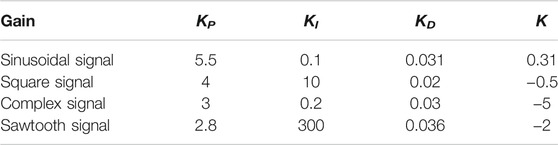
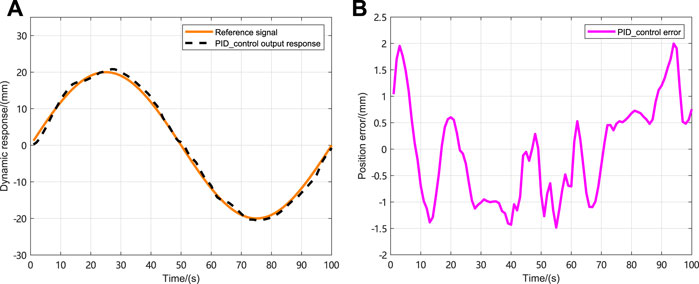
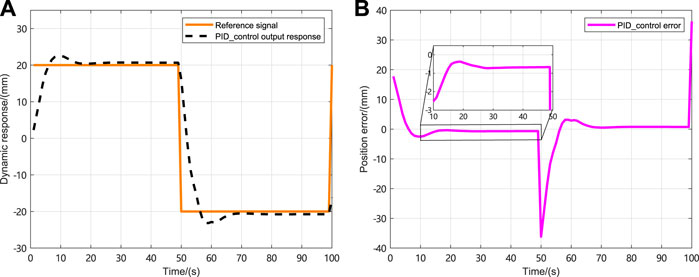
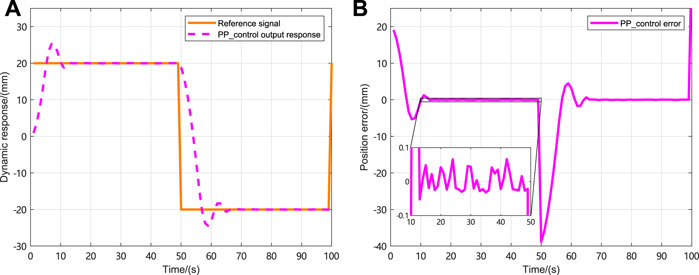
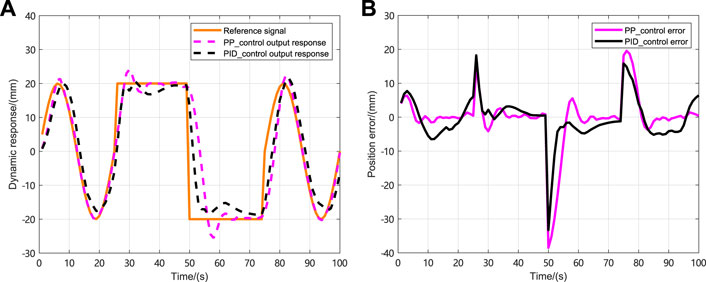
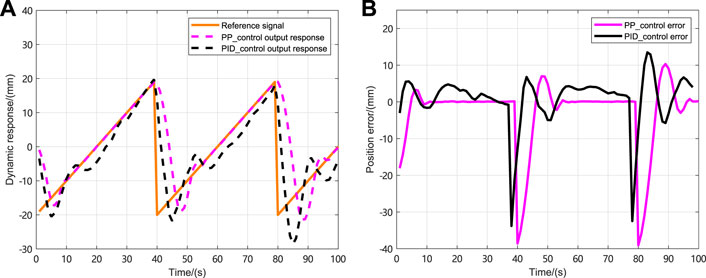
The initial state of the NLSRMS control system is x(0) = [0 0] ^T , and the observed state and control input are initially zero. Moreover, the reference signals are the sinusoidal signal, the square wave signal, the complex signal with alternating sinusoidal and square wave, and the sawtooth wave signal. The weighting factors in the cost function are γ _y = 1, γ _u = 0.1, respectively. To prevent the deviation caused by the different delay sequences in each simulation system, the same delay occurrence is set in all simulations, and there is no delay in the first transmission. The delay sequence generated in the transmission channel is shown in Figure 3. The state observer gain is L = [1.824 6,7.481 6] ^T . The PID controller parameters and PP controller gains corresponding to each simulation system are shown in Table 2, in which K _P , K _I and K _D , respectively, represent the gain of the PID controller and K represent the proportional gain of the PP controller; the selection method and the PID parameter selection method are the same. The NLSRMS with the time delay tracking sinusoidal signal adopted PID controller and PP controller are shown in Figures 4, 5, respectively. That signal amplitude and frequency are 20 mm and 0.01 Hz, respectively. Comparing the position errors in Figures 4B, 5B, it is evident that the maximum absolute value of the steady state error of the proposed PP control method is only 0.2 mm, while the PID control method is as high as 2 mm. The NLSRMS control system with the time-varying delay tracking square wave signal uses the PID controller and the PP controller shown in Figures 6, 7, respectively. That signal amplitude and frequency are 20 mm and 0.01 Hz. Comparing the position errors in Figures 6B, 7B, it is evident that the maximum absolute value of the steady state error of the proposed PP control method is only 0.07 mm; however, the PID control method is as high as 0.7 mm. The results prove that the PP control method has better stability and faster response speed than the PID control method. The NLSRM control system with random delay is followed by the sawtooth wave with an amplitude of 20 mm and a frequency of 0.025 Hz, and the complex signal alternating sinusoidal and square waves has an amplitude of 20 mm, and the frequency is 0.08 Hz and 0.04 Hz, respectively. The output response and the position error of tracking sawtooth waves are shown in Figure 8. The output response and the position error of the tracking complex signal are shown in Figure 9. These waveforms certify that the response speed of the PP control method is slightly slower than that of the PID control method when the signal jumps, but it can rapidly trend toward stabilization after the signal jumps. Therefore, the tracking effectiveness of PP control is better than that of the PID control method.

FIGURE 3

FIGURE 3. Sequence of time delay τ _κ .

TABLE 2

TABLE 2. Controller gains corresponding to each simulation system.

FIGURE 4

FIGURE 4. NLSRMS with the PID control method: (A) Output response. (B) Position error.

FIGURE 5

FIGURE 5. NLSRMS with the PP control method: (A) Output response. (B) Position error.

FIGURE 6

FIGURE 6. NLSRMS with the PID control method: (A) Output response. (B) Position error.

FIGURE 7

FIGURE 7. NLSRMS with the PP control method: (A) Output response. (B) Position error.

FIGURE 8

FIGURE 8. NLSRMS with the PP and PID control methods: (A) Output response. (B) Position error.

FIGURE 9

FIGURE 9. NLSRMS with the PP and PID control methods: (A) Output response. (B) Position error.

5 Conclusion and Discussion

In this article, the tracking control issue of the NLSRMS with time-varying delay is studied. First, the NLSRMS model was established, and the PP control strategy is proposed to achieve higher tracking accuracy of the LSRM. Then, the predictive output equation and the cost function are combined to solve the optimal control value to ensure the robustness of the closed-loop NLSRMS. Furthermore, the PP controller and the PID controller are compared; the simulation results verify that the proposed proportional predictive controller can suppress the impact of random delay and reduce the LSRM position tracking error. The influence of bandwidth limits in network communication, the greater the influence of data transmission, the larger the performance of the system, and this article only studies the way to compensate on the controller without improving network communication transmission; in future research, the event trigger mechanism (ETM) will be considered.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author Contributions

LQ: methodology, writing, and supervision. TD and XY: investigate, writing, methodology and simulation. MN: writing and revising. JP and CL: design of the system structure and supervision. All authors contributed to the article and approved the submitted version.

Funding

This work is supported by the National Natural Science Foundation of China (Grants No. 61873170, U1813225, and U1913214), in part by the Science and Technology Development Foundation of the Shenzhen Government (Grant No. JCYJ20190808144607400), the Education Department Foundation of Guangdong Province (Grant No. 2020ZDZX3005), and the Shenzhen International Cooperation Project (Grant No. GJHZ20200731095801004).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ahmad, S. S., and Narayanan, G. (2016). Linearized Modeling of Switched Reluctance Motor for Closed-Loop Current Control. IEEE Trans. Ind. Applicat. 52, 3146–3158. doi:10.1109/TIA.2016.2550521

CrossRef Full Text | Google Scholar

An, B.-R., Liu, G.-P., and Tan, C. (2018). Group Consensus Control for Networked Multi-Agent Systems with Communication Delays. ISA Trans. 76, 78–87. doi:10.1016/j.isatra.2018.03.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Cao, R., Su, E., and Lu, M. (2020). Comparative Study of Permanent Magnet Assisted Linear Switched Reluctance Motor and Linear Flux Switching Permanent Magnet Motor for Railway Transportation. IEEE Trans. Appl. Supercond. 30, 1–5. doi:10.1109/TASC.2020.2965874

CrossRef Full Text | Google Scholar

Chen, D.-L., and Liu, G.-P. (2020). A Networked Predictive Controller for Linear Multi-Agent Systems with Communication Time Delays. J. Franklin Inst. 357, 9442–9466. doi:10.1016/j.jfranklin.2020.07.020

CrossRef Full Text | Google Scholar

Daldaban, F., and Ustkoyuncu, N. (2010). A Novel Linear Switched Reluctance Motor for Railway Transportation Systems. Energ. Convers. Manage. 51, 465–469. doi:10.1016/j.enconman.2009.10.009

CrossRef Full Text | Google Scholar

Findeisen, R., and Allgöwer, F. (2004). Computational Delay in Nonlinear Model Predictive Control. IFAC Proc. Volumes 37, 427–432. doi:10.1016/S1474-6670(17)38769-4

CrossRef Full Text | Google Scholar

Han, C., Liu, X., and Zhang, H. (2008). Robust Model Predictive Control for Continuous Uncertain Systems with State Delay. J. Control. Theor. Appl. 6, 189–194. doi:10.1007/s11768-008-5227-y

CrossRef Full Text | Google Scholar

Lan, J., and Zhao, D. (2020). Robust Model Predictive Control for Nonlinear Parameter Varying Systems without Computational Delay. Int. J. Robust Nonlinear Control. 31, 8273–8294. doi:10.1002/rnc.5235

CrossRef Full Text | Google Scholar

Liu, G.-P. (2020). Coordinated Control of Networked Multiagent Systems with Communication Constraints Using a Proportional Integral Predictive Control Strategy. IEEE Trans. Cybern. 50, 4735–4743. doi:10.1109/TCYB.2019.2894264

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, Z., Du, G., and Du, F. (2017). Research Status and Development Trend of Finite Control Set Model Predictive Control in Power Electronics. Diangong Jishu Xuebao/Transactions China Electrotechnical Soc. 32, 58–69. doi:10.19595/j.cnki.1000-6753.tces.160399

CrossRef Full Text | Google Scholar

Masoudi, S., Soltanpour, M. R., and Abdollahi, H. (2018). Adaptive Fuzzy Control Method for a Linear Switched Reluctance Motor. IET electric Power Appl. 12, 1328–1336. doi:10.1049/iet-epa.2018.0059

CrossRef Full Text | Google Scholar

Miao, L., Zhang, Y., Tong, C., Xiao, X., and Wang, W. (2018). Efficiency Optimization of Permanent Magnet Synchronous Generators Based on Model Predictive Direct Torque Control. Trans. China Electrotechnical Soc. 33, 3535–3546. doi:10.19595/j.cnki.1000-6753.tces.170800

CrossRef Full Text | Google Scholar

Pan, J. F., Meng, F. J., Jiang, W., and Cheung, N. C. (2013a). “Fuzzy PID Control for the Linear Switched Reluctance Machine,” In 2013 5th International Conference on Power Electronics Systems and Applications: 2013 5th International Conference on Power Electronics Systems and Applications (PESA), 11–13. Dec. 2013, (Hong Kong (HK)), 1–4. doi:10.1109/PESA.2013.6828216

CrossRef Full Text | Google Scholar

Pan, J. F., Zou, Y., and Cao, G. (2013b). Adaptive Controller for the Double‐sided Linear Switched Reluctance Motor Based on the Nonlinear Inductance Modelling. IET electric Power Appl. 7, 1–15. doi:10.1049/iet-epa.2012.0080

CrossRef Full Text | Google Scholar

Prasad, N., Jain, S., and Gupta, S. (2020). Measurement and Optimization of Performance Parameters of Linear Switched Reluctance Motor Using Finite Element Method. Mapan 35, 251–259. doi:10.1007/s12647-019-00350-8

CrossRef Full Text | Google Scholar

Qiu, L., Shi, Y., Pan, J., and Zhang, B. (2018a). Robust Cooperative Positioning Control of Composite Nested Linear Switched Reluctance Machines with Network-Induced Time Delays. IEEE Trans. Ind. Electron. 65, 7447–7457. doi:10.1109/TIE.2017.2772186

CrossRef Full Text | Google Scholar

Qiu, L., Shi, Y., Zhang, B., Pan, J., and Lai, X. (2018b). Tracking Control of Networked Multiple Linear Switched Reluctance Machines Control System Based on Position Compensation Approach. IEEE Trans. Ind. Inf. 14, 5368–5377. doi:10.1109/TII.2018.2810538

CrossRef Full Text | Google Scholar

Song, X., Shao, Y., and Qu, Z. (2020). A Vehicle Trajectory Tracking Method with a Time-Varying Model Based on the Model Predictive Control. IEEE Access 8, 16573–16583. doi:10.1109/ACCESS.2019.2963291

CrossRef Full Text | Google Scholar

Tan, C., Li, L., and Zhang, H. (2015). Stabilization of Networked Control Systems with Both Network-Induced Delay and Packet Dropout. Automatica 59, 194–199. doi:10.1016/j.automatica.2015.06.026

CrossRef Full Text | Google Scholar

Walsh, G. C., Beldiman, O., and Bushnell, L. G. (2001). Asymptotic Behavior of Nonlinear Networked Control Systems. IEEE Trans. Automat. Contr. 46, 1093–1097. doi:10.1109/9.935062

CrossRef Full Text | Google Scholar

Wang, J.-J. (2018). Parameter Optimization and Speed Control of Switched Reluctance Motor Based on Evolutionary Computation Methods. Swarm Evol. Comput. 39, 86–98. doi:10.1016/j.swevo.2017.09.004

CrossRef Full Text | Google Scholar

Yang, R., Liu, G.-P., Shi, P., Thomas, C., and Basin, M. V. (2014). Predictive Output Feedback Control for Networked Control Systems. IEEE Trans. Ind. Electron. 61, 512–520. doi:10.1109/TIE.2013.2248339

CrossRef Full Text | Google Scholar

Yao, J., Liu, R., and Yin, X. (2018). Research on 3-vector Model Predictive Control with Low Switching Frequency of Permanent Magnet Synchronous Motor. Trans. China Electrotechnical Soc. 33, 2935–2945. doi:10.19595/j.cnki.1000-6753.tces.170617

CrossRef Full Text | Google Scholar

Yoon, Y.-H. (2016). Position Detecting Modeling of Linear Switched Reluctance Motor(LSRM) for Railway Vehicles. Trans. Korean Inst. Electr. Eng. 65, 1907–1912. doi:10.5370/kiee.2016.65.11.1907

CrossRef Full Text | Google Scholar

Zhang, X.-M., Han, Q.-L., and Yu, X. (2016). Survey on Recent Advances in Networked Control Systems. IEEE Trans. Ind. Inf. 12, 1740–1752. doi:10.1109/TII.2015.2506545

CrossRef Full Text | Google Scholar

Zhao, X., He, J., Fu, B., Shan, Z., and Xu, G. (2018). An Agc Method for Interconnected Power Grid with Two-Channel Random Delays. Dianli Xitong Baohu Yu Kongzhi/Power Syst. Prot. Control. 46, 50–57. doi:10.7667/PSPC.170573

CrossRef Full Text | Google Scholar