- 1Institute of Automatic Control, School of Electrical, Information and Media Engineering, University of Wuppertal, Wuppertal, Germany
- 2Lab-STICC, ENSTA Bretagne, Brest, France
This paper deals with the design of linear observer-based state feedback controllers with constant gains for a class of nonlinear discrete-time systems in the form of a quasi-linear representation in presence of stochastic noise. For taking into account nonlinearities in the design of linear observer-based state feedback controllers, a polytopic modeling approach is investigated. An optimization problem is formulated to reduce the sensitivity of the controlled system towards stochastic input, state, and output noise with a predefined covariance. Due to the nonlinearities, the separation principle does not hold, thus, the controller and the observer have to be designed simultaneously. For this purpose, a Lyapunov-based method is used, which provides, in addition to the controller and observer gains, a stability proof for the nonlinear closed loop in a predefined polytopic domain. In general, this leads to nonlinear matrix inequalities. To solve these nonlinear matrix inequalities efficiently, we propose an approach based on linear matrix inequalities (LMIs) with a superposed iteration rule. When using this iterative LMI approach, a minimization task can be solved additionally, which desensitizes the closed loop to stochastic noise. The proposed method additionally enables the consideration of different linear closed loop structures by a unified Lyapunov-based framework. The efficiency of the proposed approach is demonstrated and compared with a classical LQG approach for a nonlinear overhead traveling crane.
1 Introduction
The research field of linear control theory is well investigated and facilitates generalized and efficient methods to design linear controllers for linear systems. For example, LMI methods have been established for the robust controller design and used to prove asymptotic stability of the closed loop simultaneously.
However, as almost all real systems are nonlinear, these methods do not ensure stability for real-world applications. To make use of the efficiency of linear methods nonetheless, these nonlinearities, if bounded, can be expressed as polytopic domains just like (time-varying) uncertainties. For this purpose, the nonlinear model can be transformed into a quasi-linear form, whereby the bounded nonlinearities can be evaluated using interval arithmetic (Rauh and Romig, 2021; Rauh et al., 2021). For these systems, a convex LMI approach is just as applicable as for pure parameter uncertainty. In such cases, a polytopic representation of the uncertainties is required, which is bounded by the element-wise defined realizations. Hence, by taking the uncertainties into account in the controller design, stability of the nonlinear closed loop can be guaranteed.
Additionally, process and measurement noise appear in all real systems. These noise processes can lead to oscillatiosn in the control loop or to excessively large control amplitudes and therefore should be suppressed. This can be achieved for example by an observer-based state feedback structure. However, with the plant being nonlinear, the separation principle is not valid. Therefore, the controller and the observer must be designed simultaneously to ensure stability (Ibrir, 2008; Rauh et al., 2021). The problem of simultaneously designing discrete-time observers and controllers for uncertain systems is also considered, for example, in Peaucelle and Ebihara (2014); Zemouche et al. (2016). These works also make use of a Lyapunov-based LMI approach. However, noise reduction is not discussed. In Ibrir (2008) as well as in Kheloufi et al. (2014), observed-based controllers are designed for Lipschitz nonlinear systems under H∞ conditions. Another control design method for nonlinear systems with a noise and disturbance compensation based on LMI techniques is shown in Furtat (2018) such as in Yucelen et al. (2010) as a robust output feedback control on the basis of active noise control. In De Oliveira et al. (2002) and Sadabadi and Karimi (2013), LMI methods are used to design dynamic and static output feedback controllers for discrete-time systems subject to H∞ and H2 conditions. A further Lyapunov-based LMI approach with polytopic domains is shown for switched linear discrete-time systems in Phat and Ratchagit (2011); Ratchagit and Phat (2011) and Yotha and Mukdasai (2013), where delays are represented with intervals.
In the continuous-time case, a desensitization to stochastic noise is already investigated, for example, in Rauh et al. (2014); Rauh et al. (2018); Rauh and Romig (2021); Rauh et al. (2021). It is especially pointed out how standard low-pass-filtering can lead to oscillation for stochastic systems with an observer-based or a filter-based controller design. To counter such oscillations, an optimization task is presented, which minimizes the area for which stability cannot be proven. This optimization task is solved by a numerical LMI-based method, which can be applied for a filter or observer design with a previously designed controller. In Rauh and Romig (2021), this work is extended by considering bounded parameter uncertainty and a simultaneous controller and linear filter design. Thereby, the entire closed loop can be designed as insensitive as possible against parameter uncertainty and stochastic noise. The same optimization task is used in Rauh et al. (2021) to design an observer-based output feedback or an observer-based state feedback controller. The reason for the separation of those articles is the fact that the design criteria are not fully identical for the requirements of different control structures.
However, a discrete-time controller is required for the implementation on a microcomputer. Therefore, the continuous-time system is sampled, which leads to a discrete-time representation of the plant. To deal with these systems, methods are required that consider the discretization in the design.
This paper deals with a discrete-time LMI approach while simultaneously optimizing the observer and controller gains. Additionally, the article solves the issue that different closed loops lead to different design criteria. Hereby, a joint optimization algorithm is developed, which can be applied to a myriad of closed loop structures. For that purpose, we address the structured linear control (SLC) problem in which the dynamic controller is described as a structured state feedback approach in an augmented system model. In this paper, the procedure is shown explicitly for the design of an observer-based state feedback control. Through a superposed iteration rule, the LMI design parameters are the same as the parameters to be implemented. The direct discrete-time design allows the offline-computed control parameters to be transferred directly to the microcomputer. Due to the consideration of noisy output equations, leading to a direct disturbance feedthrough term, a classical H2 optimization cannot be applied. Moreover, the presence of polytopic domains invalidates the parameterization of classical LQG approaches. To overcome both limitations and to obtain a discrete-time noise-insensitive controller, we forecast the influence of noise on the closed loop behavior by discrete-time increments of the Lyapunov function candidate. This leads to the discrete-time counterpart of the Itô differential operator from Rauh and Romig (2021); Rauh et al. (2021). Thereby, the uncertainty domains are quantified and subsequently minimized.
By solving the proposed optimization task, a noise-insensitive controller is obtained. With its help, the actual state trajectories converge as closely as possible to the desired operating point. In addition, this framework has the capability to robustly prescribe the desired system dynamics in terms of a discrete-time
This paper is structured as follows. Within a problem description in Section 2, the observer-based output feedback controller is introduced. This is followed in Section 3 by the necessary basics of the work, which consist of the description of polytopic domains, robust Lyapunov stability and robust
2 Problem Statement
2.1 Desensitization of the Closed Loop to Stochastic Noise in the Continuous-Time Case
Consider the continuous-time linear noisy system
with the state vector
To prove the stability of system (Eq. 1), the time derivative L(V) in the form of its stochastic interpretation of the Lyapunov function candidate
with the augmented system matrices
2.2 Desensitization of the Closed Loop to Stochastic Noise in the Discrete-Time Case
In the following, we consider multivariable nonlinear discrete-time systems subject to noise represented by the quasi-linear form
with the same nomenclature as in Eq. 1. The nonlinearity of the system is assumed only in the state equation, i.e., the matrices
with the observer gain
with the controller gain
the augmented closed loop system
can be derived with
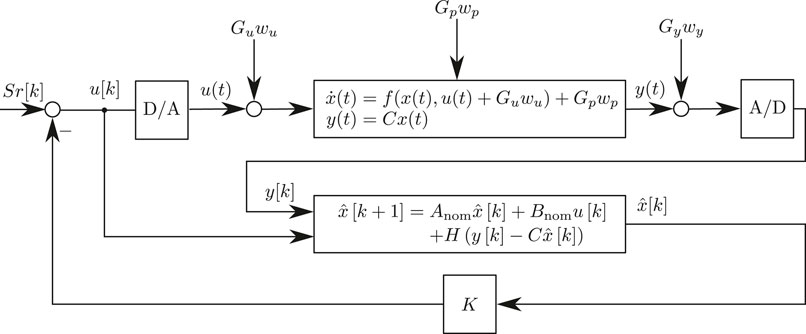
The closed loop structure is visualized in Figure 1.
3 Fundamentals for the Controller Design
3.1 Modeling with Polytopic Domains
Consider the nonlinear discrete-time system (Eq. 3). If the states
of the extremal vertex matrices Av and Bv, where nv denotes the number of independent extremal realizations for the union of all matrices included in Eq. 6. With this representation, it is possible to consider constant or time-varying uncertain parameters with known bounds (Scherer and Weiland, 1994; Boyd et al., 1997). Measurement tolerances for specific system parameters, fabrication tolerances or system nonlinearities can be accounted for by this uncertainty model. Furthermore, these uncertain parameters can be used to describe unidentifiable parts of the system dynamics or to cover different or even faulty system variants. In this work, the parameters ζv are functions of the states
with the nv extremal vertex matrices
3.2 Quadratic Lyapunov Stability
To guarantee robust stability of the autonomous closed loop (Eq. 5) with
with P = PT ≻ 0 as a free decision variable. The uncertain closed loop (Eq. 5) with the polytopic domain (Eq. 7) is robustly (quadratically) stable if the Lyapunov conditions
are fulfilled (Scherer and Weiland, 1994). Therefore, it is sufficient that the increment ΔV = V(z[k + 1]) − V(z[k]) is negative definite. Remind that
3.3 Robust
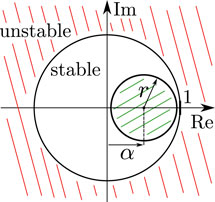
Due to the robust design procedure, a direct pole placement is not possible. This issue is resolved by robust
where |α + r|⩽1 with 0 < r < 1 and −1 < α < 1. If (Eq. 9) are satisfied, the system (Eq. 5) is robustly stable and all eigenvalues of the extremal realizations (Eq. 7) are located within the circular sub-region of the unit circle (Dehnert, 2020; Rauh, 2017; Wahab, 1994).
This transformation maps the unit circle with radius r = 1 and center at the origin α = 0 onto a circle of radius r < 1 and center at α on the real axis in the complex plane. The radius r is also called exponential decay rate and α is an eigenvalue shift operator. By minimizing this
4 Main Results
4.1 Iterative Offline Observer Based Controller Design with Robust
First we assume that w[k] = 0 is true, then the stability of the deterministic, noise-free part of the augmented system (Eq. 5) can be proven by the conditions (Eq. 9), which are equivalent to
after applying the Schur complement. To linearize the inverse of the matrix P, we consider the constant matrix
[Dehnert, 2020]. Due to P−1 ≽ L, the nonlinear matrix inequalities (Eq. 10) are always satisfied if the LMIs
are fulfilled. The proof of inequality (Eq. 11) can be found in Dehnert et al. (2015) or Dehnert (2020). Note that the inequality (Eq. 11) becomes an equality if
where l is the current iteration. This leads to a successively closer approximation of P. The initialization of the update rule (Eq. 13) can be done with
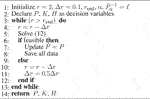
In a first step, the feasibility problem is formulated in the form of our method in Algorithm 1. This procedure ensures that a valid solution is determined, however, yet without any optimization. This solution then represents the starting point for further optimizations. By using Algorithm 1, the nonlinear problem is reduced to an iterative LMI algorithm. Algorithm 1 is essential because the initialization of
Algorithm 1 Feasibility and guarantee of desired
4.2 Convergence Study of the Iterative LMI Solution
As the convergence of the linearization P−1 = L in the iterative method is an important attribute for the solution, which is no issue in non-iterative standard methods, a convergence study will be shown in the following, based on Dehnert (2020).
Let Pco be a known and constant matrix. To numerically compute the matrix inverse
with l = 0, 1, 2, … , whereby the convergence condition can be formulated as
This method is known as Newton-Schulz iteration and was first published in Schulz (1933) and is also called Hotelling-Bodewig algorithm or hyper-power iterative method (Soleymani, 2013). The Newton-Schulz iteration exhibits quadratic convergence if the initial value
This reformulation simultaneously gives information about the radius of convergence, such that quadratic convergence holds if
with the spectral radius ρ.
However, in this article, Pco = P is an unknown decision variable of the LMI problem and thus not constant. Since P changes in each iteration, quadratic convergence can be proven for each iteration by the relation (Eq. 15) for the presented method. Thus, by using the iteration rule in combination with LMIs, a method similar to the Newton-Schulz iteration is obtained. This is used to find the origin of the matrix difference P−1 − L ≈ 0. To determine possible initial values, the condition (Eq. 16) cannot be used directly because P is unknown. However, due to the relation
4.3 Desensitization of Observer and Controller Gains via Iterative LMI Solutions
In Section 4.1, it was assumed that there is an absence of noise, thus
of the Itô differential operator (Eq. 2). This operator is the generalization of the increment ΔV = V(z[k + 1]) − V(z[k]) in the stochastic case.
Proof of the discretized Itô differential operator. To prove (Eq. 17), consider the expectation value
of ΔV. Due to causality, we can assume that w[k] and z[k] are stochastically independent and the noise process is a zero mean process, i.e., E{w[k]} = 0. It also follows that
By using the trace of matrices for the final scalar summand in Eq. 18, the reformulation trace{ABC} = trace{CAB} is valid. Therefore, it follows
Furthermore, we assume that the variance of each noise process wi[k] equals 1, which leads to
Note, a derivation of the Itô differential operator for the continuous case can be found in Senkel et al. (2016). The following relations can already be found in Rauh et al. (2021) for continuous-time systems and are reformulated here for the discrete-time case.
Due to the stochastic noise with non-zero matrices in
for each vertex realizations with
To increase the region in which stability can be proven, one option is to minimize the interior of the ellipsoids (Eq. 20). The volume of the ellipsoids is proportional to
Therefore, the cost function
shall be minimized. To be able to use LMI conditions, a reshaping of
which can be reformulated with the Schur complement to
As presented in Section 4.1, the matrix inverse can be approximated by the linearization
holds. By these reformulations and the results of Section 4.1, the cost function (Eq. 21) can be rewritten, thus the minimization task
subject to
with
can be formulated. All variables denoted by
4.3.1 Computational Complexity
The shown algorithms are implemented in Matlab using Mosek (MOSEK ApS, 2019) and the interface Yalmip (Löfberg, 2004). The controller design is performed offline using the algorithms. Therefore, computational time is not a limiting factor and not shown in detail. The number of iterations and the computation time depends on the order of the closed loop, the size and number of the decision variables and the number of vertex matrices. However, each calculation of the control parameters is done within a few seconds to minutes on a standard PC.
4.4 Improvements and Delimitation in Comparison to Preliminary Works and Existing Results
4.4.1 Parameter-Dependent Decision Variables
Due to the quadratic Lyapunov function, which is used for all nv extremal realizations
4.4.2 LMI Methods
The main disadvantage of established LMI design methods for discrete-time systems from the literature (see for example de Oliveira et al. (1999); De Oliveira et al. (2002)) is the need of a change of variables to convert the nonlinear matrix inequality into LMIs. By the iterative procedure used in this paper, the closed loop system matrix remains in its original form in the design procedure. This makes it possible to apply the method on a myriad of different types of closed loops, such as PID structures or observer-based feedback controllers and their combinations within a uniform approach, whereas other methods are solely applicable to one particular controller type. The numerical effort of the iteration rule is classified as acceptable, due to the fact that the method yields less conservative solutions, compared to existing standard methods. This is especially investigated in Dehnert et al. (2021) for saturated discrete-time linear systems. Furthermore, the observer and controller matrices can be structured independently of each other and independently of the Lyapunov matrix P without modifications of the LMI conditions. As a result, the applicability of LMI methods for real applications is increased, since a change of LMI conditions is avoided. This simplifies the design of different control structures for various real-world technical systems significantly.
The independence of the method on the actual controller types is generated by the formulation of the iteration rule. This makes it possible to avoid changing the control variables in additional LMI variables, such that
Algorithm 2 Offline Minimization of Sensitivity towards Noise (Stage 2)
5 Example: Overhead Traveling Crane
5.1 Modeling the Overhead Traveling Crane
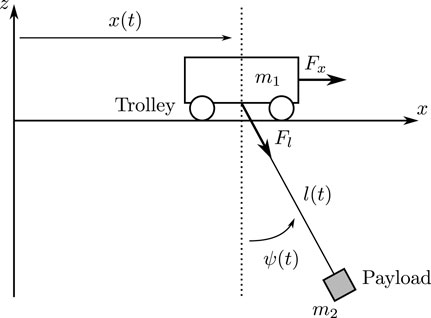
There exist several approaches to the modeling of overhead traveling cranes, which differ in complexity due to the number of inputs. As an example, Ackermann (2002) uses a simplified model, in which the rope length change cannot be manipulated. In Park et al. (2007), the modeling of a system with variable rope length is shown. In the following model, the rope length depends on a winch whose radius has to be taken into account, leading to an extension of the model from Park et al. (2007). The crane system is shown in Figure 3 and consists of a cart that can be moved along a rail with the help of a synchronous motor. The winch drive is mounted on the cart to move the weight suspended on a rope. It is assumed that the rope has vanishing elasticity. Incremental encoders are used to measure the position of the carriage, the pendulum movement and the rope length. These are the measurable outputs of the system and can be summarized in the vector
The mathematical model of the overhead traveling crane is given by the derivations of the equations of motion using Lagrange’s equations of second kind. The parameters of the model are the mass m1 = 5.5 kg of the cart, the payload with the mass m2 = 0.5 kg, the rope winch with the radius RT = 0.03 m and the mass moment of inertia θ = 0.000225 kg m2. Then, the Lagrange function is defined as the difference of kinetic and potential energy according to
with the kinetic energy
and the potential energy
where the gravitation constant is g
where Qj represents all external and non-conservative forces, which can be summarized in the vector
with the actuation forces Fx and Fl generated by the engine drum and the rope winch, respectively, as well as the friction constants of the cart
with the state vector
composed of the generalized variables (Eq. 27) and the corresponding generalized velocities
due to small pendulum angles were made. In addition, the second input for the rope length u2 has to be extended by
A possible realization of the quasi-linear representation (Eq. 28) can be given by the matrices
where the constants pi with i = 1, 2, … , 13 consist of the system parameters. These constants and their values are given in Appendix A. It is assumed that the states x and the inputs u are constrained by
In general, this allows to evaluate the respective matrix entries from Eq. 30 using interval arithmetic. For the control design, a polytopic representation in the form of Eq. 9 can be defined. For that purpose, the occurring states and nonlinearities are taken into account by introducing nδ = 5 independent parameters of the interval vector
which leads to the transformed matrices
If all vertices of the nδ independent parameters of Eq. 31 are considered, the polytopic representation
is obtained with
Due to the independence of the parameters δi, the system dynamics are embedded conservatively by this approach. Reducing the pessimism should be the subject of further researches. For example, smaller interval boxes connected in series could be used to reduce the over-approximation of Eq. 31 (Azuma et al. (1997)). If all parameters δi are monotonically decreasing or increasing functions of x, it is also possible to reduce the number of vertices (Azuma et al. (2000)).
In the following, the first order, explicit Euler approximation
with Ts = 0.015 s is used to discretize (31). This avoids the appearance of the matrix exponential function in the discretization, such that the convexity condition of Eq. 32 remains valid.
Figure 4 shows the advantage of the quasi-linear model in comparison to a linear model. For this comparison, the linear model was linearized at the operating point
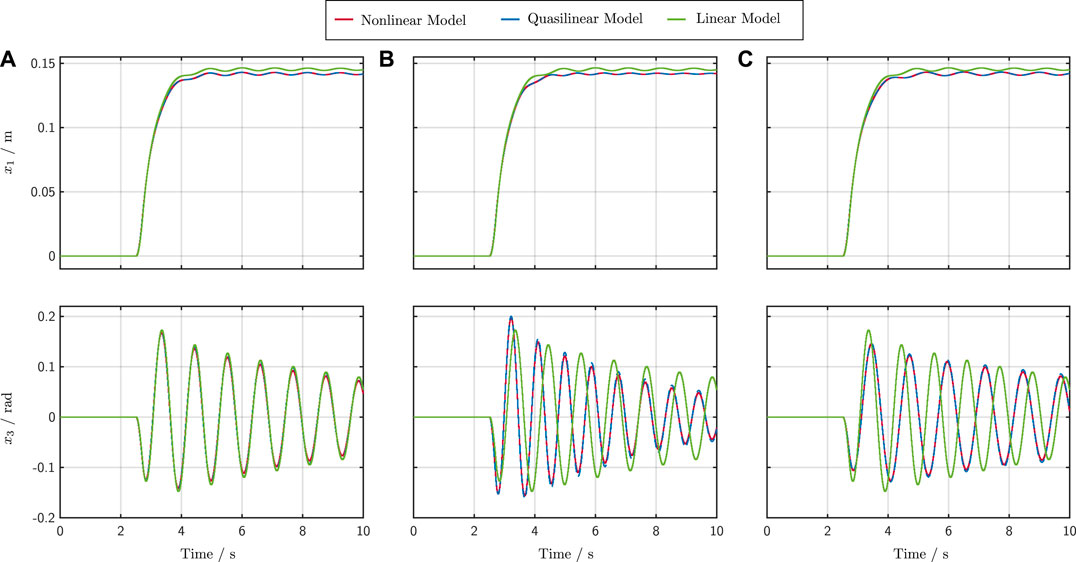
FIGURE 4. Simulation results for the nonlinear, the quasi-linear and the linear model with different rope length. Case (A) l = 0.3 m, Case (B) l = 0.2 m and Case (C) l = 0.4 m.
The nonlinear model from Appendix A is shown in red, the quasi-linear model in blue and the linear model in green. In Case (Figure 4A) all models have a constant rope length of l = 0.3 m, in Case (Figure 4B) l = 0.2 m and in Case (Figure 4C) l = 0.4 m. It can be observed that in the latter two cases large deviations occur due to the linearization and deviation from the operating point. Despite the simplifications made for small angles, a deviation from the operating point shows that the quasi-linear model behaves like the nonlinear one, while the linear model shows deviations. Due to the fact that the quasi-linear model is used, the presented approach is independent of the operating point. Only the upper and the lower bounds of the states must be known, which, however, is not a disadvantage, since these usually result from the system itself.
5.2 Control of the Overhead Traveling Crane
The presented method is to be compared with a standard approach. For this purpose, an LQG controller has been implemented additionally. Subsequently, the results of the LMI controller are compared with the standard LQG design procedure. The same control structure of both controllers ensures the comparability of the methods. Due to limited computing capacity of the implementation both controllers are linear with constant gains.
In the following, it is first described how the setting parameters of the LMI controller and the LQG controller can be selected systematically. Both LQG and LMI approaches are parameterized with the disturbance input matrices
Exactly introduced in Section 2, where the linearized model with Anom and Bnom is used in the observer (cf. Figure 1). For that purpose, and to design the LQG controller, the nonlinear model from Appendix A has been linearized at the operating point (Eq. 34) and discretized with Eq. 33. Subsequently, the LQG’s observer and controller were designed separately from each other. In the simulation shown later, which is equivalent to Figure 1 and uses the nonlinear model from Appendix A to represent the plant, the LQG controller exhibits a stable behavior during the simulation. However, due to the nonlinearities no guaranteed stability statement can be made (invalid separation theorem). Thus, there is no proof of stability for the LQG control in the nonlinear case. Furthermore, an optimal design of the LQG controller is not possible and the parameters have to be set individually and semi-empirically. To determine the parameters as systematically as possible, the covariance matrices for the design of the observer are given by
Furthermore, the controller parameterization in the LQG case was performed with the diagonal matrices
with μx,i = 1 and μu,i = 0.5.
Thus, the diagonal elements of the weighting matrices are normalized by the maximum value of the respective state or input.
For the LMI controller, there are two tuning parameters r and α, defined in Section 3.3. With these parameters, it is possible to manipulate the eigenvalue location of the extremal matrices (Eq. 31) and thus affect the dynamic behavior of the system. First, a suitable radius r is determined, with which a sufficient control gain K is available without providing high observer gains H. Therefore, α = 0 is placed and Algorithm 2 is used for various values of r. The resulting evaluation is shown in Figure 5. The parameter r represents an upper estimate of the spectral radius of all extremal matrices
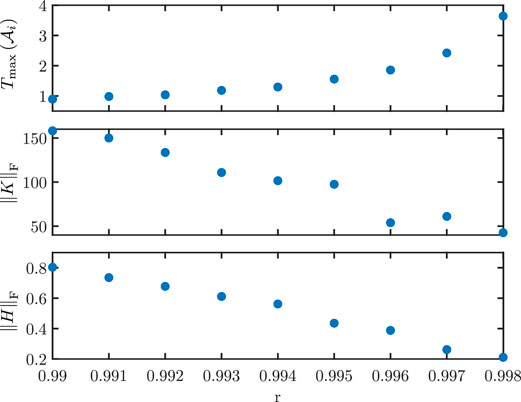
FIGURE 5. r-dependency of the maximum time constant
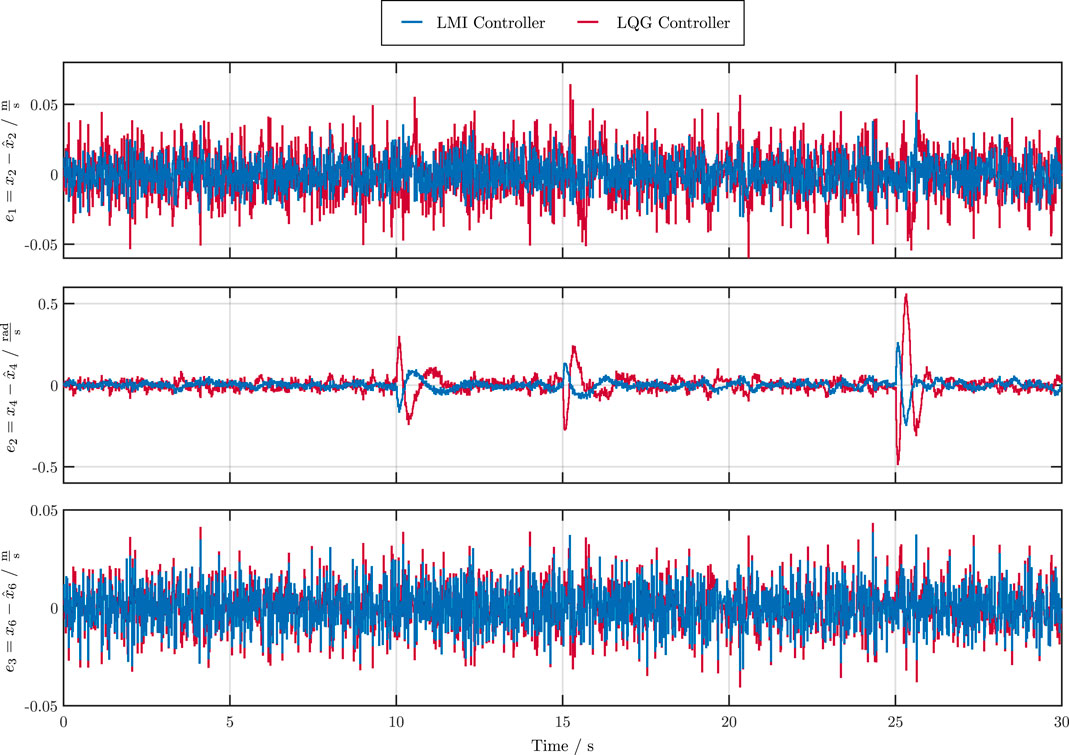
Exemplarily, a simulation result for Case 2 is shown in Figure 6; Figure 7 in comparison to the LQG controller. During the simulation, a predefined, piecewise constant, tracking profile r was applied to the overhead traveling crane system. Figure 6 shows the tracking behavior and Figure 7 the observer errors. In the following, the root mean square deviations (RMSE) values
with N = 30 s/Ts = 2000 of the simulation shown in Figure 6; Figure 7 are taken into account. Furthermore, the maximum control variables are evaluated. For this purpose, the simulation was carried out for all four cases. The results compared to the LQG controller of this analysis are shown in Table 1.
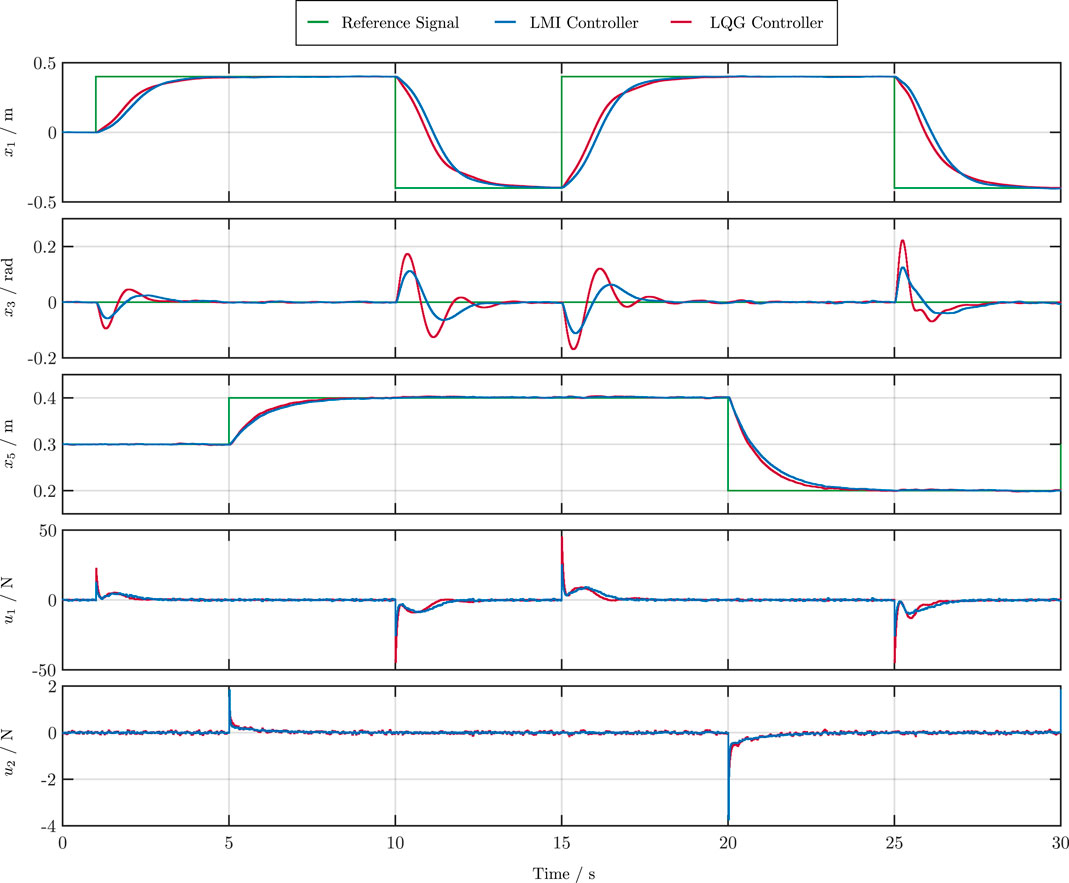
FIGURE 6. Tracking performance of the measurable states x1, x3 and x5 and control inputs u1 and u2 for the LMI and LQG controller.

TABLE 1. Comparison of the RMSE values (Eqs 35, 36) and the maximum control variables max |u| for (α + r = 0.993).
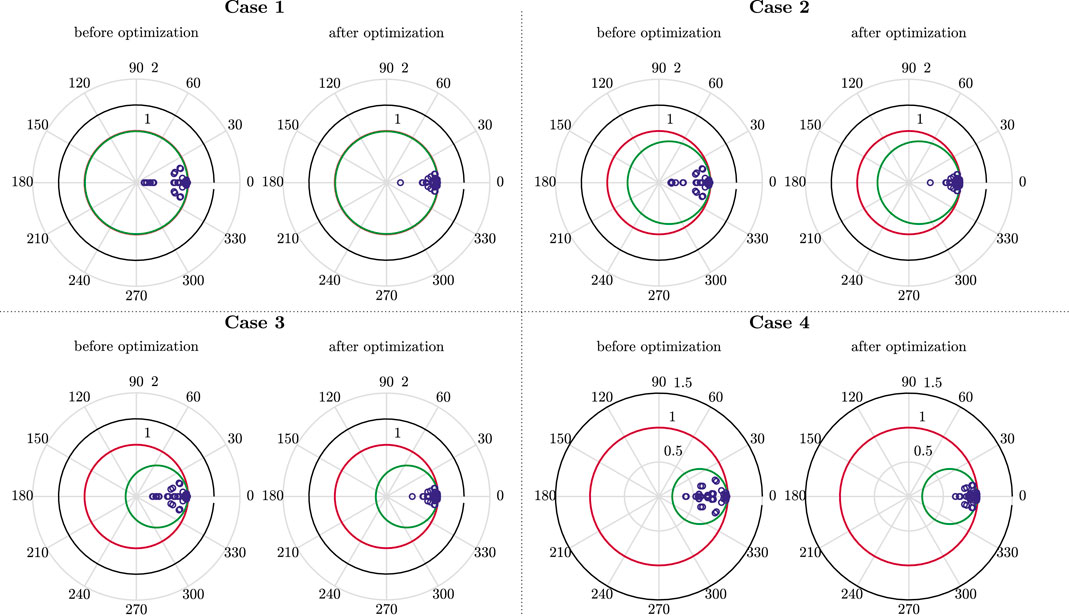
The control performance of all four cases is similar to the LQG controller. However, the observer errors of the LMI controllers (Case 1—Case 4) are strictly smaller than the LQG observer error (see also Figure 7). Furthermore, the reduction of the radius r leads to significantly smaller control variables without negatively affecting the control and observer behavior. Next, it is shown how the optimization (Eq. 22) affects the eigenvalues of the extremal matrices. For this purpose, Figure 8 shows the respective eigenvalue locations (Case 1—Case 4) before and after the optimization. The optimization effectively suppresses system noise. The proposed algorithm achieves this by reducing the gains, thus placing the eigenvalues further to the right of the r boundary. In a final summary, a further comparison of all LMI controllers (Case 1—Case 4) to the LQG approach is shown in Table 2. Therefor, all controllers are rated in terms of the RMSE values
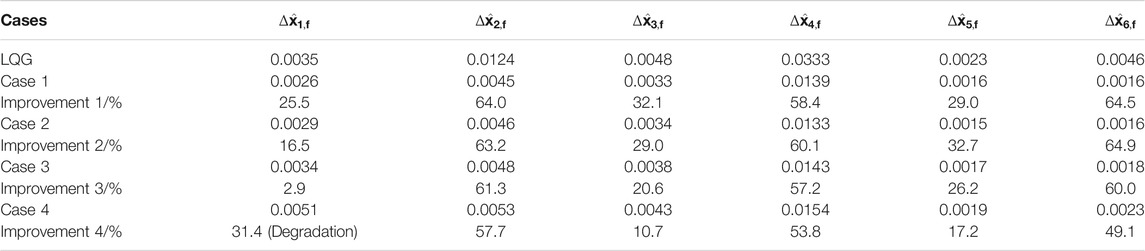
TABLE 2. Comparison for all controllers in terms of the RMSE values (Eq. 37) from all observer states
Quantifying all observer states
6 Conclusions and Outlook
In this article, a design of a linear observer-based state feedback controller based on an iterative LMI approach was developed for discrete-time systems in the presence of stochastic noise. Nonlinearities were taken into account by forming a polytopic quasi-linear representation. The verification of closed loop stability under disturbances could be provided by a discretized version of the Ito differential operator, whereby the noise was already taken into account in the control design. In addition, the proof of convergence for the method could be provided. The proposed method can also be applied to controllers with different structures without modifying the method. The example of the overhead traveling crane could be used to demonstrate the advantages of the new method in comparison with a standard LQG controller. This means that only a few setting parameters are required, which can be used for systematically adjusting the controller and observer gains. Furthermore, the impact of noise could be significantly reduced.
Further work will deal with an optimization of the control parameters to achieve enhanced damping properties and smaller tracking errors. This could include filter-based PID-controllers and parameter-dependent Lyapunov functions. Additionally, the observer matrices Anom and Bnom can be optimized if they are chosen as free decision variables. On the one hand, this implies a less conservative model in which no or less unphysical vertices exist. On the other hand, the optimized observer matrices may cause unphysical behavior in control operation. This effect can be reduced, for example, by improving the convex enclosure of the quasi-linear model, similar to the interval multisection applied in Rauh et al. (2017) for the implementation of a gain-scheduling controller, such that the over-approximation is reduced. In addition, it will be investigated how actuator saturations can be included in the optimization and how they affect it.
Data Availability Statement
Data are contained within the article.
Author Contributions
Conceptualization, RD and AR; Investigation, RD, MD, SL, and AR; Software, RD, MD, SL, and AR; Validation, RD, MD, SL, AR, and BT; Writing-original draft, RD, MD, SL, AR, and BT; Writing-review and editing, RD, MD, SL, AR, and BT. All authors have read and agreed to the published version of the manuscript.
Funding
This article is funded by the Publication Fund for Open Access Publications of the University of Wuppertal.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We acknowledge support from the Open Access Publication Fund of the University of Wuppertal.
Appendix
The nonlinear equations of the overhead traveling crane system are given by
They can be simplified with (29) to the quasi-linear model (31) with the constant terms
References
Azuma, T., Watanabe, R., and Uchida, K. (1997). “An Approach to Solving Parameter-dependent LMI Conditions Based on Finite Number of LMI Conditions,” in Proceedings of the American Control Conference, Albuquerque, NM, June 6, 1997. doi:10.1109/acc.1997.611851
Azuma, T., Watanabe, R., Uchida, K., and Fujita, M. (2000). A New LMI Approach to Analysis of Linear Systems Depending on Scheduling Parameters in Polynomial Forms. at-Automatisierungstechnik 48 (4), 199. doi:10.1524/auto.2000.48.4.199
Boyd, S., El-Ghaoui, L., Feron, E., Balakrishnan, V., and Yaz, E. (1997). Linear Matrix Inequalities in System and Control Theory. Philadelphia: SIAM: studies in applied mathematics.
Coetsee, J. (1994). Control of Nonlinear Systems Represented in Quasilinear Form. Massachusetts: Massachusetts Institute of Technology.
Daafouz, J., and Bernussou, J. (2001). Parameter Dependent Lyapunov Functions for Discrete Time Systems with Time Varying Parametric Uncertainties. Syst. Control. Lett. 43, 355–359. doi:10.1016/s0167-6911(01)00118-9
de Oliveira, M. C., Bernussou, J., and Geromel, J. C. (1999). A New Discrete-Time Robust Stability Condition. Syst. Control. Lett. 37, 261–265. doi:10.1016/s0167-6911(99)00035-3
De Oliveira, M. C., Geromel, J. C., and Bernussou, J. (2002). Extended H 2 and H Norm Characterizations and Controller Parametrizations for Discrete-Time Systems. Int. J. Control. 75, 666–679. doi:10.1080/00207170210140212
Dehnert, R. (2020). Entwurf robuster Regler mit Ausgangsrückführung für zeitdiskrete Mehrgrößensysteme. Wiesbaden: Springer Vieweg.
Dehnert, R., Lerch, S., Grunert, T., Damaszek, M., and Tibken, B. (2021). “A Less Conservative Iterative LMI Approach for Output Feedback Controller Synthesis for Saturated Discrete-Time Linear Systems,” in 25th International Conference on System Theory, Control and Computing (ICSTCC), Iasi, Romania, October 20–23, 2021. doi:10.1109/icstcc52150.2021.9607288
Dehnert, R., Lerch, S., and Tibken, B. (2020). “Robust Anti Windup Controller Synthesis of Multivariable Discrete Systems with Actuator Saturation,” in 2020 IEEE Conference on Control Technology and Applications (CCTA), Montreal: QC, Canada, August 24–26, 2020, 581–587. doi:10.1109/ccta41146.2020.9206346
Dehnert, R., Tibken, B., Paradowski, T., and Swiatlak, R. (2015). “Multivariable PID Controller Synthesis of Discrete Linear Systems Based on LMIs,” in 2015 IEEE Conference on Control Applications (CCA), Sydney, NSW, Australia, September 21–23, 2015, 1236–1241. doi:10.1109/cca.2015.7320781
Furtat, I. (2018). Control of Nonlinear Systems with Compensation of Disturbances under Measurement Noises. Int. J. Control. 93, 1–23. doi:10.1080/00207179.2018.1503723
Grunert, T., Dehnert, R., Kummert, A., Tibken, B., and Fielsch, S. (2019). “Gain Scheduled Control of Bounded Multilinear Discrete Time Systems with Uncertanties: An Iterative LMI Approach,” in 2019 IEEE 58th Conference on Decision and Control (CDC), Nice, France, December 11–13, 2019, 5199–5205. doi:10.1109/cdc40024.2019.9029623
Ibrir, S. (2008). Static Output Feedback and Guaranteed Cost Control of a Class of Discrete-Time Nonlinear Systems with Partial State Measurements. Analysis 68 (7), 1784–1792. doi:10.1016/j.na.2007.01.011
Kheloufi, H., Zemouche, A., Bedouhene, F., and Souley-Ali, H. (2014). “Robust H∞ Observer-Based Controller for Lipschitz Nonlinear Discrete-Time Systems with Parameter Uncertainties,” in 53rd IEEE Conference on Decision and Control, Los Angeles, CA, December 15–17, 2014, 4336–4341.
Lerch, S., Dehnert, R., Damaszek, M., and Tibken, B. (2021a). “Anti Windup PID Control of Discrete Systems Subject to Actuator Magnitude and Rate Saturation: An Iterative LMI Approach,” in 25th International Conference on System Theory, Control and Computing (ICSTCC), Iasi, Romania, October 20–23, 2021. doi:10.1109/icstcc52150.2021.9607157
Lerch, S., Dehnert, R., Damaszek, M., and Tibken, B. (2021b). “Static Output Feedback Controller Design of Discrete Systems Subject to Actuator Magnitude and Rate Saturation,” in 25th International Conference on System Theory, Control and Computing (ICSTCC), Iasi, Romania, October 20–23, 2021. doi:10.1109/icstcc52150.2021.9607245
Löfberg, J. (2004). “Yalmip: A Toolbox for Modeling and Optimization in MATLAB,” in 2004 IEEE International Conference on Robotics and Automation (IEEE Cat. No.04CH37508), New Orleans, LA, April 26–May 1, 2004 (New Orleans, LA: IEEE), 284–289.
MOSEK ApS (2019). The MOSEK Optimization Toolbox for MATLAB Manual. Version 9.0. Available at: https://docs.mosek.com/9.3/faq.pdf.
Park, H., Chwa, D., and Hong, K.-S. (2007). A Feedback Linearization Control of Container Cranes: Varying Rope Length. Int. J. Control Automation, Syst. 5, 379–387.
Peaucelle, D., and Ebihara, Y. (2014). LMI Results for Robust Control Design of Observer-Based Controllers, the Discrete-Time Case with Polytopic Uncertainties. IFAC Proc. Volumes 47, 6527–6532. doi:10.3182/20140824-6-za-1003.00218
Phat, V. N., and Ratchagit, K. (2011). Stability and Stabilization of Switched Linear Discrete-Time Systems with Interval Time-Varying Delay. Nonlinear Anal. Hybrid Syst. 5, 605–612. doi:10.1016/j.nahs.2011.05.006
Ratchagit, K., and Phat, V. N. (2011). Robust Stability and Stabilization of Linear Polytopic Delay-Difference Equations with Interval Time-Varying Delays. Neural, Parallel and Scientific Computations 19, 361–372.
Rauh, A., Dehnert, R., Romig, S., Lerch, S., and Tibken, B. (2021). Iterative Solution of Linear Matrix Inequalities for the Combined Control and Observer Design of Systems with Polytopic Parameter Uncertainty and Stochastic Noise. Algorithms 14, 205. doi:10.3390/a14070205
Rauh, A., Prabel, R., and Aschemann, H. (2017). “Oscillation Attenuation for Crane Payloads by Controlling the Rope Length Using Extended Linearization Techniques,” in 2017 22nd International Conference on Methods and Models in Automation and Robotics (MMAR), Miedzyzdroje, Poland, August 28–31, 2017, 307–312. doi:10.1109/mmar.2017.8046844
Rauh, A., Romig, S., and Aschemann, H. (2018). “When Is Naive Low-Pass Filtering of Noisy Measurements Counter-productive for the Dynamics of Controlled Systems,” in 2018 23rd International Conference on Methods Models in Automation Robotics (MMAR), Miedzyzdroje, Poland, August 27–30, 2018, 809–814.
Rauh, A., and Romig, S. (2021). Linear Matrix Inequalities for an Iterative Solution of Robust Output Feedback Control of Systems with Bounded and Stochastic Uncertainty. Sensors 21, 3285. doi:10.3390/s21093285
Rauh, A., Senkel, L., Gebhardt, J., and Aschemann, H. (2014). “Stochastic Methods for the Control of Crane Systems in Marine Applications,” in 2014 European Control Conference (ECC), Strasbourg, France, June 24–27, 2014, 2998–3003. doi:10.1109/ecc.2014.6862370
Rauh, A. (2017). Sensitivity Methods for Analysis and Design of Dynamic Systems with Applications in Control Engineering: Feedforward Control – Feedback Control – Robust Control – State Estimation. Aachen: Shaker.
Sadabadi, M., and Karimi, A. (2013). An LMI Formulation of Fixed Order H∞ and H2 Controller Design for Discrete-Time Systems with. Polytopic Uncertainties 75, 2453–2458. doi:10.1109/CDC.2013.6760248
Scherer, C., and Weiland, S. (1994). Linear Matrix Inequality in Control. Germany/The Netherlands: Department of Mathematics University of Stuttgart/Department of Electrical Engineering Eindhoven University of Technology.
Schulz, G. (1933). Iterative Berechung der reziproken Matrix. Z. Angew. Math. Mech. 13, 57–59. doi:10.1002/zamm.19330130111
Senkel, L., Rauh, A., and Aschemann, H. (2016). Experimental and Numerical Validation of a Reliable Sliding Mode Control Strategy Considering Uncertainty with Interval Arithmetic. Editors A. Rauh, and L. Senkel (Cham, Switzerland: Springer International Publishing), 87–122. chap. 4 part I. doi:10.1007/978-3-319-31539-3_4
Soleymani, F. (2013). On a Fast Iterative Method for Approximate Inverse of Matrices. Commun. Korean Math. Soc. 28, 407–418. doi:10.4134/ckms.2013.28.2.407
Wahab, A. (1994). Pole Assignment in a Specified Circular Region Using a Bilinear Transformation onto the Unit Circle. Int. J. Syst. Sci. 25 (7), 1113–1125. doi:10.1080/00207729408949265
Yotha, N., and Mukdasai, K. (2013). New Delay-dependent Robust Stability Criterion for LPD Discrete-Time Systems with Interval Time-Varying Delays. Discrete Dyn. Nat. Soc. 2013, 929725. doi:10.1155/2013/929725
Yucelen, T., Sadahalli, A. S., and Pourboghrat, F. (2010). “Active Noise Control in a Duct Using Output Feedback Robust Control Techniques,” in Proceedings of the 2010 American Control Conference, Baltimore, MD, June 30–July 2, 2010, 3506–3511. doi:10.1109/acc.2010.5530942
Zemouche, A., Zerrougui, M., Boulkroune, B., Rajamani, R., and Zasadzinski, M. (2016). “A New LMI Observer-Based Controller Design Method for Discrete-Time LPV Systems with Uncertain Parameters,” in 2016 American Control Conference (ACC), Boston, MA, July 6–8, 2016, 2802–2807. doi:10.1109/acc.2016.7525343
Keywords: discrete-time systems, stochastic disturbance, robust control, linear matrix inequaities (LMI), optimization, polytopic modeling
Citation: Dehnert R, Damaszek M, Lerch S, Rauh A and Tibken B (2022) Robust Feedback Control for Discrete-Time Systems Based on Iterative LMIs with Polytopic Uncertainty Representations Subject to Stochastic Noise. Front. Control. Eng. 2:786152. doi: 10.3389/fcteg.2021.786152
Received: 29 September 2021; Accepted: 29 November 2021;
Published: 09 February 2022.
Edited by:
Mudassir Rashid, Illinois Institute of Technology, United StatesReviewed by:
Fotis Nicholas Koumboulis, National and Kapodistrian University of Athens, GreeceGrienggrai Rajchakit, Maejo University, Thailand
Copyright © 2022 Dehnert, Damaszek, Lerch, Rauh and Tibken. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Robert Dehnert, ZGVobmVydEB1bmktd3VwcGVydGFsLmRl
†Present addresses: Andreas Rauh, Department of Computing Science, Carl von Ossietzky Universität Oldenburg, Group: Distributed Control in Interconnected Systems, Oldenburg, Germany
 Robert Dehnert
Robert Dehnert Michelle Damaszek
Michelle Damaszek Sabine Lerch
Sabine Lerch Andreas Rauh
Andreas Rauh Bernd Tibken
Bernd Tibken