- 1Department of Automation, Tsinghua University, Beijing, China
- 2Department of Computer Science, University of Oxford, Oxford, United Kingdom
- 3Department of Automation, Shanghai Jiao Tong University, Shanghai, China
This paper reviews the recent works on multiplayer reach-avoid (M-RA) differential games between two adversarial teams in a game region which is split into a goal region and a play region. The pursuit team aims to protect the goal region from the evasion team by cooperatively capturing the evaders which start from the play region and strive to enter the goal region. We provide a selective overview of algorithms and theoretical results for multiplayer reach-avoid differential games. Specifically, we focus on point mass holonomic players that can move freely in the game region and have simple motions as Rufus Isaacs states. We describe how the challenges due to high-dimensional continuous joint action and state spaces, as well as complex cooperations and competitions among players, can be properly resolved by a combination of qualitative and quantitative analysis of small-scale games and optimal task allocation. We finally point out the limitations of the current works and identify fruitful future research directions on theoretical studies of multiplayer reach-avoid differential games.
1 Introduction
Multi-robot systems, including self-driving cars and unmanned aerial vehicles, are becoming a topic of great interest. These systems have significant advantages over a single robot because they can share the workload and cooperatively complete complicated tasks, such as automated package delivery, disaster survivors search, infrastructure protection and region patrolling (Chen et al., 2016; Shishika and Kumar, 2018; Shishika and Kumar, 2020; Yan et al., 2022; Yan et al., 2019b; Yan et al., 2020; Shishika et al., 2020; Shishika et al., 2021; Deng et al., 2021; Guerrero-Bonilla et al., 2021; Lee and Bakolas, 2021; Von Moll et al., 2022b). Of particular relevance to this paper is a class of scenarios related to security and cooperation-competition applications. Specifically, we consider multiplayer reach-avoid (M-RA) differential games, in which multiple robots are used to protect a goal region of interest against a group of malicious robots which aim to enter the goal region without being captured.
Compared with the classical pursuit-evasion games in which the capture is the only competition goal, M-RA differential games are more complicated and have more practical significance, as the evaders aim to reach a target set and avoid the capture at the same time. According to the degree of abstraction and physical constraints, the players can be described by different mathematical models, such as simple motion (Isaacs, 1965), Dubins car with the minimum turning radius (Dubins, 1957), and Reeds–Shepp car with the backward move (Reeds and Shepp, 1990). This review focuses on the simple motion, or the first-order integrator with bounded inputs in the language of control theory, in which the player moves with a bounded speed and can change its heading instantaneously. Such a model is a suitable abstraction for mobile robots or robotic vehicles which have speed limitations and high maneuverability, for instance, humanoid robots, quadrotor unmanned aerial vehicle and small underground vehicles, and due to its simplicity, this model has been extensively studied with fruitful results in differential games (Fisac et al., 2015; Chen et al., 2018; Ibragimov et al., 2018; Yan et al., 2020; Fu and Liu, 2021; Yan et al., 2021a; Yan et al., 2021b; Liang et al., 2022; Wang et al., 2022; Yan et al., 2022).
The challenges of solving M-RA differential games with simple motions can be broadly divided into two categories: non-unique terminal conditions, and complex cooperation and competition pattern (Yan et al., 2020; Yan et al., 2022). Non-unique terminal conditions, where the game could end up with either capture or entry into the goal region, largely complicate the strategy synthesis which involves integrating backward trajectories from differential terminal surfaces (Isaacs, 1965). This results from a lack of systematic analysis methods in the presence of complicated singular surfaces occurring in the backward computation. At the inter-agent level, grouping players into two opposing teams is intrinsically accompanied with complex cooperation within team members and goal-driven inter-team competition. For instance, it is not hard to imagine a scenario where cooperation between two pursuers is necessary for winning against an evader while any one of them fails to do so (Yan et al., 2020). Like prey animals, some evaders may lure the pursuers away from the goal region or sacrifice themselves through being captured such that the other evaders successfully reach the goal region.
This review is concerned with the M-RA differential games, with a particular interest in simple motions, which were first discussed by (Mitchell et al., 2005; Margellos and Lygeros, 2011; Zhou et al., 2012) and then extended into many variations and practical applications (Huang et al., 2014; Selvakumar and Bakolas, 2019; Fu and Liu, 2020). The problem is closely related to lifeline games (Garcia et al., 2019b; Yan et al., 2021a; Yan et al., 2021b; Chen and Yu, 2022), two-target differential games (Blaquière et al., 1969; Olsder and Breakwell, 1974; Pachter and Getz, 1980; Getz and Pachter, 1981) and target guarding differential games (Mohanan et al., 2018). Moreover, the problem has high relevance to scenarios involving underground vehicles guarding a building, unmanned aerial vehicles patrolling against illegal poachers and unmanned surface vehicles patrolling around a prohibited water area.
The remainder of this paper is organized as follows. Section 2 introduces the background on simple motion, game elements and core concepts. In Section 3, we review two most common methods in M-RA differential games. We detail the barrier construction in Section 4 for several interesting M-RA differential games. We present an integer linear programming formulation for task allocation in Section 5. We review three classical strategies in Section 6. In Section 7, we discuss the limitations in the literature and possible directions for future research. Finally, Section 8 concludes the paper.
2 Background
M-RA differential games draw concepts from the fields of differential games, reachability, control and robotics. In this section, we first introduce the system dynamics, assumptions and game elements used throughout the rest of the paper in Section 2.1. Then, Section 2.2 contains a representative, but not complete, discussion of the possible applications. We conclude the section with the core concepts in differential games for qualitative and quantitative analysis in Section 2.3.
2.1 Simple motion and game elements
We consider Np + Ne players partitioned into two teams, a team of Np pursuers (also called defenders),
where
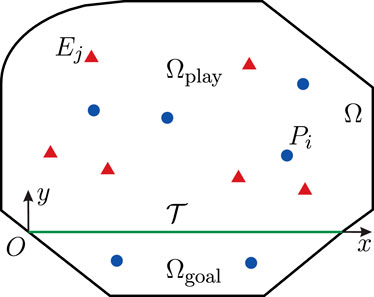
FIGURE 1. Multiplayer reach-avoid (M-RA) differential games, where multiple evaders (red) aim to enter the goal region, while the pursuers (blue) are tasked to protect the goal region by capturing the evaders (Yan et al., 2020).
2.2 Applications
As the players’ objectives imply, M-RA differential games have high relevance to the adversarial scenarios in which players compete or cooperate for a set of states in the game state space. For example, mobile ground vehicles can be employed to defend a building of interest so as to minimize some metric, such as the number of malicious vehicles entering the building (Fu and Liu, 2020; Shishika and Kumar, 2020; Shishika et al., 2021). In wildlife protection, the use of unmanned aerial vehicles against illegal poachers is a promising alternative to typical field methods. As more and more attacking boats occur in many waterside cities, deploying patrolling boats is a sensible and feasible solution to protecting stationary ferries. In path planning, a group of vehicles aim to get into some goal region or escape from a bounded region through an exit, while avoiding dangerous situations, such as collisions with moving obstacles (Yan et al., 2019b; Yan et al., 2020; Yan et al., 2022).
2.3 Barriers, winning regions and strategies
In general, the problems in M-RA differential games are classified into two categories: game of kind and game of degree. In a game of kind, the goal is, given a winning condition, to determine which team (player) can win the game, and therefore the game solution is win or lose for a team (player). If the game winner is known with the result of the game of kind, the natural question to ask is how to design strategies so as to ensure the winning and optimize some metric simultaneously, for instance, the distance to the goal region from the perspective of the evasion team if the captured cannot be avoided. Technically, such a problem leads to a game of degree, in which the focus is, given a payoff function, to find the (saddle-point) equilibrium strategies for the players.
2.3.1 Barriers and winning regions
In order to solve the game of kind systematically, Isaacs introduced the concept of barrier (Isaacs, 1965), a surface that divides the entire game state space into two disjoint parts: pursuit winning region (PWR) and evasion winning region (EWR). With a particular interest in the case of multiple pursuers against one evader, the PWR is the set of initial states, from which the pursuit team can ensure the capture before the evader enters the goal region. The EWR, complementary to the PWR, is the set of initial states, from which the evader guarantees to reach the goal region regardless. Naturally, constructing the barrier becomes the core of solving a game of kind. Formally, the PWR
which can be also described by fixing the pursuers/evaders’ positions. Due to the usefulness of knowing the game winner before the game actually runs, huge progress has been made on the study of barriers (Yan et al., 2017; Shishika and Kumar, 2018; Yan et al., 2019a; Shishika et al., 2020; Yan et al., 2020; Liang et al., 2022; Lee and Bakolas, 2021; Yan et al., 2021a; Yan et al., 2021b; Von Moll et al., 2022b; Chen and Yu, 2022).
2.3.2 Strategies
Regarding the game of degree, the strategy type has a huge impact on the approaches of seeking equilibrium strategies and the inherent computational complexity. In a nutshell, a strategy (policy) of a player resolves the choices in each game state based on its available information at the moment. There are four basic types of strategies for the players in differential games–open loop, state feedback, non-anticipative and anticipative strategies (Mitchell et al., 2005). An open loop strategy requires that each player decides its entire controls u(τ) for all
3 Methods
We begin our discussion by reviewing the two most common methods, geometric method and Hamilton-Jacobi-Isaacs (HJI) method, that are widely used in M-RA differential games with simple motions, to solve the induced games of kind and games of degree. The geometric method leverages the player dynamics, i.e., simple motion, under which the optimal trajectory of the player is a straight line in many cases (Isaacs, 1965; Yan et al., 2019b; Yan et al., 2020; Yan et al., 2022). The HJI method is more general and is able to handle with more complicated player dynamics. However, it also suffers from high computational complexity Mitchell et al. (2005); Margellos and Lygeros (2011); Chen et al. (2018); Fisac et al. (2015).
3.1 Geometric method
If the optimal trajectories of the players are known to be composed of straight lines, which is common under the simple motion, solving the game is closely related to constructing the dominance regions (Isaacs, 1965; Oyler et al., 2016), where a point in the game region is said to be dominated by one of the players if that player is able to reach the point before the other players, regardless of the other players’ best effort (the capture radius is also taken into account). A dominance region is then the set of all points dominated by a particular player. We first introduce two classical and predominant dominance regions: Voronoi cell and Apollonius circle, and then present a more general function-based dominance region.
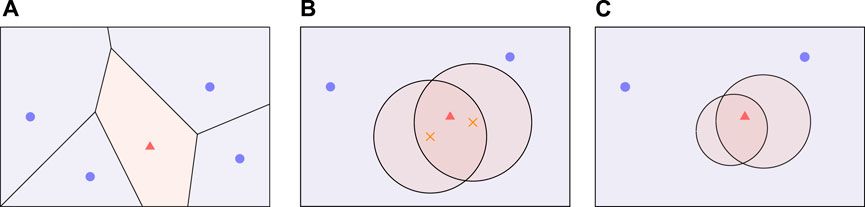
FIGURE 2. Dominance regions for multiple pursuers against one evader: Voronoi cell (A), Apollonius circle (B) and function-based (C), where the crosses are the centers of the Apollonius circles.
3.2 Hamilton-Jacobi-Isaacs method
Let
Since the M-RA differential game is zero-sum in general, the corresponding value function V(x) is the unique viscosity solution to the HJI equation
where the Hamiltonian is defined as
More specifically, we define the minimax Hamiltonian as
If V(x) is twice continuously differentiable, the equilibrium trajectories are determined by the following ELODE:
where f* is the stacked dynamics f under the minimax controls. Such equilibrium trajectories are called regular equilibrium trajectories and the corresponding optimal controls are called regular equilibrium controls. The ELODE (6) reveals that for M-RA differential games with simple-motion players, the regular equilibrium trajectories are straight lines and the regular equilibrium controls are constant, which validates geometric methods in such games. Along the regular equilibrium trajectories, it holds that
implying that the value function is constant.
The HJI method solves an M-RA differential game by integrating the ODE system (6) in inverse time initially from the boundary of
where
Apart from the computation above, the HJI method is also used as a tool to verify the value function sufficiently. Letting
1. It is continuously differentiable everywhere over
2. It satisfies the HJI Eq. 4 over
3. It equals to Φ(x) on the boundary of
4 Construction of barriers and winning regions
In this section, we review the barrier construction for multiple/single player(s) against one opponent in five interesting and representative M-RA differential games by detailing the game description and barrier construction individually. We will omit the resulting winning regions which interested readers can find in the related papers, as by definition, they follow from the barriers directly.
4.1 Two-dimensional bounded convex game region
4.1.1 Game description
The game region Ω is a two-dimensional (2D) closed convex region and the splitting hypersurface
4.1.2 Barrier construction
For this game, let x = [x,y]⊤ for any vector
and
where
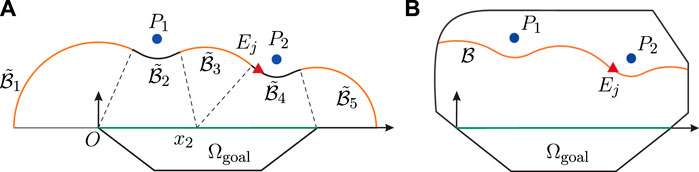
FIGURE 3. Barrier construction for two-dimensional (2D) bounded convex game region. (A) No boundary for play region; (B) Bounded play region.
4.2 Three-dimensional game region
4.2.1 Game description
The game region Ω is the whole three-dimensional (3D) space and
4.2.2 Barrier construction
We focus on the barrier for the pursuit team against one evader. The capture strategy in Yan et al. (2022) indicates that the barrier is equivalent to the case where the dominance region of the evader which is proved to be strictly convex before the capture occurs, is tangent to the goal region. Formally, the barrier can be computed as follows
Since Yan et al. (2022) proves that in Ej’s dominance region, the unique point closest to the goal region can be determined by at most three pursuers, checking the tangent property for all pursuer combinations with no more than three pursuers would be sufficient to cover all points of the barrier, improving the computational efficiency drastically. The extension to a convex play region with an exit is also discussed in Yan et al. (2022).
4.3 Limited evasion lifetime
4.3.1 Game description
The game region Ω is the whole 2D plane and
4.3.2 Barrier construction
We focus on the barrier for one pursuer against one evader. First, we compute the barrier for the game without lifetime limitation which directly follows from Section 4.1, as indicated by
and
The variable x* in (11) is as follows:
The complete barrier

FIGURE 4. Barrier construction for 2D reach-avoid differential games with limited evasion lifetime (Yan et al., 2021b).
4.4 View of the evasion team
4.4.1 Game description
The game region Ω is the 2D plane and
4.4.2 Barrier construction
The barrier in this case splits the state space into three disjoint parts: Under the players’ optimal strategies, the first one corresponds to no captured evader, the second corresponds to one captured evader and the third corresponds to two captured evaders. Since it takes the pursuer some time to capture the first-pursued evader (if the capture is guaranteed) before pursuing the second-pursued evader, the Apollonius circle is generalised to tackle the scenario where the pursuer starts to pursue the evader when the latter has already moved for a time interval δ. Formally, the dominance region accounting for a time difference between the pursuit and evasion of P and Ej, called δ-Apollonius circle, is defined as follows
If Ej moves freely before P pursues it for a time period δ, then based on the δ-Apollonius circle, the barrier is computed as follows
where
and the barrier is illustrated in Figure 5B. Then, the barrier for two evaders against one pursuer follows by combining the common one-versus-one barrier without time difference and the proposed one-versus-one barrier with a time difference, where an aiding strategy between two evaders may occur. More specifically, if P pursues E1 first and then E2, the aiding strategy describes that E1 moves away from the goal region to aid E2’s evasion, such that E2 reaches the best relative position to escape when E1 is captured. This strategy implies that one evader may need to sacrifice itself to save the other evader, which is frequently observed between prey animals. As an illustration, Figure 5C indicates that if P pursues E1 first, then the game space is divided by the orange curve into two disjoint regions

FIGURE 5. Barrier construction for 2D reach-avoid differential games with one pursuer and two evaders (Yan et al., 2021a). (A) Small time difference Δ; (B) Large time difference Δ; (C) Winning spaces when P pursues E1 first; (D) Winning spaces when P pursues E2 first.
4.5 The lady in the lake with multiple pursuers
4.5.1 Game description
We extend the classical game the Lady in the Lake (Isaacs, 1965) to multiple pursuers. The game region Ω is the whole two-dimensional plane and

FIGURE 6. The Lady in the Lake with multiple pursuers. Game description (A); the barrier does not exist (B) and the barrier occurs (C) for one pursuer and one evader.
4.5.2 Barrier construction
Since the pursuers are uniformly distributed, the goal of the evader is to penetrate
If α < α0, then
and ρ0 is the solution to the equation in (17) for θi = π/Np. We depict one pursuer case for an illustration. In Figure 6B, α < α0 holds and the red curve splits the game space into ϒ2 and ϒ3, such that E has different strategies separately as stated above, where ϒ1 is the circle that E should enter if it lies in ϒ2. In Figure 6C, α ≥ α0 holds and the (orange) barrier emerges. We refer interested readers to Yan et al. (2017) for details.
5 Task allocation
Task allocation, a popular task planning strategy, focuses on assigning groups of simple tasks to individual players for execution. When applied to M-RA differential games, the player configurations, availabilities and capabilities need to be considered (Smith et al., 2009; Bajaj and Bopardikar, 2019; Yan et al., 2020; Yan et al., 2022; Bajaj et al., 2021; Antonyshyn et al., 2022; Velhal et al., 2022). In this section, we first introduce an integer linear programming formulation for capturing the most number of evaders in Section 5.1 and then propose a polynomial approximation algorithm in Section 5.2.
5.1 Integer linear programming
From the pursuit team’s perspective, the goal is, for each evader, to designate a pursuit coalition which is capable of capturing the evader before it enters the goal region. If the barrier of the game is constructed, a pursuit coalition is adequate if the evader and the pursuit coalition lie in the PWR. In this way, we collect the outcomes of all pursuit coalition and evader pairs prior to the game execution. Then, we match pursuit coalitions with the evaders such that the most number of evaders are captured. This task allocation problem can be formulated as a 0–1 integer linear program as follows.
Suppose that the size of the pursuit coalition is less or equal to Nc (Nc ≤ Np). Then the pursuit team
where xcj = 1 indicates the assignment of pursuit coalition Pc to capture Ej, and xcj = 0 means no assignment.
5.2 Polynomial approximation algorithm
Since problem (18) is a special constrained matching problem (Tanimoto et al., 1978) and proved to be NP-hard (Yan et al., 2022), solving (18) is intractable when the number of players is large. Fortunately, Yan et al. (2022) shows that there exist constant-factor polynomial algorithms for problem (18), and further proposes a 1/Nc-approximation polynomial algorithm called Sequential Matching algorithm. In this algorithm, First, polynomial algorithms (e.g., maximum network flow) are used to compute the maximum matching of the subgraph of
6 Cooperative strategies
Based on the results of the game of kind, the game of degree needs to provide the strategies for the players to ensure their winnings and optimize some metrics at the same time. In this section, we review three types of dominance region based cooperative strategies, with a focus on the pursuers.
6.1 Voronoi-based strategy
Voronoi partitions are widely used for generating cooperative strategies for the players, usually when they all have the same speed. There are three popular Voronoi-based pursuit strategies: area-based, point-based, and relay strategies. The area-based pursuit strategy is aiming at minimizing the area of the evader’s Voronoi cell (Pan et al., 2012). The point-based pursuit strategy requires that each pursuer moves towards a specific point in the evader’s dominance region, such as the farthest point from the evader’s current position, and the point closest to the goal region (Yan et al., 2019b; Garcia et al., 2020; Yan et al., 2022). The relay pursuit strategy allows the pursuers to pursue the evader in a relay way based on whether the evader is in its dominance region against the other pursuers.
6.2 Apollonius-circle based strategy
As for unequal speed scenarios, the Apollonius circle is used to design cooperative strategies for the pursuers. Most of Apollonius-based pursuit strategies are point-based. For instance, since the evader’s dominance region, formed by the intersection of all one-to-one Apollonius circles, is strictly convex, the point on the dominance region closest to a convex goal region (if they are disjoint) is unique and thus moving towards this point under feedback strategies can ensure the pursuit winning (Yan et al., 2019b). However, the singularity needs to be resolved when the non-convex goal regions are considered Von Moll et al. (2020).
6.3 Convex optimization based strategy
It is difficult to use Voronoi-based or Apollonius-based strategies when the pursuers have positive capture radii, due to the lack of the closed-form representation of the dominance region. Inspired by the function-based dominance region, Yan et al. (2022) proposed a convex optimization based pursuit strategy which applies to both point capture and radius capture cases. For multiple pursuers against one evader, if the evader’s dominance region is disjoint from the goal region, then the point xI (may be non-unique) in the dominance region closest to the goal region is computed by solving the convex optimization problem
where fij is defined in Definition 3 and
7 Discussion
Being a relatively new field of study, many research questions remain open for M-RA differential games. In this section, we discuss the limitations in the existing literature and point out directions for future developments, from the following aspects of the games inspired by Shishika and Kumar (2020): player dynamics, sequential capture, spatial-temporal coupling, fast evaders and partial information.
7.1 Player dynamics
We assumed that each player is modelled by simple motion and thus can change its heading instantaneously. As discussed above, this dynamical model is a suitable abstraction for mobile robots or robotic vehicles which have limited speed and high maneuverability. However, such abstractions may generate strategies which fail to complete the tasks, since some constraints ignored in the abstraction have a crucial effect on the strategy synthesis. Examples of the constraints include minimum turning radius, maximum acceleration, and external forces. Taking these dynamical constraints into account will inevitably complicate the strategy synthesis.
7.2 Sequential capture
If the pursuer is allowed to capture multiple evaders sequentially, then this scenario will involve a dynamic vehicle routing problem (Bopardikar et al., 2010) in an adversarial setting. This cannot be handled with existing barrier construction methods which only focus on myopic capture, i.e., the capture of the evader being pursued without reasoning the pursuit after the capture. Taking sequential capture into consideration when synthesizing strategies will lead to many interesting strategic behaviors, and constructive results have been presented when the evaders are assumed to arrive in a probabilistic spatio-temporal manner (Smith et al., 2009; Bajaj and Bopardikar, 2019; Bajaj et al., 2021). For example, some of the evaders may lure the pursuers away from the goal region so that other evaders can reach the goal region. When constructing the barriers for capturing multiple evaders, the pursuers may chase the evaders that are further away first and the close ones afterwards.
7.3 Spatial-temporal coupling
The task allocation method in Section 5 assumes that each pursuit coalition plays a game against an evader independently. However, since all players operate in a shared environment simultaneously, the players’ trajectories in different games are coupled spatially and temporally. Such coupling may lead to future collision and can also be leveraged to design wiser strategies. Taking the coupling of the future paths between different matching pairs into account is worth studying.
7.4 Fast evaders
Most of existing results are provided when the pursuers are faster or equal to the evaders. The most significant consequence of this constraint is that the evader’s dominance region, represented by either Voronoi cell, Apollonius circle or non-negative level set of a function, is convex. This convexity property ensures that the evader dominates all points along the straight line from its current position to any goal point in its dominance region, implying a capture-free path regardless of the pursuers’ strategies. However, the game with faster evaders is fundamentally different, because the capture requires more complicated cooperation among the pursuers to offset the speed disadvantages, or leverage the characteristics of the game region (e.g, boundaries and convexity).
7.5 Partial information
The assumption in the existing works that each player has full knowledge of the positions and speeds of all other players, may be invalid in many realistic situations due to the adversarial objectives. First, the pursuers have a limited detection range out of which the information about evaders and the environment may be unavailable. Second, even if the evaders are detected, measurement errors exist and vary depending on the sensing devices. Third, if the number of evaders within the detection range is large, then counting or locating all possible evaders in a dense swarm raises a big challenge to the detection capabilities of the pursuers.
8 Conclusion
In this work, we reviewed the recent progress in M-RA differential games. We provided background on game elements, application and problems of interest. We introduced two common methods, geometric method and HJI method, for solving M-RA differential games. We presented a review of barrier construction (winning regions follow immediately) for multiple players against one opponent player in several games. We presented an integer linear programming formulation and its approximation algorithm to tackle multiple versus multiple cases using the results of multiple versus one and the maximum matching. We presented three dominance region based pursuit strategies, depending on the speed ratio and the capture radius. Finally, we discussed several limitations in the current problem formulation and identified the corresponding trends for future research.
Author contributions
RY contributed to conception, design of the study, data collection and analysis. RY wrote the first draft of the manuscript, and RD wrote Sections 3.2, 6 of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version. The work of RY was completed at Tsinghua University.
Funding
The work of RY, RD, ZS, and YZ was supported by the Science and Technology Innovation 2030-Key Project of “New Generation Artificial Intelligence” under Grant 2020AAA0108200. The work of XD was sponsored by Shanghai Pujiang Program under Grant 22PJ1404900.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Akilan, Z., and Fuchs, Z. (2017). “Zero-sum turret defense differential game with singular surfaces,” in 2017 IEEE Conference on Control Technology and Applications (CCTA), Maui, HI, 27–30 August, 2017, 2041–2048.
Antonyshyn, L., Silveira, J., Givigi, S., and Marshall, J. (2022). Multiple mobile robot task and motion planning: A survey. ACM Computing Surveys (CSUR). doi:10.1145/3564696
Bajaj, S., and Bopardikar, S. D. (2019). “Dynamic boundary guarding against radially incoming targets,” in 2019 IEEE 58th Conference on Decision and Control (CDC), Nice, France, 11–13 December, 2019 (IEEE), 4804–4809.
Bajaj, S., Torng, E., and Bopardikar, S. D. (2021). “Competitive perimeter defense on a line,” in 2021 American Control Conference (ACC), New Orleans, LA, 25–28 May, 2021 (IEEE), 3196–3201.
Blaquière, A., Gérard, F., and Leitmann, G. (1969). Quantitative and qualitative games. New York: Academic Press.
Bopardikar, S. D., Smith, S. L., Bullo, F., and Hespanha, J. P. (2010). Dynamic vehicle routing for translating demands: Stability analysis and receding-horizon policies. IEEE Trans. Autom. Control 55, 2554–2569. doi:10.1109/tac.2010.2049278
Chen, X., and Yu, J. (2022). Reach-avoid games with two heterogeneous defenders and one attacker. IET Control Theory Appl. 16, 301–317. doi:10.1049/cth2.12226
Chen, M., Zhou, Z., and Tomlin, C. J. (2016). Multiplayer reach-avoid games via pairwise outcomes. IEEE Trans. Autom. Control 62, 1451–1457. doi:10.1109/tac.2016.2577619
Chen, M., Herbert, S. L., Vashishtha, M. S., Bansal, S., and Tomlin, C. J. (2018). Decomposition of reachable sets and tubes for a class of nonlinear systems. IEEE Trans. Autom. Control 63, 3675–3688. doi:10.1109/tac.2018.2797194
Deng, R., Yan, R., Zhang, W., Shi, Z., and Zhong, Y. (2021). “Receding horizon defense strategy for reach-avoid games with uncertainties via pairwise outcomes,” in 2021 40th Chinese Control Conference (CCC), Shanghai, China, 26–28 July, 2021 (IEEE), 5401–5406.
Dubins, L. E. (1957). On curves of minimal length with a constraint on average curvature, and with prescribed initial and terminal positions and tangents. Am. J. Math. 79, 497–516. doi:10.2307/2372560
Fisac, J. F., Chen, M., Tomlin, C. J., and Sastry, S. S. (2015). “Reach-avoid problems with time-varying dynamics, targets and constraints,” in Proceedings of the 18th international conference on hybrid systems: computation and control, Seattle, Washington, April, 2015, 11–20.
Fu, H., and Liu, H. H.-T. (2020). Guarding a territory against an intelligent intruder: Strategy design and experimental verification. IEEE/ASME Trans. Mechatronics 25, 1765–1772. doi:10.1109/tmech.2020.2996901
Fu, H., and Liu, H. H.-T. (2021). An isochron-based solution to the target defense game against a faster invader. IEEE Control Syst. Lett. 6, 1352–1357. doi:10.1109/lcsys.2021.3092950
Garcia, E., Casbeer, D. W., Fuchs, Z. E., and Pachter, M. (2018). Cooperative missile guidance for active defense of air vehicles. IEEE Trans. Aerosp. Electron. Syst. 54, 706–721. doi:10.1109/taes.2017.2764269
Garcia, E., Casbeer, D. W., and Pachter, M. (2019a). Design and analysis of state-feedback optimal strategies for the differential game of active defense. IEEE Trans. Autom. Control 64, 553–568.
Garcia, E., Casbeer, D. W., Von Moll, A., and Pachter, M. (2019b). “Cooperative two-pursuer one-evader blocking differential game,” in 2019 American Control Conference (ACC), Philadelphia, PA, 10–12 July, 2019 (IEEE), 2702–2709.
Garcia, E., Casbeer, D. W., and Pachter, M. (2020). Optimal strategies for a class of multi-player reach-avoid differential games in 3D space. IEEE Robotics Autom. Lett. 5, 4257–4264. doi:10.1109/lra.2020.2994023
Garcia, E., Casbeer, D. W., Von Moll, A., and Pachter, M. (2021). Multiple pursuer multiple evader differential games. IEEE Trans. Autom. Control 66, 2345–2350. doi:10.1109/tac.2020.3003840
Getz, W. M., and Pachter, M. (1981). Two-target pursuit-evasion differential games in the plane. J. Optim. Theory Appl. 34, 383–403. doi:10.1007/bf00934679
Guerrero-Bonilla, L., Egerstedt, M., and Dimarogonas, D. V. (2021). “Area defense and surveillance on rectangular regions using control barrier functions,” in 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–01 October, 2021 (IEEE), 8166–8172.
Huang, H., Ding, J., Zhang, W., and Tomlin, C. J. (2014). Automation-assisted capture-the-flag: A differential game approach. IEEE Trans. Control Syst. Technol. 23, 1014–1028. doi:10.1109/tcst.2014.2360502
Ibragimov, G., Ferrara, M., Kuchkarov, A., and Pansera, B. A. (2018). Simple motion evasion differential game of many pursuers and evaders with integral constraints. Dyn. Games Appl. 8, 352–378. doi:10.1007/s13235-017-0226-6
Lee, Y., and Bakolas, E. (2021). “Optimal strategies for guarding a compact and convex target set: A differential game approach,” in 2021 60th IEEE Conference on Decision and Control (CDC), Austin, TX, 14–17 December, 2021 (IEEE), 4320–4325.
Liang, L., Deng, F., Peng, Z., Li, X., and Zha, W. (2019). A differential game for cooperative target defense. Automatica 102, 58–71. doi:10.1016/j.automatica.2018.12.034
Liang, L., Deng, F., Lu, M., and Chen, J. (2021). Analysis of role switch for cooperative target defense differential game. IEEE Trans. Automatic Control 66, 902–909. doi:10.1109/tac.2020.2987701
Liang, L., Deng, F., Wang, J., Lu, M., and Chen, J. (2022). A reconnaissance penetration game with territorial-constrained defender. IEEE Trans. Automatic Control 67, 6295–6302. doi:10.1109/tac.2022.3183034
Margellos, K., and Lygeros, J. (2011). Hamilton–Jacobi formulation for reach–avoid differential games. IEEE Trans. Automatic Control 56, 1849–1861. doi:10.1109/tac.2011.2105730
Mitchell, I. M., Bayen, A. M., and Tomlin, C. J. (2005). A time-dependent Hamilton-Jacobi formulation of reachable sets for continuous dynamic games. IEEE Trans. Automatic Control 50, 947–957. doi:10.1109/tac.2005.851439
Mohanan, J., Manikandasriram, S., Venkatesan, R. H., and Bhikkaji, B. (2018). Toward real-time autonomous target area protection: Theory and implementation. IEEE Trans. Control Syst. Technol. 27, 1293–1300. doi:10.1109/tcst.2018.2805295
Olsder, G. J., and Breakwell, J. V. (1974). Role determination in an aerial dogfight. Int. J. Game Theory 3, 47–66. doi:10.1007/bf01766218
Oyler, D. W., Kabamba, P. T., and Girard, A. R. (2016). Pursuit–evasion games in the presence of obstacles. Automatica 65, 1–11. doi:10.1016/j.automatica.2015.11.018
Pachter, M., and Getz, W. M. (1980). The geometry of the barrier in the game of two cars. Optim. Control Appl. Methods 1, 103–118. doi:10.1002/oca.4660010202
Pachter, M., Garcia, E., and Casbeer, D. W. (2019). Toward a solution of the active target defense differential game. Dyn. Games Appl. 9, 165–216. doi:10.1007/s13235-018-0250-1
Pan, S., Huang, H., Ding, J., Zhang, W., vić, D. M. S., and Tomlin, C. J. (2012). “Pursuit, evasion and defense in the plane,” in 2012 American Control Conference (ACC), Montreal, QC, 27–29 June, 2012 (IEEE), 4167–4173.
Reeds, J., and Shepp, L. (1990). Optimal paths for a car that goes both forwards and backwards. Pac. J. Math. 145, 367–393. doi:10.2140/pjm.1990.145.367
Selvakumar, J., and Bakolas, E. (2019). Feedback strategies for a reach-avoid game with a single evader and multiple pursuers. IEEE Trans. Cybern. 51, 696–707. doi:10.1109/tcyb.2019.2914869
Shishika, D., and Kumar, V. (2018). “Local-game decomposition for multiplayer perimeter-defense problem,” in 2018 IEEE Conference on Decision and Control (CDC), Miami, FL, 17–19 December, 2018 (IEEE), 2093–2100.
Shishika, D., and Kumar, V. (2020). “A review of multi agent perimeter defense games,” in International Conference on Decision and Game Theory for Security, College Park, MD, 28–30 October, 2020 (Springer), 472–485.
Shishika, D., Paulos, J., and Kumar, V. (2020). Cooperative team strategies for multi-player perimeter-defense games. IEEE Rob. Autom. Lett. 5, 2738–2745. doi:10.1109/lra.2020.2972818
Shishika, D., Maity, D., and Dorothy, M. (2021). “Partial information target defense game,” in 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–05 June, 2021 (IEEE), 8111–8117.
Smith, S. L., Bopardikar, S. D., and Bullo, F. (2009). “A dynamic boundary guarding problem with translating targets,” in Proceedings of the 48h IEEE Conference on Decision and Control (CDC) held jointly with 2009 28th Chinese Control Conference, Shanghai, China, 15–18 December, 2009 (IEEE), 8543–8548.
Tanimoto, S. L., Itai, A., and Rodeh, M. (1978). Some matching problems for bipartite graphs. J. ACM (JACM) 25, 517–525. doi:10.1145/322092.322093
Velhal, S., Sundaram, S., and Sundararajan, N. (2022). A decentralized multirobot spatiotemporal multitask assignment approach for perimeter defense. IEEE Trans. Robotics 38, 3085–3096. doi:10.1109/tro.2022.3158198
Von Moll, A., Garcia, E., Casbeer, D., Suresh, M., and Swar, S. C. (2020). Multiple-pursuer, single-evader border defense differential game. J. Aerosp. Inf. Syst. 17, 407–416. doi:10.2514/1.i010740
Von Moll, A., Shishika, D., Fuchs, Z., and Dorothy, M. (2021). “The turret-runner-penetrator differential game,” in 2021 American Control Conference (ACC), New Orleans, LA, 25–28 May, 2021 (IEEE), 3202–3209.
Von Moll, A., Pachter, M., Shishika, D., and Fuchs, Z. (2022a). Circular target defense differential Games$^*$. IEEE Trans. Automatic Control, 1–14. doi:10.1109/tac.2022.3203357
Von Moll, A., Shishika, D., Fuchs, Z., and Dorothy, M. (2022b). Turret-runner-penetrator differential game with role selection. IEEE Trans. Aerosp. Electron. Syst. 58, 5687–5702. doi:10.1109/taes.2022.3176599
Wang, J., Jin, X., and Tang, Y. (2022). Optimal strategy analysis for adversarial differential games. Electron. Res. Archive 30, 3692–3710. doi:10.3934/era.2022189
Yan, R., Shi, Z., and Zhong, Y. (2017). “Escape-avoid games with multiple defenders along a fixed circular orbit,” in 2017 13th IEEE International Conference on Control & Automation (ICCA), Ohrid, Macedonia, 03–06 July, 2017 (IEEE), 958–963.
Yan, R., Shi, Z., and Zhong, Y. (2019a). “Construction of the barrier for reach-avoid differential games in three-dimensional space with four equal-speed players,” in 2019 IEEE 58th Conference on Decision and Control (CDC), Nice, France, 11–13 December, 2019 (IEEE), 4067–4072.
Yan, R., Shi, Z., and Zhong, Y. (2019b). Reach-avoid games with two defenders and one attacker: An analytical approach. IEEE Trans. Cybern. 49, 1035–1046. doi:10.1109/tcyb.2018.2794769
Yan, R., Shi, Z., and Zhong, Y. (2020). Task assignment for multiplayer reach–avoid games in convex domains via analytical barriers. IEEE Trans. Robotics 36, 107–124. doi:10.1109/tro.2019.2935345
Yan, R., Shi, Z., and Zhong, Y. (2021a). Cooperative strategies for two-evader-one-pursuer reach-avoid differential games. Int. J. Syst. Sci. 52, 1–19. doi:10.1080/00207721.2021.1872116
Yan, R., Shi, Z., and Zhong, Y. (2021b). Optimal strategies for the lifeline differential game with limited lifetime. Int. J. Control 94, 2238–2251. doi:10.1080/00207179.2019.1698770
Yan, R., Duan, X., Shi, Z., Zhong, Y., and Bullo, F. (2022). Matching-based capture strategies for 3D heterogeneous multiplayer reach-avoid differential games. Automatica 140, 110207. doi:10.1016/j.automatica.2022.110207
Keywords: reach-avoid differential game, pursuit-evasion differential game, multi-agent games, cooperative control, barrier construction, winning regions, constrained matching problem
Citation: Yan R, Deng R, Duan X, Shi Z and Zhong Y (2023) Multiplayer reach-avoid differential games with simple motions: A review. Front. Control. Eng. 3:1093186. doi: 10.3389/fcteg.2022.1093186
Received: 08 November 2022; Accepted: 21 December 2022;
Published: 10 January 2023.
Edited by:
Daigo Shishika, George Mason University, United StatesReviewed by:
Shaunak Bopardikar, Michigan State University, United StatesHuiping Li, Northwestern Polytechnical University, China
Copyright © 2023 Yan, Deng, Duan, Shi and Zhong. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zongying Shi, c3p5QG1haWwudHNpbmdodWEuZWR1LmNu; Rui Yan, cnVpLnlhbkBjcy5veC5hYy51aw==
 Rui Yan
Rui Yan Ruiliang Deng1
Ruiliang Deng1