- 1Mechanical Engineering Department, George Mason University, Fairfax, VA, United States
- 2DEVCOM Army Research Laboratory, Adelphi, MD, United States
- 3Computer Vision and Robotics Laboratory (VeRLab), Department of Computer Science, Universidade Federal de Minas Gerais, Belo Horizonte, Brazil
Interesting and effective team behaviors arise when a group of agents contend with adversaries. Examples range from animal group behaviors observed in nature to strategies used in team sports. This mini review goes over literature in multiagent systems that study group control in adversarial scenarios. We identify different ways of formulating adversaries and discuss various types of teaming behavior that arise. Specifically from the perspective of multiagent task assignment, the types of tasks and the nature of assignments brought by the adversary are categorized. The frontiers of the current literature and the direction for future research are discussed at the end.
1 Introduction
Multiagent systems have been studied for various military and civilian security applications including patrolling (Czyzowicz et al., 2011), target tracking (Ramachandran et al., 2020), and interception (Garcia et al., 2020). Beyond direct use in security applications, these problems serve as a vehicle to investigate various teaming behaviors that arise due to the added challenge by the adversary. Natural swarms competing against predators (Olson et al., 2013) and team sports (Fujii, 2021) provide good examples of how sophisticated teaming behaviors emerge in order for them to survive or win. While the term adversarial could mean, in general, situations where the environment poses risks for the system to fail or malfunction, this review is focused on scenarios that involve competing teams of agents that must move in the environment to achieve their objectives.
Given that many multi-agent coordination problems can be explained as versions of task allocation (Gerkey and Matarić, 2004; Khamis et al., 2015), we discuss the types of tasks and the nature of assignments that arise in adversarial scenarios. Two key aspects that we focus are: i) the level of coupling between tasks; and ii) the dynamic and strategic nature of assignments.
A common way of utilizing multi-agent system is to solve a given problem with “divide and conquer” approach, which allows spatially distributed tasks to be executed efficiently (Cortes et al., 2004). However, the coupling between those tasks is loose in the sense that the success of one agent does not affect the success of its teammates. This is an aspect of task allocation that adversarial scenarios may potentially stress. When the overall group must work as a cohesive team to compete against another team, the task may not allow simple decomposition into independent subtasks. Instead, the agents may have to take specialized roles that augment each other.
When the adversary is modeled as another decision-making entity, the problem is often formulated as a non-cooperative dynamic game. In such formulation, the adversary may take advantage of a static or open-loop assignment strategies. Therefore, the assignment must consider the evolution of system states as well as possible adversarial actions. This is one step beyond an assignment policy based on a static analysis that is performed repeatedly over time.
In this mini review, we go over the literature on multi-agent systems with a particular focus on how the adversarial scenario pushes the teaming behavior in the above two aspects. The paper is organized as follows. The first three sections review groups of literature with different focus: Section 2 on the scalability in team size; Section 3 on adversarial decision making; and Section 4 at the intersection of the above two. Section 5 on team sports provides insights on a more complex teaming that current engineered systems are lacking. Finally, Section 6 discusses the frontiers of the current literature and the direction for future research.
2 Patrolling, routing, and tracking
The efficient allocation and coordination of resources are essential for accomplishing intricate spatially distributed tasks, such as surveillance and coverage. The spatial constraints imposed by the geometry of the environment and the movement of the adversarial agents complicate the decision-making process.
Patrolling involves systematically visiting or traversing designated areas to uphold security and monitor any possible alterations. The prevailing approaches often involve pre-determined cyclic or partition strategies (Czyzowicz et al., 2011), while some extend these paradigms to incorporate non-deterministic behaviors (Agmon et al., 2008). Such persistent surveillance task has also been modeled as a Vehicle Routing Problem (VRP) (Stump and Michael, 2011). However, successful patrolling teams demand adaptive decision-making, dynamically adjusting their strategies based on unexpected events (Portugal and Rocha, 2013) or threats. Moreover, a specific research category centers around adversarial patrolling, wherein explicit attacker models and adversary detection are taken into account (Huang et al., 2019; Basilico, 2022). The integration of such information allows for the development and analysis of effective defense mechanisms and/or countermeasure strategies (Alpern et al., 2019; Basilico and Carpin, 2020; Duan et al., 2021), significantly enhancing the system’s resilience against a wide array of potential attack scenarios.
In routing problems, the primary objective is to determine time or length-optimized paths to deliver information, goods, or services efficiently. When posed in adversarial scenarios, these problems undergo distinct formulations that introduce additional aspects and constraints. For instance, the presence of hazardous zones was considered in (Macharet et al., 2021). Perimeter (or boundary) defense is another important task where the goal is to protect a region from potential targets attempting to enter or escape. Different dynamic VRP formulations have been proposed to address the task of a single agent capturing linearly translating targets (Smith et al., 2009; Agharkar et al., 2015; Bajaj and Bopardikar, 2019). The objective is to determine an optimal path that intercepts the maximum number of targets en route before they reach the perimeter. The same concept was extended to the multi-agent case applying a partition strategy (Macharet et al., 2020) and a network flows formulation for the heterogeneous case (Chen et al., 2021).
Finally, in various real-world applications, such as surveillance, search and rescue, environmental monitoring, and military operations, the ability to efficiently and accurately detect and track targets is of utmost importance (Robin and Lacroix, 2016). These tasks require the coordinated motion of multiple robots to achieve an augmented perception of the environment and to continuously follow mobile targets. In an adversarial setting, a fundamental approach involves reconfiguring the team displacement to restore impacted capabilities (Ramachandran et al., 2020). Differently (Zhou and Kumar, 2023), presents a robust framework designed to withstand sensing and communication attacks or failures.
3 Differential games
Adversarial motion control problems, in particular, ones with direct engagement between red team and blue team have been modeled using differential games. The focus of the literature has mainly been on how to extend the strategies developed for one-vs-one scenario to team-vs-team scenarios while avoiding curse of dimensionality.
A variant of PEGs called reach-avoid game studies an engagement between a group of evaders (attackers) who seek to reach a target area and a group of pursuers (defenders) whose goal is to minimize the number of breaches by intercepting them. The solution approach is often based on agent-agent assignments (Garcia et al., 2020). It approximates the team-vs-team problem into a combination of one-vs-one problems whose solution can be obtained using traditional differential game techniques. The pairwise outcomes are then encoded into bipartite graph, which can be used to formulate assignment problems. There are existing algorithms such as Hungarian algorithm (Kuhn, 1955) that solves Maximum Matching or Minimum Linear Sum Assignment in polynomial time. The result gives which pursuer should go after which evader.
Many variants of multiagent reach-avoid games have been considered using such decomposition method, where the modification in the game environment (geometry) results in different low-level control strategy (Garcia et al., 2019; Yan et al., 2019; Garcia et al., 2020). However, at the high level, the team strategies all utilize pair-wise outcome to reduce the team coordination problem into agent-to-agent assignments.
Progress on the teaming aspect has been made by considering how a coalition of pursuers can team up against a single evader (Makkapati and Tsiotras, 2019; Yan et al., 2022), which generalizes the assignment approach. In Shishika et al. (2020) two-vs-one pincer movement was proposed for the perimeter defense game, which is a variant of reach-avoid game where the defending agents are constrained to move on the perimeter of the target. The two-vs-one result was further utilized to construct bounded regions within which n-vs-m local games were defined. While most of the multi-agent reach-avoid games considered individually greedy attacker strategies, this n-vs-m formulation showed how the subteam of attackers can team up to attack a single point so that q = m − n of them can survive and score if there are more attackers (m > n). We categorize this as a force concentration, which has tighter coupling than force distribution in a sense that the success of a subteam relies on the cooperation of its members, instead of the subteam performance being the sum of individual performance.
Turret Runner Penetrator differential game (Von Moll et al., 2022) is yet another variant where the defender is like a turret and can neutralize the attacker by turning and pointing at it. This formulation allows for the consideration of a sequence of captures similar to the routing formulation (Macharet et al., 2020). A distinct type of teaming that was studied in this problem is the heterogeneous roles that arise for the attackers. More specifically, it was shown that in certain initial conditions, it is optimal for the attackers to split into two roles: the runner and the penetrator (Von Moll et al., 2022). The runner acts as a decoy to waste as much time as possible before the turret pursues the penetrator, whereas the penetrator seeks to breach the perimeter. Such a sacrificial role employed by an agent is not something seen in homogeneous task assignment considered in majority of reach-avoid games. This work suggests a possibility of a more sophisticated type of teaming in adversarial games beyond simple divide and conquer approach.
4 Resource allocation
At a higher abstraction level, allocation of agents/resources in graph environments have been considered in the literature of Colonel Blotto (CB) games (Roberson, 2006; Powell, 2009; Kovenock and Roberson, 2018; Chandan et al., 2020). In its most standard form, CB games consider a zero-sum two-player game between two colonels each possessing a certain amount of resources that can be allocated to a given set of “battlefields.” A battlefield is won by the colonel who allocated more resources to it. The goal of each colonel is to win as many battlefield as possible by strategically allocating its resources without knowing how its opponent is going to allocate his/hers.
One type of teaming that arise in this framework is coalition formation. Among other variants of CB games, coalition CB games (Gupta et al., 2014; Heyman and Gupta, 2018) consider a scenario where there are more than two players. A special case of three-player game was considered where A and B each plays against C, while C must take care of both. What makes this decision making problem interesting is that A and B each has its own objective function, and therefore, they are selfish. Yet, there is an incentive for them to leverage the action of each other to implicitly “cooperate” and beat C together.
A problem formulated at the intersection of motion control strategies and resource allocation is the dynamic version of the CB game, which is referred to as the dynamic attacker-defender blotto (dDAB) game (Ferguson et al., 2022; Shishika et al., 2022; Chen et al., 2023). The game is played over multiple stages with sequential action. There is also an asymmetry between the two players in a sense that the attacker wins the overall game by allocating more resources at any node, whereas the defender must prevent that by maintaining numerical advantage at all the nodes. The path-guarding game (Ferguson et al., 2022; Chen et al., 2023) considered a variant of the dDAB game where the defending team is tasked with guarding a subset of nodes forming a path between two locations. Strategies that control platoons of defender resources were proposed. In these problems, coordination is necessary among defending agents to ensure that there is no gap in the defended nodes. We can categorize such teaming behavior as formation maintenance.
5 Machine learning on team sports
Humans have developed robust abilities to work together in teams to accomplish shared goals in many domains (e.g., in families, businesses, and politics). Most settings present unique challenges for analysis, including limited information, mixed-motives among agents, nonstationarity, etc. While human strategies may not always be ‘optimal’ in the language of traditional game theory due to cognitive biases (Thomas, 2018), bounded rationality (Altman, 2016), or compromises of coalition-building (Ray, 2007), they work remarkably well across a variety of settings.
Nevertheless, one human domain stands out as having the features we desire for studies of robot motion while also being constrained enough to not be immediately intractable—team sports. Team sports require coordination among teammates and are usually played against an opposing team that has a purely opposing goal (i.e., a zero-sum game). Moreover, recent advances in motion tracking technologies has enabled the collection of large quantities of human-generated sports data (Liu et al., 2023), including movement data in the form of player trajectories. These advances are recent enough that the field of leveraging this data to understand adversarial team behavior is still in relative infancy (Fujii, 2021).
One difficulty is that these games are far from the simplistic mathematical games, natively featuring a complex panoply of phenomena, including heterogeneous agents that have differing psychologies and who take on distinct roles within the team strategy. As such, some early work is in the direction of using machine learning techniques to learn player-specific action templates, which can be leveraged to understand common play concepts (Miller and Bornn, 2017; Ziyi et al., 2023). Other works aim to give a glimpse into domain knowledge of high-level intuitive concepts which may be useful to guide our development of multi-agent robot team strategies (Fernandez and Bornn, 2018). Long-term goals are to fuse the high-level concepts, like space-creating/exploiting behavior, with low-level trajectories of individual players (Terner and Franks, 2021; Chen et al., 2022). Space-creating/exploiting behavior can be linked to the concepts of zone assignment discussed in Section 2.
Ultimately, we view recent advances in the study of team sport as representing the full diversity of behavior and complexity that we would like our robotic systems to attain while operating together in adversarial environments. Thus, it is both a form of a desired endpoint for development of autonomous systems and also essentially an independent direction by which to investigate the same fundamental problems as the rest of the works in this review, only drilling down from the top-level view rather than the bottom-up approach of reasoning from a small number of idealized, mathematical agents.
6 Discussion
6.1 Types of teaming behavior
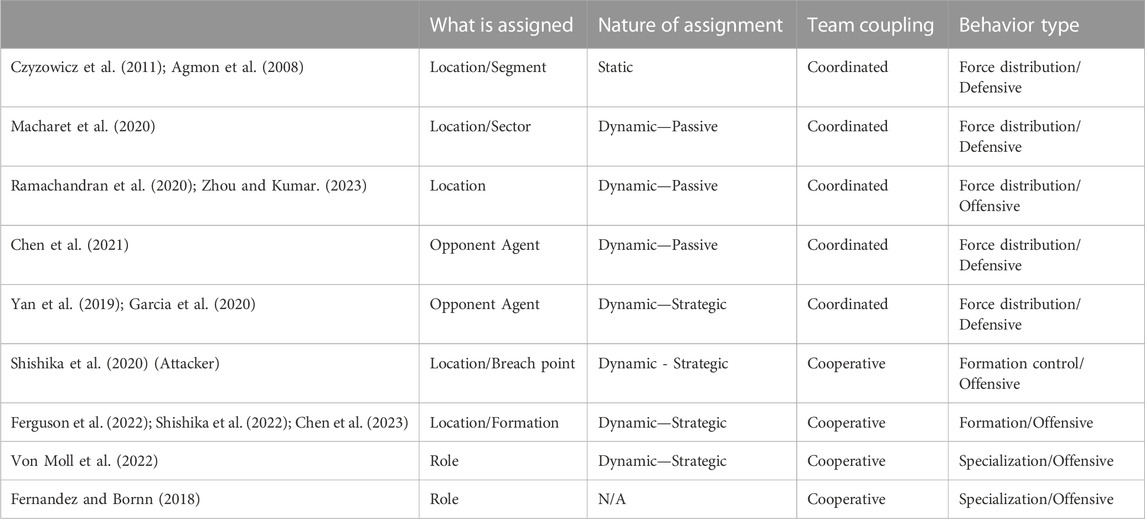
Table 1 provides some representative works in the literature with their attributes in terms of the type of tasks and assignments. The task to be assigned can have different level of abstraction. The lowest level and most concrete is a particular location that the assigned agent should move to. The next level is the assignment of a region or an opponent agent for which there is a movement strategy. The highest level of abstraction will be the assignment of roles, wherein the local objective functions corresponding to individual roles can be different.
The nature of assignment can be either static or dynamic. Within the works that consider dynamic assignment of tasks, we further categorize them into ‘passive’ and ‘strategic’. The passive ones allow re-assignments based on the time-varying situation, but the analysis is based on instantaneous optimality and does not take into account how the system will evolve over time. Whereas strategic assignments are determined based on the possible decisions to be made by the adversary as well as how it evolves over time.
As the label for the coupling between tasks or the team members, we use coordination and cooperation. The term coordination is used for loose coupling between tasks where the success of each agent/task is independent from one another. Also, the contribution of each agent to the overall team performance metric is linear or sublinear. On the other hand, cooperation is used for tasks where the failure of one agent can significantly affect the overall success of the team.
We identified the following types of teaming behavior: i) force distribution, ii) formation control, and iii) specialization. Force distribution is the most common type of teaming where the agents are given loosely coupled tasks that can be executed separately. The team performance typically consider the sum of individual utilities. The formation control, on the other hand, requires the team members to be in a particular configuration to fulfill the mission requirement. Finally, specialization occurs when the agents take heterogeneous roles.
6.2 Scalability vs. task interdependency
Figure 1 depicts the state of the current literature in two axes: scale in terms of the number of agents, and the interdependency between tasks that adds complexity in decision making.
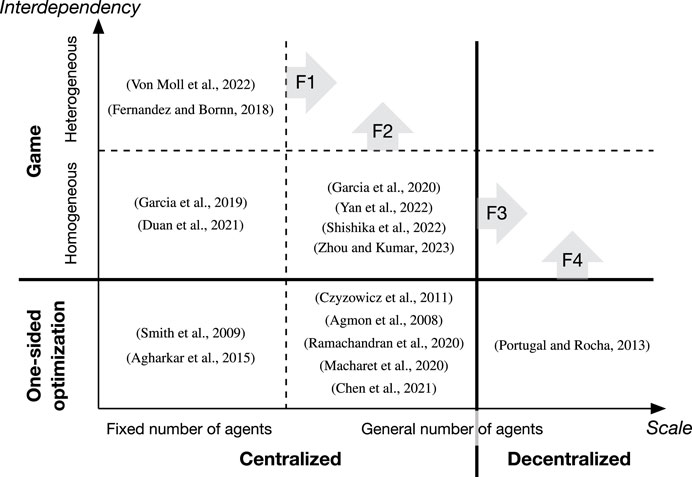
FIGURE 1. Frontiers in the current literature in terms of scalability with respect to the number of agents, and interdependency between tasks that add complexity in decision making.
Game-theoretic formulation leads to complex strategic interaction between the blue team and the red team, however, scalability is achieved by decomposing the overall problem into pairwise results where there is no coupling between team members. A more effective teaming arises when agents take heterogeneous roles. Achieving scalability while considering heterogeneous roles for tightly coupled teaming behavior is an open area for research, represented by the frontiers F1 and F2 in Figure 1.
Another gap in the current literature is that game-theoretic formulation treats the entire team as a single decision-making entity. Such a centralized approach naturally leads to limited scalability. The frontier F3 is about scaling up the centralized game theoretic analysis by decentralizing the decision making. There are some efforts in taking game-theoretic results and using machine learning techniques to decentralize the decision making (Paulos et al., 2019; Lee et al., 2023). Mean field game provides another way to achieve scalability (Lasry and Lions, 2007; Guan et al., 2022), however, the focus is on within-team interaction, and therefore, incorporating an explicit models of adversary still remains as a challenge.
The frontier F4 is concerned with the incorporation of adversarial decision making in large-scale multi-agent system that are currently formulated as one-sided optimization. The primary challenge in this pursuit lies in mitigating the computational complexities inherent in the associated combinatorial optimization. To address this challenge, a multifaceted approach is warranted, involving the deployment of online strategies that can dynamically adapt to partial and evolving information, the ability to reroute in response to unexpected obstructions in the initial plan, and the orchestration of cooperative strategies to proactively avoid potential attacks.
7 Conclusion
We review the literature on multi-agent systems operating in the presence of adversarial group of agents. From the task-assignment perspective, we categorize the type of tasks and the nature of assignment that arise in adversarial scenarios. The consideration of adversarial engagement require the assignment scheme to be dynamic and strategic, which is also supported by the literature on the analysis of team sports. Finally, we identify the frontiers in the current literature where the challenge includes: the scale up of game-theoretic strategies to large groups, enhancing the level of teaming by incorporating specialized roles, and incorporation of adversarial decision making in decentralized multiagent systems.
Author contributions
DS: Conceptualization, Writing–original draft, Writing–review and editing. MD: Conceptualization, Writing–original draft, Writing–review and editing. DM: Conceptualization, Writing–original draft, Writing–review and editing.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. DS is funded by ARL grant ARL DCIST CRA W911NF-17-2-0181.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Agharkar, P., Bopardikar, S. D., and Bullo, F. (2015). Vehicle routing algorithms for radially escaping targets. SIAM J. Control Optim. 53, 2934–2954. doi:10.1137/141000087
Agmon, N., Kraus, S., and Kaminka, G. A. (2008).Multi-robot perimeter patrol in adversarial settings, IEEE International Conference on Robotics and Automation, 15 September 2023, China. ICRA, 2339–2345. doi:10.1109/ROBOT.2008.4543563
Alpern, S., Lidbetter, T., and Papadaki, K. (2019). Optimizing periodic patrols against short attacks on the line and other networks. Eur. J. Operational Res. 273, 1065–1073. doi:10.1016/j.ejor.2018.08.050
Altman, M. (2016). “A bounded rationality assessment of the new behavioral economics,” in Routledge handbook of behavioral economics (Germany: Routledge), 179–193.
Bajaj, S., and Bopardikar, S. D. (2019). Dynamic boundary guarding against radially incoming targets. In IEEE 58th Conference on Decision and Control (CDC). December 13, 2019, USA, IEEE, 4804–4809. doi:10.1109/CDC40024.2019.9028868
Basilico, N. (2022). Recent trends in robotic patrolling. Curr. Robot. Rep. 3, 65–76. doi:10.1007/s43154-022-00078-5
Basilico, N., and Carpin, S. (2020). “Balancing unpredictability and coverage in adversarial patrolling settings,” in Algorithmic foundations of robotics XIII. Editors M. Morales, L. Tapia, G. Sánchez-Ante, and S. Hutchinson (Cham: Springer International Publishing), 762–777.
Chandan, R., Paarporn, K., and Marden, J. R. (2020). “When showing your hand pays off: announcing strategic intentions in colonel blotto games,” in IEEE American control conference. ACC). 4632–4637.
Chen, A. K., Ferguson, B. L., Shishika, D., Dorothy, M., Marden, J. R., Pappas, G. J., et al. (2023).Path defense in dynamic defender-attacker blotto games (ddab) with limited information American Control Conference. December 13, 2019, China, IEEE, 447–453.
Chen, A. K., Macharet, D. G., Shishika, D., Pappas, G. J., and Kumar, V. (2021).Optimal multi-robot perimeter defense using flow networks, Proc. of 15th International Symposium Distributed Autonomous Robotic Systems, January 5th, 2023, Germany. DARS, 282. –293. doi:10.1007/978-3-030-92790-5_22
Chen, X., Jiang, J.-Y., Jin, K., Zhou, Y., Liu, M., Brantingham, P. J., et al. (2022). Reliable: offline reinforcement learning for tactical strategies in professional basketball games. Proc. 31st ACM Int. Conf. Inf. Knowl. Manag., 3023–3032. doi:10.1145/3511808.3557105
Cortes, J., Martinez, S., Karatas, T., and Bullo, F. (2004). Coverage control for mobile sensing networks. IEEE Trans. robotics Automation 20, 243–255. doi:10.1109/tra.2004.824698
Czyzowicz, J., Gasieniec, L., Kosowski, A., and Kranakis, E. (2011). “Boundary patrolling by mobile agents with distinct maximal speeds,” in Algorithms – esa 2011. Editors C. Demetrescu, and M. M. Halldórsson (Berlin, Heidelberg: Springer Berlin Heidelberg), 701–712.
Duan, X., Paccagnan, D., and Bullo, F. (2021). Stochastic strategies for robotic surveillance as stackelberg games. IEEE Trans. Control Netw. Syst. 8, 769–780. doi:10.1109/TCNS.2021.3058932
Ferguson, B. L., Shishika, D., and Marden, J. R. (2022).Ensuring the defense of paths and perimeters in dynamic defender-attacker blotto games (ddab) on graphs, 2022 58th Annual Allerton Conference on Communication, Control, and Computing (Allerton), 27-30 Sept. 2022, USA. IEEE. 1–7.
Fernandez, J., and Bornn, L. (2018). Wide open spaces: a statistical technique for measuring space creation in professional soccer. In Sloan sports analytics conference. IEEE, China, vol. 2018
Fujii, K. (2021). Data-driven analysis for understanding team sports behaviors. J. Robotics Mechatronics 33, 505–514. doi:10.20965/jrm.2021.p0505
Garcia, E., Casbeer, D. W., Von Moll, A., and Pachter, M. (2020). Multiple pursuer multiple evader differential games. IEEE Trans. Autom. Control. doi:10.1109/TAC.2020.3003840
Garcia, E., Von Moll, A., Casbeer, D. W., and Pachter, M. (2019). “Strategies for defending a coastline against multiple attackers,” in Ieee conf. Decis. Control (China: CDC), 7319.
Gerkey, B. P., and Matarić, M. J. (2004). A formal analysis and taxonomy of task allocation in multi-robot systems. Int. J. robotics Res. 23, 939–954. doi:10.1177/0278364904045564
Guan, Y., Zhou, M., Pakniyat, A., and Tsiotras, P. (2022). “Shaping large population agent behaviors through entropy-regularized mean-field games,” in American Control Conference (ACC) (IEEE), July 12, 2024, China, (IEEE), 4429. –4435.
Gupta, A., Başar, T., and Schwartz, G. A. (2014).A three-stage colonel blotto game: when to provide more information to an adversary, Decision and Game Theory for Security: 5th International Conference, GameSec 2014, Los Angeles, CA, USA, November 6-7, 2014, 5. Springer, 216–233.
Heyman, J. L., and Gupta, A. (2018).Colonel blotto game with coalition formation for sharing resources, Decision and Game Theory for Security: 9th International Conference, GameSec 2018, Seattle, WA, USA, October 29–31, 2018, 9. Springer, 166–185.
Huang, L., Zhou, M., Hao, K., and Hou, E. (2019). A survey of multi-robot regular and adversarial patrolling. IEEE/CAA J. Automatica Sinica 6, 894–903. doi:10.1109/JAS.2019.1911537
Khamis, A., Hussein, A., and Elmogy, A. (2015). Multi-robot task allocation: a review of the state-of-the-art. Coop. robots Sens. Netw. 31–51. doi:10.1007/978-3-319-18299-5_2
Kovenock, D., and Roberson, B. (2018). The optimal defense of networks of targets. Econ. Inq. 56, 2195–2211. doi:10.1111/ecin.12565
Kuhn, H. W. (1955). The Hungarian method for the assignment problem. Nav. Res. Logist. Q. 2, 83–97. doi:10.1002/nav.3800020109
Lasry, J.-M., and Lions, P.-L. (2007). Mean field games. Jpn. J. Math. 2, 229–260. doi:10.1007/s11537-007-0657-8
Lee, E. S., Zhou, L., Ribeiro, A., and Kumar, V. (2023). Graph neural networks for decentralized multi-agent perimeter defense. Front. Control Eng. 4, 1104745. doi:10.3389/fcteg.2023.1104745
Liu, J., Huang, G., Hyyppä, J., Li, J., Gong, X., and Jiang, X. (2023). A survey on location and motion tracking technologies, methodologies and applications in precision sports. Expert Syst. Appl. 229, 120492. doi:10.1016/j.eswa.2023.120492
Macharet, D. G., Alves Neto, A., and Shishika, D. (2021). Minimal exposure dubins orienteering problem. IEEE Robotics Automation Lett. 6, 2280–2287. doi:10.1109/LRA.2021.3061004
Macharet, D. G., Chen, A. K., Shishika, D., Pappas, G. J., and Kumar, V. (2020).Adaptive partitioning for coordinated multi-agent perimeter defense, IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS’20), 29 Oct, 2020, China. IEEE.
Makkapati, V. R., and Tsiotras, P. (2019). Optimal evading strategies and task allocation in multi-player pursuit–evasion problems. Dyn. Games Appl. 9, 1168–1187. doi:10.1007/s13235-019-00319-x
Miller, A. C., and Bornn, L. (2017).Possession sketches: mapping nba strategies, Proceedings of the 2017 MIT Sloan Sports Analytics Conference, July 2019, China, 1–12. IEEE.
Olson, R. S., Hintze, A., Dyer, F. C., Knoester, D. B., and Adami, C. (2013). Predator confusion is sufficient to evolve swarming behaviour. J. R. Soc. Interface 10, 20130305. doi:10.1098/rsif.2013.0305
Paulos, J., Chen, S. W., Shishika, D., and Kumar, V. (2019). Decentralization of multiagent policies by learning what to communicate. In International Conference on Robotics and Automation (ICRA) May – 2 June 2023, China, (IEEE, 7990–7996,
Portugal, D., and Rocha, R. P. (2013). Distributed multi-robot patrol: a scalable and fault-tolerant framework. Robotics Aut. Syst. 61, 1572–1587. doi:10.1016/j.robot.2013.06.011
Powell, R. (2009). Sequential, nonzero-sum “blotto”: allocating defensive resources prior to attack. Games Econ. Behav. 67, 611–615. doi:10.1016/j.geb.2009.03.011
Ramachandran, R. K., Fronda, N., and Sukhatme, G. S. (2020). Resilience in multi-robot target tracking through reconfiguration. IEEE Int. Conf. Robotics Automation (ICRA), 4551. doi:10.1109/ICRA40945.2020.9196961
Ray, D. (2007). A game-theoretic perspective on coalition formation. Oxford: Oxford University Press.
Robin, C., and Lacroix, S. (2016). Multi-robot target detection and tracking: taxonomy and survey. Aut. Robots 40, 729–760. doi:10.1007/s10514-015-9491-7
Shishika, D., Guan, Y., Dorothy, M., and Kumar, V. (2022).Dynamic defender-attacker blotto game, 2022 American Control Conference, 8-10 June 2022, USA. ACC. 4422–4428. doi:10.23919/ACC53348.2022.9867318
Shishika, D., Paulos, J., and Kumar, V. (2020). Cooperative team strategies for multi-player perimeter-defense games. IEEE Rob. Autom. Lett. 5, 2738–2745. doi:10.1109/lra.2020.2972818
Smith, S. L., Bopardikar, S. D., and Bullo, F. (2009).A dynamic boundary guarding problem with translating targets, Proceedings of the 48h IEEE Conference on Decision and Control (CDC) held jointly with 2009 28th Chinese Control Conference, 15-18 Dec. 2009, Germany. IEEE, 8543–8548. doi:10.1109/CDC.2009.5400538
Stump, E., and Michael, N. (2011). Multi-robot persistent surveillance planning as a vehicle routing problem. In IEEE Int. Conf. Automation Sci. Eng. 569–575. doi:10.1109/CASE.2011.6042503
Terner, Z., and Franks, A. (2021). Modeling player and team performance in basketball. Annu. Rev. Statistics Its Appl. 8, 1–23. doi:10.1146/annurev-statistics-040720-015536
Thomas, O. (2018). Two decades of cognitive bias research in entrepreneurship: what do we know and where do we go from here? Manag. Rev. Q. 68, 107–143. doi:10.1007/s11301-018-0135-9
Von Moll, A., Shishika, D., Fuchs, Z., and Dorothy, M. (2022). Turret–runner–penetrator differential game with role selection. IEEE Trans. Aerosp. Electron. Syst. 58, 5687–5702. doi:10.1109/TAES.2022.3176599
Yan, R., Duan, X., Shi, Z., Zhong, Y., and Bullo, F. (2022). Matching-based capture strategies for 3d heterogeneous multiplayer reach-avoid differential games. Automatica 140, 110207. doi:10.1016/j.automatica.2022.110207
Yan, R., Shi, Z., and Zhong, Y. (2019). Task assignment for multiplayer reach–avoid games in convex domains via analytical barriers. IEEE Trans. Rob. 36, 107–124. doi:10.1109/tro.2019.2935345
Zhou, L., and Kumar, V. (2023). Robust multi-robot active target tracking against sensing and communication attacks. IEEE Trans. Robotics 39, 1768–1780. doi:10.1109/TRO.2022.3233341
Keywords: multiagent systems, cooperative control, adversarial scenarios, dynamic games, task assignment, vehicle routing, pursuit evasion, resource allocation
Citation: Shishika D, Dorothy M and Macharet DG (2023) Teaming behavior in adversarial scenarios. Front. Control. Eng. 4:1279454. doi: 10.3389/fcteg.2023.1279454
Received: 18 August 2023; Accepted: 19 October 2023;
Published: 02 November 2023.
Edited by:
Francisco J. Vargas, Federico Santa María Technical University, ChileReviewed by:
Qiang Fu, Air Force Engineering University, ChinaVenkata Ramana Makkapati, Honda Aircraft Company, United States
Copyright © 2023 Shishika, Dorothy and Macharet. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Daigo Shishika, ZHNoaXNoaWtAZ211LmVkdQ==
 Daigo Shishika
Daigo Shishika Michael Dorothy
Michael Dorothy Douglas G. Macharet
Douglas G. Macharet