Near-infrared cathodoluminescence of Xe2 excimers in dense gaseous mixtures

Borghesani, A. F.; Carugno, G.; Chiossi, F.

doi:10.3389/fdest.2025.1580297

ORIGINAL RESEARCH article

Front. Detect. Sci. Technol., 19 May 2025

Sec. Detector Physics

Volume 3 - 2025 | https://doi.org/10.3389/fdest.2025.1580297

This article is part of the Research TopicFundamentals of luminescence and electroluminescence in particle detection technologies relying on noble-gas mediaView all 7 articles

Near-infrared cathodoluminescence of excimers in dense gaseous mixtures

A. F. Borghesani^1,2*

G. Carugno²

F. Chiossi³^†

¹CNISM Unit, Department of Physics and Astronomy, Università degli Studi, Padua, Italy
²Istituto Nazionale di Fisica Nucleare, Sezione di Padova, Padua, Italy
³Department of Physics and Astronomy, Università degli Studi, Padua, Italy

We report new spectroscopic measurements of the near-infrared fluorescence band of electron-beam excited ${Xe}_{2}$ excimers as a function of the gas density in several gaseous mixtures of different Xe concentrations at room temperature. We have used He, Ar, and $N_{2}$ as buffer gases, with the Xe concentrations in the mixtures ranging from approximately $8 %$ up to $80 %$ . The investigated density range extends up to 10 times the density $N_{ig}$ of the ideal gas at standard temperature and pressure ( $N_{ig} \approx 2.5 \times 1 0^{25} m^{- 3}$ ). In all mixtures, we have observed that the wavelength of the centroid of the infrared excimer band is shifted toward longer wavelengths as the gas density is increased, in a manner similar to what was originally observed in pure Xe gas and an Ar–Xe mixture. The strength of the redshift depends on the Xe concentrations in the mixture and the nature of the buffer gas and is very well rationalized by taking into account both the classical dielectric screening effect due to the gaseous environment and the density-dependent quantum shift of the energy of the optically active electron in the ${Xe}_{2}$ molecule, provided that the contributions of the two gaseous species in the mixture are weighted by applying the laws of ideal gaseous mixtures.

1 Introduction

Xenon is chosen in several high-energy physics applications owing to its excellent fluorescence properties. Excitation of the Xe atoms is accomplished by several different techniques, including either electron- (Arai and Firestone, 1969; Lorents, 1976; Koehler et al., 1974)-, proton- (Hurst et al., 1969), ion- (Ulrich, 2012; Khasenov, 2016), or $α$ -particle beams (Mimura et al., 2009; Álvarez et al., 2013); electrical discharges (Suzuki and Kubota, 1979); and synchrotron light (Dutuit et al., 1978). In particular, Xe is experimentally found to be very efficient in shedding its excitation energy due to the electron impacts on lower-lying atomic and excimer levels (Wojciechowski and Foryś, 1999), thereby leading to intense, narrow-band fluorescence in the vacuum–ultraviolet (VUV) range. For this reason, dense Xe gas and liquid are particularly well-suited as sensitive media in ionizing particle detectors (Knoll, 1989; Gómez Cadenas et al., 2014; Zhang et al., 2023; Aalbers et al., 2022; Anton et al., 2020).

In the degradation pathway of the energy released in the detector medium, a significant amount of the energy is released in the VUV range by the de-excitation of ${X e}_{2}$ excimers from the first excited molecular level to the repulsive ground state, leading to the emission of the well-known first and second VUV continua (Tanaka and Zelikoff, 1954). The first continuum is centered at approximately $148$ nm and is observed at low gas pressure, whereas the second continuum occurs at approximately $172$ nm for higher pressures. An additional, much fainter, third continuum centered at approximately $270$ nm has also been observed (Henck and Coche, 1967; Millet et al., 1978; Leardini et al., 2022). At pressures in excess of $P ≳ 100$ Pa, it is believed that the excimer VUV emission dominates any other type of radiative emission (Moutard et al., 1988).

The processes leading to excimer fluorescence in the low-density limit have been extensively studied and are now very well-known (Millet et al., 1978; Mulliken, 1970; Salamero et al., 1984; Nowak et al., 1985; Keto et al., 1997). The excimer levels responsible for the emission of the first two VUV continua are the ${Xe}_{2}^{⋆} (1_{u}, 0_{u}^{-})$ and the ${Xe}_{2}^{⋆} (0_{u}^{+})$ (in the Hund’s c case (Atkins and Friedman, 2005)), which are produced by the collision of a neutral atom in its ground state, Xe $({}^{1}S_{0})$ , off excited atoms in the $6 s {[3 / 2]}_{2}^{o}$ and $6 s {[3 / 2]}_{1}^{o}$ levels (in Racah notation) following the reaction scheme (Millet et al., 1978; Moutard et al., 1988; Wenck et al., 1979):

\begin{matrix} X e (6 s {[3 / 2]}_{2}^{o}) + 2 X e ({}^{1}S_{0}) & \to & {X e}_{2}^{⋆} (1_{u}, 0_{u}^{-}) + X e ({}^{1}S_{0}) \\ X e (6 s {[3 / 2]}_{1}^{o}) + 2 X e ({}^{1}S_{0}) & \to & {X e}_{2}^{⋆} (0_{u}^{+}) + X e ({}^{1}S_{0}) . \end{matrix}

Eventually, the excimers may radiatively decay toward the repulsive ground state $0_{g}^{+}$ .

{X e}_{2}^{⋆} \to {X e}_{2} (0_{g}^{+}) \to 2 X e ({}^{1}S_{0}) + h ν .

The first continuum, observed at low pressure $(P < 2 \times 1 0^{4} Pa)$ , is produced by the transition from the vibrationally excited ${(0_{u}^{+})}_{v^{'} ≫ 0}$ molecular state, correlated with the resonant $6 s ({}^{3}P_{1})$ atomic state, toward the dissociative $0_{g}^{+}$ ground state. The second continuum, observed at higher pressure $(P > 5 \times 1 0^{4} Pa)$ , is the result of overlapping bound-free transitions to the repulsive ground state from the lowest, vibrationally relaxed $(1_{u}, 0_{u}^{-})$ molecular states, correlated with the metastable $6 s ({}^{3}P_{2})$ atomic state (Wenck et al., 1979; Gornik et al., 1981), along with contributions from the vibrationally relaxed bound state related to the $6 s ({}^{3}P_{1})$ atomic state (Leardini et al., 2022). For a more detailed discussion on the elementary processes leading to the emission of the VUV continua, we refer to Borghesani et al. (2001) and the references therein.

The potential energy curves of these lowest-lying excimer levels in pure Xe have been determined by both the analysis of spectroscopic experiments (Keto et al., 1997; Gornik et al., 1981; Raymond et al., 1984; Castex, 1981; Koeckhoven et al., 1995) and by theoretical calculations (Mulliken, 1970; Ermler et al., 1978; Jonin and Spiegelmann, 2002).

Although less energetic transitions may be involved in the Xe excimer de-excitation processes along the energy degradation pathway, leading to possible infrared (IR) and/or near-infrared (NIR) fluorescence, the investigation of such a possibility has been given less attention than the VUV fluorescence. NIR cathodoluminescence, produced by electron impacts, was first observed in the gaseous phase of pure Xe at a wavelength of approximately $1.28 μ$ m, corresponding to a wavenumber $\tilde{ν} \approx 7900 {cm}^{- 1}$ (Carugno, 1998). As the NIR light yield has been found to be of intensity similar to that in the UV range, its detection could be exploited to enhance the sensitivity and resolution of high-energy particle detectors (Belogurov et al., 2000).

Further investigation of this NIR band produced the de-excitation of ${Xe}_{2}$ formed by electron impacts in pure Xe gas, has provided evidence that the broad and asymmetric emission is a strong indication of an excimer-type transition from a bound molecular state to a lower-lying repulsive one. Owing to the relatively large pressure values of our experiment ( $P \geq 1 \times 1 0^{4}$ Pa), we have suggested that the emission originates from a higher-lying bound-free molecular transition involving the vibrationally relaxed, bound $(3) 0_{g}^{+}$ state related to the $6 p {[1 / 2]}_{0}$ atomic limit and the dissociative $(1) 0_{g}^{+}$ related to the $6 s {[3 / 2]}_{1}$ atomic limit (Jonin and Spiegelmann, 2002). Moreover, we have been able to reproduce the band shape by means of Franck–Condon-type calculations (Borghesani et al., 2007a; Borghesani et al., 2007b). Additional pieces of information regarding the kinetics of the de-excitation reactions leading to the NIR emission have been recently obtained, although unsolved questions remain (Piotter et al., 2023; Hammann et al., 2024).

One striking feature of the discovered NIR excimer band is that its central wavelength, i.e., the wavelength of the band maximum, $λ_{m}$ is strongly redshifted as the gas density $N$ is increased (Borghesani et al., 2001; Borghesani et al., 2005; Mogentale, 2006). Its wavenumber ${\tilde{ν}}_{m} = 1 / λ_{m}$ linearly decreases with increasing $N$ . Such a redshift, although weaker, has also been observed in an Ar $(\approx 90 %)$ -Xe $(\approx 10 %)$ mixture (Borghesani et al., 2001; Borghesani et al., 2007b). As it is well-known that excitation energy is efficiently transferred from the lighter to the heavier atomic species (Efthimiopoulos et al., 1997), it is safe to assume that the emitting species in the mixture is still the ${Xe}_{2}$ excimer.

We have been able to rationalize the experimental findings, i.e., the density-dependent redshift, by setting up a simple theoretical model that takes into account multiple scattering effects (Borghesani et al., 2001). It is only based on the knowledge of the dielectric constant of the gaseous environment and the quantum density-dependent shift $V_{0} (N)$ of the energy of the delocalized, optically active electron in the excimer. It is important to note that the presence of $V_{0} (N)$ establishes a strong and unexpected link to the seemingly unrelated topics of electron energetics and transport in dense noble gases (Borghesani et al., 1988; Borghesani et al., 1992; Borghesani, 2020; Borghesani, 2021).

This model does not contain any adjustable parameters and accurately describes the data up to higher densities and will be described in Section 3. As it depends on the properties of the gaseous environment in which the Xe atoms are immersed, we have decided to carry out measurements in gaseous mixtures in which the emitting species Xe is typically the minority component, whose dielectric constants and scattering lengths (i.e., $V_{0} (N)$ ) are different from those of Xe. We have chosen He and Ar because their $V_{0} (N)$ contributions have opposite signs and should lead to significant differences in the experimental outcomes. We have also chosen to use $N_{2}$ because its dielectric constant is quite large, but its scattering length is not known with as high an accuracy as for the aforementioned noble gases, thereby leading to the conclusion that the present technique could be an alternative method to measure the scattering length of an atomic or molecular species. We anticipate the result that the model remains valid, provided that the atomic properties of the species are taken into account using the law of ideal mixtures.

This article is organized as follows. The experimental technique is briefly described in Section 2. The phenomenology of the experimental results is presented in Section 3, and their discussion is reported in Section 4. Finally, the conclusions are drawn in Section 5.

2 Experimental details

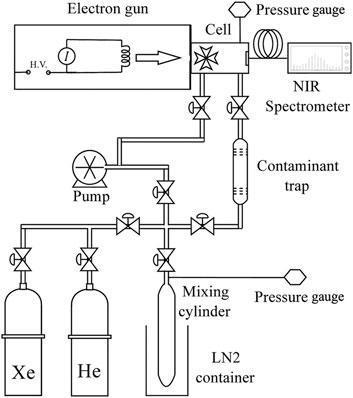
The technique and apparatus have been described accurately in Borghesani et al. (2001). We briefly summarize them here. A simplified schematic of the experimental apparatus is shown in Figure 1. The technique for exciting the gas sample has already been described in the literature (Borghesani et al., 2001). A homemade electron gun (Barcellan et al., 2011) injects $\approx 70$ keV electrons into the pressurized, stainless-steel cell through a $2 \times 2 {mm}^{2}$ wide and $10 μ$ m thin Ti window. The electron gun can be operated in either pulsed or continuous mode. In the present experiment, we operated the e-gun in the continuous mode at variance with the previous experiments (Borghesani et al., 2001). In spite of this change in the excitation mode, we did not observe any differences in the outcome.

Figure 1

Figure 1. Schematic of the experimental apparatus.

Electrons lose $\approx 10$ to $20$ keV energy upon crossing the Ti window but are still energetic enough to excite and ionize the atoms of the gas contained in the cell. An electron current of intensity up to $I_{e} \approx 30 μ$ A can be easily obtained (Barcellan et al., 2011). Under normal operating conditions, we used excitation currents in the range $0.2 μ A ≲ I_{e} < 5 μ A$ . As the energy of the injected electrons is fixed by the settings of the e-gun, an increase in the excitation current intensity only results in an increase in the number of excimers formed, leading to a proportional increase in the NIR fluorescence intensity. In any case, the electron current is weak enough not to lead to significant heating of the gas sample, as confirmed by the pressure remaining constant within an accuracy of $\approx 1$ hPa during the whole run.

${X e}_{2}$ excimers formed in the collision of a ground-state Xe atom with an excited atom (either directly excited by electron impact or in an excited state after a ${Xe}^{+}$ -electron recombination process) decay to a dissociative state. Owing to the quite large pressure used in the present experiment ( $P ≳ 1 \times 1 0^{4}$ Pa), we safely assumed that the NIR fluorescence is due to a bound-free transition between higher-lying, vibrationally relaxed molecular levels and the dissociative one.

The emitted light exited the cell through a sapphire window and was analyzed by an NIR spectrometer (Ocean Optics, mod. NIRQuest512).

The pressure cell, which was tested with pressure up to $P \approx 4$ MPa, was filled with a mixture of gases of the highest commercial purity. The procedure of producing the Xe–He gas mixture of a desired concentration is as follows: at first, Xe is introduced into a calibrated mixing chamber at a desired pressure at room temperature. Subsequently, Xe is frozen by immersing the mixing chamber in a liquid nitrogen (LN2) bath. Then, He gas is added to the refrigerated mixing chamber until a desired pressure is reached. Thereafter, the mixing chamber is heated up to room temperature.

To produce the Xe– $N_{2}$ mixtures, we use an intermediate calibrated cell to be filled at room temperature with $N_{2}$ up to the desired pressure. Then, the gas in the intermediate cell is condensed into the mixing chamber along with Xe, and finally, the mixing chamber is allowed to attain room temperature.

After waiting for enough time for the two gases to inter-diffuse, the mixture is introduced to the cell by flowing it through a trap to further remove residual oxygen and other impurities. At the temperature and pressures of the experiment ( $T \approx 300$ K and $P \leq 1$ MPa), the gases can be assumed to obey the ideal gas law, and the concentration of Xe in the mixture is computed by adopting the law of ideal gas mixtures (Guggenheim, 1966).

3 Experimental results: phenomenology

In this section, we present the experimental results obtained in the Xe–He, Xe– $N_{2}$ , and Ar–Xe gaseous mixtures for several pressure values and compare them with previously published results. In Figure 2 we report a spectrum obtained in pure Xe at $P = 0.1$ MPa with the high-resolution FT-IR interferometer (Borghesani et al., 2007a) to show how a typical spectrum appears. The continuous band in the center is the excimer spectrum. Several narrow Xe I atomic lines are also present, with their originating atomic manifolds shown in the legend. We would like to warn the interested reader not to give too much importance to the relative intensity of the atomic lines compared to that of the excimer band. We have observed that its height relative to that of the atomic lines strongly depends on the gas purity. If the gas is very pure, the excimer band is much higher than the atomic lines. On the contrary, the atomic lines overwhelm the excimer band if the gas is not so pure. Although the gas was initially introduced in the cell after being purified to a few parts per million oxygen equivalent, the continuous electron bombardment of all surfaces may lead to desorption of several impurities. Although the impurity content may be estimated in the order of some tens of parts per million, especially oxygen-based impurities, their actual amount cannot be controlled. This fact strongly and unpredictably affects the relative weight of the excimer band and the atomic lines from run to run. On the other hand, we have always observed that the features of the excimer spectrum, as far as its location and width are concerned, do not depend on the sample history and purity.

Figure 2

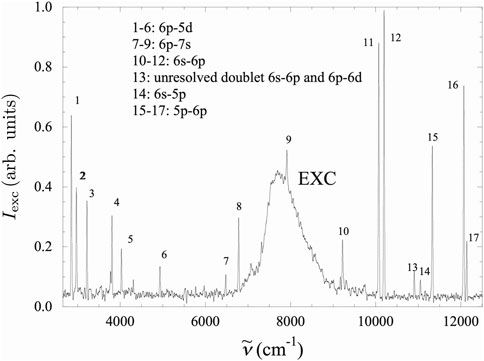
Figure 2. Typical high-resolution spectrum in Xe at $P = 0.1$ MPa. The large central feature is the excimer band. The narrow lines are atomic Xe I lines. In the legend, the atomic manifolds are reported, from which the atomic lines originate. This spectrum is obtained with the e-gun in the pulsed mode and with an FT-IR Bruker Equinox 55 interferometer equipped with an LN2-cooled InSb detector (redrawn after Borghesani et al., 2007a).

The intensity of the NIR radiation emitted by the ${Xe}_{2}$ excimers obviously depends, among other factors, on the abundance of Xe in the mixture. Thus, it is necessary to adjust the current supplied by the e-gun in order to always safely detect the NIR signal. As the electron current intensity $I_{e}$ can vary in quite a broad range, one has to check that the features of the excimer spectrum do not depend on it. Toward this goal, we first show in the top panel of Figure 3 that the total integrated light intensity of the excimer spectrum $I_{exc}$ scales linearly with the excitation current intensity $I_{e}$ .

Figure 3

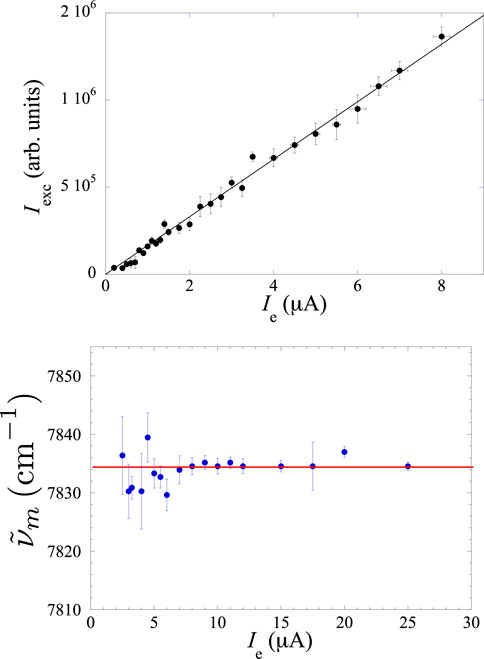
Figure 3. Top panel: linear relationship between the integrated intensity of the excimer spectrum $I_{exc}$ and the electron current intensity $I_{e}$ injected into the gas sample. Experimental conditions: pure Xe gas at $P = 99.4$ kPa. Bottom panel: the position ${\tilde{ν}}_{m}$ of the excimer band maximum is independent of the intensity of the excitation electron current $I_{e}$ . Experimental conditions: pure Xe gas at $P = 82.8$ kPa.

Another indication that the intensity of the electron current does not influence the microscopic processes leading to excimer formation and decay can be deduced by inspecting the bottom panel of Figure 3, in which the central wavenumber ${\tilde{ν}}_{m}$ of the excimer band is shown to be independent of the intensity of the current injected by the e-gun into the sample. Actually, ${\tilde{ν}}_{m}$ corresponds to the average energy of the excimer bound-free transition, and it turns out not to be altered by the excitation current intensity. Although the data presented in Figure 3 have been recorded in pure Xe gas at pressures $P = 99.4$ kPa and $82.8$ kPa, respectively, similar results are obtained in all investigated mixtures at any pressure.

Finally, we noted that the excimer spectra recorded at different electron current intensities for the same gas pressure do differ only in the intensities and not in their general features. After proper normalization at the unit area, they exactly overlap, provided that the spectra recorded at lower excitation current are less intense and, therefore, much noisier than those recorded at higher excitation current, as shown in Figure 4.

Figure 4

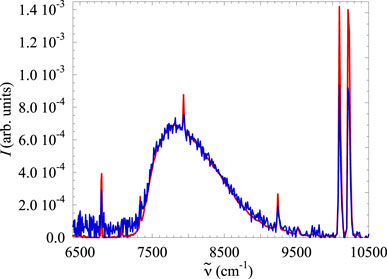
Figure 4. Normalized spectra recorded in pure Xe gas at room temperature for the same pressure $P = 18.9$ kPa, corresponding to the gas density $N \approx 4.6 \times 1 0^{24} m^{- 3}$ , with two different values of the excitation current. Red line: $I_{e} = 25 μ$ A. Blue line: $I_{e} = 2 μ$ A. The two spectra are normalized to unit area and almost perfectly overlap.

3.1 Pure Xenon gas and the Ar–Xe mixture

In pure Xe gas, the modification of the spectrum as a consequence of the variation of the gas density is the largest among all mixtures. In Figure 5 we show two spectra recorded at the lowest and highest pressures reached in the present experiment, corresponding to densities $N \approx 4.6 \times 1 0^{24} m^{- 3}$ and $N \approx 1.72 \times 1 0^{26} m^{- 3}$ , respectively. The differences between the two spectra are striking. We immediately observe that the spectrum recorded at high density is significantly shifted toward smaller wavenumbers with respect to the spectrum obtained at low density. The narrow atomic Xe I lines are suppressed at high density. Moreover, as expected, at high density, the excimer band is strongly collisionally broadened. The present measurements are in excellent agreement with our previous measurements (Borghesani et al., 2001; Borghesani et al., 2007b).

Figure 5

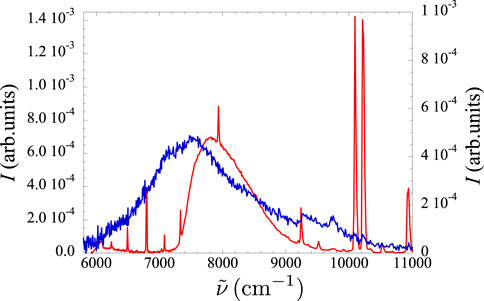
Figure 5. Spectra recorded in pure Xe gas at room temperature at two different pressure values. Red line: $P = 18.9$ kPa, $N \approx 4.6 \times 1 0^{24} m^{- 3}$ (left scale). Blue line: $P = 682$ kPa, $N \approx 1.72 \times 1 0^{26} m^{- 3}$ (right scale). Note the strong pressure-dependent redshift and broadening of the excimer band and the almost complete suppression of the narrow Xe I atomic lines at higher pressure. Each spectrum is normalized to unit area.

In the Xe–Ar mixture of nominal $10 % - 90 %$ composition, the shift is smaller than in pure Xe, as is the collisional broadening. For the sake of completeness, we report here our previous data for pure Xe and the Xe–Ar mixture. The density-dependent redshift of ${\tilde{ν}}_{m}$ is plotted in the top panel of Figure 6. We immediately note that ${\tilde{ν}}_{m}$ decreases linearly with increasing gas density $N$ and that the slope is much larger in the pure Xe gas than in the Ar–Xe mixture. The solid lines represent the prediction of the model that will be described and discussed later in this paper and are not a linear fit to the data.

Figure 6

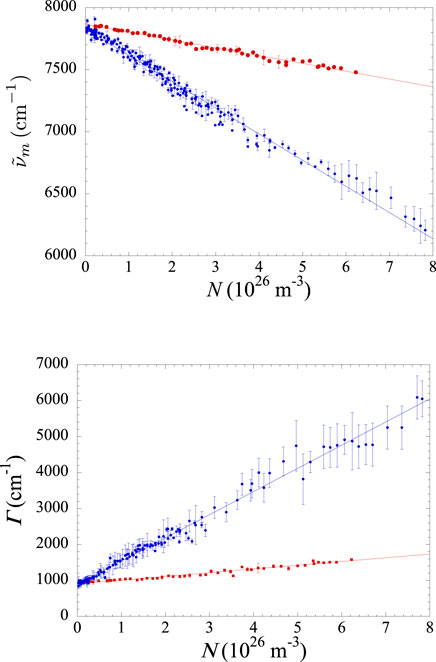
Figure 6. Top panel: density-dependent redshift of the wavenumber ${\tilde{ν}}_{m}$ of the centroid of the ${Xe}_{2}$ excimer band in pure Xe gas (blue circles) and in the Xe $(10 %)$ –Ar $(90 %)$ mixture (red circles) (redrawn after Borghesani et al., 2007b). Lines: prediction of the model, Equation 5 (see text). Bottom panel: density dependence of the full width at half maximum $Γ$ of the excimer spectrum in pure Xe gas (blue circles) and in the Xe $(10 %)$ –Ar $(90 %)$ mixture (red circles) (redrawn after Borghesani and Carugno, 2008). Lines: linear fit to the data.

The increase in density is (Equations 2, 4, 5, 6, and 7) expected to result in a higher collision frequency that reduces the lifetime of the excimer species and increases the width of the continuum. Although the excimer spectrum is a band rather than a narrow line, its width is a measure of how much the density affects the excimer lifetime. The density dependence of the full width at half height $Γ$ is reported in the bottom panel of Figure 6. First, we noted that the broadening of the excimer band linearly increases with increasing $N$ according to Equation 1 (Borghesani et al., 2007b; Borghesani and Carugno, 2008)

Γ = Γ_{0} + γ N, (1)

in which $γ = \bar{v} σ / π c$ , $c$ is the speed of light, $\bar{v} \propto T^{1 / 2}$ is the thermal velocity of the species, $T$ is the absolute temperature, $σ$ is a sort of atom–molecule collision cross section, and $N \bar{v} σ$ is the excimer–atom scattering rate. This is the typical outcome of collisional broadening and is to be expected. As the excimer continuum originates in a bound-free transition, $Γ_{0}$ is related to the energy range available to the final state. It is roughly determined by the steepness of the potential energy curve of the dissociative state and by the spatial extension of the wavefunction of the vibrational ground state of the bound potential. That is the reason why $Γ_{0}$ has the same value in both pure Xe and in the Xe–Ar mixture.

The second, and perhaps more interesting, observation is that the spectrum broadening is much larger in the pure gas than in the mixture. Apparently, the ${X e}_{2}$ –Xe collision cross-section is roughly one order of magnitude larger than that of ${X e}_{2}$ –Ar. We have suggested that this could be an effect of quantum indistinguishability of identical particles (Borghesani and Carugno, 2008), although this interpretation has been strongly criticized, especially because the measurements are carried out at room temperature, at which quantum effects should be negligible.

3.2 Xe–He mixtures

We have investigated three Xe–He mixtures of nominal Xe concentrations that were roughly $10 %$ , $36 %$ , and $69 %$ , respectively. A typical spectrum obtained from the mixture at the lowest Xe concentrations and at the highest pressure value $P = 787.8$ kPa, corresponding to a density $N \approx 1.91 \times 1 0^{26} m^{- 3}$ , is shown in Figure 7, in which it is compared with a pure Xe spectrum at low pressure $P \approx 63$ kPa, corresponding to a roughly ten times lower density $N \approx 1.54 \times 1 0^{25} m^{- 3}$ .

Figure 7

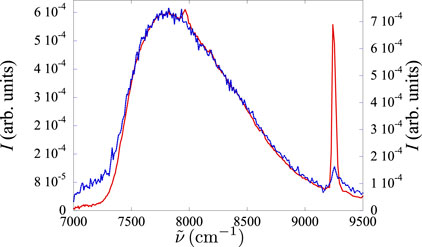
Figure 7. Spectra of a $10 %$ Xe– $90 %$ He mixture at $P = 787.8$ kPa $(N \approx 1.91 \times 1 0^{26} m^{- 3})$ (blue line, left scale) and of pure Xe at $P = 63$ kPa $(N \approx 1.54 \times 1 0^{25} m^{- 3})$ (red line, right scale). Both spectra are redshifted with respect to the spectrum in pure Xe for $P \to 0$ , but the mixture requires a larger pressure to achieve a comparable redshift. Both spectra are normalized to the unit area.

We immediately note that the redshift in the Xe–He mixture is very weak, as both spectra are almost coincident. The Xe–He mixture requires a much higher density than the pure gas to reach a similar redshift.

In the top panel of Figure 8 we report the density dependence of the central wavenumber of the spectrum for the three investigated Xe–He mixtures, along with the results obtained in pure Xe gas during the present experimental run.

Figure 8

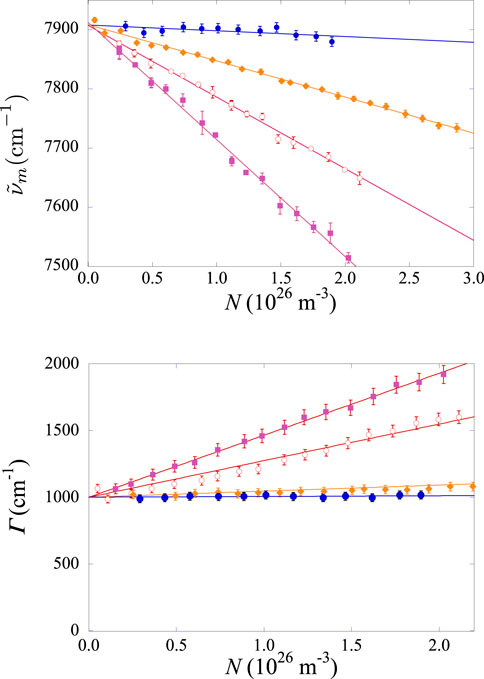
Figure 8. Top panel: density dependence of ${\tilde{ν}}_{m}$ for the Xe–He mixtures of Xe concentrations of (from the top): $\approx 12 %$ (closed circles), $\approx 36, %$ (diamonds), and $\approx 69 %$ (open circles). The ${\tilde{ν}}_{m}$ redshift in pure Xe measured during the present campaign is also shown (squares). Lines: theoretical prediction. Bottom panel: full width at half height $Γ$ of the ${Xe}_{2}$ excimer band in the Xe–He mixtures of Xe concentrations (from bottom): $\approx 12 %$ (closed circles), $\approx 36 %$ (diamonds), and $\approx 69 %$ (open circles). The excimer width $Γ$ in pure Xe measured during the present campaign is also shown (squares). Lines: linear fit to the data.

We observed that in all mixtures, ${\tilde{ν}}_{m}$ is linearly redshifted upon a density increase. The redshift increases with the increase in Xe concentrations in the mixture, eventually converging to the behavior of pure Xe gas.

The spectra also show collisional broadening. Their full width at half maximum $Γ$ is depicted in the bottom panel of Figure 8 and is described by the same linear relationship of Equation 1. We noted that the density dependence of $Γ$ is the weakest for the mixture with the lowest Xe concentrations and becomes stronger as the Xe concentrations increase.

3.3 Xe– $N_{2}$ mixtures

We investigated several Xe– $N_{2}$ mixtures of Xe concentrations $x (%) \approx$ 8, 15, 20, 25, 30, 40, 75, and 80. Two typical spectra recorded with $x \approx 25 %$ at low and high density are shown in the top panel of Figure 9, whereas in the bottom panel, two such spectra are reported for low and high density at $x = 80 %$ . These spectra qualitatively show the same features as those obtained in the other mixtures, i.e., redshift of ${\tilde{ν}}_{m}$ and collisional broadening. However, their shape is more distorted. The distortion with increasing density is even larger at higher $x$ than in other mixtures at the same $N$ and $x$ , as shown in the bottom panel of Figure 9. This phenomenon makes it difficult, at the highest $N$ , to even define the excimer bandwidth. Moreover, some of the atomic Xe I lines are almost entirely suppressed. However, at variance with mixtures with different buffer gases of comparable concentration and density, the atomic lines stemming from transitions within the 6s–6p manifold in the wavenumber range $9 \times 1 0^{3} {c m}^{- 1} \leq \tilde{ν} \leq 1 0^{4} {c m}^{- 1}$ are not suppressed at all and, at high Xe concentrations, are affected by density in a still unexplained way. They are extremely broadened, and their integrated intensity becomes almost comparable to that of the excimer. We do not know if low nitrogen concentrations may lead to the appearance of satellites around the Xe I atomic lines, which are not resolved in the present experiment, or if another emission continuum, possibly originating from the formation and de-excitation of ${XeN}_{2}$ exciplex, is appearing in the spectral range shared with the atomic lines. So far, we have no convincing explanation for this behavior.

Figure 9

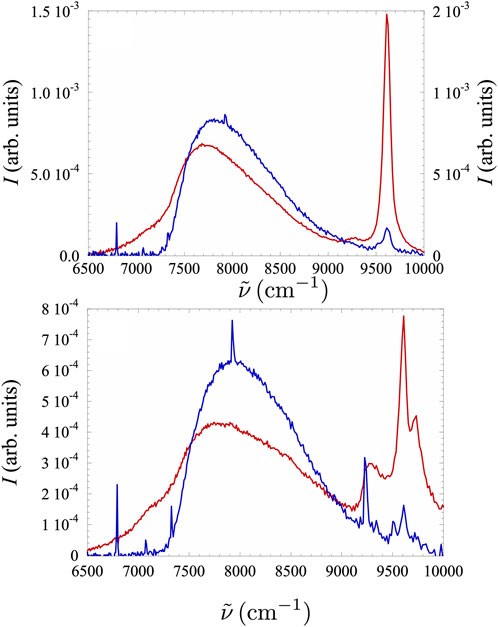
Figure 9. Typical spectra in Xe– $N_{2}$ mixtures. Top panel: spectra at $x = 25 %$ . Blue line: $P = 20$ kPa and $N = 4.86 \times 1 0^{24} m^{- 3}$ . Red line: $P = 718$ kPa and $N = 1.75 \times 1 0^{26} m^{- 3}$ . Bottom panel: spectra at $x = 80 %$ . Blue line: $P = 20$ kPa and $N \approx 4.90 \times 1 0^{24} m^{- 3}$ . Red line: $P = 740$ kPa and $N = 1.80 \times 1 0^{26} m^{- 3}$ . At high pressure, the spectrum is heavily distorted with respect to its low-pressure shape. The lines stemming from atomic transitions within the 6p–6s manifold in the range $9,000 {cm}^{- 1} < \tilde{ν} < 1 0^{4} {cm}^{- 1}$ are not suppressed and are strongly affected by the density, especially in the Xe-richer mixture. All spectra are normalized to the unit area.

For all Xe concentrations, ${\tilde{ν}}_{m}$ linearly decreases with increasing $N$ , as shown in the top panel of Figure 10. Once again, the strength of the redshift is minimal for the mixture with the lowest Xe concentration and increases with the increase in the Xe concentration, monotonically approaching the strength obtained in pure Xe gas.

Figure 10

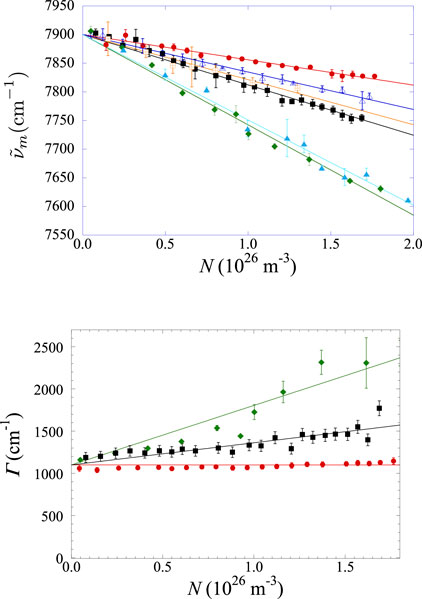
Figure 10. Top panel: density-dependence of ${\tilde{ν}}_{m}$ in the Xe– $N_{2}$ mixtures of Xe concentrations (from the top): $x (%) = 8$ , 20, 30, $40$ , $75$ , and 80. Lines: theoretical prediction. Bottom panel: full width at half height $Γ$ of the ${Xe}_{2}$ excimer band as a function of the gas density for the Xe– $N_{2}$ mixtures of Xe concentrations of (from the top): $x (%) = 80$ , 40, and 8. The data for the other mixtures are not plotted to avoid cluttering. Lines: linear fit to the data.

The quantification of the collisional broadening of the spectra is shown in the bottom panel of Figure 10, in which the full width at half height $Γ$ is reported as a function of the gas density for some mixtures. Once more, the largest broadening occurs for the mixture with the highest Xe concentration, whereas the minimum broadening is obtained when the Xe concentration is the lowest. Again, we suggest that this effect could be a consequence of the quantum indistinguishability of identical particles (Gasiorowicz, 1974). If the ${Xe}_{2}$ excimer collides with an Xe atom, the scattering cross-section might be larger than if it were colliding with a different atomic species, as it occurs in the case of $H_{2}$ –H collisions at low energy (Krstic and Schultz, 1999). However, this hypothesis is questionable, as quantum effects hardly manifest themselves at high temperatures.

Finally, we want to provide evidence regarding the large uncertainty on the width at the highest Xe concentration. As previously noted, the spectra in the Xe– $N_{2}$ mixtures at high Xe concentrations are so much more distorted than in the mixtures based on different gases that the individuation of the width might be very difficult, thereby making $Γ$ quite meaningless at high density.

4 Discussion

The most interesting feature of our experimental observation is that the NIR excimer spectrum is always shifted toward lower wavenumbers, i.e., it is redshifted, if the density of the gas is increased. This phenomenon may affect the way in which Xe is used in the field of high-energy particle detection. However, most significantly in our opinion, it may shed light on the (unexpected) correlation between two different realms involving very low-energy electrons in a dense environment: loosely bound electron states in a molecule and quasi-free electron transport in dense gases.

We noted that, in the limit of the negligibly small density, ${\tilde{ν}}_{0} = \lim_{N \to 0} {\tilde{ν}}_{m}$ and $Γ_{0}$ converge to the same values for all investigated mixtures, which is precisely the one observed in the pure Xe gas. This is a very convincing clue that the emitting species is the ${X e}_{2}$ excimer in all samples. Thus, a possible explanation of the experimental outcome for the pure gas should act as a guide for understanding the behavior observed in the different mixtures.

We were able to set up a theoretical model that explains the experimentally observed redshift in pure Xe gas without any adjustable parameters (Borghesani et al., 2001). We are now in the position to extend this successful model to the case of the mixtures. We will see that all the features of the model maintain their validity and that the extension of the pure gas model to the mixtures is straightforward, provided that the mixtures are dealt with by exploiting the law of the ideal mixtures. Thus, in this section, we will recapitulate the model we have devised and show how it is successfully extended to mixtures.

4.1 Derivation of the model for pure Xe gas

The electronic structure of an isolated homonuclear excimer is accurately described in terms of an ionic core plus a (largely) delocalized electron in a diffuse Rydberg orbital whose radius is much larger than the internuclear separation (Mulliken, 1970). Such a description also retains its validity in a dense gaseous environment, provided that the density is low enough to lead to a negligibly low scattering rate of the electron off the surrounding atoms. Stated differently, the mean free path of a quasi-free electron in the gas must be larger than the size of the Rydberg orbital. This condition is fulfilled in pure Xe gas as the mean free path at the density of our experiment is several nanometers long (Huang and Freeman, 1978). It is also fulfilled in $N_{2}$ (Wada and Freeman, 1981), Ar (Huang and Freeman, 1981), and He (Bartels, 1975). A rough estimate of an upper limit on the value of the Rydberg orbital radius $R$ can be easily obtained by enforcing the condition that the quasi-free electron mean free path $ℓ = 1 / N σ$ , in which $σ$ is the momentum-transfer scattering cross-section, is much longer than the circumference $2 π R$ of the Rydberg orbital, $2 π R N σ ≲ 1$ . For Xe gas atoms, in the 10 meV energy range, $σ \approx 5 \times 1 0^{- 20} m^{2}$ (McEachran and Stauffer, 2014). For the highest density $N \approx 8 \times 1 0^{26} m^{- 3}$ reached in the previous experiment in pure Xe (Borghesani et al., 2001), we get $R ≲ 3.8$ nm.

High-extravalence excitations of atomic impurities in highly polarizable media are known to be redshifted and are assumed to have a probable parentage with Wannier impurity states in liquids (Messing et al., 1977a; Messing et al., 1977b). Thus, the excimer energy spectrum can be computed in analogy with that of these Wannier states.

Two main effects influence the excimer energy spectrum. The first one is a classical dielectric screening effect. It has been shown that the electron energy eigenvalues in a point-like Coulomb potential immersed in a medium of a relative dielectric constant $K (N)$ , (Equation 2), are reduced by a factor $K^{2} (N)$ (Herman et al., 1956). In a naive picture, we can envision this effect by assuming that many atoms of the environment can be accommodated within the wide electron orbit, thereby screening the ionic core–electron Coulomb interaction.

In the present case, the excimer band originates from the transition from the high-lying, vibrationally relaxed, bound $(3) 0_{u}^{+}$ molecular state, described by the potential energy curve $V_{u}$ , toward the dissociative $(1) 0_{g}^{+}$ state, described by the potential energy curve $V_{g}$ (Borghesani et al., 2007a).

As a consequence of dielectric screening, the average energy difference between the initial and final states is reduced by the factor $K^{2} (N)$ . The relative dielectric constant is computed via the Lorentz–Lorenz formula

\frac{K - 1}{K + 2} = (\frac{α}{3 ϵ_{0}}) N, (2)

in which $α = 4.45 \times 1 0^{- 40}$ F $\cdot$ m is the Xe atomic polarizability (see Table 1) and $ϵ_{0}$ is the vacuum permittivity.

Table 1

Table 1. Physical properties of the gases.

Owing to the smallness of $α$ and the not-so-large density reached in the present experiment, $1 / K^{2} (N)$ can be expressed as a Taylor expansion by keeping only the first-order term without any loss of accuracy. Thus, the wavenumber ${\tilde{ν}}_{m}$ at the center of the excimer band is obtained as

{\tilde{ν}}_{m} = \frac{⟨ V_{u} - V_{g} ⟩}{2 π ℏ c K^{2} (N)} \approx {\tilde{ν}}_{0} (1 - \frac{2 α}{ϵ_{0}} N) = {\tilde{ν}}_{0} - {\tilde{ν}}_{0} \frac{2 α}{ϵ_{0}} N, (3)

In Equation 3 $ℏ$ is the reduced Planck’s constant and ${\tilde{ν}}_{0} = ⟨ V_{u} - V_{g} ⟩ / 2 π ℏ c$ , which can approximately be estimated to be ${\tilde{ν}}_{0} \approx 7900 {cm}^{- 1}$ (Borghesani et al., 2007a; Borghesani et al., 2007b). Unfortunately, there are no precise theoretical estimates, and thus, the value of ${\tilde{ν}}_{0}$ must be deduced from the experiment. This dielectric screening effect is linear in $N$ , but the slope $2 α {\tilde{ν}}_{0} / ϵ_{0}$ approximately contributes only one-half of the measured slope.

The second, equally relevant contribution to the density dependence of ${\tilde{ν}}_{m}$ is given by a quantum multiple scattering effect that also affects the transport properties of quasi-free electrons in dense noble gases (Borghesani et al., 1992). The Rydberg electron in the excimer is so largely delocalized that it can be treated as if it were almost quasi-free. Its wavefunction spans over many surrounding atoms at once, and its energy is shifted by the density-dependent quantity $V_{0} (N)$ that was first computed by Fermi (Fermi, 1934),

V_{0} (N) = \frac{2 π ℏ^{2}}{m} N a, (4)

In Equation 4 $m$ is the electron mass and $a$ is the electron–atom scattering length. This contribution only affects the energy of the electron in the upper bound state, whereas it is absent in the final state, in which the electron is no longer widely delocalized.

By adding this contribution to the first one, we finally get the density-dependent shift of ${\tilde{ν}}_{m}$ as

{\tilde{ν}}_{m} = {\tilde{ν}}_{0} - ({\tilde{ν}}_{0} \frac{2 α}{ϵ_{0}} - \frac{ℏ a}{m c}) N, (5)

which turns out to be linear in $N$ . We stress the fact that the model, Equation 5, does not contain any adjustable parameters.

The Xe scattering length is $a = - 3.09 \times 1 0^{- 10}$ m (see Table 1) and adds to the effect of the dielectric screening by reducing the energy difference of the bound–free transition. This leads to the observed strong redshift of the spectra in pure Xe. The solid line in the top panel of Figure 5 is the theoretical prediction given by Equation 5.

In the case of the Xe $(10 %)$ –Ar $(90 %)$ mixture, Xe is mainly surrounded by Ar atoms. Thus, by using the values of atomic polarizability $α = 1.827 \times 1 0^{- 40}$ F $\cdot$ m and scattering length $a = - 0.86 \times 1 0^{- 10}$ m relative to Ar, Equation 5 also describes the mixture redshift satisfactorily well, as shown by the solid line in the top panel of Figure 5.

While the dielectric screening effect, although of different strengths in different gases, always acts in the same direction by reducing the transition energy, thereby shifting the excimer spectrum toward longer wavelengths, the contribution of the multiple scattering effect (Equation 4) may be positive or negative depending on the sign of the scattering length $a$ . Thus, it may amplify or diminish the redshift of the excimer spectrum. In low atomic mass noble gases such as He and Ne, $a$ has a positive value, whereas it is negative in heavier noble gases. For these reasons, we expect that the redshift of the ${X e}_{2}$ excimer spectrum in the mixtures is significantly smaller than that in pure Xe. The goal of the present experiment is exactly to test this prediction.

4.2 Extension of the model to Xe-based mixtures

The aim of Section 4.2 is to extend the interpretative model to gaseous mixtures for the redshift. The energy transfer from the lighter to the heavier noble gases is a well-known process (Efthimiopoulos et al., 1997). Therefore, Xe is always excited either by direct or indirect processes, and it is safe to assume that ${Xe}_{2}$ excimers, although Xe may be the less abundant species, are the emitting species in the investigated spectral range.

In a mixture, the ${Xe}_{2}$ excimer is mostly surrounded by atoms or molecules of different species. It then interacts with them, and not only with other Xe atoms. As a consequence, Equation 5 must accordingly be modified by taking into account the probability that the Xe neighbors are different. The easiest way to pursue this goal is to simply adopt the concept of the ideal mixtures (Guggenheim, 1966) and assume that the average polarizability and scattering length of any mixture are the sum of these properties of the individual species, weighted by their relative abundances.

We have to remember that at the temperature and pressures of the present experiment, all gases follow the law of the ideal gas quite accurately¹. Therefore, the average density $N$ of any mixture does not significantly differ from the density of the ideal gas at the same $T$ and $P$ .

Let $α_{i}$ , $a_{i}$ , and $x_{i}$ with $i = 1,2$ be the polarizability, scattering length, and relative abundance of the two species present in the mixture, respectively. Moreover, let $x_{1} = x$ , and $x_{2} = 1 - x$ . Equation 5 is then modified to yield

{\tilde{ν}}_{m} = {\tilde{ν}}_{0} - \{\frac{2 {\tilde{ν}}_{0}}{ϵ_{0}} [x α_{1} + (1 - x) α_{2}] - \frac{ℏ}{m c} [x a_{1} + (1 - x) a_{2}]\} N \equiv {\tilde{ν}}_{0} - β N, (6)

with the slope $β$ given by

β = \{\frac{2 {\tilde{ν}}_{0}}{ϵ_{0}} [x α_{1} + (1 - x) α_{2}] - \frac{ℏ}{m c} [x a_{1} + (1 - x) a_{2}]\} . (7)

The main result is that ${\tilde{ν}}_{m}$ is still linearly dependent on the density $N$ , although its value now depends on the properties of the two species in the mixture. Equation 6 is represented by the straight lines in the top panel of Figure 6 for the Ar–Xe mixture and in the top panels of Figure 8 and Figure 10 for the Xe–He and Xe– $N_{2}$ mixtures, respectively.

The values of polarizability $α$ and scattering length $a$ of the gases at hand are found in the literature and summarized in Table 1. Once the polarizability and scattering length of the species used in our experiment are known, it is an easy task to compute the expected values for the slope $β$ via Equation 7. In Table 2 we compare the values of $β$ obtained with a linear fit to the experimental ${\tilde{ν}}_{m}$ data with the theoretical prediction. The uncertainty $δ$ on the theoretical determination of $β$ is due to the uncertainty of the mixture concentration and the uncertainty of the values of the scattering length found in the literature, whereas the uncertainty of the experimental determination of the slope is the statistical uncertainty of the weighted linear fit to the experimental data.

Table 2

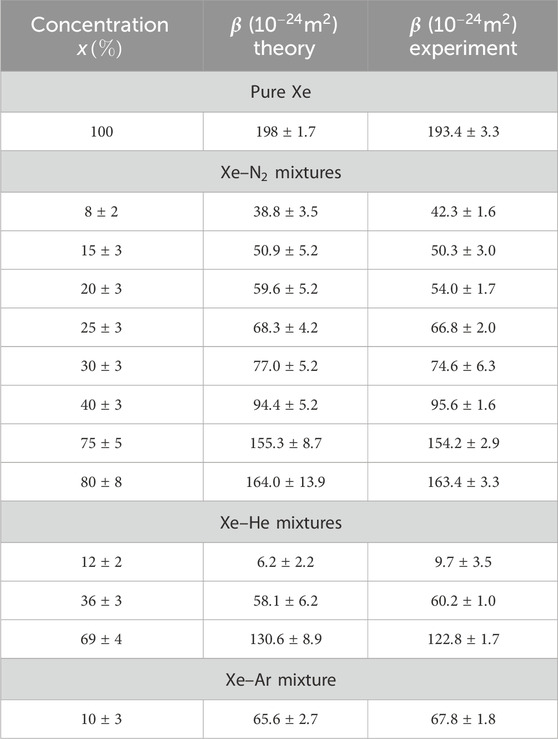
Table 2. Comparison of the experimentally measured values of the linear coefficient $β$ (Equation 7) of the density-dependent redshift of the ${Xe}_{2}$ excimer band centroid with the theoretically expected ones for the investigated Xe– $N_{2}$ and Xe–He mixtures of different Xe concentrations $x$ . Literature data for pure Xe and the Xe–Ar mixture are reported (Borghesani et al., 2001).

We noted that the proposed extension of the original model for the pure gas accounts for the experimental results for the mixtures in an excellent way. The experimental data, within the uncertainty, are very close to the theoretical values for all mixtures. A visual way to ascertain how the experimental data of the slope are close to the predicted values is shown in Figure 11. Here, the experimental $β_{th}$ values of all the mixtures are plotted as a function of the normalized distance from the theoretical value, $y = (β_{th} - β_{exp}) / δ$ . Although this way of displaying the results is not statistically rigorous, nonetheless, it suggests how well the experimental values are aligned with the theoretical prediction.

Figure 11

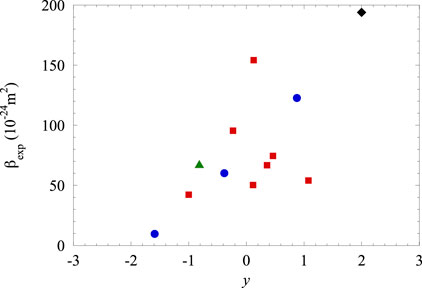
Figure 11. Experimental values of the shift slope $β_{exp}$ versus the normalized distance between the theoretical and experimental slope values $y = (β_{th} - β_{exp}) / δ$ , in which $δ$ is the uncertainty in the theoretical value. Mixtures: Xe– $N_{2}$ (squares), Xe–He (circles), Xe–Ar (triangle), and pure Xe (diamond).

Some additional general remarks can be made by examining the table. The Xe–He mixtures show the lowest $β_{exp}$ values among all mixtures of comparable Xe concentrations. This is because the polarizability of He is the least, and its scattering length is also relatively small. He shows the least polarizability among all investigated gases, thereby yielding the weakest contribution to the redshift due to the dielectric screening effect. Additionally, its scattering length is positive and quite large, leading to a multiple scattering effect contribution, that is, acting to increase the energy difference in the transition, thereby inducing a blueshift that greatly reduces the overall redshift. In addition, the scattering length of the $N_{2}$ molecule is positive but much smaller than that of He (moreover it is known with quite a large uncertainty (Chang, 1981; Song et al., 2023)), and its blueshift contribution is overwhelmed by the redshift induced by its very large polarizability. We can spot this differences between the two mixtures by observing Figure 12, in which the experimental slope values $β_{exp}$ for the Xe–He and Xe– $N_{2}$ mixtures are reported as a function of the Xe concentration. Notably, in the limit of the negligibly small Xe concentrations, $\lim_{x \to 0} β_{exp} (x) < 0$ for the Xe–He mixtures, thereby indicating that if the Xe excimer were only surrounded by He atoms, its emission, would be shifted to higher wavenumbers, i.e., a blueshift of the excimer band would be observed.

Figure 12

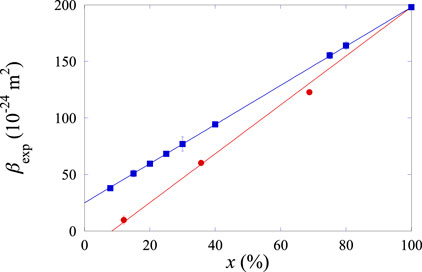
Figure 12. Dependence of the experimental slope $β_{exp}$ on the Xe concentration $x$ for the Xe– $N_{2}$ mixtures (squares) and for the Xe–He mixtures (circles).

On the contrary, for the Xe– $N_{2}$ mixtures, we still have $\lim_{x \to 0} β_{exp} (x) > 0$ . In this case, the polarizability of the nitrogen molecule is so large that it obscures the opposing effect of its scattering length, and the excimer band would still be redshifted.

5 Conclusion

The investigation of the NIR fluorescence of ${Xe}_{2}$ excimers produced by electron impact has led to very interesting discoveries. In the pure Xe gas we have observed a broad NIR emission centered around the wavenumber ${\tilde{ν}}_{m} \approx 7,900 {cm}^{- 1}$ , which we have attributed to a bound–free transition between higher-lying molecular levels. The number of NIR photons emitted per unit energy released in the gas by energetic particles has been proved to be comparable to that of UV photons emitted in the same excitation process, thereby suggesting that the exploitation of the radiation emitted in this band could help improve the sensitivity and energy resolution of high-energy particle detectors based on Xe.

We have unexpectedly found that in addition to the expected collisional broadening, the excimer band is redshifted, i.e., its centroid linearly shifts to smaller wavenumbers, as the gas density increases. We have been able to rationalize the experimental observations by devising a model in which the optically active electron in the molecule in its high-lying energy state is largely delocalized. In this way, it can be treated almost as if it were a quasi-free electron.

According to our model, two effects act to modify the transition energy. The first one is based on the effect of classical dielectric screening: many surrounding atoms are contained in the extremely extended electron orbit and screen the Coulomb electron–nucleus interaction, thereby reducing the difference between the energy levels.

The second one, on the contrary, is a quantum multiple scattering effect. The wavefunction of the delocalized electron has such a wide spatial extension that it spans over several surrounding atoms at a time. As a result, the electron energy is altered by a density-dependent quantum shift $V_{0} (N)$ of its energy at the bottom of the conduction band. For relatively low and intermediate gas densities, this shift is linear with the density itself and depends on the electron–atom scattering length. For the heavier noble gases, the electron–atom scattering length is negative, and so is $V_{0} (N)$ , whereas both are positive for the lighter He and Ne atoms. This effect can, thus, amplify or reduce the influence of the dielectric screening effect.

It is extremely interesting to note that $V_{0} (N)$ influences the energetics and dynamics of excess electrons of very low energy (a few meV) in dense noble gases and liquids and determines their transport regime, where they either drift through the medium as highly mobile quasi-free particles or get self-localized in cavities and consequently move as very slow hydrodynamic objects (Reininger et al., 1983; Borghesani et al., 1991; Borghesani, 2007).

Thus, the spectroscopic measurements may give useful pieces of information on how a delocalized electron interacts with its high-density surroundings. The leading proposal of the present measurements is that the environment could be modified by embedding the probe, i.e., the ${Xe}_{2}$ excimer, in different gases. Gas mixtures have proven to be the best solution. The choice of the gases to be used has been dictated by the values of their physical properties. Moreover, at the temperature and pressure of the present experiment, they can be mixed uniformly in all proportions and behave as ideal gases.

The experimental outcome in the mixture turns out to be qualitatively similar to what is observed for pure Xe gas. The excimer band is always redshifted, i.e., its central wavenumber linearly decreases with increasing gas density, but the shift strength depends on the concentration and type of gases in the mixture.

We have extended the equation of the model to the mixtures by simply applying the law of ideal gas mixtures and assuming that the mixture can be treated as a simple gas whose effective scattering length and effective polarizability are given by the contributions of the individual properties of the two species in the mixture, weighted by their relative abundance.

This extended model is able to describe with great accuracy the experimental results without any adjustable parameters and, thus, has great predictive power. For instance, this spectroscopic technique could be used as an alternative way to measure the scattering length of some gases such as, for instance, some highly polarizable gases such as ${CH}_{3}$ CN (Mikulski et al., 1997), methanol (Krebs and Lang, 1996), or ammonia (Krebs and Wantschik, 1980), which are not known to have equal accuracy as their dielectric constant is, instead of carrying out precision electron scattering experiments at very low energy.

The outcome of the present experiment could have some implications on liquefied noble gas detectors operated in the two-phase mode, such as for liquid Ar mixed with a small concentration of Xe (Kim et al., 2004; Neumeier et al., 2015a), because redshifted luminescence in the gas phase could help correlate the scintillation signal from the liquid. Additionally, the understanding of the processes leading to the NIR shift of the luminescence in the dense gas could also help shed light on the microscopic processes leading to scintillation in liquefied noble gases and/or their mixtures (Neumeier et al., 2015b; Szydagis et al., 2025).

Some puzzling questions remain unsolved. The most critical one is how the collisional broadening of the excimer band correlates with the properties of the individual gases. Although the full width at half length of the excimer band linearly increases with an increase in the gas density, thereby strongly indicating a collision-induced reduction of the excimer lifetime, nonetheless, it is not clear why the coefficient $γ$ in Equation 1 is so large and why the reduction in the Xe concentrations diminishes the density-dependent broadening. For the latter effect, we have proposed the hypothesis of a possible quantum effect of the indistinguishability of identical particles, although the high temperature in the experiment indicates that it might hardly be the case (Borghesani and Carugno, 2008).

Another puzzling question is the effect of nitrogen on some of the Xe I atomic lines, especially at low nitrogen concentrations, as shown in Figure 9. Is their broadening due to the formation of red and blue satellites that are not resolved in our setup? Or is the apparent broadening due to an underlying broad continuum caused by the emission of a possible ${XeN}_{2}$ exciplex? Further measurements at low (and accurately determined) nitrogen concentrations could help in understanding this phenomenon. Unfortunately, this remains an unsolved question so far.

Possible future developments of the experiment will be to pursue the possibility of increasing the gas densities to possibly bridge the gap with the liquid, in which similar NIR luminescence has been detected (Neumeier et al., 2014), and to investigate mixtures with different noble gases in order to test the validity of our heuristic model.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors without undue reservation.

Author contributions

AFB: conceptualization, data curation, formal analysis, investigation, methodology, supervision, validation, visualization, writing – original draft, writing – review and editing, resources, and software. GC: conceptualization, investigation, methodology, resources, supervision, writing – review and editing, and project administration. FC: conceptualization, investigation, writing – review and editing, formal analysis, data curation, methodology, and validation, and visualization.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Acknowledgments

The authors acknowledge useful discussion with Prof. D. Iannuzzi of Vrije Universiteit Amsterdam (The Netherlands). They also gratefully acknowledge technical assistance by G. Galeazzi, E. Berto, and G. Galet.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers at the time of submission. This had no impact on the peer review process and the final decision.

Generative AI statement

The authors declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹https://webbook.nist.gov/chemistry/fluid/

References

Aalbers, J., AbdusSalam, S. S., Abe, K., Aerne, V., Agostini, F., Ahmed Maouloud, S., et al. (2022). A next-generation liquid xenon observatory for dark matter and neutrino physics. J. Phys. G Nucl. Part. Phys. 50, 013001. doi:10.1088/1361-6471/ac841a