A New Impedance Sensor Based on Electronically Implemented Chaotic Coupled van der Pol and Damped Duffing Oscillators

The chaotic behaviour of a system depends on the parameter values, and when the system exhibits such a chaotic behaviour, it is sensitive to the initial conditions. This feature can be used for manufacturing high sensitivity sensors. Sensors based on chaotic circuits have already been used for measuring water salinity, inductive effects, and both noise and weak signals. This article investigates an impedance sensor based on the van der Pol and Duffing damped oscillators. The calibration process is a key point and therefore the folding behaviour of signal periods was also explored. A sensitivity of 0.15 kΩ/Period was estimated over a range from 89.5 to 91.6 kΩ. This range can be adjusted according to the application by varying the gain of the operational amplifier used in this implementation. The development of this type of sensor might be used in medical and biological engineering for skin impedance measurements, for example. This type of chaotic impedance sensor has the advantage of sensing small disturbances and then rapidly detecting small impedance changes within biological materials.

1 Introduction

Many experiments in the biological, engineering and physical sciences have shown that a fundamental implicit property of chaos is a sensitive dependence on the initial conditions. According to Arshad et al. (2020) and Teodorescu, (2017), the change in a dynamic non-linear system due to small changes in its parameters is also sensitive to the initial conditions. This might occur if the dynamic variables of the initial conditions are selected inside the instability region of the system; hence, small perturbations over the parameter values set will significantly affect the system’s dynamics. Therefore, the parameter’s sensitively depend on the initial conditions. Characteristic improvements in sensory systems can be achieved by exploring these attributes. Small changes in system’s parameters may cause different results when the initial conditions are precisely chosen for that purpose, in contrast to linear oscillators whose changes are at the same magnitude according to the defined variation Karimov et al. (2019). For this reason, sensors based on chaotic circuits have been increasingly studied and used in the sensing area. Among some examples, this approach has been used to determine the salinity of water Teodorescu and Cojocaru, (2012), in inductive sensors Karimov et al. (2019), noise-activated non-linear sensors Gammaitoni and Bulsara, (2002), Gammaitoni and Bulsara, (2003), Korneta and Gomes, (2017), weak signal detection sensors Farxodovich, (2021), Ling et al. (2019) and impedance sensors Korneta et al. (2018). There are several ways to implement a chaotic circuit for sensing Gammaitoni and Bulsara, (2002) provided a description of the system dynamic, which allows for the use of a measurement technique based on monitoring the permanence time of the system in its stationary states. Brown et al. (1992) presented three different case studies that explored the sensitivity dependence on the initial conditions to build a sensory device that can be implemented in hardware. One of the experiments used control manifold theory to build a sensor that used the change in the character of a fixed point from elliptical to hyperbolic as a detection mechanism. A second experiment used the escape from the basin of attraction from a fixed point as a detection mechanism. Finally, a third one used a bifurcation event to obtain a change of state in a duplication oscillator. Bifurcation theory studies and classifies phenomena characterised by sudden changes in behaviour resulting from small variations in the imposed conditions, analysing how the qualitative nature of the equation solutions depends on the system parameters Hoff (2014). In a system of equations dependent on parameters, the qualitative structure of the flow can change by varying its parameters. In order to better understand these dynamic changes, it is necessary to briefly define the period, equilibrium point and chaos within the context of nonlinear dynamics. Period in nonlinear dynamics means that the chaotic system can have sequences of values for the evolution of variables that are repeated at a regular interval, providing periodic behaviour from any point in that sequence Marcondes, (2017). In particular, equilibrium points can be created or destroyed, or have their stability altered. These qualitative changes in dynamics are called bifurcations and the parameter values in which they occur are called bifurcation points. In other words, bifurcation is a change in the topological type of the system when its parameters pass through a critical value. Bifurcations are scientifically important, as they provide models of transitions and instabilities when some parameters are varied Hoff, (2014).

There are some types of bifurcation in continuous dynamic systems, in which equilibrium points can be created or destroyed, or have their stability altered by varying one or more parameters Pedro, (2019). In continuous dynamic systems, there are two main bifurcations by which an equilibrium has its stability altered by varying one or more parameters: the saddle-node bifurcation and the Hopf bifurcation. The saddle-node bifurcation is the basic mechanism for creating and destroying equilibrium points, and is also called the fold, tangent, limit point or return point bifurcation. The Hopf bifurcation of a system implies in the generation of a limit cycle.

If Hopf bifurcation evolves by adequately varying the system parameters, it can generate a limit cycle or an attractor. In addition to the equilibrium, the most common form of behaviour is a limit cycle. A limit cycle is an isolated closed path, isolated in the sense that neighbouring paths are not closed, so they spiral towards or away from the limit cycle. Stable limit cycles are very scientifically important, as they model systems that exhibit self-sustaining oscillations. In other words, these systems oscillate even without periodic external forces.

One of the possible bifurcations of a limit cycle generated by Hopf bifurcation is the period doubling bifurcation. The original limit cycle becomes unstable as a family of duplicate period solutions emerges. In general, a series of n duplications may arise after each 2ⁿT period limit cycle is obtained. Several systems have an infinite series of bifurcations with a finite accumulation point; the associated movement beyond that point is chaotic, characterising a route to chaos via a period doubling or Feigenbaum’s scenario Hoff (2014).

Impedance sensors are very well-established in the industry due to their versatility and their main appeal for being non-invasive and non-contact. The first attribute is given by the adjustable penetration of the electric field in matter, while the latter is due to charge induction (capacitive coupling). Impedance sensors can either be individually classified as capacitive and inductive for single frequency applications. In the case of multifrequency systems, impedance sensors measure a spectrum in a wide frequency range. Therefore, impedance sensors can measure the change in either resistance (the real part of the impedance) or reactance (the imaginary part of the impedance) or both. It is known that resistance depends mostly on the resistivity of the material and electrode (sensor) geometry Carminati, (2017). Many biological applications use the phase angle given by arctan (reactance/resistance) in order to characterise the sample under study. Therefore, this type of sensor can have great applicability within the context of biomedical engineering, since skin hydration levels are typically characterised by measurements of electrical skin impedance or thermal conductivity, or by optical spectroscopic techniques, including reflectivity. Mechanical or geometric properties can be evaluated by indirect methods, such as electrical impedance. It is among the most robust, simple and low cost technique Huang et al. (2012).

Impedance sensors based on chaotic circuits are of great interest, for example: 1) monitoring of skin hydration and temperature changes by Huang et al. (2012); 2) investigations of skin nonlinear properties by Pabst, (2018); 3) investigations related to bioelectrical impedance analysis (BIA) by Bertemes-Filho et al. (2010); 4) optimisation of bio-oscillators by Shitiri et al. (2018) and Huertas et al. (2015). The second application suffers from low sensitivity when measuring its properties. Signal sensitivity may also be related to precision and/or accuracy. Either precision or accuracy of the measured output voltage depends on many things, such as movement artifacts. These artifacts (noise) significantly change the skin impedance which, in turns, cannot not be separated from the total measured impedance. It is known from Sinclair, (2000) that skin has a memristive characteristic, where the skin delivered charge depends on the applied voltage used to characterize it. Therefore, a low output voltage may imply a low resistance change; standard impedance sensors may have difficulties in measuring these changes. In the case of chaotic sensor, coupled analogue or digital filters can be used to analyse the signal as a function of time by using the theory of non-linear dynamic systems in order to remove external noise.

Chaotic sensors are cheap and easy to implement. In addition, They can be implemented to have a high sensitivity to the sample’s resistivity change and analysed by a simpler bifurcation diagram in comparison to the one presented in Brown et al. (1992). Therefore, based on the sensitivity offered by chaotic circuits, this article proposes an active impedance sensor based on the chaotic van der Pol and damped Duffing coupled circuits with different attractors. The transition from periodic to other regular dynamics is found through chaotic dynamics in a weak coupling, resulting in windows of regularity immersed in chaos in the parameter space. The chaotic region is also shown for the position of periodic window islands, some of which exhibit period doubling phenomena. The latter case, in turn, can be analyzed using an experimentally obtained bifurcation diagram which will provide a relationship between the resistance representing one of the system parameters and the periodic attractor described by Pedro (2019).

2 Materials and Methods

In order to better understand the electrical implementation of the sensor proposed here, some basic equations are presented in the following for justifying the electrical circuit simulated in this article. The dynamics of the system that linearly couples the van der Pol and damped Duffing oscillators is given by:

$\ddot{x}-\mu \left(1-x^2\right)\dot{x}+x-k\left(y-x\right)=0(1)$

$\ddot{y}+\alpha \dot{y}-y+y^3-k\left(x-y\right)=0(2)$

where μ is a positive parameter that controls one of the model’s nonlinear behaviours, α corresponds to the dissipation term and k is the coupling constant.

For k = 0, both oscillators are decoupled. The van der Pol exhibits a limit cycle while the Duffing circuit presents a damped oscillatory movement. Certainly, coupling can be seen as the disturbance which proportionally arises from the difference in their positions.

Considering that x = x₁, y = y₁, $\dot{x}=x_2$ and $\dot{y}=y_2$, then the system can be rewritten as:

${\dot{x}}_1=x_2(3)$

${\dot{x}}_2=\mu \left(1-x_1^2\right)x_2-x_1+k\left(y_1-x_1\right)(4)$

${\dot{y}}_1=y_2(5)$

${\dot{y}}_2=-\alpha y_2+y_1-{y_1}^3+k\left(x_1-y_1\right)(6)$

Thereby, an integrating circuit can be built following the schematic shown in Figure 1, where τ is the time of integration (R_b = 100 kΩ and C_b = 10 nF). The circuit was built with the k coupling constant = 0.5, μ = 0.8 and $\alpha =\frac{R_{sensor}}{R_b}$. TL074 operational amplifiers were implemented together with AD633 analogue multipliers.

FIGURE 1

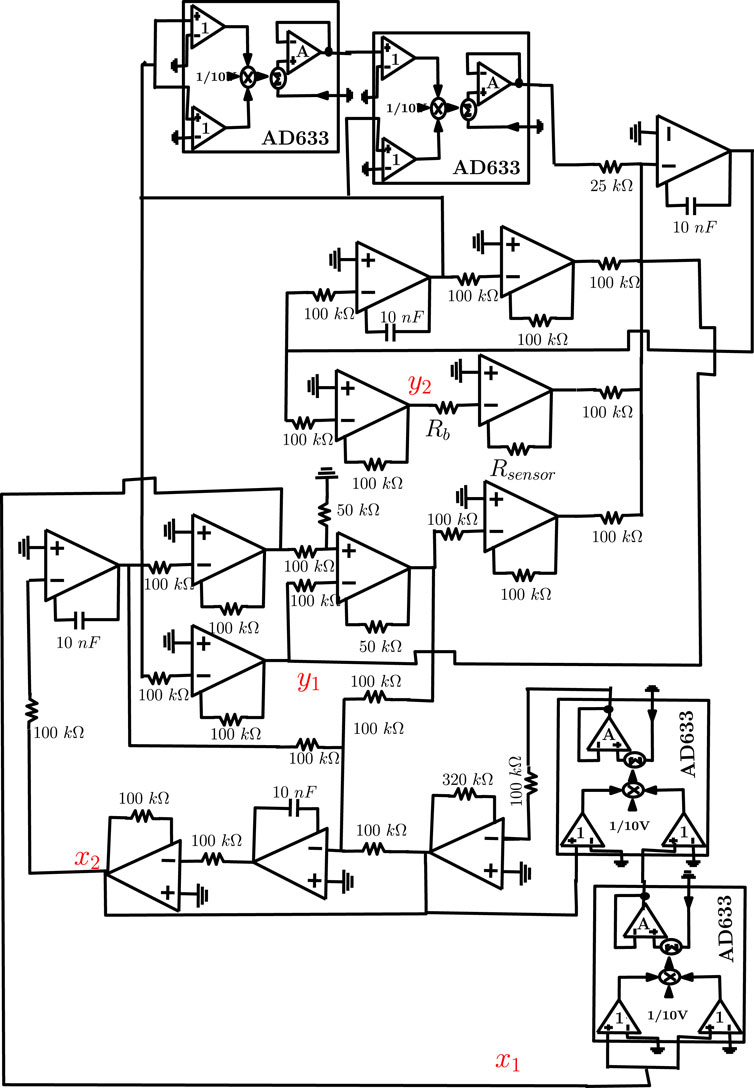
FIGURE 1. Schematic integrated circuit of the van der Pol and Duffing damped oscillators coupled system, where A, B and C represent the transfer equations.

Figure 2 shows the block diagram of the measuring system. A National Instruments data acquisition board read the voltages at a maximum rate of 180 kS/s ¹ and also wrote parameters at a maximum rate of 100 kS/s. The board contains eight analogue inputs, two outputs for parameter control and 20 digital I/O ports. The control of the initial conditions was done by relays connected to each capacitor of the operational amplifier. Analog outputs were in the range of −10 to 10 V at a resolution of 16 bits, as well as the analog inputs. Measured voltages are filtered and then controlled by an algorithm programmed the Python language¹.

FIGURE 2

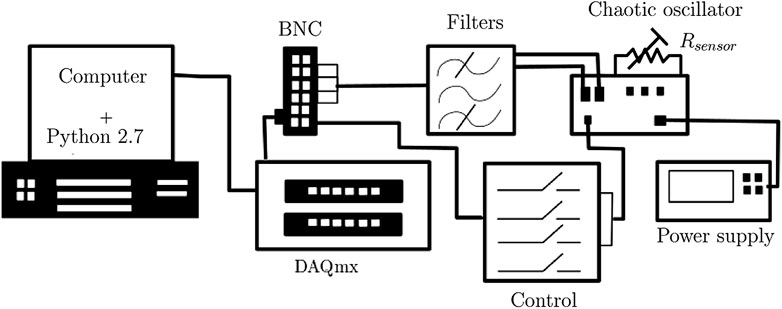
FIGURE 2. Block diagram of the measuring system showing all equipment and connections implemented in the laboratory, where BNC are connectors.

Both integrated circuits (TL074 and AD633) have a flat frequency response within the working bandwidth of the proposed sensor. Therefore, the voltage amplitude must be less than $\sqrt[3]{10}$ and ${y_1}^3$ should be kept below 10 V, assuring good linearity working room for the multiplier AD633. R_sensor is recommended to range from 100 kΩ to 10 MΩ (see Figure 2), resulting in a voltage gain from 0.1 to 1.0 (=$\frac{R_{sensor}}{R_b}$). The SNR was adjusted so that all voltages in the circuit were kept between 0.001 and 3 V, preventing any instability and nonlinearity response of the Opamps. Both voltage pairs X1/X2 and Y1/Y2 were measured by an oscilloscope (BK Precision, model 2,534) in order to monitor the respective Lissajous curves. It was observed that the measured Lissajous curves had the same behaviour compared to the numerical results.

A 100 kΩ (±10 Ω) potentiometer was used to characterise the α parameter (see Eq. 6). 100 points were collected within the chosen resistance range. These points were linearly spaced and collected manually; that is, for each increment in the resistance value. A code algorithm in the Python language was implemented for updating the voltage value of y₂ (see Figure 1).

3 Results

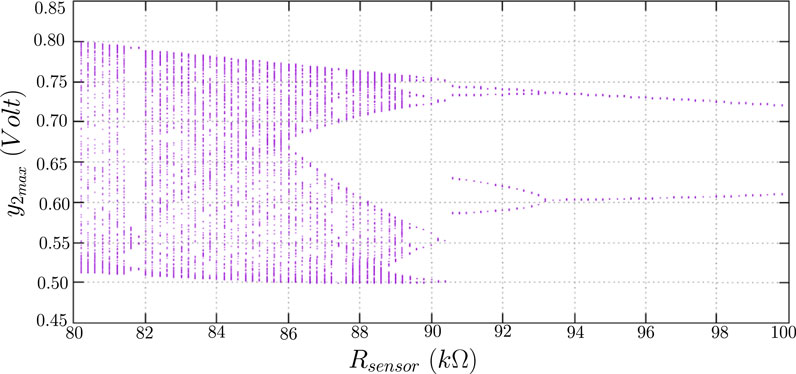
An experimental bifurcation diagram was obtained from the coupled van der Pol and Duffing damped oscillators integrated circuit, as shown in Figure 3.

FIGURE 3

FIGURE 3. Experimental bifurcation diagram of the coupled van der Pol and damped Duffing circuit.

Based on the numerical data and the technique presented by Woafo et al. (1996), the resistance range was chosen to be between 80 and 100 Ω. This range comprises the chaotic region where the phenomenon called period doubling happens, which is a point in the bifurcation diagram in which the phase space starts to present a period orbit duplicate to the previous one.

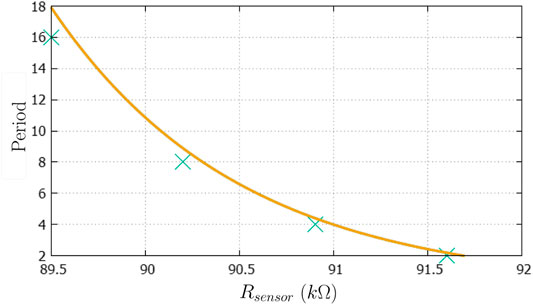
Table 1 shows four points extracted at the region nearby the period doubling, as shown in the bifurcation diagram of Figure 3.

TABLE 1

TABLE 1. Nearby-period-doubling points from Figure 3 showing their respective periods.

A fitting curve was done to best represent the data shown in Table 1, which used a Taylor series model nearby the fixed points. It should be emphasised that there are many types of bifurcation, each one may have a specific equation according to Onias, (2012). In this work, it was used the model proposed by Tresser et al. (2014), was used, in which an exponential function was used for the fitting process, such as:

$P\left(R\right)=a\cdot e^{\left(-b\cdot R+c\right)}(7)$

where P represents the system period, R is the sensor resistance and a, b and c are the coefficients of the fitting equation.

The correlation between the points and their respective periods was done by via visual inspection, either using the measured voltage by the DAQ or by the oscilloscope through the Lissajous curve. The results are shown in Figure 4; resistance can be written as a function of period P, so that:

$R\left(P\right)=92.10-In\left(\frac{P}{1.237}\right)(8)$

The resistance given by Eq. 8 has a confidence range from 89.87 to 90.13 kΩ with a fitting correlation coefficient of −0.96 kΩ. Therefore, the sensor sensitivity can be calculated based on its resistance curve. Generically, sensitivity is defined as a variation of the output signal for a given variation of the physical input parameter. According to work done by Limited, (2021), the sensitivity S of a transducer can be calculated as:

$S=\frac{RFS}{PFS}(9)$

where RFS is the full-scale resistance and PFS is the measured full-scale period, resulting in a sensitivity of 150 Ω/Period, according to the data shown in Table 1.

FIGURE 4

FIGURE 4. Curve adjustment of Eq. 7 to the experimental data shown in Table 1.

4 Discussions

Even with various ways for implementing chaotic circuits for sensing mentioned in Gammaitoni and Bulsara, (2002) and Brown et al. (1992), none of these are focused on impedance sensing for bioimpedance applications. The development of this type of sensor could be applied both to beauty therapy areas, where there is a need to measure the levels of moisture and oiliness Fábrica do Micropimentador (2021), as well as to the biomedical field Ferreira, (2006), with importance in investigating thermoregulation, haemodynamic control and metabolite excretion functions. In addition, the presence of elements from the peripheral nervous system in the dermis layer of the skin means it should be considered an organ for capturing sensory information (heat, cold, pressure, pain and touch) of key importance in researche.

A methodology for measuring impedance is electrical impedance spectroscopy (EIS). Most EIS designers prototype systems for larger bandwidth, lower cost, power excitation control and best portability and usability for users. These systems work with voltage controlled current source VCCS circuits, which have a very high output impedance into compared to the unknown load. This special characteristic gives a sufficient stability in the transfer function over a large frequency range, but it depends on the size of the unknown load and on the characteristics of the Opamps used in the implementation. Hence, chaotic sensing circuits might overcome this required specification.

An EIS-based VCCS system consists of applying a sinusoidal current of multiple frequencies and constant amplitude to the tissue sample, measuring the resulting potential and then calculating the transfer impedance, as shown by Bertemes-Filho et al. (2012). In terms of measuring biological impedance, three advantages of this proposed sensor can be identidied, such as: 1) there is no need of any type of source for exciting the sample under study; 2) it can be used either for sensing grounded or floating loads without the presence of fluctuation due to common voltage; 3) larger working frequency bandwidth in comparison to the standard EIS.

Over the last 20 years, biosensors have been used in wearable applications for measuring electrochemical properties in the human body, such as bioimpedance. There are still technical limitations to be overcome when developing electrochemical impedance spectroscopy measuring systems, including low sensitivity, the impossibility of using non-disposable electrodes (sensors) and of measuring small molecules in a tiny biological sample. Therefore, we believe that the proposed chaotic impedance sensor will overcome these disadvantages over biosensors, with high sensitivity, reusabiliry as an impedance sensor, frequency independence and tunability according to the sample under study.

Although the implemented resistance was on the order of kΩ, other values can be easily investigated. This can be done by exchanging the R_b resistance of the chaotic oscillator (see Figure 1) by a potentiometer (R_bsensor), as shown in Figure 5. This can provide a method for measuring the impedance range most used for this type of application. However, it is required to keep the $R_{sensor}/R_{b_{sensor}}$ ratio in the range of 0.1–1.0.

FIGURE 5

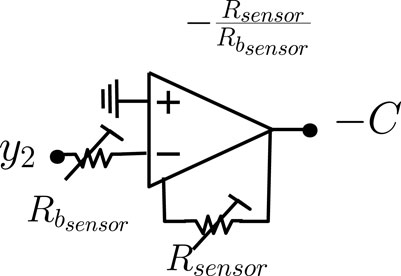
FIGURE 5. Schematic circuit proposal for working with a larger range of biological sample resistance.

We have investigated here a new impedance sensor to indirectly measure a sample’s impedance, whether biological or not, by means of a known mathematical relationship. The main advantage of this implementation is the absence of either a voltage or current source in the measuring system. It can be observed in Figure 1 that the circuits of the oscillator are only powered by a continuous-current supplier, but generating an alternate-current voltage with a period that varies with the impedance of the samples in contact to the proposed sensor. It can be observed in Figure 3 that small variations in the sample’s impedance dramatically changes the dynamic response of the chaotic oscillation system. It should also be pointed out that different regions of the parameter space have different types of bifurcations, allowing sensor sensitivity to be adjusted according to the application under study. It must be emphasised that only one application was investigated among many other phenomena in dynamic systems.

Further investigations are required; for example, the stochastic resonance phenomena for sensor optimisation, as described by Barreto, (2015). This is due to the fact that the coupling of van der Pol and damped Duffing oscillators could act as a noise signal, which is simultaneously feed back to the measuring system. Therefore, the hypothesis that the coupling constant can improve the sensor’s ability to identify signals through the stochastic resonance phenomenon might be plausible.

Regarding chaotic sensors for commercial applications, care should be taken, and more investigations carried out. An alternative is to use a discrete peak detector circuit and a counter for detecting the number of peaks of y₂. This should be carefully studied, since coupling chaotic circuits working with auxiliary circuits may add several difficulties due to noise. However, the visual inspection of folding periods in the bifurcation diagram given by the routines in Python might be considered a feasible solution to characterize the impedance change of a sample under study.

Finally, it should be expected that the system dynamics from a certain finite amount of doubling period will lead to chaos. We believe that the behaviour presented by the bifurcation diagram shown in Figure 3 is such a case. It can be noticed that there is no visual way to count the doubling periods after the fourth step, unless a magnification is done to possibly find further steps until chaos is reached. Future works will use the TISEAN routine in order to read longer periods that occur on a smaller parameter variation. TISEAN is a software package for analysing time series with methods based on nonlinear dynamic systems according to Hegger et al. (1999) and Kantz and Schreiber, (2004). There are open-source electronic prototyping platforms (e.g., Arduino) capable of performing automated data processing routines which might be useful for this application.

It should be emphasised that the presented model was not intended to implement a practical device, but to propose the modelling of an impedance sensor based on the van der Pol and Duffing damped oscillators. Although the sensor sensitivity (=150 Ω/Period) may be low for practical applications, bioimpedance solutions are more complex and expensive which, in turn, use signal generators, current sources and voltage meters to calculate impedance by means of electrodes placed on the skin surface.

5 Conclusion

This work brought a proposal for an impedance sensor based on the coupling of the van der Pol and damped Duffing circuits. It was observed that small variations might be identified using chaotic oscillators. Most disturbances have magnitudes as great as the signal variation desired to be measured, then a chaotic sensor may be able to sense only the signal variation disregarding the disturbance (e.g., noise). The findings from this work might be used in the development of a portable, real time, low-power consumption and low-cost device for detecting very small impedance changes in real life applications. It must be emphasised that practical tests with different types of samples, including biological ones, must be done before exploiting the applicability and usability of the proposed sensor.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

BGP made the main contributions to the conception of the work and the creation of new analytical models used in the work. PB-F drafted the work, substantively revised it and agrees to be personally accountable for the first author’s own contributions and for ensuring that questions related to the accuracy or integrity of any part of the work, even ones in which the author was not personally involved, are appropriately investigated, resolved, and documented in the literature.

Funding

This project was funded by UDESC (State University of Santa Catarina) grant number 092384469-46.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank the State University of Santa Catarina (UDESC) for the institutional support and the Coordination for the Improvement of Higher Education Personnel (CAPES) for the financial support by means of PROAP-AUXPE.

Footnotes

¹S/s = samples per second.

References

Arshad, A. A. E. A. S. S. A., Shaukat, S., and Ahmad, J. (2020). Chaos Theory and its Application: An Essential Framework for Image Encryption. Chaos Theory Appl. 2 (1), 17–22.

Google Scholar

Barreto, M. A. (2015). Aplicação de ressonância estocástica em medidas eletrofisiológicas.. Available at: http://www.cc.faccamp.br/Dissertacoes/Marco_2015.pdf

Google Scholar

Bertemes-Filho, P., Negri, L. H., Felipe, A., and Vincence, V. C. (2012). Mirrored Modified Howland Circuit for Bioimpedance Applications: Analytical Analysis. J. Phys. Conf. Ser. 407, 012030. doi:10.1088/1742-6596/407/1/012030

CrossRef Full Text | Google Scholar

Bertemes-Filho, P., Valicheski, R., Pereira, R. M., and Paterno, A. S. (2010). Bioelectrical Impedance Analysis for Bovine Milk: Preliminary Results. J. Phys. Conf. Ser. 224, 012133. doi:10.1088/1742-6596/224/1/012133

CrossRef Full Text | Google Scholar

Brown, R., Chua, L., and Popp, B. (1992). Is Sensitive Dependence on Initial Conditions Nature's Sensory Device? Int. J. Bifurc. Chaos 02, 193–199. doi:10.1142/s0218127492000185

CrossRef Full Text | Google Scholar

Carminati, M. (2017). Advances in High-Resolution Microscale Impedance Sensors. J. Sensors. doi:10.1155/2017/7638389

CrossRef Full Text | Google Scholar

[Dataset] Fábrica, do Micropimentador (2021). Analisador de pele digital bio impedância oleosidade umidade. Available at: https://www.fabricadomicropigmentador.com.br/produtos/analisador-de-pele-digital-bio-impedancia-oleosidade-umidade/ (Accessed Oct 16, 2021).

Google Scholar

Farxodovich, I. J. (2021). Using a Chaotic Generator as a Detector of Weak Periodic Signals. Archive Conf. 13, 93–97.

Google Scholar

Ferreira, D. M. (2006). Impedância Elétrica na Determinação de alterações da Pele Provocadas por Substâncias Irritantes. Ph.D. thesis, UFRJ. Available at: http://www.peb.ufrj.br/teses/Tese0040_2006_08_25.pdf (Accessed Oct 16, 2021).

Google Scholar

Gammaitoni, L., and Bulsara, A. R. (2002). Noise Activated Nonlinear Dynamic Sensors. Phys. Rev. Lett. 88, 230601. doi:10.1103/PhysRevLett.88.230601

PubMed Abstract | CrossRef Full Text | Google Scholar

Gammaitoni, L., and Bulsara, A. R. (2003). Nonlinear Sensors Activated by Noise. Phys. A Stat. Mech. its Appl. 325, 152–164. doi:10.1016/s0378-4371(03)00194-8

CrossRef Full Text | Google Scholar

Hegger, R., Kantz, H., and Schreiber, T. (1999). Practical Implementation of Nonlinear Time Series Methods: The Tisean Package. Chaos 9, 413–435. doi:10.1063/1.166424

PubMed Abstract | CrossRef Full Text | Google Scholar

[Dataset] Hoff, A. (2014). Estruturas de bifurcação em sistemas dinâmicos quadridimencionais. Available at: https://www.udesc.br/arquivos/cct/id_cpmenu/877/dissertacao_david_15162081954893_877.pdf.

Google Scholar

Huang, X., Yeo, W.-H., Liu, Y., and Rogers, J. A. (2012). Epidermal Differential Impedance Sensor for Conformal Skin Hydration Monitoring. Biointerphases 7, 52. doi:10.1007/s13758-012-0052-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Huertas, G., Maldonado, A., Yúfera, A., Rueda, A., and Huertas, J. L. (2015). The Bio-Oscillator: A Circuit for Cell-Culture Assays. IEEE Trans. Circuits Syst. II 62, 164–168. doi:10.1109/tcsii.2014.2386233

CrossRef Full Text | Google Scholar

Kantz, H., and Schreiber, T. (2004). Nonlinear Time Series Analysis, 7. Cambridge University Press.

Google Scholar

Karimov, T., Nepomuceno, E. G., Druzhina, O., Karimov, A., and Butusov, D. (2019). Chaotic Oscillators as Inductive Sensors: Theory and Practice. Sensors 19, 4314. doi:10.3390/s19194314

PubMed Abstract | CrossRef Full Text | Google Scholar

Korneta, W., and Gomes, I. (2017). Noise Activated Bistable Sensor Based on Chaotic System with Output Defined by Temporal Coding and Firing Rate. Chaos 27, 111103. doi:10.1063/1.5006564

PubMed Abstract | CrossRef Full Text | Google Scholar

Korneta, W., Iacyel, G., Rodrigo, P., and Zabovsky, M. (2018). “Nonlinear Sensor Driven by Chaotic Dynamics,” in ANNA’18; Advances in Neural Networks and Applications 2018 (VDE), 1–4.

Google Scholar

[Dataset] Limited, G. I. (2021). Calculating Sensitivity and Full Scale Output. Available at: http://www.gdsinstrumentspp.com/SUPPORT%20SITE/Product%20Helpsheets/125%20-%20Hardware%20-%20Transducers%20-%20Calculating%20sensitivity%20and%20full%20scale%20output.pdf (Acessed Nov 29, 2021).

Google Scholar

Ling, Y.-f., Chen, C.-x., Niu, D.-z., and Chen, T. (2019). Weak Signal Detection Using Double-Well Duffing-van der Pol Oscillator and Formulation of Detection Statistics. J. Phys. Soc. Jpn. 88, 044001. doi:10.7566/jpsj.88.044001

CrossRef Full Text | Google Scholar

[Dataset] Marcondes, D. C. (2017). Controle de parâmetros via tensão contínua: uma aplicação em dinâmica não-linear. Available at: https://www.udesc.br/arquivos/cct/id_cpmenu/877/dissertacao_david_15162081954893_877.pdf.

Google Scholar

[Dataset] Onias, H. H. S. (2012). Bifurcações Dinâmicas Em Circuitos Eletrônicos. Available at: https://repositorio.ufpe.br/handle/123456789/11087.

Google Scholar

Pabst, O. (2018). Rectifying Memristor Bridge Circuit Realized with Human Skin. J. Electr. Bioimpedance 9, 184–192. doi:10.2478/joeb-2018-0023

PubMed Abstract | CrossRef Full Text | Google Scholar

[Dataset] Pedro, B. G. (2019). Acoplamento dos osciladores van der pol e duffing amortecido: Uma abordagem experimental. Available at: https://www.udesc.br/arquivos/cct/id_cpmenu/877/Disserta__o_Bruna_15705659818779_877.pdf.

Google Scholar

Shitiri, E., Vasilakos, A., and Cho, H.-S. (2018). Biological Oscillators in Nanonetworks-Opportunities and Challenges. Sensors 18, 1544. doi:10.3390/s18051544

PubMed Abstract | CrossRef Full Text | Google Scholar

Sinclair, I. (2000). Sensors and Transducers. Elsevier.

Google Scholar

Teodorescu, H.-N. L., and Cojocaru, V. P. (2012). “Biomimetic Chaotic Sensors for Water Salinity Measurements and Conductive Titrimetry,” in 2012 Third International Conference on Emerging Security Technologies (IEEE), 182–185. doi:10.1109/est.2012.42

CrossRef Full Text | Google Scholar

Teodorescu, H.-N. L. (2017). “Sensors Based on Nonlinear Dynamic Systems—A Survey,” in 2017 International Conference on Applied Electronics (AE) (IEEE), 1–10.

Google Scholar

Tresser, C., Coullet, P., and Faria, E. (2014). Period Doubling. Scholarpedia 9, 3958. doi:10.4249/scholarpedia.3958

CrossRef Full Text | Google Scholar

Woafo, P., Chedjou, J. C., and Fotsin, H. B. (1996). Dynamics of a System Consisting of a van der pol Oscillator Coupled to a Duffing Oscillator. Phys. Rev. E 54, 5929–5934. doi:10.1103/physreve.54.5929

PubMed Abstract | CrossRef Full Text | Google Scholar