Overshoot-tolerant primary frequency control of battery energy storage system for battery aging mitigation

Battery energy storage systems (BESSs) are required to provide frequency support to the grid in some cases, which increases the charge-discharge cycles of battery and accelerates its aging, especially in primary frequency control (PFC). However, the conventional PFC of BESS mainly focuses on the frequency support performance without adequately considering battery health. This paper proposes an adaptive PFC of BESS for battery aging mitigation, which adopts a novel overshoot-tolerant principle to recover the state of energy (SOE) of battery. Once the frequency support demand aligns with the SOE recovery demand, the BESS responds to the frequency deviation in a reverse way. Then, the battery can be charged or discharged more vigorously, and the SOE of battery can be adequately maintained at an ideal level. A multi-objective online optimization model is proposed to update the optimal PFC coefficient, which is solved by the non-dominated sorting genetic algorithm (NSGA-II). The simulation results verify the proposed method, which can effectively recover the SOE of battery with an improved frequency support performance. Moreover, the case study results also validate that the aging of battery can be mitigated by recovering the SOE.

1 Introduction

Battery energy storage systems (BESSs) have become increasingly important in modern power systems due to their rapid response speed, high energy density, and flexible deployment. They can provide auxiliary services to the grid, where the frequency support is crucial (Pusceddu et al., 2021; Shu et al., 2024). However, frequency control, especially primary frequency control (PFC) will accelerate the aging of the battery and shorten its life. The operational costs of BESSs are then increased, limiting their wide application (National Standardization Administration, 2021; Xiang et al., 2023; Zhai et al., 2017).

Specifically, battery aging consists of calendar aging and cycle aging (Xia et al., 2018; Zhang et al., 2018). The calendar aging reflects the natural degradation of battery capacity over time, while the cycle aging represents the battery capacity loss in charge-discharge cycles. As the frequency disturbance is relatively irregular, the battery would be randomly and frequently charged or discharged to meet the grid demand. The state of energy (SOE) of battery may fluctuate within a random range in this case, which largely aggravates the aging of battery (Perez et al., 2016; Grimaldi et al., 2023). However, the aging mechanism of battery is impacted by multiple factors, e.g., temperature, charge-discharge rate, SOE level, which are complicated to quantify. Then, the mitigation of battery aging in PFC scenario is challenging. Fortunately, it has been found that battery aging, including the calendar and the cycle aging, can be comprehensively alleviated when the SOE is shallowly charged around an intermediate level (Wei et al., 2022). Then, controlling the SOE could be a reasonable solution to mitigate the battery aging in PFC scenario, and how to incorporate the SOE management in the PFC is the key.

PFC adjusts the battery output power in response to frequency dynamic via certain control coefficients (Kottick et al., 1993; Wang et al., 2019; Rui et al., 2020). Different with synchronous generators, the PFC coefficient of BESS can be flexibly regulated, and the performance of PFC is greatly dependent on the parameter tuning. For example, by applying an adaptive fuzzy blending algorithm to adjust the BESS output power, the emulation of inertia and frequency damping (i.e., frequency droop) can be realized (Xing et al., 2021; Wang et al., 2020). Then, the frequency regulation capability of grid is enhanced. The PFC coefficient can also be regulated piecewise. For example, the inertia control and frequency droop control can be enabled in the frequency decrease stage and frequency recovery stage, respectively (Li et al., 2022a). In this way, the key indices, e.g., the rate of change of frequency (RoCoF) and the maximum frequency deviation, of frequency quality can be comprehensively improved. However, the PFC coefficient regulation of BESS is for improving the frequency quality, while the battery health is barely considered. Moreover, those control methods may stimulate a sudden and large change in battery output power. The long-term operation under such conditions will largely shorten the life of battery (Stroe et al., 2017; Xu et al., 2018a).

Several studies have incorporated battery aging into frequency control. Certain studies focus on economically managing the SOE of battery by fully considering battery aging (Shi et al., 2018; Zheng et al., 2023; Li et al., 2023). The goal is to maximize the profit of BESS in frequency regulation markets within battery lifespan constraints. However, the models developed face challenges arising from the dynamic changes of policies in the power market, particularly differences across regions and countries. Therefore, relying on regulation through the economics of the electricity market may hinder the overall improvement of battery lifespan and the applicability of health management. To enhance the improvement of BESS operation, it is perhaps more effective to directly mitigate battery aging based on the fundamental principles of frequency control (Li et al., 2022b; Tan et al., 2020). Some methods adaptively adjust the PFC coefficient according to the SOE level. For example, the PFC coefficient can be reduced when the SOE gradually deviates from the median (Tan et al., 2020; Liu et al., 2013). The change rate of SOE and further the charge-discharge ratio can be constrained in this way. However, reducing PFC coefficients decreases the performance of frequency support. It makes the design of control law difficult considering the tradeoff between battery aging mitigation and frequency support performance. Moreover, as battery aging is also impacted by SOE level in addition to the SOE change rate, the mitigation performance of battery aging by only reducing SOE change rate requires further verification.

As discussed before, maintaining the SOE around an intermediate level exhibits lower battery aging. Thus, an idea of SOE recovery is further proposed. The SOE of battery in PFC scenario is conventionally recovered when the frequency enters into the PFC dead band (PFC-DB), where the BESS does not need to provide frequency support and the PFC is suspended (Fu et al., 2022; Zhu and Zhang, 2019). Unfortunately, although the previous studies can recover SOE to a preferable range, the recovery is only activated in the PFC-DB. In this case, the SOE may have already accumulated to a certain extent before entering the PFC-DB. Then, a large depth of charge and discharge (DOD/C) of battery will be generated to recover the SOE, which will aggravate the aging of battery. To achieve more efficient SOE recovery, it should be conducted along with the PFC process (i.e., outside the PFC-DB), instead of within the PFC-DB. Nevertheless, it is difficult to realize the SOE recovery in the PFC process, as the conventional PFC methods adjust the BESS output power in a unidirectional way. Specifically, the BESS increases its output power when the frequency deviation is negative (indicating a power shortage of grid) and decreases the output power when the frequency deviation is positive. In this way, there is limited adjustment space for the BESS to recover SOE along with the PFC process.

To overcome the limitation of existing PFC methods in terms of battery aging mitigation, this paper proposes an adaptive control mode with tolerance to overshoot frequency response, which is solved by a multi-objective online optimization model. The proposed method reforms the conventional PFC where the BESS responds to the frequency deviation in a unidirectional way. It also overthrows the convention that the SOE should be recovered within the PFC-DB. Then, more adjustment space is released for BESS to achieve balance between frequency support and battery lifespan. The rest of this paper is organized as follows. Section 2 presents the conventional PFC for BESS. Section 3 discusses the principle of the overshoot-tolerant adaptive PFC. Case studies are presented in Section 4. Finally, conclusions are given in Section 5.

2 Conventional primary frequency control for BESS

The BESS can participate in PFC through droop control. Specifically, when the grid frequency deviates from its nominal value, the BESS automatically adjusts its power output based on the droop coefficient to mitigate frequency deviations. This control strategy enables the BESS to respond rapidly to grid frequency disturbances: during frequency drops, the BESS discharges to provide additional power support; during frequency rises, it charges to absorb excess power. In this way, the BESS achieves effective frequency regulation. In this process, the active power output of the BESS can be expressed as in Equation 1.

$P_{\text{BESS}}\left(t\right)=-K_{\mathrm{B}}\left(SOE\right)\Delta f\left(t\right),(1)$

where K_B(SOE) is the PFC coefficient that adjusts with the battery’s SOE, which aims to prevent rapid depletion or saturation of the SOE during prolonged PFC, ∆f(t) represents the grid’s frequency deviations at time t. This formulation enables the BESS to dynamically adjust its power output in response to grid frequency disturbances while effectively controlling the SOE levels.

The PFC coefficient of the BESS is established to ensure that the battery’s power output remains within its energy limitations. This coefficient, composed of a discharge component K_d and a charge component K_c, adjusts dynamically based on the battery SOE. When the SOE is low, K_c is set to its maximum value to maximize charging and frequency control, while K_d is reduced and decreases further as the SOE lowers. Conversely, when the SOE is high, K_d is maximized to enhance discharging for frequency support, whereas K_c is minimized and diminishes as the SOE increases. The relationships between K_d, K_c, and the battery SOE are formulated in Equation 2 (Tan et al., 2020; Liu et al., 2013).

$\left\{\begin{array}{l}{K}_{\mathrm{d}}=\frac{K_{\text{Bmax}}}{1+100K_{\text{Bmax}}{e}^{1-\frac{m\left(SOE-SO{E}_{\min }\right)}{SO{E}_{\text{low}}-SO{E}_{\min }}}}\\ K_{\mathrm{c}}=\frac{K_{\text{Bmax}}}{1+100K_{\text{Bmax}}{e}^{1-\frac{m\left(SO{E}_{\max }-SOE\right)}{SO{E}_{\max }-SO{E}_{\text{high}}}}}\end{array}\right.,(2)$

where K_Bmax is the maximum value of the PFC coefficient, SOE_min and SOE_max are the minimum and maximum values of battery SOE, SOE_low and SOE_high are the lower and higher values of battery SOE, and m is the adaptive coefficient of the curve and is normally set to 25 (Tan et al., 2020).

Figure 1 gives the visualization of determining values of K_B(SOE) with the change of SOE. The curve constrains the discharging power coefficient of BESS to maintain SOE when its level is low. When the battery SOE is high, reducing the charging power coefficient prevents BESS from overcharging. The amplitude of the PFC coefficient K_Bmax is related to the rated power of BESS and the adjustment rate, as shown in Equation 3.

$K_{\text{Bmax}}=\frac{P_N^{\text{BESS}}}{{\delta }_{\text{BESS}}{f}_N},(3)$

where $P_N^{\text{BESS}}$ is rated power of BESS, δ_BESS is the adjustment rate of BESS and f_N is the rated frequency of power grid.

Figure 1

Figure 1. PFC coefficient of BESS considering SOE limitation.

3 Adaptive PFC with tolerance to overshoot frequency response for battery aging mitigation

In this paper, a novel adaptive PFC with tolerance to overshoot frequency response is proposed to mitigate battery aging. The principle of the adaptive PFC will be demonstrated in this section, and the online optimization method for solving the coefficient will be developed.

3.1 Principle of adaptive PFC for battery aging mitigation

The comparison of the conventional PFC and the proposed adaptive PFC about the principles of SOE recovery is shown in Figure 2. As shown in the left area of Figure 2, the conventional PFC adjusts the BESS output power in a unidirectional way in response to the frequency dynamic, which limits the adjustment space of BESS for SOE recovery. Specifically, the power imbalance in the grid results in frequency fluctuation, and the BESS regulates its output power in proportion to the frequency deviation. With this control law, the BESS increases its output power when the frequency deviation is negative (indicating a power shortage of grid) and decreases the output power when the frequency deviation is positive. The conventional PFC usually sets the dead band to prevent unnecessary frequent actions. Once the frequency turns back to the predefined dead band (i.e., PFC-DB), it indicates that the frequency is relatively stable, and the PFC is not needed provisionally. Thus, the PFC is suspended in the PFC-DB. In the conventional PFC, the SOE is usually recovered within the PFC-DB to avoid conflict with frequency support. However, this principle separates the functionalities of BESS in terms of frequency regulation and SOE recovery, which is inefficient.

Figure 2

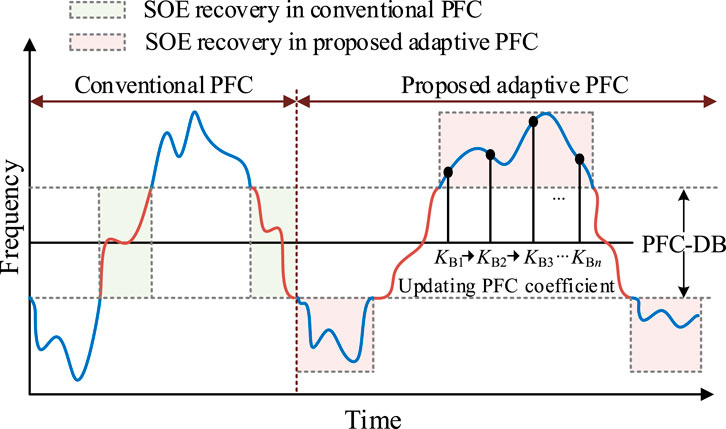
Figure 2. SOE recovery schemes of conventional PFC and proposed adaptive PFC, where K_B1-K_Bn are the example PFC coefficients in the proposed PFC.

In this paper, the SOE recovery is conducted along with the PFC, i.e., out of the PFC-DB, which is realized by adaptively adjusting the PFC coefficient, which is shown in the right area of Figure 2. With the proposed PFC, the frequency regulation and SOE recovery can be efficiently coordinated, and the battery aging can be mitigated without violating the frequency support performance. It is worth mentioning that the frequency deviation in the proposed method is not unidirectional compared to the conventional PFC. Instead, the frequency deviation can be responded in a reverse way, striving for more adjustment room for the BESS to recover the SOE.

The regulation principles of the conventional PFC and the proposed PFC in different SOE and frequency deviation states are shown in Figure 3. As shown in Figure 3, under the conventional PFC, the output power direction of BESS is always consistent with the direction of frequency deviation, despite the SOE level. Then, the amplitude of frequency deviation can be reduced. Differently, the output power of BESS in under the proposed PFC is determined by the SOE in addition to the frequency deviation. For instance, if the grid frequency deviation is negative, indicating a power shortage, the battery is supposed to be discharged to compensate for the power shortage. Here two cases are considered. First, the SOE of battery is below the reference, as shown in case I in Figure 3. It denotes that the frequency support demand conflicts with the SOE recovery demand (which means the battery should be charged for SOE recovery). In this case, the frequency support demand is guaranteed as a matter of priority, and the battery will be discharged as the same in the conventional PFC to compensate for the power shortage. Another case is that the SOE is larger than the reference, which means the frequency support demand aligns with the SOE recovery demand. In this context, a moderately larger discharging power can be applied to recover the SOE in a more efficient way, and the frequency deviation may cross the zero axis (as indicated by P₂ in case VI). The adjustment principle is the same when the frequency deviation is positive. A smaller charging power is applied when the SOE is larger than the reference (case III in Figure 3), while an adaptively larger charging power is designed when the SOE is smaller than the reference (case II in Figure 3).

Figure 3

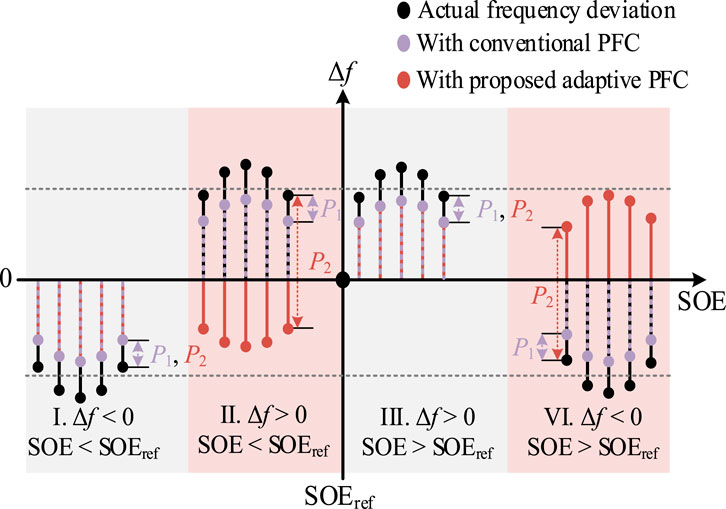
Figure 3. Frequency regulation principles of conventional PFC and proposed adaptive PFC, where Δf is the frequency deviation and SOE_ref is the SOE reference, P₁ and P₂ are the output power of BESS in response to frequency deviation under the conventional PFC and the proposed PFC, respectively.

In all, if the frequency support demand aligns with the SOE recovery demand, the proposed PFC allows overshoot-tolerant response of frequency deviation of BESS for SOE recovery. It should be noted that the reversed frequency deviation should also be constrained by the operational thresholds. That is to say, the frequency deviation is expected to be restricted within a band, instead of approaching zero as close as possible. This adaptive PFC can make full use of the adjustment room of BESS. Then, it can recover the SOE of battery more efficiently by improving the frequency support performance.

3.2 Optimization model for solving adaptive PFC coefficient

As demonstrated, the proposed method allows the PFC respond to the frequency deviation in a reverse manner, leading to a wide range of PFC coefficients. In this case, the design of the PFC coefficient is important. A multi-objective optimization model is developed in this paper to solve the coefficient of the proposed PFC. To facilitate the analysis of long-period PFC, the grid frequency is sampled with a certain period, and the PFC coefficient is updated periodically, as shown in Figure 2. The sampled frequency deviation of each period will be input to the optimization model, and the optimal PFC coefficient of this period can be solved. Figure 4 demonstrates the periodic operation of the proposed PFC method, which will be explained in the following.

Figure 4

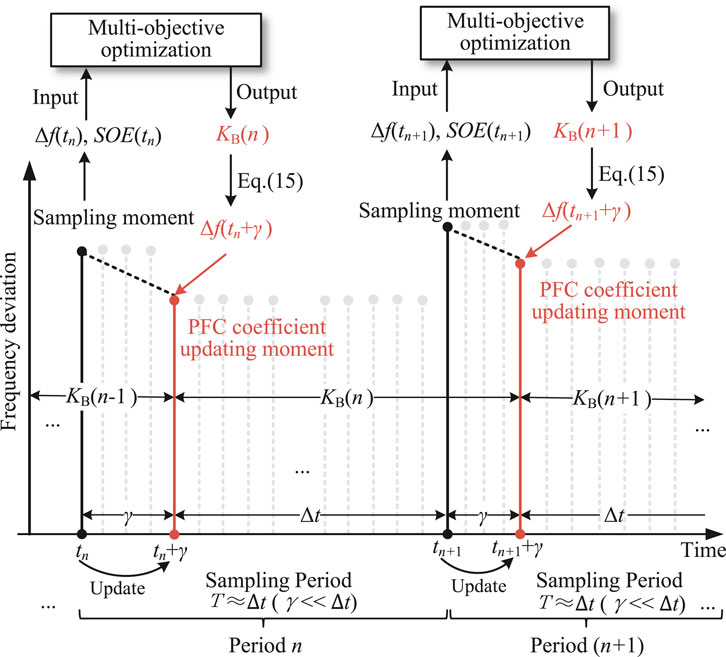
Figure 4. The periodic operation of the adaptive PFC, where t_n and t_n+1 are the start moments of control period n and n+1, respectively, T is frequency sampling period, γ is the duration time for PFC coefficient calculation, ∆t is the duration time from PFC coefficient updating moment to the next frequency sampling moment, and K_B is the adaptive PFC coefficient.

The grid frequency deviation at the moment t_n (the start moment at nth sampling period) is calculated by Equation 4.

$\Delta f\left(t_n\right)=f\left(t_n\right)-f_N,(4)$

where f is the actual frequency, f_N is the rated grid frequency, and Δf is the frequency deviation.

Defining the PFC coefficient to be optimized as K_B, the change of frequency deviation can be obtained according to the BESS output power increment under PFC, as shown in Equation 5.

$\Delta f\left(t_n+\gamma \right)-\Delta f\left(t_n\right)=\frac{K_{\mathrm{B}}\left(n-1\right)\Delta f\left(t_n\right)-K_{\mathrm{B}}\left(n\right)\Delta f\left(t_n+\gamma \right)}{K_{\mathrm{G}}},(5)$

where K_B(n) is the PFC coefficient to be optimized in the nth sampling period, K_G is the frequency modulation coefficient of the grid, which is given by Equation 6.

$K_{\mathrm{G}}=\frac{P_N^{\text{Grid}}}{{\delta }_{\text{Grid}}{f}_N},(6)$

where $P_N^{\text{Grid}}$ is the rated power of grid and δ_Grid is the adjustment rate of synchronous generators in the grid.

After simplifying Equation 5, a transform coefficient between the sampling data and the supposed value can be extracted, then the sampling grid frequency deviation will change as given in Equation 7.

$\Delta f\left(t_n+\gamma \right)=\frac{K_{\mathrm{B}}\left(n-1\right)+K_{\mathrm{G}}}{K_{\mathrm{B}}\left(n\right)+K_{\mathrm{G}}}\Delta f\left(t_n\right).(7)$

As shown in Figure 4, one sampling period can be divided into two parts as given in Equation 8.

$T=\gamma +\Delta t.(8)$

During the sampling period, battery will be charged or discharged under the PFC. Assuming that the frequency deviation is consistent with previous moment except at both the sampling moment and PFC coefficient updating moment. Thus, the SOE of battery at the next sampling moment (t_n+1) can be calculated by Equation 9.

$SOE\left(t_{n+1}\right)=SOE\left(t_n\right)+\frac{K_{\mathrm{B}}\left(n-1\right)\Delta f\left(t_n\right)\gamma +K_{\mathrm{B}}\left(n\right)\Delta f\left(t_n+\gamma \right)\Delta t}{E_{\text{BESS}}},(9)$

where E_BESS is the capacity of BESS.

Since γ is greatly smaller than ∆t, Equation 9 can be further simplified by Equation 10.

$SOE\left(t_{n+1}\right)=SOE\left(t_n\right)+\frac{K_{\mathrm{B}}\left(n\right)\Delta f\left(t_n+\gamma \right)\Delta t}{E_{\text{BESS}}}.(10)$

Then, the optimization objectives for solving the adaptive PFC coefficient can be determined. The first optimization objective is to maintain the frequency stability. It is realized by minimizing the frequency deviation, which is expressed by Equation 11.

$J_1\left(n\right)=\left|\Delta f\left(t_n+\gamma \right)\right|.(11)$

Another objective is to mitigate battery aging. As illustrated previously, battery aging can be efficiently alleviated by maintaining the SOE of battery within the desired range. In this paper, this principle is adopted. The objective for battery aging mitigation is expressed as in Equation 12.

$J_2\left(n\right)=\left|SOE\left(t_{n+1}\right)-SO{E}_{\text{ref}}\right|,(12)$

where SOE_ref is the predefined SOE reference.

It is worth mentioning that recovering the SOE does not only benefit the battery aging mitigation but also help to maintain the frequency modulation capability of BESS.

The adjustment of the PFC coefficient is constrained by several conditions, including the capacity of BESS, the threshold of transform coefficient, and the threshold of SOE for security consideration. Those constraints are given in Equations 13–15

$\left|K_{\mathrm{B}}\left(n\right)\right|\le \frac{P_N^{\text{BESS}}}{{\delta }_{\text{BESS}}{f}_N},(13)$

$\left|\frac{K_{\mathrm{B}}\left(n-1\right)+K_{\mathrm{G}}}{K_{\mathrm{B}}\left(n\right)+K_{\mathrm{G}}}\right|\le 1-\frac{P_N^{\text{BESS}}}{P_N^{\text{Grid}}},(14)$

$SO{E}_{\text{low}}\le SOE\left(t_{n+1}\right)\le SO{E}_{\text{high}},(15)$

where $P_N^{\text{BESS}}$ is the rated power of BESS, δ_BESS is the minimum adjustment rate of BESS, SOE_low and SOE_high are the upper and lower limits of SOE, respectively.

Note that if a severe grid fault drives the measured frequency deviation beyond the safety range specified by power grid. The proposed controller immediately abandons the optimization loop and executes an emergency strategy. The PFC coefficient is saturated at its maximum value, and the battery should fully provide frequency support without considering the optimization, as given by Equation 16.

$K_{\mathrm{B}}\left(n\right)=\frac{P_N^{\text{BESS}}}{{\delta }_{\text{BESS}}{f}_N}.(16)$

Under this condition, the BESS operates in a constant-power mode: it injects or absorbs the full available power without regard to SOE recovery or optimization objectives. Once the frequency returns within the permissible range, the controller seamlessly re-engages the multi-objective optimization, restoring the coordinated regulation of frequency support and SOE restoration.

According to the above, the optimal coefficient of the adaptive PFC can be solved by minimizing the objectives given by Equations 11, 12 subjected to constraints given by Equations 13–15, i.e.,

$\underset{K_{\mathrm{B}}}{\min }{J}_1\left(n\right),J_2\left(n\right).(17)$

subjected to Equations 13–15.

3.3 Online solving of optimization model

In multi-objective optimization, due to the trade-offs between different objectives, there are often multiple feasible solutions that satisfy the constraints (known as the Pareto front). This paper employs the Non-Dominated Sorting Genetic Algorithm II (NSGA-II) to determine the Pareto front for optimizing the PFC coefficient. NSGA-II is suitable for dynamic optimization of PFC coefficients as it can search the entire population with fewer design parameters and lower computational costs (Mohammadi et al., 2020). After obtaining the Pareto front, a weighted sum of the objective values corresponding to the Pareto solutions is calculated. This approach comprehensively filters the results to minimize frequency deviation and SOE deviation, ultimately selecting the solution with the smallest combined deviation as the optimal PFC coefficient.

The basic principle of NSGA-Ⅱ is to sort the individuals of the population through the non-dominated relationship of them and select individuals which is the closest to the value of the objective. Then, the optimal solution of each step can more likely retain the advantages of the last iteration. Taking the objective functions J₁ (frequency deviation) and J₂ (SOE deviation) as an example, the Pareto front includes several solutions that satisfy the constraints. All the solutions in the set can be referred to as the optimal solution corresponding to comprehensively minimized J₁ and J₂. Then, the most optimal solution in the solution set is searched according to the designer’s preference for different control targets. For example, different objective functions can be weighted and summed up to a composite objective. Then, the optimal composite objective can be picked up, based on which the optimal solution can be extracted. The adaptive PFC coefficient is just optimized in this manner.

Since J₁ and J₂ may have great differences in amplitude, the data in the Pareto solution set need to be normalized at first, as shown in Equation 18.

$\left\{\begin{array}{l}{j_1}^{*}\left(m\right)=\frac{j_1\left(m\right)}{\max \left\{j_1\left(m\right)\right\}}\\ {j_2}^{*}\left(m\right)=\frac{j_2\left(m\right)}{\max \left\{j_2\left(m\right)\right\}}\end{array}\right.,(18)$

where j₁(m) is the mth value of J₁ in the Pareto solution set, j₁^*(m) is the normalized value of j₁(m), j₂(m) is the mth value of J₂ in the Pareto solution set, j₂^*(m) is the normalized value of j₂(m).

With the normalized values of J₁ and J₂, the weighted composite objective is formed in Equation 19.

$j=\min \left\{\alpha {j_1}^{*}\left(m\right)+\beta {j_2}^{*}\left(m\right)\right\},(19)$

where α and β are the weight factors for j₁^*(m) and j₂*(m), respectively, and j is the minimum composite objective. The weight factors can be set according to actual situation, where α+β = 1 in all cases.

After obtaining the minimum composite objective by Equation 19, the corresponding optimal PFC coefficient can be determined.

4 Case studies

This paper applies the frequency data of the UK power grid (National Grid ESO) in entire year of 2021 (National Grid ESO, 2020) to verify the proposed method. In the case study, $P_N^{\text{BESS}}$ is 2.5 MW, PGrid N is 10 MW, PFC-DB is set to ±0.05 Hz (National Standardization Administration, 2021), SOE_ref is 0.5, δ_Grid is 5%, δ_BESS is 0.5% (National Standardization Administration, 2021), SOE_low is 0.1, SOE_high is 0.9, α and β both are 0.5.

4.1 Assessment of PFC performance and battery aging

In the case studies, the performance of the proposed PFC will be assessed from the perspectives of control performance and the economics feasibility. The assessment framework is demonstrated in the following.

4.1.1 Assessment of control performance

Aiming at continuous power disturbance and PFC in a long-term timescale, the root mean square (RMS) of frequency deviation and SOE deviation are applied as the performance assessment indices, which are given in Equation 20.

$\left\{\begin{array}{l}{\text{RMS}}_f=\sqrt{\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\left(f_i-f_n\right)}^2}\\ {\text{RMS}}_{\text{SOE}}=\sqrt{\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\left({\mu }_i-{\mu }_{\text{ref}}\right)}^2}\end{array}\right.,(20)$

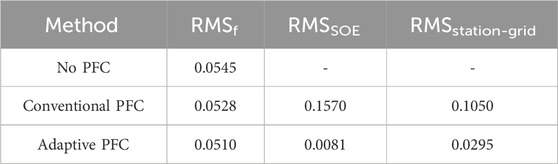
where RMS_f and RMS_SOE are the root mean square values of frequency deviation and SOE deviation, respectively, f_i and μ_i are the frequency and SOE of sampling point i, and N is the total number of sampling points. The smaller the two index values are, the lower the deviation of frequency and SOE, indicating better performance in frequency support and battery aging mitigation.

The two indices are combined to obtain a comprehensive index as given in Equation 21.

${\text{RMS}}_{\text{station}-\text{grid}}=\frac{{\text{RMS}}_f+{\text{RMS}}_{\text{SOE}}}{2},(21)$

where RMS_station-grid is the comprehensive assessment index, which evaluates the effect of PFC from the perspectives of grid support and battery aging mitigation.

4.1.2 Assessment of battery aging

To further validate the effectiveness of the proposed method for suppressing battery aging, the aging model for lithium-ion batteries of Xu et al. (2018b) is adopted to assess the capacity degradation, considering both the calendar and cyclic aging process. The loss of battery capacity can be calculated by Equation 22.

$\left\{\begin{array}{l}L=1-{\alpha }_{\text{SEI}}{e}^{-{\beta }_{\text{SEI}}{g}_{\mathrm{d}}}-\left(1-{\alpha }_{\text{SEI}}\right)e^{-g_{\mathrm{d}}}\\ SOH={\alpha }_{\text{SEI}}{e}^{-{\beta }_{\text{SEI}}{g}_{\mathrm{d}}}-\left(1-{\alpha }_{\text{SEI}}\right)e^{-g_{\mathrm{d}}}\end{array}\right.,(22)$

where L is the extend of battery aging, SOH is the battery state of health, α_SEI, β_SEI are empirical coefficients, which depend on the specific surface area of the graphite (Laresgoiti et al., 2015; Han et al., 2014), g_SEI and g_d are the degradation rates of battery during SEI formation and after this period, respectively.

Since evaluating battery aging is not the focus of this research, this model is not specified in this paper, and the detailed information can be found in Xu et al. (2018b).

4.1.3 Economic analysis of battery aging mitigation

Based on the estimated SOH of battery, this paper further utilizes levelized cost of storage (LCOS) index (Beltran et al., 2019) to evaluate the economics of battery aging mitigation, which is given by Equation 23.

$LCOS=\frac{I_0\times E_{\text{BESS}}+{\sum }_0^y\left(O{p}_{\text{cost}}\times W_y\right)}{\sqrt{\beta }\times {\sum }_0^{y}SOH\left(y\right)},(23)$

where I₀ is the initial construction investment of the BESS (¥/kWh), y is the test duration which converts to years, Op_cost is the operating cost (¥/kWh) of BESS, W_y is the amount of electricity consumed (kWh) during the test duration, and β is the energy conversion efficiency of BESS converter. A lower LCOS indicates improved economic performance.

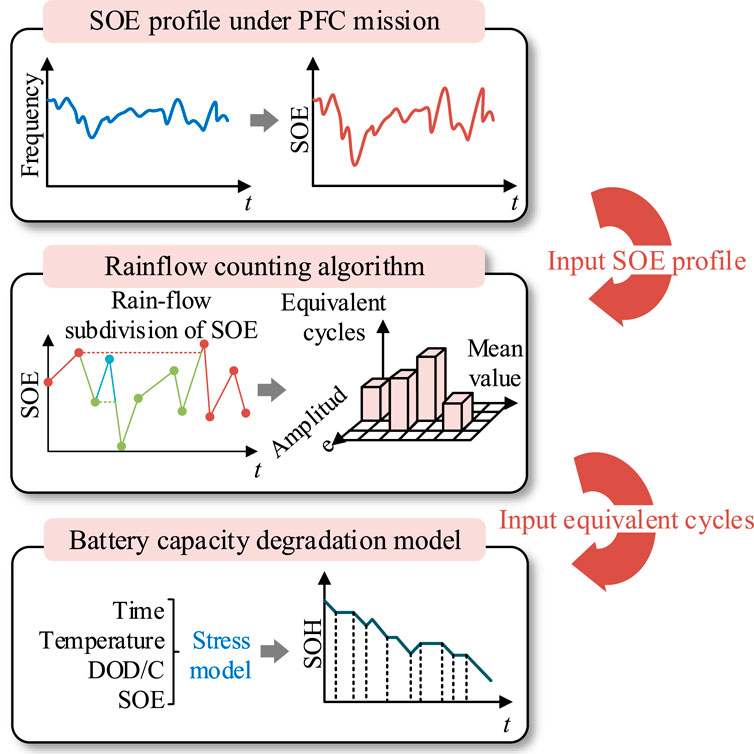
The process of battery aging assessment is shown in Figure 5. First, the output profile of BESS with PFC is obtained according to frequency data, which is then used to obtain the SOE profile of battery under PFC mission. The SOE profile is then input to the program of rain flow counting algorithm (RFCA). The RFCA method can decompose the historical load data into multiple cycles by considering both dynamic and static strength. This process benefits capturing the inherent characteristics of fatigue load and is commonly applied for estimating the fatigue life of battery. Thus, the RFCA method can provide the equivalent number of charging and discharging cycles that the battery undergoes during PFC. Finally, the battery aging model introduced in Section 2 is employed to evaluate the results, and the battery aging is quantitively assessed.

Figure 5

Figure 5. Battery aging assessment under PFC mission.

4.2 Single step optimization process of adaptive PFC analysis

The multi-objective online optimization model includes two objective functions, i.e., frequency deviation and SOE deviation. To understand the optimization mechanism accurately, the single-step optimization process of the PFC coefficient is demonstrated as an example. In the following analysis, t_n and t_n+1 represent the start moment of the nth and (n+1) th sampling periods, respectively. According to Figure 4, Δf (t_n), K_B(n−1), SOE (t_n) are the inputs of the optimization model, while K_B(n) is the PFC coefficient to be optimized. SOE (t_n+1) and Δf (t_n+γ) are recorded to assess the performance of the optimized control under K_B(n).

Table 1 shows the example of PFC coefficient optimization under different SOE states and frequency deviation in a single step. For instance, when ∆f (t_n) is −0.1 Hz, indicating a power shortage in the grid, the BESS needs to be discharged to supply the grid for frequency stability. However, it conflicts with the SOE recovery when the SOE is lower than the reference (0.5 sis applied in this paper), as shown in the last line in Table 1. In such cases, the priority is given to the grid frequency support, and the SOE recovery requirement is laid aside. Conversely, if the SOE is higher than the reference when ∆f (t_n) is 0.1 Hz, the demand for SOE recovery aligns with the frequency support demand (i.e., the battery needs to be discharged), as shown in the first three lines in Table 1. In this case, the optimal PFC coefficient can be obtained via the NSGA-Ⅱ program. As shown in Table 1, through this inverse frequency deviation response pattern, the absolute values of the frequency deviation under the proposed method can be achieved lower than the actual sampled frequency deviation.

Table 1

Table 1. Single step optimization result analysis.

Figure 6 shows the three-dimensional distribution of objective function J₁ (frequency deviation) and objective function J₂ (SOE deviation) under different initial conditions, i.e., with different current SOE and different previous PFC coefficient. As shown in Figure 6, different initial conditions lead to various distribution of objective values. It should be mentioned that according to Equation 7, the value of objective function will increase indefinitely when K_B(n) equals -K_G. For the sake of legibility, a polar region between (−3, −5) of K_B axis is set in Figure 6. The values of the two objective functions under the initial settings (i.e., Δf (t_n) = −0.1 Hz, K_B(n−1) = −1 MW/Hz, and SOE (t_n) = 0.4/0.6) corresponding to the results in Table 1 are marked with red dots in Figure 6. The corresponding K_B(n) is the optimal PFC coefficient to be updated in this single step.

Figure 6

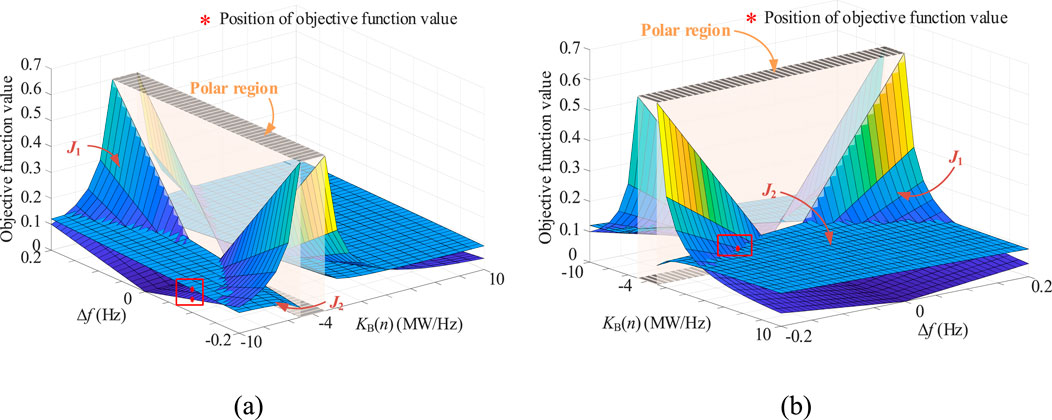
Figure 6. Three-dimensional distribution of objective function values J₁ and J₂ under different initial conditions: (a) Δf (t_n) = −0.1 Hz, K_B(n−1) = −1 MW/Hz, SOE (t_n) = 0.6 and (b) Δf (t_n) = −0.1 Hz, K_B(n-1) = −1 MW/Hz, SOE (t_n) = 0.4.

The experimental platform for NSGA-II online optimization runs on the Windows 10 X64 operating system with an Intel i5-7500 CPU. For ensuring real-time performance, the NSGA-II algorithm is configured with specific parameters tailored to balance optimization accuracy and computational efficiency: the population size is set to 50 individuals, the maximum number of generations is limited to 10, the crossover probability is 0.9, and the mutation probability is 0.1. According to the statistics, the time scale for the update periodicity of PFC coefficient typically falls within the range of 10⁻³∼10⁻²s level seconds. Within this brief timeframe, BESS performs frequency control by using the previous updated PFC coefficient in the last period, as illustrated in Figure 4. Since the fluctuations in grid frequency during this timescale are negligible in real-world engineering scenarios (National Standardization Administration, 2021), the transient delay resulting from the PFC coefficient update barely has impact on the quality of frequency control.

4.3 Distribution of adaptive PFC coefficient

When K_B(n-1) is set to −8.5 MW/Hz as the initial condition for the entire PFC, the optimal PFC coefficients under different frequency deviation and SOE are solved by the NSGA-Ⅱ program, and their distribution is shown in Figure 7.

Figure 7

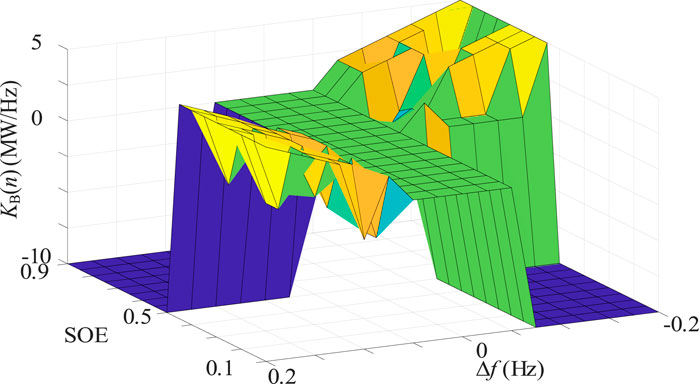
Figure 7. Distribution of optimal PFC coefficient with different frequency deviation and SOE when K_B(n−1) is −8.5 MW/Hz.

Based on the distribution characteristic of the optimal PFC coefficient, they can be classified into four areas, i.e., Area Ⅰ: ∆f > 0.05, SOE>0.5, Area Ⅱ: ∆f > 0.05, SOE<0.5, Area Ⅲ: ∆f < −0.05, SOE<0.5, and Area Ⅳ: ∆f < −0.05, SOE>0.5. The region with ∆f∈[−0.05, 0.05] Hz is PFC-DB, where PFC is not activated, and the PFC coefficient is zero. In both Area Ⅰ and Ⅲ, the BESS mainly responds to the frequency support demand, thus K_B(n) remains unchanged to provide full frequency support. The battery is charged in Area Ⅰ and discharged in Area Ⅲ. Differently, in Area Ⅱ and Ⅳ, the SOE recovery demand aligns with the frequency support demand. In such cases, K_B(n) is no longer fixed but a varying value adapting to real-time frequency deviation and SOE, making the distribution surface of K_B(n) oscillate irregularly as shown in Figure 7.

Currently, many research studies have proposed using logistic functions to adjust PFC coefficient (Tan et al., 2020; Liu et al., 2013). These methods divide the PFC coefficient into charging and discharging coefficients. Specifically, the value of the discharging coefficient increases with increasing battery SOE, allowing the BESS to have sufficient power to address frequency drops. On the other hand, the charging coefficient declines as the SOE increases to prevent overcharging during PFC. These studies aim to achieve stable BESS output by limiting the rate of SOE variation during PFC, thereby avoiding accelerated battery aging. To validate the effectiveness of the proposed strategy in this paper, the approach proposed in Tan et al. (2020) is adopted as a comparison method (defined as the conventional PFC) in this case study. To visualize the differences between the conventional PFC and the proposed adaptive PFC, this paper uses K-means method to cluster all K_B data sets of the two methods, the data points with similar values are clustered and marked with the same color. The spatial distributions of K_B under the two PFC methods are shown in Figure 8. It can be observed in Figure 8b that the distribution interval of K_B of the adaptive PFC is wider than that of the conventional PFC, while K_B of conventional PFC only distributes in the positive area in Figure 8a. The reason is that the conventional PFC refers to the differential adjustment mode of traditional generator units, which adjusts its output power in the same direction as the frequency deviation, and the output space is quite limited. Differently, the adaptive PFC gets rid of the passive control mode and responds to the frequency deviation with an overshoot-tolerant manner. It flexibly adjusts the PFC coefficient to be positive or negative according to frequency support demand and SOE recovery demand, as explained in Section 3.

Figure 8

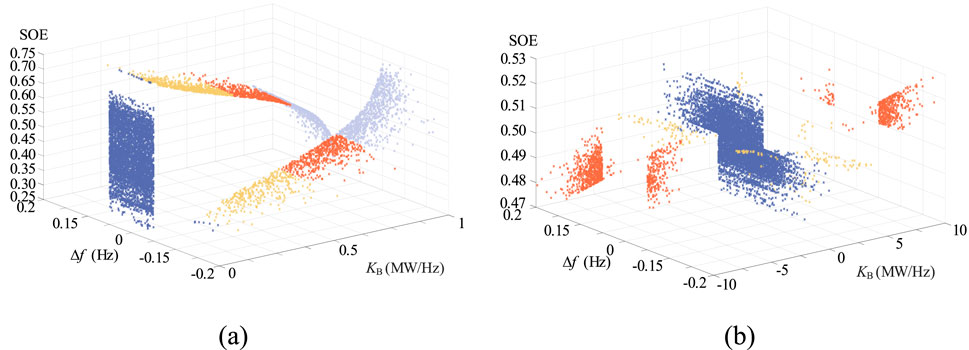
Figure 8. Spatial distribution of K_B under adaptive PFC: (a) conventional PFC and (b) proposed adaptive PFC.

4.4 Performance of adaptive PFC

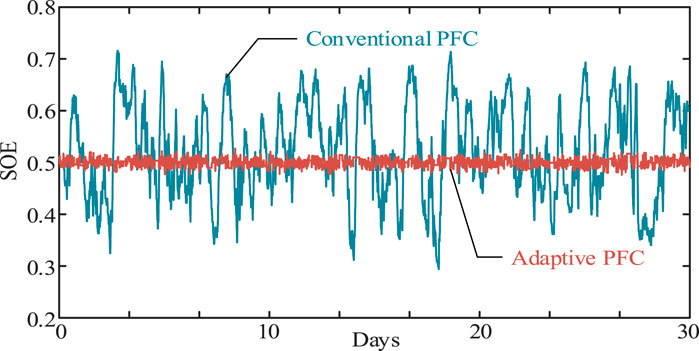
In the context of a 10 MW grid capacity, to ensure BESS can continuously provide frequency support and to better demonstrate the control effects of the proposed method in simulations, the capacity of BESS (i.e., E_BESS) is set to 4 MWh in this case study. It is worth mentioning that the proposed method is versatile for BESS across a range of capacities. The dynamics of battery SOE under the proposed adaptive PFC and the conventional PFC are shown in Figure 9. It can be seen from Figure 9 that the amplitude of SOE fluctuation under the conventional PFC is larger than that under the adaptive PFC. It indicates that the battery faces overcharging or discharging risks, and the battery aging is accelerated. Differently, the adaptive PFC considers the SOE recovery as one of the optimization objectives when designing the PFC coefficient, thus leading to a more stable SOE dynamic around the reference value. As shown in Figure 9, the highest SOE deviation under the conventional PFC is 21.48%, which turns to be 2.68% under the proposed adaptive PFC, exhibiting an 87.5% improvement.

Figure 9

Figure 9. Dynamics of battery SOE under the proposed adaptive PFC and the conventional PFC.

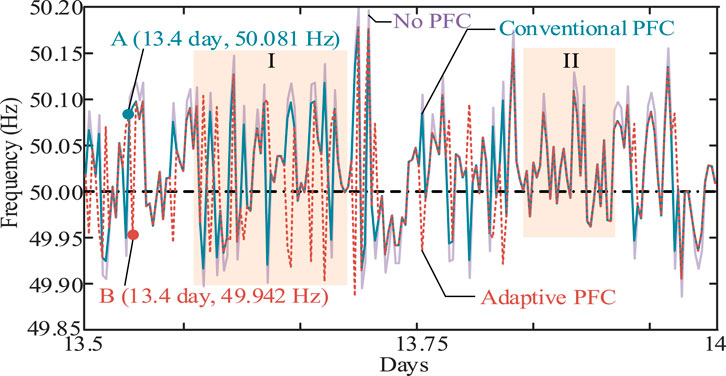
In terms of the frequency support, the frequency dynamics under the conventional and the proposed PFC methods are shown in Figure 10. Note that at some sampling points, the frequency is reversed under the adaptive PFC, as indicated by points A and B in Figure 10. This is due to the principle of the adaptive PFC that allows overshoot response to frequency deviation if the SOE recovery demand is consistent with the frequency regulation demand. It is worth mentioning that the absolute value of frequency deviation at point B is smaller than that at point A, indicating an improved frequency support performance. Then, observing area I in Figure 10 can realize that the frequency deviation is reverse with the same amplitude under the proposed adaptive PFC at some point. Also, the results in area II show that there are sampling points where the frequency dynamic under the proposed PFC is exactly consistent with that of the conventional PFC. The results validate the merit of the proposed PFC, i.e., improving the SOE recovery performance with improved frequency support performance.

Figure 10

Figure 10. Grid frequency dynamics under the proposed adaptive PFC and conventional PFC.

The frequency support performance is further quantitatively analyzed through the assessment indices presented in Section 4. A. The results are shown in Table 2. It can be seen from Table 2 that with the help of NSGA-Ⅱ optimization, the adaptive PFC can not only diminish the frequency deviation further but also significantly reduce the RMS of battery SOE. This demonstrates that the adaptive PFC achieves more comprehensive control performance compared to conventional methods.

Table 2

Table 2. Assessment indices of the proposed adaptive PFC and conventional PFC.

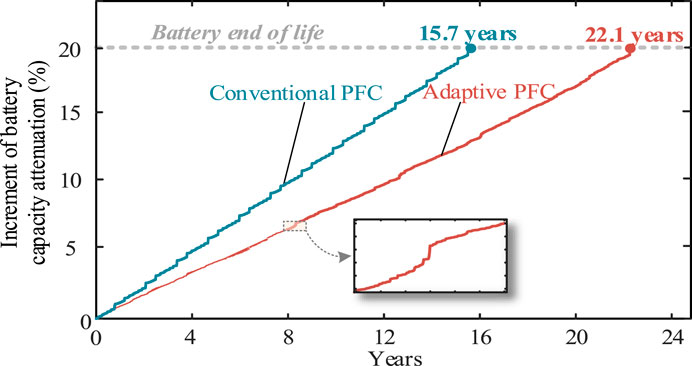
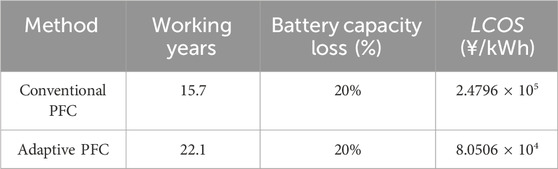
However, the battery lifetime normally measured in years, and acquiring long-term data sets to simulate the aging process of battery over several decades is challenging. To further validate the long-term effects of battery aging mitigation under the proposed strategy, this paper addresses the scarcity of long-term battery output datasets by utilizing the continuous cycling of battery SOE under PFC throughout the year 2021 (Stroe et al., 2016). The analysis focuses on extended periods of battery operation. The cycling process will cease when the empirical model (Xu et al., 2018b) determines that the battery has reached its end of life (EOL) (Liu et al., 2023; Meng et al., 2023), which is defined as the point where the remaining useful capacity of the battery is 80% of its initial capacity. Figure 11 shows the increments of battery capacity attenuation under the proposed adaptive PFC and the conventional PFC during prolonged operation. It can be seen from Figure 11 that the adaptive PFC significantly reduces the attenuation of battery capacity compared with the conventional PFC. The estimated lifetime of battery under the adaptive PFC is 22.1 years, which exhibits 6.4 years improvement compared to conventional PFC. It is important to note that this improvement is demonstrated for lithium-ion battery chemistry with an SOE set point of 50%. However, the core control logic of the framework remains universally applicable for other types of batteries: the aging model parameters and SOE reference value can be recalibrated for other battery chemistries without modifying the underlying control architecture. This ensures that the framework retains its ability to provide effective primary frequency support while mitigating aging across diverse energy storage technologies. The results further validate the performance of the proposed adaptive PFC in terms of battery aging mitigation. From an economic perspective, when β is 0.9 (Beltran et al., 2019), I₀ and Op_cost are set to 1,200¥/kWh and 0.8¥/kWh respectively (Zhao et al., 2015), the results of LCOS are shown in Table 3. It is evident that the LCOS can be reduced by approximately 1.6 × 10⁵ ¥/kWh throughout the battery’s lifespan by implementing the adaptive PFC to alleviate battery aging.

Figure 11

Figure 11. Increments of battery capacity attenuation under long-term cycle.

Table 3

Table 3. Analysis of battery aging mitigation.

5 Conclusion

An adaptive PFC of BESS with tolerance to overshoot frequency response is proposed in this paper to mitigate the battery aging. The battery aging mitigation is realized by recovering the SOE of battery. By assessing the real-time frequency deviation and SOE, the cases where the frequency support demand is in accordance with the SOE recovery demand can be identified. In those cases, the proposed method implements a reverse PFC coefficient that turns the frequency to the opposite side of the rated value, and the battery is charged or discharged more vigorously. This overshoot response principle is validated to be effective in recovering the SOE and enlarging the adjustment room of battery with improved frequency quality. The PFC coefficient is periodically updated based on a multi-objective optimization model, which is solved by the NSGA-Ⅱ algorithm. The case study results verify the proposed method in long-term frequency support and SOE recovery, which is comprehensively improved to a large extent compared to the conventional unidirectional PFC. Moreover, the case study results also validate that battery aging can be efficiently reduced by recovering the SOE. While the current study assumes a homogeneous BESS to enable initial validation, future work will embed a hierarchical allocation layer that dynamically distributes the aggregate PFC command among heterogeneous modules according to their real-time battery aging and response dynamics. Furthermore, future work should also address practical implementation considerations for large-scale deployment, such as providing guidelines for industrial-grade hardware, including the selection of appropriate Real-Time Operating Systems (RTOS) and the potential for FPGA acceleration to enhance the real-time performance of the control algorithm. Moreover, a more holistic approach to battery aging mitigation, incorporating factors such as temperature and charge/discharge rates, promises to further refine the control efficacy and extend the longevity of BESS in frequency regulation applications.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

TG: Writing – original draft, Data curation, Methodology, Conceptualization. YW: Visualization, Writing – original draft, Validation. YL: Writing – review and editing, Formal Analysis, Methodology. QF: Writing – review and editing, Visualization. QP: Writing – review and editing, Visualization, Conceptualization.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by the Guizhou Provincial Science and Technology Support Plan [(2023) General 293] and the Science and Technology Project of Guizhou Power Grid Co., LTD [GZKJXM20232529].

Conflict of interest

Authors TG, YW, and QF were employed by Electric Power Research Institute of Guizhou Power Grid Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The authors declare that this study received funding from the Science and Technology Project of Guizhou Power Grid Co., LTD. The funder had the following involvement in the study: study design.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Beltran, H., Tomás García, I., Alfonso-Gil, J. C., and Pérez, E. (2019). Levelized cost of storage for Li-Ion batteries used in PV power plants for ramp-rate control. IEEE Trans. Energy Convers. 34 (1), 554–561. doi:10.1109/tec.2019.2891851

CrossRef Full Text | Google Scholar

Fu, H., Tong, X., Pan, Z., Liu, F., Wang, F., and Zhang, W. (2022). “Research on BESS participating in power system primary frequency regulation control strategy considering state-of-charge recovery,” in 2022 5th International Conference on Energy, Electrical and Power Engineering (CEEPE), Chongqing, China (IEEE), 1234–1238.

CrossRef Full Text | Google Scholar

Grimaldi, A., Minuto, F. D., Perol, A., Casagrande, S., and Lanzini, A. (2023). Ageing and energy performance analysis of a utility-scale lithium-ion battery for power grid applications through a data-driven empirical modelling approach. J. Energy Storage 65, 107232. doi:10.1016/j.est.2023.107232

CrossRef Full Text | Google Scholar

Han, X., Ouyang, M., Lu, L., Li, J., Zheng, Y., and Li, Z. (2014). A comparative study of commercial lithium ion battery cycle life in electrical vehicle: aging mechanism identification. J. Power Sources 251, 38–54. doi:10.1016/j.jpowsour.2013.11.029

CrossRef Full Text | Google Scholar

Kottick, D., Blau, M., and Edelstein, D. (1993). Battery energy storage for frequency regulation in an island power system. IEEE Trans. Energy Convers. 8 (3), 455–459. doi:10.1109/60.257059

CrossRef Full Text | Google Scholar

Laresgoiti, I., Käbitz, S., Ecker, M., and Sauer, D. U. (2015). Modeling mechanical degradation in lithium ion batteries during cycling: solid electrolyte interphase fracture. J. Power Sources 300, 112–122. doi:10.1016/j.jpowsour.2015.09.033

CrossRef Full Text | Google Scholar

Li, S., Xu, Q., Xia, Y., and Hua, K. (2022a). Comprehensive set-ting and optimization of dead-band for BESS participate in power grid primary frequency regulation. Int. J. Electr. Power Energy Syst. 141, 108195. doi:10.1016/j.ijepes.2022.108195

CrossRef Full Text | Google Scholar

Li, S., Zhao, P., Gu, C., Li, J., Cheng, S., and Xu, M. (2022b). Online battery protective energy management for energy-transportation nexus. IEEE Trans. Industrial Inf. 18 (11), 8203–8212. doi:10.1109/tii.2022.3163778

CrossRef Full Text | Google Scholar

Li, S., Zhao, P., Gu, C., Li, J., Huo, D., and Cheng, S. (2023). Aging mitigation for battery energy storage system in electric vehicles. IEEE Trans. Smart Grid 14 (3), 2152–2163. doi:10.1109/tsg.2022.3210041

CrossRef Full Text | Google Scholar

Liu, H., Hu, Z., Song, Y., and Lin, J. (2013). Decentralized vehicle-to-grid control for primary frequency regulation considering charging demands. IEEE Trans. Power Syst. 28 (3), 3480–3489. doi:10.1109/tpwrs.2013.2252029

CrossRef Full Text | Google Scholar

Liu, Y., Wang, L., Li, D., and Wang, K. (2023). State-of-health estimation of lithium-ion batteries based on electro-chemical impedance spectroscopy: a review. Prot. Control Mod. Power Syst. 8 (3), 41–17. doi:10.1186/s41601-023-00314-w

CrossRef Full Text | Google Scholar

Meng, J., Yue, M., and Diallo, D. (2023). A degradation empirical-model-free battery end-of-life prediction framework based on gaussian process regression and kalman filter. IEEE Trans. Transp. Electrification 9 (4), 4898–4908. doi:10.1109/tte.2022.3209629

CrossRef Full Text | Google Scholar

Mohammadi, A. S., Trovão, J. P. F., and Antunes, C. H. (2020). Component-level optimization of hybrid excitation synchronous machines for a specified hybridization ratio using NSGA-II. IEEE Trans. Energy Convers. 35 (3), 1596–1605. doi:10.1109/tec.2020.2990283

CrossRef Full Text | Google Scholar

National Grid ESO (2020). Historic frequency data. Available online at: https://www.nationalgrideso.com/industry-information/balancing-services/frequency-response-services/historic-frequency-data (Accessed December 01, 2022).

Google Scholar

National Standardization Administration (2021). Guide for technology and test on primary frequency control of grid-connected power resource, GB/T 40595-2021. China: National Standardization Administration.

Google Scholar

Perez, A., Moreno, R., Moreira, R., Orchard, M., and Strbac, G. (2016). Effect of battery degradation on multi-service portfolios of energy storage. IEEE Trans. Sustain. Energy 7 (4), 1718–1729. doi:10.1109/tste.2016.2589943

CrossRef Full Text | Google Scholar

Pusceddu, E., Zakeri, B., and Gissey, G. C. (2021). Synergies between energy arbitrage and fast frequency response for battery energy storage systems. Appl. Energy 283, 116274. doi:10.1016/j.apenergy.2020.116274

CrossRef Full Text | Google Scholar

Rui, W., Qiuye, S., Pinjia, Z., Yonghao, G., Dehao, Q., and Peng, W. (2020). Reduced-order transfer function model of the droop-controlled inverter via Jordan continued-fraction expansion. IEEE Trans. Energy Convers. 35 (3), 1585–1595. doi:10.1109/tec.2020.2980033

CrossRef Full Text | Google Scholar

Shi, Y., Xu, B., Wang, D., and Zhang, B. (2018). Using battery storage for peak shaving and frequency regulation: joint optimization for super linear gains. IEEE Trans. Power Syst. 33 (3), 2882–2894. doi:10.1109/tpwrs.2017.2749512

CrossRef Full Text | Google Scholar

Shu, H., Li, W., Wang, G., Han, Y., Li, J., and Tang, Y. (2024). Online collaborative estimation technology for SOC and SOH of frequency regulation of a lead-carbon battery in a power system with a high proportion of renewable energy. Prot. Control Mod-ern Power Syst. 9 (1), 52–64. doi:10.23919/pcmp.2023.000232

CrossRef Full Text | Google Scholar

Stroe, D.-I., Swierczynski, M., Stroe, A.-I., Laerke, R., Kjaer, P. C., and Teodorescu, R. (2016). Degradation behavior of lithium-ion batteries based on lifetime models and field measured frequency regulation mission profile. IEEE Trans. Industry Appl. 52 (6), 5009–5018. doi:10.1109/tia.2016.2597120

CrossRef Full Text | Google Scholar

Stroe, D.-I., Knap, V., Swierczynski, M., Stroe, A.-I., and Teodorescu, R. (2017). Operation of a grid-connected Lithi-um-Ion battery energy storage system for primary frequency regulation: a battery lifetime perspective. IEEE Trans. Industry Appl. 53 (1), 430–438. doi:10.1109/tia.2016.2616319

CrossRef Full Text | Google Scholar

Tan, Z., Li, X., He, L., Li, Y., and Huang, J. (2020). Primary frequency control with BESS considering adaptive SOC recovery. Int. J. Electr. Power and Energy Syst. 117, 105588. doi:10.1016/j.ijepes.2019.105588

CrossRef Full Text | Google Scholar

Wang, R., Sun, Q., Gui, Y., and Ma, D. (2019). Exponential-function-based droop control for islanded microgrids. J. Mod. Power Syst. Clean Energy 7 (4), 899–912. doi:10.1007/s40565-019-0544-3

CrossRef Full Text | Google Scholar

Wang, Z., Shi, L., Wu, F., Peng, Y., Lou, B., and Lee, K. Y. (2020). “Coordinated droop and virtual inertia control of wind farm for frequency regulation,” in 2020 IEEE Power and Energy Society General Meeting (PESGM), Montreal, QC, Canada (IEEE), 1–5.

CrossRef Full Text | Google Scholar

Wei, Y., Yao, Y., Pang, K., Xu, C., Han, X., Lu, L., et al. (2022). A comprehensive study of degradation characteristics and mechanisms of commercial Li(NiMnCo)O-2 EV batteries under vehicle-to-grid (V2G) services. Batteries-Basel 8 (10), 188. doi:10.3390/batteries8100188

CrossRef Full Text | Google Scholar

Xia, Q., Wang, Z., Ren, Y., Sun, B., Yang, D., and Feng, Q. (2018). A reliability design method for a lithium-ion battery pack considering the thermal disequilibrium in electric vehicles. J. Power Sources 386, 10–20. doi:10.1016/j.jpowsour.2018.03.036

CrossRef Full Text | Google Scholar

Xiang, M., Yang, Z., and Yu, J. (2023). Hierarchical AGC dis-patch with detailed modeling of energy storage system behaviors. IEEE Trans. Power Syst. 38 (2), 1689–1701. doi:10.1109/tpwrs.2022.3178432

CrossRef Full Text | Google Scholar

Xing, W., Wang, H., Lu, L., Han, X., Sun, K., and Ouyang, M. (2021). An adaptive virtual inertia control strategy for distributed battery energy storage system in microgrids. Energy 233, 121155. doi:10.1016/j.energy.2021.121155

CrossRef Full Text | Google Scholar

Xu, B., Shi, Y., Kirschen, D. S., and Zhang, B. (2018a). Optimal battery participation in frequency regulation markets. IEEE Trans. Power Syst. 33 (6), 6715–6725. doi:10.1109/tpwrs.2018.2846774

CrossRef Full Text | Google Scholar

Xu, B., Oudalov, A., Ulbig, A., Andersson, G., and Kirschen, D. S. (2018b). Modeling of lithium-ion battery degrada-tion for cell life assessment. IEEE Trans. Smart Grid 9 (2), 1131–1140. doi:10.1109/tsg.2016.2578950

CrossRef Full Text | Google Scholar

Zhai, Q., Meng, K., Dong, Z. Y., and Ma, J. (2017). Modeling and analysis of lithium battery operations in spot and frequency regulation service markets in Australia electricity market. IEEE Trans. Industrial Inf. 13 (5), 2576–2586. doi:10.1109/tii.2017.2677969

CrossRef Full Text | Google Scholar

Zhang, L., Mu, Z., and Sun, C. (2018). Remaining useful life prediction for lithium-ion batteries based on exponential model and particle filter. IEEE Access 6, 17729–17740. doi:10.1109/access.2018.2816684

CrossRef Full Text | Google Scholar

Zhao, P., Wang, J., and Dai, Y. (2015). Capacity allocation of a hybrid energy storage system for power system peak shaving at high wind power penetration level. Renew. Energy 75, 541–549. doi:10.1016/j.renene.2014.10.040

CrossRef Full Text | Google Scholar

Zheng, N., Qin, X., Wu, D., Murtaugh, G., and Xu, B. (2023). Energy storage state-of-charge market model. IEEE Trans. Energy Mark. Policy Regul. 1 (1), 11–22. doi:10.1109/tempr.2023.3238135

CrossRef Full Text | Google Scholar

Zhu, D., and Zhang, Y.-J. A. (2019). Optimal coordinated control of multiple battery energy storage systems for primary frequency regulation. IEEE Trans. Power Syst. 34 (1), 555–565. doi:10.1109/tpwrs.2018.2868504

CrossRef Full Text | Google Scholar