Analytical prediction of thermomechanical shear strain in solder joints with FEA validation in electronic packaging

This paper presents a closed-form analytical model for predicting shear strain in chip-on-board assemblies with an array of solder balls. While the classical analytical formula estimates shear strain based on a configuration with a single solder joint at each end of the chip, it fails to account for the distributed nature of real assemblies. By applying compatibility conditions along the chip/solder ball and PCB/solder ball interfaces, and employing beam theory, the proposed model incorporates key geometric and material parameters, including chip and PCB dimensions, solder ball diameter, height, pitch, and elastic moduli, enabling accurate prediction of mechanical response under thermal loading. Results show that the classical model overestimates shear strain by more than 50 times compared to finite element analysis (FEA), whereas the proposed method yields results consistent with FEA. Hence, the proposed analytical solution presented in the paper demonstrates a significant improvement over the classical formula in prediction of shear strain. The new model reveals that in a fully populated array layout, the maximum shear strain at the outermost solder joint remains nearly constant with increasing chip size. The analysis also indicates that inner solder joints contribute minimally to mechanical support, suggesting that depopulated array designs may not compromise reliability. Additional parametric studies demonstrate that reducing the thickness or stiffness of the chip or PCB decreases overall strain levels. These findings are validated by finite element simulations. The paper concludes with a discussion of future work to address normal strain effects and inelastic behaviors in solder joints.

1 Introduction

Predominant failures in packaged electronic devices often arise from cracking or interface delamination, particularly thermal fatigue failures in solder balls. Emerging technologies such as 2.5D/3D integration, hybrid bonding, wafer- and panel-level packaging, chip stacking, fan-out, package-on-package (PoP), system-in-package (SiP), chiplets, and heterogeneous integration present additional challenges on thermomechanical fatigue of solder balls (Lau and Fan, 2025). The mismatch in the coefficients of thermal expansion (CTE) between different materials, most notably the silicon chip and the printed circuit board (PCB), induces cyclic deformation in the solder balls subject to thermal loads. Over time, this repeated deformation leads to crack initiation and propagation, ultimately causing joint failure. Solder balls serve as the primary mechanical and electrical interconnects between PCB and the semiconductor packages, such as chip-on-board (COB) and ball grid array (BGA) assemblies. Failures in these solder joints can lead to catastrophic malfunction of the entire system, making their mechanical integrity a key determinant of package reliability and product lifespan.

The reliability of solder joints has long been a persistent challenge for the electronic packaging community, particularly as electronic devices continue to shrink in size while increasing in functionality (Schubert et al., 2003; Lau et al., 2003; Paul et al., 2022; Paul, 2017; Wong et al., 1988; Wiese, 2003; Syed, 2001; Syed, 2004; Cheng et al., 2017; Bhate et al., 2008; Qiang, 2007; Darveaux, 2002; Darveaux, 2014; Yi and Jones, 2020; Wong et al., 2016; Wong, 2019; Cheng et al., 2001). Due to the complex geometry of solder joints and the heterogeneous material configurations involved, finite element analysis (FEA) has become the primary tool for assessing the mechanical response of solder joints under various loading conditions (Syed, 2001; Syed, 2004; Darveaux, 2002; Darveaux, 2014; Yi and Jones, 2020). Solder materials undergo plastic or creep deformation during thermal cycling to experience fatigue failure. Viscoplastic and creep models are essential in describing the time-dependent deformation behavior of materials under stress, particularly at elevated temperatures (Schubert et al., 2003; Lau et al., 2003; Paul et al., 2022; Paul, 2017; Wong et al., 1988; Wiese, 2003; Cheng et al., 2017; Bhate et al., 2008; Wong et al., 2016; Wong, 2019; Cheng et al., 2001). FEA enables the calculation of stresses, strains, and inelastic strain energy densities, which are directly correlated with fatigue life (Syed, 2001; Darveaux, 2002; Zhang et al., 2006; Fan et al., 2005; Fan et al., 2010; Fan et al., 2006; Bhatti et al., 2006; Vasudevan et al., 2007; Pei et al., 2006; Vasudevan and Fan, 2008; Varia and Fan, 2011). However, despite its widespread use, FEA has significant limitations. High-fidelity models require fine meshing, detailed material characterizations, and complex boundary conditions, all of which increase computational time and resource demands. Moreover, running extensive parametric studies using FEA to explore the effects of package design variables on solder joint reliability can be prohibitively time-consuming. These challenges limit its practicality for gaining fundamental physical insights or for rapid design iterations during early stages of development.

In contrast, analytical models can offer closed-form expressions that reveal underlying physical mechanisms and provide quick estimates of critical mechanical quantities such as shear strain. These models are particularly valuable for understanding trends, validating numerical simulations, and guiding design decisions (Suhir et al., 2017). However, such closed-form analytical solutions for an array of solder balls, even in the framework of linear elastic analysis, do not exist. The classical analytical formula for estimating shear strain in solder balls is based on highly simplified assumptions with a single solder ball at each end (Lau and Fan, 2025). In addition, such a solution does not meet the continuity or compatibility condition along the interfaces. To address this deficiency, our previous work developed an improved analytical model that incorporated the compatibility condition along the interface (Khanal et al., 2024). The predicted shear strains using this enhanced model showed better agreement with FEA results, thereby demonstrating the importance of including continuity condition in analytical formulations. However, that earlier study focused on a simplified system involving a single solder ball at each end under idealized conditions.

In this study, we extend our analytical methodology to consider an array of solder balls connecting a chip to a PCB in a typical chip-on-board assembly. We derive a comprehensive analytical solution that captures the deformation behavior of solder joints under thermomechanical loading, including the contributions from shear forces, bending moments, and geometric factors associated with the array configuration. The theoretical predictions are validated through detailed finite element simulations. Furthermore, we conduct a series of parametric studies to explore the influence of key design variables, such as solder joint pitch, chip size, and CTE mismatch, on the resulting shear strain. These results provide deeper insights into the fundamental mechanisms governing solder joint failure and offer practical guidance for improving the reliability of future electronic packages.

2 Theory

2.1 Assumptions

To facilitate a closed-form analytical solution, the following assumptions are made in this study:

1. Linear Elasticity: All materials in the assembly, including the solder joints, are assumed to behave as linear elastic throughout the analysis. Nonlinear effects such as creep, plasticity, and time-dependent behaviors of the solder material are not considered within the scope of this model.

2. Point Contact: The solder joints are idealized as having point contact at both the chip/solder (top) and PCB/solder (bottom) interfaces. This simplification enables analytical tractability while capturing the essential mechanical interaction at the interfaces.

3. Neglect of Solder Material’s Normal Force and Bending: Normal force and bending deformation within the solder joints is neglected in the derivation of shear strain. The model focuses solely on shear deformation.

2.2 Classical formula

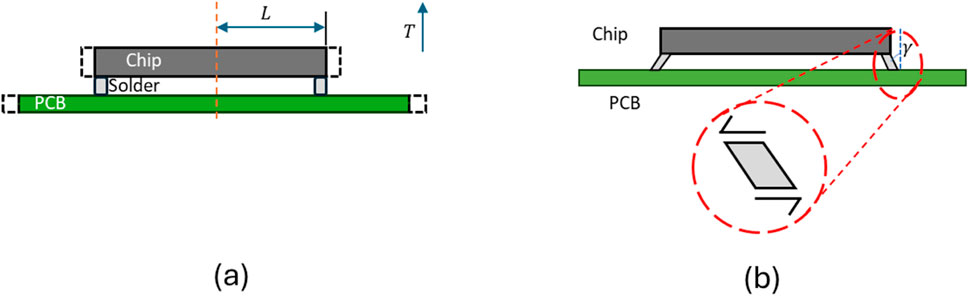
Figure 1a shows a schematic of a simplified chip on board assembly, in which $L$ denotes the half length of the chip and $h_S$ represents the solder’s height. In this configuration, only one solder connection at the each end of the chip is considered. Additionally, only a slice of the chip on board is considered so that the problem is treated as a 2D problem with plane stress condition. As the temperature increases from the stress-free reference state, both the chip and the PCB undergo thermal expansion. Due to the mismatch in their thermal expansion coefficients, shear stress and strain are induced in the solder joints, as shown in Figure 1b. Neglecting the constraint condition and considering the free thermal expansions of the chip and PCB, the estimated shear strain, according to the classical formula (Lau and Fan, 2025), can be calculated as follows.

${\gamma }_s=\frac{\left({\alpha }_P-{\alpha }_C\right)∆TL}{h_S}(1)$

where ${\alpha }_P$ and ${\alpha }_C$ are the CTEs of PCB and chip. This simplified equation clearly shows that the shear strain is proportional to the thermal mismatch $\left({\alpha }_P-{\alpha }_C\right)∆T$ and the size of the chip L. Since a silicon chip typically has a rectangular shape, the diagonal represents the longest dimension. Based on this equation, for a long time, it has shown that one of the most critical parameters influencing solder ball reliability is the half-diagonal length of the chip. The equation also implies that the shear strain in a solder ball is inversely proportional to its height, i.e., increasing the height can help reduce the strain. However, it is important to note that in deriving this equation, the contribution of shear forces acting on the solder balls was not considered. This means that the compatibility, or continuity condition along the solder/chip and solder/PCB interfaces is not met. As a result, this classical approach significantly overestimates the actual strain values (Khanal et al., 2024).

Figure 1

Figure 1. Figure showing chip-solder-PCB (a) Before deformation (b) After deformation.

2.3 New formula

We now present a more accurate derivation of the shear strain for the configuration shown in Figure 1. Before analyzing an array of solder balls, we first simplify the problem by considering a single solder joint, as in the classical formulation in Section 2.1. Figure 2 shows the free-body diagrams of the individual components: the chip, solder joint, and PCB, respectively. Due to symmetry, only half of each component is illustrated. Since the shear forces develop at the interface of solder joints rather than at the neutral axes of the chip and the PCB, equivalent bending moments are used. Consequently, bending moments and axial forces are introduced in both the chip and the PCB, as the shear force P, acting at the interfaces, is transferred to the mid-planes of the chip and PCB. Based on equilibrium conditions, the following equations can be established.

$M_P=\frac{P{h}_P}{2}(\mathrm{2a})$

$M_C=\frac{P{h}_C}{2}(\mathrm{2b})$

where $h_P$ and $h_C$ are the height (or often referred as to the thickness) of PCB and chip. The height of the solder is denoted as $h_S$. The interface area is $A_S$ at both the chip and PCB interfaces. The chip and PCB (or any other materials) are treated as beam components, each with heights $h_P$ and $h_C$, rectangular cross-section area of $A_P$ and $A_C$, and the moment of inertia $I_P$ and $I_C$, respectively.

Figure 2

Figure 2. Free-body diagrams of each component in a simplified chip-on-board assembly.

Based on these assumptions, the displacements of the PCB and chip at the solder joint location when temperature rises can be expressed as follows, according to the free-body diagrams in Figure 2.

$\Delta L_{\mathrm{P}}={\alpha }_{\mathrm{P}}\Delta TL-\frac{L}{A_P{E}_P}P-\frac{h_P^{2}L}{4I_P{E}_P}P={\alpha }_{\mathrm{P}}\Delta TL-\frac{4L}{A_P{E}_P}P(\mathrm{3a})$

$\Delta L_C={\alpha }_C\Delta TL+\frac{L}{A_C{E}_C}P+\frac{h_C^{2}L}{4I_C{E}_C}P={\alpha }_C\Delta TL+\frac{4L}{A_C{E}_C}P(\mathrm{3b})$

where $\Delta T$ represents the temperature change, $\alpha$ denotes the coefficient of thermal expansion, E stands for Young’s modulus, $L$ corresponds to the half-length of the chip or PCB, and $I=\frac{b{h}^3}{12}$, where b is the width of the assembly (in this analysis, the width of the assembly is the diameter of solder d_s).

To solve the unknown shear force P, we use the continuity equation (or called compatibility equation) as follows

${\gamma }_S=\frac{\Delta L_P-\Delta L_C}{h_S}=\frac{P}{A_S{G}_S}(4)$

where ${\gamma }_S$ is the averaged shear strain in the solder ball and $G_S$ is the shear modulus of the solder material, $G_s=\frac{E_s}{2\left(1+{\nu }_s\right)}.$ Using Equations 3a, b, 4, the shear force P is solved, as follows.

$P=\frac{\left({\alpha }_P-{\alpha }_C\right)\Delta TL}{\frac{h_S}{A_S{G}_S}+4L\left(\frac{1}{A_P{E}_P}+\frac{1}{A_C{E}_C}\right)}(5)$

Equation 5 can be rewritten as

$FP=D(6)$

where

$F=\frac{h_S}{A_S{G}_S}+4L\left(\frac{1}{A_P{E}_P}+\frac{1}{A_C{E}_C}\right)(7)$

is a compliance coefficient that depends on the system’s geometry and material properties, and

$D=\left({\alpha }_P-{\alpha }_C\right)\Delta TL(8)$

is the thermal mismatch displacement. Then, based on Equation 4, the new shear strain formula is obtained as follows.

${\gamma }_s=\frac{P}{A_s{G}_s}=\frac{\left({\alpha }_P-{\alpha }_C\right)\Delta TL}{h_s+4L{A}_s{G}_s\left(\frac{1}{A_P{E}_P}+\frac{1}{A_C{E}_C}\right)}(9)$

Compared to Equation 1, Equation 9 introduces a more sophisticated term in the denominator, in addition to the solder ball height $h_s$. This term incorporates the half-length of the chip, the cross-sectional areas of both the chip and the PCB, the elastic moduli of the PCB, chip, and solder, as well as the interface area $A_s$. All of these parameters contribute to determining the shear strain in the solder joint.

2.4 Shear strains for multiple solder joints

Now, let’s consider there are arrays of solder joints between the chip and the PCB. Figure 3 shows a schematic representation of the system under consideration for a 2D slice model. As the model exhibits symmetry, only half of the system is analyzed while deriving the analytical solution, as illustrated in Figure 4. Hence, n represents the total number of solders in the half-sliced-model. In this study, the pitch of the solder ball is represented by s, as shown in Figure 3. Solder numbering starts with i = 1 at the outermost edge and increases sequentially towards the center, with the solder nearest to the line of symmetry having the highest value of n. Index i is used to represent specific solder under investigation, ranging from 1 to n. For simplicity, it is assumed that the connection between the solder and the components (chip and PCB) is located in a single point on the outer edge of the solder. Likewise, to make derivation of analytical solution simple, it is assumed that only shear force is transferred through these points. However, in reality, there exist a transfer of normal force as well as bending moment between the solder and the components to maintain the solder joint in equilibrium. Figure 5a shows free-body diagrams illustrating the transfer of forces between the solder, chip, and PCB based on these assumptions. Since the shear forces develop at the interface of solder joints rather than at the neutral axes of the chip and the PCB, equivalent bending moments - equal to shear force multiplied by half the thickness of the component - are induced, as shown in Figure 5b. These moments, termed as M_Ci for chips and M_Pi for PCB, are developed at each n number of solder joints, where i ranges from 1 to n, similar to the expressions given in Equations 2a, b. These assumptions give only one unknown shear force per solder. After calculating the shear forces in each solder joint, the corresponding strains can be evaluated using force-stress and constitutive relationships.

Figure 3

Figure 3. Schematic diagram of a chip-on-board assembly with a full array of solder joins with a pitch of s.

Figure 4

Figure 4. Half-model of the system due to symmetry.

Figure 5

Figure 5. Free body diagram showing (a) Load transfer between chip, solder, and PCB, (b) Equivalent moment induced.

For a given n number of solder joints, there will be n unknown shear forces denoted by load vector $\left.\left\{P\right.\right\}$ as represented in Equation 10.

$\left.\left\{P\right.\}=\left\{P_1\right.,\cdots ,P_i,\cdots P_n\right\}(10)$

As a natural extension, Equation 6 can be extended to multiple solder joints, and the equation becomes a matrix form.

$\left.\left[F\right]\left\{P\right.\}=\left\{D\right.\right\}(11)$

where $\left[F\right]$ is the compliance matrix of order n × n with elements F_ij. The expressions for F_ij can be derived in a similar manner shown in Section 2.2 for a single joint in half-model, as follows.

$F_{ij}=\left\{\begin{array}{l}\frac{h_s}{A_s{G}_s}+4\left[\frac{1}{A_C{E}_C}+\frac{1}{{A_{P}E}_P}\right]\left[L-\left(i-1\right)s\right],\text{for\hspace{0.17em}}i=j\\ 4\left[\frac{1}{A_C{E}_C}+\frac{1}{A_P{E}_P}\right]\left[L-\left(j-1\right)s\right],\text{for\hspace{0.17em}}i\ne j\end{array}\right.$

$F_{ij}=F_{ji}i,j=1,n(12)$

where s represents the pitch of solder joints.

Similarly, Equation 8 can be extended to the multiple joints as follows.

$D_i=\left({\alpha }_P-{\alpha }_C\right)∆T\left[L-\left(i-1\right)s\right]i=1,n(13)$

which is the thermal displacement vector with order n × 1 at each solder joint’s location. Finally, upon solving for the shear force vector $\left.\left\{P\right.\right\}$ by Equation 11, the shear strains in each of the solder are calculated using Equation 9. The shear strain vector with shear strains at each of the solders is given by Equation 15.

$\left\{{\gamma }_s\right\}=\frac{1}{A_s{G}_s}\left\{P\right\}(14)$

where,

$\left.\left\{{\gamma }_s\right.\}=\left\{{\gamma }_{s,1}\right.,\cdots {\gamma }_{s,i},\cdots {\gamma }_{s,n}\right\}(15)$

For Equations 12, 13, in the case of single solder joint, i.e., n = 1, they are reduced to Equations 7, 8, respectively. Equations 12, 13 are obtained through the superposition by each force or moment component, as well as the compatibility condition of Equation 4 for each joint.

3 Finite element analysis

3.1 Finite element model

Since the analytical model illustrated in Figure 3 is based on a two-dimensional sliced representation under plane stress conditions, a corresponding 2D plane stress finite element model is developed in ANSYS to validate the analytical results. The use of a full three-dimensional (3D) finite element model is not required for this purpose. All components of the system are modeled with quadratic PLANE183 elements under the plane stress assumption. Each element consists of eight nodes, with each node possessing two degrees of freedom, i.e., translations along x- and y-axis. Owing to geometric symmetry, only half of the model is analyzed, with a symmetric boundary condition applied along the center plane (x = 0). Additional displacement constraints are imposed to eliminate rigid body motion. A uniform temperature change, ΔT, is applied throughout the model. Figure 6 illustrates the finite element mesh for the case of n = 10, corresponding to a full assembly containing 20 solder joints.

Figure 6

Figure 6. An example of finite element model for the chip-on-board assembly (n = 10 in the half model).

3.2 Extraction of shear strain

As the analytical approach assumes solder/chip and solder/PCB connection occurring at discrete points, the shear strain calculated from Equation 14 represents an average shear strain, rather than a continuum shear strain. However, in the finite element model, shear strain distribution in solder joints is obtained. Hence, to ensure consistency with the analytical assumption, the finite element analysis utilizes an average shear strain instead of using a single nodal value. Our previous study (Khanal et al., 2024) calculated area-averaged shear strain taken from elements on the top layer of the solder. However, these results may be affected by mesh sensitivity and corner-node stress concentration, thereby affecting the validity of results. For this reason, nodal shear strain values along the midplane of the solder are used to compute the average shear strain. A path along the midplane of the solder as shown in Figure 7, to extract the nodal shear strain values. The average shear strain is then calculated by using a weighted sum of nodal strains as follows.

${\gamma }_{\text{avg}}=\frac{\left[{\gamma }_1\frac{l_e}{2}+\left({\gamma }_2+{\gamma }_3+\cdots +{\gamma }_k\right)l_e+{\gamma }_{k+1}\frac{l_e}{2}\right]}{d_s}(16)$

where k denotes the number of mesh divisions along the solder length, γ₁ to γ_k+1 are the nodal shear strains, l_e represents the spacing between nodes, t_s is the thickness of the plane stress element, while d_s is the solder ball length. Figure 8 illustrates a schematic of the nodal shear strain distribution along the midplane of the solder, based on a mesh element size with six segments along its length. Similar procedure can be followed to find the average shear strain along top and bottom layer.

Figure 7

Figure 7. Path created along the midplane of the solder ball for calculating the shear strain.

Figure 8

Figure 8. Nodal shear strain along the midplane of the solder for a given mesh size.

Furthermore, from the finite element analysis, the shear force along each interface for each solder joint can be extracted to compare with the analytical solutions Equation 5 or Equation 11. Alternatively, the averaged shear strain can also be obtained directly from the shear force from finite element analysis and then converted to shear strain using Equation 14.

4 Results and discussions

4.1 Shear strain distribution and mesh dependency

To show shear strain distribution in a solder joint, we first performed finite element analysis and studied a simplified chip-on-board assembly involving a single solder ball at each end, as illustrated in Figure 1. The geometry and material properties used in this case are shown in Table 1. The temperature change of ΔT = 100 °C is assumed.

Table 1

Table 1. Material and geometric properties of the system used for evaluating shear strain distribution and mesh dependency.

The shear strain contour in the solder is presented in Figure 9, which shows an overall uniform distribution. The shear strain distribution along the top, middle, and bottom layers of the solder is shown in Figure 10. As shown in the figure, the shear strain distribution appears irregular in the top and bottom layers. This behavior is attributed to stress singularities at the corners of solder-chip and solder-PCB interfaces (Vellukunnel et al., 2023; Fan et al., 2001; Ye et al., 2022). Therefore, obtaining shear strain at specific points along the solder interface regions may result in inaccurate results and should be avoided. However, the distribution is smoother in the middle layer, with zero values at both ends due to free surfaces.

Figure 9

Figure 9. Shear strain contour for single solder joint (n = 1), showing stress concentration at the top-left and bottom-left corners (blue). ‘Min’ label in ANSYS indicates maximum negative strain.

Figure 10

Figure 10. Shear strain distribution along the top, middle, and bottom layer of solder for single joint case (n = 1).

As the shear strain distribution along the top and bottom exhibits significant irregularities due to stress singularities (Fan et al., 2001), the results are likely to be highly mesh dependent. In order to assess the mesh dependency, shear strain distributions were computed for two different mesh sizes: 0.01 mm and 0.005 mm. The shear strain distributions for the top, bottom, and middle layers are illustrated in Figures 11–13 respectively. The plots show that the shear strain values at top and bottom interfaces of the solder, differ significantly between the two mesh sizes at both ends of the interfaces, indicating the mesh dependency of the results. The top left and bottom left portions typically experience higher strain, as indicated by the blue region of strain contour in Figure 9. However, as shown in Figure 13, the strain distribution in the middle layer remains nearly identical for both the mesh sizes, indicating that the mesh size does not affect the shear strain distribution in the middle layer.

Figure 11

Figure 11. Shear strain distribution along the top layer of solder for two mesh sizes.

Figure 12

Figure 12. Shear strain distribution along the bottom layer of solder for two mesh sizes.

Figure 13

Figure 13. Shear strain distribution along the middle layer of solder for two mesh sizes.

Furthermore, the average shear strain values for the top, middle and bottom layers of solder are calculated for both mesh sizes using Equation 16. As illustrated in Table 2, despite variation in shear strain distribution across the layers and mesh sensitivity in top and bottom layers, the average shear strain values for all three layers is identical. This suggests that the mesh size has no impact on average shear strain, but the strain at particular points can vary significantly. In the subsequent analysis and discussions, we will use the averaged strain from the finite element analysis to verify the analytical solutions.

Table 2

Table 2. Averaged shear strain obtained from the shear strain distribution along the top, middle, and bottom layer for two mesh sizes.

4.2 Analytical results versus FEA

Based on the material properties and geometric dimensions in Table 1, the shear strain results from the proposed analytical method given by Equation 9, the classical solution given by Equation 1, and FEA results are obtained and illustrated in Table 3. As seen in Table 3, the shear strain results from the proposed analytical method closely match with those obtained from FEA model. On the other hand, the classical formula yields the shear strain value over 50 times greater than the FEA result, suggesting a significant overestimation of shear strain in the solder. Hence, the proposed analytical solution presented in the paper demonstrates a significant improvement over the classical formula in prediction of shear strain, as validated with FEA results. In Table 3, the results of the shear force are also obtained based on the FEA analysis and Equation 5. Using the shear force value from finite element analysis, the shear strain is also obtained and is the same as shown in the table. The use of shear force (resultant force at a surface) in FEA can also effectively minimize the effect of meshing density and stress singularity.

Table 3

Table 3. Shear strain and shear force values obtained from three different models: proposed analytical model, Classical model, and FE model.

Now, let’s consider a fully populated array of solder joints with the parameters given in Table 4. The pitch used here is 0.5mm, and the solder diameter is 0.3 mm. For n = 10 in a half-model, this corresponds to a configuration with a fully populated array of 20 $\times$ 20 solder balls. In the analytical model, we consider a half-sliced model with 10 solder balls of 0.3 mm diameter with a pitch of 0.5 mm. In finite element model, to minimize the possible edge effect (Vellukunnel et al., 2023), the finite element model includes an “overhang” portion, which also reflects the actual situation in real applications, as shown in Figure 14. Such an overhang, however, does not affect the analytical results using Equation 14.

Table 4

Table 4. Parameters for a case study of a fully populated array of solder joints.

Figure 14

Figure 14. Finite element model with a overhang portion for an array of solder joints (n = 10).

The shear strain values for each solder joints, indexed form i = 1 to 10, computed from both the analytical model and FEA model are shown in Figure 15. The corresponding shear force P for both the analytical model and FEA model are shown in Figure 16. The figures demonstrate that the shear strain and shear force predicted by the analytical model show similar trends with the FEA results across all solder joints. A notable discrepancy is observed between the FEA and analytical results, for instance, at the edge solder joint (i = 1), the analytical results (both shear force and shear strain) exceed FEA results by a factor of about 1.6. In the current analytical model, only shear force is transferred through these points. However, in reality, there exist a transfer of normal force as well as bending moment between the solder and the components to maintain the solder joint in equilibrium. We believe this is the reason for the discrepancy. Despite the observed difference, the analytical results achieve the same order of magnitude compared to the finite element analysis.

Figure 15

Figure 15. Comparison of shear strain value obtained from analytical solutions with average shear strain obtained from plane stress FEA for all ten solder joints (The results are obtained based on the materials properties in Table 2 and the geometrical parameters in Table 4, with ΔT = 100 °C).

Figure 16

Figure 16. Comparison of shear strain value obtained from analytical solutions with average shear strain obtained from plane stress FEA for all ten solder joints (The results are obtained based on the materials properties in Table 2 and the geometrical parameters in Table 4, with ΔT = 100 °C).

Another notable observation from Figures 15, 16 is that the result is highest at the outermost solder joint and subsequently diminishes exponentially for inner solders, eventually approaching zero. These findings indicate that the outermost solder joint is the most critical and prone to failure. For the solder joints with index i ≥ 5, the values are almost negligible, suggesting that these joints are not engaged in load bearing. This implies that a depopulated array design will not affect the solder joint reliability. Figure 17 plots the schematic designs of a fully populated array with a depopulated array. According to the predictions shown above, the depopulated array design will not affect the overall solder joint reliability.

Figure 17

Figure 17. (a) A fully populated ball layout vs. (b) a depopulated ball layout.

4.3 Parametric study

Figure 18 presents the maximum shear strain in solder joints as a function of the chip’s half-length, using three different analytical approaches. When Equation 1 is applied, the shear strain increases linearly with chip’s length, but the results significantly overestimate the actual strain in the solder joints. In contrast, Equation 9 yields a nonlinear increase in strain with chip length, as shown in the figure. Furthermore, when considering a fully populated array layout with a given pitch and solder ball diameter, Equation 14 predicts that the maximum shear strain is nearly independent of chip length. We also performed the finite element analysis for the fully populated array layout, which confirms this trend, as shown in the figure. The reason is that as the chip length increases, the number of solder joints beneath the chip increases, consequently the shear strain at the outermost joint remains virtually unchanged. The three curves in Figure 18 using three analytical formulas, Equations 1, 9, 14, predict entirely different trends for shear strain versus chip size, highlighting the importance of the analytical development presented in this work. Among the three, this paper offers the most realistic prediction, validated by the finite element analysis.

Figure 18

Figure 18. Plot between maximum shear strain and chip length for three analytical approaches and FEA solution (ΔT = 100 °C, material properties are given in Table 2. For Equation 1; Equation 9, chip length a variable, while for Equation 14, s = 0.5 mm is fixed as chip-length is a variable. All other geometric parameters are shown in Table 4 excluding chip-length).

Figures 19a,b plot the maximum shear strain against the thickness (or height) of the chip and PCB. As the thickness of the chip or PCB decreases, the overall assembly becomes more flexible, therefore the solder joint strain decreases.

Figure 19

Figure 19. Plot using the analytical solution of Equation 14 showing the relationship between maximum shear strain and: (a) Chip thickness, varying from 0.10 mm to 0.50 mm in 0.05 mm increments (b) PCB thickness, varying from 0.50 mm to 1.20 mm in 0.10 mm increments (ΔT = 100 °C, material properties are given in Table 2, and the geometric information are given in Table 4 except for the variations of PCB and chip thickness variations shown above).

Figure 20 presents the results for the maximum shear strain versus the PCB modulus. As PCB modulus increases, the shear strain decreases. This also demonstrates that reducing PCB modulus will increase the overall flexibility of the assembly, therefore, the solder strain can be reduced.

Figure 20

Figure 20. Graph using the analytical solution of Equation 14 showing the relationship between maximum shear strain and PCB modulus, with the modulus varying from 15 GPa to 25 GPa in 1 GPa increments. (ΔT = 100 °C, material properties are given in Table 2, and the geometric information are given in Table 4 except for the variations of PCB and chip thickness variations shown).

5 Concluding remarks

This paper presents a closed-form analytical model to predict shear strain in chip-on-board assemblies with an array of solder balls, using linear elastic analysis based on beam theory. The model extends classical single-ball formulations by deriving a compliance matrix-based solution and is validated through finite element analysis (FEA). Unlike the classical formula, which can overestimate solder ball strain by a factor of 50 or more, the present model yields more realistic predictions for array configurations. Several important findings have been made:

1. Model Accuracy: The shear strain predictions for each solder joint in a full-array layout are generally consistent with FEA results, achieving the same order of magnitude. However, notable discrepancies appear at the edge joints, where the analytical model overestimates strain by a factor of approximately 1.6. While the model accounts for shear forces at the solder/chip and solder/PCB interfaces, it still does not consider normal forces or bending moments, which are part of the equation for full equilibrium of the solder joint.

2. Effect of Array Layout: For a fully populated solder ball array, the shear strains in the inner rows are found to be almost negligible, indicating that these joints contribute minimally to mechanical support, as shown in Figures 15, 16, as the strains or shear force on the inner joints are virtually zero. This suggests that a depopulated array design will not significantly impact solder joint reliability. Depending on the design parameters, the analytical model can estimate how many inner rows effectively provide no mechanical support.

3. Effect of Chip Size: When the solder ball pitch and size are fixed, increasing the chip size leads to a corresponding increase in the number of solder joints. However, the maximum shear strain at the outermost solder ball remains virtually unchanged. This finding fundamentally contrasts with predictions based on the classical formula, which suggests a linear increase in shear strain with chip size.

4. Assembly Flexibility: Reducing the thickness of the chip or PCB, or lowering the modulus of the PCB, results in a more flexible assembly. Consequently, the shear strain in the solder joints decreases.

The proposed model offers valuable insights into the mechanical behavior of solder joints and provides useful guidance for material selection and early-stage design optimization. It is particularly beneficial for identifying design trends and validating numerical simulations. Nonetheless, limitations remain. The current model assumes linear elastic behavior and cannot account for the nonlinearities inherent in solder materials, such as creep, viscoplastic deformation, or variations in actual solder joint geometry. Additionally, the analysis is limited to shear strain, whereas in reality, both shear and normal strains interact and influence joint reliability. Since the solder joint is considered as a point contact, the effect of the actual shape of solder joints or the effect of fillet cannot be captured. Future work will focus on incorporating normal strain effects, more rigorously enforcing equilibrium conditions, and exploring coupled shear-normal deformation along with inelastic behavior to improve model fidelity. Furthermore, the analytical framework will be extended from the current 2D sliced model to a full 3D representation using plate theory in place of beam theory. Once the 3D analytical model is established, it will enable the development of design guidelines - for example, defining acceptable depopulation ranges as a function of PCB stiffness or chip length.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

UB: Writing – original draft, Validation, Methodology, Investigation, Writing – review and editing. JZ: Validation, Writing – review and editing, Supervision, Writing – original draft. XF: Writing – original draft, Investigation, Data curation, Conceptualization, Validation, Writing – review and editing, Methodology, Supervision.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bhate, D., Chan, D., Subbarayan, G., Chiu, T. C., Gupta, V., and Edwards, D. R. (2008). Constitutive behavior of Sn3.8Ag0.7Cu and Sn1.0Ag0.5Cu alloys at creep and low strain rate regimes. IEEE Trans. Components Packag. Technol. 31 (3), 622–633. doi:10.1109/tcapt.2008.2001165

CrossRef Full Text | Google Scholar

Bhatti, P. K., Pei, M., and Fan, X. (2006). “Reliability analysis of SnPb and SnAgCu solder joints in FC-BGA packages with thermal enabling preload,” in 56th electronic components and technology conference 2006, San Diego, CA, USA, 30 May 2006 - 02 June 2006 (IEEE), 6.

Google Scholar

Cheng, Z., Becker, K., and Wilde, J. (2001). Applying Anand model to represent the viscoplastic deformation behavior of solder alloys. ASME J. Electron. Packag. 123, 247–253. doi:10.1115/1.1371781

CrossRef Full Text | Google Scholar

Cheng, S., Huang, C.-M., and Pecht, M. (2017). A review of lead-free solders for electronics applications. Microelectron. Reliab. 75, 77–95. doi:10.1016/j.microrel.2017.06.016

CrossRef Full Text | Google Scholar

Darveaux, R. (2002). Effect of simulation methodology on solder joint crack growth correlation and fatigue life prediction. J. Electron. Packag. 124 (3), 147–154. doi:10.1115/1.1413764

CrossRef Full Text | Google Scholar

Darveaux, R. (2014). “Thermal cycle fatigue life prediction for flip chip solder joints,” in 2014 IEEE 64th Electronic Components and Technology Conference (ECTC), Orlando, FL, USA, 27-30 May 2014 (IEEE).

CrossRef Full Text | Google Scholar

Fan, X., Wang, H. B., and Lim, T. B. (2001). Investigation of the underfill delamination and cracking in flip-chip modules under temperature cyclic loading. IEEE Trans. Compon. Packag Technol. 24 (1), 84–91. doi:10.1109/6144.910806

CrossRef Full Text | Google Scholar

Fan, X., Rasier, G., and Vasudevan, V. S. (2005). Effects of dwell time and ramp rate on lead-free solder joints in FCBGA packages electronic components and technology. ECTC 2005, 901–906. doi:10.1109/ECTC.2005.1441379

CrossRef Full Text | Google Scholar

Fan, X., Pei, M., and Bhatti, P. K. (2006). “Effect of finite element modeling techniques on solder joint fatigue life prediction of flip-chip BGA packages,” in 56th electronic components and technology conference 2006, San Diego, CA, USA, 30 May 2006 - 02 June 2006 (IEEE), 9.

Google Scholar

Fan, X., Varia, B., and Han, Q. (2010). Design and optimization of thermo-mechanical reliability in wafer level packaging. Microelectron. Reliab 50 (4), 536–546. doi:10.1016/j.microrel.2009.11.010

CrossRef Full Text | Google Scholar

Khanal, M., Zhou, J., and Fan, X. (2024). “Accurate prediction of solder stresses/strains in multi-layered electronics packages during temperature cycling,” in 2024 IEEE 74th electronic components and technology conference (ECTC), Denver, CO, USA, 28-31 May 2024 (IEEE).

CrossRef Full Text | Google Scholar

Lau, J., and Fan, X. (2025). Hybrid bonding, advanced substrates, failure mechanisms, and thermal management for chiplets and heterogeneous integration. doi:10.1007/978-981-96-4166-6

CrossRef Full Text | Google Scholar

Lau, J., Dauksher, W., and Vianco, P. (2003). “Acceleration models, constitutive equations and reliability of lead-free solders and joints,” in IEEE Electronic Components and Technology Conference Proceedings, New Orleans, Louisiana, 27-30 May 2003 (IEEE), 229–236.

Google Scholar

Paul, T. V. (2017). Understanding the reliability of solder joints used in advanced structural and electronics applications: Part 2-reliability performance. Weld. J. 96. Available online at: https://www.osti.gov/pages/biblio/1356221.

Google Scholar

Paul, V., and Neilsen, M. (2022). “Processing and reliability of solder interconnections in stacked packaging,” in From architectures to applications (Li and goyal). Editor 16 Chapter (Springer), 471–526.

Google Scholar

Pei, M., Fan, X., and Bhatti, P. K. (2006). “Field condition reliability assessment for SnPb and SnAgCu solder joints in power cycling including mini cycles,” in Proceedings of the electronic components and technology conference (ECTC), San Diego, CA, USA, 30 May 2006 - 02 June 2006 (IEEE), 899–905.

Google Scholar

Qiang, W. (2007). “Experimental determination and modification of Anand model constants for Pb-free material 95.5Sn4.0Ag0.5Cu,” in EUROSIME Conf. IEEE, London, UK, 16-18 April 2007 (IEEE).

CrossRef Full Text | Google Scholar

Schubert, A., Dudek, R., Auerswald, E., Gollhardt, A., Michel, B., and Reichl, H. (2003). “Fatigue life models for SnAgCu and SnPb solder joints evaluated by experiments and simulation,” in IEEE Electronic Components and Technology Conference Proceedings, New Orleans, LA, USA, 27-30 May 2003 (IEEE), 603–610.

CrossRef Full Text | Google Scholar

Suhir, E., Yi, S., and Ghaffarian, R. (2017). How many peripheral solder joints in a surface mounted design experience inelastic strains? J. Electron. Mater. 46 (3), 1747–1753. doi:10.1007/s11664-016-5224-8

CrossRef Full Text | Google Scholar

Syed, A. (2001). Predicting solder joint reliability for thermal, power, and bend cycle within 25% accuracy. 51st ECTC, 255–263. doi:10.1109/ECTC.2001.927732

CrossRef Full Text | Google Scholar

Syed, A. (2004). “Accumulated creep strain and energy density based thermal fatigue life prediction models for SnAgCu solder joints,” in 2004 Proceedings. 54th electronic components and technology conference, Las Vegas, NV, USA, 04-04 June 2004 (IEEE).

CrossRef Full Text | Google Scholar

Varia, R., and Fan, X. (2011). “Reliability enhancement of wafer level packages with nano-column-like hollow solder ball structures,” in Proceedings of 61st electronic components and technology conference (61st ECTC), Orlando, Florida, May 31–June 3, 2011 (IEEE), 754–760.

CrossRef Full Text | Google Scholar

Vasudevan, V., and Fan, X. (2008). “An acceleration model for lead-free (SAC) solder joint reliability under thermal cycling,” in Proceedings of the electronic components and technology conference (58th ECTC), Lake Buena Vista, FL, USA, 27-30 May 2008 (IEEE), 139–145.

Google Scholar

Vasudevan, V., Fan, X., Liu, T., and Young, D. (2007). “Slow cycle fatigue creep performance of Pb-free (LF) solders,” in Proceedings of the electronic components and technology conference (ECTC), Sparks, NV, USA, 29 May 2007 - 01 June 2007 (IEEE), 116–123.

CrossRef Full Text | Google Scholar

Vellukunnel, M. T., Khanal, M., and Fan, X. (2023). “Thermal stresses in a bi-layer assembly in electronics packaging,” in 2023 24th international conference on thermal, mechanical and multi-physics simulation and experiments in microelectronics and microsystems (EuroSimE), Graz, Austria, 16-19 April 2023 (IEEE), 1–7.

CrossRef Full Text | Google Scholar

Wiese, S. (2003). Microstructural dependendence of constitutive properties of eutectic SnAg and SnAgCu solders. 197–206.

Google Scholar

Wong, E. H. (2019). A new creep fatigue model for solder joints. Microelectron. Reliab. 98, 153–160. doi:10.1016/j.microrel.2019.05.012

CrossRef Full Text | Google Scholar

Wong, B., Helling, D. E., and Clark, R. W. (1988). A creep-rupture model for two-phase eutectic solders. IEEE Trans. CMPT 11 (3), 284–290. doi:10.1109/33.16655

CrossRef Full Text | Google Scholar

Wong, E. H., van Driel, W. D., Dasgupta, A., and Pecht, M. (2016). Creep fatigue models of solder joints: a critical review. Microelectron. Reliab. 59, 1–12. doi:10.1016/j.microrel.2016.01.013

CrossRef Full Text | Google Scholar

Ye, G., Fan, X., and Zhang, G. (2022). Practical aspects of thermomechanical modeling in electronics packaging: a case study with a SiC power package. Microelectron. Reliab 132, 114514. doi:10.1016/j.microrel.2022.114514

CrossRef Full Text | Google Scholar

Yi, S., and Jones, R. (2020). Machine learning framework for predicting reliability of solder joints. Solder. and Surf. Mt. Technol. 32.2, 82–92. doi:10.1108/ssmt-04-2019-0013

CrossRef Full Text | Google Scholar

Zhang, G. Q., van Driel, W. D., and Fan, X. (2006). Mechanics of microelectronics. Springer Science and Business Media.

Google Scholar