On Using Lagrangian Drift Simulations to Aid Interpretation of in situ Monitoring Data

One key challenge of marine monitoring programs is to reasonably combine information from different in situ observations spread in space and time. In that context, we suggest the use of Lagrangian transport simulations extending both forward and backward in time to identify the movements of water bodies from the time they were observed to the time of their synopsis. We present examples of how synoptic maps of salinity generated by this method support the identification and tracing of river plumes in coastal regions. We also demonstrate how we can use synoptic maps to delineate different water masses in coastal margins. These examples involve quasi-continuous observations of salinity taken along ferry routes. A third application is the synchronization of measurements between fixed stations and nearby moving platforms. Both observational platforms often see the same water body, but at different times. We demonstrate how the measurements from a fixed platform can be synchronized to measurements from a moving platform by taking into account simulation-based time shifts.

1. Introduction

In situ observations from FerryBoxes installed on ships of opportunity provide measurements for a large number of different parameters with high temporal resolution. In this study, we address a couple of examples that refer to FerryBox observations in the southern North Sea (Petersen, 2014). Localized in situ observations are, however, only limited snapshots of an ongoing evolution of water masses, ranging from the large-scale ocean circulation on the order of years (Sheehan et al., 2017) to the smaller meso- and submeso-scale structures (Oka et al., 2014; Schubert et al., 2019). Proper interpretation of oceanographic measurements often requires knowledge about the origin and history of the regional water masses. Naturally, this would be analyzed within a Lagrangian framework. In this study, we demonstrate the usefulness of such an approach with three examples.

High-quality quasi-continuous data being available along frequent 1D ship transects entails a certain imbalance between high temporal resolution on one hand and low spatial coverage in a 2D domain on the other. Satellite pictures might be employed to achieve some spatial extrapolation. Another kind of complementary information are hydrodynamic currents derived from high-frequency radar observations, altimetry, or numerical models. Based on such current fields, the Lagrangian approach follows the pathways of individual water parcels. Integrating tracer trajectories back in time provides information on an analyzed water parcel's origin. Retrospectively, future drift paths can also be specified.

Concepts that combine observational data (either in situ or satellite based) with Lagrangian advection have already been applied in the past. Jönsson et al. (2009), for instance, based their Lagrangian approach on output from a coastal circulation model, aiming at a dynamic interpolation between satellite data at different times. Each data point taken on a moving platform like a ferry or research vessel refers to a different location in both space and time. Knowing the movements of water parcels, however, enables the generation of virtual observations at the time of an intended synopsis, shifting existing real measurements in both space and time. If tracers can be assumed to behave passively, originally nonsimultaneous data will be combined into one single map that refers to a specific time of interest. Widening the time interval from which observations are combined will increase the number of data points in this map.

Most variables, however, are not passive and their values will change during the tracer's journey. Nonetheless, Jönsson et al. (2009) used Lagrangian diagnostics to separate the effects of dilution and biogeochemical processing within the water column from the influence of advection. The differences between two observations at different times (but in the same water body) allow to estimate rates of either growth or depletion of constituents like chlorophyll a, for instance. Even when the underlying processes cannot be described in detail, Lagrangian advection nevertheless sets a general framework that spatially structures their occurrence. As d'Ovidio et al. (2015) state, the Lagrangian approach can help disentangle temporal from spatial biogeochemical variability.

Lagrangian simulations can also help to understand the origins and behaviors of organisms and particles in highly dynamic and diverse environments, like the land to sea boundary (Cahill et al., 2008; Pérez-Ruzafa et al., 2019). Huhn et al. (2012) analyzed patterns of advection to link the observed Madagascar plankton bloom to a nutrient source at the southern tip of Madagascar. With a similar approach, d'Ovidio et al. (2015) studied the effects of natural iron enrichment on phytoplankton blooms in the vicinity of the Kerguelen Plateau in the Southern Ocean. The authors used the Lagrangian approach for adapting their sampling strategy to the estimated location of the plume with high iron concentrations, the presumed precondition for the occurrence of algae blooms.

Peacock and Haller (2013) gave a nice overview of Lagrangian coherent structures (LCSs; Haller, 2001), which they call a hidden dynamical skeleton behind the aforementioned organization and accumulation of tracer particles. LCSs derived from Lagrangian simulations support a description of both small and large-scale features in the marine system. Studies showed altimetry-derived mesoscale surface transports to be relevant for the organization of planktonic communities in terms of delimited patches or elongated plumes (Lehahn et al., 2007; d'Ovidio et al., 2010; Olascoaga et al., 2013). Studying small-scale structures in coastal waters, Hernández-Carrasco et al. (2018) used currents measured by a high-frequency radar system that were not constrained by the assumption of geostrophic balance. Again they found LCSs to shape patchiness of chlorophyll a concentrations.

Within a monitoring framework, backward trajectories identify the origins of probed water bodies. Recently, Callies (2021) demonstrated enhanced separation of backward trajectories in simulated German Bight surface currents (i.e., convergence in the usual passage of time) due to a very high sensitivity on seeding positions on either side of linear structures. These lines of enhanced separation were shown to be highly variable in time, moving, disappearing, or newly arising depending on the recent history of atmospheric forcing. Such time-dependent pronounced spatial structuring impedes a purely statistical description of uncertainty. For a dynamic time-interpolation of high-resolution observational data, however, the accuracy of hydrodynamic currents is the decisive factor. Simulated Lagrangian drift paths accumulate uncertainties and at some stage the accumulated errors may transfer a tracer parcel to another sub-mesoscale regime, which lets the simulated trajectory further diverge from reality. Unfortunately, suitable observations on Lagrangian transports in the southern North Sea region are very sparse. Model validations based on drift experiments were reported in Callies et al. (2017b) and Callies et al. (2019). Unavoidably, however, uncertainty is very much situation dependent so that no strict measure of uncertainty can be provided. Other types of information must be included for assessing consistency the overall puzzle.

In this study, we present three examples of combining oceanographic observations from ships of opportunity with Lagrangian simulations of forward and backward trajectories. We argue that this is an effective and simple method to infer time-dependent 2D patterns and structures, such as the origin and evolution of water masses in coastal regions, from high-resolution observations along just 1D transects. All our examples will refer to salinity as an approximately passive tracer. Modeling salinity is notoriously error-prone due to uncertainties in freshwater supply and a long-term accumulation of errors due to salinity's passive behavior. Combining observed salinity with simulated Lagrangian transports can therefore be seen as an attempt to beneficially combine reliable components from the worlds of modeling and in situ observations.

The paper is organized as follows: We start with a description of observational platforms and example data sets we use. We then summarize our drift modeling approach and how synoptic maps are derived from a collection of observations distributed in time. Illustrative results from three prototypical examples are presented in more detail, followed by a more general discussion and a summary of main conclusions.

2. Materials and Methods

2.1. Observations

2.1.1. FerryBox Observations

FerryBoxes were developed within the GOOS (Global Ocean Observing System) and EuroGOOS framework (Petersen, 2014). They allow for routine measurements of standard oceanographic parameters such as temperature, salinity, turbidity, oxygen, and chlorophyll fluorescence, as well as pH, nutrients (ammonium, nitrate/nitrite, phosphate, silicate), and main algal classes. The depth of a FerryBox intake is typically within the first 3–5 m of the water surface (Petersen and Colijn, 2017). FerryBox systems have been installed on different ships of opportunity (both ferries and cargo vessels), as summarized by Petersen (2014).

In example A, we will analyze data from a FerryBox installed on the M/V Funny Girl (Voynova et al., 2017) within the Coastal Observing System for Northern and Arctic Seas (COSYNA; Baschek et al., 2017). From the end of April through September, the ferry travels twice a day between the island of Helgoland and Büsum, Germany (Figure 1). Comprehensive FerryBox records for salinity, temperature, pH, dissolved oxygen, chlorophyll fluorescence, and colored dissolved organic matter are available for the years 2012–2014, allowing to quantify the impact of the summer flood event in June 2013 along this ship's route (Voynova et al., 2017). Here, we use salinity as an indicator of river plume progression on the coast during and after the large flood.

FIGURE 1

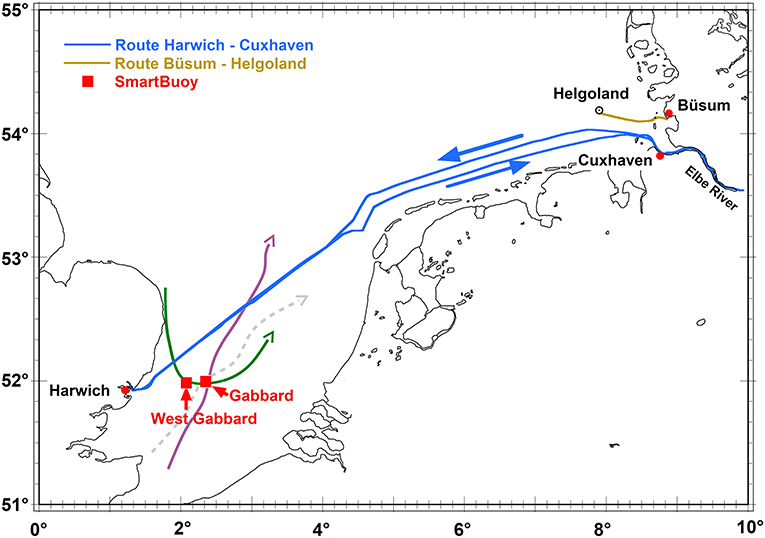
Figure 1. Ferry routes between Helgoland and Büsum, between Cuxhaven and Harwich and locations of the SmartBoy stations Gabbard and West Gabbard. Example trajectories are drawn that illustrate different pathways of water parcels either from Gabbard to the ferry transect (purple) or from the ferry transect to Gabbard (green). The colors agree with the color map used in Figure 7. Finally, the dashed gray line provides the example of a water parcel being probed at Gabbard but never seen by the FerryBox system.

Within the EU-funded project FerryBox (2002–2005), a ferry operated in the southern North Sea between Cuxhaven (Germany) and Harwich (Great Britain) was equipped with a FerryBox (Figure 1). In examples B and C, we will refer to salinity data recorded by that ferry (Petersen et al., 2011), deriving useful information on the large-scale salinity distribution.

2.1.2. Station (West) Gabbard

In December 2000, the Centre for Environment, Fisheries and Aquaculture Science (CEFAS) deployed a moored intelligent, automated, multi-parameter recording platform for marine environmental data collection (SmartBuoy¹) at Gabbard (52°00'N/2°20'E) in the North Sea, a location with about 45 m water depth. Measuring instruments were attached at about 1 m depth. In August 2002, the Gabbard SmartBuoy was moved to a site, which is about 9 nautical miles closer to shore (West Gabbard, 51°59'N/2°05'E, water depth about 32 m). Locations of the SmartBuoy relative to the FerryBox transect are shown in Figure 1.

The buoy is part of the National Marine Monitoring Programme (NMMP) funded by the UK Government's Department for Environment, Food and Rural Affairs (Defra). The monitoring program's main objective is to observe nutrient and phytoplankton dynamics in the region. The SmartBuoy also takes observations of other parameters such as temperature, suspended sediment concentration, and light penetration, which help to interpret the biogeochemical parameter variations. Surface salinity data in 2002 from this buoy was used to compare to FerryBox data collected over the same period.

2.2. Lagrangian Drift Modeling

The Lagrangian drift module PELETS-2D (Program for the Evaluation of Lagrangian Ensemble Transport Simulations) conducts offline simulations based on pre-calculated 2D current fields (Callies et al., 2011). Optionally, winds may be used as additional forcing. The Lagrangian transport algorithm of PELETS was developed for hydrodynamic fields being defined on irregular triangular grids. Velocities are updated by linear interpolation in time and space every time a tracer particle is transferred to another triangular grid cell. Velocities are also updated when time steps would otherwise exceed a limit of 15 min. In all examples of the present study, a simple Euler forward scheme was used. In the 2D setup with small time steps, results hardly change when a higher order Runge–Kutta solver is used (employed by Callies, 2021, for a similar German Bight setup).

The examples we present use Eulerian hydrodynamic currents from two different models. The first model is the 2D barotropic version of the finite element model TELEMAC (Hervouet and van Haren, 1996). Multi-decadal hourly simulations for the North Sea (Weisse and Plüß, 2006; Weisse et al., 2009, 2014) are available from the database coastDat (Plüß and Weisse, 2012). These simulations with TELEMAC-2D were forced with NCEP/NCAR re-analyzed wind fields (Kistler et al., 2001) that were dynamically downscaled with the nested regional climate model SN-REMO (Meinke et al., 2004).

The second set of pre-calculated currents comes from the 3D finite difference model BSHcmod, which is run operationally by the Federal Maritime and Hydrographic Agency (BSH) (Dick et al., 2001; Dick and Kleine, 2007). Depending on the application, we extract either vertical mean or surface currents from the archived BSHcmod model output, available with roughly 900 m grid resolution in the inner German Bight and roughly 5 km grid resolution further west. Surface fields are representative of a 5 m deep surface layer. Atmospheric forcing on an hourly basis is provided by the regional model COSMO-EU (Consortium for Small-Scale Modeling; Schulz and Schättler, 2014), which is run operationally by the German Meteorological Service (Deutscher Wetterdienst [DWD]). Wind stress is included using the parameterization by Smith and Banke (1975). No extra Stokes drift is taken into account in the archived model outputs.

BSHcmod flow fields are defined on a regular grid, so that to be used with PELETS their topology must be pre-processed, introducing diagonals that subdivide each rectangular grid cell into two triangles. A more general triangulation process can also deal with the transition between nested grids with different resolution. In no case does the transformation affect the information content of the flow fields.

2.3. Synoptization

In our simulations, we initialize one passive tracer particle at the location and time of each in situ measurement. The trajectory of this water parcel is then integrated both forward and backward in time using hourly (TELEMAC-2D) or 15-min (BSHcmod) current fields. We then produce synoptic spatial maps that combine information from all trajectories (if applicable), each trajectory contributing one pixel that describes the location of the respective drifter at the time of the map (Figure 2).

FIGURE 2

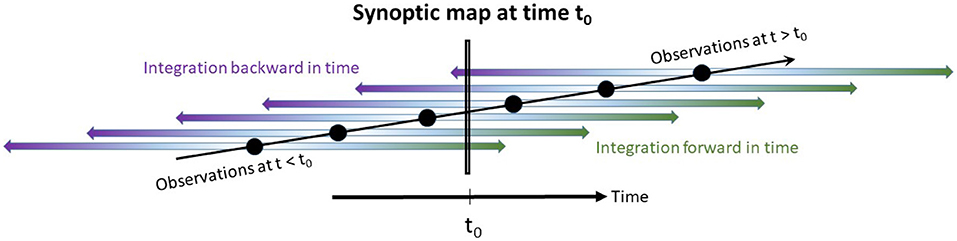
Figure 2. A sketch of how a synoptic plot is generated, assembling snapshots from different trajectories initialized at different times (when corresponding observations were taken) and integrated both backward and forward in time. The vertical coordinate in the graph has no physical meaning, it was introduced to avoid trajectories attached to different observations being plotted on top of each other.

Lipphardt et al. (2006) obtained a large ensemble of Lagrangian trajectories synchronized in time by attaching trajectories to each point of a regular grid covering an area of interest (in their study: Monterey Bay). On this pre-defined grid, they color coded characteristics (e.g., residence time, origin, or fate of the respective trajectory) of trajectories emerging from each node. In our monitoring-oriented approach, initial locations are irregular, corresponding to shipborne observations and trajectories. Trajectories are initialized each time an observation is taken. The measurement at the point of a trajectory's origin is assumed to remain conserved along the simulated trajectory (passive tracer). If data are recorded on a moving platform like a ship of opportunity, for instance, at most one observation will be taken at exactly the time of the synoptic plot. All other pixels in the plot come from trajectories integrated either forward or backward in time (see Figure 2). Pixels in the synoptic map will be distributed irregularly, and the number of pixels depends on how many overlapping trajectories are active at the time the plot refers to.

3. Results

Three different examples illustrate the use of model-based Lagrangian transports to improve interpretation of observational data. The first example aims at the identification of the fresh water plume in a coastal region after an extreme Elbe river flood in June 2013. FerryBox data collected on the coast near the Elbe captured unusually low salinities. Using salinity as an indicator, the Elbe river plume shape could be estimated using simulated Lagrangian transports. The second example deals with FerryBox data recorded along a route between the mouth of the Elbe River Estuary at Cuxhaven, Germany, and Harwich, Great Britain. Synoptic maps help to identify the angle, at which the ship route cuts through the salinity front. The third example refers to a comparison of the same FerryBox data with salinity measurements from the CEFAS Gabbard Buoy, a fixed station adjacent to the ferry route. In this case, Lagrangian simulations enable a dynamic synchronization of the two salinity records.

3.1. Example A

In this example, we try to delineate the area, which is potentially influenced by the Elbe river plume after an extreme river flood. For this purpose, FerryBox salinity observations attached to surface tracer parcels are considered passive in the further course of the parcel drift. Although this assumption is not strictly valid due to vertical mixing, tracers labeled by low observed salinity nevertheless carry the information of being influenced by low salinity water, which is essential for our purpose. This approach is feasible due to the large gradients in salinity in this coastal region.

In June 2013, an Elbe River flood event discharged a large amount of estuarine water to the German Bight. A plume of low salinity water extended from the Elbe estuary along the coast to the north (Voynova et al., 2017). FerryBox observations on board the Funny Girl detected the arrival of low salinity water around the middle of June (Figure 3). However, although the Hovmöller diagram in Figure 3 combines two coordinates representing space and time, it nevertheless remains strictly confined to a linear transect between Büsum and Helgoland. Along its ordinate, Figure 3 provides for each point on the ferry route the corresponding time series of salinity. Figure 4C replicates one of these time series for some nearshore location. However, proper interpretation of these observations requires a wider context.

FIGURE 3

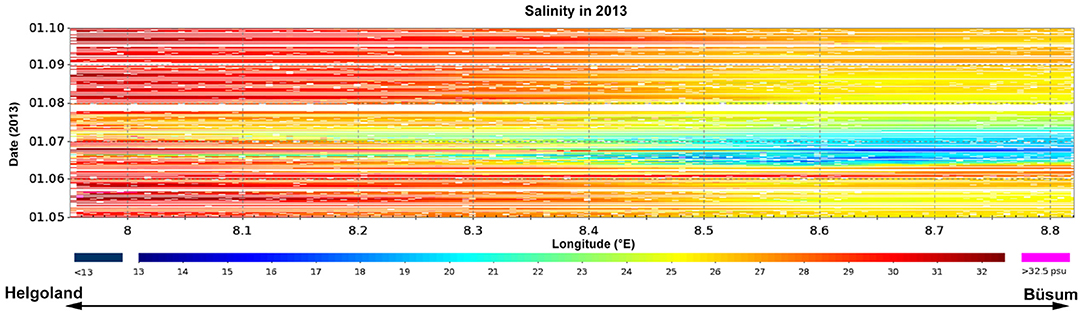
Figure 3. A Hovmöller diagram combining salinity observations from all ferry cruises between Büsum and Helgoland during May to September 2013.

FIGURE 4

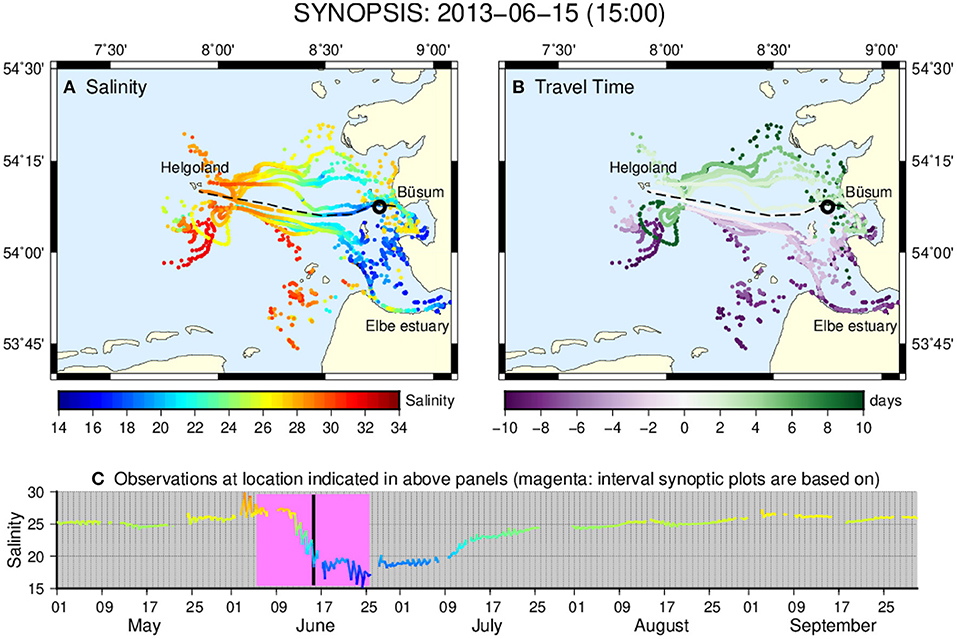
Figure 4. (A) Synopsis of salinity data collected within the period June 15, 2013 (15:00) UTC ±10 days. Drift trajectories were calculated based on surface currents from BSHcmod. (B) Differences between the time of the synopsis and times of observations. Green (purple) indicates observations to be taken earlier (later) than June 15, 2013 (15:00) UTC (see the conceptual Figure 2). Dashed lines in panels A and B represent the ferry route along which all measurements were taken. (C) Time series of FerryBox observations at the location indicated by black circles in (A,B). The vertical black line indicates the time of the synoptic plot, and the magenta colored bar covers the time interval from which data contribute. An animation of this figure is provided as a Supplementary Video 1.

The Elbe estuary is located about 30 km to the south of the ferry transect (see Figure 4), so whether or not the fresh water can be seen by the ferry depends on the weather conditions and the corresponding orientation of coastal ocean currents during the days prior. In a retrospective analysis, (simulated) hydrodynamic fields will be known and these can be used (calculating backward trajectories) to specify the present location of water bodies that will cross the ferry transect at some later time. In the same way, it will be possible to specify the present location of water bodies previously seen by the ferry (see Figure 2).

An example focusing on June 15, 2013 (15:00) is shown in Figure 4A. Considering a symmetric interval of 10 days before and 10 days after, the set of measurements included corresponds to a narrow horizontal band in Figure 3, centered around June 15. Figure 4A replicates these salinity values, but moves them from the ferry transect to their location valid on June 15, assuming that salinity is a passive tracer. Lagrangian drift modeling was based on pre-calculated BSHcmod surface currents. The synoptic salinity map is complemented by a map of travel times (Figure 4B), which denotes the differences between the time stamp of the synoptic plot and the times at which contributing asynchronous observations were taken. Positive (negative) travel times mean that trajectories had to be calculated forward (backward) in time because observations were made earlier (later) than the time the synoptic map refers to (cf. Figure 2, which uses the same color code for travel time). Figure 4 describes the situation at a specific instant of time (on June 15, 2013). An animation of the full time evolution with hourly resolution is provided as a Supplementary Video 1.

According to Figure 4A, data recorded along a linear transect within a 20 day period are spread across a large portion of the south-east German Bight neighboring the Elbe Estuary. The drift model locates water bodies with low salinity (according to FerryBox observations) along a coastal stretch originating from the Elbe estuary. Most of the low salinity water parcels reached the ferry transect up to 10 days after the time stamp of the synoptic plot (negative travel times according to Figure 4B). That the minimum salinity observations will be seen in the near future can also be deduced from the local time series shown in Figure 4C.

Due to a primarily cyclonic (counterclockwise) circulation in the German Bight at that time, most water bodies that have been seen by the ferry within the last 10 days (positive travel times) are located to the north of the ferry transect (Figure 4B). However, near Helgoland positive travel times occur also to the south of the ferry transect, suggesting that waters are advected from the north, in a direction opposite to the predominant flow observed near the coast.

3.2. Example B

Traveling between Cuxhaven (Germany) and Harwich (UK) on a daily basis, the MS Duchess of Scandinavia persistently measured low salinity (<33) near the coastal Dutch and German waters between 2002 and 2005 (Petersen et al., 2018). A characteristic pattern the ferry sees on each of its passages is the salinity front it crosses near the Dutch and German coastal waters. However, salinity measurements along this one-dimensional transect cannot inform about the orientation of the front the ferry cuts through. This information can be gained by combining each measurement with two trajectories integrated forward and backward in time.

Taking into account the larger spatial scale of this application, we calculated trajectories of 40 days in length and thereby substantially increased the time window, from which observations may contribute to the synoptic maps. Combining synchronous pixels of all overlapping trajectories into one map provides synopses like the one shown in Figure 5. Preparing such synopses at regular times reveals the time evolution of spatially distributed water bodies that were or will be in contact with the FerryBox observational system. Considering the very large time interval we chose, absolute salinity values in Figure 5 should be considered with caution. Instead, the emphasis is put on the spatial structure. Narrowing the time interval from which data contribute would narrow the spatial range around the ferry transect in Figure 5.

FIGURE 5

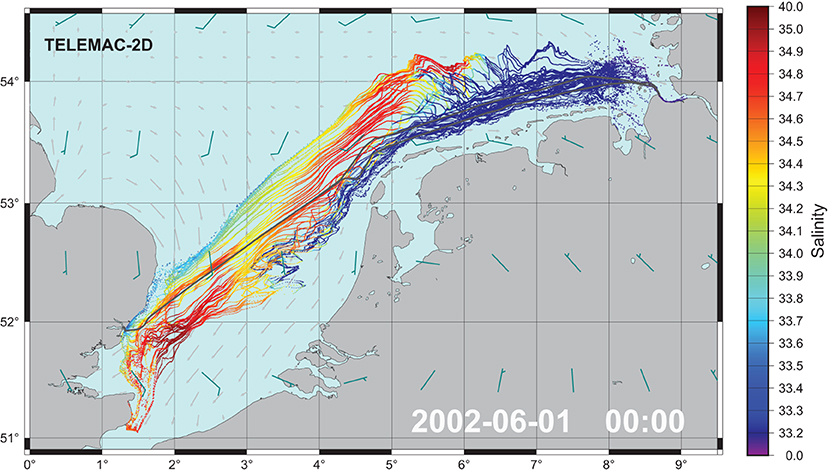
Figure 5. Salinity observations collected on the ferry transect Cuxhaven–Harwich within the period June 1, 2002 ± 40 days. Based on hydrodynamic fields from TELEMAC-2D, each water body was transported either forward or backward in time (maximum travel time 40 days) to estimate its position at the time of the map shown. Gray arrows indicate marine currents, and winds are represented by blue wind barbs.

The synoptic map in Figure 5 (similar to Figure 4) outlines the area (changing in time) within which the FerryBox observations could be compared to other data sources. If data from additional measurements exist, and they are located within the coverage of the synoptic map, respective FerryBox data directly comparable to these additional observations can be identified. The following example C illustrates this approach.

3.3. Example C

This example combines FerryBox observations with observations at station Gabbard. The ferry route passes by Gabbard within approximately 32 or 23 km, depending on the SmartBuoy position before and after August 2002 (see Figure 1). Figure 6 shows salinity measured at Gabbard together with corresponding FerryBox data observed at the time when the ferry was closest to the buoy. Nearly all of the time the ferry sees lower salinity than Gabbard, which can be explained by the larger distance of Gabbard from the British coast. There are, however, also peaks in the FerryBox data that reach the salinities seen at Gabbard. The large variability in the FerryBox data could indicate the presence of frontal structures so that salinity values observed at a given location may depend on the tidal phase.

FIGURE 6

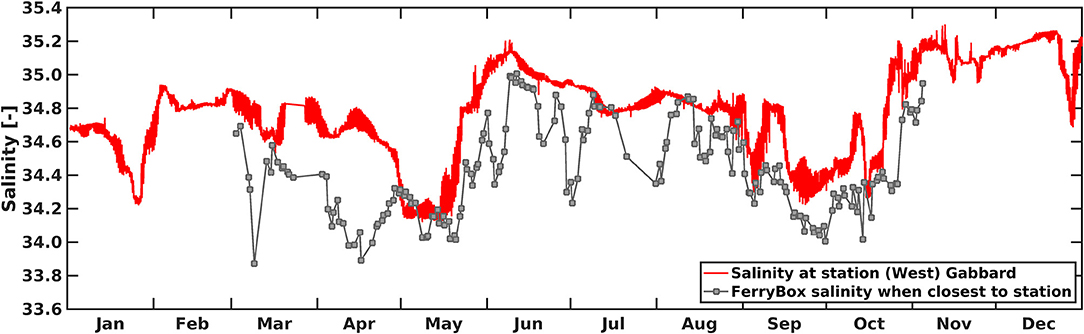
Figure 6. Red: Salinity values observed at station Gabbard in the year 2002. Small gray circles represent corresponding FerryBox measurements each time the ferry was closest to the stationary buoy (cf. Figure 1).

Based on drift simulations (TELEMAC-2D), we were able to identify those water bodies that have been seen by both in situ measurement systems. Like in example A (see Figure 4), time delays between the two observations of the same sample are identified. Example trajectories in Figure 1 illustrate three different ways how observations at Gabbard and along the ferry transect can be related to each other. One trajectory (purple) is first seen at Gabbard and then moves in a north-east direction, crossing the ferry transect a couple of days later. Another water body (green) first meets the ferry near the coast before it continues on its way toward Gabbard. Finally, the dashed gray trajectory does not cross the ferry transect at any time before or after it reaches Gabbard. In this case, a Gabbard observation will not have a direct FerryBox counterpart.

Technically, trajectories extending both forward and backward in time were attached to each FerryBox (rather than Gabbard) observation. By construction, this approach avoids the (highly probable) situation that test trajectories started at Gabbard would cross the ferry transect at times when the ferry is not there. To disentangle the different situations outlined in Figure 1, we labeled water parcels as being seen at Gabbard when they entered a circular region with a radius of 500 m from Gabbard. Taking the Gabbard time series as a reference, the time a trajectory had to be integrated before it reached station Gabbard defines the time interval by which the FerryBox time series must be shifted for a direct comparison of data points. Results are shown in Figure 7. Small squares represent FerryBox records that are time shifted in agreement with the aforementioned analysis of Lagrangian transports. The color code indicates the time delay that has been compensated for in the plot. In other words, while Gabbard observations were made at the time specified on the abscissa of Figure 7, the corresponding FerryBox observations were taken at this time minus an offset represented by the color code (negative values indicate backward integration of trajectories starting from "future" FerryBox observations). Note that the same colors were also applied in the schematic drawing in Figure 1. Tracking water parcels based on barotropic current fields from TELEMAC-2D reveals that travel times between the buoy and the ferry route may amount to up to 1 month.

FIGURE 7

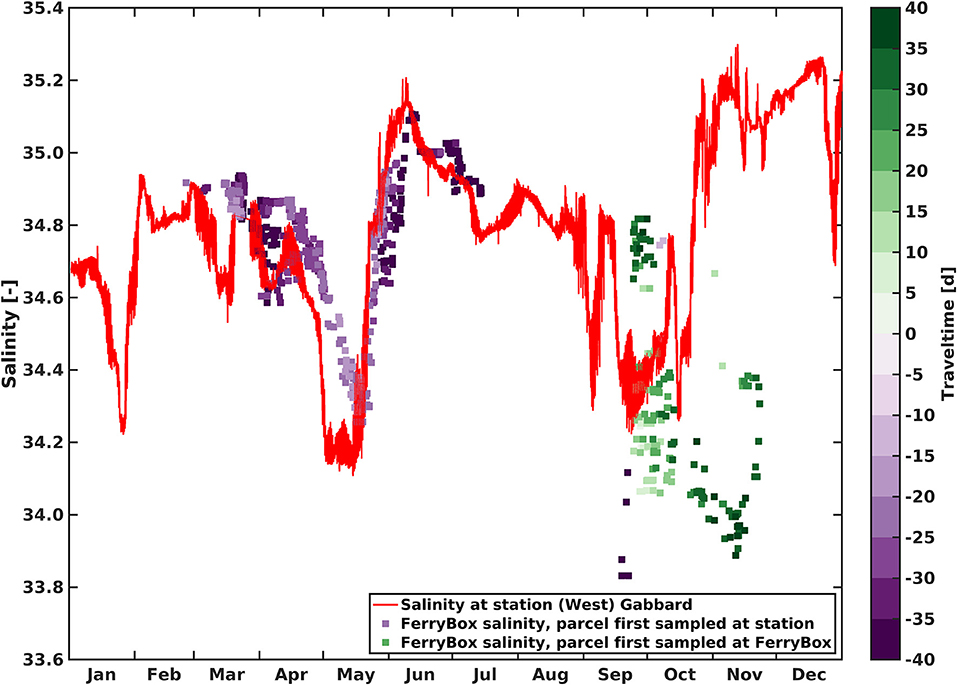
Figure 7. Red: Salinity values observed at station Gabbard in the year 2002, copied from Figure 6. Color-coded pixels indicate FerryBox observations for those water parcels that were also seen near Gabbard according to drift simulations based on hydrodynamic fields from TELEMAC-2D. The color code specifies estimated travel times either from the ferry transect to Gabbard (positive values, green) or from Gabbard to the ferry transect (negative values, purple). Compare the corresponding example trajectories shown in Figure 1.

In Figure 7, three different situations can be distinguished that are shown schematically in Figure 1. First, there are periods (e.g., February and August) in which Gabbard observations are not "replicated" by the ferry. Second, between March and July, the transformed ferry data match the Gabbard data very well. The drift corrected FerryBox analogues provide a smooth time series without the pronounced oscillations of salinity values observed when the ferry is closest to Gabbard (see Figure 6). During this period, the water drifts from Gabbard toward the ferry, crossing the ferry transect further north (see purple trajectory in Figure 1). A third situation occurs during October–November, when the transformed ferry data do not match Gabbard observations. In this latter period, the water mass is first observed by the ferry, and then by Gabbard (see the green trajectory drafted in Figure 1). Small-scale patchiness of salinity and/or insufficient model resolution of marine flows in the coastal region might be the reasons for the unsuccessful data synchronization in this case.

Distributions in Figure 8 statistically summarize the differences between salinity observations taken by the two in situ systems. Diagrams in Figures 8A,B were derived from Figure 6, considering FerryBox observations that were taken when the ferry was closest to Gabbard. The two different diagrams arise from a distinction between situations when simulated trajectories move from Gabbard to the ferry transect (Figure 8A) or vice versa (Figure 8B). The same color code has been used in Figure 7 and also for the example trajectories in Figure 1. By contrast, the distributions in Figures 8C,D were derived from Figure 7, i.e., considering asynchronous FerryBox observations that were taken at the locations identified by Lagrangian drift simulations based on TELEMAC-2D current fields.

FIGURE 8

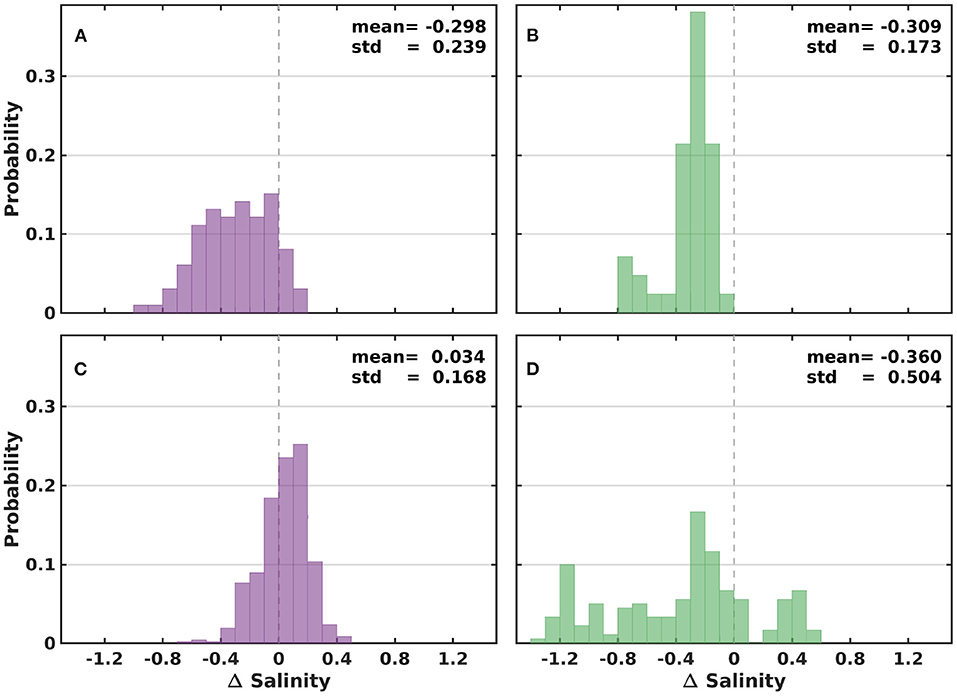
Figure 8. Probability distributions of salinities observed by the FerryBox system minus those observed at Gabbard. (A,B) refer to FerryBox measurements taken when the ferry was closest to Gabbard (derived from the time series shown in Figure 6), while (C,D) refer to FerryBox observations at locations and times that were identified by simulated drift trajectories (see Figure 7). The two purple histograms comprise all those cases when simulated trajectories move from Gabbard to the ferry transect (same color code as in Figures 1 and 7), while the two green histograms combine all cases in which simulated trajectories move from the ferry toward Gabbard.

A comparison of Figures 8A,C shows that when Gabbard saw the water parcel first (purple trajectory in Figure 1), using the drift model interface reduces both the mean and the standard deviation of differences between the two in situ observations. Figure 8C even tends to underestimate the procedure success, at times with a steep change in salinity (see May–June in Figure 7), when even a small discrepancy between the timings of these events would result in large instantaneous differences. A simple standard deviation cannot fully represent such specific behavior.

The situation is clearly the opposite for Figures 8B,D. As already mentioned, the most likely reason for the model's failure is that in this situation FerryBox observations are taken at very nearshore locations (see Figure 1). According to Figure 6, FerryBox observations from the autumn period underlying Figure 8B lack the pronounced and steep changes observed earlier in the year. It remains unclear to which extent this difference could possibly depend on the buoy's relocation from Gabbard to West Gabbard in August 2002 (see section 2.1.2 and Figure 1), which also moves the reference point where the ferry is closest to the buoy.

4. Discussion

A key challenge of any observing network is to spatially extrapolate localized observations. Schulz-Stellenfleth and Stanev (2010) addressed this problem for the example of water level, applying optimal linear estimation based on Kalman filter theory. Assumed sources of observational evidence were either tide gauges or satellite altimeters. Grayek et al. (2011) applied a similar technique to FerryBox data recorded on the ferry route Cuxhaven (Germany)-Immingham (Great Britain), trying to extrapolate one-dimensional data of surface temperature and salinity into the German Bight area. Their study contributed to a larger coastal observing and forecasting system implemented in the German Bight (Stanev et al., 2011; Baschek et al., 2017).

We provided three examples that illustrate how already a much simpler combination of FerryBox observations with drift simulations could offer an added value. A straightforward application of drift simulations is using them to identify the histories of water bodies prior to when they were sampled. Petersen et al. (2011) employed this technique to substantiate the hypothesis that the nutrient-rich freshwater the ferry observed is of fluvial origin (Rhine River). Similarly, Lucas et al. (2016) used the approach to substantiate the assumption that advection of coastal water from the Elbe estuary triggered a change in bacterial communities. The depth of a FerryBox intake, 3–5 m (Petersen and Colijn, 2017), would capture the signature of buoyant plumes, which extend down to 10 m (Garvine and Monk, 1974; Whitney and Garvine, 2005; Cahill et al., 2008; Li et al., 2018). In 2013, the Elbe river estuary buoyant outflow extended to at least 10 m depth and was spread out over the German Bight for at least 2 months (Voynova et al., 2017; Kerimoglu et al., 2020).

The approach we propose is based on similar techniques, but goes one step further. In example A, drift simulations substantiated the influence of the extreme Elbe River flood event on observations from the ferry between Büsum and the island of Helgoland. In addition, however, Figure 4A also reveals the extent to which FerryBox observations are informative about the river plume's location in the German Bight at the time of the synopsis. This information is relevant when the objective is to design a monitoring network made up of different observational platforms. To which extent would data from a second ferry, for instance, overlap with the data already available? It should be noted that the pattern shown in Figure 4A is not constant but changes with weather induced changes in residual currents (Callies et al., 2017a). Therefore, a sound study of the aforementioned question would need the consideration of a large manifold of synopses in the format in Figure 4. Such animated synopses with hourly resolution are made available as a Supplementary Video 1.

Our use of Lagrangian advection for the purpose of dynamic synchronization of observations differs from the objective of Desprès et al. (2011), who generated mesoscale and sub-mesoscale patterns of sea surface salinity (SSS) in the North Atlantic Ocean based on altimetry-derived surface velocities. Starting from a smooth large-scale SSS climatology, their approach produced fronts in reasonable statistical agreement with in situ observations from a ship of opportunity. Also Dencausse et al. (2014) aimed at an optimum representation of fine-scale structures in a statistical sense, which needed proper adjustment of tracer parcel integration times. Focusing on sea surface temperature (SST) and salinity in the Southern Ocean, they initialized tracer parcels with values from weekly smooth objective analyses of Argo floats and other in situ data. Small-scale features arose as a result of the stirring by Lagrangian advection superimposed on large-scale latitudinal gradients of SST or SSS. In contrast, all our examples were based on observations taken at a much higher frequency (seconds to minutes) so that generation of small scales features was not an issue.

To assign salinities to the locations of tracer particles in the synoptic map (e.g., Figure 4A), one would have to assume a strictly passive behavior neglecting, for instance, any changes by turbulent sub-grid scale mixing. Such assumption is questionable in dynamic coastal waters. However, the main intention of Figure 4A is a specification of spatial structures rather than a provision of precise salinity values. A labeling of water parcels in relation to estuarine water benefits from the large horizontal salinity gradients that prevail in this coastal region. Thereby, the analyzed location and spread of the Elbe estuary plume is less sensitive to vertical mixing, which cannot be dealt with in the 2D setup. The plume can be expected to precondition ecosystem changes due to an enhanced import of nutrients, for instance. As in d'Ovidio et al. (2015), the age of the water body (here: the estimated time since its discharge on the coast, see Figure 4B) can be a relevant unit for subsequent process-oriented studies.

Keeping in mind the aforementioned restrictions, example C nevertheless addressed the use of simulated Lagrangian transports for a synchronization of data recorded at different locations. Relating observations from different platforms is one common approach for data validation. Haller et al. (2015), for instance, compared FerryBox data with observations taken at MARNET station Deutsche Bucht, a station located approximately 10 km to the west of the ferry port on Helgoland. If reliable hydrodynamic simulations are available, corresponding drift calculations provide the time lags that must be accounted for to identify matching segments of two (or more) time series. Petersen et al. (2008) employed drift simulations to synchronize FerryBox measurements with remote sensing data from a satellite overpass neighboring in time. However, the maximum time differences they dealt with in their study did not exceed 19 h. Drift simulations also help to identify those observations that might be independent from each other in the sense that they refer to different water bodies.

In example C, two periods could well be distinguished with regard to the method's success (see Figure 7). During the first period (approximately March–July 2002), drift trajectories from Gabbard toward the northeast (purple in Figure 1) successfully compensated for the seeming discrepancies between a relatively smooth Gabbard time series and the oscillating salinity values observed by the ferry at locations closest to the buoy (see Figures 8A,C). The drift simulations suppose that the relevant FerryBox observations were made in the open sea. In contrast, TELEMAC-2D drift simulations could not match FerryBox to Gabbard salinities at the end of the year, according to the histograms in Figures 8B,D. Figure 1 outlines the special situation (green-colored trajectory) that distinguishes flow conditions at that time. According to the simulations, water masses met the ferry transect in a coastal area, before they continued toward Gabbard further southeast. The drift model likely fails to adequately capture flow variabilities in dynamic coastal regions, including small-scale eddies and mixing processes. An intense tracer dispersion can also be recognized in Figure 4 near the island of Helgoland. Due to limited numerical resolution, the localized stirring by the island within a region with large tidal excursions will necessarily generate much uncertainty. From Figure 4, it can be seen how such uncertainty will be exported to a wider region. In the example of the English coast, small-scale changes of salinity in the nearshore area may also enhance variability of FerryBox observations.

Insufficient accuracy of hydrodynamic flow simulations can be a general limitation to the proposed approach. On a small scale, experiments show that drifters released pairwise may separate quickly (Callies et al., 2019). This sets an upper limit for the predictability of drift trajectories. Turbulent movements underlying such pair separation can be simulated using a stochastic model (e.g., LaCasce, 2008). In Figure 4, such random dispersion was disregarded. The smoothing of random dispersion is shown in Figure 9A. Instead of only one, 10 trajectories per observation were released and dispersed by adding a random velocity component with an eddy diffusivity of about 1 m²/s, adjusted to the resolution of the discretized marine current fields (Callies et al., 2011). Comparing Figures 4A, 9A shows that large-scale patterns, in particular the estimated location and extent of the Elbe plume, are not influenced by adding particle dispersion.

FIGURE 9

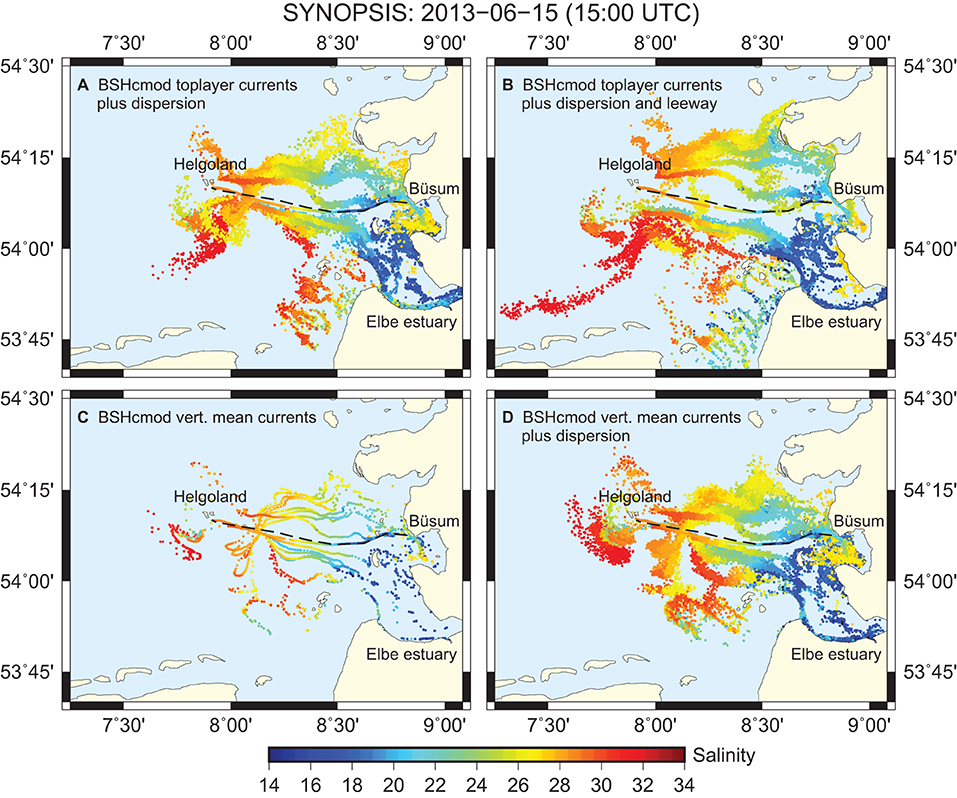
Figure 9. As in Figure 4A, but generated with modified model setups: (A) Based on BSHcmod surface currents augmented with stochastic particle dispersion. In this setup, ten tracer particles per observation were released. (B) As in A, but additionally using a leeway of 0.6% of 10 m winds. (C) Simulations based on vertical mean currents. (D) As C, but adding stochastic particle dispersion. Dashed lines represent the ferry route along which all measurements were taken.

To reproduce drifter trajectories observed in drifter experiments, it turned out that BSHcmod surface currents should be complemented by an additional leeway of 0.6% of the 10 m wind velocity (Callies et al., 2017b, 2019). Figure 9B shows the consequences of using this leeway in combination with dispersion. Given frequent westerly winds, backward trajectories expand further west, as expected. In any case, it is important to see that the shape of the river plume on the coast for the most part does not depend on whether the additional wind drag is assumed or not. Figures 9C,D illustrate the consequences of choosing vertically average (rather than surface) current fields, with and without modeling water parcel dispersion. Again it can be observed that the shape and location of the Elbe river plume does not depend on this choice.

Undeniably drift simulations involve substantial uncertainties, possibly depending on weather conditions and also the specific region of interest. Callies et al. (2017b) successfully used BSHcmod surface currents for a reproduction of experimental long-term drifter trajectories in the German Bight region. The outcome of drift simulations may depend on the specific choice of the underlying hydrodynamic model, so it may be useful to compare the result from different models (Callies et al., 2011; Hufnagl et al., 2017) or different setups like those presented in Figure 9, for instance. In Figure 10, we show an example of discrepancies between synopses based on two different models (TELEMAC-2D and BSHcmod), a corresponding animation for a 9-month period is provided as a Supplementary Video 2. Despite the fact that meteorological forcing was provided by different institutions (NCEP and DWD), the two synoptic maps share essential features. However, there are also substantial differences regarding, for instance, the quantitative spatial spreading of information.

FIGURE 10

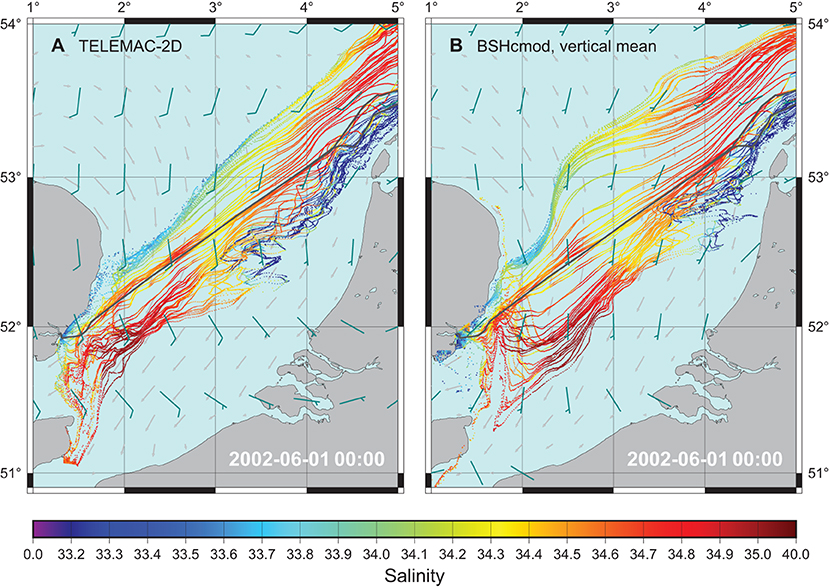
Figure 10. (A) Zooming into the western part of Figure 5. Simulations were performed based on TELEMAC-2D simulations. (B) Same setup, except that drift simulations are now based on vertical mean currents from the operational 3D model BSHcmod. An animation of this figure is provided as a Supplementary Video 2.

Synopses like those in Figure 10 could also be valuable for an assessment of model differences with regard to their general transport behavior in different regions. In Figure 10, a certain discrepancy does not come as a surprise, as simulations based on 2D currents are compared to those based on the vertical means of currents from a full 3D model. With regard to example C, data synchronization based on BSHcmod simulations was less successful than that based on TELEMAC-2D shown in Figure 7. This might be related to the higher spatial resolution of the 2D unstructured grid.

For distributing localized information across a wider spatial domain, statistical methods like optimal interpolation or kriging could be used, closely related to data assimilation schemes. In this case, model output delivers a prior synoptic field for a variable of interest, which then becomes updated based on existing data. Background statistics (covariance matrices) are mostly analyzed from numerical simulations. Grayek et al. (2011) applied this approach to assimilate FerryBox surface temperature and salinity data. The less sophisticated non-statistical approach we propose avoids specifications of proper error covariance matrices. However, no complete fields of the variables of interest can be provided. This disadvantage is compensated by the fact that the spatial spreading of localized observations is based on the specific flow conditions exactly at the time of interest. In their statistical approach, Grayek et al. (2011) did not explicitly correct for variations in the measured data that arose from tidal oscillations in the presence of spatial gradients. This correction is, however, an integral part of the analysis we propose.

An interesting question is whether the two concepts could somehow be profitably combined. To further illustrate this idea, Figure 11A presents an overlay of surface salinity simulations from BSHcmod with FerryBox observations, synchronized using drift simulations based on BSHcmod surface currents. Model output and observations are displayed using the same color table, so that the time-shifted trajectories would become invisible if the relocated observations were in perfect agreement with model predictions. The FerryBox data are obviously useful for keeping the model on track. Salinities in the coastal region tend to be underestimated in BSHcmod, a deficiency Haller et al. (2015) analyzed based on FerryBox observations within the period January 2009–April 2012, also for a more recent model version of BSHcmod.

FIGURE 11

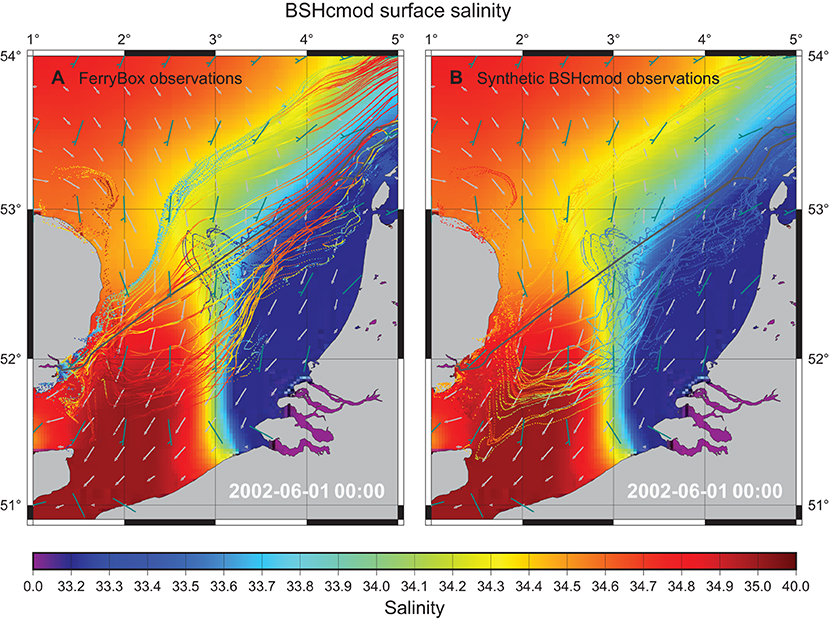
Figure 11. (A) Composite of a surface salinity field from BSHcmod (1 June 0:00) and the corresponding synoptic map derived by combining FerryBox observations within ±40 days with BSHcmod surface currents (cf. Figure 10B). (B) The same composite but replacing real FerryBox salinity observations by their simulated counterparts (same location and time) from BSHcmod.

To check out a hypothetical reference situation with “perfect” data, we replaced observed salinity values by synthetic data copied from BSHcmod salinity fields. Results of this numerical experiment are shown in Figure 11B. Agreement is much better than in Figure 11A but still not perfect. A possible reason is the fact that Lagrangian transports completely suppress diffusion of salinity. Also vertical mixing particularly in coastal regions is not dealt with in simulated transports based on 2D surface current fields. It should be noted that salinity values plotted for displaced tracer particles are those observed up to 40 days before or after the time of the synoptic plot. The best choice of the time slot taken into account is not a priori clear.

5. Conclusions

In this study, we propose using Lagrangian transport simulations to infer 2D spatial structures from 1D FerryBox data with high temporal resolution. Synoptic spatial patterns at given times are generated combining data from a time slot centered around the time of interest. Hydrodynamic drift calculations are used to move all water parcels sampled within this time slot either forward or backward in time. In this way, FerryBox data collected during several cruises along a set transect become expanded into a larger spatial “corridor”. Examples we showed addressed localizing an estuarine water plume, identifying the orientation of a salinity front and synchronizing time series measured by two different platforms.

We applied the proposed method to observations of salinity, for which the assumption of passive behavior can be justified. However, our 2D Lagrangian simulations did not take into consideration either horizontal or vertical mixing processes. That is likely the reason why even double twin experiments using virtual observations extracted from the top layer of 3D model simulations did not show perfect agreement with the simulated “truth”. Unresolved sub-grid scale processes will generally be a source of uncertainty in the synopses established.

Identification of regions of origin of water masses is generally of great help for the interpretation of monitoring data. For such an analysis, the simplistic treatment of salinity as a passive tracer may not be a crucial constraint. For other variables like chlorophyll, for instance, the constraint might be relaxed and replaced by a simple parameterization of algal growth. Alternatively, observations from an independent second platform might be used to estimate rates of change in the drifting water body.

Data Availability Statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://codm.hereon.de/codm/.

Author Contributions

YV and WP collected the field data. MK and UC conducted numerical drift simulations. UC prepared the manuscript with contributions from all three co-authors. All authors contributed to the article and approved the submitted version.

Funding

FerryBox activities were partly supported by the EU projects FerryBox (Grant Agreement EVK2-2002-00144) and JERICO (Grant Agreement # 262584), as well as funding from the Helmholtz Association.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Barotropic simulations of North Sea currents with TELEMAC-2D were provided by Andreas Plüß, Federal Waterways Engineering and Research Institute (BAW), in the context of the EU project HIPOCAS. Simulations with BSHcmod were provided by the Federal Maritime and Hydrographic Agency (BSH). We thank all those who helped obtain, analyze, and enumerate the FerryBox data. We thank the Cassen Eils shipping company, which operates the MV Funny Girl, and DFDS shipping company, which operated MV Duchess of Scandinavia for helping us collect FerryBox data. We also thank the crews onboard both vessels. We thank the numerous past and present Hereon scientists and engineers who helped to obtain and verify the FerryBox data. We thank Naomi Greenwood (CEFAS) for providing Gabbard station data. We also thank three reviewers for their helpful comments.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2021.666653/full#supplementary-material

Footnotes

1. ^See http://data.cefas.co.uk/#/View/66, last access May 17, 2021.

References

Baschek, B., Schroeder, F., Brix, H., Riethmüller, R., Badewien, T. H., Breitbach, G., et al. (2017). The coastal observing system for northern and arctic seas (COSYNA). Ocean Sci. 13, 379–410. doi: 10.5194/os-13-379-2017

CrossRef Full Text | Google Scholar

Cahill, B., Schofield, O., Chant, R., Wilkin, J., Hunter, E., Glenn, S., et al. (2008). Dynamics of turbid buoyant plumes and the feedbacks on nearshore biogeochemistry and physics. Geophys. Res. Lett. 35:L10605. doi: 10.1029/2008GL033595

CrossRef Full Text | Google Scholar

Callies, U. (2021). Sensitive dependence of trajectories on tracer seeding positions-coherent structures in German Bight backward drift simulations. Ocean Sci. 17, 527–541. doi: 10.5194/os-17-527-2021

CrossRef Full Text | Google Scholar

Callies, U., Carrasco, R., Floeter, J., Horstmann, J., and Quante, M. (2019). Submesoscale dispersion of surface drifters in a coastal sea near offshore wind farms. Ocean Sci. 15, 865–889. doi: 10.5194/os-15-865-2019

CrossRef Full Text | Google Scholar

Callies, U., Gaslikova, L., Kapitza, H., and Scharfe, M. (2017a). German Bight residual current variability on a daily basis: principal components of multi-decadal barotropic simulations. Geo Mar. Lett. 37, 151–162. doi: 10.1007/s00367-016-0466-2

CrossRef Full Text | Google Scholar

Callies, U., Groll, N., Horstmann, J., Kapitza, H., Klein, H., Maßmann, S., et al. (2017b). Surface drifters in the German Bight: model validation considering windage and Stokes drift. Ocean Sci. 13:799–827. doi: 10.5194/os-13-799-2017

CrossRef Full Text | Google Scholar

Callies, U., Plüß, A., Kappenberg, J., and Kapitza, H. (2011). Particle tracking in the vicinity of Helgoland, North Sea: a model comparison. Ocean Dyn. 61, 2121–2139. doi: 10.1007/s10236-011-0474-8

CrossRef Full Text | Google Scholar

Dencausse, G., Morrow, R., Rogeé, M., and Fleury, S. (2014). Lateral stirring of large-scale tracer fields by altimetry. Ocean Dyn. 64, 61–78. doi: 10.1007/s10236-013-0671-8

CrossRef Full Text | Google Scholar

Desprès, A., Reverdin, G., and d'Ovidio, F. (2011). Mechanisms and spatial variability of meso scale frontogenesis in the northwestern subpolar gyre. Ocean Model 39, 97–113. doi: 10.1016/j.ocemod.2010.12.005

CrossRef Full Text | Google Scholar

Dick, S., and Kleine, E. (2007). The BSH new operational circulation model using general vertical co-ordinates. Environ. Res. Eng. Manag. 3, 18–24.

Google Scholar

Dick, S., Kleine, E., Müller-Navarra, S. H., Klein, H., and Komo, H. (2001). The Operational Circulation Model of BSH (BSHcmod) - Model Description and Validation. Berichte des Bundesamtes für Seeschifffahrt und Hydrographie 29/2001. Hamburg: BSH.

Google Scholar

d'Ovidio, F, Della Penna, A, Trull, T. W., Nencioli, F., Pujol, M.-I., Rio, M.-H., et al. (2015). The biogeochemical structuring role of horizontal stirring: Lagrangian perspectives on iron delivery downstream of the Kerguelen Plateau. Biogeosciences 12, 5567–5581. doi: 10.5194/bg-12-5567-2015

CrossRef Full Text | Google Scholar

d'Ovidio, F., De Monte, S., Alvain, S., Dandonneau, Y., and Lévy, M. (2010). Fluid dynamical niches of phytoplankton types. Proc. Natl. Acad. Sci. U.S.A. 107, 18366–18370. doi: 10.1073/pnas.1004620107

PubMed Abstract | CrossRef Full Text | Google Scholar

Garvine, R. W., and Monk, J. D. (1974). Frontal structure of a river plume. J. Geophys. Res. 79, 2251–2259. doi: 10.1029/JC079i015p02251

CrossRef Full Text | Google Scholar

Grayek, S., Staneva, J., Schulz-Stellenfleth, J., Petersen, W., and Stanev, E. V. (2011). Use of FerryBox surface temperature and salinity measurements to improve model based state estimates for the German Bight. J. Mar. Syst. 88, 45–59. doi: 10.1016/j.jmarsys.2011.02.020

CrossRef Full Text | Google Scholar

Haller, G. (2001). Distinguished material surfaces and coherent structures in three-dimensional fluid flows. Physica D 149, 248–277. doi: 10.1016/S0167-2789(00)00199-8

CrossRef Full Text | Google Scholar

Haller, M., Janssen, F., Siddorn, J., Petersen, W., and Dick, S. (2015). Evaluation of numerical models by FerryBox and fixed platform in situ data in the southern North Sea. Ocean Sci. 11, 879–896. doi: 10.5194/os-11-879-2015

CrossRef Full Text | Google Scholar

Hernández-Carrasco, I., Orfila, A., Rossi, V., and Garçon, V. (2018). Effect of small scale transport processes on phytoplankton distribution in coastal seas. Sci. Rep. 8:8613. doi: 10.1038/s41598-018-26857-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Hervouet, J. M., and van Haren, L. (1996). TELEMAC2D Version 3.0 Principle Note. Rapport EDF HE-4394052B, Electricité de France, Département Laboratoire National d'Hydraulique, Chatou CEDEX.

Hufnagl, M., Payne, M., Lacroix, G., Bolle, L. J., Daewel, U., Dickey-Collas, M., et al. (2017). Variation that can be expected when using particle tracking models in connectivity studies. J. Sea Res. 127, 133–149. doi: 10.1016/j.seares.2017.04.009

CrossRef Full Text | Google Scholar

Huhn, F., von Kameke, A., Pérez-Mu nuzuri, V., Olascoaga, M. J., and Beron-Vera, F. J. (2012). The impact of advective transport by the South Indian Ocean Countercurrent on the Madagascar plankton bloom. Geophys. Res. Lett. 39:L06602. doi: 10.1029/2012GL051246

CrossRef Full Text | Google Scholar

Jönsson, B. F., Salisbury, J. E., and Mahadevan, A. (2009). Extending the use and interpretation of ocean satellite data using Lagrangian modelling. Int. J. Remote Sens. 30, 3331–3341. doi: 10.1080/01431160802558758

CrossRef Full Text | Google Scholar

Kerimoglu, O., Voynova, Y. G., Chegini, F., Brix, H., Callies, U., Hofmeister, R., et al. (2020). Interactive impacts of meteorological and hydrological conditions on the physical and biogeochemical structure of a coastal system. Biogeosciences 17, 5097–5127. doi: 10.5194/bg-17-5097-2020

CrossRef Full Text | Google Scholar

Kistler, R., Kalnay, E., Collins, W., Saha, S., White, G., Wollen, J., et al. (2001). The NCEP-NCAR 50-year reanalysis: monthly means CD-ROM and documentation. Bull. Am. Meteorol. Soc. 82:247–268. doi: 10.1175/1520-0477(2001)082<0247:TNNYRM>2.3.CO;2

CrossRef Full Text | Google Scholar

LaCasce, J. H. (2008). Statistics from Lagrangian observations. Progress in Oceanography 77:1–29. doi: 10.1016/j.pocean.2008.02.002

CrossRef Full Text | Google Scholar

Lehahn, Y., d'Ovidio, F., Lévy, M., and Heifetz, E. (2007). Stirring of the northeast Atlantic spring bloom: A Lagrangian analysis based on multisatellite data. J. Geophys. Res. 112:C08005. doi: 10.1029/2006JC003927

CrossRef Full Text | Google Scholar

Li, Q. P., Zhou, W., Chen, Y., and Wu, Z. (2018). Phytoplankton response to a plume front in the northern South China Sea. Biogeosciences 15, 2551–2563. doi: 10.5194/bg-15-2551-2018

CrossRef Full Text | Google Scholar

Lipphardt, Jr. B. L., Small, D., Kirwan, A., Wiggins, S., Ide, K., Grosch, C., et al. (2006). Synoptic Lagrangian maps: application to surface transport in Monterey Bay. J. Mar. Res. 64:221–247. doi: 10.1357/002224006777606461

CrossRef Full Text | Google Scholar

Lucas, J., Koester, I., Wichels, A., Niggemann, J., Dittmar, T., Callies, U., et al. (2016). Short-term dynamics of North Sea bacterioplankton-dissolved organic matter coherence on molecular level. Front. Microbiol 7:321. doi: 10.3389/fmicb.2016.00321

PubMed Abstract | CrossRef Full Text | Google Scholar

Meinke, I., von Storch, H., and Feser, F. (2004). A validation of the cloud parameterization in the regional model SN-REMO. J. Geophys. Res. 109:D13205. doi: 10.1029/2004JD004520

CrossRef Full Text | Google Scholar

Oka, E., Uehara, K., Nakano, T., Suga, T., Yanagimoto, D., Kouketsu, S., et al. (2014). Synoptic observation of central mode water in its formation region in spring 2003. J. Oceanogr. 70, 521–534. doi: 10.1007/s10872-014-0248-2

CrossRef Full Text | Google Scholar

Olascoaga, M. J., Beron-Vera, F. J., Haller, G., Tri nanes, J., Iskandarani, M., Coelho, E. F., et al. (2013). Drifter motion in the Gulf of Mexico constrained by altimetric Lagrangian coherent structures. Geophys. Res. Lett. 40:6171–6175. doi: 10.1002/2013GL058624

CrossRef Full Text | Google Scholar

Peacock, T., and Haller, G. (2013). Lagrangian coherent structures: the hidden skeleton of fluid flows. Phys. Today 66, 41–47. doi: 10.1063/PT.3.1886

CrossRef Full Text | Google Scholar

Pérez-Ruzafa, A., Pascalis, F. D., Ghezzo, M., Quispe-Becerra, J. I., Hernández-García, R., Muñoz, I., et al. (2019). Connectivity between coastal lagoons and sea: asymmetrical effects on assemblages' and populations' structure. Estuar. Coast. Shelf Sci. 216, 171–186. doi: 10.1016/j.ecss.2018.02.031

CrossRef Full Text | Google Scholar

Petersen, W. (2014). FerryBox systems: state-of-the-art in Europe and future development. J. Mar. Syst. 140, 4–12. doi: 10.1016/j.jmarsys.2014.07.003

CrossRef Full Text | Google Scholar

Petersen, W., and Colijn, F. (2017). Ferrybox White Paper. EuroGOOS AISBL. Available online at: https://eurogoos.eu/download/publications/EuroGOOS_Ferrybox_whitepaper_2017.pdf

Petersen, W., Reinke, S., Breitbach, G., Petschatnikov, M., Wehde, H., and Thomas, H. (2018). FerryBox data in the North Sea from 2002 to 2005. Earth Syst. Sci. Data 10, 1729–1734. doi: 10.5194/essd-10-1729-2018

CrossRef Full Text | Google Scholar

Petersen, W., Schroeder, F., and Bockelmann, F.-D. (2011). FerryBox - Application of continuous water quality observations along transects in the North Sea. Ocean Dyn. 61, 1541–1554. doi: 10.1007/s10236-011-0445-0

CrossRef Full Text | Google Scholar

Petersen, W., Wehde, H., Krasemann, H., Colijn, F., and Schroeder, F. (2008). FerryBox and MERIS-Assessment of coastal and shelf sea ecosystems by combining in situ and remotely sensed data. Estuar. Coast. Shelf Sci. 77, 296–307. doi: 10.1016/j.ecss.2007.09.023

CrossRef Full Text | Google Scholar

Plüß, A., and Weisse, R. (2012). coastdat-1 Tide-Surge North Sea hydrodynamic hindcast (1958–2004). World Data Center for Climate (WDCC) at DKRZ. doi: 10.1594/WDCC/coastDat-1_Tide-Surge

CrossRef Full Text | Google Scholar

Schubert, R., Schwarzkopf, F. U., Baschek, B., and Biastoch, A. (2019). Submesoscale impacts on mesoscale Agulhas dynamics. J. Adv. Model. Earth Syst. 11:2745–2767. doi: 10.1029/2019MS001724

CrossRef Full Text | Google Scholar

Schulz, J.-P., and Schättler, U. (2014). Kurze Beschreibung des Lokal-Modells Europa COSMO-EU (LME) und seiner Datenbanken auf dem Datenserver des DWD. Report, Deutscher Wetterdienst, Offenbach. Available online at: https://www.dwd.de/SharedDocs/downloads/DE/modelldokumentationen/nwv/cosmo_eu/cosmo_eu_dbbeschr_201406.pdf?__blob=publicationFile&v=3

Schulz-Stellenfleth, J., and Stanev, E. V. (2010). Statistical assessment of ocean observing networks - a study of water level measurements in the German Bight. Ocean Model. 33, 270–282. doi: 10.1016/j.ocemod.2010.03.001

CrossRef Full Text | Google Scholar

Sheehan, P. M. F., Berx, B., Gallego, A., Hall, R. A., Heywood, K. J., and Hughes, S. L. (2017). Thermohaline forcing and interannual variability of northwestern inflows into the northern North Sea. Cont. Shelf Res. 138, 120–131. doi: 10.1016/j.csr.2017.01.016

CrossRef Full Text | Google Scholar

Smith, S., and Banke, E. (1975). Variation of the sea surface drag coefficient with wind speed. Q. J. R. Meteor. Soc. 101, 665–673. doi: 10.1002/qj.49710142920

CrossRef Full Text | Google Scholar

Stanev, E. V., Schulz-Stellenfleth, J., Staneva, J., Grayek, S., Seemann, J., and Petersen, W. (2011). Coastal observing and forecasting system for the German Bight - estimates of hydrophysical states. Ocean Sci. 7, 569–583. doi: 10.5194/os-7-569-2011

CrossRef Full Text | Google Scholar

Voynova, Y. G., Brix, H., Petersen, W., Weigelt-Krenz, S., and Scharfe, M. (2017). Extreme flood impact on estuarine and coastal biogeochemistry: the 2013 Elbe flood. Biogeosciences 14, 541–557. doi: 10.5194/bg-14-541-2017

CrossRef Full Text | Google Scholar

Weisse, R., Gaslikova, L., Geyer, B., Groll, N., and Meyer, E. (2014). CoastDat-model data for science and industry. Die Küste 81, 5–18. Available online at: https://henry.baw.de/handle/20.500.11970/101679

Google Scholar

Weisse, R., and Plüß, A. (2006). Storm-related sea level variations along the North Sea coast as simulated by a high-resolution model 1958-2002. Ocean Dynamics 56, 16–25. doi: 10.1007/s10236-005-0037-y

CrossRef Full Text | Google Scholar

Weisse, R., von Storch, H, Callies, U., Chrastansky, A., Grabemann, I., Günther, H., et al. (2009). Regional meteo-marine reanalyses and climate projections: results for Northern Europe and potentials for coastal and offshore applications. Bull. Am. Meteorol. Soc. 90, 849–860. doi: 10.1175/2008BAMS2713.1

CrossRef Full Text | Google Scholar

Whitney, M. M., and Garvine, R. W. (2005). Wind influence on a coastal buoyant outflow. J. Geophys. Res. 110:C03014. doi: 10.1029/2003JC002261

CrossRef Full Text | Google Scholar