- 1College of Oceanography, Hohai University, Nanjing, China
- 2Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing, China
- 3Key Laboratory of Marine Hazards Forecasting, Ministry of Natural Resources (MNR), Hohai University, Nanjing, China
- 4State Key Laboratory of Numerical Modeling for Atmospheric Sciences and Geophysical Fluid Dynamics, Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing, China
- 5Southern Laboratory of Ocean Science and Engineering Guangdong Laboratory, Zhuhai, China
Oceanic mesoscale eddies are associated with large thermodynamic anomalies, yet so far they are most commonly studied in terms of surface temperature and in the sense of composite mean. Here we employ an objective eddy identification and tracking algorithm together with a novel matching and filling procedure to more thoroughly examine eddy-induced thermodynamic anomalies in the North Pacific, their relationship with eddy amplitude (SSH), and the percentage of variability they explain on various timescales from submonthly to interannual. The thermodynamic anomalies are investigated in terms of sea surface temperature (SST), isothermal layer depth (ITD), and upper ocean heat content (HCT). Most eddies are weak in amplitude and are associated with small thermodynamic anomalies. In the sense of composite mean, anticyclonic eddies are generally warm eddies with deeper isothermal layer and larger heat content, and the reverse is true for cyclonic eddies. A small fraction of eddies, most probably subsurface eddies, exhibits the opposite polarities. Linear relationships with eddy amplitude are found for each of the thermodynamic parameters but with different level of scatter and seasonality. HCT-amplitude relation scatters the least and has the smallest seasonal difference, ITD-amplitude relation has the largest scatter and seasonality, while SST-amplitude relation is in between. For the Kuroshio and Oyashio Extension region, the most eddy-rich region in the North Pacific, eddies are responsible for over 50% of the total SSH variability up to the intra-seasonal scale, and ITD and HCT variability up to interannual. Eddy-induced SST variability is the highest along the Oyashio Extension Front on the order of 40–60% on submonthly scales. These results highlight the role of mesoscale eddies in ocean thermodynamic variability and in air-sea interaction.
Introduction
Mesoscale eddies are ubiquitous in the global oceans. They are coherent rotating vortices on horizontal scales of O(100 km) and temporal scales of O(100 days). Surface eddies are characterized by sea level rise or fall that are associated with significant geostrophic velocity anomalies and therefore can be detected and tracked from sea level height maps (Morrow and Le Traon, 2012; Chelton, 2013; Petersen et al., 2013). Thanks to the advancement of satellite altimeter observations and objective eddy detection and tracking algorithms, we now have some knowledge about the spatial, statistical, and temporal distribution of some of the key dynamic and kinematic properties of eddies (Hwang et al., 2004; Itoh and Yasuda, 2010; Cheng et al., 2014). From the perspective of energetics, kinetic energy of eddies accounts for a considerable fraction of the total kinetic energy (e.g., Wyrtki et al., 1976; Richardson, 1983; Zhou and Cheng, 2021b), dynamically adjusted by interaction with the time-mean flow (Ferrari and Wunsch, 2009; Qiu and Chen, 2010; Waterman et al., 2011; Yang and Liang, 2016; Sérazin et al., 2018; Yang et al., 2018). In the North Pacific, the Kuroshio Extension and the Subtropical Counter Current are two of the most eddy-energetic regions with dynamic interactions between eddies and the time-mean flow. Other regions, such as along the eastern boundary and in the Gulf of Alaska, are also abundant with eddies, although there eddies are generally weaker (Cheng et al., 2014).
Besides dynamic anomalies like sea surface height and velocity, eddies are also associated with thermodynamic and biogeochemical perturbations at the surface and beneath, and in their atmospheric imprints. Satellite-based studies showed that on average, mesoscale eddies can cause temperature anomalies at the surface on the order of 0.5°C (Frenger et al., 2013; Faghmous et al., 2015; Chen et al., 2017). Dong et al. (2014) used Argo profiles to show that eddy-induced temperature anomalies extends to about 1,000 m below surface, maximized at the thermocline, having huge impacts on the upper ocean heat content. Remarkable eddy-signature in salinity and chlorophyll is also found (Chelton et al., 2011; Gaube et al., 2013; Wang et al., 2018; Zhao et al., 2021). It is also established that ocean mesoscale eddies can modulate the air temperature, wind velocity, and precipitation in the atmospheric boundary layer directly above (e.g., O’Neill, 2012; Frenger et al., 2013; Putrasahan et al., 2017; Sugimoto et al., 2017), and may even be able to change the free atmospheric circulation as well as atmospheric transient eddy activity (e.g., Ma et al., 2015, 2017; Zhou et al., 2015; Zhang et al., 2019, 2020; Liu X. et al., 2021).
However, our current understanding on eddy-induced dynamic and thermodynamic anomalies is still poor. First, most studies only examined temperature perturbations on the sea surface, while eddies’ impact on subsurface temperature in the upper ocean is mostly untouched. Lack of high-resolution subsurface observations is the main reason. Second, eddy-induced temperature anomalies are commonly studied in the sense of composite mean over a large number of eddies. Although some studies presented the statistical distribution (or at least a standard deviation besides the mean) of height anomalies, such distributions of temperature anomalies are rarely investigated. The relationship between dynamic and thermodynamic anomalies, moreover, is still to be explored. Third, aside from the absolute values, it remains unknown how important the eddy-induced perturbations are relative to the total variability of dynamic and thermodynamic quantities on various timescales. This problem is of particular importance in, e.g., midlatitude air-sea interaction. It is historically under debate as to what extent is the midlatitude surface temperature variability on interannual and shorter timescales driven by atmospheric forcing, and to what extent by ocean internal processes that can potentially force atmospheric responses. Recent studies started to highlight the ocean control on surface temperature (Smirnov et al., 2014; Bishop et al., 2017), based on autoregressive models linearized using either observed or model-simulated temperature and heat flux. These studies extend the conventional stochastic climate model proposed by Hasselmann (1976) and Frankignoul and Hasselmann (1977) by enabling ocean noise forcing, yet they still rely on statistical fitting, and the shortest timescale investigated is limited to monthly due to data resolution. Direct description of eddy-induced anomalies and multi-scale variability down to submonthly timescales is therefore in keen interest.
This paper is an attempt to tackle the above issues using direct eddy identification and matching approaches. It answers the following key questions: (a) how are eddy morphologic, kinematic, and thermodynamic parameters statistically related to eddy amplitude; (b) how much dynamic and thermodynamic variability do the eddy-induced anomalies explain. These questions are important to ocean dynamics and air-sea interaction, but have not been thoroughly investigated. Here by thermodynamic parameters, we consider both surface temperature and subsurface heat anomalies in terms of isothermal layer depth and upper ocean heat content. The rest of the paper is organized as follows: In section “Data and Methods” we introduce the data used in this work, and the eddy identification and tracking method. Section “Results” presents the results in three subsections: Statistical relationship of eddy morphologic and kinematic parameters with eddy amplitude (section “Detected Eddy Properties”); eddy-induced thermodynamic anomalies and their statistical relationship with the amplitude (section “Eddy-Induced Anomalies”); and the relative importance of eddy-induced variability on different timescales (section “Eddy-Induced Variabilities”). Section “Conclusion and Discussion” includes a summary of the results and a brief discussion.
Data and Methods
Data
In this study, we make use of daily sea surface height (SSH) and sea surface temperature (SST) data provided by the Estimating the Circulation and Climate of the Ocean, phase II, project (Menemenlis et al., 2008) on a spatial grid of 1/4°× 1/4°. The study domain is the North Pacific (120°E–90°W, 10°–60°N). Ocean sub-surface potential temperature and salinity from the same dataset with 3-day interval are used to estimate the isothermal layer depth and upper ocean heat content, which are then interpolated into daily records. There are 50 levels in the vertical from 5 m to 6150 m with the layer thickness ranging from 10 m below the surface to 456 m near the bottom. The time range of all data is 2008–2017 (10 years).
The reasons for using the ECCO2 reanalysis product are twofold. First, there lacks long-term Eulerian observations of ocean sub-surface temperature necessary for estimating isothermal layer depth and upper ocean heat content. Argo floats do a good job of measuring sub-surface temperature, but they drift around with the ocean currents. Second, this paper aims at examining both dynamic and thermodynamic anomalies of eddies, and relies on matching the temperature anomalies with eddies detected from SSH maps, thus physical consistency between SSH and the surface and sub-surface temperature is essential. Satellite observations of SSH and SST are based on different hardware platforms with different retrieval methodologies and therefore cannot guarantee physical consistency. Reanalysis datasets commonly employ certain data assimilation techniques that introduce unphysical jumps and artificial sources/sinks. Although also a reanalysis, the ECCO2 project estimates the ocean state by a least square fit of the Massachusetts Institute of Technology General Circulation Model (Marshall et al., 1997) to available satellite (e.g., altimeter for SSH, radiometer for SST) and in-situ data, including Argo floats. Using a Green function approach (Menemenlis et al., 2005), the fit is applied for a number of control parameters (e.g., the initial and boundary conditions, vertical viscosity, and bottom drag), and the model is integrated forward freely without observational data injection, hence ensuring dynamic and thermodynamic consistency along with accuracy (Wunsch et al., 2009). The ECCO2 dataset has been employed to diagnose eddy dynamics and energetics in various parts of the world oceans (Fu, 2009; Chen et al., 2014; Qiu et al., 2017; Yang et al., 2017, 2018). The following study is based on anomalies defined as the deviation from the 10-year climatological annual cycle. For simplicity hereafter we drop the word “anomaly” in this sense and reserve it to indicate the eddy anomaly, i.e., the difference of a quantity inside and outside an eddy, as elaborated in section “Eddy-Induced Anomalies.”
Eddy Identification and Tracking
Over the past decades, a number of autonomous eddy detection algorithms has been developed, based on either observational or modeling data (Chelton et al., 2007, 2011; Doglioli et al., 2007; Chaigneau et al., 2008; Nencioli et al., 2010; Dong et al., 2011; Faghmous et al., 2015; Zhang C. et al., 2015). We use the objective autonomous eddy identification algorithm developed by Faghmous et al. (2015). This algorithm first detects eddy centers by finding local SSH extrema, and then defines the outermost closed contours around the extrema as eddy boundaries. It is free of expert parameters that must be determined a priori. This algorithm provides eddy boundary information, which is of particular importance to this study in calculating eddy-induced anomalies. It should be noted that as in previous studies (e.g., Cheng et al., 2014; Faghmous et al., 2015; Liu et al., 2020), no strict distinction between mesoscale eddies and long baroclinic Rossby waves are made, since the two are both manifested as SSH extrema and they often coincide (Pingree and Sinha, 2001; Oliveira and Polito, 2013; Polito and Sato, 2015). Eddy trajectories are found by searching for similar eddies between the adjacent timesteps within a search radius determined by the maximum eddy propagation speed—the phase speed of long baroclinic Rossby waves. To account for data complexity, here we allow the eddies to disappear for 1 day in its trajectory, thus not counting its re-appearance in the next day as a different eddy. This algorithm has been successfully used in the past to detect and track mesoscale eddies in the world oceans (Putrasahan et al., 2017; Ding et al., 2018; Liu et al., 2020).
Recently, eddies maximizing below the sea surface start to attract more research interests. These subsurface eddies are being observed in various parts of the global oceans (Pelland et al., 2013; Pegliasco et al., 2015; Zhang Z. et al., 2015, 2017; Song et al., 2019; Zhu et al., 2021), and simulated in ocean models (Chiang et al., 2015; Wang, 2017; Xu et al., 2019, 2020). Only some of the subsurface eddies exert imprints on SSH, particularly the intra-thermocline eddies whose isopycnals outcrop the sea surface, and some relatively shallow sub-thermocline eddies that make contact with the mixed layer on top which transfers the eddy-induced anomalies to the surface (Assassi et al., 2016). These surface signals of subsurface eddies, however, are expected to be weak, thus the detection quality of these eddies is compromised. Deep sub-thermocline eddies with the “lens” shape are associated with anomalies of the opposite sign above and below its core, and therefore have very little surface imprint. In this work we use sea surface perturbations to detect eddies, and thereby restrict ourselves to those eddies that are detectable from the surface. Deep sub-thermocline eddies are left for future research.
Results
Detected Eddy Properties
In the 3653 days of 2008–2017, an average number of 524 cyclonic and 506 anticyclonic eddies are detected per day in the North Pacific basin, which, respectively, fall into 110,615 and 106,140 trajectories. Figure 1A shows a snapshot of the SSH field and the detected eddy boundaries. It is clear that the eddies correspond well to the SSH contours. Eddies in the Kuroshio Extension (KE, 140–170°E, 30–40°N) region are largest in size and strongest in amplitude, followed by the Subtropical Counter Current (STCC, 125°E–155°W, 15–25°N) region and along the eastern boundary and the Aleutian Islands. The distribution of eddy lifespan averaged across 1°× 1° cells is show in Figure 1B. Long-living eddies are mostly generated in the eastern basin, whereas KE and STCC eddies are short. This is presumably due to the strong baroclinic and barotropic interaction with the background flow (Ferrari and Wunsch, 2009; Waterman et al., 2011; Waterman and Jayne, 2011; Bishop, 2013; Chen et al., 2014; Yang and Liang, 2016; Yang et al., 2017, 2018; Ji et al., 2018). The trajectories of eddies longer than 180 days are shown in Figure 1C, which reveals that eddies travel longer (shorter) distances near the equator (at higher latitudes), as a result of the poleward decreasing Rossby wave speed. Eddies in the subarctic North Pacific (in the Gulf of Alaska and along the Aleutian Islands) are long-living and quasi-stationary, exhibiting the shortest travel distance (Di Lorenzo et al., 2005; Rogachev et al., 2007; Saito et al., 2014; Rogachev and Shlyk, 2018, 2019). Active eddy generation is noticeable along the eastern boundary, where coastal Kelvin waves from the tropics are transformed into Rossby waves propagating westward away from the boundary (Clarke and Shi, 1991; Fu and Qiu, 2002). These above results agree quantitatively with the work by Cheng et al. (2014) based on altimeter data, which confirms the credibility of the eddy identification and tracking results.
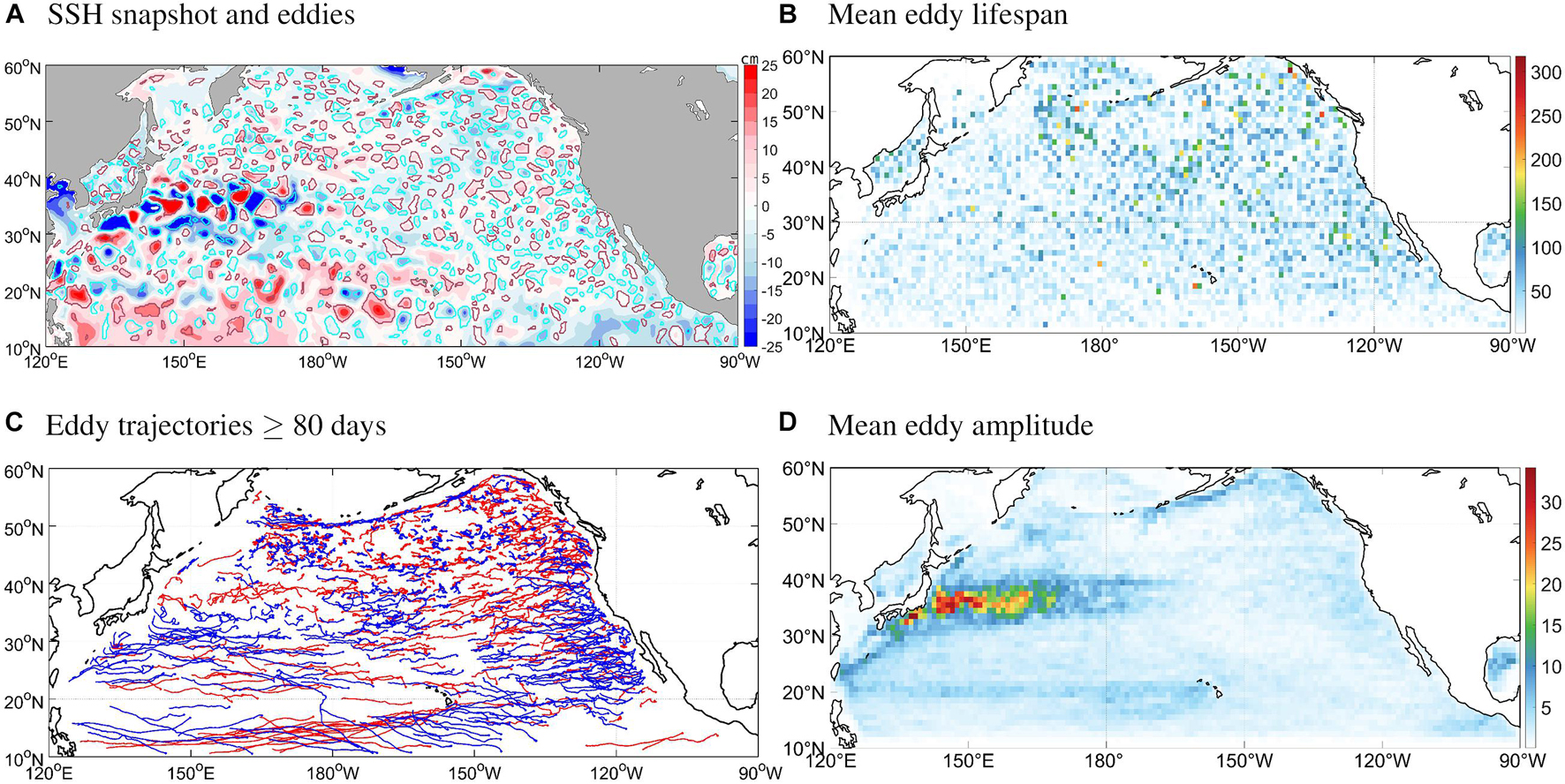
Figure 1. (A) Snapshot of the SSH anomaly (cm) field on January 1, 2008 (shading). Anomaly is defined as the departure from the climatological annual cycle. Areas enclosed by the red (cyan) curve represents the identified anticyclonic (cyclonic) eddies. (B) Mean eddy lifespan (days) averaged within 1°×1° grid cells organized by the generation location of eddies. (C) Trajectories of eddies with lifespan longer than 180 days detected on January 1, 2008. Red (blue) curves represent the trajectories of anticyclonic (cyclonic) eddies. (D) Mean eddy amplitude (i.e., SSHA, cm) averaged within 1°×1° grid cells organized by the instantaneous location of eddies. Shown are the absolute values averaged across cyclonic and anticyclonic eddies.
We define for each eddy an equivalent circle having the same area as the eddy, the equivalent circle’s radius as the eddy radius, and then the eddy-induced SSH anomaly (SSHA) as the difference between the SSH extrema within the eddy boundary and the average SSH outside the eddy but within three radii. This definition is similar to, but not the same as, the one employed by Frenger et al. (2013), who took the inside value as the average within two eddy radii, and the ambient value as the average within three radii. Their definition of interior value includes anomalies outside the eddy boundary, and their ambient value includes areas inside. Cheng et al. (2014) used the same inside SSH as ours, but calculated the ambient SSH as the average along the boundary. This definition suffers from contamination by residual large-scale imprints surviving the removal of the climatological means (e.g., in the STCC in Figure 1A). Our definition arguably does a better job in accurately representing both the interior and ambient values. The eddy-induced SSHA is referred to as the eddy amplitude in this work. Figure 1D shows the spatial distribution of mean eddy amplitude, which agrees well with Cheng et al. (2014) in terms of pattern and magnitude. Eddy-induced anomalies of other quantities are defined in the same way. It should be noted that in this study, in order to assess eddy-induced variability on the smallest possible scales, we do not apply any filtering criterion on e.g., eddy size or lifetime, as commonly did in literature studies (Frenger et al., 2013, 2015; Cheng et al., 2014; Chen et al., 2017; Liu et al., 2020). This results in a tremendous number of weak eddies.
To have a better overview on the detected eddies, we plot in Figure 2 the relationship between the eddies’ SSHA and their morphologic and kinematic parameters. Some previous studies (e.g., Cheng et al., 2014) investigated statistical distributions of these parameters, yet their relationship with the amplitude is seldom examined. First, Figure 2A shows that on the first order, eddy amplitude and radius exhibit a linear relationship. Large scatter, however, is present especially for moderate-amplitude eddies with radius ranging from as small as a few tens of km to as large as 350 km. The strongest eddies (| SSHA| > 60 cm) scatter less, having radius of ∼100–200 km. The most abundant weak eddies (| SSHA| < 4 cm) are at most 150 km large. Next, in Figure 2B we present the distribution of eddy deformation ratio defined as the area of the deviation between the eddy boundary and its equivalent circle relative to the eddy area following Kurian et al. (2011). Most of the strong eddies are moderately deformed, while weak eddies span over a large scatter, from near-regular to severely distorted. As for lifespan, it is found that strong eddies, mostly in the KE and STCC according to Figure 1D, are basically shorter than about a season (Figure 2C), while weak eddies can be anything between transient (a few days) and quasi-permanent (a few years) depending on their location. The translation speed of eddies is shown in Figure 2D, normalized by the theoretical value of the phase speed of long baroclinic Rossby waves at the eddies’ latitude given by Qiu et al. (1997). Note that theoretical Rossby wave speed is slightly slower than observed, thus the ratio shown in this figure is slightly higher. Large scatter is noticed in the figure, with weak eddies ranging from very slow to very fast, while strong eddies tend to travel at a speed closer to the Rossby wave speed. In terms of travel direction defined as the azimuth of the end point of a track relative to the starting point, there exists a preferred westward propagation direction (Figure 2E), same as found previously (Pingree and Sinha, 2001; Palacios and Bograd, 2005; Chelton et al., 2011). However, it is particularly interesting to note that taking all eddies into account, the dominance of westward propagation is not as obvious as for long-lived eddies, and eddies can travel to virtually every direction (Figure 2F). To further examine this point, we plot in Figure 3A the spatial distribution of mean propagation direction of all eddies, and in Figure 3B only the ones persisting for at least 150 days. The generation location of the non-westward (especially the eastward) propagating eddies largely agrees with the location of strong eddies (Figure 1C). Since the strong eddies are mostly short-lived ones (Figure 2C), raising the threshold of lifespan filters out the strong eddies that propagate to the east or other directions. The association between strong eddies and eastward propagation indicates that the simple theory of westward propagation required by conservation of potential vorticity and the beta effect (Nof, 1981; Cushman-Roisen et al., 1990) breaks up in areas with strong advection by eastward background flow (Hughes, 1996; Holland and Mitchum, 2001; Fang and Morrow, 2003; Morrow et al., 2003).
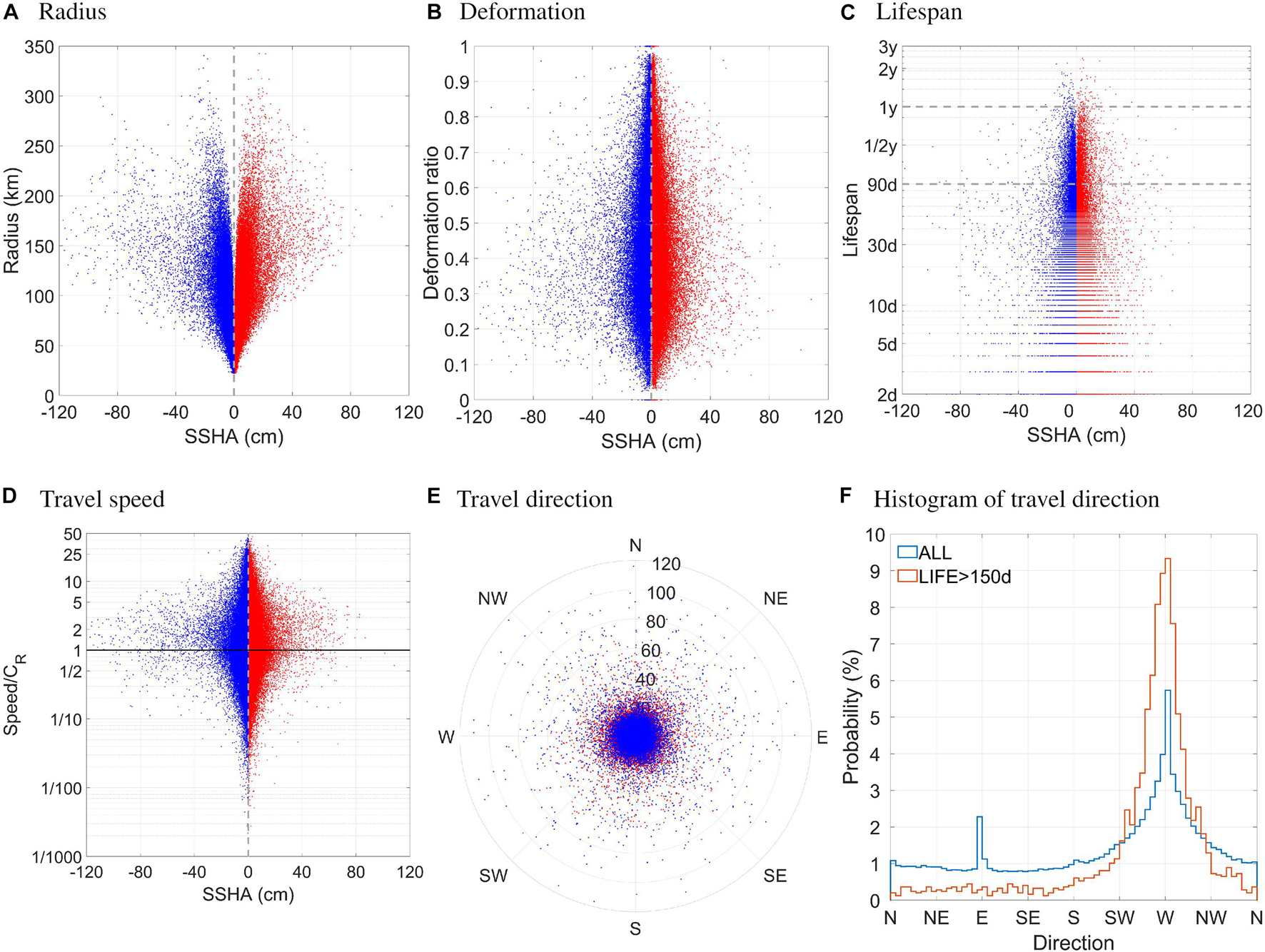
Figure 2. Scatter plots showing the statistical relationship between eddy amplitude (cm) and (A) radius (km), (B) deformation ratio, (C) lifespan (days; note the logarithmic y-axis; amplitude is taken at the eddies’ half-life), (D) the ratio between travel speed defined as the track length divided by the lifespan and the theoretical speed of long baroclinic Rossby wave (note the logarithmic y-axis), and (E) travel direction defined as the azimuth of eddy termination location relative to the generation location. Red (blue) dots represent anticyclonic (cyclonic) eddies. The radial axis indicates eddy amplitude in cm. (F) Histogram of eddy travel direction. Red stairs represent the histogram over all eddies, and blue stars are for eddies persisting for longer than 150 days.
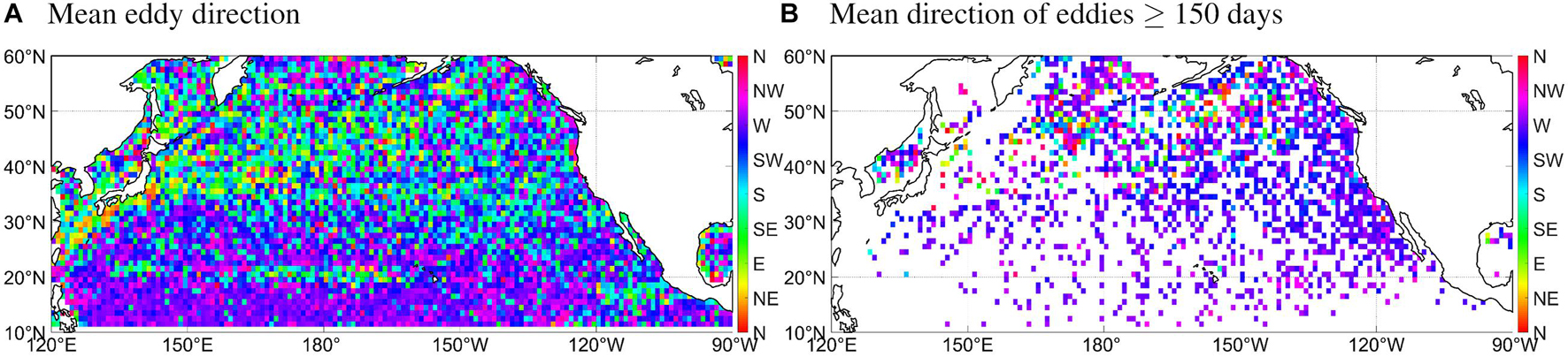
Figure 3. Mean eddy direction defined as the azimuth of eddy termination location relative to the generation location, averaged within 1°×1° grid cells, organized by the generation location. (A) Shows mean eddy direction across all eddies in a grid cell, and (B) show mean direction across eddies persisting for longer than 150 days.
Eddy-Induced Anomalies
We next investigate thermodynamic anomalies induced by mesoscale eddies in terms of SST, isothermal layer depth (ITD), and upper ocean heat content (HCT), along with SSH. Here the ITD is calculated as the depth where seawater temperature decreases by 0.2°C from the temperature at 10 m below the surface. This definition has been widely used in literature studies (de Boyer Montégut et al., 2004; Breugem et al., 2008; Pang et al., 2019). The HCT is defined over the upper 400 m as , where T is temperature, c is specific heat capacity, and ρ is density. c and ρ are calculated from temperature and salinity using the polynomial algorithm of Fofonoff and Millard (1983). The choose of the upper 400 m is in accordance with many literature works (Vivier et al., 2002; Doney et al., 2007; Song et al., 2014), based on the consideration that the upper 400 m is thermodynamically the most energetic layer of the ocean. It has been shown that about 52% of surface-intensified eddies extend to less than 400 m in the vertical (Liu et al., 2020). An alternative limit of 700 m does not change our findings qualitatively.
Eddy-induced anomalies to the quantities under study [i.e., SST anomaly (SSTA), ITD anomaly (ITDA) and HCT anomaly (HCTA)] are calculated in the same way as the SSHA (as differences between the extrema inside the eddy and mean value outside the eddy but within 3 radii). The spatial distribution of mean eddy-induced thermodynamic anomalies is shown in Figure 4. On average, eddies in the Kuroshio and Oyashio Extension region are most effective in changing the SST, with mean SSTA of more than 2°C (Figure 4A). The largest SSTA appears in the confluence region between the Kuroshio and the Oyashio, reflecting the vigorous poleward heat transport by mesoscale eddies (Sugimoto and Hanawa, 2011; Seo et al., 2014; Sugimoto et al., 2014; Masunaga et al., 2016), and along the KE and Oyashio Extension currents. This is also where the eddies are the strongest (Figure 1D). Eddy-induced ITDA is the largest in the northwest, especially along the Kuril-Kamchatka Trench and around the Kuril Straits where the average | ITDA| is about 300 m (Figure 4B) and extreme values concentrate (Figure 4C). Climatologically, the background ITD in subpolar western North Pacific is known to be quite large in winter (∼1,000–3,000 m, Figure 4B contours). This is because of the strong vertical temperature inversion driven by the combination of intense surface cooling and the maintenance of the shallow thermocline by heavy precipitation and Ekman suction (de Boyer Montégut et al., 2007). The subsurface water, which is well-mixed due to the deep intense tidal mixing there (Kawasaki and Hasumi, 2010; Tanaka et al., 2010; Yagi and Yasuda, 2013; Kawasaki et al., 2021), is thus kept relatively warm, protected from the surface cooling. In this work the ITD is defined as the depth where temperature is 0.2°C lower than the SST, which means that it must be searched for beneath the large body of well-mixed warm water and is hence very deep. Mesoscale eddies traveling through these areas advect water mass from somewhere else and can thus bring along quite large ITDAs, even though their amplitudes are small. Such deep climatological ITD is not present in summer because of the surface heating and the seasonal thermocline, and so are the extreme eddy-induced ITDAs. Besides the western subpolars, the strong eddies in the KE region are also characterized with large ITDAs. We also calculated eddy-induced anomalies of mixed layer depth, which is almost identical to ITDA except in the temperature inversion regions where the mixed layer is shallow (not shown). Eddy-induced HCTA, as indicated by Figure 4D, exhibits a similar pattern with the eddy amplitude, which is not surprising since theoretically the eddy SSH anomaly is linearly related to heat content anomaly due to the thermal expansion effect (e.g., Stephenson et al., 2013).
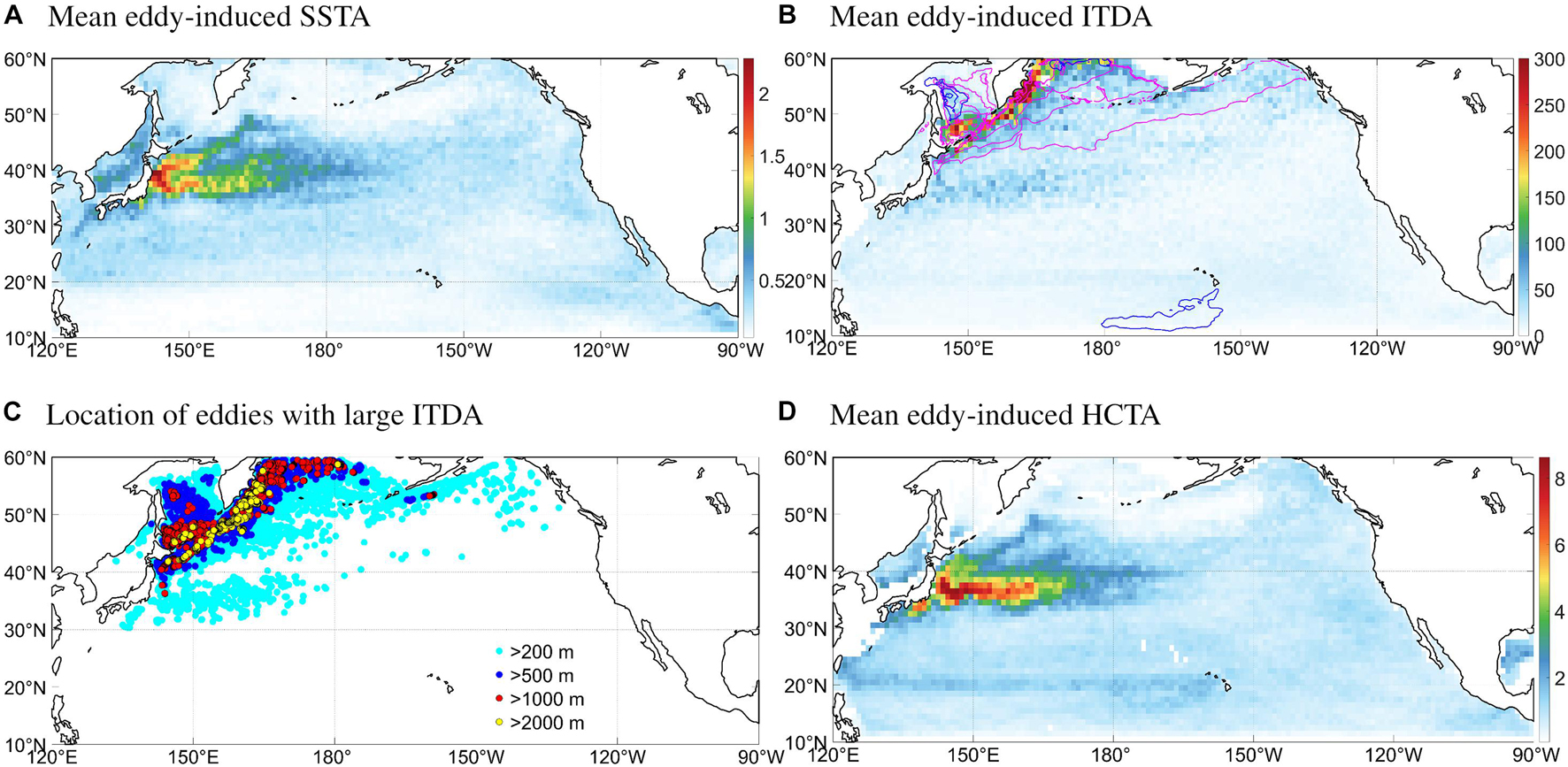
Figure 4. Mean eddy-induced (A) SSTA (°C) (B) ITDA (m) averaged within 1°×1° grid cells, organized by the instantaneous location of eddies. Shown are the absolute values averaged across cyclonic and anticyclonic eddies. In (B), contours show the climatological mean ITD averaged across 1993–2019. Magenta contours are for winter (DJF) at 200, 500, 1,000, and 2,000 m levels, and blue contours are for summer (JJA) at 50, 100, and 150 m levels. (C) Location of eddies with | ITDA| >200 m (cyan), 500 m (blue), 1,000 m (red), and 1,500 m (yellow). (D) Same as (A,B) but for HCTA (GJ/m2).
It is a good start to examine the statistical distribution of eddy anomalies in the sense of composite mean. To do this, we follow Frenger et al. (2013) and Chen et al. (2017) to normalize the eddies according to their respective radius, but do not rotate them, with no restriction on eddy size or lifetime whatsoever. The results are shown in Figure 5. The composite-mean SSHA and SSTA confirm that generally, anticyclonic (cyclonic) eddies are associated with positive (negative) SSHA and higher (lower) temperature, which is in qualitative agreement with previous studies (Frenger et al., 2013; Faghmous et al., 2015; Chen et al., 2017), but is much weaker in amplitude as a result of the inclusion of the large number of weak eddies. The composite-mean eddy ITDA and HCTA are consistent with SSTA, indicating warmer and deeper isothermal layer containing more heat associated with anticyclonic eddies and vice versa. On average, a typical eddy with 8 cm SSHA would induce SSTA of 0.5°C, ITDA of 7 m, and HCTA of 1 GJ/m2. The eddy impact maximizes near the eddy center and is basically isotropic. Cyclonic and anticyclonic eddies show general symmetry.
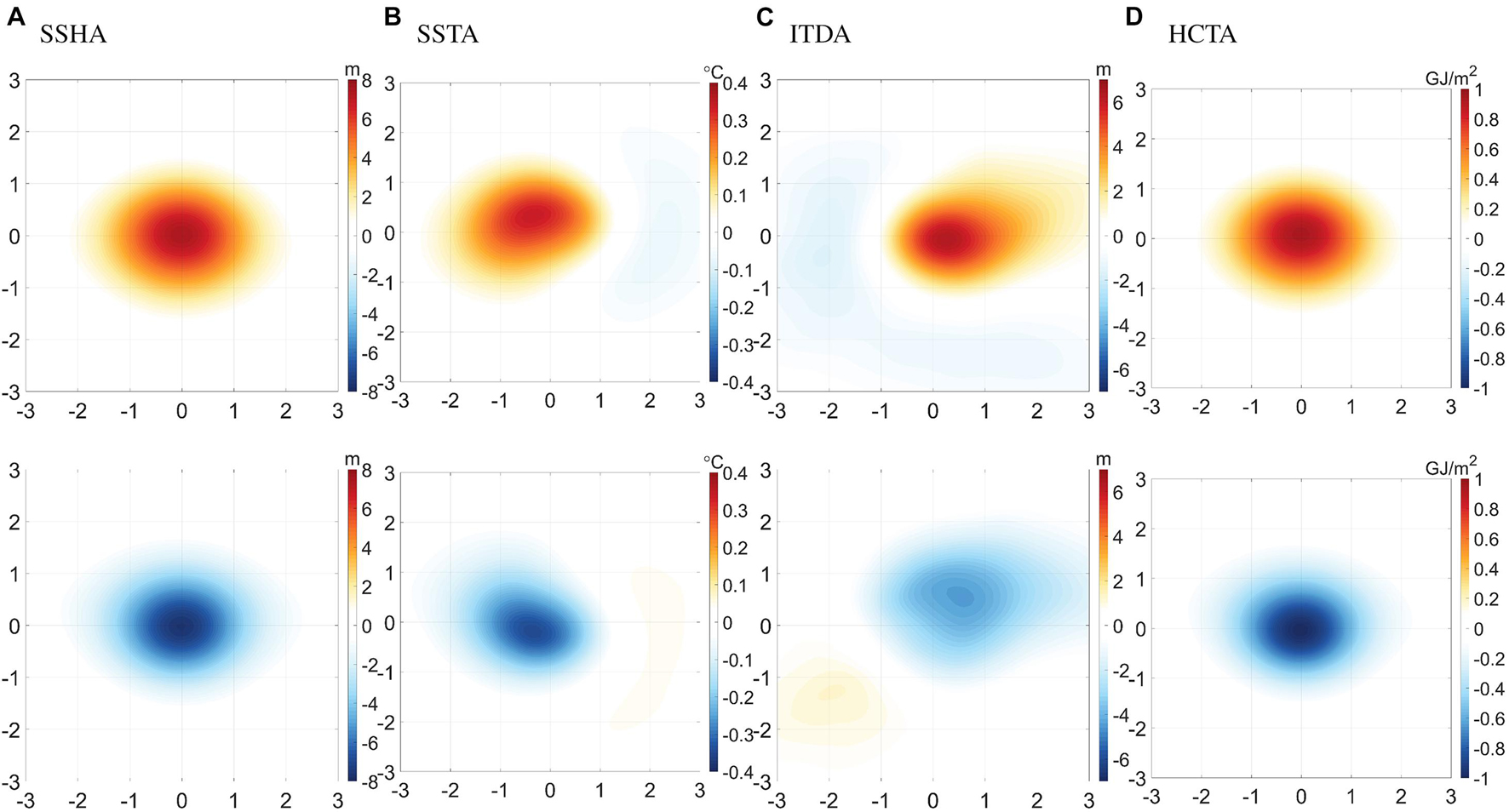
Figure 5. Eddy-induced (A) SSHA (cm), (B) SSTA (°C), (C) ITDA (m), (D) HCTA (GJ/m2) averaged over all eddies. The upper (lower) row is for anticyclonic (cyclonic) eddies. Eddies are scaled relative to their respective radius. Shown are the distribution of the indicated quantities within 3 times the eddy radius in each direction.
On the other hand, histograms of the parameters (Figure 6) indicate that the vast majority of eddies are very weak (P[| SSHA| < 4 cm] = 81%), and are associated with weak SSTA (P[| SSTA| < 0.4°C] = 80%), ITDA (P[| ITDA| < 20 m] = 69%), and HCTA (P[| HCTA| < 1 GJ/m2] = 64%). This is a result of the absence of eddy screening in this work. Here, for ITDA, we excluded the eddies in the western subpolar regions because of their very weak amplitude and very large ITDA. It is shown that eddy-induced ITDA elsewhere exhibits distinct seasonality (Figures 6D,E). In summer about 99% of the ITDA is below ± 20 m, while in winter this percentage is 53%. Further, the statistical relationship between eddy amplitude (SSHA) and eddy-induced SSTA is illustrated in Figure 7A. The maximum SSTA can reach ∼ ± 6°C, and average SSTA for strong eddies with |SSHA| > 40 cm is on the order of ± 2°C. Despite some scatters, a statistically significant linear relationship is still visible (linear coefficient = 0.033°C/cm). Seasonal differences are also shown in Figures 7B,C. It could be inferred that in summer, the SSHA-SSTA relation is flatter, with a larger number of strong eddies associated with weak SSTA, indicating that the mesoscale eddies are less capable at changing the SST in summer. This is presumably due to the formation of the shallow seasonal thermocline, which leads to easier SST disturbance by other forcing terms like solar radiation and cloud cover. Moreover, it is noticeable that about 20% of the eddies, mostly weak ones, have inconsistent SSHA and SSTA, i.e., anticyclonic eddies being cold eddies and vice versa. These eddies are also known as abnormal eddies (Liu Y. et al., 2021). The presence of such abnormality is most probably due to subsurface eddies. Recently, Bashmachnikov et al. (2013) and Assassi et al. (2016) showed that surface eddies have SSTAs of the same sign as the SSHA, while for subsurface eddies that do have surface imprints, the two anomalies have the opposite sign. Since subsurface eddies maximizes beneath the surface, their surface signatures are expected to be weak. Other processes, e.g., baroclinic instability, surface flooding or mixing etc., may also generate abnormal eddies (Liu Y. et al., 2021).
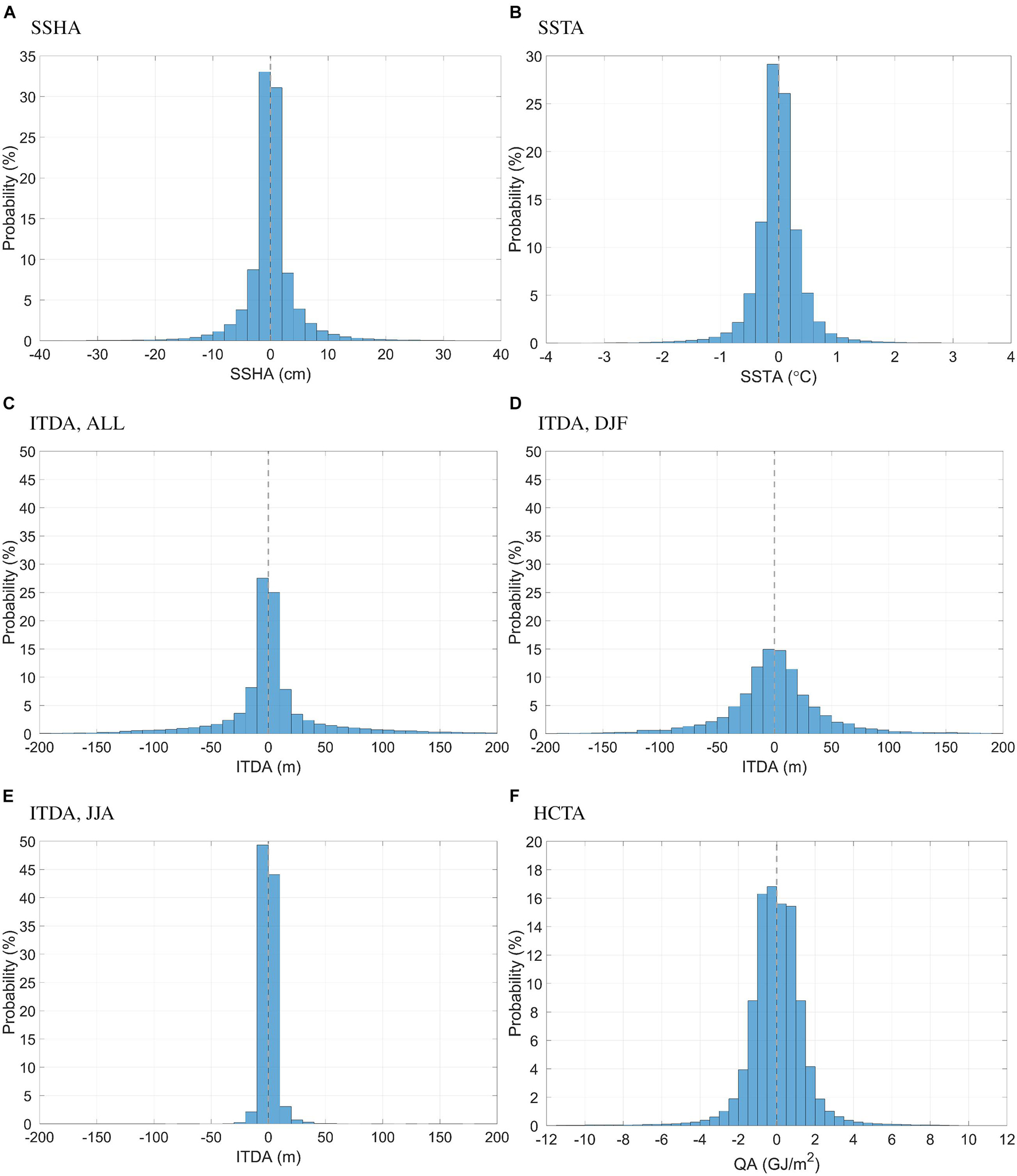
Figure 6. Histograms of eddy-induced (A) SSHA (cm), (B) SSTA (°C), (C) overall ITDA (m), (D) ITDA in winter (DJF, m), (E) ITDA in summer (JJA, m), (F) HCTA (GJ/m2).
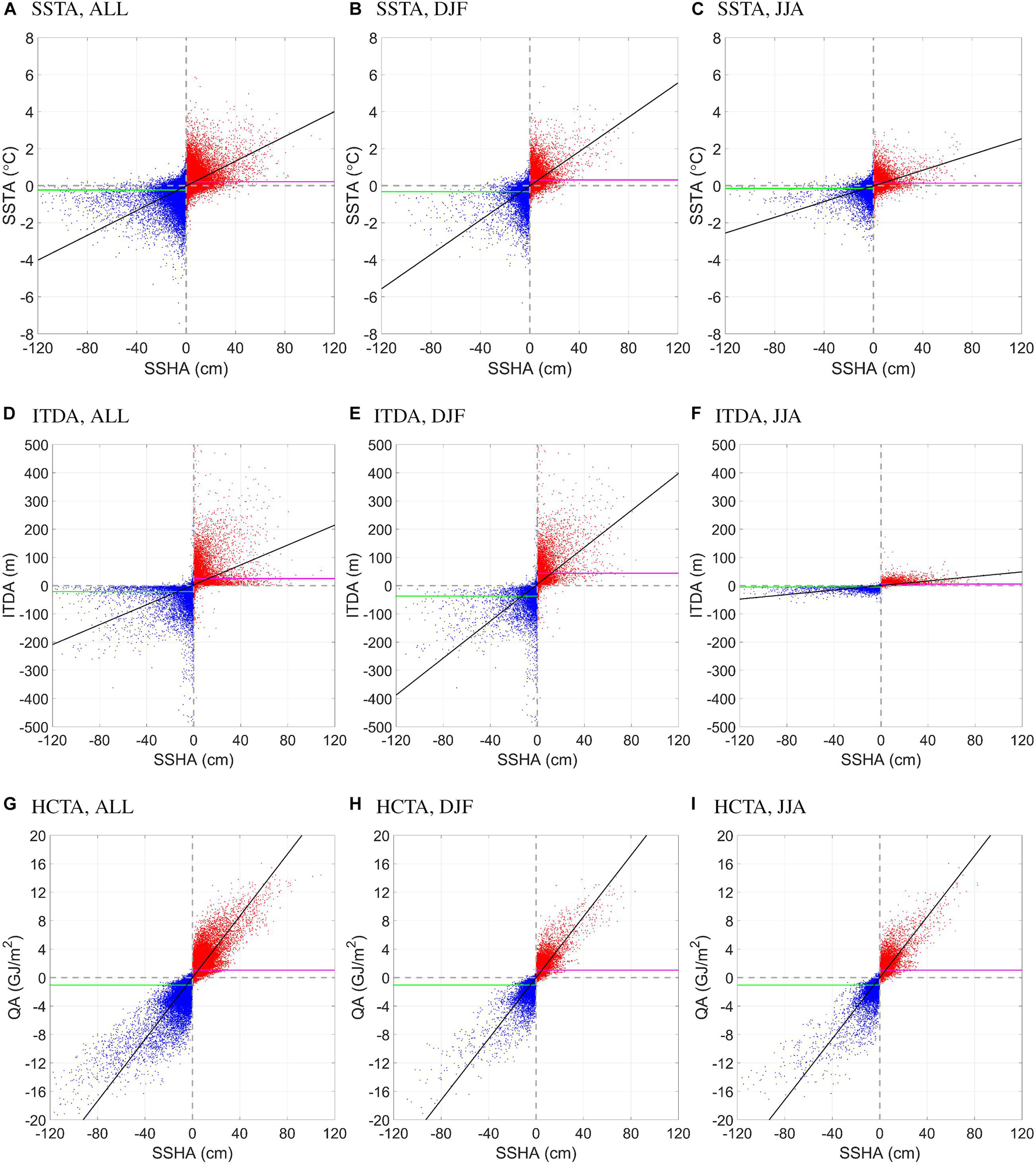
Figure 7. Scatter plots showing statistical relationship between eddy amplitude (SSHA, cm) and (A–C) SSTA (°C), (D–F) ITDA (m), (G–I) HCTA (GJ/m2) over all time (1st column), winter (DJF, second column), and summer (JJA, last column). The magenta (green) line represents the average over all anticyclonic (cyclonic) eddies. The black line is the linear relationship calculated by least square fitting.
The eddy-induced ITDA, as shown in Figure 7D, can be as large as over 1,800 m, even though the western subpolar regions are excluded. The extreme values are, of course, scarce. For clarity, Figure 7D only shows | ITDA| ≤ 500 m. A closer look on winter and summer results (Figures 7E,F) reveals that most of the large-ITDA eddies are found in winter, while summer ITDAs are very weak (<50 m), regardless of eddy amplitude. The wintertime SSHA-ITDA relationship is on the first order linear, with a coefficient of 3.3 m/cm. A similar control of mesoscale features on mixed layer depth has been recently found in a modeling study for the Southern Ocean (Bachman et al., 2017). The very weak eddy-induced ITDA in summer is again suggestive of eddies’ reduced capability in changing the upper ocean temperature, and can be attributed to the same reasons as for SSTA. The excluded eddies in the western subpolar region, as mentioned about, also exhibit significant seasonality in ITDA (not shown), as a result of the disappearance of the very deep background ITD in summer. As for SSTA, abnormal SSHA-ITDA relationship is also noticed.
Finally, eddy-induced HCTA is shown as a function of eddy amplitude in Figure 7G. A better (less-scattered) linear relationship than for SSTA and ITDA is evident, with a coefficient of 0.22 GJ/cm. This is a result of HCT being a vertical integral representing the entire upper layer’s heat content, which is partially related to surface elevation due to thermal expansion. Mesoscale eddies are 3D structures (Dong et al., 2014; Liu et al., 2020), and are therefore more capable in modulating HCT than SST and ITD which depend on additional driving forces such as air-sea heat and freshwater fluxes. Seasonal contrast for eddy-induced HCTA is not obvious (Figures 7H,I), indicating less control on HCTA by the seasonally varying surface fluxes. Despite the better linear relationship, scatters do exist, and there are also some eddies with abnormal sign of HCTA.
Eddy-Induced Variabilities
In the above we have investigated the eddy-induced anomalies in terms of their mean values and statistical relationship with the eddy amplitude. However, it remains unknown how much variability do the eddies explain on different timescales. In this section we further examine this problem by reconstructing fields of eddy-induced time series. To do so, at each time step, areas within the individual eddy boundaries are filled with the anomaly values induced by the respective eddies, while areas not belonging to any eddies are set to zero. For each eddy, the eddy-induced anomaly value calculated above is assigned to the eddy’s body center, and from there the anomalies gradually reduce to zero along the radial direction toward the boundary. See Figure 8 for a schematic diagram of this “matching and filling” procedure. In this way, eddy boundaries always have zero anomaly, and large-scale signatures are prevented because the eddy-induced anomaly is already the difference between the interior maximum and the ambient mean. Here no eddy screening is made whatsoever, and there is no presumption on the shape of the eddy boundary and/or its symmetry. A simpler way, i.e., directly set eddy interior values to be the same as the original field, is subject to residual large-scale anomalies that the eddy anomalies superimpose on.
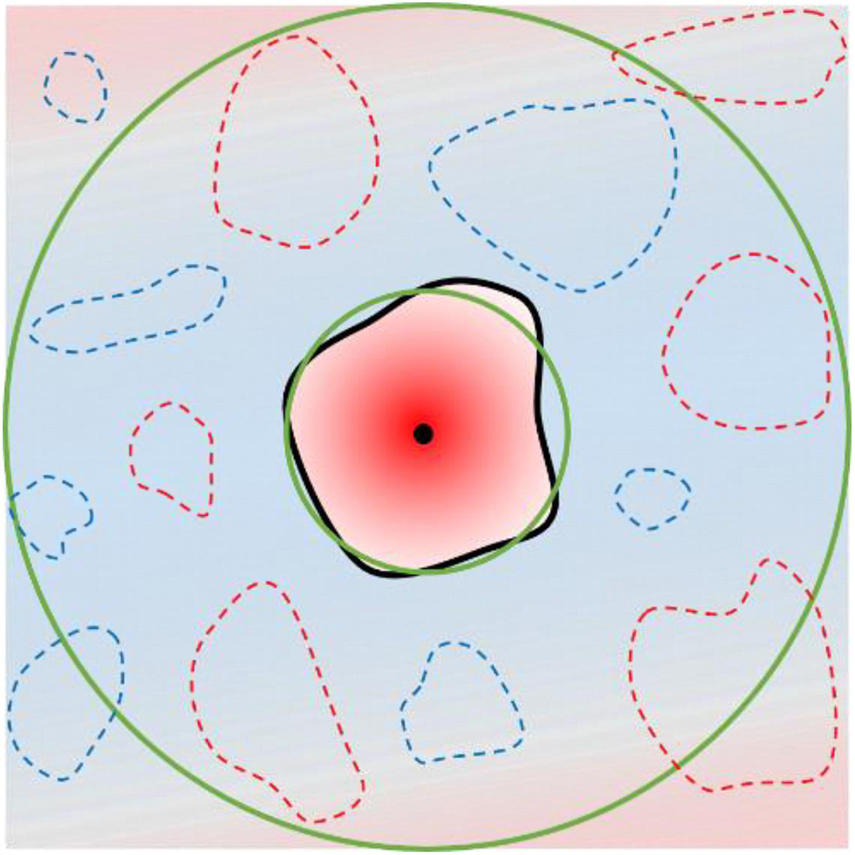
Figure 8. Schematic diagram showing the eddy reconstruction process. The eddy under study is indicated by the area enclosed by the thick black curve, with the black dot representing its body center. The two green circles show the equivalent circle and the ambient circle, i.e., a circle with 3 times the radius of the equivalent circle. When reconstructing, the eddy anomaly is assigned to the body center, and decreases linearly in the radial direction toward the boundary. Dashed curves indicate other eddies, either with positive (red) or negative (blue) anomalies. The shading in the background is to indicate the large-scale imprint left over after removing the climatology, and is not present in the reconstructed eddy field.
Conventionally, spatial filtering is more often employed to extract the mesoscale from the background. However, the filtering approach is subject to several difficulties and is therefore believed less suitable for this study. (A) First, filters are usually not capable of separating the scales in a clear-cut manner, instead the resultant scales are interdependent. Such spectral leakage can be large for some filters, for instance the universally employed simple boxcar running mean filter. See Zhou and Cheng (2021b) for more discussions about filters. (B) Second, since large meanders of the background currents, oceanic fronts, and mesoscale eddies are all mesoscale features, spatial filtering is not efficient in separating them (Zhang et al., 2019). To alleviate this problem, elongating the filtering window in the zonal direction, say, to 15°× 5°, could yield some improvement, but cleaner separation could only be achieved by using eddy detection approaches (Zhou and Cheng, 2021a). (C) Third, spatial filters are built on the assumption of homogeneity, which means the characteristics of perturbations on different scales must not change over space, and are therefore better used in a small area. Assassi et al. (2016), e.g., showed that the size of the filtering window and the length scales of the eddy and the background current are all important. In reality, length scales of eddies and the background current vary significantly over the large basin of the North Pacific. Using a moving window with adaptable size according to local eddy properties may be helpful to lessen this problem, but it is too complicated to implement and is subject to other problems due to e.g., the a priori determination of eddy properties. (D) Last, mesoscale fields of different variables extracted by the same filter are not necessarily physically consistent. For example, mesoscale eddies with closed SSHA contours do not necessarily have SSTAs with closed contours too. It is thus difficult to interpret the results involving different variables. In contrast, the matching and filling method used in this work is free from all these kinds of problems because it is based on individual eddy processes instead of statistical tools.
Figure 9A shows an example snapshot of the reconstructed SSHA, in comparison with the original field shown in Figure 1A. It is obvious that the reconstructed SSHA captures the mesoscale features but leaves out the larger-scale imprint. As a confirmation to this, the 2D spatial spectra in the KE region shown in Figure 9B exhibits spectral peaks at wavelengths of a few degrees in both the zonal and meridional directions. In the meridional there also exists a peak at about 10–15° length scale reflecting the spatial inhomogeneity of eddy activity, which would be a problem for conventional filtering approach. The original and reconstructed time series at a selected grid point (150°E, 35°N) in the KE region are shown in Figure 9C. It could be inferred that at this point, mesoscale eddies are responsible for many of the negative SSHA events and some of the positive events, both in terms of magnitude and timing. The time-domain power spectra in Figure 9D indicates that at this point, eddy-induced SSH variability is more energetic than the original signal in the high-frequency band of 2–10 days. The reason for the overestimate is because of the intermittency of eddies in the Eulerian sense. For a certain grid point, SSHA in the eddy-vacant periods are exactly zero, but when an eddy approaches, it plunges or rises abruptly. The same happens when an eddy leaves. Faster, smaller, stronger eddies cause more abruptness in the resultant reconstructed time series. Moreover, eddies sometimes disappear from the detection algorithm at one time step but reappear at the next, presumably due to background signals that interfere the detection (Faghmous et al., 2015). This introduces even more intermittency and abruptness. When estimating the spectra using Fourier transform, therefore, harmonics at the highest frequencies are overly energetic. Applying smoothing to the reconstructed time series beforehand would of course reduce the abruptness and hence the overestimated spectral power, but the time series in the eddy-occupied periods, not only around the arrivals/departures, would also be smoothed and thus the high-frequencies are still unrealistic. In the future, improvements to the spatial and temporal resolutions are expected to lessen this problem. We investigated a large number of geographical points and found that lower frequencies than 1/10 cpd are mainly free from the overestimate problem (not shown), hence the band of 2–10 days, which is known as the synoptic scale, is discarded in the following analysis.
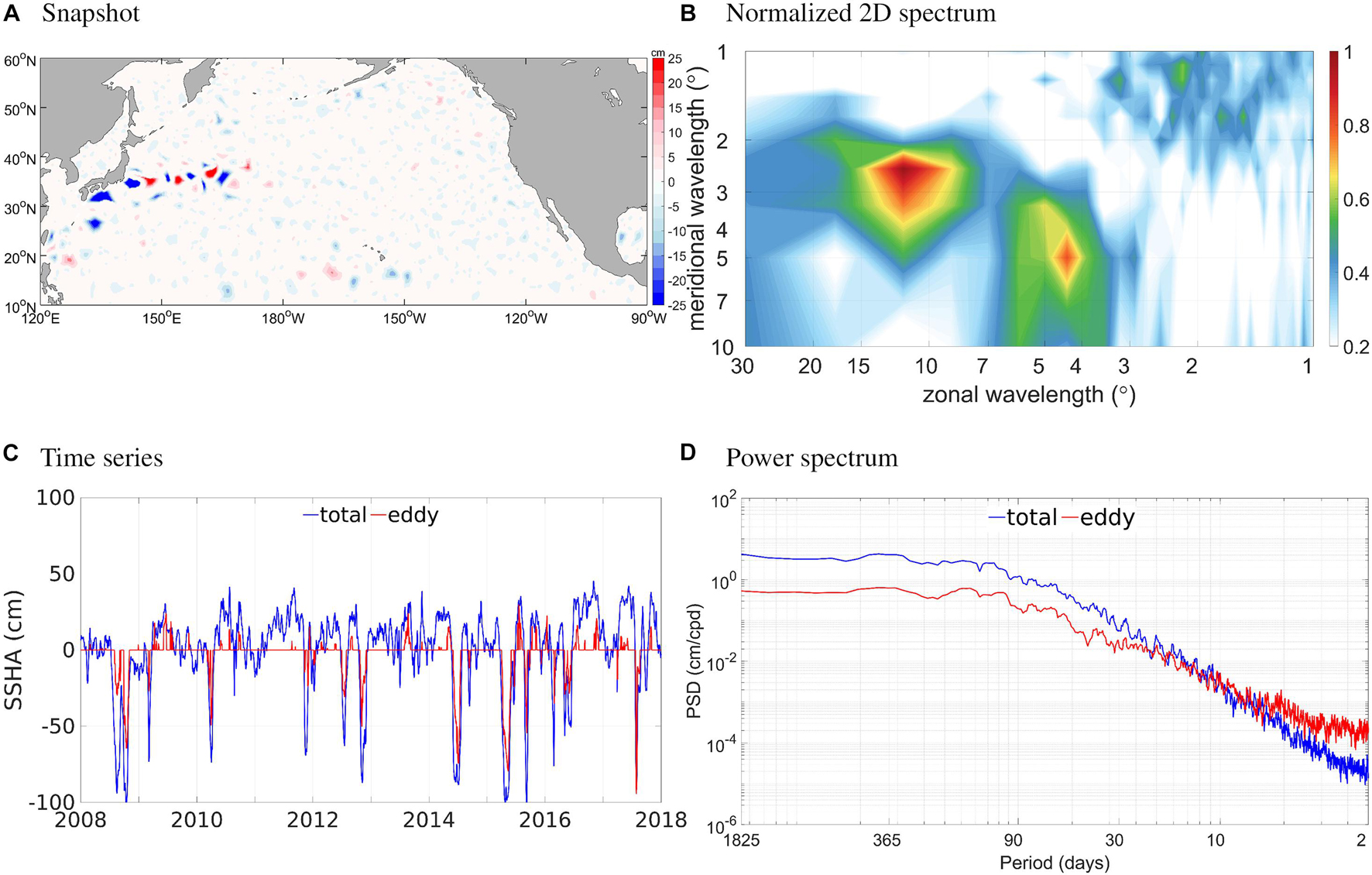
Figure 9. (A) Snapshot of the reconstructed eddy-induced SSH (cm) field on January 1, 2008. (B) Normalized 2D power spectrum of reconstructed SSH in the Kuroshio Extension region (145°–180°E, 30°–40°N), averaged over the year 2008. (C) Time series of the original and reconstructed eddy-induced SSH (cm) at 150°E, 35°N. (D) Power spectral density of the original and reconstructed time series shown in (C).
We then investigate the horizontal distribution of mesoscale eddies’ contribution to the variability of the studied quantities. Bandpass filters are applied on the original and reconstructed fields to extract the variability on submonthly (10–30 days), intra-seasonal (30–90 days), intra-annual (90 days to 1 year), and interannual (1–5 year) timescales. Eddies’ contribution is then measured as the ratio between the standard deviations of eddy-induced and original fields. The results are shown in Figures 10, 11.
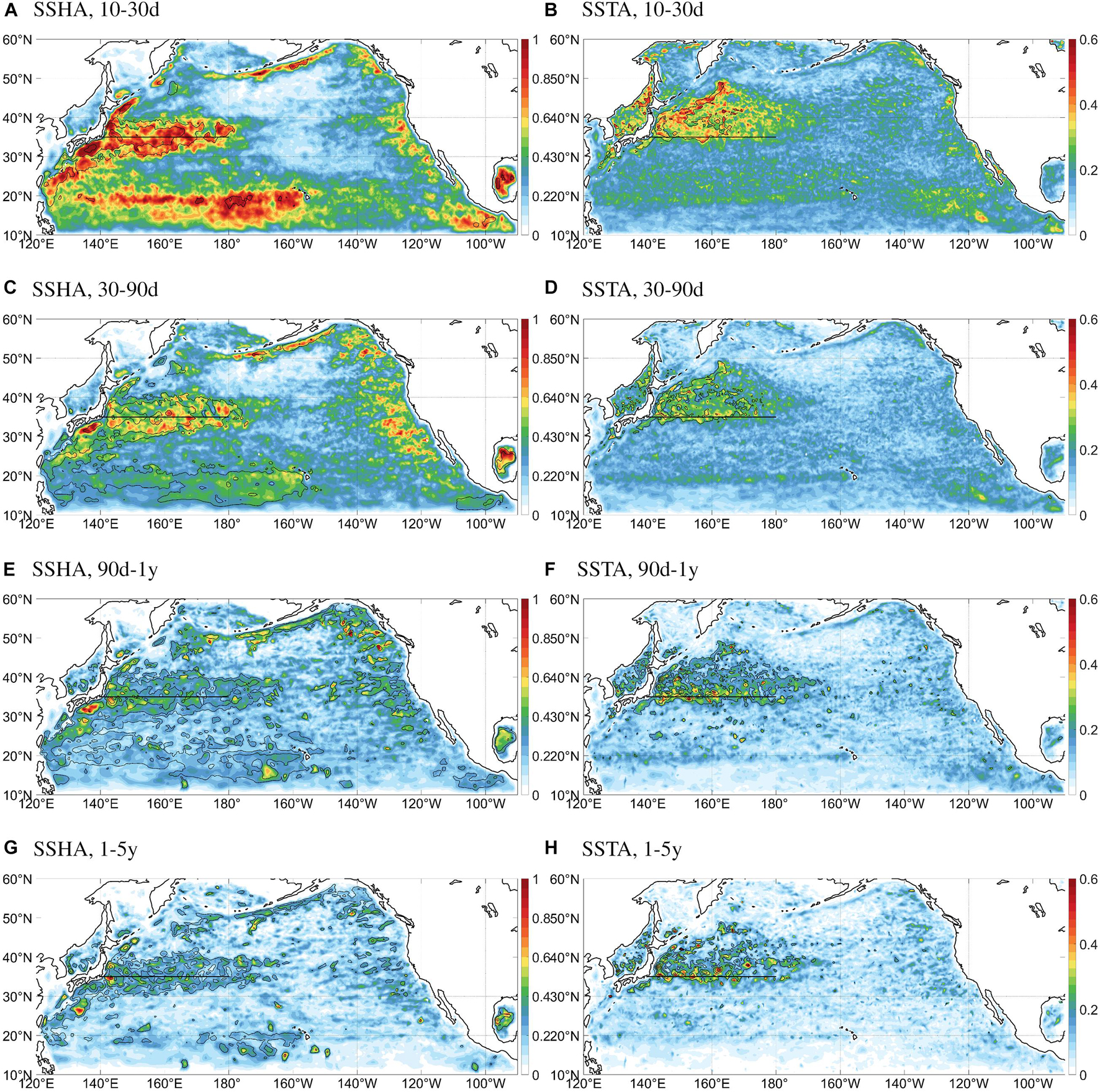
Figure 10. Ratio of standard deviation of eddy-induced and original variability for (A,C,E,G) SSHA, and (B,D,F,H) SSTA on (A,B) sub-monthly (10–30 days), (C,D) intraseasonal (30–90 days), (E,F) intra-annual (90 days–1 year), and (G,H) inter-annual (1–5 years) timescales. The black line indicates the climatological position of the KE jet at 35°N. Note the different color scale for SSTA. Contours show the standard deviation of the eddy-induced fields.
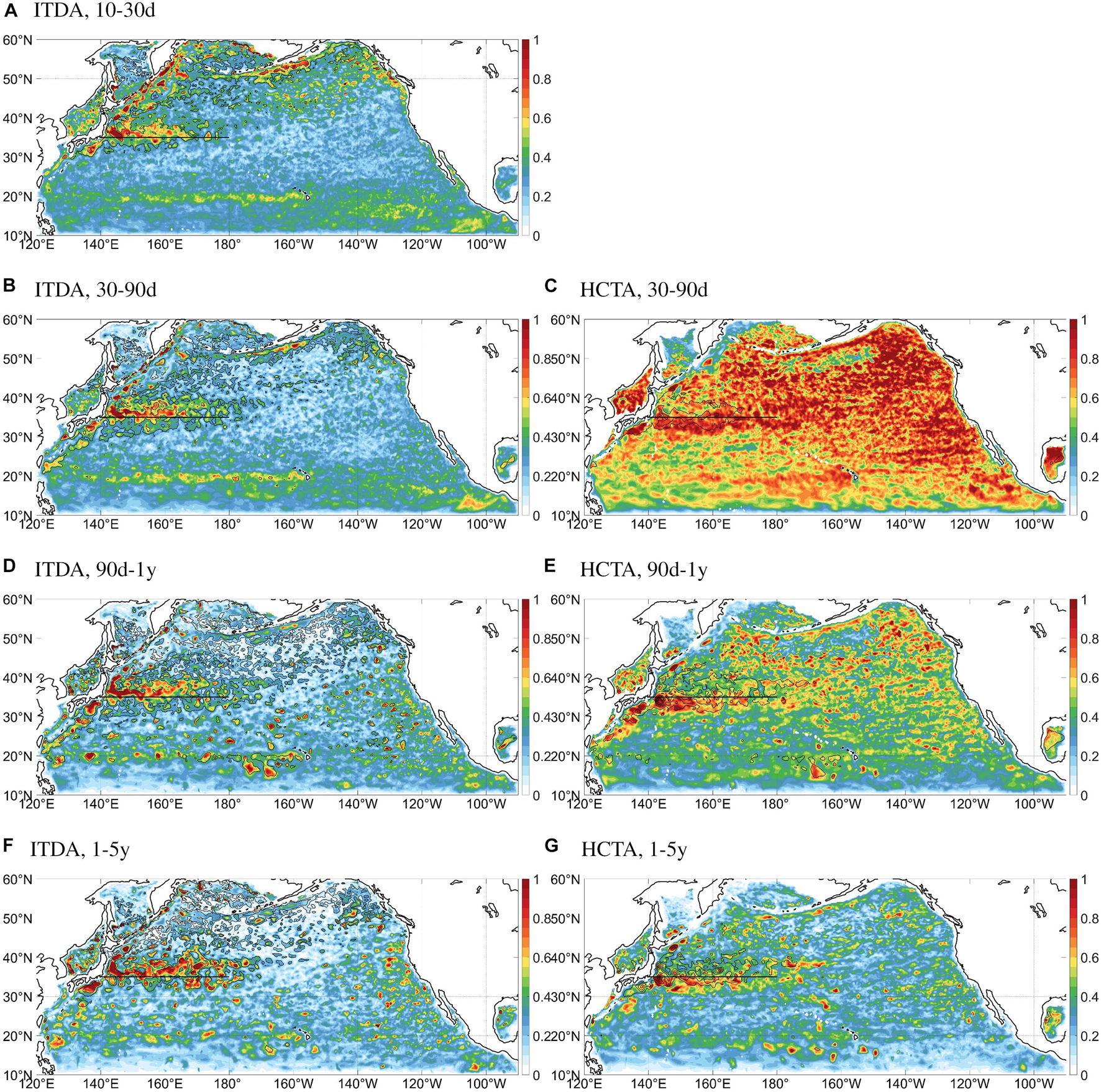
Figure 11. Ratio of standard deviation of eddy-induced and original variability for (A,B,D,F) ITDA, and (C,E,G) HCTA on (A) sub-monthly (10–30 days), (B,C) intraseasonal (30–90 days), (D,E) intra-annual (90 days–1 year), and (F,G) inter-annual (1–5 year) timescales. The black line indicates the climatological position of the KE jet at 35°N. Contours show the standard deviation of the eddy-induced fields.
For SSH, it is evident that eddy-induced variability explains much or nearly all of the submonthly SSH variability in the regions with vigorous eddy activity, i.e., along the Kuroshio and its extension, the STCC, and along the Aleutian Islands (Figure 10A). Some high percentages could also be found along the North American coast, where active Kelvin wave-Rossby wave conversion takes place (Clarke, 1983; Clarke and Shi, 1991; Fu and Qiu, 2002). In the tropical eastern Pacific, tropical instability waves are responsible for a large fraction of the submonthly SSH variability too. In the subtropical and subarctic ocean interior, where eddy activity is less pronounced, the explained standard deviation is close to zero. The pattern of explained SSH variability resembles the pattern of absolute mean eddy amplitude (Figure 1D), except that in the less pronounced eddy active regions than the KE (e.g., the STCC), the weaker eddies do explain a large fraction of total variability. Eddy contribution then decays toward sub-seasonal and longer scales except for some spots along the Kuroshio and in the Gulf of Alaska (Figure 10, left column), respectively, associated with the large meanders of the former (Sugimoto and Hanawa, 2012; Usui et al., 2013) and the quasi-permanent eddies in the latter (Di Lorenzo et al., 2005; Saito et al., 2014).
In terms of SST, eddies’ contribution on submonthly scales is the largest around Japan, especially along the Oyashio Extension Front oriented SW-NE to the west of 170°E where eddies account for as much as 40–60% of the total standard deviation (Figure 10B). The Oyashio Extension Front region is characterized with the strongest SST gradient, and the most vigorous short-term SST variability in the North Pacific (Kida et al., 2015; Zhou et al., 2015; Zhou and Cheng, 2021a). High eddy contribution is also found in the Kuroshio and Oyashio Confluence region, in the northern Japan Sea, in southeast North Pacific, and along the North American coast. Comparing the eddy contribution and the absolute mean eddy-induced SSTA (Figure 4A), it could be inferred that the eddy poleward heat transport plays a more important role in the submonthly SST variability along the Oyashio Extension front than it does in the KE and Kuroshio-Oyashio Confluence region. It is thus indicative that the Oyashio Extension front, which is a quasi-permanent feature, has a significant eddy signature in the high frequency. With increasing time scale, however, eddy contribution in the Oyashio Extension decays monotonically (Figure 10, right column). The KE along 35°N, on the other hand, exhibits relatively high percentage of eddy-explained SST variability on almost every timescale up to interannual, probably due to the temperature advection by the pinched-off eddies from the highly vibrant jet axis. The absolute value of explained variability for SST is smaller than for SSH almost everywhere on corresponding timescales, indicating the greater complexity of other processes including atmospheric forcing in driving SST variability.
Eddy contribution on ITD variability (Figure 11, left column) highlights the KE, the Kuril-Kamchatka Trench, the Aleutian Island Chain, and the STCC. Particularly, in the KE region on the north flank of the climatological KE jet at 35°N, there are the largest eddy contribution (∼100%) on every time scale up to interannual, indicating the dominant role of eddy activity on ITD variability there. South of 35°N, however, eddy-induced ITDA variability is not large. We will come back to this point later after having introduced the eddy contribution to HCTA variability. Along the Kuril-Kamchatka Trench and the Aleutian Island Chain, eddies are responsible for large fractions of ITD variability on submonthly timescales, but their contribution decreases toward the longer scales. This is most likely related to the short lifespan of eddies there, as shown in Figure 1B. The fraction in the STCC is moderate on submonthly and intra-seasonal scales but becomes too patch on longer scales. Near the eastern boundary, high percentage of ITD variability is explained by eddies north of the Vancouver Island on submonthly and intra-seasonal scales but moves to the central and southern part on intra-annual and interannual scales.
Moreover, HCT variability on submonthly scales is almost entirely explained by eddies everywhere and is therefore not shown. This is reflective of the HCT’s lack of high-frequency variability because of the huge thermal inertia of the upper ocean, and the fact that eddies can induce significant heat transport as a result of their movement (Dong et al., 2014). Such high percentage is still present in the intra-seasonal band over most of the basin except for the subarctic and the subtropics where it is on the order of 40–50% (Figure 11C). On intra-annual scales, as can be inferred from Figure 11E, eddies are responsible for over 80% of the total variability in eddy-active regions on the south flank of the KE, in the Japan Sea, and near the eastern boundary. Explained percentages remain high south of the KE on inter-annual timescales while elsewhere they reduce to less than 20% expect for some patchy spots (Figure 11G). The high contribution of eddy-induced HCTA south of the KE on every timescale up to interannual indicates that variability of the subsurface thermal structure is almost entirely determined by eddies there, instead of the low frequency basic flow, i.e., the KE jet and its southern recirculation. It is known that the KE jet, an inertial jet that maximizes below the mixed layer (Mizuno and White, 1983; Kida et al., 2015), exhibits significant variability on decadal timescales (Qiu and Chen, 2005, 2010; Taguchi et al., 2007; Ceballos et al., 2009; Sugimoto and Hanawa, 2009; Kelly et al., 2010; Sugimoto et al., 2014; Qiu et al., 2017). Therefore it is expected that the eddy contribution to HCT will further decrease on decadal timescales.
At this point one might wonder why mesoscale eddies with lifespan on the order of weeks to months can explain some of the variability on longer scales. In the KE region, this is actually a reflection of the low-frequency interaction between eddies and the jet. Extensive studies have shown that the KE jet can force violent eddy generation due to baroclinic and barotropic instability (Waterman et al., 2011; Bishop, 2013; Chen et al., 2014; Fang and Yang, 2016; Yang et al., 2017, 2018; Ji et al., 2018), and the eddies can also feed back to the jet), forming a closed feedback loop on interannual-decadal timescales. Near the eastern boundary, on the other hand, the reason is that the generation of westward-propagating Rossby waves is sensitive, on interannual timescales, to ENSO-generated SSH anomalies that travel northward as coastally-trapped Kelvin waves (e.g., Kessler, 1990; Fu and Qiu, 2002).
Now we focus on the KE region and examine the relationship between eddy-induced SST, ITD, and HCT variabilities. We have noticed that the highest area of SST variability explained by eddies lies along 35°N, whereas for ITD it is on the north flank, and for HCT it is on the south flank. This means eddies can change SST on both sides, but they are more effective in changing the ITD than HCT in the north, and the opposite is true for the south. Our results are thus indicative that the mesoscale eddies are deeper (shallower) south (north) of the mean jet axis. This conclusion is consistent with the observational study of Zhang Z. et al. (2017) and the modeling study of Xu et al. (2019), which both favored concentrated subsurface eddies south of the KE. We also verified the distribution of subsurface eddies in the ECCO2 reanalysis using the criterion proposed by Assassi et al. (2016), which relies on the sign relationship between eddy-induced SSHA and density anomalies, and found similar results (not shown). Liu et al. (2020), however, gave the opposite distribution of eddy depth around the KE axis, but they only focused on surface eddies. It is thus inferable that the southern (northern) region has shallower (deeper) surface eddies and more (less) subsurface eddies.
Conclusion and Discussion
This work examined eddy-induced surface and subsurface thermodynamic anomalies, and quantitatively studied their statistical relations with eddy amplitude. This is a step forward from literature studies on eddy dynamic parameters only, or eddy-induced SST perturbation in the sense of composite mean. Further, the multi-scale assessment on eddies’ contribution to the total variability is novel and instructive. It is now clear that mesoscale eddies can induce large anomalies in upper ocean temperature on various scales. These thermodynamic anomalies can explain a large portion of the total variability. Of the entire basin, the Oyashio Extension exhibits the largest eddy-explained SST on submonthly timescales. The Kuroshio Extension region is highlighted for the largest percentage of ITD and HCT variabilities induced by eddies on every timescale up to interannual. For submonthly timescales, particularly, the percentage of eddy-induced SST variability (∼40%) is close to the previously proposed ratio of ocean internal variability relative to the total SST variability (∼50%, Smirnov et al., 2014), indicating eddies’ dominance among all kinds of ocean internal processes at this scale. Future research on upper ocean thermodynamic variability and air-sea interaction should better acknowledge the role played by ocean mesoscale eddies.
We also used altimeter SSH observations from the AVISO project (Ducet et al., 2000), and blended satellite and buoy SST observations from the NOAA OI-SST dataset (Reynolds et al., 2007), both having the same resolution as the ECCO2, to perform the same studies on the same time range. The results are similar to the ECCO2 results presented above and are therefore omitted. Furthermore, it must be noted that the 1/4°grid size of the ECCO2 and satellite datasets can only partially resolve the heat perturbations due to mesoscale eddies. Recent studies found that the eddies redistribute heat via two major physical mechanisms: water mass trapping within the eddy body, and advective effects by the large velocities around the eddy rim (Xu et al., 2014, 2016). The trapping effect is on a larger scale that is resolvable here, whereas the advection effect needs a much higher resolution. This is thus indicative of the need of submesoscale-resolving observations, modeling results, and reanalysis for better studying eddy thermal effects.
Our results suggest that in the Kuroshio and Oyashio Extension region, mesoscale eddies contribute to about 40–50% of SST variability on monthly to intra-annual timescales. Related to this, Smirnov et al. (2014) used the statistical tool of linear inverse model and proposed that on the corresponding timescales and in the same area, SST variability induced by intrinsic oceanic processes is about 50%. Although they used different data and methodology as this work, it is still useful to compare the findings. Since mesoscale eddies are just one component of intrinsic oceanic process, that the contribution of eddies is smaller than the total oceanic intrinsic process is understandable, and also indicative of the dominant role of eddies among other oceanic processes on the intra-annual and smaller timescales. Moreover, Bishop et al. (2017) concluded, also using a statistical model, that the explained SST variability by oceanic processes in western boundary current regions increases with timescale, in contrast to our finding of monotonically decreasing eddy contribution. This suggests that as the timescale grows, other oceanic intrinsic processes than mesoscale eddies, e.g., interannual variability of western boundary currents, take over and play more important roles in air-sea interaction.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.
Author Contributions
JZ performed the data analysis and wrote the initial draft. GZ proposed the main ideas, took part in the data analysis, and dramatically modified the manuscript. HL, ZL, and XC participated to the discussions and contributed to the improvement of the manuscript. All authors contributed to the article and approved the submitted version.
Funding
GZ was supported by the National Natural Science Foundation of China (grant no. 41906001), the Natural Science Foundation of Jiangsu Province (Grant No. BK20190501), and the Fundamental Research Funds for the Central Universities (Grant No. B210202137). HL was supported by the National Natural Science Foundation of China (Grant No. 41931183). ZL was supported by the Fundamental Research Funds for the Central Universities (Grant No. B19020044) and 2020 Jiangsu Shuangchuang (Mass Innovation and Entrepreneurship) Talent Program (Grant No. 2020–30448).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Assassi, C., Morel, Y., Vandermeirsch, F., Chaigneau, A., Pegliasco, C., Morrow, R., et al. (2016). An index to distinguish surface- and subsurface-intensified vortices from surface observations. J. Phys. Oceanogr. 46, 2529–2552. doi: 10.1175/JPO-D-15-0122.1
Bachman, S. D., Taylor, J. R., Adams, K. A., and Hosegood, P. J. (2017). Mesoscale and submesoscale effects on mixed layer depth in the southern ocean. J. Phys. Oceanogr. 47, 2173–2188. doi: 10.1175/JPO-D-17-0034.1
Bashmachnikov, I., Boutov, D., and Dias, J. (2013). Manifestation of two meddies in altimetry and sea-surface temperature. Ocean Sci. 9, 249–259. doi: 10.5194/os-9-249-2013
Bishop, S. P. (2013). Divergent eddy heat fluxes in the kuroshio extension at 144°–148°E. Part II: spatiotemporal variability. J. Phys. Oceanogr. 43, 2416–2431. doi: 10.1175/JPO-D-13-061.1
Bishop, S. P., Small, R. J., Bryan, F. O., and Tomas, R. A. (2017). Scale dependence of midlatitude air-sea interaction. J. Clim. 30, 8207–8221. doi: 10.1175/JCLI-D-17-0159.1
Breugem, W.-P., Chang, P., Jang, C. J., Mignot, J., and Hazeleger, W. (2008). Barrier layers and tropical Atlantic SST biases in coupled GCMs. Tellus A Dyn. Meteorol. Oceanogr. 60, 885–897. doi: 10.1111/j.1600-0870.2008.00343.x
Ceballos, L. I., Di Lorenzo, E., Hoyos, C. D., Schneider, N., and Taguchi, B. (2009). North Pacific gyre oscillation synchronizes climate fluctuations in the eastern and western boundary systems. J. Clim. 22, 5163–5174. doi: 10.1175/2009JCLI2848.1
Chaigneau, A., Gizolme, A., and Grados, C. (2008). Mesoscale eddies off Peru in altimeter records: identification algorithms and eddy spatio-temporal patterns. Prog. Oceanogr. 79, 106–119. doi: 10.1016/j.pocean.2008.10.013
Chelton, D. (2013). Ocean-atmosphere coupling: Mesoscale eddy effects. Nat. Geosci. 6, 594–595. doi: 10.1038/ngeo1906
Chelton, D. B., Schlax, M. G., and Samelson, R. M. (2011). Global observations of nonlinear mesoscale eddies. Prog. Oceanogr. 91, 167–216. doi: 10.1016/j.pocean.2011.01.002
Chelton, D. B., Schlax, M. G., Samelson, R. M., and de Szoeke, R. A. (2007). Global observations of large oceanic eddies. Geophys. Res. Lett. 34:L15606. doi: 10.1029/2007GL030812
Chen, L., Jia, Y., and Liu, Q. (2017). Oceanic eddy-driven atmospheric secondary circulation in the winter Kuroshio Extension region. J. Oceanogr. 73, 295–307. doi: 10.1007/s10872-016-0403-z
Chen, R., Flierl, G. R., and Wunsch, C. (2014). A description of local and nonlocal eddy–mean flow interaction in a global eddy-permitting state estimate. J. Phys. Oceanogr. 44, 2336–2352. doi: 10.1175/JPO-D-14-0009.1
Cheng, Y.-H., Ho, C.-R., Zheng, Q., and Kuo, N.-J. (2014). Statistical characteristics of mesoscale eddies in the North Pacific derived from satellite altimetry. Remote Sens. 6, 5164–5183. doi: 10.3390/rs6065164
Chiang, T.-L., Wu, C.-R., Qu, T., and Hsin, Y.-C. (2015). Activities of 50-80 day subthermocline eddies near the Philippine coast. J. Geophys. Res. Ocean. 120, 3606–3623. doi: 10.1002/2013JC009626
Clarke, A. J. (1983). The reflection of equatorial waves from oceanic boundaries. J. Phys. Oceanogr. 13, 1193–1207.
Clarke, A. J., and Shi, C. (1991). Critical frequencies at ocean boundaries. J. Geophys. Res. Ocean 96, 10731–10738. doi: 10.1029/91JC00933
Cushman-Roisen, B., Chassignet, E. P., and Tang, B. (1990). Westward motion of mesoscale eddies. J. Phys. Oceanogr. 20, 758–768.
de Boyer Montégut, C., Madec, G., Fischer, A. S., Lazar, A., and Iudicone, D. (2004). Mixed layer depth over the global ocean: an examination of profile data and a profile-based climatology. J. Geophys. Res. 109, 1–20. doi: 10.1029/2004JC002378
de Boyer Montégut, C., Mignot, J., Lazar, A., and Cravatte, S. (2007). Control of salinity on the mixed layer depth in the world ocean: 1. General description. J. Geophys. Res. 112:C06011. doi: 10.1029/2006JC003953
Di Lorenzo, E., Foreman, M. G. G., and Crawford, W. R. (2005). Modelling the generation of Haida Eddies. Deep Sea Res. Part II Top. Stud. Oceanogr. 52, 853–873. doi: 10.1016/j.dsr2.2005.02.007
Ding, M., Lin, P., Liu, H., and Chai, F. (2018). Increased eddy activity in the Northeastern Pacific during 1993–2011. J. Clim. 31, 387–399. doi: 10.1175/JCLI-D-17-0309.1
Doglioli, A. M., Blanke, B., Speich, S., and Lapeyre, G. (2007). Tracking coherent structures in a regional ocean model with wavelet analysis: application to Cape Basin eddies. J. Geophys. Res. 112:C05043. doi: 10.1029/2006JC003952
Doney, S. C., Yeager, S., Danabasoglu, G., Large, W. G., and McWilliams, J. C. (2007). Mechanisms governing interannual variability of upper-ocean temperature in a global ocean hindcast simulation. J. Phys. Oceanogr. 37, 1918–1938. doi: 10.1175/JPO3089.1
Dong, C., McWilliams, J. C., Liu, Y., and Chen, D. (2014). Global heat and salt transports by eddy movement. Nat. Commun. 5:3294. doi: 10.1038/ncomms4294
Dong, C., Nencioli, F., Liu, Y., and McWilliams, J. C. (2011). An automated approach to detect oceanic eddies from satellite remotely sensed sea surface temperature data. IEEE Geosci. Remote Sens. Lett. 8, 1055–1059. doi: 10.1109/LGRS.2011.2155029
Ducet, N., Le Traon, P. Y., and Reverdin, G. (2000). Global high-resolution mapping of ocean circulation from TOPEX/Poseidon and ERS-1 and –2. J. Geophys. Res. Ocean. 105, 19477–19498. doi: 10.1029/2000JC900063
Faghmous, J. H., Frenger, I., Yao, Y., Warmka, R., Lindell, A., and Kumar, V. (2015). A daily global mesoscale ocean eddy dataset from satellite altimetry. Sci. Data 2:150028. doi: 10.1038/sdata.2015.28
Fang, F., and Morrow, R. (2003). Evolution, movement and decay of warm-core Leeuwin Current eddies. Deep Sea Res. Part II Top. Stud. Oceanogr. 50, 2245–2261. doi: 10.1016/S0967-0645(03)00055-9
Fang, J., and Yang, X.-Q. (2016). Structure and dynamics of decadal anomalies in the wintertime midlatitude North Pacific ocean–atmosphere system. Clim. Dyn. 47, 1989–2007. doi: 10.1007/s00382-015-2946-x
Ferrari, R., and Wunsch, C. (2009). Ocean circulation kinetic energy: reservoirs, Sources, and Sinks. Annu. Rev. Fluid Mech. 41, 253–282. doi: 10.1146/annurev.fluid.40.111406.102139
Fofonoff, N. P., and Millard, R. C. Jr. (1983). Algorithms for Computation of Fundamental Properties of Seawater. Paris: UNESCO, 58.
Frankignoul, C., and Hasselmann, K. (1977). Stochastic climate models, part II application to sea-surface temperature anomalies and thermocline variability. Tellus 29, 289–305.
Frenger, I., Gruber, N., Knutti, R., and Münnich, M. (2013). Imprint of Southern Ocean eddies on winds, clouds and rainfall. Nat. Geosci. 6, 608–612. doi: 10.1038/ngeo1863
Frenger, I., Münnich, M., Gruber, N., and Knutti, R. (2015). Southern Ocean eddy phenomenology. J. Geophys. Res. Ocean. 120, 7413–7449. doi: 10.1002/2015JC011047
Fu, L.-L. (2009). Pattern and velocity of propagation of the global ocean eddy variability. J. Geophys. Res. 114:C11017. doi: 10.1029/2009JC005349
Fu, L. L., and Qiu, B. (2002). Low-frequency variability of the North Pacific Ocean: the roles of boundary- and wind-driven baroclinic Rossby waves. J. Geophys. Res. Ocean 107:3220. doi: 10.1029/2001JC001131
Gaube, P., Chelton, D. B., Strutton, P. G., and Behrenfeld, M. J. (2013). Satellite observations of chlorophyll, phytoplankton biomass, and Ekman pumping in nonlinear mesoscale eddies. J. Geophys. Res. Ocean. 118, 6349–6370. doi: 10.1002/2013JC009027
Hasselmann, K. (1976). Stochastic climate models Part I. Theory. Tellus 28, 473–485. doi: 10.1111/j.2153-3490.1976.tb00696.x
Holland, C. L., and Mitchum, G. T. (2001). Propagation of big island eddies. J. Geophys. Res. 106, 935–944.
Hughes, C. W. (1996). The Antarctic circumpolar current as a waveguide for Rossby Waves. J. Phys. Oceanogr. 26, 1375–1387.
Hwang, C., Wu, C.-R., and Kao, R. (2004). TOPEX/Poseidon observations of mesoscale eddies over the subtropical countercurrent: kinematic characteristics of an anticyclonic eddy and a cyclonic eddy. J. Geophys. Res. Ocean 109:C08013. doi: 10.1029/2003JC002026
Itoh, S., and Yasuda, I. (2010). Characteristics of mesoscale eddies in the kuroshio–oyashio extension region detected from the distribution of the sea surface height anomaly. J. Phys. Oceanogr. 40, 1018–1034. doi: 10.1175/2009JPO4265.1
Ji, J., Dong, C., Zhang, B., Liu, Y., Zou, B., King, G. P., et al. (2018). Oceanic eddy characteristics and generation mechanisms in the Kuroshio Extension region. J. Geophys. Res. Ocean. 123, 8548–8567. doi: 10.1029/2018JC014196
Kawasaki, T., and Hasumi, H. (2010). Role of localized mixing around the Kuril Straits in the Pacific thermohaline circulation. J. Geophys. Res. 115:C11002. doi: 10.1029/2010JC006130
Kawasaki, T., Hasumi, H., and Tanaka, Y. (2021). Role of tide–induced vertical mixing in the deep Pacific Ocean circulation. J. Oceanogr. 77, 173–184. doi: 10.1007/s10872-020-00584-0
Kelly, K. A., Small, R. J., Samelson, R. M., Qiu, B., Joyce, T. M., Kwon, Y.-O., et al. (2010). Western boundary currents and frontal air–sea interaction: gulf stream and Kuroshio Extension. J. Clim. 23, 5644–5667. doi: 10.1175/2010JCLI3346.1
Kessler, W. S. (1990). Observations of long Rossby waves in the northern tropical Pacific. J. Geophys. Res. Ocean. 95, 5183–5217. doi: 10.1029/JC095iC04p05183
Kida, S., Mitsudera, H., Aoki, S., Guo, X., Ito, S., Kobashi, F., et al. (2015). Oceanic fronts and jets around Japan: a review. J. Oceanogr. 71, 469–497. doi: 10.1007/s10872-015-0283-7
Kurian, J., Colas, F., Capet, X., McWilliams, J. C., and Chelton, D. B. (2011). Eddy properties in the California Current System. J. Geophys. Res. 116:C08027. doi: 10.1029/2010JC006895
Liu, X., Ma, X., Chang, P., Jia, Y., Fu, D., Xu, G., et al. (2021). Ocean fronts and eddies force atmospheric rivers and heavy precipitation in western North America. Nat. Commun. 12:1268. doi: 10.1038/s41467-021-21504-w
Liu, Y., Zheng, Q., and Li, X. (2021). Characteristics of global ocean abnormal mesoscale eddies derived from the fusion of sea surface height and temperature data by deep learning. Geophys. Res. Lett. 48:e2021GL094772. doi: 10.1029/2021GL094772
Liu, Z., Liao, G., Hu, X., and Zhou, B. (2020). Aspect ratio of eddies inferred from argo floats and satellite altimeter data in the ocean. J. Geophys. Res. Ocean 125:e2019JC015555. doi: 10.1029/2019JC015555
Ma, X., Chang, P., Saravanan, R., Montuoro, R., Hsieh, J. S., Wu, D., et al. (2015). Distant influence of Kuroshio Eddies on North Pacific weather patterns? Sci. Rep. 5:17785. doi: 10.1038/srep17785
Ma, X., Chang, P., Saravanan, R., Montuoro, R., Nakamura, H., Wu, D., et al. (2017). Importance of resolving kuroshio front and eddy influence in simulating the north pacific storm track. J. Clim. 30, 1861–1880. doi: 10.1175/JCLI-D-16-0154.1
Marshall, J., Adcroft, A., Hill, C., Perelman, L., and Heisey, C. (1997). A finite-volume, incompressible Navier Stokes model for studies of the ocean on parallel computers. J. Geophys. Res. Ocean. 102, 5753–5766. doi: 10.1029/96JC02775
Masunaga, R., Nakamura, H., Miyasaka, T., Nishii, K., and Qiu, B. (2016). Interannual modulations of oceanic imprints on the wintertime atmospheric boundary layer under the changing dynamical regimes of the Kuroshio Extension. J. Clim. 29, 3273–3296. doi: 10.1175/JCLI-D-15-0545.1
Menemenlis, D., Campin, J.-M., Heimbach, P., Hill, C. N., Lee, T., Nguyen, A. T., et al. (2008). ECCO2: high resolution global ocean and sea ice data synthesis. Mercat. Ocean Q. Newslett. 31, 13–21.
Menemenlis, D., Fukumori, I., and Lee, T. (2005). Using Green’s functions to calibrate an ocean general circulation model. Mon. Weather Rev. 133, 1224–1240. doi: 10.1175/MWR2912.1
Mizuno, K., and White, W. B. (1983). Annual and interannual variability in the kuroshio current system. J. Phys. Oceanogr. 13, 1847–1867.
Morrow, R., Fang, F., Fieux, M., and Molcard, R. (2003). Anatomy of three warm-core Leeuwin Current eddies. Deep Sea Res. 2 Top. Stud. Oceanogr. 50, 2229–2243. doi: 10.1016/S0967-0645(03)00054-7
Morrow, R., and Le Traon, P.-Y. (2012). Recent advances in observing mesoscale ocean dynamics with satellite altimetry. Adv. Space Res. 50, 1062–1076. doi: 10.1016/j.asr.2011.09.033
Nencioli, F., Dong, C., Dickey, T., Washburn, L., and McWilliams, J. C. (2010). A vector geometry–based eddy detection algorithm and its application to a high-resolution numerical model product and high-frequency radar surface velocities in the southern california bight. J. Atmos. Ocean. Technol. 27, 564–579. doi: 10.1175/2009JTECHO725.1
Nof, D. (1981). On the β-induced movement of isolated Baroclinic eddies. J. Phys. Oceanogr. 11, 1662–1672.
Oliveira, F. S. C., and Polito, P. S. (2013). Characterization of westward propagating signals in the South Atlantic from altimeter and radiometer records. Remote Sens. Environ. 134, 367–376. doi: 10.1016/j.rse.2013.03.019
O’Neill, L. W. (2012). Wind speed and stability effects on coupling between surface wind stress and SST observed from buoys and satellite. J. Clim. 25, 1544–1569. doi: 10.1175/JCLI-D-11-00121.1
Palacios, D. M., and Bograd, S. J. (2005). A census of Tehuantepec and Papagayo eddies in the northeastern tropical Pacific. Geophys. Res. Lett. 32:L23606. doi: 10.1029/2005GL024324
Pang, S., Wang, X., Liu, H., Zhou, G., and Fan, K. (2019). Decadal variability of the barrier layer and forcing mechanism in the Bay of Bengal. J. Geophys. Res. Ocean. 124, 5289–5307. doi: 10.1029/2018JC014918
Pegliasco, C., Chaigneau, A., and Morrow, R. (2015). Main eddy vertical structures observed in the four major Eastern Boundary Upwelling Systems. J. Geophys. Res. Ocean. 120, 6008–6033. doi: 10.1002/2015JC010950
Pelland, N. A., Eriksen, C. C., and Lee, C. M. (2013). Subthermocline eddies over the Washington continental slope as observed by seagliders, 2003–09. J. Phys. Oceanogr. 43, 2025–2053. doi: 10.1175/JPO-D-12-086.1
Petersen, M. R., Williams, S. J., Maltrud, M. E., Hecht, M. W., and Hamann, B. (2013). A three-dimensional eddy census of a high-resolution global ocean simulation. J. Geophys. Res. Ocean. 118, 1759–1774. doi: 10.1002/jgrc.20155
Pingree, R., and Sinha, B. (2001). Westward moving waves or eddies (Storms) on the Subtropical/Azores Front near 32°N? Interpretation of the Eulerian currents and temperature records at moorings 155 (35.5°W) and 156 (34.4°W). J. Mar. Syst. 29, 239–276.
Polito, P. S., and Sato, O. T. (2015). Do eddies ride on Rossby waves? J. Geophys. Res. Ocean. 120, 5417–5435. doi: 10.1002/2015JC010737
Putrasahan, D. A., Kamenkovich, I., Le Hénaff, M., and Kirtman, B. P. (2017). Importance of ocean mesoscale variability for air-sea interactions in the Gulf of Mexico. Geophys. Res. Lett. 44, 6352–6362. doi: 10.1002/2017GL072884
Qiu, B., and Chen, S. (2005). Variability of the Kuroshio Extension jet, recirculation gyre, and mesoscale eddies on decadal time scales. J. Phys. Oceanogr. 35, 2090–2103. doi: 10.1175/JPO2807.1
Qiu, B., and Chen, S. (2010). Eddy-mean flow interaction in the decadally modulating Kuroshio Extension system. Deep Sea Res. 2 Top. Stud. Oceanogr. 57, 1098–1110. doi: 10.1016/j.dsr2.2008.11.036
Qiu, B., Chen, S., and Schneider, N. (2017). Dynamical links between the decadal variability of the Oyashio and Kuroshio Extensions. J. Clim. 30, 9591–9605. doi: 10.1175/JCLI-D-17-0397.1
Qiu, B., Miao, W., and Müller, P. (1997). Propagation and decay of forced and free Baroclinic Rossby Waves in off-equatorial oceans. J. Phys. Oceanogr. 27, 2405–2417.
Reynolds, R. W., Smith, T. M., Liu, C., Chelton, D. B., Casey, K. S., and Schlax, M. G. (2007). Daily high-resolution-blended analyses for sea surface temperature. J. Clim. 20, 5473–5496. doi: 10.1175/2007JCLI1824.1
Richardson, P. L. (1983). Eddy kinetic energy in the North Atlantic from surface drifters. J. Geophys. Res. 88:4355. doi: 10.1029/JC088iC07p04355
Rogachev, K., Shlyk, N., and Carmack, E. (2007). The shedding of mesoscale anticyclonic eddies from the Alaskan Stream and westward transport of warm water. Deep Sea Res. Part II Top. Stud. Oceanogr. 54, 2643–2656. doi: 10.1016/j.dsr2.2007.08.017
Rogachev, K. A., and Shlyk, N. V. (2018). The role of the aleutian eddies in the kamchatka current warming. Russ. Meteorol. Hydrol. 43, 43–48. doi: 10.3103/S1068373918010065
Rogachev, K. A., and Shlyk, N. V. (2019). Characteristics of the Kamchatka Current eddies. Russ. Meteorol. Hydrol. 44, 416–423. doi: 10.3103/S1068373919060062
Saito, R., Yamaguchi, A., Yasuda, I., Ueno, H., Ishiyama, H., Onishi, H., et al. (2014). Influences of mesoscale anticyclonic eddies on the zooplankton community south of the western Aleutian Islands during the summer of 2010. J. Plankton Res. 36, 117–128. doi: 10.1093/plankt/fbt087
Seo, Y., Sugimoto, S., and Hanawa, K. (2014). Long-term variations of the Kuroshio Extension path in winter: meridional movement and path state change. J. Clim. 27, 5929–5940. doi: 10.1175/JCLI-D-13-00641.1
Sérazin, G., Penduff, T., Barnier, B., Molines, J.-M., Arbic, B. K., Müller, M., et al. (2018). Inverse cascades of kinetic energy as a source of intrinsic variability: a global OGCM study. J. Phys. Oceanogr. 48, 1385–1408. doi: 10.1175/JPO-D-17-0136.1
Smirnov, D., Newman, M., and Alexander, M. A. (2014). Investigating the role of ocean-atmosphere coupling in the North Pacific ocean. J. Clim. 27, 592–606. doi: 10.1175/JCLI-D-13-00123.1
Song, B., Wang, H., Chen, C., Zhang, R., and Bao, S. (2019). Observed subsurface eddies near the Vietnam coast of the South China Sea. Acta Oceanol. Sin. 38, 39–46. doi: 10.1007/s13131-019-1412-8
Song, W., Lan, J., Liu, Q., Sui, D., Zeng, L., and Wang, D. (2014). Decadal variability of heat content in the South China Sea inferred from observation data and an ocean data assimilation product. Ocean Sci. 10, 135–139. doi: 10.5194/os-10-135-2014
Stephenson, G. R., Gille, S. T., and Sprintall, J. (2013). Processes controlling upper-ocean heat content in Drake Passage. J. Geophys. Res. Ocean. 118, 4409–4423. doi: 10.1002/jgrc.20315
Sugimoto, S., Aono, K., and Fukui, S. (2017). Local atmospheric response to warm mesoscale ocean eddies in the Kuroshio–Oyashio Confluence region. Sci. Rep. 7:11871. doi: 10.1038/s41598-017-12206-9
Sugimoto, S., and Hanawa, K. (2009). Decadal and interdecadal variations of the aleutian low activity and their relation to upper oceanic variations over the North Pacific. J. Meteorol. Soc. Japan. Ser. II 87, 601–614. doi: 10.2151/jmsj.87.601
Sugimoto, S., and Hanawa, K. (2011). Roles of SST anomalies on the wintertime turbulent heat fluxes in the Kuroshio-Oyashio confluence region: influences of warm eddies detached from the Kuroshio Extension. J. Clim. 24, 6551–6561.
Sugimoto, S., and Hanawa, K. (2012). Relationship between the path of the Kuroshio in the south of Japan and the path of the Kuroshio Extension in the east. J. Oceanogr. 68, 219–225. doi: 10.1007/s10872-011-0089-1
Sugimoto, S., Kobayashi, N., and Hanawa, K. (2014). Quasi-decadal variation in intensity of the western part of the winter subarctic SST front in the Western North Pacific: the influence of Kuroshio Extension path state. J. Phys. Oceanogr. 44, 2753–2762. doi: 10.1175/JPO-D-13-0265.1
Taguchi, B., Xie, S. P., Schneider, N., Nonaka, M., Sasaki, H., and Sasai, Y. (2007). Decadal variability of the Kuroshio Extension: observations and an eddy-resolving model hindcast. J. Clim. 20, 2357–2377. doi: 10.1175/JCLI4142.1
Tanaka, Y., Hibiya, T., and Niwa, Y. (2010). Assessment of the effects of tidal mixing in the Kuril Straits on the formation of the North Pacific intermediate water. J. Phys. Oceanogr. 40, 2569–2574. doi: 10.1175/2010JPO4506.1
Usui, N., Tsujino, H., Nakano, H., and Matsumoto, S. (2013). Long-term variability of the Kuroshio path south of Japan. J. Oceanogr. 69, 647–670. doi: 10.1007/s10872-013-0197-1
Vivier, F., Kelly, K. A., and Thompson, L. A. (2002). Heat budget in the Kuroshio Extension region: 1993–99. J. Phys. Oceanogr. 32, 3436–3454.
Wang, Q. (2017). Three-dimensional structure of mesoscale eddies in the western tropical Pacific as revealed by a high-resolution ocean simulation. Sci. China Earth Sci. 60, 1719–1731. doi: 10.1007/s11430-016-9072-y
Wang, Y., Zhang, H.-R., Chai, F., and Yuan, Y. (2018). Impact of mesoscale eddies on chlorophyll variability off the coast of Chile. PLoS One 13:e0203598. doi: 10.1371/journal.pone.0203598
Waterman, S., Hogg, N. G., and Jayne, S. R. (2011). Eddy–mean flow interaction in the Kuroshio Extension region. J. Phys. Oceanogr. 41, 1182–1208. doi: 10.1175/2010JPO4564.1
Waterman, S., and Jayne, S. R. (2011). Eddy-mean flow interactions in the along-stream development of a western boundary current jet: an idealized model study. J. Phys. Oceanogr. 41, 682–707. doi: 10.1175/2010JPO4477.1
Wunsch, C., Heimbach, P., Ponte, R., and Fukumori, I. (2009). The global general circulation of the ocean estimated by the ECCO-consortium. Oceanography 22, 88–103. doi: 10.5670/oceanog.2009.41
Wyrtki, K., Magaard, L., and Hager, J. (1976). Eddy energy in the oceans. J. Geophys. Res. 81, 2641–2646. doi: 10.1029/JC081i015p02641
Xu, A., Yu, F., and Nan, F. (2019). Study of subsurface eddy properties in northwestern Pacific Ocean based on an eddy-resolving OGCM. Ocean Dyn. 69, 463–474. doi: 10.1007/s10236-019-01255-5
Xu, A., Yu, F., Nan, F., and Ren, Q. (2020). Characteristics of subsurface mesoscale eddies in the northwestern tropical Pacific Ocean from an eddy-resolving model. J. Oceanol. Limnol. 38, 1421–1434. doi: 10.1007/s00343-020-9313-4
Xu, L., Li, P., Xie, S. P., Liu, Q., Liu, C., and Gao, W. (2016). Observing mesoscale eddy effects on mode-water subduction and transport in the North Pacific. Nat. Commun. 7:10505. doi: 10.1038/ncomms10505
Xu, L., Xie, S.-P., McClean, J. L., Liu, Q., and Sasaki, H. (2014). Mesoscale eddy effects on the subduction of North Pacific mode waters. J. Geophys. Res. Ocean. 119, 4867–4886. doi: 10.1002/2014JC009861
Yagi, M., and Yasuda, I. (2013). A modified method for estimating vertical profiles of turbulent dissipation rate using density inversions in the Kuril Straits. J. Oceanogr. 69, 203–214. doi: 10.1007/s10872-012-0165-1
Yang, H., Qiu, B., Chang, P., Wu, L., Wang, S., Chen, Z., et al. (2018). Decadal variability of eddy characteristics and energetics in the Kuroshio Extension: unstable versus stable states. J. Geophys. Res. Ocean. 123, 6653–6669. doi: 10.1029/2018JC014081
Yang, Y., and Liang, X. S. (2016). The instabilities and multiscale energetics underlying the mean–interannual–eddy interactions in the Kuroshio Extension region. J. Phys. Oceanogr. 46, 1477–1494. doi: 10.1175/JPO-D-15-0226.1
Yang, Y., Liang, X. S., Qiu, B., and Chen, S. (2017). On the decadal variability of the eddy kinetic energy in the Kuroshio Extension. J. Phys. Oceanogr. 47, 1169–1187. doi: 10.1175/JPO-D-16-0201.1
Zhang, C., Li, H., Liu, S., Shao, L., Zhao, Z., and Liu, H. (2015). Automatic detection of oceanic eddies in reanalyzed SST images and its application in the East China Sea. Sci. China Earth Sci. 58, 2249–2259. doi: 10.1007/s11430-015-5101-y
Zhang, C., Liu, H., Li, C., and Lin, P. (2019). Impacts of mesoscale sea surface temperature anomalies on the meridional shift of North Pacific storm track. Int. J. Climatol. 39, 5124–5139. doi: 10.1002/joc.6130
Zhang, C., Liu, H., Xie, J., Lin, P., Li, C., Yang, Q., et al. (2020). North Pacific storm track response to the mesoscale SST in a global high-resolution atmospheric model. Clim. Dyn. 55, 1597–1611. doi: 10.1007/s00382-020-05343-x
Zhang, Z., Li, P., Xu, L., Li, C., Zhao, W., Tian, J., et al. (2015). Subthermocline eddies observed by rapid-sampling Argo floats in the subtropical northwestern Pacific Ocean in spring 2014. Geophys. Res. Lett. 42, 6438–6445. doi: 10.1002/2015GL064601
Zhang, Z., Zhang, Y., and Wang, W. (2017). Three-compartment structure of subsurface-intensified mesoscale eddies in the ocean. J. Geophys. Res. Ocean. 122, 1653–1664. doi: 10.1002/2016JC012376
Zhao, D., Xu, Y., Zhang, X., and Huang, C. (2021). Global chlorophyll distribution induced by mesoscale eddies. Remote Sens. Environ. 254:112245. doi: 10.1016/j.rse.2020.112245
Zhou, G., and Cheng, X. (2021b). On the errors of estimating oceanic eddy kinetic energy. J. Geophys. Res. Ocean 126:e2020JC016449. doi: 10.1029/2020JC016449
Zhou, G., and Cheng, X. (2021a). Impacts of oceanic fronts and eddies in the Kuroshio-Oyashio Extension region on the atmospheric general circulation and storm track. Adv. Atmos. Sci. doi: 10.1007/s00376-021-0408-4
Zhou, G., Latif, M., Greatbatch, R. J., and Park, W. (2015). Atmospheric response to the North Pacific enabled by daily sea surface temperature variability. Geophys. Res. Lett. 42, 7732–7739. doi: 10.1002/2015GL065356
Keywords: mesoscale eddy, sea surface temperature, upper ocean heat content, isothermal layer depth, sea surface height
Citation: Zhou J, Zhou G, Liu H, Li Z and Cheng X (2021) Mesoscale Eddy-Induced Ocean Dynamic and Thermodynamic Anomalies in the North Pacific. Front. Mar. Sci. 8:756918. doi: 10.3389/fmars.2021.756918
Received: 11 August 2021; Accepted: 25 October 2021;
Published: 12 November 2021.
Edited by:
Zhiyu Liu, Xiamen University, ChinaReviewed by:
Lixiao Xu, Ocean University of China, ChinaDi Dong, Southern Ocean Science and Engineering Guangdong Laboratory, China
Linlin Zhang, Institute of Oceanology, Chinese Academy of Sciences (CAS), China
Copyright © 2021 Zhou, Zhou, Liu, Li and Cheng. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Guidi Zhou, Z3VpZGkuemhvdUBoaHUuZWR1LmNu
 Jiang Zhou
Jiang Zhou Guidi Zhou
Guidi Zhou Hailong Liu
Hailong Liu Zhuhua Li
Zhuhua Li Xuhua Cheng
Xuhua Cheng