- 1College of Oceanography, Hohai University, Nanjing, China
- 2Navigation Technology Institute, Jiangsu Maritime Institute, Nanjing, China
- 3Vessel Division, Digital Engineering Technology Research Center for Maritime Safety and Security, Nanjing, China
- 4College of Meteorology and Oceanography, National University of Defense Technology, Changsha, China
- 5Geodetic Datum and MarineTechnology Center, Jiangsu Province Surveying and Mapping Engineering Institute, Nanjing, China
Among various vertical coordinate systems, the sigma coordinate—a terrain-following approach fitted to seabed topography—has been most widely used in coastal and continental shelf seas. However, it can induce notable simulation errors in the baroclinic pressure gradient (BPG) and baroclinic currents over steep-sloped terrain. In this study, a continuous layer index function, λ, was adopted as a generalized vertical coordinate to replace the sigma coordinate in the FVCOM model. By adapting seawater motion equations suitable for the λ coordinate system, multiple forms of vertical coordinates could be flexibly configured in the FVCOM model. We designed three types of generalized terrain-following coordinates that combine conventional sigma and z coordinates for the FVCOM model (named FVCOM-gtsz) and proposed a BPG calculation scheme by subtracting the local average density stratification. Two sets of idealized seamount numerical simulation experiments demonstrated that the new coordinate systems significantly reduced simulation errors in the BPG and baroclinic currents around steep seamounts. Compared to the conventional method of subtracting area-averaged density stratification, the proposed BPG scheme more effectively eliminated errors caused by density stratification. The FVCOM-gtsz was implemented in the South China Sea, demonstrating strong performance in simulating circulation patterns, mesoscale eddy activity, and vertical thermal stratification. We further investigated the feasibility of designing density-feature-informed hybrid coordinates based on the λ coordinate system, along with other vertical coordinate formulations, which can substantially improve the FVCOM model’s adaptive operational capacity in coastal and shelf marine environments.
1 Introduction
Ocean numerical models employ diverse vertical coordinate systems (Pacanowski et al., 1991; Haidvogel and Beckmann, 1999; Pietrzak et al., 2002; Moll and Radach, 2003; Li et al., 2013; Carton et al., 2018). Currently, three types of vertical coordinates are widely used. For example, the Modular Ocean Model (MOM) (Bryan, 1969) and MIT General Circulation Model (MITgcm) (Marshall et al., 1997) implement z coordinate; the Princeton Ocean Model (POM) (Mellor et al., 2002; Xia et al., 2006; Wang et al., 2021) and Regional Ocean Modeling System (ROMS) (Shchepetkin and McWilliams, 2005; Haidvogel et al., 2008; Yang et al., 2011) rely on sigma (σ) coordinate; Miami Isopycnic Coordinate Ocean Model (MICOM) (Bleck et al., 1992), uses isopycnic coordinate. The choice of vertical coordinates has a significant impact on the performance of ocean model (Gangopadhyay and Robinson, 2002).
The movement of seawater is generally quasi-horizontal, with horizontal velocity much greater than vertical velocity. Vertical variations and gradients of temperature and salinity are also greater than their horizontal counterparts. In general, the z coordinate aligns more closely with the motion of seawater and the distribution of temperature and salinity. However, the use of z coordinate in spatial discretization can produce unnatural stepped bottom topography, which leads to computational errors in the near-bottom physical processes (Gary, 1973; Ezer and Mellor, 2004; Ivanov et al., 2004). Ezer (2016) found that the artificial seafloor topography generated by z-coordinate models negatively impacts simulations of western boundary currents and large-scale circulations. Additionally, z-coordinate model contains only a few vertical layers in shallow waters, making it is not convenient to simulate the vertical structure of ocean hydrology. In contrast, isopycnic-coordinate models have many vertical layers in highly stratified areas, aiding the simulation of vertical temperature and salinity structures (Bleck and Boudra, 1981). However, the isopycnic coordinate also produce step-like seafloor topography, which is not convenient for describing physical processes near the sea bottom (Hirose, 2011).
The sigma coordinate, also known as a terrain-following coordinate, ensures that both the sea surface and seafloor coincide with vertical layers. Regardless of water depth, sigma-coordinate models contain the same number of vertical layers, which facilitates shallow-water simulations. This approach accurately reflects the influence of seafloor topography and boundary layers on seawater movement, as the sea bottom aligns with a sigma layer. However, the use of sigma coordinate in strongly stratified water on steep terrain may cause large baroclinic pressure gradient (BPG) errors (Mellor et al., 2002). Various methods have been proposed to reduce BPG errors, such as subtracting the average density stratification (Mellor et al., 1998), reverting to z layers to calculate BPG (Shi and Zhu, 2000), and designing high-order difference schemes (McCalpin, 1994). However, none has been able to fully resolve the problem. To overcome the shortcomings of z and sigma coordinates, some ocean models use mixed sigma–z coordinates. For example, the NCOM (Mask and Preller, 2007) and SELFE (Zhang and Baptista, 2008) models use sigma coordinates in the upper layers and z coordinates in the lower layers. The use of mixed sigma and z coordinates is believed to help in reducing BPG errors (Zhuang et al., 2018; Bruciaferri et al., 2018).
The Finite Volume Coastal Ocean Model (FVCOM), originally developed by Chen et al. (2003), is a prognostic, unstructured-grid, finite-volume, free-surface, three-dimensional primitive equation community ocean model. Its finite-volume approach combines the geometric flexibility of finite-element methods with the computational efficiency and structural simplicity of finite-difference methods. This study develops a generalized terrain-following coordinate system for FVCOM to enhance its numerical simulation capabilities over steep submarine topography.
The structure of this paper is as follows: Section 1 introduces the main vertical coordinates used in ocean models, along with their respective merits and limitations; Section 2 implements a λ-coordinate-based generalized terrain-following system in FVCOM, designing three hybrid sigma–z generalized coordinates and proposing a modified BPG calculation method by removing local average density stratification; Section 3 presents numerical experiments on idealized steep seamount topography, systematically evaluating the effects of vertical coordinates on BPG and baroclinic current simulations; Section 4 applies the enhanced FVCOM model to the South China Sea (SCS); and Section 5 assesses the feasibility of designing multiple vertical coordinate configurations under the λ-coordinate framework.
2 Enhancing FVCOM through a generalized terrain-following coordinate system
As detailed in the Appendix, the sigma-coordinate system, defined as where , with η representing the surface elevation, H the static water depth, and D the total water depth, enables precise terrain-following discretization in the FVCOM (Chen et al., 2003). To enhance the model’s adaptability under generalized terrain-following coordinates, we introduced a vertical layer index λ as the independent variable. The relationship between the and z coordinates is defined as:
Here, is a variable whose mathematical expression can be arbitrarily defined. Vertical layers are conventionally discretized as discontinuous integers, whereas this framework establishes a continuous layer index function of λ applicable to the arbitrary position between layers. The vertical velocity in the coordinate system is defined as:
The relationship between and the vertical velocity in the z coordinate system is given by:
where the subscript notation denotes partial derivatives:
Using Equations 1–3 and Equations A.1–A.5 in the z coordinate system given in the Appendix, derive the following equations:
Using Equation 1, we can obtain the following transformations of the BPG:
The λ-coordinate system represents a generalized vertical coordinate framework. Various vertical coordinate configurations can be derived by specifying distinct mathematical formulations of
in Equation 1. This study proposed a generalized terrain-following formulation of:
where ranges from −1 at the seabed to 0 at the sea surface, thereby satisfying the terrain-following criteria.
We presented six expressions for . The first three expressions adopt the traditional sigma coordinate form, which neglects spatial variation of in x and y directions. These are respectively referred to as A1, A2, and A3 coordinates. The A1 coordinate features uniform σ layers and is expressed as follows:
Here, kb denotes the total number of vertical layers. The A2 coordinate employs an exponential formulation for layer distribution:
where the exponent controls the layer concentration near the surface and seafloor. A3 is a σ coordinate based on a hyperbolic function, which is expressed as follows:
where and are used to adjust the layer concentration near the surface and seafloor, respectively. Figure 1 provides a schematic of the vertical coordinates under steep terrain, Figure 1A shows a schematic of a tall seamount, and Figures 1B–D present the vertical stratification of the A1–A3 coordinates, respectively.
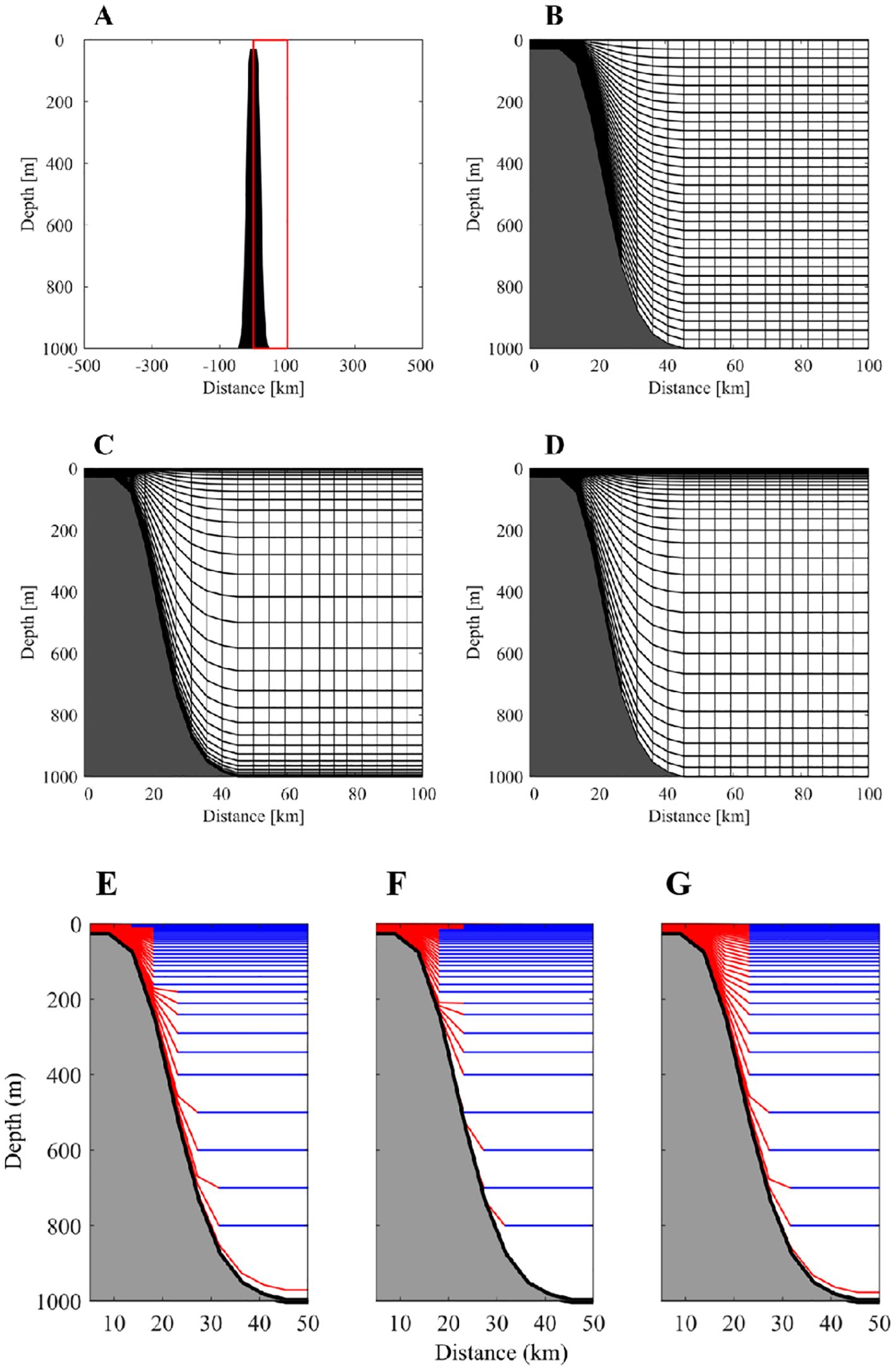
Figure 1. Schematic showing the topography (A) A1 coordinate (B) A2 coordinate (C) A3 coordinates (D) B1 coordinate (E) B2 coordinate (F) and B3 coordinate near a tall seamount. In the B1-B3 coordinate panels (E–G), red lines indicate conventional sigma layers, and the blue lines are z layers.
The remaining three vertical coordinate formulations have spatial variations of in and directions. These generalized terrain-following coordinates are constructed by hybridizing traditional sigma coordinates with selective z-plane layers. The vertical position of the z layer is denoted as , whose sigma value is determined by:
where is the initial sea surface elevation, is the total number of z layers serves as a coupling parameter linking z-layers with conventional sigma layers. The B1 coordinate fully couples z-layers to uniform -layers of the A1 coordinate. The expression of uniform layer is shown in Equation 12. The hybrid scheme operates as:
where is another coupling parameter. The B2 coordinate hybridizes z-layers with the exponential -layers of A2 coordinate:
The B3 coordinate fully mixes z-layers with hyperbolic -layers of the A3 coordinate:
Figures 1E, F illustrate the B1–B3 coordinate configurations. We designate this enhanced model as FVCOM with generalized terrain-following sigma-z coordinates (FVCOM-gtsz). Notably, the conventional sigma coordinates constitute special cases of this generalized formulation and remain fully compatible with FVCOM-gtsz.
As stated in the Appendix, the scheme of subtracting average density stratification is used in the FVCOM model to reduce BPG calculation error. In this study, we propose an alternative scheme that subtracts the local average density stratification. An illustration of the unstructured triangular grid is shown in Figure 2. The variables of u and v are placed at the centroid of triangular, and H, , , D, S, T, km, and kh are located at the node. The Bx and By of BPG have the same location as u and v. The integral of Bx on the triangular grid is calculated using the finite-volume method:
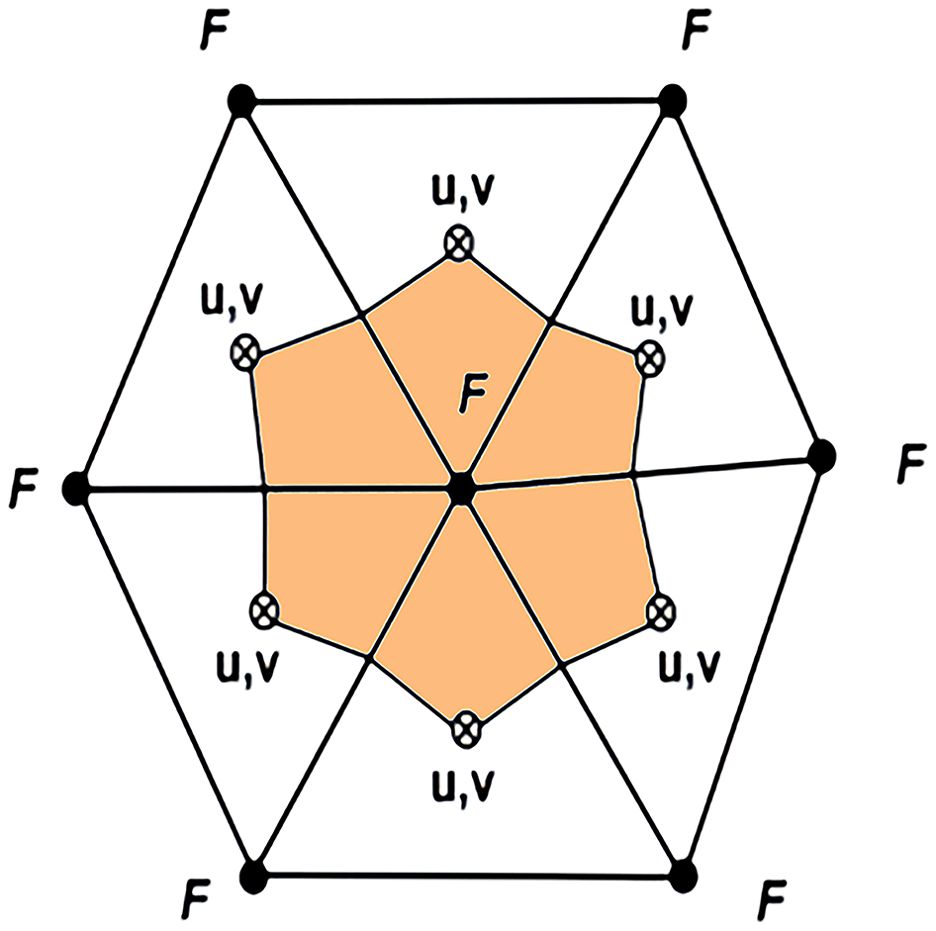
Figure 2. Illustration of the unstructured triangular grid. Variable locations: Node • for F and centroid ⨂ for u and v. F represents H, , , D, S, T, , km, kh and other tracer variables.
where and are the averages of and on the triangular grid, respectively. In Equation 16, the integral of on the triangular grid (namely )is transformed to the integral of along its closed edges (namely ) through Green’s theorem. The integral of is treated similarly as that of . The calculation of is similarly written as:
Using the scheme of subtracting average density stratification, in Equations 17, 18 is replaced by the residual density. . is given by:
where is the area average density stratification in the whole calculation domain. In the calculations of Bx and By at one centroid, only the densities at the triangular grid surrounding the centroid are used. Therefore, the triangular grid is taken as a local area for the BPG calculation, in Equations 17, 18 can be replaced by the residual density , which is obtained by removing the local average density stratification from . is given as:
where is the local average density stratification. It should be noted that the centroid and the three nodes of each triangle form a local domain, and the local average density is defined as the average density within that triangle. When multiple triangles share a common node, the residual density at that node varies across triangles due to differences in local averages.
3 Performance assessments of the FVCOM-gtsz on an ideal seamount
3.1 Numerical experiments to examine the vertical coordinates
3.1.1 Experimental setup
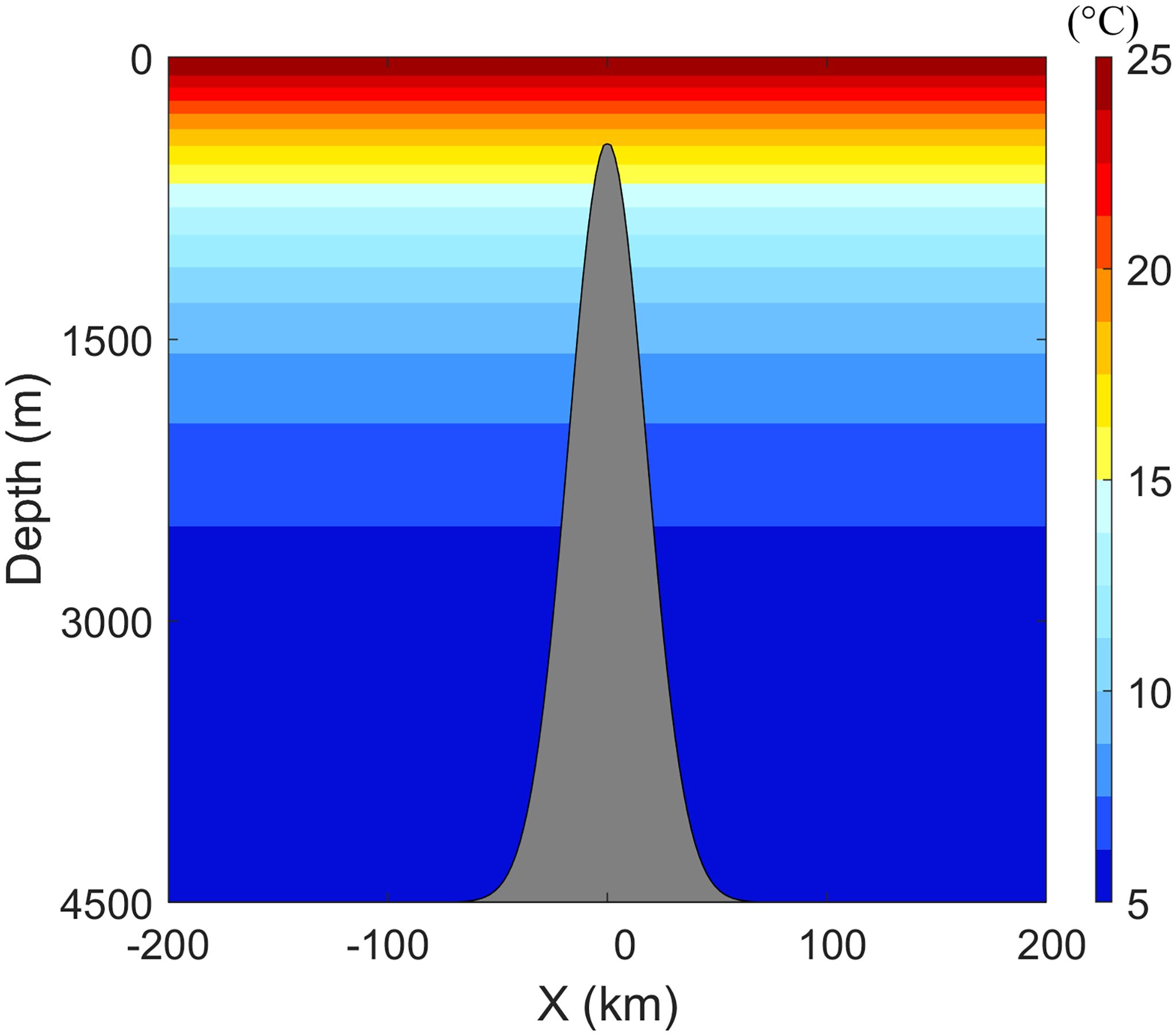
The FVCOM-gtsz model was applied to calculate BPGs and baroclinic currents in an idealized seamount setting originally proposed by Beckmann and Haidvogel (1999). The computational domain is a circular area with a diameter of 400 km and a maximum water depth of 4500 m. The domain has closed boundaries. As shown in Figure 3, there is a steep seamount in the area. The water depth near the seamount is defined by:
where L equals 36,000 m, and r is the radial distance from the seamount center. The maximum slope of the seamount is 13.8:100. The unit of depth in Equation 20 is m. The water temperature is given by:
The unit of temperature in Equation 21 is °C. The variable z denotes the vertical position, defined as positive upwards, with z = 0 at the still water level and negative values below this level. This purely vertical thermal gradient is visualized in Figure 3. A constant salinity field () is prescribed. The water is stationary at the initial moment, with no external forcing. Theoretically, the system is expected to remain stationary throughout the simulation.
We constructed an unstructured triangular mesh comprising 14,763 vertices and 28,922 elements. The grid resolution varies from 10 km to 20 km, with finer grids near the seamount. All numerical experiments use 41 vertical layers, but each one has different vertical settings. The temperature and salinity are fixed in the calculations. The internal time step of the model is 60.0 s, which is ten times the external time step. The horizontal diffusion is parameterized using the Smagorinsky eddy parameterization method (Smagorinsky, 1963), and the vertical diffusion is given by the Mellor–Yamada level 2.5 turbulent closure model (Mellor & Yamada, 1982).
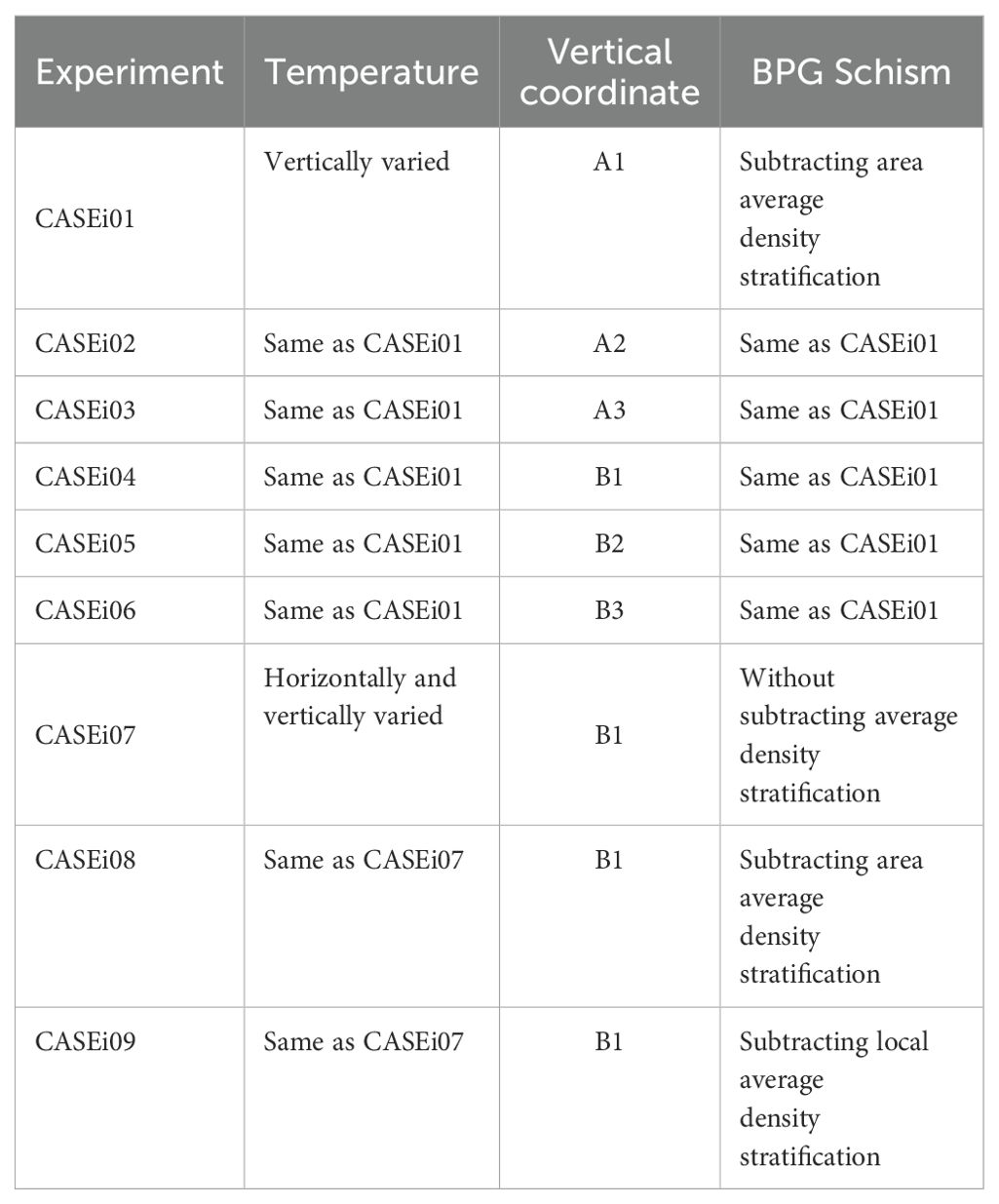
Six numerical experiments with different vertical coordinates were conducted to calculate the BPGs and baroclinic currents. Their configurations are detailed in Table 1. Experiments CASEi01, CASEi02, and CASEi03 used the conventional sigma coordinates of A1, A2, and A3, respectively. In CASEi02, the parameter of A2 coordinate was given a value of 2 after evaluating its impact on the calculation of BPG, which can increase the vertical layers in the upper and lower parts of the water column. In CASEi03, we adjusted the values of and in the A3 coordinate, and found the best selection of and to encrypt the vertical layers in the upper part alone. The novel hybrid coordinate systems (B1, B2 and B3) proposed in this study were applied in the experiments of CASEi04–06, respectively. These hybrid systems integrate 40 z-layers, whose vertical positions are -2, -4, -6, -8, -10, -15, -22, -30, -39, -50, -64, -81, -100, -120, -140, -160, -180, -200, -222, -248, -278, -312, -352, -400, -456, -522, -600, -692, -802, -934, -1092, -1278, -1498, -1762, -2078, -2450,-2890, -3418, and -4000 m.
3.1.2 Results
Figure 4 shows the temporal evolution of the maximum velocity errors () in the calculated baroclinic currents from the six experiments. In CASEi01, CASEi02 and CASEi03, the values of increase from zero to 33.40, 34.83 and 34.06 cm/s, respectively, within a one-day run, after which the values stabilize. In contrast, the growth time of in CASEi04, CASEi05, and CASEi06 is approximately 2 days before stabilizing at 14.97, 9.70, and 16.71 cm/s, respectively. The errors of made by the B1, B2 and B3 coordinates are only 44.8%, 27.8%, and 49.1% of those generated using the A1, A2, and A3 coordinates. Figure 5 presents the calculated BPGs along the east–west transect at y = 0. The BPGs should be 0 because the temperature has no horizontal variation. However, as shown in Figures 5A–C, the calculated BPGs are not zero on the seamount in the experiments of CASEi01, CASEi02, and CASEi03, which are the components of . Their absolute maximum values are 1.73×10-4, 1.81×10-4, and 1.87×10-4N/kg, respectively. Panels D–F in Figure 5 demonstrate that the hybrid coordinate systems (CASEi04–06) produce significantly smaller BPG artifacts compared to conventional sigma coordinates (CASEi01–03). The absolute maximum errors of BPG in the subsequent three experiments are only 0.23×10-4, 0.12×10-4, and 0.19×10–4 N/kg, respectively. The maximum BPG errors generated by the B1, B2, and B3 coordinate systems are 13.29%, 6.63%, and 10.16%, respectively, of those induced by the A1, A2, and A3 systems. Figure 6 shows the calculated surface currents after a 32-day run in the six experiments. Although the theoretical result is a stationary state with zero surface currents, non-zero values are observed. The maximum values of the surface current in CASEi01, CASEi02, and CASEi03 are 24.89, 29.46, and 22.36 cm/s, with mean values of 0.58, 0.66, and 0.52 cm/s, respectively. In contrast, CASEi04, CASEi05, and CASEi06 yield maximum surface current velocities of 2.60, 2.24, and 2.61 cm/s, and mean values of 0.12, 0.11, and 0.12 cm/s, respectively. Collectively, Figures 4-6– demonstrate that the hybrid coordinate systems (B1–B3) significantly reduce BPG errors and suppress spurious baroclinic currents when compared to conventional sigma coordinates (A1–A3).
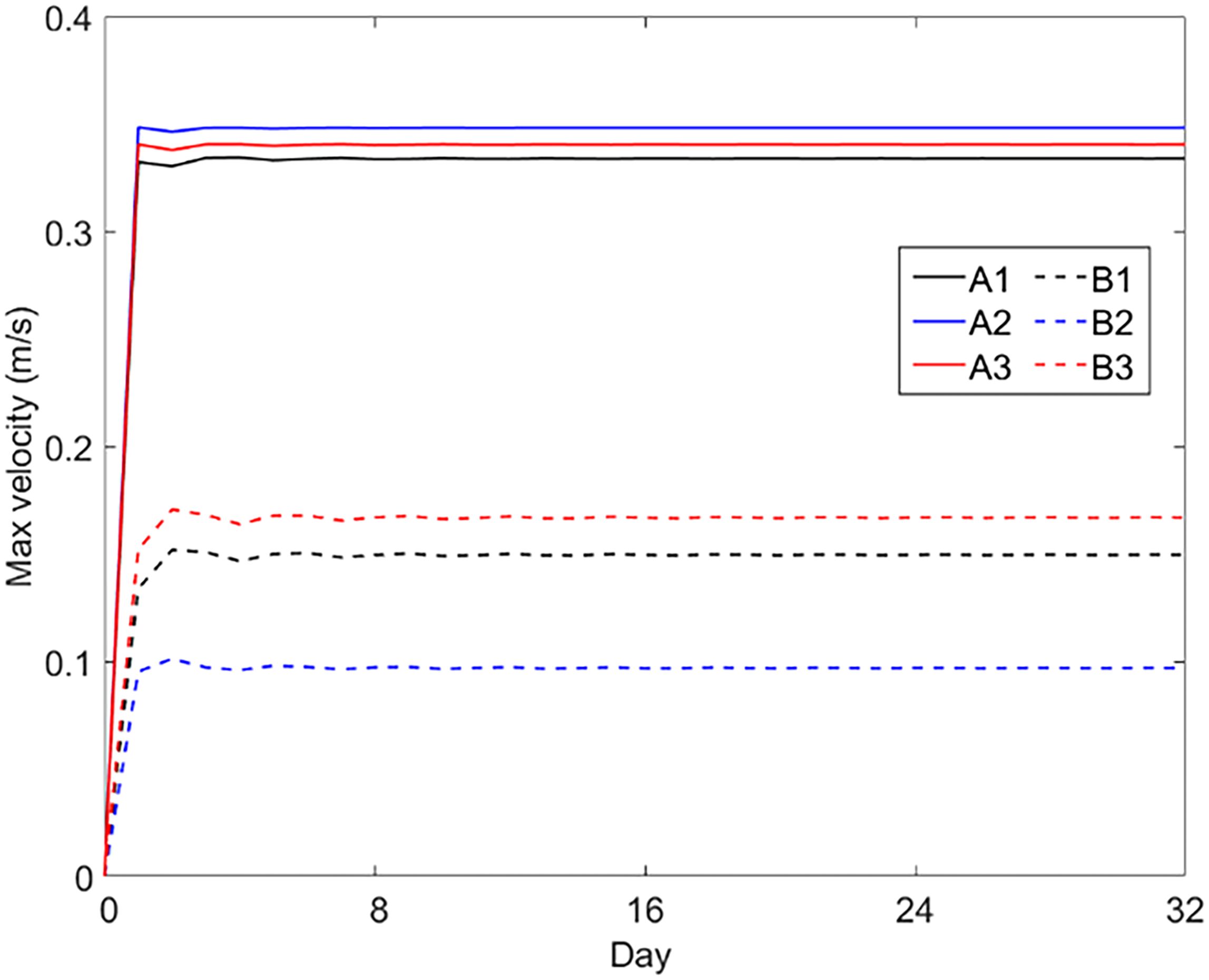
Figure 4. The maximum velocity in numerical experiments using different vertical coordinates. The A1, A2, A3, B1, B2, and B3 coordinates were applied in the experiments of CASEi01 to CASEi06.
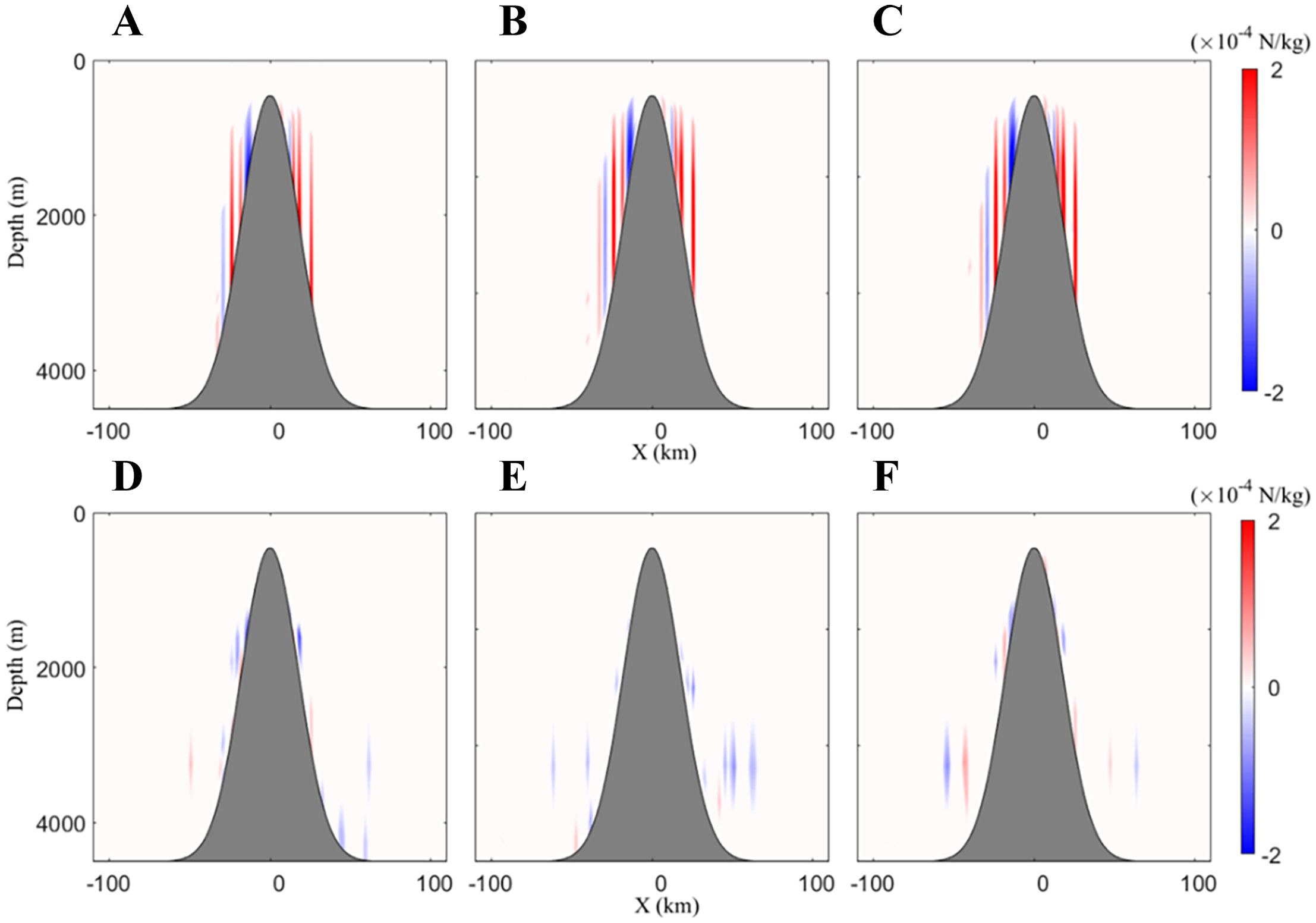
Figure 5. Calculated BPGs along the east–west transect through the seamount in the experiments of (A) CASEi01, (B) CASEi02, (C) CASEi03, (D) CASEi04, (E) CASEi05 and (F) CASEi06.
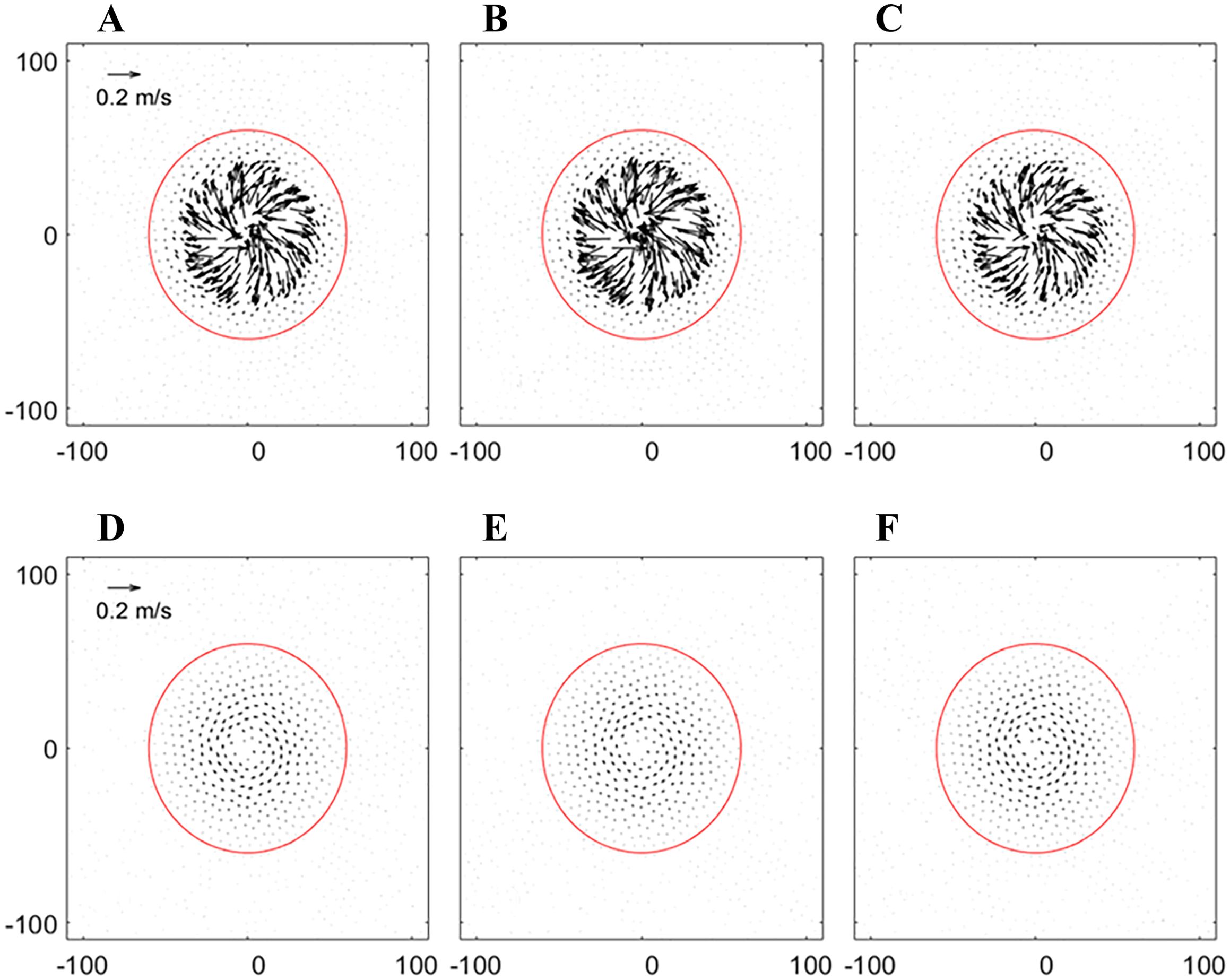
Figure 6. The surface currents on a 32-day run in the experiments of (A) CASEi01, (B) CASEi02, (C) CASEi03, (D) CASEi04, (E) CASEi05, and (F) CASEi06.
3.2 Numerical experiments to examine the BPG schemes of subtracting density stratification
3.2.1 Experimental setup
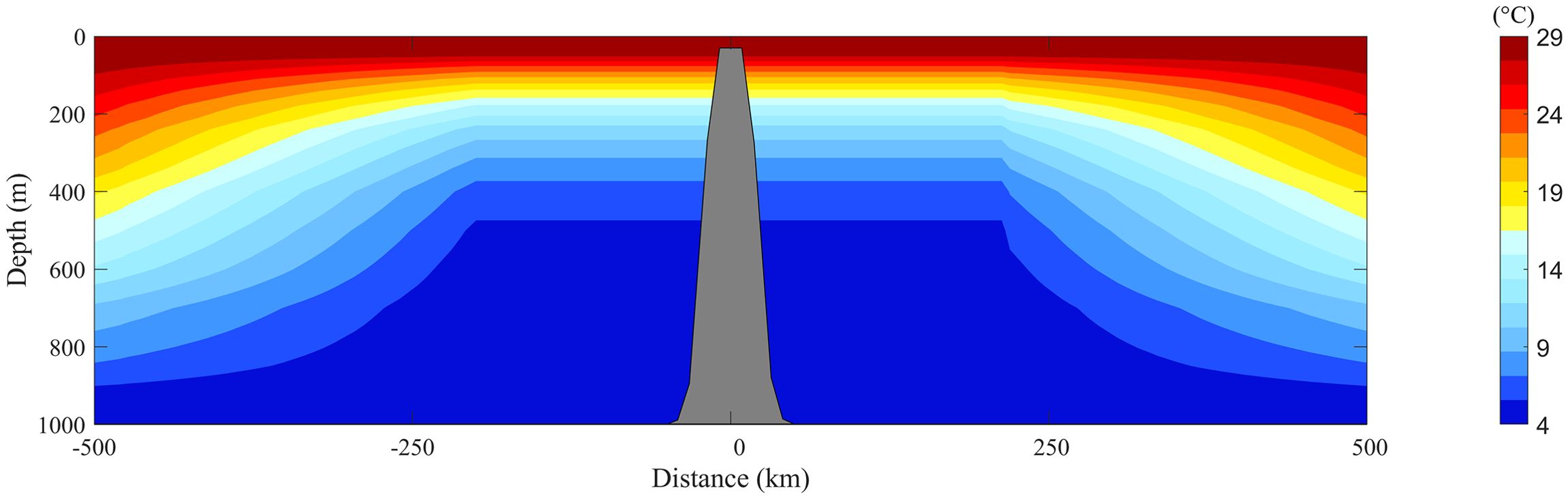
Unlike the previous numerical experiments, here we use a temperature field with horizontal variation to examine the BPG schemes that subtract density stratification. The computational domain is a circular area with a diameter of 500 km, with a seamount located at its center. To ensure model stability during the simulation, the seamount’s terrain was adjusted. As shown in Figure 7, the static water depth is defined by:
where =1000m, , and . is the distance to the center of the circular area. The maximum slope of the seamount is 5.6:100. Figure 7 also shows the temperature profile through the center. The temperature remains horizontally uniform near the seamount but varies with distance farther away. The temperature across the entire domain is defined by:
where and . The vertical position z in Equation 23 follows the same definition as in Equation 21, increasing upward with z = 0 at the still water level. The salinity is taken as a constant of 35 psu.
Three numerical experiments—CASEi07, CASEi08, and CASEi09—were conducted, with their configurations detailed in Table 1. The B1 coordinate system was applied in all three experiments. Analogous to CASEi04, a set of discrete z-layers was hybridized with a uniform sigma coordinate system. In CASEi07, the BPG scheme was applied without subtracting the average density stratification. Notably, the BPG schemes for subtracting area average density stratification and subtracting local average density stratification were used in CASEi08 and CASEi09, respectively. The average densities were first calculated on the z-layers and then interpolated to the B1 coordinate system for subtraction. All other model settings were consistent with those used in CASEi01.
3.2.2 Results
The BPG near the seamount should theoretically vanish due to the absence of horizontal temperature gradients. However, as demonstrated in Figure 8, all three numerical experiments (CASEi07–09) generated spurious BPG signals. The maximum BPG errors observed were of 3.17×10–4, 1.08 ×10-4, and 0.09×10–5 N/kg, respectively. The BPG errors originate from two components. The first component arises from the average density stratification, while the second component stems from the residual density removing the average density stratification. Comparing Figures 8A, B shows that the domain-average density subtraction scheme (CASEi08) yields smaller BPG errors than the non-subtraction scheme (CASEi07). However, discrepancies between domain-average and local stratification introduce residual BPG errors in CASEi08. By applying local-average density subtraction, CASEi09 reduces BPG errors to near zero (Figure 8C), highlighting the effectiveness of spatial-scale matching in mitigating numerical artifacts. Figure 9 presents the simulated surface currents of CASEi07, CASEi08, and CASEi09 after a 32-day integration. As shown in Figures 9A–C, all experiments exhibit consistent far-field cyclonic circulation (~2 m/s, counterclockwise rotation). In contrast, near-seamount currents display marked sensitivity to BPG correction schemes: CASEi07 generates strong residual flows with maximum velocity 1.06 m/s and mean velocity 0.40 m/s, while CASEi08 (domain-average correction) reduces these values to 0.27 m/s and 0.03 m/s respectively. Most notably, CASEi09 (local correction) achieves near-complete suppression of residual flows, limiting the maximum and mean velocities to 0.03 m/s and 0.002 m/s respectively a two-order-of-magnitude improvement over CASEi07. Due to the spatial separation between near-seamount and far-field currents, the former are predominantly attributed to BPG errors. It is evident that the BPG scheme incorporating local-average density stratification subtraction achieves minimal errors in both pressure gradient and velocity errors.
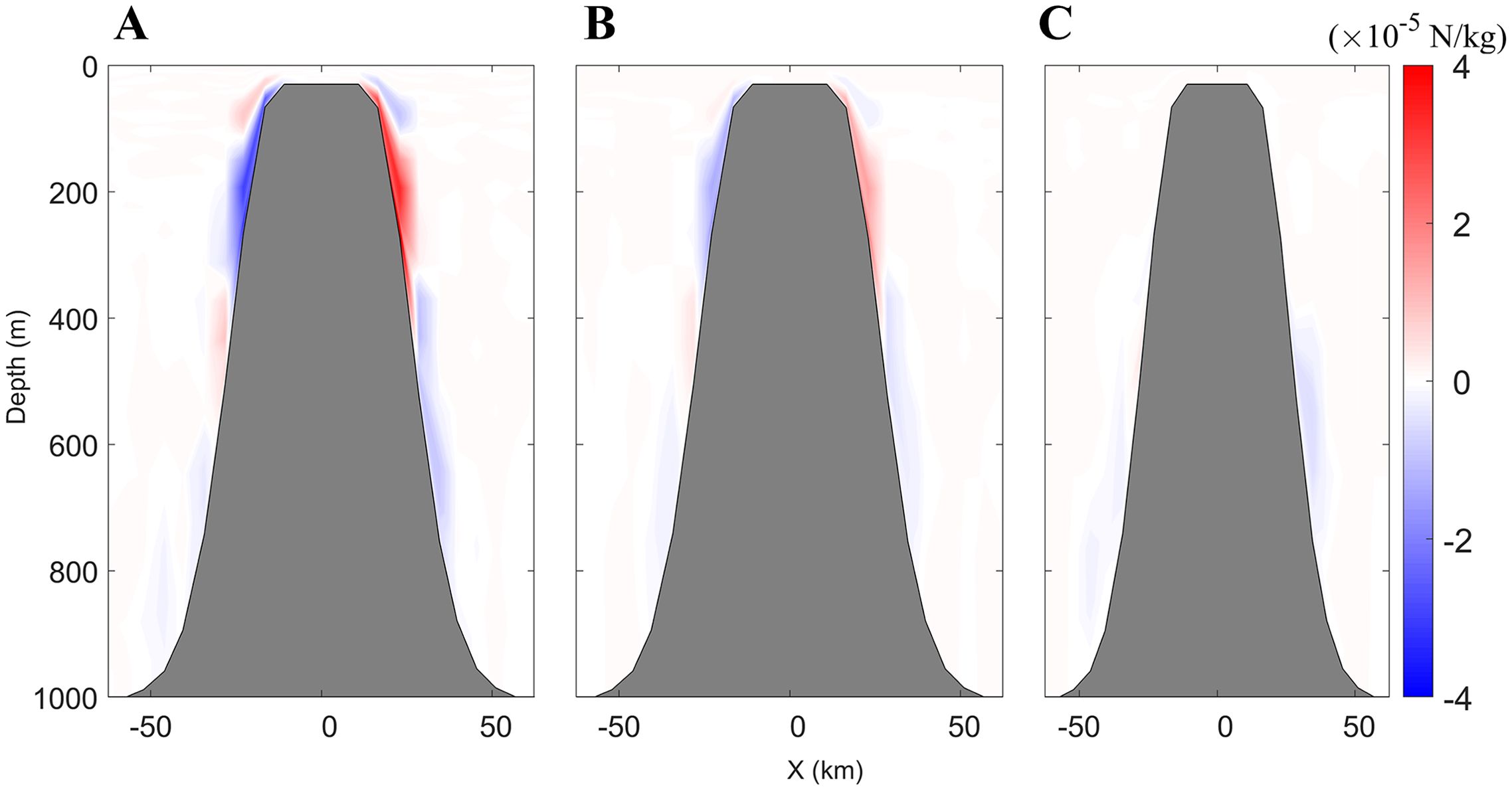
Figure 8. The results of BPG along the east–west transect through the seamount in the experiments of CASEi07 (A), CASEi08 (B) and CASEi09 (C).
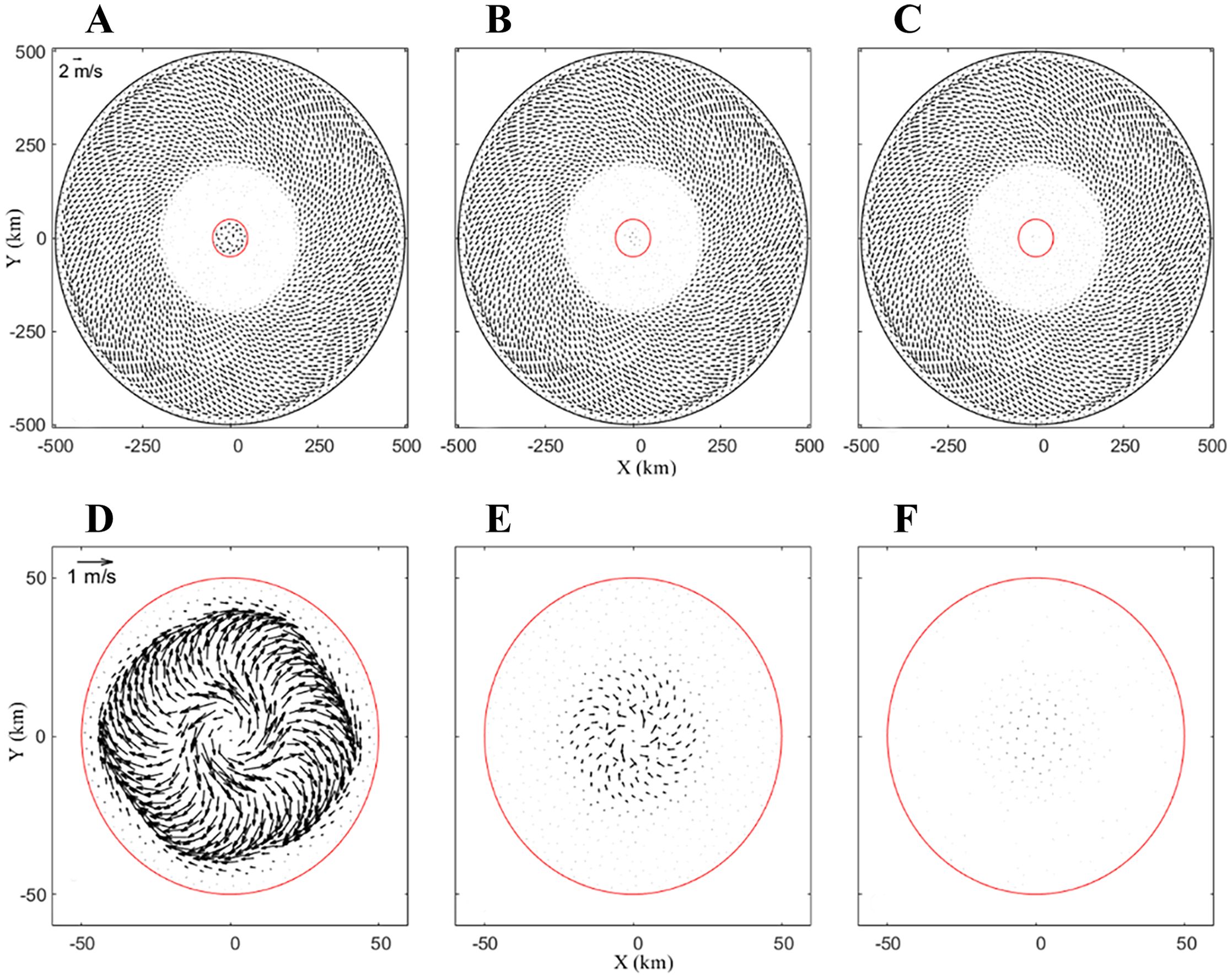
Figure 9. The calculated surface current on a 32-day run in the whole area of CASEi07 (A), CASEi08 (B) and CASE09 (C), and near the seamount of CASEi07 (D), CASEi08 (E) and CASEi09 (F).
4 Summary application of the FVCOM-gtsz in the South China Sea
4.1 Experimental setup
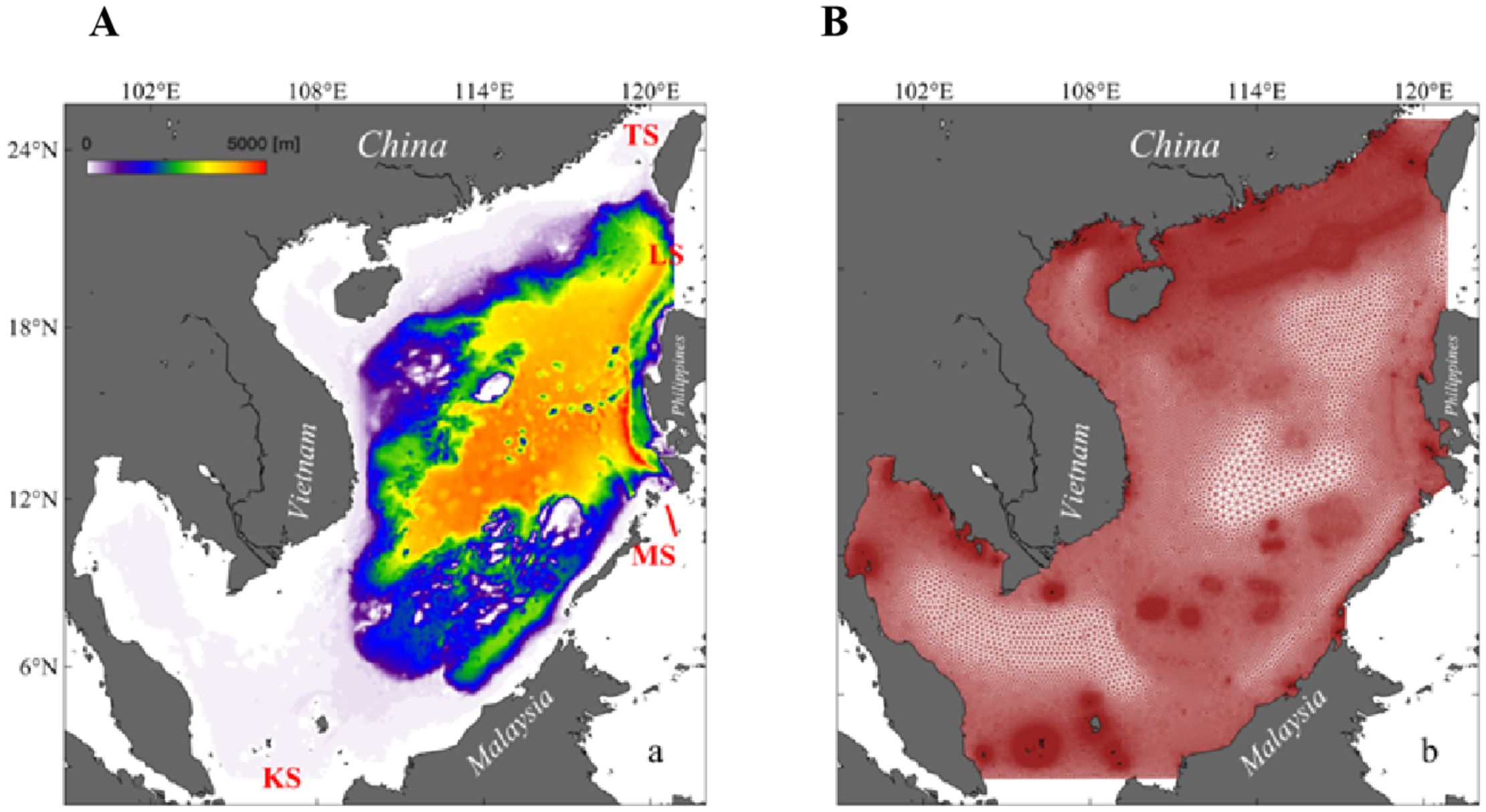
The South China Sea (SCS) is an important marginal sea of China. Its water movements have great influences on ocean engineering, local weather, and climate variations. Ocean models are an important way to study currents in the SCS. As shown in Figure 10, the topography of the South China Sea exhibits significant variations, with shallow waters near the continental shelf being only a few meters deep, while the central basin reaches depths of several thousand meters. We applied the FVCOM-gtsz model in SCS. The model domain extends from 0°N to 25°N in the north–south direction and from 99°E to 123°E in the east–west direction. There are 133,147 triangular elements with resolutions ranging from 3 km to 20 km. Seven numerical experiments were configured; their setups are shown in Table 2. The first six experiments (CASEs01-06) utilized the A1–A3 and B1–B3 vertical coordinate systems respectively, with a total of 51 vertical layers distributed across the water column. The B1–B3 coordinate systems incorporate a hybrid sigma-z configuration, where z-layers are vertically aligned with the HYCOM reanalysis data stratification (https://www.hycom.org). Bathymetric data were obtained from the GEBCO database at 0.5’ × 0.5’ resolution. The model simulation spanned from 1 April to 30 June 2010, with initial and open boundary conditions for oceanic currents, temperature, and salinity derived from HYCOM datasets. Meteorological forcing terms including wind stress, shortwave radiation, longwave radiation, latent heat flux, and sensible heat flux were obtained from the NCEP Climate Forecast System Reanalysis (CFSR; https://www.ncei.noaa.gov/products/weather-climate-models/climate-forecast-system). The seventh experiment (CASEs07) utilized the B1 coordinate system and additionally assimilated AVISO satellite altimetry data (https://www.aviso.altimetry.fr/en/data.html) and GHRSST remote sensing sea surface temperature (SST) products (https://www.ncei.noaa.gov).
4.2 Results
Figure 11A shows the surface geostrophic currents on June 9 derived from AVISO altimeter data, revealing a prominent anticyclonic eddy offshore Vietnam centered near (112°E, 14°N) with a radius exceeding 200 km, alongside smaller vortices in other regions. Figure 11B presents the HYCOM-simulated surface currents, revealing a northward coastal flow along Vietnam and a counterflow to the south near (112°E, 14°N), where a weak cyclonic circulation appears to be nearly established. Figure 12 presents FVCOM-gtsz simulated surface currents from CASEs01–06. Panels 12A–C correspond to simulations using the A1–A3 coordinate systems: A1 and A2 coordinates show incipient eddy formation trends offshore Vietnam with underdeveloped vortical structures, while A3 fails to reproduce any eddy features. Panels 12D–F depict results from B1–B3 coordinates, all successfully simulating anticyclonic eddies offshore Vietnam. The B1-simulated eddy center aligns closely with the AVISO-observed position (112°E, 14°N), whereas B2 and B3 displace the eddy southward to approximately 11°N. Overall, the B1–B3 configurations outperform A1–A3 in eddy simulations. While B1 achieves optimal accuracy, it still underrepresents smaller vortices evident in the AVISO data (Figure 11A). Figure 13 gives simulated cross-sectional velocity (i.e., v-component) perpendicular to the 14°N transect in the SCS using A1–A3 and B1–B3 coordinate systems. The B1 coordinate system effectively simulates the mesoscale eddy near (112°E, 14°N); thus, the flow west of 112°E in Figure 13D is predominantly northward (positive v-component), while the flow east of 112°E is mainly southward (negative v-component). The flow velocities across the section simulated by the other five coordinate configurations exhibit marked discrepancies compared to those in Figure 13D. Figure 12G presents the simulated surface currents from CASEs07, which reproduce most of the eddy features observed in Figure 11A. In addition to the strong mesoscale eddy offshore Vietnam, coherent vortices are simulated near (110°E, 5°N), (114°E, 7°N), (109°E, 9°N), (116°E, 12°N), (115°E, 14°N), (119°E, 15°N), (116°E, 18°N), and (119°E, 21°N). However, significant discrepancies in both eddy positions and rotational directions exist between Figure 12G and Figure 11A in China’s coastal waters. The geostrophic currents in Figure 11A, derived from satellite altimetry, may not adequately represent eddy structures in shallow coastal regions where wind-driven currents dominate and actual flow fields deviate substantially from geostrophic balance. In contrast, Figure 12G depicts flow fields incorporating combined effects of surface winds, sea surface height, and thermohaline processes, resulting in fundamentally different dynamics.
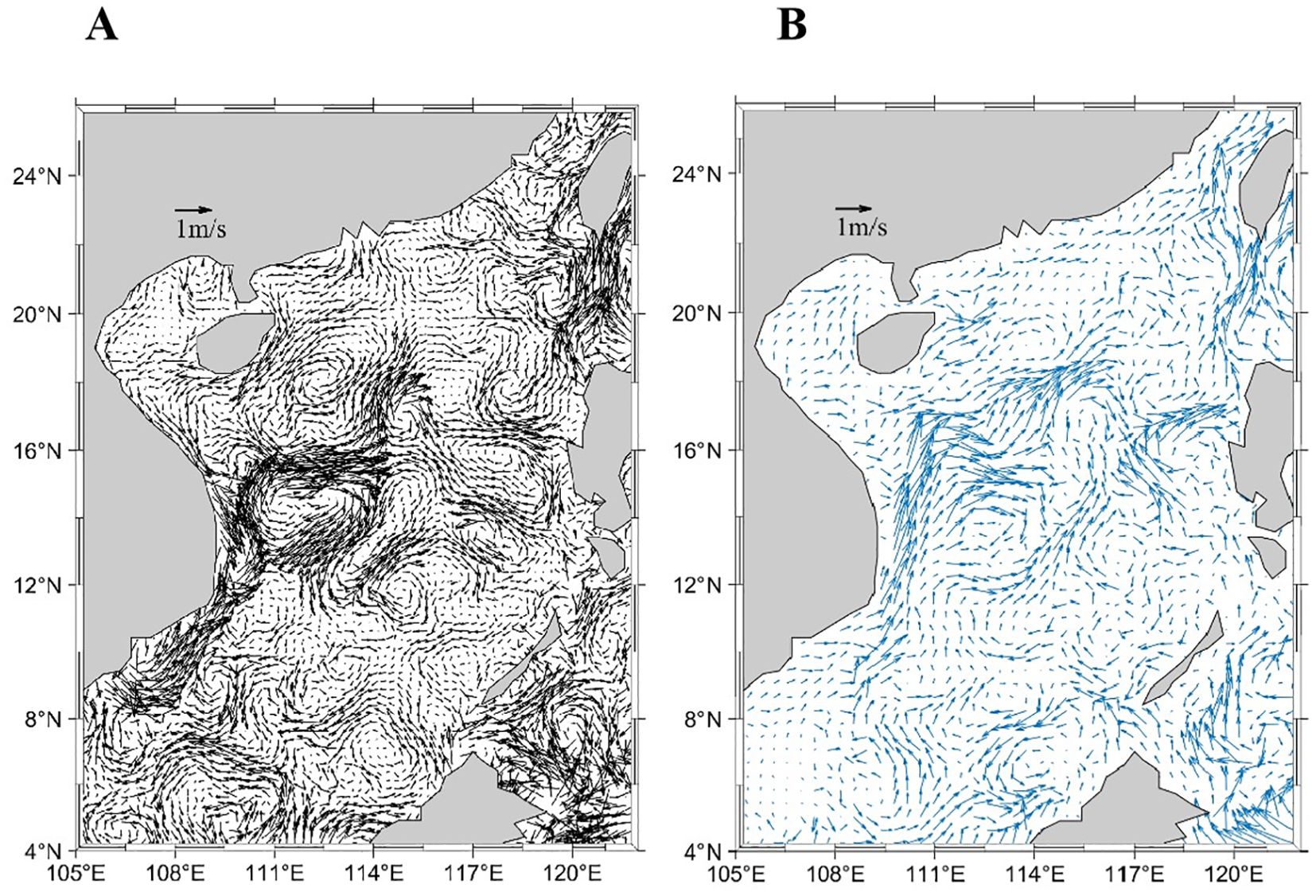
Figure 11. The geostrophic flow deduced by satellite altimeter data (A), the simulated currents by HYCOM (B).
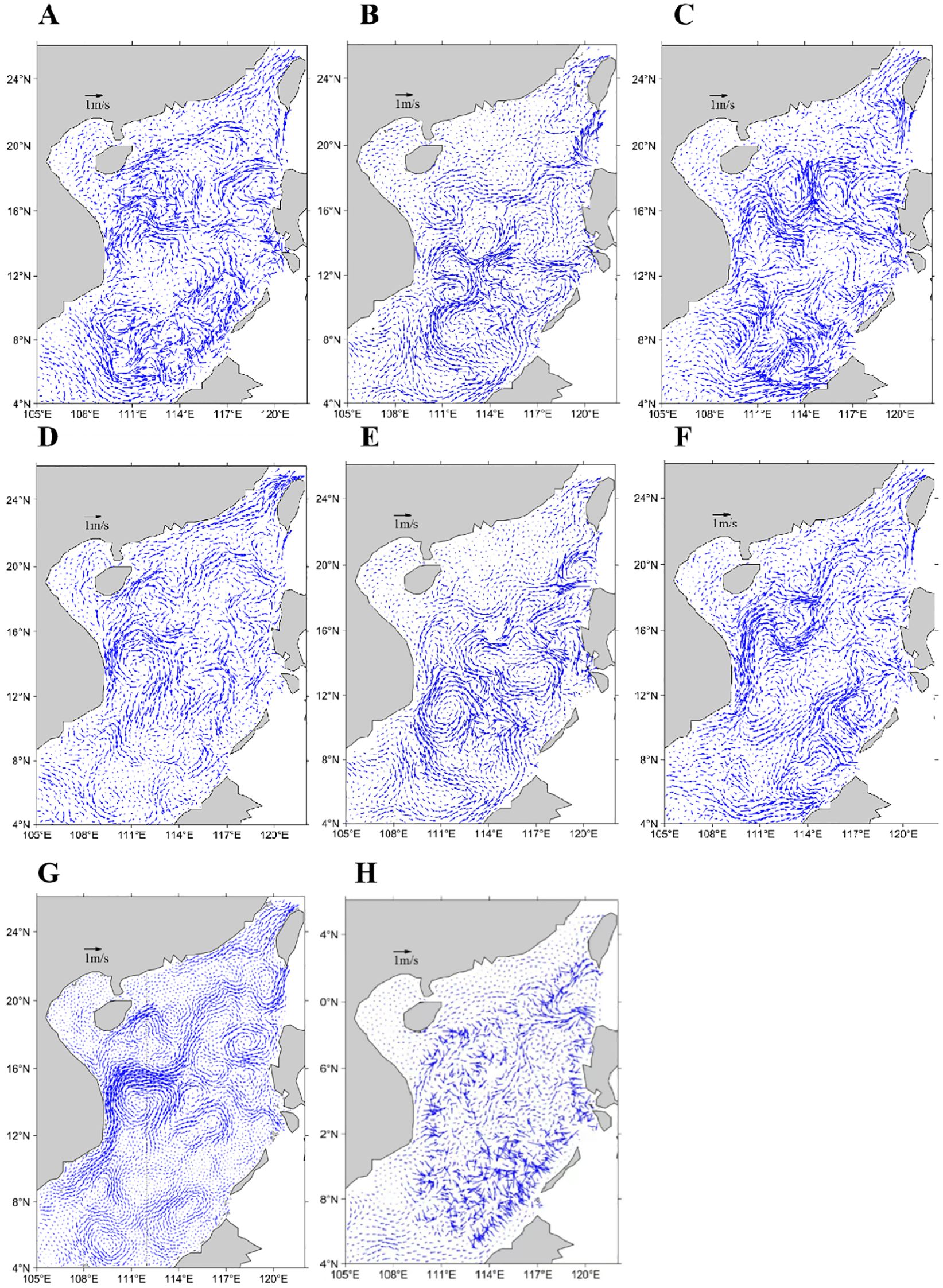
Figure 12. Simulated surface currents in the SCS on June 9, 2010, under different configurations: (A–F) FVCOM-gtsz model with coordinates A1, A2, A3, B1, B2, and B3; (G) FVCOM-gtsz model (B1 coordinate) assimilating altimeter and SST data; (H) FVCOM model (B1 coordinate).
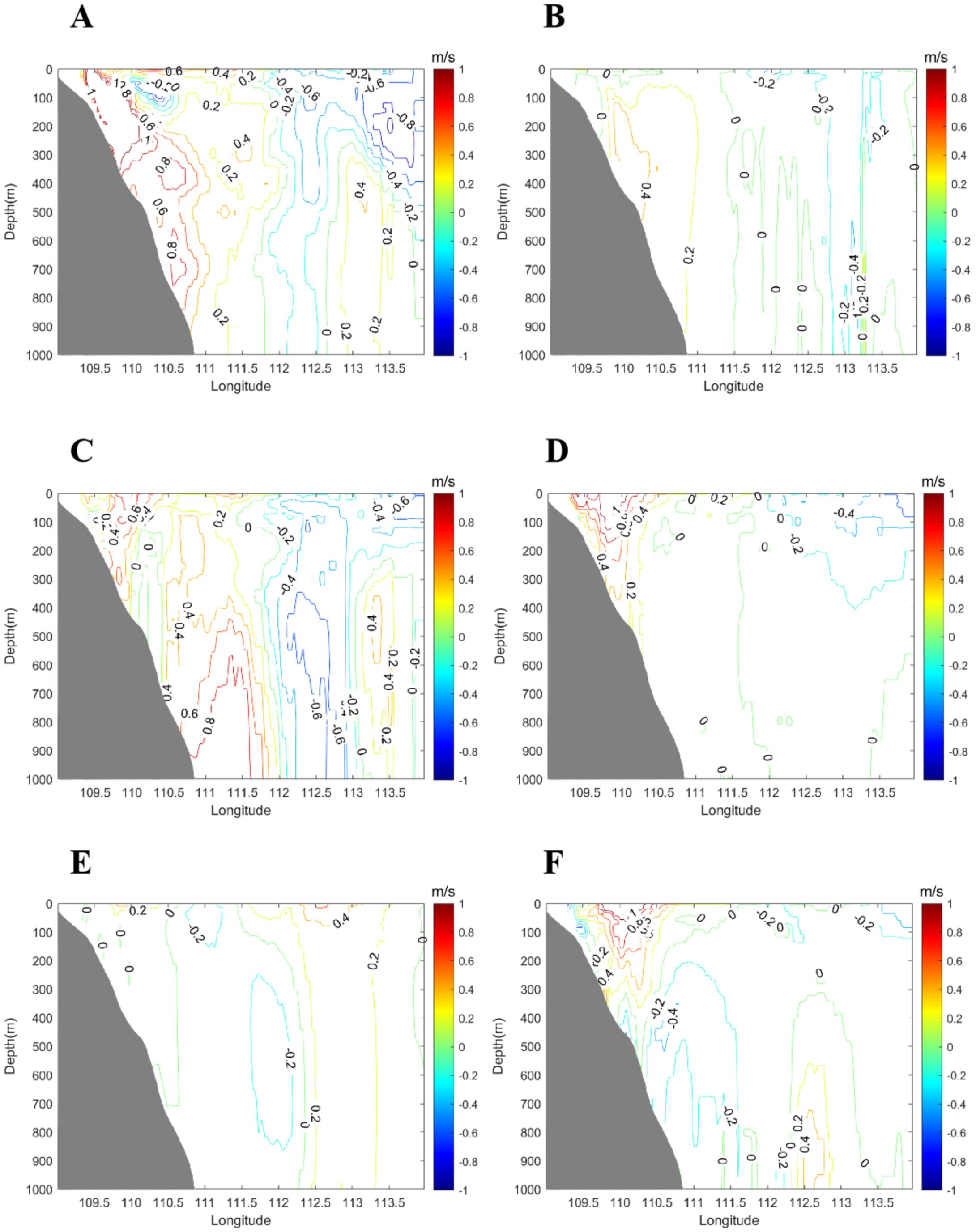
Figure 13. Simulated cross-sectional velocity (i.e., v-component) perpendicular to the 14°N transect in the SCS by the FVCOM-gtsz model with the A1 (A), A2 (B), A3 (C), B1 (D), B2 (E) and B3 (F) coordinates on June 9, 2010.
Figure 14 compares monthly mean sea surface height anomalies between satellite observations and numerical simulations in June, showing broadly consistent spatial patterns with a mean difference of 4.2 cm. Figure 15 validates simulated sea temperature profiles against Argo float observations on June 8 at two locations: (119.30°E, 17.35°N) and (115.58°E, 15.02°N). The model successfully replicates vertical thermal structures, yielding mean temperature errors of 0.42°C and 1.05°C, respectively.
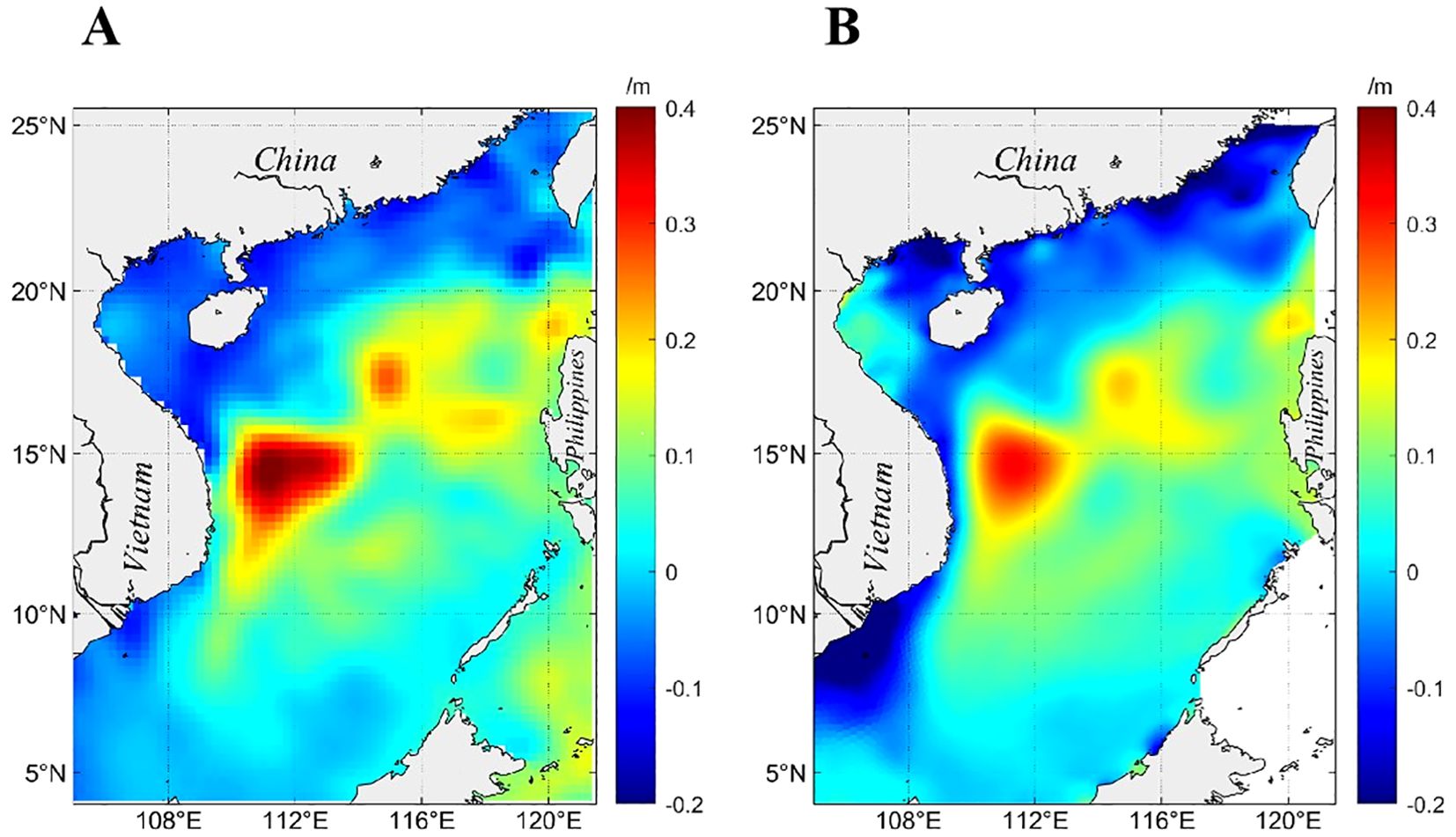
Figure 14. Monthly mean sea surface height anomalies between satellite observations (A) and numerical simulations (B) in June 2010.
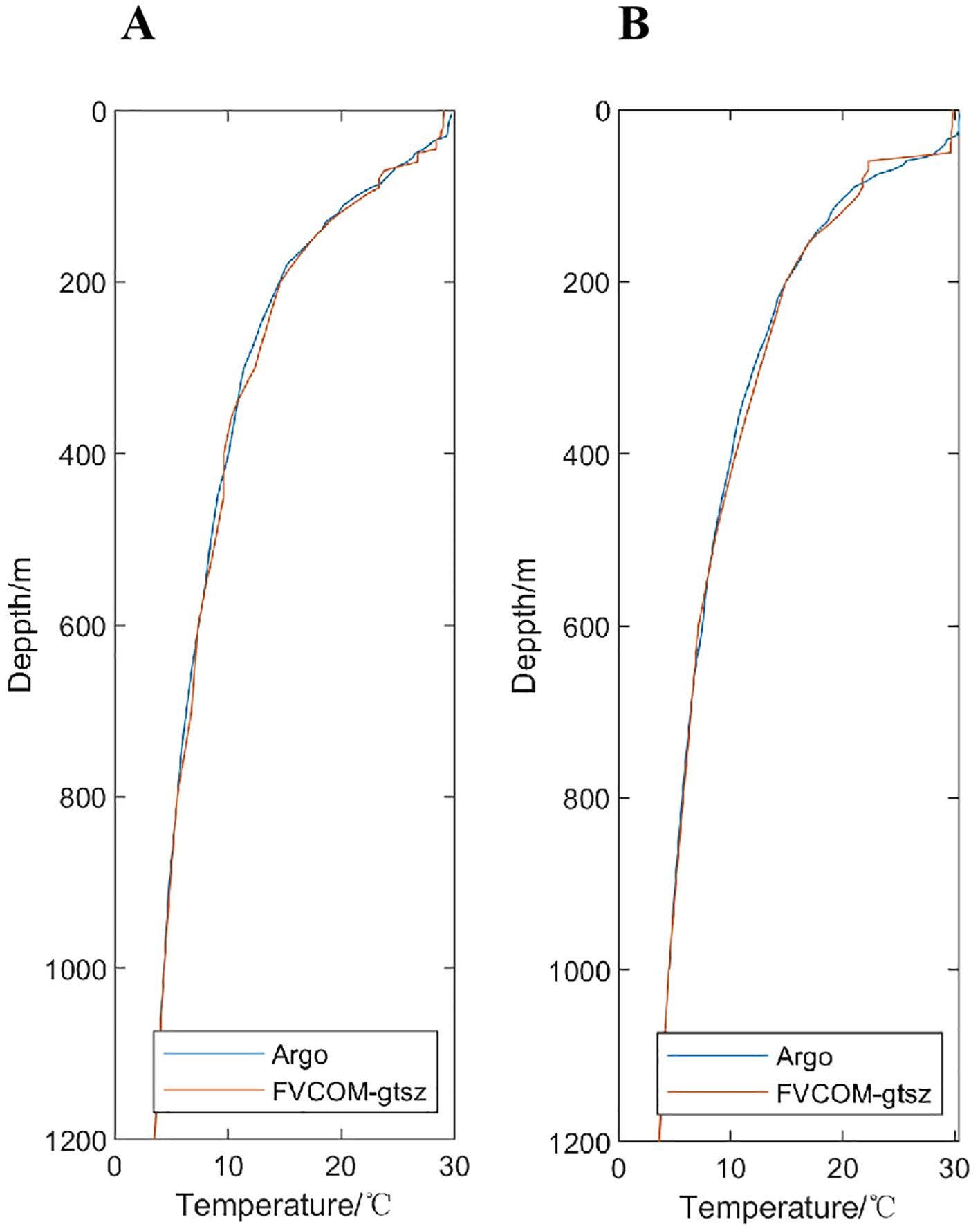
Figure 15. Simulated and observed sea temperature profiles on June 8, 2010, at Argo float locations: (A) 119.30°E, 17.35°N and (B) 115.58°E, 15.02°N.
5 Discussions
5.1 The relationship of dynamical equations in conventional sigma coordinates and generalized terrain-following coordinates
This study employed Equation 11 to define a terrain-following λ-coordinate system, based on which six vertical coordinates (A1–A3, B1–B3) were given. The A1–A3 coordinates represent traditional sigma coordinates with constant σ values across each vertical layer, whereas the B1–B3 coordinates are generalized terrain-following coordinates where σ values vary spatially with (x, y). The governing equations for seawater motion under traditional sigma coordinates are provided in Equations A.11–A.17 of the Appendix, while those for the λ-coordinate system are derived in Equations 4–10 of Section 2. By jointly analyzing Equations A.11–A.17 and 4–10, we systematically elucidate the hydrodynamic relationships between traditional sigma coordinates and generalized terrain-following coordinates.
Equation 11 leads to the following partial derivatives:
For a generic variable F (where F denotes variables such as ), the chain rule gives:
For the traditional sigma coordinates, since is independent of , Equation 11 can be rewritten as:
The horizontal gradients and are derived as:
Using these relations, it can be demonstrated that the governing equations of the generalized coordinate system (Equations 4–10) are mathematically consistent with those of the traditional sigma coordinate system Equations A.11–A.17.
For the generalized terrain-following coordinates defined in Equation 11, where varies with , i.e.,
In the generalized coordinates, since and , the horizontal gradients become:
Using the relationships derived above, it can be demonstrated that Equations 4–10 are inconsistent with Equations A.11–A.17 in the Appendix.
From the analysis above, it is evident that the traditional sigma coordinate can be regarded as a special case of the generalized terrain-following coordinate and is compatible with the generalized system’s governing equations and ocean models. Conversely, while the generalized terrain-following coordinate can be expressed in a form similar to the traditional sigma coordinate, it is incompatible with the governing equations and ocean models formulated for the traditional sigma coordinate.
This study conducted two additional numerical experiments in the SCS using the original FVCOM model. The first experiment (CASEs08) employed the A1 coordinate system, while the second (CASEs09) utilized the B1 coordinate system, with all simulation configurations consistent with those in Section 4. The results of CASEs08 demonstrated that the simulation outputs from the original FVCOM model were identical to those of the FVCOM-gtsz model (figures omitted). In contrast, CASEs09 revealed significant discrepancies between the results of the original FVCOM model and those of the FVCOM-gtsz model. Figure 12H presents the simulated surface current field from CASEs09 based on the FVCOM model with the B1 coordinate setup, which is markedly distinct from Figure 12A. The flow field exhibits a highly disorganized structure, lacking discernible circulation patterns or vortical features.
5.2 Feasibility of designing multiple vertical coordinates based on the coordinate system
Within the λ-coordinate framework, we developed a novel generalized terrain-following system through the hybridization of sigma and z coordinates. This approach preserves the terrain-following advantages of the sigma coordinate while reducing vertical layer slopes in steep topographic regions via z-coordinate integration, thereby mitigating BPG calculation errors. Both z-coordinate and traditional sigma coordinate systems exhibit spurious cross-isopycnal mixing and lack flexibility for vertical layer refinement near pycnoclines. In contrast, density coordinates minimize cross-isopycnal mixing and enable high-resolution layering around pycnoclines. The HYbrid Coordinate Ocean Model (HYCOM) employs a hybrid coordinate system that combines terrain-following coordinates in shallow seas, quasi-z coordinates in the upper mixed layer of deep oceans, and density coordinates in deeper strata, demonstrating advantages for both shallow and deep marine environments (Chassignet et al., 2006). However, HYCOM still encounters challenges in designing vertical coordinates for shelf-slope transition zones, where the system must simultaneously adhere to bottom topography through terrain-following coordinate, refine vertical layers near pycnoclines using density coordinate, configure mixed-layer vertical layers with z-coordinate, and mitigate steep topographic slopes via z-coordinate adjustments at abrupt bathymetric features. To address this, we propose a terrain-following λ-coordinate framework that hybridizes sigma, z-, and density coordinates. In Section 2, we derived a hybrid sigma-z coordinate by comparing σ-value distributions between traditional sigma and z-coordinate layers. Future work will extend this methodology by comparing σ-value distributions across sigma, z-, and density coordinate layers to develop a unified sigma-z-density hybrid system for seamless vertical discretization across diverse ocean regimes.
Terrain-following coordinates typically require the same number of vertical layers in both shallow and deep-water regions. While this enhances vertical resolution and simulation accuracy in shallow seas, it leads to unnecessary computational costs. To address this, He et al. (2022) developed a generalized piecewise terrain-following coordinate system that employs traditional sigma coordinates in shallow seas, z-coordinates in deep regions, and hybrid sigma-z coordinates in shelf-slope transition zones. By leveraging the generalized formulation of the λ-coordinate in Equation 1, this framework can be extended to incorporate density coordinates, enabling a unified generalized piecewise terrain-following system that synergistically combines sigma, z-, and density coordinates for optimized vertical discretization across varied marine environments.
6 Conclusions
Current ocean models primarily utilize sigma, z, and density coordinates, each exhibiting distinct strengths and limitations. The sigma coordinate, known for its terrain-following capability, is the most widely used vertical system in coastal and continental shelf seas. However, it faces a well-recognized limitation: steeply sloped terrains can induce significant errors in the simulation of BPGs and baroclinic currents due to exaggerated vertical layer slopes.
In this study, we adopted the vertical layer index λ as the vertical coordinate. Traditionally, λ is treated as a discrete integer. In this study, we redefined it as a continuously varying parameter by assigning distinct λ values to any position between vertical layers. This redefinition transforms the λ-coordinate system into a generalized vertical coordinate framework. Seawater motion equations were formulated for the λ system through a generalized coordinate transformation. The traditional sigma coordinate emerges as a special case of this λ-coordinate system. The governing equations in the λ system are compatible with those in the traditional sigma coordinate system. The λ coordinate enables the design of multiple types of vertical coordinates. We proposed three types of generalized terrain-following coordinates that integrate traditional sigma and z coordinates. Additionally, we explored the feasibility of designing generalized terrain-following coordinates incorporating density, sigma, and z coordinates, and examined the viability of developing a generalized piecewise terrain-following system through combinations of multiple coordinate approaches.
This study introduced the seawater motion equations in the λ-coordinate system into the FVCOM model, and implemented the generalized terrain-following coordinates that integrate traditional sigma and z coordinates, resulting in an enhanced model version: FVCOM-gtsz. This model offers improved adaptability to regional hydrodynamic variations. We designed two sets of idealized seamount numerical experiments. The first set compared BPG and baroclinic flow errors between traditional sigma coordinates and sigma-z hybrid terrain-following coordinates. The results demonstrated that all three sigma-z hybrid terrain-following coordinate schemes significantly reduced BPG and baroclinic flow simulation errors in steep seamount regions. The second set evaluated BPG and baroclinic flow errors under different mean density stratification subtraction schemes. The local-average density stratification subtraction method was most effective in eliminating density-induced errors. The λ-coordinate system and the local-average subtraction scheme can be applied independently or jointly, with combined implementation yielding the best results. The FVCOM-gtsz model was also applied to the SCS, where it successfully simulated circulation structures, mesoscale eddy activity, and vertical thermal stratification—demonstrating robust application capabilities.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding authors.
Author contributions
YB: Writing – original draft, Writing – review & editing, Conceptualization, Validation. YC: Conceptualization, Formal Analysis, Funding acquisition, Investigation, Methodology, Resources, Validation, Writing – original draft, Writing – review & editing. SZ: Formal Analysis, Validation, Visualization, Writing – review & editing. WZ: Validation, Writing – review & editing. GC: Formal Analysis, Validation, Writing – review & editing. ZD: Data curation, Writing – review & editing.
Funding
The author(s) declare that financial support was received for the research and/or publication of this article. This research was funded by the National Natural Science Foundation of China (Nos.41076048, 41376012, and 41206163) and Natural Science Foundation of the Jiangsu Higher Education Institutions of China (Grant No. 24KJB170003).
Acknowledgments
The author visited the FVCOM research group led by Chen Changsheng of the University of Massachusetts Dartmouth in the United States for a year and received enthusiastic guidance from Chen Changsheng, Qi Jianhua, and Xu Qichun for the improvement of FVCOM in 2017.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Bleck R. and Boudra D. (1981). Initial testing of a numerical ocean circulation model using a hybrid (Quasi-isopycnic) vertical coordinate. J. Phys. Oceanogr. 11, 755–770. doi: 10.1175/1520-0485(1981)011<0755:ITOANO>2.0.CO;2
Bleck R., Rooth C., Hu D., and Smith L. (1992). Salinity-driven thermocline transients in a wind- and thermohaline-forced isopycnic coordinate model of the north atlantic. J. Phys. Oceanogr. 22, 1486–1505. doi: 10.1175/1520-0485(1992)022<1486:SDTTIA>2.0.CO;2
Bruciaferri D., Shapiro G. I., and Wobus F. (2018). A multi-envelope vertical coordinate system for numerical ocean modelling. Ocean. Dyn. 68, 1239–1258. doi: 10.1007/s10236-018-1189-x
Bryan K. (1969). A numerical method for the study of the circulation of the world ocean. J. Comput. Phys. 4, 347–376. doi: 10.1016/0021-9991(69)90004-7
Carton J., Chepurin. G. A., and Chen. L. (2018). SODA3: A new ocean climate reanalysis. J. Clim. 31, 6967–6983. doi: 10.1175/JCLI-D-18-0149.1
Chassignet E., Hurlburt H., and Smedstad O. (2006). Ocean prediction with the hybrid coordinate ocean model (HYCOM). Ocean Weather Forecasting 6, 413–426. doi: 10.1007/1-4020-4028-8_16
Chen C., Liu. H., and Beardsley R. C. (2003). An unstructured grid, finite volume primitive equation coastal ocean model: Application to coastal ocean and estuaries. J. Atmos. Ocean. Tech. 20, 159–186. doi: 10.1175/1520-0426(2003)020<0159:AUGFVT>2.0.CO;2
Ezer T. (2016). Revisiting the problem of the Gulf Stream separation: on the representation of topography in ocean models with different types of vertical grids. Oxf 104, 15–27. doi: 10.1016/j.ocemod.2016.05.008
Ezer T. and Mellor G. (2004). A generalized coordinate ocean model and a comparison of the bottom boundary layer dynamics in terrain-following and in z-level grids. Ocean. Model. 6, 379–403. doi: 10.1016/S1463-5003(03)00026-X
Gangopadhyay A. and Robinson A. R. (2002). Feature-oriented regional modeling of oceanic fronts. Dyn. Atmos. Oceans 36, 201–232. doi: 10.1016/S0377-0265(02)00032-5
Gary J. (1973). Estimate of truncation error in transformed coordinate, primitive equation atmospheric models. J. Atmos. Sci. 30, 223–233. doi: 10.1175/1520-0469(1973)030<0223:EOTEIT>2.0.CO;2
Haidvogel D., Arango H., and Budgell W. (2008). Ocean forecasting in terrain-following coordinates: formulation and skill assessment of the regional ocean modeling system. J. Comput. Phys. 227, 3595–3624. doi: 10.1016/j.jcp.2007.06.016
Haidvogel D. and Beckmann A. (1999). Numerical ocean circulation modeling Vol. 49 (Covent Garden, London, England: Imperial College Press), 344–352. doi: 10.1142/p097
He Z., Zhu S., Sheng J., and Wang B. (2022). Applications of generalized vertical coordinates in ocean circulation models. Ocean. Model. 175, 102025. doi: 10.1016/j.ocemod.2022.102025
Hirose N. (2011). Inverse estimation of empirical parameters used in a regional ocean circulation model. J. Oceanogr. 67, 323–326. doi: 10.1007/s10872-011-0041-4
Ivanov V., Shapiro G., and Huthnance J. (2004). Cascades of dense water around the world ocean. Prog. Oceanogr. 0, 47–98. doi: 10.1016/j.pocean.2003.12.002
Li J., Wei H., Zhang Z., and Lu Y. (2013). A modelling study of inter-annual variation of Kuroshio intrusion on the shelf of East China Sea. J. Ocean. U China 12, 537–548. doi: 10.1007/s11802-013-2203-z
Marshall J., Adcroft A., and Hill C. (1997). A finite-volume, incompressible Navier Stokes model for studies of the ocean on parallel computers. J. Geophys 102, 5753–5766. doi: 10.1029/96JC02775
Mask A. and Preller R. (2007). A numerical simulation of the East Asian Seas in March 2002: Effect of vertical grid choice. Oxf 18, 81–96. doi: 10.1016/j.ocemod.2007.02.007
McCalpin J. (1994). A comparison of second-order and fourth-order pressure gradient algorithms in a sigma-coordinate ocean model. Int. J. Numer 18, 361–383. doi: 10.1002/fld.1650180404
Mellor G., Häkkinen S., and Ezer T. (2002). A generalization of a sigma coordinate ocean model and an intercomparison of model vertical grids. Ocean. Forecast. 55-72. doi: 10.1007/978-3-662-22648-3_4
Mellor G., Oey L., and Ezer T. (1998). Sigma coordinate pressure gradient errors and the seamount problem. J. Atmos. Ocean. Tech. 15, 1122–1131. doi: 10.1175/1520-0426(1998)015<1122:SCPGEA>2.0.CO;2
Mellor G. and Yamada T. (1982). Development of a turbulence closure model for geophysical fluid problems. Rev. Geophys. 20, 851-875. doi: 10.1029/RG020i004p00851
Moll A. and Radach G. (2003). Review of three-dimensional ecological modelling related to the North Sea shelf system: Part 1. Models and their results. Prog. Oceanogr. 57, 175–217. doi: 10.1016/S0079-6611(03)00067-3
Pacanowski R., Dixon K., and Rosati A. (1991). The GFDL modular ocean model users guide. GFDL Ocean. Group Tech. Rep. 2, 142.
Pietrzak J., Jakobson J. B., and Burchard. H. (2002). A three-dimensional hydrostatic model for coastal and ocean modelling using a generalized topography following coordinate system. Oxf 4, 173–205. doi: 10.1016/S1463-5003(01)00016-6
Shchepetkin A. and McWilliams J. C. (2005). The regional oceanic modeling system (ROMS): a split-explicit, free-surface, topography-following-coordinate oceanic model. Oxf 9, 347–404. doi: 10.1016/j.ocemod.2004.08.002
Shi F. and Zhu S. (2000). Numerical study on residual current and its impact on mass transport in the Hangzhou Bay and the Changjiang Estuary I. A 3-D joint model of the Hangzhou Bay and the Changjiang Estuary. Haiyang Xuebao (in Chinese). 22, 1–12.
Smagorinsky J. (1963). General circulation experiments with the primitive equations: I. Basic Experiment Monthly Weather Rev. 91, 99–164. doi: 10.1175/1520-0493(1963)0912.3.CO;2
Wang B., Wu L., and Zhao N. (2021). Summer wind effects on coastal upwelling in the southwestern Yellow Sea. J. Mar. Sci. Eng. 9, 1021. doi: 10.3390/jmse9091021
Xia C., Qiao. F., Yang. Y., and Ma. J. (2006). Three-dimensional structure of the summertime circulation in the Yellow Sea from a wave-tide-circulation coupled model. J. Geophys 111. doi: 10.1029/2005JC003218
Yang D., Yin. B., Liu Z., and Feng X. (2011). Numerical study of the ocean circulation on the East China Sea shelf and a Kuroshio bottom branch northeast of Taiwan in summer. J. Geophys 116. doi: 10.1029/2010JC006777
Zhang Y. and Baptista A. M. (2008). SELFE: A semi-implicit Eulerian–Lagrangian finite-element model for cross-scale ocean circulation. Ocean Model. 21 (3–4), 71-96. doi: 10.1016/j.ocemod.2007.11.005
Zhuang Z., Yuan. Y., and Yang. G. (2018). An ocean circulation model in σs-z-σb hybrid coordinate and its validation. Ocean. Dyn. 68, 159–175. doi: 10.1007/s10236-017-1124-6
Appendix
Chen et al. (2003) gave the governing equations of momentum, continuity, temperature and salinity for the ocean waters in z coordinate as following:
where is the elevation; f is the Coriolis parameter; is the vertical turbulent diffusion coefficient; is the vertical turbulent mixing coefficient; and are the items of baroclinic pressure gradient (BPG); is the solar radiation; , , and are the horizontal diffusion terms of turbulence. and are parameterized by the Mellor and Yamada (1982) level-2.5 (MY-2.5) turbulent closure scheme. The expressions of BPG in Equations A.1, A.2 of z coordinate system are:
where g is gravitational acceleration, is the ocean water density, and is the standard density.
In the FVCOM model, the sigma coordinate transformation was used in the vertical in order to obtain a smooth representation of irregular bottom topography (Chen et al., 2003). The sigma coordinate transformation is defined as:
where is the static water depth. The vertical velocity is defined as
The relation between and is:
Then Equations A.1-A.7 are given as:
(A.14)
Regarding the sigma coordinate of Equation A.8, the following applies:
Equations (A.16)-(A.17) require that every vertical layer has constant value, which is named as conventional sigma coordinate in this paper. The translations of (A.16)-(A.17) are used in Equations (A.11)-(A.12) of sigma coordinate system to calculate the BPG.
In maritime areas with steep terrains and notable density stratifications, and are two major counter terms, but the algebraic sum of is a minor term. General temperature and salinity errors lead to errors in the calculations of and , which may result in serious errors in the algebraic sum of . To reduce the BPG calculation errors, in Equations A.16-A.17 can be replaced by residual density by removing the average density stratification.
Keywords: FVCOM, λ coordinate, generalized terrain-following coordinate, baroclinic pressure gradient, ocean circulation model
Citation: Bu Y, Chen Y, Zhu S, Zhang W, Cao G and Ding Z (2025) Development of generalized terrain-following FVCOM model for the steep terrain seas. Front. Mar. Sci. 12:1441840. doi: 10.3389/fmars.2025.1441840
Received: 31 May 2024; Accepted: 11 July 2025;
Published: 06 August 2025.
Edited by:
Donald B. Olson, University of Miami, United StatesReviewed by:
Tarang Khangaonkar, Pacific Northwest National Laboratory (DOE), United StatesLiying Wan, National Marine Environmental Forecasting Center, China
Copyright © 2025 Bu, Chen, Zhu, Zhang, Cao and Ding. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yang Chen, Y3lAaGh1LmVkdS5jbg==; Shouxian Zhu, emh1c2hvdXhpYW5AdmlwLnNpbmEuY29t
 Yixuan Bu
Yixuan Bu Yang Chen
Yang Chen Shouxian Zhu1*
Shouxian Zhu1*