Dynamic motion response of a large-scale steel aquaculture cage during towing

As global aquaculture ventures further into offshore environments, the safe transport of large-scale aquaculture net cages across varied marine conditions has become a critical technical concern. This study conducts a detailed numerical simulation of the wet towing process for an octagonal aquaculture cage using AQWA software, systematically examining the effects of towline length, towing speed, towing configuration, and environmental factors on the cage’s dynamic response and towline load characteristics. The findings reveal that towline length and towing speed are pivotal in determining the pitch amplitude of the cage and the resulting towline tension. Compared to a towline length of 200 m, using a towline length of 150 m combined with a towing speed of 0.5 m/s reduces pitch amplitude by 51.6% and towline tension by 24.8%. Additionally, an interval towing arrangement significantly enhances cage stability while minimizing towline stress. Under conditions of low wave height and longer wave period, the cage’s motion response remains stable, contributing to enhanced transport safety. This research offers critical theoretical foundations and optimization strategies for the wet towing design considerations of offshore aquaculture cages, providing valuable insights to advance transport safety in challenging marine environments.

1 Introduction

With rising global living standards and increasing demand for fish protein, nearshore aquaculture is nearing its production capacity. Consequently, offshore aquaculture net cages have emerged as vital marine farming infrastructure, providing an effective solution to spatial constraints and environmental sustainability challenges in coastal areas (Dong et al., 2024). Compared to nearshore farming, offshore aquaculture offers advantages such as improved water quality, larger farming areas, and enhanced seafood quality (Froehlich et al., 2017). However, offshore operations are often located in open ocean environments where aquaculture platforms are vulnerable to typhoons, large waves, and strong currents. To mitigate these challenges, offshore net cages are typically constructed with steel structures, which increase their resistance to wind and waves, ensuring the safety and productivity of aquaculture activities.

Offshore net cages build on traditional floating net cage designs, integrating technical advancements from floating marine engineering platforms and innovating to meet the specific demands of offshore aquaculture. This approach overcomes the structural limitations faced by traditional aquaculture platforms in offshore environments, representing a significant strategic shift from nearshore to offshore aquaculture (Ding et al., 2023). Since offshore net cages are designed to be positioned far from shore, they are typically constructed on land, where the towing system is first deployed at a designated location before transporting (Figure 1) and securing the cage offshore (Lira et al., 2019). For instance, the ‘Deep Blue one’ tilting incident, which involved significant damage during towing operations, underscores the importance of ensuring safe towing methods for these platforms. Current research primarily focuses on the dynamic response, structural strength, and fatigue resistance of net cage towing systems, with relatively little attention given to the safety of cage transport. Ensuring safety during towing is crucial for the overall structural integrity of net cages. While studies on the transport of offshore net cages remain limited, existing literature on marine structure dynamics and engineering provides a solid foundation for the design and optimization of net cage transport systems.

Figure 1

Figure 1. The towing process of (A) Ocean Farm one and (B) Deep Blue one (photo courtesy of www.salmar.no and sd.ifeng.com).

Since the 1950s, detailed analyses have been conducted on towing systems for floating structures and the factors affecting towing operations, both domestically and internationally. Wet towing has been widely applied in marine engineering and has been extensively studied as a critical technology. The feasibility of the wet towing method for the offshore substation WSBJF has been confirmed through experimental and numerical studies (Wang et al., 2023). The allowable pressure range for the Composite Bucket Foundation (CBF) during offshore transport has been analyzed using the finite element method, highlighting its potential for offshore applications (Li et al., 2024). Strategies for reducing installation costs in offshore projects have been proposed through investigations into the wet towing transport method for the “jacket + three-bucket foundation” structure in offshore wind farms (Yan et al., 2021). The safety of air-buoyancy structures during transport has been verified through physical experiments, which observed the floating behavior of the CBF under varying speeds, wave heights, and wind conditions (Ding et al., 2020). The air-buoyancy towing behavior of multi-bucket foundation platforms (MBFPs) has been studied using MOSES numerical simulation software, demonstrating that towing stability can be significantly improved by reducing towing speed and selecting appropriate sea conditions (Le et al., 2013). These studies collectively emphasize the essential role of wet towing in ensuring the safe and stable transport of marine structures.

The composition of the towing system is also critical to the safety of net cages. In 1958, (Holmstrom, 1982) studied towing systems based on linear theory and found that adjusting the position of the towline configuration and the length of the towline could improve the stability of the towing system (Yasukawa and Yamada, 2009) enhanced the safety of towing systems for floating wind turbines by adjusting the towline position and length. (Li et al., 2020) used MOSES to examine the static stability of floating wind turbines under different environmental conditions. (Le et al., 2021) conducted model tests and found that towing speed and wave height significantly impact the towing stability and drag of tension-leg platforms. (Fitriadhy et al., 2013) discovered that towline elasticity and the weight of the towed structure play crucial roles in the directional stability of towing systems (Shin, 2011)further analyzed the effect of elastic towlines on towing stability. Through simulation studies (Shi, 2011)investigated the combined effects of towline length, water depth in the towing area, and current speed on the towing system, noting that towing against the current causes greater system drift, with water depth having a more substantial effect than towline length. (Han et al., 2017) used a multibody dynamics approach to analyze the impact of wind, waves, and currents on the towing stability of floating wind turbines, concluding that pitch motion is more affected by wind and waves than roll and heave motions. These studies underscore the importance of towline length and towing speed for the safe transport of net cages, providing essential theoretical support for maintaining stability during the towing process.

In offshore aquaculture, the shape of the net cage plays a critical role in its stability and adaptability. Octagonal cages are commonly used in offshore farming due to their unique geometric structure. Compared to traditional circular or square cages, octagonal cages offer superior hydrodynamic stability, enabling them to more effectively distribute the forces exerted by ocean currents and waves (Fan et al., 2023). This shape has been widely adopted (e.g., in Ocean Farm one and Deep-Blue one) and not only helps to reduce stress concentrations in dynamic environments but also provides greater internal space, optimizing the growth conditions for fish.

Therefore, this study focuses on an octagonal steel cage, using a combination of physical experiments and numerical simulations to analyze in detail the effects of various towing configurations on cage stability. Key variables, including towline length, towing speed, and marine environmental conditions, are comprehensively considered to explore their impact on the dynamic response characteristics during towing. The structure of this paper is as follows: Section 2 provides an overview of the platform, model, and towline geometry, detailing the geometric structure and physical properties. Based on hydrodynamic theory, the equations of motion and forces acting on the net cage in a marine environment are established. Section 3 verifies the accuracy of the numerical simulations through comparisons with physical model tests. Section 4 discusses the steady-state stability of the net cage under different towing points. The influence of key factors such as towline length, towing speed, wave period, and wave height on towing stability is then examined. The subsequent section presents the main insights of this study, along with a grounded discussion on potential directions for future research. Finally, conclusions are summarized in Section 6.

2 Materials and methods

Numerical simulation and laboratory experiments are employed to investigate the effects of towing position, towing length, towing speed, wave period, and wave height on the dynamic response characteristics of a newly built cage. In this study AQWA is utilized to develop a numerical model for simulating the towing process of a fish farm, focusing on analyzing the effects of towing point position and wave loads on its dynamic response.

2.1 Experimental setup

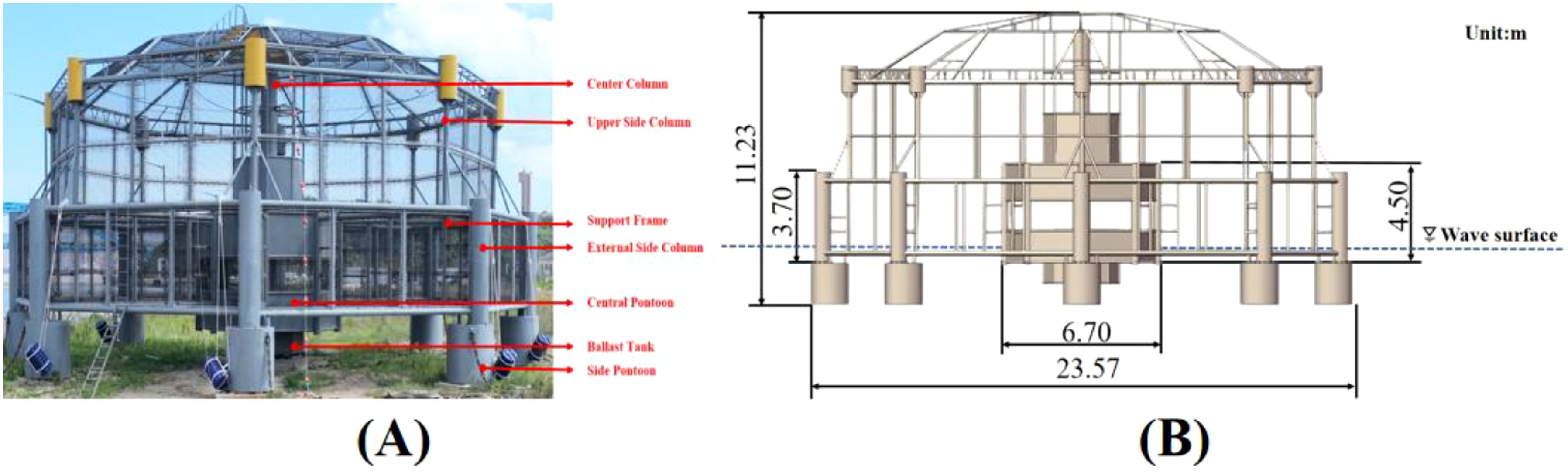
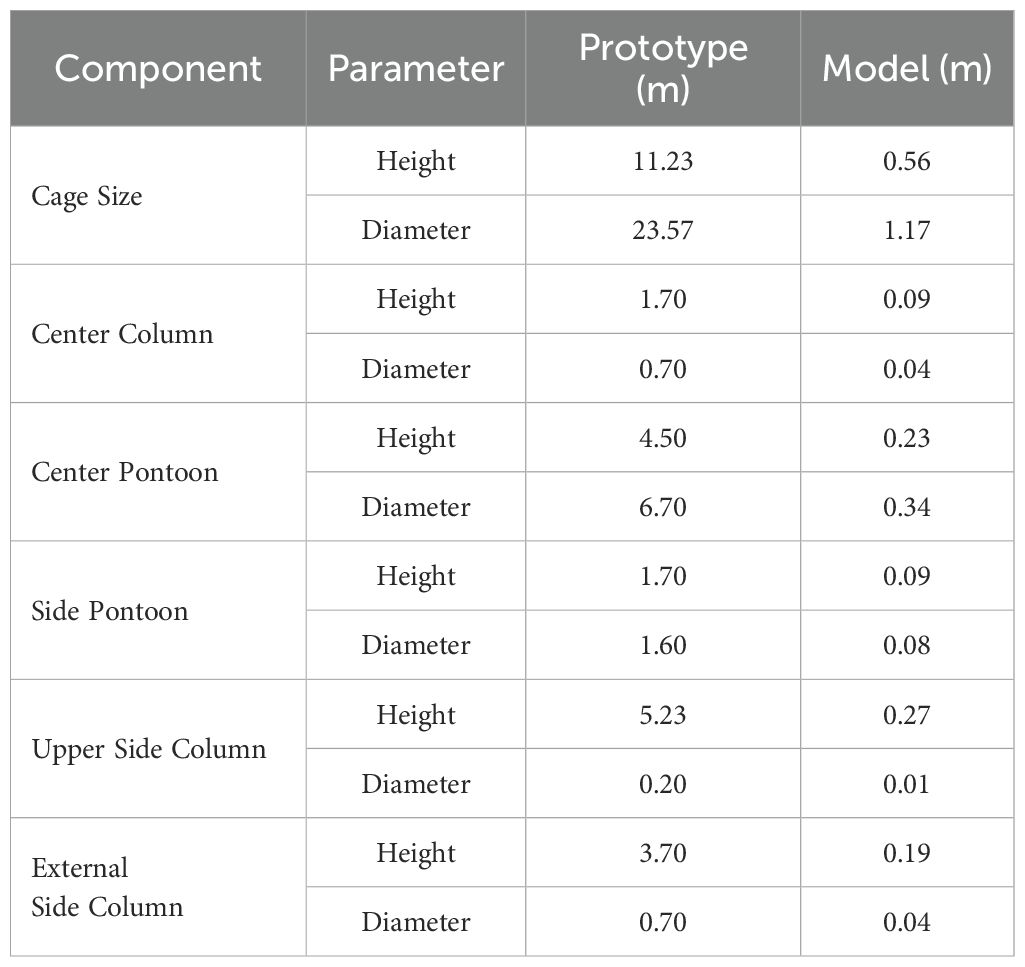
The net cage is designed an octagonal structure (Figure 2A), primarily consisting of external edge columns, a central column, and supporting trusses. The external frame is divided into two parts: side pontoons and external edge columns. Eight side pontoons are arranged in a regular octagonal layout around the perimeter of the net cage and are connected to the central float by cylindrical trusses. An octagonal ballast tank is installed at the lowest part of the net cage, to lower the center of gravity and enhance its stability. The net cage has an overall height of 11.23 m, a width of 23.57 m, and a draft depth of 2.2 m. The side pontoons have a diameter of 1.6 m and a height of 1.7 m, while the central float has a diameter of 6.7 m and a height of 4.5 m (Figure 2B). The main parameters are provided in Table 1 for reference.

Figure 2

Figure 2. Photo: (A) Net cage prototype; (B) Geometric dimension.

Table 1

Table 1. Principal parameters of the model.

2.1.1 Equations of motion for towed body

The planar motion equations are typically used to describe the behavior of objects moving in a two-dimensional plane. The forces acting on the net cage can be categorized into externally applied forces, damping forces, and restoring forces. The combined effect of these forces determines the motion state of the net cage. When the net cage moves in water, the resultant force can be expressed as:

$$F_{total}=F_{ext}+F_{damping}+F_{restoring}$$

Where $F_{ext}$ represents the externally applied forces, $F_{damping}$ represents the damping forces, and $F_{restoring}$ represents the restoring forces. The damping force is typically proportional to velocity and can be expressed as:

$$F_{damping}=- c·V$$

Where $F_{damping}$ is the damping force, c is the damping coefficient, and V is the velocity. The restoring moment is related to displacement and is typically expressed as:

$$F_{restoring}=- k·X$$

Where $F_{restoring}$ is the elastic force, k is the stiffness coefficient, and X is the displacement. Substituting the above equations into Newton’s second law and simplifying yields:

$$M_{trans}·\frac{d^{2}X}{d{t}^2}+C_{trans}·\frac{dX}{dt}+D_{trans}(X)+F_{ext,trans}=0$$

Where $M_{trans}$ is the translational mass matrix, $D_{trans}$ is the translational damping matrix, $D_{trans}$ is the translational restoring force, and $F_{ext,trans}$ is the translational external force (wave force). Based on this, the rotational motion equation further describes the behavior of the object during rotation.

During the rotational process, the expression for the resultant moment can be represented as:

$$M_{total}=M_{ext}+M_{damping}+M_{restoring}$$

Where $M_{total}$ is the total moment applied, $M_{ext}$ is the external moment, $M_{damping}$ is the damping moment, and $M_{restoring}$ is the restoring moment. The damping moment is typically proportional to the angular velocity and can be expressed as:

$$M_{damping}=-c_{rot}·\Omega$$

The restoring moment is related to angular displacement and is typically expressed as:

$${\text{M}}_{restoring}=-k_{rot}·\Theta$$

By substituting the above equations into the rotational equation and simplifying, we obtain:

$$I·\frac{d^2\Theta }{d{t}^2}+C_{rot}·\frac{d\Theta }{dt}+D_{rot}(\Theta )=0$$

Where I is the rotational inertia, $C_{rot}$ is the rotational damping matrix, $\Omega$ is the angular acceleration, $k_{rot}$ is the rotational restoring coefficient, and $\Theta$is the angular displacement of the net cage.

In the practical application of net cages, there exists a coupling relationship between translational and rotational motion. The coupled motion equation can be used to describe the interaction between these two types of motion, as follows:

$$F_{couple}=M_{couple}·A+C_{couple}·V+D_{couple}(X)$$

Where $M_{couple}$ is the coupled mass matrix, A is the acceleration vector, V is the velocity vector, and $D_{couple}(X)$ is the coupled restoring force.

2.2 Towing system

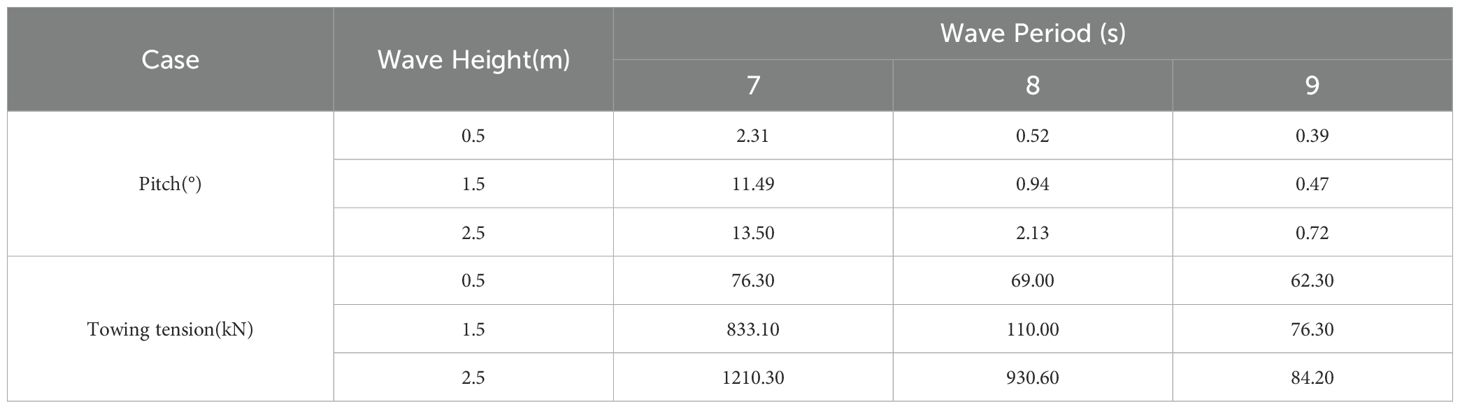
Based on the octagonal structure of the net cage, this experiment adopts two towing configurations: the adjacent fixation configuration and the spaced fixation configuration. In the adjacent fixation configuration, two towlines are symmetrically fixed to two adjacent side pontoons, while in the spaced fixation configuration, two towlines are symmetrically fixed to alternate side pontoons, with the other ends secured to the stern of the tugboat (Figure 3).

Figure 3

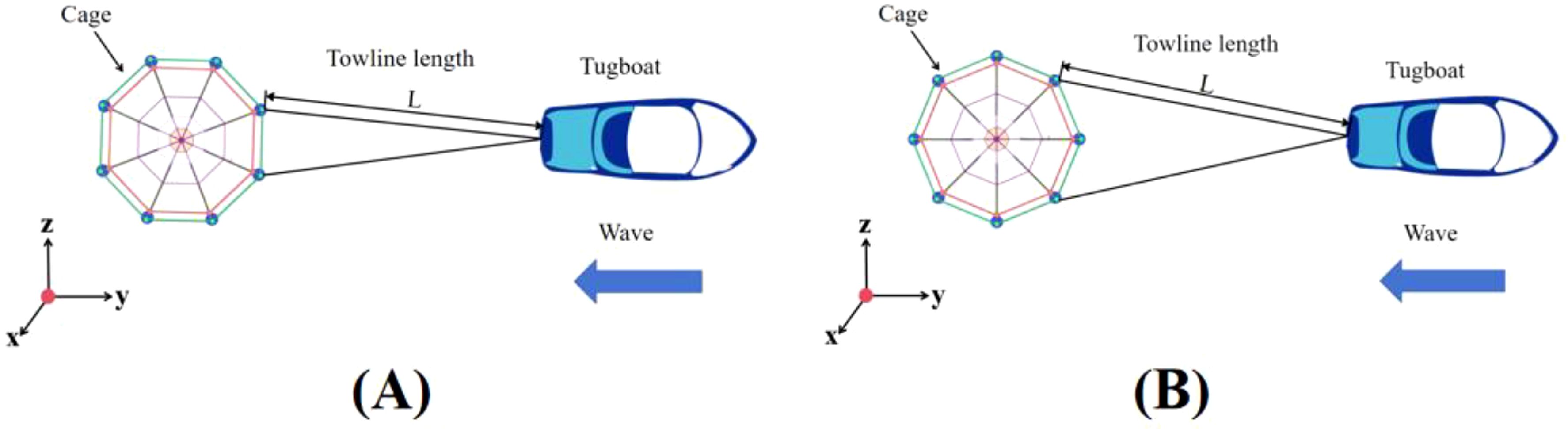
Figure 3. Top view of the towing systems with towline fixed on two: (A) adjacent pontoons; (B) spaced pontoons.

2.2.1 Towing length

The towline is an important factor affecting the motion of the net cage. In towing analysis, the dynamic response of the towline can be calculated by considering its stiffness and damping coefficients. The calculation formula for the towline force is as follows:

$$F_{cable}=k_{cable}\Delta L+c_{cable}\frac{d}{dt}\left(\Delta L\right)$$

Where $F_{cable}$ is represents the stiffness of the towline, indicating its ability to resist stretching, $\Delta L$ is the elongation of the towline, $c_{cable}$ is the damping coefficient of the towline, describing energy dissipation during towing.

According to international maritime regulations, the minimum safe length of the main towline must be calculated (Solas, 2002). The formula for calculating the minimum safe length of the main towline is as follows:

$$L=\left(L_1+L_2\right)·K$$

Where L represents the minimum safe length of the main towline, $L_1$ represents the total length of the tugboat, $L_2$ represents the total length of the towed vessel, and K is the wind and wave coefficient. Based on weather conditions, the value of K ranges from 2.3 to 3.3, with 2.3 used for favorable weather and 3.3 for rough conditions. In this analysis, the wind and wave coefficient K is set to 2.3, and the length of the tugboat $L_1$ is 23 m. Therefore, the minimum safe length of the main towline is calculated as 100 m (rounded).

2.3 Numerical simulation analysis

This study uses Airy wave theory to describe wave motion by setting reasonable parameters such as wave height, period, and wavelength to construct a wave environment for simulating the dynamic response of the net cage during towing. The wave model not only effectively reflects the wave motion characteristics under actual sea conditions but also provides a reliable theoretical foundation for analyzing the dynamic behavior of the towing system.

2.3.1 Frequency domain analysis

In the frequency domain, the equations of motion can be transformed into the complex domain for solving. By solving the Frequency Response Function (FRF), the response characteristics of the structure under different wave frequencies can be obtained.

$$\widehat{\mathit{\xi }}(\mathit{\omega })=\frac{\widehat{\mathit{F}}(\mathit{\omega })}{(-{\mathit{\omega }}^{\mathbf{2}}\mathit{M}+i\omega C+\mathit{K})}$$

Where $\widehat{\xi }\left(\omega \right)$ denotes the frequency response, and $\widehat{F}\left(\omega \right)$ represents the wave force in the frequency domain.

2.3.2 Time domain analysis

Time domain analysis solves the equations of motion using numerical integration methods, which are suitable for simulating complex nonlinear problems, especially under real wave conditions.

$$M\ddot{\xi }\left(t\right)+C\dot{\xi }\left(t\right)+K\xi \left(t\right)=F\left(t\right)$$

In the above equation, M represents the mass matrix, describing the system’s mass characteristics and its effect on motion; C represents the damping matrix, describing the system’s damping characteristics, i.e., friction or energy dissipation; K represents the stiffness matrix, describing the system’s stiffness characteristics, i.e., its resistance to deformation; $\xi \left(t\right)$ denotes the displacement vector, representing the system’s displacement state at time t; $\dot{\xi }\left(t\right)$ denotes the velocity vector, which is the derivative of displacement with respect to time, reflecting the system’s motion speed; $\ddot{\xi }\left(t\right)$ denotes the acceleration vector, which is the second derivative of displacement with respect to time, reflecting the system’s acceleration;

In the time domain analysis module of AQWA, the wave propagation time step is set to 0.1 s, and the total simulation time is 1000 s to observe the long-term motion response of the net cage.

2.4 Simulation conditions

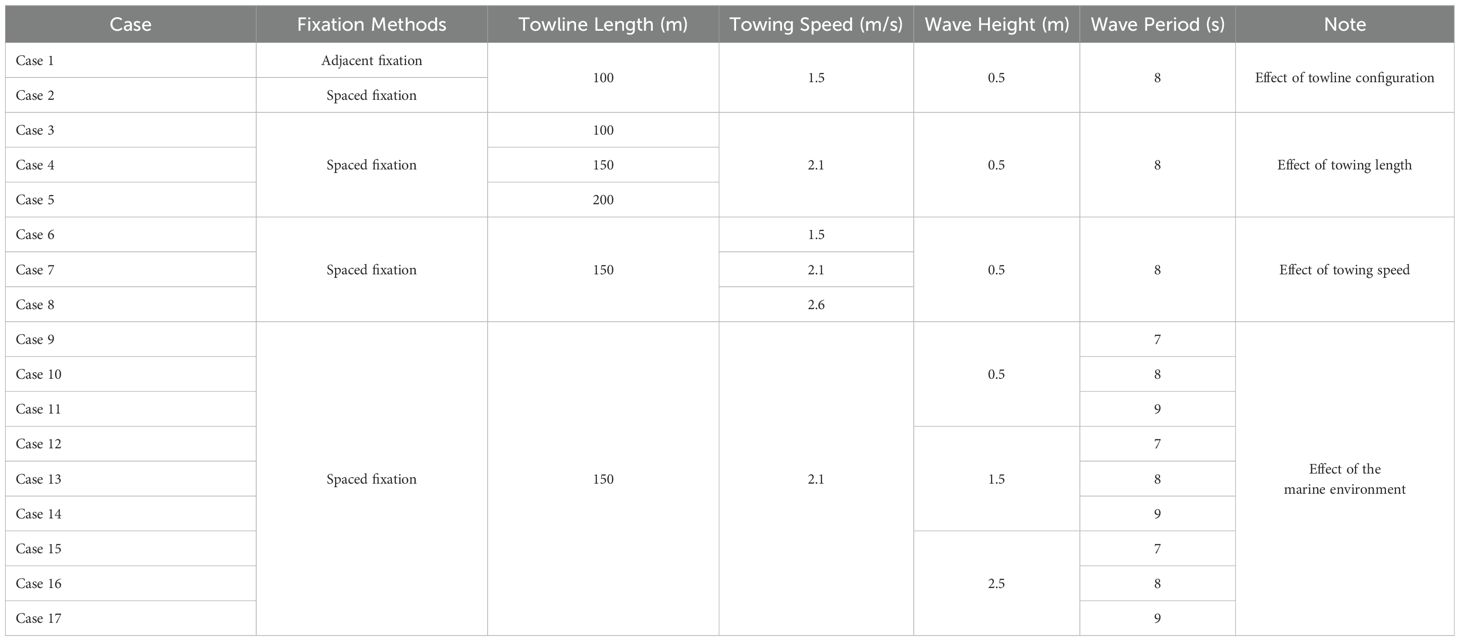
To comprehensively evaluate the effects of various factors on the stability of the towing system, this study designs a series of simulation scenarios. Given the significant impact of towing method, towing length, towing speed, and sea state on system stability and efficiency, simulations were conducted under 17 distinct conditions using sea state data provided by the China Oceanic Information Network (COIN). The simulations analyzed the time varying motion response of the net cage across different scenarios, as presented in Table 2. Comparisons were made to assess the effects of varying towing speeds (3 knots, 4 knots, 5 knots), towing lengths, and sea state levels (3, 4, 5) on the motion response.

Table 2

Table 2. Conditions of the simulation test.

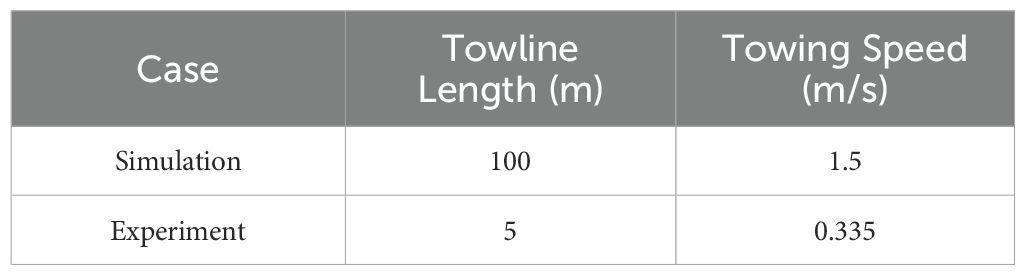
3 Model validation

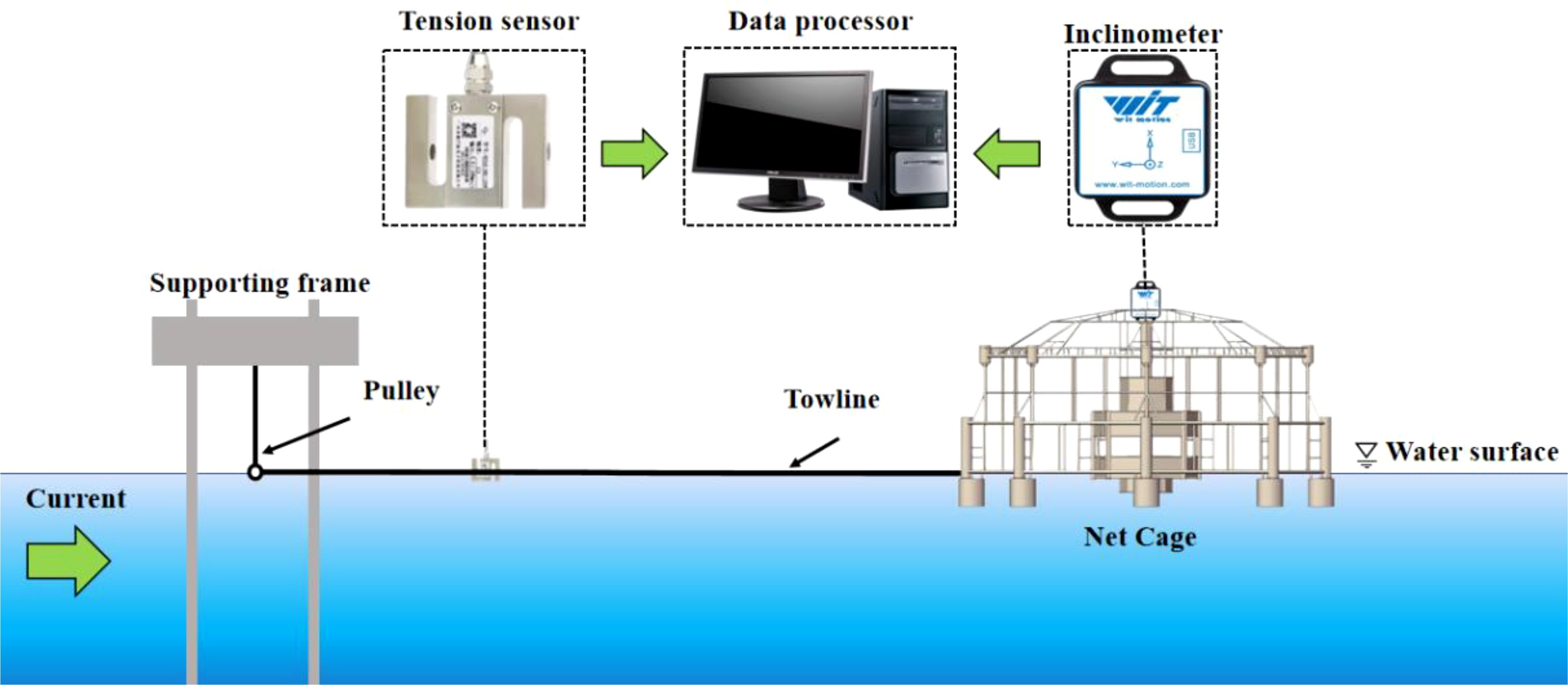
The experiments were conducted in a flume tank at Zhejiang Ocean University (Figures 4, 5). This flume tank featured a horizontal, square water channel with flow generated by axial-flow pumps. The test section had dimensions of 6.0 meters in length, 1.5 meters in width, and 1.2 meters in water depth. For model validation, a series of experiments were carried out on an octagonal cage model at a Froude scale of 1:20, with the results compared to numerical simulations conducted under identical environmental conditions. The specific environmental load conditions used in the experiments, including a spaced fixation configuration, a towline length of 100 meters, and a towing speed of 1.5 m/s, are summarized in Table 3. A comparison of the longitudinal pitching motion between the numerical simulations and experimental results is presented in Figure 6.

Figure 4

Figure 4. Schematic diagram of the towing experiments.

Figure 5

Figure 5. Photo of the experiment in the recirculating flume tank.

Table 3

Table 3. Parameters of test conditions for numerical model verification.

Figure 6

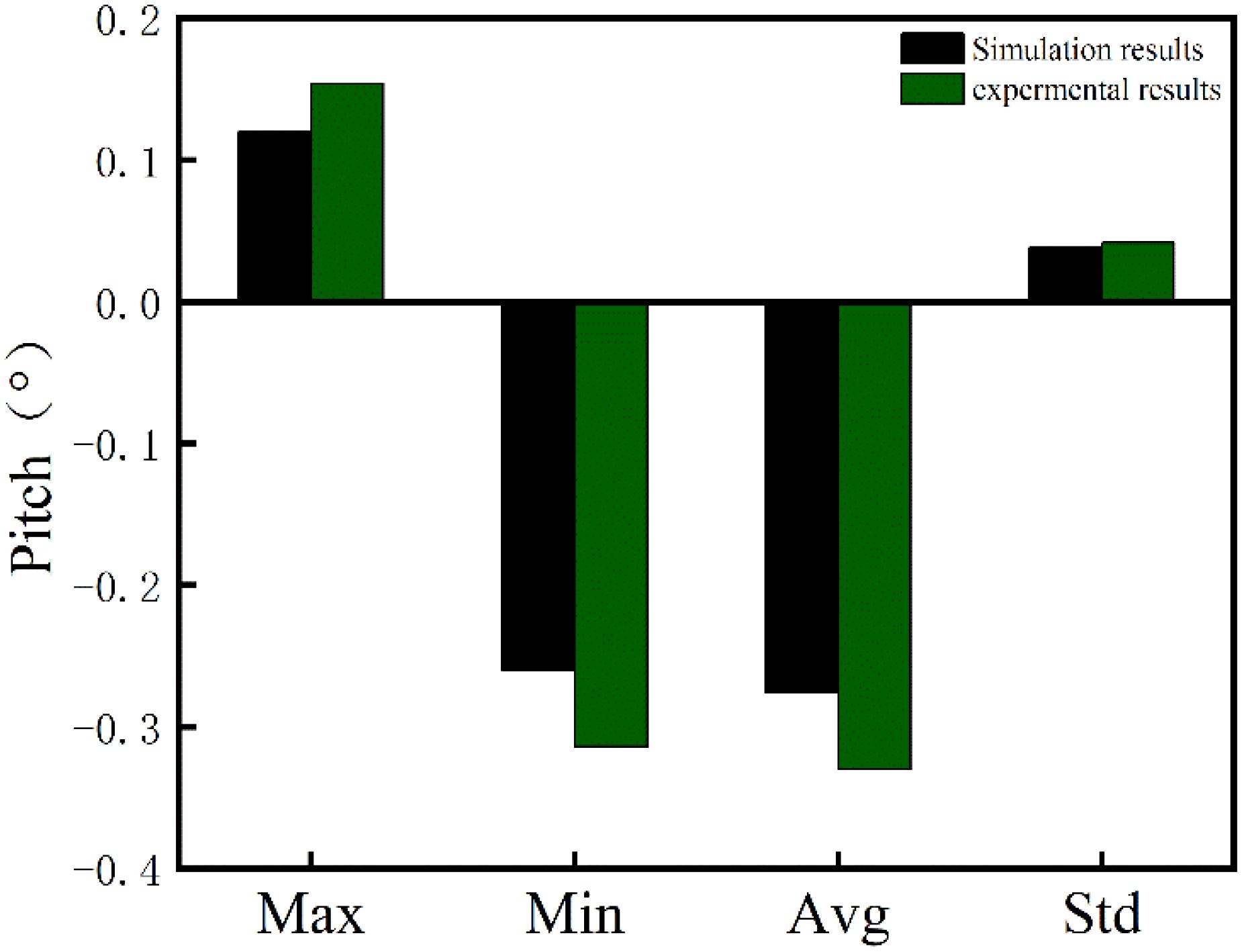
Figure 6. Comparisons of the pitch results from simulation and experiment. (Max., Min., Avg., and Std are the abbreviations for maximum, minimum, average, and standard deviation dataset).

The experimental results were compared with the simulation results, with the standard deviation for the simulation results being 0.038°, while the standard deviation for the experimental results is 0.041°. The maximum difference remained within 10%, indicating a close agreement between the two sets of data. This close alignment demonstrates that the numerical simulation can accurately predict towing responses.

4 Results

4.1 Effect of the towline configuration

The position of the towing configuration exerts a substantial influence on the motion amplitude of the net cage during towing operations. To quantify this effect, a comparative analysis was conducted on two experimental configurations, as outlined in Table 2 (Adjacent fixation and Spaced fixation). Figure 7 presents a statistical comparison of the roll and heave motions of the net cage across the different towing configurations.

Figure 7

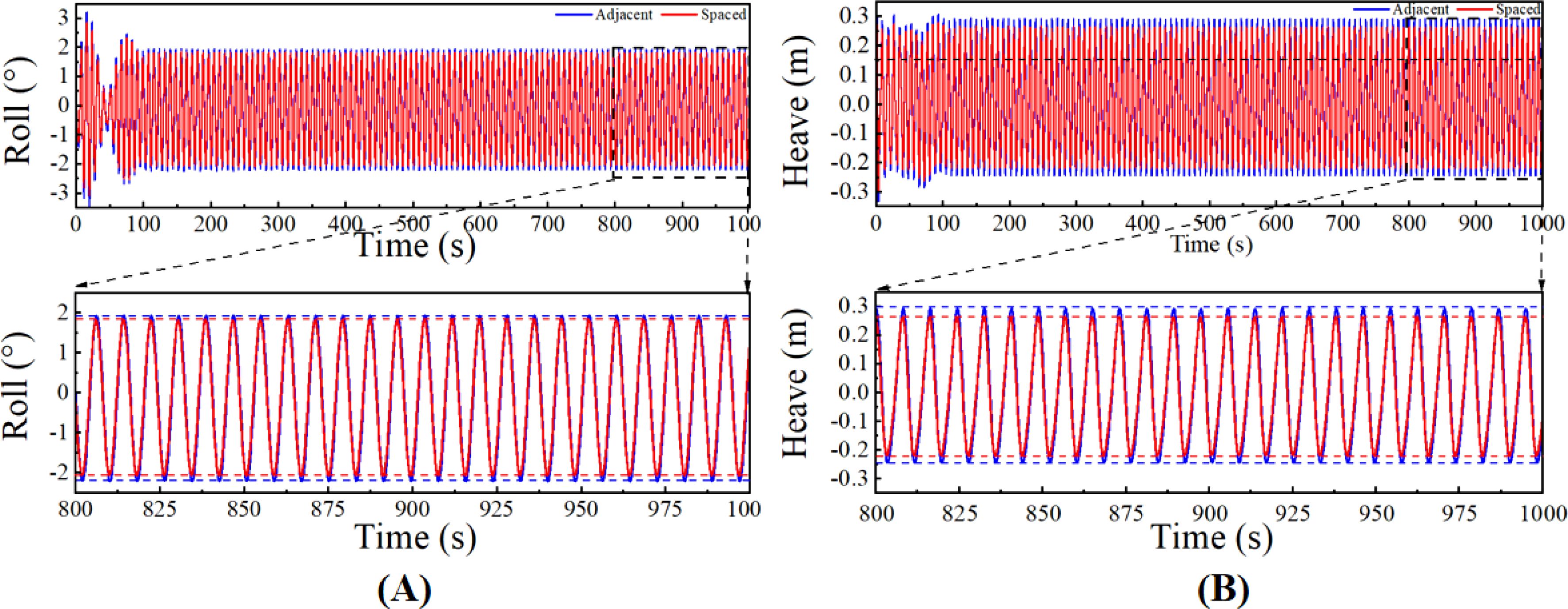
Figure 7. Dynamic response of (A) Roll and (B) Heave of the net cage for different towing configurations.

The comparison reveals that the towing position has minimal influence on the roll and heave responses of the net cage. Under both configurations, the roll and heave amplitudes remain stable at approximately 5.5° and 0.55 m, respectively. This finding demonstrates that different choices of towing points exert an insignificant effect on roll and heave responses, aligning with the conclusions of (Chen et al., 2024; Huynh and Kim, 2024) study similarly found that variations in towing position during towing have negligible impacts on heave and roll, likely due to the small geometric dimensions and shallow draft of the towed structure, resulting in limited motion differences.

Comparatively, the pitch motion is markedly influenced by the towing position. Figure 8 presents the pitch time history curves for different towing configurations, showing that the numerical simulation stabilizes after 400 seconds, with Adjacent fixation exhibiting significantly higher pitch values than Spaced fixation. A focused analysis of the pitch amplitude over the 800–1000 second interval indicates that, in Adjacent fixation, the pitch amplitude fluctuates between -0.35° and 0.51°, while in Spaced fixation, the range is notably reduced to -0.16° to 0.24°, representing a 53.49% decrease relative to Adjacent fixation. This reduction is attributed to the optimized towing position in Spaced fixation, where the tow cable’s configuration are positioned more laterally, leading to a more uniform force distribution and a corresponding decrease in longitudinal moment impact on the net cage.

Figure 8

Figure 8. Dynamic response of the pitch of the net cage with different towing configurations.

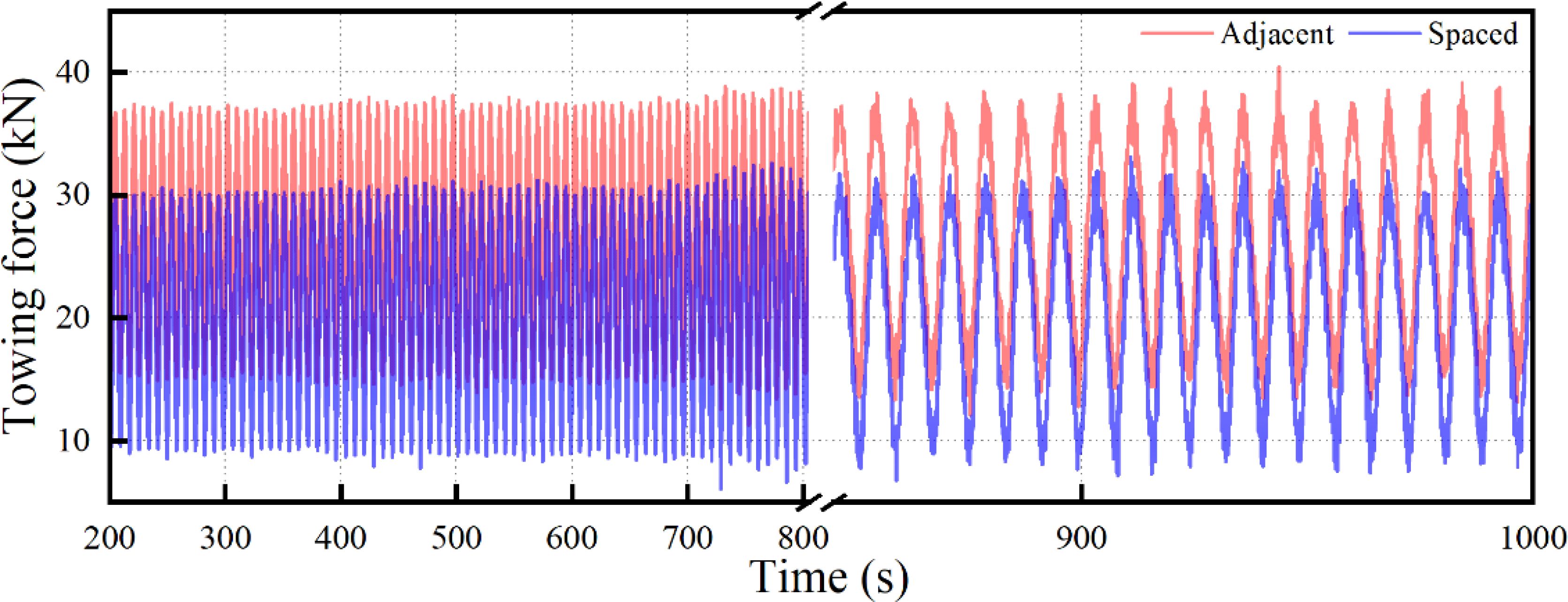
Figure 9 provides a detailed illustration of the variation in towline tension under different towing configurations. It is evident from the figure that the towline tension in Adjacent fixation is significantly higher than that in Spaced fixation, with greater fluctuations, indicating more severe load variations in the system under Adjacent fixation, where the maximum tension reaches 37.43 kN. In contrast, Spaced fixation shows a maximum tension of 31.11 kN, with relatively smoother tension fluctuations. A comparison reveals that the towline tension in Spaced fixation is reduced by 16.88% compared to Adjacent fixation, likely due to the smaller towing angle in Adjacent fixation, causing uneven loading on the net cage during towing. Spaced fixation, with a lower towline load, demonstrates higher stability. Under identical sea conditions, the towing configuration in Spaced fixation proves safer than that in Adjacent fixation.

Figure 9

Figure 9. Dynamic response of the towing force at different towing configurations.

4.2 Effect of the towing length

In engineering applications, the towline serves as a critical variable in the towing system, where its length significantly impacts the motion response of the net cage. Consequently, this section considers towing length as the primary variable (Table 2) to examine its effect on the motion behavior of the net cage.

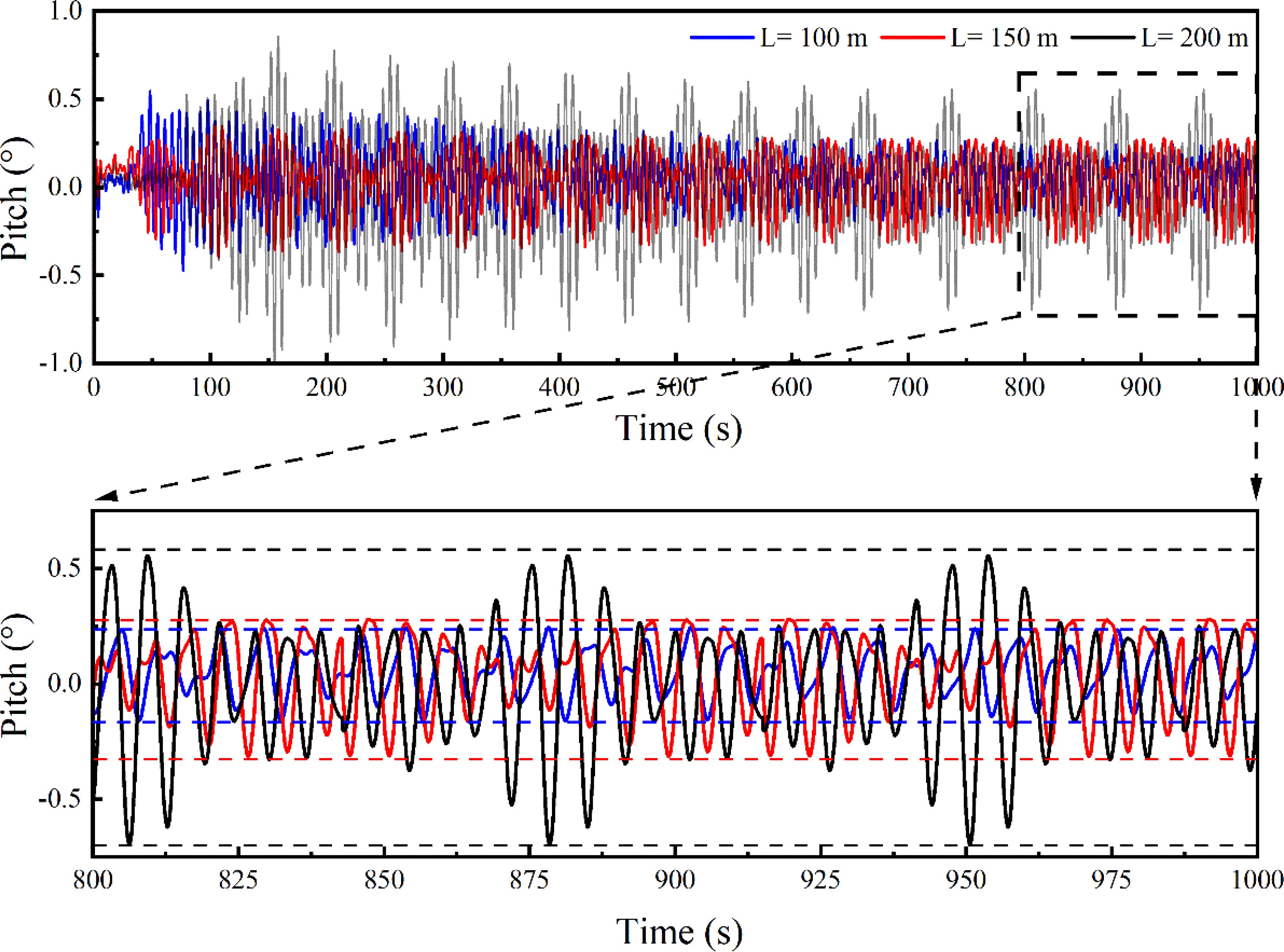
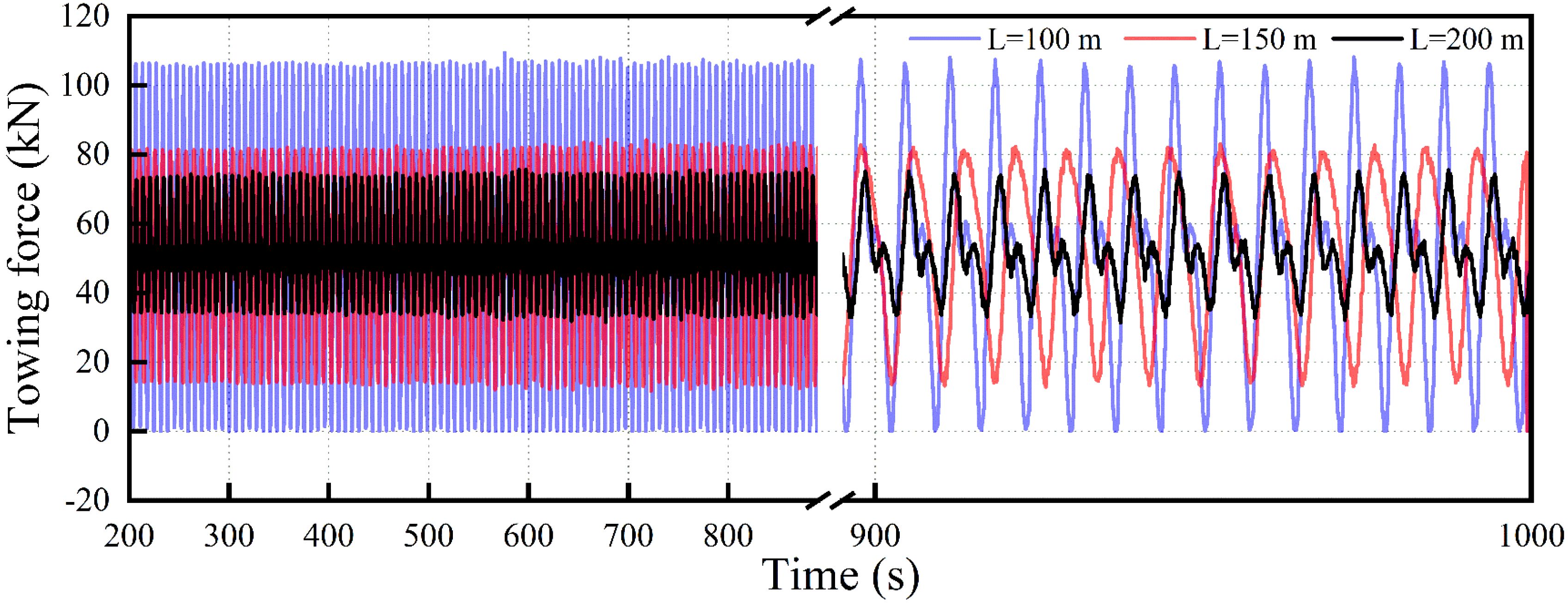
The time history of the pitch angle of the net cage at various towing lengths is illustrated in Figure 10. As the cable length increases, the pitch angle gradually rises, exhibiting periodic fluctuations across all lengths. Generally, towing length is inversely proportional to oscillation frequency. At a cable length of 100 m, the pitch angle exhibits minor fluctuations, around 0.38°, with a relatively high oscillation frequency. When extended to 150 m, the pitch amplitude increases to approximately 0.61°, accompanied by a slight decrease in frequency. At 200 m, the pitch amplitude increases considerably, with fluctuations reaching up to 1.26° and the lowest frequency recorded. Therefore, selecting an optimal towing length can effectively minimize pitch amplitude, allowing the net cage to reach a steady state more rapidly and maintain stability during towing.

Figure 10

Figure 10. Dynamic response of the pitch of the net cage with different towing lengths.

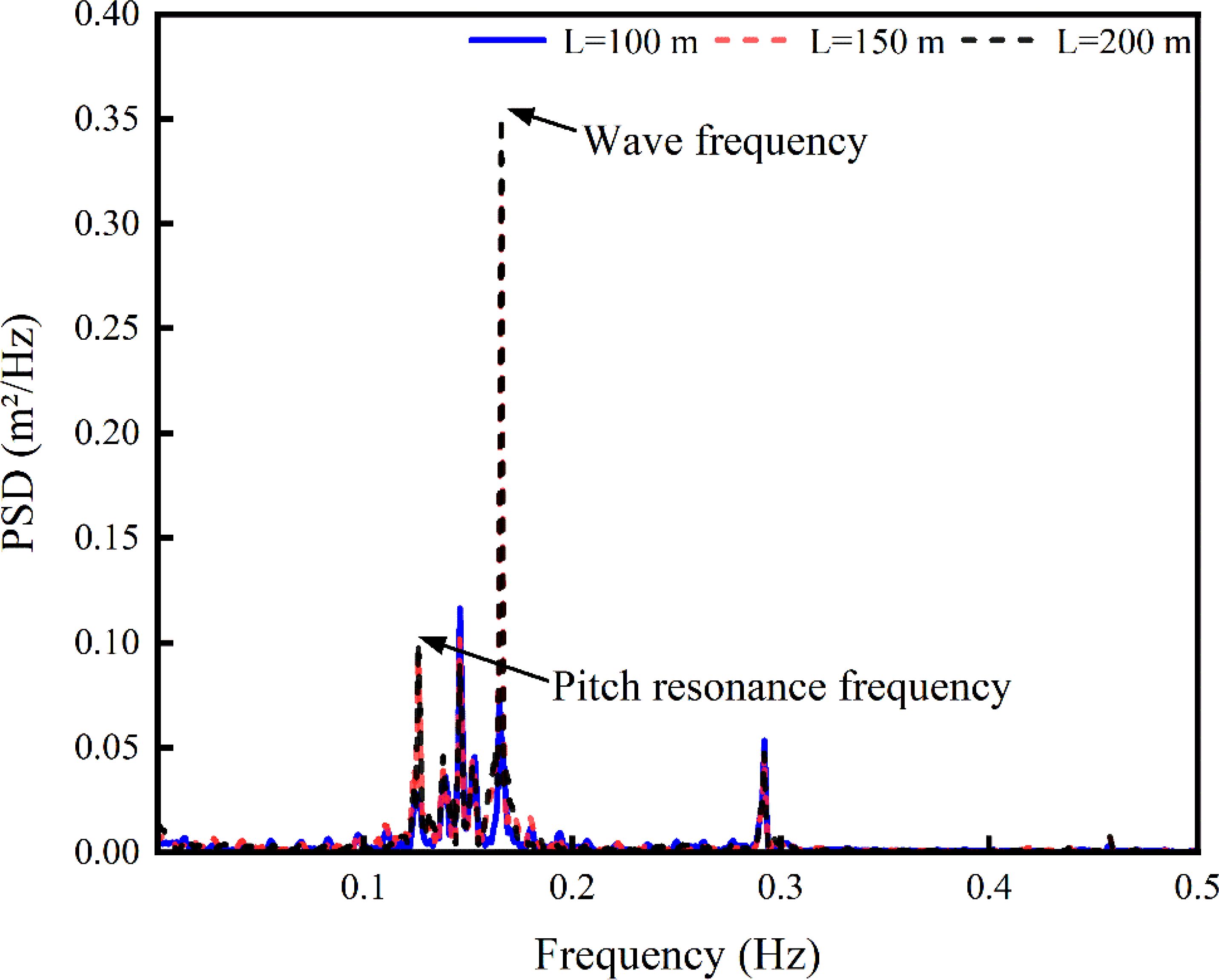
Figure 11 provides an illustration of the power spectral density (PSD) variation of pitch motion across three conditions as a function of frequency for different towing lengths. At the resonance frequency of 0.3 Hz and wave frequency of 0.17 Hz, cable length significantly influences the net cage’s pitch response. A shorter cable exhibits lower PSD values at these frequencies, indicating a smaller pitch response. As the cable length extends to 150 m, the PSD rises, reflecting an increase in vibration response. At a length of 200 m, the PSD reaches peak values at both resonance and wave frequencies, suggesting that a longer cable intensifies the net cage’s response to external disturbances, especially at wave frequency, where the pitch amplitude is greatest. Thus, increasing the cable length leads to stronger low-frequency vibration responses, which impacts the towing system’s stability.

Figure 11

Figure 11. Power spectra of net cage pitch motion with different towing lengths.

Figure 12 shows the effect of towing length on towing tension. The figure indicates that towing tension decreases as cable length increases. At a cable length of 100 m, the tension reaches its peak at approximately 109 kN; when the length extends to 150 m, the tension fluctuations reduce. At 200 m, the tension further declines to 75 kN, representing a 31.19% reduction compared to the 100 m length. This result suggests that shorter towlines are more susceptible to external environmental influences, leading to unstable force distribution and increased system complexity and risk. As the cable length increases, the variation in towing tension diminishes, enhancing the overall safety of the towing system.

Figure 12

Figure 12. Dynamic response of the towing force at different towing lengths.

4.3 Effect of the towing speed

Given the substantial volume of the aquaculture net cage, its wetted surface and horizontal plane are subject to considerable variation under intense motion. Table 2 provides a comparative analysis of selected towing speeds (1.5 m/s, 2.1 m/s, and 2.6 m/s) to assess the influence of towing speed on the net cage under representative marine conditions, including a wave height of H=0.5m, wave period of T=8s, towing length of 150 m, and a head on wave direction.

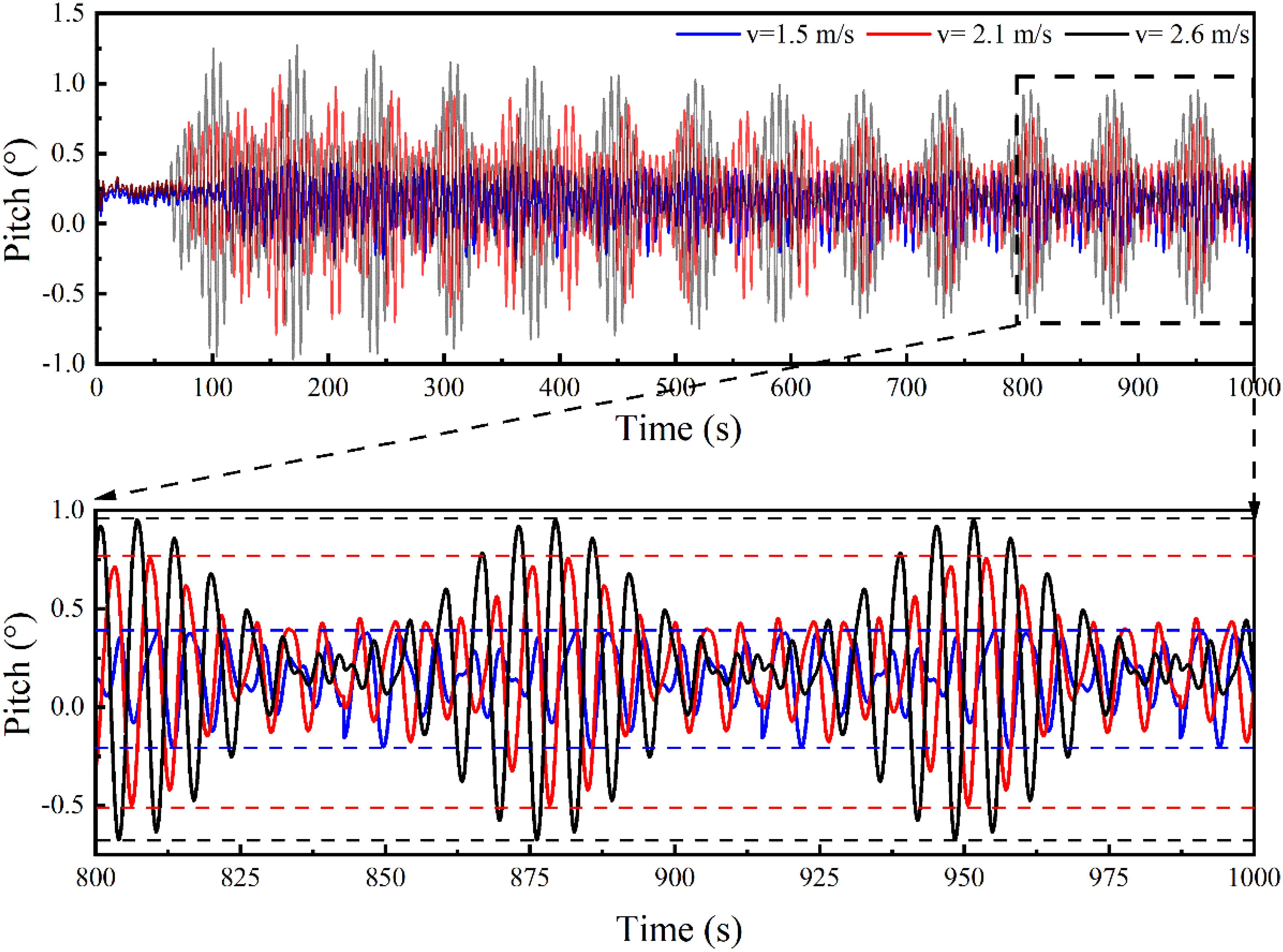
Figure 13 presents the time dependent trend of the vessel’s pitch angle under different towing speeds. The pitch amplitude and frequency both increase significantly with higher towing speeds. At 1.5 m/s, the pitch angle displays minor and steady fluctuations, indicating stable vessel motion at lower speeds. At 2.1 m/s, the pitch amplitude and fluctuation range expand. When the towing speed reaches 2.6 m/s, the pitch angle of the net cage shows intense fluctuations in both frequency and amplitude, highlighting the pronounced effect of high towing speeds on vessel motion.

Figure 13

Figure 13. Dynamic response of the pitch of the net cage under different towing speeds.

An expanded view between 800 s and 1000 s provides insight into the pitch angle’s detailed variations post stabilization under different speeds. At 1.5 m/s, the net cage exhibits small, consistent fluctuations with an amplitude of around 0.51°. With an increase to 2.1 m/s, the fluctuation amplitude rises to 1.22°. At 2.6 m/s, the pitch amplitude peaks at 1.62°, indicating intense motion. These observations reflect a nonlinear increase in pitch amplitude with rising towing speed, especially at higher speeds. It can be inferred that elevated speeds substantially affect net cage stability, intensifying the dynamic response of the system and potentially increasing structural fatigue risks.

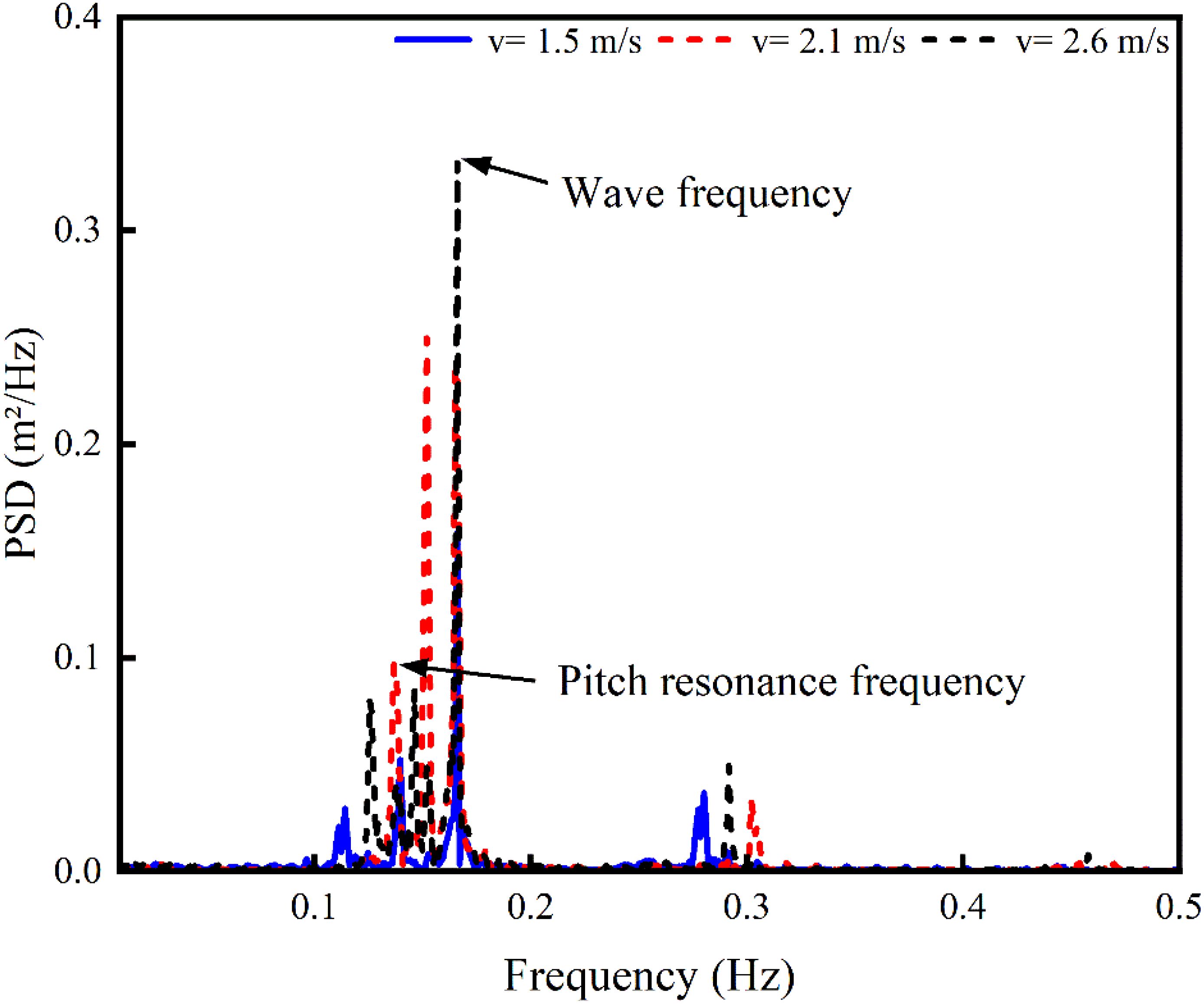
The frequency distribution of the power spectral density (PSD) for the vessel’s pitch angle under different towing speeds is presented in Figure 14, revealing the vibration response characteristics of the vessel at various frequencies. A prominent resonance frequency is observed around 0.15 Hz, with peaks present across all speeds, and power values increasing progressively with higher towing speeds. At low speed (1.5 m/s), the power at this frequency is minimal, indicating a weaker pitch response; however, at moderate (2.1 m/s) and high speeds (2.6 m/s), the peak power increases significantly, suggesting that the vessel is more prone to resonance at this frequency under higher speeds. Thus, as towing speed increases, the vessel’s vibration response at the pitch resonance frequency is markedly enhanced, with the pitch response becoming more intense, especially under high-speed towing conditions.

Figure 14

Figure 14. Power spectra of net cage pitch motion under different towing speeds.

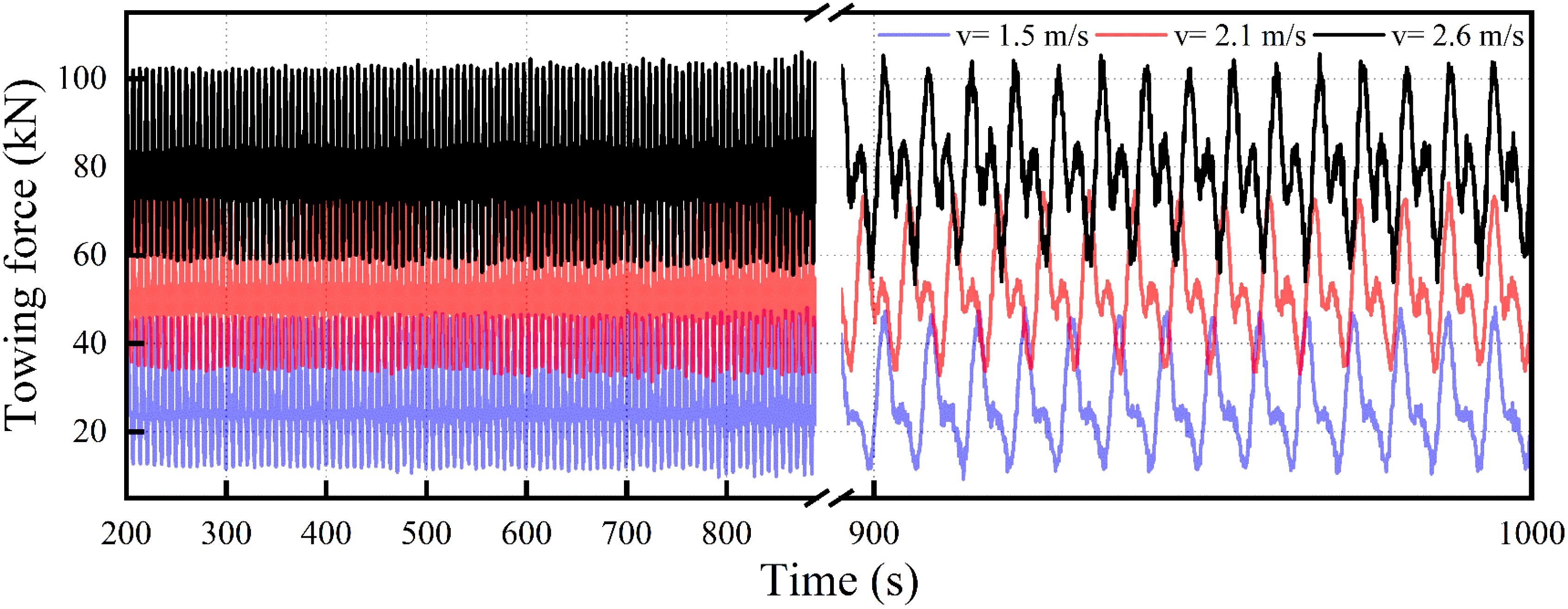
Figure 15 shows the variation in towline tension across different towing speeds. An increase in towing speed correlates with a rise in cable tension. At lower speeds, the tension remains steady around 48 kN; as the speed increases to 2.6 m/s, the tension reaches a peak of 73 kN. At this speed, the maximum fluctuation in tension is observed at 106 kN. These results suggest that higher towing speeds contribute to increased instability in cable tension, thereby adding complexity to the forces acting on the net cage.

Figure 15

Figure 15. Dynamic response of the towing force at different towing speeds.

4.4 Effect of the wave conditions

To investigate the effect of various marine environments on the towing of an octagonal cage, nine random sea states were selected through an orthogonal combination of different wave heights (H = 0.5 m, 1.5 m, and 2.5 m) and periods (T = 7 s, 8 s, and 9 s), Data were compiled to summarize the pitch motion response amplitude and towline tension under different marine conditions, and a comprehensive analysis of the results is provided in Table 4.

Table 4

Table 4. Summary of pitch motion response and towing tension.

Figure 16 shows the time-history curves of the net cage’s pitch motion under various conditions, illustrating how pitch motion amplitude fluctuates with changes in wave height and period:

Figure 16

Figure 16. Dynamic response of the pitch of the net cage under wave heights: (A) 0.5 m; (B) 1.5 m; (C) 2.5 m.

When the wave height is 0.5 m and the wave period is 7 s, the system exhibits large pitch angle fluctuations, with a maximum amplitude of approximately 2.51°, indicating an unstable state. Increasing the wave period to 8 s markedly reduces the pitch angle, with a maximum amplitude of 0.52°, and stabilizes the net cage motion, resulting in decreased fluctuation amplitude and frequency. At a wave period of 9 s, the maximum amplitude further reduces to 0.39°, producing smoother motion;

For a wave height of 1.5 m and a wave period of 7 s, the system reaches a maximum amplitude of 11.49°, which represents a 150.21% increase over the 0.5 m case. Increasing the wave period to 8 s reduces the pitch amplitude significantly to approximately 0.94°. When the period increases to 9 s, the maximum amplitude further declines to about 0.47°, indicating a 20.51% increase compared to the 0.5 m wave height condition;

In cases with a wave height of 2.5 m, the dynamic response of the system becomes even more pronounced. At a wave period of 7 s, the maximum amplitude approaches 13.50°, representing a 17.67% increase over the 1.5 m wave height case, highlighting more severe motion under high-wave conditions. Extending the wave period to 8 s decreases the pitch amplitude to 2.13°, an 81.24% reduction, with some fluctuations persisting. At a wave period of 9 s, the pitch amplitude decreases further, showing pitch angles similar to the 1.5 m wave height case.

Through an analysis of the changes in pitch angles under varying wave heights and periods, it becomes clear that the wave period significantly influences the pitch motion of the net cage. As wave height increases, the motion response of the net cage gradually intensifies; however, at higher wave periods, the system’s response appears more stable. Notably, under conditions of high waves and long periods, the net cage demonstrates a more stable dynamic response.

The towline tension curves under various marine environments are presented in Figure 17. A comprehensive analysis reveals that fluctuations in towline tension significantly increase with changes in wave height and wave period.

Figure 17

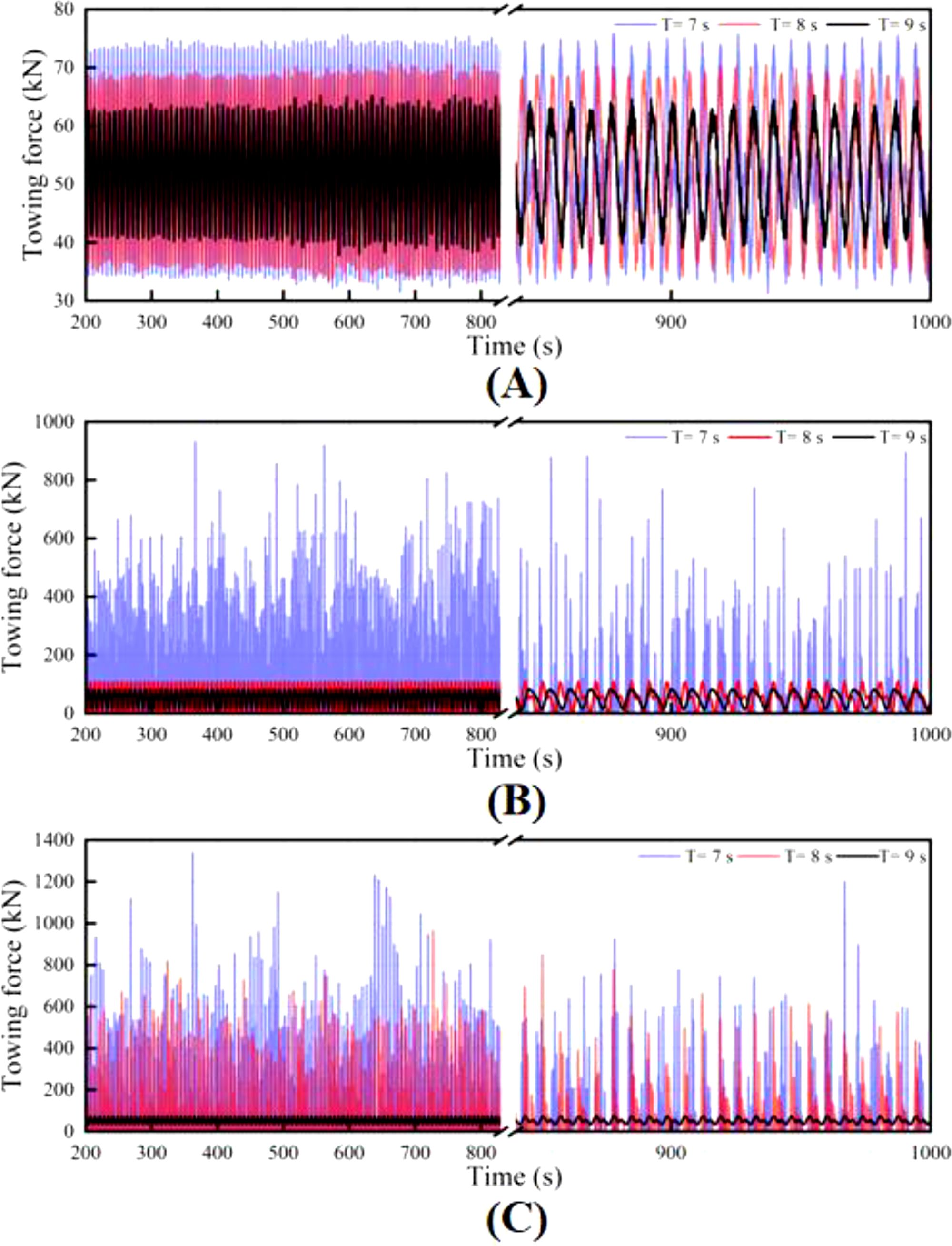
Figure 17. Dynamic response of the towing force under different wave heights: (A) 0.5 m; (B) 1.5 m; (C) 2.5 m.

When the wave height is 0.5 m, the towing force remains relatively stable, with a maximum fluctuation range of approximately 76.3 kN and minimal fluctuation amplitude, indicating that under low wave height conditions, the influence of wave period on towline tension is limited. However, as the wave height increases to 1.5 m, the fluctuation amplitude of the towing force increases significantly, reaching a maximum of 810.4 kN, which represents a 90.48% increase. Particularly at a wave period of 7 s, the fluctuations in towline tension become more intense, indicating that the influence of wave period is more pronounced under higher wave height conditions.

When the wave height increases to 2.5 m, the fluctuation amplitude of the towline tension reaches its maximum value of approximately 1210 kN, representing a 93.7% increase compared to the wave height of 0.5 m. At a wave period of 7 s, the towing force of the system reaches its peak, with extremely intense fluctuations, indicating that the combination of high wave height and short-wave period has the most significant impact on the dynamic stability of the system.

An analysis of towline tension and pitch angle under varying marine conditions indicates that changes in wave height and wave period significantly impact the towline tension and pitch angle of the octagonal cage. In general, a combination of high wave height and short-wave period increases net cage instability, resulting in substantial fluctuations in towline tension and marked intensification of pitch angle. This combination may lead to structural fatigue, thereby increasing the risk of damage. As wave height rises, the system’s pitch angle also increases significantly due to stronger hydrodynamic forces exerted by higher waves, which intensifies the system’s dynamic response. Conversely, under low wave height conditions, both the pitch angle and towline tension decrease significantly, contributing to greater system stability.

Additionally, wave period has a pronounced effect. Under identical wave height conditions, a longer wave period effectively reduces pitch amplitude and towline tension, suggesting that a longer wave period mitigates the system’s dynamic response and enhances towing stability.

5 Discussion

Large steel net cages are essential for marine aquaculture. These cages are typically installed on land and then towed by tugboats to the operational sea area. Unlike conventional cylindrical foundation platforms, the large size and high center of gravity of net cage platforms result in a higher water surface elevation under the same draft conditions. This increases the risk of tipping during long-distance towing operations. For example, the Deep Blue one net cage platform experienced two towing tilt incidents, leading to significant economic losses. As a result, the towing safety of large floating net cage platforms is a critical engineering issue (Shi, 2019). During towing, the dynamic performance of the net cage platform is influenced by factors such as towing configuration, towline length, and towing speed. These factors not only determine the platform’s motion response but also affect the distribution of towline tension and overall towing stability.

5.1 The impact of towing method on the towing performance of net cage platforms

The towing position (towline configuration) directly impacts the pitch angle of the net cage platform. The V-shaped towing configuration is commonly used in offshore wet towing operations. The choice of towing points has little effect on roll and heave responses, as noted by Liu et al (2024). Similarly, Huynh and Kim, (2024) found that changes in towing position have minimal effects on heave and roll during towing, likely due to the smaller dimensions and shallow draft of the towed structure, resulting in limited motion differences. However, this study compares two towing configurations: spaced and adjacent. The results show that spaced towing results in smaller motion amplitudes than adjacent towing. This agrees with Wang et al (2024), where the difference is attributed to the larger towline angle in the spaced configuration, which leads to a more balanced force distribution during towing and enhances stability. In contrast, for net cage platforms with large dimensions, the lateral force area is significant, which can cause substantial oscillations and create instability. The V-shaped towing configuration optimizes the towline’s distribution and angle, effectively dispersing lateral forces, thus improving resistance to tipping and enhancing overall towing stability.

In towing systems, the net cage platform is connected to the tugboat by a towline, and the length of the towline is a key factor affecting the dynamic performance of the net cage platform. This study demonstrates that increasing the towline length effectively mitigates the impact tension within the towline, a finding that is highly consistent with the conclusions of Fitriadhy and Yasukawa (2011), further validating the positive role of towline length in damping vibrations. However, this study also delves into the low-frequency vibration issues that may arise from excessive towline length. The phenomenon of low-frequency vibrations is consistent with the findings of Shin (2011), who noted that while longer towlines significantly reduce instantaneous stress, they may also increase the risk of system vibrations. Additionally, in tests using a 200-meter towline, an increase in pitch amplitude was observed, which contradicts the theoretical expectation that longer towlines should reduce system fluctuations. Analysis shows that when the towline length exceeds a critical threshold, low-frequency vibrations may be amplified, significantly complicating the system’s dynamic response. This finding aligns with the research of Xu et al (2024), further revealing the low-frequency dynamic challenges potentially induced by excessively long towlines and highlighting the importance of properly controlling towline length to ensure the safety and stability of the towing system.

Additionally, towing speed has a direct impact on the wet towing operation of the net cage platform. According to the statistical analysis of the pitch angle and towline tension, as the towing speed increases, the towing resistance of the net cage platform also increases, resulting in higher towline tension. This is consistent with the findings of Neisi et al (2024). regarding floating wind turbines. Furthermore, as the towing speed increases further, the amplitude and frequency of the pitch motion of the net cage platform significantly rise, demonstrating stronger nonlinear dynamic responses. This phenomenon is in line with the results observed by Zhang et al (2019) under high towing speed conditions, where increased towing speed significantly induces fluctuations in the pitch angle, increasing the dynamic load on the system and placing higher demands on the structural design of the net cage.

5.2 The impact of marine environment on the towing performance of net cage platforms

Wave parameters are key factors influencing the towing performance of net cage platforms, especially under harsh sea conditions, where towing operations can easily result in excessive motion response or even cable failure. According to the statistical analysis of pitch angle and towline tension, the effects of significant wave height and wave period on the towing performance of the net cage platform have been found to be particularly significant. As the effective wave height increases, wave forces are intensified, causing a simultaneous increase in the platform’s motion response and towline tension, which significantly reduces the stability of the net cage platform during towing. This finding is consistent with the results reported by Wang et al (2023); Zhang et al (2017), and Soares and Das (2009) regarding the hydrodynamics of cylindrical foundation towing, confirming that wave conditions are considered one of the primary external factors affecting towing stability.

Moreover, the wave period plays a crucial role in the dynamic response characteristics of the net cage platform. Short-period waves are more likely to induce high-frequency vibrations in the platform, resulting in significant fluctuations in both the pitch angle and towline tension during towing. In contrast, long-period waves tend to mitigate the effects of wave loads to some extent, thereby reducing the amplitude of the platform’s dynamic response and enhancing system stability. This phenomenon is consistent with the findings of Zhai et al (2023) in their study on large prefabricated sinking boxes, and it has also been further corroborated by the research of Sun et al (2023) on offshore wind turbine jacket foundations. They noted that, under conditions of high wave heights and short-period waves, the hydrodynamic loads on floating structures increase significantly, which can lead to structural risks during towing. Therefore, in order to meet towline tension requirements and ensure towing safety, several studies recommend limiting the sea conditions for towing offshore structures to sea states no higher than level 4.

Although the findings of this study provide valuable guidance for the towing of octagonal cages, certain limitations remain. Firstly, the study primarily focused on the effects of towing length, towing speed, and towing position, while the influence of draft depth on the net cage’s motion response under varied sea conditions was not fully explored. Variations in draft depth may significantly affect the interaction between the net cage and the marine environment, particularly in complex wave and towing scenarios, where the coupling between the net cage submerged section and hydrodynamic forces could lead to distinct motion characteristics. Additionally, the effect of wind-current coupling was not included in the analysis, even though, in practical operations, the interaction between wind forces and ocean currents could substantially impact system stability and towline tension. Future research should incorporate the effects of draft depth and wind-current coupling to conduct a more comprehensive analysis of the towing system, enhancing the understanding of dynamic responses under complex ocean conditions and providing more precise theoretical support for offshore towing operations.

6 Conclusions

Through numerical simulations, the motion response of an octagonal offshore aquaculture net cage during towing was analyzed under various towing lengths, towing speeds, marine conditions, and towing configurations. Key findings show that spaced towing configurations significantly reduce pitch amplitude and towline tension by evenly distributing external forces, thereby enhancing the system’s stability. An optimal towing length of 150 m minimizes pitch motion and maintains stable tension, though excessively long cables may introduce complications due to increased sag. The 150 m towline is most effective under moderate sea states, with wave heights ranging from 0.5 to 1.5 meters and wave periods around 7 seconds. In more extreme conditions, a shorter towline may be more suitable for maintaining stability. Towing speed significantly affects the dynamic response, with higher speeds increasing pitch and tension fluctuations, while lower speeds promote greater stability. Additionally, wave height and period play critical roles in the system’s behavior; higher wave heights and short-period waves amplify motion and increase towing risks, while long-period waves help stabilize the system by reducing dynamic responses.

Comprehensive analysis shows that optimizing towing length, towing position, and towing speed, along with accurate assessment of wave period and height, is essential for ensuring the safety of wet towing operations for offshore net cages. This study provides theoretical foundations and practical guidelines for enhancing the stability in the transport of marine aquaculture equipment.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding authors.

Ethics statement

Informed consent was obtained from all subjects involved in the study.

Author contributions

SN: Conceptualization, Investigation, Writing – original draft, Writing – review & editing. ZW: Conceptualization, Writing – original draft, Writing – review & editing. LG: Methodology, Writing – original draft, Writing – review & editing. LT: Data curation, Writing – original draft, Writing – review & editing. TG: Software, Writing – original draft, Writing – review & editing. CC: Software, Writing – original draft, Writing – review & editing. DF: Project administration, Writing – original draft, Writing – review & editing. FG: Funding acquisition, Project administration, Writing – original draft, Writing – review & editing. XY: Funding acquisition, Resources, Supervision, Writing – original draft, Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. National Key Research and Development Program (Grant No.2020YFE0200100), National Natural Science Foundation of China (Grant No. 42306229), Natural Science Foundation of Zhejiang Province (Grant No. LQ24D060003).

Acknowledgments

The authors would like to thank all the reviewers who participated in the review.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chen M., Chen Y., Li T., Tang Y., Ye J., Zhou H., et al. (2024). Analysis of the wet-towing operation of a semi-submersible floating wind turbine using a single tugboat. Ocean Eng. 299, 117354. doi: 10.1016/j.oceaneng.2024.117354

Crossref Full Text | Google Scholar

Ding H., Feng Z., Zhang P., Le C., and Guo Y. (2020). Floating performance of a composite bucket foundation with an offshore wind tower during transportation. Energies 13, 882. doi: 10.3390/en13040882

Crossref Full Text | Google Scholar

Ding W. W., Jiang J. Q., Yue W. Z., Li Y. Z., Wang W. S., Sheng S. W., et al. (2023). Numerical study on hydrodynamic performance of a new semi-submersible aquaculture platform. Appl. Sci. 13, 12652. doi: 10.3390/app132312652

Crossref Full Text | Google Scholar

Dong S. L., Dong Y. W., Huang L. Y., Zhou Y. G., Cao L., Tian X. L., et al. (2024). Advancements and hurdles of deeper-offshore aquaculture in China. Rev. Aquaculture 16, 644–655. doi: 10.1111/raq.12858

Crossref Full Text | Google Scholar

Fan Z. Q., Liang Y. H., and Yun-Peng Z. (2023). Review of the research on the hydrodynamics of fishing cage nets. Ocean Eng. 276, 114192. doi: 10.1016/j.oceaneng.2023.114192

Crossref Full Text | Google Scholar

Fitriadhy A., Yasukawa H., and Koh K. K. (2013). Course stability of a ship towing system in wind. Ocean Eng. 64, 135–145. doi: 10.1016/j.oceaneng.2013.02.001

Crossref Full Text | Google Scholar

Fitriadhy A. and Yasukawa H. (2011). Course stability of a ship towing system. Ship Technol. 58 (1), 4–23. doi: 10.1016/j.oceaneng.2013.02.001

Crossref Full Text | Google Scholar

Froehlich H. E., Gentry R. R., Rust M. B., Grimm D., and Halpern B. S. (2017). Public perceptions of aquaculture: evaluating spatiotemporal patterns of sentiment around the world. PLoS One 12, e0169281. doi: 10.1371/journal.pone.0169281

PubMed Abstract | Crossref Full Text | Google Scholar

Han Y. Q., Ding H. Y., and Zhang P. Y. (2017). Environmental impact analysis of floating wind turbine towing based on multibody dynamics. J. Tianjin Univ. 50, 1055–1061. doi: 10.1063/1.4982742

Crossref Full Text | Google Scholar

Holmstrom J. T. (1982). Custom designing winches for deep tow survey use. Sea Technol. 23, 10–1061.

Google Scholar

Huynh T. and Kim Y. B. (2024). Control system design for offshore floating platform transportation by combination of towing and pushing tugboats. J. Marine Sci. Eng. 12 (3), 459. doi: 10.3390/jmse12030459

Crossref Full Text | Google Scholar

Le C. H., Ding H. Y., and Zhang P. Y. (2013). Air-floating towing behaviors of multi-bucket foundation platform. China ocean Eng. 27, 645–658. doi: 10.1007/s13344-013-0054-4

Crossref Full Text | Google Scholar

Le C., Ren J., Wang K., Zhang P., and Ding H. (2021). Towing performance of the submerged floating offshore wind turbine under different wave conditions. J. Marine Sci. Eng. 9, 633. doi: 10.3390/jmse9060633

Crossref Full Text | Google Scholar

Li X., Lian J., Jia Z., Wu H., He S., Zhang X., et al. (2024). Allowable differential air pressure during offshore transportation of composite bucket foundation. Ships Offshore Structures 19, 338–347. doi: 10.1080/17445302.2023.2169064

Crossref Full Text | Google Scholar

Li L., Ruzzo C., Collu M., Gao Y., Failla G., and Arena F. (2020). Analysis of the coupled dynamic response of an offshore floating multi-purpose platform for the Blue Economy. Ocean Eng. 217, 107943. doi: 10.1016/j.oceaneng.2020.107943

Crossref Full Text | Google Scholar

Lira A. D., Pinheiro M., Leuwen J. V., Seij M., and Goetheer R. (2019). P-67: Review of Dry Transportation of FLNG’s/FSRU’s/FPSO’s (Offshore Technology Conference Brasil), D011S014R001. OTC.

Google Scholar

Liu C., Zhang Y., Xin Y., Yin J., Chen C., and Hao J. (2024). Towing hydrodynamic characteristics of semi-submersible cage platform. China Fisheries Sci. 31, 1151–1162. doi: 10.12264/JFSC2024-0123

Crossref Full Text | Google Scholar

Neisi A., Ghassemi H., and Iranmanesh M. (2024). Dynamic response of three different floating platform (OC4, BSS, GVA) using multi-segment mooring system. Appl. Ocean Res. 153, 104301. doi: 10.1016/j.apor.2024.104301

Crossref Full Text | Google Scholar

Shi L. (2011). Research on Towing Performance of Large Floating Body Based on Aqwa (Dalian: Dalian University of Technology).

Google Scholar

Shi L. (2019). Dynamic analysis of semi-submersible offshore fish farm operated in China East Sea. New York: NTNU.

Google Scholar

Shin S. M. (2011). Simulation of fluid-structure interaction of a towed body using an asymmetric tension model. J. Comput. fluids Eng. 16, 7–13. doi: 10.6112/kscfe.2011.16.1.007

Crossref Full Text | Google Scholar

Soares C. G. and Das P. K. (Eds.) (2009). Analysis and design of marine structures. (Boca Raton: CRC).

Google Scholar

Solas I. M. O. (2002). International convention for the safety of life at sea (solas) (London: International Maritime Organization).

Google Scholar

Sun K., Xu Z., Li S., Jin J., Wang P., Yue M., et al. (2023). Dynamic response analysis of floating wind turbine platform in local fatigue of mooring. Renewable Energy 204, 733–749. doi: 10.1016/j.renene.2022.12.117

Crossref Full Text | Google Scholar

Wang H., Liu C., Guo Y., Zhao Y., Li X., and Lian J. (2023). Experimental and numerical research on the wet-towing of wide-shallow bucket jacket foundation for offshore substation. Ocean Eng. 275, 114126. doi: 10.1016/j.oceaneng.2023.114126

Crossref Full Text | Google Scholar

Wang H., Xiang G., Xiang X., and Ahmed F. (2024). Motion characteristics and T-foil based optimization of marine towed-cage in swell. Appl. Ocean Res. 147, 103992. doi: 10.1016/j.apor.2024.103992

Crossref Full Text | Google Scholar

Xu H., Wang J., Ling-ke R., Wang J., Cheng S., and Liang X. (2024). Cable length prediction for towing models of reverse towing systems based on the cable deployment process. Ocean Eng. 313, 119331. doi: 10.1016/j.oceaneng.2024.119331

Crossref Full Text | Google Scholar

Yan C., Wang H., Guo Y., Wang Z., and Liu X. (2021). Laboratory study of integrated wet-towing of a triple-bucket jacket foundation for far-offshore applications. J. Marine Sci. Eng. 9, 1152. doi: 10.3390/jmse9111152

Crossref Full Text | Google Scholar

Yasukawa H. and Yamada R. (2009). Course stability and yaw response of tow and towed ships. Trans. Japan Soc. Naval Architects Ocean Engineers 9, 167–176. doi: 10.2534/jjasnaoe.9.167

Crossref Full Text | Google Scholar

Zhai Q., Wang P., Wang H., Yan S., Hu X., and Zhao H. (2023). Analysis of towing stability and seakeeping of large prefabricated caisson in sea. Res. Adv. A Ser. Water dynamics 01), 114–123. doi: 10.16076/j.cnki.cjhd.2023.01.015

Crossref Full Text | Google Scholar

Zhang P., Liang D., Ding H., Le C., and Zhao X. (2019). ). Floating state of a one-step integrated transportation vessel with two composite bucket foundations and offshore wind turbines. J. Marine Sci. Eng. 7, 263. doi: 10.3390/en13040882

Crossref Full Text | Google Scholar

Zhang H., Xie Z., Fang G., and Kong L. (2017). Investigation on the impact tension characteristics of taut mooring lines. Ocean Eng. 35, 23–32. doi: 10.16483/j.issn.1005-9865.2017.05.003

Crossref Full Text | Google Scholar