Simplified polyp-canal system of stony coral Seriatopora hystrix protects its branching areas in the flow field

The polyp-canal system is vital for the growth, budding, and mineralization of scleractinian corals. Seriatopora hystrix displays a unique structural trait, with its calices and canals making up only about 15% of the colony volume, lower than the 40-50% observed in other widely distributed genera such as Acropora, Montipora, Pocillopora, or Stylophora. We used micro-computed tomography to visualize the polyp-canal system of S. hystrix, quantify its growth parameters, and simulate the dynamic processes of polyp budding and movement. It reveals that the polyps in S. hystrix follow the budding pattern of unilateral extension along the growth axis and radiates within the horizontal plane, which simplifies its polyp-canal system. Through the finite element analyses under average and maximum wave velocities of South China Sea, we measured the stress distribution in coral models with varying canal volume proportions. We found that the lower volume proportion of polyp-canal system in S. hystrix reduces the VonMises stress at the branching areas by approximately 40-50%, ensuring the continual construction of branchlets in high speed flow field. This study enhances our understanding of Seriatopora coral growth patterns and their adaptation to marine environments, contributing to the species selection in coral reef restoration.

Introduction

Coral reefs are among the most biodiverse ecosystems on Earth, holding immense value for both the environment and human society (Ferrario et al., 2014; Cinner et al., 2016; Hughes et al., 2017; Li et al., 2022a). Seriatopora hystrix is a branching coral species widely distributed across the Indo-Pacific region (Dana, 1846). It is known for its rapid growth and can be found at depths ranging from 0 to 60 meters (Shlesinger, 1985). S. hystrix is commonly found in the rear-reef, reef flat, and lagoon, and abundant in the fore-reef (Nir et al., 2011). Its fast growth rate and morphological plasticity allow it to provide high-quality, complex habitats for marine life (Dai, 1989).

Current studies on coral growth primarily encompasses two areas: multi-omics and morphology (Li et al., 2020; Wang et al., 2024). With the rapid advancement of sequencing technologies, an increasing number of growth mechanisms have been uncovered through multi-omics studies (Black and Burris, 1983; Maier et al., 2001; Underwood et al., 2006; Chen et al., 2008; Maier et al., 2009; Mayfield et al., 2012; Nakajima et al., 2017). Recent morphological research has focused on the patterns of polyp-canal system construction and its regulatory effects on coral growth (Li et al., 2020; Lin and Chen, 2022; Li et al., 2023). Studying coral growth based on the morphological structure of the polyp-canal system provides valuable insights into the polyp, skeleton, and canal, which are essential components of coral colonies (Li et al., 2021a; Li et al., 2024). This approach helps to reveal the differential mechanisms of polyp distribution, movement, budding, and mineralization across various coral species (Li et al., 2021a; Li et al., 2021b).

Compared to other common coral species, the polyp-canal system of S. hystrix is particularly unique. Unlike Pocillopora and Stylophora, which belong to the same family (Rachmilovitz et al., 2024); the branching coral Acropora (Loh et al., 2001); and Montipora, which also have strong lateral expansion ability (Veron, 2000), the polyp-canal system in S. hystrix is highly simplified, with a canal volume proportion of less than 15%, significantly lower than the 40-60% observed in the aforementioned corals (Li et al., 2021a). As the canals are small in volume and few in number, early morphological studies suggested that biological tissues in S. hystrix only distributed on the colony surface (Yost et al., 2013). However, our previous research has identified regularly arranged canals within the colony that correspond closely to the positions of coral calices, indicating that these canals play a role in the growth process of coral colony (Li et al., 2021a). Therefore, to investigate the growth patterns of S. hystrix, it is crucial to explore the formation of its simplified polyp-canal system and its regulatory role in the growth process.

In this work, we reconstructed the polyp-canal system of S. hystrix through micro-computed tomography (micro-CT), and visualized the dynamic process of polyp budding and movement. We compared the budding patterns of S. hystrix with those of other common coral species to understand the reasons behind its construction of a simplified polyp-canal system. To analyze the protection of the simplified polyp-canal system in the flow field for the coral colony, we also simulated the effects of varying seawater flow velocities on coral models using the finite volume method. We analyzed how corals with different porosity ratios are influenced by both the average and maximum flow velocities in the South China Sea. The resulting pressure distribution on the coral structures is then incorporated into structural mechanics analysis. Using finite element analysis, we assess their stress states during loading, calculating the stress distribution and pressure variations during the loading process. This work aims to deepen our understanding of the growth, budding, and mineralization patterns of S. hystrix from a morphological perspective, and explored the influence of the ocean current field environment on growth patterns, which helps to promote the study on coral growth-external environment interactions, providing strong evidence for species selection in coral reef restoration.

Result

Structure change of polyp-canal system during S. hystrix branching

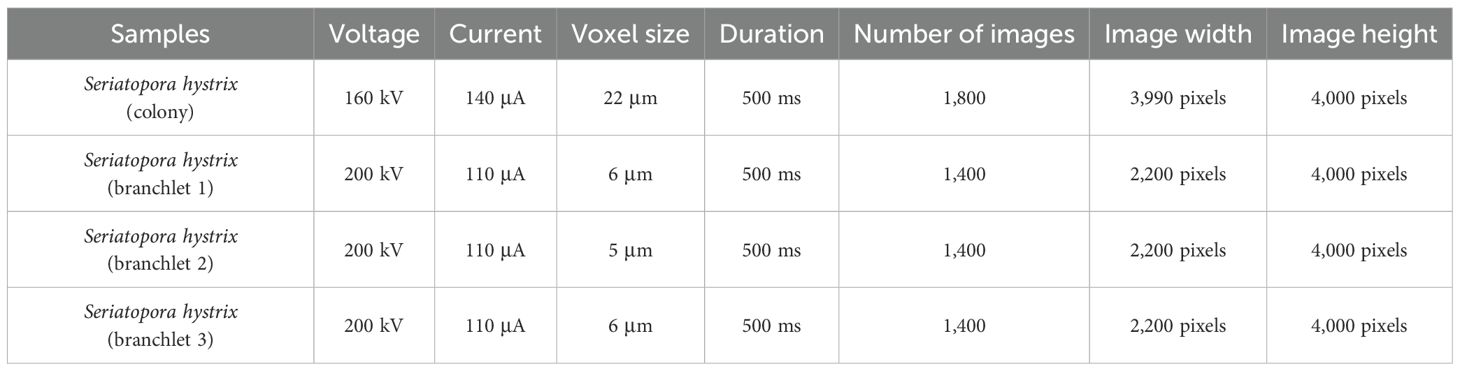
As S. hystrix grows, its polyp-canal system undergoes a gradual simplification and uniformization, with the canal volume proportion within the colony progressively decreasing due to biomineralization. This simplification process of the polyp-canal system encompasses four distinct structural stages, which reveal the patterns of polyp budding and movement in S. hystrix (Figure 1).

Figure 1

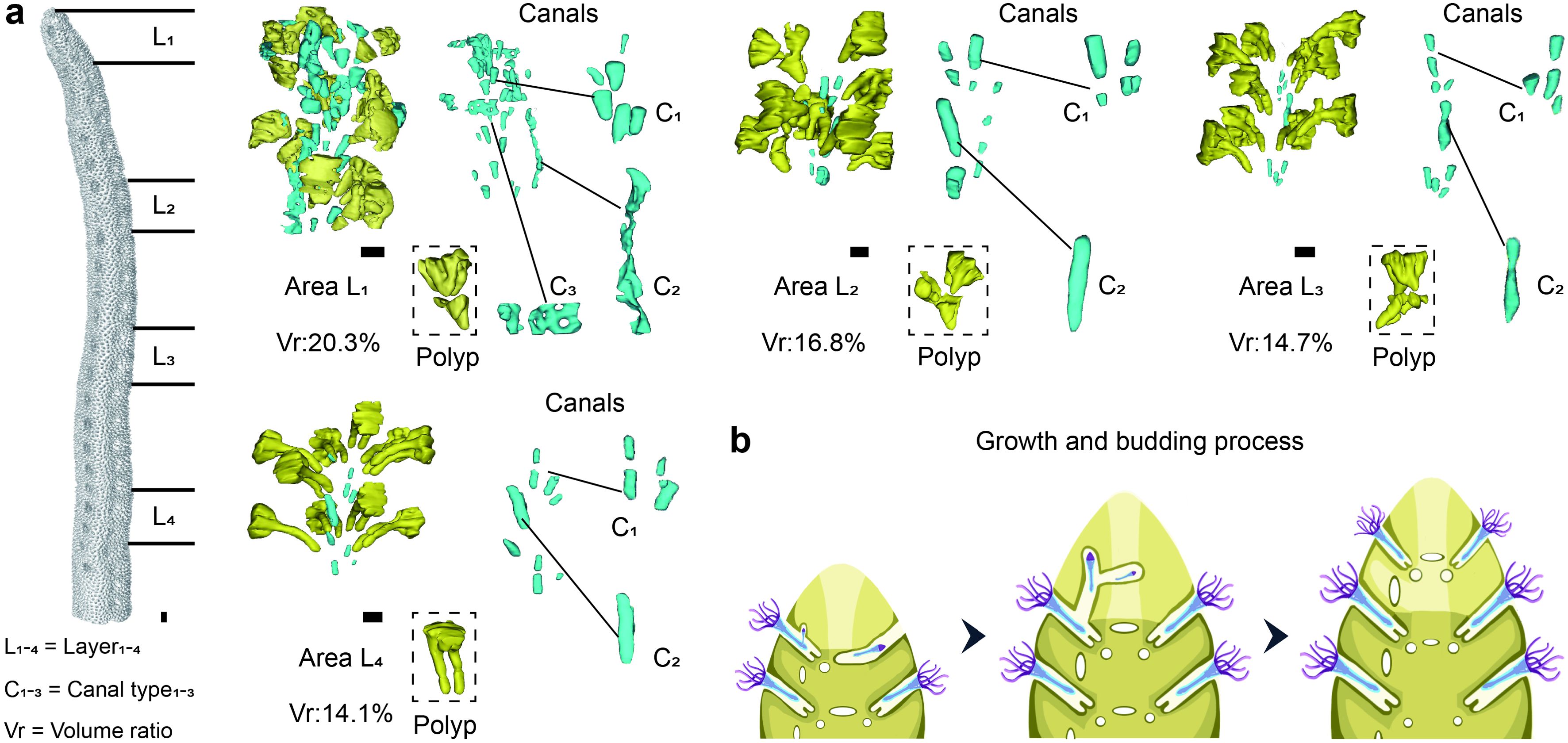
Figure 1. Structural changes and developmental stages of the polyp-canal system in S. hystrix during growth. (a) Four distinct stages of the polyp-canal system, progressing from the branchlet tips towards the colony base, are characterized by a gradual simplification and reduction in canal volume due to biomineralization. Area L₁ (0–6 mm from branchlet tips) exhibits the highest canal volume (>20%) and greatest structural diversity, including three types of canals (C₁, C₂, and C₃). In subsequent stages, the canal volume decreases progressively: Area L₂ (15–20 mm from branchlet tips) with 16.8% volume and no C₃ canals; Area L₃ (29–34 mm from tips) with 14.7% volume, and Area L₄ (43–48 mm from tips) with 14.1% volume, where the calices and C₁ canals become uniform in size. The main growth parameters of the coral samples in this study are as follows. In the coral colony, the main branch diameter is approximately 1 cm, while the branchlet diameter ranges from 0.4 to 0.6 cm, with an aspect ratio between 1.6 and 2.5. The wall thickness in the majority of colony reaches or exceeds 1 mm, while a small number of areas are below 0.5 mm. The widest area of the calices has a diameter of about 1 mm, while the narrowest area is 0.2 mm, with a volume of approximately 0.7 mm³. The C₁ type canal diameter is about 0.1–0.2 mm, approximately spherical, with a volume in the range of 0.003–0.005 mm³. The total length of the C₂ canal is about 1–3 mm, with a diameter of approximately 0.3 mm, and a volume in the range of 0.1–0.2 mm³. The total length of the C₃ canal is about 1–1.5 mm, with a diameter of 0.1–0.3 mm, and a volume in the range of 0.05–0.1 mm³. (b) Simulated growth process of S. hystrix demonstrating polyp budding, movement, and canal formation along the growth axis. The C₃ canals disappear due to biomineralization, and the uniformity of calices and canals increases as branchlet growth proceeds. Scale bars: 0.5 mm.

The first stage is located within 0–6 mm from the tips of the branchlets, where the canal volume proportion is the highest in the entire colony, exceeding 20% (Figure 1a). This area also displays the greatest diversity in canal structures. We refer to this region as Area L₁. In this region, eight polyps are arranged in two layers, with coral calices shaped like inverted cones that vary noticeably in structure among individuals. Canals within the branchlet center, among the calices, are categorized into three types based on their distribution and structural differences. C₁ refers to small, spherical canals near the base of the calices, typically located at the pointed end of the inverted cone, with each calyx corresponding to one or two such canals. C₂ represents a longitudinal tubular canal, with only one present in this region, positioned between two vertically aligned calices. C₃ describes transverse, band-like canals situated between adjacent coral calices within the same horizontal plane.

The second stage, Area L₂, is approximately 10 mm away from the first stage, located 15–20 mm from the branchlet tips, where the canal volume proportion decreases to about 16.8% (Figure 1a). The arrangement of polyps in Area L₂ is similar to that in Area L₁, however, there are no C₃ canals between adjacent calices. At this stage, each calyx base corresponds to a single spherical C₁ canal. A longitudinal C₂ canal exists between two vertically adjacent calices, positioned on the same side of the branchlet as in Area L₁, but the canal volume is reduced. The third stage, Area L₃, is found 29–34 mm from the branchlet tips, where the canal volume proportion further decreases to 14.7%, close to the average for a S. hystrix colony. This region contains only calices, C₁ and C₂ canals. At this stage, the calices start to change structurally, with the upper half becoming cubic and the lower half forming two parallel tubes. By the fourth stage, Area L₄, is located 43–48 mm from the branchlet tips, where the canal volume proportion slightly decreases to 14.1%. Here, the shapes and volumes of the eight calices become nearly uniform, and the corresponding C₁ canals for each calyx are also similar in size. All C₂ canals between polyps of each horizontal plane on the same branchlet side vertically connect calices along the growth direction.

Budding process of the simplified polyp-canal system in S. hystrix

We simulated the dynamic growth, polyp budding, and movement processes of S. hystrix by integrating the structural changes of the polyp-canal system across different developmental stages (Figure 1b). Coral branchlet growth is centered on one side, serving as the growth core where polyps are responsible for budding, while new polyps simultaneously radiating within the same horizontal plane and extending vertically. At each horizontal level, newly budded polyps migrate into their respective calices via C₃ canals. During vertical extension, new polyps enter calices on the same side of the newly formed branchlet tips through C₂ canals aligned with the growth axis. As the branchlets grow, C₃ canals gradually disappear due to infilling by biomineralization, while the structures and volumes of the calices become uniform, each with a similarly sized C₁ canal at the base. The volume of C₂ canals connecting calices on the growth core side decreases but remains present.

This growth and budding pattern simplifies the polyp-canal system of S. hystrix, resulting in a canal volume proportion lower than that of other common coral genera like Montipora, Acropora, Pocillopora, and Stylophora (Figure 2). In Montipora, coral calices are arranged along fan-shaped lines radiating from a central growth axis, with budding relationships between polyps on the same line, necessitating extensive canal connections and a high canal volume proportion of around 50%. In Pocillopora and Stylophora, polyps bud in growth bundles aligned along the growth axis. Polyps near the center of the bundle continuously bud and move upward into newly formed calices, while peripheral polyps do not bud, resulting in a canal volume proportion of about 40%. In Acropora, the axial canal of each branchlet contains a polyp that serve as the growth core, continuously budding and moving along the growth axis toward the branchlet tip. This pattern reduces the need for canals during the budding process, but due to the large size of the axial canals, the canal volume proportion still reaches 35-40%. In S. hystrix, the coral calices and C₂ canals on the growth core side collectively fulfill the function of the axial canal in Acropora, further simplifying the polyp-canal system. The C₃ canals used for polyp movement at the same horizontal level become completely filled as growth proceeds. These two regulations resulting in a canal volume proportion of only about 15% or even lower for S. hystrix.

Figure 2

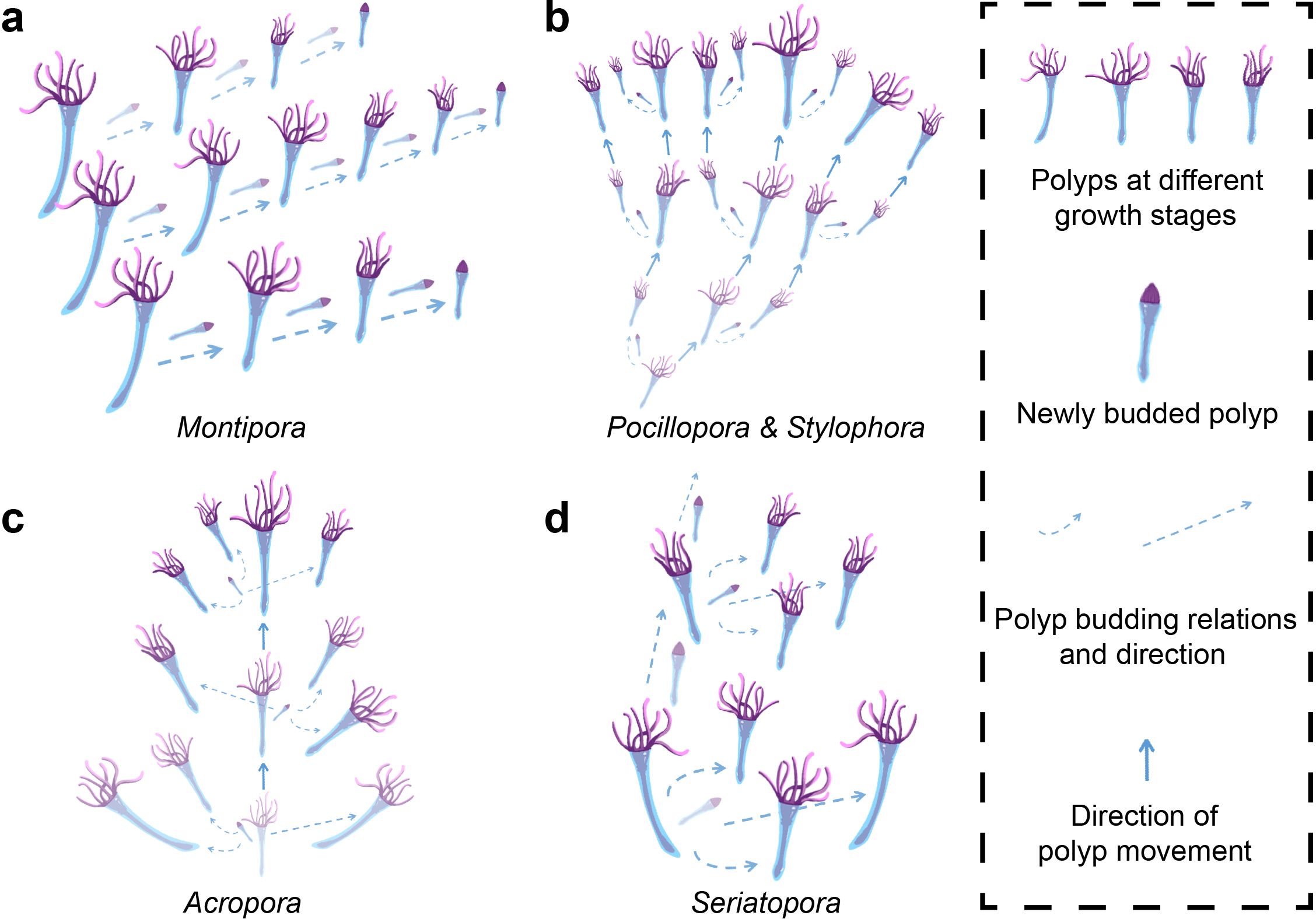
Figure 2. Comparison of polyp-canal systems and canal volume proportions among coral genera. (a) In Montipora, fan-shaped calice arrangements radiating from a central axis necessitate extensive canal connections, resulting in a canal volume proportion of about 50%. (b) Pocillopora and Stylophora exhibit bundled polyp budding along the growth axis, leading to a canal volume proportion of about 40%. (c) In Acropora, a large axial canal allows for continuous polyp budding and movement, maintaining a canal volume of 35-40%. (d) The polyp-canal system of S. hystrix exhibits lowest canal volume proportion (no more than 15%) compared to other common coral genera due to its simplified growth and budding patterns. S. hystrix replaces the axial canal with smaller C₂ canals, and the complete filling of C₃ canals during growth further reduces the canal volume proportion.

Mechanical responses of stony coral models under flow conditions

To quantify the changes in mechanical properties brought about by the simplified polyp-canal system of S. hystrix in a flow field, we constructed four Y-shaped coral models with canal volume proportions of 10%, 20%, 30%, and 40%. These models mimic the bifurcated branching pattern of S. hystrix and consist of a main branch and two branchlets connected through a branching area. We conducted finite element analysis on these models under flow velocities of 10.3 cm/s and 56.6 cm/s, representing the average and maximum flow velocities recorded in the coral reef regions of the South China Sea in 2023.

Based on the Reynolds number calculation formula, with a seawater flow velocity of 10.3 cm/s, the Reynolds number is determined to be 1,027.94. According to the principles of fluid dynamics, when the Reynolds number is less than 2,000, viscous forces have a greater impact on the flow field than inertial forces. In such a flow regime, velocity disturbances are attenuated due to viscous forces, resulting in a stable fluid flow. Therefore, the fluid domain is set to laminar flow. The velocity contour plot under this condition is shown in Figure 3a. For coral models with different canal volume proportions, the overall deformation distribution in the flow field is similar, with a gradual increase from the main branch to the branching areas and further to the tips of the branchlets (Figure 3b). The model with a 10% canal volume proportion exhibits the lowest total deformation, with the maximum value of remaining three groups showing increases of approximately 1.3-2.8% over this model. Aside from the areas where the model connects to the base, the VonMises stress at branching area is higher than other parts of those four models, and this difference becomes more pronounced with increasing canal volume proportion (Figure 3c).

Figure 3

Figure 3. Finite element analysis of S. hystrix coral models with varying canal volume proportions under a flow velocity of 10.3 cm/s. (a) Velocity contour plot of the flow field showing laminar flow characteristics due to a Reynolds number of 1,027.94. The parameters of the coral model are as follows. In the coral model, the main branch diameter is 1 cm, the branchlet diameter is 0.5 cm, and the aspect ratio is 2. The canal diameter is 0.5 mm, with a volume of about 0.07 mm³, and the wall thickness ranges from 0.2 to 1 mm. The angle between the coral branchlets is 120°. (b) Deformation distribution of the four coral models, with 10%, 20%, 30%, and 40% canal volume proportions. Deformation increases from the main branch to the branchlets, with the 10% canal volume model exhibiting the lowest total deformation. (c) VonMises stress distribution, showing higher stress in the branching areas, with stress increasing as canal volume proportion rises.

Similarly, with a seawater flow velocity of 56.6 cm/s, the Reynolds number is calculated to be 5,648.68. Since this value exceeds 2,000, inertial forces predominate over viscous forces in the flow field, leading to less stable fluid motion. Small variations in velocity are likely to escalate, resulting in a chaotic turbulent flow field. Consequently, the fluid domain is classified as turbulent, with the velocity contour plot shown in Figure 4a. Compared to the flow velocity of 10.3 cm/s, the total deformation and stress values for each sample increased by approximately 35 to 40 times at higher velocities, but the gradient distribution remained generally consistent (Figures 4b, c). The only notable difference in distribution is that for samples with a 10% canal volume proportion, high-stress regions are concentrated around the branching area and the upper surfaces of branchlets, while the stress values range from about 1,000-6,000 Pa. In contrast, for the other three samples, high-stress regions are more concentrated around the branching area and adjacent lower surfaces of branchlets, with the maximum value exceeding 12,000 Pa for the 40% model.

Figure 4

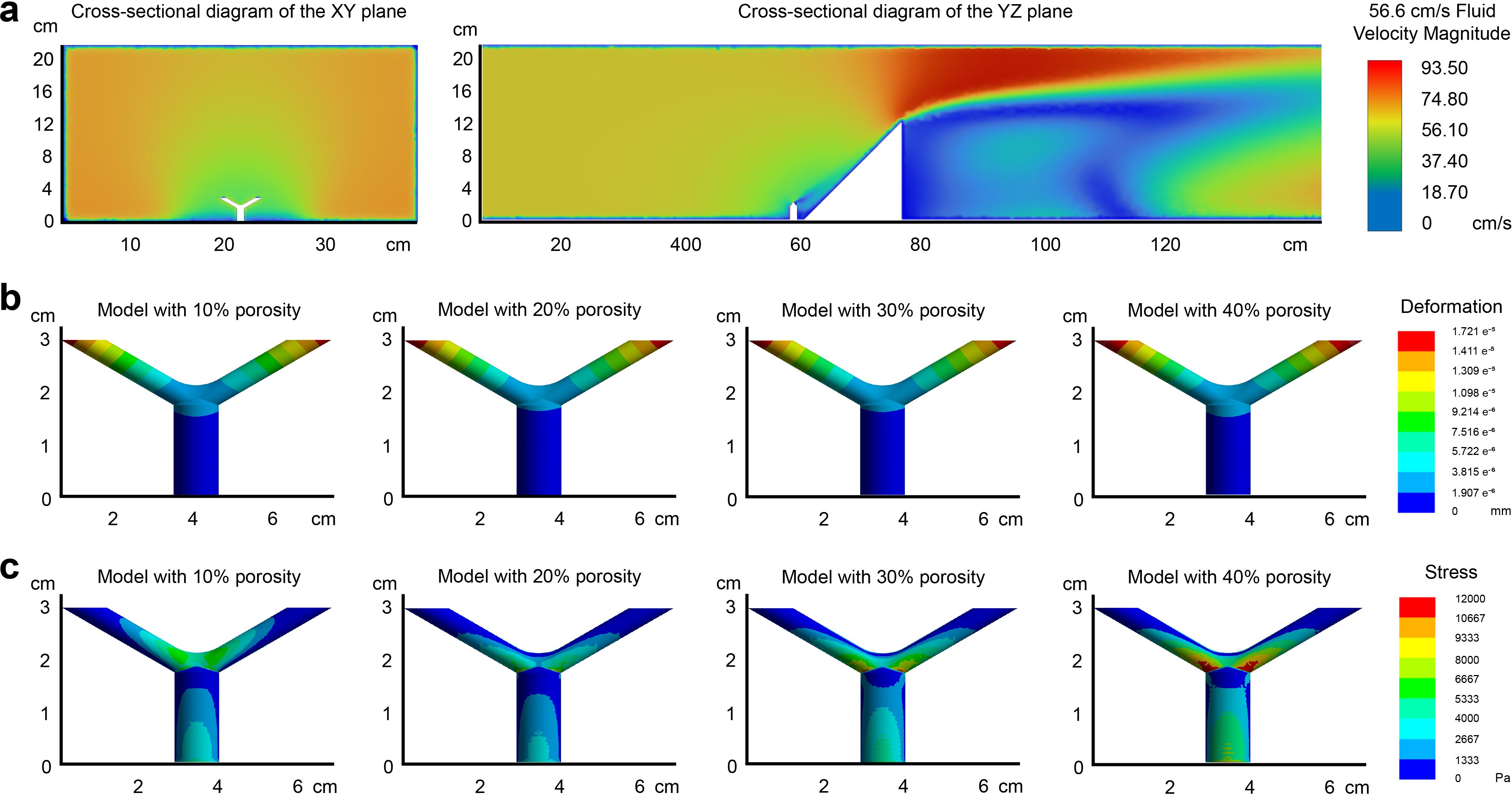
Figure 4. Finite element analysis of S. hystrix coral models under a flow velocity of 56.6 cm/s. (a) Velocity contour plot under turbulent flow conditions with a Reynolds number of 5,648.68. The parameters of the growth model are consistent with those in Figure 3. (b) Deformation distribution of the coral models, showing a 35–40 fold increase compared to 10.3 cm/s, though gradient patterns remain similar. (c) VonMises stress distribution, with the 40% canal volume model showing the highest stress, particularly in the angular regions between the branching areas and the branchlets.

We selected three representative stress points to place probes for quantitative measurements, including mid-branchlet, branching area, and mid-main branch (Figure 5). At a flow velocity of 10.3 cm/s, the coral model with a 40% canal volume proportion showed an overall deformation increase of 4.7 e^-8 cm at the mid-branchlet, compared to the model with a 10% canal volume, an increase of approximately 18.4% (Figure 5a). In the branching area, the deformation increased by 5.6 e^-9 cm, or about 5.8%. Although the mid-main branch in the model with a 40% canal volume proportion exhibited an overall deformation increase of 1.61 e^-8 cm, representing a 48.2% rise compared to the model with a 10% canal volume proportion, the small deformation values across all four models meant there was no obvious difference. The VonMises stress differences in the coral models were more pronounced, especially in the branching area (Figure 5c). The stress in the 40% model increased by 7.81 Pa, about 77.2%, compared to the 10% model. At the mid-branchlet, the increase was 2.94 Pa, or about 24.3%, while at the mid-main branch, the difference was minor, with an increase of only 1.26 Pa, or about 7.7%.

Figure 5

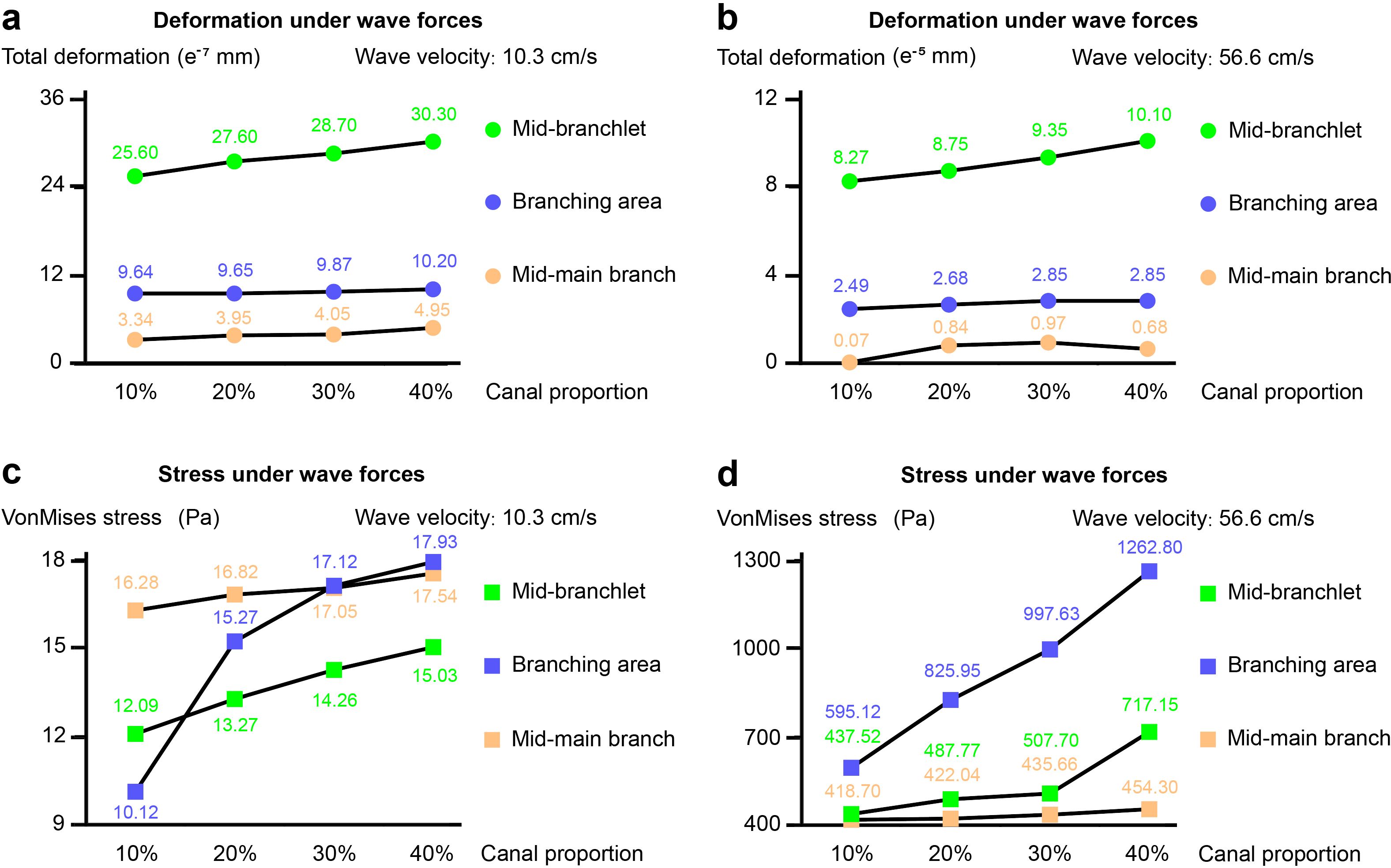
Figure 5. Quantitative measurements of deformation and VonMises stress at three representative points under flow velocities of 10.3 cm/s and 56.6 cm/s. (a, b) Deformation at the mid-branchlet, branching area, and mid-main branch across models with different canal volume proportions. At both flow velocities, the 40% canal volume model shows the largest deformation, particularly at the mid-branchlet. (c, d) VonMises stress distribution at the same points. Stress increases are most pronounced at the branching area, especially as canal volume proportion rises from 10% to 40%. Stress in the 40% model is up to 112.2% higher than in the 10% model at the higher flow velocity. The one-way ANOVA revealed significant differences in means among Group 10%, Group 20%, Group 30%, and Group 40%.

At a flow velocity of 56.6 cm/s, the 40% model exhibited an overall deformation at the mid-branchlet that was 1.83 e^-6 cm greater than that of the 10% model, an increase of approximately 22.1% (Figure 5b). Differences in deformation at the branching area and mid-main branch were minimal, with the largest difference at the branching region being only 3.6 e^-7 cm, or about 14.5%. All four measurements for the mid-main branch were below 1.00 e^-6 cm, showing no notable difference. The stress distribution showed little change at the mid-main branch, as the canal volume proportion increased from 10% to 40%, the VonMises stress rose by only 35.6 Pa, an increase of 8.5% (Figure 5d). At the mid-branchlet, the stress values for canal volumes of 10%, 20%, and 30% were relatively similar, at 437.52 Pa, 487.77 Pa, and 507.70 Pa, respectively. However, when the canal volume proportion reached 40%, the stress increased to 717.15 Pa, a 63.9% increase compared to the 10% model. The changes were even more pronounced in the branching area, compared to a stress of 595.12 Pa at 10% model, the stress increased by 38.8%, 67.6%, and 112.2% for models with canal volume proportion of 20%, 30%, and 40%, respectively.

In summary, variations in the canal volume proportion of the coral model have a minor effect on total deformation but substantially impact VonMises stress values, particularly in the branching area. As the flow velocity increases, the stress difference at the branching area between coral models with 10% and 40% canal volume proportions becomes further amplified.

Discussion

The budding patterns of S. hystrix simplify its polyp-canal system

Different reef-building corals exhibit diverse patterns of polyp budding and movement, driven by their varying requirements during coral growth. Among them, S. hystrix adopts a budding pattern that leads to the most simplified polyp-canal system, which is the primary reason its calices and canals constitute less than 15% of the colony volume (Figure 1). In contrast, in Montipora, each polyp possesses budding capability, with one-to-one budding relationships among calices (Figure 2a). This pattern facilitates rapid horizontal expansion of the foliose colony but also results in the highest canal volume proportion among these representative coral species. For Pocillopora, Stylophora, Acropora, and Seriatopora, which have needs for vertical niche expansion in their massive, and branching colonies, the differentiation in budding capability among polyps becomes evident (Figures 2b-d). Only polyps in the core growth region participate in budding, while polyps in other regions lack this ability, reducing the overall volume of the polyp-canal system. In Pocillopora and Stylophora, the core growth region is located at the center of each growth bundle (Figure 2b). In Acropora, the core growth region is concentrated at the axial canal, giving it precise directional control for axial growth (Figure 2c).

In comparison, the growth, budding, and mineralization patterns of S. hystrix adhere to a strategy that minimizes the volume proportion of the polyp-canal system as much as possible (Figure 2d). Each branchlet has one side that serves as the growth core, where vertically adjacent polyps along this side have budding ability. After budding, some polyps move into other calices within the same horizontal plane, while one polyp continues along the growth axis, entering the adjacent coral calyx in this core growth region, thereby continuing the budding process. After the budding and movement processes, the C₃ canals used for horizontal polyp transport are completely filled, and the volume of C₂ canals used for vertical transport gradually decreases. The role of C₁ canals remains unclear, which needs further studies, but their volume and number also decrease during growth. The calices gradually transform from their initially large inverted conical shape to a form with an upper half that is nearly cuboidal and a lower half connected by two thin tubular structures, thereby reducing the overall volume. This budding and mineralization pattern allows S. hystrix to maximize the simplification of its polyp-canal system while still meeting essential growth requirements, resulting in the lowest overall volume proportion of coral calices and canals. Moreover, within the same horizontal plane, the shape, volume, and number of coral calices and C₁ canals of S. hystrix gradually become uniform during growth, demonstrating the regulatory role of the polyp-canal system in controlling the growth of the entire colony (Figure 1a).

Simplified polyp-canal system protects S. hystrix branching in high flow

Under both average and maximum water flow velocities, the deformation of coral models with varying canal volume proportions in a flow field remains minimal, with maximum values not exceeding 2 μm, an amount negligible for coral growth. This indicates that the flow environment does not exert sufficient pressure to cause direct rigid deformation of the coral colony. However, the equivalent stress experienced by the coral varies substantially with flow speed. At a water flow velocity of 10.3 cm/s, the equivalent stress for all four models is below 300 Pa. When the flow velocity increases to 56.6 cm/s, the equivalent stress rises dramatically to several thousand, even tens of thousands of pascals. In the branching regions of the model with a 40% canal volume, the maximum equivalent stress exceeds 12,000 Pa. This suggests that when the flow velocity surpasses the average speed, the resulting increase in flow leads to a substantial rise in equivalent stress within the coral, particularly in the branching regions.

At a flow velocity of 56.6 cm/s, between the angles of two branchlets, the stress values range from 700 to 2,000 Pa for coral models with canal volumes of 10-20%. In contrast, when the canal volume reaches 40%, the stress increases to 2,000-4,000 Pa, more than doubling. Similarly, in the angle between the branchlets and the main branch, the stress is 1,000-2,000 Pa at a 10% canal volume, 2,600-5,300 Pa at 20%, and rises sharply to 10,000-12,000 Pa at 40%, representing a 3–10 fold increase. Even at the locations with the smallest differences, such as where stress probes are embedded within the skeleton, the difference is still around twofold. This demonstrates that in high-flow environments, the low canal volume proportion of S. hystrix, below 15% and approaching 10% as biomineralization progresses, substantially reduces the equivalent stress in its branching regions compared to other major coral species with canal volumes exceeding 40%. This reduction in stress makes the branching regions less susceptible to physical damage from external forces.

For S. hystrix, a bushy branching coral species, the branching process is crucial for occupying ecological space and increasing the effective light absorption area. However, the branching region is also the most vulnerable part of the coral. If this region suffers physical damage, such as breakage, the coral could lose multiple branchlets. Even if, as some researchers speculate, S. hystrix possesses a fragmentation reproduction ability similar to that of Acropora, the newly formed branchlets containing only a few polyps are struggle to thrive in natural environments after fragmentation, seriously affecting the growth and expansion of the colony (Ayre and Dufty, 1994; Miller and Ayre, 2008). The simplified polyp-canal system of S. hystrix reduces its overall canal volume proportion, which, in turn, lowers the equivalent stress under high-flow conditions. This adaptation ensures the successful progression of the branching process and maintains mechanical strength in the branching regions after branching is complete, thereby protecting the survival and growth of coral colony in high-velocity flow environments. Given S. hystrix’s simplified polyp-canal system reducing mechanical stress in high-flow environments, it is an ideal candidate for coral reef restoration in areas with strong water currents, ensuring survival under challenging hydrodynamic conditions. As research integrating micro-CT technology and finite element analysis expands to more coral species, we believe it will provide theoretical guidance for the environmental adaptation and population selection in coral reef restoration areas based on actual flow field conditions.

Methods

Sample collection

The S. hystrix samples were collected from the Nansha Islands (3°35′N to 11°55′N, 109°30′E to 117°50′E) in 2023. The average flow velocity recorded in the coral reef areas was 10.3 cm/s, with a maximum flow velocity of 56.6 cm/s. Samples were collected from depths of approximately 5–10 meters at the fore-reefs. At this depth, S. hystrix exhibits thicker branches and a more robust colony structure (Nir et al., 2011), which provide enhanced resistance to waves and storms. The daily mean temperatures ranged from 28 to 32°C. Before the experiments, samples were maintained in a laboratory coral tank for at least three months under conditions mimicking their South China Sea habitat.

Micro-CT test

S. hystrix samples were analyzed using 3D models constructed with a 230 kV latest-generation X-ray microfocus computed tomography system (Phoenix v|tome|x m; General Electric, GE; at Yinghua NDT, Shanghai, China, Table 1). Two-dimensional image reconstructions of each specimen from the matrices of scan slices were assembled using proprietary software from GE. For the visual reconstructions of polyp budding patterns in Pocillopora, Stylophora, Acropora, and Montipora, we utilized the micro-CT data from our previously established coral structural database (Li et al., 2021a).

Table 1

Table 1. Parameters of the micro-CT tests.

Micro-CT offers remarkable advancements over traditional imaging techniques in studying coral morphology and growth process. The key advantages include: 1) High-resolution 3D visualization: Micro-CT enables non-invasive, three-dimensional reconstruction of complex internal structures, such as polyp-canal networks and skeletal porosity, which are inaccessible to conventional methods like optical microscopy or scanning electron microscopy (SEM). This capability is critical for analyzing opaque coral skeletons, where traditional techniques fail to resolve hidden anatomical details. 2) Non-destructive analysis: Unlike destructive methods (e.g., SEM or physical sectioning), micro-CT preserves sample integrity, allowing repeated examinations of the same specimen over time. This is particularly valuable for longitudinal studies of growth dynamics. 3) Quantitative volumetric and structural metrics: Micro-CT facilitates precise quantification of parameters such as skeleton-void ratios, canal volumes, and mineral density gradients. These metrics are essential for understanding mechanical properties of coral skeletons. 4) Dynamic process tracking: The technology captures temporal changes in coral structures, such as the budding and movement of polyps. This reveals mechanisms of calcium transport and skeletal repair that are invisible to static imaging methods.

3D reconstructions of polyp-canal systems

Slice data derived from the scans were then analyzed and manipulated using 3D reconstruction software. Reconstructions of polyp-canal systems were performed using VG Studio Max (Li et al., 2021a; Zhu et al., 2022) (v3.3.0). The 3D reconstructions were created following the method previously described (Zhu et al., 2022). Images of the reconstructions were exported from Mimics and VG Studio Max and finalized in Adobe Photoshop CC 2019 and Adobe Illustrator CC 2019.

Simulation of coral budding processes and patterns

Each small branchlet in our samples contained hundreds of polyps. We obtained growth information for these polyps through 3D reconstruction encompassing various budding stages. By comparing and sorting these reconstructions, we simulated changes in polyp distribution during the budding and transit processes. This method allows characterization of dynamic coral growth processes from static sample reconstructions.

Skeleton to void ratio measurement

The calculation of the skeletal matter to void volumetric ratio of coral samples, called the ‘skeleton to void ratio,’ was conducted using VG Studio Max 3.3 (Li et al., 2022b). In this study, we employed this method to measure the canal proportion in Seriatopora (15.1%, 14.7%, 14.4%), Pocillopora (38.7%, 41.2%, 40.6%), Stylophora (40.8%, 42.1%, 39.6%), Acropora (39.3%, 38.5%, 40.1%), and Montipora (53.2% 53.6%, 53.0%). A one-way analysis of variance (ANOVA) revealed significant differences in means among Seriatopora (14.73%), Pocillopora (40.17%), Stylophora (40.83%), Acropora (39.30%), and Montipora (53.27%), with F(4,10)=508.58, p<0.0001. We also measured the proportion of canals at different positions of the small branches in Figure 1 (Area L₁ is 20.3%, Area L₂ is 16.8%, Area L₃ is 14.7%, Area L₄ is 14.1%). All measurements are the averages of three different samples. The specific procedures are as follows. Initially, the ‘surface determination’ function was used to differentiate between the areas of reconstructed skeleton and the canal system in the colony. We then calculated the volume of the reconstructed skeleton and used the ‘erode/dilate’ mode to encompass the entire area of both the skeleton and canals. Next, the ‘porosity/inclusion analysis module’ was used to reconstruct the lumen of the canal system for volume calculation. With the volumes of the skeleton and canal system, we determined a skeleton-void ratio for each sample.

Simulation of coral models in wave fields

Under controlled conditions of varying seawater flow velocities, we investigated the impact of differing porosity ratios on coral models by examining their deformation (total displacement) and stress (VonMises stress) responses in a simulated flow environment. The objective of this study was to analyze stress variation patterns, thereby elucidating the stress distribution and hydrodynamic resistance of corals with different porosity ratios.

In this study, we employed a finite volume approach to simulate the effects of varying flow velocities representative of average and maximum flow conditions observed in the South China Sea. The resulting pressure distribution on coral structures was then incorporated into a structural mechanics analysis to evaluate deformation and stress. Using finite element analysis, physical material properties were defined for Y-shaped coral structures, and stress states during simulated flow loading were assessed. The material properties of the coral model in the finite element analysis are based entirely on the real values of the coral (e.g., Poisson’s ratio: 0.38, Elastic modulus: 9.7 ± 2.9 GPa, Compressive strength: 18.6 ± 2.0 MPa, Tensile strength: 0.8 ± 0.1 MPa, Density: 2.83 g/cm³). The Static Structure module was utilized to establish boundary conditions, including interface connections, applied loads, and constraints, to simulate structural loading and determine stress and pressure distribution across the coral structures. The model consisted of three main components: the Coral Model, the Dam Body and the Fluid Domain. The coral models were categorized into four distinct types with porosity ratios of 10%, 20%, 30%, and 40%, respectively. Different fluid domains were created to simulate varying seawater flow rates, and flow regimes were characterized based on Reynolds number calculations, using the following equation:$R_e=\frac{\rho vd}{\mu }$.

For the finite element analysis, pressure loads derived from the fluid simulation were applied uniformly across the coral model. A fixed boundary condition was set at the base of the coral model, while a fluid-solid interaction boundary was imposed on the surface of the coral model. The coral models were meshed using ANSYS WORKBENCH Mechanical solver, employing Solid 186 high-order 3D, 20-node solid elements, with a total mesh count of approximately 1,200,000, and mesh size ranging from 0.05 mm to 0.3 mm. The simulation results demonstrated deformation and stress patterns across the four coral models under two distinct flow conditions. In addition, three specific points on the coral structures, the mid-main branch, branching area, and mid-branchlet, were selected for further analysis, allowing for detailed examination of deformation and stress probe readings to assess the impact of flow conditions on coral structural stability and growth.

In addition to the primary analysis presented, we also conducted simulations of the four coral models under two flow conditions with the lateral side of the coral models oriented in the flow direction. The observed stress and deformation distributions were consistent with those described earlier. Specifically, when the canal volume proportion was 10% or 20%, stress attenuation from the branching area to the mid-branchlet was more pronounced compared to that observed for the 40% porosity model. Due to the redundancy of these results, they are not included in the main text.

In finite element analysis, model accuracy is directly influenced by the resolution of micro-CT imaging. Optimal results are achieved when the resolution is at least 1/2 or lower than the target sample structure size (for example, when the resolution is 50μm, the minimum size of the target sample should be no less than 100μm) (Van Rietbergen et al., 1996). In this study, the smallest canal diameter in S. hystrix is approximately 100μm (i.e., 0.1 mm, as shown in Figure 1), and the micro-CT resolution used in the experiment ranged from 5 to 22μm, meeting this standard.

Significance analysis

A one-way ANOVA was employed to evaluate differences in means across four independent groups (10%, 20%, 30%, 40%), each with three observations (Figure 5). This method assesses whether group means differ significantly by comparing the variance between groups to the variance within groups. The F-statistic and corresponding p-value were calculated to test the null hypothesis that all group means are equal, with significance determined at the 0.05 level.

Limitations

The study on the simplified polyp-canal system of S. hystrix has several limitations that should be considered for a complete understanding. Below, we outline these constraints and suggest areas for future research.

1) Comparison with homogeneous models

We did not directly compare the mechanical properties of the actual coral skeleton with those of a homogeneous model having the same overall porosity. This comparison could help determine whether the specific structure of the polyp-canal system or just the overall porosity plays a more important role in determining the mechanical strength of the coral skeleton. Future research could explore this by creating and testing homogeneous models alongside actual coral skeletons to isolate the effects of canal structure versus overall porosity.

2) Depth range and generalizability

Our study focused on samples collected from a specific depth range (5–10 meters) in the Nansha Islands, where S. hystrix exhibits a robust structure adapted for wave and storm resistance. This focus limits the generalizability of our findings to other depth ranges or different coral reef systems. Investigating the skeletal structure of S. hystrix along a bathymetric gradient could provide a more comprehensive understanding of how the polyp-canal system adapts to varying environmental conditions, such as different flow velocities and light levels.

3) Flow velocity and environmental complexity

While we considered average and maximum flow velocities (10.3 cm/s and 56.6 cm/s, respectively) in our simulations, the actual flow conditions in the coral’s natural environment are complex and can vary over time. More detailed measurements of flow velocity and other environmental parameters at the sampling sites could enhance our understanding of how the coral’s structural adaptations correlate with specific environmental factors, providing a richer context for our findings.

4) Ecological validation and distribution

Our study did not compare the distribution of S. hystrix with that of other coral species in different flow environments. Such a comparison could provide ecological validation of our hypothesis that the simplified polyp-canal system allows S. hystrix to thrive in high-flow conditions, offering insights into its competitive advantages in various marine ecosystems.

In conclusion, while our research offers valuable insights into the growth patterns and mechanical properties of S. hystrix, further studies are needed to fully explore the interplay between the coral’s polyp-canal system and its environmental context, ensuring a more holistic understanding of coral adaptation.

Data availability statement

The HRCT data supporting this study’s findings are available in Figshare: https://figshare.com/s/a3a6d8b9070ce750aca5; https://figshare.com/s/379c8ebb05928b76cba5.

Ethics statement

The manuscript presents research on animals that do not require ethical approval for their study.

Author contributions

YL: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Validation, Visualization, Writing – original draft, Writing – review & editing. ZL: Software, Supervision, Writing – review & editing. YZ: Resources, Writing – review & editing. CH: Resources, Software, Supervision, Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This research was supported by the China Postdoctoral Science Foundation, Grant Number: 2023M740483; the Postdoctoral Fellowship Program of CPSF, Grant Number: GZB20230100; and the Fundamental Research Funds for the Central Universities, Grant Number: DUT24BS070.

Acknowledgments

We thank Ms. Chenyi Wang for support and assistance throughout the manuscript revision and submission process. This research work is supported by the Big Data Computing Center of Southeast University.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ayre D. J. and Dufty S. (1994). Evidence for restricted gene flow in the viviparous coral seriatopora hystrix on Australia’s great barrier reef. Evolution 48, 1183–1201. doi: 10.2307/2410377

PubMed Abstract | Crossref Full Text | Google Scholar

Black C. C. and Burris J. E. (1983). Diurnal carbon-14 partitioning between zooxanthellae and the coral animal tissue of intact Seriatopora hystrix colonies. Marine Biol. 75, 117–120. doi: 10.1007/BF00405993

Crossref Full Text | Google Scholar

Chen C., Dai C. F., Plathong S., Chiou C. Y., and Chen C. A. (2008). The complete mitochondrial genomes of needle corals, Seriatopora spp. (Scleractinia: Pocilloporidae):: An idiosyncratic atp8, duplicated trnW gene, and hypervariable regions used to determine species phylogenies and recently diverged populations. Mol. Phylogenet. Evol. 46, 19–33. doi: 10.1016/j.ympev.2007.09.013

PubMed Abstract | Crossref Full Text | Google Scholar

Cinner J., Huchery C., MacNeil M. A., Graham N. A. J., McClanahan T. R, Maina J., et al. (2016). Bright spots among the world’s coral reefs. Nature 535, 416. doi: 10.1038/nature18607

PubMed Abstract | Crossref Full Text | Google Scholar

Dai C. F. (1989). Scleractinia of Taiwan 1. Families astroceniidae and pocilloporidae. Acta Oceanogr. Taiwanica 22, 83–101.

Google Scholar

Dana J. D. (1846). Zoophytes. US Exploratory Expeditions 1836–1842 7, 1–740. doi: 10.5962/bhl.title.70845

Crossref Full Text | Google Scholar

Ferrario F., Beck M. W., Storlazzi C. D., Micheli F., Shepard C. C., and Airoldi L. (2014). The effectiveness of coral reefs for coastal hazard risk reduction and adaptation. Nat. Commun. 5, 3794. doi: 10.1038/ncomms4794

PubMed Abstract | Crossref Full Text | Google Scholar

Hughes T. P., Barnes M. L., and Bellwood D. R. (2017). Coral reefs in the anthropocene. Nature 546, 82–90. doi: 10.1038/nature22901

PubMed Abstract | Crossref Full Text | Google Scholar

Li Y., Gao Y., Zheng X., Liu H., and Chen K. (2022a). Generation mechanism and evaluation method of coral reef ecosystem functions. J. Appl. Oceanogr. 41, 475–482.

Google Scholar

Li Y., Han T., Bi K., Liang K., Chen J., Lu J., et al. (2020). The 3D reconstruction of Pocillopora colony sheds light on the growth pattern of this reef-building coral. iScience 23, 101069. doi: 10.1016/j.isci.2020.101069

PubMed Abstract | Crossref Full Text | Google Scholar

Li Y., Liao X., Bi K., Han T., Chen J., Lu J., et al. (2021a). Micro-CT reconstruction reveals the colony pattern regulations of four dominant reef-building corals. Ecol. Evol. 11, 16266–16279. doi: 10.1002/ece3.v11.22

PubMed Abstract | Crossref Full Text | Google Scholar

Li Y., Liao X., He C., and Lu Z. (2021b). Calcium transport along the axial canal in acropora. Diversity-Basel 13, 407. doi: 10.3390/d13090407

Crossref Full Text | Google Scholar

Li Y., Liao X., Wang X., Li Y., Zhao H., Zhao Y., et al. (2023). Polyp-canal reconstruction reveals evolution towards complexity in corals. Research 6, 0166. doi: 10.34133/research.0166

PubMed Abstract | Crossref Full Text | Google Scholar

Li Y., Wang F., Liu Z., Jiang J., Han T., Liao X., et al. (2022b). The formation of biogenic reef stone: from coral skeleton to reef rubble. J. Oceanogr. 78, 135–149. doi: 10.1007/s10872-022-00636-7

Crossref Full Text | Google Scholar

Li Y., Zhao H., Zhao Y., Liao X., Chen J., He C., et al. (2024). bioRxiv. doi: 10.1101/2024.05.25.595876

Crossref Full Text | Google Scholar

Lin Z. and Chen J. (2022). Morphology of coral symbiosome and skeleton of Galaxea fascicularis. J. Appl. Oceanogr. 41, 34–41. doi: 10.1007/s10872-022-00636-7

Crossref Full Text | Google Scholar

Loh W. K. W., Loi T., Carter D., and Hoegh-Guldberg O. (2001). Genetic variability of the symbiotic dinoflagellates from the wide ranging coral species Seriatopora hystrix and Acropora longicyathus in the Indo-West Pacific. Marine Ecol. Prog. Ser. 222, 97–107. doi: 10.3354/meps222097

Crossref Full Text | Google Scholar

Maier E., Tollrian R., and Nürnberger B. (2001). Development of species-specific markers in an organism with endosymbionts:: microsatellites in the scleractinian coral Seriatopora hystrix. Mol. Ecol. Notes 1, 157–159. doi: 10.1046/j.1471-8278.2001.00058.x

Crossref Full Text | Google Scholar

Maier E., Tollrian R., and Nürnberger B. (2009). Fine-scale analysis of genetic structure in the brooding coral Seriatopora hystrix from the Red Sea. Coral Reefs 28, 751–756. doi: 10.1007/s00338-009-0497-5

Crossref Full Text | Google Scholar

Mayfield A. B., Chan P. H., Putnam H. M., Chen C. S., and Fan T. Y. (2012). The effects of a variable temperature regime on the physiology of the reef-building coral Seriatopora hystrix: results from a laboratory-based reciprocal transplant. J. Exp. Biol. 215, 4183–4195. doi: 10.1242/jeb.071688

PubMed Abstract | Crossref Full Text | Google Scholar

Miller K. J. and Ayre D. J. (2008). Population structure is not a simple function of reproductive mode and larval type: insights from tropical corals. J. Anim. Ecol. 77, 713–724. doi: 10.1111/j.1365-2656.2008.01387.x

PubMed Abstract | Crossref Full Text | Google Scholar

Nakajima Y., Nishikawa A., Iguchi A., Nagata T., Uyeno D., Sakai K., et al. (2017). Elucidating the multiple genetic lineages and population genetic structure of the brooding coral Seriatopora (Scleractinia: Pocilloporidae) in the Ryukyu Archipelago. Coral Reefs 36, 415–426. doi: 10.1007/s00338-017-1557-x

Crossref Full Text | Google Scholar

Nir O., Gruber D. F., Einbinder S., and Tchernov D. (2011). Changes in scleractinian coral Seriatopora hystrix morphology and its endocellular Symbiodinium characteristics along a bathymetric gradient from shallow to mesophotic reef. Coral Reefs 30, 1089–1100. doi: 10.1007/s00338-011-0801-z

Crossref Full Text | Google Scholar

Rachmilovitz E. N., Shaish L., Douek J., and Rinkevich B. (2024). Population genetics assessment of two pocilloporid coral species from the northern red sea: Implications for urbanized reef sustainability. Marine Environ. Res. 199, 106580. doi: 10.1016/j.marenvres.2024.106580

PubMed Abstract | Crossref Full Text | Google Scholar

Shlesinger Y. (1985). Reproduction and juvenile growth in stony corals. Department of Zoology, Tel-Aviv University, Tel-Aviv.

Google Scholar

Underwood J. N., Souter P. B., Ballment E. R., Lutz A. H., and van Oppen M. J. H. (2006). Development of 10 polymorphic microsatellite markers from herbicide-bleached tissues of the brooding pocilloporid coral Seriatopora hystrix. Mol. Ecol. Notes 6, 176–178. doi: 10.1111/j.1471-8286.2005.01183.x

Crossref Full Text | Google Scholar

Van Rietbergen B., Weinans H., Huiskes R., and Polman B. J. W. (1996). Computational strategies for iterative solutions of large FEM applications employing voxel data. Int. J. Numerical Methods Eng. 39, 2743–2767. doi: 10.1002/(SICI)1097-0207(19960830)39:16<2743::AID-NME974>3.0.CO;2-A

Crossref Full Text | Google Scholar

Veron J. E. N. (2000). Corals of the world Vol. 2 (Townsville: Australian Institute of Marine Science).

Google Scholar

Wang C. Y., Roeroe K. A., Zhou Z., Niu G. F., Du J. G., Hu W. J., et al. (2024). Gene expression plasticity governing symbiosis during natural coral bleaching. Sci. Total Environ. 953, 176046. doi: 10.1016/j.scitotenv.2024.176046

PubMed Abstract | Crossref Full Text | Google Scholar

Yost D. M., Wang L. H., Fan T. Y., Chen C. S., Lee R. W., Sogin E., et al. (2013). Diversity in skeletal architecture influences biological heterogeneity and Symbiodinium habitat in corals. Zoology 116, 262–269. doi: 10.1016/j.zool.2013.06.001

PubMed Abstract | Crossref Full Text | Google Scholar

Zhu Y., Li Q., Lu J., Chen Y., Wang J., Gai Z., et al. (2022). The oldest complete jawed vertebrates from the early Silurian of China. Nature 609, 954–958. doi: 10.1038/s41586-022-05136-8

PubMed Abstract | Crossref Full Text | Google Scholar