Abstract
Compared to structured ocean environments, unstructured ocean environments are inherently more complex. In such unstructured environments, the presence of narrow waterways poses unique navigational hurdles for autonomous surface vehicles (ASVs) due to their restricted connectivity. Current path planning algorithms designed for unstructured environments, particularly those characterized by narrow spaces, often face difficulties in efficiently exploring the target area while producing high-quality paths. In this study, we tackle the aforementioned complexities by incorporating progressive sampling and point cloud clustering, which jointly expedite the detection of constrained waterways in unstructured marine environments. More specifically, we generate multiple random trees from these sampling points, thereby bolstering both navigational accuracy and overall computational efficiency. Building upon these core techniques, we introduce a novel extension of the traditional rapidly-exploring random trees (RRT) connect algorithm—referred to as multiple RRT-connect (multi-RRT-connect)—aimed at swiftly determining a viable path between prescribed start and goal coordinates. As the number of samples expands, the random trees gradually enlarge and interlink, mirroring the functionality of classic RRT-connect and ultimately forming a continuous corridor. Subsequently, the derived path undergoes iterative refinement and optimization, culminating in a significantly reduced trajectory length.We subjected the proposed algorithm to rigorous testing through comprehensive simulations alongside meticulous comparisons with established state-of-the-art solutions. The results highlight the algorithm’s distinct advantages across multiple dimensions such as path construction success, computational efficiency, and trajectory refinement quality, thereby underscoring its potential to advance autonomous navigation in challenging maritime settings.
1 Introduction
1.1 Background
Autonomous surface Vehicles (ASVs) have emerged as indispensable tools across a spectrum of disciplines owing to their unparalleled capacity to navigate autonomously in complex terrains. These platforms assume pivotal roles in marine transportation (Wibowo and Deng, 2012; Xiao et al., 2024), oceanographic research (Yoo and Kwon, 2012; Sloyan et al., 2019), environmental surveillance (Szpak and Tapamo, 2011; Peters, 2017), and maritime archaeological endeavours (McCarthy, 2006; Fraga et al., 2015). In facilitating human engagement with the oceanic realm, ASVs frequently necessitate bespoke navigation strategies to navigate environmental activities in oceanic settings adeptly. Hence, there is a growing interest in enhancing ASV navigation systems to minimize human errors and support intelligent navigation. Central to this pursuit is the development of autonomous collision avoidance and efficient path planning solutions.
ASV path planning involves strategically generating optimal or nearly optimal routes that avoid collisions. This process accounts for multiple factors, including obstacles, vehicle dynamics, and specified performance metrics (Subramani et al., 2017; Singh et al., 2018). In transport and rescue missions within the ocean environments, as shown in Figure 1.
Figure 1
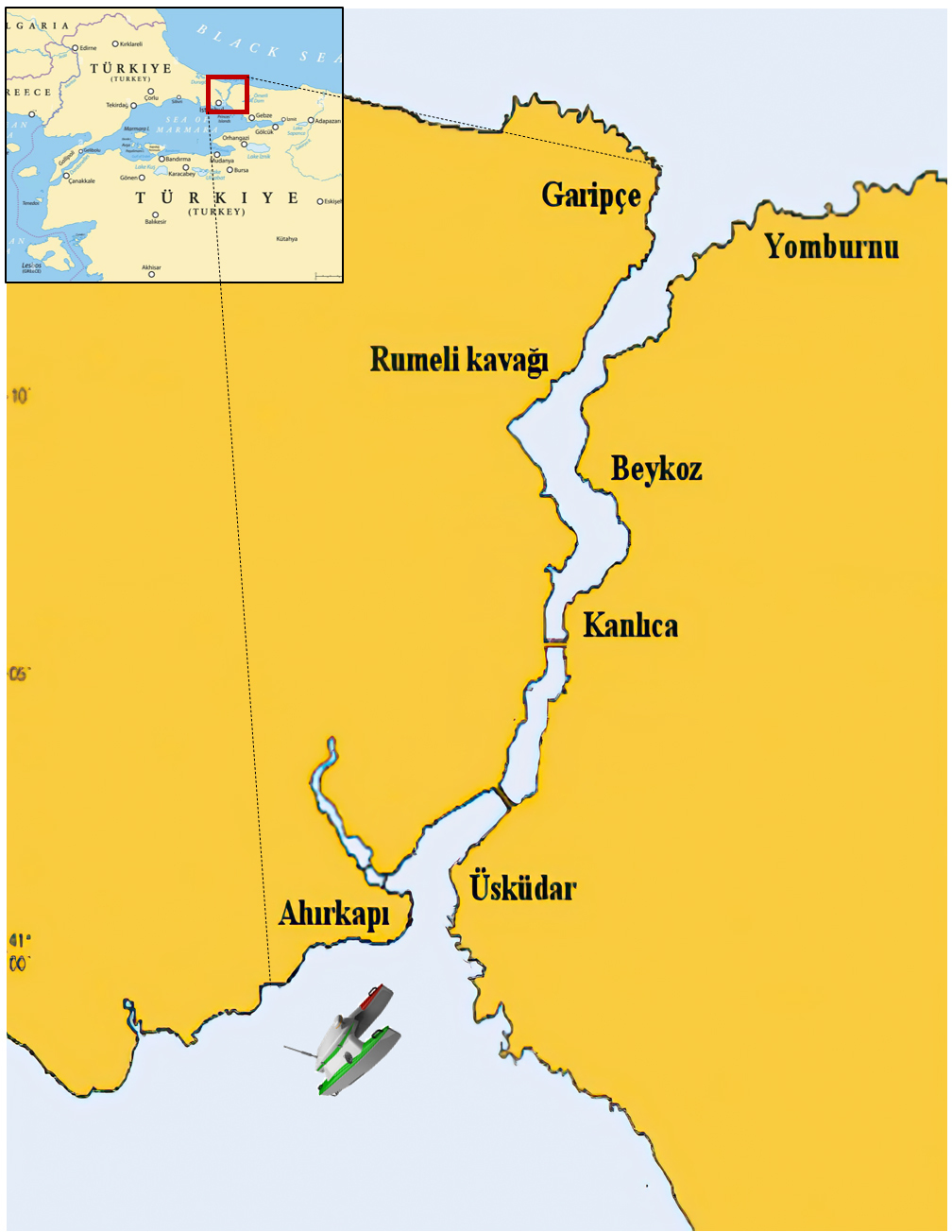
tASVs navigate the strait, where the narrow waterways present heightened challenges for continuous, obstacle-avoidance navigation (Altan and Otay, 2017).
ASVs often encounter unstructured settings characterized by narrow waterways. Such conditions lead to poor connectivity in free space, greatly heightening the difficulty of creating continuous paths that avoid obstacles. Sampling-based planners, like the probabilistic roadmap (PRM) (Kavraki and Latombe, 1994; Hsu et al., 2003) and rapidly-exploring random trees (RRT) (Jang and Joo-sung, 2022; LaValle, 1998), have shown impressive effectiveness in solving complex ASV path planning challenges. These frameworks generate random state samples and perform explicit collision detection to assess sample feasibility. However, planners using a random sampling approach may become exceedingly time-intensive when attempting to connect two nodes located in separate components linked by a narrow passage. When contrasted with the entirety of the configuration space, the volume occupied by narrow passages is notably limited. Consequently, the probability of sampling positions within these specific regions on the map is diminished, resulting in the subpar performance of planners in these areas. This significantly affects convergence speed and can substantially hinder the overall effectiveness of the planners.
In this paper, we focus on generating connected obstacle-avoidance paths in ocean environments with narrow waterways. To address this challenge, we introduce an enhanced version of the rapidly exploring random tree (RRT), termed multiple RRT-connect (multi-RRT-connect). This method incorporates progressive sampling and point cloud clustering strategies to manage path planning within narrow regions effectively. In detail, the process is structured into two distinct phases: pre-processing and search. In the pre-processing phase, a significant challenge arises when attempting to attain an adequate number of sampling points within narrow passages. To overcome this limitation, we propose a novel sampling strategy, termed progressive sampling, which seamlessly integrates random and local circular sampling techniques. By employing this innovative approach, we aim to expedite the process of accurately locating narrow passages. This proposed approach not only overcomes the challenges associated with traditional random sampling techniques but also advances path planning algorithms by enhancing their efficiency in navigating complex environments. Following the pre-processing phase, we proceed to cluster these sampling points and establish multiple local trees based on this clustered data. In the search phase, leveraging the established foundations, we present a groundbreaking variation of RRT-connect. This innovative approach enables the swift identification of a viable path linking the start and goal points. Notably, as the sample size increases, the random trees systematically expand and interconnect, mirroring the behaviour of the traditional RRTconnect algorithm, ultimately resulting in the construction of a complete path. Our algorithm guarantees an accelerated convergence rate and significantly enhances memory utilization compared to the traditional sampling-based methods. Furthermore, the resulting path undergoes rigorous refinement and optimization procedures, ultimately leading to the attainment of a substantially shorter trajectory. Figure 2 illustrates the simulation result, providing an illustrative example of our method’s performance. The outcomes unequivocally highlight the exceptional capabilities of our algorithm.
Figure 2
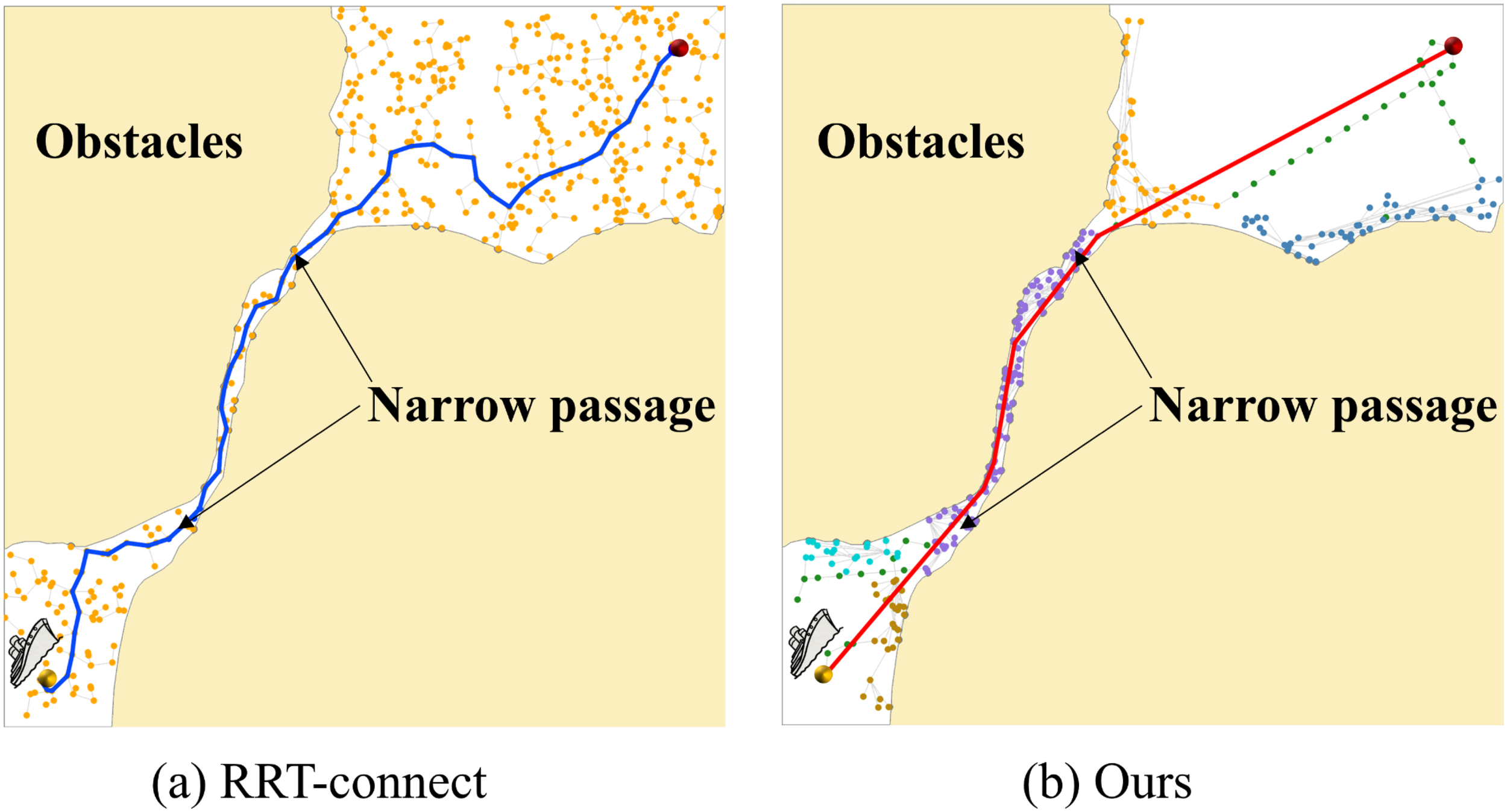
The path planning procedures within confined spaces leverage the RRT-connect method proposed by Kuffner and LaValle (Kuffner and M LaValle, 2000) in subfigure (a) and a novel approach presented by this study in subfigure (b). Our method achieves a significant path length of 1298, completing the task in just 0.09 seconds. In stark contrast, the RRT-connect method necessitates 0.31 seconds and yields a considerably longer path length of 1448.
1.2 Literature review
The realm of path planning algorithms (Wang et al., 2020; Zhang et al., 2024) for ASVs has been extensively explored in numerous scholarly publications, underscoring the field’s significance. This section embarks on an in-depth investigation of path planning, focusing specifically on the intricate challenge of navigating narrow passages. In scenarios where narrow passages exist within the configuration space , obtaining sufficient information for path planning methods (Ruan et al., 2022; Guo et al., 2023; Tu et al., 2024) becomes challenging. These narrow passages provide limited information, representing only a small portion of the total free space. As a result, algorithms experience slower convergence rates and, in certain instances, may struggle to converge entirely. Traditional methods (Yu et al., 2017; Li and Yang, 2020; Yu et al., 2024) struggle to adequately model the configuration space and establish a comprehensive map that connects these narrow passages. As a result, generating a seamless obstacle avoidance path through these constrained areas becomes impracticable. In response to these challenges, researchers have undertaken numerous endeavours aimed at enhancing the capacity of path planning algorithms to navigate narrow passages.
An established strategy is to analyze the topology of configuration spaces to directly derive connectivity paths within narrow passages. For instance, Lien et al. (Lien et al., 2003) introduced a path planning method relying on random sampling along intermediate axes. This approach greatly improves the likelihood of detecting road markers in narrow passageways. Similarly, Bhattacharya et al. (Bhattacharya and Gavrilova, 2008) introduced a method based on Voronoi diagrams to facilitate the generation of interconnected pathways within restricted passages. This method subsequently integrates these pathways with the RRT-connect algorithm to formulate trajectories conducive to obstacle avoidance. Additionally, Rodriguez et al. (Rodriguez et al., 2006) capitalized on the topological attributes of obstacles to enhance the efficacy of narrow passage exploration. Moreover, Liu et al. (Miyombo et al., 2022) employed corrosion thinning techniques in image processing to pinpoint the spatial distribution of confined passages. Nonetheless, these methods typically exhibit applicability primarily within low-dimensional environments for addressing the trajectory planning challenge in narrow passages. This limitation arises due to the requisite analysis of configuration space topology and the concomitant computational intensity.
Diverging from the approach of scrutinizing the topology of configuration space, an alternative strategy involves the design of varied sampling methods to enhance the likelihood of sampling pertinent waypoints within narrow passages. Boor et al. (Boor et al., 1999) employed a Gaussian sampling technique to effectively sample the perimeter of obstacles, thereby augmenting the probability of sampling road markings within these constrained pathways. Nevertheless, the Gaussian sampling method tends to produce numerous redundant sampling points concentrated along the boundary of obstacles rather than within the narrow passages themselves. To refine sampling precision within narrow passages, Hsu (Hsu et al., 2003) introduced the randomized bridge builder (RBB) technique for acquiring path points. Subsequently, Sun et al. (Sun et al., 2005) integrated the RBB method with uniform random sampling to systematically sample free space, thereby constructing a comprehensive path map delineating the entirety of the unobstructed area. While the RBB method notably enhances the precision of narrow passage determinations, it is worth noting that not all road marking points generated by the RBB method are situated within narrow passages. Guo et al. (Guo et al., 2023) presents the grid bridge method for narrow passage detection, wherein each grid point’s status within a narrow passage is sequentially determined by utilizing a stationary orthogonal bridge with a fixed direction over the grid map. Additionally, several alternative methods exist for addressing path planning within narrow corridors. For instance, the hybrid planner (Lien, 2008) integrates a random sampling approach with Minkowski sum computations, thereby enhancing the likelihood of detecting narrow regions. Dalibard et al. (Dalibard and Laumond, 2009) proposed the principle component analysis (PCA) technique to discern the preferred direction within narrow passages, leveraging collision-free samples obtained during the process.
Diverging from the prior research cited above, this paper introduces a novel sampling technique, called progressive sampling, designed to efficiently identify narrow regions and precisely distribute points within them. Subsequently, we employ a novel variation of the RRT-connect algorithm, known as multiple RRT-connect, to progressively expand and interconnect random trees, facilitating the swift determination of a feasible path from the starting point to the destination. For a comprehensive understanding of these methods, please refer to Section 3.
1.3 Motivation and contribution
This paper presents a cutting-edge path planning framework specifically developed for ASVs operating in unstructured maritime environments dominated by narrow channels. The primary contributions of this research can be summarized as follows:
-
In the preliminary stage, we introduce a novel progressive sampling scheme that dexterously merges random sampling with local circular sampling to ensure an adequately dense set of points in constrained corridors. This innovative approach accelerates the detection of narrow passageways and surpasses the limitations of traditional uniform random sampling by focusing attention on regions with heightened navigational difficulty. Consequently, it stands as a significant enhancement for path planning algorithms in complex settings.
-
In the subsequent search phase, we adopt a modified RRT-connect method, which expeditiously establishes a feasible path between the start and goal positions. As the sample size increases, the random trees grow and mutually intersect in a structured manner, ultimately converging on a continuous route. This improvement not only facilitates efficient pursuit of feasible solutions but also broadens the algorithm’s applicability to diverse practical scenarios.
-
We provide a rigorous theoretical assessment of the multi-RRT-connect approach proposed herein. The algorithm showcases a time complexity of O(n log n) and a space complexity of O(n) in effectively computing a collision-free path. Here, n signifies the total number of samples. Mathematical scrutiny of the proposal reveals that its time complexity aligns with that of the original RRT-connect. However, it notably reduces the number of n to achieve a similar level of optimality.
Our work is outlined in detail below: Section 2 provides comprehensive background information on sampling strategies for narrow regions, as well as the rapidly-exploring random tree (RRT) and its variant. In Section 3, we elucidate the path planning framework for navigating narrow waterways, encompassing progressive sampling, point clustering, and multiple RRT-connect to identify feasible paths. Finally, Section 4 showcases the simulation outcomes and their analysis.
2 Preliminaries
Strategies for sampling the configuration space C, especially in narrow areas, as well as the application of the RRT algorithm and its variations, are crucial components in path planning for ASVs navigating complex marine environments. We present a comprehensive exploration of these methods in the following sections.
2.1 Sampling strategies for narrow regions
In order to obtain the connectivity of the environment map, researchers often discretize the environment by sampling points. A well-designed sampling method can yield a greater amount of connectivity information within the environment map using a reduced number of points, thus expediting path searches and enabling the acquisition of higher-quality routes. Conversely, poor sampling outcomes may indirectly result in longer and more circuitous paths, ultimately leading to wasted time in the overall ASV navigation process. In order to address the “narrow passage” challenge, a multitude of sampling strategies have been thoroughly examined over the years, with a specific focus on capturing local features around obstacles. The representative strategies encompass Gaussian sampling, randomized bridge builder (RBB) and randomized star builder (RSB).
Gaussian sampling (Boor et al., 1999; Lin, 2006) entails gathering landmark points in the vicinity of obstacle edges, as depicted in Figure 3a. For a random point within the obstacle, a collected point at a distance of σ in a random direction is obtained. When a point is located within the clear space, it is labeled as a landmark. By carefully selecting the step size σ, a greater number of landmarks can be sampled around obstacles, facilitating rapid obstacle identification. Gaussian sampling in narrow passages can yield a significant number of landmark points, thereby significantly improving the sampling efficiency for such confined spaces. Nonetheless, this method also produces a significant number of unnecessary sampling points scattered along the obstacle’s edge instead of within the narrow passage itself, resulting in decreased sampling precision for the passage. Randomized bridge builder (RBB) (Hsu et al., 2003; Sun et al., 2005) is shown in Figure 3C. In an n-dimensional space, a narrow passage implies that there is at least one direction v where the robot’s mobility is severely limited. Even slight movements along this direction are highly likely to result in collision with obstacles. To avoid collisions, the robot can only move in directions that are orthogonal to the constrained pathway. From this viewpoint, the RBB concept stipulates that when two landmark points lie within an obstacle yet their midpoint resides in free space, those midpoints are deemed landmark points within the narrow passage, as illustrated in Figure 3b. Generating a free-space road marking point using the RBB method involves three collision detections, compared to just one in the conventional uniform random sampling method. As a result, the RBB method substantially increases the duration of collision detection. Randomized star builder (RSB) (Zhong and Su, 2011; Li et al., 2012). The essence of RSB lies in integrating orthogonal bridges alongside the singular bridge detection of RBB (with the quantity of orthogonal bridges dependent on the dimensionality of the free space). By additionally scrutinizing whether the terminals of these supplementary orthogonal bridges reside within obstacles, various regions like narrow passages, depressions, and corners can be more accurately delineated. Although the RSB method offers improved accuracy in identifying narrow passages, the greater number of bridges it employs means it demands more time for collision detection compared to the RBB method. Furthermore, similar to the RBB approach, the RSB method still grapples with the issue of inefficient sampling.
Figure 3
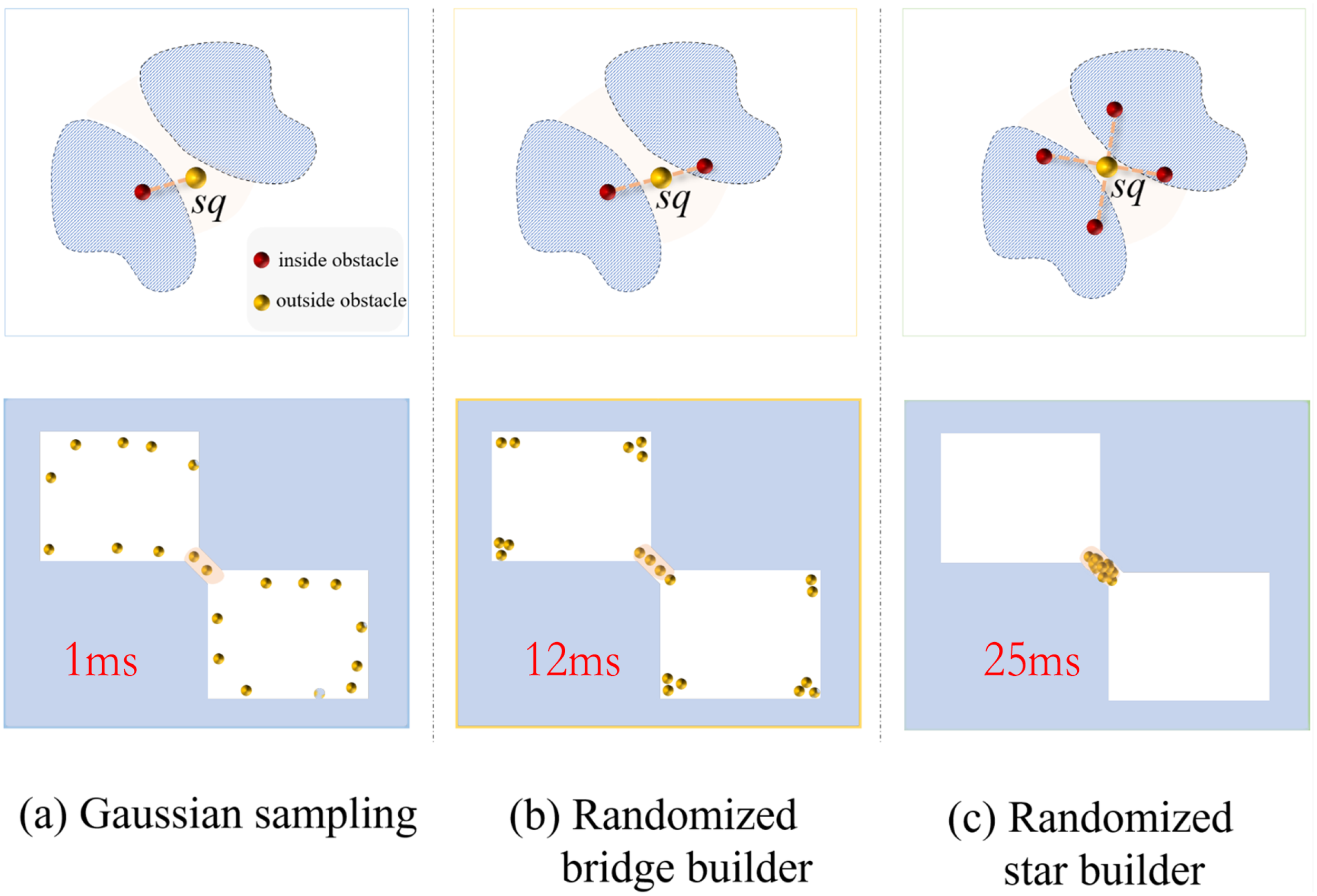
We acquire 20 points employing representative sampling methods. sq signifies the valid sampling point. (a) Gaussian sampling (left column); (b) Randomized bridge builder (middle column); and (c) Randomized star builder (right column).
The objective of sampling is to gather extensive connectivity information within free space to facilitate the identification of optimal paths. However, prevalent sampling methods frequently encounter challenges, including excessive sampling in narrow spaces and ineffective sampling results. In response, the paper proposes hybrid sampling strategies, incorporating both random and local circular sampling methods, which seamlessly integrate obstacle information within the environment. This innovative approach targets efficient sampling in narrow spaces, effectively tackling the aforementioned challenges. Further elaboration on these strategies can be found in Section 3.1.
2.2 Rapidly-exploring random tree and its variant
The rapidly-exploring random tree (RRT) algorithm (LaValle, 1998; Noreen et al., 2016; Meng et al., 2023) is a path planning algorithm commonly used in autonomous systems. The method operates by incrementally constructing a tree T, rooted at the start position ps, through random sampling of points in the space, with the objective of efficiently exploring extensive regions of the configuration space . Each new sampled point is linked to the closest node within the tree, thereby expanding it towards uncharted regions. This process continues until the tree reaches the goal position pgor a predefined stopping condition is met as shown in Figure 4a. However, RRT has some limitations, particularly in narrow spaces. In such environments, the algorithm can struggle to find a path because the random sampling often results in points that fall outside the narrow passage, making it difficult to grow the tree effectively in the constrained area. This inefficiency leads to slower convergence and may require a large number of samples to successfully navigate through tight spaces, resulting in increased computation time and decreased overall performance. In these scenarios, more specialized algorithms tailored for constrained spaces or alternative techniques such as RRT-connect may be more effective for successful planning.
Figure 4
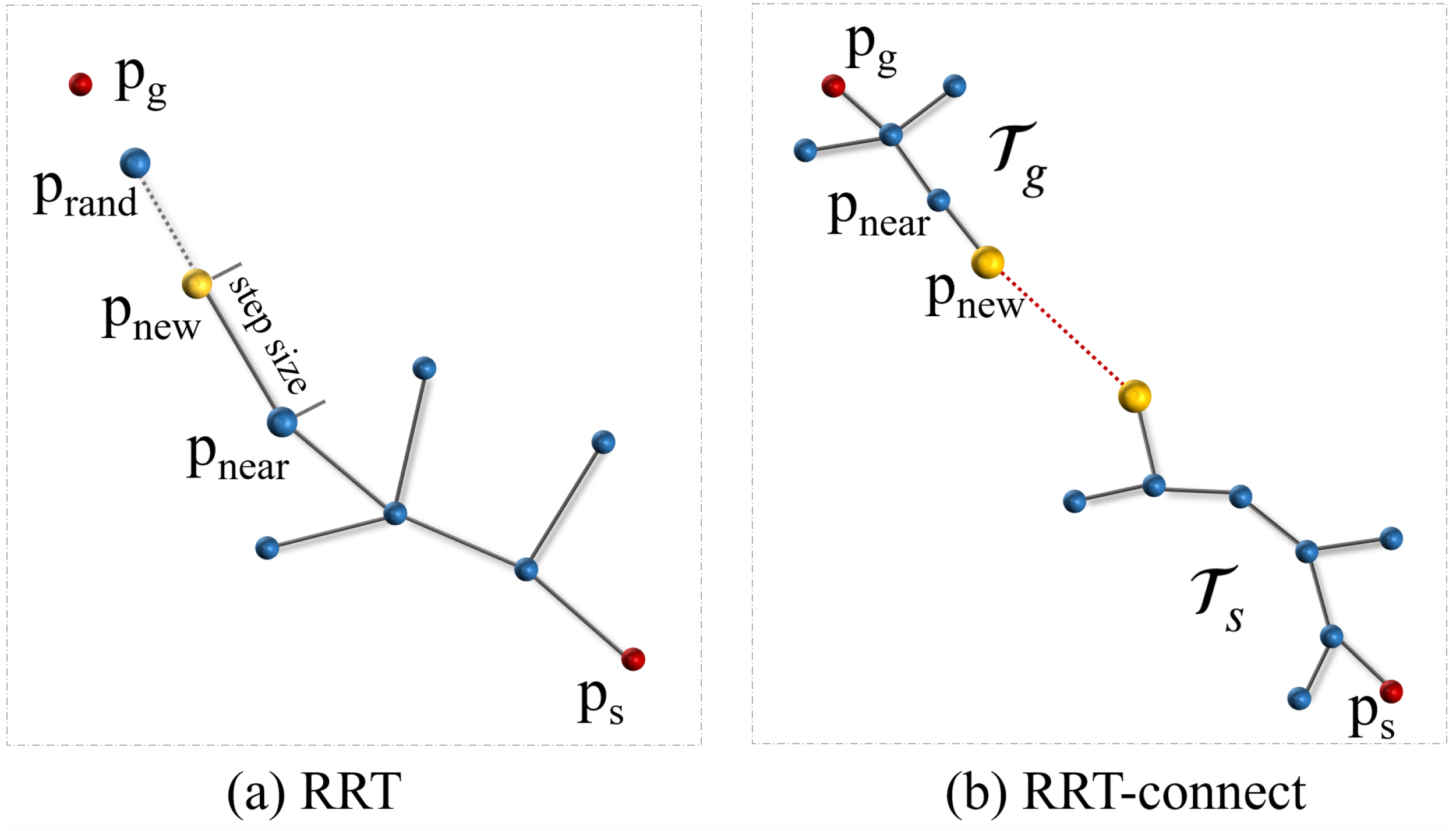
The RRT and RRT-connect algorithms exhibit distinctive traits in their planning tree structures. (a) RRT algorithm initiates a single tree and incrementally expands by randomly selecting points within the configuration space . (b) RRT-connect algorithm commences with the initialization of two trees, denoted as Tsand Tg, which then converge towards each other.
The RRT-connect algorithm, a variation of the rapidly-exploring random tree method proposed by Kuffner and LaValle (Kuffner and M LaValle, 2000), excels in efficiently identifying paths between a starting configuration psand a goal configuration pgwithin narrow spaces. The algorithm initializes two trees, Tsrooted at psand Tgrooted at pg. The trees grow iteratively by randomly selecting points in the configuration space and extending towards them, as illustrated in Figure 4b. In order to link the trees, it searches for obstacle-free trajectories among their nodes, slowly connecting the initial and final configurations. The standard RRT algorithm emphasizes navigating from the beginning to the endpoint, whereas RRT-connect simultaneously searches for a path from both the start and finish points towards the center. This strategy markedly amplifies path search efficiency while diminishing the requisite number of samples. Particularly in constrained environments with narrow passages, the conventional RRT method may incur substantial time costs when traversing such areas via random sampling. In contrast, RRT-connect showcases superior efficacy in promptly and effectively navigating through narrow passages by leveraging dual-sided exploration towards the central region, outperforming the traditional RRT approach.
In this paper, we present an adaptation of the RRT-connect algorithm called multiple RRT-connect. Drawing inspiration from the conventional RRT-connect framework, multi-RRT-connect is designed to rapidly identify a viable path in intricate environments characterized by narrow passages. Notably, depending on the complexity of the environment map, multiple random trees are generated. As the sampling count rises, these trees grow and link up with each other. This characteristic distinguishes multi-RRT-connect from the traditional RRT-connect method and contributes to its superior convergence rate in establishing a comprehensive path between the initial and destination configurations. For further information, kindly consult Section 3.
3 Path planning framework featuring narrow passages
This paper presents an innovative path planning method designed specifically for ASVs operating within unstructured marine environments, particularly those characterized by narrow waterways. The environmental space is discretized into a grid, which is then mapped onto continuous space to facilitate navigation. The algorithm is based on the following assumptions: (1) Obstacles and ASVs are assumed to operate on the same horizontal plane. (2) ASVs are equipped with a sonar system, enabling them to acquire environmental information, including the positions of obstacles. This paper employs the Micron DST, a compact digital imaging sonar model developed by Tritech, to construct environmental maps and detect relevant information (Cao et al., 2018).
Let denote the configuration space, and represent the region occupied by obstacles. The set is referred to as the obstacle-free space. A path in is described by a continuous function . This path is deemed collision-free if for all . The path planning problem involves minimizing the search for feasible trajectories given a cost function , as follows:
In this paper, constrained by Equation 1, we aim to efficiently find a feasible path in unstructured marine environments characterized by narrow passages.
In detail, the multi-RRT-connect algorithm is designed to expedite convergence by simultaneously developing numerous random trees across space. Improving the convergence speed of multi-RRT-connect requires the implementation of effective sampling and growth strategies. The strategic placement of sampling nodes at crucial locations, including narrow passage entrances and exits, has the potential to expedite tree growth within confined spaces, ultimately facilitating swift algorithmic convergence. In contrast to the straightforward single-tree growth associated with RRT-based techniques, the growth process inherent in multi-RRT-connect is significantly more complex, requiring careful deliberation of growth sequence, connectivity among trees, and termination criteria. In summary, the method delineated in this study comprises four primary components: progressive sampling, points clustering, multi-RRT-connect growth, and path optimization, as described in Figure 5.
Figure 5
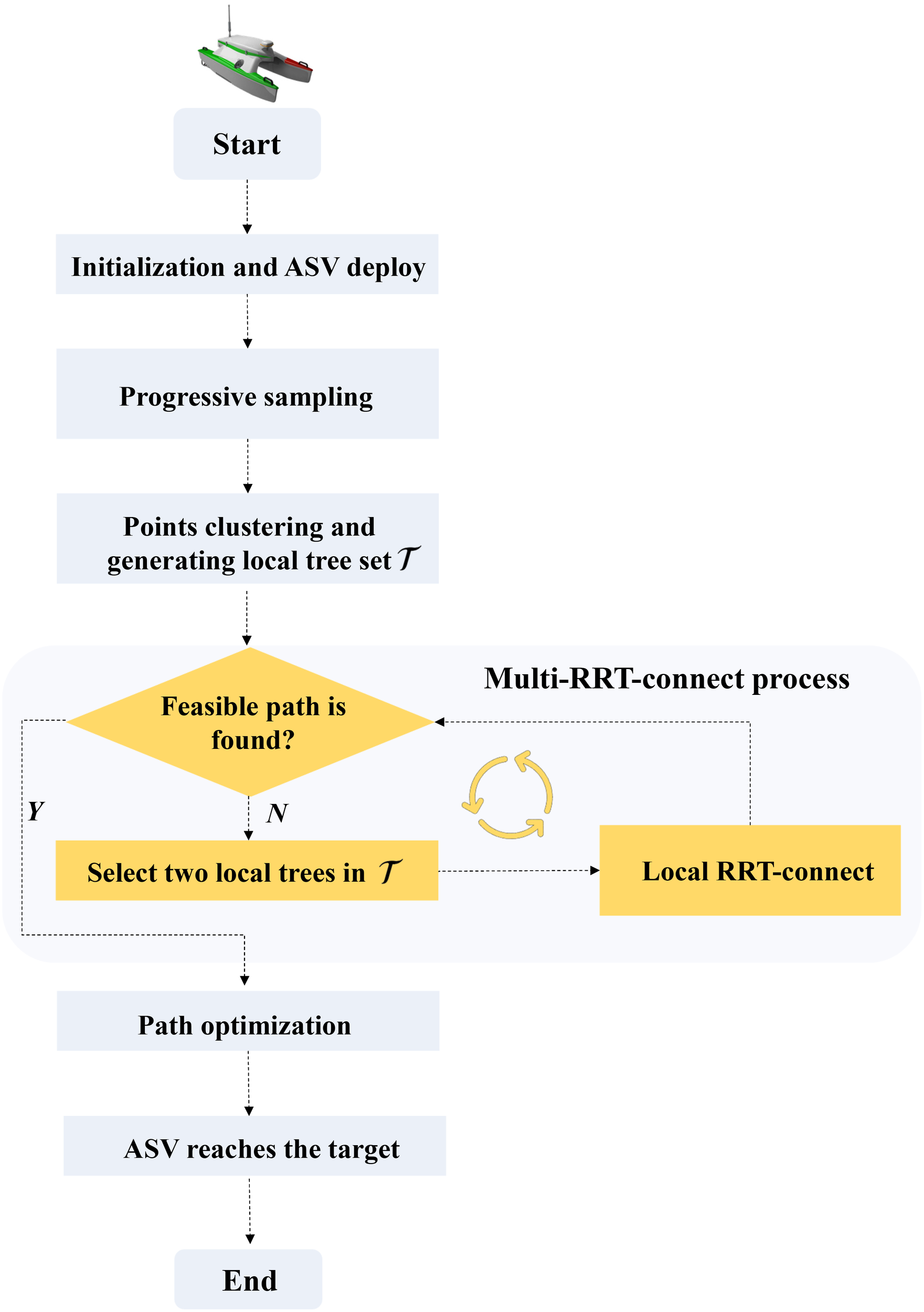
Flowchart illustrates the path planning process for ASV in uncharted marine environments with narrow passages.
3.1 Progressive sampling
The purpose of sampling is to gather connectivity information within confined regions to address the sluggish convergence issue encountered by conventional methods. The optimal distribution of sampling points entails a sparse dispersion in open regions and a dense clustering in narrow spaces. This paper integrates a progressive sampling technique frequently employed in terrain sampling within the realm of geographic information systems. The progressive sampling strategy is grounded in obstacle information to promptly discern and delineate narrow spaces. The sampling procedure can be divided into two stages, comprising random sampling in the configuration space and local circular sampling based on obstacles.
3.1.1 Random sampling
This step is aimed at obtaining approximate spatial information. To guarantee that sampling points are evenly distributed across the configuration space while maintaining a degree of randomness, we employ the Hammersley pseudo-random sampling strategy (Kalagnanam and Diwekar, 1997). This approach enables us to effectively capture the overall distribution of obstacles using a limited number of points. Specifically, given the sample size N, the sampling point is determined by Equation 2:
The Van der Corput sequence , where represent the individual digits of when expressed in binary form. and are constants representing the size of the target map.
3.1.2 Local circular sampling
After the initial sampling, a set of sample points is generated within the configuration space. ., alongside a corresponding set of sample point states. . Here,. . denotes that the sample point resides within an obstacle, while signifies its location in free space. . As regions with significant connectivity information are typically near obstacles, and all sample points with are confined within obstacles, strategically sampling around these points satisfying via sample point testing can augment the sample count within narrow regions. This sampling strategy substantially reduces testing time compared to indiscriminate sampling across the entire space. In detail, for all points where , randomly sample within a circle centered at point p, one by one. To determine the sampling circle adaptively, the radius r is established by measuring the distance from the sampled point p to the closest obstacle point on the map. Please refer to Algorithm 1 for the detailed procedure of the local circular sampling.
Algorithm 1 Local circular sampling.

Figure 6 illustrates the progressive sampling process, which encompasses random sampling and local circular sampling techniques. By leveraging this novel sampling strategy, it facilitates the rapid identification and delineation of confined areas, mitigating the challenges associated with conventional sampling approaches. Moreover, this method fosters advancements in the subsequent path planning algorithm proposed in this paper, augmenting its efficacy in navigating intricate and narrow environments.
Figure 6
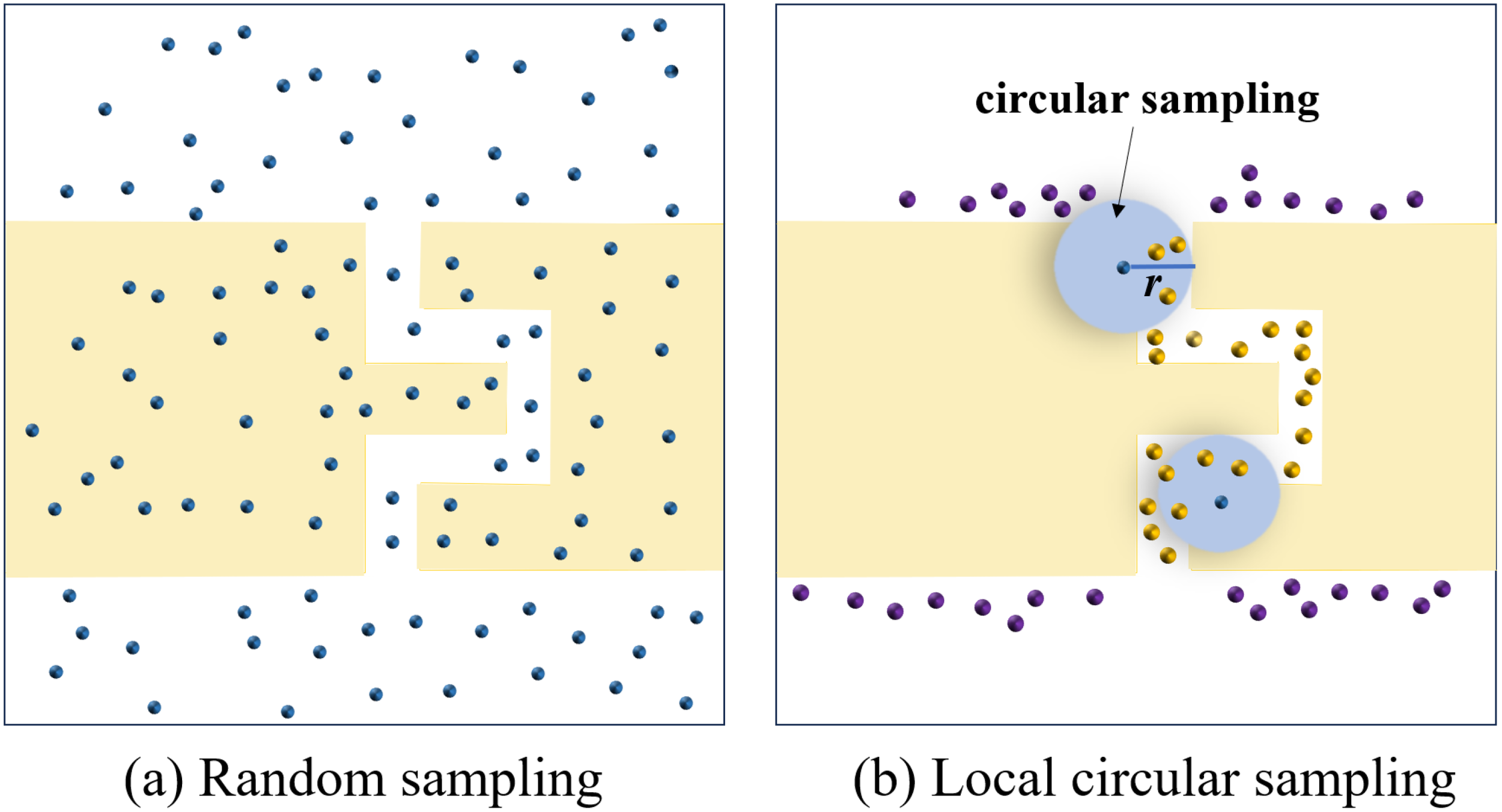
The progressive sampling process. (a) Random sampling with 120 points; (b) Local circular sampling with 25 points (highlighted in yellow) in the narrow passage.
3.2 Points clustering
The sampling point set often concentrates within specific narrow areas in the spatial domain , thereby reflecting the spatial distribution of these confined regions. In order to identify these narrow regions, the point set necessitates partitioning into distinct parts through a clustering process. As depicted in Figure 7a, the distance between separate clusters is notably larger than the distance between points belonging to the same cluster. We employ the Manhattan clustering method as described by Tu et al. (Tu et al., 2024) to implement the aforementioned process. The core idea behind this clustering algorithm lies in categorizing two points as belonging to the same group, provided that their Manhattan metric is below a predefined threshold. To improve the clustering algorithm’s efficiency, we employ the kd-tree method, which accelerates the clustering procedure and reduces the computational burden. The kd-tree is constructed according to the data attributes, thereby establishing closer connections between data objects with high similarity and facilitating a faster searching process. For structured point sets, the Manhattan clustering approach is both effective and convenient. By navigating through the branches of the kd-tree, the clustering procedure can be efficiently carried out. The outcomes of the clustering are represented as C = (c1,c2,…,cm).
Figure 7
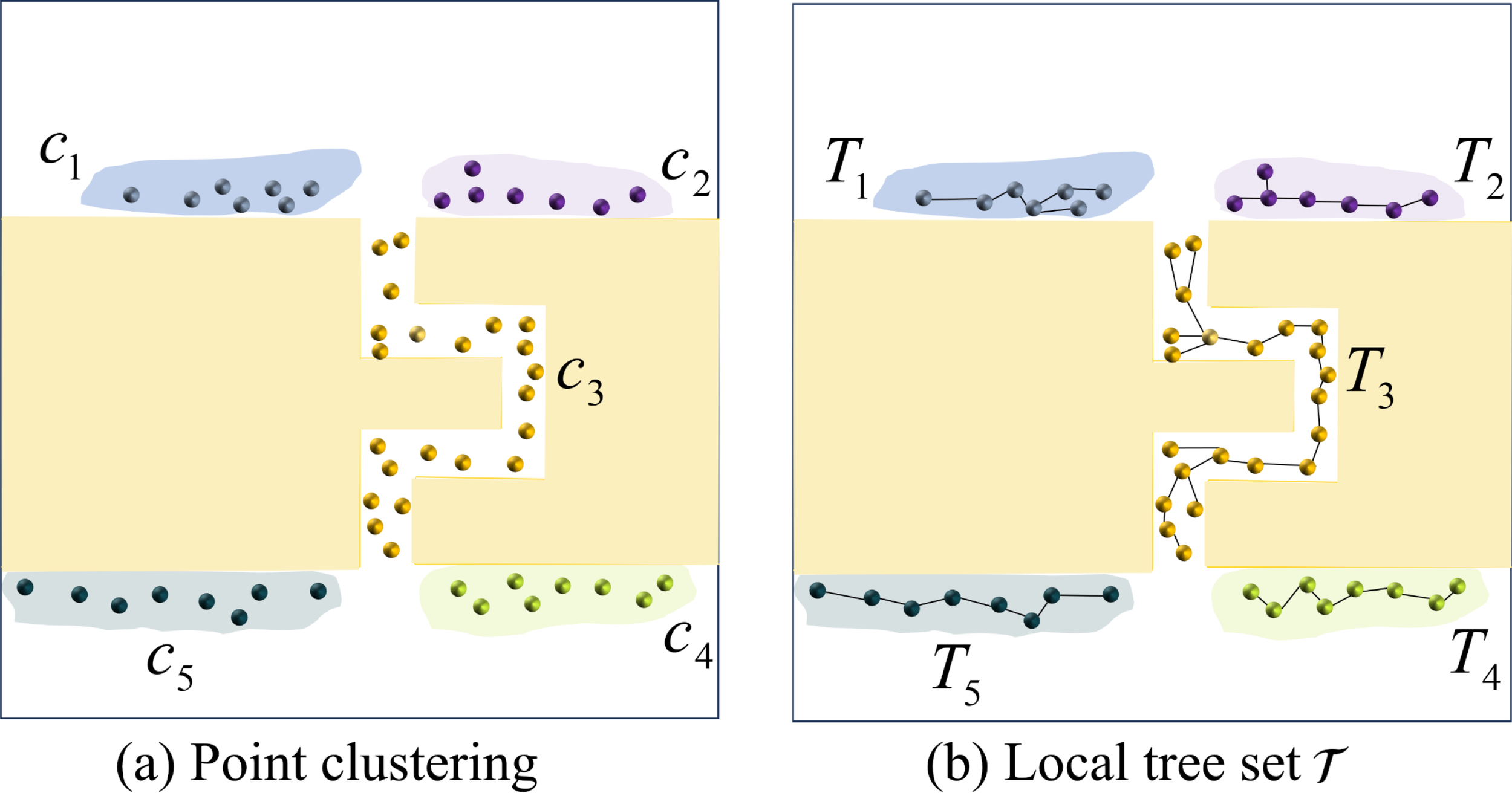
Point clustering and the generation of the local tree set . (a) Utilizing the Manhattan clustering method, five clusters C = (c1,c2,c3,c4,c5) are generated; (b) The local tree set is derived from clustering the points in (a).
Based on the clustering results, we identify sampling points and establish multiple local trees. ., as depicted in Figure 7b. These local trees are purposefully placed in proximity to narrow passageways, mirroring their spatial arrangement for improved efficiency in path planning. Further elaboration on the utilization of local trees is provided in the subsequent section.
3.3 Multiple RRT-connect to find feasible path
By executing sampling and clustering operations, we obtain a set of local trees denoted as . We incorporate the two trees Tsand Tgsourced from the start point and goal point, resulting in a total of (n + 2) trees. Building upon the well-established foundations, we introduce a pioneering variation of RRT-connect called multiple RRT-connect (multi-RRT-connect). This innovative approach enables the rapid identification of a feasible path that links both the starting point and the destination. Remarkably, as the sample size increases, the random trees systematically expand and interconnect, leading to the eventual construction of a comprehensive path. The multi-RRT-connect algorithm is implemented as depicted in Algorithm 2.
Algorithm 2 Multi-RRT-connec.

In detail, we randomly sample a point prandin the configuration space and determine the tree Ts(Tg) denoted as Tparentthat has the minimum Euclidean distance to prand(Line 3-9). After inserting the point pnew, steered by prand, into the selected tree Tparent(Line 10-11), a local RRT-connect operation between Tparentand the near tree Tnearin tree set will be triggered. The near tree is selected according to the distance-triggering criterion (Line 13). The criterion for triggering must not exceed the predefined length Ltri, constrained by Equation 3,
If more than one tree. . is triggered simultaneously, the algorithm selects the nearest tree Tnear. Subsequently, it locates node pnfrom tree Tnear, which is nearest to pnew. Following this step, the LocalConnect procedure endeavors to establish a connection with pnewand pnon Tnearin order to update its current best solution (line 16). The LocalConnect procedure is similar to RRT-connect (Kuffner and M LaValle, 2000). It involves iteratively growing the current two trees Tparentand Tneartowards each other by randomly sampling nodes, extending the trees towards these nodes, and checking for a connection between the trees. Once the LocalConnect process is completed, the local tree Tnearwill undergo a merging process with tree Tparentand consequently be eliminated from the tree set . Through iterative execution of the above steps, the tree set undergoes a progressive merging process as the number of sampling instances grows. Upon the convergence of tree Tsat the endpoint with tree Tgat the starting point, a viable trajectory is determined, thereby concluding the growth process. The pipeline of the multi-RRT-connect algorithm is visualized in Figure 8.
Figure 8
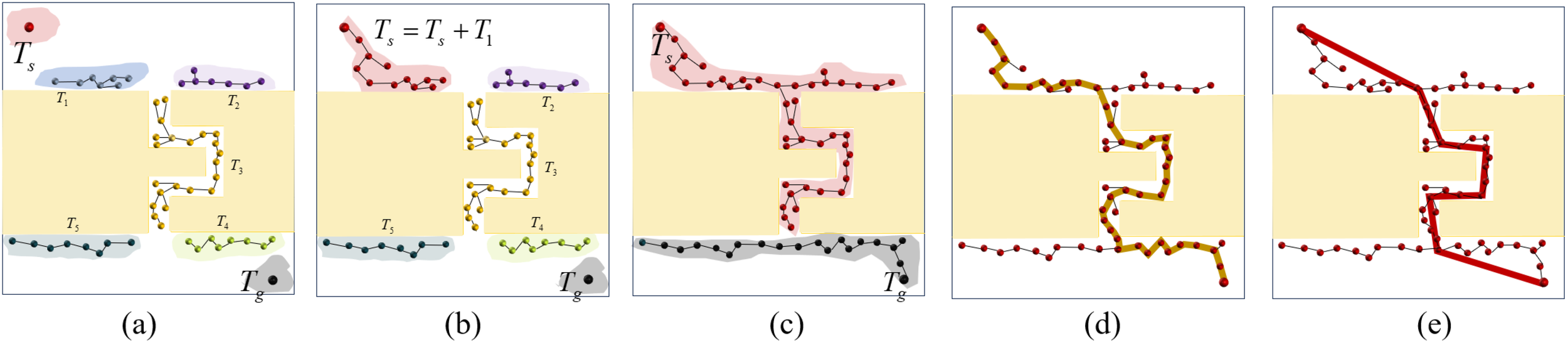
Illustration of multi-RRT-connect algorithm. (a) Integration of the trees Tsand Tgwith the local tree set , resulting in a total of n + 2 trees; (b) In the LocalConnect process, we merge Tswith Tifrom and generate updated Ts; (c) Through iterative execution of LocalConnect, the tree set undergoes a progressive merging process until only trees Tsand Tgremain; (d) Upon the convergence of tree Tswith tree Ts, a feasible path of length 256 is identified. (e) The refined path result in a shorter length of 194.
3.4 Path optimization
The findings from the experimentation disclose that the trajectory produced by Algorithm 2 demonstrates inferior quality, characterized by numerous unnecessary detours. To address this issue, we employ the redundant node elimination method to enhance trajectory precision. This straightforward approach requires only a minimal number of collision detections to filter redundant nodes from the path, achieving a more concise and direct trajectory. Consider the path denoted by Π:= (p1,p2,…,pn) as the initial trajectory. The refined algorithm systematically navigates through all path nodes from the initial point to the destination. Nodes are classified as redundant if they can be linked in a collision-free trajectory. Conversely, in the event of a detected collision, the validity of the parent node is affirmed, and it is subsequently retained within the optimized trajectory. Figure 8e visually depicts the process, showcasing the refined trajectory as a red line. Through meticulous algorithmic adjustments, redundant nodes are substantially eliminated, resulting in a path with minimized unnecessary detours and enhanced overall quality. Notably, the optimized trajectory predominantly comprises straight sections, punctuated by only a few strategic turning points, thereby optimizing its suitability for ASV navigation.
We conducted a rigorous evaluation of our algorithm’s performance through comprehensive simulations and comparative analyses against established elegant methods. The superiority of the algorithm in multiple aspects is unambiguously shown by the experimental results, encompassing the success rate of path construction, computational efficiency, and path optimization. For a comprehensive comparative analysis of our algorithm against elegant related methods, please refer to Section 4.
3.5 Theoretical analysis
In this part, our goal is to assess the theoretical viability and effectiveness of multi-RRT-connect by conducting a thorough analysis.
DEFINITION 1. (Probabilistic completeness.) Provided with the start point ps and a collection of target points Pg, The path planning problemis deemed feasible if it meets the subsequent condition, determined byEquation 4,
where denotes the nodes at planning iteration n. The algorithm is considered to be probability complete.
LaValle et al. (LaValle, 1998) demonstrated that RRT guarantees probabilistic completeness. Subsequently, the probabilistic completeness of RRT-connect (Kuffner and M LaValle, 2000) was inferred. Property 3.1 establishes the probabilistic completeness of the proposed algorithm, multi-RRT-connect.
PROPERTY 3.1. For a given triplet representing a feasible path planning problem, the probability of discovering a viable solution is delineated asEquation 5.
As the iteration count n approaches infinity, the probability of discovering a feasible solution, provided it exists, converges to one.
PROOF. To establish the above theorem, we present the following three arguments: (1) The tree generated randomly through multi-RRT-connect must contain psamong its nodes. Furthermore, The goal node pgneeds to be contained within the specified set of target goal nodes Pg. This condition can be expressed as σ(0)multi−RRT−connect = ps and σ(1)multi−RRT−connect = pg ∈ Pg, which aligns with the criteria of RRT-connect; (2) The random trees generated by the multi-RRT-connect algorithm, similar to those in RRT-connect, are connected. Specifically, whenever a node is randomly sampled, it becomes connected to its nearest neighbour node within the particular tree selected for growth by the multi-RRT-connect method; (3) The multi-RRT-connect algorithm specifies the goal node from the set of desired goals Pg. Consequently, with infinite random sampling, the probability that the multi-RRT-connect algorithm generates a random tree reaching the target region approaches one.
Multi-RRT-connect internally employs distinct space-filling trees, each of which fulfills the properties of a classic RRT tree. The algorithm alternates and independently expands each tree, ensuring that both trees satisfy criterion 5. Given the preceding reasoning, we can demonstrate that multi-RRT-connect is capable of discovering a viable path for the specified path planning problem and converging to a probability of 1 as the sample size grows indefinitely. Therefore, multi-RRT-connect guarantees probabilistic completeness.
PROPERTY 3.2. When it comes to planning a path for an ASV travelling from a given start point ps to a specified goal point pg, the multi-RRT-connect algorithm has shown a time complexity of O(nlogn) and a space complexity of O(n), enabling the swift determination of a collision-free route between the origin and the intended destination.
PROOF. The multi-RRT-connect method is based on the RRT-connect algorithm. The key elements of the algorithm comprise sampling and searching for the nearest tree (and ), establishing local connections between and , and updating the set of local trees . Let denote the overall iteration counts, and let represent the size of . In every iteration of the algorithm, the sampling operation is simple and can be completed in time . The search for and requires a time cost of and , respectively. Additionally, the local connection process between and exhibits a time complexity of , mirroring that of the classic RRT-connect approach. The computational complexity of the path-planning process with multi-RRT-connect is characterized by , which can be approximated as . Therefore, the time complexity of the multi-RRT-connect algorithm is generally limited by . Given a fixed total number of sampling nodes, denoted as , the analysis of space complexity for the multi-RRT-connect algorithm entails summing up the memory needs of every node and edge. This computational process results in . As a result, the space complexity of the multi-RRT-connect algorithm is concisely expressed as .
Kuffner et al. (Kuffner and M LaValle, 2000) state that the time complexity of RRT-connect is O(n log n). The mathematical analysis we conducted on multi-RRT-connect reveals that its time complexity is still comparable to the original RRT-connect. The proposed method excels in quickly identifying narrow passages, thereby significantly reducing the value of n required to achieve similar optimality levels compared to RRT-connect. This capability improves the convergence speed of path-planning algorithms, particularly in environments with confined regions. Comprehensive experimental results supporting these findings are illustrated in Section 4.
4 Simulation and analysis
This section presents the experimental findings, which demonstrate the viability and energy efficiency of our planning method in various scenarios. The simulations were all carried out using Microsoft Visual C++ 2022, without relying on external numerical libraries. To ensure consistency and reproducibility in the study, all tests were executed on a system furnished with a 2.50 GHz AMD Ryzen 9 CPU and accompanied by 16 GB of RAM.
4.1 Simulation settings
In this section, we begin by introducing a rigorous criterion for defining the narrow regions. For a given region R, if the proportion of free space to obstacle space falls below a specified threshold ∈, denoted as Equation 6, then the region is considered a narrow region.
Quantitatively speaking, supposing the presence of a hyper-spherical region SR(pc,r) centered at node pccontaining n nodes, denoted by P = {p1,p2,…,pn}. A pair (ACi,SCi) is employed to denote the extension status of node pi, where ACiand SCirespectively represent the attempted extension count and successful extension counts. The blocking rate BRi (Zhou et al., 2023), as defined in Equation 7, represents the degree of obstruction experienced by a node pi. A lower value of BRiindicates a more difficult extension for node pi, suggesting a more intricate narrow environment.
Furthermore, we can define a metric, regional complexity (REC), as depicted in Equation 8. This metric quantifies the average level of node extension obstruction within the vicinity of pc. A lower REC value signifies a greater prevalence of obstacles, suggesting an increased likelihood of the region being classified as narrow.
In order to showcase the effectiveness of our suggested approach, we applied it to four benchmark scenarios, which are outlined in detail in Figure 9. These scenarios exhibit differing levels of region complexity (REC), where some present more significant challenges compared to others. For each benchmark, we conducted comparative analyses against the most pertinent existing methods listed below.
-
PRM + Gaussian sampling (Ref (Boor et al., 1999).), which incorporates the collection of landmark points located near the edges of obstacles. By meticulously selecting the step size σ, it becomes possible to sample a larger number of landmarks around obstacles, thereby facilitating expedited narrow passage identification.
-
PRM + RBB sampling (Ref (Sun et al., 2005).) creates a road marking point in free space that depends on three collision detections for precise localization of narrow areas.
-
RRT-connect (Ref (Kuffner and M LaValle, 2000).), which is a variation of the rapidly-exploring random tree (RRT) approach, shows effectiveness in maneuvering through tight spaces. This is achieved through dual-sided exploration towards the central region, surpassing the performance of the traditional RRT approach.
-
LGM-BRRT* (Ref (Shu et al., 2019).) which integrates an enhanced bridge-test technique with a locally guided novel search strategy to tackle path planning challenges in clustered environments featuring narrow passages.
Figure 9
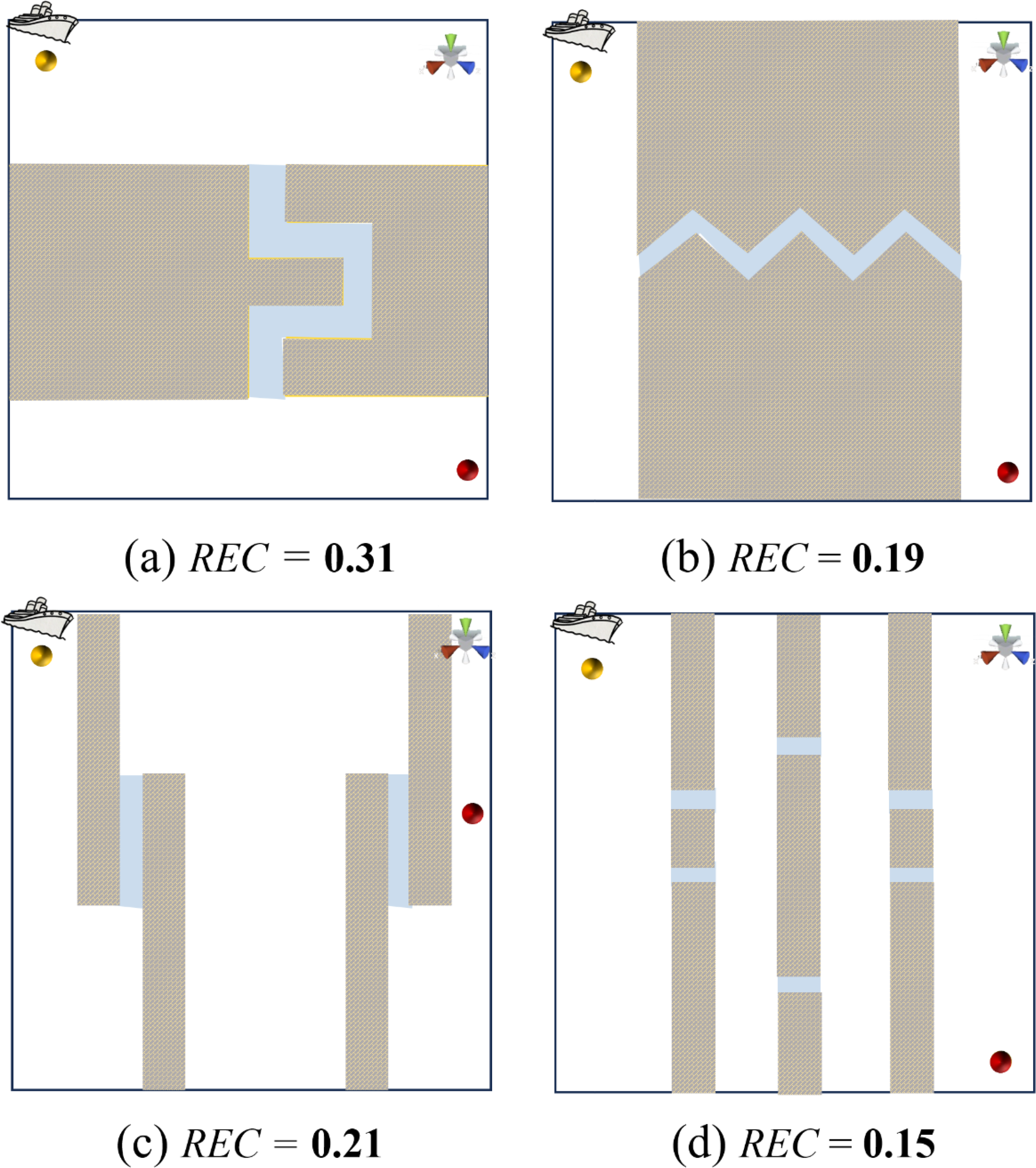
Four maps depicting varying degrees of regional complexity (REC) are displayed to demonstrate the efficacy of the suggested approach in constricted areas. Yellow and red spheres denote the starting and destination points, respectively, whereas the blue areas signify the existence of tight corridors, as determined by Equation 7. (a, b) represent the single-channel scenarios, while (c, d) correspond to the multichannel scenarios.
To address the inherent unpredictability of sampling-based methods, we performed 50 trials for each benchmark. For each trial, we recorded the average computation time, path length, and success rate in navigating narrow environments.
4.2 Performance
Table 1 presents a comprehensive performance comparison of five path planning methods across diverse map benchmarks with varying regional complexity (REC). The metrics evaluated include average time (in seconds), average path length, and success rate (%). Our proposed method demonstrates superior performance across all benchmarks. It consistently achieves a 100% success rate, indicating its robustness in navigating complex environments. Notably, our method exhibits the lowest average execution time, ranging from 0.091 to 0.118 seconds, highlighting its efficiency. While the average path length varies across maps, it remains competitive with other methods. In contrast, PRM + Gaussian (Boor et al., 1999) and PRM + RBB (Sun et al., 2005) exhibit significantly higher execution times, often exceeding several seconds. Although PRM + Gaussian maintains a high success rate, PRM + RBB demonstrates lower success rates in certain benchmarks. Both methods also yield longer path lengths compared to our approach. RRT-connect (Kuffner and M LaValle, 2000) achieves a 100% success rate and relatively low execution times, comparable to our method. However, it produces significantly longer path lengths, indicating a potential trade-off between speed and optimality. LGM-BRRT* (Shu et al., 2019) also maintains a 100% success rate and generates competitive path lengths. However, its execution times are considerably higher than our proposed method, suggesting a higher computational cost. Overall, our method offers a favorable balance between efficiency, path optimality, and robustness.
Table 1
| Map Method | Assessment | Figure 9a | Figure 9b | Figure 9c | Figure 9d |
|---|---|---|---|---|---|
| Ours | Average Time (s) | 0.118 | 0.103 | 0.116 | 0.091 |
| Average Length | 1820 | 1578 | 1954 | 1591 | |
| success rate | 100% | 100% | 100% | 100% | |
| PRM+Gaussian(Ref (Boor et al., 1999).) | Average Time (s) | 4.781 | 3.265 | 4.004 | 4.256 |
| Average Length | 1832 | 1602 | 1996 | 1638 | |
| success rate | 94% | 96% | 100% | 98% | |
| PRM+PBB(Ref (Sun et al., 2005).) | Average Time (s) | 5.404 | 5.016 | 5.024 | 6.315 |
| Average Length | 1854 | 1610 | 2013 | 1600 | |
| success rate | 86% | 96% | 98% | 96% | |
| RRT-connect(Ref (Kuffner and M LaValle, 2000).) | Average Time (s) | 0.138 | 0.103 | 0.122 | 0.132 |
| Average Length | 2150 | 1864 | 2432 | 2049 | |
| success rate | 100% | 100% | 100% | 100% | |
| LGM-BRRT*(Ref (Shu et al., 2019).) | Average Time (s) | 3.451 | 4.036 | 4.789 | 5.053 |
| Average Length | 1731 | 1503 | 1883 | 1545 | |
| success rate | 100% | 100% | 100% | 100% |
A comparative evaluation of four related methods applied to diverse maps with different levels of regional complexity (REC).
Bold font indicates that the method achieves the best performance on the corresponding metric among all methods.
Its low execution times and high success rates make it a promising candidate for real-time applications in complex and dynamic environments.
4.2.1 Sampling evaluation
In the pre-processing stage of the method, we implement a progressive sampling strategy to swiftly identify narrow regions that critically affect the subsequent path planning process, utilizing the multi-RRTconnect algorithm. In this section, we compare representative sampling strategies, including simple random sampling, Gaussian sampling, and RBB sampling, as depicted in Figure 10 and summarized in Table 2.
Figure 10
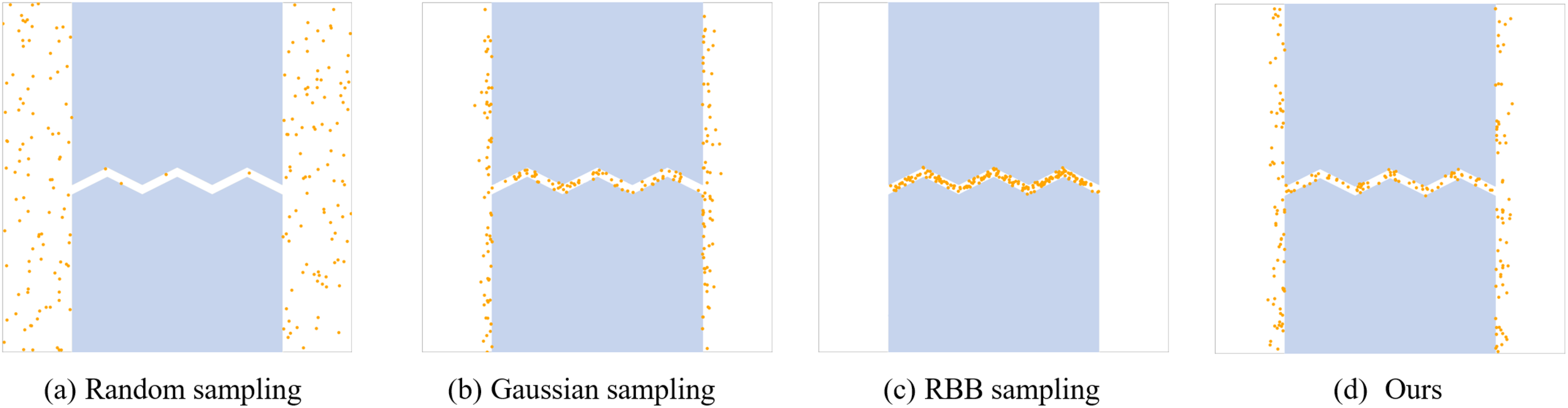
Visualization of Sampling Results. Here, represents the number of sampling points within narrow regions, and Tavgdenotes the average sampling time per point within these regions. (a) Random sampling: , Tavg= 0.001ms; (b) Gaussian sampling: , Tavg= 0.007;(c) RBB sampling: , Tavg= 0.352ms and (d) Prograssive sampling (Ours): , Tavg= 0.005ms.
Table 2
| Assessment Method | Tavg | ||
|---|---|---|---|
| Ours | 200 | 92 | 0.005ms |
| Simple random sampling | 200 | 4 | 0.001ms |
| Gaussian sampling | 200 | 74 | 0.007ms |
| RBB sampling | 200 | 200 | 0.352ms |
Sampling performance statistics.
We compare three elegant sampling methods using three detailed criteria. represents the total number of sampling points, while denotes the number of sampling points specifically within narrow regions. Additionally, Tavgis defined as the average sampling time per point within these narrow regions.
Bold font indicates that the method achieves the best performance on the corresponding metric among all methods.
Based on the findings shown in Table 2, it is evident that to achieve roughly 90 points in narrow areas, we need to generate a total of 200 sampled points using our method. Moreover, the average sampling time per point within these narrow regions is remarkably low, at only 0.005ms. In contrast, Gaussian sampling yields 74 points in the same narrow regions but requires an average sampling time of 0.007ms. While it is worth noting that all points obtained using RBB sampling are within the confined regions, the average sampling time per point in this case is significantly higher, at 0.352ms. This value is approximately 70 times greater than the average sampling time achieved by our method. Gaussian sampling and RBB sampling necessitate two and three collision tests per sample in narrow passages, respectively, making these methods particularly time-consuming. This high computational demand indirectly contributes to the low convergence of path planning methods based on these sampling strategies.
4.2.2 Evaluation of different narrow levels
We evaluate the scenarios characterized by differing degrees of regional complexity (REC), ranging from 0.006 to 0.23. A lower REC value indicates a higher probability of the region being classified as narrow, whereas a higher REC value suggests the region is more likely to be classified as wide. We performed a comparison of the aforementioned elegant methods in the same scenario but with varying degrees of narrowness, as illustrated in Figure 11. Based on our results, the time performance advantage becomes increasingly pronounced as the metric REC decreases. For example, when REC = 0.23, our method requires only 0.12 seconds to generate a path with a length of 2138, whereas the RRT-connect algorithm needs 0.34 seconds to generate a path of length 2469. When the scenario is set with an extremely narrow metric where REC is 0.006, the RRT-connect method takes 3.72 seconds to generate paths of length 2516. Our method only takes 0.39 seconds, approximately one-tenth of the time required by RRT-connect, to generate a short path of length 2316. Clearly, our method exhibits a significant advantage in narrow spaces, especially under extremely narrow conditions.
Figure 11
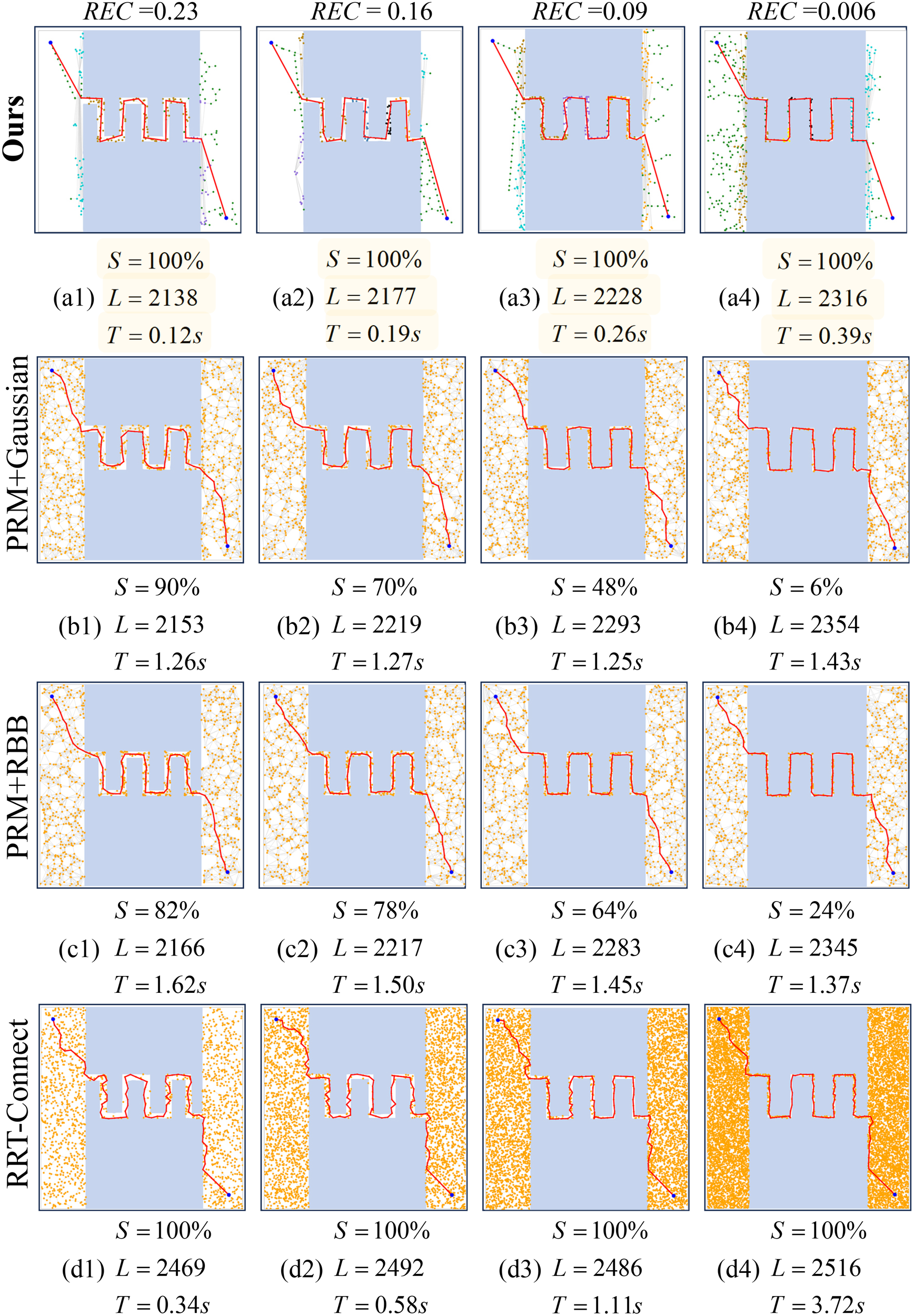
We evaluated the same scenario characterized by varying degrees of narrowness, quantified by REC values of 0.23, 0.16, 0.09, and 0.006, conducting 50 trials for each case. The comparison methods included PRM with Gaussian sampling (b1∼b4), PRM with RBB sampling (c1∼c4), RRT-connect (d1∼d4), and our proposed method (a1∼a4). In this context, S represents the success rate, L denotes the average path length, and T indicates the average time cost.
Furthermore, in our study involving 50 trials on the map with an exceptionally narrow level REC = 0.006, as illustrated in Figure 11, both the PRM method utilizing Gaussian sampling and RBB sampling demonstrated an approximate 80% failure rate in identifying a feasible path between specified start and goal points. In contrast, our method consistently found paths successfully in all 50 trials. This characteristic enhances the popularity of the proposed algorithm in the path-planning process within marine environments that contain narrow passages.
4.3 Quantitative comparison
In this part, we carry out a comparison between our method and four other elegant methods in the field that resemble ours, highlighting the distinct advantages of our approach.
4.3.1 Comparison to Boor et al.’s work
They (Boor et al.,1999) introduced a path planning algorithm that builds a graph by randomly sampling points in the configuration space C, assessing their feasibility, and linking them to create a roadmap of feasible paths. Gaussian sampling enhances this process by generating sample pairs from Gaussian distributions, thereby increasing the probability of placing nodes in crucial areas such as narrow passages. Nevertheless, Gaussian sampling often generates numerous redundant sampling points concentrated near the boundary of obstacles rather than within the narrow passages themselves. Additionally, each sampling requires two collision tests, which reduces overall sampling efficiency. In contrast to Gaussian sampling, our progressive sampling fully utilizes obstacle information and requires only one collision test to determine each sampling point. As shown in Figure 12, it takes 4.0 seconds to generate a path with sampling 48 points in the narrow regions using 0.16 seconds. In contrast, our proposed method achieves a shorter feasible path in only 0.12 seconds by sampling 121 points in the narrow regions using 0.003 seconds.
Figure 12
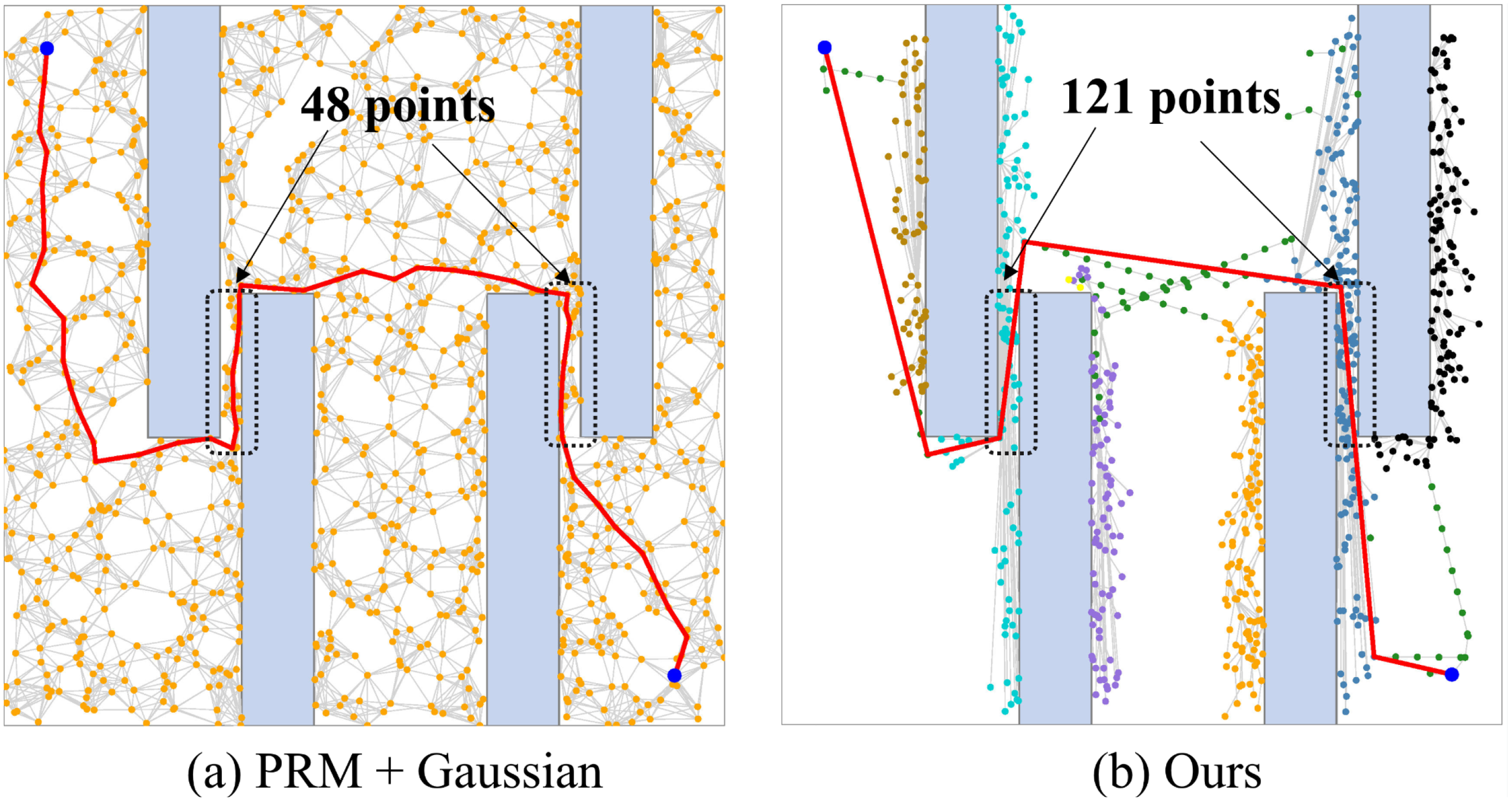
We evaluated the performance of our proposed method shown in subfigure (b) against PRM method utilizing Gaussian sampling shown in subfigure (a). Our approach has a superior ability to detect points in narrow regions more efficiently, significantly accelerating algorithm convergence.
4.3.2 Comparison to Sun et al.’s work
This paper (Sun et al., 2005) introduces the PRM method with the RBB (Randomized Bridge Builder) sampling strategy to enhance the path-planning process by prioritizing sample generation in narrow passages. The RBB strategy operates by establishing “bridges” between random points: initially, two random points are sampled, and if both fall within obstacles, a midpoint is computed. This midpoint is then validated for free space and incorporated into the roadmap. By augmenting sample density in crucial regions, RBB sampling significantly enhances the success rate of PRM. However, this method may face challenges in effectively navigating narrow passages or areas with high obstacle density due to its dependence on random sampling. The randomized Bridge Builder sampling strategy can be computationally expensive and inefficient in environments with narrow passages, as it may necessitate a large number of samples to discover valid paths. For further details, kindly consult Table 1.
4.3.3 Comparison to Kuffner et al.’s work
Kuffner and colleagues (Kuffner and M LaValle, 2000) have introduced the RRT-connect algorithm, an enhanced variant of the rapidlyexploring random tree approach, which is particularly adept at finding pathways between an initial point psand a target point pgin constrained environments. The algorithm initializes two trees, Tsrooted at psand Tgrooted at pg, and iteratively expands these trees by randomly selecting points in the configuration space and extending towards them. Notably, RRT-connect demonstrates efficacy in promptly navigating through narrow passages by leveraging dual-sided exploration towards the central region, thus outperforming the traditional RRT approach. Despite its advantages, the RRT-connect algorithm exhibits inefficiency in detecting confined regions when compared to our proposed method. As illustrated in Figure 2, our method requires only 0.091 seconds, including 0.007 seconds for identifying narrow regions, to generate a path of 1298 length. In contrast, the RRT-connect algorithm lacks a specialized mechanism for locating narrow regions, resulting in increased time expenditure for detection and path search, which takes 0.314 seconds time and produces a path of 1448 length.
4.3.4 Comparison to Shu et al.’s work
They (Shu et al., 2019) presented the LGM-BRRT* approach, a locally guided multiple bi-RRT* method that refines solutions via an enhanced bridge-test and a search strategy grounded in local guidance. This method accelerates success rates and optimizes memory usage compared to bidirectional RRT* (Ge et al., 2021) while maintaining ease of implementation. Extensive evaluations across various scenarios have verified its success rates. Results indicate that LGM-BRRT* is particularly advantageous for path planning in environments characterized by clustered regions and narrow passages. In contrast to our proposed method, LGM-RRT* exhibits challenges in efficiently locating an initial solution within a clustered environment featuring narrow passages. Furthermore, the reliance on bridge-test to identify narrow regions can impede algorithmic convergence. For comprehensive details, please refer to Table 1.
4.4 Simulation experiments on the ROS platform
The limitations in equipment availability hindered our ability to apply the algorithm in marine environments characterized by narrow regions. Nonetheless, we validated the algorithm’s performance within a simulated narrow-region environment. This study carried out simulation experiments utilizing the Rviz visualization tool within the robot operating system (ROS). The initial step involved setting up a robot simulation environment in Gazebo, where the turtlebot model equipped with a 360-degree scanning sonar system was selected as the simulated robot. Notably, the robot’s motion was constrained by specific limits on its linear and angular velocities, defined as v ∈ (0,5 m/s] and ω ∈ (−0.15,0.15 rad/s], respectively.
In the Rviz visualization tool as shown in Figure 13a, the Gmapping algorithm was employed to construct the environment map. The starting point was set at coordinates (258, 42, 0), and the target point was defined at (256, 60, 0). The paths planned by the classic RRT-connect algorithm were displayed in black, and those generated by the proposed algorithm were shown in red. Figure 13b presents the path created using the classic RRT-connect algorithm as the planner, whereas Figure 13c illustrates the path produced by the proposed algorithm. The simulation results demonstrate that the proposed algorithm is notably more efficient in path planning, particularly in navigating narrow passages, producing shorter paths that allow the robot to reach its destination more quickly. These findings substantiate the proposed method’s potential for efficient application in real-world scenarios.
Figure 13
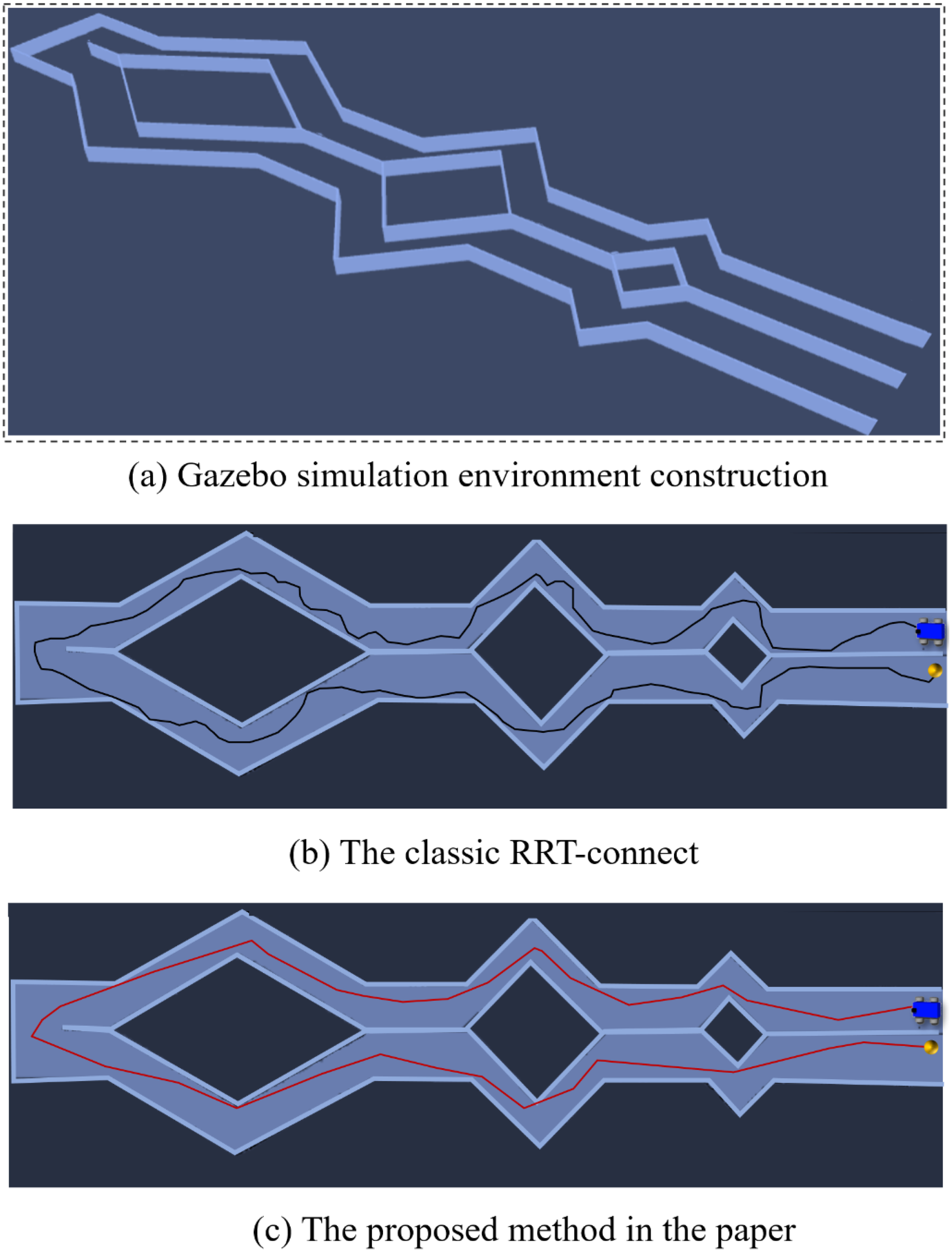
The path planning procedures for navigating narrow passages were evaluated within the robot operating system (ROS) framework shown in subfigure (a). Operating under constraints on the robot’s linear and angular velocities, the proposed method demonstrated superior performance shown in subfigure (c), achieving a significantly shorter path length of 612 and completing the task in just 84.81 seconds. In comparison, the classic RRT-Connect algorithm required 118.46 seconds to complete the same task and produced a notably longer path with a length of 706 shown in subfigure (b).
5 Conclusion
This paper tackles the issue of ASV path planning in unstructured ocean settings, with a particular emphasis on navigating through narrow waterways. To tackle these complexities, we introduced an innovative approach that combines progressive sampling and point cloud clustering to efficiently identify narrow passages within the configuration space . Our proposed method, called multiple RRT-connect, builds upon the traditional RRT-connect by growing multiple random trees based on the identified sampling points. This strategy enhances navigational precision and efficiency, allowing for the rapid identification of feasible paths between start and goal points. As the sample count increases, these random trees expand and interconnect to form a complete path, which is subsequently refined and optimized to produce significantly shorter trajectories. By conducting thorough simulations and comparing our approach to cutting-edge methods, we’ve showcased the outstanding performance of our algorithm. The results underscore its benefits in path construction success, computational speed, and overall optimization.
Future work. In our forthcoming research, we intend to comprehensively incorporate ASV kinematic constraints to improve both path feasibility and energy efficiency. Specifically, we plan to design an advanced controller capable of simulating the path-tracking process of real-world ASVs, thereby integrating motion planning with precise control in our next phase. In addition, we aim to embed dynamic ASV models to construct a more realistic framework that accurately reflects physical and kinematic limitations. Furthermore, the algorithm’s practicality will be enhanced by incorporating the inherent physical and hydrodynamic characteristics of ASVs into simulation studies, alongside refining path optimization to adhere to stringent maritime safety standards. We will also address the challenges posed by multi-target missions, dynamic obstacle management, and harsh oceanic conditions to thoroughly evaluate adaptability and robustness. Collision risks will be quantitatively assessed and balanced with efficiency objectives, while rigorous validation of prototypes in near-real or actual sea environments will underpin reliability and drive continual improvements in autonomous maritime applications.
Statements
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
WM: Funding acquisition, Methodology, Supervision, Writing – original draft, Writing – review & editing. RK: Data curation, Software, Visualization, Writing – original draft, Writing – review & editing. YP: Software, Validation, Writing – original draft, Writing – review & editing. XS: Validation, Visualization, Writing – original draft, Writing – review & editing. YG: Funding acquisition, Investigation, Writing – original draft, Writing – review & editing.
Funding
The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported in part by the Natural Science Foundation of Shandong Province (ZR2023QF122), in part by the National Natural Science Foundation of China (62302124), and in part by the Youth Teacher Development Foundation of Harbin Institute of Technology (IDGA10002143).
Acknowledgments
The authors would like to thank the reviewers for their valuable suggestions.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1
Altan Y. C. Otay E. N. (2017). Maritime traffic analysis of the strait of istanbul based on ais data. J. Navigation70, 1367–1382. doi: 10.1017/S0373463317000431
2
Bhattacharya P. Gavrilova M. L. (2008). Roadmap-based path planning-using the voronoi diagram for a clearance-based shortest path. IEEE Robotics Automation Magazine15, 58–66. doi: 10.1109/MRA.2008.921540
3
Boor V Overmars M. H. Stappen A.F. (1999). “The gaussian sampling strategy for probabilistic roadmap planners,” in Proceedings 1999 IEEE international conference on robotics and automation (Cat. No. 99CH36288C), vol. 2. (Detroit, MI, USA: IEEE), 1018–1023.
4
Cao X. Sun H. Jan G. E (2018). Multi-auv cooperative target search and tracking in unknown underwater environment. Ocean Eng.150, 1–11. doi: 10.1016/j.oceaneng.2017.12.037
5
Dalibard S Laumond J.P. (2009). “Control of probabilistic diffusion in motion planning,” in Algorithmic foundation of robotics VIII: selected contributions of the eight international workshop on the algorithmic foundations of robotics (Berlin: Springer), 467–481.
6
Fraga T. M. Fonseca C Coelho I. Freire J. Carvalho P Teixeira A et al . (2015). “Research in maritime archaeology in Portugal: A view of the past and present,” in Shipwrecks around the world: revelations of the past (Delta Book World, New Delhi), 450–485.
7
Ge Q. Li A. Li S. Du H. Huang X. Niu C. (2021). Improved bidirectional rrt* path planning method for smart vehicle. Math. Problems Eng.2021, 6669728. doi: 10.1155/2021/6669728
8
Guo P. Sun C. Li Q. (2023). “Obstacle avoidance path planning in unstructured environment with narrow passages,” in IEEE transactions on intelligent vehicles (Beijing China: IEEE).
9
Hsu D. Jiang T. Reif J. Sun Z. (2003). “The bridge test for sampling narrow passages with probabilistic roadmap planners,” in 2003 IEEE international conference on robotics and automation (cat. no. 03CH37422) (Taipei, Taiwan: IEEE), 4420–4426.
10
Jang D.-u. Joo-sung K. (2022). Development of ship route-planning algorithm based on rapidlyexploring random tree (rrt*) using designated space. J. Marine Sci. Eng.10, 1800–1815. doi: 10.3390/jmse10121800
11
Kalagnanam J. R. Diwekar U. M. (1997). An efficient sampling technique for off-line quality control. Technometrics39, 308–319. doi: 10.1080/00401706.1997.10485122
12
Kavraki L. Latombe J.-C. (1994). “Randomized preprocessing of configuration for fast path planning,” in Proceedings of the 1994 IEEE international conference on robotics and automation (San Diego, CA, USA: IEEE), 2138–2145.
13
Kuffner J. J. M LaValle S. (2000). “Rrt-connect: An efficient approach to single-query path planning,” in Proceedings 2000 ICRA. Millennium conference. IEEE international conference on robotics and automation. Symposia proceedings (Cat. No. 00CH37065), vol. 2. (San Francisco, CA, USA: IEEE), 995–1001.
14
LaValle S. (1998). “Rapidly-exploring random trees: A new tool for path planning,” in Research Report (Iowa State: Iowa State University), 9811.
15
Li D. Li Q. Cheng N. Song J. (2012). “Extended rrt-based path planning for flying robots in complex 3d environments with narrow passages,” in 2012 IEEE international conference on automation science and engineering (CASE) (Seoul, Korea (South): IEEE), 1173–1178.
16
Li J. Yang C. (2020). “Auv path planning based on improved rrt and bezier curve optimization,” in 2020 IEEE international conference on mechatronics and automation (ICMA) (Beijing, China: IEEE), 1359–1364.
17
Lien J.-M. (2008). “Hybrid motion planning using minkowski sums,” in Robotics: science and systems (Orlando USA: George Mason University).
18
Lien J.-M. Thomas S. L. Amato N. M. (2003). “A general framework for sampling on the medial axis of the free space,” in 2003 IEEE international conference on robotics and automation (Cat. No. 03CH37422), vol. 3. (Taipei, Taiwan: IEEE), 4439–4444.
19
Lin Y.-T. (2006). “The gaussian prm sampling for dynamic configuration spaces,” in 2006 9th international conference on control, automation, robotics and vision (Singapore: IEEE), 1–5.
20
McCarthy M. (2006). “Maritime archaeology in australasia: reviews and overviews,” in Maritime archaeology: Australian approaches (Adelaide, South Australia, Australia: Springer), 1–11.
21
Meng W. Gong Y Xu F. Tao P. Bo P. Xin S. (2023). Efficient path planning for auvs in unmapped marine environments using a hybrid local–global strategy. Ocean Eng.288, 116227. doi: 10.1016/j.oceaneng.2023.116227
22
Miyombo M. E. Liu Y.-k. Angu N. Y. A. Ayodeji A. (2022). Minimum dose path planning during reactor coolant system maintenance with corrosion product activity. Nuclear Eng. Design396, 111897. doi: 10.2139/ssrn.4020155
23
Noreen I. Khan A. Habib Z. (2016). A comparison of rrt, rrt* and rrt*-smart path planning algorithms. Int. J. Comput. Sci. Network Secur. (IJCSNS)16, 20.
24
Peters K. (2017). “Tracking (im) mobilities at sea: Ships, boats and surveillance strategies,” in The mobilities of ships (Detroit: Routledge), 88–105.
25
Rodriguez S. Tang X. Lien J.-M. Amato N. M. (2006). “An obstacle-based rapidlyexploring random tree,” in Proceedings 2006 IEEE international conference on robotics and automation, 2006. ICRA 2006. (Orlando, FL, USA: IEEE), 895–900.
26
Ruan S. Poblete K. L. Wu H. Ma Q. Chirikjian G. S. (2022). Efficient path planning in narrow passages for robots with ellipsoidal components. IEEE Trans. Robotics39, 110–127. doi: 10.1109/TRO.2022.3187818
27
Shu X. Ni F. Zhou Z. Liu Y. Liu H. Zou T. (2019). “Locally guided multiple bi-rrt for fast path planning in narrow passages,” in 2019 IEEE international conference on robotics and biomimetics (ROBIO) (Dali, China: IEEE), 2085–2091.
28
Singh Y. Sharma S. Sutton R. Hatton D. Khan A. (2018). A constrained a* approach towards optimal path planning for an unmanned surface vehicle in a maritime environment containing dynamic obstacles and ocean currents. Ocean Eng.169, 187–201. doi: 10.1016/j.oceaneng.2018.09.016
29
Sloyan B. M. Wanninkhof R. Kramp M. Johnson G. C. Talley L. D. Tanhua T. et al . (2019). The global ocean ship-based hydrographic investigations program (go-ship): a platform for integrated multidisciplinary ocean science. Front. Marine Sci.6, 445. doi: 10.3389/fmars.2019.00445
30
Subramani D. N. Jr P. J.H. Lermusiaux P. F. J. (2017). Energy-optimal path planning in the coastal ocean. J. Geophysical Research: Oceans122, 3981–4003. doi: 10.1002/2016JC012231
31
Sun Z. Hsu D. Jiang T. Kurniawati H. Reif J. H. (2005). Narrow passage sampling for probabilistic roadmap planning. IEEE Trans. Robotics21, 1105–1115. doi: 10.1109/TRO.2005.853485
32
Szpak Z. L. Tapamo J. R. (2011). Maritime surveillance: Tracking ships inside a dynamic background using a fast level-set. Expert Syst. Appl.38, 6669–6680. doi: 10.1016/j.eswa.2010.11.068
33
Tu H. Deng Y. Li Q. Song M. Zheng X. (2024). Improved rrt global path planning algorithm based on bridge test. Robotics Autonomous Syst.171, 104570. doi: 10.1016/j.robot.2023.104570
34
Wang J. Xiao Y. Li T. Chen C. L. P. (2020). A survey of technologies for unmanned merchant ships. IEEE Access8, 224461–224486. doi: 10.1109/Access.6287639
35
Wibowo S. Deng H. (2012). Intelligent decision support for effectively evaluating and selecting ships under uncertainty in marine transportation. Expert Syst. Appl.39, 6911–6920. doi: 10.1016/j.eswa.2012.01.003
36
Xiao G. Wang Y. Wu R. Li J. Cai Z. (2024). Sustainable maritime transport: A review of intelligent shipping technology and green port construction applications. J. Marine Sci. Eng.12, 1728. doi: 10.3390/jmse12101728
37
Yoo S.-H. Kwon S.-J. (2012). Non-market benefits of building the large oceanographic research ship. Ocean Polar Res.34, 175–183. doi: 10.4217/OPR.2012.34.2.175
38
Yu L. Wei Z. Wang Z. Hu Y. Wang H. (2017). “Path optimization of auv based on smooth-rrt algorithm,” in 2017 IEEE international conference on mechatronics and automation (ICMA) (Takamatsu, Japan: IEEE), 1498–1502
39
Yu Y. Zheng H. Xu W. (2024). “Learning and sampling-based informative path planning for auvs in ocean current fields,” in IEEE transactions on systems, man, and cybernetics: systems (Memphis Amherst USA: IEEE).
40
Zhang D. Chu X. Liu C. He Z. Zhang P. Wu W. (2024). A review on motion prediction for intelligent ship navigation. J. Marine Sci. Eng.12, 107. doi: 10.3390/jmse12010107
41
Zhong J. Su J. (2011). “Narrow passages identification for probabilistic roadmap method,” in Proceedings of the 30th Chinese control conference (Yantai, China: IEEE), 3908–3912.
42
Zhou L. Ding J. Fan X. (2023). “An adaptive rrt algorithm based on narrow passage recognition for assembly path planning,” in 2023 IEEE international conference on industrial engineering and engineering management (IEEM) (Singapore, Singapore: IEEE), 0203–0208.
Summary
Keywords
autonomous surface vehicles, unstructured marine environments, constricted waterways, rapidly exploring random tree, point cloud clustering
Citation
Meng W, Ku R, Pu Y, Shi X and Gong Y (2025) Efficient collision-avoidance navigation strategy for autonomous surface vehicles in unstructured and constricted marine environments. Front. Mar. Sci. 12:1555262. doi: 10.3389/fmars.2025.1555262
Received
04 January 2025
Accepted
09 April 2025
Published
12 May 2025
Volume
12 - 2025
Edited by
Agnieszka Lazarowska, Gdynia Maritime University, Poland
Reviewed by
Zhiping Xu, Jimei University, China
Botao Zhang, Hangzhou Dianzi University, China
Józef Lisowski, Gdynia Maritime University, Poland
Updates
Copyright
© 2025 Meng, Ku, Pu, Shi and Gong.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wenlong Meng, wenlongmenghit@163.com
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.