TSeq-GAN: a generalized and robust blind source separation framework for AIS signals of unmanned surface vehicles

Autonomous Identification System (AIS) enables unmanned surface vehicles (USVs) to sense their surrounding environment, enhancing safe navigation. However, AIS signals may collide in congested waterways, degrading sensing performance. Conventional statistical blind source separation (BSS) algorithms struggle to isolate signals lacking strictly non-Gaussian features in complex communication environments. Due to Gaussian filtering in AIS signal modulation, essential higher-order statistics are lost, often leading to low accuracy and instability with conventional methods. To this end, this paper develops a time sequence generative adversarial network (TSeq-GAN)-enabled BSS method. The proposed approach replaces an ordered training set with a randomly constructed AIS mixed signal matrix and incorporates a spatialtemporal feature extraction network paired with a generative adversarial framework to capture multidimensional signal characteristics and reconstruct the original signals. Furthermore, a global multi-objective optimization strategy is applied to the loss function to balance error minimization and signal quality. Under a 5 dB signal-to-noise ratio (SNR) and varying numbers of mixed signals, experimental results show that the method reduces mean squared error (MSE) by at least 9.84%, improves signal-to-interference ratio (SIR) by 10.03%, and increases continuous mutual information (cMI) by at least 4.11% compared to existing techniques, validating its robust and accurate extraction of AIS signals.

1 Introduction

Unmanned Surface Vehicles (USVs) are a quintessential example of intelligent vessels. Due to their compact size, autonomous operation, high intelligence, and strong maneuverability, USVs have become critical in marine exploration and environmental monitoring (Yan et al., 2010, Wang et al., 2024a). They achieve functions such as pattern recognition, autonomous navigation, and automatic docking/undocking by integrating multi-source sensor fusion, multimodal target detection and recognition, and real-time path planning (Wang et al., 2025). However, these capabilities impose stringent demands on navigation efficiency, decision-making, and obstacle avoidance. Current USV surface intelligent identification systems include radar, ultrasonic sensors, optical cameras, and AIS (Cheng et al., 2023, Xiao et al., 2025). Radar and ultrasonic sensors are prone to false or missed detections under severe weather conditions such as strong waves or high winds; they are expensive, difficult to maintain, and ultrasonic sensors are limited to short-range detection, which hinders target discrimination and local detail capture in complex or densely populated environments (Ma et al., 2022, Wang et al., 2024b). Optical cameras similarly suffer under adverse weather and have limited fields of view, making them vulnerable to occlusion and localized interference (Zhu et al., 2023). In contrast, the Automatic Identification System (AIS) is a novel navigational aid and one of the most critical sensing devices on vessels. Utilizing Very High Frequency (VHF) radio communication, AIS offers stable anti-interference performance, low power consumption, and long-range coverage (Sun et al., 2024) (Liu et al., 2022b), thus providing substantial value for comprehensive environmental perception (Yang et al., 2019). W. et al. addressed the requirement for realtime vessel positioning and dynamic monitoring during navigation by fusing AIS data with tracking radar data (Kazimierski and Stateczny, 2013). Mohamed et al. proposed the fuzzy function dependency (FFD) method to mitigate uncertainties and data inconsistencies in the fusion of AIS and over-the-horizon (OTH) radar data (Mohamed Mostafa et al., 2019). Larson et al. employed autonomous navigation algorithms and obstacle-avoidance strategies to enable USVs to navigate complex environments autonomously (Larson et al., 2006). However, owing to the self-organizing time-division multiple-access (SO-TDMA) scheme used by AIS and the ever-increasing number of vessels and corresponding communication demands, slot collisions among AIS receivers within the same time slot have become increasingly prevalent in hightraffic-density regions. Consequently, the probability of detecting AIS signals in these areas is substantially reduced, markedly elevating collision risk and posing a serious threat to navigational safety.Consequently, there is a growing demand for efficient and accurate separation of original signals from mixed AIS signals to enhance USV safety and operational efficiency (Yu et al., 2021) (Mei et al., 2024).

BSS refers to the extraction of source signals from mixed signals without any prior knowledge of the mixing process, and it has been applied in various fields, including speech signal separation (Khan et al., 2020). Aapo et al. proposed a fast ICA algorithm (FastICA) based on fixed-point iteration, which efficiently achieves blind source separation by maximizing the non-Gaussianity of the signals, thereby significantly accelerating both computation and convergence compared to conventional ICA algorithms (Hyvärinen and Oja, 1997). E et al. introduced Tukey’s M-estimator to overcome the tendency of the standard FastICA algorithm to become trapped in local optima when separating complex-valued signals, thus enhancing its stability and robustness in complex-valued scenarios (Jianwei et al., 2021). Cardoso et al. presented the Joint Approximate Diagonalization of Eigen-matrices (JADE) algorithm, which performs blind source separation by jointly diagonalizing multiple covariance or higher-order statistic matrices, this approach addresses the limitations of traditional BSS methods when source signals exhibit statistical correlation, offering a more robust separation framework (Cardoso, 1998). Traditional blind source separation algorithms, such as FastICA and JADE, rely on nonlinear functions to amplify the non-Gaussian characteristics of the mixed signals to recover the original sources, under the prerequisite that the source signals are non-Gaussian and the mixtures approximate Gaussian distributions (Rieta et al., 2004) (Hyvärinen and Oja, 1997).However, AIS signals undergo Gaussian Minimum Shift Keying (GMSK) modulation, where the baseband signal is passed through a Gaussian low-pass filter (Meng et al., 2018). The smoothing effect of the filter alters the original statistical properties of the source signal, leading to a partial loss of its non-Gaussian features (Lin et al., 2006). Consequently, traditional Independent Component Analysis (ICA) algorithms face inherent limitations when processing AIS signals compared to other types of signals. In contrast, neural networks can partially overcome the absence of these prior conditions in AIS mixed signals and can automatically adjust model parameters across different noise environments without the need for additional denoising networks, thereby enhancing the suppression of complex noise interference (Galvan, 1996). Kumar et al. introduced the use of capsule networks (CapsNet) to separate speech sources in underdetermined convolutive mixtures (Kumar and Jayanthi, 2020). Xu et al. proposed a novel two-step approach for underdetermined blind source separation (UBSS): first, the law of large numbers is employed to estimate both the number of sources and the mixing matrix; second, the separated signals are recovered via a minimum angular separation rule (Xu et al., 2020). Li et al. presented a single-source detection criterion based on vector transformations of the mixture signals, using an improved density-peak clustering algorithm to adaptively estimate initial cluster centers across different application scenarios (Li et al., 2020). Xie et al. developed an underdetermined blind source separation method for speech mixtures grounded in compressed sensing, thereby addressing the signal reconstruction challenge (Xie et al., 2021). Niknazar et al. proposed a blind source separation technique for nonlinear and chaotic signals by leveraging dynamic similarity measures combined with a relaxed non-Gaussianity assumption, successfully handling the separation of Gaussian components (Niknazar et al., 2021). Li et al. further introduced a D-CNN model that effectively mitigates structural redundancy, functional ambiguity, and amplitude uncertainty in underwater acoustic source separation under complex environmental conditions.In contrast to other signal modalities such as audio and speech, AIS signals possess an intermittent framing structure (Li et al., 2024). By integrating dedicated temporal and spatial feature-extraction modules, the network can simultaneously capture local spatial patterns and long-range temporal dependencies, thereby aligning more naturally with the characteristics of AIS training sequences and data frames (Shao et al., 2020, Gu et al., 2023, Jiang et al., 2024). Considering that AIS signals are typically transmitted in marine environments and are severely affected by multipath effects, noise interference, and potential multi-channel interference, the introduction of GAN networks can further optimize the statistical properties of the separated signals (Sun et al., 2022, Liu et al., 2022a).

Therefore, to address the issue of low AIS signal separation accuracy in USVs operating in complex waters, this paper proposes a TSeq-GAN-based BSS algorithm. By accurately separating AIS source signals, the algorithm enhances the recognition and perception capabilities of USVs in complex environments, thereby improving their autonomous navigation. The main contributions of this paper are as follows:

1. To address the susceptibility of AIS signals to multipath propagation, shadow fading, and waveinduced interference in maritime environments, the proposed algorithm integrates a parallel CNN-LSTM architecture into the GAN-based generative-adversarial framework, enabling effective filtering of localized noise bursts and sustained suppression of short-term disturbances.

2. The proposed algorithm constructs a randomized AIS signal dataset by substituting conventionally ordered training corpora with data streams generated using varied pseudo-random seeds, diverse source signals, and multiple sequence lengths. This strategy effectively mitigates mode collapse and reduces both dictionary bias and overfitting.

3. The proposed algorithm is grounded in the principle of multi-objective optimization, incorporating mean squared error loss, interference suppression loss, and statistical correlation loss to enable the network to adaptively satisfy multidimensional constraints, thereby balancing the requirements of multiple task objectives.

4. Under low SNR conditions, we conducted simulations to separate random signals with varying numbers of mixtures, validating the effectiveness, robustness, and generalizability of our method. Our approach outperforms other BSS algorithms by at least 9.841%.

2 The proposed method

2.1 Brief introduction of BSS model

The traditional model for linear mixing and separation of signals is that the source signals $S={[s_1,s_2,\dots ,s_m]}^{\top }$ and noise $N={[n_1,n_2,\dots ,n_m]}^{\top }$ are input into the channel. In this case, the noise is predominantly additive white noise, and the effect of the channel on the mixed signal is abstracted as the matrix A. Thus, the instantaneous mixing model is X = AS + N (in this paper, the noise signal is considered part of the channel’s influence, which is incorporated into A), where X represents the mixed signal observed by the receiver from M sources. Therefore, by estimating the channel matrix, i.e., the separation matrix W, the separation of the mixed signal can be achieved. After passing through the separation matrix, the instantaneous mixing model becomes $Y={[y_1,y_2,\dots ,y_m]}^{\top }=WX=WAS$, where W = A^⊤, thus enabling the separation of the mixed signal (Cardoso, 1999).

Traditional linear mixing models are suitable for open water environments with high signal-to-noise ratios and low interference. However, in complex maritime environments, signal propagation for USVs is affected by various nonlinear factors, such as multipath effects, Doppler shifts, sea waves, weather changes, and electromagnetic interference between vessels. Therefore, in intelligent USV navigation scenarios, blind source separation often involves nonlinear mixing problems. The source continuous signals S(t) = [s₁ (t),s₂ (t),…,s_n(t)] are mixed through a nonlinear system and arrive at the receiver. The resulting received mixed continuous signals are denoted as X(t) = [x₁ (t),x₂ (t),…,x_m(t)], and the nonlinear mixing model can be expressed as Equation (1):

$\begin{array}{ll}\{\begin{array}{c}X(t)=f(S(t))\\ \forall i\ne j,I(s_i(t);s_j(t))=0\end{array}& (1)\end{array}$

where S(t) represents the vector form of n source signals, X(t) denotes the m-dimensional mixed signals, f() is a nonlinear vector function indicating that each observed signal x_i(t) is the result of a nonlinear transformation applied to all source signals, and I() represents the mutual information among the signals.

2.2 TSeq-GAN structure design and analysis

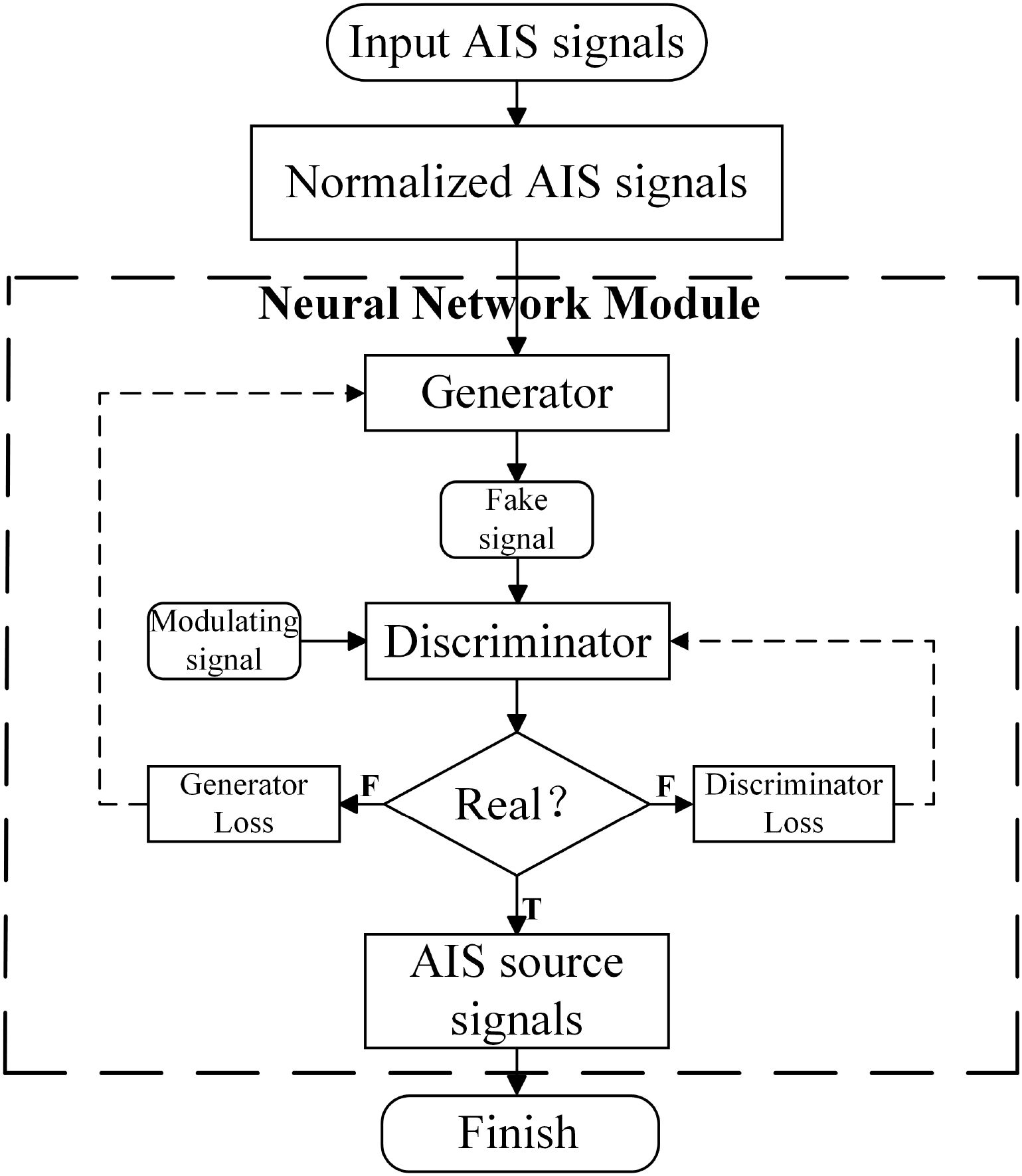
This paper addresses the limitations of conventional BSS algorithms in processing nonlinear mixing models, including restrictive assumptions on nonlinear mixing, insufficient handling of correlations and dynamic variations among source signals, and high sensitivity to noise and interference. To overcome these issues, a TSeq-GAN network is proposed for the separation of mixed AIS signals under a nonlinear mixing model. The flowchart of the proposed BSS algorithm is presented in Figure 1. Upon receiving the raw AIS mixed signal with added noise, the signal is normalized to render it suitable for neural network input. The generator then combines the processed signal with random noise and attempts to generate a counterfeit signal resembling the true AIS source signal. Since AIS signals are modulated using GMSK, the GMSKmodulated signal is considered most similar to the source signal; hence, it is used as the real signal, which, together with the generator-produced counterfeit signal, is fed into the discriminator. The discriminator determines whether the generated signal is genuine or counterfeit. Through this adversarial process, the generator continuously refines its network parameters to produce signals that closely approximate the real source signals, while the discriminator simultaneously improves its ability to distinguish between genuine and counterfeit signals. When the discriminator can no longer differentiate between them, the source signal is effectively obtained (Goodfellow et al., 2020).

Figure 1

Figure 1. AIS signals blind source separation flow chart.

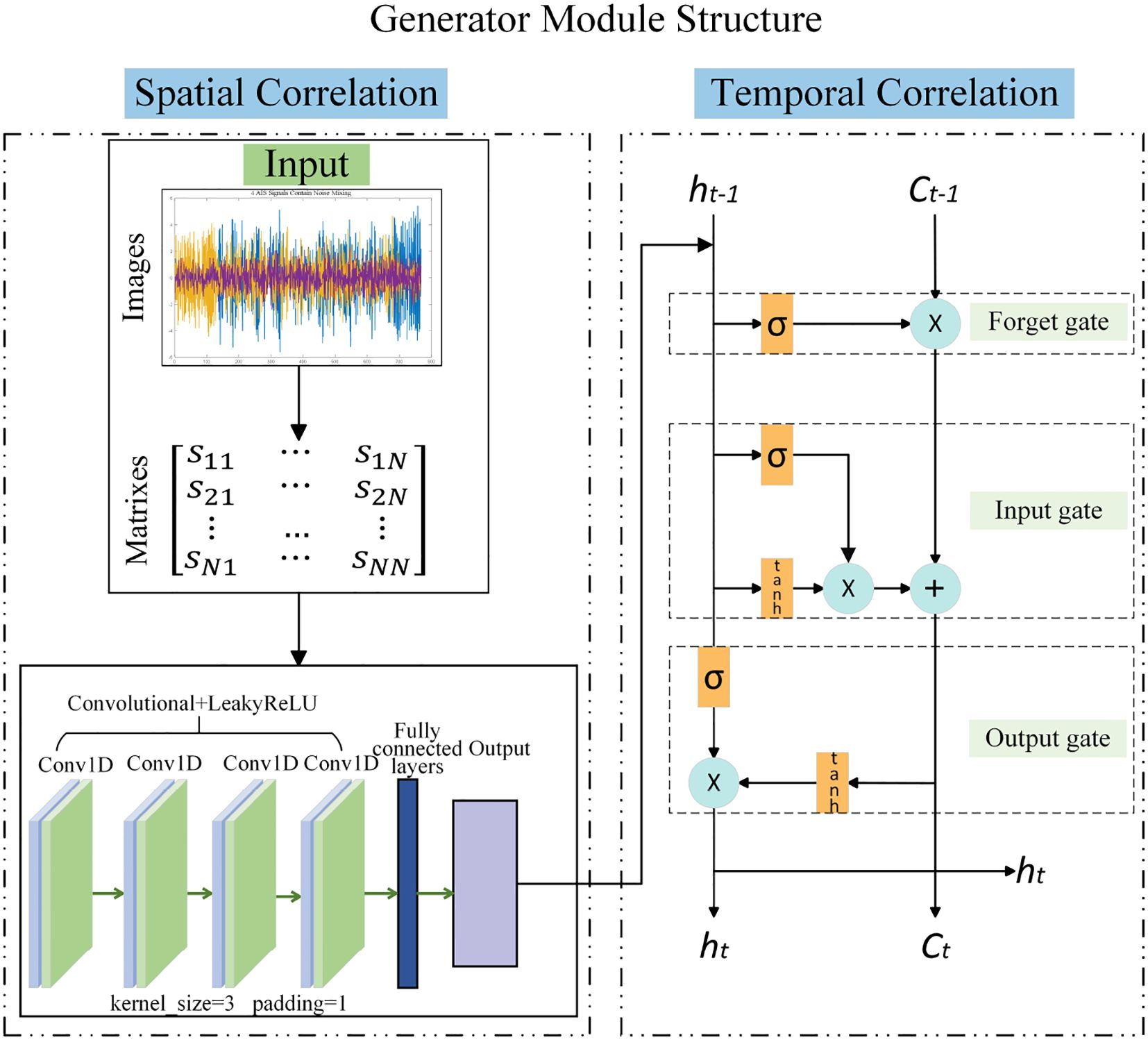
The traditional GAN generator consists of a multilayer perceptron (MLP) architecture with fully connected neurons, meaning each neuron is connected to all neurons in the preceding layer. This simple fully connected structure limits the MLP’s ability to effectively capture spatial structures or temporal dependencies in sequential data. Therefore, this work introduces CNN and LSTM networks into the generator of the conventional GAN framework to optimize the MLP architecture. The TSeq-GAN network structure is illustrated in Figure 2. This novel architecture can automatically capture multidimensional temporal and spatial features from the raw input during end-to-end training. These features not only contain information about the source signals but also implicitly represent noise characteristics, thereby naturally achieving a denoising effect during the separation process.In the TSeq-GAN network, the CNN extracts local features of the signal via convolutional kernels, learning features across multiple scales, which facilitates the recognition of AIS signals under low signal-to-noise ratio conditions. Furthermore, the translation invariance and local connectivity of convolution operations help suppress Gaussian and impulse noise. The LSTM, a neural network specialized for sequential data processing, captures temporal correlations between preceding and succeeding signal frames (Hochreiter and Schmidhuber, 1997), compensating for CNN’s lack of temporal memory. More importantly, in the presence of time-slot collisions, the LSTM enhances signal structure modeling and reduces the risk of pseudo-separation.The GAN framework approximates the distributional characteristics of the signals rather than merely fitting point-to-point mappings. Therefore, the proposed TSeq-GAN separation algorithm relies on the CNN front-end to filter out high-frequency noise, the LSTM to model contextual dependencies, and adversarial training in GAN to eliminate pseudo-noise outputs, thereby effectively countering noise interference.

Figure 2

Figure 2. TSeq-GAN structure diagram.

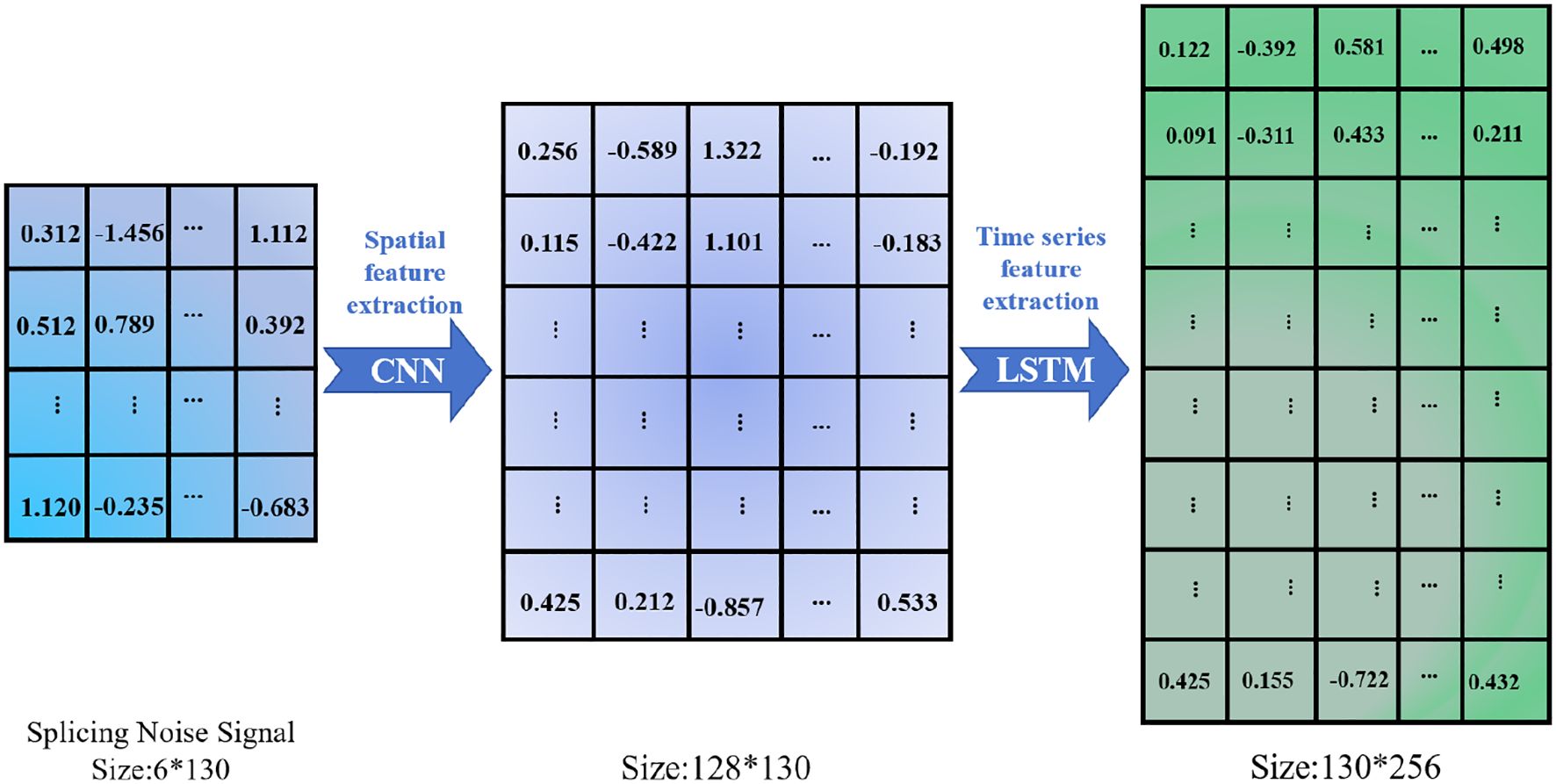
Firstly, the mixed AIS signals are transformed into a matrix format, which, on one hand, enhances the network’s ability to process complex, variable, and noisy signals, and on the other hand, fully leverages the CNN’s local feature extraction, the LSTM’s temporal sequence modeling, and the GAN’s adversarial training capabilities, particularly when dealing with highly nonlinear and multimodal signals. Figure 3 illustrates the internal structure of the generator. The generator receives as input two components: a random noise vector $Z(Z\in {ℝ}^{(d_s)})$ and a mixed signal matrix $S(S\in {ℝ}^{(N*N)})$.The matrix S is flattened into a vector $S\in {ℝ}^{(N*N)}$, which is then concatenated with the random noise vector S, resulting in the combined input, as shown in Equation (2):

Figure 3

Figure 3. Diagram of the internal structure of the generator.

$\begin{array}{ll}I=\left[\begin{array}{c}Z\\ S\end{array}\right](I\in {ℝ}^{(d_z+N^2)})& (2)\end{array}$

The combined input is fed into the generator, where random noise is introduced to enhance the diversity of the generated signals, while the mixed signal provides useful features to guide the generator’s learning. The combined signal I is expanded into a three-dimensional vector I_3D and input into the CNN layer. The CNN layer consists of four 1D convolutional neural network layers. The convolution operation in the first layer is given by the following Equation (3):

$\begin{array}{ll}{X}^{(l)}=Leaky\text{Re}LU(Conv1D^{(l)}({\mathbf{X}}^{(l-1)}))& (3)\end{array}$

the output size of the convolution operation is given by $X^{(l)}\in {ℝ}^{N\times C^{(l)}\times T^{(l)}}$, where $C^{(l)}$ represents the number of channels and $T^{(l)}$ is the temporal length, such that ${\mathbf{\text{X}}}_{CNN}\in {ℝ}^{N\times C^{128}\times T}$. In the first convolutional layer, the input channel is set to 1, the output channel is 16, and the kernel size is 1 ∗ 3 to extract basic low-level local temporal features. In the subsequent layers, the input channels are sequentially 16, 32, and 64, and the output channels are 32, 64, and 128, respectively. All convolutional layers use a kernel size of 1 ∗ 3. These three convolutional layers progressively increase the abstraction level of the features, capturing higher-level signal patterns. After each convolutional layer, LeakyReLU, as shown as Equation (4) is used as the activation function, with the following formula for LeakyReLU:

$\begin{array}{ll}Leaky\text{Re}LU=\{\begin{array}{ll}x\hfill & if x>0\hfill \\ \alpha x\hfill & if x\le 0\hfill \end{array}& (4)\end{array}$

this activation function introduces non-linearity while retaining negative value information. After feature extraction, to adapt to the LSTM layer, X_CNN is transposed to a dimension of N × T × 128, as shown in equation: $X_{(LSTM-in)}=X_{CNN}^{\top }\in {ℝ}^{N\times T\times 128}$.

The input X is fed into an LSTM layer with 256 hidden units. The LSTM layer is used to process the high-dimensional features extracted by the convolutional layers, leveraging its memory mechanism to capture long-term dependencies. The two stacked LSTM layers provide powerful temporal modeling capabilities. The temporal data processed by the LSTM is given by Equation (5):

$\begin{array}{ll}{h}_t,c_t=LSTM(X_{(LSTM-in)},h_{t-1},c_{t-1})& (5)\end{array}$

where $h_t\in {ℝ}^{256}$ represents the hidden state used to capture temporal features, c_t represents the current cell state, $h_{t-1}$ represents the hidden state from the previous time step, and $c_{t-1}$ represents the cell state from the previous time step. The output of the LSTM layer is the hidden state at the final time step, $h_{\mathit{\text{final}}}=h_T\in {ℝ}^{N\times 256}$,which represents the global feature of the entire sequence, where h_T is the hidden state at the last time step.

The output of the LSTM layer is passed through two fully connected layers. The first layer maps the high-dimensional features, while the second layer outputs signal data that matches the dimensionality of the real source signal. Each fully connected layer uses the Tanh activation function to constrain the output within the range of [−1,1], simulating the characteristics of the real signal. The Equation (6) for the Tanh function is:

$\begin{array}{ll}Tanh(x)=\frac{\exp (x)-\exp (-x)}{\exp (x)+\exp (-x)}& (6)\end{array}$

the Tanh activation function normalizes the amplitude of the generated signal, facilitating the comparison with the actual target signal for loss computation. The output h_final from the LSTM layer is mapped through the fully connected layer as Equation (7):

$\begin{array}{ll}{X}_{output}=Tanh(w_2·Leaky\text{Re}LU(w_1·h_{final}+b_1)+b_2)& (7)\end{array}$

where w₁ and b₁ are the weight matrix and bias term of the first fully connected layer, and w₂ and b₂ are the weight matrix and bias term of the second fully connected layer, The signal network feature extraction is shown in Figure 4.

Figure 4

Figure 4. AIS signal spatial feature and time feature extraction schematic diagram.

The discriminator adopts a straightforward architecture: real and generated signals are both input and then passed through three fully connected layers that progressively reduce the feature dimensionality. The first layer projects the input into a 256-dimensional feature space; the second layer further compresses it to 128 dimensions; and the third layer outputs a single probability, representing the confidence that the input is a genuine AIS signal.In this work, we use the AIS physical-layer Gaussian Minimum Shift Keying (GMSK) waveform as the “real” signal in the discriminator alongside the generator’s synthetic outputs. This design is justified by two factors. First, the AIS protocol uniformly employs 9.6 kbps GMSK modulation at the physical layer, so using the native GMSK waveform as the ground truth guarantees that our evaluation metrics align exactly with the operational AIS standard. Second, GMSK’s continuous-phase nature—characterized by a constant envelope, high spectral efficiency, and robustness to multipath—ensures that the baseband waveform faithfully preserves the signal’s critical time- and frequency-domain features. Consequently, our chosen metrics can accurately quantify deviations between the separated output and the standard modulated signal.For nonlinear representation, each hidden layer uses a LeakyReLU activation, and the final output layer applies a Sigmoid function to yield a [−1,1] probability for binary classification.

Finally, we employ Mean Squared Error (MSE), Signal-to-Interference Ratio (SIR), and continuous Mutual Information (cMI) as objective metrics to assess the quality of the separated signals.

2.3 The introduction of adaptive multidimensional constraint mechanism

The loss function of TSeq-GAN consists of both generator and discriminator losses. The generator loss comprises adversarial loss, mean squared error loss, interference suppression loss, and statistical correlation loss. The adversarial loss is the conventional GAN loss function that drives the adversarial game between the generator and the discriminator, thereby improving the quality of the generated model. The discriminator’s output, confined within the range [0,1], represents an evaluation of the “realness” of the input samples; hence, the cross-entropy loss function is employed.

To meet the demands of multi-source sensing in scenarios with high traffic density and suboptimal communication conditions for USVs, the generated samples must closely approximate the distribution of real samples. Therefore, this paper implements a multidimensional constraint mechanism within the generator by jointly introducing mean squared error loss, interference suppression loss, statistical correlation loss, and adversarial loss. The overall loss is then backpropagated to update the generator’s training parameters. The integration of these multidimensional constraints optimizes the generator’s performance from multiple perspectives, thereby enabling high-quality BSS of AIS signals.The network adversarial loss in this algorithm is defined as Equation (8):

$\begin{array}{ll}{L}_{adv}=-E_{z{P}_Z(z)}[\log D(G(z))]& (8)\end{array}$

Here, z denotes the noise distribution, G(z) represents the sample generated by the generator G upon receiving z, and D (G(z)) is the discriminator D’s output for G(z), which is a probability value ranging from 0 to 1. The generator aims to minimize the discriminator’s ability to distinguish the generated samples, driving the output of the generated samples as close to 1 as possible. The mean squared error (MSE) loss is defined as Equation (9):

$\begin{array}{ll}{L}_{MSE}=\frac{1}{N}{\displaystyle \sum _{i=1}^N}{(y_i-G(z))}^2& (9)\end{array}$

where y_irepresents the GMSK signal. The interference suppression loss is defined as Equation (10):

$\begin{array}{ll}{L}_{SIR}=10{\log }_{10}(\frac{\Vert y_i{\Vert }_2^2}{{\Vert y_i-G(z)\Vert }_2^2+ϵ})& (10)\end{array}$

where∥·∥₂ represents the Euclidean norm, and ϵ is set to a small constant to prevent division by zero. The statistical correlation loss is defined as Equation (11):

$\begin{array}{ll}{L}_{cMI}={\displaystyle \iint p(y_i,G(z))\log }\frac{p(y_i,G(z))}{p(y_i)p(G(z))}d{y}_{i}dG(z)& (11)\end{array}$

where, $p(y_i,G(z))$ is the joint probability density function of y_iand G(z), while p(y_i) and p(G(z)) are their respective marginal probability density functions. In the simulation program, the mutual-inforegression function from scikit-learn is used to estimate the mutual information between continuous variables. Different loss components in the loss function may have varying numerical scales; if one loss term has a significantly larger magnitude, it could lead the model to overly optimize that specific objective during convergence, thereby neglecting other objectives and causing convergence difficulties or instability during training. To meet the requirements of multi-objective tasks and ensure training stability, optimal weight parameters for each loss term have been determined through parameter tuning experiments. The overall loss calculation for the generator network is detailed as follows as Equation (12):

$\begin{array}{ll}{L}_G={\lambda }_1{L}_{MSE}+{\lambda }_2{L}_{SIR}+{\lambda }_3{L}_{cML}+{\lambda }_4{L}_{adv}.& (12)\end{array}$

Since the discriminator’s objective is to distinguish real samples from generated samples as accurately as possible, this study employs the cross-entropy loss function to compute the loss for real samples L_real as shown as equation (14), and generated samples L_fake as shown as equation (15), separately, and then sums them to obtain the total discriminator loss L_D as Equation (13):

$\begin{array}{ll}{L}_D=L_{real}+L_{fake}& (13)\end{array}$

$\begin{array}{ll}{L}_{real}=-E_{y{p}_{data}(y)}[\log D(y_i)]& (14)\end{array}$

$\begin{array}{ll}{L}_{fake}=-E_{z{p}_Z(z)}[\log (1-D(G(z)))].& (15)\end{array}$

3 Experimental

This section primarily compares the proposed algorithm with the FastICA (Jianwei et al., 2021), JADE (Deville et al., 2004), Successive Interference Cancellation (SIC) (Ristaniemi and Huovinen, 2006), Higher-order Statistics Algorithms (Lu et al., 2015), and AGAN network (Sun et al., 2022) through comparative experiments, as well as conducts ablation experiments with GAN, CNN-GAN, and CNNLSTM configurations. The experimental results demonstrate that the separation performance of the TSeq-GAN network employed in this paper is significantly superior.

3.1 Experimental detail

This algorithm was trained for 1000 epochs on a computer equipped with a 2.40 GHz Intel I5-9300H CPU, GTX 1650 GPU, and 8GB of RAM, requiring approximately 86.1667 minutes. During the initialization and preparation stages, the Adam optimizer was used to update the parameters of both the generator and the discriminator, with an initial learning rate set to 0.0002. The training loop consisted of multiple epochs, and within each epoch, both the discriminator and the generator were trained in batches of 128.

In the experiments, specific weight parameters were assigned to each component of the generator loss. The weight λ₁ for the MSE loss was set to 0.4 to ensure that the generator prioritizes the accuracy of signal generation, making the generated signal as similar as possible to the target signal. The weight λ₂ for the interference suppression loss was set to 0.01 to prevent the loss function from overemphasizing SIR, thereby avoiding the excessive optimization of SIR at the expense of other loss components. The weight λ₃ for the statistical correlation loss was set to 0.5, which helps the generated signal capture more signal structure and features rather than merely minimizing the MSE. Finally, the weight λ₄ for the adversarial loss was set to 0.05 to balance the training process, ensuring that the generator does not merely produce signals that satisfy the discriminator without being close to the actual source signals.

3.2 Establishment of the AIS signal simulation dataset

Because fixed datasets contain only a limited set of message formats, coding schemes, and channel conditions, models trained on them tend to overfit to these “seen” samples. Although the AIS message format and modulation are standardized, the VHF channel is subject to multidimensional variation—multipath fading, noise, interference, antenna orientation, etc.—that changes dynamically in both space and time. Consequently, a static dataset cannot fully represent the true transmission environment. Moreover, the GAN-based separation network proposed here is prone to mode collapse if the training data lack diversity; in contrast, a dataset with richer variability forces the generator to “cover” a wider distribution of real signals and reduces the risk of memorizing specific examples, yielding a more robust mapping.

To this end, our AIS signal corpus is generated via a stochastic process that introduces maximal diversity in message content, temporal structure, channel conditions, and noise statistics. Each signal instance begins with a binary payload produced by a pseudo-random number generator (PRNG), which is then encoded and modulated using Gaussian Minimum Shift Keying (GMSK). The modulated symbols are concatenated with a fixed control sequence to create distinct message payload structures. To emulate realistic transmission impairments, we inject additive white Gaussian noise (AWGN) at randomly selected SNR levels and simulate channel mixing via randomly generated noise matrices. As a result, the dataset exhibits inherent randomness at every generation and mixing stage, ensuring that each simulation run produces novel signal realizations that satisfy the prerequisites of blind source separation.To evaluate robustness, we benchmark the separation performance under a channel SNR of 5 dB. Furthermore, to assess the network’s behavior in dense maritime traffic scenarios, we conduct experiments with varying numbers of simultaneously mixed signals, thereby validating the algorithm’s ability to disentangle AIS streams under different vessel-density conditions.

The baseband signal, after undergoing HDLC bit stuffing, synchronization-sequence insertion with buffering, and NRZI encoding, is then passed through a Gaussian low-pass filter to impart Gaussian characteristics. The time-domain impulse response of the Gaussian low-pass filter as Equation (16):

$\begin{array}{ll}g(t)=\frac{1}{\sqrt{2\pi }\sigma }\exp (-\frac{t^2}{2{\sigma }^2})& (16)\end{array}$

where σ represents the standard deviation of the Gaussian function, which determines the extent of the pulse response’s spread. After passing through the Gaussian low-pass filter, the signal is modulated using Minimum Shift Keying (MSK) to generate the AIS signal. The time-domain impulse response of the Gaussian low-pass filter as Equation (17):

$\begin{array}{ll}s(t)=\cos (2\pi f_{c}t+\varphi (t))& (17)\end{array}$

where f_c is the carrier frequency and ϕ(t) is the instantaneous phase of the signal. The carrier frequency band for AIS signal modulation are 161.975MHz (international standard channel) and 162.025MHz (some countries have expanded their channels), and in this paper, the carrier frequency is set to 161.975MHz. Therefore, the GMSK signal can be represented as Equation (18):

$\begin{array}{ll}S(t)=\cos (2\pi f_{c}t+\pi h{\displaystyle {\int }_{-\infty }^t}b(\tau )h_g(\tau )d\tau )& (18)\end{array}$

where the modulation index h is used to characterize the modulation intensity of the signal, b(t) represents the baseband signal, and the pulse shaping function h_g(t) is used to filter the baseband signal, thereby limiting the signal bandwidth and controlling its signal characteristics.

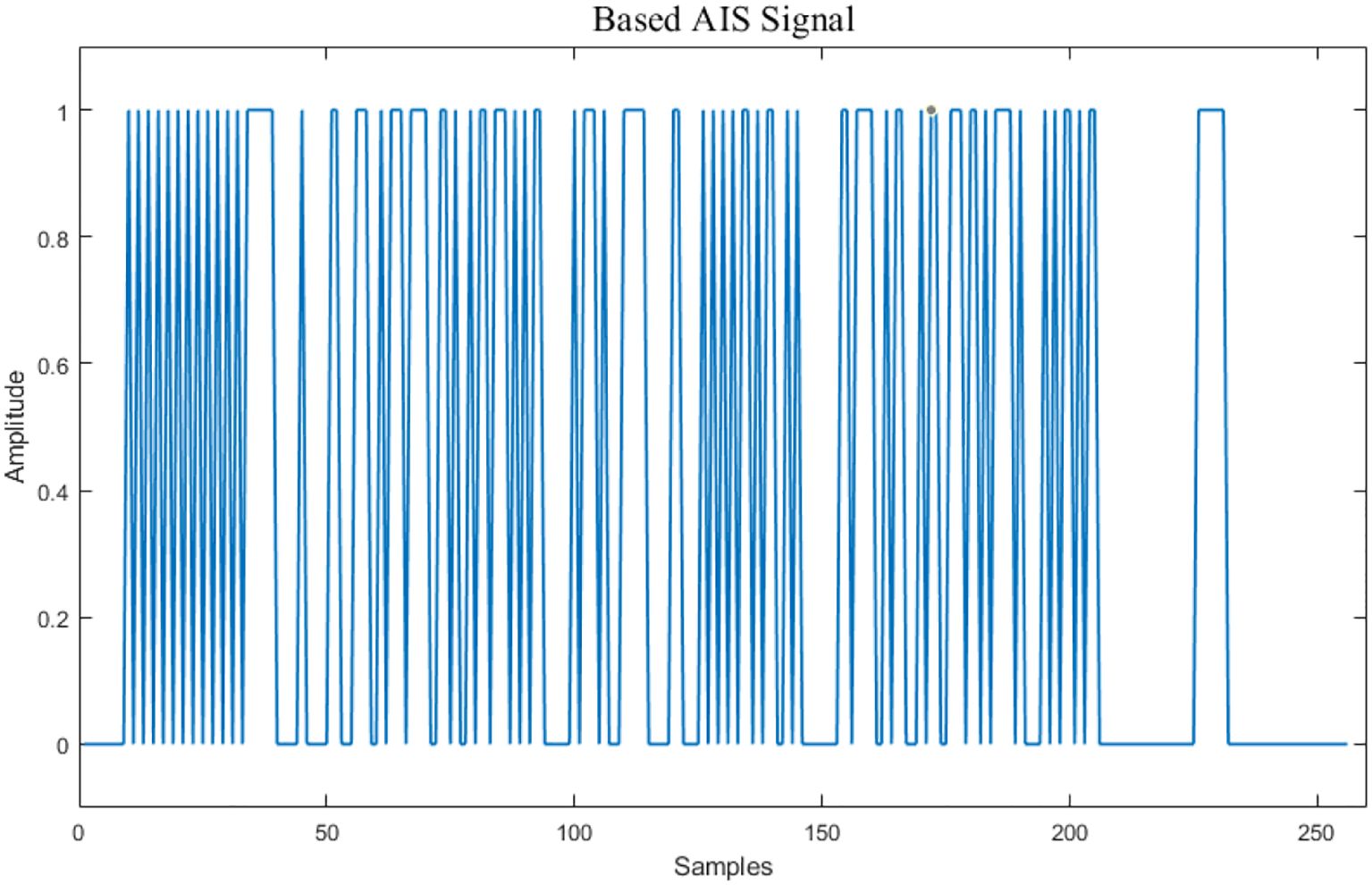
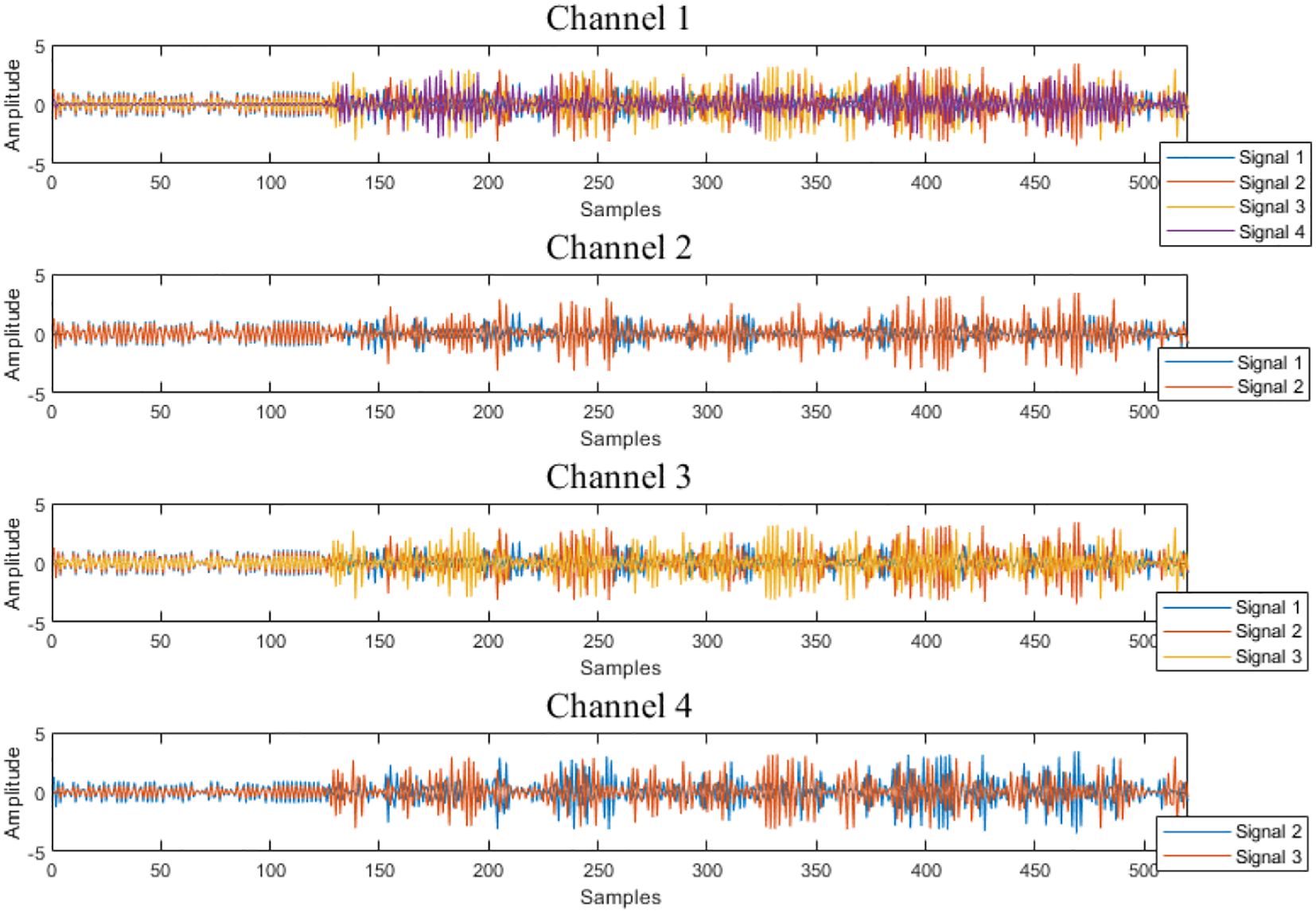
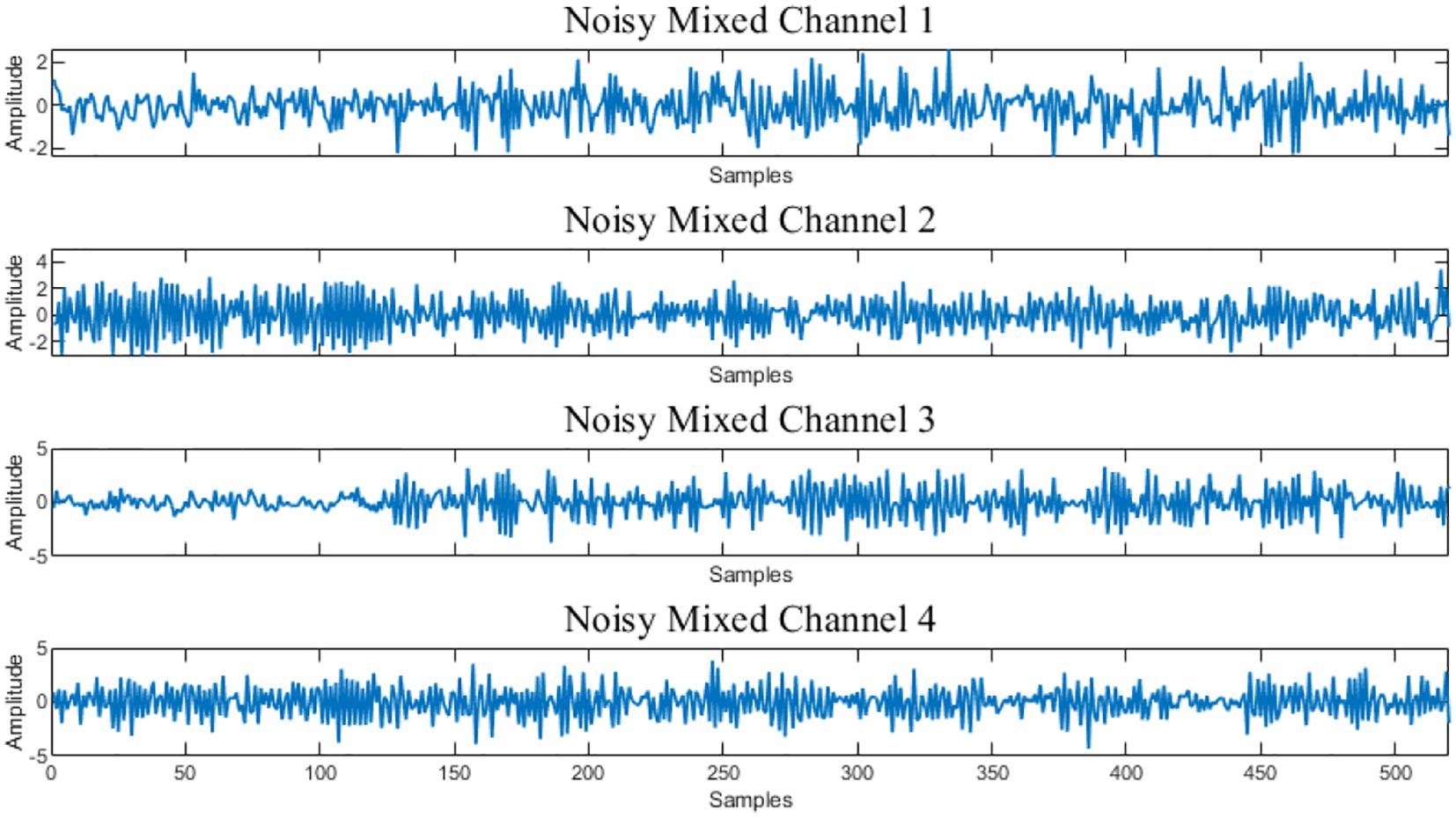
To simulate the unpredictable Gaussian white noise interference in real channel environments, the signal data is processed through a Gaussian noise network for noise addition. Figure 5 illustrates the baseband AIS signal, Figure 6 shows the GMSK-modulated signal, and Figure 7 the schematic illustration of the modulated AIS signal mixture (when there are four signal sources). Figure 8 depicts the schematic illustration of the AIS signal mixture after noise interference (four signals combined).

Figure 5

Figure 5. AIS baseband signal diagram.

Figure 6

Figure 6. GMSK modulation signal diagram.

Figure 7

Figure 7. Positive-definite mixture observation diagram for four signal sources.

Figure 8

Figure 8. Positive-definite mixture observation diagram with added noise for four signal sources.

3.3 Comparison of experimental analysis

The comparative experiments are conducted in scenarios where the channel conditions for USV navigation are poor, in order to verify the separation performance of different algorithms for source signals. In this study, the FastICA, JADE, SIC, Higher-order statistics algorithms, AGAN, and TSeq-GAN networks are sequentially applied to separate blind signals with 4, 6, 8, and 10 mixed source signals. Meanwhile, MSE, SIR, and cMI are used as evaluation metrics for the performance of the algorithms.

Figure 9A illustrates the changes in MSE for mixed signals separated by six different algorithms after mixing with varying numbers of source signals. Overall, the error between the mixed signals and the source signals increases as the number of source signals rises. The TSeq-GAN network proposed in this study shows MSE values of 0.1488, 0.1627, 0.1876, and 0.2321 for 4, 6, 8, and 10 mixed source signals, respectively, with a reduction of at least 35.5252% in MSE compared to the mixed signals. Figure 9B shows the changes in SIR for mixed signals separated by the six algorithms. Generally, the coherence of the separated signals decreases as the number of mixed signals increases. The TSeq-GAN network proposed in this study achieves coherence values of 9.3806, 8.0132, 7.8426, and 7.0178 for 4, 6, 8, and 10 mixed source signals, respectively, with an improvement of at least 1.2287 times in the signal coherence. Figure 9C illustrates the changes in cMI for mixed signals separated by the six algorithms. Overall, the similarity between the separated signals and the source signals decreases as the number of mixed signals increases. The TSeq-GAN network proposed in this study achieves cMI values of 2.1801, 1.6323, 1.4221, and 1.2073 for 4, 6, 8, and 10 mixed source signals, respectively, with a 3.5084-fold increase in continuous mutual information. Therefore, based on the robustness reflected by MSE, SIR, and cMI evaluation metrics, the TSeq-GAN network outperforms the other algorithms in signal separation.

Figure 9

Figure 9. Separation results of different algorithms. (A) Comparison results of MSE for different algorithms. (B) Comparison results of SIR for different algorithms. (C) Comparison results of cMI for different algorithms.

The experimental results show that the TSeq-GAN network continuously adjusts the model through endto-end joint optimization, rather than relying solely on analytical derivation or local optimization. Unlike other algorithms in the comparative experiments, the CNN and LSTM structures within the TSeq-GAN network effectively capture local temporal dependencies and long-term relationships in the random signals. The adversarial mechanism between the generator and discriminator allows for adaptive model adjustment. This network structure and joint optimization mechanism enable better extraction of features from random signal sequences, making the algorithm highly robust and generalized.

3.4 Ablation experiment analysis

In this section, we conduct an in-depth investigation into the influence of each module within the TSeqGAN network on the performance of the separation algorithm. The experiments are carried out under a SNR of 5 dB. By selectively removing different layer structures in the TSeq-GAN network, we verify that each module employed in this work contributes significantly to enhancing the network’s overall performance.

The experimental data are divided into three parts for verification. The first part involves a source signal mix of 3–4 signals, representing a scenario where the USV operates in a open and sparse water environment. The experimental results are shown in Table 1. The second part involves a source signal mix of 5–6 signals, representing a scenario where the USV operates in a low-traffic-density water environment. The experimental results are shown in Table 2. The third part involves a source signal mix of 7–8 signals, representing a scenario where the USV operates in a medium-traffic-density water environment. The experimental results are shown in Table 3. The fourth part involves a source signal mix of 9–10 signals, representing a scenario where the USV operates in a crowded water environment. The experimental results are shown in Table 4. MSE is used to measure the error between the generated signal and the true signal, SIR is used to assess the strength of the separated source signals, and cMI is used to evaluate the similarity between the extracted signals and the true signals.

Table 1

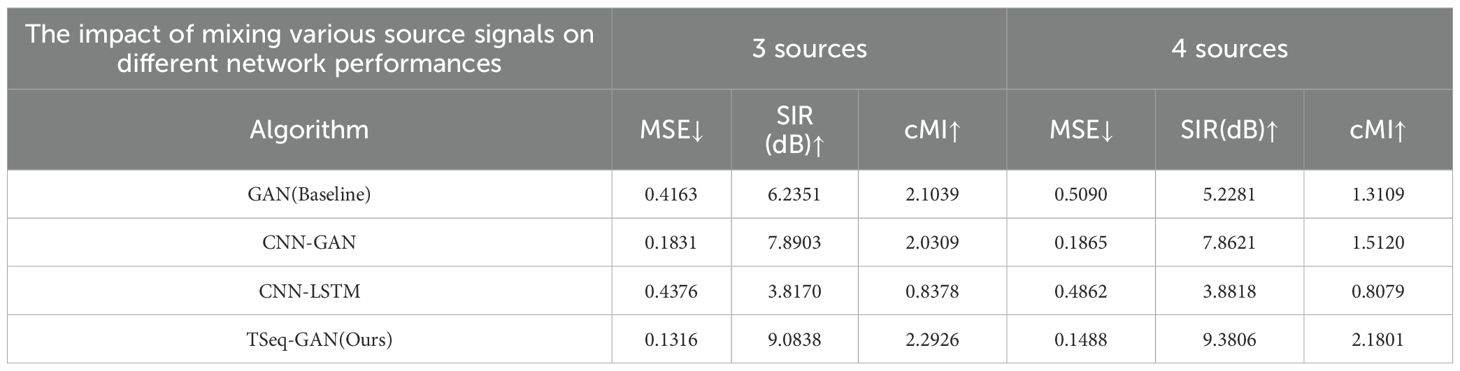
Table 1. The separation performance table of each network when the mixed number of source signals is 3 to 4.

Table 2

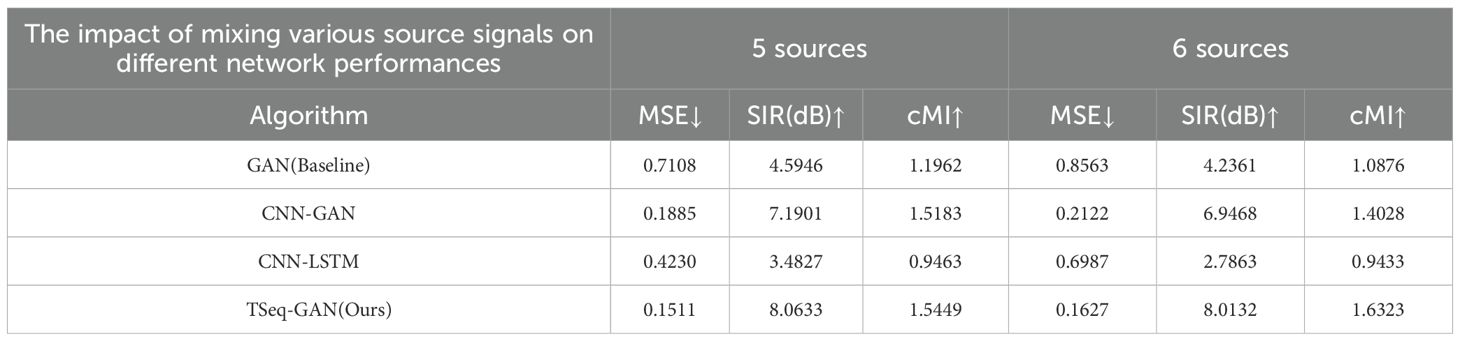
Table 2. The separation performance table of each network when the mixed number of source signals is 5 to 6.

Table 3

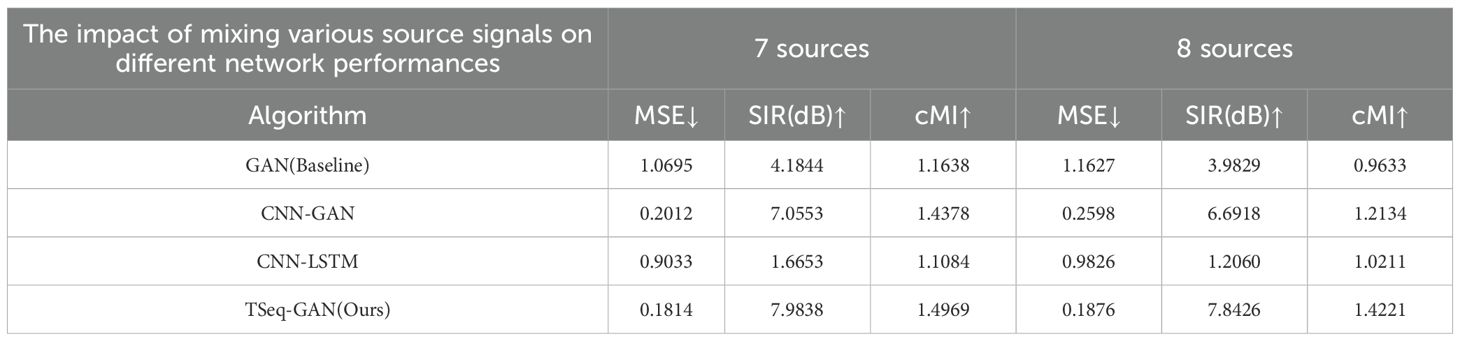
Table 3. The separation performance table of each network when the mixed number of source signals is 7 to 8.

Table 4

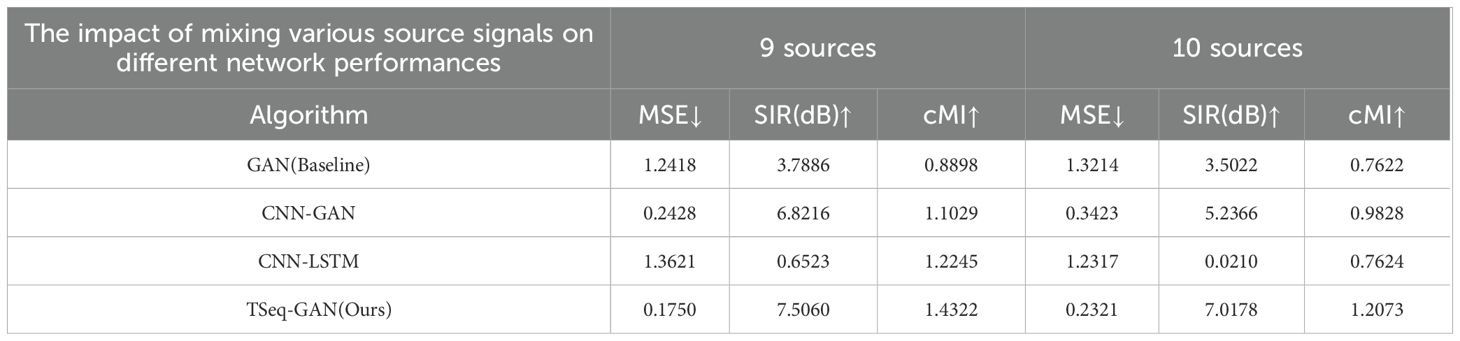
Table 4. The separation performance table of each network when the mixed number of source signals is 9 to 10.

In the open water environment, this network reduces MSE by at least 28.1267%, improves SIR by at least 15.1262%, and enhances cMI by at least 8.9196 compared to the other three networks. In lower traffic density water environments, the network reduces MSE by at least 19.8408%, increases SIR by at least 12.1445%, and improves cMI by at least 1.752% compared to the other three networks. In moderate traffic density water environments, the TSeq-GAN network outperforms the others by reducing MSE by at least 9.841%, increasing SIR by at least 13.1603%, and improving cMI by at least 4.1104%. Similarly, when the USV operates in crowded water areas, the network shows significant improvements in MSE, SIR, and cMI compared to the other three networks, with MSE decreasing by at least 27.9242%, SIR increasing by at least 10.0328%, and cMI improving by at least 16.962%.

As demonstrated by some of the experiments, the multi-level feature structure of the TSeq-GAN network proposed in this study enables the network to simultaneously handle both short-term and long-term dependencies of signals, while adaptively learning to generate separation results that align with the true distribution of the signals. This multi-level feature extraction and generation capability makes the model more powerful in BSS tasks compared to other independent network structures. Furthermore, through adversarial training, the TSeq-GAN network can effectively learn the separation characteristics of signals even in high-noise environments, complex interference, and nonlinear signal mixtures, ensuring that the model possesses good robustness and generalization capabilities. In contrast, other independent network structures are relatively weaker in handling complex noise and interference within the signals.

3.5 Analysis of network time complexity

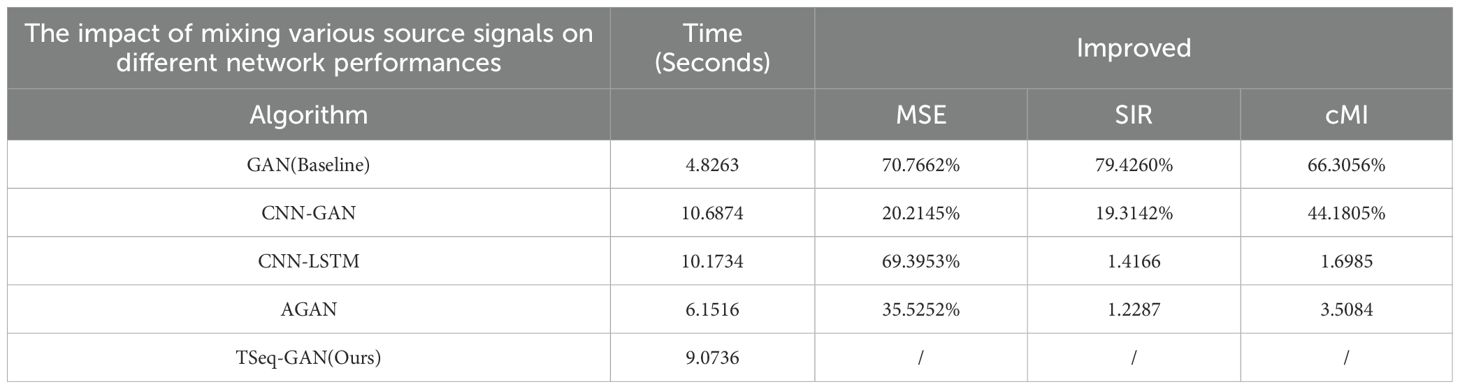
Due to the significant efficiency differences among various network architectures, this section presents a time performance comparison experiment between the TSeq-GAN network and other networks, such as the Attentional GAN, when the number of mixed sources is 4, as shown in Table 5.

Table 5

Table 5. Comparison of the timeliness of AIS blind signal separation by neural networks.

Although the TSeq-GAN network is not the most optimal in terms of computational efficiency, its signal extraction accuracy improves by up to 70.7662%, the quality of generated signals improves by up to 1.2287 times, and the similarity with the source signals increases by up to 3.5084 times. Considering the complex scenarios that USVs encounter during autonomous navigation, which are subject to varying degrees of noise, interference, and multipath effects, the accuracy of AIS signal separation directly influences the USV’s ability to assess the positions of surrounding vessels. Therefore, while timeliness is important for real-time signal processing, in BSS tasks in this scenario, if the accuracy of the algorithm cannot be guaranteed, the results of real-time processing will be meaningless.

3.6 Sensitivity analysis of TSeq-GAN parameters

Figures 10A, B illustrate the variations in MSE, SIR, and cMI, respectively, as the loss weights are adjusted. In this experiment, a global sensitivity analysis method is employed. Based on the correspondence between the magnitudes of the different loss functions and the overall performance, parameters λ₁ and λ₄ are adjusted simultaneously to observe changes in the overall model performance, while parameters λ₂ and λ₃ are adjusted concurrently to assess the overall performance variations. Consequently, a total of four sets of comparative experiments are conducted: in one scenario, with λ₁ and λ₄ held constant, one group increases λ₂ and λ₃ to 0.05 and 0.7, respectively, while another group increases them to 0.1 and 0.9; in another scenario, with λ₂ and λ₃ fixed, one group decreases λ₁ and λ₄ to 0.05 and 0.005, respectively, and another group increases them to 0.1 and 0.01, respectively.

Figure 10

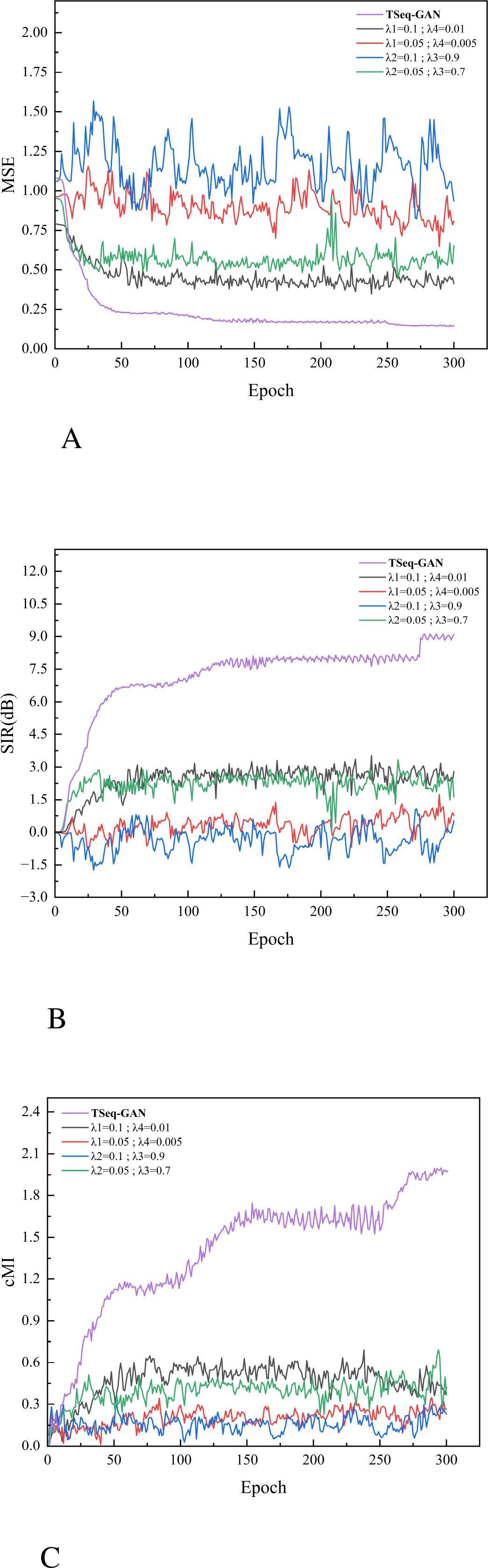
Figure 10. Separation performance under different parameters. (A) The Impact of Changes in Loss Weights on MSE. (B) The Impact of Changes in Loss Weights on SIR. (C) The Impact of Changes in Loss Weights on cMI.

4 Conclusion

In summary, to address the perception challenges faced by USVs operating in complex traffic environments and adverse channel conditions—particularly the limitations of traditional BSS algorithms in modeling capability and separation stability—this study constructs a randomly generated AIS signal dataset tailored for complex interference scenarios and innovatively proposes a TSeq-GAN-based blind source separation method. This approach integrates temporal modeling and spatial feature extraction mechanisms into the generator structure of a GAN, significantly enhancing the model’s robustness to strong noise interference and time-slot collisions without relying on additional denoising modules. Moreover, this architecture improves the model’s deep understanding and representation of AIS signal features, effectively achieving high-precision separation of target signals in low signal-to-noise ratio environments.The proposed method not only demonstrates a fusion-based innovation in model architecture but also achieves significant breakthroughs in algorithm performance and adaptability to practical scenarios, revealing broad application potential in maritime intelligent perception.

The experimental results indicate that, compared to traditional algorithms, the network proposed in this paper shows significant improvement in the extraction of source signals from mixed AIS signals. The MSE, SIR, and cMI performance have all been notably enhanced. Therefore, this network to some extent overcomes the traditional BSS algorithms’ excessive reliance on the assumption that source signals are independent and mixed signals are not independent, offering higher robustness and generalization capability. Additionally, the improvement in AIS signal BSS with this network will further enhance the decision-making ability of USVs in complex waters, improve the ability of USVs to accurately identify the positions and dynamics of surrounding vessels, and provide real-time decision support to enhance their autonomous navigation capabilities.

Furthermore, improvements in AIS signal blind source separation are expected to enhance USV decisionmaking in complex waters, improving its accuracy in identifying the positions and dynamics of surrounding vessels and providing real-time decision support to boost autonomous navigation capabilities. However, limitations remain in handling real noisy signal data deficiencies and underdetermined scenarios. Therefore, future work will focus on two key aspects: first, validating network separation performance using real-world incomplete signal data; second, achieving high-precision separation of underdetermined mixed signals while further lightening the neural network and reducing the number of antennas required on USVs, thereby contributing to more precise autonomous navigation.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding author.

Author contributions

JZ: Writing – review & editing, Software, Conceptualization. YP: Software, Writing – original draft, Writing – review & editing. BH: Writing – review & editing, Conceptualization. XM: Funding acquisition, Writing – review & editing. HL: Software, Writing – original draft. YL: Writing – review & editing, Supervision, Investigation.

Funding

The author(s) declare financial support was received for the research and/or publication of this article. This work was supported by the National Natural Science Foundation of China (Grant No. 52471379), the National Natural Science Foundation of China (Grant No. 52201401) and Chenguang Program of Shanghai Education Development Foundation and Shanghai Municipal Education Commission (Grant No. 24CGA52).

Acknowledgments

We sincerely thank the Merchant Marine College, Shanghai Maritime University, for their invaluable assistance in the development of the computational model. Their professional expertise was crucial to the successful realization of this model. We also gratefully acknowledge Merchant Marine College, Shanghai Maritime University, for providing the experimental facilities, which constituted essential external support for the completion of this work.

Conflict of interest

Author BH was employed by the company Shanghai Ship and Shipping Research Institute CO.LTD.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Cardoso J.-F. (1998). Blind signal separation: statistical principles. Proc. IEEE 86, 2009–2025. doi: 10.1109/5.720250

Crossref Full Text | Google Scholar

Cardoso J.-F. (1999). High-order contrasts for independent component analysis. Neural Comput. 11, 157–192. doi: 10.1162/089976699300016863, PMID: 9950728

PubMed Abstract | Crossref Full Text | Google Scholar

Cheng C., Liu D., Du J.-H., and Li Y.-Z. (2023). Research on visual perception for coordinated air–sea through a cooperative usv-uav system. J. Mar. Sci. Eng. 11, 1978. doi: 10.3390/jmse11101978

Crossref Full Text | Google Scholar

Deville Y., Puigt M., and Albouy B. (2004). “Time-frequency blind signal separation: extended methods, performance evaluation for speech sources,” in 2004 IEEE International Joint Conference on Neural Networks (IEEE Cat. No. 04CH37541), Vol. 1. 255–260 (IEEE).

Google Scholar

Galvan J. (1996). An unsupervised recurrent neural network for noise identification. J. Syst. Eng. (London) 6, 177–185.

Google Scholar

Goodfellow I. J., Pouget-Abadie J., Mirza M., Xu B., Warde-Farley D., Ozair S., et al. (2020). Generative adversarial nets. (ACM New York, NY, USA) Adv. Neural Inf. Process. Syst. 63, 139–144.

Google Scholar

Gu H.-Q., Liu X.-X., Xu L., Zhang Y.-J., and Lu Z.-M. (2023). Dsss signal detection based on cnn. Sensors 23, 6691. doi: 10.3390/s23156691, PMID: 37571474

PubMed Abstract | Crossref Full Text | Google Scholar

Hochreiter S. and Schmidhuber J. (1997). Long short-term memory. Neural Comput. 9, 1735–1780. doi: 10.1162/neco.1997.9.8.1735, PMID: 9377276

PubMed Abstract | Crossref Full Text | Google Scholar

Hyvärinen A. and Oja E. (1997). A fast fixed-point algorithm for independent component analysis. Neural Comput. 9, 1483–1492. doi: 10.1162/neco.1997.9.7.1483

Crossref Full Text | Google Scholar

Jiang M., Zhou F., Shen L., Wang X., Quan D., and Jin N. (2024). Multilayer decomposition denoising empowered cnn for radar signal modulation recognition. IEEE Access 12, 31652–31661. doi: 10.1109/ACCESS.2024.3369180

Crossref Full Text | Google Scholar

Jianwei E., Ye J., He L., and Jin H. (2021). Performance analysis for complex-valued fastica and its improvement based on the tukey m-estimator. Digital Signal Process. 115, 103077. doi: 10.1016/j.dsp.2021.103077

Crossref Full Text | Google Scholar

Kazimierski W. and Stateczny A. (2013). “Fusion of data from ais and tracking radar for the needs of ecdis,” in 2013 Signal Processing Symposium (SPS). 1–6 (IEEE).

Google Scholar

Khan J. B., Jan T., Khalil R. A., and Altalbe A. (2020). Hybrid source prior based independent vector analysis for blind separation of speech signals. IEEE Access 8, 132871–132881. doi: 10.1109/ACCESS.2020.3010342

Crossref Full Text | Google Scholar

Kumar M. and Jayanthi V. (2020). Underdetermined blind source separation using capsnet. Soft Computing 24, 9011–9019. doi: 10.1007/s00500-019-04430-4

Crossref Full Text | Google Scholar

Larson J., Bruch M., and Ebken J. (2006). “Autonomous navigation and obstacle avoidance for unmanned surface vehicles,” in Unmanned systems technology VIII (Orlando (Kissimmee), Florida, SPIE), Vol. 6230. 53–64.

Google Scholar

Li S., Yu Z., Wang P., Sun G., and Wang J. (2024). Blind source separation algorithm for noisy hydroacoustic signals based on decoupled convolutional neural networks. Ocean Eng. 308, 118188. doi: 10.1016/j.oceaneng.2024.118188

Crossref Full Text | Google Scholar

Li Y., Wang Y., and Dong Q. (2020). A novel mixing matrix estimation algorithm in instantaneous underdetermined blind source separation. Signal Image Video Process. 14, 1001–1008. doi: 10.1007/s11760-019-01632-z

Crossref Full Text | Google Scholar

Lin B.-S., Lin B.-S., Chong F.-C., and Lai F. (2006). A functional link network with higher order statistics for signal enhancement. IEEE Trans. Signal Process. 54, 4821–4826. doi: 10.1109/TSP.2006.882075

Crossref Full Text | Google Scholar

Liu R. W., Guo Y., Nie J., Hu Q., Xiong Z., Yu H., et al. (2022a). Intelligent edge-enabled efficient multisource data fusion for autonomous surface vehicles in maritime internet of things. IEEE Trans. Green Commun. Networking 6, 1574–1587. doi: 10.1109/TGCN.2022.3158004

Crossref Full Text | Google Scholar

Liu R. W., Liang M., Nie J., Yuan Y., Xiong Z., Yu H., et al. (2022b). Stmgcn: Mobile edge computingempowered vessel trajectory prediction using spatio-temporal multigraph convolutional network. IEEE Trans. Ind. Inf. 18, 7977–7987. doi: 10.1109/TII.2022.3165886

Crossref Full Text | Google Scholar

Lu G., Xiao M., Wei P., and Zhang H. (2015). A new method of blind source separation using single-channel ica based on higher-order statistics. Math. Problems Eng. 2015, 439264. doi: 10.1155/2015/439264

Crossref Full Text | Google Scholar

Ma L., Liu X., Zhang Y., and Jia S. (2022). Visual target detection for energy consumption optimization of unmanned surface vehicle. Energy Rep. 8, 363–369. doi: 10.1016/j.egyr.2022.01.204

Crossref Full Text | Google Scholar

Mei X., Han D., Saeed N., Wu H., Han B., and Li K.-C. (2024). Localization in underwater acoustic iot networks: Dealing with perturbed anchors and stratification. IEEE Internet Things J 10, 17757–17769. doi: 10.1109/JIOT.2024.3360245

Crossref Full Text | Google Scholar

Meng X., Liu C., Teng J., and Ma S. (2018). Frequency offset estimation of satellite-based ais signals based on interpolated fft. Wireless Pers. Commun. 99, 35–45. doi: 10.1007/s11277-017-5035-0

Crossref Full Text | Google Scholar

Mohamed Mostafa M. A. R., Vucetic M., Stojkovic N., Lekić N., and Makarov A. (2019). Fuzzy functional dependencies as a method of choice for fusion of ais and othr data. Sensors 19, 5166. doi: 10.3390/s19235166, PMID: 31779096

PubMed Abstract | Crossref Full Text | Google Scholar

Niknazar H., Nasrabadi A. M., and Shamsollahi M. B. (2021). A new blind source separation approach based on dynamical similarity and its application on epileptic seizure prediction. Signal Process. 183, 108045. doi: 10.1016/j.sigpro.2021.108045

Crossref Full Text | Google Scholar

Rieta J. J., Castells F., Sánchez C., Zarzoso V., and Millet J. (2004). Atrial activity extraction for atrial fibrillation analysis using blind source separation. IEEE Trans. Biomed. Eng. 51, 1176–1186. doi: 10.1109/TBME.2004.827272, PMID: 15248534

PubMed Abstract | Crossref Full Text | Google Scholar

Ristaniemi T. and Huovinen T. (2006). “Joint multipath delay tracking and interference cancellation in ds-cdma systems using successive ica for oversaturated data,” in 2006 1st International Symposium on Wireless Pervasive Computing. 1–5 (IEEE).

Google Scholar

Shao G., Chen Y., and Wei Y. (2020). Deep fusion for radar jamming signal classification based on cnn. IEEE Access 8, 117236–117244. doi: 10.1109/Access.6287639

Crossref Full Text | Google Scholar

Sun S., Lyu H., Gao Z., and Yang X. (2024). Grid map assisted radar target tracking in a detection occluded maritime environment. IEEE Trans. Instrumentation Measurement 73, 1–11. doi: 10.1109/TIM.2024.3381495

Crossref Full Text | Google Scholar

Sun X., Xu J., Ma Y., Zhao T., Ou S., and Peng L. (2022). Blind image separation based on attentional generative adversarial network. J. Ambient Intell. Humanized Computing 13, 1397–1404. doi: 10.1007/s12652-020-02637-0

Crossref Full Text | Google Scholar

Wang T., Xiao G., Li Q., and Biancardo S. A. (2025). The impact of the 21st-century maritime silk road on sulfur dioxide emissions in chinese ports: based on the difference-in-difference model. Front. Mar. Sci. 12, 1608803. doi: 10.3389/fmars.2025.1608803

Crossref Full Text | Google Scholar

Wang C., Zhang X., Gao H., Bashir M., Li H., and Yang Z. (2024a). Colergs-constrained safe reinforcement learning for realising mass’s risk-informed collision avoidance decision making. Knowledge-Based Syst. 300, 112205. doi: 10.1016/j.knosys.2024.112205

Crossref Full Text | Google Scholar

Wang C., Zhang X., Gao H., Bashir M., Li H., and Yang Z. (2024b). Optimizing anti-collision strategy for mass: A safe reinforcement learning approach to improve maritime traffic safety. Ocean Coast. Manage. 253, 107161. doi: 10.1016/j.ocecoaman.2024.107161

Crossref Full Text | Google Scholar

Xiao G., Amamoo-Otoo C., Wang T., Li Q., and Biancardo S. A. (2025). Evaluating the impact of eca policy on sulfur emissions from the five busiest ports in America based on difference in difference model. Front. Mar. Sci. 12, 1609261. doi: 10.3389/fmars.2025.1609261

Crossref Full Text | Google Scholar

Xie Y., Xie K., and Xie S. (2021). Underdetermined blind source separation of speech mixtures unifying dictionary learning and sparse representation. Int. J. Mach. Learn. Cybernetics 12, 3573–3583. doi: 10.1007/s13042-021-01406-5

Crossref Full Text | Google Scholar

Xu P., Jia Y., Wang Z., and Jiang M. (2020). Underdetermined blind source separation for sparse signals based on the law of large numbers and minimum intersection angle rule. Circuits Systems Signal Process. 39, 2442–2458. doi: 10.1007/s00034-019-01263-2

Crossref Full Text | Google Scholar

Yan R.-j., Pang S., Sun H.-b., and Pang Y.-j. (2010). Development and missions of unmanned surface vehicle. J. Mar. Sci. Appl. 9, 451–457. doi: 10.1007/s11804-010-1033-2

Crossref Full Text | Google Scholar

Yang D., Wu L., Wang S., Jia H., and Li K. X. (2019). How big data enriches maritime research–a critical review of automatic identification system (ais) data applications. Transport Rev. 39, 755–773. doi: 10.1080/01441647.2019.1649315

Crossref Full Text | Google Scholar

Yu K., Liang X.-f., Li M.-z., Chen Z., Yao Y.-l., Li X., et al. (2021). Usv path planning method with velocity variation and global optimisation based on ais service platform. Ocean Eng. 236, 109560. doi: 10.1016/j.oceaneng.2021.109560

Crossref Full Text | Google Scholar

Zhu J., Yang Y., and Cheng Y. (2023). A millimeter-wave radar-aided vision detection method for water surface small object detection. J. Mar. Sci. Eng. 11, 1794. doi: 10.3390/jmse11091794

Crossref Full Text | Google Scholar