Physics-guided deep neural networks for bathymetric mapping using Sentinel-2 multi-spectral imagery

Satellite-derived bathymetry (SDB) based on multi-spectral imagery data has been a critical tool for large-scale water depth in shallow water regions. Traditional SDB models primarily rely on known laws relating the exponential attenuation of light with the path length it traveled. In the past few years, deep computer vision models have emerged as valuable new technologies for bathymetry measurement. However, due to the black-box nature of these deep models, they may produce bathymetry results that are inconsistent with physical laws and exhibit limited generalizability across diverse areas. In this paper, we propose a novel hybrid architecture, HybridBathNet, that integrates UNet (extracting spatial and spectral feature) with a physical bathymetry network (ensuring physical relationships). By embedding physical constraints directly into the model architecture, HybridBathNet achieves improved bathymetric inversion accuracy while maintaining consistency with established optical attenuation laws. Experimental results demonstrate that the proposed model delivers high-quality bathymetric estimations across diverse island regions. Comparative evaluations against state-of-the-art methods further validate the superior accuracy and generalization capability of HybridBathNet. The code of HybridBathNet is available at https://github.com/qiushibupt/HybridBathNet.

1 Introduction

Traditional bathymetric measurement methods primarily rely on acoustic equipment such as sonar, which, despite their high precision, face challenges including low measurement efficiency, high costs, and limited coverage (Constantinoiu et al., 2024; de Moustier, 1988). Additionally, these large survey vessels often cannot access shallow waters, resulting in a scarcity of nearshore bathymetric data. In recent years, with advancements in technology and satellite payload capabilities, there has been a significant increase in Earth observation satellite launches, providing various high-quality observational data (Philpot, 1989; Manessa et al., 2016). Among various remote sensing platforms available for bathymetric mapping, Landsat series satellites, with their extensive temporal archive dating back to the 1970s and free data policy, have been widely applied in satellite-derived bathymetry (SDB) applications (Jagalingam et al., 2015; Duan et al., 2022). High-resolution commercial satellites such as WorldView-2 and WorldView-3 offer superior spatial resolution (2–3 meters) and additional spectral bands, enabling more precise bathymetric inversion in shallow waters within 6 meters depth, though their commercial nature limits widespread accessibility (Evagorou et al., 2022; Wicaksono et al., 2024). In the field of bathymetric inversion, publicly available 10-meter resolution Sentinel-2 multispectral imagery has been widely utilized, with its 10-meter spatial resolution effectively enhancing the capability to identify seafloor features (Spoto et al., 2012; Immitzer et al., 2016). Furthermore, the combination of free data access and regular acquisition schedules makes Sentinel-2 particularly suitable for long-term monitoring applications and climate change impact assessments. As remote sensing technology develops, Satellite-Derived Bathymetry (SDB) methods based on remote sensing imagery have gradually become an important supplementary approach for shallow water depth measurement due to their advantages of large coverage area, rapid acquisition, and low cost.

The principle of Satellite-Derived Bathymetry (SDB) based on multispectral imagery data is to construct a bathymetric inversion model that utilizes the correlation between spectral imagery captured by satellites and water depth to estimate water depth. Currently, SDB methods are mainly divided into two categories: physics-based methods and empirical model-based methods. Physics-based methods primarily establish a direct relationship between reflectance and water depth by considering the propagation of light in water bodies, taking into account imagery of both the water column and the seafloor. In 1970s, researchers use reflectance from different bands to correct for seafloor albedo, constructing the log-transformed linear band model for water depth derivation (Lyzenga, 1978, 1981). To address the issue of excessive parameters requiring fitting, the logarithmic band ratio model (LBR) is more widely used. It employs a linear fit to the logarithm of the ratio between the blue and green bands for water depth, reducing the impact of seafloor variations and offering greater robustness (Stumpf et al., 2003). Building on this, the polynomial logarithmic band ratio model (PLBR) is also proposed to further capture non-linear relationships (Han et al., 2023). For shallow water SDB tasks, advanced statistical filtering methods have been employed to accurately identify the reflection times of light at the water surface and seafloor, thereby enhancing SDB performance (Degnan, 2002; Chen et al., 2021, 2022). Subsequent research has leveraged absorption and backscattering coefficients derived from multispectral satellite imagery to enhance the performance of SDB models (Lee et al., 2016). Moreover, the incorporation of Tobler’s First Law of Geography has been shown to reduce statistical bias in model predictions (Traganos et al., 2018). These physics-based methods typically require complex mathematical derivations, and their prediction results are highly dependent on high-quality input imagery.

Compared to physics-based methods, empirical methods directly fit the relationship between reflectance and water depth. In this line, traditional machine learning-based methods can accept inputs from more spectral bands and use in-situ data for fitting, allowing them to establish more complex fitting functions. This capability leads to better bathymetric inversion performance, as demonstrated by models based on support vector regression (Hamilton et al., 1993; Mateo-Pérez et al., 2020), multilayer perceptron (Le et al., 2022), and random forest (Misra et al., 2018). Additionally, researchers employ the K-nearest neighbors (KNN) algorithm to assign optimal linear regression models to different subspaces, each with appropriate band combinations, thereby improving the accuracy (Niroumand-Jadidi et al., 2020). However, these methods operate on a per-pixel basis, which constrains their receptive fields and hinders the exploitation of spatial context. As research progressed, researchers discover that spatial information contained in multispectral imagery is critical. For example, experiments from three different areas demonstrate notable improvements in SDB accuracy when spatial information is incorporated (Cahalane et al., 2019). The recent progress of computer vision technologies–such as scene classification (Chollet, 2017), object detection (Bochkovskiy et al., 2020), and semantic segmentation (Sun et al., 2019)–demonstrate the effectiveness of deep network architectures in capturing complex spatial patterns, which holds great promise for enhancing SDB accuracy. Early efforts in this direction apply Convolutional Neural Networks (CNNs) to multispectral imagery from satellites such as ZY-3, GF-1, and WorldView-2, resulting in SDB models based on single-layer convolutional architectures (Ai et al., 2020). Building on this foundation, more advanced deep architectures–such as U-Net and RefineNet–are later adapted for SDB applications to better capture hierarchical spatial features (Mandlburger et al., 2021; Sun et al., 2023). Recently, to effectively integrate multi-scale spatial features and enhance generalization, researchers introduce a multi-scale center-aligned hierarchical resampling module, which enables reliable performance even with limited in-situ data (Qin et al., 2024). Although SDB methods based on deep learning have achieved certain successes, direct application of these black-box models encounters two major challenges. (1) Physical inconsistency. Physics-based SDB methods are grounded in established physical principles and incorporate domain-specific prior knowledge, allowing them to explicitly model the physical processes involved in light propagation through water. In contrast, deep learning methods operate as black-box models and do not explicitly account for the underlying physical laws. As a result, they may generate bathymetric estimates that are inconsistent with the physics of light attenuation in ocean environments. (2) Limited generalization. Relationships learned by deep learning-based SDB models are primarily data-driven. As such, their predictions are often constrained by the distribution of the training data and may degrade in scenarios that differ significantly from those seen during training. For instance, a deep learning model trained on clear shallow waters may produce inaccurate or unreliable depth estimates when applied to complex environments.

To address these challenges, this paper proposes a novel deep learning framework that integrates domain knowledge and physical principles into SDB. A straightforward strategy for enforcing physical consistency in SDB is to incorporate physics-based loss functions into the training objective, as inspired by approaches in other domains [e.g (Daw et al., 2022; Beucler et al., 2019; Raissi et al., 2019)]. However, the inclusion of such loss functions alone is not enough to address the above limitations in the SDB filed. To this end, we go beyond the use of physics-based loss functions by embedding physical principles of SDB directly into the network architecture, and propose a novel framework–HybridBathNet (Hybrid Architecture for Physically Consistent Bathymetry). Specifically, we first process the Sentinel-2 image data to remove noise such as clouds and sun glint, and then match it with airborne LiDAR Bathymetry (ALB) elevation data to the same dimensions to construct the dataset. Second, this study pioneers the integration of a physical network module within a deep learning framework specifically for bathymetric inversion. Unlike conventional approaches that impose soft constraints via loss function regularization, HybridBathNet simultaneously predicts the Water Depth Index (WDI) from radiative transfer theory as an intrinsic part of the network. Moreover, through a feature fusion module explicitly designed based on prior physical knowledge, HybridBathNet enforces physical constraints at the feature level. By embedding physical priors directly into the network architecture, this method not only enhances interpretability but also substantially improves the model’s fitting accuracy and generalization capability. The contributions of this paper are threefold:

● We develop a novel hybrid SDB model, HybridBathNet, capable of automatically learning the mapping rules between water surface radiance features and water depth from multispectral satellite imagery and in-situ data, performing well in various complex areas.

● By introducing a physical bathymetry network in HybridBathNet, we explicitly incorporate physics guidance into the deep learning model. Unlike approaches that rely solely on physics-based loss functions, our method embeds physical knowledge directly into the model structure, thereby tailoring the network specifically for bathymetric inversion. This internal incorporation of physical constraints enhances the model’s generalization capability. As a result, HybridBathNet achieves higher accuracy and improved robustness across diverse and complex seabed topographies.

● We selected a total of five research areas located in the Atlantic Ocean, Caribbean Sea, and Pacific Ocean to construct training and testing data, as well as real-world dataset. Training data comes from Oahu Island, while real-world dataset come from St. Croix Island, Saipan Island, Tinian Island, and Vieques Island. Analysis of the test datasets and real-world dataset demonstrates that HybridBathNet consistently outperforms traditional physics-based models (e.g., PLBR) and deep learning-based approaches (e.g., UNet++) in terms of accuracy (RMSE) and reliability (R²).

2 Data

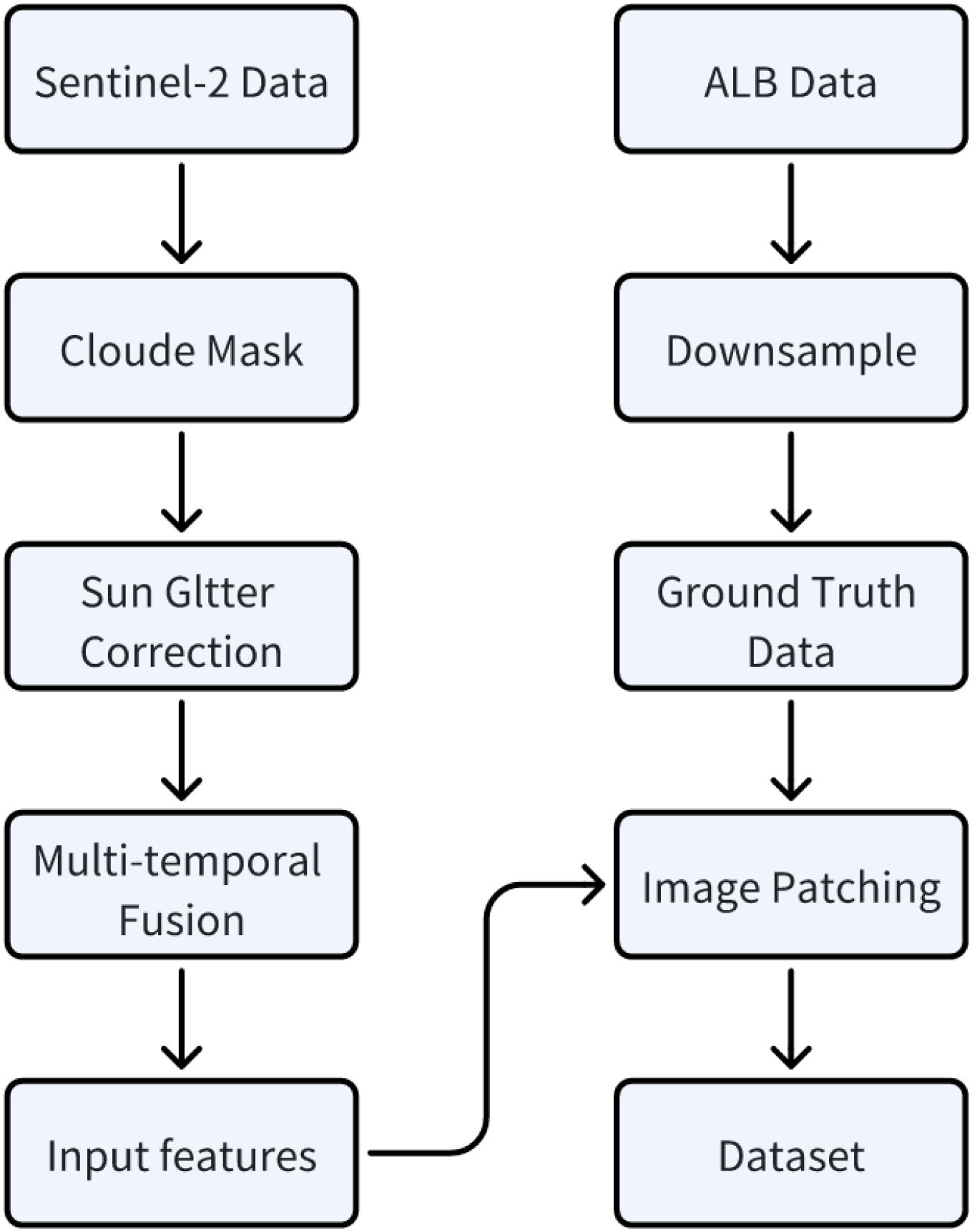
In our research, data preprocessing can be broadly divided into the processing of Sentinel-2 multispectral imagery data and ALB data. The processing of Sentinel-2 imagery includes the removal of interference pixels and the filling of invalid pixels, which determines the quality of the model input data. For ALB data, due to the resolution differences between it and satellite imagery data, we downsampled it to the corresponding resolution for matching. Figure 1 illustrates the detailed data preprocessing workflow for constructing our dataset.

Figure 1

Figure 1. The workflow of data preprocessing for dataset construction.

2.1 Sentinel-2 multispectral imagery data

Sentinel-2 is an Earth observation mission under the European Space Agency’s “Copernicus Programme”, consisting of two polar-orbiting satellites (Sentinel-2A and Sentinel-2B) designed to provide continuous high-resolution optical imagery for global land and coastal areas. The Multi-Spectral Instrument (MSI) they carry can acquire 13 spectral bands covering visible, near-infrared, and short-wave infrared spectral regions. This includes 4 bands (B2, B3, B4, and B8) with 10-meter spatial resolution, 6 bands (B5, B6, B7, B8a, B11, and B12) with 20-meter resolution, and 3 bands (B1, B9, and B10) with 60-meter resolution. We use atmospherically corrected L2A Surface Reflectance (SR) data processed by Sen2Cor for satellite-derived bathymetry research. Although Sentinel-2 L2A data has undergone preliminary atmospheric correction, the original images still contain interference from clouds, shadows, and sun glint. This noise affects the accuracy of water depth and surface feature analysis. Therefore, we use band information along with three auxiliary Sentinel-2 products in Google Earth Engine (GEE) to further address these issues: the Scene Classification Layer (SCL), the Cloud Probability Layer (MSK_CLDPRB), and the Quality Assessment Layer (QA60). To mitigate the effects of sun glint, we calculate the ratio of NIR to SWIR reflectance. If this ratio exceeds a threshold of 2, the pixel is considered part of a sun glint area and is subsequently masked out.

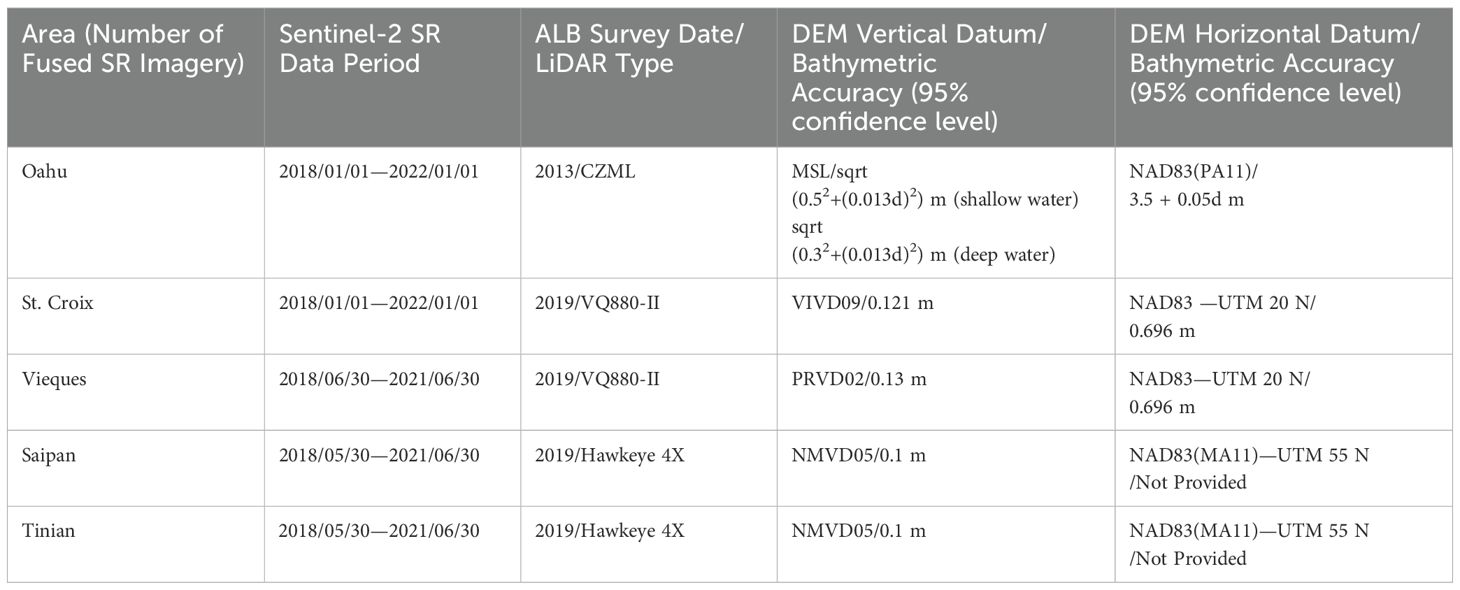
In several recent studies, researchers have applied median filtering to multi-temporal surface reflectance imagery to better eliminate noise effects, thereby generating fused surface reflectance data (Han et al., 2023; Xu et al., 2023). Here, we similarly use Google Earth Engine (GEE) to implement efficient multi-temporal data fusion. For Oahu Island, which serves as our training and testing dataset, we integrate L2A data acquired from January 2018 to January 2022 into one fused surface reflectance images. This operation reduces interference caused by factors such as variations in inherent optical properties and cloud cover, enhancing the clarity and stability of the surface reflectance imagery. Similarly, for all study areas, we construct one fused surface reflectance image for each region. Detailed information on the multi-temporal Sentinel-2 surface reflectance image fusion for each study area is shown in Table 1.

Table 1

Table 1. The information of SR data and ALB data are used in this study for water depth.

2.2 ALB data

The in-situ data used in this study are ALB data collected by the National Oceanic and Atmospheric Administration (NOAA), which can be downloaded from the internet (https://coast.noaa.gov/dataviewer/). The ALB data are Digital Elevation Model (DEM) raster data that can be used after appropriate processing and include not only underwater topography but also partial land terrain elevation data. Detailed information about the ALB data is shown in Table 1. The original spatial resolution of these Digital Elevation Models is 1 meter; during data preprocessing, we downsampled them to a 10meter resolution to facilitate spatial alignment with Sentinel-2 L2A surface reflectance imagery. This multi-temporal fusion strategy is specifically designed to address temporal inconsistencies in satellite observations and mitigate the effects of variable atmospheric conditions, seasonal changes in water optical properties, and transient environmental factors. By creating a temporally stable composite, we obtain a more representative characterization of seafloor reflectance properties that is less susceptible to short term variations, thereby improving the reliability of bathymetric inversion. The median filtering process effectively removes transient atmospheric effects and temporal noise while preserving the underlying spectral-depth relationships that are fundamental to satellite-derived bathymetry.

2.3 Study areas

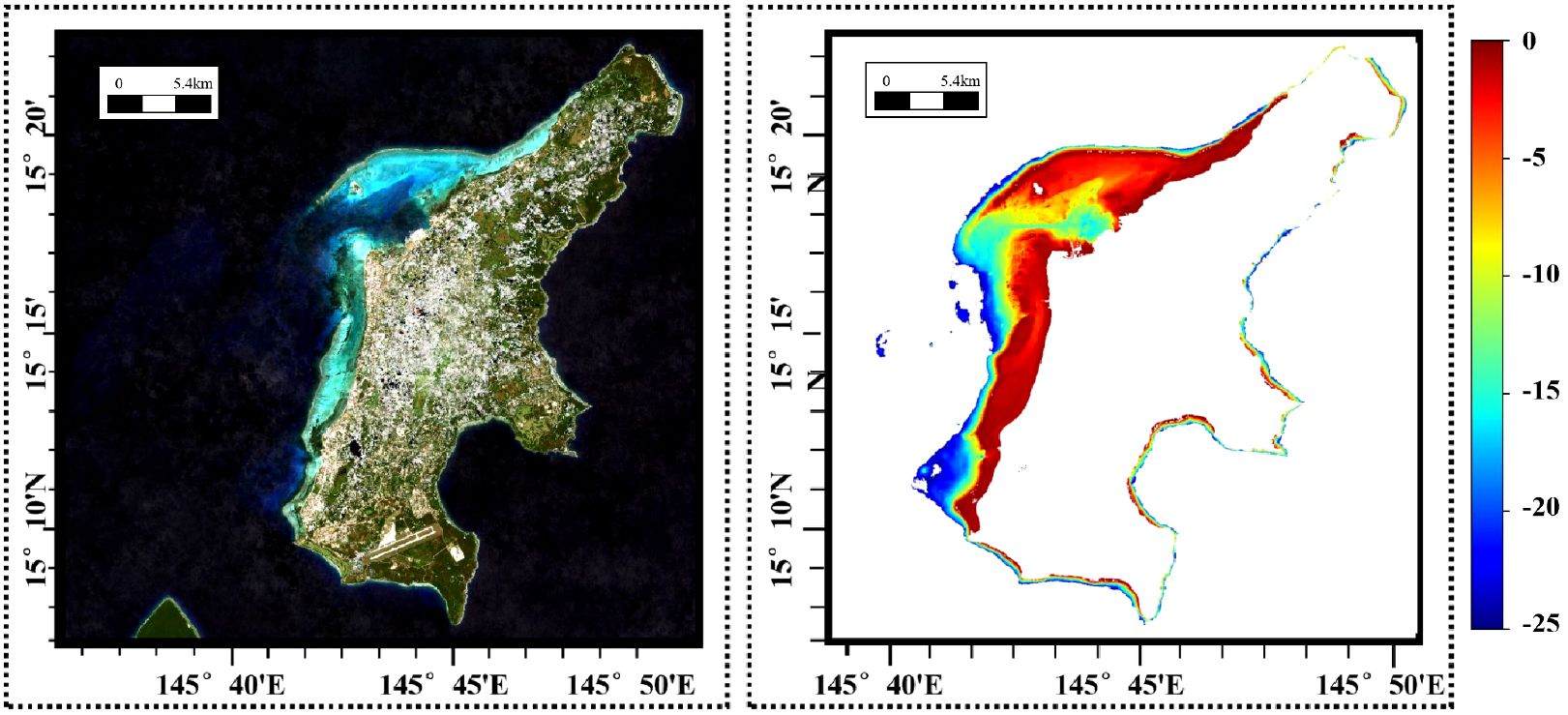
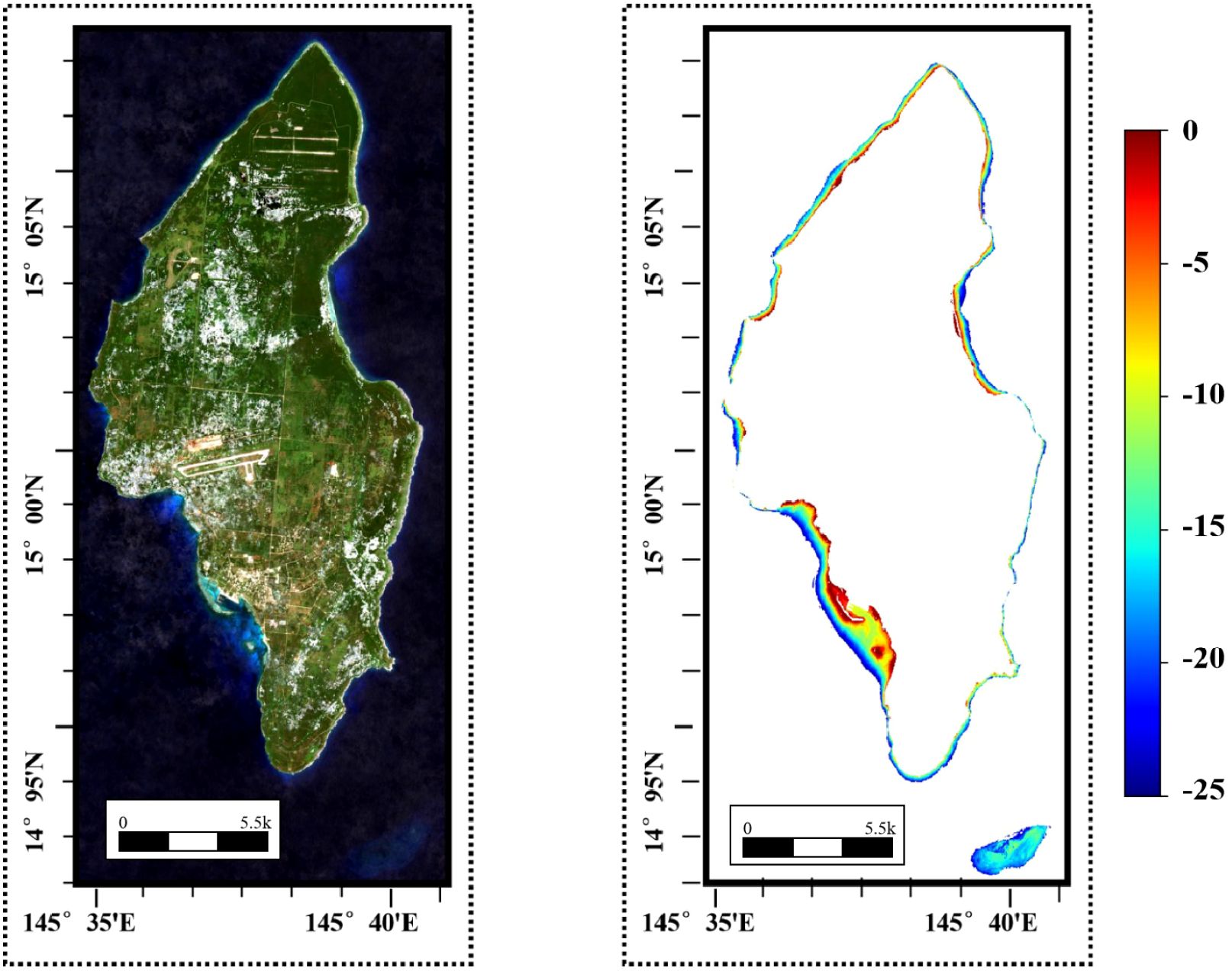
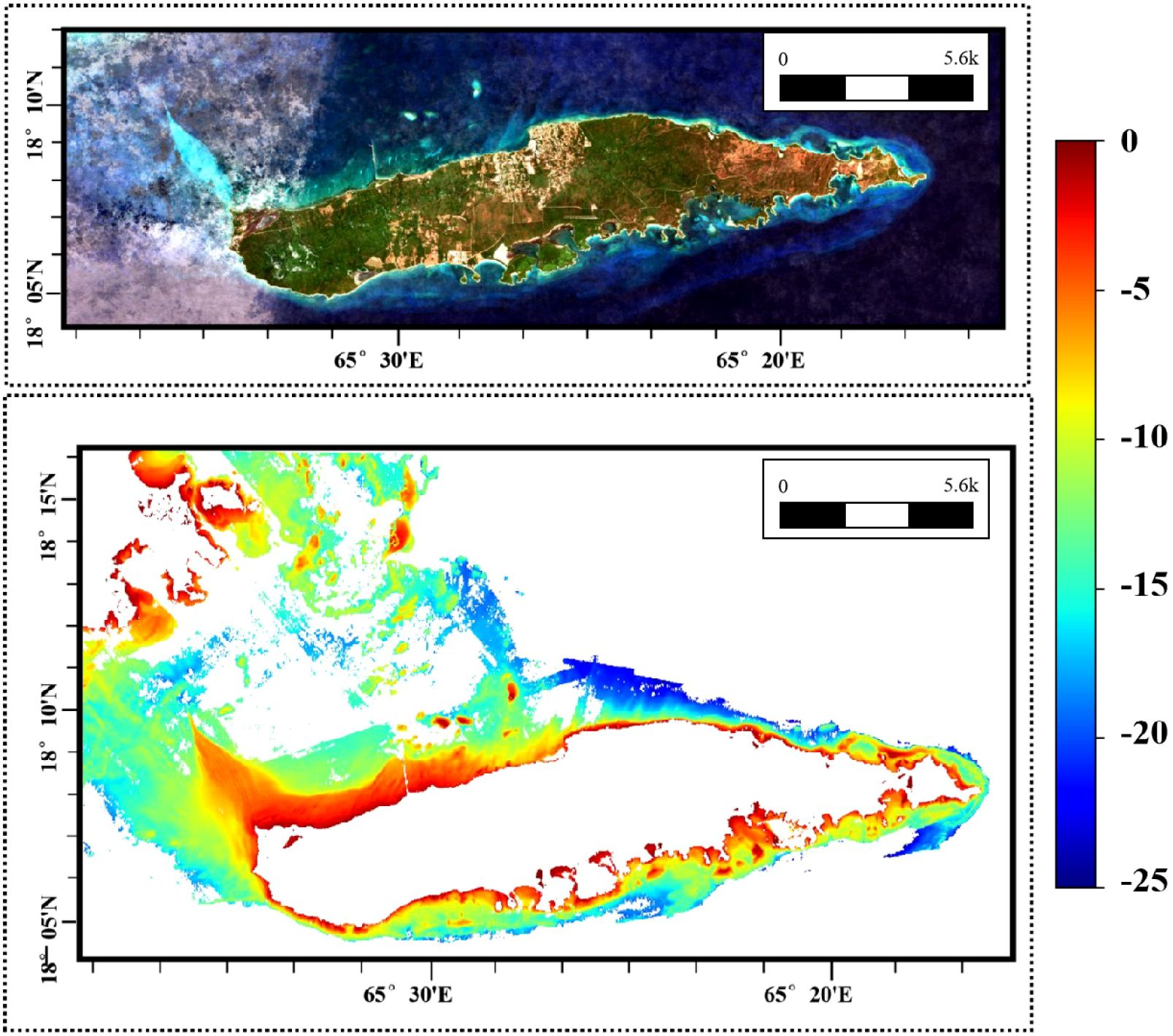
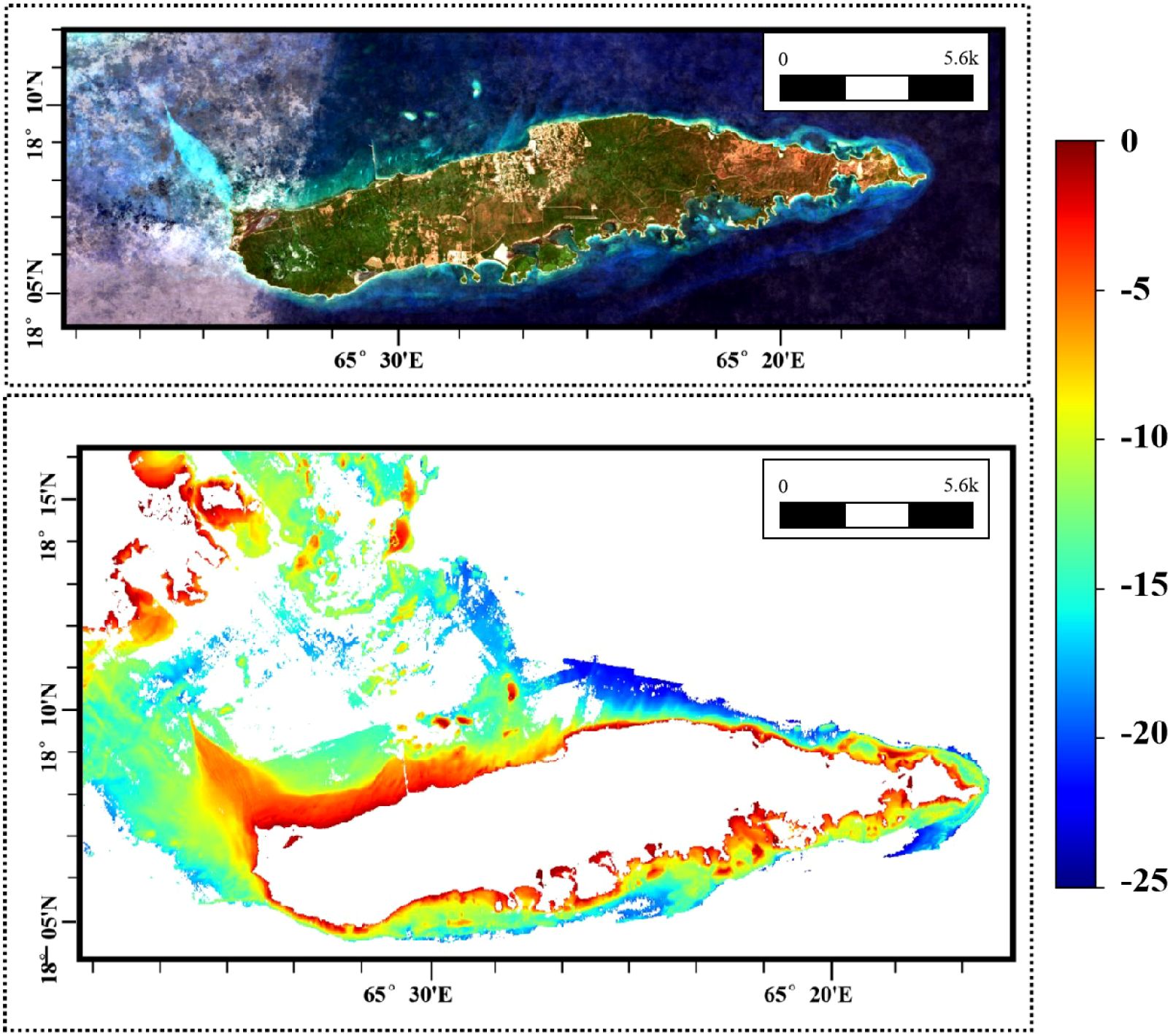
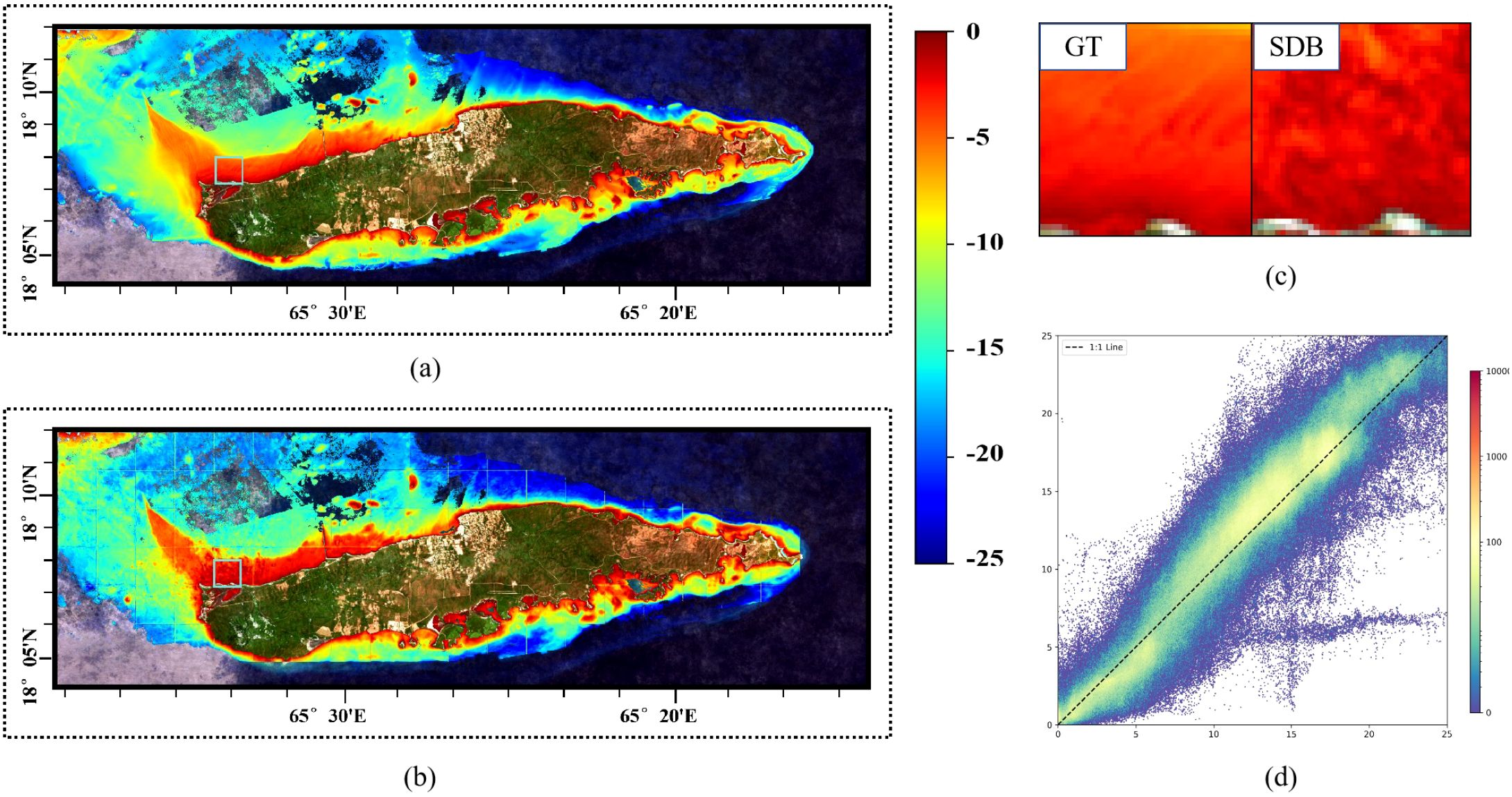
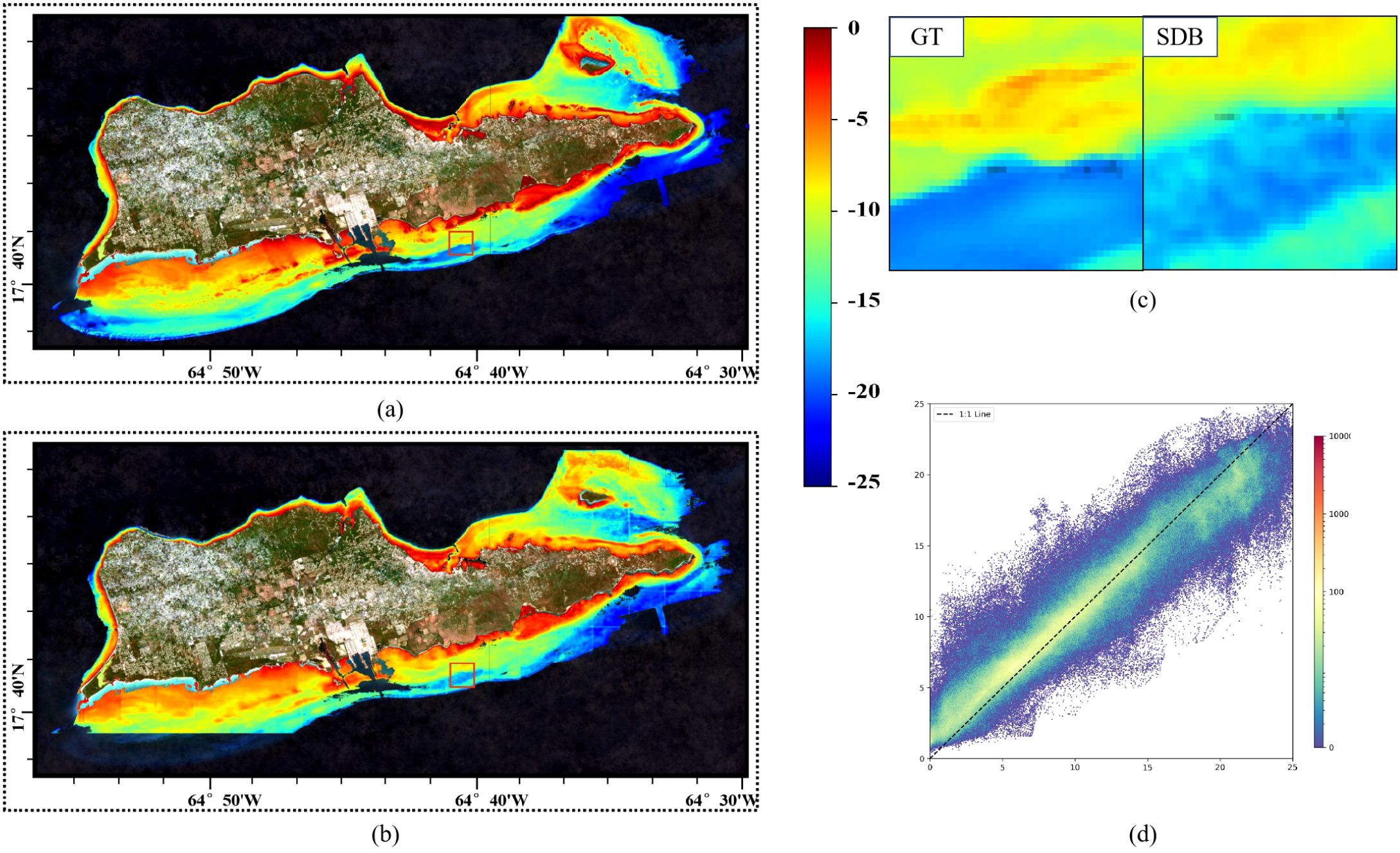
Figure 2 shows the global distribution and topographical conditions of the study areas. We select Oahu Island for the training and testing datasets, with the remaining four islands constituting the real-world dataset for inference. Oahu Island has the largest number of water depth samples, with over 3,000,000 effective points, making it the most extensive study area among the five datasets. The division of the training and test sets is shown in Figure 3. The bathymetric ground truth data for validation consist of high-precision ALB datasets from these four geographically distributed study areas spanning two ocean basins. The independent validation datasets from St. Croix and Vieques (Caribbean Sea) and Saipan and Tinian (Western Pacific) provide comprehensive spatial coverage for assessing model generalization across diverse bathymetric environments including steep underwater slopes, coral reef systems, shallow lagoons, and complex nearshore topographies. All ALB datasets were acquired by NOAA using state-of-the-art airborne LiDAR systems with bathymetric accuracies ranging from 0.1 to 0.696 meters at 95% confidence levels, with collection timeframes spanning from 2013 to 2019 as detailed in Table 1. The eastern side of Oahu Island has extensive coral reef coverage, with numerous artificial structures along the shore, creating complex topography. The fused SR imagery and DBM in the real-world dataset are shown in Figures 4–7. St. Croix Island is located in the Caribbean Sea of the Western Atlantic Ocean; its northwestern side has steep underwater slopes, while its southern side features a relatively flat seafloor, offering diverse underwater topography. Vieques Island is also located in the Caribbean Sea and is geographically and topographically very similar to St. Croix Island, with uniformly smooth underwater topography and clear water conditions. Saipan Island and Tinian Island are located in the Commonwealth of the Northern Mariana Islands in the Western Pacific, distinctly isolated from other study areas in the real-world dataset. Among the two, Saipan Island has unique topographical features: its underwater topography differs significantly between the eastern and western sides. The eastern side has steep slopes, while the western side features a large lagoon formed by coral debris, extending more than 4 kilometers offshore. In contrast, the underwater topography around Tinian Island is primarily steep, except for its southwestern part; areas with water depth less than 25 meters are typically within 500 meters of the coastline.

Figure 2

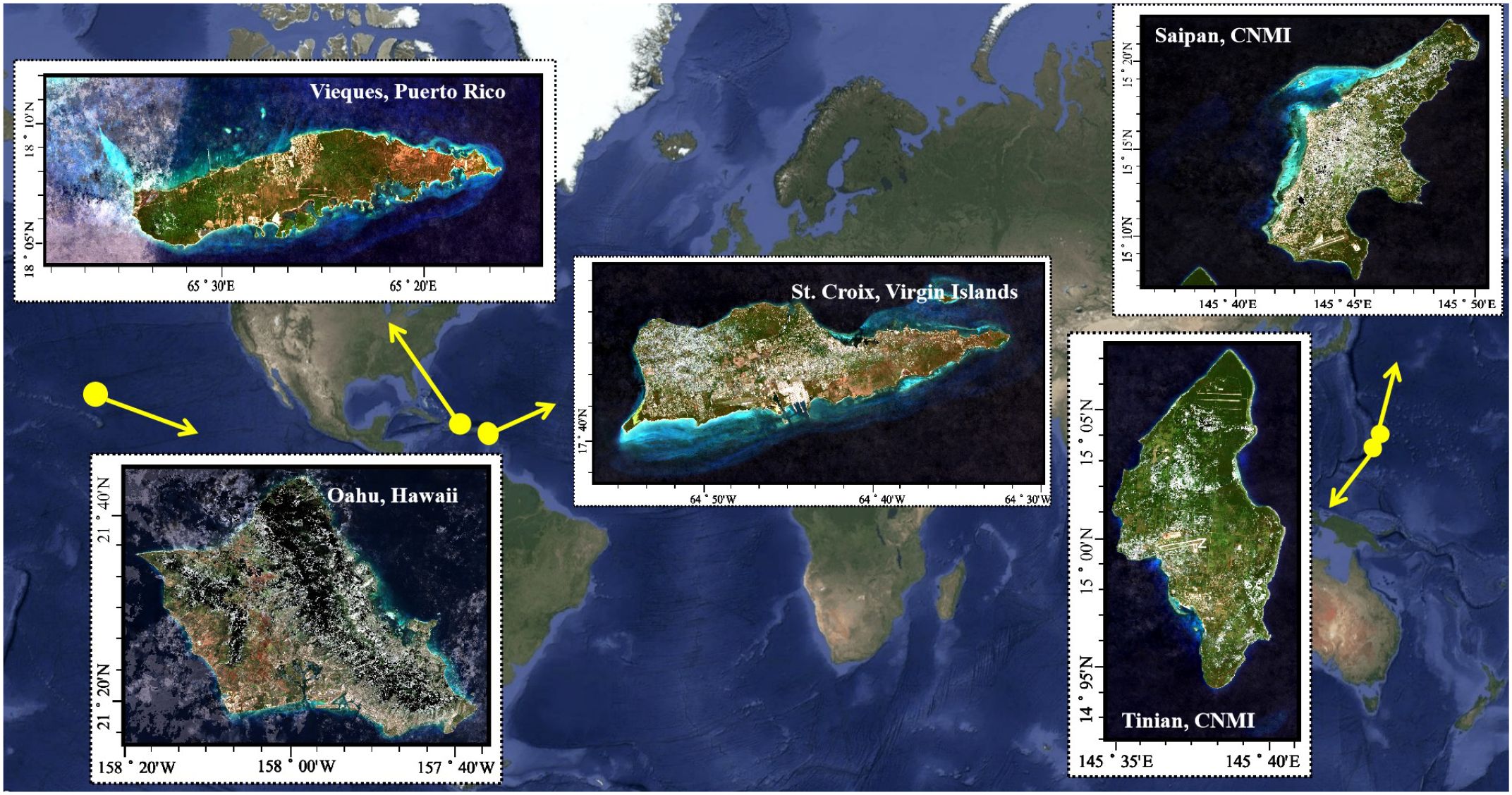
Figure 2. Geographic distribution of the study areas used in our research, including Oahu, St. Croix, Vieques, Saipan, and Tinian. Oahu is selected as the training and testing dataset.

Figure 3

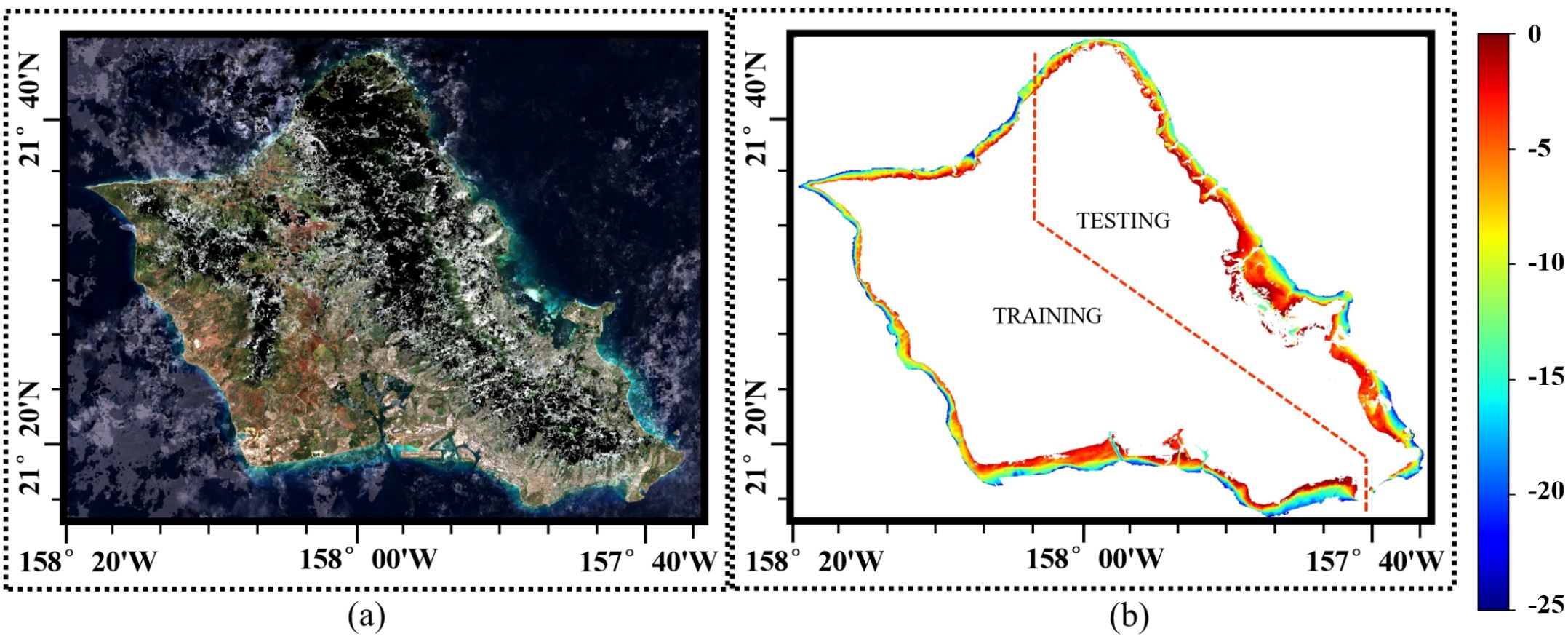
Figure 3. (a) Fused SR imagery of Oahu, and (b) its corresponding DBM and the partition of the training dataset and testing dataset.

Figure 4

Figure 4. The fused SR imagery and DBM of Saipan.

Figure 5

Figure 5. The fused SR imagery and DBM of Tinian.

Figure 6

Figure 6. The fused SR imagery and DBM of St. Croix.

Figure 7

Figure 7. The fused SR imagery and DBM of Vieques.

3 Method

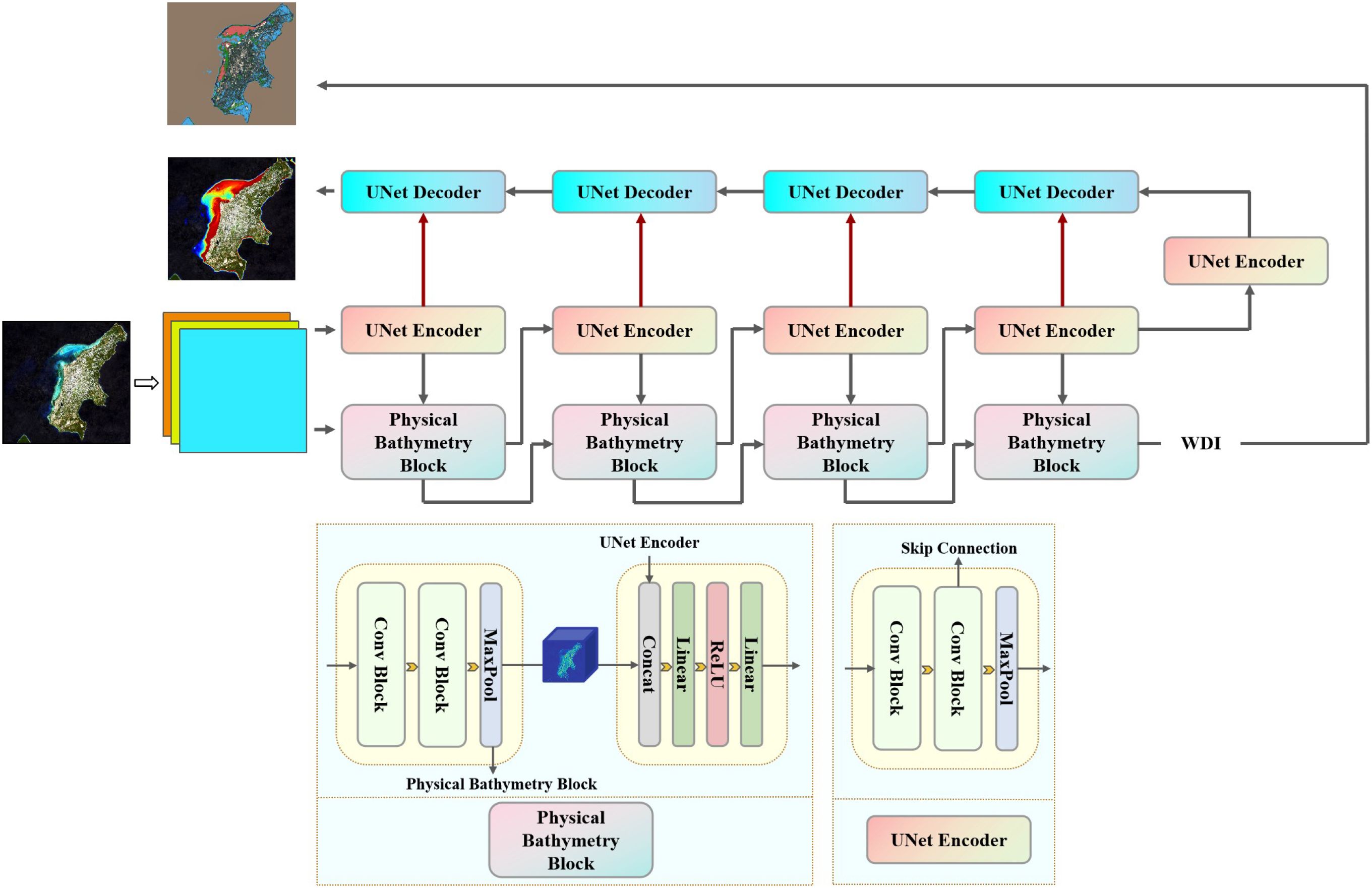
This study proposes a novel neural network architecture HybridBathNet, which integrates prior physical laws to improve inversion accuracy while achieving better generalization. As shown in Figure 8, HybridBathNet consists of the following two main components:

1. A U-Net-based model for predicting water depth Z from input features.

2. A physical bathymetry network that ensures physical relationship between reflectance and depth.

Figure 8

Figure 8. The structure of HybridBathNet.

The input to the model is a multispectral remote sensing image patch of size 64 × 64. Specifically, we utilize Bands 2, 3, and 4 from the Sentinel-2 L2A product, resulting in an input tensor with dimension 64×64×3. The architecture of HybridBathNet consists of two main components: a UNet-based Backbone for spatial feature extraction, and a Physical Bathymetry Network, which comprises a Water Depth Index Prediction Branch and a Feature Fusion Module. In the following sections, we detail the design of each component and introduce an end-to-end learning strategy for training the complete HybridBathNet framework.

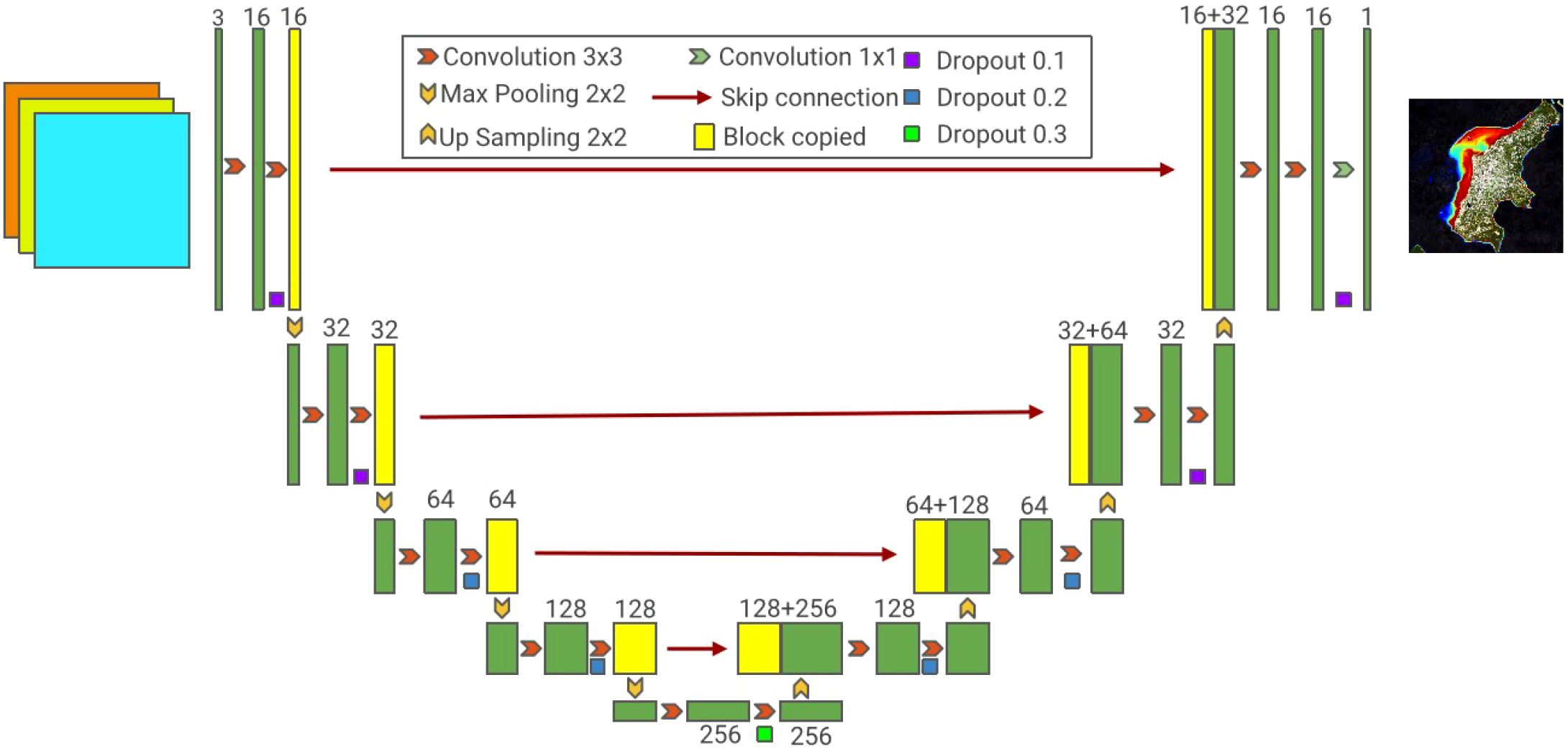
3.1 UNet-based backbone

The U-Net architecture was originally proposed for biomedical image segmentation (Ronneberger et al., 2015) and has achieved significant success in various segmentation tasks where the output has the same spatial resolution as the input. Its encoder-decoder structure and skip connections effectively capture multi-scale contextual information. As shown in Figure 9, its encoder path reduces spatial resolution while increasing the number of feature channels to capture hierarchical features of the input, and the decoder path symmetrically upsamples the feature maps to restore spatial details. The model’s skip connections fuse high-resolution features from the encoder output with corresponding upsampled features in the decoder, mitigating the loss of spatial details during the downsampling process.

Figure 9

Figure 9. The structure of U-Net.

The U-Net architecture is well-suited for dense prediction tasks such as Satellite-Derived Bathymetry (SDB), as it effectively integrates high-level semantic information with low-level spatial details. In our framework, U-Net takes multispectral satellite imagery as input and produces a single-band output image of the same spatial dimensions, where each pixel represents the estimated water depth at the corresponding location. While traditional U-Net can effectively learn the mapping from spectral features to depth through data-driven training, it does not incorporate the underlying physical principles governing light propagation in water. As a result, its generalization ability degrades when applied to data distributions that differ significantly from those seen during training.

3.2 Physical bathymetry network

To explicitly incorporate physical priors and enhance generalization, our Physical Bathymetry Network is designed with two key components: the Water Depth Index Prediction Branch and the Feature Fusion Module.

3.2.1 Water depth index from reflectance

Existing physics-based methods primarily establish the relationship between satellite imagery and water depth by directly leveraging principles derived from physical models, such as radiative transfer theory. The log-transformation linear band model is a classic physics-based water depth inversion scheme (Lyzenga, 1978):

$\begin{array}{ll}{R}_w=(A_d-R_{\infty })\exp (-gZ)+R_{\infty }& (1)\end{array}$

where $R_w$ is the observed reflectance, $R_{\infty }$ is the reflectance of optically deep water, A_d is the bottom albedo, Z is the depth, and g is a function of the diffuse attenuation coefficients for downwelling and upwelling light. Rearranging Equation 1, we get:

$\begin{array}{ll}Z=g^{-1}[\ln (A_d-R_{\infty })-\ln (R_w-R_{\infty })]& (2)\end{array}$

To eliminate the dependence on bottom albedo A_d, using two spectral bands with different attenuation properties can provide a solution. By applying Equation 2 to two bands and eliminating the albedo term through algebraic manipulation, the depth can be expressed as a linear combination of the log-transformed reflectances from both bands. Since reflectance values typically vary across different spectral bands due to their different absorption and scattering characteristics in water, the use of two bands with distinct attenuation coefficients allows for the separation of depth-related signal variations from bottom albedo variations. The differential attenuation between bands provides the necessary information to solve for depth while compensating for variable bottom types (Equation 3):

$\begin{array}{ll}Z=a_0+a_i{X}_i+a_j{X}_j& (3)\end{array}$

where $X_k=\text{ln}[R_w({\lambda }_k)-R_{\infty }({\lambda }_k)]$ (for k = i,j), and constants a₀, a_i, and a_j are determined through multivariate linear regression. A key limitation of the log-transformation linear band model lies in its reliance on empirically determining five variables for the linear transformation, which substantially increases the computational burden, particularly for large-scale water bodies. Additionally, the model encounters numerical instability when $R_w-R_{\infty }$ becomes negative, as the logarithmic function is undefined in such cases. To address these issues, the Log-Band Ratio (LBR) model introduces improvements by fitting water depth using the logarithmic ratio of the blue and green spectral bands, as shown in Equation 4:

$\begin{array}{ll}Z=m_1\frac{\ln (n{R}_w({\lambda }_i))}{\ln (n{R}_w({\lambda }_j))}-m_0& (4)\end{array}$

where m₁ and m₀ are model coefficients, n is a fixed constant, and Z is the prior water depth of the model. It has been demonstrated that this logarithmic ratio varies significantly with water depth while being relatively insensitive to bottom reflectance. This implies that, at a constant depth, variations in bottom type produce only minor changes in the ratio. Owing to this property, the ratio is referred to as the Water Depth Index (WDI), as defined in Equation 5:

$\begin{array}{ll}W=\frac{\ln (n\times R_{\text{blue}})}{\ln (n\times R_{\text{green}})}& (5)\end{array}$

where $R_{\text{blue}}$ and $R_{\text{green}}$ represent the surface reflectance of the blue and green bands after denoising, respectively, and n is a constant, typically set around 1500 to avoid negative values in the logarithm. However, in nearshore shallow water regions, the LBR model often deliver unsatisfactory performance. To improve accuracy under such conditions, the Polynomial Log-Band Ratio (PLBR) model has been proposed, which extends LBR by incorporating higher-order terms, as shown in Equation 6:

$\begin{array}{ll}Z=a\times W^2+b\times W+c& (6)\end{array}$

Additionally, some studies have explored exponential relationship fitting (Hsu et al., 2021), which has demonstrated promising results in certain regions.

These methods, grounded in physical knowledge, offer interpretability and stability. A critical component of such approaches is the relationship between the Water Depth Index (WDI) and actual water depth, which serves as the foundation for accurate depth estimation. However, accurately modeling this relationship remains challenging due to its potential nonlinearity and sensitivity to environmental conditions. Traditional fitting approaches may fall short in capturing such complexity, thereby motivating the use of our following architecture to learn this mapping more effectively.

3.2.2 Water depth index prediction branch

To explicitly encode the relationship between the Water Depth Index (WDI) and actual water depth, we introduce a WDI Prediction Branch designed to estimate the WDI value W from the same multispectral input. As illustrated in Figure 8, this branch adopts the encoder structure of the U-Net architecture. Since predicting W is a relatively simpler task than directly estimating water depth, a full U-Net is not required. Therefore, the WDI Prediction Branch excludes the decoder and skip connections, retaining only the encoder. This design ensures that the extracted features during WDI prediction are aligned in scale and semantics with the encoder outputs of the water depth estimation branch, thereby facilitating effective and physically meaningful feature fusion in subsequent stages.

Compared to directly calculating the WDI W and inputting it as a feature to the model, the WDI prediction branch has the following advantages. First, compared to directly feeding the WDI as an input feature, the WDI Prediction Branch enables the extraction of hierarchical features aligned with the encoder levels of the U-Net backbone. Through feature fusion, the backbone network is able to more effectively leverage WDI-related information during training. This joint architecture facilitates multi-task learning, allowing the network to simultaneously learn meaningful representations of both WDI W and water depth Z. Due to information sharing and strong correlation between tasks, the backbone network can extract features beneficial to both tasks. Second, the feature fusion between the WDI Prediction Branch and the U-Net encoder can be explicitly controlled through the architectural design of the Feature Fusion Module. This structural flexibility enables the model to embed physical priors more systematically.

3.2.3 Feature fusion module

To enhance the model’s ability to capture the complex nonlinear relationship between WDI and water depth, we design a Feature Fusion Module that fuse features from two branches (U-Net backbone branch and WDI prediction branch) at multiple levels. Unlike traditional models that rely on fixed empirical functions (e.g., polynomial or exponential functions), our approach introduces learnable nonlinear relations within the fusion process, enabling the network to flexibly adapt to diverse environmental conditions. By aligning feature representations from the WDI Prediction Branch and the U-Net backbone at corresponding encoder stages, the FFM facilitates the extraction of joint representations that retain both physical interpretability and nonlinear modeling capacity. This design empowers HybridBathNet to generalize effectively across regions with varying bathymetric characteristics. The feature fusion is defined in following formulas:

$$F_{\text{intermediate}}^l=\text{Activation}({\text{Linear}}_1(\text{Concat}(F_Z^l,F_W^l)))$$

$$F_{\text{fused}}^l={\text{Linear}}_2(F_{\text{intermediate}}^l)$$

where $F_Z^l$ and $F_W^l$ are feature maps generated at the same level l by the U-Net backbone and the WDI prediction branch, respectively. The resulting fused features $F_{\text{fused}}^l$ are forwarded as input to the next encoder module (level l + 1) of the backbone network, enabling the progressive integration of multi-modal information throughout the encoding process. In contrast, the WDI prediction branch does not incorporate the fused features, but instead uses the original features $F_W^l$ as input for its subsequent encoder modules. This design ensures that the WDI prediction branch remains focused solely on the task of estimating W.

The relationship between water depth Z and the WDI W, as characterized by physics-based approaches, constitutes a fundamental physical constraint within the domain of SDB. In the proposed HybridBathNet, we explicitly embed this constraint into the network architecture through the Feature Fusion Module. Unlike purely data-driven approaches that rely on the model to infer dependencies in an unconstrained manner, our design imposes a physically motivated structure that explicitly regulates feature relationship across multiple levels. This form of architectural guidance enables the network to learn physically consistent representations more efficiently and mitigates the risk of overfitting, particularly in scenarios with sparse in-situ depth data.

3.3 End-to-end learning procedure

For the prediction of water depth Z and Water Depth Index W, mean squared error (MSE) is adopted as the loss function, given its suitability for regression tasks. The overall training loss is formulated as a weighted sum of the individual losses associated with the two prediction branches (Equations 7–9), enabling joint optimization,

$\begin{array}{ll}\text{MSE}(Z)=\frac{1}{N}\sum _{i=1}^N{(Z_i-{\widehat{Z}}_i)}^2& (7)\end{array}$

$\begin{array}{ll}\text{MSE}(W)=\frac{1}{N}\sum _{i=1}^N{(W_i-{\widehat{W}}_i)}^2& (8)\end{array}$

$\begin{array}{ll}\text{Loss}={\lambda }_1\text{MSE}(Z)+{\lambda }_2\text{MSE}(W)& (9)\end{array}$

where λ₁ and λ₂ are adjustable hyperparameters used to balance the importance of the two tasks. W_i is calculated using the formula from the LBR method (Equation 5).

To account for invalid or missing data in the model input–such as regions where the water depth is out of range, data is unavailable, or the pixel corresponds to a non-water body–we introduce a binary mask matrix to selectively filter these pixels during training (Equation 10). Each element in the mask matrix indicates the validity of the corresponding pixel in the ground truth map, where a value of 0 denotes an invalid (i.e., masked-out) pixel. This mechanism ensures that the loss computation and gradient updates are performed only on valid water pixels:

$\begin{array}{ll}\text{Mask}(m,n)=\{\begin{array}{ll}0,\hfill & \text{if}\hspace{0.33em}y(m,n)=\text{null}\hspace{0.33em}\text{value}\hfill \\ 1,\hfill & \text{if}\hspace{0.33em}y(m,n)\ne \text{null}\hspace{0.33em}\text{value}\hfill \end{array}& (10)\end{array}$

Subsequently, the masked loss is computed by performing an element-wise multiplication between the original loss map and the binary mask matrix, followed by averaging over all valid (unmasked) pixels (Equation 11):

$\begin{array}{ll}Los{s}^{\prime }=\frac{{\displaystyle \sum (Los{s}_{\mathrm{p}\mathrm{i}\mathrm{x}\mathrm{e}\mathrm{l}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}}\odot \mathrm{M}\mathrm{a}\mathrm{s}\mathrm{k})}}{{\displaystyle \sum \mathrm{M}\mathrm{a}\mathrm{s}\mathrm{k}}}& (11)\end{array}$

For the training configuration, the batch size is set to 64. The learning rate is adjusted using a cosine annealing learning rate scheduler, with an initial learning rate of 1 × 10⁻⁴ and a minimum learning rate of 1 × 10⁻⁷. The number of training epochs is set to 50, using the AdamW optimizer. Data augmentation techniques are also applied during training, including vertical flipping, horizontal flipping, and random rotation.

3.4 Model evaluation metrics

To evaluate model performance, we use the following three evaluation metrics commonly used for regression tasks: Root Mean Square Error (RMSE), Mean Absolute Error (MAE), and Coefficient of Determination (R²). These metrics are defined in the following formulas:

$\begin{array}{ll}\text{RMSE}=\sqrt{\frac{1}{N}{\displaystyle \sum _{i=1}^N}{(Z_i-{\widehat{Z}}_i)}^2}& (12)\end{array}$

$\begin{array}{ll}\text{MAE}=\frac{1}{N}\sum _{i=1}^N|Z_i-{\widehat{Z}}_i|& (13)\end{array}$

$\begin{array}{ll}{R}^2=1-\frac{{\sum }_{i=1}^N{(Z_i-{\widehat{Z}}_i)}^2}{{\sum }_{i=1}^N{(Z_i-\overline{Z})}^2}& (14)\end{array}$

Root Mean Square Error (RMSE) quantifies the average magnitude of the error between predicted and observed values, with better sensitivity to larger deviations (Equation 12). Mean Absolute Error (MAE), in contrast, assigns equal weight to all errors (Equation 13). R² represents the proportion of variance in the true values that can be explained by the predicted values (Equation 14). Lower RMSE and MAE values, along with a higher R² value, indicate better model performance in water depth mapping.

4 Results and discussion

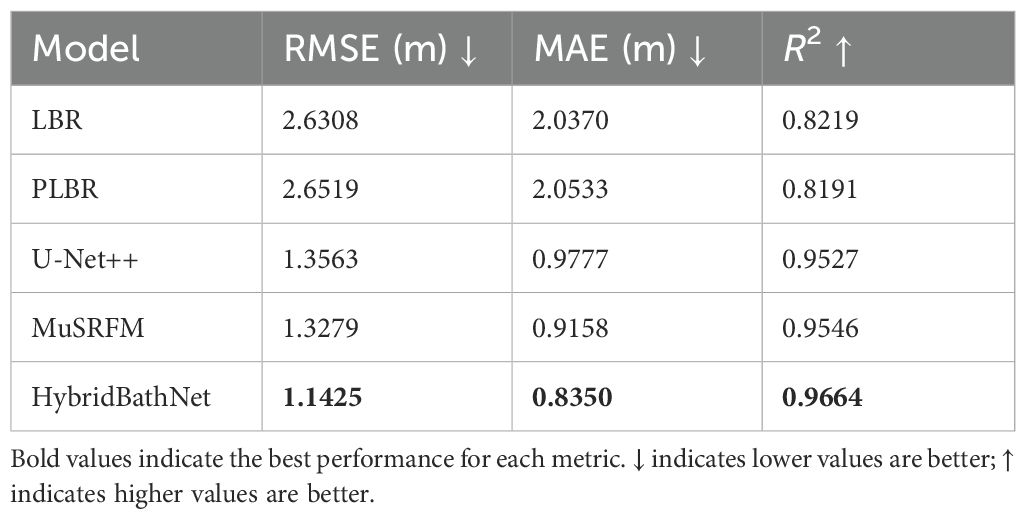
To comprehensively evaluate the performance of HybridBathNet, we reproduced four representative Satellite-Derived Bathymetry (SDB) models as baselines, comprising two classical physics-based approaches and two deep learning-based models. Among the physics-based methods, the Logarithmic Band Ratio (LBR) model has been extensively adopted in prior studies (Stumpf et al., 2003), utilizing the logarithmic ratio of blue and green spectral bands to establish the relationship between spectral reflectance and water depth. The Polynomial Logarithmic Band Ratio (PLBR) model (Han et al., 2023) is regarded as a refinement of the original LBR model, incorporating quadratic terms to capture non-linear relationships and offering improved accuracy in many practical applications. Deep learning-based models have recently gained attention in the field of SDB. U-Net++, an enhanced version of the original U-Net architecture, introduces redesigned skip connections that increase model capacity. Owing to its superior performance in various segmentation tasks, it has also been adopted for SDB applications (Sun et al., 2023). MuSRFM (Qin et al., 2024) is a recent deep learning model specifically designed for SDB, capable of fusing hierarchical features from different ranges, and has shown good fitting accuracy and generalization capability across different regions.

4.1 Results on the test dataset

During model training, we use the constructed training dataset to complete training and parameter calibration, followed by performance evaluation on the test dataset. The prediction results are shown in Table 2. As deep learning models, U-Net++, MuSRFM, and HybridBathNet exhibit training result variations due to randomness; therefore, the results in Table 2 represent the optimal values of the R² metrics obtained from three consecutive repeated experiments. Given the inherent randomness in training deep learning models (U-Net++, MuSRFM and HybridBathNet), the reported results correspond to the best R² values obtained over three consecutive independent runs. The prediction results are masked by the corresponding ground truth water depth images.

Table 2

Table 2. Performance comparison of different models on the test dataset.

The following conclusions can be drawn from the results. First, the LBR and PLBR models, which are entirely physics-based, exhibited relatively lower inversion accuracy, with RMSE values of 2.6308 m and 2.6519 m, respectively. These outcomes indicate that simple linear and polynomial regression models struggle to adequately fit the relationship between surface reflectance and water depth in these complex regions. Second, deep learning-based models significantly outperformed the above two models, with U-Net++ and MuSRFM achieving substantially lower RMSE values of 1.3563 m and 1.3279 m, respectively. Second, deep learning-based models outperform the physics-based models, with U-Net++ and MuSRFM achieving lower RMSE values of 1.3563 m and 1.3279 m, respectively. This improvement can be attributed to the higher model complexity inherent in deep learning architectures, which enables them to more effectively capture the nonlinear relationships between spectral imagery and water depth. Moreover, these deep learning methods are capable of leveraging spatial information embedded in the input imagery, further enhancing their predictive performance. Finally, HybridBathNet achieved a lower RMSE of 1.1425 m, outperforming the other deep learning models. While inheriting the powerful data-driven learning capabilities, HybridBathNet further enhances model interpretability and embeds physical priors, enabling it to learn more robust and generalizable SDB patterns. This advantage is particularly evident given that the training and testing regions are geographically distant and independent.

To provide a more intuitive evaluation of model performance, we further analyze and visualize the prediction results of each SDB model on the test dataset. As shown in Figure 10, the predictions for U-Net++, MuSRFM, and HybridBathNet correspond to the models that achieved the highest R² scores across three repeated experiments. Figures 10a, b, which depict the results of the LBR and PLBR models, are consistent with the quantitative metrics reported in Table 2, exhibiting a relatively scattered distribution between predicted and actual values and a weak alignment along the 1:1 line. In contrast, Figures 10c–e show that deep learning-based methods demonstrate a much tighter fit, with R² values exceeding 0.95. These models exhibit better point density near the 1:1 line and reduced dispersion. As illustrated in Figure 10e, the prediction results of HybridBathNet are more tightly clustered around the 1:1 reference line, with a noticeably lower frequency of large-error outliers compared to the other two deep learning models. This indicates a more compact and accurate prediction distribution, highlighting HybridBathNet’s robustness and reliability in water depth estimation. For all three deep learning models, notable prediction errors emerge when the actual water depth exceeds 24 meters. This can be attributed to two primary factors: first, the quality of satellite multispectral imagery degrades with increasing depth due to water turbidity; second, the number of training samples within this depth range is substantially lower, limiting the models’ ability to capture the complex relationship between spectral reflectance and water depth. As shown in Figure 11, the variance of residuals clearly increases beyond 24 meters, indicating greater uncertainty in model predictions. Additionally, in regions where the depth exceeds 7 meters, HybridBathNet tends to slightly overestimate the true values. A possible explanation is that, due to the relatively smaller sample size in deeper waters, the physical prior introduced via the Feature Fusion Module exerts a stronger influence during training, leading to a slight bias in the predicted values.

Figure 10

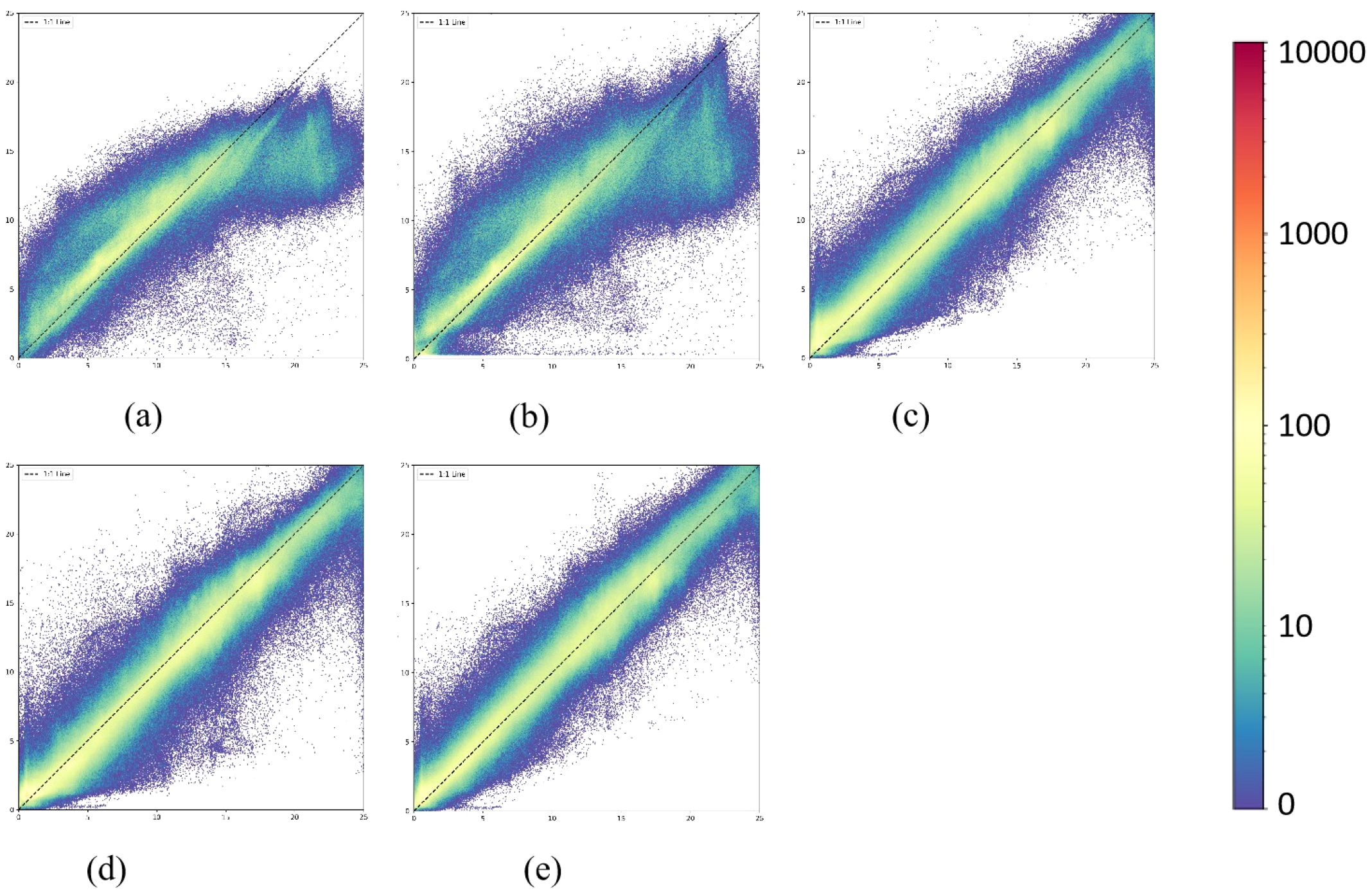
Figure 10. Density scatter plots of the models used on the test dataset: (a) LBR, (b) PLBR, (c) UNet++, (d) MuSRFM and (e) HybridBathNet.

Figure 11

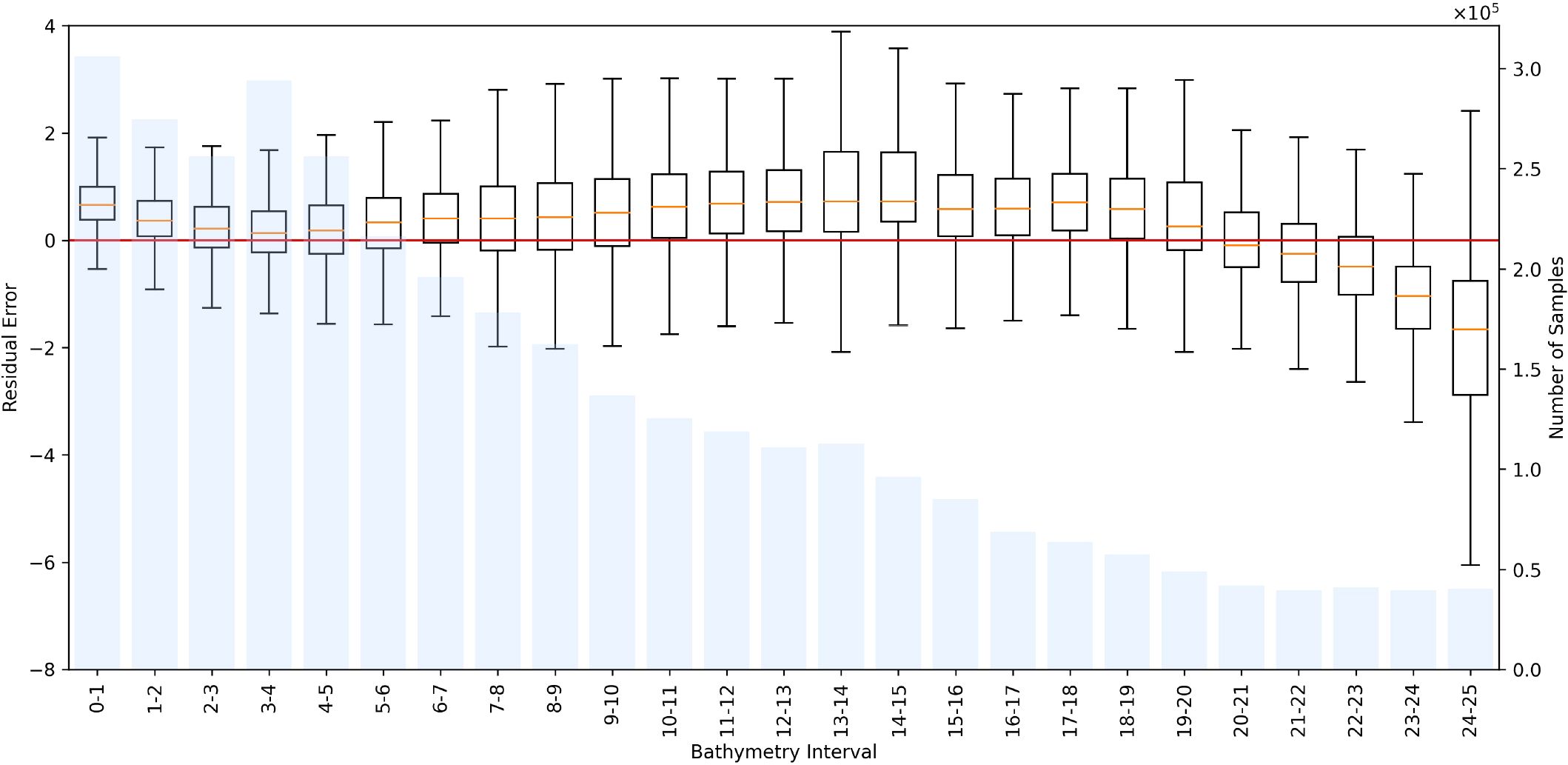
Figure 11. Distribution of residual errors of HybridBathNet and the number of training samples in bathymetric intervals with a range of 1 m on the test dataset.

Figure 12 displays the bathymetry maps obtained by inverting the surface reflectance imagery from the test dataset. As shown in Figure 13, for non-deep learning models, their bathymetry maps show significant influence from pulse noise compared to the ground truth water depth, with obvious numerous point anomalies and poor spatial continuity. These models have receptive fields limited to individual pixels and cannot capture spatial information in the input imagery. Consequently, they can only map relationships between individual pixels and their corresponding water depths. Deep learning-based models can capture richer spatial features, have a broader feature perception ability, and produce smoother bathymetry maps in similar areas that more closely resemble the actual images. Since deep learning models predict based on individual image patches, the inverted bathymetry maps from these models are noticeably affected by the boundaries of each patch, with relatively obvious prediction depth scale differences between adjacent image patches, while physics-based inversion methods are not affected by this. It can be clearly seen in Figure 14 that the inverted images from U-Net++ and MuSRFM exhibit grid-like patterns, which is determined by the input-output format of model training and prediction. Although HybridBathNet’s output water depth inversion map still has visible grid errors due to its use of a physical network, the errors are significantly smaller than those of the other two deep learning models. This is because for boundary regions of cropped images, although HybridBathNet’s backbone model struggles to capture effective global and local spatial features, the physical network is not limited by spatial position, allowing HybridBathNet to perform better in these boundary regions than other models that rely solely on deep learning networks.

Figure 12

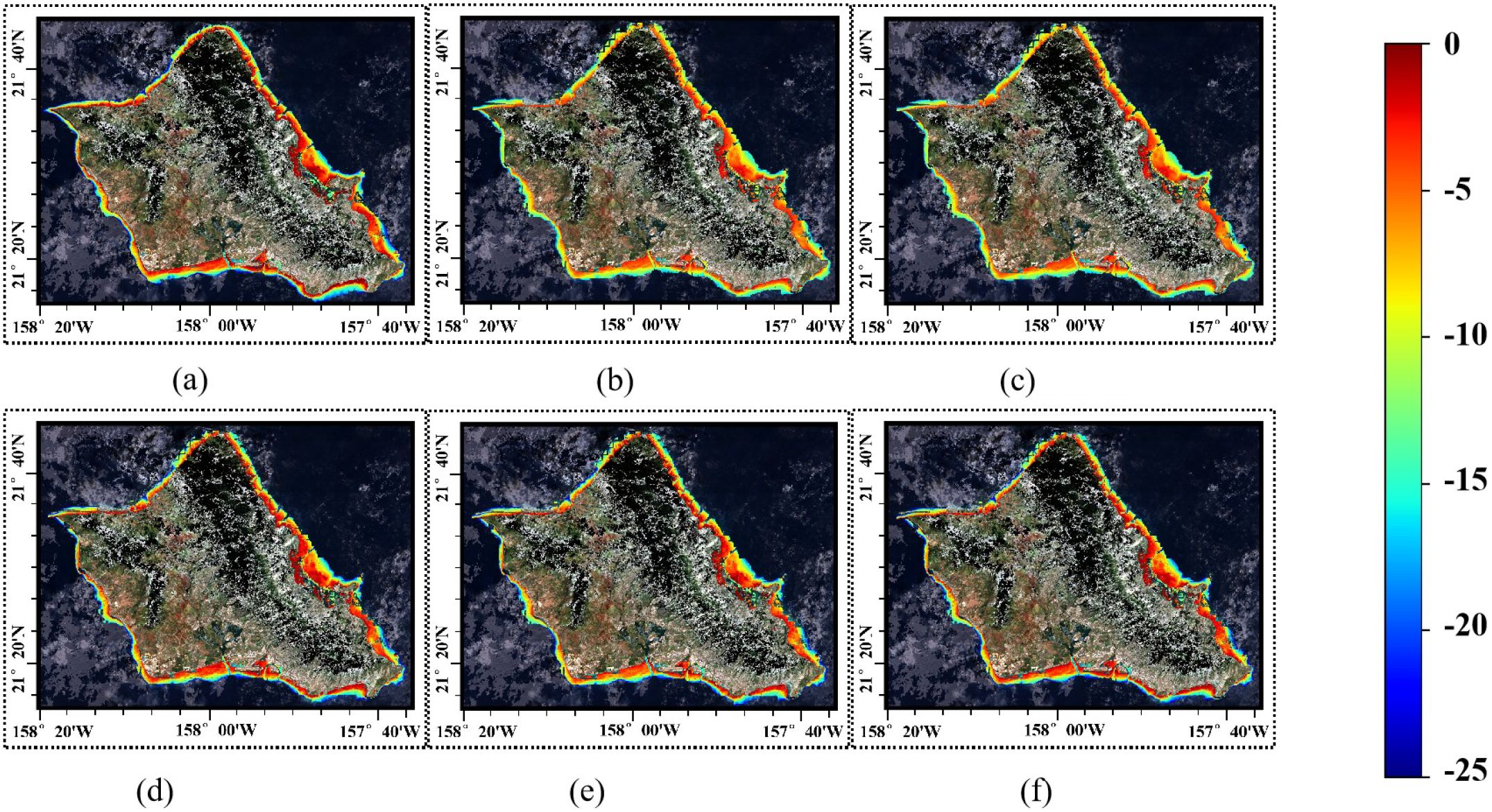
Figure 12. The bathymetry maps of the testing dataset area, which are (a) GT, (b) LBR, (c) PLBR, (d) UNet++, (e) MuSRFM and (f) HybridBathNet.

Figure 13

Figure 13. The bathymetry map details of the northeastern part of the testing dataset. (a) Ground truth, (b) LBR method, (c) PLBR method, (d) UNet++ method, (e) MuSRFM method, (f) HybridBathNet (our proposed method).

Figure 14

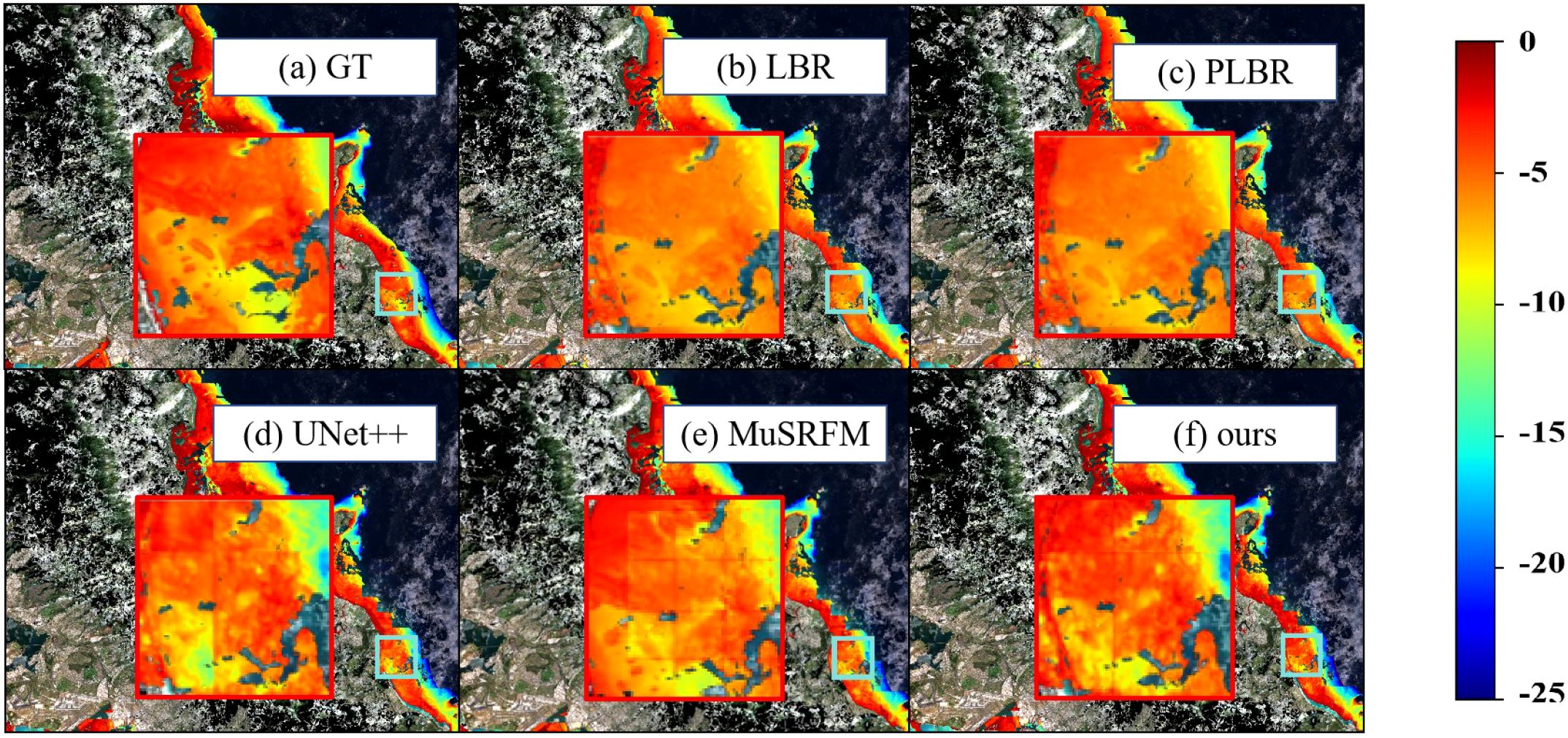
Figure 14. The bathymetry map details of the southeastern part of the testing dataset. (a) Ground truth, (b) LBR method, (c) PLBR method, (d) UNet++ method, (e) MuSRFM method, (f) HybridBathNet (our proposed method).

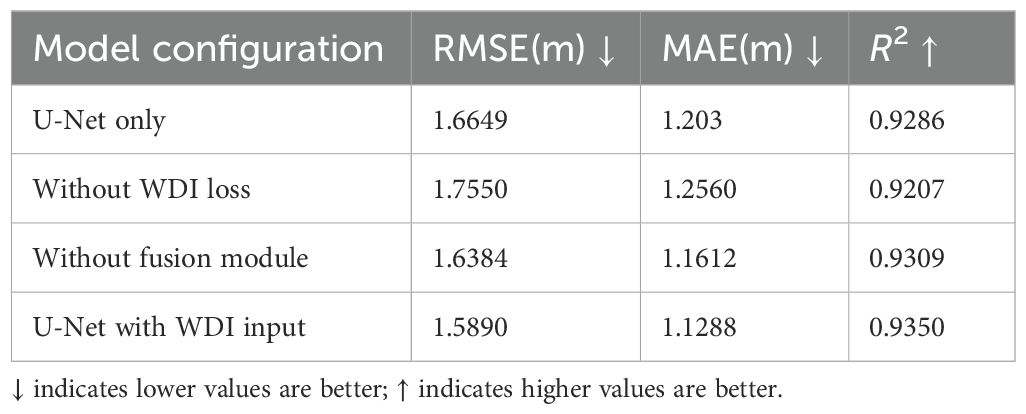
4.2 Ablation study results

The ablation experiments presented here aim to evaluate the contribution of each HybridBathNet component to its overall accuracy. As shown in Figure 8, HybridBathNet can be roughly divided into two components: the backbone network and the physical network(including the WDI prediction branch and the Feature Fusion Module). Accordingly, we designed four ablation experiments:

1. Retaining only the backbone network, completely removing the WDI prediction branch (U-Net only).

2. Retaining the WDI branch but using only simple feature concatenation, without the Feature Fusion Module (without fusion module).

3. Retaining the WDI branch and Feature Fusion Module but not using loss constraints on the WDI (without WDI loss).

4. Retaining only the backbone network and directly inputting the WDI W as a channel to the model (U-Net with W input).

Similar to the previous experiments, the highest metrics were obtained through three consecutive repeated experiments to objectively evaluate each sub-model in the ablation study.

The ablation experiment results in Table 3 confirm the effectiveness of our physical network. After removing the WDI prediction branch from HybridBathNet, it degraded to the backbone U-Net structure, and its average root mean square error substantially increased from 1.1425 m to 1.6649 m. Similarly, the model that retained the WDI branch and Feature Fusion Module but did not use loss constraints on the WDI (Without WDI loss) showed similar metrics, with a root mean square error of 1.7550 m. This is because without using loss to constrain the WDI, HybridBathNet’s physical network cannot be properly trained, demonstrating the effectiveness of the WDI prediction branch in HybridBathNet. Additionally, replacing the Feature Fusion Module with simple feature concatenation (Without fusion module) increased the root mean square error to 1.6384 m, while directly inputting the WDI W into the model (U-Net with WDI input) resulted in a root mean square error of 1.5890 m. This indicates that the Feature Fusion Module performs deeper integration of the WDI and backbone network features at the feature level, verifying its effectiveness.

Table 3

Table 3. Ablation study results for HybridBathNet components.

4.3 Results on the real-world datasets

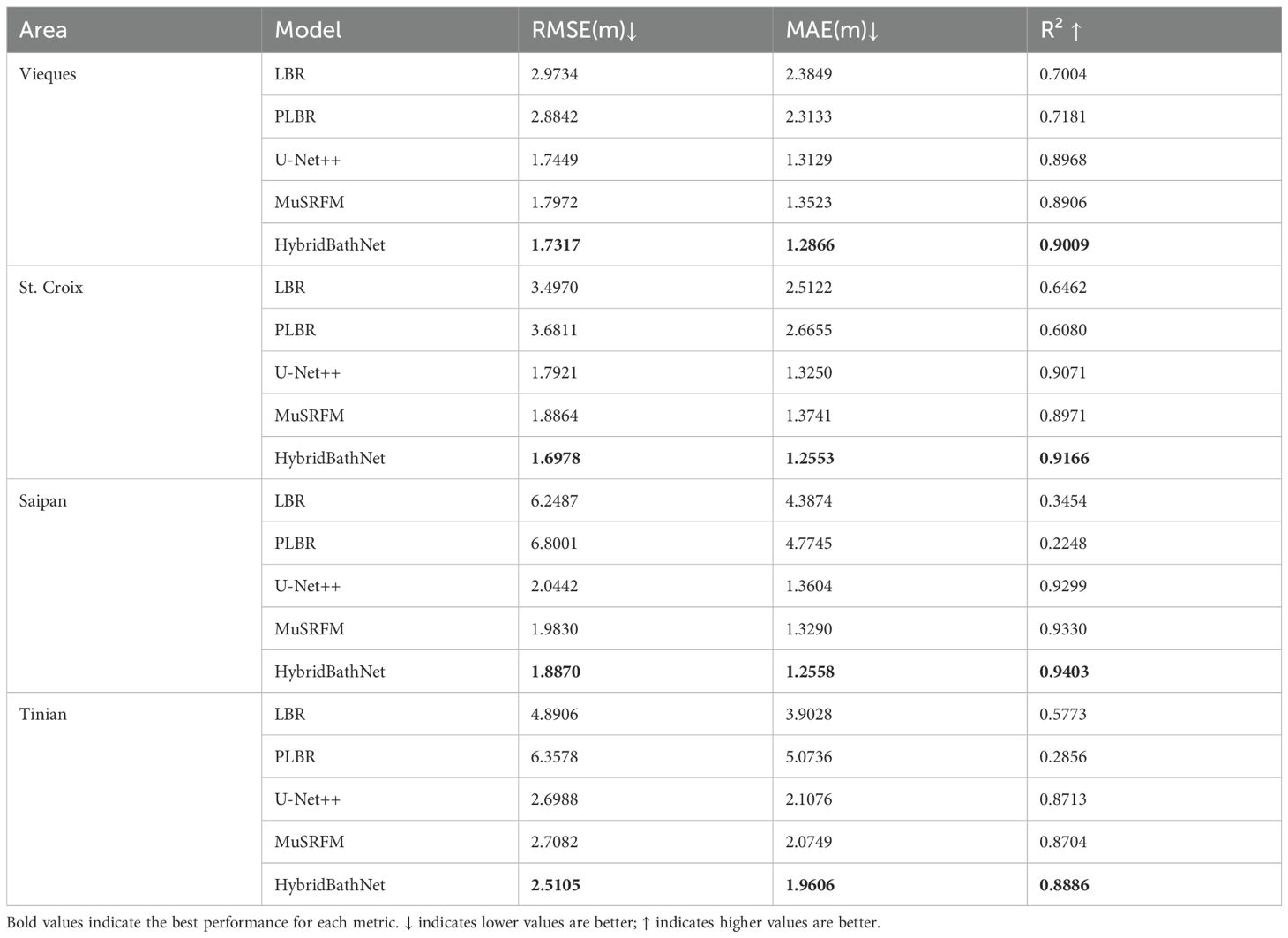
The real-world dataset consists of data from four different study areas, with detailed descriptions of their sources and various characteristics in Section 2.3. The purpose of using an extensive real-world dataset is to evaluate the performance of satellite-derived bathymetry models across a broader range, assessing their generalization and transfer capabilities in different regions, which cannot be fully represented by the data features of a limited test dataset. The HybridBathNet model used in this section is likewise the model with the best R² metric from three experiments. Table 4 presents the inference results of various satellite-derived bathymetry models on the real-world dataset.

Table 4

Table 4. Performance comparison of different models across various areas in the real-world dataset.

Overall, HybridBathNet outperformed the other four satellite-derived bathymetry models across all four study areas. In general, the inversion accuracy of each model showed a certain degree of decline in other regions, as the data distribution in different islands differs notably from that of Oahu Island. In the Saipan Island and Tinian Island regions, the LBR and PLBR models were almost ineffective; in terms of optical properties, the waters around these two islands differ significantly from those of Oahu Island, making simple linear fitting almost inapplicable in these regions. St. Croix Island and Vieques Island have far more usable data than the first two islands and more complex topography, yet the LBR and PLBR performed better in these two regions than in the Saipan and Tinian. Deep learning models still far outperformed physics-based methods on these islands because deep learning models can learn more complex and deeper connections between water depth and satellite imagery, maintaining good generalization despite significant topographical differences. Compared to other deep learning models, HybridBathNet also demonstrated a clear advantage in R².

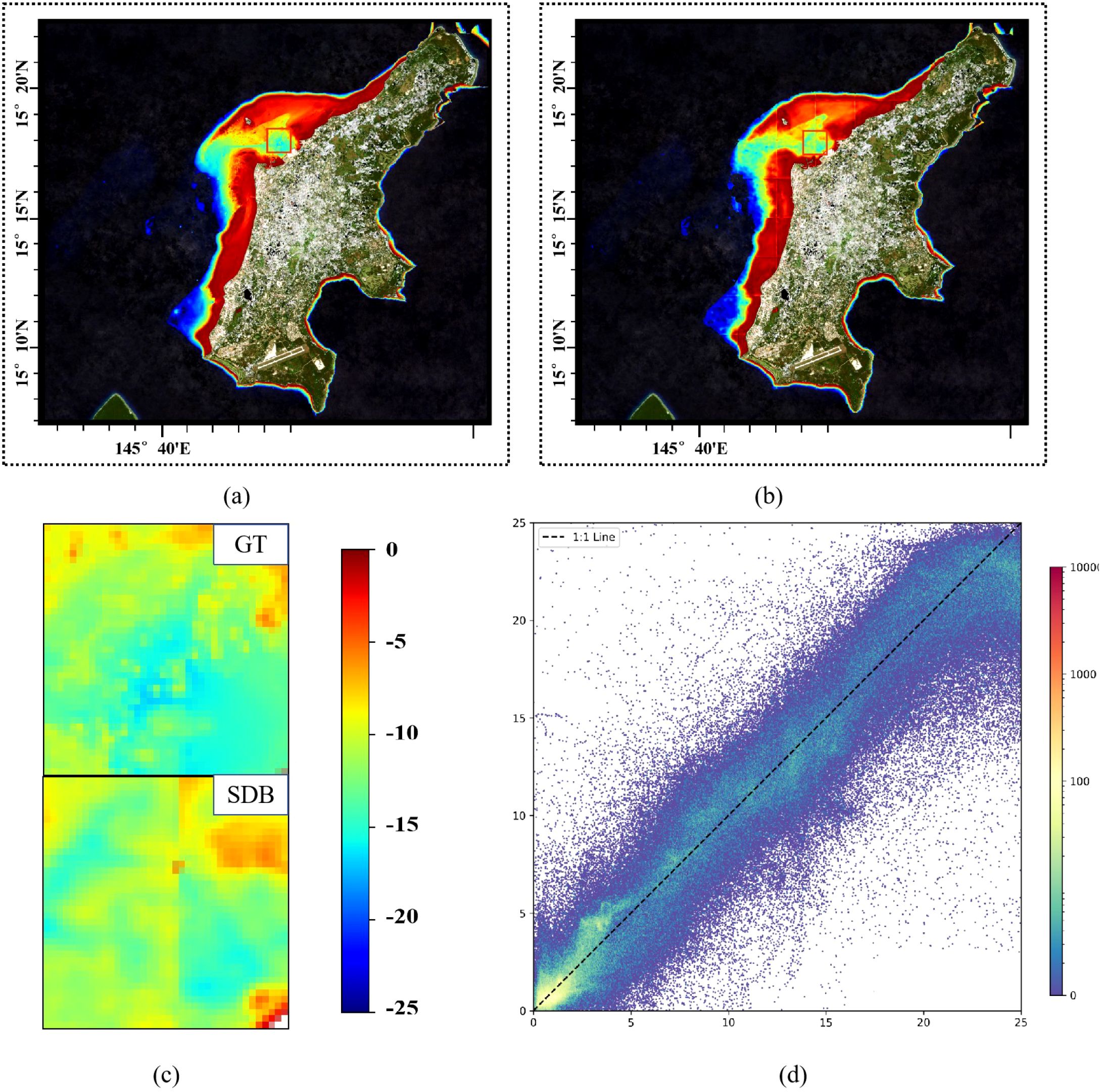
As shown in Figures 15, 16, in the inverted images of Saipan Island and Tinian Island, grid-like water depth inversion errors became evident again, further indicating that the waters of these two islands differ significantly in optical properties from the training region. However, compared to the almost complete failure of LBR and PLBR, HybridBathNet’s performance in these two regions still remained ahead of other deep learning models. This is because the fusion mode of bathymetric imagery and Water Depth Index W at the feature level, learned by the Feature Fusion Module, is not limited to simple linear or quadratic relationships but can adjust to some extent based on the data. This allows the physical network to still play a role in the water depth inversion process. As shown in Figure 16, there is a large lagoon on the northwest side of Saipan Island, a topography that did not appear in the training data. Facing this abrupt topographical environment, HybridBathNet’s performance in the bathymetry map still did not differ much from the ground truth data. However, there is a port on the southwest side of Tinian Island, a topography that also did not appear in the training data, with even greater topographical changes. HybridBathNet’s inversion results here are deficient, with a more obvious underestimation of water depth. As can also be seen in Figure 15, in these steep slope topographies (referring to Tinian), the model underestimates the water depth across the entire area.

Figure 15

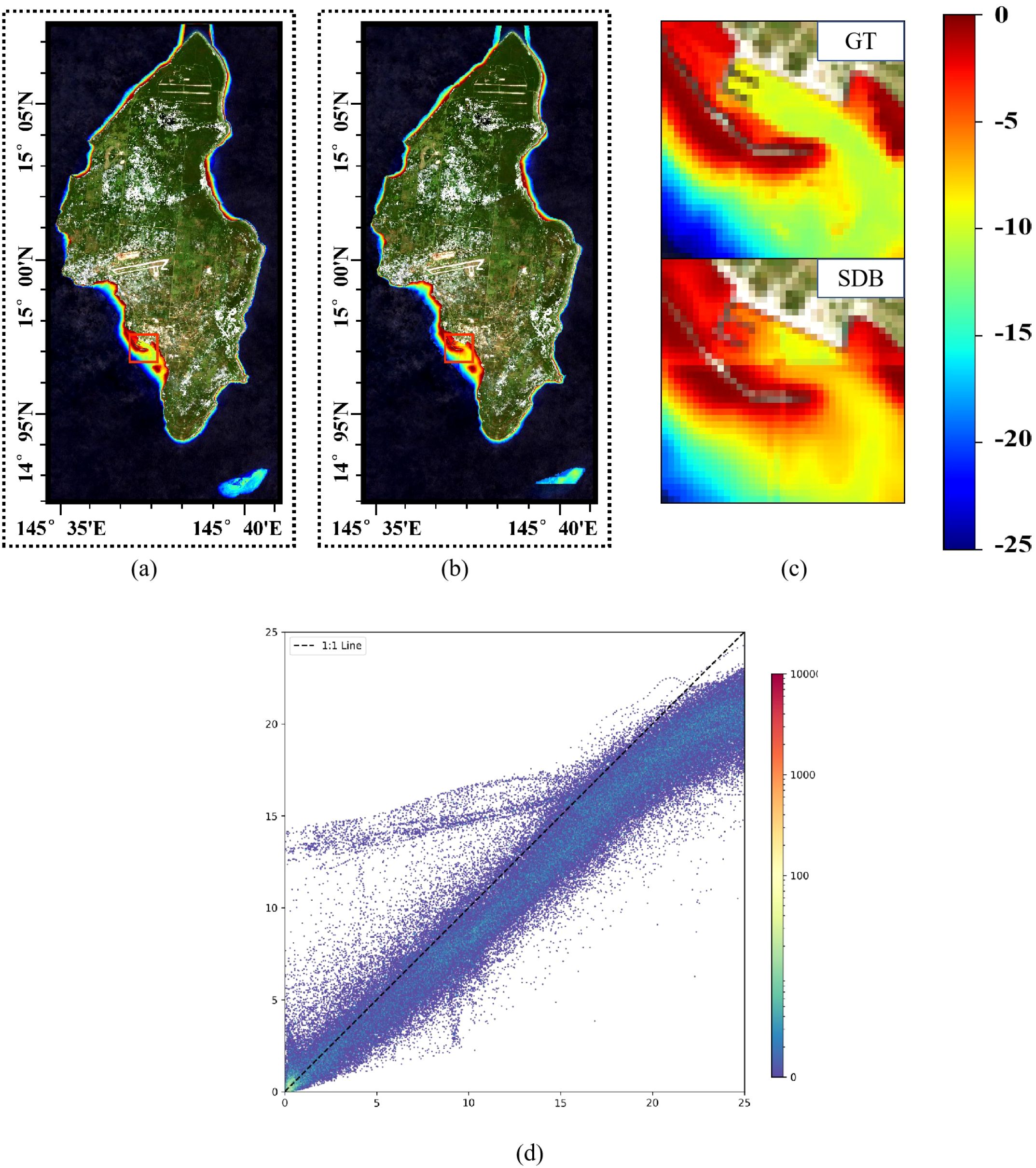
Figure 15. The bathymetry maps of the Tinian area. (a) Ground truth bathymetry map for the entire island, (b) SDB prediction for the entire island, (c) Local enlarged view showing detailed comparison between GT and SDB results, (d) Density scatter plot of HybridBathNet predictions on the test dataset.

Figure 16

Figure 16. The bathymetry maps of the Saipan area.

As shown in Figure 17, for Vieques Island, HybridBathNet has high inversion accuracy for medium-depth areas near the coast, but for deep-water areas farther from the island, the model tends to overestimate water depth. This occurs because marine areas farther from land appear differently in satellite imagery and are also affected differently by factors such as ocean waves. Additionally, the lower proportion of deep water data in the training dataset is another reason for the model’s insufficient accuracy in deep water areas. In the beach areas on the western side of Vieques, HybridBathNet significantly underestimates water depth in some areas. We believe this may occur because the U-Net backbone network, when capturing surrounding spatial information, is influenced by the beach and nearby shallow water areas. Additionally, the water around Vieques Island is clearer compared to the training area, which may also cause the model to misjudge water depth.

Figure 17

Figure 17. The bathymetry maps of the Vieques area.

In St. Croix Island, as shown in Figure 18, since its geographical location is close to Vieques Island and the topography is very similar, there are similar errors in the inversion for deeper and shallower waters. As shown in Figure 18 (referring to details within the St. Croix map), also for waters farther from land, HybridBathNet’s inversion results show significantly smaller errors in medium-depth areas than in deep-water areas. This further validates the possibility that the error is attributable to the non-uniform distribution of training data.

Figure 18

Figure 18. The bathymetry maps of the St. Croix area.

After evaluating the SDB models on the real-world dataset, it can be seen that HybridBathNet not only outperforms traditional physics-based models in terms of accuracy and generalization but also surpasses other deep learning models. These experimental results confirm the superiority of the HybridBathNet architecture and the feasibility of introducing physical knowledge into deep learning architectures.

4.4 Experimental results under varying sample sizes

In practical applications of bathymetric inversion, another important factor limiting inversion accuracy is the sample size of training data. For most regions, only limited in-situ data can be obtained, making models that can achieve good performance with minimal in-situ training data of higher practical value. To simulate such scenarios, we randomly masked 90% of the data in the Oahu Island training set, retaining only 10% of the original effective data, and then retrained the models to observe their performance. In the specific experiments, we first obtained the mask matrix representing valid value positions, then randomly invalidated 90% of the points, and applied the new mask matrix to the training data. The model results used in this section represent the average performance across three repetitions of the above experiments. Table 5 shows the experimental results of various Satellite-Derived Bathymetry models under varying sample sizes.

Table 5

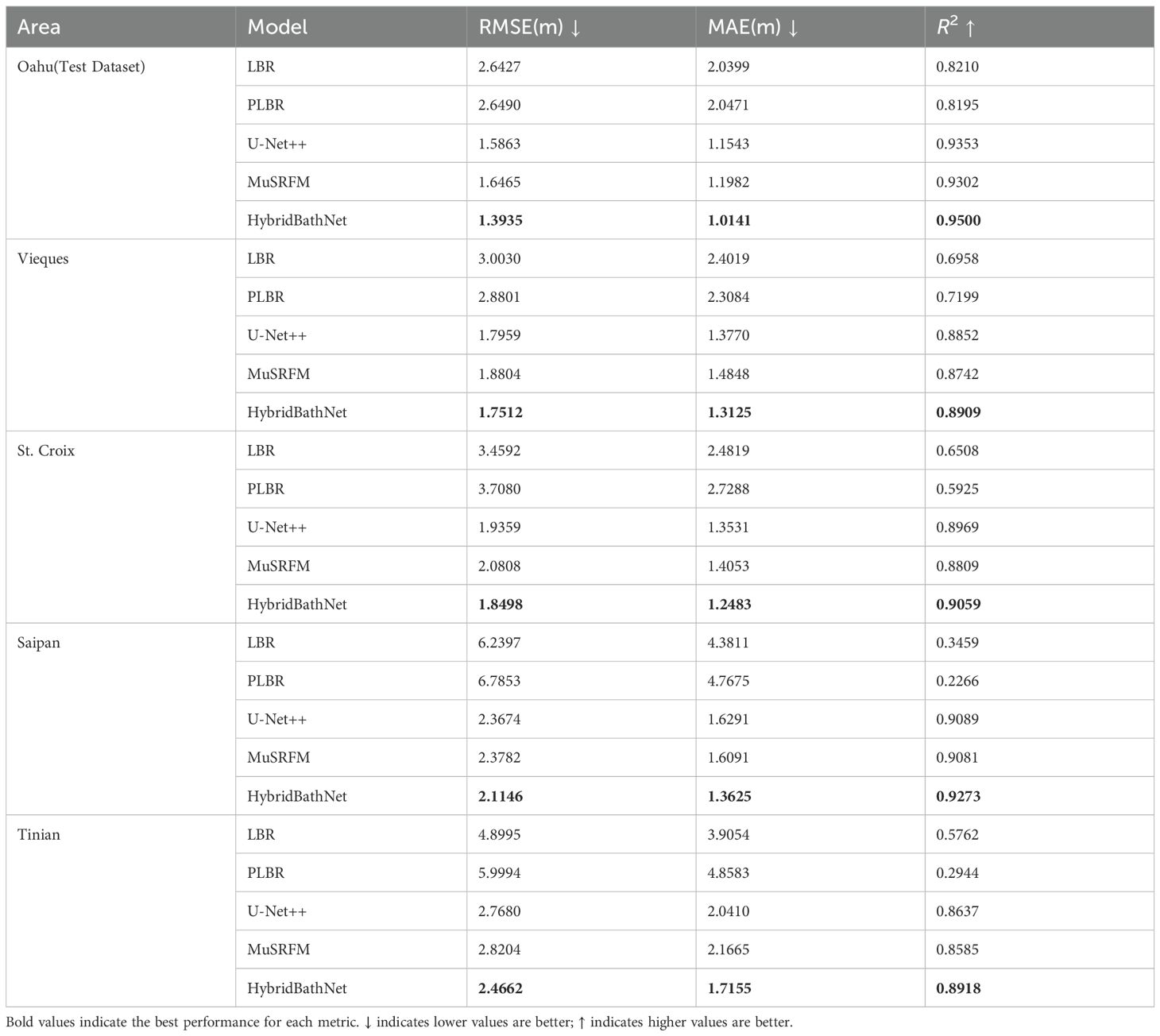
Table 5. Performance comparison of different models under reduced training sample size (10% of original data).

First, when using only 10% of the training data, the LBR and PLBR models showed virtually no change in performance on both the test dataset and real-world datasets. The essence of these models is polynomial fitting, and their results depend only on the statistical distribution of the data. Since the training data contains samples on the order of millions, the randomly sampled 10% of training data maintains a distribution consistent with the original training data. For deep learning-based models, U-Net++ and MuSRFM showed varying degrees of performance degradation across all test regions, as these data-driven models are more sensitive to training sample size. Notably, when using fewer training samples, these two deep learning models experienced the most significant performance decline on Saipan Island data, where they originally performed well, with R² decreases of 0.0210 and 0.0249, respectively. This may be attributed to the reduced ability to fit diverse terrains after retaining only limited in-situ data, and the learned spatial dependencies were also affected due to significantly sparser training data. These two deep learning models also showed obvious performance degradation on the Oahu test dataset, with R² decreases of 0.0174 and 0.0244, respectively. This further confirms that the models cannot learn some originally learnable complex terrains under sparse data conditions.

Compared to U-Net++ and MuSRFM, although HybridBathNet was also affected when using less data, its performance across all metrics was significantly superior to these two deep learning models. Unlike the previous two models, the region where HybridBathNet experienced the most performance decline was the Oahu test dataset, with R² decrease of 0.0164, yet even the degraded metrics approached the results of the other two models using full data. This is because the Physical Bathymetry Network in HybridBathNet, as a physics-constrained network, can exhibit characteristics similar to LBR and PLBR, maintaining higher stability when sample size is significantly reduced. Notably, when using only 10% of the training data, HybridBathNet’s performance metrics on Tinian Island actually showed slight improvement. This may be because some complex terrains in Tinian Island waters differ significantly from Oahu Island, and with significantly reduced in-situ data, the U-Net-based backbone of HybridBathNet was less influenced by the complex terrain of Oahu Island, resulting in slightly improved inversion accuracy for similar terrains between the two islands, while the physical constraints of the Physical Bathymetry Network ensured no significant errors occurred in complex terrain areas.

Overall, when the sample size of training data was significantly reduced, HybridBathNet demonstrated better performance compared to other deep learning models, benefiting from the stability provided by physics-based constraints. The experimental results indicate that for regions where only limited training data can be obtained, the physics-guided architecture of HybridBathNet exhibits better generalizability than purely data-driven models.

5 Discussion

Although HybridBathNet performs well in most regions and exhibits good generalization for seabed conditions not encountered in the training set, it still has some limitations in areas with significant topographical differences from the training set. For instance, in regions such as the port of Tinian Island, the effectiveness of the physical network is compromised due to substantial differences in topography and optical properties compared to the training areas. In contrast, in areas where the geographical and optical characteristics are broadly consistent with the training set, the integration of physical priors markedly improves model performance. For example, the waters surrounding Oahu Island used for training are characterized by clear water conditions, with extensive coral reef coverage on the eastern side of the island. The water quality around Vieques Island and St. Croix Island is very similar to that of Oahu Island, featuring uniformly smooth underwater topography, clear water, and minimal terrestrial suspended matter, resulting in good inversion accuracy in both regions. The western side of Saipan Island contains a lagoon formed by coral debris. Although this topographical feature was not present in the training set, the optical properties of the water body in this area are similar to those in the training set, resulting in considerable prediction accuracy in this region. For Tinian Island, despite its geographical proximity to Saipan Island, the surrounding marine terrain is quite steep with numerous artificial structures and relatively turbid water, which has affected prediction accuracy to some extent.

Notably, in the training data from the waters surrounding Oahu Island, regions with water depths exceeding 23 meters comprise only a small proportion of the dataset. Despite this, the model maintains relatively high inversion accuracy for deep-water zones. The experimental results in the Experimental Results Under Varying Sample Sizes section also demonstrate that when using only 10% of the training data, HybridBathNet actually showed slight improvement in inversion accuracy on Tinian Island compared to using the full dataset. This suggests that physics-guided deep learning models such as HybridBathNet may achieve effective generalization to new, yet similar, environments even with limited training data. In future research, we will continue to explore the generalization capabilities of HybridBathNet on diverse seabed conditions under conditions of extremely limited in-situ data. Meanwhile, for marine areas with geographical and optical characteristics that differ significantly from the training regions, physics-guided models may achieve high inversion accuracy with only minimal in-situ data for fine-tuning alignment.

Furthermore, HybridBathNet’s backbone network and the physical network module both have high requirements for the quality of input multispectral satellite imagery. In this study, several pixels on the northern and western coasts of Oahu Island–the region used for model training–were partially obscured by shadows. Although preprocessing steps such as applying the Scene Classification Layer and the Quality.

Assessment Layer were employed on the Sentinel-2 imagery, residual noise likely remained. This could have, to some extent, affected HybridBathNet’s performance during training. In similar seabed conditions, data denoising continues to present a persistent challenge in the SDB domain. Additionally, Sentinel-2 data has a spatial resolution of 10 m, while the ALB data used as in-situ data in the dataset has a spatial resolution of 1 m. The downsampling process for resolution alignment results in a loss of ALB data precision, which also affects model performance. Addressing this issue may require not only the development of more advanced denoising techniques to ensure higher-quality datasets but also efforts to improve the model’s robustness against noisy or imperfect inputs.

6 Conclusion

In this study, we proposed HybridBathNet, a novel physics-guided deep learning framework for bathymetric inversion that integrates domain-specific physical constraints directly into the network architecture. To our knowledge, this represents the first attempt to explicitly embed physical priors within a deep neural model for Satellite-Derived Bathymetry (SDB). By coupling the representational power of CNNs with water depth index from reflectance through a dedicated physical network module, HybridBathNet not only improves predictive accuracy but also enhances generalization and interpretability. Experimental results demonstrate that HybridBathNet consistently outperforms both traditional physics-based models and purely data-driven deep learning models in terms of accuracy (as measured by RMSE) and reliability (as measured by R²), across both training and geographically distinct testing regions. These results underscore the potential and effectiveness of incorporating physical knowledge into deep learning frameworks for SDB.

While HybridBathNet demonstrates notable generalization capability in regions beyond the training area, its performance may still degrade in environments with extreme topographical and optical differences compared to the training set. Future research should further investigate the generalization capacity of our model under conditions of scarce in-situ data. Moreover, like most SDB models, HybridBathNet relies heavily on the quality of input multispectral satellite imagery. Persistent noise-particularly in areas affected by shadows, atmospheric effects, or water turbidity-can compromise model performance. Thus, developing more advanced denoising techniques or designing models with enhanced robustness to noisy inputs presents an important direction for future work.

Data availability statement

The dataset combines publicly available data sources: 1. Sentinel-2 L2A Surface Reflectance data - Freely available through Google Earth Engine under the Copernicus Programme terms of use; 2. NOAA Airborne LiDAR Bathymetry (ALB) data - Publicly accessible through NOAA’s Data Access Viewer (https://coast.noaa.gov/dataviewer/) under NOAA’s data usage policies. Dataset is specific to five island regions (Oahu, St. Croix, Vieques, Saipan, and Tinian). Requests to access the datasets should be directed to SQ, bGx5eW1ybEBnbWFpbC5jb20=.

Author contributions

SQ: Writing – original draft, Validation, Data curation. YC: Writing – original draft, Data curation. WW: Writing – original draft, Writing – review & editing. GZ: Writing – review & editing. LL: Writing – review & editing. ZH: Writing – review & editing. YW: Writing – review & editing.

Funding

The author(s) declare financial support was received for the research and/or publication of this article. This work is supported by National Natural Science Foundation of China under grants 62076232 and 62172049.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ai B., Wen Z., Wang Z., Wang R., Su D., Li C., et al. (2020). Convolutional neural network to retrieve water depth in marine shallow water area from remote sensing images. IEEE J. Selected Topics Appl. Earth Observations Remote Sens. 13, 2888–2898.

Google Scholar

Beucler T., Rasp S., Pritchard M., and Gentine P. (2019). Achieving conservation of energy in neural network emulators for climate modeling. arXiv preprint arXiv:1906.06622.

Google Scholar

Bochkovskiy A., Wang C.-Y., and Liao H.-Y. M. (2020). Yolov4: Optimal speed and accuracy of object detection. arXiv preprint arXiv:2004.10934.

Google Scholar

Cahalane C., Magee A., Monteys X., Casal G., Hanafin J., and Harris P. (2019). A comparison of landsat 8, rapideye and pleiades products for improving empirical predictions of satellite-derived bathymetry. Remote Sens. Environ. 233, 111414.

PubMed Abstract | Google Scholar

Chen Y., Le Y., Wu L., Li S., and Wang L. (2022). An assessment of waveform processing for a single-beam bathymetric lidar system (sbls-1). Sensors 22, 7681.

PubMed Abstract | Google Scholar

Chen Y., Le Y., Zhang D., Wang Y., Qiu Z., and Wang L. (2021). A photon-counting lidar bathymetric method based on adaptive variable ellipse filtering. Remote Sens. Environ. 256, 112326.

Google Scholar

Chollet F. (2017). “Xception: Deep learning with depthwise separable convolutions,” in Proceedings of the IEEE conference on computer vision and pattern recognition. 1251–1258.

Google Scholar

Constantinoiu L.-F., Tavares A., Cândido R. M., and Rusu E. (2024). Innovative maritime uncrewed systems and satellite solutions for shallow water bathymetric assessment. Inventions 9, 20.

Google Scholar

Daw A., Karpatne A., Watkins W. D., Read J. S., and Kumar V. (2022). “Physics-guided neural networks (pgnn): An application in lake temperature modeling,” in Knowledge guided machine learning (Chapman and Hall/CRC), 353–372.

Google Scholar

Degnan J. J. (2002). Photon-counting multikilohertz microlaser altimeters for airborne and spaceborne topographic measurements. J. Geodynamics 34, 503–549.

Google Scholar

de Moustier C. (1988). State of the art in swath bathymetry survey systems.

Google Scholar

Duan Z., Chu S., Cheng L., Ji C., Li M., and Shen W. (2022). Satellite-derived bathymetry using landsat-8 and sentinel-2a images: assessment of atmospheric correction algorithms and depth derivation models in shallow waters. Optics Express 30, 3238–3261.

PubMed Abstract | Google Scholar

Evagorou E., Argyriou A., Papadopoulos N., Mettas C., Alexandrakis G., and Hadjimitsis D. (2022). Evaluation of satellite-derived bathymetry from high and medium-resolution sensors using empirical methods. Remote Sens. 14, 772.

Google Scholar

Hamilton M. K., Davis C. O., Rhea W. J., Pilorz S. H., and Carder K. L. (1993). Estimating chlorophyll content and bathymetry of lake tahoe using aviris data. Remote Sens. Environ. 44, 217–230.

Google Scholar

Han T., Zhang H., Cao W., Le C., Wang C., Yang X., et al. (2023). Cost-efficient bathymetric mapping method based on massive active–passive remote sensing data. ISPRS J. Photogrammetry Remote Sens. 203, 285–300.

Google Scholar

Hsu H.-J., Huang C.-Y., Jasinski M., Li Y., Gao H., Yamanokuchi T., et al. (2021). A semi-empirical scheme for bathymetric mapping in shallow water by icesat-2 and sentinel-2: A case study in the south China sea. ISPRS J. Photogrammetry Remote Sens. 178, 1–19.

Google Scholar

Immitzer M., Vuolo F., and Atzberger C. (2016). First experience with sentinel-2 data for crop and tree species classifications in central europe. Remote Sens. 8, 166.

Google Scholar

Jagalingam P., Akshaya B., and Hegde A. V. (2015). Bathymetry mapping using landsat 8 satellite imagery. Proc. Eng. 116, 560–566.

Google Scholar

Le Y., Hu M., Chen Y., Yan Q., Zhang D., Li S., et al. (2022). Investigating the shallow-water bathymetric capability of zhuhai-1 spaceborne hyperspectral images based on icesat-2 data and empirical approaches: A case study in the south China sea. Remote Sens. 14, 3406.

Google Scholar

Lee Z., Shang S., Qi L., Yan J., and Lin G. (2016). A semi-analytical scheme to estimate secchi-disk depth from landsat-8 measurements. Remote Sens. Environ. 177, 101–106.

Google Scholar

Lyzenga D. R. (1978). Passive remote sensing techniques for mapping water depth and bottom features. Appl. optics 17, 379–383.

PubMed Abstract | Google Scholar

Lyzenga D. R. (1981). Remote sensing of bottom reflectance and water attenuation parameters in shallow water using aircraft and landsat data. Int. J. Remote Sens. 2, 71–82.

Google Scholar

Mandlburger G., Kölle M., Nübel H., and Soergel U. (2021). Bathynet: A deep neural network for water depth mapping from multispectral aerial images. PFG–Journal Photogrammetry Remote Sens. Geoinformation Sci. 89, 71–89.

Google Scholar

Manessa M. D. M., Kanno A., Sekine M., Haidar M., Yamamoto K., Imai T., et al. (2016). Satellitederived bathymetry using random forest algorithm and worldview-2 imagery. Geoplanning: J. Geomatics Plann. 3, 117.

Google Scholar

Mateo-Pérez V., Corral-Bobadilla M., Ortega-Fernández F., and Vergara-González E. P. (2020). Port bathymetry mapping using support vector machine technique and sentinel-2 satellite imagery. Remote Sens. 12, 2069.

Google Scholar

Misra A., Vojinovic Z., Ramakrishnan B., Luijendijk A., and Ranasinghe R. (2018). Shallow water bathymetry mapping using support vector machine (svm) technique and multispectral imagery. Int. J. Remote Sens. 39, 4431–4450.

Google Scholar

Niroumand-Jadidi M., Bovolo F., and Bruzzone L. (2020). Smart-sdb: Sample-specific multiple band ratio technique for satellite-derived bathymetry. Remote Sens. Environ. 251, 112091.

Google Scholar

Philpot W. D. (1989). Bathymetric mapping with passive multispectral imagery. Appl. optics 28, 1569–1578.

PubMed Abstract | Google Scholar

Qin X., Wu Z., Luo X., Shang J., Zhao D., Zhou J., et al. (2024). Musrfm: Multiple scale resolution fusion based precise and robust satellite derived bathymetry model for island nearshore shallow water regions using sentinel-2 multi-spectral imagery. ISPRS J. Photogrammetry Remote Sens. 218, 150–169.

Google Scholar

Raissi M., Perdikaris P., and Karniadakis G. E. (2019). Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 378, 686–707.

Google Scholar

Ronneberger O., Fischer P., and Brox T. (2015). U-net: Convolutional networks for biomedical image segmentation. Springer. p. 234–241.

Google Scholar

Spoto F., Sy O., Laberinti P., Martimort P., Fernandez V., Colin O., et al. (2012). “Overview of sentinel-2,” in 2012 IEEE international geoscience and remote sensing symposium (IEEE). 1707–1710.

Google Scholar

Stumpf R. P., Holderied K., and Sinclair M. (2003). Determination of water depth with high-resolution satellite imagery over variable bottom types. Limnology Oceanography 48, 547–556.

Google Scholar

Sun S., Chen Y., Mu L., Le Y., and Zhao H. (2023). Improving shallow water bathymetry inversion through nonlinear transformation and deep convolutional neural networks. Remote Sens. 15, 4247.

Google Scholar

Sun K., Xiao B., Liu D., and Wang J. (2019). “Deep high-resolution representation learning for human pose estimation,” in Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. 5693–5703.

Google Scholar

Traganos D., Poursanidis D., Aggarwal B., Chrysoulakis N., and Reinartz P. (2018). Estimating satellite-derived bathymetry (sdb) with the google earth engine and sentinel-2. Remote Sens. 10, 859.

Google Scholar

Wicaksono P., Harahap S. D., and Hendriana R. (2024). Satellite-derived bathymetry from worldview-2 based on linear and machine learning regression in the optically complex shallow water of the coral reef ecosystem of kemujan island. Remote Sens. Applications: Soc. Environ. 33, 101085.

Google Scholar

Xu N., Wang L., Zhang H.-S., Tang S., Mo F., and Ma X. (2023). Machine learning based estimation of coastal bathymetry from icesat-2 and sentinel-2 data. IEEE J. Selected Topics Appl. Earth Observations Remote Sens. 17, 1748–1755.

Google Scholar