Enhancing underwater acoustic orthogonal frequency division multiplexing based channel estimation: a robust convolution-recurrent neural network framework with dynamic signal decomposition

Introduction: Underwater acoustic (UWA) communication systems confront significant challenges due to the unique, dynamic, and unpredictable nature of acoustic channels, which are impacted by low signal-to-noise ratio (SNR), severe multipath propagation, latency, Doppler spread, and a shortage of real-world data. Orthogonal frequency division multiplexing (OFDM) is essential for establishing resilient and reliable data transmission in these challenging environments, but accurate channel estimation remains a critical barrier to unlocking its full potential—especially given the limitations of conventional estimation methods in adapting to UWA channel dynamics.

Methods: This work introduces a Convolution-Recurrent Neural Network (CRNet) estimator integrated with dynamic signal decomposition (DSD) techniques (e.g., Local Mean Decomposition, LMD; Empirical Mode Decomposition, EMD) to estimate UWA-OFDM channel characteristics and mitigate noise-induced distortions in received signals. The CRNet architecture combines convolutional layers (to capture spatial features) and recurrent layers (to model temporal dependencies), enabling it to learn complex UWA channel dynamics. The model is trained using paired data: received pilot symbols, transmitted pilots, and accurate channel impulse responses (CIR). Post-training, CRNet operates using only the received signal as input, eliminating the need for supplementary channel characteristics like SNR. To ensure real-world relevance, training and testing datasets are generated via the Bellhop ray-tracing model, which simulates diverse UWA environments (shallow coastal and continental shelf).

Results: Numerical findings demonstrate that the proposed CRNet model consistently outperforms benchmark methods—including least squares (LS), minimal mean square error (MMSE), and backpropagation neural network (BPNN)—across key metrics: bit error rate (BER), amplitude error, and phase error. CRNet exhibits superior performance with QPSK modulation compared to QAM, and maintains robustness even with a small number of pilot symbols. Performance evaluations on both training and unseen datasets confirm its resilience and flexibility in demanding UWA environments, validating its ability to generalize to dynamic channel conditions beyond training scenarios.

Discussion: The CRNet estimator addresses critical limitations of conventional UWA-OFDM channel estimation methods: its dual focus on spatial and temporal features (via convolutional-recurrent layers) overcomes the static linear constraints of LS/MMSE, while DSD-driven noise mitigation enhances input signal quality for more accurate estimation. By eliminating reliance on post-training supplementary channel data (e.g., SNR), CRNet simplifies real-world deployment. Its superior BER performance and adaptability to diverse UWA environments (shallow coastal, continental shelf) position it as a robust solution for improving the reliability and efficiency of UWA communication systems.

1 Introduction

UWA communication channels are widely recognized as some of the most complex and challenging environments for data transmission. Unlike typical terrestrial wireless channels, UWA communication is significantly affected by a range of environmental conditions such as variations in temperature, salinity, and pressure, as well as limited available bandwidth, multipath propagation, Doppler shifts, signal attenuation, and ambient ocean noise Stojanovic and Preisig (2009). These adverse conditions impose stringent demands on the design of reliable and efficient communication systems. The growing need for underwater wireless communication systems driven by applications like environmental monitoring, search-and-rescue operations, and deep-sea exploration has highlighted these challenges Preisig (2007). Acoustic wave propagation in water is inherently slow and suffers from high transmission losses. The foundational experimental and theoretical research conducted by Deng et al. Deng et al. (2023) on underwater sound emission from elastic Mindlin plates provided insight into the impact of boundary reflections and material interactions on acoustic propagation. These findings provide a crucial physical basis for understanding the distortions caused by multipath and reflection in UWA-OFDM systems. Furthermore, the presence of reflections from the ocean surface and seabed leads to multiple delayed signal paths, contributing to inter-symbol interference. This delay sensitivity, combined with Doppler-induced frequency shifts, makes the UWA channel highly dynamic and doubly selective in both time and frequency domains Stojanovic (2003). Achieving reliable communication underwater is substantially more difficult than in radio-frequency-based terrestrial systems. Under extremely SNR conditions, signals in UWA communication systems become significantly attenuated, posing serious reliability issues. To address this challenge, multicarrier transmission methods particularly OFDM, have gained attention for enhancing transmission robustness in such adverse environments Zhang et al. (2022b). A common variant, OFDM with cyclic prefix (CP), is especially advantageous in underwater environment Khan et al. (2020) due to its ability to handle severe multipath propagation. CP-OFDM not only mitigates inter-symbol interference (ISI) but also enables efficient spectrum utilization and supports cost-effective transceiver designs. OFDM has become increasingly adopted in UWA systems for its capacity to counteract the effects of multipath fading and delay spread. By dividing the overall channel bandwidth into numerous orthogonal narrowband subcarriers, OFDM allows each subcarrier to be modulated using conventional schemes at lower data rates. This approach maintains the overall data throughput comparable to a single-carrier system while offering improved resistance to channel impairments Zhang et al. (2019). OFDM provides both high-speed transmission and enhanced spectral efficiency, making it a compelling solution for reliable communication in complex UWA channels.

Accurate channel estimation Khan et al. (2020) is fundamental for ensuring reliable communication in UWA systems. Since the receiver must possess precise channel state information (CSI) to decode transmitted signals effectively, pilot-assisted estimation techniques are commonly employed. In this method, a set of known pilot symbols is transmitted alongside data-bearing subcarriers, enabling the receiver to infer the channel’s characteristics and improve signal detection reliability Murad et al. (2021).

In UWA-OFDM systems, the transmitted signal undergoes significant distortion due to multipath propagation, making it essential to estimate the CIR accurately. Pilot symbols, known in advance to the receiver, provide the necessary reference for estimating the CIR using algorithms such as LS and MMSE Khan et al. (2020). While the LS estimator is straightforward and widely used, it often suffers from limited accuracy. Conversely, the MMSE estimator offers improved performance by minimizing the mean squared error, but it requires prior knowledge of the channel statistics Jiang et al. (2019) and involves higher computational complexity, which can hinder its practical deployment.

In recent years, deep neural networks (DNNs) have demonstrated considerable potential across various domains Zhang et al. (2022a), including wireless communication. Applied to channel estimation, DNN based approaches aim to learn the nonlinear mapping between received signals and channel parameters. However, their application in UWA environments remains limited due to challenges such as overfitting and poor generalization capabilities. Similar deep learning based inverse modeling has been effectively utilized for subsurface imaging tasks; for instance, Lei et al. Lei et al. (2024) combined reverse time migration with neural architectures to enhance localization precision in complex underwater environments, offering significant advantages for UWA channel reconstruction. These limitations primarily stem from the scarcity of real-world underwater Zhang et al. (2022b) channel data required to train complex deep learning models effectively. Without sufficient training data that accurately reflects real UWA conditions, models are prone to underperform when exposed to new or dynamic scenarios. Therefore, developing methods to generate or simulate diverse channel conditions is essential to improve the training process and enhance model robustness for underwater applications.

The main Contributions of paper are listed as follows:

This research presents a CRNet model for channel estimation in UWA-OFDM systems. The suggested method is designed to address intricate and fluctuating underwater channel conditions, including nonlinear distortions and environmental interferences. Before estimation, DSD methods are applied on the incoming signals to significantly reduce noise and improve the quality of the input for the neural network. The suggested CRNet model is trained on representative data to comprehend the fundamental attributes of UWA multipath channels. Comprehensive simulations are conducted to evaluate the efficacy of the proposed model across various modulation methods. The performance of BER in relation to SNR is specifically examined among standard estimators LS, MMSE, and BPNN, alongside the novel CRNet method using QAM and QPSK modulation techniques in two different underwater environments i.e. Shallow coastal and Shelf continental channels. The main contributions of this paper are summarized as follows:

1. We have introduced a CRNet estimator for channel estimation in UWA OFDM systems. By combining convolutional and recurrent layers, the model effectively captures both spatial characteristics and temporal relationships inherent in the received signal. This dual capacity facilitates a more thorough comprehension of the intricate and dynamic characteristics of UWA channels. The suggested methodology has robust estimating capabilities, even under difficult circumstances, and provides a substantial enhancement compared to conventional techniques. Additionally, we provide a theoretical explanation and establish a mathematical framework to characterize the performance and effectiveness of the CRNet model for UWA channel estimation.

2. We employ dynamic signal decomposition techniques including Local Mean Decomposition (LMD) and Empirical Mode Decomposition (EMD) on the received signals to suppress noise and isolate meaningful signal components. These techniques enhance the overall quality of the input fed into the neural network, thereby improving the robustness and accuracy of the channel estimation process. Theoretical foundations and mathematical modeling are also provided to support the proposed methodology and demonstrate its effectiveness in challenging underwater environments.

3. In order to generate the training and testing datasets, we replicate the UWA communication environments using the Bellhop ray tracing model that enables us to include a broad spectrum of channel conditions exhibiting the multipaths propagation and complexities characteristic of underwater environments. We conduct thorough experiments to evaluate the performances of QPSK and QAM modulation schemes inside the CRNet-based estimation framework. Additionally, we evaluate our proposed estimator against traditional channel estimate techniques, namely LS, MMSE, and BPNN, across the two specified bellhop channels—Shallow Coastal and Continental Shelf across range of SNRs for robustness and versatility in our analysis. The findings clearly demonstrate the improved performance of our technique in several metrics, including estimate accuracy, enhancement of BER with fewer pilots, and adaptation to diverse modulation schemes and channel conditions in difficult UWA environments.

The rest of this article is structured as follows. In Section 1.1, we provide a thorough examination of the related works. Section 2 provides a detailed description of the proposed approach. The simulation setups are presented in Section 3. Section 4 presents results and discussions. Ultimately, Section 5 concludes this article.

1.1 Related works

This section presents a detailed review of existing literature focused on supervised learning-based channel estimation and pilot-assisted techniques, along with dynamic signal decomposition techniques providing the necessary context and alignment with the methodological direction of our proposed approach. To ensure reliability and fidelity inside underwater devices accurate UW channel estimation is very important the author in Zhang et al. (2022c) proposed a channel estimation techniques in communication systems which are generally categorized into three main approaches. The first is pilot-assisted estimation, where known pilot symbols are transmitted alongside data subcarriers to facilitate channel state information (CSI) recovery Jiang et al. (2019). The second approach, blind estimation, eliminates the need for pilots and instead relies on the statistical properties of the received signals to estimate the channel. The third, known as semiblind estimation, combines elements of both methods by using partial knowledge of the transmitted data along with statistical characteristics to infer the channel. For instance, the author in Murad et al. (2021) proposed pilot-assisted schemes, in which pilot symbol placement typically follows two configurations: comb-type and block-type. In the comb-type configuration, pilot symbols are regularly spaced throughout the frequency domain, allowing continuous tracking of channel variations and facilitating synchronization. In contrast, block-type pilots in Jiang et al. (2019) are placed on specific subcarriers within dedicated OFDM symbols, making them especially effective in handling frequency-selective fading. Each configuration offers unique advantages depending on the channel conditions and system requirements. Enhancing the performance of underwater communication systems relies heavily on advanced signal processing techniques. In addition, the author in Jiang et al. (2019) investigated a range of methods, including effective channel estimation algorithms and modulation schemes specifically tailored for UWA environments. Furthermore, the work in Kari et al. (2017) introduced a new set of adaptive robust channel estimators specifically designed for underwater acoustic multipath channels. The objective is to address the unique issues posed by this environment, such as non-stationarity and impulsive noise. In order to tackle these problems, the authors used adaptive filtering approaches that revolve upon a logarithmic cost function. This approach aims to improve the speed of convergence and stability, particularly in scenarios where impulsive noise is present. Unlike DL-based approaches, the study in Farzamnia et al. (2017) focused on the simulation of block-type channel estimation algorithms in multipath fading environments. It also proposed a sparse channel estimation technique based on the LS method, demonstrating improved estimation performance. The authors recommended extending this work by evaluating OFDM systems with multiple users under the LS-based sparse estimation framework. Similarly, in Chen et al. (2010), LS was employed for channel estimation, where the channel frequency response of pilot symbols was used to adjust subsequent data symbols through a weighted averaging mechanism.

In Liu et al. (2021a) the issue of severe multipath fading in UWA OFDM systems was addressed by the authors, which is primarily caused by significant propagation delays and reflections from the seabed. These conditions can result in outdated CSI and reduced estimation accuracy. To mitigate this, the authors proposed the CsiPreNet model a hybrid framework combining CNN and LSTM architectures to improve CSI prediction and enhance the reliability of channel estimation in such environments. In the context of MIMO-OFDM channel estimation. Moreover, the authors in Jiang et al. (2019) highlighted the critical role of accurate CSI acquisition. By utilizing received pilot symbols and CIR, deep learning models were trained for this task. The proposed methods demonstrated improved performance over LS and backpropagation-based neural networks in terms of BER and normalized mean square error, showing results comparable to the MMSE approach. However, when constrained by shallow network depth, the DNN models exhibited lower estimation accuracy but offered advantages in memory efficiency and computation speed. To overcome the limitations in conventional OFDM channel estimation techniques, recently DL has brought transformative improvements to communication systems, particularly in OFDM, where conventional models struggle to handle channel complexities. The author in Bithas et al. (2019) highlighted the application of DL techniques to enhance system performance under challenging conditions. Notably, architectures such as CNNs and LSTM networks have emerged as prominent tools for tackling the unique difficulties posed by UWA channels. In a related communication domain, Yao et al. Yao et al. (2023) enhanced OFDM based automobile radar systems functioning in spectrally crowded vehicle situations. Their optimization methodology reduced interference and enhanced spectral efficiency issues that are logically comparable to underwater OFDM channels, where multipath effects and bandwidth limitations equally limit reliable data transmission.

In Ye et al. (2017) the authors introduced a deep learning-based approach for channel estimation and symbol detection in an OFDM system. To tackle the problems in conventional methods for channel estimation and symbol detection that are not robust enough to handle wireless channels in severe distortion and interference. The proposed solution is to train a deep learning model offline using simulated data that views OFDM and wireless channels as black boxes. The methodology involves analyzing the impact of variations in channel model statistics during training and deployment stages and comparing the performance of the DL-based approach with traditional methods. The results show that the deep learning-based approach is more robust and can detect transmitted symbols with performance comparable to the minimum MSE estimator.

In addition to, the authors in Ling et al. (2009) examined the fundamental elements of MIMO systems in the context of UWA communications, with a specific emphasis on channel estimates and signal identification. The research proposed a novel method for improving channel estimation by proposing a cyclic strategy for generating training sequences. Additionally, the paper presents the Iterative Adaptive Strategy (IAA) algorithm, which, when combined with the Bayesian Information Criterion (BIC), may produce sparse channel estimates. Furthermore, the integration of the RELAX algorithm serves to boost the performance. The results showcased the propposed system ability to achieve low bit error rates at different payload data speeds in underwater conditions that are characterized by delay spread.

In MIMO-OFDM communication, where standard estimate techniques are computationally difficult and scale poorly, accurate CSI collection is crucial for multi-antenna system performance. Researchers are increasingly using DL to overcome these constraints. For instance, Balevi and Gitlin in Balevi et al. (2020) developed a scalable deep learning architecture for estimating massive MIMO channels, achieving higher performance in high-dimensional antenna systems with manageable complexity. Additionally, in Qiao et al. (2019) the authors did a thorough performance and complexity study of MIMO-OFDM channel estimation methods, including classical and learning-based approaches, revealing trade-offs. Furthermore, in Lu et al. (2020) authors developed an end-to-end framework for channel categorization, estimation, and signal detection, improving system efficiency and flexibility in dynamic contexts. However, in Tabata et al. (2020) the authors have created an offline-trained DNN-based model for underwater environment classification, enhancing channel estimation accuracy by adapting to UWA channel propagation characteristics. These contributions demonstrate that deep learning may increase estimation accuracy and allow integrated and scalable solutions for complicated communication settings.

An adaptive denoising method was also proposed in Cho and Ko (2020), using dual pilot sets, one for CIR estimation and the other for optimal window selection, showing superior accuracy in time-varying UWA channels, particularly at low SNRs. Other efforts in Li et al. (2020) explored blind and semiblind estimation strategies to reduce complexity and improve spectral efficiency. To tackle high PAPR and computational cost in UWA OFDM, an M-ary spread spectrum model using LSTM was introduced in Qiao et al. (2022) and validated through both simulations and experimental setups. Additionally, the authors in Raza et al. (2021) addressed nonlinear distortion in UWA OFDM by employing DNNs to suppress such effects while reducing PAPR. A DL-based receiver was proposed in Zhang et al. (2019) that bypasses explicit channel estimation and equalization, simplifying the overall processing in UWA OFDM systems.

Various denoising techniques have been proposed in recent literature to enhance the quality of UWA signals, which are often degraded by non-stationary and nonlinear noise sources such as wind, marine life, and ship machinery. EMD combined with frequency-domain thresholding has been shown effective in isolating intrinsic mode functions (IMFs) and reducing ambient noise in Veeraiyan et al. (2013). Advanced approaches integrate signal decomposition with machine learning models for instance, Correlation-based Variational Mode Decomposition (CVMD) coupled with Least Squares Support Vector Machine (LSSVM) and Gaussian Process Regression (GPR) improves prediction and denoising by adaptively selecting decomposition parameters as proposed in Yang et al. (2020a). Additionally, in Yang et al. (2020b) a hybrid framework like MIVMD-mvMDE-LWTD-SG leverages mutual information-based VMD multiscale entropy, and wavelet-based filtering was proposed to handle complex, chaotic, and ship-radiated noise components more effectively.

1.2 Research motivation

In the above discussion, we noticed that UWA communication faces significant challenges such as low SNR, high computational complexity, and the reliance on accurate CSI. LS estimation remains computationally simple but is highly sensitive to noise, particularly in low-SNR environments. MMSE estimation improves performance but demands precise knowledge of channel and noise statistics Jiang et al. (2019); Khan et al. (2020); Zhang et al. (2022a), which is difficult to obtain in underwater settings. Alternatively, BPNN offers robustness by learning nonlinear channel characteristics and has demonstrated improved accuracy over classical approaches. However, their effectiveness is limited by training complexity, risk of overfitting, and sensitivity to changing environments. This study compares LS, MMSE, and BPNN with a proposed model, aiming to enhance channel estimation along with dynamic signal decomposition to reduce BER in dynamic UWA conditions.

2 Proposed methodology

The methodology of the suggested system model is explained in the following subsections.

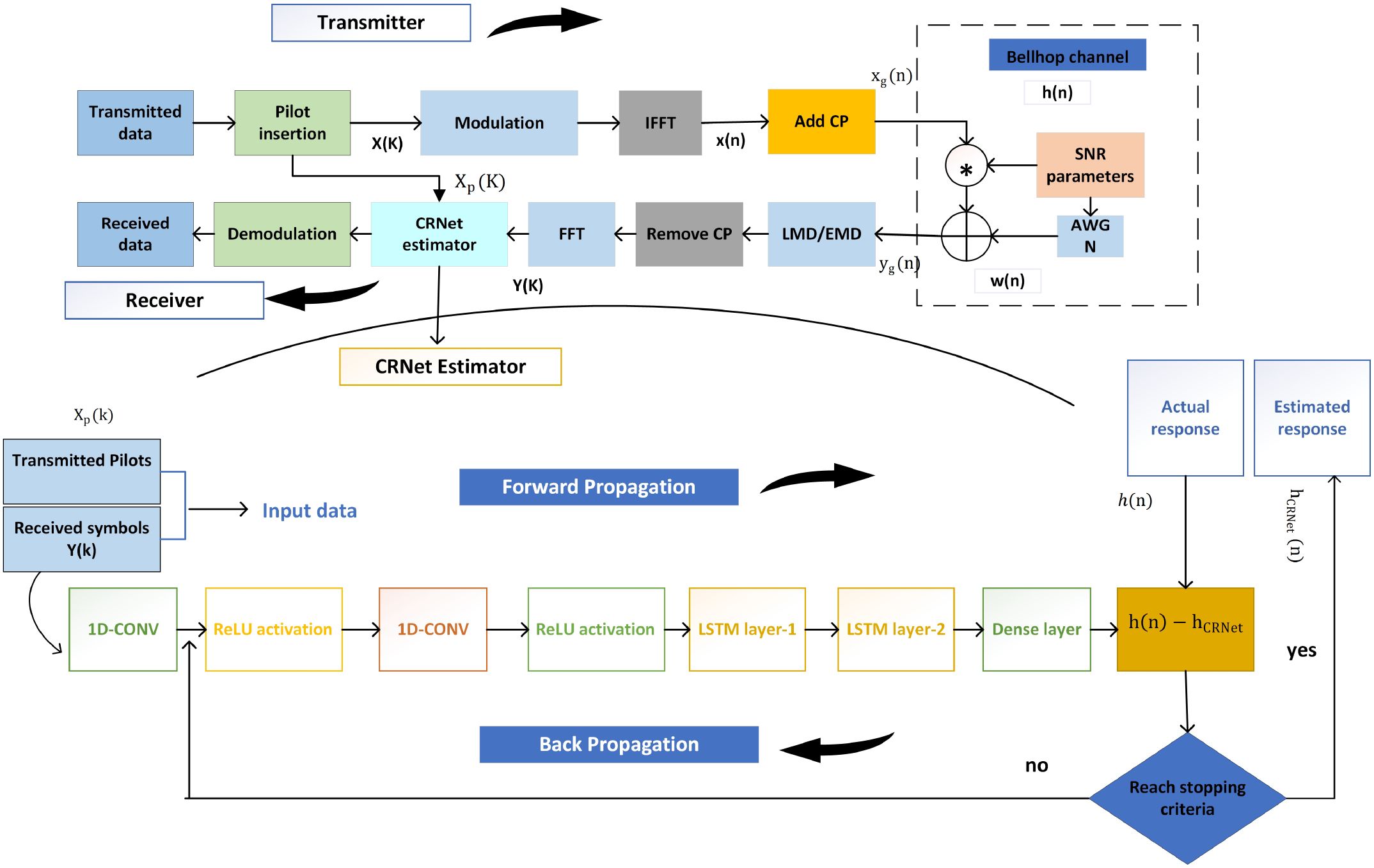
A schematic of the UWA-OFDM system Chen et al. (2017); Wang et al. (2017); Jiang et al. (2019) is shown in Figure 1. The system starts with the generation of a binary data stream, to which pilot tones are added for CIR estimation. The data is encoded with quadrature amplitude modulation (QAM). An Inverse Fast Fourier Transform (IFFT) is then employed to convert the modulated data from the frequency domain to the time domain across N orthogonal subcarriers as in Equation 1. The resultant time-domain signal x(n) is derived from the frequency-domain components X(k), as specified in Jiang et al. (2019):

Figure 1

Figure 1. Proposed system model architecture.

$\begin{array}{ll}x(n)=\text{IFFT}\{X(k)\}=\frac{1}{N}\sum _{k=0}^{N-1}X(k)e^{j\frac{2\pi nk}{N}},n=0,\dots ,N-1& (1)\end{array}$

Following the IFFT operation, the resulting N parallel subcarriers are serialized, and a cyclic prefix is appended as in Equation 2 to each OFDM symbol to mitigate ISI. The resulting time-domain transmit signal with the cyclic prefix can be expressed as Jiang et al. (2019):

$\begin{array}{ll}{x}_g(n)=\{\begin{array}{ll}x(N+n),\hfill & n=-N_g,-N_g+1,\dots ,-1\hfill \\ x(n),\hfill & n=0,1,\dots ,N-1\hfill \end{array}& (2)\end{array}$

Here, N_g denotes the length of the cyclic denotes the length of the cyclic prefix. This implies that the last N_g samples of the OFDM symbol x_g(n) are duplicated and prepended to form the extended signal resulting in a total symbol length of N + N_g. After transmission through the UWA channel, the received signal y_g(n) as in Equation 3 can be expressed as Jiang et al. (2019):

$\begin{array}{ll}{y}_g(n)=x_g(n)\otimes h(n)+w(n),-N_g\le n\le N-1& (3)\end{array}$

Here, the operator ⊛ denotes circular convolution and w(n) represents additive white Gaussian noise (AWGN) with zero mean. The term h(n) refers to the channel impulse response as in Equation 4, which is defined as Jiang et al. (2019):

$\begin{array}{ll}h(n)=\sum _{i=0}^{r-1}{h}_i\delta (n-{\tau }_i)& (4)\end{array}$

In this context, σ(n) denotes the unit impulse function, r is the total number of multipath components, and h and τ_i represent the complex gain and time delay associated with the ith path, respectively. At the receiver side, the cyclic prefix is removed as in Figure 1 and the resulting time-domain signal y(n) is transformed into the frequency domain using the Fast Fourier Transform (FFT) as in as in Equation 5, as expressed by the following equation Jiang et al. (2019):

$\begin{array}{ll}Y(k)=\text{FFT}\{y(n)\}=\frac{1}{N}\sum _{n=0}^{N-1}y(n)e^{-j\frac{2\pi nk}{N}},k=0, 1,\dots ,N-1& (5)\end{array}$

Hence, if the ISI is reduced fully, the received signal as in Equation 6 may be expressed as Jiang et al. (2019):

$\begin{array}{ll}Y(k)=X(k)H(k)+W(k),k=0, 1,\dots ,N-1& (6)\end{array}$

The frequency-domain representations of the CIR h(n) and noise w(n) are given by H(k) and W(k), respectively. In an UWA communication system, the relationship between the transmitted and received signals is effectively captured using these frequency-domain components.

2.1 Proposed model for underwater acoustic channel estimation

In this subsection, we present our CRNet approach for accurate estimation of UWA channels. The proposed model architecture consists of an input layer, followed by a sequence of convolutional layers to capture local spatial features and recurrent layers to model temporal dependencies inherent in the channel and fully connected dense layer to capture complex channel gain, culminating in a fully connected output layer for channel response prediction.

2.1.1 Network architecture

The architecture of the proposed CRNet model is tailored to estimate complex channel gains for each subcarrier in an OFDM-based UW communication system. The model integrates the following key components:

Initially, The model is trained with received symbols Y (K) along with transmitted pilot symbols X_p(k) in a pair, and the label would be the corresponding CIR. The suggested model structure for OFDM channel estimation has multiple layers intended for mapping the input data with their corresponding output. The model starts with an input layer that receive a pair of data. After that, there are two Conv1D layers, each consisting of 64 filters, a kernel size of 3, and ReLU activation functions. The purpose of these convolutional layers is to capture spatial dependencies within the input data. Subsequently, two LSTM layers are utilized; the initial LSTM layer comprises 64 units and generates sequences, enabling it to effectively handle the temporal characteristics of the data across all samples. The second LSTM layer is also composed of 64 units, it essentially condenses and summarizes the temporal information that was learned from the prior layer. After the LSTM layers, a Dense layer is included to further process the data. This Dense layer consists of 128 units. The Proposed model architecture consists of a combination of convolutional and recurrent layers, which allows it to successfully learn and represent the intricate relationships found in UWA-OFDM channel estimation.

The first 1D convolution layer having $W_i^{(1)}\in {ℝ}^{K\times C}$ be the kernel for the i-th filter. The convolution operation at time t is given by as in Equation 7:

$\begin{array}{ll}{z}_t^{(1)}[i]=\sum _{j=0}^{K-1}\sum _{k=0}^{C-1}{W}_i^{(1)}[j,k]·x_{t+j-k}[k]+b_i^{(1)}& (7)\end{array}$

Where: $W_i^{(1)}\in {ℝ}^{K\times C}$ is the convolutional kernel of size K for the i-th filter, x_t+j−k[k] is the k-th channel (real or imaginary) at position $t+j-k$, $b_i^{(1)}\in ℝ$ is the bias term, $z_t^{(1)}[i]$ is the pre-activation output at time t for filter i.

Furthermore, ReLU activation layer as in Equation 8 applied to introduce non-linearity using element wise operation to the output of previous convolutional layer, having output shape as in Equation 9.

$\begin{array}{ll}{a}_t^{(1)}[i]=\max (0,z_t^{(1)}[i])& (8)\end{array}$

$\begin{array}{ll}{A}^{(1)}\in {ℝ}^{T\times F_1}& (9)\end{array}$

Where F₁ as in Equation 12 is the number of filters (i.e., feature maps) learned in this layer. These features help extract local multipath patterns in the UWA channel.

Following the first 1D Conv layer, second and 1D convolution layer as in Equation 10 takes A⁽¹⁾ as input and applies filters $W_i^{(2)}\in {ℝ}^{K\times F_1}$ for each i-th filter as follows:

$\begin{array}{ll}{z}_t^{(2)}[i]=\sum _{j=0}^{K-1}\sum _{k=0}^{F_1-1}{W}_i^{(2)}[j,k]·a_{t+j-k}^{(1)}[k]+b_i^{(2)}& (10)\end{array}$

Here, $W_i^{(2)}\in {ℝ}^{K\times F_1}$ are learned weights for the second convolutional layer, $a_{t+j-k}^{(1)}[k]$ is the output of the first layer at offset $t+j-k$, $b_i^{(2)}$ is the bias for the i-th filter.

Moreover, output of the previous convolutional layer exhibit an element wise ReLU activation function layer as Equation 11:

$\begin{array}{ll}{a}_t^{(2)}[i]=\text{max}(0,z_t^{(2)}[i])& (11)\end{array}$

$\begin{array}{ll}{A}^{(2)}\in {ℝ}^{T\times F_2}& (12)\end{array}$

Where F₂ as in Equation 12 is the number of filters in this layer. This step refines the receptive field, enhancing temporal resolution for channel fluctuations.

Following convolutional layers, 1st LSTM layer processes the sequence $a_t^{(2)}\in {ℝ}^{F_2}$ at each time step t, computing the hidden state h_t∈ R^H using the standard LSTM Equation 13:

$$f_t=\sigma (W_f[h_{t-1},a_t^{(2)}]+b_f)$$

$$i_t=\sigma (W_i[h_{t-1},a_t^{(2)}]+b_i)$$

$${\tilde{c}}_t=\text{tanh}(W_c[h_{t-1},a_t^{(2)}]+b_c)$$

$$c_t=f_t\odot c_{t-1}+i_t\odot {\tilde{c}}_t$$

$$o_t=\sigma (W_o[h_{t-1},a_t^{(2)}]+b_o)$$

$\begin{array}{ll}{h}_t=o_t\odot \text{tanh}(c_t)& (13)\end{array}$

Here: $a_t^{(2)}\in {ℝ}^{F_2}$ is the current input vector from Conv2, $h_{t-1}\in {ℝ}^H$ is the previous hidden state, c_t is the memory cell, ⊙ is element-wise multiplication, σ(·) is the sigmoid activation, W_∗, b_∗ are learned weights and biases. The LSTM captures long-term dependencies due to delayed multipath propagation common in underwater environments.

After that the second LSTM layer condenses the sequence into a fixed-size vector as in Equation 14:

$\begin{array}{ll}{h}_{\text{final}}=h_T\in {ℝ}^H& (14)\end{array}$

It outputs only the last hidden state, which summarizes the entire received OFDM frame. Following second LSTM layer, a fully connected dense layer maps the final LSTM output to predicted time-domain channel coefficients as in Equation 15:

$\begin{array}{ll}{z}_{\text{dense}}=W_{\text{dense}}·h_{\text{final}}+b_{\text{dense}},z_{\text{dense}}\in {ℝ}^{N·C}& (15)\end{array}$

Where: $W_{\text{dense}}\in {ℝ}^{(N·C)\times H}$ is the dense layer weight, and N is the number of subcarriers, C = 2 for real and imaginary output parts.

The final layer of the network is called the output layer, which give us channel estimates of CRNet model. In the OFDM framework, each output neuron is associated with an individual subcarrier, enabling the network to estimate the corresponding complex channel coefficient. This layer generates the output as in Equation 16 by computing:

$\begin{array}{ll}{\widehat{h}}_i=\sum _{d=1}^D(W_{i,d}^{(r)}+j{W}_{i,d}^{(i)})h_d^{\text{final}}+b_i^{(r)}+j{b}_i^{(i)},i=1,\dots ,N& (16)\end{array}$

Where:

● ${\widehat{h}}_i$ is the estimated complex channel coefficient for the i-th subcarrier.

● $h_d^{\text{final}}$ is the d-th element of the LSTM’s final hidden state.

● $W_{i,d}^{(r)}$, $W_{i,d}^{(i)}$ are the weights of the dense layer for the real and imaginary parts, respectively.

● $b_i^{(r)}$, $b_i^{(i)}$ are the bias terms for the real and imaginary parts.

● D denotes the dimensionality of the LSTM hidden output.

● N is the total number of subcarriers in the OFDM system.

The network output delivers the estimated channel impulse response for specified subcarriers.

2.1.2 Model training process

The CRNet model is trained using a supervised learning approach, where each training instance consists of an input-output pair. The input includes both the received OFDM signals and their corresponding pilot symbols, while the output represents the true channel characteristics. During training, the model iteratively updates its internal parameters such as weights and biases to accurately map the input data to the desired channel responses. The overall functionality and processing pipeline of the CRNet framework are illustrated in Figure 1 and formally described in Algorithm 1 for clarity and reproducibility.

Algorithm 1. CRNet-based channel estimation for UWA-OFDM

2.1.3 Data generation and training parameters

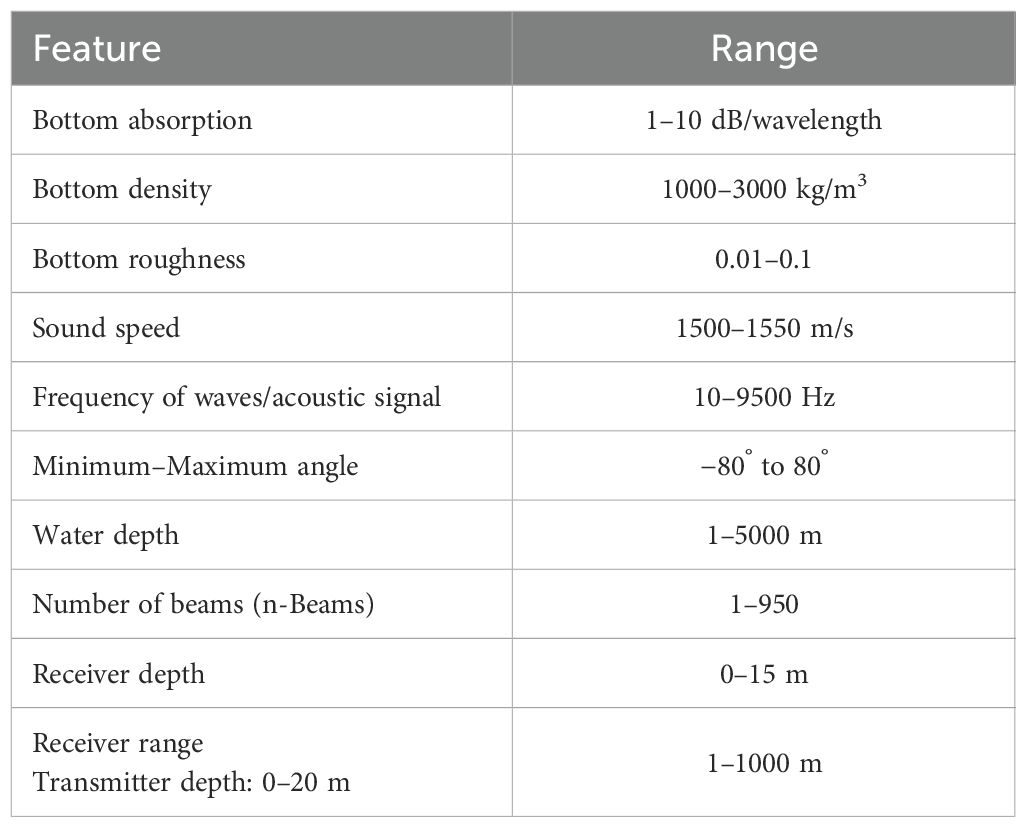
The dataset used for training and testing the CRNet model was generated using the Bellhop ray-tracing model, which mimics sound propagation in dynamic underwater environments. To accurately depict the spatial variability of the marine environment, several critical parameters were modified across various simulation combinations as illustrated in Table 1, including sound speed (1500–1550 m s⁻¹), bottom absorption (1–10 dB per wavelength), bottom density (1000–3000 kg m⁻³), seabed roughness (0.01–0.1), transmitter depths (0–20 m) and receiver depths (0–15 m), acoustic frequencies (10–9500 Hz), angles (−80–80^°), and receiver range (1–1000 m). These variations illustrate a range of underwater topographies from shallow coastal areas to continental shelf environments, capturing temporal dynamics of UWA channels such as Doppler shifts, delays, and multipath propagation. Both shallow-coastal and continental shelf channel data sets, generated through the Bellhop ray-tracing simulation, comprises 6,000 samples collected during the simulation phase. The input shape for each training sample of the received signal is (Nt, Nfft, num) = (1152, 1024, 10). Nt represents the quantity of samples, Nfft denotes the received signal as input features, and num indicates the number of iterations.

Table 1

Table 1. Underwater acoustic channel parameter ranges.

To accurately represent the spatial variability present in real marine environments, the Bellhop model is further adjusted to simulate both horizontal and vertical gradients in environmental characteristics: vertical sound speed profiles (SSPs) integrate depth dependent temperature gradients (5–25 ^°C) and salinity levels (30–35 ppt), with shallow coastal areas displaying a surface duct (an increase in sound speed with depth up to 10m) and Continental shelf conditions characterized by a sound channel (minimum sound speed at depths of 50–100 m); the seabed is depicted as a spatially heterogeneous medium, with transitions between sand (near shore) and silt (continental shelves) occurring at random horizontal intervals (50–200 m); horizontal ambient noise gradients also fluctuate, with near shore regions incorporating ship noise contributions (10–20 dB higher at 1–5 kHz) continental shelf areas mainly influenced by both marine life noise and ships (peaking at 10–100 Hz). These modifications ensure the model capacity to generalize across diverse underwater scenarios, reflecting the dynamic attributes of the aquatic environment.

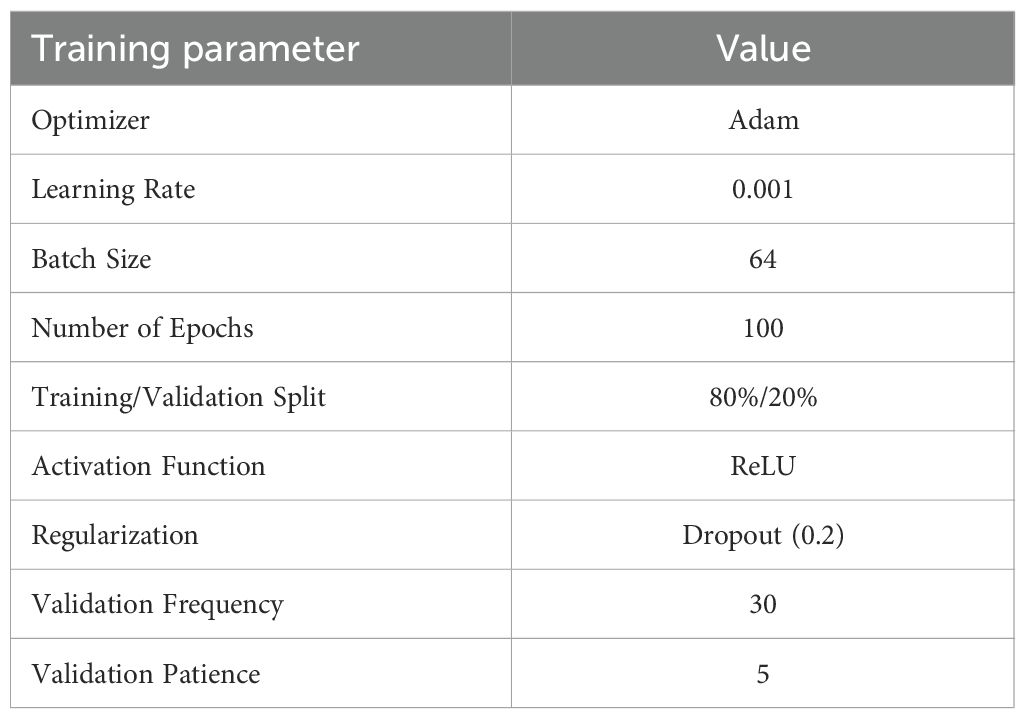
The CRNet model was optimized utilizing the Adam optimizer with a learning rate of 1 × 10⁻³, a batch size of 64 over 100 epochs, an 80%/20% training/validation split, dropout regularization set at 0.2, ReLU activation in hidden layers, performance evaluation every 30 steps, and early stopping with a patience of 5 epochs to guarantee convergence. Table 2 provide combination of these options for CRNet Model ensuring comprehensive set of training data representing real world UW channel complexities such as temperature gradients, salinity fluctuations, and seabed structure enhances the CRNet model robustness across varied environmental conditions, allowing it to effectively learn and predict UWA channel responses, reduce pilot workload, and maintain reliable communication even in adverse underwater propagation scenarios.

Table 2

Table 2. Model training options for proposed CRNet model.

2.2 Channel equalization via convolution-recurrent network estimates

The channel equalization technique is essential for mitigating the distortion caused by the underwater acoustic channel. The CRNet model presents a notable advancement by integrating convolutional and recurrent layers to effectively capture spatial and temporal relationships in channel response. This dual strategy allows the model to learn and adapt to the highly dynamic characteristics of UWA channels, offering enhanced resilience relative to conventional techniques. CRNet ability of performing precise channel estimate with a reduced number of pilot symbols and to manage time-varying channel circumstances illustrates its significant superiority over LS, MMSE, and BPNN.The mathematical expression as in Equation 17 for the equalization procedure of the kth subcarrier is as follows: CRNet directly supplies the frequency response estimate ${\widehat{H}}_{\text{CRNet}}(k)$ for each sub-carrier k; one-tap LS equalization is then simply.

$\begin{array}{ll}{Y}_{\text{eq}}(k)=Y(k)/{\widehat{H}}_{\text{CRNet}}(k).& (17)\end{array}$

● Y (k) – received frequency-domain signal on sub-carrier k;

● ${\widehat{H}}_{\text{CRNet}}(k)$– complex channel response estimated by CRNet on sub-carrier k;

● Y_eq(k) – equalized symbol after one-tap compensation on sub-carrier k.

Although LS, MMSE, and BPNN are popular benchmark algorithms for channel equalization, their foundational principles limit their effectiveness in practical UWA environments. LS and MMSE depend on static linear estimates and are incapable of adapting dynamically to the non-stationary and nonlinear characteristics of multipath UWA channels, whereas BPNN is deficient in the temporal memory necessary to grasp sequential relationships in acoustic signals. The proposed CRNet presents an integrated framework that merges dynamic signal decomposition architecture including convolutional and recurrent layers. This design allows CRNet to learn spatial correlations and temporal evolutions of channel coefficients, facilitating adaptive equalization under diverse propagation situations. Thus, CRNet signifies a significant progression beyond traditional equalizers by offering a physically informed, data driven methodology capable at effectively simulating the time varying dynamics of UWA channels.

3 Simulation results with critical analysis

This section outlines the experimental setup, beginning with an overview of the simulation environment that employs the Bellhop channel model, as described in Section 3.1. Section 3.2 elaborates on the implementation of various benchmark techniques. The performance evaluation criteria are presented in Section 3.3. Section 4 provides a comprehensive discussion of the experimental outcomes and their analysis. Finally, Section 5 concludes the study.

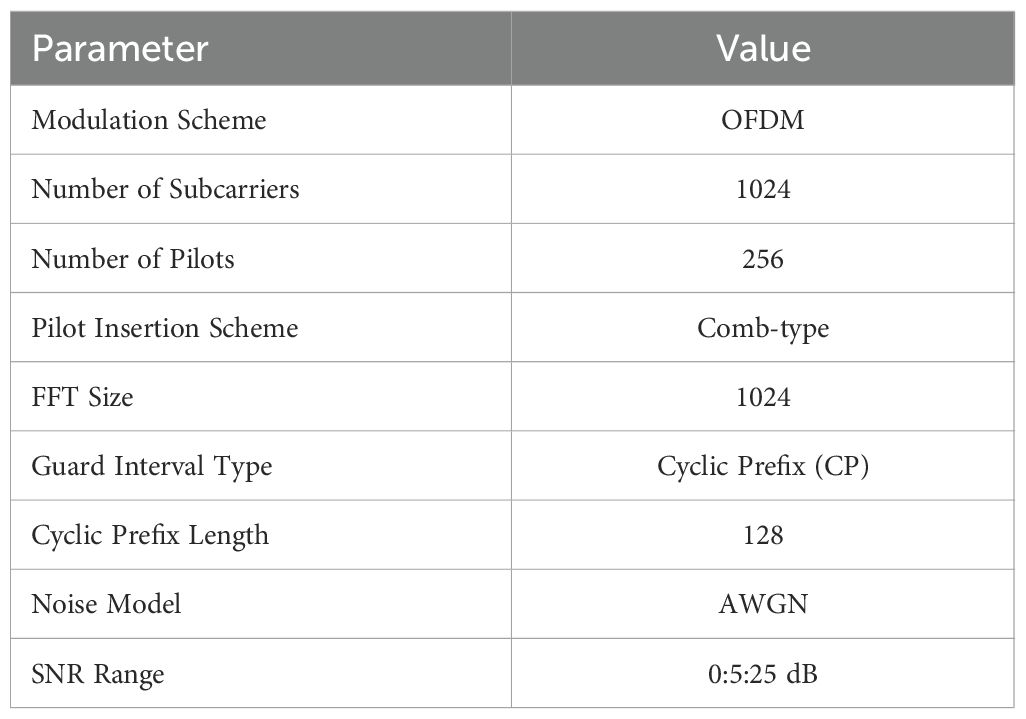
The proposed model have been executed in Python, and the simulation includes a series of essential parameters detailed in Table 3. This concise table offers a thorough summary of essential characteristics, including the modulation technique, subcarrier count, pilot configuration, FFT dimensions, and the use of a CP as a guard interval. Comb-type pilot insertion is used for its spectral efficiency and simple channel estimation procedure. It ensures uniform pilot spacing over the frequency range, hence simplifying the interpolation of the channel response and effectively compensating for Doppler shifts, common in UWA communications. The latest release of Python 3.14.0 was used to create the Bellhop-based UWA channel simulation pipelines, dynamic signal decomposition modules, and the CRNet model. Every experiment was carried out on a Windows 11 Pro Education system that had a 64-bit x64 configuration, an AMD Ryzen 7 5800H processor (3.20 GHz), 16.0 GB of RAM, and no pen or touch input prerequisites.

Table 3

Table 3. Simulation parameters for UWA-OFDM system.

3.1 Simulation environment based on bellhop

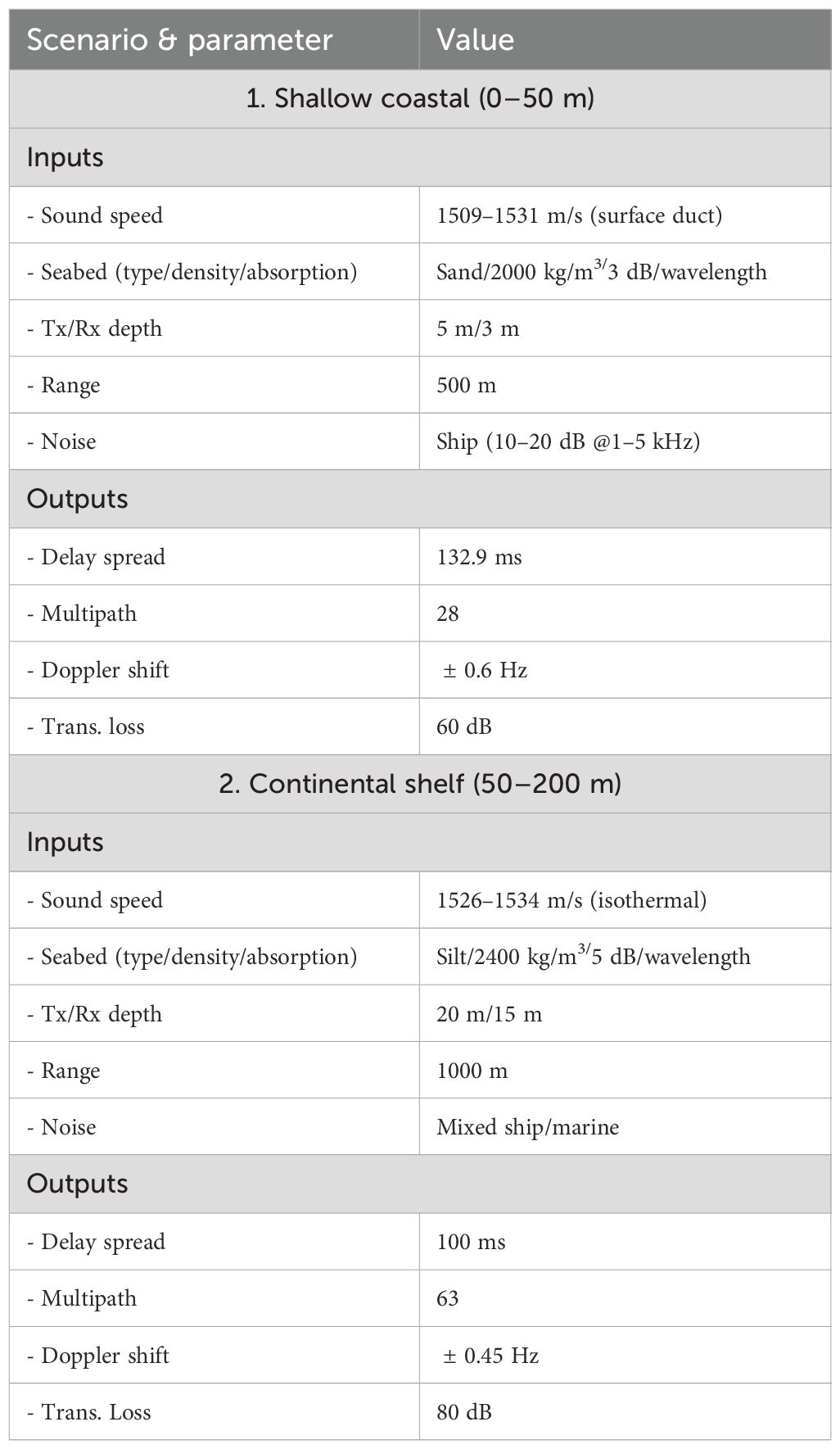
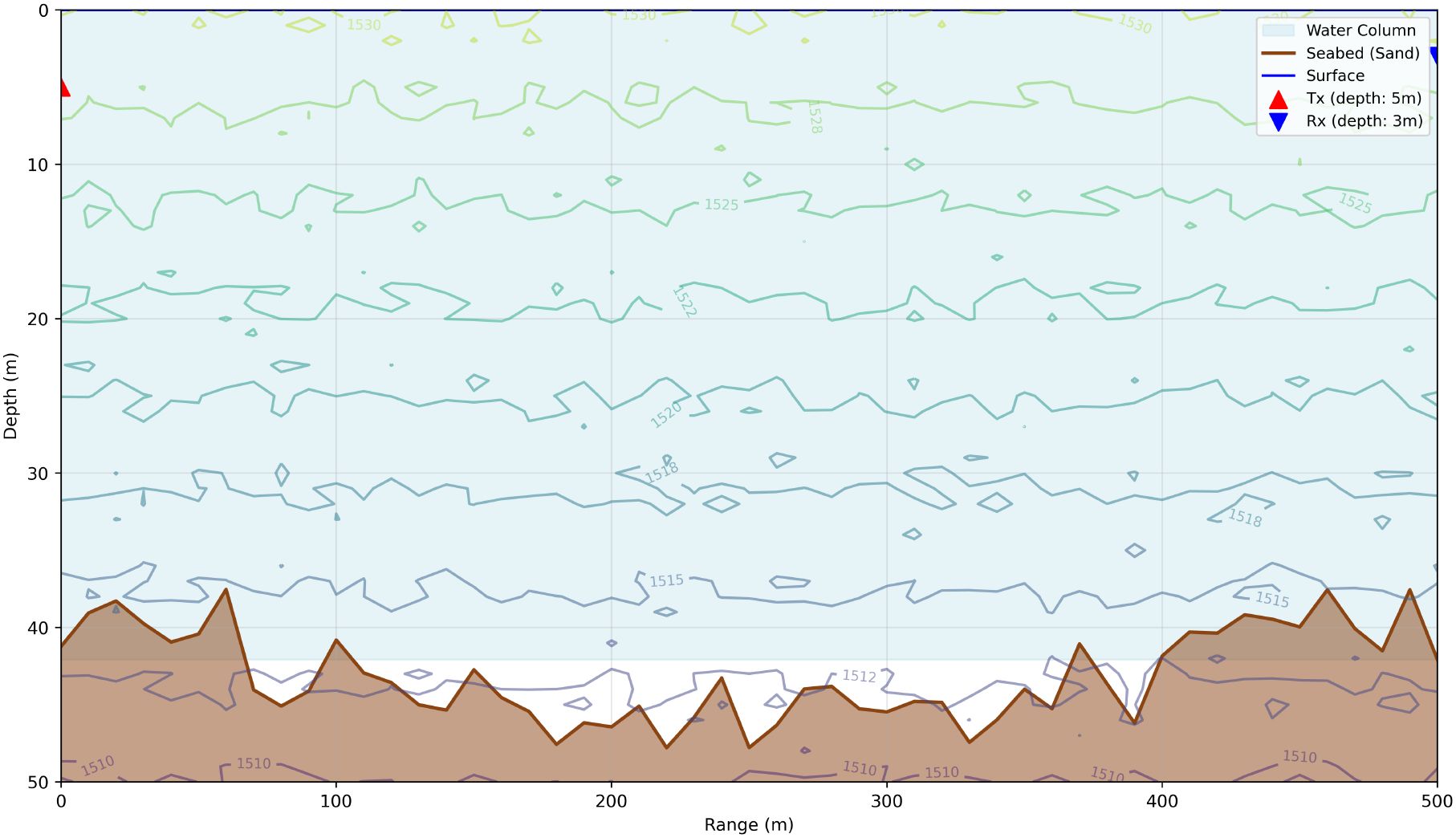
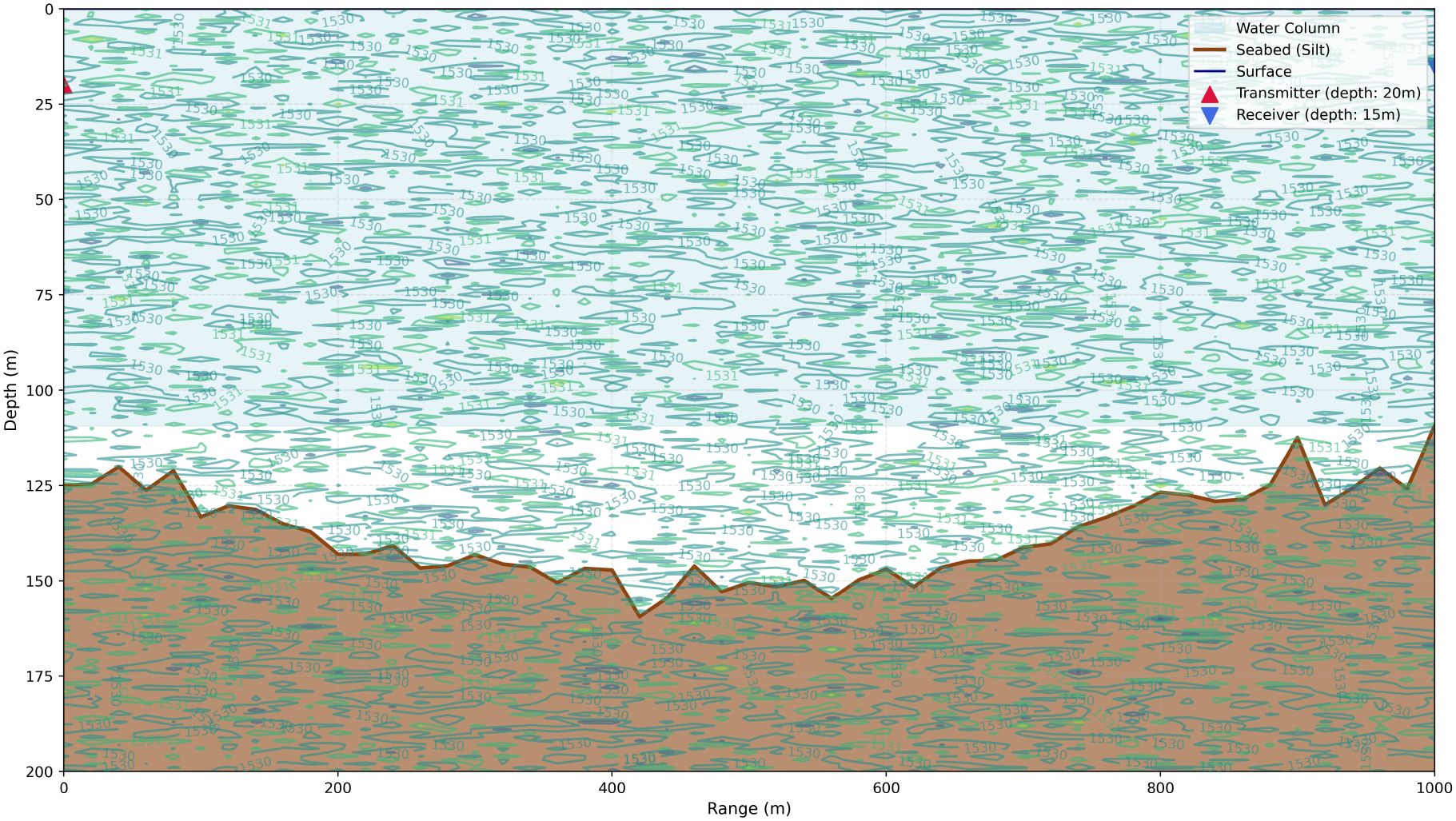
The dataset used for training and testing the CRNet model was generated using the Bellhop, a well-validated tool for modeling underwater sound propagation in dynamic marine environments. Bellhop solves the wave equation for discrete eigenrays to produce essential outputs that define UWA channel complexity, including multipath components (their amplitudes, delays, and angles of arrival), transmission loss (dB), and eigenray trajectories all crucial for simulating real acoustic propagation phenomena such as surface and bottom reflections, sound speed fluctuations, and depth-dependent attenuation. In order to ensure that the CRNet model is assessed against spatially and temporally varied UWA channels, Bellhop is set up with specific input parameters for the training and testing datasets. For testing 20% of the entire dataset, two scenario specific channel configurations are created to simulate genuine underwater environments, with precise Bellhop inputs and associated channel characteristics outlined in Table 4. Each test scenario is carefully designed to prevent overlap with training conditions (e.g., incorporating intermittent ship noise in shallow water tests. Two typical environments were examined Shallow Coastal (0–50 m) and Continental Shelf (50–200 m). In the shallow coastal environment as shown in Figure 2, the sound speed ranged from 1509 to 1531 m/s owing to a surface duct, with a sandy bottom exhibiting a density of 2000 kg/m³ and an absorption rate of 3 dB per wavelength. The transmitter and receiver were positioned at depths of 5 m and 3 m, respectively, over a distance of 500 m. Environmental noise was characterized as ship-induced, varying from 10 to 20 dB within the 1–5 kHz frequency range. Bellhop simulations produced a delay spread of 132.9 ms, 28 multipath components, a Doppler shift of ±0.6 Hz, and a transmission loss of 60 dB. While for continental shelf environment as depicted in Figure 3, the sound velocity ranged from 1526 to 1534 m/s under near-isothermal circumstances, characterized by a silt bottom (density 2400 kg/m³, absorption 5 dB per wavelength). The transmitter and receiver were positioned at depths of 20 m and 15 m, respectively, over a range of 1000 m. The noise profile included both maritime and marine sources. Analysis of the bellhop for this environment revealed a delay spread of 100 ms, 63 multipath components, a Doppler shift of ±0.45 Hz, and a transmission loss of 80 dB. These meticulously designed simulation scenarios provide genuine UWA channels, including essential propagation properties, multipath diversity, and Doppler effects, which are vital for assessing the efficacy of channel estimate methods in real-world situations. These configurations ensures that test channels accurately represent the real world dynamics of UWA conditions, which is essential for evaluating CRNet adaptability to time-varying situations.

Table 4

Table 4. Bellhop input parameters & test channel characteristics.

Figure 2

Figure 2. Demonstration of Bellhop ray model in shallow water.

Figure 3

Figure 3. Demonstration of Bellhop ray model in continental shelf water.

3.2 Benchmark system and models

Benchmarks such as LS, MMSE, and BP-NN estimators represent established techniques for UWA channel estimation, each presenting unique advantages and constraints. These models serve as traditional references and are discussed in the subsequent subsections for comparative evaluation.

3.2.1 Least squares estimator

The LS algorithm is a commonly used conventional method for channel estimation as in Equation 18. The aim is to reduce the squared error between the received and sent pilot symbols. This is accomplished by optimizing the subsequent cost function Cho et al. (2010).

$\begin{array}{ll}{\widehat{H}}_{\text{LS}}[k]=Y[k]/X[k],k=0,\dots ,N-1,& (18)\end{array}$

where $X[k]$ and $Y[k]$ are the known pilot and received symbol on sub-carrier $k$, respectively. Its MSE is ${\sigma }_Z^2/{\sigma }_X^2$; hence it serves only as a lower-bound reference for the proposed CRNet.

3.2.2 Minimum mean square error estimator

MMSE estimator improves upon the LS approach by addressing its sensitivity to noise through the integration of statistical information about both the channel and the noise. It aims to minimize the MSE between the actual channel H and its estimate $\widehat{H}$. This approach requires the computation of the channel autocorrelation and noise variance, which can be particularly challenging and computationally intensive in underwater acoustic environments, thus limiting its feasibility for real time implementation. The estimator is formulated by determining an optimal linear weighting matrix W that minimize the expected error between $H$ and $\overline{H}$. Consider the LS solution in Equation 18 we can compute Equation 19 for MMSE as in Liu et al. (2025):

$\begin{array}{ll}{\widehat{H}}_{\text{MMSE}}=R_{HH}{(R_{HH}+\frac{{\sigma }_Z^2}{{\sigma }_X^2}I)}^{-1}{\widehat{H}}_{\text{LS}}.& (19)\end{array}$

Because $R_{HH}$ and ${\sigma }_Z^2$ are rarely known a priori in UWA channels, MMSE need prior channel statistics which is challenging in UWA environment.

3.2.3 Back-propagation neural network

We include a fully-connected BP-NN Jiang et al. (2019) solely to quantify the gain offered by the proposed CRNet. BP-NN learns a non-linear pilot-to-CIR mapping but suffers from vanishing gradients and over-fitting in highly non-stationary UWA channels. CRNet overcomes these limitations through complex-valued convolutions and residual LSTM paths.

3.3 Performance evaluation metrics

In UWA communication, various evaluation metrics are used to assess system and model performance. Among these, MSE is a widely adopted standard as in Equation 20, particularly valuable for evaluating DL models. MSE measures the average of the squared differences between predicted and actual values, thereby indicating the extent of prediction errors. It is often used in regression tasks and is proficient in assessing the precision of signal reconstruction or channel estimation in UWA systems. Additionally, it is standard practice to present BER versus SNR and BER versus the number of pilot symbols, both of which offer critical insights into communication quality and overall system performance. One limitation of MSE, however, is its sensitivity to outliers since the error values are squared, larger deviations have a disproportionately greater impact on the final score. The MSE is calculated as Liu et al. (2021b).

$\begin{array}{ll}\text{MSE}=\frac{1}{N}\sum _{i=1}^N{(y_i-{\widehat{y}}_i)}^2& (20)\end{array}$

Furthermore, SNR and BER are critical performance metrics in signal processing for UWA communication. SNR represents the ratio of the signal power to the background noise power and serves as a key indicator of signal clarity and robustness against interference. A higher SNR implies a cleaner, more reliable signal, whereas a lower SNR reflects greater vulnerability to noise Zhang et al. (2022b), which is a common challenge in underwater environments. On the other hand, BER measures the proportion of bits received incorrectly compared to the total number of transmitted bits, offering a direct assessment of transmission accuracy. Monitoring BER is essential for evaluating the reliability and effectiveness of data communication systems operating in complex and noisy underwater conditions.

4 Results and discussions

Simulation results are explained in the following subsections:

4.1 Proposed model performance in channel estimation

The proposed model incorporates a convolutional recurrent architecture that enables each layer to capture both spatial and temporal dependencies by combining convolutional layers with recurrent units. This design promotes efficient feature reuse and enhances gradient flow during backpropagation, addressing issues like vanishing or exploding gradients. The recurrent connections provide shorter and more stable paths for information and gradient propagation, resulting in more effective and stable training. The proposed CRNet model learns feature maps that capture the frequency, temporal, and noise characteristics of underwater acoustic signals. By training on paired data of transmitted OFDM pilot symbols X_p(k) and received symbols Y (k), the network effectively learns the mapping between the received signal and the channel impulse response CIR. Visualizing these feature maps reveals how the model distinguishes between different signal components, guided by actual channel responses across varying underwater environments.

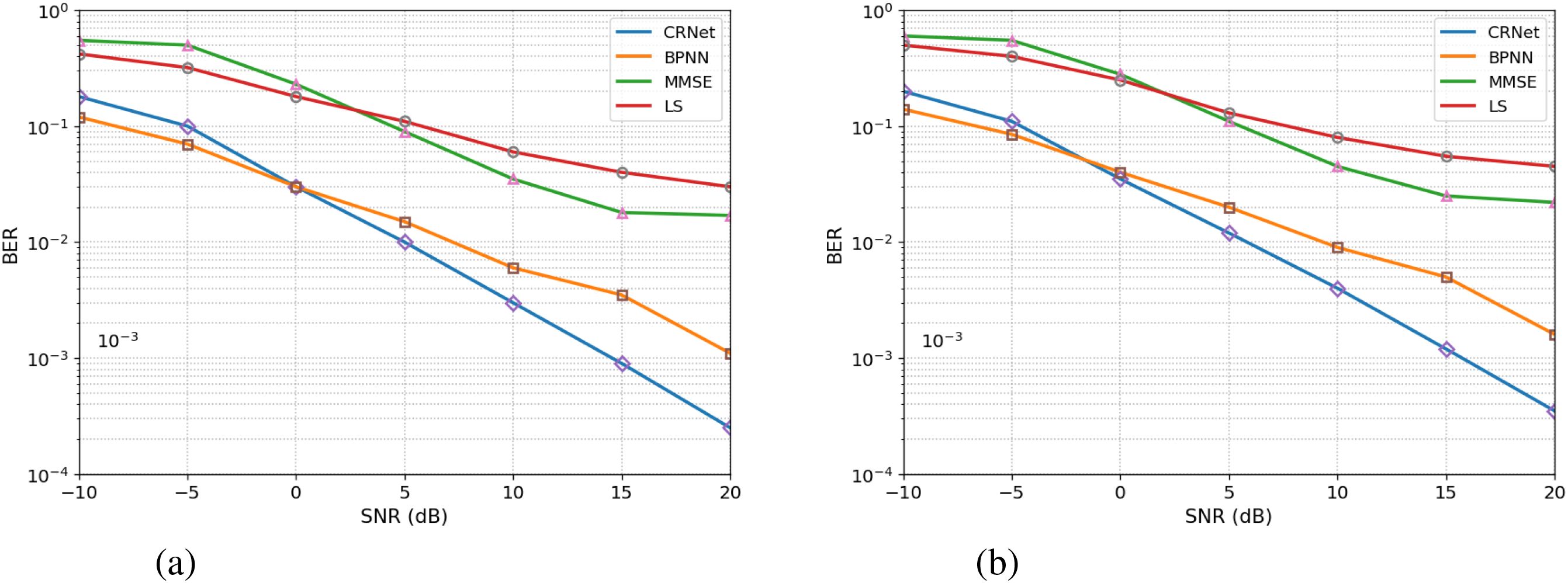
The QPSK modulation method exhibits a notable improvement in BER performance as SNR grows, especially when using the CRNet model for channel estimation. In the shallow coastal environment, marked by significant multipath reflections, surface scattering, and considerable temporal variability owing to the shallow sea depth (0–50 m), the BER for QPSK modulation stays notably elevated throughout the SNR spectrum, particularly at lower SNR values as depicted in Figure 4. At −10 dB SNR, all models (LS, MMSE, BPNN, and CRNet) show elevated BER values, with LS and MMSE reporting values of 0.42 and 0.55, respectively, indicating substantial noise and multipath interference. With an increase in SNR, CRNet performance markedly improves, attaining a BER of 0.18 at 0 dB, in contrast to 0.32 for LS, 0.50 for MMSE, and 0.07 for BPNN. At 10 dB, CRNet achieves a BER of 0.03, illustrating its proficiency in managing nonlinearities and surpassing other models. At 20 dB, CRNet attains 0.00025, demonstrating its exceptional noise resistance and strong performance in a channel characterized by intricate multipath effects, while BPNN obtains 0.0011, and both MMSE and LS exhibit comparatively higher error rates, about 0.017 and 0.03, respectively.

Figure 4

Figure 4. Impact of QPSK modulation using (a) shallow coastal and (b) continental shelf channels.

Conversely, the continental shelf environment in Figure 3, characterized by increased depth (50–200 m) and more robust acoustic propagation pathways. At −10 dB SNR, LS and MMSE exhibit values of 0.50 and 0.60, respectively, however BPNN and CRNet demonstrate superior performance with values of 0.14 and 0.20. As the SNR rises to 0 dB, CRNet attains a performance metric of 0.11, followed by BPNN at 0.085, MMSE at 0.55, and LS at 0.40. This demonstrates that data-driven models consistently surpass linear estimators, but with a reduced performance disparity relative to the shallow coastal scenario. At 10 dB, CRNet achieves 0.035, whilst BPNN attains 0.04, and MMSE and LS provide 0.28 and 0.25, respectively. At 20 dB, CRNet attains a value of 0.00035, followed by BPNN at 0.0016, MMSE at 0.022, and LS at 0.045, demonstrating CRNet dominance over other models, although the margin is narrower in the continental shelf environment owing to the decreased complexity of the channel. The findings indicate that CRNet has superior performance in both scenarios, with a more noticeable advantage in the shallow coastal channel, where multipath-induced distortions are more prominent.

4.2 Impact of high order modulation schemes

This study primarily focused on assessing BER under varying SNR conditions across different modulation schemes, such 16,32 and 64 QAM for both shallow coastal and continental shelf channels.

The BER vs SNR curve for 16-QAM, as shown in Figure 5, highlights the effectiveness of the proposed CRNet model relative to traditional LS, MMSE, and BPNN estimators in both channels. In the shallow coastal environment, the 16-QAM BER stays comparatively high throughout the SNR spectrum, particularly at low SNR values. At −10 dB, all models have increased BERs, with LS and MMSE presenting BER values of 0.55 and 0.45, respectively, whilst BPNN and CRNet perform more favorably with values of 0.35 and 0.25. With an increase in SNR, CRNet demonstrates substantial enhancement, reducing to 0.18 at 0 dB, further declining to 0.03 at 10 dB, and eventually achieving 0.0010 at 20 dB, reflecting a 90% improvement over LS (0.015) and a 75% enhancement over BPNN (0.0045). Conversely, the continental shelf environment, characterized by more steady propagation and less multipath interference (50–200 m depth), demonstrates a significant increase in BER across all models, with CRNet consistently surpassing the others. At −10 dB, LS and MMSE exhibit BERs of 0.58 and 0.48, however BPNN and CRNet demonstrate superior performance with 0.38 and 0.28, respectively. As the SNR rises to 0 dB, CRNet attains a value of 0.18, and at 20 dB, it hits 0.0015, demonstrating a 90% enhancement over LS (0.015) and an 80% enhancement over MMSE (0.0100). The findings confirm that CRNet regularly achieves the lowest BER, demonstrating a more significant advantage in shallow coastal channels where multipath-induced distortions are more prominent.

Figure 5

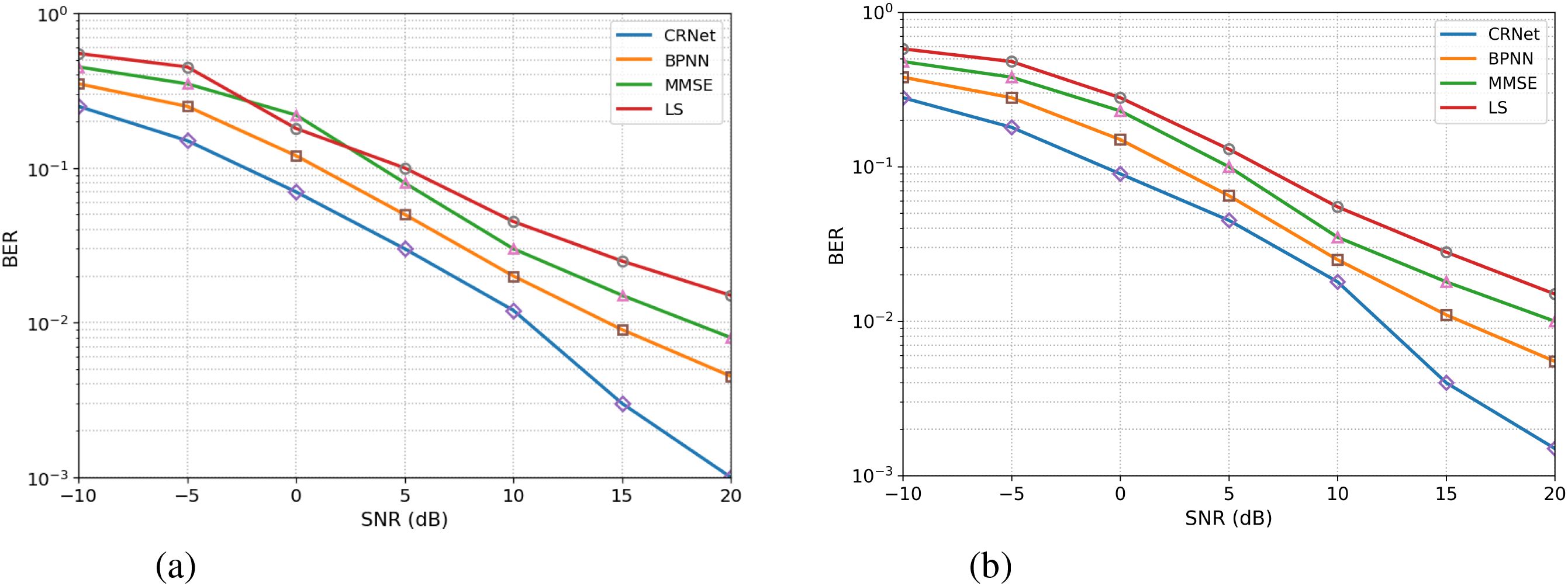
Figure 5. Comparison of 16-QAM BER vs SNR for (a) shallow coastal and (b) continental shelf channels.

Furthermore, In Figure 6 The BER for 32-QAM grows substantially throughout the SNR spectrum in comparison to 16-QAM, indicating the heightened complexity associated with higher order modulation. At −10 dB, all models exhibit increased BERs, with LS and MMSE presenting BERs of 0.60 and 0.50, respectively, whilst BPNN and CRNet show superior performance at 0.30 and 0.32. With an increase in SNR, CRNet demonstrates significant enhancement, achieving 0.18 at 0 dB, 0.03 at 10 dB, and 0.0025 at 20 dB. In the continental shelf environment, 32-QAM has elevated BERs compared to 16-QAM, but the performance disparity diminishes. At −10 dB, LS and MMSE exhibit values of 0.65 and 0.55, respectively, whilst BPNN and CRNet have worse performance with values of 0.42 and 0.38. As the SNR ascends to 0 dB, CRNet attains a value of 0.34, and at 20 dB, it obtains 0.0040. These findings indicate that while 32-QAM modulation yields a larger BER than 16-QAM owing to more signal complexity.

Figure 6

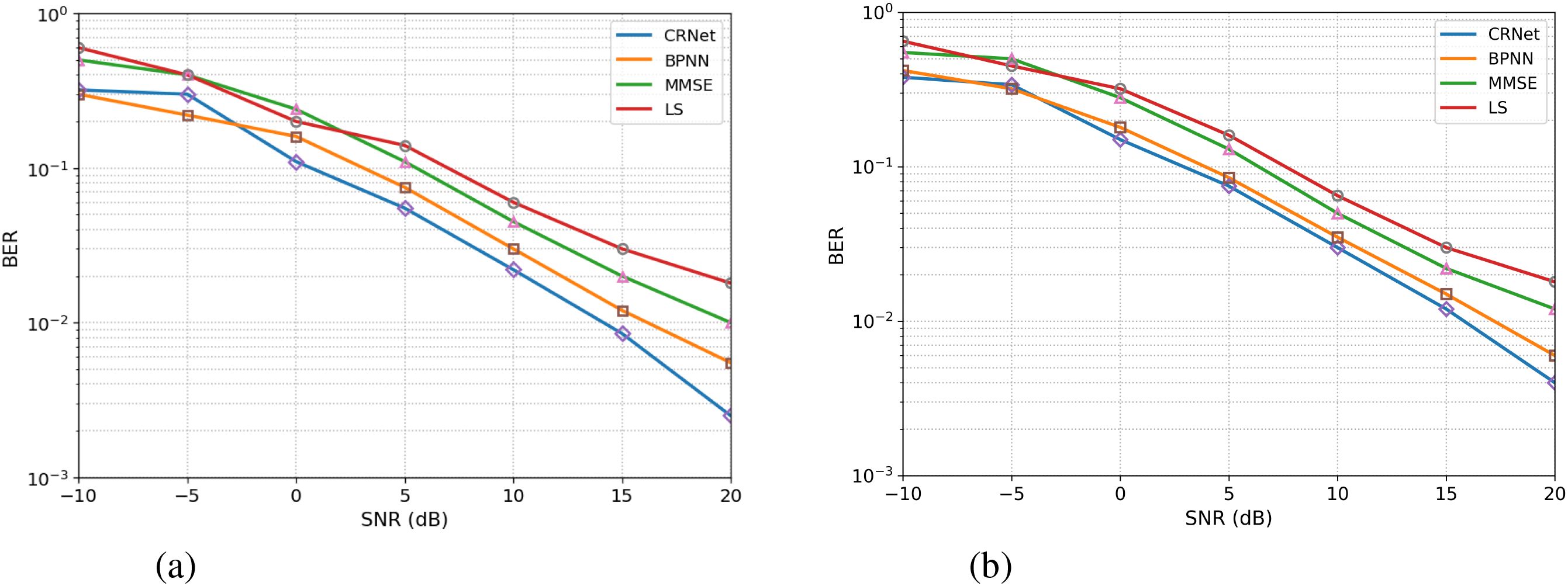
Figure 6. Comparison of 32-QAM BER vs SNR for (a) shallow coastal and (b) continental shelf channels.

As shown in Figure 7 the 64-QAM BER values are notably elevated throughout the SNR spectrum, indicating the raised signal complexity of 64-QAM coupled with the adverse channel conditions of multipath reflections, surface scattering, and significant temporal variability typical of shallow waters. At −10 dB, LS and MMSE show increased BERs of 0.68 and 0.58, respectively, however BPNN and CRNet display superior performance with BERs of 0.40 and 0.30, respectively. With an increase in SNR, CRNet markedly surpasses other models, achieving scores of 0.18 at 0 dB, 0.095 at 10 dB, and 0.0080 at 20 dB. Conversely, the continental shelf environment, distinguished by more consistent propagation and less multipath interference (50–200 m depth), exhibits superior overall BER performance across all models. At −10 dB, LS and MMSE exhibit values of 0.70 and 0.60, respectively, whilst BPNN and CRNet have worse performance with values of 0.40 and 0.32, respectively. With an increase in SNR, CRNet attains a BER of 0.11 at 0 dB and 0.0075 at 20 dB. The results demonstrate that CRNet consistently surpasses the other models in both environments, where multipath induced distortions are more severe.

Figure 7

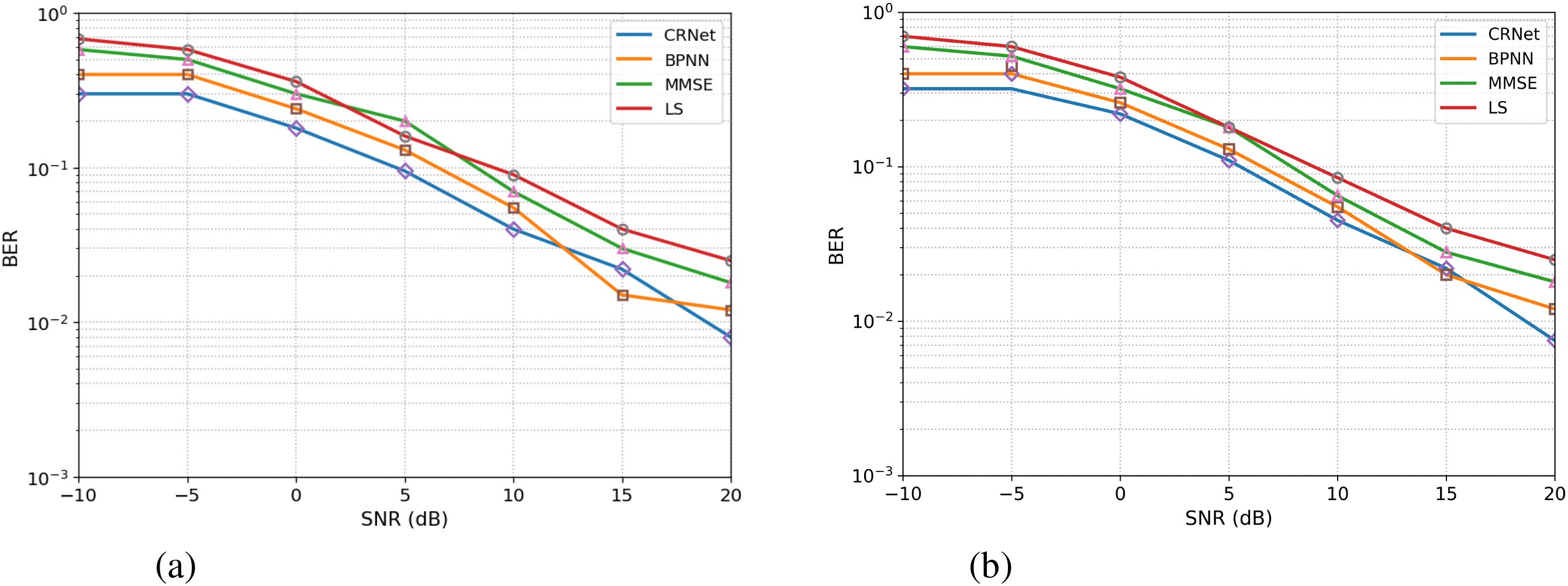
Figure 7. Comparison of 64-QAM BER vs SNR for (a) shallow coastal and (b) continental shelf channels.

We have specifically assessed the BER performance of these approaches for two distinct modulation schemes i.e. QPSK and QAM. Our results demonstrate that for all SNR levels, the BER of QPSK modulation surpasses that of QAM modulation. This indicates that QPSK has enhanced performance relative to QAM in our experimental setup.

Figures 8, 9 illustrates amplitude and phase error, demonstrating the enhanced performance of CRNet in estimation of different channels relative to conventional estimators such as LS, MMSE, and BPNN. The amplitude error for CRNet is markedly reduced across different SNR levels, illustrating its proficiency in reliable estimating channel amplitudes even in difficult UWA conditions, characterized by multipath interference and Doppler shifts. Conversely, LS and MMSE show more amplitude errors, particularly at low SNRs, highlighting their inadequacies in managing the dynamic and noisy characteristics of underwater channels. Likewise, the phase error for CRNet is persistently minimal, even at low SNRs, ensuring precise phase estimate essential for coherent signal detection. Conversely, LS and MMSE exhibit more phase errors, underscoring their vulnerability to noise and inadequacy in accurately representing intricate channel features. The CRNet model capacity to reduce both amplitude and phase errors highlights its durability and accuracy, establishing it as the optimal selection for reliable UWA communication.

Figure 8

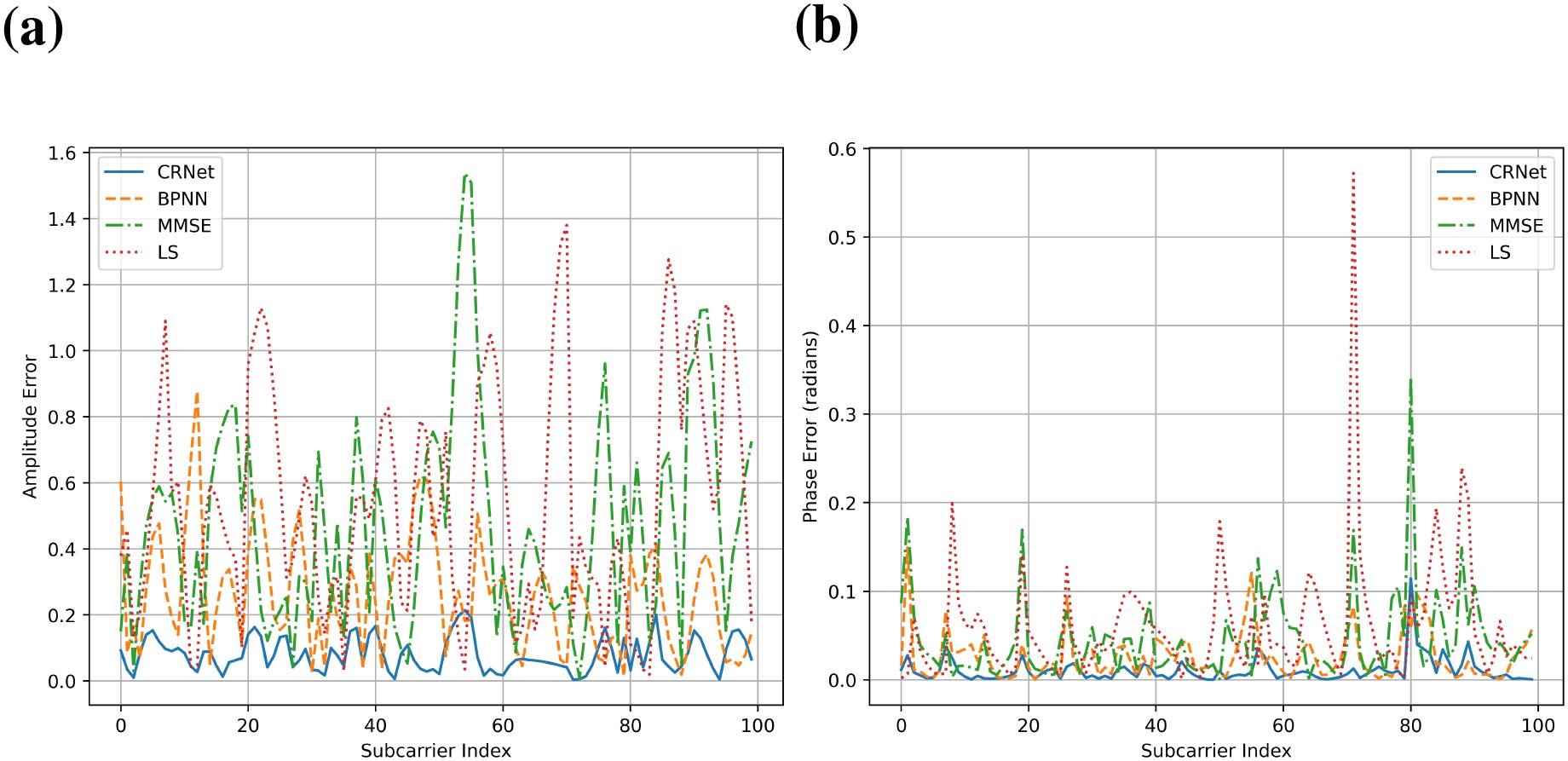
Figure 8. Amplitude error and phase error in estimation of Shallow coastal. (a) Amplitude error. (b) Phase error.

Figure 9

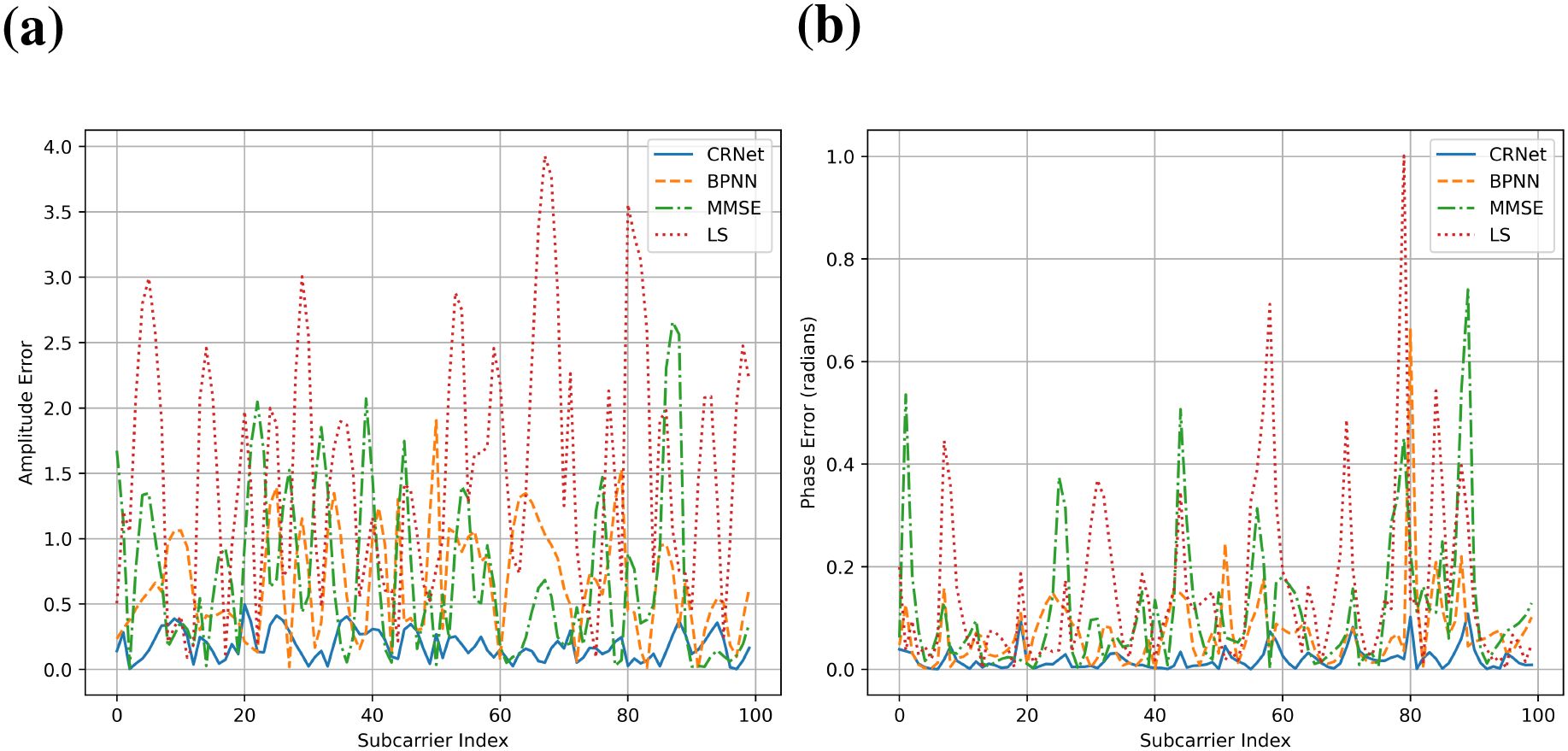
Figure 9. Amplitude error and phase error in estimation of continental shelf. (a) Amplitude error. (b) Phase error.

4.3 Mean square error analysis of proposed scheme

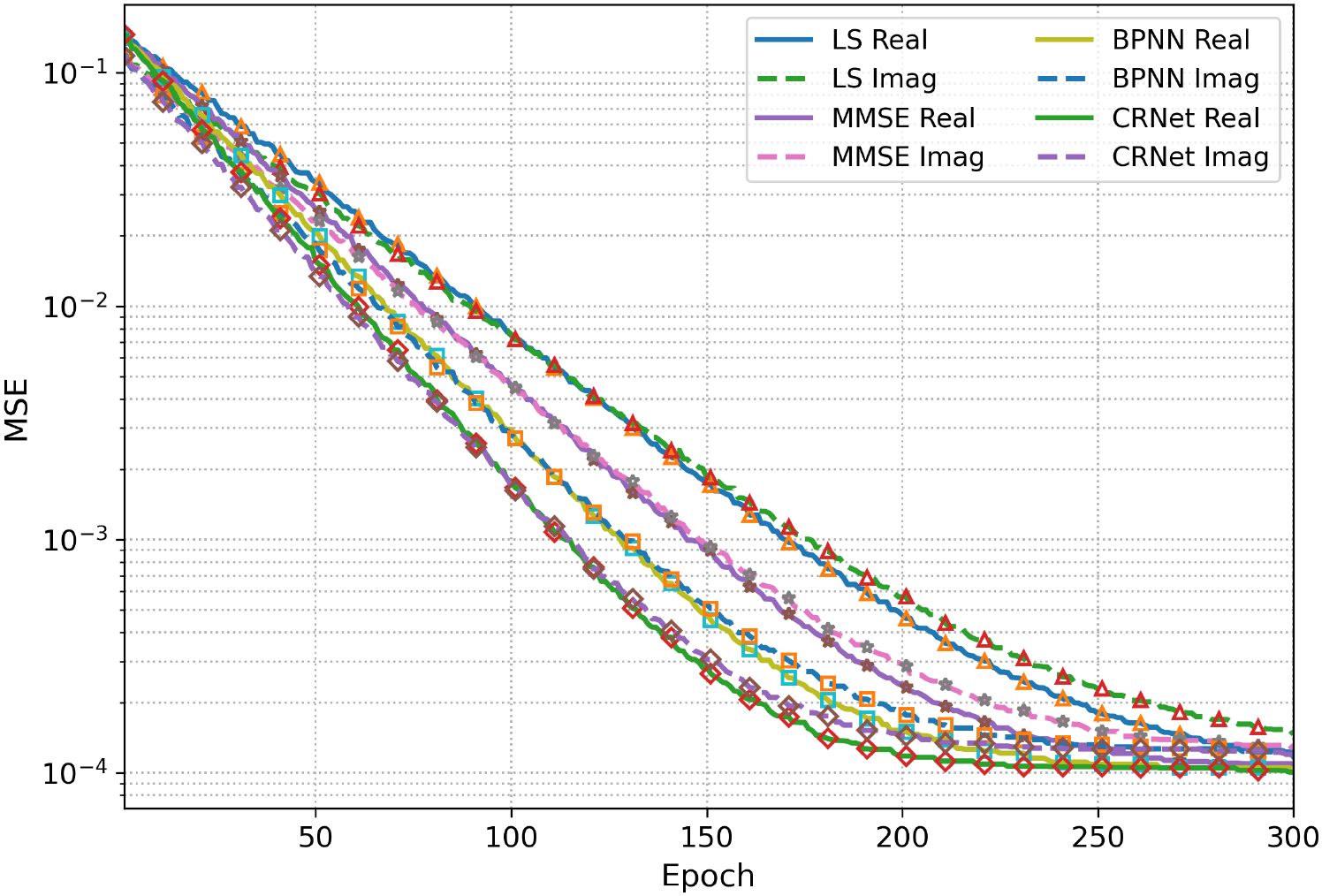
The MSE performance of the proposed CRNet model and benchmark estimators, including LS, MMSE, and BPNN, was assessed in two UWA channel environments: shallow coastal and continental shelf. Results depict the fluctuation of MSE with training epochs for the real and imaginary components of the channel coefficients. The findings illustrate the convergence characteristics and overall estimation precision of each model across various channel circumstances. A similar reduction in MSE is found in both configurations as the number of epochs grows, indicating that all models successfully learn to represent the fundamental channel dynamics over time. Nonetheless, the extent of enhancement and the ultimate steady-state MSE differ significantly between conventional and learning based methodologies. Overall, neural estimators, especially CRNet, demonstrate faster convergence and attain much lower MSE values compared to traditional linear estimators like LS and MMSE. In the shallow coastal environment, marked by significant multipath propagation, elevated reflection losses, and fluctuating interference within a limited sea depth, precise channel estimation proves to be extremely difficult. As demonstrated in Figure 10 LS and MMSE estimators initially exhibit high MSE values (about 10⁻¹) and demonstrate gradual convergence rates. After 300 epochs, the LS estimator stabilizes at 10⁻³, whilst the MMSE attains a marginally lower final error of around 2 × 10⁻⁴. The constraint of both approaches lies in their linear modeling characteristics, which inadequately account for nonlinear distortions resulting from surface scattering and phase variations. The BPNN model significantly outperforms LS and MMSE by acquiring nonlinear input–output relationships from the data. The MSE constantly decreases throughout training, reaching roughly 1.5 × 10⁻⁴ after 300 epochs. Nonetheless, the convergence is somewhat slower and less stable owing to gradient vanishing and network saturation in intricate multipath scenarios. Despite these advancements, BPNN continues to demonstrate constraints in adjusting to extremely dynamic channel situations.

Figure 10

Figure 10. MSE loss of CRNet along with traditional models in shallow coastal channel.

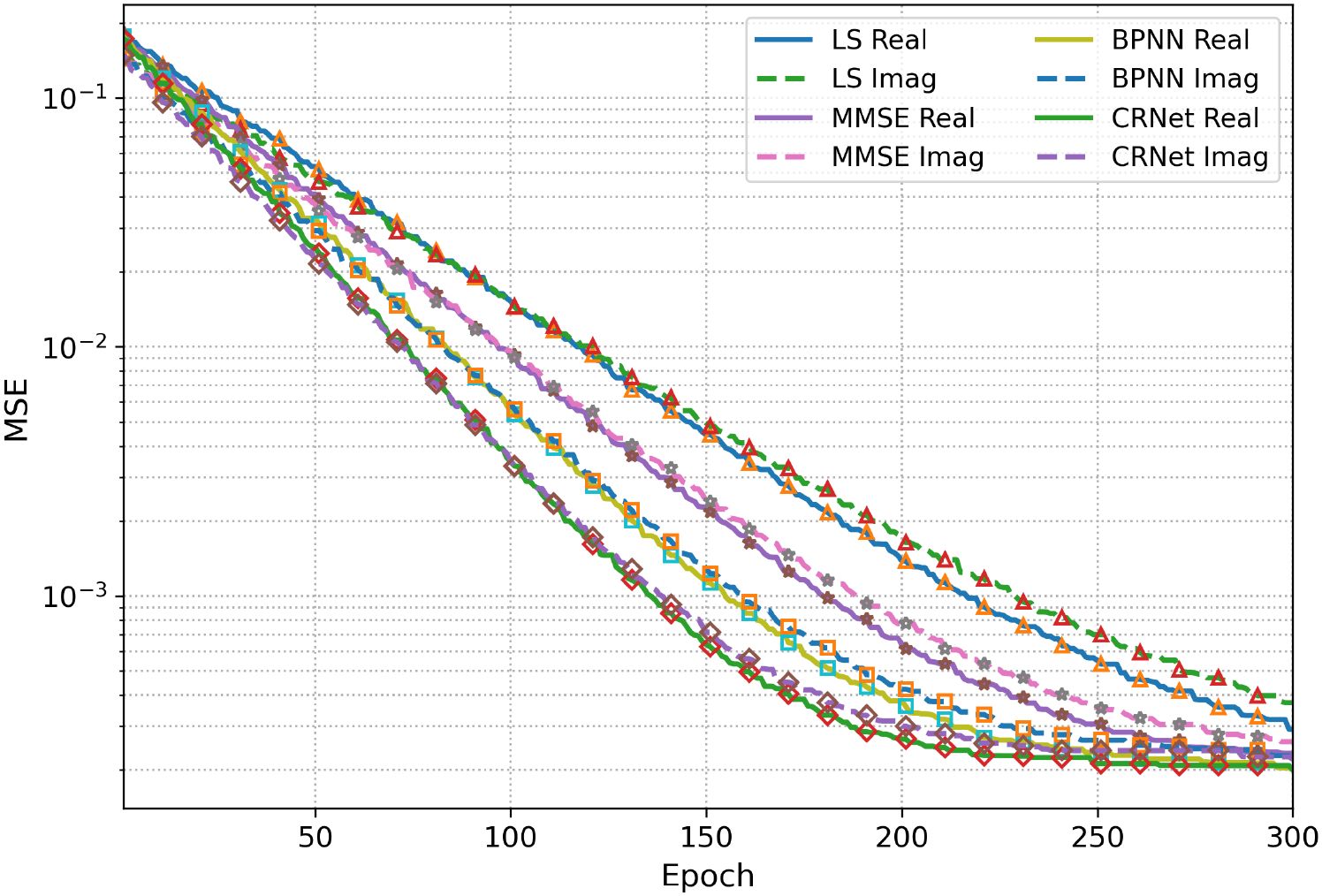
Conversely, the CRNet model attains the lowest overall MSE and the quickest convergence rate among all evaluated estimators. Both the real and imaginary components attain steady-state MSE approaching 8 × 10⁻⁵ after about 200 epochs. This exceptional performance is due to two main architectural benefits: first, the complex-valued representation enables CRNet to simultaneously model amplitude and phase relationships present in underwater channels; and second, residual connections improve gradient flow, facilitating efficient and stable training. As a result, CRNet has exceptional proficiency in alleviating multipath interference and simulating nonlinear acoustic propagation effects. The MSE loss in continental shelf environment as shown in Figure 11 has a considerably deeper area characterized by steady acoustic pathways and multipath variability. In these circumstances, all estimators demonstrate enhanced convergence and more gradual error reduction relative to the shallow coastal scenario. The LS and MMSE estimators exhibit superior performance, achieving final MSE values of around 1 × 10⁻³ and 1.5 × 10⁻⁴, respectively. The stability of this environment minimizes random dispersion, therefore enhancing the precision of linear estimating methods. The BPNN model excels in this context, with accelerated convergence and a final MSE of around 1 × 10⁻⁴. This enhancement signifies that neural models have more reliability when the channel displays less abrupt temporal or spatial fluctuations. Nevertheless, the performance of BPNN continues to be poor compared to CRNet for both convergence speed and ultimate accuracy. CRNet consistently surpasses all baseline models, achieving quick convergence and sustaining the lowest steady-state MSE of less than 1 × 10⁻⁴ for both the real and imaginary components. Despite the reduction in performance disparity between CRNet and MMSE/BPNN in a shallow setting, CRNet continually proves to be the most precise and reliable estimator.

Figure 11

Figure 11. MSE loss of CRNet along with traditional models in continental shelf channel.

4.4 Impact of dynamic signal decomposition techniques

UWA communication is significantly impacted by ambient noise from sources like wind-driven surface activity, marine vessels, and aquatic life. This noise is non-stationary and varies with factors such as location, sea depth, wind speed, and acoustic propagation conditions. Enhancing signal quality through effective denoising can improve the performance of UWA systems. This study utilizes the denoised signal derived from the suggested DSD techniques as input for the CRNet architecture, therefore integrating the denoising and learning phases into an efficient pipeline for channel estimation as depicted in Figure 1.

4.4.1 Local mean decomposition

LMD is used as a denoising at the receiver to boost the accuracy of UWA channel estimates by extracting relevant information from noisy signals Jan et al. (2023). LMD decomposes the received signal into a series of intrinsic mode functions (IMFs) as depicted in Algorithm 2, each representing a separate frequency component as depicted in Figure 12. By assessing and choosing relevant IMFs, LMD successfully isolates the channel-induced distortions from the actual signal. This selective separation of components assists in separating the underlying channel characteristics, decreasing noise interference, and eventually enhancing the accuracy of channel estimates, which is vital for robust UW communicatsystems. ems. The received UWA signal be denoted as in Equation 21:

Algorithm 2. Local mean decomposition (LMD) for UWA signal.

Figure 12

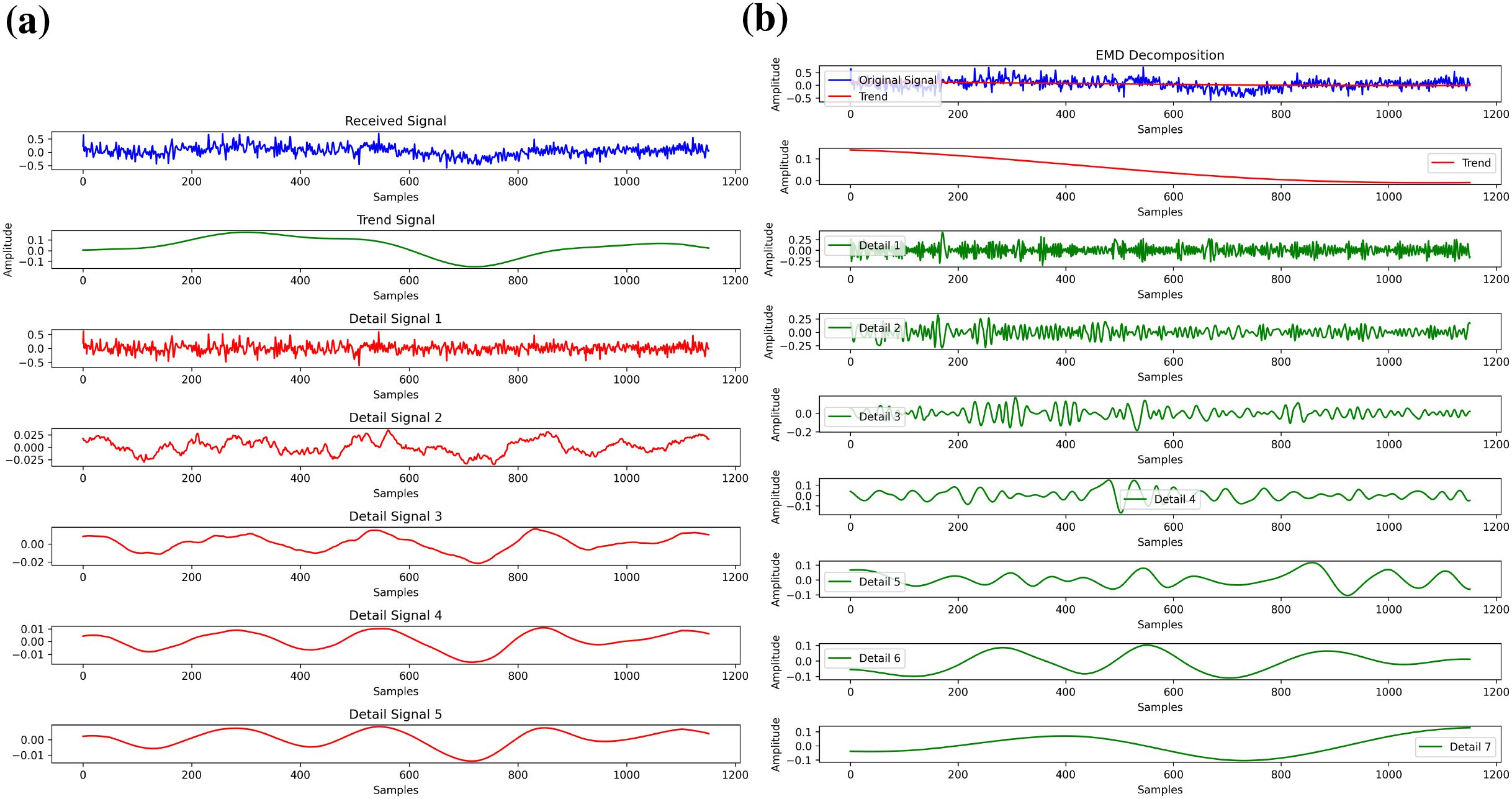
Figure 12. Dynamic signal decomposition techniques (a) Local mean decomposition (b) Empirical model decomposition.

$\begin{array}{ll}y(t)=s(t)+w(t)& (21)\end{array}$

where:

● y(t) is the observed received signal,

● s(t) is the useful signal component transmitted through the UWA channel,

● w(t) is the additive noise (typically modeled as AWGN or colored noise).

The goal of LMD is to decompose y(t) into a set of product functions (PFs) that represent amplitude and frequency modulated components of the signal. Unlike previous denoising methods. Our proposed LMD strategy is explicitly tailored to address the dynamic and intricate characteristics of UWA communication. In Jan et al. (2023) the authors concentrated on chirp-based UWA estimation using limited datasets, neglecting pilot and OFDM subcarrier effects, while Lu et al. (2021) tackled the denoising of marine mammal data, specifically targeting bioacoustic signals from species such as dolphins and whales, without accounting for actual communication complexities. In contrast, our approach specifically addresses channel distortions resulting from multipath propagation and Doppler shifts. Hence, the suggested LMD proficiently separates essential signal components from noisy received signal, hence ensuring enhanced accuracy and robustness in UWA channel estimation.

The received UWA signal as in Equation 22 is denoted by y(t). The LMD decomposes y(t) into K product functions (PFs), and a residual r_K(t) in Lu et al. (2021) is defined as

$\begin{array}{ll}y(t)=\sum _{k=1}^{K}P{F}_k(t)+r_K(t)& (22)\end{array}$

Each product function PF_k(t) captures a mono-component AM-FM signal structure as in Equation 23 and is defined as:

$\begin{array}{ll}P{F}_k(t)=a_k(t)\text{ cos }({\int }_0^t{\omega }_k(\tau )d\tau )& (23)\end{array}$

where:

● a_k(t) is the instantaneous amplitude of the k-th PF,

● ω_k(t) is the instantaneous angular frequency, derived from phase variations,

● The integral ${\int }_0^t{\omega }_k(\tau )d\tau$ represents the instantaneous phase of the signal component.

After PF, the local mean and envelope estimation process as in Equation 25 for each decomposition step k applied to the UWA received signal:

1. Identify all local extrema (peaks and troughs) of the signal y_k(t).

2. Estimate the local mean as in Equation 24 m_k(t) by averaging adjacent extrema as in Lu et al. (2021):

$\begin{array}{ll}{m}_k(t)=\frac{x_i(t)+x_{i+1}(t)}{2}& (24)\end{array}$

where x_i(t) and x_{i+ 1}(t) are successive extrema.

3. Estimate the local envelope e_k(t) using

$\begin{array}{ll}{e}_k(t)=\left|\frac{x_i(t)-x_{i+1}(t)}{2}\right|& (25)\end{array}$

4. Extract the frequency-modulated signal component as in Equation 26:

$\begin{array}{ll}{h}_k(t)=\frac{y_k(t)-m_k(t)}{e_k(t)}& (26)\end{array}$

This isolates the oscillatory behavior normalized by the local envelope.

5. Calculate the instantaneous phase as in Equation 27:

$\begin{array}{ll}{\varphi }_k(t)={\cos }^{-1} (h_k(t))& (27)\end{array}$

6. Reconstruct the product function as in Equation 28:

$\begin{array}{ll}P{F}_k(t)=a_k(t) \text{cos }({\varphi }_k(t)),\text{\hspace{1em}where\hspace{0.33em}}{a}_k(t)=e_k(t)& (28)\end{array}$

This PF captures both amplitude and frequency modulation effects of the k-th component.

7. Update the signal as in Equation 29 for the next iteration as in Lu et al. (2021):

$\begin{array}{ll}{y}_{k+1}(t)=y_k(t)-P{F}_k(t)& (29)\end{array}$

Repeat this process until the residual r_K(t) = y_{K+ 1}(t) becomes a monotonic trend.

At the end, the final reconstruction as depicted in Figure 13 and Equation 30 the denoised UWA signal using LMD are expressed as

Figure 13

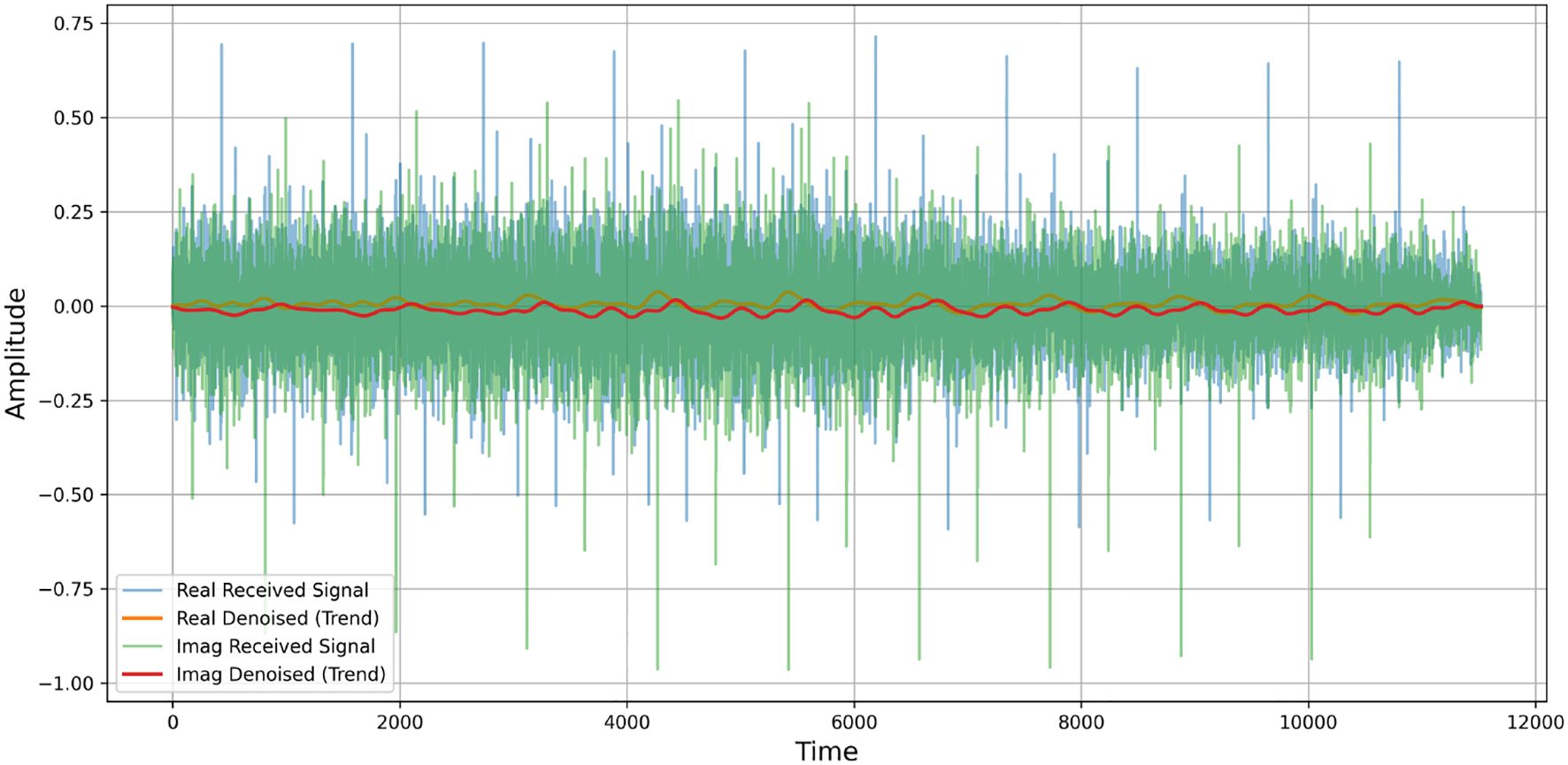
Figure 13. Comparison of the received and denoised signal using the LMD technique. The denoised signal shows improved smoothness and reduced high-frequency noise.

$\begin{array}{ll}y(t)=\sum _{k=1}^K{a}_k(t)\text{ cos }({\int }_0^t{\omega }_k(\tau )d\tau )+r_K(t)& (30)\end{array}$

where:

● a_k(t) and ω_k(t) reflect the adaptive amplitude and frequency of underwater signal components,

● r_K(t) captures the residual, usually interpreted as trend or background noise after decomposition.

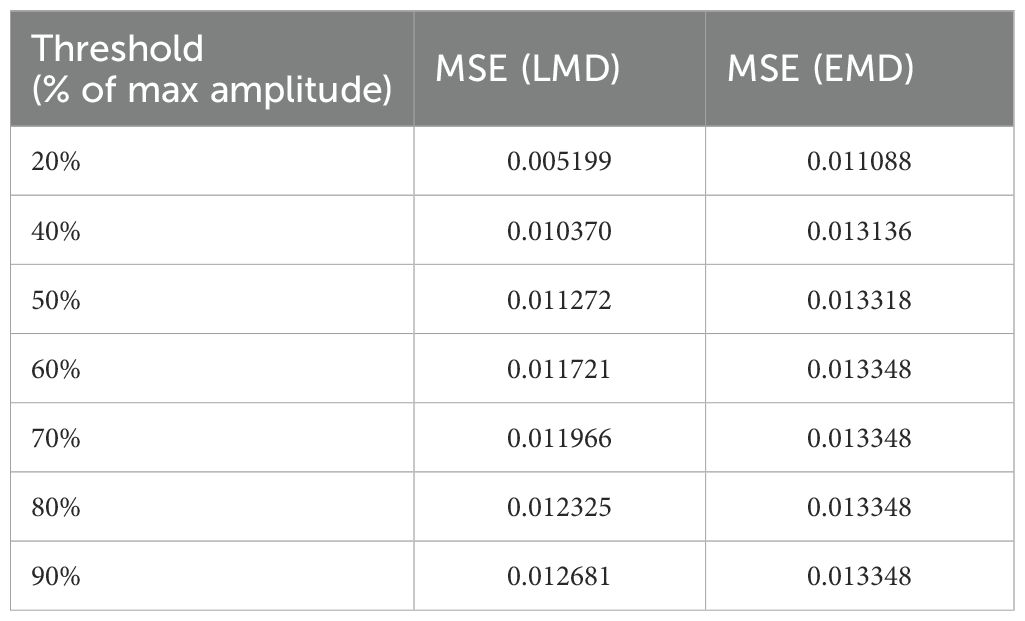
Table 5 shows the MSE values for LMD and EMD denoising methods across different amplitude thresholds. LMD consistently attains a lower MSE than EMD across all threshold values, ranging from 20% to 90% of the maximum amplitude. This signifies that LMD is superior in maintaining the original signal while attenuating noise. Significantly, at the 20% threshold, LMD decreases the MSE by almost 50% relative to EMD (0.005199 vs. 0.011088) and continues to exhibit superior performance at elevated thresholds, demonstrating its durability in UWA signal denoising. Moreover, Figure 13 demonstrates the efficiency of LMD denoising techniques on both real and imaginary received and trend signals.

Table 5

Table 5. Comparison of MSE between LMD and EMD denoising techniques at different thresholds.

4.5 Analysis on impact of pilot number

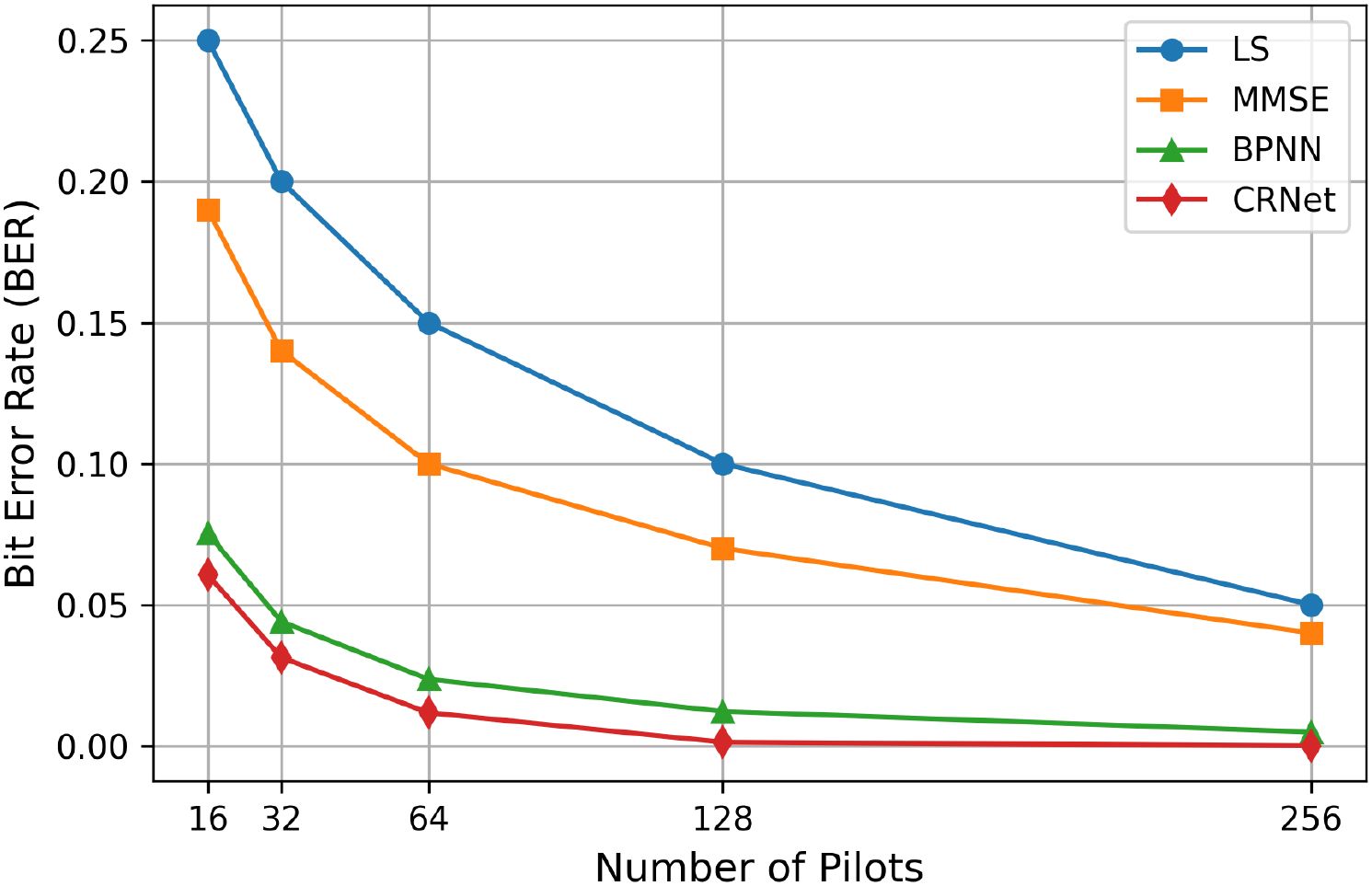
Pilots play a very crucial role in the correlation between BER performance and the number of pilot symbols. For an accurate channel estimation, it is necessary for the system to use a minimum number of pilots for the enhancement of spectral efficiency and overall system performance. As shown in Figure 14. As the number of pilots increases from 16 to 32 and then to 256, the BER performance of all pilot-assisted algorithms, except BPNN and CRNet, deteriorates significantly. Despite the decreased pilot tone, the CRNet estimator can maintain its BER at about 10⁻³, whereas the LS and MMSE estimators exhibit a failure with a BER of roughly 10⁻².

Figure 14

Figure 14. Impact on pilot number.

4.6 Evaluation of proposed model on training and unseen data

Figure 15 illustrates the CRNet BER performance in relation to SNR (0–20 dB) for the shallow-coastal and continental-shelf channels. Across the shallow-coastal link, CRNet reduces the training BER from 0.25 at 0 dB to 0.001 at 20 dB, while the unseen-data BER slightly trails at 0.0011, resulting in a 10% relative gap at the lowest SNR and an almost negligible gap at higher levels, demonstrating effective generalization despite significant, rapid multipath variations. In the continental-shelf link, the training BER decreases from 0.28 to 0.002, while the test BER attains 0.0025 at 20 dB, indicating a 12.5% enhancement; the improved train-test concordance signifies the more gradual and stable fading of the deeper-water channel. In both cases, CRNet achieves a BER of less than 10–³ at 15 dB SNR with a generalization cost of around 15%, surpassing linear and traditional non-linear estimators.

Figure 15

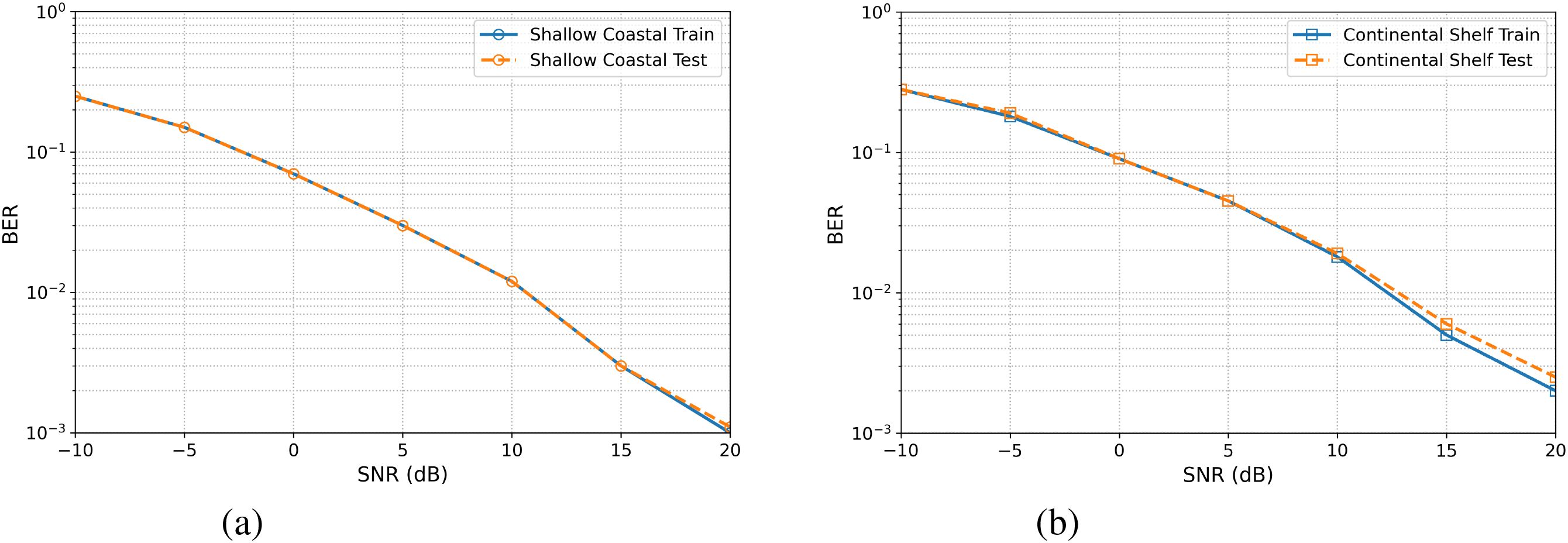
Figure 15. CRNet BER performance for (a) Shallow Coastal and (b) Continental Shelf Channels on training and testing data channel.

5 Conclusion

In this work, we thoroughly addressed the intricate channel estimation issue in UWA-OFDM communication systems. We have examined the impact of various modulation methods and pilot quantities on channel estimation approaches. Our distinctive CRNet-based estimator is designed to manage the complex structure of UWA channels. We explained the design and training of the CRNet model and illustrate the capabilities of CRNet estimator via extensive experiments using the BELLHOP data set, collected from shallow coastal and continental shelf environments. Experiments demonstrate that DenseNet surpasses traditional methodologies. The CRNet model exhibits a significant improvement in BER performance, achieving up to a 90% reduction in error rates at elevated SNRs compared to conventional linear and non-linear estimators such as LS, MMSE, and BPNN, demonstrating its exceptional generalization capability and resilience in both shallow coastal and continental shelf UWA channels. Our findings demonstrate that QPSK outperforms QAM in modulation schemes at low SNR levels. This underscores the importance of selecting the appropriate modulation approach for UWA-OFDM systems. We also integrated dynamic signal decomposition techniques, namely LMD and EMD, to denoise the received signals before estimation. The results show that LMD outperformed EMD, providing more effective noise suppression and signal clarity. The CRNet-based estimator surpasses traditional methods because of its adaptability. Our research investigates the impact of pilot signals on the performance of the CRNet estimator and maintains acceptable BER levels with reduced pilot resources, which is crucial for UW communication applications. The CRNet-based estimator demonstrates flexibility, resilience, and superior performance compared to previous channel estimation techniques, representing a significant advancement in underwater communication systems. The CRNet concept has the potential to enhance the reliability and efficiency of UW communication networks by addressing the specific challenges posed by dynamic and unpredictable environments. In the future, we want to conduct experiments using real-world sea data for thorough testing, aimed at improving the model generalization skills over a broader spectrum of underwater acoustic environments.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://github.com/EngrMansoorJan/UWA-OFDM-CE-A-Robust-CRNet-Framework.

Author contributions

MJ: Writing – original draft, Data curation, Methodology, Software, Validation, Investigation, Writing – review & editing, Conceptualization. MA: Data curation, Methodology, Conceptualization, Supervision, Writing – review & editing, Software. SHM: Writing – review & editing, Funding acquisition, Project administration, Resources. SMM: Project administration, Writing – review & editing, Resources. FK: Methodology, Conceptualization, Writing – review & editing, Funding acquisition, Supervision.

Funding

Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2025R300), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor HH declared a past co-authorship with the author SAHM.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2025.1671853/full#supplementary-material

References

Balevi E., Doshi A., and Andrews J. G. (2020). Massive mimo channel estimation with an untrained deep neural network. IEEE Trans. Wireless Commun. 19, 2079–2090. doi: 10.1109/TWC.2019.2962474

Crossref Full Text | Google Scholar

Bithas P. S., Michailidis E. T., Nomikos N., Vouyioukas D., and Kanatas A. G. (2019). A survey on machine-learning techniques for uav-based communications. Sensors 19, 5170. doi: 10.3390/s19235170, PMID: 31779133

PubMed Abstract | Crossref Full Text | Google Scholar

Chen W., Qi L., and Yanjun F. (2010). “An improved least square channel estimation algorithm for underwater acoustic ofdm systems,” in 2010 2nd International Conference on Future Computer and Communication, Vol. 3. V3–577 (3 Park Avenue, New York City, NY: IEEE). doi: 10.1109/IBCAST59916.2023.10713000

Crossref Full Text | Google Scholar

Chen P., Rong Y., Nordholm S., He Z., and Duncan A. J. (2017). Joint channel estimation and impulsive noise mitigation in underwater acoustic ofdm communication systems. IEEE Trans. Wireless Commun. 16, 6165–6178. doi: 10.1109/TWC.2017.2720580

Crossref Full Text | Google Scholar

Cho Y. S., Kim J., Yang W. Y., and Kang C. G. (2010). MIMO-OFDM wireless communications with MATLAB (Hoboken, New Jersey, USA: John Wiley & Sons).

Google Scholar

Cho Y.-H. and Ko H.-L. (2020). Channel estimation based on adaptive denoising for underwater acoustic ofdm systems. IEEE Access 8, 157197–157210. doi: 10.1109/ACCESS.2020.3018474

Crossref Full Text | Google Scholar

Deng J., Gao N., Chen X., Pu H., and Guo J. (2023). Underwater sound radiation from a mindlin plate with an acoustic black hole. Ocean Eng. 278, 114376. doi: 10.1016/j.oceaneng.2023.114376

Crossref Full Text | Google Scholar

Farzamnia A., Hlaing N. W., Haldar M. K., and Rahebi J. (2017). “Channel estimation for sparse channel ofdm systems using least square and minimum mean square error techniques,” in 2017 international conference on engineering and technology (ICET). 1–5 (3 Park Avenue, New York City, NY: IEEE). doi: 10.1109/ICEngTechnol.2017.8308193

Crossref Full Text | Google Scholar

Jan M., Mazhar S., Adil M., Muhammad A., and Gang Q. (2023). “Integration of deep neural networks and local mean decomposition for accurate underwater acoustic channel estimation,” in 2023 20th International Bhurban Conference on Applied Sciences and Technology (IBCAST). 866–871 (3 Park Avenue, New York City, NY: IEEE). doi: 10.1109/IBCAST59916.2023.10713000

Crossref Full Text | Google Scholar

Jiang R., Wang X., Cao S., Zhao J., and Li X. (2019). Deep neural networks for channel estimation in underwater acoustic ofdm systems. IEEE Access 7, 23579–23594. doi: 10.1109/ACCESS.2019.2899990

Crossref Full Text | Google Scholar

Kari D., Marivani I., Khan F., Sayin M. O., and Kozat S. S. (2017). Robust adaptive algorithms for underwater acoustic channel estimation and their performance analysis. Digital Signal Process. 68, 57–68. doi: 10.1016/j.dsp.2017.05.006

Crossref Full Text | Google Scholar

Khan M. R., Das B., and Pati B. B. (2020). Channel estimation strategies for underwater acoustic (uwa) communication: An overview. J. Franklin Institute 357, 7229–7265. doi: 10.1016/j.jfranklin.2020.04.002

Crossref Full Text | Google Scholar

Lei J., Fang H., Zhu Y., Chen Z., Wang X., Xue B., et al. (2024). Gpr detection localization of underground structures based on deep learning and reverse time migration. NDT E Int. 143, 103043. doi: 10.1016/j.ndteint.2024.103043

Crossref Full Text | Google Scholar

Li Y., Wang B., Shao G., Shao S., and Pei X. (2020). Blind detection of underwater acoustic communication signals based on deep learning. IEEE Access 8, 204114–204131. doi: 10.1109/ACCESS.2020.3036883

Crossref Full Text | Google Scholar

Ling J., Yardibi T., Su X., He H., and Li J. (2009). Enhanced channel estimation and symbol detection for high speed multi-input multi-output underwater acoustic communications. J. Acoustical Soc. America 125, 3067–3078. doi: 10.1121/1.3097467, PMID: 19425650

PubMed Abstract | Crossref Full Text | Google Scholar

Liu S., Adil M., Ma L., Mazhar S., and Qiao G. (2025). Densenet-based robust channel estimation in ofdm for improving underwater acoustic communication. IEEE J. Oceanic Eng. 50 (2), 1518–1537. doi: 10.1109/JOE.2024.3510929

Crossref Full Text | Google Scholar

Liu L., Cai L., Ma L., and Qiao G. (2021a). Channel state information prediction for adaptive underwater acoustic downlink ofdma system: Deep neural networks based approach. IEEE Trans. Vehicular Technol. 70, 9063–9076. doi: 10.1109/TVT.2021.3099797

Crossref Full Text | Google Scholar

Liu Z., Tan Z., and Bai F. (2021b). Adaptive modulation based on steady-state mean square error for underwater acoustic communication. EURASIP J. Wireless Commun. Networking 2021, 70. doi: 10.1186/s13638-021-01956-w

Crossref Full Text | Google Scholar

Lu H., Jiang M., and Cheng J. (2020). Deep learning aided robust joint channel classification, channel estimation, and signal detection for underwater optical communication. IEEE Trans. Commun. 69, 2290–2303. doi: 10.1109/TCOMM.2020.3046659

Crossref Full Text | Google Scholar

Lu T., Yu F., Wang J., Wang X., Mudugamuwa A., Wang Y., et al. (2021). Application of adaptive complementary ensemble local mean decomposition in underwater acoustic signal processing. Appl. Acoustics 178, 107966. doi: 10.1016/j.apacoust.2021.107966

Crossref Full Text | Google Scholar

Murad M., Tasadduq I. A., and Otero P. (2021). Pilot-assisted ofdm for underwater acoustic communication. J. Mar. Sci. Eng. 9, 1382. doi: 10.3390/jmse9121382

Crossref Full Text | Google Scholar

Preisig J. (2007). Acoustic propagation considerations for underwater acoustic communications network development. ACM SIGMOBILE Mobile Computing Commun. Rev. 11, 2–10. doi: 10.1145/1347364.1347370

Crossref Full Text | Google Scholar

Qiao G., Babar Z., Ma L., and Ahmed N. (2019). Channel estimation and equalization of underwater acoustic mimo-ofdm systems: A review estimation du canal et l’égalisation des systèmes mems-mrof acoustiques sous-marins: Une revue. Can. J. Electrical Comput. Eng. 42, 199–208. doi: 10.1109/CJECE.2019.2897587

Crossref Full Text | Google Scholar

Qiao G., Liu Y., Zhou F., Zhao Y., Mazhar S., and Yang G. (2022). Deep learning-based m-ary spread spectrum communication system in shallow water acoustic channel. Appl. Acoustics 192, 108742. doi: 10.1016/j.apacoust.2022.108742

Crossref Full Text | Google Scholar

Raza W., Ma X., and Bilal M. (2021). Long short-term memory neural network assisted peak to average power ratio reduction for underwater acoustic orthogonal frequency division multiplexing communication. J. Acoustical Soc. America 150, A319–A319. doi: 10.1121/10.0008433

Crossref Full Text | Google Scholar

Stojanovic M. (2003). Acoustic (underwater) communications. Wiley Encyclopedia Telecommunications. doi: 10.1002/0471219282.eot110

Crossref Full Text | Google Scholar

Stojanovic M. and Preisig J. (2009). Underwater acoustic communication channels: Propagation models and statistical characterization. IEEE Commun. magazine 47, 84–89. doi: 10.1109/MCOM.2009.4752682

Crossref Full Text | Google Scholar

Tabata Y., Ebihara T., Ogasawara H., Mizutani K., and Wakatsuki N. (2020). Improvement of communication quality using compressed sensing in underwater acoustic communication system with orthogonal signal division multiplexing. Japanese J. Appl. Phys. 59, SKKF04. doi: 10.35848/1347-4065/ab8be5

Crossref Full Text | Google Scholar

Veeraiyan V., Velayutham R., and Philip M. M. (2013). Frequency domain based approach for denoising of underwater acoustic signal using emd. J. Intelligent Syst. 22, 67–80. doi: 10.1515/jisys-2012-0021

Crossref Full Text | Google Scholar

Wang Z., Wu H., and Liu S. (2017). “An improved sparse underwater acoustic ofdm channel estimation method based on joint sparse model and exponential smoothing,” in 2017 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC). 1–6 (3 Park Avenue, New York City, NY: IEEE). doi: 10.1109/ICSPCC.2017.8242418

Crossref Full Text | Google Scholar

Yang H., Gao L., and Li G. (2020a). Underwater acoustic signal prediction based on correlation variational mode decomposition and error compensation. IEEE Access 8, 103941–103955. doi: 10.1109/ACCESS.2020.2994895

Crossref Full Text | Google Scholar

Yang H., Li L., and Li G. (2020b). A new denoising method for underwater acoustic signal. IEEE Access 8, 201874–201888. doi: 10.1109/ACCESS.2020.3035403

Crossref Full Text | Google Scholar

Yao Y., Shu F., Cheng X., Liu H., Miao P., and Wu L. (2023). Automotive radar optimization design in a spectrally crowded v2i communication environment. IEEE Trans. Intelligent Transportation Syst. 24, 8253–8263. doi: 10.1109/TITS.2023.3264507

Crossref Full Text | Google Scholar

Ye H., Li G. Y., and Juang B.-H. (2017). Power of deep learning for channel estimation and signal detection in ofdm systems. IEEE Wireless Commun. Lett. 7, 114–117. doi: 10.1109/LWC.2017.2757490

Crossref Full Text | Google Scholar

Zhang Y., Li J., Zakharov Y., Li X., and Li J. (2019). Deep learning based underwater acoustic ofdm communications. Appl. Acoustics 154, 53–58. doi: 10.1016/j.apacoust.2019.04.023

Crossref Full Text | Google Scholar

Zhang Y., Wang H., Li C., and Meriaudeau F. (2022a). “Complex-valued deep network aided channel tracking for underwater acoustic communications,” in OCEANS 2022-Chennai. 1–5 (3 Park Avenue, New York City, NY: IEEE). doi: 10.1109/OCEANSChennai45887.2022.9775455

Crossref Full Text | Google Scholar

Zhang Y., Wang H., Li C., and Meriaudeau F. (2022b). Data augmentation aided complex-valued network for channel estimation in underwater acoustic orthogonal frequency division multiplexing system. J. Acoustical Soc. America 151, 4150–4164. doi: 10.1121/10.0011674, PMID: 35778218

PubMed Abstract | Crossref Full Text | Google Scholar

Zhang Y., Zhang S., Wang B., Liu Y., Bai W., and Shen X. (2022c). Deep learning-based signal detection for underwater acoustic otfs communication. J. Mar. Sci. Eng. 10, 1920. doi: 10.3390/jmse10121920

Crossref Full Text | Google Scholar