Slot sharing for container shipping liners under service competition and demand uncertainty

This study investigates the slot–sharing strategies of two container shipping liners (CSLs) engage in service competition within a shipping market characterized by uncertain demand. We develop a game–theoretic model where CSLs decide whether to enter a slot–sharing agreement and determine their service quality levels. Three typical agreements, namely, transfer–payment, revenue–sharing, and cost–sharing, are examined, with slot–sharing arrangements and transactions are implemented after demand uncertainty is realized. Equilibrium service quality levels and profits under different agreements are derived, and numerical experiments analyze the impacts of key parameters. We find that the transfer–payment agreement generally yields higher profits than the other two but reduces service quality due to diminished competition. Interestingly, we find that slot–sharing does not always outperform no slot–sharing. When service competition is intense and transfer–payment prices are low, the CSLs may achieve higher profits by operating independently. In addition, we demonstrate that slot–sharing can achieve a win–win situation where both service quality and CSL profits improve under moderate service competition and balanced transfer–payment prices.

1 Introduction

In the era of globalization, container liner shipping serves as the bedrock of international trade. It transports over 80% of the global trade volume and functions as a vital link connecting economies around the world¹. According to the Global Trade Update report released by UNCTAD (United Nations Conference on Trade and Development), the global trade volume was estimated to reach approximately $31 trillion by the end of 2023². However, container shipping liners (CSLs) have no control over the demand in the shipping market. This demand is highly volatile and significantly impacts the CSLs’ profitability. In recent years, unexpected events such as the increasing pressures on key chokepoints like the Suez and Panama Canals and the Red Sea due to geopolitical tensions and climate change, deglobalization (Zahoor et al., 2023; Chen et al., 2023b), and trade barriers have all contributed to a significant increase in demand volatility in the shipping market¹. This uncertain demand subjects CSLs to high risks in shipping service operations, particularly in slot operations. Given that shipping schedules have limited short–term flexibility, it is relatively difficult to increase or adjust slots in a short time. This leads to inflexible supply–demand dynamics in the shipping market.

To achieve better supply–demand matching, mitigate risks related to demand fluctuations, and boost overall operational efficiency, capacity sharing is extensively implemented in various sectors, including aviation, retail, and ride–hailing services (Guo and Wu, 2018; Li and Shi, 2024; Huang et al., 2023). In the shipping market, slot sharing is also commonly regarded as a means to alleviate supply–demand imbalances and further enhance the profitability of CSLs. In 2023, MSC, the world’s largest container shipping company, reached an alliance agreement with ZIM, ranked tenth and headquartered in Haifa, on multiple routes³. This agreement involved vessel sharing, slot purchase, and slot exchange arrangements. For instance, MSC announced a vessel–sharing agreement with ZIM for the Nordic and Israeli routes, deploying five 6,700–TEU vessels, with ZIM providing two of them. It’s worth noting that the MSC Group not only owns its own shipping company but also operates the logistics service provider MEDLOG. Similarly, ZIM combines its shipping operations with its subsidiary logistics company, Zim Logistics. Intuitively, such a slot–sharing agreement can assist CSLs in better managing cargo slots in a volatile shipping market, thus reducing the risk stemming from demand uncertainty. However, whether CSLs can gain benefits from slot–sharing depends on the specific mechanisms within the agreement, such as the transfer–payment price of surplus slots.

Unlike unscheduled shipping, CSLs have fixed schedules and routes, along with relatively stable freight rates⁴. To increase their market share in the container shipping market, CSLs strive for better service quality, rendering the shipping market highly competitive. For example, Maersk and IBM jointly developed TradeLens, a neutral, blockchain–based platform for digitalizing container logistics⁵. Logistics service providers like DKSH⁶ and Time: Matters⁷ offer end–to–end logistics services. In this context, cost competition is often minimized, and service quality is a primary competitive differentiator (Lee et al., 2015; Huang et al., 2025; Jiang et al., 2025). On specific routes, MSC and ZIM can jointly operate vessels, while their respective subsidiary logistics companies, MEDLOG and Zim Logistics, can sell the slots and engage in intense service competition. Under demand uncertainty, these two CSLs may encounter either excess or insufficient capacity. The above–mentioned slot–sharing practices among CSLs in the shipping market prompt us to raise the following research questions: (1) In the face of demand uncertainty, should CSLs reach a slot–sharing agreement? (2) What is the performance of different slot–sharing agreements such as transfer–payment, revenue–sharing, and cost–sharing? (3) How does service competition impact CSLs’ slot–sharing strategies?

To address these questions, we consider two CSLs engage in service competition within a shipping market characterized by uncertain demand. The two CSLs decide whether to reach a slot–sharing agreement with each other and then determine their service quality. We consider three typical slot–sharing agreements between the CSLs, namely, transfer–payment, revenue–sharing, and cost–sharing agreement. After demand uncertainty is realized, slot–sharing based on specific agreement is implemented. Our focus lies in comparing the performance of these three distinct agreements and investigating whether the CSLs should opt for a slot–sharing agreement.

We present a summary of our key findings in response to the research questions. First, in comparing the three slot–sharing agreements, we show that the transfer–payment agreement is more profitable for CSLs compared to the other two. However, the service quality under the transfer–payment agreement is relatively low because of the weak competition between CSLs. Thus, we recommend that CSLs consider using the transfer–payment agreement when sharing cargo slots. Second, regarding whether CSLs should reach a slot–sharing agreement, taking the transfer–payment agreement as an example, we find that the decision depends on the degree of service competition and the transfer–payment price. Specifically, when service competition is intense and the transfer–payment price is low, reaching a transfer–payment agreement results in lower profits for CSLs compared to not sharing slots. Conversely, under other circumstances, reaching a transfer–payment agreement to share cargo slots benefits the CSLs. Intriguingly, we also show that in some cases, reaching a transfer–payment agreement can improve both the service quality and the profits of the two CSLs, creating a win–win situation for both CSLs and shippers. Third, service competition has a two–fold impact on the performance of the slot–sharing agreement. For instance, we demonstrate that the change in profit after adopting slot–sharing agreements can be either positively or negatively influenced by the degree of service competition.

The contributions of this paper are threefold. First, we formulate a sequential game–theoretic model to explore the slot–sharing strategies of CSLs, taking into account service competition and demand uncertainty. Most prior studies focus on micro–level operational challenges using optimization–based methodologies, while our research shifts to strategic–level analysis by employing game–theoretic modelling for revenue management problems (Liu et al., 2024; Song and Wang, 2022; Ting and Tzeng, 2004; Wang et al., 2020; Zurheide and Fischer, 2015). Second, we establish and compare different slot–sharing agreements, such as transfer–payment, revenue–sharing, and cost–sharing. Notably, CSLs distribute the total revenue or costs based on the Shapley value, which differs from most existing research that assumes an exogenous sharing ratio (Herbon and David, 2023; Wang et al., 2024a). Third, we create a stylized model for CSLs managers to assess the performance of slot–sharing agreements. The analytical results offer several operational strategies for the shipping managers. For example, we identify the specific conditions regarding the degree of service competition and the transfer–payment price under which reaching a transfer–payment agreement is advantageous for the CSLs.

The rest of this paper is organized as follows. Section 2 reviews the literature relevant to our research. Section 3 presents the model, including a no slot–sharing benchmark and three slot–sharing agreements. Section 4 provides an analysis to answer the research questions. In Section 5, we present the conclusions and major findings, along with managerial implications and suggestions for future research directions. Detailed derivations and proofs of the analytical results are included in the Appendix.

2 Literature review

Our work is related with three fundamental research streams: (1) revenue management in liner shipping, (2) competition and cooperation of CSLs, and (3) contract design and coordination mechanism. Next, we briefly review the relevant studies within these domains.

2.1 Revenue management in liner shipping

In the field of revenue management for liner shipping operations, earlier studies primarily focus on micro–level operational issues. These works typically employ optimization–based techniques to tackle challenges such as slot allocation, capacity control, and pricing. For example, Choi et al. (2020) systematically review revenue management models applied in container liner shipping, contrasting them with those in the airline sector. Ting and Tzeng (2004) propose a conceptual liner revenue management framework integrating ship scheduling, demand forecasting, inventory and slot allocation, and pricing. Subsequent advancements include static capacity control models like booking limit and bid–price approaches (Zurheide and Fischer, 2012, Zurheide and Fischer, 2015), along with dynamic programming models for dynamic capacity adjustment (Maragos and Spyriodon, 1994; Lee et al., 2009). Several studies also incorporate demand uncertainty and stochasticity into revenue management models (Tao et al., 2023; Wang et al., 2016; Song and Wang, 2022; Wang et al., 2020; Zhou et al., 2025b).

However, these classical studies are predominantly characterized by static or single–carrier frameworks, myopic or deterministic booking–control rules, and limited consideration of demand uncertainty, strategic competition, or dynamic interactions among carriers. Recent research has increasingly incorporated dynamic programming, rolling–horizon optimization, robust and stochastic modelling techniques, as well as slot–inventory joint control, thereby reflecting the growing complexity and uncertainty in the operational environment of container shipping lines (Liang et al., 2024, Liang et al., 2023; Mehrzadegan et al., 2022; Wang and Tian, 2024b; Zhang et al., 2025). Notable advancements include dynamic slot allocation under stochastic and time–varying demand (Liang et al., 2024, Liang et al., 2023; Wang et al., 2024b; Xing et al., 2023; Xiong et al., 2024), explicit modelling of cancellation/no–show behaviors and overbooking mechanisms (Ao et al., 2024; Gu et al., 2025; Yang et al., 2024), and cooperative slot management frameworks based on alliances with network–level capacity sharing (Liang et al., 2025; Xin et al., 2023, Xin et al., 2023; Zhang et al., 2025; Zhou et al., 2024, Zhou et al., 2025a). Despite these advancements, relatively few studies have comprehensively addressed strategic service competition and capacity/slot allocation among multiple carriers using game–theoretic or macro–level models. While some existing works explore competitive pricing or service–quality setting from a game–theory perspective (Najafi and Zolfagharinia, 2021; Zhou et al., 2025a), they often lack integration with operational–level revenue management or fail to specifically model the joint determination of capacity control, slot allocation, and service competition within a stochastic or dynamic framework suitable for liner shipping.

To address this research gap, this study examines revenue management strategies for container shipping liners in the context of service competition. It explicitly models competitive interactions among multiple carriers using game–theoretic frameworks. By endogenizing both service decisions and slot allocation decisions within a competitive setting and leveraging recent advancements in stochastic and cooperative revenue management, our approach extends prior research and sheds light on new strategic dimensions of liner shipping revenue management.

2.2 Competition and cooperation of CSLs

In the container shipping market, extensive research conduct on competition among CSLs, including price competition (Chen et al., 2016; Choi et al., 2020; Song et al., 2023; Yu and Liu, 2021; Xu et al., 2025a) and service–level competition (Liu and Wang, 2019; Wang and Liu, 2019; Zhou et al., 2023; Xu et al., 2025b). Regarding cooperation among CSLs, the literature can be broadly categorized into two levels: tactical operational and strategic decision–making. At the tactical operational level, a growing body of research explores various collaboration forms, such as slot chartering (Chen et al., 2023; Shi et al., 2008; Xu et al., 2025c), slot co–chartering or exchange (Chen et al., 2024, Chen et al., 2022; Zhuo et al., 2025), joint fleet deployment (Chen and Yahalom, 2013; Wang et al., 2025), and vessel pooling (Liang et al., 2025; Papachristidis and Papachristidis, 2015). At the strategic decision level, some studies use exogenous sharing ratios to allocate profits or costs, while others employ cooperative game theory to endogenously model CSL cooperation. Among the former, Liu and Wang (2019); Song et al. (2021) and Sun et al. (2025) analyze horizontal alliances between two CSLs. For example, Song et al. (2021) use a game–theoretic approach to examine how two CSLs—differentiated by endogenous service quality and exogenous price levels—may form partial–route or full–route alliances. Vertical cooperation among CSLs and other stakeholders (e.g., river carriers and ports) is widely investigated (Sun et al., 2025; Wang et al., 2024d; Zheng and Luo, 2021). For example, Wang et al. (2024a) propose a vertical structure model to address competitive and cooperative interactions among ports, river carriers, and sea carriers, where river–sea direct services compete with transhipment–based alliances. A sequential Stackelberg game is employed to capture asymmetric market power, with profit–sharing ratios endogenously determined based on this power structure. In contrast, another research stream uses cooperative game theory to endogenize coalition formation and profit allocation, employing concepts such as the core, stable set, Shapley value, and coalition structure value. Yang et al. (2011) apply cooperative game theory and core theory to analyze the stability of liner shipping alliances by examining both market–level collective rationality and intra–alliance individual rationality. They show that the core may be empty due to non–convex cost functions and uneven profit distribution under joint services using mega–container ships. Wen et al. (2019) investigate centralized horizontal cooperation via a shipping pool, exploring how to maximize joint profits through discrete event simulation and dynamic ship routing. They apply cooperative game theory methods—including the Shapley value, nucleolus, and proportional rules—to ensure fair profit allocation among participants. Rau and Spinler (2017) develop an integrated cooperative game theory simulation model for container shipping, incorporating a real options investment approach and comparing its performance against individual and collective discounted cash flow methods. Using the coalition structure value concept, they analyze potential alliance formations and their evolution under market volatility, competitive intensity, lead times, and alliance complexity. Our study contributes to this research stream by examining strategic competition and cooperation among CSLs, focusing on three distinct cooperative schemes. Unlike prior studies that model cooperation primarily through transfer price negotiations or exogenous sharing ratios, we leverage cooperative game theory—specifically the Shapley value—to propose two alternative mechanisms: a profit–sharing scheme and a cost–sharing scheme, both under service–level competition.

2.3 Contract design and coordination mechanism

Contract design and coordination mechanisms serve as essential tools to align incentives among participating firms, enhance overall system efficiency, and mitigate risks stemming from demand uncertainty and operational frictions. In sectors such as the shipping industry and supply chain management, various contract types and mechanisms (e.g., Wholesale Price Contract, Revenue–Sharing Contract, Cost–Sharing Contract, Quantity Discount Contract) have been proposed to facilitate cooperation, coordinate decision–making, and achieve mutually beneficial outcomes (Cai et al., 2017; Chakraborty et al., 2019, Chakraborty et al., 2015; Gallego and Talebian, 2019; Ghosh and Shah, 2015; Zhang et al., 2019; Zhao et al., 2022).

Chakraborty et al. (2015) investigate a supply chain involving two competing manufacturers selling through a common retailer, modelling their interactions as a Stackelberg game under a wholesale price contract. They further propose a revenue–sharing contract to coordinate the supply chain and enhance system efficiency in a manufacturer encroachment setting. Zhao et al. (2022) examine two competing supply chains under demand uncertainty, where each manufacturer, acting as a Stackelberg leader, chooses between offering a wholesale price contract or a revenue–sharing contract to its retailer. Their results identify the market conditions under which each contract type is preferred, highlighting that revenue sharing can achieve win–win outcomes under low competition and low demand uncertainty. Zhang et al. (2019) analyze an e–commerce logistics market where two competing logistics service providers (LSPs) decide on order quantities and service quality levels under both centralized and decentralized settings, comparing equilibrium outcomes across Cournot and Stackelberg competition structures. To achieve effective horizontal coordination, they propose a revenue–sharing contract in which one LSP pays the other a transfer price plus a negotiated share of service revenue, treating the sharing ratio as a decision variable reflecting the LSPs’ relative bargaining power. Chakraborty et al. (2019) study how a retailer and two competing manufacturers can benefit from collaborative product quality improvement strategies in a supply chain. They develop a game–theoretic model to analyze three contractual settings: both manufacturers using wholesale price contracts, both adopting cost–sharing contracts, and one using a cost–sharing contract while the other retains a wholesale price contract. Their results show that cost–sharing mechanisms between the retailer and manufacturers incentivize quality investment, leading to higher product quality and greater overall supply chain profits compared to wholesale price contracts. Gallego and Talebian (2019) examine contracting between a single retailer and multiple suppliers offering substitutable products, modelling their interaction as a Stackelberg game where suppliers act as leaders and the retailer as a follower. They characterize the equilibrium contracts—including all–unit and marginal–unit quantity discounts—and demonstrate that such nonlinear contracts (i.e., quantity discount contracts) can coordinate the supply chain and achieve profit splits where each supplier earns its marginal contribution to the overall chain profit. Cai et al. (2017) examine contract design in a VMI supply chain with service–sensitive demand, showing that a pure revenue–sharing contract, where the retailer shares a portion of sales revenue with the supplier, may create competition among supply chain members and fail to achieve coordination. To address this, they propose three flexible subsidy contracts based on revenue sharing: one that subsidizes all surplus products, another that subsidizes only unsold inventory exceeding the target level, and a third that subsidizes all inventory exceeding the target level regardless of whether it is sold. These contracts enhance service quality levels, improve overall supply chain performance, and achieve Pareto–improving supply chain coordination.

Our contribution involves comparing the effects of three distinct slot–sharing contracts on the service quality levels and profits of CSLs. Unlike prior research that offers limited game–theoretic insights into slot–sharing agreements, our analysis not only integrates the operational context of container shipping liners but also redesigns revenue–sharing and cost–sharing contracts using cooperative game theory.

2.4 Summary of the literature

Overall, the literature has extensively examined revenue management in liner shipping operations, competition and cooperation among CSLs, and various contract designs and coordination mechanisms to facilitate collaboration among them. However, existing studies primarily focus on micro–level operational optimization or assume exogenous sharing arrangements when analyzing CSL cooperation. Few have explored the strategic design of slot–sharing agreements using game–theoretic approaches, especially under service competition and demand uncertainty. In this context, our study contributes to bridging these gaps by adopting a macro–level perspective to investigate the impacts of three distinct slot–sharing agreements—transfer–payment, revenue–sharing, and cost–sharing—on CSLs’ equilibrium service quality levels and profits. Specifically, we integrate the operational realities of container shipping lines and leverage cooperative game theory to redesign revenue–sharing and cost–sharing agreements, providing managerial insights into effective slot–sharing collaboration under competitive markets with demand volatility.

3 Model

We consider two container shipping lines (CSLs), namely CSL 1 and CSL 2. These two CSLs are in a shipping alliance and jointly operate an identical shipping route. The slot capacity of each CSL is denoted as $I_i(i=1,2)$ and each unit of cargo slot is provided at a marginal cost $c$ (e.g., shipping cost) and sold at the price $p$ by the two CSLs. Although they are in a shipping alliance, they provide services, such as freight forwarding service, with different service qualities $s_i$ to attract market demand. This incurs a service cost given as $k{s}_i^2$, where $k$ is the cost coefficient. Due to the highly uncertain market demand, under– or over–booking frequently occurs. As a result, the CSLs reach an agreement on slot sharing to address the uncertain market demand. To be specific, the CSLs can utilize each other’s surplus slots through a predetermined contract in such an agreement. If unfulfilled demand volumes exist, the CSLs will postpone orders to the next shipping period and pay delay compensation, regardless of the existence of a slot–sharing agreement. The delay compensation paid is represented as $\delta$, and the CSLs do not want the overbooked cargos to cause a loss, i.e., $c+\delta \le p$. Intuitively, the market demand $D_i$ for CSL $i$ rises with its own service quality level $s_i$ and declines as the service quality level $s_j(j=1,2)$ of the competing CSL increases (Guo and Jiang, 2022). Thus, the market demand $D_i$ is specified Equations 1 and 2 as follows:

$\begin{array}{ll}\begin{array}{c}{D}_i={ϵ}_i{d}_i(s_i,s_j), i,j=1,2 andi\ne j, where\end{array}& (1)\end{array}$

$\begin{array}{ll}\begin{array}{c} d_i(s_i,s_j)=\alpha +\beta (s_i-s_j).\end{array}& (2)\end{array}$

Here, ${ϵ}_i$ is a random variable in the range $[0,1]$, capturing demand uncertainty. Note that $d_i(s_i,s_j)$ represents the deterministic part of the demand function, which depends on the service quality level of the two CSLs. In this context, $\alpha$ represents the basic market potential, and $\beta$ reflects the sensitivity of demand to service quality levels, which can be used to measure the degree of service competition between the CSLs. Typically, CSLs with larger market shares provide a greater slot capacity. For simplicity and without loss of generality, we assume $\alpha =1/2$ and $I_1=I_2=I$, indicating that both CSLs have equal market shares and an identical quantity of cargo slots. In addition, we assume that ${ϵ}_i$ and ${ϵ}_j$ follow the same probability distribution, with the probability density function $g({ϵ}_i)$. The mean of ${ϵ}_i$ is given by $\mu ={{\displaystyle \int }}_0^1{ϵ}_{i}g\left({ϵ}_i\right)d{ϵ}_i$. Note that ${ϵ}_i$ and ${ϵ}_j$ can be either correlated or independent, and their joint probability density function is denoted as $g_{12}({ϵ}_1,{ϵ}_2)$.

The event sequence is as follows. First, the CSLs decide whether to reach an agreement on slot sharing and corresponding sharing schemes such as transfer–payment, profit–sharing, and cost–sharing. Second, the CSLs set their respective service quality levels, namely, $s_i$ and $s_j$. Third, the uncertain demand in the shipping market is realized, that is, ${ϵ}_1$ and ${ϵ}_2$ are determined. Finally, if the two CSLs have reached a slot–sharing agreement, the CSL with a shortage of cargo slots will first seek surplus slots from the other CSL. Any remaining unfilled demand will be postponed to the next shipping period, accompanied by delay compensation paid to the shippers. If no slot–sharing agreement exists, each CSL’s unfilled demand will be postponed to the next shipping period with the same delay compensation paid to the shippers.

Before discussing the typical slot–sharing agreements, we briefly summarize the notations and definitions in the following table for easy reference (Table 1).

Table 1

Table 1. Notations and definitions.

3.1 Benchmark–no slot sharing

We consider a benchmark case where the two CSLs do not reach an agreement in cargo slot sharing. A superscript $N$ is added to the parameters to denote this case, which is named as scenario N. Intuitively, the profit function for CSL $i$ is given in Equation 3 as follow:

$\begin{array}{ll}\begin{array}{c}{\pi }_i^N(s_i,I_i\mid s_j) =pE[{ϵ}_i{d}_i]-(c+\delta )E[{({ϵ}_i{d}_i-I_i)}^{+}] -k{s}_i^2-c{I}_i.\end{array}& (3)\end{array}$

The first term in the profit function stands for the revenue from selling cargo slots. The second term represents the slot cost and the delay compensation cost of the unfulfilled excess demand volumes. The third term reflects the service cost of CSL $i$’s service cost, and the fourth term represents the CSL $i$’s slots cost that it owns in the current shipping period. Without slot sharing, the equilibrium is summarized in the following lemma.

Lemma 1. Without slot sharing, the equilibrium service quality levels and the profits are $s_1^N=s_2^N=\frac{\beta [p\mu -(c+\delta ){{\displaystyle \int }}_{2I}^1ϵg(ϵ)dϵ]}{2k}$ and ${\pi }_1^N={\pi }_2^N=\frac{1}{2}p\mu -\left(c+\delta \right){{\displaystyle \int }}_{2I}^1\left(\frac{{ϵ}_i}{2}-I\right)g\left({ϵ}_i\right)d{ϵ}_i-k{\left[s^N(I)\right]}^2-cI$

3.2 Three slot–sharing agreements

We develop three typical slot–sharing schemes between the CSLs and evaluate their impacts on the profits of the shipping alliance. These schemes are transfer–payment, revenue–sharing, and cost–sharing. Next, we illustrate these three slot–sharing schemes in detailed one by one.

3.2.1 Transfer–payment agreement

When CSL $i$ has insufficient cargo slots, it can purchase the remaining cargo slots from CSL $j$ at a transfer–payment price $t$ to meet the excess demand. Both CSLs, when setting $t$, wish for the cost of purchasing cargo slots not to exceed the sum of slots operational cost and delay compensation, i.e., $0\le t\le c+\delta$. A superscript $T$ is added to the parameters to denote the transfer–payment agreement, which is named as scenario T. Under this agreement, the profit function for CSL $i$ is defined in Equation 4 as follows:

$\begin{array}{ll}\begin{array}{c}{\pi }_i^T(s_i,I_i\mid s_j,I_j)=pE[{ϵ}_i{d}_i(s_i,s_j)]+tE[{(\text{min}\{I_i-{ϵ}_i{d}_i,{ϵ}_j{d}_j-I_j\})}^{+}]\hfill \\ -tE[{(\min \{{ϵ}_i{d}_i-I_i,I_j-{ϵ}_j{d}_j\})}^{+}]\hfill \\ -(c+\delta )E\left[{({({ϵ}_i{d}_i-I_i)}^{+}-{(I_j-{ϵ}_j{d}_j)}^{+})}^{+}\right]-k{s}_i^2-c{I}_{i.}\hfill \end{array}& (4)\end{array}$

In the profit function, the first term stands for the revenue that CSL $i$ gets from selling cargo slots. The second term represents CSL $i$’s revenue generated by selling its surplus cargo slots to CSL $j$ which has a shortage of slots. The third term is the cost for CSL $i$ to buy cargo slots from CSL $j$ when it has a shortage. The fourth term is for the slot cost and the delay compensation cost that CSL $i$ incurs because of unfulfilled excess demand after slot sharing. The fifth term is the service cost for CSL $i$, and the sixth term is CSL $i$’s slots cost that it originally owns in the current shipping period.

3.2.2 Revenue–sharing agreement

In this type of agreement, if one CSL has a cargo slot shortage while another has surplus slots, the CSL with the shortage can utilize the surplus slots of the other. Then, the two CSLs share the total revenue according to the Shapley value. A superscript $R$ is added to the parameters to represent this revenue–sharing agreement, which is named as scenario R. Under this agreement, the profit function for CSL $i$ is defined in Equations 5, 6 and 7 as follows:

$\begin{array}{ll}\begin{array}{c}{\pi }_i^R(I)=\frac{1}{2}V(\{i\})+\frac{1}{2}[V(\{i,j\})-V(\left\{j\right\})],\end{array}& (5)\end{array}$

$\begin{array}{ll}\begin{array}{c}V(\{i\})=pE[{ϵ}_i{d}_i]-(c+\delta )E[{({ϵ}_i{d}_i-I_i)}^{+}]-k{s}_i^2-c{I}_i,\end{array}& (6)\end{array}$

$\begin{array}{ll}\begin{array}{c}V(\{i,j\})=pE[{ϵ}_i{d}_i+{ϵ}_j{d}_j]-(c+\delta )E\left[{({ϵ}_i{d}_i+{ϵ}_j{d}_j-I_i-I_j)}^{+}\right]\hfill \\ -k{s}_i^2-k{s}_j^2-c{I}_i-c{I}_j.\hfill \end{array}& (7)\end{array}$

In Equation 5, $V(\{i\})$ is the total revenue with only CSL $i$ in the alliance. Also, $V(\{i,j\})$ denotes the total alliance revenue with both CSLs are in the alliance. In Equation 6, the first term represents the revenue that CSL $i$ obtains from selling cargo slots. The second term is the slot cost and delay compensation cost for unfulfilled excess demand volumes. The third term is the service cost at service quality level $s_i$. The fourth term is the CSL $i$’s slots cost that it owns originally in the current shipping period. In Equation 7, the first term represents the total revenue earned by the two CSLs from selling cargo slots. The second term accounts for the slot cost and delay compensation cost for the alliance’s total unfulfilled excess demand volumes. The third and fourth terms are the service costs for CSL $i$ and CSL $j$, respectively. The fifth and sixth terms are the slot costs that CSL $i$ and CSL $j$ own originally, respectively.

3.2.3 Cost–sharing agreement

The cost herein refers to the specific cost resulting from empty or overbooked cargo slots within the alliance. In a shipping alliance with a cost–sharing agreement, if one CSL has a slot shortage while the other has a surplus, the CSL with a shortage can use the surplus slots of the other. The losses of the alliance due to empty or overbooked cargo slots are shared between the two CSLs according to the Shapley value. A superscript $C$ is added to the parameters to represent this cost–sharing agreement, which is named as scenario C. Under this agreement, the profit function for CSL $i$ is defined in Equations 8 and 9 as follows:

$\begin{array}{ll}\begin{array}{c}V(\{i\})=cE[{(I_i-{ϵ}_i{d}_i)}^{+}]+\delta E[{({ϵ}_i{d}_i-I_i)}^{+}].\end{array}& (8)\end{array}$

$\begin{array}{ll}\begin{array}{c}V(\{i,j\})=cE\left[{(I_i+I_j-{ϵ}_i{d}_i-{ϵ}_j{d}_j)}^{+}\right]+\delta E\left[{({ϵ}_i{d}_i+{ϵ}_j{d}_j-I_i-I_j)}^{+}\right].\end{array}& (9)\end{array}$

In Equation 8, the first term represents the cost of the unsold cargo slots when CSL $i$ operates independently, and the second term stands for the delay compensation cost for unfulfilled excess demand volumes. In Equation 9, the first term represents the cost of unsold cargo slots within the alliance, while the second term represents the delay compensation cost for the unfulfilled excess demand volumes after slot–sharing. We use the Shapley value method to allocate the alliance’s costs resulting from empty or overbooked cargo slots between the two CSLs. Similar to the revenue–sharing agreement, the cost borne by CSL $i$ is given in Equations 10 as follows:

$\begin{array}{ll}\begin{array}{c}{\phi }_i(V)=\frac{1}{2}V(\{i\})+\frac{1}{2}[V(\{i,j\})-V(\left\{j\right\})].\end{array}& (10)\end{array}$

Consequently, we can solve the equilibrium under these three agreements and the results are presented in the following lemma. A detailed derivation and the Values of the intermediate parameters like $A,B,A_3$ and $B_3$ are presented in Appendix A.

Lemma 2. (a) Under transfer–payment agreement, we have $s_1^T=s_2^T=\frac{\beta (p\mu -A-B)}{2k}$ and ${\pi }_1^T={\pi }_2^T=pE\left[\frac{{ϵ}_i}{2}\right]-(c+\delta )E[{(\frac{{ϵ}_i}{2}-I-{(I-\frac{{ϵ}_i}{2})}^{+})}^{+}]-k{\left[s^T\right(t,I\left)\right]}^2-cI=\frac{1}{2}p\mu -(c+\delta ){\displaystyle {\int }_0^{2I}{\int }_{4I-{ϵ}_2}^1}(\frac{{ϵ}_1}{2}+\frac{{ϵ}_2}{2}-2I)g_{12}({ϵ}_1,{ϵ}_2)d{ϵ}_{1}d{ϵ}_2-(c+\delta ){\displaystyle {\int }_{2I}^1{\int }_{2I}^1}(\frac{{ϵ}_1}{2}-I)g_{12}({ϵ}_1,{ϵ}_2)d{ϵ}_{1}d{ϵ}_2-k{\left[s^T\right(t,I\left)\right]}^2-cI$.

(b) Under revenue–sharing agreement, we have $s_1^R=s_2^R=\frac{\beta \left[p\mu -\left(c+\delta \right){{\displaystyle \int }}_{2I}^1ϵg\left(ϵ\right)dϵ\right]}{k}$ and ${\pi }_1^R={\pi }_2^R=pE\left[\frac{{ϵ}_i}{2}\right]-(c+\delta )E\left[{(\frac{{ϵ}_i}{2}-I-{(I-\frac{{ϵ}_j}{2})}^{+})}^{+}\right]-k{\left[s^R\right(I\left)\right]}^2-cI=\frac{1}{2}p\mu -(c+\delta ){\displaystyle {\int }_0^{2I}{\int }_{4I-{ϵ}_2}^1}(\frac{{ϵ}_1}{2}+\frac{{ϵ}_2}{2}-2I)g_{12}({ϵ}_1,{ϵ}_2)d{ϵ}_{1}d{ϵ}_2-(c+\delta ){\displaystyle {\int }_{2I}^1{\int }_{2I}^1}(\frac{{ϵ}_1}{2}-I)g_{12}({ϵ}_1,{ϵ}_2)d{ϵ}_{1}d{ϵ}_2-k{\left[s^R\right(I\left)\right]}^2-cI.$

(c) Under cost–sharing agreement, we have $s_1^C=s_2^C=\frac{\beta (p\mu -A_3-B_3)}{2k}$ and ${\pi }_1^C={\pi }_2^C=pE[\frac{{ϵ}_i}{2}]-(c+\delta )E[{(\frac{{ϵ}_i}{2}-I-{(I-\frac{{ϵ}_i}{2})}^{+})}^{+}]-k{[s^C(I)]}^2-cI=\frac{p\mu }{2}-(c+\delta )[{\int }_0^{2I}{\int }_{4I-{ϵ}_2}^1(\frac{{ϵ}_1}{2}+\frac{{ϵ}_2}{2}-2I)g_{12}({ϵ}_1,{ϵ}_2)d{ϵ}_{1}d{ϵ}_2+{\int }_{2I}^1{\int }_{2I}^1(\frac{{ϵ}_1}{2}-I)g_{12}({ϵ}_1,{ϵ}_2)d{ϵ}_{1}d{ϵ}_2]-k{[s^C(I)]}^2-cI$.

4 Analysis

In this section, we first compare the equilibrium service quality levels and profits of the CSLs under the three slot–sharing agreements. This allows us to identify which slot–sharing agreement performs better than the others. Then, we address the question of whether the CSLs should reach a slot–sharing agreement. If so, under what conditions?

4.1 Comparison of the three agreements

When the CSLs reach an agreement, a natural question is that how the agreements affect the equilibrium service quality levels and the profits of the CSLs. Under the transfer–payment agreement, each CSL decides on its service quality level to maximize its expected profit. However, under revenue–sharing and cost–sharing agreements, each CSL not only strives to maximize the alliance’s total profit but also aims to maximize its share of the alliance’s profit distribution. To be specific, under revenue–sharing agreement, each CSL maximize its contribution to the alliance’s profit. While under cost–sharing agreement, each CSL minimize its contribution to the alliance’s total shared costs. Considering these factors, each CSL decides on its service quality level to maximize its own profit. We compare the equilibrium among the different agreements and the results are summarized in the following proposition.

Proposition 1. By comparing the equilibrium under the different agreements, we have $s^R⩾s^C⩾s^T$and ${\pi }_i^R⩽{\pi }_i^C⩽{\pi }_i^T$.

Proposition 1 shows that among the three agreements, the transfer–payment agreement leads to the lowest equilibrium service quality level but the highest profit for each CSL. The driving forces are as follows. Under the revenue–sharing and cost–sharing agreements, the CSLs not only compete in terms of market demand volumes but also in their contributions to the alliance’s profits or the total shared costs. Thus, the market competition is more intense under these two agreements, leading to a higher equilibrium service quality level. Moreover, under the revenue–sharing agreement, one of the goals of each CSL is to generate more profit for the alliance. So, CSLs tend to be more aggressive in selling cargo slots (even if the profit from overselling cargo is less than that when cargo slots are within capacity, it is still positive), resulting in a significant increase in service quality levels. However, under the cost–sharing agreement, one of the goals of each CSL is to minimize the alliance’s total shared costs. The CSLs tend to moderate their cargo–slot sales (overselling can lead to delay compensation, while underbooking can result in losses from empty cargo slots). Consequently, the transfer–payment agreement leads to the lowest equilibrium service quality level, while the revenue–sharing agreement results in the highest one.

Therefore, we show that transfer–payment agreement is the most profitable scheme for the CSLs to share cargo slots. The agreements of revenue– and cost– sharing are less profitable due to the competition of CSLs in their contributions to the alliance’s profits or the total shared costs. Consequently, when CSLs choose to reach an agreement in slot sharing in a shipping alliance, transfer–payment is the most beneficial one, but leading to a lowest service quality level. For example, in the CMA CGM/Marfret Vessel Sharing Agreement for the PAD service (FMC Agreement No. 011931–010), the two CSLs agree to share vessel space based on their respective capacity contributions⁸. The agreement allows for slot sales between parties at a pre–agreed slot rate, a typical form of transfer–payment mechanism. Such arrangements demonstrate how CSLs in practice adopt transfer–payment–based slot sharing to flexibly manage capacity and balance utilization.

4.2 To reach a slot–sharing agreement or not

We have demonstrated that the transfer–payment agreement is the most advantageous for the CSLs to share cargo slots. In this section, we take transfer–payment agreement as an example to examine that whether the CSLs should reach a slot–sharing agreement or not. To be specific, we compare the equilibrium between the transfer–payment agreement and the benchmark, and the results are summarized in the following propositions. The results from comparing service quality levels are summarized in the following proposition.

Proposition 2. We have $s^T(t,I)>s^N(I)$ if $t<\frac{c+\delta }{2}$; otherwise, $s^T(t,I)\le s^N(I)$.

Proposition 2 indicates that reaching a transfer–payment agreement can result in either a higher or lower service quality level, depending on the transfer–payment price. To be specific, when the transfer–payment price is low (i.e., $t<\frac{c+\delta }{2}$), reaching a transfer–payment agreement leads to a higher service quality level than no slot–sharing. This is because a low transfer–payment price drives each CSL to compete for more demand volumes by improving the service quality level. In this situation, the cost of purchasing slots from the other CSL under overselling is low, thereby resulting in a higher equilibrium service quality level. In contrast, when the transfer–payment price is high (i.e., $t>\frac{c+\delta }{2}$), reaching a transfer–payment agreement leads to a lower service quality level than no slot–sharing, mainly due to the high costs of purchasing slots from the other CSL under overselling. We identify such a threshold value of the transfer–payment price and demonstrate that it is influenced by the slot cost (i.e., $c$) and the delay compensation cost (i.e., $\delta$) of a unit cargo slot. This is because they are the two typical costs of the overselling cargo slots.

Next, we explore the equilibrium profits between the transfer–payment agreement and no slot–sharing, and the results are summarized in the following proposition.

Proposition 3. (a) We have ${\pi }_i^T(t,I)<{\pi }_i^N(I)$ if $t<\frac{c+\delta }{2}$ and $\beta >\hat{\beta }(t)$; otherwise, ${\pi }_i^T(t,I)\ge {\pi }_i^N(I)$, where $\hat{\beta }(t)=\sqrt{\frac{R^T(t,I)-R^N(I)}{k[{(s^T(t,I))}^2-{(s^N(I))}^2]}}$ (The definition of the term $R^T(t,I)-R^N(I)$ can be seen in Appendix). (b) When $t<\frac{c+\delta }{2}$ and $\beta <\widehat{\beta }(t)$, reaching a transfer–payment leads to improved service quality levels and profits of the two CSLs.

Proposition 3 indicates that reaching a transfer–payment agreement also can result in either a higher or lower profit, depending on the transfer–payment price $t$ and the degree of service competition $\beta$. To be specific, when the transfer–payment price is low (i.e., $t<\frac{c+\delta }{2}$) and the degree of service competition $\beta$ is high (i.e., $\beta >\hat{\beta }(t)$), reaching a transfer–payment agreement leads to a lower profit for the CSLs than no slot–sharing. The driving forces are as follows. In this situation, a high degree of service competition $\beta$ indicates intense service competition between the CSLs. Moreover, a low transfer–payment price (i.e., $t<\frac{c+\delta }{2}$) further intensifies this service competition because a low transfer–payment price helps the CSLs better handle demand uncertainty. These two driving forces lead to high equilibrium service quality levels as shown in Proposition 2, and then increase the service costs. Consequently, a transfer–payment agreement under such conditions hurts both CSLs due to the intense service competition. As graphically shown in Figure 1, region A represents the area where a transfer–payment agreement makes both CSLs worse off due to the fierce service competition.

Figure 1

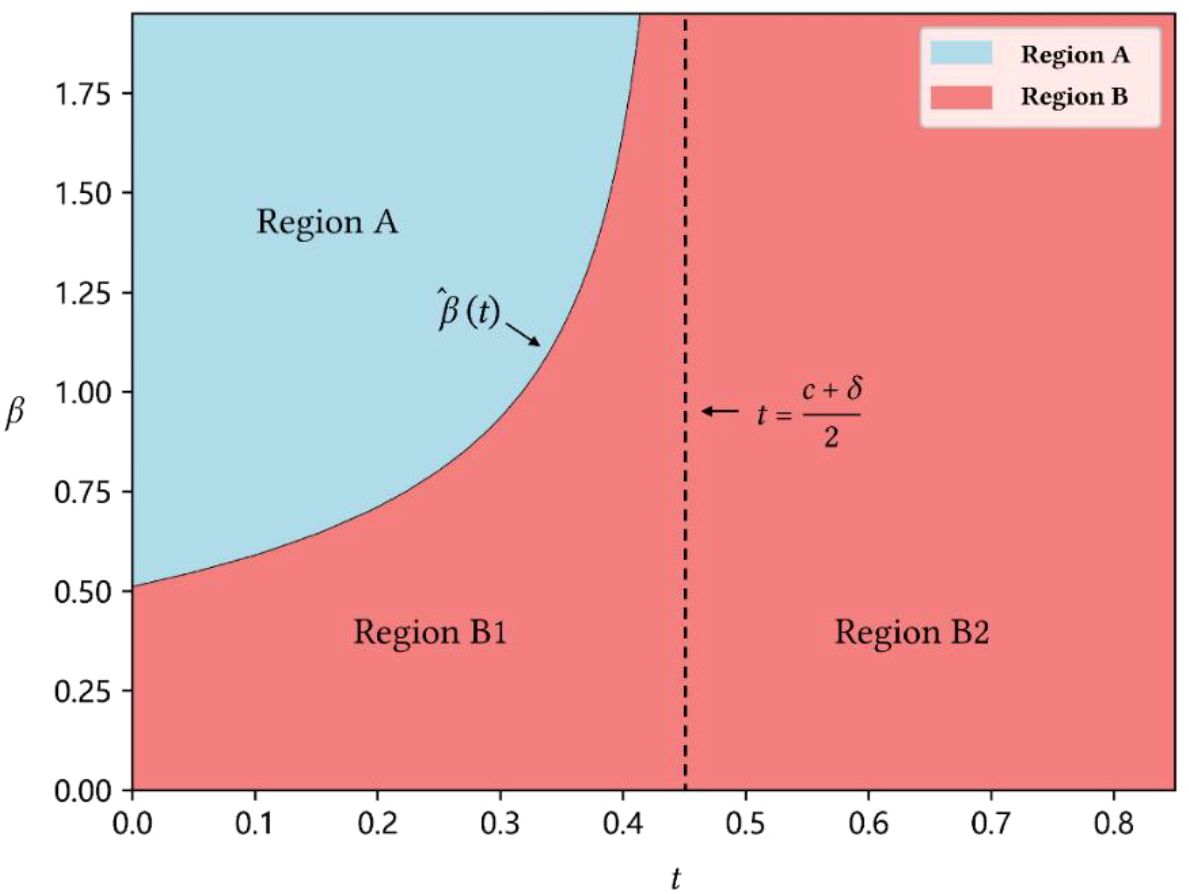
Figure 1. Profit comparison between scenarios T and N. Th parameter setting is $p=1, c=0.3, \delta =0.6, I=0.4,$ and $k=1$. In addition, in all the figures in this study, we have $g(x)=1$ and ${ɡ}_{12}(x, y)= g(x)·g(y)$, where $x, y\in [0,1]$.

As Figure 1 shows, the region B can be divided into two regions, namely, region B1 (i.e., $t<\frac{c+\delta }{2}$ and $\beta <\widehat{\beta }(t)$) and region B2 (i.e., $t>\frac{c+\delta }{2}$). In region B2, we have $t>\frac{c+\delta }{2}$, which indicates that the impact of transfer–payment price is more significant. A high transfer–payment price decreases the CSLs’ ability to handle the uncertain demand volumes by sharing slots, thereby weakening the service competition. This leads to a decline of service costs and consequently benefits the CSLs. However, as presented in Proposition 3(b), an interesting situation occurs in region B1 when $t<\frac{c+\delta }{2}$ and $\beta <\widehat{\beta }(t)$, in which reaching a transfer–payment leads to improved service quality levels and profits of the two CSLs. Intuition suggests that an improved service quality level will increases the service costs and then hurts the profit of the CSLs. In this situation, the low degree of service competition $\beta$ (i.e., $\beta <\widehat{\beta }(t)$) and transfer–payment price (i.e., $t<\frac{c+\delta }{2}$) do lead to fierce service competition, which increase the service costs of the CSLs. However, the benefits form slot–sharing to handle uncertain demand volumes with a low transfer–payment price compensate the loss from service costs. Consequently, reaching a transfer–payment agreement results in a win–win outcome for the CSLs and the shippers, in which the CSLs obtain larger profits and the shippers enjoy higher service quality levels. We graphically characterize this interesting situation in region B1 in Figure 1

Next, we examine the how the regions A and B in Figure 1 affected by the key parameters like transfer–payment price $t$ and degree of service competition $\beta$. The analytical results are summarized in the following corollary.

Corollary 1. By defining $\Delta {\pi }_i^T={\pi }_i^T(t,I)-{\pi }_i^N(I)$, we have (a) $\Delta {\pi }_i^T$ increases in $t$; (b) $\Delta {\pi }_i^T$ decreases in $\beta$ if $t<\frac{c+\delta }{2}$ whereas increases in $\beta$ if $t>\frac{c+\delta }{2}$; (c) $\Delta {\pi }_i^T>0$ if $t>\frac{c+\delta }{2}$.

As shown in Corollary 1(a), as the transfer–payment price $t$ rises, the competition between the CSLs weakens. This leads to a decrease in the service quality level, followed by a reduction in service costs, and consequently, an increase in the CSLs’ profits. Thus, an increase in the transfer–payment price promotes an increase in the profit difference $\text{Δ}{\pi }_i^T$ as defined in Corollary 1. In particular, when $t>\frac{c+\delta }{2}$, the value of profit difference $\text{Δ}{\pi }_i^T$ is always positive, indicating that reaching a transfer–payment agreement to share cargo slots always benefits the CSLs, as shown in Corollary 1(c).

Corollary 1(b) shows that the degree of service competition $\beta$ has a two–sided impact. Intuitively, a high degree of service competition $\beta$ leads to more intense market competition and a high equilibrium service quality level, which is then followed by an increase in service costs. When $t<\frac{c+\delta }{2}$, reaching a transfer–payment agreement results in more intense market competition than not sharing slots. Thus, the CSLs are more sensitive to the coefficient $\beta$. As a result, the profit difference $\text{Δ}{\pi }_i^T$ decreases in the degree of service competition $\beta$ and the value of $\text{Δ}{\pi }_i^T$ may become negative with a specific degree of service competition $\beta$. This indicates that reaching a transfer–payment agreement to share cargo slots may result in a loss of benefit, which is consistent with the results in Proposition 3. When $t>\frac{c+\delta }{2}$, the CSLs are less sensitive to the coefficient $\beta$ due to weaker market competition. Consequently, the value of profit difference $\text{Δ}{\pi }_i^t$ increases in the degree of service competition $\beta$ and the CSLs are better off by reaching a transfer–payment agreement for sharing cargo slots.

Based on the above discussion, a natural question arises, it is if the CSLs can reach a transfer–payment agreement, what is the optimal transfer–payment price? The answer for this question is summarized in the following proposition.

Proposition 1. When two CSLs reach a transfer–payments agreement, the optimal transfer price is $t^{*}=c+\delta$, and both CSLs are willing to share cargo slots at $t^{*}$.

When the CSLs reach a transfer–payment agreement, we have $\frac{\partial {\pi }_i^T(t,I)}{\partial t}=-2k{s}^T·\frac{\partial s^T(t,I)}{\partial t}>0$, which indicates that each CSL’s profit increases in the transfer price $t$. Hence, when the CSLs reach a transfer–payment agreement, the optimal transfer–payment price is $t^{*}=c+\delta$. Such a transfer–payment price satisfies the slot–sharing constraint $t\le c+\delta$ and weakens the competition between the CSLs. It also helps the CLSs to better handle the demand uncertainty, thereby maximizing the profit of the CSLs. According to Proposition 3, we can easily derive that ${\pi }_i^T(t,I)\ge {\pi }_i^N(I)$, indicating that reach a transfer–payment agreement to share cargo slots are beneficial for the CSLs. However, according to Proposition 1, such a transfer–payment price leads to a decline of service quality level. Proposition 4 provides a theoretical foundation for determining a key parameter in slot-sharing contracts. It suggests that an optimal transfer price naturally emerges from the CSLs’ cost structures and risk profiles, acting as a catalyst for cooperation. This price makes the agreement mutually beneficial. It underscores that pricing in cooperative agreements is not merely transactional but strategic. An appropriately set transfer price can act as a structural element that underpins and stabilizes the alliance by aligning the economic interests of competing entities.

4.3 Numerical experiment

In this section, we perform numerical experiments to analyze the impacts of key parameters on the equilibrium profits of CSLs. To be specific, we examine how equilibrium profits respond to changes in the service quality level demand sensitivity $\beta$, the unit delay compensation cost $\delta$, and the initial slot capacity $I$. These experiments aim to offer managerial insights into how market characteristics and operational factors affect CSLs’ performance under various slot–sharing agreements.

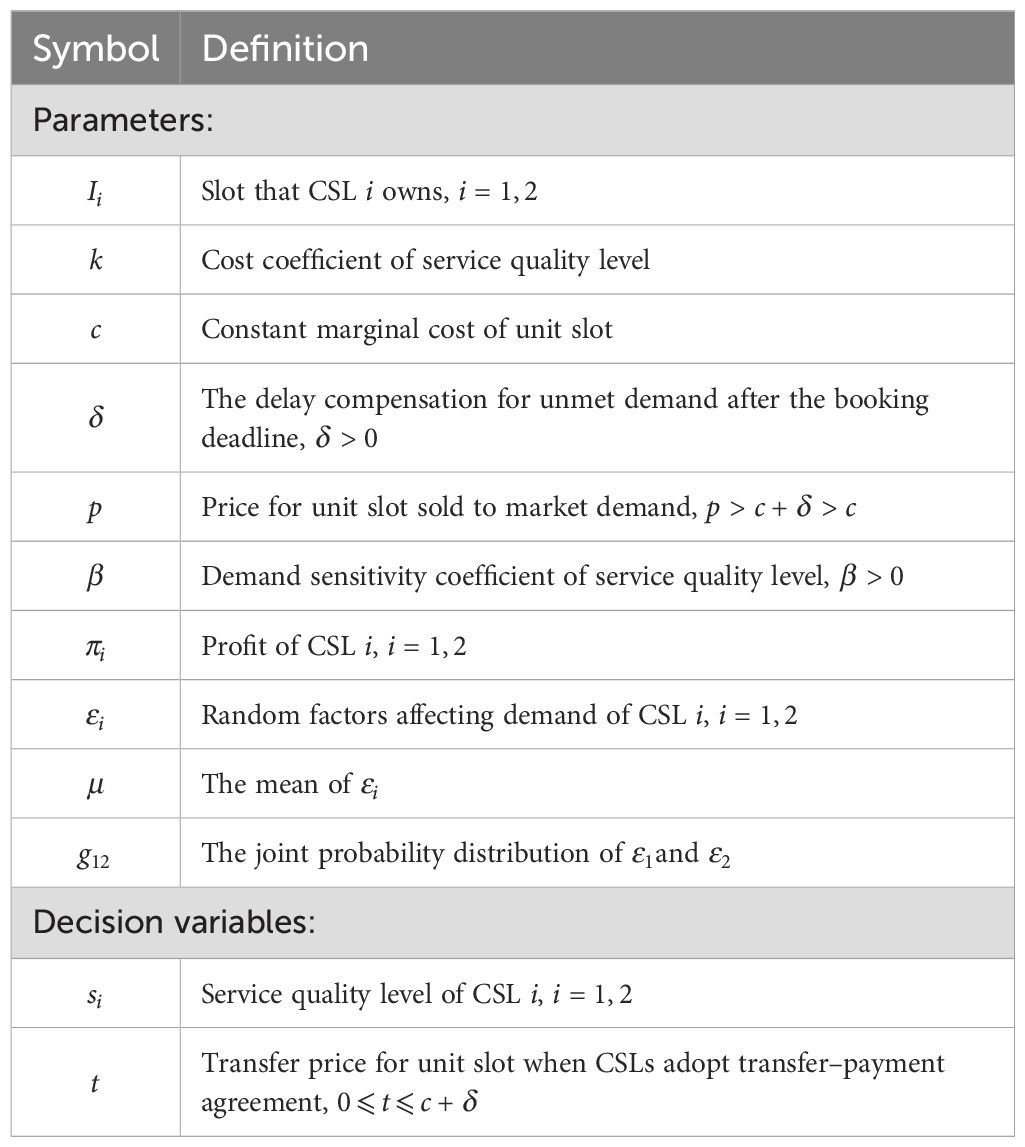
First, we consider the impact of demand sensitivity on CSLs’ profits by examining how different cooperation mechanisms perform under varying levels of $\beta$. In the numerical analysis presented in Figure 2, when there is no service competition between the CSLs (i.e., $\beta =0$), all three slot–sharing agreements outperform the no–sharing scenario. This occurs because slot sharing mitigates inventory risks without exacerbating market competition, leading to higher profits. As $\beta$ increases, service competition under revenue–sharing and cost–sharing contracts intensifies rapidly, causing profits to drop below those under no slot sharing when $\beta$ is high. In Figure 2A, since $t>(c+\delta )/2$, The relatively high transfer price under the transfer–payment contract mitigates the intensification of market competition, thereby keeping profits at a level higher than that in the no–sharing scenario. However, in Figure 2B, since $t<(c+\delta )/2$, the relatively low transfer price in the transfer–payment contract encourages CSLs to be more proactive in securing cargo, thereby intensifying market competition. Consequently, the rise in service costs may exceed the benefits derived from reduced inventory risk through slot sharing. Therefore, when the degree of service competition $\beta$ is high, the profits under the transfer–payment agreement may even be lower than those without slot sharing.

Figure 2

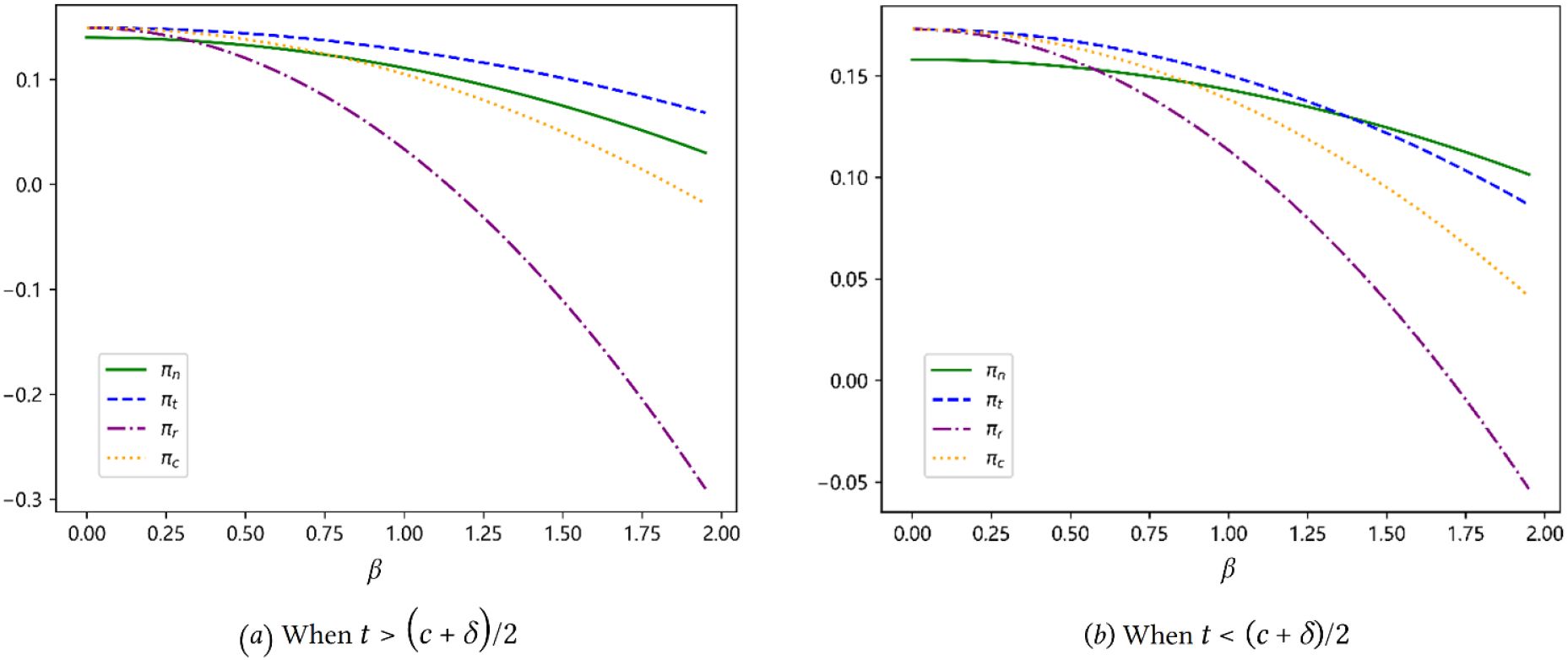
Figure 2. Sensitivity analysis of profit ${\pi }_i$ regarding $\beta$. The parameter setting in (A) is $p=1, c=0.3, \delta =0.2, t=0.4, I=0.3$, and $k=1$ (with $t>(c+\delta )/2$). The parameter setting in (B) is $p=1, c=0.2, \delta =0.6, t=0.22, I=0.3$, and $k = 1$ (with $t<(c+\delta )/2$).

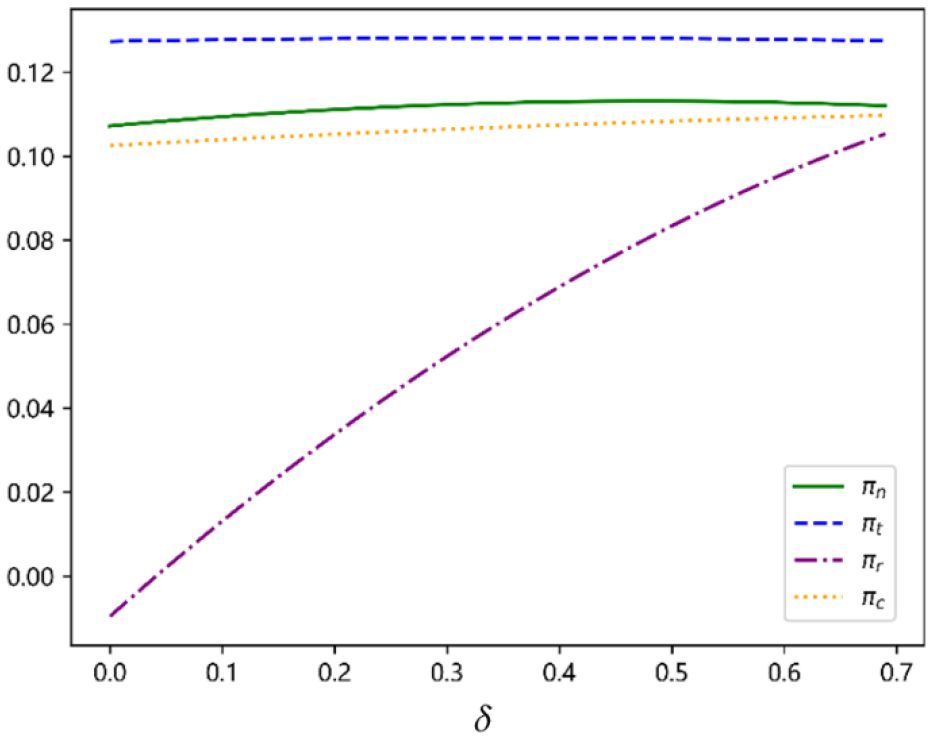
Next, we examine the impact of unit slot delay compensation on CSLs’ profits. As shown in Figure 3, with an increase in unit compensation, CSLs become more cautious in securing cargo. This caution weakens market competition, reduces service quality levels, and ultimately lowers costs and boost profits. Especially for CSLs under the revenue–sharing agreement, as the unit compensation increases, the profit from unfulfilled excess demand (i.e., $p-c-\delta$) decreases. Consequently, the cost savings from lowering service quality levels exceed the reduced profit from unfulfilled excess demand. This leads to a rapid mitigation of previously intense market competition and a significant profit increase. However, under other slot–sharing agreements, although CSLs become more cautious in cargo securing, thereby decreasing service quality levels and saving costs. The cost savings may slightly exceed the reduced profit from unmet excess demand and consequently, the overall change in profit remains negligible.

Figure 3

Figure 3. Sensitivity analysis of Profit ${\pi }_i$ regarding $\delta$. The parameter setting is $p=1, c=0.3, \beta =1, t=0.4, I=0.3$, and $k = 1$.

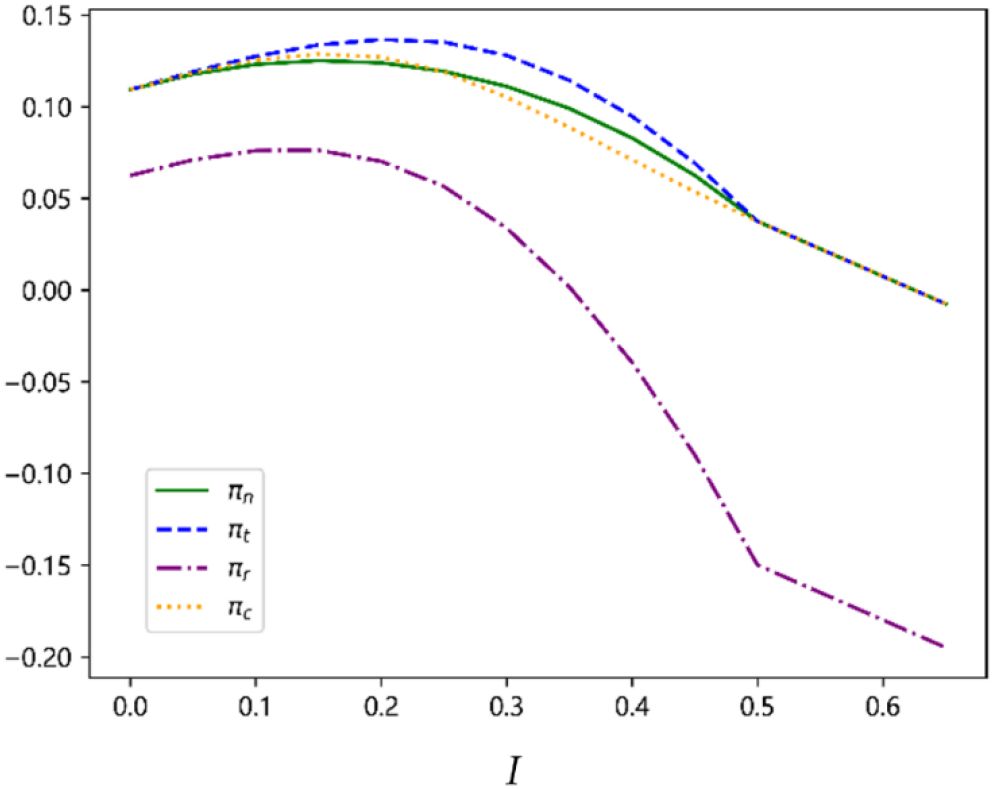
In addition, we examine how CSLs’ profits respond to changes in initial slot capacity, which is presented in Figure 4. As initial slot capacity increases, CSLs can gradually meet shippers’ demand, leading to more transactions and higher profits. However, when slot capacity exceeds a certain threshold, demand uncertainty causes surplus slots, thereby incurring empty slot losses. Under such circumstances, slot–sharing agreement helps mitigate these empty slot losses, yielding higher profits under the transfer–payment agreement than without slot sharing. When slot capacity exceeds 0.5—the maximum potential market demand for each CSL—excess slots inevitably lead to waste. Furthermore, as both CSLs have surplus capacity, they cease competing by improving service quality levels, causing profits to decline linearly.

Figure 4

Figure 4. Sensitivity analysis of Profit ${\pi }_i$ regarding $I$. The parameter setting is $p=1, c=0.3, \delta =0.2, \beta =1, t=0.4$, and $k = 1$.

5 Conclusion

In recent years, unexpected events, de–globalization, and trade barriers have significantly increased demand volatility in the shipping market. Facing such demand volatility, CSLs are seen to form alliances and reach slot–sharing agreements on specific shipping routes. In this study, we develop a sequential game–theoretic model where two CSLs engage in service competition in a shipping market with uncertain demand. We consider three typical slot–sharing agreements among the CSLs: transfer–payment, revenue–sharing, and cost–sharing agreements. The two CSLs first decide whether to reach a slot–sharing agreement with each other, and then determine their service quality levels. We focus on the performance of the slot–sharing agreements and the impact of service competition. Specifically, we aim to answer the question of whether the CSLs should reach a slot–sharing agreement. Our analysis has produced some interesting and notable findings.

When comparing the three slot–sharing agreements, we find that the transfer–payment agreement yields the highest profits among the three, with a relatively lower service quality level. In contrast, under revenue–sharing and cost–sharing agreements, CSLs compete not only for market demand but also in their contributions to the alliance’s total profit or shared costs, resulting in higher service quality levels but lower profits. It is worth noting that although the service quality under transfer–payment is the lowest among the three agreements, it may still exceed that under no slot–sharing scenario. Therefore, while transfer–payment is the most profitable slot–sharing scheme for CSLs, it achieves this with a moderate level of service quality.

When comparing the transfer–payment agreement with no slot–sharing, we find that its impact on CSLs’ service quality and profits depends on the transfer–payment price and the demand sensitivity to service quality. Specifically, when the transfer–payment price is low and demand is highly sensitive to service quality (i.e., competition is intense), the agreement intensifies competition, resulting in higher service quality but lower profits. Conversely, when demand sensitivity is low, a low transfer–payment price can achieve a win–win outcome by improving both service quality and profits. Moreover, we find that the optimal transfer–payment price equals the sum of the unit slot cost and the delay compensation cost, which maximizes CSLs’ profits by balancing competition intensity and risk–sharing efficiency.

When examining the numerical results, we find that when demand is insensitive to service quality, all three slot–sharing agreements perform equally well and yield higher profits than no slot sharing, as slot sharing mitigates inventory risks without intensifying market competition. As sensitivity coefficient of demand to service quality increases, competition under revenue–sharing and cost–sharing agreements escalates rapidly, causing profits to fall below those under no slot sharing at high sensitivity levels. In contrast, under the transfer–payment agreement, a relatively high transfer price suppresses market competition, maintaining profits above the no–sharing scenario. Moreover, an increase in delay compensation leads CSLs to adopt more cautious cargo–securing strategies, weakening competition, reducing service quality levels, and increasing profits. Finally, as initial slot capacity rises, profits first increase as CSLs better meet shippers’ demand, but beyond a certain capacity threshold, surplus slots under demand uncertainty lead to empty slot losses. When capacity exceeds the maximum potential market demand, these excess slots inevitably cause wastage; although service competition persists, it no longer intensifies, leading to a linear decline in profits.

Our model has certain limitations, and we identify several issues and areas for future research. First, for simplicity, our model only considers a single shipping period for the CSLs. However, unfilled cargos are postponed to the next shipping period. Thus, future studies could consider a multiple–shipping–period model to further explore the CSLs’ decision–making processes. Second, we have considered three typical agreements for the CSLs to share cargo slots. In the future, more slot–sharing agreements emerging from practice can be investigated. Finally, our findings are based on a stylized model that emphasizes key factors in the container shipping market. To verify the robustness of our analytical results, future research could utilize simulation–based or empirical analyses.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

SZ: Software, Writing – review & editing, Methodology, Investigation, Writing – original draft, Funding acquisition, Formal Analysis, Validation, Resources, Conceptualization. JH: Writing – original draft, Software, Formal Analysis, Data curation. XZ: Conceptualization, Validation, Funding acquisition, Writing – review & editing, Resources, Writing – original draft. FW: Formal Analysis, Writing – review & editing, Methodology, Funding acquisition, Resources.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was funded by the National Natural Science Foundation of China (Grant No. 72271251, 72371252), the Natural Science Foundation of Guangdong Province, China (Grant No.2023A1515010683).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

1. ^ “ Review of Maritime Transport 2024”. Available from: https://unctad.org/publication/review–maritime–transport–2024 (accessed on May 4, 2025).
2. ^ “Global trade expected to shrink by nearly 5% in 2023 amid geopolitical strains and shifting trade patterns”. Available from: https://unctad.org/news/global–trade–expected–shrink–nearly–5–2023–amid–geopolitical–strains–and–shifting–trade (accessed on May 4, 2025).
3. ^ “MSC and ZIM Form an Alliance; Maersk Responds”. Available from: https://www.longsailing.net/News.html?NewsInfoId=1424 (accessed on May 4, 2025).
4. ^ “Why Sailing Schedule Changes Matter – More Than Shipping”. Available from: https://www.morethanshipping.com/why–sailing–schedule–changes–matter/ (accessed on May 4, 2025).
5. ^ “TradeLens available in China through collaboration with China Unicom Digital Tech”. Available from: https://www.maersk.com/news/articles/2021/05/10/tradelens–available–in–china–through–collaboration–with–china–unicom–digital–tech (accessed on May 4, 2025).
6. ^ “E2E Bridge – DKSH Pegasus Case Study”. Available from: https://www.uml.org/uml_success_stories/2008–06–10_E2E_Case_Study_on_DKSH_Pegasus.pdf (accessed on May 4, 2025).
7. ^ “What does end–to–end logistics mean?”. Available from: https://www.time–matters.com/emergency–logistics–glossary/end–to–end–logistics/ (accessed on May 4, 2025).
8. ^ “ CMA CGM / MARFRET VESSEL SHARING AGREEMENT FOR PAD SERVICE”. Available from: https://www.lawinsider.com/contracts/1RPAKk1n4Jb (accessed on June 25, 2025).

References

Ao R., Fu H., and Simchi-Levi D. (2024). Two-stage online reusable resource allocation: reservation, overbooking and confirmation call. arXiv preprint arXiv:2410.15245.

Google Scholar

Cai J., Hu X., Tadikamalla P. R., and Shang J. (2017). Flexible contract design for VMI supply chain with service-sensitive demand: Revenue-sharing and supplier subsidy. Eur. J. Oper. Res. 261, 143–153.

Google Scholar

Chakraborty T., Chauhan S. S., and Ouhimmou M. (2019). Cost-sharing mechanism for product quality improvement in a supply chain under competition. Int. J. Prod. Econ. 208, 566–587.

Google Scholar

Chakraborty T., Chauhan S. S., and Vidyarthi N. (2015). Coordination and competition in a common retailer channel: Wholesale price versus revenue-sharing mechanisms. Int. J. Prod. Econ. 166, 103–118.

Google Scholar

Chen R., Dong J.-X., and Lee C.-Y. (2016). Pricing and competition in a shipping market with waste shipments and empty container repositioning. Transp. Res. Part B. Methodol. 85, 32–55.

Google Scholar

Chen J., Liu X., Zhou S., and Kang J. (2023a). Knowledge mapping analysis of shipping network resilience using CiteSpace. Ocean Coast. Management 244, 106775.

Google Scholar

Chen J., Xu Q., Zhang H., Wan Z., and Yu M. (2022). Bilateral slot exchange and co-allocation for liner alliance carriers of containerized maritime logistics. Adv. Eng. Inform. 51, 101479.

Google Scholar

Chen J., Xu J., Zhou S., and Liu A. (2023b). Slot co-chartering and capacity deployment optimization of liner alliances in containerized maritime logistics industry. Adv. Eng. Inform. 56, 101986.

Google Scholar

Chen J. and Yahalom S. (2013). Container slot co-allocation planning with joint fleet agreement in a round voyage for liner shipping. J. Navig. 66, 589–603.

Google Scholar

Chen J., Ye J., Liu A., Fei Y., Wan Z., and Huang X. (2024). Robust optimization of liner shipping alliance fleet scheduling with consideration of sulfur emission restrictions and slot exchange. Ann. Oper. Res. 343, 1013–1043.

Google Scholar

Choi T.-M., Chung S.-H., and Zhuo X. (2020). Pricing with risk sensitive competing container shipping lines: Will risk seeking do more good than harm? Transp. Res. Part B. Methodol. 133, 210–229.

Google Scholar

Gallego G. and Talebian M. (2019). Oligopolistic contracting: Channel coordination under competition. Nav. Res. Logist. NRL 66, 619–631.

Google Scholar

Ghosh D. and Shah J. (2015). Supply chain analysis under green sensitive consumer demand and cost sharing contract. Int. J. Prod. Econ. 164, 319–329.

Google Scholar

Gu Y., Wang Y., and Wang T. (2025). An approximate dynamic programming approach to dynamic slot allocation of spot containers with random arrivals, cancellations, and no-shows. Transp. Res. Part E Logist. Transp. Rev. 193, 103837.

Google Scholar

Guo X. and Jiang B. (2022). Inventory sharing under service quality competition.

Google Scholar

Guo L. and Wu X. (2018). Capacity sharing between competitors. Manage. Sci. 64, 3554–3573.

Google Scholar

Herbon A. and David I. (2023). Optimal manufacturer’s cost sharing ratio, shipping policy and production rate – A two-echelon supply chain. Oper. Res. Perspect. 10, 100264.

Google Scholar

Huang W., Hu J., Zhou S., and Zhao M. (2023). Demand prediction and sharing strategy in resilient maritime transportation: Considering price and quality competition. Ocean Coast. Manage. 58, 106676.

Google Scholar

Huang W., Huang G., and Zhou S. (2025). Integrated optimization of dynamic lane allocation and signal timing at urban intersections. Transportmetr. B.: Transp. Dynamics. 13, 2474656.

Google Scholar

Jiang G., Fan Q., Zhang Y., Xiao Y., Xie J., and Zhou S. (2025). A tradable carbon credit incentive scheme based on the public-private-partnership. Transport. Res. Part E: Logistics Transport. Rev. 197, 104039.

Google Scholar

Lee L. H., Chew E. P., and Sim M. S. (2009). A revenue management model for sea cargo. Int. J. Oper. Res. 6, 195–222.

Google Scholar

Lee C.-Y., Tang C. S., Yin R., and An J. (2015). Fractional price matching policies arising from the ocean freight service industry. Prod. Oper. Manage. 24, 1118–1134.

Google Scholar

Li X. and Shi J. (2024). Capacity sharing for ride-sourcing platforms under competition. Transp. Res. Part E Logist. Transp. Rev. 182, 103397.

Google Scholar

Liang J., Li L., Zheng J., and Tan Z. (2023). Service-oriented container slot allocation policy under stochastic demand. Transp. Res. Part B. Methodol. 176, 102799.

Google Scholar

Liang J., Ma Z., Wang S., Liu H., and Tan Z. (2024). Dynamic container slot allocation with empty container repositioning under stochastic demand. Transp. Res. Part E Logist. Transp. Rev. 187, 103603.

Google Scholar

Liang J., Zhou Y., Wang S., and Zheng J. (2025). Container slot allocation policy in vessel pool alliance under stochastic demand. Comput. Oper. Res. 180, 107074.

Google Scholar

Liu J. and Wang J. (2019). Carrier alliance incentive analysis and coordination in a maritime transport chain based on service competition. Transp. Res. Part E Logist. Transp. Rev. 128, 333–355.

Google Scholar

Liu X., Zhou S., Zhuo X., Chen J., and Deng L. (2024). Editorial: Opportunities and challenges of EU ETS to the global marine industry. Front. Mar. Sci. 5, 18–23.

Google Scholar

Maragos S. A. and Spyriodon A. (1994). Yield management for the maritime industry (Doctoral dissertation, Massachusetts Institute of Technology).

Google Scholar

Mehrzadegan E., Ghandehari M., and Ketabi S. (2022). A joint dynamic inventory-slot allocation model for liner shipping using revenue management concepts. Comput. Ind. Eng. 170, 108333.

Google Scholar

Najafi M. and Zolfagharinia H. (2021). Pricing and quality setting strategy in maritime transportation: Considering empty repositioning and demand uncertainty. Int. J. Prod. Econ. 240, 108245.

Google Scholar

Papachristidis B. and Papachristidis P. B. (2015). “Pools in international shipping,” in HSBA handbook on ship finance. Eds. SChinas O., Grau C., and Johns M. (Springer, Berlin, Heidelberg), 269–281.

Google Scholar

Rau P. and Spinler S. (2017). Alliance formation in a cooperative container shipping game: Performance of a real options investment approach. Transp. Res. Part E Logist. Transp. Rev. 101, 155–175.

Google Scholar

Shi X., Meersman H., and Voss S. (2008). The win-win game in slot-chartering agreement among the liner competitors and collaborators. In Proceedings of the IAME 2008 Conference Sustainability in International Shipping, Port and Logistics Industries and the China Factor (Vol. 3, p. D2).

Google Scholar

Song Z., Tang W., and Zhao R. (2021). Liner alliances with heterogeneous price level and service competition: Partial vs. Full Omega 103, 102414.

Google Scholar

Song C. and Wang Y. (2022). Slot allocation and exchange for container shipping alliance under profit-sharing agreement and uncertain demand. Ocean Coast. Manage. 229, 106335.

Google Scholar

Song W., Yang H., Li D., and Yang Z. (2023). Dynamic pricing and competition of container liner shipping services in a duopoly spot market. Comput. Ind. Eng. 185, 109613. doi: 10.1016/j.cie.2023.109613

Crossref Full Text | Google Scholar

Sun H., Geng L., Gao Y., and Qu C. (2025). Cooperation and coordination strategy of the online container supply chain considering service quality competition. Res. Transp. Bus. Manage. 59, 101297.

Google Scholar

Tao Y., Wang M., and Zhou S. (2023). Pricing and contract preference in maritime supply chains with downstream competition: Impact of risk-aversion and contract unobservability. Ocean Coast. Management 58, 106691.

Google Scholar

Ting S.-C. and Tzeng G.-H. (2004). An optimal containership slot allocation for liner shipping revenue management. Marit. Policy Manage. 31, 199–211.

Google Scholar

Wang Z., Dai Q., and Kong Y. (2024d). Vertical structure selection and evolution in shipping supply chains under bilateral bargaining. Expert Syst. Appl. 238, 122032.

Google Scholar

Wang L, Fu X., and Xiong Y. (2024a). Revenue-sharing in the alliance of inland river and sea carriers: Formulation and a case study. Transp. Res. Part E Logist. Transp. Rev. 183, 103419.

Google Scholar

Wang J. and Liu J. (2019). Vertical contract selection under chain-to-chain service competition in shipping supply chain. Transp. Policy 81, 184–196.

Google Scholar

Wang S., Liu Z., and Qu X. (2016). Minimax regret model for liner Shipping Fleet Deployment with Uncertain Demand. Transp. Res. Rec. J. Transp. Res. Board 2549, 45–53. doi: 10.3141/2549-06

Crossref Full Text | Google Scholar

Wang M. and Tian X. (2024b). Dynamic container slot allocation for a liner shipping service. Transp. Res. Part B. Methodol. 179, 102874.

Google Scholar

Wang T., Tian X., and Wang Y. (2020). Container slot allocation and dynamic pricing of time-sensitive cargoes considering port congestion and uncertain demand. Transp. Res. Part E Logist. Transp. Rev. 144, 102149.

Google Scholar

Wang Y., Zhang H., Wang T., and Liu J. (2025). Heterogeneous vessel fleet co-management for liner alliances under profit-sharing agreement and weekly-dependent demand. Transp. Res. Part E Logist. Transp. Rev. 194, 103880.

Google Scholar

Wen M., Larsen R., Ropke S., Petersen H. L., and Madsen O. B. G. (2019). Centralised horizontal cooperation and profit sharing in a shipping pool. J. Oper. Res. Soc. 70, 737–750.

Google Scholar

Xin X., Wang X., Zhang T., Chen H., Guo Q., Zhou S., et al. (2023). Liner alliance shipping network design model with shippers’ choice inertia and empty container relocation. Electron. Res. Arch. 31, 5509–5540. doi: 10.3934/era.2023280

Crossref Full Text | Google Scholar

Xing W., Yan L., and Zhou S. (2023). Strategic logistics service procurement in shipping supply chains. Ocean Coast. Manage. 242, 106714.

Google Scholar

Xiong C., Wang C., Zhou S., and Song X. (2024). Dynamic rolling scheduling model for multi-AGVs in automated container terminals based on spatio-temporal position information. Ocean Coast. Management 58, 107349.

Google Scholar

Xu L., Huang J., Fu S., and Chen J. (2025c). Evaluation of navigation capacity in the Northeast Arctic passage: evidence from multiple factors. Marit. Policy Manag. 523, 497–513.

Google Scholar

Xu L., Li X., Yan R., and Chen J. (2025a). How to support shore-to-ship electricity constructions: Trade off between government subsidy and port competition. Transport. Res. Part E. 201, 104258.

Google Scholar

Xu L., Li X., Yan R., and Chen J. (2025b). Is international shipping in right direction towards carbon emissions control? Transp. Policy 166, 189–201.

Google Scholar

Yang D., Liu M., and Shi X. (2011). Verifying liner Shipping Alliance’s stability by applying core theory. Res. Transp. Econ. 32, 15–24.

Google Scholar

Yang S., Zhang J., and Zhou S. (2024). The cost transportation game for collaboration among transportation companies. Ann. Operations Res. 336, 1479–1503. doi: 10.1007/s10479-023-05466-4

Crossref Full Text | Google Scholar

Yu M. and Liu H. (2021). “Ocean Carrier Price Competition with Bulk Cargo transportation and empty container repositioning,” in Advances in artificial systems for logistics engineering. Eds. Hu Z., Zhang Q., Petoukhov S., and He M. (Springer International Publishing, Cham), 180–189.

Google Scholar

Zahoor N., Wu J., Khan H., and Khan Z. (2023). De-globalization, international trade protectionism, and the reconfigurations of global value chains. Manage. Int. Rev. 63, 823–859.

Google Scholar

Zhang M., Fu Y., Zhao Z., Pratap S., and Huang G. Q. (2019). Game theoretic analysis of horizontal carrier coordination with revenue sharing in E-commerce logistics. Int. J. Prod. Res. 57, 1524–1551.

Google Scholar

Zhang T., Wang S., and Xin X. (2025). Liner fleet deployment and slot allocation problem: A distributionally robust optimization model with joint chance constraints. Transp. Res. Part B. Methodol. 197, 103236.

Google Scholar

Zhao H., Chen J., and Ai X. (2022). Contract strategy in the presence of chain to chain competition. Int. J. Prod. Res. 60, 1913–1931.

Google Scholar

Zheng S. and Luo M. (2021). Competition or cooperation? Ports’ strategies and welfare analysis facing shipping alliances. Transp. Res. Part E Logist. Transp. Rev. 153, 102429.

Google Scholar

Zhou S., Guo Z., Chen J., and Jiang G. (2025a). Large containership stowage planning for maritime logistics: A novel meta-heuristic algorithm to reduce the number of shifts. Adv. Eng. Inf. 64, 102962.

Google Scholar

Zhou Y., Li G., Zhou S., Hu D., Zhang S., and Kong L. (2023). Spatio-temporal differences and convergence analysis of green development efficiency of marine economy in China. Ocean Coast. Manage. 238, 106560.

Google Scholar

Zhou S., Liao Q., and Chen J. (2024). A novel metaheuristic approach for AGVs scheduling problem with battery constraints in an automated container terminal. J. Sea Res. 202, 102536.

Google Scholar

Zhou S., Liu X., Chen J., Zhao M., Wang F., and Wu L. (2025b). Joint optimization of slot and empty container co-allocation for liner alliances with uncertain demand in maritime logistics industry. Transport. Res. Part E: Logistics Transport. Rev. Forthcoming 204, 104437.

Google Scholar

Zhuo X., Sun Y., and Zhou S. (2025). Impact of consumers traceability awareness on blockchain adoption in supply chains. IEEE Trans. Eng. Manage. 72, 140–1153.

Google Scholar

Zurheide S. and Fischer K. (2012). A revenue management slot allocation model for liner shipping networks. Marit. Econ. Logist 14, 334–361.

Google Scholar

Zurheide S. and Fischer K. (2015). Revenue management methods for the liner shipping industry. Flex. Serv. Manuf. J. 27, 200–223.

Google Scholar

Appendix

Appendix A. Derivation of equilibrium outcome.

First, we consider the scenario T (i.e., slot sharing under transfer–payment agreement). For CSL $i$, its expected profit is

$$\begin{array}{c}{\pi }_i(s_i,I_i|s_j,I_j)=p·E[{ϵ}_i{d}_i(s_i,s_j)]+t·E[{(\min \{I_i-{ϵ}_i{d}_i,{ϵ}_j{d}_j-I_j\})}^{+}]\hfill \\ -t·E[{(\text{mim}\{{ϵ}_i{d}_i-I_i,I_j-{ϵ}_j{d}_j\})}^{+}]-(c+\delta )·E[(({ϵ}_i{d}_i\hfill \\ -I_i{)}^{+}-(I_j-{ϵ}_j{d}_j{)}^{+}{)}^{+}]-k{s}_i^2-\text{c}{I}_i\hfill \end{array}$$

From the first order condition $\{\begin{array}{c}\frac{d{\pi }_1^t(s_1,I|s_2,I)}{d{s}_1}=0\\ \frac{d{\pi }_2^t(s_2,I|s_1,I)}{d{s}_2}=0\end{array}$, we can gain the equilibrium service quality level in scenario $T$:

$$s_1^T(t,I)=s_2^T(t,I)=\frac{\beta (p\mu -A-B)}{2k}=\frac{\beta ({\int }_0^{1}pϵg(ϵ)dϵ-A-B)}{2k}$$

where

$$\begin{array}{c}A={\displaystyle {\int }_0^{2I}}[{\displaystyle {\int }_{2I}^{4I-{ϵ}_2}t{ϵ}_1{g}_{12}({ϵ}_1,{ϵ}_2)d{ϵ}_1}\hfill \\ +{\displaystyle {\int }_{4I-{ϵ}_2}^1(t{ϵ}_2+(c+\delta )({ϵ}_1-{ϵ}_2))}{g}_{12}({ϵ}_1,{ϵ}_2)d{ϵ}_1]d{ϵ}_2\hfill \\ B={\displaystyle {\int }_{2I}^1}[{\displaystyle {\int }_{4I-{ϵ}_2}^{2I}t{ϵ}_1{g}_{12}({ϵ}_1,{ϵ}_2)d{ϵ}_1}\hfill \\ +{\displaystyle {\int }_0^{4I-{ϵ}_2}t{ϵ}_2{g}_{12}({ϵ}_1,{ϵ}_2)d{ϵ}_1}{\displaystyle {\int }_{2i}^1(c+\delta )}{ϵ}_1{g}_{12}({ϵ}_1,{ϵ}_2)d{ϵ}_1]d{ϵ}_2\hfill \end{array}$$

From the second order condition, it can be proved that the profit function ${\pi }_i(s_i,I_i\mid s_j,I_j)$ is concave. Given the optimal service quality level $s_1^T(t,I)=s_2^T(t,I)$, we can find that $\frac{\partial {\pi }_i^T(t,I)}{\partial t}=-2k{s}_i^T·\frac{\partial s_i^T(t,I)}{\partial t}>0$, where $\frac{\partial s_i^T(t,I)}{\partial t}=-\frac{\beta }{2k}[{\int }_0^{2I}{\int }_{2I}^{4I-{ϵ}_2}{ϵ}_1{g}_{12}({ϵ}_1,{ϵ}_2)d{ϵ}_{1}d{ϵ}_2+{\int }_0^{2I}{\int }_{4I-{ϵ}_2}^1{ϵ}_2{g}_{12}({ϵ}_1,{ϵ}_2)d{ϵ}_{1}d{ϵ}_2]<0$. Therefore, we can obtain the optimal transfer price $t^{*}=c+\delta$, which maximize the profit of CSL i under transfer–payment agreement.

Second, let’s consider the scenario $R$ (i.e., slot sharing under revenue–sharing agreement). For CSL $i$, based on the rule of Sharply Value, its service quality level in scenario expected profit is

$${\pi }_i^R(I)=\frac{1}{2}V(\{i\})+\frac{1}{2}[V(\{i,j\})-V(\left\{j\right\})]$$

where $V(\{i\})=pE[v]-(c+\delta )E[{({ϵ}_i{d}_i-I_i)}^{+}]-k{s}_i^2-c{I}_i$ (only CSL $i$ in the alliance) and $V(\{i,j\})=pE[{ϵ}_i{d}_i+{ϵ}_j{d}_j]-(c+\delta )E[{({ϵ}_i{d}_i+{ϵ}_j{d}_j-I_i-I_j)}^{+}]-k{s}_i^2-k{s}_j^2-c{I}_i-c{I}_j$ (CLS $i$ and $j$ in the alliance)

From the first order condition $\{\begin{array}{c}\frac{d{\pi }_1^R(s_1,I|s_2,I)}{d{s}_1}=0\\ \frac{d{\pi }_2^R(s_2,I|s_1,I)}{d{s}_2}=0\end{array}$, we can gain the equilibrium service quality level in scenario $R$:

$$s_1^R=s_2^R=\frac{\beta [p\mu -(c+\delta ){\int }_{2I}^1ϵg(ϵ)dϵ]}{k}$$

The stable existence of the alliance requires that the total revenue of the alliance exceeds the sum of the revenues of each logistics company when competing individually in the market (i.e., scenario $N$), and that the revenue of each logistics company is higher than when it competes alone in the market.

$$V(\left\{i,j\right\})>V(\left\{i\right\})+V(\left\{j\right\})$$

$${\pi }_i^R(I)>V(\left\{i\right\})$$

$${\pi }_j^R(I)>V(\left\{j\right\})$$

The above–mentioned conditions regarding the stability of the alliance can be proven to hold true.

Third, let’s consider the scenario $C$ (i.e., slot sharing under revenue–sharing agreement). Based on the rule of Sharply Value, the expected cost the CSL $i$ shares is:

$${\phi }_i(V)=\frac{1}{2}V(\left\{i\right\})+\frac{1}{2}[V(\left\{i,j\right\})-V(\left\{j\right\})]$$

where

$V(\left\{i\right\})=cE[{(I_i-{ϵ}_i{d}_i)}^{+}]+\delta E[{({ϵ}_i{d}_i-I_i)}^{+}]$

$$V(\left\{i,j\right\})=cE[{(I_i+I_j-{ϵ}_i{d}_i-{ϵ}_j{d}_j)}^{+}]+\delta E[{({ϵ}_i{d}_i+{ϵ}_j{d}_j-I_i-I_j)}^{+}]$$

Thus, the profit the CSL $i$ earns under scenario $C$:

$$\begin{array}{c}{\pi }_i=p·E[{ϵ}_i{d}_i]-c·E[min\{{ϵ}_i{d}_i,I_i\}]-c·E[{({ϵ}_i{d}_i-I_i-{(I_j-{ϵ}_j{d}_j)}^{+})}^{+}]\hfill \\ --\frac{1}{2}[V(\left\{i\right\})-V(\left\{j\right\})]-c·E[{(min\{I_i-{ϵ}_i{d}_i,-{ϵ}_j{d}_j-I_j\})}^{+}]\hfill \\ -k{s}_i^2\hfill \end{array}$$

From the first order condition $\{\begin{array}{c}\frac{d{\pi }_1^C(s_1,I|s_2,I)}{d{s}_1}=0\\ \frac{d{\pi }_2^C(s_2,I|s_1,I)}{d{s}_2}=0\end{array}$, we can gain the equilibrium service quality level in scenario $C$:

$$s_1^C=s_2^C=\frac{\beta (p\mu -A_3-B_3)}{2k}$$

where

$A_3= (c+\delta ){\int }_0^{2I}{\int }_{4I-{ϵ}_2}^1({ϵ}_1-{ϵ}_2)g_{12({ϵ}_1, {ϵ}_2)d{ϵ}_{1}d{ϵ}_2}$

$$B_3= (c+\delta ){\int }_{2I}^1{\int }_{2I}^1{ϵ}_1{g}_{12({ϵ}_1, {ϵ}_2)d{ϵ}_{1}d{ϵ}_2}$$

We can prove the existence of parameters under which a cost–sharing alliance can exist stably. Unlike scenario N, this requires that the alliance’s cost must be lower than the sum of the costs incurred by each logistics company when they independently participate in market competition. Additionally, the cost for each logistics company within the alliance must be lower than its cost when competing independently in the market, as follows:

$$V(\left\{i,j\right\})<V(\left\{i\right\})+V(\left\{j\right\})$$

$${\phi }_i(V)<V(\left\{i\right\})$$

$${\phi }_j(V)<V(\left\{j\right\})$$

Appendix B. Proofs.

Proof of Proposition 1.

From Appendix A, we obtain the equilibrium service quality levels and profits under the three different scenarios, respectively.

$$s^T(t,I)=\frac{\beta (p\mu -A-B)}{2k}$$

$$s^R=\frac{\beta [p\mu -(c+\delta ){\int }_{2I}^1ϵg(ϵ)dϵ]}{k}$$

$$s_2^C=\frac{\beta (p\mu -A_3-B_3)}{2k}$$

$$\begin{array}{c}{\pi }_i^T= p·E[\frac{{ϵ}_i}{2}]- (c+\delta )E[{(\frac{{ϵ}_i}{2}- I - {(I -\frac{{ϵ}_j}{2})}^{+})}^{+}]- k{[s^T(t, I)]}^2\hfill \\ - cI\hfill \end{array}$$

$$\begin{array}{c}{\pi }_i^R= p·E[\frac{{ϵ}_i}{2}]- (c+\delta )E[{(\frac{{ϵ}_i}{2}- I - {(I -\frac{{ϵ}_j}{2})}^{+})}^{+}]- k{[s^R(I)]}^2\hfill \\ - cI\hfill \end{array}$$

$$\begin{array}{c}{\pi }_i^C= p·E[\frac{{ϵ}_i}{2}]- (c+\delta )E[{(\frac{{ϵ}_i}{2}- I - {(I -\frac{{ϵ}_j}{2})}^{+})}^{+}]- k{[s^C(I)]}^2\hfill \\ - cI\hfill \end{array}$$

By simple mathematical calculations, we can obtain $s^R\geqq ̸s^C\geqq ̸s^T$ and then ${\pi }_i^R\leqq ̸{\pi }_i^C\leqq ̸{\pi }_i^T$.

Proof of Proposition 5. By simple mathematical calculations, we have

$$s^T(t,I)-s^N(I)=\frac{\beta (p\mu -A-B)}{2k}-\frac{p\mu \beta -(c+\delta )\beta {\displaystyle {\int }_{2I}^1ϵg(ϵ)dϵ}}{2k}=\frac{(c+\delta -2t)\beta {\displaystyle {\int }_0^{2I}}{\displaystyle {\int }_{2I}^{4I-{ϵ}_2}{ϵ}_1{g}_{12({ϵ}_1-{ϵ}_2)d{ϵ}_{1}d{ϵ}_2}}+{\displaystyle {\int }_0^{2I}}{\displaystyle {\int }_{4I-{ϵ}_2}^1{ϵ}_2{g}_{12({ϵ}_1-{ϵ}_2)d{ϵ}_{1}d{ϵ}_2}}}{2k}$$

Obviously, we have $s^T\left(t,I\right)>s^N\left(I\right)$ if $t<\frac{c+\delta }{2}$; otherwise, $s^T\left(t,I\right)\le s^N\left(I\right)$ Proof of Proposition 1. We compare ${\pi }_i^T$ with ${\pi }_i^N$ and obtain $\text{Δ}{\pi }_i^T= {\pi }_i^T\left(t,I\right)- {\pi }_i^N\left(I\right)= R^T\left(t,I\right)- R^N\left(I\right)- k\left[{\left(s^T\left(t,I\right)\right)}^2- {\left(s^N\left(I\right)\right)}^2\right]$, where $R^T\left(t,I\right)= -\left(c+\delta \right){\int }_0^{2I}{\int }_{4I-{ϵ}_2}^1\left(\frac{{ϵ}_1}{2}+\frac{{ϵ}_2}{2}-2I\right)g_{12\left({ϵ}_1,{ϵ}_2\right)d{ϵ}_{1}d{ϵ}_2}-\left(c+\delta \right){\int }_{2I}^1{\int }_{2I}^1\left(\frac{{ϵ}_1}{2}-I\right)g_{12\left({ϵ}_1,{ϵ}_2\right)d{ϵ}_{1}d{ϵ}_2}$ and $R^N\left(I\right)= -\left(c+\delta \right){\int }_{2I}^1\left(\frac{{ϵ}_i}{2}-I\right)g\left({ϵ}_i\right)d{ϵ}_i$. Then, we have $R^T\left(t,I\right)-R^T\left(I\right)= \left(c+\delta \right){\int }_0^{2I}{\int }_{2I}^{4I-{ϵ}_2}\left(\frac{{ϵ}_1}{2}+I\right)g_{12}\left({ϵ}_1,{ϵ}_2\right)d{ϵ}_{1}d{ϵ}_2-\left(c+\delta \right){\int }_0^{2I}{\int }_{4I-{ϵ}_2}^1\left(I-\frac{{ϵ}_2}{2}\right)g_{12}\left({ϵ}_1,{ϵ}_2\right)d{ϵ}_{1}d{ϵ}_2$. It is easy to demonstrate that $R^T\left(t,I\right)- R^N\left(I\right)$ is always positive and independent of $t$ and $\beta$.

Similarly, we have

$$\begin{array}{c}{\left(s^T\left(t,I\right)\right)}^2- {\left(s^N\left(I\right)\right)}^2\hfill \\ = {\beta }^2\left[{\left(\frac{p\mu -A-B}{2k}\right)}^2- {\left(\frac{p\mu -\left(c+\delta \right){\int }_{2I}^1ϵg\left(ϵ\right)dϵ}{2k}\right)}^2\right]\hfill \\ = {\beta }^2\left[{\left(S^T\left(t,I\right)\right)}^2- {\left(S^N\left(I\right)\right)}^2\right]\text{.,}\hfill \end{array}$$

where $S^T\left(t,I\right)=\frac{p\mu -A-B}{2k}$ and $S^N\left(I\right)=\frac{p\mu -\left(c+\delta \right){\int }_{2I}^1ϵg\left(ϵ\right)dϵ}{2k}$. Since $\partial s^t\left(t, I\right)/\partial t < 0$, the term $-k\left[\left(s\left(t, I\right)\right)² - \left(s^N\left(I\right)\right)²\right]$ increases monotonically with respect to $t$. It’s easy to draw that when $t<\frac{c+\delta }{2}$, $\Delta {\pi }_i^T$is monotonically decreasing in $\beta$; when $t>\frac{c+\delta }{2}$, $\Delta {\pi }_i^T$ is monotonically increasing in $\beta$, and $\Delta {\pi }_i^T>0$.

Therefore, by the Intermediate Value Theorem, there exists a $\widehat{t}(\beta )\in [0,\frac{c+\delta }{2}]$ such that when $t>\widehat{t}(\beta )$, $\Delta {\pi }_i^T(t,I)>0$; and when $t<\widehat{t}(\beta )$, $\Delta {\pi }_i^T(t,I)<0$. Let $\Delta {\pi }_i^T(t,I)=0$, we obtain that:

When$t<\frac{c+\delta }{2}$, there exists $\hat{\beta }(t)=\sqrt{\frac{R(t,I)-R^N(I)}{k{[{(s^T(t,I))}^2-{(s^N(I))}^2]}^2}}$, such that $\begin{array}{rr}\hfill & \hfill \text{Δ}{\pi }_i^T(t,I)\langle 0,\text{ when }\beta \rangle \hat{\beta }(t)\\ \hfill & \hfill \text{Δ}{\pi }_i^T(t,I)>0,\text{ when }\beta <\hat{\beta }(t)\end{array}$Hence, Proposition 7 (a) is proved.

From above discussion, we know that when $t<\frac{c+\delta }{2}$ and $\beta <\widehat{\beta }(t)$, $\text{Δ}{\pi }_i^T(t,I)>0$ (i.e., ${\pi }_i^T>{\pi }_i^N$). From Proposition 8, we know that when $t<\frac{c+\delta }{2}$, $s^T(t,I)>s^N(I)$. Therefore, service quality levels and profits of the two CSLs are improved, meaning that Proposition 9 (b) is proved.

Proof of Corollary 2. The results are obvious based on the Proof of Proposition 10.

Proof of Proposition 11. In Appendix A, we prove that the optimal transfer price is $t^{*}=c+\delta$ under a transfer–payments agreement. According to Proof of Proposition 12, $t^{*}=c+\delta >\frac{c+\delta }{2}$ means that $\text{Δ}{\pi }_i^T(t,I)>0$ (i.e., ${\pi }_i^T>{\pi }_i^N$). The CSLs gains more profit than that in scenario $N$, so both CSLs are willing to share cargo slots at $t^{*}$.