- 1Department of Electrical Engineering, Indian Institute of Technology Bombay, Powai, Mumbai, India
- 2Center of Excellence in Quantum Information, Computation, Science and Technology, Indian Institute of Technology Bombay, Powai, Mumbai, India
- 3Low Temperature Laboratory, Department of Applied Physics, Aalto University, Aalto, Finland
- 4QTF Centre of Excellence, Department of Applied Physics, Aalto University, Aalto, Finland
- 5MESA+ Institute for Nanotechnology, University of Twente, Enschede, Netherlands
The non-Abelian state has garnered considerable interest in the field of fundamental physics and future applications in quantum computing. In this review, we introduce the basic ideas of constructing the non-Abelian states in various systems from 1D to 3D and discuss the possible approaches to detect these states, including the Majorana bound states in a hybrid device and the v = 5/2 state in a fractional quantum Hall system.
1 Introduction
Topological quantum computing aims to utilize non-Abelian anyons and their manipulation to realize qubit operations with the ultimate goal of fault-tolerant quantum computing. However, it has been shown that such states can be formed, detected, and manipulated theoretically. However, the experimental progress has been impeded by complications in the real materials, such as unwanted doping, random disorders, and inhomogeneous potential profiles Therefore, besides the existing semiconductor material-based platforms, topological materials have also been vastly investigated. The goal of this mini-review is to introduce various topological material systems as novel platforms for hosting non-Abelian states.
We will start with the one-dimensional platform as a basic model for realizing the topological states in combination with superconductivity. Then, we will extend the concepts to higher dimensions and various material platforms. It is useful to first introduce several theoretical concepts related to topological materials.
1.1 Quantum topology: a brief introduction
Different symmetries give rise to different types of topological materials. A practical way to identify the possible topological phases is to calculate the topological invariants. For the topological states concerning the
In general, one starts with an understanding of the Chern number, whose definition stems from the Berry phase in the momentum space. The Berry phase can, in general, be calculated on a parameter R(t) that changes very slowly along a closed path in the parameter space, where the quantum state of the system should be described by the time-dependent Schrödinger equation:
The wave function is then |Φ(t)⟩ = eiθ(t)|un(R(t))⟩. The phase θ(t) is expressed as follows (see also Shen (2012)):
The first term on the right-hand side is the dynamic phase, and the second term is the so-called Berry phase γc. The vector An(R) = i⟨n, R|∇R|n, R⟩ is called Berry connection or Berry vector potential because it is an analog to a vector potential in an electromagnetic field. If the change along a closed path is adiabatic, the wave function should have a gauge transformation |n, R⟩ = eiχ(R)|n, R⟩ and a phase difference γc = 2mπ, and the integer number m is the so-called Chern number. It is a topological invariant, i.e., independent of the details of the Hamiltonian.
Using Stoke’s theorem,
the Berry curvature from the Berry connection is defined as
Reverting to the momentum space in which we will define these quantities, based on Bloch’s theorem, a Bloch wave is the wave function of an electron in a periodic potential
where |un,k(r)⟩ is the cell-periodic eigenstate of
In the Brillouin zone, points k and k + K are the same, where K is the reciprocal lattice vector. So, the Berry phase across the Brillouin zone becomes
The aforementioned equation is easy to manipulate in a 1D system and is referred to as the Zak phase. One considers a typical two-band Hamiltonian written in the Dirac form as
where
One can further extend the concept of the winding number to more than one dimension, via the skyrmion number, and use the concept of Berry curvature to derive the expression for the Berry phase, intricately connected to the Hall conductivity via the Chern number. One can recast the expression for the Chern number and hence the Hall conductance in terms of the unit vector
The quantity inside the integrand is often referred to as a skyrmion number and is indeed a winding number that indicates the number of winding onto a sphere. In fact, quantum Hall conductivity is related to the Chern number C via TKNN relation (Thouless et al., 1982)
Here,
1.2 Anyons
The quantum statistics of identical particles are intrinsic to their mutual exchange. For example, with the exchange of two indistinguishable particles, the phase factor eiαπ is added to their composite wave functions.
Here, α is a statistical parameter. Furthermore, with the double exchange, both particles return to their initial states, i.e.,
Then, this implies that e2iαπ = 1 and the phase factor gain after a single exchange eiαπ = ±1. In general, this equation holds for the three-dimensional (3D) world, where +1 is for bosons and −1 is for fermions. More specifically in statistical parameter terms, α = 1 for fermions and α = 0 for bosons 1. However, this is not true for the two-dimensional (2D) world, where α ∈ [0, 1], and thus the fractional value of α gives rise to fractional statistics different from fermions and bosons (Leinaas and Myrheim, 1977; Wilczek, 1982) (Figure 1). These particles are called anyons (Wilczek, 1990). Similar to fermions, with the exchange of two anyons, the exchange phase απ is subsequently added, and with n exchange, the composite states wave function is
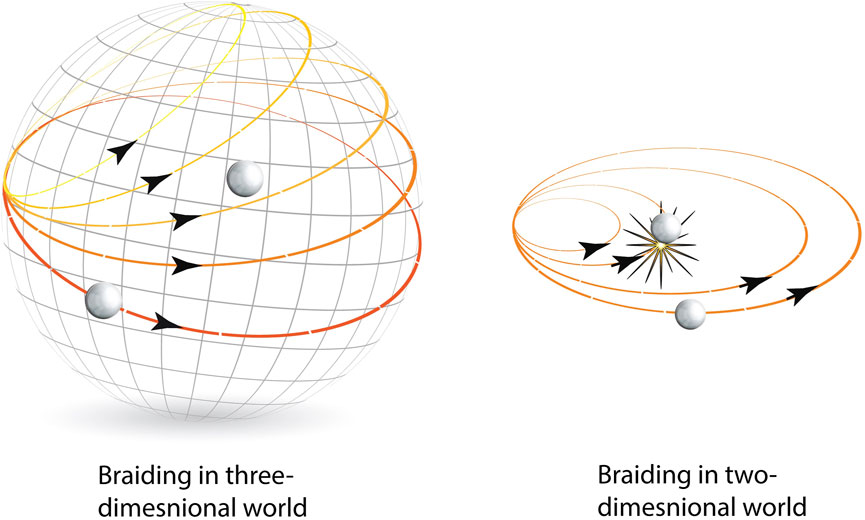
FIGURE 1. Braiding of two indistinguishable particles. The exchange of two particles is equivalent to braiding, i.e., circling one particle around another. As long as the path is continuous, all paths encircling another particle are equivalent. In a three-dimensional world, the paths can be continuously deformed to a point. This is equivalent to remaining stationary in time. All these paths result in the double exchange of the particles (see text for explanation a). However, in a two-dimensional plane, the continuous deformation of the path could not be employed. For a certain path, two particles will interact. In the case of fermions, the Pauli exclusion principle forbids such hard wall interactions, and thus braiding in 3D and 2D is not equivalent, giving birth to the third kind of particle, i.e., anyons. Adapted with permission from Najjar (2020).
Thus, with the double exchange unlike fermions, anyons with fractional values for statistical parameters will never return to the initial state. The number of times particles will exchange without crossing each other in a 2D plane defines the topological number of that particle. Thus, fractional statistics is the topological property of particles in the 2D plane. These are Abelian anyons.
The excitations in anyons are separated from the ground states by an energy gap. However, if the ground state carries the degeneracy, then it does not obey simpler Abelian braid statistics but rather non-Abelian braid statistics (Moore and Seiberg, 1988; Frölich and Gabbiani, 1990). The difference between the two braid statistics is found from the fusion rule they obey. Anyons are identified with the exchange statistics which depends on their topological order. For Abelian anyons, the fusion product is unique and defined as
where
1.3 FQHE anyons
The classical example of quantum particles in the three-dimensional world is electrons and photons belonging to the fermionic and bosonic groups. However, this is not true when they are confined in the 2D plane, and they may create emergent quasiparticle excitations upon perturbation. These quasiparticles may have anyonic quantum statistics. The FQH states are one such system where anyonic excitations with fractional electronic charge can be created. Halperin and subsequently by Arovas, Schrieffer, and Wilczek for the first time propose the existence of anyonic topological order in FQH states (Arovas et al., 1984; Halperin, 1984).
For the simpler Laughlin FQH states with the filling fraction ν = 1/m with the quantum of charge q = e/m, it will carry the phase π/m or simply πν.
The origin of the fractional statistics comes from the topological part of the Berry phase, which is proportional to the phase accumulated by the quasiparticle trajectory enclosing magnetic flux. When a quasihole moves in a closed loop, every quasiparticle it encircles will contribute a phase of 2πν. If it encircles only one quasiparticle, then the total phase will be 2πν. Here, since ν < 1, the gain in phase is an intermediate between 0 and π, thus making quasihole as anyons. The fractional charge and fractional statistics form two important constituents of anyonic excitations in FQH states. The fractional charge has been measured in several experiments (Goldman and Su, 1995; Saminadayar et al., 1997). However, fractional statistics remained elusive. The experimental approach to probe the fractional statistics was chosen to be interferometry, but so far results were always debated. However, Bartolomei et al. (2020) demonstrated fractional statistics in two-particle collider geometry. Simultaneously, in Fabry–Pérot interferometry, Nakamura et al. (2020) showed the anyonic phase in the interferometric signal. Both experiments were performed on the filling factor of ν = 1/3 having Abelian anyonic statistics. The non-Abelian quantum statistics are still abetting the experimental demonstration (Feldman and Halperin, 2021).
1.4 Majorana zero modes
A special group of non-Abelian anyons of great interest worldwide is the Majorana bound states, which inherently are tied to topological superconductivity. Unlike the free Majorana fermion, originally proposed by Ettore Majorana in 1937, the Majorana bound state (MBS), or the Majorana zero mode (MZM), is not a free fermion. The bound nature of such a state arises from being “connected” to the bulk as an edge mode of topological nature. Such modes can be exchanged using non-Abelian statistics and hence can potentially be braided as required in topological quantum computation. The edge modes are a simple consequence of the quantum topology of the band structure of topological superconductors. The basic minimal model for this was developed in the groundbreaking paper of Kitaev, in which a prototypical 1D p-wave superconductor serves a physical realization of the p-wave model (Kitaev, 2001).
The topological characterization of this model is quite straightforward (Leumer et al., 2020). We start with the calculation of the winding number from the energy–momentum (dispersion) relationship. The real space description of this “spinless” model typically seems like a linear chain with the p-wave pairing potential between nearest neighbors, as shown in Figure 2A. The special point t = Δ, where t is the hopping energy and Δ is the pairing potential, marks a special condition called the Kitaev point (Leumer et al., 2020). This gives rise to the disjointed Majorana modes at the ends of the chain, and when written based on Majorana modes, one can think of these end modes as a single fermion. A description of various critical cases in real space is depicted in Figure 2A.
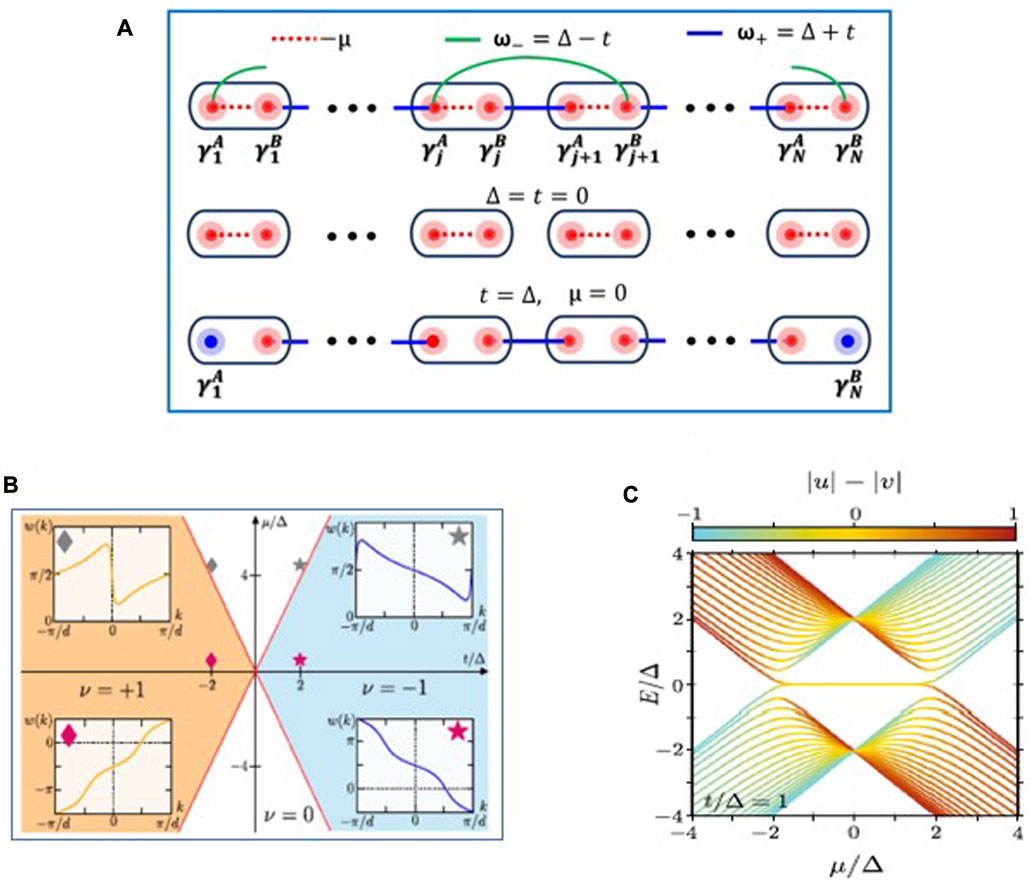
FIGURE 2. Edge modes and the topological phase space. (A) Simple description of the site basis of the Kitaev model for topological superconductivity. The special Kitaev point when t = Δ, for μ =0 corresponds to the case of disjoint Majorana edge modes at the ends of the chain. (B) Topological phase space with insets showing the azimuth function w(k). (C) Energy spectrum of the Kitaev point clearly showing the topological transition at μ =±2t. The plot also shows the color variation in |u|−|v|, which gives the difference between the electronic and the hole contribution of the excitation spectrum. Note that the zero energy mode has a precisely zero value for this quantity, indicating a neutral excitation. (B) Reproduced under CC-BY-4.0 from Leumer et al. (2020). (C) Reproduced with permission from Leumer et al. (2021).
However, the topological phase space is more complex and includes a parametric regime involving the chemical potential μ, the hopping t, and the pairing parameter Δ. This regime is depicted in Figure 2B, in which the area enclosed within |μ| = |2t| represents the topological phase space. It is important to note that this region gives a finite winding number when integrated over the Brillouin zone, as shown in the enclosed w(k) plots. Within this phase space, one is expected to observe the Majorana edge modes or the Majorana zero modes at zero energy, as shown in the energy spectrum of the Kitaev point in Figure 2C. The plot also shows the color variation in |u| − |v|, which gives the difference between the electronic and the hole contribution of the excitation spectrum. Note that the zero energy mode has a precisely zero value for this quantity, indicating a neutral excitation. This summarizes the appearance of MZMs within this simple model.
Of course, this model can be realized on a realistic s-wave system by introducing two important ingredients: the Rashba spin–orbit coupling and a Zeeman field (Lutchyn et al., 2010). As explained in many excellent overviews, this combination introduces the helical states and mimics a “spinless” model above a critical Zeeman field. This model, as it turns out, can be realized in superconducting hybrid systems featuring a Rashba nanowire with proximatized superconductivity and an externally applied Zeeman field. Here, the detection of the MZMs in this setup will involve transport experiments in the form of conductance spectroscopy which will be discussed in the following section.
2 Hybrid quantum platforms for anyonic states
In order to construct, detect, and manipulate the desired non-Abelian states, we need to combine the properties from different materials and enable electronic transport. Therefore, it is efficient to design and realize hybrid quantum devices. Here, we will first discuss the one-dimensional semiconductor nanowire-based hybrid devices based on Andreev reflection.
2.1 1D Rashba nanowire-superconducting hybrid systems
The Kitaev model provides a basic backbone for the understanding of topological superconductivity and how MZMs occur at the edges of such a chain. An early proposal for the realization of the same featured the material combination of Rashba spin–orbit coupling in a 1D wire coupled with an axial Zeeman field (Lutchyn et al., 2010) over which s-wave superconductivity is induced. Hence, these quasi 1D Rashba nanowire-superconductor hybrids (Alicea, 2010; Lutchyn et al., 2010) are currently leading candidates for the detection and manipulation of MZMs (Kitaev, 2001). The past few years have witnessed tremendous experimental advancements (Mourik et al., 2012; Deng et al., 2016; Nichele et al., 2017; Gül et al., 2018; Zhang et al., 2021) aimed at the ascertained detection of MZMs. Before graduating toward the actual manipulation or harnessing of MZMs (Zhang et al., 2019; Prada et al., 2020), many unresolved aspects exist that include the possibility of a non-topological origin of the zero-bias conductance as well as understanding the role of interactions within the topological superconductor channel (Stanescu and Tewari, 2013; Liu et al., 2017a; Moore et al., 2018a; Moore et al., 2018b; Deng et al., 2018; Liu et al., 2018; Chiu and Das Sarma, 2019; Vuik et al., 2019; Pan and Sarma, 2020). Before we discuss the Rashba nanowire model and how this emulates the Kitaev chain, let us review the basic ingredients of how conductance measurements are currently used to detect the MZMs.
The primary method for detecting MZMs is via conductance measurements, with the zero-bias conductance quantization as a possible telltale signature. The zero-bias conductance peak (ZBCP) of measure 2e2/h arising out of a coherent and perfect Andreev reflection (Prada et al., 2020) is regarded as a strong signature of the MZM. This signature is expected from a local conductance measurement in a normal–topological superconductor (N–TS) link (Zhang et al., 2018; Zhang et al., 2019; Prada et al., 2020; Zhang et al., 2021). The so-called telltale signature was that the local conductance measured at one end of the device would equal the conductance quantum that arises from a perfect Andreev reflection. Before moving on to describe the hybrid system, we will now review the bare minimum theoretical concepts related to the current experimental scenario.
2.1.1 Andreev processes
We need to clarify the meaning of “proximity inducing” clearly here. There are many subtleties involved in the process of “induced superconductivity,” many of which have been discussed in detail in the classic works of de Gennes. It is possible that the induced superconductivity that is measured via spectroscopy is basically an induced gap inside the normal region, which, for practical purposes, acts as the gap that we concern ourselves with for the rest of the discussion. This implies that Δ = Δind, which is different from the gap of the parent superconductor. A detailed understanding of the induced gap in these systems is still lacking but can be microscopically understood via local Andreev reflection processes.
Let us make a quick understanding of the Andreev phenomena. There are excellent references for this including classic textbooks (de Gennes, 1999), but here we provide a brief synopsis.
Quasiparticles in systems comprising of inhomogeneous superconductors and related hybrid junctions like the ones we consider here with other kinds of conductors are described by the stationary states of the Bogoliubov–de Gennes (BdG) equation (Datta and Bagwell, 1999; de Gennes, 1999) given by
where H is the one-electron Hamiltonian, which represents the channel without superconducting interactions, with the electrochemical potential μ, with the electrostatic potential U and the pairing potential Δ evaluated via a mean-field technique such as the self-consistent field method. Figures 3A,B pictorially depict the transformation in momentum space. We are normally used to looking at two bands for up-spin and down-spin that are filled up to the Fermi energy or electrochemical potential μ in a metallic system. In order to explain the pairing, one performs a clever trick, i.e., flips the down-spin band to effectively make it a “hole” band and retains the electronic status for the up-spins. Under this transformation, in the absence of the superconducting pairing Δ, the bands of the up-spin electrons and flipped down-spin holes pictorially look like the depiction in Figure 3B.
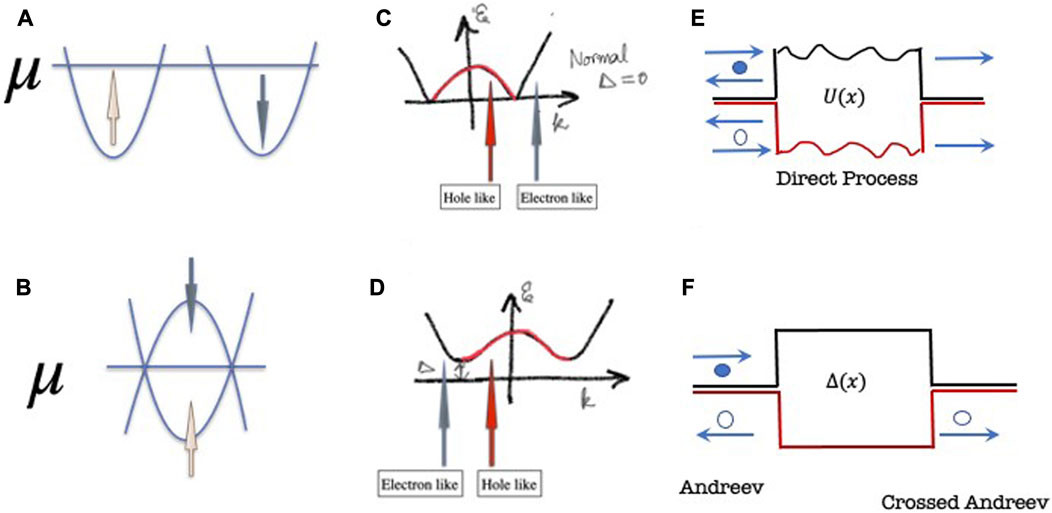
FIGURE 3. Understanding of the superconductor–semiconductor hybrid systems. (A) Schematic of typical metallic bands represented by the up-spin and down-spin states filled up to the electrochemical potential μ. (B) Same under the BdG transformation, where the down-spin band is flipped to form a hole-like band. (C) BdG spectrum in the excitation picture of a normal metal state. (D) Excitation picture of a superconducting state where the pairing potential introduces the gap Δ. (E) Example of the spatial variation of the electrostatic potential U. This accounts for the direct reflection/transmission processes. (F) Schematic of a spatial variation in the pairing potential Δ. This variation is responsible for Andreev processes which include the local Andreev reflection and the crossed Andreev reflection. In (C) and (D), we assume incidence from the left side.
One often represents this using the so-called “excitation picture” taking only one-half of the spectrum given that the (15) possesses electron–hole symmetry. In this picture, in the absence of pairing, the ungapped metallic spectrum looks like what is shown in Figure 3B. When pairing is introduced via superconducting interactions via the term Δ, a gap opens here and the excitation spectrum now can be broadly schematized as shown in Figure 3 (d). With the introduction of the superconducting pairing Δ, the eigenstates of the BdG Hamiltonian in (15) can be represented as a superposition of electron-like states and hole-like states with coefficients u and v from (15). In other words, quasiparticle excitations that are eigenstates of (15) can be represented as, for instance,
Two kinds of potentials are evident from the BdG equation in (15). First is the regular electrostatic potential, which, in real space, would translate to barriers and inhomogeneities within the material stack, as schematically shown in Figure 3E. These barriers give rise to what we term the direct reflection processes and refer to the standard reflection and transmission in heterostructures or tunnel barriers that one encounters in standard quantum mechanics. The position dependence U(x) is often referred to as the “band diagram” in device physics and refers to the spatial variation at the bottom (top) of the conduction (valence) band, within the structure. Since we also have the hole block in the lower block of the Hamiltonian in (15), Figure 3E also depicts the mirror reflection of the potential and the reflection process schematic.
The second type of potential is the pairing term Δ, whose spatial dependence comes as an off-diagonal component in (15), and this gives rise to the Andreev processes. This off-diagonal contribution is a bit non-trivial to plot in real space, but one can, just like how we describe the band-diagram U, use the minimum of the excitation spectrum shown in Figure 3D, to map out a spatial variation of Δ, a simple schematic of which is shown in Figure 3F. This term mathematically couples the electron and hole blocks, and, consequently, any reflection process that involves the spatial variation of Δ will mix electrons and holes. This is roughly speaking the Andreev process. Let us now turn our attention to Figure 3F, in which we schematize a typical spatial profile where a superconducting region of finite Δ is sandwiched between two normal regions with Δ = 0. Here, an incident electron from the normal region gets partially reflected as an electron and partially as a hole. Not only this, but as the particles exit the superconductor on the other side, a similar process happens where a partial transmission happens as a hole. The latter process is called the crossed Andreev reflection (CAR) and will prove to be a crucial ingredient in the topological gap protocol (Pikulin et al., 2021; Aghaee et al., 2022), which will be used to detect the non-locality of true MZMs. One can also use these processes to microscopically understand induced superconductivity. Due to the presence of Andreev reflection, the semiconducting section achieves a gap that resembles a superconducting gap. However, this gap is not the standard “forbidden energy” gap associated with a periodic system but simply the fact that Andreev reflection “depletes” the semiconductor of its states that lie within the parent superconductor’s gap.
It is worth remarking at this stage that all this has led to a side-by-side strong theoretical push (Stanescu and Tewari, 2013; Liu et al., 2017a; Moore et al., 2018a; Moore et al., 2018b; Deng et al., 2018; Liu et al., 2018; Chiu and Das Sarma, 2019; Vuik et al., 2019; Pan and Sarma, 2020), where a lot of focus has been on resolving the issue of the origins of the observed ZBCP. In parallel, there is also a strong need to push for theoretical works that go beyond minimal 1D models in order to include multi-mode effects (Lahiri et al., 2018; Sriram et al., 2019; Prada et al., 2020), realistic potentials (Vuik et al., 2016; Domínguez et al., 2017; Antipov et al., 2018; Mikkelsen et al., 2018; Pan et al., 2019; Winkler et al., 2019), the inclusion of disorder (Moore et al., 2018b; Deng et al., 2018; Chiu and Das Sarma, 2019; Pan and Sarma, 2020), and also scattering and relaxation effects (Liu et al., 2017b).
2.1.2 Conductance spectroscopy in Rashba nanowire hybrid setups: the topological gap protocol
Let us now discuss conductance spectroscopy in detail. The MZMs form edge states as dictated by the bulk boundary correspondence of a one-dimensional (1D) topological superconductor phase. This phase is realizable using a quasi-1D system, the semiconducting Rashba nanowire, in which a topological phase transition could be introduced via the application of a magnetic field on a Rashba nanowire coupled to a “proximity-inducing” superconductor (Lutchyn et al., 2010).
The Rashba nanowire with Zeeman splitting is a prerequisite for achieving topological superconductivity and hence the presence of MZMs. This is well explained in several references (Lutchyn et al., 2010), which we succinctly detail now. As detailed in many reviews (Cayao, 2017), in order to mimic the Kitaev-style p-wave superconductivity using induced s-wave superconductivity and hence an existing spin-texture, one has to first obtain an effective p-wave interaction. This can be performed by exploiting the spin texture that comes via the combination of Rashba interaction and the Zeeman field, as succinctly depicted in Figure 4A. The bands shown here are a result of the displaced up-spin and down-spin bands due to the Rashba interaction followed by the Zeeman interaction. Following a critical field VZ > Vc, one has a single effective spin-band at the Fermi energy and an odd number of pairs of points crossing the Fermi energy (Cayao, 2017). This also corresponds to the Majorana number index being equal to unity. A schematic depiction of a ground-state setup with an impression of the fermionic mode corresponding to the two Majoranas at the edges is shown in Figure 4 (b).
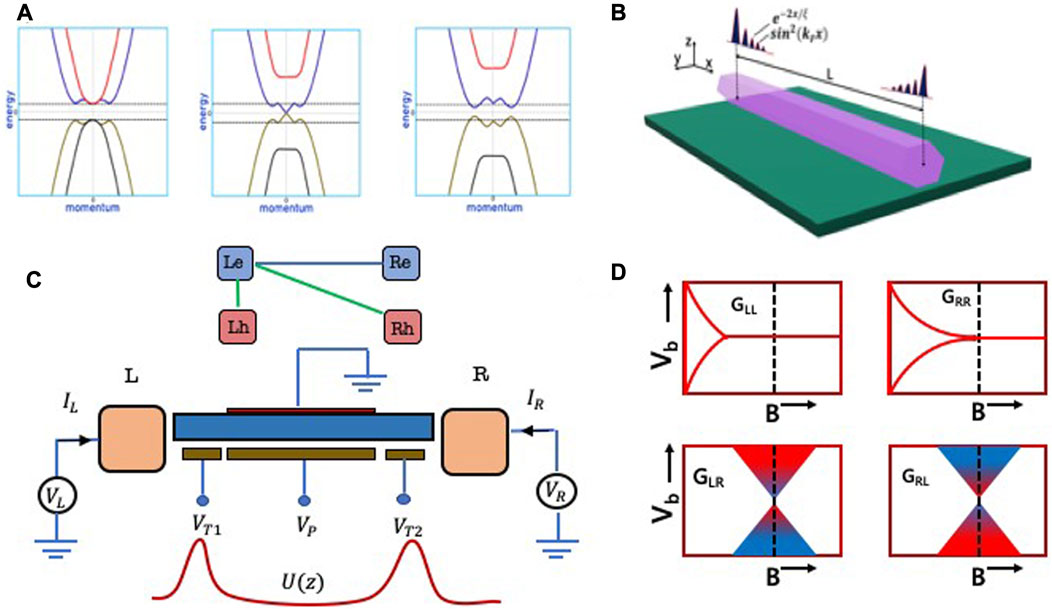
FIGURE 4. Rashba hybrid system and transport spectroscopy setup for MZM detection. (A) Schematic band structures of the Rashba nanowire with a Zeeman energy VZ. This combination creates the desired spin texture to induce a p-wave-like pairing using the s-wave-induced superconductivity. Above a critical field, one can achieve a topological phase transition. (B) A typical MZM appears as localized edge states as a result of proximity-induced superconductivity on a Rashba nanowire. A topological transition is induced via an axial magnetic field. These edge states can be detected via transport spectroscopy in which a set of conductance measurements can ascertain the MZM presence. (C) Schematic of a current setup that probes the conductance matrix, which includes the local conductance and non-local conductance (upper panel) The local conductance and non-local conductance depend on three processes: direct transmission, the local Andreev reflection, and the crossed Andreev reflection. (D) Typical schematic plot showing the topological gap protocol that uses the local and non-local spectra to gauge the presence of MZMs.
Until recently, the primary method for detecting MZMs was via a local conductance measurement, with the zero-bias conductance quantization as a possible telltale signature. The zero-bias conductance peak (ZBCP) of measure 2e2/h arising out of a coherent and perfect Andreev reflection (Prada et al., 2020) is expected from a local conductance measurement in a normal–topological superconductor (N–TS) link (Zhang et al., 2018; Zhang et al., 2019; Prada et al., 2020; Zhang et al., 2021). The so-called telltale signature so far was that the local conductance measured at one end of the device would equal the conductance quantum that arises from a perfect Andreev reflection. However, as we shall briefly detail, such signatures may be easily reproduced as false positives via close to zero sub-gap states arising from disorder. Probing true Majoranas will therefore require exploiting their non-local features (see the schematic in Figure 4A).
Following a theoretical proposal (Rosdahl et al., 2018), in recent times, there has also been a keen interest in pursuing transport measurements across a three-terminal normal–topological superconductor–normal (N–TS–N) configuration (Ménard et al., 2020; Puglia et al., 2021), where non-local conductance signatures (Rosdahl et al., 2018) could augment the certainty of MZM detection. These ideas have further been recently cemented via the proposal for the topological gap protocol (Pikulin et al., 2021), which has recently been quantified experimentally in InAs–Al hybrid setups (Aghaee et al., 2022). A typical transport spectroscopy setup that is used to realize this is schematized in Figure 4B. The Rashba nanowire is depicted in dark blue and is coated with a parent superconductor shown in red, which induces a superconducting gap inside the nanowire. This setup has three gates, one plunger gate VP and two tunnel gates VT1 and VT2, on the two sides. The plunger gate controls the overall chemical potential μ of the setup, and the tunnel gates modulate the coupling to the two normal contacts L and R. A sample of the electrostatic potential profile is schematized in the lower panel of Figure 4B. Using operational amplifiers (not shown here), voltages VL and VR can be applied to either terminal and currents IL or IR which can be separately measured. With this setup, it is possible to define the conductance matrix as follows:
A theoretical understanding of the aforementioned necessitates an evaluation of the terminal currents. We can derive the terminal currents using the Keldysh current operator (Datta, 1997). For instance, the terminal electronic current at the left contact can be derived in the Landauer–Büttiker form as
where
where the last term
from which we note that the non-local conductance can also be negative (Rosdahl et al., 2018). This is an important aspect of the topological gap protocol.
The topological gap protocol is summarized via sample plots taken from Pikulin et al. (2021) and Aghaee et al. (2022) in Figure 4D. The latest consensus is that a combination of the local and the non-local conductance traces will form the experimental test for the presence of MZMs. We may recall, as shown in Figure 4B, that local potential variations, both the smooth part that is induced via gates VP, VT1, and VT2, and the irregular variations induced via impurities, can induce close to zero energy sub-gap states. These can indeed mimic the local measurements, and hence one must measure both GLL and GRR at the two ends. A conductance gap closure in both GLL and GRR as shown in the upper panel of Figure 4D sets the first stage. This at least implies the presence of edge states. However, the edge states may also be uncorrelated.
For this, we turn to the non-local conductance spectra, which can be measured by applying a voltage across a terminal and measuring currents across the other. We note from (19) that the expression for the non-local conductance indeed has an attached relative negative sign between the direct and the crossed-Andreev components. Most importantly, it does not have the local Andreev component, implying that at zero bias, in the presence of a true MZM, the non-local conductance vanishes. This also implies that the non-local conductance changes its sign at this crossing point. By comparing the upper and lower panel of Figure 4D, we notice that the gap closure of the non-local spectrum is quite different from the local conductance spectrum. The gap of the local conductance spectrum typically closes when the zero energy modes form, due to either the presence of localized impurities or the actual topological transition. The zero-bias conductance line then appears through the extent of the topological phase. However, the non-local conductance, on the other hand, must show a gap closing and re-opening. This is because the non-local conductance does not have the local Andreev component and remains identically zero around where zero-bias conductance manifests. However, there may be other effects near zero bias for finite lengths due to the parity crossings as discussed in recent theoretical works.
It is worth mentioning that the requirement on strong Rashba interaction and the well-aligned Zeeman field places many restrictions on the setup given the necessity for scalable architecture in the future. In this regard, recent proposals include new geometries with the addition of a magnetic insulator, which can, in effect, minimize the Zeeman field requirement. Recent works in this direction have proposed several structural optimizations (Khindanov et al., 2021; Liu et al., 2021; Maiani et al., 2021; Escribano et al., 2022) and quantum transport calculations (Singh and Muralidharan, 2023) along with the experimental ascertaining (Liu et al., 2020; Vaitiekėnas et al., 2021) of achieving topological superconductivity at minuscule Zeeman fields.
Having discussed the aforementioned works, we summarize this section with the following quick takeaway message. The evolving search for MZMs in quasi-1D systems has indeed currently culminated with a systematic protocol based on a thorough investigation of the local and non-local conductance, thereby leading to a possible sighting of true MZMs via this method. It must be remarked that other methods should indeed be devised in addition to the regular conductance spectroscopy to augment these protocol-based examinations. In a later part of this review, we will also cover the Josephson effect-based detection of MZMs, which are also being investigated in this platform.
2.2 Non-abelian anyons in fractional quantum Hall states and designer 2D platform
The excitation in FQH states carries fractional quantum statistics, either with Abelian or non-Abelian topological order. The wave function of Abelian anyons may acquire an arbitrary phase after moving one quasiparticle around another on the plane. Even more remarkable, the exchange of non-Abelian anyons will not only alter the phase of their wave functions but also change the ground state of the whole system. This unique property of non-Abelian anyons might offer a possible route for designing quantum devices with topological protection against decoherence (Nayak et al., 2008). There are quite a few material platforms hosting non-Abelian states. Here, we will limit the discussion to the quantum Hall platform.
2.2.1 Majorana edge modes
Like other quantum Hall and fractional states, the charges in ν = 5/2 are carried by the edge modes. Here, the two chiral edge modes carrying one electron each contribute to a quantum conductance of σxy = 2e2/h, and co-propagating bosonic charge modes contribute to σxy = e2/2h. However, the presence of the Majorana modes complicates the edge structure, resulting in several possible degenerate ground states (Kitaev, 2006; Ma and Feldman, 2019). These chiral Majorana edge modes are charge-neutral and thus do not contribute to the total quantum of conductance. However, they carry half quanta of heat (Kane and Fisher, 1997). The three well-studied topological states of ν = 5/2 are shown in Figure 5. Pfaffian states have a single co-propagating Majorana neutral mode, while the anti-Pfaffian mode has three counter-propagating chiral modes. The chirality and number of Majorana modes are shown in Table 1.
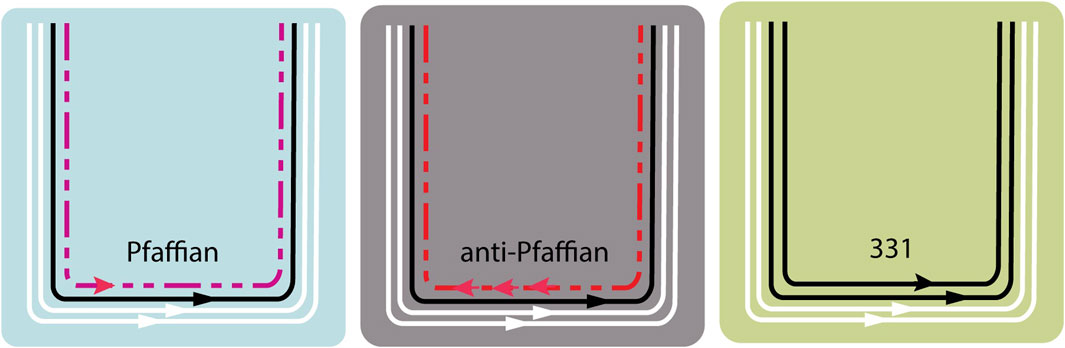
FIGURE 5. Edge structure for proposed ν =5/2 states—electron edge mode with charge q =1 (white), charge mode carrying charge of q =1/2 (black), and charge neutral Majorana modes (red dash line). The Pfaffian and anti-Pfaffian are non-Abelian states differing in the number of Majorana modes, and 331 is an Abelian state with no Majorana modes present. Adapted with permission from Mross et al. (2018).
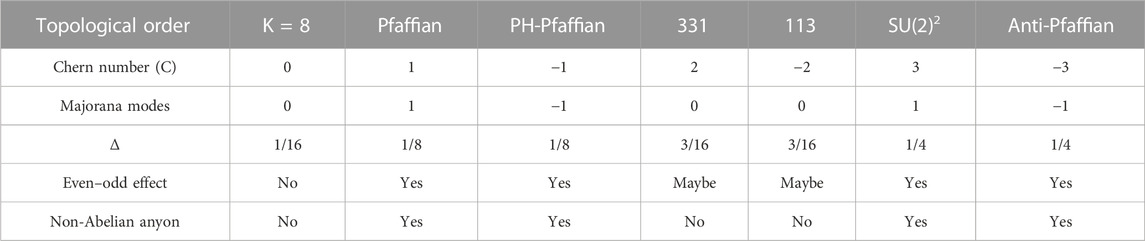
TABLE 1. Most interesting topological ground states of ν =5/2. The second row shows the Chern number of the edge. The negative Chern number (C) is due to the presence of upstream neutral modes. The third row depicts the unpaired Chiral Majorana edge modes. Note that a pair of Majorana could combine to form the Bose mode. In the absence of unpaired Majorana modes, the topological order of spin-polarized ν =5/2 is Abelian. The third row shows the expected scaling dimension Δ for the fundamental quasiparticle of charge q = e/4. The scaling dimension is related to the tunneling coefficient by gT =2Δ. The fourth row shows the expected results of the even–odd effect in Fabry–Pérot interferometry. All non-Abelian topological orders are expected to show odd–even effects. However, apart from K =8, both 331 and 113 may show similar odd–even effects if they possess flavor symmetry.
2.2.2 Brief introduction to the filling factor = 5/2
The even-denominator FQH state, observed in several high-quality 2-DEG may host non-Abelian anyons (Lin et al., 2008). The half-filled states (ν = 1/2) in the N = 0 Landau level are quasiparticle excitations called composite fermions. These are quasiparticles of electrons bounded with an even number of flux quanta. At ν = 1/2, they behave like weakly interacting particles, almost like electrons at the zero magnetic fields (Jain, 2015; Laitinen et al., 2018). Unlike ν = 1/2, the even-denominator FQH states formed at higher Landau levels (N > 0) are topologically distinct. Among these even-denominator FQH states, the ν = 5/2 FQH state is the most acknowledged state. Since its first observation by Willett et al. (1987), the identity ν = 5/2 has been under intense theoretical and experimental debate.
The most viable explanation of ν = 5/2 is Moore–Read states, a Px + iPy spin-triplet superconducting state of the composite fermions (Willett et al., 1991; Read and Green, 2000). The Moore–Read states have Pfaffian wave function. Other competing descriptions of the ground state of ν = 5/2 include hole conjugate anti-Pfaffian (Lee et al., 2007), particle–hole symmetric Pfaffian (Levin et al., 2007), the alternating stripe of Pfaffian and anti-Pfaffian (Mross et al., 2018), and Abelian 331 (Yang and Feldman, 2013), summing up a total topological order state to 16. Thus, the ν = 5/2 state belongs to topological states of 16-fold way (Ma and Feldman, 2019). Based on Kitaev’s classification, the order states with even Chern numbers will have Abelian topological order and states with odd Chern numbers will have non-Abelian topological order (Kitaev, 2006). Thus, there are eight non-Abelian and eight Abelian topological states. The seven lowest Chern number topological states of ν = 5/2 are listed in Table 1:
The key experimental approaches include the spin-polarization measurement in the tilted magnetic field (Eisenstein et al., 1988; Stern et al., 2010), tunneling experiment for interaction parameters “g” (Radu et al., 2008; Fu et al., 2016), scattering (Dolev et al., 2008; Venkatachalam et al., 2011), and interferometry experiment (Willett et al., 2009; Willett et al., 2010; Willett et al., 2013; Willett et al., 2019) for the charge and quantum statistics detection of the quasiparticles. All the experimental results confide more to the non-Abelian nature of ν = 5/2, but the results are still inconclusive. The thermal quantum Hall measurement is another probe that measures the quanta of heat carried by the topological edges (Banerjee et al., 2018; Dutta et al., 2022). Each chiral edge carries a single quantum of heat, while a Majorana chiral edge carries half quanta of heat; thus, the signature of fractional thermal quanta indicates the presence of Majorana states. In the thermal quantum Hall experiment (Banerjee et al., 2018), the observation of the fractional thermal conductance quanta kxy ≈ 5/2 is intriguing, not fully consistent with either the Pfaffian or anti-Pfaffian order, and may indicate the role of disorder in the stabilization of the ν = 5/2 state (Mross et al., 2018; Wang et al., 2018). The experimental determination of the ν = 5/2 ground state requires more effort (Dutta et al., 2022). Until now, the smoking gun signature for non-Abelian states is missing.
In this review, we will limit the discussion to electronic charge transport. The device schematics of three key experimental approaches for detecting quantum statistics and the charge of quasiparticles covered in this review are shown in Figure 6.
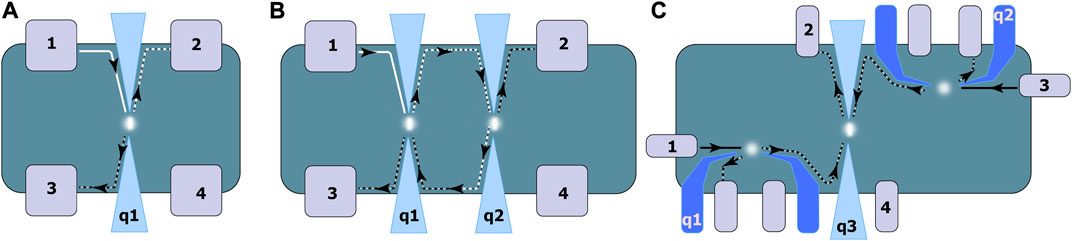
FIGURE 6. Tunneling probes for non-Abelian anyons. (A) Single QPC geometry where tunneling between the two counter-propagating edge states is initiated at the QPC (q1). The measure of the tunneling resistance with respect to DC bias current and temperature gives the measure of the interaction parameter gT. Note that the same geometry could be used to measure the fractional charge of the quasiparticle via shot noise in a weak backscattering current limit. (B) Interferometer device with a Fabry–Pérot cavity is defined by two QPCs. The phase-coherent transport across the Fabry–Pérot cavity is measured with respect to the change in the number of quasiparticles in the cavity. This is achieved via sweeping the magnetic field. The closed loop path defined by the two QPCs enclosed the Aharonov–Bohm fluxes which carry the signature of both quasiparticle charge and braiding statistics. (C) Two particle interferometer geometry with three quantum point contacts: q1, q2, and q3. The input QPCs q1 and q2 create quasiparticles at the two counter-propagating edges. At the QPC q3, they collide, and collision output is measured via the cross-correlation technique at ohmic contacts 2 and 4. The two-particle interference at the QPC q3 carries the signature of the quantum statistics.
Tunneling experiment: The random partitioning of the current is related to the charge of the quasiparticle excitations and interaction parameter “gT.” The tunneling experiment provides excellent settings to probe them in the FQH environment. This could be set up in the single QPC geometry, shown in Figure 6 (a). At the QPC, two counter-propagating edges are close enough to interact. In the weak backscattering limit, FQH edges interact weakly, leading to the tunneling of a small fraction of edge current from one edge to other. Based on Wen’s model, the interaction between weakly coupled fractional quantum Hall liquids leads to power law-dependent tunneling conductance with respect to. temperature:
However, due to dissipation at the edges, inter-edge long-range interaction and edge reconstruction lead to renormalization of gT (Chang, 2003). Thus, so far, the identification of the topological order via interaction parameter lacks an experimental basis. It has been proposed to probe the scaling dimension via shot noise (Snizhko and Cheianov, 2015). The noise generated at the QPC carries the signature of the charge of the quasiparticle and the scaling dimension. For a typical experimental relevant regime of T ≫ kBT,
In the shot noise experiments, the quasiparticle charge was found to be e/4 but is not sufficient proof for ν = 5/2 being non-Abelian (Dolev et al., 2008; Dolev et al., 2010). Resolving the scaling dimension in such measurements requires high-quality experimental accuracy. However, the recent proposal highlights the significance of the scaling dimension in shot noise measurement, where the temperature instead of biasing voltage is a control knob. The case of the two counter-propagating edges at different temperatures may give rise to intriguing phenomena of negative excess noise, also dubbed as negative delta-T noise (Rech et al., 2020). Here, the scaling dimension alone determines the negative Fano factor. However, the scaling dimension is not universal as it is thought to be. It is easily perturbed via a non-equilibrium process, like the presence of counter-propagating neutral edge modes in FQH states with complex edge structures, which will lead to the renormalization of the scaling dimension. Nevertheless, the Fano factor in the tunneling experiment could be pivotal in identifying the topological order of the FQH states.
Fabry–Pérot interferometer: The quantum statistics of the particle are defined in terms of a phase factor accumulated by the particle when they have looped around another or the position of the two particles is exchanged (Figure 6B). The simplest and ideal experimental platform for probing quantum statistics would be a confined geometry where one could employ the chiral edge property of edge states to encircle the particles in the bulk. Furthermore, the Fabry–Pérot interferometer is such geometry where at quantum point contacts (QPCs), the counter-propagating edge states interact.
In the weak interaction regime, tunneling processes are dominated by quasiparticles (Dolev et al., 2010). In the phase-coherent limit, the interaction between the two paths, the back-reflected signal and loop path, across the interferometer will give an interference signal which is sensitive to the Aharonov–Bohm (AB) phase and the statistical phase (Halperin et al., 2011; Rosenow and Stern, 2020). θ ∼θAB + ϕs, where θAB = qAB/eϕ0 is the Aharonov–Bohm phase which is sensitive to the charge q of quasiparticle (Goldman and Su, 1995; Willett et al., 2009). ϕs is the statistical phase gained by the quasiparticle looping around the quasiparticle in the bulk of the interferometer of area A. The change in magnetic flux through the interferometer by a single flux quantum ϕ0 = h/e leads to the addition or removal of a single quasiparticle from the bulk. This results in a jump in phase defined by ϕs. The experimental signature of this phase shift is the key signature of the statistical phase of the anyons (Rosenow and Stern, 2020).
Furthermore, in the non-Abelian case, the Aharonov–Bohm phase is influenced by the “even–odd effect” (Das Sarma et al., 2005; Bonderson et al., 2006a; Stern and Halperin, 2006). The even–odd effect is related to the parity of the number of quasiparticles in the interferometer. Specifically for ν = 5/2, an odd number of the quasiparticles in the interferometer will give 2ϕ0 periodicity in the magnetic field contrary to the 4ϕ0 periodicity for an even number of particles. In addition, the statistical phase of the quasiparticle will depend on the topological order of the quasiparticle; for example, for the Pfaffian state (particle–hole symmetric anti-Pfaffian state) with fixed fermion parity, ϕs = 1ϕ0(ϕs = 1.5ϕ0) and for the state without fixed fermion parity, ϕs = 2ϕ0(ϕs = 3ϕ0) (von Keyserlingk et al., 2015).
The Fabry–Pérot interferometer could probe the charge of the quasiparticle excitations and their quantum statistics. It looks simpler, but device fabrication is more complicated due to its conflicting design constraint of weak Coulomb blockade and phase coherency. In the recent design, the GaAs/AlGaAs 2-DEG is epitaxially grown in between two auxiliary metallic layers. The screening layers drastically reduced the Coulomb charging energy and suppressed the bulk–edge interaction, allowing for an Aharonov–Bohm physics-dominated interference pattern in gate vs. magnetic field sweep. The jumps in the interference pattern are seen at Δθ ∼ 0.3 × 2π, which is closer to the theoretical value of π/3 for fractional quantum Hall states ν = 1/3 (Nakamura et al., 2020).
Similar phase jumps may result due to the interaction of quasiparticles localized at the impurity sites close to the physical edge of the interferometer. However, these random interactions will unlikely give phase jumps closer to the expected value of statistical phase jumps. More experimental signatures are needed to exclude these effects, and, above all, the probe for the quantum statistics of other fractional states (ν = 1/5, 2/5) will provide a better understanding of the quantum statistics of anyons. A similar geometry designed for non-Abelian anyons of ν = 5/2 might resolve the odd–even effect.
Two-particle interferometer: The quantum statistics of the particle can also be determined in the two-particle interferometer. In analogy to quantum optics, if the two-quantum particle collides at a beam splitter, the outcome of the collision depends on the exclusion statistics of the colliding particles. For example, in the case of bosonic particle-like photons, the photons will bunch together, while in the case of electrons that obey Fermi statistics, the electrons tend to be anti-bunch. This behavior could be observed in fluctuation measurement. In the case of electronic excitations, the Pauli exclusion principle enforces the single occupancy of quantum states in the outgoing beam, resulting in negligible fluctuations in cross-correlation measurement due to sequential tunneling of the electrons in output beams.
On the other hand, fractional excitations, which obey intermediary statistics to fermions and bosons, will obey lesser exclusion and thus cause randomness in the occupancy of quantum states in outgoing beams. This results in finite fluctuations in correlation measurement. The statistical signature in the cross-correlation is revealed by the power law decay of the wave function at the edges, which, in fact, measures the spatial correlation at the beam splitter. Although the measurement of exclusion statistics is an indirect measurement of quantum statistics, it is also related to the braiding of quantum particles in the bulk (Rosenow et al., 2016). This scheme was successfully implemented for the identification of Abelian anyonic statistics of fractional excitations carrying charge q = e/3 (Bartolomei et al., 2020).
However, the presence of more than one edge channel complicates the physics involved in the collision experiment. The ν = 2/5 states have two edge states with inner and outer edges carrying fractional charges of q = 1/3 and q = e/5, respectively. The collision experiment performed on the inner edge channel of ν = 2/5 carrying q = e/3 charge shows similar evolution in the exclusion statistics to that in ν = 1/3. On the other hand, partitioning of the outer edge channel, which carries the fractional charge of q = e/5, has shown a reduction of spatial exclusion as expected for anyons but with a lesser agreement with the theory. This deviation may arise due to interactions between co-propagating edges (Ruelle et al., 2023).
Recently, the Andreev correlation between the transmitted quasiparticle and quasihole at the QPC has been proposed (Glidic et al., 2023). For example, in the string backscattering regime, the impinging of quasiparticle of charge q = e/3 at QPC will create the reflected hole of q = −2e/3. This Andreev-like process involving both transmitted quasiparticle and quasihole could result in the double exchange at the QPC and thus reveal the exchange statistics. In a recent experiment with two-QPC geometry, the exchange statistics for ν = 1/3 are probed (Hong et al., 2022). However, a time-domain experiment on anyons where the time delay between the anyons impinging at the QPC could be varied will give a better picture of the double-exchange processes (Jonckheere et al., 2022). Furthermore, a similar experimental setup can be used for revealing non-topological order states of ν = 5/2 (Lee and Sim, 2022).
Moreover, there is a more involved geometry with a hole in bulk is the Mach–Zehnder interferometer. In this type of device, the presence of the metallic contact (drain) in the bulk of the FQH liquid usually suppresses the Coulomb-dominated physics. Here, the Aharonov–Bohm physics is independent of the number of quasiparticles in the bulk, making it an attractive alternative to the Fabry–Pérot interferometer. However, the larger size of the interferometer, the equilibration process due to the presence of non-topological neutral modes, and inferior interior drain contacts make the interference of the fractional charges less visible. In the recent experiment, the flux periodicity of ϕs = ϕ0 for both integer and fractional states is observed. This is also consistent with Kundu et al. (2022). However, the true significance of the quantum statistics should be seen from the power law behavior of flux-dependent tunneling current which has a topological origin. However, this has not been reported yet.
There are other fractional states with non-Abelian topological order. For example, ν = 7/2 is expected to have hole-conjugate non-Abelian topological order of ν = 5/2. Additionally, FQH states ν = 12/5 and 19/8 are predicted to have non-Abelian topological order and only observed in very high-quality samples (Eisenstein et al., 2002; Bonderson et al., 2006b; Pan et al., 2008). In higher Landau levels, the charge density waves in the form of stripe and bubble phases compete with FQH states. In the GaAs/AlGaAs heterostructure, the Landau level and the fractional quantum Hall states are no longer favored (Gervais et al., 2004). However, in graphene due to the spinor nature of Landau levels, the formation of the FQH state is more favorable. In the recent experiment, the even denominator fractional states are observed (Kim et al., 2019). Still, a detailed study on the ground state of these states is missing. Moreover, a study of these states in QPC-confined geometry will be required for further controlled manipulation of these states.
2.2.3 Designer non-Abelian states: parafermions
The non-Abelian excitation’s topological degeneracy of their ground state makes them stand out from other conventional abelian excitations. These degenerate ground states could also be engineered within conventional systems by fabricating defects with fractional topological-ordered phases. The non-Abelian defects are zero energy modes arising from two different gapping processes at the edges. These defects are called parafermions (Alicea and Fendley, 2016). There are multiple ways to create parafermions, for example, via the gapping in edge states: In quantum Hall bilayer, the edge states are gapped by inter-layer electron tunneling processes (Vaezi and Barkeshli, 2014), and in abelian fractional quantum Hall states, edges are gapped by coupling them with the superconducting order parameter (Clarke et al., 2014). Here, we described the following two approaches:
a. Quantum Hall bilayer
The two layers will have either FQH filling factors with the same charge polarity (ν1 = ν2) or with opposite polarity (ν1 = −ν2); the two layers are coupled by tunneling at the edges, while the bulk of the two layers remains pristine. A trench cut through the two layers will create a unique system where two types of tunneling processes will dominate: inter-layer tunneling (top–top layers) and intra-layer tunneling (between the top and bottom layers). The electronic tunneling in these processes will create a gap at the boundary of the trench and thus coherently connect two layers via a tunneling plane. The endpoints of this plane host a pair of topological defects. In the Hall bilayer with an opposite filling factor, the inter-layer tunneling between two counter-propagating edge modes will create a gap at the boundary of the same side of the trench and thus form the (vacuum) hole in quantum Hall planes in both layers. In this construction, for creating the topological defects, two layers needed to be coupled via a superconductor (Barkeshli, 2016). However, if two layers have the same polarity of filling factors, then the tunneling plane forms the cross geometry. The inter-layer tunneling process leads to the creation of the parafermions with the topological dimension of
The 2DEGs in GaAs/AlGaAs, graphene families, and other quantum materials with an internal degree of freedom of spins and layers form the interesting platform quantum Hall bilayer. In the experiment, the total filling factor of νT = 1, νT = 1/2, and νT = 2/3 are studied in double-quantum-well structures fabricated in the GaAs/AlGaAs (Lay et al., 1997; Spielman et al., 2000; Shabani et al., 2013; Mueed et al., 2015; Mueed et al., 2016). νT = 1 supports the excitonic condensation with inter-layer phase coherence (Eisenstein, 2014), and ground states of νT = 1/2 are still under debate (Zhao et al., 2021). It is expected that in the absence of inter-layer tunneling, νT = 1/2 stabilizes to Halperin 331 states via tuning inter-layer and intra-layer Coulomb interactions (He et al., 1993).
However, when in the presence of inter-layer tunneling, the ground states can be tuned continuously from Abelian Halperin 331 to Moore–Read Pfaffian, a non-Abelian state (Papić et al., 2009a; Papić et al., 2009b; Zhu et al., 2016). This phase transition depends on two parameters: the d, the separation between the two layers, and
The tunneling parameter could measure the topological order; g = 3/8(1/4) is the Halperin 331 (Moore Read Pfaffian) state (Radu et al., 2008; Baer et al., 2014). The tunneling experiment requires a combination of local and global gates to tune the density of electrons locally and globally (Figure 7). Most of the experiments are limited to tunneling in a single-layer system, and measured “g” shows a wide range of values, strongly depending on the device geometry (Fu et al., 2016). In the recent experiment, inter-layer tunneling is locally induced via a QPC for the excitonic νT = 1 quantum Hall bilayer (Zhang et al., 2020). A similar tunneling experiment is to be reported for νT = 1/2 yet.
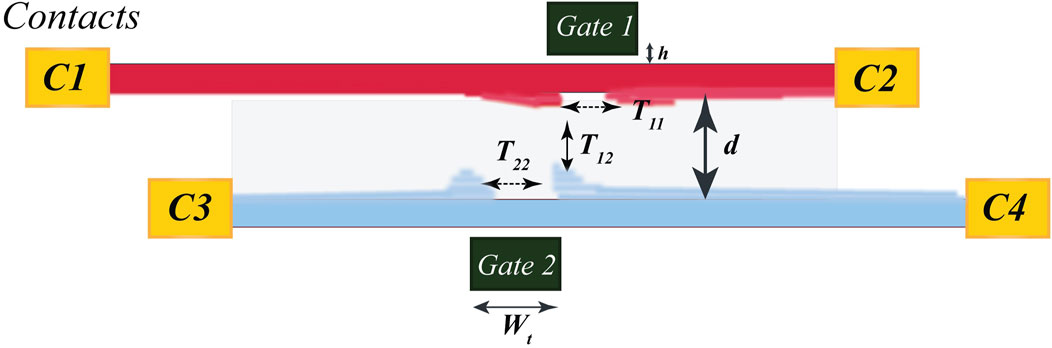
FIGURE 7. Tunneling process in the quantum Hall bilayer. Inter-layer T12 tunneling induced by the local top and bottom gates. The electronic wave function extends in the vertical direction tunneling the electrons across the two layers in the vertical direction. The inter-layer tunneling process T11, T22 across the gates dominates transport within the same layer. The interplay between these two processes is controlled by the inter-layer distance d and magnetic length lb, leading to the formation of non-Abelian topological defects. Adapted from Barkeshli and Qi (2014), licensed under CC BY 3.0. b. Quantum Hall/superconductor hybrids
In a separate experiment, the inter-layer tunneling between two graphene layers separated by WSe2 has been studied via current–voltage characteristics (Fu et al., 2016). The enhanced inter-layer coherence and band alignment of WSe2 with graphene facilitate inter-layer tunneling (Burg et al., 2018). Such geometrical construction with local QPC could provide a platform for probing “g.” Another experimental probe for the non-Abelian MR Pfaffian state could be seen in the quantum Hall drag conductance measurement where the non-quantized value will be the starring signature against quantized Hall drag conductance for the Halperin 331 states (Zhu et al., 2016; Regan et al., 2022). νT = 2/3 is more interesting than νT = 1/2. Here, spin-charge separation leads to many different non-Abelian phases (Vaezi and Barkeshli, 2014). In this type of system, the non-Abelian ground states could be distinctly studied in tunnel-coupled quantum dot geometry via temperature-dependence tunneling processes (Fiete et al., 2008). The novel non-Abelian phases in the quantum Hall bilayer make them an attractive playground. With the advent of sample quality and nanofabrication techniques, it would be interesting to experimentally realize the topological defects in such a system.
b. Quantum Hall/superconductor hybrids
The two different gapping mechanisms, namely, the tunneling of electrons and superconducting proximity-induced pairing of an electron across counter-propagating edge states are key to the fabrication of topological defects in quantum Hall/superconducting hybrids. The physical realization of this hybrid platform can be implemented by creating a trench in the quantum Hall fluid and filling the trench with the superconductor (Alicea and Fendley, 2016).
The trench in the quantum Hall fluid will enforce the propagation of the chiral edge states along the trench, and only electron tunneling across the trench will be feasible (see Figure 8). Even for the fractional filling, only electron tunneling across the trench will be allowed. Furthermore, in the second process, the pairing of the quasiparticle via copper pair condensate will lead to the conversion of the quasiparticle to a quasihole via perfect crossed-Andreev reflections (CARs). In addition, to open the gap, the condition for the spin symmetry of the edge states must be broken, and thus a strong spin–orbit interaction is needed. This may be achieved either by the spin–orbit interaction of the superconductor or by local ferromagnetic interaction within the edge states (Clarke et al., 2013). Recently, it has also been demonstrated that magnetic field bending at the edges of the superconductor with wedge geometry could lead to the counter in-plane magnetic field components at the two edges of the trench. The in-plane magnetic field provides the necessary Zeeman energy to open the gap in the chiral edge states (Galambos et al., 2022).
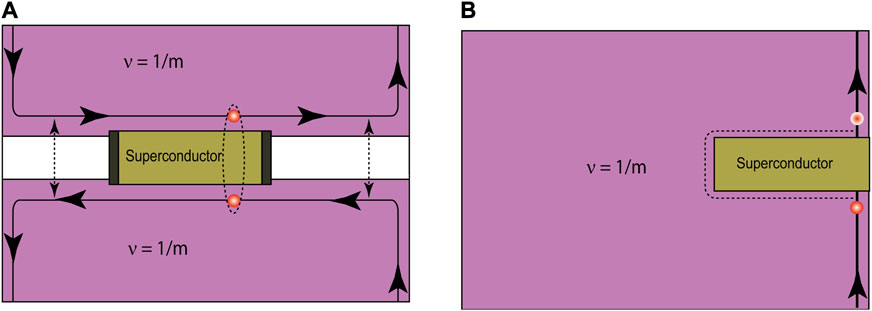
FIGURE 8. Quantum Hall/superconductor hybrid construction for engineering parafermions at the domain defined by trench, superconductor, and fractional quantum Hall fluid (shown in dark gray) (A). The experimental setup was studied to probe the parafermions (refs Lee et al., 2017; Gül et al., 2022) in non-local measurement. This measurement scheme suffers from vortex-induced dissipative processes, giving similar negative conductance signatures in non-local transport measurement (B). See the text for the details. Adapted with permission from Alicea and Fendley (2016).
Though for parafermions, one needs to have fractional excitations. However, even Laughlin filling ν = 1 could set the platform for p-wave symmetric topological states due to CAR processes at the edges of the superconductor, a necessary ingredient for the Majorana modes. In the non-local tunneling experiment, the negative signature in conductance demonstrates these superconducting correlations. However, this is not the unique signature for the formation of MZMs.
The formation of quantum Hall states requires a high magnetic field and usually, the superconductors, for example, molybdenum–rhenium alloys and niobium nitrate with high upper critical fields HC2. This leads to the formation of Abrikosov vortices in the superconductor (de Gennes, 1999; Tinkham, 2004). The hybridization of these vortices with the sub-gap Caroli–de Gennes–Matricon states could also mimic the negative signature in non-local conductance measurement (Caroli et al., 1964), similar to the one due to the presence of MZMs (Galambos et al., 2022).
Recently, the quantum transport probe in graphene (Lee et al., 2017; Gül et al., 2022) and InAs (Hatefipour et al., 2022) coupled with a superconductor showed negative conductance in such a quantum Hall/superconductor hybrid. However, the role of vortices in this quantum transport could not be negated. This is observed in the suppression of the CAR signature (lower negative conductance than the theoretically predicted value). Despite this, the experiment by Gül et al. (2022) shows the increase in the CAR signature with the decrease in temperature for fractional excitations. In contrast, for the quantum Hall CAR signal is largely temperature-independent. This distinction between the two may arise due to the different dissipation processes of fractional excitations from that of electronic excitations (Schiller et al., 2022b). This may indicate condensation of parafermions in the fractional quantum Hall/superconductor hybrid system. Nevertheless, probing the non-Abelian nature of these topological defects requires a different approach, for example, finite frequency noise (Smirnov, 2019; Smirnov, 2022), current correlation (Bignon et al., 2005), and entropy measurements (Sela et al., 2019).
The experimental realization of the parafermions in the designer quantum Hall hybrid platform may seem to be challenging. They will support topological quantum computation. Compared to ν = 5/2, Moore–Read state, and MZMs, parafermions will provide a much richer platform for universal quantum computation with careful engineering.
2.3 3D higher-order topological insulator systems
2.3.1 Symmetry-protected topological states
In the past decay, the concept of the topological state has been established and widely extended. To identify such a state, one needs to define a topological invariant based on the wave function of the state. For a topological state, its topological invariant is quantized and remains unchanged upon certain perturbations. Quantum Hall system and superfluid helium 3 have been recognized as the first experimental realizations of topological states. In the 2000s, the discovery of topological insulators deepened the understanding of the topological phases in condensed matter.
All topological states eventually originate from certain symmetries. The presence of the symmetries in the system “protects” the corresponding states from adiabatic changes. For example, the typical
a. Topological invariant
Different symmetries give rise to different types of topological materials. As introduced in the beginning, the topological invariants are useful indicators for identifying the topology in the materials. These topological invariants are numbers that do not change under an adiabatic deformation of the Hamiltonian of the system. For the topological states concerning the
b. Tenfold symmetry classification
A useful tool to identify the TIs is the tenfold symmetry classification (Ryu et al., 2010). It considers three essential symmetries: time-reversal symmetry
2.3.2 Topological crystalline insulator
Recent progress in theory and experiment shows that it is possible to go beyond these three symmetries. For instance, if we consider the spatial/crystalline symmetries, we will be able to define a new type of topological state, namely, the topological crystalline insulator (TCI) (Ando and Fu, 2015). The full classification of TCI has not been attained yet and is an active area of current research. An example is the class of materials whose topological properties are protected by mirror symmetry. The mirror symmetry
The first predicated real material of TCI is SnTe (Hsieh et al., 2012). At room temperature, SnTe has a simple rock salt structure, and its band gaps are located at four equivalent L points in the face-centered-cubic (FCC) Brillouin zone. These gaps are inverted relative to PbTe, while the alloy Pb1−xSnxTe gradually closes and re-opens the gap as a function of the doping percentage x Figure 9. The intrinsic distinction between PbTe and SnTe is that the cation/anion character of the conduction/valence bands is switched. This corresponds to a sign change in the mass term in the k · p theory Hamiltonian (Mitchell and Wallis, 1966). Eventually, SnTe is determined to be topological (PbTe is not) with microscopic band structures analysis. The main evidence is that the band gap of the SnTe changes non-monotonically as a function of the lattice constant: the gap closes and re-opens, indicating a topological phase transition (Shchennikov and Ovsyannikov, 2003).
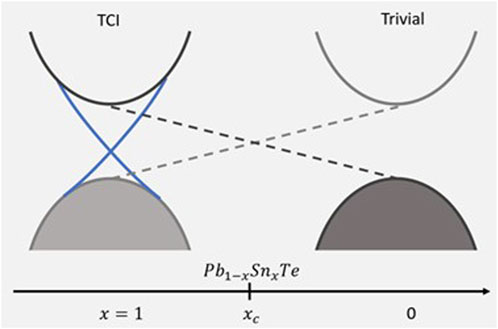
FIGURE 9. Phase transition between SnTe and PbTe. By changing the compound ratio between the Pb and Sn atoms, the material transit between a TCI and a non-topological semiconductor is shown.
More specified classification based on the crystalline point group symmetry has been proposed (Cornfeld and Chapman, 2019), which can help find and identify the topological crystalline insulators.
2.3.3 Higher-order topological states
In the previous cases, when the systems are in d-dimension, the d-1-dimensional boundary can host gapless topological states. These states belong to the first-order topological states, according to the classification that is introduced by Schindler et al. (2018a). If the d-1-dimensional states are generically gapped, the second-order topological states will emerge as d-2-dimensional states, e.g., corners for a 2D system or hinge states in a 3D system. This can be achieved by spontaneously breaking certain symmetries in the system, for example, SnTe with strain (Schindler et al., 2018a) or in an electric field. These topological materials are therefore referred to as higher-order topological insulators (HOTIs). In some sense, the HOTIs can be considered an extension of the concept of TCI.
The first evidence of HOTIs was observed in bismuth crystals (Drozdov et al., 2014; Li et al., 2014; Murani et al., 2017; Jäck et al., 2019) even before the theory was established (Schindler et al., 2018a; Schindler et al., 2018b). The 1D hinge states were protected locally by the time-reversal symmetry and globally by the crystalline structure’s threefold rotation symmetry and inversion symmetry. A more systematic study on the HOTI is performed (Benalcazar et al., 2017a; Benalcazar et al., 2017b).
2.3.4 Topological 3D Weyl/Dirac semimetal
Furthermore, since the realization of graphene and its 1D states along the zigzag edges, identifying bulk-gapless systems with topological boundary modes has attracted attention. For example, for a Weyl semimetal in which the time-reversal symmetry or inversion symmetry is broken, the bulk hosts one or more pairs of gapless Weyl points. At the momenta away from these points, the system is generically gapped. Therefore, it is possible to define the topological invariants at the closed Brillouin zone surfaces. It is shown that the topological invariants in Weyl semimetals are non-trivial and result in the topological surface Fermi arcs. The disconnected surface Fermi-arc contours connect two Weyl points with opposite chirality and then reconnect through the bulk at the Weyl points (Figure 10).
A Dirac semimetal, in contrast, has both time-reversal and inversion symmetries. It can be understood as two degenerate Weyl fermions with opposite chirality. The crystal symmetries protect the two Weyl cones from hybridizing. Although similar Fermi arcs were observed in Dirac semimetals (Wang et al., 2013; Xu et al., 2015; Moll et al., 2016), it was not clear whether they are topologically protected (Kargarian et al., 2016) because the surface Fermi arcs can be removed without breaking symmetry or closing an energy gap. It remained an open question whether there is topologically protected bulk-boundary correspondence in the 3D Dirac semimetals.
Recently, a sophisticated study on the bulk-boundary correspondence using topological quantum chemistry (Elcoro et al., 2021) clarified this question: the topological Dirac semimetals exhibit one-dimensional higher-order hinge Fermi arcs (HOFAs) as a universal and direct consequence of their bulk 3D Dirac points. A spinful quadruple insulator model was introduced to verify and predict the properties of the HOFA states (Wieder et al., 2020). The predicted material candidates are Cd3As2 and PtO2. More recently, this method is proven to be an efficient way of searching non-trivial materials in a generic base. An open website has been built by the relevant theory groups, providing an extremely large database for the topological materials (Mois et al., 2023).
2.3.5 Experimental observations of higher-order topological states
In this section, we will focus on the experimental progress of the higher-order topological states in various systems and the possible detection of Majorana states in such systems.
Several 3D materials have been identified with their higher-order topological hinge states. A direct manner to observe the hinge states is by STM measurement, for example, in bismuth (Drozdov et al., 2014; Schindler et al., 2018a). Nevertheless, because of the spin–momentum locking property of the hinge states, the backscattering processes are forbidden. Therefore, the induced superconducting states in Josephson-type devices have much longer coherence lengths, and larger supercurrent densities can flow in the hinge states. Such particular current density distribution is illustrated in Figure 11A. Furthermore, the corresponding field dependence of the critical current is shown in the following section. The experimental results of Cd3As2 and Bi-based Josephson junctions are shown in Figures 11B, C.
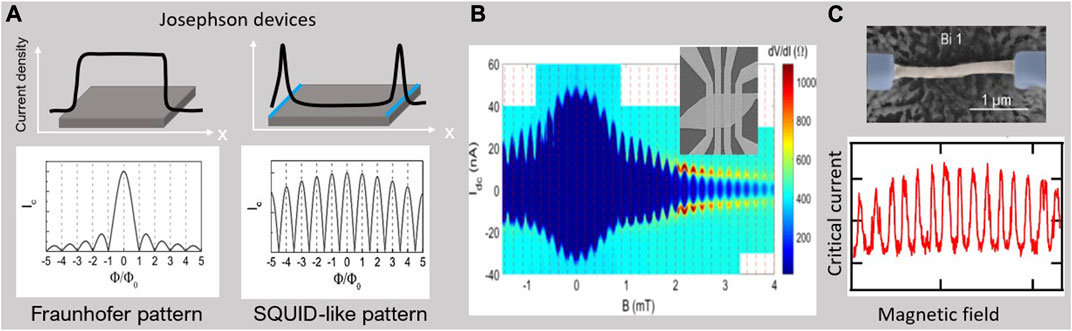
FIGURE 11. Detecting the hinge states with Josephson devices. (A) Magnetic field dependence of the critical current with different density distributions. (B, C) SQUID-like oscillations observed in the Cd3As2 nanoplate [adapted with permission from Li et al. (2020). Copyrighted by the American Physical Society.] and Bi-nanowire [adapted with permission from Li et al. (2014). Copyrighted by the American Physical Society.].
The presence of the hinge states in Josephson devices results in higher current density at the edges of the junction. Therefore, the magnetic field dependence of the critical current changes from a conventional Fraunhofer pattern to a SQUID-like pattern. Such critical current oscillation was first observed in bismuth single-crystal nanowires (Li et al., 2014; Murani et al., 2017) and then recently in Cd3As2 (Li et al., 2020) and WTe2 (Choi et al., 2020) nanoplates.
2.3.6 Higher-order topological states and Majorana bound states
2.3.6.1 a.c. Josephson effect and fractional Shapiro steps
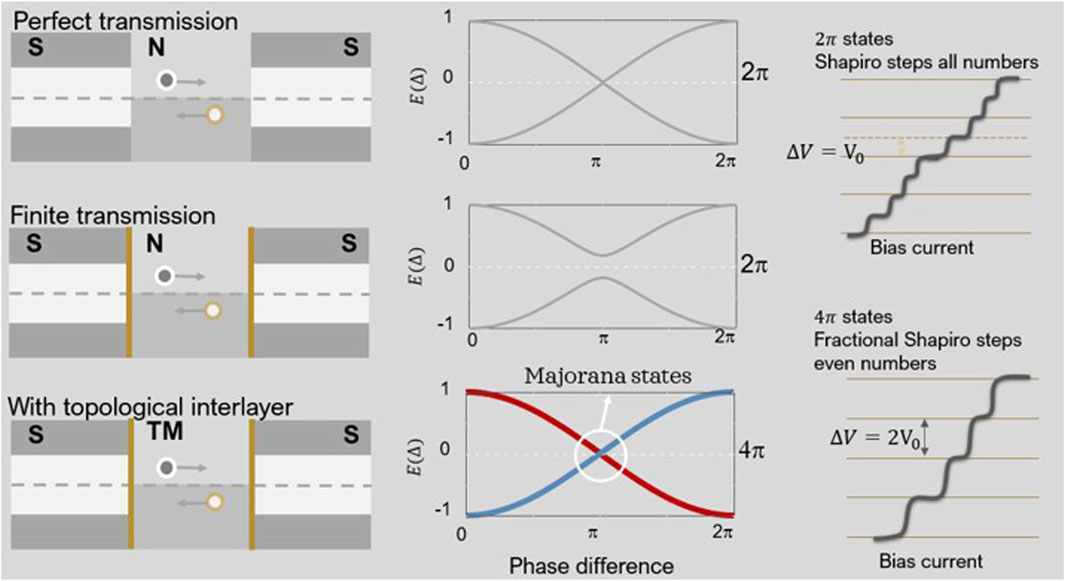
Originally, the topological insulators were predicted to be the suitable platform for realizing braiding in combination with an s-wave superconductor using the proximity effect (Fu and Kane, 2008). The Hamiltonian of the proximitized material is similar to the p-wave superconductor. Because the spin of the charge is locked to its momentum, backscattering is suppressed in such systems, known as spin–momentum locking. The topologically protected Andreev bound states prevent the relaxation of the quasiparticle; therefore, the corresponding energy spectrum is 4π-periodic instead of 2π, and the Majorana state is present at the zero energy. Due to the inverse a.c. Josephson effect, the IV characteristic of the junction becomes quantized under radio-frequency irradiation. These are the so-called Shapiro steps. The step height is given by hf/2e, where f is the frequency of the irradiation signal. When the Majorana zero energy state is present, the spectrum becomes 4π-periodic, and the step height is doubled (hf/e), namely, fractional Shapiro steps (San-Jose et al., 2012; Badiane et al., 2013) (Figure 12). In most 3D systems, supercurrent is carried by multiple modes on the surface or in the bulk. Most of these channels have a finite incident angle to the NS interface, except one mode which is perpendicular to the interface. This mode hosts the Majorana state and enables a 4π-periodic supercurrent to flow. Therefore, there are two types of supercurrent that coexist in the junction device—2pi- and 4pi-periodic states. The first signature of the fractional Shapiro steps was observed in 2D TI HgTe (Wiedenmann et al., 2016; Bocquillon et al., 2017), followed by many works in 3D TIs (Le Calvez et al., 2019; Schüffelgen et al., 2019; de Ronde et al., 2020), including an emission measurement of a.c. Josephson effect (Deacon et al., 2016) and 3D Dirac semimetals (Li et al., 2018; Wang et al., 2018).
Particularly, in 3D topological nanowires, the surface states forming a conducting cylinder in the state are quantized due to the confinement. The lowest level has a finite gap at the zero energy because of the Berry phase π. It is necessary to apply a parallel field that shifts the degenerate states and forms a gapless Dirac state as the lowest level (Cook and Franz, 2011; Jauregui et al., 2016).
To note that, due to finite quasiparticle relaxation time (Badiane et al., 2013), joule heating (Le Calvez et al., 2019), and capacitive coupling to the environment (Houzet et al., 2013), sometimes the higher level steps become hf/2e, except the lowest n = 1 level. This could sometimes be confused with a high re-trapping current, which hides the lowest level of the Shapiro steps. However, most recent research shows that despite all types of perturbations, similar signatures of the 4π-periodic supercurrent and the fractional Shapiro steps can also be observed in trivial Josephson junctions with extremely high transparency (Dartiailh et al., 2021). Such findings suggest the importance of cross-checking the results with different measurement methods for searching Majorana bound states.
2.3.6.2 e–e interaction and Majorana Kramer pairs
The higher-order topological states in the TCI and Dirac semimetals are time-reversal invariant, which is similar to the 2D quantum spin Hall states. The formed Majorana states are also degenerate. This is, however, detrimental for the Majorana braiding since the two states cancel each other’s phase changes exactly. To lift this degeneracy, one option is to break the time-reversal symmetry by applying an external magnetic field or making the material magnetic (Qi et al., 2010). Another possibility is by taking into account the electron–electron interaction in Rashba nanowires (Klinovaja and Loss, 2014; Thakurathi et al., 2018), time-reversal invariant topological superconductors (Zhang et al., 2013), or higher-order topological insulators (Hsu et al., 2018), forming Majorana Kramer pairs (MKPs) or parafermions (PFs). The key point of this approach is to realize an enhanced cross-Andreev pairing in two nanowires or hinge states. This enhancement is predicted to be sufficiently large when a modest e–e interaction is present. The feasibility of using MKPs or PFs for braiding and computing has been studied (Gao et al., 2016; Wölms et al., 2016; Schrade and Fu, 2022).
3 Conclusion and outlook
We have introduced several material systems from one-dimensional to three-dimensional, which can be employed for exploring Majorana physics. Furthermore, we explained the basic principles for forming and detecting the non-Abelian states in the designed hybrid devices based on these materials. Instead of detecting MZMs directly, it requires sometimes more effort in understanding the intrinsic topological properties of the material itself. Nevertheless, these novel systems and states open the door to a fascinating field in condensed matter and provide rich resources for finding different approaches to realizing the non-Abelian states. Similarly, for detecting the non-Abelian states, the experimental measurement methods have been adapted and developed in various regimes, including tunneling spectroscopy, Coulomb blockade spectroscopy, Shapiro steps, and spectroscopy in the RF regime. Particularly, the interferometer techniques can be applied to the FQH systems.
As has been already mentioned, trivial states can generate “false-positive” signals in different ways. For instance, in the case of the Rashba nanowire hybrid setup, while the topological gap protocol establishes some guidelines, it is still completely based on linear-response transport spectroscopy. Particularly, the disorders can play an unexpectedly important role in suppressing the non-local signals and potentially make false-positive signals with the combination of trivial ABS ((Hess et al., 2023a) and the discussions (Hess et al., 2023b; Sarma and Pan, 2023)). Going beyond conductance spectroscopy might settle for more stringent conditions that could bypass some of the issues caused by local defects and the resulting false positives. Many measurements also invoke the use of Coulomb blockade spectroscopy (Lai et al., 2021) via adjacent quantum dot that is coupled as well as using shot noise signatures. These ideas strongly connect with recent theoretical explorations on the possibility of more robust theoretical constructs that include entanglement spectra (Smirnov, 2021a; Smirnov, 2021b; Kejriwal and Muralidharan, 2022) and parity fluctuations (Pöyhönen et al., 2022). Therefore, it is very important to “cross-check” the same states with different measurement methods (in different regimes) and compare the output of the same measurement method in different material systems. We also believe that in the field, there is a strong drive to enhance the quality of materials beyond their current state for the next phase. Simultaneously, both theoretical and experimental aspects need to evolve in tandem, ultimately working toward achieving the objective of braiding and demonstrating non-Abelian statistics.
The 2D platform, particularly the 2-DEG systems, boasts a considerable advantage due to its gate tunability in defining the device configuration. This advantage not only facilitates the amalgamation of various measurement techniques into one single device but also provides better control over the system. Recent development in such systems (Hell et al., 2017; Pientka et al., 2017) has demonstrated the possibility of using the 2D systems as the platform for Majorana physics. Nevertheless, the issues like disorders and metallization can still persist in these material platforms, potentially leading to similar challenges that have hindered the conclusive validation of MBS.
Author contributions
The authors contributed equally to writing the manuscript. BM wrote Section 2.1, MK wrote Section 2.2, and CL wrote Section 2.3. All authors contributed to the article and approved the submitted version.
Funding
MK acknowledges the funding from the Academy of Finland grant (338872), Finnish Indian Consortia for Research and Education (FICORE), and QuantERA II Program that has received funding from the European Union’s Horizon 2020 Research and Innovation Programme under Grant Agreement Nos 731473 and 101017733. CL thanks the Netherlands Organization for Scientific Research (NWO) for the funding through a Vidi grant (203.047). BM acknowledges the support by the Science and Engineering Research Board (SERB), Government of India, Grant No. CRG/2021/003102, and the Ministry of Human Resource Development (MHRD), Government of India, Grant No. STARS/APR2019/NS/226/FS under the STARS scheme.
Acknowledgments
The authors are grateful to Alexander Zyuzin for the scientific discussions.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Aghaee, M., Akkala, A., Alam, Z., Ali, R., Ramirez, A. A., Andrzejczuk, M., et al. (2022). Inas-al hybrid devices passing the topological gap protocol. Phys. Rev. B 107, 245423. doi:10.1103/PhysRevB.107.245423
Alicea, J., and Fendley, P. (2016). Topological phases with parafermions: theory and blueprints. Annu. Rev. Condens. Matter Phys. 7, 119–139. doi:10.1146/annurev-conmatphys-031115-011336
Alicea, J. (2010). Majorana fermions in a tunable semiconductor device. Phys. Rev. B 81, 125318. doi:10.1103/physrevb.81.125318
Ando, Y., and Fu, L. (2015). Topological crystalline insulators and topological superconductors: from concepts to materials. Annu. Rev. Condens. Matter Phys. 6, 361–381. doi:10.1146/annurev-conmatphys-031214-014501
Antipov, A. E., Bargerbos, A., Winkler, G. W., Bauer, B., Rossi, E., and Lutchyn, R. M. (2018). Effects of gate-induced electric fields on semiconductor majorana nanowires. Phys. Rev. X 8, 031041. doi:10.1103/physrevx.8.031041
Arakane, T., Sato, T., Souma, S., Kosaka, K., Nakayama, K., Komatsu, M., et al. (2012). Tunable Dirac cone in the topological insulator Bi2-xSbxTe3-ySey. Nat. Comm. 3, 636. doi:10.1038/ncomms1639
Arovas, D., Schrieffer, J. R., and Wilczek, F. (1984). Fractional statistics and the quantum Hall effect. Phys. Rev. Lett. 53, 722–723. doi:10.1103/physrevlett.53.722
Badiane, D. M., Glazman, L. I., Houzet, M., and Meyer, J. S. (2013). Ac Josephson effect in topological Josephson junctions. Comptes Rendus Phys. 14, 840–856. doi:10.1016/j.crhy.2013.10.008
Baer, S., Rössler, C., Ihn, T., Ensslin, K., Reichl, C., and Wegscheider, W. (2014). Experimental probe of topological orders and edge excitations in the second Landau level. Phys. Rev. B 90, 075403. doi:10.1103/physrevb.90.075403
Banerjee, M., Heiblum, M., Umansky, V., Feldman, D. E., Oreg, Y., and Stern, A. (2018). Observation of half-integer thermal Hall conductance. Nature 559, 205–210. doi:10.1038/s41586-018-0184-1
Barkeshli, M. (2016). Charge 2e/3 superconductivity and topological degeneracies without localized zero modes in bilayer fractional quantum Hall states. Phys. Rev. Lett. 117, 096803. doi:10.1103/PhysRevLett.117.096803
Barkeshli, M., and Qi, X.-L. (2014). Synthetic topological qubits in conventional bilayer quantum Hall systems. Phys. Rev. X 4, 041035. doi:10.1103/physrevx.4.041035
Bartolomei, H., Kumar, M., Bisognin, R., Marguerite, A., Berroir, J.-M., Bocquillon, E., et al. (2020). Fractional statistics in anyon collisions. Science 368, 173–177. doi:10.1126/science.aaz5601
Benalcazar, W. A., Bernevig, B. A., and Hughes, T. L. (2017b). Electric multipole moments, topological multipole moment pumping, and chiral hinge states in crystalline insulators. Phys. Rev. B 96, 245115. doi:10.1103/physrevb.96.245115
Benalcazar, W. A., Bernevig, B. A., and Hughes, T. L. (2017a). Quantized electric multipole insulators. Science 357, 61–66. arXiv:1611.07987. doi:10.1126/science.aah6442
Bignon, G., Houzet, M., Pistolesi, F., and Hekking, F. (2005). Realizing controllable quantum states. Singapore: World Scientific, 23–28.
Bocquillon, E., Deacon, R., Wiedenmann, J., Leubner, P., Klapwijk, T., Brüne, C., et al. (2017). Gapless Andreev bound states in the quantum spin Hall insulator HgTe. Nat. Nanotechnol. 137, 137–143. doi:10.1038/nnano.2016.159
Bonderson, P., Kitaev, A., and Shtengel, K. (2006a). Detecting non-abelian statistics in theν=5/2fractional quantum Hall state. Phys. Rev. Lett. 96, 016803. doi:10.1103/physrevlett.96.016803
Bonderson, P., Shtengel, K., and Slingerland, J. K. (2006b). Probing non-abelian statistics with quasiparticle interferometry. Phys. Rev. Lett. 97, 016401. doi:10.1103/physrevlett.97.016401
Burg, G. W., Prasad, N., Kim, K., Taniguchi, T., Watanabe, K., MacDonald, A. H., et al. (2018). Strongly enhanced tunneling at total charge neutrality in double-bilayer graphene-WSe2 heterostructures. Phys. Rev. Lett. 120, 177702. doi:10.1103/physrevlett.120.177702
Caroli, C., De Gennes, P., and Matricon, J. (1964). Bound Fermion states on a vortex line in a type II superconductor. Phys. Lett. 9, 307–309. doi:10.1016/0031-9163(64)90375-0
Cayao, J. (2017). Hybrid superconductor-semiconductor nanowire junctions as useful platforms to study majorana bound states. arXiv:1703.07630 [cond-mat.mes-hall] Available at: https://doi.org/10.48550/arXiv.1703.07630.
Chang, A. M. (2003). Chiral Luttinger liquids at the fractional quantum Hall edge. Rev. Mod. Phys. 75, 1449–1505. doi:10.1103/revmodphys.75.1449
Chiu, C.-K., and Das Sarma, S. (2019). Fractional Josephson effect with and without Majorana zero modes. Phys. Rev. B 99, 035312. doi:10.1103/physrevb.99.035312
Choi, Y. B., Xie, Y., Chen, C. Z., Park, J., Song, S. B., Yoon, J., et al. (2020). Evidence of higher-order topology in multilayer WTe2 from Josephson coupling through anisotropic hinge states. Nat. Mater. 19, 974–979. doi:10.1038/s41563-020-0721-9
Clarke, D. J., Alicea, J., and Shtengel, K. (2014). Exotic circuit elements from zero-modes in hybrid superconductor–quantum-Hall systems. Annu. Rev. Condens. Matter Phys. 10, 877–882. doi:10.1038/nphys3114
Clarke, D. J., Alicea, J., and Shtengel, K. (2013). Exotic non-Abelian anyons from conventional fractional quantum Hall states. Nat. Commun. 4, 1. doi:10.1038/ncomms2340
Cook, A., and Franz, M. (2011). Majorana fermions in a topological-insulator nanowire proximity-coupled to an s-wave superconductor. Phys. Rev. B - Condens. Matter Mater. Phys. 84, 1. doi:10.1103/PhysRevB.84.201105
Cornfeld, E., and Chapman, A. (2019). Classification of crystalline topological insulators and superconductors with point group symmetries. Phys. Rev. B 99, 075105. doi:10.1103/physrevb.99.075105
Dartiailh, M. C., Cuozzo, J. J., Elfeky, B. H., Mayer, W., Yuan, J., Wickramasinghe, K. S., et al. (2021). Missing Shapiro steps in topologically trivial Josephson junction on InAs quantum well. Nat. Commun. 12, 78. arXiv:2005.00077. doi:10.1038/s41467-020-20382-y
Das Sarma, S., Freedman, M., and Nayak, C. (2005). Topologically protected qubits from a possible non-abelian fractional quantum Hall state. Phys. Rev. Lett. 94, 166802. doi:10.1103/physrevlett.94.166802
Datta, S., and Bagwell, P. F. (1999). Superlattices Microstruct. 25, 1233–1250. doi:10.1006/spmi.1999.0747
Datta, S. (1997). Electronic transport in mesoscopic systems. Cambridge: Cambridge University Press.
De Gennes, P. (1999). “Superconductivity of metals and alloys,” in Advanced books classics series (Colorado: Westview Press).
de Ronde, B., Li, C., Huang, Y., and Brinkman, A. (2020). Induced topological superconductivity in a BiSbTeSe2-based Josephson junction. Nanomaterials 10, 794. doi:10.3390/nano10040794
Deacon, R. S., Wiedenmann, J., Bocquillon, E., Klapwijk, T. M., Leubner, P., Brüne, C., et al. (2016). Josephson radiation from gapless andreev bound states in HgTe-based topological junctions. Condens. Matter - Mesoscale Nanoscale Phys. 7, 021011. doi:10.1103/PhysRevX.7.021011
Deng, M.-T., Vaitiekėnas, S., Prada, E., San-Jose, P., Nygård, J., Krogstrup, P., et al. (2018). Nonlocality of Majorana modes in hybrid nanowires. Phys. Rev. B 98, 085125. doi:10.1103/physrevb.98.085125
Deng, M. T., Nygard, J., Hansen, E., Danon, J., Leijnse, M., Flensberg, K., et al. (2016). Majorana bound state in a coupled quantum-dot hybrid-nanowire system. Science 354, 1557–1562. doi:10.1126/science.aaf3961
Dolev, M., Gross, Y., Chung, Y. C., Heiblum, M., Umansky, V., and Mahalu, D. (2010). Dependence of the tunneling quasiparticle charge determined via shot noise measurements on the tunneling barrier and energetics. Phys. Rev. B 81, 161303. doi:10.1103/physrevb.81.161303
Dolev, M., Heiblum, M., Umansky, A., Stern, V., and Mahalu, D. (2008). Observation of a quarter of an electron charge at the ν = 5/2 quantum Hall state. Nature 452, 829–834. doi:10.1038/nature06855
Domínguez, F., Cayao, J., San-Jose, P., Aguado, R., Yeyati, A. L., and Prada, E. (2017). Zero-energy pinning from interactions in Majorana nanowires. npj Quantum Mater. 2, 13. doi:10.1038/s41535-017-0012-0
Drozdov, I. K., Alexandradinata, A., Jeon, S., Nadj-Perge, S., Ji, H., Cava, R. J., et al. (2014). One-dimensional topological edge states of bismuth bilayers. Nat. Phys. 10, 664–669. doi:10.1038/nphys3048
Duse, C., Sriram, P., Gharavi, K., Baugh, J., and Muralidharan, B. (2021). Role of dephasing on the conductance signatures of Majorana zero modes. J. Phys. Condens. Matter 33, 365301. doi:10.1088/1361-648x/ac0d16
Dutta, B., Yang, W., Melcer, R., Kundu, H. K., Heiblum, M., Umansky, V., et al. (2022). Distinguishing between non-abelian topological orders in a quantum Hall system. Science 375, 193–197. doi:10.1126/science.abg6116
Eisenstein, J. (2014). Exciton condensation in bilayer quantum Hall systems. Annu. Rev. Condens. Matter Phys. 5, 159–181. doi:10.1146/annurev-conmatphys-031113-133832
Eisenstein, J. P., Cooper, K. B., Pfeiffer, L. N., and West, K. W. (2002). Insulating and fractional quantum Hall states in the first excited Landau level. Phys. Rev. Lett. 88, 076801. doi:10.1103/physrevlett.88.076801
Eisenstein, J. P., Willett, R., Stormer, H. L., Tsui, D. C., Gossard, A. C., and English, J. H. (1988). Collapse of the even-denominator fractional quantum Hall effect in tilted fields. Phys. Rev. Lett. 61, 997–1000. doi:10.1103/physrevlett.61.997
Elcoro, L., Wieder, B. J., Song, Z., Xu, Y., Bradlyn, B., and Bernevig, B. A. (2021). Magnetic topological quantum chemistry. Nat. Commun. 12, 4. doi:10.1038/s41467-021-26241-8
Escribano, S. D., Maiani, A., Leijnse, M., Flensberg, K., Oreg, Y., Levy Yeyati, A., et al. (2022). Semiconductor-ferromagnet-superconductor planar heterostructures for 1D topological superconductivity. npj Quantum Mater. 7, 81. doi:10.1038/s41535-022-00489-9
Feldman, D. E., and Halperin, B. I. (2021). Fractional charge and fractional statistics in the quantum Hall effects. Rep. Prog. Phys. 84, 1. doi:10.1088/1361-6633/ac03aa
Fiete, G. A., Bishara, W., and Nayak, C. (2008). Multichannel kondo models in non-abelian quantum Hall droplets. Phys. Rev. Lett. 101, 176801. doi:10.1103/physrevlett.101.176801
Fu, H., Wang, P., Shan, P., Xiong, L., Pfeiffer, L. N., West, K., et al. (2016). Competing ν = 5/2 fractional quantum Hall states in confined geometry. Science 113, 12386–12390. doi:10.1073/pnas.1614543113
Fu, L., and Kane, C. (2008). Superconducting proximity effect and majorana fermions at the surface of a topological insulator. Phys. Rev. Lett. 100, 096407. doi:10.1103/physrevlett.100.096407
Galambos, T. H., Ronetti, F., Hetényi, B., Loss, D., and Klinovaja, J. (2022). Crossed Andreev reflection in spin-polarized chiral edge states due to the Meissner effect. Phys. Rev. B 106, 075410. doi:10.1103/physrevb.106.075410
Gao, P., He, Y. P., and Liu, X. J. (2016). Symmetry-protected non-Abelian braiding of Majorana Kramers pairs. Phys. Rev. B 94, 1. arXiv:1603.09331. doi:10.1103/PhysRevB.94.224509
Gervais, G., Engel, L. W., Stormer, H. L., Tsui, D. C., Baldwin, K. W., West, K. W., et al. (2004). Competition between a fractional quantum Hall liquid and bubble and wigner crystal phases in the third Landau level. Phys. Rev. Lett. 93, 266804. doi:10.1103/physrevlett.93.266804
Glidic, P., Maillet, O., Piquard, A., Aassime, C., Cavanna, A., Jin, Y., et al. (2023). Quasiparticle Andreev scattering in the \nu 1/3 fractional quantum Hall regime. Nat. Commun. 14, 1. doi:10.1038/s41467-023-36080-4
Goldman, V. J., and Su, B. (1995). Resonant tunneling in the quantum Hall regime: measurement of fractional charge. Science 267, 1010–1012. doi:10.1126/science.267.5200.1010
Gül, O., Ronen, Y., Lee, S. Y., Shapourian, H., Zauberman, J., Lee, Y. H., et al. (2022). Andreev reflection in the fractional quantum Hall state. Phys. Rev. X 12, 021057. doi:10.1103/physrevx.12.021057
Gül, Ö., Zhang, H., Bommer, J. D. S., de Moor, M. W. A., Car, D., Plissard, S. R., et al. (2018). Ballistic Majorana nanowire devices. Nat. Nanotechnol. 13, 192–197. doi:10.1038/s41565-017-0032-8
Halperin, B. I. (1984). Statistics of quasiparticles and the hierarchy of fractional quantized Hall states. Phys. Rev. Lett. 52, 1583–1586. doi:10.1103/physrevlett.52.1583
Halperin, B. I., Stern, A., Neder, I., and Rosenow, B. (2011). Theory of the Fabry-Pérot quantum Hall interferometer. Phys. Rev. B 83, 155440. doi:10.1103/physrevb.83.155440
Hatefipour, M., Cuozzo, J. J., Kanter, J., Strickland, W. M., Allemang, C. R., Lu, T.-M., et al. (2022). Induced superconducting pairing in integer quantum Hall edge states. Nano Lett. 22, 6173–6178. doi:10.1021/acs.nanolett.2c01413
He, S., Das Sarma, S., and Xie, X. C. (1993). Quantized Hall effect and quantum phase transitions in coupled two-layer electron systems. Phys. Rev. B 47, 4394–4412. doi:10.1103/physrevb.47.4394
Hell, M., Leijnse, M., and Flensberg, K. (2017). Two-dimensional platform for networks of majorana bound states. Phys. Rev. Lett. 118, 107701. doi:10.1103/physrevlett.118.107701
Hess, R., Legg, H. F., Loss, D., and Klinovaja, J. (2023b). Reply to comment on ’trivial andreev band mimicking topological bulk gap reopening in the nonlocal conductance of long rashba nanowires. arXiv:2306.16853 [cond-mat.mes-hall] Available at: https://doi.org/10.48550/arXiv.2306.16853.
Hess, R., Legg, H. F., Loss, D., and Klinovaja, J. (2023a). Trivial andreev band mimicking topological bulk gap reopening in the nonlocal conductance of long rashba nanowires. Phys. Rev. Lett. 130, 207001. doi:10.1103/physrevlett.130.207001
Hsieh, D., Xia, Y., Qian, D., Wray, L., Meier, F., Dil, J. H., et al. (2009). Observation of time-reversal-protected single-Dirac-cone topological-insulator states inBi2Te3andSb2Te3. Phys. Rev. Lett. 103, 146401. doi:10.1103/physrevlett.103.146401
Hsieh, T. H., Lin, H., Liu, J., Duan, W., Bansil, A., and Fu, L. (2012). Topological crystalline insulators in the SnTe material class. Nat. Commun. 3, 1969. doi:10.1038/ncomms1969
Hsu, C. H., Stano, P., Klinovaja, J., and Loss, D. (2018). Majorana kramers pairs in higher-order topological insulators. Phys. Rev. Lett. 121, 196801. doi:10.1103/physrevlett.121.196801
Jäck, B., Xie, Y., Li, J., Jeon, S., Bernevig, B. A., and Yazdani, A. (2019). Observation of a Majorana zero mode in a topologically protected edge channel. Science 364, 1255–1259. doi:10.1126/science.aax1444
Jain, J. (2015). Composite fermion theory of exotic fractional quantum Hall effect. Annu. Rev. Condens. Matter Phys. 6, 39–62. doi:10.1146/annurev-conmatphys-031214-014606
Jauregui, L. A., Pettes, M. T., Rokhinson, L. P., Shi, L., and Chen, Y. P. (2016). Magnetic field-induced helical mode and topological transitions in a topological insulator nanoribbon. Nat. Nanotechnol. 11, 345–351. doi:10.1038/NNANO.2015.293
Jonckheere, T., Rech, J., Grémaund, B., and Martin, T. (2022). Anyonic statistics revealed by the hong-ou-mandel dip for fractional excitations. Available at: https://doi.org/10.1103/PhysRevLett.130.186203.
Kane, C. L., and Fisher, M. P. A. (1997). Quantized thermal transport in the fractional quantum Hall effect. Phys. Rev. B 55, 15832–15837. doi:10.1103/physrevb.55.15832
Kargarian, M., Randeria, M., and Lu, Y. M. (2016). Proc. Natl. Acad. Sci. U. S. A. 113, 8648–8652. doi:10.1073/pnas.1524787113
Kejriwal, A., and Muralidharan, B. (2022). Nonlocal conductance and the detection of Majorana zero modes: insights from von Neumann entropy. Phys. Rev. B 105, L161403. doi:10.1103/physrevb.105.l161403
Khindanov, A., Alicea, J., Lee, P., Cole, W. S., and Antipov, A. E. (2021). Topological superconductivity in nanowires proximate to a diffusive superconductor–magnetic-insulator bilayer. Phys. Rev. B 103, 134506. doi:10.1103/physrevb.103.134506
Kim, Y., Balram, A. C., Taniguchi, T., Watanabe, K., Jain, J. K., and Smet, J. H. (2019). Even denominator fractional quantum Hall states in higher Landau levels of graphene. Nat. Phys. 15, 154–158. doi:10.1038/s41567-018-0355-x
Kitaev, A. (2006). Anyons in an exactly solved model and beyond. Ann. Phys. 321, 2–111. doi:10.1016/j.aop.2005.10.005
Kitaev, A. Y. (2001). Unpaired Majorana fermions in quantum wires. Physics-Uspekhi 44, 131–136. doi:10.1070/1063-7869/44/10s/s29
Klinovaja, J., and Loss, D. (2014). Time-reversal invariant parafermions in interacting Rashba nanowires. Phys. Rev. B - Condens. Matter Mater. Phys. 90, 045118. doi:10.1103/physrevb.90.045118
Kundu, H. K., Biswas, S., Ofek, N., Umansky, V., and Heiblum, M. (2022). Anyonic interference and braiding phase in a mach-zehnder interferometer. Nat. Phys. 19, 515–521. doi:10.1038/s41567-022-01899-z
Lahiri, A., Gharavi, K., Baugh, J., and Muralidharan, B. (2018). Nonequilibrium Green's function study of magnetoconductance features and oscillations in clean and disordered nanowires. Phys. Rev. B 98, 125417. doi:10.1103/physrevb.98.125417
Lai, Y.-H., Das Sarma, S., and Sau, J. D. (2021). Theory of Coulomb blockaded transport in realistic Majorana nanowires. Phys. Rev. B 104, 085403. doi:10.1103/physrevb.104.085403
Laitinen, A., Kumar, M., and Hakonen, P. J. (2018). Weak antilocalization of composite fermions in graphene. Phys. Rev. B 97, 075113. doi:10.1103/physrevb.97.075113
Lay, T. S., Jungwirth, T., Smrčka, L., and Shayegan, M. (1997). One-component to two-component transition of theν=2/3fractional quantum Hall effect in a wide quantum well induced by an in-plane magnetic field. Phys. Rev. B 56, R7092–R7095. doi:10.1103/physrevb.56.r7092
Le Calvez, K., Veyrat, L., Gay, F., Plaindoux, P., Winkelmann, C. B., Courtois, H., et al. (2019). Joule overheating poisons the fractional ac Josephson effect in topological Josephson junctions. Commun. Phys. 2, 1. doi:10.1038/s42005-018-0100-x
Lee, G.-H., Ko-Fan, H., Efetov, D. K., Wei, D. S., Lee, S. H., Watanabe, K., et al. (2017). Inducing superconducting correlation in quantum Hall edge states. Nat. Phys. 13, 693–698. doi:10.1038/nphys4084
Lee, J.-Y. M., and Sim, H.-S. (2022). Non-Abelian anyon collider. Nat. Commun. 13 (6660), 1. doi:10.1038/s41467-022-34329-y
Lee, S.-S., Ryu, S., Nayak, C., and Fisher, M. P. A. (2007). Particle-hole symmetry and theν=52Quantum Hall state. Phys. Rev. Lett. 99, 236807. doi:10.1103/physrevlett.99.236807
Leinaas, J. M., and Myrheim, J. (1977). On the theory of identical particles. Il Nuovo Cimento B 37, 1–23. doi:10.1007/bf02727953
Leumer, N., Grifoni, M., Muralidharan, B., and Marganska, M. (2021). Linear and nonlinear transport across a finite Kitaev chain: an exact analytical study. Phys. Rev. B 103, 165432. doi:10.1103/physrevb.103.165432
Leumer, N., Marganska, M., Muralidharan, B., and Grifoni, M. (2020). Exact eigenvectors and eigenvalues of the finite Kitaev chain and its topological properties. J. Phys. Condens. Matter 32, 445502. doi:10.1088/1361-648x/ab8bf9
Levin, M., Halperin, B. I., and Rosenow, B. (2007). Particle-hole symmetry and the pfaffian state. Phys. Rev. Lett. 99, 236806. doi:10.1103/physrevlett.99.236806
Li, C.-Z., Wang, A.-Q., Li, C., Zheng, W.-Z., Brinkman, A., Yu, D.-P., et al. (2020). Reducing electronic transport dimension to topological hinge states by increasing geometry size of Dirac semimetal Josephson junctions. Phys. Rev. Lett. 124, 156601. doi:10.1103/physrevlett.124.156601
Li, C., de Boer, J. C., de Ronde, B., Ramankutty, S. V., van Heumen, E., Huang, Y., et al. (2018). 4π-periodic Andreev bound states in a Dirac semimeta. Nat. Mater. 17, 875–880. doi:10.1038/s41563-018-0158-6
Li, C., Kasumov, A., Murani, A., Sengupta, S., Fortuna, F., Napolskii, K., et al. (2014). Magnetic field resistant quantum interferences in Josephson junctions based on bismuth nanowires. Phys. Rev. B 90, 245427. doi:10.1103/physrevb.90.245427
Lin, X., Du, R., and Xie, X. (2008). Recent experimental progress of fractional quantum Hall effect: 5/2 filling state and graphene. Natl. Sci. Rev. 1, 564–579. doi:10.1093/nsr/nwu071
Liu, C.-X., Sau, J. D., and Das Sarma, S. (2018). Distinguishing topological Majorana bound states from trivial Andreev bound states: proposed tests through differential tunneling conductance spectroscopy. Phys. Rev. B 97, 214502. doi:10.1103/physrevb.97.214502
Liu, C.-X., Sau, J. D., and Das Sarma, S. (2017b). Role of dissipation in realistic Majorana nanowires. Phys. Rev. B 95, 054502. doi:10.1103/physrevb.95.054502
Liu, C.-X., Sau, J. D., Stanescu, T. D., and Das Sarma, S. (2017a). Andreev bound states versus Majorana bound states in quantum dot-nanowire-superconductor hybrid structures: trivial versus topological zero-bias conductance peaks. Phys. Rev. B 96, 075161. doi:10.1103/physrevb.96.075161
Liu, C.-X., Schuwalow, S., Liu, Y., Vilkelis, K., Manesco, A. L. R., Krogstrup, P., et al. (2021). Electronic properties of InAs/EuS/Al hybrid nanowires. Phys. Rev. B 104, 014516. doi:10.1103/physrevb.104.014516
Liu, Y., Vaitiekėnas, S., Martí-Sánchez, S., Koch, C., Hart, S., Cui, Z., et al. (2020). Semiconductor–ferromagnetic insulator–superconductor nanowires: stray field and exchange field. Nano Lett. 20, 456–462. doi:10.1021/acs.nanolett.9b04187
Lutchyn, R. M., Sau, J. D., and Das Sarma, S. (2010). Majorana fermions and a topological phase transition in semiconductor-superconductor heterostructures. Phys. Rev. Lett. 105, 077001. doi:10.1103/physrevlett.105.077001
Ma, K. K. W., and Feldman, D. E. (2019). The sixteenfold way and the quantum Hall effect at half-integer filling factors. Phys. Rev. B 100, 035302. doi:10.1103/physrevb.100.035302
Maiani, A., Seoane Souto, R., Leijnse, M., and Flensberg, K. (2021). Topological superconductivity in semiconductor–superconductor–magnetic-insulator heterostructures. Phys. Rev. B 103, 104508. doi:10.1103/physrevb.103.104508
Mélin, R., Bergeret, F. S., and Yeyati, A. L. (2009). Self-consistent microscopic calculations for nonlocal transport through nanoscale superconductors. Phys. Rev. B 79, 104518. doi:10.1103/physrevb.79.104518
Ménard, G. C., Anselmetti, G. L. R., Martinez, E. A., Puglia, D., Malinowski, F. K., Lee, J. S., et al. (2020). Conductance-matrix symmetries of a three-terminal hybrid device. Phys. Rev. Lett. 124, 036802. doi:10.1103/physrevlett.124.036802
Mikkelsen, A. E. G., Kotetes, P., Krogstrup, P., and Flensberg, K. (2018). Hybridization at superconductor-semiconductor interfaces. Phys. Rev. X 8, 031040. doi:10.1103/physrevx.8.031040
Mitchell, D. L., and Wallis, R. F. (1966). Theoretical energy-band parameters for the lead salts. Phys. Rev. 151, 581–595. doi:10.1103/physrev.151.581
Hong, C., Alkalay, N., Schiller, T., Umansky, V., Heiblum, M., et al. (2022). Partitioning of diluted anyons reveals their braiding statistics. Nat. Vol. 617, 277–281. doi:10.1038/s41586-023-05883-2
Mois, A., Andrei, B. B., Barry, B., Jennifer, C., Luis, E., Claudia, F., et al. (2023). topologicalquantumchemistry. Available at: https://www.topologicalquantumchemistry.com.
Moll, P. J., Nair, N. L., Helm, T., Potter, A. C., Kimchi, I., Vishwanath, A., et al. (2016). Transport evidence for Fermi-arc-mediated chirality transfer in the Dirac semimetal Cd3As2. Nature 535, 266–270. arXiv:1505.02817. doi:10.1038/nature18276
Moore, C., Stanescu, T. D., and Tewari, S. (2018a). Two-terminal charge tunneling: disentangling Majorana zero modes from partially separated Andreev bound states in semiconductor-superconductor heterostructures. Phys. Rev. B 97, 165302. doi:10.1103/physrevb.97.165302
Moore, C., Zeng, C., Stanescu, T. D., and Tewari, S. (2018b). Quantized zero-bias conductance plateau in semiconductor-superconductor heterostructures without topological Majorana zero modes. Phys. Rev. B 98, 155314. doi:10.1103/physrevb.98.155314
Moore, G., and Seiberg, N. (1988). Polynomial equations for rational conformal field theories. Phys. Lett. B 212, 451–460. doi:10.1016/0370-2693(88)91796-0
Mourik, V., Zuo, K., Frolov, S., Plissard, S., Bakkers, E., and Kouwenhoven, L. (2012). Signatures of majorana fermions in hybrid superconductor-semiconductor nanowire devices. Science 336, 1003–1007. doi:10.1126/science.1222360
Mross, D. F., Oreg, Y., Stern, A., Margalit, G., and Heiblum, M. (2018). Theory of disorder-induced half-integer thermal Hall conductance. Phys. Rev. Lett. 121, 026801. doi:10.1103/physrevlett.121.026801
Mueed, M. A., Kamburov, D., Hasdemir, S., Shayegan, M., Pfeiffer, L. N., West, K. W., et al. (2015). Geometric resonance of composite fermions near the ν=1/2 fractional quantum Hall state. Phys. Rev. Lett. 114, 236406. doi:10.1103/PhysRevLett.114.236406
Mueed, M. A., Kamburov, D., Pfeiffer, L. N., West, K. W., Baldwin, K. W., and Shayegan, M. (2016). Geometric resonance of composite fermions near bilayer quantum Hall states. Phys. Rev. Lett. 117, 246801. doi:10.1103/physrevlett.117.246801
Murani, A., Kasumov, A., Sengupta, S., Kasumov, Y. A., Volkov, V. T., Khodos, I. I., et al. (2017). Ballistic edge states in Bismuth nanowires revealed by SQUID interferometry. Nat. Commun. 8, 1. doi:10.1038/ncomms15941
Nakamura, J., Liang, S., Gardner, G. C., and Manfra, M. J. (2020). Direct observation of anyonic braiding statistics. Nature 16, 931–936. doi:10.1038/s41567-020-1019-1
Nayak, C., Simon, S. H., Stern, A., Freedman, M., and Das Sarma, S. (2008). Non-Abelian anyons and topological quantum computation. Rev. Mod. Phys. 80, 1083–1159. doi:10.1103/revmodphys.80.1083
Nichele, F., Drachmann, A. C. C., Whiticar, A. M., O’Farrell, E. C. T., Suominen, H. J., Fornieri, A., et al. (2017). Scaling of majorana zero-bias conductance peaks. Phys. Rev. Lett. 119, 136803. doi:10.1103/physrevlett.119.136803
Pan, H., and Sarma, S. D. (2020). Physical mechanisms for zero-bias conductance peaks in Majorana nanowires. Phys. Rev. Res. 2, 013377. doi:10.1103/physrevresearch.2.013377
Pan, H., Sau, J. D., Stanescu, T. D., and Das Sarma, S. (2019). Curvature of gap closing features and the extraction of Majorana nanowire parameters. Phys. Rev. B 99, 054507. doi:10.1103/physrevb.99.054507
Pan, W., Xia, J. S., Stormer, H. L., Tsui, D. C., Vicente, C., Adams, E. D., et al. (2008). Experimental studies of the fractional quantum Hall effect in the first excited Landau level. Phys. Rev. B 77, 075307. doi:10.1103/physrevb.77.075307
Papić, Z., Möller, G., Milovanović, M. V., Regnault, N., and Goerbig, M. O. (2009b). Fractional quantum Hall state at ν=1/4 in a wide quantum well. Phys. Rev. B 79, 245325. doi:10.1103/PhysRevB.79.245325
Papić, Z., Regnault, N., and Das Sarma, S. (2009a). Interaction-tuned compressible-to-incompressible phase transitions in quantum Hall systems. Phys. Rev. B 80, 201303. doi:10.1103/physrevb.80.201303
Pientka, F., Keselman, A., Berg, E., Yacoby, A., Stern, A., and Halperin, B. I. (2017). Topological superconductivity in a planar Josephson junction. Phys. Rev. X 7, 021032. doi:10.1103/physrevx.7.021032
Pikulin, D., van Heck, B., Karzig, T., Martinez, E. A., Nijholt, B., Laeven, T., et al. (2021). Protocol to identify a topological superconducting phase in a three-terminal device. arXiv Available at: https://doi.org/10.48550/arXiv.2103.12217.
Pöyhönen, K., Moghaddam, A. G., and Ojanen, T. (2022). Many-body entanglement and topology from uncertainties and measurement-induced modes. Phys. Rev. Res. 4, 023200. doi:10.1103/physrevresearch.4.023200
Prada, E., San-Jose, P., de Moor, M. W. A., Geresdi, A., Lee, E. J. H., Klinovaja, J., et al. (2020). From Andreev to Majorana bound states in hybrid superconductor–semiconductor nanowires. Nat. Rev. Phys. 2, 575–594. doi:10.1038/s42254-020-0228-y
Puglia, D., Martinez, E. A., Ménard, G. C., Pöschl, A., Gronin, S., Gardner, G. C., et al. (2021). Closing of the induced gap in a hybrid superconductor-semiconductor nanowire. Phys. Rev. B 103, 235201. doi:10.1103/physrevb.103.235201
Qi, X.-L., Hughes, T. L., and Zhang, S.-C. (2010). Chiral topological superconductor from the quantum Hall state. Phys. Rev. B 82, 184516. doi:10.1103/physrevb.82.184516
Radu, I. P., Miller, J. B., Marcus, C. M., Kastner, M. A., Pfeiffer, L. N., and West, K. W. (2008). Quasi-particle properties from tunneling in the v = 5/2 fractional quantum Hall state. Science 320, 899–902. doi:10.1126/science.1157560
Read, N., and Green, D. (2000). Paired states of fermions in two dimensions with breaking of parity and time-reversal symmetries and the fractional quantum Hall effect. Phys. Rev. B 61, 10267–10297. doi:10.1103/physrevb.61.10267
Rech, J., Jonckheere, T., Grémaud, B., and Martin, T. (2020). Negative delta-T noise in the fractional quantum Hall effect. Phys. Rev. Lett. 125, 086801. doi:10.1103/physrevlett.125.086801
Regan, E. C., Wang, D., Paik, Y., MacDonald, A. H, Zeng, Y., Zhang, L., et al. (2022). Emerging exciton physics in transition metal dichalcogenide heterobilayers. Nat. Rev. Mater. 7, 778–795. doi:10.1038/s41578-022-00440-1
Rosdahl, T. O., Vuik, A., Kjaergaard, M., and Akhmerov, A. R. (2018). Andreev rectifier: a nonlocal conductance signature of topological phase transitions. Phys. Rev. B 97, 045421. doi:10.1103/physrevb.97.045421
Rosenow, B., Levkivskyi, I. P., and Halperin, B. I. (2016). Current correlations from a mesoscopic anyon collider. Phys. Rev. Lett. 116, 156802. doi:10.1103/physrevlett.116.156802
Rosenow, B., and Stern, A. (2020). Flux superperiods and periodicity transitions in quantum Hall interferometers. Phys. Rev. Lett. 124, 106805. doi:10.1103/physrevlett.124.106805
Ruelle, M., Frigerio, E., Berroir, J.-M., Plaçais, B., Rech, J., Cavanna, A., et al. (2023). Comparing fractional quantum Hall Laughlin and jain topological orders with the anyon collider. Phys. Rev. X 13, 011031. doi:10.1103/physrevx.13.011031
Ryu, S., Schnyder, A. P., Furusaki, A., and Ludwig, A. W. (2010). Topological insulators and superconductors: tenfold way and dimensional hierarchy. New J. Phys. 12, 065010. doi:10.1088/1367-2630/12/6/065010
Saminadayar, L., Glattli, D. C., Jin, Y., and Etienne, B. (1997). Nature 389, 162. doi:10.1103/PhysRevLett.79.2526
San-Jose, P., Prada, E., and Aguado, R. (2012). Ac Josephson effect in finite-length nanowire junctions with majorana modes. Phys. Rev. Lett. 108, 1. doi:10.1103/PhysRevLett.108.257001
Sarma, S. D., and Pan, H. (2023). Disorder effects on the so-called andreev band in majorana nanowires. arXiv:2306.10041 [cond-mat.mes-hall] Available at: https://doi.org/10.48550/arXiv.2306.10041.
Schiller, N., Katzir, B. A., Stern, A., Berg, E., Lindner, N. H., and Oreg, Y. (2022b). Interplay of superconductivity and dissipation in quantum hall edges.
Schiller, N., Oreg, Y., and Snizhko, K. (2022a). Extracting the scaling dimension of quantum Hall quasiparticles from current correlations. Phys. Rev. B 105, 165150. doi:10.1103/physrevb.105.165150
Schindler, F., Cook, A. M., Vergniory, M. G., Wang, Z., Parkin, S. S., Andrei Bernevig, B., et al. (2018b). Higher-order topological insulators. Sci. Adv. 4, eaat0346. doi:10.1126/sciadv.aat0346
Schindler, F., Wang, Z., Vergniory, M. G., Cook, A. M., Murani, A., Sengupta, S., et al. (2018a). Higher-order topology in bismuth. Nat. Phys. 14, 918–924. doi:10.1038/s41567-018-0224-7
Schrade, C., and Fu, L. (2022). Quantum computing with majorana kramers pairs. Phys. Rev. Lett. 129, 227002. doi:10.1103/physrevlett.129.227002
Schüffelgen, P., Rosenbach, D., Li, C., Schmitt, T. W., Schleenvoigt, M., Jalil, A. R., et al. (2019). Selective area growth and stencil lithography for in situ fabricated quantum devices. Nat. Nanotechnol. 14, 825–831. doi:10.1038/s41565-019-0506-y
Sela, E., Oreg, Y., Plugge, S., Hartman, N., Lüscher, S., and Folk, J. (2019). Detecting the universal fractional entropy of majorana zero modes. Phys. Rev. Lett. 123, 147702. doi:10.1103/physrevlett.123.147702
Shabani, J., Liu, Y., Shayegan, M., Pfeiffer, L. N., West, K. W., and Baldwin, K. W. (2013). Phys. Rev. B 88, 245413. doi:10.1103/PhysRevB.88.245413
Shchennikov, V. V., and Ovsyannikov, S. V. (2003). Thermoelectric power, magnetoresistance of lead chalcogenides in the region of phase transitions under pressure. Solid State Commun. 126, 373–378. doi:10.1016/s0038-1098(03)00210-2
Shen, S.-Q. (2012). Topological insulators: Dirac equation in condensed matters. Berlin, Germany: Springer.
Shytov, A. V., Levitov, L. S., and Halperin, B. I. (1998). Tunneling into the edge of a compressible quantum Hall state. Phys. Rev. Lett. 80, 141–144. doi:10.1103/physrevlett.80.141
Singh, R., and Muralidharan, B. (2023). Conductance spectroscopy of Majorana zero modes in superconductor-magnetic insulator nanowire hybrid systems. Commun. Phys. 6, 36. doi:10.1038/s42005-023-01147-7
Smirnov, S. (2021b). Majorana ensembles with fractional entropy and conductance in nanoscopic systems. Phys. Rev. B 104, 205406. doi:10.1103/physrevb.104.205406
Smirnov, S. (2021a). Majorana entropy revival via tunneling phases. Phys. Rev. B 103, 075440. doi:10.1103/physrevb.103.075440
Smirnov, S. (2019). Majorana finite-frequency nonequilibrium quantum noise. Phys. Rev. B 99, 165427. doi:10.1103/physrevb.99.165427
Smirnov, S. (2022). Revealing universal Majorana fractionalization using differential shot noise and conductance in nonequilibrium states controlled by tunneling phases. Phys. Rev. B 105, 205430. doi:10.1103/physrevb.105.205430
Snizhko, K., and Cheianov, V. (2015). Scaling dimension of quantum Hall quasiparticles from tunneling-current noise measurements. Phys. Rev. B 91, 195151. doi:10.1103/physrevb.91.195151
Spielman, I. B., Eisenstein, J. P., Pfeiffer, L. N., and West, K. W. (2000). Resonantly enhanced tunneling in a double layer quantum Hall ferromagnet. Phys. Rev. Lett. 84, 5808–5811. doi:10.1103/physrevlett.84.5808
Sriram, P., Kalantre, S. S., Gharavi, K., Baugh, J., and Muralidharan, B. (2019). Supercurrent interference in semiconductor nanowire Josephson junctions. Phys. Rev. B 100, 155431. doi:10.1103/physrevb.100.155431
Stanescu, T. D., and Tewari, S. (2013). Majorana fermions in semiconductor nanowires: fundamentals, modeling, and experiment. J. Phys. Condens. Matter 25, 233201. doi:10.1088/0953-8984/25/23/233201
Stern, A., and Halperin, B. I. (2006). Proposed experiments to probe the non-abelianν=5/2quantum Hall state. Phys. Rev. Lett. 96, 016802. doi:10.1103/physrevlett.96.016802
Stern, M., Plochocka, P., Umansky, V., Maude, D. K., Potemski, M., and Bar-Joseph, I. (2010). Optical probing of the spin polarization of theν=5/2quantum Hall state. Phys. Rev. Lett. 105, 096801. doi:10.1103/physrevlett.105.096801
Taskin, A. A., Ren, Z., Sasaki, S., Segawa, K., and Ando, Y. (2011). Observation of Dirac holes and electrons in a topological insulator. Phys. Rev. Lett. 107, 016801. doi:10.1103/physrevlett.107.016801
Thakurathi, M., Simon, P., Mandal, I., Klinovaja, J., and Loss, D. (2018). Phys. Rev. B 97, 1. doi:10.1103/PhysRevB.98.245404
Thouless, D. J., Kohmoto, M., Nightingale, M. P., and den Nijs, M. (1982). Quantized Hall conductance in a two-dimensional periodic potential. Phys. Rev. Lett. 49, 405–408. doi:10.1103/physrevlett.49.405
Vaezi, A., and Barkeshli, M. (2014). Fibonacci anyons from abelian bilayer quantum Hall states. Phys. Rev. Lett. 113, 236804. doi:10.1103/physrevlett.113.236804
Vaitiekėnas, S., Liu, Y., Krogstrup, P., and Marcus, C. M. (2021). Zero-bias peaks at zero magnetic field in ferromagnetic hybrid nanowires. Nat. Phys. 17, 43–47. doi:10.1038/s41567-020-1017-3
Venkatachalam, V., Yacoby, A., Pfeiffer, L., and West, K. (2011). Local charge of the ν = 5/2 fractional quantum Hall state. Nature 469, 185–188. doi:10.1038/nature09680
von Keyserlingk, C. W., Simon, S. H., and Rosenow, B. (2015). Enhanced bulk-edge Coulomb coupling in fractional fabry-perot interferometers. Phys. Rev. Lett. 115, 126807. doi:10.1103/physrevlett.115.126807
Vuik, A., Eeltink, D., Akhmerov, A. R., and Wimmer, M. (2016). Effects of the electrostatic environment on the Majorana nanowire devices. New J. Phys. 18, 033013. doi:10.1088/1367-2630/18/3/033013
Vuik, A., Nijholt, B., Akhmerov, A. R., and Wimmer, M. (2019). Reproducing topological properties with quasi-Majorana states. SciPost Phys. 7, 61. doi:10.21468/SciPostPhys.7.5.061
Wang, A. Q., Li, C. Z., Li, C., Liao, Z. M., Brinkman, A., and Yu, D. P. (2018). 4π-Periodic supercurrent from surface states in Cd3As2 nanowire-based Josephson junctions. Phys. Rev. Lett. 121, 237701. doi:10.1103/physrevlett.121.237701
Wang, Z., Weng, H., Wu, Q., Dai, X., and Fang, Z. (2013). Phys. Rev. B - Condens. Matter Mater. Phys. 88, 1. doi:10.1103/PhysRevB.88.125427
Wen, X.-G. (2007). Quantum field theory of many-body systems: From the origin of sound to an origin of light and electrons. Oxford: Oxford Academic.
Wiedenmann, J., Bocquillon, E., Deacon, R. S., Hartinger, S., Herrmann, O., Klapwijk, T. M., et al. (2016). 4π-periodic Josephson supercurrent in HgTe-based topological Josephson junctions. Nat. Commun. 7, 1. doi:10.1038/ncomms10303
Wieder, B. J., Wang, Z., Cano, J., Dai, X., Schoop, L. M., Bradlyn, B., et al. (2020). Electric-field-driven non-volatile multi-state switching of individual skyrmions in a multiferroic heterostructure. Nat. Commun. 11, 1. doi:10.1038/s41467-020-17354-7
Wilczek, F. (1990). Fractional statistics and anyon superconductivity. Ser. Dir. Condens. Matter Phys. 10, 1. doi:10.1142/0961
Wilczek, F. (1982). Quantum mechanics of fractional-spin particles. Phys. Rev. Lett. 49, 957–959. doi:10.1103/physrevlett.49.957
Willett, R., Eisenstein, J. P., Störmer, H. L., Tsui, D. C., Gossard, A. C., and English, J. H. (1991). Nucl. Phys. B 360, 362.
Willett, R., Eisenstein, J. P., Störmer, H. L., Tsui, D. C., Gossard, A. C., and English, J. H. (1987). Observation of an even-denominator quantum number in the fractional quantum Hall effect. Phys. Rev. Lett. 59, 1776–1779. doi:10.1103/PhysRevLett.59.1776
Willett, R. L., Nayak, C., Shtengel, K., Pfeiffer, L. N., and West, K. W. (2013). Magnetic-field-tuned aharonov-bohm oscillations and evidence for non-abelian anyons atν=5/2. Phys. Rev. Lett. 111, 186401. doi:10.1103/physrevlett.111.186401
Willett, R. L., Pfeiffer, L. N., and West, K. W. (2010). Alternation and interchange of e/4 and e/2 period interference oscillations consistent with filling factor 5/2 non-Abelian quasiparticles. Phys. Rev. B 82, 205301. doi:10.1103/physrevb.82.205301
Willett, R. L., Pfeiffer, L. N., and West, K. W. (2009). Measurement of filling factor 5/2 quasiparticle interference with observation of charge e/4 and e/2 period oscillations. PNAS 106, 8853–8858. doi:10.1073/pnas.0812599106
Willett, R. L., Shtengel, K., Nayak, C., Pfeiffer, L. N., Chung, Y. J., Peabody, M. L., et al. (2019). Interference measurements of non-abelian e/4 and abelian e/2 quasiparticle braiding. Available at: https://doi.org/10.1103/PhysRevX.13.011028.
Winkler, G. W., Antipov, A. E., van Heck, B., Soluyanov, A. A., Glazman, L. I., Wimmer, M., et al. (2019). Unified numerical approach to topological semiconductor-superconductor heterostructures. Phys. Rev. B 99, 245408. doi:10.1103/physrevb.99.245408
Wölms, K., Stern, A., and Flensberg, K. (2016). Braiding properties of majorana kramers pairs. Phys. Rev. B 93, 045417. arXiv:1507.02881. doi:10.1103/physrevb.93.045417
Xu, S. Y., Liu, C., Kushwaha, S. K., Sankar, R., Krizan, J. W., Belopolski, I., et al. (2015). Observation of Fermi arc surface states in a topological metal. Science 347, 294–298. doi:10.1126/science.1256742
Yang, G., and Feldman, D. E. (2013). Influence of device geometry on tunneling in the \nu = 5/2 quantum Hall liquid. Phys. Rev. B 88, 085317. doi:10.1103/PhysRevB.88.085317
Zhang, D., Falson, J., Schmult, S., Dietsche, W., and Smet, J. H. (2020). Quasiparticle tunneling across an exciton condensate. Phys. Rev. Lett. 124, 246801. doi:10.1103/physrevlett.124.246801
Zhang, F., Kane, C. L., and Mele, E. J. (2013). Time-reversal-invariant topological superconductivity and majorana kramers pairs. Phys. Rev. Lett. 111, 056402. doi:10.1103/physrevlett.111.056402
Zhang, H., de Moor, M. W. A., Bommer, J. D. S., Xu, D., Wang, G., van Loo, N., et al. (2021). Large zero-bias peaks in insb-al hybrid semiconductor-superconductor nanowire devices. arXiv:2101.11456 [cond-mat.mes-hall], Available at: https://doi.org/10.48550/arXiv.2101.11456.
Zhang, H., Liu, C.-X., Gazibegovic, S., Xu, D., Logan, J. A., Wang, G., et al. (2018). Retracted article: quantized majorana conductance. Nature 556, 74–79. doi:10.1038/nature26142
Zhang, H., Liu, C.-X., Qi, X.-L., Dai, X., Fang, Z., and Zhang, S.-C. (2009). Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nat. Phys. 5, 438–442. doi:10.1038/nphys1270
Zhang, H., Liu, D. E., Wimmer, M., and Kouwenhoven, L. P. (2019). Next steps of quantum transport in Majorana nanowire devices. Nat. Commun. 10, 5128. doi:10.1038/s41467-019-13133-1
Zhang, J., Chang, C. Z., Zhang, Z., Wen, J., Feng, X., Li, K., et al. (2011). Band structure engineering in (Bi(1-x)Sb(x)(2)Te(3) ternary topological insulator. Nat. Commun. 2, 1. doi:10.1038/ncomms1588
Zhao, T., Faugno, W. N., Pu, S., Balram, A. C., and Jain, J. K. (2021). Origin of the ν=1/2 fractional quantum Hall effect in wide quantum wells. Phys. Rev. B 103, 155306. doi:10.1103/physrevb.103.155306
Keywords: Majorana bound state, superconducting proximity effect, non-Abelian state, 5/2 fractional quantum Hall state, topological superconductivity, higher-order topological states
Citation: Muralidharan B, Kumar M and Li C (2023) Emerging quantum hybrid systems for non-Abelian-state manipulation. Front. Nanotechnol. 5:1219975. doi: 10.3389/fnano.2023.1219975
Received: 09 May 2023; Accepted: 31 August 2023;
Published: 13 October 2023.
Edited by:
Syed Arshad Hussain, Tripura University, IndiaReviewed by:
Mitsuki Ito, National Institute of Technology, Kushiro College, JapanNarayan Mohanta, Indian Institute of Technology Roorkee, India
Copyright © 2023 Muralidharan, Kumar and Li. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Chuan Li, Y2h1YW4ubGlAdXR3ZW50ZS5ubA==
 Bhaskaran Muralidharan
Bhaskaran Muralidharan Manohar Kumar
Manohar Kumar Chuan Li
Chuan Li