- 1Plutonium Fuel Development Center, Sector of Nuclear Fuel, Decommissioning and Waste Management Technology Development, Japan Atomic Energy Agency, Tokai-Mura, Ibaraki, Japan
- 2Nuclear Plant Innovation Promotion Office, Japan Atomic Energy Agency, Oarai-Machi, Japan
The diffusion phenomena in uranium–plutonium mixed oxides U1−yPuyO2 dictate the physicochemical properties of mixed oxides (MOX) nuclear fuel throughout manufacturing, irradiation, and storage. More precisely, it is paramount to estimate the cation interdiffusion insofar as it dovetails with the actinide redistribution during sintering and under irradiation. This paper draws a critical review of the existing experimental data of U and Pu interdiffusion coefficients in MOX fuel.
1 Introduction
The diffusion phenomena in solids dictate their physicochemical properties, such as redox behavior, melting point, recrystallization, creep, sintering, and ionic conductivity, among others. In the nuclear industry, these diffusion properties are of paramount interest since they directly impact the in-pile performances of the fuel and hence the safety of the reactor. For instance, uranium–plutonium U1−yPuyO2 mixed oxides (MOX), with various compositions, are used for decades for nuclear power all over the world (Olander, 2009; Baron et al., 2020; Kato et al., 2020; Dudarev, 2022; Kato and Machida, 2022). During their lifetime, MOX fuel pellets undergo the harshest temperature, atmosphere, and irradiation conditions. More precisely, green compacts are sintered at elevated temperature, usually around 2,000 K, in highly reducing atmosphere (hydrogen-containing gas mixture) (Ramaniah, 1982; Okita et al., 2000; Vauchy et al., 2014a). Under irradiation, because of the concomitant fission reactions and the coolant’s action, a thermal gradient (up to ∼300 K/mm) occurs along the MOX pellet radius and induces a rapid restructuring of the fuel (Bober et al., 1973; Noirot et al., 2008; Maeda et al., 2009a; Maeda et al., 2009b; Van Uffelen et al., 2010; Ishimi et al., 2019; Kato and Greenspan, 2021; Ozawa et al., 2021). During both these high temperature stages, actinide cations migrate to mix up and segregate, respectively. MOX fuels are therefore always subjected to strong chemical gradients (oxygen and cations). Due to their outstanding atomic weight (MU−Pu ≥ 238 u), these actinides hardly move and need a significant addition of energy to diffuse, hence the extreme sintering temperature.
As their chemical and radiological toxicities are potentially lethal (International Commission on Radiological Protection, 1996; Voeltz, 2000; Rodriguez and Wexler, 2014), Pu-bearing solids need to be handled in dedicated confined environments (glove boxes); thus, they are challenging to study. Only a handful of diffusion coefficients in actinide-bearing oxides are published, anionic and cationic combined. Particularly, the physicochemical processes associated with cation diffusion are remarkably complex, and their scanty migration is hardly measurable. Within this frame, this paper draws a review of the available experimental data on cation interdiffusion coefficients in U–Pu dioxides, since they are the very key for manufacturing and in-pile behaviors.
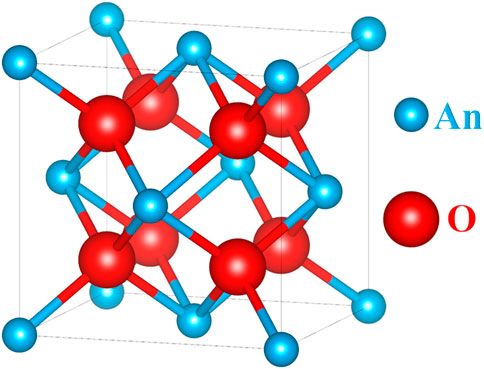
2 Crystal structure and defect chemistry of actinide dioxides
Actinide dioxides (AnO2) are known to crystallize in a fluorite structure (CaF2 type), space group
Even at room-temperature, this crystal structure can accommodate large deviations from oxygen stoichiometry (O/An = 2) as evidenced in the pure poles UO2+x (Geønvold and Haraldsen, 1948), PuO2−x (Gardner et al., 1965), AmO2−x (Chikalla and Eyring, 1968), CmO2−x (Mosley, 1972), BkO2−x (Baybarz, 1968), and CfO2−x (Baybarz et al., 1972) as well as in the respective solid solutions, the most studied being U1−yPuyO2±x Markin and Street, 1967), U1−yAmyO2±x (Bartscher and Sari, 1983), and Pu1−yAmyO2−x (Vauchy et al., 2017).
These deviations from stoichiometry and irradiation defects both induce severe lattice defects and can also enhance atomic diffusion (Kilner et al., 1981; Matzke, 1983a; Ferry et al., 2005; Smirnov and Elmanov, 2016). Due to the large mass of the actinide atoms, cationic vacancies and/or interstitials are unprobeable; thus, only the anion sub-lattice (oxygen) supports the defects (Belle, 1961; Atlas et al., 1966; Matzke and Sørensen, 1981; Matzke, 1987), namely, oxygen vacancies (
3 Interdiffusion vs. self-diffusion
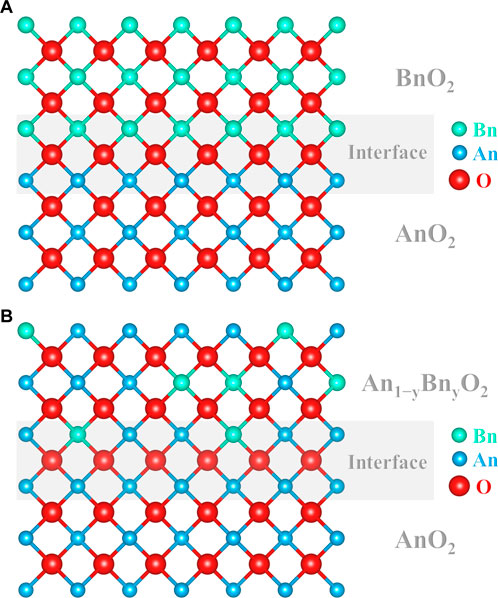
Diffusion in binary substitutional solid solutions is called interdiffusion. This corresponds to the thermally activated atomic transport of species in a chemical potential field as they tend to rearrange to uniformize the molecular distribution in the medium. Interdiffusion then describes the tendency of two materials of different chemical compositions (usually as a diffusion couple) to homogenize as a function of thermodynamic conditions. Figures 2A,B schematically illustrates two examples of diffusion couples, AnO2/BnO2 and AnO2/An1−yBnyO2, respectively (An and Bn having different Z numbers). In both cases, a cationic chemical gradient exists between the two lattices and hence can be defined as interdiffusion.
Once the chemical equilibrium is established, i.e., no chemical gradient remains, the diffusion phenomena that take place in such a medium only correspond to the Brownian motion of the constituting atom. This is known as the self-diffusion (Crank, 1957; Murch, 2001; Mehrer, 2007).
Studies on actinide dioxides often report “tracer diffusion” of a given species, which are claimed to be “self-diffusion.” Figure 3 shows a schematic representation of the three experimental cases encountered in the literature for cation “self-diffusion” measurements in AnO2.
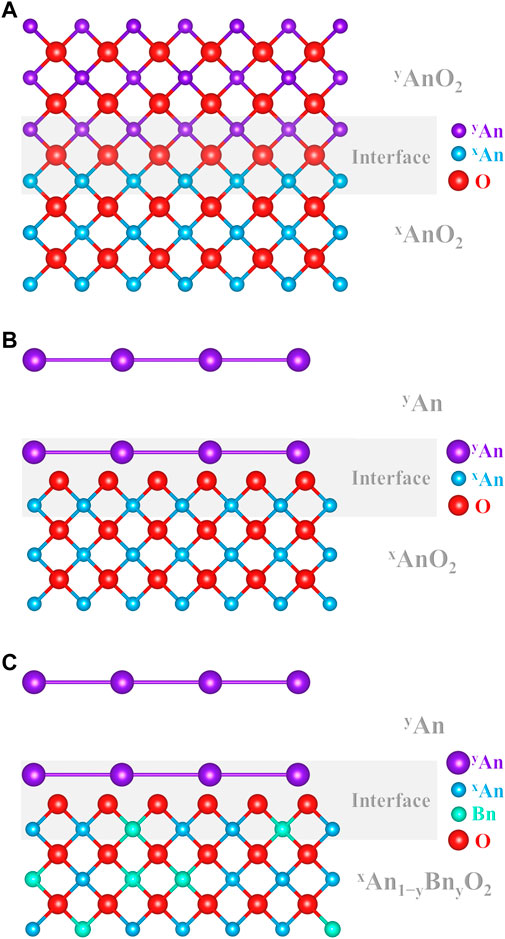
FIGURE 3. Schematic representation of (A) isotopic self-diffusion between yAnO2 and xAnO2, (B) tracer layer deposition yAn on xAnO2, and (C) tracer layer deposition yAn on xAn1−yBnyO2.
The first case (Figure 3A) corresponds to contacting two samples of the exact same chemical composition AnO2 but with different isotopic compositions, one being enriched in a given isotope yAn compared with the host material (xAn). The couple is then annealed, allowing yAnO2 to diffuse in xAnO2, and the yAn/xAn diffusion profile is analyzed. To the best of our knowledge, this is the very definition of measuring self-diffusion. Unfortunately, this type of experimental study is rarely carried out on actinide dioxides (Nagels et al., 1966; Sabioni et al., 1998). Albeit being of prime importance, these results are excluded from the discussion as this review focuses on interdiffusion.
On the other hand, a chemical gradient cannot be excluded in the next two examples of “tracer diffusion” experiments. The associated published data on (U, Pu)O2 will then be considered in this review, in addition to the “real” interdiffusion measurements.
The second case (Figure 3B) shows the typical experimental procedure proposed in the literature to investigate An self-diffusion in AnO2 (Auskern and Belle, 1961; Schmitz and Lindner, 1963; Alcock et al., 1966; Yajima et al., 1966; Matzke, 1969; Matzke, 1973; Matzke, 1983b; Glasser-Leme and Matzke, 1983; Ma, 2017). Normally, this technique consists in depositing a thin layer (by evaporation/condensation) of a pure isotope yAn (usually more α-active than xAn, e.g., 238Pu or 233U) on a polished surface of a specimen xAnO2 (UO2, PuO2, or their solid solution), and the migration of this species is observed in the host lattice using α-spectrometry (Marin and Coniglio, 1966; Hawkins and Alcock, 1968). It is very unlikely that the deposited layer and the substrate material are of the same chemical composition. Indeed, the deposition process is operated in a high vacuum and induces the condensation of a metallic layer on the substrate (Schmitz and Lindner, 1963; Wade, 1971; Wade et al., 1978). An obvious oxygen chemical gradient is then present between the substrate and the layer and may dramatically enhance the diffusion of An in AnO2. One may accept these data as self-diffusion due to the claimed infinitesimal thickness of the said layer and/or due to its hypothetical oxidation, regardless of the published studies that show it is metallic. However, we believe that the associated results cannot be accepted as pure self-diffusion.
The third case (Figure 3C) and the second case are very similar, except the small, yet important, difference in the chemical composition of the host lattice. Indeed, yAn is deposited on the surface of a xAn1−yBnyO2 material (An and Bn being different elements). Regrettably, this technique is also widely used to determine “self-diffusion” coefficients of a species An in a host material (Schmitz and Lindner, 1965; Lindner et al., 1967; Riemer and Scherff, 1971; Matzke, 1973; Matzke and Lambert, 1974; Schmitz, Marajofsky; Lambert, 1978; Matzke, 1983a; Matzke, 1983b; Noyau, 2012; Noyau et al., 2012). For some reason, even if one may consider that the second example is suitable for An self-diffusion in AnO2, this simplification cannot be accepted here. Even in the ideal case of a spontaneously oxidized layer to the same O/An ratio than that of the substrate, the presence of another atom Bn in the cation sub-lattice makes it impossible to accept it as self-diffusion. Neglecting or denying the existence of this chemical gradient may induce severe experimental biases when interpreting the data as pure “self-diffusion.” Indeed, interdiffusion coefficients are of several orders of magnitude larger than that of self-diffusion (Matzke, 1990). When these experimental values of the so-called self-diffusion are used for calculations and/or fuel performance codes, this may be especially problematic.
4 Determination of the interdiffusion coefficients
4.1 Bulk vs. grain boundary diffusion
A polycrystalline material is often considered as a semi-infinite medium composed of adjacent crystals that are separated by grain boundaries. Most of the uranium–plutonium MOX studied are polycrystalline specimens, and the influence of both lattice and grain boundary diffusions needs to be described.
Bulk, or lattice, diffusion refers to the migration of atoms within the volume of a crystal (grain). In the case of interdiffusion measurements, bulk diffusion corresponds to the net mass transport through the surface of the grains. Figure 4 shows an illustration with contacted single crystals with species A diffusing in the B lattice.
Harrison proposed three types of grain boundary diffusion kinetics in polycrystalline materials (Harrison, 1961). Figure 5 illustrates these kinetics with species A diffusing (considered infinite) in the B lattice.
The first type (Figure 5A) corresponds to the situation where bulk diffusion is negligible and where a significant grain boundary diffusion occurs. A sharp composition transition is observed between the grain boundaries and the bulk of the grains. This type of diffusion behavior is observed in the first steps of an interdiffusion experiment.
The second type (Figure 5B) corresponds to the situation where the lattice diffusion cannot be considered as negligible anymore. A composition gradient is then established between the grain boundaries and the bulk of the grains. This type of diffusion behavior is observed when the annealing time and/or temperature increases compared to the first type.
The last type (Figure 5C) corresponds to the situation where the grain boundary and bulk diffusion kinetics are similar. Only a slight composition gradient remains between the grain boundaries and the bulk of the grains. Usually, this type of behavior is observed when the diffusion distance is much larger than the grain size and the diffusion fields of the neighboring grains overlap.
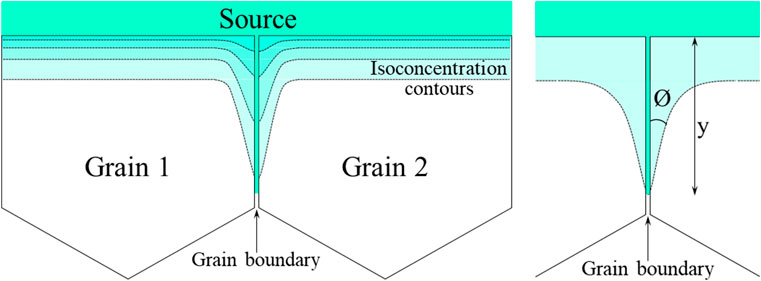
In most experiments, the second type of diffusion is observed and is quantified by measuring the isoconcentration contours in adjacent grains along the boundaries (Figure 6).
Bulk and grain boundary diffusions can be very different in polycrystalline materials, the latter being known to be “pathways” or “shortcuts” for atomic transport (Fisher, 1951; Knorr et al., 1989). Indeed, differences of several orders of magnitude are usually reported between these two types of diffusion resulting from the high level of disorientation of the atoms located along the grain boundaries. In practice, authors rarely differentiate these two effects, and averages are usually calculated in polycrystalline materials. On the other hand, some studies involving single crystals are also reported. Studying such materials allows extracting the bulk diffusion due to the nonexistence of grain boundaries; however, it could also raise questions of preferential penetrations with respect to crystal orientation. This problem is being ignored in polycrystals as a result of the random grain orientation.
For example, Figure 7 shows real EPMA elemental mappings of a diffusion couple A–B (arbitrary gray levels), corresponding to the second case of grain boundary diffusion (Figure 5B).
The grain boundary diffusion can usually be determined by three different means (Le Claire, 1963; Peterson, 1983):
- Measuring the distance of the diffusion apex from the surface (“y” in Figure 6).
- Measuring the angle (“Ø” in Figure 6) between the grain boundary and the tangent to a concentration contour.
- Measuring the amount of diffusing species in slices parallel to the interface plane.
4.2 Experimental techniques
In crystalline materials, the interdiffusion coefficients are usually determined directly via the preparation of diffusion couples and subsequent annealing. Each specimen is polished to obtain a surface roughness appropriate for contact. The samples are then annealed to allow species diffusion, and their concentration is determined as a function of their depth of penetration, usually by electron probe microanalysis (EPMA) (Oishi et al., 1981; Sakka et al., 1982; Dean and Goldstein, 1986; Léchelle et al., 2012) or ion beam analysis [e.g., Rutherford backscattering spectrometry, nuclear reaction analysis or secondary ion mass spectrometry (Ishigaki et al., 1987; Vauchy et al., 2015a; Jeynes and Colaux, 2016)]. The “diffusion profile” is the variation in the elemental concentration with the perpendicular distance from the interface plane (see Figure 7). Other ion beam analysis techniques are also encountered for depth profiling.
4.3 Mathematical approach
Solids submitted to a spatial concentration gradient (herein, chemical gradient) tend to homogenize with time and temperature. The resulting flux of atoms (of the same species) is usually noted as
where
Figure 8 shows a representation of the evolution of composition–distance curves with annealing time tn in an ideal A–B interdiffusion couple.
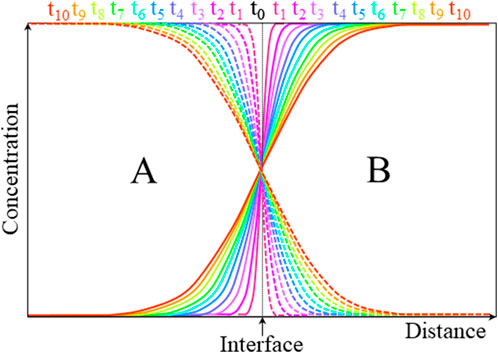
FIGURE 8. Evolution of ideal interdiffusion profiles of species A (dashed) and B (solid) in their mutual lattice with annealing time tn.
If the atomic transport of species A and B is equal and opposite, the lattice structure remains unchanged by the diffusion process, directly leading to the interdiffusion coefficient
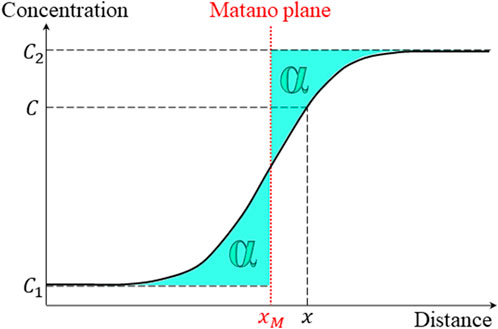
The Boltzmann–Matano method (Boltzmann, 1894; Matano, 1933) is widely used to calculate the interdiffusion coefficients from the elemental depth profiles (one dimensional) shown in Figure 8. The Matano plane is defined as the abscissa at which the two areas α under the diffusion profile curve are equal (Figure 9).
From this representation, Eq. 3 gives the resolution of the diffusion equation:
In practice, species A and B rarely have the same diffusion rates, and their interpenetration induces a shift of the lattice planes called the Kirkendall effect (Kirkendall, 1942). The individual diffusion coefficients of A and B (
where
In this same case, an alternative (and more relevant) method consists in measuring both A and B elemental profiles and resolving the second Fick’s law (Eq. 2). The interdiffusion coefficients of the two species are then directly obtained.
5 Uranium–plutonium interdiffusion coefficients
5.1 Reviewed studies
An exhaustive investigation of the published U–Pu interdiffusion coefficients in their dioxide was attempted in this review (Schmitz and Lindner, 1963; Davies and Novak, 1964; Schmitz and Lindner, 1965; Lindner et al., 1967; Theisen and Vollath, 19671967; Riemer and Scherff, 1971; Schmitz, Marajofsky; Chilton and Edwards, 1978; Lambert, 1978; Glasser-Leme and Matzke, 1982; Matzke, 1983b; Glasser-Leme and Matzke, 1984; Verma, 1984; Glasser-Leme, 1985; Jean-Baptiste and Gallet, 1985; Marin, 1988; Mendez; Kutty et al., 1999; Sato et al., 2010; Noyau, 2012; Berzati, 2013). Most of the available data are from the 1970s–1980s, and recent studies are scarce. Table 1 gives the main details about the studies reviewed here.
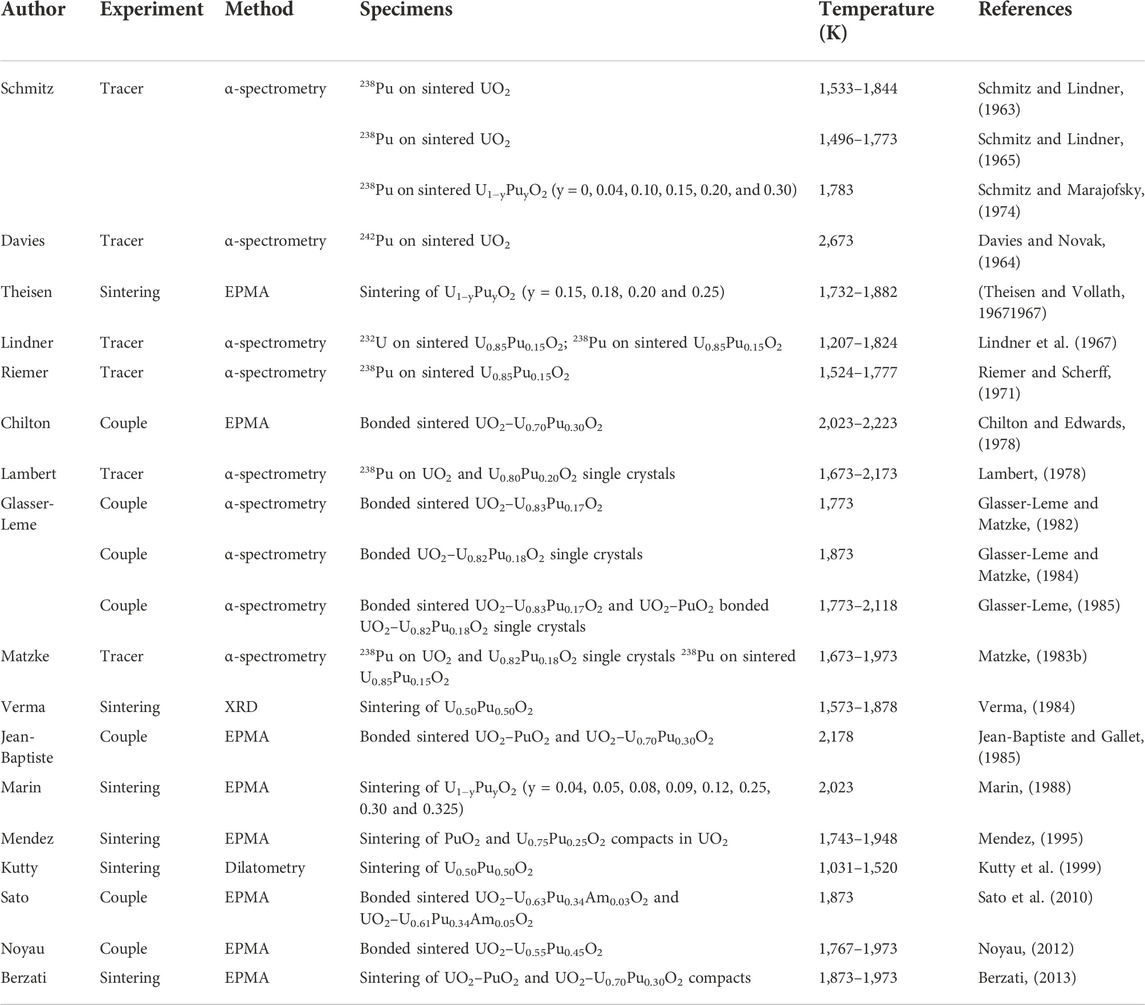
TABLE 1. Description of the type of experiment, analysis method, specimens and temperature ranges of the reviewed studies.
5.2 Relation between
All the available data are gathered in Figure 10 as an Arrhenius diagram. The color of the data points refers to the analysis techniques used.
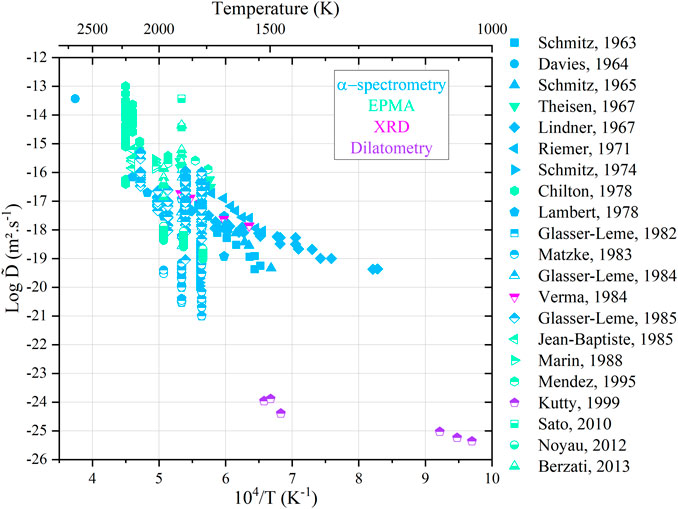
FIGURE 10. Arrhenius diagram for cation interdiffusion coefficients against the reciprocal of the temperature.
The large scattering in the available data may have resulted from the differences in experimental techniques and analysis procedure, among others. However, most of the authors agree that the cationic composition (Pu content) has only a minor influence on the interdiffusion coefficients. A common trend also emerges, i.e.,
For a given temperature, it can be seen clearly that the interdiffusion coefficients can vary by a factor of 108. Indeed, diffusion in oxides is first governed by temperature but also by the oxygen activity in the surrounding gas mixture. In a previous study, we have shown that even if a composition change is not experimentally noticeable between different conditions (T, pO2), significant variations in diffusion coefficients are possible (Vauchy et al., 2015a). A more suitable representation is the variation in
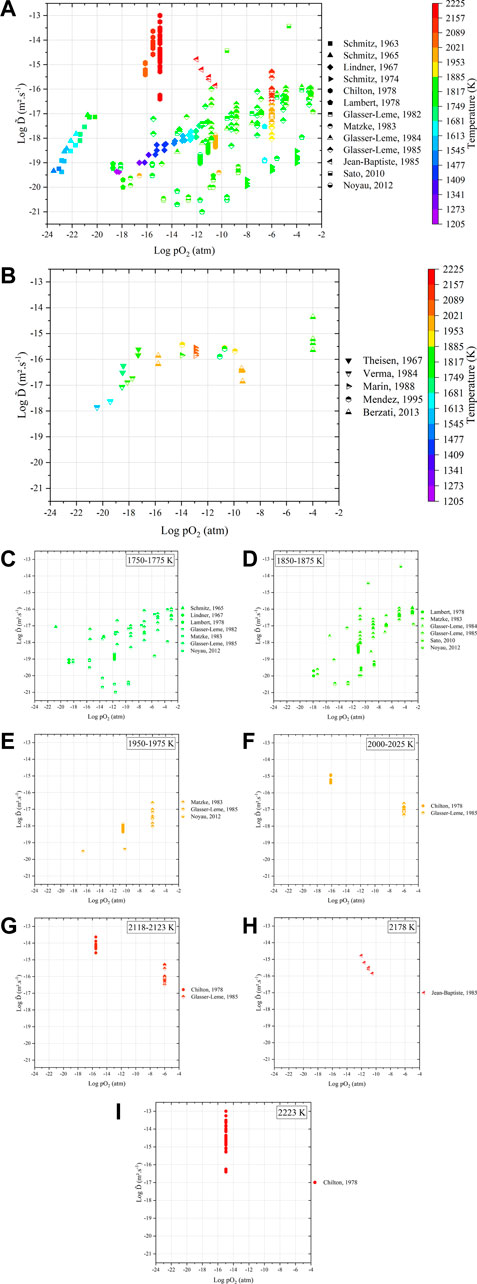
FIGURE 11. Variations in interdiffusion coefficients as a function of temperature and oxygen partial pressure obtained (A) from dense samples and (B) after sintering of green specimens. Details of the variation in
Even in this representation, the experimental results on dense materials remain largely scattered (Figure 11A). As a general trend among the same study, interdiffusion coefficients increase with both pO2 and T (except Chilton et al. and Jean-Baptiste et al.).
Concerning the “sintering” experiments (Figure 11B), the values seem less scattered (10−18–10−14 m2.s−1), but the available data are also more restricted. The values of
5.3 Relation between
To provide a complete understanding of the interdiffusion phenomena, the O/M ratio of the samples studied in the literature was either tabulated or calculated from the Pu content, temperature, and atmosphere conditions with the relation given in (Hirooka et al., 2022). Figure 12 plots the dependence of
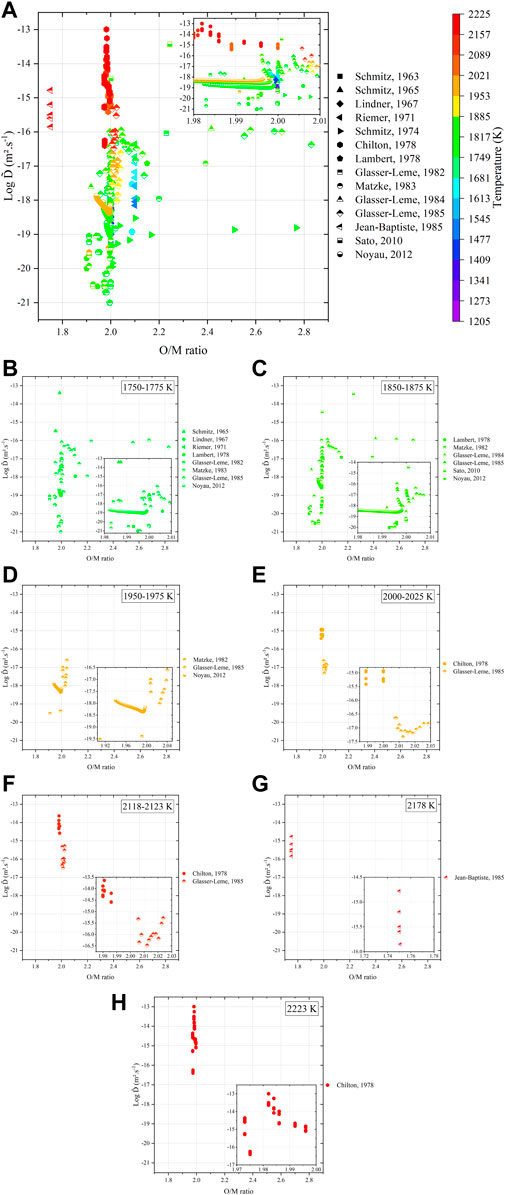
FIGURE 12. Variations in interdiffusion coefficients as a function of (A) O/M ratio of the specimens (tabulated or calculated) and temperature with details at (B) 1,750 K–1,775 K, (C) 1,850 K–1,875 K, (D) 1,950 K–1,975 K, (E) 2,000 K–2,025 K, (F) 2,118 K–2,123 K, (G) 2,178 K, and (H) 2,223 K, respectively.
Regardless of the representation, the literature data still remain largely scattered. One must consider a critical analysis of these data with respect to the experimental procedures. Within this context, the values from Matzke (Matzke, 1983b) and Glasser-Leme (Glasser-Leme and Matzke, 1982; Glasser-Leme and Matzke, 1984) can be considered as doubtful. Indeed, they were carried out on “single crystals” obtained from arc-melted powders, and the melted pool was subsequently cut and polished to obtain a surface suitable for vapor-phased tracer deposition. The problem with this technique (beyond the questions raised in Section 3) resides in the fact that the “crystal” was arbitrary cut, without taking into account its orientation. It is known that the crystal orientation has a strong influence on diffusion properties (Turnbull and Hoffman, 1954; Burriel et al., 2016; Holby, 2019). Therefore, measuring diffusion coefficients without referring to the Miller indices of the associated crystal planes is useless. Furthermore, the “tracer diffusion” experiments, namely, Schmitz (Schmitz and Lindner, 1963; Schmitz and Lindner, 1965; Schmitz, Marajofsky), Lindner (Lindner et al., 1967), Riemer (Riemer and Scherff, 1971), and Lambert (Lambert, 1978), should also be rejected as the nature (composition, thickness, etc.) of the deposited layer is really questionable, and the α-degradation energy method used allows probing only the first atomic layers as the path of α particles in such dense and heavy materials is very restricted. The data obtained by means of this technique cannot be considered as representative of bulk diffusion properties. Unfortunately, only the five investigations, namely, that of Chilton (Chilton and Edwards, 1978), Glasser-Leme (Glasser-Leme, 1985), Jean-Baptiste (Jean-Baptiste and Gallet, 1985), Sato (Sato et al., 2010), and Noyau (Noyau, 2012), are acceptable (Figure 13).
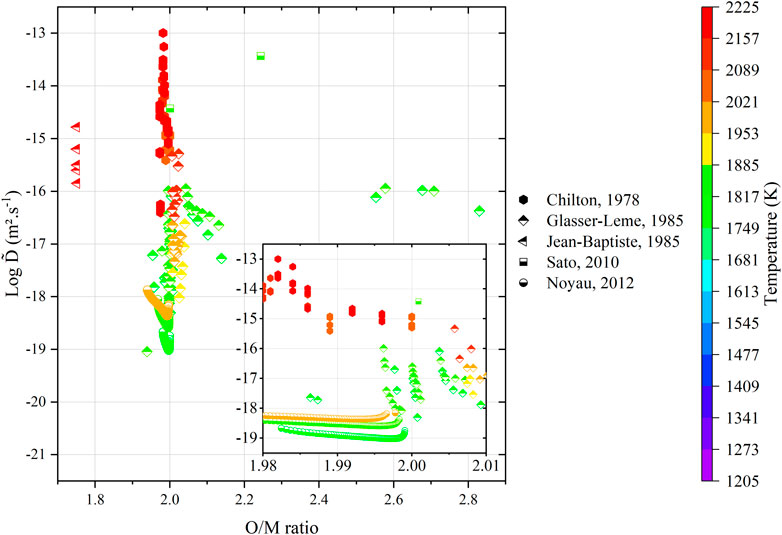
FIGURE 13. Variations in the acceptable interdiffusion coefficients from the literature as a function of O/M ratio of the specimens (tabulated or calculated) and temperature.
As the number of data points is extremely small and scattered, it seems unreasonable to make a direct comparison of the associated
6 Oxygen/metal ratio, oxygen potential, points defects, clusters, and (inter) diffusion
As already detailed, the driving force for interdiffusion in fluorite structures, hence AnO2, is the migration of free oxygen vacancies (in AnO2−x) or interstitials (in AnO2+x) by the hopping process. However, recent studies seem to suggest that some complex cationic charge-compensation mechanisms can take place in U1−yPuyO2±x (Martin et al., 2022), similarly to what was clearly observed in U1−yAmyO2±x mixed oxides (Epifano et al., 2019). Such a behavior could have an effect on the diffusion mechanisms as the crystal lattice would be distorted due to the difference in ionic size of the cations. As these new results need to be confirmed and because they were never experimentally evidenced at elevated temperatures, we will not further discuss their effects on the cation interdiffusion in MOX fuels.
Thus, in hypostoichiometry, the greater the concentration of vacancies, the larger the interdiffusion coefficient. However, the reality is a little different. Indeed, increasing the number of oxygen vacancies induces a reduction of An(IV) to An(III) to keep electroneutrality. These trivalent cations trap the oxygen vacancies, forming uncharged cluster defects (Anderson, 1971; Ando and Oishi, 1983; Bevan et al., 1986; Nakayama and Martin, 2009; Yoshida et al., 2011; Vinograd, Bukaemskiy, Modolo, Deissmann, Bosbach).
For instance, at a given temperature, a decrease in the oxygen potential of a U1−yPuyO2 MOX leads to a decrease in its oxygen/metal ratio by the partial reduction of Pu(IV)–Pu(III) (Kato et al., 2017b; Hirooka et al., 2022). Due to the attractive Coulomb (electrostatic) interaction, trivalent plutonium atoms trap oxygen vacancies, forming the clusters
In hyperstoichiometric (O/M > 2.00) U1−yPuyO2 MOX, the presence of oxygen atoms
The Brouwer diagram given in Figure 14A shows the variations in the concentrations of point defects in U1−yPuyO2, at temperature T, as a function of the oxygen partial pressure. For O/M < 2, decreasing pO2 leads to larger deviations from stoichiometry and thus to a higher concentration in oxygen vacancies. However, these defects (single or double-charged oxygen vacancies,
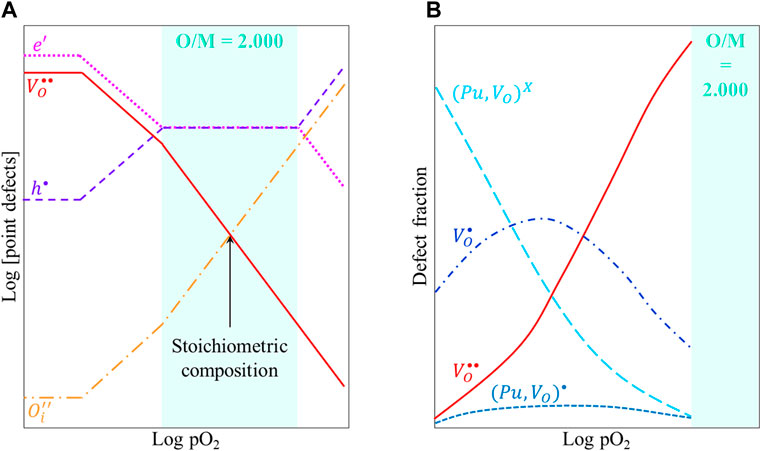
FIGURE 14. (A) Schematic Brouwer diagram and (B) defects fraction as a function of pO2 in U1−yPuyO2±x at a given temperature.
This trapping process can explain the experimental observations of enhanced U–Pu interdiffusion in near stoichiometric compositions, as compared to lower O/M ratios.
More generally, the free-point-defects-mediated diffusion mechanism not only impacts cations but is generic for atomic transport, both in hypo- and hyperstoichiometry. Indeed, oxygen chemical diffusion in AnO2±x was shown to be enhanced at compositions close to O/M = 2.00 (Chereau and Wadier, 1973; Sari, 1978; Bayoǧlu and Lorenzelli, 1979; Bayoǧlu and Lorenzelli, 1984; Stan and Cristea, 2005) as a result of preponderant clustering when the deviation from stoichiometry is increased. This observation remains under discussion among the community as some other studies suggest either an increase or a stagnation in the oxygen chemical diffusion coefficient when the deviation from stoichiometry is increased (Woodley and Gibby, 1973; Kim and Olander, 1981; Kato et al., 2009; Kato et al., 2013; Vauchy et al., 2015b; Watanabe et al., 2015; Watanabe et al., 2017).
7 Diffusion mechanism in AnO2±x fluorite structure
7.1 Empirical crystallographic approach
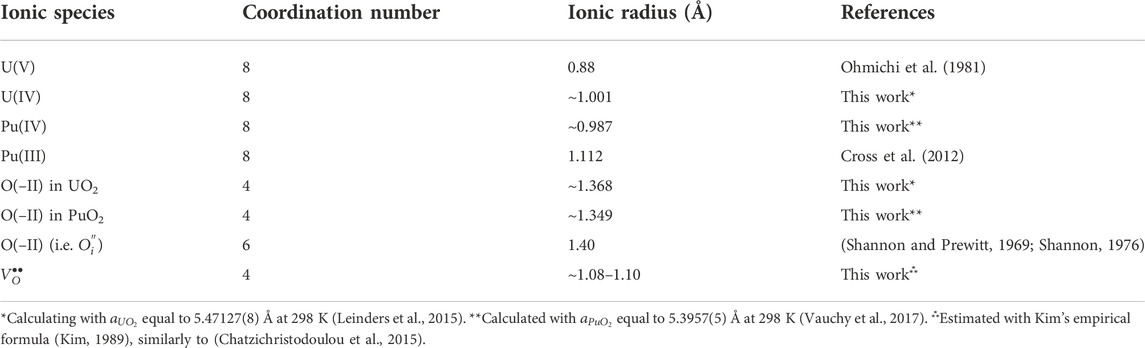
In this section, we propose a diffusion mechanism in AnO2±x based on the crystallographic oxygen defects that the fluorite lattice can accommodate. As the actinide dioxides are known to be ionic crystals, the ionic radii of the constitutive species of the fluorite AnO2±x structure (herein adapted to U1−yPuyO2±x) are either tabulated from the literature or calculated from the respective values in pure, stoichiometric dioxides UO2 and PuO2. Albeit being a very simplistic model, the ions are considered to be contacting hard spheres (sphere packed), since the structure of stoichiometric AnO2 is the lowest-energy configuration.
Thus, in the fluorite structure of the pure, stoichiometric, AnO2 dioxide, the O(–II) ionic radius
As the lattice parameter
Figure 15 schematically shows the resulting fluorite structure of hypo- and hyperstoichiometric actinide dioxide AnO2±x.
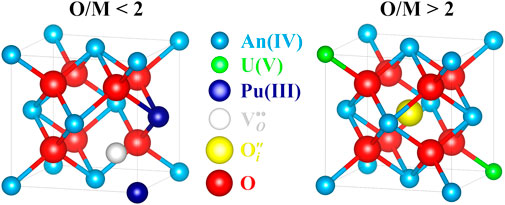
FIGURE 15. Hypo- and hyperstoichiometry lattice defects in AnO2±x (U1−yPuyO2±x) fluorite structure (atoms drawn proportionally to their ionic radii). The cluster
7.1.1 Interdiffusion in hypostoichiometry (O/M < 2)
Hypostoichiometry in AnO2 is defined as an O/M ratio lower than the reference value 2. In this composition range, the concentration in oxygen vacancies is larger than that of interstitial oxygen atoms, the metal lattice being conserved (see Section 2). Contrary to some common beliefs, the size of oxygen vacancies is smaller than that of the anion. The lattice locally collapses around the vacancy due to the electrostatic interactions (repulsions) between the constitutive ions of the crystal (Marrocchelli et al., 2013; Chatzichristodoulou et al., 2015). As explained before, the cations have to accommodate the charge of the oxygen vacancy and form trivalent ions. This reduction is also accompanied by an increase in the ionic radius of the metal atom (see Table 2), reverberating its effect as a local swelling of the lattice due to steric effects. Usually, the magnitude of the increase in the cation radius is larger than that of the local collapse of the lattice due to the presence of the oxygen vacancy. This competition creates large local distortions in the crystal structure. Macroscopically, the lattice swells proportionally to the magnitude of deviation from stoichiometry (Markin and Street, 1967; Kato and Konashi, 2009; Vauchy et al., 2014b; Vauchy et al., 2017; Tracy et al., 2018).
As explained before, interdiffusion in hypostoichiometric U1−yPuyO2−x is governed by the migration of free oxygen vacancies. As shown in Figure 15, the formation of a doubly charged oxygen vacancy is only possible if at least two plutonium atoms are contiguous. As U1−yPuyO2−x is considered as a solid solution, i.e., that the cations are randomly dispersed in the lattice, not all Pu sites are equivalent in their propensity to form these clusters. Indeed, if doubly charged oxygen vacancies are considered to be formed, the presence of U ions in the first metal shell of Pu atoms tends to stabilize Pu(IV) by decreasing the probability to form an oxygen vacancy, hence of
7.1.2 Interdiffusion in hyperstoichiometry (O/M > 2)
Hyperstoichiometry in AnO2 is defined as an O/M ratio larger than the reference value 2. In this composition range, the interstitial oxygen atoms become predominant with respect to the concentration in oxygen vacancies, the metal lattice being again conserved (see Section 2). Compared to the atom in its “normal” site (Table 2), these interstitial oxygens have a larger ionic radius. The lattice then locally expands due to the steric hindrance. The presence of such interstitials is balanced by the metal lattice by inducing a partial oxidation of the cations to the pentavalent state. These oxidized ions have a smaller ionic radius than that of the tetravalent ones (Table 2), inducing a local shrinkage of the crystal cell. Again, the ambivalence of these defects creates tremendous local lattice distortions. The contraction induced by the formation of An(V) is greater than the local swelling generated by the presence of the interstitial anion. Macroscopically, the lattice shrinks proportionally to the magnitude of deviation from stoichiometry (Brett and Fox, 1966; Markin and Street, 1967; Sali et al., 2016).
Cation interdiffusion in hyperstoichiometric U1−yPuyO2+x is mediated by the migration of free oxygen interstitials [presumably indirect mechanism (Dorado et al., 2010)]. The clustering effect of interstitial oxygen atoms becomes preponderant when the deviation from stoichiometry is increased. As a result, they become less mobile within the crystal structure, and the cation interdiffusion is then either stabilized or declined.
7.2 Computational approach
Carrying experimental studies on materials containing transuranium elements is difficult and can only be operated in specific, and very limited, nuclear facilities around the world (Vauchy et al., 2016b). Computation is a convenient complementary approach for appraising the diffusion mechanisms that take place in actinide dioxides.
Point defect chemistry is one of the tools used to interpret the diffusion phenomena in the fluorite structure of U1−yPuyO2±x. The formation and migration energies of the crystal defects are either used (when available) or computed to estimate their mobility in the solid, hence providing information on the diffusion of these species. One common representation of the mixed oxide relies on the interconnection of three distinct sub-lattices: [U(III), U(IV), U(V), Pu(III), Pu(IV)]1[O’(−II), Va]2[O’(−II), Va]1 standing for the normal cation, the normal anion and the interstitial anion lattices, respectively. This formalism is used for thermodynamic computations using the CALPHAD method and the TAF-ID database (Guéneau et al., 2011; Guéneau et al., 2021) and more recently for calculating diffusion properties with the cBΩ model (Chroneos et al., 2015; Saltas et al., 2016) and the DICTRA code (Moore et al., 2017; Chakraborty et al., 2020).
Atomistic approaches are also investigated using first-principles calculations based on density functional theory (DFT), often coupled to the Hubbard’s model (DFT + U), or empirical potentials (EPs). Molecular dynamics (MD) simulations can subsequently be carried out for computing the diffusivity of some species in actinide dioxides (Freyss et al., 2005; Dorado et al., 2010; Boyarchenkov et al., 2013; Cooper et al., 2015; Matthews et al., 2019; Wang et al., 2019; Nekrasov et al., 2021; Chen and Kaltsoyannis, 2022; Cooper, 2022).
Although being very useful for interpreting some fundamental properties, these studies focused on self-diffusion and/or on oxygen chemical diffusion phenomena. However, the underlying diffusion mechanisms may possibly be used for interpreting the experimental interdiffusion data.
Eventually, and as a direct engineering application, disposing of reliable experimental cation interdiffusion coefficients can be used for modeling the macroscopic U−Pu homogenization that occur during sintering using a finite elements method (FEM) (Léchelle et al., 2001; Léchelle et al., 2012; Dempowo et al., 2022).
8 Conclusion
Where are we now in the determination of cation interdiffusion in uranium–plutonium mixed oxide fuels? Answering this question remains difficult. Indeed, despite being studied for decades, experimental determinations of U–Pu interdiffusion coefficients in MOX fuel are scarce and highly scattered. The lack of a more systematic investigation of these diffusion properties is clear. A critical review of the literature data unfortunately led to exclude most of the proposed studies as the associated results were doubtful due to experimental approximations and biases, among others. Diffusion being a thermally activated phenomenon, interdiffusion is enhanced, at the first order, by an increase in temperature. Oxygen partial pressure also plays a major role in interdiffusion. In hypostoichiometry, cation diffusion is mediated by free oxygen vacancies, and an excessive decrease in pO2 can induce severe clustering effects (oxygen vacancy traps), reverberating as a barrier to cation migration. In hyperstoichiometry, oxygen in the interstitial positions greatly enhance diffusion properties until reaching a plateau due to the competition between formation, coalescence, and dissociation of clusters. As a general conclusion, more reliable experiments are needed to properly understand the cation interdiffusion in MOX fuels, either for precisely tailoring sintering or for predicting in-pile behavior. At the light of this critical review of the published data, the preparation of new interdiffusion couples from dense sintered pellets and subsequent EPMA analysis appears to be the most relevant method to obtain the true interdiffusion coefficients of U and Pu in MOX fuels. Finally, the role of americium in the diffusion processes needs to be further discussed as most of the studies simply omit the presence of this daughter element of plutonium.
Author contributions
RV: conceptualization, data collection, formal analysis, writing, and original draft. SH: conceptualization, data collection, and formal analysis. TM: conceptualization, data collection, and formal analysis. MK: conceptualization, funding acquisition.
Acknowledgments
The visualization of crystal structures was performed with VESTA (Momma and Izumi, 2011).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Alcock, C. B., Hawkins, R. J., Hills, A. W. D., and McNamara, P. (1966). “A study of cation diffusion in stoichiometric UO2 using α-ray spectrometry,” Journal of Nuclear Materials, 26, 1, 112-122.
Anderson, J. S. (1971). “Defects in oxides,” Solid state chemistry (Gaithersburg, Maryland, USA: National Bureau of Standards), 364, 295–317.
Ando, K., and Oishi, Y. (1983). Diffusion characteristics of actinide oxides. J. Nucl. Sci. Technol. 20 (12), 973–982. doi:10.1080/18811248.1983.9733499
Atlas, L. M., Schlehman, G. J., and Readey, D. W. (1966). Defects in PuO2–x: Density measurements at high temperature. J. Am. Ceram. Soc. 49 (11), 624. doi:10.1111/j.1151-2916.1966.tb13182.x
Auskern, A. B., and Belle, J. (1961). Uranium ion self-diffusion in UO2. J. Nucl. Mater. 3 (3), 311–319. doi:10.1016/0022-3115(61)90199-4
Baron, D., Hallstadius, L., Kulacsy, K., Largenton, R., and Noirot, J. (2020). “2.02 - fuel performance of light water reactors (uranium oxide and MOX)”, Comprehensive nuclear materials. Editors R. J. M. Konings, and R. E. Stoller. 2nd ed. (Oxford, England: Elsevier), 35–71.
Bartscher, W., and Sari, C. (1983). A thermodynamic study of the uranium-americium oxide U0.5Am0.5O2±x. J. Nucl. Mater. 118 (2), 220–223. doi:10.1016/0022-3115(83)90228-3
Baybarz, R. D., Haire, R. G., and Fahey, J. A. (1972). On the californium oxide system. J. Inorg. Nucl. Chem. 34 (2), 557–565. doi:10.1016/0022-1902(72)80435-4
Baybarz, R. D. (1968). The berkelium oxide system. J. Inorg. Nucl. Chem. 30 (7), 1769–1773. doi:10.1016/0022-1902(68)80352-5
Bayoǧlu, A. S., and Lorenzelli, R. (1979). Etude de la diffusion chimique de l’oxygene dans PuO2−x par dilatometrie et thermogravimetrie. J. Nucl. Mater. 82 (2), 403–410. doi:10.1016/0022-3115(79)90022-9
Bayoǧlu, A. S., and Lorenzelli, R. (1984). Oxygen diffusion in fcc fluorite type nonstoichiometric nuclear oxides MO2±x. Solid State Ionics 12, 53–66. doi:10.1016/0167-2738(84)90130-9
Belle, J. (1961). Uranium dioxide: Properties and nuclear applications. Nav. React. Div. React. Dev. U. S. Atomic Energy Comm. Washington, D.C. USA
Berzati, S. (2013).Influence du potentiel d’oxygène sur la microstructure et l’homogénéité U−Pu des combustibles U1−yPuyO2±x PhD thesis, 1. [CEA Cadarache], Bordeaux, France .
Bevan, D. J. M., Grey, I. E., and Willis, B. T. M. (1986). The crystal structure of β-U4O9−y. J. Solid State Chem. 61 (1), 1–7. doi:10.1016/0022-4596(86)90002-2
Bober, M., Schumacher, G., and Geithoff, D. (1973). Plutonium redistribution in fast reactor mixed oxide fuel pins. J. Nucl. Mater. 47 (2), 187–197. doi:10.1016/0022-3115(73)90101-3
Boltzmann, L. (1894). Zur Integration der Diffusionsgleichung bei variabeln Diffusionscoefficienten. Ann. Phys. 289 (13), 959–964. doi:10.1002/andp.18942891315
Boyarchenkov, A. S., Potashnikov, S. I., Nekrasov, K. A., and Aya, K. (2013). Investigation of cation self-diffusion mechanisms in UO2±x using molecular dynamics. J. Nucl. Mater. 442 (1), 148–161. doi:10.1016/j.jnucmat.2013.08.030
Brett, N. H., and Fox, A. C. (1966). Oxidation products of plutonium dioxide-uranium dioxide solid solutions in air at 750°C. J. Inorg. Nucl. Chem. 28, 1191–1203. doi:10.1016/0022-1902(66)80445-1
Brincat, N. A., Molinari, M., Parker, S. C., Allen, G. C., and Storr, M. T. (2015). Computer simulation of defect clusters in UO2 and their dependence on composition. J. Nucl. Mater. 456, 329–333. doi:10.1016/j.jnucmat.2014.10.001
Burriel, M., Téllez, H., Chater, R. J., Castaing, R., Veber, P., Zaghrioui, M., et al. (2016). Influence of crystal orientation and annealing on the oxygen diffusion and surface exchange of La2NiO4+δ. J. Phys. Chem. C 120, 17927–17938. doi:10.1021/acs.jpcc.6b05666
Caglak, E., Govers, K., Lamoen, D., Labeau, P-E., and Verwerft, M. (2020). Atomic scale analysis of defect clustering and predictions of their concentrations in UO2+x. J. Nucl. Mater. 541, 152403. doi:10.1016/j.jnucmat.2020.152403
Catlow, C. R. A. (1981). “2 - defect clustering in nonstoichiometric oxides,” Nonstoichiometric oxides. O. T. Sørensen (Academic Press), 61–98. Cambridge, Massachusetts
Chakraborty, P., Guéneau, C., and Chartier, A. (2020). Modelling of plutonium diffusion in (U, Pu)O2±x mixed oxide. Solid State Ionics 357, 115503. doi:10.1016/j.ssi.2020.115503
Chatzichristodoulou, C., Norby, P., Hendriksen, P. V., and Mogensen, M. B. (2015). Size of oxide vacancies in fluorite and perovskite structured oxides. J. Electroceram. 34 (1), 100–107. doi:10.1007/s10832-014-9916-2
Cheik Njifon, I. (2018). Modélisation des modifications structurales, électroniques et thermodynamiques induites par les défauts ponctuels dans les oxydes mixtes à base d’actinides (U,Pu)O2 [PhD thesis]. Aix-Marseille, France: [CEA Cadarache.
Chen, J-L., and Kaltsoyannis, N. (2022). DFT + U study of uranium dioxide and plutonium dioxide with occupation matrix control. J. Phys. Chem. C 126 (27), 11426–11435. doi:10.1021/acs.jpcc.2c03804
Chereau, P., and Wadier, J-F. (1973). Mesures de resistivite et de cinetique d’oxydation dans PuO2−x. J. Nucl. Mater. 46 (1), 1–8. doi:10.1016/0022-3115(73)90116-5
Chikalla, T. D., and Eyring, L. (1968). Phase relationships in the americium-oxygen system. J. Inorg. Nucl. Chem. 30 (1), 133–145. doi:10.1016/0022-1902(68)80072-7
Chilton, G. R., and Edwards, J. (1978). The solid-state diffusion of plutonium in uranium dioxide. J. Nucl. Mater. 78 (1), 182–191. doi:10.1016/0022-3115(78)90516-0
Chroneos, A., Fitzpatrick, M. E., and Tsoukalas, L. H. (2015). Describing oxygen self-diffusion in PuO2 by connecting point defect parameters with bulk properties. J. Mat. Sci. Mat. Electron. 26 (5), 3287–3290. doi:10.1007/s10854-015-2829-2
Cooper, M. W. D. (2022). Ceramic nuclear fuel performance and the role of atomic scale simulations. J. Nucl. Mater. 561, 153531. doi:10.1016/j.jnucmat.2022.153531
Cooper, M. W. D., Grimes, R. W., Fitzpatrick, M. E., and Chroneos, A. (2015). Modeling oxygen self-diffusion in UO2 under pressure. Solid State Ionics 282, 26–30. doi:10.1016/j.ssi.2015.09.006
Crank, J. (1957). Diffusion coefficients in solids, their measurement and significance. Discuss. Faraday Soc. 23 (0), 99–104. doi:10.1039/df9572300099
Cristea, P., Stan, M., and Ramirez, J. C. (2007). Point defects and oxygen diffusion in fluorite type oxides. J. Optoelectron. Adv. Mater. 9 (6), 1750–1756.
Cross, J. N., Villa, E. M., Wang, S., Diwu, J., Polinski, M. J., and Albrecht-Schmitt, T. E. (2012). Syntheses, structures, and spectroscopic properties of plutonium and americium phosphites and the redetermination of the ionic radii of Pu(III) and Am(III). Inorg. Chem. 51 (15), 8419–8424. doi:10.1021/ic300958z
Davies, J. H., and Novak, P. E. (1964). Diffusion of plutonium and uranium in oxide fuel at 2400°C. Trans. Am. Nucl. Soc. 7 (2), 393.
Dean, D. C., and Goldstein, J. I. (1986). Determination of the interdiffusion coefficients in the Fe−Ni and Fe−Ni−P systems below 900°C. Metall. Mater Trans. A 17 (7), 1131–1138. doi:10.1007/bf02665311
Dempowo, N. C., Valdivieso, F., Bruchon, J., and Léchelle, J. (2022). One-dimensional modeling of bulk cationic interdiffusion in mixed oxides (U, Pu)O2 and analysis of homogenization within a microstructure using a finite difference method. J. Nucl. Mater. 568, 153850. doi:10.1016/j.jnucmat.2022.153850
Dorado, B., Durinck, J., Garcia, P., Freyss, M., and Bertolus, M. (2010). An atomistic approach to self-diffusion in uranium dioxide. J. Nucl. Mater. 400 (2), 103–106. doi:10.1016/j.jnucmat.2010.02.017
Dorado, B., Garcia, P., Carlot, G., Davoisne, C., Fraczkiewicz, M., Pasquet, B., et al. (2011). First-principles calculation and experimental study of oxygen diffusion in uranium dioxide. Phys. Rev. B 83 (3), 035126. doi:10.1103/physrevb.83.035126
Dudarev, S. L. (2022). Grand challenges in nuclear engineering. Front. Nucl. Eng. 1. 945270 doi:10.3389/fnuen.2022.945270
Epifano, E., Naji, M., Manara, D., Scheinost, A. C., Hennig, C., Lechelle, J., et al. (2019). Extreme multi-valence states in mixed actinide oxides. Commun. Chem. 2 (1), 59–11. doi:10.1038/s42004-019-0161-0
Fahey, J. A., Turcotte, R. P., and Chikalla, T. D. (1974). Thermal expansion of the actinide dioxides. Inorg. Nucl. Chem. Lett. 10 (6), 459–465. doi:10.1016/0020-1650(74)80067-x
Ferry, C., Lovera, P., Poinssot, C., and Garcia, P. (2005). Enhanced diffusion under alpha self-irradiation in spent nuclear fuel: Theoretical approaches. J. Nucl. Mater. 346 (1), 48–55. doi:10.1016/j.jnucmat.2005.04.072
Fisher, J. C. (1951). Calculation of diffusion penetration curves for surface and grain boundary diffusion. J. Appl. Phys. 22 (1), 74–77. doi:10.1063/1.1699825
Freyss, M., Petit, T., and Crocombette, J-P. (2005). Point defects in uranium dioxide: Ab initio pseudopotential approach in the generalized gradient approximation. J. Nucl. Mater. 347 (1–2), 44–51. doi:10.1016/j.jnucmat.2005.07.003
Gardner, E. R., Markin, T. L., and Street, R. S. (1965). The plutonium–oxygen phase diagram. J. Inorg. Nucl. Chem. 27 (3), 541–551. doi:10.1016/0022-1902(65)80259-7
Geønvold, F., and Haraldsen, H. (1948). Oxidation of uranium dioxide (UO2). Nature 162 (4106), 69–70. doi:10.1038/162069a0
Glasser-Leme, D., and Matzke, H. (1982). Interdiffusion and chemical diffusion in the UO2−(UPu)O2 system. J. Nucl. Mater. 106 (1–3), 211–220. doi:10.1016/0022-3115(82)90350-6
Glasser-Leme, D., and Matzke, H. (1984). Dependence upon oxygen potential of the interdiffusion in single crystalline UO2−(U, Pu)O2. Solid State Ionics 12, 217–225. doi:10.1016/0167-2738(84)90150-4
Glasser-Leme, D., and Matzke, H. (1983). The diffusion of uranium in U3O8. J. Nucl. Mater. 115 (2–3), 350–353. doi:10.1016/0022-3115(83)90330-6
Glasser-Leme, D. (1985). Interdifusão catiônica nos sistemas UO2−(U,Pu)O2 e UO2–PuO2 [PhD thesis]. Brazil, USA: São PauloIstitutos de Pesquisas Energeticas e Nucleares.
Guéneau, C., Dupin, N., Kjellqvist, L., Geiger, E., Kurata, M., and Gossé, S., (2021). TAF-ID: An international thermodynamic database for nuclear fuels applications. Calphad 72, 102212. doi:10.1016/j.calphad.2020.102212
Guéneau, C., Dupin, N., Sundman, B., Martial, C., Dumas, J-C., Gossé, S., et al. (2011). Thermodynamic modelling of advanced oxide and carbide nuclear fuels: Description of the U–Pu–O–C systems. J. Nucl. Mater. 419 (1), 145–167. doi:10.1016/j.jnucmat.2011.07.033
Harrison, L. G. (1961). Influence of dislocations on diffusion kinetics in solids with particular reference to the alkali halides. Trans. Faraday Soc. 57 (0), 1191–1199. doi:10.1039/tf9615701191
Hawkins, R. J., and Alcock, C. B. (1968). A study of cation diffusion in UO2+x and ThO2 using α-ray spectrometry. J. Nucl. Mater. 26 (1), 112–122. doi:10.1016/0022-3115(68)90162-1
Hirooka, S., Matsumoto, T., Sunaoshi, T., and Hino, T. (2022). Relative oxygen potential measurements of (U, Pu)O2 with Pu = 0.45 and 0.68 and related defect formation energy. J. Nucl. Mater. 558, 153375. doi:10.1016/j.jnucmat.2021.153375
Holby, E. F. (2019). Crystallographic orientation effects of hydrogen diffusion in α-uranium from DFT: Interpreting variations in experimental data. J. Nucl. Mater. 513, 293–296. doi:10.1016/j.jnucmat.2018.10.022
International Commission on Radiological Protection (1996). Age-dependent doses to members of the public from intake of radionuclides: Part 5. Compilation of ingestion and inhalation dose coefficients. Ann. ICRP 26 (1), 1–91. doi:10.1016/s0146-6453(00)89192-7
Ishigaki, T., Yamauchi, S., and Fueki, K. (1987). Diffusion profile measurement using SIMS in La0.9Sr0.1FeO3 and La0.9Sr0.1CoO3. Yogyo-Kyokai-Shi 95 (10), 99–101.
Ishimi, A., Katsuyama, K., and Furuya, H. (2019). Restructure behavior analysis in fast breeder reactor MOX fuel by X-ray CT. J. Nucl. Sci. Technol. 56 (11), 981–987. doi:10.1080/00223131.2019.1633967
Jean-Baptiste, P., and Gallet, G. (1985). Interdiffusion des cations dans les oxydes mixtes (U, Ce)O2−x et (U, Pu)O2−x: Influence de la teneur en uranium, de la température et de l’écart a la stoechiométrie. J. Nucl. Mater. 135 (1), 105–114. doi:10.1016/0022-3115(85)90442-8
Jeynes, C., and Colaux, J. L. (2016). Thin film depth profiling by ion beam analysis. Analyst 141 (21), 5944–5985. doi:10.1039/c6an01167e
Kato, M. (2021). “Fuel design and fabrication: Pellet-type fuel”, Encyclopedia of nuclear energy. E. Greenspan (Oxford, England: Elsevier), 298–307.
Kato, M., and Konashi, K. (2009). Lattice parameters of (U, Pu, Am, Np)O2−x. J. Nucl. Mater. 385 (1), 117–121. doi:10.1016/j.jnucmat.2008.09.037
Kato, M., and Machida, M. (2022). Materials science and fuel technologies of uranium and plutonium mixed oxide [internet]. 1st Edition (Boca Raton, Florida, USA: CRC Press), 182. doi:10.1201/9781003298205
Kato, M., Maeda, S., Abe, T., and Asakura, K.. 2.01 - uranium oxide and MOX production, R. J. M. Konings, and R. E. Stoller, Comprehensive nuclear materials. 2nd ed. Oxford, England: Elsevier; 2020. p. 1–34.
Kato, M., Morimoto, K., Tamura, T., Sunaoshi, T., Konashi, K., Aono, S., et al. (2009). Oxygen chemical diffusion in hypo-stoichiometric MOX. J. Nucl. Mater. 389 (3), 416–419. doi:10.1016/j.jnucmat.2009.02.018
Kato, M., Nakamura, H., Watanabe, M., Matsumoto, T., and Machida, M. (2017). Defect Chemistry and Basic Properties of Non-Stoichiometric PuO2. Defect Diffusion Forum 375, 57–70. doi:10.4028/www.scientific.net/ddf.375.57
Kato, M., Uchida, T., and Sunaoshi, T. (2013). Measurement of oxygen chemical diffusion in PuO2-x and analysis of oxygen diffusion in PuO2-x and (Pu, U)O2-x. Phys. Status Solidi C 10 (2), 189–192. doi:10.1002/pssc.201200454
Kato, M., Watanabe, M., Matsumoto, T., Hirooka, S., and Akashi, M. (2017). Oxygen potentials, oxygen diffusion coefficients and defect equilibria of nonstoichiometric (U, Pu)O2±x. J. Nucl. Mater. 487, 424–432. doi:10.1016/j.jnucmat.2017.01.056
Kilner, J. A., and Steele, B. C. H. (1981). “5 - mass transport in anion-deficient fluorite oxides,” Nonstoichiometric oxides. O. T. Sørensen (Academic Press), Cambridge, Massachusetts 233–269.
Kim, D-J. (1989). Lattice parameters, ionic conductivities, and solubility limits in fluorite-structure MO2 oxide [M = Hf4+, Zr4+, Ce4+, Th4+, U4+] solid solutions. J. Am. Ceram. Soc. 72 (8), 1415–1421. doi:10.1111/j.1151-2916.1989.tb07663.x
Kim, K. C., and Olander, D. R. (1981). Oxygen diffusion in UO2−x. J. Nucl. Mater. 102 (1–2), 192–199. doi:10.1016/0022-3115(81)90559-6
Kirkendall, E. O. (1942). Diffusion of zinc in alpha brass. Transactions of the American Institute of Mining and Metallurgical Engineers, 147, 104–110.
Knorr, D. B., Cannon, R. M., and Coble, R. L. (1989). Overview no. 84: An analysis of diffusion and diffusional creep in stoichiometric and hyperstoichiometric uranium dioxide. Acta Metall. 37 (8), 2103–2123. doi:10.1016/0001-6160(89)90136-3
Kutty, T. R. G., Hegde, P. V., Keswani, R., Khan, K. B., Majumdar, S., and Purushotham, D. S. C. (1999). Densification behaviour of UO2−50%PuO2 pellets by dilatometry. J. Nucl. Mater. 264 (1–2), 10–19. doi:10.1016/s0022-3115(98)00490-5
Lambert, R. A. (1978). The diffusion of plutonium in uranium/plutonium mixed oxide single crystals at varying oxygen to metal ratio [PhD thesis]. Guildford, UK: University of Surrey.
Le Claire, A. D. (1963). The analysis of grain boundary diffusion measurements. Br. J. Appl. Phys. 14 (6), 351–356. doi:10.1088/0508-3443/14/6/317
Léchelle, J., Noyau, S., Aufore, L., Arredondo, A., and Audubert, F. (2012). Volume interdiffusion coefficient and uncertainty assessment for polycrystalline materials. Diffus. Fundam. 17 (2), 1–39.
Léchelle, J., Boyer, R., and Trotabas, M. (2001). A mechanistic approach of the sintering of nuclear fuel ceramics. Mater. Chem. Phys. 67 (1–3), 120–132. doi:10.1016/s0254-0584(00)00429-6
Leinders, G., Cardinaels, T., Binnemans, K., and Verwerft, M. (2015). Accurate lattice parameter measurements of stoichiometric uranium dioxide. J. Nucl. Mater. 459, 135–142. doi:10.1016/j.jnucmat.2015.01.029
Lindner, R., Reimann, D. K., and Schmitz, F. (1967). “Diffusion in mixed U/Pu oxides”, Proceedings of a symposium (Brussels, Belgium: International Atomic Energy Agency), 265–272.
Ma, Y. (2017). A study of point defects in UO2+x and their impact upon fuel properties [PhD thesis]. Université Aix-Marseille. Marseille, France.
Maeda, K., Sasaki, S., Kato, M., and Kihara, Y. (2009). Short-term irradiation behavior of minor actinide doped uranium plutonium mixed oxide fuels irradiated in an experimental fast reactor. J. Nucl. Mater. 385 (2), 413–418. doi:10.1016/j.jnucmat.2008.12.041
Maeda, K., Sasaki, S., Kato, M., and Kihara, Y. (2009). Radial redistribution of actinides in irradiated FR-MOX fuels. J. Nucl. Mater. 389 (1), 78–84. doi:10.1016/j.jnucmat.2009.01.010
Manes, L., and Manes-Pozzi, B. (1975). “A unified model for defects in substoichiometric plutonium dioxide and uranium-plutonium mixed oxides,” in 5th international conference on plutonium and other actinides 1975 proceedings of the conference. Baden baden, Germany. (Amsterdam: North-Holland Publ.), 145–163.
Marin, J-M. (1988). Phénoménologie de l’homogénéisation U−Pu dans les combustibles nucléaires [PhD thesis]. Aix-Marseille, France: [CEA CadaracheI.
Marin, J. F., and Coniglio, M. (1966). Determination des coefficients d’autodiffusion par spectrometrie α. Nucl. Instrum. Methods 42 (2), 302–304. doi:10.1016/0029-554x(66)90207-2
Markin, T. L., and Street, R. S. (1967). The uranium–plutonium–oxygen ternary phase diagram. J. Inorg. Nucl. Chem. 29 (9), 2265–2280. doi:10.1016/0022-1902(67)80281-1
Marrocchelli, D., Bishop, S. R., and Kilner, J. (2013). Chemical expansion and its dependence on the host cation radius. J. Mat. Chem. A Mat. 1 (26), 7673–7680. doi:10.1039/c3ta11020f
Martin, P. M., Medyk, L., Fouquet-Métivier, P., Epifano, E., Lebreton, F., Hunault, M. O. J. Y., et al. (2022). “Extreme multi-valence states in mixed actinide oxides U1–yMyO2±x,” Plutonium futures – the science (Avignon, France).
Matano, C. (1933). On the relation between the diffusion coefficients and concentrations of solid metals (the nickel-copper system). Jpn. J. Phys. 8, 109–113.
Matthews, C., Perriot, R., Cooper, M. W. D., Stanek, C. R., and Andersson, D. A. (2019). Cluster dynamics simulation of uranium self-diffusion during irradiation in UO2. J. Nucl. Mater. 527, 151787. doi:10.1016/j.jnucmat.2019.151787
Matzke, H. (1987). Atomic transport properties in UO2 and mixed oxides (U, Pu)O2. J. Chem. Soc. Faraday Trans. 2 83 (7), 1121–1142. doi:10.1039/f29878301121
Matzke, Hj (1981). “4 - diffusion in nonstoichiometric oxides,” Nonstoichiometric oxides. O. T. Sørensen (Academic Press), Cambridge, Massachusetts, 155–232.
Matzke, Hj (1990). Atomic mechanisms of mass transport in ceramic nuclear fuel materials. Faraday Trans. 86 (8), 1243–1256. doi:10.1039/ft9908601243
Matzke, Hj (1983). Diffusion processes and surface effects in non-stoichiometric nuclear fuel oxides UO2+x, and (U, Pu)O2±x. J. Nucl. Mater. 114 (2), 121–135. doi:10.1016/0022-3115(83)90249-0
Matzke, Hj, and Lambert, R. A. (1974). The evaporation behavior and metal self-diffusion processes in (U, Pu)C and (U, Pu)O2. J. Nucl. Mater. 49 (3), 325–328. doi:10.1016/0022-3115(74)90045-2
Matzke, Hj (1969). On uranium self-diffusion in UO2 and UO2+x. J. Nucl. Mater. 30 (1–2), 26–35. doi:10.1016/0022-3115(69)90165-2
Matzke, Hj (1983). Radiation enhanced diffusion in UO2 and (U, Pu)O2. Radiat. Eff. 75 (1–4), 317–325. doi:10.1080/00337578308224715
Mehrer, H. (2007). Diffusion in solids, fundamentals, methods, materials, diffusion-controlled processes. 1st ed.. Heidelberg, Germany: Springer BerlinSpringer Series in Solid-State Sciences, 654.
Mendez, S. (1995). Etude de l’inerdiffusion U−Pu appliquée au combustible MOX [PhD thesis]. CEA Cadarache Science des Matériaux III: Aix-Marseille, France.
Middleburgh, S. C., Lumpkin, G. R., and Grimes, R. W. (2013). Accommodation of excess oxygen in fluorite dioxides. Solid State Ionics 253, 119–122. doi:10.1016/j.ssi.2013.09.020
Momma, K., and Izumi, F. (2011). VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 44 (6), 1272–1276. doi:10.1107/s0021889811038970
Moore, E., Guéneau, C., and Crocombette, J-P. (2017). Oxygen diffusion model of the mixed (U, Pu)O2±x: Assessment and application. J. Nucl. Mater. 485, 216–230. doi:10.1016/j.jnucmat.2016.12.026
Mosley, W. C. (1972). Phases and transformations in the curium–oxygen system. J. Inorg. Nucl. Chem. 34 (2), 539–555. doi:10.1016/0022-1902(72)80434-2
Murch, G. E. (2001). “Diffusion kinetics in solids,” Phase transformations in materials (John Wiley & Sons), Hoboken, NJ, USA, 171–238.
Nagels, P., Van Lierde, W., De Baptist, R., Denayer, M., De Jonghe, L., and Gevers, R. (1966). “Migration and re-orientation of oxygen interstitials, and migration and self-diffusion of uranium in UO2,” Thermodynamics vol II (Vienna, Austria: International Atomic Energy Agency).
Nakamichi, S., Hirooka, S., Kato, M., Sunaoshi, T., Nelson, A. T., and McClellan, K. J. (2020). Effect of O/M ratio on sintering behavior of (Pu0.3U0.7)O2−x. J. Nucl. Mater. 535, 152188. doi:10.1016/j.jnucmat.2020.152188
Nakayama, M., and Martin, M. (2009). First-principles study on defect chemistry and migration of oxide ions in ceria doped with rare-Earth cations. Phys. Chem. Chem. Phys. 11 (17), 3241–3249. doi:10.1039/b900162j
Nekrasov, K. A., Galashev, A. E., Seitov, D. D., and Gupta, S. K. (2021). Diffusion of oxygen in hypostoichiometric uranium dioxide nanocrystals. A molecular dynamics simulation. Chim. Tech. Acta 8 (1), 20218107. doi:10.15826/chimtech.2021.8.1.07
Noirot, J., Desgranges, L., and Lamontagne, J. (2008). Detailed characterisations of high burn-up structures in oxide fuels. J. Nucl. Mater. 372 (2–3), 318–339. doi:10.1016/j.jnucmat.2007.04.037
Norris, D. I. R. (1977). Thermomigration of oxygen in (U, Pu)O2−x described by a cluster model. J. Nucl. Mater. 68 (1), 13–18. doi:10.1016/0022-3115(77)90211-2
Noyau, S. (2012). Etude des phénomènes d’autodiffusion et d’interdiffusion du plutonium dans les céramiques de type U₁₋ᵧPuᵧO₂₋ₓ [PhD thesis]. Limoges, France: CEA Cadarache.
Noyau, S., Garcia, P., Pasquet, B., Roure, I., Audubert, F., and Maître, A. (2012). Towards Measuring the Pu Self-Diffusion Coefficient in Polycrystalline U0.55Pu0.45O2±x. Defect Diffusion Forum 323–325, 203–208. doi:10.4028/www.scientific.net/ddf.323-325.203
Ohmichi, T., Fukushima, S., Maeda, A., and Watanabe, H. (1981). On the relation between lattice parameter and O/M ratio for uranium dioxide-trivalent rare Earth oxide solid solution. J. Nucl. Mater. 102 (102), 40–46. doi:10.1016/0022-3115(81)90544-4
Oishi, Y., Sakka, Y., and Ando, K. (1981). Cation interdiffusion in polycrystalline fluorite-cubic solid solutions. J. Nucl. Mater. 96 (1–2), 23–28. doi:10.1016/0022-3115(81)90214-2
Okita, T., Aono, S., Asakura, K., Aoki, Y., and Ohtani, T. (2000). Operational experiences in MOX fuel fabrication for the FUGEN advanced thermal reactor. Int. At. Energy Agency (IAEA), 60 109–117.
Olander, D. (2009). Nuclear fuels – present and future. J. Nucl. Mater. 389 (1), 1–22. doi:10.1016/j.jnucmat.2009.01.297
Ozawa, T., Hirooka, S., Kato, M., Novascone, S., and Medvedev, P. (2021). Development of fuel performance analysis code, BISON for MOX, named Okami: Analyses of pore migration behavior to affect the MA-bearing MOX fuel restructuring. J. Nucl. Mater. 553, 153038. doi:10.1016/j.jnucmat.2021.153038
Peterson, N. L. (1983). Grain-boundary diffusion in metals. Int. Met. Rev. 28 (1), 65–91. doi:10.1179/imtr.1983.28.1.65
Ramaniah, M. V. (1982). Analytical chemistry of fast reactor fuels - a review. Pure Appl. Chem. 54 (4), 889–908. doi:10.1351/pac198254040889
Riemer, G., and Scherff, H. L. (1971). Plutonium diffusion in hyperstoichiometric mixed uranium-plutonium dioxides. J. Nucl. Mater. 39 (2), 183–188. doi:10.1016/0022-3115(71)90023-7
Rodriguez, Y. R. (2014). “Plutonium,” Encyclopedia of toxicology. Editor P. Wexler. 3rd ed. (Oxford, England: Academic Press), 982–985.
Sabioni, A. C. S., Ferraz, W. B., and Millot, F. (1998). First study of uranium self-diffusion in UO2 by SIMS. J. Nucl. Mater. 257 (2), 180–184. doi:10.1016/s0022-3115(98)00482-6
Sakka, Y., Oishi, Y., and Ando, K. (1982). Cation interdiffusion in polycrystalline fluorite-cubic MgO–ZrO2 solid solution. Bull. Chem. Soc. Jpn. 55 (2), 420–422. doi:10.1246/bcsj.55.420
Sali, S. K., Kulkarni, N. K., Phatak, R., and Agarwal, R. (2016). Oxidation behaviour of plutonium rich (U, Pu)C and (U, Pu)O2. J. Nucl. Mater. 479, 623–632. doi:10.1016/j.jnucmat.2016.07.062
Saltas, V., Chroneos, A., Cooper, M. W. D., Fitzpatrick, M. E., and Vallianatos, F. (2016). Investigation of oxygen self-diffusion in PuO2 by combining molecular dynamics with thermodynamic calculations. RSC Adv. 6 (105), 103641–103649. doi:10.1039/c6ra24575g
Sari, C. (1978). Oxygen chemical diffusion coefficient of uranium-plutonium oxides. J. Nucl. Mater. 78 (2), 425–426. doi:10.1016/0022-3115(78)90465-8
Sato, I., Tanaka, K., and Arima, T. (2010). “Diffusion behaviors of plutonium and americium in polycrystalline urania,” IOP conference series: Materials science and engineering (San-Francisco, California, USA, 012005.
Schmitz, F., and Lindner, R. (1965). Diffusion of heavy elements in nuclear fuels: Actinides in UO2. J. Nucl. Mater. 17 (3), 259–269. doi:10.1016/0022-3115(65)90169-8
Schmitz, F., and Lindner, R. (1963). Diffusion of Pu in U02. Radiochim. Acta. 1, 218–220. doi:10.1524/ract.1963.1.4.218
Schmitz, F., and Marajofsky, A. (1974). “Autodiffusion du plutonium dans (U, Pu)O2–x: Role du potentiel d’oxygène et de la teneur en plutonium,” Proceedings of a symposium (Vienna, Austria: International Atomic Energy Agency), 1, 457–467.Proceedings series
Shannon, R. D., and Prewitt, C. T. (1969). Effective ionic radii in oxides and fluorides. Acta Crystallogr. Sect. B 25 (5), 925–946. doi:10.1107/s0567740869003220
Shannon, R. D. (1976). Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Cryst. Sect. A 32 (5), 751–767. doi:10.1107/s0567739476001551
Smirnov, E., and Elmanov, G. (2016). Radiation enhanced diffusion processes in UO2 and (U, Pu)O2. IOP Conf. Ser. Mat. Sci. Eng. 130, 012063. doi:10.1088/1757-899x/130/1/012063
Stan, M., and Cristea, P. (2005). Defects and oxygen diffusion in PuO2−x. J. Nucl. Mater. 344 (1–3), 213–218. doi:10.1016/j.jnucmat.2005.04.044
Takeuchi, K., Kato, M., and Sunaoshi, T. (2011). Influence of O/M ratio on sintering behavior of (U0.8, Pu0.2)O2±x. J. Nucl. Mater. 414 (2), 156–160. doi:10.1016/j.jnucmat.2011.02.050
Talla Noutack, M. S. (2019). First-principles study of the effect of americium content in mixed oxide fuels [PhD thesis]. Aix-Marseille, France: CEA Cadarache.
Theisen, R., and Vollath, D. (1967).Plutonium distribution and diffusion in UO2−PuO2 ceramics, Plutonium as a React. fuel Proc. a symposium, 13-17, 253–264.
Tracy, C. L., Lang, M., Zhang, F., Park, S., Palomares, R. I., and Ewing, R. C. (2018). Review of recent experimental results on the behavior of actinide-bearing oxides and related materials in extreme environments. Prog. Nucl. Energy 104, 342–358. doi:10.1016/j.pnucene.2016.09.012
Turnbull, D., and Hoffman, R. E. (1954). The effect of relative crystal and boundary orientations on grain boundary diffusion rates. Acta Metall. 2 (3), 419–426. doi:10.1016/0001-6160(54)90061-9
Van Uffelen, P., Konings, R. J. M., Vitanza, C., and Tulenko, J. (2010). “Analysis of reactor fuel rod behavior,” Handbook of nuclear engineering. D. G. Cacuci (Boston, MA, USA: Springer), 1519–1627.
Vauchy, R., Belin, R. C., Richaud, J-C., Valenza, P. J., Adenot, F., and Valot, C. (2016). Studying radiotoxic materials by high temperature X-ray diffraction. Appl. Mater. Today 3, 87–95. doi:10.1016/j.apmt.2016.03.005
Vauchy, R., Belin, R. C., Robisson, A-C., and Hodaj, F. (2014). High temperature X-ray diffraction study of the kinetics of phase separation in hypostoichiometric uranium–plutonium mixed oxides. J. Eur. Ceram. Soc. 34 (10), 2543–2551. doi:10.1016/j.jeurceramsoc.2014.02.028
Vauchy, R., Belin, R. C., Robisson, A-C., Lebreton, F., Aufore, L., Scheinost, A. C., et al. (2016). Actinide oxidation state and O/M ratio in hypostoichiometric uranium–plutonium–americium U0.750Pu0.246Am0.004O2–x mixed oxides. Inorg. Chem. 55 (5), 2123–2132. doi:10.1021/acs.inorgchem.5b02533
Vauchy, R., Joly, A., and Valot, C. (2017). Lattice thermal expansion of Pu1−y Am y O2−x plutonium–americium mixed oxides. J. Appl. Crystallogr. 50 (6), 1782–1790. doi:10.1107/s1600576717014832
Vauchy, R., Robisson, A-C., Audubert, F., and Hodaj, F. (2014). Ceramic processing of uranium−plutonium mixed oxide fuels (U1−yPuy)O2 with high plutonium content. Ceram. Int. 40, 10991–10999. doi:10.1016/j.ceramint.2014.03.104
Vauchy, R., Robisson, A-C., Belin, R. C., Martin, P. M., Scheinost, A. C., and Hodaj, F. (2015). Room-temperature oxidation of hypostoichiometric uranium–plutonium mixed oxides U1−yPuyO2−x – a depth-selective approach. J. Nucl. Mater. 465, 349–357. doi:10.1016/j.jnucmat.2015.05.033
Vauchy, R., Robisson, A-C., Bienvenu, P., Roure, I., Hodaj, F., and Garcia, P. (2015). Oxygen self-diffusion in polycrystalline uranium–plutonium mixed oxide U0.55Pu0.45O2. J. Nucl. Mater. 467, 886–893. doi:10.1016/j.jnucmat.2015.11.003
Vauchy, R., Robisson, A-C., Martin, P. M., Belin, R. C., Aufore, L., Scheinost, A. C., et al. (2015). Impact of the cation distribution homogeneity on the americium oxidation state in the U0.54Pu0.45Am0.01O2−x mixed oxide. J. Nucl. Mater. 456, 115–119. doi:10.1016/j.jnucmat.2014.09.014
Verma, R. (1984). Study of homogenisation and cation interdiffusion in mixed UO2−PuO2 compacts by X-ray diffraction. J. Nucl. Mater. 120 (1), 65–73. doi:10.1016/0022-3115(84)90171-5
Vinograd, V. L., Bukaemskiy, A. A., Modolo, G., Deissmann, G., and Bosbach, D. (2021). Thermodynamic and structural modelling of non-stoichiometric ln-doped UO2 solid solutions, Ln = {La, Pr, Nd, Gd}. Front. Chem. 9, 705024. doi:10.3389/fchem.2021.705024
Wade, W. Z., Short, D. W., Walden, J. C., and Magana, J. W. (1978). Self-diffusion in plutonium metal. Metall. Mater Trans. A 9 (7), 965–972. doi:10.1007/bf02649841
Wade, W. Z. (1971). The self-diffusion of plutonium in a Pu/1 wt% Ga alloy. J. Nucl. Mater. 38 (3), 292–302. doi:10.1016/0022-3115(71)90058-4
Wang, J., Ewing, R. C., and Becker, U. (2014). Average structure and local configuration of excess oxygen in UO2+x. Sci. Rep. 4 (1), 4216. doi:10.1038/srep04216
Wang, L-F., Sun, B., Liu, H-F., Lin, D-Y., and Song, H-F. (2019). Thermodynamics and kinetics of intrinsic point defects in plutonium dioxides. J. Nucl. Mater. 526, 151762. doi:10.1016/j.jnucmat.2019.151762
Watanabe, M., Kato, M., and Matsumoto, T. (2015). Oxygen chemical diffusion coefficients of (Pu,Am)O2 fuels. Nuclear Energy Agency of the OECD NEA, Paris, France, 386–390.
Watanabe, M., Sunaoshi, T., and Kato, M. (2017). Oxygen Chemical Diffusion Coefficients of (U, Pu)O2-X. Defect Diffusion Forum 375, 84–90. doi:10.4028/www.scientific.net/ddf.375.84
Willis, B. T. M. (1963). Positions of the oxygen atoms in UO2.13. Nature 197 (4869), 755–756. doi:10.1038/197755a0
Woodley, R. E., and Gibby, R. L. (1973). Room-temperature oxidation of (U, Pu)O2−x. At. Energy Comm.. 465, 349-357.
Yajima, S., Furuya, H., and Hirai, T. (1966). Lattice and grain-boundary diffusion of uranium in UO2. J. Nucl. Mater. 20 (2), 162–170. doi:10.1016/0022-3115(66)90004-3
Yoshida, K., Arima, T., Inagaki, Y., Idemitsu, K., Osaka, M., and Miwa, S. (2011). Oxygen potential of hypo-stoichiometric La-doped UO2. J. Nucl. Mater. 418 (1–3), 22–26. doi:10.1016/j.jnucmat.2011.06.045
Keywords: diffusion, interdiffusion, uranium-plutonium mixed oxide, actinides, atomic transport, nuclear fuel, MOX, self-diffusion
Citation: Vauchy R, Hirooka S, Matsumoto T and Kato M (2022) Cation interdiffusion in uranium–plutonium mixed oxide fuels: Where are we now?. Front. Nucl. Eng. 1:1060218. doi: 10.3389/fnuen.2022.1060218
Received: 03 October 2022; Accepted: 14 November 2022;
Published: 09 December 2022.
Edited by:
Jacques Lechelle, Commissariat à l’Energie Atomique et aux Energies Alternatives (CEA), FranceReviewed by:
Jianwei Wang, Louisiana State University, United StatesRené Bes, University of Helsinki, Finland
Copyright © 2022 Vauchy, Hirooka, Matsumoto and Kato. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Romain Vauchy, dmF1Y2h5LnJvbWFpbkBqYWVhLmdvLmpw
 Romain Vauchy
Romain Vauchy Shun Hirooka
Shun Hirooka Taku Matsumoto1
Taku Matsumoto1 Masato Kato
Masato Kato