Mechanistic assessment of aerosol transport in SFR cover gas space post HCDA conditions

With the growing emphasis on safety in next-generation reactors, along with the necessity to practically eliminate large doses to the public from severe accidents, a mechanistic assessment of such accidents becomes very important problem. The present manuscript attempts to address the source term assessment, focusing on the release behaviour of the aerosol from the roof-slab leak paths post-Core Disruptive Accident (CDA) conditions (known as interface source term or cover gas source term). Following a CDA, after possible Na leak through the gap between rotating plugs and major components, the cover gas space could be in contact with the containment atmosphere through these open leak paths. Additionally, the impact of sodium slug to roof-slab could have caused roof-slab cooling line failure. The present study assesses the release behaviour of the aerosols from the roof-slab leak paths, with respect to aerosol size under various cases of roof-slab cooling line failure. Sodium aerosols are used as representative aerosols for studying the radionuclide (RN) aerosol release behaviour. The assessment indicates that most of the aerosol leaking from roof-slab leak paths are of the diameter between 5 and 25 $\mu m$, with leak rates peaking in the range of 17–23 $\mu m$. Furthermore, with respect to air ingress concern, it is observed that the air ingress from the containment atmosphere was found only in the annular leak paths and it is not mixing into cover gas. However, this ingress was limited to the annular leak path only. It is seen that higher leak rates are observed in the case of complete failure of the roof-slab cooling system. Hence, it is important to maintain the roof-slab bottom plate temperatures within limits to avoid larger aerosol leak rates.

Highlights

• The release behaviour of aerosols from the cover gas to the RCB post-CDA is studied for the first time.

• Various cases of roof-slab cooling line failure and its effect of release of aerosols from roof-slab leak paths are studied.

• Most of the aerosols leaking roof-slab leak paths are of a size less than 25 $\mu m$.

• Air ingress from RCB atmosphere was found in annular leak-paths; however, these ingress was limited to annular leak paths only.

1 Introduction

Due to the involvement of multi-physics phenomena modelling, determining the severe accident source term is one of the most complex aspects of reactor design analysis, yet it remains critical for meeting licensing requirements. Historically, these analyses have been performed for postulated bounding accident scenarios, with conservative release fraction assumptions derived either from experimental observations or past reactor experiences (Grabaskas et al., 2015). It was expected that the choice of the bounding accident scenario with conservative assumptions would lead to conservative release fractions.

With the advent of advanced computational resources, mechanistic assessments of the severe accident source term has become desirable, particularly for Gen-IV reactors (Grabaskas et al., 2015). Since Gen-IV Sodium Cooled Fast Reactors (SFRs) are in their early deployment stage, such analyses are expected to provide crucial feedback to safety design systems and aid in improving Severe Accident Management Guidelines (SAMGs). For oxide fuelled pool-type SFRs, Unprotected Loss of Flow Accident (ULOFA) is of interest, where significant core damage is postulated due to the loss of flow caused by the unavailability of both primary pumps and all engineered safety systems. Though such accidents are of low probability (for metal-fuelled pool-type SFRs, conservative ULOF the long-term response is pretty benign (Harish et al., 2009; Grabaskas et al., 2017)), such accidents are postulated for the bounding radionuclide (RN) release estimates and affirming the adequacy of the engineered and passive safety systems.

Following a ULOFA, failure of the roof-slab seals is expected (Velusamy et al., 2011). This failure results in the ejection of approximately 350 kg of sodium, along with RNs released into the primary sodium and cover gas¹. This phase is referred to as the “instantaneous interface source term” (refer to Figure 1). Following this phase, the release of RNs would primarily occur through the evaporation of the primary sodium pool, a phase known as the “delayed interface source term,” which may persist for several hours, depending on the plugging time of the roof-slab leak paths (Balard and Carluec, 1996; Berthoud et al., 1987). In addition to the evaporative release, sodium fires may also occur depending on the availability of oxygen in the cover gas due to Reactor Containment Building (RCB) air ingress (Velusamy et al., 2011) (refer Figure 1). In the current manuscript, sodium fires resulting from air ingress into the cover gas have not been considered. Literature related to instantaneous and delayed interface source term is given in the following section.

Figure 1

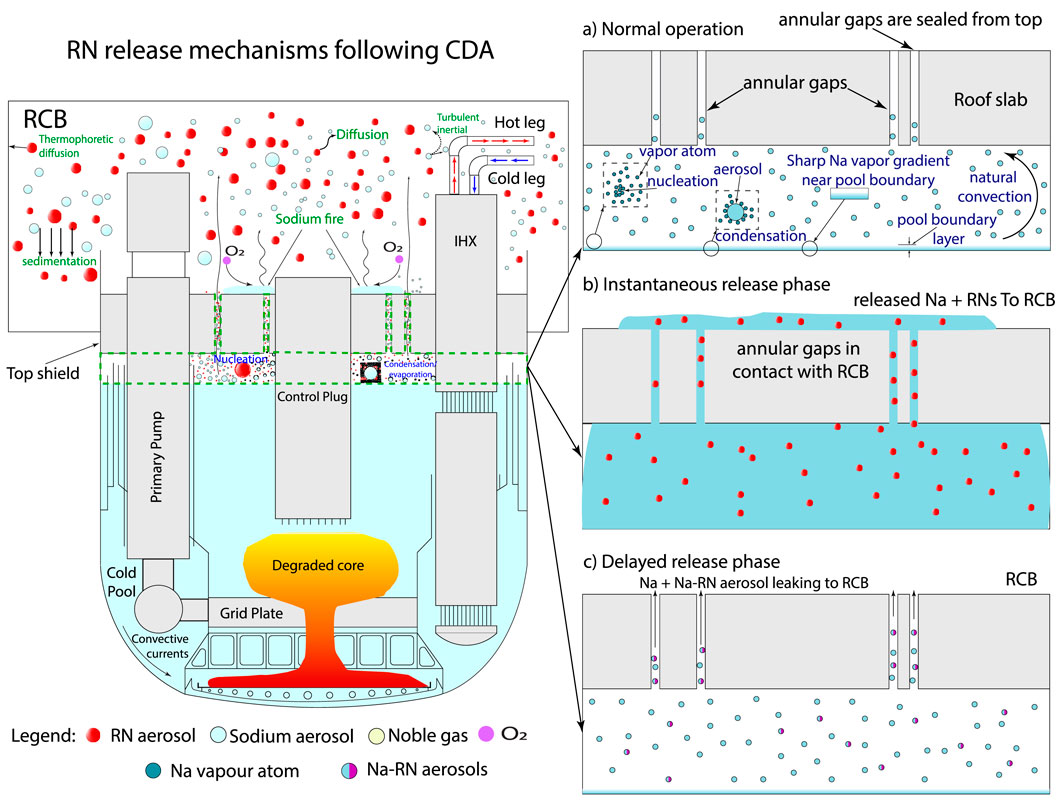
Figure 1. Illustration of RN release mechanisms from the cover gas to the RCB following a CDA. The boundary marked by the green dashed line indicates the cover gas region. (a) Normal operation: During normal operation, the sodium vapour present in cover gas nucleates, condenses, and is transported via natural convection. The resulting aerosol disperses in the cover gas and may also be transported to the annular gaps. (b) Instantaneous release phase: Sodium released through the annular leak paths leads to the release of RN aerosols into the RCB. (c) Delayed release phase: Following sodium release, sodium from the primary pool evaporates, forming sodium aerosols. Due to the high concentration of sodium aerosols, RNs are expected to bind to these Na aerosols.

1.1 Literature of related works

The literature on the interface source term can be broadly classified into two categories: 1) studies related to the determination of the instantaneous source term, and 2) studies related to the determination of the delayed source term. Most experiments concerning both the instantaneous and delayed source terms were conducted in the 1980s (Berthoud et al., 1987; Petrykowski and Longest, 1985).

For the instantaneous interface source term, the experiments primarily focused on RN release during the core bubble expansion and subsequent oscillation phases. Detailed studies on the instantaneous interface source term can be found in various works (Berthoud et al., 1987; Balard and Carluec, 1996).

To date, very limited experimental work has been carried out to understand the delayed release of the RNs post-severe accident, mostly through experiments carried out at NALA, PAVE and NACOWA facilities. These were small-scale facilities [e.g., Minges and Schütz (Minges and Schütz, 1994)] where RN release from hot sodium into an inert gas atmosphere, as well as sodium fires, were examined, effectively simulating delayed source term scenarios in the cover gas.

In the NALA experimental program (Balard and Carluec, 1996; Berthoud et al., 1987), the release behaviour of the Cs, I, Sr, U from hot sodium into an inert gas atmosphere, sodium evaporation, and sodium aerosol behaviour were studied in terms of the enrichment factors². The experiment series included laboratory-scale (few grams of sodium) to technical-scale experiments ($\sim 1$ kg sodium) to study the released quantity of RN. A very high retention factor of Uranium was observed (about $10^4$). For Strontium, the retention factor was about $\sim$ 500. For Iodine and Cesium, the retention factors were very low (for I, RF: 1–10, for Cs RF: <1). The PAVE experimental series aimed to study the release of the insoluble fission products from the sodium during the sodium fire and under neutral atmospheric conditions that are expected to occur in the cover gas during a severe accident scenario. For the SrO, ${\mathrm{C}\mathrm{e}\mathrm{O}}_2$ and ruthenium, the retention factors at the boiling temperature were 300, 100 and 180 respectively (Balard and Carluec, 1996).

Minges and Shutz (Minges and Schütz, 1994) studied the release and deposition behaviours of volatile RNs such as Cs and iodine. It was found that the release was proportional to the vapour pressure of the Cs and iodine. This is expected since Cs would be in elemental form in the primary sodium pool and have higher volatility. Additionally, much larger enrichment factors were found in several cold spots of the roof slab.

1.2 Objective and structure of the manuscript

As observed from the literature, except for highly volatile species such as Cs and I, most RN releases from the sodium pool would be similar to sodium aerosols. This is anticipated due to the significantly lower ratio of RNs in the primary sodium inventory (RNs are on the order of kilograms, while the primary sodium inventory is on the order of hundreds of tonnes). Hence, the release of the volatile RN is expected to be tightly bound to sodium evaporation.

In the present manuscript, we mainly study sodium aerosol formation due to evaporation (from the primary sodium pool), nucleation, condensation, and dispersion in the cover gas space, driven by natural convective currents. These aerosols would eventually be released through leak paths in the annular gaps. Since these aerosols are generated through evaporation of the RN-sodium, they would be internally/externally mixed³ and their behaviour will be dictated by the effective density of the aerosol.

Consideration of all RNs with their effective density would be numerically intensive (as there will be multicomponent internally/externally mixed aerosols). For the current analysis, sodium aerosols have been considered as representative to study the release behaviour from the roof-slab leak paths, with a focus on the release characteristics relative to different aerosol sizes.

The present manuscript is an extension of (Patel et al., 2023), where the evolution and transport of the aerosols in cover gas under reactor operation conditions were studied in detail. In that study, extensive validation of the modified Aerosolved code was also provided. In the current manuscript, we analyse the aerosol evolution and transport in cover gas and roof-slab annular leak paths for a CDA resulting from the ULOF sequence. The study brings out the aerosol transport behaviour and quantifies the effective aerosol size released to the RCB from the annular leak paths in the roof slab.

The manuscript is structured as follows: Section 2 offers a concise overview of the governing equations used in the model. Section 3 provides a brief description of the validation experiments conducted by Furukawa et al. (Furukawa et al., 1984). Section 4 outlines the ULOF accident sequence. Section 5 details the geometric aspects of the reference reactor cover gas. Section 6 discusses various release scenarios considered for the assessment, along with boundary conditions and results from the numerical analysis. Finally, Section 7 concludes our key findings.

2 Model description

2.1 Governing equations

Post-CDA, the temperature in the primary sodium pool would be maintained with Safety Grade Decay Heat Removal System (SGDHRS). For the reference reactors, SGDHRS are designed with a frequency of loss of Decay Heat Removal (DHR function ¡$10^{-7}$/reactor year. For the current analysis, the primary sodium temperature is expected to stabilize at a steady-state temperature of approximately 823 K due to decay heat removal by means of SGDHRS. At such high temperatures, nucleation and condensation of RN-sodium vapour lead to the formation of RN-sodium aerosol. Such RN-sodium aerosols may externally mixed or internally mixed depending on the properties of the RN. (Anderson, 1991). The generated sodium aerosol would grow further via condensation of the RN-sodium vapour. The generated aerosol would be advected to the cover gas (Kumar et al., 2016). The present section provides a brief overview of the governing equations. For the detailed description of the governing equation, the readers are referred to (Frederix et al., 2017; Patel et al., 2023).

Let us consider $\mathcal{S}$ species containing vapour phases (primarily sodium vapor) and condensed phases (mostly sodium aerosols) in volume $\mathcal{V}$. The condensed phase has in ppm concentration with discrete particulate size within the volume. The typical aerosol size ranges from 1 nm to several tens of $\mu m$.

The vapour species are denoted by $f_j^c$, where index j represents the ${\mathrm{j}}^{\mathrm{t}\mathrm{h}}$. Similarly, condensed species are denoted by $f_j^d$. For mass conservation, the sum of the condensed fraction and vapor fraction should be one (Frederix, 2016; Patel et al., 2023),

${\displaystyle \sum _j}\left(f_j^c+f_j^d\right)=1(1)$

The continuity equation for all species can be given as,

$\frac{\partial \rho }{\partial t}+\nabla .\left(\rho \mathbf{u}\right)+\nabla .\left[\mathit{\varphi }\left(1-\gamma \right)\right]=0(2)$

Where $\rho$ is the mixture density and $\mathbf{u}$ is the mixture velocity. Where the third term takes care of the change in the mass due to the removal/addition of the aerosols. $\gamma ={\rho }^v/{\rho }^d$ with ${\rho }^v$ being the local mean vapour density and ${\rho }^d$ being the local mean dispersed phase density (Frederix et al., 2017).

The equation for the conservation of momentum in the mixture can be written as:

$\frac{\partial \left(\rho \mathbf{u}\right)}{\partial t}+\nabla .\left(\rho \mathbf{u}\mathbf{u}\right)=-\nabla p+\nabla .\left(\mu \tau \right)(3)$

Where p is system pressure and $\mu$ is mixture viscosity. $\tau$ is the strain rate tensor (Frederix et al., 2017).where $\mathbf{I}$ denotes the identity tensor. The energy conservation equation for the mixture can be expressed as:

$C_p\frac{\partial \left(\rho T\right)}{\partial t}+C_p\nabla .\left(\rho T\mathbf{u}\right)=\nabla .\left(k\nabla T\right)+\mu \tau \left(\nabla \mathbf{u}\right)+\frac{Dp}{Dt}(4)$

T is the temperature of the mixture. $C_p$ and k are the specific heat capacity and thermal conductivity, respectively. Where, $\frac{D}{Dt}$ is the material derivative $\frac{D}{Dt}≔\frac{\partial }{\partial t}+\mathbf{u}.\nabla$.

The momentum equation for the particle velocity can be expressed as (Ohira, 2003),

$\frac{\partial {\mathbf{u}}_{\mathbf{droplet}}\left(s\right)}{\partial t}+{\mathbf{u}}_{\mathbf{droplet}}\left(s\right)\nabla .{\mathbf{u}}_{\mathbf{droplet}}\left(s\right)=-\frac{1+0.158R{e}_d^{0.687}}{{\tau }_d}\left[{\mathbf{u}}_{\mathbf{droplet}}\left(s\right)-\mathbf{u}\right]+\left(1-\gamma \right)\mathbf{g}(5)$

Where,

${\tau }_d=\frac{{\rho }_p{d}^2}{18\mu }$

$u_{\mathit{droplet}}$(s) is size dependent aerosol velocity, defined as,

${\mathbf{u}}_{\mathbf{d}\mathbf{r}\mathbf{o}\mathbf{p}\mathbf{l}\mathbf{e}\mathbf{t}}\left(s\right)=\mathbf{u}+\mathbf{w}\left(s\right)$

Where, s is the mass of the aerosol. $\mathbf{w}(s)$ is the relative velocity of the aerosol with respect to the motion of the gas mixture (Patel et al., 2023).

${\rho }_p$ represents the particle material density, g is the gravitational acceleration, d denotes the representative particle diameter, and $\gamma$ refers to the ratio of the continuum phase density to the condensed phase density. The aerosol Reynolds number can be expressed as:

$R{e}_d=\frac{\rho d|\mathbf{w}\left(s\right)|}{\mu }$

The species transport equation for condensed and continuous phases can be given as below,

$\frac{\partial }{\partial t}\left(\rho f_j^d\right)+\nabla .\left(\rho \mathbf{u}{f}^d\right)+\nabla .\left({\left(f^d\right)}^{-1}\mathit{\varphi }{f}_j^d\right)={\mathfrak{J}}_j(\mathrm{6a})$

$\frac{\partial }{\partial t}\left(\rho f_j^c\right)+\nabla .\left(\rho \mathbf{u}{f}^c\right)+\nabla .\left({\left(f^c\right)}^{-1}{\mathit{\varphi }}^{\prime }{f}_j^c\right)={\mathfrak{R}}_j(\mathrm{6b})$

Where,

$\mathit{\varphi }={\int }_0^{\infty }s\mathbf{w}\left(\mathbf{s}\right)n\left(s,\mathbf{x},t\right)ds-{\int }_0^{\infty }s\mathbb{D}\left(s\right)\nabla n\left(s,\mathbf{x},t\right)ds(7)$

Where, $\mathbb{D}$ is the aerosol diffusivity, which can be expressed as,

$\mathbb{D}=\frac{K_{b}T{C}_c}{3\pi \mu d}(8)$

Where, ${\mathfrak{J}}_j$ and ${\mathfrak{R}}_j$ are the source term for the condensed/dispersed phase and vapor phase. ${\mathit{\varphi }}^{\prime }$ = $\gamma \mathit{\varphi }$ is the vapor correction flux. The sectional formulation for General Dynamic Equation (GDE) can be given as,

$\frac{\partial }{\partial t}\left(\rho {\mathcal{M}}_i\right)+\nabla .\left(\rho \mathbf{u}{\mathcal{M}}_i\right)+\nabla .\left(\rho \mathbf{w}\left(s\right){\mathcal{M}}_i\right)=\nabla .\left(\mathbb{D}\nabla \rho {\mathcal{M}}_i\right)+J_{{\mathcal{M}}_i}(9)$

Where, $J_{{\mathcal{M}}_i}$ represents the source term, accounting for evaporation, nucleation, and condensation. A detailed expression for the nucleation and condensation can be found in Patel et al. (Patel et al., 2023). ${\mathcal{M}}_i=N_i/\rho$ and $N_i$ represents the number concentration in the ${\mathrm{i}}^{\mathrm{t}\mathrm{h}}$ size bin. Since, here we are examining aerosol size ranging from few nm to 100 $\mu m$, the aerosol size bin structure is chosen such that size bins are spread geometrically over the given size range. For the current analysis, the aerosol size distribution has been divided into 40 size bins, with the minimum aerosol size set to 1 nm and the maximum aerosol size set to 100 $\mu m$. The aerosol size range has been determined based on small-scale experiments and previous numerical studies (Kumar et al., 2016; Patel et al., 2023; Huang and He, 2019). The above set of equations (Equations 1–9) was solved in modified Aersolved (Frederix, 2016; Lucci et al., 2022), which is written using the OpenFOAM framework.

3 Validation

Before conducting a detailed assessment for accidental conditions, the modified solver was validated with experiments performed in small-scale cover gas facilities. The detailed results were presented in Patel et al. (Patel et al., 2023). A summary of the validation results is presented in this section for completeness.

As presented in Table 1, two experimental facilities were considered for validation: the SILVERINA cover gas facility (Kumar et al., 2015) and the cover gas facility reported by Furukawa et al. The details of the cover gas facilities can be found in (Kumar et al., 2015) and (Furukawa et al., 1984). The experimentally observed average mass concentration and temperatures were compared with numerically calculated average values. In some experiments reported by Furukawa et al., average temperatures were not provided; however, the numerically calculated values showed good agreement with the average temperatures obtained by averaging the rooftop temperature and the sodium pool temperature, which represent the approximate average temperature in cover gas (Kumar et al., 2016). Post validation, aerosolEulerFoam would be used to analyze aerosol transport in cover gas during accident conditions post CDA. The subsequent section gives a brief summary of the ULOF accident sequence.

Table 1

Table 1. Validation of average mass concentration and temperature in scaled down cover gas facilities. For current validation two experimental facilities are considered: 1) SILVERINA cover gas facility (Chandramouli et al., 2006) 2) Facility reported by Furukawa et al. (1984).

4 ULOF accident sequence

For the current analysis, the loss of AC power to both primary pumps, along with the failure of engineered safety features, is considered as the initiating event. Initially, due to the loss of flow and subsequent loss of heat removal from the core, the fuel temperature rises. Due to axial and radial expansion, the overall reactivity would be effectively negative and effective power would decrease (Harish et al., 2009).

As the power-to-flow ratio eventually increases, the temperature of both the fuel and coolant will continue to rise, ultimately causing the fuel element clad to fail and releasing non-condensible fission gases (such as Xe and Kr) from the plenum inventory into the coolant. Relatively volatile RN can be transported to the cover gas space along with the non-condensible fission gas bubbles. This would be the first source of the RN release in the cover gas space.

A subsequently high power-to-flow ratio causes sodium voiding in the central top region of the core, which spreads axially downward and radially outward, leading to positive overall reactivity. This effective positive reactivity increases the power and temperature of the fuel sub-assembly, ultimately causing clad failures and initiating fuel melt in the highly rated fuel channels. This molten fuel can be swept away in the primary pool. Due to uncertainty in the modeling, it is assumed that the all molten fuel slumps, leading to large reactivity insertion, power surge, and eventual core disassembly (Harish et al., 2009). This results in conservative estimates. Up to this stage, several RN can be transported along with non-condensable gases and may also evaporate into the cover gas space along with primary sodium. These RN-sodium aerosols can mechanically deposit on various surfaces of the cover gas space. These deposited aerosols can re-evaporate if temperature changes.

At the end of disassembly, about $\sim 54\%$ of the core is in molten form and $\sim 40\%$ of the core volume is in vapor form and the pressure in the molten fuel bubble would be about 4 MPa (Chellapandi et al., 2003). The molten core bubble starts expanding and transfers its energy to the coolant via heat transfer and mechanical work against the vessel wall and roof-slab. It is estimated that during the core bubble expansion phase, the cover gas peak pressure increases to 1.5 MPa and is assumed to fail the seals and elongated bolts on the top shield, leading to the formation of the leak paths in the roof-slab structure. At the end of the first phase, the core bubble does not have further energy to cause any further vessel deformation. This residual core bubble pressure is in quasi-static equilibrium with the surrounding sodium (Chellapandi et al., 2013). The quasi-static pressure is 0.2 MPa.

This quasi-static pressure acts as the driving force for subsequent sodium release into the containment. For the reference reactor, the amount of sodium expelled into the RCB has been estimated through thermal-hydraulic calculations, assuming quasi-static pressure as the driving force, to be approximately 350 kg (Chellapandi et al., 2003). Moreover, several RNs released to cover gas during the fuel melt phase are likely to be ejected into the containment.

Upon the release of sodium, the instantaneous source of RNs within the RCB would comprise the steady-state cover gas inventory and RNs released during fuel melt phase (referred to as the instantaneous interface source term).

Subsequently, the RN release rate to the containment will depend on both the release rate from the fuel into the coolant and the evaporation rate from the coolant surface, as well as the leak rate through the roof slab (referred to as the delayed interface source term). The present manuscript address delayed interface source term, where characteristics of RN releasing for long term to containment and their release rates are quantified.

5 Geometric detail of the reference reactor cover gas

The cover gas region serves as an inert isolation space, bounded by the surface of the primary sodium pool at the bottom and the bottom plate of the roof-slab at the top. During normal reactor operations, the average temperature of the primary sodium pool is approximately 823 K, while the temperature of the roof-slab bottom plate is maintained at around 393 K through air cooling. The cover gas space is connected to annular gaps within the roof-slab, which are provided for manufacturing tolerances between component penetrations and the roof-slab itself. During reactor operation, the annular gaps between the roof-slab and penetrating components (such as Large Rotating Plug (LRP), and Small Rotating Plug (SRP)) are sealed from the top to avoid any leakage.

For the current assessment, the cover gas geometry is based on that of the Prototype Fast Breeder Reactor (PFBR), with some simplifications. The inner diameter of the cover gas was about 12.9 m. The cover gas (i.e., the space comprising between the primary sodium pool and roof-slab bottom plate) height is about 0.8 m. The roof-slab thickness is about 1.8 m, and its bottom plate surface is in contact with argon cover gas.

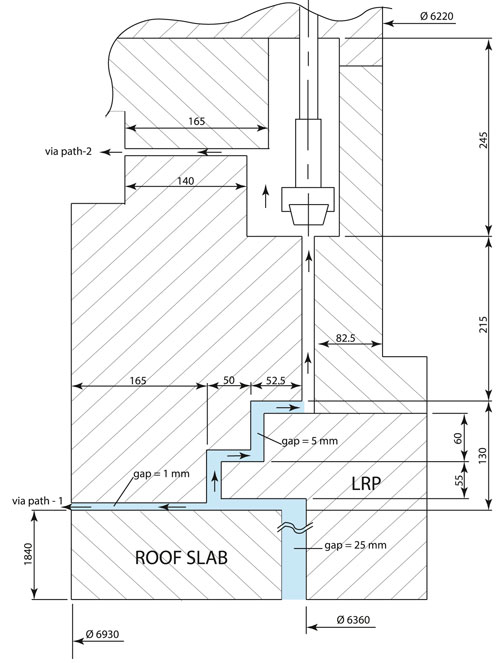
Several components, including the Intermediate Heat Exchanger (IHX), Pump, Decay Heat Exchanger (DHX), and Large Rotating Plug (LRP), are mounted on the roof-slab. The annular gaps between these components and the roof-slab vary from 10 mm to 50 mm, depending on the specific penetration. These gaps are primarily provided to accommodate manufacturing tolerances. For the present analysis, a uniform annular gap of 10 mm has been assumed. Additionally, only the major structural penetrations—namely, the IHX, Pump, DHX, and LRP—are considered for the modelling. A detailed annotated geometrical model is illustrated in Figure 2. The details of the computational framework are given in a subsequent section.

Figure 2

Figure 2. (a) Geometrical information for full reference reactor cover gas and roof-slab domain. (b) Domain considered for numerical analysis. The structural penetration in cover gas are not modeled, only fluid domain (i.e., annular gaps) are modeled. Further, for the geometrical simplification, all annular gaps are considered to be 10 mm. The annulus penetration of LRP-SRP and CP annular gaps are not considered.

6 Post-CDA aerosol evolution in cover gas

During severe accidents such as CDA, the impact of a sodium slug on the roof-slab is expected to cause the displacement of components mounted on the roof-slab. Although some of these components may settle back onto the roof slab following sodium release, the leak area through the bearings of LRP and SRP would remain open even after they return to their normal positions. For the reference reactor, these leak paths in the rotating plugs contribute 80% of the total leak paths area. Hence, the cover gas would be in contact with the RCB after sodium release (Velusamy et al., 2011).

The subsequent release of RNs would be influenced by the available oxygen content within the cover gas space. If the oxygen content is insufficient to sustain or ignite a sodium fire, the RN release would primarily occur through sodium evaporation. These sodium-bound RN aerosols would then be transported to the RCB via the leak paths. A typical leak path formed between the LRP and roof-slab is depicted in Figure 3. As shown, the leak paths in the roof-slab contain multiple bends, which may promote inertial deposition. However, for the current analysis, the effect of these bends is neglected, resulting in conservative release estimates.

Figure 3

Figure 3. Simplified schematic of leak path from RS-LRP for reference reactor.

In this analysis, it is assumed that RN and sodium release occur through the evaporation of the sodium pool, followed by aerosol formation. These aerosols are then transported and released through the leak paths. This assumption is justified, as the sodium pool would be at a significantly higher temperature compared to the RCB, creating a pressure differential that drives the flow outward (with the cover gas at approximately 12 kPa gauge pressure, higher than the RCB pressure). For modelling the leak behaviour from the roof-slab, sodium aerosols are taken as representative aerosols. This assumption is valid because most of the RN release is expected to be tightly bound to sodium evaporation, and a significant portion of the fission products are dissolved in the liquid sodium aerosol present in the cover gas (Balard and Carluec, 1996).

The roof-slab cooling system consists of several cooling lines injecting the air to maintain the roof-slab bottom plate and annular walls temperature at 393 K. The cooling air enters the top shield at 363 K through inlet pipes and cools the roof-slab bottom plate by impinging it as a jet. The coolant leaving the bottom plates flows in a vertical cooling passage around the component penetration shell to cool the annular walls of the shell (IGCAR, 2010). During CDA, the forces imposed on the internal components and the vertical shells can lead to closure of the vertical cooling passages around the component penetrations leading to failure of heat rejection from the cover gas space.

For the current analysis, we have considered the failure of various sections of roof-slab air cooling system, which fails to heat rejection from the cover gas. The behaviour of the aerosol release from the leak path due to these failures is examined. We have studied the failure of three sections viz., 1) failure of the cooling lines near annular walls of the roof-slab at both pump penetrations leading to failure of heat rejection from these locations, 2) failure of the cooling lines near annular walls of the roof-slab in all component penetrations, and 3) failure of the cooling linear near the roof-slab bottom plate and annular walls of the all the component penetrations, enveloping most of the failure scenarios. All three cases are depicted in Figure 4. The failure of the cooling line is depicted via violet blocks. The details of the boundary conditions for each case are given in the following section.

Figure 4

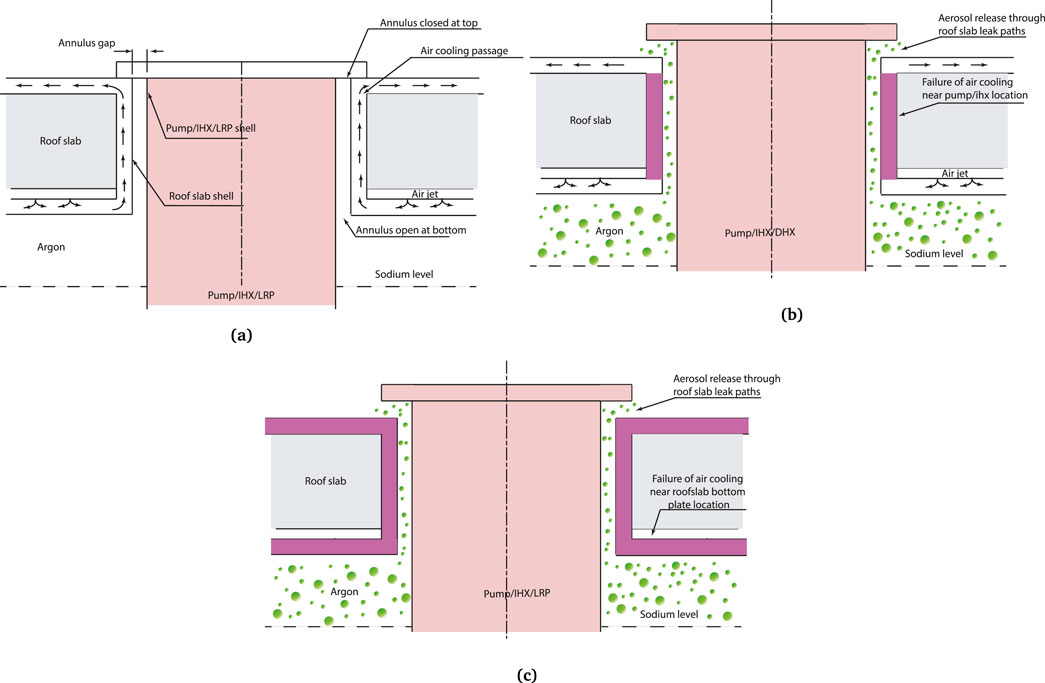
Figure 4. Illustration of cover gas dynamics in roof-slab annular gaps during operation and accident conditions. (a) Illustration of cover gas dynamics during operation conditions. and DHX penetrations (case 1 & 2). (b) Illustration of failure of heat removal to the annular walls of pump/IHX. (c) Illustration of failure of heat removal to roof-slab walls and component penetration annular walls (case-3).

6.1 Boundary condition

The primary sodium pool was subject to a Dirichlet boundary condition (fixedValue). For the side walls of the cover gas region, a Neumann boundary condition (zeroGradient) was imposed. In the absence of explicit temperature data for various component shells, representative pump temperature profiles were assigned to all component shells, as referenced in (Chauhan, 2021; Patel et al., 2023). Furthermore, the temperature boundary conditions for the roof-slab bottom plate and its annular walls were implemented in accordance with the case-specific considerations detailed in Section 6. For example, in case-1, the failure of the cooling lines near the annular wall of the pump is assumed. Hence, adiabatic boundary conditions were applied to the annular walls. Similarly, for the case-2 annular walls of the pump, IHX and DHX were assigned adiabatic boundary conditions. In case-3, adiabatic boundary conditions were applied to all annular walls of the roof-slab and the bottom plate of the roof-slab.

The velocity boundary conditions at the outlet of the annular walls were set to zeroGradient, while no-slip boundary conditions were applied to the cover gas side walls and the roof-slab bottom plate walls. The sodium vapour mass fraction at the roof-slab bottom plate and pool surface is kept constant at one, assuming these surfaces are saturated by sodium vapour. As reported in experiments conducted by A. Anderson (Anderson, 1991), the deposition of aerosol particles onto the cover gas side walls is minimal. Thus, a zeroGradient boundary condition is applied to the cover gas side walls for the aerosol number densities. At the roof-slab bottom plate and annular walls, the number concentration is fixed to zero, assuming complete deposition at the roof-slab bottom plate (Huang and He, 2019). The Neumann boundary condition was applied to define the number densities at the pool surface and the component shell wall within the cover gas, while turbulence was modeled using the standard k-$ϵ$ model.

6.2 Failure of the cooling section near the annular walls of the roof-slab near primary pump penetrations

In the reference reactor, the primary pump is a centrifugal and mechanical pump with about 20 m height housing in the standpipe of the inner vessel penetrating in the cold pool (IGCAR, 2010). During CDA, there is a possibility of deformation of the internal components during core bubble expansion (Chellapandi et al., 2003). The few mm pump displacement would essentially block the cooling lines near the pump annular gaps, leading to a ceasing or reduction in heat rejection from the cover gas to the cooling lines present in roof-slab. Hence, it is necessary to study all possible annular gap cooling section failure scenarios. In the present section, analysis is performed for the failure of the pump annular gap cooling lines. The subsequent section discusses the failure of both the pump and IHX annular gap cooling lines.

Figure 5a shows the total mass flow rates (consisting of dispersed and continuous phases) at each leak path at the rooftop. The highest leak rate is from the LRP-RS leak path $\sim 1.24$ g/s. Which constitutes about 35% of the total mass flow rate. This is expected, as the LRP annular gaps leak area for the current reference reactor is about 0.2133 ${\mathrm{m}}^{\mathrm{2}}$, compared to other leak paths (e.g., DHX: 0.01791 ${\mathrm{m}}^{\mathrm{2}}$, Pump: 0.0688 ${\mathrm{m}}^{\mathrm{2}}$).

Figure 5

Figure 5. (a) Total mass flow rate from the various leak paths, comprising both aerosol phase and gas phase (argon and sodium vapour). (b) Phase-wise mass flow rate from the leak paths, where the inert phase consists of both argon and sodium vapour. (c) Aerosol size-wise leak rate at the leak-path outlet. The leak rates were determined by multiplying the aerosol mass flux by the leak-path outlet area. In this context, the aerosol leak rate is positive for aerosols with sizes <20 $\mu m$, whereas aerosols >20 $\mu m$ exhibits a negative leak rate. The negative leak rate for larger aerosols is attributed to gravitational force.

Figure 5b shows mass flow rates for both inert and dispersed phases. As shown in the figure, effective positive mass outflow is for the inert phase only. Whereas, the dispersed phase is having effective negative mass flow rate. The negative mass flow rate might be due to inertia force of the large aerosol particles due to effective downward force. The effective leak rates for the dispersed phase are about 0.02–0.05 g/s for most of the leak paths.

Figure 5b depicts aerosol size-wise mass flow rates at the leak path outlet, which gives better understanding regarding aerosol size leaking out from the leak path. The aerosol size less than $\sim$ 20 $\mu m$ are having positive mass flux at the outlet of the leak-path. The peak positive mass flux is about 3 mg/s for the particle size of 17 $\mu m$ at the LRP leak path outlet. The peak negative mass flux is about 25 mg/s for the particle size of the 40 $\mu m$ aerosols at the LRP leak path outlet. The maximum mass flux rate is found for the RS-LRP leak path, which is expected as the RS-LRP has the highest leak path area compared to other component penetrations. Figure 6 shows the flow distribution of the mixture in the pump’s annular gaps. As seen in the figure, there is air ingress from the RCB atmosphere. However, the air ingress is limited to the annular gaps only.

Figure 6

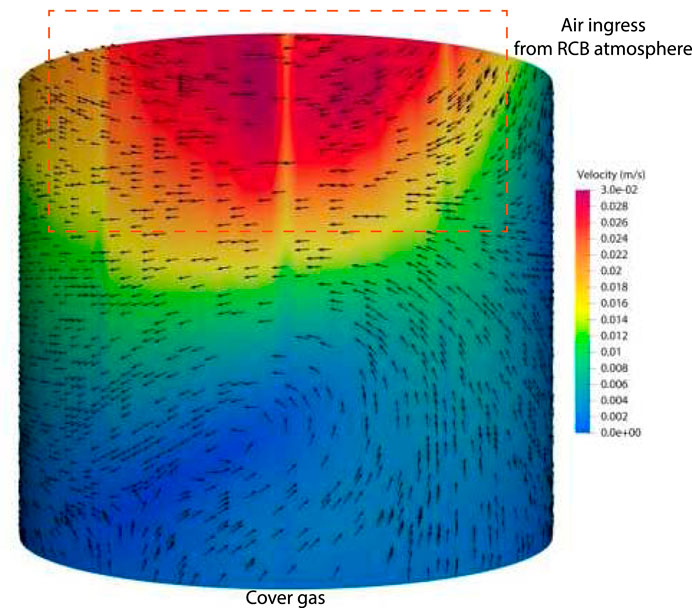
Figure 6. Illustration of air ingress from RCB atmosphere. The RCB air mixing is limited to the annular gaps only. The effective mass flow rate is positive at the outlet.

The average temperature in the cover gas is about 630 K. The average mass concentration in the cover gas region is about 45–50 g/${\mathrm{m}}^{\mathrm{3}}$. Whereas, the average mass concentration in the annular regions varies about 45–65 g/${\mathrm{m}}^{\mathrm{3}}$. The Count Mean Diameter in the annular regions of the pump, LRP, DHX and IHX varies from 7–11 $\mu m$.

6.3 Failure of the cooling section near the annular walls of the roof-slab in the all component penetrations

Figure 7a shows the steady state total mass flow rates (considering the contribution from both phases, i.e., the inert and dispersed phases). As shown in the figure, the leak rates are not consistent with the leak path area (the leak rate in some of the DHX leak paths is higher compared to LRP leak paths). To determine the reason behind the lower leak rates from the LRP leak paths compared to the DHX leak paths, the temperature gradient in the annular gaps were compared. From the temperature gradient in the annular gaps, it is seen that LRP, IHX and pump temperature gradients are about 70 k/m. Whereas, DHX temperature gradient is about 100 k/m. This higher temperature gradient could cause higher buoyancy in the annular gaps and eventual higher leak rates in the DHX annular gaps compared to LRP annular gaps. Whereas, for the pump annular gaps failure case, the temperature gradient in the annular gaps is comparable (about 100–120 k/m) to the other annular leak paths, leading to mass flow rates consistent with the leak area. Additionally, there were more convection loops compared to the pump annular gap failure case.

Figure 7

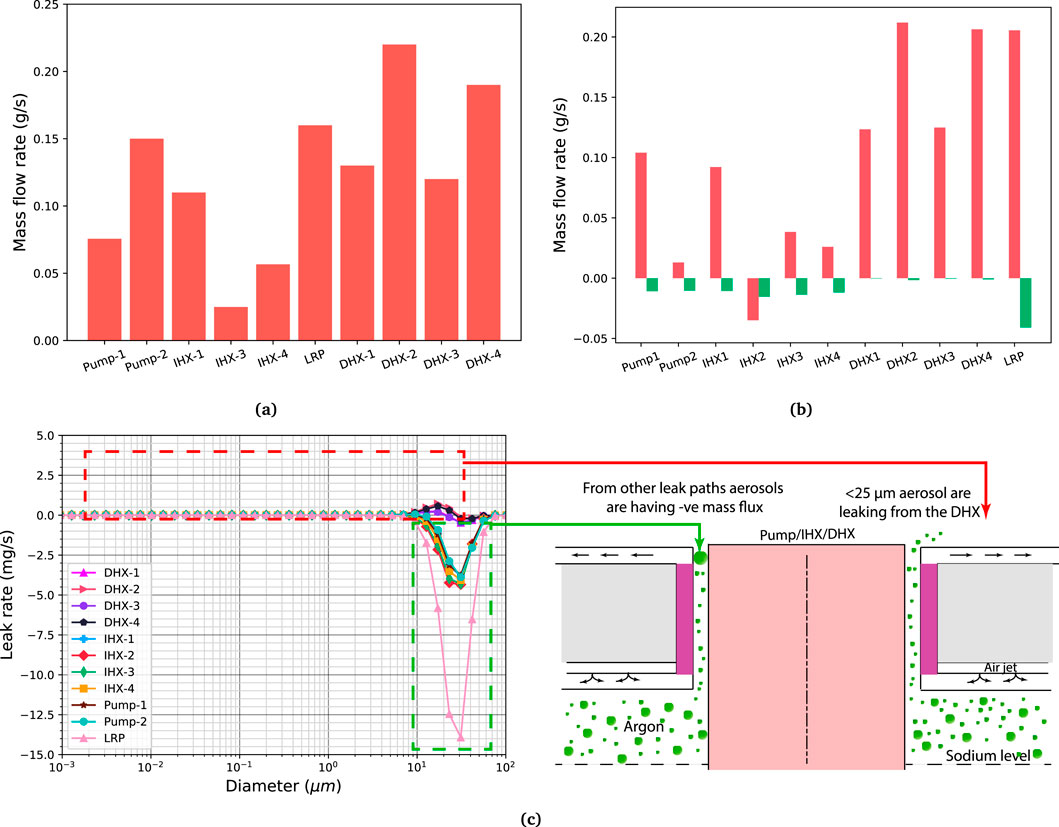
Figure 7. (a) Total mass flow rate from the various leak paths, comprising both aerosol phase and gas phase (argon and sodium vapour). (b) Phase-wise mass flow rate from the leak paths, where the inert phase consists of both argon and sodium vapour. (c) Aerosol size-wise leak rate at the leak-path outlet. The leak rates were determined by multiplying the aerosol mass flux by the leak-path outlet area. In this context, the aerosol leak rate is positive for aerosols with sizes <25 $\mu m$, whereas aerosols >25 $\mu m$ exhibits a negative leak rate. The negative leak rate for larger aerosols is attributed to gravitational force.

The mass flow rates for the inert and dispersed phases are shown in Figure 7b. As shown in the figure, except for IHX-2, the effective positive mass outflow is for the inert phase only. Whereas, the dispersed phase has effective negative mass flow rates. The effective leak rates for the dispersed phase are about 0.01–0.04 g/s for most of the leak paths.

Figure 7c depicts aerosol size-wise mass flow rates. As shown in the figure, the positive leak rate is seen for only DHX leak paths. Leak rates for other component annular leak paths are negative. The leaking aerosols from the DHX are less than 25 $\mu m$. The peak positive leaked mass is observed for about 17–23 $\mu m$ aerosols. The peak negative leak rates are for about 31 $\mu m$ aerosols. Where for LRP annular leak paths the leak rates are about 14 mg/s and for other leak paths the leak rates are about 3–4 mg/s.

The average temperature in the cover gas is about 640 K. The average aerosol concentration in the cover gas region is about 40 g/${\mathrm{m}}^{\mathrm{3}}$. Whereas, in the annular gap region, the aerosol concentration varies from about 30–35 g/${\mathrm{m}}^{\mathrm{3}}$. The CMD of aerosol in the annular regions of the pump, LRP and IHX varies from 8–9 $\mu m$.

6.4 Failure of the cooling section near the roof-slab bottom plate and annular walls of all the component penetrations

Figure 8a shows the total mass flow rate at the outlet of the leak path. As shown in the figure, the maximum mass flow rate is for the LRP annular leak path (about 2 g/s), which is the highest among all the failure scenarios. The mass flow rate for the pump/IHX leak path is about 0.5 g/s. For DHX, the mass flow rates are about 0.125 g/s. The mass flow rates are consistent with the leak path area. Figure 8b shows the mass flow rates for the dispersed phase and inert phase. The dispersed phase mass flow rates are very low. This might be due to the effective downward force on the larger particles. Figure 8c, shows the aerosol size-wise leak rates for various annular leak paths. The positive leak rates are for aerosol sizes less than 25 $\mu m$. The peak positive leak rate for most of the annular gaps is about 17 $\mu m$. The highest positive leak rate is for the LRP leak path, about 8 mg/s for 17 $\mu m$. The peak negative aerosol leak rate is for 40 $\mu m$ particles (about 20 mg/s).

Figure 8

Figure 8. (a) Total mass flow rate from the various leak paths, comprising both aerosol phase and gas phase (argon and sodium vapour). (b) Phase-wise mass flow rate from the leak paths, where the inert phase consists of both argon and sodium vapour. (c) Aerosol size-wise leak rate at the leak-path outlet. The leak rates were determined by multiplying the aerosol mass flux by the leak-path outlet area. In this context, the aerosol leak rate is positive for aerosols with sizes <25 $\mu m$, whereas aerosols >25 $\mu m$ exhibits a negative leak rate. The negative leak rate for larger aerosols is attributed to gravitational force.

The average temperature in the cover gas is about 820 K. This was expected since for this case it is assumed that all annular cooling paths and roof-slab bottom plate cooling sections failed, leading to continuous temperature rise in the cover gas. Eventually, the cover gas space would be in equilibrium with the sodium pool temperature. The average aerosol mass concentration in the cover gas is about 28–30 g/${\mathrm{m}}^{\mathrm{3}}$, which is lower than the other two cases (case-1: about 45–50 g/$m^3$ and case-2: about 40 g/$m^3$). The reason behind the lower aerosol concentration may be due to the higher average temperatures of the cover gas, leading to a lower chance of condensation in the cover gas compared to the other two cases. To confirm, we checked the average sodium vapour mass fraction in the cover gas. We found that for the failure of the cooling section near the roof-slab bottom plate and annular wall of the other roof-slab penetrations, the sodium vapour mass fraction was about 0.05, whereas, for the failure of the cooling section near the pump annular wall, the sodium vapour mass fractions were about $10^{-5}$. For the failure of the cooling section near pump-IHX-DHX annular walls in the roof slab, the sodium vapour mass fractions were observed in the range of $10^{-3}$ to $10^{-7}$. Where near sodium pool the sodium vapour mass fractions were observed about $10^{-3}$ and near roof-slab it was about $10^{-7}$.

The present analysis is performed with sodium aerosols as a representative aerosol to the RN-sodium aerosol mixture. Though the present analysis does provide useful insights regarding aerosol behaviour concerning aerosol size and various scenarios involving failure of the different cooling sections in the roof-slab, we believe it is a first step towards multi-component aerosol analysis. It should be noted that the aerosol size is one of the most important parameters governing the aerosol transport behaviour. The above analysis shows that most of the aerosols leaking from the roof-slab leak paths have a size of less than 25 $\mu m$. These results differs from the operating condition observation, where we observed aerosol having <1 $\mu m$ would be in upper region of the annular gap. The reason behind presence of higher aerosols during accident conditions might be due to open leak paths and air ingress from the RCB atmosphere, which promotes the aerosol growth in the annular gaps. The aerosols of size 17–23 $\mu m$ have peak mass flux at the roof-slab outlet, whereas the aerosols of size 31–40 $\mu m$ are having negative mass flux at the roof slab outlet. Further, it is seen that higher leak rates are observed in the case of complete failure of the roof-slab cooling system. Hence, the roof-slab cooling system as well as cover gas systems should remain functional post-accident scenario.

7 Conclusion

This study presents a mechanistic assessment of the delayed interface source term, focusing on post-accident aerosol release through roof-slab leak paths. Sodium aerosols are used as a representative for RN-sodium mixtures to reduce computational complexity. The analysis investigates size-dependent aerosol transport across three failure scenarios viz., 1) roof-slab cooling line failure near primary pump penetrations, 2) failure of cooling line near all component penetrations, and 3) failure of cooling line near all component penetrations and the roof-slab bottom wall.

Simulations reveal that most of the aerosols released through roof-slab leak paths are less than 25 $\mu m$ in size, differing from operating conditions where sub-micron aerosols (less than 1 $\mu m$) dominate in the upper annular gap. The presence of larger particles post-accident at roof-slab leak paths is attributed to open leak paths and air ingress from the RCB atmosphere, promoting in-gap aerosol growth. However, the air ingress from RCB was found to be limited to annular leak paths only. Lower aerosol concentrations were observed in scenarios with complete roof-slab cooling failure due to higher temperatures converting sodium aerosol into vapor. This resulted in increased mass fluxes of aerosol and vapor at the leak paths outlets.

These findings emphasize the critical role of roof-slab coolability in mitigating aerosol release to the RCB post-accident. Maintaining roof-slab bottom plate temperatures within limits is essential to minimize leak rates. Currently, sodium aerosols are used to study the aerosol release behavior from RCB. In future it will be interesting to study multi-component RN-sodium aerosols behavior and its validation with simulated experiment observations.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

PP: Investigation, Methodology, Software, Validation, Writing – original draft, Writing – review and editing. AK: Conceptualization, Investigation, Supervision, Writing – review and editing. AA: Project administration, Resources, Supervision, Writing – review and editing.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Gen AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹Cover gas refers to the inert isolation layer provided in SFRs.

²The enrichment factor was defined as the ratio of the RN concentration in the released sodium to the RN concentration in the sodium pool.

³A single aerosol particle may be composed of many chemical species and the aerosol may consist of mixed particle of multicomponent aerosols. If all particle in aerosols are of the same chemical composition, the aerosol is said to be internally mixed. If the particles in the aerosol are chemically different, then the aerosol is said to be externally mixed (Friedlander, 2000).

References

Anderson, A. (1991). Studies of aerosol characteristics, heat transfer and mass transfer with application to the cover gas region of sodium cooled Fast reactors. Manchester: University of Manchester. Ph.D. thesis.

Google Scholar

Balard, F., and Carluec, B. (1996). “Evaluation of the LMFBR cover gas source term and synthesis of the associated R and D,” in Evaluation of radioactive materials and sodium fires in Fast reactors (Japan).

Google Scholar

Berthoud, G., Longest, A. W., Wright, A. L., and Schütz, W. P. (1987). Experiments on liquid-metal fast breeder reactor aerosol source terms after severe accidents. Nucl. Technol. 81 (2), 257–277. doi:10.13182/nt88-a34096

CrossRef Full Text | Google Scholar

Chandramouli, S., Sakthivel, S., Vijayamohana Rao, P., Gurumoorthy, K., Rajan, K. K., Kalyanasundaram, P., et al. (2006). “Commissioning and operation of SILVERINA sodium loop,” in Proceedings of national conference on operating experience of nuclear reactors and power plants (Mumbai: BARC), 203–209.

Google Scholar

Chauhan, A. K. (2021). Thermal analysis of PSP of PFBR. Internal report PFBR/32110/DN/1144/Rev.A, indira gandhi center for atomic research, kalpakkam.

Google Scholar

Chellapandi, P., Srinivasan, G. S., and Chetal, S. C. (2013). Primary containment capacity of Prototype Fast Breeder Reactor against core disruptive accident loadings. Nucl. Eng. Des. 256, 178–187. doi:10.1016/j.nucengdes.2012.12.014

CrossRef Full Text | Google Scholar

Chellapandi, P., Velusamy, K., Chetal, S. C., Bhoje, S. B., Lal, H., and Sethi, V. S. (2003). “08-17/2003-08-22. Analysis for mechanical consequences of a core disruptive accident in prototype fast breeder reactor,” in 17th international conference on structural mechanics in reactor technology (SMiRT 17), 17–22.

Google Scholar

Frederix, E., Kuczaj, A., Nordlund, M., Veldman, A., and Geurts, B. (2017). Eulerian modeling of inertial and diffusional aerosol deposition in bent pipes. Comput. and Fluids 159, 217–231. doi:10.1016/j.compfluid.2017.09.018

CrossRef Full Text | Google Scholar

Frederix, E. M. A. (2016). Eulerian modeling of aerosol dynamics. Netherlands: University of Twente. Ph.D. thesis.

Google Scholar

Friedlander, S. K. (2000). Smoke, dust, and haze: fundamentals of aerosol dynamics. 2nd Edition. New York: Oxford University Press.

Google Scholar

Furukawa, O., Furutani, A., Hattori, N., and Iguchi, T. (1984). Experimental study of heat transfer through cover gas in the LMFBR. Exp. Study Heat Transf. through Cover Gas LMFBR 1, 451–458.

Google Scholar

Grabaskas, D., Bucknor, M., and Jerden, J. (2017). A mechanistic source term calculation for a metal fuel sodium Fast reactor. Argonne, IL: Argonne National Laboratory. (ANL).

Google Scholar

Grabaskas, D. S., Brunett, A. J., Bucknor, M. D., Sienicki, J. J., and Sofu, T. (2015). “Regulatory technology development plan sodium fast reactor,” in Mechanistic source term development. ANL-ART–3. Argonne, IL United States: Argonne National Laboratory ANL.

Google Scholar

Harish, R., Srinivasan, G., Riyas, A., and Mohanakrishnan, P. (2009). A comparative study of unprotected loss of flow accidents in 500MWe FBR metal cores with PFBR oxide core. Ann. Nucl. Energy 36 (8), 1003–1012. doi:10.1016/j.anucene.2009.06.004

CrossRef Full Text | Google Scholar

Huang, X., and He, S. (2019). Numerical modelling of cover gas thermal hydraulics in Sodium-cooled Fast Reactors. Nucl. Eng. Des. 355, 110347. doi:10.1016/j.nucengdes.2019.110347

CrossRef Full Text | Google Scholar

IGCAR (2010). “PFBR final safety analysis report,” in Scientific report internal report, indira gandhi center for atomic research. Kalpakkam.

Google Scholar

Kumar, A., Subramanian, V., Krishnakumar, S., Baskaran, R., Chandramouli, S., and Venkatraman, B. (2015). Characterisation of sodium aerosol in cover gas region of SILVERINA loop. Aerosol Air Qual. Res. 15 (5), 1813–1822. doi:10.4209/aaqr.2014.09.0193

CrossRef Full Text | Google Scholar

Kumar, A., Venkatesan, S., Krishnakumar, S., Ramakrishnan, B., Chandramouli, S., and Balasubramaniam, V. (2016). Studies on geometrical effect on sodium aerosol characteristics in cover gas region. Aerosol Air Qual. Res. 16, 1832–1840. doi:10.4209/aaqr.2016.01.0010

CrossRef Full Text | Google Scholar

Lucci, F., Frederix, E., and Kuczaj, A. K. (2022). AeroSolved: computational fluid dynamics modeling of multispecies aerosol flows with sectional and moment methods. J. Aerosol Sci. 159, 105854. doi:10.1016/j.jaerosci.2021.105854

CrossRef Full Text | Google Scholar

Minges, J., and Schütz, W. (1994). Experiments on the enrichment of cesium in the cover gas aerosol of the European Fast Reactor EFR. Nucl. Eng. Des. 147 (1), 17–22. doi:10.1016/0029-5493(94)90251-8

CrossRef Full Text | Google Scholar

Ohira, H. (2003). Numerical simulation of aerosol behavior in turbulent natural convection: verification of an advanced model. J. Nucl. Sci. Technol. 40 (5), 307–316. doi:10.3327/jnst.40.307

CrossRef Full Text | Google Scholar

Patel, P. R., Kumar, D. A., and Arul, A. J. (2023). Mechanistic assessment of aerosol transport in an SFR cover gas space under operating condition. Aerosol Sci. Technol. 57 (9), 842–860. doi:10.1080/02786826.2023.2232428

CrossRef Full Text | Google Scholar

Petrykowski, J. C., and Longest, A. W. (1985). “LMFBR source term experiments in the fuel aerosol simulant test (FAST) facility,” in Proceeding of the international topical meeting on Fast reactor safety (Knoxville, Tennessee, United States: Oak Ridge National Laboratory).

Google Scholar

Velusamy, K., Chellapandi, P., Satpathy, K., Verma, N., Raviprasan, G. R., Rajendrakumar, M., et al. (2011). A fundamental approach to specify thermal and pressure loadings on containment buildings of sodium cooled fast reactors during a core disruptive accident. Ann. Nucl. Energy 38 (11), 2475–2487. doi:10.1016/j.anucene.2011.07.002

CrossRef Full Text | Google Scholar

Nomenclature

CDA Core Disruptive Accident

CFD Computational Fluid Dynamics

DHX Deacay Heat Exchanger

IHX Intermediate Heat Exchanger

LOCA Loss of Coolant Accident

LRP Large Rotating Plug

PFBR Prototype Fast Breeder Reactor

RCB Reactor Containment Building

RN Radionuclide

SAMG Severe accident management guidelines

SFR Sodium cooled Fast Reactor

SGDHRS Safety Grade Decay Heat Removal System

SRP Small Rotating Plug

ULOF Unprotected Loss of Flow

Greek symbols

$\mathit{\gamma }$ interphase mass transfer term

${\mathit{C}}_{\mathit{p}}$ specific heat capacity of the mixture (J/kg/k)

$\mathit{\mu }$ mixture viscosity(Pa S)

${\mathit{\nu }}^{\mathit{turbulence}}$ turbulent viscosity (Pa S)

$\mathit{\rho }$ Mixture density (kg/${\mathrm{m}}^{\mathrm{3}}$)

$\mathit{\tau }$ stress tensor

$\mathbf{u}$ velocity of mixture (m/s) c continuum

Subscripts/superscripts

d discrete

i bin index

j Species index

p particle

v vapor

Other symbols

$\mathit{f}$ mass fraction

D diffusion coefficient ($m^2$/s)

g gravitational acceleration (m/$s^2$)

I identity tensor

J Nucleation rate (#/$m^3$/s)

K Coagulation kernel k thermal conductivity (W/m/K)

n, N aerosol number concentration (#/${\mathrm{m}}^{\mathrm{3}}$)

p pressure (N/${\mathrm{m}}^{\mathrm{2}}$)

Re Reynolds number s aerosol mass (kg)

T Temperature of mixture (K)

w(s) Relative velocity of the aerosol with respect to motion of the gas (m/s)

x, y aerosol volume $({\mathrm{m}}^{\mathrm{3}})$