Hybrid solvers for reactor modelling: matrix-based and matrix-free approaches on voxel-dominated meshes

Simulating neutronics and thermal hydraulics within nuclear reactor cores is computationally intensive, not only because of the complexity of the governing equations but also because of the intricate geometries involved. Solving the Boltzmann transport and Navier-Stokes equations for a full core representation typically relies on unstructured meshes, which, while highly flexible, can substantially increase computational costs regarding memory and solving time. Cartesian meshes with Finite Elements (FE) offer a faster alternative, potentially improving computational speed by an order of magnitude due to direct memory addressing. However, they necessitate finer grids to accurately capture the boundary details of non-Cartesian surfaces, which can offset these gains by increasing solver times. To address this challenge, a new meshing algorithm is proposed in conjunction with hybrid, matrix-based and matrix free, solver technologies. It employs a geometry-conforming boundary method using voxel-dominated Cartesian meshes. This method enables accurate boundary representation at arbitrary resolutions, which can be adjusted to resolve the physics to the desired level of accuracy rather than strictly to capture geometric detail. This is combined with a hybrid solver for fluid flows to different regions of a problem in order to increase efficiency when resolving the boundary. This article demonstrates the method’s application to Computational Fluids Dynamics (CFD) and neutronics problems relevant to reactor physics, showcasing its accuracy, convergence, numerical stability, and suitability for handling complex geometries.

Highlights

$•$ Voxel-dominant meshes are built from Signed Distance Functions (SDF), allowing for accurate surface representation.

$•$ A hybrid matrix-free and matrix-based FEA solver was developed to accelerate computations associated with voxel-dominant meshes

1 Introduction

Simulating neutron transport and thermal hydraulics within nuclear reactor cores is computationally intensive. The complexity of the governing equations combined with the intricate geometries involved often lead us to use simplifications, whether that be to the equations or the problem domains, that often sacrifices numerical accuracy for reduced computational costs. Often the thermal hydraulics are resolved at the sub-channel scale using coupled one-dimensional models that are highly parameterised and fine tuned to experimental data. Other examples include the use of diffusion theory for resolving the neutron distribution, perhaps with a few groups resolving the energy domain with smeared cross-sections homogenising the heterogeneous structures making a core.

High fidelity models are of course used today and are still being developed by various research bodies throughout the world to improve the quality of numerical approximations. Finite element, spectral element and control volume models are popular choices as they offer a flexible route to capturing geometries, and have been developed extensively over the last few decades. Examples of their use in thermal hydraulics include Paul et al. (2008), and similarly Fang et al. (2021), providing full FEM solutions of the Navier-Stokes LES equations for reactor analysis. Others have proposed hybrid methods, such as Liu et al. (2019), Liu et al. (2022), that aim to combine CFD calculations with sub-channel models to enhance accuracy whilst retaining the computational speed of the sub-channel model. A recent review of methods in CFD in nuclear thermal hydraulics can be found in Wang M. et al. (2021). Similarly, for neutron transport, FEM solutions on both structured (Evans et al., 2010) and unstructured grids (Wang Y. et al., 2021; Nguyen et al., 2025) have been developed and are in use in many industry and research codes and meshing tools (Tautges and Jain, 2012).

Unstructured mesh methods are best suited to handle complex geometries composing a core that include fuel pins, spacer grids among other supporting structures. Structured meshes, say with Finite Elements, have also been proposed as a faster alternative, offering the potential to improve computational speed by an order of magnitude due to their reduced memory access requirements and structured solver implementations. However, their primary limitation lies in handling complex geometries, particularly in the presence of curved boundaries and irregular features. Unlike unstructured meshes, which conform naturally to boundaries, Cartesian grids approximate curved surfaces with step-like edges. This stair-casing effect leads to significant accuracy loss, particularly in the BTE, where geometric fidelity plays a critical role in determining neutron streaming paths and scattering effects.

To mitigate the stair-casing issue, several Cartesian-based solver techniques have been developed for general PDEs, including applications in fluid flow, solid mechanics. These methods include:

$•$ Immersed boundary methods (Peskin, 2002; Verzicco, 2023; Yang et al., 2018; Yang, 2018), which treats the boundary/interface as a forcing term on the smeared-interface surface. It either use the Dirac delta or Heaviside distribution.

$•$ Cut-cell approaches (Ingram et al., 2003; Meinke et al., 2013; Xie, 2022), where the geometry cuts through the Cartesian grid or block-structured adaptive mesh refinement (AMR) grid (Barad et al., 2009; Salih et al., 2019), and cells that intersect the boundary are trimmed to match the geometry. It strongly enforces the boundary. But it may lead to small elements or irregular cuts.

$•$ Unfitted boundary methods (Lesueur et al., 2022; Martorell and Badia, 2024), which uses background grids with weakly enforced boundary constraints.

Other approaches include the development of iso-parametric elements that can be used in combination with both structured and unstructured meshes to conform exactly to structures such including fuel pins (Owens et al., 2016).

From an implementation point of view, there are two ways to implement an FEA solver: the matrix-based method and the matrix-free method (Johan and Hughes, 1991; Davydov et al., 2020; Martínez-Frutos and Herrero-Pérez, 2015). The matrix-based approach assembles the global stiffness matrix, which can be memory-intensive for large sparse systems, and the assembly cost grows with the problem size. On the other hand, the matrix-free approach does not assemble the global matrix; instead, it computes matrix–vector products on the fly. This results in much lower memory usage and faster performance for large-scale problems, e.g., on GPUs.

There are two type of geometry modelling approaches, explicit modelling or implicit modelling. Explicit modeling describes geometry through direct parameterisation, where surfaces and boundaries are explicitly defined. This approach is widely used in Computer-Aided Design (CAD) systems, which rely on representations such as Non-Uniform Rational B-Splines (NURBS) and triangle meshes to create and manipulate complex structures.

Implicit modelling, on the other hand, defines geometry indirectly using mathematical functions, typically representing surfaces as level sets of scalar fields (Li et al., 2018). This approach is particularly advantageous for handling complex, topologically evolving shapes, such as those found in fluid simulations, medical imaging (MRI/CT scans), and volumetric datasets (e.g., VDB data (Museth, 2013)). It can be generated via implicit geometry kernel or library, including nTop Inc. (2024), LEAP71 (2024).

This article explores implicit geometric modelling techniques, specifically by leveraging the signed distance function (SDF) to efficiently represent complex geometries. In addition, the proposed method addresses the challenge of using structured meshes that still conform to geometries of arbitrary shape. The method (named implicit geometry-conforming meshing (IGCM)) employs a voxel-dominated Cartesian mesh, that maintains as much structure as possible, but for a few elements that are perturbed so that element surfaces are fitted to an internal body’s boundary, or a problem’s exterior domain. In addition, this article also proposes a hybrid solver for CFD that, in particular, can be used in combination with the meshing tool. This approach ensures a balance between computational efficiency and geometric fidelity, allowing fine-scale resolution where necessary while maintaining the performance benefits of a structured mesh. In contrast to the hex-core meshing algorithm, the mesh will be exported in unstructured format. Our solver will leverage the Cartesian data structure and design the associated solver.

The following sections are set out as follows. Section 2 details the voxel dominated meshing tool together with the hybrid solver for CFD. Section 3 presents a range of numerical examples applying the proposed tools to a range of applications and benchmarks including neutron transport and CFD of fuel assemblies. Section 4 completes the article with a conclusion.

2 Voxel dominated mesh with hybrid solver

This section describes the voxel-dominated displaced boundary mesh method, along with the hybrid solver for efficient CFD simulations.

Two variants of the meshing approach are proposed for capturing the geometric details of arbitrary bodies. The first applies when only the external or internal region of the domain is needed, such as in CFD calculations for flow around solid bodies. The second resolves both the internal and external regions of a structure, which is typically required for neutron transport and fluid-structure interaction calculations. This approach is often referred to as multi-material with interface.

In both cases, the goal is to preserve a uniform Cartesian grid across as much of the domain as possible, modifying or displacing elements only where necessary to conform to the surface of the body. The method is illustrated in Figure 1, which shows a Cartesian voxel mesh initially discretising a square domain containing a circular region whose surface is to be preserved. Maintaining the Cartesian structure throughout but filtering out the internal elements of the circle (assuming here the exterior is to be resolved) results in the mesh of 1b where clearly the surface is approximated with the step-like structure and resemblance of the surface is only achieved when sufficient, and perhaps excessive, resolution is applied.

Figure 1

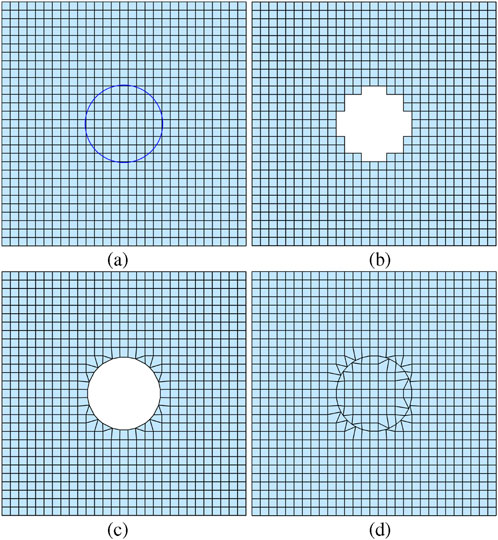
Figure 1. (a) Initial voxel grid with circle indicated; (b) Cartesian mesh with internal elements removed; (c) Unfitted boundary method for external domain with mixed Cartesian and unstructured grid; (d) Unfitted boundary method preserving internal/external domains using only quadrilateral elements in Cartesian coordinates.

Instead, the method introduced here begins with structured Cartesian voxel mesh (or background mesh) of Figure 1a with element size $\mathrm{\Delta }x$. An internal geometry, such as the circle here, is then represented through a signal distance field (SDF), which holds the minimum distance between any position within the domain to the surface of the object, denoted here as ${\mathrm{\Gamma }}_S$.

From this, a transformation map, ${\phi }_{\mathbf{d}}$, is defined on the nodes of the background mesh that map the set of closest nodes to the surface, to the nearest position on the surface. That is, for the given set of nodes on the original background mesh, denoted as $\{{\mathbf{x}}_i\}$, for $i\in \{\mathrm{1,2},\dots N\}$ ($N$ being the total number of mesh nodes), a new set of point positions $\{{\widehat{\mathbf{x}}}_i\}$ are formed by,

${\widehat{\mathbf{x}}}_i={\phi }_{\mathbf{d}}\left({\mathbf{x}}_i\right)=\left\{\begin{array}{cc}{\mathbf{x}}_i+\mathbf{d}\left({\mathbf{x}}_i\right),\hfill & \text{if\hspace{0.17em}}{\mathbf{x}}_i\in {\mathrm{\Gamma }}_M,\hfill \\ {\mathbf{x}}_i,\hfill & \text{otherwise}.\hfill \end{array}\right.(1)$

In Equation 1 the term ${\mathrm{\Gamma }}_M$ denotes the interface region between the surface and the background mesh which contains positions within $\frac{\mathrm{\Delta }x}{2}$ from the surface. The term $\mathbf{d}({\mathbf{x}}_i)$ is the vector of shortest distance between the node $i$ and the surface ${\mathrm{\Gamma }}_S$. That is $\mathbf{d}({\mathbf{x}}_i)≔{\mathbf{x}}_{S,i}-{\mathbf{x}}_i$, with ${\mathbf{x}}_i\in {\mathrm{\Gamma }}_M$, and ${\mathbf{x}}_{S,i}\in {\mathrm{\Gamma }}_S$ being the closest position to the surface.

The set of nodes $\{{\widehat{\mathbf{x}}}_i\}$ define the nodes of the mesh used in the CFD simulations of this article. Note the element and node connectivity remains the same, and that the elements with changed shape are those with nodes that have been moved. In the cases where a moved element has an edge in line with the structure, no further changes are made. Those elements where the object’s surface cuts through the element’s volume (i.e., cutting through two opposite nodes of the quadrilateral), the element is partitioned into two triangles, with the joining edge aligning with the internal body’s surface. The internal triangle is then removed from the mesh, together with all other internal quadrilateral elements of the unchanged background mesh, resulting in the mesh presented in Figure 1c. As can be seen, the regular mesh is preserved but for the set of quadrilateral and triangle elements surrounding the surface of the internal body. This approach is used in this article for the CFD calculations.

For neutron transport problems, the solution domain includes both internal and external regions relative to a surface—such as when resolving fuel pins and surrounding moderator. In this situation, meshes must preserve the volumes of both internal and external regions. To achieve this, the method presented here uses the SDF function, as before, to define distances between a surface and the nodes of an initial background Cartesian mesh. The initial node movement described in Equation 1 is again applied; however, internal elements of the body are retained. At this stage, modified elements surrounding the surface either preserve the surface along an edge or have the surface cutting through their volume. In the former case, no more modifications are necessary. In the latter case, a further modification is applied to the element’s nodes to preserve the surface while maintaining the quadrilateral structure of the overall mesh. A single node not in contact with the surface is identified and moved onto it. As presented in Figure 1d, the resulting mesh preserves both the surface and the Cartesian quadrilateral mesh structure.

2.1 Hybrid region FEM solver

For time dependent CFD solutions, a hybrid matrix-based and matrix-free solver is implemented for the proposed voxel-dominant meshes that is composed of a structured (Cartesian) and unstructured component. More specifically, the domain $\mathrm{\Omega }$ is decomposed into two sub-domains $\mathrm{\Omega }={\mathrm{\Omega }}_C\cup {\mathrm{\Omega }}_U$, where ${\mathrm{\Omega }}_C$ represents the Cartesian mesh region, and ${\mathrm{\Omega }}_U$ represents the unstructured mesh region. Each component is treated separately in terms of data storage, memory addressing and, if stored, matrix assembly. A node pairing between local Cartesian grid ${\mathrm{\Omega }}_C$ and unstructured mesh ${\mathrm{\Omega }}_U$ is imposed to enforce solution continuity.

For the Cartesian mesh region $({\mathrm{\Omega }}_C)$, where the discretisation uses hexahedral (in 3D) or quadrilateral (in 2D) elements, the nodes and elements are stored in a Cartesian grid format. The shape functions and element stiffness matrices follow standard FEA for structured meshes with trilinear/bilinear elements.

For the unstructured mesh region $({\mathrm{\Omega }}_U)$, the mesh consists of four types of linear elements that includes hexahedral, tetrahedra, pyramids and wedge. Here the standard finite element assembly process is used, storing global system matrices.

The solver treats each region separately, where for the Cartesian grid it employs the previous work developed in Yang et al. (2016), Yang et al. (2019), Nillama et al. (2022). In essence this is a stabilised explicit, matrix-free, solver designed to reduce memory access cost of indirect addressing by relying on the structured nature of the grid. For the unstructured grid component, the solver relies on matrix-based approaches which, whilst fast, does require more memory. However, due to the voxel-dominant mesh structure, the unstructured part is restricted to the interface/boundary region which is typically a small proportion of the whole domain. Thus the larger proportion of the domain is treated with minimal storage. Overall, this may provide an even balance of memory usage and efficient computation.

3 Numerical results

This section provides a number of numerical examples using the proposed methods in diffusion-based applications, CFD and neutron transport to demonstate the accuracy and stability.

3.1 Poisson problem: circle embedded in a square domain with analytical solution

This numerical example evaluates the accuracy of the proposed meshing method in solving Poisson’s equation, given by:

$-\nabla \cdot \nabla u\left(r,\theta \right)=f\left(r,\theta \right),$

where the solution variable $u(r,\theta )$ is expressed in polar coordinates.

The problem is defined over a square domain $[-\mathrm{1,1}]\times [-\mathrm{1,1}]$, with a circular boundary of radius $R=1/3$ centered at the origin. A Neumann boundary condition is imposed on the circle, $\frac{\partial u}{\partial n}=0$, where $n$ denotes the outward pointing normal to the surface. The source term $f(r,\theta )$ is defined as

$f\left(r,\theta \right)=\frac{24}{r}\sin \left(-5\theta \right),$

On the outer square boundary, a Dirichlet boundary condition is applied to match the analytical solution:

$u\left(r,\theta \right)=r\sin \left(-5\theta \right)+\frac{1}{5}{\left(r/R\right)}^{-6}r\sin \left(-5\theta \right).$

The problem is solved on two different mesh types: 1. Voxel-Dominated Mesh–A geometry-conforming mesh where the circular boundary is fully resolved. 2. Standard Cartesian Mesh–A structured Cartesian grid where elements overlapping with the circle are removed.

The computed solutions and errors for both mesh types, using a $30\times 30$ element resolution, are presented in Figure 2. The results show that while both meshes yield similar solutions, the voxel-dominated mesh significantly reduces maximum errors and suppresses the extent of the largest error regions by better conforming to the geometry.

Figure 2

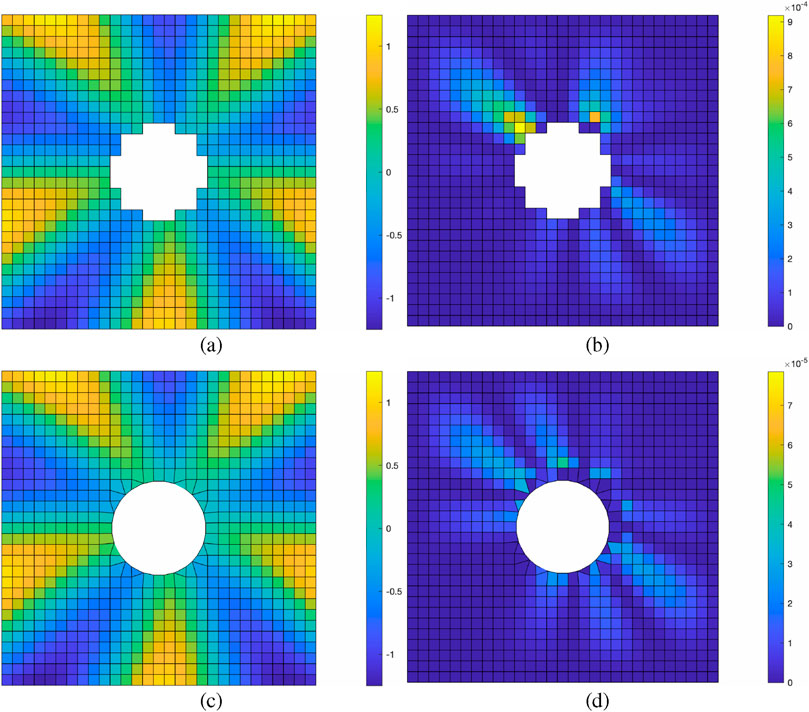
Figure 2. (a,b) Solution and error using the voxel grid. (c,d) Solution and error using the voxel-dominant grid. Both sets of results are based on a $30\times 30$ quadrilateral element mesh.

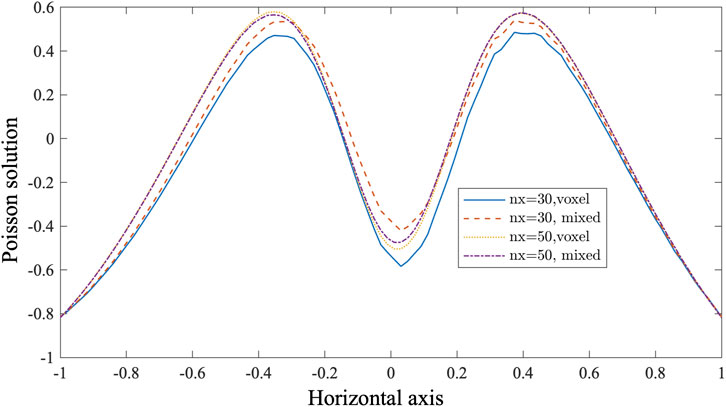
This improvement is further illustrated in Figure 3, which plots the solution along the horizontal line at $y=0.5$. The figure compares results for both mesh types at resolutions of $30\times 30$ and $50\times 50$. The geometry-conforming mesh demonstrates improved accuracy, particularly in regions close to the embedded circular boundary.

Figure 3

Figure 3. Solution along the horizontal line at $y=0.5$ x-axis: horizontal axis. y-axis: solutions.

In the two simulations presented, the solver iterations (see Section 3.6) required to reach convergence were closely comparable. The voxel and voxel-dominant meshes required 80 and 82 solver iterations for tolerance $10^{-8}$. Since the mesh sizes are nearly identical and CPU solver iterations have the same cost, this demonstrates that the meshing approach allows geometries to be resolved without increasing the computational cost of solving the discretised equations.

3.2 Fixed source neutron transport simulation of fuel pin and PWR assembly

This numerical example provides a demonstration of the meshing tool for use in resolving neutron transport problems at the pin-level scale. The analysis is focused on the ability of the meshing tool to capture domain surfaces accurately, but which also remains numerically stable when used in combination with typical FEM discretisations. For this demonstration both the single energy group fixed source and multi-group eigenvalue versions of the Boltzmann transport equations are solved. The latter of these is given by,

$\begin{array}{ll}\hfill \mathrm{\Omega }\cdot \nabla {\psi }_g\left(\vec{r},\mathrm{\Omega }\right)+{\mathrm{\Sigma }}_{t,g}\left(\vec{r}\right){\psi }_g\left(\vec{r},\mathrm{\Omega }\right)& -{\displaystyle \sum _{g^{\prime }=1}^G}{\int }_{{\mathrm{\Omega }}^{\prime }}{\mathrm{\Sigma }}_{s,g^{\prime }\to g}\left(\vec{r},{\mathrm{\Omega }}^{\prime }\to \mathrm{\Omega }\right){\psi }_{g^{\prime }}\left(\vec{r},{\mathrm{\Omega }}^{\prime }\right)d{\mathrm{\Omega }}^{\prime }\hfill \\ \hfill & =\frac{{\chi }_g}{4\pi k_{\mathit{eff}}}{\displaystyle \sum _{g^{\prime }=1}^G}{\int }_{{\mathrm{\Omega }}^{\prime }}\nu {\mathrm{\Sigma }}_{f,g^{\prime }}\left(\vec{r}\right){\psi }_{g^{\prime }}\left(\vec{r},{\mathrm{\Omega }}^{\prime }\right)d{\mathrm{\Omega }}^{\prime },\hfill \end{array}$

for $g\in \{\mathrm{1,2},\dots ,G\}$. The solution yields the angular flux for each energy group $g,{\psi }_g(\vec{r},\mathrm{\Omega })$, in direction $\mathrm{\Omega }$ at position $\vec{r}$ together with the multiplication factor $k_{\mathit{eff}}$. The terms $\nu {\mathrm{\Sigma }}_{f,g^{\prime }}$ and ${\mathrm{\Sigma }}_{s,g^{\prime }\to g}$ denote the production (via fission from group $g^{\prime }$) and group to group scattering material cross-sections, respectively, and ${\chi }_g$ denotes the fission spectrum.

In the following analysis standard numerical technques for discretising the space-angle dimensions of the BTE are employed. This includes a discontinuous Galerkin FEM spatial discretisation using bi-linear basis functions on quadrilateral element meshes. This is combined with a simple, zero-order structured discrete ordinate-$S_N$ method, based on equal solid-angle quadrature for discretising the angular domain in the Boltzmann transport equation, the details of which can be found in Adigun et al. (2018).

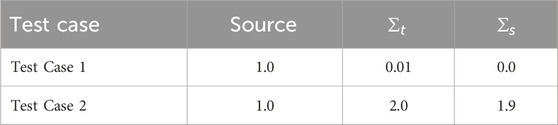
The first demonstration uses a 2-dimensional single fuel pin of radius 0.418 cm, encapsulated within a square domain, with side lengths 1.26 cm, bounded by reflective surfaces. Two sets of single group cross-sections and neutron sources are used which are not designed to represent anything physical but, moreover, are used to test numerical stability using the geometry capturing meshes over different material regimes. In both problems, the material and sources in the fuel and moderator remain constant, as listed in Table 1, with the scattering and total cross-sections set to examine mesh performance in the transparent and diffuse material regimes. As the analytical solutions yield a constant flux, it would be expected the solutions to be resolved to within machine precision and solver tolerances, regardless of the mesh resolution. Thus numerical instabilities arising from the mesh and element shape will most likely be exposed when capturing the circular pin geometry. Noting that all calculations were performed using double precision, this investigation is not focused on other instabilities, causing solution divergence, including those due to poor element shape and lower precision computations. Figure 4 present the absolute relative scalar flux errors using meshes ranging from FEM grids of $8\times 8$ to $100\times 100.$ In all cases, whilst the largest errors occur around the pin interface, the errors are to within typical round-off limits and solver tolerances as they do not exceed $10^{-8}$. This demonstrates that the numerical methods remain stable when used in combination with the meshing techniques for the extreme transport regimes in radiation transport.

Table 1

Table 1. Source and material cross-sections used in the neutron transport test cases.

Figure 4

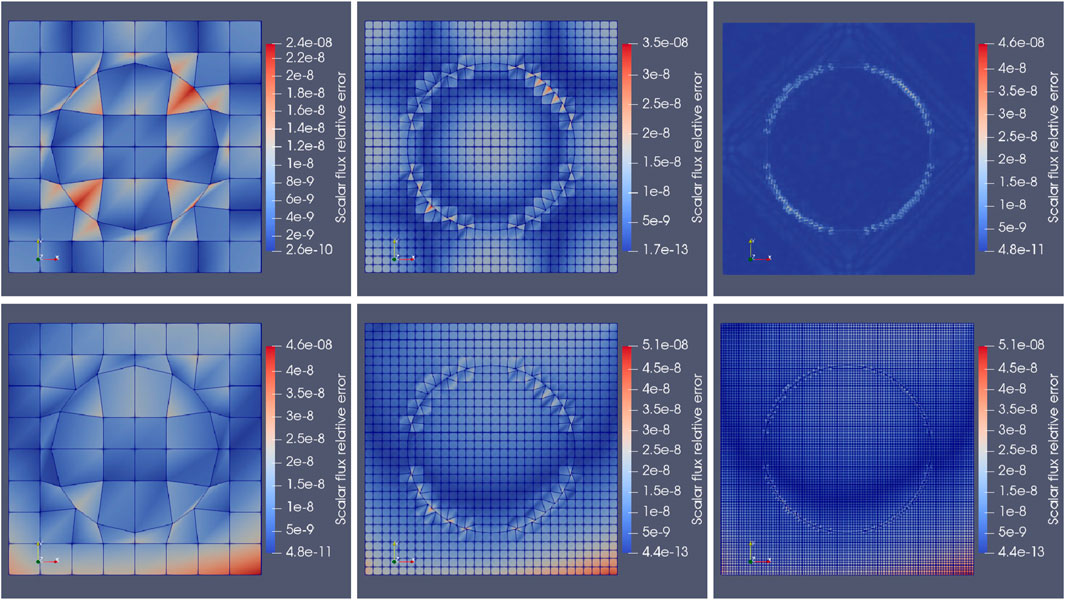
Figure 4. ${\text{S}}_{16}$ Scalar flux solution absolute relative errors to the void (top) and scatter (bottom) pin problem. Left to right, using a spatial mesh of $8\times 8$, $30\times 30$, and $100\times 100$, quadrilateral elements.

The following investigation evaluates mesh performance in resolving fuel pins within a representative reactor geometry. A single fuel pin and its surrounding moderator were modeled using the dimensions and material cross-sections for uranium dioxide (${\text{UO}}_2$) fuel and moderator from the C5G7 benchmark Nuclear Energy Agency (2003). Thermal flux solutions for group 7, obtained using meshes of varying resolutions from coarse to fine, are presented in Figure 5. Additionally, Figure 6 shows the scalar flux profiles for groups 1 and 7 along the diagonal of the domain (from position (0,0),cm to (1.26,1.26),cm). This figure also includes the 2-norm errors of the scalar flux along the same diagonal. The reference solution was computed using a fine mesh of $400\times 400$ elements, and errors are shown for meshes ranging from $8\times 8$ to $200\times 200$ elements. These results indicate that the solutions remain stable across the different mesh resolutions. While oscillations appear in the coarse mesh, particularly in the fast flux, these are expected due to insufficient resolution rather than poor mesh performance. That is, the coarse elements simply lack the ability to capture the finer solution details observed in higher-resolution meshes. Increasing the resolution mitigates these oscillations, with the fine mesh solution exhibiting smooth contours, except for small blips in the fast flux, which result from ray effects. The error convergence graphs show that the errors do converge at a rate in close agreements with first-order convergence, which again should be expected due to the use of linear FEM functions.

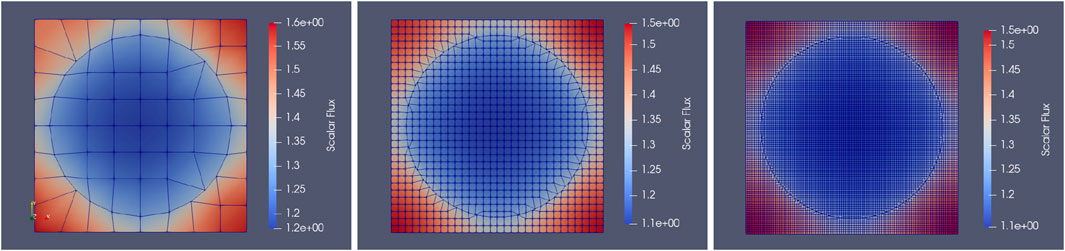
Figure 5

Figure 5. ${\text{S}}_{32}$ Group 7 scalar flux solution profiles single pin of C5G7. Left to right, using a spatial mesh of $8\times 8$, $30\times 30$, and $100\times 100$, quadrilateral elements.

Figure 6

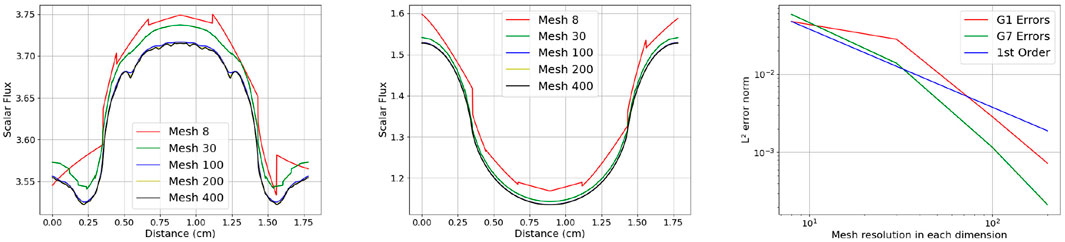
Figure 6. Left and middle: ${\text{S}}_{32}$ Scalar flux group 1 and group 2 solution profiles to the single pin of C5G7 for varying resolution meshes. Legend number indicated number of elements in each dimension. Line plots were taken through the diagonal from positions (0,0)cm to (1.26,1.26)cm. Right: Group 1 and 7 - 2-norm error plotted against mesh resolution in each dimension.

In summary, this numerical example provides evidence the meshing algorithm is suitable for resolving fuel pins across transparent and diffuse material regimes, and for those typical found in reactor physics benchmarks.

3.3 Two dimensional CFD benchmark

The 2D lid-driven cavity flow (Ghia et al., 1982) at $Re=1000$ is a well-established numerical benchmark in computational fluid dynamics (CFD). It involves an incompressible, viscous flow inside a square cavity, where the top boundary moves at a constant velocity $v=1$ while the other three walls remain stationary. This setup generates a primary vortex in the cavity centre, along with secondary vortices near the corners. The case serves as an ideal benchmark for assessing numerical schemes, solution accuracy. It is a convection-dominated problem, where stabilised FE is used (Yang et al., 2016).

To validate the hybrid solver, we rotate the computational domain by 45°, intentionally introducing a stair-casing issue. This test evaluates the solver’s ability to handle both Cartesian and unstructured grids while ensuring accurate vorticity transport and solution consistency.

Figure 7 presents the computational meshes and their corresponding velocity solutions under a $50\times 50$ resolution. The voxel-dominant mesh demonstrates superior accuracy in capturing viscous boundary layers, leading to more accurate results compared to a purely voxel-based approach. Figure 8 further illustrates the velocity profiles along the horizontal and vertical centerlines of the cavity, comparing the obtained solutions against established reference data.

Figure 7

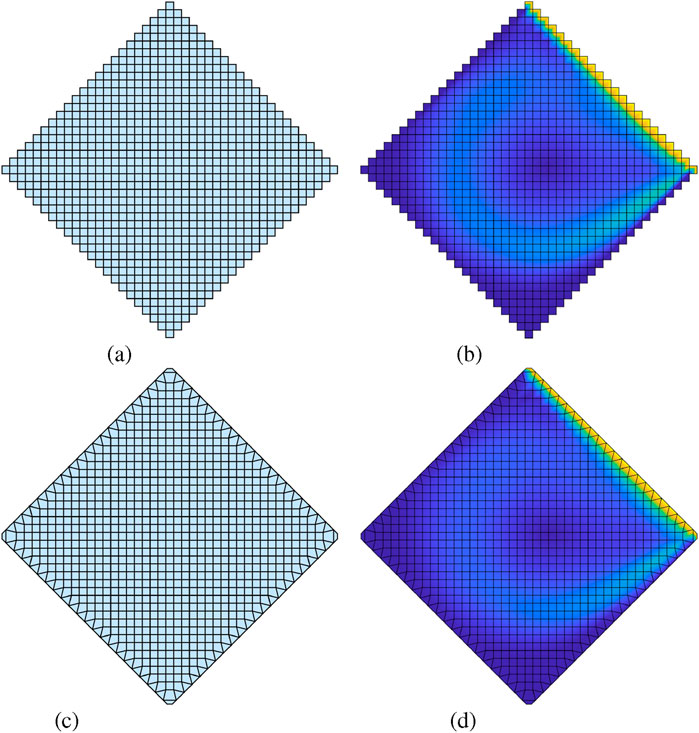
Figure 7. Lid driven flow benchmark case for $\mathrm{R}\mathrm{e}=1000$ using voxel-grid (a, b) and voxel-dominant mesh (c, d) with hybrid solver with $50\times 50$.

Figure 8

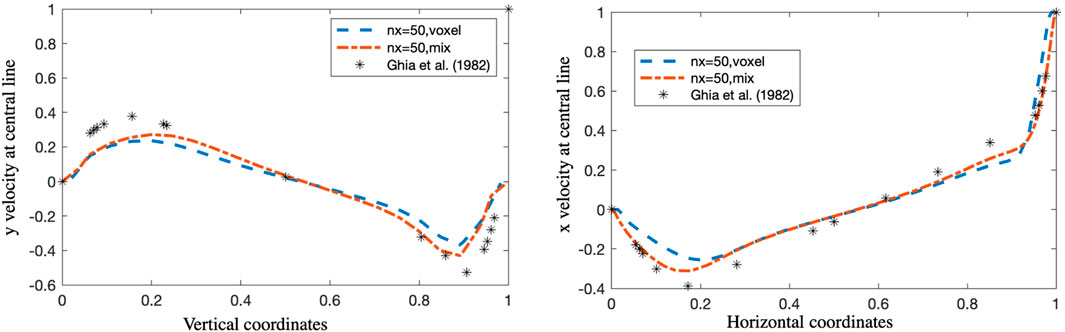
Figure 8. Vertical and horizontal velocity through the horizontal centerline and vertical of the cavity at Re = 1,000 using n = 50 solution in the original coordinates before rotation.

3.4 Three dimensional CFD CANDU fuel assembly

This study presents a CFD analysis of a three-dimensional CANDU fuel assembly (Torgerson et al., 2006), focusing on pressure distribution and velocity profiles. The CANDU (Canada Deuterium Uranium) reactor utilizes heavy water moderation, with fuel bundles immersed in pressurized coolant. Accurately modeling the flow behavior around the fuel rods is essential for optimising heat transfer efficiency and minimising pressure drop (Piro et al., 2016).

A typical CANDU fuel bundle, illustrated in Figure 9, consists of 37 fuel elements, concentrically arranged and mounted on two end plates. The bundle has a total length of approximately 500 mm and a diameter of about 100 mm. The CFD simulation provides insights into velocity distribution, flow separation, and pressure variations within the assembly. These results help assess flow uniformity and identify potential recirculation zones, ensuring an optimized thermal-hydraulic performance of CANDU fuel bundles during reactor operation. The simulation is conducted for a single-phase flow, excluding heat transfer and chemical reactions.

Figure 9

Figure 9. Isometric view of a 37 element CANDU fuel bundle modelled in nTOP, left: whole view, right: close view.

To analyse the effects of mesh resolution, surface and volume meshes were generated at three levels of refinement with mesh size of 0.2868 cm, 0.1434 cm, 0.0717 cm, with a refinement factor of two at each level. Figure 10 shows the surface and volume meshes at three resolutions. All simulations used a mass flow rate of 20.9 kg/s as used in (Bhattacharya et al., 2012). The pressure drop for each simulation of increasing mesh resolutions was calculated as 11.22 KPa, 11.02 kPa, 10.78 kPa showing these values to be converging to within 0.2 kPa. Figure 11 presents the flow velocities pressure profiles using the small and large meshes. Again, this shows closely converging solution details.

Figure 10

Figure 10. Surface and volume meshes at three resolutions: 0.2868 cm, 0.1434 cm, and 0.0717 cm, corresponding to a refinement factor of two between successive levels.

Figure 11

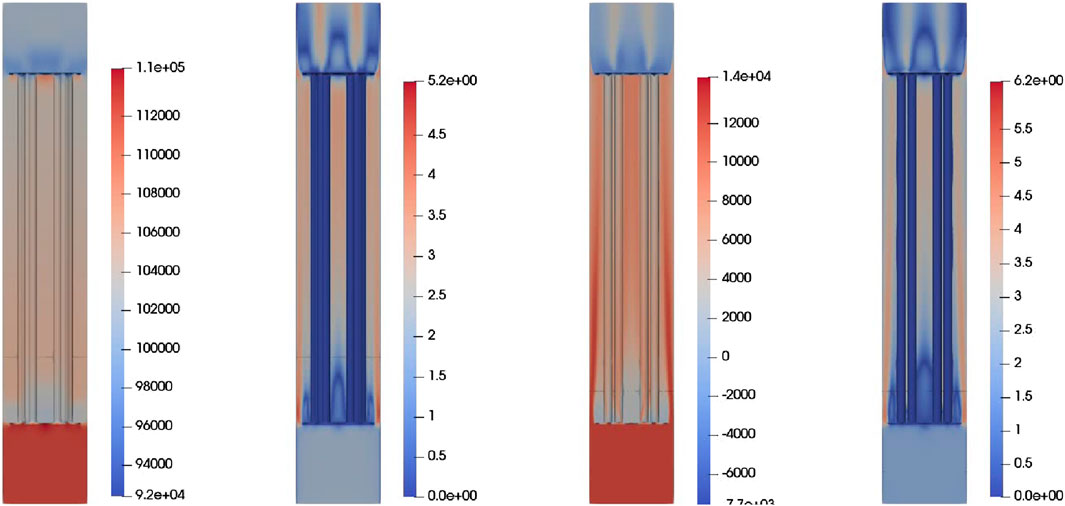
Figure 11. Contour plots of pressure distribution and velocity magnitude at coarse (0.2868 cm) and fine (0.0717 cm) grid resolutions, under a mass flow rate of 20.9 kg/s. Left: coarse grid results. Right: fine grid results.

3.5 Illustration of computational efficiencies

The use of meshes constructed predominantly of structured elements offer significant memory savings compared to fully unstructured meshes, in part this is due to the absence of indirect addressing and mesh-connectivity storage. Additionally, the repetition of element shapes eliminates the need to compute and store spatial integrals for each individual element. Although quadrilateral and hexahedral elements involve more nodes per element, the overall number of elements is substantially lower, by factors of approximately 6 in 2D and 20 in 3D, resulting in a net reduction in memory and computational costs. Thus the effectiveness of the method presented will be driven by the fraction of unperturbed elements.

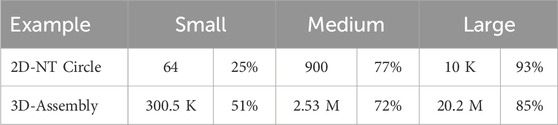
Table 2 presents the fraction of unperturbed elements used in the 2D reactor pincell problems and the 3D CANDU reactor geometry for varying mesh sizes. In the 2D case, the number of unperturbed element is quite low for the smallest mesh, the eight by eight grid resulting in just 25% of elements being unperturbed. However, one can see from Figure 5 the pin occupies a large proportion of the domain and so the large elements tend to intersect the surface on a regular basis. As mesh resolution is increased the unperturbed fraction quickly rises and reaches over 93% for the 100 by 100 mesh. Similarly the three meshes used for the CANDU geometry show increasing unperturbed fractions, initially starting from 51% for the lowest mesh of 300.5 K elements, and rising to 85% for the large mesh with 20.2 M elements.

Table 2

Table 2. Fraction of perturbed elements for the 2D neutron transport and 3D CANDU reactor.

3.6 CFD and BTE solver information

The CFD and BTE solver used here was based on an in-house code (Buchan et al., 2021), written in Fortran-90 and compiled as a python library. The CFD solver used a continuous linear FEM with VMS stabilisation, and a generalized minimal residual method (GMRES) solver with a Jacobi preconditioner. The BTE solver used discontinuous linear FEM with a sweep based solutions scheme. For the eigenvalue problems, a Power method was employed. Both solvers have been developed with MPI parallelism and the CFD solver has the additional OpenMP capability which was used in the calculation of the CANDU assembly.

4 Conclusion

This study presents a hybrid solver framework integrated with a voxel-dominated Cartesian meshing approach to efficiently solve the Boltzmann Transport Equation and Navier-Stokes equations in complex nuclear reactor simulations. Traditional unstructured meshing techniques, while flexible, impose significant computational burdens due to high memory consumption and solver inefficiencies. In contrast, structured Cartesian methods offer computational advantages but suffer from stair-casing errors, particularly in handling curved geometries.

To overcome these limitations, the implicit geometry-conforming meshing (IGCM) method was introduced within a voxel-dominated Cartesian mesh. This approach is coupled with a hybrid solver, applying structured solvers in voxel regions while using adaptive numerical treatments near complex boundaries. The combination of these methods enables high computational efficiency while preserving accuracy in neutron transport and thermal hydraulics simulation. The demonstration provided here showed that complex geometries can be resolved through the simulation of a CANDU assembly. The proposed hybrid solver and meshing framework provides a promising direction for accelerating full-core reactor simulations while ensuring the accuracy of boundary interactions. Future work will focus on benchmarking the solver against high-fidelity reference solutions and extending its applicability to multi-physics coupling, including neutron transport, thermal radiation, and turbulence modelling.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

LY: Software, Writing – original draft, Formal Analysis, Funding acquisition, Methodology. JY: Methodology, Writing – review and editing. JP: Formal Analysis, Writing – review and editing. AB: Funding acquisition, Methodology, Software, Writing – original draft.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. STFC funded through grant: Parallel solvers for voxel-dominant meshes for the Boltzmann Transport Equation.

Acknowledgments

Authors acknowledge the support of the STFC-funded Digital BIC program. The authors thank nTOP for providing the free academic license to use CAD modelling software to model the CANDU fuel bundle.

Conflict of interest

Authors LY and JY were employed by Voxshell Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adigun, B. J., Buchan, A. G., Adam, A., Dargaville, S., Goffin, M. A., and Pain, C. C. (2018). A haar wavelet method for angularly discretising the boltzmann transport equation. Prog. Nucl. Energy 108, 295–309. doi:10.1016/j.pnucene.2018.05.023

CrossRef Full Text | Google Scholar

Barad, M. F., Colella, P., and Schladow, S. G. (2009). An adaptive cut-cell method for environmental fluid mechanics. Int. J. Numer. methods fluids 60, 473–514. doi:10.1002/fld.1893

CrossRef Full Text | Google Scholar

Bhattacharya, A., Yu, S., and Kawall, G. (2012). Numerical simulation of turbulent flow through a 37-element candu fuel bundle. Ann. Nucl. energy 40, 87–105. doi:10.1016/j.anucene.2011.10.017

CrossRef Full Text | Google Scholar

Buchan, A. G., Yang, L., Welch, D., Brenner, D. J., and Atkinson, K. D. (2021). Improved estimates of 222 nm far-uvc susceptibility for aerosolized human coronavirus via a validated high-fidelity coupled radiation-cfd code. Sci. Rep. 11, 19930. doi:10.1038/s41598-021-99204-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Davydov, D., Pelteret, J.-P., Arndt, D., Kronbichler, M., and Steinmann, P. (2020). A matrix-free approach for finite-strain hyperelastic problems using geometric multigrid. Int. J. Numer. Methods Eng. 121, 2874–2895. doi:10.1002/nme.6336

CrossRef Full Text | Google Scholar

Evans, T. M., Stafford, A. S., Slaybaugh, R. N., and and, K. T. C. (2010). Denovo: a new three-dimensional parallel discrete ordinates code in scale. Nucl. Technol. 171, 171–200. doi:10.13182/NT171-171

CrossRef Full Text | Google Scholar

Fang, J., Shaver, D. R., Tomboulides, A., Min, M., Fischer, P., Lan, Y.-H., et al. (2021). Feasibility of full-core pin resolved cfd simulations of small modular reactor with momentum sources. Nucl. Eng. Des. 378, 111143. doi:10.1016/j.nucengdes.2021.111143

CrossRef Full Text | Google Scholar

Ghia, U., Ghia, K. N., and Shin, C. (1982). High-re solutions for incompressible flow using the navier-stokes equations and a multigrid method. J. Comput. Phys. 48, 387–411. doi:10.1016/0021-9991(82)90058-4

CrossRef Full Text | Google Scholar

Ingram, D. M., Causon, D. M., and Mingham, C. G. (2003). Developments in cartesian cut cell methods. Math. Comput. Simul. 61, 561–572. doi:10.1016/s0378-4754(02)00107-6

CrossRef Full Text | Google Scholar

Johan, Z., and Hughes, T. J. (1991). A globally convergent matrix-free algorithm for implicit time-marching schemes arising in finite element analysis in fluids. Comput. Methods Appl. Mech. Eng. 87, 281–304. doi:10.1016/0045-7825(91)90009-u

CrossRef Full Text | Google Scholar

LEAP71 (2024). PicoGK: a compact and robust open-source geometry kernel for computational engineering.

Google Scholar

Lesueur, M., Rattez, H., and Colomés, O. (2022). μct scans permeability computation with an unfitted boundary method to improve coarsening accuracy. Comput. and Geosciences 166, 105118. doi:10.1016/j.cageo.2022.105118

CrossRef Full Text | Google Scholar

Li, Q., Hong, Q., Qi, Q., Ma, X., Han, X., and Tian, J. (2018). Towards additive manufacturing oriented geometric modeling using implicit functions. Vis. Comput. Industry, Biomed. Art 1, 9–16. doi:10.1186/s42492-018-0009-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, B., He, S., Moulinec, C., and Uribe, J. (2019). Sub-channel cfd for nuclear fuel bundles. Nucl. Eng. Des. 355, 110318. doi:10.1016/j.nucengdes.2019.110318

CrossRef Full Text | Google Scholar

Liu, B., He, S., Moulinec, C., and Uribe, J. (2022). A multiscale model of a rod bundle using subchannel cfd. Nucl. Eng. Des. 393, 111793. doi:10.1016/j.nucengdes.2022.111793

CrossRef Full Text | Google Scholar

Martínez-Frutos, J., and Herrero-Pérez, D. (2015). Efficient matrix-free gpu implementation of fixed grid finite element analysis. Finite Elem. Analysis Des. 104, 61–71. doi:10.1016/j.finel.2015.06.005

CrossRef Full Text | Google Scholar

Martorell, P. A., and Badia, S. (2024). High order unfitted finite element discretizations for explicit boundary representations. J. Comput. Phys. 511, 113127. doi:10.1016/j.jcp.2024.113127

CrossRef Full Text | Google Scholar

Meinke, M., Schneiders, L., Günther, C., and Schröder, W. (2013). A cut-cell method for sharp moving boundaries in cartesian grids. Comput. and Fluids 85, 135–142. doi:10.1016/j.compfluid.2012.11.010

CrossRef Full Text | Google Scholar

Museth, K. (2013). Vdb: high-resolution sparse volumes with dynamic topology. ACM Trans. Graph. (TOG) 32, 1–22. doi:10.1145/2487228.2487235

CrossRef Full Text | Google Scholar

Nguyen, K. H., DeHart, M. D., Hanophy, J. T., and Wang, Y. (2025). Development of a griffin model of the advanced test reactor. Ann. Nucl. Energy 211, 111012. doi:10.1016/j.anucene.2024.111012

CrossRef Full Text | Google Scholar

Nillama, L. B. A., Yang, J., and Yang, L. (2022). An explicit stabilised finite element method for navier-stokes-brinkman equations. J. Comput. Phys. 457, 111033. doi:10.1016/j.jcp.2022.111033

CrossRef Full Text | Google Scholar

nTop Inc (2024). nTop documentation, release 4.0: implicit and other models. nTop Inc. Available online at: https://ntop.com.

Google Scholar

Nuclear Energy Agency (2003). NEA/NSC/DOC(2003)16. Paris, France: Nuclear Energy Agency, Organisation for Economic Co-operation and Development.

Google Scholar

Owens, A., Welch, J., Kópházi, J., and Eaton, M. (2016). Discontinuous isogeometric analysis methods for the first-order form of the neutron transport equation with discrete ordinate (sn) angular discretisation. J. Comput. Phys. 315, 501–535. doi:10.1016/j.jcp.2016.03.060

CrossRef Full Text | Google Scholar

Paul, F., Fischer, J. W. L., and Kerkemeier, S. G. (2008). nek5000 web page. Available online at: http://nek5000.mcs.anl.gov.

Google Scholar

Peskin, C. S. (2002). The immersed boundary method. Acta Numer. 11, 479–517. doi:10.1017/s0962492902000077

CrossRef Full Text | Google Scholar

Piro, M., Wassermann, F., Grundmann, S., Leitch, B., and Tropea, C. (2016). Progress in on-going experimental and computational fluid dynamic investigations within a candu fuel channel. Nucl. Eng. Des. 299, 184–200. doi:10.1016/j.nucengdes.2015.07.009

CrossRef Full Text | Google Scholar

Salih, S. Q., Aldlemy, M. S., Rasani, M. R., Ariffin, A., Ya, T. M. Y. S. T., Al-Ansari, N., et al. (2019). Thin and sharp edges bodies-fluid interaction simulation using cut-cell immersed boundary method. Eng. Appl. Comput. Fluid Mech. 13, 860–877. doi:10.1080/19942060.2019.1652209

CrossRef Full Text | Google Scholar

Tautges, T. J., and Jain, R. (2012). Creating geometry and mesh models for nuclear reactor core geometries using a lattice hierarchy-based approach. Eng. Comput. 28, 319–329. doi:10.1007/s00366-011-0236-8

CrossRef Full Text | Google Scholar

Torgerson, D., Shalaby, B. A., and Pang, S. (2006). Candu technology for generation iii+ and iv reactors. Nucl. Eng. Des. 236, 1565–1572. doi:10.1016/j.nucengdes.2006.04.020

CrossRef Full Text | Google Scholar

Verzicco, R. (2023). Immersed boundary methods: historical perspective and future outlook. Annu. Rev. Fluid Mech. 55, 129–155. doi:10.1146/annurev-fluid-120720-022129

CrossRef Full Text | Google Scholar

Wang, M., Wang, Y., Tian, W., Qiu, S., and Su, G. (2021a). Recent progress of cfd applications in pwr thermal hydraulics study and future directions. Ann. Nucl. Energy 150, 107836. doi:10.1016/j.anucene.2020.107836

CrossRef Full Text | Google Scholar

Wang, Y., Schunert, S., Ortensi, J., Laboure, V., DeHart, M., Prince, Z., et al. (2021b). Rattlesnake: a moose-based multiphysics multischeme radiation transport application. Nucl. Technol. 207, 1047–1072. doi:10.1080/00295450.2020.1843348

CrossRef Full Text | Google Scholar

Xie, Z. (2022). An implicit cartesian cut-cell method for incompressible viscous flows with complex geometries. Comput. Methods Appl. Mech. Eng. 399, 115449. doi:10.1016/j.cma.2022.115449

CrossRef Full Text | Google Scholar

Yang, L. (2018). One-fluid formulation for fluid–structure interaction with free surface. Comput. Methods Appl. Mech. Eng. 332, 102–135. doi:10.1016/j.cma.2017.12.016

CrossRef Full Text | Google Scholar

Yang, L., Badia, S., and Codina, R. (2016). A pseudo-compressible variational multiscale solver for turbulent incompressible flows. Comput. Mech. 58, 1051–1069. doi:10.1007/s00466-016-1332-9

CrossRef Full Text | Google Scholar

Yang, L., Gil, A. J., Carreño, A. A., and Bonet, J. (2018). Unified one-fluid formulation for incompressible flexible solids and multiphase flows: application to hydrodynamics using the immersed structural potential method (ispm). Int. J. Numer. Methods Fluids 86, 78–106. doi:10.1002/fld.4408

CrossRef Full Text | Google Scholar

Yang, L., Yang, J., Boek, E., Sakai, M., and Pain, C. (2019). Image-based simulations of absolute permeability with massively parallel pseudo-compressible stabilised finite element solver. Comput. Geosci. 23, 881–893. doi:10.1007/s10596-019-09837-4

CrossRef Full Text | Google Scholar